Сборник контрольных работ по алгебре, (10 класс)
Контрольная работа № 1
по теме «Функции и их свойства»
Цель: проверить уровень усвоение ГОСО
— умение находить значение функции в точке;
— умение находить область определения функции;
— умения строить эскиз графика функции и находить по эскизу промежутки
возрастания и убывания , экстремумы функции, точки пересечения с осями
координат;
— знания свойств четных и нечетных функций.
1. Вычислите:
y = f(x) является нечетной y = f(x) является четной
2 f(-4) + f(3) f(-3) + 2 f(1)
eсли f(4)=1, f(-3)=2 eсли f(3)=4, f(-1)=2
2. Найдите значение функции в точке X0.
X0 = -2 и X0 = 4 X0 = -3 и X0 = 1
3. Постройте эскиз функции и найдите координаты точек его пересечения с осями координат.
4. Найдите область определения функции
5. Найдите промежутки возрастания и убывания и экстремумы функции.
Критерии оценки.
0-10 баллов – «2»
11-14баллов – «3»
15-19 баллов – «4»
20-21 баллов – «5»
Распределение заданий по содержанию и видам деятельности.
| Содержательные линии | Воспроизведение знаний | Применение знаний | Интеграция знаний | Процентное Соотношение в тексте |
| Четные и нечетные функции. | №1 | 20% | ||
| Значения функции в точке | №2 | 20% | ||
| График функции и ее свойства | №3,4 | №5 | 40% | |
| Процентное Соотношение в тексте | 40% | 40% | 20% | 100% |
Критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемого элемента | Балл за выполнение задания |
| 1 | Свойства четных и нечетных функций. | Знания свойств четных и нечетных функций | 2 | 3 |
| Запись ответа | 1 | |||
| 2 | Значение функции в точке | Правильно подставил | 2 | 3 |
| Вычисления | 1 | |||
| 3 | График функции и ее свойства | Построение эскиза графика | 2 | 5 |
| Пересечение с осью абсцисс | 1 | |||
| Пересечение с осью ординат | 2 | |||
| Запись ответа | 1 | |||
| 4 | Область определения функции | Составление условий для нахождения области определения | 2 | 5 |
| Решение неравенства | 1 | |||
| Запись ответа | 2 | |||
| 5 | Промежутки возрастания , убывания и экстремумы функции | Вершина параболы | 1 | 5 |
| Свойства модуля | 1 | |||
| Эскиз графика | 2 | |||
| Запись ответа | 1 |
Контрольная работа № 2
по теме «Тригонометрические функции»
Цель: проверить уровень усвоение ГОСО
— умение находить период тригонометрических функций;
— уменияупрощать тригонометрические выражения с помощью основных формул
тригонометрии;
— знание значений тригонометрических функций;
— умения строить графики тригонометрических функций;
— умения по графику определять свойства тригонометрических функций;
1. Найдите наименьший положительный период функции
2. Вычислите значение выражения
3. Постройте график функции
4. Не выполняя построений, найдите область определения и область значений функции.
5. Вычислите:
cos(2 arcsin1\3) cos(2 arcsin1\5)
Критерии оценки.
0-10 баллов – «2»
11-14 баллов – «3»
15-19 баллов – «4»
20-21 баллов – «5»
Распределение заданий по содержанию и видам деятельности.
| Содержательные линии | Воспроизведение знаний | Применение знаний | Интеграция знаний | Процентное Соотношение в тексте |
| График и свойства тригонометрической функции | №1 | №3,4 | №5 | 80% |
| Преобразование тригонометрических выражений | №2 | 20% | ||
| Процентное Соотношение в тексте | 40% | 40% | 20% | 100% |
Критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемого элемента | Балл за выполнение задания |
| 1 | Определение периода функции | Знание наименьшего периода тригонометрических функций | 1 | 3 |
| Нахождение периода по формуле | 1 | |||
| Запись ответа | 1 | |||
| 2 | Нахождение значения выражения, содержащего обратные тригонометрические функции | Определение обратных тригонометрических функций положительного аргумента | 1 | 3 |
| Определение обратных тригонометрических функций отрицательного аргумента | 1 | |||
| Вычисление значения выражения | 1 | |||
| 3 | График тригонометрической функции | Сдвиг по оси абсцисс | 1 | 5 |
| Растяжение по оси ординат | 1 | |||
| Аккуратность построения | 1 | |||
| Нули функции | 1 | |||
| Промежутки возрастания(убывания) | 1 | |||
| 4 | Область значений тригонометрических функций | Область определения | 1 | 5 |
| Область значений | 2 | |||
| Выбор ответа | 1 | |||
| Запись ответа | 1 | |||
| 5 | Свойства монотонности | Знание радианной меры | 1 | 5 |
| Промежутки монотонности | 3 | |||
| Запись ответа | 1 |
Контрольная работа № 3
по теме «Тригонометрические уравнения и неравенства»
Цель: проверить уровень усвоение ГОСО
— умение находить значение обратных тригонометрических функций;
— умение решать простейшие тригонометрические уравнения;
— умения решать однородные тригонометрические уравнения;
— умения преобразовывать уравнения с помощью основных формул тригонометрии.
— умения решать системы тригонометрических уравненийи неравенств;
1. Решите уравнение
а) а)
б) б)
2. Решите уравнение
а) а)
б) б)
3. Решите неравенство
4. Решите систему уравнений
5. Решите систему неравенств
Критерии оценки.
0-12 баллов – «2»
13-16 баллов – «3»
17-21 баллов – «4»
22-23 баллов – «5»
Распределение заданий по содержанию и видам деятельности.
| Содержательные линии | Воспроизведение знаний | Применение знаний | Интеграция знаний | Процентное Соотношение в тексте |
| Тригонометрические уравнения | №1 | №2 | 40% | |
| Тригонометрические неравенства | №3 | 20% | ||
| Системы тригоно-метрических урав-нений и неравенств | №4 | №5 | 40% | |
| Процентное Соотношение в тексте | 40% | 40% | 20% | 100% |
Критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемого элемента | Балл за выполнение задания |
| 1 | Решение тригонометрических уравнений | Решение простейших тригонометрических уравнений | 2 | 5 |
| Применение формул суммы тригонометрических функций | 1 | |||
| Решение однородных тригонометрических уравнений первой степени | 1 | |||
| Выбор ответа | 1 | |||
| 2 | Решение тригонометрических уравнений | Выбор способа решения тригонометрического уравнения | 3 | 5 |
| Решение квадратного уравнения | 1 | |||
| Вычисления и выбор ответа | 1 | |||
| Решение неравенств | 2 | |||
| Выбор ответа | 1 | |||
| Запись ответа | 1 | |||
| 3 | Решение тригонометрических неравенств | Преобразование неравенства | 1 | 3 |
| Решение неравенства | 1 | |||
| Выбор ответа | 1 | |||
| 4 | Решение системы тригонометрических уравнений | Применение метода подстановки | 1 | 5 |
| Применение формулы произведения тригонометрических функций | 1 | |||
| Решение тригонометрических уравнений | 2 | |||
| Запись ответа | 1 | |||
| 5 | Решениесистемы тригонометрических неравенств | Решение простейшего тригонометрического неравенства | 2 | 5 |
| Определение общего решения | 3 |
Контрольная работа № 4
по теме «Определение производной функции. Геометрический и физический смысл производной»
Цель: проверить уровень усвоения ГОСО
— знание формул и правил нахождения производных, уравнения касательной;
— умения применять таблицу и правила нахождения производных;
— умение составлять уравнение касательной к графику функции;
— умения находить производную в точке;
— умения составлять уравнения и неравенства с производной и решать их*
— умения применять производную при решении физических задач.
1. Найти производную функции:
а) а) б) — 8х3 б) )+ 3х5
2. Составьте уравнение касательной к графику функции f(x) в точке x0.
, x0=-1 , x0 = 1
3. Решите уравнение:
если если
4. Составьте и решите неравенство
5.Материальная точка движется по закону
x(t)= 5t + 6t2 – t3 x(t) = – t2 + 2t – 4
( х – метров, t – в секундах)
Определите
скорость точки в момент, когда ускорение точки в момент, когда
ее ускорение равно нулю. ее скорость равна 1м/с
Критерии оценки.
0-12 баллов – «2»
13-16 баллов – «3»
17-21 баллов – «4»
22-23 баллов – «5»
Распределение заданий по содержанию и видам деятельности.
| Содержательные линии | Воспроизведение знаний | Применение знаний | Интеграция знаний | Процентное Соотношение в тексте |
| Нахождение производной | №1 | №3,4 | 60% | |
| Геометрический смысл производной | №2 | 20% | ||
| Физический смысл производной | №5 | 20% | ||
| Процентное Соотношение в тексте | 40% | 40% | 20% | 100% |
Критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемого элемента | Балл за выполнение задания |
| 1 | Нахождение производной | Знание таблицы производных | 1 | 3 |
| Производная произведения | 1 | |||
| Производная степенной функции | 1 | |||
| 2 | Составление уравнения касательной к графику функции | Знание уравнения касательной к графику функции | 1 | 5 |
| Нахождение производной | 1 | |||
| Нахождение значений функции и производной в точке | 1 | |||
| составление уравнения касательной к графику функции | 1 | |||
| Запись ответа | 1 | |||
| 3 | Составление и решение уравнения с производной. | Нахождение производной дроби | 1 | 5 |
| Нахождение производной в точке | 1 | |||
| Составление уравнения | 1 | |||
| Решение уравнения | 1 | |||
| Вычисления и запись ответа | 1 | |||
| 4 | Составление и решение неравенства с производной. | Нахождение производной | 1 | 5 |
| Составление неравенства | 1 | |||
| Решение неравенства | 2 | |||
| Запись ответа | 1 | |||
| 5 | Применение производной при решении физических задач | Нахождение скорости | 1 | 5 |
| Нахождение ускорения | 1 | |||
| Составление уравнения для нахождения времени | 2 | |||
| Нахождение конечного ответа | 1 |
Контрольная работа № 5
по теме «Производные сложных и тригонометрических функции»
Цель: проверить уровень усвоение ГОСО
— знание формул и правил нахождения производных тригономкерических функций,;
— умения находить производную сложной функции;
— умения составлять уравнения и неравенства с производной и решать их.
1. Найти производную функции:
б) ,
xn--j1ahfl.xn--p1ai
| Контрольная работа № 1 | |
| 1 вариант 1). Для функции f (х) = х3 + 2х2 – 1. Найти f (0), f (1), f (-3), f (5). 2). Найти D(у), если: 3). Построить график функции: а). у = – х + 5 б). у = х2 – 2 По графику определить : а). Монотонность функции; б). Ограниченность функции; в). Минимальное ( максимальное ) значение функции 4). Для заданной функции найти обратную: | 2 вариант 1). Для функции f (х) = 3х2 – х3 + 2. Найти f (0), f (1), f (-3), f (5). 2). Найти D(у), если: 3). Построить график функции: а). у = х – 7 б). у = – х2 + 2 По графику определить : а). Монотонность функции; б). Ограниченность функции; в). Минимальное ( максимальное ) значение функции 4). Для заданной функции найти обратную: |
| Контрольная работа № 2 | |
| 1 вариант 1). Вычислите: 2). Упростите:
3). Известно, что: . Вычислить . 4). Решите уравнение: . 5). Докажите тождество: . | 2 вариант 1). Вычислите: 2). Упростите: 3). Известно, что: . Вычислить . 4). Решите уравнение: . 5). Докажите тождество: . |
| Контрольная работа № 3 | |
| 1 вариант 1). Найти наименьшее и наибольшее значения функций: на отрезке ; на отрезке . 2). Упростить выражение: 3). Исследуйте функцию на четность: 4). Постройте график функции: 5). Известно, что . Докажите, что . | 2 вариант 1). Найти наименьшее и наибольшее значения функций: на отрезке ; на отрезке . 2). Упростить выражение: 3). Исследуйте функцию на четность: 4). Постройте график функции: 5). Известно, что . Докажите, что . |
| Контрольная работа № 4 | |
| 1 вариант 1). Решить уравнение: 2). Найти корни уравнения на отрезке . 3). Решить уравнение: 4). Найти корни уравнения , принадлежащие отрезку . | 2 вариант 1). Решить уравнение: 2). Найти корни уравнения на отрезке . 3). Решить уравнение: 4). Найти корни уравнения , принадлежащие отрезку . |
| Контрольная работа № 5 | |
| 1 вариант 1). Вычислить: 2). Упростить выражение: 3). Доказать тождество: 4). Решить уравнение а). 5). Зная, что и , найти . | 2 вариант 1). Вычислите: 2). Упростить выражение: 3). Доказать тождество: 4). Решить уравнение а). 5). Зная, что и , найти . |
| Контрольная работа № 6 | |
| 1 вариант 1). Найдите производную функции: а). ; б). ; в). ; г). ; д). . 2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции в точке х0 = 1. 3). Прямолинейное движение точки описывается законом . Найдите ее скорость в момент времени с. 4). Дана функция . Найдите: а). Промежутки возрастания и убывания функции; б). Точки экстремума; в). Наибольшее и наименьшее значения функции на отрезке . | 2 вариант 1). Найдите производную функции: а). ; б). ; в). ; г). ; д). . 2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции в точке х0 = 1. 3). Прямолинейное движение точки описывается законом . Найдите ее скорость в момент времени t = 2с. 4). Дана функция . Найдите: а). Промежутки возрастания и убывания функции; б). Точки экстремума; в). Наибольшее и наименьшее значения функции на отрезке . |
| Контрольная работа № 7 ( итоговая ) | |
| 1 вариант 1). Дана функция. Составить уравнение касательной к графику в точке с абсциссой . Установить, в каких точках промежутка касательная к графику данной функции составляет с осью Ох угол 600. 2). Решите уравнение: 3). Упростите выражение: а). ; б). . 4). Постройте график функции с полным исследованием функции . | 2 вариант 1). Дана функция. Составить уравнение касательной к графику в точке с абсциссой . Установить точки минимума и максимума, а также наибольшее и наименьшее значение на промежутке . 2). Решите уравнение: 3). Упростите выражение: а). ; б). . 4). Постройте график функции с полным исследованием функции . |
infourok.ru
| +Контрольная работа № 1 | |
| 1 вариант 1). Для функции f (х) = х3 + 2х2 – 1. Найти f (0), f (1), f (-3), f (5). 2). Найти D(у), если: 3). Построить график функции: а). у = – х + 5 б). у = х2 – 2 По графику определить : а). Монотонность функции; б). Ограниченность функции; в). Минимальное ( максимальное ) значение функции 4). Для заданной функции найти обратную: | 2 вариант 1). Для функции f (х) = 3х2 – х3 + 2. Найти f (0), f (1), f (-3), f (5). 2). Найти D(у), если: 3). Построить график функции: а). у = х – 7 б). у = – х2 + 2 По графику определить : а). Монотонность функции; б). Ограниченность функции; в). Минимальное ( максимальное ) значение функции 4). Для заданной функции найти обратную: |
| Контрольная работа № 2 | |
| 1 вариант 1). Вычислите: 2). Упростите: 3). Известно, что: . Вычислить . 4). Решите уравнение: . 5). Докажите тождество: . | 2 вариант 1). Вычислите: 2). Упростите: 3). Известно, что: . Вычислить . 4). Решите уравнение: . 5). Докажите тождество: . |
| Контрольная работа № 3 | |
| 1 вариант 1). Найти наименьшее и наибольшее значения функций: на отрезке ; на отрезке . 2). Упростить выражение: 3). Исследуйте функцию на четность: 4). Постройте график функции: 5). Известно, что . Докажите, что . | 2 вариант 1). Найти наименьшее и наибольшее значения функций: на отрезке ; на отрезке . 2). Упростить выражение: 3). Исследуйте функцию на четность: 4). Постройте график функции: 5). Известно, что . Докажите, что . |
| Контрольная работа № 4 | |
| 1 вариант 1). Решить уравнение: 2). Найти корни уравнения на отрезке . 3). Решить уравнение: 4). Найти корни уравнения , принадлежащие отрезку . | 2 вариант 1). Решить уравнение: 2). Найти корни уравнения на отрезке . 3). Решить уравнение: 4). Найти корни уравнения , принадлежащие отрезку . |
| Контрольная работа № 5 | |
| 1 вариант 1). Вычислить: 2). Упростить выражение: 3). Доказать тождество: 4). Решить уравнение а). 5). Зная, что и , найти . | 2 вариант 1). Вычислите: 2). Упростить выражение: 3). Доказать тождество: 4). Решить уравнение а). 5). Зная, что и , найти . |
| Контрольная работа № 6 | |
| 1 вариант 1). Найдите производную функции: а). ; б). ; в). ; г). ; д). . 2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции в точке х0 = 1. 3). Прямолинейное движение точки описывается законом . Найдите ее скорость в момент времени с. 4). Дана функция . Найдите: а). Промежутки возрастания и убывания функции; б). Точки экстремума; в). Наибольшее и наименьшее значения функции на отрезке . | 2 вариант 1). Найдите производную функции: а). ; б). ; в). ; г). ; д). . 2). Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции в точке х0 = 1. 3). Прямолинейное движение точки описывается законом . Найдите ее скорость в момент времени t = 2с. 4). Дана функция . Найдите: а). Промежутки возрастания и убывания функции; б). Точки экстремума; в). Наибольшее и наименьшее значения функции на отрезке . |
| Контрольная работа № 7 ( итоговая ) | |
| 1 вариант 1). Дана функция. Составить уравнение касательной к графику в точке с абсциссой . Установить, в каких точках промежутка касательная к графику данной функции составляет с осью Ох угол 600. 2). Решите уравнение: 3). Упростите выражение: а). ; б). . 4). Постройте график функции с полным исследованием функции . | 2 вариант 1). Дана функция. Составить уравнение касательной к графику в точке с абсциссой . Установить точки минимума и максимума, а также наибольшее и наименьшее значение на промежутке . 2). Решите уравнение: 3). Упростите выражение: а). ; б). . 4). Постройте график функции с полным исследованием функции . |
infourok.ru
Контрольные работы по алгебре, 10 класс
10 класс. Диагностическая контрольная работа по алгебре
№
Задание
№
Задание
І вариант
ІІ вариант
1.
Сравнить числа х и у, если разность х – у равна (-7).
1.
Сравнить числа х и у, если разность х – у равна (+9).
А. х > у Б. х = у В. х < у Г. Другой ответ
2.
Решить систему неравенств:

2.
Решить систему неравенств:
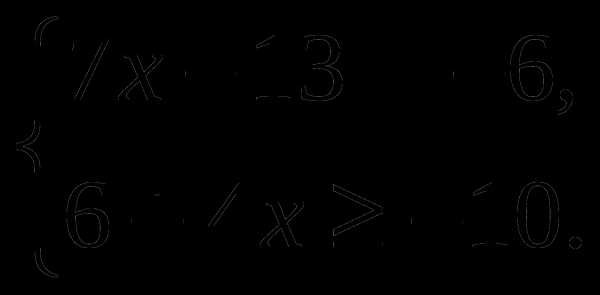
А. (-3; 7] Б. (-2; 4] В. [-4; 1) Г. (-2; -4]
3.
Указать точку, через которую проходит график функции: у = 2х² + 5х -1
3.
Указать точку, через которую проходит график функции: у = 2х² + 3х -5
А. (-1; -6) Б. (1; 6) В. (3; 0) Г. (2; 11)
4.
Указать координаты вершины параболы
у = (х +1)² — 3?
4.
Указать координаты вершины параболы
у = (х -1)² + 3?
А. (-2; 3) Б. (1; 3) В. (-1; -3) Г. (2; -3)
5.
Решить графически систему уравнений:

5.
Решить графически систему уравнений:
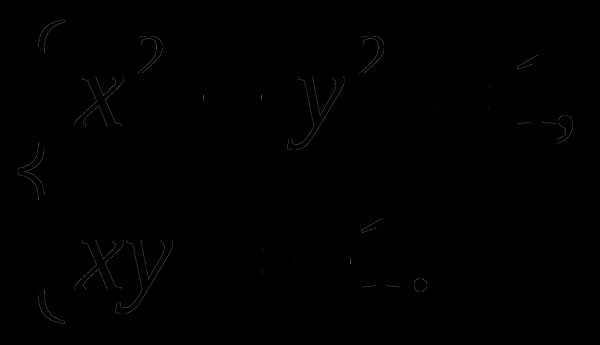
6.
Постройте график функции у = -х² + 2х + 8. Используя график: а) решите неравенство
-х² + 2х + 8 0;
0;
б) определите промежутки возрастания и убывания функции.
6.
Постройте график функции у = х² + 2х — 3. Используя график: а) решите неравенство х² + 2х — 3 0;
0;
б) определите промежутки возрастания и убывания функции.
7.
В геометрической прогрессии (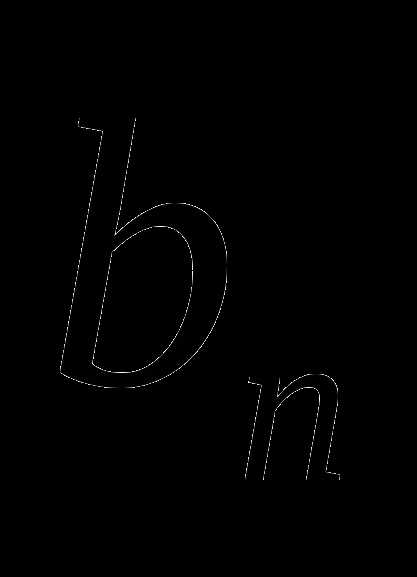 )
) 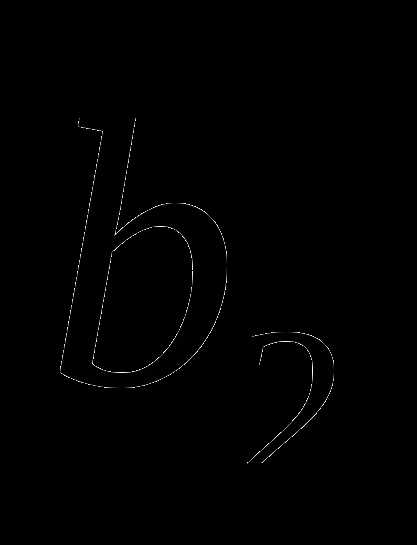 =6,
=6,  =486, q>0. Найдите
=486, q>0. Найдите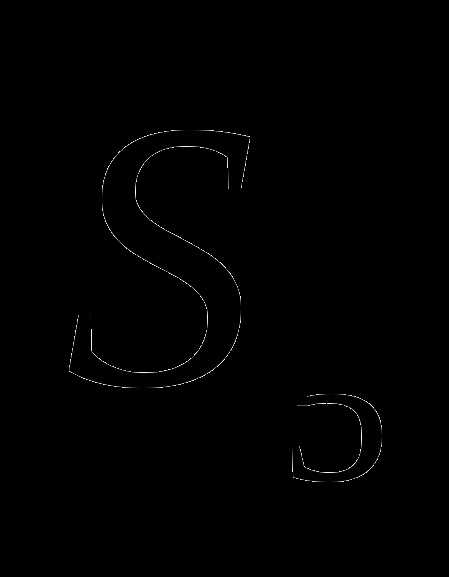 .
.
7.
В геометрической прогрессии (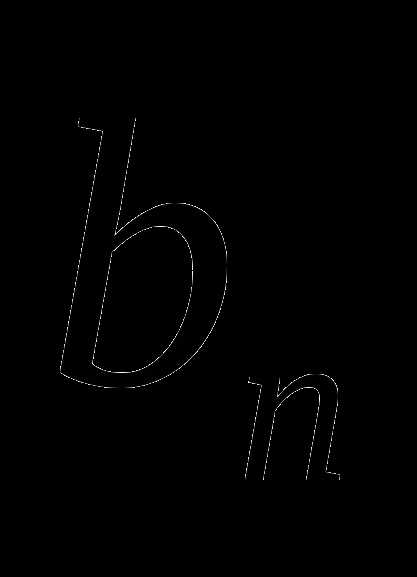 )
) 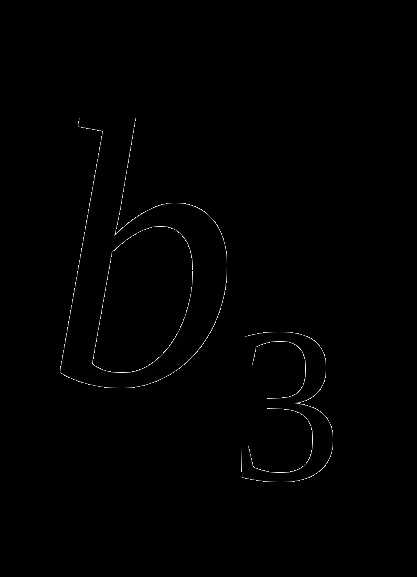
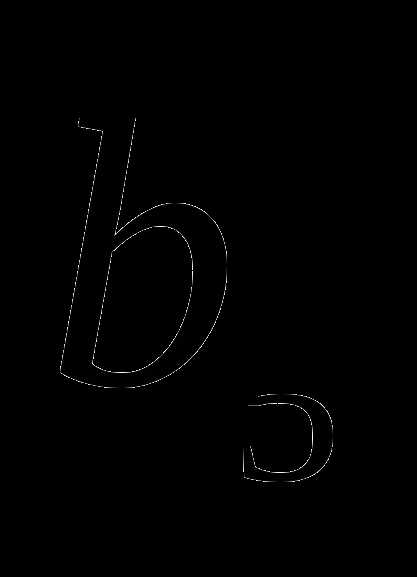 =162, q<0. Найдите
=162, q<0. Найдите 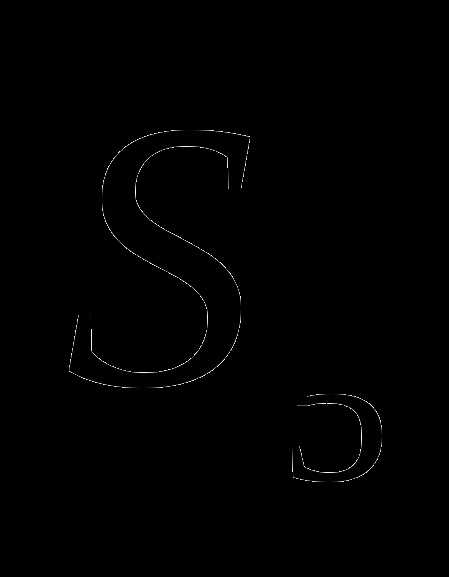 .
. 8.
Сумма первого и второго членов арифметической прогрессии равна  , а разность между первым членом и разностью d этой арифметической прогрессии равна
, а разность между первым членом и разностью d этой арифметической прогрессии равна  . Найдите третий член и номер члена, который равен
. Найдите третий член и номер члена, который равен
(-3).
8.
Сумма первого и третьего членов арифметической прогрессии равна 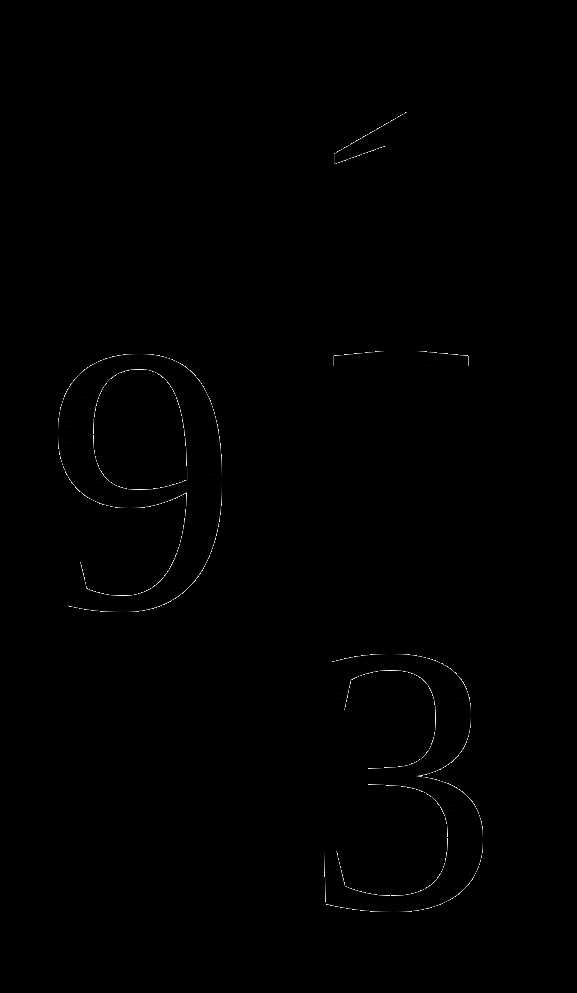 , а разность между первым и третьим членами этой арифметической прогрессии равна
, а разность между первым и третьим членами этой арифметической прогрессии равна 
Оценивание: 1-5 по 1 баллу; 6,7 по 2 балла; 8 – 3 балла.
10 класс. Тематическая контрольная работа по алгебре «Числовые множества. Функции».
№
Задание
1 вариант
№
Задание
2 вариант
1
Записать множество способом перечисления его элементов:
а) правильные дроби со знаменателем 7;
б) решения уравнения х² + 6х -7 = 0;
в) гласные буквы украинского алфавита.
1
а) неправильные дроби, числитель которых равен 6;
б) решения уравнения х² +х – 12 = 0;
в) дни недели.
2
Записать все подмножества множества
В = {m, n, k}.
Записать все подмножества множества
С = {5, 6, 7}.
3
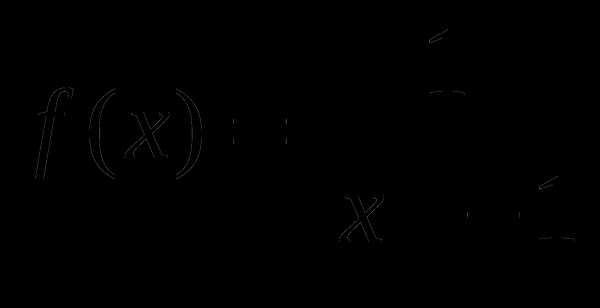 , найти f(-2), f(-1), f(0), f(1), f(2).
, найти f(-2), f(-1), f(0), f(1), f(2).
3
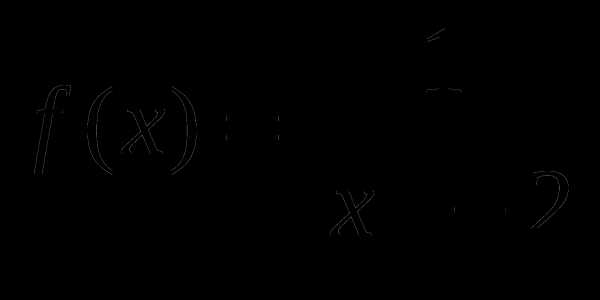 , найти f(-2), f(-1), f(0), f(1), f(2).
, найти f(-2), f(-1), f(0), f(1), f(2).
4
Найти область определения функций:
а) у =  б) у =
б) у = 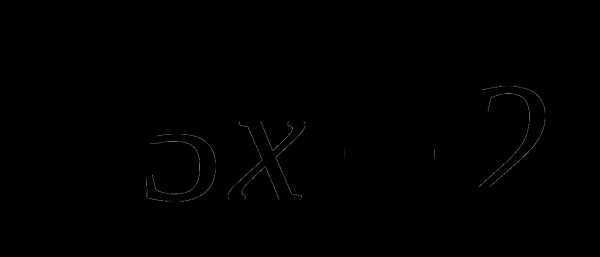 .
.
4
Найти область определения функций:
а) у = 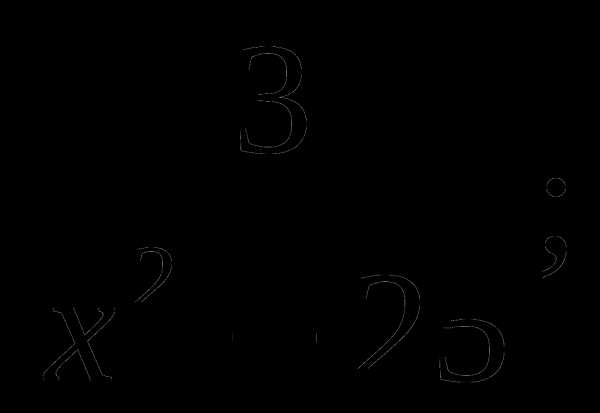 б) у =
б) у = 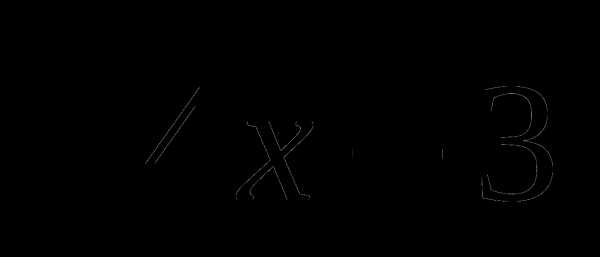 .
.
5
Указать множество значений функций:
а) у = 16х – 5; б) у = 23; в) у = х² — 9.
5
Указать множество значений функций:
а) у = -5х + 7; б) у = 32; в) у = х² — 7.
6
Доказать, что функция у = 7х – 3 возрастает на всей области определения.
6
Доказать, что функция у = -2х + 5 убывает на всей области определения.
7
Определить четность или нечетность функций: а) у = |х| + х²; б) у = х³·|х|.
7
Определить четность или нечетность функций: а) у = х (5 -|х|) ; б) у =  .
.
8
Построить графики функций: а) у = |х| — 5;
б) у = 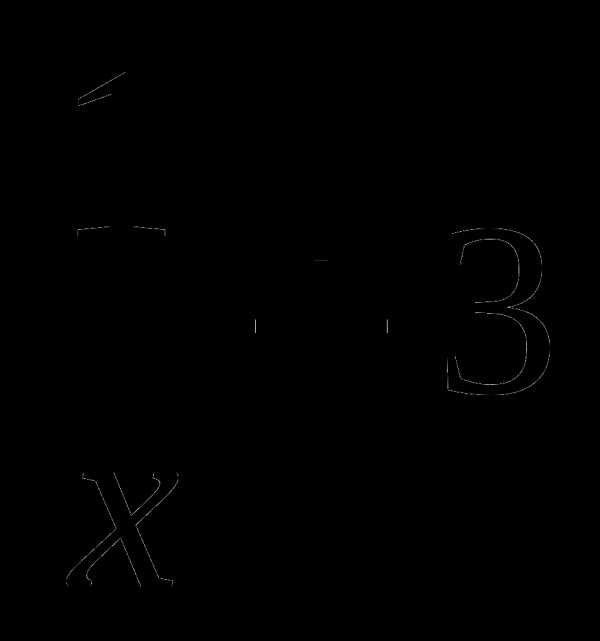 .
.
8
Построить графики функций: а) у = 5 — |х|;
б) у =  .
.
Оценивание: 1 – 4 задания – по 1 баллу;
5 – 8 задания – по 2 балла.
10 класс. Тематическая контрольная работа по алгебре №3 «Уравнения и неравенства» (учебник Е.П.Нелин, 10 класс, §3,4,5).
№
Задание
1 вариант
№
Задание
2 вариант
1
Какие из уравнений равносильны уравнению 3 —  =0?
=0?
А) 1–3х=0, Б) 
В)  Г) 3х–1=0.
Г) 3х–1=0.
1
Какие из уравнений равносильны уравнению 
А) 1–7х=0, Б) 
В) 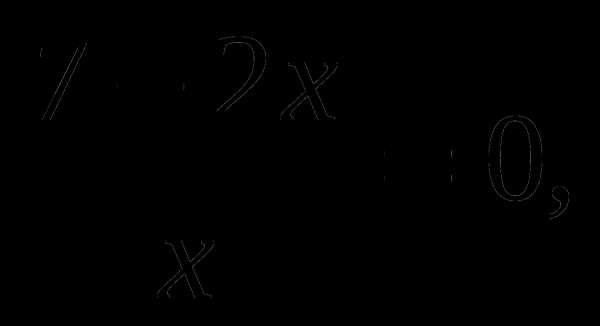 Г) 7х–2=0.
Г) 7х–2=0.
2
Решите уравнение и укажите, какое преобразование могло бы привести к нарушению равносильности.
.
2
Решите уравнение и укажите, какое преобразование могло бы привести к нарушению равносильности.
.
3
Применяя свойства функций, решите уравнения:
а)
б) |х²+4х-21| +|49-х²| +|2х+14| = 0;
в) х +  + х³ = 70.
+ х³ = 70.
Применяя свойства функций, решите уравнения:
а)
б) |х²-х-20| +|25-х²| +|2х-10| = 0;
в) х +  + х² = 93.
+ х² = 93.
4
Решить неравенство методом интервалов:
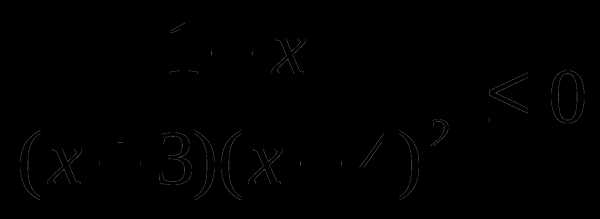
4
Решить неравенство методом интервалов:
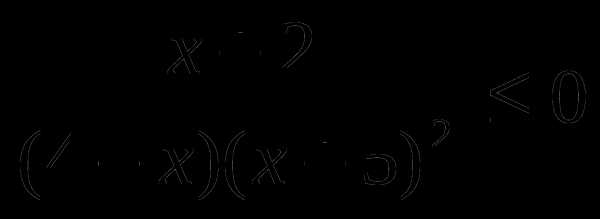
5
Решить уравнения:
а) |12-х| = 5;
б) | х-3 | — | 2х + 4 | = 2.
5
Решить уравнения:
а) |х — 7| = 8;
б) | х +3 | — | 6 – 3х | = 1.Оценивание: 1 – 1 балл;
2 – 2 балла;
3,4,5 – по 3 балла.
10 класс. Контрольная работа №4 «Уравнения и неравенства с параметрами. Графики уравнений и неравенств».
№
І вариант
№
ІІ вариант
1
Решить уравнение с параметром а относительно переменной х:
|х² -6|х|| = а.
1
Решить уравнение с параметром а относительно переменной х:
|х² -8|х|| = а.
2
Решить неравенство с параметром а относительно переменной х:
4х + 3а≥ 6 – ах.
2
Решить неравенство с параметром а относительно переменной х:
2ах — 3≤ а – х.
3
Построить график неравенства:
(х-2)² + у² ≤16.
3
Построить график неравенства:
х² + (у-1)² ≥36.
4
Выполнить деление многочлена
А(х) = на В(х)=.
4
Выполнить деление многочлена
А(х) = на В(х)=.
5
Используя схему Горнера, проверить являються ли числа 1 и (-2) корнями многочлена: х³ + х² — 3х – 2.
5
Используя схему Горнера, проверить являються ли числа (-1) и 2 корнями многочлена: х³ — х² — 5х – 3.
10 класс. Контрольная работа по алгебре и началам анализа №5 «Метод математической индукции. Корень п-ой степени».
№
І вариант
№
ІІ вариант
1
Используя метод математической индукции, доказать:
1
Используя метод математической индукции, доказать:
1 + 2 + 3 +…+ n = 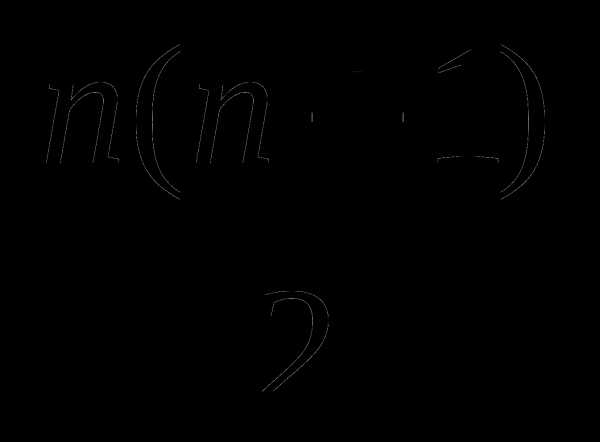
2
Установить соответствие:
1.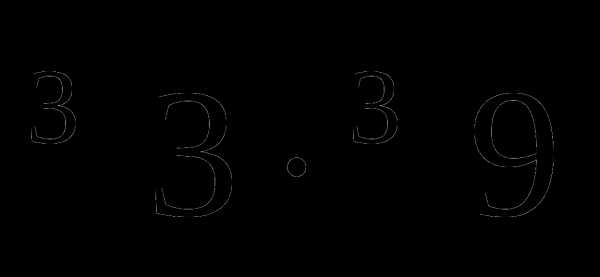 А 1
А 1
2.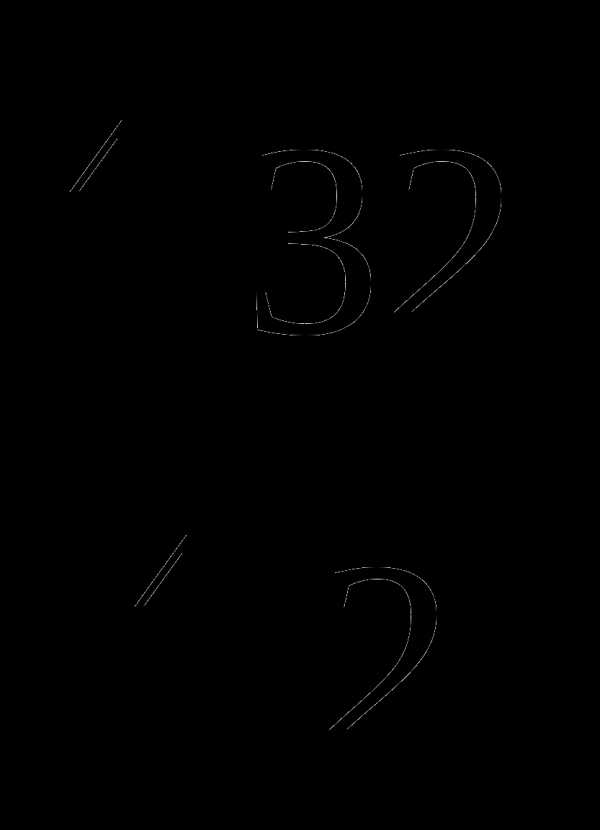 Б 2
Б 2
3. 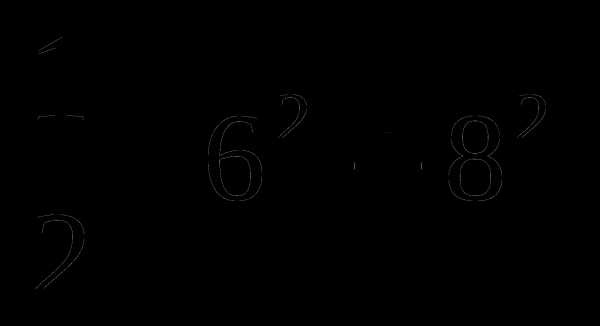 В 3
В 3
4. 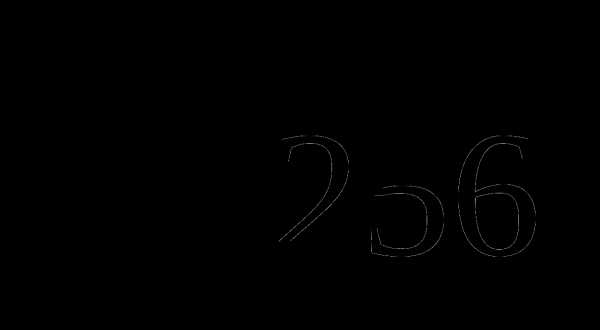 Г 4
Г 4
Д 5
2
Установить соответствие:
1. А 1
А 1
2.  Б 2
Б 2
3. 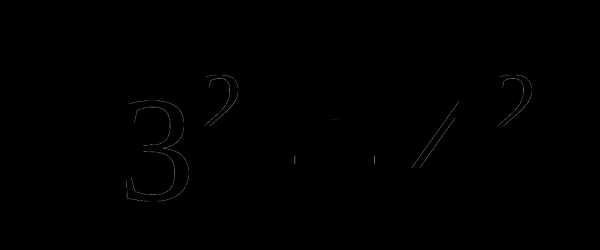 В 3
В 3
4.  Г 4
Г 4
Д 5
3
Разместить числа в порядке убывания:  ;
; 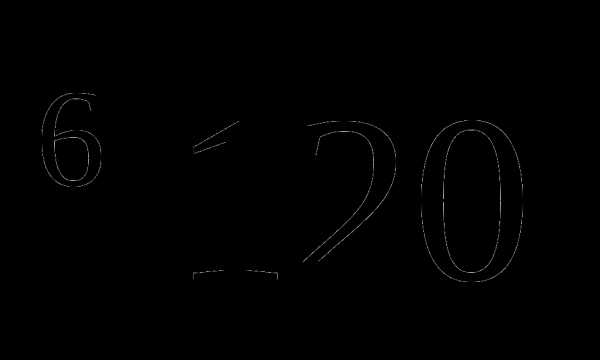 ;
; 
3
Разместить числа в порядке возрастания:
 ;
; 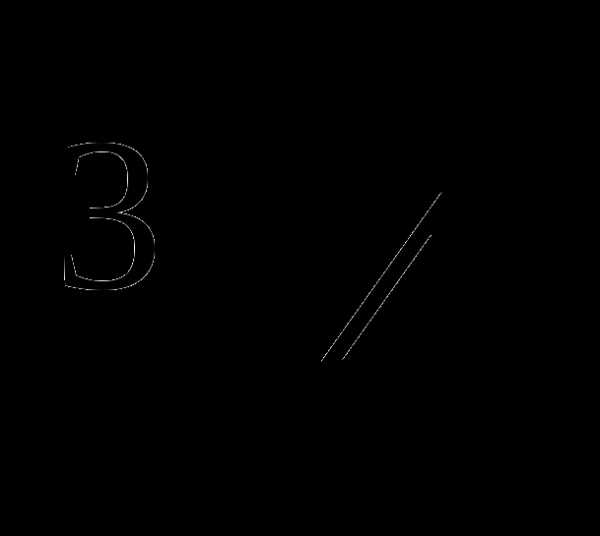 ;
; 
4
Вычислить:
4
Вычислить:
5
Сравнить:  и
и 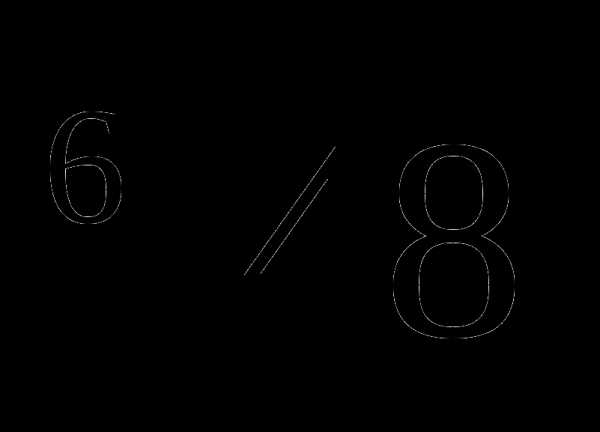 .
.
5
Сравнить: 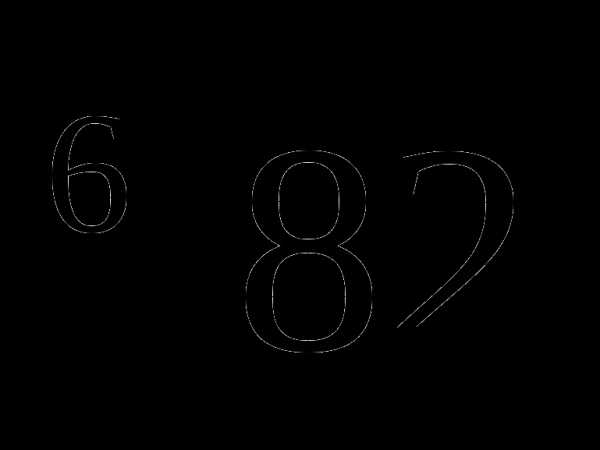 и
и  .
.
10 класс. Контрольная работа по алгебре и началам анализа №6
№
І вариант
№
ІІ вариант
1.
Вычислить: а)  б)
б) 
1.
Вычислить: а)  б)
б) 
2.
Решить уравнение: х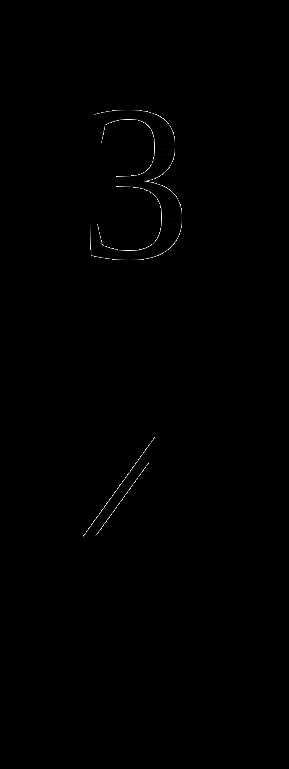 = 81.
= 81.
2.
Решить уравнение: х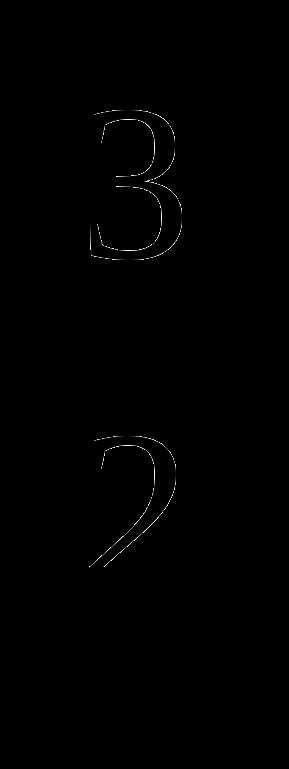 = 64.
= 64.
3.
Установить соответствие между функциями, заданными формулами, (1 – 4) и их графиками (А – Д).
1) у = х
2) у = х
3) у = х
4) у = х
3.
Установить соответствие между функциями, заданными формулами, (1 – 4) и их графиками (А – Д).
1) у = х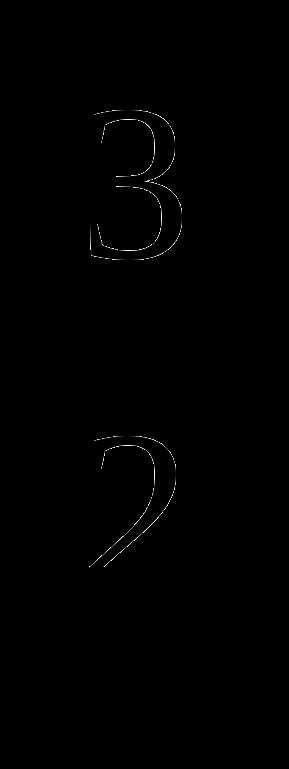
2) у = х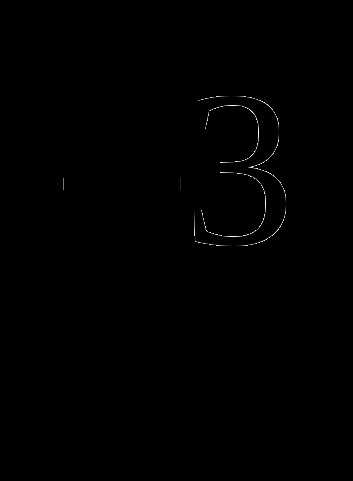
3) у = х
4) у = х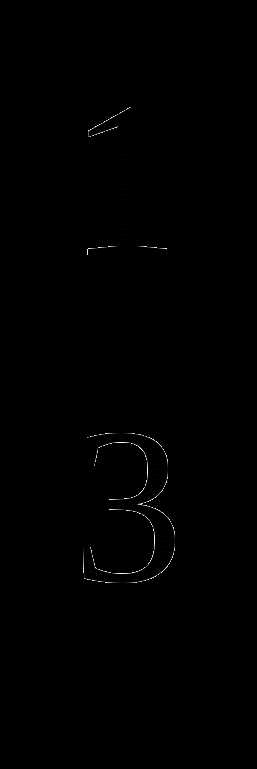
4.
Сократить дробь:
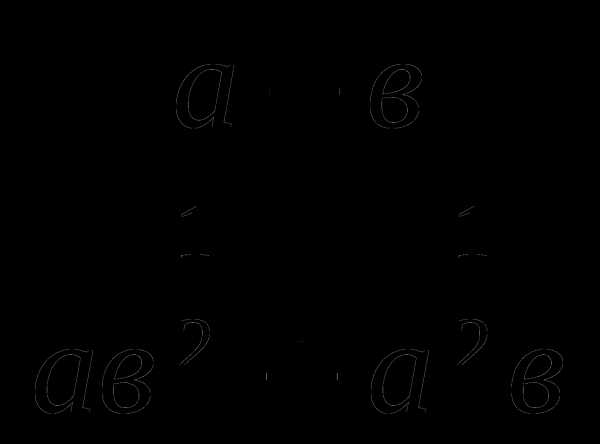
4.
Сократить дробь:
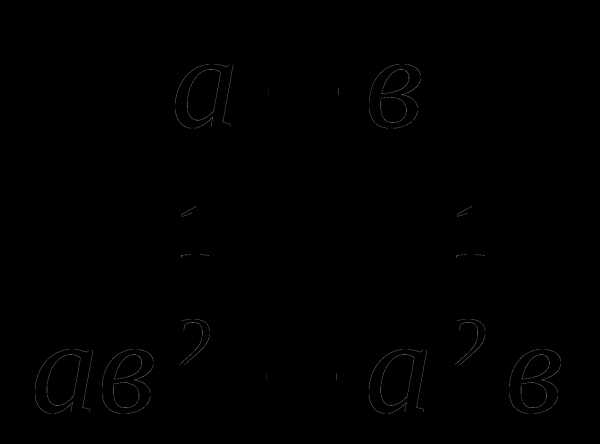
5.
Упростить:
5.
Упростить: .
10 класс. Контрольная работа по алгебре и началам анализа №6
№
І вариант
№
ІІ вариант
1.
Вычислить: 27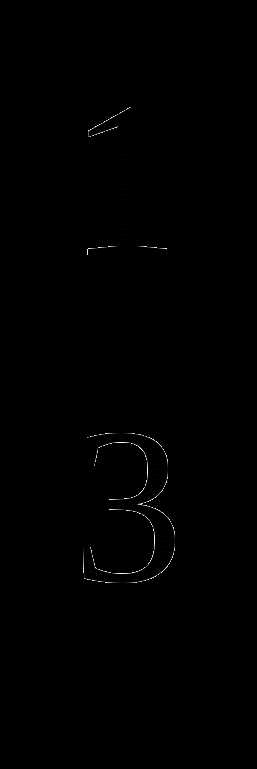
1.
Вычислить: 8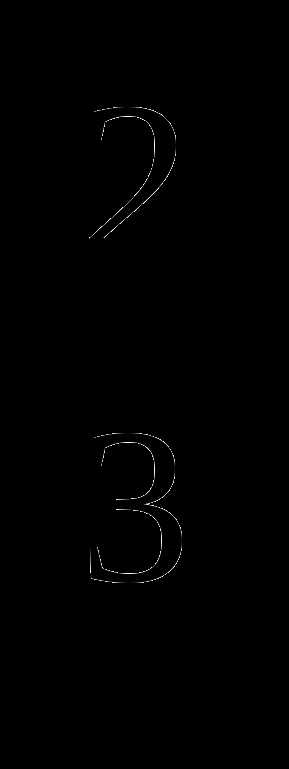
2.
Решить уравнение: х = 81.
= 81.
2.
Решить уравнение: х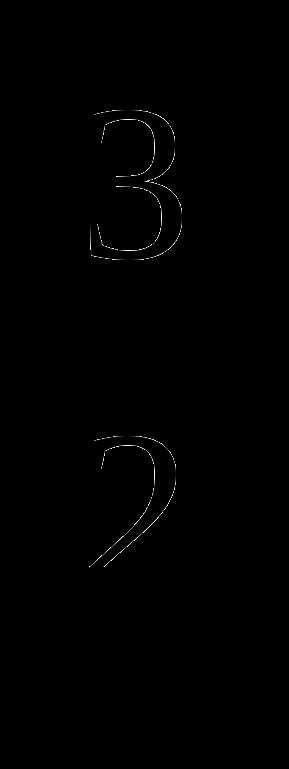 = 64.
= 64.
3.
Установить соответствие между функциями, заданными формулами, (1 – 4) и их графиками (А – Д).
1) у = х
2) у = х
3) у = х
4) у = х
3.
Установить соответствие между функциями, заданными формулами, (1 – 4) и их графиками (А – Д).
1) у = х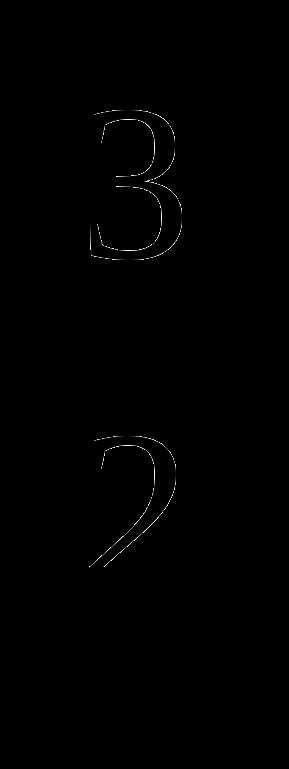
2) у = х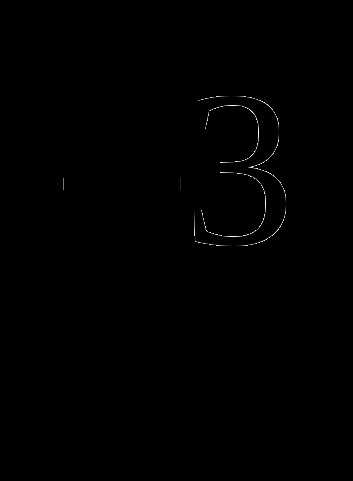
3) у = х
4) у = х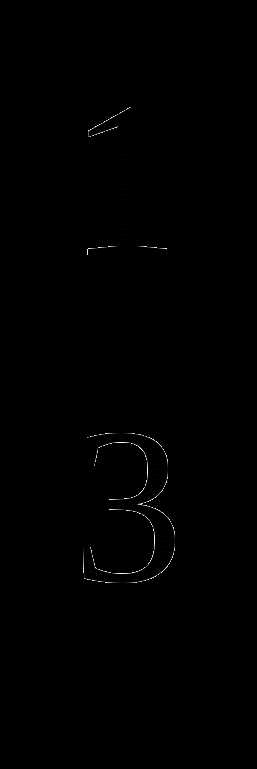
4.
Сократить дробь:
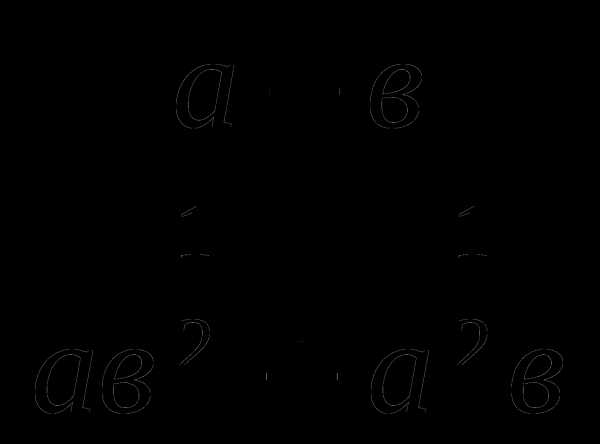
4.
Сократить дробь:
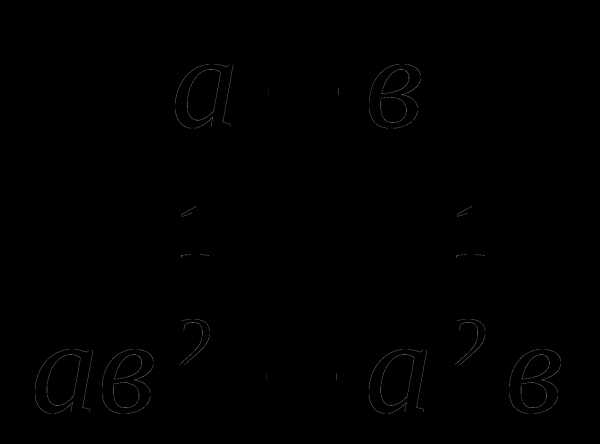
5.
Решить уравнение:
5.
Решить уравнение:
6.
Решить неравенство:
6.
Решить неравенство:
10 класс. Алгебра. Контрольная работа №7 «Иррациональные уравнения и неравенства»
№
І вариант
№
ІІ вариант
1
Сколько корней имеет уравнение .
1
Сколько корней имеет уравнение .
2
Установить соответствие между функциями, заданными формулами (1-4), и их областями определения (А-Д):
1. у =  А. (-∞; 0)
А. (-∞; 0)
2. у =  Б. [0; +∞)
Б. [0; +∞)
3. у = 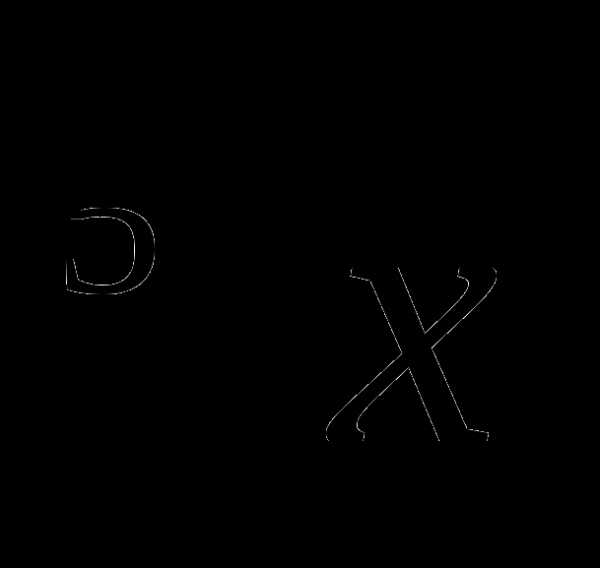 В. (0; +∞)
В. (0; +∞)
4. у =  Г. (-∞; +∞)
Г. (-∞; +∞)
Д. (-∞; 0) U (0; +∞)
2
Установить соответствие между функциями, заданными формулами (1-4), и их областями определения (А-Д):
1. у = 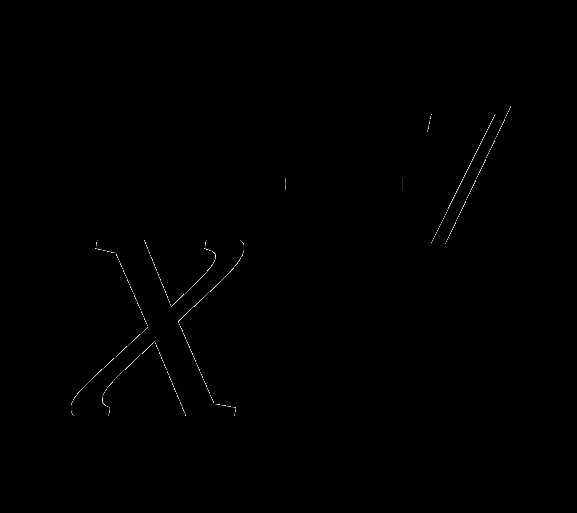 А. (-∞; 0)
А. (-∞; 0)
2. у =  Б. (0; +∞)
Б. (0; +∞)
3. у = 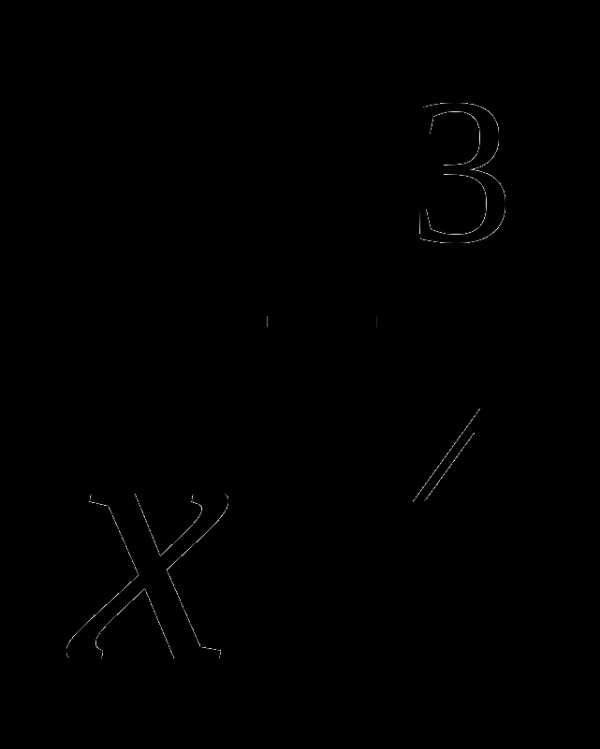 В. [0; +∞)
В. [0; +∞)
4. у =  Г. (-∞; +∞)
Г. (-∞; +∞)
Д. (-∞; 0) U (0; +∞)
3
Решить уравнения:
.
3
Решить уравнения:
.
4
Решить систему уравнений:
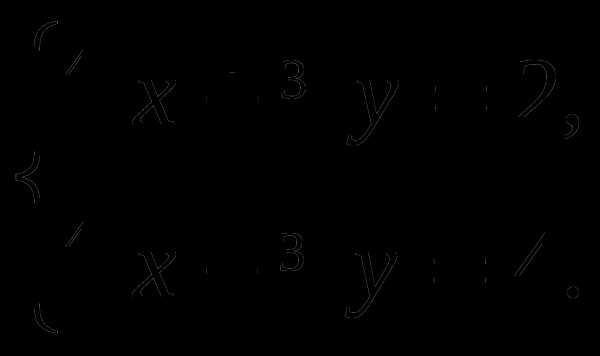
4
Решить систему уравнений:

5
Решить неравенства:
а) ;
б)  < 0.
< 0.
5
Решить неравенства:
а) ;
б) 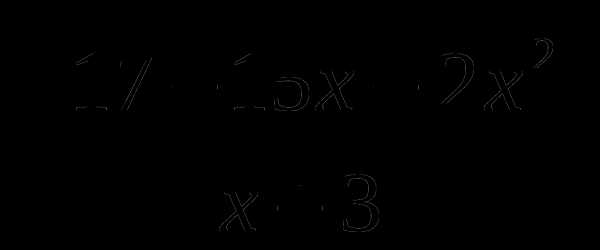 > 0.
> 0.
Оценивание: 1, 2 – по 0,5 балла; 3, 4 – по 1 баллу; 5 – 2 балла.
10 класс. Контрольная работа №8 «Тригонометрические функции и их графики»
№
І вариант
№
ІІ вариант
1
Записать в порядке возрастания:
sin(-1), sin , sin 135º, sin(-30º).
, sin 135º, sin(-30º).
Записать в порядке убывания:
cos , cos(-1), cos(-30º), cos 135º.
, cos(-1), cos(-30º), cos 135º.
2
Построить график функции 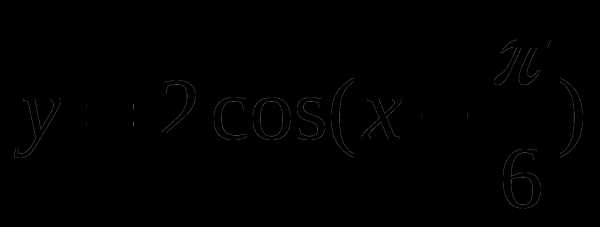 . Записать промежутки возрастания и убывания функции.
. Записать промежутки возрастания и убывания функции.
2
Построить график функции 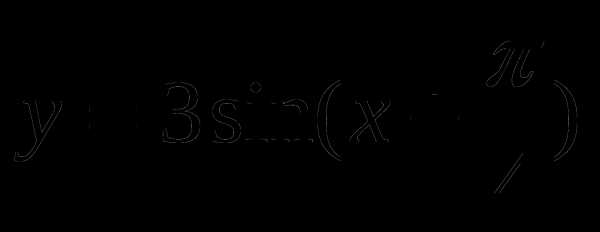 . Записать промежутки возрастания и убывания функции.
. Записать промежутки возрастания и убывания функции.
3
Найти значение выражения 
3
Найти значение выражения 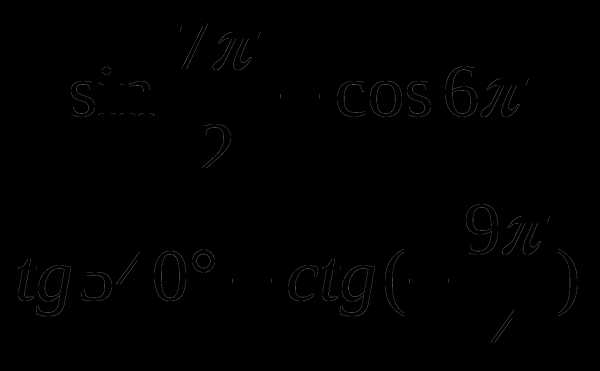
10 класс. Годовая контрольная работа.
І вариант
ІІ вариант
1.
Известно, что множество А=, В=.
Найти 1) АUВ; 2)А∩В.
1.
Известно, что множество А=, В=.
Найти 1) АUВ; 2)А∩В.
2.
Определить четность или нечетность функции у =  .
.
2.
Определить четность или нечетность функции у = х (4 -|х|).
3.
Решить неравенство методом интервалов:

3.
Решить неравенство методом интервалов:

4.
Решить уравнение:
а) 2| х-3 | — | 3 — х | = 5.
б) .
4.
Решить уравнение:
а) 5| х – 4 | — 2| 4 – х | = 4.
б) .
5.
Докажите тождество:
.
5.
Докажите тождество:
.
infourok.ru
ГДЗ по алгебре за 10 класс контрольные работы Глизбург В.И. Базовый уровень
GDZ.RU-
1 класс
- Математика
- Английский язык
- Русский язык
- Информатика
- Литература
- Окружающий мир
- Человек и мир
-
2 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Белорусский язык
- Информатика
- Литература
- Окружающий мир
- Человек и мир
-
3 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Белорусский язык
- Информатика
- Литература
- Окружающий мир
- Испанский язык
-
4 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Окружающий мир
- Испанский язык
-
5 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Белорусский язык
- Французский язык
- Биология
- История
- Информатика
- География
gdz.ru
|
РАЗРАБОТКИ |
10 классВ категории разработок: 18 Фильтр по целевой аудитории — Целевая аудитория -для 1 классадля 2 классадля 3 классадля 4 классадля 5 классадля 6 классадля 7 классадля 8 классадля 9 классадля 10 классадля 11 классадля учителядля классного руководителядля дошкольниковдля директорадля завучейдля логопедадля психологадля соц.педагогадля воспитателя Представлено 4 варианта экзаменационной работы. Цель экзамена: проверка уровня предметной компетентности учащихся 10 класса по математике за курс 10 класса в рамках проведения промежуточной аттестации. Целевая аудитория: для 10 класса Представлена контрольная работа по алгебре для учеников 10 класса по учебнику Алимова Целевая аудитория: для 10 класса В работе представлены 4 варианта. Работа составлена в форме теста с кратким ответом и состоит из двух частей: Часть1 – 7 заданий базового уровня сложности с кратким ответом, часть 2 – 3 задания повышенного уровня сложности. Структура теста аналогична структуре КИМ ЕГЭ, что позволит не только проверить знания, умения и навыки учащихся за курс 10 класса, но и постепенно подготовить к работе с подобным материалом при подготовке и сдаче экзамена. На выполнение работы отводится 45 минут. Целевая аудитория: для 10 класса
Итоговая контрольная работа по алгебре и началам математического анализа за курс 10 класса составлена в соответствии с учебником: Целевая аудитория: для 10 класса
Итоговая контрольная работа по геометрии за курс 10 класса составлена в соответствии с учебником: Геометрия, 10-11: учебник для общеобразовательных учреждений. / Атанасян Л.С., Бутузов В.Ф. и др. – М.: Просвещение, 2009 — 2013. Целевая аудитория: для 10 класса 4 варианта + демонстрационный вариант. Ко всем вариантам даны ответы. Целевая аудитория: для 10 класса Данный материал содержит 9 теоретических самостоятельных работ по геометрии за курс 10 класса, к учебнику Л.С.Атанасян. Данные работы рекомендуется проводить на второй урок после изучения нового. Такая работа займет не много времени, 5-7 минут. Задания подобраны с разным уровнем сложности. Целевая аудитория: для 10 класса Планирование,контрольные работы,справочный материал по учебнику Мордковича,алгебра-10 Целевая аудитория: для 10 класса Данная контрольная работа выполнена в форме малого ЕГЭ, содержит 15 различных вариантов по 15 вопросов в каждом. Каждый вариант разбит на 2 части. Часть 1: Задания B1 — B10 Часть 2: Задания B11 — B15. Ко всем вариантам есть ответы и критерии оценивания. Целевая аудитория: для 10 класса
В дидактических материалах предоставлены теоретические материалы по теме «Показательные уравнения», рассмотрены методы решения уравнений, предложены задания для самостоятельного изучения и закрепления новых знаний и умений. Это пособие поможет подготовиться к ЕГЭ по математике. Цель работы направлена на обучение решения показательных уравнений стандартного вида. При подготовке к ЕГЭ эти задачи входят в группы А и В. Целевая аудитория: для 10 класса |
Конкурсы Диплом и благодарность каждому участнику! |
www.uchportal.ru
Нулевая контрольная работа по алгебре 10 класс(1-2 вариант)
Проверочная контрольная работа на начало учебного года по алгебре в 10 классе
Просмотр содержимого документа
«Нулевая контрольная работа по алгебре 10 класс(1-2 вариант)»
Проверочная контрольная работа по алгебре 10 класс
Вариант 1.
1. Найдите значение выражения: .
2. Найдите значение выражения: .
3. Решите уравнение: .
4. Геометрическая прогрессия задана условиями , . Найдите .
5. Найдите значение выражения: при , .
6. При каких значениях значения выражения больше значения
выражения 3х — 6?
7. Сократите дробь: .
8. Два велосипедиста одновременно отправляются в 60-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым.
9. Постройте график функции
и определите, при каких значениях прямая имеет с графиком ровно две общие точки.
10. Найдите сумму шести первых членов геометрической прогрессии,
если в2 = 4 и в4 = 1.
11. Найдите сумму шестнадцати первых членов арифметической прогрессии:
— 8; — 4; 0;…
12. Найдите область допустимых значений функции:
13. Вычислите:.
14. Найдите значение , если и
15. Доказать:
Проверочная контрольная работа по алгебре 10 класс
Вариант 2.
1. Найдите значение выражения:
2. Найдите значение выражения: .
3. Решите уравнение: .
4. Арифметическая прогрессия задана условиями: , .Найдите
5.Найдите значение выражения: при .
6. Решите неравенство: ?
7. Сократите дробь: .
8. Два автомобиля отправляются в 340-километровый пробег. Первый едет со скоростью на 17 км/ч большей, чем второй, и прибывает к финишу на 1 ч раньше второго. Найдите скорость первого автомобиля.
9.Постройте график функции
и определите, при каких значениях прямая имеет с графиком ровно две общие точки.
10. Найдите сумму пяти первых членов геометрической прогрессии,
если в5 = 81 и в3 = 36.
11. Найдите сумму восемнадцати первых членов арифметической прогрессии:
7; 11; 15;…
12. Найдите область допустимых значений функции:
13. Вычислите:
14. Найдите значение , если и
15. Доказать: 
kopilkaurokov.ru
