Итоговая контрольная работа по математике (10 класс)
Вариант 1
А1 Упростить: 5sin 2α – 4 + 5cos2α
1) 1 2) 9 3) -9 4) -4
А2 Найти все решения уравнения:
 + 2πn , где n; 2) 2πn , где n; 3) πn , где n; 4) π +2πn , где n
+ 2πn , где n; 2) 2πn , где n; 3) πn , где n; 4) π +2πn , где n
А3 Указать множество значений функции: y = 2 cos x – 1
1) [-1; 1 ] 2) ( -∞; ∞) 3) [-1; 3 ] 4) [-3; 1 ]
А4 Найти значение выражения: 5cos2x + 1 , если sin2x = 0,3
А5 Найти значение выражения: 2 – tg2x∙ cos2 x, если sin x = 0,2
1) 1,2 2) 1,96 3) 1,04 4) 1,6
А6. Укажите производную функции у = х4 – 
1)4х — 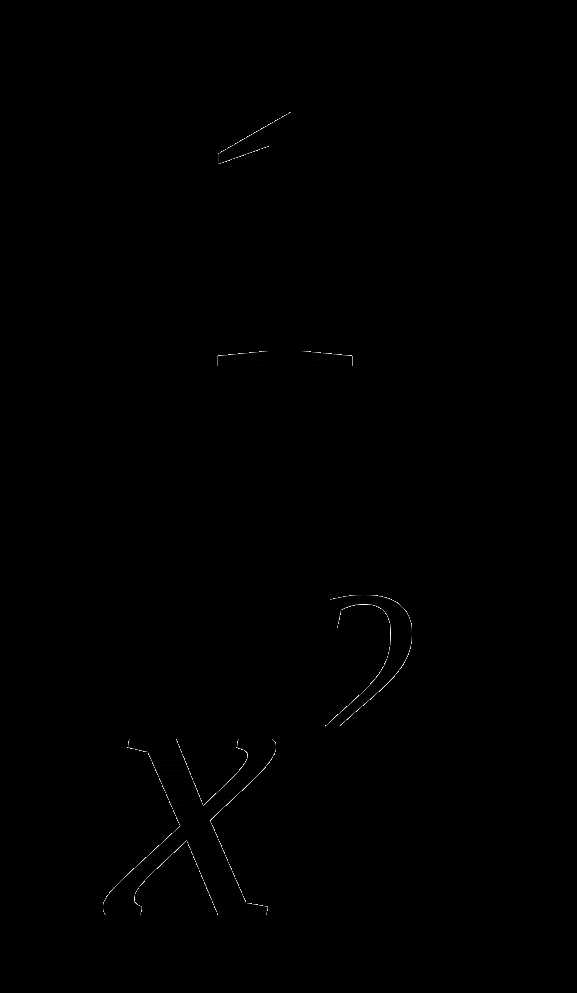 2) 4х3 —
2) 4х3 —  3) 4х3 +
3) 4х3 +  4) 4х +
4) 4х + 
А7. Найдите производную функции у = 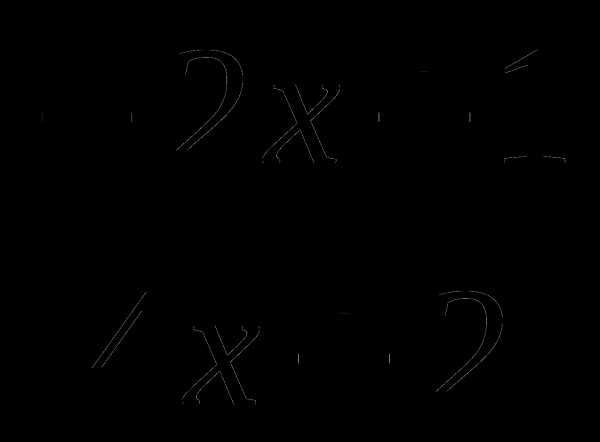
1) – 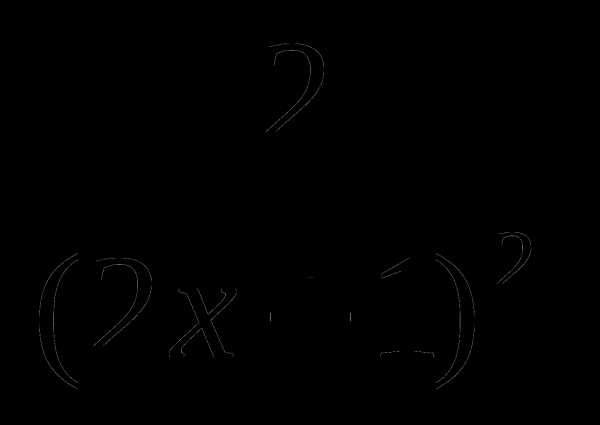 2)
2) 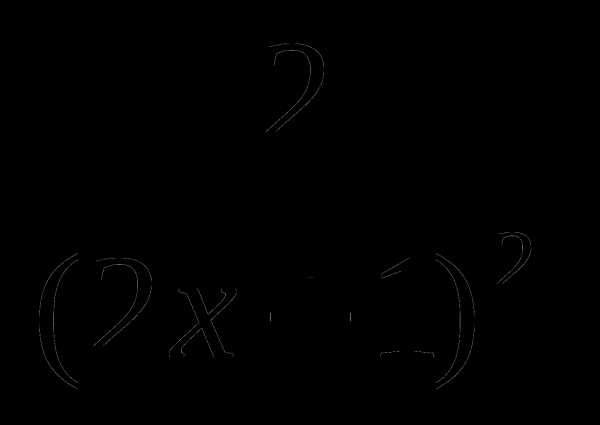 3)
3) 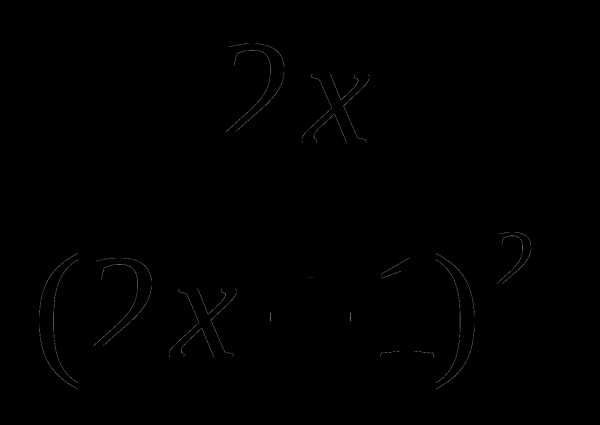 4) —
4) — 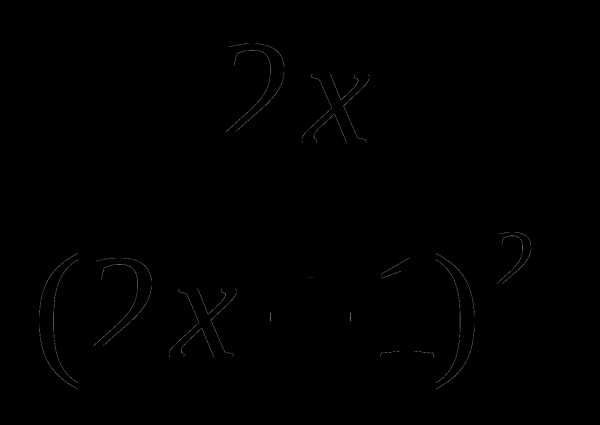
А8. Найдите тангенс угла наклона касательной, проведенной к графику функции у = 4 – х2 в точке с абсциссой х0 = — 3
1) 0 2)6 3) -6 4) -5
А9. Найдите производную функции у = х3 + sin x
1) y‘ =3x2+cosx 2) y‘= x2 + cos x 3) y‘=x2-sinx 4) y‘=3x2-cosx
А10. Найдите точку максимума функции у = х3 – 2х2
1) -1 2) 2 3) -2 4) 0
— — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — —
В1. Найдите наибольшее значение функции f(x) = x3 – 3x на отрезке [0;3].
В 2.
За время t тело перемещается по прямой на расстояние S(t) = 2,5t2 – 11t +17. Через сколько секунд скорость точки будет равна 14?
В 3. Найдите значение выражения: 21 ∙ sinα ∙ ctg(π-α), если cosα =
∙ sinα ∙ ctg(π-α), если cosα =
B4. На рисунке изображен 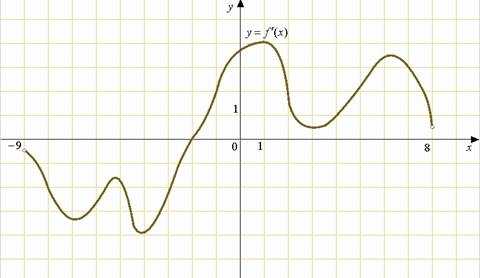 график производной функции , определенной на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней.
график производной функции , определенной на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней.
В5. Найти сумму корней уравнения 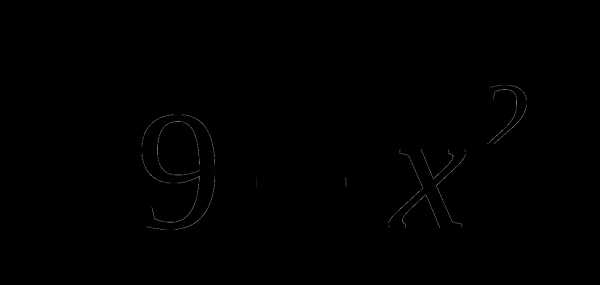 ∙ sin2x = 0
∙ sin2x = 0
В6. Найдите минимум функции g(x) = 3х 5 – 5х3.
В7
С1. Решите уравнение
С2. Определите размеры бассейна с квадратным дном и объёмом 32 м3 таким образом,
чтобы сумма площади боковой поверхности и площади дна была минимальной. В
ответе укажите площадь боковой поверхности.
С3
Вариант 2
А1 Упростить:
1) 1 2 ) ctg2α 3) tg2α 4) 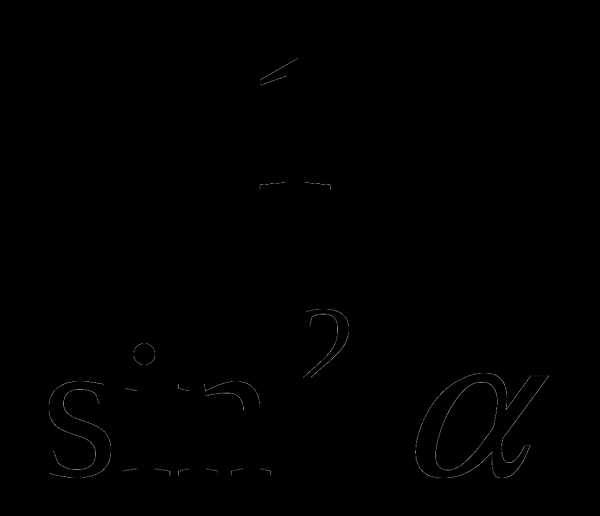
А2 Найти все решения уравнения: (tg2х + 1)∙ tg х =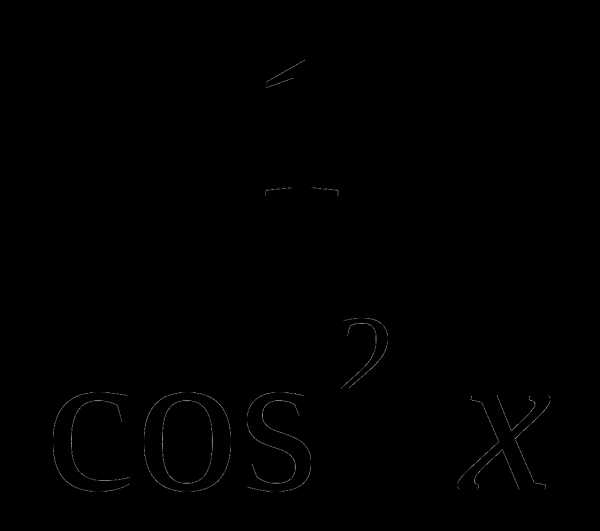
1)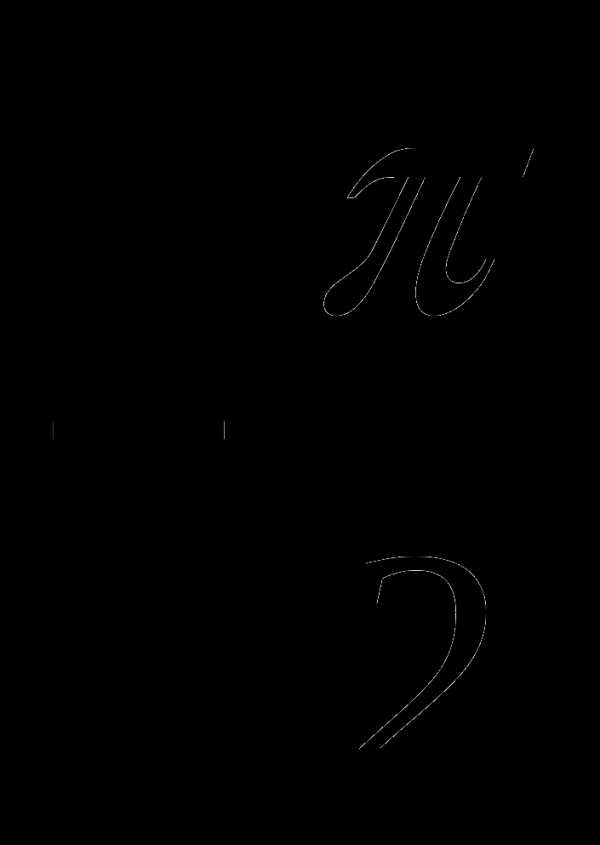 + 2πn
+ 2πn
 + πn , где n; 4) —
+ πn , где n; 4) — + πn, где n
+ πn, где n А3 Указать множество значений функции: y = sin x – 3
1) [-4; -2 ] 2) [-10; 4 ] 3 )[-4; 4 ] 4) [-10; 10 ]
А4 Найти значение выражения: 3 sin2x – 1, если cos2 х = 0,5
1) 0,5 2) 1,25 3) -1,5 4) -0,5
А5 Найти значение выражения : 3 + 2tg2 x∙ cos2 x, если sin x = 0,3
1) 4,82 2) 3,6 3)4,8 4) 3,18
А6. Укажите производную функции : у = х2 + cosx.
1) 2х+sin x 2) 2x – sin x 3) x – sin x 4) x + sin x
А7. Найдите производную функции : у = 3х2 ∙ cosx.
1) -6xsinx 2) x3cosx + 3x2sinx 3) 6xcosx + 3x2sinx 4) 6xcosx – 3x2sinx
А8. Найдите тангенс угла наклона касательной, проведенной к графику функции у = 2х – х2 в его точке с абсциссой х0 = -2
1) 0 2) 6 3) -2 4) -8
А9. Найдите производную функции: у = (х+1)(х+2) – (х-1)(х-3)
1) 7 2) — 7 3) -1 4) 1
А10. Найдите точку минимума функции: у = х2 – 1.
1) 0 2) 0,5 3) 1 4) -1
В1. Найдите наименьшее значение функции : f(х) = х3 – 3х на отрезке [-3;3].
В2. За время t тело перемещается по прямой на расстояние S(t) = 3t2 — 4,5t + 5.
Через сколько секунд скорость будет 13,5?
В3. Найти значение выражения : 3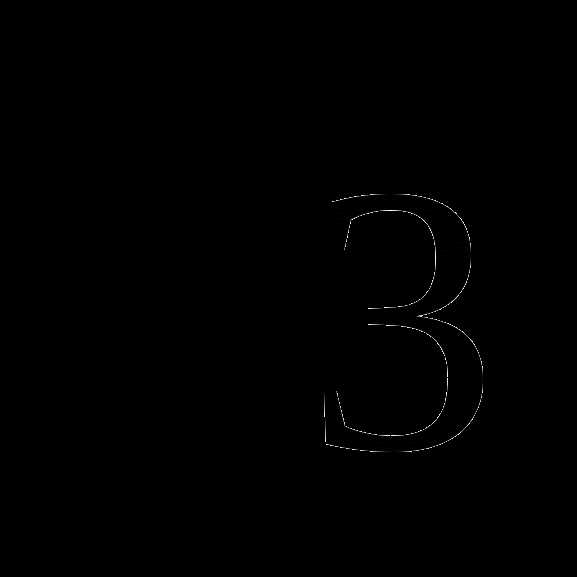 ∙ tgα ∙ cos2(π-α), если sin2α =
∙ tgα ∙ cos2(π-α), если sin2α = 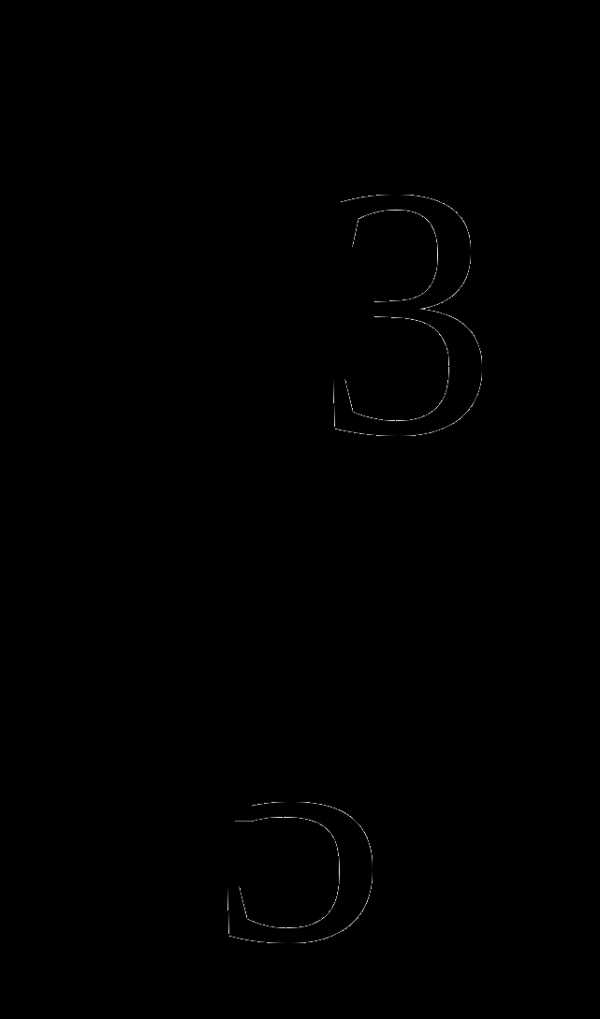 .
.
В4. Функция у = f (х) определена на промежутке (-8;8). График её производной изображен на рисунке. Укажите число промежутков возрастания функции.
В5. Найти сумму корней уравнения 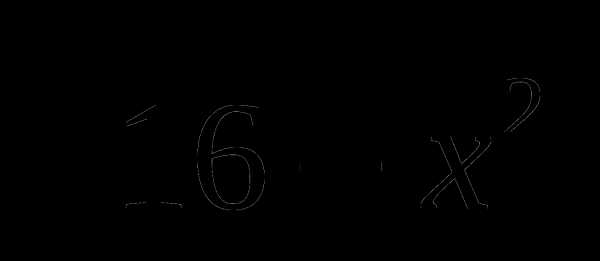 ∙ cos2x = 0
∙ cos2x = 0
В6. Найдите максимум функции у =  +
+ — 2х — 2
— 2х — 2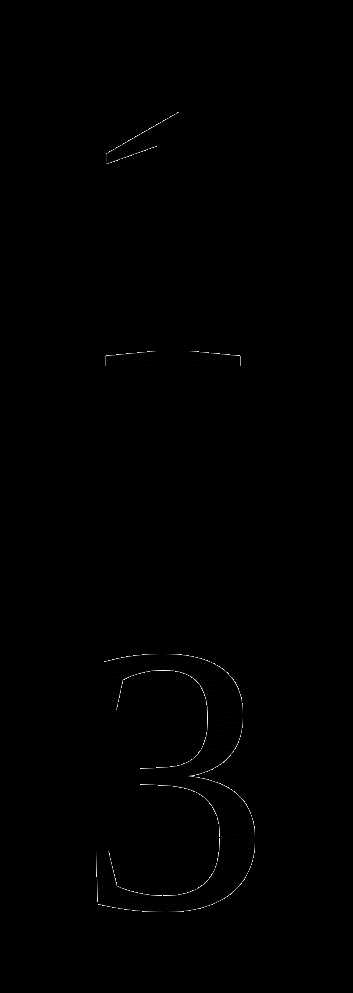 .
.
В7
С1. Решите уравнение :
С2. Рассматриваются всевозможные прямоугольные параллелепипеды, объём каждого
из которых равен 32 см3, а одна из боковых граней является квадратом. Найдите среди них параллелепипед с наименьшим периметром основания. В ответе укажите этот периметр.
С3

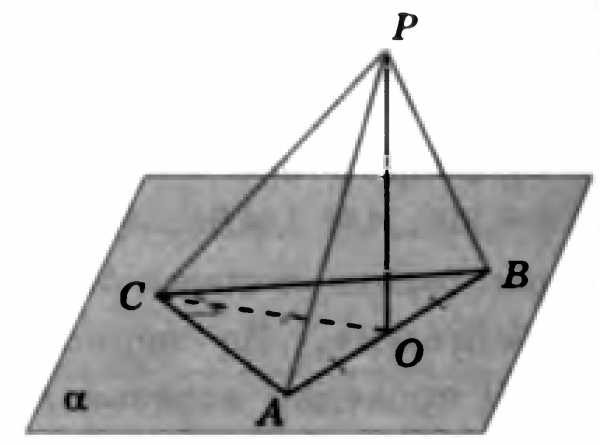
Вариант 3.
А1. Упростить: cos4x + sin2x ∙ cos2x
1) cos2x 2) 2sin2x 3) cos4x. 4) cos2x
А2. Найдите все решения уравнения: 2sinx ∙( tg2x + 1) = 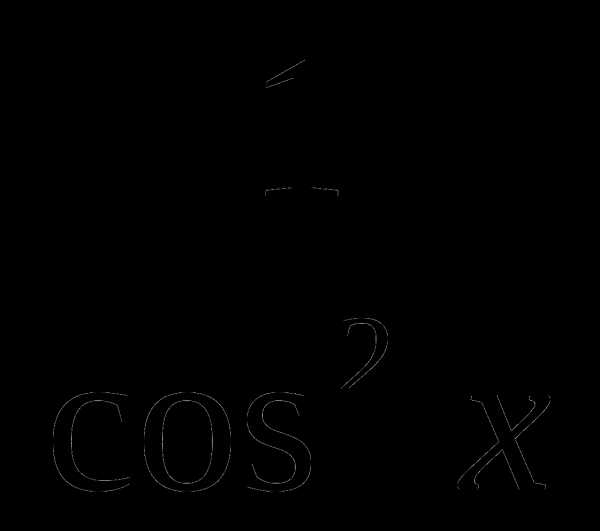
1) πn, n z 2)(-1)n
z 2)(-1)n  + πn, n
+ πn, n z 3)
z 3) 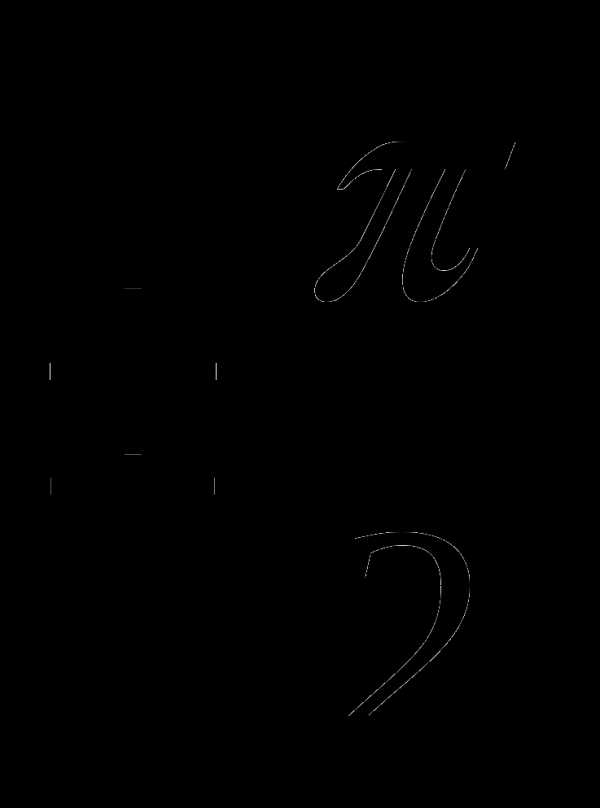 +
+  n, n
n, n z 4)
z 4)  + 2
+ 2 n, n
n, n z
z
А3. Найдите множество значений функции: у = cosх -10
1)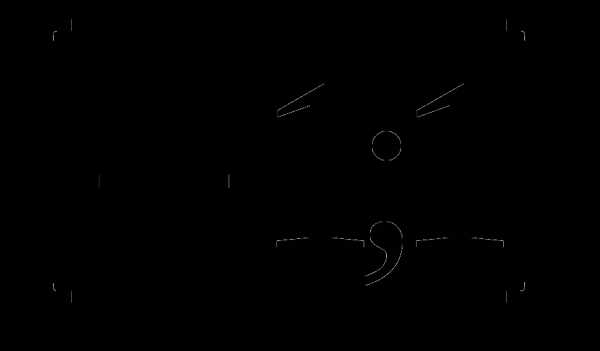 2)
2) 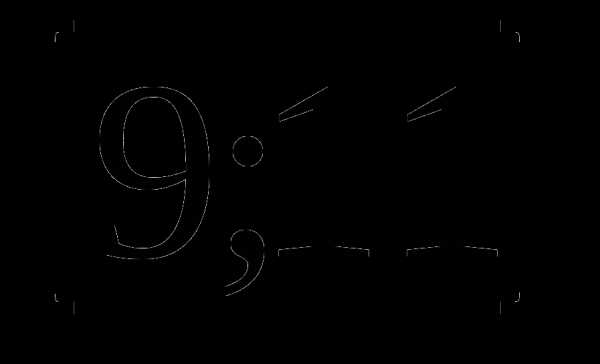 3)
3)  4)( -∞; + ∞)
4)( -∞; + ∞)
А4. Найдите значение выражения: 3 – 2tg2x ∙ cos2x, если sinx = 0,1
1) 2,98 2) 1,02 3) 2,8 4) 3,02
А5. Найдите значение выражения: 3cos2x – 2, если sin2x = 0,1
1) 1,3 2) 0,7 3) — 0,5 4) –1,7
А6. Укажите производную функции : у = х2 –sinx
1) 2x — cosx 2) 2x + cosx 3)  + cosx 4)
+ cosx 4)  — cosx
— cosx
А7. Найдите производную функции: у = -3,6х2 ∙ cosx
1) -7,2xcosx — 3,6x2sinx 2) -7,2xcosx +3,6x2sinx 3) -1,2x3cosx + 3,6x2sinx
4) 7,2xsinx
А8. Найдите тангенс угла наклона касательной, проведённой к графику функции у = -0,5х2 в его точке с абсциссой х0 = -3.
1) -3 2) 3 3) -4,5 4) 0.
А9. Найдите производную функции: у = 9 – 9х8 —  х5
х5
1) у’ = 9х – х9 —  х6 2) у’ = 9х – 72х7 – 5х4 3) у’ = -17х7 — 6х4 4) у’ = -72х7 – 6х4
х6 2) у’ = 9х – 72х7 – 5х4 3) у’ = -17х7 — 6х4 4) у’ = -72х7 – 6х4
А10. Найдите точку максимума функции: у = х3 – 3х + 2
1) 1 2) 0 3) -1 4) 4.
В1. Найдите наименьшее значение: f(x) = х3 + 3х на отрезке 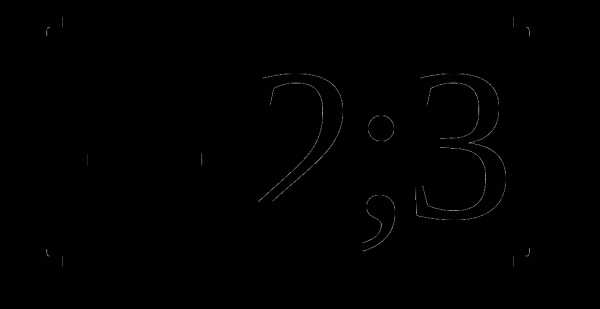 .
.
В2
Точка движется по координатной прямой согласно закону х(t) = t2 — 5t – 7, где х(t)-координата точки в момент времени t. Найдите её скорость при t = 3.
t2 — 5t – 7, где х(t)-координата точки в момент времени t. Найдите её скорость при t = 3.
В3. Найдите значение выражения
18 ∙ sinα ∙ ctg(
∙ sinα ∙ ctg( — α), если cosα =
— α), если cosα =  .
.
В4. Функция у = f(х) определена на промежутке (-10;2). График её производной изображён на рисунке. Сколько точек экстремума имеет функция у = f(х) на этом промежутке?
В5. Сколько корней имеет уравнение: 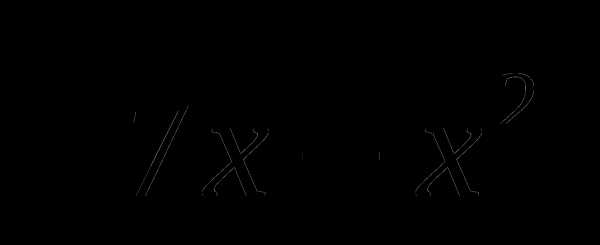 ∙ (2cosx – 1) = 0.
∙ (2cosx – 1) = 0.
В6. Найдите минимум функции: f(х) =  .
.
В7
С1. Решите уравнение :
С2. Рассматриваются всевозможные прямоугольные параллелепипеды, объем каждого
из которых равен 4 см3, а одна из боковых граней является квадратом. Найдите
среди них параллелепипед с наименьшим периметром основания. В ответе укажите
этот периметр.
С3

Вариант 4.
А1. Упростить: 1 – sinα ∙ ctgα ∙ cosα
1) 0 2) cos2α 3) sin2α 4) 1 – sin2α
А2. Найдите все решения уравнения: ctg2x ∙ (1 — cos2x) = 0
1)  +
+ n, n
n, n z. 2)
z. 2)  n, n
n, n z 3)
z 3)  n, n
n, n z 4)
z 4)  +
+  n, n
n, n z
z
А3. Найдите множество значений функции: у = 6cos3x
1)  2)
2) 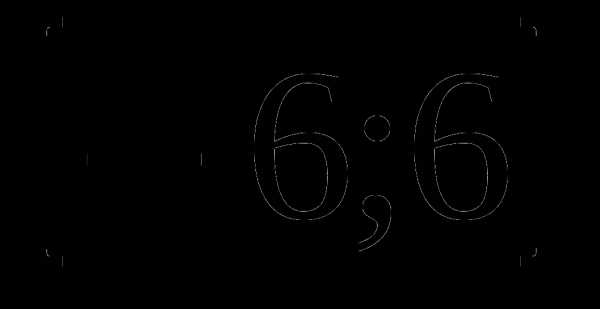 3)
3) 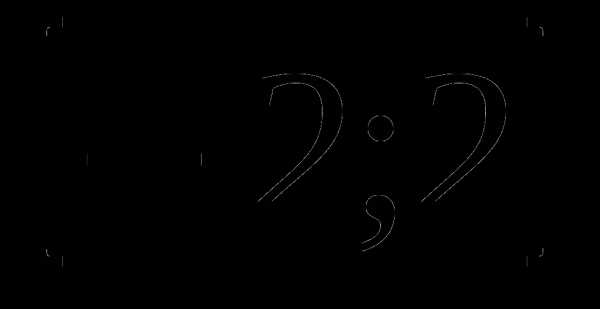 4)
4) 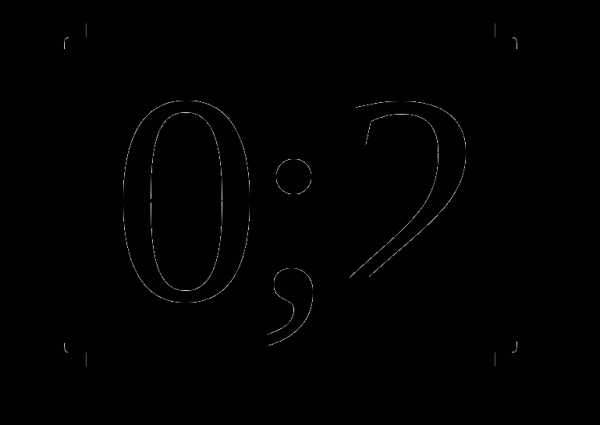
А4. Найдите значение выражения: 4 + 5tg2x ∙ cos2x, если sinx = 0,4
1) 6 2) 4,8 3) 4,4 4) 9,2
А5. Найдите значение выражения: 14sin2x – 3, если cos2x = 0,7
1)-2,58 2) 39 3) 1,2 4) 6,8.
А6. Укажите производную функции: у = х2 + cosx
1) 2x + sinx 2)  — sinx 3)
— sinx 3)  + sinx 4) 2x – sinx
+ sinx 4) 2x – sinx
А7. Найдите производную функции : у = 5х2 sinx
1) y’ = 10xcosx 2) y’=10xsinx — 5x2cosx 3) y’=10xsinx + 5x2cosx
4) y’ = 10xcosx + 5x2sinx
А8. Найдите тангенс угла наклона касательной, проведенной к графику функции у = 2х2 в его точке с абсциссой х0 = -1
1) 4 2) 2 3) -2 4) — 4
А9. Найдите производную функции: у = 8 -5х4 + 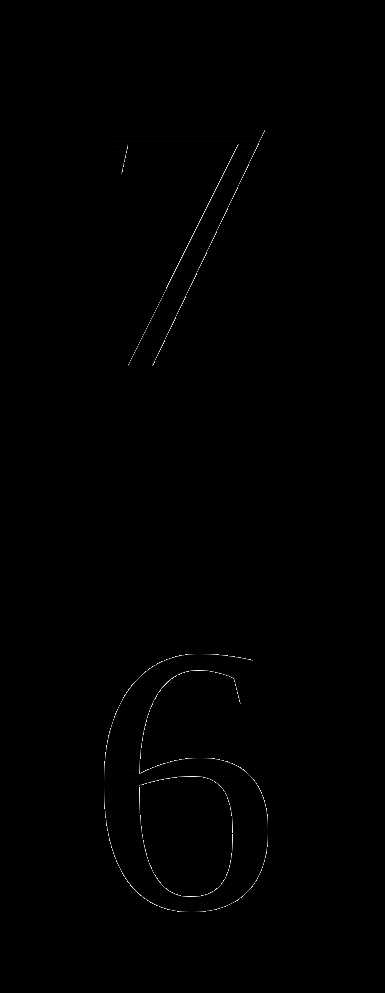 х6
х6
1) у’ = -20х3 + 7х5 2) у’ = 8х – 20х5 + 7х7 3) у’ = 8х – х5 + х7
х7
4) у’ = -20х3 + 7х4.
А10. Найдите точку максимума функции: у = 4х – х4
1) 1 2) -1 3) 0 4) -2.
В1. Найдите наибольшее значение функции: f(x) = -х3 – 3х на отрезке 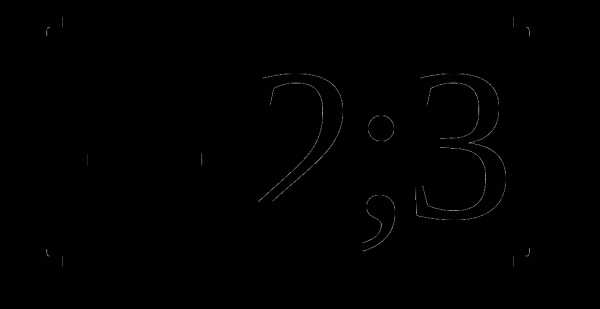 .
.
В2.
За время t тело перемещается по прямой на расстояние S(t) = 0,5t2 – 7t + 23. Через сколько секунд скорость точки будет равна 6?
В3. Найдите значение выражения: 6 ∙ tgα ∙ cos2(
∙ tgα ∙ cos2( — α), если sin2α =
— α), если sin2α =  .
.
В4. Функция у = f(x) определена на промежутке (-4;10). График её производной изображён на рисунке. Укажите наибольшую длину промежутка возрастания функции
у = f(х).
В5. Сколько корней имеет уравнение ( sinx + cosx )2 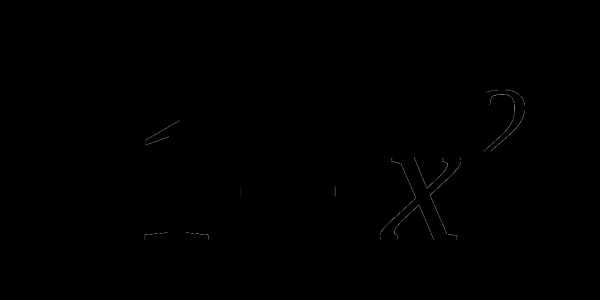 =0 ?
=0 ?
В6. Найдите максимум функции у = х3 – 2х2 – 7х + 3.
В7 Найдите наибольшее значение функции у=9х – 8 sin х +7 на отрезке
С1. Решите уравнение.
С2. Закрытый металлический бак с квадратным дном должен иметь объём 216 м3.
При каких размерах на его изготовление пойдет наименьшее количество материала?
С3 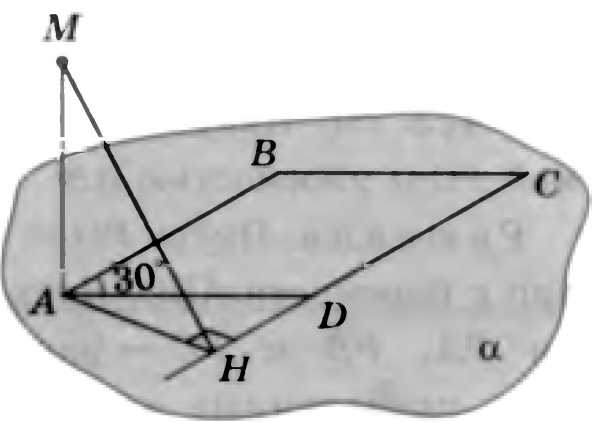
infourok.ru
|
РАЗРАБОТКИ |
В категории разработок: 162 Фильтр по целевой аудитории — Целевая аудитория -для 1 классадля 2 классадля 3 классадля 4 классадля 5 классадля 6 классадля 7 классадля 8 классадля 9 классадля 10 классадля 11 классадля учителядля классного руководителядля дошкольниковдля директорадля завучейдля логопедадля психологадля соц.педагогадля воспитателя Задания можно использовать в качестве переводного экзамена или итоговой работы в конце 8 класса или в качестве мониторинга остаточных знаний в начале 9 класса. Линия УМК под редакцией Ю.М.Колягина Алгебра. 8 класс, УМК под редакцией Л.С.Атанасяна. Геометрия 7-9 класс.
Целевая аудитория: для 8 класса 4 варианта по 11 заданий. Ответы прилагаются.
Целевая аудитория: для 9 класса Контрольная работа содержит 2 варианта по пять заданий в каждом. Тексты контрольной работы разбиты по пяти уровням сложности. Каждая задача варианта соответствует своему уровню сложности. Создана контрольная работа в текстовом редакторе MicrosoftWord. Для удобства приведены правильные ответы.
Целевая аудитория: для 10 класса Контрольная работа содержит 2 варианта по пять заданий в каждом. Тексты контрольной работы разбиты по пяти уровням сложности. Каждая задача варианта соответствует своему уровню сложности. Создана контрольная работа в текстовом редакторе MicrosoftWord. Для удобства приведены правильные ответы.
Целевая аудитория: для 10 класса На выполнение ВПР по математике в 6 классе даётся 60 минут. Работа содержит 13 заданий. В заданиях 1–8, 10 необходимо записать только ответ. В задании 12 нужно изобразить рисунок или требуемые элементы рисунка. В заданиях 9, 11, 13 требуется записать решение и ответ. При необходимости можно пользоваться черновиком. Записи в черновике проверяться и оцениваться не будут.
Целевая аудитория: для 6 класса На выполнение Всероссийской проверочной работы по математике 2018 дается 60 минут. Проверочная работа содержит 14 заданий.
Источник: Всероссийские проверочные работы
Целевая аудитория: для 5 класса Книга посвящена особому классу задач, который называют «софизмами». Суть их в том, что требуется найти ошибку в заведомо ложном доказательстве. Последнее иногда оказывается довольно сложно. Не случайно с греческого «софизм» можно перевести как хитрая выдумка, уловка. Некоторые софизмы возникли еще в античном мире, скорее всего в результате ошибок в серьезных рассуждениях. Но история происхождения большей их части навсегда останется тайной. Зачем нужны такие задачи? На этот вопрос ответил в предисловии к одной из своих книг известный популяризатор науки, профессор Геттингенского университета немецкий математик Карл Литцман: «Серьезное значение изучения ошибок и софизмов для воспитания математического мышления, как кажется автору, еще недостаточно осознано. Не только учитель должен иметь дело с ошибками, которые делают его ученики; сами учащиеся зачастую научаются большему на примере разъясненной ошибки, чем даже при правильном выполнении по готовым образцам задач и упражнений»
Целевая аудитория: для 11 класса Предлагаю Вашему вниманию 4 варианта административной контрольной работы по математике для 6 класса (УМК С.М.Никольский и др.). В каждом варианте по 5 номеров. Ответы прилагаются. Целевая аудитория: для 6 класса Экзаменационная работа предназначена для учителей математики и учеников 5 классов. Целевая аудитория: для 5 класса Сборник содержит контрольные и самостоятельные работы по темам «Делимость. НОК и НОД». В каждой работе 40 вариантов заданий. Для каждой работы приведены листы с ответами по каждому варианту.
Целевая аудитория: для 6 класса |
Конкурсы Диплом и благодарность каждому участнику! |
www.uchportal.ru
Контрольная работа по математике за первую четверть 10 кл.
Контрольная работа по математике за 1 четверть
10 класс
Вариант 1.
А1. Какая функция является возрастающей?
; 2) у = 3-7х; 3) у =; 4) у = -х .
А2. Вычислите f(3), если
А3. Найдите область определения функции
А4. Через две пересекающиеся прямые
1) можно провести только одну плоскость;
2) нельзя провести плоскость;
3) можно провести бесконечно много плоскостей.
А5. Две прямые называются скрещивающимися, если они
1) лежат в одной плоскости и не пересекаются;
2) не пересекаются;
3) не пересекаются и не параллельны.
_____________________________________________________________________________
В1. sin ά= ½, . ά- угол первой четверти.
Найдите значения остальных тригонометрических функций
В2. Вычислите 16* ( cos2x – sin2x), если.
С1. Постройте график функции .
Контрольная работа по математике за 1 четверть
10 класс.
Вариант 2.
А1. Какая функция является убывающей?
1); 2) у = 2х+6; 3) у =; 4) у = .
А2. Вычислите f(-2), если
А3. Найдите область определения функции
.А4. Если две плоскости имеют общую точку, то они
1) называются пересекающимися;
2) пересекаются по прямой, проходящей через эту точку;
3) параллельны.
А5 Через прямую и не лежащую на ней точку
1) проходит плоскость и притом только одна;
2) проходит бесконечно много плоскостей;
3) нельзя провести плоскость.
_______________________________________________________________________
В1. cos ά = -1/2 . ά- угол второй четверти.
Найдите значения остальных тригонометрических функций
В2. Вычислите 8 *( sin2x — cos2x) , если .
С1. Постройте график функции .
xn--j1ahfl.xn--p1ai
Контрольные работы по математике 10 класс со спецификациями
2. Упростите выражение: .
3. Вычислить .
4. Вычислить:
5. Упростить выражение:
6. Доказать тождество:
7. Решить уравнение
Контрольная работа по теме «Тригонометрические формулы»
Форма контрольной работы: контрольная работа
Вид контроля: тематический
Спецификация контрольной работы по математике
по теме «Тригонометрические уравнения» для обучающихся 10 классов
1.Назначение контрольно-измерительных материалов контрольной работы.
Контрольно-измерительные материалы позволяют оценить уровень подготовки по математике обучающихся 10 классов МБОУО лицей №6 в объеме, установленном обязательным минимумом содержания образования
2.Документы, определяющие содержание контрольно-измерительных материалов контрольной работы.
Содержание работы определяется на основе следующих документов:
Федеральный компонент государственного стандарта общего образования. Математика. Среднее (полное) общее образование (приказ Минобразования России №1089 от 05.03.2004) .Содержание контрольной работы по математике рассчитано на обучающихся 10 классов общеобразовательных учреждений, изучающих математику, в соответствии с Федеральным компонентом государственного стандарта среднего (полного) общего образования по математике, по учебнику (Ю.М Колягин, Ю.В.Сидоров и др. «Алгебра и начала анализа-10»,М. «Мнемозина) и учебно-методическим комплексом к ним, имеющими гриф Министерства образования и науки Российской Федерации.
3.Структура контрольной работы.
Работа состоит из одной части, которая направлена на проверку овладения содержанием курса математики на уровне углубленной подготовки. Эта работа содержит 5 заданий и предусматривает развернутый ответ с записью решения. Работа включает задания по темам «Показательная функция», «Показательные уравнения», «Показательные неравенства».
4.Обобщенный план варианта контрольно-измерительных материалов контрольной работы по математике для обучающихся 10 классов.
5.Оценивание работыДля оценивания результатов выполненных работ обучающихся используется общий балл. Максимальный балл работу в целом – 10. Задание оценивается в 1 балл и считается выполненными верно, если приведено верное решение и записан верный ответ
6.Дополнительные материалы и оборудование: не используются.7.Инструкция по выполнению работы.
Время выполнение работы-45 минут (1урок). Все задания выполняются с полным пояснением
Контрольная работа по теме «Тригонометрические уравнения»
Вариант 1
1. Решите уравнение:
2. Найдите решение уравнения на отрезке .
3. Решите уравнение:
; в)
4. Решите уравнение:
а)
в)
5.Решите систему уравнений:
Контрольная работа по теме «Тригонометрические уравнения»
Вариант 2
1. Решите уравнение:
а)
2. Найдите решение уравнения на отрезке .
3. Решите уравнение:
в)
4. Решите уравнение:
а)
в)
Решите систему уравнений:
.
Контрольная работа по теме «Тригонометрические функции»
Форма контрольной работы: контрольная работа
Вид контроля: тематический
Спецификация контрольной работы по математике
по теме «Тригонометрические функции» для обучающихся 10 классов
1.Назначение контрольно-измерительных материалов контрольной работы.
Контрольно-измерительные материалы позволяют оценить уровень подготовки по математике обучающихся 10 классов МБОУО лицей №6 в объеме, установленном обязательным минимумом содержания образования
2.Документы, определяющие содержание контрольно-измерительных материалов контрольной работы.
Содержание работы определяется на основе следующих документов:
Федеральный компонент государственного стандарта общего образования. Математика. Среднее (полное) общее образование (приказ Минобразования России №1089 от 05.03.2004) .Содержание контрольной работы по математике рассчитано на обучающихся 10 классов общеобразовательных учреждений, изучающих математику, в соответствии с Федеральным компонентом государственного стандарта среднего (полного) общего образования по математике, по учебнику (Ю.М Колягин, Ю.В.Сидоров и др. «Алгебра и начала анализа-10»,М. «Мнемозина) и учебно-методическим комплексам к ним, имеющими гриф Министерства образования и науки Российской Федерации.
3.Структура контрольной работы.
Работа состоит из одной части, которая направлена на проверку овладения содержанием курса математики на уровне углубленной подготовки. Эта работа содержит 6 заданий и предусматривает развернутый ответ с записью решения. Работа включает задания по темам «Тригонометрические функции, их графики и свойства»
4.Обобщенный план варианта контрольно-измерительных материалов контрольной работы по математике для обучающихся 10 классов.
5.Оценивание работыДля оценивания результатов выполненных работ обучающихся используется общий балл. Максимальный балл работу в целом – 6. Задание оценивается в 1 балл и считается выполненными верно, если приведено верное решение и записан верный ответ
6.Дополнительные материалы и оборудованиеКалькуляторы не используются.
7.Инструкция по выполнению работы.
Время выполнение работы-45 минут (1урок). Все задания выполняются с полным пояснением
Контрольная работа по теме «Тригонометрические функции»
Вариант 1
Найдите область определения функции .
Найдите область значений функции . Укажите, при каких значениях аргумента функция достигает наибольшего и наименьшего значения (если таковые существуют).
Какие из указанных ниже функций являются четными: какие нечетными и какие не являются ни четными, ни нечетными:
а) ; б) ; в) .
Постройте график функции . Опишите ее свойства (D(f), E(f), нули функции, промежутки знакопостоянства, промежутки возрастания и убывания).
Запишите все решения уравнения , принадлежащие промежутку .
Запишите все решения неравенства , принадлежащие промежутку .
Контрольная работа по теме «Тригонометрические функции»
Вариант 2
Найдите область определения функции .
2. Найдите область значений функции . Укажите, при каких значениях аргумента функция достигает наибольшего и наименьшего значения (если таковые существуют).
3. Какие из указанных ниже функций являются четными: какие нечетными и какие не являются ни четными, ни нечетными:
а) ; б) ; в) .
Постройте график функции . Опишите ее свойства (D(f), E(f), нули функции, промежутки знакопостоянства, промежутки возрастания и убывания)
Запишите все решения уравнения , принадлежащие промежутку .
Запишите все решения неравенства , принадлежащие промежутку .
Контрольная работа по теме «Параллельность в пространстве»
Форма контрольной работы: контрольная работа
Вид контроля: тематический
Спецификация контрольной работы по математике
по теме «Параллельность в пространстве» для обучающихся 10 классов
1.Назначение контрольно-измерительных материалов контрольной работы.
Контрольно-измерительные материалы позволяют оценить уровень подготовки по математике обучающихся 10 классов МБОУО лицей №6 в объеме, установленном обязательным минимумом содержания образования
2.Документы, определяющие содержание контрольно-измерительных
материалов контрольной работы.
Содержание работы определяется на основе следующих документов:
Федеральный компонент государственного стандарта общего образования. Математика. Среднее (полное) общее образование (приказ Минобразования России №1089 от 05.03.2004) .Содержание контрольной работы по математике рассчитано на обучающихся 10 классов общеобразовательных учреждений, изучающих математику, в соответствии с Федеральным компонентом государственного стандарта среднего (полного) общего образования по математике, по учебнику (Геометрия, 10-11: учебник для общеобразовательных учреждений/ Л.С. Атанасян, В.Ф, Бутузов, С.Б. Кадомцев и др. – Москва: Просвещение, 2010) и учебно-методическим комплексам к ним, имеющими гриф Министерства образования и науки Российской Федерации.
3.Структура контрольной работы.
Работа состоит из одной части, которая направлена на проверку овладения содержанием курса математики на уровне углубленной подготовки. Эта работа содержит 3 заданий и предусматривает развернутый ответ с записью решения. Работа включает задания по темам «Параллельность прямых», «Параллельность прямой и плоскости», «Параллельность плоскостей».
4.Обобщенный план варианта контрольно-измерительных материалов контрольной работы по математике для обучающихся 10 классов.
5.Оценивание работыДля оценивания результатов выполненных работ обучающихся используется общий балл. Максимальный балл работу в целом – 3. Задание оценивается в 1 балл и считается выполненными верно, если приведено верное решение и записан верный ответ .
6.Дополнительные материалы и оборудование: не используются.7.Инструкция по выполнению работы.
Время выполнение работы-45 минут (1урок). Все задания выполняются с полным пояснением
Контрольная работа ПО ТЕМЕ «пАРАЛЛЕЛЬНОСТЬ В ПРОСТРАНСТВЕ»
Вариант I
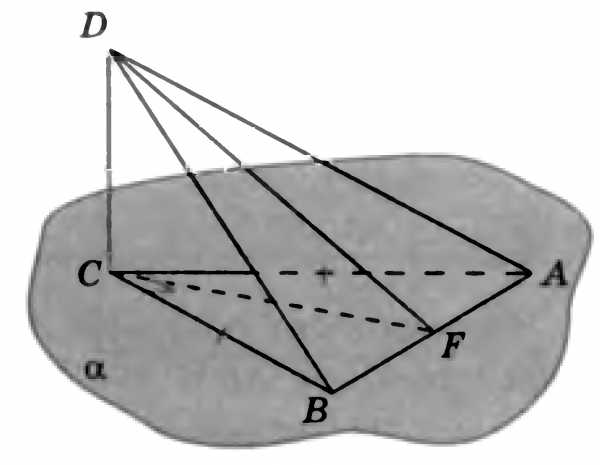
1. Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А2В2, если А1В1 = 12 см, В1О : ОВ2 = 3 : 4.
2. В тетраэдре DABC точки М и N-середины ребер DA и DВ. Постройте сечение тетраэдра, проходящей через точки M, N параллельно прямой DС. Определите вид построенного сечения.
3.Найдите площадь сечения единичного куба ABCDA1B1C1D1 плоскостью, проходящей через вершины A1, C1 и середину ребра DС.
Контрольная работа ПО ТЕМЕ «пАРАЛЛЕЛЬНОСТЬ В ПРОСТРАНСТВЕ»
Вариант II
1. Через точку О, не лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А1В1, если А2В2 = 15 см, ОВ1 : ОВ2 = 3 : 5.
2. В тетраэдре DABC точки М и К-середины ребер DA и ВС соответственно. Постройте сечение тетраэдра, проходящей через точки M, К параллельно прямой DС. Определите вид построенного сечения.
3.Найдите площадь сечения единичного куба ABCDA1B1C1D1 плоскостью, проходящей через вершины A, C и середину ребра A1D1
Контрольная работа по теме «Перпендикулярность в пространстве»
Форма контрольной работы: контрольная работа
Вид контроля: тематический
Спецификация контрольной работы по математике
по теме «Перпендикулярность в пространстве» для обучающихся 10 классов
1.Назначение контрольно-измерительных материалов контрольной работы.
Контрольно-измерительные материалы позволяют оценить уровень подготовки по математике обучающихся 10 классов МБОУО лицей №6 в объеме, установленном обязательным минимумом содержания образования
2.Документы, определяющие содержание контрольно-измерительных материалов контрольной работы.
Содержание работы определяется на основе следующих документов:
Федеральный компонент государственного стандарта общего образования. Математика. Среднее (полное) общее образование (приказ Минобразования России №1089 от 05.03.2004) .Содержание контрольной работы по математике рассчитано на обучающихся 10 классов общеобразовательных учреждений, изучающих математику, в соответствии с Федеральным компонентом государственного стандарта среднего (полного) общего образования по математике, по учебнику (Геометрия, 10-11: учебник для общеобразовательных учреждений/ Л.С. Атанасян, В.Ф, Бутузов, С.Б. Кадомцев и др. – Москва: Просвещение, 2010) и учебно-методическим комплексам к ним, имеющими гриф Министерства образования и науки Российской Федерации.
3.Структура контрольной работы.
Работа состоит из одной части, которая направлена на проверку овладения содержанием курса математики на уровне углубленной подготовки. Эта работа содержит 2 задания и предусматривает развернутый ответ с записью решения. Работа включает задания по темам «Перпендикулярность прямых», «Перпендикулярность прямой и плоскости», «Перпендикулярность плоскостей», «Угол между прямыми, прямой и плоскостью, плоскостями».
4.Обобщенный план варианта контрольно-измерительных материалов контрольной работы по математике для обучающихся 10 классов.
Геометрическая задача на нахождение:а)измерений параллелепипеда (куба)
б)синуса (косинуса) угла между прямой и плоскостью
2
2
2
Геометрическая задача на нахождение:
а)расстояния от точки до плоскости
б)линейный угол двугранного угла
в)синуса угла между плоскостями
3
5.Оценивание работы
Для оценивания результатов выполненных работ обучающихся используется общий балл. Максимальный балл работу в целом – 5. Задание оценивается в 1 балл и считается выполненными верно, если приведено верное решение и записан верный ответ
6.Дополнительные материалы и оборудование: нет7.Инструкция по выполнению работы.Время выполнение работы-45 минут (1урок). Все задания выполняются с полным пояснением
Контрольная работа теме «Перпендикулярность в пространстве»
Вариант 1
1. Диагональ куба равна 6 см. Найдите:
а) ребро куба;
б) косинус угла между диагональю куба и плоскостью одной из его граней.
2. Сторона АВ ромба ABCD равна a, один из углов равен 60°. Через сторону АВ проведена плоскость α на расстоянии от точки D.
а) Найдите расстояние от точки С до плоскости α.
б) Покажите на рисунке линейный угол двугранного угла DABM,
М α.
в) Найдите синус угла между плоскостью ромба и плоскостью α.
Контрольная работа теме «Перпендикулярность в пространстве»
Вариант 1
1. Основанием прямоугольного параллелепипеда служит квадрат; диагональ параллелепипеда равна 2 см, а его измерения относятся как 1 : 1 : 2. Найдите:
а) измерения параллелепипеда;
б) синус угла между диагональю параллелепипеда и плоскостью его основания.
2. Сторона квадрата ABCD равна а. Через сторону AD проведена плоскость α на расстоянии от точки В.
а) Найдите расстояние от точки С до плоскости α.
б) Покажите на рисунке линейный угол двугранного угла BADM,
М α.
в) Найдите синус угла между плоскостью квадрата и плоскостью α.
Итоговая контрольная работа
Форма контрольной работы: контрольная работа
Вид контроля: итоговый
Спецификация итоговой контрольной работы по математике
для обучающихся 10 классов
1.Назначение контрольно-измерительных материалов контрольной работы.
Контрольно-измерительные материалы позволяют оценить уровень подготовки по математике обучающихся 10 классов МБОУО лицей №6 в объеме, установленном обязательным минимумом содержания образования
2.Документы, определяющие содержание контрольно-измерительных
материалов контрольной работы.
Содержание работы определяется на основе следующих документов:
Федеральный компонент государственного стандарта общего образования. Математика. Среднее (полное) общее образование (приказ Минобразования России №1089 от 05.03.2004) .Содержание контрольной работы по математике рассчитано на обучающихся 10 классов общеобразовательных учреждений, изучающих математику, в соответствии с Федеральным компонентом государственного стандарта среднего (полного) общего образования по математике, по учебнику (Ю.М Колягин, Ю.В.Сидоров и др. «Алгебра и начала анализа-10»,М. «Мнемозина; Геометрия, 10-11: учебник для общеобразовательных учреждений/ Л.С. Атанасян, В.Ф, Бутузов, С.Б. Кадомцев и др. – Москва: Просвещение, 2010) и учебно-методическим комплексам к ним, имеющими гриф Министерства образования и науки Российской Федерации.
3.Структура контрольной работы.
Работа состоит из двух частей, которые направлены на проверку овладения содержанием курса математики на уровне углубленной подготовки. Первая часть содержит 12 заданий базового уровня. К каждому заданию 1-6 и 8-12 требуется дать краткий ответ, при выполнении задания 7 необходимо сделать выбор верных утверждений. Вторая часть включает 2 задания (13,14) повышенного уровня и 1 задание (15) высокого уровня сложности с развернутым ответом. Работа включает задания по темам «Выражения и преобразования», «Уравнения и неравенства», «Функции и их свойства», «Геометрические задачи»
4.Обобщенный план варианта контрольно-измерительных материалов контрольной работы по математике для обучающихся 10 классов.
5.Оценивание работы
Для оценивания результатов выполненных работ обучающихся используется общий балл. Максимальный балл работу в целом – 19. Верное выполнение заданий 1-12 оценивается 1 баллом. Выполнение заданий с развернутым ответом повышенного уровня (13, 14) в зависимости от полноты решения и правильности ответа оценивается от 0 до 2 баллов, а высокого уровня (15) – от 0 до 3 баллов
6.Дополнительные материалы и оборудование
Калькуляторы не используются.
7.Инструкция по выполнению работы.
Время выполнение работы-90минут (2урока). Все задания выполняются с полным пояснением
Итоговая контрольная работа по математике
Вариант 1
1. Вычислите + 0,5-1.
2. Упростите выражение .
3. Найдите значение выражения .
4. На одной из граней двугранного угла величиной 30о взята точка, находящаяся на расстоянии 56 см от ребра данного двугранного угла. Найдите расстояние от указанной точки до другой грани этого двугранного угла.
5. Найдите корень уравнения log3(x + 2) = log3(2x2 — 8) .
6. Найдите , если .
7. Выберите верные утверждения.
1) Через любые две точки пространства можно провести прямую.
2) Через любые три точки пространства можно провести плоскость.
3) Через любые четыре точки пространства можно провести плоскость.
4) Для любых двух плоскостей в пространстве найдутся две параллельные прямые, каждая из которых содержится ровно в одной из указанных плоскостей.
8. Решите уравнение 2x-1 + 2x+1 = 2,5.
9. Найти область определения функции .
10. Упростите выражение .
11. Упростите выражение .
12. На рисунке изображен график функции y = f(x) ,
определенной на (-4;8). Найдите сумму точек экстремума функции f(x)
13. Решите уравнение
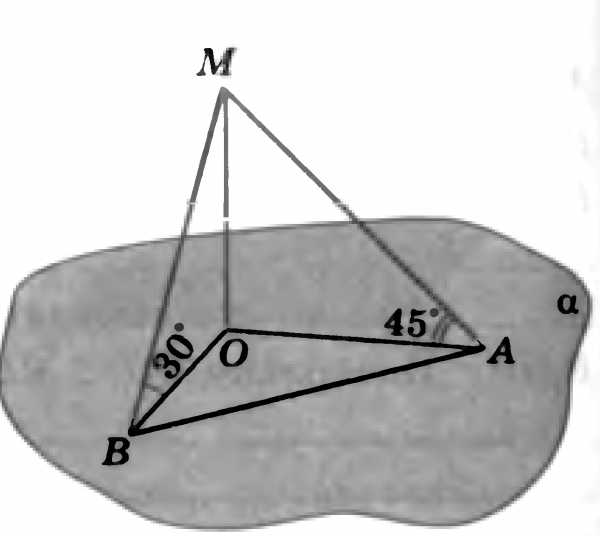
14. В правильной четырёхугольной призме площадь основания 16 см2, а высота 2 см. Найдите диагональ призмы и угол между прямой, содержащей эту диагональ, и плоскостью боковой грани.
15. Решите неравенство:
Итоговая контрольная работа по математике
Вариант 2
1. Вычислите — 0,25-2
2. Упростите выражение .
3. Найдите значение выражения 44.
4. На одной из граней двугранного угла величиной 30о взята точка, находящаяся на расстоянии 38 см от другой грани данного двугранного угла. Найдите расстояние от указанной точки до ребра этого двугранного угла.
5. Найдите корень уравнения log3(x2 + 4) = log3(2x + 7).
6. Найдите , если .
7. Выберите венные утверждения.
1) Любая прямая в пространстве имеет общую точку хотя бы с одной плоскостью.
2) Любые две непараллельные прямые в пространстве имеют общую точку.
3) Любые две непараллельные плоскости в пространстве имеют общую точку.
4) Для любых двух прямых в пространстве найдутся две параллельные плоскости, каждая из которых содержит ровно одну из данных прямых.
8. Решите уравнение 41-x + 42—x = 1,25.
9. Найдите область определения функции у=.
10. Упростите выражение .
11. Упростите выражение .
12. На рисунке изображен график функции y = f(x), определенной на (-7;5) . Найдите сумму точек экстремума функции f(x).
13. Решить уравнение
14. В основании прямой треугольной призмы АВСА1В1С1 лежит прямоугольный треугольник с прямым углом С и катетами 8 и 6 см. Площадь боковой поверхности призмы 120 см 2 . Найдите длину бокового ребра призмы и угол между прямой С1М , где М – середина АВ, и плоскостью основания призмы.
15. Решите неравенство:
infourok.ru
