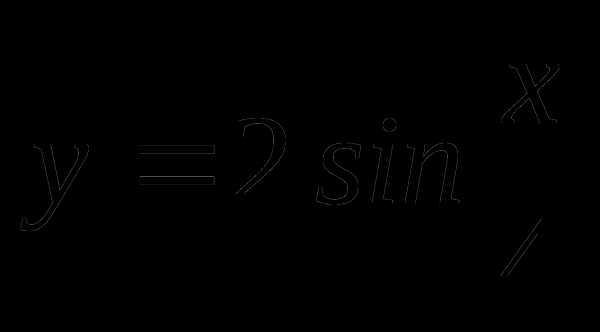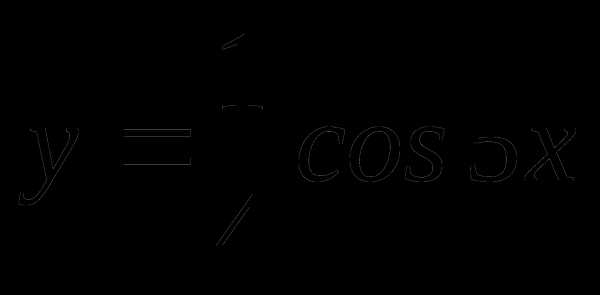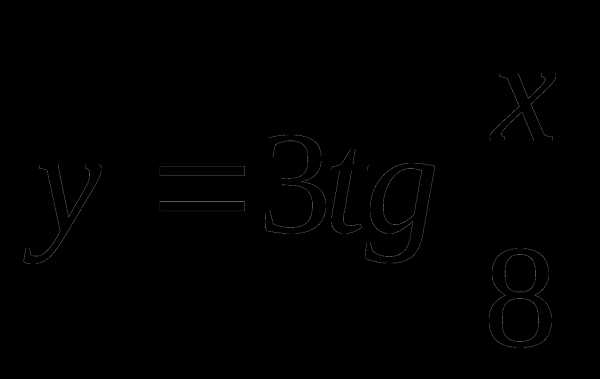Контрольная по тригонометрии 11 класс – Учебно-методический материал по алгебре (11 класс) на тему: Контрольная работа по теме «Тригонометрические функции» | скачать бесплатно

Контрольная работа по Математике «Тригонометрические уравнения» 10-11 класс

Контрольная работа по теме «Тригонометрические уравнения»

Вариант 1

1. Решить уравнения, сводящиеся к квадратным:

а) ; б) ;

в) ; г) .

2. Решить уравнение разложением на множители:

а) ; б) .

3. Решить однородное уравнение первой степени:

а) ; б) .

4. Решить однородное уравнение второй степени:

.

5. Решить неоднородное уравнение:

.

Контрольная работа по теме «Тригонометрические уравнения»

Вариант 2

1. Решить уравнения, сводящиеся к квадратным:

а) ; б) ;

в) ; г) .

2. Решить уравнение разложением на множители:

а) ; б) .

3. Решить однородное уравнение первой степени:

а) ; б) .

4. Решить однородное уравнение второй степени:

.

5. Решить неоднородное уравнение:

.

Контрольная работа по теме «Тригонометрические уравнения»

Вариант 1

1. Решить уравнения, сводящиеся к квадратным:

а) ; б) ;

в) ; г) .

2. Решить уравнение разложением на множители:

а) ; б) .

3. Решить однородное уравнение первой степени:

а) ; б) .

4. Решить однородное уравнение второй степени:

.

5. Решить неоднородное уравнение:

.

Контрольная работа по теме «Тригонометрические уравнения»

Вариант 2

1. Решить уравнения, сводящиеся к квадратным:

а) ; б) ;

в) ; г) .

2. Решить уравнение разложением на множители:

а) ; б) .

3. Решить однородное уравнение первой степени:

а) ; б) .

4. Решить однородное уравнение второй степени:

.

5. Решить неоднородное уравнение:

.

doc4web.ru

Контрольная работа по алгебре 11 кл «Тригонометрические функции» 8 вариантов

Контрольная работа № 1 ВАРИАНТ 1 А 11

1. Найти область определения и множество значений функции y = sin x + 2.

2. Выяснить, является ли функция

y = x² + cos x чётной или нечётной.

3. Доказать, что наименьший положительный период функции y = cos 2 x равен π.

4. Найти принадлежащие отрезку [- π; π] корни уравнения 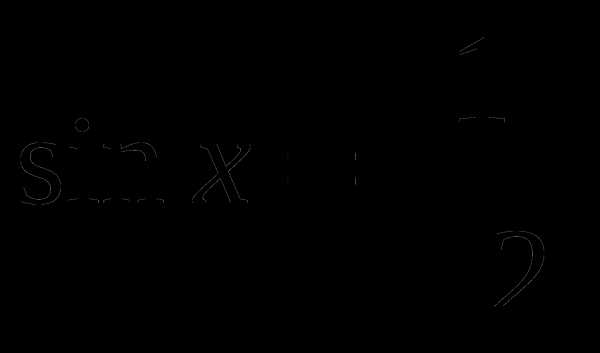с помощью графика функции.

5. Построить график функции y = cos x

   — 1 и найти значение аргумента, при которых функция возрастает, принимает наибольшее значение.

_________________________________________

Контрольная работа № 1 ВАРИАНТ 2 А 11

1. Найти область определения и множество значений функции y = 3 cos x.

2. Выяснить, является ли функция y = x³ sin x чётной или нечётной.

3. Доказать, что наименьший положительный период функции 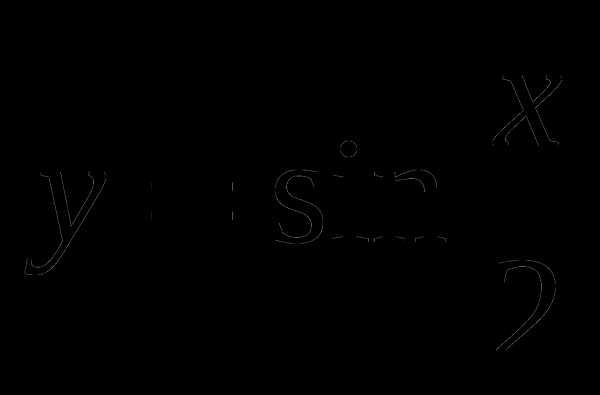равен 4π.

4. Найти принадлежащие отрезку [0; 2,5π] корни уравнения 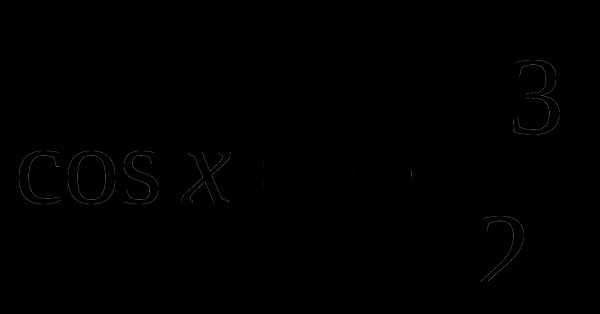с помощью графика функции.

5. Построить график функции

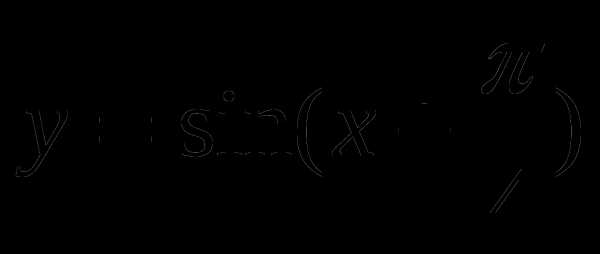   и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.

_________________________________________

Контрольная работа № 1 ВАРИАНТ 3 А 11

1. Найти область определения и множество значений функции y = — sin x +3.

2. Выяснить, является ли функция

y = x — cos x чётной или нечётной.

3. Доказать, что наименьший положительный период функции y = sin 2x равен π.

4. Найти принадлежащие отрезку [- π/2; π] корни уравнения 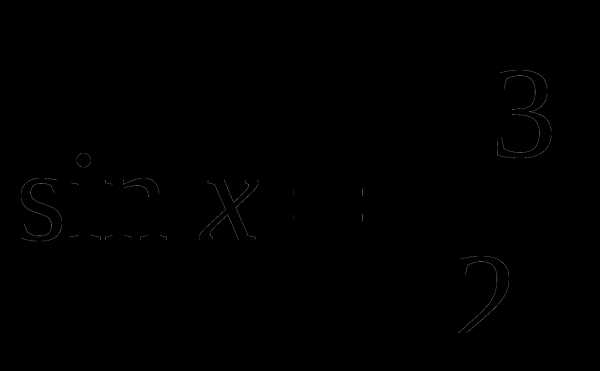с помощью графика функции.

5. Построить график функции y = cos x +2 и найти значение аргумента, при которых функция возрастает, принимает наибольшее значение.

_________________________________________

Контрольная работа № 1 ВАРИАНТ 4 А 11

1. Найти область определения и множество значений функции y = -5 cos x.

2. Выяснить, является ли функция y = —x² + sin x чётной или нечётной.

3. Доказать, что наименьший положительный период функции 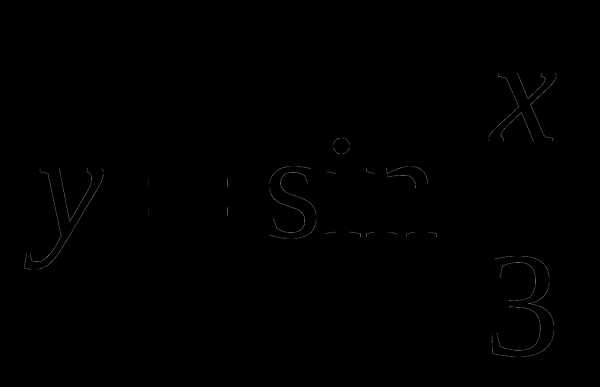равен 6π.

4. Найти принадлежащие отрезку [- π/2; 2,5π] корни уравнения

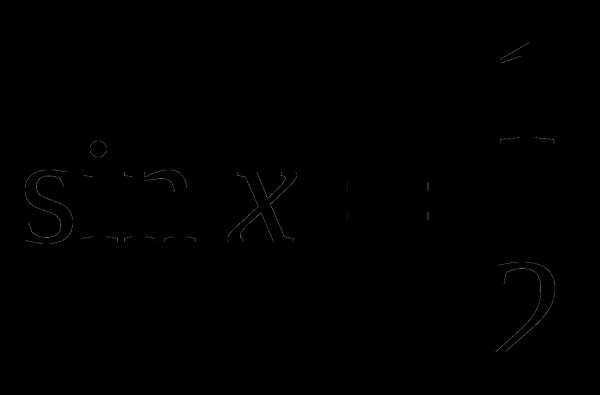   с помощью графика функции.

5. Построить график функции 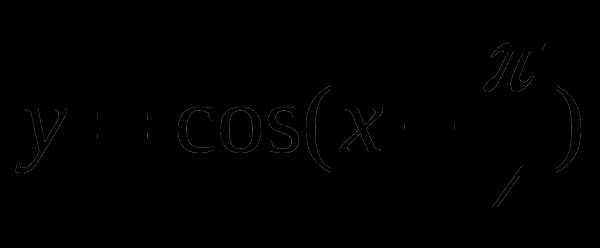и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.

_________________________________________

Контрольная работа № 1 ВАРИАНТ 5 А 11

1. Найти область определения и множество значений функции y = cos x -1.

2. Выяснить, является ли функция

y = sin x –x² чётной или нечётной.

3. Доказать, что наименьший положительный период функции равен 10π.

4. Найти принадлежащие отрезку [0; 2π] корни уравнения с помощью графика функции.

5. Построить график функции y = cos x +3 и найти значение аргумента, при которых функция возрастает, принимает наибольшее значение.

_________________________________________

Контрольная работа № 1 ВАРИАНТ 6 А 11

1. Найти область определения и множество значений функции y = -2 sin x.

2. Выяснить, является ли функция y = —x⁴ cos x чётной или нечётной.

3. Доказать, что наименьший положительный период функции

   равен 4π.

4. Найти принадлежащие отрезку [- π/2; π] корни уравнения 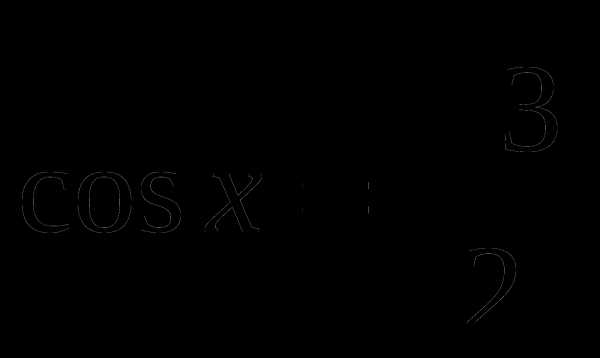с помощью графика функции.

5. Построить график функции 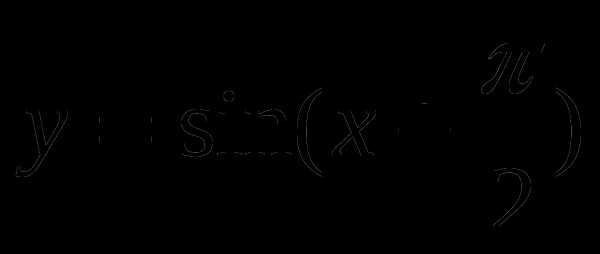и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.

_________________________________________

Контрольная работа № 1 ВАРИАНТ 7 А 11

1. Найти область определения и множество значений функции y = — cos x -2.

2. Выяснить, является ли функция

y = x³ + cos x чётной или нечётной.

3. Доказать, что наименьший положительный период функции y = sin 4 x равен π.

4. Найти принадлежащие отрезку [- π; π/2] корни уравнения 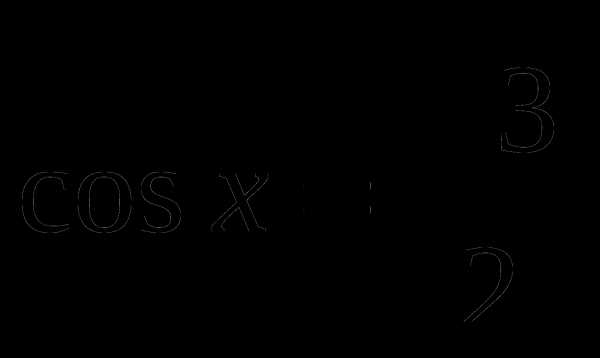с помощью графика функции.

5. Построить график функции y = sin x +2 и найти значение аргумента, при которых функция возрастает, принимает наибольшее значение.

_________________________________________

Контрольная работа № 1 ВАРИАНТ 8 А 11

1. Найти область определения и множество значений функции y = -5 sin x.

2. Выяснить, является ли функция y = x² +sin x чётной или нечётной.

3. Доказать, что наименьший положительный период функции равен 6π.

4. Найти принадлежащие отрезку [- π/2; 2,5π] корни уравнения 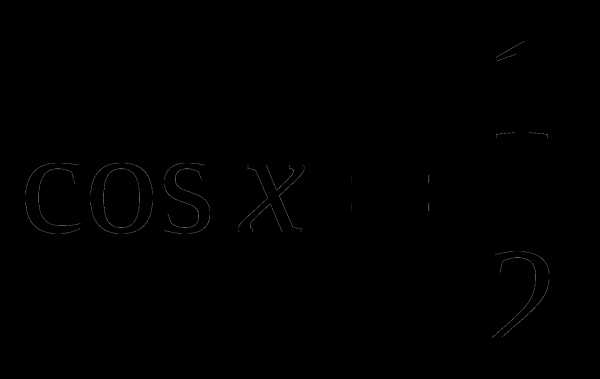с помощью графика функции.

5. Построить график функции 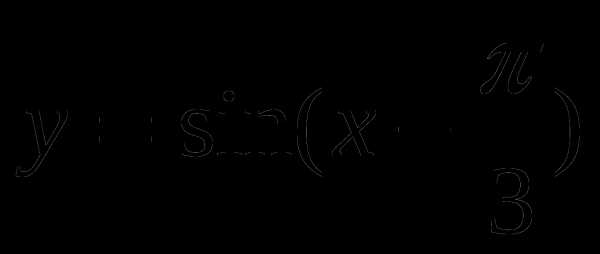и найти значение аргумента, при которых функция убывает, принимает наименьшее значение.

_________________________________________

infourok.ru

Контрольная работа по теме «Тригонометрические функции»

Просмотр содержимого документа
«Контрольная работа по теме «Тригонометрические функции»»

Вариант 1.

1. Найти область определения функции

1) у=sin 2) у=cos 3) y= 4)y=lgsinx

2.Найти множество значений функции

1) у=2cos2x+3 2) y= x+cos2x

3.Найти наименьшее и наибольшее значение функции

1)y=1-2 2)y=cos3x sin3x

4. Сравните величины и объясните

1) arcsin и arcsin0,2 2) arccos и arccos 0,1

3) sin1 и соs2

5.Найти количество корней уравнения

1) соsx=arctgx 2) arcsinx=ctgx

6.a) решите уравнение

б) найдите все его корни, принадлежащие промежутку

Вариант 2.

1. Найти область определения функции

1) у=сos 2) у=cos 3) y= 4)y=log ₂cosx

2.Найти множество значений функции

1) у=5sin2x-3 2) y= x -cos ²2x

3.Найти наименьшее и наибольшее значение функции

1)y=1-2 2)y=2cos3x sin5x- 2cos5x sin3x

4. Сравните величины и объясните

1) arctg и arctg0,3 2) arccos и arccos 0,9

3) sin2 и tg2

5.Найти количество корней уравнения

1) sinx=arccosx 2) arcsinx=arcctgx

6.a) решите уравнение

б) найдите все его корни, принадлежащие промежутку

multiurok.ru

тригонометрические функции 11 класс (контрольная работа)

Чтобы посмотреть этот PDF файл с форматированием и разметкой, скачайте его и откройте на своем компьютере.
Контрольная работа 11 класс

III

вариант

1)

Найти

D

(
f
):

а
)
y = sin
x

+ 3 cos
x

б
)
y = 3 tg
в
)
y = cos (
)

2)
Найти

E (f)
:

а
)
y = 6 sin 3x

–

8

б
)
y = 8
–

5 sin
x

· cos x

*
в
)
y

=
sin

x

–

2
cos

x

3)
Построить графики:

а
)
y
=
—
3 cos x

+ 2

б
)
y

=
tg

(
x

+
)

4)

Решить уравнение

на

Sin

x

=

5)
sin

x

‹

на

*
6)

sin

2
x

= ­

на

Контрольная работа 11 класс

I

вариант

1)

На
йти
D (f)
:

а
)
y

= 3
sin

x

б
)
y

=
tg

2
x

в
)
y

=

2)
Найти

E

(
f
):

а
)
y

= 3
sin

x

+ 1
б
)
y

= 5
–

3
sin

x

cos

x

*
в)
y

= 4
sin

x

–

6
cos

x

3)

Построить графики:

а
)
y

=
sin

x

+ 1
б
)
y

= 3
cos x
–

2

4)

Решить урав
нение

на промежутке

Sin

x

=
—

5)

Решить неравенство

на промежутке

Sin

x

≤
—

*6)
Sin

3
x

=
—

на

Контрольная работа 11 класс

IV

вариант

1)
Найти
D

(
f
):

а
)
y = 4 cos x

–

3
sin 2

б
)
y = tg 7
x

в
)
y = sin

2)

Найти

E

(
f
):

а
)
y

= 7
cos

10
x

–

13

б
)
y = 4
–

8 sin

x

·
cos x

*
в
)
y

= 3
sin

x

–

4
cos

x

3)

Построить графики:

а
)
y

=
—
2 sin
x

–

1

б
)
y =

tg (x

—

)

4)

Решить уравнение

на

Cos

x

=

5)
cos

x

≥

на

*6)
cos

3
x

=

на

Контрольная работа 11 класс

II

вариант

1)
Найти
D

(
f
)
:

а
)
y

=
cos

4
x

б
)
y

=
tg

4
x

в)
y

=

2)

Найти

E (f)
:

а
)
y = 10 cos 2x
–

12
б
)
y = 8 sin x cos x + 7

*
в
)
y

= 3
cos

x

+ 7
sin

x

3)

Построить графики:

а
)
y = cos x
–

1
б
)
y = 2 sin x + 1,5

4)

Решить уравнение
на

Cos

x

=

5)

Решить неравенство

на про
межутке

Cos

x

*
6)Cos 2 x =
—

на

Приложенные файлы

schoolfiles.net

Контрольная работа по алгебре и началам анализа 11 класс `Тригонометрические функции`

1 вариант
№ 1 Найти область определения и множество значений функции
У=sin2x+π4-3
У=2tg(x+π)№2 Исследовать функцию на четность или нечетность
У=sinx+x∙cosxУ=tg(x)x№3 Доказать, что функция у=cosx4 периодическая и найти ее наименьший положительный период.
№4 Найти все принадлежащие отрезку ⦋0;3π⦌корни уравнения sinx=22
№5 Найти все принадлежащие отрезку⦋-π;2π⦌ решения неравенства соsx≥-122 вариант
№ 1 Найти область определения и множество значений функции
У=sin4x+π2+3
У=3сtg(x+π)№2 Исследовать функцию на четность или нечетность
У=cosx+x∙sinxУ=ctg(x)x2№3 Доказать, что функция у=cos3x периодическая и найти ее наименьший положительный период.
№4 Найти все принадлежащие отрезку ⦋-2π;π⦌корни уравнения sinx=32
№5 Найти все принадлежащие отрезку⦋-3π;0⦌ решения неравенства соsx≤-123 вариант
№ 1 Найти область определения и множество значений функции
У=cosx+π5-1
У=2sinx∙ctgx№2 Исследовать функцию на четность или нечетность
У=sin2xУ=tg(x)х2+1№3 Доказать, что функция у=cosx3 периодическая и найти ее наименьший положительный период.
№4 Найти все принадлежащие отрезку ⦋-1.5π;2π⦌корни уравнения sinx=-22
№5 Найти все принадлежащие отрезку⦋-2π;π⦌ решения неравенства соsx≥124 вариант
№1 Найти область определения и множество значений функции
У=sinx3У=cosx№2 Исследовать функцию на четность или нечетность
У=cos2xУ=cosx+х4№3 Доказать, что функция у=sinx4 периодическая и найти ее наименьший положительный период.
№4 Найти все принадлежащие отрезку ⦋0;3π⦌корни уравнения cosx=22
№5 Найти все принадлежащие отрезку⦋-0.5π;2.5π⦌ решения неравенства sinx≤125 вариант
№1 Найти область определения и множество значений функции
У=cos(x-π2)У=2cos²x-1№2 Исследовать функцию на четность или нечетность
У=sinx(1+cosx)У=x3∙tg2x№3 Доказать, что функция у=tgx4 периодическая и найти ее наименьший положительный период.
№4 Найти все принадлежащие отрезку ⦋0;3π⦌корни уравнения cosx=12
№5 Найти все принадлежащие отрезку⦋-π;2π⦌ решения неравенства соsx≥326 вариант
№1 Найти область определения и множество значений функции
У=2sinxcosx
У=2ctg(x+π2)№2 Исследовать функцию на четность или нечетность
У=(2×2+cosx)∙cosxУ=x∙ctgх№3 Доказать, что функция у=sin2x периодическая и найти ее наименьший положительный период.
№4 Найти все принадлежащие отрезку ⦋-2.5π;0.5π⦌корни уравнения sinx=-12
№5 Найти все принадлежащие отрезку⦋-2π;π⦌ решения неравенства tgx≥1
7 вариант
№1 Найти область определения и множество значений функции
У=cos2x+π2+1
У=sinx№2 Исследовать функцию на четность или нечетность
У=sinx+х∙sinxУ=x3-tgx№3 Доказать, что функция у=sinx2 периодическая и найти ее наименьший положительный период.
№4 Найти все принадлежащие отрезку ⦋0;3π⦌корни уравнения sinx=-32
№5 Найти все принадлежащие отрезку⦋-π;2π⦌ решения неравенства tgx≥-18 вариант
№1 Найти область определения и множество значений функции
У=sin²x-cos²xУ=2cosx∙tgx№2 Исследовать функцию на четность или нечетность
У=sinx(x5-tgx)У=(1+2×4)cosx№3 Доказать, что функция у=tg2x периодическая и найти ее наименьший положительный период.
№4 Найти все принадлежащие отрезку ⦋-3π;0⦌корни уравнения cosx=-22
№5 Найти все принадлежащие отрезку⦋-2π;π⦌ решения неравенства соsx≤22

Приложенные файлы

schoolfiles.net

Контрольная работа №1 по теме»Тригонометрические функции»

Вариант1 1.Найти область определения и множество значений функции у=5 cos х . 2. Выяснить является функция у=2sin x – tg x четной или нечетной? 3.Изобразить график функции у= sin x на интервале ( — 2п; 2п) и решить уравнение sin x = 0,5. 4.Найти наибольшее и наименьшее значения функции у= 6sin x cos х + 3 5. Построить график функции у= cos х + 2. При каких значениях функция убывает; возрастает?

Вариант2 1.Найти область определения и множество значений функции у=0,5 sin х . 2. Выяснить является функция у=2cos x – x четной или нечетной? 3.Изобразить график функции у= cos x на интервале ( — 2п; 2п) и решить уравнение cos x = -0,5. 4.Найти наибольшее и наименьшее значения функции у= 6cosx — 6sinх + 3 5. Построить график функции у= sin х + 2. При каких значениях функция убывает; возрастает?

Вариант3 1.Найти область определения и множество значений функции у= cos х + 4 2. Выяснить является функция у = 3sin x + tg x четной или нечетной? 3.Изобразить график функции у= sin x на интервале ( — 2п; 2п) и решить уравнение sin x = -1. 4.Найти наибольшее и наименьшее значения функции у= 8sin x cos х — 2 5. Построить график функции у= cos х — 1. При каких значениях функция убывает; возрастает?

Вариант6 1.Найти область определения и множество значений функции у=sin х — 3 2. Выяснить является функция у = cos x +3 x четной или нечетной? 3.Изобразить график функции у= cos x на интервале ( — 2п; 2п) и решить уравнение cos x = -1. 4.Найти наибольшее и наименьшее значения функции у= 5cosx — 5sinх + 2 5. Построить график функции у= sin х — 1. При каких значениях функция убывает; возрастает?

Вариант5 1.Найти область определения и множество значений функции у= 5cos х . 2. Выяснить является функция у=sin x –5 tg x четной или нечетной? 3.Изобразить график функции у= sin x на интервале ( — 2п; 2п) и решить уравнение sin x = 1. 4.Найти наибольшее и наименьшее значения функции у= 10sin x cos х + 2 . 5. Построить график функции у= cos х + 1. При каких значениях функция убывает; возрастает?

Вариант6 1.Найти область определения и множество значений функции у=sin х + 2 2. Выяснить является функция у=2cos x – x четной или нечетной? 3.Изобразить график функции у= cos x на интервале ( — 2п; 2п) и решить уравнение cos x = 1. 4.Найти наибольшее и наименьшее значения функции у= 8cosx — 8sinх + 3 5. Построить график функции у= sin х + 1. При каких значениях функция убывает; возрастает?

Вариант7 1.Найти область определения и множество значений функции у=cos х + 11 2. Выяснить является функция у=sin x –2tg x четной или нечетной? 3.Изобразить график функции у= sin x на интервале ( — 2п; 2п) и решить уравнение sin x = 1. 4.Найти наибольшее и наименьшее значения функции у= 6sin x cos х + 3 5. Построить график функции у= cos х + 3. При каких значениях функция убывает; возрастает?

Вариант8 1.Найти область определения и множество значений функции у=0,5 sin х . 2. Выяснить является функция у=2cos x – x четной или нечетной? 3.Изобразить график функции у= cos x на интервале ( — 2п; 2п) и решить уравнение cos x = -1. 4.Найти наибольшее и наименьшее значения функции у= 6cosx — 6sinх + 3 5. Построить график функции у= sin х +3. При каких значениях функция убывает; возрастает?

kopilkaurokov.ru

Контрольная работа по алгебре и началам анализа Тема: Тригонометрические функции

Контрольная работа по алгебре и началам анализа

Тема: Тригонометрические функции

(учебник алгебры и начал анализа 10-11, авторов Ш.А.Алимова и др.)

Вариант I

1. Найти область определения функции:

2. Найти множество значений функции:

3. Найти наименьший положительный период функции:

4. Решить графически уравнение. Найти все корни уравнения, принадлежащие промежутку :

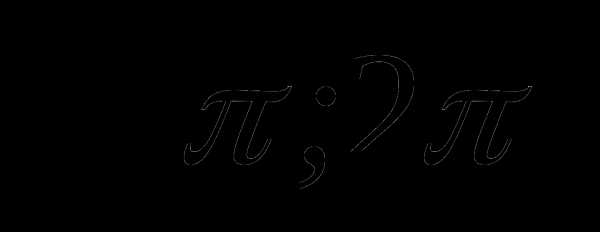5. Решить уравнение:

6. Решить графически неравенство:

Контрольная работа по алгебре и началам анализа

Тема: Тригонометрические функции

(учебник алгебры и начал анализа 10-11, авторов Ш.А.Алимова и др.)

Вариант II

1. Найти область определения функции

2. Найти множество значений функции

3. Найти наименьший положительный период функции:

4. Решить графически уравнение. Найти все корни уравнения, принадлежащие промежутку :

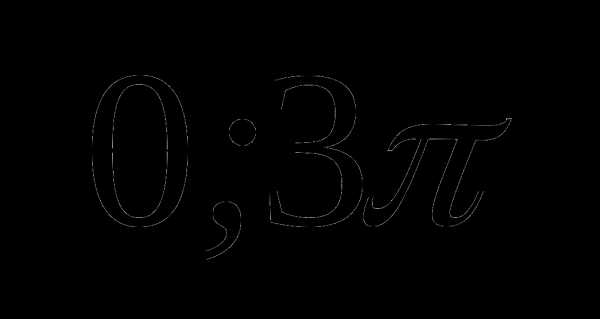5. Решить уравнение:

6. Решить графически неравенство:

refdb.ru