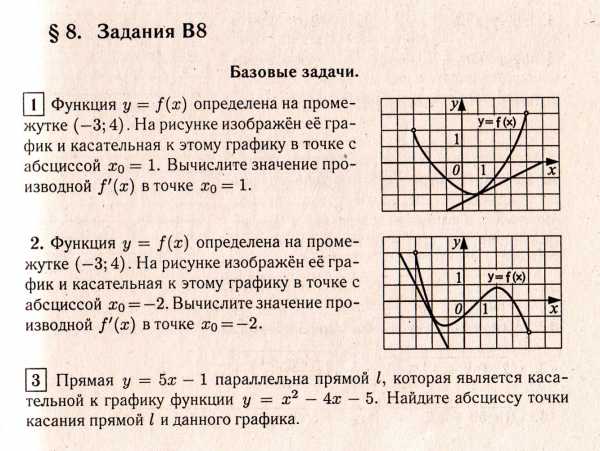
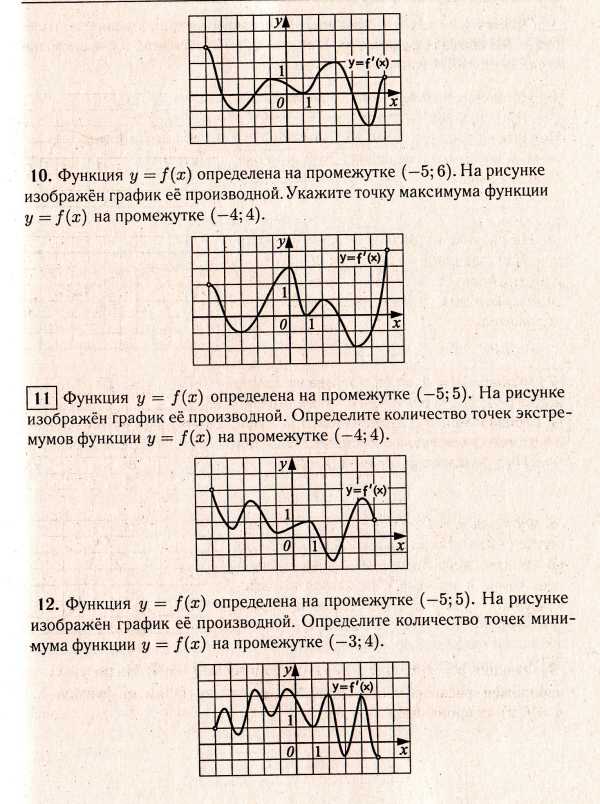
Итоговая контрольная работа по математике 10 класс
Олимпиадные задания по математике 10 класс.
№ 1. Найдите меньший катет прямоугольного треугольника, если его гипотенуза равна 20, а периметр 48.
А) 12
Б) 6
В) 18
Г) 24
№ 2. Решите неравенство:
А)
Б)
В)
Г)
№ 3. Найдите значение выражения:
А) -34
Б)
В) 63
Г) 56
№ 4. Известно, что ABCD-ромб, найдите его площадь, если А(-3; 4), В(7;9), С(5; -2) и D(-5;-7).
А) 125
Б) 200
В) 256
Г) 100
№ 5. Парабола задана формулой . Определите координаты её вершины.
А) (-1; 9)
Б) (1; -9)
В) (1;9)
Г) (-1; -9)
№ 6. Последовательность(аn) задана формулой . Найдите квадрат суммы её второго и четвёртого членов.
А)
Б) 121
В)
Г) 16
№ 7. Вычислите радиус окружности с центром в начале координат, если она проходит через точку С(-12; -5).
А)
Б) 17
В) 13
Г) 169
№ 8. Найдите значение выражения:
А) 1,75
Б)
В) 3
Г) 5,2
№ 9. Принтер печатает одну страницу за 2с. Сколько страниц напечатает принтер за 3мин?
А) 180
Б) 50
В) 90
Г) 120
№ 10. Выпускники школы выбрали 3 разных специальности: 19-учитель, 31-врач и 15-юрист. Найдите вероятность того, что случайно встреченный выпускник этой школы юрист.
А)
Б) 0,3
В)
Г) 65
№ 11. Приведите к тригонометрической функции угла из промежутка (00; 900):
А)
Б)
В)
Г)
№ 12. Треугольники АВС и ADC лежат в разных плоскостях и имеют общую сторону АС. ЕМ- средняя линия треугольника АВС с основанием АС. Найдите угол между прямыми ЕМ и АВ, если угол С 500, угол В 900.
А) 700
Б) 400
В) 600
Г) 1400
№ 13. Решите уравнение:
А)
Б)
В)
Г)
№ 14. Известно, что ABCDA1B1C1D1-прямоугольный параллелепипед. Найдите DF, если DE=8, DK=10, DB=12.
А)
Б)
В)
Г) 6
№ 15. Найдите значение производной функции в точке х0=2, если .
А) 0
Б) -1
В) 2
Г) 4
infourok.ru
РАЗРАБОТКИ | 10 классВ категории разработок: 18 Фильтр по целевой аудитории — Целевая аудитория -для 1 классадля 2 классадля 3 классадля 4 классадля 5 классадля 6 классадля 7 классадля 8 классадля 9 классадля 10 классадля 11 классадля учителядля классного руководителядля дошкольниковдля директорадля завучейдля логопедадля психологадля соц.педагогадля воспитателя Представлена контрольная работа по алгебре для учеников 10 класса по учебнику Алимова Целевая аудитория: для 10 класса Целевая аудитория: для 10 класса 4 варианта + демонстрационный вариант. Ко всем вариантам даны ответы. Целевая аудитория: для 10 класса Целевая аудитория: для 10 класса Планирование,контрольные работы,справочный материал по учебнику Мордковича,алгебра-10 Целевая аудитория: для 10 класса Планирование,контрольные,самостоятельные работы,зачеты,коллоквиумы по учебнику Атанасяна Целевая аудитория: для 10 класса В дидактических материалах предоставлены теоретические материалы по теме «Показательные уравнения», рассмотрены методы решения уравнений, предложены задания для самостоятельного изучения и закрепления новых знаний и умений. Это пособие поможет подготовиться к ЕГЭ по математике. Цель работы направлена на обучение решения показательных уравнений стандартного вида. При подготовке к ЕГЭ эти задачи входят в группы А и В. Целевая аудитория: для 10 класса Данная практическая работа может быть использована для проверки или отработки навыков умения решать простейшие тригонометрические уравнения. Целевая аудитория: для 10 класса В работе представлены 4 варианта. Работа составлена в форме теста с кратким ответом и состоит из двух частей: Часть1 – 7 заданий базового уровня сложности с кратким ответом, часть 2 – 3 задания повышенного уровня сложности. Структура теста аналогична структуре КИМ ЕГЭ, что позволит не только проверить знания, умения и навыки учащихся за курс 10 класса, но и постепенно подготовить к работе с подобным материалом при подготовке и сдаче экзамена. На выполнение работы отводится 45 минут. Целевая аудитория: для 10 класса Итоговая контрольная работа по алгебре и началам математического анализа за курс 10 класса составлена в соответствии с учебником: Целевая аудитория: для 10 класса | Конкурсы Диплом и благодарность каждому участнику! |
www.uchportal.ru
Полугодовая контрольная работа по математике 10 класс
Контрольная работа по алгебре и началам анализа за 1 полугодие
10 класс.
1 вариант.
Часть1.
А1. Вычислить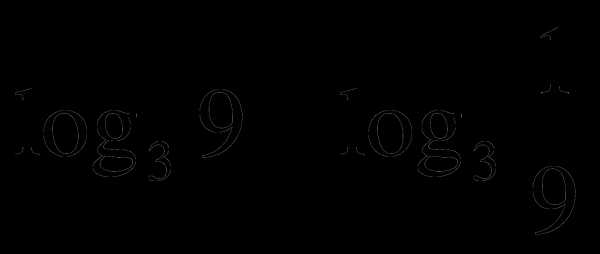 
.
А2. Решить уравнение 
А3. Вычислите 9 +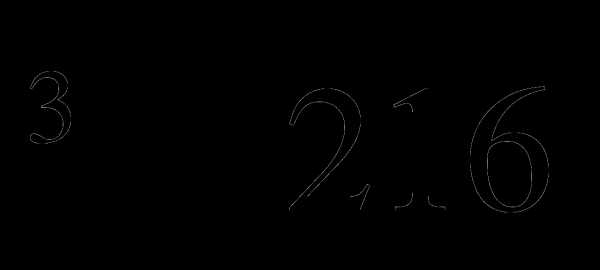 
.
А4. Решить уравнение 
.
А5. Вычислить
А6. Найдите значение выражения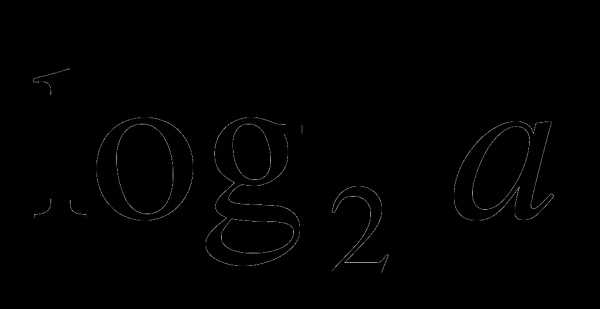 
, если .
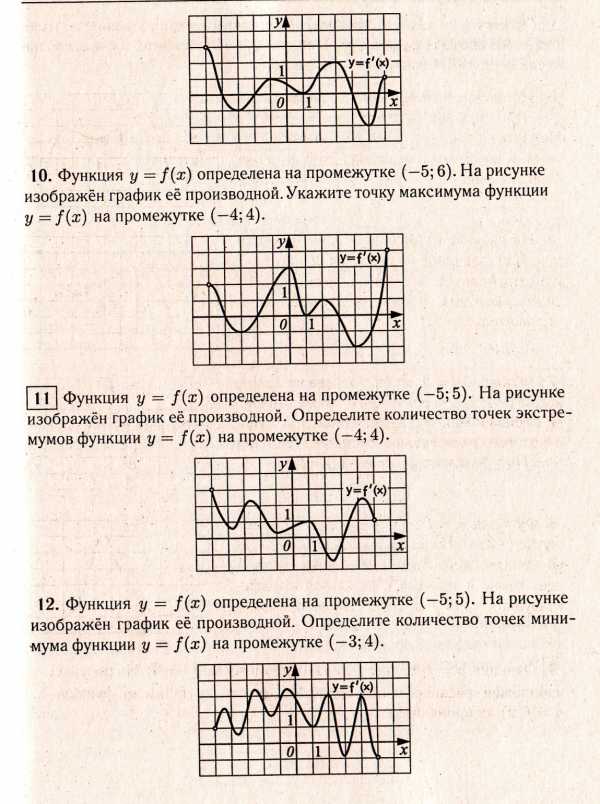
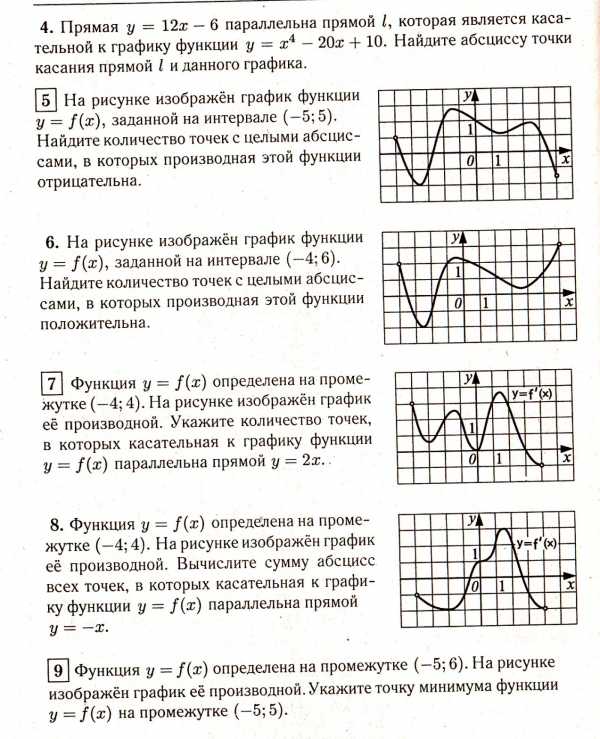
А7. На одном из рисунков изображен график функции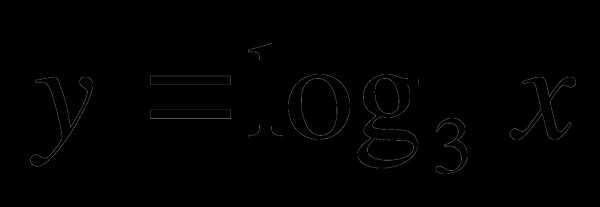 
. Укажите этот рисунок.
1
2
2
3
3
4
4
А8. Найдите область определения функции .
А9. Найдите произведение корней уравнения .
А10. Решить уравнение .
Часть2. В1. Найдите наибольшее целое число, являющееся решением неравенства .
В2. Найдите значение выражения 5х0, где х0 — наибольшее целое число, являющееся решением неравенства
В3 Вычислите значение числового выражения
В4. Решите уравнение . В ответе запишите корень уравнения или сумму корней, если их несколько.
В5. Решите уравнение .
В6. При каком значении переменной х равны дроби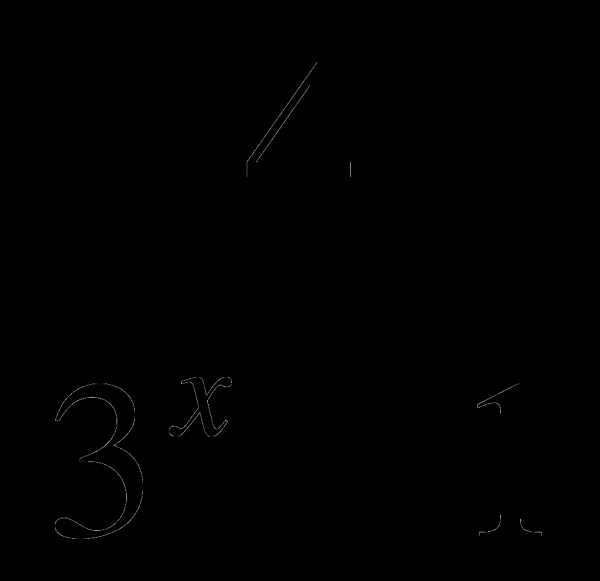 
и 
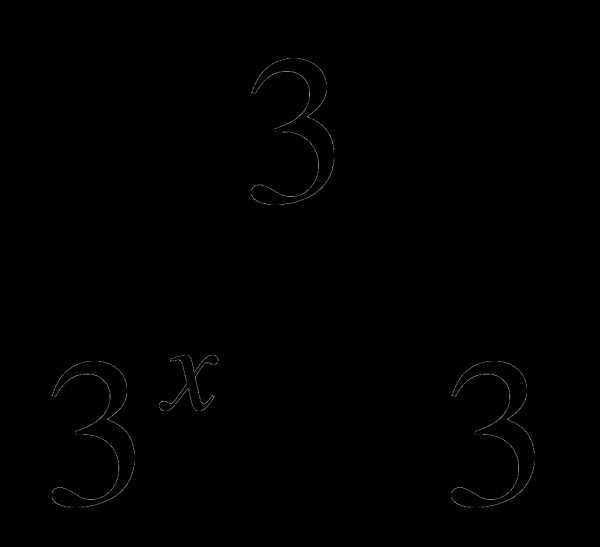
Часть 3.
С1. Решите уравнение .
С2. Решите неравенство: .
Контрольная за 1 полугодие.
10 класс.
2 вариант.
Часть1.
А1. Вычислить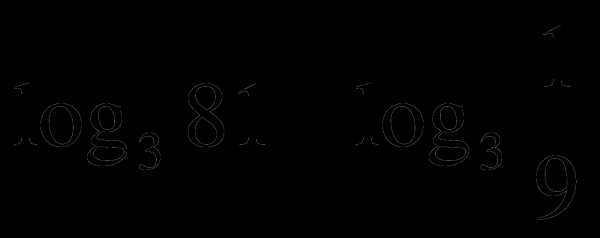 
.
А2. Решить уравнение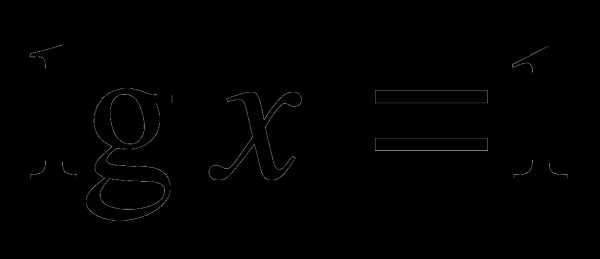 
А3. Вычислите 7 +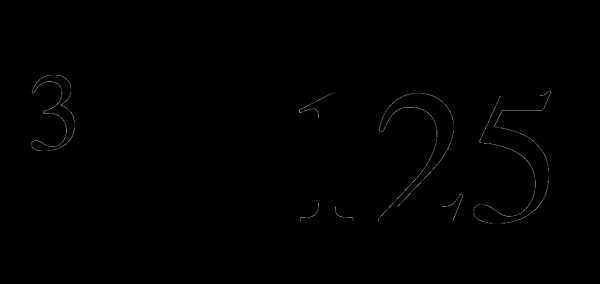 
.
А4. Решить уравнение 
.
А5. Вычислить
А6. Найдите значение выражения 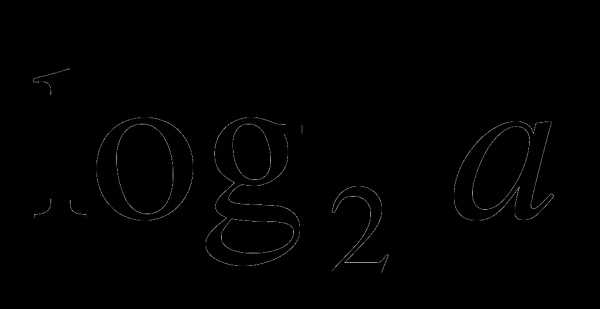, если .
А7. На одном из рисунков изображен график функции 
. Укажите этот рисунок.
1
2
2
3
3
4
4
А8. Найдите область определения функции .
А9. Найдите произведение корней уравнения .
А10. Решить уравнение .
Часть2.
В1. Найдите наибольшее целое число, являющееся решением неравенства .
В2. Найдите значение выражения 4х0, где х0 — наибольшее целое число, являющееся решением неравенства .
В3 Вычислите значение числового выражения .
В4. Решите уравнение . В ответе запишите корень уравнения или сумму корней, если их несколько.
В5. Решите уравнение .
В6. При каком значении переменной х равны дроби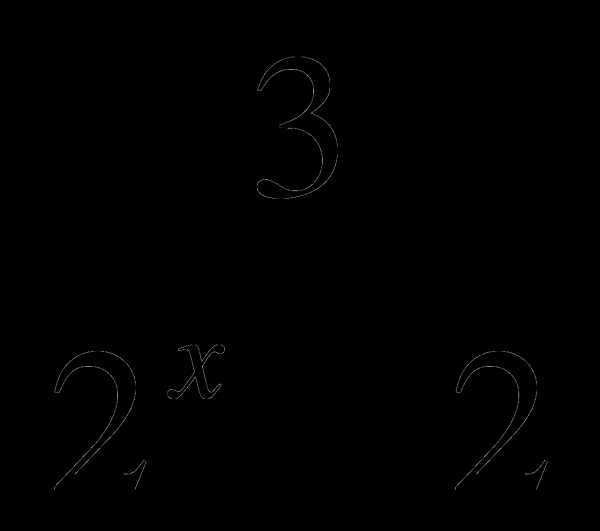 
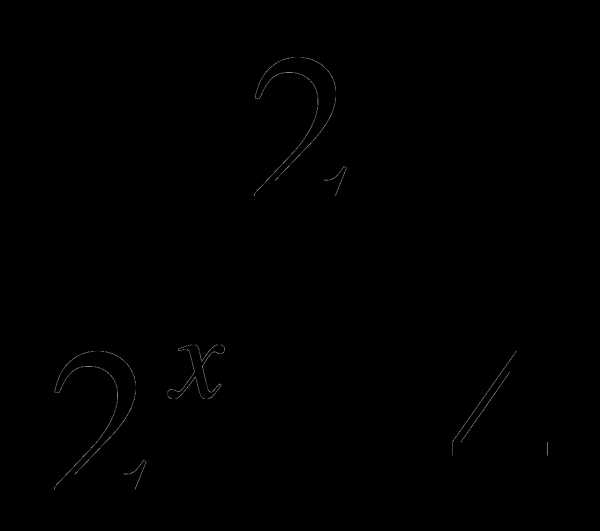?Часть 3.
С1. Решите уравнение .
С 2.
Решите неравенство: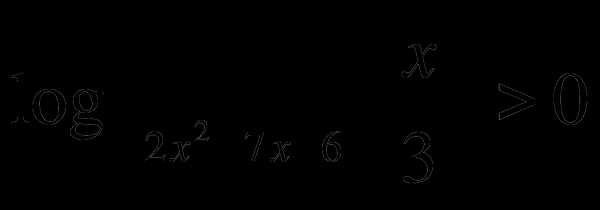 
.
Контрольная за 1 полугодие.
10 класс.
3 вариант.
Часть1.
А1. Вычислить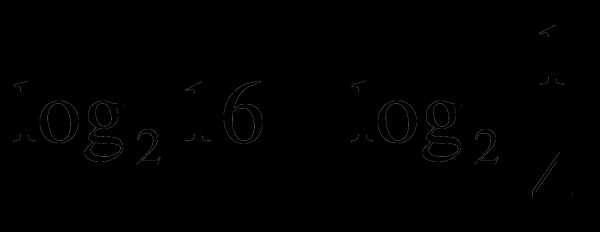 
.
А2. Решить уравнение 
А3. Вычислите 4 +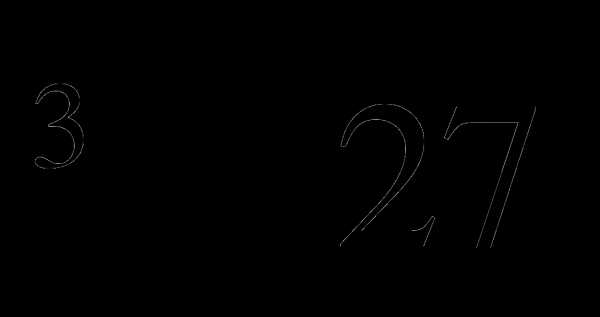 
.
А4. А4. Решить уравнение 
.
А5. Вычислить
А6. Найдите значение выражения 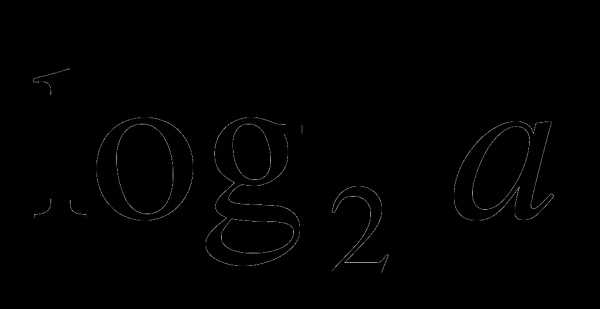, если .
А7. На одном из рисунков изображен график функции 
. Укажите этот рисунок.
1
2
2
3
3
4
4
А8. Найдите область определения функции .
А9. Найдите сумму корней уравнения .
А10. Решить уравнение .
Часть2.
В1. Найдите наибольшее целое число, являющееся решением неравенства .
В2. Найдите значение выражения 5х0, где х0 — наибольшее целое число, являющееся решением неравенства
В3 Вычислите значение числового выражения
В4. Решите уравнение . В ответе запишите корень уравнения или сумму корней, если их несколько.
В5. Решите уравнение .
В6. При каком значении переменной х равны дроб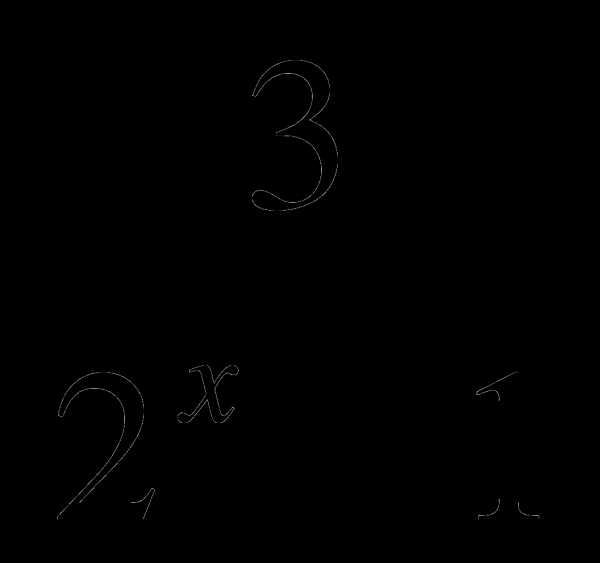и 
и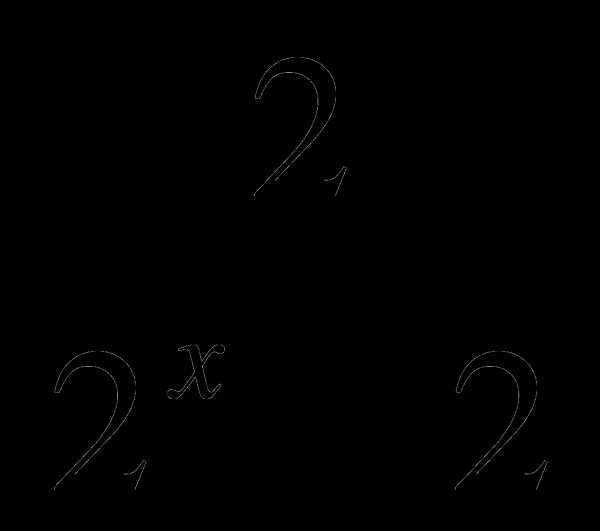 
?
С1. Решите уравнение .
С2.
Решите неравенство: .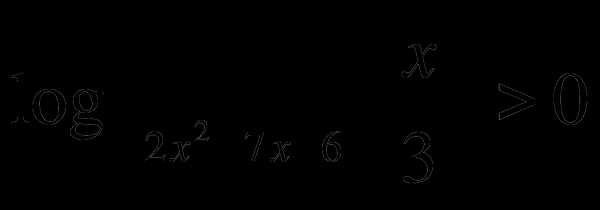
Контрольная за 1 полугодие.
10 класс.
4 вариант.
Часть1.
А1. Вычислить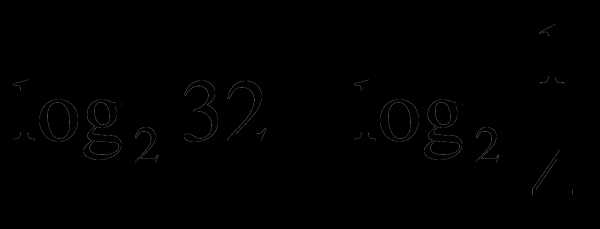 
.
А2. Решить уравнение 
А3. Вычислите 5 +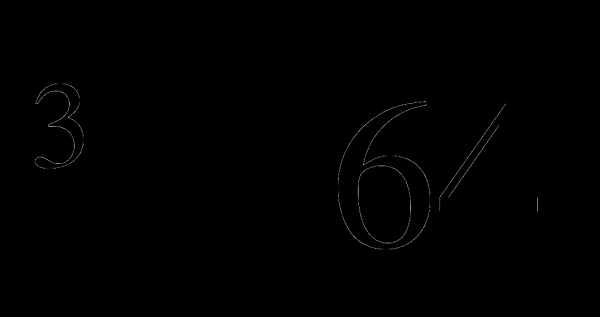 
.
А4. Решить уравнение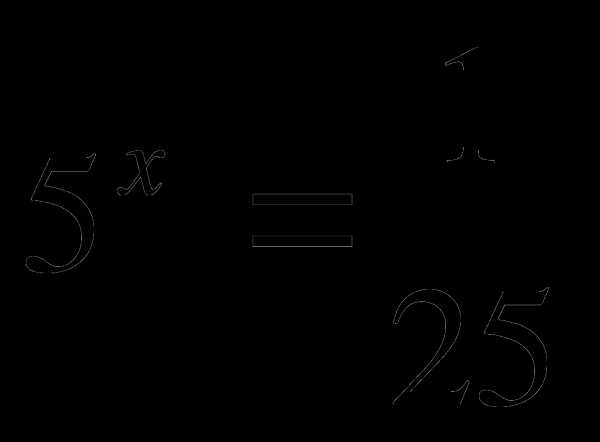 
.
А5. Вычислить
А6. Найдите значение выражения 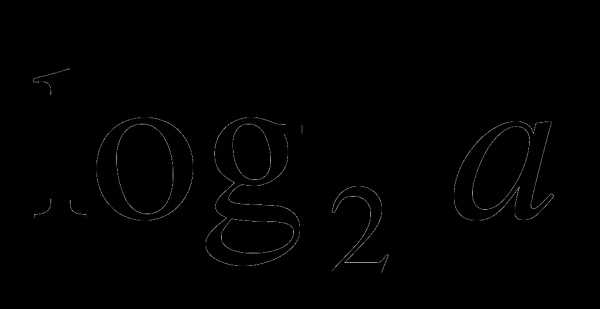, если .
А7. На одном из рисунков изображен график функции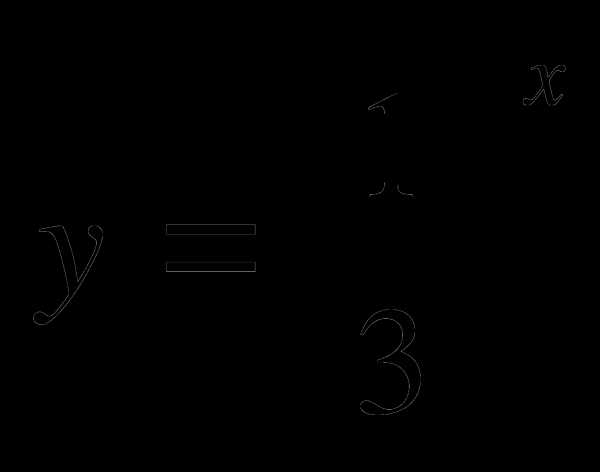 
. Укажите этот рисунок.
1
2
2
3
3
4
4
А8. Найдите область определения функции .
А9. Найдите сумму корней уравнения .
А10. Решить уравнение .
Часть2.
В1. Найдите наибольшее целое число, являющееся решением неравенства .
В2. Найдите значение выражения 4х0, где х0 — наибольшее целое число, являющееся решением неравенства .
В3 Вычислите значение числового выражения .
В4. Решите уравнение . В ответе запишите корень уравнения или сумму корней, если их несколько.
В5. Решите уравнение .
В6. При каком значении переменной х равны дроб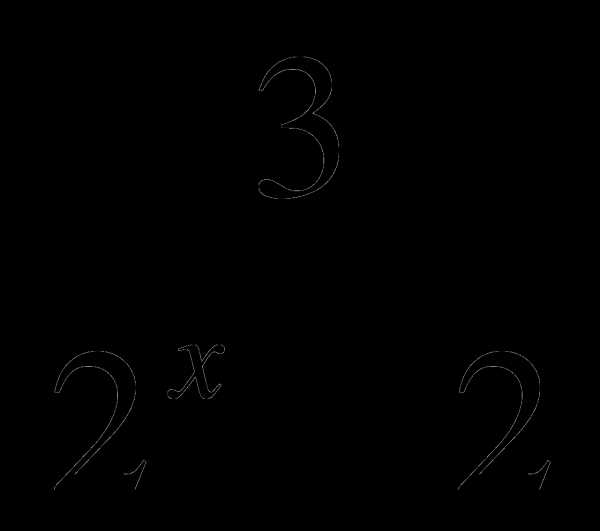и 
и ?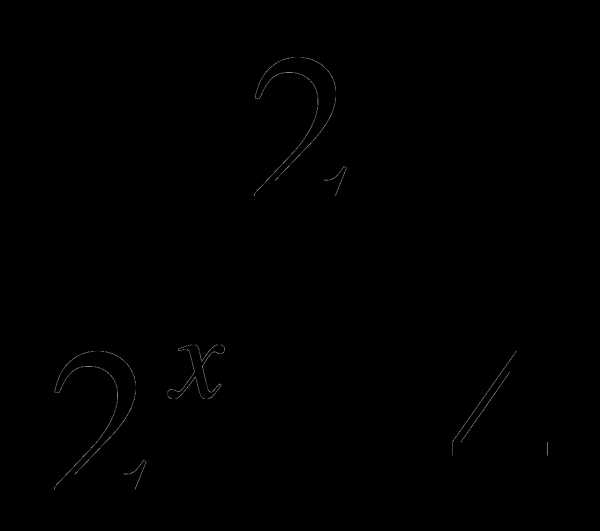
Часть 3.
С1. Решите уравнение .
С2. Решите неравенство: .
infourok.ru
Итоговая контрольная работа по математике (10 класс)
Лукоянова
Наталья Анатольевна,
учитель математики
МБОУ Гимназия в г. Новый Уренгой
Итоговая контрольная работа по математике (10 класс)
Вариант №1
1. Понятие действительного числа.
2. Скрещивающиеся прямые. Признак скрещивающихся прямых. Угол между скрещивающимися прямыми.
3. Найдите значение выражения .
4. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
Вариант №2
1. Множества чисел. Свойства действительных чисел.
2. Параллельность двух плоскостей. Признак параллельности двух плоскостей.
3. Найдите значение выражения .
4. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 9 и 12, и боковым ребром, равным 5.
Вариант №3
1. Рациональные выражения. Схема Горнера, теорема Безу.
2. Перпендикулярность прямой и плоскости. Признак перпендикулярности прямой и плоскости.
3. Найдите значение выражения .
4. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.
Вариант №4
1. Рациональные уравнения. Системы рациональных уравнений.
2. Теорема о трёх перпендикулярах.
3. Найдите , если и .
4. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
Вариант №5
1. Арксинус. Арккосинус. Формулы для арксинуса и арккосинуса.
2. Перпендикулярность двух плоскостей. Признак перпендикулярности двух плоскостей.
3. Найдите корень уравнения:
4. В прямоугольном параллелепипеде ABCDA1B1C1D1 ребро BC = 4, ребро АВ = , ребро BB1 = 4. Точка K — середина ребра CC1. Найдите площадь сечения, проходящего через точки B1, A1 и K.
Вариант №6
1. Метод интервалов решения неравенств. Общий метод интервалов решения неравенств.
2. Прямоугольный параллелепипед. Теорема о свойстве диагонали прямоугольного параллелепипеда.
3. Решите уравнение .
4. В прямоугольном параллелепипеде ABCDA1B1C1D1ребро CD = 2, ребро ВС = , ребро CC1 = 2. Точка K — середина ребра DD1. Найдите площадь сечения, проходящего через точки C1, B1 и K.
Вариант №7
1. Арктангенс. Арккотангенс. Формулы для арктангенса и арккотангенса.
2. Понятие призмы. Теорема о площади боковой поверхности прямой призмы.
3. Найдите корень уравнения
4. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.
Вариант №8
1. Рациональные неравенства. Нестрогие неравенства. Системы рациональных неравенств.
2. Понятия пирамиды, правильной пирамиды. Теорема о площади боковой поверхности
правильной пирамиды.
3. Найдите , если .
4. В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.
Вариант №9
1. Тригонометрические функции у = sin α, у = cos α и их свойства.
2. Усеченная пирамида. Теорема о площади боковой поверхности правильной
усеченной пирамиды.
3. Найдите , если .
4. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы.
Вариант №10
1. Формулы для двойных и половинных аргументов. Формулы для тангенсов.
2. Сложение и вычитание векторов. Два правила сложения векторов и два правила вычитания векторов.
3. Решите уравнение . Если уравнение имеет более одного корня, в ответе укажите меньший из них.
4. Площадь поверхности правильной треугольной призмы равна 6. Какой будет площадь поверхности призмы, если все ее ребра увеличить в три раза?
Вариант №11
1. Понятие функции и её графика. Функция .
2. Правило параллелепипеда для сложения трех некомпланарных векторов.
3. Найдите корень уравнения .
4. В правильной треугольной пирамиде SABC точка M – середина ребра AB, S – вершина. Известно, что BC = 3, а площадь боковой поверхности пирамиды равна 45. Найдите длину отрезка SM.
Вариант №12
1. Простейшие тригонометрические уравнения.
2. Умножение вектора на число, определение и свойства.
3. Найдите значение выражения .
4. В правильной треугольной пирамиде SABC точка L — середина ребра AC, S — вершина. Известно, что BC = 6, а SL = 5. Найдите площадь боковой поверхности пирамиды.
Вариант №13
1. Понятие корня степени п. Корни чётной и нечётной степеней.
2. Аксиомы стереометрии и следствия из них.
3. Найдите , если .
4. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
Вариант №14
1. Арифметический корень. Свойства корней степени п.
2. Параллельные плоскости. Свойства параллельных плоскостей.
3. Найдите значение выражения .
4. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
Вариант №15
1. Степень с рациональным показателем. Свойства степени с рациональным показателем.
2. Правильные многогранники, определение и виды.
3. Найдите корни уравнения: В ответ запишите наибольший отрицательный корень.
4. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в два раза?
Вариант №16
1. Показательная функция. Свойства показательной функции.
2. Параллельные прямые в пространстве. Параллельность трех прямых.
3. Найдите значение выражения при .
4. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.
Вариант №17
1. Понятие логарифма. Свойства логарифмов.
2. Параллельность прямой и плоскости. Признак параллельности прямой и плоскости.
3. Найдите , если при .
4. Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер.
Вариант №18
1. Логарифмическая функция. Свойства логарифмической функции.
2. Компланарные векторы.
3. Найдите значение выражения при .
4. В правильной треугольной пирамиде боковое ребро равно 5, а тангенс угла между боковой гранью и плоскостью основания равен Найти сторону основания пирамиды.
Вариант №19
1. Показательные уравнения. Способы решения показательных уравнений.
2. Угол между прямой и плоскостью.
3. Решите уравнение . В ответе напишите наибольший отрицательный корень.
4. В правильной четырёхугольной пирамиде боковое ребро равно 22, а тангенс угла между боковой гранью и плоскостью основания равен Найти сторону основания пирамиды.
Вариант №20
1. Логарифмические уравнения. Способы решения логарифмических уравнений.
2. Двугранный угол. Линейный угол двугранного угла.
3. Найдите значение выражения .
4. В правильной четырёхугольной пирамиде SABCD высота SO равна 13, диагональ основания BD равна 8. Точки К и М — середины ребер CD и ВС соответственно. Найдите тангенс угла между плоскостью SMK и плоскостью основания AВС.
Вариант №21
1. Понятие угла. Радианная мера угла.
2. Разложение вектора по трем некомпланарным векторам.
3. Решите уравнение .
4. В правильной четырёхугольной пирамиде все рёбра равны 1. Найдите площадь сечения пирамиды плоскостью, проходящей через середины боковых рёбер.
Вариант №22
1 Определение синуса, косинуса, тангенса и котангенса угла. Основные формулы для sin α,
cos α, tg α и ctg α.
2. Углы с сонаправленными сторонами. Угол между прямыми.
3. Найдите корень уравнения .
4. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы.
Вариант №23
1. Простейшие показательные и логарифмические неравенства.
2. Расстояние от точки до плоскости.
3 Найдите , если . При .
4. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
Вариант № 24
1. Однородные уравнения.
2. Понятие вектора в пространстве. Равенство векторов.
3. Найдите корень уравнения .
4. В правильной четырёхугольной пирамиде боковое ребро равно 22, а тангенс угла между боковой гранью и плоскостью основания равен Найти сторону основания пирамиды.
Вариант № 25
1. Тригонометрические функции у = tg α, y = ctg α и их свойства.
2. Тетраэдр. Параллелепипед. Сечения тетраэдра и параллелепипеда плоскостью.
3. Найдите корень уравнения .
4. В прямоугольном параллелепипеде ABCDA1B1C1D1 ребро BC = 4, ребро АВ = , ребро BB1 = 4. Точка K — середина ребра CC1. Найдите площадь сечения, проходящего через точки B1, A1 и K.
infourok.ru
Контрольная работа по математике для 10 класса по теме «Функции и их свойства»
Контрольная работа № 1
по теме «Функции и их свойства»
Цель: проверить уровень усвоение ГОСО
— умение находить значение функции в точке;
— умение находить область определения функции;
— умения строить эскиз графика функции и находить по эскизу промежутки
возрастания и убывания , экстремумы функции, точки пересечения с осями
координат;
— знания свойств четных и нечетных функций.
1. Вычислите:
y = f(x) является нечетной y = f(x) является четной
2 f(-4) + f(3) f(-3) + 2 f(1)
eсли f(4)=1, f(-3)=2 eсли f(3)=4, f(-1)=2
2. Найдите значение функции в точке X0.
X0 = -2 и X0 = 4 X0 = -3 и X0 = 1
3. Постройте эскиз функции и найдите координаты точек его пересечения с осями координат.
4. Найдите область определения функции
5. Найдите промежутки возрастания и убывания и экстремумы функции.
Критерии оценки.
0-10 баллов – «2»
11-14баллов – «3»
15-19 баллов – «4»
20-21 баллов – «5»
Распределение заданий по содержанию и видам деятельности.
Содержательные линии
Воспроизведение знаний
Применение знаний
Интеграция знаний
Процентное
Соотношение в тексте
Четные и нечетные функции.
№1
20%
Значения функции в точке
№2
20%
График функции и ее свойства
№3,4
№5
40%
Процентное
Соотношение в тексте
40%
40%
20%
100%
Критерии оценивания
№
задания
Характеристика задания
Проверяемые элементы
Балл за выполнение проверяемого элемента
Балл за выполнение задания
1
Свойства четных и нечетных функций.
Знания свойств четных и нечетных функций
2
3
Запись ответа
1
2
Значение функции в точке
Правильно подставил
2
3
Вычисления
1
3
График функции и ее свойства
Построение эскиза графика
2
5
Пересечение с осью абсцисс
1
Пересечение с осью ординат
2
Запись ответа
1
4
Область определения функции
Составление условий для нахождения области определения
2
5
Решение неравенства
1
Запись ответа
2
5
Промежутки возрастания , убывания и экстремумы функции
Вершина параболы
1
5
Свойства модуля
1
Эскиз графика
2
Запись ответа
1
infourok.ru
Итоговая контрольная работа по математике за курс 10 класса
Итоговая контрольная работа за 10 класс Вариант 1 А1. Найдите , если (1 балл) А2. Найдите производную функции: а) б) в) ( по 1 баллу за каждый пример) А3. (1 балл) А4. (1 балл) В1. Упростите выражение: (1 балл) В2. .Составьте уравнение касательной к графику функции в точке (1 балл) В3. Площадь прямоугольника 36 дм2. Какую длину должны иметь его стороны, чтобы периметр был наименьшим? (1 балл) В4. (1 балл) С1. а) Решите уравнение: 4sin2x — 4sinx + 1 = 0. (1 балл) б) найдите все корни этого уравнения, принадлежащие промежутку (. (1 балл) С2. При каких значениях параметра а уравнение х4 – 2х2 = а имеет ровно три корня? (2 балла) |
Вариант 2
А1. Найдите , если (1 балл)
А2. Найдите производную функции:
а)
б)
в)
( по 1 баллу за каждый пример)
А3. (1 балл)
А4. (1 балл)
В1. Упростите выражение: (1 балл)
В2. Составьте уравнение касательной к графику функции в точке (1 балл)
В3. Число 16 представьте в виде произведения двух положительных множителей, сумма квадратов у которых наибольшая. (1 балл)
В4. (1 балл)
С1. а) Решите уравнение: 4sin2x + 4sinx + 1 = 0. (1 балл)
б) найдите все корни этого уравнения, принадлежащие отрезку . (1 балл)
С2. При каких значениях параметра а уравнение 2х3 – 3х2 – 36х + 3 = а имеет ровно два корня?
(2 балла)
Итоговая контрольная работа за 10 классВариант 3
А1. Найдите , если (1 балл)
А2. Найдите производную функции:
а)
б)
в)
( по 1 баллу за каждый пример)
А3. (1 балл)
А4. (1 балл)
В1. Упростите выражение: (1 балл)
В2. Составьте уравнение касательной к графику функции в точке (1 балл)
В3. Сумма катетов прямоугольного треугольника равна 15см. Каковы должны быть их длины, чтобы гипотенуза треугольника была наименьшей? (1 балл)
В4. (1 балл)
С1. а) Решите уравнение: 3cos2x – sin2x + 4sinx = 0. (1 балл)
б) найдите все корни этого уравнения, принадлежащие отрезку . (1 балл)
С2. При каких значениях параметра а уравнение х3 – 3х2 = а имеет ровно три корня? (2 балла)
Итоговая контрольная работа за 10 классВариант 4
А1. Найдите , если (1 балл)
А2. Найдите производную функции:
а)
б)
в)
( по 1 баллу за каждый пример)
А3. (1 балл)
А4. (1 балл)
В1. Упростите выражение: (1 балл)
В2. Составьте уравнение касательной к графику функции в точке (1 балл)
В3. Число 9 представьте в виде двух положительных слагаемых так, чтобы произведение квадрата одного из них на утроенное другое было наибольшим. (1 балл)
В4. (1 балл)
С1. а) Решите уравнение: 8sin2x – 2cosx -5 = 0. (1 балл)
б) найдите все корни этого уравнения, принадлежащие промежутку (. (1 балл)
С2. При каких значениях параметра а уравнение х3 – 3х2 — 24х + а = 0 имеет ровно два различных корня? (2 балла)
infourok.ru
Контрольная работа по математике 10 класс. Базовый уровень. 1 полугодие.
Контрольная работа по математике за 1 полугодие, 10 класс (базовый уровень)
Вариант 1
Вариант 2
Вычислите
а), б), в), г), д), е), ж),
з)
Вычислите
а), б), в), г), д), е), ж),
з)
При каких значениях имеет смысл выражение
а), б), в) ?
При каких значениях имеет смысл выражение
а), б), в) ?
Упростите выражение
а), б)
при х6
Упростите выражение
а), б)
при х
Решите уравнение
а) х3-5х2-5х+1=0
б) 6х3-х2-20х+12=0
Решите уравнение
а) 2х3+3х2+3х+2=0
б) 6х3-13х2+4=0
Плоскость проходит через середины боковых сторон AB и CD трапеции ABCD – точки М и К.
а)Докажите, что AD параллельна .
б)Найдите ВС, если AD=10см, МК=8см.
Плоскость проходит через основание AD трапеции ABCD. М и К — середины боковых сторон трапеции.
а)Докажите, что МК параллельна .
б)Найдите AD, если ВС=4см, МК=6см.
Прямая а параллельна плоскости , а прямая в лежит в плоскости .
Определите, могут ли прямые а и в
а)быть параллельными, б)пересекаться,
в)быть скрещивающимися.
Прямая а параллельна плоскости , а прямая в пересекает плоскость .
Определите, могут ли прямые а и в
а)быть параллельными,
б)пересекаться,
в) быть скрещивающимися.
Решите неравенства
а)
б) 
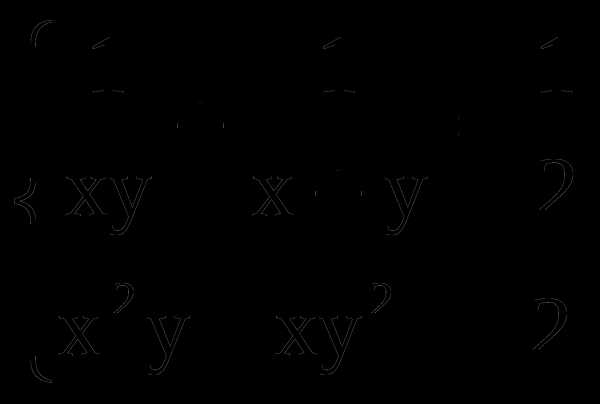
Решите неравенства
а)
в)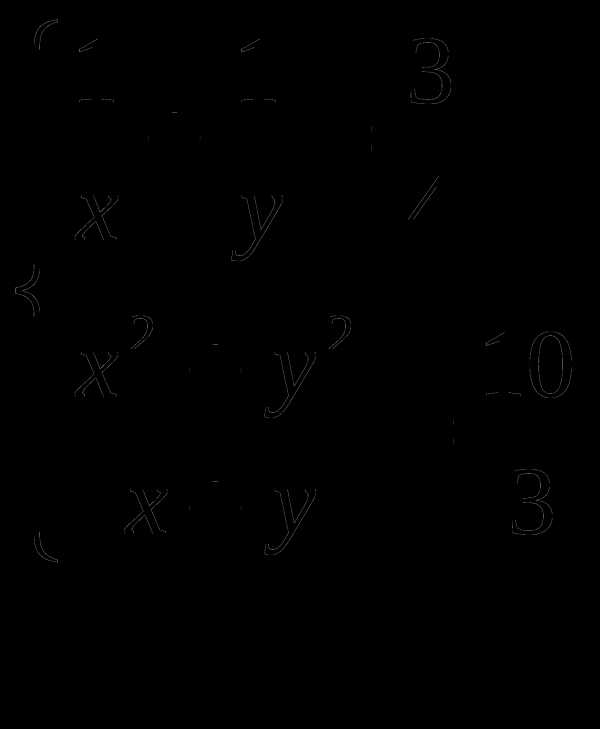
Выполните действия
Выполните действия
Решить графически уравнение
Решить графически уравнение
Подготовительный вариант контрольной работы по математике за 1 полугодие,
10 класс
В классе
Д/з
Вычислите
а), б), в), г), д), е), ж),
з)
Вычислите
а), б), в), г), д), е), ж),
з)
При каких значениях имеет смысл выражение
а), б), в) ?
При каких значениях имеет смысл выражение
а), б), в) ?
Упростите выражение
а), б)
при х8
Упростите выражение
а), б)
при х
Решите уравнение
а), б),
в), г) ,
д) 4
Решите уравнение
а), б),
в), г),
д) 6
Плоскость проходит через середины боковых сторон AB и CD трапеции ABCD – точки М и К.
а)Докажите, что BC параллельна .
б)Найдите AD, если BC=6см, МК=8см.
Плоскость проходит через основание ВС трапеции ABCD. М и К — середины боковых сторон трапеции.
а)Докажите, что МК параллельна .
б)Найдите ВС, если AD=8см, МК=6см.
Прямая а параллельна плоскости , и прямая в параллельна плоскости .
Определите, могут ли прямые а и в
а) быть параллельными, б) пересекаться,
в) быть скрещивающимися.
Прямая а пересекает плоскость и прямая в пересекает плоскость .
Определите, могут ли прямые а и в
а)быть параллельными,
б)пересекаться,
в) быть скрещивающимися.
Решите неравенства
а), б)
Решите неравенства
а), б)
Выполните действия
Выполните действия
Решить графически уравнение
Решить графически уравнение
infourok.ru
