система счисления. Виды систем счисления
В курсе информатики, вне зависимости, школьном или университетском, особое место уделяется такому понятию как системы счисления. Как правило, на него выделяют несколько уроков или практических занятий. Основная цель — не только усвоить основные понятия темы, изучить виды систем счисления, но и познакомиться с двоичной, восьмеричной и шестнадцатеричной арифметикой.
Что это значит?
Начнем с определения основного понятия. Как отмечает учебник «Информатика», система счисления — это система записи чисел, в которой используется специальный алфавит или определенный набор цифр.
В зависимости от того, меняется ли значение цифры от ее положения в числе, выделяют две: позиционную и непозиционную системы счисления.
В позиционных системах значение цифры меняется вместе с ее положением в числе. Так, если взять число 234, то цифра 4 в ней означает единицы, если же рассмотреть число 243, то тут она будет уже означать десятки, а не единицы.
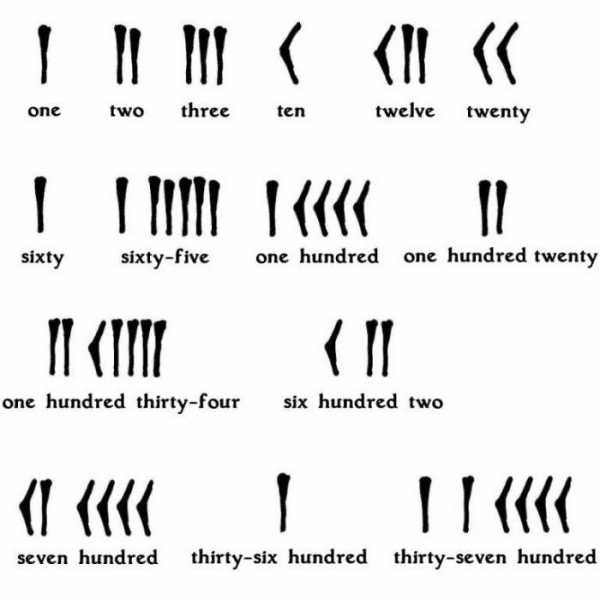
В непозиционных системах значение цифры статично, вне зависимости от ее положения в числе. Наиболее яркий пример – палочковая система, где каждая единица обозначается с помощью черточки. Неважно, куда вы припишите палочку, значение числа измениться лишь на единицу.
Непозиционные системы
К непозиционным системам счисления относятся:
- Единичная система, которая считается одной из первых. В ней вместо цифр использовались палочки. Чем их было больше, тем больше было значение числа. Встретить пример чисел, записанных таким образом, можно в фильмах, где речь идет о потерянных в море людях, заключенных, которые отмечают каждый день с помощью зарубок на камне или дереве.
- Римская, в которой вместо цифр использовались латинские буквы. Используя их, можно записать любое число. При этом его значение определялось с помощью суммы и разницы цифр, из которых состояло число. Если слева от цифры находилось меньшее число, то левая цифра вычиталась из правой, а если справа цифра была меньше или равна цифре слева, то их значения суммировались. Например, число 11 записывалось как XI, а 9 – IX.
- Буквенные, в которых числа обозначались с помощью алфавита того или иного языка. Одной из них считается славянская система, в которой ряд букв имел не только фонетическое, но и числовое значение.
- Вавилонская система счисления, в которой использовалось всего два обозначения для записи – клинья и стрелочки.
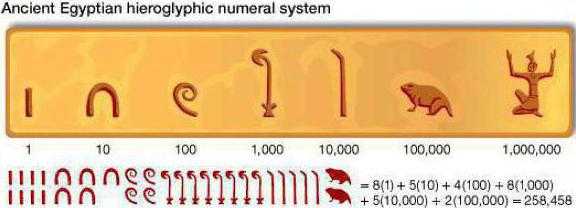
- В Египте тоже использовались специальные символы для обозначения чисел. При записи числа каждый символ мог использоваться не более девяти раз.
Позиционные системы
Большое внимание уделяется в информатике позиционным системам счисления. К ним относятся следующие:
- двоичная;
- восьмеричная;
- десятичная;
- шестнадцатеричная;
- шестидесятеричная, используемая при счете времени (к примеру, в минуте — 60 секунд, в часе — 60 минут).
Каждая из них обладает своим алфавитом для записи, правилами перевода и выполнения арифметических операций.
Десятичная система
Данная система является для нас наиболее привычной. В ней используются цифры от 0 до 9 для записи чисел. Они также носят название арабских. В зависимости от положения цифры в числе, она может обозначать разные разряды – единицы, десятки, сотни, тысячи или миллионы. Ее мы пользуемся повсеместно, знаем основные правила, по которым производятся арифметические операции над числами.
Двоичная система
Одна из основных систем счисления в информатике – двоичная. Ее простота позволяет компьютеру производить громоздкие вычисления в несколько раз быстрее, нежели в десятичной системе.
Для записи чисел используется лишь две цифры – 0 и 1. При этом, в зависимости от положения 0 или 1 в числе, его значение будет меняться.
Изначально именно с помощью двоичного кода компьютеры получали всю необходимую информацию. При этом, единица означала наличие сигнала, передаваемого с помощью напряжения, а ноль – его отсутствие.

Восьмеричная система
Еще одна известная компьютерная система счисления, в которой применяются цифры от 0 до 7. Применялась в основном в тех областях знаний, которые связаны с цифровыми устройствами. Но в последнее время она употребляется значительно реже, так как на смену ей пришла шестнадцатеричная система счисления.
Двоично-десятичная система
Представление больших чисел в двоичной системе для человека – процесс довольно сложный. Для его упрощения была разработана двоично-десятичная система счисления. Используется она обычно в электронных часах, калькуляторах. В данной системе из десятичной системы в двоичную преобразуется не все число, а каждая цифра переводится в соответствующий ей набор нулей и единиц в двоичной системе. Аналогично происходит и перевод из двоичной системы в десятичную. Каждая цифра, представленная в виде четырехзначного набора нулей и единиц, переводится в цифру десятичной системы счисления. В принципе, нет ничего сложного.
Для работы с числам в данном случае пригодится таблица систем счисления, в которой будет указано соответствие между цифрами и их двоичным кодом.
Шестнадцатеричная система
В последнее время все большую популярность приобретает в программировании и информатике система счисления шестнадцатеричная. В ней используются не только цифры от 0 до 9, но и ряд латинских букв – A, B, C, D, E, F.

При этом, каждая из букв имеет свое значение, так A=10, B=11, C=12 и так далее. Каждое число представляется в виде набора из четырех знаков: 001F.
Перевод чисел: из десятичной в двоичную
Перевод в системах счисления чисел происходит по определенным правилам. Наиболее часто встречается перевод из двоичной в десятичную систему и наоборот.
Для того, чтобы перевести число из десятичной системы в двоичную, необходимо последовательно делить его на основание системы счисления, то есть, число два. При этом, остаток от каждого деления необходимо фиксировать. Так будет происходить до тех пор, пока остаток от деления не будет меньше или равен единице. Проводить вычисления лучше всего в столбик. Затем полученные остатки от деления записываются в строку в обратном порядке.
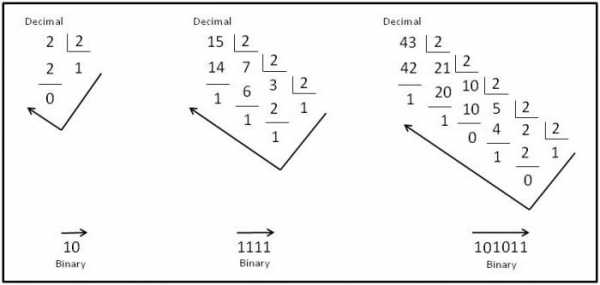
Например, переведем число 9 в двоичную систему:
Делим 9, так как число не делится нацело, то берем число 8, остаток будет 9 – 1 = 1.
После деления 8 на 2 получаем 4. Снова делим его, так как число делится нацело – получаем в остатке 4 – 4 = 0.
Проводим ту же операцию с 2. В остатке получаем 0.
В итоге деления у нас получается 1.
Далее записываем все полученные нами остатки в обратном порядке, начиная с итога деления: 1001.
Вне зависимости от итоговой системы счисления, перевод чисел из десятичной в любую другую будет происходить по принципу деления числа на основу позиционной системы.
Перевод чисел: из двоичной в десятичную
Довольно легко переводить числа и в десятичную систему счисления из двоичной. Для этого достаточно знать правила возведения чисел в степень. В данном случае, в степень двойки.
Алгоритм перевода следующий: каждую цифру из кода двоичного числа необходимо умножить на двойку, причем, первая двойка будет в степени m-1, вторая – m-2 и так далее, где m – количество цифр в коде. Затем сложить результаты сложения, получив целое число.
Для школьников этот алгоритм можно объяснить проще:
Для начала берем и записываем каждую цифру, умноженную на двойку, затем проставляем степень двойки с конца, начиная с нуля. Потом складываем полученное число.
Для примера разберем с вами полученное ранее число 1001, переведя его в десятичную систему, и заодно проверим правильность наших вычислений.
Выглядеть это будет следующим образом:
1*23 + 0*22+0*21+1*20= 8+0+0+1 =9.
При изучении данной темы удобно использовать таблицу со степенями двойки. Это существенно уменьшит количество времени, необходимое для проведения вычислений.
Другие варианты перевода
В некоторых случаях перевод может осуществляться между двоичной и восьмеричной системой счисления, двоичной и шестнадцатеричной. В таком случае можно пользоваться специальными таблицами или же запустить на компьютере приложение калькулятор, выбрав во вкладке вид вариант «Программист».
Арифметические операции
Вне зависимости от того, в каком виде представлено число, с ним можно проводить привычные для нас вычисления. Это может быть деление и умножение, вычитание и сложение в системе счисления, которую вы выбрали. Конечно, для каждой из них действуют свои правила.
Так для двоичной системы разработаны свои таблицы для каждой из операций. Такие же таблицы используются и в других позиционных системах.
Заучивать их необязательно – достаточно просто распечатать и иметь под рукой. Также можно воспользоваться калькулятором на ПК.

Одна из важнейших тем в информатике – система счисления. Знание этой темы, понимание алгоритмов перевода чисел из одной системы в другую – залог того, что вы сможете разобраться в более сложных темах, таких как алгоритмизация и программирование и сможете самостоятельно написать свою первую программу.
fb.ru
Системы счисления
СИСТЕМЫ СЧИСЛЕНИЯ
Система счисления — это знаковая система, в которой числа записываются по определенным правилам, с помощью символов некоторого алфавита.
Символы алфавита, которые используют для записи чисел, называют цифрами.
Цель создания системы счисления — выработка наиболее удобного способа записи количественной информации.
Удобная система счисления должна обладать следующими свойствами:
простота и краткость записи на материальном носителе
однозначность представления
удобство выполнения арифметических операций над числами
легкость и наглядность обучения основам работы с числами
Системы счисления бывают:
Позиционные (десятичная)
Непозиционные (римская)
В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен.
Изобретение позиционной нумерации, основанной на поместном значении цифр, приписывается шумерам и вавилонянам; развита была такая нумерация индусами и имела неоценимые последствия в истории человеческой цивилизации. К числу таких систем относится современная десятичная система счисления, возникновение которой связано со счётом на пальцах. В средневековой Европе она появилась через итальянских купцов, в свою очередь заимствовавших её у мусульман.
Причины, по которой она оказалась общепринятой, совсем не математического характера. Десять пальцев рук – вот тот первоначальный аппарат для счета, которым человек пользовался с доисторических времен. По пальцам удобно считать от одного до десяти. Сосчитав до десяти, т.е. использовав до конца возможности нашего природного «счетного аппарата», естественно принять само число 10 за новую, более крупную единицу (единицу следующего разряда).
В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе. При этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания.
Каноническим примером непозиционной системы счисления является римская, в которой в качестве цифр используются латинские буквы.
Системы счисления, используемые в компьютерах:
Двоичная система счисления.
Для записи чисел используются только две цифры – 0 и 1. Выбор двоичной системы объясняется тем, что электронные элементы, из которых строятся ЭВМ, могут находиться только в двух хорошо различимых состояниях. По существу эти элементы представляют собой выключатели. Как известно выключатель либо включен, либо выключен. Третьего не дано. Одно из состояний обозначается цифрой 1, другое – 0.
Благодаря таким особенностям двоичная система стала стандартом при построении ЭВМ.
Восьмеричная система счисления.
Для записи чисел используется восемь чисел 0,1,2,3,4,5,6,7.
Шестнадцатеричная система счисления.
Для записи чисел в шестнадцатеричной системе необходимо располагать уже шестнадцатью символами, используемыми как цифры. В качестве первых десяти используются те же, что и в десятичной системе. Для обозначения остальных шести цифр (в десятичной они соответствуют числам 10,11,12,13,14,15) используются буквы латинского алфавита – A,B,C,D,E,F.
Перевод чисел из одной системы счисления в другую.
Перевод чисел из любой системы счисления в десятичную.
Правило перевода чисел из системы с основанием М в десятичную:
Для того чтобы число из любой системы счисления перевести в десятичную систему счисления, необходимо его представить в развернутом виде и произвести вычисления.
(Развернутая форма числа — это запись, которая представляют собой сумму произведений цифр числа на значение позиций.)
Перевод чисел из десятичной системы счисления в другую.
Правило перевода целых чисел из десятичной системы счисления в систему с основанием N:
Последовательно выполнять деление исходного числа и получаемых частных на N до тех пор, пока не получим частное, меньшее делителя.
Полученные при таком делении остатки – цифры числа в системе счисления N – записать в обратном порядке (снизу вверх).
Правило перевода дробных чисел из десятичной системы счисления в систему с основанием N:
Последовательно выполнять умножение исходного числа и получаемые дробные части на N до тех пор, пока дробная часть не станет равна нулю или не достигнем требуемую точность.
Полученные при таком умножении целые части — числа в системе счисления N – записать в прямом порядке (сверху вниз).
Правило перевода произвольных (смешанных) чисел из десятичной системы счисления в систему с основанием N:
Перевод произвольных чисел, то есть чисел, содержащих целую и дробную части, осуществляют в два этапа. Отдельно переводится целая часть, отдельно – дробная. В итоговой записи полученного числа целая часть отделяется от дробной запятой.
studfiles.net
Компьютерные системы счисления
От системы счисления, используемой в компьютере, зависят объем памяти, скорость вычислений и сложность выполнения ал- горитмов. В компьютерах используются двоичная, восьмеричная, десятичная и шестнадцатеричная системы счисления.
В жизни мы в основном пользуемся десятичной системой счис- ления (арабская нумерация).
Начало этой системе счисления было положено в Вавилоне и Древнем Египте. Цифры 1234567890 сложились в Индии около 400 г. н.э. Арабы стали пользоваться подобной нумерацией около 800 г. н.э. после перевода работ математика Мухаммеда Аль Хорезми. Цифры арабской нумерации уже были немного похожи на наши:
Примерно в 1200 г. н.э. европейцы, заимствовав нумерацию у арабов, называли ее арабской. Это исторически неправильное название удерживается и поныне.
Форма индийских цифр претерпевала многообразные изменения, форма, которой мы пользуемся сейчас, установилась в XVI в.
В компьютерах десятичная система счисления используется для ввода и вывода информации.
В 1703 г. немецкий математик Лейбниц (1646—1716) ввел двоичную систему счисления 1936 г. американский инженер и математик предложил использовать ее для конструирования электронных схем.
В настоящее время двоичная система счисления является стандартной при создании компьютеров, т.к. в ней наиболее просто выполняются арифметические и логические операции.
Восьмеричная и шестнадцатеричная системы счисления используются в компьютере для составления программ на языке машинных кодов. Шведский король Карл XII в 1717 г. увлекся восьмеричной системой и собирался ввести ее как общегосударственную.
Шестнадцатеричная система счисления используется и сейчас: столовые сервизы на 12 персон, в пачке 12 фломастеров, в году 12 месяцев и прочее.
xn—-7sbfhivhrke5c.xn--p1ai
Конспект урока «Компьютерные системы счисления» для учащихся 10 класса
Цели:
Образовательные:
- изучение и усвоение нового материала: компьютерные СС – 2,8,16 СС;
- изучение и усвоение нового материала: перевод чисел из 2СС в 8,16 СС и наоборот.
Воспитательные:
- повышение мотивации учащихся путем использования нестандартных задач;
- обеспечение сознательного усвоения материала.
Развивающие:
- развитие мышления при помощи задач, в том числе из КИМ ЕГЭ;
- совершенствование умственной деятельности с привлечением устного счета.
Опорные понятия:
- система счисления
- позиционная и непозиционная системы
- основание системы
- алфавит
- кодирование информации
Задачи учителя:
- познакомить с компьютерными системами счисления;
- научить переводу чисел из двоичной в восьмеричную и шестнадцатеричную системы счисления и наоборот.
План урока:
- Организационный момент.
- Проверка пройденного материала. (Фронтальный опрос)
- Что такое системы счисления?
- Какие бывают системы счисления? Приведите примеры.
- Основные характеристики позиционной системы счисления (0, разряд)
- Что такое основание и алфавит позиционной системы счисления?
- С помощью какого носителя осуществляется кодирование в компьютере? Какие два устойчивых состояния есть?
В основе кодирования информации в компьютере лежит то, что электрический ток имеет всего два устойчивых состояния – есть ток и нет тока. Для удобства принято обозначать наличие тока 1, а отсутствие – 0.
0 и 1 это цифры какой системы счисления?
И так, основная компьютерная система счисления – двоичная, основание 2, цифры 0 и 1. Что же в ней такого особенного? Используя известные правила перевода, переведите число 3710 в 2СС (все в тетради, один у доски). Ответ: 1001012. Обратите внимание на то, что у двузначного числа 3710 двоичное представление получилось 6-тиразрядным. Давайте посмотрим, как увеличится разрядность двоичного числа, если десятичное увеличится всего на один разряд. Переведем число 38910 в 2СС (один у доски). Ответ: 110000101.
Мы видим, что разрядность увеличилась основательно. А ведь 398 не самое большое число, обрабатываемое на компьютере. Основная проблема, возникающая при работе с двоичными числами, это их длинная запись. Поэтому ученые – теоретики решили ввести промежуточные компьютерные системы счисления. Как вы думаете, какие основания предложили использовать? (8,16).
Естественно, для перевода чисел ил 10СС в 8 и 16 СС и обратно, можно использовать знакомые вам правила. Но чаще приходится выполнять переводы из 2СС в 8 и 16 СС и обратно. Как это можно сделать?
Когда я спросила, какие основания взяли для промежуточных СС, вы предположи 8 и 16. Совершенно не зря взяли эти числа. Дело в том, что они очень удачно связаны со степенями двойки.
Связь между основаниями компьютерных СС.
2СС – 8СС
23 = 8
Правила перевода: заданное двоичное число делят на группы по три разряда, начиная с права. Каждую группу переводят в десятичную цифру. Полученные десятичные цифры образуют искомое восьмеричное число.
(На слайде – пример перевода. Использование шпоргалки: обратить внимание на то, что цифры больше чем 7 не получится.)
Обратный перевод: Каждая цифра восьмеричного числа представляется тремя двоичными цифрами. Они составляют двоичное представление заданного числа.
(На слайде пример перевода).
Задание для самостоятельной работы (все в тетради, один у доски)
2СС – 16СС
24 = 16
На какие группы в данном случае будет делиться двоичное число?
Предлагаю вам самостоятельно попробовать перевести число 101110101011112 в 16СС и доработать шпоргалку для работы с 16ричными цифрами. (1 минута сами работают, потом 1 к доске проверять).
Итак, восьмеричная и шестнадцатеричная СС используются для более короткой записи чисел в двоичном коде. Вы могли видеть такие записи при выводе сообщения об ошибке по адресу. Попробуем решить задачи из контрольно – измерительных материалов ЕГЭ по информатике. В сборниках страница 14, № 33, 34 Рефлексия: задания 2 варианта, взаимопроверка (3 ответа – 5, 2 ответа – 4, 1 ответ – 3, нет ответов – неуд).
1 вариант | 2 вариант |
1. Если осуществлять перевод из 2СС в 32СС, то на какие по длине группы будет делиться двоичное число? | 1. Если осуществлять перевод из 2СС в 64СС, то на какие по длине группы будет делиться двоичное число? |
2. Некое двоичное число перевели в 16СС, получив 4-х разрядное число. Сколько разрядов было в исходном двоичном числе? | 2. Некое двоичное число перевели в 8СС, получив 6-ти разрядное число. Сколько разрядов было в исходном двоичном числе? |
3. Почему в компьютере используется двоичная, а не какая-нибудь иная СС? | 3. Что физически в компьютере обозначают цифры двоичной СС 1 и 0? |
Оценки за урок, ДЗ
Используется литература:
«ЕГЭ 2009. Информатика. Сборник экзаменационных материалов». Москва, Эксмо, 2009 г.
04.10.2010
Дополнительно:
Демонстрационный материал к уроку презентация на тему: «Компьютерные системы счисления»Слайд 3

Слайд 9

Здесь представлены лишь скриншот презентации. Полный вариант содержит 13 слайдов.
www.metod-kopilka.ru
Урок информатики. Тема: «Компьютерные системы счисления»
Разделы: Информатика
Цели:
- Образовательные:
- изучение и усвоение нового материала: компьютерные СС – 2,8,16 СС;
- изучение и усвоение нового материала: перевод чисел из 2СС в 8,16 СС и наоборот.
- Воспитательные:
- повышение мотивации учащихся путем использования нестандартных задач;
- обеспечение сознательного усвоения материала.
- Развивающие:
- развитие мышления при помощи задач, в том числе из КИМ ЕГЭ;
- совершенствование умственной деятельности с привлечением устного счета.
Опорные понятия:
- система счисления
- позиционная и непозиционная системы
- основание системы
- алфавит
- кодирование информации
Задачи учителя:
- познакомить с компьютерными системами счисления;
- научить переводу чисел из двоичной в восьмеричную и шестнадцатеричную системы счисления и наоборот.
ХОД УРОКА
1. Организационный момент. (Презентация. Слайд 1)
2. Проверка пройденного материала. (Фронтальный опрос)
- Что такое системы счисления?
- Какие бывают системы счисления? Приведите примеры.
- Основные характеристики позиционной системы счисления (0, разряд)
- Что такое основание и алфавит позиционной системы счисления?
- С помощью какого носителя осуществляется кодирование в компьютере? Какие два устойчивых состояния есть?
3. Тема урока: Компьютерные системы счисления. (Слайд 2)Объяснение нового материала.
В основе кодирования информации в компьютере
лежит то, что электрический ток имеет всего два
устойчивых состояния – есть ток и нет тока. Для
удобства принято обозначать наличие тока 1, а
отсутствие – 0.
0 и 1 это цифры какой системы счисления? (Слайд 3)
Итак, основная компьютерная система счисления –
двоичная, основание 2, цифры 0 и 1. Что же в ней
такого особенного?
Используя известные правила перевода, переведите число 3710 в 2СС (все в тетради, один у доски). Ответ: 1001012.
Обратите внимание на то, что у двузначного числа 3710 двоичное представление получилось 6-тиразрядным. Давайте посмотрим, как увеличится разрядность двоичного числа, если десятичное увеличится всего на один разряд. Переведем число 38910 в 2СС (один у доски). Ответ: 110000101.
Мы видим, что разрядность увеличилась основательно. А ведь 398 не самое большое число, обрабатываемое на компьютере. Основная проблема, возникающая при работе с двоичными числами, это их длинная запись. Поэтому ученые – теоретики решили ввести промежуточные компьютерные системы счисления. Как вы думаете, какие основания предложили использовать? (8,16).
Мы с вами составим таблицу, которая содержит основную информацию о СС с основаниями 2,8 и 16. (Слайд 4)
Естественно, для перевода чисел ил 10СС в 8 и 16 СС и обратно, можно использовать знакомые вам правила. Но чаще приходится выполнять переводы из 2СС в 8 и 16 СС и обратно. Как это можно сделать?
Когда я спросила, какие основания взяли для промежуточных СС, вы предположи 8 и 16. Совершенно не зря взяли эти числа. Дело в том, что они очень удачно связаны со степенями двойки.
Связь между основаниями компьютерных СС. (Слайд 5)
2СС – 8СС
23 = 8
Правила перевода: заданное двоичное число делят на группы по три разряда, начиная с права. Каждую группу переводят в десятичную цифру. Полученные десятичные цифры образуют искомое восьмеричное число.
(На слайде – пример перевода. Использование
шпоргалки: обратить внимание на то, что цифры
больше чем 7 не получится.)
Обратный перевод: (Слайд 6)
Каждая цифра восьмеричного числа представляется тремя двоичными цифрами. Они составляют двоичное представление заданного числа. (На слайде пример перевода).
Задание для самостоятельной работы (все в тетради, один у доски) (Слайд 7)
(Слайд 8)
2СС – 16СС
24 = 16
На какие группы в данном случае будет делиться двоичное число?
Предлагаю вам самостоятельно попробовать перевести число 101110101011112 в 16СС и доработать шпоргалку для работы с 16ричными цифрами. (1 минута сами работают, потом 1 к доске проверять).
Итак, восьмеричная и шестнадцатеричная СС используются для более короткой записи чисел в двоичном коде. Вы могли видеть такие записи при выводе сообщения об ошибке по адресу.
4. Попробуем решить задачи из контрольно – измерительных материалов ЕГЭ по информатике. (Слайд 9)
5. Рефлексия: задания 2 варианта (Слайд 10), взаимопроверка (Слайд 11) (3 ответа – 5, 2 ответа – 4, 1 ответ – 3, нет ответов – неуд).
| 1 вариант | 2 вариант |
| 1. Если осуществлять перевод из 2СС в 32СС, то на какие по длине группы будет делиться двоичное число? | 1. Если осуществлять перевод из 2СС в 64СС, то на какие по длине группы будет делиться двоичное число? |
| 2. Некое двоичное число перевели в 16СС, получив 4-х разрядное число. Сколько разрядов было в исходном двоичном числе? | 2. Некое двоичное число перевели в 8СС, получив 6-ти разрядное число. Сколько разрядов было в исходном двоичном числе? |
| 3. Почему в компьютере используется двоичная, а не какая-нибудь иная СС? | 3. Что физически в компьютере обозначают цифры двоичной СС 1 и 0? |
6. Оценки за урок, ДЗ (Слайд 12)
7. Если остается время на уроке, можно порассуждать на тему: почему 10система счисления принята во всем мире. И какая система скорей всего принята у героев фантастического фильма «Аватар»? (Слайд 13)
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
4. Представление числовой информации в компьютере
4.1. Компьютерная система счисления
Система счисления — это способ записи чисел с помощью заданного набора специальных знаков (цифр).
Существуют позиционные и непозиционные системы счисления.
В непозиционных системах вес цифры (т. е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти.
Алфавит системы: I,V,X,L,C,D,M. Изменение весовых значений цифр алфавита определяется циклической последовательностью: умножить на 5, а затем удвоить, тогда таблица весовых значений имеет вид:
|
I |
V |
X |
L |
C |
D |
M |
|
1 |
5 |
10 |
50 |
100 |
500 |
1000 |
Число 672 можно представить в римском изображении: 600+70+2=DCLXXII. Возможна запись любых положительных чисел в диапазоне от 1 до 3999. Для изображения чисел больших по весу используется над- или подстрочный индекс. Например,: 5325=VMCCCXXV=VMCCCXXV.
Достоинства непозиционных систем:
использование в качестве цифр букв основной для римлян разговорной системы;
возможность выделения некоторой информации в ряду другой нетрадиционной.
Недостатки:
громоздкость записи;
непонятность выполнения правил действий над числами, даже простейших арифметических.
Исходя из изложенного, римская, как и другие непозиционные системы, используется редко, в основном для обозначения веков, знаменательных дат.
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая – 7 единиц, а третья – 7 десятых долей единицы.
Сама же запись числа 757,7 означает сокращенную запись выражения:
700 + 50 + 7 + 0,7 = 7•102 + 5•101 + 7•100 + 7•10-1 = 757,7.
Любая позиционная система счисления характеризуется своим основанием.
Основание позиционной системы счисления — это количество различных знаков или символов, используемых для изображения цифр в данной системе.
В качестве основания системы счисления можно использовать любое значение Р в диапазоне:
.
Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т. д. Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения
an-1 qn-1 + an-2 qn-2+ … + a1 q1 + a0 q0 + a-1 q-1 + … + a-m q-m,
где ai – цифры системы счисления; n и m – число целых и дробных разрядов, соответственно.
Например:
Разряды 3 2 1 0 -1
Число 1 0 1 1, 12 = 1∙23+0∙22+1∙21+1∙20+1∙2-1 = 10,510
Разряды 2 1 0 -1 -2
Число 2 7 6, 5 48 = 2∙82+7∙81+6∙80+5∙8-1+ 4∙8-2 = 190,687510
В каждой системе счисления цифры упорядочены в соответствии с их значениями: 1 больше 0, 2 больше 1 и т. д.
Промежуточная – это система счисления, основание которой кратно 2 в целой положительной степени (n). Следовательно, основания любой промежуточной системы вычисляются зависимостью: Р=2n, т.е. Р=4, Р=8, Р=16, Р=32 и т.д. В настоящее время широко используются 2 промежуточные системы: восьмеричная (Р=8) и шестнадцатиричная (Р=16).
Продвижением цифры называют замену её следующей по величине. Продвинуть цифру 1, значит, заменить её на 2, продвинуть цифру 2, значит, заменить её на 3 и т. д. Продвижение старшей цифры (например, цифры 9 в десятичной системе) означает замену её на 0. В двоичной системе, использующей только две цифры – 0 и 1, продвижение 0 означает замену его на 1, а продвижение 1 – замену её на 0.
Для образования целого числа, следующего за любым данным целым числом, нужно продвинуть самую правую цифру числа; если какая-либо цифра после продвижения стала нулем, то нужно продвинуть цифру, стоящую слева от неё.
Применяя это правило, можно записать первые десять целых чисел
в двоичной системе: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001;
в троичной системе: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100;
в пятеричной системе: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14;
восьмеричной системе: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.
в десятичной системе 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В шестнадцатеричной системепервые 36 числел:0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1A, 1B, 1C, 1D, 1E, 1F, 20, 21, 2216.
Люди предпочитают десятичную систему, вероятно, потому, что с древних времен считали по пальцам, а пальцев у людей по десять на руках и ногах. Не всегда и не везде люди пользуются десятичной системой счисления. В Китае, например, долгое время пользовались пятеричной системой счисления.
Из всех систем счисления особенно проста и поэтому интересна для технической реализации в компьютерах двоичная система счисления.
Компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:
для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т. п.), а не, например, с десятью, — как в десятичной;
представление информации посредством только двух состояний надежно и помехоустойчиво;
возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
двоичная арифметика намного проще десятичной.
Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел.
Двоичная система, удобная для компьютеров, но для человека же наоборот неудобна из-за ее громоздкости и непривычной записи.
Полезно запомнить запись в различных системах счисления первых семнадцати целых чисел:
|
10ая |
2ая |
5ая |
8ая |
16ая |
|
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
0 1 10 11 100 101 110 111 1000 1001 1010 1011 1100 1101 1110 1111 10000 |
0 1 2 3 4 10 11 12 13 14 20 21 22 23 24 30 31 |
0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 20 |
0 1 2 3 4 5 6 7 8 9 A B C D E F 10 |
studfiles.net
Системы счисления — Компьютер для новичков

В настоящее время подавляющее число людей являются грамотными и умеют считать. Тем не менее, далеко не все в курсе, что за время человеческой цивилизации было придумано большое количество самых разнообразных систем счисления. Разные народы в различные исторические периоды использовали разные системы счета, которые видоизменялись с течением времени.
Считается, что самая первая система счета у всех народов состояла всего из одного числа, единицы. Соответственно для обозначения, какого то другого числа ее следовало повторить соответствующее количество раз. В качестве обозначения могло выступать что угодно, черточки, крестики и любые другие символы. Отсутствие письменности тоже не помеха, ведь можно использовать камешки, ракушки, плоды, веточки, делать зарубки, вязать узелки и так далее.
Таким образом, для записи числа 4 требовалось собрать 4 камешка или поставить 4 черточки: ||||. Это так называемая единичная система счисления, из которой впоследствии сформировались остальные. Все предельно просто, но очень не удобно для более менее больших чисел. Через какое то время люди догадались упростить запись, объединяя какое то количество элементов в группы и обозначая их другим символом. Чаще всего встречалась группировка по 3 и 5 элементов.
Таким образом, если договориться, что черные камни обозначают единицы, а один белый камень равен 3 черным, то для обозначения допустим 8 чужаков надо показать ●●●●●●●● черных камней или ○ белый и ●●●●● черных или ○○ белых и ●● черных. Любая из этих комбинаций обозначает в нашей условной системе число 8. Такой прием, конечно, заметно упрощал счет. Впоследствии многие народы использовали в качестве обозначения чисел буквы своего алфавита.
Римская система счисления
Одной из таких систем счисления является римская, которая до сих пор находит применение, например, для обозначения веков, цифр на циферблате аналоговых часов, разделов в документе и так далее. В ее основе лежат следующие числа и соответствующие им буквы латинского алфавита.
- 1 — I
- 5 — V
- 10 — X
- 50 — L
- 100 — C
- 500 — D
- 1000 — M
Все остальные числа получаются их комбинацией в соответствии с определенными правилами, причем 0 в римской системе отсутствует. Хотя сейчас правила довольно вольные и существует множество вариантов их трактовки отличающиеся различной степенью строгости. Мы не будем их расписывать, желающие могут найти их самостоятельно. Приведем лишь несколько примеров записи чисел в римской системе счисления.
- II — 2
- IV — 4
- XVI — 16
- XXIII — 23
- XLVIII — 48
Десятичная система счисления
Однако сейчас нам привычна система счисления основанная на цифрах от 1 до 9 и 0, это так называемые арабские цифры, хотя с исторической точки зрения это не совсем так. В итоге получается 10 цифр, поэтому она называется десятичной системой счисления с основанием системы равным 10. Считается, что она обязана своему появлению количеству пальцев на руках, что сильно упрощало жизнь. Ее особенностью является то, что в зависимости от местоположения цифры в числе меняется ее значение. Например, в числе 152 цифра 5 имеет значение 50, поскольку стоит в разряде десятков, а цифра 1 имеет значение 100 так как обозначает сотни. Это так называемая позиционная система счисления.
Так же существуют непозиционные системы, где значение цифр не зависит от их места в числе, а так же смешанные системы. Примером непозиционной системы может служить единичная система счета и с некоторой оговоркой римская.
Впрочем, еще относительно недавно в историческом масштабе, вплоть до конца XVIII века на Руси применялась пятеричная система, в которой были только цифры 0, 1, 2, 3, 4 и вытесненная из обихода современной десятичной.
Помимо уже названных систем счисления имеется множество других существовавших в разное время, а так же использующих в настоящее время в разных сферах деятельности человека. Для пересчета чисел из одной системы счисления в другую, вы можете воспользоваться онлайн конвертером систем счисления в конце статьи. Дальше мы рассмотрим несколько таких систем счисления применяющихся в компьютерной технике и программном обеспечении.
Двоичная система счисления
Почти все электронные вычислительные устройства, в том числе компьютеры используют вовсе не привычную для нас десятичную, а двоичную систему счисления, где основанием системы является 2. В ее основе лежит использование всего двух чисел 0 и 1. Это очень удобно для электронных устройств в силу технических причин, поскольку соответствует всего двум состояниям включено (1) и выключено (0) или высокий и низкий сигнал или «истина» и «ложь» и так далее. Наличие всего двух состояний упрощает техническую реализацию, повышает надежность работы, уменьшает габариты и обеспечивает высокую помехоустойчивость цифровых схем, в сравнение с аналоговыми.
В итоге любые числа представлены в виде комбинаций нулей и единиц. Например, число 4 в двоичной системе счисления записывается как 100, но читается каждый символ в отдельности, то есть «один ноль ноль». Это может запутать, поскольку запись числа 4 в двоичной системе счисления внешне не отличается от числа 100 из десятичной. В некоторых ситуациях из-за этого может возникнуть путаница. В таких случаях справа от числа подстрочным шрифтом принято указывать систему счисления, к которой относится данной число в десятичном формате. Числа из нашего примера можно записать следующим образом 410 и соответственно 1002. Так же встречается вариант указания перед двоичным числом префиксов 0b или &, то есть 0b100 или &100.
Чтобы перевести десятичное число в двоичное, можно воспользоваться калькулятором расположенным ниже или применить метод Горнера. Для этого нужно десятичное число последовательно делить на основание системы, в данном случае 2. Если результат получается с остатком, то остаток отбрасываем, пишем 1 и снова делим на 2. Если результат получается без остатка, то пишем 0 и снова делим на 2. Запись нулей и единиц осуществляется справа налево, а деление продолжается пока в частном не получится ноль. Рассмотрим это на примере и преобразуем число 1110 в двоичный вид.
11/2=5 остаток 1 5/2=2 остаток 1 2/2=1 остаток 0 1/2=0 остаток 1
В частном получился ноль, осталось записать получившиеся цифры справа налево от первой к последней и в итоге получаем, что 1110=10112
Для обратной конвертации двоичных в десятичные, можно складывать последовательно цифры слева на право, умножая получившейся в предыдущем шаге результат на 2. Пересчитаем наш пример в обратную сторону.
Дано: &1011 1+0*2=1 (на первом шаге предыдущая сумма отсутствует, поэтому 0*2 ) 0+1*2=2 1+2*2=5 1+5*2=11 Результат: 1110
Чтобы окончательно вас запутать, стоит упомянуть, что для записи чисел может применяться двоичный код, а система счета при этом использоваться десятичная. Такая комбинация называется двоично-десятичное кодирование и так же находит применение в вычислительной технике.
Шестнадцатеричная система счисления
Неудобством двоичных чисел является их громоздкость и трудность визуального восприятия человеком. Поэтому для представления двоичного кода в информатике широко используется шестнадцатеричная система счисления. Как вы уже наверно догадались, в ней используется шестнадцать символов, цифры от 0 до 9 и латинские буквы A, B, C, D, E, F соответствующие числам от 10 до 15 в десятичной системе. Шестнадцатеричное число может обозначаться словом hex.
Благодаря основанию системы равному 16 для записи 1 байта требуется всего 2 цифры в этой системе, для символов юникода требуется 4 шестнадцатеричных числа (иногда больше). Может использоваться для обозначения цветов в цветовой модели RGB, в програмировании, записи адресов IPv6, представления MAC-адреса сетевого оборудования, кодов ошибок операционных систем, записи хешей, и так далее.
Чтобы перевести десятичное число в шестнадцатеричное используйте онлайн калькулятор систем счисления в конце статьи или воспользуйтесь алгоритмом, приведенным в примере с двоичной системой. Для примера пересчитаем число 38210
382/16=23 остаток 14, пишем E 23/16=1 остаток 7, пишем 7 1/16=0 остаток 1, пишем 1 Результат: 17E16=38210
Чтобы пересчитать шестнадцатеричное число в десятичное, нужно разбить его на разряды и цифру каждого разряда умножить на 16 в степени соответствующего разряда и сложить получившиеся числа. Проще понять на примере, для этого выполним обратную операцию: 17E16=1*162+7*161+14*160=1*256+7*16+14*1=38210
Кроме рассмотренных систем существует и большое количество позиционных систем счисления с другими основаниями. Так в компьютерах одно время использовалась система с основанием 8, а такая древняя система счисления как шестидесятеричная, используется и в наше время для обозначения времени, координат и углов.
Калькулятор систем счисления
Работает только с целыми положительными числами.
beginpc.ru
