1. Перевод дробных чисел из одной системы счисления в другую
Каждый знает, что дроби бывают обыкновенные и десятичные. Обыкновенная дробь представляет собой отношение целого числа к натуральному. Поэтому ее перевод в другую систему счисления трудности не представляет: надо отдельно перевести в новую систему счисления числитель и знаменатель, затем записать их отношение. Запись числа десятичной дробью — это распространение позиционного принципа вправо от разряда единиц. Вспомните: при переходе на один разряд влево «вклад» цифры увеличивается в \(10\) раз, а при переходе на один разряд вправо уменьшается в \(10\) раз. Так что запись \(1,38054\) обозначает число: 1⋅100+3⋅10−1+8⋅10−2+0⋅10−3+5⋅10−4+4⋅10−5.
Легко понять, что и здесь вместо числа \(10\) можно использовать любое другое натуральное число \(b\), большее \(1\). Скажем, 1,38054b=1⋅b0+3⋅b−1+8⋅b−2+0⋅b−3+5⋅b−4+4⋅b−5.
По аналогии с десятичными дробями будем называть такую запись дробного числа b-ичной дробью. Так же как и для целых чисел, каждая цифра, используемая в записи b-ичной дроби, должна быть меньше \(b\). Как же переводить десятичную дробь в b-ичную? Для того что-бы найти алгоритм, запишем b-ичную дробь c=0,a1a2…an в виде суммы разрядных слагаемых: c=a1⋅b−1+a2⋅b−2+…+an−1⋅bn−1+an⋅b−n.
Из этой записи видно, что целая часть числа bc=a1,a2…an дает первую цифру после запятой в указанном представлении числа \(c\). Выделив в \(bc\) дробную часть, поступим с ней точно так же умножим на \(b\). Таким образом мы получим еще одну цифру — a2. И так далее. Вот пример перевода десятичной дроби \(0,36\) в пятеричную систему:
Ответ: 0,145.
А теперь попытаемся перевести ту же дробь в семеричную систему счисления:
Обратите внимание: после четвертого умножения мы снова получили дробь \(0,36\). Это значит, что дальше процесс будет повторяться и никогда не закончится! Тем самым после перевода числа \(0,36\) в семеричную систему счисления получается бесконечная периодическая дробь: 0,23432343…7= 0,(2343)7. При переводе конечной b-ичной дроби в десятичную систему тоже может получиться бесконечная дробь. К примеру, запись 0,13 представляет одну треть и, следовательно, в десятичной системе будет выглядеть как бесконечная десятичная дробь 0,33333…=0,(3).
Как вы знаете, бесконечные дроби нередко округляют, оставляя такое количество разрядов, которое обеспечивает необходимую точность.
Напомним, что в десятичной системе правило округления таково: если цифра в разряде, с которого производится округление, меньше \(5\), то цифра в предшествующем разряде не меняется, в противном случае она увеличивается на \(1\).
Для b-ичной дроби правило нужно модифицировать: если цифра в разряде, с которого производится округление, меньше \(b/2\), то цифра в предшествующем разряде не меняется, в противном случае она увеличивается на \(1\).
Например, дробь 0,23432343…7 при округлении до третьего разряда после запятой дает 0,2347, а при округлении до шестого разряда после запятой даёт 0,2343247.Гейн А. Г., Ливчак А. Б., Сенокосов А. И. Информатика и ИКТ. 11 класс. М. : Просвещение, 56 с.
www.yaklass.ru
Десятичные дроби и смешанные числа в разных системах счисления
Автор — Лада Борисовна Есакова.
Перевод целых чисел из одной системы счисления в другую обычно не вызывает проблем. А вот необходимость перевести десятичную дробь или смешанное число (число с целой и дробной частью) из системы в систему часто ставит в тупик даже сильных учеников.
1. Перевод смешанного числа в десятичную систему счисления из любой другой.
Для перевода смешанного числа в десятичную систему из любой другой следует пронумеровать разряды числа, начиная с нуля, справа налево от младшего целого разряда. Разряды дробной части нумеруются слева направо от -1 в убывающем порядке. Теперь представим число в виде суммы произведений его цифр на основание системы в степени разряда числа и ответ готов.
Пример 1.
Переведите число 105,4 из восьмеричной системы в десятичную.
Решение:
Пронумеруем целые разряды числа справа налево от 0, дробные – слева направо от -1 :
Посчитаем сумму произведений цифр числа на 8 (основание системы) в степени разряда числа:
Ответ:
2. Перевод десятичных дробей из десятичной системы счисления в любую другую.
Для перевода десятичной дроби из десятичной системы в любую другую следует умножать дробь, а затем дробные части произведений, на основание новой системы пока дробная часть не станет равной 0 или до достижения указанной точности. Затем целые части выписать, начиная с первой.
Переведите десятичное число 0,816 в двоичную систему с точностью до сотых.
Решение:
Умножаем дробь 0,816, а затем дробную часть произведения (0,632) на 2 и выписываем целые части, начиная с первой:
Ответ:
Пример 3.
Переведите десятичное число 0,8125 в восьмеричную систему.
Решение:
Умножаем дробь 0,8125, а затем дробную часть произведения (0,5) на 8 и выписываем целые части, начиная с первой:
Ответ:
3. Перевод смешанных чисел из десятичной системы счисления в любую другую
Если необходимо перевести смешанное число из десятичной системы в любую другую, следует перевести целую и дробную части, а затем записать, разделив десятичной запятой.
Пример 4.
Сколько единиц в двоичной записи десятичного числа 14,125?
Решение:
Переведем целую часть числа в двоичную систему:
Переведем дробную часть числа в двоичную систему:
Соединим целую и дробную части:
14,12510 = 1110,0012
Количество единиц равно 4.
Ответ: 4
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Перевод дробных чисел из одной системы счисления в другую
После того, как я сделал несколько калькуляторов для перевода между разными системами счисления — вот список от первой до последней версии, от самого простого к сложному: Перевод числа в другие системы счисления, Перевод из десятичной системы счисления, Перевод из одной системы счисления в другую — в комментариях стали периодически спрашивать — а что же, мол, дробные числа, как же их переводить? И когда спросили больше трех раз, я таки решил изучить этот вопрос.
Результатом стал калькулятор, который вы видите ниже, он умеет переводить и дробные числа в том числе. Как водится, для любознательных под калькулятором немного теории.
Основание системы счисления исходного числа
Основание системы счисления переведенного числа
Точность вычисленияЗнаков после запятой: 8
Переведенное число
Детали перевода
Исходное число в десятичной системе счисления
Переведенное число в десятичной системе счисления
Погрешность перевода (в десятичном выражении)
Максимальная погрешность перевода (в десятичном выражении)
Сохранить share extension
Теперь теория. Я, честно говоря, думал, что вопрос довольно сложный, но при ближайшем рассмотрении все оказалось проще простого. Надо было только держать в голове тот факт, что речь идет о позиционных системах счисления.
Все просто, не так ли? Та же самая простота сохраняется и при записи дробного числа в любой другой системе счисления. Возьмем, например, горячо любимую каждым программистом двоичную систему и число, например, 110.001. Эта запись есть не что иное как
Да-да, число для примера было выбрано не просто так. То есть, 110.001 в двоичной системе есть 6.125 в десятичной. Принцип, я думаю, ясен.
Есть только одно но — все-таки из-за того, что здесь участвую дроби с разными знаменателями, не всегда одно и тоже число можно одинаково точно выразить в разных системах счисления. Что я имею в виду?
Возьмем, например, число . Отлично смотрится в десятичной системе счисления. Но вот если попробовать получить запись этого числа в двоичной системе счисления — будут проблемы. Попробуем, пока не устанем
Продолжать можно еще довольно долго, но уже сейчас видно, что 0.8 в десятичной системе это 0.11001100…(дальше очень много цифр) в двоичной. Если честно, то это периодическое число с перидом 1100, так что мы никогда не сможем выразить его точно в двоичной системе счисления. 110011001100… будет продолжаться до бесконечности.
Поэтому перевод дробного числа из одной системы счисления в другую чаще всего дает погрешность. Погрешность эта зависит от того, сколько разрядов мы используем для записи дробной части переведенного числа. Возьмем пример с числом 0.8 и используем для записи его двоичного представления шесть разрядов после запятой — 0.110011. Полученное число вовсе не 0.8, а 0.796875, разница при этом составляет 0.003125. Это и есть наша погрешность перевода десятичного числа 0.8 в двоичный вид при использовании шести разрядов после запятой.
Вес крайнего правого разряда (самого младшего разряда) называется разрешением (resolution) или точностью (precision), и определяет наименьшее неравное нулю число, которое может быть представлено данным числом разрядов. Для нашего примера это . При этом максимально возможная погрешность представления числа, как нетрудно сообразить, не превышает половины этого веса, или 0.0078125. Так что для 0.8 мы имеем еще и не самую плохую погрешность.Вот, собственно, и все.
planetcalc.ru
перевод дробных чисел
Наименование УО: МБОУ СОШ с. Захаровка
Учитель: Вавин Александр Викторович
Предмет: Информатика и ИКТ
Класс: 11А класс
Тема урока: Перевод дробных чисел из одной СС в другую
Цели урока
Научиться переводить дробные числа из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную;
Научиться оформлять алгоритм перевода дробных чисел из десятичной системы счисления в любую другую;
Отработать полученные знания на практике;
Развивать мышление, логику, память.
Тип урока: Изучение нового материала.
Ход урока
I. Организационный момент: приветствие. (2 мин)
Проверка готовности учащихся к уроку, отметка отсутствующих.
II. Постановка темы и целей урока.(1 мин)
III. Фронтальный опрос. (3 мин)
Алгоритм перевода чисел из десятичной системы счисления в любую другую?
IV. Решение примеров на повторение (5 минут)
Переведите числа 19,44, 129 из десятичной системы счисления в двоичную и шестнадцатеричную.
V. Объяснение нового материала. (15 мин)
Алгоритм перевода дробных чисел из десятичной системы счисления в любую другую :
Можно сформулировать алгоритм перевода правильной дроби с основанием p в дробь с основанием q:
1. Основание новой системы счисления выразить цифрами исходной системы счисления и все последующие действия производить в исходной системе счисления.
2. Последовательно умножать данное число и получаемые дробные части произведений на основание новой системы до тех пор, пока дробная часть произведения не станет равной нулю или будет достигнута требуемая точность представления числа.
3. Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
4. Составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.
Пример 1. Перевести число 0,6562510 в восьмеричную систему счисления.
|
0, |
65625 * 8 |
|
5 |
25000 * 8 |
|
2 |
00000 |
Получаем: 0,6562510=0,528
Пример 2. Перевести в двоичную систему счисления десятичную дробь 0.710.
|
0, |
7 *2 |
|
1 |
4 *2 |
|
0 |
8 *2 |
|
1 |
6 *2 |
|
1 |
2 |
. . .
Очевидно, что этот процесс может продолжаться бесконечно, давая все новые и новые знаки в изображении двоичного эквивалента числа 0,710. Так, за четыре шага мы получаем число 0,10112, а за семь шагов число 0,10110012, которое является более точным представлением числа 0,710 в двоичной системе счисления, и т.д. Такой бесконечный процесс обрывают на некотором шаге, когда считают, что получена требуемая точность представления числа.
Алгоритм перевода произвольных чисел из десятичной системы счисления в любую другую:
Перевод произвольных чисел, т.е. чисел, содержащих целую и дробную части, осуществляется в два этапа. Отдельно переводится целая часть, отдельно — дробная. В итоговой записи полученного числа целая часть отделяется от дробной запятой (точкой).
VI. Решение задач у доски. (6 минут)
Пример 1. Перевести число 17,2510 в двоичную систему счисления.
|
Переводим целую часть: |
Переводим дробную часть: |
|
17 2 1 8 2 0 4 2 0 2 2 0 1 |
0, 25 ×2 0 50 ×2 1 00 |
Получаем: 17,2510=1001,012
Пример 2. Перевести число 124,2510 в восьмеричную систему.
|
Переводим целую часть: |
Переводим дробную часть: |
|
124 8 4 15 8 7 1 |
0, 25 ×8 2 00 |
Получаем: 124,2510=174,28
Пример 3. Перевести число 0,6562510 в шестнадцатеричную систему счисления.
|
0, |
65625 * 16 |
|
10 (А) |
50000 * 16 |
|
8 |
00000 |
Получаем: 0,6562510=0,А816
Пример 4. Перевести десятичную дробь 0,562510 в двоичную систему счисления.
|
0, |
5625 * 2 |
|
1 |
1250 * 2 |
|
0 |
2500 * 2 |
|
0 |
5000 * 2 |
|
1 |
0000 |
Получаем: 0,562510=0,10012
VII. Самостоятельная работа. (5 мин)
Перевести числа из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную:
1 вариант: 243,11
2 вариант: 275,13
Самопроверка и выставление оценок в тетради.
VIII.Подведение итогов и выставление отметок. (3 минуты)
Давайте подведем итог урока. Итак, что открыли для себя нового на сегодняшнем уроке?
IX. Домашнее задание. (4мин)
Перевести числа из десятичной системы счисления в данную:
105, 34 и 358, 25 в двоичную
500, 12 и 675,24 в восьмеричную
167,001 и 113, 005 в шестнадцатеричную
Давайте подведем итог урока. Итак, что открыли для себя нового на сегодняшнем уроке?
Всем спасибо за урок, до свидания! (1мин)
studfiles.net
Перевод правильной десятичной дроби в любую другую позиционную систему счисления
Основные понятия
Система счисления – это совокупность правил наименования и изображения чисел с помощью набора символов, называемых цифрами.
Используются три типа систем счисления:
· позиционная – представление числа зависит от порядка записи цифр.
· непозиционная – представление числа не зависит от порядка записи цифр
· смешанная – нет понятия «основание»: либо оснований несколько, либо оно вычисляемое
В непозиционных системах вес цифры (т.е. тот вклад, который она вносит в значение числа) не зависит от ее позициив записи числа.
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая – 7 единиц, а третья – 7 десятых долей единицы.
Сама же запись числа 757,7 означает сокращенную запись выражения
700 + 50 + 7 + 0,7 = 7∙102 + 5∙101 + 7∙100 + 7∙10-1 = 757,7.
Любая позиционная система счисления характеризуется своим основанием.
Основание позиционной системы счисления — это количество различных знаков или символов, используемых для изображения цифр в данной системе.
За основание системы можно принять любое натуральное число — два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д. Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения
an-1 qn-1 + an-2 qn-2+ … + a1 q1 + a0 q0 + a-1 q-1 + … + a—m q—m,
где ai – цифры системы счисления; n и m – число целых и дробных разрядов, соответственно.
Таблица 1. Эквиваленты чисел в различных системах счислений
| Системы счисления | |||
| Десятичная | Двоичная | Восьмеричная | Шестнадцатеричная |
| A | |||
| B | |||
| C | |||
| D | |||
| E | |||
| F |
Преобразование чисел из одной системы счисления в другую
Перевод целого числа из десятичной системы в другую позиционную систему счисления
При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q–1. Число в системе с основанием q записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего.
a. в двоичную:
7510 = 1 001 0112 2610=110102
b. в восьмеричную:
7510= 1138 24110=3618
c. в шестнадцатеричную:
7510= 4B16 362710=Е2В16
Перевод правильной десятичной дроби в любую другую позиционную систему счисления
При переводе правильной десятичной дроби в систему счисления с основанием q необходимо сначала саму дробь, а затем дробные части всех последующих произведений последовательно умножать на q, отделяя после каждого умножения целую часть произведения. Число в новой системе счисления записывается как последовательность полученных целых частей произведения.
Умножение производится до тех пор, пока дробная часть произведения не станет равной нулю. Это значит, что сделан точный перевод. В противном случае перевод осуществляется до заданной точности.
a. в двоичную:
0,3510 = 0,010112 0,562510=0,10012
или
0,84710=0,11012
b. в восьмеричную:
0,3510 = 0,2638 0,6562510=0,528
c. в шестнадцатеричную:
0,3510= 0,5916 0,84710=0,D8D16
megaobuchalka.ru
Как перевести обыкновенную дробь в десятичную
Рассмотрим, как перевести обыкновенную дробь в десятичную. Не всегда можно записать обыкновенную дробь в виде конечной десятичной. Таким образом, перевод обыкновенной дроби в десятичную в процессе вычислений может привести к неточному результату.
Правило:
Чтобы обыкновенную дробь перевести в десятичную, нужно ее числитель разделить на знаменатель.
Примеры:
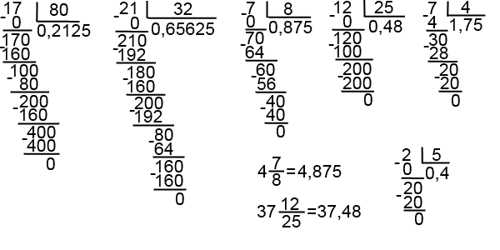
Однако, при делении, например, 2 на 7, мы получим бесконечную дробь:
Результат можно округлить с той или иной точностью:
Но в математике, как правило, требуются не приближенные, а точные значения. Поэтому полезно помнить, когда перевод обыкновенной дроби в десятичную приводит к получению точного ответа.
Любое число можно разделить на 2, 5 и числа, которые можно разложить на множители только из двоек и пятерок.
Например, 4=2∙2, 8=2∙2∙2, 10=2∙5, 16=2∙2∙2∙2, 20=2∙2∙5, 25=5∙5, 32=2∙2∙2∙2∙2∙2, 40=2∙2∙2∙5, 50= 2∙5∙5, 64==2∙2∙2∙2∙2∙2, 80=2∙2∙2∙2∙5, 100=2∙5∙2∙5 и т.д.
Таким образом, при выполнении действий, содержащих и десятичные, и обыкновенные дроби, перевести обыкновенную дробь в десятичную удобно только в том случае, когда знаменатель обыкновенной дроби представляет собой произведение только двоек и пятерок. В остальных случаях следует от десятичной дроби перейти к обыкновенной.
www.uznateshe.ru
Перевести обыкновенную дробь в десятичную дробь
Перевод обыкновенной дроби в десятичную дробь
Несократимую дробь можно преобразовать в десятичную только тогда, когда разложение знаменателя b на простые множители не содержит чисел, отличных от 2 и 5.
В результате преобразования получается бесконечная периодическая десятичная дробь .
Простой способ преобразования
Воспользуйтесь калькулятором, разделите числитель дроби на знаменатель в результате получите десятичную дробь.
Пример Преобразовать дробь в десятичную дробь
Разделим с помощью калькулятора числить на знаменатель, получим .
Альтернативный метод преобразования
Привести знаменатель дроби к 10, 100, 1000, 10000 и т.д. Найдите число которое преобразует знаменатель к числу из списка (10, 100, 1000, и т.д.). Умножьте числитель и знаменатель на данное число, затем запишите числитель в виде десятичной дроби, расположив запятую(точку) в зависимости от количества нулей в знаменателе.
В примере показано как переводить дробь в десятичную дробь ручным способом.
Пример Преобразовать дробь в десятичную.
.
.
calcs.su
