Гвэ по математике 9 – Консультация по математике (9 класс) на тему: Задания для подготовки к ГВЭ (9 класс) | скачать бесплатно

ГВЭ по математике 9класс

ГВЭ-9 по математике 1 вариант

1. Найдите значение выражения .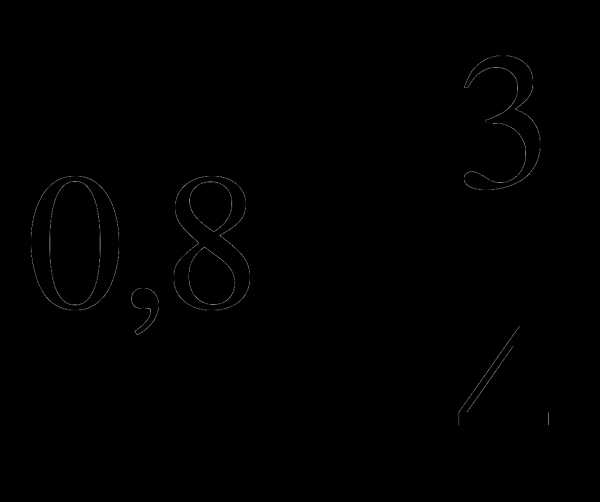

Ответ: ___________________________.

2. Решите уравнение .

Ответ: ___________________________.

3. Найдите значение выражения 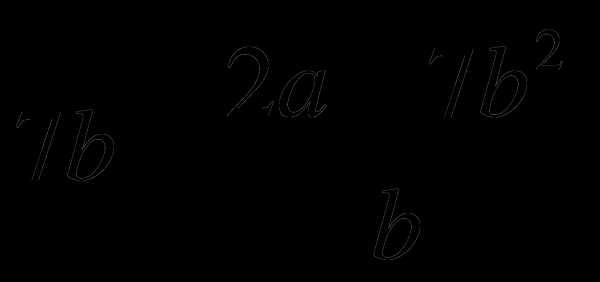при .

Ответ: ___________________________.

4. Установите соответствие между графиками функций и формулами, которые их задают.

1) 2)

3)

В таблице под каждой буквой, соответствующей графику, впишите номер формулы, которая его задаёт.

5. Решите систему неравенств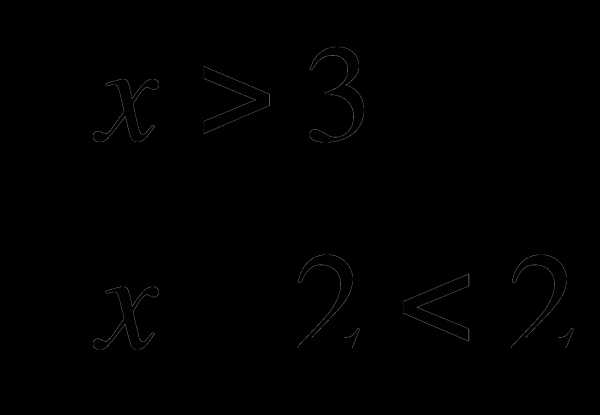

На каком рисунке изображено множество её решений?

Ответ:

6. В равнобедренном треугольнике АВС с основанием АС внешний угол при вершине А равен 144º. Найдите величину угла ВСА. Ответ дайте в градусах.

Ответ: ___________________________.

7. Длина хорды окруж­но­сти равна 12, а рас­сто­я­ние от цен­тра окруж­но­сти до этой хорды равно 8. Най­ди­те радиус окруж­но­сти.

Ответ: ___________________________.

8. Укажите номера верных утверждений.

1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

2) Диа­го­на­ли квад­ра­та делят его углы по­по­лам.

3) Если угол ост­рый, то смеж­ный с ним угол также яв­ля­ет­ся ост­рым.

Ответ: ___________________________.

9. По­сту­пив­ший в про­да­жу в ап­ре­ле мо­биль­ный те­ле­фон стоил 4000 руб­лей. В сен­тяб­ре он стал сто­ить 2560 руб­лей. На сколь­ко про­цен­тов сни­зи­лась цена на мо­биль­ный те­ле­фон в пе­ри­од с ап­ре­ля по сен­тябрь?

Ответ: ___________________________.

10. В ко­роб­ке 14 па­ке­ти­ков с чёрным чаем и 6 па­ке­ти­ков с зелёным чаем. Павел на­у­гад вы­ни­ма­ет один па­ке­тик. Ка­ко­ва ве­ро­ят­ность того, что это па­ке­тик с зелёным чаем?

Ответ: ___________________________.

Для записи решений заданий 11 и 12 и ответов к ним используйте дополнительный лист. Запишите сначала номер задания, затем чётко и разборчиво решение и ответ.

11. Ту­ри­сты про­плы­ли на лодке от ла­ге­ря не­ко­то­рое рас­сто­я­ние вверх по те­че­нию реки, затем при­ча­ли­ли к бе­ре­гу и, по­гу­ляв 3 часа, вер­ну­лись об­рат­но через 5 часов от на­ча­ла пу­те­ше­ствия. На какое рас­сто­я­ние от ла­ге­ря они от­плы­ли, если ско­рость те­че­ния реки равна 2 км/ч, а соб­ствен­ная ско­рость лодки 8 км/ч?

12. В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC = ED. Докажите, что данный параллелограмм — прямоугольник.

infourok.ru

Подготовка к ГВЭ-9 по математике

ГВЭ-9 по математике 1 вариант

Инструкция по выполнению работы

Экзаменационная работа состоит из 12 заданий, из которых 10 заданий базового уровня сложности с кратким ответом и 2 задания повышенного уровня сложности с развёрнутым ответом.

На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).

Ответы к заданиям 1–10 записываются в виде целого числа или конечной десятичной дроби.

При выполнении заданий 11 и 12 требуется записать полное решение и ответ.

Все бланки заполняются яркими чёрными чернилами. Допускается использование гелевой, или капиллярной, или перьевой ручки.

При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.

Баллы, полученные Вами за выполненные задания, суммируются.

Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.

Желаем успеха!

1. Найдите значение выражения .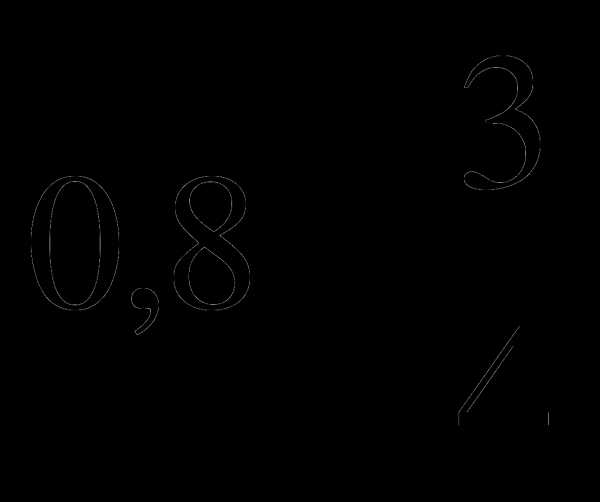

Ответ: ___________________________.

2. Решите уравнение .

Ответ: ___________________________.

3. Найдите значение выражения 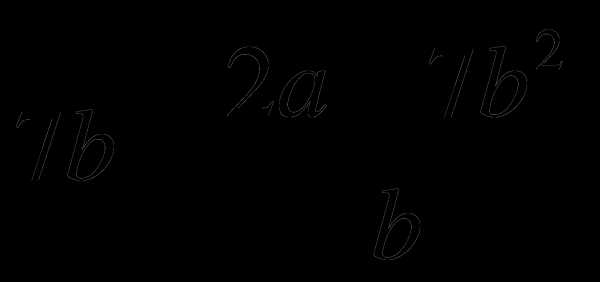при .

Ответ: ___________________________.

4. Установите соответствие между графиками функций и формулами, которые их задают.

1) 2) 3)

В таблице под каждой буквой, соответствующей графику, впишите номер формулы, которая его задаёт.

5. Решите систему неравенств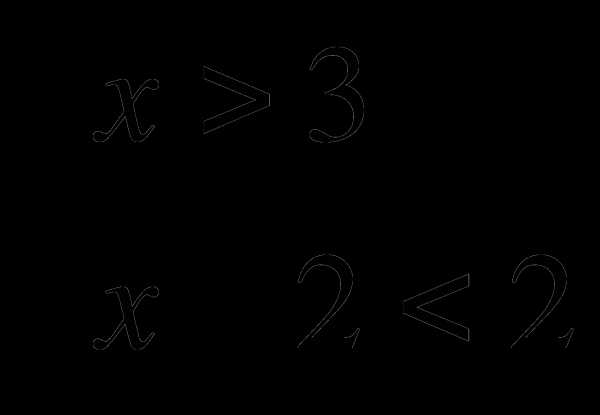

На каком рисунке изображено множество её решений?

Ответ:

6. В равнобедренном треугольнике АВС с основанием АС внешний угол при вершине А равен 144º. Найдите величину угла ВСА. Ответ дайте в градусах.

Ответ: ___________________________.

7. Длина хорды окруж­но­сти равна 12, а рас­сто­я­ние от цен­тра окруж­но­сти до этой хорды равно 8. Най­ди­те радиус окруж­но­сти.

Ответ: ___________________________.

8. Укажите номера верных утверждений.

1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

2) Диа­го­на­ли квад­ра­та делят его углы по­по­лам.

3) Если угол ост­рый, то смеж­ный с ним угол также яв­ля­ет­ся ост­рым.

Ответ: ___________________________.

9. По­сту­пив­ший в про­да­жу в ап­ре­ле мо­биль­ный те­ле­фон стоил 4000 руб­лей. В сен­тяб­ре он стал сто­ить 2560 руб­лей. На сколь­ко про­цен­тов сни­зи­лась цена на мо­биль­ный те­ле­фон в пе­ри­од с ап­ре­ля по сен­тябрь?

Ответ: ___________________________.

10. В ко­роб­ке 14 па­ке­ти­ков с чёрным чаем и 6 па­ке­ти­ков с зелёным чаем. Павел на­у­гад вы­ни­ма­ет один па­ке­тик. Ка­ко­ва ве­ро­ят­ность того, что это па­ке­тик с зелёным чаем?

Ответ: ___________________________.

Для записи решений заданий 11 и 12 и ответов к ним используйте дополнительный лист. Запишите сначала номер задания, затем чётко и разборчиво решение и ответ.

11. Ту­ри­сты про­плы­ли на лодке от ла­ге­ря не­ко­то­рое рас­сто­я­ние вверх по те­че­нию реки, затем при­ча­ли­ли к бе­ре­гу и, по­гу­ляв 3 часа, вер­ну­лись об­рат­но через 5 часов от на­ча­ла пу­те­ше­ствия. На какое рас­сто­я­ние от ла­ге­ря они от­плы­ли, если ско­рость те­че­ния реки равна 2 км/ч, а соб­ствен­ная ско­рость лодки 8 км/ч?

12. В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC = ED. Докажите, что данный параллелограмм — прямоугольник.

infourok.ru

МАтематика. Подготовка к ГВЭ — математика, тесты

Тренировочные работы составлены по типу  образца экзаменационной работы  для проведения государственного выпускного экзамена по математике для обучающихся, освоивших образовательные программы основного общего образования.

Экзаменационные работы включают 10 заданий: одно задание по арифметике, одно задание по теории вероятностей, семь заданий по алгебре, одно задание по геометрии. Задания являются стандартными для курса математики основной школы. Все они относятся к заданиям с развернутым ответом и требуют записи решения задачи, демонстрирующей умение обучающегося математически грамотно излагать ход решения, приводя при этом необходимые пояснения и обоснования.

Просмотр содержимого документа
«2 вариант»

Просмотр содержимого документа
«3 вариант»

Просмотр содержимого документа
«4 вариант»

Просмотр содержимого документа
«5 вариант»

Просмотр содержимого документа
«6 вариант»

Просмотр содержимого документа
«7 вариант»

Просмотр содержимого документа
«7 вариантов»

Просмотр содержимого документа
«8 вариант»

Просмотр содержимого документа
«9 вариант»

kopilkaurokov.ru

Пробный ГВЭ-9 по математике (для обучающихся с ОВЗ)(К)

Начало формы

Конец формы

Пробный ГВЭ-9 по математике (для обучающихся с ОВЗ)(К)

1 вариант

1. Решите уравнение .

2. Упростите выражение , найдите его значение при ; . В ответ запишите полученное число.

3.  Упростите выражение    и найдите его значение при  . В ответе запишите полученное число.

4. Какое из чисел от­ме­че­но на ко­ор­ди­нат­ной пря­мой точ­кой A? 

В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та. 

1) 2) 3) 4)

5. Най­ди­те зна­че­ние вы­ра­же­ния  

6. На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наибольшее значение атмосферного давления во вторник.

7. В фирме такси в данный момент свободно 20 машин: 9 черных, 4 желтых и 7 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.

8. Плата за те­ле­фон со­став­ля­ет 340 руб­лей в месяц. В сле­ду­ю­щем году она уве­ли­чит­ся на 2%. Сколь­ко придётся пла­тить еже­ме­сяч­но за те­ле­фон в сле­ду­ю­щем году?

9. В таб­ли­це даны ре­зуль­та­ты за­бе­га маль­чи­ков 8-го клас­са на ди­стан­цию 60 м. 

Номер до­рож­ки

1

2

3

4

Время (с)

10,3

10,7

11,0

9,1

Зачёт вы­став­ля­ет­ся, если по­ка­за­но время не хуже 10,5 с. Вы­пи­ши­те но­ме­ра до­ро­жек, по ко­то­рым бе­жа­ли маль­чи­ки, по­лу­чив­шие зачёт. 

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

10. В рав­но­бед­рен­ном тре­уголь­ни­ке ABC с ос­но­ва­ни­ем AC внеш­ний угол при вер­ши­не C равен 123°. Най­ди­те ве­ли­чи­ну угла ABC. Ответ дайте в гра­ду­сах.

Пробный ГВЭ-9 по математике (для обучающихся с ОВЗ)(К)

Вариант 2

1. Най­ди­те корни урав­не­ния

2. Упростите выражение  и найдите его значение при . В ответ запишите полученное число.

3.  Найдите значение выражения    при  .

4. Одна из точек, от­ме­чен­ных на ко­ор­ди­нат­ной пря­мой, со­от­вет­ству­ет числу  

Какая это точка? В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.

1) точка A 2) точка B 3) точка C 4) точка D

5. Най­ди­те зна­че­ние вы­ра­же­ния 

6. На ри­сун­ке по­ка­за­но, как из­ме­ня­лась тем­пе­ра­ту­ра воз­ду­ха на про­тя­же­нии одних суток. По го­ри­зон­та­ли ука­за­но время суток, по вер­ти­ка­ли — зна­че­ние тем­пе­ра­ту­ры в гра­ду­сах Цель­сия. Най­ди­те раз­ность между наи­боль­шим и наи­мень­шим зна­че­ни­ем тем­пе­ра­ту­ры в пер­вой по­ло­ви­не этих суток. Ответ дайте в гра­ду­сах Цель­сия.

7. Миша с папой решили покататься на колесе обозрения. Всего на колесе двадцать четыре кабинки, из них 5 — синие, 7 — зеленые, остальные — красные. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Миша прокатится в красной кабинке.

8. Плата за те­ле­фон со­став­ля­ет 220 руб­лей в месяц. В сле­ду­ю­щем году она уве­ли­чит­ся на 10%. Сколь­ко придётся пла­тить еже­ме­сяч­но за те­ле­фон в сле­ду­ю­щем году?

9. В таб­ли­це даны ре­зуль­та­ты за­бе­га маль­чи­ков 9-го клас­са на ди­стан­цию 60 м.

Номер до­рож­ки

1

2

3

4

Время(с)

10,0

9,7

9,9

9,2

Зачёт вы­став­ля­ет­ся, если по­ка­за­но время не хуже 9,8 с. Вы­пи­ши­те но­ме­ра до­ро­жек, по ко­то­рым бе­жа­ли маль­чи­ки, по­лу­чив­шие зачёт.

10. В тре­уголь­ни­ке ABC , AC = BC. Внеш­ний угол при вер­ши­не B равен 146°. Най­ди­те угол C. Ответ дайте в градусах.

infourok.ru

Пробные варианты ГВЭ по математике 9 класс 2016

Вариант 1

Часть1

1. Запишите в ответе номера выражений, значения которых положительны.

Номера запишите в порядке возрастания без пробелов, запятых и других дополнительных символов.

1)

2)

3)

4)

Ответ: ______________________________.

Решение.

Найдём значения выражений:

 

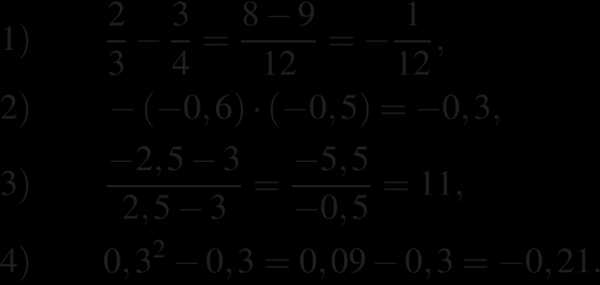
Таким образом, искомое выражение указано под номером 3.

Ответ: 3

2. Решите уравнение  .

Если корней несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: ______________________________.

Решение.

Поскольку число отрицательно, и . Число положительно и больше 1. Поэтому оно является наибольшим.

 

Правильный ответ указан под номером 3.

Ответ: 3

3. Установите соответствие между графиками функций и формулами, которые их задают.

1. 2) 3) 4)

 

Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке.

А

Б

В

 

 

 

Решение.

Упростим дробь:

 

Правильный ответ указан под номером 3.

Ответ: 3

4. Найдите значение выражения    при  

Решение.По теореме, обратной теореме Виета — сумма корней равна 5, а их произведение равно −14.

Ответ: ______________________________.

Тем самым, это числа −2 и 7.

Ответ: −2; 7.

Ответ: -2; 7

Решение.

Определим вид графика каждой из функций.

1)   уравнение параболы, ветви которой направленны вверх.

2)   уравнение прямой.

3)   уравнение верхней ветви параболы, направленной вправо.

4)   уравнение гиперболы.

Тем самым найдено соответствие: A — 1, Б — 4, В — 2.

 

Ответ: 142.

Ответ: 142

Решение.

Определим разность арифметической прогрессии:

 

 

Член арифметической прогрессии с номером может быть найден по формуле

 

 

Поэтому

 

Ответ: 414.

Ответ: 414

Решение.

Упростим выражение:

 

 

При , значение полученного выражения равно 16.

 

Ответ: 16.

Ответ: 16

5. Решите систему неравенств

На каком из рисунков изображено множество её решений?

Ответ: ______________________________.

Решение.

Решим систему:

 

 

Правильный ответ указан под номером 3.

Ответ: 3

Решение.

Сумма углов выпуклого четырёхугольника равна 360°. Имеем: Так как , и  — общая треугольника ABD и BDC. Из равенства треугольников следует, что . Таким образом, .

 

Ответ: 95.

Ответ: 95

6. Найдите  , если градусные меры дуг    и    равны 112° и 170° соответственно.

Ответ: ______________________________.

Решение.

Так как вписанный угол равен половине дуги на которую он опирается, имеем , а . В треугольнике OKM , .

 

Ответ: 39.

Ответ: 39

7. Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 60°. Найдите площадь параллелограмма, делённую на .

Ответ: ______________________________.

Решение.

Площадь параллелограмма равна произведению сторон на синус угла между ними, имеем:

 

 

Ответ: 30.

 

———-

В открытом банке иррациональный ответ.

Ответ: 30

Решение.

Опустим перпендикуляр BH. Треугольник ABH — прямоугольный. Таким образом,

 

Ответ: 3.

Ответ: 3

8. Какие из следующих утверждений верны?

1) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на синус угла между ними.

2) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.

3) Треугольник ABC, у которого AB = 5, BC = 6, AC = 7, является остроугольным.

4) В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: ______________________________.

Решение.

Суточная норма потребления углеводов мужчины лежит в пределах 257−586 г. Потребление 488 г жиров в сутки соответствует норме.

 

Правильный ответ указан под номером 1.

Ответ: 1

Решение.

Автобус проехал 240 км за 5 часов. Таким образом, его скорость равна 48 км/ч. Автомобиль проехал это же расстояние за 3 часа со скоростью 80 км/ч. Таким образом, скорость автомобиля больше скорости автобуса на 32 км/ч.

Ответ: 32

Решение.

Все участвовавшие в олимпиаде делятся на три группы: участники, получившие дипломы, участники, получившие сертефикаты, участники, получившие похвальные грамоты. Известно что всех участников получили дипломы, следовательно, оставшаяся часть составила от общего числа участников. Из участников, получивших дипломы, участников были награждены похвальными грамотами, оставшиеся участников составили 144 человека. Пусть x — общее число участников, тогда:

 

 

Тем самым, в олимпиаде участвовал 231 учащийся.

 

Ответ: 231.

Ответ: 231

9. Короткое плечо шлагбаума имеет длину 1 м, а длинное плечо – 3 м. На какую высоту (в метрах) опустится конец короткого плеча, когда конец длинного плеча поднимается на 1,8 м?

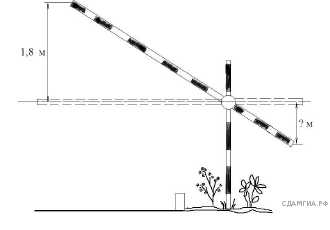
Ответ: ______________________________.

Решение.

Найдём синус угла, на который поднимается длинное плечо:

 

 

Угол подъема длинного плеча равен углу на который опустится короткое плечо. Пусть x — высота, на которую опустится короткое плечо, имеем:

 

 

Таким образом, короткое плечо опустится на 0,6 м.

 

Ответ: 0,6.

Ответ: 0,6

 Решение.

Разъясним каждый вариант ответа:

1) Очевидно, что пользователей из России больше, чем пользователей из Украины и Белоруссии вместе.

2) Сектор «Украина» занимает большую площадь диаграммы, чем сектор «Другие страны», а т. к. «Латвия» включена в «Другие страны», имеем: пользователей из Украины больше, чем пользователей из Латвии.

3) Сектор в две трети диаграммы отсекается углом в 2·360°/3 = 240°. Очевидно, что угол, отсекающий сектор «Россия» примерно равен 240°, значит примерно две трети общего числа пользователей — из России.

4) Видно, что пользователей из Украины меньше четверти всех пользователей, значит, меньше 12/4=3 миллионов.

Ответ: 4.

Ответ: 4

10. В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.

Ответ: ______________________________.

Часть 2

Решение.

Выразим высоту трапеции из формулы площади:

 

 

Подставляя, получаем:

 

 

 

Ответ: 4.

 

Приведём другое решение.

Подставим в формулу известные значения величин:

 

 

Ответ: 4

Решение.

Имеем:

 

.

 

Ответ: .

11. Два оператора, работая вместе, могут набрать текст газеты объявлений за 8 ч. Если первый оператор будет работать 3 ч, а второй 12 ч, то они выполнят только 75% всей работы. За какое время может набрать весь текст каждый оператор, работая отдельно?

Решение.

Пусть первый оператор может выполнить данную работу за    часов, а второй за    часов. За один час первый оператор выполняет    часть всей работы, а второй  . Составим систему уравнений:

 

 

 

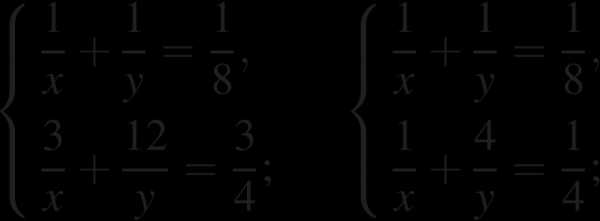
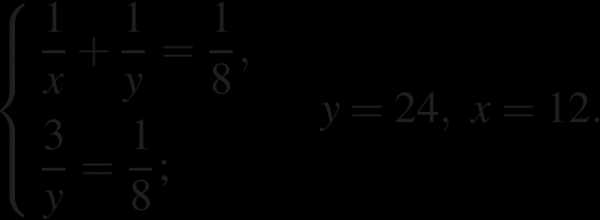
Ответ: первый оператор за 12 ч, второй оператор за 24 ч.

Решение.

Сумма    принимает наименьшее значение, равное 0, только в том случае, когда оба слагаемых одновременно равны 0. Получаем систему уравнений

 

Решим её:

 

Ответ: 0; (2;1).

Решение.

Проведём радиус OA. Треугольник AOC — прямоугольный, ∠A = 90°. ∠COA = 180° − ∠AOD = 180° − 140° = 40°; ∠ACO = 90° − 40° = 50°.

Ответ: 50.

12. В окружности с центром проведены две равные хорды и . На эти хорды опущены перпендикуляры и . Докажите, что и равны.

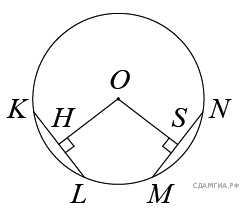
infourok.ru

Дополнительные материалы и оборудование

Необходимые справочные материалы для выполнения экзаменационной работы ГВЭ-9 (письменная форма) по математике выдаются вместе с текстом экзаменационной работы (см. приложение 1). Они аналогичны справочным материалам ОГЭ по математике.

При выполнении заданий разрешается пользоваться линейкой.

Продолжительность гвэ-9 по математике

На выполнение экзаменационной работы по математике (с маркировкой «А» и «К») даётся 3 часа 55 минут (235 минут). В продолжительность выполнения экзаменационной работы по учебным предметам не включается время, выделенное на подготовительные мероприятия (инструктаж обучающихся, вскрытие пакетов с экзаменационными материалами, заполнение регистрационных полей экзаменационной работы, настройка технических средств).

При продолжительности выполнения экзаменационной работы 4 и более часа организуется питание обучающихся.

Для обучающихся с ОВЗ, обучающихся детей-инвалидов и инвалидов, а также тех, кто обучался по состоянию здоровья на дому, в образовательных организациях, в том числе санаторно-курортных, в которых проводятся необходимые лечебные, реабилитационные и оздоровительные мероприятия для нуждающихся в длительном лечении, продолжительность выполнения экзаменационной работы увеличивается на 1,5 часа.

Система оценивания выполнения отдельных заданий и экзаменационной работы в целом гвэ-9 (письменная форма) по математике Оценивание экзаменационной работы гвэ-9 по математике, маркированного буквой «а»

Каждое из заданий 1–10 с кратким ответом считается выполненным, если записанный ответ совпадает с верным ответом. Задания 11 и 12 оцениваются 2 баллами, если обоснованно получен верный ответ; 1 баллом, если верно построена математическая модель и получен неверный ответ из-за арифметической ошибки или в доказательстве математического утверждения содержатся неточности, и 0 баллов в других случаях.

Задание с развернутым ответом оценивается экспертом с учетом правильности и полноты ответа. Максимальный первичный балл за задание с развернутым ответом – 2. К заданию приводится подробная инструкция для экспертов, в которой указывается, за что выставляется каждый балл – от нуля до максимального балла. В экзаменационном варианте перед каждым типом задания предлагается инструкция, в которой приведены общие требования к оформлению ответов.

Максимальный балл за всю работу – 14. Рекомендуется следующая шкала перевода суммы первичных баллов в пятибалльную систему оценивания.

Шкала пересчета первичного балла за выполнение экзаменационной работы в отметку по пятибалльной шкале (гвэ-9 по математике с маркировкой буквой «а»)

Отметка по пятибалльной шкале	«2»	«3»	«4»	«5»
Общий балл	0–3	4–6	7–9	10–14

Оценивание экзаменационной работы ГВЭ-9 по математике, маркированного буквой «К»

Каждое из заданий 1–10 с кратким ответом считается выполненным, если записанный ответ совпадает с верным ответом.

Максимальный балл за всю работу – 10. Рекомендуется следующая шкала перевода суммы первичных баллов в пятибалльную систему оценивания.

Шкала пересчета первичного балла за выполнение экзаменационной работы ГВЭ-9 по математике (с маркировкой буквой «К») в отметку по пятибалльной шкале

Отметка по пятибалльной шкале	«2»	«3»	«4»	«5»
Общий балл	0–2	3–5	6–8	9–10

Образцы экзаменационных материалов ГВЭ-9 (письменная форма) по математике

Ниже приведены образцы экзаменационных работ для проведения ГВЭ-9 по математике.

Следует иметь в виду, что образцы предназначены для того, чтобы дать возможность составить представление о структуре будущей экзаменационной работы, числе, форме и уровне сложности заданий, и не отражает всех элементов содержания, которые будут проверяться с помощью вариантов экзаменационной работы.

Образец экзаменационного варианта для проведения ГВЭ-9 (письменная форма) по математике (с маркировкой буквой «А»)

Инструкция по выполнению работы

Экзаменационная работа состоит из 12 заданий, из которых 10 заданий базового уровня сложности с кратким ответом и 2 задания повышенного уровня сложности с развёрнутым ответом.

На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).

Ответы к заданиям 1–10 записываются в виде целого числа или конечной десятичной дроби.

При выполнении заданий 11 и 12 требуется записать полное решение и ответ.

Все бланки заполняются яркими чёрными чернилами. Допускается использование гелевой, или капиллярной, или перьевой ручки.

При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.

Баллы, полученные Вами за выполненные задания, суммируются.

Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.

studfiles.net

Варианты 14-15 заданий для подготовки к ГВЭ по математике в 9 классе

Вариант 14

Часть 1

1. Найдите значение выражения при и

2. Упростите выражение: .

3. Решите уравнение: .

4. Решите двойное неравенство: и укажите два каких-нибудь числа, являющихся его решениями.

5. Постройте график функции . Укажите промежуток, в котором функция убывает.

6. Даны три первых члена геометрической прогрессии: 6; -12; 24. Найти знаменатель и седьмой ее член.

7. Найдите номера верных утверждений.

1). Серединный перпендикуляр к хорде проходит через центр окружности.

2). Точка касания двух окружностей лежит на линии центров.

3). Угол между двумя секущими, пересекающимися вне круга, равен полусумме дуг, высекаемых секущими на окружности.

1. В треугольнике КОМ угол К равен 40°, угол О равен 30°. Найдите внешний угол при вершине М.

1. Катя, Настя, Игорь, Даша и Андрей бросали жребий – кому начать игру. Найдите вероятность того, что начинать игру будет мальчик?

2. Число хвойных деревьев в парке относится к числу лиственных как 1:4. Сколько процентов деревьев в парке составляют лиственные?

Часть 2

1. В озеро впадает две реки. Лодка отплывает от пристани А на первой реке, плывет 36 км вниз до озера, далее 19 км по озеру (в озере нет течения) и 24 км по второй реке против течения до пристани В, затратив 8 часов на весь путь от А до В. Из этих 8 часов 2 часа лодка плывет по озеру. Скорость течения первой реки на 1 км/ч больше, чем скорость течения второй реки. Найти скорость течения каждой реки.

2. Наклонная балка поддерживается тремя столбами, стоящими вертикально на равном расстоянии друг от друга. Длина двух меньших столбов 60см и 90см. Найдите длину большего столба.

Вариант 15

Часть 1

1. Упростите выражение: :.

2. Решите уравнение: .

3. Решите неравенство: .

4. Выполните действие: . Результат запишите в виде десятичной дроби.

5. Постройте график функции . При каких значениях х функция принимает положительные значения?

6. В арифметической прогрессии , найдите .

7. Прямоугольный газон обнесен изгородью длиной 30м. Площадь газона . Найдите длины сторон газона.

8. Найдите номера верных утверждений.

1). Если при пересечении двух прямых третьей образуются равные соответственные углы, то прямые параллельны.

2). Если гипотенуза одного прямоугольного треугольника равна гипотенузе другого прямоугольного треугольника, то такие треугольники равны.

3). Точка пересечения медиан треугольника- центр описанной окружности.

1. Определите по приведенным ниже диаграммам, в каком из продуктов содержится 25% белка. Какой составляющей больше всего во всех трех продуктах? В каком из продуктов наименьшее количество углеводов?

1. Расход электроэнергии по социальной норме составляет 110квт, стоимость 1квт электроэнергии по социальной норме 1 рубль 52 копейки, а стоимость электроэнергии потребленной свыше социальной нормы на 70% больше. Сколько должен заплатить потребитель за 180квт?

Часть 2

1. В 19 часов от двух пристаней, расстояние между которыми 3 км, одновременно в одном направлении отошли два быстроходных катера. Скорость одного из них была 48км/ч, а другой догонял его со скоростью 54км/ч. В котором часу второй катер догонит первый?

2. Вершина В ромба ABCD соединена с серединой стороны AD в точке К. Найдите площадь четырехугольника KBCD, если площадь ромба ABCD равна 28 см2.

multiurok.ru