Словарь геометрических понятий 7-8 класс
Геометрия,7-9 Основные определения, теоремы, формулы
7 класс Глава I Начальные геометрические сведения
Первичные понятия: точка, прямая, плоскость, пространство, отрезок, луч, угол, равные фигуры, середина отрезка, биссектриса угла, измерение отрезков, измерение углов
Отрезок-часть прямой, ограниченная двумя точками.
Луч-часть прямой,ограниченная точкой с одной стороны и неограниченная с другой стороны.
Угол-часть плоскости, ограниченная двумя лучами, выходящими из одной точки.
Равные фигуры-фигуры, которые совпадают при наложении друг на друга.
Середина отрезка-точка на отрезке, делящая его пополам.
Биссектриса угла-луч, выходящий из вершины угла и делящий его пополам.
Единицы измерения длины отрезка: миллиметры, сантиметры, дециметры, метры, километры.
Единицы измерения углов
Длина отрезка-количество единиц измерения длины, вмещающихся между двумя концами отрезка.
Градусная мера угла-количество единиц измерения углов, вмещающихся между сторонами угла.
Прямой угол-угол,градусная мера которого равна 900.
Острый угол-угол,градусная мера которого меньше 900.
Тупой угол-угол,градусная мера которого больше 900,но меньше 1800.
Развёрнутый угол-угол,градусная мера которого равна 1800.
Смежные углы – это два угла, у которых одна сторона общая,а две других образуют прямую линию.
Свойство: сумма смежных углов равна 1800.
Вертикальные углы-два угла, у которых стороны одного угла являются продолжением сторон другого.
Свойство: вертикальные углы равны.
Перпендикулярные прямые-прямые, которые при пересечении образуют прямой угол.
Параллельные прямые-прямые, лежащие в одной плоскости и не имеющие общих точек.
Глава II Треугольники
Треугольник-фигура, состоящая из трёх точек, соединённых между собой отрезками.Точки-вершины треугольника, отрезки-стороны треугольника.
Периметр – сумма длин всех сторон.
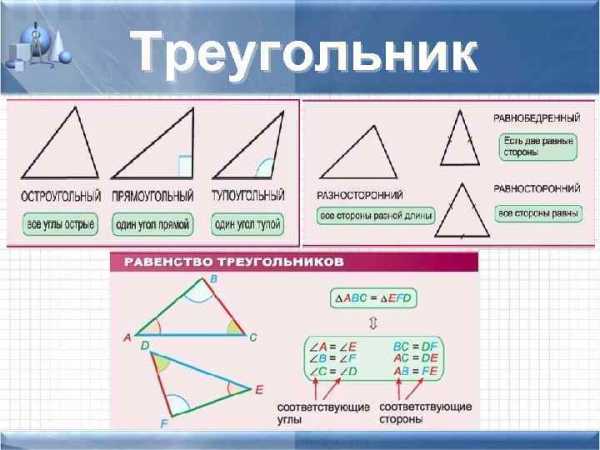
Теорема(первый признак равенства треугольников): если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Теорема: из точки,не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Медиана треугольника— это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса треугольника— отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Высота треугольника— перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
Равнобедренный треугольник-треугольник, у которого две стороны равные. Равные стороны – боковые, третья сторона – основание.
Равносторонний треугольник— треугольник, у которого все стороны равны.
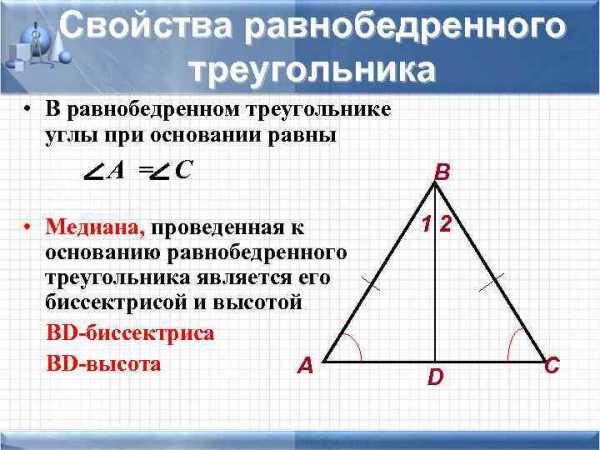
Свойство:в равнобедренном треугольнике углы при основании равны.
Свойство:в равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Теорема(второй признак равенства треугольников): если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Теорема(третий признак равенства треугольников): если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
Окружность-геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки-центра.
Радиус окружности-отрезок,соединяющий любую точку окружности с её центром.
Хорда-отрезок, соединяющий две любые точки окружности.
Диаметр-хорда, проходящая через центр.
Дуга – часть окружности, ограниченная двумя точками.
Основные задачи на построение циркулем и линейкой:
построение отрезка, равного данному
построение угла, равного данному
построение биссектрисы угла
построение середины отрезка
построение перпендикулярных прямых
Глава III Параллельные прямые
При пересечении двух прямых третьей прямо-секущей образуются следующие виды углов:
накрест лежащие углы
односторонние углы
соответственные углы
Теорема(первый признак параллельности прямых):если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Теорема(второй признак параллельности прямых):если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Теорема(третий признак параллельности прямых):если при пересечении двух прямых секущей сумма внутренних односторонних углов равна углы равна 1800, то прямые параллельны.
Аксиома: через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Теорема:если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
Теорема:если две прямые параллельны третьей прямой, то они параллельны.
Теорема:если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Теорема:если две параллельные прямые пересечены секущей, то соответственные углы равны.
Теорема:если две параллельные прямые пересечены секущей, то сумма внутренних односторонних углов равна 1800.
Глава IV Соотношения между сторонами и углами треугольника
Теорема: сумма внутренних углов треугольника равна 1800.
Внешний угол треугольника-угол, смежный с каким-либо внутренним углом треугольника.
Остроугольный треугольник-это треугольник, все внутренние углы которого острые.
Тупоугольный треугольник-это треугольник, у которого один из углов тупой.
Прямоугольный треугольник-это треугольник, у которого один из углов прямой.
Гипотенуза-это сторона прямоугольного треугольника, лежащая напротив прямого угла.
Катеты-это стороны прямоугольного треугольника, образующие прямой угол.
Теорема:в треугольнике против большего угла лежит большая сторона.
Следствие:в прямоугольном треугольнике гипотенуза всегда больше катета.
Теорема(признак равнобедренного треугольника):если в треугольнике два угла равны, то он равнобедренный.
Теорема(неравенство треугольника):каждая сторона треугольника меньше суммы двух других сторон.
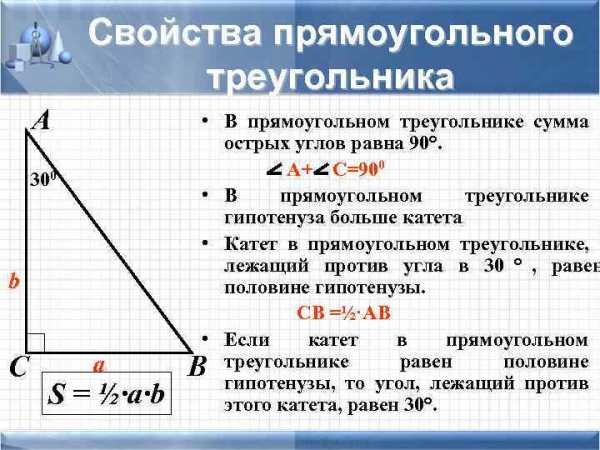
Свойство:сумма двух острых углов треугольника равна 900.
Свойство:катет прямоугольного треугольника, лежащий против угла в 300, равен половине гипотенузы.
Свойство:если катет прямоугольного треугольника равен половине гипотенузы, то он лежит напротив угла в 300.
Теорема(признак равенства прямоугольных треугольников):если катеты одного прямоугольного треугольника равны катетам другого прямоугольного треугольника, то такие треугольники равны.
Теорема(признак равенства прямоугольных треугольников):если катет и прилежащий к нему острый угол одного прямоугольного треугольника равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.
Теорема(признак равенства прямоугольных треугольников):если гипотенуза и острый угол одного прямоугольного треугольника равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Теорема(признак равенства прямоугольных треугольников):если катет и гипотенуза одного прямоугольного треугольника равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.
Расстояние от точки до прямой – это длина перпендикуляра, опущенного из этой точки на прямую.
Теорема:все точки каждой из двух параллельных прямых равноудалены от другой прямой.
8 класс. Глава V Четырёхугольники
Многоугольник
Диагональ-это отрезок, соединяющий две несоседних вершины многоугольника.
Выпуклый многоугольник— это многоугольник, который весь лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
Теорема:Сумма внутренних углов выпуклого n-угольника равна (n-2)*1800.
Параллелограмм— это четырёхугольник, у которого противоположные стороны попарно параллельны.
Свойство:в параллелограмме противоположные стороны равны и противоположные углы равны.
Свойство:диагонали параллелограмма точкой пересечения делятся пополам.
Теорема(признак параллелограмма):Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.
Теорема(признак параллелограмма):Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм.
Теорема(признак параллелограмма):Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.
Трапеция-это четырёхугольник, у которого две стороны параллельны, а две другие не параллельны.Параллельные стороны-основания, непараллельные стороны-боковые.
Равнобедренная трапеция-это трапеция, у которой боковые стороны равны.
Прямоугольная трапеция-это трапеция, у которой один из углов прямой.
Теорема Фалеса: если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пресекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Прямоугольник-это параллелограмм, у которого все углы прямые.
Свойство: диагонали прямоугольника равны.
Ромб-это параллелограмм, у которого все стороны равны.
Свойство: диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Квадрат-это прямоугольник, у которого все стороны равны.
Глава VI Площадь
Площадь плоской фигуры-это количество единичных квадратов, вмещающихся в данную фигуру.
Единицы измерения площади: мм2,см2, дм2, м2, ар=100м2, км2 , га=100км2.
Площадь квадрата равна квадрату его стороны.
Площадь прямоугольника равна произведению его смежных сторон.
Площадь параллелограмма равна произведению его основания на высоту.
Площадь треугольника равна половине произведения его основания на высоту.
Площадь прямоугольного треугольника равна произведению его катетов.
Если высоты двух треугольников равны, то их площади относятся как основания.
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Площадь трапеции равна полусумме её оснований на высоту.
Теорема Пифагора:в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Теорема(обр.):если квадрат одной стороны треугольника равен сумме квадратов двух других его сторон, то треугольник прямоугольный.
Глава VII Подобные треугольники
Отрезки m и n пропорциональны отрезкам m1и n1,если отношения их длин равны m:m1= n: n1.
Подобные треугольники— это треугольники,у которых соответственные углы равны, а сходственные стороны пропорциональны.
Коэффициент подобия- это число, равное отношению сходственных сторон подобных треугольников.
Теорема: Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Свойство биссектрисы тр-ка: биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
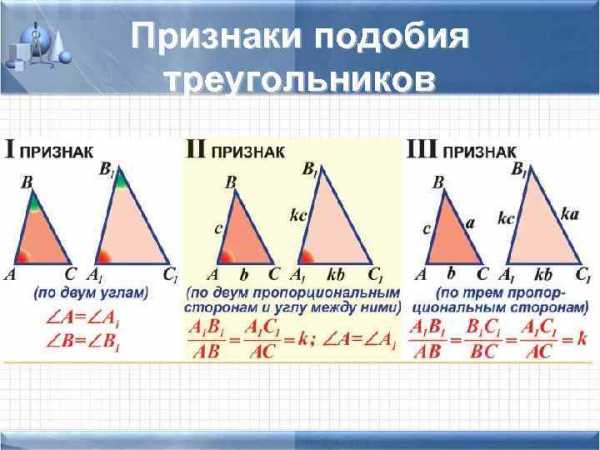
Теорема(первый признак подобия треугольников):если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Теорема(второй признак подобия треугольников):если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.
Теорема(первый признак подобия треугольников):если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон.
Теорема:Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
Среднее пропорциональное(среднее геометрическое)двух величин – это квадратный корень из произведения этих величин.
С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
С. Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы,заключённым между катетом и высотой, проведённой из вершины прямого угла.
Синус острого угла прямоугольного треугольника- это отношение противолежащего катета к гипотенузе.
Косинус острого угла прямоугольного треугольника- это отношение прилежащего катета к гипотенузе.
Тангенс острого угла прямоугольного треугольника- это отношение противолежащего катета к прилежащему .
Котангенс острого угла прямоугольного треугольника- это отношение прилежащего катета к противолежащему .
Глава VIII Окружность
Касательная к окружности – это прямая, имеющая с окружностью только одну общую точку.
Т. Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
Т.(обр.) Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
Центральный угол – это угол с вершиной в центре окружности.
Дуга окружности измеряется центральным углом, который на неё опирается.
Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Т.Вписанный угол равен половине дуги, на которую он опирается.
С. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
С. Вписанный угол, опирающийся на полуокружность, — прямой.
Т. Если две хорды окружности пересекаются, произведение отрезков одной хорды равно произведению отрезков другой хорды.
9 класс
Средняя линия трапеции— это отрезок, соединяющий середины её боковых сторон.
Теорема:средняя линия трапеции равна полусумме её оснований и параллельна им.
infourok.ru
Справочник по геометрии 7 -9 класс Треугольник
Справочник по геометрии 7 -9 класс
Треугольник
Треугольник В Основные формулы A + B+ C=1800 с а P = a + b + c; ha S = ½·a·ha; А S = ½·a·b·sin. C; b С 1/22/2018 5
Свойства равнобедренного треугольника • В равнобедренном треугольнике углы при основании равны А = С В • Медиана, проведенная к 12 основанию равнобедренного треугольника является его биссектрисой и высотой ВD-биссектриса ВD-высота А С D
Признаки равенства треугольников СУС УСУ ССС По двум По стороне и По трём сторонам и углу двум сторонам между ними прилежащим к ней углам
Признаки равенства прямоугольных треугольников
Свойства прямоугольного треугольника A • В прямоугольном треугольнике сумма острых углов равна 90°. A+ C=900 300 • В прямоугольном треугольнике гипотенуза больше катета • Катет в прямоугольном треугольнике, лежащий против угла в 30 ° , равен b половине гипотенузы. CB =½·AB • Если катет в прямоугольном C a B треугольникето угол, лежащий против гипотенузы, равен половине S = ½·a·b этого катета, равен 30°.
Соотношения между сторонами и углами треугольника В В треугольнике АВD: • против большего угла лежит M большая сторона ; N • против большей стороны лежит А С больший угол • Каждая сторона треугольника меньше суммы двух других его сторон: АВ
Признаки подобия треугольников
Пропорциональные отрезки в прямоугольном треугольнике b a h bc ac h= или h 2 = ac· bc ; b= или b 2 = c · bc ; a= или a 2 = c · ac ;
Теорема Пифагора Теорема: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов с 2 =а 2+b 2 b с Обратная теорема : Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то этот треугольник прямоугольный а
Признаки параллельности прямых
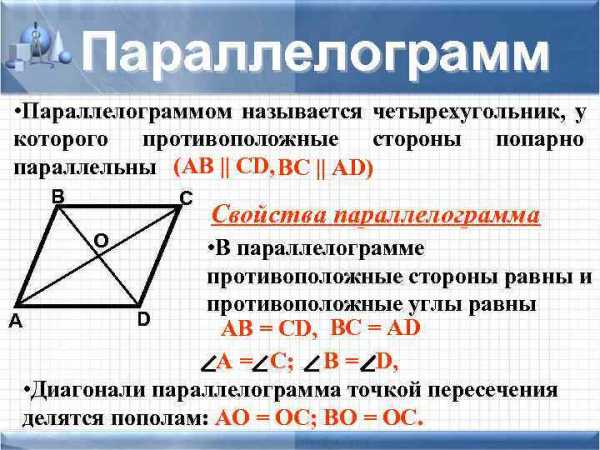Параллелограмм • Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны (АB || CD, BC || AD) В Свойства параллелограмма О • В параллелограмме противоположные стороны равны и противоположные углы равны А D АB = CD, BC = AD А = С; B = D, • Диагонали параллелограмма точкой пересечения делятся пополам: АО = ОС; ВО = ОС.
Параллелограмм Признаки параллелограмма • Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм • Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм • Если в четырехугольнике диагонали пересекаются и и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм Основные формулы В С A + B + C + D = 1800 b ha О P = 2(a + b) S = a·ha А a D S = a·b·sin. A
Квадрат • Квадрат — это прямоугольник, у которого все стороны равны. • Квадрат обладает всеми свойствами и признаками параллелограмма, прямоугольника, ромба Основные формулы В С A = B = C = D = 900 (R-радиус описанной окружности) а P = 4 a S = a 2 S = ½·P·r А а D(r-радиус вписанной окружности)
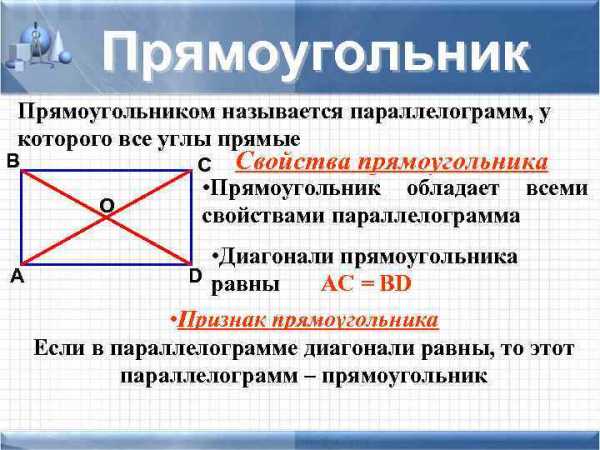Прямоугольником называется параллелограмм, у которого все углы прямые В С Свойства прямоугольника • Прямоугольник обладает всеми O свойствами параллелограмма • Диагонали прямоугольника А D равны AC = BD • Признак прямоугольника Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник
Прямоугольником называется параллелограмм, у которого все углы прямые В Основные формулы b O С A = B = C = D = 900 А a D P = 2(a + b) S = a·b
Ромбом называется параллелограмм, у В которого все стороны равны Свойства ромба • Все стороны ромба равны АВ=ВС=СД=ДА. А С Противолежащие углы ромба равны • О • Диагонали ромба точкой пересечения делятся пополам: АО=ОС, ВО=ОД. D • Диагонали ромба взаимно перпендикулярны АС ВД. ВД • Диагонали ромба являются биссектрисами его углов
Ромбом называется параллелограмм, у В которого все стороны равны Основные формулы d 2 О AВ = BС = CD = AD = a А С d 1 P = 4 a a S = ½·d 1·d 2 D
Трапеция • Четырехугольник, у которого две B b C стороны параллельны, а две другие нет, называется трапецией. M N • BC, AD–основания трапеции, ВС║АD h • AB, CD – боковые стороны a A D • MN –средняя линия трапеции • В равнобедренной трапеции углы при основаниях равны • В равнобедренной трапеции диагонали равны Свойства Основные формулы средней линии трапеции: P = АВ+ВС+СD+AD
2. 1 Основные утверждения и теоремы 1) Верное 11) Неверное 21) Неверное 31) Неверное 2) Верное 12) Неверное 22) Неверное 32) Верное 3) Неверное 13) Верное 23) Неверное 33) Неверное 4) Неверное 14) Неверное 24) Неверное 34) Неверное 5) Верное 15) Верное 25) Верное 35) Верное 6) Неверное 16) Неверное 26) Верное 36) Верное 7) Верное 17) Неверное 27) Неверное 37) Неверное 8) Неверное 18) Неверное 28) Неверное 38) Верное 9) Неверное 19) Верное 29) Верное 39) Неверное 10) Верное 20) Неверное 30) Неверное 40) Неверное 1/22/2018 27
present5.com
Геометрия. 7 — 9 классы. Атанасян Л.С. и др.
В этом учебнике геометрии много задач: есть задачи и практические задания к каждому параграфу, дополнительные задачи к каждой главе и, наконец, задачи повышенной трудности. Основными являются задачи к параграфу. Более трудные задачи отмечены звездочкой. В конце книги к задачам даны ответы и указания.Учебник для 7 — 9 классов общеобразовательных учреждений.
ОГЛАВЛЕНИЕ
Введение 3
Глава I
Начальные геометрические сведения 5
§ 1. Прямая и отрезок —
1. Точки, прямые, отрезки —
2. Провешивание прямой на местности 6
Практические задания 7
§ 2. Луч и угол 8
3. Луч —
4. Угол —
Практические задания и вопросы 10
§ 3. Сравнение отрезков и углов —
5. Равенство геометрических фигур —
6. Сравнение отрезков и углов 11
Вопросы и задачи 12
§4. Измерение отрезков 13
7. Длина отрезка —
8. Единицы измерения. Измерительные инструменты 15
Практические задания 16
Вопросы и задачи 17
§ 5. Измерение углов 18
9. Градусная мера угла —
10. Измерение углов на местности 20
Практические задания —
Вопросы и задачи 21
§6. Перпендикулярные прямые 22
11. Смежные и вертикальные углы —
12. Перпендикулярные прямые —
13. Построение прямых углов на местности 23
Практические задания 24
Вопросы и задачи —
Вопросы для повторения к главе I 25
Дополнительные задачи 26
Глава II
Треугольники 28
§ 1. Первый признак равенства треугольников —
14. Треугольник —
15. Первый признак равенства треугольников 29
Практические задания 30
Вопросы и задачи 31
§ 2. Медианы, биссектрисы и высоты треугольника 32
16. Перпендикуляр к прямой —
17. Медианы, биссектрисы и высоты треугольника 33
18. Свойства равнобедренного треугольника 35
Практические задания 36
Задачи —
§ 3. Второй и третий признаки равенства треугольников 38
19. Второй признак равенства треугольников —
20. Третий признак равенства треугольников 39
Задачи 41
§ 4. Задачи на построение 43
21. Окружность —
22. Построения циркулем и линейкой 44
23. Примеры задач на построение 45
Вопросы и задачи 48
Вопросы для повторения к главе II 49
Дополнительные задачи 50
Глава III
Параллельные прямые 54
§ 1. Признаки параллельности двух прямых —-
24. Определение параллельности прямых —
25. Признаки параллельности двух прямых 55
26. Практические способы построения параллельных прямых .. 57
Вопросы и задачи 58
§ 2. Аксиома параллельных прямых 59
27. Об аксиомах геометрии —
28. Аксиома параллельных прямых 60
29. Теоремы об углах, образованных двумя параллельными прямыми и секущей 63
Вопросы и задачи 65
Вопросы для повторения к главе III 68
Дополнительные задачи —
Глава IV
Соотношения между сторонами и углами треугольника 70
§ 1. Сумма углов треугольника —
30. Теорема о сумме углов треугольника —
31. Остроугольный, прямоугольный и тупоугольный треугольники 71
Задачи —
§ 2. Соотношения между сторонами и углами треугольника 72
32. Теорема о соотношениях между сторонами и углами треугольника —
33. Неравенство треугольника , 74
Вопросы и задачи —
§ 3. Прямоугольные треугольники 76
34. Некоторые свойства прямоугольных треугольников —
35. Признаки равенства прямоугольных треугольников 77
36. Уголковый отражатель 79
Задачи —
§ 4. Построение треугольника по трем элементам 82
37. Расстояние от точки до прямой. Расстояние между параллельными прямыми —
38. Построение треугольника по трем элементам 84
Вопросы и задачи —
Задачи на построение : 87
Вопросы для повторения к главе IV 89
Дополнительные задачи 90
Задачи повышенной трудности 92
Задачи к главе I —
Задачи к главе II 93
Задачи к главам III и IV —
Задачи на построение 95
Глава V
Четырехугольники 98
§ 1. Многоугольники —
39. Многоугольник —
40. Выпуклый многоугольник 99
41. Четырехугольник —
Вопросы и задачи 100
§ 2. Параллелограмм и трапеция 101
42. Параллелограмм —
43. Признаки параллелограмма 102
44. Трапеция 103
Задачи 104
§3. Прямоугольник, ромб, квадрат 108
45. Прямоугольник —
46. Ромб и квадрат 109
47. Осевая и центральная симметрии 110
Вопросы и задачи 113
Вопросы для повторения к главе V 114
Дополнительные задачи 115
Глава VI
Площадь 117
§ 1. Площадь многоугольника —
48. Понятие площади многоугольника —
49. Площадь квадрата 120
50. Площадь прямоугольника 122
Вопросы и задачи —
§ 2. Площади параллелограмма, треугольника и трапеции 124
51. Площадь параллелограмма —
52. Площадь треугольника 125
53. Площадь трапеции 126
Задачи 127
§ 3. Теорема Пифагора 129
54. Теорема Пифагора —
55. Теорема, обратная теореме Пифагора 131
Задачи 132
Вопросы для повторения к главе VI 133
Дополнительные задачи 134
Глава VII
Подобные треугольники 138
§ 1. Определение подобных треугольников —
56. Пропорциональные отрезки —
57. Определение подобных треугольников —
58. Отношение площадей подобных треугольников 139
Вопросы и задачи 140
§ 2. Признаки подобия треугольников 142
59. Первый признак подобия треугольников —
60. Второй признак подобия треугольников 143
61. Третий признак подобия треугольников —
Вопросы и задачи 144
§ 3. Применение подобия к доказательству теорем и решению задач 146
62. Средняя линия треугольника —
63. Пропорциональные отрезки в прямоугольном треугольнике … 147
64. Практические приложения подобия треугольников 149
65. О подобии произвольных фигур 152
Вопросы и задачи 153
Задачи на построение 155
§ 4. Соотношения между сторонами и углами прямоугольного треугольника 15($
66. Синус, косинус и тангенс острого угла прямоугольного треугольника
67. Значения синуса, косинуса и тангенса для углов 30°, 45° и 60° 158
Задачи 159
Вопросы для повторения к главе VII 160
Дополнительные задачи 161
Глава VIII
Окружность 164
§ 1. Касательная к окружности —
68. Взаимное расположение прямой и окружности —
69. Касательная к окружности 166
Задачи 168
§ 2. Центральные и вписанные углы 169
70. Градусная мера дуги окружности —
71. Теорема о вписанном угле 171
Задачи 173
§ 3. Четыре замечательные точки треугольника 176
72. Свойства биссектрисы угла и серединного перпендикуляра к отрезку —
73. Теорема о пересечении высот треугольника 179
Задачи 180
§ 4. Вписанная и описанная окружности 181
74. Вписанная окружность —
75. Описанная окружность 183
Задачи 185
Вопросы для повторения к главе VIII 187
Дополнительные задачи 188
Глава IX
Векторы 192
§ 1. Понятие вектора —
76. Понятие вектора —
77. Равенство векторов 194
78. Откладывание вектора от данной точки 196
Практические задания —
Вопросы и задачи —
§ 2. Сложение и вычитание векторов 198
79. Сумма двух векторов —
80. Законы сложения векторов. Правило параллелограмма 200
81. Сумма нескольких векторов 201
82. Вычитание векторов 202
Практические задания 204
Вопросы и задачи —
§ 3. Умножение вектора на число. Применение векторов к решению задач 206
83. Произведение вектора на число —
84. Применение векторов к решению задач 208
85. Средняя линия трапеции 210
Практические задания —
Задачи 211
Вопросы для повторения к главе IX 213
Дополнительные задачи 214
Задачи повышенной трудности 215
Задачи к главе V —
Задачи к главе VI 217
Задачи к главе VII 219
Задачи к главе VIII 221
Задачи к главе IX 224
Глава X
Метод координат 227
§ 1. Координаты вектора —
86. Разложение вектора по двум неколлинеарным векторам —
87. Координаты вектора 229
Задачи 232
§ 2. Простейшие задачи в координатах 234
88. Связь между координатами вектора и координатами его начала и конца —
89. Простейшие задачи в координатах 236
Задачи 238
§ 3. Уравнения окружности и прямой 241
90. Уравнение линии на плоскости —
91. Уравнение окружности 242
92. Уравнение прямой 243
Задачи 245
Вопросы для повторения к главе X 249
Дополнительные задачи 250
Глава XI
Соотношения между сторонами и углами треугольника
Скалярное произведение векторов 252
§ 1. Синус, косинус, тангенс угла —
93. Синус, косинус, тангенс —
94. Основное тригонометрическое тождество. Формулы приведения 253
95. Формулы для вычисления координат точки 254
Задачи 255
§ 2. Соотношения между сторонами и углами треугольника 256
96. Теорема о площади треугольника —
97. Теорема синусов —
98. Теорема косинусов 257
99. Решение треугольников 258
100. Измерительные работы 260
Задачи 261
§ 3. Скалярное произведение векторов 264
101. Угол между векторами —
102. Скалярное произведение векторов —
103. Скалярное произведение в координатах 266
104. Свойства скалярного произведения векторов 268
Задачи 269
Вопросы для повторения к главе XI 271
Дополнительные задачи 272
Глава XII
Длина окружности и площадь круга 275
§ 1. Правильные многоугольники —
105. Правильный многоугольник —
106. Окружность, описанная около правильного многоугольника —
107. Окружность, вписанная в правильный многоугольник 276
108. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности 278
109. Построение правильных многоугольников 279
Вопросы и задачи 281
§ 2. Длина окружности и площадь круга 283
110. Длина окружности —
111. Площадь круга 285
112. Площадь кругового сектора 286
Вопросы и задачи 287
Вопросы для повторения к главе XII 290
Дополнительные задачи —
Глава XIII
Движения 293
§ 1. Понятие движения —
113. Отображение плоскости на себя —
114. Понятие движения 294
115. Наложения и движения 296
Задачи 299
§ 2. Параллельный перенос и поворот 300
116. Параллельный перенос —
117. Поворот 301
Задачи 302
Вопросы для повторения к главе XIII 303
Дополнительные задачи 304
Глава XIV
Начальные сведения из стереометрии 307
§ 1. Многогранники —
118. Предмет стереометрии —
119. Многогранник 309
120. Призма 311
121. Параллелепипед 312
122. Объем тела 314
123. Свойства прямоугольного параллелепипеда 316
124. Пирамида 319
Вопросы и задачи 321
§ 2. Тела и поверхности вращения 327
125. Цилиндр —
126. Конус 328
127. Сфера и шар 330
Вопросы и задачи 331
Вопросы к главе XIV 335
Дополнительные задачи 336
Задачи повышенной трудности 338
Задачи к главе X —
Задачи к главе XI 340
Задачи к главе XII 341
Задачи к главе XIII 342
Задачи к главе XIV 343
Приложения 344
1.
proresheno.ru
Справочник по геометрии 7-9 класс
Выполнил:
ученик 9А класса
средней школы №
135
Матвеев Евгений.
Руководитель проекта:
О
черетина
Т.В.
Казань 2004 г.
7 класс.
Глава
I
.
Точки, прямые, отрезки.
Через любые две точки Если две прямые имеют общую
можно провести прямую, точку, то они пересекаются.
и притом только одну.
Прямая а и точки А и В.
Прямая а и b пересекаются в точке О.
Две прямые либо имеют только одну общую точку,
либо не имеют общих точек.
Угол.
Угол – это геометрическая фигура, Угол называется развёрнутым, которая состоит из точки и двух лучей, если обе его стороны
исходящих из этой точки. лежат на одной прямой.
Угол с вершиной О и сторонами h и k. Развёрнутый угол с вершиной С
и сторонами p и q.
Развёрнутый угол = 180º; Неразвёрнутый угол < 180º .
Луч, исходящий из вершины угла и Два угла, у которых одна общая
делящий его на два равных угла, сторона общая, а две другие
называется биссектриса угла. являются продолжениями одна
другой, называются смежными.
Два угла, называются вертикальными,
если стороны одного угла являются Сумма смежных углов = 180º.
продолжениями сторон другого.
Две пересекающиеся прямые
Вертикальные углы равны. называются перпендикулярными,
если они образуют 4 прямых угла.
Глава
I I.
Треугольники.
Треугольник – геометрическая фигура, Р
АВС
= АВ+ВС+СА.
кот-ая состоит из 3 точек, не лежа-
щих на 1 прямой, соединённых отрезками.
В равных треугольниках против
Треугольник с вершинами А, В, С и соответственно равных сторон
Сторонами а, b, c. лежат равные углы, также против
соответственно равных равных
углов лежат равные стороны.
Теорема:
Если 2 стороны и угол
Теорема:
Из точки, не лежа-
между ними 1-го треугольника щей на прямой, можно провести
соответственно равны 2 сторонам перпендикуляр к этой, и притом
и углу между ними другого только один.
треугольника, то треугольники равны.
Отрезок, соединяющий вершину треуг- Отрезок бисс-сы угла треуг-ка,
ка с серединой противоположной сто- соединяющий вершину треуг-ка
роны, называется медианой треуг-ка. с точкой противоположной сторо- ны, называется бисс-сой треуг-ка.
Перпендикуляр, проведённый из верши-
ны треуг-ка к прямой, содержащей Треуг-к, у кот-го 2 стороны равны,
противоположную сторону, называ- называется равнобедренным.
ется высотой треуг-ка.
Теорема:
В равнобедренном треуг-ке
ВН — высота треуг-ка АВС. углы при основании равны.
Теорема:
В равнобедренном Высота равнобедренного треуг-ка, про-
треуг-ке бисс-са, проведённая ведённая к основанию, является медианой
к основа-нию, является и бисс-сой.
медианой и высотой.
Медиана, проведённая к основанию, явля-
ется высотой и бисс-сой.
Теорема:
Если сторона и 2
Теорема:
Если три стороны 1го
прилежащих к ней угла 1го треуг-ка соответственно равны 3ём
треуг-ка соответственно рав- сторонам другого треуг-ка, то такие
ны стороне и 2 прилежащим к треуг-ки равны.
ней углам другого треуг-ка, то
такие треуг-ки равны.
Определение:
Окружность называется геометр-ая фигура, состоя-щая из всех точек, располож-ых на заданном расс-нии от данной точки.
Глава
I I I.
Параллельные прямые.
Определение:
Две прямые
Теорема:
Если при пересечении 2 пря-
на плоскости параллельны, мых секущей накрест лежащие углы рав-
если они не пересекаются. ны, то прямые параллельны.
Теорема:
Если при пересечении 2 пря-
Накрест лежащие – 3 и 5, 4 и 6. мых секущей соответственные углы рав-
Односторонние – 4 и 5, 3 и 6. ны, то прямые параллельны.
Соответственные – 1 и 5, 4 и 8,2 и 6, 3 и 7.
Теорема:
Если при пересече-
Теорема:
Если две параллельные пря-
нии 2 прямых секущей сумма мые пересечены секущей, то накрест
односторонних углов равна лежащие углы равны.
180º, то прямые параллельны.
Теорема:
Если две прямые пересечены
Теорема:
Если две парал- секущей, то сумма односторонних углов
лельные прямые пересечены равна 180º.
секущей, то соответствен-
ные углы равны.
Глава
IV.
Соотношения между сторонами
и углами треугольника.
Теорема:
Сумма углов Внешний угол треуг-ка = сумме двух углов тре-
треуг-ка = 180º. уг-ка, не смежных с ним.
В любом треугольнике либо Теорема:
В треуг-ке против большей сто-
все углы острые, либо два роны лежит больший угол, против большего
два угла острые, а третий угла лежит большая сторона.
тупой или прямой.
В прямоугольном треуг- ке гипотенуза Если два угла треуг-ка равны, то больше катета. треуг-к – равнобедренный.
Теорема:
Каждая сторона Для любых 3 точек А,В,С, не лежащих на
треугольника меньше суммы одной прямой, справедливы неравенства:
2 других сторон. АВ<
AB
+
BC
, ВС<ВА+АС, АС<АВ+ВС.
Сумма двух острых углов пря- Катет прямоугольного треуг-ка, лежащий
моугольного треуг-ка = 90º. против угла в 30º, равен ½ гипотенузы.
Если катет прямоугольного треуг- Если катеты 1го прямоугольного треуг-
ка = ½ гипотенузы, то угол, лежа- ка соответственно = катетам другого
щий против этого катета, = 30º. , то такие треуг-ки равны.
Если катет и прилежащий к нему Теорема:
Если гипотенуза и острый
острый угол 1го прямоугольного угол 1го прямоугольного треуг-ка соот-
треуг-ка соответственно равны ветственно равны гипотенузе и остро-
катету и прилежащему к нему му углу другого, то такие треуг-ки равны. острому углу другого, то такие
треугольники равны. Теорема:
Если гипотенуза и катет 1го
прямоугольного треуг-ка соответствен-
Теорема:
Все точки каж- но равны гипотенузе и катету другого,
дой из 2 параллельных прямых то такие треугольники равны.
равноудалены от другой прямой.
Расстояние от произвольной точки 1ой из параллельных прямых до
другой прямой называется прямой называется расстоянием между
этими прямыми.
8 класс.
Глава
V
.
Многоугольники.
Сумма углов выпуклого
n
-угольника В параллелограмме противоположные
= (
n
-2)180º. стороны равны и противоположные
углы равны.
Диагонали параллелограмма точ-
кой пересечения делятся пополам. Если в 4-угольнике 2 стороны равны и
параллельны, то этот 4-угольник – па-
раллелограм.
Если в 4-угольнике противопо-
ложные стороны попарно равны, Если в 4-угольнике диагональю пересе-
то этот 4-угольник – параллело- каются и точкой пересечения делятся
грамм. пополам, то этот 4-угольник – парал-
лелограмм.
Трапецией называется 4-угольник,
у кот-го 2 стороны параллельны, а Прямоугольником называется парал-
2 другие стороны не параллельны. лелелограмм, у кот-го все углы прямые.
Диагонали прямоугольника равны. Если в параллелограмме дигонали равны,
то этот параллелограмм – прямоуголь-
Ромбом называется параллело- ник.
грамм, у кот-го все стороны
равны. Диагонали ромба взаимно перпендикуляр-
ны и делят его углы пополам.
Квадкатом называется прямо-
угольник, у кот-го все стороны Все углы квадрата равны.
равны.
Диагонали квадрата равны, взаимно
Фигура называется симметричной перпендикулярны, точкой пересечения
относительно прямой а, если для делятся пополам и делят углы
каждой точки фигуры симметричная квадрата пополам.
ей точка относительно прямой а
также принадлежит этой фигуре. Прямая а называется осью симметрии.
Фигура называется симметричной Точка О называется центром симмет-
относительно точки О, если для рии фигуры.
каждой точки фигуры симметрич-
ная ей точка относительно точки О
также принадлежит этой фигуре.
Глава
VI
.
Площадь.
Равные многоугольники имеют
S
квадрата равна квадрату его стороны.
Равные
S
.
Если многоугольник составлен из Теорема:
S
прямоугольника = про-
нескольких многоугольников, то изведению его смежных сторон.
Его
S
= сумме площадей этих
многоугольников. Теорема:
S
параллелограмма = про-
изведению его основания на высоту.
Теорема:
S
треугольника =
= произведению его основания
S
прямоугольного треугольника = 1/2
на высоту. произведения его катетов.
Если высоты 2ух 3-угольников
coolreferat.com
Определения и теоремы геометрия 7 класс
Геометрия 7 класс
Определения
Отрезок-часть прямой, ограниченная двумя точками.
Концы отрезка-точки, ограничивающие прямую.
Луч-прямая, имеющая начало в точке, но не имеющая конца.
Угол-геометрическая фигура, состоящая из точки и двух лучей, исходящих из этой точки.
Стороны угла-лучи, составляющие угол.
Вершина угла-точка, из которой берут начало стороны угла.
Развернутый угол, если обе его стороны лежат на одной прямой.
Середина отрезка-точка, делящая отрезок пополам.
Прямой угол=900. Острый угол<900. 1800>Тупой угол>900.
Смежные-два угла, у которых одна сторона общая, а две другие-это продолжения друг друга.
Вертикальные-два угла, если стороны одного угла-это продолжение сторон другого.
Перпендикулярные-две пересекающиеся прямые, образующие четыре прямых угла.
Периметр-сумма длин всех сторон фигуры.
Перпендикуляр АН-отрезок, соединяющий точку А с точкой Н, лежащей на прямой. Этот отрезок с прямой образует прямой угол.
Биссектриса-луч, исходящий из вершины угла и делящий его на два равных угла.
Медиана-отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
Высота-перпендикуляр, проведенный из вершины угла к прямой, содержащей противолежащую сторону.
Равнобедренный треугольник, если две его стороны равны.
Окружность-геометрическая фигура, состоящая из множества точек, которые находятся на одинаковом расстоянии от одной единственной точки-центр окружности.
Радиус r — отрезок, соединяющий центр окружности с любой точкой, лежащей на этой окружности.
Хорда-отрезок, соединяющий две точки, лежащие на окружности.
Диаметр-хорда, проходящая через центр окружности.
Дуга-часть окружности, полученная делением этой окружности двумя точками.
Параллельные прямые-две не пересекающиеся на плоскости прямые.
Параллельные отрезки, если они лежат на параллельных прямых.
Секущая к двум прямым-прямая, пересекающая данные прямые в двух точках.
Гипотенуза-сторона прямоугольного треугольника, лежащая напротив прямого угла. Две другие стороны прямоугольного треугольника-катеты.
Неравенства треугольника: АВ<АС+СВ, АС<АВ+ВС, ВС<ВА+АС.
Расстояние от точки до прямой-длина перпендикуляра, проведенного из точки к прямой.
Расстояние между прямыми-расстояние от любой точки одной из параллельных прямых до другой прямой.
Правила и теоремы
Через любые две точки можно провести только одну прямую.
Две прямые имеют либо одну общую точку, либо ни одной.
Две геометрические фигуры называются равными, если их можно совместить наложением.
Равные отрезки имеют равные длины.
Сумма смежных углов равна 1800.
Вертикальные углы равны.
Развернутый угол равен 1800. Неразвернутый меньше 1800.
Две прямые, перпендикулярные к третьей, не пересекаются.
Признаки равенства треугольников:
Теорема 1 (по двум сторонам и углу). Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.
Теорема 2 (по стороне и двум углам). Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то эти треугольники равны.
Теорема 3 (по трём сторонам). Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то эти треугольники равны.
2.2.Теорема (о перпендикуляре к прямой). Из точки, не лежащей на прямой, можно провести только один перпендикуляр к этой прямой.
2.3. Медиана делит сторону на два равных отрезка.
2.4. Свойства равнобедренного треугольника:
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Теорема 2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
3.1. Признаки параллельности двух прямых (обратные теоремы тоже справедливы):
Теорема 1. Если при пересечении двух прямых секущей накрест лежащие углы равны, то данные прямые параллельны.
Теорема 2. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Теорема 3. Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то прямые параллельны.
3.2. Аксиома параллельных прямых. Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Следствия из аксиомы:
10. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
20. Если две прямые параллельны третьей, то все три прямые параллельны.
4.1. Теорема (о сумме углов треугольника). Сумма углов треугольника равно 1800.
4.2. В любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.
4.5. Теорема (о соотношении между сторонами и углами треугольника). В треугольнике против большей стороны лежит больший угол и против большего угла лежит большая сторона.
Следствия из теоремы:
10. В прямоугольном треугольнике гипотенуза больше катета.
20. Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).
4.6. Каждая сторона треугольника меньше суммы двух других сторон.
4.7. Свойства прямоугольного треугольника:
10. Сумма двух острых углов прямоугольного треугольника равна 900.
20. Катет прямоугольного треугольника, лежащий напротив угла в 300, равен половине гипотенузы.
30. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий напротив этого катета, равен 300.
4.8. Признаки равенства прямоугольных треугольников:
1. Если катеты одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то эти треугольники равны.
2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему углу другого треугольника, то эти треугольники равны.
Теорема 1. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузы и острому углу другого прямоугольного треугольника, то эти треугольники равны.
Теорема 2. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
4.9. Угол падения равен углу отражения.
4.10. Теорема. Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
infourok.ru
