Формулы геометрии. Площади фигур. — материалы для подготовки к ЕГЭ по Математике
Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!
Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.
Ты нашел то, что искал? Поделись с друзьями!
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.
1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
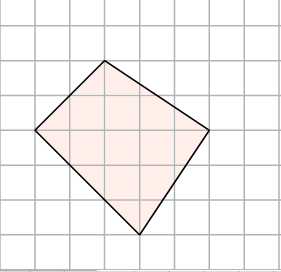
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Ответ: .
2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
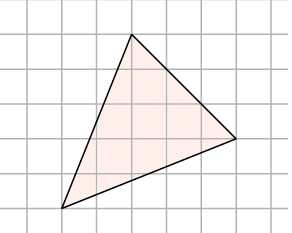
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Ответ: .
3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
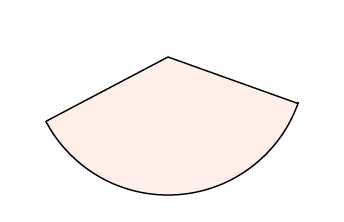
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Ответ: .
Читайте также о задачах на тему «Координаты и векторы». Для их решения вспомните, что такое абсцисса точки (это ее координата по ) и что такое ордината (координата по ). Пригодятся также такие понятия, как координаты вектора и длина вектора (она находится по теореме Пифагора), синус и косинус угла, угловой коэффициент прямой, уравнение прямой, а также сумма, разность и скалярное произведение векторов, угол между векторами.
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
|
Треугольник |
|
Площадь треугольника равна половине произведения его стороны на высоту, проведённую к этой стороне. |
|
|
Треугольник |
|
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними. |
|
|
Треугольник |
|
Площадь треугольника равна корню квадратному из произведения полупериметра этого треугольника и разностей полупериметра и всех его сторон. |
|
|
Треугольник |
|
Площадь треугольника равна отношению произведения квадрата его стороны на синусы прилежащих углов к удвоенному синусу противолежащего угла. |
|
|
Треугольник |
|
Площадь треугольника равна отношению произведения квадрата его высоты на синус угла, из вершины которого проведена эта высота, к удвоенному произведению синусов двух других углов. |
|
|
Треугольник |
|
Площадь треугольника равна произведению квадрата его полупериметра на тангенсы половин всех углов треугольника. |
|
|
Прямоугольный треугольник |
|
Площадь прямоугольного треугольника равна половине произведения его катетов. |
|
|
Равнобедренный треугольник |
|
Площадь равнобедренного треугольника равна половине произведения его основания на корень квадратный из разности квадратов боковой стороны и половины основания. |
|
|
Равносторонний треугольник |
|
Площадь равностороннего треугольника равна четверти произведения квадрата стороны этого треугольника и квадратного корня из трёх. |
|
|
Равносторонний треугольник |
|
Площадь равностороннего треугольника равна отношению квадрата его высоты к квадратному корню из трёх. |
|
|
Треугольник |
|
Площадь треугольника равна отношению произведения всех его сторон к четырём радиусам, описанной около него окружности. |
|
|
Треугольник |
|
Площадь треугольника равна удвоенному произведению квадрата радиуса, описанной около него окружности, и синусов всех его углов. |
|
|
Треугольник |
|
Площадь треугольника (многоугольника) равна произведению его полупериметра и радиуса окружности, вписанной в этот треугольник (многоугольник). |
|
|
Треугольник |
|
Площадь треугольника равна произведению квадрата радиуса вписанной окружности на котангенсы половин всех углов треугольника. |
|
|
Прямоугольник |
|
Площадь прямоугольника равна произведению двух соседних его сторон. |
|
|
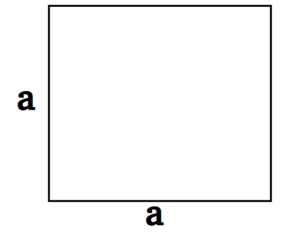
Квадрат |
|
Площадь квадрата равна квадрату его стороны. |
|
|
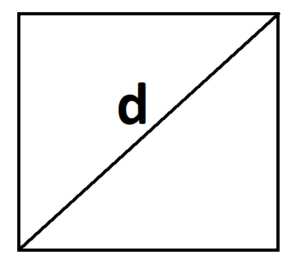
Квадрат |
|
Площадь квадрата равна половине квадрата его диагонали. |
|
|
Параллелограмм |
|
Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне. |
|
|
Параллелограмм |
|
Площадь параллелограмма равна произведению двух соседних его сторон на синус угла между ними. |
|
Ромб |
|
Площадь ромба равна произведению квадрата его стороны на синус одного из его углов. |
|
|
Ромб (дельтоид) |
|
Площадь ромба (как и дельтоида) равна половине произведения его диагоналей. |
|
|
Трапеция |
|
Площадь трапеции равна произведению полусуммы её оснований на высоту. |
|
|
Трапеция |
|
Площадь трапеции равна произведению её средней линии на высоту. |
|
|
Выпуклый четырёхугольник |
|
Площадь выпуклого четырёхугольника равна половине произведения его диагоналей на синус угла между ними. |
|
|
Вписанный четырёхугольник |
|
Площадь четырёхугольника, вписанного в окружность, равна корню квадратному из произведения разностей полупериметра этого четырёхугольника и всех его сторон. |
|
|
Круг |
|
Площадь круга равна произведению числа «пи» на квадрат радиуса. |
|
|
Круг |
|
Площадь круга равна четверти произведения числа «пи» на квадрат диаметра. |
|
|
Круговой сектор |
формулы для случаев градусной и радианной мер центральных углов |
Площадь кругового сектора равна произведению площади единичного сектора (сектор, соответствующий центральному углу с мерой равной единице) на меру центрального угла, соответствующего данному сектору. |
|
|
Круговое кольцо |
|
Площадь кругового кольца равна произведению числа «пи» на разность квадратов внешнего и внутреннего радиусов. |
|
| Круговое кольцо |
|
Площадь кругового кольца равна четверти произведения числа «пи» на разность квадратов внешнего и внутреннего диаметров. |
|
| Круговое кольцо |
|
Площадь кругового кольца равна удвоенному произведению числа «пи», среднего радиуса кольца и его ширины. |
math4school.ru
Формула вычисления площади для всех геометрических фигур
Стандартное обозначение площади — S
Площадь
Пусть длина стороны квадрата равна a, тогда формул квадрата:
S = a ⋅ a = a2
Прямоугльник
Пусть длины сторон прямоугольника равны a и b
S = a ⋅ b
Параллелограмм
Пусть длины сторон параллелограмма равны a и b и
ha это высота на сторону a,
и hb это высота на сторону b
Формула площади параллелограмма:
S = a ⋅ ha = b ⋅ hb
Трапеция
Допустим, что длины параллельных сторон трапеции имеют длину a и b и расстояние между двумя основами s h(the trapezoid altitude). Тогда формула площади:
$S = \frac{(a + b)\cdot h}{2}$
Площадь круга
$P = \pi\cdot r^2$
$\pi=3,14$
Площадь прямоугольного треугольника
$S=\frac{a \cdot b}{2}$
$S=\frac{c \cdot h_c}{2}$
Площадь треугольника — калькулятор
Стороны треугольника:Треугольник
ABC — треугольник
длина его сторон: a, b, c и длина его высот: ha, hb и hc.
S = ½(a ⋅ ha) = ½(b ⋅ hb) = ½(c ⋅ hc)S = ½(ab ⋅ sinC) = ½(ac ⋅ sinB) = ½(bc ⋅ sinA)
p = ½(a + b + c)
S = √p(p — a)(p — b)(p — c) — формула Герона
$S = R^2\sin(A) \cdot \sin(B) \cdot \sin(C) = \frac{abc}{4R}$
где R — радиус описанной окружностиПлощадь параллелограмма(ромба)
$S = AB\cdot DE = BC \cdot DF$
$S = AB \cdot AD \sin \alpha$
$S = \frac12 AC \cdot BD \sin \gamma$
Площадь выпуклого четырехугольника
$S = \frac12 AC \cdot BD \sin \varphi $
Площадь правильного многоугольника
$S = \frac14 n\cdot a^2\cdot \text{ctg}(\frac{\pi}{n})$
n — число ребер(вершин).
$\pi=3,14159265359$
www.math10.com
Формулы площадей всех основных фигур
1. Формула площади равнобедренной трапеции через стороны и угол
b — верхнее основание
a — нижнее основание
c — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2. Формула площади равнобокой трапеции через радиус вписанной окружности
R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α, β — углы трапеции
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α, β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
m — средняя линия трапеции
c — боковая сторона
α, β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
b — верхнее основание
a — нижнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):
www-formula.ru
Как найти площадь геометрических фигур? – boeffblog.ru
Что такое площадь?
Площадь – характеристика замкнутой геометрической фигуры (круг, квадрат, треугольник и т.д.), которая показывает ее размер. Площадь измеряется в квадратных сантиметрах, метрах и т.д. Обозначается буквой S (square).
Как найти площадь треугольника?
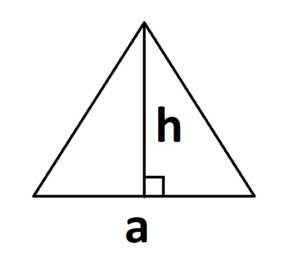
1. Самая известная формула площади треугольника по стороне и высоте:
S = a · h
где a – длина основания, h – высота треугольника, проведенная к основанию.
Причем, основание не обязательно должно находиться снизу. Так тоже сойдет. 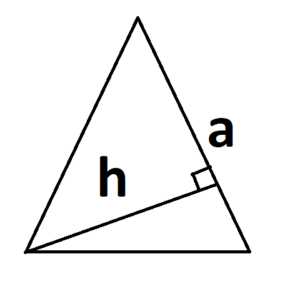
Если треугольник тупоугольный, то высота опускается на продолжение основания:
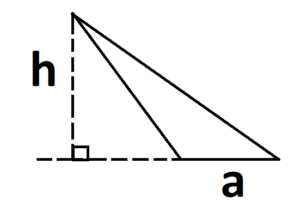
Если треугольник прямоугольный, то основанием и высотой являются его катеты:
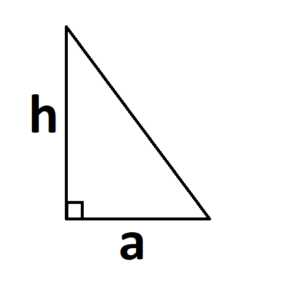
2. Другая формула, которая является не менее полезной, но которую почему-то всегда забывают:
S = a · b · sinα
где a и b – две стороны треугольника, sinα – синус угла между этими сторонами.
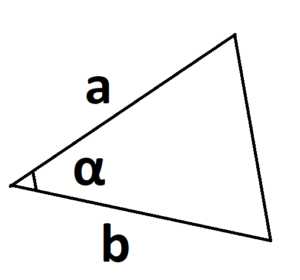
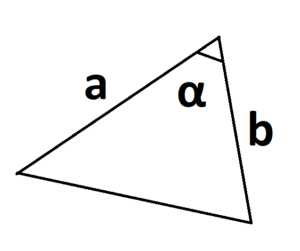
Главное условие – угол берется между двумя известными сторонами.
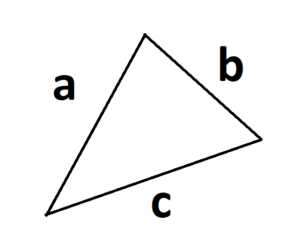
3. Формула площади по трем сторонам (формула Герона):
S =
где a, b и с – стороны треугольника, а р – полупериметр. p = (a + b + c)/2.
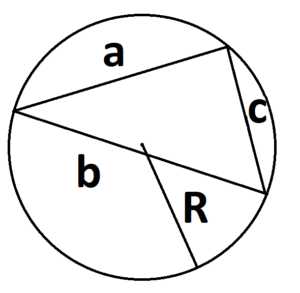
4. Формула площади треугольника через радиус описанной окружности:
S =
где a, b и с – стороны треугольника, а R – радиус описанной окружности.
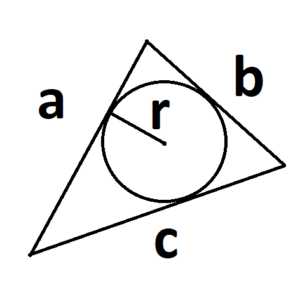
5. Формула площади треугольника через радиус вписанной окружности:
S =p · r
где р – полупериметр треугольника, а r – радиус вписанной окружности.
Как найти площадь прямоугольника?
1. Площадь прямоугольника находится довольно-таки просто:
S = a · b
Никаких подвохов.
Как найти площадь квадрата?
1. Так как квадрат является прямоугольником, у которого все стороны равны, то к нему применяется такая же формула:
S = a · a = a2
2. Также площадь квадрата можно найти через его диагональ:
S = d2
Как найти площадь параллелограмма?
1. Площадь параллелограмма находится по формуле:
S = a · h
Это связано с тем, что если от него отрезать прямоугольный треугольник справа и приставить его слева, получится прямоугольник:
2. Также площадь параллелограмма можно найти через угол между двумя сторонами:
S = a · b · sinα
Как найти площадь ромба?
Ромб по своей сути является параллелограммом, у которого все стороны равны. Поэтому для него применяются те же формулы площади.
1. Площадь ромба через высоту:
S = a · h
2. Площадь ромба через угол между сторонами:
S = a · a sinα = a2 · sinα
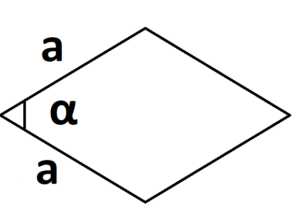
3. Площадь ромба через диагонали:
S = d1 · d2
Как найти площадь трапеции?
1. Площадь трапеции находится по следующей формуле:
S = · h
Как найти площадь круга?
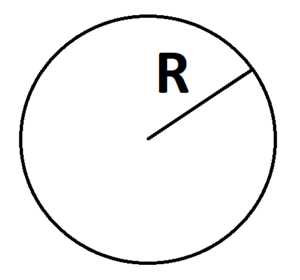
1. Площадь круга можно найти через радиус:
S = π r2
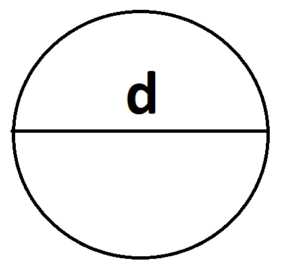
2. Площадь круга можно найти через диаметр:
S = πd2/4
boeffblog.ru
| Главная > Учебные материалы > Математика: Формулы площадей и объемов геометрических фигур | |||||||||||||||||||||||||
|
|||||||||||||||||||||||||
Формулы площадей 1.Площадь многоугольника. Формулы объемов1.Объем куба.2.Объем параллелепипеда. 3.Объем призмы. 4.Объем пирамиды. 5.Объем усеченной пирамиды. 6.Объем цилиндра. 7.Объем правильной треугольной пирамиды. 8.Объем конуса. 9.Объем усеченного конуса. 10.Объем тетраэдра. 11.Объем шара. 12.Объем шарового сегмента и сектора. Примеры решений С1. Видео. |
|||||||||||||||||||||||||
| 1 2 3 4 5 6 7 8 | |||||||||||||||||||||||||
Площадь многоугольника |
|||||||||||||||||||||||||
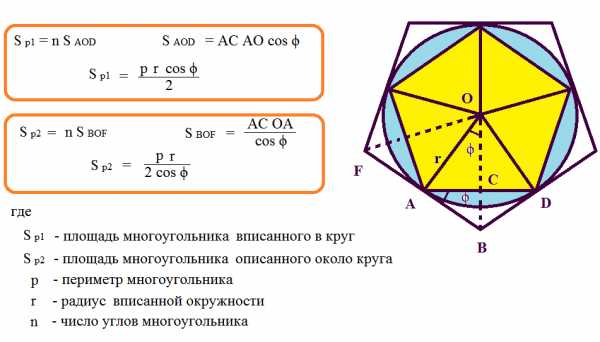 |
|||||||||||||||||||||||||
Рассчитать площадь многоугольника вписанного в круг и описанного около круга |
|||||||||||||||||||||||||
Площадь треугольника |
|||||||||||||||||||||||||
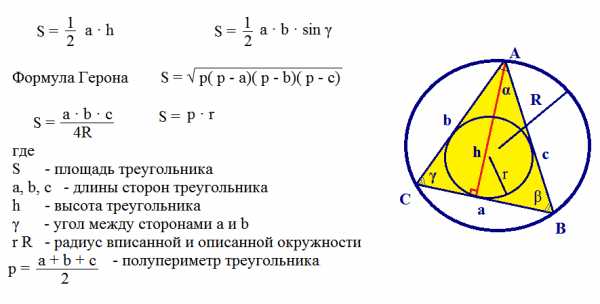 |
|||||||||||||||||||||||||
Рассчитать площадь треугольника |
|||||||||||||||||||||||||
Площадь квадрата |
|||||||||||||||||||||||||
Рассчитать площадь квадрата |
|||||||||||||||||||||||||
Площадь прямоугольника |
|||||||||||||||||||||||||
Рассчитать площадь прямоугольника |
|||||||||||||||||||||||||
Площадь параллелограмма |
|||||||||||||||||||||||||
Рассчитать площадь параллелограмма |
|||||||||||||||||||||||||
Площадь ромба |
|||||||||||||||||||||||||
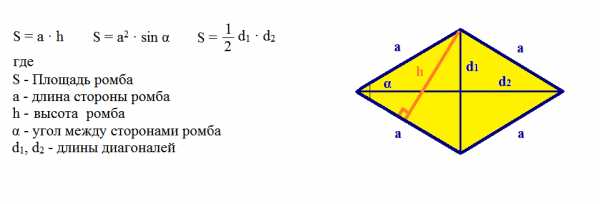 |
|||||||||||||||||||||||||
Рассчитать площадь ромба |
|||||||||||||||||||||||||
Площадь трапеции |
|||||||||||||||||||||||||
 |
|||||||||||||||||||||||||
Рассчитать площадь трапеции |
|||||||||||||||||||||||||
Площадь четырехугольника |
|||||||||||||||||||||||||
Рассчитать площадь четырехугольника |
|||||||||||||||||||||||||
Площадь круга |
|||||||||||||||||||||||||
Рассчитать площадь круга, длину окружности |
|||||||||||||||||||||||||
Площадь кругового сектора, длина дуги |
|||||||||||||||||||||||||
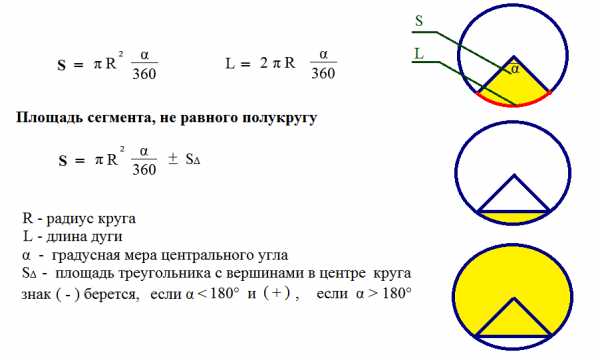 |
|||||||||||||||||||||||||
Рассчитать площадь кругового сектора, длину дуги |
|||||||||||||||||||||||||
Площадь эллипса |
|||||||||||||||||||||||||
Рассчитать площадь эллипса |
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
Объем куба |
|||||||||||||||||||||||||
Рассчитать объем и площадь поверхности куба |
|||||||||||||||||||||||||
Объем параллелепипеда |
|||||||||||||||||||||||||
Рассчитать объем параллелепипеда |
|||||||||||||||||||||||||
Объем призмы |
|||||||||||||||||||||||||
Рассчитать объем призмы |
|||||||||||||||||||||||||
Объем пирамиды |
|||||||||||||||||||||||||
Рассчитать объем пирамиды |
|||||||||||||||||||||||||
Объем усеченной пирамиды |
|||||||||||||||||||||||||
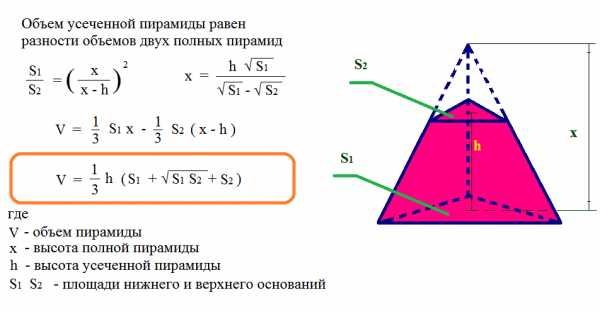 |
|||||||||||||||||||||||||
Рассчитать объем усеченной пирамиды |
|||||||||||||||||||||||||
Объем цилиндра |
|||||||||||||||||||||||||
Рассчитать объем цилиндра |
|||||||||||||||||||||||||
Объем правильной треугольной пирамиды |
|||||||||||||||||||||||||
Рассчитать объем правильной треугольной пирамиды |
|||||||||||||||||||||||||
Объем конуса |
|||||||||||||||||||||||||
Рассчитать объем конуса |
|||||||||||||||||||||||||
Объем усеченного конуса |
|||||||||||||||||||||||||
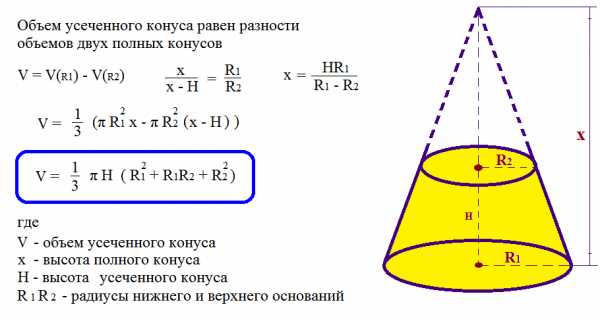 |
|||||||||||||||||||||||||
Рассчитать объем усеченного конуса |
|||||||||||||||||||||||||
Объем тетраэдра |
|||||||||||||||||||||||||
Рассчитать объем тетраэдра |
|||||||||||||||||||||||||
Объем шара |
|||||||||||||||||||||||||
Рассчитать объем и площадь поверхности шара |
|||||||||||||||||||||||||
Объем шарового сегмента и сектора |
|||||||||||||||||||||||||
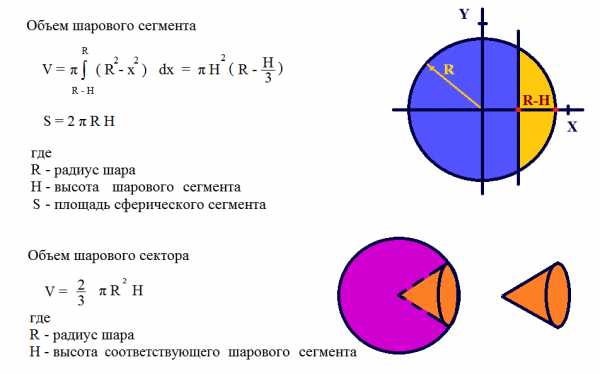 |
|||||||||||||||||||||||||
Рассчитать объем шарового сегмента |
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
| 1 2 3 4 5 6 7 8 | |||||||||||||||||||||||||
www.mathtask.ru
Площади фигур | Формулы с примерами
Площади фигур формулыПлощадь квадрата
Площадь прямоугольника
Площадь параллелограмма
Площадь ромба
Площадь треугольника

Площадь правильного треугольника
Площадь полупериметра
Площадь трапеции
Площадь описанного n угольника
Площадь произвольного четырехугольника
Площадь окружности
Площадь круга
formula-xyz.ru