Самостоятельная работа по математике «Формулы приведения»
Самостоятельные работы по теме «Преобразования тригонометрических выражений» для 10-х классов физико-математического профиля
САМОСТОЯТЕЛЬНАЯ РАБОТА
Тема: «Формулы приведения».
Вариант 1.
Упростить выражение:
а) ;
б) .
Вычислить:
а )
б) .
САМОСТОЯТЕЛЬНАЯ РАБОТА
Тема: «Формулы приведения».
Вариант 2.
1. Упростить выражение:
а) ;
б) .
2. Вычислить:
а) ;
б) .
САМОСТОЯТЕЛЬНАЯ РАБОТА
Тема: «Формулы приведения».
Вариант 3.
1. Упростить выражение:
а) ;
б) .
2. Вычислить:
а );
б) .
САМОСТОЯТЕЛЬНАЯ РАБОТА
Тема: «Формулы приведения».
Вариант 4.
1. Упростить выражение:
а) ;
б) .
2. Вычислить:
а)
б) .
Ответы к самостоятельной работе «Формулы приведения».
Вариант 1
Вариант 2
Вариант 3
Вариант 4
videouroki.net
Зачет по алгебре 10 класса на тему «Формулы приведения» (тригонометрия)
1- вариант
1) cos(π + x)=
2) sin(½π – x)=
3) tg(2π + x)=
4) ctg(3/2π –x)=
5) cos2(2π — x)=
6) — sin( 3/2π +x)=
7) 2tg(½π – x)=
8) ¼ ctg(2π –x)=
9) cos(x – π)=
10) sin2(½π + x)=
__________________________________
3- вариант
1) sin(π + x)=
2) cos(3/2π –x)=
3) ctg(2π+x)=
4) tg(½π – x)=
5) sin2(x – π)=
6) cos3(3/2π +x)=
7) 4tg(½π + x)=
8) ctg(2π — x)=
9) – sin(x — ½π)=
10) cos(-π-x)=
2 — вариант
1) cos(x – π)=
2) sin(3/2π +x)=
3) tg2(2π — x)=
4) — ctg(½π + x)=
5) 3cos(π + x)=
6) sin3(3/2π –x)=
7) tg(2π + x)=
8) ctg(½π – x)=
9) – cos(-2π – x)=
10) sin(-½π + x)=
___________________________________
4 — вариант
1) sin(½π + x)=
2) cos(π + x)=
3) tg(
4) ctg(2π + x)=
5) sin2(½π – x)=
6) cos2(π– x)=
7) tg3(3/2π –x)=
8) ctg3 (2π — x)=
9) — cos(-½π – x) =
10) 5sin(-2π — x)=
6 — вариант
1) cos(½π – x)=
2) sin(π–x)=
3) tg(3/2π –x)=
4) ctg(2π — x)=
5) cos(½π + x)=
6) sin(π + x)=
7) tg(3/2π +x)=
8) ctg2(2π + x)=
9) — cos(x – π)=
10) -3sin3(-3/2π –x)=
____________________________
8 — вариант
1) tg(½π + x)=
2) ctg(π + x)=
3) cos(3/2π +x)=
4) sin(2π + x)=
5) tg (½π + x)=
6) ctg2(½π – x)=
7) — cos3(-x + π)=
8) 6sin(4π — x)=
9) tg(- 3/2
π –x)=10) ctg( 7/2π + x)=
5- вариант
1) tg(2π — x)=
2) ctg(3/2π –x)=
3) cos(π–x)=
4) sin(-2π — x)=
5) tg(9 /2π + x)=
6) ctg(π + x)=
7) cos2(3/2π +x)=
8) sin(2π + x)=
9) – tg3(x – π)=
10) ctg(6π — x)=
_________________________________
7 — вариант
1) ctg (½π + x)=
2) tg (π + x)=
3) sin (3/2π +x)=
4) cos (2π + x)=
5)-2 ctg (½π – x)=
6) tg (π–x)=
7) sin (3/2π –x)=
8) -cos2 (x – π)=
9) ctg (-8π — x)=
10) tg (5π + x)=
10 — вариант
1) ctg(3/2π –x)=
2) tg (½π + x)=
3) sin (π–x)=
4) cos (2π + x)=
5) ctg (½π – x)=
6) tg (3/
7) sin2 (π + x)
8) -cos (2π — x)=
9) sin (-6π + x)=
10) cos3 (-9 /2π – x)=
12 — вариант
1) ctg (3/2π +x)=
2) tg (½π + x)=
3) sin (π + x)=
4) -4cos (2π + x)=
5) ctg (-3/2π –x)=
6) tg (-½π – x)
7) sin2 (π–x)=
8) cos3 (2π — x)=
9) -ctg (½π – x)
10) tg (x –3 π)=
11 — вариант
1) ctg (π + x)=
2) tg (2π + x)=
3) — sin (½π + x)=
4) cos (3/2π +x)=
5) tg (x – π)=
6) -ctg (x -2π) =
7) sin2 (-½π – x)=
8) cos3 (-3/2π –x)=
9) -5 tg (6π + x)=
10) sin (4π — x)=
__________________________________
9- вариант
1) tg (π–x)=
2) ctg (2π — x)=
3) sin (½π – x)=
4) cos (- 3/2π –x)=
5) tg (5π + x)=
6) ctg (2π + x)=
7) sin2 (x – π)=
8) — cos (3/2π +x)=
9) — tg3 (½π – x)=
10) ctg (-8π — x)=
multiurok.ru
Конспект урока «Формулы приведения» 10 класс
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа №5 г. Курганинска
Разработка урока дифференцированного обучения для 11 класса для подготовки к ЕГЭ «Формулы приведения»
Автор:Писаренко Галина Павловна
учитель математики МБОУ СОШ №5, высшая квалификационная категория
г. Курганинск, 2011 г.
Урок дифференцированного обучения:
«Формулы приведения»
Тип урока: комбинированный.
Цели урока:
• Обучающая: выработать у учащихся умения применять формулы приведения при преобразовании тригонометрических выражений; обобщить и систематизировать знания учащихся по теме «Преобразования тригонометрических выражений».
• Развивающая: развивать навыки самоконтроля, умения сравнивать, анализировать, делать выводы, применять полученные знания на практике.
• Воспитательная цель: воспитывать самостоятельность, чувства коллективизма, интереса к предмету.
Техническое обеспечение урока: мультимедийное оборудование.
Ход урока:
1. Организационный момент.
2. Устная работа (проверка усвоения материала базового уровня).
Разминка:
• Продолжить: sin30 = cos =
cos 45 =sin =
sin60 =cos =
tg 45 =ctg =
• Углом какой четверти являются следующие углы:275 ,520 ,,-75̊̊̊
•Какой знак имеют тригонометрические функции в четвертях: sin х, cos х, tg x .
Мнемоническое правило формул приведения (УЗИ):
Угол (находим какой четверти принадлежит данный угол)
Знак (определяем знак функции данного угла)
Имя (-Имя функция меняет? Кивок головой на вопрос отвечает: да- )
3.Работа у доски:
Вычислите: 1) sin150+cos315-tg225
Решение.
2) sin135+tg45
3)-2cos(
Задания самостоятельной работы аналогичны. Учащимся предлагается самим определиться с выбором группы.
4. Работа в группах:
Задания для группы «Всезнайки»
1.Вычислить:sin150 +tg45
2. Вычислите: sin 330 + ctg 585
3. Упростите:
4. Вычислить:
5.Упростите: (1+ соs(-x))2+(1-sin(3+x))2 -4сos2x
Задания для группы «Знатоки»
1. Вычислите:sin 90 – cos 120
3. Упростите:cos (+x)+ tg (-x)+ctg(2+x)+sin(-x)
4. Вычислить:
5. Упростите: 1-sin2(3\2-x) +sin2(-x)
Задания для группы «Почемучки»
1.Вычислите: сos 0 +sin 330: 2.Вычислите:cos 120 –tg 135 3. Вычислите: 4.Вычислить: -2сos(360 при х=15 5. Упростите: cos2(sin2()
Учащимся со «слабым» уровнем знаний материала преподаватель оказывает помощь. После выполнения заданий выбранной группы, можно выполнять задания следующего уровня.
5. Самопроверка самостоятельной работы:
1) 1,5
2) 0,5
3) -sin x
4) -0,5
5) 2sin2x
Правильный ответ задания оценивается «+». «Всезнайки» получают «отлично» при пяти правильных ответах, «хорошо» -при четырех. «Знатоки»: « хорошо» — при пяти правильных ответах. Для получения оценки «отлично» необходимо решение 2 задания из вышестоящей группы. «Почемучки» — «хорошо» при выполнении пяти заданий.
6. Подведение итогов, выставление оценок за урок.
7. Домашнее задание:
1). Сделать работу над ошибками самостоятельной работы.
2). Придумать примеры с применением формул приведения (УЗИ) и решить их (5 примеров).
3). Выполнить задания из учебника: .№ 26.10(г),26.12(а), 26.21(в,г)
infourok.ru
Самостоятельная работа по математике «Формулы приведения»
Формулы приведения
Вариант 1
Вычислите: sin2400 + cos1500.
Ответ: 1) -; 2) 0; 3) ; 4)
Вычислите:
Ответ: 1) 0; 2) ; 3) 2; 4)
Упростите:
Ответ: 1) 1; 2) tgβ; 3) -1; 4) 0
Упростите: tg(2700+) — ctg(2700-)
Ответ: 1) ; 2) ; 3) 0; 4) tgα
Вычислите: tg410 tg420 …
Формулы приведения
Вариант 2
Вычислите: sin2400 + cos1500.
Ответ: 1) -; 2) 0; 3) ; 4)
Вычислите:
Ответ: 1) 0; 2) ; 3) 2; 4)
Упростите:
Ответ: 1) 1; 2) tgβ; 3) -1; 4) 0
Упростите: tg(2700+) — ctg(2700-)
Ответ: 1) ; 2) ; 3) 0; 4) tgα
Вычислите: tg410 tg420 …
Формулы приведения
Вариант 3
Вычислите: sin2400 + cos1500.
Ответ: 1) -; 2) 0; 3) ; 4)
Вычислите:
Ответ: 1) 0; 2) ; 3) 2; 4)
Упростите:
Ответ: 1) 1; 2) tgβ; 3) -1; 4) 0
Упростите: tg(2700+) — ctg(2700-)
Ответ: 1) ; 2) ; 3) 0; 4) tgα
Вычислите: tg410 tg420 …
Формулы приведения
Вариант 4
Вычислите: sin2400 + cos1500.
Ответ: 1) -; 2) 0; 3) ; 4)
Вычислите:
Ответ: 1) 0; 2) ; 3) 2; 4)
Упростите:
Ответ: 1) 1; 2) tgβ; 3) -1; 4) 0
Упростите: tg(2700+) — ctg(2700-)
Ответ: 1) ; 2) ; 3) 0; 4) tgα
Вычислите: tg410 tg420 …
videouroki.net
Контрольная работа по теме «Формулы приведения и сложения» для 10 класса
Контрольная работа №1
по теме: «Формулы приведения и формулы сложения»
ВАРИАНТ I
Вычислите:
а) sin150º;
б) cos29ºcos16º — sin29ºsin16º;
в) sin240º + cos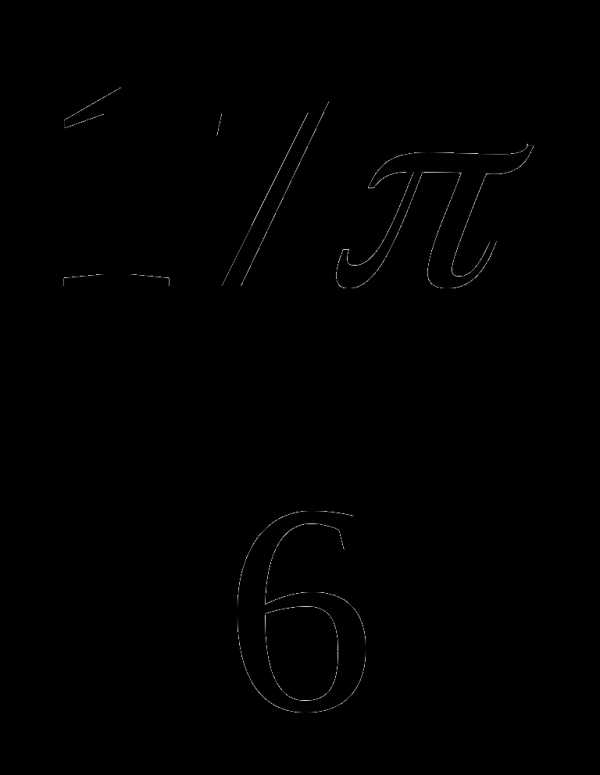 ;
;
г) ;
д) ctg1ºctg2ºctg3º…ctg88◦ctg89º
Найдите значение трех других тригонометрических функций угла
 :
:
cosα=  и
и 
Упростите выражение:
а) ;
б) ;
в) 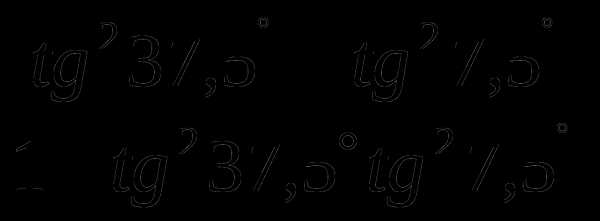
Найдите наибольшее значение выражения
Вычислите при данных условиях
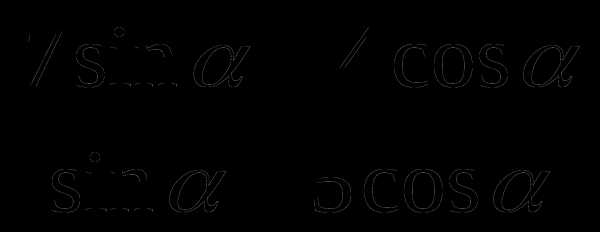 , если tg
, если tg =2
=2
_________________________________________________________________________
Контрольная работа №1
по теме: «Формулы приведения и формулы сложения»
ВАРИАНТ II
Вычислите:
а) cos240º;
б) sin29ºcos16º +sin16ºcos29º;
в) cos150º + sin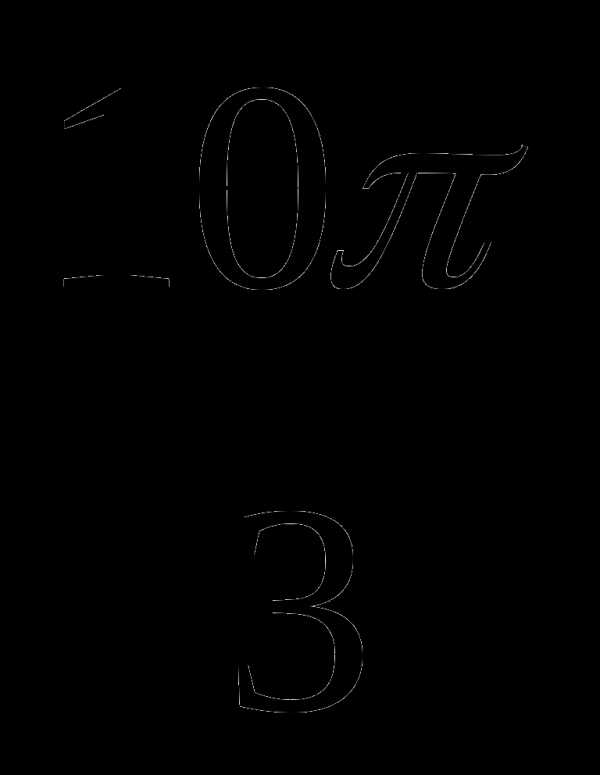 ;
;
г) ;
д) tg1ºtg3ºtg5º…tg89º
Найдите значение четырех основных тригонометрических функций угла
 :
:
sinα= и
и 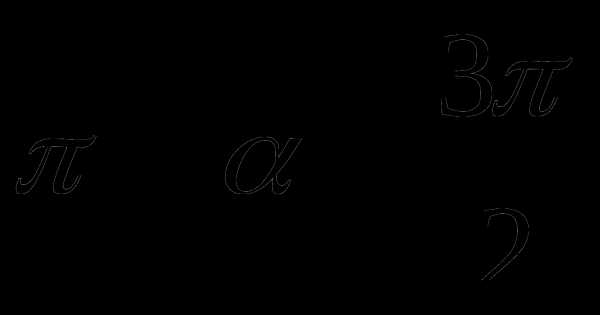
Упростите выражение:
а) ;
б) ;
в) 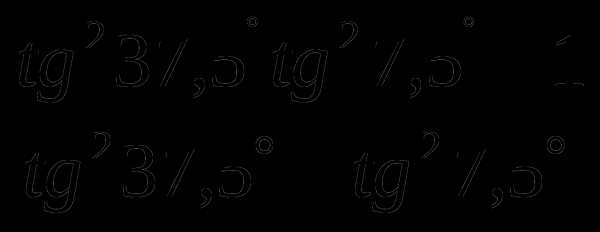
Найдите наибольшее значение выражения
Вычислите при данных условиях
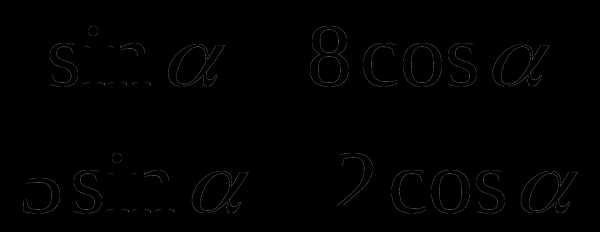 , если tg
, если tg =3
=3
Контрольная работа №1
по теме: «Формулы приведения и формулы сложения»
ВАРИАНТ III
Вычислите:
а) sin390º;
б) cos76ºcos31º + sin76ºsin31º;
в) sin530º — cos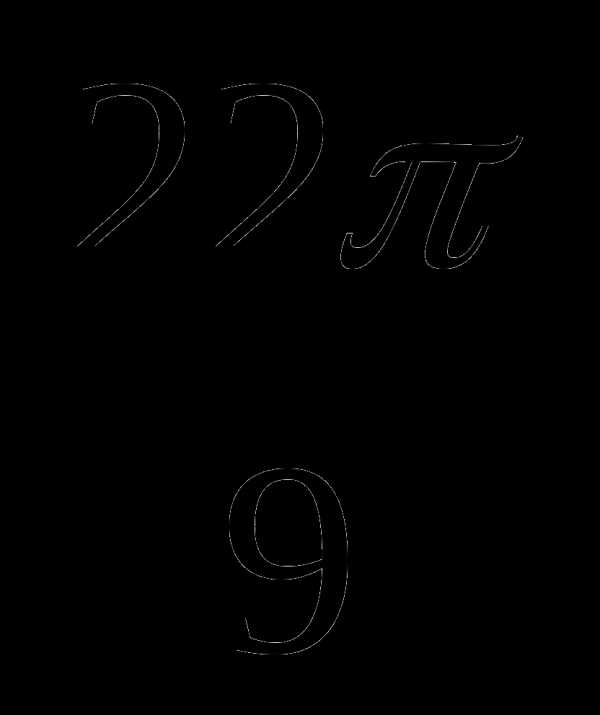 ;
;
г) ;
д) tg88ºtg86ºtg84º…tg2º
Найдите значение четырех основных тригонометрических функций угла
 :
:
25sin² + 5sin
+ 5sin — 12 = 0 и
— 12 = 0 и 
Упростите выражение:
а) ;
б) ;
в) 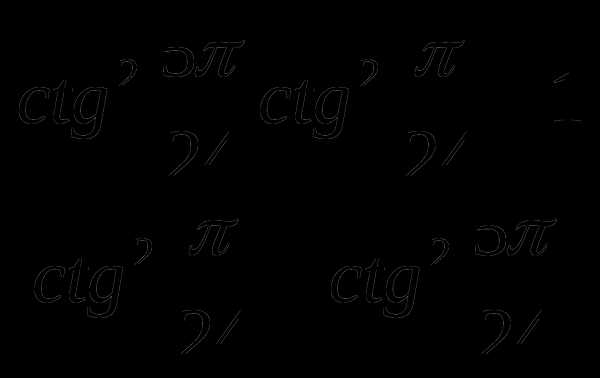
Найдите наибольшее значение выражения
Вычислите при данных условиях
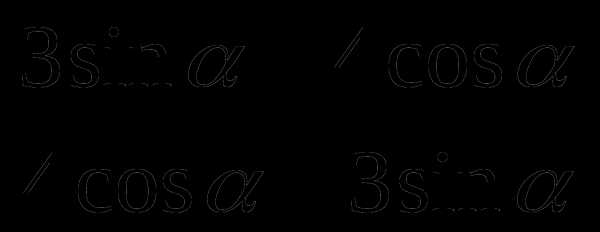 , если сtg
, если сtg =
=
_____________________________________________________________________________
Контрольная работа №1
по теме: «Формулы приведения и формулы сложения»
ВАРИАНТ IV
Вычислите:
а) cos420º;
б) sin76ºcos31º — sin31ºcos76º;
в) cos770º — sin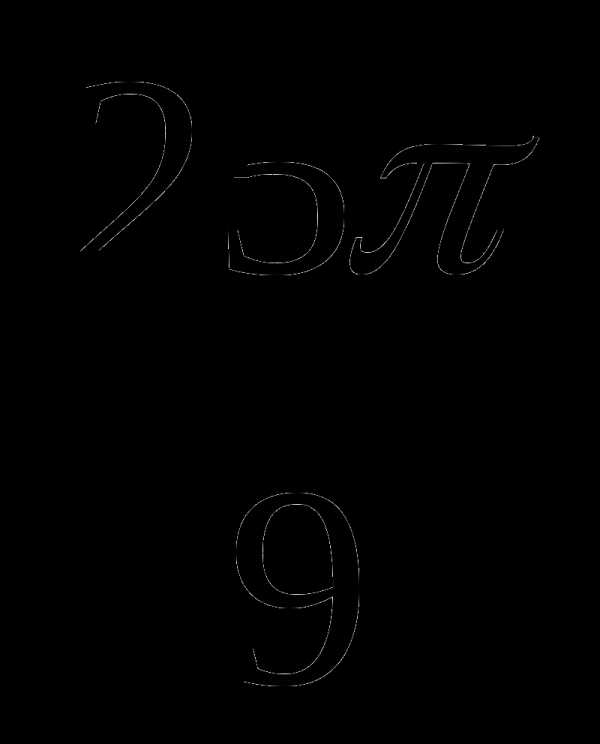 ;
;
г) ;
д) ctg2ºctg4ºctg6º…ctg88º
Найдите значение четырех основных тригонометрических функций угла
 :
:
25cos² — 5cos
— 5cos — 12 = 0 и
— 12 = 0 и 
Упростите выражение:
а) ;
б) ;
в) 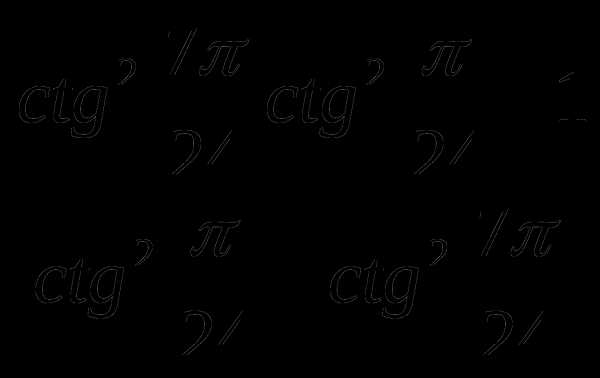
Найдите наибольшее значение выражения
Вычислите при данных условиях
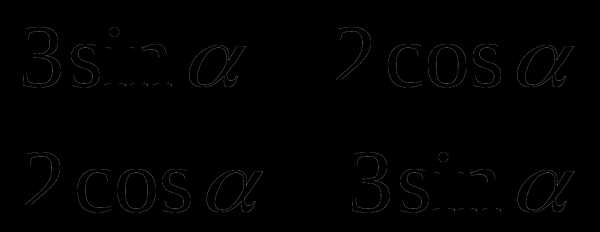 , если tg
, если tg =
=
infourok.ru
| Самостоятельная работа в 10 классе Из данных молекулярных формул выпишите амины, составьте их структурные формулы, дайте названия | Самостоятельная работа по теме : «Валентность» Составьте формулы сложных веществ, определив значения индексов Х и У: FexCly, NaxSy, CrxOy, HxNy, AgxOy | ||
| Самостоятельная работа по теме У какого из простых веществ, образованных элементами №11, 12, 13 наиболее ярко выражены металлические свойства ? Почему? Напишите… | Самостоятельная работа №1 (6 ч.) Самостоятельная работа №1 (6 ч.) Слушателя: Баранецкой Олеси Михайловны, г. Долгопрудный, мбоу школа №3 | ||
| Самостоятельная работа по теме «Химические формулы. Относительная молекулярная масса. Массовая доля элемента в веществе» Какое из соединений – халькозин (Сu2 S) или куприт (Сu2O) – богаче медью? Ответ подтвердите расчетом | Документи 1. /Алимов/КУС Производная.doc 2. /Алимов/Контрольная… | ||
| План урока по алгебре и началам анализа в 11 классе по теме «Степень с рациональным показателем» Применяемые формы работы: фронтальная работа, индивидуальная самостоятельная работа, работа в парах | Общая характеристика методов обучения Традиционные: рассказ, беседа лекция, семинар, семинар-практикум, практикум, практическая работа, лабораторная работа, экскурсия,… | ||
| Урок по алгебре и началам анализа в 10 классе по теме Методы обучения: словесный, наглядный, решение задач, самостоятельная работа, работа в группах | Основы мировых религиозных культур Республика Бурятия, г. Улан-Удэ, мбоу «Курумканская средняя общеобразовательная школа №1» Знакомство, работа с картой, беседа, путешествие в слово «Родина», комментированное чтение, устный рассказ на тему, работа с иллюстративным… | ||
| Урок по русскому языку в 3 классе на тему: «Правописание безударных гласных в корне слова» Приемы: фронтальный опрос, самостоятельная работа, комментирование, беседа, взаимопроверка, работа в группах |
lib2.podelise.ru
Разноуровневый урок закрепления знаний по теме «Формулы приведения». Алгебра, 10 класс.
Посысалова Л.Н. (ст. Ярославская, Мостовского района, СОШ №14)
Разноуровневый урок закрепления знаний по теме
«Формулы приведения».
Урок разработан для учащихся 10 классов, является вторым в теме «Формулы приведения».
Цель урока: закрепление формул приведения, выработка навыков их применения при нахождении углов больше 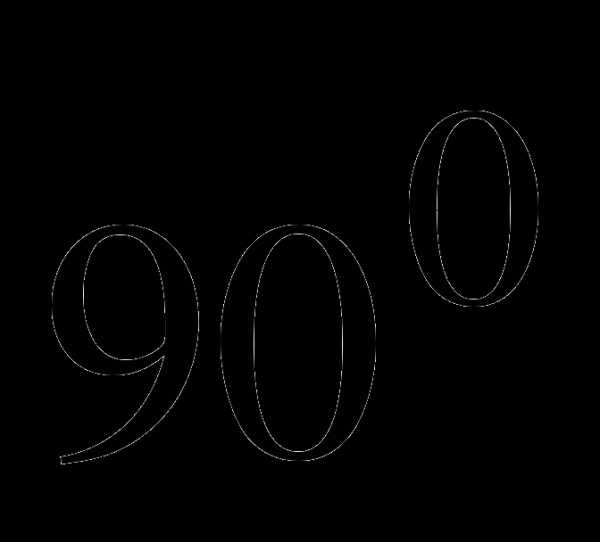 , преобразовании тригонометрических выражений. Рассмотреть методы решения тригонометрических выражений базового и повышенного уровней сложности.
, преобразовании тригонометрических выражений. Рассмотреть методы решения тригонометрических выражений базового и повышенного уровней сложности.
Организовать работу по теме на уровне, соответствующем уровню уже сформированных знаний.
1 этап урока – организационный (1 минута).
Учитель сообщает учащимся тему урока, цель и обращает внимание на раздаточный материал, который находится на столах и будет использован в ходе урока.
2 этап урока (5 минут).
Повторение теоретического материала по теме
«Тригонометрические выражения».
Учитель задает учащимся вопросы:
-что называется синусом, косинусом, тангенсом и котангенсом ?
-назовите знаки синуса, косинуса, тангенса и котангенса по четвертям;
-сформулируйте основное тригонометрическое тождество;
— выразите из основного тригонометрического тождества синус и косинус;
— чему равно произведение тангенса угла на котангенс того же угла?
-чему равны синус, косинус, тангенс и котангенс угла  .
.
3 этап урока (5 минут)
Устная работа по решению простейших задач по теме
«Тригонометрические выражения».
Учащимся предлагается лист приложения №1 с заданиями для устного счета.
Учитель предлагает учащимся самостоятельно выполнить задания (кроме задания №8), записав ответы, а затем по очереди отвечать на вопросы, комментируя свои ответы ссылкой на соответствующий теоретический факт.
4 этап урока (10 минут)
Повторение теоретического материала по теме
«Формулы приведения».
Перед решением задач необходимо повторить выборочно формулы приведения и правило, позволяющее их запомнить без особого труда.
Сформулируйте правило, позволяющее переходить от углов больше 900 к углам от 00 до 900. Выполнить задание №8 устного счета.
8.Упростите выражения:
а)  в)
в)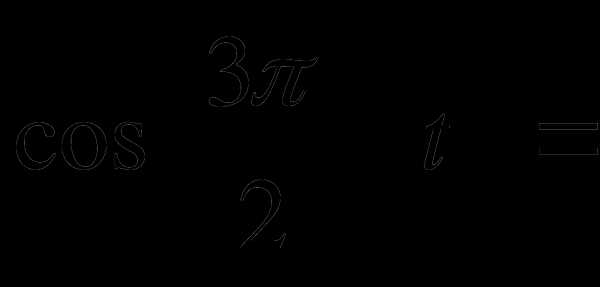 д) ж)
д) ж)
б) г) е) з)
К доске вызываются три ученика, которые решают задания базового уровня. Ученики каждого ряда работают соответственно с одним из учеников. После окончания работы рассматриваются ошибки, допущенные в ходе выполнения заданий.
Затем к доске вызывается один ученик, которому предлагается решить более сложное задание.
1.Найдите значение выражения:
Ученикам предлагается вспомнить способы доказывания тождеств и предлагается ( по желанию ученика) доказать тождество.
2. Докажите тождество:
5 этап урока ( 15 минут)
Разноуровненвая самостоятельная работа.
Ученикам предлагаются карточки с разноуровневыми самостоятельными работами. Один из учеников выполняет свою работу у доски.
6 этап урока (2 минуты).
Обсуждение ошибок, допущенных в работе.
На этом этапе рассматривается решение заданий учеником у доски и обсуждение допущенных ошибок.
7 этап урока (2 минуты).
Подведение итогов урока, постановка домашнего задания.
Учитель еще раз обращает внимание, на те типы заданий и теоретические факты, которые рассматривались на уроке, говорит о необходимости выучить их, дает оценку работы учащихся на уроке, выставляет отметки.
В качестве домашнего задания учащиеся должны повторить параграфы 26,27,31, задания на карточках.
Задания для устного счета.
1.Упростите выражение:
а) 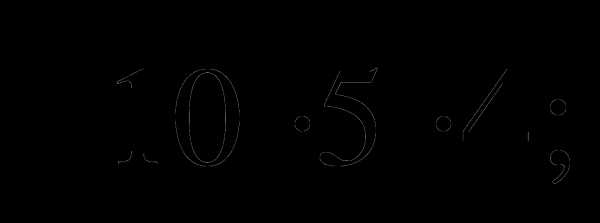 б)
б) 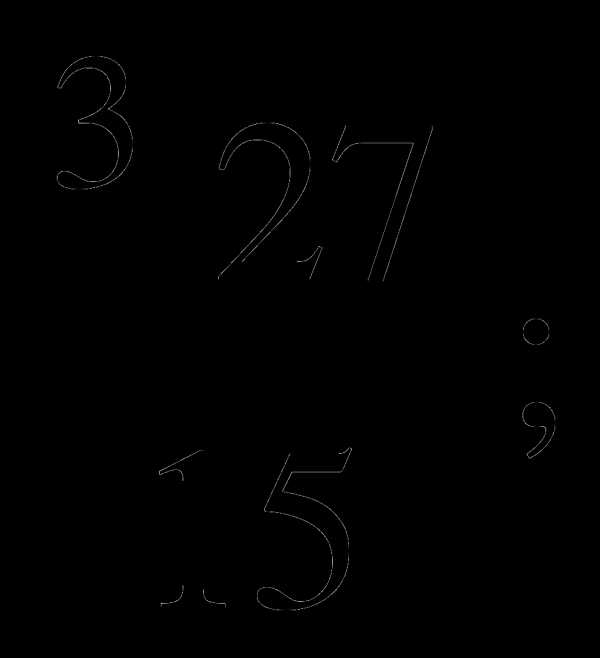 в)
в) 
2.Упростите выражение:
а) 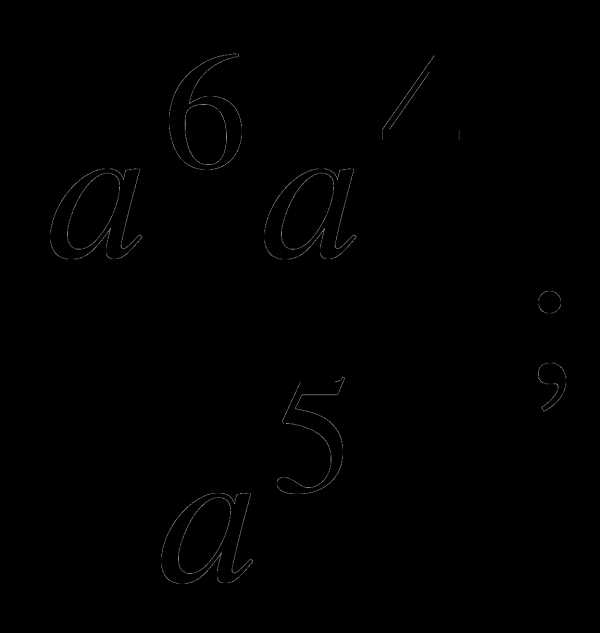 б)
б) 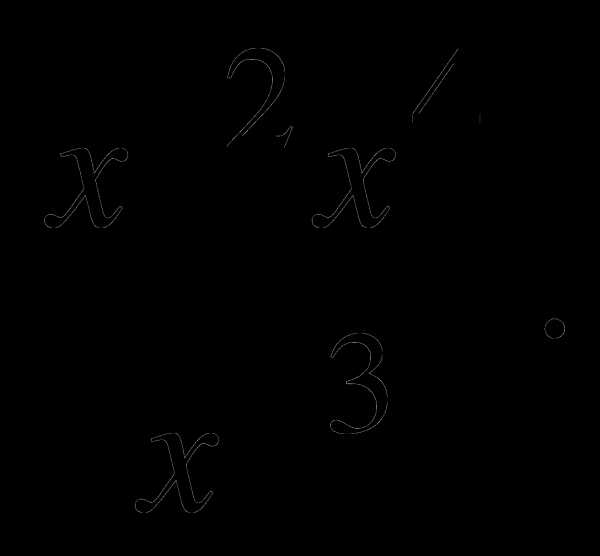
3.Переведите из градусной меры в радианную:
а)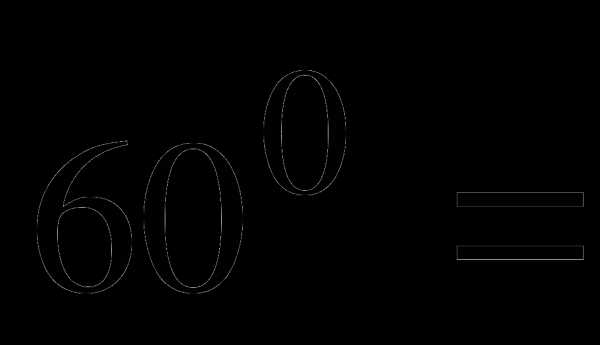 б)
б) 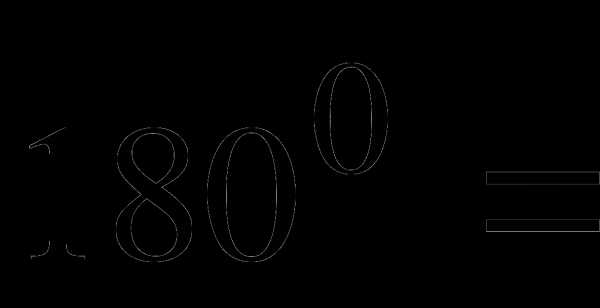 в)
в) 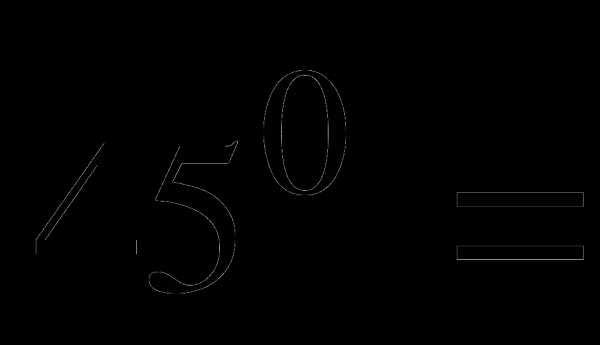 г) 2700=
г) 2700=
4.Переведите из радианной меры в градусную:
а) 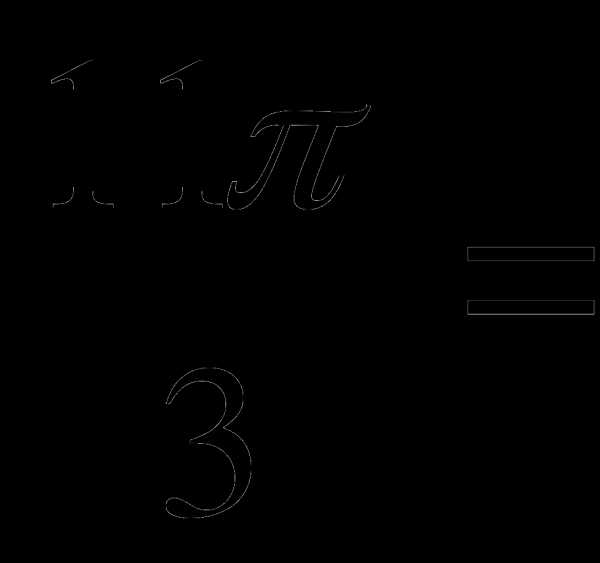 б)
б)  в)
в)  г)
г) д)
д) 
5.Определите четверть, если:
а) б)
6. Вычислите:
а) 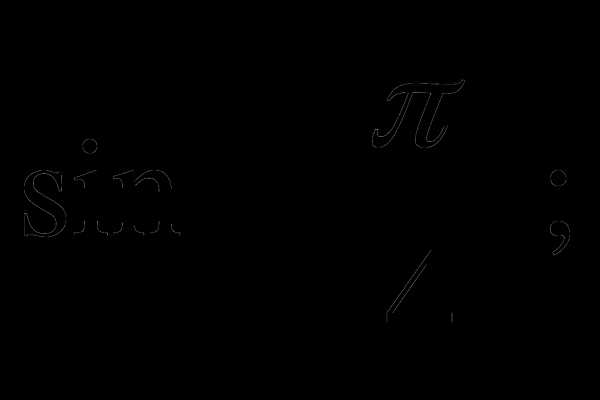 б)
б) 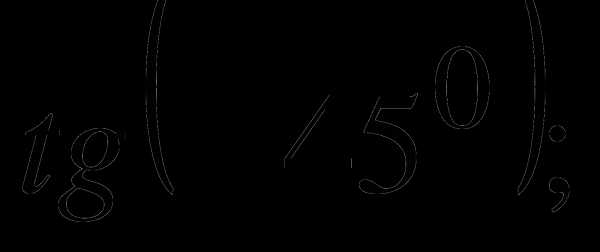 в)
в)  г)
г) 
7.Упростите выражение.
а) в)
в)
б) г)
8.Упростите выражения:
а)  в)
в)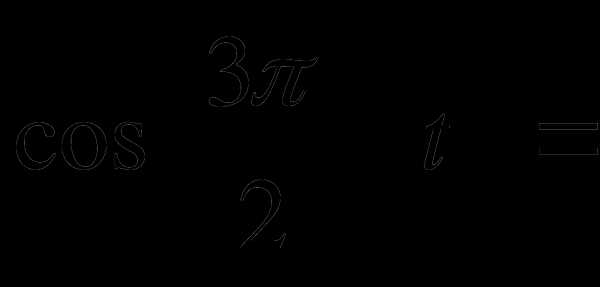 д) ж)
д) ж)
б) г) е) з)
Работа у доски.
__________________________________________________________________________________
Вариант1.
1.Вычислить с помощью формул приведения.
а) 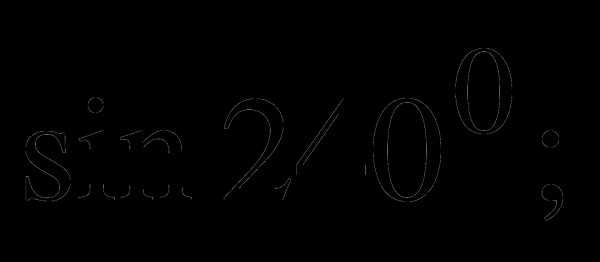 б)
б) 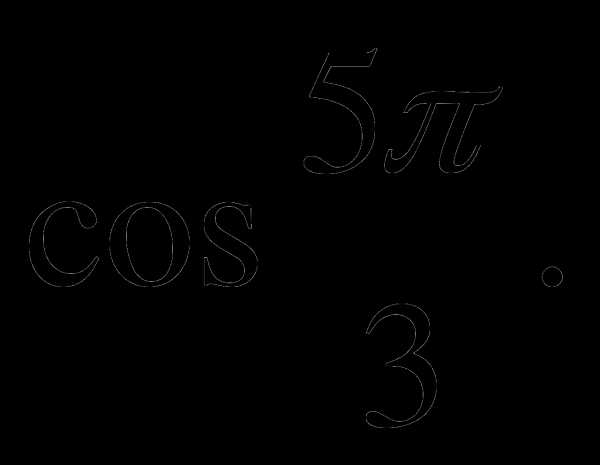
2.Упростить выражение:
3.Вычислите:
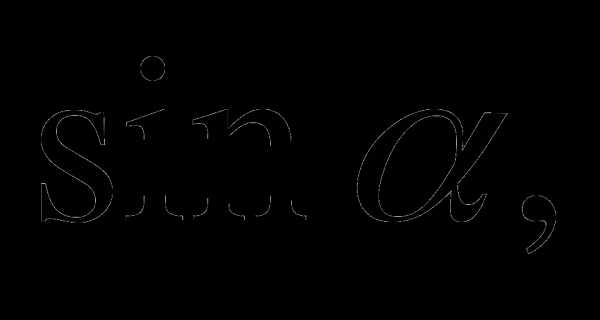 если
если 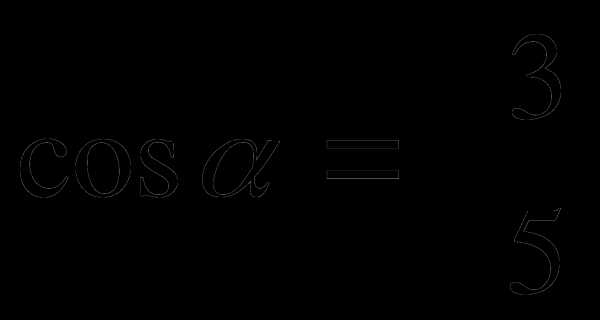 и
и 
__________________________________________________________________________________
Вариант2.
1.Вычислить с помощью формул приведения.
а) 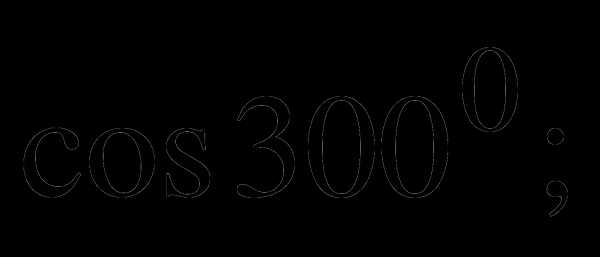 б)
б) 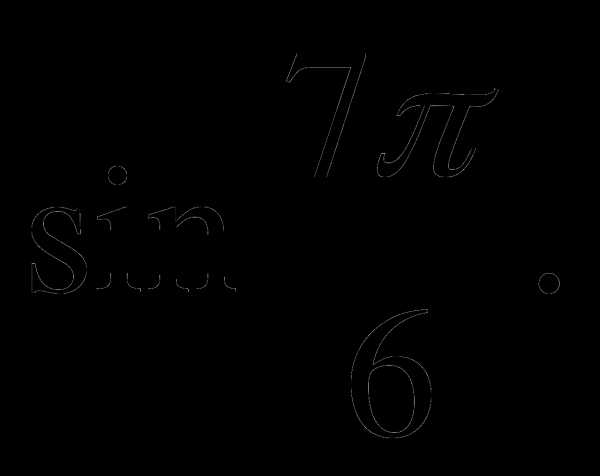
2.Упростить выражение:
3.Вычислите:
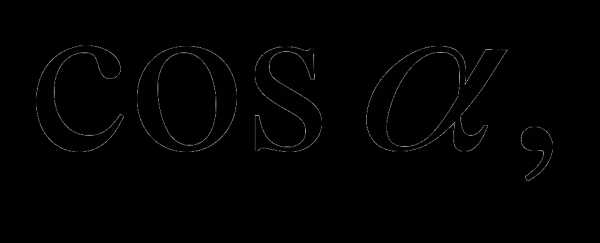 если
если 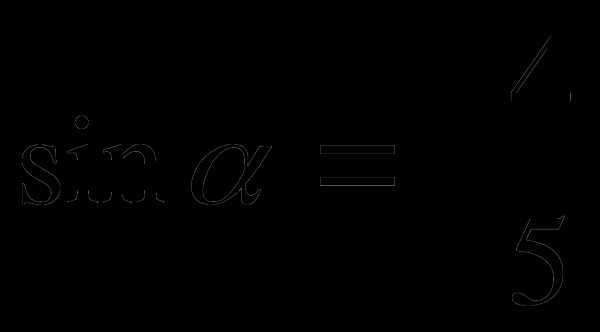 и
и 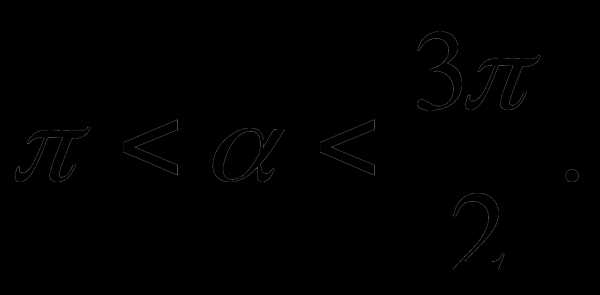
__________________________________________________________________________________
Вариант 3.
1.Вычислить с помощью формул приведения.
а) 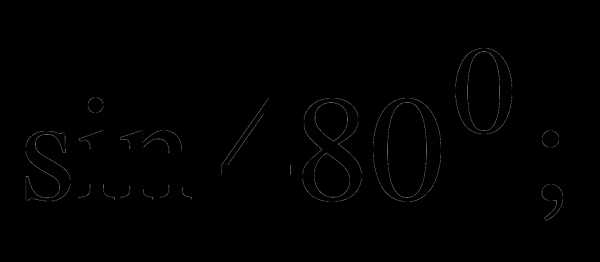 б)
б) 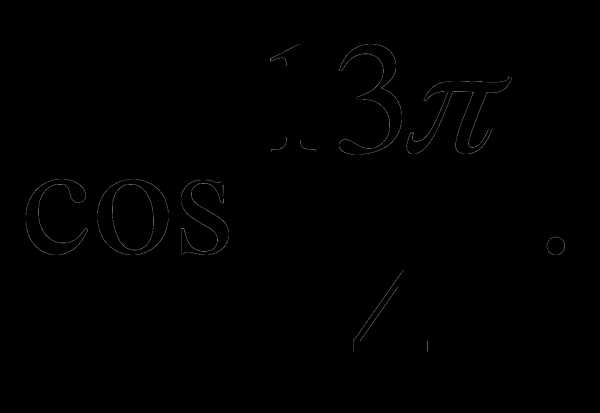
2.Упростить выражение:
3.Вычислите:
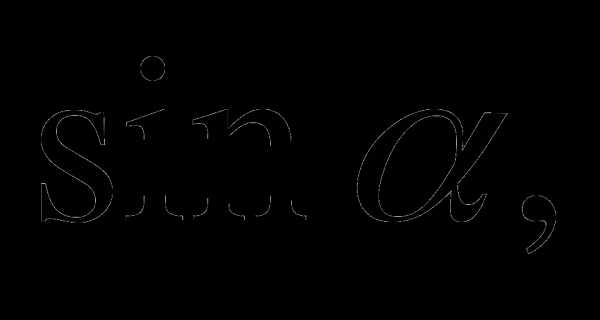 если
если 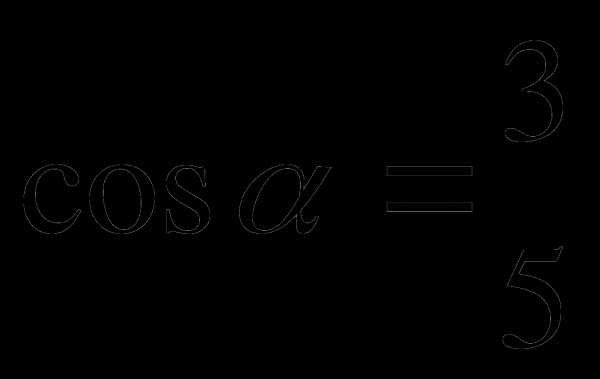 и
и 
__________________________________________________________________________________
1.Найдите значение выражения:
2. Докажите тождество:
1 уровень.
Работа у доски.
Вариант1.
1.Вычислить с помощью формул приведения.
а) 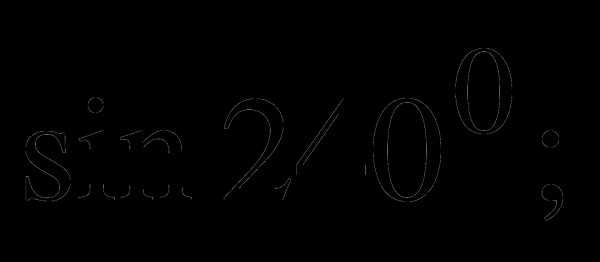 б)
б) 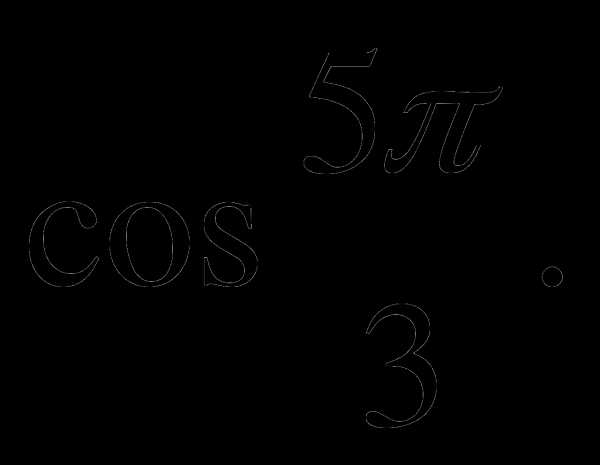
2.Упростить выражение:
3.Вычислите:
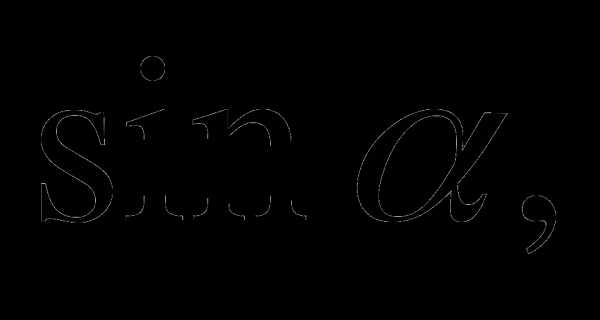 если
если 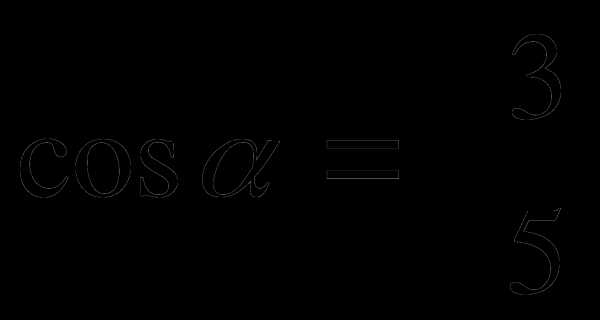 и
и 
_____________________________________________________________________________
1.Найдите значение выражения:
2. Докажите тождество:
_____________________________________________________________________________
Самостоятельная работа.
Вариант 1.
1.Переведите из градусной меры в радианную:
а) 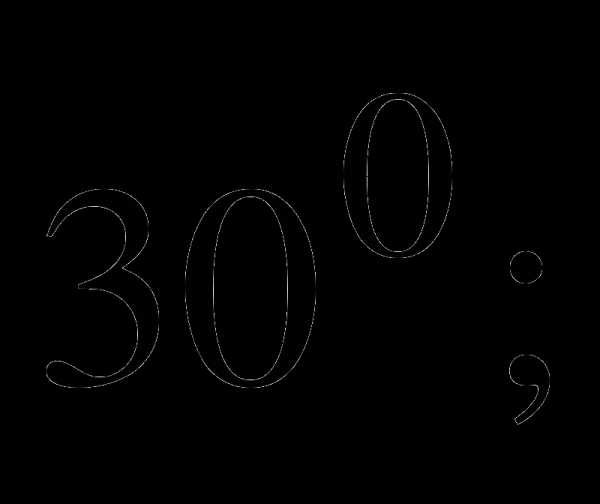 б) 1500.
б) 1500.
2.Переведите из радианной меры в градусную:
а)  б)
б) 
3. Преобразуйте с помощью формул приведения:
а)  б)
б)
4.Вычислите с помощью формул приведения:
а) 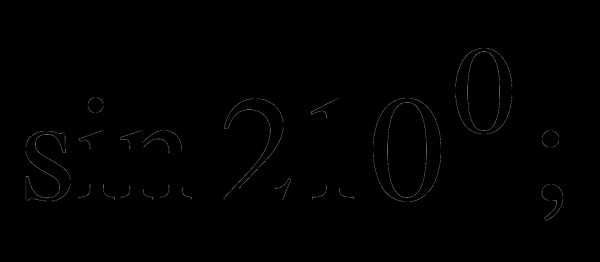 б)
б) 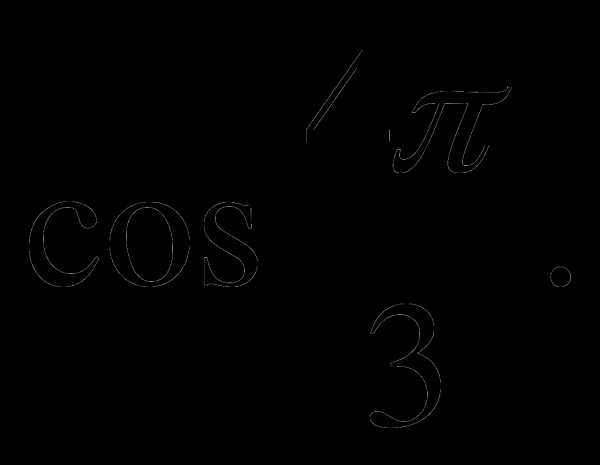
5.Найдите значение выражения:
1 уровень.
Вариант1.
1.Вычислить с помощью формул приведения.
а) 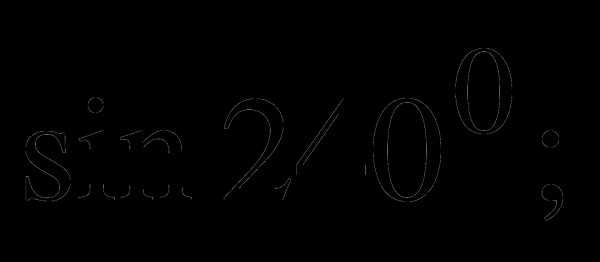 б)
б) 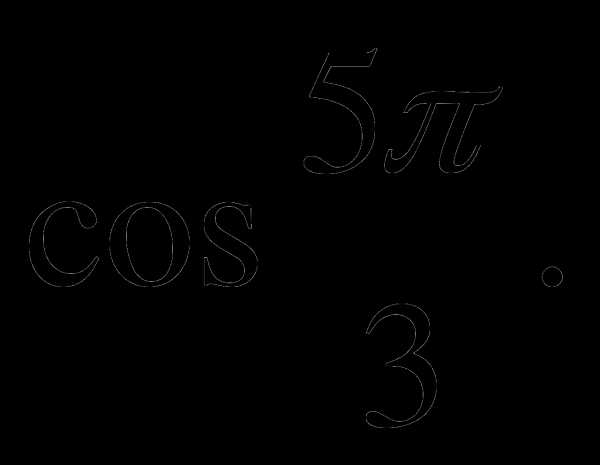
2.Упростить выражение:
3.Вычислите:
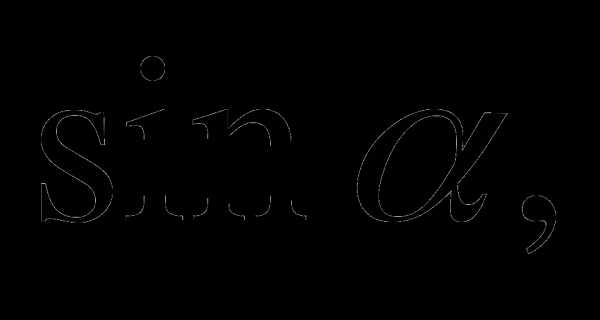 если
если 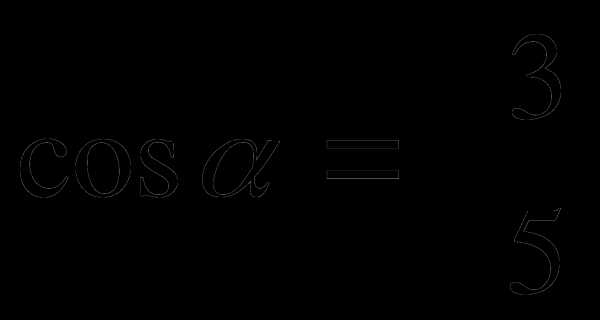 и
и 
_____________________________________________________________________________
1.Найдите значение выражения:
2. Докажите тождество:
_____________________________________________________________________________
Самостоятельная работа.
Вариант 2.
1.Переведите из градусной меры в радианную:
а) 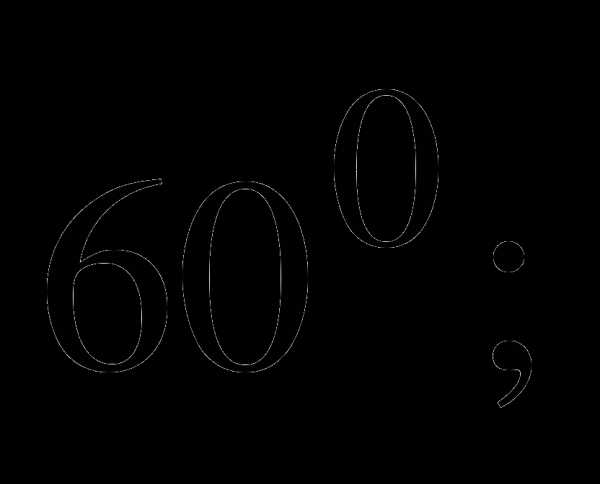 б) 2400.
б) 2400.
2.Переведите из радианной меры в градусную:
а)  б)
б) 
3. Преобразуйте с помощью формул приведения:
а) б) 
4.Вычислите с помощью формул приведения:
а) 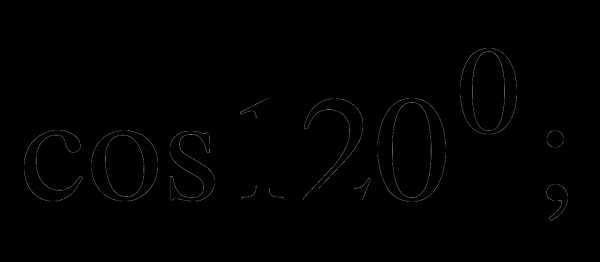 б)
б) 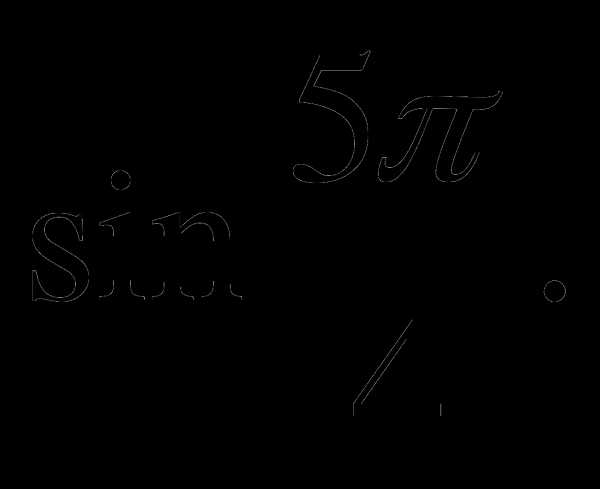
5.Найдите значение выражения:

2 уровень.
Работа у доски.
Вариант2.
1.Вычислить с помощью формул приведения.
а) 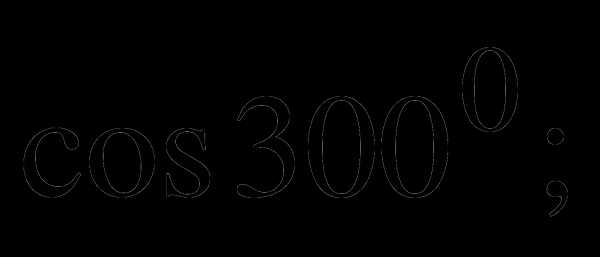 б)
б) 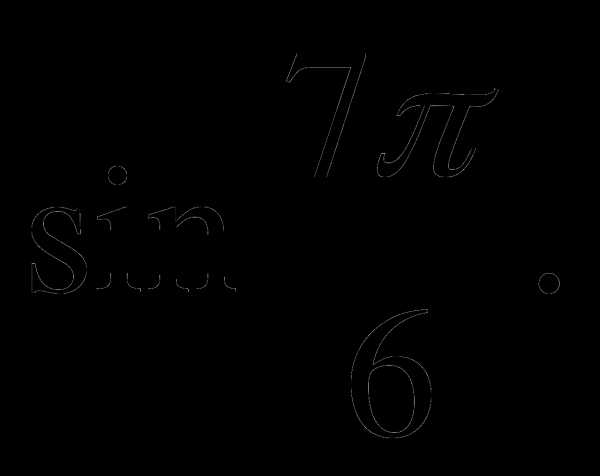
2.Упростить выражение:
3.Вычислите:
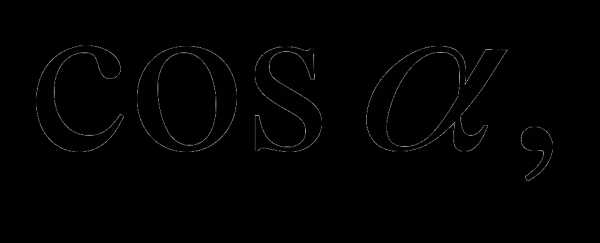 если
если 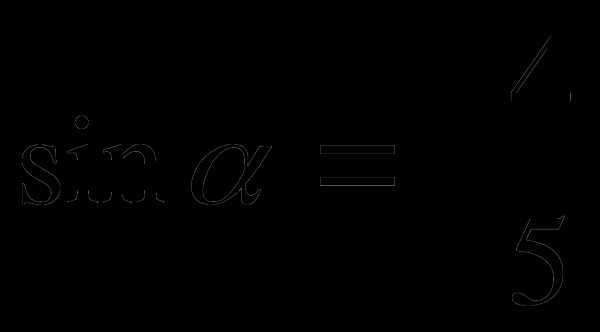 и
и 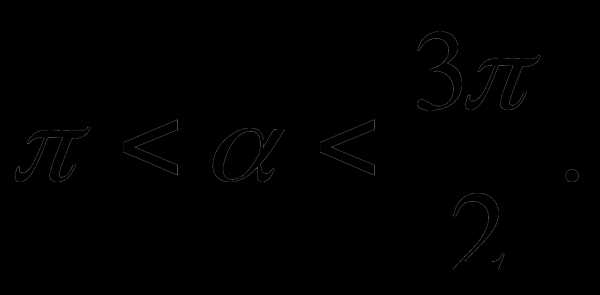
__________________________________________________________________________________
1.Найдите значение выражения:
2. Докажите тождество:
__________________________________________________________________________________
Самостоятельная работа.
Вариант1.
1.Преобразуйте с помощью формул приведения:
а)  в)
в)
б) 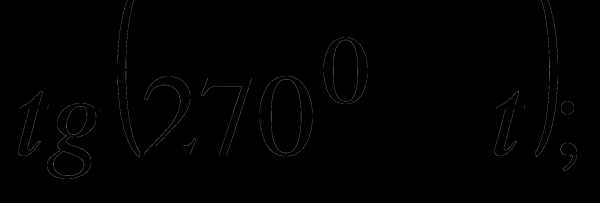 г)
г)
2.Найдите значение выражения:
3.Упростите выражение:
2 уровень.
Работа у доски.
Вариант2.
1.Вычислить с помощью формул приведения.
а) 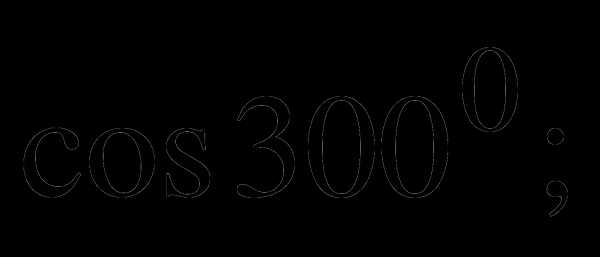 б)
б) 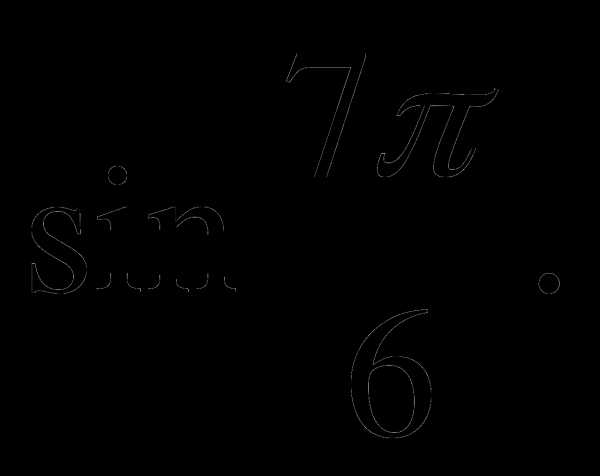
2.Упростить выражение:
3.Вычислите:
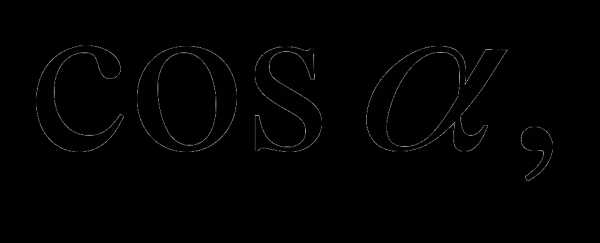 если
если 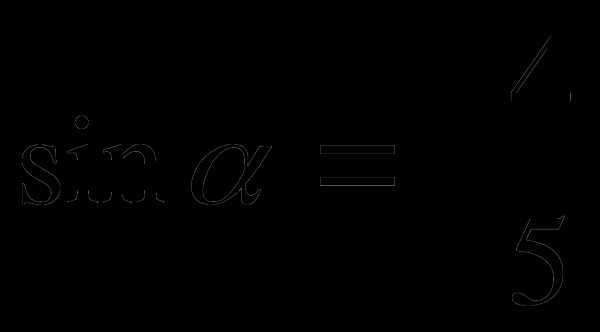 и
и 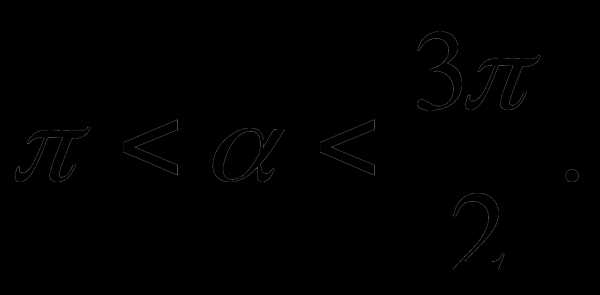
__________________________________________________________________________________
1.Найдите значение выражения:
2. Докажите тождество:
__________________________________________________________________________________
Самостоятельная работа.
Вариант 2.
1.Преобразуйте с помощью формул приведения:
а) в)
б)  г)
г)
2.Найдите значение выражения:
3.Упростите выражение:
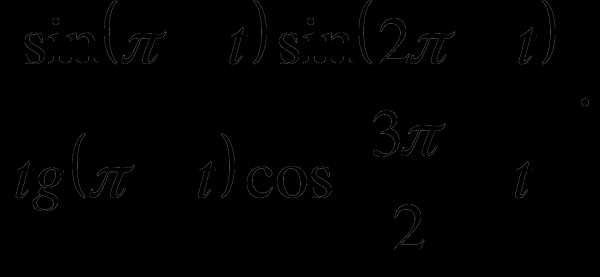
3 уровень
Работа у доски.
Вариант 3.
1.Вычислить с помощью формул приведения.
а) 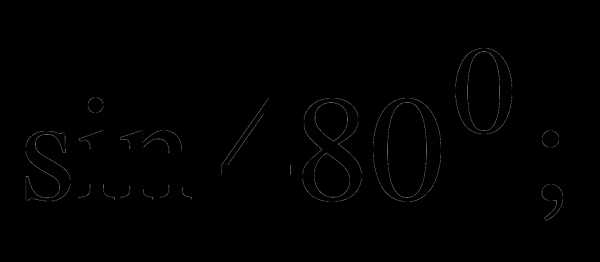 б)
б) 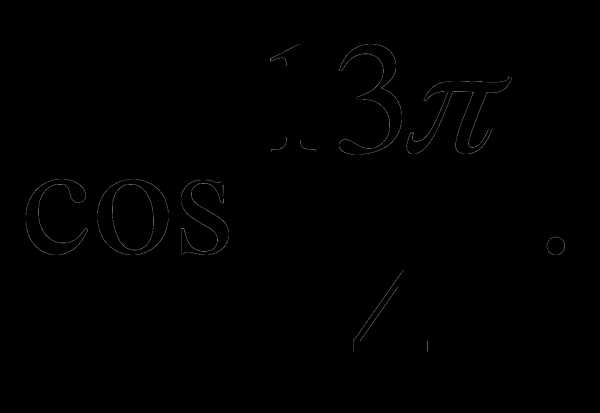
2.Упростить выражение:
3.Вычислите:
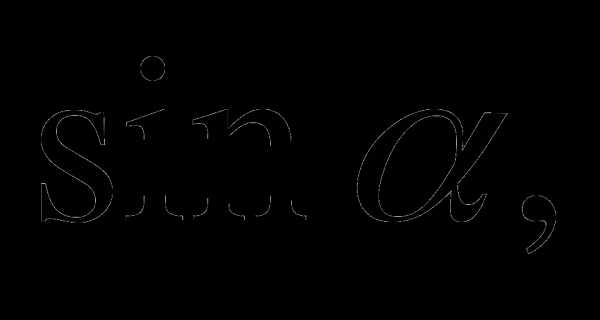 если
если 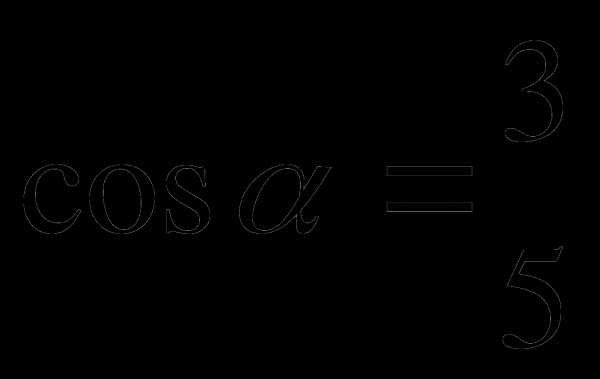 и
и 
__________________________________________________________________________________
1.Найдите значение выражения:
2. Докажите тождество:
_________________________________________________________________________________
Самостоятельная работа.
Вариант 1.
1.Вычислите: 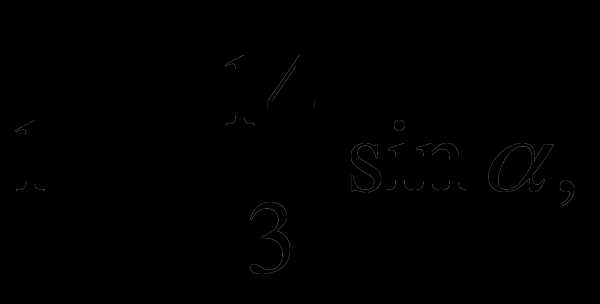 если
если
2.Найдите значение выражения:
3.Упростите выражение: 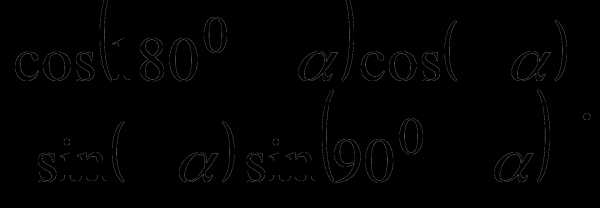
4.Докажите тождество: 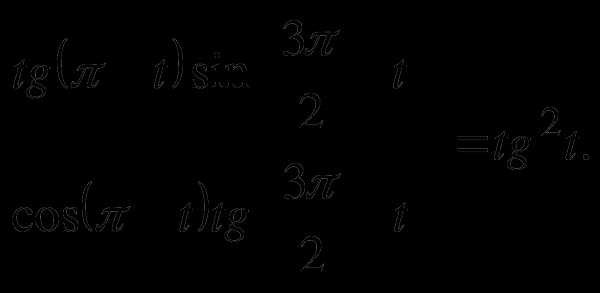
3 уровень
Работа у доски.
Вариант 3.
1.Вычислить с помощью формул приведения.
а) 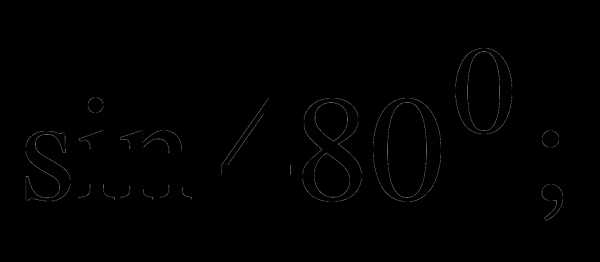 б)
б) 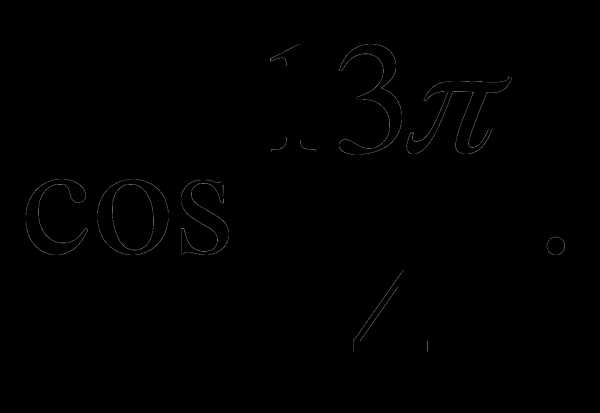
2.Упростить выражение:
3.Вычислите:
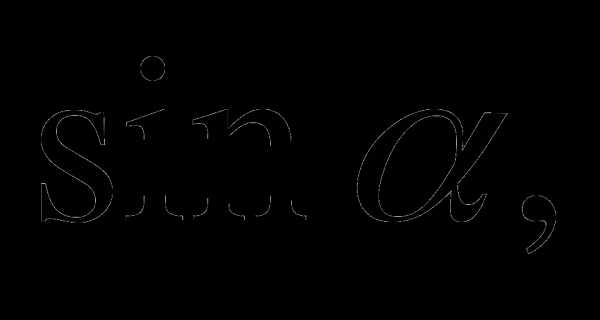 если
если 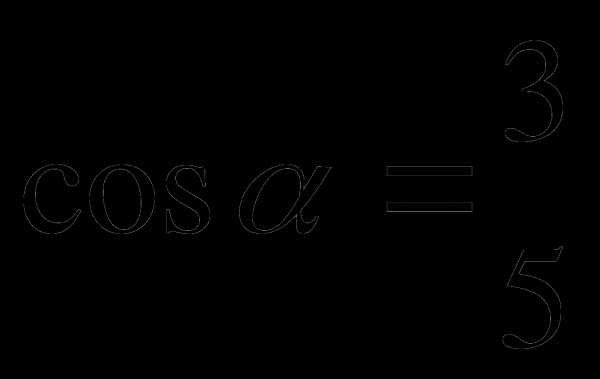 и
и 
__________________________________________________________________________________
1.Найдите значение выражения:
2. Докажите тождество:
_________________________________________________________________________________
Самостоятельная работа.
Вариант 2.
1.Вычислите: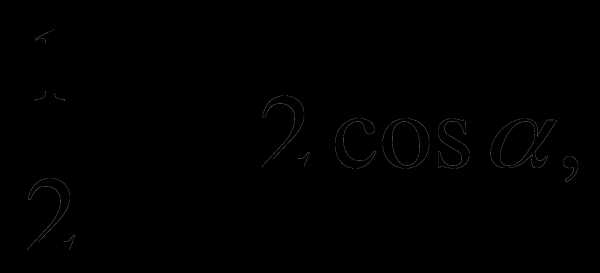 если
если
2.Найдите значение выражения:
3.Упрстите выражение:
4.Докажите тождество: 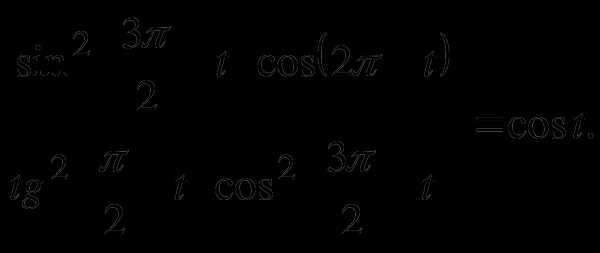
infourok.ru
