Основные формулы геометрия 7-11 класс
Сумма площадей боковых граней
Призма прямая
Пирамида
Сумма площадей боковых граней

Цилиндр
Конус

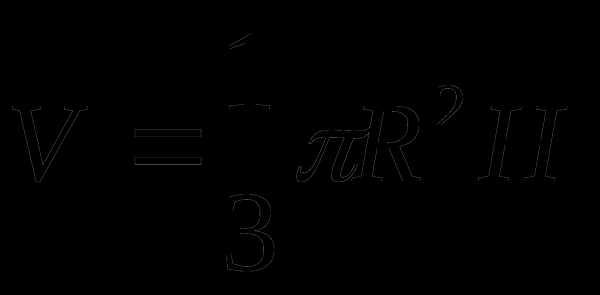
Шар, сфера
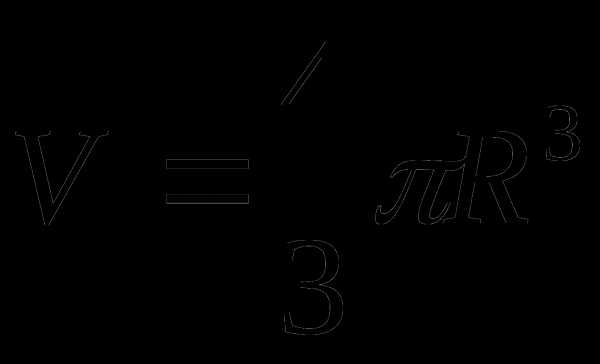
Тетраэдр


d – длина диагонали
Прямоугольник

a,b – длина стороны
d – длина диагонали
Параллелограмм

a, b – длина стороны
h – высота
d – диагональ
Ромб

а – сторона
h – высота
d — диагональ
Треугольник
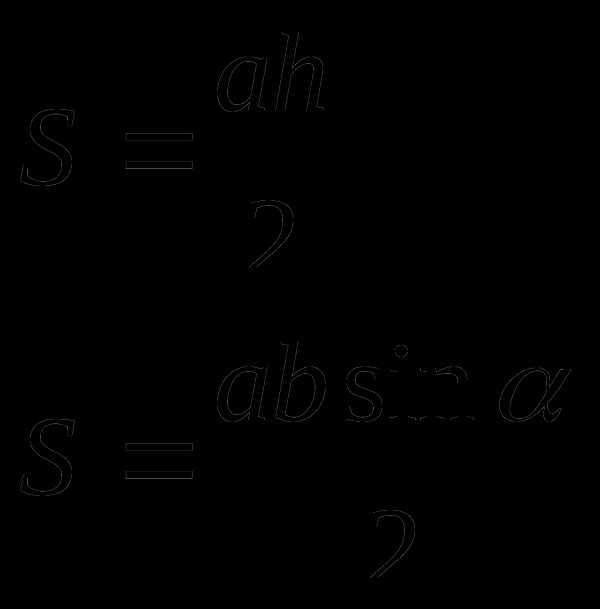
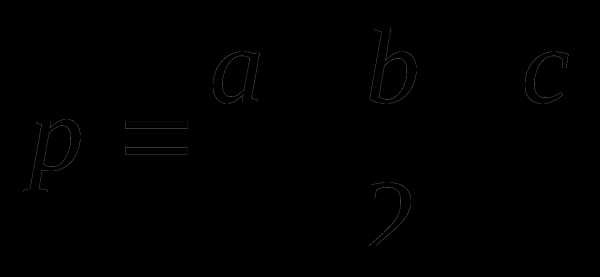

a, b, c – стороны треугольника
h – высота треугольника
p – полупериметр
R – радиус вписанной окружности
R – радиус описанной окружности
Прямоугольный треугольник
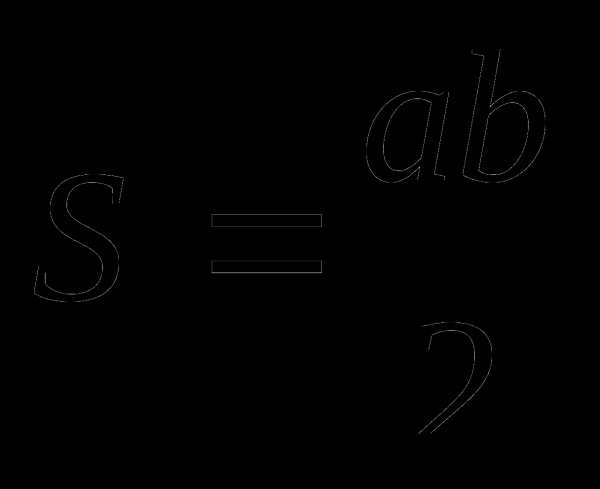
Теорема Пифагора
a, b – катеты
c – гипотенуза
Трапеция


a,b – основания трапеции
h – высота трапеции
l – средняя линия трапеции
Круг
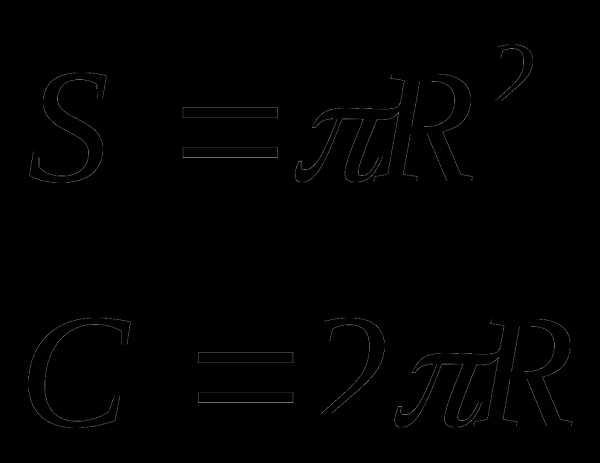
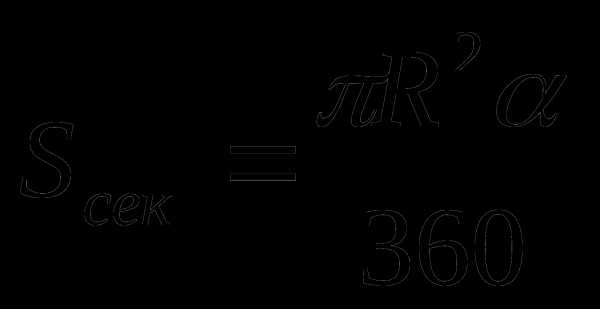
R – радиус окружности
C – длина окружности
Правильные многоугольники
infourok.ru
Основные формулы, используемые в геометрии — ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ 10-11 КЛАССОВ — ПОУРОЧНЫЕ РАЗРАБОТКИ ПО ГЕОМЕТРИИ 11 класс — разработки уроков — авторские уроки — план-конспект урока
ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ 10-11 КЛАССОВ
(уроки 55-68)
Основные формулы, используемые в геометрии
Площади поверхностей и объемов тел.
Призма. (Рсеч. — периметр сечения перпендикулярного боковому ребру. АА1 — боковое ребро).
(Н — высота призмы).
Прямая призма. (Росн. — периметр основания, АА1 — боковое ребро).
(АА1 — боковое ребро (высота)).
Прямоугольный параллелепипед. (АА1 — соответствующее боковое ребро).
(а, b, с — ребра параллелепипеда).
Куб. (а — ребро куба).
Правильная пирамида. (p — полупериметр основания, h — апофема).
(H — высота пирамиды)
Правильная усеченная пирамида. (p1 и р2 — полупериметры оснований, h — высота боковой грани).
(S1 и S2 — площади оснований).
(H — высота пирамиды. S1 и S2 — площади оснований).
Цилиндр. (R — радиус основания, H — высота).
Конус. (R — радиус основания, l — образующая).
(H — высота конуса).
Усеченный конус. (R и r — радиусы оснований, l — образующая).
Шар.
Шаровой сегмент. (R — радиус шара, H — высота сегмента).
Шаровой сектор. (R — радиус шара, H — высота шарового сектора).
Справочник по геометрии 11 класс. Формулы площадей плоских
Documents войти Загрузить ×- No category
Related documents
Document 4898178

Тема II «Преобразование алгебраических выражений

Площади фигур

Звук — Большой театр кукол

8 — 9 класс 1. Определите радиус шара с водой масса которого

шпаргалки

Задание 4

Материал полиэфирный эластомер, Hytrel
Выпускное отверстие для воздуха Внутренняя резьба 19,05 мм

Самолет пролетает над погрузившейся на небольшую глубину

Неинерциальные системы отсчёта

Химия, 9-10 класс, 1 этап с решениями
Решение задний В9
belyeva_se_ivanova_la_st_peterburg_fest_14
Скачать studydoc.ruПОУРОЧНЫЕ РАЗРАБОТКИ ПО ГЕОМЕТРИИ 11 класс — разработки уроков — авторские уроки — план-конспект урока
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ УЧЕБНОГО МАТЕРИАЛАЕ
Глава V. МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ
§ 1. Координаты точки и координаты вектора
Урок 1. Прямоугольная система координат в пространстве
Урок 2. Координаты вектора
Урок 3. Координаты вектора
Урок 4. Связь между координатами векторов и координат точек
Урок 5. Простейшие задачи в координатах
Урок 6. Простейшие задачи в координатах
Урок 7. Простейшие задачи в координатах. Контрольная работа № 1
§ 2. Скалярное произведение векторов
Урок 8. Угол между векторами. Скалярное произведение векторов
Урок 9. Угол между векторами. Скалярное произведение векторов
Урок 10. Вычисление углов между прямыми и плоскостями
Урок 11. Повторение вопросов теории и решение задач
§ 3. Движения
Урок 12. Движения. Центральная симметрия. Зеркальная симметрия. Осевая симметрия. Параллельный перенос
Урок 13. Решение задач по теме «Движения»
Урок 14. Контрольная работа № 5.2 по теме «Скалярное произведение векторов в пространстве. Движения»
Урок 15. Зачет по теме «Метод координат в пространстве»
Глава VI. ЦИЛИНДР, КОНУС И ШАР
§ 1. Цилиндр
Урок 16. Понятие цилиндра
Урок 17. Цилиндр. Решение задач
Урок 18. Цилиндр. Решение задач
§ 2. Конус
Урок 19. Конус
Урок 20. Конус
Урок 21. Усеченный конус
§ 3. Сфера
Урок 22. Сфера. Уравнение сферы
Урок 23. Взаимное расположение сферы и плоскости
Урок 24. Касательная плоскость к сфере
Урок 25. Площадь сферы
Урок 26. Разные задачи на многогранники, цилиндр, конус и шар
Урок 27. Разные задачи на многогранники, цилиндр, конус и шар
Урок 28. Разные задачи на многогранники, цилиндр, конус и шар
Урок 29. Зачет по теме: «Тела вращения»
Урок 30. Зачет по теме: «Тела вращения»
Урок 31. Обобщение по теме: «Цилиндр, конус, сфера и шар»
Урок 32. Самостоятельное решение задач
Глава VII. ОБЪЕМЫ ТЕЛ
§ 1. Объем прямоугольного параллелепипеда
Урок 33. Понятие объема. Объем прямоугольного параллелепипеда
Урок 34. Объем прямоугольного параллелепипеда. Объем прямоугольной призмы, основанием которой является прямоугольный треугольник
Урок 35. Объем прямоугольного параллелепипеда
§ 2. Объем прямой призмы и цилиндра
Урок 36. Объем прямой призмы
Урок 37. Объем цилиндра
Урок 38. Объем цилиндра
§ 3. Объем наклонной призмы, пирамиды и конуса
Урок 39. Вычисление объемов тел с помощью интеграла
Урок 40. Объем наклонной призмы
Урок 41. Объем пирамиды
Урок 42. Объем пирамиды
Урок 43. Объем пирамиды
Урок 44. Объем конуса
Урок 45. Решение задач на нахождение объема конуса
Урок 46. Контрольная работа № 4
§ 4. Объем шара и площадь сферы
Урок 47. Объем шара
Урок 48. Объем шара
Урок 49. Объем шарового сегмента, шарового слоя, сектора
Урок 50. Объем шарового сегмента, шарового слоя и шарового сектора
Урок 51. Площадь сферы
Урок 52. Решение задач по темам «Объем шара и его частей», «Площадь сферы». Подготовка к контрольной работе
Урок 53. Контрольная работа по темам «Объем шара» и «Площадь сферы»
Урок 54. Зачет по темам «Объем шара, его частей» и «Площадь сферы»
ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ 10-11 КЛАССОВ
Урок 55. Аксиомы стереометрии. Повторение
Урок 56. Повторение. Параллельность прямых, параллельность прямой и плоскости. Скрещивающиеся прямые. Параллельность плоскостей
Урок 57. Повторение. Перпендикулярность прямой и плоскости. Теорема о трех перпендикулярах. Угол между прямой и плоскостью
Урок 58. Повторение. Двугранный угол. Перпендикулярность плоскостей
Урок 59. Многогранники: параллелепипед, призма, пирамида, площади их поверхностей
Урок 60. Многогранники: параллелепипед, призма, пирамида
Урок 61. Повторение. Векторы в пространстве. Действия над векторами. Скалярное произведение векторов
Урок 62. Повторение. Цилиндр, конус и шар, площади их поверхностей
Урок 63. Повторение по теме: «Объемы тел»
Основные формулы, используемые в геометрии
Урок 64. Повторение по теме: «Объемы тел»
Урок 65. Повторение по теме: «Многогранники»
Урок 66. Повторение по теме: «Тела вращения»
Урок 67. Повторение по теме: «Комбинации с описанными сферами»
Урок 68. Повторение по теме: «Комбинации с вписанными сферами»
ПРИЛОЖЕНИЕ. КОНТРОЛЬНЫЕ И САМОСТОЯТЕЛЬНЫЕ РАБОТЫ
Урок 3. Координаты вектора
Урок 5. Простейшие задачи в координатах
Урок 6. Простейшие задачи в координатах
Урок 7. Простейшие задачи в координатах
Урок 9. Угол между векторами. Скалярное произведение векторов
Урок 13. Решение задач по теме «Движения»
Урок 14. Контрольная работа № 5.2 по теме «Скалярное произведение векторов в пространстве. Движения»
Урок 15. Зачет по теме «Метод координат в пространстве»
Урок 18. Цилиндр. Решение задач
Урок 20. Конус
Урок 22. Сфера. Уравнение сферы
Урок 23. Взаимное расположение сферы и плоскости
Урок 28. Разные задачи на многогранники, цилиндр, конус и шар
Урок 29. Зачет по теме: «Тела вращения»
Урок 30. Зачет по теме: «Тела вращения»
Урок 31. Обобщение по теме: «Цилиндр, конус, сфера и шар»
Урок 38. Объем цилиндра
Урок 43. Объем пирамиды
Урок 45. Решение задач на нахождение объема конуса
Урок 46. Контрольная работа № 4
Урок 50. Объем шарового сегмента, шарового слоя и шарового сектора
Урок 52. Решение задач по темам «Объем шара и его частей», «Площадь сферы». Подготовка к контрольной работе
Урок 53. Контрольная работа по темам «Объем шара» и «Площадь сферы»
Урок 54. Зачет по темам «Объем шара, его частей» и «Площадь сферы»
Урок 56. Повторение. Параллельность прямых, параллельность прямой и плоскости. Скрещивающиеся прямые. Параллельность плоскостей
Урок 57. Повторение. Перпендикулярность прямой и плоскости. Теорема о трех перпендикулярах. Угол между прямой и плоскостью
Урок 60. Многогранники: параллелепипед, призма, пирамида
Урок 65. Повторение по теме «Многогранники»
Урок 66. Повторение по теме: «Тела вращения»
Урок 67. Повторение по теме: «Комбинации с описанными сферами»
Урок 68. Повторение по теме: «Комбинации с вписанными сферами»
compendium.su
Основные формулы по геометрии и их свойства.
Основные формулы по геометрии и свойства
Радиус описанной окружности трапеции по сторонам и диагонали
a — боковые стороны трапеции
c — нижнее основание
b — верхнее основание d — диагональ
h – высота p = (a+d+c)/2
Радиус вписанной окружности в равнобочную трапецию
с — нижнее основание
b — верхнее основание
a — боковые стороны
h — высота
Найти радиус описанной окружности треугольника, формула
a, b, c — стороны треугольника
p — полупериметр, p= (a+b+c)/2
Найти радиус описанной окружности равностороннего треугольника по стороне
a — сторона треугольника
Формулы вычисления площади треугольника (если даны все стороны треугольника):
I формула Герона
p — полупериметр p=(a+b+c)|2
II формула Герона.
Формула расчета площади треугольника
h — высота треугольника
a — основание
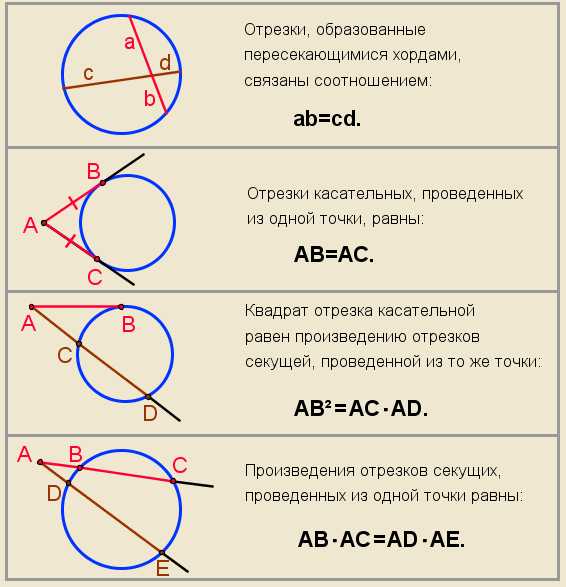

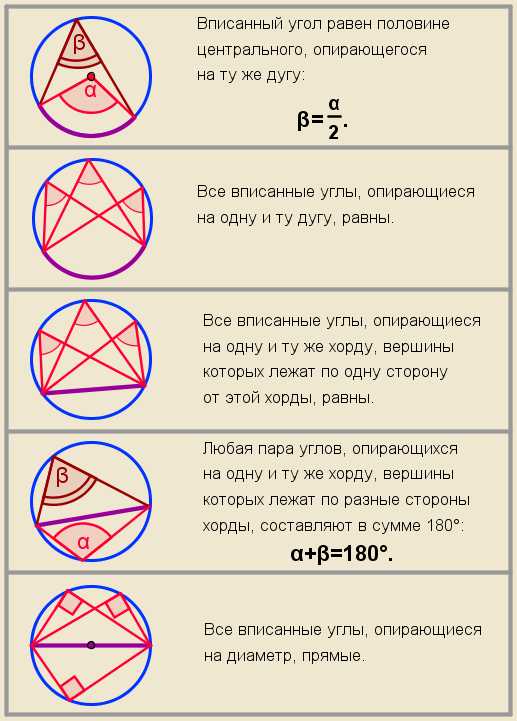

Центральным называется угол с вершиной в центре окружности.
Центральный угол равен градусной мере дуги, на которую опирается. Поэтому углом в один радиан называется центральный угол, который опирается на дугу в один радиан.
Вписанным называется угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.
Вписанный угол равен половине градусной меры дуги, на которую опирается.
Две различные точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности.
Дугою в один градус называется дуга окружности, длина которой равняется части его длины. Дугою в один радиан (1 рад) называется дуга окружности, длина которой равняется радиусу этой окружности.
Переход от градусной меры углов и дуг к радианной, и наоборот, осуществляется по формулам:
рад.
В частности:
рад.
рад.
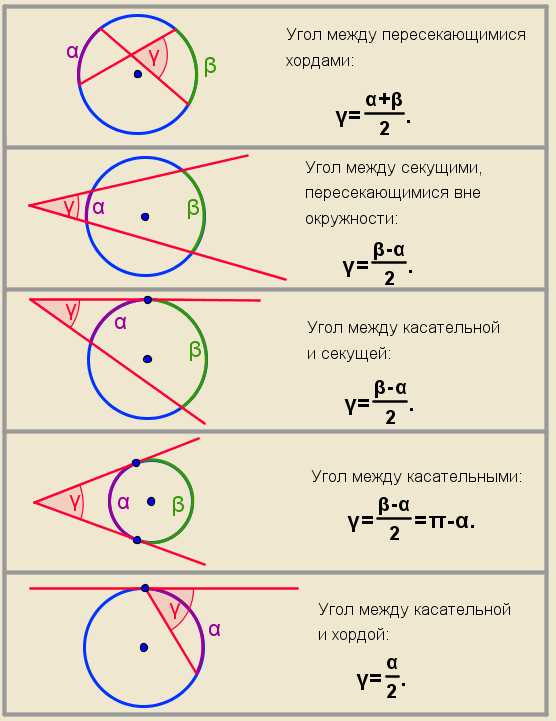
Формула площади параллелограмма через сторону и высоту
a, b — стороны параллелограмма
Hb — высота на сторону b
Ha — высота на сторону a
Формула площади трапеции через основания и высоту
a — нижнее основание
b — верхнее основание
m — средняя линия
h — высота трапеции
2. Формула площади трапеции через четыре стороны
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
Формула площади трапеции, (S ):
Вычислить площадь ромба
a — сторона ромба
D — большая диагональ
d — меньшая диагональ
Формулы площади ромба через диагонали и углы между сторонами ( S ):
a — сторона ромба h — высота
r — радиус вписанной окружности
Радиус вписанной окружности в шестиугольник
a — сторона шестиугольника
Радиус вписанной окружности в равнобедренный треугольник
a, b — стороны треугольника
Радиус вписанной окружности в равносторонний треугольник
a — сторона треугольника
Радиус вписанной окружности в треугольник
a, b, c — стороны треугольника
p — полупериметр, p=(a+b+c)/2
Радиус вписанной окружности в прямоугольный треугольник
Радиус вписанной окружности в ромб
r — радиус вписанной окружности
a — сторона ромба
D, d — диагонали
h — высота ромба
Радиус вписанной окружности в квадрат
a — сторона квадрата
Радиус вписанной окружности в равнобочную трапецию
с — нижнее основание
b — верхнее основание
a — боковые стороны
h — высота
Радиусы описанной окружности
Радиус описанной окружности правильного шестиугольника
a — сторона шестиугольника
d — диагональ шестиугольника
Найти радиус описанной окружности треугольника, формула
p= (a+b+c)/2
Найти радиус описанной окружности прямоугольного треугольника по катетам
Радиус описанной окружности прямоугольника по стороне
a, b — стороны прямоугольника
d — диагональ
Найти радиус описанной окружности около квадрата
Найти радиус описанной окружности равностороннего треугольника по стороне
найти радиус описанной окружности равнобедренного треугольника по сторонам
Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.
infourok.ru
АЛГЕБРА Формулы — Справочник — Все формулы по математике за 11 класс
приобрестиСправочник — Все формулы по математике за 11 класс
скачать (156.5 kb.)
Доступные файлы (1):
n1.doc
АЛГЕБРАФормулы
Формулы сложения
Формулы двойного аргумента
Формулы половинного аргумента
Ф-лы преобразования суммы в произведение
Ф-лы преобразования произведения в сумму
Соотношения м/у функциями
Ф-лы тройного аргумента
Третья степень
Arcsin…
Производная
Прогрессии
Квадратное уравнение ax2+bx+c=0 (a?0)
Первообразная
Интеграл
Логарифмы
Степени
ГЕОМЕТРИЯ
1. Соотношение м/у углами и сторонами треугольника.
2. Площади плоских фигур.
Площадь треугольника:
Площадь равностороннего треугольника:
Площадь прямоугольного треугольника:
Площадь четырёхугольника:
Площадь трапеции:
Площадь параллелограмма:
Площадь круга:
Площадь ромба:
3. Объёмы и площади объёмных фигур.
Прямая призма:
Прямоугольный параллелепипед:
Куб:
Пирамида:
Правильная пирамида:
Правильная усечённая пирамида:
Цилиндр:
Конус:
Усечённый конус:
4. Векторы.
Равные векторы:
Сложение и вычитание:
Компланарные векторы:
Координаты векторов:
Коллинеарные векторы:
Некоторые формулы на координаты:
1. Координаты
2. Координаты середины отрезка AB
3. Длина вектора
Скалярное произведение векторов:
АЛГЕБРА Формулы
nashaucheba.ru
| Главная > Учебные материалы > Математика: Формулы геометрии | |||||||||||||||||||||||
|
|||||||||||||||||||||||
|
1.Признаки параллельности прямых.
|
|||||||||||||||||||||||
| 1 2 3 4 5 6 7 8 | |||||||||||||||||||||||
Признаки параллельности прямых |
|||||||||||||||||||||||
Признаки равенства треугольников |
|||||||||||||||||||||||
 |
|||||||||||||||||||||||
Теорема Пифагора |
|||||||||||||||||||||||
 |
|||||||||||||||||||||||
Рассчитать стороны прямоугольного треугольника
|
|||||||||||||||||||||||
Радиус вписанной и описанной окружностей правильных многоугольников |
|||||||||||||||||||||||
 |
|||||||||||||||||||||||
Рассчитать радиус вписанной и описанной окружностей |
|||||||||||||||||||||||
Теорема синусов |
|||||||||||||||||||||||
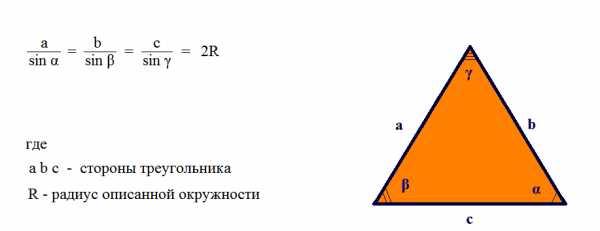 |
|||||||||||||||||||||||
Рассчитать сторону треугольникаРассчитать угол треугольника
|
|||||||||||||||||||||||
Теорема косинусов |
|||||||||||||||||||||||
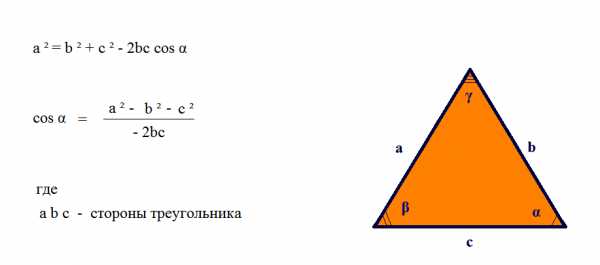 |
|||||||||||||||||||||||
Рассчитать сторону треугольникаРассчитать угол треугольника |
|||||||||||||||||||||||
Радиус вписанной и описанной окружностей |
|||||||||||||||||||||||
 |
|||||||||||||||||||||||
| 1 2 3 4 5 6 7 8 | |||||||||||||||||||||||
www.mathtask.ru
