Движение по окружности, угловая скорость, частота, период, центростремительное ускорение. Формулы, определения, пояснения
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T — это время, за которое тело совершает один оборот.
Частота вращение — это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.
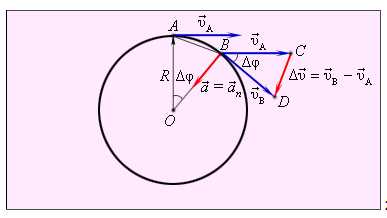
Разница векторов есть . Так как , получим
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
fizmat.by
Угловая и линейная скорости, формулы и примеры
В системе СИ угловая скорость измеряется в рад/с.
Основные характеристики и формулы
Так как за период угловое перемещение рад, угловая скорость связана с периодом и частотой вращения:
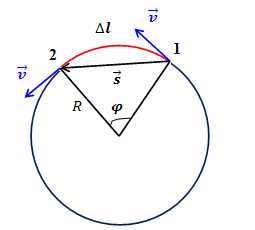
Рис.1. Линейное и угловое перемещение при равномерном движении точки по окружности
Наряду с понятием угловой скорости для характеристики равномерного движения по окружности сохраняет смысл привычное для нас понятие скорости движения точки вдоль траектории, которое в данном случае называется линейной скоростью.
Модуль линейной скорости равен отношению длины дуги окружности к промежутку времени, за который эта дуга пройдена.
Линейная скорость тела, которое движется по окружности, не изменяется по модулю, а все время изменяется по направлению, и в любой точке траектории направлена по касательной к дуге этой окружности (рис.1).
Угловая и линейная скорости связаны между собой соотношением:
где радиус окружности.
Кинематическое уравнение или закон движения точки по окружности:
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Вращательное движение (движение тела по окружности) | Формулы и расчеты онлайн
Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних следующие замены:
Если:
перемещение s — угловое перемещение (угол поворота) φ,
скорость u — угловая скорость ω,
ускорение a — угловое ускорение α
Вращательное движение, характеристики
| Вращательное движение | Угловая скорость | Угловое ускорение |
|---|---|---|
| Равномерное | Постоянная | Равно нулю |
| Равномерно ускоренное | Изменяется равномерно | Постоянно |
| Неравномерно ускоренное | Изменяется неравномерно | Переменное |
Угол поворота
Во всех уравнения вращательного движения углы задаются в радианах, сокращенно (рад).
Если
φ — угловое перемещение в радианах,
между сторонами угла поворота,
r — радиус,
то по определению радиана
\[ φ = \frac{s}{r} \]
Соотношение между единицами угла
\[ \frac[-1.35]{φ_{рад}}{φ_{°}} = \frac[-1.2]{π}{180°} \]
|
$ 1 рад = 57.3° $ |
$ 1° = 17.45 мрад $ |
$ 1´ = 291 мкрад $ |
Обратите внимание: Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков
(1рад = 1м/ 1м = 1), он не имеет размерности.
Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ω от t). Поэтому графику можно определить, какой угловой скоростью обладает тело в тот или иной момент времени и на какой угол с момента начала движения оно повернулось (он характеризуется площадью под кривой).
Кроме того, для представления соотношений между названными величинами используют график углового перемещения (зависимость φ от t) и график углового ускорения (зависимость α от t).
Число оборотов
Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.
Единица СИ частоты (или числа оборотов)
\[ [n] = [f] = \frac{Обороты}{Секунда} = \frac{(об)}{с} = \frac{1}{c} = Герц \]
В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.
Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.
Если
n — число оборотов,
f — частота,
T — продолжительность одного оборота, период,
φ — угловое перемещение,
N — полное число оборотов,
ω — угловая частота,
то
Период
\[ T = \frac{1}{f} = \frac{1}{n} \]
Угловое перемещение
Угловое перемещение равно произведению полного числа оборотов на 2π:
\[ φ = 2 π N \]
Угловая скорость
Из формулы для одного оборота следует:
\[ ω = 2 π f = \frac{2π}{T} \]
Обратите внимание:
• формулы (1)—(6) справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
• вопреки своему названию число оборотов n — это не число, а физическая величина.
• следует различать число оборотов n и полное число оборотов N.
В помощь студенту
Вращательное движение (движение тела по окружности) |
стр. 421 |
|---|
www.fxyz.ru
1.1.8 Движение тела по окружности. Угловая и линейная скорости точки. Центростремительное ускорение точки
Видеоурок: Движение по окружности
Лекция: Движение тела по окружности. Угловая и линейная скорости точки. Центростремительное ускорение точки
Движение по окружности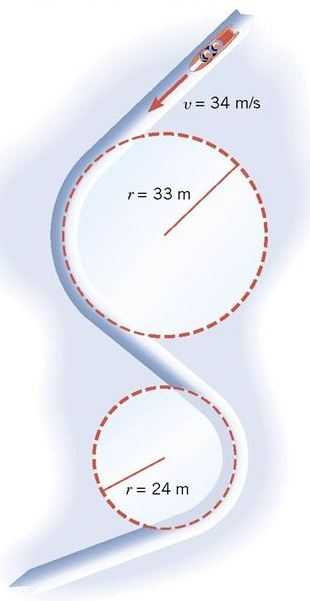
Траектория движения — окружность.
Так как скорость — векторная величина, то она зависит не только от модуля значения, но и от направления. Поэтому движение тела по окружности можно назвать равноускоренным. Даже если тело будет двигаться с постоянной по величине скоростью, её направление будет постоянно изменяться.
Любое криволинейное движение можно свести к нескольким движениям по окружности. Примером данного движения является бег по стадиону, ход стрелки часов, прогулка на корде лошади и другое.Основные характеристики движения
1. Линейная скорость
 Мгновенная скорость (линейная) — на протяжении всего движения меняет свое направление вдоль касательной к траектории.
Мгновенная скорость (линейная) — на протяжении всего движения меняет свое направление вдоль касательной к траектории.Так как траектория движения точки — окружность, то в качестве пути в числителе находится формула длины перемещения.
Поэтому формула мгновенной скорости приобретает следующий вид, где Т — период:
2. Центростремительное ускорение
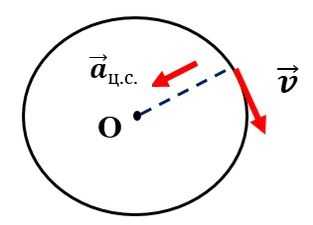 Направлено перпендикулярно к линейной скорости на протяжении всего движения.
Направлено перпендикулярно к линейной скорости на протяжении всего движения.Центростремительное ускорение определяется по формуле:
3. Период вращения
Период вращения — это величина, определяющая время, за которое тело делает одно полное вращение.
Период — это скалярная величина. Основной единицей периода является [Т]=1с.
Период определяется по формуле:
где N — количество оборотов, t — время, за которое они были совершены.
4. Частота вращения
Определяет, насколько часто совершаются обороты в единицу времени.
Частота — скалярная величина. Измеряется в [n] = 1с-1.
Частота определяется по формуле:
5. Угловое перемещение
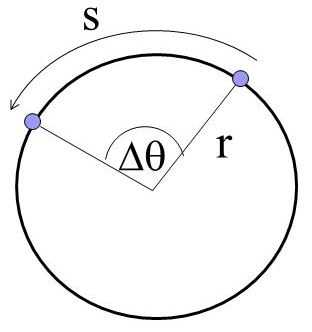
Угловое перемещение — величина, которая определяется углом поворота радиуса, соединяющего центр описываемой окружности, с точкой, где находится тело, относительно начального его положения.
Данная величина может измеряться в градусной или радианной мере углов.
6. Угловая скорость
Это значение, которое определяет, насколько изменяется угловое перемещение со временем.
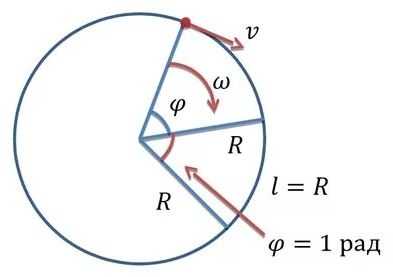 Измеряется в 1 рад/с.Определяется по формуле:
Измеряется в 1 рад/с.Определяется по формуле:где
— угловая скорость материальной точки, 1/с
— угол поворота радиус — вектора, рад- промежуток времени, с
Угловое перемещение связано с линейной скоростью и центростремительным ускорением следующей формулой:
cknow.ru
Угловая скорость. Формула угловой скорости :: SYL.ru
Расстояние и время, которое уходит на преодоление этого расстояния, связывает физическое понятие – скорость. И у человека, как правило, не вызывает вопросов определение этой величины. Все понимают, что двигаться на автомобиле со скоростью 100 км/ч — значит за один час проехать 100 километров.

А как быть, если тело вращается? Например, обычный бытовой вентилятор делает с десяток оборотов в секунду. И в то же время скорость вращения лопастей такова, что их запросто можно остановить рукой без вреда для себя. Земля вокруг своей звезды – Солнца — делает один оборот за целый год, а это более 30 миллионов секунд, но скорость её движения по околозвёздной орбите составляет около 30 километров за одну секунду!
Как же связать привычную скорость с быстротой вращения, как выглядит формула угловой скорости?
Понятие угловой скорости
Понятие угловой скорости используется в изучении законов вращения. Оно применяется ко всем вращающимся телам. Будь то вращение некоторой массы вокруг другой, как в случае с Землёй и Солнцем, или же вращение самого тела вокруг полярной оси (суточное вращение нашей планеты).
Отличие угловой скорости от линейной в том, что она фиксирует изменение угла, а не расстояния в единицу времени. В физике угловую скорость принято обозначать буквой греческого алфавита «омега» — ω.
Классическая формула угловой скорости вращения рассматривается так.
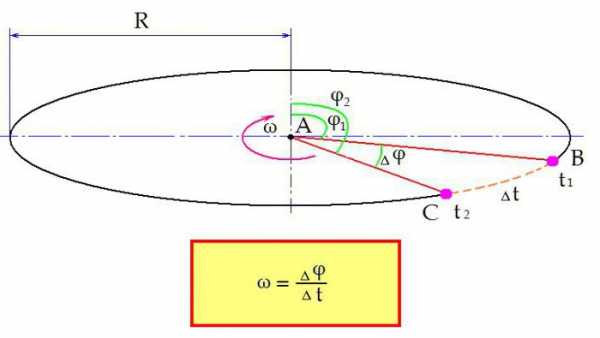
Представим, что вокруг некоторого центра А вращается физическое тело с постоянной скоростью. Его положение в пространстве относительно центра определяется углом φ. В некоторый момент времени t1 рассматриваемое тело находится в точке В. Угол отклонения тела от начального φ1.
Затем тело перемещается в точку С. Оно находится там в момент времени t2. Время, понадобившееся для данного перемещения:
∆t = t2 – t1.
Меняется и положение тела в пространстве. Теперь угол отклонения равен φ2. Изменение угла за период времени ∆t составило:
∆φ = φ2 – φ1.
Теперь формула угловой скорости формулируется следующим образом: угловая скорость определяется как отношение изменения угла ∆φ за время ∆t.
Единицы измерения угловой скорости
Скорость движения тела линейная измеряется в разных величинах. Движение автотранспорта по дорогам привычно указывают в километрах в час, морские суда делают узлы – морские мили в час. Если же рассматривать движение космических тел, то тут чаще всего фигурируют километры в секунду.
Угловая скорость в зависимости от величины и от предмета, который вращается, также измеряется в разных единицах.
Радианы в секунду (рад/с) – классическое мерило скорости в международной системе единиц (СИ). Показывают – на сколько радиан (в одном полном обороте 2 ∙ 3,14 радиан) успевает повернуться тело за одну секунду.
Обороты в минуту (об/мин) – самая распространённая единица для обозначения скоростей вращения в технике. Валы двигателей как электрических, так и автомобильных выдают именно (достаточно посмотреть на тахометр в своём автомобиле) обороты в минуту.
Обороты в секунду (об/с) – используется реже, прежде всего в образовательных целях.
Период обращения
Иногда для определения скорости вращения удобнее пользоваться другим понятием. Периодом обращения принято называть время, за которое некое тело делает оборот 360° (полный круг) вокруг центра вращения. Формула угловой скорости, выраженная через период обращения, принимает вид:
ω = 2П / Т.
Выражать периодом обращения быстроту вращения тел оправдано в случаях, когда тело вращается относительно медленно. Вернёмся к рассмотрению движения нашей планеты вокруг светила.
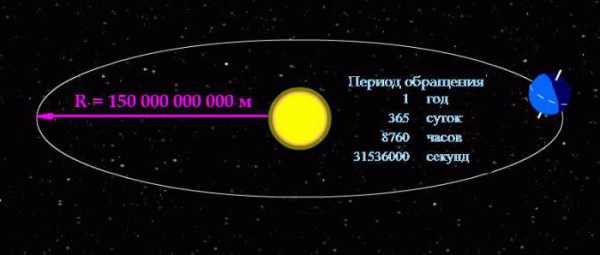
Формула угловой скорости позволяет вычислить её, зная период обращения:
ω = 2П/31536000 = 0,000000199238499086111 рад/с.
Глядя на полученный результат, можно понять, почему, рассматривая вращение небесных тел, удобнее пользоваться именно периодом обращения. Человек видит перед собой понятные цифры и наглядно представляет себе их масштаб.
Связь угловой и линейной скоростей
В некоторых задачах должны быть определены линейная и угловая скорость. Формула трансформации проста: линейная скорость тела равняется произведению угловой скорости на радиус вращения. Как это показано на рисунке.
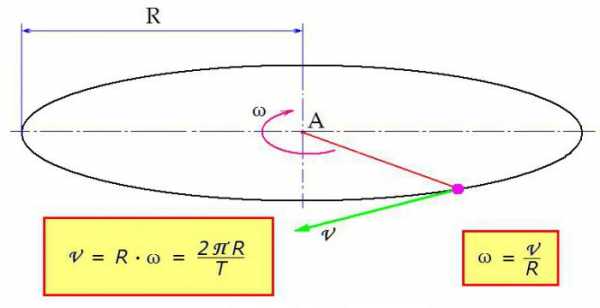
«Работает» выражение и в обратном порядке, с его помощью определяется и угловая скорость. Формула через скорость линейную получается путём несложных арифметических манипуляций.
www.syl.ru
Период обращения | Все формулы
Период обращения — Время, за которое тело совершает один оборот, т.е. поворачивается на угол 2 пи, называется периодом обращения
Сидерические периоды обращения планет Солнечной системы:
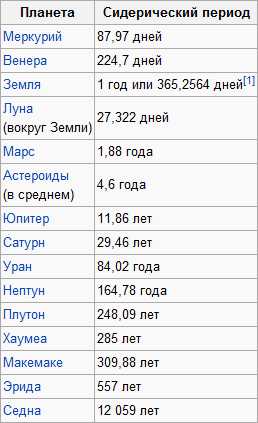
Найдем период обращения:
Если, например, за время t = 4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения. Обозначается он буквой Т и определяется по формуле
Найдем частоту обращения:
Если, например, за время t = 4 с тело совершило n = 20 оборотов,то за 1 с оно успевало совершить 5 оборотов. Это число и выражает частоту обращения. Обозначается она греческой буквой V (читается: ню) и определяется по формуле:
За единицу частоты обращения в СИ принимают частоту обращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: 1/с или с-1 (читается: секунда в минус первой степени).
В формуле мы использовали :
— Период обращения
— Частота обращения
— Число оборотов
xn--b1agsdjmeuf9e.xn--p1ai
Равномерное движение тела по окружности – FIZI4KA

1. Движением тела по окружности называют движение, траекторией которого является окружность. По окружности движутся, например, конец стрелки часов, точки лопасти вращающейся турбины, вращающегося вала двигателя и др.
При движении по окружности направление скорости непрерывно изменяется. При этом модуль скорости тела может изменяться, а может оставаться неизменным. Движение, при котором изменяется только направление скорости, а её модуль сохраняется постоянным, называется равномерным движением тела по окружности. Под телом в данном случае имеют в виду материальную точку.
2. Движение тела по окружности характеризуется определёнными величинами. К ним относятся, прежде всего, период и частота обращения. Период обращения тела по окружности \( T \) — время, в течение которого тело совершает один полный оборот. Единица периода — \( [\,T\,] \) = 1 с.
Частота обращения \( (n) \) — число полных оборотов тела за одну секунду: \( n=N/t \). Единица частоты обращения — \( [\,n\,] \) = 1 с-1 = 1 Гц (герц). Один герц — это такая частота, при которой тело совершает один оборот за одну секунду.
Связь между частотой и периодом обращения выражается формулой: \( n=1/T \).
Пусть некоторое тело, движущееся по окружности, за время \( t \) переместилось из точки А в точку В. Радиус, соединяющий центр окружности с точкой А, называют радиусом-вектором. При перемещении тела из точки А в точку В радиус-вектор повернётся на угол \( \varphi \).
Быстроту обращения тела характеризуют угловая и линейная скорости.
Угловая скорость \( \omega \) — физическая величина, равная отношению угла поворота \( \varphi \) радиуса-вектора к промежутку времени, за которое этот поворот произошел: \( \omega=\varphi/t \). Единица угловой скорости — радиан в секунду, т.е. \( [\,\omega\,] \) = 1 рад/с. За время, равное периоду обращения, угол поворота радиуса-вектора равен \( 2\pi \). Поэтому \( \omega=2\pi/T \).
Линейная скорость тела \( v \) — скорость, с которой тело движется вдоль траектории. Линейная скорость при равномерном движении по окружности постоянна по модулю, меняется по направлению и направлена по касательной к траектории.
Линейная скорость равна отношению пути, пройденному телом вдоль траектории, ко времени, за которое этот путь пройден: \( \vec{v}=l/t \). За один оборот точка проходит путь, равный длине окружности. Поэтому \( \vec{v}=2\pi\!R/T \). Связь между линейной и угловой скоростью выражается формулой: \( v=\omega R \).
Из этого равенства следует, что чем дальше от центра окружности расположена точка вращающегося тела, тем больше её линейная скорость.
4. Ускорение тела равно отношению изменения его скорости ко времени, за которое оно произошло. При движении тела по окружности изменяется направление скорости, следовательно, разность скоростей не равна нулю, т.е. тело движется с ускорением. Оно определяется по формуле: \( \vec{a}=\frac{\Delta\vec{v}}{t} \) и направлено так же, как вектор изменения скорости. Это ускорение называется центростремительным ускорением.
Центростремительное ускорение при равномерном движении тела по окружности — физическая величина, равная отношению квадрата линейной скорости к радиусу окружности: \( a=\frac{v^2}{R} \). Так как \( v=\omega R \), то \( a=\omega^2R \).
При движении тела по окружности его центростремительное ускорение постоянно по модулю и направлено к центру окружности.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. При равномерном движении тела по окружности
1) изменяется только модуль его скорости
2) изменяется только направление его скорости
3) изменяются и модуль, и направление его скорости
4) не изменяется ни модуль, ни направление его скорости
2. Линейная скорость точки 1, находящейся на расстоянии \( R_1 \) от центра вращающегося колеса, равна \( v_1 \). Чему равна скорость \( v_2 \) точки 2, находящейся от центра на расстоянии \( R_2=4R_1 \)?
1) \( v_2=v_1 \)
2) \( v_2=2v_1 \)
3) \( v_2=0,25v_1 \)
4) \( v_2=4v_1 \)
3. Период обращения точки по окружности можно вычислить по формуле:
1) \( T=2\pi\!Rv \)
2) \( T=2\pi\!R/v \)
3) \( T=2\pi v \)
4) \( T=2\pi/v \)
4. Угловая скорость вращения колеса автомобиля вычисляется по формуле:
1) \( \omega=a^2R \)
2) \( \omega=vR^2 \)
3) \( \omega=vR \)
4) \( \omega=v/R \)
5. Угловая скорость вращения колеса велосипеда увеличилась в 2 раза. Как изменилась линейная скорость точек обода колеса?
1) увеличилась в 2 раза
2) уменьшилась в 2 раза
3) увеличилась в 4 раза
4) не изменилась
6. Линейная скорость точек лопасти винта вертолёта уменьшилась в 4 раза. Как изменилось их центростремительное ускорение?
1) не изменилось
2) уменьшилось в 16 раз
3) уменьшилось в 4 раза
4) уменьшилось в 2 раза
7. Радиус движения тела по окружности увеличили в 3 раза, не меняя его линейную скорость. Как изменилось центростремительное ускорение тела?
1) увеличилось в 9 раз
2) уменьшилось в 9 раз
3) уменьшилось в 3 раза
4) увеличилось в 3 раза
8. Чему равен период обращения коленчатого вала двигателя, если за 3 мин он совершил 600 000 оборотов?
1) 200 000 с
2) 3300 с
3) 3·10-4 с
4) 5·10-6 с
9. Чему равна частота вращения точки обода колеса, если период обращения составляет 0,05 с?
1) 0,05 Гц
2) 2 Гц
3) 20 Гц
4) 200 Гц
10. Линейная скорость точки обода велосипедного колеса радиусом 35 см равна 5 м/с. Чему равен период обращения колеса?
1) 14 с
2) 7 с
3) 0,07 с
4) 0,44 с
11. Установите соответствие между физическими величинами в левом столбце и формулами для их вычисления в правом столбце. В таблице под номером физической
величины левого столбца запишите соответствующий номер выбранной вами формулы из правого столбца.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
А) линейная скорость
Б) угловая скорость
В) частота обращения
ФОРМУЛА
1) \( 1/T \)
2) \( v^2/R \)
3) \( v/R \)
4) \( \omega R \)
5) \( 1/n \)
12. Период обращения колеса увеличился. Как изменились угловая и линейная скорости точки обода колеса и её центростремительное ускорение. Установите соответствие между физическими величинами в левом столбце и характером их изменения в правом столбце.
В таблице под номером физической величины левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) угловая скорость
Б) линейная скорость
B) центростремительное ускорение
ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ
1) увеличилась
2) уменьшилась
3) не изменилась
Часть 2
13. Какой путь пройдёт точка обода колеса за 10 с, если частота обращения колеса составляет 8 Гц, а радиус колеса 5 м?
Ответы
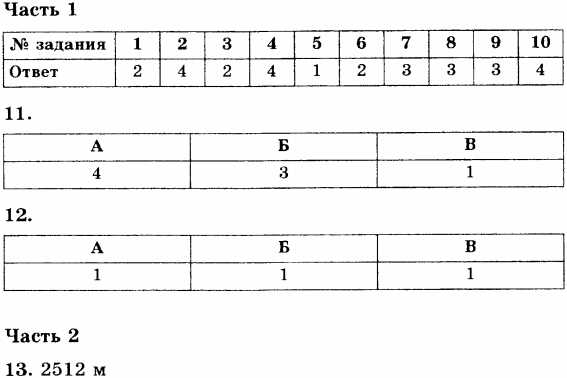
Равномерное движение тела по окружности
5 (100%) 1 votefizi4ka.ru
