Период и частота обращения | Физика
Равномерное движение по окружности характеризуют периодом и частотой обращения.
Период обращения — это время, за которое совершается один оборот.
Если, например, за время t=4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения. Обозначается он буквой T и определяется по формуле
Итак, чтобы найти период обращения, надо время, за которое совершено n оборотов, разделить на число оборотов.
Другой характеристикой равномерного движения по окружности является частота обращения.
Частота обращения — это число оборотов, совершаемых за 1 с. Если, например, за время t = 2 с тело совершило n = 10 оборотов, то легко сообразить, что за 1 с оно успевало совершить 5 оборотов. Это число и выражает частоту обращения. Обозначается она греческой буквой ν (читается: ню) и определяется по формуле
Итак, чтобы найти частоту обращения, надо число оборотов разделить на время, в течение которого они произошли.
За единицу частоты обращения в СИ принимают частоту обращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: 1/с или с-1 (читается: секунда в минус первой степени). Раньше эту единицу называли «оборот в секунду», но теперь это название считается устаревшим.
Сравнивая формулы (6.1) и (6.2), можно заметить, что период и частота — величины взаимно обратные. Поэтому
Формулы (6.1) и (6.3) позволяют найти период обращения T, если известны число n и время оборотов t или частота обращения ν. Однако его можно найти и в том случае, когда ни одна из этих величин неизвестна. Вместо них достаточно знать скорость тела v и радиус окружности r, по которой оно движется. Для вывода новой формулы вспомним, что период обращения — это время, за которое тело совершает один оборот, т. е. проходит путь, равный длине окружности (lокр
= 2πr, где π≈3,14— число «пи», известное из курса математики). Но мы знаем, что при равномерном движении время находится делением пройденного пути на скорость движения. Таким образом,Итак, чтобы найти период обращения тела, надо длину окружности, по которой оно движется, разделить на скорость его движения.
1. Что такое период обращения? 2. Как можно найти период обращения, зная время и число оборотов? 3. Что такое частота обращения? 4. Как обозначается единица частоты? 5. Как можно найти частоту обращения, зная время и число оборотов? 6. Как связаны между собой период и частота обращения? 7. Как можно найти период обращения, зная радиус окружности и скорость движения тела?
phscs.ru
Период обращения | Все формулы
Период обращения — Время, за которое тело совершает один оборот, т.е. поворачивается на угол 2 пи, называется периодом обращения
Сидерические периоды обращения планет Солнечной системы:
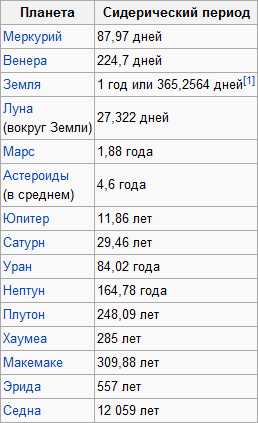
Найдем период обращения:
Если, например, за время t = 4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения. Обозначается он буквой Т и определяется по формуле
Найдем частоту обращения:
Если, например, за время t = 4 с тело совершило n = 20 оборотов,то за 1 с оно успевало совершить 5 оборотов. Это число и выражает частоту обращения. Обозначается она греческой буквой V (читается: ню) и определяется по формуле:
За единицу частоты обращения в СИ принимают частоту обращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: 1/с или с-1 (читается: секунда в минус первой степени).
В формуле мы использовали :
— Период обращения
— Частота обращения
— Число оборотов
xn--b1agsdjmeuf9e.xn--p1ai
Период обращения – Формулы по физике.рф
Период обращения — Время, за которое тело совершает один оборот, т.е. поворачивается на угол 2 пи, называется периодом обращения
Сидерические периоды обращения планет Солнечной системы:
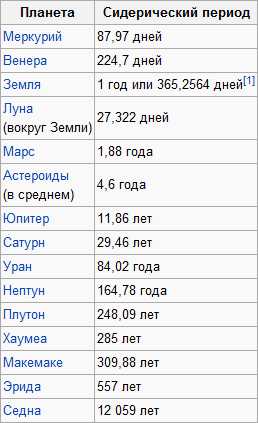
Найдем период обращения:
Если, например, за время t = 4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения. Обозначается он буквой Т и определяется по формуле
Найдем частоту обращения:
Если, например, за время t = 4 с тело совершило n = 20 оборотов,то за 1 с оно успевало совершить 5 оборотов. Это число и выражает
За единицу частоты обращения в СИ принимают частоту обращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: 1/с или с-1 (читается: секунда в минус первой степени).
В формуле мы использовали :
— Период обращения
— Частота обращения
— Число оборотов
xn--e1adcbkcgpcji1bjh6h.xn--p1ai
Период обращения – Формулы по физике.рф
Период обращения — Время, за которое тело совершает один оборот, т.е. поворачивается на угол 2 пи, называется периодом обращения
Сидерические периоды обращения планет Солнечной системы:

Найдем период обращения:
Если, например, за время t = 4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения. Обозначается он буквой Т и определяется по формуле
Найдем частоту обращения:
Если, например, за время t = 4 с тело совершило n = 20 оборотов,то за 1 с оно успевало совершить 5 оборотов. Это число и выражает частоту обращения. Обозначается она греческой буквой V (читается: ню) и определяется по формуле:
За единицу частоты обращения в СИ принимают частоту обращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: 1/с или с-1 (читается: секунда в минус первой степени).
В формуле мы использовали :
— Период обращения
— Частота обращения
— Число оборотов
1.2. Равномерное движение по окружности. Период и частота обращения — Phystech.Academy
Движение по окружности с постоянной по модулю скоростью называют равномерным движением по окружности. Из (3) следует, что при таком движении угловая скорость `omega` тоже постоянна. В этом случае её называют также циклической частотой.
Для описания равномерного движения по окружности наряду с циклической частотой `omega` удобно использовать период обращения `T`, определяемый как время, в течение которого совершается один полный оборот, и частоту `nu` обращения `nu=1/T`, которая численно равна числу оборотов радиус-вектора точки за единицу времени. В связи с этим говорят, что частота измеряется в оборотах в секунду.
Из определения (2) угловой скорости следует, что при равномерном движении по окружности величины `omega`, `T` и `nu` связаны соотношениями
`omega=(2pi)/T=2pinu`. (4)
Размерности `omega` и `nu` одинаковы (`1//»с»`), так как эти величины различаются лишь числовым множителем `2pi`.
Рассмотрим два примера, иллюстрирующих применение введённых величин.
Считая, что Земля движется вокруг Солнца по круговой орбите радиуса `R=150` млн км, найдите линейную скорость `v` Земли в её годичном движении вокруг Солнца.
Будем считать, что Земля совершает один полный оборот вокруг Солнца за `365` суток. Тогда период обращения Земли `T=3,15*10^7` с. Далее из (3) и (4) находим
`v=(2pi)/T R=(2*3,14)/(3,15*10^7)*150*10^9~~30*10^3` м/с.
Рельсы игрушечной железной дороги образуют кольцо радиуса `R`. Вагончик `M` перемещается по рельсам, подталкиваемый стержнем `AB`, который вращается с постоянной угловой скоростью `omega_1` вокруг оси, перпендикулярной плоскости рисунка и проходящей через точку `A`,которая лежит внутри кольца почти у самых рельсов (рис. 2). Как зависит от времени линейная скорость `v(t)` вагончика? Считайте `0<=varphi_1<pi//2`.
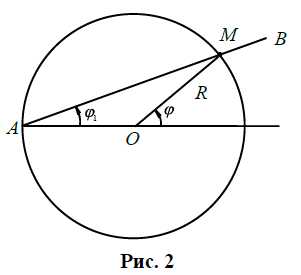
Будем считать, что угол `varphi_1` отсчитывается от направления, задаваемого радиусом `AO` (точка `O` — центр окружности, по которой движется вагончик). Стержень вращается с постоянной угловой скоростью `omega_1`, следовательно, угол `varphi_1` растёт со временем по линейному закону `varphi_1=omega_1t`. Найдём зависимость от времени `t` угла `varphi` поворота радиус-вектора вагончика. Для этого заметим, что треугольник `AOM` равнобедренный, тогда `/_OAM=varphi_1`. Внешний угол треугольника равен сумме двух внутренних, с ним не смежных, отсюда `varphi=2varphi_1=2omega_1t`. Заметим, что угол `varphi(t)` растёт со временем по линейному закону и что угловая скорость `omega` вагончика при движении по рельсам постоянна и вдвое больше угловой скорости `omega_1`, с которой вращается стержень, т. е. `omega=2omega_1`. Следовательно, вагончик движется по окружности равномерно, его линейная скорость от времени не зависит и равна
`v=omega*R=2*omega_1*R`.
phystech.academy
Период обращения и частота обращения.
Период обращения и частота обращения.Прямолинейное равномерное движение. Скорость равномерного прямолинейного движения. Уравнение прямолинейного равномерного движения. Графическое описание прямолинейного равномерного движения.
ПРД — это движение, при котором тело за любые одинаковые промежутки времени проходит одинаковые пути.
Для удобства при ПРД ось координат направляют вдоль траектории тела, при этом:
a=ax=0
V=Vx=Δrx/Δt=const, => Δrx=Vx*Δt
X(t)=x0+Δrx=x0+Vx*Δt – уравнение ПРД
5. 5.Неравномерное движение. Средняя и средняя путевая скорости. Мгновенная скорость. Ускорение.
НД — Движение, при котором за равные промежутки времени тело совершает неравные перемещения
При НД скорость тела меняется и у него есть ускорение.
Средняя скорость МТ – это скорость равная отношению перемещения МТ за некоторый промежуток времени к этому промежутку времени.
Средняя путевая скорость. Vcp = l/ Δt = l1 + 12 + l3/ Δt1 + Δt2 + Δt3
Средняя путевая скорость – скалярная величина.
Знание средней скорости не позволяет определить положение тела, если тело движется не равномерно. Для этого нужно определять скорость на каждом участке траектории. Чем меньше промежуток времени мы выберем, тем точнее будет результат. Если Δt стремиться к 0 (т.е. значение промежутка времени очень близко к 0), то скорость будет называется мгновенной.
Мгновенная скорость МТ(скорость) – это скорость МТ в данный момент времени в данной точке траектории, равная отношению перемещения тела за бесконечно малый промежуток времени к этому промежутку времени.
при Δt→0
Ускорение тела – это величина быстроты изменения скорости тела, равная отношению изменения скорости тела за малый промежуток времени, к этому промежутку времени.
ускорение тела.
В СИ [a]= (Тело за 1 секунду изменяет скорость на 1 м/с).
6. Равноускоренное движение. Уравнение прямолинейного равноускоренного движения. Графическое описание прямолинейного равноускоренного движения.
Равноускоренное движение — движение, при котором ненулевой вектор ускорения остаётся неизменным по модулю и направлению.
ПРУД – движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково.
При ПРУД для удобства ось координат направляют вдоль траектории движения тела, при этом:
a=ax= const
График уравнения проекции мгновенной скорости на ось ох от времени. Площадь фигуры, ограниченной графиком (трапеции), численно равна проекции перемещения на ось ох.
Получаем 2ое на картинке уравнение. Подставляем вэ икс от т (1 уравн.) и сокращаем.
7. Равномерное движение по окружности. Линейная и угловая скорости. Центростремительное ускорение.
Движение по окружности называется равномерным, если модуль вектора скорости остаётся неизменным. Вектор скорости направлен по касательной к траектории в данной точке. Криволинейное движение можно представить как движение по дугам некоторых (к обоим предложениям рисунки).
Линейная скорость — скорость, с которой движется тело вдоль криволинейной траектории. (формула, вел. в формуле, единица и сказать, что при Δt=T V=2πR/T)
Угловая скорость- это скорость изменения угла поворота модуля радиус-вектора (угол между его начальным положением радиус-вектора и последующим положением).
Векторы скорости всё время направлены в разные стороны, значит, всегда есть изменение скорости, а значит, есть и ускорение. Ускорение при равномерном движении по окружности наз. центростремительным (обозначение).
Вывести формулу цен. ускор.
Период обращения и частота обращения.
Равномерное движение по окружности характеризуют периодом и частотой обращения.
Если, например, за время t = 4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения.
Период обращения – это величина, равная промежуткувремени, за которойтело совершило один полный оборот.
Т – период обращение тела
[T]= 1 c
Например: период обращения секундной стрелки часов = 60 секунд.
Частота обращения – это величина, равная числу оборотов,совершаемых телом за единицу времени.
n– частота обращения тела
[n]= 1 c-1 = 1 Гц(Герц)
Δt– промежуток временидвижения тела
N─ число полных оборотов
9. Неравномерное движение по окружности. Полное ускорение. Угловое ускорение.
Движение по окружности называется неравномерным, если модуль скорости со временем изменяется. При таком движении кроме центростремительного ускорения есть тангенциальное.
Рисуем тока не пишем формулу ац*
Сумма векторов тан. и цен. ускорений называется полным ускорением.
a=aτ + aц (всё со стрелками) назвать величины во всех формулах (2 на рисунке, и написанная)
Дата добавления: 2015-07-08; просмотров: 503 | Нарушение авторских прав
mybiblioteka.su — 2015-2018 год. (0.005 сек.)
mybiblioteka.su
Период и частота
Физика > Период и частота
Как найти период и частоту – определение и формула. Читайте, что такое угловая частота, цикл, частоты синусоидальных волн, единицы измерения, уравнения.
Период – продолжительность цикла повторяющегося события, а частота – количество циклов за временной промежуток.
Задача обучения
- Преобразование между частотой и периодом.
Основные пункты
- Регулярно повторяющееся движение – периодическое. Одно полное повторение – цикл.
- Продолжительность цикла – период.
- Частота отображает число циклов, осуществленное за определенный временной промежуток. Это обратная величина периода и определяется формулой f = 1/T.
- Некоторые перемещения лучше всего характеризовать угловой частотой (ω). Она относится к угловому смещению за временной промежуток. Вычисляется по формуле: ω = 2πf.
Термины
- Угловая частота – угловое смещение за временной промежуток.
- Период – длительность одного цикла в повторяющемся событии.
- Частота – соотношение количества раз (n) периодического явления за временную единицу (t): f = n/t.
Пример
Когда-то существовал викторианский трюк. Человеку нужно было вслушаться в звук мухи, воспроизвести музыкальную ноту на пианино и сказать, сколько раз летучая мышь ударила крыльями за секунду. Если это 200 раз в секунду, то частота движения – f = 200/1 с = 200 Гц. Период составляет 1/200-ю секунду: T = 1/f = (1/200) с = 0.005 с.
Период и частота
Эти термины используют для выражения повторного движения. Период – время, которое тратится на одно повторение. Один полноценный проход – цикл. Частота – количество циклов за конкретный временной промежуток (f).
Синусоидальные волны разных частот. Нижние обладают более высокими частотами, а горизонтальная ось отображает время.
Понятия выражаются в формуле: F = 1/T.
Допустим, частота сердца новорожденного составляет 120 раз в минуту, а период – половина секунды. Если вы отточите интуицию на ожидание сопряженности больших частот с короткими периодами (и наоборот), то избежите ошибок.
Единицы
Чаще всего частота рассчитывается в герцах (Гц). 1 Гц указывает на то, что событие происходит раз в секунду. Традиционная единица, применимая во вращающихся механических приборах, – обороты в минуту (об/мин). Единица периода – секунда.
Угловая частота
Частота периодического движения лучше всего передается через угловую частоту – ω. Она относится к угловому смещению на единицу времени или скорости перемены состояния синусоидальной формы волны. В виде формулы:

Колеса совершают вращение с частотой f циклов в секунду, что можно описать как ω радиан в секунду. Механическая связь позволяет линейным колебаниям поршней парового двигателя руководить колесами
у (t) = sin(θ(т)) = sin(ωt) = sin(2πft)
ω = 2πf
Угловая частота часто отображается в радианах на секунду.
v-kosmose.com
