Факториал
ФАКТОРИАЛ.
Факториал – так называют часто встречающуюся в практике функцию, определённую для целых неотрицательных чисел. Название функции происходит от английского математического термина factor – «сомножитель». Обозначается она n!. Знак факториала «!» был введён в1808 году во французском учебнике Хр. Крампа.
Для каждого целого положительного числа n функция n! равна произведению всех целых чисел от 1 до n.
Например:
4! = 1*2*3*4 = 24.
Для удобства полагают по определению 0! = 1. О том, что нуль – факториал должен быть по определению равен единице, писал в 1656 году Дж. Валлис в «Арифметике бесконечных».
Функция n! растёт с увеличением n очень быстро. Так,
1!=1,
2!=2,
3!=6,
4!=24,
5!=120,
…..,
10!=3 628 800.
При преобразовании выражений, содержащих факториал, по лезно использовать равенство
(n + 1)! = (n + 1) • n! = (n + 1) • n • (n – 1)! (1)
Английский математик Дж. Стирлинг в 1970г. предложил очень удобную формулу для приближённого вычисления функции n!:
n! ≈ ( | n | ) | n | * √ 2¶ n , |
е |
где е = 2,7182… — основание натуральных логарифмов.
Относительная ошибка при пользовании этой формулой очень невелика и быстро падает при увеличении числа n.
Способы решения выражений, содержащих факториал, рассмотрим на примерах.
Пример 1. (n! + 1)! = (n! + 1) • n!.
Пример 2. Вычислить 10! 8!
Решение. Воспользуемся формулой (1):
10! =10*9*8! = 10*9=90 8! 8!
Пример 3. Решить уравнение (n + 3)! = 90 (n + 1)!
Решение. Согласно формуле (1) имеем
= (n + 3)(n + 2) = 90.
(n + 3)! =(n + 3)(n + 2)(n+1)! (n + 1)! (n + 1)!
Раскрыв скобки в произведении, получаем квадратное уравнение
n2 + 5n — 84 = 0, корнями которого являются числа n = 7 и n = -12. Од нако факториал определен только для неотрицательных целых чисел, т. е. для всех целых чисел n ≥ 0. Поэтому число n = -12 не удовлетворя ет условию задачи. Итак, n = 7.
Пример 4. Найти хотя бы одну тройку натуральных чисел х, у и z, для которой верно равенство х! = y! • z!.
Решение. Из определения факториала натурального числа n сле дует, что
(n+1)! = (n + 1) • n!
Положим в этом равенстве n + 1 = у! = х, где у — произвольное нату ральное число, получим
x!=y! • (x-1)!
Теперь видим, что искомые тройки чисел можно задать в виде
(y!;y;y!-1) (2)
где y- натуральное число, больше 1.
Например, справедливы равенства
2! = 2! • 1!
6! = 3! • 5!
24! = 4! • 23!
Пример 5. Определить, сколькими нулями оканчивается деся тичная запись числа 32!.
Решение. Если десятичная запись числа Р = 32! оканчивается k нулями, то число Р можно представить в виде
Р = q • 10k,
где число q не делится на 10. Это означает, что разложение числа q на простые множители не содержит одновременно 2 и 5.
Поэтому, чтобы ответить на поставленный вопрос, попробуем опреде лить, с какими показателями в произведение 1 • 2 • 3 • 4 • … • 30 • 31 • 32 входят числа 2 и 5. Если число k — наименьший из найденных показателей, то число Р будет оканчиваться k нулями.
Итак, определим, сколько чисел среди натуральных чисел от 1 до 32 делятся на 2. Очевидно, что их количество равно 32/2 = 16. Затем определим, какое количество среди найденных 16 чисел делится на 4; затем — какое количество из них делится на 8 и т. д. В результате получим, что среди тридцати двух первых натуральных чисел на 2 делится 16 чисел,
из них на 4 делятся 32/4 = 8 чисел, из них на 8 делятся 32/8 = 4 числа, из них на 16 делятся 32/16 = 2 числа и, наконец, из них на 32 делятся 32/32=1, т.е. одно число. Понятно, что сумма полученных количеств:
16 + 8 + 4 + 2 + 1 = 31
равна показателю степени, с которым число 2 входит в 32!.
Аналогично определим, сколько чисел среди натуральных чисел от 1 до 32 делятся на 5, а из найденного количества на 10. Разделим 32 на 5.
Получим 32/5 = 6,4. Следовательно, среди натуральных чисел от 1 до 32
существует 6 чисел, которые делятся на 5. Из них на 25 делится одно
число, так как 32/25 = 1,28. В результате число 5 входит в число 32! с пока зателем, равным сумме 6+1 = 7.
Из полученных результатов следует, что 32!= 231 • 57 • т, где число т не делится ни на 2, ни на 5. Поэтому число 32! содержит множитель
107 и, значит, оканчивается на 7 нулей.
Итак, в данном реферате определено понятие факториала.
Приведена формула английского математика Дж Стирлинга для приближённого вычисления функции n!
При преобразовании выражений, содержащих факториал, по лезно использовать равенство
(n + 1)! = (n + 1) • n! = (n + 1) • n • (n – 1)!
На примерах подробно рассмотрены способы решения задач с факториалом.
Факториал используется в различных формулах в комбинаторике, в рядах и др.
Например, количество способов выстроить n школьников в одну шеренгу равняется n!.
Число n! равно, например, количеству способов, которыми можно n различных книг расставить на книжной полке, или, например, число 5! равно количеству способов, которыми пять человек можно рассадить на одной скамейке. Или, например, число 27! равно количеству способов, которыми наш класс из 27 учеников можно выстроить в ряд на уроке физкультуры.
Рязановский А.Р., Зайцев Е.А.
Математика. 5-11 кл.: Дополнительные материалы к уроку математики. –М.:Дрофа, 2001.- (Библиотека учителя).
Энциклопедический словарь юного математика. /Сост. А.П.Савин.-М.:Педагогика, 1985
Математика. Справочник школьника. /Сост. Г.М. Якушева.- М.: Филолог. об-во «Слово», 1996.
studfiles.net
Факториал — Википедия
Материал из Википедии — свободной энциклопедии
Факториа́л — функция, определённая на множестве неотрицательных целых чисел. Название происходит от лат. factorialis — действующий, производящий, умножающий; обозначается n!, произносится эн факториа́л. Факториал натурального числа n определяется как произведение всех натуральных чисел от 1 до n включительно:
- n!=1⋅2⋅…⋅n=∏k=1nk{\displaystyle n!=1\cdot 2\cdot \ldots \cdot n=\prod _{k=1}^{n}k}.
Например,
- 5!=1⋅2⋅3⋅4⋅5=120{\displaystyle 5!=1\cdot 2\cdot 3\cdot 4\cdot 5=120}.
Из определения факториала следует соотношение (n−1)!=n!n{\displaystyle (n-1)!={\frac {n!}{n}}}, откуда при n=1{\displaystyle n=1} формально находим
- 0!=1{\displaystyle 0!=1}.
Последнее равенство обычно принимают в качестве соглашения, хотя, как показано выше, оно следует из определения факториала для натуральных чисел при условии, что все значения функции связаны единым рекуррентным соотношением.
| n | n! |
|---|---|
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5040 |
| 8 | 40 |
ru.wikipedia.org
Таблица факториалов
Таблица факториалов| 1! | 1 |
| 2! | 2 |
| 3! | 6 |
| 4! | 24 |
| 5! | 120 |
| 6! | 720 |
| 7! | 5 040 |
| 8! | 40 320 |
| 9! | 362 880 |
| 10! | 3 628 800 |
| 11! | 39 916 800 |
| 12! | 479 001 600 |
| 13! | 6 227 020 800 |
| 14! | 87 178 291 200 |
| 15! | 1 307 674 368 000 |
| 16! | 20 922 789 888 000 |
| 17! | 355 687 428 096 000 |
| 18! | 6 402 373 705 728 000 |
| 19! | 121 645 100 408 832 000 |
| 20! | 2 432 902 008 176 640 000 |
| 21! | 51 090 942 171 709 440 000 |
| 22! | 1 124 000 727 777 607 680 000 |
| 23! | 25 852 016 738 884 976 640 000 |
| 24! | 620 448 401 733 239 439 360 000 |
| 25! | 15 511 210 043 330 985 984 000 000 |
| 26! | 403 291 461 126 605 635 584 000 000 |
| 27! | 10 888 869 450 418 352 160 768 000 000 |
| 28! | 304 888 344 611 713 860 501 504 000 000 |
| 29! | 8 841 761 993 739 701 954 543 616 000 000 |
| 30! | 265 252 859 812 191 058 636 308 480 000 000 |
— версия для печати
- Определение (что такое факториал)
- Факториал числа — результат последовательного умножения числа на все натуральные числа меньшие данного числа и большие единицы. Обозначается факториал восклицательным знаком после числа — «n!».
- Факториал натурального числа n можно также определить как рекуррентную функцию F (n). Определяется она следующим образом: F (0) = F (1) = 1; F (n) = n * F (n-1).
- Пример:
- 7! = 7×6×5×4×3×2×1 = 5040
- Не стоит забывать
- По общепринятой договоренности 0! = 1 (факториал нуля равен единице). Этот факт важен, к примеру, для вычисления биномиальных коэффициентов.
- Полезный факт
- Факториал числа, функцию от натурального аргумента можно продолжить на все действительные числа с помощью т.н. Гамма-функции (важно отметить, что для этого требуется определенный математический аппарат). В таком случае, мы сможем посчитать факториал любого действительного числа. Например, факториал (или, Гамма-функция, что математически правильнее) числа Пи Π! приблизительно равен 2.28803779534. Факториал числа Эйлера, другого трансцендентного числа, Γ(e) ~ 1.567468255 (упрощенно, факториал числа e).
| Если у вас есть мысли по поводу данной страницы или предложение по созданию математической (см. раздел «Математика») вспомогательной памятки, мы обязательно рассмотрим ваше предложение. Просто воспользуйтесь обратной связью. |
© Школяр. Математика (при поддержке «Ветвистого древа») 2009—2016
scolaire.ru
Таблица факториалов до 50
Таблица факториалов до 50Главная > ф >
Факториа́л числа n (лат. factorialis — действующий, производящий, умножающий; обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел от 1 до n включительно.Например: 4! = 4 × 3 × 2 × 1 = 24.
Принято: 0! = 1.
В таблице приведены значения факториалов для чисел от 0 до 50.
| число | факториал числа |
|---|---|
| 0! | 1 |
| 1! | 1 |
| 2! | 2 |
| 3! | 6 |
| 4! | 24 |
| 5! | 120 |
| 6! | 720 |
| 7! | 5040 |
| 8! | 40320 |
| 9! | 362880 |
| 10! | 3628800 |
| 11! | 39916800 |
| 12! | 479001600 |
| 13! | 6227020800 |
| 14! | 87178291200 |
| 15! | 1307674368000 |
| 16! | 20922789888000 |
| 17! | 355687428096000 |
| 18! | 6402373705728000 |
| 19! | 121645100408832000 |
| 20! | 2432902008176640000 |
| 21! | 51090942171709440000 |
| 22! | 1124000727777607680000 |
| 23! | 25852016738884976640000 |
| 24! | 620448401733239439360000 |
| 25! | 15511210043330985984000000 |
| 26! | 403291461126605635584000000 |
| 27! | 10888869450418352160768000000 |
| 28! | 304888344611713860501504000000 |
| 29! | 8841761993739701954543616000000 |
| 30! | 265252859812191058636308480000000 |
| 31! | 8222838654177922817725562880000000 |
| 32! | 263130836933693530167218012160000000 |
| 33! | 8683317618811886495518194401280000000 |
| 34! | 295232799039604140847618609643520000000 |
| 35! | 10333147966386144929666651337523200000000 |
| 36! | 371993326789901217467999448150835200000000 |
| 37! | 13763753091226345046315979581580902400000000 |
| 38! | 523022617466601111760007224100074291200000000 |
| 39! | 20397882081197443358640281739902897356800000000 |
| 40! | 815915283247897734345611269596115894272000000000 |
| 41! | 33452526613163807108170062053440751665152000000000 |
| 42! | 1405006117752879898543142606244511569936384000000000 |
| 43! | 60415263063373835637355132068513997507264512000000000 |
| 44! | 2658271574788448768043625811014615890319638528000000000 |
| 45! | 119622220865480194561963161495657715064383733760000000000 |
| 46! | 5502622159812088949850305428800254892961651752960000000000 |
| 47! | 258623241511168180642964355153611979969197632389120000000000 |
| 48! | 12413915592536072670862289047373375038521486354677760000000000 |
| 49! | 608281864034267560872252163321295376887552831379210240000000000 |
| 50! | 30414093201713378043612608166064768844377641568960512000000000000 |
comments powered by HyperComments
tab.wikimassa.org
Двойной факториал — это… Что такое Двойной факториал?
Факториа́л числа n (обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел до n включительно:
- .
По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел.
Эта функция часто используется в комбинаторике, теории чисел и функциональном анализе.
Иногда словом «факториал» неформально называют восклицательный знак.
Свойства
Комбинаторное определение
В комбинаторике факториал определяется как количество перестановок множества из n элементов. Например, элементы множества {A,B,C,D} можно линейно упорядочить 4!=24 способами:
ABCD BACD CABD DABC ABDC BADC CADB DACB ACBD BCAD CBAD DBAC ACDB BCDA CBDA DBCA ADBC BDAC CDAB DCAB ADCB BDCA CDBA DCBA
Связь с гамма-функцией
Факториал связан с гамма-функцией от целочисленного аргумента соотношением:
- n! = Γ(n + 1)
Таким образом, гамма-функцию рассматривают как обобщение факториала для положительных вещественных чисел. Путём аналитического продолжения её также расширяют и на всю комплексную плоскость, исключая особые точки при .
Формула Стирлинга
Формула Стирлинга — асимптотическая формула для вычисления факториала:
см. O-большое. Коэффициенты этого разложения дают последовательность A001163 в OEIS (числители) и последовательность A001164 в OEIS (знаменатели).
Во многих случаях для приближенного значения факториала достаточно рассматривать только главный член формулы Стирлинга:
При этом можно утверждать, что
Разложение на простые числа
Каждое простое число p входит в разложение n! на простые в степени
Таким образом,
- ,
где произведение берется по всем простым числам.
Другие свойства
- x!2 > xx > x! > = x, при x>1
Обобщения
Двойной факториал
Двойной факториал числа n обозначается n!! и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же чётность что и n. Таким образом,
По определению полагают 0!! = 1.
Убывающий факториал
Убывающим факториалом (или неполным факториалом) называется выражение
Убывающий факториал дает число размещений из n по k.
Возрастающий факториал
Возрастающим факториалом называется выражение
Праймориал или примориал
Примориал (англ. Primorial) числа n обозначается n# и определяется как произведение простых чисел, не превышающих n. Например,
Последовательность праймориалов начинается так:
- 2, 6, 30, 210, 2310, 30030, 510510, 9699690, … (последовательность A002110 в OEIS)
Суперфакториалы
Основная статья: Большие числа
Нейл Слоан и Саймон Плоуф (англ.) в 1995 году определили суперфакториал как произведение первых n факториалов. Согласно этому определению суперфакториал четырёх равен (поскольку устоявшегося обозначения нет, используется функциональное)
В общем
Последовательность суперфакториалов начинается (с n = 0) с
- 1, 1, 2, 12, 288, 34560, 24883200, … (последовательность A000178 в OEIS)
Идея была обобщена в 2000 Генри Боттомли (англ.), что привело к гиперфакториалам (англ. Super-duper-factorial), которые являются произведением первых n суперфакториалов. Первые члены (с n = 0) равны:
- 1, 1, 2, 24, 6912, 238878720, 5944066965504000, … (последовательность A055462 в OEIS)
Продолжая рекуррентно, можно определить факториал кратного уровня, где m-уровневый факториал n — произведение первых n (m − 1)-уровневых факториалов, то есть
где для n > 0 и .
Субфакториал
Субфакториал определяется как количество беспорядков порядка , то есть перестановок -элементного множества без неподвижных точек.
Ссылки
См. также
Wikimedia Foundation. 2010.
dic.academic.ru
Онлайн калькулятор: Факториал
Факториал числа n (обозначается n!) — произведение всех натуральных чисел до n включительно:
По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел.
Поскольку в вычислениях иногда бывает довольно трудно перемножать все числа входящие в факториал, используется так называемая формула Стирлинга:
приближенная формула для вычисления факториала.
Во многих случаях для упрощения рассматривают только главный член формулы
При этом утверждается, что
Калькулятор рассчитывает «честный» факториал, факториал по формуле Стирлинга, а также нижнюю и верхнюю границу (из неравенства). К сожалению, из-за ограниченных вычислительных способностей Javascript максимально возможный факториал для калькулятора — 170!
Знаков после запятой: 2
Граница снизу
Формула Стирлинга
Граница сверху
Сохранить share extension
planetcalc.ru
Десять букв: Факториал дробных чисел
Вычислим факториалы нескольких натуральных чисел и отметим точки (1, 1), (2, 2), (3, 6), (4, 24) и т.д.на прямоугольной системе координат.
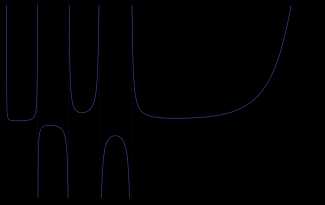Что если попробовать плавной линией соединить эти точки и найти функцию, график которой имел бы такой вид? Тогда можно было бы вычислять факториал от любых чисел, не только от натуральных.
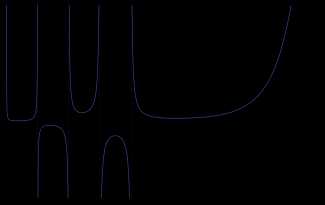Об этом математики задумались в начале XVIII века. Если такая функция f(x) существует, она должна удовлетворять условию f(x) = x f(x-1), т.е. рекурсивному определению факториала. В 1729 году Леонард Эйлер нашёл способ получить факториал в виде бесконечного произведения, в которое в качестве аргумента можно было подставлять и дробные числа.Вот как будет работать эта формула для n = 4, например:
Сходится произведение довольно медленно, я проверил в Экселе. Для того, чтобы произведение превысило 23, нужно взять 139 множителей, а чтобы добраться до 23,5, множителей нужно уже 283. На 1435-м шагу произведение доходит до 23,4, ну а в бесконечности будет равно 24
Я выложил лист для вычисления факториала в гугл доки. Меняете n и смотрите, к чему будут стремиться частичные произведения.
Чуть позже Эйлер выразил факториал в виде несобственного интеграла:
Применим к нему метод интегрирования частями, взяв u = (-ln x)n, dv = dx:
Требуемое свойство выполняется.
Заменой t = −ln x этот интеграл принимает используемый в настоящее время вид и известен как гамма-функция.
Аргументами её могут быть не только дробные или даже отрицательные числа, но и комплексные.
Для натуральных аргументов Г(n) = (n-1)!
Шотландский математик Джеймс Стирлинг был современником Эйлера и вывел формулу, позволяющую приближённо вычислять факториал для больших чисел.
.
desyatbukv.blogspot.com
