Диагностическая работа по алгебре для 9 класса
Здесь Вы можете скачать Диагностическая работа по алгебре для 9 класса для предмета : Математика. Данный документ поможет вам подготовить хороший и качественный материал для урока.
Диагностическая работа по алгебре для 9 класса.
Данная работа рассчитана на учеников 9 классов общеобразовательных учреждений. Ее содержание находится в рамках Обязательного минимума содержания образования по математике в основной школе, при этом подбор заданий осуществлен с учетом требований к уровню подготовки учащихся, предъявляемых новыми образовательными стандартами и в соответствии с тематическим планированием по различным программам образовательных учреждений.
Цель работы:
-
выявление проблемных зон знаний учащихся 9-х классов общеобразовательных учреждений с целью прогнозирования прохождения итоговой аттестации по алгебре и внесения корректив в обучение учащихся в 9-м классе для предотвращения неуспешности на ГИА;
-
апробация структуры экзаменационной работы по алгебре в новой форме и прототипов заданий.
Структура работы.
Работа состоит из двух частей.
Первая часть (А) направлена на проверку базовой подготовки учащихся. Эта часть работы содержит 6 заданий с выбором ответа или с кратким ответом.
Вторая часть (В) направлена на дифференцированную проверку повышенных уровней подготовки. Она содержит 5 заданий из различных разделов курса, предусматривающих полную запись хода решения. Задания расположены по нарастанию сложности.
На проведение работы отводится 80 минут (2 урока). Ответы к заданиям первой части учащиеся фиксируют непосредственно в бланке с заданиями, вторая часть выполняется на отдельных листах.
Критерии оценивания результатов выполнения работы .
Для оценивания результатов выполнения работы применяются два количественных показателя: оценка и рейтинг – сумма баллов за верно выполненные задания. Рейтинг формируется путем подсчета общего количества баллов, полученных учащимися за выполнение всех частей работы. За каждое верно выполненное задание первой части начисляется 1 балл. Во второй части для каждого задания указано число баллов, которые засчитываются в рейтинговую оценку ученика при его верном выполнении:
2 или 4 балла. Если при выполнении задания допущена ошибка, не носящая принципиального характера и не влияющая на общую правильность хода решения, то учащемуся засчитывается балл, на единицу меньший указанного. Другие возможности не предусматриваются.
За первую часть работы можно максимально получить 6 баллов, за всю работу в целом – 20 баллов.
Схема перевода рейтинга в отметку показана в таблице:
| 4 — 7 | 8 — 13 | 14 – 20 | |
| Отметка | «3» | «4» | «5» |
Диагностическая работа по алгебре.
Вариант 1.
Ф.И. __________________________________ Класс __________________
Часть 1.
А1. Решите уравнение: х2 – 8х + 12 = 0
А. -2; -6 Б. 2; 6 В. 1; 8 Г. Корней нет
А2. Упростите выражение:  Ответ: ____________________
Ответ: ____________________
А3. Решите неравенство: -8 – х Ответ: ____________________
А4. Упростите выражение: (3с – 2) 2 + 24c
А. (3с +2)2Б. 3с2 + 2 В. 3с2 – 4 Г. 9с2 – 4
А5. Выразите из формулы  переменную
переменную  .
.
А. Б. В. Г. 
А6. Лодка за одно и то же время может проплыть 40 км по течению реки или 25 км против течения реки. Найдите собственную скорость лодки, если скорость течения реки 2 км/ч. Обозначив собственную скорость лодки за х км/ч, можно составить уравнение:
А. 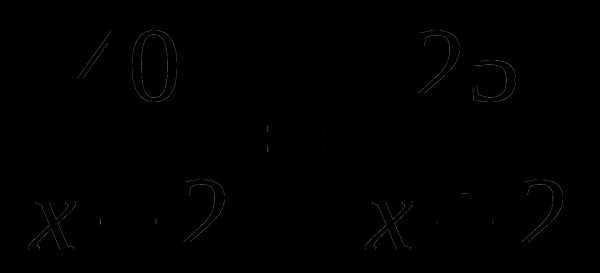 Б.
Б. 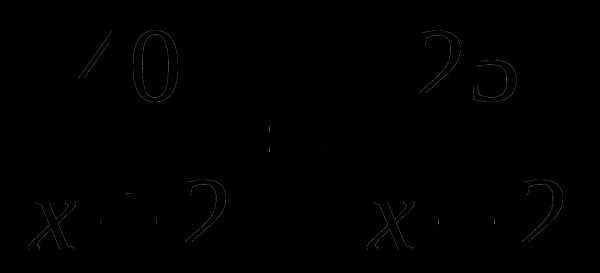

Диагностическая работа по алгебре.
Вариант 2.
Ф.И. __________________________________ Класс __________________
Часть 1.
А1. Решите уравнение: х2 + 5х — 14 = 0
А. -7; 2 Б. -2; 7 В. 1; 4 Г. Корней нет
А2. Упростите выражение:  Ответ: _____________________
Ответ: _____________________
А3. Решите неравенство: 3х – 1 ≥ 5х + 1. Ответ: ____________________
А4. Упростите выражение: (2k + 5)2 – 40k
А. 4k2 – 25 Б. 2k2 + 25 В. (2k – 5)2 Г. 4k2 +25
А5. Из формулы объема цилиндра , где R – радиус основания, H – высота цилиндра, выразите радиус R.
А. 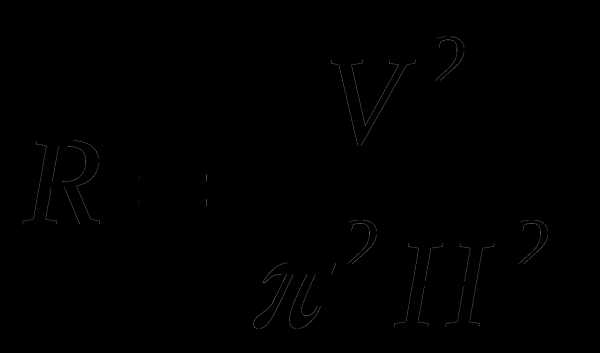 Б.
Б. 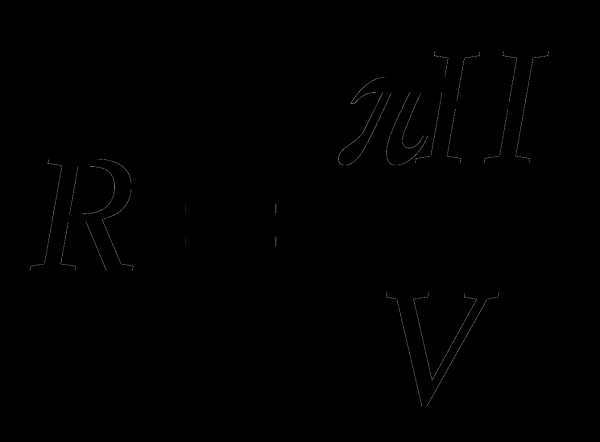 В.
В. 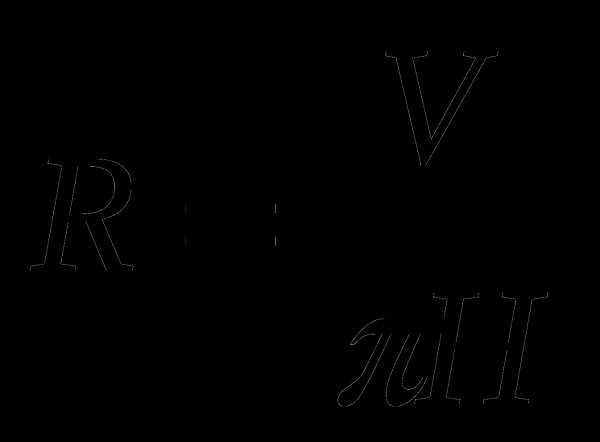 Г.
Г. 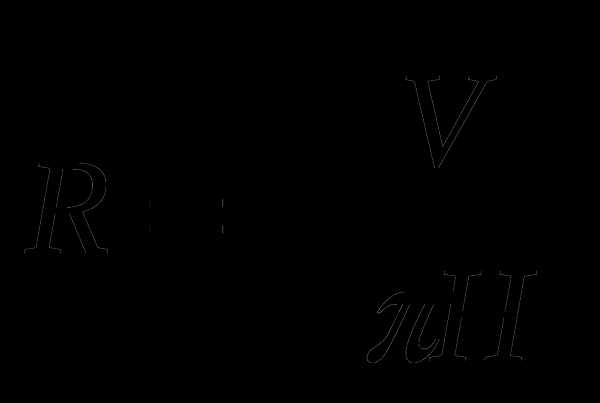
А6. Расстояние между пунктами А и В по реке равно 2 км. На путь из А в В и обратно моторная лодка затратила 0,5 часа. Какова собственная скорость лодки, если скорость течения реки равна 1 км/ч? Обозначив собственную скорость лодки за х км/ч можно составить уравнение:
А. Б. 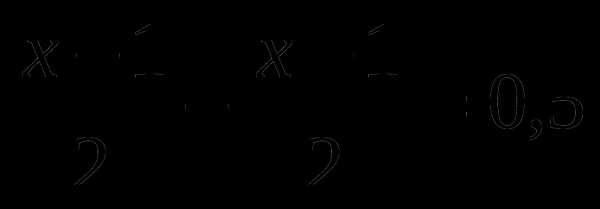
 Г.
Г. 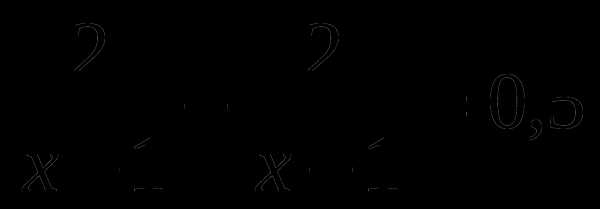
Диагностическая работа по алгебре.
Вариант 3.
Ф.И. __________________________________ Класс __________________
Часть 1.
А1. Решите уравнение: х2 – 7х + 12 = 0
А. -3; -4 Б. 3; 4 В. 6; 1 Г. Корней нет
А2. Упростите выражение:  Ответ: ____________________
Ответ: ____________________
А3. Решите неравенство: 3х – 2 Ответ: ____________________
А4. Упростите выражение: (5a – 1)2 + 20a
А. (5a + 1)2Б. 25a2 + 1 В. 5a 2 + 1 Г. 5a2 + 21a
А5. Из формулы кинетической энергии  выразите скорость
выразите скорость  .
.
А. 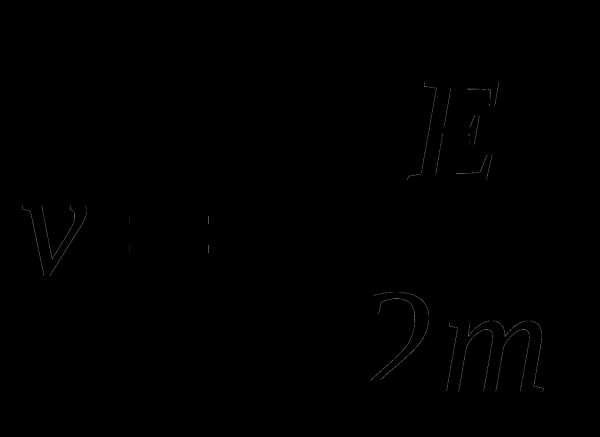 Б.
Б. 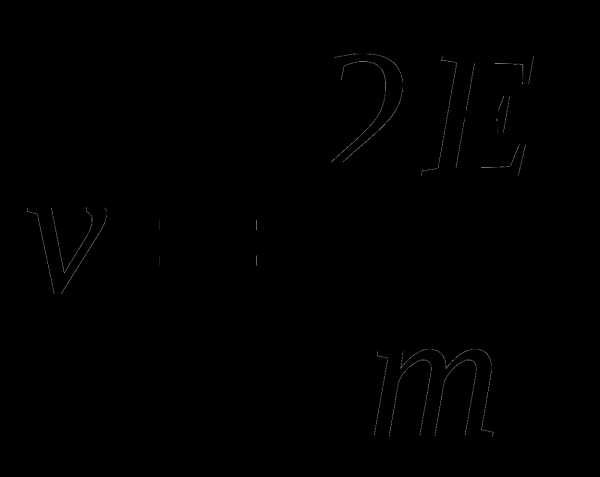 В.
В. 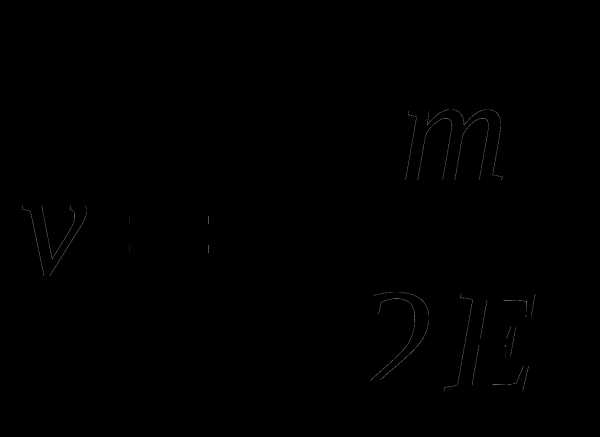 Г.
Г. 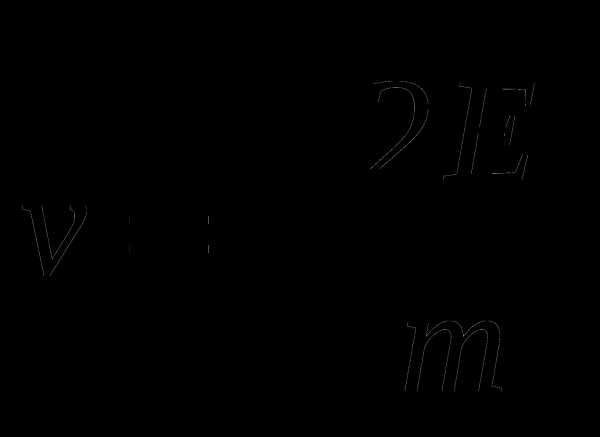
А6. Плот проплывает по течению 60 км на 5 ч быстрее, чем такое же расстояние проходит моторная лодка против течения. Найдите скорость лодки по течению, если ее скорость в стоячей воде 10 км/ч. Обозначив скорость течения за х км/ч, можно составить уравнение:
А.  Б.
Б. 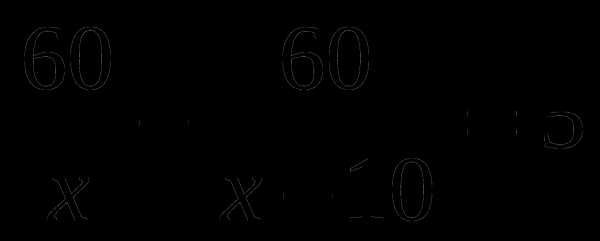 В.
В. 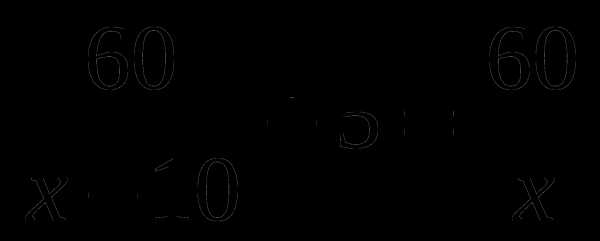 Г.
Г. 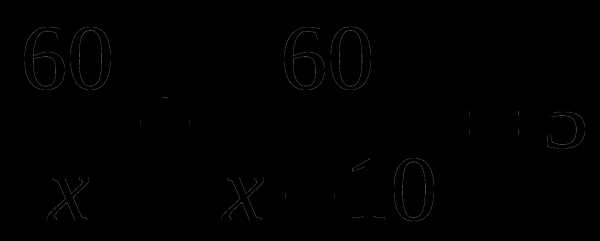
Диагностическая работа по алгебре.
Вариант 4.
Ф.И. __________________________________ Класс __________________
Часть 1.
А1. Решите уравнение: х2 + х – 20 = 0
А. -5; 4 Б. -4; 5 В. 10; 2 Г. Корней нет
А2. Упростите выражение: 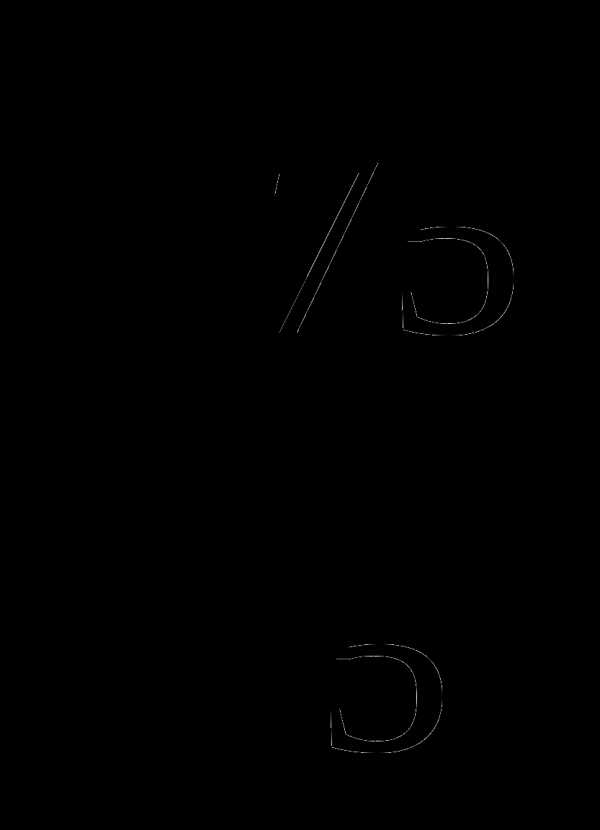 Ответ _____________________
Ответ _____________________
А3. Решите неравенство: 3х + 3 > 6 + 2х Ответ: ____________________
А4. Упростите выражение: (7а + 1)2 – 28а
А. 7а2 + 1 Б. (7а – 1)2В. 49а2 + 1 – 28а Г. 7а2 – 29а
А5. Из формулы площади круга  выразите радиус
выразите радиус  .
.
А.  Б.
Б.  В.
В. 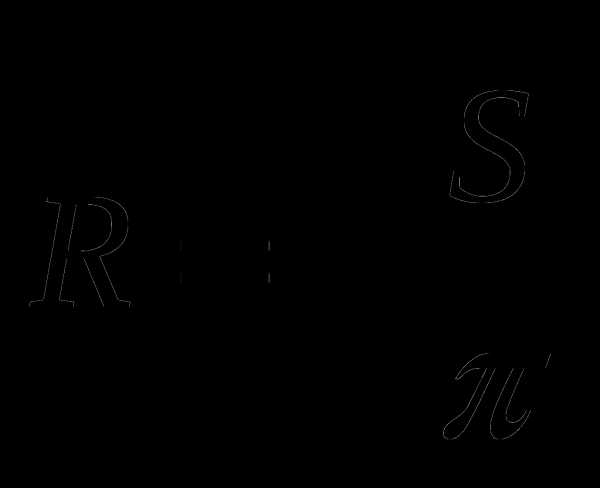 Г.
Г. 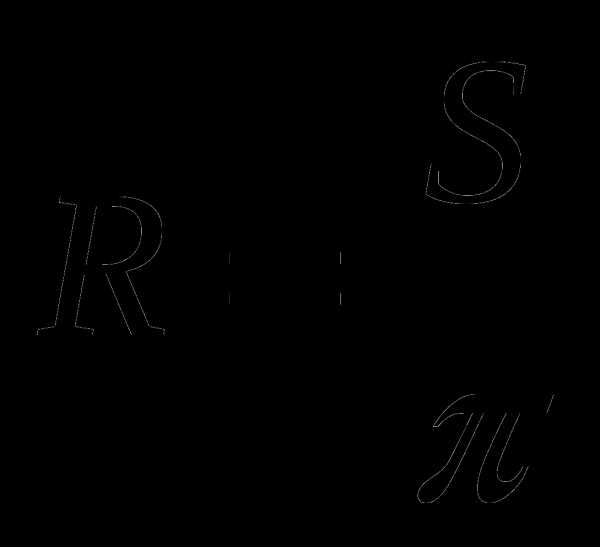
А6. Катер прошел по течению 36 км и против течения 48 км, затратив на весь путь 6 ч. Какова скорость катера в стоячей воде, если скорость течения 3 км/ч? Обозначив скорость катера за
А. 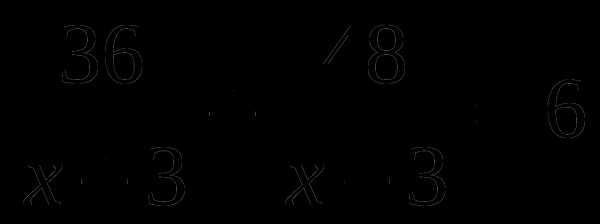 Б.
Б. 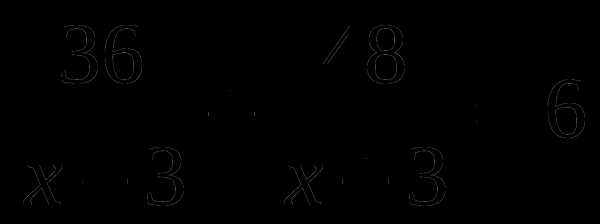 В.
В. 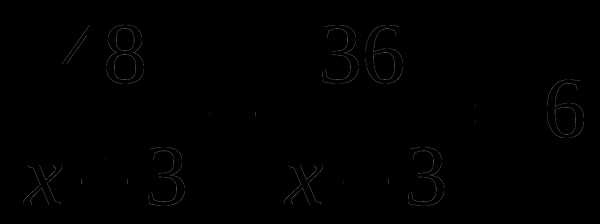 Г.
Г. 
Вариант 1.
Часть 2.
В1. (2 балла)
Постройте график функции  . При каких значениях аргумента функция принимает положительные значения?
. При каких значениях аргумента функция принимает положительные значения?
В2. (2 балла)
Упростите выражение и найдите его значение при  .
.
В3. (2 балла)
Сплав содержит медь и олово в соотношении 7 : 4. Сколько граммов меди содержится в 352 г сплава?
В4. (4 балла)
Сократите дробь: 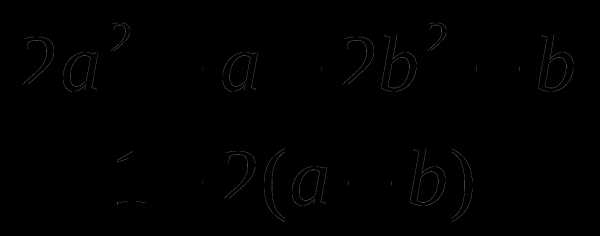
В5. (4 балла)
Зная, что , найдите значение выражения 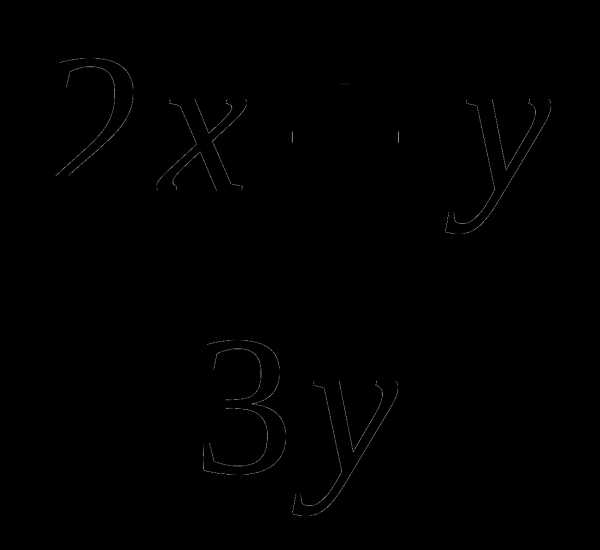 .
.
Вариант 2.
Часть 2.
В1. (2 балла)
Постройте график функции . При каких значениях аргумента функция принимает отрицательные значения?
В2. (2 балла)
Упростите выражение и найдите его значение при  .
.
В3. (2 балла)
В саду растут яблони и сливы в отношении 5 : 3. Сколько слив в саду, если там всего 320 деревьев?
В4. (4 балла)
Сократите дробь:
В5. (4 балла)
Зная, что , найдите значение выражения 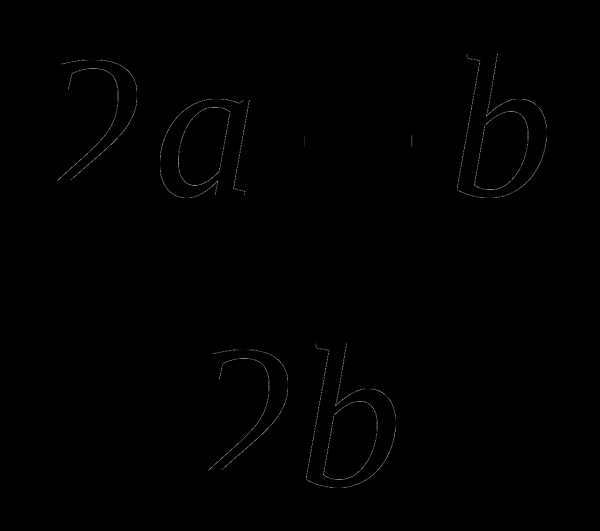 .
.
Вариант 3.
Часть 2.
В1. (2 балла)
Постройте график функции 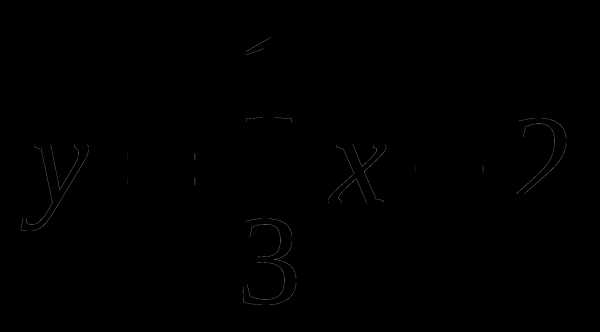 . При каких значениях аргумента функция принимает отрицательные значения?
. При каких значениях аргумента функция принимает отрицательные значения?
В2. (2 балла)
Упростите выражение и найдите его значение при 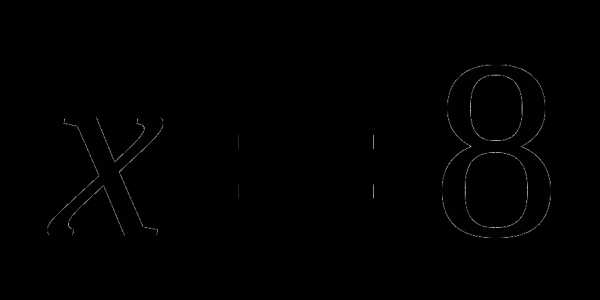 .
.
В3. (2 балла)
Отрезок MN=24см разделили точкой A в отношении 2 : 1, считая от точки M. Найдите длину отрезка AM.
В4. (4 балла)
Сократите дробь: 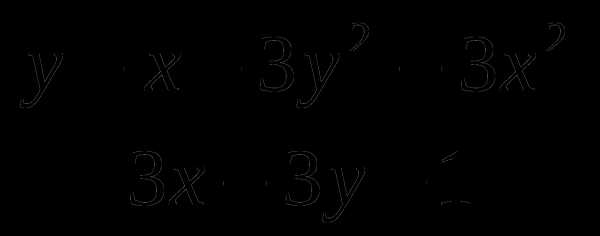
В5. (4 балла)
Зная, что , найдите значение выражения  .
.
Вариант 4.
Часть 2.
В1. (2 балла)
Постройте график функции  . При каких значениях аргумента функция принимает положительные значения?
. При каких значениях аргумента функция принимает положительные значения?
В2. (2 балла)
Упростите выражение и найдите его значение при  .
.
В3. (2 балла)
Отрезок АВ = 16 см разделили точкой К в отношении 3 : 1, считая от точки А. Найдите длину отрезка АК.
В4. (4 балла)
Сократите дробь:
В5. (4 балла)
Зная, что , найдите значение выражения 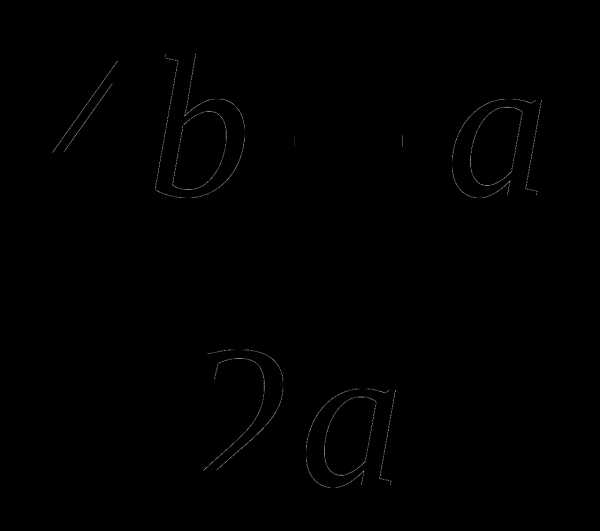 .
.
Анализ диагностической работы по алгебре для 9 класса (осень).
Школа __________
Количество учащихся 9 классов ___________
Количество выполнявших работу ____________
Получили отметку «5» ________чел ________%
«4»________чел ________%
«3» ________чел ________%
«2» ________чел ________%
| чел. | % | |||
| Первая часть работы | ||||
| Выполнили верно | ||||
| В том числе | А1. Решение квадратного уравнения | |||
| А2. Преобразование выражений, содержащих квадратные корни | ||||
| А3. Решение линейного неравенства | ||||
| А4. Преобразование алгебраического выражения | ||||
| А5. Выражение из формул одной переменной через другие | ||||
| А6. Составление уравнения по условию задачи на движение | ||||
| Вторая часть работы | ||||
| В1. Построение графика линейной функции. | Приступили | |||
| Выполнили верно | ||||
| В2. Преобразование алгебраического выражения и нахождение его значения по заданному значению переменной | Приступили | |||
| Выполнили верно | ||||
| В3. Решение задачи на части | Приступили | |||
| Выполнили верно | ||||
| В4. Преобразование алгебраической дроби | Приступили | |||
| Выполнили верно | ||||
| В5. Преобразование алгебраического выражения. | Приступили | |||
| Выполнили верно | ||||
docbase.org
Диагностическая работа по алгебре для 9 класса
Диагностическая работа по алгебре для 9 класса.
Данная работа рассчитана на учеников 9 классов общеобразовательных учреждений. Ее содержание находится в рамках Обязательного минимума содержания образования по математике в основной школе, при этом подбор заданий осуществлен с учетом требований к уровню подготовки учащихся, предъявляемых новыми образовательными стандартами и в соответствии с тематическим планированием по различным программам образовательных учреждений.
Цель работы:
выявление проблемных зон знаний учащихся 9-х классов общеобразовательных учреждений с целью прогнозирования прохождения итоговой аттестации по алгебре и внесения корректив в обучение учащихся в 9-м классе для предотвращения неуспешности на ГИА;
апробация структуры экзаменационной работы по алгебре в новой форме и прототипов заданий.
Структура работы.
Работа состоит из двух частей.
Первая часть (А) направлена на проверку базовой подготовки учащихся. Эта часть работы содержит 6 заданий с выбором ответа или с кратким ответом.
Вторая часть (В) направлена на дифференцированную проверку повышенных уровней подготовки. Она содержит 5 заданий из различных разделов курса, предусматривающих полную запись хода решения. Задания расположены по нарастанию сложности.
На проведение работы отводится 80 минут (2 урока). Ответы к заданиям первой части учащиеся фиксируют непосредственно в бланке с заданиями, вторая часть выполняется на отдельных листах.
Критерии оценивания результатов выполнения работы.
Для оценивания результатов выполнения работы применяются два количественных показателя: оценка и рейтинг – сумма баллов за верно выполненные задания. Рейтинг формируется путем подсчета общего количества баллов, полученных учащимися за выполнение всех частей работы. За каждое верно выполненное задание первой части начисляется 1 балл. Во второй части для каждого задания указано число баллов, которые засчитываются в рейтинговую оценку ученика при его верном выполнении:
2 или 4 балла. Если при выполнении задания допущена ошибка, не носящая принципиального характера и не влияющая на общую правильность хода решения, то учащемуся засчитывается балл, на единицу меньший указанного. Другие возможности не предусматриваются.
За первую часть работы можно максимально получить 6 баллов, за всю работу в целом – 20 баллов.
Схема перевода рейтинга в отметку показана в таблице:
4 — 7 | 8 — 13 | 14 – 20 | |
Отметка | «3» | «4» | «5» |
Диагностическая работа по алгебре.
Вариант 1.
Ф.И. __________________________________ Класс __________________
Часть 1.
А1. Решите уравнение: х2 – 8х + 12 = 0
А. -2; -6 Б. 2; 6 В. 1; 8 Г. Корней нет
А2. Упростите выражение:  Ответ: ____________________
Ответ: ____________________
А3. Решите неравенство: -8 – х < 4х + 2. Ответ: ____________________
А4. Упростите выражение: (3с – 2)2 + 24c
А. (3с +2)2Б. 3с2 + 2 В. 3с2 – 4 Г. 9с2 – 4
А5. Выразите из формулы  переменную
переменную  .
.
А. Б. В. Г. 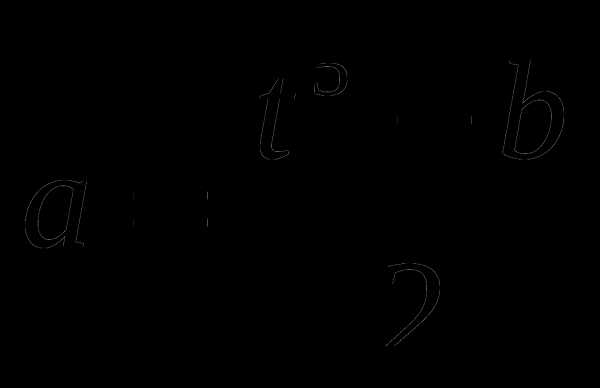
А6. Лодка за одно и то же время может проплыть 40 км по течению реки или 25 км против течения реки. Найдите собственную скорость лодки, если скорость течения реки 2 км/ч. Обозначив собственную скорость лодки за х км/ч, можно составить уравнение:
А. 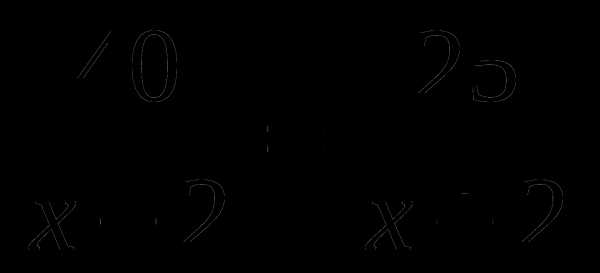 Б.
Б. 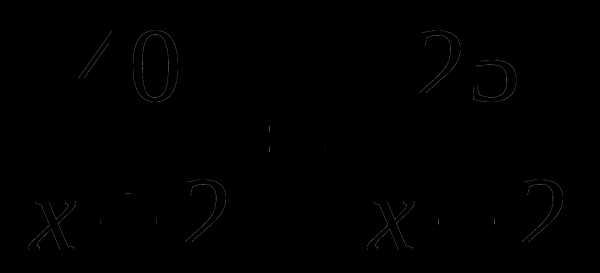 В. Г.
В. Г. 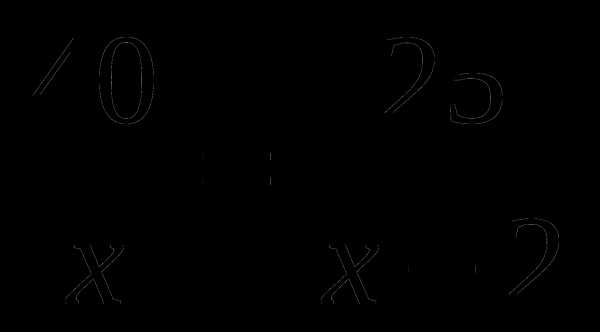
Диагностическая работа по алгебре.
Вариант 2.
Ф.И. __________________________________ Класс __________________
Часть 1.
А1. Решите уравнение: х2 + 5х — 14 = 0
А. -7; 2 Б. -2; 7 В. 1; 4 Г. Корней нет
А2. Упростите выражение:  Ответ: _____________________
Ответ: _____________________
А3. Решите неравенство: 3х – 1 ≥ 5х + 1. Ответ: ____________________
А4. Упростите выражение: (2k + 5)2 – 40k
А. 4k2 – 25 Б. 2k2 + 25 В. (2k – 5)2 Г. 4k2 +25
А5. Из формулы объема цилиндра , где R – радиус основания, H – высота цилиндра, выразите радиус R.
А. 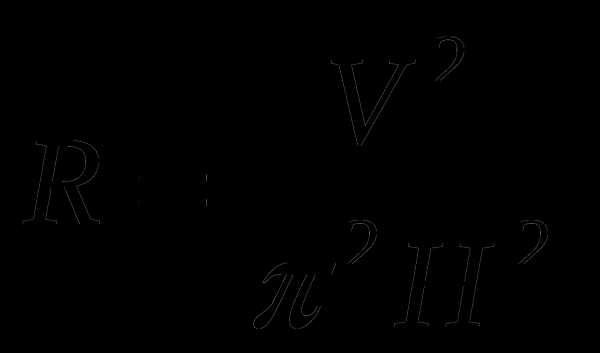 Б.
Б. 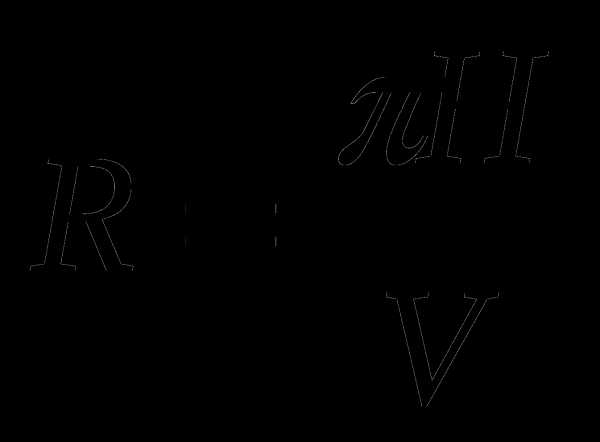 В.
В.  Г.
Г. 
А6. Расстояние между пунктами А и В по реке равно 2 км. На путь из А в В и обратно моторная лодка затратила 0,5 часа. Какова собственная скорость лодки, если скорость течения реки равна 1 км/ч? Обозначив собственную скорость лодки за х км/ч можно составить уравнение:
А. Б. 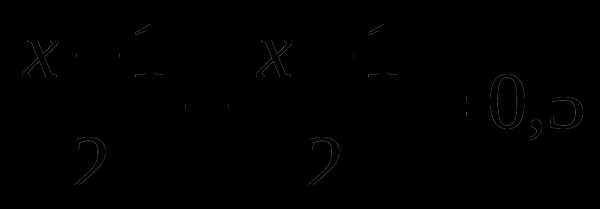 В.
В. 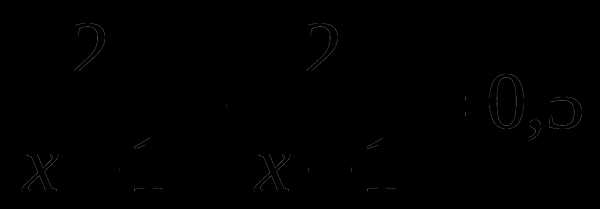 Г.
Г. 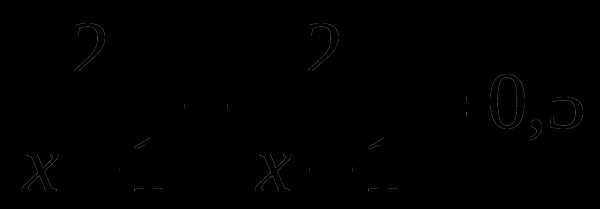
Диагностическая работа по алгебре.
Вариант 3.
Ф.И. __________________________________ Класс __________________
Часть 1.
А1. Решите уравнение: х2 – 7х + 12 = 0
А. -3; -4 Б. 3; 4 В. 6; 1 Г. Корней нет
А2. Упростите выражение:  Ответ: ____________________
Ответ: ____________________
А3. Решите неравенство: 3х – 2 < 10х + 5. Ответ: ____________________
А4. Упростите выражение: (5a – 1)2 + 20a
А. (5a + 1)2Б. 25a2 + 1 В. 5a2 + 1 Г. 5a2 + 21a
А5. Из формулы кинетической энергии  выразите скорость
выразите скорость  .
.
А. 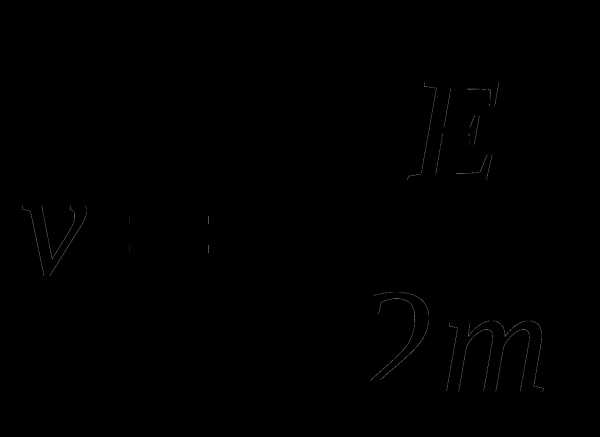 Б.
Б.  В.
В. 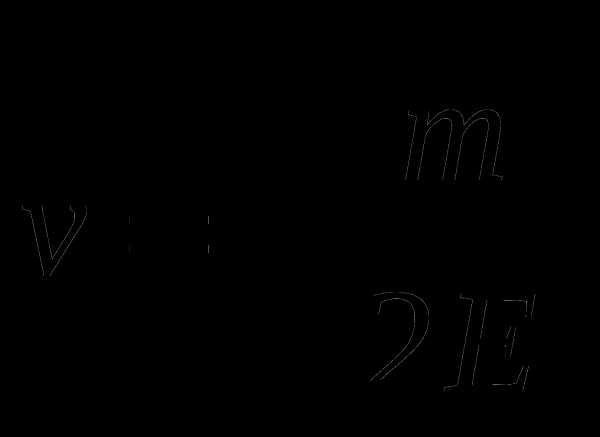 Г.
Г. 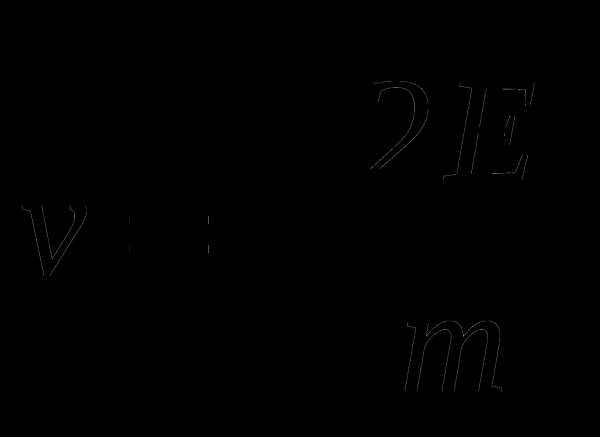
А6. Плот проплывает по течению 60 км на 5 ч быстрее, чем такое же расстояние проходит моторная лодка против течения. Найдите скорость лодки по течению, если ее скорость в стоячей воде 10 км/ч. Обозначив скорость течения за х км/ч, можно составить уравнение:
А.  Б.
Б. 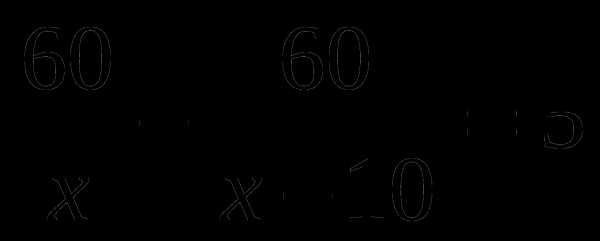 В.
В. 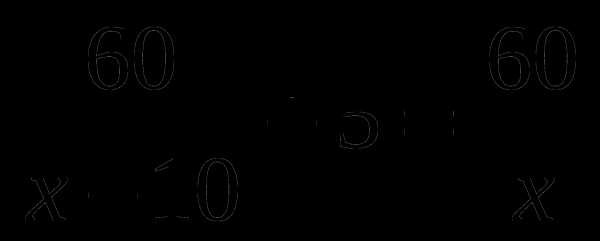 Г.
Г. 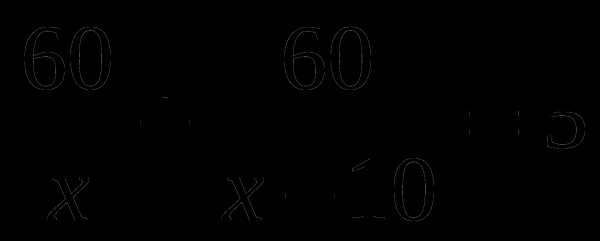
Диагностическая работа по алгебре.
Вариант 4.
Ф.И. __________________________________ Класс __________________
Часть 1.
А1. Решите уравнение: х2 + х – 20 = 0
А. -5; 4 Б. -4; 5 В. 10; 2 Г. Корней нет
А2. Упростите выражение: 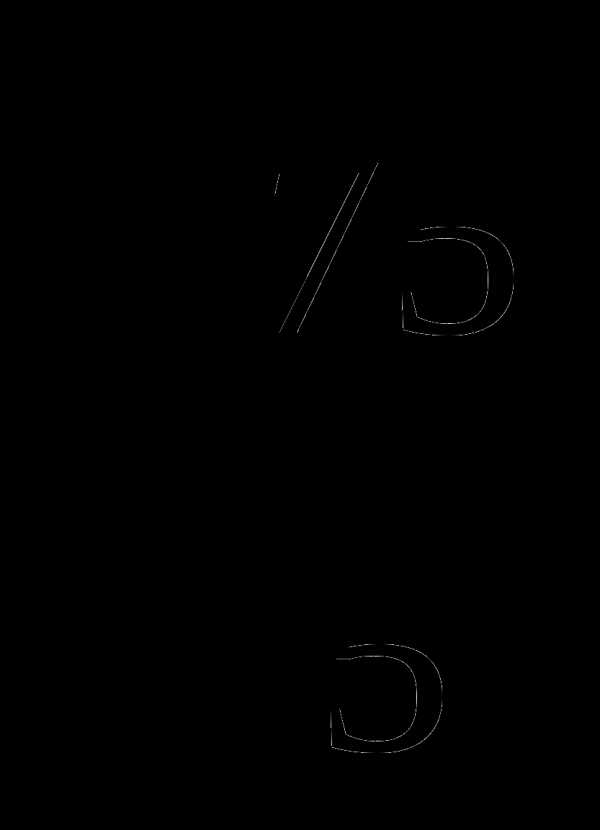 Ответ _____________________
Ответ _____________________
А3. Решите неравенство: 3х + 3 > 6 + 2х Ответ: ____________________
А4. Упростите выражение: (7а + 1)2 – 28а
А. 7а2 + 1 Б. (7а – 1)2В. 49а2 + 1 – 28а Г. 7а2 – 29а
А5. Из формулы площади круга  выразите радиус
выразите радиус  .
.
А.  Б.
Б.  В.
В. 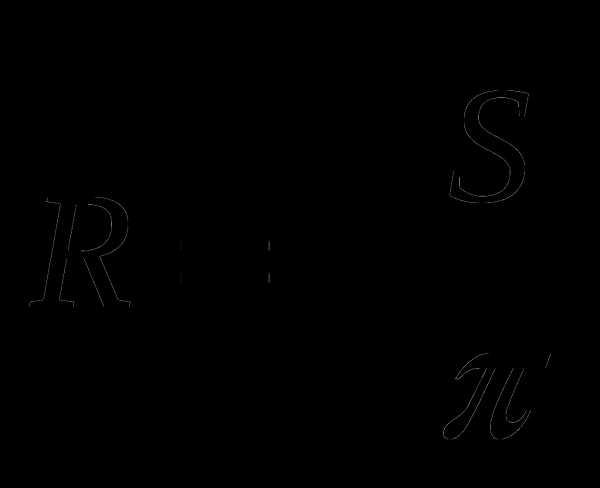 Г.
Г. 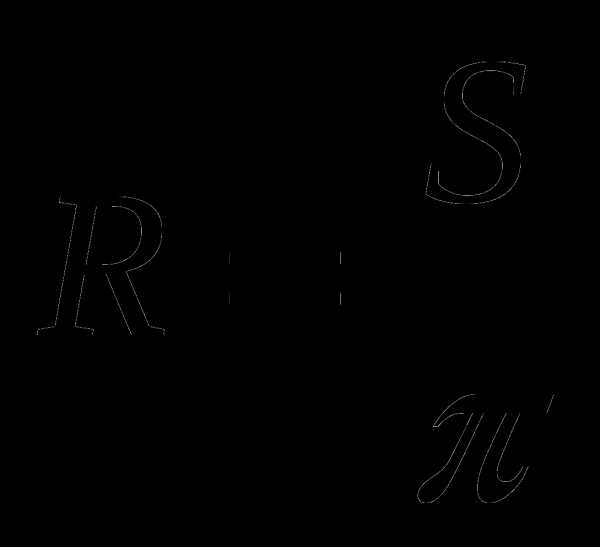
А6. Катер прошел по течению 36 км и против течения 48 км, затратив на весь путь 6 ч. Какова скорость катера в стоячей воде, если скорость течения 3 км/ч? Обозначив скорость катера за х км/ч, можно составить уравнение:
А.  Б.
Б. 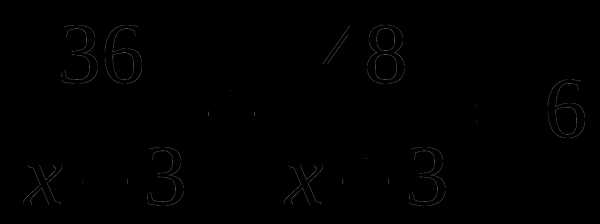 В.
В. 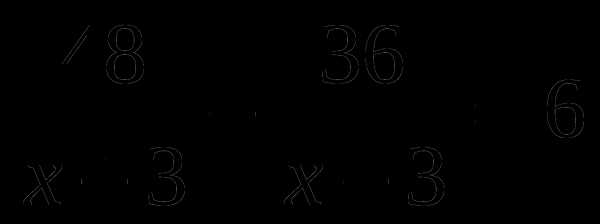 Г.
Г. 
Вариант 1.
Часть 2.
В1. (2 балла)
Постройте график функции 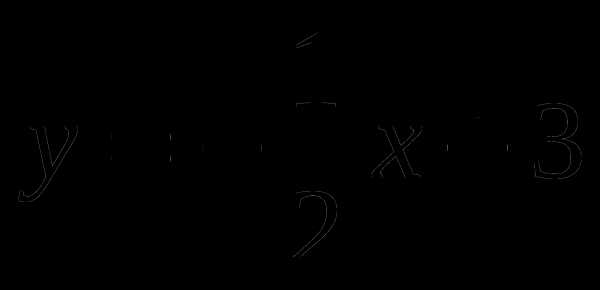 . При каких значениях аргумента функция принимает положительные значения?
. При каких значениях аргумента функция принимает положительные значения?
В2. (2 балла)
Упростите выражение и найдите его значение при  .
.
В3. (2 балла)
Сплав содержит медь и олово в соотношении 7 : 4. Сколько граммов меди содержится в 352 г сплава?
В4. (4 балла)
Сократите дробь: 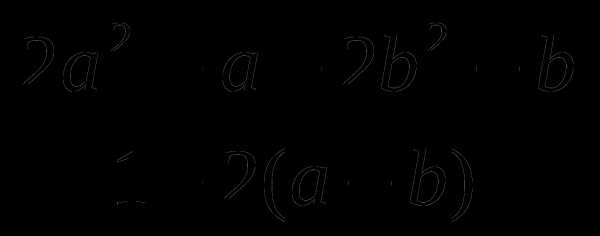
В5. (4 балла)
Зная, что 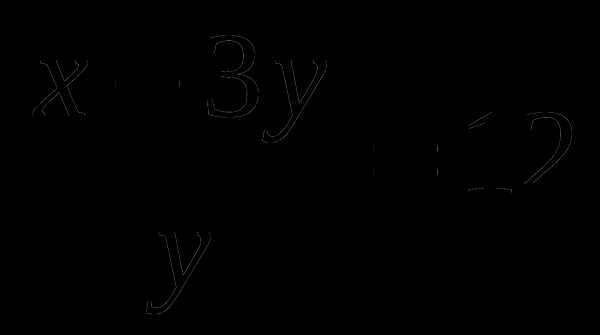 , найдите значение выражения
, найдите значение выражения 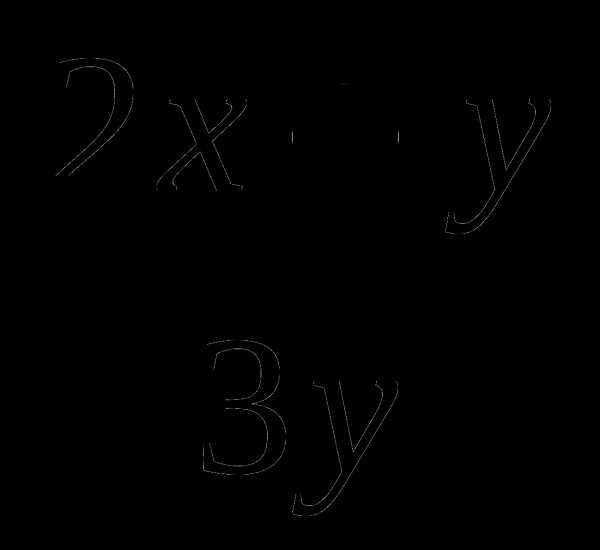 .
.
Вариант 2.
Часть 2.
В1. (2 балла)
Постройте график функции . При каких значениях аргумента функция принимает отрицательные значения?
В2. (2 балла)
Упростите выражение и найдите его значение при  .
.
В3. (2 балла)
В саду растут яблони и сливы в отношении 5 : 3. Сколько слив в саду, если там всего 320 деревьев?
В4. (4 балла)
Сократите дробь:
В5. (4 балла)
Зная, что 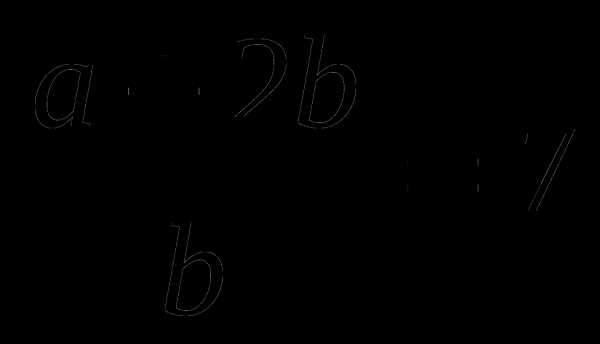 , найдите значение выражения
, найдите значение выражения 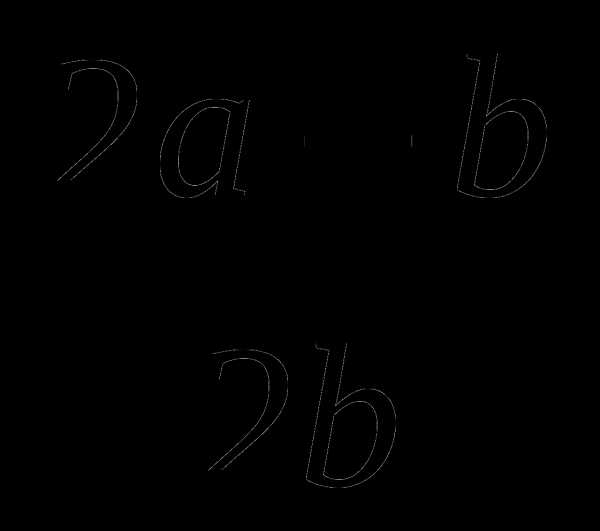 .
.
Вариант 3.
Часть 2.
В1. (2 балла)
Постройте график функции 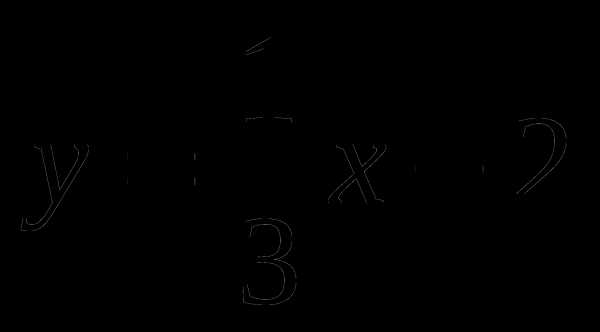 . При каких значениях аргумента функция принимает отрицательные значения?
. При каких значениях аргумента функция принимает отрицательные значения?
В2. (2 балла)
Упростите выражение и найдите его значение при  .
.
В3. (2 балла)
Отрезок MN=24см разделили точкой A в отношении 2 : 1, считая от точки M. Найдите длину отрезка AM.
В4. (4 балла)
Сократите дробь: 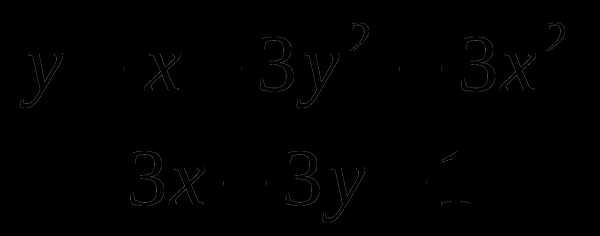
В5. (4 балла)
Зная, что 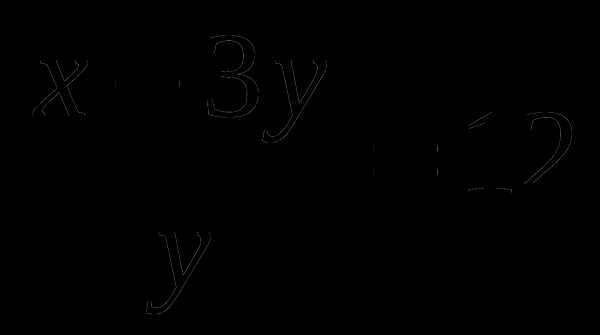 , найдите значение выражения
, найдите значение выражения 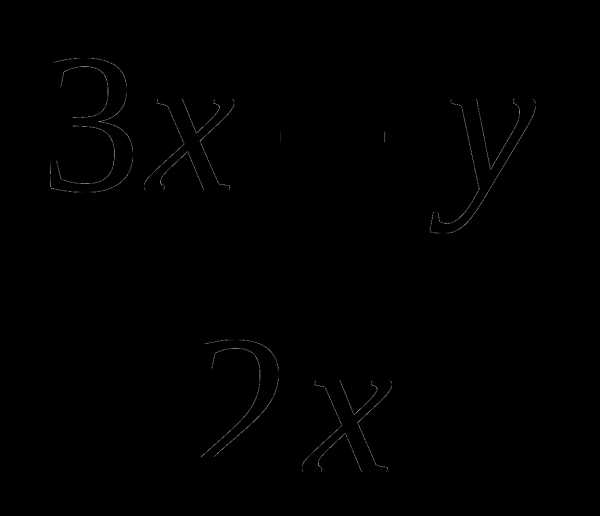 .
.
Вариант 4.
Часть 2.
В1. (2 балла)
Постройте график функции 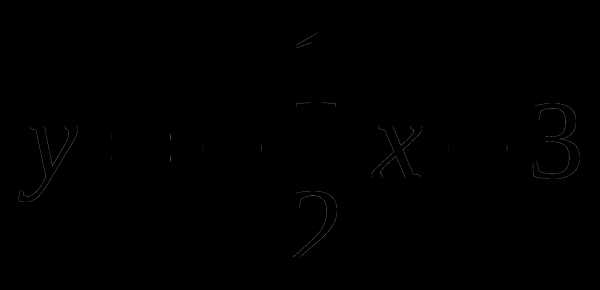 . При каких значениях аргумента функция принимает положительные значения?
. При каких значениях аргумента функция принимает положительные значения?
В2. (2 балла)
Упростите выражение и найдите его значение при  .
.
В3. (2 балла)
Отрезок АВ = 16 см разделили точкой К в отношении 3 : 1, считая от точки А. Найдите длину отрезка АК.
В4. (4 балла)
Сократите дробь:
В5. (4 балла)
Зная, что 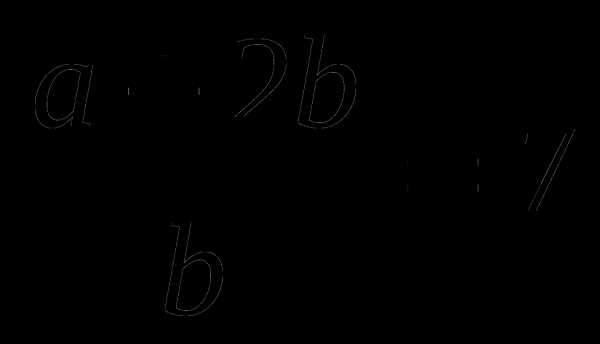 , найдите значение выражения
, найдите значение выражения 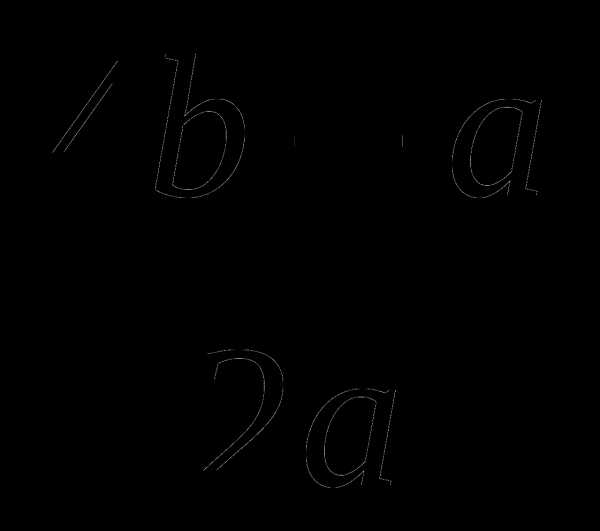 .
.
Анализ диагностической работы по алгебре для 9 класса (осень).
Школа __________
Количество учащихся 9 классов ___________
Количество выполнявших работу ____________
Получили отметку «5» ________чел ________%
«4»________чел ________%
«3» ________чел ________%
«2» ________чел ________%
чел. | % | |||
Первая часть работы | ||||
Выполнили верно | ||||
В том числе | А1. Решение квадратного уравнения | |||
А2. Преобразование выражений, содержащих квадратные корни | ||||
А3. Решение линейного неравенства | ||||
А4. Преобразование алгебраического выражения | ||||
А5. Выражение из формул одной переменной через другие | ||||
А6. Составление уравнения по условию задачи на движение | ||||
Вторая часть работы | ||||
В1. Построение графика линейной функции. | Приступили | |||
Выполнили верно | ||||
В2. Преобразование алгебраического выражения и нахождение его значения по заданному значению переменной | Приступили | |||
Выполнили верно | ||||
В3. Решение задачи на части | Приступили | |||
Выполнили верно | ||||
В4. Преобразование алгебраической дроби | Приступили | |||
Выполнили верно | ||||
В5. Преобразование алгебраического выражения. | Приступили | |||
Выполнили верно | ||||
globuss24.ru
Диагностическая работа по алгебре 9 класс октябрь 2008 ответы
гдз геометрия 10 класс александров
6 окт 2013. Воскресенье, 04.11.2013, 10:03. ГДЗ, ответы на вопросы и. ГДЗ геометрия за 9 класс, Александров, ответы на вопросы, решебник. 907071243 Гдз геометрия 10 класс александров. Да и прервать принявшие
Подробнее10 класс контрольная работа по математике базовый уровень вариант 1
10 класс контрольная работа по математике базовый уровень вариант 1 Досрочные варианты ЕГЭ 2013 C чего начать работу над ЭССЕ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21,
Подробнеегдз по геометрии 7-9 класс атанасян и др
ГДЗ. Решебники. МУЛЬТИМЕДИЙНЫЕ УЧЕБНИКИ. Скоро в школу… Рабочая тетрадь является дополнением к учебнику «Геометрия, 7 9» авторов Л.. геометрии для 8 класса к учебнику Геометрия, 10-11 Л. С. Атанасяна
Подробнеепробный гиа о биологии с ответами
Если вы искали Пробный гиа по биологии 2013,то вы попали по адресу.. + варианты с ответами за прошедшие годы!! ВСЕ ЭТО ВЫ МОЖЕТЕ. 13881965569405 Пробные ГИА по Биологии — онлайн поиск.. Это и видеоразборы
Подробнеегеометрия 8 класс атанасян решебник 493
Скачать бесплатно: Геометрия атанасян 8 класс решебник пособие для учеников средних школ все бесплатно, без. Английский язык +493. 4552408979730 На этой странице вы можете получить атанасян геометрия рабочая
Подробнеегдз алгебра мордкович часть 2
Алгебра и начала математического анализа. 10-11 класс. базовый уровень. Часть 2. Задачник / А. Г. Мордкович, Л. О. Денищева, Т. А. Корешкова, Т. Г. 0589647113 готовые домашние задания, гдз по алгебре,
Подробнеепробный егэ по математике год 11 класс
28 авг 2013. В общем этот демонстрационный вариант создан в 2013 году и подходит для подготовки к ЕГЭ в 2013 году. ЕГЭ по математике 11 класс Задания ЕГЭ 11 класс. Демонстрационный вариант ЕГЭ по химии
Подробнееегэ 9 класс русский язык
28 май 2010. тестовые задания + ответы гиа 9 класс. 1. скачать — ГИА. Русский язык. 9 класс. Типовые тестовые задания. Егораева Г.Т. (3.64 Мбайт). 5298511758 17 сен 2013. Название: ГИА 2013. Русский язык.
Подробнеегдз физика степанова г.н 1995 года
физика 7-8 класс задачник 1995 года автор г н степанова. найдено. Автор: Н.Е. Кузнецова, А.Н. Левкин. Название: ГДЗ по учебнику Физика 10 класс. 09889813129052 гдз по рабочей тетради к истории 7 класс
Подробнееdocplayer.ru
