Алгоритм перевода чисел из одной системы счисления в другую
⇐ ПредыдущаяСтр 3 из 21Следующая ⇒
1. Из десятичной системы счисления:
o разделить число на основание переводимой системы счисления;
o найти остаток от деления целой части числа;
o записать все остатки от деления в обратном порядке;
2. Из двоичной системы счисления
o Для перевода в десятичную систему счисления необходимо найти сумму произведений основания 2 на соответствующую степень разряда;
o Для перевода числа в восьмеричную необходимо разбить число на триады.
Например, 1000110 = 1 000 110 = 1068
o Для перевода числа из двоичной системы счисления в шестнадцатеричную необходимо разбить число на группы по 4 разряда.
Например, 1000110 = 100 0110 = 4616
Таблицы для перевода:
| Двоичная СС | |
| A | |
| B | |
| C | |
| D | |
| E | |
| F |
| Двоичная СС | Восьмеричная СС |
Рассмотрим основные правила перевода.
1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней двойки:
Таблица 4. Степени числа 2
| n (степень) | |||||||||||
Пример .Число перевести в десятичную систему счисления.
2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней восьмерки:
Таблица 5. Степени числа 8
| n (степень) | |||||||
Пример .
Число перевести в десятичную систему счисления.
3. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней числа 16:
Таблица 6. Степени числа 16
| n (степень) | |||||||
Пример .Число перевести в десятичную систему счисления.
Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
Пример.Число перевести в двоичную систему счисления.
Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример.Число перевести в восьмеричную систему счисления.
Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример.Число перевести в шестнадцатеричную систему счисления.
7. Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой (табл. 3).
Пример.Число перевести в восьмеричную систему счисления.
8. Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей восьмеричной цифрой (табл. 3).
Пример.Число перевести в шестнадцатеричную систему счисления.
Пример.Число перевести в двоичную систему счисления.
Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой.
Пример.Число перевести в двоичную систему счисления.
Читайте также:
lektsia.com
Алгоритмы перевода чисел из одной позиционной системы исчисление в другую — Документ
Лабораторная работа
Системы счисления
Правило счета.
Целые числа в любой системе счисления порождаются с помощью правила счета: Для образования целого числа, следующего за любым данным целым числом, нужно продвинуть самую правую цифру числа; если какая-либо цифра после продвижения стала нулем, то нужно продвинуть цифру, стоящую слева от неё.
Продвинуть цифру 1 значит заменить её на 2, продвинуть цифру 2 значит заменить её на 3 и т.д. Продвижение старшей цифры (например, цифры 9 в десятичной системе) означает замену её на 0. В двоичной системе, использующей только две цифры – 0 и 1, продвижение 0 означает замену его на 1, а продвижение 1 – замену её на 0.
Пример 1. Применяя правило счета, запишем первые десять целых чисел:
в двоичной системе: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001;
в троичной системе: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100;
в пятеричной системе: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14;
в восьмеричной системе: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.
Алгоритмы перевода чисел из одной позиционной системы исчисление в другую.
Чтобы перевести целое десятичное число в двоичную (восьмеричную, шестнадцатеричную) систему счисления, нужно последовательно делить с остатком это число, а затем получаемые частные на основание новой системы счисления до тех пор, пока частное не станет меньше основания. При переводе запись двоичного (восьмеричного, шестнадцатеричного) числа следует начинать со старшего значащего разряда, а заканчивать записью младшего значащего разряда (см. пример 2).
Для перевода правильной дроби из десятичной системы счисления в двоичную (восьмеричную, шестнадцатеричную) нужно умножить исходную дробь и дробные части получающихся произведений на основание, представленное в десятичной системе. Целые части получающихся произведений дают последовательность цифр, которая является представлением дроби в двоичной (восьмеричной, шестнадцатеричной) системе счисления (см. пример 3).
Для чисел, имеющих как целую, так и дробную части, перевод из десятичной системы счисления в другую осуществляется отдельно для целой и дробной частей по правилам, указанным выше.
Пример 2. Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
Пример 3. Переведем число 0,36 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
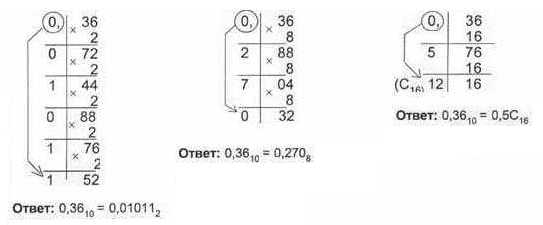
Обратный перевод числа в десятичную систему осуществляется по формуле:
где:
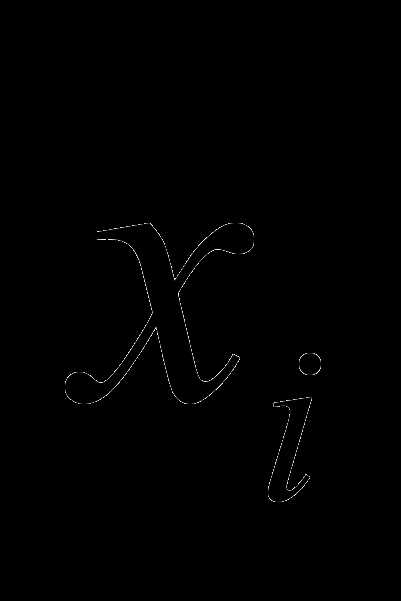 – i-я цифра числа;
– i-я цифра числа;

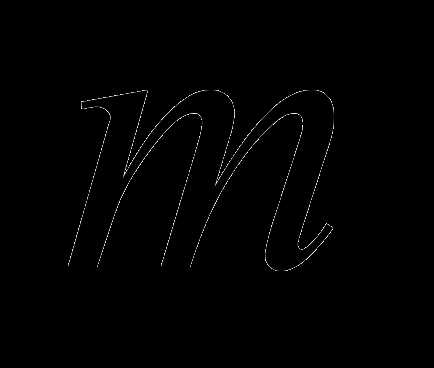 – количество цифр в дробной части числа;
– количество цифр в дробной части числа;
 – основание системы счисления.
– основание системы счисления.
Пример 4. Выполним перевод числа
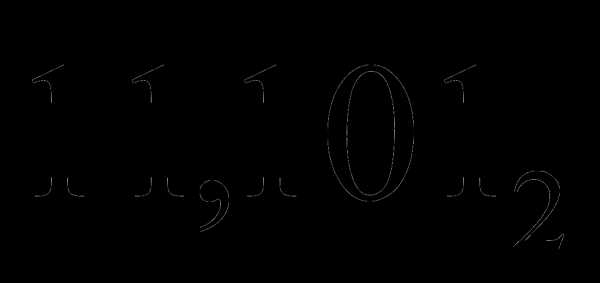 из двоичной системы счисления в
десятичную.
из двоичной системы счисления в
десятичную.
Имеем: .
Чтобы перевести восьмеричное (шестнадцатеричное) число в двоичную систему, нужно заменить каждую цифру восьмеричного (шестнадцатеричного) числа соответствующим трехразрядным (четырехразрядным) двоичным числом. Затем необходимо удалить крайние нули слева, а при наличии точки – и крайние нули справа.
Пример 5.
Чтобы перевести двоичное число в восьмеричную (шестнадцатеричную) систему счисления нужно двигаясь от точки влево, а затем вправо, разбить двоичное число на группы по три (четыре) разряда, дополняя, при необходимости, нулями крайние левую и правую группы. Затем каждую группу из трех (четырех) разрядов следует заменить соответствующей восьмеричной (шестнадцатеричной) цифрой (см. таблица 1).
Пример 6.
Таблица 1
Первые 16 натуральных чисел записанных в десятичной,
двоичной, восьмеричной и шестнадцатеричной системах счисления
|
10 |
2 |
8 |
16 |
|
0 |
0000 |
0 |
0 |
|
1 |
0001 |
1 |
1 |
|
2 |
0010 |
2 |
2 |
|
3 |
0011 |
3 |
3 |
|
4 |
0100 |
4 |
4 |
|
5 |
0101 |
5 |
5 |
|
6 |
0110 |
6 |
6 |
|
7 |
0111 |
7 |
7 |
|
8 |
1000 |
10 |
8 |
|
9 |
1001 |
11 |
9 |
|
10 |
1010 |
12 |
A |
|
11 |
1011 |
13 |
B |
|
12 |
1100 |
14 |
C |
|
13 |
1101 |
15 |
D |
|
14 |
1110 |
16 |
E |
|
15 |
1111 |
17 |
F |
gigabaza.ru
Алгоритм перевода чисел из любой системы счисления в десятичную
Для того, чтобы число из любой системы счисления перевести в десятичную систему счисления, необходимо его записать в виде многочлена (полинома), состоящего из произведений цифр числа и соответствующей степени числа основы, и вычислить по правилам десятичной арифметики:
Пример 1. Перевести число 101,012 из двоичной системы счисления в десятичную.
101,012 X10
Решение:
2 1 0 -1 -2
1 0 1, 0 1 = 1*22 + 0*21 + 1*20+0*2-1+1*2-2 =4+0+1+0+0,25 = 5,2510
Ответ: 101,012 = 5,2510
Алгоритм перевода чисел из десятичной системы счисления в другую
Последовательно выполнить деление данного числа и получаемых неполных частных на основание новой системы счисления до тех пор, пока не получите неполное частное, меньшее делителя;
полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
составить число в новой системе счисления, записывая его, начиная с последнего частного.
Пример 2. Перевести 47510в двоичную систему счисления.
47510 X2
|
475 |
2 | |||||||
|
474 |
237 |
2 | ||||||
|
1 |
236 |
118 |
2 | |||||
|
1 |
118 |
59 |
2 | |||||
|
0 |
58 |
29 |
2 | |||||
|
1 |
28 |
14 |
2 | |||||
|
1 |
14 |
7 |
2 | |||||
|
0 |
6 |
3 |
2 | |||||
|
1 |
2 |
1 | ||||||
|
1 | ||||||||
Читая остатки от деления снизу вверх, получим 1110110112.
Проверка:
8 7 6 5 4 3 2 1 0
1110110112= 1*28+ 1*27 + 1*26 + 0*25 + 1*24 + 1*23 + 0*2 2 + 1*21 + 1*20=1 + 2 + 8 + 16 + 64 + 128 + 256 = 47510.
Пример 3. Перевести десятичное число 352 в восьмеричную и 315 в шестнадцатеричную системы счисления:
|
352 |
8 | |||
|
352 |
44 |
8 | ||
|
0 |
40 |
5 | ||
|
4 | ||||
|
315 |
16 | |||
|
304 |
19 |
16 | ||
|
11 |
16 |
1 | ||
|
3 | ||||
Отсюда следует: 35210 = 4738 , 31510= 13В16.
Напомним, что 1110 = В16.
Правило перевода дробных чисел из десятичной системы счисления в систему с основаниемq:
Последовательно выполнять умножение исходного числа и получаемых дробные части на qдо тех пор, пока дробная часть не станет равна нулю или не достигнем требуемую точность.
Полученные при таком умножении целые части – числа в системе счисления q– записать в прямом порядке (сверху вниз).
Пример 4. Перевести число 0,37510в двоичную СС.
0,37510 X2
|
0 |
375 |
× 2 |
|
0 |
750 |
× 2 |
|
1 |
500 |
× 2 |
|
1 |
000 |
Полученный результат – 0,0112.
Пример 5.Выполнить перевод из десятичной системы счисления в шестнадцатеричную числа 35525,84710. Перевод выполнять до трех значащих цифр после запятой.
Представим исходное число как сумму целого числа и правильной дроби:
35525,847 = 35525 + 0,847.
Выполнить перевод числа 3552510в шестнадцатеричную систему счисления:
|
35525 |
16 | ||
|
35520 |
2220 |
16 | |
|
5 |
2208 |
138 |
16 |
|
12 |
128 |
8 | |
|
10 | |||
Таким образом, 3552510=8AC516.
Выполнить перевод числа 0,847 в шестнадцатеричную систему счисления. Перевод выполнить до трех значащих цифр.
|
0 |
847 *16 |
|
13 8 13 |
552 *16 832 *16 312 *16 |
0,847 ≈ 0,D8D16.
Тогда имеем:
35525 + 0,847 = 8AC516+ 0,D8D16≈ 8AC5,D8D16.
Таким образом, 35525,84710≈ 8AC5,D8D16.
studfiles.net
Алгоритмы перевода чисел из одной системы счисления в другую, арифметика в различных системах счисления
Вот видео на эту тему:https://www.youtube.com/watch?v=xdT1cOHiZLc&list=UUWCGpoRrnJmmYnxO09Ix2RQ
А вот статьи:
http://vestikinc.narod.ru/AB/index.htm
======================================
Алгоритмы перевода чисел из одной системы в другую.
В программировании используются три системы счисления: двоичная, десятичная и шестнадцатеричная.
Поэтому, должно быть пять алгоритмов перехода:
1. Из двоичной в десятичную;
2. Из двоичной в шестнадцатеричную;
3. Из десятичной в двоичную;
4. Из десятеричной в шестнадцатеричную;
5. Из шестнадцатеричной в двоичную;
6. Из шестнадцатеричной в десятичную.
Теперь, сами алгоритмы:
1. Допустим есть число в двоичной системе исчисления:
1010. Его нужно перевести в десятичную.
Нужно умножить поразрядно каждую цифру на основание в степени разряда. Какое основание в двоичной системе? Ответ: два. Основание определили. Теперь, как
это умножить на степень разряда? Разряды в числе считаются справа налево. Т. е. в числе 1010 это 0-первый разряд, 1-второй, 0-третий, 1-четвёртый. Как это
выглядит? 0*2^0 + 1*2^1 + 0*2^2 + 1*2^3 = 0 + 2 + 0 + 8 = 10. Т. е. 1010 в двоичной системе = 10 в десятеричной.
2. Перевести из двоичной в шестнадцатеричную.
1110. Число уже другое. Не 1010.
Точно так же.
0*2^0 + 1*2^1 + 1*2^2 + 1*2^2 = 0 + 2 + 4 + 8 = E
3. Нужно перевести из десятичной системы в двоичную.
Есть число 15. Нужно перевести в двоичную систему. Алгоритм такой:
Делим 15 и (12) на два и остаток записываем.
15 / 2 = 7 (и остаток 1)12 / 2 = 6 (и остаток 0)
7 / 2 = 3 (и остаток 1)6 / 2 = 3 (и остаток 0)
3 / 2 = 1 (и остаток 1)3 / 2 = 1 (и остаток 1)
1 / 2 = 0 (и остаток 1)1 / 2 = 0 (и остаток 1)
Записываем остатки 1111Записываем остатки 1100
Остатки записываются снизу вверх.
4. Теперь нужно перевести из десятичной системы в шестнадцатеричную.
Есть число 68 и 157 в десятичной системе.
68 / 16 = 4 (и остаток 4)157 / 16 = 9 (и остаток 13 или D (D=13))
4 / 16 = 0 (и остаток 4)9 / 16 = 0 (и остаток 9)
Записываем остатки 44.Записываем 9D
5. Теперь осталась только шестнадцатеричная система счисления.
Как из неё переводить числа? Допустим 157 и 8FD нужно перевести в двоичную систему. Это самый простой алгоритм из перечисленных. Для перевода нужно
каждую цифру заменяем её эквивалентом в двоичной системе. Как расчитать эквивалент? Нужно помнить, что на каждую цифру из шестнадцатеричной системы
приходится четыре цифры в двоичной. Например, 7 это 0111 или F (т. е. 15) это 1111 или D (т. е. 13) это 1101
Т. е. цифры 1, 5 и 7 это 0001, 0101 и 0111. А вместе это 157 и 000101010111
Или 8, F и D это 1000, 1111 и 1101 А вместе это 8FD и 100011111101
6. Последний алгоритм это из шестнадцатеричной ситстемы перевести в десятичную.
Например 157 и 8FD Нужно перевести в 10-тичную.
Нужно перевести цифры в десятичную систему, потому умножить их на основание шестнадцатеричной системы (*16) в степени разряда цифры. Например, число 157
7*16^0 + 5*16^1 + 1*16^2 = 7*1 + 5*16 + 1*256 = 343
Или число 8FD нужно перевести в десятичную систему, тогда
D(13)*16^0 + F(15)*16^1 + 8(8)*16^2 = 13*1 + 15*16 + 8*256 = 2301
otvet.mail.ru
Правила перевода чисел из одной системы счисления в другую
⇐ ПредыдущаяСтр 2 из 3Следующая ⇒
Из 16 или 8 в 2
| Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр) (см. таблицу). | |||||||
| Двоичная (Основание 2) | Восьмеричная (Основание 8) | Десятичная (Основание 10) | Шестнадцатиричная (Основание 16) | ||||
| триады | тетрады | ||||||
| 0 1 | 0 1 2 3 4 5 6 7 | 000 001 010 011 100 101 110 111 | 0 1 2 3 4 5 6 7 8 9 | 0 1 2 3 4 5 6 7 8 9 A B C D E F | 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 |
Например:
а) Перевести 305.48 «2» с.с.
б) Перевести 7B2.E16«2» с.с.
16А16=1 0110 10102 3458=11 100 1012
Из 2 в 16 или 8
| Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой. |
Например:
а) Перевести 1101111001.11012 «8» с.с.
б) Перевести 11111111011.1001112 «16» с.с.
10001010100101012=1000 1010 1001 0101=8A9516= 1 000 101 010 010 101=1052258
Из 16 в 8 и обратно
Перевод из восьмеричной в шестнадцатеричную систему и обратно осуществляется через двоичную систему с помощью триад и тетрад.
Например:
Перевести 175.248 «16» с.с.
Результат: 175.248 = 7D.516.
Из 10 в любую с.с.
| При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q–1. Число в системе с основанием q записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего. |
Например:
а) Перевести 18110 «8» с.с.
Результат: 18110 = 2658
б) Перевести 62210 «16» с.с.
Результат: 62210 = 26E16
Перевод правильных дробей
Для перевода правильной десятичной дроби в другую систему эту дробь надо последовательно умножать на основание той системы, в которую она переводится. При этом умножаются только дробные части. Дробь в новой системе записывается в виде целых частей произведений, начиная с первого.
Например:
Перевести 0.312510 «8» с.с.
Результат: 0.312510 = 0.248
Замечание. Конечной десятичной дроби в другой системе счисления может соответствовать бесконечная (иногда периодическая) дробь. В этом случае количество знаков в представлении дроби в новой системе берется в зависимости от требуемой точности.
Например:
Перевести 0.6510 «2» с.с. Точность 6 знаков.
Результат: 0.6510 0.10(1001)2
Для перевода неправильной десятичной дроби в систему счисления с недесятичным основанием необходимо отдельно перевести целую часть и отдельно дробную.
Например:
Перевести 23.12510 «2» с.с.
| 1) Переведем целую часть: | 2) Переведем дробную часть: |
Таким образом: 2310 = 101112; 0.12510 = 0.0012.
Результат: 23.12510 = 10111.0012.
Необходимо отметить, что целые числа остаются целыми, а правильные дроби — дробями в любой системе счисления.
Из 2, 8 или 16 в 10
| При переводе числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную надо это число представить в виде суммы степеней основания его системы счисления. |
Например:
a)10101101.1012 = 1 27+ 0 26+ 1 25+ 0 24+ 1 23+ 1 22+ 0 21+ 1 20+ 1 2-1+ 0 2-2+ 1 2-3 = 173.62510
б) Перевести 703.048 «10» с.с.
703.048 = 7 82+ 0 81+ 3 80+ 0 8-1+ 4 8-2 = 451.062510
в) Перевести B2E.416 «10» с.с.
B2E.416 = 11 162+ 2 161+ 14 160+ 4 16-1 = 2862.2510
Схема перевода чисел из одной системы счисления в другую
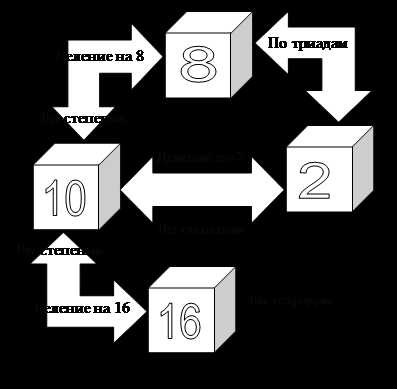
Aрифметические операции в позиционных системах счисления
Рассмотрим основные арифметические операции: сложение, вычитание, умножение и деление. Правила выполнения этих операций в десятичной системе хорошо известны — это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным системам счисления. Только таблицами сложения и умножения надо пользоваться особыми для каждой системы.
Сложение
При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево
| Таблица двоичного сложения | Таблица двоичного вычитания | Таблица двоичного умножения |
| 0+0=0 0+1=1 1+0=1 1+1=10 | 0-0=0 1-0=1 1-1=0 10-1=1 | 0 0=0 0 1=0 1 0=0 1 1=1 |
При сложении двоичных чисел в каждом разряде производится сложение цифр слагаемых и переноса из соседнего младшего разряда, если он имеется. При этом необходимо учитывать, что 1+1 дают нуль в данном разряде и единицу переноса в следующий.
Например:
Выполнить сложение двоичных чисел:
а) X=1101, Y=101;
Результат 1101+101=10010.
б) X=1101, Y=101, Z=111;
Результат 1101+101+111=11001.
Таблица сложения в 8-ой системе счисления
| 2+2=4 | 3+2=5 | 4+2=6 | 5+2=7 | 6+2=10 | 7+2=11 |
| 2+3=5 | 3+3=6 | 4+3=7 | 5+3=10 | 6+3=11 | 7+3=12 |
| 2+4=6 | 3+4=7 | 4+4=10 | 5+4=11 | 6+4=12 | 7+4=13 |
| 2+5=7 | 3+5=10 | 4+5=11 | 5+5=12 | 6+5=13 | 7+5=14 |
| 2+6=10 | 3+6=11 | 4+6=12 | 5+6=13 | 6+6=14 | 7+6=15 |
| 2+7=11 | 3+7=12 | 4+7=13 | 5+7=14 | 6+7=15 | 7+7=16 |
Таблица сложения в 16-ой системе счисления
| + | A | B | C | D | E | F | ||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | A | B | C | D | E | F | ||||||||||
| B | B | C | D | E | F | 1A | ||||||||||
| C | C | D | E | F | 1A | 1B | ||||||||||
| D | D | E | F | 1A | 1B | 1C | ||||||||||
| E | E | F | 1A | 1B | 1C | 1D | ||||||||||
| F | F | 1A | 1B | 1C | 1D | 1E |
Вычитание
Читайте также:
lektsia.com
Алгоритм перевода целого числа из десятичной системы счисления в систему счисления с произвольным основанием (р)
Для перевода целого числа нужно делить его на произвольное основание (р) до получения целого частного. Полученный остаток, в том числе ноль, будет младшим разрядом числа в новой системе счисления. Полученное частное нужно опять разделить на произвольное основание (р) до получения целого частного и продолжать этот процесс до тех пор, по частное не станет нулем. Полученные остатки будут разрядами числа в новой системе счисления. Число в системе счисления с основанием р получается выписыванием в обратно порядке полученных остатков. Все действия выполняются по правилам десятичной системы счисления.
Пример:
39:2=19 целых и 1 в остатке, значит =1
19:2=9 целых и 1 в остатке, значит =1
9:2=4 целых и 1 в остатке, значит=1
4:2=2 целых и 0 в остатке, значит =0
2:2=1 целых и 0 в остатке, значит =0, результат от деления=1
-
_39 ∟2
38 19 ∟2
1 18 9 ∟2
1 8 4∟2
1 4 2 ∟2
0 21 ∟2
0 0 0
1
Ответ:
Алгоритм перевода целого числа из системы счисления с произвольным основанием (р) в десятичную систему счисления
Для перевода из системы счисления с основанием р в десятичную систему счисления нужно представить число в виде многочлена и вычислить значение этого многочлена по правилам арифметики десятичной системы счисления
Пример: Перевести число 100111 из двоичной в десятичную систему счисления:
Удобно вычислять значение многочлена, используя схему Горнера
N=,
Тогда N==
=(…()
Пример:
((((1∙2+0)∙2+0)∙2+1)∙2+1)∙2+1
|
11 |
00 |
00 |
11 |
11 |
11 | |
|
2 |
21 |
42 |
84 |
19 |
319 |
339 |
Перевод дробных чисел из одной системы счисления в другую Алгоритм перевода правильной дроби с основанием р в дробь с основаниемq
Основание новой системы счисления выразить цифрами исходной системы счисления и все последующие действия производить в исходной системе счисления.
2. Последовательно умножать данное число и получаемые дробные части произведений на основание новой системы до тех пор, пока дробная часть произведения не станет равной нулю или будет достигнута требуемая точность представления числа.
Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
Составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.
Пример. Перевести число 0,6562510в восьмеричную систему счисления.
-
0,
65625
х 8
5
25000 х 8
2
00000
Ответ: 0,6562510=0,528.
studfiles.net
Учебный курс «Информатика»
Как мы уже отмечали, человек привык работать в десятичной системе счисления, а ЭВМ ориентирована на двоичную систему. Поэтому общение человека с машиной невозможно без создания простых и надёжных алгоритмов перевода чисел из одной системы в другую и наоборот. Итак, как осуществить перевод чисел из десятичной системы в двоичную?
Допустим, надо перевести число 11 в двоичную систему счисления. Разделим 11 на 2. Получим частное 5 и остаток 1. Следовательно, в двоичной записи числа 11 последняя цифра равна 1. Для нахождения второй цифры разделим найденное нами частное 5 снова на 2. Получим частное 2 и остаток 1. Следовательно, вторая цифра с конца в двоичной записи числа 11 тоже равна 1. Частное 2 снова делим на 2. Получим 1 и 0 в остатке. Полученная 1 и есть первая цифра в двоичной записи числа 11. Остаток от последнего деления 0 — вторая цифра.
Если необходимо преобразовать нецелое число — десятичную дробь, то производим следующие действия:
1. Целую часть числа преобразовываем в двоичную систему способом, описанным выше.
2. Дробную часть необходимо преобразовывать умножением на основание системы, в которую мы переводим число.
В результате умножения дробной части — числа 0,7 на основание системы — число 2 получим 1,4. Целую часть данного числа (цифру 1) выделяем, а дробную часть — число 0,4 снова умножаем на 2.
Очевидно, что процесс перевода числа 0,7 может продолжаться бесконечно. Действительно, за шесть шагов мы можем получить число 0,101100, а за семь шагов получили бы 0,1011001, которое является более точным представлением числа 0,7 в двоичной системе. Такой бесконечный процесс обрывают на некотором шаге, когда считают, что получена требуемая точность представления числа. В результате перевода получим ответ:
Для перевода десятичных чисел в другие позиционные системы счисления пользуются теми же правилами, лишь меняется лишь основание системы, в которую надо перевести числа.
Перевод чисел из двоичной системы счисления в системы, родственные двоичной и обратно. Большие числа в двоичной системе счисления имеют очень громоздкие записи. Конечно, можно перевести число в десятичную систему и записать его в таком виде, а потом, когда оно понадобится, перевести его обратно, но все эти переводы очень трудоёмки. На помощь приходят системы, родственные двоичной — восьмеричная и шестнадцатеричная. Перевод из родственной системы в двоичную и обратно может быть мгновенно выполнен в уме.
Системами счисления родственными двоичной считаются такие системы, основания которых являются значением степени числа 2.
Например, четверичная, восьмеричная и шестнадцатеричная системы счисления являются системами, родственными двоичной.
Для перевода чисел из двоичной системы счисления в системы, родственные двоичной, необходимо выполнить следующие действия:
1.Разбить число на некоторое количество разрядов, равное степени числа 2 основания системы, в которую переводим.
2.Если в старших и младших разрядах после разбиения не хватает знаков, то добавить их нулями.
3.По таблице определить значение пары, триады, тетрады и т.п. разрядов, записанных в двоичной системе счисления, соответственно значению в той системе, в которую переводим.
Например, дано число 1111010111010,0111, записанное в двоичной системе счисления. Для перевода его в восьмеричную систему счисления разобьём число на триады (т.к. основание числа 2 равно 3), начиная от запятой, вправо и влево: 1.111.010.111.010,011.1 . Разбиение показано точками. В старшей и младшей триадах не хватает разрядов. Дополним их нулями: 001.111.010.111.010,011.100. По таблице определим восьмеричные цифры, соответствующие триадам. Получается восьмеричное число 17272,34.
Рассмотрим ещё один пример: дано число 1111010111010,0111, записанное в двоичной системе счисления. Для перевода его в шестнадцатеричную систему счисления разобьём число на тетрады (т.к. основание числа 2 равно 4): 1.1110.1011.1010,0111. В старшей тетраде не хватает разрядов. Дополним их нулями: 0001.1110.1011.1010,0111. По таблице определим шестнадцатеричные знаки, соответствующие тетрадам. Получается шестнадцатеричное число 1EBA,7.
Пусть дано то же число. Для перевода его в четверичную систему счисления разобьём число на пары (т.к. основание числа 2 равно 2): 1.11.10.10.11.10.10,01.11. В старшей паре не хватает одного разряда. Дополним его нулём: 01.11.10.10.11.10.10,01.11. Определим четверичные цифры, соответствующие парам. Получается четверичное число 1322322,13.
Пусть дано число 73,62 , записанное в восьмеричной системе счисления. Необходимо перевести его в двоичную систему. Для этого каждую цифру числа запишем в виде триады из 0 и 1, соответствующей значению восьмеричной цифры в двоичной системе счисления: 111.011,110.010.
Рассмотрим ещё один пример: дано число 7В3,Е6, записанное в шестнадцатеричной системе счисления. Необходимо перевести его в двоичную систему. Для этого каждую цифру шестнадцатеричного числа запишем в виде тетрады из 0 и 1,соответствующей значению знака в двоичной системе счисления: 0111.1011.0011,1110.0110.
Перевод чисел из р-ичной позиционной системы счисления в десятичную.Все позиционные системы счисления, о которых мы говорили выше, строятся по одному общему принципу. Выбирается некоторое число р — основание системы счисления, и каждое число N представляется в виде комбинации его степеней с коэффициентами, т.е. произвольное число в системе счисления с основанием р имеет вид:
Если необходимо перевести двоичное число 1011011,11 в десятичную систему, воспользуемся этой формулой. Основание системы р=2, к — коэффициент, указывающий количество знаков в числе влево от запятой, к=7; а — знаки числа с соответствующими им коэффициентами.
Воспользуемся формулой для перевода шестнадцатеричного числа ВF,1D в десятичную систему. Основание системы р=16, к=2.
Пусть необходимо перевести восьмеричное число 254,262 в десятичную систему. Основание системы р=8, к=3


infolike.narod.ru
