Примеры решения задач по теме «Кинематика твёрдого тела»
Примеры решения задач по теме «Кинематика твёрдого тела»
«Физика — 10 класс»
При решении задач по этой теме обращайте внимание на связь кинематических характеристик поступательного и вращательного движений. При этом могут быть в одних случаях одинаковыми угловые скорости (например, задача 2), а в других — линейные скорости движения (например, задача 1).
Задача 1.
Два шкива соединены ременной передачей, передающей вращение от одного шкива к другому. Ведущий шкив вращается с частотой ν1 = 3000 об/мин, ведомый шкив — с частотой ν2 = 600 об/мин. Ведомый шкив имеет диаметр D2 = 500 мм. Какой диаметр D1 у ведущего шкива?
Р е ш е н и е.
Ведущий шкив вращается с угловой скоростью ω1 = 2πν1, а ведомый — со скоростью ω2 = 2πν2. Скорость приводного ремня равна линейной скорости точек окружностей того и другого шкива: υ = ω
Отсюда Следовательно, искомый диаметр
Задача 2.
Колесо, радиус которого 40 см, катится по горизонтальной дороге со скоростью 2 м/с. Определите скорости относительно дороги точек колеса, находящихся на концах его вертикального и горизонтального диаметров, а также ускорения этих точек.
Р е ш е н и е.
Точка О1 неподвижна относительно земли (рис. 1.64), следовательно, υ1 = 0. Если считать, что через точку О1 проходит мгновенная ось вращения, то относительно неё скорости всех точек, согласно уравнению (1.29), будут равны υ = ωr, где r — расстояние от точки O1 до выбранной точки обода. Угловая скорость вращения ω = υ0/R.
Тогда υc = υD = ωR√2 = υ0√2 ≈ 2,8 м/с.
Скорость точки A υA = 2ωR = 2υ0 = 4 м/с.
Все точки обода относительно оси вращения движутся с одинаковыми линейными скоростями и, следовательно, с одинаковым ускорениями
Заметим, что эту задачу также можно решить на основе закона сложения скоростей. Так, например, скорость точки D равна сумме скорости 0 подвижной системы отсчёта, связанной с осью колеса, и скорости 1 точки обода D относительно этой оси.
Задача 3.
Катушка с намотанной на неё нитью может катиться по поверхности горизонтального стола без скольжения. С какой скоростью υ0 и в каком направлении будет перемещаться ось катушки, если конец нити тянуть в горизонтальном направлении со скоростью υ? Радиус внутренней части катушки r, внешней — R (рис. 1.65).
Р е ш е н и е.
Скорость υ — скорость движения нити — совпадает со скоростью точки А внутренней части катушки. Омгн — мгновенная ось вращения. Угловая скорость относительно мгновенной оси вращения ω = υ/(R — r), так как расстояние О
Очевидно, что катушка перемещается в направлении движения конца нити. Скорость перемещения катушки будет больше, чем скорость нити.
Задача 4.
Шарик радиусом r катится со скоростью υ0 по двум рельсам, расположенным на расстоянии 2а друг от друга. Определите скорости точек А и В относительно рельсов (рис. 1.66, а).
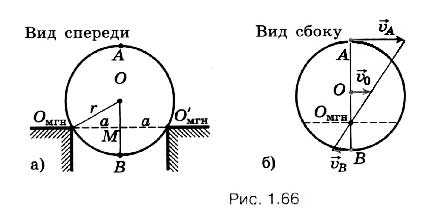
Р е ш е н и е.
Мгновенная ось вращения Омгн в данном случае показана на рисунке 1.66, б. Угловая скорость поворота шарика относительно этой оси ω = υ0/OM,
где
Отсюда
следовательно,
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Кинематика — Физика, учебник для 10 класса — Класс!ная физика
Физика и познание мира — Что такое механика — Механическое движение. Система отсчёта — Способы описания движения — Траектория. Путь. Перемещение — Равномерное прямолинейное движение. Скорость. Уравнение движения — Примеры решения задач по теме «Равномерное прямолинейное движение» — Сложение скоростей — Примеры решения задач по теме «Сложение скоростей» — Мгновенная и средняя скорости — Ускорение — Движение с постоянным ускорением — Определение кинематических характеристик движения с помощью графиков — Примеры решения задач по теме «Движение с постоянным ускорением» — Движение с постоянным ускорением свободного падения — Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» — Равномерное движение точки по окружности — Кинематика абсолютно твёрдого тела. Поступательное и вращательное движение — Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями — Примеры решения задач по теме «Кинематика твёрдого тела»
class-fizika.ru
Решение задач по теме «Кинематика». Видеоурок. Физика 10 Класс
Первая задача, которую мы рассмотрим, будет посвящена равномерному движению вдоль одной оси. Эта задача будет связана с относительностью движения тел.
Условие:
Из точки в точку и обратно движется вертолет. В первый раз из точки в точку и обратно он летит в безветренную погоду. А второй раз он летит уже при ветре, направление которого совпадает с направлением первоначального движения, то есть из точки в точку . В каком случае – в первом, когда безветренная погода, или во втором случае, когда есть ветер – вертолет затратит больше времени на преодоление этого расстояния?
Решение:
Обозначим скорость вертолета как , а скорость ветра – . А расстояние из точки до точки обозначим буквой . В результате нам надо исследовать, во сколько раз время будет больше, чем время . То есть найти отношение .
Чтобы найти время , то есть время, за которое вертолет летит из точки в точку и обратно в безветренную погоду, мы запишем следующее выражение:
– это время полета из точки в точку , а – время полета из точки в точку , когда вертолет летит обратно.
Учитывая, что движение равномерное, можно записать:
Рассмотрим теперь второй случай. Запишем выражение для времени полета из точки в точку и обратно при наличии ветра:
– это время полета из точки в точку при условии, что ветер дует по направлению движения вертолета. – это время полета при условии, что ветер дует против направления движения вертолета.
Обратите внимание, что время определяется как , поскольку скорости направлены в одну сторону. А определяете как . То есть ветер тормозит движение вертолета, замедляет его движение, поэтому в данном случае мы берем разность скоростей (рис. 1).
Рис. 1. Направление скоростей вертолета и ветра
Обратите внимание на то, что если бы скорость ветра была больше скорости вертолета, то время получилось бы отрицательным, а это значит, что вертолет обратно бы никогда не прилетел.
Сложим полученные выражения:
Найдем отношение к :
Видно, что числитель больше, чем знаменатель, значит, отношение будет больше единицы . Следовательно, можно говорить о том, что время полета в первом случае меньше времени полета во втором случае. Так что при наличии ветра вертолет будет в любом случае двигаться медленнее и затратит большее количество времени.
Также эту задачу можно было решить другим способом, с помощью вычисления средней скорости.
Ответ: .
Вторая задача связана с равнопеременным движением вдоль прямой. То есть движение будет с постоянным ускорением.
Условие:
Материальная точка движется вдоль прямой согласно уравнению . Определите пройденный путь этой точкой за секунды.
Решение:
Сравним уравнение Галилея с уравнением движения данной материальной точки.
Рассматривая эти два уравнения, можно сделать вывод, что . Точка начинает свое движение из начала координат. Начальная скорость – это величина, которая стоит перед буквой . В нашем случае начальная скорость будет равна . Обратите внимание, что эта скорость положительна и, следовательно, тело начинает движение вдоль оси в том же самом направлении, что и сама ось .
Рассматривая ускорение, мы можем записать следующее: . Это означает, что ускорение равно . В данном случае знак минус говорит о том, что ускорение направлено против оси . Движение является замедленным (рис. 2).
Рис. 2. Направление скорости и ускорения материальной точки
Также мы можем записать уравнение скорости .
Для определения пройденного пути необходимо исследовать траекторию движения.
Итак, для того чтобы исследовать траекторию движения тела, нужно определить, в какой же точке произойдет остановка тела, то есть скорость тела будет равна нулю. Для этого в уравнение скорости подставим конечную скорость, равную нулю, и получим время .
То есть это означает, что тело через 2,5 секунды остановится. Определим координату точки, в которой тело остановится:
То есть, пройдя расстояние 1,25 метра, тело остановилось.
Следующий шаг, который мы должны сделать для исследования траектории, это определить конечную координату, то есть координату тела по истечении 4 секунд движения.
То есть координата точки в конце движения составит .
Обратите внимание на то, что если бы мы сразу определили конечную координату, то, следуя формуле, мы должны были бы сказать, что тело прошло 0,8 метра, хотя это совсем не так. Ведь – это проекция перемещения. Она совпадает с пройденным путем только в том случае, если направление скорости не изменяется, а в нашей задаче направление скорости через 2,5 секунды меняется на противоположное.
Итак, траектория движения тела является ломаной линией. Тело первые секунды двигалось в одну сторону, затем оно остановилось и при сохранении ускорения начало движение в противоположную сторону (рис. 3).
Рис. 3. Пройденный путь материальной точки
Пройденный путь определяется:
Ответ: .
Третья задача посвящена равномерному движению по окружности, то есть движению по окружности с постоянной скоростью.
Условие:
Имеется вращающийся с постоянной скоростью диск некоторого радиуса. При этом крайние точки этого диска обладают линейной скоростью . А точки, которые располагаются на ближе к центру вращения, обладают скоростью . Необходимо определить центростремительное ускорение крайних точек этого диска (рис. 4).
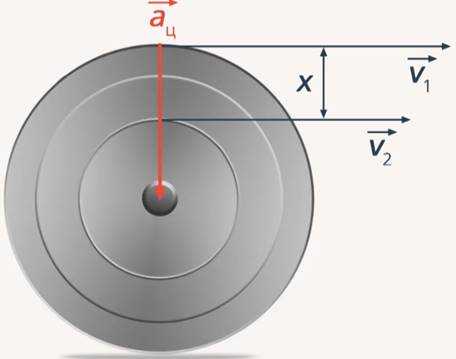
Рис. 4. Иллюстрация к задаче № 3
Решение:
Угловая скорость всех точек на этом вращающемся теле будет одинакова, поэтому для крайних точек мы записываем уравнение:
Аналогично для точек, которые смещены к центру, можно записать:
Разница радиусов равна:
Отсюда можно выразить :
Исходя из того, что угловая скорость одинакова для всех точек, можно записать:
Решая это уравнение, мы можем найти радиус траектории крайних точек:
А для определения центростремительного ускорения достаточно использовать формулу:
interneturok.ru
Методы решения кинематических задач
Наиболее распространенным в кинематике является координатный метод решения задач, который уже применялся выше. Суть его отражается в пунктах следующего предписания.- Выберите систему: тело отсчета, начало отсчета времени. Свяжите с телом отсчета систему координат.
- Изобразите в выбранной системе отсчета все кинематические характеристики движения каждого из рассматриваемых тел в начальный, конечный, промежуточные моменты времени – координаты, перемещения, скорости, ускорения.
- Запишите для каждого из рассматриваемых тел уравнения движения в координатной форме
- Запишите для каждого из рассматриваемых тел уравнение скорости в проекциях на выбранные направления (υx = υ0x + ax ∙ Δt).
- При необходимости запишите дополнительные уравнения.
- Решите полученную систему уравнений относительно неизвестных величин.
Следует иметь в виду, что данное предписание содержит лишь пункты, касающиеся только кинематической части задачи. В нем отсутствуют такие обязательные для решения каждой задачи пункты, как, например, анализ условия, поиск рационального или оригинального подхода к решению, поверка ответа. Кроме того, надо отдавать себе отчет в том, что данное предписание не является алгоритмом и не дает никакой гарантии на получение результата в случае его точного исполнения. Более того, некоторые указания в конкретных случаях могут и не выполняться. Например, если отсутствует требование найти скорость тела в заданный момент времени, четвертый пункт может быть опущен. Может не изображаться на чертеже часть кинематических характеристик. Вместе с тем, следование предписанию может оказаться весьма полезным.
|
Пример 1Задача об автомобиле |
|
|
Казалось бы, задачу можно решить просто, воспользовавшись известной формулой
Однако по приведенной формуле находится перемещение тела. Путь же, даже при прямолинейном движении тела не всегда численно совпадает с его перемещением.
Не будем торопиться и применим к решению приведенное выше предписание.
Будем решать задачу в системе отсчета, неподвижной относительно Земли. Начнем отсчитывать время с момента появления у автомобиля ускорения.
Свяжем точку отсчета с положением автомобиля в этот момент времени. Ось координат направим в сторону начальной скорости автомобиля.
Отобразим на чертеже все необходимые кинематические характеристики движения тела (координаты, перемещения, скорости и ускорения) в начальный, конечный и промежуточные моменты времени.
Начальная координата автомобиля 0, в этот момент времени у автомобиля имеется скорость направленная по оси X, и в этот же момент у автомобиля появляется ускорение направленное в противоположную выбранной оси сторону. Знак минус говорит о том, что ускорение направлено против установленного нами направления. И не более того.
Автомобиль, двигаясь с ускорением –2 м/с2, уменьшает свою скорость.
Прежде, чем рассуждать дальше, произведем несложные расчеты.
Скорость автомобиля уменьшается и через одну секунду она будет равна 8 м/с, через 2 секунды – 6 м/с, через 3 секунды – 4 м/с, через 4 секунды – 2 м/с. Через 5 секунд автомобиль остановится.
Может показаться, что раз автомобиль остановился, то условие задачи сформулировано неверно.
В связи с этим, один из вариантов решения рассматриваемой задачи может быть таким: мы, воспользовавшись данным уравнением, подставляем в него значение времени 5 с, в течение которого, как нам кажется, автомобиль двигался, и рассчитываем перемещение. Это можно сделать устно. Производим подстановку значений в уже использованную ранее формулу. После несложных вычислений получаем
Но на самом деле текст задачи несколько иной. В задаче четко сказано, что автомобиль двигался не 5, а 6 секунд, и требуется найти путь, пройденный им в течение 6 секунд.
Одним из вариантов такого движения, когда автомобиль действительно мог бы двигаться еще одну секунду, является движение автомобиля в горку.
Представим себе следующую ситуацию. Автомобиль разогнался и у основания горки водитель выключил двигатель. Автомобиль въезжает на горку, его скорость действительно уменьшается, он движется с отрицательным ускорением. Через 5 с автомобиль останавливается и начинает двигаться назад, то есть скатываться с горки. Он может двигаться еще некоторое время: секунду, две, три и так далее, но он движется уже назад. При этом скорость автомобиля по величине возрастает. Вектор же ускорения направлен против оси, и поэтому даже для случая увеличения скорости, мы обязаны считать это ускорение отрицательным.
Отобразим на чертеже координату точки остановки. В этой точке ускорение у автомобиля все равно есть, оно по-прежнему направлено против оси и равно –2 м/с2.
В нашем случае автомобиль через 5 с остановился, потом начал движение в обратном направлении и через секунду он оказалось ближе к началу координат.
Автомобиль совершил перемещение до остановки, потом он совершил перемещение в обратном направлении.
Пройденный автомобилем путь оказался равным сумме модулей перемещений и
Сначала мы рассчитываем по формуле, которую уже использовали, перемещение автомобиля за 5 с (это перемещение мы уже определили – оно равно 25 м).
Затем решаем вторую задачу.
|
Воспользуемся тем же самым уравнением, только начальную скорость примем равной нулю. Рассчитаем перемещение
Окончательно: L = 25 м + 1 м = 26 м.
|
Необходимость следования предписанию по решению задач, а также влияние выбора системы отсчета на ход решения ярко проявляется при анализе следующей задачи.
|
Пример 2Задача о воздушном шаре. |
|
|
Очень часто такую задачу решают поэтапно:
Такое решение является достаточно простым. Но основные рассуждения при его выполнении построены на знании скорости подъема шара. Стоит из условия задачи исключить данные об этой скорости, как решение данным способом уже не может быть выполнено. Следовательно, приведенные рассуждения иллюстрируют всего лишь частный подход к решению одной конкретной задачи. Этот подход не распространяется на решение других задач и поэтому служит лишь иллюстрацией того, как не следует решать кинематические задачи.
Универсальным для решения задач по кинематике является координатный метод. Проиллюстрируем его применительно к данной задаче.
Свяжем точку отсчета с поверхностью Земли. Начнем отсчет времени в тот момент, когда предмет отделился от шара. Координатную ось направим вертикально вверх.
Запишем уравнения движения шара и тела в системе отсчета, связанной с Землей:
По условию задачи, в искомый момент времени
Отсюда: Численно:
Задача имеет и более рациональное решение.
Если связать систему отсчета с движущимся шаром и ось 0Y направить вертикально вниз, то уравнение движения тела запишется: H = 125 м.
Такое решение редко приводится в силу того, что мы «привыкли» связывать систему отсчета с Землей, каким-то неподвижным телом.
Координатный метод позволяет решать и более сложные задачи на движение тела, брошенного под углом к горизонту. Одной из таких задач является следующая.
|
Пример 3Задача о движении тела, брошенного под углом к горизонту. |
|
|
При решении задачи учитывать сопротивление воздуха не будем. Сразу оговоримся, что в реальных условиях пренебрегать сопротивлением воздуха можно только при очень небольших скоростях, сообщаемых брошенным под углом к горизонту телам, да и то, если нас интересуют лишь приближенные ответы на поставленные выше вопросы. При больших же начальных скоростях тел сопротивление их движению настолько велико, что реальные значения искомых величин значительно отличаются от соответствующих теоретических значений, полученных без учета сопротивления воздуха. Однако, чтобы научиться решать реальные сложные задачи, надо начать с анализа более простых идеализированных ситуаций. Именно такой анализ и представлен в данной задаче.
Свяжем систему отсчета с местом броска камня. Начнем отсчитывать время в момент броска. Камень участвует в сложном движении. Он одновременно смещается горизонтально и движется в вертикальном направлении, сначала поднимается вверх, потом падает.
Горизонтальное и вертикальное движения происходят независимо друг от друга, что следует из принципа независимости движений. Данный принцип позволяет рассмотреть вместо сложного движения два простых: движение горизонтальное и движение вертикальное.
В связи с этим, ось абсцисс направим горизонтально вправо, ось ординат – вертикально вверх. Вектор начальной скорости разложим на две векторных составляющих: и спроецируем эти составляющие на выбранные направления.
Вдоль оси абсцисс тело движется равномерно со скоростью υ0x = υ0 ∙ cos α.
Вдоль оси ординат тело движется с ускорением a = g = –9,8 м/с2. Ускорение отрицательно и на восходящем, и на нисходящем участках траектории, поскольку его вектор направлен против оси 0Y. Вертикальная составляющая начальной скорости равна υ0y = υ0 ∙ sin α.
Запишем уравнения движения для двух его составляющих в проекциях на выбранные направления:
С учетом того, что перепишем уравнения в виде:
Из второго уравнения находим время:
Из решения следует, что на высоте h камень окажется дважды: на восходящем и нисходящем участках траектории.
Если конечная координата тела вдоль оси 0Y равна нулю, то второе уравнение перепишем:
Из этого уравнения получаем:
Подставляя значение времени полета в уравнение движения тела вдоль горизонтальной оси, имеем:
Поскольку то
Если угол α = 45°, то sin 90° = 1. Это означает, что при броске под данным углом дальность полета камня максимальна. Она равна:
|
|
Максимальной высоты тело достигнет через время в два раза меньшее общего времени полета: Подставляя значение этого времени в уравнение для нахождения высоты подъема тела, имеем:
Кроме того, если в уравнение для высоты подъема тела подставить время, выраженное из уравнения для дальности полета в горизонтальном направлении, получим:
Сопоставление этого уравнения с уравнением позволяет утверждать, что траекторией тела, брошенного под углом к горизонту, является парабола.
Наряду с координатным методом решения кинематических задач, удобно пользоваться векторным методом. Суть этого метода заключается в следующем.
Записывается уравнение для расчета перемещения тела в виде
Вектор равен геометрической сумме двух векторов и
Одной из распространенных операций над векторами является их сложение по правилу треугольника
Решение кинематических задач векторным методом начинается с построения треугольника, сторонами которого являются вектора
Далее мы «забываем», что имеем дело с векторами и решаем обычную геометрическую задачу.
При решении геометрической задачи часто приходится выполнять дополнительные построения. Желательно, чтобы при этом на чертеже появились прямоугольные треугольники, соотношение между сторонами которых проще, чем для косоугольных треугольников.
Применим приведенные рассуждения, например, к нахождению времени движения камня, брошенного под углом к горизонту, до заданной точки.
Камень брошен из точки O и движется по параболе. Через некоторое время t он оказывается в точке A на высоте h. Нарисуем три вектора: Вектор перемещения соединяет начальную точку O и заданную точку A. Вектор имеет начало в точке броска O и сонаправлен с вектором начальной скорости. Вектор направлен вертикально вниз и оканчивается в заданной точке A. Все три вектора образуют треугольник OAB.
Опустив из точки A перпендикуляр на горизонтальное направление, получаем прямоугольный треугольник OAC. Катет, противолежащий углу равен
Он связан с гипотенузой соотношением:
Это уравнение можно переписать в более привычном виде: В общем виде, уравнение имеет два корня. Как уже пояснялось выше, на высоте h, камень может находиться дважды: на восходящем и на нисходящем участках траектории.
Рассмотрим, как векторный метод применяется к решению более сложной задачи.
|
Пример 4Задача о теннисном шаре |
|
|
Выполним чертеж.
β = β′, т. к. угол падения равен углу отражения.
α = β, как углы с взаимно перпендикулярными сторонами.
Шарик, по условию задачи, касается плоскости дважды, пусть в точках A и B. При этом он совершает перемещение
Так как движение происходит в поле тяжести, то a = g и
О векторе мы знаем, что он направлен вертикально вниз и заканчивается в точке B.
О векторе мы знаем, что он направлен вдоль вектора и длина его ограничивается точкой пересечения с вектором
Достроим чертеж. Опустим из точки C на основание треугольника ABC перпендикуляр.
ACD = α, как вертикальные накрест лежащие.
CAD = π/2 – α.
CBD = π/2 – α.
Отсюда: CAD = CBD.
Это означает, что ΔACB – равнобедренный.
Таким образом,
Это и есть ответ к данной задаче. Но так как нам неизвестна начальная скорость шарика при отскоке, но известна высота, с которой он упал, необходимо решить еще одну задачу, которая позволила бы установить связь между этими величинами. Для этого можно воспользоваться уравнением, связывающим начальную скорость тела (в данном случае она равна нулю), конечную скорость (скорость непосредственно перед ударом о плоскость), и ускорение движения тела (ускорением свободного падания): α = β.
Окончательно: S = 8 ∙ h ∙ sin α.
files.school-collection.edu.ru
Решение задач по кинематике
Решение задач по кинематике равнопеременного движения традиционно вызывает у учащихся затруднения, что связано в основном с тем, что здесь впервые встает проблема формализации физической задачи, т.е. перевода ее с языка “текстовой задачи” по физике на язык математики. До этого учащимся приходилось в основном решать задачи, если можно так выразиться, “по формулам”, а теперь необходимо осмыслить задачу не только с точки зрения физики, но и суметь записать ее в терминах уравнений кинематики и затем из этих уравнений, опираясь на условие задачи, получить нужные “формулы”. В настоящей работе представлен ход обзорного урока по этой теме.
Чтобы научиться решать задачи по кинематике нужно прежде всего уметь правильно выбрать систему отсчета (СО), которая включает в себя:
- Точку отсчета (выбираем произвольно из соображений удобства)
- Систему координат, связанную с точкой отсчета
- Начало отсчета времени (счетчик времени, выбираем из соображений удобства).
Вообще важно, чтобы учащиеся отдавали себе отчет, что для решения задач по кинематике необходимо:
Выбрать СО подходящим образом, чтобы в этой СО уравнения кинематики принимали наиболее простой вид. Обязательно обратить внимание на выбор начала отсчета времени.
Сделать чертеж, иллюстрирующий описанное в условии задачи явление: начертить систему координат, траекторию движения, вектора скоростей и ускорений.
Записать основные уравнения кинематики равнопеременного движения в выбранной СО для произвольного момента времени:
где x0,y0 – начальное положение тела, v0x, v0y – проекции начальной скорости тела, ax, ay – проекции ускорений.
4. Записать уравнения (1)-(4) для характерных моментов времени, из которых находить требуемые в условии задачи величины, т.е. получить рабочие формулы.
Важно, чтобы учащиеся понимали, что можно получить решение любой задачи кинематики равнопеременного движения, если записаны основные уравнения (1)-(4). Важно также, чтобы они осознавали, что вид этих уравнений меняется в зависимости от выбора СО. В связи с этим, решим несколько задач, иллюстрирующих сказанное.
Задача 1. Теннисист при подаче запускает мяч с высоты h над землей. На каком расстоянии от подающего мяч ударится о землю, если начальная скорость равна v0 и направлена вверх под углом к горизонту?
Решение: а). Точку отсчета (начало координат) поместим в точку на поверхности земли, где стоял теннисист в момент удара. Время начнем отсчитывать от момента удара по мячу. На рис.1 изображена система координат XOY, траектория движения мяча, вектора скорости и ускорения.
Рис. 1
В выбранной СО начальные условия имеют вид: x0 = 0, y0 = h, ax = 0, ax = — g,
и кинематические уравнения (1)-(4) запишутся в виде:
Требуемое в условии задачи расстояние D (дальность полета) найдем из условия: D = x(tn), где время полета tn определяется из соотношения y(tn) = 0, т.е.можем записать уравнение:
При решении этого квадратного уравнения удобнее записывать его в приведенном виде x2 + 2qx + + q = 0 и находить корни по формуле
Опыт показывает, что учащиеся зачастую не знают этого и находят корни такого уравнения по общей формуле, что осложняет выкладки. Перепишем уравнение в виде
тогда его решение
Т.к. t >= 0, то физический смысл имеет корень
Теперь из условия D =x(tn) получим рабочую формулу
б). Решим эту задачу, выбрав за точку отсчета (начало координат) точку, где находился мяч в момент удара. Время по-прежнему отсчитываем от момента удара по мячу. На рис.2 изображена система координат XOY, траектория движения мяча, вектора скорости и ускорения.
Рис. 2
В выбранной СО начальные условия имеют вид: x0 = 0, y0 = 0, ax = 0, ax = — g,
Кинематические уравнения (1)-(4) теперь запишутся так
и время полета tn мяча до земли найдется из условия: y(tn) = — h. Дальше решение задачи повторяет способ а).
В рассмотренной задаче было безразлично, где поместить начало координат, однако в задачах, где высота, на которой происходит событие, не задана, начало координат лучше всего помещать именно в эту точку на неизвестной высоте. Направление осей выбирается из соображений удобства.
Задача 2. Тело, свободно падающее с некоторой высоты, последние h м пути прошло за время с. Какое время и с какой высоты падало тело?
Решение: Начало координат поместим в точку на неизвестной высоте H, ось Y направим вертикально вниз. Время начнем отсчитывать с момента начала падения тела. На рис.3 изображена система координат и ускорение свободного падения тела.
Рис. 3
В выбранной СО v0y = 0, y0 = 0, ay = g и уравнения кинематики (1)-(4) сведутся к двум
Т.к. в условии задачи речь идет о свободном падении тела, то в любой момент времени его координата будет равна пройденному пути. Выразим из уравнения для координаты отрезки пути H и h. Из рис.3 очевидно, что
где tn – время падения тела на землю. Получили два уравнения с двумя неизвестными H и tn. Уравнение (6) после преобразований принимает вид
Откуда
Подставляя найденное tn в (5), получим искомое выражение для высоты
Таким образом, требуемые в задаче величины определены.
Следует отметить, что если на размещение начала отсчета и направление осей системы координат учащиеся еще обращают внимание, то выбор начала отсчета времени обычно ускользает из их поля зрения. Это особенно заметно при решении задач, где в движении участвует несколько тел.
Если тела начинают свое движение одновременно, то отсчет времени начинается с момента начала движения тел, а кинематические уравнения пишутся для каждого из тел.
Задача 3. Два тела, расстояние между которыми l, начинают одновременно двигаться навстречу друг другу: первое — равномерно со скоростью v, а второе – из состояния покоя равноускоренно с ускорением a. Через какое время тела встретятся?
Решение: Поместим начало координат в точку, где находилось первое тело в начальный момент, ось OX направим по движению первого тела. Отсчет времени начнем с момента начала движения тел. На рис.4 изображена ось ОХ, вектора скоростей и ускорений обоих тел.
Рис. 4
В этой СО x10 = 0, x20 = l. Уравнение движения для первого тела
Уравнение движения для второго тела
В момент встречи x1(t) = x2(t), t – время в пути до встречи, т.е.
откуда
Задача 4. Лифт поднимается с ускорением a. В тот момент, когда его скорость стала равна v, с потолка кабины лифта начал падать болт. Высота кабины лифта h. Вычислить время падения болта.
Решение: Свяжем начало неподвижной системы координат с точкой, в которой находится пол лифта в момент, когда болт начинает падать. Время начнем отсчитывать от момента начала падения болта. На рис.5 изображена система координат (ось ОY), вектора скоростей и ускорений.
Рис. 5
Пусть yk vk — координата и проекция скорости кабины лифта, yб vб - координата и проекция скорости болта. Для кабины лифта основные уравнения (1) — (4) запишутся в виде
а для болта примут вид
Когда болт упадет на пол, будет выполняться: yk (t) = yб (t), где t – время падения болта:
Наибольшие затруднения вызывает у учащихся выбор начала отсчета времени, и особенно запись уравнений кинематики в случае, когда тела, участвующие в движении, начинают двигаться неодновременно.
Задача 5. Тело с начальной скоростью v0 и ускорением a1 начинает двигаться из некоторой точки по прямолинейной траектории. Через время из той же точки вслед за первым телом начинает двигаться другое тело без начальной скорости с ускорением a2. Через какое время после выхода первого тела второе тело его догонит?
Решение: Начало координат свяжем с точкой, из которой начинают двигаться тела. Ось ОХ направим по движению тел. Время начнем отсчитывать от начала движения первого тела. На рис.6 изображена система координат, вектора скоростей и ускорение.
Рис.6
В этой СО уравнения кинематики для первого тела имеют вид
а для второго тела, с учетом того, что оно начало свое движение на секунд позже первого, запишутся в виде
На запись этих уравнений нужно особенно обратить внимание учащихся. В момент, когда второе тело догонит первое, будет выполняться x1(t) = x2(t), т.е.
Получаем квадратное уравнение для определения времени t
С учетом того, что t >= 0 находим
Задача 6. Два тела брошены вертикально вверх с поверхности Земли из одной точки вслед друг за другом с интервалом времени , с одинаковыми начальными скоростями v0. Определить, через какое время тела встретятся.
Решение: Начало отсчета поместим в точку бросания. Ось OY направим вертикально вверх. Отсчет времени начнем с момента бросания первого тела. На рис.7 изображена ось OY и вектора начальной скорости и ускорения свободного падения.
Рис. 7
В выбранной СО y10 = y20 = 0, v01y = v02y = v0, a1y = a2y = -g. Уравнения кинематики для первого тела имеют вид
Основные уравнения кинематики для второго тела с учетом того, что оно начала свое движение на секунд позже первого, запишутся в виде
Тела “встретятся”, когда y1 (t)= y2 (t), т.е. получаем уравнение для нахождения искомого времени “встречи”
откуда
urok.1sept.ru
Решение графических задач по теме «Кинематика»
Пояснительная записка к уроку.
ФИО
Сырова Ольга Юрьевна
Место работы
государственное бюджетное общеобразовательное учреждение Самарской области средняя общеобразовательная школа с. Новый Сарбай муниципального района Кинельский Самарской области
Должность
Учитель математики и физики
Класс
9
Предмет, кол-во часов в неделю
Физика, 2
Тема и номер урока в теме
Решение задач по теме «Кинематика», урок № 10
Базовый учебник
А.В. Перышкин. Физика. 9 класс: Учебник для общеобразовательных учреждений. – М.: «Дрофа», 2010
9.
Тип урока
Закрепление изученного
10.
Формы контроля
Фронтальный опрос, тест, самоконтроль
11.
Виды контроля
Текущий, предварительный
Цель урока:
закрепить знания, полученные по теме «Основы кинематики»,
Задачи:
сформировать навыки решения качественных, расчетных задач, закрепить навыки чтения и построения графиков движения.
Метапредметные результаты:
формирование умений воспринимать, перерабатывать и предъявлять информацию в словесной, образной, символической формах, анализировать и перерабатывать полученную информацию в соответствии с поставленными задачами, выделять основное содержание прочитанного текста, находить в нем ответы на поставленные вопросы и излагать его;
развитие монологической и диалогической речи, умения выражать свои мысли и способности выслушивать собеседника, понимать его точку зрения, умение работать в группе, объективно оценивать результат своей деятельности.
Предметные результаты:
знание формул
умения обнаруживать зависимости между физическими величинами, объяснять полученные результаты и делать выводы;
умения читать графики зависимости физических величин;
умения применять теоретические знания для решения качественных задач.
Средства обучения: разноуровневый печатный материал — заготовка, доска.
Связи:
межпредметные: математика — линейная зависимость, график линейной функции; квадратичная функция и ее график;
внутрипредметные: равномерное и равноускоренное движение.
Технологическая карта урока.
Этап урока
Вид работы контроля
Деятельность преподавателя
Деятельность учащихся
Планируемые результаты обучения
Время, мин
Метапредметные
Предметные
Организационный
Приветствие учителя
Подготовка рабочих мест
1
Актуализация знаний
Работа в группах. Фронтальный опрос.
Поясняет действия к выполнению задания «Физический диктант»
Работают в группах. Из предложенного набора карточек формируют физические формулы, прикрепляя их магнитами к доске
Умеют предъявлять информацию в образной форме, умеют работать в группе.
Знают физические формулы
2
Постановка учебной задачи
Беседа
Подводит к теме урока. Предлагает раздаточный материал
Выделяют цели урока. Знакомятся с предложенным материалом.
Умеют воспринимать, перерабатывать и предъявлять информацию в словесной форме, развивают монологическую и диалогическую речь
1
Проверка теоретических знаний
Фронтальный опрос
Корректирует работу учащихся
Отвечают на вопросы качественных задач. Дополняют ответы друг друга.
Применяют знания по физике в жизни, осознают связь теории с практикой; умеют выражать свои мысли и выслушивать собеседника
Умеют применять теоретические знания для решения качественных задач.
2-3
Исследовательский (Исследование зависимости скоростей двух тел, движущихся ускоренно и равномерно)
1.Индивидуальная траектория обучения
2. Работа в группах
Вовлечение нескольких учащихся в решение задания №2 (а,б) раздаточного материала у доски.
Корректирует работу учащихся.
Решают расчетные задачи задания №2 (а,б).
Возможна индивидуальная работа сильных учащихся на опережение (работы учащихся у доски)
Строят графики зависимостей физических величин задание №2 (в)
(три уровня сложности), с последующей проверкой на доске)
Понимают важность межпредметных связей физики и математики
(математика — линейная зависимость, график линейной функции; квадратичная функция и ее график)
Умеют работать в группе.
Умеют обнаруживать зависимости между физическими величинами; умеют объяснять полученные результаты и делать выводы
Умеют строить графики зависимости физических величин;
20
Рефлексия деятельности
Самоконтроль (взаимоконтроль)
Раздает тест
Выполняют минитест, с последующей проверкой. Выставляют оценку. Система оценивания
5 правильных ответов«5»
4 — «4»
3 – «3»
1-2 ответа – «2»
Оценивают результат своей деятельности
5-6
Подведение итогов урока.
Фронтальный опрос
Комментирует ответы учащихся
Анализируют работу класса.
Высказывают мнения о своей работе: что вызвало затруднение? какие задания выполняли с уверенностью? Сдают тетради на проверку.
Развивают монологическую и диалогическую речи, пробуют выражать свои мысли, выслушивают собеседника.
3-5
Домашнее задание
Записывают д/з.
Подготовиться к контрольной работе по теме «Кинематика»
Дополнительно (по желанию) подготовить доклад на тему «Великие изобретения прошлого» или «Изобретения будущего»
1
Приложение 3.
Ответы в качественным задачам.
1. Земля вращается с запада на восток. Почему же, подпрыгивая вверх, мы попадаем на то же место, а не смещаемся к западу?
Ответ: Потому, что в системе отсчета, связанной с Землей, человек покоится.
2. Какова траектория движения точек винта самолета по отношению к летчику? по отношению к Земле?
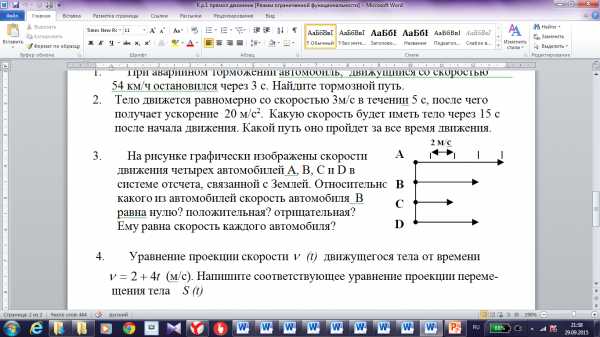Ответ: Окружность, винтовая линия
3. На рисунке графически изображены скорости движения четырех автомобилей А, В, С и D в системе отсчета, связанной с Землей. Относительно какого из автомобилей скорость автомобиля В равна нулю? положительная? отрицательная?
Ответ: относительно D, относительно С, относительно А
4. Даны графики, характеризующие движение пешехода. Опишите это движение, пользуясь обоими графиками.
а б
Ответ: Рисунок 3, а представляет собой график изменения координаты, а рисунок 3, б — график пути. На первом графике показано, что пешеход вернулся в то место, откуда он начал движение; на втором по ординате точки С можно определить весь пройденный им путь. Отрезки ОА и ВС соответствуют движению; АВ — остановке. В обоих направлениях скорость движения одинакова. Это видно по наклону прямых ОА и ВС к оси времени.
Ответы к тесту.
- 2 вариант
Система оценивания
1) 4
1) 1
5 правильных ответов«5»
4 — «4»
3 – «3»
1-2 ответа – «2»
2) 2,4
2) 2,4
3) 2
3) 1
4) 1
4) 2
5) 1
5) 3
infourok.ru
Задачи по кинематике с решениями — Задачи по кинематике с решениями
Задачи по кинематике с решениями
скачать (256.5 kb.)
Доступные файлы (1):
содержание
1.doc
Реклама MarketGid:Задачи по кинематике с решениями
Задачи с решениями по кинематике по следующим темам:
Равномерное прямолинейное движение: 13 задач
Равноускоренное (равнозамедленное) движение: 2 задачи
Свободное падение: 1 задача
Криволинейное движение: 3 задачи
Движение по окружности: 3 задачи
1. Равномерное прямолинейное движение
1.1.Решение задачи 1 о графике зависимости координаты от времени
| | На рисунке представлены графики зависимости координаты двух тел от времени. Графики каких зависимостей показаны? Какой вид имеют графики зависимости скорости и пути пройденного телом, от времени? |
Решение
На рисунке показаны графики равномерного движения тел.
1) В начальный момент времени t = 0 первое тело имеет начальную координату хо1 = 1 м, второе тело — координату хо2 = 0.
2) Оба тела движутся в направлении оси Х, так как координата возрастает с течением времени.
3) Уравнение движения для равномерного прямолинейного движения имеет вид: x=xо+vхt.
Тогда для первого, второго тела соответственно:
x1=xо1+v1хt и x2=xо2+v2хt
или x1=1+v1хt, x2=v2хt.
Определим скорости первого и второго тела:
| v1x | = | x1 − 1 | = | 2 − 1 | = 0,5 м/с. |
| t | 2 |
| v2x | = | x2 | = | 1 | = 0,5 м/с. |
| t | 2 |
Уравнения скорости имеют вид: v1х=v2х=0,5 м/с.
Так как S=vхt, то уравнение пути S=0,5t.
^
| | Графики каких движений показаны на рисунке? Как отличаются скорости движения этих тел? В какой момент времени тела встретились? Какие пути тела прошли до встречи? |
Решение
Так как изменение координаты тела происходит прямо пропорционально времени, то можно утверждать, что движение равномерное и прямолинейное. По отношению к точке отсчета (0; 0) у первого тела координата убывает, а у второго наоборот — возрастает. Первое тело движется против оси х, второе — по направлению оси координат.
а) Чтобы ответить на вопрос об отличии скоростей, определим их из уравнения координаты:
| vx | = | x − xo | , тогда |
| t |
| v1x | = | 3 − 6 | м/с = −0.75 м/с. |
| 4 |
| v2x | = | 3 − 0 | м/с = 0.75 м/с. |
| 4 |
Скорости тел равны по абсолютному значению, но противоположны по направлению.
б) Зная также, что v=tg α (геометрический смысл скорости) и сравнивая углы наклонов графиков движения тел к оси t, приходим к выводу, что углы одинаковы, следовательно, скорости равны.
в) Точка пересечения двух прямых означает, что тела встретились в одно и то же время в одной и той же точке, т. е. время встречи t = 4 c, а координата x = 3 м.
г) Так как движение равномерное и прямолинейное, то S = x − xo. Находим пути, пройденные телами до встречи:
S1= | x1 − xo1 | = | (3−6) м | = 3 м,
S2= | x2 − xo2 | = | (3−0) м | = 3 м.
Оба тела, двигаясь с одинаковыми скоростями, за одно и тоже время прошли равное расстояние.
^
Точка движется с постоянной скоростью vo под углом α к оси x. В начальный момент времени t = 0 точка имела координаты (хo; уo). Написать уравнения движения точки и уравнение траектории.
Решение
уравнение движения имеет вид:
x = xo + vxt по оси x и
y = yo + vyt по оси Y.
Начальные координаты заданы xo, yo. Проекции скорости найдем из прямоугольного треугольника АВС:
vx = −vocos α, знак минус указывает на то, что направление проекции вектора скорости не совпадает с направлением оси x;
vy = vosin α, проекция скорости положительна, так как направление вектора скорости, совпадает с направлением оси Y.
Тогда, подставляя проекции скоростей в соответствующие уравнения движения, имеем:
x = xo − vot·cos α,
y = yo + vot·sin α.
Решая совместно эти два уравнения, напишем уравнение траектории. Для этого из уравнения движения точки вдоль оси x выразим время и подставим в уравнение движения точки вдоль оси Y:
| t = | xo − x | , тогда |
| vo cos α |
| y = yo + vo sin α | xo − x | = | yo + xotg α − x tg α. |
| vo cos α |
^
Даны уравнения движения тела: x = vxt и y = yo + vyt. Запишите уравнение траектории и постройте график, если vx = 25 см/с, vy = 1 м/с, yo = 0,2 м.
Решение
решая совместно уравнения x = vxt и y = yo+vyt,
получим уравнение траектории:
Если теперь мы подставим исходные данные, то уравнение траектории примет вид: y = 0.2 + 4x.
Сравним уравнение траектории с уравнением вида y = kx + b. Проводя аналогию, делаем вывод, что траектория движения тела представляет собой прямую.
Начальное положение точки при t = 0 xo = 0.2 м, вторую точку возьмем, например, при t = 1 c у = 4.2 м.
^
Первую половину пути автомобиль проехал со средней скоростью v1 = 60 км/ч, а вторую — со средней скоростью v2 = 40 км/ч. Определить среднюю скорость V автомобиля на всем пути.
Решение: проанализируем условие задачи: первую половину пути автомобиль проехал со скоростью 60 км/ч и затратил время, равное
Вторую половину пути автомобиль проехал со скоростью 40 км/ч и затратил время, равное
По определению, средняя скорость V при равномерном прямолинейном движении равна отношению всего пройденного пути ко всему затраченному времени.
Подставляя значения скорости в формулу средней скорости, получим:
| V = | 2 • 60 • 40 | = 48 км/ч. |
| 60 + 40 |
Средняя скорость равна 48 км/ч.
^
Первую половину времени автомобиль двигался со средней скоростью v1 = 40 км/ч, а вторую — со средней скоростью v2 = 60 км/ч. Определить среднюю скорость автомобиля на всем пути.
Решение: в отличие от предыдущий задачи, автомобиль движется первую половину времени с одной скоростью 40 км/ч, а вторую половину времени — со скоростью 60 км/ч. Следовательно, автомобиль проходит за равные промежутки времени разные расстояния.
и
тогда средняя скорость
| V = | S1 + S2 | = | v1t/2 + v2t/2 | = | v1 + v2 | . |
| t | t | 2 |
Средняя скорость для этого случая оказалась равной среднему арифметическому значению скоростей.
Подставим значения скоростей и проведем вычисления:
| V = | 40 + 60 | = 50 км/ч. |
| 2 |
Средняя скорость равна 50 км/ч.
^
Автомобиль проходит первую треть пути со скоростью v1, а оставшуюся часть пути — со скоростью v2 = 50 км/ч. Определить скорость на первом участке пути, если средняя скорость на всем пути V = 37,5 км/ч.
Решение: обозначим весь путь через S; время, затраченное на прохождение первого участка пути, — через t1; время движения на втором участке пути — через t2. Очевидно, что
| t1 + t2 | = | S | + | 2S | . |
| 3v1 | 3v2 |
Отсюда
| v1 | = | Vv2 | = 25 км/ч. |
| 3v2 − 2V |
^
Катер прошел первую половину пути со средней скоростью в n = 2 раза большей, чем вторую. Средняя скорость на всем пути составила Vc = 4 км/ч. Каковы скорости катера на первой и второй половинах пути?
Решение: катер проходит одинаковые отрезки пути с разной скоростью, следовательно, будет разным и затраченное время. Примем скорость на втором участке пути за v, тогда на первом участке скорость 2v. Средняя скорость на всем пути:
где
| t1 | = | S | | и | t2 | = | S | . |
| 2·2v | 2v |
Подставляем в формулу средней скорости время:
| Vc | = | S | = | 4vv | = | 4v | . |
| S/(4v) + S/(2v) | 3v | 3 |
Из последней формулы выразим скорость второго участка пути:
Подставляя значение средней скорости на всем пути в последнюю формулу, имеем v = 3 км/ч, тогда скорость на первом участке пути в v = 2 раза больше, чем на втором, и равна 6 км/ч.
^
Катер, двигаясь вниз по течению, затратил время в n = 3 раза меньше, чем на обратный путь. Определить, с какими скоростями относительно берега двигался катер, если средняя скорость на всем пути составила V = 3 км/ч.
Решение: двигаясь вниз по течению, катер затратил время в n = 3 раза меньше, т. к. его скорость относительно берега равна сумме его скорости относительно воды (собственная скорость) и скорости течения v1=vk+vT. Путь, проходимый катером, одинаков туда и обратно, обозначим его через S. Время, затраченное им при движении по течению вниз:
Обратно катер плывет против течения и его скорость относительно берега будет равна разности собственной скорости и скорости течения v2=vk−vT. Тогда затраченное время при движении катера против течения равно:
По условию задачи время движения катера против течения в три раза больше времени движения катера по течению:
| t2 | = | S(vk + vT) | = | vk + vT | | и | vk + vT | = 3. |
| t1 | S(vk − vT) | vk − vT | vk − vT |
Упрощая эти уравнения, находим, что vk=2vT (формула 1).
Теперь найдем среднюю скорость при движении катера на всем пути:
| V = | S | = | 2S | = | 2S | . |
| t | t1 + t2 | S/(vk + vT) + S/(vk − vT) |
Здесь учтем (1), тогда
| V = | 2 | = | 3 | VT, |
| 1/(3vk) + 1/vT | 2 |
отсюда находим скорость течения: vT = (2/3)V, а vk = (4/3)V.
После вычислений окончательно имеем: vT = (2/3)3 = 2 км/ч и vk = (4/3)3 = 4 км/ч.
^
Пассажир едет в поезде, скорость которого 80 км/ч. Навстречу этому поезду движется товарный поезд длиной 1 км со скоростью 40 км/ч. Сколько времени товарный поезд будет двигаться мимо пассажира?
Решение:
1-й способ. Cистему отсчета свяжем с Землей. Наблюдатель находится в точке O с координатой x = 0. Координата хвоста товарного поезда xT = 1 км. Уравнение движения обоих тел имеет вид: x1 = v1t и x2 = xT − v2t. В момент встречи хвоста поезда с пассажиром x1 = x2 или v1t = xT − v2t, отсюда время встречи равно
^ Свяжем систему координат с товарным поездом, тогда скорость пассажира в поезде, по отношению к неподвижной системе координат (товарный поезд), равна vo=v1+v2. Так как длина поезда l=1 км, то пассажир проедет мимо него, следовательно, и будет наблюдать в течение времени
После подстановки t = 30 c.
^
Формула x=20t. Необходимо:
определить характер движения;
найти начальную координату точки;
выявить модуль и определить направление скорости;
найти графический и аналитический смысл x через 15 секунд;
определить время (t), когда x=100 м.
Решение:
1. Уравнение x = xo + vt — это равномерное прямолинейное движение.
2. Начальная координата точки xo = 0.
3. Скорость точки — это коэффициент при t, то есть v = 20 м/с. Скорость положительна, следовательно, точка движется вдоль выбранного направления оси координат x.
4. Через ^ координата точки будет равна x = 300 м. Графически — нарисовать в осях координат x(t) по точкам прямую, которая будет проходить через точки (0 с; 0 м) и (15 с; 300 м). Через 15 с координата (по графику) будет 300 м.
5. При x = 100 м: 100 = 20t, отсюда t = 5 c.
^
Зависимость скорости от времени движущегося тела задана следующей формулой: v = 2 + 0,5t. Опишите это движение (укажите значение характеризующих его величин). Постройте график v(t).
Решение:
Зависимость скорости от времени движущегося тела задана следующей формулой: v = 2 + 0,5t. Опишите это движение (укажите значение характеризующих его величин). Постройте график v(t).
Уравнение скорости (назовем его 1) для равноускоренного движения имеет вид:
Сопоставляя уравнение, заданное по условию задачи, с уравнением (1), находим: vo = 2 м/с, a = 0,5 м/с2.
Тело движется вдоль оси координат с начальной скоростью 2 м/с равноускоренно с ускорением 0,5 м/с. Знак скорости «+» указывает на направление движения (вдоль выбранной оси координат). Так вектора скорости и ускорения совпадают, то тело разгоняется. Остановки не предвидится.
Для построения графика воспользуемся аналогией y = b + kx, что соответствует линейной функции. Для построения графика достаточно двух точек:
1) t = 0, v = 2 м/с;
2) t = 2 c, v = 3 м/с.
^
Теплоход плывет по реке из точки А в точку Б в течение 3 часов, а обратно — в течение 5 часов. Собственная скорость теплохода одинакова в обоих случаях. За какое время из точки А в точку Б доплывет плот?
Решение:
Обозначим скорость теплохода как vт, а скорость реки как vр.
Время движения теплохода по течению равно:
Время движения теплохода против течения:
Выражаем S из обоих уравнений и приравниваем правые части:
| t1(vт + vр) = t2(vт − vр). |
Получаем: vт = 4vр.
По сути получается, что теплоход без течения преодолеет это расстояние за 4 часа, по течению — за 3 часа и против — за 5 часов.
Скорость теплохода, плывущего против течения относительно берега равна 3-м скоростям течения.
Ответ: плот проплывет данное растояние за 15 часов.
2. Равноускоренное (равнозамедленное) движение.
^
Наблюдатель, стоящий на платформе, определил, что первый вагон электропоезда прошёл мимо него в течение ^ , а второй — в течение 5 с. После этого передний край поезда остановился на расстоянии 75 м от наблюдателя. Считая движение поезда равнозамедленным, определить его начальную скорость, ускорение и время замедленного движения.
Решение:
Составим уравнение движения для первого вагона:
| L = vot1 − | at12 | , |
| 2 |
для двух вагонов сразу:
| 2L = vo(t1 + t2) − | a(t1 + t2)2 | . |
| 2 |
Нам понадобится еще одно уравнение, в котором будет скорость и ускорение:
Таким образом, мы имеем систему из трех уравнений, решая которую (поупражняйтесь в математике самостоятельно), выйдем на конечную формулу:
| a = | 8S(t2 − t1)2 | = 0.25 | м | . |
| (2t1t2 + t22 − t12)2 | с2 |
^
Тело, двигаясь прямолинейно с постоянным ускорением, прошло последовательно два равных участка пути, по 20 м каждый. Первый участок пройден за 1.06 с, а второй — за 2.2 с. Определить ускорение тела, скорость в начале первого и в конце второго участков пути, путь, пройденный телом от начала движения до остановки. Начертить графики зависимости пройденного пути, скорости и ускорения от времени.
Решение:
Анализ условия задачи: так как второй участок (равный первому) пройден за большее время, то тело движется равнозамедленно.
Чтобы определить ускорение тела a, его скорость в начале первого vo и в конце второго участков пути v, запишем уравнение пути для первого участка:
| S = vot1 − | at12 | . |
| 2 |
Методом укрупнения запишем уравнение пути для двух участков:
| 2S = vo(t1 + t2) − | a(t1 + t2)2 | . |
| 2 |
После решения этих уравнений относительно искомых vo и a, получим: vo = 22 м/с, a = −6 м/с2.
Для определения скорости в конце второго участка v запишем уравнение скорости:
Здесь время t — это 1.06 + 2.2 = 3.26 c. Проведя вычисления, получим v = 2.44 м/с.
Для определения общего пути Sобщ до остановки воспользуемся формулой:
| Sобщ = | vкон2 − vo2 | = | −vo2 | = | vo2 | . |
| −2a | −2a | 2a |
Здесь конечная скорость vкон = 0, поскольку тело в конце пути остановилось. Ускорение и начальную скорость мы определили чуть выше.
Получим Sобщ = 40.33 м.
Уравнение пути: S = 22t − 3t2,
скорости: v = 22 − 6t,
ускорения: a = −6 м/с2.
Ответ: vo = 22 м/с, a = −6 м/с2, Sобщ = 40.33 м.
3. Свободное падение.
^
Тело, брошенное вертикально вниз с начальной скоростью 5 м/с, в последние 2 с падения прошло путь вдвое больший, чем в две предыдущие 2 с. Определить время падения и высоту, с которой тело было брошено. Построить график зависимости пройденного пути, ускорения и скорости от времени.
Решение:
Сделаем рисунок к задаче и введем следующие обозначения:
h1 — расстояние пройденное телом в две предыдущие секунды, тогда
2h1 — расстояние пройденное телом за последние две секунды,
t — время падения с высоты H.
Высота падения тела H равна:
| H = vot + | gt2 | (1), |
| 2 |
а высота h (без четырех секунд) равна:
| h = vo(t − 4) + | g(t − 4)2 | (2). |
| 2 |
Вычитая из уравнения (1) уравнение (2), получим:
| 3h1 = 4vo + | gt2 | − | g(t − 4)2 | . |
| 2 | 2 |
То есть:
| h1 = | 4 | vo + | gt2 | − | g(t − 4)2 | (3). |
| 3 | 6 | 6 |
Составим еще одно уравнение высоты:
| h + h1 = vo(t − 2) + | g(t − 2)2 | (4). |
| 2 |
Вычитая из уравнения (1) уравнение высоты (4), получим в конце (формула исправлена):
| h1 = vo + | gt2 | − | g(t − 2)2 | (5). |
| 4 | 4 |
Приравнивая правые части уравнений (3) и (5), имеем (после преобразований) t = 4,5 c, тогда высоту, с которой падало тело, можно рассчитать по формуле (1). Высота равна 123,75 м.
Для построения графиков составим уравнения пути H(t), g(t) и v(t):
H = 5t +5t2, g = 10 м/с2 = const, v = 5 + 10t.
Примечание: начало отсчета выбиралось в точке бросания тела, и ось направлялась вертикально вниз (по вектору начальной скорости и ускорения), что видно из графиков.
4. Криволинейное движение:
^
Если камень, брошенный под углом 30° к горизонту, находился в полете 2 с, то с какой скоростью он упал на землю?
Решение:
Если камень был в полете ^ , то в силу симметрии 1 с он летел до максимальной точки подъема и 1 с падал вниз (сопротивлением воздуха мы пренебрегаем). В максимальной точке подъема камень имеет только горизонтальную составляющую Vx скорости V. Свободно падая с максимальной высоты подъема, за 1 с камень приобретет вертикальную скорость Vy, равную:
Vy = gt
Скорость бросания равна скорости падения тела, которая связана с вертикальной составляющей в момент падения:
| V = | vy | = | gt |
| sin α | sin α |
Искомая скорость равна V = 20 м/с.
Ответ: камень упал на землю со скоростью 20 м/с.
^
С вершины наклонной плоскости, образующей с горизонтом угол 60°, бросают тело в горизонтальном направлении. Если через 3,5 с тело ударилось о плоскость, то с какой начальной скоростью оно было брошено?
Решение:
Высоту полета тела H определим по формуле:
Дальность полета по горизонтали ^ будет равна:
S = vot.
Отношение высоты полета тела H к дальности полета по горизонтали S равно:
Находим vo:
Если принять g = 10 м/с2, то vo = 10.1 м/с.
Ответ: начальная скорость тела равна 10.1 м/с.
^
С башни брошено тело в горизонтальном направлении со скоростью 15 м/с. Пренебрегая сопротивлением воздуха, определить радиус кривизны траектории тела через 2 с после начала движения.
Решение:
Радиус кривизны траектории — это радиус окружности ^ , по которой в этот момент движется тело.
Через две секунды тело приобретет скорость v, в которой вертикальная составляющая равна vy= gt:
| v = √(vx2 + vy2) = √(vx2 + (gt)2). | (1) |
Нормальное ускорение тела an:
откуда радиус окружности R равен:
Нормальное ускорение an связано соотношением:
где
тогда:
Подставляя (3) и (1) в (2), получим:
| R = | vv2 | = | √(vx2 + (gt)2) | • (vx2 + (gt)2). |
| gvx | gvx |
После вычислений R = 104,2 м.
Ответ: радиус кривизны через 2 с составляет 104,2 м.
5. Движение по окружности
^
Колесо, вращаясь равнозамедленно, при торможении уменьшило за 1 минуту частоту вращения от 300 до 180 об/мин. Момент инерции колеса равен 2 кг•м2. Найти:
1) угловое ускорение колеса;
2) тормозящий момент;
3) работу сил торможения;
4) число оборотов, сделанных колесом за эту минуту.
Решение:
При равнозамедленном вращении колеса имеем изменение угловой скорости:
| Δw = w2 − w1 = 2πn2 − 2πn1 = 2π(n2 − n1). |
Угловое ускорение равно отношению изменения угловой скорости ко времени
| ε = | Δw | = | 2π(n2 − n1) | . |
| t | t |
Момент торможения (тормозящий момент) будет равен:
| M = Jε = J | 2π(n2 − n1) | . |
| t |
Работа сил торможения равна изменению кинетической энергии:
| −A = W2 − W1 = | Jw12 | − | Jw12 | = | J(2πn2)2 | − | J(2πn1)2 | = 2π2J(n22 − n12). |
| 2 | 2 | 2 | 2 |
То есть:
Наконец, число оборотов можно определить так (поскольку движение равнозамедленное):
Проведем расчеты:
ε = −0.21 рад/с2; М = −0.42 Н•м; A = 631 Дж; N = 240 оборотов.
^
На краю горизонтальной платформы стоит человек массой 80 кг. Платформа представляет собой круглый однородный диск массой 160 кг, вращающийся вокруг вертикальной оси, проходящий через ее центр, с частотой 6 об/мин. Сколько оборотов в минуту будет делать платформа, если человек перейдет от края платформы к ее центру? Момент инерции рассчитывать как для материальной точки.
Решение:
Система «человек–платформа» замкнута в проекции на ось ^ , т. к. моменты сил Mm1g= 0 и Mm2g= 0 на эту ось. Следовательно, можно воспользоваться законом сохранения момента импульса. В проекции на ось Y:
где J1 — момент инерции платформы с человеком, стоящим на ее краю, J2 — момент инерции платформы с человеком, стоящим в центре, w1 и w2 — угловые скорости платформы в обоих случаях. Здесь
| J2 = | m2R2 | , (2) |
| 2 |
где m1, m2 — массы человека и платформы соответственно, R — радиус платформы.
Подставляя (2) в (1) и учитывая, что w = 2πn, где n — частота вращения платформы, получим:
| ( | m2R2 | + m1R2)2πn1 = | m2R2 | 2πn2. |
| 2 | 2 |
Решаем последнее уравнение относительно неизвестной частоты вращения «платформы-человек» n2:
После вычислений: n2 = 0.2 (об/с) = 12 об/мин. Задача это ВУЗовская и решена здесь по просьбе посетителей в виде исключения.
^
Экваториальный радиус Земли равен 6370 км. Определить линейную и угловую скорости движения точек экватора при вращении Земли вокруг оси.
Решение:
Линейная скорость вращения ν точек земного экватора:
а угловая скорость вращения w всех точек Земли равна:
После вычислений будем иметь: ν = 463 м/с, w = 7,3×10−5 рад/с.
Скачать файл (256.5 kb.)
gendocs.ru
Как научиться решать задачи по физике? Часть 1 Кинематика.
Зависимость скорости от времени
И В Яковлев Материалы по физике MathUsru Равноускоренное движение Темы кодификатора ЕГЭ: виды механического движения, скорость, ускорение, уравнения прямолинейного равноускоренного движения, свободное
ПодробнееПРОБНЫЙ ЭКЗАМЕН по теме 1. КИНЕМАТИКА
ПРОБНЫЙ ЭКЗАМЕН по теме. КИНЕМАТИКА Внимание: сначала попытайтесь ответить на вопросы и решить задачи самостоятельно, а потом проверьте свои ответы. Указание: ускорение свободного падения принимать равным
ПодробнееОсновные законы и формулы
1.1. Кинематика материальной точки Основные законы и формулы При движении материальной точки в пространстве радиус-вектор, проведённый из начала координат к точке, и координаты этой точки, представляющие
Подробнее/ /15
1. Задание 1 7777 Вариант 3580273 Небольшое тело движется в пространстве. На рисунке показаны графики зависимости от времени t проекций V x, V y и V z скорости этого тела на оси OX, OY и OZ от времени
ПодробнееКИНЕМАТИКА задания типа В Стр. 1 из 5
КИНЕМТИК задания типа В Стр. 1 из 5 1. Тело начало движение вдоль оси OX из точки x = 0 с начальной скоростью v0х = 10 м/с и с постоянным ускорением a х = 1 м/c 2. Как будут меняться физические величины,
ПодробнееФИЗИКА Формулы, понятия, определения
Серия «Библиотека школьника» Э.Н. Гришина И.Н. Веклюк ФИЗИКА Формулы, понятия, определения Издание третье Ростов-на-Дону «Феникс» 14 УДК 373.167.1:53 ББК.3я7 КТК 444 Г85 Гришина Э.Н. Г85 Физика. Формулы,
Подробнееесли υ 0 а — движение ускоренное
Кинематика Механическое движение изменение положения тела в пространстве с течением времени относительно других тел. Поступательное движение движение, при котором все точки тела проходят одинаковые траектории.
ПодробнееКинематика 1 1) 1 2) 2 3) 3 4) 4
Кинематика 1 1 Точка движется по окружности радиусом 2 м, и ее перемещение равно по модулю диаметру. Путь, пройденный телом, равен 1) 2 м 2) 4 м ) 6,28 м 4) 12,56 м 2 Камень брошен из окна второго этажа
ПодробнееЗадачи 29 и 30 (бывшие С2 и С3)
Задачи 29 и 30 (бывшие С2 и С3) Задача 29 (по новой нумерации, которую вводят в ЕГЭ с 2015 года) это расчетная задача на механику. До 2014 года включительно она фигурировала под номером «С2». Это может
Подробнееt, с. 2015г.
Уравнения и графики кинематики (методика решения тестов и задач), м/с 1 8 6 4 1 3 4 5, с 6 7 8 Составили: Жаганюк М., Киргизов А. Мягков А., Неделько М., Шарипов М. Руководитель: учитель МОУ СОШ 31 Лукина
Подробнее1. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
1. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА 1.. Кинематика. Кинематика это часть теоретической механики, в которой изучается механическое движение материальных точек и твердых тел. Механическое движение это перемещение
ПодробнееКИНЕМАТИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ
КИНЕМАТИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ПРЕДИСЛОВИЕ Физика является одной из тех наук, знание которой необходимо для успешного изучения общенаучных и специальных дисциплин При изучении курса физики студенты
ПодробнееМЕТОДИЧЕСКИЕ УКАЗАНИЯ
Министерство общего и профессионального образования Российской Федерации ОРЕНБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Кафедра физики Т.М. Чмерева М.Р. Ишмеев МЕТОДИЧЕСКИЕ УКАЗАНИЯ к лабораторной работе 104
ПодробнееДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
Министерство образования Российской Федерации Государственное образовательное учреждение высшего профессионального образования «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Кафедра «МЕХАНИКА» ДИНАМИКА
ПодробнееМатериальная точка. Система отсчета
Неравномерное Учебник Касьянов В.А. Автор: Шипкина Е.А. 10 класс. Модуль 1 по теме «Кинематика» — 15 часов Материальная точка Система отсчета Механическое движение Равномерное Периодическое Криволинейное
ПодробнееЦДО «Уникум» РУДН ОЛИМПИАДА ПО ФИЗИКЕ
ЦДО «Уникум» РУДН ОЛИМПИАДА ПО ФИЗИКЕ Задание 1. Дальность полета снаряда, летящего по навесной траектории, равна максимальной высоте подъема. Какова максимальная высота настильной траектории при той же
Подробнее= 1 е) f(9) = 27; f(1) = 3
Глава 8 ФУНКЦИИ И ГРАФИКИ Алгоритмы А- Задание стандартных функций А- Понятие функции. График функции А-3 Каноническая запись зависимостей А- Задание стандартных функций. К стандартным функциям отнесем
ПодробнееПодготовка к ОГЭ ЧАСТЬ 1
Подготовка к ОГЭ ЧАСТЬ 1 МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ-1 1.Кинематика 1. Буксирный катер за ч проплыл 5 км. Определите скорость катера..тело, двигаясь из состояния покоя, равноускоренно за первую секунду проходит
ПодробнееСПРАВОЧНИК ПО ФИЗИКЕ классы
СПРАВОЧНИК ПО ФИЗИКЕ 7 11 классы МОСКВА «ВАКО» 017 УДК 37853 ББК 746 С74 6+ Издание допущено к использованию в образовательном процессе на основании приказа Министерства образования и науки РФ от 0906016
ПодробнееКурсы подготовки к ЕГЭ по физике
Курсы подготовки к ЕГЭ по физике Механика. Задание 9 Учитель физики: Бабчик И.И. Учебное заведение: МБОУ лицей 1 г. Сургут, 019 г. Задание 9. Основные вопросы 1 1. Кинематика Задача 1 Задача 7. Движение
ПодробнееИТТ Вариант 2 ОСНОВЫ КИНЕМАТИКИ
ИТТ- 10.1.2 Вариант 2 ОСНОВЫ КИНЕМАТИКИ 1.Предложены две задачи: 1) Определить среднюю скорость самолёта по известному расстоянию между двумя городами и времени полёта. 2) Определить путь, пройденный самолётом
ПодробнееПРЕДИСЛОВИЕ генератором тестов
ПРЕДИСЛОВИЕ Пособие предназначено для учащихся средних школ, колледжей и техникумов и может быть использовано как при изучении физики, так и при подготовке к ЕГЭ. В пособии представлено 816 разноуровневых
Подробнее, а путь за десятую секунду равен S10
класс. Муниципальный тур. 06/7 учебный год. Лазарев А.Н. Задача. Полезное соотношение. За третью секунду свободного падения тело пролетело /0 всего пути. Какой путь оно пролетело за последнюю секунду падения.
ПодробнееФизика, 10 класс, муниципальный этап
Задача. (0 баллов) Департамент образования Ярославской области Всероссийская олимпиада школьников 07/08 учебного года Физика, 0 класс, муниципальный этап Возможные решения задач Шарик, подвешенный на нити
ПодробнееS ср. Для равноускоренного движения. . t
1.10. Равноускоренное движение и средняя скорость Большое количество задач, как на равноускоренное движение тела, так и на свободное падение тела, можно решить через формулу для средней скорости тела.
ПодробнееУДК :53 ББК 22.3я72 Д30
УДК 373.167.1:53 ББК 22.3я72 Д30 Учебное пособие «Я сдам ЕГЭ!» Физика. Модульный курс. Практикум и диагностика» предназначено для подготовки обучающихся 10 11 классов к единому государственному экзамену
ПодробнееСВЕРДЛОВСКАЯ ОБЛАСТЬ
МУНИЦИПАЛЬНЫЙ ЭТАП ВСЕРОССИЙСКОЙ ОЛИМПИАДЫ ШКОЛЬНИКОВ ПО ФИЗИКЕ СВЕРДЛОВСКАЯ ОБЛАСТЬ 015-016 УЧЕБНЫЙ ГОД 10 класс Решение задач, рекомендации по проверке Задача 1. (10 баллов) Максимальная дальность полета
Подробнееdocplayer.ru
