Лукина Галина Степановна, автор-составитель
Учимся решать физические задачи
Относительность движения
Нельзя наблюдать и определить
движение тела, имеющего конечную
величину, не определяя сначала,
какое движение имеет каждая его
маленькая частичка или точка.
Л. ЭЙЛЕР
1. Расчет средней скорости переменного движения
В предыдущих номерах журнала уже разбирались некоторые методы и подходы к решению задач по кинематике. Но вступительные экзамены в высшие учебные заведения показали, что задачи на расчет средней скорости неравномерного движения по-прежнему решаются неверно очень многими учащимися. Затруднения вызывают и задачи, в которых решение значительно упрощается переходом в удобную систему отсчета. Поэтому мы еще раз возвращаемся к вопросам кинематики и предлагаем учащимся 9-11 классов внимательно отнестись к предложенным темам..
Итак, движения разделяются:
по характеру траектории – на прямолинейное и криволинейное;
по наличию ускорения – на равномерное, переменное и равнопеременное.
Равномерное прямолинейное движение – это движение с постоянной скоростью, то есть V = const, a = 0. Обратите внимание, что скорость постоянна и по модулю и по направлению.
Переменное движение может быть прямолинейным и криволинейным. Одной из характеристик прямолинейного переменного движения является средняя путевая скорость, которую часто называют просто средней скоростью движения. Для определения средней скорости движения мы истинное сложное движение мысленно заменяем равномерным движением, при котором тот же путь проходится за то же время.
, где S – весь пройденный путь, t – все время движения.
Обратите внимание, что в физике вводятся два различных понятия средней скорости: векторная средняя скорость, вычисляемая по вектору перемещения тела за определенное время движения Vср = S/t, и скалярная средняя скорость, определяемая длиной пути вдоль траектории, которую мы и называем путевой скоростью. По модулю эти скорости не совпадают, поэтому при решении задач желательно уточнять, о какой средней скорости ведется речь. В приведенных ниже примерах мы будем иметь в виду путевую среднюю скорость. Но иногда в задачах движение задается графиком скорости. Вот тогда уточнение того, о какой средней скорости идет речь, обязательно.
Обратите внимание на еще один момент в вычислении средней скорости неравномерного движения.
Только в том случае, когда тело движется прямолинейно с постоянным ускорением а, возможно применение формулы Vср = (V1 + V2)/2. Объясняется это тем, что на графике скорости прямолинейное движение с постоянным ускорением (равнопеременное движение) (рис. 1) может быть представлено линейной зависимостью скорости от времени V = V0 + at
Так как площадь под графиком скорости численно равна длине пути S за промежуток времени от 0 до t1, то для равноускоренного движения по формуле площади трапеции находим S = (Vо+V)·t1/2. Отсюда сравнением с формулой расчета длины пути S=Vср t1 получаем формулу для расчета средней скорости прямолинейного равнопеременного движения Vср = (V0 + V)/2 или Vср = (V1 + V2)/2, где V1 и V2 соответственно скорости в начале и в конце прямолинейного участка движения.
То есть мы фактически заменили данное движение равномерным со скоростью Vср и площадью под линией графика, равной пройденному пути S (рис. 2)
Если же не выполняется хотя бы одно из оговоренных условий: либо движение не прямолинейное, либо скорость зависит от времени не линейно (то есть движение не равнопеременное), применять выведенную выше формулу расчета средней скорости Vср = (V1 + V2)/2 нельзя!
В таком случае необходимо пользоваться общей формулой расчета средней скорости
где S – весь пройденный телом путь, S = S1 + S2 + S3+ S4 + …,
t – все время движения, включая остановки; t = t1+ t2+ t3+ t4+…
Среднюю скорость можно определять и по графику зависимости пути от времени (рис 3)
Средняя скорость, равная Vср = Δl / Δt, на этом графике определяется тангенсом угла наклона прямой, соединяющей начальную и конечную точки рассматриваемого участка движения, к оси времени. По этому графику легко можно судить об изменении средней скорости в зависимости от выбора интервала времени. Кроме того, можно определить тот момент времени, когда мгновенная скорость будет по модулю равна средней скорости на заданном участке движения. Для этого нужно параллельным переносом полученного отрезка АВ до касания с линией графика найти точку касания С. Ее координаты и будут соответствовать искомому моменту времени и пройденному к этому моменту времени пути.
Задача 1. Первую четверть пути автомобиль двигался со скоростью 30 км/ч, вторую четверть — со скоростью 40 км/ч, а оставшийся путь — со скоростью 80 км/ч. Определить среднюю скорость движения автомобиля на всем пути.
Дано: S1=1/4 S S2=1/4 S S3=1/2 S V1=30 км/ч V2=40 км/ч V3=80 км/ч | Решение. |
Vср = ? | Средняя скорость движения равна |
Здесь t1 = ; t2 = ; t3 = .
Получаем (t1 + t2 + t3) = ++=.
Тогда Vср=; Vср= км/ч.
Ответ: средняя скорость движения автомобиля 48 км/ч.
Примечание. Еще раз обратите внимание на расчет средней скорости движения. При неравномерном движении ни в коем случае нельзя рассчитывать среднюю скорость как среднюю арифметическую скорость. Решая подобную задачу, учащиеся часто допускают ошибку, рассчитывая среднюю скорость как , что совершенно не допустимо!
Задача 2. Автомобиль двигался по ровной дороге 1 мин со скоростью 90 км/ч, а затем 2 мин на подъеме со скоростью 60 км/ч и под уклон 0,5 мин со скоростью 120 км/ч. Определить среднюю скорость движения автомобиля за это время.
Дано: t1=1=1/60 ч V1=90 км/ч t2=2 мин=1/30 ч V2=60 км/ч t3=0,5 мин=1/120 ч V3=120 км/ч | Решение.Средняя скорость движения автомобиля равна , где S1=V1*t1; S2=V2*t2; S3=V3*t3. Получаем . Подставив данные, получаем Vср=77 км/ч. |
Vср -? | Ответ: средняя скорость движения автомобиля 77 км/ч. |
Примечание. 1. Эту задачу можно решать и графически с помощью графика скорости. Для этого необходимо построить в одной системе координат (V, t) графики скорости для каждого интервала времени, затем рассчитать весь пройденный путь как площадь под общим графиком за весь промежуток времени (рис. 4).
Средняя скорость может быть найдена отношением всего пройденного пути ко всему промежутку времени .
Задача 3. Велосипедист проехал первую половину пути со скоростью 12 км/ч, а второю половину пути – со скоростью 20 км/ч. Определить среднюю скорость движения велосипедиста.
Дано: S1=S2=1/2 S V1=12 км/ч V1=20 км/ч | Решение. Средняя скорость движения велосипедиста равна Vср=, где t1=, t2=. Тогда (t1+t 2)=. |
Vср-? | ; км/ч. |
Ответ: средняя скорость движения велосипедиста 15 км/ч.
Задача 4. Первую половину времени велосипедист двигался со скоростью 12 км/ч, а вторую половину времени – со скоростью 20 км/ч. Определить среднюю скорость велосипедиста за все время движения.
Дано: t1=t2=1/2 t V1=12 км/ч V1=20 км/ч | Решение. Средняя скорость движения велосипедиста равна , где ; ; t=t1+t2. Тогда S1+S2= |
Vср-? | ; Vср=16 км/ч. |
Ответ: средняя скорость движения велосипедиста 16 км/ч.
Примечание. Обратите внимание на разницу в условиях задачи № 3 и № 4 и разные значения средней скорости. При этом подход к решению и в том и в другом случаях одинаков.
studfiles.net
Презентация к уроку по физике (9 класс) на тему: Решение задач по кинематике.
Слайд 1
Решение задач по кинематики.Слайд 2
Задача №1 Уравнение движения тела имеет вид x=2+10t . Опишите это движение (укажите значения характеризующих его величин), постройте график x(t) .
Слайд 3
Задача №2 Зависимость проекции скорости от времени движущегося тела задана формулой Опишите это движение, постройте график ( t ). По графику определите модуль перемещения через 1с после начала движения.
Слайд 4
Задача №3 Электропоезд отходящий от станции, в течении 0,5 мин двигался с ускорением 0,8 м/ . Определите путь, который он прошел за это время, и скорость в конце этого пути.
Слайд 5
На рисунке представлены графики зависимости координаты двух тел от времени. Графики каких зависимостей показаны? Какой вид имеют графики зависимости скорости и пути пройденного телом, от времени?
Слайд 6
. . . Решение На рисунке показаны графики равномерного движения тел. 1) В начальный момент времени t = 0 первое тело имеет начальную координату х о1 = 1 м, второе тело — координату х о2 = 0 . 2) Оба тела движутся в направлении оси Х, так как координата возрастает с течением времени 3) Уравнение движения для равномерного прямолинейного движения имеет вид: x= x о +v х t Тогда для первого, второго тела соответственно: x 1 =x о1 +v 1х t и x 2 =x о2 +v 2х t или x 1 =1+v 1х t, x 2 =v 2х t. Определим скорости первого и второго тела: v 1x = x 1 − 1 = 2 − 1 = 0,5 м/с. t 2 v 2x = x 2 = 1 = 0,5 м/с. t 2 Уравнения скорости имеют вид: v 1х =v 2х =0,5 м/с. Так как S= v х t , то уравнение пути S=0,5 t
Слайд 7
Задача №5 Первую половину пути автомобиль проехал со средней скоростью v1 = 60 км/ч, а вторую — со средней скоростью v2 = 40 км/ч. Определить среднюю скорость V автомобиля на всем пути.
Слайд 8
Решение: проанализируем условие задачи: первую половину пути автомобиль проехал со скоростью 60 км/ч и затратил время, равное Вторую половину пути автомобиль проехал со скоростью 40 км/ч и затратил время, равное . По определению, средняя скорость V при равномерном прямолинейном движении равна отношению всего пройденного пути ко всему затраченному времени. = = Подставляя значения скорости в формулу средней скорости, получим: Средняя скорость равна 48 км/ч.
nsportal.ru
Разбор задач тренировочных заданий по кинематике
В большинстве компьютерных вариантов заданий для каждого участника генерируются свои наборы данных
Задание 1 «С какой скоростью движется вторая машина относительно первой (4 балла)».
Две машины приближаются к перекрестку, двигаясь под прямым углом друг к другу со скоростями 54 км/ч и 72 км/ч. С какой скоростью движется вторая машина относительно первой?
|
Дано: |
Перевод единиц: |
|
v1 = 54 км/ч |
15 м/с |
|
v2 = 72 км/ч |
20 м/с |
|
= ? |
|
Решение. Скорости, заданные в условии, измерены относительно системы отсчета, связанной с землей. Уточним обозначение этих скоростей:
, .
Скорость второй машины относительно первой — это скорость второй машины измеренная в системе отсчета, связанной с первой машиной (например, водителем первой машины). Если первая машина двигается относительно земли со скоростью , то в системе отсчета первой машины земля двигается с такой же по величине скоростью, но в обратном направлении:
.
Для водителя первой машины скорость второй машины будет складываться из ее скорости относительно земли и скорости земли в системе отсчета первой машины:
.
Величина относительной скорости второй машины v21 равна гипотенузе прямоугольного треугольника, образованного скоростями машин относительно земли. По теореме Пифагора находим:
.
Заметим, если относительная скорость окажется направленной по линии, соединяющей машины, то продолжая двигаться с такими скоростями, они неминуемо столкнутся!
Ответ: 25 м/с.
Задание 2 «Вычислите среднюю скорость движения человека (8 баллов)»
Вычислите среднюю скорость движения человека, если первую треть пути он шел со скоростью 1,5 м/с, а оставшуюся часть пути со скоростью 1,0 м/с.
|
Дано: |
|
v1 = 1,5 м/с |
|
v2 = 1,0 м/с |
|
= ? |
Решение. Согласно общему определению средней скорости:
,
где S — весь пройденный путь, а t — все время движения.
Времена t1 и t2 прохождения первой трети пути и остальных двух третей равны, соответственно
, .
Учитывая, что t = t1 + t2 находим
.
Ответ: 1,125 м/с.
Задание 3 «Найдите ускорение и путь автомобиля (8 баллов)»
Автомобиль, движущийся со скоростью 36 км/ч, разгоняется в течение десяти секунд до 108 км/ч и затем за полминуты сбрасывает скорость до нуля. Считая движение при разгоне и торможении равнопеременным, найдите ускорение и путь для каждого из промежутков времени.
|
Дано: |
Перевод единиц: |
|
v1 = 36 км/ч |
10 м/с |
|
t1 = 10 c |
|
|
v2 = 108 км/ч |
30 м/с |
|
t2 = 0,5 мин |
30 c |
|
a1, S1, a2, S2 = ? |
|
Решение. Применяя формулу скорости для равноускоренного движения в течение времени t1, получим
,
откуда
.
Находим путь, пройденный на участке разгона:
.
Скорость при торможении машины меняется по формуле
v = v2 – a2t, (1)
убывая за время t2 до v = 0. Подставляя нуль в правую часть уравнения (1), и выражая величину ускорения, получаем
.
Отметим, что в данном случае проекция ускорения на ось OX отрицательна: a2x = —a2 = –1 м/с2.
Соответствующий путь составляет
.
Ответ: a1 = 2 м/с2, S1 = 200 м, a2 = 1 м/с2 (a2x = –1 м/с2), S2 = 450 м.
Задание 4 «Вычислите максимальную высоту подъема тела, брошенного под углом к горизонту (8 баллов)»
Вычислите максимальную высоту подъема тела, брошенного под углом 30 к горизонту со скоростью 20 м/с. Сопротивлением воздуха пренебрегите.
|
Дано: |
|
= 30 |
|
v0 = 20 м/с |
|
hmax = ? |
Решение. Проанализируем, как изменяется со временем проекция скорости на ось OY. Cуществует такой момент времени t1 = v0y/g, при котором проекция vy обращается в нуль. До этого момента времени vy положительна, то есть тело движется вверх. После момента времени проекция vy становится отрицательной, то есть тело движется вниз.
Очевидно, что в этот момент времени достигается максимальная высота hmax.:
.
Используя численные данные, находим:
.
Ответ: 5 м.
Задание 5 «Модель: Измерьте скорость тележки (8 баллов)»
Задание: Измерьте с помощью оптических
датчиков скорость тележки. Занесите результаты в отчёт (меню в верхней части
программы) и отошлите отчёт на сервер.
Стойки с датчиками расположите так, чтобы они фиксировали моменты прохождения
тележки. Позицию датчиков можно менять мышью или с помощью пункта ввода.
Конечный результат округляйте до сотых. Пример округления: 0,605 можно
округлять до 0,60 или до 0,61.
Рис.1 Начальное состояние системы
Для измерения скорости следует установить стойки с датчиками, например, на позиции с координатами x1=0.2 м и x2=0.8 м и нажать кнопку “Пуск”. Тележка доедет до противоположной стенки и остановится, а на датчиках появятся показания (рис.2).
Рис.2 Конечное состояние системы
Скорость находим как отношение пути между x2 и x1 к затраченному времени t2-t1:
v=(x2-x1)/(t2-t1)
При этом пусть мы сначала ошибемся и напишем v= (0.8-0.2)/(2.5-0.278) м/с = 0.6/2.222 м/с = 0.270027 … м/с
(вместо x2=0.9 м написали x2=0.8 м). Округляем до сотых: v=0.27 м/с
Открываем пункт меню “Отчёт…” в верхней части программы, и в появившемся окне вводим это значение (рис.3):
Рис.3 Отсылка отчёта
Нажимаем кнопку “Отправить результаты на сервер” и получаем отзыв с сервера с информацией о неправильном решении:
Рис.4 Результат проверки со стороны сервера
При нажатии кнопки “Закрыть” любая информация в окне отчета сохраняется и показывается вновь при открытии отчета. При нажатии кнопки “Очистить” восстанавливается первоначальное состояние окна отчета с пустыми пунктами ввода.
Мы можем нажать кнопку “Очистить”, затем кнопку “Закрыть”, проверить правильность наших действий и вычислений.
Например, заново проделать измерения при тех же или других расстояниях между датчиками. Обнаруживаем ошибку и исправляем ее:
v=(x2-x1)/(t2-t1) = (0.9-0.2)/(2.5-0.278) м/с = 0.7/2.222 м/с = 0.360036 … м/с
Округляем до сотых: v=0.36 м/с.
Открываем отчет, вводим ответ, отсылаем отчет на сервер и получаем:
Рис.5 Результат проверки нового результата
Итоговый балл за выполнение задания получился 7 из 8 возможных, так как имелась одна дополнительная попытка отсылки результатов на сервер.
Задание 6 «Тест: Кинематика (16 вопросов, 25 баллов)»
Тест будет разбираться в отдельном документе.
Задание 7 «Модель: Измерьте среднюю и мгновенную скорость тележки (12 баллов)»
Задание: По наклонному рельсу из точки с координатой х=0 из состояния покоя начинает равноускоренно двигаться тележка. Определите время движения тележки до её удара о стенку, а также её среднюю и конечную скорость на отрезке от x=0 до x=0.5
Время определите с точностью до тысячных, а остальные величины до сотых, и отошлите результаты на сервер. В промежуточных вычислениях сохраняйте не менее 4 значащих цифр.
Оптические датчики срабатывают при пересечении светового луча датчика флажком тележки. Положение ворот с оптическими датчиками можно изменять при помощи мыши или задавая значения их координат х1 и х2 при помощи клавиатуры.
На рис.6 показано начальное состояние системы.
Рис.6 Начальное состояние системы
Первую стойку передвигаем в позицию x1=0.5 м, вторую (с помощью пункта ввода для x2) — в позицию x2=0.99999 м (если x2=1 м тележка не пересекает луч, поэтому ставим стойку очень близко к x=1 м). Нажимаем кнопку “Пуск” и получаем, например, t1=1.443 с, t2=2.041 с (рис.7).
Рис.7 Конечное состояние системы
Полное время движения равно t2. Средняя скорость vср движения на отрезке от x=0 м до x=0.5 м равна x1/t1. Конечная скорость v1 движения на этом отрезке в два раза больше, так как при равноускоренном движении vср=(v0+v1)/2, а v0=0. То есть v1 проще вычислить чем измерить с достаточной точностью.
distolymp2.spbu.ru
Примеры решения задач по кинематике
Пример 1. Найти по величине и
направлению относительно берега скорость
человека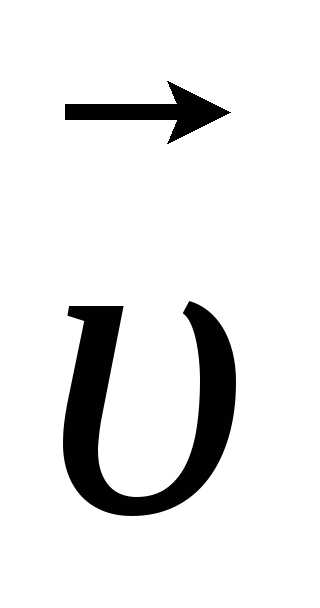
,
движущегося поперек парохода со скоростью2 м/с, пароход движется со скоростью
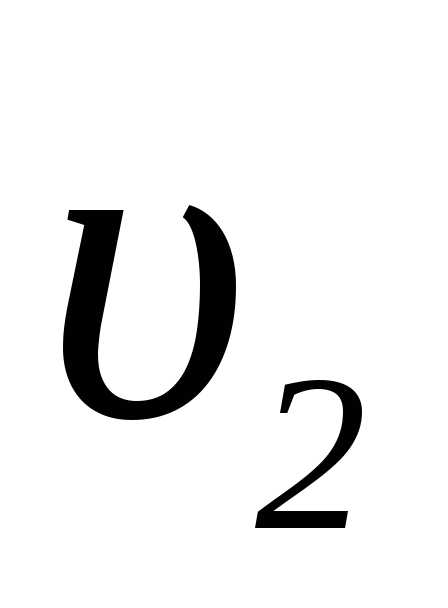=8 м/с.
Решение:
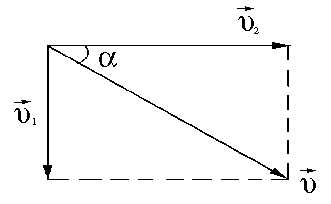
Рисунок 4 – Пример 1
Скорость 
человека
относительно берега является векторной
суммой скоростей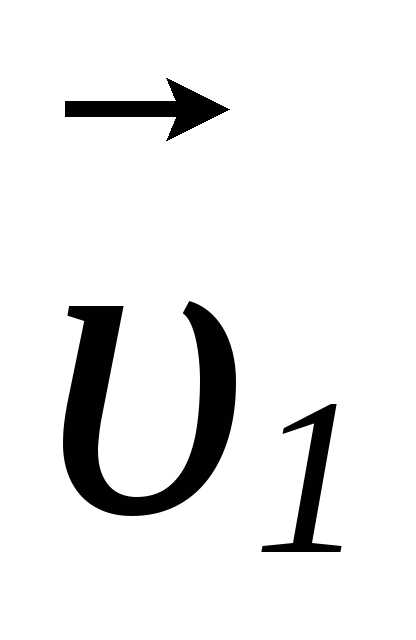
и
:
=
+
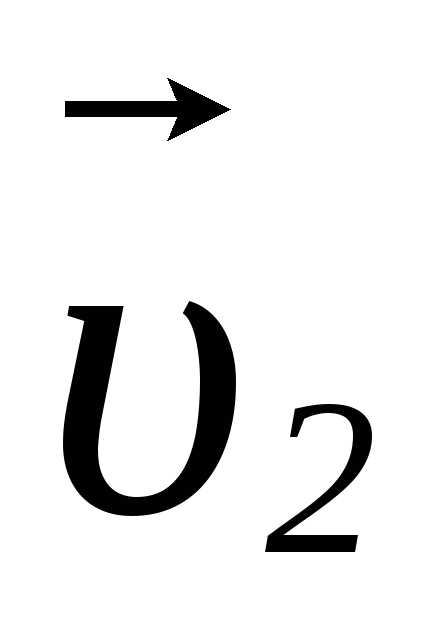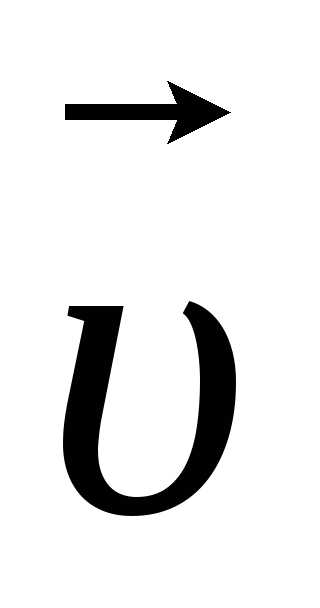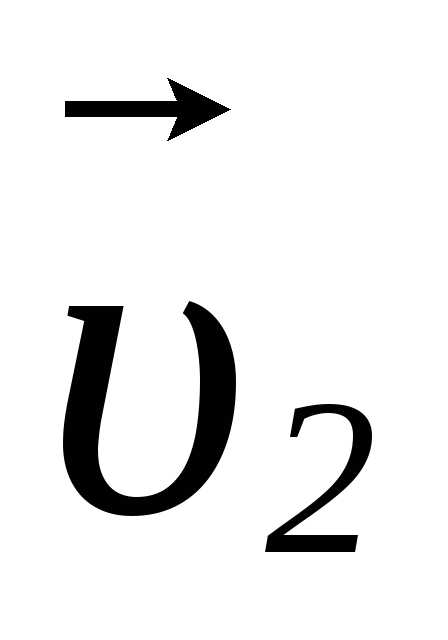(12)
Численное значение скорости
определяется:
=
=
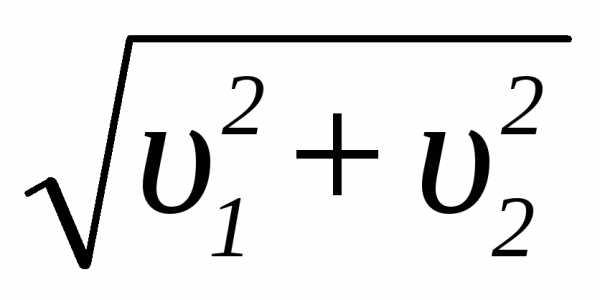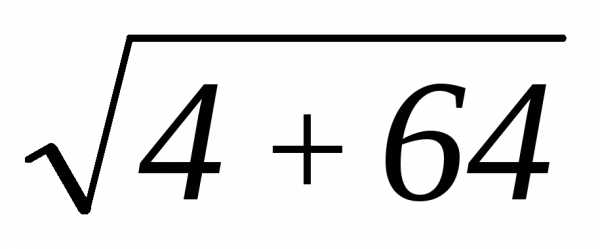=8,25м/с.
Направление скорости 
определяется
углом, который
она составляет с направлением движения
парохода: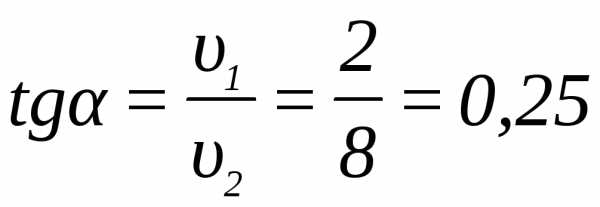
,
отсюда=1403.
Пример 2. Камень, брошенный вертикально вверх, достигает высоты30м. Через сколько времени он достигает этой высоты и через сколько времени он упадет обратно на землю? Какую начальную скорость ему надо сообщить?
Решение:
Движение камня вверх равнозамедленно, его ускорение а = — g, авысота поднятия
,
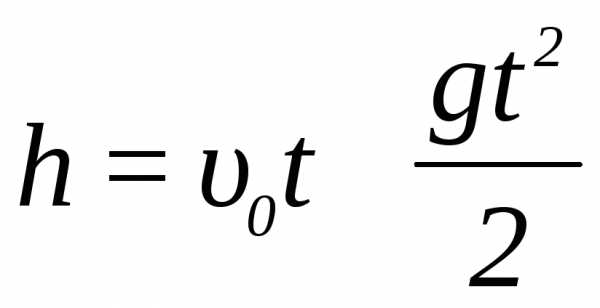(13)
где 
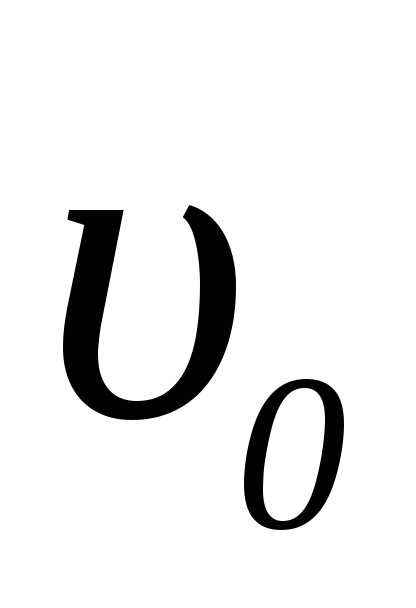— начальная скорость камня;
—
время, в течение которогоон
поднимается вверх.
Начальная скорость определяется из условия, что скорость в высшей точке поднятия равна нулю, то есть
,
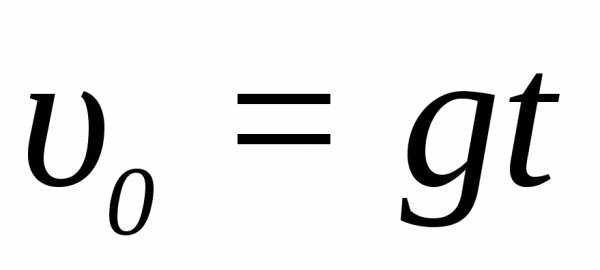(14)
Подставляя (14) в (13), имеем
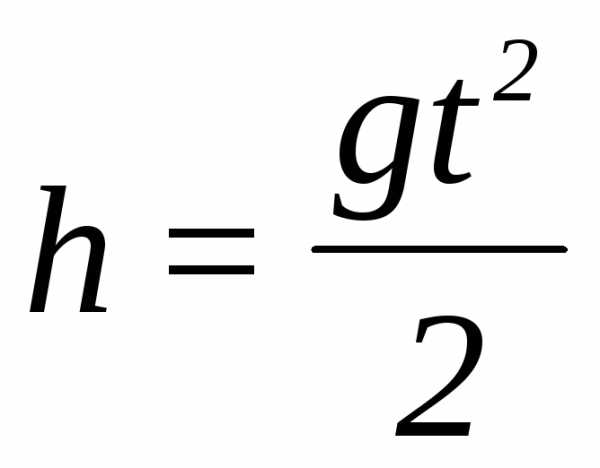(15)
Искомое время поднятия определяется
из (15). Так как время подъема и падения
равны, то камень вернется на землю через 
.
,
.
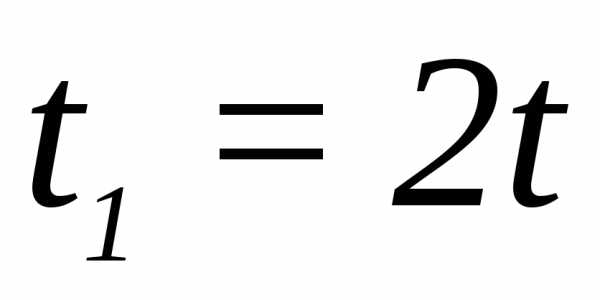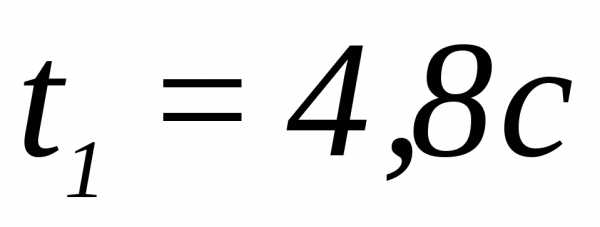Начальная скорость вычисляется по уравнению (14)
Пример 3. Точка движется по кривой
согласно уравнению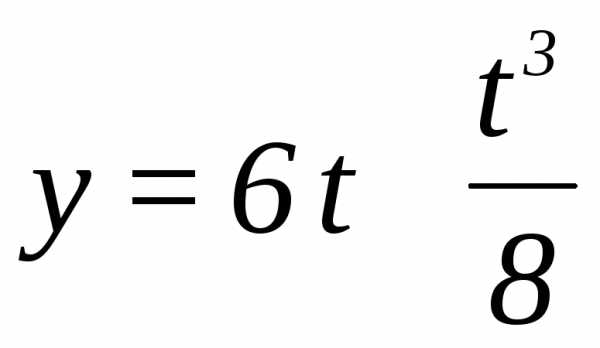
.
Найти среднюю скорость движения точки
в промежутке времени от 
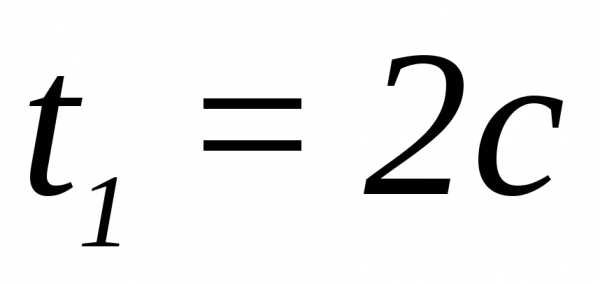и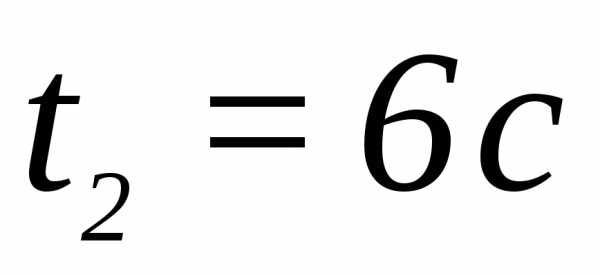
.
Решение:
Среднее значение модуля скорости точки
в промежутке времени от t до
равно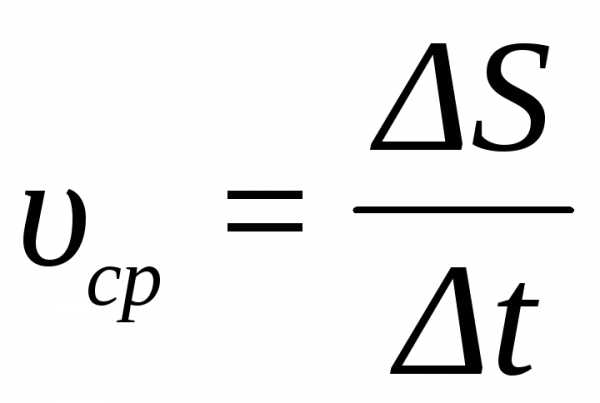
,
где
—
путь, пройденный точкой за время
.
По условию задачиy—
криволинейная координата движущейся
точки, а задача сводится к вычислению
пути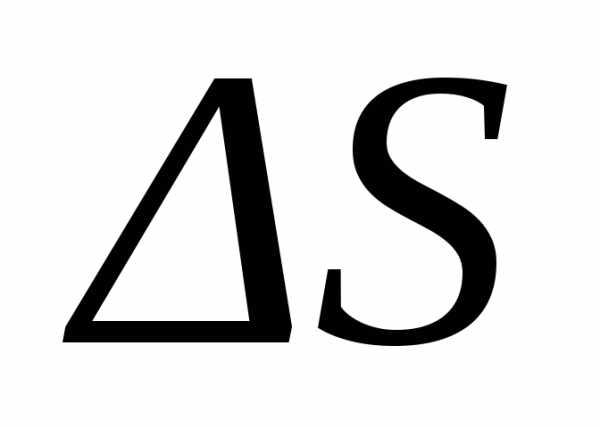
,
пройденного точкой за промежуток времени
=t2 – t1.
Предположим, что точка двигалась по
кривой в течение всего промежутка
времени в одном направлении, то есть
= 
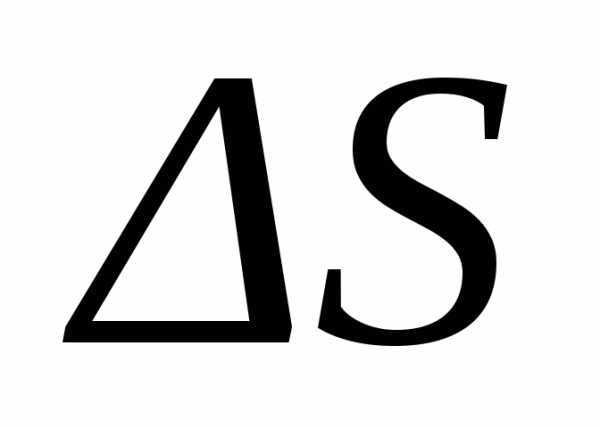=y2 — y1;
.
Движение твердого тела
Твёрдым телом называется совокупность материальных точек, расстояние между которыми постоянно. Поэтому его движение сводится к движению составляющих точек. Движение каждой точки описывается тремя функциями (координатами). Если твёрдое тело состоит из Nточек, то его движение должно описываться3Nкоординатами. Однако нет необходимости использовать три функции, так как большинство из них взаимно зависимы. Число независимых функций, которыми определяется движение некоторой совокупности материальных точек, называется числом её степеней свободы. Движение материальной точки описывается тремя параметрами, и поэтому число её степеней свободы равно трём.
Если две материальные точки жёстко связаны между собой некоторым стержнем неизменной длины l, то независимых координат останется пять, они описывают движение рассматриваемой системы.
Чтобы найти положение твёрдого тела, необходимо задать шесть независимых параметров, то есть число степеней свободы твёрдого тела i = 6.
Эти шесть независимых параметров можно задать различным образом.
Удобно использовать три параметра для указания положения какой-либо точки твёрдого тела, а оставшимися тремя параметрами описывать положение твёрдого тела, закреплённого в этой точке.
Кинематика движения точки была уже проанализирована, а движение твёрдого тела, закреплённого в точке, рассматривается относительно системы координат, жёстко связанной с твёрдым телом.
Поступательным движениемтвёрдого тела называется такое, при котором все его точки движутся по одинаковым траекториям. Это означает, что скорости всех точек тела в любой момент времени одинаковы.
Любая прямая, проведённая между какими-либо точками тела, перемещается параллельно самой себе.
Это движение полностью характеризуется заданием движения какой- либо одной точки тела, то есть поступательно движущееся тело имеет три степени свободы. В кинематическом отношении это движение полностью эквивалентно движению материальной точки.
Плоское движениетвёрдого тела наблюдается тогда, когда траектории всех точек лежат в параллельных плоскостях. Движение тела в этом случае полностью определяется движением одного из его сечений, в какой-либо из параллельных плоскостей, а положение сечения – положением двух точек этого сечения.
Положение двух точек на плоскости характеризуется четырьмя координатами. Между этими параметрами имеется одно соотношение, выражающее постоянство расстояний между двумя точками. Следовательно, имеются лишь три независимых параметра, то есть число степеней свободы равно трём.
Вращательное движение– это такое, при котором две точки тела остаются всё время неподвижными. Прямая, проходящая через эти точки, называется осью вращения. Все точки твёрдого тела, лежащие на оси вращения, неподвижны.
Другие точки твёрдого тела движутся по окружности в плоскостях, перпендикулярных оси вращения.
Если начало отсчёта радиуса – вектора 
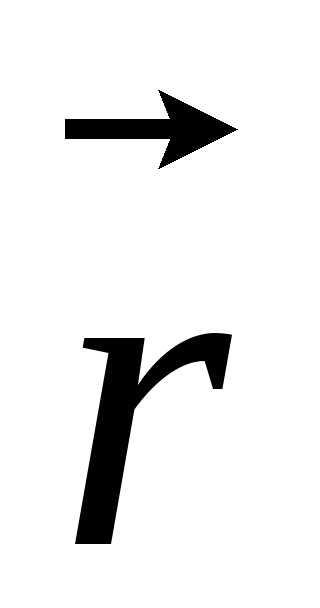расположить
на оси вращения, то скорость любой точки
вращающегося твёрдого тела определится
так:
=
,
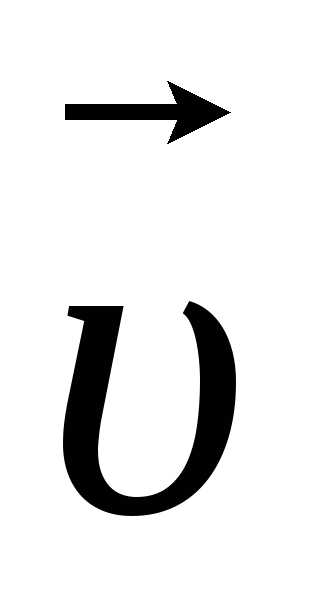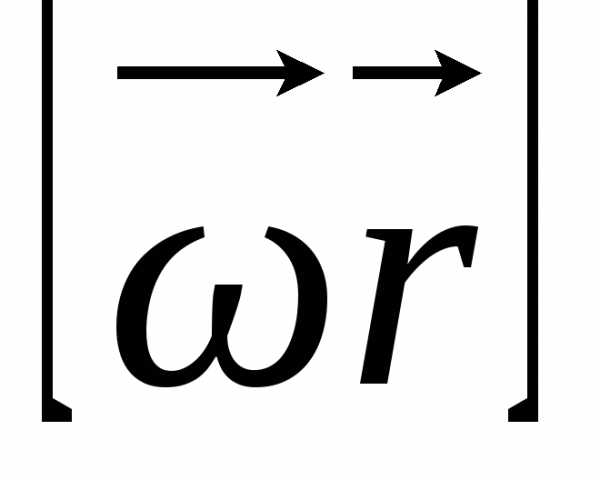(16)
где — 
—
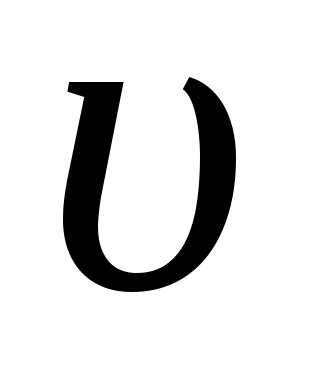линейная скорость;
—
угловая скорость.
Рисунок 5
Если расстояние точки твёрдого тела от оси вращения равно R(рисунок 5), то для нормального, тангенциального и полного ускорения имеем следующие соотношения:
(17)
В векторной форме ускорение точек твёрдого тела, ось вращения которого не изменяет направления в пространстве, определяется, как и в случае движения точки по окружности, то есть по формуле
=
+
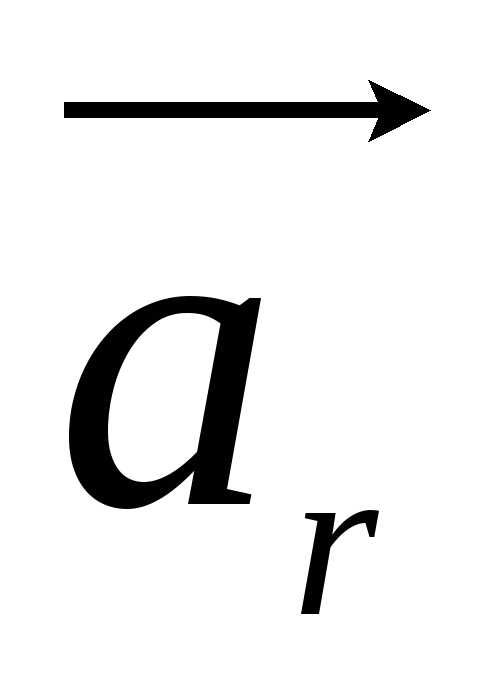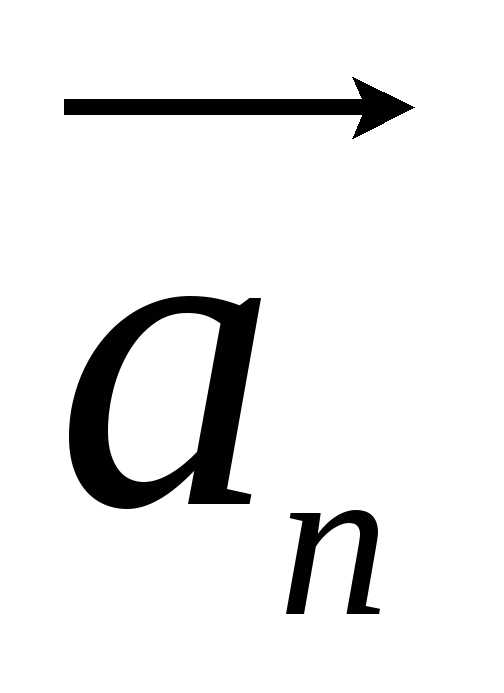(18)
studfiles.net
Методическая разработка по физике (9 класс) по теме: Разработки к урокам физики для 9 кл. по теме «Кинематика материальной точки»
УРОК 1. МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ.
МАТЕРИАЛЬНАЯ ТОЧКА. СИСТЕМА ОТСЧЕТА.
ТРАЕКТОРИЯ И ПЕРЕМЕЩЕНИЕ
К р а т к и й т е о р е т и ч е с к и й м и н и м у м
1. Механическое движение и его описаниа.
2. Характеристики движения-координата,траектория,путь,скорость.
3. Материальная точка-модель тела.
4. Критерии замены тела материальной точкой.
5. Система отсчёта.
6. Перемещение.
Механика – наука, изучающая движение тел, состоящее в перемещении их относительно друг друга. Название «механика» происходит от греческого слова mechanik, что означает наука о машинах, искусство постройки машин.
Английский физик Ньютон,опираясь на работы Г.Галилея и его современников,а так же на результаты своих собственных исследований, создал цельное учение о механическом движении и взаимодействии тел, котороеполучило название классической механики. Классическая механика состоит из трёх частей: к и н е м а т и к а, д и н а м и к а, с т а т и к а.
Кинематика – раздел механики, в котором изучается движение тел без учета действующих на них сил.
Динамика – раздел механики, в котором изучается движение тел под действием сил.
Статика — раздел механики, в котором изучается равновесие абсолютно твёрдых тел.
Основными задачами кинематики являются:
а) Описание с помощью математических формул, графиков или таблиц совершаемых телом движений.
б) Определение кинематических величин, характеризующих это движение.
Для описания движения в кинематике вводятся специальные понятия (материальная точка, система отсчёта,траектория) и величины (путь,перемещение,скорость,ускорение), которые важны не только в кинематике, но и в других разделах физики.
Первое,что бросается в глаза при наблюдении окружающего мира,-это его изменчивость
-Какие изменения вы замечаете?(ночь меняет день, вода при охлаждении замерзает,падают капли,едет автомобиль…)
-Подведём итог: наиболее частые ответы связаны с изменением положения тел относительно друг друга.
Механическое движение – изменение положения тела в пространстве относительно других тел с течением времени.
Однако одно и то же тело одновременно может и двигаться и не двигаться, если наблюдать его относительно разных тел отсчёта.
Тело отсчета – тело, относительно которого рассматривают движение других тел.
Пример: В купе вагона на столе лежит яблоко. Пассажир видит, что расстояние до яблока с течением времени сохраняется. Яблоко не совершает механического движения.Но с точки зрения провожающего,яблоко движется, так как расстояние от яблока до перронас течением времени растёт.
Из примеров следует: нет, и не может быть абсолютно твёрдых тел.
Даже самое простое движение тела оказывается сложным для изучения.Для того, чтобы облегчить исследования,вводят ряд упрощений.
Поступательное движение – движение тела, при котором все его точки движутся одинаковым образом, или движение тела, при котором прямая линия, соединяющая любые две его точки, остается параллельной самой себе.
Материальная точка – тело, размерами и формой которого в данных условиях движения можно пренебречь.
-Как же определить положение тела(материальной точки)?
Для этого необходимо тело отсчёта.Если через него провести оси координат,то положение тела в пространстве можно задать его координатами. Но при движении тела его положение меняется с течением времени. Значит, нужен прибор для измерения временит (часы), связанные с телом отсчёта.
Все вместе: а) тело отсчёта, б) система координат, в) прибор для измерения времени,-образуют систему отсчёта.
Система отсчёта может быть: а)одномерной, б) двухмерной, в) трёхмерной.
Для описания механического движения необходимо ввести ещё одно понятие- траектория.
Траектория – линия в пространстве, описываемая материальной точкой при её движении. В зависимости от траектории движения могут быть прямолинейными и криволинейными.
Прямолинейное и криволинейное движение – движение точки, при котором траекторией является прямая или кривая линия соответственно.Путь – длина участка траектории, пройденного точкой в течение рассматриваемого отрезка времени.
С изменением координат связана первая из величин, вводимых для описания движения,- перемещение.
Перемещение – направленный отрезок прямой (вектор), соединяющий начальное и конечное положение точки. Перемещение — величина векторная.
Векторная величина – величина, имеющая кроме численного значения (модуля) еще и направление (перемещение, ускорение, скорость, импульс, сила и т. д.).
Скалярная величина – величина, имеющая только численное значение (путь, время, объем, плотность, энергия и т. д.).
Модуль перемещения и путь могут совпадать по значению только в том случае,если тело движется вдоль прямой в одном направлении.
Проекция вектора на ось.
Проекцию считают положительной,если от проекции начала вектора к проекции его конца нужно идти по направлению оси.
В противном случае проекция вектора отрицательна.
Если вектор перпендикулчрен оси,то при любом направлении вектора его проекция на ось равна нулю.
К о н т р о л ь н ы е в о п р о с ы
1. Что изучает механика? Какие три раздела включает она в себя?
2. Что называют механическим движением тела? Приведите примеры.
3. Дайте определение кинематики, динамики и статики.
4. Какое тело называют телом отсчета? Приведите примеры тел отсчета. Сколько может быть тел отсчета при описании движения тела?
5. Дайте два определения поступательного движения тела, Приведите примеры поступательного движения тел.
6. Какое тело называют материальной точкой? Приведите примеры движения тела, при котором его можно принять за материальную точку.
7. Дайте определение траектории. Какие два вида траекторий описывают механическое движение тел? Приведите примеры траекторий движения некоторых тел.
8. Что такое путь? Чем он отличается от траектории?
9. Дайте определение системы отсчета. Опишите движение какого-либо тела в выбранной Вами системе отсчета.
10. Что называют перемещением? Изобразите на пояснительном рисунке прямолинейную или криволинейную траекторию движения какой-либо материальной точки и вектор ее перемещения за некоторый отрезок времени.
11. Чем отличаются путь и перемещение? Могут ли совпасть модуль вектора перемещения точки и пройденный ею путь? В каком случае? Приведите примеры.
12. Какие величины называются векторными? По каким правилам складываются (вычитаются) векторы? Изобразите на пояснительном рисунке несколько примеров сложения (вычитания) векторов.
13. Какие величины называются скалярными? Приведите примеры скалярных величин.
О б р а з ц ы р е ш е н и я з а д а ч
1. Вагон движется в одном направлении по прямолинейному участку железнодорожного полотна. Можно ли назвать движение вагона поступательным? Почему? Сравните путь и перемещение вагона за некоторый отрезок времени. Сравните путь и перемещение в случае, если вагон, двигаясь по этому же полотну, вернется в точку, из которой он начал движение.
Решение. Движение вагона можно назвать поступательным, так как прямая, проведенная через любые две точки движущегося вагона, остаётся параллельной самой себе. Модуль перемещения вагона за некоторый отрезок времени и пройденный им за это же время путь одинаковы, так как траектория движения вагона – прямая линия (этот вывод справедлив только при условии неизменного направления движения вагона). В случае возвращения вагона в исходную точку его перемещение принимает нулевое значение, а путь становится равным удвоенному значению расстояния, пройденного вагоном до точки изменения направления движения.
2. Материальная точка движется с неизменной скоростью по окружности радиуса R. Сравните путь и перемещение точки за четверть, половину и три четверти её оборота.
Решение. Величина пути , пройденного точкой за четверть оборота, равна длине дуги АВ (рис. 1).
.
Модуль перемещения точки равен длине гипотенузы АВ прямоугольного треугольника ОАВ.
Тогда
.
Путь , пройденный точкой за половину оборота, равен длине дуги АВС.
.
Модуль перемещения точки равен диаметру окружности (отрезок АС): .
Тогда
.
Путь , пройденный точкой за три четверти оборота, равен длине дуги АВСD.
.
Модуль перемещения точки равен длине гипотенузы АD прямоугольного треугольника ОАD.
.
Тогда
.
О б р а з ц ы р е ш е н и я з а д а ч
3. Тело переместилось из точки А с координатами х1 = 4 м, у1 = 2 м в точку В с координатами х2 = 6 м, у2 = – 2 м. Сделать пояснительный рисунок, найти величину (модуль) перемещения тела и проекции вектора перемещения на оси координат.
Решение. Изобразим декартову прямоугольную систему координат хоу и отметим на ней точки А и В (рис. 2).
Нарисуем вектор перемещения тела. Для этого соединим отрезком прямой точки А и В. Стрелку поставим у точки В, так как это – конечное положение тела.
Найдем проекцию перемещения тела на оси х и у:
;
.
Определим модуль вектора перемещения тела:
.
4. Группа туристов, выйдя из лагеря, прошла 3 км в направлении на северо-восток. Затем туристы стали двигаться в направлении на восток и прошли еще 2 км. Последний отрезок пути длиной 4 км они двигались в северном направлении. Сделать пояснительный рисунок, на котором указать результирующее перемещение группы туристов. Вычислить модуль результирующего перемещения и его направление (т. е. угол между вектором перемещения и направлением на север). Чему равен пройденный туристами путь?
Решение. Сделаем пояснительный рисунок (рис. 3). При этом учтем, что направление на северо-восток составляет угол 45 с направлением на север и такой же угол с направлением на восток.
Воспользуемся соотношениями, известными из курса математики:
,
где – проекции перемещения группы на ось х на первом, втором и третьем участке движения соответственно.
,
где – проекции перемещения группы на ось у на первом, втором и третьем участке соответственно.
;
;
;
Тогда
;
Используем численные значения модулей векторов перемещений:
;
Тогда
– модуль результирующего перемещения.
Вычислим угол .
; – направление результирующего перемещения.
Вычислим путь, пройденный туристами:
.
К о н т р о л ь н ы е з а д а н и я
5. Определить модуль перемещения тела и пройденный им путь в следующих случаях:
а) пловец переплыл бассейн длиной 50 метров по прямой водной дорожке туда и обратно;
б) мяч поднялся вверх на высоту 5 метров а потом спустился вниз на 2 метра;
в) пешеход, двигаясь по прямым улицам, прошел 3 квартала на запад, а потом 4 квартала на юг;
г) лифт прошел при спуске с некоторой высоты 15 метров, а потом поднялся на 20 метров;
О т в е т: а) 0, 100 м; б) 3 м, 7 м; в) 5 кв., 7 кв.; г) 5 м, 35 м.
6. Тело преодолело подъем длиной 100 метров с углом наклона к горизонту 60° . Определить численные значения проекций перемещения тела на горизонтальную и вертикальную координатные оси.
О т в е т: 50 м, 86,6 м.
nsportal.ru
Презентация к уроку по физике (9 класс) на тему: Как решать задачи по кинематике
Как решать задачи по кинематике?
Не существует универсального метода решения задач по физике, но существует универсальный подход к решению задач. Когда грамотный физик, а мы собираемся стать грамотными физиками, решает задачу, то его действия можно поделить на три больших этапа:
1. Постановка задачи;
2. Решение задачи;
3. Анализ решения.
При постановке задачи и анализе решения мы являемся физиками, при решении задачи мы математики.
Постановка задачи – наиболее важный, а в школьных задачах, и наиболее трудный этап. Мы должны понять физику явления, сформулировать физическую модель, а затем перевести ее в математическую. Конечным результатом этого этапа должна быть система уравнений и неравенств.
При решении задач по кинематике этот этап разбивается на четыре ступени:
1.Внимательно, не торопясь, прочитайте условие задачи. Подумайте, о каком физическом явлении идет речь. Какие физические величины известны, а какие надо найти? (Когда задача сложная, не следует особенно стремиться получить ответ. Надо последовательно, аккуратно ставить задачу, а ответ придет сам, куда ему деваться?)
2.Изобразите на рисунке (схематически) рассматриваемые тела, изобразите их движения.
3.Выберите систему отсчета. Для этого надо построить систему координат, т. е. задать ее начало и положительные направления координатных осей. Кроме того, надо выбрать начало отсчета времени. Без выбора системы отсчета описать движение полностью невозможно.
Для описания прямолинейного движения достаточна одна координатная ось, совмещенная с траекторией движения. Если движение происходит в одной плоскости, то потребуются две оси, для 3-х мерного движения необходима 3-х мерная система координат.
Выбор системы отсчета произволен и не влияет на конечный результат решения задачи. Но удачный выбор системы отсчета упрощает решение задачи.
На этом мы заканчиваем построение физической модели и нам надо превратить ее в математическую модель. Помните, математика – язык физики.
4.Запишите уравнения, описывающие движения всех тел. В случае кинематики в школьных задачах это будут уравнения для зависимости координат материальных точек от времени. Далее от уравнений для значений координат и проекций заданных величин надо перейти к уравнениям для их модулей. Это непростой момент, рисунок должен Вам помочь.
5.Сформулируйте на языке математики так называемые «начальные» и «скрытые» условия. В качестве начальных условий обычно выступают значения координат и скоростей в начальный момент времени, а вот нахождение скрытых условий – это самый деликатный момент в решении задачи. В кинематике в качестве скрытых условий может быть, например, встреча двух тел в момент времени tв, т. е. их координаты в этот момент равны. Это условие дает уравнение:
x1(tв) = x2(tв).
Общее число уравнений должно равняться числу неизвестных.
6.На этом заканчивается этап постановки задачи. Мы получили систему уравнений, может быть, систему уравнений и неравенств, которые являются математической моделью решаемой нами задачи. В последний момент мы смотрим, а что, собственно, нам надо найти в этой задаче, и из состояния «физик» мы переходим в состояние «математик» и решаем эту систему в общем (буквенном) виде. Решать в общем виде – это строго обязательно. Всякая подстановка численных значений до получения общего ответа – это серьезное нарушение. Оценка за это снижается немилосердно!
7.После того, как получен ответ в общем виде, мы снова переходим в состояние «физик» и занимаемся анализом задачи. Полезно посмотреть, к каким последствиям приводит увеличение или уменьшение величин, заданных в условии задачи. Посмотрите области допустимых значений. Проследите, чтобы размерности правой и левой части уравнений были одинаковы. Если у Вас метры складываются с секундами, идите в начало задачи и ищите ошибку. Замечательно, что Вы ошиблись, поиск своих или чужих ошибок – самый эффективный способ обучения. Когда все получается с первого раза – чему тогда учиться?
8.Подставьте в буквенный ответ числовые значения заданных физических величин с наименованием их единиц. Предварительно надо выразить все числовые значения в одной системе единиц. Выполните вычисления и получите ответ. Пользуйтесь правилами приближенных вычислений. Следите, чтобы точность полученного ответа не превосходила точности заданных величин. К сожалению, составители задач редко правильно задают точность исходных величин.
Перечисленные рекомендации не надо считать абсолютно жесткими, неизменными. Всего не предусмотришь. В некоторых случаях отдельные пункты можно опустить, иногда приходится вводить новые. Многие задачи проще решать графически. Но на первых этапах мы должны придерживаться этой схемы. Если где-то мы отходим от нее, то делать это надо осознанно. Когда Вы станете большими мастерами в решении задач по физике, тогда Вы можете импровизировать. А эталон, к чему надо стремиться, сформулировал Р.Фейнман
Физик, это тот, кто видит решение задачи, еще не решая ее.
Приступаем к решению задач. Понятно, что первые задачи будут несложными. Надо привыкнуть к последовательному выполнению этапов решения задач по кинематике.
Задача 1
Тело движется равномерно вдоль оси Х. Со скоростью v = 2 м/с противоположно положительному направлению оси Х. Найдите положение тела в момент времени t1 = 10 с после начала движения, если начальная координата x0 = 5 м. Чему равен путь, пройденный телом?
Решение.
Выписываем в левом верхнем углу «Дано» и делаем рисунок. Иногда это полезно делать одновременно.
Дано: v = 2 м/с t1 = 10 с x0 = 5 м x(t1) = ? s(t1) = ? t1 |
Из условия задачи видно, что физической моделью задачи является материальная точка, двигающаяся по прямой с постоянной скоростью.Математической моделью такого процесса является математическое уравнение для координат материальной точки:
x = x0+ vxt.
По условию задачи vx= -v и формула для координаты принимает вид:
x = x0 — vt.
Пройденный телом путь равен
s = vt.
В этих уравнениях t – параметр, переменная величина. Уравнения показывают, как изменяется координата материальной точки и пройденный ею путь со временем t. Можно для большей ясности писать x(t) и s(t). Смотрим в условие задачи, что нам нужно найти. Координату и пройденный путь в момент времени t1. Физика закончилась. Переходим в состояние «математик» и смотрим, что нам предстоит решить. В этой задаче работы для математика нет. Надо подставить вместо t ее численное значение t1 и подсчитать численный ответ. Обратите внимание, t — переменная величена, а t1 – число. В школьных задачах по физике, как правило, не бывает сложной математики. Поэтому когда Вы оформляете решение задачи в чистовике, математическую часть можно излагать предельно кратко. Леша Щекин на контрольных и олимпиадах выписывал исходную систему уравнений, потом сразу выписывал ответ в общем виде и численный ответ. Это правильно. Но когда Саша Головко записывал «Дано», потом замирал на какое-то время, а потом сразу писал ответ, то это уже слишком. Так поступать не следует. Экзаменатор может подумать, что Вы списали.
Итак, мы имеем:
x(t1) = x0 – vt1 = 5 м – 2 м/с∙10 с = -15 м.
Пройденный телом путь равен
s(t1) = vt1 = 2 м/с∙10 с = 20 м.
Анализ решения.
Из уравнение для координаты видно, что тело из +? движется к началу координат, в момент времени t = 0 оно проходит координатуx0 = 5 м, в момент времени 2,5 с оно проходит через начало координат и уходит в -?. С размерностями величин все в порядке. Поэтому у нас есть основания надеяться, что мы правильно решили задачу.
Задача 2
Из пунктов А и В, расстояние между которыми l = 55 км, одновременно начали двигаться с постоянными скоростями навстречу друг другу по прямому шоссе два автомобиля. Скорость первого автомобиля v1 = 50 км/ч, а второго v2 = 60 км/ч. Через сколько времени после начала движения автомобили встретятся? Найдите пути, пройденные каждым автомобилем за это время.
Решение.
Дано: l = 55 км v1 = 50 км/ч v2 = 60 км/ч t1 = ? s1= ? s1= ? |
Представим движение автомобилей как движение материальных точек.
Примем пункт А за начало координат и направим координатную ось Х в сторону пункта В (см.рис.). Движение автомобилей будет описываться уравнениями:
x1(t) = x01 + v1xt,
x2(t) = x02 + v2xt.
Начальные условия:
x01 = 0,x02 = l.
Так как вектор скорости первого автомобиля направлен в положительном направлении, а второго – в отрицательном, то
v1x = v1,v2x = -v2.
Поэтому первые два уравнения перепишем в виде:
x1(t) = v1t,
x2(t) = l – v2t.
Когда в момент времени t1 автомобили встретятся, они будут иметь равные координаты:
x1(t1) = x2(t1),
или
v1t1 = l – v2t1.
Откуда
t1 =l/(v1 + v2) = 0,5 ч.
Пройденные пути равны
s1 =v1t1 = 25 км,s2 = v2t1 = 30 км.
Анализ задачи.
Задача слишком простая, чтобы что-то еще анализировать. Можно сложить s1 + s2, получается 55 км, значит, решили правильно, скорее всего.
Задача 3
Движение точки на плоскости описывается уравнениями
х = 6 м + 3 м/с ∙t,
y = 4 м/с ∙t.
Определить траекторию движения точки и построить ее на плоскости XOY.
Решение.
Исключим из обоих уравнений параметр t. Для этого выразим время из первого уравнения и подставим во второе, получим:
y = 4x/3 – 8 м.
Это уравнение прямой линии с угловым коэффициентом 4/3 и пересекающая ось OY в точке –8. Можно построить ее по точкам,
при х = 0y = -8 ми при y = 0х = 6 м.
Направление скорости движения точки укажем стрелкой.
Задача 4
На рисунке изображен график зависимости от времени координаты точки, движущейся вдоль оси Х. Как двигалась точка? Постройте графики модуля v и проекции vxскорости, а также пути в зависимости от времени.
Решение.
В течение первых 3 с координаты точки изменялись от 2 м до – 4 м, следовательно, точка двигалась противоположно положительному направлению оси Х. Проекция скорости равна
V1x = (- 4 – 2 )/ 3 м/c = — 2 м/c,
А модуль скорости равен v1 = 2 м/с.
Следующие 4 с точка не двигалась, ее координаты не изменялись, v2x = v2 = 0. Потом в течение 2 с точка двигалась в положительном направлении оси Х о пришла в начало координат (х = 0).Проекция и модуль скорости соответственно равны
v3x = v3 = (0 – (-4))/2 м/с = 2 м/с.
На рисунке «а» изображен график проекции скорости, на рисунке «б» – график модуля скорости, на рисунке «в» — график пути. При построении графика пути не забывайте, что путь не может быть отрицательным и при движении не убывает.
Задача 5
С подводной лодки, погружающейся равномерно, испускаются звуковые импульсы длительностью t1 = 30,1 с. Длительность импульса, принятого на лодке после его отражения от дна, равна t2 = 29,9 с. Определите скорость погружения лодки v. Скорость звука в воде с = 1500 м/с.
Решение.
Звуковой импульс не является материальной частицей, однако уравнения движения звукового импульса такие же, как и у материальной точки, поэтому можно применять законы кинематики материальной точки.
За время t1 лодка переместится на расстояние vt1, поэтому расстояние в воде между началом импульса и его концом равно
L = ct1 – vt1.
Такая длина сигнала сохранится и после отражения от дна. Прием импульса закончится в тот момент, когда лодка встретится с задним концом импульса. Поскольку скорость их сближения равна с + v, то продолжительность приема равна
t2 = L/(c + v)
Решая эти уравнения совместно, получим
v = = 5 м/с.
nsportal.ru
Решение типовых задач по физике. Механика. Кинематика :: Класс!ная физика
На этой странице представлены условия типовых задач по физике из сборника задач Бендрикова Г.А. для школьников 9-11 классов и студентов.
Решения этих задач даны на плейлисте видео — СМОТРИ ЗДЕСЬ —
Номера задач здесь и на плейлисте совпадают.
Счастливого разбора «полетов»!
Задачи на прямолинейное равномерное и равнопеременное движение
1. Товарный поезд идет со скоростью 10 м/с. Спустя 30 мин. с той же станции по тому же направлению вышел экспресс со скоростью 20 м/с. Через какое время после выхода товарного поезда и на каком расстоянии от станции экспресс догонит товарный поезд.
2. Из городов А и В, расстояние между которыми равно 54 км одновременно выехали навстречу друг другу две автомашины со скоростями 4 м/с и 6 м/с. Через какое время и на каком расстоянии от города, находящемся на полпути между А и В встретятся автомашины?
3. Стержень АВ длины l опирается концами о пол и стену. Найти зависимость координаты y — конца стержня В от времени t при движении конца стержня А с постоянной скоростью v в направлении, указанном на рисунке.
4. Товарный поезд длины 630 м и экспресс длины 120 м идут по двум параллельным путям в одном направлении со скоростями 13 м/с и 28 м/с соответственно. В течении какого времени экспресс будет обгонять товарный поезд?
5. Два поезда идут навстречу друг другу со скоростями 10 м/с и 15 м/с. Пассажир в первом поезде замечает, что второй поезд проходит мимо него в течении 6 секунд. Какова длина второго поезда?
6. Теплоход, имеющий длину 300 м, движется по прямому курсу в неподвижной воде со скоростью v. Катер, имеющий скорость 25 м/с, проходит расстояние от кормы движущегося теплохода до его носа и обратно, за 37,5 секунды. Найти скорость v теплохода.
7. На наклонную плоскость, составляющую с линией горизонта угол альфа, опирается стержень, который может перемещаться только по вертикали, благодаря направляющему устройству АВ. С какой скоростью поднимается стержень?
8. Капли дождя на окнах неподвижного трамвая оставляют полосы, наклоненные под углом 30 градусов к вертикали. При движении трамвая со скоростью 5 м/с полосы от дождя вертикальные. Найти скорость капель дождя в безветренную погоду и скорость ветра.
9. Пловец переплывает реку, имеющую ширину h. Под каким углом альфа к направлению течения он должен плыть, чтобы переправиться на противоположный берег в кратчайшее время?
10. Лодочник, переправляясь через реку ширины H, из пункта А в пункт В все время направляет лодку под углом альфа к берегу. Найти скорость лодки относительно воды, если скорость течения реки равна u, а лодку снесло ниже пункта В на расстояние l.
11. Корабль идет на запад со скоростью v. Известно, что ветер дует с юго-запада. Скорость ветра, измеренная на палубе корабля, равна u0. Найти скорость ветра u относительно Земли.
12. Тело 1 начинает двигаться из точки А по направлению к точке В со скоростью V1. Одновременно тело 2 начинает двигаться из точки В по направлению к точке С со скоростью V2. Расстояние AB=L. Острый угол ABC равен альфа. В какой момент времени t расстояние r между телами 1 и 2 будет минимальным, и каково это расстояние?
13. Один поезд шел первую половину пути S1 со скоростью 80 км/ч, а вторую половину — со скоростью 40 км/ч. Второй поезд шел первую половину времени со скоростью 80 км/ч, а вторую половину времени со скоростью 40 км/ч. Какова средняя скорость каждого поезда?
14. Тело, имея начальную скорость v1=2 м/с двигалось в течении времени t1=3c равномерно, t2=2 cекунды с ускорением а2=2 м/с2, t3=5 cекунд с ускорением а3=1 м/с2. Найти среднюю скорость на этом пути.
15. Самолет, летящий горизонтально со скоростью V, попадает в полосу дождя, капли которого падают вертикально со скоростью омега. Кабина пилота имеет два стекла: верхнее горизонтальное и переднее, наклоненное к горизонту под углом альфа. Каждое из стекол имеет площадь S. Найдите отношение числа капель воды, падающих в единицу времени на переднее стекло к числу капель, падающих в единицу времени на верхнее стекло.
16. Тело, имея начальную скорость v0 = 1 м/с, двигалось равноускоренно и приобрело, пройдя некоторое расстояние, скорость v = 7 м/с. Какова была скорость тела у на половине этого расстояния?
17. Тело, имея некоторую начальную скорость, движется равноускоренно из некоторого положения. Известны координаты тела, отсчитанные вдоль направления движения от произвольного начала отсчета в моменты времени. Найти ускорение тела.
18. Парашютист спускается с постоянной скоростью v = 5 м/с. На расстоянии h = 10 м от земли у него выпал предмет. На сколько позже приземлится парашютист, чем этот предмет? Сопротивлением воздуха для падающего предмета пренебречь. Считать ускорение свободного падения g = 10 м/с2.
19. Тело, имея некоторую начальную скорость, движется равноускоренно. За время t тело прошло путь s, причем его скорость увеличилась в n раз. Найти ускорение тела.
20. По одному направлению из одной точки одновременно начали двигаться два тела: одно — равномерно со скоростью v = 980 см/с, а другое — равноускоренно без начальной скорости с ускорением а = 9,8 см/с2. Через какое время второе тело догонит первое?
21. Два поезда прошли одинаковый путь s за одно и то же время /, однако один поезд, имея начальную скорость, равную нулю, прошел весь путь с ускорением а = 3 см/с2, а другой поезд половину пути шел со скоростью v, = 18 км/ч, а половину пути — со скоростью v2 = 54 км/ч. Найти путь s, пройденный поездами.
22. Автомобиль, трогаясь с места, едет с ускорением а. Достигнув скорости v, он некоторое время едет равномерно, а затем тормозит с ускорением а2 до остановки. Найти время t движения автомобиля, если он прошел путь s.
23. Поезд прошел путь s = 60 км за время t = 52 мин. Сначала он шел с ускорением +а, в конце с ускорением -а, остальное время с максимальной скоростью v =72 км/ч. Найти модуль ускорения, если начальная и конечная скорости равны нулю.
24. Какая предельная скорость приземления v парашютиста допустима, если человек, не имея парашюта, может безопасно прыгать с высоты 2 м?
25. Камень брошен с высоты h = 28 м вертикально вверх с начальной скоростью v0 = 8 м/с. Найти скорость v падения камня на землю.
26. Тело падает без начальной скорости с высоты h = 45 м. Найти среднюю скорость падения на второй половине пути.
27. За какое время t свободно падающее без начальной скорости тело пройдет сотый сантиметр своего пути?
28. Свободно падающее без начальной скорости тело в последнюю секунду падения прошло 2/3 своего пути. Найти путь s, пройденный телом.
29. Тело брошено с некоторой высоты вертикально вверх с начальной скоростью v0 = 30 м/с. Найти координату h и скорость v тела через время t = 10 с, а также пройденный за это время путь Считать ускорение свободного падения g = 10 м/с2.
30. Свободно падающее без начальной скорости тело спустя некоторое время после начала падения находилось на высоте h2 = 1100 м, а еще через время t1 = 10 с — на высоте h3 = 120 м над поверхностью земли. С какой высоты h падало тело?
31. Тело, брошенное вертикально вверх, дважды проходит через точку на высоте h. Промежуток времени между этими прохождениями равен At. Найти начальную скорость тела v0 и время t0 от начала движения тела до возврата в начальное положение.
32. Одно тело брошено вертикально вверх с начальной скоростью v0, другое падает с высоты h без начальной скорости. Движения начались одновременно и происходят по одной прямой. Найти зависимость расстояния s между телами от времени t.
33. С башни, имеющей высоту h, бросают одновременно два шарика: один — вертикально вверх со скоростью v1, другой — вертикально вниз со скоростью v2. Найти промежуток времени At, отделяющий моменты их падения на землю.
34. С крыши падают одна за другой две капли. Через время t2 = = 2 с после начала падения второй капли расстояние между каплями стало равным s = 25 м. На сколько раньше первая капля оторвалась от крыши?
35. С высоты /i] = 10 м без начальной скорости падает камень. Одновременно с высоты h3 = 5 м вертикально вверх бросают другой камень. С какой начальной скоростью и{) брошен второй камень, если камни встретились на высоте h = 1 над землей?
36. Два тела брошены вертикально вверх с одинаковыми начальными скоростями с интервалом времени At. С какой скоростью будет двигаться второе тело относительно первого?
37. Лодка подтягивается к высокому берегу озера при помощи веревки, которую наматывают с постоянной скоростью v = 1 м/с на цилиндрический барабан, находящийся на высоте h = 6 м над уровнем воды . Найти зависимость скорости лодки от длины веревки . Найти также скорость лодки в момент времени, когда I = 10 м, и перемещение лодки из этого положения за время t = 1 с.
38. По наклонной плоскости одновременно начали двигаться два тела: одно — вверх с начальной скоростью ц, = 0,5 м/с, другое — вниз без начальной скорости. Через какое время t тела встретятся и какой будет их относительная скорость в месте встречи, если первоначальное расстояние между телами I = 2,5 м?
39. По наклонной плоскости одновременно начали двигаться два тела: одно — вверх с начальной скоростью ц, = 0,5 м/с, другое — вниз без начальной скорости. Через какое время t тела встретятся и какой будет их относительная скорость в месте встречи, если первоначальное расстояние между телами I = 2,5 м?
40. Стальной шарик, упавший с высоты h = 1,5 м на стальную доску, отскакивает от нее с потерей 25% скорости. Найти время t, которое проходит от начала движения шарика до его второго падения на доску.
41. Мяч свободно падает с высоты h — 120 м на горизонтальную плоскость. При каждом отскоке скорость его уменьшается вл = 2 раза. Построить график скорости и найти пройденный мячом путь от начала движения до остановки.
42. На движущуюся вертикально вверх со скоростью и горизонтальную гладкую плиту свободно падает шарик. Расстояние от точки начала падения шарика до его места встречи с плитой равна h0- На какую высоту h от этого места подскочит шарик после соударения с плитой? Плита, обладая очень большой массой, не изменяет своей скорости в результате соударения с шариком. Считать соударение абсолютно упругим.
РЕШЕНИЯ ЭТИХ ЗАДАЧ даны на плейлисте видео — СМОТРИ ЗДЕСЬ —
Номера задач здесь и на плейлисте совпадают.
www.class-fizika.narod.ru
