задачи по физике, примеры решения
Столкнувшись с задачами по физике на внутреннюю энергию, главное, основательно разобраться во всех процессах, указанных в условиях, и использовать ранее изученные формулы по этой теме.
Каким образом можно изменить внутреннюю энергию в физике
Чтобы условия задачи всегда были ясны, важно детально разобраться с понятием, точно знать, что это такое, от чего зависит и на что влияет.
Понятие, определение
Внутренней энергией называется энергия движения и взаимодействия частиц, составляющих тело, соответственно, она складывается из кинетической энергии, возникающей при движении молекул тела, и потенциальной энергии взаимодействия его частиц.
В международной системе обозначается большой латинской буквой U и измеряется в Джоулях.
Внутренняя энергия тела зависит:
- От температуры. Чем выше температура тела, тем активнее движутся частицы внутри него, тем больше его внутренняя энергия.

- От его массы.
- От агрегатного состояния вещества (вода/лед).
Изменить внутреннюю энергию можно:
- С помощью работы, совершаемой над телом или совершенной им. Причем, внутренняя энергия объекта уменьшается, если он совершает работу, и, наоборот, увеличивается, если работа совершается над ним.
- При помощи теплопередачи.
Теплопередача — это один из способов изменения внутренней энергии объекта, при котором происходит передача энергии от объекта к объекту или от одной части тела к другой без совершения работы.
Основные формулы и их применение
Основными формулами, которые понадобятся для решения задач по данной теме, являются:
- \(U=E_к+E_п\), где \(E_к\) — кинетическая энергия, а \(E_п\) — потенциальная.

- \(\Delta U=A+Q\), где \(A\) — это работа, \(Q\) — количество теплоты. Данное уравнение выражает первый закон термодинамики: изменение внутренней энергии при переходе системы из одного состояния в другое будет равняться сумме работы внешних сил и количества теплоты переданной системе.
Примеры решения качественных задач по теме
Для решения задач по данной теме термодинамики чаще всего нужны следующие формулы:
Источник: infourok.ruЧтобы окончательно разобраться с темой, рассмотрим решение нескольких типовых задач.
Задача №1
Какова внутренняя энергия гелия, который заполняет аэростат объемом 50 м
Решение
- Записываем известные нам данные: p=80 кПа, V=50 м3, U=?
- Приводим единицы измерения давления к общепринятым — Па, p=8х104 Па.
- Для одноатомного идеального газа U вычисляется по формуле: \(U=\frac32\times\frac mM\times R\times T\)
- Для решения этой задачи нам понадобится уравнение Менделеева-Клапейрона: \(p\times V=\frac mM\times R\times T\)
- Соответственно, \(U=V=\frac32\times p\times V\)
- Подставляем числовые значения в формулу и получаем ответ: 6 МДж.

Задача №2
Насколько изменилась внутренняя энергия гелия, если его масса 200 грамм, а температура увеличилась на 20 Кельвинов?
Решение
- Записываем вводные данные: m= 200 гр., T=20 К, R=8,31 Дж х моль/К, M=0,004 кг/моль, U=?
- Для решения данной задачи потребуется одна формула — для идеального газа: \(U=\frac32\times\frac mM\times R\times T\)
- Производим несложные математические действия и получаем ответ: 12,5 кДж.
Задача №3
Газ находится в закрытом баллоне. При охлаждении газа его внутренняя энергия снизилась на 500 Дж. Какое количество теплоты при этом отдал газ и совершал ли он работу?
Решение
- Это задача скорее теоретическая, поэтому давайте рассуждать: так как газ находится в закрытом баллоне, следовательно, его объем не меняется, т.е. \(\Delta V=0\)
- Работа определяется по формуле: \(\Delta V=0\), \(А=0\), а это значит, что газ работу не совершал.

- По первому закону термодинамики, \(Q=A+\Delta U=\Delta U= — 500\) Дж.
Мордехай Тульчинский — Качественные задачи по физике в средней школе и не только… читать онлайн бесплатно
Е. М. Тульчинский
Качественные задачи по физике в средней школе и не только…
Я считаю, что понял смысл уравнения, если в состоянии представить себе общий вид его решения, не решая его непосредственно.
Поль Дирак, один из величайших физиков-теоретиков XX века© ООО «Издательство АСТ», 2021
© Иллюстрации Подобед В., 2021
Перед вами сборник качественных задач по физике. Слово «качественные» здесь говорит вовсе не о качестве этих задач (хотя они и были тщательно подобраны), а противопоставляет их количественным задачам, то есть задачам, для решения которых требуются расчеты.
К сожалению, преподавание физики в школе порой создает ложное представление о том, как решаются физические задачи: «Нужно найти подходящую формулу, подставить в нее числа и выполнить расчеты». В такой картине мира, конечно, для качественных рассуждений не остается места, поскольку физик здесь выглядит чем-то средним между справочником и приложением к калькулятору. Однако на самом деле решению почти любой содержательной количественной, расчетной физической задачи предшествует решение качественной задачи: физик должен разобраться в явлении, понять, какими физическими законами оно управляется, и составить 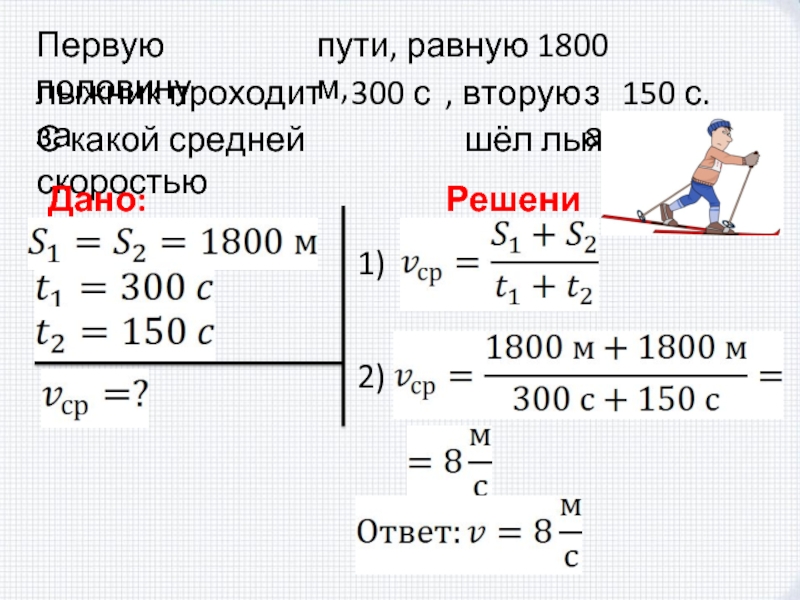 И лишь после этого начинаются вычисления – но иногда в них уже нет необходимости (именно об этом говорил Поль Дирак, слова которого вынесены в эпиграф). Другими словами, умение справляться с качественными задачами – очень важный навык настоящего физика, а само противопоставление качественных и количественных задач довольно искусственно.
И лишь после этого начинаются вычисления – но иногда в них уже нет необходимости (именно об этом говорил Поль Дирак, слова которого вынесены в эпиграф). Другими словами, умение справляться с качественными задачами – очень важный навык настоящего физика, а само противопоставление качественных и количественных задач довольно искусственно.
Чтобы решить качественную задачу, нужно, конечно, хорошо знать и понимать законы физики. Но еще нужно уметь выделять главное и отодвигать в сторону второстепенное, видеть взаимосвязи, рассуждать логически. Вот этому в меру возможности и научит вас сборник задач, который вы держите в руках.
Расположение задач в сборнике в целом повторяет структуру курса физики в средней школе, однако такое деление все же условно и сделано для ориентира: некоторые задачи допускают несколько разных подходов, для решения других нужно скомбинировать физические законы из разных разделов.
В некоторых задачах есть подвох или неожиданный поворот, чтобы напомнить, что физик всегда имеет дело с реальным миром и должен быть готов к тому, что этот мир не вполне укладывается в готовые схемы. По той же причине условия задач далеки от рафинированного «тело массы m равномерно движется по абсолютно гладкой поверхности…». Даже когда герои задачи выдуманы (здесь вас ждут и три поросенка, и Золушка, и Гэндальф с Бильбо Бэггинсом, и вездесущий Мюнхгаузен, и друзья-физики Винкель и Нуллибер – кстати, догадаетесь ли вы, откуда взялись их имена?), сама физическая ситуация вполне реалистична. Физик должен уметь прокладывать путь от практической ситуации к теоретической модели, которая позволит ему применить свои знания физических законов.
По той же причине условия задач далеки от рафинированного «тело массы m равномерно движется по абсолютно гладкой поверхности…». Даже когда герои задачи выдуманы (здесь вас ждут и три поросенка, и Золушка, и Гэндальф с Бильбо Бэггинсом, и вездесущий Мюнхгаузен, и друзья-физики Винкель и Нуллибер – кстати, догадаетесь ли вы, откуда взялись их имена?), сама физическая ситуация вполне реалистична. Физик должен уметь прокладывать путь от практической ситуации к теоретической модели, которая позволит ему применить свои знания физических законов.
Все задачи в этом сборнике (их ровно 200) сопровождаются подробным разбором. Этот разбор если и не приводит прямиком к ответу, то по крайней мере указывает путь. Однако не торопитесь обращаться к разбору – попытайтесь решить задачу самостоятельно. Не отчаивайтесь, если не добьетесь успеха с первой попытки: пользу приносит не обладание ответом, а его поиск. Попробуйте сами задать себе «наводящие» вопросы:
– С какими физическими явлениями имеют дело герои задачи? Какие физически законы управляют этими явлениями?
– Что мне известно? Какие выводы я могу сделать из того, что мне известно?
– Что мне нужно выяснить? Как я мог бы это выяснить? Какая информация мне помогла бы?
Ответы помогут вам совершить следующий шаг.
Усилия, которые вы приложите, даже если они и не приведут вас к ответу, сделают вас немножко более тренированным. Более того, если вы теперь обратитесь к готовому решению (это совершенно не зазорно после того, как вы потратили на обдумывание задачи достаточно сил и времени), вы воспримете его совершенно иначе: «Ах вот в чем тут было дело!» или «Вот чего мне не хватало!». Это и значит, что вы научились чему-то новому для себя.
Чтобы усилить этот эффект, большинство задач в сборнике сделаны многослойными, наподобие луковицы или матрешки: читая разбор задачи, вы «в нагрузку» к ответу получаете новые вопросы, которые потребуют дальнейшего обдумывания, а возможно, расчетов или даже углубления теоретических познаний.
Хочется надеяться, что работа с этим сборником поможет вам лучше разглядеть красоту, многогранность и практичность физики и понять, почему для многих она становится делом жизни. Может быть, и вы присоединитесь к их числу!
Условия задач
I. Знакомство с физикой
1. Физические измерения
Физические измерения
1. Приумножить и измерить
Представьте себе, что вам понадобилось измерить толщину троса, но никакого измерительного прибора, кроме линейки, у вас под рукой не оказалось, а точность «плюс-минус миллиметр» вас не устраивает. Как провести точное измерение толщины троса обычной линейкой?
2. Винкель на диете
Винкель по настоянию врача сел на диету. Среди условий диеты есть ограничение на количество черешни (которую Винкель, как назло, очень любит): врач настоятельно рекомендовал ему съедать не больше 200 мл черешни в день. Винкель, конечно, мог бы просто насыпать черешню в обычный стакан, объем которого как раз 200 мл, однако в стакане между ягодами есть пустоты. Винкель не готов нарушать предписания врача, но и пустоты его очень огорчают: ведь это означает, что объем черешни в стакане меньше 200 мл. Помогите Винкелю отмерить нужное количество черешни.
2. Строение вещества
3. Дружные стекла
Дружные стекла
Почему трудно отделить друг от друга два больших стекла, сложенных вместе?
4. Горячий и сладкий
Почему сахар быстрее растворяется в горячем чае, чем в холодном?
5. Можно ли сделать из мухи слона?
В фильмах ужасов и фантастических фильмах нередко появляются насекомоподобные существа очень крупных размеров (размером с человека или даже больше). Может ли теоретически существовать муха размером со слона (скажем, как результат генетической мутации)?
Читать дальшеФизические задачи как средство развития обучащихся
1. Классификация физических задач
С решением физических задач как с одним из необходимых элементов учебной работы ребята знакомятся уже на первых уроках физики в 7 классе. Решение задач – это то, что пугает многих, хотя сам процесс решения любой задачи может стать увлекательным и является очень полезным: ведь в жизни человек постоянно сталкивается с необходимостью решать «задачи жизненные».
По мнению А.В.Усовой, задачи имеют большое значение для конкретизации знаний учащихся, для привития им умения видеть различные конкретные проявления общих законов. Без такой конкретизации знания остаются книжными, не имеющими практической ценности. Решение задач способствует более глубокому и прочному усвоению физических законов, развитию логического мышления, сообразительности, инициативы, воли и настойчивости в достижении поставленной цели, вызывает интерес к физике, помогает приобретению навыков самостоятельной работы и служит незаменимым средством для развития самостоятельности в суждениях. …Решение задач – одно их важнейших средств повторения, закрепления и проверки знаний учащихся. [20, с. 92-93].
Одними из первых определение физической учебной задачи дали С.Е.Каменецкий и В.П.Орехов: физической задачей в учебной практике обычно называют небольшую проблему, которая в общем случае решается с помощью логических умозаключений, математических действий и эксперимента на основе законов и методов физики. По существу на занятиях по физике каждый вопрос, возникший в связи с изучением учебного материала, является для учащихся задачей. Активное целенаправленное мышление «всегда есть решение задач» в широком понимании этого слова.
По существу на занятиях по физике каждый вопрос, возникший в связи с изучением учебного материала, является для учащихся задачей. Активное целенаправленное мышление «всегда есть решение задач» в широком понимании этого слова.
Вместе с тем, С.Е.Каменецкий и В.П.Орехов подчеркивают, что с сущностью физических явлений учащихся знакомят различными методами: путем рассказа, демонстрации опытов, постановки лабораторных работ, проведения экскурсий и т.д. При этом активность учащихся, а следовательно, глубина и прочность их знаний будут наибольшими тогда, когда создается «проблемная ситуация». В ряде случаев ей может быть придана форма задачи, в процессе решения которой ученик «переоткрывает» для себя физическую закономерность, а не получает ее в готовом виде. В этом случае задача выступает как средство изучения физического явления. С этой целью можно использовать качественные, расчетные, экспериментальные и другие задачи. [10, с. 6-7].
Чаще всего самим учащимся ответить на вопрос: «Что же такое задача?» сложно.-reshenie-173.jpg) На вопрос: «Какими бывают физические задачи?», ребята отвечают в основном: «…простыми и сложными». А ведь понимание сущности физической задачи, возможность определения ее структуры, умение отнести данную для решения задачу к определенному типу помогут учащемуся определить способ дальнейшей деятельности по ее решению.
На вопрос: «Какими бывают физические задачи?», ребята отвечают в основном: «…простыми и сложными». А ведь понимание сущности физической задачи, возможность определения ее структуры, умение отнести данную для решения задачу к определенному типу помогут учащемуся определить способ дальнейшей деятельности по ее решению.
Кроме того, образовательные стандарты нового поколения «… трактуют понятие «результат образования» с позиции деятельностного подхода, …» [1]. И уже все понимают, что качество образования обучающегося будет оцениваться не по количеству знаний, приобретенных им в школе, а по умению выполнять различные виды деятельности, находить пути решения и решать различные по сути задачи.
Владение способами деятельности делает обучение активным и действенным. Поэтому очень важно, чтобы обучающийся смог соотнести данную ему для решения задачу к определенному классу, отличив ее по каким-либо признакам.
В методической и учебной литературе описан широкий ряд классификаций физических задач по различным признакам.
А.В.Усовой и Н.Н.Тулькибаевой подробно описаны способы классификации задач.
По их мнению по содержанию задачи делят на:
- текстовые;
- графические;
- экспериментальные;
- задачи-рисунки.
По основному способу решения:
- логические;
- вычислительные;
- графические;
- геометрические;
- экспериментальные.
По степени сложности:
- простые;
- сложные.
По характеру и методу исследования:
- качественные;
- количественные.
По характеру используемого материала выделяют:
- задачи, для решения которых достаточно знаний определенной темы, раздела;
- комплексные задачи, требующие применения знаний из различных разделов одного учебного предмета;
- задачи, требующие применения знаний из нескольких учебных дисциплин.
 [21, 10-11].
[21, 10-11].
С.Е.Каменецкий и В.П.Орехов подчеркивают, что задачи по физике классифицируют по многим признакам:
- по содержанию;
- целевому назначению;
- глубине исследования вопроса;
- способам решения;
- способам задания условия;
- степени трудности и т.д.
По содержанию задачи следует разделить прежде всего в зависимости от их физического материала. Различают задачи по:
- механике;
- молекулярной физике;
- электричеству и т.д.
Такое деление условно в том отношении, что нередко в условии задачи используются сведения из нескольких разделов физики.
Различают задачи с абстрактным и конкретным содержанием. Примером с абстрактным содержанием может быть следующая задача: какую силу нужно приложить, чтобы поднять по наклонной плоскости тело массой m, если длина плоскости l, а высота h? Трением пренебречь. Какова сила давления тела на плоскость?
Какова сила давления тела на плоскость?
Если же в задаче будет указано, какая именно используется наклонная плоскость, что за тело и как оно поднимается по ней, то это будет уже физическая задача с конкретным содержанием.
Достоинство абстрактных задач состоит в том, что в них выделяется и подчеркивается физическая сущность, выяснению которой не мешают несущественные детали. Главное достоинство конкретных задач — большая наглядность и связь с жизнью.
Задачи, содержащие материал о технике, промышленном сельскохозяйственном производстве, транспорте и связи, называют задачами с политехническим содержанием. Эти задачи должны составлять значительную часть задач по физике.
Ряд задач содержит сведения исторического характера: данные о классических физических опытах, открытиях, изобретениях или даже исторических легендах. Такие задачи называют задачами с историческим содержанием.
Широкое распространение получили также занимательные задачи. Отличительной чертой их содержания является использование необычных парадоксальных или занимательных фактов и явлений. Их решение оживляет уроки, повышает интерес учащихся к физике.
Отличительной чертой их содержания является использование необычных парадоксальных или занимательных фактов и явлений. Их решение оживляет уроки, повышает интерес учащихся к физике.
…По способу решения различают:
- устные;
- экспериментальные;
- вычислительные;
- графические задачи. [10, 9-10]
2. Общие вопросы методики решения физических задач
Мы видим, что как по содержанию, так и по дидактическим целям физические задачи очень разнообразны. Также, зачастую разным является и уровень подготовки учащихся в пределах одного классного коллектива. Кроме того, на начальном этапе изучения физики или отдельного физического раздела очень важен порядок решения задач разных типов: во многих случаях для понимания и выяснения физической сущности того или иного физического явления целесообразно начинать с решения задач качественных (задач-вопросов) и экспериментальных и только потом переходить к задачам вычислительным и графическим.
Курс физики без умения решать физические задачи не может быть усвоен в полном объеме. Очень многие учащиеся испытывают значительные затруднения при решении задач, что сказывается на их выборе своей будущей профессии и дальнейшего жизненного пути. Поэтому научить обучающегося решать физические задачи – одна из важнейших педагогических задач, но и вместе с этим — сложнейшая педагогическая проблема.
Тем не менее, сложность данного вида занятий для обучащихся может быть существенно уменьшена путем достаточного подбора учебных задач и применения ряда общих положений для их решения.
Как правило, в классе на уроке решение задачи начинают с ее внимательного чтения, желания понять о чем идет речь, то есть определить с каким физическим явлением мы будем иметь дело. После прочтения можно попросить кого-нибудь из обучащихся повторить условие задачи своими словами и постараться определить тип предложенной задачи:
- задача-вопрос;
- вычислительная задача;
- графическая и т.
 д.,
д.,
то есть дальше мы должны определить способ деятельности: будем ли мы что-то считать, работать с графиком или рассуждать.
После прочтения и пересказа условие задачи обучащимися может быть понято не до конца, поэтому желательно задать им несколько вопросов, например таких:
- Какие факты изложены в задаче, причины и следствия, может быть о чем-то не сказано, почему?
- О каком физическом явлении (или явлениях), физическом теле (телах) идет речь? Что с ними происходит?
- Какие физические законы (формулы) мы сможем использовать для объяснения происходящего в задаче?
- Почему тело изменило свое положение и как? назвать причины.
- Вспомнить, может что-то подобное встречалось на уроках?
После такой непродолжительной беседы обучающимся можно предложить задачу «нарисовать», показать «что было и что стало», ведь все-таки, наиболее часто приходится иметь дело с текстовыми задачами и только лишь запись «Дано:» не всегда может помочь делу.
Общие подходы к решению физических задач разных типов изложены в трудах ученых-методистов: А.В.Усовой, Н.Н.Тулькибаевой, С.Е.Каменецкого, В.П.Орехова, М.Е.Тульчинского и др.
А.В.Усова поясняет, что при решении задач-вопросов требуется объяснить, что то или иное физическое явление или предсказать, как оно будет протекать в определенных условиях. Как правило, в содержании таких задач отсутствуют числовые данные.
Например:
- На груди и на спине водолаза помещают толстые свинцовые пластины, а к башмакам приделывают свинцовые подошвы. Зачем это делают?
- Почему волосок электрической лампочки накаливается добела, в то время как провода остаются холодными, хотя по ним проходит такой же ток?
Отсутствие вычислений при решении задач-вопросов позволяет сосредоточить внимание учащихся на физической сущности. Необходимость обоснования ответов на поставленные вопросы приучает школьников рассуждать, помогает глубже осознать сущность физических законов. Решение задач-вопросов выполняют, как правило, устно, за исключением тех случаев, когда задача содержит графический материал. Ответы могут быть выражены и рисунками. Например, ответ к задаче: «Нарисуйте шар, плавающий на поверхности жидкости, плотность которой вдвое больше плотности вещества шара» — может быть выражен только рисунком.
Решение задач-вопросов выполняют, как правило, устно, за исключением тех случаев, когда задача содержит графический материал. Ответы могут быть выражены и рисунками. Например, ответ к задаче: «Нарисуйте шар, плавающий на поверхности жидкости, плотность которой вдвое больше плотности вещества шара» — может быть выражен только рисунком.
К задачам-вопросам тесно примыкают задачи — рисунки. В них требуется устно дать ответы на вопрос или изобразить новый рисунок, являющийся ответом на рисунок задачи. Решение таких задач способствует воспитанию у учащихся внимания, наблюдательности и развитию графической грамотности.
Количественные задачи — это задачи, в которых ответ на поставленный вопрос не может быть получен без вычислений. При решении таких задач качественный анализ так же необходим, но его дополняют еще и количественным анализом с подсчетом тех или иных числовых характеристик процесса. Количественные задачи разделяют по трудности на простые и сложные.
Под простыми задачами понимают задачи, требующие несложного анализа, и простых вычислений, обычно в одно — два действия. …Для решения количественных задач могут быть применены разные способы: алгебраический, геометрический, графический. Алгебраический способ решения задач заключается в применении формул и уравнений. При геометрическом способе используют теоремы геометрии, а при графическом — графики.
…Эксперимент в задачах используют по разному. В одних случаях из опыта, проводимого на демонстрационном столе, или из опытов, выполняемых учащимися самостоятельно, находят данные необходимые для решения задачи. В других случаях задача может быть решена на основе данных, указанных в условиях задачи. Опыт в таких случаях используют для иллюстрации явлений и процессов, описанных в задаче, или для проверки правильности решения. Но если эксперимент применяется только для проверки решения, задачу неправомерно называть экспериментальной. Существенным признаком экспериментальных задач является то, что при их решении и данные берутся из опыта. В процессе решения экспериментальных задач у учащихся развивается наблюдательность, совершенствуются навыки обращения с приборами. При этом школьники глубже познают сущность физических явлений и законов.
В процессе решения экспериментальных задач у учащихся развивается наблюдательность, совершенствуются навыки обращения с приборами. При этом школьники глубже познают сущность физических явлений и законов.
В графических задачах в процессе решения используют графики. По роли графиков в решении задач различают такие, ответ, на который может быть получен на основе анализа уже имеющего графика, и в которых требуется графически выразить функциональную зависимость между величинами. Решение графических задач способствует уяснению функциональной зависимости между величинами, привитию навыков работы с графиком. В этом их познавательное и политехническое знание.
Физические задачи, в условии которых не хватает данных, для их решения называют задачами с неполными данными. Недостающие данные для таких задач находят в справочниках, таблицах и в других источниках. С такими задачами учащиеся будут часто встречаться в жизни, в связи с этим решение в школе подобных задач очень ценно.
Для того, чтобы проявить учащимся интерес к решению задач необходимо их умело подбирать. Содержание задач должно быть понятным и интересным, кратко и четко сформулированным. Математические операции в задаче не должны затушевывать ее физический смысл, необходимо избегать искусственности и устаревших числовых данных в условиях задач.
Содержание задач должно быть понятным и интересным, кратко и четко сформулированным. Математические операции в задаче не должны затушевывать ее физический смысл, необходимо избегать искусственности и устаревших числовых данных в условиях задач.
Начинать решение задач по темам нужно с простейших, в которых внимание учащихся сосредотачивается на закономерности, изучаемой в данной теме, или на уточнении признаков нового понятия, установлении его связи с другими понятиями. Затем постепенно следует переходить к более трудным задачам. [20, с. 93]
3. Решение текстовых задач: качественных и количественных
В учебном процессе по физике наиболее часто используют текстовые задачи, в которых условие выражено словесно, текстуально, причем в условии есть все необходимые данные, кроме физических постоянных. По способам решения их разделяют на задачи — вопросы и расчетные (количественные).
Задачи-вопросы решают устно. Для решения, как правило:
- не требуется никаких расчетов;
- требуется сообразительность и находчивость;
- необходимо отчетливое понимание сущности физических явлений и закономерностей.

Решение качественной задачи – это построение рассуждения, приводящее к ответу на поставленный вопрос. Чтобы научить осознанно подходить к решению качественных задач, нужна определенная система работы учителя и продуманная методика обучения.
Прежде всего это — правильный подбор задач. Наиболее доступны для начала задачи, в которых предлагается дать объяснение физическим явлениям, или фактам, известным обучащимся из личного опыта. Решение качественных задач включает три этапа: чтение условия, анализ задачи и решение. При анализе содержания задачи используют, прежде всего, общие закономерности, известные обучащимся по данной теме. После этого выясняют, как конкретно должно быть объяснено то явление, которое описано в задаче. Ответ к задаче получают как завершение проведенного анализа. В качественных задачах анализ условия тесно сливается с получением нужного обоснованного ответа.
Пример:
На цоколе лампы карманного фонаря написано: «0,28 А».
Что это означает? Что произойдет если по спирали лампы пропустить меньшую силу тока? Что произойдет, если сила тока в спирали будет значительно больше?
Речь идет о протекании тока в участке цепи – спирали лампы карманного фонаря. А что такое электрический ток? Направленное движение заряженных частиц, а сила тока в соответствии с формулой-определением – это количество заряда, перенесенное по спирали в единицу времени. Следовательно, если увеличить силу тока, увеличится и количество заряда, перенесенное по проводнику в единицу времени. В данной задаче три вопроса, поэтому и ответов должно быть тоже 3:
- Это означает, что при нормальной работе лампы по ее спирали за каждую секунду переносится заряд в 0,28 Кл;
- Если по спирали лампы пропустить меньшую силу тока, будет переносится и меньший заряд, т.е. накал лампы уменьшится;
- Если сила тока в спирали будет значительно больше, то и заряд, переносимый в единицу времени увеличится, увеличится накал спирали и спираль может перегореть.

Решение расчетных задач – это умение получать новое знание в процессе применения формул.
Простые расчетные задачи – это задачи «на подстановку»: краткая запись условия, перевод в СИ, решение в общем виде, постановка данных в формулу и анализ результата.
Решение более сложных расчетных задач требует осуществления трех важных шагов:
- выяснить, о каком физическом явлении идет речь в тексте задачи;
- смоделировать ситуацию, описанную в тексте задачи, и представить модель ситуации в виде рисунка;
- подобрать законы или составить уравнения, которые описывают эту модель и позволяют получить ответ на вопрос задачи.
Поэтому начинать решение следует с анализа задачи по схеме:
Явление – Модель — Законы
Для этого необходимо:
I. Распознать явления, которым соответствует описанная в задаче ситуация:
- Выделить объекты (анализ), с которыми происходят изменения, и их характеристики в начальном состоянии;
- Выделить конечное состояние каждого объекта и его характеристики;
- Установить воздействия, которые привели к изменению состояния каждого объекта;
II.-reshenie-332.jpg) Построить модель ситуации (выполнить рисунок, схему или чертеж («нарисовать» задачу), описанной в задаче;
Построить модель ситуации (выполнить рисунок, схему или чертеж («нарисовать» задачу), описанной в задаче;
III. Составить уравнения, описывающие построенную модель.
Прежде всего необходимо научиться различать явления, которым соответствует ситуация задачи. Выполним это на примере анализа условия задачи по теме «Постоянный ток»:
Источник замкнули сначала на один резистор, а потом на другой, затем на оба, соединенные последовательно. В первом случае сила тока – 3А, во втором – 2А, в третьем – 1,5А. Какова сила тока, проходящего через источник при параллельном соединении этих сопротивлений?
Итак, объекты в начальном состоянии – замкнутая цепь с разными потребителями: первый резистор, второй резистор, последовательно соединенные резисторы.
Конечное состояние – замкнутая цепь с параллельно соединенными резисторами.
Воздействие – не указано.
Явление – электрический ток в замкнутой цепи, при последовательном и параллельном соединении потребителей.
Таким образом, начиная уже с 7 класса надо приучать обучающихся решать расчетные задачи по такому простому плану:
- Явление;
- Рисунок;
- Формула (или уравнение для классов постарше).
Такая систематическая работа способствует развитию логического мышления обучающихся, и воспитывает сознательный подход к решению задач. Ели обучающийся заранее знает план, по которому ему придется действовать, то и сам процесс для него становится психологически комфортным.
Анализ условия задачи на уроке можно проводить в виде беседы, в ходе которой обсуждаются логически связанные между собой вопросы, что постепенно подводит обучащихся к наиболее рациональному способу решения задачи. Иногда полезно разобрать несколько вариантов решения одной и той же задачи, сопоставить их, и выбрать наиболее рациональный. Нужно систематически приучать обучащихся самостоятельно анализировать задачи, требуя от них вполне сознательного и обоснованного рассуждения.
4. Операции сравнения, анализа и синтеза при решении физических задач
В современных условиях развивающего обучения важнейшим критерием успешного освоения курса физики является развитие логического мышления. Именно систематическое решение физических задач способствует формированию таких мыслительных операций как сравнение, анализ и синтез, которые в свою очередь позволят решить любую даже не физическую задачу.
Часто, основными средствами обучения решению задач по физике являются:
- решение «по образцу»;
- решение в соответствии с определенным алгоритмом решения.
Оба эти способа активно пропагандируются также и в различных авторских рабочих тетрадях на печатной основе. Но надо учитывать:
- решать «по образцу» учащиеся привыкают быстро и настолько сильно, что стоит немного изменить условие задачи – сразу начинаются трудности;
- решение по алгоритму дает хороший результат при решении задач из некоторых разделов, например, из кинематики, и для сложных творческих задач подобрать определенный алгоритм практически невозможно.

Кроме того, оба эти метода не решают главную педагогическую задачу – они не развивают учащегося, его учебную инициативу и самое главное: не обеспечивают успешности в случае его абсолютно самостоятельной работы.
По заключению ученых-методистов гораздо более сложным способом решения физических задач, но вместе с тем и достаточно универсальным способом (методом) решения практически любой физической задачи является применение мыслительных операций.
По мнению А.В.Усовой, аналитико-синтетический метод — основной метод решения задач по физике в средней школе во всех классах. Удачное применение его в учебном процессе позволяет вести учащихся по правильному пути отыскания решения задачи, и способствует развитию их логического мышления.
В методических пособиях по физике довольно часто анализ, и синтез рассматривают как два самостоятельных метода. Однако такое разделение нельзя понимать буквально. Синтез и анализ также неразделимы, как индукция и дедукция в процессе мышления. При решении физических задач используют анализ и синтез, взятые в совокупности, т.е. практически применяют аналитико-синтетический метод.
При решении физических задач используют анализ и синтез, взятые в совокупности, т.е. практически применяют аналитико-синтетический метод.
При этом методе решения путем анализа, начиная с вопроса задачи, выясняют, что необходимо знать для ее решения, и, постепенно расчленяя сложную задачу на ряд простых, доходят до известных величин, данных в условии.
Затем с помощью синтеза рассуждения проводят в обратном порядке: используя известные величины, и подбирая необходимые соотношения, производят ряд действий, в результате которых находят неизвестное.
Поясним это на примере следующей задачи: «Найдите давление на почву гусеничного трактора массой 10 т, если длина опорной части гусеницы 2 м, а ширина 50 см».
Анализ: чтобы определить давление трактора на почву, необходимо знать действующую на него силу тяжести, и площадь опоры. Сила тяжести в задаче не дана, площадь опоры не указана. Для определения общей площади опоры, т. е. площади опорной части двух гусениц, необходимо узнать площадь опоры одной гусеницы и умножить ее на два. Площадь одной части одной гусеницы можно определить, так как известны ее ширина и длина. Силу тяжести, действующую на трактор, можно найти по известной его массе.
е. площади опорной части двух гусениц, необходимо узнать площадь опоры одной гусеницы и умножить ее на два. Площадь одной части одной гусеницы можно определить, так как известны ее ширина и длина. Силу тяжести, действующую на трактор, можно найти по известной его массе.
Синтез: рассуждение ведут в обратном порядке, в его ходе составляют план решения и производят необходимые вычисления. Последовательность рассуждения примерно следующая.
Зная ширину длину опорной части гусеницы, можно определить опорную площадь одной гусеницы. Для этого необходимо длину на ширину. Зная опорную площадь одной гусеницы, можно определить общую площадь опоры трактора. Для этого необходимо найденную площадь, т.е. площадь опорной части одной гусеницы, умножить на два. Зная массу трактора, находят силу тяжести, действующую на него. По силе тяжести и площади опоры можно определить давление трактора на почву. Для этого силу тяжести необходимо разделить на площадь опоры [20, с. 96-97].
Тульчинский М.Е. также поясняет: чтобы связать данное явление с одним или несколькими физическими законами, надо расчленить сложное явление на ряд простых, т.е. применить анализ. Для соединения в общий вывод следствий, полученных из отдельных законов, используется синтез [19, с. 5].
Каменецкий С.Е. и Орехов В.П. описывают применение аналитического и синтетического способов рассуждения при решении задач следующим образом: при аналитическом способе рассуждения начинают с определения искомой величины, выясняют, как связана эта величина с другими величинами и, последовательно применяя физические формулы, приходят кратчайшим путем к искомой величине.
При синтетическом способе рассуждения сначала устанавливают промежуточные зависимости между данными физическими величинами, стараясь подготовить почву для определения искомой величины. В итоге всех операций, часть из которых может оказаться лишней, получают выражение, из которого и находят искомую величину.
Учащиеся чаще всего становятся на путь синтетического решения: они пробуют различные зависимости между величинами, пока не установят такую, которая дает возможность найти искомую величину. При этом, естественно, вначале возможны пути, не приводящие к желаемому результату. Синтетический, способ решения наиболее простой, но не всегда короткий.
Аналитический способ труден, так как требует строгой логической последовательности в действиях, но он быстрее приводит к конечной цели.
При решении задач, особенно в старших классах, предпочтение нужно отдать аналитическому способу, так как этот способ имеет большое значение для развития логического мышления.
Приведем пример решения задачи аналитическим и синтетическим способами.
Продолжение статьи
В настоящий момент информационное общество нуждается в человеке «обучаемом», а не только «обученном»: способном самостоятельно учиться и многократно переучиваться в течение своей жизни, быть готовым к самостоятельным действиям и принятию решений.
Основу деятельностного подхода в обучении составляет теория поэтапного формирования умственных действий. Реализация учебной деятельности в современных условиях достигается формированием у обучащихся теоретического мышления путем специального построения учебного процесса и особой организации познавательной деятельности. Учитель должен не просто излагать систему знаний, а способствовать формированию у обучающихся научного стиля мышления.
Одной из основных целей учебного предмета «Физика» для каждого учителя должно стать развитие мышления обучающихся, прежде всего абстрактного-логического; формирование у обучащихся качеств мышления и качеств личности, необходимых для полноценного функционирования человека в современном обществе.
Список использованной литературы
- Федеральный государственный образовательный стандарт Основного общего образования http:// standart.edu.ru/catalog.aspx?CatalogId=2588.
- Большой энциклопедический словарь.
 — 2-е изд., перераб. и доп. — М.: Большая Российская энциклопедия; СПб.: Норинт, 2001. — 1456 с.
— 2-е изд., перераб. и доп. — М.: Большая Российская энциклопедия; СПб.: Норинт, 2001. — 1456 с. - В.Е.Столяренко. Психология и педагогика: учебник / Л.Д.Столяренко, С.И.Самыгин,– Изд. 4-е. – Ростов н/д : Феникс, 2014. – 636 с. – (Высшее образование).
- Волькенштейн В.С. Все решения к «Сборнику задач по общему курсу физики» В 2 кн. Кн. 2 – М.: Олимп: ООО «Фирма «Издательство АСТ», 1999 г. – 592 с. – (Готовимся к экзаменам).
- Выготский Л.С. Проблемы развития психики, собр. соч. в 6-ти тт. Т.З / Под ред A.M. Матюшкина. — М.: Педагогика, 1983. — 368 с.
- Гальперин П.Я. Лекции по психологии: Учебное пособие для студентов вузов. – М: Книжный дом «Университет»: Высшая школа, 2002.
- Громцева О.И. Сборник задач по физике: 10-11 классы — М.: Издательство «Экзамен», 2015. – 208 с.
- Зверева Н.М., Володарский В.Е., Вакс И.З., Коршак Е.В., Легкий М.П. Об активизации мышления учащихся при постановке физических задач//Физика в школе. — №2, 1977.
 — С. 34-42.
— С. 34-42. - Зимняя И.А. Педагогическая психология: Учеб. пособие. — Ростов-на-Дону: Феникс, 1997.-480 с.
- Каменецкий С.Е., Орехов В.П. Методика решения задач по физике в средней школе. Пособие для учителей. /; М., «Просвещение», 1971. – 448 с.
- Каменецкий С.Е., Пурышева Н.С., Важеевская Н.Е. и др.
Учеб. пособие для студ. высш. пед. учеб. заведений. — Под ред. С.Е. Каменецкого, Н.С. Пурышевой. — М.: Изд. центр «Академия», 2000. — 368 с. - Касаткина И.Л. Репетитор по физике: электромагнетизм, колебания и волны, оптика, элементы теории относительности, физика атома и атомного ядра. / И.Л. Касаткина. – Изд-е 10-е, перераб. и доп. / Под ред. Т.В. Шкиль. — Ростов н/Д: идательство «Феникс», 2009 – 844 с. : ил.
- Менчинская Н.А. Проблема учения и умственного развития школьника. — М.: Педагогика, 1989. — 223 с.
- Рубинштейн С.Л. О мышлении и путях его исследования. — М.: АН СССР, 1958.-147 с.
- Рубинштейн С.Л. Основы общей психологии.
 — С.-Пб.: Питер Ком, 1998. — 688 с.
— С.-Пб.: Питер Ком, 1998. — 688 с. - Столяренко Л.., Самыгин С.И. Психология и педагогика: учебник/ Изд. 4-е. – Ростов н/д: Феникс, 2014. – 636 с. (Высшее образование).
- Тарасов Л.В., Тарасова Н.Н.. Вопросы и задачи по физике.- М.:Высш. шк., 1968. — 238с.
- Тульчинская Г.М. Формирование умений учащихся по применению сравнений в курсе физики средней школы. — Дисс. …к.п.н, — М.: МПГУ, 1991.-176 с.
- Тульчинский М.Е. Качественные задачи по физике в средней школе. Пособие для учителей. Изд. 4-е, переработ. И доп. М., «Просвещение», 1972. 240 с. с ил.
- Усова А.В., Орехов В.П., Каменецкий С.Е. Методика преподавания физики в 7-8 классах средней школы: Пособие для учителя / и др.; Под редакцией А.В.Усовой. – 4-е изд., перераб. – М.: Просвещение, 1990. – 319 с.
- Усова А.В., Тулькибаева Н.Н. Практикум по решению физических задач: Для студентов Физ.-Мат. фак. /. – 2-е изд. – М.: Просвещение, 2001. – 206 с.: ил.
- Фаликман М.
 Виды мышления: видеолекция / Мария Фаликман (к. п. н.) // ПостНаука: проект. — 16.10.2015. — 14 мин 35 с.
Виды мышления: видеолекция / Мария Фаликман (к. п. н.) // ПостНаука: проект. — 16.10.2015. — 14 мин 35 с. - Физика 8 класс: рабочая тетрадь к учебнику А.В.Перышкина / Т.А.Ханнанова. – М.: Дрофа, 2014. – 127, [1] с.: ил.
- Фридман Л.М., Волков К.Н. Психологическая наука — учителю. — М.: Просвещение, 1985, — 224 с.
- http://files.school-collection.edu.ru/.
- Одинцова Н.И. Поурочное планирование по физике к Единому государственному экзамену / Н.И. Одинцова, Л.А.Прояненкова. – М.: Издательство «Экзамен», 2009. – 414, (Серия «УМК»).
- Материалы курса «Как научить решать задачи по физике (основная школа). Подготовка к ГИА»: лекции 5-8. – М.: Педагогический университет «Первое сентября», 2010. – 128 с.
Необычные задачи по физике развивающие научное мышление (для школьников) / Хабр
Возможно вы уже читали мои статьи:
А сегодня я хочу поделиться своим давним но интересным проектом и его идеей.
Когда я учился в аспирантуре, и работал в “Лаборатории методики преподавания физики” при Харьковском национального университета им. В.Н.Каразина, я обеспечивал свою семью за счет репетиторств. Хотелось давать ученикам возможность увидеть физику не только в учебнике но и в реальной жизни, удивить и завлечь их наукой. Тогда и пришла идея сделать простенький сайт, в помощь мне и учителям, которые приходили в нашу лабораторию на курсы повышения квалификации.
В.Н.Каразина, я обеспечивал свою семью за счет репетиторств. Хотелось давать ученикам возможность увидеть физику не только в учебнике но и в реальной жизни, удивить и завлечь их наукой. Тогда и пришла идея сделать простенький сайт, в помощь мне и учителям, которые приходили в нашу лабораторию на курсы повышения квалификации.
С тех пор прошло более 10 лет, сайт не развивался, но актуальность свою сохранил. Данный пост будет интересен как преподавателям, так и родителям, которые хотят, чтоб их ребенок любил и знал физику. Заодно сможете проверить и свои навыки.
В чем суть?
Существует огромное количество хороших и качественных задачников по физики содержащие правильно подобранные и разбитые по темам задачи разного уровня сложности. Вся, причем только необходимая, информация имеется в задачи, и, разумеется, есть один единственный и точный ответ.
Решение классических задач безусловно необходимый элемент обучения, но останавливаться только на них нельзя, ведь в реальном мире мы вынуждены сами определять важные исходные данные из множества, сами выбирать наиболее оптимальные методы решения, и мириться с их неточностями.
Я искал интересные статьи, которые могли бы привлечь внимание школьника (про суперкар, слона прыгающего на батуте, или про дом поднятый в небо при помощи шаров с гелием). Почти всегда удавалось найти новость по изучаемому разделу физики. Ребенок оказывался на месте инженера, и должен был искать ответы на поставленные вопросы. Методы решения ученик выбирал сам, а все необходимые данные он искал в статье, или в просторах интернета. Некоторые данные можно было получить из фотографий.
Фото к задаче о роботе-блохе
Таким образом дети приучались к самостоятельной исследовательской работе, начинали замечать физику вокруг себя и просто получали удовольствие от занятий. На базе таких задач и появился сайт 15 Минут науки.
Проверь свои силы
Занятия с периодическим применением сайта детям понравились. Однако оказалось, что даже сильные ученики и победители олимпиад, не всегда могут правильно ответить даже на простые вопросы, из-за того что привыкли к “идеализированным” задачам. Попробуйте сами определить скорость этой улитки (считая ширину кадра равной 12 см.):
Попробуйте сами определить скорость этой улитки (считая ширину кадра равной 12 см.):
Видео из
этого поста.
Определили? Оставьте свой вариант ответа в опросе (в конце поста).
Правильный ответ тут, но приглашаю голосовать честноОколо 45 см/мин. Улитка проползла пути 12 см за 16 секунд.
Многие ошибочно засекают время между тем, как улитка появилась и исчезла, но правильно зафиксировать внимание на конкретной точке улитки.
Или вот задача про маятниковые часы, какой период колебаний маятника? Как будете определять? Насколько точным будет результат?
Ответ и пояснение
Многие дети запускают секундомер на часах но, разумеется, не могут мгновенно запустить и остановить по завершению колебания. Тогда и появляется идея делать замер для десяти, или более колебаний за раз.
А вот еще одна задача из того-же поста:
Для тонкой подстройки периода колебаний маятника из “башни Елизаветы”, сверху на маятник клали (или снимали) пенни – старинная английская монета.Одна монетка способна скорректировать точность часов на 0,4 секунды за сутки. Почему это происходит, ведь период колебаний не зависит от массы маятника?
Подсказок не будет хочется увидеть ваши версии в комментарии. Кто знает правильный ответ — прячьте его под спойлер, пожалуйста.
Еще немножко про сайт и послесловие
Сайт не требует регистраций, пожертвований и не содержит рекламы, это принципиальная позиция автора. Взамен прошу понять и простить массу ошибок, они были допущены, так как сайт писался ночью после трех работ и учебы. Если пришлете замечания, я постараюсь максимально быстро внести правки.
Ответов на задачи не будет, зато по ссылке “ответы и подсказки” находится интересный дополнительный материал по теме.
Стоит обратить, что разбиение на классы соответствует старой программе украинских школ. Обновлять на новую, или добавлять российские программы не буду поскольку они постоянно меняются и одновременно актуальными могут быть сразу несколько программ. Ориентируйтесь не по классам, а по темам, или по разделам физики.
Ориентируйтесь не по классам, а по темам, или по разделам физики.
Также есть желание написать про учебный прибор по молекулярной физике, который был создан в нашей лаборатории и который может повторить каждый, и про некоторые другие простые эксперименты по физики. Есть ли читатели, которым интересна данная тема?
ЕГЭ. Физика. Электродинамика. Квантовая физика. Качественные задачи.500 задач с решениями и ответами. Ответы — Учебник 2021 — 2022 год
Авторы: Демидова Марина Юрьевна, Грибов Виталий Аркадьевич, Гиголо Антон Иосифович
Издательство: Экзамен
ЕГЭ. Физика. Электродинамика. Квантовая физика. Качественные задачи.500 задач с решениями и ответами
«Задания по физике, аналогичные заданиям из банка заданий ЕГЭ.
В серию входит два сборника, содержащие суммарно более 950 заданий Единого государственного экзамена по темам «»Механика»», «»Молекулярная физика»», «»Электродинамика»», «»Квантовая физика»» и «»Качественные задачи»». В пособии приведены ответы ко всем заданиям, а также решения всех сложных задач, требующих развернутого ответа.
Пособие необходимо учителям, учащимся старших классов, их родителям, а также методистам и членам приемных комиссий.
В пособии приведены ответы ко всем заданиям, а также решения всех сложных задач, требующих развернутого ответа.
Пособие необходимо учителям, учащимся старших классов, их родителям, а также методистам и членам приемных комиссий.
На этой странице вы можете бесплатно скачать правильные ответы к новому сборнику для 1 полугодия и 2 полугодия обучения в школе. Новый сборник — решебник предназначен для учащихся, учителей школы и родителей, которые хотят помочь своим детям освоить предмет на хорошую оценку! Надеемся, что новые задания из сборника ГДЗ подойдут для следующего 2023 — 2024 учебного года. Полную версию учебника с ответами можно бесплатно скачать в формате ВОРД или PDF и потом распечатать на принтере, а так же читать онлайн. Также здесь можно скачать и распечатать ответы для родителей на домашнее задание, примеры, решения, страница, вопросы, пояснения и объяснения к онлайн заданиям из нового учебника.
Купить этот сборник недорого наложенным платежом за наличный или безналичный расчет с доставкой можно в Интернет-магазине или просто нажать кнопку КУПИТЬ
Официальный сайт. 2021 — 2022 учебный год. Открытый банк заданий. Полная версия. КДР. РДР. Тренажер. ВПР. ФИПИ ШКОЛЕ. ФГОС. ОРКСЭ. МЦКО. ФИОКО. ОГЭ. ЕГЭ. ГИА. Школа России. Школа 21 век. ГДЗ. Решебник. Перспектива. КРС. Школа 2100. Таблица. Планета знаний. Страница. Россия. Беларусь. Казахстан. РБ
2021 — 2022 учебный год. Открытый банк заданий. Полная версия. КДР. РДР. Тренажер. ВПР. ФИПИ ШКОЛЕ. ФГОС. ОРКСЭ. МЦКО. ФИОКО. ОГЭ. ЕГЭ. ГИА. Школа России. Школа 21 век. ГДЗ. Решебник. Перспектива. КРС. Школа 2100. Таблица. Планета знаний. Страница. Россия. Беларусь. Казахстан. РБ
Вид поставки: Электронная книга. Лицензия. Полная версия издательства с картинками
Способ доставки: электронная доставка, наложенный платеж
Язык книги: Русский
Варианты формата книги: Word, PDF, TXT, EPUB, FB2, PDF, MOBI, DOC, RTF, DJVU, LRF
Категория: Учебная, методическая литература и словари | Книги для школы | Физика. Астрономия | ЕГЭ по физике
СКАЧАТЬ ОТВЕТЫ | КУПИТЬ | ЧИТАТЬ ОНЛАЙН | ОТЗЫВЫ | ОБСУДИТЬ
Презентация «Решение качественных задач на тему «Механическая энергия»» 7 класс
Качественные задачи
по теме
«Потенциальная и кинетическая энергия»
7 класс
Каким видом механической энергии обладает заведенная пружина механической игрушки?
На полу лежат медные чайник и миска одинаковой массы. Их подняли и поставили на стол. Одинаково ли при этом изменилась их потенциальная энергия?
Их подняли и поставили на стол. Одинаково ли при этом изменилась их потенциальная энергия?
Если скорость тела увеличить в 3 раза, во сколько раз изменится его кинетическая энергия?
Во сколько раз изменилась скорость тела, если его кинетическая энергия уменьшилась в 16 раз?
Почему в походе опытный турист предпочитает перешагнуть через упавшее дерево, вместо того чтобы сначала наступить на него, а затем спрыгнуть?
Как меняется потенциальная энергия воздуха в футбольном мяче при ударе по мячу ногой?
Ударившийся о землю мяч подпрыгивает несколько раз. Почему при каждом последующем прыжке он подскакивает на меньшую высоту?
На соревнованиях по прыжкам в воду спортсмен сначала прыгает на доску-трамплин, а затем вверх. Почему при этом прыжок получается более высоким?
В какой точке траектории движения искусственного спутника потенциальная энергия его относительно Земли наибольшая; наименьшая? Что можно сказать о кинетической энергии спутника в этих точках?
Двигаясь по сыпучему песку или рыхлому снегу, мы затрачиваем больше энергии, чем при движении по твердой дороге. Объясните почему.
Объясните почему.
В какой реке — горной или равнинной — каждый кубический метр текущей воды обладает большей кинетической энергией? Почему?
Морские волны совершают большую работу по разрушению берегов. Какой энергией они обладают и что является источником этой энергии?
Объясните физический смысл поговорки «Что тратишь, поднимаясь в гору, вернёшь на спуске».
Тело массой m поднимают на высоту h. Одинаковой ли будет потенциальная энергия тел, если опыт проводить на Земле и на Луне?
Камень брошен вертикально вверх. Опишите, какие превращения энергии происходят при полёте камня.
Интересные камни
Почему не падают?
https://www.youtube.com/watch?v=88gd8Z8nZL0
(PDF) Подход к решению проблем в множественных представлениях качественных и количественных задач кинематики движения
90 Jurnal Ilmiah Pendidikan Fisika Al-BiRuNi, 08 (1) (2019) 89-98
В решении физических задач,
sпредставление состоят из графика, символа,
вербального и диаграммы, которые имеют
подход к их решению и решению каждой
задачи в различных представлениях
зависит от способности учащихся
понимать каждое представление (Aviani &
Я, 2015). В задачах физики
В задачах физики
представление имеет несколько типов, включая
вербальную или лингвистическую, диаграммную,
изобразительную, графическую, символическую и
математическую формы. Если у учащихся есть способность
во многих представлениях, можно сказать, что
говорят, что учащиеся обладают способностями к множеству представлений (Hung & Wu,
2018). Предыдущее исследование показало, что
учащихся, которые могут переводить вербальные задачи
в диаграммы, лучше умеют решать
задачи, чем студенты, которые не могут
переводить задачу (Bollen, Kampen, Baily,
Kelly, & Cock, 2017).
Различные подходы к решению
качественных и количественных задач это
важно для улучшения решения задач
способности решать физические задачи
(Kustusch, 2016; Marshman & Singh,
2015). Если студенты предпочитают предметы, связанные с
исчислением, они будут склонны решать задачи
с использованием количественных методов, в то время как
студенты, которым не нравится исчисление, обычно
будут стремиться решать задачи качественным
способом (Сусак, Бубич). , Kazotti, Planinic, &
, Kazotti, Planinic, &
Palmovic, 2018).Хороший решатель задач
решает проблемы с качественным и
количественным подходом во всех видах задач,
но начинающий
решает проблемы только с количественным подходом
или просто с исчислением. Хороший решатель задач
, у которого есть все возможности представления
, это имя является кратным представлением
и оценивает свою работу
с помощью графического анализа (Susac, Bubic,
Martinjak, Planinic, & Palmovic, 2017).
Индонезийские учащиеся способны только
запоминать факты, термины и научные законы
только решать задачи, но не могут
использовать анализ рассуждений задачу, которая
встречается в повседневной жизни (Супено, Субики и
Рома, 2018). Поэтому большинство студентов в
индонезийских студентов считают
физику чем-то трудным, потому что она использует слишком
много формул и должна запоминать, если
хочет решать в ней задачи (Azizah et
al. , 2015). Это создает препятствия при решении задач
, 2015). Это создает препятствия при решении задач
с использованием нескольких представлений
(Nieminen, Savinainen, & Viiri, 2010).
Источник этой проблемы на самом деле не
только мы можем дать ученикам, а
роль учителя здесь очень важна
(Fahmi, 2017; Scherr, Plisch, & Goertzen,
2017). Большинство учителей, давая ученикам задачи
, не видят проблем в каждой категории представления
(Bunawan,
Setiawan, Rusli, & Nahadi, 2015).
Иногда учителя слишком много внимания уделяют
проблемам, которые обычно появляются на
выпускном экзамене. Это приводит к тому, что учащиеся
не привыкают к решению задач в различных
типах представлений. В результате
учащихся будут запутаны при решении
задач в разных представлениях, даже
, хотя иногда вопросы
относительно легкие (Bollen et al., 2017).
Иногда в умах школьников бывает
что мы запоминаем их с помощью физических
формул. При запоминании формулы
При запоминании формулы
по физике завершение количественного анализа
облегчит решение задачи
, потому что учащиеся ищут только
неизвестных значений в уравнении физики
(Rusilowati, 2017). Проблемы в некоторых
репрезентациях трудно решить с
только количественным подходом, иногда
требующим качественного подхода (Docktor
et al., 2015). Например, графы и
представления символов, студенты должны
качественных аналитических навыков, чтобы иметь возможность
представить события, которые происходят в задачах.
Предыдущее исследование, проведенное
(Ibrahim & Rebello, 2012), показало, что
учащихся манипулировали уравнениями только в
физических задачах в различных видах
представлений. Более того,
учащиеся редко использовали качественные решения для решения физических
задач.В проведенном исследовании они
использовали задачи на символьное представление,
графические и вербальные с качественными и
количественными вопросами по кинематике и
Шаблон решения задач для интеграции качественной и количественной физики Инструкция по JSTOR
Абстрактный Резюме Шаблон решения проблем позволяет использовать методологию обучения, которая объединяет аспекты как последовательного, так и концептуального обучения. Он предназначен для улучшения навыков критического мышления при использовании в рамках личностно-ориентированного подхода к обучению, когда регулярная и тщательная оценка обучения учащихся является ключевым компонентом учебной программы.
Он предназначен для улучшения навыков критического мышления при использовании в рамках личностно-ориентированного подхода к обучению, когда регулярная и тщательная оценка обучения учащихся является ключевым компонентом учебной программы.
Journal of General Education: A Curricular Commons of the Humanities and Sciences посвящен идеям и идеалам науки, которые просвещают понимание учебной программы, выходящее за рамки дисциплинарной и профессиональной концентрации, чтобы обеспечить достояние студенческого образования.Исследования, эссе, форумы и обзоры журнала вовлекают академические круги и других лиц в дискуссии об экспериментах и инновациях в общем образовании, а также об оценках общего образования, истории, философии и теоретической перспективе. Журнал ценит общее образование как краеугольный камень искусства свободы и социальной справедливости и как хранитель просвещенного участия.
Информация об издателе Являясь частью Пенсильванского государственного университета и подразделением библиотек и научных коммуникаций Пенсильванского государственного университета, Penn State University Press служит университетскому сообществу, гражданам Пенсильвании и ученым во всем мире, продвигая научное общение в основных гуманитарных дисциплинах. и социальные науки.Пресса объединяется с выпускниками, друзьями, преподавателями и сотрудниками, чтобы вести хронику жизни и истории университета. И как часть учреждения, предоставляющего землю и поддерживаемого государством, Press выпускает как научные, так и популярные публикации о Пенсильвании, призванные способствовать лучшему пониманию истории, культуры и окружающей среды штата.
и социальные науки.Пресса объединяется с выпускниками, друзьями, преподавателями и сотрудниками, чтобы вести хронику жизни и истории университета. И как часть учреждения, предоставляющего землю и поддерживаемого государством, Press выпускает как научные, так и популярные публикации о Пенсильвании, призванные способствовать лучшему пониманию истории, культуры и окружающей среды штата.
%PDF-1.4 % 184 0 объект > эндообъект внешняя ссылка 184 115 0000000016 00000 н 0000003522 00000 н 0000003792 00000 н 0000003818 00000 н 0000003870 00000 н 0000003905 00000 н 0000004417 00000 н 0000004578 00000 н 0000004746 00000 н 0000004915 00000 н 0000005093 00000 н 0000005171 00000 н 0000005247 00000 н 0000005326 00000 н 0000005404 00000 н 0000005482 00000 н 0000005559 00000 н 0000005636 00000 н 0000005713 00000 н 0000005790 00000 н 0000005867 00000 н 0000005944 00000 н 0000006021 00000 н 0000006098 00000 н 0000006175 00000 н 0000006252 00000 н 0000006329 00000 н 0000006406 00000 н 0000006483 00000 н 0000006560 00000 н 0000006637 00000 н 0000006714 00000 н 0000006791 00000 н 0000006868 00000 н 0000006944 00000 н 0000007694 00000 н 0000008031 00000 н 0000008738 00000 н 0000008979 00000 н 0000009584 00000 н 0000009831 00000 н 0000010262 00000 н 0000010339 00000 н 0000018158 00000 н 0000018723 00000 н 0000019102 00000 н 0000025746 00000 н 0000026178 00000 н 0000026555 00000 н 0000026844 00000 н 0000027661 00000 н 0000027927 00000 н 0000028258 00000 н 0000028400 00000 н 0000028952 00000 н 0000029215 00000 н 0000029533 00000 н 0000029638 00000 н 0000030536 00000 н 0000031248 00000 н 0000032075 00000 н 0000032867 00000 н 0000033028 00000 н 0000033830 00000 н 0000034302 00000 н 0000039120 00000 н 0000039475 00000 н 0000039852 00000 н 0000040063 00000 н 0000040927 00000 н 0000041759 00000 н 0000042464 00000 н 0000065575 00000 н 0000079844 00000 н 0000081660 00000 н 0000081926 00000 н 0000083404 00000 н 0000083650 00000 н 0000083985 00000 н 0000084080 00000 н 0000084513 00000 н 0000084727 00000 н 0000085013 00000 н 0000085078 00000 н 0000085135 00000 н 0000085306 00000 н 0000085404 00000 н 0000085501 00000 н 0000085645 00000 н 0000085769 00000 н 0000085885 00000 н 0000085996 00000 н 0000086114 00000 н 0000086259 00000 н 0000086396 00000 н 0000086504 00000 н 0000086698 00000 н 0000086831 00000 н 0000086950 00000 н 0000087077 00000 н 0000087259 00000 н 0000087370 00000 н 0000087536 00000 н 0000087643 00000 н 0000087776 00000 н 0000087923 00000 н 0000088062 00000 н 0000088217 00000 н 0000088344 00000 н 0000088494 00000 н 0000088593 00000 н 0000088709 00000 н 0000088850 00000 н 0000088954 00000 н 0000002596 00000 н трейлер ]>> startxref 0 %%EOF 298 0 объект>поток xb«`f`6b`g«[ ̀
Курсы физики — Колледж Шабо
Эти списки взяты из Curricunet, и некоторые курсы могут не предлагаться каждый семестр. Для получения дополнительной информации свяжитесь с академическим отделом, поговорите с консультантом или обратитесь к текущему расписанию занятий и каталогу колледжей.
Для получения дополнительной информации свяжитесь с академическим отделом, поговорите с консультантом или обратитесь к текущему расписанию занятий и каталогу колледжей.
PHYS 11 — Описательная физика ( 4,00 единицы )
Движение, гравитация, тепло, свет, звук, электричество, магнетизм, атомы и ядра. Современные научные проблемы и разработки, такие как альтернативные источники энергии, солнечная энергия, ядерная энергия, лазеры, теория относительности и черные дыры.Предназначен для лиц, не специализирующихся в области физических наук. Включает введение в лабораторию, принципы и методы с акцентом на основные концепции, обсуждаемые в классе. Может не получить кредит, если Физика 10 или Физика 10L была завершена.
Результаты обучения учащихся (SLO)
- Продемонстрировать мастерство выполнения лабораторного отчета по учебной программе по физике 11 наук (включая физику, химию, науки о Земле, геологию, метеорологию и астрономию), конкретно определяя части научного процесса, включая данные наблюдений, прошлые исследования, проверяемые гипотезы, результаты экспериментов, анализ данных, поддержку или опровержение предшествующей теории , рецензирование и публикация.

PHYS 122 — Дополнительная инструкция по физике (0,50–1,00 ед.)
Индивидуальный курс с учебным пособием от инструктора, наставника студентов, по основным вычислениям по физике, предназначенный для развития уверенности в себе и подготовки студента к решению проблем при обычной навигации по курсам физики.
Результаты обучения учащихся (SLO)
- Применение концепций и решение задач по физике
- Совместное решение проблем
- Демонстрация повышенной осведомленности о стилях обучения для повышения успеха в физике
PHYS 18 — Подготовительная физика ( 3.00 единиц )
Основные методы решения задач в механике как основа для Физики 2А и Физики 4А. Методы и стратегии, используемые для решения задач количественной физики. Предназначен для студентов, изучающих математику, инженерию и физику. Акцент на групповых действиях по решению проблем, разнообразии подходов к решению проблем и подробном устном и письменном представлении решений.
Результаты обучения учащихся (SLO)
- Демонстрация математических способностей и способности рассуждать, необходимые для решения вводных физических аналитических и концептуальных задач
PHYS 25 — Вычислительные методы для инженеров и ученых ( 3.00 единиц )
Методология и приемы решения инженерных/научных задач с использованием компьютерно-прикладных программ численного анализа MATLAB, SimuLink, MuPad и EXCEL. Технические расчеты и визуализация с использованием программного обеспечения MATLAB. Примеры и приложения из прикладной математики, физической механики, электрических цепей, биологии, тепловых систем, жидкостных систем и других областей науки и техники. Может не получить зачет, если инженерное дело 25 или математика 25 были завершены.
Результаты обучения учащихся (SLO)
- Учащиеся будут решать ВРУЧНУЮ, используя дифференциальное исчисление, для независимой переменной, которая оптимизирует/минимизирует/максимизирует некоторую величину зависимой переменной, полученную в результате анализа реальной ситуации-сценария.

- Имея набор данных, который можно смоделировать либо с помощью степенной функции, либо с помощью экспоненциальной функции, учащиеся должны линеаризовать данные, а затем выполнить линейную регрессию с использованием программного обеспечения MATLAB или EXCEL, чтобы определить наилучшие константы аппроксимации m и б.
- Учащиеся будут использовать среду программирования MATLAB на основе SimuLink InterConnected-Icon для создания диаграммы SimuLink FeedBack Diagram, которая создает график численного решения нелинейного, неоднородного дифференциального уравнения второго порядка.
- Учащиеся будут использовать команды base-MATLAB для создания файла сценария, который создает график численного решения нелинейного, неоднородного дифференциального уравнения второго порядка.
- Учащиеся будут использовать родное «ПРИЛОЖЕНИЕ» MATLAB, MuPad, для решения СИМВОЛИЧЕСКОГО уравнения линейного неоднородного дифференциального уравнения второго порядка.
PHYS 27 — Введение в беспилотные полеты и ракетостроение ( 3,00 единицы )
Этот курс знакомит студентов с физикой, лежащей в основе, а также с созданием и эксплуатацией беспилотных летательных аппаратов, таких как ракеты, воздушные шары и беспилотные летательные аппараты (дроны), которые собирают данные об атмосфере в полете, которые затем анализируются и представляются.
Результаты обучения учащихся (SLO)
- Создайте рабочую печатную плату, которая точно собирает атмосферные данные во время полета беспилотного летательного аппарата.
- Соберите работающий беспилотный автомобиль, который будет подниматься и приземляться с неповрежденной платой.
- Проанализируйте полученные в полете данные.
PHYS 3A — Колледж физики A ( 4,00 единицы )
Введение в основные принципы классической механики с использованием исчисления для студентов, изучающих науки о жизни и архитектуру. Включает в себя: научный метод и социальную ответственность ученого, ньютоновскую механику, энергию, гравитацию, жидкости, термодинамику и вибрационные волны.
Результаты обучения учащихся (SLO)
- 70% учащихся смогут записать по памяти пифагорейские тождества, взаимные тождества, формулы двойного угла для синуса и косинуса, а также формулы суммы и разности для синуса и косинуса
- 70% учащихся смогут использовать закон синусов и закон косинусов для решения косоугольных треугольников
- 70% учащихся смогут строить графики тригонометрических функций
PHYS 3B — Колледж физики B
( 4. 00 единиц )
00 единиц )
Введение в основные принципы ЭЛЕКТРОМАГНИТИЗМА И СОВРЕМЕННОЙ ФИЗИКИ с использованием исчисления для студентов, изучающих науки о жизни и архитектуру. Включает электростатику, электросхемы, электромагнитные волны, оптику, теорию относительности, атомную и ядерную физику и социальную ответственность ученого и архитектора.
Результаты обучения учащихся (SLO)
- 70 % учащихся смогут работать на стандартном лабораторном оборудовании
- 70 % учащихся смогут анализировать лабораторные данные
- 70 % учащихся смогут составлять подробные лабораторные отчеты
PHYS 4A — Общая физика I ( 5.00 единиц )
Введение в принципы ньютоновской механики с использованием исчисления по мере необходимости. Векторы, кинематика, динамика, энергия, импульс, вращение, колебания и гравитация.
Результаты обучения учащихся (SLO)
- Оценить улучшение успеваемости учащихся по физике 4A в течение семестра с использованием опросника Force Concept Inventory с опросом до и после занятий и нормализованным приростом («NG»)
- PHYS 4A – Учащиеся должны уметь читать, переводить, составлять схемы и успешно решать качественно ключевые словесные задачи, связанные с понятиями кинематики в одном, двух и трех измерениях, законами движения Ньютона, гравитацией, работой и энергией, импульсом, вращательным движением и динамикой, статическим равновесием , и колебания.

- Демонстрация качественного владения физическими понятиями 4A в области механики, энергии, вращения, статики и/или гравитации посредством презентаций, групповых проектов, научных работ и/или домашних заданий
- Демонстрация мастерства физики 4A лабораторный отчет со всеми присутствующими элементами требований, включая реферат; введение; материалы, методы и процедуры; данные и анализ; Результаты и обсуждение; использованная литература; таблицы данных.
- Тест FCI до/после сравнения базовой механики с использованием нормализованного усиления 100% X [(после — до)/(30-до)]
PHYS 4B — Общая физика II ( 5.00 единиц )
Электрические поля, электрические токи, магнитные поля, индукционные токи, переменные цепи, уравнения Максвелла, электромагнитные волны.
Результаты обучения учащихся (SLO)
- Продемонстрировать качественное владение физическими понятиями 4B в области электричества, напряжения, цепей, конденсаторов и/или магнетизма с помощью презентаций, групповых проектов, научных работ и/или домашних заданий.

- Демонстрация мастерства физики 4B лабораторный эксперимент путем подачи полного лабораторного отчета со всеми присутствующими элементами требований, включая реферат; введение; материалы, методы и процедуры; данные и анализ; Результаты и обсуждение; использованная литература; таблицы данных.
- Продемонстрировать количественное владение концепциями физики 4B в E&M с помощью теста CSEM до/после.
- Чтение, перевод, составление диаграмм и успешное решение количественных задач с ключевыми словами, связанных с понятиями Закона Кулона, Закона Гаусса, сохранения энергии; определения емкости, тока и сопротивления, законы магнетизма, закон индукции Фарадея и концепция цепей переменного тока.
- Успешно решить качественно ключевые слова, связанные с понятиями Закона Кулона; Закон Гаусса; сохранение энергии; определения емкости, тока и сопротивления; законы магнетизма, закон индукции Фарадея и концепция цепей переменного тока.
- Продемонстрировать владение качественными аспектами электромагнетизма с помощью домашних заданий и/или экзаменационных задач.

- Продемонстрировать качественное владение концепциями Physics 4B в Enull с помощью теста CSEM до/после.
PHYS 4C — Общая физика III (5,00 единиц)
Колебания, жидкости, звуковые волны, термодинамика, электромагнитный спектр, оптика, включая отражение, преломление, дифракцию, интерференцию, поляризацию.
Результаты обучения учащихся (SLO)
- Демонстрация качественного владения физическими понятиями 4C в области волн, термодинамики и/или оптики посредством презентаций, групповых проектов, научных работ и/или домашних эссе
- Демонстрация мастерства физики 4C лабораторный эксперимент путем представления полного лабораторного отчета со всеми присутствующими элементами требований, включая реферат; введение; материалы, методы и процедуры; данные и анализ; Результаты и обсуждение; использованная литература; таблицы данных.
- Демонстрирует владение количественными аспектами понятий физики 4C в области волн, термодинамики и оптики с помощью домашних заданий и/или экзаменационных задач
PHYS 5 — Современная физика ( 3,00 единицы )
Специальная теория относительности и современная физика, включая фотоны, квантовую механику, атомы, твердые тела, ядерную физику, физику элементарных частиц и космологию.
Результаты обучения учащихся (SLO)
- Демонстрирует владение количественными и качественными аспектами Физики 5: концепции и методы теории относительности, квантовой механики и ядерной физики.
- Демонстрирует владение количественными и качественными аспектами Физики 5: концепции и методы теории относительности, квантовой механики и ядерной физики посредством презентаций, групповых проектов, исследовательских работ и/или домашних заданий.
- Читать, переводить, составлять диаграммы и успешно решать количественные задачи с ключевыми словами, связанные с концепциями теории относительности, ядерной физики и квантовой механики.
- Качественно решать ключевые задачи, связанные с понятиями электрического тока и сопротивления, законами магнетизма, законами индукции, геометрической и волновой оптикой и современной физикой.
Использование компьютеров для получения информации
Использование компьютеров для получения информацииВыдержки из предложения
Лаборатория вычислительной физики: Использование компьютеров для получения информации
представлен в NSF Instrumentation и программа усовершенствования лабораторий
Мы предлагаем предложить новый курс под названием «Введение в вычислительную технику».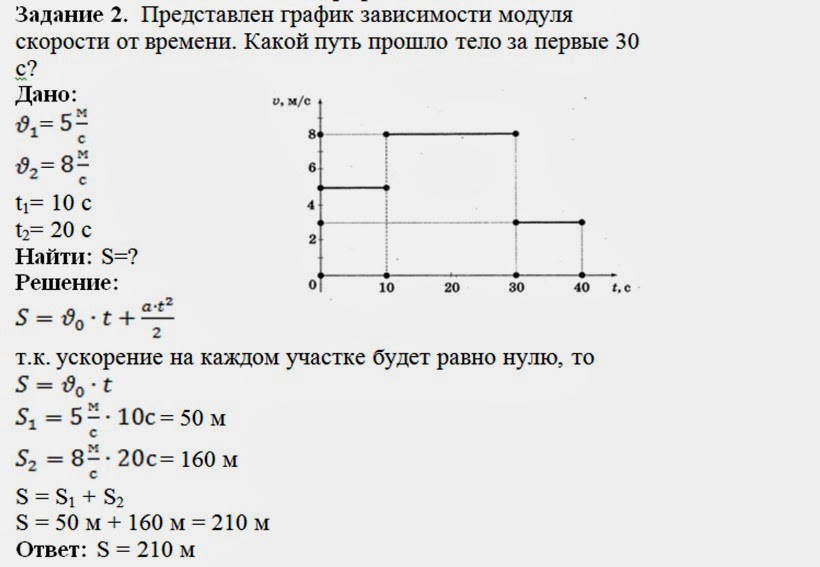 Физика.» Этот курс использует преимущества многих случаев, в которых
физический вопрос и его алгоритмическое решение тесно связаны между собой, поэтому
физика и алгоритм освещают друг друга.Потому что он использует это
ссылку на самую полную, в курсе только один пререквизит по физике, и
таким образом, студенты будут сдавать их уже на первом курсе. Курс
будет 1) волновать и привлекать студентов на раннем этапе обучения в колледже
карьеры, 2) позволяют правильно использовать вычисления во всей физике
учебная программа, и 3) развивать физическое понимание студентов.
Физика.» Этот курс использует преимущества многих случаев, в которых
физический вопрос и его алгоритмическое решение тесно связаны между собой, поэтому
физика и алгоритм освещают друг друга.Потому что он использует это
ссылку на самую полную, в курсе только один пререквизит по физике, и
таким образом, студенты будут сдавать их уже на первом курсе. Курс
будет 1) волновать и привлекать студентов на раннем этапе обучения в колледже
карьеры, 2) позволяют правильно использовать вычисления во всей физике
учебная программа, и 3) развивать физическое понимание студентов.
А. Текущая ситуация
Oberlin College предлагает стандартную подготовку к аспирантуре. учебный план, который можно найти в любом первоклассном колледже или университете.Мы делаем не хочу принижать эту учебную программу: она стала стандартной именно потому что он зарекомендовал себя настолько успешным. Однако в стандарте есть общепризнанные недостатки, такие как:- Студенты должны проработать четыре тяжелых года, прежде чем они начнут видеть
текущие исследовательские приложения в их формальной курсовой работе.
 Много студентов
выпадать по пути.
Много студентов
выпадать по пути.
- Стандартная учебная программа утвердилась до появления
компьютер, так
этот самый практичный из физических инструментов в значительной степени игнорируется.В Оберлине для
например, физиков призывают изучать компьютерный язык, но большинство
те, кто это делает, применяют это знание только к одной или двум проблемам релаксации.
которые могут или не могут быть заданы в курсе электродинамики.
- Учебная программа имеет тенденцию выпускать выпускников, которые манипулируют символы скорее чем понимать физику. Например, любой старшеклассник по физике сможет представить периодическую функцию в виде ряда Фурье с частотами, идущими от от +\бесконечности до -\бесконечности, но немногие смогут объяснить значение отрицательные частоты.
Это предложение является попыткой устранения недостатков сохраняя при этом разнообразные и очевидные преимущества стандартной учебной программы.
Б. Курс философии
Типичный курс вычислительной физики предлагается юниорам или для пожилых людей как курс с добавленной стоимостью: учащиеся уже знакомы с физические задачи и с аналитическими методами их решения, и они научил новому набору методов, алгоритмическим методам, приклеивать Уже известно.-reshenie-24.jpg) Поскольку этот курс начинается так поздно в учебной программе, он дает
впечатление, что численные методы второсортны и должны
б/у только
когда аналитические методы не работают. Этот подход игнорирует тот факт, что во многих
случаях 90 444 алгоритмическое решение задачи напрямую связано с
фундаментальное понятие проблемы и, таким образом, знание алгоритмического
Решение фактически помогает студенту понять фундаментальную концепцию. В виде
Например, рассмотрим задачу с начальным значением dx/dt = x, x(0) = 1.То
аналитический (манипулирующий символами) метод решения этой проблемы опирается на факты
такие как \integral dx/x = ln(x), которые концептуально очень далеки от
фундаментальная идея о том, что производная является наклоном. В отличие от алгоритмического
метод (скажем, Рунге-Кутта) есть прямое воплощение этой фундаментальной идеи. От
понимание метода Рунге-Кутты и кодирование его в программу,
студент не только строит практический инструмент для решения дифференциальных уравнений,
но также строит собственное понимание идеи производной.
Поскольку этот курс начинается так поздно в учебной программе, он дает
впечатление, что численные методы второсортны и должны
б/у только
когда аналитические методы не работают. Этот подход игнорирует тот факт, что во многих
случаях 90 444 алгоритмическое решение задачи напрямую связано с
фундаментальное понятие проблемы и, таким образом, знание алгоритмического
Решение фактически помогает студенту понять фундаментальную концепцию. В виде
Например, рассмотрим задачу с начальным значением dx/dt = x, x(0) = 1.То
аналитический (манипулирующий символами) метод решения этой проблемы опирается на факты
такие как \integral dx/x = ln(x), которые концептуально очень далеки от
фундаментальная идея о том, что производная является наклоном. В отличие от алгоритмического
метод (скажем, Рунге-Кутта) есть прямое воплощение этой фундаментальной идеи. От
понимание метода Рунге-Кутты и кодирование его в программу,
студент не только строит практический инструмент для решения дифференциальных уравнений,
но также строит собственное понимание идеи производной. Этот
ситуация, когда обучение алгоритму на ранней стадии поможет
концептуальное развитие студента и будет строить его физическое понимание.
[Примечание: никто не станет отрицать многочисленные преимущества аналитического метода над числовым.
решений (например, невозможно выбрать неправильный размер шага в
аналитическое решение), и никто не станет отрицать, что иногда алгоритмическое
метод , а не концептуально поучительный (например, QR-алгоритм для
проблема собственных значений). Предлагаемый здесь подход , а не вылечит все болезни.Ничего не будет. Вместо этого мы ожидаем, что два вида инструкций будут дополнять друг друга.
и усиливают друг друга.]
Этот
ситуация, когда обучение алгоритму на ранней стадии поможет
концептуальное развитие студента и будет строить его физическое понимание.
[Примечание: никто не станет отрицать многочисленные преимущества аналитического метода над числовым.
решений (например, невозможно выбрать неправильный размер шага в
аналитическое решение), и никто не станет отрицать, что иногда алгоритмическое
метод , а не концептуально поучительный (например, QR-алгоритм для
проблема собственных значений). Предлагаемый здесь подход , а не вылечит все болезни.Ничего не будет. Вместо этого мы ожидаем, что два вида инструкций будут дополнять друг друга.
и усиливают друг друга.]
Наш предлагаемый курс вычислительной физики использует преимущества таких
взаимовыгодных ситуациях для обучения алгоритмам в качестве вспомогательных средств для
понимания физики, а не как (несколько неприятных) механизмов для
получение ответов. Для развития связи между формальными
подходы и неформальные, физические (и в основном изобразительные) подходы,
курс будет использовать компьютерную графику существенным образом. Курс будет иметь
только одно обязательное условие, а именно вводная «Механика и теория относительности»
курс (который, в свою очередь, требует одного семестра исчисления). Таким образом
студенты будут готовы к курсу уже во втором семестре
на первом курсе (если они поступают в колледж с углубленным изучением математики, как
многие делают). В этом положении мы будем использовать курс, чтобы ввести волнение,
исследовательские проблемы и понимание физики на раннем этапе обучения студента-физика.
карьера. Также в этой должности она будет полезна студентам смежных профессий.
таких наук, как химия, информатика и геология.Мы выберем
примеры, чтобы сделать курс привлекательным для таких студентов.
Курс будет иметь
только одно обязательное условие, а именно вводная «Механика и теория относительности»
курс (который, в свою очередь, требует одного семестра исчисления). Таким образом
студенты будут готовы к курсу уже во втором семестре
на первом курсе (если они поступают в колледж с углубленным изучением математики, как
многие делают). В этом положении мы будем использовать курс, чтобы ввести волнение,
исследовательские проблемы и понимание физики на раннем этапе обучения студента-физика.
карьера. Также в этой должности она будет полезна студентам смежных профессий.
таких наук, как химия, информатика и геология.Мы выберем
примеры, чтобы сделать курс привлекательным для таких студентов.
C. Краткое содержание курса
Курс состоит из четырех равноценных разделов: 1) базовые, 2) обычные дифференциальные уравнения и хаос, 3) спектральный анализ и 4) гармонический функции. В разделе Основы представлены инструкции на языке FORTRAN. языка с помощью простых приложений к поиску нуля в многочленах. FORTRAN был выбран вместо Pascal или C, потому что i) он имеет относительно
простой синтаксис, ii) он обладает необходимыми языковыми функциями для
поддерживают числовую работу, и iii) это стандарт де-факто для научных
Работа.Мы сможем сжать реальное обучение языку в три этапа.
недель, потому что многие функции, такие как символьные переменные, указатели и
рекурсия, не будет преподаваться.
FORTRAN был выбран вместо Pascal или C, потому что i) он имеет относительно
простой синтаксис, ii) он обладает необходимыми языковыми функциями для
поддерживают числовую работу, и iii) это стандарт де-факто для научных
Работа.Мы сможем сжать реальное обучение языку в три этапа.
недель, потому что многие функции, такие как символьные переменные, указатели и
рекурсия, не будет преподаваться.
Раздел обыкновенного дифференциального уравнения построит непосредственно
на
студентка курса «Механика и теория относительности». Числовой
преподаваемая техника будет Рунге-Кутта, а примеры будут взяты из
поле хаоса. Это поле, конечно, будет способствовать возбуждению, но
также ценно в построении физического понимания студента.Хаос сильно зависит
по методам визуализации, таким как сечение Пуанкаре, вся
цель состоит в том, чтобы создать хорошую качественную картину движения. Эти
методы также ценны для построения качественного понимания в
ситуации, когда доступны аналитические решения. Они не обычно
используется как таковое просто потому, что аналитическое решение используется как костыль для
избежать глубокого качественного понимания ситуации.
Они не обычно
используется как таковое просто потому, что аналитическое решение используется как костыль для
избежать глубокого качественного понимания ситуации.
Каждый профессиональный физик имеет качественное понимание из спектральных анализ .Студенты обычно этого не делают, потому что вводятся методы Фурье. сопровождается такой какофонией сложных интегралов и сходимости теоремы о том, что учащийся упускает фундаментальный качественный момент. Эти темы необходимы для второй встречи с предметом, но для нашего Введение подчеркнем примерами и качественными картинками. Эта секция придаст курсу столь необходимый экспериментальный компонент.
Последний раздел обычно называют «решениями задачи Лапласа».
уравнение», но наши ученики даже не будут знать, что такое частная производная!
Вместо этого мы будем говорить о гармонических функциях , определенных в этих точках.
которые удовлетворяют
отношение среднего значения.Не более таинственно сказать, что
температура пластины должна быть гармонической функцией, чем можно сказать, что
температура подчиняется уравнению Лапласа. Отношение среднего значения приводит непосредственно
к методам релаксации, а затем к методам случайного блуждания. Мультисетка
будут введены методы (применяющие релаксацию к сеткам разного размера).
как для ускорения вычислений, так и для укрепления качественного понимания
составляющих длин волн, разработанных в секции спектрального анализа.
Отношение среднего значения приводит непосредственно
к методам релаксации, а затем к методам случайного блуждания. Мультисетка
будут введены методы (применяющие релаксацию к сеткам разного размера).
как для ускорения вычислений, так и для укрепления качественного понимания
составляющих длин волн, разработанных в секции спектрального анализа.
Качественные и количественные методы для дифференциальных уравнений, возникающих в математической физике
Дифференциальные уравнения являются ключевым инструментом в моделировании физических явлений.Большинство физических законов естественных наук выражаются в терминах дифференциальных уравнений, например, законы баланса массы или энергии и импульса. Кроме того, дифференциальные уравнения также используются при моделировании динамики населения, болезней и т. д.
В этом специальном выпуске мы сосредоточимся на объединении приложений и теоретических разработок дифференциальных уравнений, ориентированных на проблемы, возникающие в физических науках. С этой целью этот выпуск послужит форумом для изучения достижений в качественных и количественных методах решения обыкновенных дифференциальных уравнений, уравнений в частных производных, дифференциальных уравнений дробного порядка, интегродифференциальных уравнений и разностных уравнений.
С этой целью этот выпуск послужит форумом для изучения достижений в качественных и количественных методах решения обыкновенных дифференциальных уравнений, уравнений в частных производных, дифференциальных уравнений дробного порядка, интегродифференциальных уравнений и разностных уравнений.
Потенциальные темы этого специального выпуска включают симметрии, дифференциальные уравнения и приложения; оптимальный контроль; преобразования эквивалентности и классические и неклассические симметрии; методы и решения сокращения и линеаризация; сохраняющиеся величины в природных явлениях; вполне интегрируемые уравнения в математической физике; операторы рекурсии, бесконечная иерархия симметрий и/или законы сохранения; уравнения, допускающие слабые солитонные решения; модели загрязнения воздуха и подземного загрязнения; математические методы расширенной термодинамики; численные методы решения задач, возникающих при моделировании физических процессов; специальные методы для решения.
Реакция на этот специальный выпуск превзошла все наши ожидания. Мы получили 53 статьи для рассмотрения для публикации, которые относятся к разным областям вышеупомянутых областей исследований. Все рукописи, представленные в этом специальном выпуске, прошли строгий процесс рецензирования. На основании отчетов рецензентов 8 оригинальных научных статей наконец-то приняты к публикации. Ниже мы кратко опишем значение ключевых вкладов в этот специальный выпуск.
Мы получили 53 статьи для рассмотрения для публикации, которые относятся к разным областям вышеупомянутых областей исследований. Все рукописи, представленные в этом специальном выпуске, прошли строгий процесс рецензирования. На основании отчетов рецензентов 8 оригинальных научных статей наконец-то приняты к публикации. Ниже мы кратко опишем значение ключевых вкладов в этот специальный выпуск.
В «Численном моделировании контроля выбросов загрязняющих веществ в атмосферу вблизи промышленной зоны», стр.Ойджинда и Н. Почай предлагают модель атмосферной диффузии для описания концентрации загрязнителей воздуха, выбрасываемых промышленным предприятием. Для аппроксимации концентрации загрязнителя воздуха используется явный метод конечных разностей. Авторы предполагают, что уровни концентрации загрязняющих веществ в воздухе для каждой точки мониторинга контролируются на уровне или ниже национального стандарта качества воздуха, близкого к индексу промышленной зоны.
В «Численных решениях связанных систем дифференциальных уравнений в частных производных дробного порядка» Ю. Ли и К. Шах разработали систематический численный метод, используя сдвинутые полиномы Лежандра для построения приближенных решений класса связанных систем дифференциальных уравнений в частных производных дробного порядка. С помощью операционных матриц интегрирования и дифференцирования дробного порядка рассматриваемая система преобразуется в систему легко решаемых алгебраических уравнений типа Сильвестра. Отработанная методика демонстрируется некоторыми тестовыми задачами, а также проводится анализ ошибок.
Ли и К. Шах разработали систематический численный метод, используя сдвинутые полиномы Лежандра для построения приближенных решений класса связанных систем дифференциальных уравнений в частных производных дробного порядка. С помощью операционных матриц интегрирования и дифференцирования дробного порядка рассматриваемая система преобразуется в систему легко решаемых алгебраических уравнений типа Сильвестра. Отработанная методика демонстрируется некоторыми тестовыми задачами, а также проводится анализ ошибок.
X. Jiang и X. Wang в статье «Глобальная корректность для класса волновых систем типа Кирхгофа» исследуют корректность волновой системы типа Кирхгофа с нелинейными источниками, диссипативными и вязкоупругими членами, с учетом больших начальные граничные условия.Для докритического случая глобальные решения существуют при условии, что начальное значение принадлежит устойчивому множеству, а разрушение за конечное время имеет место для случая, когда начальное значение принадлежит неустойчивому множеству. Для сверхкритического случая соответствующее решение дует вверх за конечное время при некоторых заданных условиях на начальные значения.
Для сверхкритического случая соответствующее решение дует вверх за конечное время при некоторых заданных условиях на начальные значения.
В «Геометрической/физической интерпретации сохраняющихся величин, соответствующих нётеровским симметриям плоскосимметричного пространства-времени» Б. Джамиль и др. исследовать нётеровские симметрии геодезических лагранжианов плоских симметричных пространств-времен и соответствующие им сохраняющиеся величины. Они обеспечивают количество нётеровых симметрий, которое может допускать плоское симметричное пространство-время. В частности, наибольшее число нётеровских симметрий достигается для пространства-времени Минковского.
В работе «Теплообмен в пористом радиальном ребре: анализ численно полученных решений» Р.Джоома и К. Харли изучают модель, описывающую теплообмен в пористом радиальном ребре с численной точки зрения. А именно, авторы используют метод Крэнка-Николсона с предиктором-корректором Ньютона-Рафсона и без него для выполнения своего анализа. Полуаналитические стационарные решения получены методом дифференциального преобразования. Также представлены сравнения между результатами, полученными в этой статье, и другими недавними сообщениями в литературе.
Полуаналитические стационарные решения получены методом дифференциального преобразования. Также представлены сравнения между результатами, полученными в этой статье, и другими недавними сообщениями в литературе.
В «Итерационный метод решения связанных уравнений кондуктивно-излучательного теплообмена в диэлектрических слоях» В.Чекурина и Ю. Бойчука авторы рассматривают математическую модель, описывающую комбинированный кондуктивно-излучательный теплообмен в диэлектрическом слое, который излучает, поглощает и рассеивает ИК-излучение как в своем объеме, так и на границе. Сформулирована нелинейная стационарная краевая задача для связанных уравнений переноса тепла и излучения для слоя, обменивающегося энергией с внешней средой за счет конвекции и излучения. В случае оптически толстого слоя, когда его толщина намного больше длины пробега фотонов, задача становится сингулярно возмущенной.В обратном случае оптически тонкого слоя задача является регулярно возмущенной и становится регулярной (невозмущенной) при толщине слоя порядка нескольких пробегов фотонов. Разработан итерационный метод решения невозмущенной задачи и проверена его сходимость. С помощью этого метода исследовано температурное поле и потоки излучения.
Разработан итерационный метод решения невозмущенной задачи и проверена его сходимость. С помощью этого метода исследовано температурное поле и потоки излучения.
В «Быстром неявном методе конечных разностей для дробных уравнений адвекции-дисперсии с дробными производными граничными условиями» Т.Лю и М. Хоу рассматривают дробные уравнения адвекции-дисперсии, моделирующие перенос пассивных трассеров, переносимых потоком жидкости в пористой среде. Для этих уравнений с граничными условиями с дробной производной авторы развивают неявный метод конечных разностей. Доказаны непротиворечивость первого порядка, разрешимость, безусловная устойчивость и сходимость первого порядка метода. Затем они демонстрируют быстрый итерационный метод для неявной конечно-разностной схемы, который требует только хранения и вычислительных затрат .Обычно метод исключения Гаусса требует хранения и вычислительных затрат .
В своей статье «Канонические формы и их интегрируемость для систем из трех ОДУ 2-го порядка» С. Захида и др. строят дифференциальные инварианты и соответствующие им канонические формы для систем из трех ОДУ 2-го порядка, обладающих трехмерными алгебрами Ли. Получено расширение до системы трех ОДУ 2-го порядка, исследована особенность в инвариантной структуре канонических форм и обсуждается интегрируемость этих канонических форм.Показаны некоторые физические примеры из системы механики частиц.
Захида и др. строят дифференциальные инварианты и соответствующие им канонические формы для систем из трех ОДУ 2-го порядка, обладающих трехмерными алгебрами Ли. Получено расширение до системы трех ОДУ 2-го порядка, исследована особенность в инвариантной структуре канонических форм и обсуждается интегрируемость этих канонических форм.Показаны некоторые физические примеры из системы механики частиц.
Благодарности
Мы благодарим всех авторов за их ценный вклад в этот специальный выпуск. Мы благодарим уважаемых рецензентов за их время, усилия и сотрудничество при рассмотрении всех представленных статей.
Рехана Наз
Мариано Торриси
Игорь Лейте Фрейре
Имран Наим
Авторские права
Авторские права © 2017 Rehana Naz et al. Эта статья находится в открытом доступе и распространяется в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.
Учебник по физике: уравнение зеркала
Диаграммы лучей можно использовать для определения местоположения, размера, ориентации и типа изображения, которое формируется при размещении объектов в заданном месте перед вогнутым зеркалом. Использование этих диаграмм было продемонстрировано ранее в Уроке 3. Лучевые диаграммы предоставляют полезную информацию об отношениях объект-изображение, но не предоставляют информацию в количественной форме. Хотя лучевая диаграмма может помочь определить приблизительное местоположение и размер изображения, она не дает числовой информации о расстоянии до изображения и размере объекта.Чтобы получить этот тип числовой информации, необходимо использовать уравнение зеркала и уравнение увеличения . Уравнение зеркала выражает количественную связь между расстоянием до объекта (d o ), расстоянием до изображения (d i ) и фокусным расстоянием (f). Уравнение формулируется следующим образом:
Уравнение увеличения связывает отношение расстояния до изображения и расстояния до объекта с отношением высоты изображения (h i ) и высоты объекта (h o ). Уравнение увеличения сформулировано следующим образом:
Уравнение увеличения сформулировано следующим образом:
Эти два уравнения можно объединить, чтобы получить информацию о расстоянии до изображения и высоте изображения, если известно расстояние до объекта, высота объекта и фокусное расстояние.
В качестве демонстрации эффективности уравнения зеркала и уравнения увеличения рассмотрим следующий пример задачи и ее решение.
Пример задачи №1
А 4.Лампа высотой 00 см расположена на расстоянии 45,7 см от вогнутого зеркала с фокусным расстоянием 15,2 см. Определите расстояние до изображения и размер изображения.
Как и все проблемы в физике, начните с идентификации известной информации.
| ч о = 4,0 см | д о = 45,7 см | f = 15,2 см |
Затем укажите неизвестные величины, которые вы хотите найти.
Для определения расстояния до изображения необходимо использовать уравнение зеркала. Следующие строки представляют решение расстояния изображения; показаны замены и алгебраические шаги.
1/f = 1/do + 1/d i1/(15,2 см) = 1/(45,7 см) + 1/d i
0,0658 см -1 = 0,0219 см -1 + 1/d i
0,0439 см -1 = 1/d i
Численные значения в приведенном выше решении были округлены при записи, однако во всех расчетах использовались неокругленные числа.Окончательный ответ округляется до третьей значащей цифры.
Для определения высоты изображения необходимо уравнение увеличения. Поскольку три из четырех величин в уравнении (без учета M) известны, можно вычислить четвертую величину. Решение показано ниже.
h i /h o = — d i /d oч i /(4,0 см) = — (22,8 см)/(45,7 см)
ч i = — (4. 0 см) • (22,8 см)/(45,7 см)
0 см) • (22,8 см)/(45,7 см)
Отрицательные значения высоты изображения указывают на то, что изображение является перевернутым. Как это часто бывает в физике, отрицательный или положительный знак перед числовым значением физической величины представляет информацию о направлении. В случае высоты изображения отрицательное значение всегда указывает на перевернутое изображение.
Из вычислений в этой задаче можно сделать вывод, что если предмет высотой 4,00 см поместить 45.7 см от вогнутого зеркала с фокусным расстоянием 15,2 см, то изображение будет перевернутым, высотой 1,99 см и расположенным на расстоянии 22,8 см от зеркала. Результаты этого расчета согласуются с принципами, обсуждавшимися ранее в этом уроке. В этом случае объект расположен на 90 223 за 90 224 центром кривизны (что было бы двумя фокусными расстояниями от зеркала), а изображение расположено между центром кривизны и фокальной точкой. Это относится к категории Случая 1: Объект находится за пределами С.
Теперь давайте попробуем второй пример задачи:
Пример задачи №2
Лампа высотой 4,0 см расположена на расстоянии 8,3 см от вогнутого зеркала с фокусным расстоянием 15,2 см. (ПРИМЕЧАНИЕ: это тот же объект и то же зеркало, только на этот раз объект расположен ближе к зеркалу.) Определите расстояние до изображения и размер изображения.
Опять же, начните с идентификации известной информации.
| ч о = 4,0 см | д о = 8,3 см | f = 15,2 см |
Затем укажите неизвестные величины, которые вы хотите найти.
Для определения расстояния до изображения необходимо использовать уравнение зеркала.Следующие строки представляют решение расстояния изображения; показаны замены и алгебраические шаги.
1/(15,2 см) = 1/(8,3 см) + 1/d i
0,0658 см -1 = 0,120 см -1 + 1/d i
-0,0547 см -1 = 1/d i
Численные значения в приведенном выше решении были округлены при записи, однако во всех расчетах использовались неокругленные числа.Окончательный ответ округляется до третьей значащей цифры.
Для определения высоты изображения необходимо уравнение увеличения. Поскольку три из четырех величин в уравнении (без учета M) известны, можно вычислить четвертую величину. Решение показано ниже.
h i /h o = — d i /d oч i /(4,0 см) = — (-18,2 см)/(8,3 см)
ч i = — (4.0 см) • (-18,2 см)/(8,3 см)
Отрицательное значение расстояния до изображения указывает на то, что изображение является виртуальным изображением, расположенным за зеркалом. Опять же, отрицательный или положительный знак перед числовым значением физической величины представляет информацию о направлении. В случае расстояния до изображения отрицательное значение всегда означает за зеркалом. Обратите также внимание, что высота изображения является положительным значением, что означает вертикальное изображение. Любое изображение, стоящее вертикально и находящееся за зеркалом, считается виртуальным изображением.
Опять же, отрицательный или положительный знак перед числовым значением физической величины представляет информацию о направлении. В случае расстояния до изображения отрицательное значение всегда означает за зеркалом. Обратите также внимание, что высота изображения является положительным значением, что означает вертикальное изображение. Любое изображение, стоящее вертикально и находящееся за зеркалом, считается виртуальным изображением.
Из расчетов во втором примере задачи можно сделать вывод, что если предмет высотой 4,0 см поместить на расстоянии 8,3 см от вогнутого зеркала с фокусным расстоянием 15,2 см, то изображение будет увеличенным, прямым, высотой 8,8 см. и расположен в 18,3 см за зеркалом. Результаты этого расчета согласуются с принципами, обсуждавшимися ранее в этом уроке. В этом случае объект находится перед фокусом (т. е. расстояние до объекта меньше фокусного расстояния), а изображение — за зеркалом.Это попадает в категорию Случая 5: Объект расположен перед F.
Знак +/-
Условные обозначения для заданных величин в уравнении зеркала и уравнениях увеличения следующие:
- f есть +, если зеркало вогнутое
- f is — если зеркало выпуклое
- d i равно +, если изображение является реальным изображением и расположено на стороне зеркала объекта.
- d i is — если изображение виртуальное и находится за зеркалом.
- h i +, если изображение прямое (и, следовательно, также виртуальное)
- h i is — если изображение перевернутое (а значит, и реальное)
Подобно многим математическим задачам в физике, этот навык приобретается только в результате большой личной практики. Возможно, вы хотели бы потратить некоторое время, чтобы решить задачи из раздела «Проверьте свое понимание» ниже.
Мы хотели бы предложить .
 ..
Зачем просто читать об этом и когда вы могли бы взаимодействовать с ним? Взаимодействие — это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного приложения Optics Bench или нашего интерактивного приложения Name That Image. Вы можете найти это в разделе Physics Interactives на нашем сайте.Интерактивная скамья Optics Bench предоставляет учащимся интерактивную среду для изучения формирования изображений линзами и зеркалами. Интерактивное приложение Name That Image Interactive предлагает учащимся интенсивную умственную тренировку по распознаванию характеристик изображения для любого заданного местоположения объекта перед изогнутым зеркалом.
..
Зачем просто читать об этом и когда вы могли бы взаимодействовать с ним? Взаимодействие — это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного приложения Optics Bench или нашего интерактивного приложения Name That Image. Вы можете найти это в разделе Physics Interactives на нашем сайте.Интерактивная скамья Optics Bench предоставляет учащимся интерактивную среду для изучения формирования изображений линзами и зеркалами. Интерактивное приложение Name That Image Interactive предлагает учащимся интенсивную умственную тренировку по распознаванию характеристик изображения для любого заданного местоположения объекта перед изогнутым зеркалом.
Проверьте свое понимание
1. Определите расстояние до изображения и высоту изображения для 5.Объект высотой 00 см, расположенный на расстоянии 45,0 см от вогнутого зеркала с фокусным расстоянием 15,0 см.
2. Определите расстояние до изображения и высоту изображения для объекта высотой 5,00 см, расположенного на расстоянии 30,0 см от вогнутого зеркала с фокусным расстоянием 15,0 см.
3. Определите расстояние до изображения и высоту изображения для объекта высотой 5,00 см, расположенного под номером 20.0 см от вогнутого зеркала с фокусным расстоянием 15,0 см.
4. Определите расстояние до изображения и высоту изображения для объекта высотой 5,00 см, расположенного на расстоянии 10,0 см от вогнутого зеркала с фокусным расстоянием 15,0 см.
5. Увеличенное перевернутое изображение расположено на расстоянии 32,0 см от вогнутого зеркала с фокусным расстоянием 12.0 см. Определите расстояние до объекта и скажите, является ли изображение реальным или виртуальным.
ZINGER : 6.
