Posted in Разное

Условия возникновения электрического поля: Электрический ток. Условия возникновения тока. Действия тока.

Содержание

Условие возникновения электрического тока. Электрическое поле

Ток в проводнике, т. е. направленное движение зарядов, вызывается действием сил электрического поля. Электрическое поле — это особый физический процесс, происходящий в определенной области пространства и характеризующийся, в частности, возникновением механических сил, действующих на заряды, помещенные в пространстве, охватываемом полем.

Прежде чем рассматривать поле, вызывающее электрический ток, познакомимся с полем, создаваемым неподвижными зарядами.

Мы знаем, что между любыми зарядами существуют силы притяжения и силы отталкивания.
Это объясняется тем, что около любого заряда существует электрическое поле.

Представим себе, что в поле, созданное неподвижными зарядами, внесен пробный заряд q0 (рис. 1), т. е. заряд, который настолько мал, что практически не изменяет ранее существовавшее поле.

Обследуя при помощи таких зарядов поле, мы убедимся, что сила, действующая на пробный заряд в электрическом поле, пропорциональна величине пробного заряда.


Однако при одной и той же величине пробного заряда сила, действующая на него в разных точках одного и того же поля, имеет разную величину. Следовательно, сила поля зависит от интенсивности поля в той точке, где расположен пробный заряд.

Величину, характеризующую интенсивность поля, называют напряженностью поля.
Напряженность поля численно равна отношению силы, действующей на пробный положительный заряд в данной точке поля, к величине этого заряда.

Направление напряженности поля совпадает с направлением силы, действующей на положительный пробный заряд в данной точке.

Рис. 1

Зная напряженность поля, мы можем определить величину силы, действующей на любой заряд в данной точке. Если буквой Е обозначить напряженность поля в данной точке, а буквой q—величину пробного заряда, то сила F, действующая на заряд, может быть определена по формуле F = E*q.

На рис. 1 показаны силовые линии поля около двух разноименно заряженных тел. Силовые линии начинаются у положительного заряда и кончаются у отрицательного.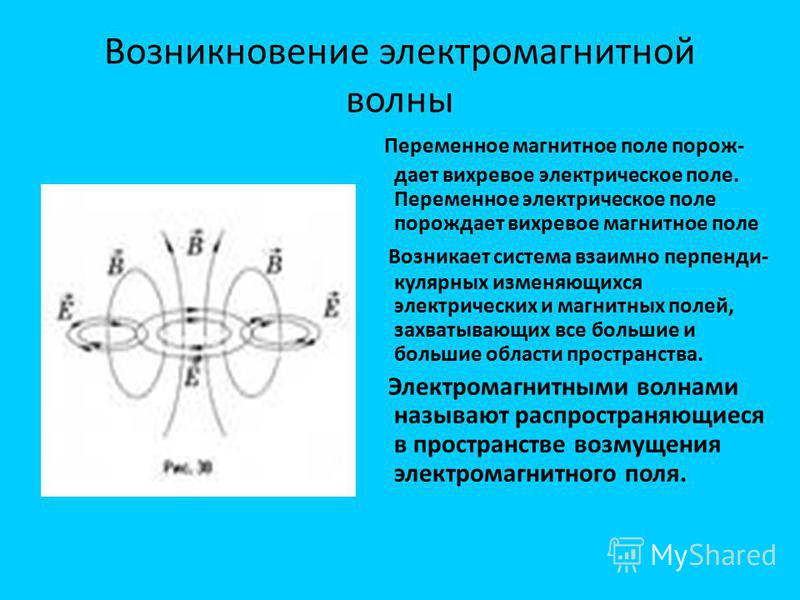

Они представляют собой пути следования пробного положительного заряда (при медленном движении) в электрическом поле. Поле около неподвижных заряженных тел называется электростатическим.

Два главных условия возникновения тока в проводнике. Условия существования электрического тока

Электрический ток — упорядоченное по направлению движение электрических зарядов. За направление тока принимается направление движения положительных зарядов.


Прохождение тока по проводнику сопровождается следующими его действиями:

* магнитным (наблюдается во всех проводниках)
* тепловым (наблюдается во всех проводниках, кроме сверхпроводников)
* химическим (наблюдается в электролитах).

Для возникновения и поддержания тока в какой-либо среде необходимо выполнение двух условий:

* наличие в среде свободных электрических зарядов

* создание в среде электрического поля.

Электрическое поле в среде необходимо для создания направленного движения свободных зарядов. Как известно, на заряд q в электрическом поле напряженностью E действует сила F = q* E, которая и заставляет свободные заряды двигаться в направлении электрического поля. Признаком существования в проводнике электрического поля является наличие не равной нулю разности потенциалов между любыми двумя точками проводника,
Однако, электрические силы не могут длительное время поддерживать электрический ток. Направленное движение электрических зарядов через некоторое время приводит к выравниванию потенциалов на концах проводника и, следовательно, к исчезновению в нем электрического поля.

Для поддержания тока в электрической цепи на заряды кроме кулоновских сил должны действовать силы неэлектрической природы (сторонние силы).

Устройство, создающее сторонние силы, поддерживающее разность потенциалов в цепи и преобразующее различные виды энергии в электрическую энергию, называется источником тока.
Для существования электрического тока в замкнутой цепи необходимо включение в нее источника тока.
основные характеристики

1. Сила тока — I, единица измерения — 1 А (Ампер).
Силой тока называется величина, равная заряду, протекающему через поперечное сечение проводника за единицу времени.
I = Dq/Dt .

Формула справедлива для постоянного тока, при котором сила тока и его направление не изменяются со временем. Если сила тока и его направление изменяются со временем, то такой ток называется переменным.
Для переменного тока:
I = lim Dq/Dt ,
Dt — 0

т.е. I = q», где q» — производная от заряда по времени.
2. Плотность тока — j, единица измерения — 1 А/м2.
Плотностью тока называется величина, равная силе тока, протекающего через единичное поперечное сечение проводника:

j = I/S .

3. Электродвижущая сила источника тока — э.д.с. (e), единица измерения — 1 В (Вольт). Э.д.с.- физическая величина, равная работе, совершаемой сторонними силами при перемещении по электрической цепи единичного положительного заряда:
e = Аст./q .

4. Сопротивление проводника — R, единица измерения — 1 Ом.
Под действием электрического поля в вакууме свободные заряды двигались бы ускоренно. В веществе они движутся в среднем равномерно, т.к. часть энергии отдают частицам вещества при столкновениях.

Теория утверждает, что энергия упорядоченного движения зарядов рассеивается на искажениях кристаллической решетки. Исходя из природы электрического сопротивления, следует, что
R = r*l/S ,

где
l — длина проводника,
S — площадь поперечного сечения,

r — коэффициент пропорциональности, названный удельным сопротивлением материала.
Эта формула хорошо подтверждается на опыте.
Взаимодействие частиц проводника с движущимися в токе зарядами зависит от хаотического движения частиц, т.е. от температуры проводника. Известно, что
r = r0(1 + a t) ,
R = R0(1 + a t) .

Коэффициент a называется температурным коэффициентом сопротивления:
a = (R — R0)/R0*t .

Для химически чистых металлов a > 0 и равно 1/273 К-1. Для сплавов температурные коэффициенты имеют меньшее значение. Зависимость r(t) для металлов линейная:

В 1911 году открыто явление сверхпроводимости, заключающееся в том, что при температуре, близкой к абсолютному нулю, сопротивление некоторых металлов падает скачком до нуля.

У некоторых веществ (например, у электролитов и полупроводников) удельное сопротивление с ростом температуры уменьшается, что объясняется ростом концентрации свободных зарядов.

Величина, обратная удельному сопротивлению, называется удельной электрической проводимостью s
s = 1/r .

5. Напряжение — U , единица измерения — 1 В.
Напряжение — физическая величина, равная работе, совершаемой сторонними и электрическими силами при перемещении единичного положительного заряда.

U = (Aст.+ Аэл.)/q .

Так как Аст./q = e, а Аэл./q = f1-f2, то
U = e + (f1 — f2) .

Электрический ток. Закон Ома

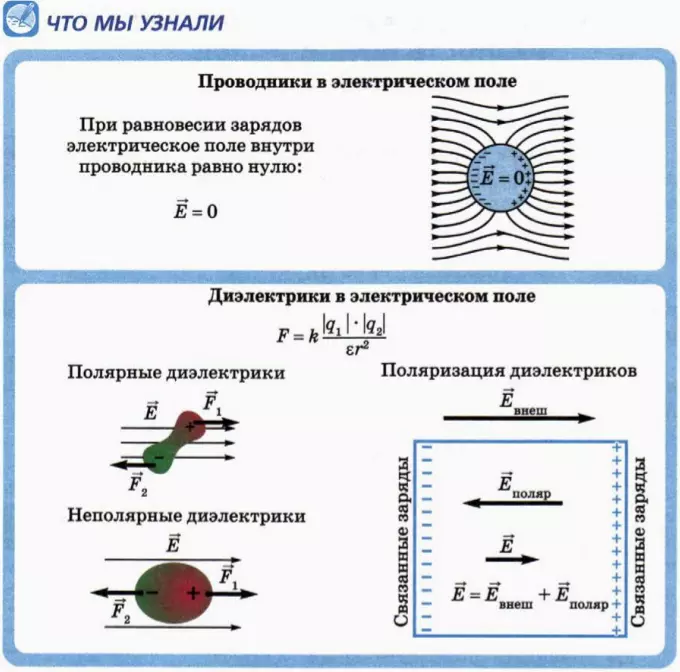
Если изолированный проводник поместить в электрическое поле то на свободные заряды q в проводнике будет действовать сила В результате в проводнике возникает кратковременное перемещение свободных зарядов.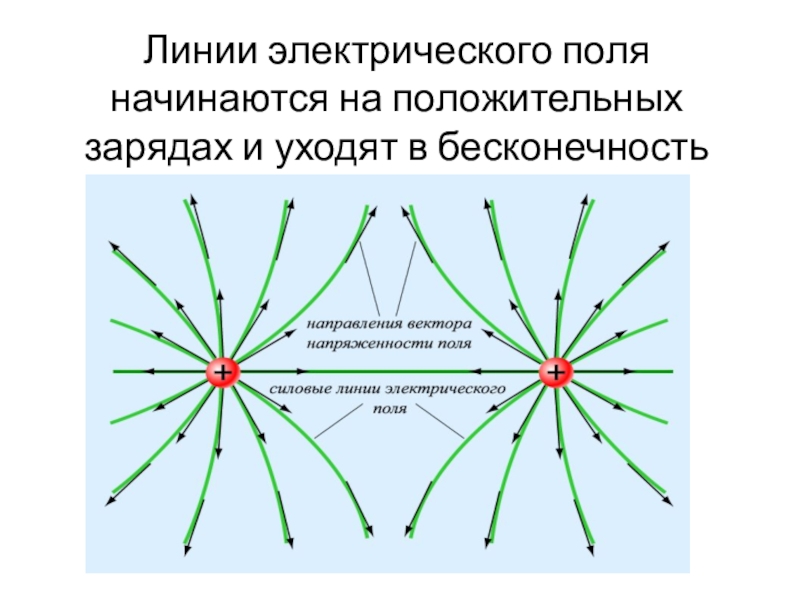 Этот процесс закончится тогда, когда собственное электрическое поле зарядов, возникших на поверхности проводника, скомпенсирует полностью внешнее поле. Результирующее электростатическое поле внутри проводника будет равно нулю (см. § 1.5).

Однако, в проводниках при определенных условиях может возникнуть непрерывное упорядоченное движение свободных носителей электрического заряда. Такое движение называется электрическим током . За направление электрического тока принято направление движения положительных свободных зарядов. Для существования электрического тока в проводнике необходимо создать в нем электрическое поле.

Количественной мерой электрического тока служит сила тока I – скалярная физическая величина, равная отношению заряда Δq , переносимого через поперечное сечение проводника (рис. 1.8.1) за интервал времени Δt , к этому интервалу времени:

В Международной системе единиц СИ сила тока измеряется в амперах (А). Единица измерения тока 1 А устанавливается по магнитному взаимодействию двух параллельных проводников с током (см. § 1.16).

Постоянный электрический ток может быть создан только в замкнутой цепи , в которой свободные носители заряда циркулируют по замкнутым траекториям. Электрическое поле в разных точках такой цепи неизменно во времени. Следовательно, электрическое поле в цепи постоянного тока имеет характер замороженного электростатического поля. Но при перемещении электрического заряда в электростатическом поле по замкнутой траектории, работа электрических сил равна нулю (см. § 1.4). Поэтому для существования постоянного тока необходимо наличие в электрической цепи устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения . Такие устройства называются источниками постоянного тока . Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются

сторонними силами .

Природа сторонних сил может быть различной. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов, в генераторах постоянного тока сторонние силы возникают при движении проводников в магнитном поле. Источник тока в электрической цепи играет ту же роль, что и насос, который необходим для перекачивания жидкости в замкнутой гидравлической системе. Под действием сторонних сил электрические заряды движутся внутри источника токапротив сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.

При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу.

Физическая величина, равная отношению работы A ст сторонних сил при перемещении заряда

q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС):

Таким образом, ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда. Электродвижущая сила, как и разность потенциалов, измеряется в вольтах (В).

При перемещении единичного положительного заряда по замкнутой цепи постоянного тока работа сторонних сил равна сумме ЭДС, действующих в этой цепи, а работа электростатического поля равна нулю.

Цепь постоянного тока можно разбить на отдельные участки. Те участки, на которых не действуют сторонние силы (т. е. участки, не содержащие источников тока), называютсяоднородными . Участки, включающие источники тока, называются неоднородными .

При перемещении единичного положительного заряда по некоторому участку цепи работу совершают как электростатические (кулоновские), так и сторонние силы. Работа электростатических сил равна разности потенциалов Δφ 12 = φ 1 – φ 2 между начальной (1) и конечной (2) точками неоднородного участка. Работа сторонних сил равна по определению электродвижущей силе 12 , действующей на данном участке. Поэтому полная работа равна

Немецкий физик Г. Ом в 1826 году экспериментально установил, что сила тока I , текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:

где R = const.

Величину R принято называть электрическим сопротивлением . Проводник, обладающий электрическим сопротивлением, называется резистором . Данное соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.

В СИ единицей электрического сопротивления проводников служит ом (Ом). Сопротивлением в 1 Ом обладает такой участок цепи, в котором при напряжении 1 В возникает ток силой 1 А.

Проводники, подчиняющиеся закону Ома, называются линейными . Графическая зависимость силы тока I от напряжения U (такие графики называются вольт-амперными характеристиками , сокращенно ВАХ) изображается прямой линией, проходящей через начало координат. Следует отметить, что существует много материалов и устройств, не подчиняющихся закону Ома, например,полупроводниковый диод или газоразрядная лампа. Даже у металлических проводников при токах достаточно большой силы наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников растет с ростом температуры.

Для участка цепи, содержащего ЭДС, закон Ома записывается в следующей форме:

По закону Ома

Сложив оба равенства, получим:

I (R + r ) = Δφ cd + Δφ ab + .

Но Δφ cd = Δφ ba = – Δφ ab . Поэтому

Эта формула выражет закон Ома для полной цепи : сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи.

Сопротивление r неоднородного участка на рис. 1.8.2 можно рассматривать каквнутреннее сопротивление источника тока . В этом случае участок (ab ) на рис. 1.8.2 является внутренним участком источника. Если точки a и b замкнуть проводником, сопротивление которого мало по сравнению с внутренним сопротивлением источника (R r ), тогда в цепи потечет ток короткого замыкания

Сила тока короткого замыкания – максимальная сила тока, которую можно получить от данного источника с электродвижущей силой и внутренним сопротивлением r . У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик и вызывать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов, используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер). Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей.

В ряде случаев для предотвращения опасных значений силы тока короткого замыкания к источнику последовательно подсоединяется некоторое внешнее сопротивление. Тогда сопротивление r равно сумме внутреннего сопротивления источника и внешнего сопротивления, и при коротком замыкании сила тока не окажется чрезмерно большой.

Если внешняя цепь разомкнута, то Δφ ba = – Δφ ab = , т. е. разность потенциалов на полюсах разомкнутой батареи равна ее ЭДС.

Если внешнее нагрузочное сопротивление R включено и через батарею протекает ток I , разность потенциалов на ее полюсах становится равной

На рис. 1.8.3 дано схематическое изображение источника постоянного тока с ЭДС равной и внутренним сопротивлением r в трех режимах: «холостой ход», работа на нагрузку и режим короткого замыкания (к. з.). Указаны напряженность электрического поля внутри батареи и силы, действующие на положительные заряды: – электрическая сила и – сторонняя сила. В режиме короткого замыкания электрическое поле внутри батареи исчезает.

Для измерения напряжений и токов в электрических цепях постоянного тока используются специальные приборы – вольтметры и амперметры .

Вольтметр предназначен для измерения разности потенциалов, приложенной к его клеммам. Он подключается параллельно участку цепи, на котором производится измерение разности потенциалов. Любой вольтметр обладает некоторым внутренним сопротивлением R B . Для того, чтобы вольтметр не вносил заметного перераспределения токов при подключении к измеряемой цепи, его внутреннее сопротивление должно быть велико по сравнению с сопротивлением того участка цепи, к которому он подключен. Для цепи, изображенной на рис. 1.8.4, это условие записывается в виде:

Это условие означает, что ток I B = Δφ cd / R B , протекающий через вольтметр, много меньше тока I = Δφ cd / R 1 , который протекает по тестируемому участку цепи.

Поскольку внутри вольтметра не действуют сторонние силы, разность потенциалов на его клеммах совпадает по определению с напряжением. Поэтому можно говорить, что вольтметр измеряет напряжение.

Амперметр предназначен для измерения силы тока в цепи. Амперметр включается последовательно в разрыв электрической цепи, чтобы через него проходил весь измеряемый ток. Амперметр также обладает некоторым внутренним сопротивлениемR A . В отличие от вольтметра, внутреннее сопротивление амперметра должно быть достаточно малым по сравнению с полным сопротивлением всей цепи. Для цепи на рис. 1.8.4 сопротивление амперметра должно удовлетворять условию

Условия существования постоянного электрического тока.

Для существования постоянного электрического тока необходимо наличие свободных заряженных частиц и наличие источника тока. в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля.

Источник тока — устройство, в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля. В источнике тока на заряженные частицы в замкнутой цепи действуют сторонние силы. Причины возникновения сторонних сил в различных источниках тока различны. Например в аккумуляторах и гальванических элементах сторонние силы возникают благодаря протеканию химических реакций, в генераторах электростанций они возникают при движении проводника в магнитном поле, в фотоэлементах — при действия света на электроны в металлах и полупроводниках.

Электродвижущей силой источника тока называют отношение работы сторонних сил к величине положительного заряда, переносимого от отрицательного полюса источника тока к положительному.

Основные понятия.

Сила тока — скалярная физическая величина, равная отношению заряда, прошедшего через проводник, ко времени, за которое этот заряд прошел.

где I — сила тока, q — величина заряда (количество электричества), t — время прохождения заряда.

Плотность тока — векторная физическая величина, равная отношению силы тока к площади поперечного сечения проводника.

где j —плотность тока , S — площадь сечения проводника.

Направление вектора плотности тока совпадает с направлением движения положительно заряженных частиц.

Напряжение — скалярная физическая величина, равная отношению полной работе кулоновских и сторонних сил при перемещении положительного заряда на участке к значению этого заряда.

где A — полная работа сторонних и кулоновских сил, q — электрический заряд.

Электрическое сопротивление — физическая величина, характеризующая электрические свойства участка цепи.

где ρ — удельное сопротивление проводника, l — длина участка проводника, S — площадь поперечного сечения проводника.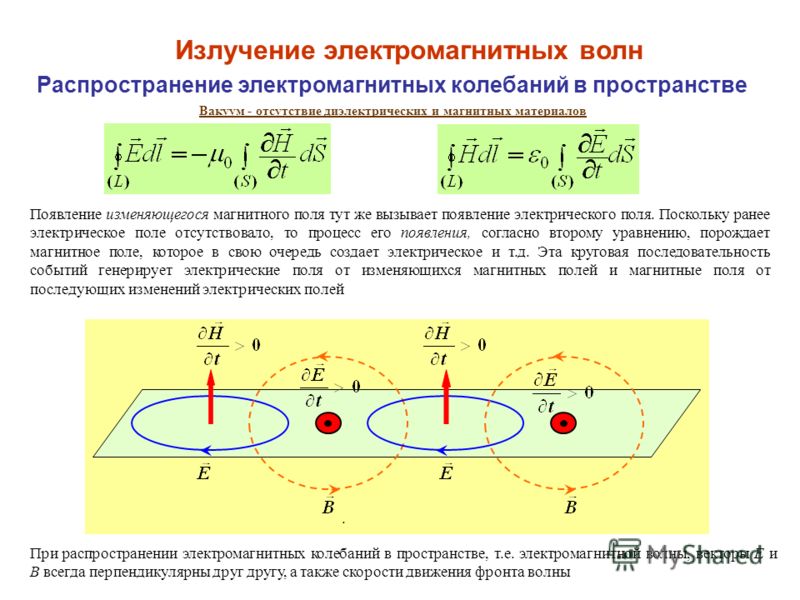

Проводимостью называется величина, обратная сопротивлению

где G — проводимость.

Без электричества невозможно представить жизнь современного человека. Вольты, Амперы, Ватты – эти слова звучат в разговоре об устройствах, которые работают от электричества. Но что это такое электрический ток и каковы условия его существования? Об этом мы расскажем далее, предоставив краткое объяснение для начинающих электриков.

Определение

Электрическим током является направленное движение носителей зарядов – это стандартная формулировка из учебника физики. В свою очередь носителями заряда называются определенные частицы вещества. Ими могут быть:

  • Электроны – отрицательные носители заряда.
  • Ионы – положительные носители заряда.

Но откуда берутся носители заряда? Для ответа на этот вопрос нужно вспомнить базовые знания о строении вещества. Всё что нас окружает – вещество, оно состоит из молекул, мельчайших его частиц. Молекулы состоят из атомов. Атом состоит из ядра, вокруг которого движутся электроны на заданных орбитах. Молекулы также хаотично движутся. Движение и структура каждой из этих частиц зависят от самого вещества и влияния на него окружающей среды, например температуры, напряжения и прочего.

Ионом называют атом, у которого изменилось соотношение электронов и протонов. Если изначально атом нейтрален, то ионы в свою очередь делят на:

  • Анионы – положительный ион атома, потерявшего электроны.
  • Катионы – это атом с «лишними» электронами, присоединившиеся к атому.

Единица измерения тока – Ампер, согласно он вычисляется по формуле:

где U – напряжение, [В], а R – сопротивление, [Ом].

Или прямопропорционален количеству заряда, перенесенному за единицу времени:

где Q – заряд, [Кл], t – время, [с].

Условия существования электрического тока

Что такое электрический ток мы разобрались, теперь давайте поговорим о том, как обеспечить его протекание.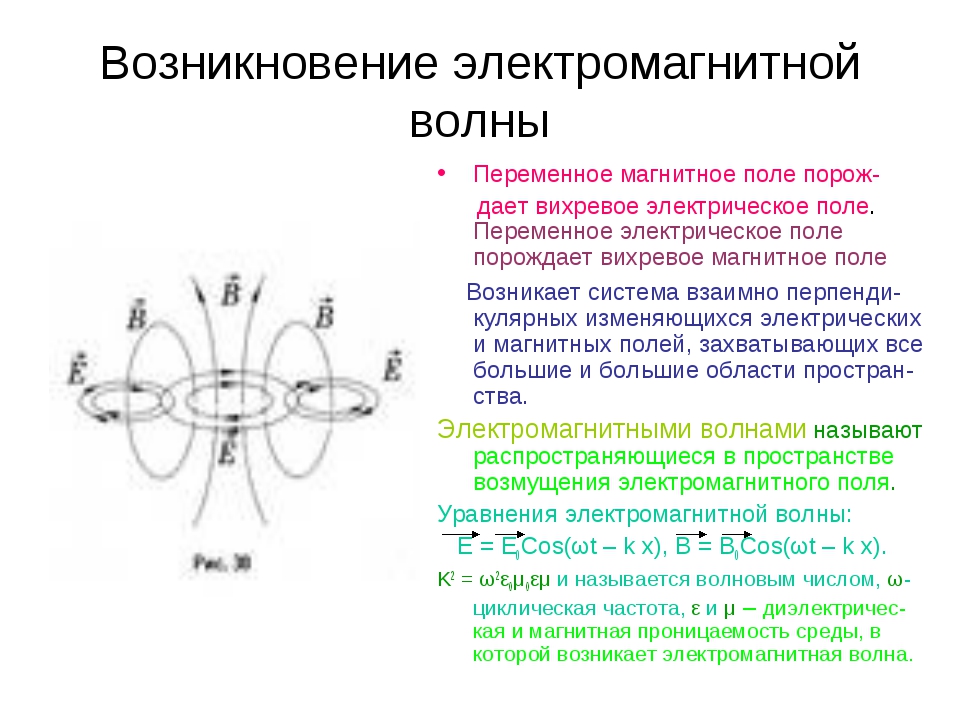 Для протекания электрического тока необходимо выполнение двух условий:

  1. Наличие свободных носителей заряда.
  2. Электрическое поле.

Первое условие существования и протекания электричества зависит от вещества, в котором протекает (или не протекает) ток, а также его состояния. Второе условие также выполнимо: для существования электрического поля обязательно наличие разных потенциалов, между которыми находится среда, в которой будут протекать носители заряда.

Напомним: Напряжение, ЭДС – это разность потенциалов. Отсюда следует, что для выполнения условий существования тока – наличия электрического поля и электрического тока, нужно напряжение. Это могут быть обкладки заряженного конденсатора, гальванический элемент, ЭДС возникшее под действием магнитного поля (генератор).

Как он возникает, мы разобрались, давайте поговорим о том, куда он направлен. Ток, в основном, в привычном для нас использовании, движется в проводниках (электропроводка в квартире, лампочки накаливания) или в полупроводниках (светодиоды, процессор вашего смартфона и другая электроника), реже в газах (люминесцентные лампы).

Так вот основными носителями заряда в большинстве случаев являются электроны, они движутся от минуса (точки с отрицательным потенциалом) к плюсу (точке с положительным потенциалом, подробнее об этом вы узнаете ниже).

Но интересен тот факт, что за направление движения тока было принято движение положительных зарядов – от плюса к минусу. Хотя фактически всё происходит наоборот. Дело в том, что решение о направлении тока было принято до изучения его природы, а также до того, как было определено за счет чего протекает и существует ток.

Электрический ток в разных средах

Мы уже упоминали о том, что в различных средах электрический ток может различаться по типу носителей заряда. Среды можно разделить по характеру проводимости (по убыванию проводимости):

  1. Проводник (металлы).
  2. Полупроводник (кремний, германий, арсенид галия и пр).
  3. Диэлектрик (вакуум, воздух, дистиллированная вода).

В металлах

В металлах есть свободные носители зарядов, их иногда называют «электрическим газом». Откуда берутся свободные носители зарядов? Дело в том, что металл, как и любое вещество, состоит из атомов. Атомы, так или иначе движутся или колеблются. Чем выше температура металла, тем сильнее это движение. При этом сами атомы в общем виде остаются на своих местах, собственно и формируя структуру металла.

В электронных оболочках атома обычно есть несколько электронов, у которых связь с ядром достаточно слабая. Под воздействием температур, химических реакций и взаимодействия примесей, которые в любом случае находятся в металле, электроны отрываются от своих атомов, образуются положительно заряженные ионы. Оторвавшиеся электроны называются свободными и двигаются хаотично.

Если на них будет воздействовать электрическое поле, например, если подключить к куску металла батарейку – хаотичное движение электронов станет упорядоченным. Электроны от точки, в которую подключен отрицательный потенциал (катод гальванического элемента, например), начнут двигаться к точке с положительным потенциалом.

В полупроводниках

Полупроводниками являются такие материалы, в которых в нормальном состоянии нет свободных носителей заряда. Они находятся в так называемой запрещенной зоне. Но если приложить внешние силы, такие как электрическое поле, тепло, различные излучения (световое, радиационное и пр.), они преодолевают запрещенную зону и переходят в свободную зону или зону проводимости. Электроны отрываются от своих атомов и становятся свободными, образуя ионы – положительные носители зарядов.

Положительные носители в полупроводниках называются дырками.

Если просто передать энергию полупроводнику, к примеру нагреть, начнется хаотичное движение носителей заряда. Но если речь идет о полупроводниковых элементах, типа диода или транзистора, то на противоположных концах кристалла (на них нанесен металлизированный слой и припаяны выводы) возникнет ЭДС, но это не относится к теме сегодняшней статьи.

Если приложить источник ЭДС к полупроводнику, то носители заряда также перейдут в зону проводимости, а также начнется их направленное движение – дырки пойдут в сторону с меньшим электрическим потенциалом, а электроны – в сторону с большим.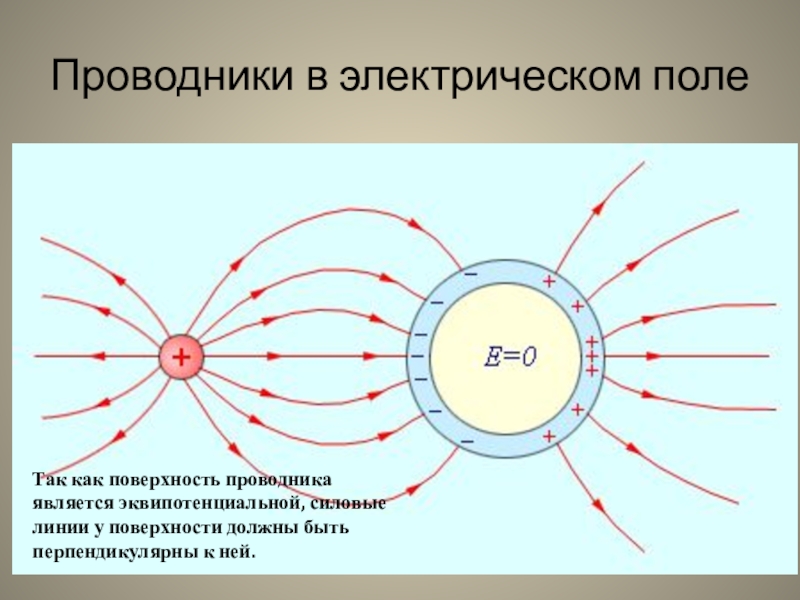

В вакууме и газе

Вакуумом называют среду с полным (идеальный случай) отсутствием газов или минимизированным (в реальности) его количеством. Так как в вакууме нет никакого вещества, то и носителям заряда браться не откуда. Однако протекание тока в вакууме положило начало электронике и целой эпохе электронных элементов – электровакуумных ламп. Их использовали в первой половине прошлого века, а в 50-х годах они начали постепенно уступать месту транзисторам (в зависимости от конкретной сферы электроники).

Допустим, что у нас есть сосуд, из которого откачали весь газ, т.е. в нём полный вакуум. В сосуд помещено два электрода, назовем их анод и катод. Если мы подключим к катоду отрицательный потенциал источника ЭДС, а к аноду положительный – ничего не произойдет и ток протекать не будет. Но если мы начнем нагревать катод – ток начнет протекать. Этот процесс называется термоэлектронной эмиссией – испускание электронов с нагретой поверхности электрона.

На рисунке изображен процесс протекания тока в вакуумной лампе. В вакуумных лампах катод нагревают расположенной рядом нитью накала на рис (Н), типа такой, как в осветительной лампе.

При этом, если изменить полярность питания – на анод подать минус, а на катод подать плюс – ток протекать не будет. Это докажет, что ток в вакууме протекает за счет движения электронов от КАТОДА к АНОДУ.

Газ также как и любое вещество состоит из молекул и атомов, это значит, что если газ будет находиться под воздействием электрического поля, то при определенной его силе (напряжение ионизации) электроны оторвутся от атома, тогда будут выполнены оба условия протекания электрического тока – поле и свободные носители.

Как уже было сказано, этот процесс называется ионизацией. Она может происходить не только от приложенного напряжения, но и при нагреве газа, рентгеновском излучении, под воздействием ультрафиолета и прочего.

Ток через воздух потечет, даже если между электродами установить горелку.

Протекание тока в инертных газах сопровождается люминесценцией газа, это явление активно используется в люминесцентных лампах.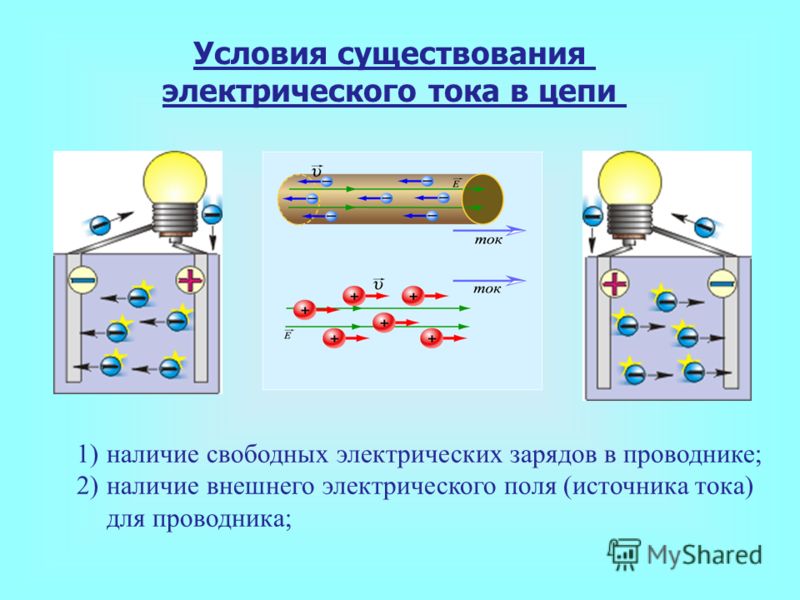 Протекание электрического тока в газовой среде называется газовым разрядом.

В жидкости

Допустим, что у нас есть сосуд с водой в который помещены два электрода, к которым подключен источник питания. Если вода дистиллированная, то есть чистая и не содержит примесей, то она является диэлектриком. Но если мы добавим в воду немного соли, серной кислоты или любого другого вещества, образуется электролит и через него начнет протекать ток.

Электролит – вещество, которое проводит электрический ток вследствие диссоциации на ионы.

Если в воду добавить медный купорос, то на одном из электродов (катоде) осядет слой меди – это называется электролиз, что доказывает что электрический ток в жидкости осуществляется за счет движения ионов – положительных и отрицательных носителей заряда.

Электролиз – физико-химический процесс, который заключается в выделении на электродах компонентов составляющих электролит.

Таким образом происходит омеднение, золочения и покрытие другими металлами.

Заключение

Подведем итоги, для протекания электрического тока нужны свободные носители зарядов:

  • электроны в проводниках (металлы) и вакууме;
  • электроны и дырки в полупроводниках;
  • ионы (анионы и катионы) в жидкости и газах.

Для того, чтобы движение этих носителей стало упорядоченны, нужно электрическое поле. Простыми словами — приложить напряжение на концах тела или установить два электрода в среде, где предполагается протекание электрического тока.

Также стоит отметить, что ток определенным образом воздействует на вещество, различают три типа воздействия:

  • тепловое;
  • химическое;
  • физическое.

Полезное

Для возникновения и поддержания тока в какой-либо среде необходимо выполнение двух условий:

В разных средах носителями электрического тока являются разные заряженные частицы.

Электрическое поле в среде необходимо для создания направленного движения свободных зарядов.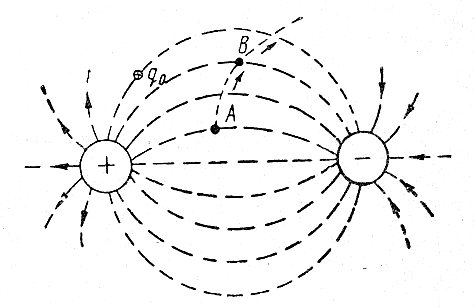 Как известно, на заряд q в электрическом поле напряженностью E действует сила F = q*E, которая и заставляет свободные заряды двигаться в направлении электрического поля. Признаком существования в проводнике электрического поля является наличие не равной нулю разности потенциалов между любыми двумя точками проводника,

Однако, электрические силы не могут длительное время поддерживать электрический ток. Направленное движение электрических зарядов через некоторое время приводит к выравниванию потенциалов на концах проводника и, следовательно, к исчезновению в нем электрического поля.

Для поддержания тока в электрической цепи на заряды кроме кулоновских сил должны действовать силы неэлектрической природы (сторонние силы).

Устройство, создающее сторонние силы, поддерживающее разность потенциалов в цепи и преобразующее различные виды энергии в электрическую энергию, называется источником тока.

Для существования электрического тока в замкнутой цепи необходимо включение в нее источника тока.

Основные характеристики

1. Сила тока — I, единица измерения — 1 А (Ампер).

Силой тока называется величина, равная заряду, протекающему через поперечное сечение проводника за единицу времени.

Формула (1) справедлива для постоянного тока, при котором сила тока и его направление не изменяются со временем. Если сила тока и его направление изменяются со временем, то такой ток называется переменным.

Для переменного тока:

Я = НтДд /Дт,(*)

т.е. = q», гдеq»- производная от заряда по времени.

2. Плотность тока — j, единица измерения — 1 А/м2.

Плотностью тока называется величина, равная силе тока, протекающего через единичное поперечное сечение проводника:

3. Электродвижущая сила источника тока — э.д.с. (e), единица измерения — 1 В (Вольт). Э.д.с.- физическая величина, равная работе, совершаемой сторонними силами при перемещении по электрической цепи единичного положительного заряда:

е = а друг. / г. (3)

4. Сопротивление проводника — R, единица измерения — 1 Ом.

Под действием электрического поля в вакууме свободные заряды двигались бы ускоренно. В веществе они движутся в среднем равномерно, т.к. часть энергии отдают частицам вещества при столкновениях.

Теория утверждает, что энергия упорядоченного движения зарядов рассеивается на искажениях кристаллической решетки. Исходя из природы электрического сопротивления, следует, что

R = R* L / S Э, (4)

l — длина проводника,

S — площадь поперечного сечения,

r — коэффициент пропорциональности, названный удельным сопротивлением материала.

Эта формула хорошо подтверждается на опыте.

Взаимодействие частиц проводника с движущимися в токе зарядами зависит от хаотического движения частиц, т.е. от температуры проводника. Известно, что

г = г 0 (1 + т), (5)

R = R 0 (1 + т).

Коэффициент a называется температурным коэффициентом сопротивления:

а = (R — R0) / R0 * т.

Для химически чистых металлов a > 0 и равно 1/273 К-1. Для сплавов температурные коэффициенты имеют меньшее значение. Зависимость r(t)для металлов линейная:

В 1911 году открыто явление сверхпроводимости , заключающееся в том, что при температуре, близкой к абсолютному нулю, сопротивление некоторых металлов падает скачком до нуля.

У некоторых веществ (например, у электролитов и полупроводников) удельное сопротивление с ростом температуры уменьшается, что объясняется ростом концентрации свободных зарядов.

Величина, обратная удельному сопротивлению, называется удельной электрической проводимостью с

с = 1 / г. (7)

5. Напряжение — U , единица измерения — 1 В.

Напряжение — физическая величина, равная работе, совершаемой сторонними и электрическими силами при перемещении единичного положительного заряда.

U = (ст. + Аэл.) / Q (8)

Так как Аст./q = e, а Аэл./q = f1-f2, то

U = е + (е1 — е2) (9)

2. 7.2 Основы электробезопасности

При эксплуатации и ремонте электрического оборудования и сетей человек может оказаться в сфере действия электрического поля или непосредственном соприкосновении с находящимися под напряжением проводками электрического тока. В результате прохождения тока через человека может произойти нарушение его жизнедеятельных функций.

Опасность поражения электрическим током усугубляется тем, что, во первых, ток не имеет внешних признаков и как правило человек без специальных приборов не может заблаговременно обнаружить грозящую ему опасность; во вторых, воздействия тока на человека в большинстве случаев приводит к серьезным нарушениям наиболее важных жизнедеятельных систем, таких как центральная нервная, сердечно-сосудистая и дыхательная, что увеличивает тяжесть поражения; в третьих, переменный ток способен вызвать интенсивные судороги мышц, приводящие к не отпускающему эффекту, при котором человек самостоятельно не может освободиться от воздействия тока; в четвертых,воздействие тока вызывает у человека резкую реакцию отдергивания, а в ряде случаев и потерю сознания, что при работе навысоте может привести к травмированию в результате падения.

Электрический ток, проходя через тело человека, может оказывать биологическое, тепловое, механическое и химическое действия. Биологическое действие заключается в способности электрического тока раздражать и возбуждать живые ткани организма, тепловое – в способности вызывать ожоги тела, механическое – приводить к разрыву тканей, а химическое – к электролизу крови.

Воздействие электрического тока на организм человека может явиться причиной электротравмы. Электротравма – это травма, вызванная воздействием электрического тока или электрической дуги. Условно электротравмы делят на местные и общие. При местных электротравмах возникает местное повреждение организма, выражающиеся в появлении электрических ожогов,

электрических знаков, в металлизации кожи, механических повреждениях и электроофтальмии (воспаление наружных оболочек глаз). Общие электротравмы, или электрические удары, приводят к поражению всего организма, выражающемуся в нарушении или полном прекращении деятельностинаиболее жизненно важных органов и систем – легких (дыхания), сердца (кровообращения).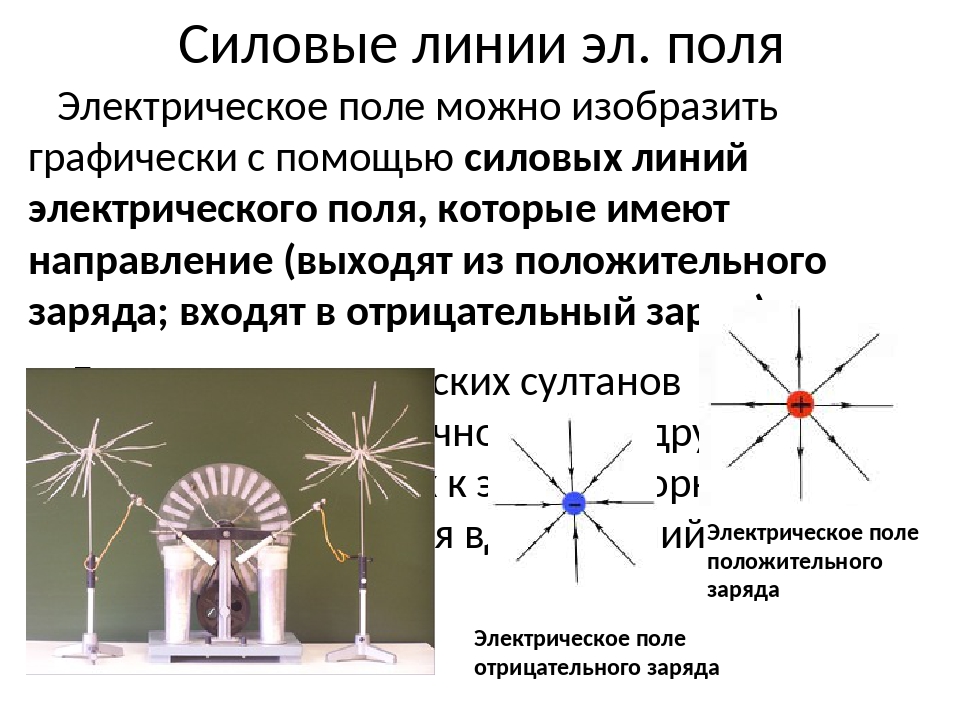

Электрический удар представляет собой возбуждение живых тканей организма проходящим через него электрическим током, сопровождающееся резкими судорожными сокращениями мышц, в том числе мышцы сердца, что может привести к остановке сердца.

Под местными электротравмами понимается повреждение кожи и мышечной ткани, а иногда связок и костей. К ним можно отнести электрические ожоги, электрические знаки, металлизацию кожи, механические повреждения.

Электрические ожоги — наиболее распространенная электротравма, возникает в результате локального воздействия тока на ткани. Ожоги бывают двух видов — контактный и дуговой.

Контактный ожог является следствием преобразования электрической энергии в тепловую и возникает в основном в электроустановках напряжением до 1 000 В.

Электрический ожог – это как бы аварийная система, защита организма, так как обуглившиеся ткани в силу большей сопротивляемости, чем обычная кожа, не позволяют электричеству проникнуть вглубь, к жизненно важным системам и органам. Иначе говоря, благодаря ожогу ток заходит в тупик.

Когда организм и источник напряжения соприкасались неплотно, ожоги образуются на местах входа и выхода тока. Если ток проходит по телу несколько раз разными путями, возникают множественные ожоги.

Множественные ожоги чаще всего случаются при напряжении до 380 В из-за того, что такое напряжение “примагничивает” человека и требуется время на отсоединение. Высоковольтный ток такой “липучестью” не обладает.

Наоборот, он отбрасывает человека, но и такого короткого контакта достаточно для серьезных глубоких ожогов. При напряжении свыше 1 000 В случаются электротравмы с обширными глубокими ожогами, поскольку в этом случае температура поднимается по всему пути следования тока.

Оценивать опасность воздействия электрического тока на человека проявляются три качественно отличные ответные реакции. Это прежде всего ощущение, более судорожное сокращение мышц (неотпускание для переменного тока и болевой эффект постоянного) и, наконец, фисрилляция сердца. Электрические токи, вызывающие соответствующую ответную реакцию, подразделяют на ощутимые, неотпускающие и фибрилляционные.

С увеличением тока четко проявляются три качественно отличные

ответные реакции. Это прежде всего ощущение, более судорожное сокращение

мышц (неотпускание для переменного тока и болевой эффект постоянного) и, наконец, фисрилляция сердца. Электрические токи, вызывающие соответствующую ответную реакцию, подразделяют на ощутимые, неотпускающие и фибрилляционные.

В целях обеспечения электробезопасности используют следующие технические способы и средства (часто в сочетании одного с другим): защитное заземление; зануление; защитное отключение; выравнивание потенциалов; малое напряжение; электрическое разделение сети; изоляцию токоведущих частей; оградительные устройства; предупредительную сигнализацию, блокировку, знаки безопасности; электрозащитные средства, предохранительные приспособления и др.

Защитное заземление — преднамеренное электрическое соединение с землей или ее эквивалентом металлических не токоведущих частей, которые могут оказаться под напряжением в результате повреждения изоляции (ГОСТ 12. 1.009-76). Защитное заземление применяется в сетях напряжением до 1000 В с изолированной нейтралью и в сетях напряжением выше 1000 В как с изолированной, так и с заземленной нейтралью.

Защитное отключение — это быстродействующая защита, обеспечивающая автоматическое отключение электроустановки (не более чем за 0,2 с) при возникновении в ней повреждения, в том числе при пробое изоляции на корпус оборудования.

Выравнивание потенциалов — метод снижения напряжений прикосновения и шага между точками электрической цепи, к которым возможно одновременное прикосновение или на которых может одновременно стоять человек.

Малое напряжение — номинальное напряжение не более 42 В, применяемое в целях уменьшения опасности поражения электрическим током.

Электрическое разделение сети — разделение сети на отдельные, электрически не связанные между собой, участки с помощью разделяющего

трансформатора. Если сильно разветвленную электрическую сеть, имеющую

большую емкость и малое сопротивление изоляции, разделить на ряд небольших сетей такого же напряжения, то они будут обладать незначительной емкостью и высоким сопротивлением изоляции. Опасность поражения током при этом резко снижается.

Изоляция в электроустановках служит для защиты от случайного прикосновения к токоведущим частям. Различают рабочую, дополнительную, двойную и усиленную электрическую изоляцию.

Оградительные устройства используются для предотвращения прикосновения или опасного приближения к токоведущим частям.

Блокировки широко применяются в электроустановках. Они бывают механическими, электрическими, электромагнитными и др. Блокировки обеспечивают снятие напряжения с токоведущих частей при попытке проникнуть к ним при открывании ограждения без снятия напряжения.

Направленное (упорядоченное) движение свободных заряженных частиц под действием электрического поля называется электрическим током .

Условия существования тока :

1. Наличие свободных зарядов.

2. Наличие электрического поля, т.е. разности потенциалов. Свободные заряды имеются в проводниках. Электрическое поле создается источниками тока.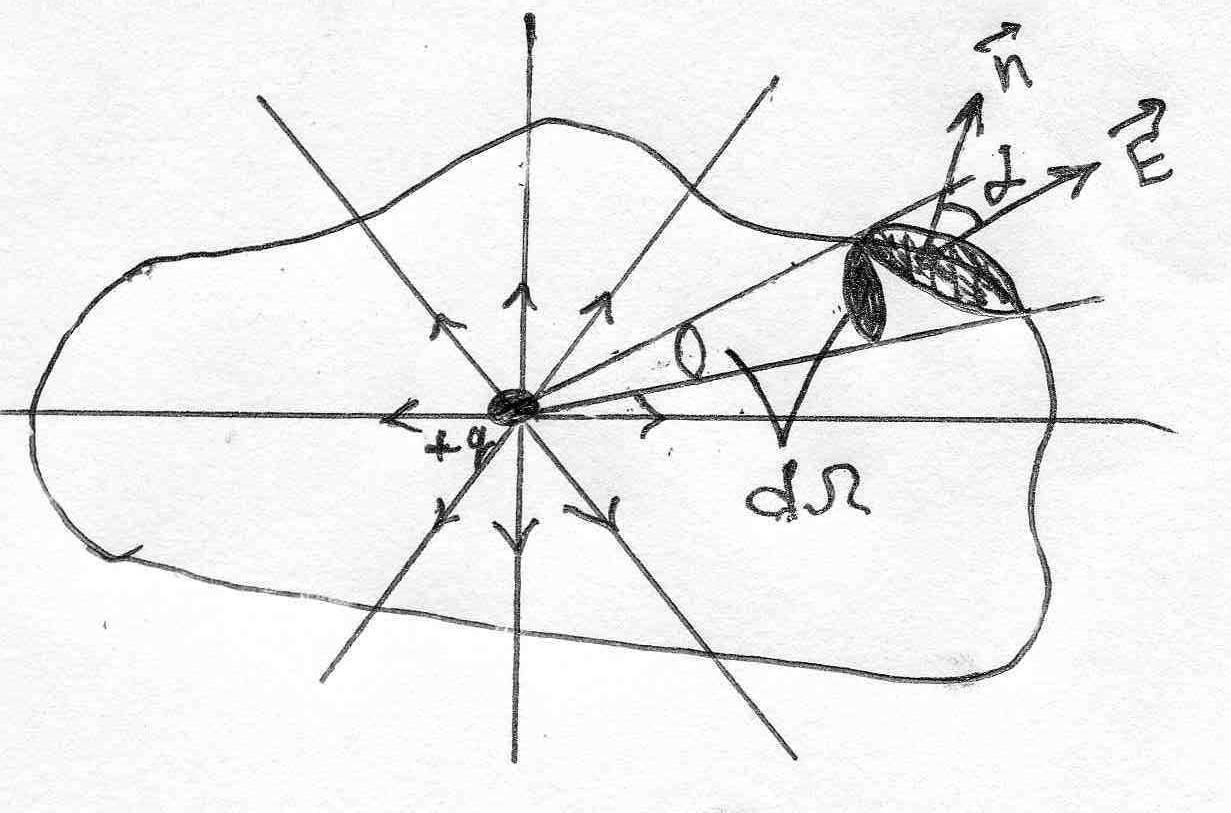

При прохождении тока через проводник он оказывает следующие действия:

· Тепловое (нагревание проводника током). Например: работа электрического чайника, утюга и т.д.).

· Магнитное (возникновение магнитного поля вокруг проводника с током). Например: работа электродвигателя, электроизмерительных приборов).

· Химическое (химические реакции при прохождении тока через некоторые вещества). Например: электролиз.

Можно также говорить о

· Световом (сопровождает тепловое действие). Например: свечение нити накала электрической лампочки.

· Механическом (сопровождает магнитное или тепловое). Например: деформация проводника при нагревании, поворот рамки с током в магнитном поле).

· Биологическом (физиологическом). Например: поражение человека током, использование действия тока в медицине.

Основные величины, описывающие процесс прохождения тока по проводнику .

1. Сила тока I — скалярная величина, равная отношению заряда, прошедшего через поперечное сечение проводника, промежутку времени, в течение которого шел ток. Сила тока показывает, какой заряд проходит через поперечное сечение проводника за единицу времени. Ток называют постоянным , если сила тока не меняется со временем. Для того чтобы ток через проводник был постоянным необходимо, чтобы разность потенциалов на концах проводника была постоянной.

2. Напряжение U . Напряжение численно равно работе электрического поля по перемещению единичного положительного заряда вдоль силовых линий поля внутри проводника.

3. Электрическое сопротивление R — физическая величина, численно равная отношению напряжения (разности потенциалов) на концах проводника к силе тока, проходящего через проводник.

60. Закон Ома для участка цепи.

Сила тока в участке цепи прямо пропорциональна напряжению на концах этого проводника и обратно пропорциональна его сопротивлению:

I = U / R;

Ом установил, что сопротивление прямо пропорционально длине проводника и обратно пропорционально площади его поперечного сечения и зависит от вещества проводника.

где ρ — удельное сопротивление, l — длина проводника, S — площадь поперечного сечения проводника.

61. Сопротивление как электрическая характеристика резистора. Зависимость сопротивления металлических проводников от рода материала и геометрических размеров.

Электри́ческое сопротивле́ние — физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношению напряжения на концах проводника к силе тока, протекающего по нему. Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления.

Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как

Где R — сопротивление; U — разность электрических потенциалов на концах проводника; I — сила тока, протекающего между концами проводника под действием разности потенциалов.

Сопротивление проводника является такой же характеристикой проводника как и его масса. Сопротивление проводника не зависит ни от силы тока в проводнике, ни от напряжения на его концах, а зависит только от рода вещества, из которого изготовлен проводник и его геометрических размеров: , где: l — длина проводника, S — площадь поперечного сечения проводника, ρ — удельное сопротивление проводника, показывающее каким сопротивлением будет обладать проводник длиной 1 м и площадью сечения 1 м 2 , изготовленный из данного материала.

Проводники, подчиняющиеся закону Ома, называются линейными. Существует много материалов и устройств, не подчиняющихся закону Ома, например, полупроводниковый диод или газоразрядная лампа. Даже у металлических проводников при достаточно больших токах наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников растет с ростом температуры.

Зависимость сопротивления проводника от температуры выражается формулой: , где: R — сопротивление проводника при температуре Т, R 0 — сопротивление проводника при температуре 0ºС, α — температурный коэффициент сопротивления.

Электрический ток. Условия, необходимые для возникновения электрического тока

Цели урока.

Обучающая:

формирование знаний учащихся об условиях возникновения и существования электрического тока.

Развивающая:

развитие логического мышления, внимания, умений использовать полученные знания на практике.

Воспитательная:

создание условий для проявления самостоятельности, внимательности и самооценки.

Оборудование.

  1. Гальванические элементы, аккумулятор, генератор, компас.
  2. Карточки (прилагаются).
  3. Демонстрационный материал (портреты выдающихся физиков Ампера, Вольта; плакаты “Электричество”, “Электрические заряды”).

Демонстрации:

  1. Действие электрического тока в проводнике на магнитную стрелку.
  2. Источники тока: гальванические элементы, аккумулятор, генератор.

План проведения урока

1. Организационный момент.

2. Вступительное слово преподавателя.

3. Подготовка к восприятию нового материала.

4. Изучение нового материала.

а) источники тока;

б) действия электрического тока;

в) физическая оперетта “Королева Электричество”;

г) заполнение таблицы “Электрический ток”;

д) меры безопасности при работе с электроприборами.

5. Подведение итогов урока.

6. Рефлексия.

7. Домашнее задание:

а) Опираясь на знания, полученные на уроках ОБЖ, спецтехнологии подготовить и записать в тетради памятку “Меры безопасности при работе с электроприборами”

б) Индивидуальное задание: Подготовить сообщение о применении источника тока в быту и технике.

Конспект урока

1. Организационный момент

Отметить наличие учащихся, назвать тему урока, цель.

2. Вступительное слово преподавателя

Со словами электричество, электрический ток мы знакомы с раннего детства. Электрический ток используется в наших домах, на транспорте, на производстве, в осветительной сети.

Но, что такое электрический ток, какова его природа, понять нелегко.

Слово электричество произошло от слова электрон, которое переводится с греческого языка как янтарь. Янтарь — это окаменевшая смола древних хвойных деревьев. Слово ток обозначает течение или движение чего-либо.

3. Подготовка к восприятию нового материала

Вопросы вводной беседы.

— Какие два типа зарядов существуют в природе? Как они взаимодействуют?

Ответ: В природе существуют два вида зарядов: положительные и отрицательные.

Носителями положительного заряда являются протоны, отрицательного электроны. Одноименно заряженные частицы отталкиваются, разноименно заряженные притягиваются

— Существует ли электрическое поле вокруг электрона?

Ответ: Да, электрическое поле вокруг электрона существует.

— Что такое свободные электроны?

Ответ: Это электроны наиболее удаленные от ядра, они могут свободно двигаться между атомами.

4. Изучение нового материала

а) Источники тока.

На столе находятся специальные устройства. Как они называются? Для чего они нужны?

Ответ: Это гальванические элементы, аккумулятор, генератор — общее название источники тока. Они необходимы для подачи электрической энергии, создают электрическое поле в проводнике.

Мы знаем, что существуют заряженные частицы, электроны и протоны, знаем, что существуют устройства, которые называются источниками тока.

Как вы считаете, что такое электрический ток?

Ответ: Электрический ток – это направленное движение заряженных частиц.

б) Действия электрического тока.

Скажите, как мы можем понять, что в цепи существует электрический ток, по каким действиям?

Ответ: Электрический ток оказывает различные виды действия:

  • Тепловое – проводник по которому идет электрический ток нагревается (электроплита, утюг, лампа накаливания, паяльник).
  • Химическое действие тока можно наблюдать при пропускании электрического тока через раствор медного купороса – выделение меди из раствора купороса, хромирование, никелирование.
  • Физиологическое – сокращение мышц человека и животных, по которым прошел электрический ток.
  • Магнитное – при прохождении электрического тока по проводнику, если рядом расположить магнитную стрелку она способна отклонится. Это действие является основным. Демонстрация опыта: аккумулятор, лампа накаливания, соединительные провода, компас.

в) Физическая оперетта “Королева Электричество”. (Приложение № 1)

Теперь девушки старшего курса представят вашему вниманию оперетту “Королева Электричество”. Не забываем русскую народную пословицу “Сказка ложь, да в ней намек, добрым молодцам урок”. То есть, вы не только слушаете и смотрите, но и берете из нее определенную информацию. Ваша задача записать как можно больше физических терминов, которые встречаются в представлении.

г) Заполнение таблицы “Электрический ток”. (Приложение № 2)

Скажите, какое одно понятие объединяет все термины, которые вы записали?

Ответ: Электрический ток.

Приступаем к заполнению таблицы “Электрический ток”.

Заполняя таблицу, давайте, обобщим полученные на уроке знания и получим новую информацию.

В процессе заполнения таблицы делаем вывод о том, какие условия необходимы для создания электрического тока.

  • Первое условие — это наличие свободных заряженных частиц.
  • Второе условие — это наличие электрического поля внутри проводника.

д) Меры безопасности при работе с электроприборами.

Где, на производственной практике, вы сталкиваетесь с применением электрического тока? Ответы учащихся.

Главная наша задача сохранить здоровье в течение всей жизни, скажите, а какие меры безопасности необходимо соблюдать при работе с электроприборами?

Ответ: При работе с электроприборами.

Запрещено.

  • Ходить по земле, держа в руках включенные в сеть электроприборы. Особенно опасно ходить босиком по влажной почве.
  • Входить в электрощитовые и другие электротехнические помещения.
  • Браться за оборванные, оголенные, висящие и лежащие на земле провода.
  • Вбивать гвозди в стену в месте, где может располагаться скрытая проводка. Смертельно опасно в этот момент заземляться на батареи центрального отопления, водопровод.
  • Сверлить стены в местах возможной электропроводки.
  • Красить, белить, мыть стены с наружной или скрытой проводкой, находящейся под напряжением.
  • Работать с включенными электроприборами вблизи батарей или водопровода.
  • Работать с электроприборами, менять лампочки, стоя на ванной.
  • Работать с неисправными электроприборами.
  • Ремонтировать необесточенные электроприборы.

5. Подведение итогов урока

— Следуя законам физики, время неумолимо движется вперед, и наш урок подошел к своему логическому завершению.

Давайте подведем итоги нашего занятия.

Как вы считаете, что такое электрический ток?

Ответ: Электрический ток – это направленное движение заряженных частиц.

Какие условия необходимы для создания электрического тока?

Ответ: Первое условие — это наличие свободных заряженных частиц.

Второе условие — это наличие электрического поля внутри проводника.

6. Рефлексия

Заполнение карточки. (Приложение № 3)

7. Домашнее задание

а) Опираясь на знания, полученные на уроках ОБЖ, спецтехнологии, подготовить и записать в тетради памятку “Меры безопасности при работе с электроприборами”.

б) Индивидуальное задание: Подготовить сообщение о применении источника тока в быту и технике. (Приложение № 2)

Электрическое поле: определение, характеристики, свойства

Есть такой термин в физике, как «Электрическое поле». Он описывает явление возникновения определенной силы вокруг заряженных тел. Оно применяется на практике и встречается в повседневной жизни. В этой статье мы рассмотрим, что такое электрическое поле и какие его свойства, а также, где оно возникает и применяется.

Определение

Вокруг заряженного тела возникает электрическое поле. Если сказать формулировку простыми словами, то это такое поле, которое действует на другие тела с определенной силой.

Основной количественной характеристикой является напряженность электрического поля. Она равна отношению силы, действующей на заряд, к величине заряда. Сила действует в каком-то направлении, значит и напряженность ЭП векторная величина. Ниже вы видите формулу напряженности:

Напряженность ЭП действует в направлении, которое вычисляется по принципу суперпозиции. То есть:

На рисунке ниже вы видите условное графическое изображение двух зарядов разной полярности и силовые линии электрического поля, возникающего между ними.

Важно! Главным условием возникновения электрического поля является то, что тело должно иметь какой-то заряд. Только тогда вокруг него возникнет поле, которое будет действовать на другие заряженные тела.

Чтобы определить величину напряженности электрического поля вокруг единичного пробного заряда используют закон Кулона, в этом случае:

Такое поле называют еще и кулоновским.

Другой важной физической величиной является потенциал электрического поля. Это уже не векторная, а скалярная величина, она прямопропорциональна энергии, приложенной к заряду:

Важно! Силовой и энергетической характеристикой электрического поля является напряженность и потенциал. Это и есть его основные физические свойства.

Он измеряется в Вольтах и численно равен работе ЭП по перемещению заряда из определенной точки в бесконечность.

Более подробно узнать о том, что такое напряженность электрического поля, вы можете из видео урока:

Виды полей

Различают несколько основных видов полей, в зависимости от того, где оно существует. Рассмотрим несколько примеров возникающих полей в различных ситуациях.

  1. Если заряды неподвижны – это статическое поле.
  2. Если заряды движутся по проводнику – магнитное (не путать с ЭП).
  3. Стационарное поле возникает вокруг неподвижных проводников с неизменяющимся током.
  4. В радиоволнах выделяют электрическое и магнитное поле, которые расположены в пространстве перпендикулярно друг другу. Это происходит, потому что любое изменение МП порождает возникновения ЭП с замкнутыми силовыми линиями.

Обнаружение электрического поля

Мы попытались вам рассказать все важные определения и условия существования электрического поля простым языком. Давайте разбираться, как его обнаружить. Магнитное обнаружить легко – с помощью компаса.

Электрическое поле мы можем обнаружить в быту. Все мы знаем, что если потереть пластиковую линейку об волосы, то мелкие бумажки начнут к ней притягиваться. Это и есть действие электрического поля. Когда вы снимаете шерстяной свитер, слышите треск и видите искорки – это оно же.

Другим способом обнаружить ЭП – поместить в него пробный заряд. Действующее поле отклонит его. Это применяется в ЭЛТ мониторах и, соответственно, лучевых трубках осциллографа, об этом поговорим позже.

Практика

Мы уже упомянули о том, что в быту электрическое поле проявляется, когда вы снимаете шерстяную или синтетическую одежду с себя и проскакивают искорки между волосами и шерстью, когда натрете пластиковую линейку и проведете над мелкими бумажками, а они притягиваются и прочее. Но это не является нормальными техническими примерами.

В проводниках малейшее ЭП вызывает движение носителей зарядов и их перераспределение. В диэлектриках, так как ширина запрещенной зоны в этих веществах большая, ЭП вызовет движение носителей зарядов только в случае пробоя диэлектрика. В полупроводниках действие находится между диэлектриком и проводником, но нужно преодолеть небольшую ширину запрещенной зоны, передав энергию порядка 0.3…0.7 эВ (для германия и кремния).

Из того, что есть в каждом доме – это электронные бытовые приборы, в том числе и блоки питания. В них есть важная деталь, которая работает благодаря электрическому полю – это конденсатор. В нём заряды удерживаются на обкладках, разделенных диэлектриком, как раз таки благодаря работе электрического поля. На картинке ниже вы видите условное изображение зарядов на обкладках конденсатора.

Другое применение в электротехнике — это полевые транзисторы или МДП-транзисторы. В их названии уже упоминается принцип действия. В них принцип работы основан на изменении проводимости СТОК-ИСТОК под воздействием на полупроводник поперечного электрического поля, а в МДП (МОП, MOSFET – одно и то же) и вовсе затвор отделен диэлектрическим слоем (окислом) от проводящего канала, так что влияние токов ЗАТВОР-ИСТОК невозможно по определению.

Другое применение уже отошедшее в быту, но еще «живое» в промышленной и лабораторной технике – электроннолучевые трубки (ЭЛТ или т.н. кинескопы). Где одним из вариантов устройства для перемещения луча по экрану является электростатическая отклоняющая система.

Если рассказать простым языком, то есть пушка, которая излучает (эмитирует) электроны. Есть система, которая отклоняет этот электрон в нужную точку на экране, для получения необходимого изображения. Напряжение прикладывается к пластинам, а на эмитированный летящий электрон воздействуют кулоновские силы, соответственно и электрическое поле. Все описанное происходит в вакууме. Тогда к пластинам прикладывают высокое напряжение, а для его формирования устанавливают трансформатор строчной развертки и обратноходовой преобразователь.

На видео ниже кратко и понятно объясняется, что такое электрическое поле и какими свойствами обладает этот особый вид материи:

Материалы по теме:

Условия, необходимые для возникновения электрического тока. Сила и плотность тока. Закон Ома

1. Условия, необходимые для возникновения электрического тока. Характеристики тока.

Закон Ома

2. Содержание:

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
Электрический ток
Сила тока
Амперметр
Напряжение
Вольтметр
Сопротивление
Омметр
Реостат, резистор, магазин сопротивления
Закон Ома
Лабораторная работа
Вопросы для самоконтроля
Список источников
Кристаллическая решетка металла
В узлах кристаллической решетки расположены «+» ионы, между
которыми хаотично движутся свободные электроны
Металлы являются хорошими проводниками благодаря свободным
заряженным частицам – электронам
Электрический ток
Электрический ток — упорядоченное (направленное)
движение заряженных частиц
Условия возникновения электрического тока в
проводнике:
1) наличие свободных заряженных частиц (электронов,
ионов)
2) электрическое поле
Направление электрического тока: от + к –
в металле:
• электроны движутся от – к +
• ток направлен в сторону, противоположную
направлению движения электронов
Сила тока
Сила тока — физическая величина, равная заряду,
прошедшему через поперечное сечение проводника
за единицу времени
Обозначение: I
Единица измерения: 1А (Ампер)
Формула:
q
I
t
Измерительный прибор: амперметр
q I t
q
I
t
q
t
I
Амперметр
А
Амперметр включается п о с л е д о в а т е л ь н о
А
При включении амперметра в цепь не имеет значения, с какой
стороны (слева или справа) от исследуемого элемента его
подключать.
Амперметр лабораторный
Шкала амперметра
Цена деления и пределы измерения прибора
Цена деления:
B A
С
n
A 50 A
B 100 A
n 10
100 50
С
5А
10
Пределы измерения:
П ниж 0 А
П верх 150 А
Принцип действия прибора
Шунт – проводник, подключаемый параллельно
амперметру для расширения пределов его измерений.
R
А
Rш
Часть измеряемого тока ответвляется и через амперметр
будет идти ток меньше измеряемого
Напряжение
Напряжение – скалярная физическая величина,
равная работе электрического поля по перемещению
единичного положительного заряда
Обозначение: U
Единица измерения в СИ: 1В (вольт)
Формула:
A
U
q
Измерительный прибор: вольтметр
A q U
A
U
q
A
q
U
Вольтметр
V
Вольтметр включается п а р а л л е л ь н о
V
Измерение напряжения
(видеофрагмент опыта)
Мультимедийное приложение к учебнику С. В. Громова и Н.А. Родиной «Физика. 9 класс» (Просвещение Медиа, Новый диск)
Вольтметр лабораторный
Вольтметр СССР, 1940 год
Шкала вольтметра
Цена деления и пределы измерения прибора
Цена деления:
B A
С
n
A 200 В
B 300 В
n 10
300 200
С
10 В
10
Пределы измерения:
П ниж 100 В
Пверх 500 В
Принцип действия прибора
Дополнительное сопротивление – проводник,
подключаемый последовательно с вольтметром для
расширения пределов его измерений
R
V
Rд
Ток через лампочку и напряжение на ней
А
V
Сопротивление
Сопротивление – скалярная физическая величина,
характеризующая свойство проводника
противодействовать электрическому току
Обозначение: R
Единица измерения: 1Ом (Ом)
Измерительный прибор: Омметр
Омметр
Измерение сопротивления
цифровым мультиметром
Причина электрического сопротивления:
взаимодействие электронов при их движении по
проводнику с ионами кристаллической решетки.
+
+
+
+
+
+
+
+
Направленному движению электронов мешают их столкновения с
колеблющимися тяжелыми и большими ионами кристаллической
решетки. Это и создает сопротивление движению электронов —
вызывает электрическое сопротивление металла.
Зависимость сопротивления проводника от его длины
(видеофрагмент опыта)
Мультимедийное приложение к учебнику С.В. Громова и Н.А. Родиной «Физика. 9 класс» (Просвещение Медиа, Новый диск)
Электрическое сопротивление металлов прямо
пропорционально длине проводника и обратно
пропорционально площади его поперечного сечения:
l
R
S
– удельное сопротивление
l – длина проводника
S – площадь поперечного сечения проводника
Удельное сопротивление – скалярная физическая
величина, численно равная сопротивлению
цилиндрического проводника единичной длины и
единичной площади поперечного сечения
Зависит от вещества и его состояния (температуры)
Единица измерения: 1 Ом м
Резистор – устройство с постоянным сопротивлением.
Реостат – устройство с переменным сопротивлением,
предназначенное для регулирования силы тока и
напряжения в электрической цепи.
Физика, 7-11 кл. Библиотека наглядных пособий (1С)
Реостат
(видеофрагмент опыта)
Мультимедийное приложение к учебнику С.В. Громова и Н.А. Родиной «Физика. 9 класс» (Просвещение Медиа, Новый диск)
Магазин сопротивлений
Зависимость силы тока
от напряжения и сопротивления
V
А
R
Результаты
I, А
Таблица 1
R=
№
1
2
3
R1
U, В
R2
I, А
R3
U, В
R1
Закон Ома
Сила тока на участке цепи прямо пропорциональна
напряжению на его концах и обратно
пропорциональна его сопротивлению
U
I
R
U
I
R
U I R
U
R
I
Закон Ома наглядно
Ампер Андре Мари
1775-1836
Алесандро Вольта
1745 — 1827
Георг Ом
1787 — 1854
Виртуальный тренажер
Содержание учебной работы: определение пределов измерения,
цены деления, погрешности измерения и показаний прибора;
запись результата измерения с учетом погрешности
«Виртуальная физика» (Д. В. Баяндин, О.И. Мухин, РЦИ ПГТУ).
Виртуальная лабораторная работа
Содержание учебной работы:
• Сборка электрической цепи
• Измерение силы, тока, напряжения, сопротивления с
помощью цифрового мультиметра.
• Исследование зависимости силы тока от напряжения и
сопротивления.
Начала электроники
Открытая физика: Часть 2 ( «Физикон»)
Вопросы для самоконтроля
1. Дайте определение электрического тока.
2. При каких условиях возникает электрический ток?
3. Чем отличается движение заряженных частиц в проводнике в
отсутствие и при наличии внешнего электрического поля?
4. Как направлен электрический ток?
5. В каком направлении движутся электроны в металлическом
проводнике, по которому протекает электрический ток?
6. Что называют силой тока?
7. Какова единица измерения силы тока?
8. Каким прибором измеряют силу тока? Как он подключается?
9. Что такое напряжение?
10.Какова единица напряжения?
11. Каким прибором измеряют напряжение? Как он подключается?
12.Что такое сопротивление? Какова причина сопротивления?
13.Какова единица сопротивления?
14.Каким прибором измеряют сопротивление? Как он
подключается?
15.Сформулируйте закон Ома для участка цепи.
Список литературы
1. Перышкин А.В. Физика. 8 класс.
2. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика. 10 класс.
Список электронных учебных изданий
1. Физика, 7-11 кл. Библиотека наглядных пособий (1С)
2. Открытая физика, ч.2 (Физикон)
3. Мультимедийное приложение к учебнику С.В. Громова и Н.А.
4. Родиной «Физика. 9 класс» (Просвещение Медиа, Новый диск)
5. «Виртуальная физика» (Д.В. Баяндин, О.И. Мухин, РЦИ ПГТУ).
6. Начала электроники (http://zeus.malishich.com )
Список ресурсов Интернет
иллюстрации
http://www.fizika.ru
http://www.go-radio.ru
http://school.xvatit.com
http://hystory.ru
http://fizportal.ru
http://radionostalgia. ca
http://slovari.yandex.ru
http://www.pribortorg.by
http://cxem.pp.ua
http://www.avito.ru
http://www.td-medstar.ru
http://omop.su
http://microschemes.pp.ua
http://www.proshkolu.ru
http://base.eworld.ru
http://masteram.com.ua
http://www.ww2.ru
http://solo-project.com
http://portal.etherway.ru

Электрический ток, сила, плотность, условия существования. Источник тока. Курсы по физике

Тестирование онлайн

  • Электрический ток. Основные понятия

  • Сила, плотность тока

Условия существования тока

Электрический ток — направленное движение заряженных частиц. Направление, в котором движутся положительно заряженные частицы, считается направлением тока. Вещества, в которых возможно движение зарядов, называются проводниками.

В металлах единственными носителями тока являются электроны. Направление тока противоположно направлению движения электронов.

Для существования тока необходимо:
1) наличие свободных заряженных частиц;
2) существование внешнего электрического поля;
3) наличие источника тока — источника сторонних сил.

Характеристики тока

Сила тока — скалярная величина, определяется по формуле

Если ток изменяется, то заряд, прошедший через поперечное сечение проводника, определяется как площадь фигуры, ограниченной зависимостью I(t).

Плотность тока — векторная величина, определяется по формуле

Прибор для измерения силы тока называется амперметром. Включается в сеть последовательно. Собственное сопротивление амперметра должно быть мало, поскольку включение амперметра не должно изменять силу тока в цепи.

В быту «источником тока» часто неточно называют любой источник электрического напряжения (батарею, генератор, розетку), но в строго физическом смысле это не так, более того, обычно используемые в быту источники напряжения по своим характеристикам гораздо ближе к источнику ЭДС, чем к источнику тока.

Примерами источника тока могут являться катушка индуктивности, вторичная обмотка трансформатора. Внутреннее сопротивление источника тока стремится к нулю.

Под действием электрического поля, созданного источником тока, свободные заряды движутся в веществе с некоторой средней скоростью — скорость дрейфа.

определение, особенности и интересные факты

В природе не существует абсолютных диэлектриков. Упорядоченное движение частиц — носителей электрического заряда, — то есть ток, можно вызвать в любой среде, однако для этого необходимы особые условия. Мы рассмотрим здесь, как протекают электрические явления в газах и как газ можно из очень хорошего диэлектрика превратить в очень хороший проводник. Нас будет интересовать, при каких условиях возникает, а также какими особенностями характеризуется электрический ток в газах.

Электрические свойства газов

Диэлектрик — это вещество (среда), в котором концентрация частиц — свободных носителей электрического заряда — не достигает сколько-нибудь значимой величины, вследствие чего проводимость пренебрежимо мала. Все газы — хорошие диэлектрики. Их изолирующие свойства используются повсеместно. Например, в любом выключателе размыкание цепи происходит, когда контакты приводятся в такое положение, чтобы между ними образовался воздушный зазор. Провода в линиях электропередач также изолируются друг от друга воздушным слоем.

Структурной единицей любого газа является молекула. Она состоит из атомных ядер и электронных облаков, то есть представляет собой совокупность электрических зарядов, некоторым образом распределенных в пространстве. Молекула газа может быть вследствие особенностей своего строения либо поляризоваться под действием внешнего электрического поля. Подавляющее большинство молекул, составляющих газ, в обычных условиях электрически нейтральны, поскольку заряды в них компенсируют друг друга.

Если приложить к газу электрическое поле, молекулы примут дипольную ориентацию, занимая пространственное положение, компенсирующее воздействие поля. Присутствующие в газе заряженные частицы под действием кулоновских сил начнут движение: положительные ионы — в направлении катода, отрицательные ионы и электроны — к аноду. Однако если поле имеет недостаточный потенциал, единый направленный поток зарядов не возникает, и можно говорить скорее об отдельных токах, настолько слабых, что ими следует пренебречь. Газ ведет себя как диэлектрик.

Таким образом, для возникновения электрического тока в газах необходима большая концентрация свободных носителей заряда и присутствие поля.

Ионизация

Процесс лавинообразного увеличения числа свободных зарядов в газе называют ионизацией. Соответственно, газ, в котором присутствует значительное количество заряженных частиц, называется ионизированным. Именно в таких газах создается электрический ток.

Процесс ионизации связан с нарушением нейтральности молекул. Вследствие отрыва электрона возникают положительные ионы, присоединение электрона к молекуле приводит к образованию отрицательного иона. Кроме того, в ионизированном газе много свободных электронов. Положительные ионы и особенно электроны — главные носители заряда при электрическом токе в газах.

Ионизация происходит, когда частице сообщается некоторое количество энергии. Так, внешний электрон в составе молекулы, получив эту энергию, может покинуть молекулу. Взаимные столкновения заряженных частиц с нейтральными приводят к выбиванию новых электронов, и процесс принимает лавинообразный характер. Кинетическая энергия частиц также возрастает, что значительно способствует ионизации.

Откуда берется энергия, затрачиваемая на возбуждение в газах электрического тока? Ионизация газов имеет несколько источников энергии, соответственно которым принято именовать и ее типы.

  1. Ионизация электрическим полем. В этом случае потенциальная энергия поля преобразуется в кинетическую энергию частиц.
  2. Термоионизация. Повышение температуры также ведет к образованию большого количества свободных зарядов.
  3. Фотоионизация. Суть данного процесса в том, что энергию электронам сообщают кванты электромагнитного излучения — фотоны, если они имеют достаточно высокую частоту (ультрафиолетовые, рентгеновские, гамма-кванты).
  4. Ударная ионизация является результатом преобразования кинетической энергии сталкивающихся частиц в энергию отрыва электрона. Наряду с термоионизацией, она служит основным фактором возбуждения в газах электрического тока.

Каждый газ характеризуется определенной пороговой величиной — энергией ионизации, необходимой для того, чтобы электрон мог оторваться от молекулы, преодолев потенциальный барьер. Эта величина для первого электрона составляет от нескольких вольт до двух десятков вольт; для отрыва следующего электрона от молекулы нужно больше энергии и так далее.

Следует учитывать, что одновременно с ионизацией в газе протекает обратный процесс — рекомбинация, то есть восстановление нейтральных молекул под действием кулоновских сил притяжения.

Газовый разряд и его типы

Итак, электрический ток в газах обусловлен упорядоченным движением заряженных частиц под действием приложенного к ним электрического поля. Наличие таких зарядов, в свою очередь, возможно благодаря различным факторам ионизации.

Так, термоионизация требует значительных температур, но открытое пламя в связи с некоторыми химическими процессами способствует ионизации. Даже при сравнительно невысокой температуре в присутствии пламени фиксируется появление в газах электрического тока, и опыт с проводимостью газа позволяет легко в этом убедиться. Надо поместить пламя горелки или свечи между обкладками заряженного конденсатора. Цепь, разомкнутая прежде из-за воздушного зазора в конденсаторе, замкнется. Включенный в цепь гальванометр покажет наличие тока.

Электрический ток в газах называется газовым разрядом. Нужно иметь в виду, что для поддержания стабильности разряда действие ионизатора должно быть постоянным, так как из-за постоянной рекомбинации газ теряет электропроводящие свойства. Одни носители электрического тока в газах — ионы — нейтрализуются на электродах, другие — электроны, — попадая на анод, направляются к «плюсу» источника поля. Если ионизирующий фактор перестанет действовать, газ немедленно снова станет диэлектриком, и ток прекратится. Такой ток, зависимый от действия внешнего ионизатора, называется несамостоятельным разрядом.

Особенности прохождения электрического тока через газы описываются особой зависимостью силы тока от напряжения — вольт-амперной характеристикой.

Рассмотрим развитие газового разряда на графике вольт-амперной зависимости. При повышении напряжения до некоторого значения U 1 ток нарастает пропорционально ему, то есть выполняется закон Ома. Возрастает кинетическая энергия, а следовательно, и скорость зарядов в газе, и этот процесс опережает рекомбинацию. При значениях напряжения от U 1 до U 2 такое соотношение нарушается; при достижении U 2 все носители зарядов достигают электродов, не успевая рекомбинировать. Все свободные заряды задействованы, и дальнейшее повышение напряжения не приводит к увеличению силы тока. Такой характер движения зарядов называется током насыщения. Таким образом, можно сказать, что электрический ток в газах обусловлен также особенностями поведения ионизированного газа в электрических полях различной напряженности.

Когда разность потенциалов на электродах достигает определенного значения U 3 , напряжение становится достаточным, чтобы электрическое поле вызвало лавинообразную ионизацию газа. Кинетической энергии свободных электронов уже хватает для ударной ионизации молекул. Скорость их при этом в большинстве газов составляет около 2000 км/с и выше (она рассчитывается по приближенной формуле v=600 U i , где U i — ионизационный потенциал). В этот момент происходит пробой газа и существенное возрастание тока за счет внутреннего источника ионизации. Поэтому такой разряд называется самостоятельным.

Наличие внешнего ионизатора в данном случае уже не играет роли для поддержания в газах электрического тока. Самостоятельный разряд в разных условиях и при различных характеристиках источника электрического поля может иметь те или иные особенности. Выделяют такие типы самостоятельного разряда, как тлеющий, искровой, дуговой и коронный. Мы рассмотрим, как ведет себя электрический ток в газах, кратко для каждого из этих типов.

В достаточно разности потенциалов от 100 (и даже меньше) до 1000 вольт для возбуждения самостоятельного разряда. Поэтому тлеющий разряд, характеризующийся малым значением силы тока (от 10 -5 А до 1 А), возникает при давлениях не более нескольких миллиметров ртутного столба.

В трубке с разреженным газом и холодными электродами формирующийся тлеющий разряд выглядит как тонкий светящийся шнур между электродами. Если продолжить откачку газа из трубки, будет наблюдаться размывание шнура, а при давлениях в десятые доли миллиметров ртутного столба свечение заполняет трубку практически полностью. Свечение отсутствует вблизи катода — в так называемом темном катодном пространстве. Остальная часть называется положительным столбом. При этом главные процессы, обеспечивающие существование разряда, локализуются именно в темном катодном пространстве и в прилегающей к нему области. Здесь происходит ускорение заряженных частиц газа, выбивающих из катода электроны.

При тлеющем разряде причиной ионизации является электронная эмиссия с катода. Испущенные катодом электроны производят ударную ионизацию молекул газа, возникающие положительные ионы вызывают вторичную эмиссию с катода и так далее. Свечение положительного столба связано в основном с отдачей фотонов возбужденными молекулами газа, и для различных газов характерно свечение определенного цвета. Положительный столб принимает участие в формировании тлеющего разряда только в качестве участка электрической цепи. Если сближать электроды, можно добиться исчезновения положительного столба, но при этом разряд не прекратится. Однако с дальнейшим сокращением расстояния между электродами тлеющий разряд не сможет существовать.

Необходимо отметить, что для данного типа электрического тока в газах физика некоторых процессов еще не прояснена полностью. Например, пока остается неясной природа сил, вызывающих при увеличении тока расширение на поверхности катода области, которая принимает участие в разряде.

Искровой разряд

Искровой пробой имеет импульсный характер.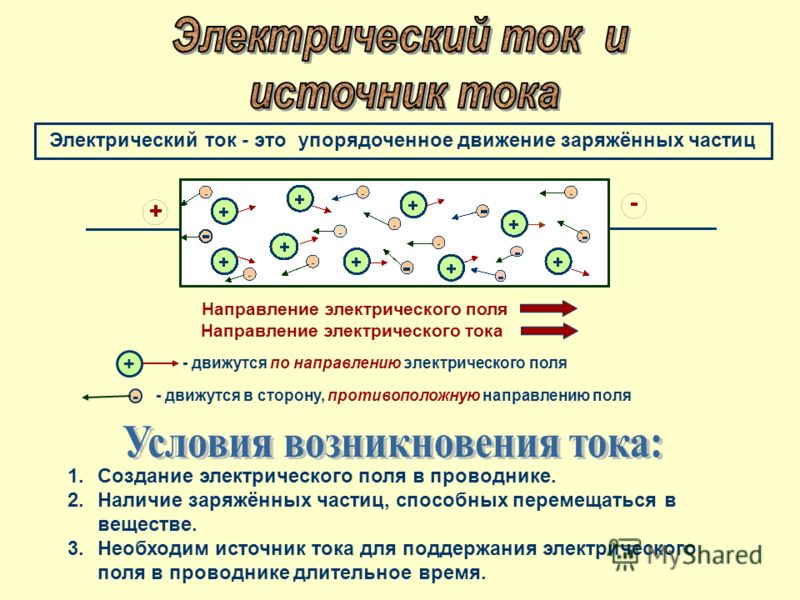 Он возникает при давлениях, близких к нормальному атмосферному, в случаях, когда мощности источника электрического поля недостаточно для поддержания стационарного разряда. Напряженность поля при этом велика и может достигать 3 МВ/м. Явление характеризуется резким возрастанием разрядного электрического тока в газе, одновременно напряжение чрезвычайно быстро падает, и разряд прекращается. Далее снова возрастает разность потенциалов, и весь процесс повторяется.

При этом типе разряда формируются кратковременные искровые каналы, рост которых может начинаться с любой точки между электродами. Это связано с тем, что ударная ионизация происходит случайным образом в местах, где в данный момент концентрируется наибольшее количество ионов. Вблизи искрового канала газ быстро нагревается и испытывает тепловое расширение, вызывающее акустические волны. Поэтому искровой разряд сопровождается треском, а также выделением теплоты и ярким свечением. Процессы лавинной ионизации порождают в искровом канале высокие давления и температуры до 10 тысяч градусов и выше.

Ярчайшим примером природного искрового разряда служит молния. Диаметр главного искрового канала молнии может составлять от нескольких сантиметров до 4 м, а длина канала достигать 10 км. Величина силы тока доходит до 500 тыс. ампер, а разность потенциалов между грозовым облаком и поверхностью Земли достигает миллиарда вольт.

Наиболее длинная молния протяженностью 321 км наблюдалась в 2007 году в Оклахоме, США. Рекордсменом по продолжительности стала молния, зафиксированная в 2012 году во Французских Альпах — она длилась свыше 7,7 секунды. При ударе молнии воздух может разогреться до 30 тысяч градусов, что в 6 раз превышает температуру видимой поверхности Солнца.

В тех случаях, когда мощность источника электрического поля достаточно велика, искровой разряд развивается в дуговой.

Этот вид самостоятельного разряда характеризуется большой плотностью тока и малым (меньше, чем при тлеющем разряде) напряжением. Дистанция пробоя невелика благодаря близкому расположению электродов. Разряд инициируется испусканием электрона с поверхности катода (для атомов металлов потенциал ионизации невелик по сравнению с молекулами газов). Во время пробоя между электродами создаются условия, при которых газ проводит электрический ток, и возникает искровой разряд, замыкающий цепь. Если мощность источника напряжения достаточно велика, искровые разряды переходят в устойчивую электрическую дугу.

Ионизация при дуговом разряде достигает почти 100%, сила тока очень велика и может составлять от 10 до 100 ампер. При атмосферном давлении дуга способна нагреваться до 5-6 тысяч градусов, а катод — до 3 тысяч градусов, что приводит к интенсивной термоэлектронной эмиссии с его поверхности. Бомбардировка анода электронами приводит к частичному разрушению: на нем образуется углубление — кратер с температурой около 4000 °C. Увеличение давления влечет за собой еще больший рост температур.

При разведении электродов дуговой разряд остается устойчивым до некоторого расстояния, что позволяет бороться с ним на тех участках электрооборудования, где он вреден из-за вызываемой им коррозии и выгорания контактов.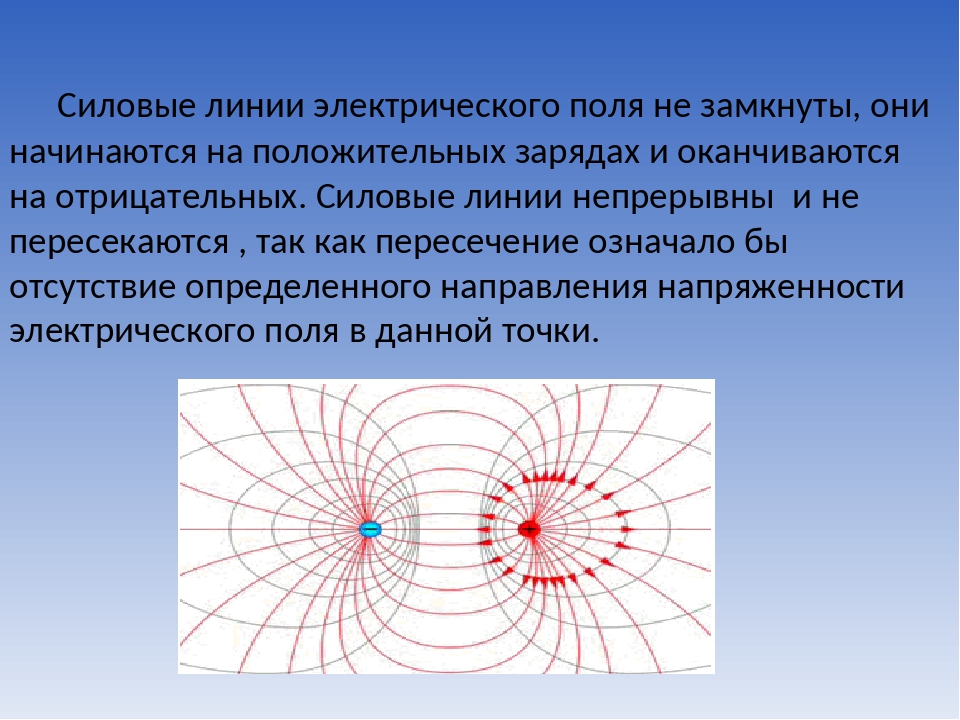 Это такие устройства, как высоковольтные и автоматические выключатели, контакторы и прочие. Одним из методов борьбы с дугой, возникающей при размыкании контактов, является использование дугогасительных камер, основанных на принципе удлинения дуги. Применяются и многие другие методы: шунтирование контактов, использование материалов с высоким потенциалом ионизации и так далее.

Развитие коронного разряда происходит при нормальном атмосферном давлении в резко неоднородных полях у электродов, обладающих большой кривизной поверхности. Это могут быть шпили, мачты, провода, различные элементы электрооборудования, имеющие сложную форму, и даже волосы человека. Такой электрод называется коронирующим. Ионизационные процессы и, соответственно, свечение газа имеют место только вблизи него.

Корона может формироваться как на катоде (отрицательная корона) при бомбардировке его ионами, так и на аноде (положительная) в результате фотоионизации. Отрицательная корона, в которой ионизационный процесс как следствие термоэмиссии направлен от электрода, характеризуется ровным свечением. В положительной короне могут наблюдаться стримеры — светящиеся линии ломаной конфигурации, могущие превратиться в искровые каналы.

Примером коронного разряда в природных условиях являются возникающие на остриях высоких мачт, верхушках деревьев и так далее. Образуются они при большой напряженности электрического поля в атмосфере, часто перед грозой или во время метели. Кроме того, их фиксировали на обшивке самолетов, попавших в облако вулканического пепла.

Коронный разряд на проводах ЛЭП ведет к значительным потерям электроэнергии. При большом напряжении коронный разряд может переходить в дуговой. Борьбу с ним ведут различными способами, например, путем увеличения радиуса кривизны проводников.

Электрический ток в газах и плазма

Полностью или частично ионизированный газ называется плазмой и считается четвертым агрегатным состоянием вещества. В целом плазма электрически нейтральна, так как суммарный заряд составляющих ее частиц равен нулю. Это отличает ее от других систем заряженных частиц, таких как, например, электронные пучки.

В природных условиях плазма образуется, как правило, при высоких температурах вследствие столкновения атомов газа на больших скоростях. Подавляющая часть барионной материи во Вселенной пребывает в состоянии плазмы. Это звезды, часть межзвездного вещества, межгалактический газ. Земная ионосфера также представляет собой разреженную слабо ионизированную плазму.

Степень ионизации является важной характеристикой плазмы — от нее зависят проводящие свойства. Степень ионизации определяется как отношение количества ионизированных атомов к общему количеству атомов в единице объема. Чем сильнее ионизирована плазма, тем выше ее электропроводность. Кроме того, ей присуща высокая подвижность.

Мы видим, таким образом, что газы, проводящие электрический ток, в пределах канала разряда являют собой не что иное, как плазму. Так, тлеющий и коронный разряды — это примеры холодной плазмы; искровой канал молнии или электрическая дуга — примеры горячей, практически полностью ионизованной плазмы.

Электрический ток в металлах, жидкостях и газах — различия и сходство

Рассмотрим особенности, которыми характеризуется газовый разряд в сравнении со свойствами тока в других средах.

В металлах ток — это направленное движение свободных электронов, не влекущее за собой химических изменений. Проводники такого типа называют проводниками первого рода; к ним относятся, кроме металлов и сплавов, уголь, некоторые соли и оксиды. Их отличает электронная проводимость.

Проводники второго рода — это электролиты, то есть жидкие водные растворы щелочей, кислот и солей. Прохождение тока сопряжено с химическим изменением электролита — электролизом. Ионы вещества, растворенного в воде, под действием разности потенциалов перемещаются в противоположные стороны: положительные катионы — к катоду, отрицательные анионы — к аноду. Процесс сопровождается выделением газа либо отложением слоя металла на катоде. Проводникам второго рода присуща ионная проводимость.

Что касается проводимости газов, то она, во-первых, временная, во-вторых, имеет признаки сходства и различия с каждым из них.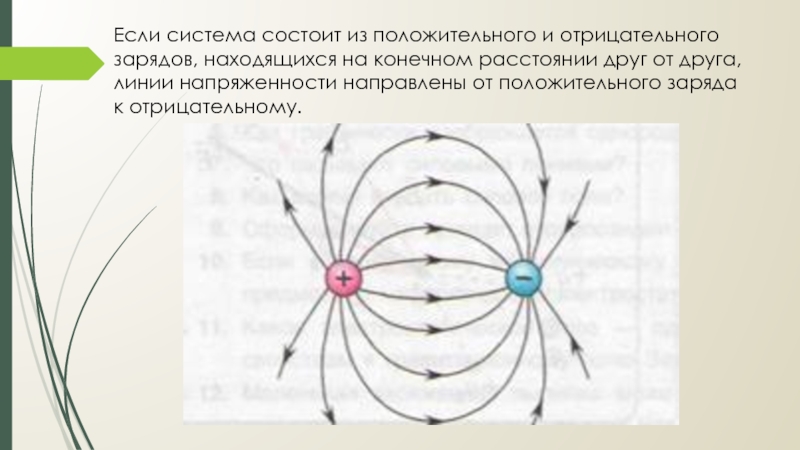 Так, электрический ток и в электролитах, и в газах — это направленный к противоположным электродам дрейф разноименно заряженных частиц. Однако в то время как электролиты характеризуются чисто ионной проводимостью, в газовом разряде при сочетании электронного и ионного типов проводимости ведущая роль принадлежит электронам. Еще одно различие электрического тока в жидкостях и в газах состоит в природе ионизации. В электролите молекулы растворенного соединения диссоциируют в воде, в газе же молекулы не разрушаются, а только теряют электроны. Поэтому газовый разряд, как и ток в металлах, не связан с химическими изменениями.

Неодинакова также и тока в жидкостях и газах. Проводимость электролитов в целом подчиняется закону Ома, а при газовом разряде он не соблюдается. Вольт-амперная характеристика газов имеет гораздо более сложный характер, связанный со свойствами плазмы.

Следует упомянуть и об общих и отличительных чертах электрического тока в газах и в вакууме. Вакуум — это почти идеальный диэлектрик. «Почти» — потому что в вакууме, несмотря на отсутствие (точнее, чрезвычайно малую концентрацию) свободных носителей заряда, тоже возможен ток. Но в газе потенциальные носители уже присутствуют, их только необходимо ионизировать. В вакуум носители заряда вносятся из вещества. Как правило, это происходит в процессе электронной эмиссии, например при нагревании катода (термоэлектронная эмиссия). Но и в различных типах газовых разрядов эмиссия, как мы видели, играет важную роль.

Применение газовых разрядов в технике

О вредном воздействии тех или иных разрядов вкратце речь уже шла выше. Теперь обратим внимание на пользу, которую они приносят в промышленности и в быту.

Тлеющий разряд применяют в электротехнике (стабилизаторы напряжения), в технологии нанесения покрытий (метод катодного распыления, основанный на явлении коррозии катода). В электронике его используют для получения ионных и электронных пучков. Широко известной областью применения тлеющего разряда являются люминесцентные и так называемые экономичные лампы и декоративные неоновые и аргоновые газоразрядные трубки. Кроме того, тлеющий разряд применяют в и в спектроскопии.

Искровой разряд находит применение в предохранителях, в электроэрозионных методах точной обработки металлов (искровая резка, сверление и так далее). Но наиболее известен он благодаря использованию в свечах зажигания двигателей внутреннего сгорания и в бытовой технике (газовые плиты).

Дуговой разряд, будучи впервые использован в осветительной технике еще в 1876 году (свеча Яблочкова — «русский свет»), до сих пор служит в качестве источника света — например, в проекционных аппаратах и мощных прожекторах. В электротехнике дуга используется в ртутных выпрямителях. Кроме того, она применяется в электросварке, в резке металла, в промышленных электропечах для выплавки стали и сплавов.

Коронный разряд находит применение в электрофильтрах для ионной очистки газов, в счетчиках элементарных частиц, в молниеотводах, в системах кондиционирования воздуха. Также коронный разряд работает в копировальных аппаратах и лазерных принтерах, где посредством его производится заряд и разрядка светочувствительного барабана и перенос порошка с барабана на бумагу.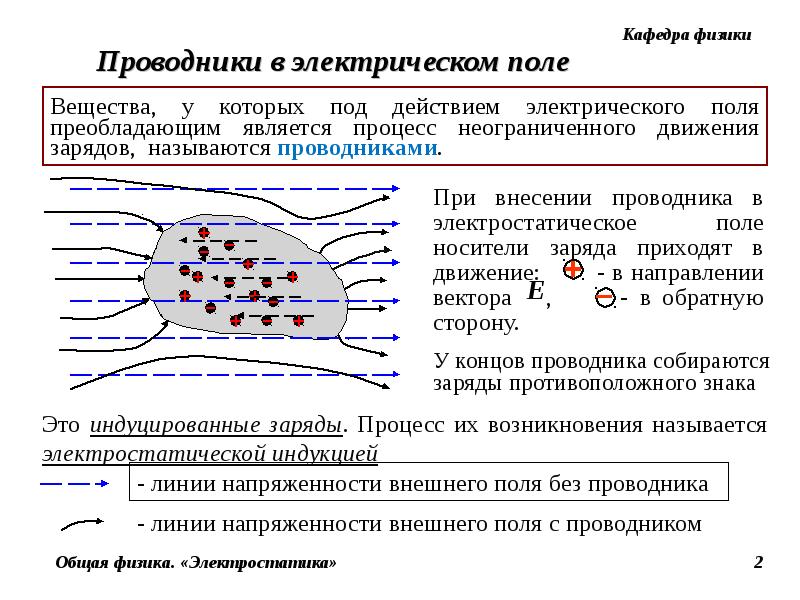

Таким образом, газовые разряды всех типов находят самое широкое применение. Электрический ток в газах успешно и эффективно используется во многих областях техники.

В обычных условиях газы не проводят электрический ток, так как их молекулы электрически нейтральны. Например, сухой воздух — это хороший изолятор, в чем мы могли убедиться с помощью самых простых опытов по электростатике. Однако воздух и другие газы становятся проводниками электрического тока, если в них тем или иным способом создать ионы.

Рис. 100. Воздух становится проводником электрического тока, если его ионизировать

Простейший опыт, иллюстрирующий проводимость воздуха при его ионизации пламенем показан на рис. 100: заряд на пластинах, сохраняющийся в течение длительного времени, быстро исчезает при внесении зажженной спички в пространство между пластинами.

Газовый разряд. Процесс прохождения электрического тока через газ обычно называют газовым разрядом (или электрическим разрядом в газе). Газовые разряды подразделяются на два вида: самостоятельные и несамостоятельные.

Несамостоятельный разряд. Разряд в газе называют несамостоятельным, если для его поддержания необходим внешний источник

ионизации. Ионы в газе могут возникать под действием высоких температур, рентгеновского и ультрафиолетового излучения, радиоактивности, космических лучей и т. д. Во всех этих случаях происходит освобождение одного или нескольких электронов из электронной оболочки атома или молекулы. В результате в газе появляются положительные ионы и свободные электроны. Освободившиеся электроны могут присоединяться к нейтральным атомам или молекулам, превращая их в отрицательные ионы.

Ионизация и рекомбинация. Наряду с процессами ионизации в газе происходят и обратные процессы рекомбинации: соединяясь между собой, положительные и отрицательные ионы или положительные ионы и электроны образуют нейтральные молекулы или атомы.

Изменение со временем концентрации ионов, обусловленное постоянным источником ионизации и процессами рекомбинации, можно описать следующим образом. Допустим, что источник ионизации создает в единице объема газа за единицу времени положительных ионов и такое же число электронов. Если в газе нет электрического тока и можно пренебречь уходом ионов из рассматриваемого объема из-за диффузии, то единственным механизмом уменьшения концентрации ионов будет рекомбинация.

Рекомбинация происходит при встрече положительного иона с электроном. Число таких встреч пропорционально как числу ионов, так и числу свободных электронов, т. е. пропорционально . Поэтому убыль числа ионов в единице объема в единицу времени может быть записана в виде , где а — постоянная величина, называемая коэффициентом рекомбинации.

При справедливости введенных предположений уравнение баланса ионов в газе запишется в виде

Мы не будем решать это дифференциальное уравнение в общем виде, а рассмотрим некоторые интересные частные случаи.

Прежде всего отметим, что процессы ионизации и рекомбинации через некоторое время должны скомпенсировать друг друга и в газе установится постоянная концентрация видно, что при

Стационарная концентрация ионов тем больше, чем мощнее источник ионизации и чем меньше коэффициент рекомбинации а.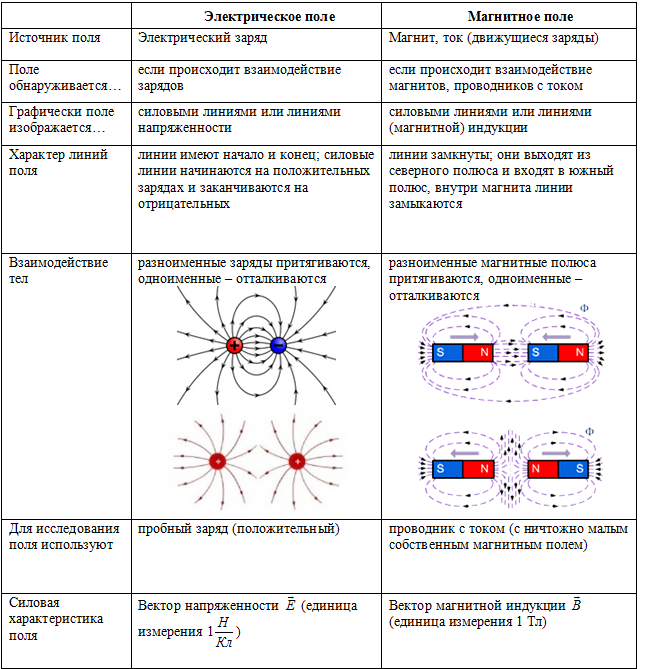

После выключения ионизатора убывание концентрации ионов описывается уравнением (1), в котором нужно положить принять в качестве начального значения концентрации

Переписав это уравнение в виде после интегрирования получаем

График этой функции показан на рис. 101. Он представляет собой гиперболу, асимптотами которой являются ось времени и вертикальная прямая Разумеется, физический смысл имеет лишь участок гиперболы, соответствующий значениям Отметим медленный характер убывания концентрации со временем в сравнении с часто встречающимися в физике процессами экспоненциального затухания, которые реализуются, когда скорость убывания какой-либо величины пропорциональна первой степени мгновенного значения этой величины.

Рис. 101. Убывание концентрации ионов в газе после выключения источника ионизации

Несамостоятельная проводимость. Процесс спадания концентрации ионов после прекращения действия ионизатора значительно ускоряется, если газ находится во внешнем электрическом поле.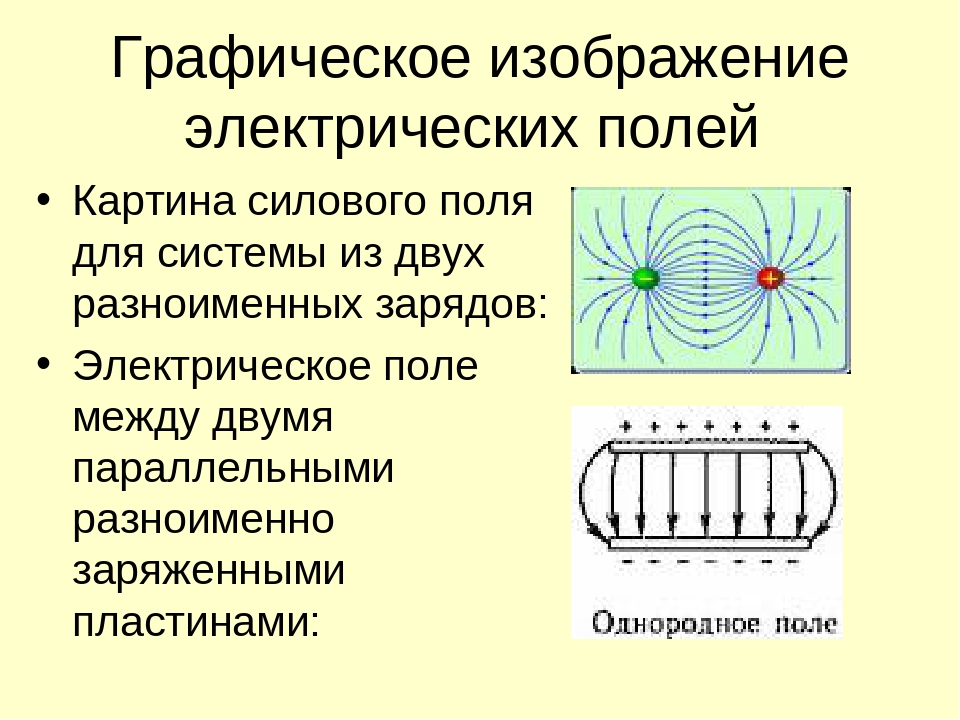 Вытягивая электроны и ионы на электроды, электрическое поле может очень быстро обратить в нуль электропроводность газа в отсутствие ионизатора.

Для уяснения закономерностей несамостоятельного разряда рассмотрим для простоты случай, когда ток в ионизуемом внешним источником газе течет между двумя плоскими электродами, параллельными друг другу. В этом случае ионы и электроны находятся в однородном электрическом поле напряженности Е, равной отношению приложенного к электродам напряжения к расстоянию между ними.

Подвижность электронов и ионов. При постоянном приложенном напряжении в цепи устанавливается некоторая постоянная сила тока 1. Это значит, что электроны и ионы в ионизованном газе движутся с постоянными скоростями. Чтобы объяснить этот факт, нужно считать, что кроме постоянной ускоряющей силы электрического поля на движущиеся ионы и электроны действуют силы сопротивления, растущие с увеличением скорости. Эти силы описывают усредненный эффект столкновений электронов и ионов с нейтральными атомами и молекулами газа.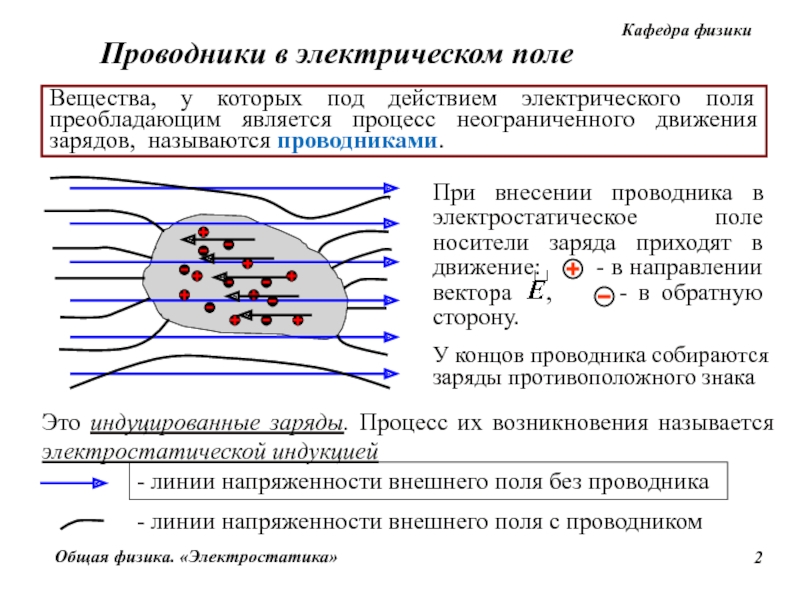 Благодаря силам сопротивления

устанавливаются в среднем постоянные скорости электронов и ионов, пропорциональные напряженности Е электрического поля:

Коэффициенты пропорциональности называются подвижностями электрона и иона. Подвижности ионов и электронов имеют разные значения и зависят от сорта газа, его плотности, температуры и т. д.

Плотность электрического тока т. е. заряд, переносимый электронами и ионами за единицу времени через единичную площадку, выражается через концентрацию электронов и ионов их заряды и скорости установившегося движения

Квазинейтральность. В обычных условиях ионизованный газ в целом электронейтрален, или, как говорят, квазинейтрален, ибо в малых объемах, содержащих сравнительно небольшое число электронов и ионов, условие электронейтральности может и нарушаться. Это значит, что выполняется соотношение

Плотность тока при несамостоятельном разряде. Чтобы получить закон изменения со временем концентрации носителей тока при несамостоятельном разряде в газе, нужно наряду с процессами ионизации внешним источником и рекомбинации учесть также уход электронов и ионов на электроды.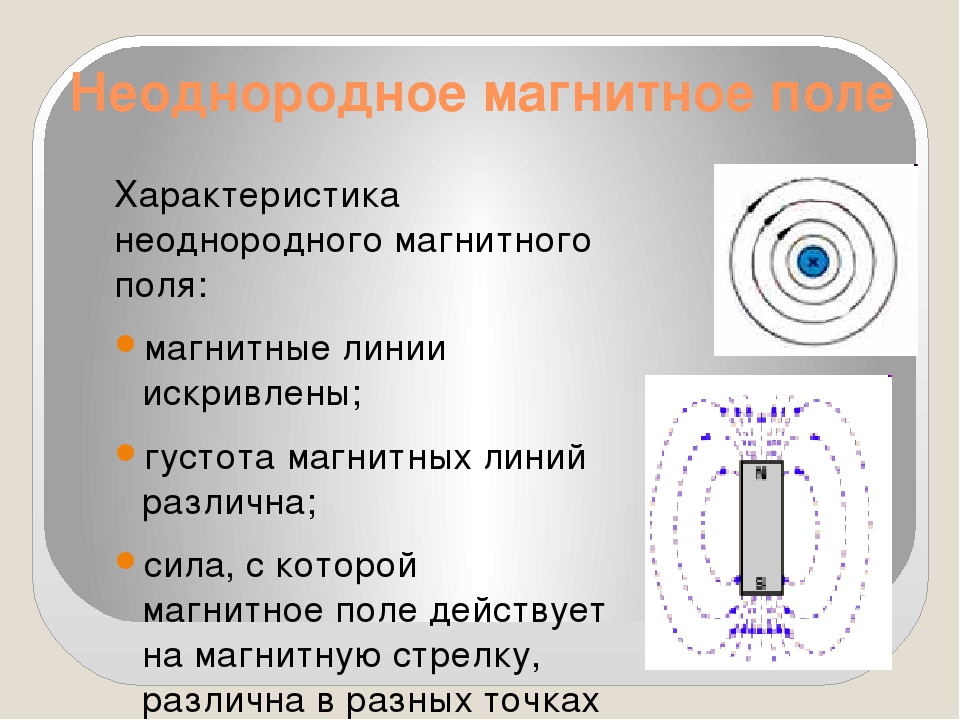 Число частиц, уходящих в единицу времени на электрод площади из объема равно Скорость убывания концентрации таких частиц мы получим, разделив это число на объем газа между электродами. Поэтому уравнение баланса вместо (1) при наличии тока запишется в виде

Для установления режима, когда из (8) получаем

Уравнение (9) позволяет найти зависимость плотности установившегося тока при несамостоятельном разряде от приложенного напряжения (или от напряженности поля Е).

Два предельных случая видны непосредственно.

Закон Ома. При низком напряжении, когда в уравнении (9) можно пренебречь вторым слагаемым в правой части, после чего получаем формулы (7) при этом имеем

Плотность тока пропорциональна напряженности приложенного электрического поля. Таким образом, для несамостоятельного газового разряда в слабых электрических полях выполняется закон Ома.

Ток насыщения. При низкой концентрации электронов и ионов в уравнении (9) можно пренебречь первым (квадратичным по слагаемым в правой части. В этом приближении вектор плотности тока направлен вдоль напряженности электрического поля, а его модуль

не зависит от приложенного напряжения. Этот результат справедлив для сильных электрических полей. В этом случае говорят о токе насыщения.

Оба рассмотренных предельных случая можно исследовать и не обращаясь к уравнению (9). Однако таким путем нельзя проследить, как при увеличении напряжения происходит переход от закона Ома к нелинейной зависимости тока от напряжения.

В первом предельном случае, когда ток очень мал, основной механизм удаления электронов и ионов из области разряда — это рекомбинация. Поэтому для стационарной концентрации можно воспользоваться выражением (2), что при учете (7) немедленно дает формулу (10). Во втором предельном случае, наоборот, пренебрегается рекомбинацией. В сильном электрическом поле электроны и ионы не успевают сколько-нибудь заметно рекомбинировать за время пролета от одного электрода до другого, если концентрация их достаточно мала. Тогда все образуемые внешним источником электроны и ионы достигают электродов и полная плотность тока равна Она пропорциональна длине ионизационной камеры, поскольку полное число производимых ионизатором электронов и ионов пропорционально I.

Экспериментальное изучение газового разряда. Выводы теории несамостоятельного газового разряда подтверждаются экспериментами. Для исследования разряда в газе удобно использовать стеклянную трубку с двумя металлическими электродами. Электрическая схема такой установки показана на рис. 102. Подвижности

электронов и ионов сильно зависят от давления газа (обратно пропорционально давлению), поэтому опыты удобно проводить при пониженном давлении.

На рис. 103 представлена зависимость силы тока I в трубке от приложенного к электродам трубки напряжения Ионизацию в трубке можно создать, например, рентгеновскими или ультрафиолетовыми лучами либо с помощью слабого радиоактивного препарата. Существенно только, чтобы внешний источник ионов оставался неизменным Линейный участок ОА вольт-амперной характеристики соответствует области применимости закона Ома.

Рис. 102. Схема установки для изучения газового разряда

Рис. 103. Экспериментальная вольт-амперная характеристика газового разряда

На участке сила тока нелинейно зависит от напряжения. Начиная с точки В ток достигает насыщения и остается постоянным на некотором участке Все это соответствует теоретическим предсказаниям.

Самостоятельный разряд. Однако в точке С снова начинается возрастание тока, сначала медленное, а затем очень резкое. Это означает, что в газе появился новый, внутренний источник ионов. Если теперь убрать внешний источник, то разряд в газе не прекращается, т. е. из несамостоятельного разряд переходит в самостоятельный. При самостоятельном разряде образование новых электронов и ионов происходит в результате внутренних процессов в самом газе.

Ионизация электронным ударом. Нарастание тока при переходе от несамостоятельного разряда к самостоятельному происходит лавинообразно и называется электрическим пробоем газа. Напряжение, при котором происходит пробой, называется напряжением зажигания. Оно зависит от рода газа и от произведения давления газа на расстояние между электродами.

Процессы в газе, ответственные за лавинообразное нарастание силы тока при увеличении приложенного напряжения, связаны с ионизацией нейтральных атомов или молекул газа свободными электронами, разогнанными электрическим полем до достаточно

больших энергий. Кинетическая энергия электрона перед очередным столкновением с нейтральным атомом или молекулой пропорциональна напряженности электрического поля Е и длине свободного пробега электрона X:

Если эта энергия достаточна для того, чтобы ионизовать нейтральный атом или молекулу, т. е. превосходит работу ионизации

то при столкновении электрона с атомом или молекулой происходит их ионизация. В результате вместо одного электрона возникают два. Они в свою очередь разгоняются электрическим полем и ионизуют встречающиеся на их пути атомы или молекулы и т. д. Процесс развивается лавинообразно и называется электронной лавиной. Описанный механизм ионизации называется ионизацией электронным ударом.

Экспериментальное доказательство того, что ионизация нейтральных атомов газа происходит в основном благодаря ударам электронов, а не положительных ионов, было дано Дж. Таунсендом. Он брал ионизационную камеру в виде цилиндрического конденсатора, внутренним электродом которого служила тонкая металлическая нить, натянутая по оси цилиндра. В такой камере ускоряющее электрическое поле сильно неоднородно, и основную роль в ионизации играют частицы, которые попадают в область наиболее сильного поля вблизи нити. Опыт показывает, что при одном и том же напряжении между электродами ток разряда больше в том случае, когда положительный потенциал подается на нить, а не на внешний цилиндр. Именно в этом случае все создающие ток свободные электроны обязательно проходят через область наиболее сильного поля.

Эмиссия электронов из катода. Самостоятельный разряд может быть стационарным лишь при условии постоянного появления в газе новых свободных электронов, так как все возникающие в лавине электроны достигают анода и выбывают из игры. Новые электроны выбиваются из катода положительными ионами, которые при движении к катоду также ускоряются электрическим полем и приобретают достаточную для этого энергию.

Катод может испускать электроны не только в результате бомбардировки ионами, но и самостоятельно, при нагревании его до высокой температуры. Такой процесс называется термоэлектронной эмиссией, его можно рассматривать как своего рода испарение электронов из металла. Обычно оно происходит при таких температурах, когда испарение самого материала катода еще мало. В случае самостоятельного газового разряда катод обычно разогревается не

нитью накала, как в электронных лампах, а из-за выделения теплоты при бомбардировке его положительными ионами. Поэтому катод испускает электроны даже тогда, когда энергия ионов недостаточна для выбивания электронов.

Самостоятельный разряд в газе возникает не только в результате перехода от несамостоятельного при повышении напряжения и удалении внешнего источника ионизации, но и при непосредственном приложении напряжения, превышающего пороговое напряжение зажигания. Теория показывает, что для зажигания разряда достаточно самого незначительного количества ионов, которые всегда присутствуют в нейтральном газе хотя бы из-за естественного радиоактивного фона.

В зависимости от свойств и давления газа, конфигурации электродов и приложенного к электродам напряжения возможны различные виды самостоятельного разряда.

Тлеющий разряд. При низких давлениях (десятые и сотые доли миллиметра ртутного столба) в трубке наблюдается тлеющий разряд. Для зажигания тлеющего разряда достаточно напряжения в несколько сотен или даже десятков вольт. В тлеющем разряде можно выделить четыре характерные области. Это темное катодное пространство, тлеющее (или отрицательное) свечение, фарадеево темное пространство и светящийся положительный столб, занимающий большую часть пространства между анодом и катодом.

Первые три области находятся вблизи катода. Именно здесь происходит резкое падение потенциала, связанное с большой концентрацией положительных ионов на границе катодного темного пространства и тлеющего свечения. Электроны, ускоренные в области катодного темного пространства, производят в области тлеющего свечения интенсивную ударную ионизацию. Тлеющее свечение обусловлено рекомбинацией ионов и электронов в нейтральные атомы или молекулы. Для положительного столба разряда характерно незначительное падение потенциала и свечение, вызываемое возвращением возбужденных атомов или молекул газа в основное состояние.

Коронный разряд. При сравнительно высоких давлениях в газе (порядка атмосферного) вблизи заостренных участков проводника, где электрическое поле сильно неоднородно, наблюдается разряд, светящаяся область которого напоминает корону. Коронный разряд иногда возникает в естественных условиях на верхушках деревьев, корабельных мачтах и т. п. («огни святого Эльма»). С коронным разрядом приходится считаться в технике высоких напряжений, когда этот разряд возникает вокруг проводов высоковольтных линий электропередачи и приводит к потерям электроэнергии. Полезное практическое применение коронный разряд находит в электрофильтрах для очистки промышленных газов от примесей твердых и жидких частиц.

При увеличении напряжения между электродами коронный разряд переходит в искровой с полным пробоем промежутка между

электродами. Он имеет вид пучка ярких зигзагообразных разветвляющихся каналов, мгновенно пронизывающих разрядный промежуток и прихотливо сменяющих друг друга. Искровой разряд сопровождается выделением большого количества теплоты, ярким голубовато-белым свечением и сильным потрескиванием. Его можно наблюдать между шариками электрофорной машины. Пример гигантского искрового разряда — естественная молния, где сила тока достигает 5-105 А, а разность потенциалов — 109 В.

Поскольку искровой разряд происходит при атмосферном (и более высоком) давлении, то напряжение зажигания весьма велико: в сухом воздухе при расстоянии между электродами 1 см оно составляет около 30 кВ.

Электрическая дуга. Специфическим практически важным видом самостоятельного газового разряда является электрическая дуга. При соприкосновении двух угольных или металлических электродов в месте их контакта выделяется большое количество теплоты из-за большого сопротивления контакта. В результате начинается термоэлектронная эмиссия и при раздвижении электродов между ними возникает ярко светящаяся дуга из сильно ионизованного хорошо проводящего газа. Сила тока даже в небольшой дуге достигает нескольких ампер, а в большой дуге — нескольких сотен ампер при напряжении порядка 50 В. Электрическая дуга широко применяется в технике как мощный источник света, в электропечах и для электросварки. слабое задерживающее поле с напряжением около 0,5 В. Это поле препятствует попаданию на анод медленных электронов. Электроны испускаются катодом К, подогреваемым электрическим током.

На рис. 105 показана полученная в этих опытах зависимость силы тока в анодной цепи от ускоряющего напряжения Эта зависимость имеет немонотонный характер с максимумами при напряжениях кратных 4,9 В.

Дискретность уровней энергии атома. Объяснить такую зависимость тока от напряжения можно лишь наличием у атомов ртути дискретных стационарных состояний. Если бы дискретных стационарных состояний у атома не было, т.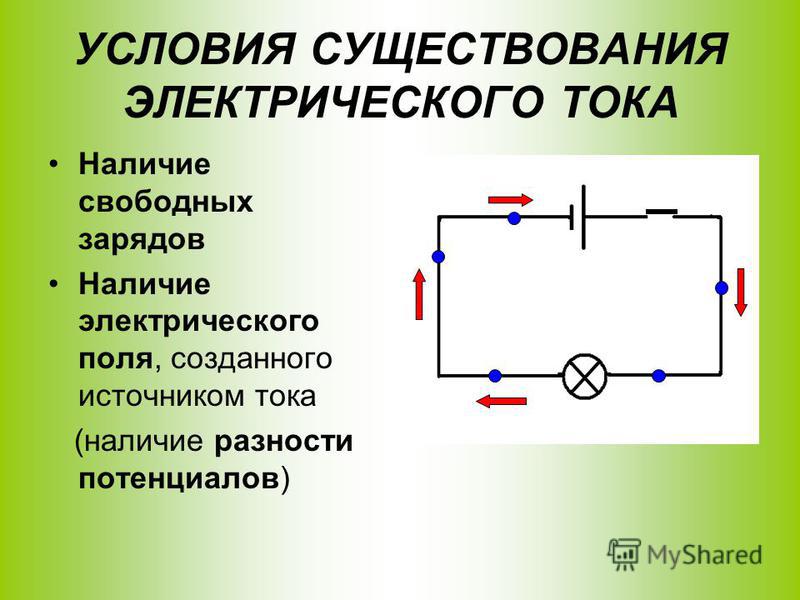 е. его внутренняя энергия могла бы принимать любые значения, то неупругие столкновения, сопровождающиеся увеличением внутренней энергии атома, могли бы происходить при любых энергиях электронов. Если же дискретные состояния есть, то столкновения электронов с атомами могут быть только упругими, пока энергия электронов недостаточна для перевода атома из основного состояния в наинизшее возбужденное.

При упругих столкновениях кинетическая энергия электронов практически не меняется, так как масса электрона много меньше массы атома ртути. В этих условиях число электронов, достигающих анода, монотонно увеличивается с ростом напряжения. Когда ускоряющее напряжение достигает значения 4,9 В, столкновения электронов с атомами становятся неупругими. Внутренняя энергия атомов скачком увеличивается, а электрон в результате соударения теряет почти всю свою кинетическую энергию.

Задерживающее поле не пропускает также медленные электроны к аноду и сила тока резко уменьшается. Она не обращается в нуль лишь потому, что часть электронов достигает сетки, не испытав неупругих соударений.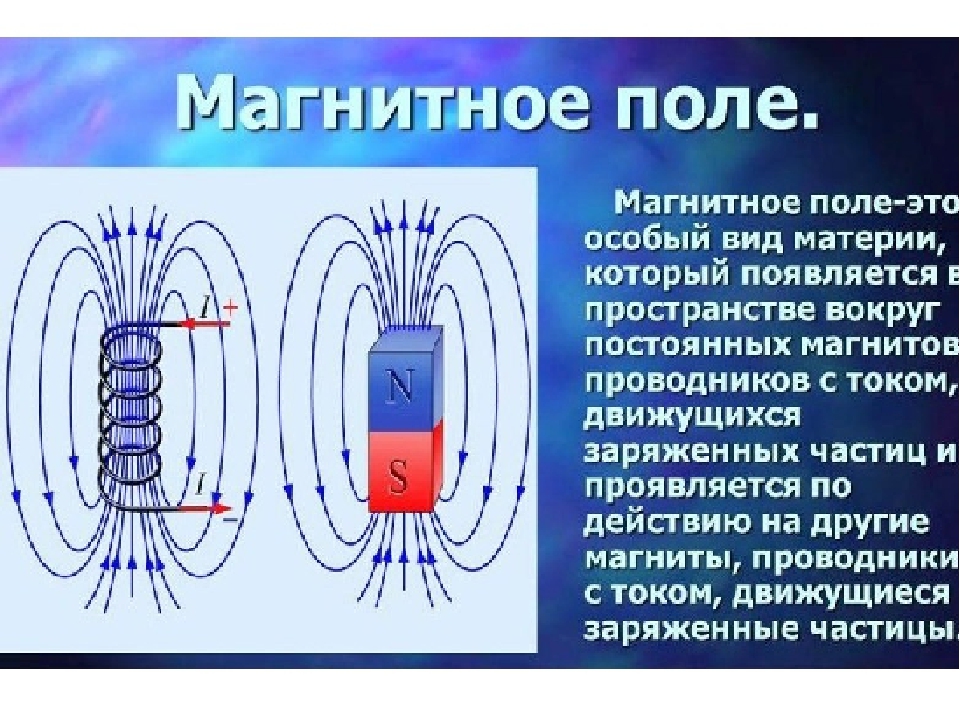 Второй и последующие максимумы силы тока получаются потому, что при напряжениях, кратных 4,9 В, электроны на пути к сетке могут испытать несколько неупругих столкновений с атомами ртути.

Итак, необходимую для неупругого соударения энергию электрон приобретает только после прохождения разности потенциалов 4,9 В. Это означает, что внутренняя энергия атомов ртути не может измениться на величину, меньшую эВ, что и доказывает дискретность энергетического спектра атома. Справедливость этого вывода подтверждается еще и тем, что при напряжении 4,9 В разряд начинает светиться: возбужденные атомы при спонтанных

переходах в основное состояние излучают видимый свет, частота которого совпадает с вычисленной по формуле

В классических опытах Франка и Герца методом электронного удара были определены не только потенциалы возбуждения, но и ионизационные потенциалы ряда атомов.

Приведите пример опыта по электростатике, из которого можно сделать вывод о том, что сухой воздух — это хороший изолятор.

Где в технике используются изолирующие свойства воздуха?

Что такое несамостоятельный газовый разряд? При каких условиях он протекает?

Поясните, почему скорость убывания концентрации, обусловленная рекомбинацией, пропорциональна квадрату концентрации электронов и ионов. Почему эти концентрации можно считать одинаковыми?

Почему для закона убывания концентрации, выражаемого формулой (3), не имеет смысла вводить понятие характерного времени, широко используемого для экспоненциально затухающих процессов, хотя и в том и в другом случае процессы продолжаются, вообще говоря, бесконечно долго?

Как по-вашему, почему в определениях подвижностей в формулах (4) для электронов и ионов выбраны противоположные знаки?

Как сила тока при несамостоятельном газовом разряде зависит от приложенного напряжения? Почему с ростом напряжения происходит переход от закона Ома к току насыщения?

Электрический ток в газе осуществляется как электронами, так и ионами. Однако на каждый из электродов приходят заряды лишь одного знака. Как это согласуется с тем, что во всех участках последовательной цепи сила тока одинакова?

Почему в ионизации газа в разряде из-за соударений наибольшую роль играют электроны, а не положительные ионы?

Опишите характерные признаки различных видов самостоятельного газового разряда.

Почему результаты опытов Франка и Герца свидетельствуют о дискретности уровней энергии атомов?

Опишите физические процессы, происходящие в газоразрядной трубке в опытах Франка и Герца, при повышении ускоряющего напряжения.

В обычных условиях газы являются диэлектриками, т.к. состоят из нейтральных атомов и молекул, и в них нет достаточного количества свободных зарядов.Газы становятся проводниками лишь тогда, когда они каким-то образом ионизированы. Процесс ионизации газов заключается в том, что под действием каких-либо причин от атома отрывается один или несколько электронов. В результате этого вместо нейтрального атома возникают положительный ион и электрон .

    Распад молекул на ионы и электроны называется ионизацией газа .

Часть образовавшихся электронов может быть при этом захвачена другими нейтральными атомами, и тогда появляются отрицательно заряженные ионы .

Таким образом, в ионизованном газе имеются носители зарядов трех сортов: электроны, положительные ионы и отрицательные.

Отрыв электрона от атома требует затрат определенной энергии — энергии ионизации W i . Энергия ионизации зависит от химической природы газа и энергетического состояния электрона в атоме. Так, для отрыва первого электрона от атома азота затрачивается энергия 14,5 эВ, а для отрыва второго электрона — 29,5 эВ, для отрыва третьего — 47,4 эВ.

Факторы, вызывающие ионизацию газа называются ионизаторами .

Различают три вида ионизации: термоионизацию, фотоионизацию и ударную ионизацию.

    Термоионизация происходит в результате столкновения атомов или молекул газа при высокой температуре, если кинетическая энергия относительного движения сталкивающихся частиц превышает энергию связи электрона в атоме.

    Фотоионизация происходит под действием электромагнитного излучения (ультрафиолетового, рентгеновского или γ-излучения), когда энергия, необходимая для отрыва электрона от атома, передается ему квантом излучения.

    Ионизация электронным ударом (или ударная ионизация ) — это образование положительно заряженных ионов в результате столкновений атомов или молекул с быстрыми, обладающими большой кинетической энергией, электронами.

Процесс ионизации газа всегда сопровождается противоположным процессом восстановления нейтральных молекул из разноименно заряженных ионов вследствие их электрического притяжения. Это явление называется рекомбинацией . При рекомбинации выделяется энергия, равная энергии, затраченной на ионизацию. Это может вызвать, например, свечение газа.

Если действие ионизатора неизменно, то в ионизованном газе устанавливается динамическое равновесие, при котором в единицу времени восстанавливается столько же молекул, сколько их распадается на ионы. При этом концентрация заряженных частиц в ионизованном газе остается неизменной. Если же прекратить действие ионизатора, то рекомбинация начнет преобладать над ионизацией и число ионов быстро уменьшится почти до нуля. Следовательно, наличие заряженных частиц в газе — явление временное (пока действует ионизатор).

При отсутствии внешнего поля заряженные частицы движутся хаотически.

Газовый разряд

При помещении ионизированного газа в электрическое поле на свободные заряды начинают действовать электрические силы, и они дрейфуют параллельно линиям напряженности: электроны и отрицательные ионы — к аноду, положительные ионы — к катоду (рис. 1). На электродах ионы превращаются в нейтральные атомы, отдавая или принимая электроны, тем самым замыкая цепь. В газе возникает электрический ток.

    Электрический ток в газах — это направленное движение ионов и электронов.

Электрический ток в газах называется газовым разрядом .

Полный ток в газе складывается из двух потоков заряженных частиц: потока, идущего к катоду, и потока, направленного к аноду.

В газах сочетается электронная проводимость, подобная проводимости металлов, с ионной проводимостью, подобной проводимости водных растворов или расплавов электролитов.

Таким образом, проводимость газов имеет ионно-электронный характер .

Реферат по физике

на тему:

«Электрический ток в газах».

Электрический ток в газах.

1. Электрический разряд в газах.

Все газы в естественном состоянии не проводят электрического тока. В чем можно убедиться из следующего опыта:

Возьмем электрометр с присоединенными к нему дисками плоского конденсатора и зарядим его. При комнатной температуре, если воздух достаточно сухой, конденсатор заметно не разряжается – положение стрелки электрометра не изменяется. Чтобы заметить уменьшение угла отклонения стрелки электрометра, требуется длительное время. Это показывает, что электрический ток в воздухе между дисками очень мал. Данный опыт показывает, что воздух является плохим проводником электрического тока.

Видоизменим опыт: нагреем воздух между дисками пламенем спиртовки. Тогда угол отклонения стрелки электрометра быстро уменьшается, т.е. уменьшается разность потенциалов между дисками конденсатора – конденсатор разряжается. Следовательно, нагретый воздух между дисками стал проводником, и в нем устанавливается электрический ток.

Изолирующие свойства газов объясняются тем, что в них нет свободных электрических зарядов: атомы и молекулы газов в естественном состоянии являются нейтральными.

2. Ионизация газов.

Вышеописанный опыт показывает, что в газах под влиянием высокой температуры появляются заряженные частицы. Они возникают вследствие отщепления от атомов газа одного или нескольких электронов, в результате чего вместо нейтрального атома возникают положительный ион и электроны. Часть образовавшихся электронов может быть при этом захвачена другими нейтральными атомами, и тогда появятся еще отрицательные ионы. Распад молекул газа на электроны и положительные ионы называется ионизацией газов.

Нагревание газа до высокой температуры не является единственным способом ионизации молекул или атомов газа. Ионизация газа может происходить под влиянием различных внешних взаимодействий: сильного нагрева газа, рентгеновских лучей, a-, b- и g-лучей, возникающих при радиоактивном распаде, космических лучей, бомбардировки молекул газа быстро движущимися электронами или ионами. Факторы, вызывающие ионизацию газа называются ионизаторами. Количественной характеристикой процесса ионизации служит интенсивность ионизации, измеряемая числом пар противоположных по знаку заряженных частиц, возникающих в единице объема газа за единицу времени.

Ионизация атома требует затраты определенной энергии – энергии ионизации. Для ионизации атома (или молекулы) необходимо совершить работу против сил взаимодействия между вырываемым электроном и остальными частицами атома (или молекулы). Эта работа называется работой ионизации A i . Величина работы ионизации зависит от химической природы газа и энергетического состояния вырываемого электрона в атоме или молекуле.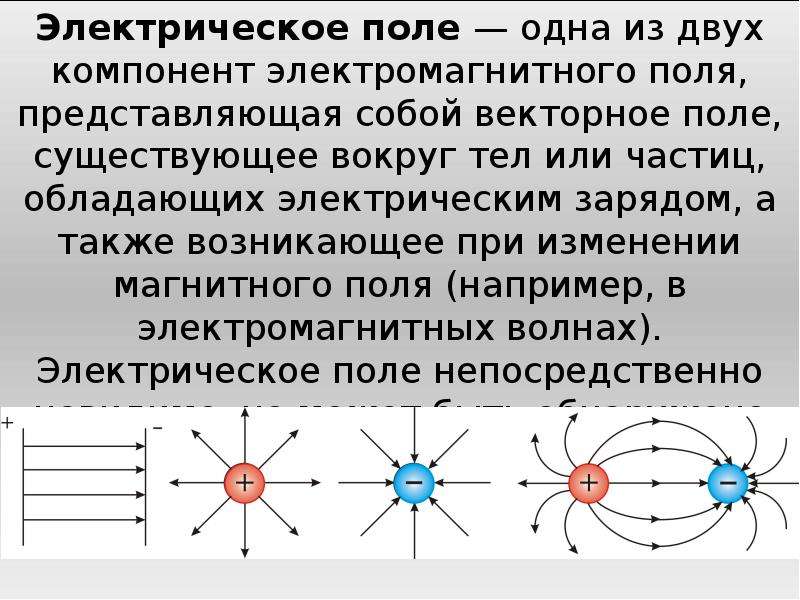

После прекращения действия ионизатора количество ионов в газе с течением времени уменьшается и в конце концов ионы исчезают вовсе. Исчезновение ионов объясняется тем, что ионы и электроны участвуют в тепловом движении и поэтому соударяются друг с другом. При столкновении положительного иона и электрона они могут воссоединиться в нейтральный атом. Точно также при столкновении положительного и отрицательного ионов отрицательный ион может отдать свой избыточный электрон положительному иону и оба иона превратятся в нейтральные атомы. Этот процесс взаимной нейтрализации ионов называется рекомбинацией ионов. При рекомбинации положительного иона и электрона или двух ионов освобождается определенная энергия, равная энергии, затраченной на ионизацию. Частично она излучается в виде света, и поэтому рекомбинация ионов сопровождается свечением (свечение рекомбинации).

В явлениях электрического разряда в газах большую роль играет ионизация атомов электронными ударами. Этот процесс заключается в том, что движущийся электрон, обладающий достаточной кинетической энергией, при соударении с нейтральным атомом выбивает из него один или несколько атомных электронов, в результате чего нейтральный атом превращается в положительный ион, а в газе появляются новые электроны (об этом будет рассмотрено позднее).

В таблице ниже даны значения энергии ионизации некоторых атомов.

3. Механизм электропроводности газов.

Механизм проводимости газов похож на механизм проводимости растворов и расплавов электролитов. При отсутствии внешнего поля заряженные частицы, как и нейтральные молекулы движутся хаотически. Если ионы и свободные электроны оказываются во внешнем электрическом поле, то они приходят в направленное движение и создают электрический ток в газах.

Таким образом, электрический ток в газе представляет собой направленное движение положительных ионов к катоду, а отрицательных ионов и электронов к аноду . Полный ток в газе складывается из двух потоков заряженных частиц: потока, идущего к аноду, и потока, направленного к катоду.

На электродах происходит нейтрализация заряженных частиц, как и при прохождении электрического тока через растворы и расплавы электролитов. Однако в газах отсутствует выделение веществ на электродах, как это имеет место в растворах электролитов.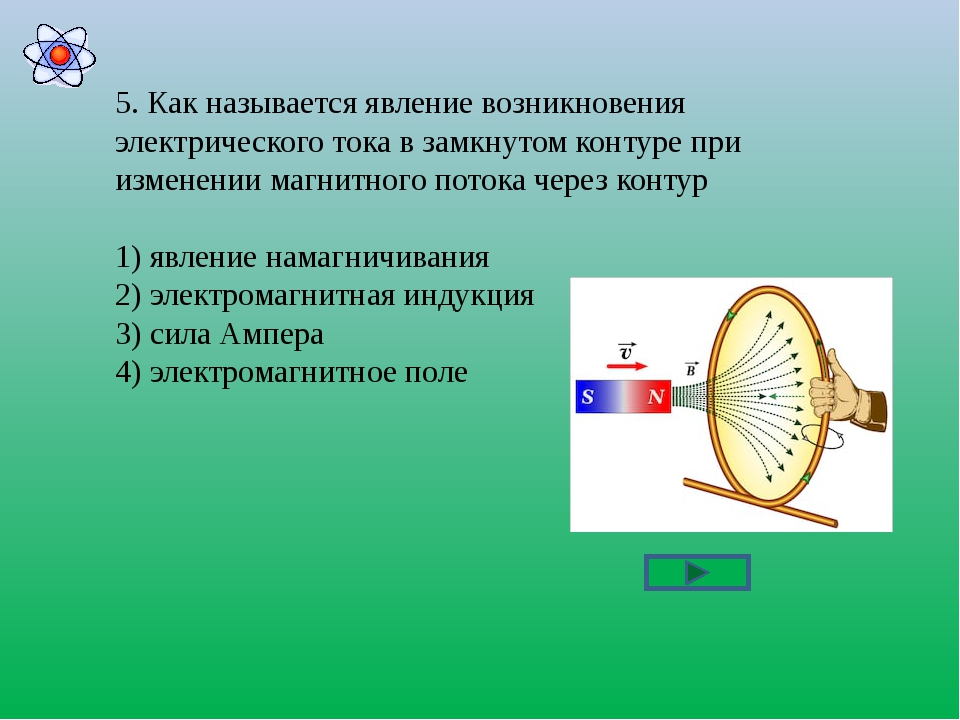 Газовые ионы, подойдя к электродам, отдают им свои заряды, превращаются в нейтральные молекулы и диффундируют обратно в газ.

Еще одно различие в электропроводности ионизованных газов и растворов (расплавов) электролитов состоит в том, что отрицательный заряд при прохождении тока через газы переносится в основном не отрицательными ионами, а электронами, хотя проводимость за счет отрицательных ионов также может играть определенную роль.

Таким образом в газах сочетается электронная проводимость, подобная проводимости металлов, с ионной проводимостью, подобной проводимости водных растворов и расплавов электролитов.

4. Несамостоятельный газовый разряд.

Процесс прохождения электрического тока через газ называется газовым разрядом. Если электропроводность газа создается внешними ионизаторами, то электрический ток, возникающий в нем, называется несамостоятельным газовым разрядом. С прекращением действия внешних ионизаторов несамостоятельный разряд прекращается. Несамостоятельный газовый разряд не сопровождается свечением газа.

Ниже изображен график зависимости силы тока от напряжения при несамостоятельном разряде в газе. Для построения графика использовалась стеклянная трубка с двумя впаянными в стекло металлическими электродами. Цепь собрана как показано на рисунке ниже.

При некотором определенном напряжении наступает такой момент, при котором все заряженные частицы, образующиеся в газе ионизатором за секунду, достигают за это же время электродов. Дальнейшее увеличение напряжения уже не может привести к увеличению числа переносимых ионов. Ток достигает насыщения (горизонтальный участок графика 1).

5. Самостоятельный газовый разряд.

Электрический разряд в газе, сохраняющийся после прекращения действия внешнего ионизатора, называется самостоятельным газовым разрядом . Для его осуществления необходимо, чтобы в результате самого разряда в газе непрерывно образовывались свободные заряды. Основным источником их возникновения является ударная ионизация молекул газа.

Если после достижения насыщения продолжать увеличивать разность потенциалов между электродами, то сила тока при достаточно большом напряжении станет резко возрастать (график 2).

Это означает, что в газе появляются дополнительные ионы, которые образуются за счет действия ионизатора. Сила тока может возрасти в сотни и тысячи раз, а число заряженных частиц, возникающих в процессе разряда, может стать таким большим, что внешний ионизатор будет уже не нужен для поддержания разряда. Поэтому ионизатор теперь можно убрать.

Каковы же причины резкого увеличения силы тока при больших напряжениях? Рассмотрим какую либо пару заряженных частиц (положительный ион и электрон), образовавшуюся благодаря действию внешнего ионизатора. Появившийся таким образом свободный электрон начинает двигаться к положительному электроду – аноду, а положительный ион – к катоду. На своем пути электрон встречает ионы и нейтральные атомы. В промежутках между двумя последовательными столкновениями энергия электрона увеличивается за счет работы сил электрического поля.

Чем больше разность потенциалов между электродами, тем больше напряженность электрического поля. Кинетическая энергия электрона перед очередным столкновением пропорциональна напряженности поля и длине свободного пробега электрона: MV 2 /2=eEl. Если кинетическая энергия электрона превосходит работу A i , которую нужно совершить, чтобы ионизировать нейтральный атом (или молекулу), т.е. MV 2 >A i , то при столкновении электрона с атомом (или молекулой) происходит его ионизация. В результате вместо одного электрона возникают два (налетающий на атом и вырванный из атома). Они, в свою очередь, получают энергию в поле и ионизуют встречные атомы и т.д.. Вследствие этого число заряженных частиц быстро нарастает, возникает электронная лавина. Описанный процесс называют ионизацией электронным ударом.

Это краткий пересказ.

Работа над полной версией продолжается


Лекция 2 1

Ток в газах

1. Общие положения

Определение: Явление прохождения электрического тока в газах называется газовым разрядом .

Поведение газов сильно зависит от его параметров, таких как температура и давление, причем эти параметры достаточно легко меняются. Поэтому, протекание электрического тока в газах является более сложным, чем в металлах или в вакууме.

Газы не подчиняются закону Ома.

2. Ионизация и рекомбинация

Газ, находящийся при нормальных условиях, состоит практически из нейтральных молекул, поэтому, крайне плохо проводит электрический ток. Однако при внешних воздействиях от атома может оторваться электрон и появляется положительно заряженный ион. Кроме того, электрон может присоединиться к нейтральному атому и образовать отрицательно заряженный ион. Таким образом, можно получить ионизованный газ, т.е. плазму.

К внешним воздействиям относятся нагрев, облучение энергичным фотонам, бомбардировка другими частицами и сильные поля, т. е. те же условия, которые необходимы для элементарной эмиссии.

Электрон в атоме находится в потенциальной яме, и чтобы вырваться оттуда, необходимо атому сообщить дополнительную энергию, которая называется энергией ионизации.

Вещество

Энергия ионизации, эВ

Атом водорода

13,59

Молекула водорода

15,43

Гелий

24,58

Атом кислорода

13,614

Молекула кислорода

12,06

Наряду с явлением ионизации наблюдается и явление рекомбинации, т.е. объединение электрона и положительного иона в нейтральный атом. Данный процесс происходит с выделением энергии, равной энергии ио низации. Эта энергия может пойти на излучение или на нагрев. Локальный нагрев газа приводит к локальному изменению давления. Что в свою очередь приводит к появлению звуковых волн. Таким образом, газовый разряд сопровождается световыми, тепловыми и шумовыми эффектами.

3. ВАХ газового разряда.

На начальных стадиях необходимо действие внешнего ионизатора.

На участке ОАВ ток существует под действием внешнего ионизатора и быстро выходит на насыщение, когда все ионизованные частицы участвуют в образовании тока. Если убрать внешний ионизатор, то ток прекращается.

Данный вид разряда называется несамостоятельным газовым разрядом. При попытке увеличить напряжение в газе появляются лавины электронов, и ток растет практически при постоянном напряжении, которое называется напряжением зажигания (ВС ).

С этого момента разряд становится самостоятельным и отпадает необходимость внешнего ионизатора. Число ионов может стать столь большим, что сопротивление межэлектродного промежутка уменьшится и соответственно упадет напряжение (СД).

Затем в межэлектродном промежутке область прохождения тока начинает сужаться, и сопротивление растет, а следовательно, растет напряжение (ДЕ).

При попытке увеличить напряжение газ становится полностью ионизованным. Сопротивление и напряжение падает до нуля, и ток вырастает во много раз. Получается дуговой разряд (Е F ).

ВАХ показывает, что газ совершенно не подчиняется закону Ома.

4. Процессы в газе

Процессы, которые могут привести к образованию лавин электронов показаны на рисунке.

Это элементы качественной теории Таунсенда .

5. Тлеющий разряд.

При низких давлениях и небольших напряжениях можно наблюдать этот разряд.

К – 1 (темное астоново пространство).

1 – 2 (светящаяся катодная пленка).

2 – 3 (темное круксово пространство).

3 – 4 (первое катодное свечение).

4 – 5 (темное фарадеево пространство)

5 – 6 (положительный анодный столб).

6 – 7 (анодное темное пространство).

7 – А (анодное свечение).

Если сделать анод подвижным, то длину положительного столба можно регулировать, практически не меняя размеры области К – 5.

В темных областях происходит разгон частиц и набор энергии, в светлых происходят процессы ионизации и рекомбинации.

Граничные условия на электрическое поле

Граничные условия на электрическое поле
Далее: Конденсаторы Вверх: Электростатика Предыдущий: Проводники
Рисунок 44:
Каким наиболее общим граничным условиям удовлетворяет электрическое поле? на интерфейсе между двумя средами: , например. , интерфейс между вакуумом а проводник? Рассмотрим интерфейс между двумя средами и .Применим прежде всего закон Гаусса,
(632)

в гауссовский дот с площадью поперечного сечения, два конца которой локально параллельно интерфейсу (см. 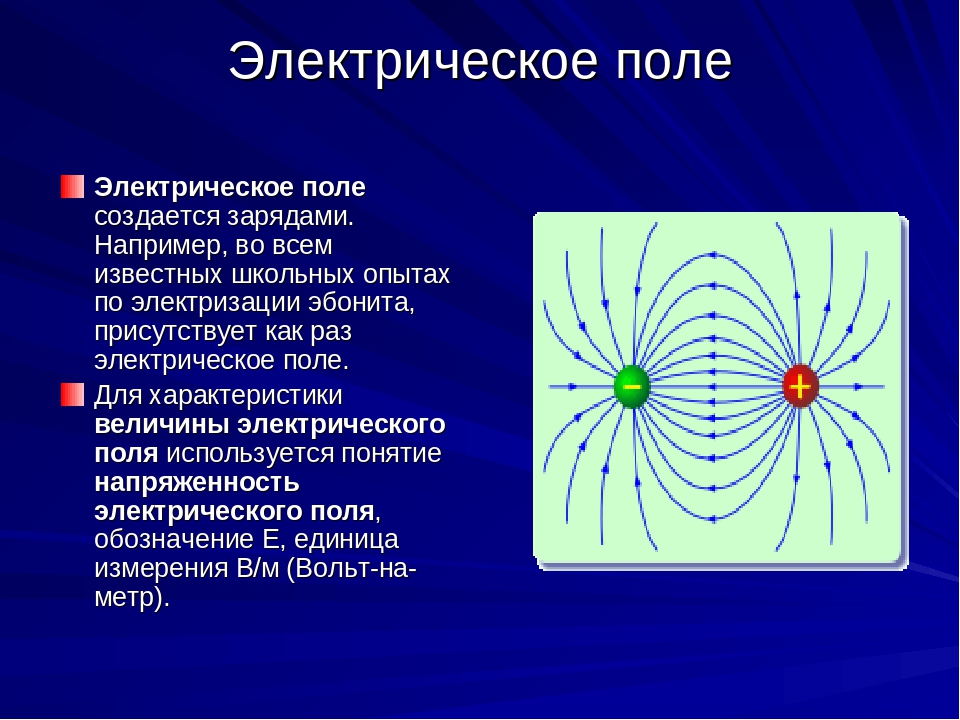рис. 44). Торцы коробки можно сделать произвольно Близко к друг другу. В этом пределе поток электрического поля из сторон коробки, очевидно, ничтожно мало. Единственный вклад в поток вносит с двух концов. По факту,
(633)

где перпендикуляр (к границе раздела) электрическое поле в средний на интерфейсе, и т.д. Заряд, заключенный в дот, просто , где плотность заряда листа на границе раздела. Обратите внимание, что любое объемное распределение заряда дает незначительный вклад в правую часть приведенного выше уравнения, в пределе, когда два концы таблетницы расположены очень близко друг к другу. Таким образом, закон Гаусса урожаи
(634)

на интерфейсе: т. е. , наличие зарядного листа на интерфейсе вызывает разрыв в перпендикулярная составляющая электрического поля.Как насчет параллельного электрического поле? Применим закон Фарадея к прямоугольному петля, чьи длинные стороны, длина , проходят параллельно интерфейсу,
(635)

(см. рис. 44). Длина коротких сторон предполагается сколь угодно малой. Доминантный вклад в петлевой интеграл дают длинные стороны:
(636)

где – параллельное (к границе раздела) электрическое поле в средний на интерфейсе, и т.д. Поток магнитного поля через петля примерно , где компонент магнитное поле, нормальное к петле, и является площадью петли. Но, поскольку короткие стороны петли сжимаются до нуля. Так, если магнитное поле не станет бесконечным (будем считать, что это не так), поток также стремится к нулю. Таким образом,
(637)

т.е. , в параллельном не может быть разрыва составляющая электрического поля на границе раздела.

Далее: Конденсаторы Вверх: Электростатика Предыдущий: Проводники
Ричард Фицпатрик 2006-02-02

Интерфейс магнитных и электрических полей

Интерфейс магнитных и электрических полей Интерфейс Magnetic and Electric Fields (mef) (), расположенный в ветке AC/DC>Electromagnetic Fields>Vector Formulations при добавлении физического интерфейса, используется для расчета распределения магнитного поля и тока, когда ток возбуждения управляется приложенным напряжением. .Стационарное моделирование и моделирование в частотной области поддерживаются в 2D и 3D.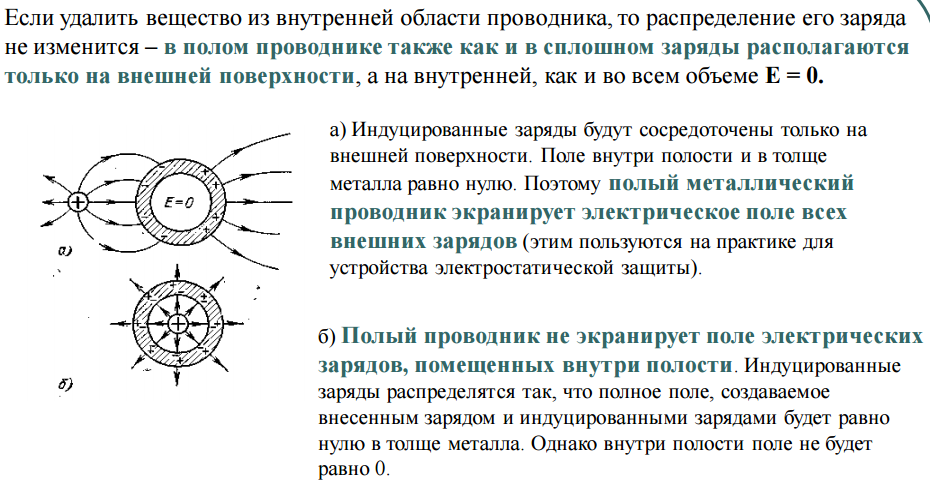 Обратите внимание, что в большинстве случаев использование интерфейса Magnetic Fields с его специальными функциями моделирования катушек является предпочтительным выбором по сравнению с использованием интерфейса Magnetic and Electric Fields. Физический интерфейс решает уравнения Максвелла, сформулированные с использованием магнитного векторного потенциала и скалярного электрического потенциала в качестве зависимых переменных. Используйте интерфейс «Магнитные и электрические поля», когда уравнение непрерывности тока необходимо везде в области моделирования.Основным узлом является функция закона Ампера и сохранения тока, которая добавляет уравнение для электрического потенциала и магнитного векторного потенциала и обеспечивает интерфейс для определения определяющих соотношений и связанных с ними свойств, таких как относительная магнитная проницаемость, относительная диэлектрическая проницаемость и электрическая проводимость. Функция закона Ампера и сохранения тока может быть переопределена функцией закона Ампера или функцией катушки, которые идентичны функциям в интерфейсе магнитных полей, удаляя электрический потенциал и уравнение сохранения тока из выбранных доменов. Когда этот физический интерфейс добавлен, эти узлы по умолчанию также добавляются в построитель моделей — закон Ампера и сохранение тока, магнитная изоляция (граничное условие по умолчанию для магнитного векторного потенциала) и начальные значения. Затем из панели инструментов Physics добавьте другие узлы, реализующие, например, граничные условия и внешние токи. Вы также можете щелкнуть правой кнопкой мыши «Магнитные и электрические поля», чтобы выбрать физические функции из контекстного меню. Сетка, управляемая физикой, управляется из окна настроек узла Mesh (если тип Sequence — это сетка, управляемая физикой).Там в таблице в разделе Physics-Controlled Mesh найдите физический интерфейс в столбце Contributor и установите или снимите флажок в столбце Use в той же строке таблицы для включения (по умолчанию) или отключения вкладов от физического интерфейса к управляемой физикой сетке. Информация из физики, такая как наличие области бесконечных элементов или периодических условий, будет использоваться для автоматической настройки соответствующей последовательности сетки.
В Справочном руководстве COMSOL Multiphysics см. раздел Сетка, управляемая физикой, для получения дополнительной информации о том, как определить сетку, управляемую физикой.
Метка — это имя физического интерфейса по умолчанию. Имя используется в основном как префикс области действия для переменных, определяемых физическим интерфейсом. Обращайтесь к таким переменным физического интерфейса в выражениях, используя шаблон <имя>.<имя_переменной>. Чтобы различать переменные, принадлежащие разным физическим интерфейсам, строка имени должна быть уникальной. В поле «Имя» разрешены только буквы, цифры и знаки подчеркивания (_).Первый символ должен быть буквой. Имя по умолчанию (для первого физического интерфейса в модели) — mef. Единственная опция, доступная в списке «Решить для», — «Полное поле».
Для 2D и 2D осесимметричных компонентов выберите Компоненты — Внеплоскостной векторный потенциал (по умолчанию), Плоскостной векторный потенциал или Трехкомпонентный векторный потенциал.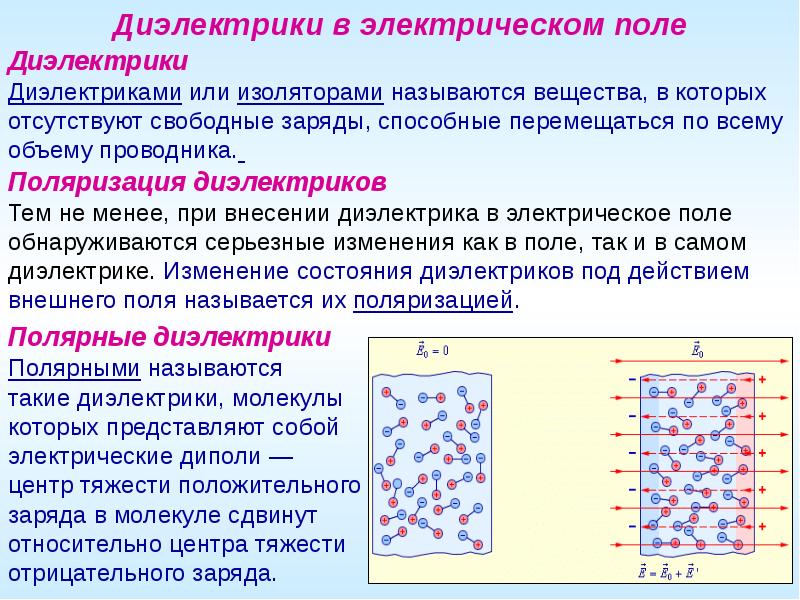 С практической точки зрения этот выбор эквивалентен решению, в каких направлениях разрешено протекание электрического тока (внеплоскостные токи, внутриплоскостные токи или токи, протекающие во всех трех координатных направлениях).
Введите значение или выражение для толщины вне плоскости d. Значение по умолчанию, равное 1 единице длины, обычно не является репрезентативным для тонкого домена.Вместо этого он описывает единичную толщину, что делает 2D-уравнение идентичным уравнению, используемому для 3D-компонентов.
Введите опорное сопротивление Zref (единица СИ: Ом). Значение по умолчанию – 50 Ом. Этот импеданс используется функциями терминала (когда для параметра Тип терминала установлено значение Terminated) и функцией экспорта файлов Touchstone. Установите флажок «Активировать входную развертку», чтобы включить развертку и вызвать параметрическую развертку по портам с сосредоточенными параметрами или терминальным узлам. Выберите вариант из списка Sweep on — Terminals или Ports. Этот параметр определяет, какие функции активируются во время развертки. Введите имя параметра развертки, чтобы указать имя параметра модели, который управляет терминалом или портом, активируемым на каждом этапе развертки. По умолчанию используется имя_порта. Заданное имя должно соответствовать параметру модели, определенному в глобальных определениях, который является объектом узла параметрического анализа в текущем исследовании. Вычисленные параметры с сосредоточенными параметрами можно экспортировать в файл Touchstone.Чтобы активировать эту функцию, введите путь к файлу или выберите файл. Выберите формат параметра (пары значений) для экспорта Touchstone — величина и угол (MA) (по умолчанию), величина в дБ и угол (DB) или действительная и мнимая части (RI). Выберите вариант из списка «Если файл существует» — «Перезаписать» или «Создать новый». Создать новую полезно, когда модель решается несколько раз с разными настройками. 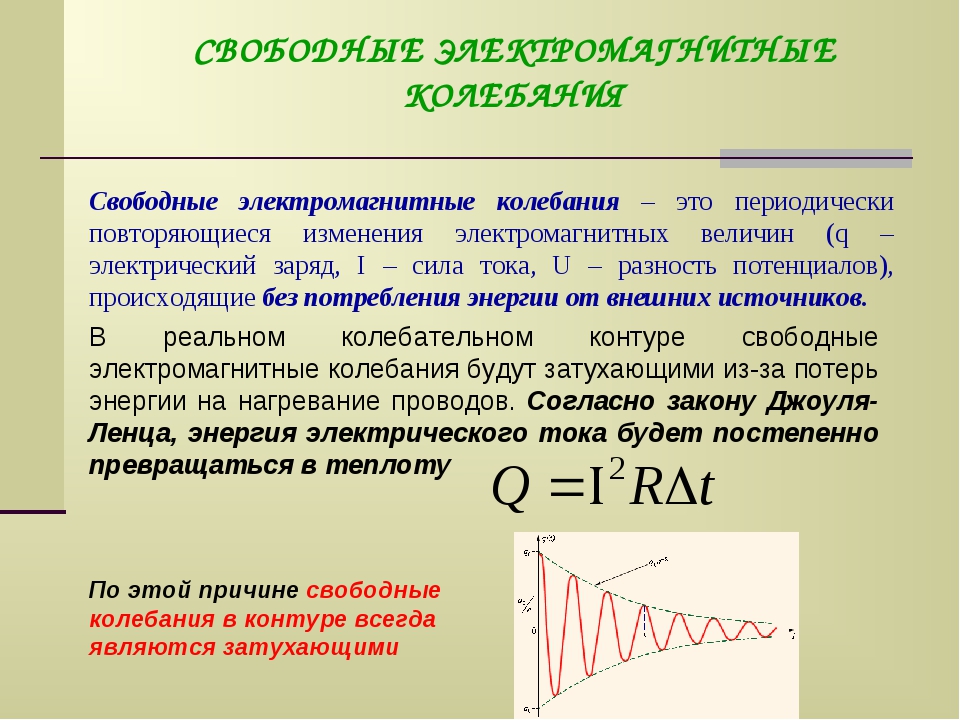Выберите параметр для экспорта — Z (по умолчанию), Y или S. Если в разделе Sweep on выбраны Terminals, также выберите параметр для экспорта — Z (по умолчанию), Y или S.Когда развертка выполняется на портах, экспортируемый параметр всегда равен S. Чтобы отобразить этот раздел, нажмите кнопку «Показать дополнительные параметры» () и выберите «Дополнительные параметры физики». Если установлен флажок Проверить применимость функций в исследовании, любые функции, несовместимые с исследованием, будут генерировать сообщение об ошибке при попытке решить или отобразить решатель по умолчанию. Решатель не будет сгенерирован. Отмените выбор, и вы сможете запустить модель, возможно, вместо этого с ошибками времени выполнения.Он доступен, чтобы позволить опытному пользователю настроить любую функцию и использовать ее за пределами предполагаемой области исследования. Зависимые переменные (полевые переменные) предназначены для электрического потенциала V и магнитного векторного потенциала A.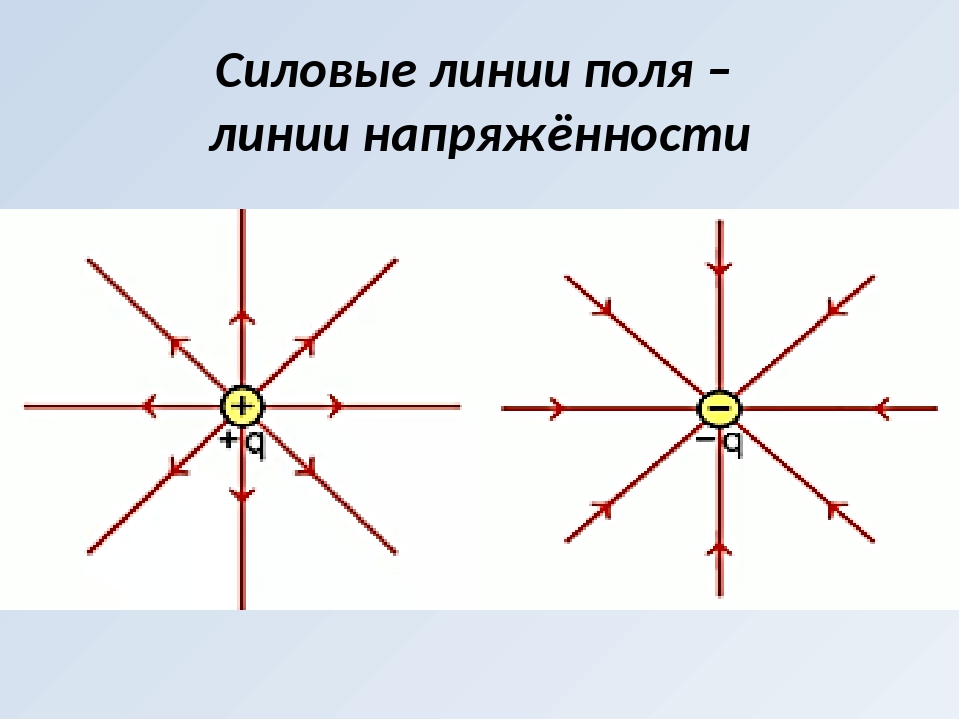 Имя можно изменить, но имена полей и зависимых переменных должны быть уникальными в рамках модели.

•

 Магнитный тормоз: путь к библиотеке приложений ACDC_Module/Motors_and_Actuators/ Magnetic_brake

Проводник в статическом электрическом поле

Введение:

Проводник — это вещество или объект, который позволяет электричеству проходить через него с низким сопротивлением.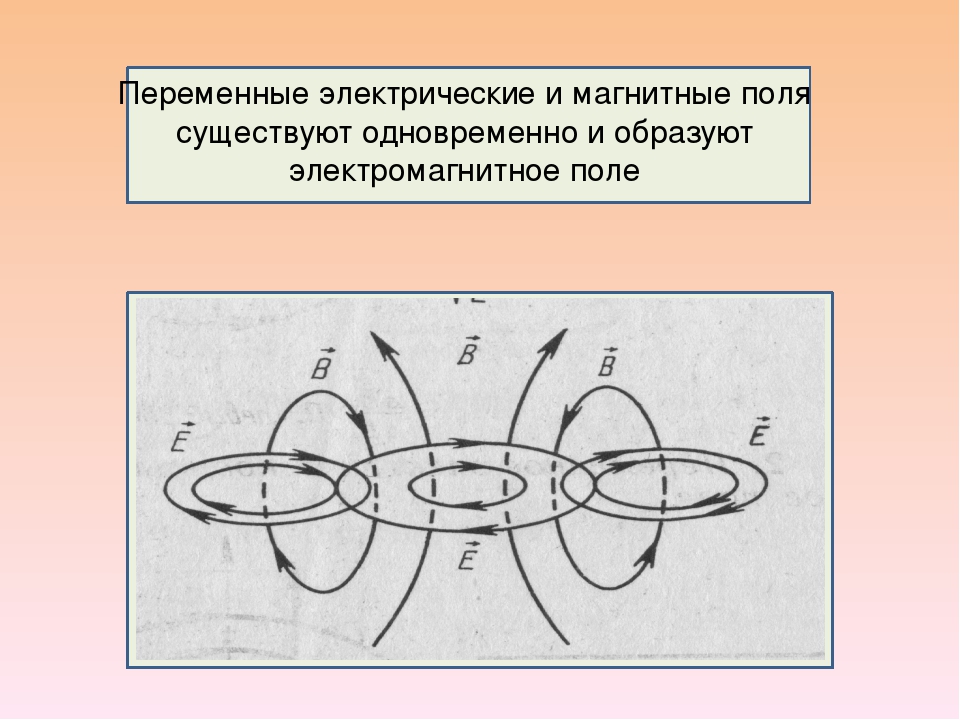 «Проводник» подразумевает, что внешние электроны атомов слабо связаны и могут свободно перемещаться через материал. Электропроводность проводников находится между полупроводниками и сверхпроводниками. В статических условиях поле Е на поверхности проводника всегда перпендикулярно поверхности.

В статическом электрическом поле:

Предположим, что внутрь проводника введены положительные (или отрицательные) заряды. В проводнике возникнет электрическое поле; поле воздействует на заряды силой и заставляет их удаляться друг от друга.Это движение будет продолжаться до тех пор, пока все заряды не достигнут поверхности проводника и не перераспределятся таким образом, что и заряд, и поле внутри исчезнут.

Поскольку поле E может быть выражено как:
E = -ΔV, если E = 0, интеграл от V должен быть постоянным, поэтому при E = 0 напряжение должно быть одинаковым везде в проводнике.

Если вначале поместить проводник в статическое электрическое поле, то электрическое поле проникнет внутрь материала. Со временем свободные электроны в проводнике будут двигаться в направлении, противоположном электрическому полю, а дырки будут двигаться в том же направлении, что и электрическое поле, что приводит к тому, что положительные и отрицательные заряды собираются на противоположных сторонах материала, создавая поле, противоположное статическому электрическому полю, и плотность тока в одном направлении с электростатическим полем. Мы можем исследовать формулу плотности тока и приведенный ниже график для лучшего понимания этих ситуаций.

В часть (1)  электрическое поле проникает через материал, создавая плотность тока в том же направлении.

 

В часть (2) в результате прохождения тока в материале возникает электрическое поле, противоположное внешнему электрическому полю, поэтому теперь проникает только часть внешнего электрического поля и величина плотности тока уменьшилась ( можно увидеть, взглянув на формулу).Электрическое поле внутри материала все еще находится в направлении + x с величиной, равной E-E i .

 

В части (3) продолжается то же действие, что и в части (2) и J становится меньше, а E i увеличивается. В результате проникающее через материал электрическое поле стало еще меньше, чем в части (2).

 

В части (4) E = E i , что означает, что в материале больше нет электрического поля и плотность тока равна нулю.Мы видим, что отрицательные заряды собираются слева, а положительные заряды справа, что создает разность потенциалов и электрическое поле E i . Мы должны помнить, что электрическое поле меняется от положительного к отрицательному, внешнее электрическое поле притягивает электроны к своему источнику и отталкивает протоны от своего источника.

Распределение заряда на материале зависит от формы материала, и на поверхности никогда не будет тангенциальной составляющей электрического поля, потому что это приведет к перемещению зарядов на поверхности.Это означает, что в статических условиях поле E на поверхности проводника всюду перпендикулярно поверхности, что делает его поверхность эквипотенциальной поверхностью.

На приведенном выше рисунке есть еще один проводник, и в статическом состоянии E равно E в , так что результирующее электрическое поле внутри материала равно нулю.

E в — это электрическое поле, созданное зарядами внутри материала, и если мы уберем внешнее электрическое поле (E), заряды перераспределятся внутри материала, сделав внутреннее электрическое поле снова равным нулю.Процесс перераспределения занимает определенное количество конечного времени в зависимости от проводимости материала.

 

Пример (1): Какими будут электрическое поле и заряд в проводнике в статических условиях?

Решение:        В статических условиях и электрический ток, и заряд в проводнике будут равны нулю.

Пример (2): чему в статических условиях будет равна нормаль и тангенциальная составляющая электрического поля на поверхности проводника?

 

Решение. В статических условиях тангенциальная составляющая электрического поля всегда равна нулю на поверхности, а нормальная составляющая равна плотности поверхностного заряда на проводнике, деленной на диэлектрическую проницаемость пространства.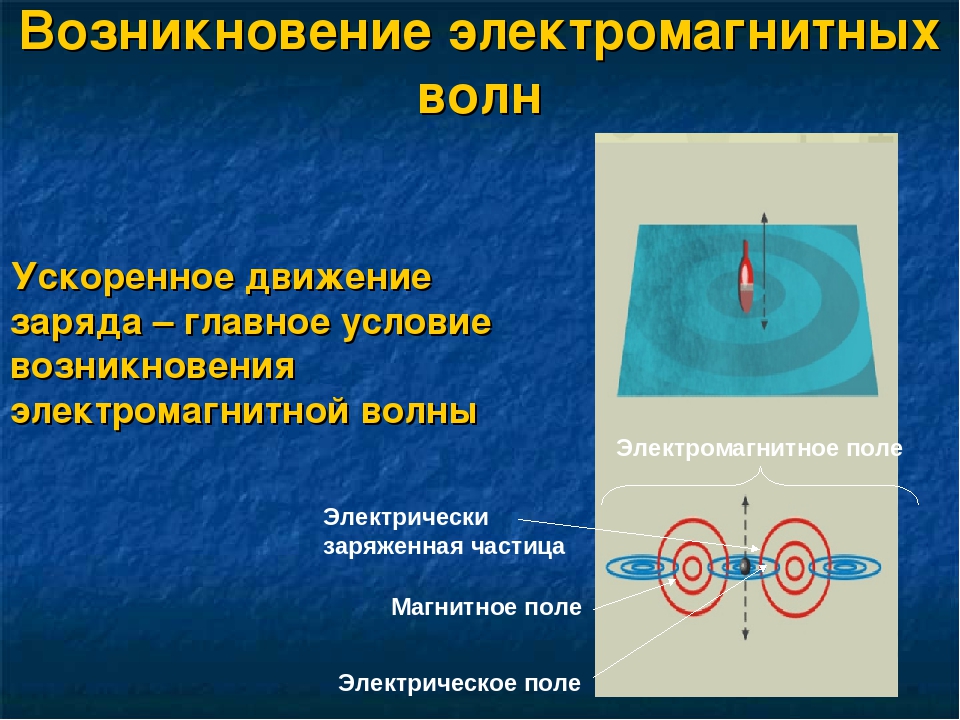

Пример (3): Где накапливается больше всего статических электрических зарядов?

(а) В медной проволоке

(b) На поверхности непроводящего материала

(с)В искре

Ответ :(б)

Пример (4): Что из следующего обычно создает статическое электричество?

(a) Протрите мокрой тряпкой пластмассовую расческу.

(b) Потрите монету пластиковой расческой

(c)Потрите пластиковую расческу кроличьим мехом.

Ответ 🙁 с)

Пример (5): Что может заставить электроны прыгать через зазор и вызывать искру?

(а) Сила большого положительного заряда по другую сторону зазора

(b) Молния вызывает множество событий

(c) Разогрев зазора

Ответ 🙁 а)

Электростатическое поле — обзор

27.4 Форма капли

Влияние электростатического поля на форму капли — хорошо известное явление, вытягивающее каплю вдоль направления поля, как показано на рис. 27.6. В 1882 году лорд Рэлей начал исследование взаимодействия зарядов и электрических полей на каплях жидкости. Он теоретически вывел критическое количество зарядов, необходимое для дестабилизации изолированной сферической капли с поверхностным зарядом. Его работа вдохновила начало электрогидродинамики (Melcher and Taylor, 1969).

За последние три десятилетия форма и устойчивость лежачих капель под действием электрических полей анализировались во многих работах. Розенкильде (1969) исследовал равновесие и устойчивость несжимаемой диэлектрической капли, находящейся в однородном электрическом поле. Считая каплю эллипсоидальной, он предложил связь между равновесной деформацией, напряженностью электрического поля, размерами капли и поверхностным натяжением. Также была представлена ​​причина нестабильности для высоких диэлектрических проницаемостей флюидов (Rosenkilde, 1969).

Миксис (1981) предложил численную модель для расчета формы осесимметричной капли в постоянном электрическом поле, что дало хорошее согласие с экспериментами.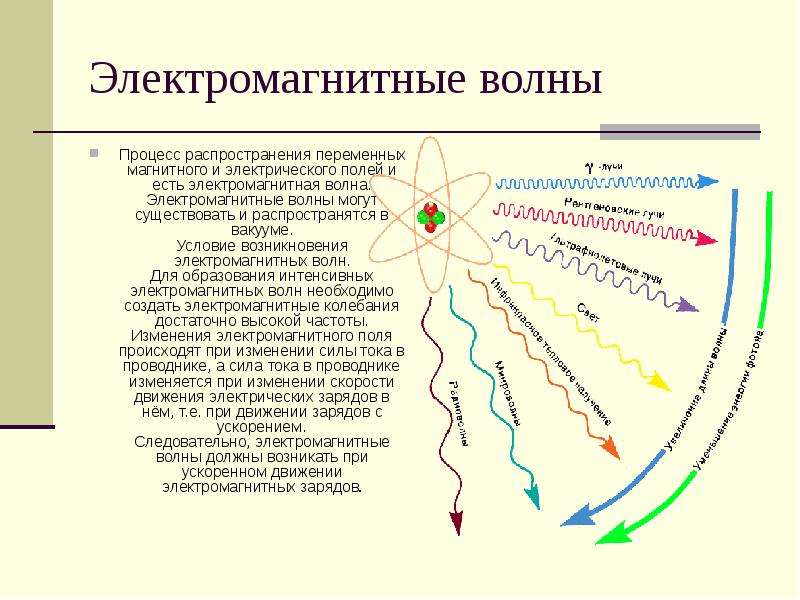 Его результаты показывают критическое значение диэлектрической проницаемости, при котором капли удлиняются и сохраняют свою первоначальную сфероидальную форму. Выше этого критического значения капля приобретала коническую форму.

В своих численных работах Basaran и Wohlhuter (Wohlhuter and Basaran, 1992; Basaran and Wohlhuter, 1992) рассчитали форму и устойчивость осесимметричных висячих и сидячих капель или пузырьков, учитывая, что линия контакта фиксирована или задана.Их первые расчеты касались предположения, что проводящие капли являются линейно поляризуемыми материалами (Wohlhuter and Basaran, 1992). Равновесная форма и устойчивость капель определяются одновременным решением уравнений Лапласа и Юнга–Лапласа. Исследование, учитывающее нелинейную поляризацию капель, было проведено путем замены уравнения Максвелла уравнением Лапласа (Basaran and Wohlhuter, 1992). Их расчеты показали важность изменения расстояния между пластинчатыми конденсаторами, которое влияет на напряженность электрического поля и размер капель.

Резник и др. (2004) выделили три сценария эволюции формы капель в сильных электрических полях, определяемых значениями электрического числа Бонда и основанных на численном решении уравнений Стокса. В слабом электрическом поле капли подвергаются напряжениям Максвелла и имеют стационарную форму. В сильных электрических полях и при малых статических краевых углах капли приобретают коническую форму и начинается струйное распыление с кончика капли. Финальный сценарий соответствует отрыву почти целой капли (т.е., явление капания), возникающее в результате сильного электрического поля и краевого угла, превышающего критическое значение. Численная модель хорошо согласовывалась с экспериментальными результатами для полимерных капель (Резник и др., 2004).

Батени и др. (2004; 2005a,b) основывали свою методологию ADSA-EF на предположении об осесимметричной форме капли. ADSA-EF можно использовать для измерения поверхностного натяжения капли в электрическом поле с эффектом гравитации и без него.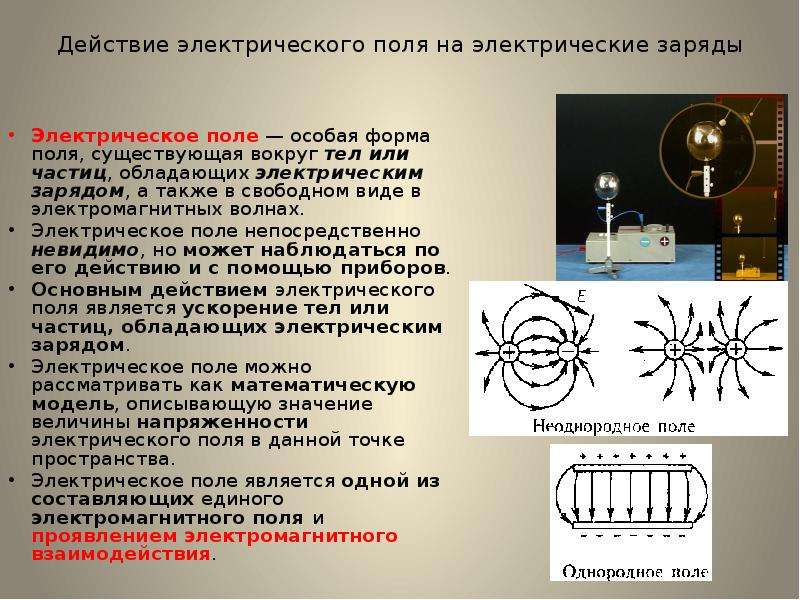 Из уравнения Юнга-Лапласа, описываемого уравнением(27.2) они рассматривали электрическое давление Δ P e , которое зависит от диэлектрической проницаемости жидкостей, напряженности и направления электрического поля следующим образом:

(27.11)ΔPe=12[ε0En(g )2−ε0(εr−1)Et2]

где E t и E n — соответственно тангенциальная и нормальная составляющие электрического поля на поверхности капли, а верхние индексы l и g относятся к капельной жидкости и окружающей жидкости, видимой как воздух, соответственно.Когда капля является проводящей жидкостью, внутри капли отсутствует электрическое поле, и уравнение Юнга–Лапласа упрощается как

Из уравнения. (27.12) и модуля электростатического поля они численно предсказали форму капли с помощью итерационной схемы, как показано на рис. 27.5.

Рисунок 27.5. Прогнозирование формы капли с помощью итерационных расчетов (Bateni et al., 2004).

Ди Марко и др.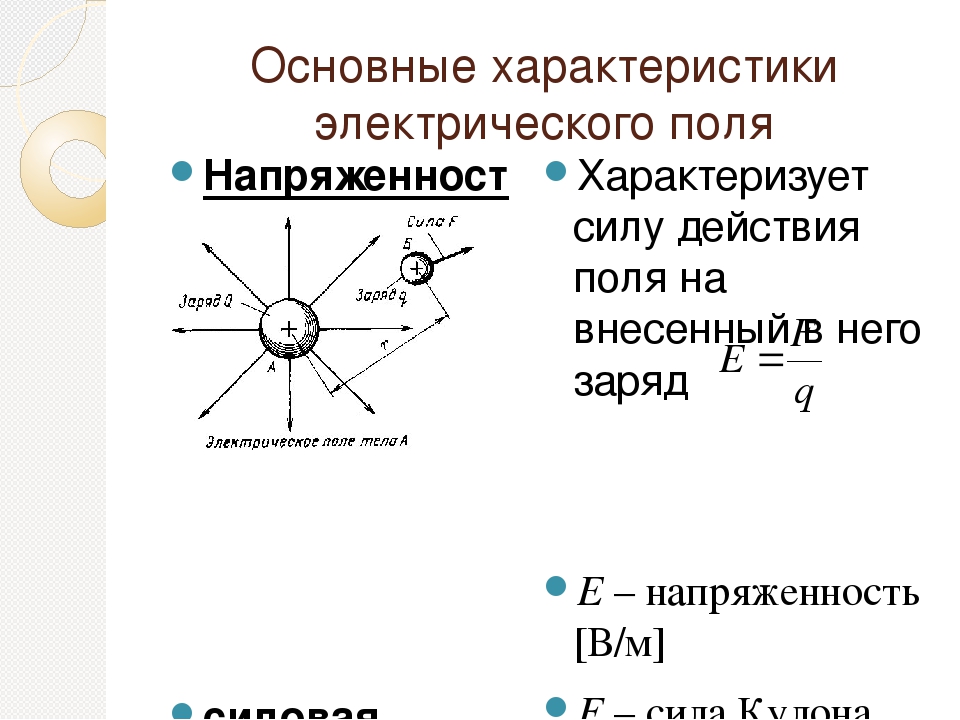 (2013) оценили электрическую силу, действующую на поверхность раздела неподвижной капли этанола, и сравнили экспериментальные результаты с теоретической моделью, основанной на равновесном действии неподвижной капли с учетом электрического поля и гравитации.Экспериментальная установка состоит из плоской алюминиевой пластины, снабженной отверстием для ввода капель. Пластина электрически заземлена и покрыта тефлоновым слоем. Электрод из нержавеющей стали в форме шайбы размером 4 мм × 15 мм уложен параллельно пластине на расстоянии 6 мм и подключен к положительному полюсу источника высокого напряжения, который может обеспечить до 8 кВ постоянного тока. Результирующее электрическое поле в резонаторе имеет среднюю напряженность 13,3×10 3 В см -1 . Форма полученных капель показана на рисунке 27.6. Капли, подвергнутые воздействию электрического поля, вытягиваются в направлении электрического поля из-за изменения кривизны границы раздела локальным электрическим напряжением, как сообщалось ранее. 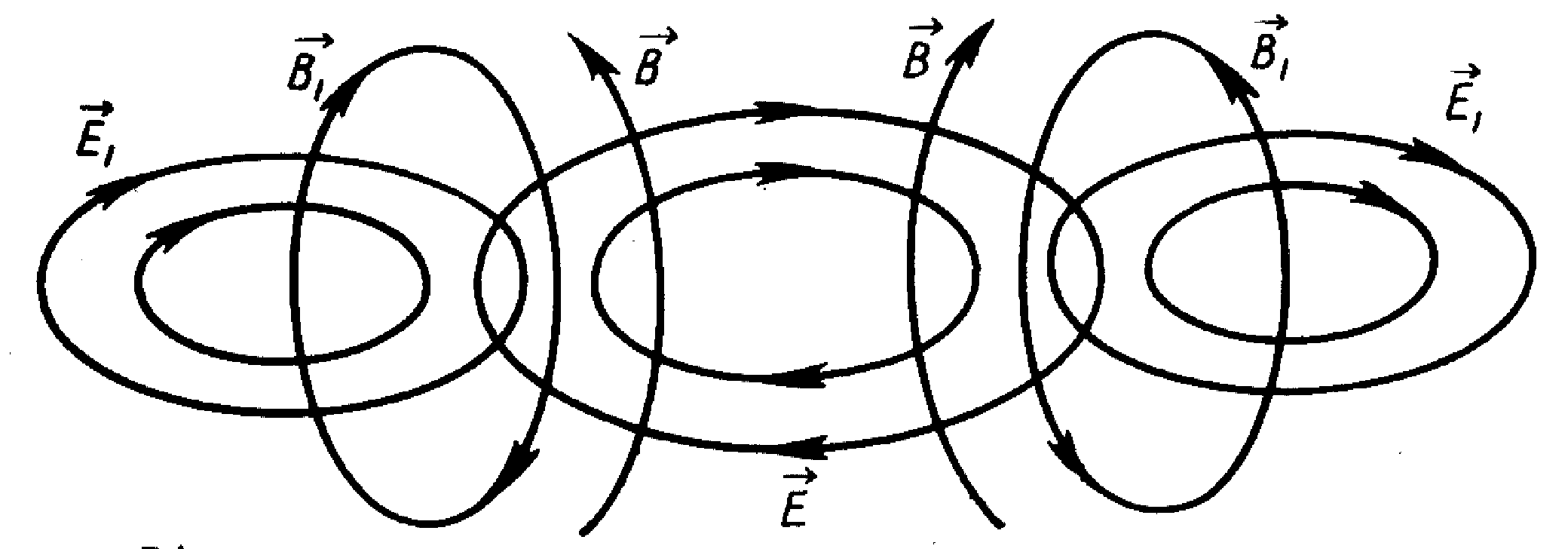Контактный угол и кривизна на вершине капли увеличиваются с увеличением напряженности электрического поля.

Рисунок 27.6. Форма капли этанола при различной напряженности электрического поля (Di Marco et al., 2013).

Профиль капель и их геометрические параметры (угол контакта, размеры капель и объем) обрабатываются специальным программным обеспечением для обработки изображений, которое может идентифицировать и интерполировать профиль капель.Эти измерения позволяют оценить результирующие силы, действующие на каплю из-за веса, адгезии и внутреннего давления. В отсутствие электрического поля экспериментальные значения силы, действующей на каплю, хорошо согласуются с теоретическими предсказаниями, что подтверждает правильность метода. Следовательно, при наличии электрического поля результирующую электрическую силу, действующую на каплю, можно оценить по разнице и сравнить с теоретическими моделями.

Конспект лекций, глава 1

Конспект лекций, глава 1
Учитывая стационарное распределение заряда мы можем, в принципе, вычислить электрическое поле:

где . 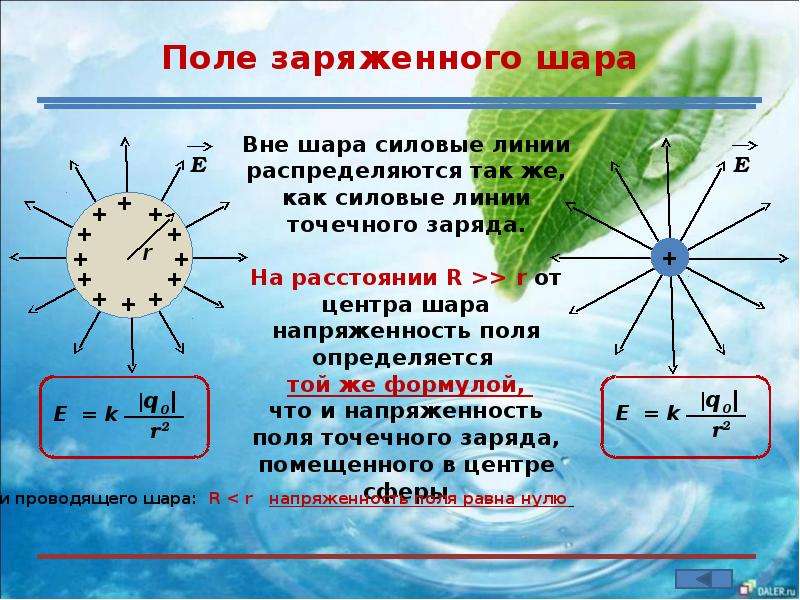Этот интеграл включает в себя вектор в качестве подынтегральной функции и, вообще говоря, его трудно вычислить. рассчитать. В большинстве случаев проще сначала оценить электростатическую потенциал В , который определяется как

поскольку подынтегральная функция интеграла является скаляром. Соответствующий электрическое поле затем можно получить из градиента V , так как

Электростатический потенциал В может быть оценен только аналитически для простейшие конфигурации заряда.Кроме того, во многих электростатических проблемы, задействованы проводники и распределение заряда ρ заранее не известен (известен только суммарный заряд на каждом проводнике).
А лучший подход к определению электростатического потенциала состоит в том, чтобы начать с Уравнение Пуассона


Очень часто мы хотим определить потенциал только в той области, где ρ = 0. В этой области уравнение Пуассона сводится к уравнению Лапласа уравнение


Существует бесконечное число функций, удовлетворяющих уравнению Лапласа и соответствующее решение выбирается путем указания соответствующего граничные условия .В этой главе основное внимание будет уделено различным методы, которые можно использовать для вычисления решений уравнения Лапласа и на граничных условиях, необходимых для однозначного определения решение.

3.1. Решения уравнения Лапласа в один, два и три Размеры

3.1.1. Уравнение Лапласа в одном измерении

В одном измерении электростатический потенциал В зависит только от одного переменная x .Электростатический потенциал В ( x ) является решением одномерного уравнения Лапласа


Общее решение этого уравнения:


где s и b — произвольные константы. Эти константы фиксируется при задании значения потенциала на двух разных позиции.

Пример
Рассмотрим одномерный мир с двумя точечные проводники, расположенные на х = 0 м и на х = 10 м.То проводник на x = 0 м заземлен ( В = 0 В) и проводник на х = 10 м находится под постоянным потенциалом 200 В. Определить В .

Граничные условия для V :


и


Первое граничное условие показывает, что b = 0 В. Второе граничное условие показывает, что с = 20 В/м.Электростатический потенциал для этой системы проводников, таким образом,


Соответствующее электрическое поле можно получить из градиента В


Используемые здесь граничные условия можно использовать для задания электростатического потенциал между x = 0 м и x = 10 м, но не в области x x > 10 м. Если бы полученное здесь решение было общее решение для всех x , тогда V будет приближаться к бесконечности, когда x приближается к бесконечности, а V приближается к минус бесконечности, когда x приближается к минус бесконечности. Таким образом, граничные условия обеспечивают информация, необходимая для однозначного определения решения уравнения Лапласа, но они же и определяют границу области, где это решение справедливо (в этот пример 0 м x

Следующие свойства верно для любого решения одномерной задачи Лапласа уравнение:

Свойство 1:
V ( x ) является средним значением V ( x + R ) и V ( x — R ) для любого R до тех пор, пока х + R и х — R расположены в области между границей точки.Это свойство легко доказать:


Это свойство сразу же предлагает мощный аналитический метод для найти решение уравнения Лапласа. Если граничные значения В


и


, то свойство 1 можно использовать для определения значения потенциала при ( а + б )/2:


Далее мы можем определить значение потенциала при x = (3 a + b )/4 и при x = ( a + 3 b )/4 :


Этот процесс можно повторить и таким образом вычислить V . 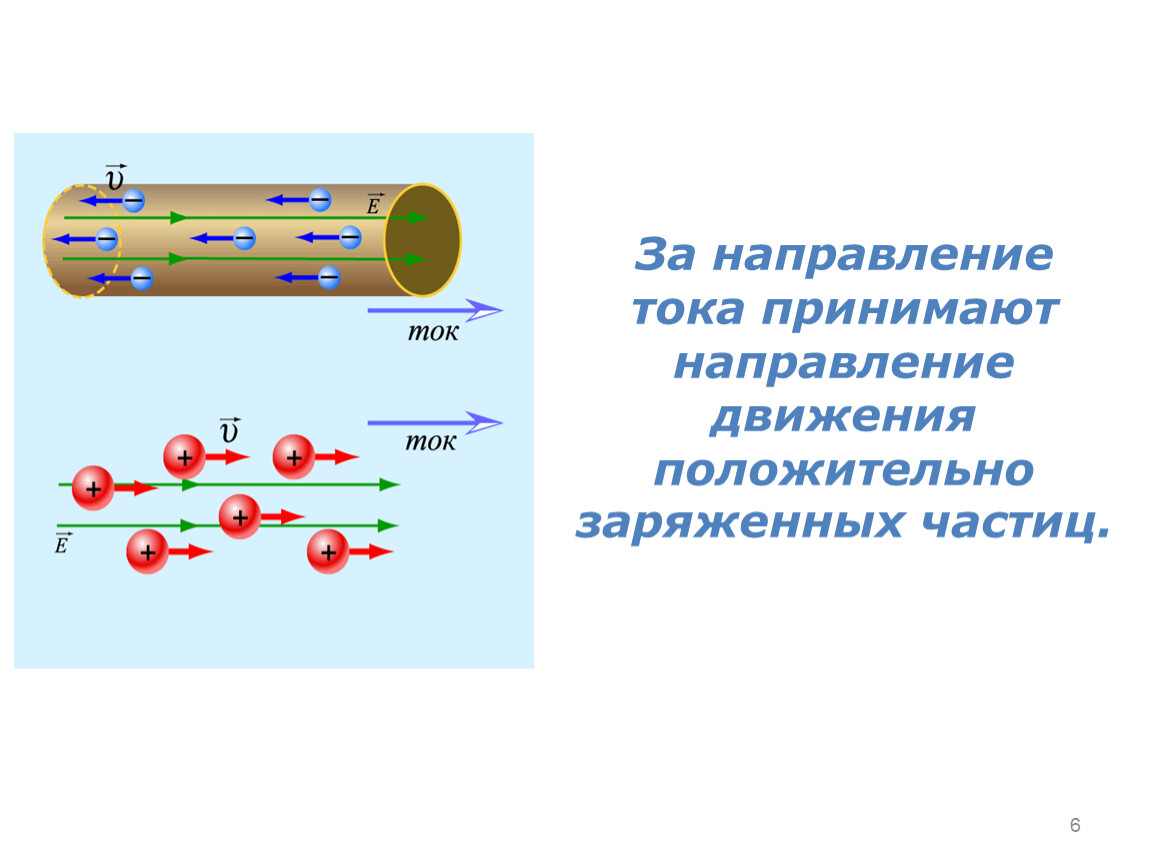в любой точке между x = a и x = b (но не в регион x > b и x a ).

Недвижимость 2:
Решение уравнения Лапласа не может иметь локальных максимумов или минимумы. Экстремальные значения должны встречаться в конечных точках (границах). Это прямое следствие свойства 1.
Свойство 2 имеет важное следствие: заряженная частица не может удерживаться в устойчивом равновесии электростатическими силами отдельно ( Теорема Эрншоу ). Частица находится в устойчивом равновесии если он расположен в положении, где потенциал имеет минимальное значение.Маленький смещение от положения равновесия увеличит электростатическую потенциал частицы, и возвращающая сила попытается сдвинуть частицу вернуться в положение равновесия. Однако, поскольку не может быть локальных максимумов или минимумы в электростатическом потенциале, частица не может удерживаться в устойчивом равновесия только электростатическими силами.

3.1.2. Уравнение Лапласа в двух измерениях

В двух измерениях электростатический потенциал зависит от двух переменных х и у .Уравнение Лапласа теперь принимает вид

.
Это уравнение не имеет простого аналитического решения, т. одномерное уравнение Лапласа делает. Однако свойства растворов одномерное уравнение Лапласа справедливо и для решений уравнения двумерное уравнение Лапласа:

Свойство 1:
Значение V в точке ( x , y ) равно среднему значению В вокруг этой точки


где интеграл по путям проходит по окружности произвольного радиуса с центром в ( x , y ) и с радиусом R .

Недвижимость 2:
V не имеет локальных максимумов и минимумов; все крайности происходят в границы.

3.1.3. Уравнение Лапласа в трех измерениях

В трех измерениях электростатический потенциал зависит от трех переменных x , y и z . Уравнение Лапласа теперь принимает вид

.
Это уравнение не имеет простого аналитического решения, т. одномерное уравнение Лапласа делает.Однако свойства растворов одномерное уравнение Лапласа справедливо и для решений уравнения трехмерное уравнение Лапласа:

Свойство 1:
Значение V в точке ( x , y , z ) равно среднему значению В вокруг этой точки


где поверхностный интеграл находится по поверхности сферы произвольной радиус, с центром в ( x , y , z ) и с радиусом Р .


Рисунок 3.1. Доказательство собственности 1.

Чтобы доказать это свойство В , рассмотрим электростатический потенциал генерируемого точечным зарядом q , расположенным на оси z , расстояние r от центра сферы радиусом R (см. рис. 3.1). Потенциал на P , создаваемый зарядом q , равен


, где d — расстояние между P и q .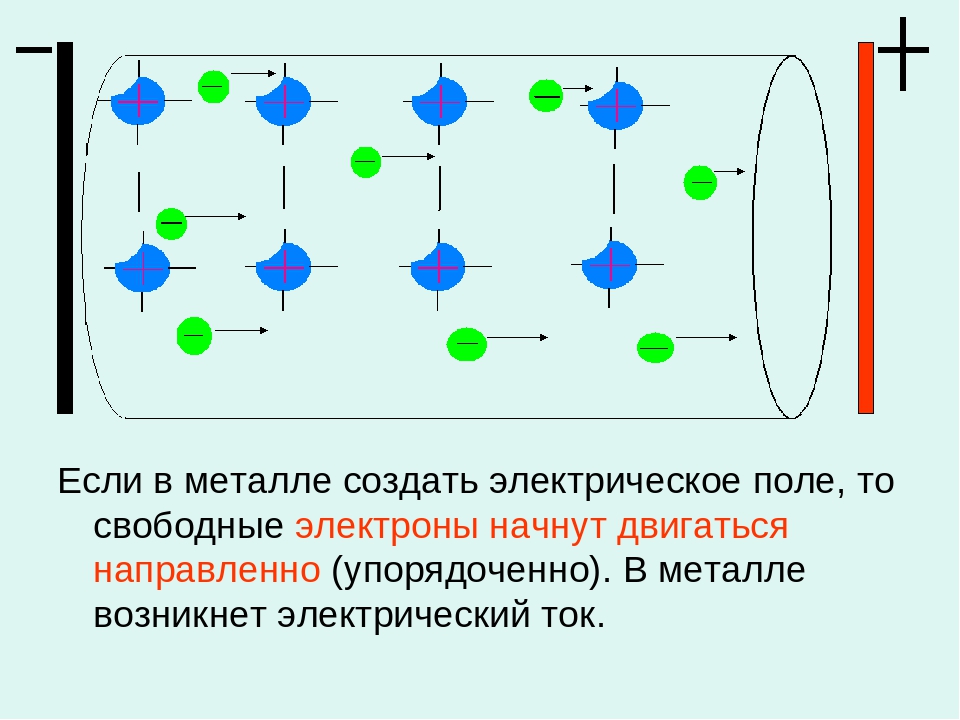 С помощью по правилу косинусов мы можем выразить d через r , R и θ


Таким образом, потенциал P из-за заряда q равен до


Средний потенциал на поверхности сферы может быть получен по формуле интегрирующий по поверхности сферы. Средний потенциал равен

который равен потенциалу из-за q в центре сфера.Применяя принцип суперпозиции, легко показать, что средний потенциал, создаваемый совокупностью точечных зарядов, равен чистому потенциал, который они производят в центре сферы.

Недвижимость 2:
Электростатический потенциал В не имеет локальных максимумов и минимумов; все крайности возникают на границах.

Пример: проблема 3.3
Найдите общее решение уравнения Лапласа в сферической координаты, для случая, когда V зависит только от r .Затем сделайте то же самое для цилиндрических координат.

Уравнение Лапласа в сферическом координаты указаны


Если V является функцией только r , то


и


Следовательно, уравнение Лапласа можно переписать как


Решение V этого дифференциального уравнения второго порядка должно удовлетворяют следующему дифференциальному уравнению первого порядка:


Это дифференциальное уравнение можно переписать как


Общее решение этого дифференциального уравнения первого порядка:


, где b — константа.Если V = 0 на бесконечности, то b должен быть равен нулю и, следовательно,



Уравнение Лапласа в цилиндрических координатах:


Если V является функцией только r , то


и


Следовательно, уравнение Лапласа можно переписать как


Решение V этого дифференциального уравнения второго порядка должно удовлетворяют следующему дифференциальному уравнению первого порядка:


Это дифференциальное уравнение можно переписать как


Общее решение этого дифференциального уравнения первого порядка:


где b — константа. Константы a и b равны определяются граничными условиями.

3.1.4. Теоремы единственности

Рассмотрим объем (см. рис. 3.2), внутри которого плотность заряда равен нулю. Предположим, что значение электростатического потенциала равно в каждой точке поверхности этого объема. Первая уникальность теорема утверждает, что в этом случае решение уравнения Лапласа есть однозначно определено.


Рисунок 3.2. Первая теорема единственности

Чтобы доказать первую теорему единственности, рассмотрим, что происходит, когда есть два решения V 1 и V 2 из Уравнение Лапласа в объеме показано на рис. 3.2. С V 1 и V 2 являются растворами Лапласа. уравнение мы знаем, что


и


Поскольку оба V 1 и V 2 являются решениями, они должны иметь одинаковое значение на границе. Таким образом, В 1 = V 2 на границе объема. Теперь рассмотрим третий функция В 3 , которая является разницей между В 1 и В 2


Функция V 3 также является решением уравнения Лапласа. Это можно легко продемонстрировать:


Значение функции В 3 равно нулю на граница объема с В 1 = В 2 есть.Однако свойство 2 любого решения уравнения Лапласа гласит, что оно может не имеют локальных максимумов или минимумов и что крайние значения решения должны происходят на границах. Поскольку V 3 является решением уравнения Лапласа уравнение и его значение равно нулю всюду на границе объема, т.е. максимальное и минимальное значение В 3 должны быть равны нулю. Следовательно, V 3 везде должно быть равно нулю. Этот сразу подразумевает, что


везде. Это доказывает, что не может быть двух разных функций V 1 и V 2 , которые являются растворами Лапласа уравнение и удовлетворяют тем же граничным условиям. Следовательно, решение Уравнение Лапласа определяется однозначно, если его значение является заданной функцией по всем границам области. Это также указывает на то, что это не имеет значения как вы пришли к своему решению: если (а) это решение уравнения Лапласа, и (б) оно имеет правильное значение на границах, то оно правильное и единственное решение.


Рисунок 3.3. Система с проводниками.
Первую теорему единственности можно применить только в тех областях, которые бесплатно и окружен границей с известным потенциалом (не обязательно постоянный). В лаборатории границы обычно являются проводниками. подключены к батареям, чтобы поддерживать их постоянный потенциал. Во многих других электростатические задачи мы не знаем потенциал на границах система. Вместо этого мы могли бы знать общий заряд на различных проводниках, которые составляют систему (примечание: знание полного заряда проводника не означает знание распределения заряда ρ , так как на него влияет наличие других проводников).В дополнение к проводникам, которые делают вверх по системе может быть распределение заряда ρ , заполняющее области между проводниками (см. рис. 3.3). Для этого типа системы первая теорема единственности неприменима. вторая теорема единственности утверждает, что электрическое поле определяется однозначно, если полный заряд на задан каждый проводник и распределение заряда в областях между проводники известны.
Доказательство второй теоремы единственности аналогично к доказательству первой теоремы единственности.Предположим, что есть два поля и которые являются решениями уравнения Пуассона в области между проводниками. Таким образом,

и


где ρ — плотность заряда в точке, где поле оценивается. Поверхностные интегралы и , оценивается с использованием поверхности, которая находится сразу за пределами одного из проводников с зарядом Q i, равны .Таким образом,

Разница между и , , удовлетворяет следующим уравнениям:


Поскольку поверхностный интеграл по поверхности проводника i равен нулю, поверхностный интеграл от по всем поверхностям проводника также будет равна нулю. Поверхностный интеграл по внешней поверхности также будет равна нулю, так как на этой поверхности.Таким образом,

Поверхностный интеграл можно переписать, используя идентификатор Грина, как
.
где интегрирование объема производится по всему пространству между проводниками и внешняя поверхность. С всегда положителен, объемный интеграл от может быть равно нулю только в том случае, если повсюду. Отсюда сразу следует, что всюду и доказывает вторую теорему единственности.

3.2. Метод изображений

Рассмотрим точечный заряд q , удерживаемый на расстоянии d над бесконечная заземленная проводящая плоскость (см. рис. 3.4). электростатический потенциал этой системы должен удовлетворять следующим двум граничным условия:


Прямой расчет электростатического потенциала не может быть выполнен так как неизвестно распределение заряда на заземленном проводнике. Примечание : распределение заряда на поверхности заземленного проводник не обязательно должен быть нулевым.


Рисунок 3.4. Метод образов.

Рассмотрим вторую систему, состоящую из двух точечных зарядов с зарядами + q и — q , расположенные по адресу z = d и z = — d соответственно (см. рисунок 3.5). Созданный электростатический потенциал по этим двум зарядам можно вычислить непосредственно в любой точке пространства.В точка P = ( x , y , 0) на плоскости xy электростатический потенциал равен



Рисунок 3.5. Зарядка и заряд изображения.

Потенциал этой системы на бесконечности будет стремиться к нулю, так как потенциал, создаваемый каждым зарядом, будет уменьшаться как 1/ r с увеличением расстояние r . Следовательно, электростатический потенциал, создаваемый двумя заряды, показанные на рисунке 3.5 удовлетворяет тем же граничным условиям, что и система показано на рисунке 3.4. Так как распределение заряда в районе z > 0 (ограничен плоской границей xy и границей на бесконечности) для две системы идентичны, следствие из первой теоремы единственности утверждает что электростатический потенциал в этой области определен однозначно. Следовательно, если мы найдем любую функцию, удовлетворяющую граничным условиям и закону Пуассона уравнение, это будет правильный ответ. Рассмотрим точку ( x , y , z ) с z > 0. Электростатический потенциал в этой точке может легко вычислить для распределения заряда, показанного на рис. 3.5. это равно


Поскольку это решение удовлетворяет граничным условиям, оно должно быть правильное решение в области z > 0 для системы, показанной на Рисунок 3.4. Этот метод использования зарядов изображения для получения электростатического потенциала в некоторой области пространства называется методом образов .
Электростатический потенциал можно использовать для расчета распределения заряда на заземленный проводник. Так как электрическое поле внутри проводника равно нуль, граничное условие для (см. главу 2) показывает, что электрическое поле снаружи проводника равно равно

где σ — поверхностная плотность заряда и — единичный вектор нормали к поверхности проводника. выражая электрическое поле через электростатический потенциал В можно переписать это уравнение как

Подставляя решение для V в это уравнение, мы находим


Только на последнем шаге этого расчета мы заменили на = 0. Распределение индуцированного заряда отрицательное, а плотность заряда наибольшая. в ( х = 0, у = 0, х = 0). Общий заряд на проводник можно рассчитать поверхностным интегрированием σ :


где . Подставляя выражение для σ в интеграл, получаем получить

В результате индуцированного поверхностного заряда на проводнике точка заряд q будет притягиваться к проводнику.Поскольку электростатический потенциал, создаваемый системой заряд-образ-заряд, одинаков как система заряд-проводник в области, где z > 0, связанное электрическое поле (и, следовательно, сила на точечном заряде q ) тоже будет так же. Сила, действующая на точечный заряд q , может быть получается непосредственно путем вычисления силы, действующей на точечный заряд со стороны имиджевый заряд. Эта сила равна


Однако есть одно важное различие между системой заряда изображения. и настоящая система.Эта разница представляет собой полную электростатическую энергию система. Электрическое поле в системе образ-заряд присутствует везде, и величина электрического поля в точках ( x , y , z ) будет быть таким же, как величина электрического поля при ( x , y , — z ). С другой стороны, в реальной системе электрическое поле будет только отлична от нуля в области с z > 0. Поскольку электростатическая энергия системы пропорциональна объемному интегралу электростатическая энергия реальной системы будет равна 1/2 электростатической энергия системы образ-заряд (лишь 1/2 всего объема имеет ненулевую электрическое поле в реальной системе).Электростатическая энергия имидж-система заряда равна

Следовательно, электростатическая энергия реальной системы равна


Электростатическую энергию реальной системы также можно получить, расчет работы, необходимой для сборки системы. Чтобы переместите заряд q в его конечное положение, мы должны будем приложить силу противоположной силе, действующей на него со стороны заземляющего проводника.Работа, проделанная для переместить заряд из бесконечности по оси z в z = d равно равно


что идентично результату, полученному с использованием электростатического потенциала энергия системы образ-заряд.

Пример: Пример 3.2 + Проблема 3.7
Точечный заряд q расположен на расстоянии s от центр заземленной проводящей сферы радиусом R (см. рис. 3.6).
а) Найдите потенциал везде.
б) Найдите индуцированный поверхностный заряд на сфере, как функция q . Интегрируйте это, чтобы получить общее индуцированное обвинение.
c) Рассчитайте электростатическую энергию этого конфигурация.


Рисунок 3.6. Пример 3.2 + Задача 3.7.

а) Рассмотрим систему, состоящую из двух зарядов q и q’ , расположены на оси z в точках z = s и z = z’ , соответственно. Если потенциал, создаваемый этой системой, везде одинаков к потенциалу, создаваемому системой, показанной на рис. 3.6, то положение точечный заряд q’ должен быть выбран таким, чтобы потенциал на поверхности сфера радиусом R с центром в начале координат равна нулю (в этом случае граничные условия для потенциала, генерируемого обеими системами, равны идентичны).
Начнем с определения правильного положения точки плата q’ .Электростатический потенциал на P (см. рис. 3.7) равен равно


Это уравнение можно переписать как



Рисунок 3.7. Система заряда имиджа.

Электростатический потенциал на Q равен


Это уравнение можно переписать как


Объединяя два выражения для q’ , мы получаем


или


Это уравнение можно переписать как


Положение заряда изображения равно


Значение заряда изображения равно


Теперь рассмотрим произвольную точку P’ на окружности. Расстояние между P’ и зарядом q составляет d и расстояние между P’ и заряд q’ равен d’ . Используя правило косинусов (см. рис. 3.7) мы можем выразить d и d’ через R , с и θ :


Электростатический потенциал в точке P’ равен


Таким образом, мы заключаем, что конфигурация заряда и заряда изображения производит электростатический потенциал, равный нулю в любой точке сферы радиусом R с центром в начале координат.Поэтому такая конфигурация заряда создает электростатический потенциал, который удовлетворяет точно той же границе условия как потенциал, создаваемый системой заряд-сфера. В регионе Таким образом, вне сферы электростатический потенциал равен электростатический потенциал, создаваемый зарядом и зарядом изображения. Рассмотрим произвольная точка . Расстояние между этой точкой и зарядом q равно d , а расстояние между этой точкой и зарядом q’ равно d’ .Эти расстояния можно выразить через r , s и θ с использованием правило косинуса:

Электростатический потенциал при поэтому будет равно

б) Плотность поверхностного заряда σ на сфере можно получить из граничных условий

, где мы использовали тот факт, что электрическое поле внутри сферы нуль.Это уравнение можно переписать как

.

Подставив в это уравнение общее выражение для V , получим получить


Полный заряд на сфере можно получить путем интегрирования σ над поверхностью сферы. Результат


в) Чтобы получить электростатическую энергию системы, мы можем определить работа, необходимая для сборки системы путем вычисления интеграла по путям силу, которую нам нужно приложить к заряду q , чтобы сдвинуть его из бесконечности в свою конечную позицию ( z = s ).Зарядка q почувствует сила притяжения, действующая на сферу со стороны индуцированного заряда. Сила эта сила равна силе на заряд q , действующей на заряд изображения q’ . Эта сила равна


Сила, которую мы должны приложить к q , чтобы переместить его из бесконечности в текущее положение противоположно . Таким образом, общая работа, необходимая для перемещения заряда, равна
.


Пример: Задача 3.10
Два полубесконечных заземления проводящие плоскости пересекаются под прямым углом. В области между ними находится точечный заряд q , расположенный, как показано на рисунке 3.8. Настроить образ конфигурации и рассчитать потенциал в этой области. Какие обвинения вы нужно, и где они должны быть расположены? Какая сила действует на q ? Как много труда потребовалось, чтобы вывести q из бесконечности?

Рассмотрим система из четырех зарядов, показанная на рис. 3.9. Электростатический потенциал генерируемое этим распределением заряда, равно нулю в каждой точке yz плоскости и в каждой точке плоскости xz .Следовательно, электростатический потенциал, создаваемый этим распределением заряда изображения, удовлетворяет тому же граничные условия как электростатический потенциал исходной системы. То потенциал, создаваемый распределением заряда изображения в области, где x > 0 и y > 0 будут идентичны потенциалу оригинальная система. Потенциал в точке P = ( x , y , z ) равно



Рисунок 3.8. Проблема 3.10.

Рисунок 3.9. Плата за изображение для задачи 3.10.

Сила, действующая на q , может быть получена путем вычисления силы воздействующие на q зарядами изображения. Суммарная сила равна векторная сумма сил, действующих на каждый из трех зарядов изображения. Сила действующий заряд изображения, расположенный в точке (- a , b , 0) направлен вдоль отрицательной оси x и равен


Сила, создаваемая образным зарядом, расположенным в точке ( a , — b , 0) направлена ​​вдоль отрицательной оси y и равна


Сила, действующая на изображение заряда, расположенного в (- a , — b , 0) направлена ​​по вектору, соединяющему (- a , — b , 0) и ( a , б , 0) и равен


Суммарная сила на заряде q есть векторная сумма , и :

Электростатическая потенциальная энергия системы в принципе может быть полученный путем вычисления интеграла по путям между бесконечностью и ( a , b , 0).Однако это не тривиально так как сила является довольно сложной функцией a и b . Более простая техника рассчитать электростатическую потенциальную энергию системы с зарядом и обвинения в изображении. Потенциальная энергия этой системы равна

Однако в реальной системе электрическое поле отлично от нуля только в области, где x > 0 и y > 0. Следовательно, сумма электростатическая потенциальная энергия реальной системы составляет всего 1/4 от полной электростатическая потенциальная энергия системы заряда изображения.Таким образом,



3.3. Разделение переменных

3.3.1. Разделение переменных: Декартовы координаты Мощный метод, очень часто используемый для решения частных дифференциальных уравнения разделение переменных . В этом разделе мы будем продемонстрировать силу этой техники, обсудив несколько Примеры.

Пример: Пример 3.3 (Гриффитс)
Два бесконечных, заземлены, металлические пластины лежат параллельно плоскости xz , одна на y = 0, другой на y = π (см. рисунок 3.10). Левый конец, на x = 0, закрыто бесконечной полосой, изолированной от двух пластин и поддерживается при заданном потенциале . Найдите потенциал внутри этой «щели».


Рисунок 3.10. Пример 3.3 (Гриффитс).

Электростатический потенциал в щели должен удовлетворять трехмерному Уравнение Лапласа. Однако, поскольку V не имеет зависимости z , трехмерное уравнение Лапласа сводится к двумерному Лапласу уравнение:


Граничные условия для решения уравнения Лапласа являются:

1. В ( x , y = 0) = 0 (заземлен снизу тарелка).

2. В ( x , y = π) = 0 (заземлен сверху тарелка).

3. В ( х = 0, у ) = V 0 ( y ) (табличка x = 0).

4. В → 0, когда x → ∞.

Эти четыре граничных условия указать значение потенциала на всех границ окружающих слота и, следовательно, достаточны для однозначного определения решения Уравнение Лапласа внутри щели.Поэтому, если мы найдем одно решение Уравнение Лапласа, удовлетворяющее этим граничным условиям, чем оно должно быть правильный. Рассмотрим решения следующего вида:


Если это решение двумерного уравнения Лапласа, то мы должны требуют, чтобы


Это уравнение можно переписать как


Первый член левой части этого уравнения зависит только от x , а второй член зависит только от y .Следовательно, если это уравнение должно выполняться для всех x и y в слоте, который мы должны потребовать что


и


Дифференциальное уравнение для X можно переписать как


Если C 1 является отрицательным числом, то это уравнение может быть переписан как


где к 2 = — С 1 .Самый общий решение этого уравнения


Однако эта функция является колебательной и не удовлетворяет граничное условие № 4, требующее, чтобы V приближалось к нулю, когда x приближается к бесконечности. Таким образом, мы заключаем, что C 1 не может быть отрицательным числом. Если C 1 положительный число, то дифференциальное уравнение для X можно записать как


Наиболее общее решение этого уравнения:


Это решение будет приближаться к нулю, когда x приближается к бесконечности, если А = 0.Таким образом,


Решение для Y можно получить, решив следующие дифференциальное уравнение:


Наиболее общее решение этого уравнения:


Таким образом, общее решение для электростатического потенциала V ( x , y ) равно


где мы поглотили константу B в константы C и Д .Константы C и D должны быть выбраны так, чтобы остальные три граничных условия (1, 2 и 3) выполнены. Первое граничное условие требует, чтобы V ( x , y = 0) = 0:


, который требует, чтобы C = 0. Второе граничное условие требует что V ( x , y = π) = 0:


что требует, чтобы .Это условие ограничивает возможные значения k положительными значениями. целые числа:

Примечание: отрицательные значения k не допускаются, поскольку exp(- kx ) стремится к нулю на бесконечности, только если k > 0. Чтобы удовлетворить границе условие #3 мы должны потребовать, чтобы


Это последнее выражение предполагает, что единственный момент времени, в который мы можем найти решение уравнения Лапласа, удовлетворяющее всем четырем граничным условиям, имеет форма это когда бывает, имеет вид .Однако, поскольку k может принимать бесконечное число значений, будет бесконечное число решений уравнения Лапласа, удовлетворяющих границе условия № 1, № 2 и № 4. Наиболее общий вид решения уравнения Лапласа уравнение будет линейной суперпозицией всех возможных решений. Таким образом,

Граничное условие № 3 теперь можно записать как


Умножение обеих сторон на sin( ny ) и интегрирование каждой части между y = 0 и y = π получаем


Интеграл в левой части этого уравнения равен нулю при все значения k кроме k = n .Таким образом,


Таким образом можно рассчитать коэффициенты D k легко:


Коэффициенты D k называются Фурье коэффициенты . Таким образом, решение уравнения Лапласа в щели равно
.

где


Теперь рассмотрим частный случай, когда .В этом случае коэффициенты D k равны

Таким образом, решение уравнения Лапласа равно



Пример: Задача 3.12
Найти потенциал в бесконечности слот примера 3.3 (Гриффитс), если граница x = 0 состоит из двух металлические полоски: одна, от y = 0 до y = π/2, удерживается на постоянный потенциал , а другой, от y = π/2 до y = π, находится в потенциале .

граничное условие при x = 0 равно


Коэффициенты Фурье функции равны

Значения первых четырех коэффициентов C :


Легко видеть, что C k + 4 = C k и поэтому мы заключаем, что


Таким образом, коэффициенты Фурье C k равны


Таким образом, электростатический потенциал равен




Пример: Задача 3.13
Для бесконечного слота (Пример 3.3 Гриффитс) определяют плотность заряда на полосе x = 0, предполагая, что это проводник с постоянным потенциалом .

электростатический потенциал в щели равен


Плотность заряда на пластине при x = 0 можно получить с помощью граничное условие для электрического поля на границе:


где направлена ​​вдоль положительной оси x .С это граничное условие можно переписать как

Дифференцирование V ( x , y ) относительно x мы получить


На границе x = 0 получаем


Таким образом, плотность заряда σ на полосе x = 0 равна равно




Пример: Двойные бесконечные слоты
Слот из примера 3.3 дюйма Гриффитс и его зеркальное отображение на негативе x разделены изоляционная полоса при x = 0. Если плотность заряда σ ( y ) на разделительной полоске дан, определяют потенциал в прорези.

граничное условие при x = 0 требует, чтобы


где направлена ​​вдоль положительной оси x . Здесь мы использовали симметрию конфигурация, которая требует, чтобы электрическое поле в районе х х > 0.С это граничное условие можно переписать как

Сначала мы определим потенциал в области x > 0. Следуя той же процедуре, что и в примере 3, получаем для электростатического потенциал


, где константы D k должны быть выбраны так, чтобы граничное условие при x = 0 выполнено. Для этого необходимо, чтобы


Так


Константы D k можно определить путем умножения обоих части этого уравнения с и интегрирование обеих сторон относительно y между y = 0 и у = π.Результат

Таким образом, константы C k равны


Таким образом, электростатический потенциал равен



3.3.2. Разделение переменных: сферические координаты Рассмотрим сферическую симметричную систему. Если мы хотим решить задачу Лапласа уравнения естественно использовать сферические координаты. Предполагая, что система имеет азимутальную симметрию ( ) Уравнение Лапласа имеет вид
.

Умножая обе части на r 2 получаем


Рассмотрим возможность того, что общим решением этого уравнения является произведение функции , которое зависит только от расстояния r , и функции , который зависит только от угла θ :

Подставляя это «решение» в уравнение Лапласа, получаем


Разделив каждый член этого уравнения на получаем

Первый член в этом выражении зависит только от расстояния r а второй член зависит только от угла θ .Это уравнение может быть истинным только для всех r и θ , если


и


Рассмотрим решение для R следующего вида:


, где A и k — произвольные константы. Замена этого выражение в дифференциальном уравнении для R ( r ) мы получить


Следовательно, константа k должна удовлетворять следующему отношение:


Это уравнение дает нам следующее выражение для k


Общее решение для таким образом, дается

, где A и B — произвольные константы.
Угол зависимая часть решения уравнения Лапласа должна удовлетворять следующему уравнение




Пример: Задача 3.18
Потенциал на поверхности сфера дается


где k — некоторая константа. Найдите потенциал внутри и снаружи сфере, а также плотность поверхностного заряда на сфере.(Предположим, что заряда нет ни внутри, ни снаружи сфере.)

Наиболее общее решение уравнения Лапласа в сферической координаты


Сначала рассмотрим область внутри сферы ( r R ). В этот регион так как иначе взорвался бы при r = 0. Таким образом,

Потенциал при r = R поэтому равен


Используя тригонометрические соотношения, мы можем переписать как

Подставляя это выражение в уравнение для получаем

Это уравнение сразу показывает, что пока не .Если затем

Таким образом, электростатический потенциал внутри сферы равен до


Теперь рассмотрим область за пределами сферы ( r > R ). В этот регион так как иначе взорвется на бесконечности. Решение уравнения Лапласа в этой области есть поэтому равно

Потенциал при r = R поэтому равен


Уравнение сразу показывает, что за исключением случаев, когда .Если затем

Таким образом, электростатический потенциал вне сферы равен


Плотность заряда на сфере можно получить с помощью границы условия для электрического поля на границе:


С это граничное условие можно переписать как

Первый член в левой части этого уравнения можно вычислить используя только что полученный электростатический потенциал:


Таким же образом получаем


Следовательно,


Таким образом, плотность заряда на сфере равна




Пример: Задача 3.19
Предположим, потенциал на поверхности шара указано, а внутри нет заряда или вне сферы. Покажите, что плотность заряда на сфере задана по

где



Большая часть решения этой задачи очень похожа на решение задачи 3.18. Сначала рассмотрим электростатический потенциал внутри сферы. Электростатический потенциал в этой области равен

.

и граничное условие


Коэффициенты можно определить, умножив обе части этого уравнения на и интегрирование по θ между θ = 0 и θ = π:

Так


В области вне сферы задан электростатический потенциал по


и граничное условие


Коэффициенты даны

Плотность заряда на поверхности сферы равно

Дифференциация по отношению к r в области r > R мы получить

Дифференциация по отношению к р в районе р р мы получить

Таким образом, плотность заряда равна


Подставляя выражения для и в это уравнение получаем

где



Пример: Задача 3.23
Решите уравнение Лапласа с помощью разделение переменных в цилиндрических координатах в предположении отсутствия зависимость от z (цилиндрическая симметрия). Убедитесь, что вы нашли все решений радиального уравнения. Соответствует ли ваш результат случае бесконечного линейного заряда?

Для системы с цилиндрической симметрией электростатический потенциал не зависит от z . Это сразу подразумевает, что . При таком предположении уравнение Лапласа имеет вид

.

Рассмотрим как возможное решение V :


Подставив это решение в уравнение Лапласа, получим


Умножив каждый член этого уравнения на r 2 и разделив от получаем

Первый член в этом уравнении зависит только от r , а второй член в этом уравнении зависит только от φ .Это уравнение может следовательно, действителен только для каждого r и каждого φ , если каждый член равно константе. Таким образом, мы требуем, чтобы


и


Сначала рассмотрим случай, когда . Дифференциальное уравнение для можно переписать как

Наиболее общее решение этого дифференциального решения


Однако в цилиндрических координатах мы требуем, чтобы любое решение для данное φ равно решению для φ + 2 π .Очевидно, что для данного решения это условие не выполняется, и мы заключаем тот . Дифференциальное уравнение для можно переписать как

Наиболее общее решение этого дифференциального решения


Условие, что требует, чтобы m было целым числом. Теперь рассмотрим радиальную функцию . Сначала рассмотрим случай, когда . Рассмотрим следующее решение для :

Подставив это решение в предыдущее дифференциальное уравнение, мы получить


Таким образом, константа k может принимать следующие два значения: значения:


Самое общее решение для при условии, что поэтому

Теперь рассмотрим решения для когда .В этом случае мы требуем, чтобы

или


Это уравнение можно переписать как


Если то решение этого дифференциального уравнения равно

Если то решение этого дифференциального уравнения равно

Объединяя решения, полученные для с решениями, полученными для делаем вывод, что наиболее общее решение для дается

Таким образом, наиболее общее решение уравнения Лапласа для системы с цилиндрической симметрией



Пример: Задача 3.25
Плотность заряда А


наклеивается на поверхность бесконечного цилиндра радиуса R . Находить потенциал внутри и снаружи цилиндра.

Электростатический потенциал можно получить, используя общее решение уравнения Лапласа для система с цилиндрической симметрией, полученная в задаче 3.24. В районе внутри цилиндр коэффициент должен быть равен нулю, иначе взорвется в .По той же причине . Таким образом,


В области вне цилиндра коэффициенты должен быть равен нулю, иначе взорвется на бесконечности. По той же причине . Таким образом,

С должен стремиться к 0, когда r приближается к бесконечности, мы также должны потребовать, чтобы равна 0. Плотность заряда на поверхности цилиндра равна до

Дифференциация в области r > R и установив r = R мы получить

Дифференциация в области r R и установив r = R мы получить

Следовательно, плотность заряда на поверхности цилиндра равна до



Для этого необходимо, чтобы


Второе отношение между и можно получить, используя условие, что электростатический потенциал равен непрерывно на любой границе.Для этого требуется, чтобы

Так


и


Теперь у нас есть два уравнения с двумя неизвестными, и , которое можно решить со следующим результатом:

и


Таким образом, электростатический потенциал внутри цилиндра равен


Таким образом, электростатический потенциал снаружи цилиндра равен



Пример: Задача 3.37
Проводящая сфера радиусом a , при потенциале , окружен тонкой концентрической сферической оболочкой радиусом 90 211 b 90 212 , над который кто-то приклеил поверхностным зарядом

где является константой.
а) Найдите электростатический потенциал в каждом область:
i) r > b
ii) a r b
b) Найти индуцированный поверхностный заряд на проводнике.
в) Каков общий заряд системы? Убедитесь, что ваш ответ согласуется с поведением V на свободе р .

а) Система имеет сферическую симметрию, поэтому мы можем использовать наиболее общее решение уравнения Лапласа в сферическом координаты:


В области внутри сферы так как иначе взорвался бы при r = 0. Следовательно,

Граничное условие для в том, что он равен в r = a :

Это сразу показывает, что для всех Кроме :

Таким образом, электростатический потенциал внутри сферы определяется как


что не должно вызывать удивления.
В области вне оболочки так как иначе взорвется на бесконечности. Таким образом,

В области между сферой и оболочкой наиболее общее решение за дается

Граничное условие для при r = a равно

Это уравнение может быть выполнено, только если


Требование непрерывности электростатического потенциала при r = b требует, чтобы


или


Это условие можно переписать как

.

Другое граничное условие для электростатического потенциала при r = b заключается в том, что он должен давать распределение заряда, указанное в задаче.Для этого необходимо, чтобы


Это условие выполняется, если


Подставив соотношение между различными коэффициентами, полученными применяя условие непрерывности, получаем


Эти уравнения показывают, что


Используя эти значения для мы можем показать, что

Граничное условие для V at r = a показывает что

Эти значения для немедленно исправить значения для :

Таким образом, потенциал в области вне оболочки равен до


Потенциал в области между сферой и оболочкой равен до


б) Плотность заряда на поверхности шара можно найти по формуле расчет наклона электростатического потенциала на этой поверхности:


в) Суммарный заряд шара равен


Суммарный заряд снаряда равен нулю.Поэтому общий заряд системы равно


Таким образом, электростатический потенциал на больших расстояниях будет примерно равно


Это равно пределу точного электростатического потенциала, когда .

3.4. Многополюсные расширения

Рассмотрим заданное распределение заряда ρ . Потенциал на точка P (см. рис. 3.11) равно


, где d — расстояние между P и бесконечно малым отрезком. распределения заряда. На рис. 3.11 показано, что d можно записать как функция r , r’ и θ :



Рисунок 3.11. Распределение заряда ρ .

Это уравнение можно переписать как


На больших расстояниях от распределения заряда и следовательно .Используя следующее расширение для :

мы можем переписать 1/ d как


Используя это расширение 1/ d , мы можем переписать электростатическую потенциал на P как


Это выражение справедливо для всех r (не только ). Однако, если тогда в потенциале P будет доминировать первый ненулевой член в это расширение.Это расширение известно как многополюсное расширение . В предел необходимо учитывать только первые члены разложения:

Первый член в этом выражении, пропорциональный 1/ r , называется монопольный термин . Второй член в этом выражении, пропорциональный 1/ r 2 , называется дипольным термином . Третий срок в это выражение, пропорциональное 1/ r 3 , называется квадрупольный терм .

3.4.1. Монопольный термин.

Если общий заряд системы отличен от нуля, то электростатический потенциал на больших расстояниях определяется монопольным членом:


где Q — общий заряд распределения заряда.
электрическое поле, связанное с монопольным членом, можно получить, вычислив градиент :

3.4.2. Дипольный член.

Если общий заряд распределения заряда равен нулю ( Q = 0), то монопольный член в мультипольном разложении будет равен нулю. В этом случае дипольный член будет доминировать над электростатическим потенциалом при больших значениях. расстояния


Поскольку θ — это угол между и мы можем переписать как

Таким образом, электростатический потенциал P можно переписать как


В этом выражении представляет собой дипольный момент распределения заряда, который определяется как

Электрическое поле, связанное с дипольным членом, может быть получено по формуле расчет градиента :


Пример
Рассмотрим систему двух точечных зарядов, показанную на рис. Рисунок 3.12. Суммарный заряд этой системы равен нулю, поэтому монопольный член равен нулю. Дипольный момент этой системы равен до


где вектор, указывающий от — q до + q .

Дипольный момент распределение заряда зависит от начала выбранной системы координат. Рассмотрим систему координат S и распределение заряда ρ . Дипольный момент этого распределения заряда равен


Вторая система координат S’ смещена на по отношению к S :

Дипольный момент распределения заряда в S’ равен до


Это уравнение показывает, что если общий заряд системы равен нулю ( Q = 0) то дипольный момент распределения заряда не зависит выбора начала системы координат.


Рисунок 3.12. Электрический дипольный момент.

Пример: Задача 3.40
Тонкий изолирующий стержень, идущий от z = — a до z = + a , содержит следующую строку сборы:
а)
б)
в)
В в каждом случае найти главный член в мультипольном разложении потенциал.

а) Суммарный заряд стержня равен


С , монопольный член будет доминировать над электростатическим потенциалом на больших расстояниях.Таким образом,

б) Полный заряд стержня равен нулю. Следовательно в электростатическом потенциале на больших расстояниях будет преобладать дипольный член (если не ноль). Дипольный момент стержня равен


Поскольку дипольный момент стержня не равен нулю, дипольный член будет преобладать электростатический потенциал на больших расстояниях. Поэтому


c) При таком распределении заряда общий заряд равен нулю, а дипольный момент равен нулю.Электростатический потенциал этого заряда в распределении преобладает квадрупольный член.


Электростатический потенциал на большом расстоянии от стержня будет равен до



Пример: Задача 3.27
Четыре частицы (одна из которых имеет заряд q , один заряд 3 q и два заряда -2 q ) размещаются как показаны на рис. 3.12, каждая на расстоянии d от начала координат.Найдите простой приблизительная формула для электростатического потенциала, действующая в точке P далеко от истока.

Суммарный заряд системы равен нулю и поэтому монопольный член в мультипольном разложении равен нулю. То дипольный момент этого распределения заряда равен


Декартовы координаты P равны

Скалярное произведение между и поэтому

Электростатический потенциал на P поэтому равен



Рисунок 3.13. Задача 3.27.


Пример: Задача 3.38
Заряд Q распределен равномерно по оси z от z = — a до z = а . Показать, что электрический потенциал в точке дается

для r > a .

Плотность заряда на этом отрезке оси z равно


Следовательно, n -й момент распределения заряда равен до


Это уравнение сразу показывает, что




Таким образом, электростатический потенциал P равен


Граничные условия электрического поля

Компоненты электрического поля:  Можно считать, что электрическое поле на любой поверхности или среде формируется из двух векторных компонентов; Тангенциальное и нормальное поле.Любое электрическое поле на поверхности можно разложить на две составляющие: тангенциальное поле и нормальное поле.

Тангенциальное поле : Тангенциальное поле или Тангенциальное электрическое поле – это векторная составляющая электрического поля, параллельная поверхности. Если E – электрическое поле вдоль поверхности,  Касательное поле обозначается следующим образом: E t .

Нормальное поле : Нормальное поле или Нормальное электрическое поле — это векторная составляющая электрического поля, которая является нормальной или перпендикулярной к поверхности.Обозначается символом: E n , если E — напряженность электрического поля на поверхности.

Граничные условия:

Когда электрическое поле распространяется более чем на одну диэлектрическую среду, граница между двумя средами оказывает некоторое влияние на электрическое поле и его компоненты. Условия, существующие на границе сред, когда одно и то же электрическое поле распространяется на эти среды, представляют интерес для изучения граничных условий электрического поля, а условия, существующие на границе, называются граничными условиями.

На границе между проводящей средой и диэлектрической средой существуют два условия:

1. Тангенциальная составляющая электрического поля равна нулю. или

2. Электрическое смещение или плотность электрического потока «D» на границе диэлектрической среды равна плотности заряда «

» на поверхности проводящей среды в этой точке. Или,

Приведенные выше граничные условия являются частным случаем, когда одна из сред является Проводником.На границе двух различных диэлектрических сред существуют следующие условия:

1. Тангенциальные составляющие электрических напряженностей равны или,

2. Нормальные составляющие электрической индукции равны или,

Закон электрического потока преломление на границе:

электрическое поле граничные условия

Здесь, Из рисунка выше , Мы видим, что:

и

А,

,

Итак,

и

Теперь, Так как;

и

Таким образом,

Или отношение тангенсов углов, образованных электрическими полями с нормалью, равно отношению их соответствующих диэлектрических проницаемостей. Это также известно как закон преломления электрического потока на границе.

Транспорт ионов натрия через эндотелиальный слой гликокаликса в условиях электрического поля: исследование молекулярной динамики: The Journal of Chemical Physics: Vol 153, No 10

A. Влияние электрического поля на транспорт Na +

Для измерения ионов натрия транспорт через EGL, разница в молярности ионов Na + между двумя тонкими слоями ниже и выше областей, богатых сахарной цепью гликокаликса, определяется следующим образом:
Δc=cb-ca=nbVb,вода-nbVa,вода. (1)
В ур. (1), c представляет собой молярность Na + , n представляет собой количество ионов Na + , а V представляет собой объем воды. Нижние индексы b и a представляют собой тонкие слои ниже и выше области, богатой SC, соответственно, а высота обоих тонких слоев составляет 4 нм. Наши предыдущие исследования 15,17 15. X. Z. Jiang, K. H. Luo, and Y. Venticos, Front. Физиол. 9 , 1667 (2018). https://doi.org/10.3389/ффиз.2018.0166717. X.Z.Jiang, Y.Ventikos, and K.H.Luo, Am. J. Physiol.: Heart Circ. Физиол. 317 , h204 (2019). https://doi.org/10.1152/ajpheart.00794.2018 продемонстрировали, что c b больше, чем c a , поэтому Δ c больше 0. На рисунке 2 показано сравнение средней молярности различия во времени между случаями, перечисленными в таблице I. На рис. 2(а) при увеличении напряженности электрического поля в направлении + z были выявлены две противоположные тенденции изменения Δ c : когда сильное электрическое поле 200 В/м, молярная разница Δ c ослабляется по мере того, как большее количество ионов Na + переносится из нижней области в верхнюю область под действием электростатической силы электрического поля; однако при наложении слабого (10 В/м) или умеренного (100 В/м) электрического поля наблюдается увеличение Δ c .При приложении электрического поля отрицательно заряженные СК движутся в противоположном направлении по отношению к ионам Na + . Изменение взаимного положения напрямую приводит к изменению межмолекулярного взаимодействия между СК и ионами. Когда на систему накладывается слабое электрическое поле, межмолекулярные взаимодействия отрицательно заряженных СК на ионах Na + преодолевают электрическое поле и изменяют движение ионов Na + снаружи внутрь, что приводит к увеличение Δ c .Таким образом, отрицательные заряды EGL приводят к существованию оптимальной напряженности электрического поля для использования электрического поля для управления транспортом Na + по EGL. Оптимальную силу можно интерпретировать, рассматривая воду и гликокаликс как континуум. Для ионов Na + электростатическая сила от электрического поля ( F E = qE , а q – суммарные заряды ионов Na + ) является движущей силой, а электростатические силы от СК ( F SC ) и ионов Cl — ( F Cl ) являются силами сопротивления.Когда только приложено электрическое поле, F SC и F Cl больше, чем F E из-за компактного пространственного распределения ионов. Под действием движущих сил электрического поля ионы Na + постепенно удаляются от отрицательно заряженных частиц, а F SC и F Cl соответственно уменьшаются. Время, когда F E преобладает над движением ионов Na + , зависит от напряженности приложенного электрического поля.Таким образом, для обеспечения транспорта ионов Na + с требуемой скоростью необходимо тщательно регулировать напряженность электрического поля, при этом соответствующее электрическое поле должно быть оптимальной напряженности. электрическое поле управляет транспортом Na + из-за пределов области, богатой SC, внутрь при всех напряженностях приложенного электрического поля. Примечательно, что в этих случаях еще сохраняются эффекты изменяющихся межмолекулярных взаимодействий от отрицательно заряженных СК на ионы Na + .Существование продемонстрировано сравнением возрастаний Δ c в случаях -100 (т.е. случай III в табл. I) и -100 м (случай IV в табл. I): в случае IV, когда отрицательные заряды СК гликокаликса выключены , увеличение Δ c по сравнению со случаем E = 0 указывает на то, что Na + транспортируется в том же направлении, что и электрическое поле, как и ожидалось; когда участвуют отрицательные заряды SC, наблюдается меньшее увеличение Δ c в случае III, что означает, что изменения межмолекулярного взаимодействия из-за SC поставили под угрозу транспорт Na + .Из-за конечной длины и растягивающихся структур СК восходящее движение СК будет уравновешиваться в относительно фиксированном положении, а это означает, что влияние СК на изменение транспорта ионов Na + посредством межмолекулярных взаимодействий ограничено. Ограниченных эффектов от SC недостаточно, чтобы изменить движение Na + , вызванное электрическим полем, что объясняет повышенное Δ c во всех случаях электрического поля на рис.

Author: alexxlab

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *