Представление чисел в компьютере. Целые числа
Будьте внимательны! У Вас есть 10 минут на прохождение теста. Система оценивания — 5 балльная. Разбалловка теста — 3,4,5 баллов, в зависимости от сложности вопроса. Порядок заданий и вариантов ответов в тесте случайный. С допущенными ошибками и верными ответами можно будет ознакомиться после прохождения теста. Удачи!Список вопросов теста
Вопрос 1
Какие числа называются целыми?
Варианты ответов
- Все числа из диапазона от (2-n; 2n)
- Это числа, которыми пользуются для счёта предметов
- Это натуральные числа, числа противоположные натуральным, и ноль
Вопрос 2
Перечислите свойства множества целых чисел, представимых в компьютереВарианты ответов
- Неограниченно
- Конечно
- Ограничено
- Бесконечно
- Дискретно
Вопрос 3
Что относится к основным правилам представления чисел в компьютере?
Варианты ответов
- Представление данных в компьютере имеет дискретную структуру
- Данные и программы в памяти компьютера хранятся в двоичном виде
- Представление информации посредством только двух состояний надёжно и помехоустойчиво
- Память компьютера не безгранична, и множество представимых в памяти компьютера величин ограничено и конечно
Вопрос 4
Какое число называют дополнительным кодом двоичного числа х в N-разрядной ячейке?
Варианты ответов
-
это новое число, дополняющее двоичное число до целого значения
-
это число, дополняющее двоичное число до значения 2N-1
-
это число, дополняющее двоичное число до значения 2N
Вопрос 5
Как выглядит внутреннее представление целого числа 248 в 2-байтовой ячейке?Варианты ответов
- 0000000010111000
- 0000000011111001
- 1000000011111000
- 0000000011111000
Вопрос 6
Чему равно самое большое целое положительное число, если под целое число выделяется ячейка памяти размером в 16 бит?
Варианты ответов
-
11111111111111112 = 215 — 1 = 3276710
-
011111111111111112 = 215 — 1 = 3276710
-
1111111111111112 = 215 = 3276810
-
1111111111111112 = 215 — 1 = 3276710
Вопрос 7
Как выглядит число 1001010 в восьмиразрядном представлении?
Варианты ответов
- 001010
- 100001010
- 01001010
- 2001010
Вопрос 8
Как выглядит внутреннее представление числа -326 в 2-байтовой ячейке?Варианты ответов
- 1000000010111011
- 0000000010111010
- 1000000010111010
Вопрос 9
Варианты ответов
Вопрос 10
Укажите диапазон значений целых чисел без знака.
Варианты ответов
-
[0; 2N]
-
[0; 2N-1]
-
[-2N-1; 2N-1]
1.
|
Целые числа
Сложность: лёгкое |
1 |
| 2. |
Восьмиразрядное представление числа
Сложность: лёгкое |
1 |
3.
|
Хранение числа в памяти компьютера
Сложность: среднее |
2 |
| 4. |
Представление числа
Сложность: среднее |
2 |
5.
|
Число в однобайтовом формате
Сложность: среднее |
2 |
| 6. |
Компьютерное представление беззнакового целого числа
Сложность: среднее |
2 |
7.
|
Экспоненциальная запись
Сложность: сложное |
3 |
| 8. |
Компьютерный способ экспоненциальной записи
Сложность: сложное |
3 |
9.
|
Определение десятичного числа
Сложность: сложное |
3 |
Урок 11. Компьютерное представление целых и вещественных чисел
Урок 11. Компьютерное представление целых и вещественных чисел
Целые числа в компьютереПравило № 4: в памяти компьютера числа хранятся в двоичной системе счисления*. С двоичной системой счисления вы знакомы из курса информатики 7-9 классов. Например, если под целое число выделяется ячейка памяти размером в 16 битов, то самое большое целое положительное число будет таким:
В десятичной системе счисления оно равно:
215 — 1 = 32 767.
* Конечно, и «внутри калькулятора» числа представляются в двоичном виде. Однако мы в это вдаваться не будем, рассмотрев лишь внешнее представление. Пример с калькулятором нам нужен был только для иллюстрации проблемы ограниченности.
Здесь первый бит играет роль знака числа. Ноль — признак положительного числа. Самое большое по модулю отрицательное число равно -32 768. Напомним (это было в курсе информатики основной школы), как получить его внутреннее представление:
1) перевести число 32 768 в двоичную систему счисления; это легко, поскольку 32 768 = 215:
1000000000000000;
2) инвертировать этот двоичный код, т. е. заменить нули на единицы, а единицы — на нули:
0111111111111111;
3) прибавить единицу к этому двоичному числу (складывать надо по правилам двоичной арифметики), в результате получим:
Единица в первом бите обозначает знак «минус». Не нужно думать, что полученный код — это «минус ноль». Этот код представляет число -32 768. Таковы правила машинного представления целых чисел. Данное представление называется дополнительным кодом.
Не нужно думать, что полученный код — это «минус ноль». Этот код представляет число -32 768. Таковы правила машинного представления целых чисел. Данное представление называется дополнительным кодом.
Если под целое число в памяти компьютера отводится N битов, то диапазон значений целых чисел:
[-2N-1, 2N~1 — 1],
т. е. ограниченность целого числа в компьютере возникает из-за ограничений на размер ячейки памяти. Отсюда же следует и конечность множества целых чисел.
Мы рассмотрели формат представления целых чисел со знаком, т. е. положительных и отрицательных. Бывает, что нужно работать только с положительными целыми числами. В таком случае используется формат представления целых чисел без знака. В этом формате самое маленькое число — ноль (все биты — нули), а самое большое число для 16-разрядной ячейки:
В десятичной системе это 216 — 1 = 65 535, примерно в два раза больше по модулю, чем в представлении со знаком.
Из всего сказанного делаем вывод: целые числа в памяти компьютера — это дискретное, ограниченное и конечное множество.
Границы множества целых чисел зависят от размера выделяемой ячейки памяти под целое число, а также от формата: со знаком или без знака. Шаг в компьютерном представлении последовательности целых чисел, как и в математическом, остается равным единице.
Рисунок 1.7 отражает то обстоятельство, что при переходе от математического представления множества целых чисел к представлению, используемому в информатике (компьютере), происходит переход к ограниченности и конечности.
Вещественные числа в компьютере
Понятие вещественного (действительного) числа в математику ввел Исаак Ньютон в XVIII веке. В математике множество вещественных чисел непрерывно, бесконечно и не ограничено. Оно включает в себя множество целых чисел и еще бесконечное множество нецелых чисел. Между двумя любыми точками на числовой оси лежит бесконечное множество вещественных чисел, что и означает непрерывность множества.
Как мы говорили выше, числа в компьютере (в том числе и вещественные) представлены в двоичной системе счисления. Покажем, что множество вещественных чисел в компьютере дискретно, ограничено и конечно. Нетрудно догадаться, что это, так же как и в случае целых чисел, вытекает из ограничения размера ячейки памяти.
Снова для примера возьмем калькулятор с десятиразрядным индикаторным табло. Экспериментально докажем дискретность представления вещественных чисел. Выполним на калькуляторе деление 1 на 3. Из математики вам известно, что 1/3 — это рациональная дробь, представление которой в виде десятичной дроби содержит бесконечное количество цифр: 0,3333333333… (3 в периоде). На табло калькулятора вы увидите:
Первый разряд зарезервирован под знак числа. После запятой сохраняется 8 цифр, а остальные не вмещаются в разрядную сетку (так это обычно называют). Значит, это не точное значение, равное 1/3, а его «урезанное» значение.
Следующее по величине число, которое помещается в разрядную сетку:
Оно больше предыдущего на 0,00000001. Это шаг числовой последовательности. Следовательно, два рассмотренных числа разделены между собой конечным отрезком. Очевидно, что предыдущее число такое:
Это шаг числовой последовательности. Следовательно, два рассмотренных числа разделены между собой конечным отрезком. Очевидно, что предыдущее число такое:
Оно тоже отделено от своего «соседа справа» по числовой оси шагом 0,00000001. Отсюда делаем вывод: множество вещественных чисел, представимых в калькуляторе, дискретно, поскольку числа отделены друг от друга конечными отрезками.
А теперь выясним вот что: будет ли шаг в последовательности вещественных чисел на калькуляторе постоянной величиной (как у целых чисел)?
Вычислим выражение 100000/3. Получим:
Это число в 100 000 раз больше предыдущего и, очевидно, тоже приближенное. Легко понять, что следующее вещественное число, которое можно получить на табло калькулятора, будет больше данного на 0,0001. Шаг стал гораздо больше.
Отсюда приходим к выводу: множество вещественных чисел, представимых в калькуляторе, дискретно с переменной величиной шага между соседними числами.
Если отметить на числовой оси точные значения вещественных чисел, которые представимы в калькуляторе, то эти точки будут расположены вдоль оси неравномерно. Ближе к нулю — гуще, дальше от нуля — реже (рис. 1.8).
Ближе к нулю — гуще, дальше от нуля — реже (рис. 1.8).
Все выводы, которые мы делаем на примере калькулятора, полностью переносятся на компьютер с переходом к двоичной системе счисления и с учетом размера ячейки компьютера, отводимой под вещественные числа. Неравномерное расположение вещественных чисел, представимых в компьютере, также имеет место.
Ответим на вопрос: ограничено ли множество вещественных чисел в памяти компьютера? Если продолжать эксперименты с калькулятором, то ответ на этот вопрос будет таким: да, множество вещественных чисел в калькуляторе ограничено.
Причиной тому служит все та же ограниченность разрядной сетки. Отсюда же следует и конечность множества.
Самое большое число у разных калькуляторов может оказаться разным. У самого простого это будет то же число, что мы получали раньше: 999999999. Если прибавить к нему единицу, то калькулятор выдаст сообщение об ошибке. А на другом, более «умном» и дорогом, калькуляторе прибавление единицы приведет к такому результату:
Данную запись на табло надо понимать так: 1 • 109.
Такой формат записи числа называется форматом с плавающей запятой, в отличие от всех предыдущих примеров, где рассматривалось представление чисел в формате с фиксированной запятой.
Число, стоящее перед буквой «е», называется мантиссой, а стоящее после — порядком. «Умный калькулятор» перешел к представлению чисел в формате с плавающей запятой после того, как под формат с фиксированной запятой не стало хватать места на табло.
В компьютере то же самое: числа могут представляться как в формате с фиксированной запятой (обычно это целые числа), так и в формате с плавающей запятой.
Но и для форматы с плавающей запятой тоже есть максимальное число. В нашем «подопытном» калькуляторе это число:
То есть 99999 • 1099. Самое большое по модулю отрицательное значение -99999 • 1099. Данные числа являются целыми, но именно они ограничивают представление любых чисел (целых и вещественных) в калькуляторе.
В компьютере все организовано аналогично, но предельные значения еще больше. Это зависит от разрядности ячейки памяти, выделяемой под число, и от того, сколько разрядов выделяется под порядок и под мантиссу.
Это зависит от разрядности ячейки памяти, выделяемой под число, и от того, сколько разрядов выделяется под порядок и под мантиссу.
Рассмотрим пример: пусть под все число в компьютере выделяется 8 байтов — 64 бита, из них под порядок — 2 байта, под мантиссу — 6 байтов. Тогда диапазон вещественных чисел, в переводе в десятичную систему счисления, оказывается следующим:
±(5 • 10-324 — 1,7 • 10308).
Завершая тему, посмотрим на рис. 1.9. Смысл, заложенный в нем, такой: непрерывное, бесконечное и не ограниченное множество вещественных чисел, которое рассматривает математика, при его представлении в компьютере обращается в дискретное, конечное и ограниченное множество.
Вопросы и задания
1. Почему множество целых чисел, представимых в памяти компьютера, дискретно, конечно и ограничено?
2. Определите диапазон целых чисел, хранящихся в 1 байте памяти в двух вариантах: со знаком и без знака.
3. Получите внутреннее представление числа 157 в 8-разрядной ячейке памяти в формате со знаком.
4. Получите внутреннее представление числа -157 в 8-разрядной ячейке памяти в формате со знаком.
5. Почему множество действительных (вещественных) чисел, представимых в памяти компьютера, дискретно, конечно и ограничено?
6. На какие две части делится число в формате с плавающей запятой?
Ключевые слова:
• разряд
• беззнаковое представление целых чисел
• представление целых чисел со знаком
• представление вещественных чисел
Оперативная память компьютера состоит из ячеек, каждая из которых представляет собой физическую систему, состоящую из некоторого числа однородных элементов. Эти элементы обладают двумя устойчивыми состояниями, одно из которых соответствует нулю, а другое — единице. Каждый такой элемент служит для хранения одного из битов — разряда двоичного числа. Именно поэтому каждый элемент ячейки называют битом или разрядом (рис. 1.2).
Эти элементы обладают двумя устойчивыми состояниями, одно из которых соответствует нулю, а другое — единице. Каждый такой элемент служит для хранения одного из битов — разряда двоичного числа. Именно поэтому каждый элемент ячейки называют битом или разрядом (рис. 1.2).
Рис. 1.2. Ячейка памяти
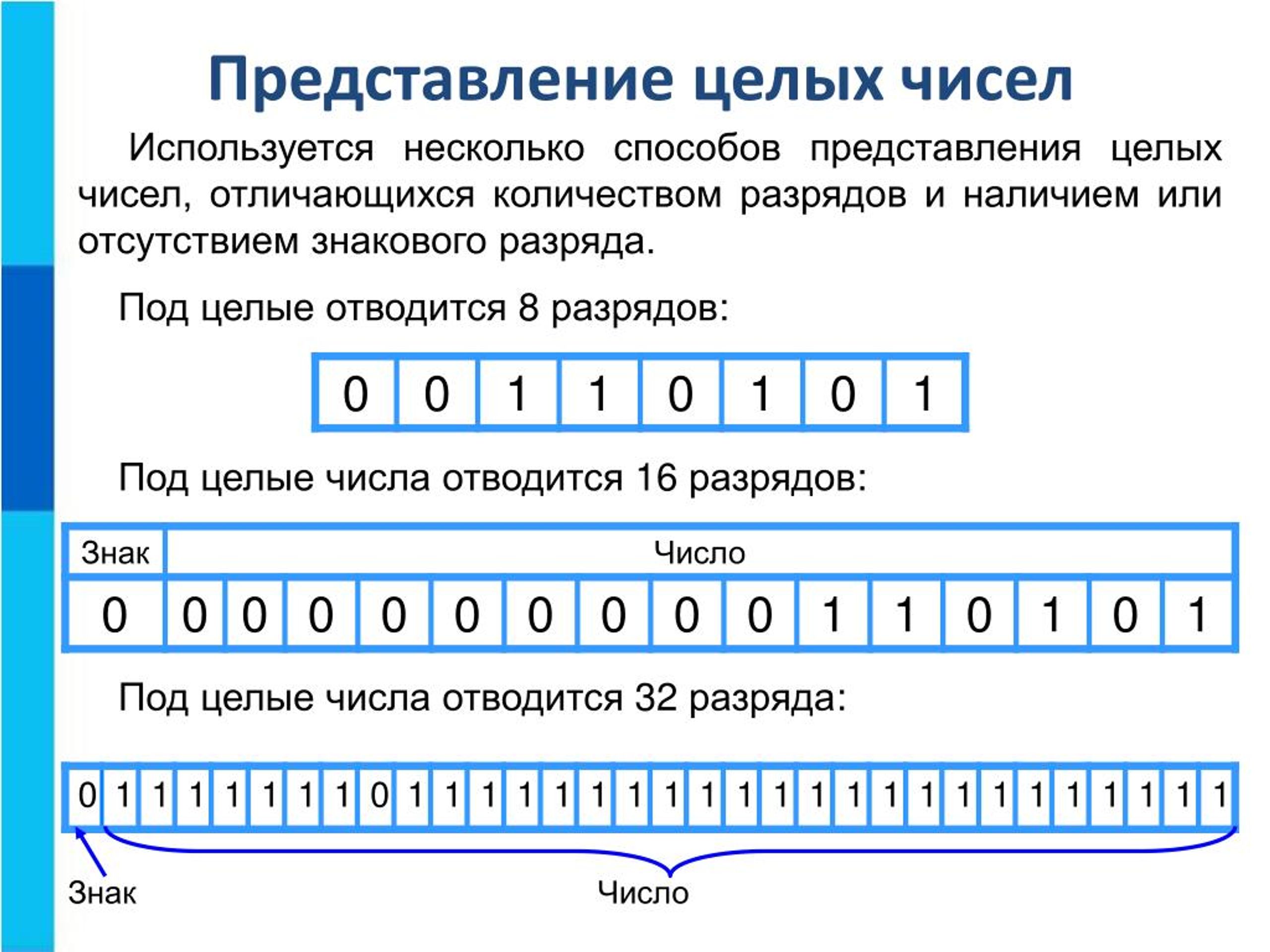
Для компьютерного представления целых чисел используется несколько различных способов, отличающихся друг от друга количеством разрядов (под целые числа обычно отводится 8, 16, 32 или 64 разряда) и наличием или отсутствием знакового разряда. Беззнаковое представление можно использовать только для неотрицательных целых чисел, отрицательные числа представляются только в знаковом виде.
Беззнаковое представление используется для таких объектов, как адреса ячеек, всевозможные счётчики (например, число символов в тексте), а также числа, обозначающие дату и время, размеры графических изображений в пикселях и т. д.
Максимальное значение целого неотрицательного числа достигается в случае, когда во всех разрядах ячейки хранятся единицы. Для n-разрядного представления оно будет равно 2n-1. Минимальное число соответствует п нулям, хранящимся в n разрядах памяти, и равно нулю.
Для n-разрядного представления оно будет равно 2n-1. Минимальное число соответствует п нулям, хранящимся в n разрядах памяти, и равно нулю.
Ниже приведены максимальные значения для беззнаковых целых n-разрядных чисел:
Для получения компьютерного представления беззнакового целого числа достаточно перевести число в двоичную систему счисления и дополнить полученный результат слева нулями до стандартной разрядности.
Пример 1. Число 5310 = 1101012 в восьмиразрядном представлении имеет вид:
Это же число 53 в шестнадцати разрядах будет записано следующим образом:
При представлении со знаком самый старший (левый) разряд отводится под знак числа, остальные разряды — под само число. Если число положительное, то в знаковый разряд помещается 0, если число отрицательное — 1. Такое представление чисел называется прямым кодом.
В компьютере прямые коды используются для хранения положительных чисел в запоминающих устройствах, для выполнения операций с положительными числами.
На сайте Федерального центра информационно-образовательных ресурсов (http://fcior.edu.ru/) размещён информационный модуль «Число и его компьютерный код». С помощью этого ресурса вы можете получить дополнительную информацию по изучаемой теме.
Для выполнения операций с отрицательными числами используется дополнительный код, позволяющий заменить операцию вычитания сложением. Узнать алгоритм образования дополнительного кода вы можете с помощью информационного модуля «Дополнительный код», размещённого на сайте Федерального центра информационно-образовательных ресурсов (http://fcior.edu.ru/).
Презентация «Представление информации в компьютере»
Презентация «Представление информации в компьютере» (Open Document Format)
Ссылки на ресурсы ЕК ЦОР
Федеральный центр информационных образовательных ресурсов:
Представление вещественных чиселЛюбое вещественное число А может быть записано в экспоненциальной форме:
где:
m — мантисса числа;
q — основание системы счисления;
p — порядок числа.
Например, число 472 ООО ООО может быть представлено так: 4,72 • 108, 47,2 • 107, 472,0 • 106 и т. д.
С экспоненциальной формой записи чисел вы могли встречаться при выполнении вычислений с помощью калькулятора, когда в качестве ответа получали записи следующего вида: 4.72Е+8.
Здесь знак «Е» обозначает основание десятичной системы счисления и читается как «умножить на десять в степени».
Из приведённого выше примера видно, что положение запятой в записи числа может изменяться.
Для единообразия мантиссу обычно записывают как правильную дробь, имеющую после запятой цифру, отличную от нуля. В этом случае число 472 ООО ООО будет представлено как 0,472 • 109.
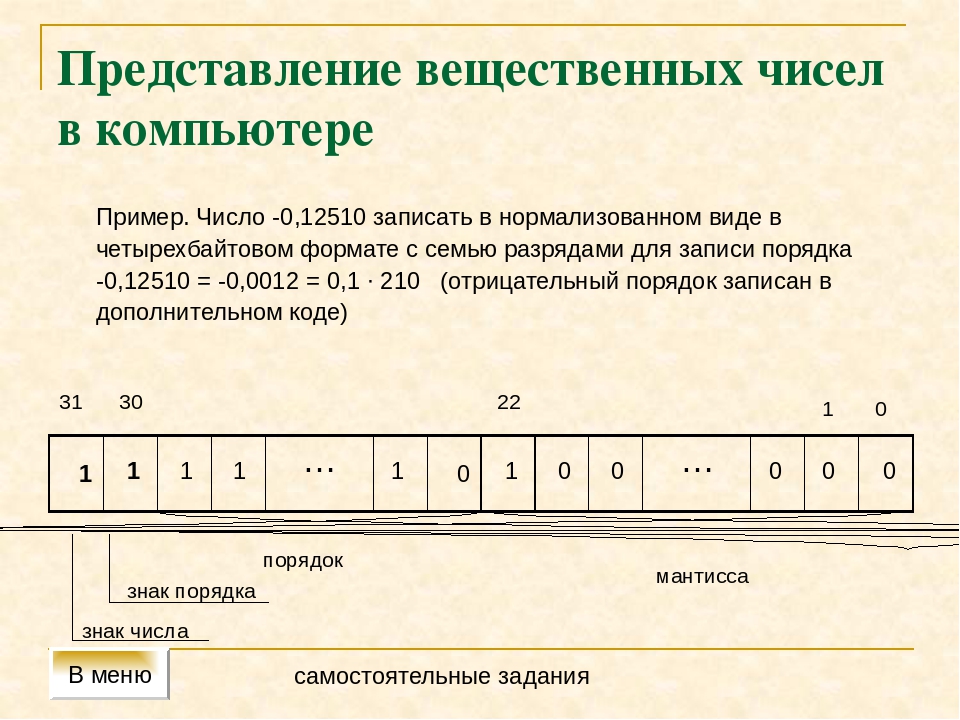
Вещественное число может занимать в памяти компьютера 32 или 64 разряда. При этом выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.
Пример:
Диапазон представления вещественных чисел определяется количеством разрядов, отведённых для хранения порядка числа, а точность определяется количеством разрядов, отведённых для хранения мантиссы.
Максимальное значение порядка числа для приведённого выше примера составляет 11111112 = 12710, и, следовательно, максимальное значение числа:
0,11111111111111111111111 • 101111111
Попытайтесь самостоятельно выяснить, каков десятичный эквивалент этой величины.
Широкий диапазон представления вещественных чисел важен для решения научных и инженерных задач. Вместе с тем следует понимать, что алгоритмы обработки таких чисел более трудоёмки по сравнению с алгоритмами обработки целых чисел.
САМОЕ ГЛАВНОЕДля компьютерного представления целых чисел используются несколько различных способов, отличающихся друг от друга количеством разрядов (8, 16, 32 или 64) и наличием или отсутствием знакового разряда.
Для представления беззнакового целого числа его следует перевести в двоичную систему счисления и дополнить полученный результат слева нулями до стандартной разрядности.
При представлении со знаком самый старший разряд отводится под знак числа, остальные разряды — под само число. Бели число положительное, то в знаковый разряд помещается 0, если число отрицательное, то 1. Положительные числа хранятся в компьютере в прямом коде, отрицательные — в дополнительном.
Бели число положительное, то в знаковый разряд помещается 0, если число отрицательное, то 1. Положительные числа хранятся в компьютере в прямом коде, отрицательные — в дополнительном.
При хранении в компьютере вещественных чисел выделяются разряды на хранение знака порядка числа, самого порядка, знака мантиссы и мантиссы. При этом любое число записывается так:
где:
m — мантисса числа;
q — основание системы счисления;
p — порядок числа.
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Используйте эти материалы при подготовке ответов на вопросы и выполнении заданий.
2. Как в памяти компьютера представляются целые положительные и отрицательные числа?
3. Любое целое число можно рассматривать как вещественное, но с нулевой дробной частью. Обоснуйте целесообразность наличия особых способов компьютерного представления целых чисел.
4. Представьте число 6310 в беззнаковом 8-разрядном формате.
Представьте число 6310 в беззнаковом 8-разрядном формате.
5. Найдите десятичные эквиваленты чисел по их прямым кодам, записанным в 8-разрядном формате со знаком:
а) 01001100;
б) 00010101.
6. Какие из чисел 4438, 1010102, 25610 можно сохранить в 8-разрядном формате?
7. Запишите следующие числа в естественной форме:
а) 0,3800456 • 102;
б) 0,245 • 10-3;
в) 1,256900Е+5;
г) 9,569120Е-3.
8. Запишите число 2010,010210 пятью различными способами в экспоненциальной форме.
9. Запишите следующие числа в экспоненциальной форме с нормализованной мантиссой — правильной дробью, имеющей после запятой цифру, отличную от нуля:
а) 217,93410;
б) 7532110;
в) 0,0010110.
10. Изобразите схему, связывающую основные понятия, рассмотренные в данном параграфе.
Электронное приложение к уроку
Презентация «Представление информации в компьютере»
Презентация «Представление информации в компьютере» (Open Document Format)
Ссылки на ресурсы ЕК ЦОР
Федеральный центр информационных образовательных ресурсов:
| Презентации, плакаты, текстовые файлы | Вернуться к материалам урока | Ресурсы ЭОР |
Cкачать материалы урока
Представление чисел в компьютере.
 Математические основы информатики
ПРЕДСТАВЛЕНИЕ
Математические основы информатики
ПРЕДСТАВЛЕНИЕЧИСЕЛ В
КОМПЬЮТЕРЕ
МАТЕМАТИЧЕСКИЕ ОСНОВЫ
ИНФОРМАТИКИ
Ключевые слова
• разряд
• беззнаковое представление целых
чисел
• представление целых чисел со
знаком
• представление вещественных чисел
Ячейки памяти
Память компьютера состоит из
ячеек, в свою очередь состоящих
из некоторого числа однородных
элементов.
Каждый такой элемент служит
для хранения одного из битов разрядов
двоичного
числа.
Именно поэтому каждый элемент
ячейки называют битом или
разрядом.
(n-1)-й разряд
0 –й разряд
ячейка из n разрядов
Представление целых чисел
Используется несколько способов представления целых
чисел, отличающихся количеством разрядов и наличием или
отсутствием знакового разряда.
Под целые отводится 8 разрядов:
0
0
1
1
0
1
0
1
Под целые числа отводится 16 разрядов:
Знак
Число
0
0 0 0 0 0 0 0 0 0 1 1 0 1 0 1
Под целые числа отводится 32 разряда:
0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
Знак
Число
Беззнаковое представление
Беззнаковое представление можно использовать только
для неотрицательных целых чисел.

Минимальное значение: во всех разрядах ячейки хранятся
нули.
Максимальное значение:
хранятся единицы (2n–1).
во всех разрядах ячейки
Количество
битов
Минимальное
значение
Максимальное значение
8
0
255 (28 – 1)
16
0
65 535 (216 – 1)
32
0
4 294 967 295 (232 – 1)
64
0
18 446 744 073 709 551 615 (264 – 1)
Пример 1. Число 5310 = 1101012 в восьмиразрядном
представлении имеет вид:
0
0
1
1
0
1
0
1
Число 53 в шестнадцатиразрядном представлении имеет
вид:
0 0 0 0 0 0 0 0 0 0 1 1 0 1 0 1
Представление чисел в памяти компьютера
Представление со знаком
При представлении со знаком самый старший (левый)
разряд отводится под знак числа, остальные разряды — под
само число.
Если число положительное, то в знаковый разряд
помещается 0, если число отрицательное, то 1.
Диапазон представления чисел — 2 n-1≤ x ≤ 2n-1-1, где n разрядность ячейки.

Минимальное значение: -2n-1.
Максимальное значение: 2n-1–1.
Количество
битов
Диапазон чисел
8
от — 27 до 27 – 1 (от -128 до 127)
16
от — 215 до 215 – 1 (от -32768 до 32767)
32
от — 231 до 231 – 1 (от -2147483648 до 2147483647)
64
от — 263 до 263 – 1 (от -9223372036854775808)
Прямой код
Пример 2. Число 7310 = 10010012.
Прямой код числа 7310 в восьмиразрядном представлении
имеет вид:
0
1
0
0
1
0
0
1
Прямой код числа -7310 в восьмиразрядном представлении
имеет вид:
1
1
0
0
1
0
0
1
Прямой код используется главным образом для записи и
выполнения операций с неотрицательными целыми числами.
Для выполнения операций с отрицательными числами
используется дополнительный код.
Представление вещественных чисел
Любое вещественное число А может быть записано в
нормальной (научной, экспоненциальной) форме:
А =±m qp, где:
m — мантисса числа;
q — основание системы счисления;
p — порядок числа.

Пример. 472 000 000 может быть представлено так:
810
76 5
4,72
47,2
4720
472 10
10
10
Запятая «плавает» по мантиссе.
Такое
представление
числа
называется
представлением в формате с плавающей запятой.
Бывают записи вида: 4.72Е+8.
Формат с плавающей запятой
Число в формате с плавающей запятой может занимать в
памяти компьютера 32 или 64 разряда.
При этом выделяются разряды для хранения
знака порядка, порядка, знака мантиссы и мантиссы.
0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
Знак и порядок
Знак и мантисса
Диапазон
представления
вещественных
чисел
определяется количеством разрядов, отведённых для
хранения порядка числа, а точность — количеством разрядов,
отведённых для хранения мантиссы.
Числа в памяти компьютера
Самое главное
Для компьютерного представления целых чисел используются
несколько различных способов, отличающихся друг от друга
количеством разрядов (8, 16, 32 или 64) и наличием или отсутствием
знакового разряда.

Для представления беззнакового целого числа его следует
перевести в двоичную систему счисления и дополнить полученный
результат слева нулями до стандартной разрядности.
При представлении со знаком самый старший разряд
отводится под знак числа, остальные разряды — под само число. Если
число положительное, то в знаковый разряд помещается 0, если
число отрицательное, то 1.
Вещественные числа в компьютере хранятся в формате с
плавающей запятой:
А = ±m qp, где:
m — мантисса числа;
q — основание системы счисления;
p — порядок числа.
Вопросы и задания
Запишите
Представьте
Найдите
Запишите
Запишите
Любое
Какие
Как виз
следующие
памяти
десятичные
целое
чисел
следующие
число
число
компьютера
443
число
числа
,эквиваленты
63
2010,0102
101010
числа
вможно
естественной
представляются
, в256
чисел
пятью
рассматривать
можно
поформе:
их
8-разрядном
различными
сохранить
целые
прямым
формекак
в
с
8
10
2беззнаковом
10 нормальной
10
вещественное,
формате.

кодам,
8-разрядном
а)
способами
нормализованной
0,3800456
записанным
положительные
в нормальной
·формате?
10
но2; с внулевой
мантиссой
8-разрядном
иформе.
отрицательные
дробной
— формате
правильной
частью.
числа?
со знаком:
дробью,
–3;
б)а)
имеющей
0,245
Обоснуйте
01001100;
· 10
после
запятой
целесообразность
цифру, отличную
наличия
от нуля: особых
способов
в)
б)
1,256900Е+5;
а)00010101.
217,93410;
компьютерного представления целых чисел.
г) 9,569120Е–3.
б) 7532110;
в) 0,0010110.
Опорный конспект
Числа в компьютере
Целое число
Положительное
Отрицательное
Вещественное число
А = ±m qp, где:
m — мантисса числа;
q — основание системы
счисления;
p — порядок числа.
Электронные образовательные ресурсы
http://files.
 school-collection.edu.ru/dlrstore/d26ca47b-943d-4dec-a853a32844cdc101/9_117.swf — Числа в памяти компьютера
school-collection.edu.ru/dlrstore/d26ca47b-943d-4dec-a853a32844cdc101/9_117.swf — Числа в памяти компьютераhttp://files.school-collection.edu.ru/dlrstore/ecf4ab69-d8ac-40a8-b26a2780aa70b33d/9_118.swf — Представление чисел в памяти
компьютера
http://files.school-collection.edu.ru/dlrstore/19d0fb95-871d-4063-961de7dc5725e555/9_121.swf — Тест двоичная система счисления и
представление чисел в памяти компьютера
|
Ваши ответы:
|
Добро пожаловать!
Ссылки:7: Интерактивные ресурсы к учебнику 7-го класса, автор Антонов А.М., НОУ школа «Ксения» г. Архангельск. Скачать для Windows или Веб-версия (только для браузера SeaMonkey)
8: Интерактивные ресурсы к учебнику 8-го класса, автор Антонов А. М., НОУ школа «Ксения» г. Архангельск. Скачать для Windows или Веб-версия (только для браузера SeaMonkey)
М., НОУ школа «Ксения» г. Архангельск. Скачать для Windows или Веб-версия (только для браузера SeaMonkey)
9: Интерактивные ресурсы к учебнику 9-го класса, автор Антонов А.М., НОУ школа «Ксения» г. Архангельск. Скачать для Windows или Веб-версия (только для браузера SeaMonkey)
Электронные образовательные ресурсы по темам
Информационное общество
Информационные технологии и общество (тренировочный тест)
Информационные технологии и общество (итоговый тест)
Информационное общество
Информация. Системы счисления.
Человек и информация (тренировочный тест)
Человек и информация (итоговый тест)
История развития систем счисления
Сложение и вычитание одноразрядных двоичных чисел
Сложение и вычитание многоразрядных двоичных чисел
Умножение и деление двоичных чисел
Двоичная система счисления и представление чисел в памяти компьютера (тренировочный тест)
Архитектура компьютера
Архитектура фон Неймана
Устройство персонального компьютера
Первое знакомство с компьютером (итоговый тест)
Первое знакомство с компьютером (тренировочный тест)
Архитектура и структура компьютера
Системный блок
Подключение устройств
Алгоритмизация и программирование
Управление и алгоритмы (тренировочный тест)
Управление и алгоритмы (итоговый тест)
Алгоритм «Почисти ковер»
Алгоритм «Погладь рубашку»
Алгоритм «Завари чай»
Алгоритм «Соберись в школу» (ветвление)
Алгоритм «Полей цветок» (ветвление)
Алгоритм «Передать сообщение по телефону» (ветвление)
Алгоритм «Погулять с другом» (ветвление)
Алгоритм «Сходить в кино» (ветвление)
Алгоритм с условным обозначением команды (цикл)
Алгоритм с условным обозначением команды (цикл)
Программное управление работой компьютера(тренировочный тест)
Программное управление работой компьютера (итоговый тест)
Информационно-коммуникационные технологии
Текстовая информация и компьютер (тренировочный тест)
Текстовая информация и компьютер (итоговый тест)
Графическая информация и компьютер. Технология мультимедиа. (тренировочный тест)
Технология мультимедиа. (тренировочный тест)
Графическая информация и компьютер. Технология мультимедиа. (итоговый тест)
Передача информации в компьютерных сетях (тренировочный тест)
Передача информации в компьютерных сетях (итоговый тест)
Табличные вычисления на компьютере (тренировочный тест)
Табличные вычисления на компьютере (итоговый тест)
Статистические функции в электронных таблицах
Логические и условные функции
Электронные таблицы. Запись формул.
Хранение и обработка информации в базах данных (тренировочный тест)
Хранение и обработка информации в базах данных (итоговый тест)
Логические задачи
Обведи фигуру одним движением (1)
Обведи фигуру одним движением (2)
Строим цепочки
Задача на переливание
Переложи спички
Переправа
6 — Представление чисел в ЭВМ
Лекция №6
Представление чисел в ЭВМ
1. Общие сведения
Общие сведения
При проектировании ЭВМ, создании инструментального и прикладного программного обеспечения разработчикам приходится решать вопрос о представлении в ЭВМ числовых данных. Для решения большинства прикладных задач обычно достаточно использовать целые и вещественные числа. Запись целочисленных данных в запоминающем устройстве ЭВМ не представляет затруднений: число переводится в двоичную систему и записывается в прямом коде. Диапазон представляемых чисел в этом случае ограничивается количеством выделенных для записи разрядов. Для вещественных данных обычно используются две формы записи: число с фиксированной точкой (ЧФТ) и число с плавающей точкой (ЧПТ).
Память ЭВМ построена из запоминающих элементов, обладающих двумя устойчивыми состояниями, одно из которых соответствует нулю, а другое — единице. Таким физическим элементом представляется в памяти ЭВМ каждый разряд двоичного числа (бит). Совокупность определенного количества эти элементов служит для представление многоразрядных двоичных чисел и составляет разрядную сетку ЭВМ.
Каждая группа из 8-ми запоминающих элементов (байт) пронумерована. Номер байта называется его адресом. Определенное число последовательно расположенных байт называется словом. Для разных ЭВМ длина слова различна — два, четыре или восемь байт. (Мне думается, что это зависит от разрядности процессора).
2. Числа с фиксированной точкой
Форма записи числа с фиксированной точкой использовалась в основном на ранних этапах развития вычислительной техники. Запись числа с фиксированной точкой обычно имеет знаковый и цифровой разряды. Фиксированная точка означает, что на этапе конструирования ЭВМ было определено, сколько и какие разряды машинного слова отведены под изображение целой и дробной частей числа. Запятая в разрядной сетке может быть зафиксирована, в принципе, после любого разряда.
Рекомендуемые файлы
Пример.
Ячейка с целой и дробной частью.
Как частный случай числа с фиксированной точкой может быть рассмотрена запись целого числа (в этом случае все разряды, кроме знакового, используются для записи целой части).
Пример.
Ячейка с записью целого числа.
К достоинствам использования чисел с фиксированной точкой относятся простота выполнения арифметических операций и высокая точность изображения чисел. К недостаткам — небольшой диапазон представления чисел.
При представлении в ЭВМ чисел в естественной форме устанавливается фиксированная длина разрядной сетки. При этом распределение разрядов между целой и дробной частями остается неизменным для любых чисел. В связи с эти в информатике существует другое название естественной формы представления чисел — с фиксированной точкой (запятой).
Работая на компьютере, мы можем вводить числа с фиксированной запятой в любом виде. Так же они будут высвечиваться на экране компьютера, но перед занесением в память компьютера они преобразуются в соответствии с разрядной сеткой и хранятся либо с запятой, фиксированной после последнего разряда (целые числа), либо с запятой перед старшим разрядом дроби.
Современные ЭВМ работают в режиме с плавающей точкой, но сохранен и режим работы с фиксированной точкой, который используется преимущемтвенно для представления целых чисел.
Обычно целые числа в ЭВМ занимают один, два или четыре байта. Один, как правило, старший бит отводится под знак числа. Знак положительного числа «+» кодируется нулем, а знак отрицательного числа «-» — единицей. Целые числа без знака в двух байтовом формате могут принимать значения от 0 до 216-1 (до 65535), а со знаком «-» от -215 до 215-1, то есть от -32768 до 32767.
Во всех разрядах всегда должно быть что-то записано, даже если это «незначащий» ноль. Число распологается так, что его самый младший двоичный разряд записывается в крайний првый бит разрядной сетки. Например, десятичное число 19 (100112) в 16-разрядной сетке записывается так:
Достоинством естественной формы являются простота и наглядность представления чисел, простота алгоритмов реализации операций, а следовательно, простота устройств и высокая скорость выполнения операций.
Существенным недостатком машин с фиксированной точкой является конечный диапазон представления величин.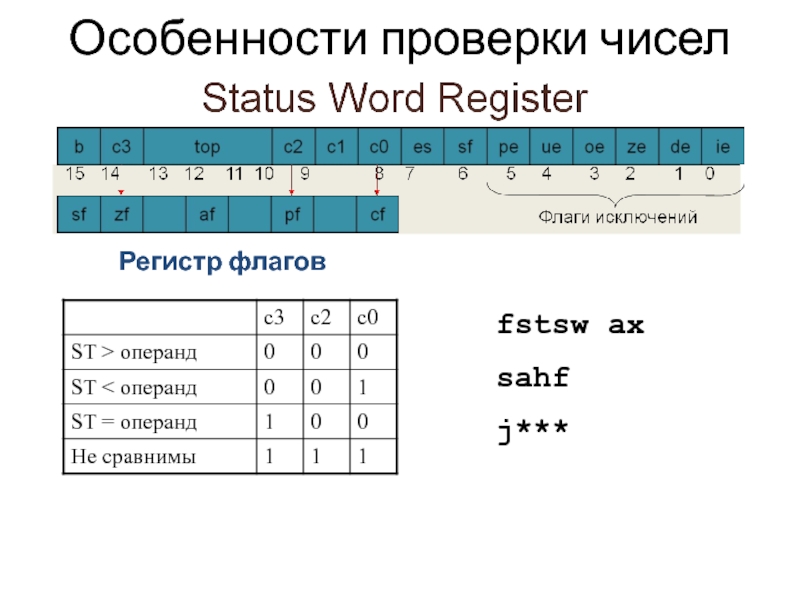 Может показаться, что это ограничивает вычислительные возможности ЭВМ. Но на самом деле короткая длина слова приводит только к снижению быстродействия машин: обработка больших чисел ведется последовательно-параллельным способом, сами числа представляются несколькими машинными словами, и для выполнения операций над ними необходимо составлять специальные программы. Поэтому если результат вычислений в естественной форме выходит за допустимые пределы, то в современных компьютерах производиться автоматический переход к представлению данных в экспотанциальной форме (но только если это оговорено программой).
Может показаться, что это ограничивает вычислительные возможности ЭВМ. Но на самом деле короткая длина слова приводит только к снижению быстродействия машин: обработка больших чисел ведется последовательно-параллельным способом, сами числа представляются несколькими машинными словами, и для выполнения операций над ними необходимо составлять специальные программы. Поэтому если результат вычислений в естественной форме выходит за допустимые пределы, то в современных компьютерах производиться автоматический переход к представлению данных в экспотанциальной форме (но только если это оговорено программой).
Применение
· Для ускорения вычислений в местах, где не требуется высокая точность. В большинстве современных процессоров ФЗ аппаратно не реализована, но даже программная ФЗ очень быстра — поэтому она применяется в разного рода игровых движках, растеризаторах[1] и т. д. Например, движок Doom для измерения расстояний использует фиксированную запятую 16,16, для измерения углов — 360°=65536.
· Чтобы обеспечить минимальную поддержку дробных чисел на целочисленном процессоре — микроконтроллера, мобильного телефона, приставок вплоть до Playstation и т. д. Если не решаются некорректные задачи и СЛАУ высокого порядка, фиксированной запятой зачастую достаточно — важно только подобрать подходящую цену (вес) младшего разряда для каждой из величин.
· Для записи чисел, которые по своей природе имеют постоянную абсолютную погрешность: координаты в программах вёрстки, денежные суммы. Например, файлы метрики шрифтов TeX используют 32-битный знаковый тип с фиксированной запятой (12,20).
o Кроме того, фиксированная запятая ведёт себя абсолютно предсказуемо — при подсчёте денег это позволяет наладить разные виды округления, а в играх — наиболее простой способ реализовать мультиплеер и запись повторов.
Задания
1. Определите максимальные значения целых чисел со знаком и без знака при их 8- и 32-разрядном представлении.
|
| 8 разрядов | 32 разряда |
| со знаком | 27-1=127 | 231-1=2,15×109 |
| без знака | 28-1=255 | 232-1=4,29×109 |
2. Представьте следующие числа в 16-разрядной сетке в формате с фиксированой точкой: 25, 801, -610.
Представьте следующие числа в 16-разрядной сетке в формате с фиксированой точкой: 25, 801, -610.
3. Числа с плавающей точкой (запятой)
Неудобство представления чисел в форме с фиксированной точкой проявляется при решении задач, в которых фигурируют как очень малые так и очень большие числа. В конкретных физических, математических и других задачах диапазон изменения величин может составлять, например от 10-30 до 1030. Можно убедиться, что в представлении с фиксированной запятой понадобились бы двоичные слова длинной около 256 бит (32 байт), по 128 бит на целую и дробную части. Однако работа ЭВМ с операндами такой длины была бы крайне неэффективной.
Точность числа определяется не его длиной, а количеством верных значащих цифр.
Например, мы хотим измерить длину отрезка линейкой с сантиметровыми делениями. Отрезок не совпадает с делениями точно — его длина между 47 и 47,5 см. На глазок прикидываем, что это 47,2 см (472 мм). Ясно, что в каких единицах ни записать длину отрезка: 472000микрон 472мм. 0,000472км — точных цифр только две: 47 при точности измерения до 1 см (ведь линейка-то сантиметровая).
Ясно, что в каких единицах ни записать длину отрезка: 472000микрон 472мм. 0,000472км — точных цифр только две: 47 при точности измерения до 1 см (ведь линейка-то сантиметровая).
Точность результата вычисления выражений, содержащих несколько чисел, определяется, как правило, точностью числа имеющего наименьшее количество верных значащих цифр. Поэтому в практических расчетах редко используют более трех значащих цифр, соответствующим образом округляя промежуточные результаты. Ясно, что для хранения в памяти ЭВМ чисел с небольшим числом значащих цифр целесообразно представлять их в экспоненциальной форме. В приведенном примере это представление может иметь вид:
4,72 х 105; 472 x 103; 4720 x 102микрон
или
4,72 х 10-4; 47,2 x 10-5;472 x 10-6км.
Из этого примера также видно, что положение запятой может изменяться. Поэтому в информатике представление в ЭВМ числа в экспотенциальной форме называются представлением с плавающей точкой (запятой).
Представление чисел в форме с плавающей точкой очень удобно для решения научных и инженерных задач. Нормализованное представление чисел не только позволяет сохранить в разрядной сетке большое количество значащих цифр, но также упрощает действие над порядками и мантисами.
Для представления чисел с плавающей точкой (ЧПТ) используется полулогарифмическая форма записи числа:
N = ± mq ± p
где q— основание системы счисления, p — порядок числа, m — мантисса числа N.
Положение точки определяется значением порядка p. С изменением порядка точка перемещается (плавает) влево или вправо.
Пример.
12510=12.5*101=1.25*102=0.125*103=0.0125*104=…
Для установления однозначности при записи чисел принята нормализованная форма записи числа. Мантисса нормализованного числа может изменяться в диапазоне: 1/q ≤ | m | < 1. Таким образом в нормализованных числах цифра после точки должна быть значащей.
Таким образом в нормализованных числах цифра после точки должна быть значащей.
Пример.
Для представления чисел в машинном слове выделяют группы разрядов для изображения мантиссы, порядка, знака числа и знака порядка:
а) представление чисел в формате полуслова
б) представление чисел в формате слова
Наиболее типично представление ЧПТ в формате слова (32 разряда).
Пример.
Число А=-3.510=-11.12=-0.111·1010
Максимальным числом представимым в формате слова будет A=(0.1111…1·101111111)2(1·2127)10.
Таким образом числа с плавающей точкой позволяют увеличить диапазон обрабатываемых чисел, но при этом точность изображения чисел определяется только разрядами мантиссы и уменьшается по сравнению с числами с фиксированной точкой. При записи числа в формате слова диапазон представимых чисел будет от -1·2127 до 1·2127 (21271038), а точность определяться мантиссой, состоящей из 23 разрядов. Точность может быть повышена путем увеличения количества разрядов мантиссы. Это реализуется путем представления чисел с так называемой двойной точностью (используется формат двойного слова):
Точность может быть повышена путем увеличения количества разрядов мантиссы. Это реализуется путем представления чисел с так называемой двойной точностью (используется формат двойного слова):
Как компьютер выполняет арифметические действия над нормализованными числами?
К началу выполнения арифметического действия операнды операции помещаются в соответствующие регистры АЛУ.
Сложение и вычитание
При сложении и вычитании сначала производится подготовительная операция, называемая выравниванием порядков.
| В процессе выравнивания порядков мантисса числа с меньшим порядком сдвигается в своем регистре вправо на количество разрядов, равное разности порядков операндов. После каждого сдвига порядок увеличивается на единицу. |
В результате выравнивания порядков одноименные разряды чисел оказываются расположенными в соответствующих разрядах обоих регистров, после чего мантиссы складываются или вычитаются. В случае необходимости полученный результат нормализуется путем сдвига мантиссы результата влево. После каждого сдвига влево порядок результата уменьшается на единицу.
В случае необходимости полученный результат нормализуется путем сдвига мантиссы результата влево. После каждого сдвига влево порядок результата уменьшается на единицу.
Пример 1. Сложить двоичные нормализованные числа 0.10111 . 2–1 и 0.11011 . 210. Разность порядков слагаемых здесь равна трем, поэтому перед сложением мантисса первого числа сдвигается на три разряда вправо:
Пример 2. Выполнить вычитание двоичных нормализованных чисел 0.10101 . 210 и 0.11101 . 21. Разность порядков уменьшаемого и вычитаемого здесь равна единице, поэтому перед вычитанием мантисса второго числа сдвигается на один разряд вправо:
Результат получился не нормализованным, поэтому его мантисса сдвигается влево на два разряда с соответствующим уменьшением порядка на две единицы: 0.1101 . 20.
Умножение
| При умножении двух нормализованных чисел их порядки складываются, а мантиссы перемножаются. |
Пример 3. Выполнить умножение двоичных нормализованных чисел:
(0.11101 . 2101) . (0.1001 . 211) = (0.11101 . 0.1001) . 2(101+11) = 0.100000101 . 21000.
В лекции «Vantage Team Builder» также много полезной информации.
Деление
| При делении двух нормализованных чисел из порядка делимого вычитается порядок делителя, а мантисса делимого делится на мантиссу делителя. Затем в случае необходимости полученный результат нормализуется. |
Пример 4. Выполнить деление двоичных нормализованных чисел:
0. 1111 . 2100 : 0.101 . 211 = (0.1111 : 0.101) . 2(100–11) = 1.1 . 21 = 0.11 . 210.
1111 . 2100 : 0.101 . 211 = (0.1111 : 0.101) . 2(100–11) = 1.1 . 21 = 0.11 . 210.
Использование представления чисел с плавающей точкой существенно усложняет схему арифметико-логического.
Представление с плавающей запятой: научные вычисления Введение: тест множественного выбора
|
Выберите наиболее подходящий ответ. |
|
|
|
|
1 квартал .
Гипотетический компьютер хранит действительные числа в формате с плавающей запятой в 8-битном формате.
слова. Первый бит используется для знака числа, второй бит для
знак экспоненты, следующие два бита для величины показателя и
следующие четыре бита — величина мантиссы. Представьте e≈2,718 в
8-битный формат.
Представьте e≈2,718 в
8-битный формат.
00010101
00011010
00010011
00101010
2 квартал . А гипотетический компьютер хранит действительные числа в формате с плавающей запятой в 8-битном формате. слова. Первый бит используется для знака числа, второй бит для знак экспоненты, следующие два бита для величины показателя и следующие четыре бита — величина мантиссы. Число по основанию 10 что (10100111) 2 представляет в приведенном выше 8-битном формате
-5.75000
-2,87500
-1,75000
-0,359375
3 квартал . А
гипотетический компьютер хранит числа с плавающей запятой в 8-битных словах. Первое
бит используется для знака числа, второй бит — для знака числа.
экспонента, следующие два бита для величины экспоненты и следующие четыре
бит для величины мантиссы. Машинный эпсилон почти
Машинный эпсилон почти
2 -7
2 -4
2 -3
2 -2
4 квартал .А машина хранит числа с плавающей запятой в 7-битном слове. Используется первый бит для знака числа, следующие три для смещенной экспоненты и следующие три для величины мантиссы. Номер (0010110) 2 представлен в база-10 — это
0,375
0,875
1,5
3,5
5 квартал . А машина хранит числа с плавающей запятой в 7-битных словах. Первый бит сохраняется для знака числа, следующие три для смещенной экспоненты и следующие три для величины мантиссы.Вас просят представить 33,35 дюйма вышеприведенное слово. В этом случае вы получите ошибку
.
переполнение
перелив
NaN
Никакой ошибки не будет зарегистрированный
Q6 . А
гипотетический компьютер хранит числа с плавающей запятой в 9-битных словах. Первое
бит используется для знака числа, второй бит — для знака числа.
экспонента, следующие три бита для величины экспоненты и следующие
четыре бита для величины мантиссы.Каждую секунду ошибка между
0.1 и его двоичное представление в 9-битном слове накапливается. В
накопленная ошибка почти за один день составляет
А
гипотетический компьютер хранит числа с плавающей запятой в 9-битных словах. Первое
бит используется для знака числа, второй бит — для знака числа.
экспонента, следующие три бита для величины экспоненты и следующие
четыре бита для величины мантиссы.Каждую секунду ошибка между
0.1 и его двоичное представление в 9-битном слове накапливается. В
накопленная ошибка почти за один день составляет
0,002344
20,25
202,5
8640
Комплексное решение
Практическое приложение для компьютерной архитектуры: представление данных
Преобразование текста в ASCII
Все компьютеры внутренне хранят текстовые данные в формате ASCII.Каждая буква английского алфавита (строчные и прописные буквы отдельно, а также числа и специальные символы) хранится как эквивалент ASCII во внутренней памяти компьютера. Код ASCII — это 8-битный длинный код, который используется для представления данных. Таблица, показанная на рисунке 01 ниже, дает таблицу преобразования кода ASCII. Показанное преобразование предназначено для традиционных символов и символов, которым требуется только 7-битное представление. Код ASCII был позже расширен до 8 битов, и 8-битные коды используются для представления расширенных символов.
Таблица, показанная на рисунке 01 ниже, дает таблицу преобразования кода ASCII. Показанное преобразование предназначено для традиционных символов и символов, которым требуется только 7-битное представление. Код ASCII был позже расширен до 8 битов, и 8-битные коды используются для представления расширенных символов.
Из таблицы кодов ASCII буква «A» имеет значение 65, а «a» — 97. Здесь 65 и 97 представлены в десятичном формате, а компьютеры не понимают никаких числовых форматов, кроме двоичного, восьмеричного или шестнадцатеричного форматов. . Десятичный эквивалент кодов ASCII используется только для удобства человека. Таким образом, преобразование 65 в двоичное даст 0100 0001 (помните, что ASCII имеет длину 8 бит), а 97 даст 0110 0001.Преобразование между десятичным и двоичным числами показано на рисунках 02 и 02B ниже. На рисунке 02C показано обратное преобразование из двоичного представления ASCII в десятичный эквивалент.
Двоичный формат кодов ASCII также может быть преобразован в восьмеричный и шестнадцатеричный формат.Восьмеричные системы счисления принимают цифры от 0 до 7 и шестнадцатеричные от 0 до F. В шестнадцатеричной системе цифры могут быть от 0 до 16 — от 0 до 9 эквивалентны десятичным эквивалентам, A представляет 10, B — 11 и т. Д. , пока F не будет равно 15. На рисунках 03 и 03B показано преобразование десятичного эквивалента кодов ASCII в восьмеричный и шестнадцатеричный форматы.
Восьмеричная цифра состоит из трех двоичных цифр, а шестнадцатеричная — из четырех.На рисунке 04 ниже показан процесс преобразования двоичных чисел в восьмеричные / шестнадцатеричные числа, а также обратный процесс. Процесс обратного преобразования из восьмеричного или шестнадцатеричного числа проще. Для восьмеричного числа просто преобразуйте каждую цифру в двоичный эквивалент. Например, восьмеричное число 101 на самом деле 01 000 001 — последняя восьмеричная цифра (слева) равна 1, и это дает двоичное 001. Вторая восьмеричная цифра — 0, а двоичный эквивалент — 000. Наконец, первая цифра — 1, а это эквивалентно 01 в двоичном формате. Здесь для первой восьмеричной цифры необходимы только две двоичные цифры, в отличие от трех для двух последних восьмеричных цифр. Причина этого в том, что код ASCII состоит ровно из восьми двоичных цифр. Для последних двух восьмеричных цифр они будут переведены в три двоичных разряда каждая. Первая восьмеричная цифра может отображаться только на две двоичные цифры, так как шесть уже заняты последними двумя восьмеричными цифрами. Таким образом, первая восьмеричная цифра может быть преобразована только в две двоичные цифры и может иметь значение только от 0 до 3.Таким образом, восьмеричное число 101 равно 0100 0001 в двоичном формате. Аналогично, для шестнадцатеричного числа 41 двоичный эквивалент определяется следующим образом. Последняя шестнадцатеричная цифра — 1, а ее двоичный эквивалент (здесь используются 4 бита) — 0001. Следующая шестнадцатеричная цифра — 4, а двоичный эквивалент — 0100. Таким образом, 41 шестнадцатеричный равен 0100 0001 в двоичном. Если внимательно присмотреться, восьмеричное число 101 на самом деле является 41 шестнадцатеричным, поскольку после преобразования оба имеют одинаковое двоичное значение.
Здесь для первой восьмеричной цифры необходимы только две двоичные цифры, в отличие от трех для двух последних восьмеричных цифр. Причина этого в том, что код ASCII состоит ровно из восьми двоичных цифр. Для последних двух восьмеричных цифр они будут переведены в три двоичных разряда каждая. Первая восьмеричная цифра может отображаться только на две двоичные цифры, так как шесть уже заняты последними двумя восьмеричными цифрами. Таким образом, первая восьмеричная цифра может быть преобразована только в две двоичные цифры и может иметь значение только от 0 до 3.Таким образом, восьмеричное число 101 равно 0100 0001 в двоичном формате. Аналогично, для шестнадцатеричного числа 41 двоичный эквивалент определяется следующим образом. Последняя шестнадцатеричная цифра — 1, а ее двоичный эквивалент (здесь используются 4 бита) — 0001. Следующая шестнадцатеричная цифра — 4, а двоичный эквивалент — 0100. Таким образом, 41 шестнадцатеричный равен 0100 0001 в двоичном. Если внимательно присмотреться, восьмеричное число 101 на самом деле является 41 шестнадцатеричным, поскольку после преобразования оба имеют одинаковое двоичное значение.
Упражнение, приведенное ниже, даст вам возможность протестировать механизм преобразования, который обсуждался ранее.Возможно, вам потребуется использовать таблицу кодов ASCII для преобразования в соответствующие коды ASCII встречающихся символов. Однако некоторые языки программирования предоставляют некоторые встроенные функции для автоматического выполнения преобразований. Например, в Java есть функция преобразования Integer.toString (
Вопрос 1
(a)
Найдите коды ASCII для следующих букв / символов A, F, Z, a, f, z,? и% — сначала в десятичном формате, затем преобразуйте их в восьмеричный и шестнадцатеричный эквиваленты.
(b)
Найдите эквиваленты кода ASCII в десятичном виде для следующих двоичных чисел — 0100 1100, 0110 1110 и 0111 1111.
(c)
Найдите эквиваленты кода ASCII в десятичном виде для следующих восьмеричных чисел — 104 , 110, 107 и 113.
(d)
Используйте информацию ниже для ответа на этот вопрос.Он показывает коды ASCII в десятичном формате. Переведите содержимое в читаемый текст в формате. Затем измените его на восьмеричный и шестнадцатеричный формат.
076 101097 114 110 105 110 103 032 099 111 109 112 117 116 101 114 115 032 105 115 032 102 117 110 033
(e)
Рассмотрим предложение, приведенное ниже. Преобразуйте его в представление ASCII в шестнадцатеричном формате, которое можно сохранить в компьютерной системе.
Быстрая коричневая лисица перепрыгивает через ленивую собаку.
Преобразование чисел в двоичные
Мы переходим к представлению целых чисел со знаком / без знака.Числа обрабатываются совсем не так, как текст. Таким образом, вполне естественно, что они хранятся по-разному. Поскольку многие математические операции могут воздействовать на числовые данные, они обычно хранятся в формате, который позволяет легко ими манипулировать. Для целых чисел со знаком / без знака широко используется представление дополнения до 2. В большинстве систем целые числа могут храниться в 16, 32 или 64 битах — длина определяет максимальное / минимальное целое число, которое может быть представлено. Здесь важно отметить, что числа также могут быть частью текста — например, предложение может быть таким: «Фут равен 12 дюймам»… ‘. Здесь 12 следует рассматривать как текст, а не число, и в этом случае он будет представлен двумя кодами ASCII, один для «1», а другой для «2».
В дополнительном представлении 2 положительные целые числа преобразуются в двоичный эквивалент с использованием метода, описанного ранее, то есть метода преобразования десятичных кодов ASCII в двоичные эквиваленты. Для отрицательных целых чисел используется немного более сложный процесс. Для отрицательных целых чисел сначала применяется тот же метод, затем все биты инвертируются и, наконец, к результату добавляется «1».Таким образом, чтобы найти представление в виде дополнения до 2 для числа, такого как -260, сначала преобразуйте 260, используя более ранний метод, который дает 0000 0001 0000 0100. Затем инвертируйте все биты, и это дает 1111 1110 1111 1011. Добавляя ‘1’ к этому дает 1111 1110 1111 1100.
Для отрицательных целых чисел используется немного более сложный процесс. Для отрицательных целых чисел сначала применяется тот же метод, затем все биты инвертируются и, наконец, к результату добавляется «1».Таким образом, чтобы найти представление в виде дополнения до 2 для числа, такого как -260, сначала преобразуйте 260, используя более ранний метод, который дает 0000 0001 0000 0100. Затем инвертируйте все биты, и это дает 1111 1110 1111 1011. Добавляя ‘1’ к этому дает 1111 1110 1111 1100.
Число с плавающей запятой сохраняется в формате, отличном от формата целого числа со знаком / без знака. Как и целые числа, числа с плавающей запятой могут храниться как 16-, 32- или 64-битные представления в зависимости от необходимой точности. Показанный здесь пример относится к представлению 16-битного числа с плавающей запятой, как указано в стандартах IEEE-754.2, 2,625 — мантисса, 2 — показатель степени. Шаги, необходимые для упражнений по преобразованию, показаны на Рисунке 06 ниже.
Вопрос 2
(a)
Найдите двоичный эквивалент дополнения до 2 следующих целых чисел 32, 58, -15, -27. Преобразуйте их также в восьмеричные и шестнадцатеричные эквиваленты.
Преобразуйте их также в восьмеричные и шестнадцатеричные эквиваленты.
(b)
Найдите представление с плавающей запятой в двоичном формате для следующих чисел: 3,5, -3,5, 25,125, 2,53, 0,33. Преобразуйте их также в восьмеричные и шестнадцатеричные эквиваленты.
(c)
16-битный двоичный эквивалент числа с плавающей запятой дается как 1 10001 1100000000. Что это за число?
================================================ ================================
Ключ ответа
Вопрос 1
(a)
A 65, 01000001, 101, 41
F 70, 01000110, 106, 46
Z 90, 01011010, 132, 5A
a 97, 01100001, 141, 61
f 102, 01100110, 146, 66
z 122, 01111010, 172, 7А
? 63, 00111111, 077, 3F
% 37, 00100101, 045, 25
(b)
0100 1100 — десятичный эквивалент 76 i.е. буква «L»
0110 1110 — десятичный эквивалент 110, т.е. буква «n»
0111 1111 — десятичный эквивалент 127, т. е. специальный символ DEL
е. специальный символ DEL
(c)
104 — десятичный эквивалент 68 для буквы «D»
110 — десятичный эквивалент 72 для буквы «H»
107 — десятичный эквивалент 71 для буквы «G»
113 — десятичный эквивалент 75 для буквы «K»
(d)
Изучение компьютеров — это весело!
(д)
54 68 65 20 71 75 69 63 6B 20 62 72 6F 77 6E 20 66 6F 78 20 6A 75 6D 70 73 20 6F 76 65 72 20 74 68 65 20 6C 61 7A 79 20 64 6F 67 46
Вопрос 2
(а)
32 0000 0000 0010 0000, 000040, 0020
58 0000 0000 0011 1010, 000072, 003A
-15 1111 1111 1111 0001, 177761, FFF1
-27 1111 1111 1110 0101, 177745, FFE5
(б)
3.5 0100001110000000, 0416000, 4380
-3,5 1100001110000000, 141600, C380
25,125 0100111100100100, 047444, 4F24
2,53 0100001010000111, 041207, 4287
0,33 0011010000111, 041207, 4287
0,33 001101036101 900 (
310321 900) 1, таким образом, число отрицательное.
 -1)] = -4 * 1.5 = -6,0
-1)] = -4 * 1.5 = -6,0
Что там со всеми единицами и нулями?
На стене в крыле информатики висит серебряная табличка. Вот его изображение:
Так что же со всеми единицами и нулями? Это просто для галочки или на самом деле что-то значит?
Я не говорю о «значении чего-то» в философском смысле. О том, действительно ли эти 1 и 0 приводят к действию и цели с нашей стороны, — это тема для другого поста. Вместо этого в этой статье я имею в виду что-то гораздо более обыденное, гораздо более банальное.Что означают единицы и 0 в нашем повседневном языке и почему компьютеры вообще говорят на этом странно ограниченном языке?
Давайте сначала рассмотрим второй вопрос. Почему компьютеры говорят в единицах и нулях? Этот язык единиц и нулей называется двоичным . Компьютеры говорят в двоичном формате из-за того, как они построены. Компьютер — это не что иное, как огромное количество переключателей. На этих странно выгравированных платах внутри компьютера находятся миллионы наноскопически маленьких электронных переключателей. Переключатель, если он не сломан, может быть включен или выключен, замкнут или разомкнут. Переключатель, который находится во «включенном» или «замкнутом» состоянии, пропускает через него электрический сигнал, в то время как выключатель, находящийся в «выключенном» или «разомкнутом» состоянии, блокирует этот сигнал. Ученые-компьютерщики представляют переключатель «включено» с цифрой 1 и переключатель «выключено» с цифрой 0.
Переключатель, если он не сломан, может быть включен или выключен, замкнут или разомкнут. Переключатель, который находится во «включенном» или «замкнутом» состоянии, пропускает через него электрический сигнал, в то время как выключатель, находящийся в «выключенном» или «разомкнутом» состоянии, блокирует этот сигнал. Ученые-компьютерщики представляют переключатель «включено» с цифрой 1 и переключатель «выключено» с цифрой 0.
Представляя данные в виде единиц и нулей, мы упаковываем их таким образом, чтобы имитировать организацию вещей внутри компьютера. Последствия этого решения глубоки и расширяют возможности, и на самом деле неясно, знали ли первые компьютерные ученые, насколько случайным окажется их решение выразить данные в виде единиц и нулей.Создавая паттерны данных точно так же, как компьютер, который их обрабатывает, они позволили компьютерам обрабатывать как данные, так и инструкции, используя одни и те же компоненты и инструменты. Позже это привело к повсеместной архитектуре фон Неймана, которой следует практически каждый современный компьютер. Невероятная вычислительная производительность и объем памяти, которыми мы сейчас пользуемся, были бы невозможны без такого способа организации компьютера и данных, которые он обрабатывает.
Невероятная вычислительная производительность и объем памяти, которыми мы сейчас пользуемся, были бы невозможны без такого способа организации компьютера и данных, которые он обрабатывает.
Давайте вернемся к нашей теме: что на самом деле означают эти 1 и 0? Компьютеры не работают напрямую с текстом.Вместо этого они получают значение только от чисел. Для построения одного числа требуется 8 из этих единиц и нулей (другими словами, 8 бит ). Например, рассмотрим этот набор из 8 бит:
0 1 0 0 1 0 0 1
Вы заметите, что это первая коллекция из 8 битов на нашей табличке, показанной на картинке. Этот набор из 8 бит называется байтом . В байте каждый бит имеет значение, связанное с ним. Это ничем не отличается от того, с чем вы привыкли работать в повседневной жизни с числами.Например, если я говорю, что я должен вам 1234 доллара, во-первых, будьте уверены, что я никогда вам не заплачу, а во-вторых, подумайте, что это значит. Каждая из этих цифр представляет собой степень 10. Самая правая цифра — это наименьшее значение, и это количество единиц. Вторая справа цифра представляет собой количество десятков. Третья справа цифра представляет собой количество сотен. Наконец, крайняя левая цифра представляет собой количество тысяч.
Самая правая цифра — это наименьшее значение, и это количество единиц. Вторая справа цифра представляет собой количество десятков. Третья справа цифра представляет собой количество сотен. Наконец, крайняя левая цифра представляет собой количество тысяч.
В нашем примере 4 в разряде единицы, 3 в разряде десятков, 2 в разряде сотен и 1 в разряде тысяч.Таким образом, общее значение этого числа составляет
.1 * 1000 + 2 * 100 + 3 * 10 4 * 1 = 1,234
Это точно такая же интерпретация, которую мы применяем к битам в байте, чтобы определить значение, которое он представляет. Единственное отличие состоит в том, что вместо каждой цифры, представляющей, сколько у нас есть определенной степени 10, каждый бит в байте представляет, сколько у нас есть определенной степени двойки. Крайний правый бит представляет, сколько у нас двойок с возведением в степень 0 (то есть сколько единиц). Бит второй справа представляет, сколько двойки в степени возведения в 1 (т. Е.е. сколько 2-х) у нас есть. Бит третий справа показывает, сколько у нас степеней двойки в степени двойки (т. Е. Сколько четверок). Четвертый-к…
Бит третий справа показывает, сколько у нас степеней двойки в степени двойки (т. Е. Сколько четверок). Четвертый-к…
Эй, заткнись, ботаник. Я умираю здесь.
ОК. Спасибо, что вытащили меня из этого. Вернемся к нашему примеру. Рассмотрим 0 1 0 0 1 0 0 1 и работаем с каждым битом, начиная с самого правого.
У нас 1 на месте.
У нас 0 в разряде 2.
У нас 0 в разряде 4.
У нас 1 в восьмерке.
У нас 0 из 16.
У нас 0 на 32 месте
У нас 1 из 64.
У нас 0 из 128.
Откуда взялись 1, 2, 4, 8, 16, 32, 64 и 128? Каждое из этих чисел является степенью двойки, что, как мы уже сказали, представляет каждый бит в байте. Каждый бит представляет одну из этих степеней двойки, и либо степень двойки присутствует в общем числе, которое представляет байт, либо ее нет. Другими словами, либо переключатель, соответствующий этому биту, закрыт, либо он открыт.Заметили идеальное соответствие между данными и структурой? Это значительно упрощает интерпретацию и представление данных, чем это было бы в противном случае.
Итак, давайте сложим, что у нас есть: 1 + 0 + 0 + 8 + 0 + 0 + 64 + 0 = 73.
Эврика, первый байт таблички миссии нашего отдела — 73! 73? Я думал, что ответ на все вопросы, имеющие космическое значение, — 42. Что такое 73?
Что ж, каждое число, которое мы получаем таким образом, фактически отображается на персонажа. Отображение определяется так называемым американским стандартным кодом обмена информацией или ASCII.Если вы выполните поиск по ASCII, одним из первых сайтов, которые вы увидите, будет самый зрелищный, интересный, информативный и потрясающе крутой сайт — www.asciitable.com. Прочтите столбец Dec, пока не найдете 73. Затем сканируйте немного вправо, пока не дойдете до столбца Chr. Вы увидите там букву «I» (большой глаз). Что это обозначает? Наша последовательность 01001001 — это байт, который переводится в число 73, которое отображается на символ I. Итак, первый символ в миссии нашего отдела — I.
Вот и все.Каждый набор из 8 бит представляет собой число, которое, в свою очередь, представляет собой символ.
Проверьте себя. Попробуйте перевести оставшуюся часть сообщения и посмотрите, сможете ли вы разобраться в остальном. Вот подсказка. В нем не говорится: «Иллинойсский футбол в этом году не будет проигран». Я оптимист, но я давно отказался от галлюциногенов.
Определение компьютерно-адаптивного теста
Компьютерные адаптивные тесты предназначены для корректировки уровня сложности — на основе предоставленных ответов — в соответствии со знаниями и способностями тестируемого.Если ученик дает неправильный ответ, компьютер задает более простой вопрос; если ученик ответит правильно, следующий вопрос будет сложнее. Компьютерные адаптивные тесты, считающиеся передовыми в технологии оценивания, представляют собой попытку более точно измерить способности отдельных учащихся, избегая при этом некоторых проблем, часто связанных с универсальным характером стандартизированных тестов. тесты.
Для студентов компьютерно-адаптивное тестирование предлагает более короткую сессию тестирования с меньшим количеством вопросов, поскольку предлагаются только те вопросы, которые считаются подходящими для учащегося. С другой стороны, разработчики тестов должны создать больший пул тестовых заданий, чтобы в системах тестирования было достаточно вопросов, чтобы соответствовать различным способностям всех учащихся, сдающих экзамен. Самые современные формы компьютерно-адаптивного тестирования, как правило, проводятся онлайн, и, поскольку система выставления оценок компьютеризирована, учителя и ученики могут получить результаты тестов быстрее, чем с помощью тестов с бумажкой и карандашом.
С другой стороны, разработчики тестов должны создать больший пул тестовых заданий, чтобы в системах тестирования было достаточно вопросов, чтобы соответствовать различным способностям всех учащихся, сдающих экзамен. Самые современные формы компьютерно-адаптивного тестирования, как правило, проводятся онлайн, и, поскольку система выставления оценок компьютеризирована, учителя и ученики могут получить результаты тестов быстрее, чем с помощью тестов с бумажкой и карандашом.
Компьютерные адаптивные тесты могут использоваться для самых разных целей, включая крупномасштабное тестирование с высокими ставками; формирующее оценивание, которое предоставляет учителям оперативную обратную связь об обучении учащихся, которую они могут использовать для изменения методик обучения; итоговое оценивание, которое преподаватели используют для определения того, что учащиеся усвоили в конце блока, семестра или года.Они также используются для выявления студентов, которым может потребоваться специализированная академическая поддержка в определенных навыках или предметных областях, таких как чтение, письмо или математика.
Поскольку компьютерно-адаптивные системы тестирования выбирают вопросы, которые должны быть достаточно сложными для каждого ученика, большинство учеников ответят примерно на половину вопросов правильно, а половина — неправильно, поэтому оценка, основанная на общем количестве или процентном соотношении правильных ответов, будет бессмысленной. Таким образом, компьютерно-адаптивная оценка основана как на количестве правильных ответов, так и на сложности выполненных заданий.Перед тем, как тесты будут назначены студентам, тестовые вопросы обычно тестируются в полевых условиях с репрезентативными выборками студентов для калибровки уровней сложности.
Реформа
Хотя компьютерно-адаптивные технологии появились сравнительно недавно, их использование в Соединенных Штатах в ближайшие годы, похоже, будет значительно расти. Например, две основные национальные инициативы по оценке, Консорциум разумной сбалансированной оценки и Партнерство по оценке готовности к поступлению в колледж и карьерный рост (PARCC), намерены использовать эту технологию. В целом, компьютерно-адаптивное тестирование внедряется в штатах и школах по следующим причинам:
В целом, компьютерно-адаптивное тестирование внедряется в штатах и школах по следующим причинам:
- Благодаря использованию более точных и эффективных оценок, на выполнение которых уходит меньше времени, учителя и ученики будут иметь больше времени для обучения и обучения, при этом получая результаты тестов, которые будут либо такими же точными, как традиционные тесты, либо более точными.
- Тесты адаптируют каждый вопрос к знаниям и способностям тестируемого, избавляя учащихся от необходимости бороться с слишком сложными вопросами или тратить время на слишком простые вопросы.
- Тесты могут предоставить более точную и быстро доступную информацию об учебных потребностях учащихся, которую учителя могут использовать для адаптации инструкций и улучшения академической поддержки учащихся.
- Безопасность теста повышена, поскольку не все участники тестирования видят одни и те же элементы.
Дебаты
Поскольку компьютерно-адаптивные тесты все еще относительно новы, дебаты об их использовании, надежности, преимуществах и недостатках только начинают возникать. Поскольку многие штаты планируют в ближайшие годы использовать новые компьютерно-адаптивные онлайн-тесты, эта технология, вероятно, станет объектом все более пристального изучения, дискуссий и дебатов.
Поскольку многие штаты планируют в ближайшие годы использовать новые компьютерно-адаптивные онлайн-тесты, эта технология, вероятно, станет объектом все более пристального изучения, дискуссий и дебатов.
В дополнение к потенциальным преимуществам, описанным выше, можно привести несколько характерных аргументов сторонников компьютерно-адаптивного тестирования:
- Тесты могут помочь определить уровень обучения учащегося более точно, чем экзамены с фиксированными вопросами, особенно для учащихся с низкими и высокими уровнями обучения.
- Адаптивные тесты дают учителям более точную информацию об учениках, которые исключительно искусны или сильно отстают в овладении ожидаемыми знаниями и навыками.
- Тесты могут повысить вовлеченность учащихся в процесс тестирования и, возможно, привести к более точным результатам, поскольку тесты короче, менее утомительны и лучше согласованы с индивидуальными способностями учащегося.
- Компьютеризированная оценка открытых вопросов и вопросов в стиле эссе становится более точной и, возможно, даже более надежной, чем человеческая оценка, что может повысить эффективность и снизить затраты на крупномасштабное стандартизованное тестирование.

Ниже приведены несколько характерных аргументов, которые могут быть выдвинуты критиками компьютерно-адаптивного тестирования:
- Сложная технология, необходимая для выставления оценок за открытые вопросы и разделы сочинений по компьютерным адаптивным тестам, еще не готова для широкого использования в школах.Системы могут быть недостаточно протестированы, а другие могут быть подвержены сбоям и ошибкам, что может привести к неточным результатам, что может поставить в невыгодное положение учащихся, проходящих тесты, что приведет к необходимости оценки человеком.
- Использование компьютеризированных тестов может поставить в невыгодное положение учащихся с более низкой технологической грамотностью и ограниченным доступом к цифровым технологиям, например учащихся из семей с низкими доходами и учащихся из сельских районов с менее надежным доступом в Интернет.
- Переход от экзаменов с использованием бумаги и карандаша к компьютерным адаптивным тестам во многих случаях влечет за собой значительные материально-технические проблемы и финансовые трудности, особенно для штатов, округов и государственных школ, испытывающих нехватку денежных средств.
 Сложное программное обеспечение, необходимое для испытаний — независимо от того, разрабатывается ли оно на заказ или является готовым продуктом — может быть дорогостоящим и потенциально непомерно дорогостоящим.
Сложное программное обеспечение, необходимое для испытаний — независимо от того, разрабатывается ли оно на заказ или является готовым продуктом — может быть дорогостоящим и потенциально непомерно дорогостоящим. - Для школ с небольшим количеством компьютеров или неадекватными компьютерными сетями — или с тем и другим — может быть непомерно сложно выделить время и компьютеры, необходимые всем учащимся для прохождения теста.
- Компьютерное адаптивное тестирование обычно требует надежной технической поддержки, потому что сломанные или неисправные системы могут сорвать администрирование тестов и существенно нарушить расписание и работу школы.
- Для округов и школ, которые все еще полагаются на бумажные документы, переход на онлайн-адаптивное тестирование может быть обременительным или невыполнимым, поскольку школа может не иметь достаточных ресурсов, устройств и технических знаний персонала.
Почему 0,1 не существует в числах с плавающей запятой
Многие начинающие программисты узнают о двоичных числах с плавающей запятой после того, как увидят, что их программы дают странные результаты: «Почему моя программа печатает 0,10000000000000001, когда я ввожу 0. 1? »; «Почему 0,3 + 0,6 = 0,89999999999999991?»; «Почему 6 * 0,1 не равно 0,6?» Подобные вопросы задают каждый день на онлайн-форумах, таких как stackoverflow.com.
1? »; «Почему 0,3 + 0,6 = 0,89999999999999991?»; «Почему 6 * 0,1 не равно 0,6?» Подобные вопросы задают каждый день на онлайн-форумах, таких как stackoverflow.com.
Ответ состоит в том, что большинство десятичных дробей имеют бесконечное количество представлений в двоичном формате. Возьмем, например, 0,1. Это один из самых простых десятичных знаков, который вы можете придумать, и все же в двоичном формате он выглядит таким сложным:
Десятичное число 0,1 В двоичном формате (до 1369 знаков)Биты продолжаются бесконечно; независимо от того, сколько из этих битов вы храните в компьютере, вы никогда не получите двоичный эквивалент десятичного 0.1.
0,1 Двоичный
0,1 — одна десятая или 1/10. Чтобы показать это в двоичном формате, то есть в двоичном формате, разделите двоичную 1 на двоичное 1010, используя двоичное длинное деление:
Вычисление одной десятой в двоичном формате Процесс деления будет повторяться вечно — как и цифры в частном, — потому что 100 («один-ноль-ноль») снова появляется как рабочая часть делимого. Осознавая это, мы можем прервать деление и записать ответ в повторяющейся двусмысленной системе счисления, например, 0,00011.
Осознавая это, мы можем прервать деление и записать ответ в повторяющейся двусмысленной системе счисления, например, 0,00011.
0.1 с плавающей точкой
0,00011 — это конечное представление бесконечного числа цифр. Это не помогает нам с плавающей запятой. Плавающая точка не представляет числа с помощью повторяющихся полос; он представляет их с фиксированным числом бит. Например, в числах с плавающей запятой двойной точности используются 53 бита, поэтому в противном случае бесконечное представление округляется до 53 значащих битов.
Давайте посмотрим, как выглядит 0,1 при двойной точности. Во-первых, давайте запишем его в двоичном формате с усечением до 57 значащих бит:
0.000110011001100110011001100110011001100110011001100110011001…
Биты 54 и выше в сумме составляют более половины значения битовой позиции 53, поэтому округляется до
0,0001100110011001100110011001100110011001100110011001101
В десятичной системе это
0,1000000000000000055511151231257827021181583404541015625
, что немного больше 0,1.
Если вы напечатаете это до 17 значащих десятичных цифр, вы получите 0,10000000000000001 (при печати результат также округляется).Обратите внимание, что если вы напечатаете менее 17 цифр, ответ будет 0,1. Но это всего лишь иллюзия — компьютер не сохранил 0,1.
Оно может быть немного больше или чуть меньше 0,1
В зависимости от того, сколько битов точности используется, приближение 0,1 с плавающей запятой может быть на минус , чем на 0,1. Например, при половинной точности, которая использует 11 значащих битов, 0,1 округляется до 0,0001100110011 в двоичной системе, что составляет 0,0999755859375 в десятичной системе.
0.1 — лишь один из многих примеров
0.1 — это наиболее часто используемый пример при обсуждении «неточностей» с плавающей запятой — поэтому я выбрал его. Но есть еще очень много примеров. Как узнать, есть ли у произвольного десятичного числа эквивалентное двоичное, которое завершается или повторяется?
Конечно, вы могли бы сделать то, что я сделал выше: преобразовать десятичную дробь в целое число, равное степени десяти, а затем выполнить двоичное деление. Если остаток равен нулю, двоичное число завершается; если вы встретите рабочий дивиденд, который вы видели раньше, двузначная дробь повторяется.Этот метод хорош, потому что вы видите, как двоичное представление разворачивается на ваших глазах. Однако это утомительно. Бинарное деление — сложная задача, даже если вы знаете, как это делать.
Если остаток равен нулю, двоичное число завершается; если вы встретите рабочий дивиденд, который вы видели раньше, двузначная дробь повторяется.Этот метод хорош, потому что вы видите, как двоичное представление разворачивается на ваших глазах. Однако это утомительно. Бинарное деление — сложная задача, даже если вы знаете, как это делать.
Существует более простой тест: десятичная дробь имеет эквивалентное завершающее двоичное число тогда и только тогда, когда десятичная дробь, записанная как правильная дробь в младших членах, имеет знаменатель, равный степени двойки. (Требуется немного теории чисел, чтобы понять, почему это работает, но объяснение похоже на то, почему десятичные дроби заканчиваются только для дробей со степенью двойки и / или степенью пяти в их знаменателе.) По этому правилу вы можете видеть, что 0,1 имеет бесконечное бикимальное число: 0,1 = 1/10, а 10 не является степенью двойки. 0.5, с другой стороны, завершается: 0.5 = 5/10 = 1/2. Если спросить, есть ли у десятичной дроби соответствующее завершающееся или повторяющееся двоичное число, это тест, который следует использовать.
Некоторые оконечные бичимальные числа не существуют и в числах с плавающей запятой
Важно отметить, что некоторые десятичные дроби с завершающими двузначными числами также не существуют в числах с плавающей запятой. Это происходит, когда битов больше, чем позволяет точность.Например,
0.500000000000000166533453693773481063544750213623046875
конвертируется в
0.100000000000000000000000000000000000000000000000000011
, но это 54 бита. Округленное до 53 бит становится
0.1000000000000000000000000000000000000000000000000001
, что в десятичной форме составляет
0.50000000000000022204460413080847263336181640625
Такие точно указанные числа вряд ли будут использоваться в реальных программах, так что это не проблема, которая может возникнуть.
Сводка
В чистой математике у каждого десятичного числа есть эквивалентное бицепсное число. В математике с плавающей запятой это совсем не так.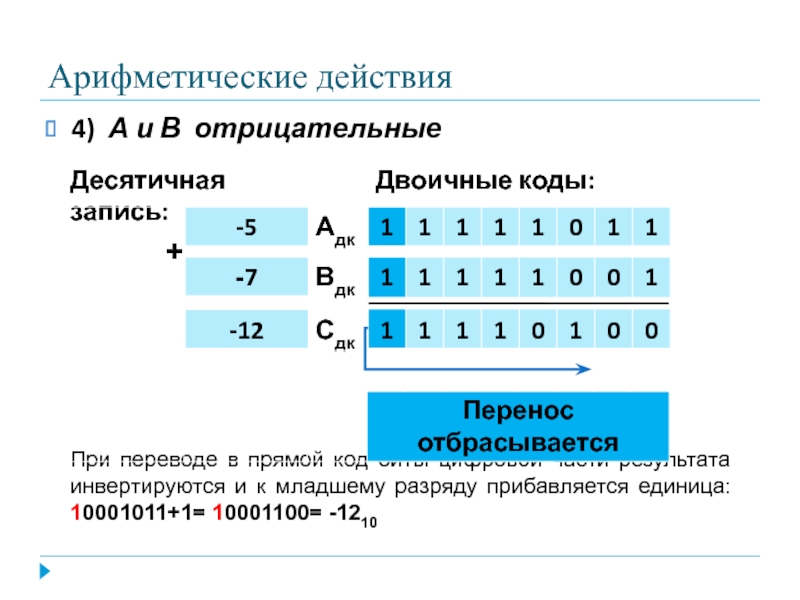
Представление данных — Полевое руководство по информатике
В этом разделе мы рассмотрим, как компьютеры представляют числа. Для начала мы рассмотрим, как работает система счисления с основанием 10, которую мы используем каждый день, а затем рассмотрим двоичную систему счисления, которая является основанием 2. После этого мы рассмотрим некоторые другие характеристики чисел, с которыми приходится иметь дело компьютерам, такие как отрицательные числа и числа с десятичной точкой.
Обычно люди используют десятичную систему счисления (также известную как десятичная). Его стоит быстро пересмотреть, потому что двоичные числа используют те же идеи, что и десятичные числа, только с меньшим количеством цифр!
В десятичном формате значение каждой цифры в числе зависит от позиции в номере.
Например, в 123 долларах 3 представляет 3 доллара, а 1 — 100 долларов.
Каждое разрядное значение в числе стоит в 10 раз больше, чем разрядное значение справа от него, т. Е. Есть «единицы», «десятки», «сотни», «тысячи», «десять тысяч», «сотня». тысячи »,« миллионы »и так далее.Кроме того, есть 10 различных цифр (0,1,2,3,4,5,6,7,8,9), которые могут быть в каждом из этих значений разряда.
Е. Есть «единицы», «десятки», «сотни», «тысячи», «десять тысяч», «сотня». тысячи »,« миллионы »и так далее.Кроме того, есть 10 различных цифр (0,1,2,3,4,5,6,7,8,9), которые могут быть в каждом из этих значений разряда.
Если бы вы могли использовать только одну цифру для представления числа, то наибольшим числом было бы 9. После этого вам понадобится вторая цифра, которая идет налево, давая вам следующие десять чисел (10, 11, 12 … 19). Это потому, что у нас есть 10 цифр, каждая из которых стоит в 10 раз больше, чем цифра справа.
Возможно, вы встречали разные способы выражения чисел в «развернутой форме».Например, если вы хотите написать число в развернутом виде, вы могли бы записать его как:
Более сложный способ записи:
Если вы знаете об экспонентах, вы можете записать это как:
Помните, что любое число в степени 0 равно 1. т.е. 8 x равно 8, потому что это 1.
Ключевые идеи, на которые следует обратить внимание:
- В десятичной системе 10 цифр — 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

- Место — это место в номере, которое представляет собой цифру, т.е.е. единицы, десятки, сотни, тысячи и так далее. Например, в числе 3 находится в разряде «сотни», 2 — в разряде «десятки» и 9 — в разряде «десять тысяч».
- Номера состоят из последовательности цифр.
- Самая правая цифра — это наименьшая ценность (в разряде «единиц»).
- Самая левая цифра имеет наибольшую ценность.
- Поскольку у нас 10 цифр, цифра в каждом месте стоит в 10 раз больше, чем цифра справа от нее.
Все это, наверное, звучит действительно очевидно, но об этом стоит задуматься осознанно, потому что двоичные числа обладают одинаковыми свойствами.
Как обсуждалось ранее, компьютеры могут хранить информацию только с использованием битов, которые имеют 2 возможных состояния.
Это означает, что они не могут представлять числа с основанием 10, используя цифры от 0 до 9, как мы записываем числа в десятичной системе счисления. Вместо этого они должны представлять числа, используя всего 2 цифры — 0 и 1.
Вместо этого они должны представлять числа, используя всего 2 цифры — 0 и 1.
Двоичный код работает так же, как десятичный, хотя поначалу может показаться, что это не так.Поскольку здесь всего 2 цифры, это означает, что каждая цифра в 2 раз больше значения, расположенного справа.
Динарная система счисленияСистему с основанием 10 (десятичную) иногда называют динарной, что больше соответствует имени двоичной системы с основанием 2. Слово «денарий» также относится к римской монете денарий, которая стоила десять ассов («ас» — медная или бронзовая монета). Термин «денарий», кажется, используется в основном в Великобритании; в США, Австралии и Новой Зеландии более распространен термин «десятичный».
Интерактивный рисунок ниже показывает, как эта двоичная система счисления представляет числа. Поиграйте с ним, чтобы увидеть, какие закономерности вы видите.
Найдите представления 4, 7, 12 и 57 с помощью интерактивного интерфейса.
Какое наибольшее число вы можете сделать с помощью интерактивного? Какой самый маленький? Есть ли какое-нибудь целое число между самым большим и самым маленьким, которое вы не можете составить? Есть ли числа с более чем одним представлением? Почему, почему нет?
Наибольшие и наименьшие числа- 000000 в двоичном формате, 0 в десятичном — наименьшее число.
- 111111 в двоичном формате, 63 в десятичном — наибольшее число.
- Все целые значения (0, 1, 2 … 63) в диапазоне могут быть представлены (и для каждого есть уникальное представление). Это то же самое, что и десятичное!
Вы, наверное, заметили из интерактивного материала, что при установке в 1 крайний левый бит («самый старший бит») добавляет 32 к общему количеству, следующий добавляет 16, а затем остальные добавляют 8, 4, 2 и 1 соответственно. .
При значении 0 бит ничего не добавляет к сумме.Итак, идея состоит в том, чтобы составить числа, сложив некоторые или все числа 32, 16, 8, 4, 2 и 1 вместе, и каждое из этих чисел может быть включено только один раз.
Выберите число меньше 61 (например, номер вашего дома, ваш возраст, возраст друга или день месяца, в котором вы родились), установите все двоичные цифры на ноль, а затем начните с самого левого digit (32), пробуя, должно ли оно быть равным нулю или единице. Посмотрите, сможете ли вы найти метод преобразования числа без особых проб и ошибок.Попробуйте разные числа, пока не найдете быстрый способ сделать это.
Определите двоичное представление для 23 без с помощью интерактивного элемента? А как насчет 4, 0 и 32? Проверьте все свои ответы в интерактивном режиме, чтобы убедиться, что они верны.
Подсчет в двоичном формате Можете ли вы придумать систематический подход к двоичному счету? т.е. начните с числа 0, затем увеличьте его до 1, затем 2, затем 3 и так далее, вплоть до максимального числа, которое может быть получено с помощью 7 бит.Попробуйте сосчитать от 0 до 16 и посмотрите, сможете ли вы определить закономерность. Подсказка: подумайте о том, как вы добавляете 1 к числу в базе 10, например. как вы работаете с 7 + 1, 38 + 1, 19 + 1, 99 + 1, 230899999 + 1 и т. д.?
Можете ли вы применить ту же идею к двоичным файлам?
Подсказка: подумайте о том, как вы добавляете 1 к числу в базе 10, например. как вы работаете с 7 + 1, 38 + 1, 19 + 1, 99 + 1, 230899999 + 1 и т. д.?
Можете ли вы применить ту же идею к двоичным файлам?
Используя свои новые знания о двоичной системе счисления, можете ли вы придумать способ считать до более 10 с помощью 10 пальцев? Какое наибольшее число вы можете изобразить своими 10 пальцами? Что, если бы вы также включили 10 пальцев ног (так что у вас есть 20 пальцев рук и ног для счета).
Подсчет в двоичном форматеДвоичное число может быть увеличено, начиная справа и меняя все последовательные биты до тех пор, пока не появится 1 (которая будет в самом первом бите в половине случаев).
Счет по пальцам в двоичном формате означает, что вы можете сосчитать до 31 на 5 пальцах и до 1023 на 10 пальцах.
На YouTube есть несколько видеороликов, на которых люди считают на пальцах двоичный код.
Один поворот состоит в том, чтобы носить белые перчатки с номерами 16, 8, 4, 2, 1 на 5 пальцах соответственно, что позволяет легко определить ценность поднятых пальцев.
Интерактивный использует ровно 6 бит. На практике мы можем использовать столько битов, сколько нам нужно, точно так же, как мы это делаем с десятичными числами. Например, при 5 битах значения разряда будут 16, 8, 4, 2 и 1, поэтому наибольшее значение будет 11111 в двоичном формате или 31 в десятичном. Представление 14 с помощью 5 бит даст 01110.
Представление чисел битамиНапишите представления для следующего. Если сделать представление невозможно, поставьте «Невозможно».
- Представляет 101 с 7 битами
- Представляет 28 с 10 битами
- Представляет 7 с 3 битами
- Представляет 18 с 4 битами
- Представляет 28299 28299 с 16 бит
Ответы (пробелы добавлены для облегчения чтения, но не обязательны).
- 101 с 7 битами: 110 0101
- 28 с 10 битами: 00 0001 1100
- 7 с 3 битами: 111
- 18 с 4 битами: Невозможно (недостаточно бит для представления значения)
- 28232 с 16 битами: 0110 1110 0100 1000
Важным понятием двоичных чисел является диапазон значений, который может быть представлен с использованием заданного числа битов. Когда у нас есть 8 бит, двоичные числа становятся полезными — они могут представлять значения от 0 до 255, поэтому достаточно сохранить чей-то возраст, день месяца и так далее.
Что такое байт? Группы из 8 бит настолько полезны, что имеют собственное имя: байт.
Компьютерная память и дисковое пространство обычно делятся на байты, а большие значения сохраняются с использованием более одного байта.
Например, двух байтов (16 бит) достаточно для хранения чисел от 0 до 65 535.
Четыре байта (32 бита) могут хранить числа до 4 294 967 295. Вы можете проверить эти числа, вычислив разрядные значения битов.
Каждый добавленный бит удваивает диапазон числа.
Вы можете проверить эти числа, вычислив разрядные значения битов.
Каждый добавленный бит удваивает диапазон числа.
На практике компьютеры хранят числа с 16, 32 или 64 битами. Это связано с тем, что это полные числа байтов (байт равен 8 битам) и позволяет компьютерам узнать, где каждое число начинается и заканчивается.
Бинарные торты — предотвращение пожаровВ свечах на праздничных тортах используется система нумерации с основанием 1, в которой каждое место стоит на 1 больше, чем то, что находится справа. Например, число 3 — 111, а 10 — 1111111111. Это может вызвать проблемы по мере взросления — если вы когда-либо видели торт со 100 свечами, вы знаете, что это серьезная опасность возгорания.
К счастью, для свечей на день рождения можно использовать двоичное представление — каждая свеча либо горит, либо не горит. Например, если вам 18 лет, двоичное представление — 10010, и вам нужно 5 свечей (при этом горят только две из них).
Есть видео об использовании двоичной системы счисления для подсчета до 1023 на руках, а также об использовании ее для праздничных тортов.
В большинстве случаев двоичные числа хранятся в электронном виде, и нам не нужно беспокоиться об их осмыслении.Но иногда бывает полезно записывать и обмениваться числами, такими как уникальный идентификатор, присвоенный каждому цифровому устройству (MAC-адрес), или цвета, указанные на странице HTML.
Запись длинных двоичных чисел утомительна — например, предположим, что вам нужно скопировать 16-битное число 0101001110010001. Широко используемый ярлык — разбить число на 4-битные группы (в данном случае 0101 0011 1001 0001), а затем записать цифру, которую представляет каждая группа (что дает 5391).Есть только одна небольшая проблема: каждая группа из 4 бит может доходить до 1111, что составляет 15, а цифры могут доходить только до 9.
Решение простое: мы вводим символы для цифр от 1010 (10) до 1111 (15), которые представляют собой просто буквы от A до F. Так, например, 16-битное двоичное число 1011 1000 1110 0001 можно более кратко записать как B8E1.
Буква «B» представляет двоичное число 1011, которое является десятичным числом 11, а буква E представляет двоичное число 1110, которое является десятичным числом 14.
Так, например, 16-битное двоичное число 1011 1000 1110 0001 можно более кратко записать как B8E1.
Буква «B» представляет двоичное число 1011, которое является десятичным числом 11, а буква E представляет двоичное число 1110, которое является десятичным числом 14.
Поскольку теперь у нас 16 цифр, это представление с основанием 16 и известно как шестнадцатеричное (или для краткости шестнадцатеричное).Преобразование между двоичным и шестнадцатеричным числами очень просто, и поэтому шестнадцатеричный — очень распространенный способ записи больших двоичных чисел.
Вот полная таблица всех 4-битных чисел и их шестнадцатеричного эквивалента:
| Двоичный | Шестигранник |
|---|---|
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | А |
| 1011 | Б |
| 1100 | С |
| 1101 | D |
| 1110 | E |
| 1111 | Ф |
Например, наибольшее 8-битное двоичное число — 11111111. Это можно записать как FF в шестнадцатеричном формате.
Оба этих представления означают 255 в нашей обычной десятичной системе (вы можете проверить это, преобразовав двоичное число в десятичное).
Это можно записать как FF в шестнадцатеричном формате.
Оба этих представления означают 255 в нашей обычной десятичной системе (вы можете проверить это, преобразовав двоичное число в десятичное).
Какие обозначения вы используете, будет зависеть от ситуации; двоичные числа представляют то, что на самом деле хранится, но могут затруднять чтение и запись; шестнадцатеричные числа — хорошее сокращение двоичного; а десятичные числа используются, если вы пытаетесь понять значение числа или выполняете обычные вычисления.Все три широко используются в информатике.
Однако важно помнить, что компьютеры только представляют числа в двоичном формате. Они не могут представлять числа непосредственно в десятичном или шестнадцатеричном формате.
Обычно числа хранятся на компьютерах в электронных таблицах или базах данных.
Они могут быть введены либо с помощью программы электронных таблиц или базы данных, либо с помощью программы, написанной вами или кем-то другим, либо с помощью дополнительного оборудования, такого как датчики, для сбора данных, таких как температура, давление воздуха или сотрясение земли.
Некоторые вещи, которые мы можем рассматривать как числа, например номер телефона (03) 555-1234, на самом деле не хранятся как числа, поскольку они содержат важные символы (например, дефисы и пробелы), а также ведущий 0. который был бы потерян, если бы он был сохранен как число (указанное выше число получилось бы как 35551234, что не совсем верно). Они сохраняются как текст , что обсуждается в следующем разделе.
С другой стороны, вещи, которые не похожи на числа (например, «30 января 2014 года»), часто сохраняются с использованием значения, которое преобразуется в формат, понятный для читателя (попробуйте ввести две даты в Excel, а затем вычтите одно из другого — результат будет полезным числом).В базовом представлении используется число. Программный код используется для преобразования базового представления в значимую дату в пользовательском интерфейсе.
Подробнее о представлении даты Разница между двумя датами в Excel — это количество дней между ними; сама дата (как и во многих системах) сохраняется как время, прошедшее с фиксированной даты (например, 1 января 1900 г. ).
Вы можете проверить это, введя дату типа «1 января 1850 года» — есть вероятность, что она не будет отформатирована как обычная дата.Точно так же дата, находящаяся достаточно далеко в будущем, может вести себя странно из-за ограниченного количества битов, доступных для хранения даты.
).
Вы можете проверить это, введя дату типа «1 января 1850 года» — есть вероятность, что она не будет отформатирована как обычная дата.Точно так же дата, находящаяся достаточно далеко в будущем, может вести себя странно из-за ограниченного количества битов, доступных для хранения даты.
Числа используются для хранения таких разнообразных вещей, как даты, оценки учащихся, цены, статистика, научные данные, размеры и размеры графики.
При сохранении чисел на компьютере необходимо учитывать следующие моменты:
- Какой диапазон чисел должен быть представлен?
- Как работать с отрицательными числами?
- Как работать с десятичными знаками и дробями?
На практике нам нужно выделить фиксированное количество битов для числа, прежде чем мы узнаем, насколько велико это число.Часто это 32 или 64 бита, хотя при необходимости можно установить 16 или даже 128 бит.
Это потому, что в противном случае компьютер не знает, где начинается и где заканчивается число.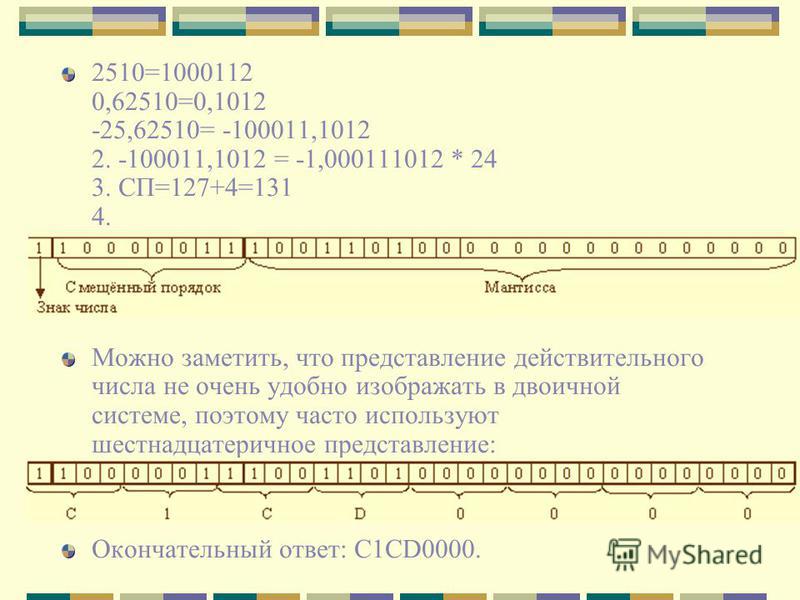
Любая система, которая хранит числа, должна идти на компромисс между количеством бит, выделенных для хранения числа, и диапазоном значений, которые могут быть сохранены.
В некоторых системах (например, в языках программирования и базах данных Java и C) можно указать, насколько точно должны храниться числа; в других — заранее (например, в таблицах).
Некоторые из них могут работать с произвольно большими числами, увеличивая пространство, используемое для их хранения по мере необходимости (например, целые числа на языке программирования Python). Однако вполне вероятно, что они все еще работают с кратным 32 бит (например, 64 бит, 96 бит, 128 бит, 160 бит и т. Д.). Если число становится слишком большим, чтобы поместиться в 32 бита, компьютер перераспределяет его, чтобы иметь до 64 бита.
В некоторых языках программирования нет проверки, когда число становится слишком большим (переполнение).Например, если у вас есть 8-битное число с использованием дополнения до двух, то 01111111 является наибольшим числом (127), и если вы добавите его без проверки, оно изменится на 10000000, что оказывается числом -128. (Не беспокойтесь о дополнении до двух, об этом позже в этом разделе.)
Это может вызвать серьезные проблемы, если не будет проверено, и является причиной варианта проблемы 2000 года, называемой проблемой 2038 года, связанной с переполнением 32-битного числа для дат во вторник, 19 января 2038 года.
(Не беспокойтесь о дополнении до двух, об этом позже в этом разделе.)
Это может вызвать серьезные проблемы, если не будет проверено, и является причиной варианта проблемы 2000 года, называемой проблемой 2038 года, связанной с переполнением 32-битного числа для дат во вторник, 19 января 2038 года.
На крошечных компьютерах, таких как те, что встроены в вашу машину, стиральную машину или крошечный датчик, который едва ли больше песчинки, нам может потребоваться более точно указать, насколько большим должно быть число.Хотя компьютеры предпочитают работать с фрагментами по 32 бита, мы могли бы написать программу (в качестве примера для датчика землетрясения), которая знает, что первые 7 бит — это широта, следующие 7 бит — это долгота, следующие 10 бит — глубина. , а последние 8 бит — это сила.
Даже на стандартных компьютерах важно хорошо подумать о количестве бит, которое вам понадобится.
Например, если у вас есть поле в вашей базе данных, которое может быть «0», «1», «2» или «3» (возможно, представляя четыре основания, которые могут встречаться в последовательности ДНК), и вы использовали 64-битное число для каждого, которое будет увеличиваться по мере роста вашей базы данных. Если в вашей базе данных 10 000 000 элементов, вы потратите 62 бита для каждого из них (для представления 4 чисел в примере требуется только 2 бита), всего 620 000 000 бит, что составляет около 74 МБ.
Если вы часто делаете это в своей базе данных, это действительно складывается — человеческая ДНК содержит около 3 миллиардов пар оснований, поэтому использовать более 2 бит для каждой из них невероятно расточительно.
Если в вашей базе данных 10 000 000 элементов, вы потратите 62 бита для каждого из них (для представления 4 чисел в примере требуется только 2 бита), всего 620 000 000 бит, что составляет около 74 МБ.
Если вы часто делаете это в своей базе данных, это действительно складывается — человеческая ДНК содержит около 3 миллиардов пар оснований, поэтому использовать более 2 бит для каждой из них невероятно расточительно.
А для таких приложений, как Google Maps, которые хранят астрономический объем данных, тратить пространство впустую — вообще не вариант!
Сколько бит вам понадобится?Действительно полезно знать примерно, сколько битов вам понадобится для представления определенного значения.Подумайте о следующих сценариях и выберите наилучшее количество бит из представленных вариантов. Вы хотите убедиться, что максимально возможное число поместится в число битов, но вы также хотите убедиться, что вы не тратите впустую пространство.
- Сохранение дня недели — а) 1 бит — б) 4 бита — в) 8 бит — d) 32 бита
- Запоминание количества людей в мире — а) 16 бит — б) 32 бита — в) 64 бита — d) 128 бит
- Сохранение количества дорог в Новой Зеландии — а) 16 бит — б) 32 бита — в) 64 бита — d) 128 бит
- Сохранение количества звезд во Вселенной — а) 16 бит — б) 32 бита — в) 64 бита — г) 128 бит
-
b(на самом деле 3 бита достаточно, так как он дает 8 значений, но с суммами, которые равномерно помещаются в 8-битные байты, легче работать) -
c(32 бита немного слишком мало, поэтому вы будете требуется 64 бита) -
b(Это сложный вопрос, но разработчику баз данных придется задуматься. В Новой Зеландии около 94 000 км дорог, поэтому, если бы средняя длина дороги составляла 1 км, было бы слишком много дорог для 16 бит. В любом случае, 32 бита было бы безопасным выбором.)
В Новой Зеландии около 94 000 км дорог, поэтому, если бы средняя длина дороги составляла 1 км, было бы слишком много дорог для 16 бит. В любом случае, 32 бита было бы безопасным выбором.) -
d(Даже 64 бит недостаточно, но 128 бит — это достаточно! Помните, что 128 бит — это не вдвое больше диапазона 64 бит.)
Представление двоичных чисел, которое мы рассмотрели до сих пор, позволяет нам представлять только положительные числа. На практике мы также захотим иметь возможность представлять отрицательные числа, например, когда баланс аккаунта становится отрицательным или температура падает ниже нуля.В нашем обычном представлении чисел с основанием 10 мы представляем отрицательные числа, помещая знак минус перед числом. Но в двоичном формате это так просто?
Мы рассмотрим два возможных подхода: добавление простого знакового бита, очень похожего на десятичную дробь, а затем более полезную систему, называемую дополнением до двух.
На компьютере у нас нет знаков минус для чисел (не очень хорошо использовать текст на основе одного при представлении числа, потому что вы не можете выполнять арифметические операции с символами), но мы можем сделать это, выделив один дополнительный бит, называемый знаком , бит, представляющий знак минус. Как и в случае с десятичными числами, мы помещаем отрицательный индикатор слева от числа — когда бит знака установлен на «0», это означает, что число положительное, а когда бит знака установлен на «1», число равно отрицательный (как будто перед ним стоит знак минус).
Как и в случае с десятичными числами, мы помещаем отрицательный индикатор слева от числа — когда бит знака установлен на «0», это означает, что число положительное, а когда бит знака установлен на «1», число равно отрицательный (как будто перед ним стоит знак минус).
Например, если бы мы хотели представить число 41 , используя 7 бит вместе с дополнительным битом, который является битом знака (чтобы получить всего 8 битов), мы бы представили его как 00101001 . Первый бит равен 0, что означает положительное число, затем оставшиеся 7 бит дают 41 , то есть число +41 .Если бы мы хотели получить -59 , это было бы 10111011 . Первый бит равен 1, что означает отрицательное число, а оставшиеся 7 бит представляют 59 , то есть число -59 .
Представление отрицательных чисел знаковым битомИспользуя 8 битов, как описано выше (один для знака и 7 для действительного числа), каковы будут двоичные представления для 1, -1, -8, 34, -37, -88 и 102?
Представление отрицательных чисел знаковым битомПробелы не обязательны, но добавлены для облегчения чтения двоичных чисел
- 1 — 0000 0001
- — 1 — 1000 0001
- — 8 — 1000 1000
- 34 — 0010 0010
- -37 — 1010 0101
- -88 — 1101 1000
- 102 — 0110 0110
Так же легко пойти другим путем. Если у нас есть двоичное число 10010111 , мы знаем, что оно отрицательное, потому что первая цифра — 1.
Числовая часть — это следующие 7 битов 0010111 , что составляет 23 .
Это означает, что это номер -23 .
Если у нас есть двоичное число 10010111 , мы знаем, что оно отрицательное, потому что первая цифра — 1.
Числовая часть — это следующие 7 битов 0010111 , что составляет 23 .
Это означает, что это номер -23 .
Какими будут десятичные значения для следующего, если предположить, что первый бит является битом знака?
- 00010011
- 10000110
- 10100011
- 01111111
- 11111111
- 00010011 равно 19
- 10000110 это -6
- 10100011 равно -35
- 01111111 равно 127
- 11111111 равно -127
А как насчет 10000000? Это преобразуется в -0 .И 00000000 — это +0 .
Поскольку -0 и +0 равны нулю, очень странно иметь два разных представления для одного и того же числа.
Это одна из причин, по которой мы не используем на практике простой знаковый бит. Вместо этого компьютеры обычно используют более сложное представление отрицательных двоичных чисел, называемое дополнением до двух .
Существует альтернативное представление, называемое два дополнения , которое позволяет избежать двух представлений для 0 и, что более важно, упрощает арифметические операции с отрицательными числами.
Представление положительных чисел с дополнением до двух
Представление положительных чисел — это тот же метод, который вы уже изучили. При использовании 8 битов крайний левый бит — это ноль, а остальные 7 бит — обычное двоичное представление числа; например, 1 будет 00000001 , а 50 будет 00110010 .
Представление отрицательных чисел с дополнением до двух
Здесь все становится интереснее. Чтобы преобразовать отрицательное число в его представление с дополнением до двух, используйте следующий процесс.
1. Преобразуйте число в двоичное (не используйте знаковый бит и представляйте, что это положительное число).
2. Инвертируйте все цифры (т.е. замените 0 на 1 и 1 на 0).
3. Добавьте 1 к результату (добавить 1 в двоичном формате легко; вы можете сделать это, сначала преобразовав в десятичное, но хорошо подумайте о том, что произойдет, когда двоичное число увеличивается на 1, попробовав несколько; в панель ниже).
Чтобы преобразовать отрицательное число в его представление с дополнением до двух, используйте следующий процесс.
1. Преобразуйте число в двоичное (не используйте знаковый бит и представляйте, что это положительное число).
2. Инвертируйте все цифры (т.е. замените 0 на 1 и 1 на 0).
3. Добавьте 1 к результату (добавить 1 в двоичном формате легко; вы можете сделать это, сначала преобразовав в десятичное, но хорошо подумайте о том, что произойдет, когда двоичное число увеличивается на 1, попробовав несколько; в панель ниже).
Например, предположим, что мы хотим преобразовать -118 в его представление с дополнением до двух. Мы будем использовать этот процесс следующим образом. 1. Двоичное число для 118 — 01110110 . 2. 01110110 с перевернутыми цифрами будет 10001001 . 3. 10001001 + 1 это 10001010 .
Следовательно, представление в виде дополнения до двух для -118 будет 10001010 .
Правило прибавления единицы к двоичному числу довольно простое, поэтому мы позволим вам выяснить это сами.Во-первых, если двоичное число заканчивается на 0 (например, 1101010), как изменится число, если вы замените последний 0 на 1? Теперь, если он заканчивается на 01, насколько он увеличится, если вы измените 01 на 10? А как насчет того, чтобы закончить на 011? 011111?
Метод добавления настолько прост, что легко собрать компьютерное оборудование, которое сделает это очень быстро.
Определение дополнения двухКаким будет представление в виде дополнения до двух следующих чисел: с использованием 8 битов ? Следуйте процедуре, описанной в этом разделе, и помните, что вам не нужно делать ничего особенного для положительных чисел.
- 19
- -19
- 107
- -107
- -92
- 19 в двоичном формате — это 0001 0011 , которое является дополнением до двух для положительного числа.
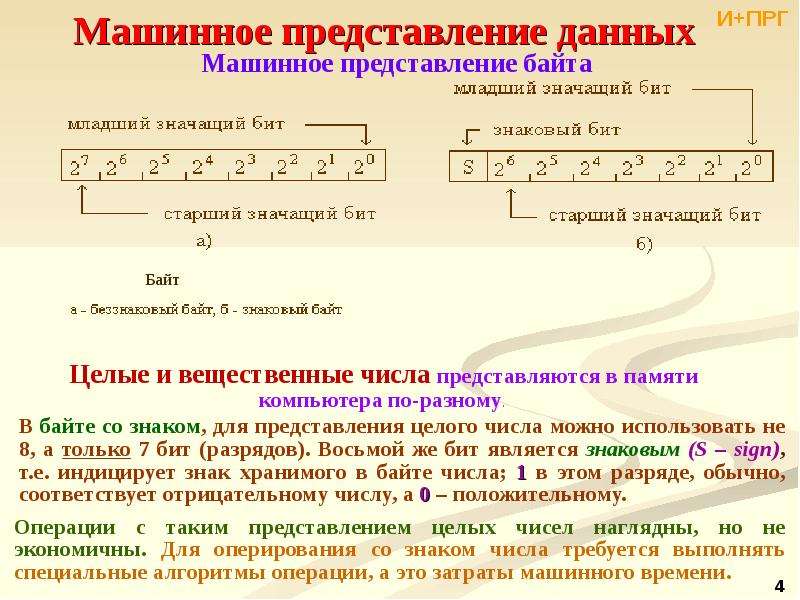
- Для -19 мы берем двоичное положительное значение 0001 0011 (см. Выше), инвертируем его в 1110 1100 и добавляем 1, получая представление 1110 1101 .
- 107 в двоичном формате — это 0110 1011 , которое является дополнением до двух для положительного числа.
- Для -107 мы берем двоичное положительное значение, равное 0110 1011 (см. Выше), инвертируем его в 1001 0100 и добавляем 1, получая представление 1001 0101 .
- Для -92 мы берем двоичное положительное значение, равное 0101 1100, инвертируем его в 1010 0011 и добавляем 1, получая представление 1010 0100 . (Если у вас это неверно, дважды проверьте, правильно ли вы увеличили на 1).
Преобразование двоичного дополнения обратно в десятичное
Чтобы обратить процесс вспять, нам нужно знать, является ли число, на которое мы смотрим, положительным или отрицательным.Для положительных чисел мы можем просто преобразовать двоичное число обратно в десятичное. Но для отрицательных чисел нам сначала нужно преобразовать их обратно в нормальное двоичное число.
Но для отрицательных чисел нам сначала нужно преобразовать их обратно в нормальное двоичное число.
Итак, как мы узнаем, положительное или отрицательное число? Оказывается (по причинам, которые вы поймете позже в этом разделе), отрицательные числа в дополнительном коде всегда начинаются с 1, а положительные числа всегда начинаются с 0. Вернитесь к предыдущим примерам, чтобы еще раз проверить это.
Итак, если число начинается с 1, используйте следующий процесс для преобразования числа обратно в отрицательное десятичное число.
- Вычтите 1 из числа.
- Обратить все цифры.
- Преобразует полученное двоичное число в десятичное.
- Поставьте перед ним знак минус.
Итак, если бы нам нужно было преобразовать 11100010 обратно в десятичное, мы бы сделали следующее.
- Вычтем 1 из 11100010 , что даст 11100001 .
- Инвертируйте все цифры, получая 00011110 .

- Преобразуйте 00011110 в двоичное число, получив 30 .
- Добавьте отрицательный знак, получив -30 .
Преобразуйте следующие два дополнительных числа в десятичные числа.
- 00001100
- 10001100
- 10111111
- 12
- 10001100 -> (-1) 10001011 -> (инвертированный) 01110100 -> (в десятичный) 116 -> (добавлен отрицательный знак) -116
- 10111111 -> (-1) 10111110 — > (инвертированный) 01000001 -> (в десятичный) 65 -> (добавлен отрицательный знак) -65
Сколько чисел можно представить с помощью дополнения до двух?
Хотя поначалу может показаться, что в качестве знакового бита нет бита, самый левый бит ведет себя как единичный.С 8 битами вы все еще можете создать только 256 возможных шаблонов из 0 и 1. Если вы попытаетесь использовать 8 бит для представления положительных чисел до 255 и отрицательных чисел до -255, вы быстро поймете, что некоторые числа были отображены на один и тот же набор битов.
Очевидно, это сделает невозможным узнать, какое число на самом деле представлено!
Если вы попытаетесь использовать 8 бит для представления положительных чисел до 255 и отрицательных чисел до -255, вы быстро поймете, что некоторые числа были отображены на один и тот же набор битов.
Очевидно, это сделает невозможным узнать, какое число на самом деле представлено!
На практике могут быть представлены числа в следующих диапазонах.
Беззнаковый диапазон — это количество чисел, которые вы можете представить, если вы разрешаете только положительные числа (знак не нужен), а два дополнения. Диапазон — это количество чисел, которые вы можете представить, если вам нужны как положительные, так и отрицательные числа.Вы можете решить это, потому что диапазон 8-битных значений, если они хранятся с использованием беззнаковых чисел, будет от 00000000 до 11111111 (то есть от 0 до 255 в десятичном формате), а диапазон дополнения до двух со знаком составляет от 10000000 (наименьшее число, — 128 в десятичной системе счисления) до 01111111 (наибольшее число, 127 в десятичной системе). Это может показаться немного странным, но это работает очень хорошо, потому что можно использовать обычное двоичное сложение, если вы используете это представление, даже если вы добавляете отрицательное число.
Это может показаться немного странным, но это работает очень хорошо, потому что можно использовать обычное двоичное сложение, если вы используете это представление, даже если вы добавляете отрицательное число.
| Номер | Диапазон без знака | Диапазон дополнения до двух |
|---|---|---|
| 8 бит | от 0 до 255 | -128 до 127 |
| 16 бит | 0 до 65 535 | -32 768 до 32 767 |
| 32 бит | 0 до 4 294 967 295 | −2 147 483 648 до 2 147 483 647 |
| 64 бит | 0 до 18 446 744 073 709 551 615 | от 9,223,372,036,854,775,808 до 9,223,372,036,854,775,807 |
Прежде чем добавлять отрицательные двоичные числа, мы рассмотрим сложение положительных чисел.Это в основном то же самое, что и методы сложения, используемые для десятичных чисел, за исключением того, что правила намного проще, потому что вы можете добавить только две разные цифры!
Вы, наверное, узнали о сложении столбцов. Например, следующее добавление столбца будет использоваться для получения 128 + 255 .
Например, следующее добавление столбца будет использоваться для получения 128 + 255 .
1 (несет)
128
+255
----
383
Когда вы добавляете 5 + 8, результат больше 9, поэтому вы помещаете 3 в столбец с единицей и переносите 1 в столбец с десятками.Точно так же работает двоичное сложение.
Сложение положительных двоичных чисел
Если вы хотите сложить два положительных двоичных числа, например 00001111 и 11001110 , вы должны выполнить аналогичный процесс сложения столбцов. Вам нужно только знать 0 + 0, 0 + 1, 1 + 0, и 1 + 1, и 1 + 1 + 1. Первые три — это то, что вы могли ожидать. Добавление 1 + 1 вызывает цифру переноса, поскольку в двоичном формате 1 + 1 = 10, что переводится в «0, переносить 1» при добавлении столбца.Последнее, 1 + 1 + 1, в двоичном формате складывается до 11, что можно выразить как «1, переносить 1». Для двух наших примеров чисел сложение работает следующим образом:
111 (несет)
11001110
+00001111
---------
11011101
Помните, что цифры могут быть только 1 или 0. Таким образом, вам нужно будет перенести 1 в следующий столбец, если сумма, которую вы получите для столбца, составляет (десятичное) 2 или 3.
Таким образом, вам нужно будет перенести 1 в следующий столбец, если сумма, которую вы получите для столбца, составляет (десятичное) 2 или 3.
Добавление отрицательных чисел с помощью простого знакового бита
С отрицательными числами, использующими знаковые биты, как мы делали раньше, это не работает.Если вы хотите сложить +11 (01011) и -7 (10111) , вы ожидаете получить ответ +4 (00100) .
11111 (несет)
01011
+10111
100010
То есть -2 .
Один из способов решения проблемы — использовать вместо этого вычитание столбцов. Но для этого потребовалось бы предоставить компьютеру аппаратную схему, которая могла бы это сделать. К счастью, в этом нет необходимости, потому что сложение с отрицательными числами работает автоматически с использованием дополнения до двух!
Сложение отрицательных чисел с дополнением до двух
Для вышеуказанного сложения (+11 + -7) мы можем начать с преобразования чисел в их 5-битную форму дополнения до двух.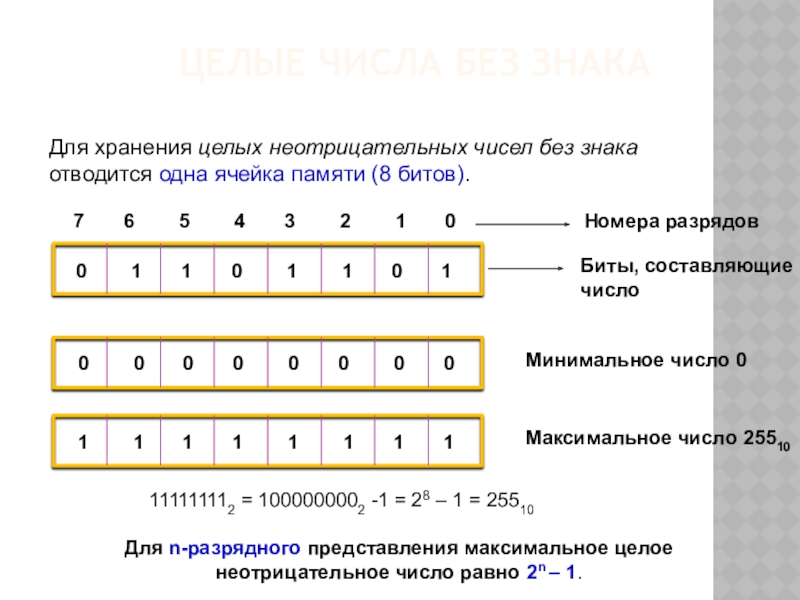 Поскольку 01011 (+11) — положительное число, изменять его не нужно.
Но для отрицательного числа 00111 (-7) (знаковый бит из перед удален, поскольку мы не используем его для дополнения до двух), нам нужно инвертировать цифры, а затем добавить 1, получив 11001 .
Поскольку 01011 (+11) — положительное число, изменять его не нужно.
Но для отрицательного числа 00111 (-7) (знаковый бит из перед удален, поскольку мы не используем его для дополнения до двух), нам нужно инвертировать цифры, а затем добавить 1, получив 11001 .
Сложение этих двух чисел работает следующим образом:
01011
11001
100100
Любые лишние биты слева (помимо того, что мы используем, в данном случае 5 бит) были усечены.Остается 00100 , что составляет 4 , как мы и ожидали.
Мы также можем использовать это для вычитания. Если мы вычитаем положительное число из положительного, нам нужно будет преобразовать вычитаемое число в отрицательное. Затем мы должны сложить два числа. Это то же самое, что и для десятичных чисел, например 5-2 = 3 то же самое, что 5 + (-2) = 3.
Это свойство дополнения до двух очень полезно.
Это означает, что положительные и отрицательные числа могут обрабатываться одной и той же компьютерной схемой, а сложение и вычитание можно рассматривать как одну и ту же операцию.
Идею использования «дополнительного» числа для замены вычитания на сложение можно увидеть, проделав то же самое в десятичной системе счисления. Дополнением к десятичной цифре является цифра, которая в сумме дает 10; например, дополнение до 4 равно 6, а дополнение до 8 равно 2. (Слово «дополнение» происходит от корня «полный» — оно завершает его до красивого круглого числа.)
Вычитание 2 из 6 — это то же самое, что добавление дополнения и игнорирование лишней 1 цифры слева.Дополнение до 2 равно 8, поэтому мы прибавляем 8 к 6, получая (1) 4.
Для больших чисел (таких как вычитание двух трехзначных чисел 255–128) дополнение — это число, которое складывается до следующей степени 10, то есть 1000–128 = 872. Убедитесь, что добавление 872 к 255 дает (почти) тот же результат, что и вычитание 128.
Вычислить дополнения в двоичном формате намного проще, потому что нужно работать только с двумя цифрами, но вычисление их в десятичном формате может помочь вам понять, что происходит.
Мы рассмотрели два различных способа представления отрицательных чисел на компьютере. На практике простой знаковый бит используется редко из-за того, что он имеет два разных представления нуля и требует другой компьютерной схемы для обработки отрицательных и положительных чисел, а также для выполнения сложения и вычитания.
Дополнение до двух широко используется, поскольку оно имеет только одно представление для нуля и позволяет обрабатывать положительные и отрицательные числа одинаково, а сложение и вычитание — как одну операцию.
Существуют и другие системы, такие как «Дополнение до одного» и «Избыток-k», но на практике наиболее широко используется дополнение до двух.
Предыдущий:Начало работы Далее:
Текст
границ | Оценка программы компьютерного обучения для улучшения навыков арифметики и представления пространственных чисел у детей начальной школы
Введение
Уже на ранней стадии развития между детьми наблюдаются значительные различия в обработке чисел и вычислении (Dowker, 2005). Трудности и недостатки, возникающие на раннем этапе обучения, потенциально могут отрицательно повлиять на дальнейший курс обучения и являются прогностическим признаком «неуспеваемости» (Jordan et al., 2003; Morgan et al., 2009). Базовые числовые навыки особенно важны для прогнозирования будущего процесса обучения (Kaufmann et al., 2005; Jordan et al., 2007; Krajewski and Schneider, 2009), а ранние различия в основных числовых навыках становятся более выраженными с возрастом во время обучения. начальная школа (Aunola et al., 2004; Гири, 2006). Результаты показывают, что помимо базовых навыков работы с числами, владение основными арифметическими операциями имеет важное значение для дальнейшего развития математических способностей в начальной школе (Mercer, Miller, 1992; Van Luit and Naglieri, 1999; Duncan et al., 2007). Эти результаты демонстрируют актуальность целевых мероприятий, которые обеспечивают достаточное развитие базовых математических навыков на ранней стадии, чтобы заложить прочную основу для будущих процессов обучения.
Трудности и недостатки, возникающие на раннем этапе обучения, потенциально могут отрицательно повлиять на дальнейший курс обучения и являются прогностическим признаком «неуспеваемости» (Jordan et al., 2003; Morgan et al., 2009). Базовые числовые навыки особенно важны для прогнозирования будущего процесса обучения (Kaufmann et al., 2005; Jordan et al., 2007; Krajewski and Schneider, 2009), а ранние различия в основных числовых навыках становятся более выраженными с возрастом во время обучения. начальная школа (Aunola et al., 2004; Гири, 2006). Результаты показывают, что помимо базовых навыков работы с числами, владение основными арифметическими операциями имеет важное значение для дальнейшего развития математических способностей в начальной школе (Mercer, Miller, 1992; Van Luit and Naglieri, 1999; Duncan et al., 2007). Эти результаты демонстрируют актуальность целевых мероприятий, которые обеспечивают достаточное развитие базовых математических навыков на ранней стадии, чтобы заложить прочную основу для будущих процессов обучения. Это исследование направлено на оценку адаптивной программы, построенной на теоретических моделях обработки чисел и численного развития.Он предлагает детям на раннем этапе возможность обучить именно тем аспектам обработки чисел и арифметическим навыкам, в которых они все еще нуждаются в поддержке.
Это исследование направлено на оценку адаптивной программы, построенной на теоретических моделях обработки чисел и численного развития.Он предлагает детям на раннем этапе возможность обучить именно тем аспектам обработки чисел и арифметическим навыкам, в которых они все еще нуждаются в поддержке.
Теоретические модели обработки чисел и численного развития
В последние годы были предложены различные модели обработки и вычисления чисел (например, McCloskey et al., 1985; Cipolotti and Butterworth, 1995). Модель тройного кода (Dehaene, 1992) в настоящее время является наиболее влиятельной моделью. Он предполагает интегративную сеть, которая определяется тремя различными модулями (вербальный, арабский и аналоговый модуль), связанных с обработкой чисел.Модули характеризуются различными репрезентативными свойствами и функциями чисел и связаны двунаправленными ссылками перекодирования. Устный модуль поддерживает подсчет и поиск фактов, визуально-арабский модуль требуется для решения письменной арифметики, а модуль аналоговой величины — для семантической обработки чисел. Dehaene et al. (1999) показали, что с помощью функциональной нейровизуализации основные компоненты математического развития можно отнести к определенным областям мозга.Что касается оценки и точного расчета, авторы выделили различные области мозга, задействованные во время обработки. Эти данные подтверждают предположения об «аналоговом представлении величин» и «слухово-вербальном представлении» (Jacobs and Petermann, 2003). Основываясь на своем метаанализе фМРТ, Арсалиду и Тейлор (2011) предложили расширение модели тройного кода. Авторы продемонстрировали актуальность вспомогательных и предметно-общих функций, задействованных при решении арифметических задач.Более того, недавние исследования показывают, что совпадение представлений чисел в различных обозначениях чисел увеличивается с возрастом, опытом и образованием (Kucian and Kaufmann, 2009; Kaufmann et al., 2011). Другие исследования фМРТ показывают, что ментальная числовая линия появляется в течение первых школьных лет в теменной доле в результате практики и опыта (Rivera et al.
Dehaene et al. (1999) показали, что с помощью функциональной нейровизуализации основные компоненты математического развития можно отнести к определенным областям мозга.Что касается оценки и точного расчета, авторы выделили различные области мозга, задействованные во время обработки. Эти данные подтверждают предположения об «аналоговом представлении величин» и «слухово-вербальном представлении» (Jacobs and Petermann, 2003). Основываясь на своем метаанализе фМРТ, Арсалиду и Тейлор (2011) предложили расширение модели тройного кода. Авторы продемонстрировали актуальность вспомогательных и предметно-общих функций, задействованных при решении арифметических задач.Более того, недавние исследования показывают, что совпадение представлений чисел в различных обозначениях чисел увеличивается с возрастом, опытом и образованием (Kucian and Kaufmann, 2009; Kaufmann et al., 2011). Другие исследования фМРТ показывают, что ментальная числовая линия появляется в течение первых школьных лет в теменной доле в результате практики и опыта (Rivera et al. , 2005; Kucian et al., 2008).
, 2005; Kucian et al., 2008).
Модель с тройным кодом представляет собой конечную стадию развития численных и вычислительных возможностей.Несколько теоретических моделей обращаются к вопросу о том, как численное познание развивается в детстве (например, von Aster, 2005; Krajewski and Schneider, 2009; Kaufmann et al., 2011). Модель развития Krajewski (2008) описывает, как способность к счету связана с количественными и количественными операциями и как приобретаются количественно-числовые компетенции на трех уровнях. Однако эта модель не отображает весь процесс развития числового познания, поскольку она ограничена младшим школьным возрастом.Четырехступенчатая модель развития (фон Астер и Шалев, 2007) основана на последних открытиях психологии развития и когнитивных наук. Он предполагает развитие различных когнитивных представлений (количество элементов, вербальная система счисления, арабская система счисления, порядковый номер), релевантных для обработки и вычисления чисел, как нейропластический процесс, который переплетается с дополнительным развитием других когнитивных областей и общих способностей области, таких как внимание или рабочая память (фон Астер и Шалев, 2007; Кауфманн и фон Астер, 2012). Согласно этой модели унаследованное представление основной системы кардинальной величины (шаг 1), которое позволяет выполнять такие функции, как субитизация и аппроксимация, обеспечивает основное значение чисел. Следующий шаг включает в себя процесс обучения ассоциированию воспринимаемого числа с устным символом, усваивающим вербальные системы (числовые слова, шаг 2) и более поздние арабские системы (цифры, шаг 3). Символизация начинается с начала развития языка. Интернализация этих систем является предпосылкой для формирования абстрактного пространственного представления чисел (ментальная числовая линия) (шаг 4) в начальной школе, что, как было установлено, необходимо для арифметического мышления (von Aster, 2005).Предполагается, что эта мысленная числовая линия развивается параллельно с освоением систем символизации и, как следствие, с растущим числом арифметических операций. Описанные в этой модели процессы нельзя рассматривать в отрыве от развития других когнитивных способностей, таких как письмо и чтение, или общих функций предметной области, таких как рабочая память или внимание.
Согласно этой модели унаследованное представление основной системы кардинальной величины (шаг 1), которое позволяет выполнять такие функции, как субитизация и аппроксимация, обеспечивает основное значение чисел. Следующий шаг включает в себя процесс обучения ассоциированию воспринимаемого числа с устным символом, усваивающим вербальные системы (числовые слова, шаг 2) и более поздние арабские системы (цифры, шаг 3). Символизация начинается с начала развития языка. Интернализация этих систем является предпосылкой для формирования абстрактного пространственного представления чисел (ментальная числовая линия) (шаг 4) в начальной школе, что, как было установлено, необходимо для арифметического мышления (von Aster, 2005).Предполагается, что эта мысленная числовая линия развивается параллельно с освоением систем символизации и, как следствие, с растущим числом арифметических операций. Описанные в этой модели процессы нельзя рассматривать в отрыве от развития других когнитивных способностей, таких как письмо и чтение, или общих функций предметной области, таких как рабочая память или внимание. Кроме того, разработка различных модулей зависит от опыта и является продуктом индивидуальной и социально-культурной истории обучения.Согласно этой модели, задержки или дефицит в развитии ранних способностей и функций приводят к трудностям в построении пространственного представления чисел, независимо от того, есть ли у ребенка дефицит базовых числовых способностей или недостатки в отображении систем символизации (словесных и / или арабских). ) (фон Астер, 2005). Основное преимущество этой модели состоит в том, что можно картировать типичное развитие, а также различные пути патологического развития (фон Астер и Шалев, 2007). Кроме того, модель позволяет предсказывать этиологические созвездия и возможные нейропсихологические дисфункции при дискалькулии, связанной с развитием (von Aster et al., 2007). Задержки и недостатки в развитии ранних способностей и функций могут происходить на разных этапах, что приводит к индивидуальным потребностям в обучении (von Aster, 2005). Более того, становится очевидным, что подходы к обучению, которые сосредоточены только на одном аспекте, например, тренировке базовых числовых способностей или повторяющейся практике арифметических операций, не решают проблем этого многоуровневого процесса.
Кроме того, разработка различных модулей зависит от опыта и является продуктом индивидуальной и социально-культурной истории обучения.Согласно этой модели, задержки или дефицит в развитии ранних способностей и функций приводят к трудностям в построении пространственного представления чисел, независимо от того, есть ли у ребенка дефицит базовых числовых способностей или недостатки в отображении систем символизации (словесных и / или арабских). ) (фон Астер, 2005). Основное преимущество этой модели состоит в том, что можно картировать типичное развитие, а также различные пути патологического развития (фон Астер и Шалев, 2007). Кроме того, модель позволяет предсказывать этиологические созвездия и возможные нейропсихологические дисфункции при дискалькулии, связанной с развитием (von Aster et al., 2007). Задержки и недостатки в развитии ранних способностей и функций могут происходить на разных этапах, что приводит к индивидуальным потребностям в обучении (von Aster, 2005). Более того, становится очевидным, что подходы к обучению, которые сосредоточены только на одном аспекте, например, тренировке базовых числовых способностей или повторяющейся практике арифметических операций, не решают проблем этого многоуровневого процесса. Эффективный подход к обучению требует курса действий, в котором иерархически организованные и частично параллельные процессы постулируемых шагов обучаются в соответствии с индивидуальным профилем способностей и знаний.
Эффективный подход к обучению требует курса действий, в котором иерархически организованные и частично параллельные процессы постулируемых шагов обучаются в соответствии с индивидуальным профилем способностей и знаний.
Компьютерные вмешательства для улучшения навыков обработки чисел и арифметики
Разработка программы для улучшения навыков обработки чисел и арифметики включает рассмотрение ряда сложных аспектов. Дети различаются по скорости обучения (Brown et al., 2003) и в разной степени получают пользу от практики (Schoppek and Tulis, 2010), что приводит к различным математическим показателям и профилям дефицита (von Aster, 2000; Geary, 2004; Wilson and Dehaene, 2007).Кроме того, дети поступают в обычную школу с очень разными предпосылками к успеваемости (Hair et al., 2006). Чтобы адекватно отреагировать на эти факторы, необходима значительная индивидуализация.
Компьютерное обучение, адаптирующееся к индивидуальному профилю обучения и уровню развития ребенка, может способствовать выполнению этих требований. Он обеспечивает оптимальный уровень сложности и скорость обучения за счет индивидуального выбора задач. Еще одно ключевое преимущество — возможность моментального отклика о правильности решаемой задачи.Прямая хронологическая близость имеет решающее значение для приобретения знаний (Krajewski and Ennemoser, 2010) и позволяет правильно моделировать решение задачи.
Он обеспечивает оптимальный уровень сложности и скорость обучения за счет индивидуального выбора задач. Еще одно ключевое преимущество — возможность моментального отклика о правильности решаемой задачи.Прямая хронологическая близость имеет решающее значение для приобретения знаний (Krajewski and Ennemoser, 2010) и позволяет правильно моделировать решение задачи.
Кроме того, компьютер представляет собой привлекательную среду обучения (Кулик и Кулик, 1991; Шоппек и Тулис, 2010), обеспечивающую интенсивное обучение в стимулирующей среде (Кулик, 2004). Компьютеризированные учебные программы могут быть специально разработаны для детей и связаны скорее с игрой, чем с обучением (Lenhard et al., 2011).
В частности, для детей, испытывающих трудности с математикой, компьютеризированное обучение обеспечивает возможность создания учебной среды, независимой от давления успеваемости и сравнения сверстников в школьном контексте, и, следовательно, предлагает менее стрессовую и безопасную среду для изучения математики (Käser and von Aster, 2013 ).
Эффективность компьютерных программ обучения
Различные метаанализы изучили влияние компьютерных инструкций по математике, выявив положительные эффекты.Например, Кулик (Кулик и Кулик, 1991; Кулик, 1994) сообщил о средней величине эффекта 0,47 для компьютерного обучения математике в начальной школе. Ли и Ма (2010) указали, что компьютерное обучение особенно полезно для учащихся с особыми потребностями, и что более значительный эффект наблюдается в начальной школе, чем в высшем образовании. Аналогичным образом, другие исследования выявили положительный эффект для компьютерного обучения математике с величиной эффекта от 0,13 до 0,8 (Khalili and Shashaani, 1994; Fletcher-Flinn and Gravatt, 1995; Kroesbergen and van Luit, 2003; Slavin and Lake, 2008; Ise и другие., 2012; Chodura et al., 2015). Помимо этих многообещающих эффектов, исследования, сравнивающие эффективность компьютерных программ с другими методами обучения математике, показали, что компьютерное обучение менее эффективно, чем прямое обучение учителя (Kroesbergen and van Luit, 2003; Ise et al. , 2012). Однако недавний метаанализ, проведенный Chodura et al. (2015) показали, что компьютерные вмешательства столь же эффективны, как и вмешательства с участием тренеров.
, 2012). Однако недавний метаанализ, проведенный Chodura et al. (2015) показали, что компьютерные вмешательства столь же эффективны, как и вмешательства с участием тренеров.
Хотя существует ряд различных компьютеризированных программ обучения математике, в большинстве программ отсутствует эмпирический анализ их эффективности (Butterworth and Laurillard, 2010; Butterworth et al., 2011) либо на теоретически обоснованной основе. Существуют компьютерные программы, которые показали свою эффективность в улучшении обработки чисел или знания арифметических фактов (Fuchs et al., 2006; Wilson et al., 2006; Lenhard and Lenhard, 2010; Kucian et al., 2011) , но доступные программы в основном ориентированы на конкретные навыки и предлагают лишь ограниченную адаптируемость. Кроме того, оценочные исследования включают только небольшие размеры выборки (Räsänen et al., 2009), а дизайн исследований включает только сравнение с нетренированной контрольной группой (Räsänen et al., 2009; Ленхард и Ленхард, 2010; Kucian et al. , 2011), тогда как сравнения с группами, получающими альтернативное обучение, отсутствуют.
, 2011), тогда как сравнения с группами, получающими альтернативное обучение, отсутствуют.
Далее представлена подборка компьютеризированных тренингов, прошедших эмпирическую оценку. «Rechenspiele mit Elfe und Mathis I» (Ленхард и Ленхард, 2010) — это программа обучения математике для детей с первого по третий класс на основе национальных образовательных стандартов. Программа состоит из пяти компонентов (количества, чисел, геометрии, словесных задач, арифметики), которые относятся к областям содержания математического класса.Оценочное исследование выявило положительный эффект обучения на успеваемость детей по математике в стандартизированном тесте по сравнению с контрольным условием у детей, посещающих обычные занятия по математике. Однако следует отметить, что управление последовательностями задач и игр не следует теоретической иерархии целей обучения, что препятствует адаптации к индивидуальным трудностям ребенка в обучении (Käser and von Aster, 2013).
Программа «Числовая гонка» (Wilson et al. , 2006) основан на предположении, что дискалькулия является результатом дефицита ядра в смысле числа или дефицита связи между чувством числа и символическим представлением чисел. Адаптивное программное обеспечение предназначено для обучения числовым сравнениям и улучшения представления количественных характеристик. Оценка программы на небольшой выборке детей в возрасте 7–9 лет с трудностями в математическом обучении продемонстрировала значительные улучшения в базовых числовых познаниях, но эффекты не распространялись на счет или арифметику (Wilson et al., 2006). Räsänen et al. (2009) сравнили «Числовую гонку» с игрой (Graphogame-Math; Mönkkönen et al., В стадии подготовки), которая тренирует соответствие словесных меток визуальным образцам и числовым символам небольших наборов точных чисел. В этом исследовании дети детского сада с низким уровнем навыков счета ( n = 30) были случайным образом отнесены к одному из двух условий обучения. Дети тренировались ежедневно в течение 3 недель.
, 2006) основан на предположении, что дискалькулия является результатом дефицита ядра в смысле числа или дефицита связи между чувством числа и символическим представлением чисел. Адаптивное программное обеспечение предназначено для обучения числовым сравнениям и улучшения представления количественных характеристик. Оценка программы на небольшой выборке детей в возрасте 7–9 лет с трудностями в математическом обучении продемонстрировала значительные улучшения в базовых числовых познаниях, но эффекты не распространялись на счет или арифметику (Wilson et al., 2006). Räsänen et al. (2009) сравнили «Числовую гонку» с игрой (Graphogame-Math; Mönkkönen et al., В стадии подготовки), которая тренирует соответствие словесных меток визуальным образцам и числовым символам небольших наборов точных чисел. В этом исследовании дети детского сада с низким уровнем навыков счета ( n = 30) были случайным образом отнесены к одному из двух условий обучения. Дети тренировались ежедневно в течение 3 недель. По сравнению с группой типично выступающих детей ( n = 30) обе обучающие группы продемонстрировали улучшенные навыки сравнения чисел, но не в других областях числовых навыков (словесный счет, сравнение чисел, счет предметов, арифметика).
По сравнению с группой типично выступающих детей ( n = 30) обе обучающие группы продемонстрировали улучшенные навыки сравнения чисел, но не в других областях числовых навыков (словесный счет, сравнение чисел, счет предметов, арифметика).
Цель программы «Rescue Calcularis» (Kucian et al., 2011) — улучшить построение и доступ к ментальной числовой линии. Обучены базовым аспектам обработки чисел, а также сложения и вычитания. Детям предлагается арабская цифра, задача на сложение / вычитание или количество точек, и задача состоит в том, чтобы с помощью джойстика расположить результат каждой задачи на числовой строке. Оценка программы выявила положительные эффекты для детей с дискалькулией развития и без нее, что было измерено с помощью нейропсихологических тестов и функциональной магнитно-резонансной томографии (фМРТ) (Kucian et al., 2011). Дети показали улучшенное пространственное представление чисел, а также улучшенные арифметические способности. Кроме того, анализ с помощью фМРТ показал, что обе группы показали снижение набора областей мозга, поддерживающих обработку чисел после обучения, что можно отнести к модуляции нейронной активации, которая облегчает обработку числовых задач.
Calcularis использует основные элементы Rescue Calcularis (Kucian et al., 2011), но представляет собой более полное обучение математическим навыкам и использует пользовательскую модель, позволяющую гибкую адаптацию.Как и в «Спасении Calcularis», программа Calcularis уделяет особое внимание созданию и доступу к ментальной числовой линии. Однако он расширен обучающими элементами для автоматизации различных представлений чисел и их взаимосвязей, а также арифметических операций при расширении диапазонов чисел. Calcularis оценивался в пилотном исследовании с небольшой выборкой ( N = 32) швейцарских детей с трудностями в изучении математики (Käser et al., 2013). Обучение представлению и вычитанию чисел принесло значительную пользу детям.
В данной статье представлена оценка Calcularis в большой выборке исследования ( N = 138) с использованием дизайна исследования с двумя контрольными группами.
Цели исследования
Основная цель настоящего исследования — оценить эффективность компьютерной обучающей программы Calcularis путем объединения двух различных подходов. Во-первых, мы стремились определить общую немедленную эффективность, сравнивая тренировочную группу Calcularis с нетренированной контрольной группой.Внедрение необученной ожидающей контрольной группы позволяет контролировать эффекты развития и обучения, а также арифметическое развитие в обычных условиях. Во-вторых, мы сравнили эффективность обучающей группы Calcularis с группой, которая прошла компьютеризированное обучение правописанию, чтобы изучить предметную специфичность обучающих эффектов. Таким образом, эффективность тренировки можно определить, принимая во внимание новизну и эффекты Хоторна, а также неспецифические эффекты тренировки на общие функции предметной области.Мы предположили, что группа Calcularis продемонстрирует повышенную арифметическую производительность (сложение, вычитание) и представление пространственных чисел (в диапазоне чисел 0–10 и 0–100) по сравнению с обеими группами с малым (компьютерное обучение правописанию) и средним (неподготовленный контроль). группа) размеры эффекта.
Во-первых, мы стремились определить общую немедленную эффективность, сравнивая тренировочную группу Calcularis с нетренированной контрольной группой.Внедрение необученной ожидающей контрольной группы позволяет контролировать эффекты развития и обучения, а также арифметическое развитие в обычных условиях. Во-вторых, мы сравнили эффективность обучающей группы Calcularis с группой, которая прошла компьютеризированное обучение правописанию, чтобы изучить предметную специфичность обучающих эффектов. Таким образом, эффективность тренировки можно определить, принимая во внимание новизну и эффекты Хоторна, а также неспецифические эффекты тренировки на общие функции предметной области.Мы предположили, что группа Calcularis продемонстрирует повышенную арифметическую производительность (сложение, вычитание) и представление пространственных чисел (в диапазоне чисел 0–10 и 0–100) по сравнению с обеими группами с малым (компьютерное обучение правописанию) и средним (неподготовленный контроль). группа) размеры эффекта.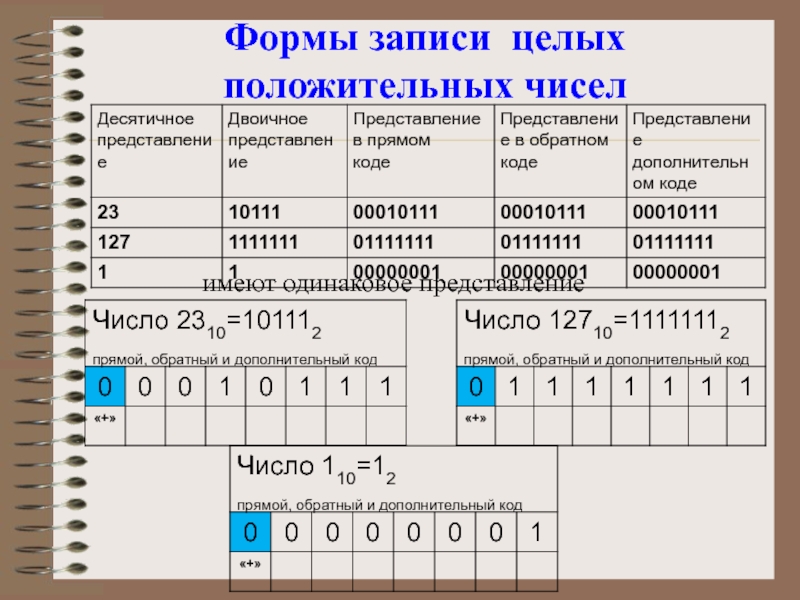
Материалы и методы
Введение в Calcularis
Calcularis — это адаптивная компьютерная программа обучения. Теоретическая основа численного познания и развития программы основана на модели трех кодов (Dehaene, 1992) и четырехступенчатой модели развития (von Aster, 2005; von Aster and Shalev, 2007).Он направлен на автоматизацию различных представлений чисел и их взаимосвязей, поддержку формирования числовой строки в уме и доступ к ней, а также на отработку арифметических операций, а также на знание арифметических фактов при расширении диапазонов чисел. Таким образом, обучение охватывает широкий спектр аспектов числового познания, что увеличивает адаптируемость программ к индивидуальным дефицитам и потребностям ребенка в обучении. Calcularis состоит из различных обучающих игр, которые иерархически структурированы в соответствии с диапазонами номеров и могут быть разделены на две части.Первая область фокусируется на различных представлениях чисел, а также на обработке чисел в целом.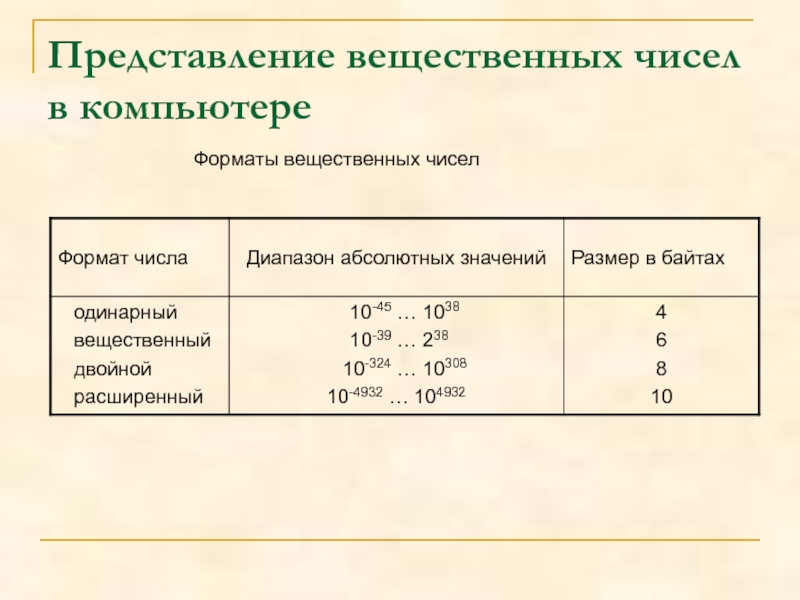 Обучаются перекодировке между альтернативными представлениями, и дети изучают три принципа понимания чисел: количество элементов, порядковость и относительность. Игры в этой области иерархически упорядочены в соответствии с четырехступенчатой моделью развития (фон Астер и Шалев, 2007). Примером первой области является игра ПОСАДКА, показанная на рисунке 1A. В этой игре детям нужно указать положение данного числа на числовой строке.Для этого необходимо управлять падающим конусом с помощью джойстика. Вторая область охватывает когнитивные операции и процедуры с числами. В этой области дети обучаются концепциям и автоматизации арифметических операций. Сложность задач определяется сложностью задачи, количеством задействованных чисел и наглядными пособиями, доступными для решения задачи. Например, в игре ПЛЮС-МИНУС (см. Рис. 1B) дети решают задачи на сложение и вычитание, используя блоки из десятков и единиц.
Обучаются перекодировке между альтернативными представлениями, и дети изучают три принципа понимания чисел: количество элементов, порядковость и относительность. Игры в этой области иерархически упорядочены в соответствии с четырехступенчатой моделью развития (фон Астер и Шалев, 2007). Примером первой области является игра ПОСАДКА, показанная на рисунке 1A. В этой игре детям нужно указать положение данного числа на числовой строке.Для этого необходимо управлять падающим конусом с помощью джойстика. Вторая область охватывает когнитивные операции и процедуры с числами. В этой области дети обучаются концепциям и автоматизации арифметических операций. Сложность задач определяется сложностью задачи, количеством задействованных чисел и наглядными пособиями, доступными для решения задачи. Например, в игре ПЛЮС-МИНУС (см. Рис. 1B) дети решают задачи на сложение и вычитание, используя блоки из десятков и единиц.
Рисунок 1.Скриншоты из компьютерной программы обучения Calcularis .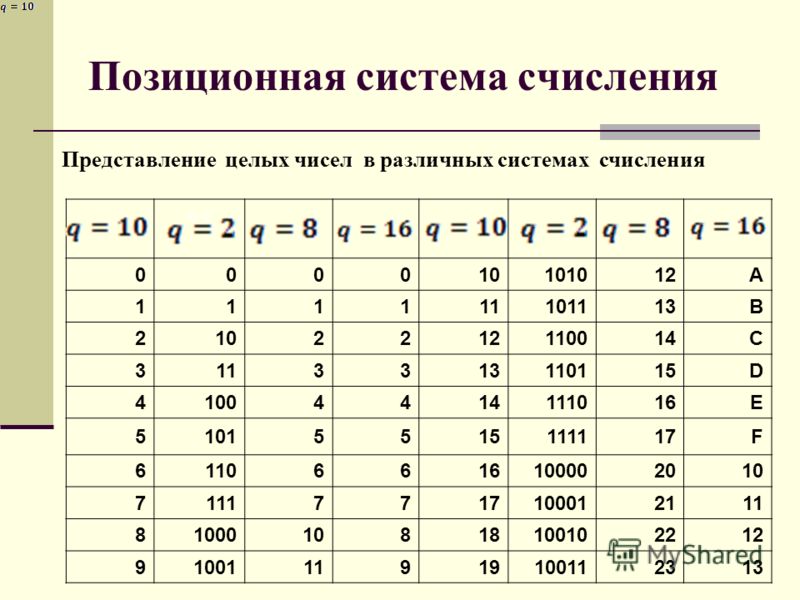 В игре «ПОСАДКА» (A) позиция отображаемого числа (29) должна быть указана в числовой строке. В игре ПЛЮС-МИНУС (B) отображаемая задача должна быть смоделирована блоками десятков и единиц.
В игре «ПОСАДКА» (A) позиция отображаемого числа (29) должна быть указана в числовой строке. В игре ПЛЮС-МИНУС (B) отображаемая задача должна быть смоделирована блоками десятков и единиц.
Ключевые компоненты (представление чисел, арифметические операции) обучаются основной и вспомогательной играм. В то время как основные игры требуют сочетания способностей, вспомогательные игры тренируют определенные навыки, которые служат предпосылками для основных игр.Последовательная система обозначений чисел, подчеркивающая их свойства, используется на протяжении всей программы обучения. Обозначения кодируются по цвету, форме и топологии. Предполагается, что такой дизайн числовых стимулов усиливает различные числовые модальности и усиливает связь между ними. Более подробное описание обучения, включая выборку примеров игр, можно найти в Käser et al. (2013), а также в Räsänen et al. (2015).
Calcularis включает пользовательскую модель, позволяющую гибкую адаптацию на основе внутренней карты обучения и профиля знаний отдельного ребенка. Все дети начинают обучение с одной и той же игры. После каждого выполненного элемента программа оценивает фактическое состояние знаний ребенка и отображает новую задачу, адаптированную к этому состоянию. Математическая структура Calcularis представляет собой модель когнитивных процессов математического развития динамической байесовской сетью. Сеть Байеса представляет собой ориентированный ациклический граф, который представляет различные математические навыки и их взаимосвязи. Модель пользователя основана на модели студента и алгоритме управления, представленном в Käser et al.(2012). Кроме того, повторение освоенных навыков (например, субитизация или арифметические операции в уже освоенных диапазонах чисел) реализовано для усиления тренированных способностей. Библиотека ошибок с типичными шаблонами ошибок позволяет предлагать целевые игры для исправления конкретных ошибок.
Все дети начинают обучение с одной и той же игры. После каждого выполненного элемента программа оценивает фактическое состояние знаний ребенка и отображает новую задачу, адаптированную к этому состоянию. Математическая структура Calcularis представляет собой модель когнитивных процессов математического развития динамической байесовской сетью. Сеть Байеса представляет собой ориентированный ациклический граф, который представляет различные математические навыки и их взаимосвязи. Модель пользователя основана на модели студента и алгоритме управления, представленном в Käser et al.(2012). Кроме того, повторение освоенных навыков (например, субитизация или арифметические операции в уже освоенных диапазонах чисел) реализовано для усиления тренированных способностей. Библиотека ошибок с типичными шаблонами ошибок позволяет предлагать целевые игры для исправления конкретных ошибок.
Инструменты
Базовая диагностика специфических нарушений развития у детей младшего школьного возраста (BUEGA)
BUEGA (Esser et al. , 2008) служил для оценки вербального и невербального интеллекта, а также навыков чтения, письма и арифметики.Эффективность чтения оценивается по скорости чтения и точности чтения. Качество письма оценивается по правильному написанию слов / графем. Подшкала «Арифметические способности» оценивает выполнение четырех основных арифметических операций (сложение, вычитание, умножение и деление), когда ребенок решает серию математических задач со словами. Коэффициенты внутренней согласованности, определенные для каждого школьного класса, достаточно высоки (от α = 0,81 до α = 0,95).
, 2008) служил для оценки вербального и невербального интеллекта, а также навыков чтения, письма и арифметики.Эффективность чтения оценивается по скорости чтения и точности чтения. Качество письма оценивается по правильному написанию слов / графем. Подшкала «Арифметические способности» оценивает выполнение четырех основных арифметических операций (сложение, вычитание, умножение и деление), когда ребенок решает серию математических задач со словами. Коэффициенты внутренней согласованности, определенные для каждого школьного класса, достаточно высоки (от α = 0,81 до α = 0,95).
HAWIK-IV (Детский тест на интеллект Гамбурга-Векслера)
Два подтеста (сходство, блочный дизайн) HAWIK-IV (тест интеллекта Гамбурга-Векслера для детей; Петерманн и Петерманн, 2007), немецкой версии WISC-IV (Шкала интеллекта Векслера для детей; Векслер, 2003) были используется для измерения вербального и невербального интеллекта.Оба субтеста показывают хорошие психометрические характеристики для детей в возрасте от 7 до 11 лет с надежностью r = 0,84–0,88 для блочного дизайна и r = 0,85–0,89 для сходства (коэффициенты разделения на половину, скорректированные Спирмена-Брауна).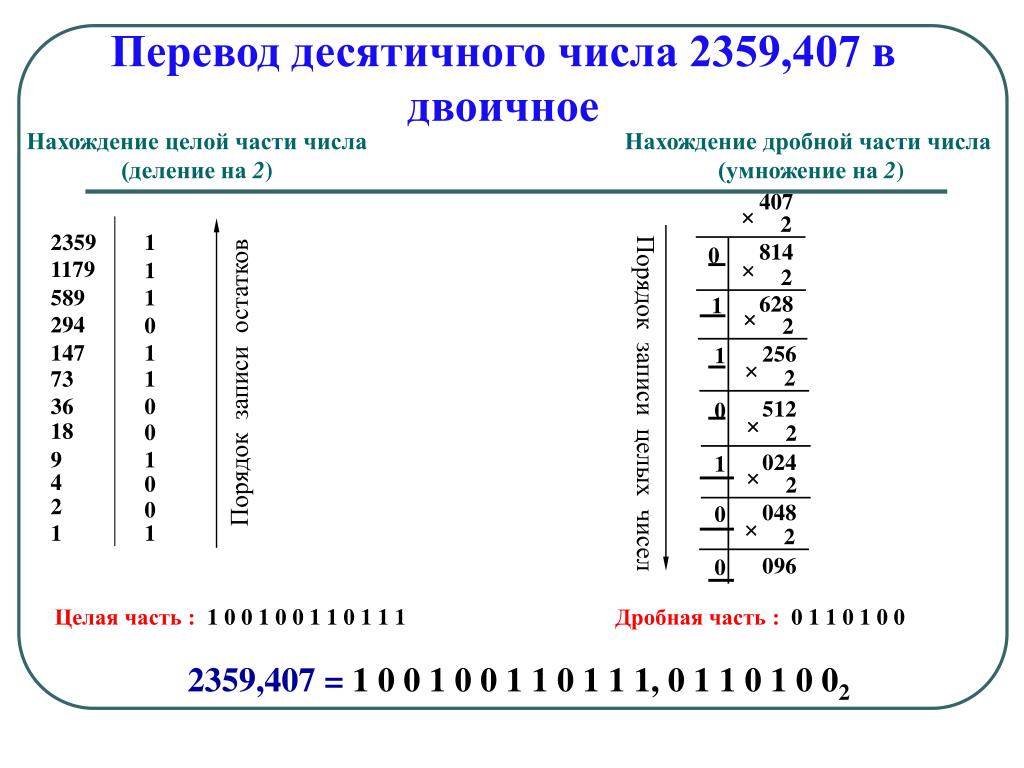
Heidelberger Rechentest 1–4 (HRT)
Арифметические действия оценивались на основе двух подшкал «сложение» и «вычитание» HRT (Haffner et al., 2005). HRT разработан как тест скорости и специально предназначен для беглости вычислений.Детям предлагается список из 40 задач на сложение / вычитание с целью решить как можно больше задач за 2 минуты. В качестве показателя надежности была рассчитана надежность повторного тестирования за двухнедельный период с высокими коэффициентами сложения ( r tt = 0,82) и вычитания ( r tt = 0,86).
Арифметический тест производительности
Тест производительности арифметики (Kucian et al., 2011) служил в качестве теста мощности, проверяющего производительность арифметики в диапазоне чисел до 100.Детям предлагается 20 заданий на сложение / вычитание без ограничения по времени. В качестве теста на мощность этот тест по арифметике нацелен на вычисление степени мастерства детей в сложении и вычитании в условиях нулевого давления времени.
Тест числовой линии
В качестве меры пространственного представления чисел дети указали расположение 20 словесно и визуально представленных чисел на числовой строке от 0 до 100. Пункты теста числовой прямой были равномерно распределены по диапазону чисел от 0 до 100 как два. были отобраны номера каждого подростка.Была рассчитана процентная абсолютная ошибка оценки (PAE) для целевого числа и указанного местоположения (оценочного числа) на числовой прямой (PAE = | оценочное число — целевое число | / шкала оценок, см. Siegler and Booth, 2004). Кроме того, чтобы оценить линейность пространственного представления, мы рассчитали коэффициент корреляции линейного соответствия ( R 2 лин) для каждого ребенка.
Компьютер-тест
Компьютерный математический тест (Käser et al., 2013) проводилась оценка арифметических характеристик и пространственного представления чисел. Этот тест на скорость включает в себя подтесты на сложение / вычитание с диапазоном чисел от 0 до 1000. Детей просят решить задачи на сложение / вычитание возрастающей сложности в течение 10 минут. Максимальное количество заданий — 76 для каждого подтеста.
Подтест для пространственного представления чисел состоит из теста числовой прямой с диапазоном чисел от 0 до 10. Число отображается на экране устно и визуально, и детей просят указать положение в числовой строке щелчком мыши.Всего в субтест 10 пунктов. Мы вычислили процентную абсолютную ошибку оценки (PAE), а также R 2 lin шаблона оценки индивидуальных числовых линий (NLE).
Мы использовали три разных теста (HRT, арифметический тест и компьютерный математический тест), исследуя производительность в задачах сложения и вычитания. Эти инструменты были реализованы, поскольку они ориентированы на конкретные аспекты (например, беглость вычислений, степень мастерства) арифметики в различных диапазонах чисел.Кроме того, они используются для сравнения результатов с результатами предыдущих исследований, изучающих эффективность компьютерных тренингов по представлению и вычислению пространственных чисел (Kucian et al., 2011; Käser et al., 2013). Для обеспечения высокой сопоставимости с предыдущими результатами Käser et al. (2013) применительно к обработке пространственных чисел была реализована задача двух числовых линий с разными диапазонами чисел (0–10, 0–100).
Анкета обратной связи
В конце исследования дети и их родители заполнили анкету для оценки обучения.Анкета включает 4 пункта, касающихся самооценки удовольствия от обучения, улучшения самооценки арифметических навыков и изменений в отношении уверенности в себе. Например, детям было предложено сказать: «Мне понравилось обучение», и они ответили по 4-балльной шкале Лайкерта в диапазоне от «не согласен» до «полностью согласен» (0–3). Коэффициенты внутренней согласованности, определенные для детей, которые тренировались с Calcularis, являются удовлетворительными (α = 0,83). Кроме того, дети оценивали уровень сложности обучения по 5-балльной шкале Лайкерта в диапазоне от «слишком просто» до «слишком сложно».Кроме того, родителей попросили оценить, насколько их ребенку понравилось обучение («Моему ребенку понравилось обучение»).
Дизайн исследования и выборка
Дизайн исследования включал три группы (группа Calcularis, группа ожидания, группа обучения орфографии). Детей случайным образом распределили в одну из трех групп. Группа Calcularis завершила 6-8-недельное обучение, в то время как ожидающая группа начала тренировку с 6-недельного периода отдыха. Группа обучения орфографии служила второй контрольной группой, проходившей обучение орфографии на компьютере (Dybuster; Kast et al., 2007) с той же продолжительностью и частотой тренировок, что и у Calcularis. Dybuster — это компьютерная программа обучения, предназначенная для улучшения навыков правописания. Оценочные исследования программы показали, что дети с дислексией, а также обычно успешные дети улучшают свои навыки правописания (Kast et al., 2007, 2011).
Дети тренировались по программе 5 раз в неделю с ежедневными 20-минутными тренировками в их собственной домашней среде. Первоначальная диагностика ( t 1 ) включала оценку арифметических действий (BUEGA, HRT, арифметический тест, компьютерный тест), а также интеллекта (HAWIK-IV, BUEGA), чтения и орфографии (BUEGA) и пространственного представление чисел (числовой тест, компьютерный тест).Все показатели арифметической производительности и пространственного представления чисел, за исключением BUEGA и HAWIK-IV, были повторно оценены во второй точке измерения ( t 2 ).
Детей набирали с помощью листовок, разосланных в начальные школы и психотерапевтические амбулатории. Все дети ходили в обычные начальные школы. Критерии включения включали как минимум средние значения IQ (минимум: 16-й процентиль, T-балл ≥ 40) (BUEGA, HAWIK-IV) и возраст 7; от 0 до 10; 11 лет.
В исследование были включены сто пятьдесят пять немецкоязычных детей. Детей случайным образом распределили по группам (группа Calcularis: n = 54, группа ожидания: n = 50, группа обучения правописанию: n = 51). В анализ данных были включены только дети, прошедшие как минимум 24 сеанса Calcularis / Dybuster в течение максимум 10-недельного периода обучения. Из-за этих критериев включения, а также других причин, таких как болезнь во время тренировки или тестовой сессии, были исключены 11 детей из группы Calcularis, 1 ребенок из группы ожидания и 5 детей из группы обучения правописанию.
Статистический анализ
Групповые различия были проанализированы с помощью дисперсионного анализа (ANOVA) и критериев хи-квадрат. Была проведена серия анализов общей линейной модели (GLM) с повторными измерениями для оценки тренировочных эффектов с точкой оценки ( t 1 — t 2 ) в качестве внутрисубъектного фактора и группы (Calcularis / ожидание / орфографии) как межпредметный фактор. Сообщается об основных эффектах группы или времени (в целом).Взаимодействие группа × время было основным интересным эффектом. В случае значительного общего взаимодействия группа × время (сравнение всех трех групп) были рассчитаны дополнительные GLM для определения эффектов взаимодействия пар групп (Calcularis против ожидания / Calcularis против обучения правописанию). Величина эффекта выражается как частные коэффициенты η 2 . Коэн (1988) постулировал, что значения η 2 от 0,06 до 0,13 являются средними эффектами, а значения η 2 больше 0.14 — большие эффекты.
Результаты
Окончательная выборка исследования состояла из 138 детей в возрасте от 7; от 0 до 10; 11 лет. Средний возраст составил 8,46 ( SD, = 0,79) года. Большинство детей посещали второй ( n = 69, 50%) и третий ( n = 53, 38,4%) классы. Четвероклассников было 13 (9,4%) и только трое пятиклассников (2,2%). В исследуемой популяции было больше девочек ( n = 95), чем мальчиков ( n = 43). Дети тренировались по программе в течение средней продолжительности обучения 6 человек.95 ( SD, = 1,23, min = 4,71, max = 9,86) недель и завершено в среднем 29,57 ( SD, = 1,75, min = 25, max = 35) тренировок. Статистический анализ не выявил существенных различий между тремя группами по полу, возрасту, арифметическим / числовым показателям или контрольным переменным (интеллект, письмо, чтение) в начальной диагностической процедуре ( t 1 ) (см. Таблицу 1). Анализ среднего интеллекта и арифметических показателей продемонстрировал высокую дисперсию в пределах выборки (средний T-показатель IQ: 50.13, SD = 5,38, мин = 41,33, макс = 73,42; математический средний T-балл: 41,90, SD = 10,22, минимум = 21,67, максимум = 71,00).
Таблица 1. Демографические и когнитивные (контрольные) характеристики [Средние, ( SD )] группы Calcularis (CAL), группы ожидания (WG) и группы обучения правописанию (ST) до вмешательства .
Используя наивысший уровень образования любого из родителей в качестве индекса социально-экономического статуса (SES), результаты показали, что 44% закончили университет ( n = 55), 21% имели право учиться в университете ( n = 26) 32% ( n = 39) получили Mittlere Reife [квалификация, полученная после 10 лет средней школы] и 3% ( n = 4) закончили Hauptschule [неполное среднее образование].Данные об уровне образования родителей отсутствовали у 14 детей. Не было значительных различий в уровне образования родителей между тремя группами с использованием критерия хи-квадрат [χ (6) 2 = 8,57, p = 0,200].
Таблица 2 суммирует средние значения и стандартные отклонения математических показателей эффективности до ( t 1 ) и после периода обучения или ожидания ( t 2 ) для трех групп.
HRT
GLM с повторными измерениями для задачи добавления HRT продемонстрировал значительный главный эффект времени [ F (1, 135) = 29.34, p <0,001, p = 0,028], но нет основного эффекта группы [ F (2, 135) = 0,062, p = 0,940]. Взаимодействие группа × время также не было значимым [ F (2, 135) = 1,92, p = 0,150].
Для вычитания ЗГТ результаты продемонстрировали значительный главный эффект времени [ F (1, 135) = 27,01, p <0,001, η 2 = 167], но никакого основного эффекта группы [ F (2, 135) = 0.11, p = 0,895]. Взаимодействие группа × время достигло значимых значений [ F (2, 135) = 7,94, p = 0,001, η 2 = 0,110], что указывает на то, что прогресс в обучении различается между группами во времени. Дальнейший анализ показал, что дети из группы Calcularis показали более высокий рост успеваемости, чем дети из ожидающей группы [ F (1, 90) = 11,07, p = 0,001, η 2 = 0,110] и группа обучения правописанию с умеренной величиной эффекта [ F (1, 87) = 13.64, p = 0,001, η 2 = 0,136].
Арифметический тест производительности
GLM выявил значительный главный эффект времени [ F (1, 135) = 6,89, p = 0,01], но не обнаружил главного эффекта группы [ F (2, 135) = 0,83 , p = 0,438] для сложения. Взаимодействие группа × время также не было значимым [ F (1, 135) = 1,77, p = 0,173].
Для вычитания результаты продемонстрировали значительный главный эффект времени [ F (1, 135) = 13.34, p <0,001, η 2 = 0,09], но нет основного эффекта группы [ F (2, 135) = 0,21, p = 0,813]. Было значимое взаимодействие группа × время [ F (2, 135) = 4,27, p = 0,016, η 2 = 0,06]. Последующий анализ показал, что дети из группы Calcularis продемонстрировали значительно большее улучшение успеваемости, чем дети из ожидающей группы [ F (1, 90) = 8.88, p = 0,001, η 2 = 0,09, средний эффект] и группа обучения правописанию [ F (1, 87) = 4,14, p = 0,045, η 2 = 0,045 , малая величина эффекта].
Тест числовой линии
Абсолютная ошибка в процентах (PAE)
Анализ числовой прямой не выявил основных эффектов времени [ F (1, 135) = 1,40, p = 0,239] и группы [ F (2, 135) = 0.81, p. = 0,445]. Взаимодействие группа × время было значимым [ F (2, 135) = 3,99, p = 0,021, η 2 = 0,056]. Дети из группы Calcularis показали более высокий прирост по сравнению с детьми из группы орфографии со средней величиной эффекта [ F (1, 87) = 6,21, p = 0,015, η 2 = 0,067]. Взаимодействие между группой × время не было значимым для сравнения между Calcularis и ожидающей группой [ F (1, 90) = 3.42, p = 0,068].
Линейность
Первоначальный анализ исследовал, лучше ли пространственное представление объяснять линейной или логарифмической функцией. Регрессии оценок детей для каждого из 20 представленных чисел были рассчитаны для каждого ребенка. Был проведен тест t с парной выборкой, сравнивающий среднее абсолютное значение остатков линейного и логарифмического соответствия для каждого ребенка. Результаты показывают, что пространственное представление чисел лучше объясняется линейным, чем логарифмическим соответствием [ t (137) = -16, 97, p <0.001], так как невязки для линейной аппроксимации меньше, чем для логарифмической. Поэтому для GLM мы использовали R 2 лин на каждого дочернего элемента. Чтобы получить представление о соответствии каждой группы, средние оценки были рассчитаны отдельно для каждой обучающей группы и нанесены на график как функция от целевого числа (рис. 2).
Рисунок 2. Шаблоны оценки для теста числовой прямой 0–100 для трех групп . Функции регрессии и коэффициенты корреляции для линейной аппроксимации (средние оценки, рассчитанные для каждой группы отдельно) показаны до (левый столбец) и после периода обучения или ожидания (правый столбец).
Анализ индивидуального R 2 lin (см. Таблицу 2) показал, что не было основного эффекта времени [ F (1, 135) = 0,20, p = 0,667] и нет основного эффекта группы [ F (2, 135) = 0,64, p = 0,531]. Взаимодействие группа × время не было значимым [ F (2, 135) = 1,12, p = 0,331].
Таблица 2. Влияние обучения (средние значения и стандартные отклонения) группы Calcularis (CAL), группы ожидания (WG) и группы обучения правописанию (ST) на арифметические показатели и пространственное представление чисел .
Компьютер-тест
Сложение и вычитание
Анализ для дополнительной задачи не выявил значимых основных эффектов времени [ F (1, 100) = 0,82, p = 0,365] или группы [ F (2, 100) = 1,56 , p = 0,215]. Взаимодействие группа × время также не было значимым [ F (2, 135) = 2,44, p = 0,093].
Для вычитания нет значимых основных эффектов времени [ F (1, 100) = 2.34, p = 0,129] или группы [ F (2, 100) = 0,73, p = 0,486]. Для вычитания наблюдалось значительное взаимодействие группа × время [ F (2, 135) = 6,82, p = 0,002, η 2 = 0,120]. Группа Calcularis показала улучшения в вычитании, тогда как ожидающая группа продемонстрировала снижение производительности в компьютерной задаче вычитания [ F (1, 66) = 14,01, p <0.001, η 2 = 0,175]. Взаимодействие группа х время не было значимым для сравнения между Calcularis и группой обучения правописанию [ F (1, 66) = 2,46, p = 0,122]. Кроме того, для сравнения между группой обучения правописанию и группой ожидания было значимое взаимодействие «группа х время» [ F (1, 68) = 4,55, p = 0,037, η 2 = 0,06]. Группа обучения правописанию продемонстрировала повышение успеваемости, в то время как дети из группы ожидания показали снижение успеваемости.
Номерная строка
Абсолютная ошибка в процентах (PAE)
Не было значимых основных эффектов времени [ F (1, 87) = 1,32, p = 0,254] и группы [ F (2, 87) = 2,44, p = 0,093 ]. Взаимодействие группа × время было значимым [ F (2, 87) = 7,76, p = 0,001, η 2 = 0,151]. Последующий анализ показал, что дети из группы Calcularis продемонстрировали значительно большее улучшение, чем дети из ожидающей группы [ F (1, 59) = 15.04, p <0,001, η 2 = 0,203, большая величина эффекта] и дети группы обучения правописанию [ F (1, 56) = 6,80, p = 0,012, η 2 = 0,108, умеренная величина эффекта].
Линейность
Размер 2 лин определялся на каждого ребенка индивидуально. GLM показал, что не было никакого основного эффекта времени [ F (1, 87) = 0,03, p = 0,868] и никакого основного эффекта группы [ F (2, 87) = 1 .48, p. = 0,233]. Взаимодействие группа × время было значимым [ F (2, 87) = 6,85, p = 0,002, η 2 = 0,136]. Последующий анализ показал, что дети из группы Calcularis продемонстрировали значительно более сильное улучшение, чем дети из ожидающей группы [ F (1, 59) = 10,99, p = 0,002, η 2 = 0,157] с большим эффектом. размер и группа обучения правописанию [ F (1, 56) = 9.39, p = 0,003, η 2 = 0,144] с большой величиной эффекта.
Хотя не было значительных различий между группами по возрасту, мы должны учитывать большие различия в возрасте. Поэтому мы повторно проанализировали данные, используя возраст в качестве ковариаты в GLM. Однако результаты показали, что не было никаких существенных изменений в результатах любого взаимодействия группа × время.
Описательный анализ анкеты обратной связи показал, что обучение было хорошо принято ( M = 2.22, SD = 0,91, n = 41): 73,2% детей указали, что им понравилось обучение. Кроме того, 78,5% детей сообщили об улучшении самооценки арифметических навыков ( M, = 2,21, SD, = 0,84), а 57,5% детей указали на более высокую уверенность в себе ( M, = 1,68, SD). = 1,12). 83,3% родителей (20 из 24) сообщили, что их ребенку понравилось обучение. Большинство детей оценили уровень сложности обучения как соответствующий (75.6%), при этом лишь немногие дети считают уровень сложности слишком высоким (7,3%) или слишком низким (17,1%).
Обсуждение
Несколько исследований демонстрируют, что значительная часть детей демонстрирует недостаточные базовые знания математики, что позволяет прогнозировать дальнейшие трудности в обучении математике (Jordan et al., 2003; Aubrey et al., 2006). Исследования развития числового познания и типичных и атипичных траекторий развития все еще находятся в зачаточном состоянии. В данной статье представлены более подробные сведения о подходах к обучению и механизмах действий, направленных на совершенствование навыков обработки чисел и арифметики на раннем этапе освоения математики.Calcularis — это программное обеспечение для адаптивного обучения, разработанное для поддержки детей в процессе обучения математике. Программа основана на прочной теоретической базе численного познания и численного развития (модель тройного кода, Dehaene, 1992; четырехступенчатая модель развития, фон Астер и Шалев, 2007) и недавних нейробиологических открытиях. Целью этого оценочного исследования было выяснить, эффективна ли программа обучения Calcularis для улучшения арифметических навыков и представления пространственных чисел.Наш план исследования дает возможность сравнить производительность обученной группы с нетренированной контрольной группой, а также с группой, прошедшей альтернативное компьютеризированное обучение.
Эффект от программы тренировок Calcularis
Calcularis Group против ожидающей группы
Результаты являются многообещающими и показали значительные улучшения по половине проанализированных мер. Это согласуется с результатами пилотного исследования с меньшей выборкой ( N = 32) швейцарских детей с трудностями в изучении математики (Käser et al., 2013). По сравнению с группой ожидания, группа Calcularis продемонстрировала большие улучшения, особенно в отношении вычитания, с умеренной и большой величиной эффекта по всем параметрам. Этот вывод считается весомым преимуществом обучения, поскольку вычитание считается сильным индикатором развития пространственного представления чисел (Dehaene, 2011). Умственная арифметика, такая как сложение и, в частности, вычитание, облегчается растущей числовой линией в уме. Это облегчает не только мысленные движения вперед и назад, но и эффективное использование стратегий вычитания, таких как «непрямое сложение» (т.е., 42 — 37 можно поменять на 37+? = 42), что требует быстрой оценки, чтобы решить, достаточно ли близки эти два числа друг к другу, чтобы косвенное добавление являлось экономической стратегией (Kaufmann and von Aster, 2012; Linsen et al., 2014).
Результаты не показали влияния на арифметические показатели производительности для сложения. Чтобы объяснить это открытие, необходимо рассмотреть иерархическую структуру Calcularis. Обучение сложению / вычитанию выполняется в возрастающих диапазонах чисел, начиная с диапазона младших чисел 0–10.Следующий более высокий диапазон чисел (0–10, 0–20, 0–100 и т. Д.) Не разблокируется до того, как ребенок продемонстрирует арифметические способности (сложение / вычитание) с определенной вероятностью. Поскольку предварительные предварительные оценки продемонстрировали, что дети лучше справляются с сложением, чем с вычитанием, программа в своем адаптивном дизайне предусмотрела больше тренировок по вычитанию, что привело к большему эффекту вычитания, чем сложения.
Что касается обработки пространственных чисел, были оценены две задачи числовой строки с разными диапазонами чисел (0–10, 0–100), чтобы получить более дифференцирующую информацию об улучшениях пространственного представления чисел, поскольку программа начинает обучение задачам мысленной числовой строки внутри числа. диапазон 0–10, а затем переходит к диапазону чисел 0–100.Группа Calcularis показала более сильные улучшения в PAE и R 2 лин, чем группа ожидания в компьютеризированном тесте числовой линии в диапазоне от 0 до 10 с большим размером эффекта. В некомпьютеризированном тесте с числовой линией группа Calcularis продемонстрировала увеличение PAE в диапазоне чисел от 0 до 100, но это увеличение не было значительно выше, чем в группе ожидания. Более того, результаты показывают, что во всех трех группах дети уже демонстрируют довольно хорошее линейное пространственное представление чисел в диапазоне чисел от 0 до 100.Этот результат согласуется с предыдущими исследованиями (например, Siegler and Booth, 2004; Kucian et al., 2011; Link et al., 2014). Однако мы не обнаружили значительного улучшения или взаимодействия группа × время для линейности в диапазоне чисел от 0 до 100. Из-за иерархической структуры программы детям предлагается серия игр, которые тренируют пространственное представление чисел в диапазоне чисел 0–10 и переходят к следующему более высокому диапазону чисел 0–100 только тогда, когда установлена определенная точность.Таким образом, эти результаты могут свидетельствовать о том, что сильные эффекты обучения были получены в отношении диапазона чисел 0–10 в течение довольно короткой продолжительности обучения, составляющей 6–8 недель, в то время как требуется дополнительное обучение, чтобы добиться значительного преимущества для представления пространственных чисел в пределах диапазон более высоких чисел 0–100. Это соответствует мнению Käser et al. (2013), которые продемонстрировали, что продление обучения с 6 недель до 3 месяцев приводит к более сильным эффектам, особенно для задачи числовой линии в диапазоне чисел от 0 до 100.Тем не менее, эти результаты показывают положительное влияние программы на построение и доступ к линии мысленных чисел, приводящее к улучшенному пространственному представлению чисел.
Этот результат особенно важен, поскольку формирование мысленной числовой линии представляет собой жизненно важный шаг в численном развитии (фон Астер и Шалев, 2007), и исследования продемонстрировали важность мысленной числовой линии для пространственного представления чисел и арифметических навыков (Зиглер и Ramani, 2009; Kucian et al., 2011). Однако следует учитывать, что это улучшение в задаче числовой линии может быть связано не только с улучшением этой основной мысленной числовой линии. Результаты недавних исследований (Ashcraft, Moore, 2012; Hurst et al., 2014; Link et al., 2014; Peeters et al., 2016) показывают, что улучшение может отражать все более широкое использование полезных стратегий, таких как использование контрольных точек. на числовой прямой (например, представив середину числовой прямой).
Поскольку исследования, которые оценивают компьютеризированные обучающие программы для улучшения арифметических действий или представления пространственных чисел, сильно различаются в отношении выборок исследования (например,g., учащиеся из группы риска или дети с дискалькулемой) и целевые показатели результатов, для адекватных сравнений доступно лишь очень ограниченное количество исследований. Обучающие исследования, демонстрирующие высокую степень сопоставимости с нашим исследованием, например, Lenhard et al. (2011) сообщили о величине эффекта от умеренного до большого для арифметической производительности для согласованных групп. Исэ и др. (2012) проанализировали исследование Fischer et al. (2008) и сообщили об улучшении арифметических навыков с большим размером эффекта после ежедневных тренировок по субитализации и визуальному счету.По сравнению с этими исследованиями и величиной эффекта, описанной в метаанализах Кулика (1994), Ли и Ма (2010), а также Славина и Лейка (2008), тренировка с Calcularis показала значительную величину эффекта: все величины эффекта (из значимых группа × время взаимодействия) продемонстрировали средние и большие размеры (η 2 = 0,06–0,20). Кроме того, наша выборка продемонстрировала высокую вариативность арифметических действий с низким и высоким уровнем успеваемости (минимум: 1-й процентиль, максимум: 98-й процентиль). Поэтому мы ожидали, что эффекты обучения будут меньше, чем размеры эффекта исследований с детьми из группы риска или с детьми с трудностями в обучении.Необходим дальнейший анализ, чтобы выяснить, кто отвечает на тренинг, а кто нет, и какие факторы влияют на наблюдаемые улучшения.
Calcularis Group против группы обучения правописанию
По сравнению с группой обучения правописанию, группа Calcularis продемонстрировала более сильные улучшения в вычитании. В отличие от результатов группы Calcularis по сравнению с группой ожидания, размер эффекта меньше. Что касается представления числовой прямой, дети из группы Calcularis продемонстрировали улучшения в диапазоне чисел от 0 до 10 (PAE, R 2 lin) и от 0 до 100 (PAE) со средней величиной эффекта по сравнению с группой, обучающей орфографии.Адекватные сравнения с другими исследованиями невозможны, поскольку в большинстве исследований отсутствует сравнение тренировочных эффектов с контрольной группой, а также с группой детей, получающих альтернативную компьютеризированную программу обучения. Однако можно принять во внимание два многообещающих исследования: Obersteiner et al. (2013), а также Fuchs et al. (2006). Obersteiner et al. (2013) использовали две модифицированные версии программы Number Race (Wilson et al., 2006) и сравнили обучающие группы с контрольной группой, получившей компьютерную программу языковой подготовки.Они сообщили, что обученные группы показали большие улучшения, чем контрольная группа, в отношении арифметических достижений с размером эффекта d = 0,40. Поскольку дизайн не включает нетренированную контрольную группу, дифференцированные сравнения с результатами нашего исследования невозможны. Обе тренировочные программы «Числовая гонка» и «Калькулярис» делают упор на мысленную числовую линию и реализовывают задачи числовой линии, но сопоставимость «Числовой гонки» и «Калькулярис» довольно ограничена. «Числовая гонка» сосредотачивается на числовых сравнениях и тренирует чувство числа у детей детского сада и дошкольного возраста, в то время как «Calcularis» стремится автоматизировать различные представления чисел и их взаимосвязь и практиковать арифметические операции, а также знание арифметических фактов в расширении диапазонов чисел у детей младшего школьного возраста. .
Fuchs et al. (2006) провели тренинг для улучшения знания арифметических фактов и сравнили обучающую группу с группой, прошедшей компьютеризированный тренинг по орфографии. Авторы сообщают, что программа была эффективна в продвижении сложения с большим размером эффекта ( d = -0,82), тогда как не было найдено никаких результатов для задач вычитания или арифметической истории. Также в этом исследовании не использовалась нетренированная контрольная группа. Что касается этих исследований, заявленные величины эффекта настоящего исследования сопоставимы.
Мы ожидали меньших размеров эффекта для сравнения Calcularis с группой обучения орфографии, чем для сравнения Calcularis с группой ожидания. Мы предполагаем, что на различные когнитивные и аффективные факторы можно повлиять, что приведет к улучшению показателей арифметических результатов в обеих группах обучения (Calcularis и обучение правописанию). Однако результаты показали, что дети из группы обучения орфографии не увеличились больше, чем группа ожидания, почти по всем заданиям, за исключением компьютерного теста на вычитание.Тем не менее, мы предполагаем, что на результаты обучения влияют некоторые важные факторы. Во-первых, ежедневные компьютеризированные тренировки могут повлиять на внимание или объем рабочей памяти. Следовательно, программа влияет на вышестоящие когнитивные функции, которые имеют решающее значение для обработки информации (например, обучение, извлечение фактов, решение проблем), что также может отражаться в улучшении арифметической производительности. Во-вторых, ежедневная практика с программой может повлиять на аффективные переменные (например,g., отношение, беспокойство, самооценка), которые также могут способствовать повышению успеваемости детей. Существует обширное исследование, демонстрирующее актуальность отношения к школьным предметам и связанных с ним академических достижений по соответствующим предметам (Ma and Kishor, 1997; Abu-Hilal, 2000). Кроме того, оценочные исследования показали, что компьютеризированные обучающие программы положительно влияют на отношение к школе (Ke, 2008) и приводят к повышению мотивации (Christmann and Badgett, 2003).Тем не менее, необходимы дальнейшие исследования, чтобы выявить, какие аспекты компьютеризированных программ обучения могут влиять на аффективные переменные, особенно на мотивацию, и какую роль эти аффективные изменения играют в отношении целей обучения и результатов обучения.
Таким образом, для получения более полной картины отдельных механизмов действий, лежащих в основе эффективного компьютеризированного обучения, необходимо принимать во внимание специфические и общие аспекты области обработки чисел и арифметики, а также аффективные переменные (Kaufmann and von Астра, 2012).
Кроме того, при интерпретации результатов необходимо учитывать, что могут существовать дополнительные факторы, влияющие на наблюдаемое прогрессирование в трех группах, которые не входили в объем данного исследования. Возможны факторы развития, которые способствуют, например, нелинейному прогрессу развития. Эти изменения в развитии могут быть обнаружены не сразу после тренировки, а позже.
Анкета обратной связи детей и их родителей показала положительные результаты, которые соответствуют опыту и впечатлениям исследовательской группы во время обучающих супервизий.Это особенно важно, поскольку Calcularis — это обучающая система, которая не встроена в сюжетную игру и не имеет реализованной системы вознаграждений. Большинство детей оценили общий уровень сложности обучения как соответствующий. Это служит индикатором качества адаптации к индивидуальному уровню и профилю успеваемости, скорости обучения и сохранения детской зоны ближайшего развития (Выготский, 1978). Кроме того, углубленный анализ пути детей через сеть навыков показал, что дети демонстрируют очень разные профили математических знаний и недостатки, ведущие к очень разным траекториям обучения, которые оптимизируют процесс обучения (Käser et al., 2012, 2013). Эти результаты подчеркивают необходимость адаптации к индивидуальному уровню знаний ребенка, с одной стороны, и доказывают эффективность и адаптируемость модели ученика и алгоритма управления, с другой.
Ограничения и показания к дальнейшим исследованиям
Следует отметить несколько важных ограничений этого исследования. Во-первых, Calcularis сочетает в себе обучение базовым навыкам работы с числами, представлению пространственных чисел и арифметическим операциям. Оценочные данные показали хорошие эффекты вычитания и пространственного представления чисел.Однако базовые навыки работы с цифрами (например, сравнение числа / количества, субитизация) не оценивались. Таким образом, невозможно определить эффекты обучения в отношении базовых числовых навыков. Кроме того, не было оценки успеваемости детей в умножении и делении, которая могла бы служить мерой для переноса обучения. Во-вторых, различимую передачу обучения невозможно было оценить, поскольку мы не оценивали нечисловые меры (например, чтение, правописание) после обучения.В-третьих, полученные результаты реагируют на немедленную эффективность. Таким образом, настоящие результаты не позволяют делать выводы о повышении математической компетентности или переносе на другие арифметические действия в долгосрочной перспективе. В-четвертых, в настоящем исследовании более двух третей исследуемой популяции составляли девочки, но соотношение полов существенно не отличалось по группам. Участников набирали с помощью рекламы, распространяемой среди профессионалов и школ. Таким образом, предложение компьютеризированной программы обучения для улучшения числового познания оказалось особенно привлекательным для девочек.Дальнейшие исследования с более крупными выборками и равным гендерным соотношением необходимы для более дифференцированного анализа возможных эффектов пола. После этого первого этапа оценки Calcularis в настоящее время проводится дополнительное оценочное исследование, которое включает в себя проведение контрольной группы, получающей традиционную интегративную обучающую терапию для детей с дискалькулией развития. Таким образом, мы стремимся понять основные процессы и механизмы действия компьютеризированной программы обучения по сравнению с некомпьютеризированными подходами к обучению.
Заключение
Это исследование демонстрирует, что адаптивную программу обучения Calcularis можно эффективно использовать для поддержки детей в их численном развитии, а также для улучшения вычитания и представления пространственных чисел. В то время как другие компьютеризированные обучающие программы показали хорошие результаты обучения арифметической деятельности (например, Fischer et al., 2008; Lenhard et al., 2011) или пространственному представлению чисел (например, Kucian et al., 2011), Calcularis продемонстрировал даже после довольно большой короткий период обучения (6–8 недель) положительный эффект для обоих.В статье поднимаются вопросы об общем принципе действия компьютеризированных программ. Необходимы дальнейшие исследования, чтобы выявить, на какие когнитивные, аффективные и мотивационные переменные влияют компьютеризированные программы, ведущие к повышению арифметической производительности. Наконец, следует отметить, что Calcularis был разработан для поддержки процессов обучения. Мы полностью согласны с Козмой (2001), который утверждает, что не существует инструмента (компьютерных программ и т. Д.), Который заменил бы хорошее обучение. Учебная программа Calcularis не ставит своей целью заменить традиционные методы обучения, но она может быть ценной возможностью дополнить и поддержать учителей и создать более дифференцированную и инклюзивную среду обучения.
Авторские взносы
GE, KK, MV и JK разработали исследование. GE, KK, MV, JK, UM, VM и TK разработали исследование. JK, LR, VM, KK, TK и UM проводили исследования. JK, LR и MV проанализировали данные. JK и LR написали рукопись.
Финансирование
Работа поддержана исследовательским грантом 01GJ1011 Федерального министерства образования и исследований Германии (BMBF).
Заявление о конфликте интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.
Благодарности
Авторы выражают благодарность детям и их родителям за участие. Мы также хотели бы поблагодарить студентов-ассистентов, которые помогли собрать данные исследования.
Список литературы
Абу-Хилал, М. М. (2000). Структурная модель отношения к школьным предметам, академическим устремлениям и достижениям. Educ. Psychol. 20, 75–84. DOI: 10.1080 / 014434100110399
CrossRef Полный текст | Google Scholar
Арсалиду, М., и Тейлор, М. Дж. (2011). 2 + 2 = 4? Мета-анализ областей мозга, необходимых для чисел и вычислений. Нейроизображение 54, 2382–2393. DOI: 10.1016 / j.neuroimage.2010.10.009
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Обри К., Даль С. и Годфри Р. (2006). Раннее развитие математики и более поздние достижения: дополнительные доказательства. Math. Educ. Res. J. 18, 27–46. DOI: 10.1007 / BF03217428
CrossRef Полный текст | Google Scholar
Аунола, К., Лескинен, Э., Леркканен, М.-К., Нурми, Ж.-Э. (2004). Динамика развития математической успеваемости от дошкольного до 2 класса. J. Educ. Psychol. 96, 699–713. DOI: 10.1037 / 0022-0663.96.4.699
CrossRef Полный текст | Google Scholar
Браун, М., Аскью, М., Ходген, Дж., Родс, В., и Уильям, Д. (2003). «Индивидуальный и когортный прогресс в обучении математике в возрасте от 5 до 11 лет: результаты 5-летнего лонгитюдного исследования Леверхалма», в материалах Proceedings of the International Conference on Science and Mathematics Learning , eds F.Л. Линь и Дж. Го (Тайбэй: Национальный Тайваньский педагогический университет), 81–109.
Баттерворт, Б., и Лорилард, Д. (2010). Низкая способность считать и дискалькулия: выявление и вмешательство. ZDM Math. Educ. 42, 527–539. DOI: 10.1007 / s11858-010-0267-4
CrossRef Полный текст | Google Scholar
Чодура, С., Кун, Дж. Т., и Холлинг, Х. (2015). Вмешательства для детей с математическими трудностями: метаанализ. Zeitschrift für Psychologie 223, 129.DOI: 10.1027 / 2151-2604 / a000211
CrossRef Полный текст | Google Scholar
Кристманн Э. и Баджетт Дж. (2003). Мета-анализ влияния компьютерных инструкций на успеваемость учащихся начальной школы. Информ. Technol. Детство просвещ. 1, 91–104.
Google Scholar
Cipolotti, L., and Butterworth, B. (1995). К модели обработки чисел с несколькими маршрутами: нарушение перекодировки номеров с сохраненными навыками вычисления. J. Exp. Psychol. Gen. 4, 375–390. DOI: 10.1037 / 0096-3445.124.4.375
CrossRef Полный текст | Google Scholar
Коэн, Дж. (1988). Статистический анализ мощности для поведенческих наук . Хиллсдейл, Нью-Джерси: Эрлбаум.
Dehaene, S. (2011). Чувство числа: как разум создает математику . Нью-Йорк, Нью-Йорк: Издательство Оксфордского университета.
Google Scholar
Dehaene, S., Spelke, E., Pinel, P., Stanescu, R., and Tsivkin, S.(1999). Источники математического мышления: данные о поведении и изображениях мозга. Наука 284, 970–974. DOI: 10.1126 / science.284.5416.970
CrossRef Полный текст | Google Scholar
Даукер, А. (2005). Индивидуальные различия в арифметике: значение для психологии, нейробиологии и образования . Хоув: Psychology Press. DOI: 10.4324 / 9780203324899
CrossRef Полный текст | Google Scholar
Дункан, Дж. Дж., Доусетт, К. Дж., Классенс, А., Магнусон, К., Хьюстон, А.С., Клебанов, П. и др. (2007). Готовность к школе и последующие достижения. Dev. Psychol. 43, 1428–1446. DOI: 10.1037 / 0012-1649.43.6.1428
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Esser, G., Wyschkon, A., and Ballaschk, K. (2008). Basisdiagnostik Umschriebener Entwicklungsstörungen im Grundschulalter (BUEGA) . Геттинген: Hogrefe.
Фишер Б., Конгетер А. и Хартнегг К. (2008). Влияние ежедневной практики на субитизацию, визуальный счет и базовые арифметические навыки. Optom. Vis. Dev. 39, 34.
Google Scholar
Флетчер-Флинн, К. М. и Граватт, Б. (1995). Эффективность обучения с помощью компьютера (CAI): метаанализ. J. Educ. Comput. Res. 12, 219–241. DOI: 10.2190 / 51D4-F6L3-JQHU-9M31
CrossRef Полный текст | Google Scholar
Фукс, Л. С., Фукс, Д., Гамлет, К. Л., Пауэлл, С. Р., Капицци, А. М., и Зиталер, П. М. (2006). Влияние компьютерных инструкций на умение комбинировать числа у первоклассников из группы риска. J. ЖЖ. Disabil. 39, 467–475. DOI: 10.1177 / 002221940603
701PubMed Аннотация | CrossRef Полный текст | Google Scholar
Гири, Д. К. (2006). «Развитие математического понимания» в Справочнике по детской психологии : Том 2. Познание, восприятие и язык, 6-е изд. . Редакторы серии У. Дэймон и Р. М. Лернер и редакторы тома Д. Кун и Р. С. Сиглер (Нью-Йорк, штат Нью-Йорк: Wiley), 777–810.
Хаффнер, Дж., Баро, К., Парзер, П., и Реш, Ф.(2005). Heidelberger Rechentest (HRT): Erfassung Mathematischer Basiskompetenzen im Grundschulalter . Геттинген: Hogrefe.
Волос, Э., Галле, Т., Терри-Хьюмен, Э., Лавель, Б., и Калкинс, Дж. (2006). Готовность детей к школе в ECLS-K: прогнозы академических, медицинских и социальных результатов в первом классе. Ранний ребенок. Res. Q. 21, 431–454. DOI: 10.1016 / j.ecresq.2006.09.005
CrossRef Полный текст | Google Scholar
Херст, М., Монахан, К.Л., Хеллер Э. и Кордес С. (2014). 123s и ABC: сдвиги в развитии логарифмической реакции на линейную отражают беглость со значениями последовательности. Dev. Sci. 6, 892–904. DOI: 10.1111 / desc.12165
CrossRef Полный текст | Google Scholar
Исэ, Э., Долле, К., Пикснер, С., и Шульте-Кёрне, Г. (2012). Effektive Förderung rechenschwacher Kinder: eine metaanalyse. Kindheit Entwicklung 21, 181–192. DOI: 10.1026 / 0942-5403 / a000083
CrossRef Полный текст
Джейкобс, К., и Петерманн, Ф. (2003). Dyskalkulie- Forschungsstand und Perspektiven. Kindheit Entwicklung 12, 197–211. DOI: 10.1026 // 0942-5403.12.4.197
CrossRef Полный текст | Google Scholar
Джордан, Н. К., Ханич, Л. Б., и Каплан, Д. (2003). Усвоение арифметических фактов у детей раннего возраста: продольное исследование. J. Exp. Детская психол. 85, 103–119. DOI: 10.1016 / S0022-0965 (03) 00032-8
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Джордан, Н.К., Каплан Д., Локуняк М. Н. и Раминени К. (2007). Прогнозирование успеваемости по математике в первом классе на основе траекторий развития. Узнай. Disabil. Res. Практик. 22, 36–46. DOI: 10.1111 / j.1540-5826.2007.00229.x
CrossRef Полный текст | Google Scholar
Käser, T., Baschera, G.-M., Kohn, J., Kucian, K., Richtmann, V., Grond, U., et al. (2013). Разработка и оценка компьютерной обучающей программы Calcularis для улучшения числового познания. Фронт.Psychol. 4: 489. DOI: 10.3389 / fpsyg.2013.00489
PubMed Аннотация | CrossRef Полный текст
Käser, T., Busetto, A. G., Baschera, G.-M., Kohn, J., Kucian, K., von Aster, M., et al. (2012). «Моделирование и оптимизация процесса обучения математике», Труды 11-й Международной конференции по интеллектуальным системам обучения , ред. С.А. Черри, В.Дж. Кланси, Г. Пападуракис и К. Панургиа (Берлин; Гейдельберг: Springer), 389– 398. DOI: 10.1007 / 978-3-642-30950-2_50
CrossRef Полный текст
Кезер, Т., и фон Астер, М. Г. (2013). «Computerbasierte Lernprogramme für Kinder mit Rechenschwäche», в Rechenstörungen bei Kindern: Neurowissenschaft, Psychologie, Pädagogik , ред. М. Г. фон Астер и Й. Х. Лоренц (Göttingen: Vandenhoeck and Ruprecht275). DOI: 10.13109 / 9783666462580.259
CrossRef Полный текст
Каст, М., Башера, Г.-М., Гросс, М., и Мейер, М. Дженке, Л. (2011). Компьютерное обучение орфографическим навыкам у детей с дислексией и без нее. Ann. Дислексия 61, 177–200. DOI: 10.1007 / s11881-011-0052-2
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Каст, М., Мейер, М., Фогели, К., Гросс, М., и Дженке, Л. (2007). Компьютерное мультисенсорное обучение у детей с дислексией развития. Рестор. Neurol. Neurosci. 25, 355–369.
PubMed Аннотация | Google Scholar
Kaufmann, L., Delazer, M., Pohl, R., Semenza, C., and Dowker, A. (2005). Эффекты специальной образовательной программы по математике у детей дошкольного возраста: экспериментальное исследование. Educ. Res. Eval. 11, 405–431. DOI: 10.1080 / 13803610500110497
CrossRef Полный текст | Google Scholar
Кауфманн, Л., Вуд, Г., Рубинштейн, О., и Хеник, А. (2011). Мета-анализ разработки, обработка и расчет. Dev. Neuropsychol. 36, 763–787. DOI: 10.1080 / 87565641.2010.549884
CrossRef Полный текст
Ке, Ф. (2008). Пример компьютерных игр для математики: увлеченное обучение на основе игрового процесса? Comput. Educ. 51, 1609–1620. DOI: 10.1016 / j.compedu.2008.03.003
CrossRef Полный текст | Google Scholar
Халили А. и Шашаани Л. (1994). Эффективность компьютерных приложений: метаанализ. J. Res. Comput. Educ. 27, 48–61. DOI: 10.1080 / 08886504.1994.10782115
CrossRef Полный текст | Google Scholar
Козьма Р. (2001). «Learning with media», в Classic Writings on Instructional Technology , ред. Д. П. Эли и Т. Пломп (Колорадо: Libraries Unlimited, Inc.), 155–188.
Krajewski, K. (2008). «Prävention der Rechenschwäche», в Handbuch der Pädagogischen Psychologie , ред. W. Schneider и M. Hasselhorn (Göttingen: Hogrefe), 360–370.
Krajewski, K., and Ennemoser, M. (2010). «Die Berücksichtigung beginzter Arbeitsgedächtnisressourcen in Unterricht und Lernförderung», в Brennpunkte der Gedächtnisforschung , ред. Х. П. Тролльдениер, В. Ленхард и П. Маркс (Göttingen: Hogrefe), 337–337.
Краевский, К., и Шнайдер, W. (2009). Раннее развитие количества к связи числа-слова как предвестник достижений математической школы и математических трудностей: результаты четырехлетнего лонгитюдного исследования. Узнай. Инструктировать. 19, 513–526. DOI: 10.1016 / j.learninstruc.2008.10.002
CrossRef Полный текст | Google Scholar
Крезберген, Э. Х., и ван Луит, Дж. Э. Х. (2003). Математическое вмешательство для детей с особыми образовательными потребностями: метаанализ. Лечебно-специальное образование. 24, 97–114. DOI: 10.1177 / 07419325030240020501
CrossRef Полный текст | Google Scholar
Kucian, K., Grond, U., Rotzer, S., Henzi, B., Schönmann, C., Plangger, F., et al. (2011). Тренировка умственной числовой линии у детей с дискалькулией развития. Нейроизображение 57, 782–795. DOI: 10.1016 / j.neuroimage.2011.01.070
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Куциан, К., и Кауфманн, Л. (2009). Модель развития числовых представлений. Behav. Brain Sci. 32, 313–373. DOI: 10.1017 / S0140525X099
CrossRef Полный текст | Google Scholar
Куциан, К., фон Астер, М., Лоеннекер, Т., Дитрих, Т., и Мартин, Э. (2008). Разработка нейронных сетей для точного и приближенного расчета: исследование фМРТ. Dev. Neuropsychol. 33, 447–473. DOI: 10.1080 / 87565640802101474
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Кулик, К.-Л. К. и Кулик Дж. А. (1991).Эффективность компьютерного обучения: обновленный анализ. Comput. Человеческое поведение. 7, 75–94. DOI: 10.1016 / 0747-5632 (91) -5
CrossRef Полный текст | Google Scholar
Кулик, Дж. А. (1994). «Метааналитические исследования результатов компьютерного обучения», в Оценка технологий в образовании и обучении , ред. Э. Л. Бейкер и Х. Ф. О’Нил (Хиллсдейл, Нью-Джерси: LEA Publishers), 9–34.
PubMed Аннотация
Кулик У. (2004).«Computerunterstützte Rechentrainingsprogramme», в Interventionen bei Lernstörungen , ред. W. Lauth, M. Grünke и J. C. Brunstein (Göttingen: Hogrefe), 329–337.
Ленхард А., Ленхард В., Шуг М. и Ковальски А. (2011). Computerbasierte Mathematikförderung mit den «Rechenspielen mit Elfe und Mathis I». Zeitschrift Entwicklungspsychologie Pädagogische Psychologie 43, 79–88. DOI: 10.1026 / 0049-8637 / a000037
CrossRef Полный текст | Google Scholar
Ленхард, В., и Ленхард, А. (2010). Rechenspiele mit Elfe und Mathis I [CD-ROM] . Геттинген: Hogrefe.
Ли, К., и Ма, X. (2010). Метаанализ влияния компьютерных технологий на изучение математики школьниками. Educ. Psychol. Ред. 22, 215–243. DOI: 10.1007 / s10648-010-9125-8
CrossRef Полный текст | Google Scholar
Link, T., Huber, S., Nuerk, H.-H., and Moeller, K. (2014). Освобождение мысленной числовой линии — новое свидетельство детского пространственного представления чисел. Фронт. Psychol. 4: 1021. DOI: 10.3389 / fpsyg.2013.01021
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Линсен, С., Вершаффель, Л., Рейнвоет, Б., и Де Смедт, Б. (2014). Связь между обработкой числовой величины у детей и умственным вычитанием многозначных чисел. Acta Psychol. 145, 75–83. DOI: 10.1016 / j.actpsy.2013.10.008
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Ма, X., и Кишор, Н.(1997). Оценка взаимосвязи между отношением к математике и достижениями в математике: метаанализ. J. Res. Математика. Educ. 28, 26–47. DOI: 10.2307 / 749662
CrossRef Полный текст | Google Scholar
Макклоски, М., Карамазза, А., и Басили, А. (1985). Когнитивные механизмы в обработке чисел и вычислении: данные о дискалькулии. Brain Cogn. 4, 171–196. DOI: 10.1016 / 0278-2626 (85) -7
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Мерсер, К.Д. и Миллер С. П. (1992). Обучение студентов с проблемами обучения математике усвоению, пониманию и применению основных математических фактов. Remed. Спец. Educ. 13, 19–35. DOI: 10.1177 / 0741932500303
CrossRef Полный текст | Google Scholar
Морган П. Л., Фаркас Г. и Ву К. (2009). Пятилетние траектории роста детей детского сада с трудностями в обучении математике. J. ЖЖ. Disabil. 42, 306–321. DOI: 10.1177 / 0022219408331037
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Оберштайнер, А., Рейсс, К., Уфер, С. (2013). Как обучение точному или приблизительному представлению чисел в уме может улучшить базовые навыки обработки чисел и арифметические навыки первоклассников. Узнай. Инструктировать. 23, 125–135. DOI: 10.1016 / j.learninstruc.2012.08.004
CrossRef Полный текст | Google Scholar
Петерс, Д., Дегранде, Т., Эберсбах, М., Вершаффель, Л., и Лювель, К. (2016). Использование детьми стратегий оценки числовой прямой. Eur. J. Psychol. Educ. 31, 117–134.DOI: 10.1007 / s10212-015-0251-z
CrossRef Полный текст | Google Scholar
Петерманн, Ф., и Петерманн, У. (2007). Hamburg-Wechsler-Intelligenztest für Kinder IV (HAWIK-IV) . Берн: Хубер.
Google Scholar
Рясанен, П., Кезер, Т., Уилсон, А., фон Астер, М., Маслов, О., Маслова, У. (2015). «Вспомогательные технологии для поддержки обучения математике», в Вспомогательные технологии для познания: Справочник для клиницистов и разработчиков , ред.О’Нил и А. Гиллеспи (Бембо: «Восход солнца»), 112–127.
Рясанен, П., Саминен, Дж., Уилсон, А. Дж., Аунио, П., и Дехаен, С. (2009). Компьютерное вмешательство для детей с низким уровнем навыков счета. Cogn. Dev. 24, 450–472. DOI: 10.1016 / j.cogdev.2009.09.003
CrossRef Полный текст | Google Scholar
Ривера, С. М., Рейс, А. Л., Эккерт, М. А., и Менон, В. (2005). Изменения в развитии ментальной арифметики: свидетельства повышенной функциональной специализации левой внутренней теменной коры. Cereb. Cortex 15, 1779–1790. DOI: 10.1093 / cercor / bhi055
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Шоппек, В., Тулис, М. (2010). Повышение эффективности арифметики и навыков решения словесных задач с помощью индивидуальной компьютерной практики. J. Educ. Res. 103, 239–252. DOI: 10.1080 / 00220670
2962
CrossRef Полный текст | Google Scholar
Зиглер, Р. С., и Рамани, Г. Б. (2009). Игра в настольные игры с линейными числами, но не в круговые, улучшает понимание чисел дошкольниками из малообеспеченных семей. J. Educ. Psychol. 101, 545–560. DOI: 10.1037 / a0014239
CrossRef Полный текст | Google Scholar
Славин Р., Лейк К. (2008). Эффективные программы по элементарной математике; синтез наилучших доказательств. Rev. Educ. Res. 78, 427–515. DOI: 10.3102 / 0034654308317473
CrossRef Полный текст | Google Scholar
Ван Луит, Дж. Э. Х. и Наглиери, Дж. А. (1999). Эффективность программы МАСТЕР для обучения специальных детей умножению и делению. J. ЖЖ. Disabil. 32, 98–107. DOI: 10.1177 / 002221949

 После ответа на все вопросы нажмите кнопку «Готово».
После ответа на все вопросы нажмите кнопку «Готово».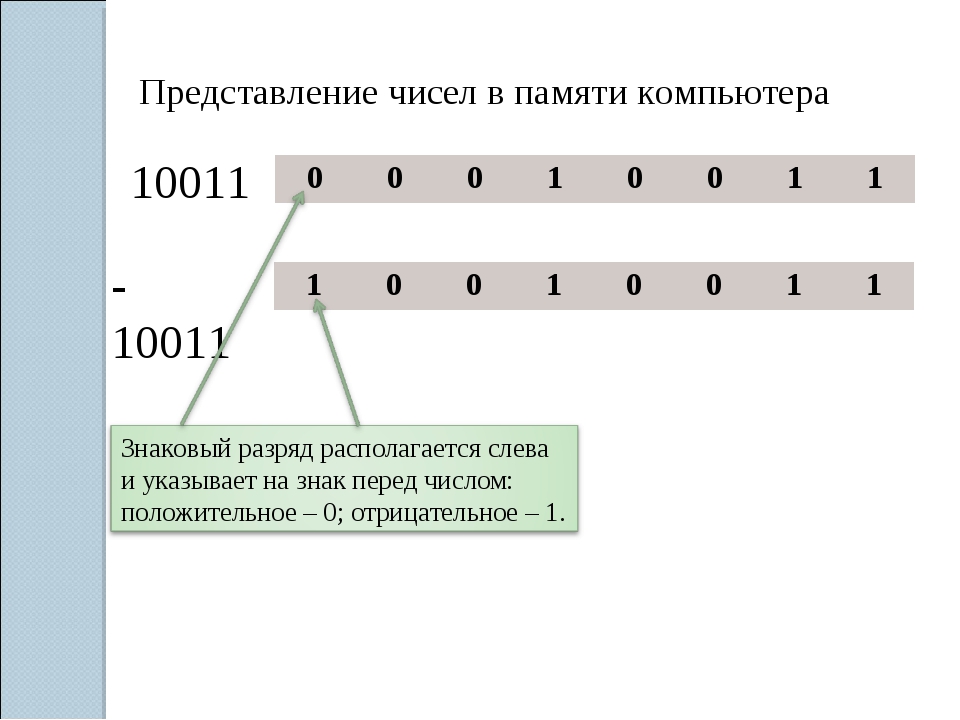 Получится:
Получится: