Тест по теме: Тригонометрия (теория)
1. Тест по теме:
Тригонометрия(теория)
Тест составила Курылева Э. Р.
МОУ « СОШ № 42» г Воркута
Начать
тест
2. Вопрос №1.
Область определения функции y=sin x:R
1;1
x 0
( 1;1)
Следующий вопрос
3. Вопрос №2.
Функция y=sin x принимает отрицательныезначения в
I и III координатных четвертях
I и II координатных четвертях
III и IV координатных четвертях
II и III координатных четвертях
Следующий вопрос
4. Вопрос №3.
Наименьший положительный периодфункции y=cos x
2
2
3
2
Следующий вопрос
5. Вопрос №4.
Нечётные тригонометрические функции:y sin x, y cos x, y tgx
y sin x, y ctgx, y tgx
y cos x, y sin x, y tgx
y sin x, y cos x, y сtgx
Следующий вопрос
6. Вопрос №5.
Множество значений функции y=sin x:R
y 0
( 1;1)
1;1
Следующий вопрос
7.
 Вопрос №6. Область определения функции y=tgx:
Вопрос №6. Область определения функции y=tgx:n n
;
2 2
x
2
x n, n Z
0;2 n
Следующий вопрос
8. Вопрос №7.
Основное тригонометрическое тождество:cos x sin x 1
cos 2 x sin 2 x 1
cos 2 x sin 2 x 1
cos x sin x 1
Следующий вопрос
9. Вопрос №8.
Продолжи формулу cos2x=:cos x sin x
cos 2 x sin 2 x
cos 2 x sin 2 x
cos x sin x
Следующий вопрос
10. Вопрос №9.
Продолжи формулу cos(x+y)=:cos x cos y sin x sin y
cos x cos y sin x sin y
cos x sin y sin x cos y
cos x sin y sin x cos y
Следующий вопрос
11. Вопрос №10.
Укажите формулу для понижения степенисинуса:
1 cos 2 x
2
1 cos x
2
sin x
2
cos 2 x 1
2
sin x
2
sin 2 x
sin 2 x
1 cos 2 x
2
Следующий вопрос
12. Вопрос №11.
Продолжи формулу cosx-cosy=:x y
x y
cos
2
2
x y
x y
2 sin
sin
2
2
x y
x y
2 sin
cos
2
2
x y
x y
2 cos
cos
2
2
2 sin
Следующий вопрос
13.
 Вопрос №12. Укажи верную формулу:
Вопрос №12. Укажи верную формулу:1
2
ctg
x 1
2
cos x
1
2
ctg
x 1
sin 2 x
1
2
tg
x 1
2
cos x
1
2
tg
x 1
2
cos x
Следующий вопрос
14. Вопрос №13.
Продолжи формулу tg(x-y)=:tgx tgy
1 tgx tgy
tgx tgy
1 tgx tgy
tgx tgy
1 tgx tgy
tgx tgy
1 tgx tgy
Следующий вопрос
15. Вопрос №14.
Продолжи формулу sinxcosy+cosxsiny=:sin( x y )
cos( x y )
sin( x y )
cos( x y )
Следующий вопрос
16. Вопрос №15.
Продолжи формулу tg2α=:tg 2
1 tg 2
2tg
1 tg 2
tg 2
1 2tg
2tg
1 2tg
Следующий вопрос
17. Вопрос №16.
Продолжи формулу sinα+sinβ=:2 sin
2 sin
2 cos
2 sin
2
cos
2
2
2
cos
cos
sin
2
2
2
2
Следующий вопрос
18. Вопрос №17.
Продолжи формулу cos²α=:2
cos 2 1
2
1 cos 2
4
1 cos 2
2
Следующий вопрос
19.
 Вопрос №18. Продолжи формулу sin²α=:
Вопрос №18. Продолжи формулу sin²α=:1
ctg 2
1 cos 2
1
1 ctg 2
2 sin cos
Следующий вопрос
20. Вопрос №19.
Продолжи формулу 2sinαcosα=:sin 2
sin 2
sin
1
sin
2
Следующий вопрос
21. Вопрос №20.
Продолжи формулу sin(α-β)=:cos cos sin sin
cos sin sin cos
cos cos sin sin
sin cos cos sin
Следующий вопрос
22. Результаты теста
Всего вопросов:Правильных ответов:
Процент правильных ответов:
Оценка:
Получить результат
Закончить тест
Аналитическая теория тригонометрических функций
Содержание:
Аналитическая теория тригонометрических функций
- Теория анализа тригонометрических функций. мы Теперь вернемся к вопросу, кратко описанному в пункте 163. На протяжении всей книги читатель был знаком с элементами тригонометрии и считал, что он свободно использовал тригонометрические или «круговые» функции cosx, sin *, tg *, … в качестве примера.
 Основа тригонометрии не так проста, как кажется читателям, знакомым с ними поначалу, и обычное изложение теории основывается на ряде предположений, которые требуют тщательного анализа.
Основа тригонометрии не так проста, как кажется читателям, знакомым с ними поначалу, и обычное изложение теории основывается на ряде предположений, которые требуют тщательного анализа.
1 °. Геометрический метод. Наиболее естественный способ — максимально точно отслеживать отображение обычных учебников и переводить используемый в них геометрический язык на язык анализа. В пункте 163 мы обсудили этот вопрос и пришли к выводу, что возникла только одна серьезная проблема. Вы должны указать, что дуга окружности связана с конкретным числом, называемым его длиной, или что сектор окружности связан с конкретным числом, называемым его областью. Выполнение одного из этих требований достаточно для строгой демонстрации всей тригонометрии.
Существует, по крайней мере, четыре очевидных способа построения теории тригонометрического анализа. Людмила Фирмаль
Они обычно следуют первым двум путям и основаны на тригонометрии, основанной на понятии длины. Но гл. Конечно, второй метод был приоритетным, потому что VII включает строгий контроль области, а не длины. 2 °. Метод бесконечной линии. Второй метод, используемый во многих курсах анализа, заключается в определении тригонометрических функций с использованием экспоненциальных функций или бесконечных рядов, таких как 223. Определите cos x и sin x как уравнения (1) потому что x = 1-sin x = x— •••• Ряд Aegis отлично сходится для всех действительных значений x и может быть умножен на ряд в пункте 223. Поэтому излучайте формулу.
Но гл. Конечно, второй метод был приоритетным, потому что VII включает строгий контроль области, а не длины. 2 °. Метод бесконечной линии. Второй метод, используемый во многих курсах анализа, заключается в определении тригонометрических функций с использованием экспоненциальных функций или бесконечных рядов, таких как 223. Определите cos x и sin x как уравнения (1) потому что x = 1-sin x = x— •••• Ряд Aegis отлично сходится для всех действительных значений x и может быть умножен на ряд в пункте 223. Поэтому излучайте формулу.
Это касательная формула сложения. Пока эта формула была доказана только при определенных ограничениях При условии, что значение переменной, т.е. если и если xr> 0 и- X-> + oo на левой стороне, x (<0 на правой стороне С ху х — * — оо и у-у? :. Таким образом, ограничения смягчены К тому, что V ,, y.2 и yt 2 должны находиться в интервале (-T * »t77) — Однако эти ограничения не являются необходимыми. Предел Y \ — ~ yy Интервал (-xv xr) не включает-.
Знак гениального определения с использованием бесконечного произведения. Третий способ — определить грех * по уравнению. Этот метод имеет много преимуществ, но, конечно, требует знания теории бесконечных произведений. 4 ° Определить обратную функцию, используя интеграл. Есть еще четвертый способ. Здесь следует отдать приоритет, так как мы почти повторили изложение логарифмической теории в первой части этой главы. Начните с определения arctgjt как уравнения X * J Tit Т + 7 * ‘ о
Эта формула однозначно определяет значение y%, соответствующее каждому действительному значению x. Поскольку подынтегральное выражение является четным, y является нечетной функцией от x. Кроме того, поскольку y непрерывен и строго возрастает, существует обратная функция jt = jc (y) согласно § 110, которая также непрерывна и строго возрастает. считать (2) x = x (y) = tgy. Определение r в уравнении (3) Тогда х (у) и 1 _ d dt 2 77 J 1 + ** ‘ о 1 ^ ^ 1 — 2 до <Y <2 * ‘
Теперь мы ставим (4) = WTU = yGFJ, Здесь подразумевается положительное значение маршрута.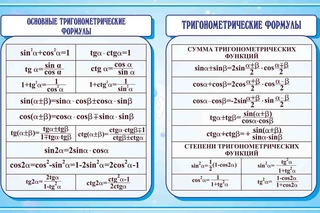 и tgy, затем через tgy мы определили уютные и греховные вещи. дуги sin a * и siny могут быть выбраны в качестве основных функций. В этом случае дуга x должна быть определена внутренним уравнением (-I, 1). 5 это Получено положительное корневое значение. синус-обратная функция; используйте g: -equality 1 г дф J. at Fra’1 2 о Уютные Tgy- отношения X cosy = y 1 «, tgy = p-r == — 4 (-1 <l: <1). Выбранный путь немного удобнее. 225.
и tgy, затем через tgy мы определили уютные и греховные вещи. дуги sin a * и siny могут быть выбраны в качестве основных функций. В этом случае дуга x должна быть определена внутренним уравнением (-I, 1). 5 это Получено положительное корневое значение. синус-обратная функция; используйте g: -equality 1 г дф J. at Fra’1 2 о Уютные Tgy- отношения X cosy = y 1 «, tgy = p-r == — 4 (-1 <l: <1). Выбранный путь немного удобнее. 225.
Теперь мы сформулировали все необходимые определения, то есть определение, представленное уравнением с номером §224. Дальнейшее развитие теории зависит от формулы сложения. Прежде всего, (1 + **) (1 + /) = 0- * Y) * + (x + Y) \ Таким образом, dx , dy (I-j-ya) dx + (l + x *) dy 1 (1-ложь) «+ — _ (1-lg) </ (dg + y) — (l: -I-y) -, vy) dz (\ -Xy) * + (x + y) * 1 + где 1-х Это приводит к отношениям Дуга tg x arc igy = дуга tg z, Однако эти функции неоднозначны и должны рассматриваться более тщательно. Put — 1 _ L (X1 4- «) 14- ^ 1 \ o олово 1-я / л-т-. = 0. *! -v «0 x *. xt -G я G ду G да «» J V + fl8 1 J «1 +» 2 • J О 0-Д «! = arc tg; c, -f- arc tg x>. Если я поставлю это сейчас y = arc tgx, y1 = arc tg *:, yy = arc tglg5 и GP trfv; y y — tgjr, + tgjf, (1) tg tVi -G-L) — * -! -s _tg yltgys ‘
= 0. *! -v «0 x *. xt -G я G ду G да «» J V + fl8 1 J «1 +» 2 • J О 0-Д «! = arc tg; c, -f- arc tg x>. Если я поставлю это сейчас y = arc tgx, y1 = arc tg *:, yy = arc tglg5 и GP trfv; y y — tgjr, + tgjf, (1) tg tVi -G-L) — * -! -s _tg yltgys ‘
Нулевые понятие про тригонометрические формулы теория. Формулы тригонометрии
Это последний и самый главный урок, необходимый для решения задач B11. Мы уже знаем, как переводить углы из радианной меры в градусную (см. урок «Радианная и градусная мера угла »), а также умеем определять знак тригонометрической функции, ориентируясь по координатным четвертям (см. урок «Знаки тригонометрических функций »).
Дело осталось за малым: вычислить значение самой функции — то самое число, которое записывается в ответ. Здесь на помощь приходит основное тригонометрическое тождество.
Основное тригонометрическое тождество. Для любого угла α верно утверждение:
sin 2 α + cos 2 α = 1.

Эта формула связывает синус и косинус одного угла. Теперь, зная синус, мы легко найдем косинус — и наоборот. Достаточно извлечь квадратный корень:
Обратите внимание на знак «±» перед корнями. Дело в том, что из основного тригонометрического тождества непонятно, каким был исходный синус и косинус: положительным или отрицательным. Ведь возведение в квадрат — четная функция, которая «сжигает» все минусы (если они были).
Именно поэтому во всех задачах B11, которые встречаются в ЕГЭ по математике, обязательно есть дополнительные условия, которые помогают избавиться от неопределенности со знаками. Обычно это указание на координатную четверть, по которой можно определить знак.
Внимательный читатель наверняка спросит: «А как быть с тангенсом и котангенсом?» Напрямую вычислить эти функции из приведенных выше формул нельзя. Однако существуют важные следствия из основного тригонометрического тождества, которые уже содержат тангенсы и котангенсы. А именно:
Важное следствие: для любого угла α можно переписать основное тригонометрическое тождество следующим образом:
Эти уравнения легко выводятся из основного тождества — достаточно разделить обе стороны на cos 2 α
(для получения тангенса) или на sin 2 α
(для котангенса).
Рассмотрим все это на конкретных примерах. Ниже приведены настоящие задачи B11, которые взяты из пробных вариантов ЕГЭ по математике 2012.
Нам известен косинус, но неизвестен синус. Основное тригонометрическое тождество (в «чистом» виде) связывает как раз эти функции, поэтому будем работать с ним. Имеем:
sin 2 α + cos 2 α = 1 ⇒ sin 2 α + 99/100 = 1 ⇒ sin 2 α = 1/100 ⇒ sin α = ±1/10 = ±0,1.
Для решения задачи осталось найти знак синуса. Поскольку угол α ∈ (π /2; π ), то в градусной мере это записывается так: α ∈ (90°; 180°).
Следовательно, угол α лежит во II координатной четверти — все синусы там положительны. Поэтому sin α = 0,1.
Итак, нам известен синус, а надо найти косинус. Обе эти функции есть в основном тригонометрическом тождестве. Подставляем:
sin 2 α + cos 2 α = 1 ⇒ 3/4 + cos 2 α = 1 ⇒ cos 2 α = 1/4 ⇒ cos α = ±1/2 = ±0,5.
Осталось разобраться со знаком перед дробью. Что выбрать: плюс или минус? По условию, угол α
принадлежит промежутку (π
3π
/2). Переведем углы из радианной меры в градусную — получим: α
∈ (180°; 270°).
Что выбрать: плюс или минус? По условию, угол α
принадлежит промежутку (π
3π
/2). Переведем углы из радианной меры в градусную — получим: α
∈ (180°; 270°).
Очевидно, это III координатная четверть, где все косинусы отрицательны. Поэтому cos α = −0,5.
Задача. Найдите tg α , если известно следующее:
Тангенс и косинус связаны уравнением, следующим из основного тригонометрического тождества:
Получаем: tg α = ±3. Знак тангенса определяем по углу α . Известно, что α ∈ (3π /2; 2π ). Переведем углы из радианной меры в градусную — получим α ∈ (270°; 360°).
Очевидно, это IV координатная четверть, где все тангенсы отрицательны. Поэтому tg α = −3.
Задача. Найдите cos α , если известно следующее:
Снова известен синус и неизвестен косинус. Запишем основное тригонометрическое тождество:
sin 2 α + cos 2 α = 1 ⇒ 0,64 + cos 2 α = 1 ⇒ cos 2 α = 0,36 ⇒ cos α = ±0,6.
Знак определяем по углу. Имеем: α
∈ (3π
/2; 2π
). Переведем углы из градусной меры в радианную: α
∈ (270°; 360°) — это IV координатная четверть, косинусы там положительны. Следовательно, cos α
= 0,6.
Имеем: α
∈ (3π
/2; 2π
). Переведем углы из градусной меры в радианную: α
∈ (270°; 360°) — это IV координатная четверть, косинусы там положительны. Следовательно, cos α
= 0,6.
Задача. Найдите sin α , если известно следующее:
Запишем формулу, которая следует из основного тригонометрического тождества и напрямую связывает синус и котангенс:
Отсюда получаем, что sin 2 α = 1/25, т.е. sin α = ±1/5 = ±0,2. Известно, что угол α ∈ (0; π /2). В градусной мере это записывается так: α ∈ (0°; 90°) — I координатная четверть.
Итак, угол находится в I координатной четверти — все тригонометрические функции там положительны, поэтому sin α = 0,2.
Справочные данные по тригонометрическим функциям синус (sin x) и косинус (cos x). Геометрическое определение, свойства, графики, формулы. Таблица синусов и косинусов, производные, интегралы, разложения в ряды, секанс, косеканс. Выражения через комплексные переменные. Связь с гиперболическими функциями.
Геометрическое определение синуса и косинуса
|BD|
— длина дуги окружности с центром в точке A
.
α
— угол, выраженный в радианах.
Определение
Синус (sin α)
— это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
Косинус (cos α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.
Принятые обозначения
;
;
.
;
;
.
График функции синус, y = sin x
График функции косинус, y = cos x
Свойства синуса и косинуса
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2 π .
Четность
Функция синус — нечетная. Функция косинус — четная.
Область определения и значений, экстремумы, возрастание, убывание
Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).
| y = sin x | y = cos x | |
| Область определения и непрерывность | — ∞ | — ∞ |
| Область значений | -1 ≤ y ≤ 1 | -1 ≤ y ≤ 1 |
| Возрастание | ||
| Убывание | ||
| Максимумы, y = 1 | ||
| Минимумы, y = -1 | ||
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы
Сумма квадратов синуса и косинуса
Формулы синуса и косинуса от суммы и разности
;
;
Формулы произведения синусов и косинусов
Формулы суммы и разности
Выражение синуса через косинус
;
;
;
.
Выражение косинуса через синус
;
;
;
.
Выражение через тангенс
; .
При ,
имеем:
;
.
При :
;
.
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
Выражения через комплексные переменные
;
Формула Эйлера
{ -∞
Секанс, косеканс
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.
Арксинус, arcsin
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Тригонометрические тождества
— это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла, которая позволяет находить любую из данных функций при условии, что будет известна какая-либо другая.
tg \alpha = \frac{\sin \alpha}{\cos \alpha}, \enspace ctg \alpha = \frac{\cos \alpha}{\sin \alpha}
tg \alpha \cdot ctg \alpha = 1
Данное тождество говорит о том, что сумма квадрата синуса одного угла и квадрата косинуса одного угла равна единице, что на практике дает возможность вычислить синус одного угла, когда известен его косинус и наоборот.
При преобразовании тригонометрических выражений очень часто используют данное тождество, которое позволяет заменять единицей сумму квадратов косинуса и синуса одного угла и также производить операцию замены в обратном порядке.
Нахождение тангенса и котангенса через синус и косинус
tg \alpha = \frac{\sin \alpha}{\cos \alpha},\enspace
Данные тождества образуются из определений синуса, косинуса, тангенса и котангенса. Ведь если разобраться, то по определению ординатой y
является синус, а абсциссой x
— косинус. Тогда тангенс будет равен отношению \frac{y}{x}=\frac{\sin \alpha}{\cos \alpha}
, а отношение \frac{x}{y}=\frac{\cos \alpha}{\sin \alpha}
— будет являться котангенсом.
Добавим, что только для таких углов \alpha , при которых входящие в них тригонометрические функции имеют смысл, будут иметь место тождества , ctg \alpha=\frac{\cos \alpha}{\sin \alpha} .
Например: tg \alpha = \frac{\sin \alpha}{\cos \alpha} является справедливой для углов \alpha , которые отличны от \frac{\pi}{2}+\pi z , а ctg \alpha=\frac{\cos \alpha}{\sin \alpha} — для угла \alpha , отличного от \pi z , z — является целым числом.
Зависимость между тангенсом и котангенсом
tg \alpha \cdot ctg \alpha=1
Данное тождество справедливо только для таких углов \alpha , которые отличны от \frac{\pi}{2} z . Иначе или котангенс или тангенс не будут определены.
Опираясь на вышеизложенные пункты, получаем, что tg \alpha = \frac{y}{x}
, а ctg \alpha=\frac{x}{y}
. Отсюда следует, что tg \alpha \cdot ctg \alpha = \frac{y}{x} \cdot \frac{x}{y}=1
. Таким образом, тангенс и котангенс одного угла, при котором они имеют смысл, являются взаимно обратными числами.
По условию \frac{\pi}{2} . Во второй четверти косинус отрицателен, поэтому \cos \alpha = -\sqrt\frac14=-\frac12 .
Для того, чтобы найти ctg \alpha , воспользуемся формулой ctg \alpha = \frac{\cos \alpha}{\sin \alpha} . Соответствующие величины нам известны.
ctg \alpha = -\frac12: \frac{\sqrt3}{2} = -\frac{1}{\sqrt 3} .
Соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом и котангенсом — задаются тригонометрическими формулами . А так как связей между тригонометрическими функциями достаточно много, то этим объясняется и обилие тригонометрических формул. Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т.д.
В этой статье мы по порядку перечислим все основные тригонометрические формулы, которых достаточно для решения подавляющего большинства задач тригонометрии. Для удобства запоминания и использования будем группировать их по назначению, и заносить в таблицы.
Для удобства запоминания и использования будем группировать их по назначению, и заносить в таблицы.
Навигация по странице.
Основные тригонометрические тождества
Основные тригонометрические тождества задают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Они вытекают из определения синуса, косинуса, тангенса и котангенса, а также понятия единичной окружности . Они позволяют выразить одну тригонометрическую функцию через любую другую.
Подробное описание этих формул тригонометрии, их вывод и примеры применения смотрите в статье .
Формулы приведения
Формулы приведения
следуют из свойств синуса, косинуса, тангенса и котангенса , то есть, они отражают свойство периодичности тригонометрических функций, свойство симметричности, а также свойство сдвига на данный угол. Эти тригонометрические формулы позволяют от работы с произвольными углами переходить к работе с углами в пределах от нуля до 90
градусов.
Обоснование этих формул, мнемоническое правило для их запоминания и примеры их применения можно изучить в статье .
Формулы сложения
Тригонометрические формулы сложения показывают, как тригонометрические функции суммы или разности двух углов выражаются через тригонометрические функции этих углов. Эти формулы служат базой для вывода следующих ниже тригонометрических формул.
Формулы двойного, тройного и т.д. угла
Формулы двойного, тройного и т.д. угла (их еще называют формулами кратного угла) показывают, как тригонометрические функции двойных, тройных и т.д. углов () выражаются через тригонометрические функции одинарного угла . Их вывод базируется на формулах сложения.
Более детальная информация собрана в статье формулы двойного, тройного и т.д. угла .
Формулы половинного угла
Формулы половинного угла
показывают, как тригонометрические функции половинного угла выражаются через косинус целого угла . Эти тригонометрические формулы следуют из формул двойного угла.
Эти тригонометрические формулы следуют из формул двойного угла.
Их вывод и примеры применения можно посмотреть в статье .
Формулы понижения степени
Тригонометрические формулы понижения степени призваны содействовать переходу от натуральных степеней тригонометрических функций к синусам и косинусам в первой степени, но кратных углов. Иными словами, они позволяют понижать степени тригонометрических функций до первой.
Формулы суммы и разности тригонометрических функций
Основное предназначение формул суммы и разности тригонометрических функций заключается в переходе к произведению функций, что очень полезно при упрощении тригонометрических выражений. Указанные формулы также широко используются при решении тригонометрических уравнений, так как позволяют раскладывать на множители сумму и разность синусов и косинусов.
Формулы произведения синусов, косинусов и синуса на косинус
Переход от произведения тригонометрических функций к сумме или разности осуществляется посредством формул произведения синусов, косинусов и синуса на косинус .
Copyright by cleverstudents
Все права защищены.
Охраняется законом об авторском праве. Ни одну часть сайта www.сайт, включая внутренние материалы и внешнее оформление, нельзя воспроизводить в какой-либо форме или использовать без предварительного письменного разрешения правообладателя.
Основные тригонометрические тождества
- Главная
- Справочник
- Тригонометрия
- Основные тригонометрические тождества
Тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла, которая позволяет находить любую из данных функций при условии, что будет известна какая-либо другая.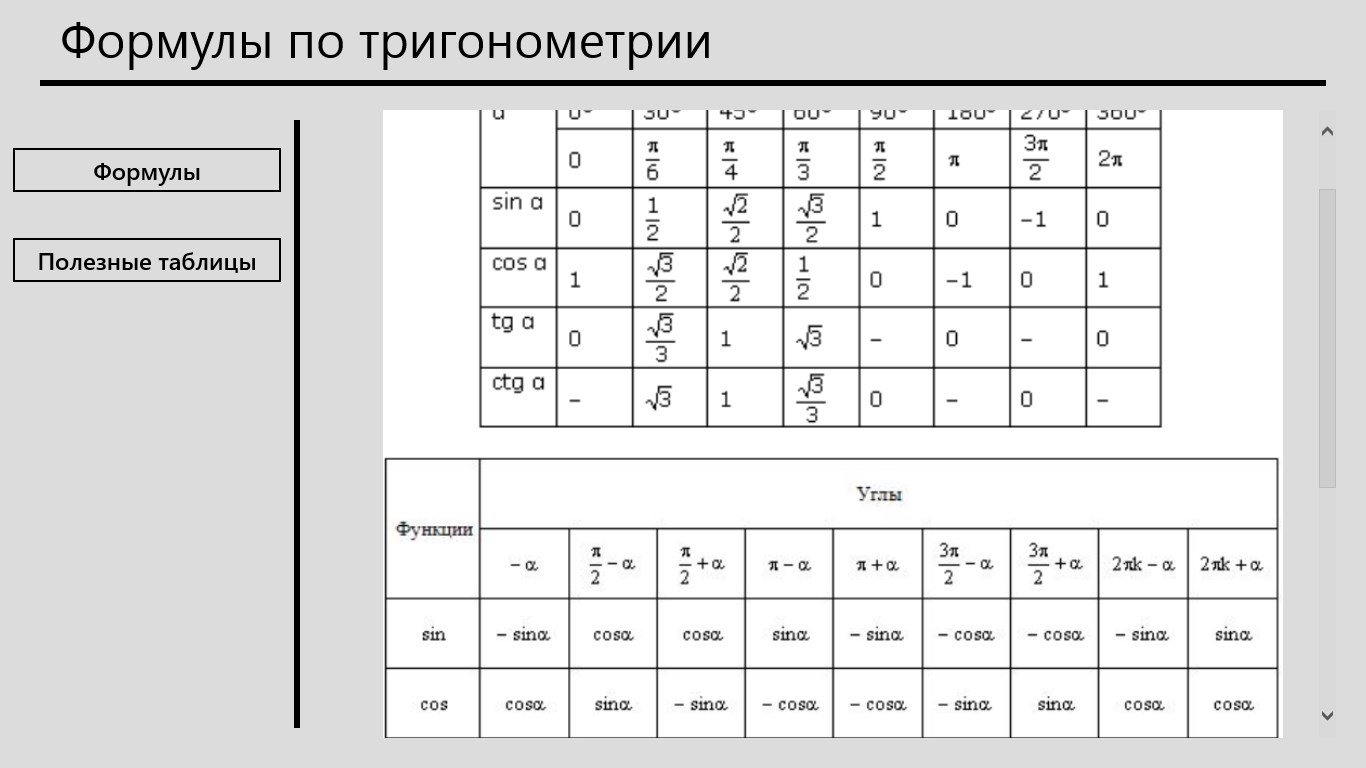
Данное тождество говорит о том, что сумма квадрата синуса одного угла и квадрата косинуса одного угла равна единице, что на практике дает возможность вычислить синус одного угла, когда известен его косинус и наоборот.
При преобразовании тригонометрических выражений очень часто используют данное тождество, которое позволяет заменять единицей сумму квадратов косинуса и синуса одного угла и также производить операцию замены в обратном порядке.
Нахождение тангенса и котангенса через синус и косинус
\[ tg \alpha = \dfrac{\sin \alpha}{\cos \alpha},\enspace ctg \alpha=\dfrac{\cos \alpha}{\sin \alpha} \]
Данные тождества образуются из определений синуса, косинуса, тангенса и котангенса. Ведь если разобраться, то по определению ординатой \( \dfrac{y}{x}=\dfrac{\sin \alpha}{\cos \alpha} \), а отношение \( \dfrac{x}{y}=\dfrac{\cos \alpha}{\sin \alpha} \) — будет являться котангенсом.
Добавим, что только для таких углов \( \alpha \), при которых входящие в них тригонометрические функции имеют смысл, будут иметь место тождества \( tg \alpha = \dfrac{\sin \alpha}{\cos \alpha} \), \( ctg \alpha=\dfrac{\cos \alpha}{\sin \alpha} \).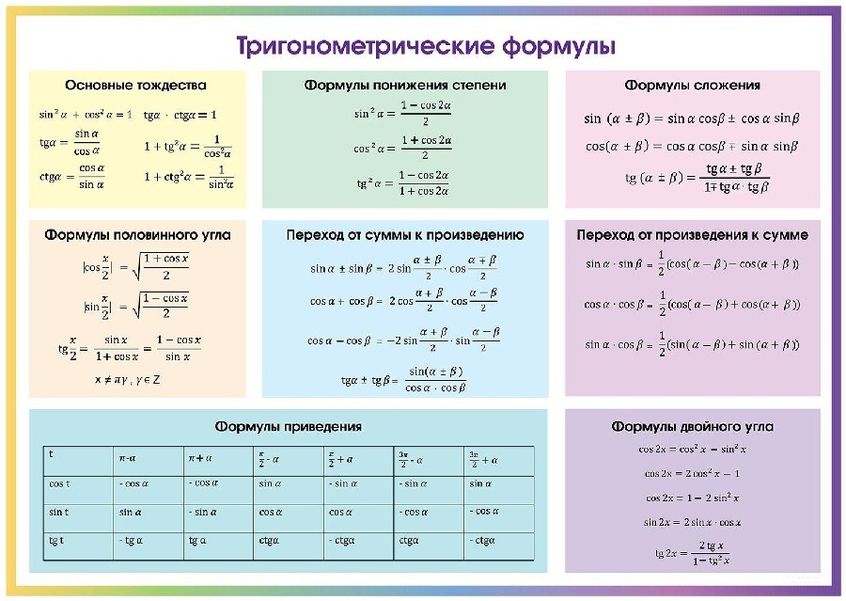
Например: \( tg \alpha = \dfrac{\sin \alpha}{\cos \alpha} \) является справедливой для углов \( \alpha \), которые отличны от \( \dfrac{\pi}{2}+\pi z \), а \( ctg \alpha=\dfrac{\cos \alpha}{\sin \alpha} \) — для угла \( \alpha \), отличного от \( \pi z \), \( z \) — является целым числом.
Зависимость между тангенсом и котангенсом
\[ tg \alpha \cdot ctg \alpha=1 \]
Данное тождество справедливо только для таких углов \( \alpha \), которые отличны от \( \dfrac{\pi}{2} z \). Иначе или котангенс или тангенс не будут определены.
Опираясь на вышеизложенные пункты, получаем, что \( tg \alpha = \dfrac{y}{x} \), а \( ctg \alpha=\dfrac{x}{y} \). Отсюда следует, что \( tg \alpha \cdot ctg \alpha = \dfrac{y}{x} \cdot \dfrac{x}{y}=1 \). Таким образом, тангенс и котангенс одного угла, при котором они имеют смысл, являются взаимно обратными числами.
Зависимости между тангенсом и косинусом, котангенсом и синусом
\( tg^{2} \alpha + 1=\dfrac{1}{\cos^{2} \alpha} \) — сумма квадрата тангенса угла \( \alpha \) и \( \alpha \), отличных от \( \dfrac{\pi}{2}+ \pi z \). {2}\alpha} \) — сумма \( \alpha \), равняется обратному квадрату синуса данного угла. Данное тождество справедливо для любого \( \alpha \), отличного от \( \pi z \).
{2}\alpha} \) — сумма \( \alpha \), равняется обратному квадрату синуса данного угла. Данное тождество справедливо для любого \( \alpha \), отличного от \( \pi z \).
Формулы приведения
sinα+2πz=sinα,cosα+2πz=cosαtgα+2πz=tgα,ctgα+2πz=ctgαsin-α+2πz=-sinα,cos-α+2πz=cosαtg-α+2πz=-tgα,ctg-α+2πz=-ctgαsinπ2+α+2πz=cosα,cosπ2+α+2πz=-sinαtgπ2+α+2πz=-ctgα,ctgπ2+α+2πz=-tgαsinπ2-α+2πz=cosα,cosπ2-α+2πz=sinαtgπ2-α+2πz=ctgα,ctgπ2-α+2πz=tgαsinπ+α+2πz=-sinα,cosπ+α+2πz=-cosαtgπ+α+2πz=tgα,ctgπ+α+2πz=ctgαsinπ-α+2πz=sinα,cosπ-α+2πz=-cosαtgπ-α+2πz=-tgα,ctgπ-α+2πz=-ctgαsin3π2+α+2πz=-cosα,cos3π2+α+2πz=sinαtg3π2+α+2πz=-ctgα,ctg3π2+α+2πz=-tgαsin3π2-α+2πz=-cosα,cos3π2-α+2πz=-sinαtg3π2-α+2πz=ctgα,ctg3π2-α+2πz=tgα
Формулы понижения степени
sin2α=1-cos2α2cos2α=1+cos2α2sin3α=3sinα-sin3α4cos3α=3cosα+cos3α4sin4α=3-4cos2α+cos4α8cos4α=3+4cos2α+cos4α8
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!Больше интересного в телеграм @calcsbox
Использование тригонометрии — Uses of trigonometry
Канадарм2 роботизированный манипулятор на Международной космической станции управляется посредством управления углами своих суставов. Расчет окончательного положения космонавта на конце руки требует многократного использования тригонометрических функций этих углов.Среди непрофессионалов, не являющихся математиками и не-учеными, тригонометрия известна главным образом своим приложением к задачам измерения, но также часто используется гораздо более тонкими способами, такими как ее место в теории музыки ; все же другие применения более технические, например, в теории чисел . Математические вопросы, связанные с рядами Фурье и преобразованиями Фурье, в значительной степени зависят от знания тригонометрических функций и находят применение в ряде областей, включая статистику .
Заявление Томаса Пейна
В главе XI «Эпохи разума» американский революционер и мыслитель эпохи Просвещения Томас Пейн писал:
-
Научные принципы, которые человек использует для получения предвидения затмения или чего-либо еще, относящегося к движению небесных тел, содержатся главным образом в той части науки, которая называется тригонометрией, или свойствами треугольника, которые: применительно к изучению небесных тел называется астрономией; когда применяется для определения курса корабля в океане, это называется навигацией; применительно к построению фигур, нарисованных линейкой и циркулем, это называется геометрией; применительно к строительству планов зданий это называется архитектурой; применительно к измерению любого участка поверхности земли это называется топографической съемкой.
 В общем, это душа науки. Это вечная истина: она содержит математическое доказательство того, о чем говорит человек, и степень ее использования неизвестна.
В общем, это душа науки. Это вечная истина: она содержит математическое доказательство того, о чем говорит человек, и степень ее использования неизвестна.
История
Большой тригонометрический обзор
С 1802 по 1871 год Великая тригонометрическая съемка была проектом по исследованию Индийского субконтинента с высокой точностью. Начиная с берега, математики и географы триангулировали огромные расстояния по стране. Одним из ключевых достижений было измерение высоты Гималайских гор и определение Эвереста как самой высокой точки на Земле.
Историческое использование умножения
В течение 25 лет, предшествовавших изобретению логарифма в 1614 году, простаферез был единственным известным общепринятым способом быстрого приближения продуктов. Он использовал тождества для тригонометрических функций сумм и разностей углов в терминах произведений тригонометрических функций этих углов.
Некоторые современные способы использования
Научные области, в которых используется тригонометрия, включают:
- акустика , архитектура , астрономия , картография , гражданское строительство , геофизика , кристаллография , электротехника , электроника , топографическая съемка и геодезия , многие физические науки , машиностроение , механическая обработка , медицинская визуализация , теория чисел , океанография , оптика , фармакология , теория вероятностей , сейсмология , статистика и визуальное восприятие
То, что эти поля включают тригонометрию, не означает, что для того, чтобы что-то о них узнать, необходимы знания тригонометрии. Это действительно означает, что некоторые вещи в этих областях не могут быть поняты без тригонометрии. Например, профессор музыки может ничего не знать о математике, но, вероятно, знает, что Пифагор был одним из первых известных авторов математической теории музыки.
Это действительно означает, что некоторые вещи в этих областях не могут быть поняты без тригонометрии. Например, профессор музыки может ничего не знать о математике, но, вероятно, знает, что Пифагор был одним из первых известных авторов математической теории музыки.
В некоторых сферах деятельности, перечисленных выше, легко представить, как можно использовать тригонометрию. Например, в навигации и топографической съемке случаи использования тригонометрии, по крайней мере, в некоторых случаях достаточно просты, чтобы их можно было описать в учебнике по тригонометрии для начинающих. В случае теории музыки применение тригонометрии связано с работой, начатой Пифагором, который заметил, что звуки, издаваемые при перещипывании двух струн разной длины, являются согласными, если обе длины являются малыми целыми кратными общей длины. Сходство формы колеблющейся струны и графика синусоидальной функции не просто совпадение. В океанографии сходство форм некоторых волн и графика синусоидальной функции также не случайно. В некоторых других областях, среди которых климатология , биология и экономика, наблюдаются сезонные периоды. Их изучение часто включает периодический характер функции синуса и косинуса.
В некоторых других областях, среди которых климатология , биология и экономика, наблюдаются сезонные периоды. Их изучение часто включает периодический характер функции синуса и косинуса.
Ряд Фурье
Многие области используют тригонометрию более продвинутыми способами, чем можно обсудить в одной статье. Часто они включают так называемые ряды Фурье в честь французского математика и физика 18-19 веков Жозефа Фурье . Ряды Фурье находят удивительно разнообразное применение во многих областях науки, в частности, во всех явлениях, связанных с сезонной периодичностью, упомянутой выше, и в волновом движении, и, следовательно, в исследовании излучения, акустики, сейсмологии, модуляции радиоизлучения. волны в электронике и электроэнергетике.
Ряд Фурье представляет собой сумму такой формы:
- ◻ + ◻ потому что θ + ◻ грех θ ⏟ 1 + ◻ потому что ( 2 θ ) + ◻ грех ( 2 θ ) ⏟ 2 + ◻ потому что ( 3 θ ) + ◻ грех ( 3 θ ) ⏟ 3 + ⋯ {\ displaystyle \ square + \ underbrace {\ square \ cos \ theta + \ square \ sin \ theta} _ {1} + \ underbrace {\ square \ cos (2 \ theta) + \ square \ sin (2 \ theta) } _ {2} + \ underbrace {\ square \ cos (3 \ theta) + \ square \ sin (3 \ theta)} _ {3} + \ cdots \,}
где каждый из квадратов ( ) — разное число, и один добавляет бесконечно много членов. Фурье использовал их для изучения теплового потока и диффузии (диффузия — это процесс, при котором, когда вы бросаете кубик сахара в галлон воды, сахар постепенно распространяется по воде, или загрязняющее вещество распространяется по воздуху, или любое растворенное вещество распространяется через любая жидкость).
◻ {\ Displaystyle \ квадрат}
Фурье использовал их для изучения теплового потока и диффузии (диффузия — это процесс, при котором, когда вы бросаете кубик сахара в галлон воды, сахар постепенно распространяется по воде, или загрязняющее вещество распространяется по воздуху, или любое растворенное вещество распространяется через любая жидкость).
◻ {\ Displaystyle \ квадрат}
Ряды Фурье применимы и к предметам, связь которых с волновым движением далеко не очевидна. Одним из распространенных примеров является цифровое сжатие, при котором изображения , аудио- и видеоданные сжимаются до гораздо меньшего размера, что делает возможной их передачу по телефону , Интернету и сетям вещания . Другой пример, упомянутый выше, — это диффузия. Среди прочего: геометрия чисел, изопериметрические задачи, повторяемость случайных блужданий, квадратичная взаимность, центральная предельная теорема, неравенство Гейзенберга .
Преобразования Фурье
Более абстрактным понятием, чем ряды Фурье, является идея преобразования Фурье . Преобразования Фурье включают в себя интегралы, а не суммы, и используются в столь же разнообразных научных областях. Многие законы природы выражаются в соотнесении скорости изменения величин с самими величинами. Например: скорость изменения численности населения иногда пропорциональна (1) существующей численности населения и (2) количеству, на которое нынешняя популяция отстает от пропускной способности . Такая связь называется дифференциальным уравнением . Если, имея эту информацию, кто-то пытается выразить численность населения как функцию времени, он пытается «решить» дифференциальное уравнение. Преобразования Фурье могут использоваться для преобразования некоторых дифференциальных уравнений в алгебраические уравнения, для которых известны методы их решения. Преобразования Фурье имеют множество применений. Практически в любом научном контексте, где встречаются слова «спектр», « гармоника» или « резонанс» , рядом есть преобразования Фурье или ряды Фурье.
Преобразования Фурье включают в себя интегралы, а не суммы, и используются в столь же разнообразных научных областях. Многие законы природы выражаются в соотнесении скорости изменения величин с самими величинами. Например: скорость изменения численности населения иногда пропорциональна (1) существующей численности населения и (2) количеству, на которое нынешняя популяция отстает от пропускной способности . Такая связь называется дифференциальным уравнением . Если, имея эту информацию, кто-то пытается выразить численность населения как функцию времени, он пытается «решить» дифференциальное уравнение. Преобразования Фурье могут использоваться для преобразования некоторых дифференциальных уравнений в алгебраические уравнения, для которых известны методы их решения. Преобразования Фурье имеют множество применений. Практически в любом научном контексте, где встречаются слова «спектр», « гармоника» или « резонанс» , рядом есть преобразования Фурье или ряды Фурье.
Статистика, в том числе математическая психология
Иногда считается, что коэффициенты интеллекта распределяются по колоколообразной кривой . Около 40% площади под кривой находится в интервале от 100 до 120; соответственно, около 40% населения набирает от 100 до 120 баллов по тестам IQ. Около 9% площади под кривой находится в интервале от 120 до 140; соответственно, около 9% населения набирает от 120 до 140 баллов по тестам IQ и т. д. Подобным образом многие другие вещи распределяются по «колоколообразной кривой», включая ошибки измерения во многих физических измерениях. Почему повсеместно распространена «колоколообразная кривая»? Для этого есть теоретическая причина, и она включает в себя преобразования Фурье и, следовательно, тригонометрические функции . Это одно из множества применений преобразования Фурье в статистике .
Около 40% площади под кривой находится в интервале от 100 до 120; соответственно, около 40% населения набирает от 100 до 120 баллов по тестам IQ. Около 9% площади под кривой находится в интервале от 120 до 140; соответственно, около 9% населения набирает от 120 до 140 баллов по тестам IQ и т. д. Подобным образом многие другие вещи распределяются по «колоколообразной кривой», включая ошибки измерения во многих физических измерениях. Почему повсеместно распространена «колоколообразная кривая»? Для этого есть теоретическая причина, и она включает в себя преобразования Фурье и, следовательно, тригонометрические функции . Это одно из множества применений преобразования Фурье в статистике .
Тригонометрические функции также применяются, когда статистики изучают сезонные периоды, которые часто представлены рядами Фурье.
Теория чисел
Есть намек на связь между тригонометрией и теорией чисел. Грубо говоря, можно сказать, что теория чисел имеет дело с качественными свойствами, а не с количественными свойствами чисел.
- 1 42 , 2 42 , 3 42 , … … , 39 42 , 40 42 , 41 год 42 . {\ displaystyle {\ frac {1} {42}}, \ qquad {\ frac {2} {42}}, \ qquad {\ frac {3} {42}}, \ qquad \ dots \ dots, \ qquad { \ frac {39} {42}}, \ qquad {\ frac {40} {42}}, \ qquad {\ frac {41} {42}}.}
Откажитесь от тех, которые не на самом низком уровне; оставляйте только те, которые находятся в самом низком плане:
- 1 42 , 5 42 , 11 42 , … , 31 год 42 , 37 42 , 41 год 42 . {\ displaystyle {\ frac {1} {42}}, \ qquad {\ frac {5} {42}}, \ qquad {\ frac {11} {42}}, \ qquad \ dots, \ qquad {\ frac {31} {42}}, \ qquad {\ frac {37} {42}}, \ qquad {\ frac {41} {42}}.}.
Затем внесите тригонометрию:
- потому что ( 2 π ⋅ 1 42 ) + потому что ( 2 π ⋅ 5 42 ) + ⋯ + потому что ( 2 π ⋅ 37 42 ) + потому что ( 2 π ⋅ 41 год 42 ) {\ displaystyle \ cos \ left (2 \ pi \ cdot {\ frac {1} {42}} \ right) + \ cos \ left (2 \ pi \ cdot {\ frac {5} {42}} \ right) + \ cdots + \ cos \ left (2 \ pi \ cdot {\ frac {37} {42}} \ right) + \ cos \ left (2 \ pi \ cdot {\ frac {41} {42}} \ right )}
Значение суммы равно -1, потому что 42 имеет нечетное количество простых множителей, и ни один из них не повторяется: 42 = 2 × 3 × 7. (Если бы было четное число неповторяющихся множителей, сумма была бы были равны 1; если бы были какие-либо повторяющиеся простые множители (например, 60 = 2 × 2 × 3 × 5), то сумма была бы равна 0; сумма — это функция Мёбиуса, вычисленная как 42.) Это намекает на возможность применение анализа Фурье к теории чисел.
(Если бы было четное число неповторяющихся множителей, сумма была бы были равны 1; если бы были какие-либо повторяющиеся простые множители (например, 60 = 2 × 2 × 3 × 5), то сумма была бы равна 0; сумма — это функция Мёбиуса, вычисленная как 42.) Это намекает на возможность применение анализа Фурье к теории чисел.
Решение нетригонометрических уравнений
С помощью тригонометрии можно решать различные типы уравнений .
Например, линейное разностное уравнение или линейное дифференциальное уравнение с постоянными коэффициентами имеет решения, выраженные через собственные значения его характеристического уравнения; если некоторые из собственных значений являются комплексными , комплексные члены могут быть заменены тригонометрическими функциями действительных членов, показывая, что динамическая переменная демонстрирует колебания .
Точно так же кубические уравнения с тремя действительными решениями имеют алгебраическое решение , которое бесполезно, поскольку оно содержит кубические корни комплексных чисел; И снова существует альтернативное решение в терминах тригонометрических функций действительных членов.
Рекомендации
Тригонометрия в искусстве | Обучонок
5. Тригонометрия в музыке
Каждая нота в рамках новой теории представляется как логарифм частоты соответствующего звука (нота «до» первой октавы, к примеру, соответствует числу 60, октава – числу 12).
Аккорд, таким образом, представляется как точка с заданными координатами в геометрическом пространстве. Аккорды сгруппированы в различные «семейства», которые соответствуют различным типам геометрических пространств.
6. Применение тригонометрии в искусстве и архитектуре
С того времени как человек стал существовать на земле, основой улучшения быта и других сфер жизни стала наука. Основы всего, что создано человеком – это различные направления в естественных и математических науках. Одна из них – геометрия.
Архитектура не единственная сфера науки, в которой используются тригонометрические формулы. Большинство композиционных решений и построений рисунков проходило именно с помощью геометрии.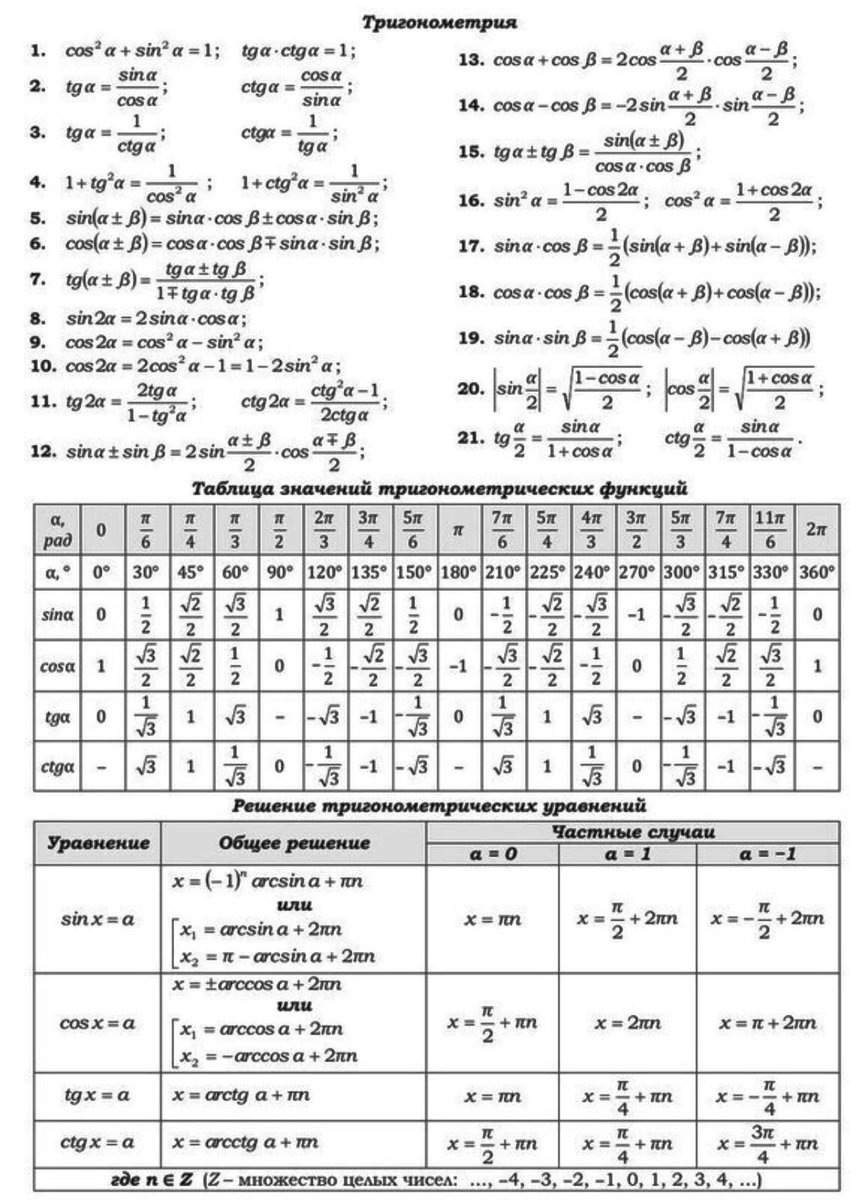 Но теоретические данные мало что значат. Рассмотрим пример на построение одной скульптуры французского мастера Золотого века искусства.
Но теоретические данные мало что значат. Рассмотрим пример на построение одной скульптуры французского мастера Золотого века искусства.
Пропорциональное соотношение в построении статуи было идеально. Однако при поднятии статуи на высокий пьедестал, она смотрелась уродливой. Скульптором не было учтено, что в перспективе к горизонту уменьшаются многие детали и при взгляде снизу вверх уже не создается впечатления ее идеальности.
Велось множество расчетов, чтобы фигура с большой высоты смотрелась пропорционально. В основном они были основаны на методе визирования, то есть приблизительного измерения, на глаз. Однако коэффициент разности тех или иных пропорций позволили сделать фигуру более приближенной к идеалу.
Таким образом, зная примерное расстояние от статуи до точки зрения, а именно от верха статуи до глаз человека и высоту статуи, можно рассчитать синус угла падения взгляда с помощью таблицы. Культовые здания во всем мире были спроектированы благодаря математике, которая может считаться гением архитектуры. Некоторые известные примеры таких зданий:Детская школа Гауди в Барселоне, Ресторан в Лос-Манантиалесе в Аргентине, мост в Сингапуре. При проектировании этих зданий не обошлось без тригонометрии.
Некоторые известные примеры таких зданий:Детская школа Гауди в Барселоне, Ресторан в Лос-Манантиалесе в Аргентине, мост в Сингапуре. При проектировании этих зданий не обошлось без тригонометрии.
Заключение
В настоящее время тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контролировать системы навигации спутников.
Также следует отметить применение тригонометрии в таких областях, как теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, медицина (включая ультразвуковое исследование (УЗИ) и компьютерную томографию), фармацевтика, химия, теория чисел, сейсмология, метеорология, океанология, картография, многие разделы физики, топография и геодезия, архитектура, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография.
Вывод:
· Мы выяснили, что тригонометрия была вызвана к жизни необходимостью производить измерения углов, но со временем развилась и в науку о тригонометрических функциях.
· Мы доказали, что тригонометрия тесно связана с физикой, биологией, встречается в природе, архитектуре и медицине.
· Мы думаем, что тригонометрия нашла отражение в нашей жизни, и сферы, в которых она играет важную роль, будут расширяться.
Литература
1. Алимов Ш.А. и др. «Алгебра и начала анализа» Учебник для 10-11 классов общеобразовательных учреждений, М., Просвещение, 2010.
2. Виленкин Н.Я. Функции в природе и техники: Кн. для внеклассного чтения IX-X кл. – 2-е изд., испр.-М: Просвещение, 1985.
3. Глейзер Г.И. История математики в школе: IX-X кл. — М.: Просвещение, 1983.
4. Маслова Т.Н. «Справочник школьника по математике»
5. Рыбников К.А. История математики: Учебник. — М.: Изд-во МГУ, 1994.
6. Учеба.ru
7. Math.ru «библиотека»
Math.ru «библиотека»
Перейти к содержанию
Исследовательской работы «Тригонометрия в окружающем мире и жизни человека»
таблица тригонометрии | Britannica
тригонометрическая таблица , табличные значения для некоторых или всех шести тригонометрических функций для различных угловых значений. Тригонометрические таблицы, которые когда-то были важным инструментом для ученых, инженеров, геодезистов и мореплавателей, устарели с появлением компьютеров. (Для справки, на рисунке показаны шесть тригонометрических функций по отношению к прямоугольному треугольнику.)
Греческий астроном Гиппарх (127 г. до н. э.) первым составил таблицу тригонометрических функций (на основе хорд в окружности). ), которые он рассчитал с шагом 7° 30′.Птолемей (145 г. н. э.) улучшил таблицы Гиппарха, рассчитывая значения с шагом 30 футов. « Альмагест » Птолемея, величайшее астрономическое произведение древности, было бы невообразимо без его таблицы аккордов.
Британская викторина
Числа и математика
A-B-C, 1-2-3… Если вы считаете, что подсчет чисел похож на чтение алфавита, проверьте, насколько свободно вы владеете языком математики в этом тесте.
Самая ранняя таблица функции синуса (хотя и не в ее современном определении) находится в Surya Siddhanta , индуистском астрономическом справочнике 4-го или 5-го века нашей эры.
Астрономы средневекового ислама были непревзойденными вычислителями, составившими таблицы всех шести тригонометрических функций в качестве основы для астрономии и астрономического хронометрирования. Венцом этого начинания стали таблицы Султана Улугбека, изданные в 1440 году в Самарканде (ныне Узбекистан).Функции синуса и тангенса (хотя до сих пор не даны их современные определения в терминах отношений), рассчитанные с шагом 1 ′, были точны до эквивалента 9 знаков после запятой.
Из мусульманской Испании тригонометрические таблицы распространились в латинскую Европу. Региомонтан (1436–1476 гг.), немецкий астроном и математик, составил первые таблицы с десятичными значениями. Точно так же Георг Иоахим Ретикус (1514–1574 гг.), ученик Николая Коперника, подготовил великолепный набор таблиц всех шести тригонометрических функций с шагом 10 дюймов с точностью до 10 знаков после запятой.Ретикус также предпринял решительные шаги по определению тригонометрических функций в терминах углов, а не дуг, и в виде отношений, а не длин.
Французский математик Франсуа Виет опубликовал таблицы всех шести тригонометрических функций в Canon Mathematicus (1579). Однако ценность этой работы заключалась не в таблицах, в которых он вычислял функции с шагом в 1 ′ с точностью до пяти знаков после запятой. Наоборот, работа Виета была важна, потому что он открыл различные тригонометрические соотношения, с помощью которых продемонстрировал, как использовать тригонометрию для решения уравнений третьей степени и выше. Отныне тригонометрические таблицы использовались не только в геодезии, астрономии и навигации, но и в алгебре.
Отныне тригонометрические таблицы использовались не только в геодезии, астрономии и навигации, но и в алгебре.
Кульминация построения тригонометрических таблиц в этот период приходится на немца Бартоломео Питискуса. Именно Питискус придумал слово тригонометрия , а его Thesaurus Mathematicus (1615) содержали таблицы синусов и косинусов, рассчитанные с интервалом в 10 футов, с точностью до 15 знаков после запятой. Позже были построены еще более точные таблицы с помощью логарифмов, изобретенных Джоном Нейпиром в 1614 году.
Тригонометрия — Энциклопедия Нового Света
Робот-манипулятор Canadarm2 на Международной космической станции управляется за счет управления углами его суставов. Вычисление конечного положения космонавта на конце руки требует многократного использования тригонометрических функций этих углов. Тригонометрия (от греческого Τριγωνομετρία «tri = три» + «gon = угол» + «metr[y] = измерять») — раздел математики, изучающий треугольники, в частности те плоские треугольники, в которых один угол имеет 90 градусов (прямоугольных треугольников) . Тригонометрия имеет дело с отношениями между сторонами и углами треугольников и с тригонометрическими функциями, которые описывают эти отношения.
Тригонометрия имеет дело с отношениями между сторонами и углами треугольников и с тригонометрическими функциями, которые описывают эти отношения.
Тригонометрия применяется как в чистой математике, так и в прикладной математике, где она необходима во многих областях науки и техники. Обычно его преподают в средних школах либо как отдельный курс, либо как часть курса предварительного исчисления. Тригонометрия неофициально называется «тригонометрия» или «триго».
Раздел тригонометрии, называемый сферической тригонометрией, изучает треугольники на сферах и играет важную роль в астрономии и навигации.
Все тригонометрические функции угла θ могут быть построены геометрически в терминах единичного круга с центром в точке O .История
Таблица тригонометрии, 1728 Cyclopaedia Тригонометрия была разработана для использования в парусном спорте в качестве навигационного метода, используемого в астрономии. [1] Истоки тригонометрии можно проследить до цивилизаций Древнего Египта, Месопотамии и долины Инда (Индия), более 4000 лет назад. Обычная практика измерения углов в градусах, минутах и секундах происходит от вавилонской системы счисления с основанием шестьдесят.
Обычная практика измерения углов в градусах, минутах и секундах происходит от вавилонской системы счисления с основанием шестьдесят.
Первое зарегистрированное использование тригонометрии принадлежит эллинистическому математику Гиппарху [2] c. 150 г. до н. э. , который составил тригонометрическую таблицу, используя синус для решения треугольников. Птолемей развил тригонометрические расчеты c. 100 C.E.
Древние сингальцы на Шри-Ланке при строительстве водохранилищ в царстве Анурадхапура использовали тригонометрию для расчета градиента водного потока. Археологические исследования также предоставляют доказательства использования тригонометрии в других уникальных гидрологических сооружениях, датируемых 4 г. до н.э.CE
Индийский математик Арьябхата в 499 г. дал таблицы полуаккордов, которые сейчас известны как таблицы синусов, наряду с таблицами косинусов. Он использовал зя для синуса, котизя для косинуса, и открам зя для обратного синуса, а также ввел версинус. Другой индийский математик, Брахмагупта, в 628 году использовал интерполяционную формулу для вычисления значений синусов вплоть до второго порядка интерполяционной формулы Ньютона-Стирлинга.
Другой индийский математик, Брахмагупта, в 628 году использовал интерполяционную формулу для вычисления значений синусов вплоть до второго порядка интерполяционной формулы Ньютона-Стирлинга.
В десятом веке персидский математик и астроном Абул Вафа ввел функцию тангенса и усовершенствовал методы расчета тригонометрических таблиц.Он установил тождества сложения углов, например, sin ( a + b ), и открыл формулу синуса для сферической геометрии:
- грехAsina=sinBsinb=sinCsinc.{\displaystyle {\frac {\sin A}{\sin a}}={\frac {\sin B}{\sin b }}={\frac {\sin C}{\sin c}}.}
Также в конце десятого и начале одиннадцатого веков египетский астроном Ибн Юнус выполнил множество тщательных тригонометрических вычислений и продемонстрировал формулу
- cosacosb=cos(a+b)+cos(a−b)2.{2}+2000} и нашел положительный корень этой кубической формулы, рассмотрев пересечение прямоугольной гиперболы и окружности. Затем путем интерполяции в тригонометрических таблицах находилось приближенное численное решение.

Подробные методы построения таблицы синусов для любого угла были даны индийским математиком Бхаскарой в 1150 году вместе с некоторыми формулами синуса и косинуса. Бхаскара также разработал сферическую тригонометрию.
Персидский математик тринадцатого века Насир ад-Дин Туси, наряду с Бхаскарой, вероятно, был первым, кто рассматривал тригонометрию как отдельную математическую дисциплину.Насир ад-Дин Туси в своем «Трактате о четырехугольнике » был первым, кто перечислил шесть различных случаев прямоугольного треугольника в сферической тригонометрии.
В четырнадцатом веке персидский математик аль-Каши и тимуридский математик Улугбек (внук Тимура) составили таблицы тригонометрических функций в рамках своих астрономических исследований.
Математик Бартоломеус Питискус опубликовал влиятельную работу по тригонометрии в 1595 году, в которой, возможно, появилось само слово «тригонометрия».
Обзор
В этом прямоугольном треугольнике: sin A = a / c ; cos A = b / c ; загар А = а / б .
Если один угол треугольника равен 90 градусов и известен один из других углов, то третий тем самым фиксирован, потому что сумма трех углов любого треугольника составляет 180 градусов. Таким образом, два острых угла в сумме составляют 90 градусов: это дополнительные углы. Форма прямоугольного треугольника полностью определяется с точностью до подобия углами.Это означает, что если один из других углов известен, отношения различных сторон всегда одинаковы, независимо от общего размера треугольника. Эти отношения задаются следующими тригонометрическими функциями известного угла A, , где a, b, и c относятся к длинам сторон на прилагаемом рисунке:
- Функция синуса (sin), определяемая как отношение стороны, противоположной углу, к гипотенузе.
- sinA = гипотенуза напротив = ac. }}\,.}
- Функция косинуса (cos), определяемая как отношение прилежащего катета к гипотенузе.
- потому чтоA=adjacenthypotenuse=bc.
 {\displaystyle \cos A={\frac {\textrm {adjacent}}{\textrm {hypotenuse}}}={\frac {b}{\,c\, }}\,.}
{\displaystyle \cos A={\frac {\textrm {adjacent}}{\textrm {hypotenuse}}}={\frac {b}{\,c\, }}\,.}
- Функция тангенса (tan), определяемая как отношение противоположного катета к соседнему катету.
- tanA=противоположный соседний=ab=sinAcosA.{\displaystyle \tan A={\frac {\textrm {напротив}}{\textrm {смежный}}}={\frac {a} {\,b\,}}={\frac {\sin A}{\cos A}}\,.}
Гипотенуза — это сторона, противоположная углу 90 градусов в прямоугольном треугольнике; это самая длинная сторона треугольника и одна из двух сторон, примыкающих к углу A . Смежный отрезок представляет собой другую сторону, примыкающую к углу A . Противоположная сторона — это сторона, противоположная углу A .Термины перпендикулярно и основание иногда используются для противоположной и смежной сторон соответственно. Многим легко запомнить, какие стороны прямоугольного треугольника равны синусу, косинусу или тангенсу, заучив слово SOH-CAH-TOA (см.
 ниже в разделе «Мнемоника»).
ниже в разделе «Мнемоника»).
Обратные величины этих функций называются косекансом (csc или cosec), секансом (sec) и котангенсом (cot) соответственно. Обратные функции называются арксинусом , арккосинусом , арктангенсом и , соответственно.Между этими функциями существуют арифметические соотношения, известные как тригонометрические тождества.
С помощью этих функций можно ответить практически на все вопросы о произвольных треугольниках, используя закон синусов и закон косинусов. Эти законы можно использовать для вычисления оставшихся углов и сторон любого треугольника, если известны две стороны и угол или два угла и сторона или три стороны. Эти законы полезны во всех разделах геометрии, поскольку каждый многоугольник можно описать как конечную комбинацию треугольников.
Расширение определений
Графики функций sin (x) и cos (x) , где угол x измеряется в радианах. Графический процесс y = sin (x) с использованием единичного круга. Графический процесс y = tan (x) с использованием единичного круга.
Графический процесс y = csc (x) с использованием единичного круга.
Графический процесс y = tan (x) с использованием единичного круга.
Графический процесс y = csc (x) с использованием единичного круга.
Приведенные выше определения применимы только к углам от 0 до 90 градусов (0 и π/2 радиан).Используя единичный круг, их можно распространить на все положительные и отрицательные аргументы (см. тригонометрическую функцию). Тригонометрические функции являются периодическими с периодом 360 градусов или 2π радиан, за исключением тангенса и котангенса, у которых π является наименьшим периодом. Это означает, что их значения повторяются через эти интервалы.
Тригонометрические функции могут быть определены другими способами помимо геометрических определений, приведенных выше, с использованием инструментов исчисления и бесконечных рядов. С помощью этих определений тригонометрические функции могут быть определены для комплексных чисел.{ix}.}
См. формулы Эйлера и де Муавра.
Мнемотехника
Студенты часто используют мнемотехнику для запоминания фактов и отношений в тригонометрии. Например, отношения синуса , косинуса и тангенса в прямоугольном треугольнике можно запомнить, представив их в виде строк букв, как в SOH-CAH-TOA.
Например, отношения синуса , косинуса и тангенса в прямоугольном треугольнике можно запомнить, представив их в виде строк букв, как в SOH-CAH-TOA.
- S ine = O pposite ÷ H ypotenuse
- C осин = A djacent ÷ H ypotenuse
- T angent = O pposite ÷ A djacent
В качестве альтернативы можно составить предложения, состоящие из слов, начинающихся с букв, которые необходимо запомнить.Например, чтобы вспомнить, что Тан = Противоположный/Смежный, нужно запомнить буквы Т-О-А. Подойдет любая запоминающаяся фраза, состоящая из слов, начинающихся с букв Т-О-А.
Представляет этнографический интерес отметить, что мнемоника TOA-CAH-SOH может быть переведена на местный сингапурский хоккиенский диалект как «большеногая женщина», что служит дополнительным учебным пособием для студентов в Сингапуре. [3]
Другой тип мнемоники описывает факты простым и запоминающимся способом, например: «Плюс вправо, минус влево; положительная высота, отрицательная глубина», что относится к тригонометрическим функциям, генерируемым вращающейся линией. .
.
Вычисление тригонометрических функций
Тригонометрические функции были одними из первых применений математических таблиц. Такие таблицы были включены в учебники по математике, и студентов учили искать значения и интерполировать между перечисленными значениями для повышения точности. Логарифмические линейки имели специальные шкалы для тригонометрических функций.
Современные научные калькуляторы имеют кнопки для вычисления основных тригонометрических функций (sin, cos, tan и иногда cis) и их обратных функций.Большинство из них позволяют выбирать методы измерения углов, градусы, радианы и, иногда, грады. Большинство языков программирования предоставляют библиотеки функций, включающие тригонометрические функции. Аппаратное обеспечение модуля с плавающей запятой, встроенное в микропроцессорные микросхемы, используемые в большинстве персональных компьютеров, имеет встроенные инструкции для вычисления тригонометрических функций.
Применение тригонометрии
Подобные морские секстанты используются для измерения угла наклона солнца или звезд по отношению к горизонту. Затем с помощью тригонометрии и морского хронометра положение корабля можно определить по нескольким таким измерениям.
Затем с помощью тригонометрии и морского хронометра положение корабля можно определить по нескольким таким измерениям.
Существует огромное количество приложений тригонометрии и тригонометрических функций. Например, метод триангуляции используется в астрономии для измерения расстояний до ближайших звезд, в географии для измерения расстояний между ориентирами и в спутниковых навигационных системах. Функции синуса и косинуса лежат в основе теории периодических функций, таких как те, которые описывают звуковые и световые волны.
Области, в которых используется тригонометрия или тригонометрические функции, включают астрономию (особенно для определения видимого положения небесных объектов, в которой необходима сферическая тригонометрия) и, следовательно, навигацию (в океанах, на самолетах и в космосе), теорию музыки , акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, биология, медицинская визуализация (компьютерная томография и УЗИ), фармация, химия, теория чисел (и, следовательно, криптология), сейсмология, метеорология, океанография, многие физические науки, землеустройство и геодезия, архитектура, фонетика, экономика, электротехника, машиностроение, гражданское строительство, компьютерная графика, картография, кристаллография и разработка игр.
Общие формулы
Некоторые уравнения, включающие тригонометрические функции, верны для всех углов и известны как тригонометрических тождеств. Многие выражают важные геометрические соотношения. Например, пифагорейские тождества являются выражением теоремы Пифагора. Вот некоторые из наиболее часто используемых тождеств, а также наиболее важные формулы, соединяющие углы и стороны произвольного треугольника. Чтобы узнать больше о тождествах, см. Тригонометрическое тождество.{2}\alpha \end{aligned}}}
Идентичность суммы и произведения
Сумма к произведению
- sinα±sinβ=2sin(α±β2)cos(α∓β2)cosα+cosβ=2cos(α+β2)cos(α−β2)cosα− потому что β = -2sin (α + β2) грех (α-β2) {\ displaystyle {\ begin {align} \ sin \ alpha \ pm \ sin \ beta & = 2 \ sin \ left ({\ frac { \alpha \pm \beta}{2}}\right)\cos\left({\frac {\alpha\mp\beta}{2}}\right)\\\cos\alpha+\cos\beta &= 2\cos\left({\frac {\alpha +\beta}{2}}\right)\cos\left({\frac {\alpha -\beta}{2}}\right)\\\cos\ альфа — \ cos \ бета & = — 2 \ грех \ влево ({\ гидроразрыва {\ альфа + \ бета} {2}} \ вправо) \ грех \ влево ({\ гидроразрыва {\ альфа — \ бета} {2} }\right)\end{выровнено}}}
Произведение на сумму
[4]- cosαcosβ=12[cos(α−β)+cos(α+β)]sinαsinβ=12[cos(α−β)−cos(α+β)] cosαsinβ=12[sin(α+β)−sin(α−β)]sinαcosβ=12[sin(α+β)+sin(α−β)]{\ displaystyle {\ begin {align} \ cos \ alpha \, \ cos \ beta & = {\ frac {1} {2}} [\ cos (\ alpha — \ beta ) + \ cos (\ alpha + \ beta )] \\\ грех \ альфа \, \ грех \ бета & = {\ гидроразрыва {1} {2}} [\ соз (\ альфа — \ бета) — \ соз (\ альфа + \ бета)] \\\ соз \ альфа \, \ грех \ бета & = {\ гидроразрыва {1} {2}} [\ грех (\ альфа + \ бета) — \ грех (\ альфа — \ бета)] \\\ грех \ альфа \, \ соз \beta &={\frac {1}{2}}[\sin(\alpha +\beta )+\sin(\alpha -\beta )]\end{aligned}}}
Синус, косинус и тангенс суммы
- sin(α±β)=sinαcosβ±cosαsinβcos(α±β)=cosαcosβ∓sinαsinβtan(α±β)=tanα± загар β1∓танαtanβ {\ displaystyle {\ begin {align} \ sin (\ alpha \ pm \ beta) & = \ sin \ alpha \ cos \ beta \ pm \ cos \ alpha \ sin \ beta \\ \ cos (\ alpha \ pm \ beta ) & = \ cos \ alpha \ cos \ beta \ mp \ sin \ alpha \ sin \ beta \\\ tan (\ alpha \ pm \ beta ) & = {\ frac {\ tan \alpha \pm \tan \beta }{1\mp \tan \alpha \tan \beta }}\end{aligned}}}
Полуугольные тождества
Обратите внимание, что ±{\displaystyle \pm} является правильным, это означает, что это может быть любой из них, в зависимости от значения A/2 . {2}}} \\\ end {выровнено}}}
{2}}} \\\ end {выровнено}}}
, где T = tanα2 {\ displaystyle T =\загар {\ гидроразрыва {\ альфа} {2}}}.{2}}{2аб}}}
В следующих тождествах A, B, и C — углы треугольника, а a, b, и c — длины сторон треугольника, противоположных соответствующим углам.
Закон синусов
Закон синусов (также известный как «правило синусов») для произвольного треугольника гласит:
- asin A = bsin B = csin C = 2R, {\ displaystyle {\ frac {a} {\ sin A}} = {\ frac {b} {\ sin B}} = {\ frac {c }{\sin C}}=2R,}
, где R — радиус описанной окружности треугольника.{2}}{2ab}}.\,}
Закон касательных
Закон касательных :
- а + ba-b = загар [12 (A + B)] загар [12 (AB − B)] {\ displaystyle {\ frac {a + b} {ab}} = {\ frac {\ tan \left[{\tfrac {1}{2}}(A+B)\right]}{\tan \left[{\tfrac {1}{2}}(AB)\right]}}}
Примечания
Ссылки
Ссылки ISBN поддерживают NWE за счет реферальных сборов
- Хилл, Тим.
 Основы тригонометрии: самоучитель . В поисках полевки, 2013.ISBN 978-1937842161
Основы тригонометрии: самоучитель . В поисках полевки, 2013.ISBN 978-1937842161 - Лиал, Маргарет Л., Джон Хорнсби и Дэвид И. Шнайдер. Тригонометрия, 9-е изд. Бостон, Массачусетс: Pearson/Addison-Wesley, 2008. ISBN 0321528859.
- Линтон, Кристофер М. От Евдокса до Эйнштейна: история математической астрономии. Кембридж, Великобритания: Издательство Кембриджского университета, 2004. ISBN 978-0521045711.
- Веснер, Терри Х. Тригонометрия с приложениями . Вт. К. Браун, 1994. ISBN 978-0697122926
Внешние ссылки
Все ссылки получены 16 декабря 2021 г.
| Основные области математики | Править |
|---|---|
| Логика | Теория множеств | Комбинаторика | Вероятность | Математическая статистика | Теория чисел | Оптимизация | Линейная алгебра | Абстрактная алгебра | теория категорий | Алгебраическая геометрия | Геометрия | Топология | Алгебраическая топология | анализ | Дифференциальные уравнения | Функциональный анализ | Числовой анализ | |
Кредиты
Энциклопедия Нового Света авторов и редакторов переписали и дополнили статью Википедии
в соответствии со стандартами New World Encyclopedia . Эта статья соответствует условиям лицензии Creative Commons CC-by-sa 3.0 (CC-by-sa), которая может использоваться и распространяться с надлежащим указанием авторства. Упоминание должно быть выполнено в соответствии с условиями этой лицензии, которая может ссылаться как на авторов New World Encyclopedia , так и на самоотверженных добровольных участников Фонда Викимедиа. Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних вкладов википедистов доступна исследователям здесь:
Эта статья соответствует условиям лицензии Creative Commons CC-by-sa 3.0 (CC-by-sa), которая может использоваться и распространяться с надлежащим указанием авторства. Упоминание должно быть выполнено в соответствии с условиями этой лицензии, которая может ссылаться как на авторов New World Encyclopedia , так и на самоотверженных добровольных участников Фонда Викимедиа. Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних вкладов википедистов доступна исследователям здесь:
История этой статьи с момента ее импорта в New World Encyclopedia :
Примечание. На использование отдельных изображений, лицензированных отдельно, могут распространяться некоторые ограничения.
приложений тригонометрии в реальной жизни
Тригонометрия — это область математики, которая анализирует соотношения между треугольниками, углами и длинами. Его концепции помогали древним исследователям отслеживать звезды и ориентироваться в океанах, а реальные приложения тригонометрии теперь можно найти повсюду. Хотя вы можете подумать, что тригонометрия редко используется за пределами классной комнаты, вы будете поражены тем, как много примеров и применений тригонометрии можно найти в повседневной жизни.Прежде чем мы углубимся в реальные приложения тригонометрии, давайте убедимся, что вы понимаете основы тригонометрии.
Хотя вы можете подумать, что тригонометрия редко используется за пределами классной комнаты, вы будете поражены тем, как много примеров и применений тригонометрии можно найти в повседневной жизни.Прежде чем мы углубимся в реальные приложения тригонометрии, давайте убедимся, что вы понимаете основы тригонометрии.
** цитата
В школе вы, возможно, узнали, что тригонометрия состоит из двух греческих слов: «ТРИГОН», что означает треугольник, и «МЕТРИЯ», что означает «мера».
История тригонометрии
Треугольники впервые были изучены в египетской и вавилонской математике во втором тысячелетии до нашей эры. Они также широко использовались в кушитской математике.Систематическое изучение тригонометрических функций зародилось в эллинистической математике и проникло в Индию как эллинистическая астрономия. Изучение тригонометрических функций процветало в индийской астрономии на протяжении всего периода Гупта благодаря Арьябхате, который разработал функцию синуса.
[Читайте: Отец математики]
Тригонометрия была важной темой изучения исламской математики в Средние века, о чем свидетельствуют такие математики, как Аль-Хорезми и Абу аль-Вафа.В исламском мире, где были признаны все шесть тригонометрических функций, это стало отдельной дисциплиной. Начиная с Региомонтана в эпоху Возрождения, переводы арабских и греческих сочинений привели к тому, что тригонометрия была признана дисциплиной на латинском Западе. Современная тригонометрия развивалась в западную эпоху Просвещения, начиная с математики 17-го века (Исаак Ньютон и Джеймс Стирлинг) и заканчивая Леонардом Эйлером (1748).
[Читайте: самые известные математики в мире]
Современная тригонометрия
Современная тригонометрия находится под сильным влиянием вавилонских, шумерских, греческих и индийских астрономов.Астрономия перешла от качественной наблюдательной науки к предсказательной количественной науке с открытием тригонометрии. Это преобразование популяризировало применение тригонометрии, продемонстрировав возможность математического представления природных явлений. Данные наблюдений могут быть впервые переведены в математические модели. Таким образом, «Альмагест» Птолемея стал переломным моментом, служа практической математике, как «Начала» Евклида — теоретической математике.
Данные наблюдений могут быть впервые переведены в математические модели. Таким образом, «Альмагест» Птолемея стал переломным моментом, служа практической математике, как «Начала» Евклида — теоретической математике.
[Читайте: математика в повседневной жизни]
Понятия и примеры тригонометрии
По своей сути тригонометрия относится к измерению треугольника. Как известно, треугольник состоит из шести частей: трех углов и трех сторон. Их имена и аббревиатуры:
- Синус (sin)
- Косинус (cos)
- Тангенс (tan)
- Котангенс (cot)
- Секанс (sec)
- Косеканс (CSC)
2 приложения к вычислениям.Итак, измерение треугольника – это сумма его сторон и углов. Это помогает в определении углов и расстояний между структурами и фокусируется на прямоугольных треугольниках, то есть треугольниках, включающих один угол, равный 90 градусам.
Категории тригонометрии
Есть две категории тригонометрии, которые помогают понять, как вы можете применять концепции в реальной жизни. Отношение сторон прямоугольного треугольника к их углам является предметом базовой тригонометрии.
Отношение сторон прямоугольного треугольника к их углам является предметом базовой тригонометрии.
- Плоская тригонометрия используется для вычисления углов плоского треугольника.
- С другой стороны, сферическая тригонометрия используется для вычисления углов треугольников, нарисованных на сфере.
Применение тригонометрии в реальной жизни
Теперь мы рассмотрим историческое использование тригонометрии и различные приложения тригонометрии в реальной жизни.
Механическая структура, такая как мост или здание, является простым примером тригонометрии. План архитектора включает в себя множество тригонометрических элементов, результаты которых сравниваются для внедрения в план.
[Читать: Исчисление в повседневной жизни]
Астрономия
Загадки Солнечной системы привлекали людей с самого начала цивилизации. На протяжении всей истории астрономы использовали тригонометрию для расчета расстояний от звезд и планет до Земли. Сегодня ученые НАСА используют его для создания и запуска космических кораблей и ракет. Люди никогда бы не добрались до Луны без тригонометрии.
Сегодня ученые НАСА используют его для создания и запуска космических кораблей и ракет. Люди никогда бы не добрались до Луны без тригонометрии.
Звуковые волны
Тригонометрия также важна в музыкальной теории и производстве.Звуковые волны движутся по повторяющемуся волновому паттерну, который можно визуально представить синусоидальной и косинусоидальной функциями. Синусоидальная кривая может представлять одну ноту, и многие синусоидальные кривые могут использоваться в комбинации для моделирования аккорда. Графическое представление музыки позволяет компьютерам генерировать и понимать звуки. Это также позволяет звукорежиссерам просматривать звуковые волны, изменяя громкость, высоту тона и другие факторы для получения желаемых звуковых эффектов.
[Читать: Вероятность в реальной жизни]
Навигация
Контроль и мониторинг движущихся транспортных средств исследуются в различных формах навигации.
Эти формы включают:
- Морская навигация
- Авиационная навигация
- Космическая навигация
- Наземная навигация
Изучение движущихся объектов известно как навигация, и угол или расстояние, измеренные в это время, выполняются с помощью тригонометрии. Компас, точечные вехи, тригонометрические соотношения и различные формулы используются для определения точного местоположения движущегося тела.
Компас, точечные вехи, тригонометрические соотношения и различные формулы используются для определения точного местоположения движущегося тела.
Морская биология
Морские биологи изучают морскую жизнь, такую как растения, животные и другие виды, обитающие в океане.Тригонометрия используется в морской биологии, чтобы предвидеть, как далеко и под каким углом находится существо или растение от ученого. Угол может быть углом наклона или углом возвышения, в зависимости от того, где находится наблюдатель. Уровень воды считается основанием прямоугольного треугольника, а глубина предмета считается наклонным расстоянием по высоте.
[Читать: Алгебра в реальной жизни]
Авиация
Когда самолет летит, ветер играет неотъемлемую роль в интеграции безопасности и технологий.Две перпендикулярные стороны прямоугольного треугольника показывают направление ветра. Итак, мы можем вычислить расстояние от самолета до пункта назначения, применяя определение тригонометрических отношений.
Обрабатывающая промышленность
Тригонометрия широко используется в обрабатывающей промышленности, позволяя производителям делать все, от автомобилей до зигзагообразных ножниц. Инженеры используют тригонометрические отношения для прогнозирования размеров и углов механических частей, используемых в машинах, инструментах и оборудовании.Это жизненно важно в автомобилестроении, поскольку позволяет производителям транспортных средств точно определять размеры каждого элемента и обеспечивать их безопасную совместную работу.
Швеи также используют его для определения угла вытачек или длины ткани, необходимой для создания определенной формы юбки или блузки.
Расследование преступлений
Криминалисты и криминальные детективы используют функции тригонометрии, чтобы сделать выводы о том, что произошло на месте преступления, изучить брызги крови, анализировать огнестрельные отверстия, чтобы установить угол падения, и использовать навигационные технологии, чтобы точно определить местонахождение преступника.
Медицинская визуализация и фармация
В ортопедии тригонометрия определяет степень искривления позвонка и наличие повреждений нервов. Он также используется для придания формы протезам рук и ног, поскольку пропорции подбираются таким образом, чтобы облегчить работу с максимально возможной функциональностью. Точно так же диагностика и лечение заболеваний с использованием различных методов визуализации, ультразвука, ядерной медицины и магнитно-резонансных методов являются использованием тригонометрии. Они также используют его для расчета точных углов, что позволяет каждому лучу точно нацеливаться на злокачественные клетки.Диагностическая радиология позволяет врачам наблюдать за структурами вашего тела.
Еще несколько примеров широкого применения методов тригонометрии: оптика, статистика, электротехника, машиностроение, компьютерная графика, разработка игр, гражданское строительство, картография (создание карт) и кристаллография (изучение расположения атомов в кристаллическом твердом теле). ).
).
В BYJU’S FutureSchool учащимся предлагается обширная учебная программа, которая поможет освоить концепции тригонометрии и преодолеть страх перед математикой.Эта специально разработанная курсовая работа придаст вам уверенности в решении любой математической задачи, которая встретится вам на пути. Запишитесь на БЕСПЛАТНОЕ пробное занятие в среде 1:1 с выделенным инструктором, чтобы проверить его.
Развитие теории оптимального управления с использованием тригонометрии для решения сложных аэрокосмических задач
Теория оптимального управления (OCT) существует с 1950-х годов. Однако с появлением современных компьютеров сообщество дизайнеров делегировало задачу решения задач оптимального управления (ЗОП) в основном прямым методам с интенсивными вычислениями вместо методов, использующих ОКТ.Некоторые недавние работы показали, что решатели, использующие OCT, могут использовать ресурсы параллельных вычислений для более быстрого выполнения. Таким образом, потребность в высококачественных решениях для OCP, работающих практически в реальном времени, возродила интерес к OCT в дизайнерском сообществе. Однако все еще существуют определенные проблемы, которые запрещают его использование для решения сложных практических аэрокосмических задач, таких как безопасная посадка полезных грузов человеческого класса на Марс.
Однако все еще существуют определенные проблемы, которые запрещают его использование для решения сложных практических аэрокосмических задач, таких как безопасная посадка полезных грузов человеческого класса на Марс.
В целях продвижения OCT в этой диссертации представлен метод регуляризации Epsilon-Trig, позволяющий просто и эффективно решать релейные и сингулярные задачи управления.Метод Epsilon-Trig решает проблемы, связанные с традиционным методом регуляризации сглаживания. Некоторые контрольные задачи из литературы, включая осциллятор Ван дер Поля, задачу о лодке и задачу о ракете Годдарда, проверяли и подтверждали метод регуляризации Эпсилон-Триг с использованием GPOPS-II.
Это исследование также представляет и развивает использование тригонометрии для включения контрольных границ и смешанных ограничений управления состоянием в OCP и называет это тригонометризацией.Результаты из литературы и GPOPS-II подтвердили и утвердили метод тригонометрии с использованием определенных эталонных OCP. В отличие от традиционной OCT, тригонометрия преобразует OCP с ограничениями в двухточечную краевую задачу, а не в многоточечную граничную задачу, что значительно снижает вычислительные затраты, необходимые для ее формулирования и решения. В этой работе тригонометрия используется для решения некоторых сложных аэрокосмических задач, включая быстрый глобальный удар, минимизацию шума для авиации общего назначения, проблему повторного входа шаттла и проблему ограничения перегрузки для ударного элемента.Будущая работа по этой диссертации включает разработку метода тригонометризации для OCP с ограничениями чистого состояния.
В отличие от традиционной OCT, тригонометрия преобразует OCP с ограничениями в двухточечную краевую задачу, а не в многоточечную граничную задачу, что значительно снижает вычислительные затраты, необходимые для ее формулирования и решения. В этой работе тригонометрия используется для решения некоторых сложных аэрокосмических задач, включая быстрый глобальный удар, минимизацию шума для авиации общего назначения, проблему повторного входа шаттла и проблему ограничения перегрузки для ударного элемента.Будущая работа по этой диссертации включает разработку метода тригонометризации для OCP с ограничениями чистого состояния.
Тип
Тип
Доктор философия
Отдел
Аэронавтика и астронавтика
Кампус
West Lafayette
Консультант / руководитель / Комитет Coit
Dr. Michael J. Grant
Дополнительный комитет Участник 2
DR Dengfeng Sun
Дополнительный член комитета 3
Dr. Кэролин Э. Фрю
Кэролин Э. Фрю
Дополнительный член комитета 4
Доктор Этирадж ВенкатапатиТеория воображаемая геометрия вместе тригонометрия воображаемая | Исторические математические тексты
Джон Ли Смитман Хаттон (1865–1933) был британским математиком и педагогом. В течение 40 лет он работал над новаторским образовательным проектом в Восточном Лондоне, который начинался как Народный дворец и в конечном итоге стал Колледжем королевы Марии в Лондонском университете. Хаттон был его директором с 1908 по 1933 год.Эта книга, опубликованная в 1920 году, исследует отношения между воображаемой и реальной неевклидовой геометрией посредством графического представления воображаемых объектов в соответствии с различными соглашениями. Эта связь важна, поскольку точки со сложными определяющими элементами присутствуют как в воображаемой, так и в реальной геометрии. Хаттон использует концепции, включая использование методов координат, для развития и иллюстрации этой взаимосвязи, и концентрируется на идее, что единственные различия между реальными и воображаемыми точками существуют исключительно по отношению к другим точкам. Этот отчетливо написанный том иллюстрирует тип исследования неевклидовой геометрии, актуальный на момент публикации.
Этот отчетливо написанный том иллюстрирует тип исследования неевклидовой геометрии, актуальный на момент публикации.
Отзывы покупателей
Еще не просмотрено
Будьте первым, кто оставит отзыв
Отзыв не был опубликован из-за ненормативной лексики
×Информация о продукте
- Дата публикации: февраль 2011 г.
- формат: Мягкая обложка
- isbn: 9781108013109
- длина: 230 страниц
- размеры: 216 x 140 x 133 кг
- наличие: В наличии
Содержание
Предисловие
1. Воображаемые точки и длины на реальных прямых. Воображаемые прямые. Свойства полуреальных фигур
2. Окружность с реальной ветвью. Коника с реальной ветвью
3. Углы между воображаемыми прямыми. Измерение мнимых углов и длин на воображаемых прямых. Теоремы, связанные с проекцией. 4. Общая коника
5. Мнимая коника
6.Начертание коник и прямых
7. Воображаемое в пространстве
Индексы.
Автор
Джон Ли Смитман Хаттон
Использование тригонометрии — Academic Kids
От академических детей
Тригонометрия имеет огромное множество применений. Те, которые прямо упоминаются в учебниках и курсах по тригонометрии, — это ее использование в практических усилиях, таких как навигация, землеустройство, строительство и тому подобное.Он также широко используется в ряде академических областей, прежде всего в математике, естественных науках и технике.
Среди неспециалистов, не являющихся математиками и учеными, тригонометрия известна главным образом своим приложением к задачам измерения, но также часто используется гораздо более тонкими способами, такими как ее место в теории музыки; все же другие применения носят более технический характер, например, в теории чисел. Математические темы рядов Фурье и преобразований Фурье, в значительной степени опирающиеся на знание тригонометрических функций, находят применение в ряде областей, включая статистику.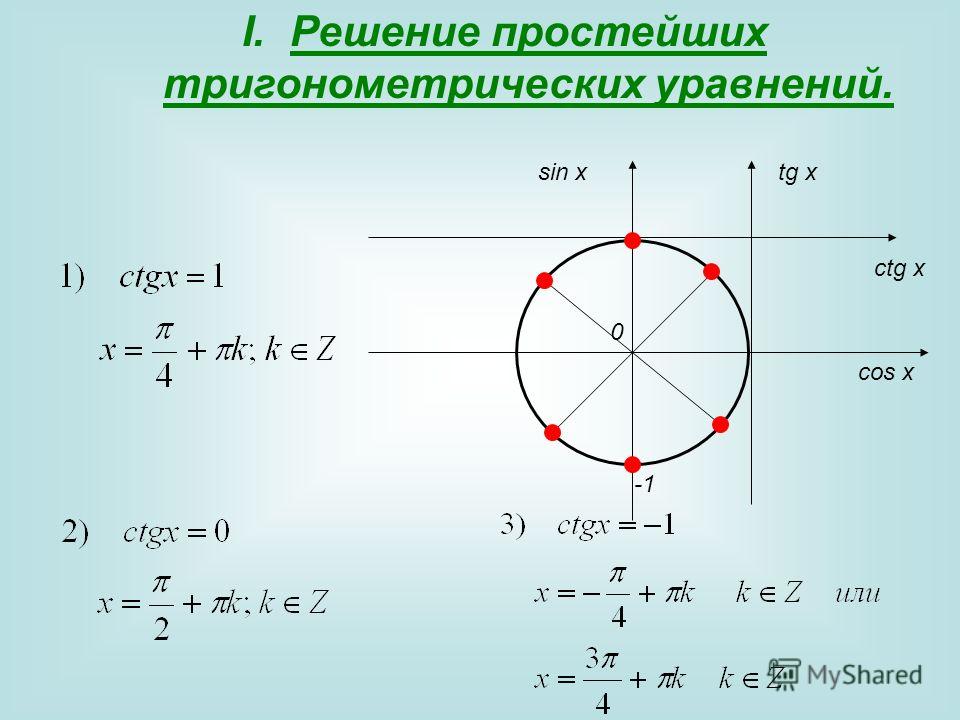
Некоторые поля, к которым применяется тригонометрия
Среди научных областей, в которых используется тригонометрия, следующие:
- акустика, архитектура, астрономия (и, следовательно, навигация, на океанах, в самолетах и в космосе; в связи с этим см. расстояние по большому кругу), биология, картография, химия, гражданское строительство, компьютерная графика, геофизика, кристаллография, экономика (в частности, при анализе финансовых рынков), электротехника, электроника, геодезия и геодезия, многие физические науки, машиностроение, медицинская визуализация (компьютерная томография и ультразвук), метеорология, теория музыки, теория чисел (и, следовательно, криптография), океанография. , оптика, фармакология, фонетика, теория вероятностей, психология, сейсмология, статистика и зрительное восприятие.
Как эти поля взаимодействуют с тригонометрией
Тот факт, что эти поля используют тригонометрию, не означает, что знание тригонометрии необходимо, чтобы что-то о них узнать. означает ли , что некоторые вещей в этих областях не могут быть поняты без тригонометрии. Например, профессор музыки, возможно, ничего не знает о математике, но, вероятно, знает, что Пифагор был самым ранним известным автором математической теории музыки.
означает ли , что некоторые вещей в этих областях не могут быть поняты без тригонометрии. Например, профессор музыки, возможно, ничего не знает о математике, но, вероятно, знает, что Пифагор был самым ранним известным автором математической теории музыки.
В некоторых областях деятельности, перечисленных выше, легко представить, как можно было бы использовать тригонометрию. Например, в навигации и геодезии случаи использования тригонометрии, по крайней мере в некоторых случаях, достаточно просты, чтобы их можно было описать в учебнике по тригонометрии для начинающих. В случае теории музыки применение тригонометрии связано с работой, начатой Пифагором, который заметил, что звуки, издаваемые перещипыванием двух струн разной длины, согласны, если обе длины являются небольшими целыми кратными общей длины.Сходство между формой вибрирующей струны и графиком функции синуса не случайно. В океанографии сходство форм некоторых волн с графиком синусоидальной функции также не случайно. В некоторых других областях, среди которых климатология, биология и экономика, существуют сезонные периодичности. Их изучение часто связано с периодической природой функций синуса и косинуса.
В некоторых других областях, среди которых климатология, биология и экономика, существуют сезонные периодичности. Их изучение часто связано с периодической природой функций синуса и косинуса.
Ряд Фурье
Многие области используют тригонометрию более продвинутым способом, чем можно обсудить в одной статье.Часто они включают так называемые ряды Фурье в честь французского математика и физика 18-го и 19-го веков Жозефа Фурье. Ряды Фурье имеют удивительно разнообразное применение во многих областях науки, в частности, во всех явлениях, связанных с сезонными периодами, упомянутыми выше, и в волновом движении, а значит, в изучении излучения, акустики, сейсмологии, модуляции радиоволн. волны в электронике и электроэнергетике.
Ряд Фурье представляет собой сумму следующего вида:
- <математика>\begin{матрица}
\square+\underbrace{\square\cos\theta+\square\sin\theta}_{1}+ \underbrace{\square\cos(2\theta)+\square\sin(2\theta)}_ {2}+ \\ \\ \ underbrace{\square\cos(3\theta)+\square\sin(3\theta)}_{3}+\,\cdots\\ \end{матрица} <математика>
, где каждый из квадратов (
Ряды Фурье применимы и к предметам, связь которых с волновым движением далеко не очевидна. Одним из распространенных примеров является цифровое сжатие, при котором изображения, аудио- и видеоданные сжимаются до гораздо меньшего размера, что делает возможной их передачу по телефону, Интернету и широковещательным сетям.Другим примером, упомянутым выше, является диффузия. Среди прочих: геометрия чисел, изопериметрические задачи, повторяемость случайных блужданий, квадратичная взаимность, центральная предельная теорема, неравенство Гейзенберга.
Преобразование Фурье
Более абстрактной концепцией, чем ряды Фурье, является идея преобразования Фурье. Преобразования Фурье включают интегралы, а не суммы, и используются в столь же разнообразных научных областях. Многие законы природы выражаются посредством соотнесения скоростей изменения величин с самими величинами.Например: скорость изменения численности населения иногда совместно пропорциональна (1) существующему населению и (2) величине, на которую существующее население отстает от пропускной способности. Такая связь называется дифференциальным уравнением. Если, имея эту информацию, мы попытаемся выразить население как функцию времени, мы попытаемся «решить» дифференциальное уравнение. Преобразования Фурье могут быть использованы для преобразования некоторых дифференциальных уравнений в алгебраические уравнения, для которых известны методы их решения.Преобразования Фурье имеют множество применений. Почти в любом научном контексте, в котором вы встречаете слова спектр, гармоника или резонанс, рядом стоят преобразования Фурье или ряды Фурье.
Преобразования Фурье включают интегралы, а не суммы, и используются в столь же разнообразных научных областях. Многие законы природы выражаются посредством соотнесения скоростей изменения величин с самими величинами.Например: скорость изменения численности населения иногда совместно пропорциональна (1) существующему населению и (2) величине, на которую существующее население отстает от пропускной способности. Такая связь называется дифференциальным уравнением. Если, имея эту информацию, мы попытаемся выразить население как функцию времени, мы попытаемся «решить» дифференциальное уравнение. Преобразования Фурье могут быть использованы для преобразования некоторых дифференциальных уравнений в алгебраические уравнения, для которых известны методы их решения.Преобразования Фурье имеют множество применений. Почти в любом научном контексте, в котором вы встречаете слова спектр, гармоника или резонанс, рядом стоят преобразования Фурье или ряды Фурье.
Статистика, включая математическую психологию
Некоторые психологи утверждают, что коэффициенты интеллекта распределяются в соответствии со знаменитой колоколообразной кривой. Около 40% площади под кривой приходится на интервал от 100 до 120; соответственно, около 40% населения набирает от 100 до 120 баллов по тестам IQ.Около 9% площади под кривой приходится на интервал от 120 до 140; соответственно, около 9% населения набирает от 120 до 140 баллов по тестам IQ и т. д. Точно так же многие другие вещи распределяются по «колоколообразной кривой», включая ошибки измерений во многих физических измерениях и количество раз, когда вы получаете орел когда подбрасываешь монету 10000 раз. Почему вездесущность «колоколообразной кривой»? Для этого есть теоретическая причина, и она включает в себя преобразования Фурье и, следовательно, тригонометрические функции).Это одно из множества применений преобразования Фурье к статистике.
Около 40% площади под кривой приходится на интервал от 100 до 120; соответственно, около 40% населения набирает от 100 до 120 баллов по тестам IQ.Около 9% площади под кривой приходится на интервал от 120 до 140; соответственно, около 9% населения набирает от 120 до 140 баллов по тестам IQ и т. д. Точно так же многие другие вещи распределяются по «колоколообразной кривой», включая ошибки измерений во многих физических измерениях и количество раз, когда вы получаете орел когда подбрасываешь монету 10000 раз. Почему вездесущность «колоколообразной кривой»? Для этого есть теоретическая причина, и она включает в себя преобразования Фурье и, следовательно, тригонометрические функции).Это одно из множества применений преобразования Фурье к статистике.
Тригонометрические функции также применяются, когда статистики изучают сезонные периодичности, которые часто представляются рядами Фурье.
Простой эксперимент с поляризационными очками
Получите две пары одинаковых поляризованных солнцезащитных очков (поляризованные очки и здесь не подойдут). Поместите левую линзу одной пары поверх правой линзы другой, выровняв обе одинаково. Медленно поверните одну пару, и вы заметите, что количество проходящего света уменьшается до тех пор, пока две линзы не окажутся под прямым углом друг к другу, когда свет не проходит.Когда угол, на который поворачивается одна пара, равен θ, какая часть света, проникающего при угле, равном 0, проходит? Ответ: это cos 2 θ. Например, когда угол равен 60 градусам, только 1/4 часть света проходит через серию из двух
линзы как при угле 0 градусов, так как косинус 60 градусов равен 1/2.
Поместите левую линзу одной пары поверх правой линзы другой, выровняв обе одинаково. Медленно поверните одну пару, и вы заметите, что количество проходящего света уменьшается до тех пор, пока две линзы не окажутся под прямым углом друг к другу, когда свет не проходит.Когда угол, на который поворачивается одна пара, равен θ, какая часть света, проникающего при угле, равном 0, проходит? Ответ: это cos 2 θ. Например, когда угол равен 60 градусам, только 1/4 часть света проходит через серию из двух
линзы как при угле 0 градусов, так как косинус 60 градусов равен 1/2.
Теория чисел
Есть намек на связь между тригонометрией и теорией чисел. Грубо говоря, можно сказать, что теория чисел имеет дело с качественными, а не с количественными свойствами чисел.Центральным понятием в теории чисел является делимость на (например, 42 делится на 14, но не на 15). Идея представления дроби в наименьшем числе также использует понятие делимости: например, 15/42 не является наименьшим числом, потому что 15 и 42 оба делятся на 3. Посмотрите на последовательность дробей.
Посмотрите на последовательность дробей.
- <математика>
\frac{1}{42}, \qquad \frac{2}{42}, \qquad \frac{3}{42}, \qquad \dots\dots, \qquad \frac{39}{42}, \qquad \frac{40}{42}, \qquad \фракция{41}{42}.<математика>
Отбрасывать те, которые не в самых низких условиях; оставьте только те, которые находятся в самых низких условиях:
- <математика>
\frac{1}{42}, \qquad \frac{5}{42}, \qquad \frac{11}{42}, \qquad \dots, \qquad \frac{31}{42}, \qquad \frac{37}{42}, \qquad \фракция{41}{42}. <математика>
Затем введите тригонометрию:
- <математика>
\cos\left(2\pi\cdot\frac{1}{42}\right)+ \cos\left(2\pi\cdot\frac{5}{42}\right)+ \cdots+ \cos\left(2\pi\cdot\frac{37}{42}\right)+ \cos\left(2\pi\cdot\frac{41}{42}\right) <математика>
Значение суммы равно −1.Откуда мы это знаем? Поскольку 42 имеет нечетных простых делителей, и ни один из них не повторяется: 42 = 2 × 3 × 7. (Если бы было четных неповторяющихся делителей, то сумма была бы равна 1; если если бы были повторяющиеся простые множители (например, 60 = 2 × 2 × 3 × 5), то сумма была бы равна 0. Это упрощает расчеты, поскольку сводит тригонометрические тождества к применению правил манипулирования показателями степени. Конечно есть! В математике, как только мы что-то изобретаем, мы начинаем с этим играться, находим вариации и новые выводы, изобретаем новые вещи. После построения синусоидальных кривых y = sin x и y = cos x мы работаем над другими триггерными функциями y = tan x, y = sec x, y = csc x и y = cot x. Все они периодические, но также имеют регулярные разрывы (разрывы) и вертикальные асимптоты.-x)/2 Из них можно определить гиперболический тангенс, секанс и т.д. Это не совсем триггерные функции, но они ведут себя странно похожим образом. Если вы спрашиваете, потому что вам надоела тригонометрия и вы просто хотите увидеть ее конец, аааа. . . . Извините но нет. Если вы продолжите заниматься математикой, она будет возвращаться к вам, поэтому освойте ее сейчас и научитесь с ней справляться.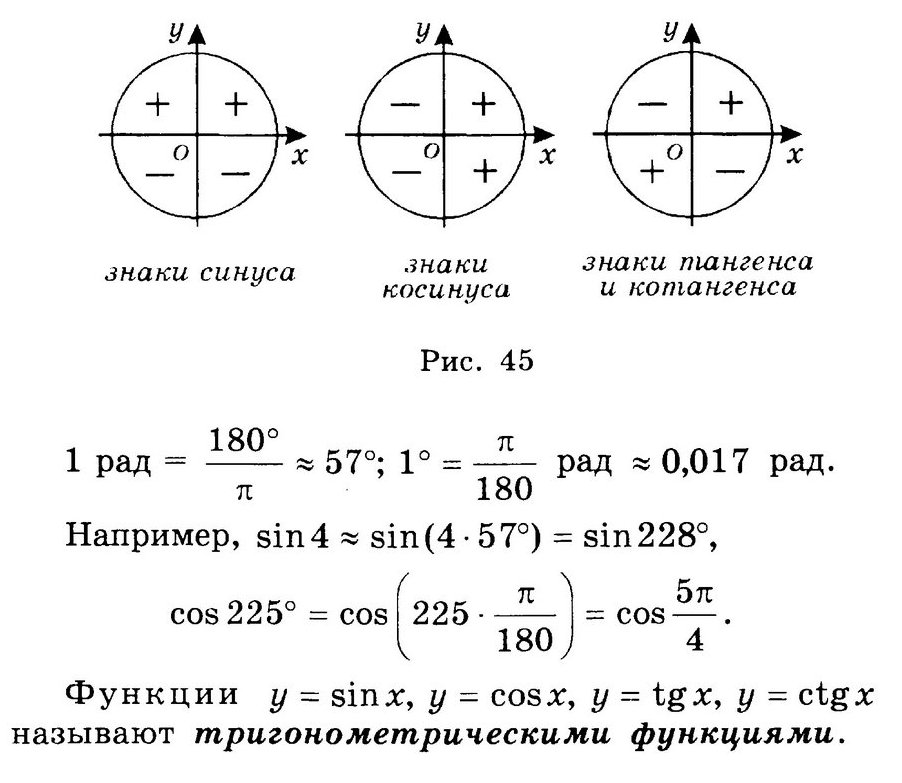 {-ix} \over 2i}
{-ix} \over 2i} Существует ли какая-либо теория тригонометрии помимо синусоидальных кривых?

