1.1.3. Знакомство с языком Pascal. Разработка обучающей программы, поддерживающей изучение темы «Структуры данных»
Похожие главы из других работ:
Content management system (CMS) система wordpress
3. Знакомство с wordpress
сайт контент denwer wordpress В этом разделе рассмотрим некоторые принципы работы в данной программе. Представленный ниже скриншот показывает стандартное завершение установки, так будет выглядеть Ваш блог…
Графический редактор Photoshop
1. Знакомство с Adobe Photoshop
…
Интерактивные средства аудио и видео взаимодействия
Первое знакомство
Программа Skype распространяется бесплатно, ее можно скачать с официального сайта или нашего файлового архива. В разделе загрузки (Download) можно выбрать для какой операционной системы вы хотите скачать программу…
Исследование возможностей Microsoft Word 2007
1.1 Знакомство с информацией
Знакомство с информацией я начала с записи в библиотеку. Здесь меня ожидало небольшое разочарование: мне нельзя было забирать литературу домой. Можно было работать только в читальном зале…
Здесь меня ожидало небольшое разочарование: мне нельзя было забирать литературу домой. Можно было работать только в читальном зале…
Исследование возможностей операционной системы Windows
2.1 Знакомство с информацией
…
Компьютерное моделирование игры в шахматы
2.2 Знакомство со средой программирования Турбо Паскаль
Для создания компьютерной модели важен выбор оптимальной среды программирования, которая позволит не только произвести все необходимые расчеты с введенными данными, вывести правильный результат…
Оперциаонные системы ASP Linux и Windows
Тема 1.2. Знакомство с графическим интерфейсом ASP Linux
…
Разработка автоматизированного рабочего места (АРМ) учителя муниципального общеобразовательного учреждения Вечерняя (сменная) общеобразовательная школа
1.1 Общее знакомство с МОУ В (с) ОШ и применяемыми информационными технологиями
Название: Муниципальное общеобразовательное учреждение вечерняя (сменная) общеобразовательная школа (МОУ В (с) ОШ). Территориальное расположение: 140560, Московская обл, Озерский р-н, Озеры г, Ленина ул, 63…
Территориальное расположение: 140560, Московская обл, Озерский р-н, Озеры г, Ленина ул, 63…
Разработка автоматизированной системы «Автомастер»
1) знакомство с предприятием;
2) изучение должностных обязанностей менеджера заказов; 3) изучение процесса составление наряда на ремонт…
Разработка автоматизированной системы «Автомастер»
3.1 Знакомство с предприятием
…
Разработка комплекса лабораторных работ по технологиям компьютерных сетей с помощью симулятора Cisco Packet Tracer
4.2 Лабораторная работа №1. Знакомство со средой Cisco Packet Tracer
Цель работы: познакомиться с интерфейсом симулятора, изучить режим реального времени, основные операции c устройствами. Программа работы: 1. Создание топологии сети; 2. Добавление конечных узлов; 3…
Ресурсное планирование
1. ЗНАКОМСТВО С ПРОГРАММОЙ MS Projeсt
Прежде чем перейти непосредственно к ресурсам проекта, необходимо познакомиться с удивительной программой, я бы даже сказала, в некотором роде, помощником в создании и управлении проектами.
Теория управления в информационных системах
1.1 Знакомство с программой Vissim
Цели и задачи Цель работы: знакомство с графическим интерфейсом программы Vissim, а также приобретение навыков создания и моделирования простейших структур, текстового и графического оформления диаграмм…
Электронное пособие по программированию (Pascal)
2.5.3 Turbo Pascal и Object Pascal от Borland, Microsoft Pascal
В 1989 году объектное расширение языка было добавлено фирмой Borland в Turbo Pascal версии 5.5 (начиная со следующей версии, среда была переименована в Borland Pascal). Объектные средства были позаимствованы из Object Pascal от Apple…
Язык структурированных запросов SQL. Использование SQL в прикладном программировании
3.2 Использование SQL в Pascal (на примере Pascal Lazarus)
Pascal, не являясь популярным языком разработки коммерческих приложений, тем не менее, очень распространен в учебных заведениях по причине наглядности многих его аспектов.
°â€œ°»°°°²°° II °â€™°â€™°â€¢°â€°â€¢°â€Œ°©°â€¢ °â€™ °° °â€°â€œ° °¯°“°“°©° °â€°â€™°¯°â€Œ°©°â€¢files.lbz.ru/authors/informatika/2/semakin-9-gl2-8-11.pdf¢
61
Глава II ВВЕДЕНИЕ В ПРОГРАММИРОВАНИЕ
Здесь вы узнаете:
• что такое программирование • как строятся вычислительные алгоритмы • как составляются программы на языке Паскаль
Введение в программированиеII
62
§ 8 Что такое программирование
Основные темы параграфа: кто такие программисты; что такое язык программирования; что такое система программирования.
Кто такие программисты
Теперь вам предстоит ближе познакомиться еще с одним разде- лом информатики, который называется «Программирование».
Назначение программирования — разработка программ управления компьютером с целью решения различных информационных задач.
Специалисты, профессионально занимающиеся программиро-
ванием, называются программистами.
Может возникнуть впечатление, что программисты теперь уже и не нужны! Но кто же тогда будет создавать все операци- онные системы, редакторы, графические пакеты, компьютерные игры и многое другое? Программисты, безусловно, нужны, при- чем задачи, которые им приходится решать, со временем стано- вятся все сложнее.
Программирование принято разделять на системное и при-
кладное. Системные программисты занимаются разработкой
системного программного обеспечения: операционных систем,
утилит и пр.
Что такое программирование § 8
63
В данной главе вы познакомитесь с простейшими правилами и приемами программирования, заглянете в эту ак туаль ную и престижную профессиональную область.
Что такое язык программирования
Для составления программ существуют разнообразные языки программирования.
Язык программирования — это фиксированная систе- ма обозначений для описания алгоритмов и структур данных.
За годы существования ЭВМ было создано много языков программирования. Наиболее известные среди них: Фортран, Паскаль, Бейсик, С (Си) и др. Распространенными языками программирования сегодня являются C++, Java, Pascal, Basic, Python.
Что такое система программирования
Для создания и исполнения на компьютере программы, напи-
санной на языке программирования, используются системы про-
граммирования.
Система программирования — это программное обес пе- чение компьютера, предназначенное для разработки, отладки и исполнения программ, записанных на опреде ленном языке программирования.
Существуют системы программирования на Паскале, Бейсике и других языках.
В данной главе речь будет идти о средствах и способах уни- версального программирования — не ориентированного на какую-то узкую прикладную область. Примером узкоспециали- зированного программирования является веб-программирование, ориентированное на создание веб-сайтов. Для этих целей, на- пример, используется язык Java Script. Языки Паскаль, Бейсик, Си относятся к числу универсальных языков программирова- ния.
Разработка любой программы начинается с построения алго- ритма решения задачи. Ниже мы обсудим особенности алгорит- мов решения задач обработки информации на ком пьютере.
Введение в программированиеII
64
Коротко о главном
Программирование — область информатики, посвященная раз-
работке программ управления компьютером с целью решения
различных информационных задач.
Программирование бывает системным и прикладным.
Паскаль, Бейсик, Си, Фортран — это универсальные языки программирования.
Система программирования — это программное обеспече- ние компьютера, предназначенное для разработки, отладки и исполнения программ, записанных на определенном языке программиро вания.
Вопросы и задания
1. Что такое программирование? 2. Какие задачи решают системные и прикладные программисты? 3. Назовите наиболее распространенные языки программирования. 4. В чем состоит назначение систем программирования?
ЕК ЦОР: часть 2, глава 6, § 32. ЦОР № 2, 5.
§ 9 Алгоритмы работы с величинами
Основные темы параграфа: компьютер как исполнитель алгоритмов; величины: константы и переменные; система команд; команда присваивания; команда ввода; команда вывода.
Компьютер как исполнитель алгоритмов
Вам уже известно, что всякий алгоритм составляется для кон-
кретного исполнителя. Теперь в качестве исполнителя мы
будем рассматривать компьютер, оснащенный системой про-
граммирования на определенном языке.
Алгоритмы работы с величинами § 9
65
Компьютер-исполнитель работает с определенными данными по определенной программе. Данные — это множество величин.
Величины: константы и переменные Компьютер работает с информацией, хранящейся в его памя- ти. Отдельный информационный объект (число, символ, строка, таб лица и пр.) называ
Контрольная работа по информатике 9 класс 3 четверть — 6 Апреля 2015
Пример работы программы:
Входные данные
Выходные данные
23
80
5
Контрольная работа. Знакомство с языком Паскаль. 9 класс. Вариант 3.
1. С какими типами числовых величин работает язык программирования Паскаль?
2. Что такое составной оператор?
3. Напишите программу, которая выводит на экран имя вашего любимого киногероя.
4. В алгоритме, записанном ниже, используются целочисленные переменные k и m. Определите значение переменной m после исполнения данного алгоритма:
k:=3
m:=k+1
k:=m*m+5
k:=k — 10
5. Определите значение переменной m после выполнения следующего фрагмента программы:
Определите значение переменной m после выполнения следующего фрагмента программы:
m:=0;
for i:=1 to 10 do
begin
n:=i+2;
if n>10 then m:=n+m*2
else m:=m+1;
end;
6. Напишите эффективную программу, которая по двум данным натуральным числам a и b, не превосходящим 30000, подсчитывает количество натуральных чисел, кратных числу a, на отрезке [a,b] (включая концы отрезка).
Программа получает на вход два натуральных числа a и b, при этом гарантируется, что 1≤a≤b≤30000. Программа должна вывести одно число: количество натуральных чисел кратных числу a на отрезке [a,b]
Пример работы программы:
Входные данные
Выходные данные
7
23
3
Контрольная работа. Знакомство с языком Паскаль. 9 класс. Вариант 4.
1. Как записываются операторы ввода и вывода в Паскале?
2. Какими средствами программируется диалог между пользователем и компьютером?
3. Напишите инструкцию вывода значения переменной a (тип real) с тремя цифрами в дробной части.
4. В алгоритме, записанном ниже, используются целочисленные переменные a и b. Определите значение переменной m после исполнения данного алгоритма:
a:=32
b:=a/4-5
a:=3+b*4
b:=b-a
5. Определите значение переменной y после выполнения следующего фрагмента программы:
x:=25;
y:=-20;
while x*y
begin
x:=x-5;
y:=y+2
end;
6. Напишите эффективную программу, которая по двум данным натуральным числам m и n, не превосходящим 30000, подсчитывает количество натуральных чисел с последней цифрой 0 на отрезке [m,n] (включая концы отрезка)
Программа получает на вход два натуральных числа m и n, при этом гарантируется, что 1≤m≤n≤30000. Программа должна вывести одно число: количество натуральных чисел с последней цифрой 0 на отрезке [m,n].
Пример работы программы:
Входные данные
Выходные данные
17
50
4
Контрольная работа. Знакомство с языком Паскаль. 9 класс. Вариант 5.
Вариант 5.
1. Что такое оператор присваивания?
2. Как программируется цикл с предусловием на Паскале? (Цикл пока)
3. Напишите в виде инструкции присваивания формулу вычисления площади треугольника.
4. В алгоритме, записанном ниже, используются целочисленные переменные c и d. Определите значение переменной c после исполнения данного алгоритма:
c:=5
d:=c*2+4
c:=(d-c)/3*2
c:=c+d
5. Определите значение переменной s после выполнения следующего фрагмента программы:
s:=24;
m:=3456;
while s>10 do
begin
m:=m mod 10;
s:=s-m
end;
s:=s+m
6. Напишите эффективную программу, которая по двум данным натуральным числам p и q, не превосходящим 30000, подсчитывает количество натуральных чисел с последней цифрой 0 на интервале (p,q) (не включая концы интервала).
Программа получает на вход два натуральных числа p и q, при этом гарантируется, что 1≤p Пример работы программы: Входные данные Выходные данные 23 80 5 Контрольная работа. 1. Как записывается раздел описания переменных в языке программирования Паскаль? 2. Как программируется цикл с постусловием на Паскале? (Цикл до) 3. Запишите в виде инструкции присваивания формулу вычисления значения функции y = -0,35×2-1,4. 4. В алгоритме, записанном ниже, используются целочисленные переменные. Определите значение переменной y после исполнения данного алгоритма: y:=-1 x:=y*5-10 y:=y div 2 +x 5. Определите значение переменной x после выполнения следующего фрагмента программы: x:=10; y:=1; f:=true; repeat x:=x div 3; y:=y+1; if x+y=4 then f:=false until (x=0) or not f 6. Напишите эффективную программу, которая по двум данным натуральным числам a и b, не превосходящим 30000, подсчитывает количество натуральных чисел, кратных числу a, на отрезке [a,b] (включая концы отрезка). Программа получает на вход два натуральных числа a и b, при этом гарантируется, что 1≤a≤b≤30000. Пример работы программы: Входные данные Выходные данные 7 23 3
Знакомство с языком Паскаль. 9 класс. Вариант 6.
 Программа должна вывести одно число: количество натуральных чисел кратных числу a на отрезке [a,b]
Программа должна вывести одно число: количество натуральных чисел кратных числу a на отрезке [a,b]
Треугольник Паскаля
Одним из самых интересных числовых узоров является треугольник Паскаля (названный в честь Блеза Паскаля , известного французского математика и философа).
Чтобы построить треугольник, начните с «1» вверху, затем продолжайте размещать цифры под ним в виде треугольника.
Каждое число представляет собой сложенные вместе числа, находящиеся непосредственно над ним.
(Здесь я подчеркнул, что 1+3 = 4)
Паттерны внутри треугольника
Диагонали
Первая диагональ это, конечно же, просто «1»
На следующей диагонали находятся Счетные числа (1,2,3 и т.д.).
Третья диагональ имеет треугольные числа
(Четвертая диагональ, не выделенная, имеет четырехгранные числа. )
)
Симметричный
Треугольник также симметричен. Числа на левой стороне имеют одинаковые совпадающие числа на правой стороне, как зеркальное отражение.
Горизонтальные суммы
Что вы заметили в горизонтальных суммах?
Есть шаблон?
Они удваивают каждый раз (степень двойки).
Экспоненты числа 11
Каждая строка также представляет собой степени (показатели) числа 11:
- 11 0 =1 (первая строка просто «1»)
- 11 1 =11 (вторая строка «1» и «1»)
- 11 2 =121 (третья строка «1», «2», «1»)
- и т.д.!
Но что происходит с 11 5 ? Простой! Цифры просто перекрываются, вот так:
То же самое происходит с 11 6 и т.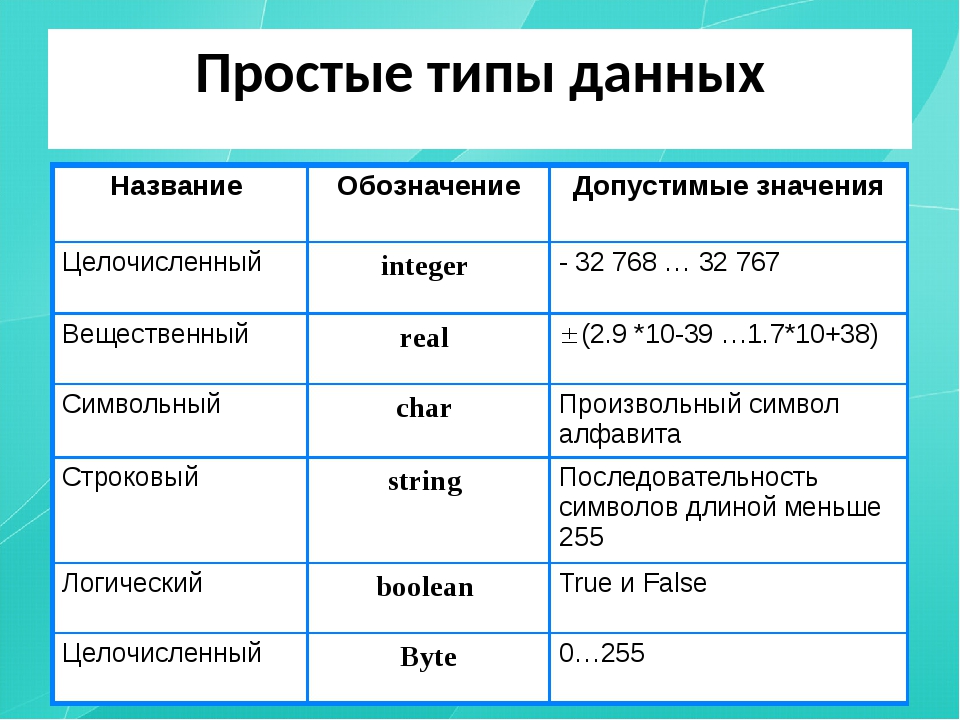 д.
д.
Квадраты
Для второй диагонали квадрат числа равен сумме чисел рядом с ним и под обоими из них.
Примеры:
- 3 2 = 3 + 6 = 9,
- 4 2 = 6 + 10 = 16,
- 5 2 = 10 + 15 = 25,
- …
Есть и веская причина… вы можете подумать об этом? (Подсказка: 4 2 =6+10, 6=3+2+1 и 10=4+3+2+1)
Последовательность Фибоначчи
Попробуйте следующее: создайте фигуру, двигаясь вверх и вниз, затем сложите значения (как показано на рисунке)… вы получите последовательность Фибоначчи.
(Последовательность Фибоначчи начинается с «0, 1», а затем продолжается добавлением двух предыдущих чисел, например, 3+5=8, затем 5+8=13 и т. д.)
Шансы и четы
Если мы раскрасим нечетные и четные числа, мы получим узор, аналогичный треугольнику Серпинского
Пути
Каждая запись также является количеством различных путей сверху вниз.
Пример: есть только один путь сверху вниз к любой «1»
И мы видим, что есть 2 разных пути к «2»
То же самое вверх, есть 3 разных пути из 3:
Ваша очередь, посмотрите, сможете ли вы найти все пути вниз к «6»:
Использование треугольника Паскаля
Орел и решка
Треугольник Паскаля показывает нам, сколько способов может сочетаться орел и решка.Затем это может показать нам вероятность любой комбинации.
Например, если вы подбросите монету три раза, только одна комбинация даст три орла (HHH), но есть три комбинации, которые дадут два орла и одну решку (HHT, HTH, THH), а также три комбинации, которые дадут одна голова и две решки (HTT, THT, TTH) и одна для всех решек (TTT). Это паттерн «1,3,3,1» в треугольнике Паскаля.
| Подбрасывает | Возможные результаты (сгруппированные) | Треугольник Паскаля |
|---|---|---|
| 1 | Х Т |
1, 1 |
| 2 |
HH HT TH TT |
1, 2, 1 |
| 3 |
HHH HHT, HTH, THH HTT, THT, TTH TTT |
1, 3, 3, 1 |
| 4 |
HHHH HHHT, HHTH, HTHH, THHH HHTT, HTHT, HTTH, THHT, THTH, TTHH HTTT, THTT, TTHT, TTTH TTTT |
1, 4, 6, 4, 1 |
. .. и т.д… .. и т.д… |
Пример. Какова вероятность того, что при 4 подбрасываниях монеты выпадет ровно два орла?
Существует 1+4+6+4+1 = 16 (или 2 4 = 16) возможных результатов, и 6 из них дают ровно два орла. Таким образом, вероятность равна 6/16, или 37,5%
.Комбинации
Треугольник также показывает нам, сколько комбинаций объектов возможно.
Пример: У вас есть 16 шаров для бильярда. Сколькими способами можно выбрать только 3 из них (игнорируя порядок их выбора)?
Ответ: спуститься к началу 16 строки (верхняя строка 0), а затем по 3 местам (первое место 0) и значение там будет вашим ответом, 560 .
Вот выдержка из строки 16:
1 14 91 364 ... 1 15 105 455 1365 ... 1 16 120 560 1820 4368 ...
Формула для любого входа в треугольник
На самом деле существует формула из Комбинаций для определения значения в любом месте треугольника Паскаля:
|
Это обычно называется «n выбрать k» и пишется так: |
н! к!(н-к)! = ( н к ) |
Обозначение: «n выбирает k» также может быть записано как C(n,k) , n C k или n C k 9.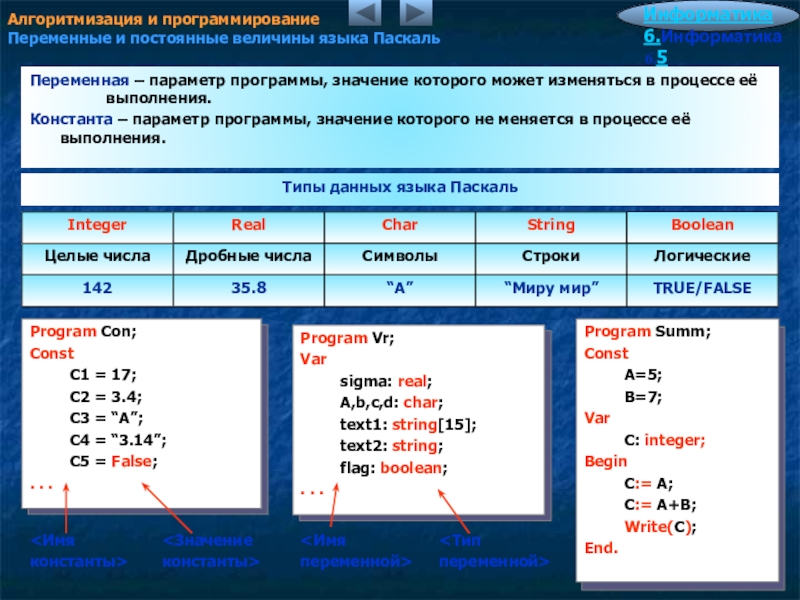 0285
0285
| ! |
«!» является «факториалом» и означает умножение ряда убывающих натуральных чисел. Примеры:
|
Таким образом, Треугольник Паскаля также может быть треугольником
и «n выбрать k» , подобным этому.
(Обратите внимание, что верхняя строка — это нулевая строка
, а также крайний левый столбец — ноль)
Пример: Строка 4, член 2 в треугольнике Паскаля равен «6» …
… посмотрим, сработает ли формула:
( 4 2 ) = 4! 2!(4−2)! = 4! 2!2! = 4×3×2×1 2×1×2×1 = 6
Да, работает! Попробуйте другое значение для себя.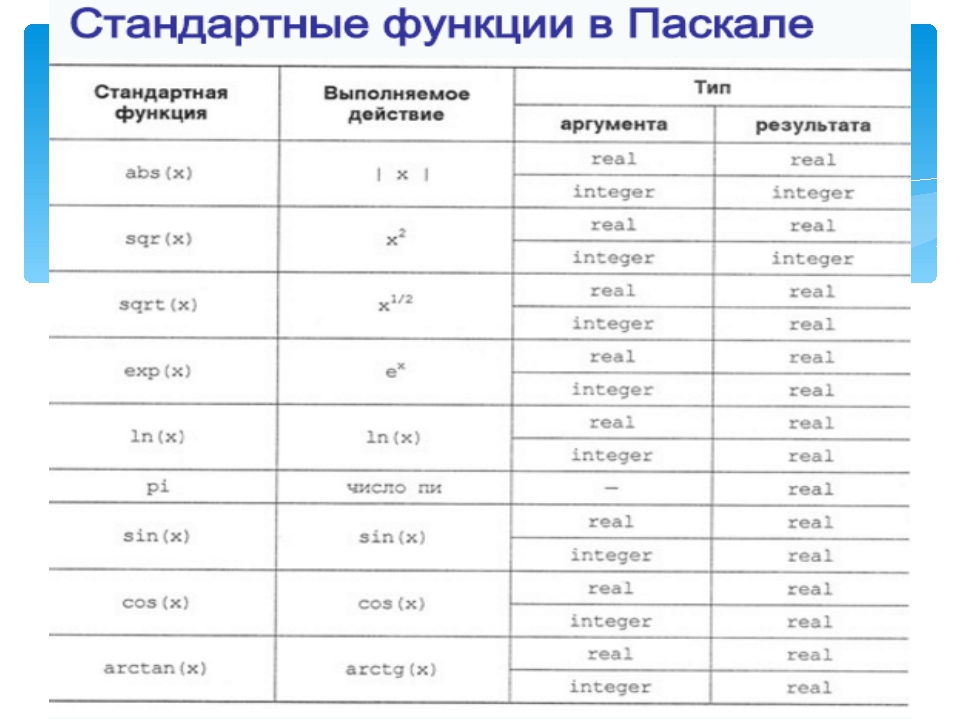
Это может быть очень полезно… теперь мы можем найти любое значение в Треугольнике Паскаля непосредственно (без вычисления всего треугольника над ним).
Многочлены
Треугольник Паскаля также показывает нам коэффициенты в биномиальном разложении:
| Мощность | Биномиальное расширение | Треугольник Паскаля |
|---|---|---|
| 2 | (х + 1) 2 = 1 х 2 + 2 х + 1 | 1, 2, 1 |
| 3 | (x + 1) 3 = 1 x 3 + 3 x 2 + 3 x + 1 | 1, 3, 3, 1 |
| 4 | (x + 1) 4 = 1 x 4 + 4 x 3 + 6 x 2 x + 4 x + 1 | 1, 4, 6, 4, 1 |
. .. и т.д… .. и т.д… |
Первые 15 строк
Для справки я включил ряды с 0 по 14 треугольника Паскаля
.1
9
36
84
126
126
84
36
9
1
1
10
45
120
210
252
210
120
45
10
1
1
11
55
165
330
462
462
330
165
55
11
1
1
12
66
220
495
792
924
792
495
220
66
12
1
1
13
78
286
715
1287
1716
1716
1287
715
286
78
13
1
1
14
91
364
1001
2002
3003
3432
3003
2002
1001
364
91
14
1
Китайцы знали об этом
Этот рисунок озаглавлен «Таблица старого метода семи умножающих квадратов». Просмотреть полное изображение
Просмотреть полное изображение
Это обложка книги Чу Ши-Чие « Ссу Юань Юй Цзянь» (Драгоценное Зеркало Четырех Элементов) , написанной в году нашей эры 1303 (более 700 лет назад и более 300 лет до Паскаля!) , а в книге написано, что треугольник был известен примерно за два с лишним века до этого.
Квинконс
Удивительная маленькая машина, созданная сэром Фрэнсисом Гальтоном, представляет собой треугольник Паскаля, сделанный из колышков. Называется Квинканкс.
Мячи падают на первый стержень, а затем отскакивают к нижней части треугольника, где собираются в маленькие корзины.
Сначала это выглядит совершенно случайным (и это так), но затем мы обнаруживаем, что шары складываются в красивый узор: нормальное распределение.
1297, 2467, 2468, 1298, 8366, 8367, 8368, 8369, 8370, 8371, 8372
Треугольник Паскаля | математика | Британика
Треугольник Паскаля , в алгебре треугольное расположение чисел, которое дает коэффициенты в разложении любого биномиального выражения, например ( x + y ) n .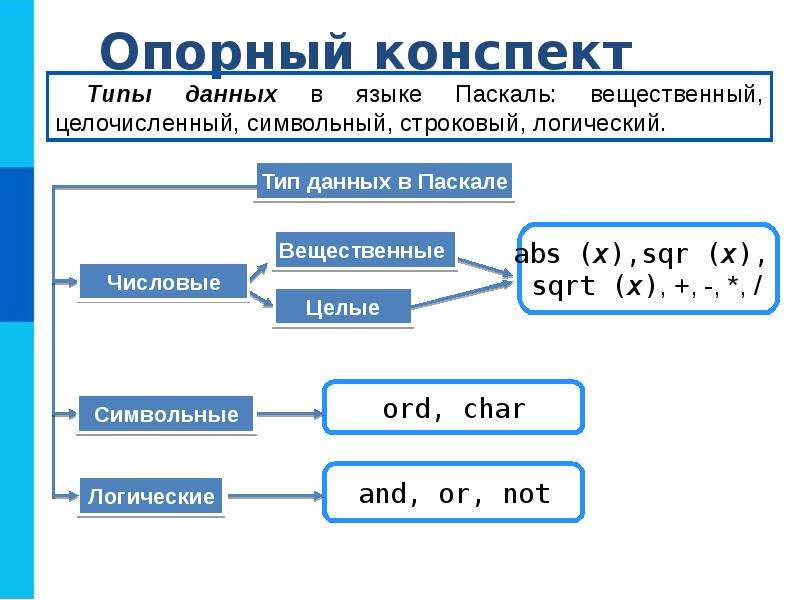 Он назван в честь французского математика 17-го века Блеза Паскаля, но он намного старше. Китайский математик Цзя Сянь разработал треугольное представление коэффициентов в 11 веке. Его треугольник в дальнейшем изучал и популяризировал китайский математик Ян Хуэй в 13 веке, по этой причине в Китае его часто называют треугольником Янхуэй. Он был включен в качестве иллюстрации в книгу китайского математика Чжу Шицзе Siyuan yujian (1303; «Драгоценное зеркало четырех элементов»), где он уже назывался «Старый метод».Замечательную закономерность коэффициентов изучал еще в XI веке персидский поэт и астроном Омар Хайям.
Он назван в честь французского математика 17-го века Блеза Паскаля, но он намного старше. Китайский математик Цзя Сянь разработал треугольное представление коэффициентов в 11 веке. Его треугольник в дальнейшем изучал и популяризировал китайский математик Ян Хуэй в 13 веке, по этой причине в Китае его часто называют треугольником Янхуэй. Он был включен в качестве иллюстрации в книгу китайского математика Чжу Шицзе Siyuan yujian (1303; «Драгоценное зеркало четырех элементов»), где он уже назывался «Старый метод».Замечательную закономерность коэффициентов изучал еще в XI веке персидский поэт и астроном Омар Хайям.
Треугольник можно построить, сначала поставив 1 (китайский «-») вдоль левого и правого краев. Затем треугольник можно заполнить сверху, сложив вместе два числа чуть выше слева и справа от каждой позиции в треугольнике. Таким образом, в индийско-арабских цифрах третий ряд — это 1 2 1, четвертый ряд — это 1 4 6 4 1, пятый ряд — это 1 5 10 10 5 1 и так далее.Первая строка, или просто 1, дает коэффициент для расширения ( x + y ) 0 = 1; вторая строка, или 1 1, дает коэффициенты для ( x + y ) 1 = x + y ; Третий ряд, или 1 2 1, дает коэффициенты для ( x + x 2 + 2 x y + y 2 ; и так далее.
Британская викторина
Числа и математика
A-B-C, 1-2-3… Если вы считаете, что подсчет чисел похож на чтение алфавита, проверьте, насколько свободно вы владеете языком математики в этом тесте.
В треугольнике много интересных узоров. Например, рисование параллельных «неглубоких диагоналей» и сложение чисел на каждой линии вместе дает числа Фибоначчи (1, 1, 2, 3, 5, 8, 13, 21,…,), которые впервые были отмечены средневековым итальянцем. математик Леонардо Пизано («Фибоначчи») в его Liber abaci (1202; «Книга счетов»).
Сложение чисел вдоль каждой «неглубокой диагонали» треугольника Паскаля дает последовательность Фибоначчи: 1, 1, 2, 3, 5,….
Encyclopædia Britannica, Inc. Другим интересным свойством треугольника является то, что если все позиции, содержащие нечетные числа, заштрихованы черным, а все позиции, содержащие четные числа, закрашены белым, фрактал, известный как гаджет Серпинского, после 20-го века будет сформирован польский математик Вацлав Серпинский.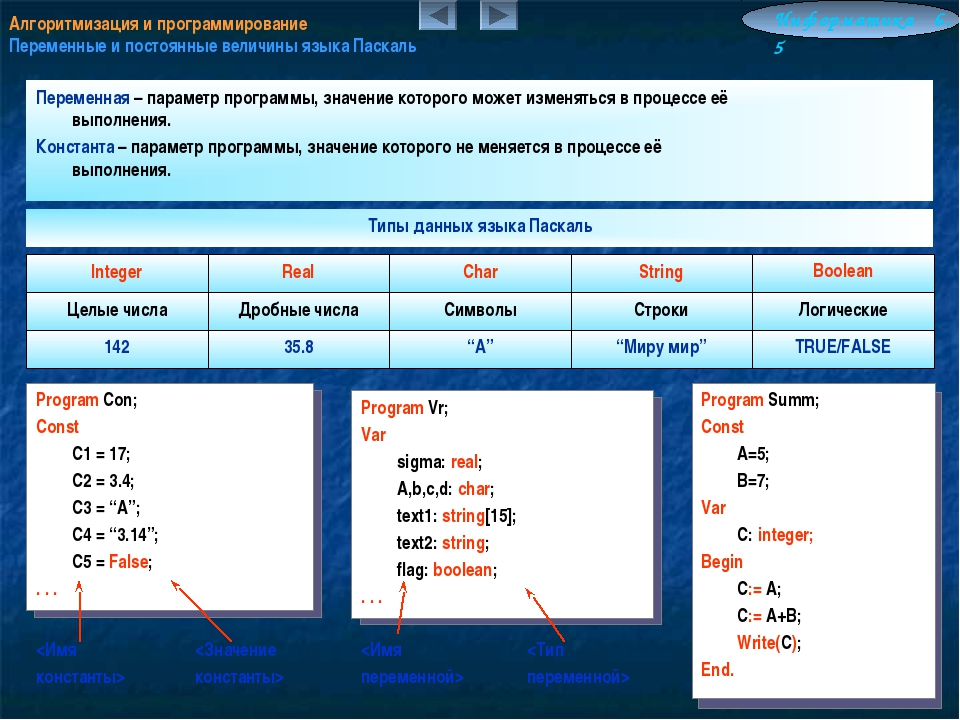
Польский математик Вацлав Серпинский описал фрактал, который носит его имя, в 1915 году, хотя дизайн как художественный мотив восходит как минимум к Италии 13-го века.Начните с сплошного равностороннего треугольника и удалите треугольник, образованный соединением средних точек каждой стороны. Середины сторон получившихся трех внутренних треугольников можно соединить, чтобы сформировать три новых треугольника, которые можно удалить, чтобы сформировать девять меньших внутренних треугольников. Процесс вырезания треугольных частей продолжается бесконечно, создавая область с размерностью Хаусдорфа чуть больше 1,5 (что указывает на то, что это больше, чем одномерная фигура, но меньше, чем двумерная фигура).
Британская энциклопедия, Inc. Уильям Л. ХошЧисловой тип данных — обзор
23.2 Функция SUM()
Эта функция работает только с числовыми значениями. Вам также следует обратиться к руководствам по вашему конкретному продукту, чтобы узнать точность результатов для точных и приблизительных числовых типов данных. Это реализация, определенная в стандартах SQL.
Это реализация, определенная в стандартах SQL.
SUM([ALL] < выражение-значение >) возвращает числовое значение всех известных значений. NULL удаляются до того, как произошло суммирование.Пустой набор возвращает пустой набор результатов, а не ноль. Если в списке SELECT есть другие столбцы, то этот пустой набор будет преобразован в NULL.
SUM(DISTINCT < value expression >) возвращает числовое значение всех известных уникальных значений. NULL и все избыточные дубликаты были удалены до того, как произошло суммирование. Пустой набор возвращает пустой набор результатов, а не ноль.
Это последнее правило трудно увидеть людям. Если в списке SELECT есть другие столбцы, то этот пустой результирующий набор будет преобразован в NULL.Это справедливо и для остальных стандартных агрегатных функций.
— нет строк
SELECT SUM(x)
FROM Empty_Table;
—одна строка с (0, NULL)
SELECT COUNT(*), SUM(x)
FROM Empty_Table;
Суммирование набора чисел выглядит так, как будто это должно быть легко, но это не так. Создайте две таблицы с одним и тем же набором положительных и отрицательных приблизительных числовых значений, но поместите одну в случайном порядке, а другую отсортируйте по абсолютному значению.Отсортированная таблица даст более точные результаты. Причина проста; положительные и отрицательные значения одной и той же величины будут складываться вместе и получат возможность компенсировать друг друга. Также меньше вероятность ошибки переполнения или потери значимости во время вычислений. Большинство реализаций SQL для ПК и множество реализаций для мэйнфреймов не используют этот трюк, потому что он потребует сортировки для каждого оператора SUM() и займет много времени.
Создайте две таблицы с одним и тем же набором положительных и отрицательных приблизительных числовых значений, но поместите одну в случайном порядке, а другую отсортируйте по абсолютному значению.Отсортированная таблица даст более точные результаты. Причина проста; положительные и отрицательные значения одной и той же величины будут складываться вместе и получат возможность компенсировать друг друга. Также меньше вероятность ошибки переполнения или потери значимости во время вычислений. Большинство реализаций SQL для ПК и множество реализаций для мэйнфреймов не используют этот трюк, потому что он потребует сортировки для каждого оператора SUM() и займет много времени.
Всякий раз, когда точному числовому присваивается точное или приблизительное числовое значение, оно может не поместиться в отведенном для него хранилище.SQL говорит, что механизм базы данных будет использовать аппроксимацию, сохраняющую значащие начальные цифры исходного числа после округления или усечения. Однако выбор между усечением или округлением определяется реализацией. Это может привести к некоторым неожиданностям, когда вам нужно переместить данные между реализациями SQL или значения хранения из программы основного языка в таблицу SQL. Вероятно, хорошей идеей будет создать столбцы с одним десятичным знаком больше, чем вам нужно.
Это может привести к некоторым неожиданностям, когда вам нужно переместить данные между реализациями SQL или значения хранения из программы основного языка в таблицу SQL. Вероятно, хорошей идеей будет создать столбцы с одним десятичным знаком больше, чем вам нужно.
Усечение определяется как усечение в сторону нуля; это значит что 1.5 усекается до 1, а — 1,5 усекается до — 1. Это верно не для всех языков программирования; все соглашаются с усечением положительных чисел в сторону нуля, но вы обнаружите, что отрицательные числа могут усекаться от нуля (например, — 1,5 будет усечено до — 2). SQL также нечетко относится к округлению, оставляя реализацию свободной для определения своего метода. Существует два основных типа округления: научный метод и коммерческий метод, которые обсуждаются в других местах этой книги.
Блез Паскаль: материалы, изобретения и факты — видео и стенограмма урока
Изобретения Паскаля
В 1642 году, в возрасте 18 лет, Паскаль изобрел калькулятор, чтобы помочь своему отцу. Этот калькулятор назывался Pascaline и имел колесо с восемью подвижными частями для набора номера. Каждая часть соответствовала определенной цифре числа. Например, число 368 будет набрано тремя частями с цифрами три, шесть и восемь соответственно для сотен, десятков и единиц.Паскалин мог складывать, вычитать, умножать и даже делить. Это была ранняя форма ныне стандартного цифрового калькулятора.
Этот калькулятор назывался Pascaline и имел колесо с восемью подвижными частями для набора номера. Каждая часть соответствовала определенной цифре числа. Например, число 368 будет набрано тремя частями с цифрами три, шесть и восемь соответственно для сотен, десятков и единиц.Паскалин мог складывать, вычитать, умножать и даже делить. Это была ранняя форма ныне стандартного цифрового калькулятора.
Также в 1640-х годах, возясь с атмосферным давлением, Блез Паскаль изобрел шприц и гидравлический пресс. Сегодня мы повсюду видим шприцы в медицинских учреждениях, а гидравлические прессы используются в автомагазинах для подъема автомобилей и во многих других случаях. Другим изобретением Паскаля была рулетка в 1655 году. На самом деле это изобретение было случайностью, когда Паскаль попытался изобрести вечный двигатель, производящий энергию.
Интересные факты
Блез Паскаль прожил всего 39 лет, но эти 39 лет были полны открытий, обучения и творчества. Родившийся 19 июня 1623 года во Франции, Блез Паскаль потерял мать лишь через три года после этого в 1626 году. Сам он умер 19 августа 1662 года в Париже.
Сам он умер 19 августа 1662 года в Париже.
Удивительно, но отец Паскаля не позволял своему маленькому сыну изучать геометрию в ранние годы. Поскольку геометрия и математика были запрещены, юный Паскаль чувствовал еще большее желание изучать эти предметы.Итак, когда ему было всего 12 лет, он начал самостоятельно изучать геометрию. Он даже вычислил, что сумма углов треугольника в сумме составляет 180 градусов.
Поскольку отец увидел, насколько он умен, Паскалю наконец разрешили изучать математику. Он даже ходил на встречи, проводимые в парижской математической академии. Именно в этой академии Паскаль представил свои первые теоремы, когда ему было всего 16 лет.
Итоги урока
Давайте повторим. Блез Паскаль за свои короткие 39 лет жизни сделал много вкладов и изобретений в различных областях.Он хорошо известен как в области математики, так и в области физики. В математике он известен тем, что внес свой вклад в теорию треугольника Паскаля и теорию вероятностей. Он также изобрел ранний цифровой калькулятор и рулетку.
Он также изобрел ранний цифровой калькулятор и рулетку.
В области физики Блейз внес свой вклад в изучение атмосферного давления, обнаружив, что вакуум реален и существует в реальном мире. Изучая атмосферное давление, он изобрел шприц и гидравлический пресс. Хотя он известен своим вкладом и изобретениями в области математики и физики, отец Паскаля фактически не позволял ему изучать математику в детстве.Но Паскаль был любопытен и проложил собственный путь, став вундеркиндом.
Результаты обучения
После этого урока вы сможете:
- Обобщить жизнь Блеза Паскаля и важность его работы
- Вспомните примеры важного вклада Паскаля в математику, физику и философию
- Определите четыре изобретения Паскаля
Java vs Pascal
Многие из вас уже изучали Pascal, и им просто нужно выучить синтаксис Java.Паскаль и Java, только отдаленно связанные, имеют много отличий. Этот документ пытается обобщить различия.
Общий
В целом, Java — гораздо более лаконичный язык. это ставит
это красиво. Грубо говоря, его синтаксис жесток. Для исторических
причины, по которым синтаксис заимствован из C, который еще более жесток
синтаксис. Это то, с чем мы должны мириться.
это ставит
это красиво. Грубо говоря, его синтаксис жесток. Для исторических
причины, по которым синтаксис заимствован из C, который еще более жесток
синтаксис. Это то, с чем мы должны мириться.
Первое жестокое замечание по синтаксису Java — это случай символов в Java имеет важное значение, поэтому имена переменных «i» и «Я» различны.Вы, естественно, не должны называть переменные где важен только регистр.
Другое существенное различие между Паскалем и Java заключается в том, что в Паскаль точка с запятой разделяет операторы , в то время как в Java точка с запятой завершает инструкций. Итак, в то время как в Паскале один может опустить точку с запятой для оператора, непосредственно предшествующего «конец», точка с запятой обязательна в Java для выражений предшествующий его эквиваленту «}».
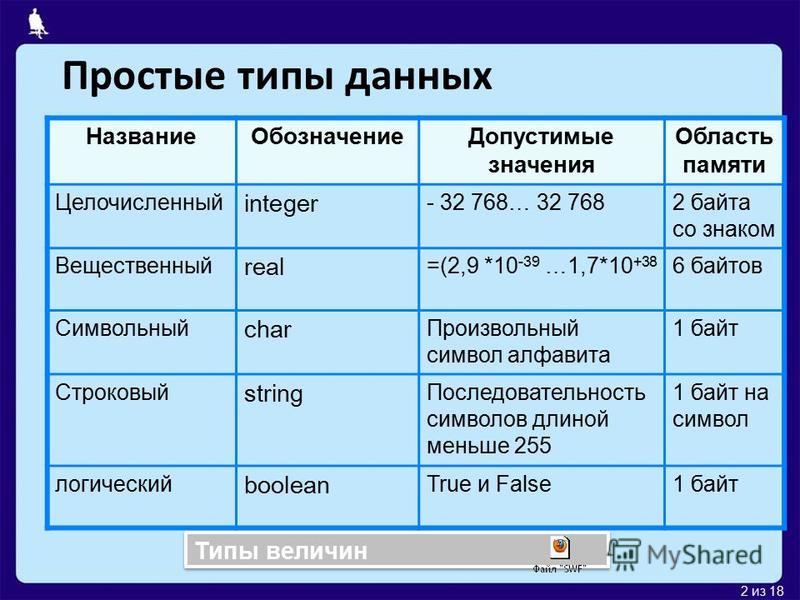
Типы данных
Основные используемые типы Java: char, int, и двойной.Они соответствуют символу Паскаля, целое и действительное.
Массивы Pascal и Java очень разные. В Java тип массива
пишется char[]. Границы массивов неявно варьируются
от нуля до единиц меньше длины массива. Вы не можете
определить границы массива самостоятельно.
В Java тип массива
пишется char[]. Границы массивов неявно варьируются
от нуля до единиц меньше длины массива. Вы не можете
определить границы массива самостоятельно.
Функции
В Паскале можно было бы написать такую функцию.
функция FuncName(параметры): returnType;
вар
Объявления переменных;
начинать
тело функции;
конец;
Аналогичная вещь в Java заключается в следующем.
public static returnType FuncName (параметры) {
Объявления переменных;
тело функции;
}
Для целей этого класса ключевые слова «public static»
необходимы.
В отличие от Паскаля функции не могут быть вложенными. Это упрощает видимость переменных значительно: видны только переменные те, которые объявлены внутри функции, и те, которые объявлены так, чтобы вся программа может их видеть, и мы игнорируем последние в этом класс.
Вызовы функций такие же, как в Паскале.
Процедуры
Java не имеет конструкции процедуры Java. Скорее, чем
процедура, используйте функцию, возвращаемое значение которой имеет тип
«пустота».
Скорее, чем
процедура, используйте функцию, возвращаемое значение которой имеет тип
«пустота».
public static void ИмяПроцедуры (параметры) {
}
Вы можете выйти из этой функции либо с оператором return без выражение («return;») или дойдя до закрывающей скобки функция.
Вы можете вызывать это как в Паскале.
Параметры
Список параметров в Java также значительно отличается от Паскаль.Параметры представляют собой список типов и параметров, разделенных запятыми. название. Например,
public static returnType FuncName (int parm1, double parm2, int parm3) {
// ...
}
Вы не можете комбинировать типы, как в Паскале. То есть, если у вас есть два
целочисленные параметры, расположенные рядом друг с другом, вы должны ввести «int
парм1, инт парм2».
Паскаль допускает возможность вызова по ссылке, используя объявление функции
function funcName(var a: integer) : real;Все параметры базовых типов Java вызываются по значению.
 Здесь нет
способ использования вызова по ссылке.
Здесь нет
способ использования вызова по ссылке.
С другой стороны, все массивы в некотором смысле вызываются по ссылке. То есть, если вы измените элемент массива, значение будет изменено в вызывающей функции.
Переменные и выражения
Переменные
Чтобы объявить переменную в Java, введите тип, а затем имя переменной, за которым следует точка с запятой:
тип_переменнойимя_переменной;Или, более конкретно, чтобы объявить целое число i, вы должны использовать
инт я;
Имена переменных в Java могут состоять из любого количества букв, цифр, и подчеркивания («_»).Однако первый символ должен быть письмо. Обратите внимание еще раз, что регистр букв значительный.
Массивы
Массивы немного сложнее, но не возмутительно. Массив декларация будет
arrayEntryType variableName = new arrayEntryType[arrayLength];Будет объявлен массив из тридцати символов с именем arr.
char[] arr = новый char[30];Обратите внимание еще раз, что массивы индексируются от 0 до единицы меньше, чем длина массива.
 Это означает, что arr[0] существует, пока
обр[30] нет! (Вы не можете, как в Паскале, изменить массив
границы, чтобы начать в другом месте.)
Это означает, что arr[0] существует, пока
обр[30] нет! (Вы не можете, как в Паскале, изменить массив
границы, чтобы начать в другом месте.)
Естественно, возможны многомерные массивы. Декларация было бы
arrayEntryType[][] variableName = new arrayEntryType[numberOfRows][rowLength];Тогда двумерная матрица вещественных чисел 4 на 5, называемая матом, будет объявлено
двойной[][] коврик = новый двойной[4][5];
Чтобы получить доступ к элементу массива, вы используете скобки, как в Паскале.arr[20], то это 21-й символ в arr. За многомерные массивы, однако вы используете отдельные скобки для каждого индекс, а не запятая. Таким образом, первый элемент мата мат[0][0].
Выражения
Java позволяет использовать многие из тех же арифметических операторов, что и в Pascal. То
`*’, `/’, `+’ и `-‘ остаются
то же самое, за исключением того, что `/’ то же самое, что и `div’, когда оба
стороны целые. (Всегда думайте дважды при делении, чтобы застраховать
что вы получите то, что хотите. )
)
Оператор `mod’ записывается как `%’ в Java.
Доступ к многомерным массивам отличается от Pascal. Подробнее см. в разделе о массивах.
литералов в языках программирования
Этот документ охватывает история и использование литералов (или констант) в языках программирования, начиная с от начала программирования до наших дней. Литералы во многих программах обсуждаются языки, в том числе современные языки, такие как C, Java, сценарии языки и более старые языки, такие как Ада, КОБОЛ и ФОРТРАН. Проблемы дизайна, типы литералов и проблемы с проиллюстрированы литералы.Литералы различаются в разных языках гораздо больше, чем большинство ожидали программисты.
литералов. 1
Целое число Литералы. 2
Дизайн Проблемы с целочисленными константами. 3
Ада Целые числа. 3
Размер целого числа 4
С Семья. 4
произвольно Длинные целые числа. 4
визуальный
БЕЙСИК 6.0 и QBasic. 4
4
визуальный Основные обозначения типов .NET. 5
база или основание целых чисел.5
вопроса. 7
Реальный Литералы. 7
Дизайн Проблемы с константами с плавающей запятой. 7
Десятичный Размещение точки 7
Точность реалов. 8
Комплекс Числа. 8
Что удваивается?. 9
ФОРТРАН 90 Добрых чисел. 10
вопроса. 11
вопроса. 11
логическое значение Литералы. 11
Дизайн Вопросы для Boolean. 11
Персонаж Строковые литералы. 13
Дизайн Проблемы со строками символов.13
Строка Разделители. 14
Строка Эскейп-последовательности. 14
Перл и строки символов оболочки UNIX. 16
Перл Альтернативные цитаты. 16
Перл Дополнительные Escape-последовательности. 17
ЮНИКС Цитаты. 17
Специальный Литералы = = где. 18
С# Дословные литералы Sting. 18
Питон
Строки в тройных кавычках. 18
18
здесь Документы. 19
Дата Литералы. 20
Массив Литералы.20
Строка Сравнение == перейти к строкам. 21
Повторение Литералы. 21
Заключение. 21
вопроса. 22
Новый Объявления FORTRAN, почему здесь, переместите в главу типа??. 24
Copyright Dennie Van Tassel 2004.
Пожалуйста, присылайте предложения и комментарии по адресу [email protected]
Литералы или константы — это значения, которые мы записываем в общепринятой форме.
ценность которых очевидна.В отличие от переменных, литералы (123, 4.3, «привет»)
не измениться в стоимости. Их также называют явными .
константы или манифеста
константы . я тоже видел такие
называются чистыми константами, но я не уверен, что эта терминология согласована. В
На первый взгляд может показаться, что все языки программирования печатают свои литералы
так же. Хотя в разных языках существует много общих соглашений
есть интересные отличия.
|
Буквальный |
Пояснение |
|
285 |
Типичное целое число |
|
34.67 |
Типичный реальный |
|
4.23Е-4 |
Типовой научный |
|
140_345 |
Целое число в Perl или Ada |
|
правда |
Типичное логическое значение |
|
0x1b или З»1Б» |
Шестнадцатеричный литерал |
|
«Б» |
Типовой символ |
|
«Здравствуйте» или «Здравствуйте» |
Типичная строка символов |
|
5HПривет |
Старая строка Холлерита FORTRAN |
|
ноль НОЛЬ |
Специальные литералы |
Различные литералы на разных языках
Стол х. 1
1
Литералы представляют возможные варианты в примитивных типах для этого языка. Некоторые из вариантов типов литералов часто являются целыми числами, с плавающей запятой, логические значения и строки символов. Каждый из них будет обсуждаться в этой главе.
Целые числа обычно описываются как числа без десятичной точки или степени. Еще одно описание для integerliterals — это строка десятичных цифр без десятичная точка.31 1 (поскольку нам нужно использовать один бит для отрицательных чисел).
Есть еще две целочисленные константы доступно на некоторых языках:
Ранний C не допускал +45, т.к.
целые числа без знака, например просто 45, по умолчанию положительны, поэтому унарные
использовался положительный знак. Таким образом, C имел унарный отрицательный оператор, но не имел унарного
положительный оператор. Но многие более поздние компиляторы C и Java допускают ненужные
положительные знаки констант. Немногие другие языки на самом деле запрещают унарные положительные
знаки.
Немногие другие языки на самом деле запрещают унарные положительные
знаки.
Последняя константа 5e2, которая оценка до 500 будет значением с плавающей запятой в C и FORTRAN. Их правило константа с плавающей запятой имеет десятичную точку ИЛИ показатель степени или и то, и другое. Таким образом, 5.0, 5e0 и 5.0e0 будут одинаковыми числами с плавающей запятой 5.0. Но в Аде целые числа могут иметь положительных показателя степени, поэтому 5e2 (или 5e+2) равно целому числу 500. Отрицательные показатели не допускаются для Ады. целые числа.Таким образом, 5е-3 — ошибка в Аде, но 5.0e-3 является константой с плавающей запятой.
Проблемы проектирования целочисленных констант
Есть несколько проблем с дизайном целые числа. Они:
- Что доступны размеры целочисленных констант? Например, у нас есть короткий целое число, обычные целые числа и длинные целые числа?
- Как мы указываем конкретный тип требуемой целочисленной константы?
- Что
основания целых чисел доступны? Примеры, которые могут быть доступны, кроме
десятичное число может быть восьмеричным, шестнадцатеричным или любым основанием.
 31 1. Сегодня широко распространены 64-битные целые числа. К сожалению, компьютерные целые числа
не может иметь эти полезные запятые для обозначения тысяч.
31 1. Сегодня широко распространены 64-битные целые числа. К сожалению, компьютерные целые числа
не может иметь эти полезные запятые для обозначения тысяч.
Но это чрезмерное упрощение так как мы можем иметь шестнадцатеричные целые числа, и они используют буквы. И мы можем захотеть восьмеричные значения и какой-то способ указать желаемый размер наших целых чисел. Также, определение целого числа в предыдущем абзаце верно не для всех языки.
Целые числа Ады
Например, в Adab как целые, так и действительные литералы могут иметь показатель степени.Таким образом в Аде целочисленный литерал 2100 также может быть записано как:
Но во многих других языках экспонента будет указывать на то, что приведенные выше литералы с плавающей запятой. За целые числа, показатель степени должен быть положительным. Ада позволяет нам использовать подчеркивание, чтобы улучшить читаемость. Знак подчеркивания часто используется для разделения числа на группы.
 из трех цифр, таких как запятые, используются в областях, не связанных с программированием. Вот некоторые
примеры:
из трех цифр, таких как запятые, используются в областях, не связанных с программированием. Вот некоторые
примеры: В большинстве приведенных выше номеров подчеркивание ставится там, где обычно должна быть запятая, но подчеркивание может быть размещается в любом удобном месте.Perl и Ruby также допускают подчеркивание в своих целые числа.
Семейство C
Если у нас есть более одного размера целых чисел, нам нужно каким-то образом указать точность целочисленной константы. Семейство C использует Lor l (ell) после целого числа для обозначения длинное целое число. Таким образом, 12 л используется в течение длительного времени. целое число. Мы можем использовать строчную букву l, но немногие могут отличить 12l (12 и L) или 121 (12 и один), поэтому мы всегда используем заглавную букву L. Эти суффиксы полезны, чтобы заставить арифметику особая точность.
Помимо длинных целых чисел, у нас есть беззнаковые целые числа в C, которые используйте суффикс u или U.
 16-1.
16-1.Если мы говорим на языке с длинными целыми числами, то как мы используем их? Например, если мы напишем 123456789012, мы не хотим получить с целочисленным переполнением или усечением. Хороший компилятор автоматически сохранить это целое как длинное целое, но мы можем захотеть помочь ему (или нам) с помощью 123456789012л.
В большинстве языков длинные целые числа ограничены некоторым большим размером. Python использует тот же L для обозначения длинного целого числа, например, 12345678
4567890L, но Python длинные целые числа могут быть сколь угодно большими.Другие языки например, диалекты Ruby и Lisp имеют эти произвольные длинные целые числа и называются системами bignum .Visual BASIC 6.0 и QBasic
Эти формы BASIC имеют два типа целых чисел. Два типа: целое число и длинное целое число . В раннем Бейсике не было типов для чисел. Там было нет различия между целыми числами и числами с плавающей запятой.
 Но теперь у нас есть несколько
числовые типы. Для числовых констант к числу используется суффикс, указывающий на тип.Вот что они используют:
Но теперь у нас есть несколько
числовые типы. Для числовых констант к числу используется суффикс, указывающий на тип.Вот что они используют: Числовой тип
Суффикс
Байт памяти
Целое число
%
2
Длинное целое
и
4
Одинарная точность
нет или !
4
Двойная точность
#
8
Типы в BASIC
Стол х.
 2
2 Таким образом, 15% — это целое число , в то время как 15&длина целое число, а 15 (или 15!) — число с плавающей запятой, одиночное число с плавающей запятой . По умолчанию все номера вещественный (с плавающей запятой) одиночный точность. Если мы хотим двойной точность float15, затем мы набираем 15#.
Обозначения типов Visual Basic .NET
VB .NET отделился от своих родителей BASIC и изменил символы-обозначения типов, которые они добавляют к числовым литералам.Целые числа (без десятичных точек) имеют тип Целое число а числа с десятичной точкой имеют тип Double . В остальном они используют метод, аналогичный предыдущим диалектам Бейсика, но используют различные коды для изменения типа по умолчанию. Коды VB .NET следующие:
S Короткий целое число
I Целое число
L Длинный целое число
F Одноместный -прецизионный с плавающей запятой
R Двойной — точный с плавающей запятой
D Десятичный
Итак, у них есть три типа целых чисел.
 и два типа с плавающей запятой.Они используют Десятичный
для десятичных дробей, таких как доллары и центы. Таким образом, 45S — это Short integer, 45I (или 45) — Integer , а 45L — Long integer. И 234.5F — это литерал с плавающей запятой Single -precision.
а 234,5R (или 234,5) — это Double — точность.
литерал с плавающей запятой. Наконец, 780.23D — это литерал валютного типа Decimal .
и два типа с плавающей запятой.Они используют Десятичный
для десятичных дробей, таких как доллары и центы. Таким образом, 45S — это Short integer, 45I (или 45) — Integer , а 45L — Long integer. И 234.5F — это литерал с плавающей запятой Single -precision.
а 234,5R (или 234,5) — это Double — точность.
литерал с плавающей запятой. Наконец, 780.23D — это литерал валютного типа Decimal . Диапазон значений для VB .Net намного больше, чем предыдущие языки.18. C# .NET имеет похожие типы и диапазоны значений.
Основание или основание целых чисел
Семейство С
Иногда нам нужно другое основание или основание наших констант, кроме основания 10. Основание 8 и основание 16 полезно для адресов хранения. Семейство C позволяет указать восьмеричные константы, предваряя число нулем. Таким образом, 012 — это восьмеричное число 12, а не десятичная двенадцать.
 Для восьмеричных значений диапазон цифр 0-7.
Для восьмеричных значений диапазон цифр 0-7. Итак, совместив это с тем, что мы узнали в предыдущем разделе, что мы можем использовать завершающую L, чтобы сделать константа Long и U, чтобы сделать его беззнаковым.Таким образом, 012UL является беззнаковым длинным восьмеричное значение 12 или эквивалент десятичного значения 10.
Для шестнадцатеричных значений нам нужно перед номером ставится 0x или 0X. Таким образом, 0x12 является шестнадцатеричным 12, а не десятичное 12. Теперь диапазон допустимых «цифр» 0 1 2 3 … 9 A B E F. Мы можем использовать прописные или строчные буквы a-f. Снова мы можем использовать длинное целое число индикатор «L» на них тоже. Таким образом, 07L — длинная восьмеричная семерка, а 0x7L — длинная восьмеричная семерка. представляет собой длинную шестнадцатеричную семерку. Мы также можем использовать завершающую букву U, чтобы сделать его без подписи.Таким образом, 0XFUL представляет собой длинное шестнадцатеричное значение без знака F, которое эквивалентно десятичному значению 15.

Ruby делает то же самое для восьмеричного и шестнадцатеричного литералы, как это делает C, но Ruby добавил 0b для двоичных чисел. Итак, в Ruby мы можем иметь шестнадцатеричные значения, такие как 0x12, восьмеричные значения, такие как 012, и двоичные значения вроде 0b1001.
ФОРТРАН 90
FORTRAN 90 делает это немного по-другому. Они допускают основание (основание числа) 2, 8 или 16.Они начинают значение с буквы B для двоичной или системы счисления 2, буквы O(oh) для восьмеричной и буквы Z для шестнадцатеричной. Затем за номером следует строка цифр, заключенная в двойные или одинарные кавычки. Диапазон цифр должен быть приемлемым для желаемого основания (никаких 8 или 9 в восьмеричных числах). Целочисленное значение 200 будет B «11001000» по основанию два, O»310″ для основания восемь и Z»C8″ для основания 16. Я очень стараюсь не быть шовинистический, но мне определенно больше нравится метод C в этом случае.
Это решение FORTRAN 90 иллюстрирует проблема добавления функции к существующему языку.
 Они не могут просто
решить использовать решение C, что все числа, начинающиеся с нуля, являются восьмеричными
ценности. Миллионы старых программ FORTRAN больше не будут работать правильно, когда
скомпилировано на новых компиляторах FORTRAN 90, поскольку 012 будет восьмеричным числом 12 вместо
десятичное число 12. С положительной стороны этого изменения, тысячи старых
программисты внезапно получили бы работу.
Они не могут просто
решить использовать решение C, что все числа, начинающиеся с нуля, являются восьмеричными
ценности. Миллионы старых программ FORTRAN больше не будут работать правильно, когда
скомпилировано на новых компиляторах FORTRAN 90, поскольку 012 будет восьмеричным числом 12 вместо
десятичное число 12. С положительной стороны этого изменения, тысячи старых
программисты внезапно получили бы работу. Ада
Ада, будучи язык всегда немного больше, делает то же, что и C и FORTRAN, но добавил больше баз и использует другой синтаксис.Целое число может быть выражено в любом основании от 2 до 16, поставив перед числом его основание, а затем заключив число в квадратные скобки в пределах # символов. Таким образом, десятичное значение 35 может быть выражено в различных основаниях. следующим образом:
2#100011# 4#203# 8#43# 10#35# 16#23#
Хотя это довольно интересно, я не вижу особого смысла в основание 7 или 11, но явно кто-то сделал.
 Кроме того, C и FORTRAN 90 могут только
использовать восьмеричные или шестнадцатеричные целые константы; Ада
позволяет использовать константы с плавающей запятой в этих разных базах.Таким образом, 23,45 может быть
выражено в базе 16 или другой базе от 2 до 16
Кроме того, C и FORTRAN 90 могут только
использовать восьмеричные или шестнадцатеричные целые константы; Ада
позволяет использовать константы с плавающей запятой в этих разных базах.Таким образом, 23,45 может быть
выражено в базе 16 или другой базе от 2 до 16 1. Предположим, вы хотите добавить больше базы на Java или C++. В настоящее время эти языки могут обрабатывать только десятичные, восьмеричное и шестнадцатеричное. Ада люди разрабатывали свои методы в самом начале, но ФОРТРАН должен был добавить его на существующий язык. Попробуйте выяснить, как вы могли бы добавить больше баз в C++ или Java, не ломая миллионы старых программ.
реалов числа с десятичной точкой, таким образом, 4.3 — настоящий литерал. Действительные числа называются числа с плавающей запятой или с плавающей запятой в некоторых языках. Другим описанием вещественных чисел является число с десятичной точкой или показателем степени (или оба), таким образом, 2e2 будет настоящим литералом, используя это определение.
 Как целое
литералы, перед числом может стоять положительный или отрицательный знак, запятые не ставятся.
позволил. Таким образом, некоторые реальные литералы:
Как целое
литералы, перед числом может стоять положительный или отрицательный знак, запятые не ставятся.
позволил. Таким образом, некоторые реальные литералы: Если язык принимает оба нижних и в верхнем регистре, «е» для показателя степени может быть в нижнем или верхнем регистре.Это может зависит от языка, если допустимо 4e-3, или нам может понадобиться 4.0e-3 (с десятичным точка). «е» означает показатель степени и означает умножение на 10 значения, которое следует. Таким образом,
Научное обозначение полезно для выражающие очень маленькие числа или очень большие значения (например, ваши шансы на выигрыш лотерея или государственный долг).
Есть несколько проблем с дизайном константы с плавающей запятой.Вот некоторые:
- Что размеры констант с плавающей запятой доступны? Например, есть ли у нас float, double и long double?
- Как мы указываем конкретный тип константы с плавающей запятой, которую мы хотим?
- Какие базы
с плавающей запятой доступны? Примеры, которые могут быть доступны, кроме
десятичное число может быть восьмеричным, шестнадцатеричным и, возможно, другим.

- Есть есть ли доступный разделитель, например запятая, используемая для тысяч?
На все вышеперечисленные вопросы есть интересные ответы в какой-то язык, и разные языки имеют разные ответы.
Размещение десятичной точки
В начале этой главы, когда мы обсуждали целочисленные литералы, мы отметили, что целочисленные литералы также могут иметь экспоненты. Итак, для Ады настоящие литералы должны иметь десятичная точка. Другая Ада Правило состоит в том, что реальные литералы должны иметь цифру с каждой стороны десятичной точки. Таким образом 4. (или .05) не являются законными Ада реально, но 4.0 приемлемо. КОБОЛ имеет похожие, но разные ограничения на литералы с плавающей запятой. В КОБОЛ буквальный .25 в порядке, но 25. не в порядке, и должно быть изменено на 25,0, так как точка завершает операторы, когда за ними следует пробел. В Паскале .04 нет допустимо, так как нам нужна цифра перед запятой, например 0,04.

Точность реалов
Семейство С
Семейство C имеет три типа реалов: поплавок , двойной , и длинный двойной . И они позволяют указать тип реального литерала. Реальные константы такие как 3.4, 2.0 и 4.564e-2 по умолчанию сохраняются как double . Если мы хотим, чтобы 4.3 хранился как float (вместо double ), мы можем добавить f или F после постоянная вроде этой 3.4F или 3.4f. Если мы хотим, чтобы 3.4 хранилось как long double , то мы используем l (нижний регистр L) или L, как мы делаем с целыми числами. Таким образом, 3,4 как long double будет 3,4 л или 3,4 л, но последний выглядит много. как три целых сорок один вместо 3,4 л. Все эти суффиксы полезны для контроля объема памяти. использования и точности результата.
1.0/3.0 // использует двойную точность .
1,0 л/3,0 л // используется длинный двойная точность .
Для примера с плавающей запятой , нам нужны обе константы float , в противном случае арифметика выполнялась бы в более высоком типе, т.
 е. в двойном. За
длинная точность, только одна из констант в long double заставит арифметику использовать long double. Это
объяснено больше в разделе о Принуждении в главе Арифметика.
е. в двойном. За
длинная точность, только одна из констант в long double заставит арифметику использовать long double. Это
объяснено больше в разделе о Принуждении в главе Арифметика.ФОРТРАН
В FORTRAN тип по умолчанию: одинарная точность (например, float в C). Мы можем ввести 4.3, что является одинарной точностью. real, но мы можем захотеть сохранить его как вещественное число с двойной точностью. ФОРТРАН использует суффикс D или d для обозначения двойной точности. Таким образом, мы может написать 4.3D0 или .43d1, чтобы указать, что это действительное значение двойной точности. Это простой способ заставить арифметику использовать двойную точность. Например:
х = 1/3d0
даст нам двойную точность деление, потому что 3d0 — двойная точность.
FORTRAN IV имеет комплексные числа. Данные сложного типа представлен двумя числами в скобках, разделенными запятой. Осталось число запятой — действительная часть, а число справа от запятой представляет собой мнимую часть комплексного числа.
 Таким образом, комплексная константа 3 + 2i
можно присвоить комплексной переменной x следующим образом:
Таким образом, комплексная константа 3 + 2i
можно присвоить комплексной переменной x следующим образом: х = (3, 2)
Fortran имеет все необходимые операции и функции для обработки сложные значения.Интересно, как рано в истории вычислений комплексные значения были обработаны Fortran. Ruby использует аналогичный синтаксис для своих сложных константы.
В Python комплексные числа состоят из двух чисел с плавающей запятой. действительная часть и мнимая часть и кодируются путем добавления J или j к мнимая часть. Таким образом, мы можем написать 3,0 + 4,3J для комплексного числа. Несколько других языков имеют встроенные комплексные числа и необходимые арифметические операторы и функции.31. Как вы видели самый большой, самый маленький, а количество целочисленных типов зависит от языка и машины. Но это довольно верно для многих языков.
языковые целые числа
размер
Ситуация становится гораздо более зависимой от машины и языка для значений с плавающей запятой.
 Для реалов есть два
части, кроме знака, экспоненты и мантиссы. Таким образом, для 3.45e-2 3.45 является
мантисса и -2 показатель степени. Мантисса обычно состоит из 7 знаков.
наименьший поплавок, 15 мест для следующего по величине поплавка и, наконец, 31 место для
самый большой поплавок. Не все языки имеют три размера. Ранние языки имели только один
размер. Новые языки, как правило, имеют три размера, особенно когда язык
используется для научного программирования.
Для реалов есть два
части, кроме знака, экспоненты и мантиссы. Таким образом, для 3.45e-2 3.45 является
мантисса и -2 показатель степени. Мантисса обычно состоит из 7 знаков.
наименьший поплавок, 15 мест для следующего по величине поплавка и, наконец, 31 место для
самый большой поплавок. Не все языки имеют три размера. Ранние языки имели только один
размер. Новые языки, как правило, имеют три размера, особенно когда язык
используется для научного программирования. Вопросы
1.Ваш Кандидатская диссертация должна показать, как расширить C++ или Java, чтобы эти языки могли указать желаемую точность для констант или переменных. Читать предыдущий раздел о добрых числах FORTRAN 90. Если ваш метод нарушает все предыдущие C++ программы вы не получите докторскую степень.
2. Perl и ранний BASIC не различают целые числа. и плавает. Эти два языка просто имеют числа. Как вы думаете, это хорошо подход? Должны ли мы делать это в OPL? Почему или почему нет?
1.
 Мы
видели несколько типов числовых литералов или констант. Какой числовой
константы, как вы думаете, мы должны иметь в OPL?
Мы
видели несколько типов числовых литералов или констант. Какой числовой
константы, как вы думаете, мы должны иметь в OPL? 2. Выполнить мы хотим разрешить разные целочисленные литералы? Например, короткий или длинный целые числа? Нужны ли нам один, два, три или более типов целых чисел? И как мы указываем, что требуется, когда мы вводим целое число?
3. Выполнить мы хотим разрешить разные реальные литералы? Например, float, double или длинный двойной.Нужны ли нам один, два, три или более типов реальных литералов? Как мы должны написать эти разные формы в OPL?
4. Что основание или основание целых чисел мы допустим: двоичные, восьмеричные, шестнадцатеричные, другие? У семейства C один путь, у FORTRAN 90 — другой, а у Ada есть третий метод. И как мы будем писать разные числа в OPL?
5. Большинство или все языки не позволяют использовать запятые в числовых литералах, например 1234.
 Это
ограничение все еще необходимо? Как вы думаете, мы должны разрешить запятые в числе для
ОПЛ? Обратите внимание, как с этим справляется Ада.
Это
ограничение все еще необходимо? Как вы думаете, мы должны разрешить запятые в числе для
ОПЛ? Обратите внимание, как с этим справляется Ада. Нам нужен литерал для истинного и ложного. Это называется Булевы или логические, в зависимости от языка. Некоторые языки имеют зарезервированное или ключевое слово для этих значений. Булевы значения порядковые значения и обычно false меньше истинное . То нормальные операции и , или и не .
Проблемы проектирования для логического значения
Есть несколько решений и отличий для Boolean ценности. Вот несколько вопросов:
- Ар там специальные зарезервированные или ключевые слова для булевых значений?
- Ар логические значения упорядочены? То есть ложно < правда или наоборот?
- Булевы значения порядковые значения? Можно ли их использовать для выбора в коммутаторе утверждение?
- Когда
говоря о логических значениях, мы используем заглавные
Булевы значения или булевы значения в нижнем регистре? Оба
версии распространены в книгах.
 Это, наверное, самая сложная проблема,
поскольку сложность задачи часто обратно пропорциональна ее
важность.
Это, наверное, самая сложная проблема,
поскольку сложность задачи часто обратно пропорциональна ее
важность.
ФОРТРАН
Все версии FORTRAN используют .TRUE. и .ЛОЖЬ. для их логические константы. А в ФОРТРАНЕ они называются логическими вместо булевых. Поскольку FORTRAN не имеет зарезервированных слов, FORTRAN использует период до и после этих логических литералов, чтобы отличить их от переменные ИСТИНА и ЛОЖЬ.Если мы напечатаем логическую переменную FORTRAN, она напечатает либо T, либо F, и эти это то, что нам нужно для ввода при чтении логических данных в программу.
Ада, Паскаль, ALGOL и Java используют true и false для своих логических литералов.
Ввод и вывод логических значений беспорядочны в большинство языков. Если мы хотим использовать целое число 123, мы можем использовать его именно так. как литеральная константа в программе, читать целое число или печатать целое число и это все равно.
 С логическими литералами все не так просто.
С логическими литералами все не так просто. Некоторые языки не имеют удобного способа ввода или вывода Логические значения. Например, в FORTRAN логические печатать как F или T. Но когда мы хотим прочитать значение для истинности, мы можем использовать буква т, или период и t (т.е. .t), или период и слово true (т.е. .true), или любая строка, начинающаяся с буквы t или точки, буквы t, тогда что-либо. Таким образом, ввод, вывод и внутренняя часть программы потенциально отличается для логики FORTRAN.
Семейство С
Семейство языков C не использует именованные константы для логические значения. Вместо этого они используют 0 (ноль) для false и 1 (один) для true в качестве результат реляционных или логических выражений. Таким образом, если мы попытаемся напечатать 4< 3 мы получили бы ноль, а 4 < 3 дали бы нам 1.
cout << "true=" << 3<4 << и ;
cout << "ложь=" << 4<3 << и ;
Пока это работает на C++, что-то подобное можно сделать и на других языках, чтобы проверить, и что печатает.
 Ситуация немного сложнее, так как значение
ноль эквивалентен ложному, а любое другое значение эквивалентно истинному. Итак,
Ситуация немного сложнее, так как значение
ноль эквивалентен ложному, а любое другое значение эквивалентно истинному. Итак, если (Икс) . . .
будет быть ложным, когда x равен нулю, и ложным в противном случае. Хотя это может быть благо, когда мы знаем, что делаем, это также общий источник плохого программные ошибки, когда мы не осторожны. Java оторвалась от своего фона C и не допускает этого.
Строки символов являются следующим типом литералов. Характер строка представляет собой группу символов, склеенных вместе. Пример наш ныне известный:
«Привет, мир».
Но все начиналось не так просто. На самом деле было небольшая доступность любого типа использования символов на очень ранних компьютерах. FORTRAN представил строку Холлерита, которая была назван в честь Германа Холлерита, изобретателя перфорированного карточное оборудование для U.
 С. Бюро переписи населения. Теперь мы будем использовать его как
следует
С. Бюро переписи населения. Теперь мы будем использовать его как
следует 13Ч ПРИВЕТ, МИР.
Цифра 13H означает, что за ней следуют тринадцать символов. Они использовались в операторах формата вывода. Таким образом, мы могли бы иметь что-то вроде следующего:
ЗАПИСАТЬ (5, 10)
10 ФОРМАТ(13HHELLO WORLD.)
Не было символьных переменных или каких-либо способов манипулирования строки символов.
Есть несколько проблем с дизайном строки символов. константы. Они:
- Как строки символов разделены? Примеры способов использования double или одинарные кавычки.
- Как мы используем разделитель внутри строки символов?
- Делать строки символов имеют escape-последовательности и переменную интерполяцию?
Таким образом, символов строки представляют собой последовательность символов, заключенных в совпадающие одинарные или двойные цитаты.
 Строки символов также называются просто строками, символьными константами или нечисловыми литералами. Каждый символ использует один байт
хранения.
Строки символов также называются просто строками, символьными константами или нечисловыми литералами. Каждый символ использует один байт
хранения. Одно интересное соображение заключается в том, как разграничивать строки, которые есть, укажите начало и конец строки. Далее нам нужно знать, как использовать разделитель внутри самой строки. Например, если мы используем кавычки для заключать строку, то как нам поставить кавычку в строку? Кроме того, можем ли мы иметь строки, которые простираются на одну строку, или мы ограничены только одной строкой? Наконец, нам нужны строковые операторы и функции для поиска, сравнения и поиска. построить строки.Существует почти столько же способов конкатенации символов строки, так как существуют языковые группы.
Строка Разделители
Кавычки или апострофы являются общим разделителем или разделительный знак для строк символов. Кавычки часто называют двойными цитаты, в то время как апострофы часто называют одинарными кавычками.
 Некоторые языки, такие как
Java или C используют только кавычки («»). Другие языки, такие как Pascal и
FORTRAN использует только {) апострофы.И все же другие языки, такие как HTML, xxx
разрешать либо кавычки, либо апострофы, если оба они используются для
конкретная строка. Таким образом, мы можем использовать «Hello world» (цитаты) или Hello world. (апострофы), но мы не можем использовать «Привет
World (кавычка в начале и апостроф в конце). я не знаю ни одного языка
это позволяет это, но я буду следить за своей электронной почтой для кого-то, кто знает об этом.
Некоторые языки, такие как
Java или C используют только кавычки («»). Другие языки, такие как Pascal и
FORTRAN использует только {) апострофы.И все же другие языки, такие как HTML, xxx
разрешать либо кавычки, либо апострофы, если оба они используются для
конкретная строка. Таким образом, мы можем использовать «Hello world» (цитаты) или Hello world. (апострофы), но мы не можем использовать «Привет
World (кавычка в начале и апостроф в конце). я не знаю ни одного языка
это позволяет это, но я буду следить за своей электронной почтой для кого-то, кто знает об этом. Выход из строки Последовательности
Если мы используем кавычки (одинарные или двойные) для заключения строк, то нам нужен какой-то способ вставить ту же кавычку внутри строки, не нарушая строка символов.Экранирующий символ используется для аннулирования специального значения следующий персонаж. Есть два распространенных решения этой проблемы. Одно решение использовать два символа (кавычки) для обозначения одного.
 Другой метод заключается в использовании
escape-символ для защиты цитаты.
Другой метод заключается в использовании
escape-символ для защиты цитаты. FORTRAN использует апострофы для строк и использует первый решение. Таким образом, в FORTRAN, если мы хотим НЕ ДЕЛАТЬ ЭТОГО, мы должны что-то сделать. похожий на этот
ПЕЧАТЬ *, НЕ ДЕЛАЙТЕ ЭТОГО! использует два апострофа
, который изменяет DONT на DONT при его обработке.Использование COBOL, Pascal, Ada и BASIC это удвоение метод . Повторение заключенную цитату иногда называют цитатой начинка .
Ада необычная поскольку он не требует вставки кавычек или escape-символа для защиты символ кавычки, когда это один символ. Ада имеет символьные литералы, заключенные в одинарные кавычки, и любой символ может быть заключено, включая одинарную кавычку. Таким образом, x в порядке, но также Это хорошо.Большинство языков требуют или \ для защиты прилагаемого одинарная цитата.
 Если подумать об этом, кажется вполне возможным сделать это на Аде.
способом, но никакие другие языки, похоже, не делают этого.
Если подумать об этом, кажется вполне возможным сделать это на Аде.
способом, но никакие другие языки, похоже, не делают этого. Java и C используют escape-символы. Обратная косая черта используется, чтобы «избежать» специального значения следующий персонаж. Таким образом, мы могли бы напечатать подобную фразу следующим образом:
cout << "Использовать \" для строк." << endl ;
Здесь у нас есть кавычки внутри строки символов, используя кавычки.Такое использование escape-символа позволяет нам заключать другие символы, которые обычно вызывают проблемы внутри строки символов, например \n для новой строки. За escape-символом может следовать шестнадцатеричный или восьмеричное значение для генерации любого символа, даже непечатаемого. С языки и другие программы UNIX широко используют этот последний метод. В таблице x.x приведен список управляющих символов, которые работают с Языки семейства C и программы UNIX.
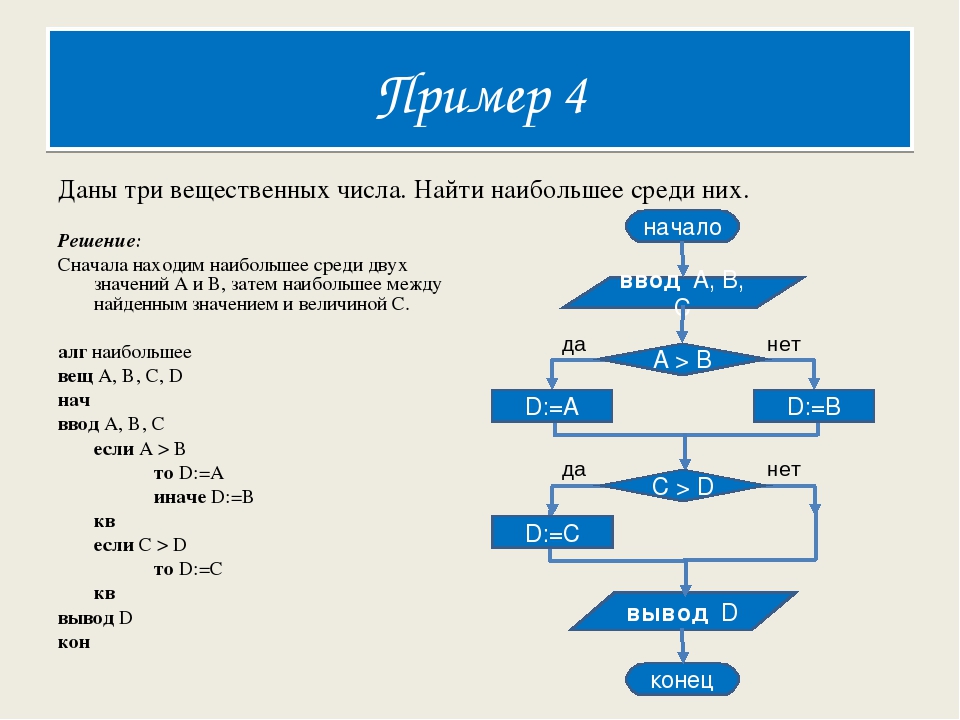 С# в основном использует один и тот же экран
персонажи как С.
С# в основном использует один и тот же экран
персонажи как С.Последовательность выхода
Описание
Декабрь
Шестигранник
Октябрь
\
Будильник/звонок (BEL)
7
\x07
\007
\б
Backspace (БС)
8
\x08
\010
\ф
Подача бумаги (FF)
12
\x0C
\014
\n
Новая линия (LF)
10
\x0A
\012
\г
Возврат каретки (CR)
13
\x0D
\015
\т
Горизонтальная вкладка (TAB)
9
\x09
\011
\v
Вертикальная вкладка (VT)
11
\x0B
\013
\»
» двойная кавычка
34
\x22
\042
\’
‘одинарная кавычка
39
\x27
\047
\
\ обратная косая черта
92
\x5C
\134
\032
Восьмеричный символ
\xff
Шестнадцатеричный символ
\ (Введите ключ)
Продолжение новой строки
Краткая таблица управляющих символов
Стол х.
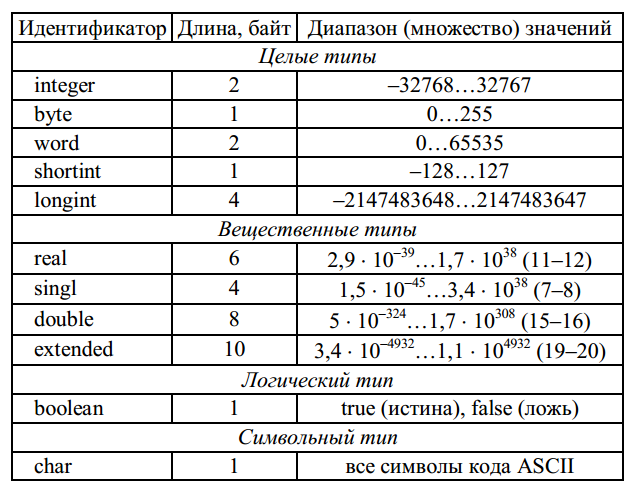 1
1 HTML и XML используют угловые скобки «» для их команды. Затем им нужен способ вставки угловых скобок. XML использует ссылки на символы, которые начинаются с символа & и заканчиваются точкой с запятой. Затем нужный именуется ссылкой или -символьный ссылочный номер . Таким образом мы можем получить <, используя либо < (что означает l ess t han) или < какой номер символа для <.Мы можем не только получить персонажей, которые в противном случае возникнут такие проблемы, как <, < и &, но мы можем получить символы других языков, которых нет на нашей клавиатуре.
Третье частичное решение необходимости цитаты внутри Строка символов допускает любой тип кавычек. Этот метод используется в версии BASIC, SQL, COBOL и HTML. Это позволяет нам сделать следующее:
Апостроф «Не» внутри кавычки
Использовать » для котировок кавычка внутри апострофа
У нас все еще есть проблема, что делать, когда нам действительно нужно или хотите, чтобы одна и та же кавычка внутри строки в кавычках и один из двух выше используются методы.
 Например, «Использовать» или для кавычек.
Например, «Использовать» или для кавычек. Из предыдущего обсуждения видно, что есть уровни активности в строках символов и зависит от языка. На самом низком уровне уровне существует проблема использования разделителя кавычек внутри строка символов. Использовались два метода: либо не или нет. По мере того, как мы продвигаемся от в основном мертвых строк символов (внутри строки нет активности), мы найдем язык, который имеет длинный или короткий список escape-символов, как указано выше таблица и интерпретация переменных в языках UNIX и родственных им языках.Эти последние строки символов я обозначу как живых строк символов , так как внутри может происходить много действий. строка символов.
Perl и строки символов оболочки UNIX
Языки программирования оболочки Perl и UNIX обрабатывают символы строки, но есть несколько важных отличий от других языков. Строки могут быть разделены соответствующими кавычками или апострофами.
 Когда строки символов заключены в апострофы, обрабатываются все символы.
как литералы.Когда строки символов
в кавычках, почти
все символы рассматриваются как литералы, за исключением переменной
замены и специальные escape-последовательности. Например, в Перле
переменные интерпретируются:
Когда строки символов заключены в апострофы, обрабатываются все символы.
как литералы.Когда строки символов
в кавычках, почти
все символы рассматриваются как литералы, за исключением переменной
замены и специальные escape-последовательности. Например, в Перле
переменные интерпретируются: $х = 45;
print ‘x = $x’ # вывод на печать x = $x
print «x = $x» # вывод x = 45
Итак, $x — это переменная Perl, и она интерпретируется, когда в двойных кавычках, но не интерпретируется при заключении в одинарные кавычки.Точно так же управляющие последовательности обрабатываются в кавычках, но не апострофы:
напечатать ‘привет\nпока’; # вывод на печать привет\nпока
напечатать «привет\nпока»; # интерпретирует новую строку \n
# и печатает две строки.
Есть много названий управляющие символы, и любой символ может быть обработан десятичным, восьмеричным или шестнадцатеричное значение.
 См. xxx в zzzz.
См. xxx в zzzz. ==== проверить все это в Perl ====
Perl Альтернативные котировки
Если методы цитирования UNIX окажутся неадекватными или слишком запутанными, Perl предоставляет следующую альтернативную форму цитирования:
.- q представляет одинарные кавычки.
- qq представляет собой двойные кавычки.
- qx представляет обратные кавычки.
Строка, которая будет заключена в кавычки, должна быть заключена в соответствие разделители. Здесь мы используем косую черту, но можно использовать и другие совпадающие символы. б/у:
print qq/Он сказал: «Не делай it.»\n/; # менее сложный
Знак доллара является специальным символом в Perl и должен быть цитируется в одинарных кавычках.
Дополнительные Escape-последовательности Perl
Помимо всех escape-последовательностей, используемых C и UNIX, Perl имеет дополнительные управляющие последовательности.
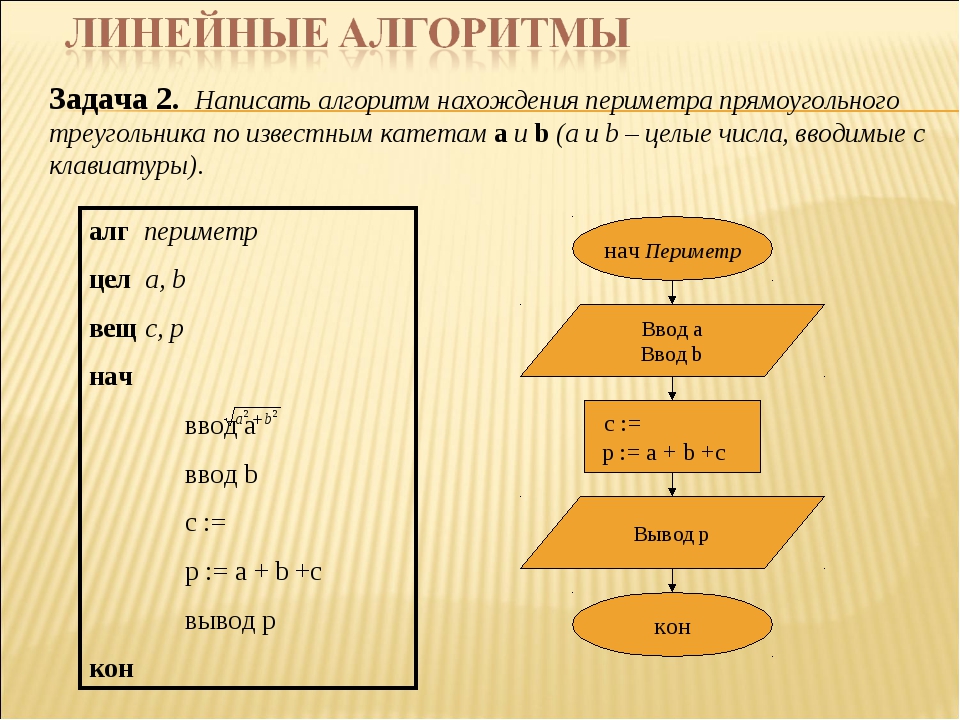 Вот еще Перл
escape-последовательности:
Вот еще Перл
escape-последовательности: Последовательность выхода
Описание
\с[
Управляющий символ
\л
Следующий символ преобразуется в нижний регистр.
\
Следующий символ преобразуется в верхний регистр.
\л
Следующие символы преобразуются в нижний регистр, пока \E не будет нашел.
\У
Следующие символы преобразуются в верхний регистр, пока \E не будет нашел.
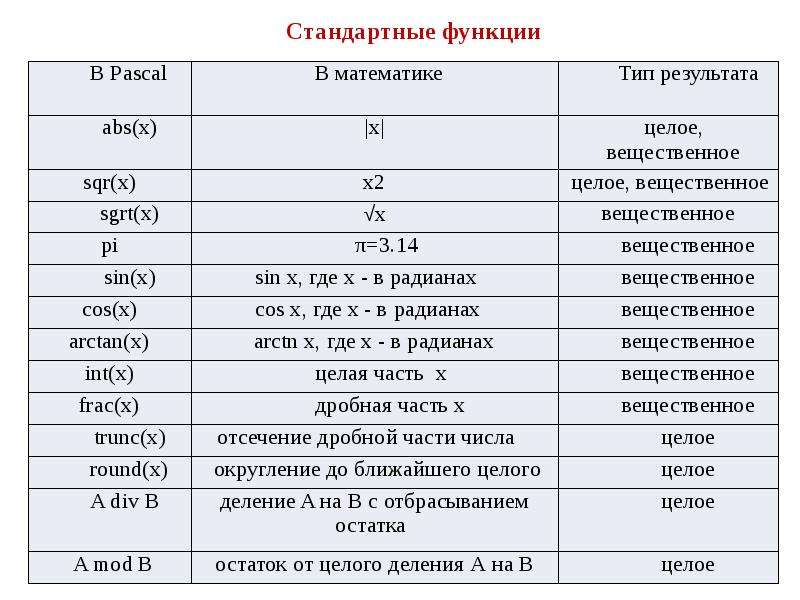
Дополнительные Escape-последовательности Perl
Стол х.2
Обратные кавычки UNIX
Специальные литералы = = где
Во многих языках есть свои специальные литералы. Примеры eof или null в C, ZERO и SPACE в COBOL и __LINE__ и __FILE__ в Perl. Эти специальные литералы обсуждаются в разделе «Именованные константы» главы «Переменные».
Литералы строк символов, которые не используют escape-последовательности полезны для адресов файлов, вставки специальных символов, таких как перевод строки и вкладки, и другие грязные ситуации.Например, у нас обычно было бы что-то похожее на это:
string strFileName = «c:\\Mydocs\\Graphics\\dennie.gif»;
, чтобы указать на мою большую фотографию.
 Но нам нужно убежать от всех
обратная косая черта. С дословной строкой C#
литерал , мы можем избежать двойного
обратную косую черту следующим образом:
Но нам нужно убежать от всех
обратная косая черта. С дословной строкой C#
литерал , мы можем избежать двойного
обратную косую черту следующим образом: строка strFileName = @»c:\Mydocs\Graphics\dennie.гифка»;
Python имеет два новых типа строк. First — это строки в тройных кавычках, в которых все находится между совпадающими группами. из трех одинарных или двойных кавычек, включая другие кавычки и строку возвращается. Это похоже на метод Perl qq/. Этот это простой способ определить строку как с одним и двойные кавычки, как qq/…/ в Perl.
«»»»А кавычка используется для начала строки,
можно использовать либо или «.»»»
UNIX, PHP и Perl имеют здесь документов (или heredoc ), которые похожи на Python тройные кавычки или необработанные строки. Название документа происходит от того факта, что документ находится здесь.
 Мы могли бы сделать предыдущий пример Python на Perl как
следует:
Мы могли бы сделать предыдущий пример Python на Perl как
следует: Цитата используется для начала строки,
либо или » можно использовать.
ЭОФ
Символы << используются для указать начало здесь документа.Слово, следующее непосредственно за (в этом случае EOF) используются чтобы указать, что искать в конце документа здесь. Закрытие индикатор (например, EOF) должен быть включен отдельная строка без пробелов перед ней. Документ здесь похож на строка в двойных кавычках, так как обычные управляющие последовательности будут интерполированы. Уведомление точка с запятой в конце первой строки в Perl пример выше. В приведенном ниже примере PHP в последней строке стоит точка с запятой. но не первая строка.
Здесь есть еще кое-что документа, и разные языки обрабатывают документ по-разному в зависимости от если строка терминатора заключена в двойные кавычки («EOF»), одинарные кавычки (EOF) или обратные кавычки.
 если ты
вам нужно посмотреть, как с этим справляются оболочки Perl и UNIX. PHP
и делает здесь документы но они немного отличаются. Вот тот же пример в
PHP:
если ты
вам нужно посмотреть, как с этим справляются оболочки Perl и UNIX. PHP
и делает здесь документы но они немного отличаются. Вот тот же пример в
PHP: Цитата используется для начала строки,
либо или » можно использовать.
EOF ; # здесь точка с запятой.
PHP использует три левых угловых скобки вместо два, а последняя строка заканчивается точкой с запятой. Различные оболочки UNIX также используют вот документы и вот откуда они взялись.
В некоторых языках есть литералы даты. Первая проблема заключается в том, как мы вводим дату, чтобы она распознавалась как дата. Visual Basic .NET использует знаки # приложить дату следующим образом:
Литерал даты может быть использован в операторе присваивания. как и другие литералы:
Дим objMyBirthday Дата = 15.
 12.1981#
12.1981# Переменные даты C# всегда предполагают время, даже если это не так. учитывая один, поэтому сохраненное выше значение будет
15.12.1981 00:00:00
VB предоставляет широкий спектр функций для управления даты, такие как добавление интервала к дате, вычитание двух дат и форматирование вывода даты.Если вам интересно какие операции можно сделать с датами, вы можете посмотреть на VB или посмотреть на приложения, такие как электронные таблицы или программы базы данных, чтобы увидеть, что возможно.
Некоторые языки имеют специальные литералы для инициализации массивы. Они будут кратко рассмотрены здесь и рассмотрены более подробно в Глава Массив. В Perl есть литералы списков, которые используются для массивов. Примеры:
(1, 2, 3, 4) # массив из четырех значений 1, 2, 3 и 4.
(1 ..4) # массив из четырех значений 1, 2, 3 и 4.
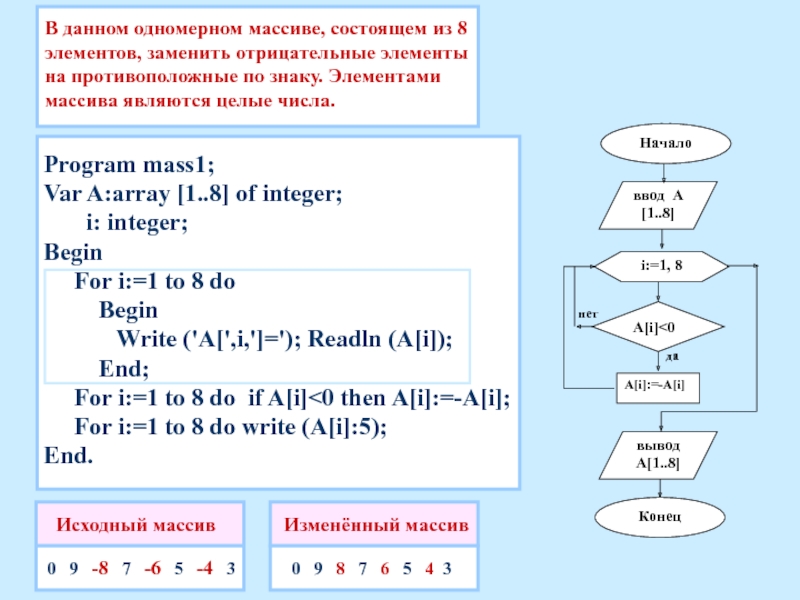
(1.5 .. 4.5) # массив из четырех значений 1.5, 2.5 и т.д.
В Perl доступно гораздо больше, поэтому пропустите главу «Массив», если интересно. ФОРТРАН и Ада также имеет обширные методы массива.
Сравнение строк == перемещение к строкам
При сравнении строк символов, что представляет собой равенство представляет интерес. Главный вопрос, что делают лишние пробелы с правой стороны к сравнению? Если мы сравним строки «привет» и «привет», они равны? Нет пробелов после первое «привет», но это пробелы после второй строки.
В QBASIC два строковых выражения считаются равными, если они одинаковой длины и содержат одинаковая последовательность символов. В COBOL строки равны, если все символы равны, и любое более длинное поле имеет только пробелы справа. Таким образом, в COBOL для сравнения пробелы дополняются. правая сторона более короткого поля. Таким образом, в QBasic строки символов «Hi» и «Hi» будут равны , а не , но в COBOL они будут оцениваться как равные .
 Возможно, мы сможем найти закономерность
где языки бизнес-программирования будут игнорировать лишние крайние справа пробелы,
но не деловые языки — нет.
Возможно, мы сможем найти закономерность
где языки бизнес-программирования будут игнорировать лишние крайние справа пробелы,
но не деловые языки — нет. В некоторых языках есть оператор для повторения строковых констант. Например, PL/I имеет следующий метод:
который даст вам город Уолла Валла которые вы, вероятно, много печатаете. (Быстро назовите другие города одинаковыми словами.) Это повторение можно использовать для присвоения значения строке символов PL/I как следует:
ГОРОД = (2)Уолла ;
Perl использует оператор «x» для повторения строк, а Python и Ruby использует оператор «*» для повторения строк.Если бы мы хотели сгенерировать строка хахаха, мы могли бы сделать это следующим образом:
PL/I
Перл
Python/Ruby
(3)га
га x 3
га * 3
Мало языков, кроме этих языков есть какие-то способы сделать это.
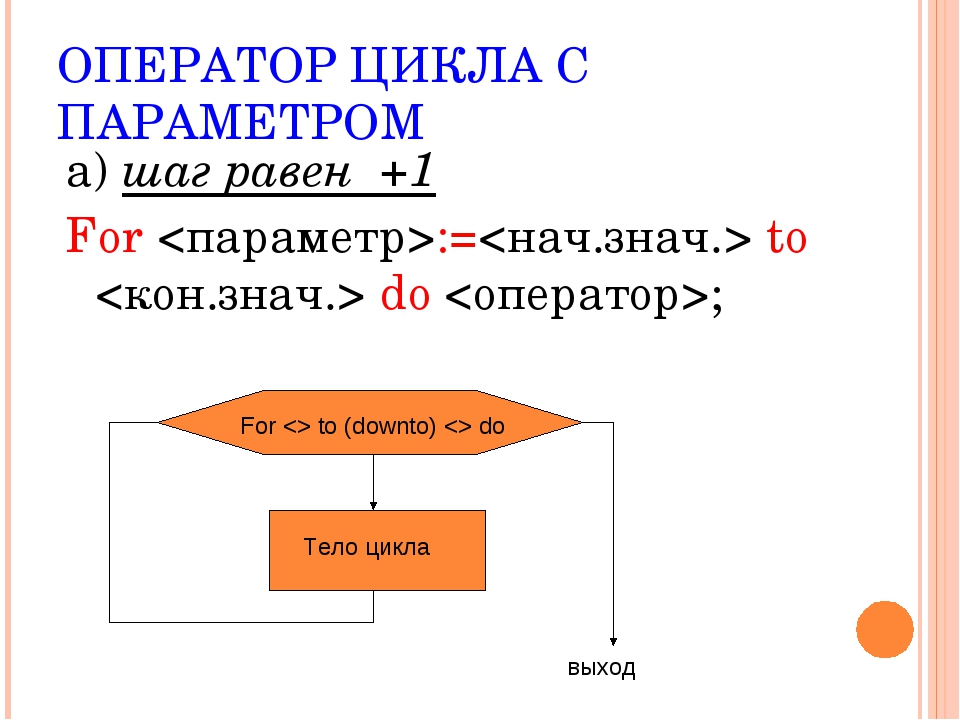 Но я подозреваю, что кто-то напишет по электронной почте о другом языке, который я пропустил.
Но я подозреваю, что кто-то напишет по электронной почте о другом языке, который я пропустил. В этой главе я рассмотрел литералы во многих языках. В простейшие литералы уровней очень похожи во многих языках, но когда мы смотрим в подробнее мы находим много интересных отличий. Некоторые языки позволяют подчеркивание в числах, как запятая используется для обозначения тысяч и миллионов. И когда мы добираемся до символьных строк, есть много различий. Цитирование и интерпретация строк символов сильно различается, особенно в сценариях языки.И есть несколько способов обработки длинных строк символов и специальные символы в них, включая символы новой строки.
- Два
обсуждались способы обработки логических значений.
Один метод заключался в том, что мы использовали зарезервированные слова, такие как true и false в
Фортран и Паскаль. Второй способ заключался в использовании нуля вместо ложного и одного (или
ничего, кроме нуля) для true в C.
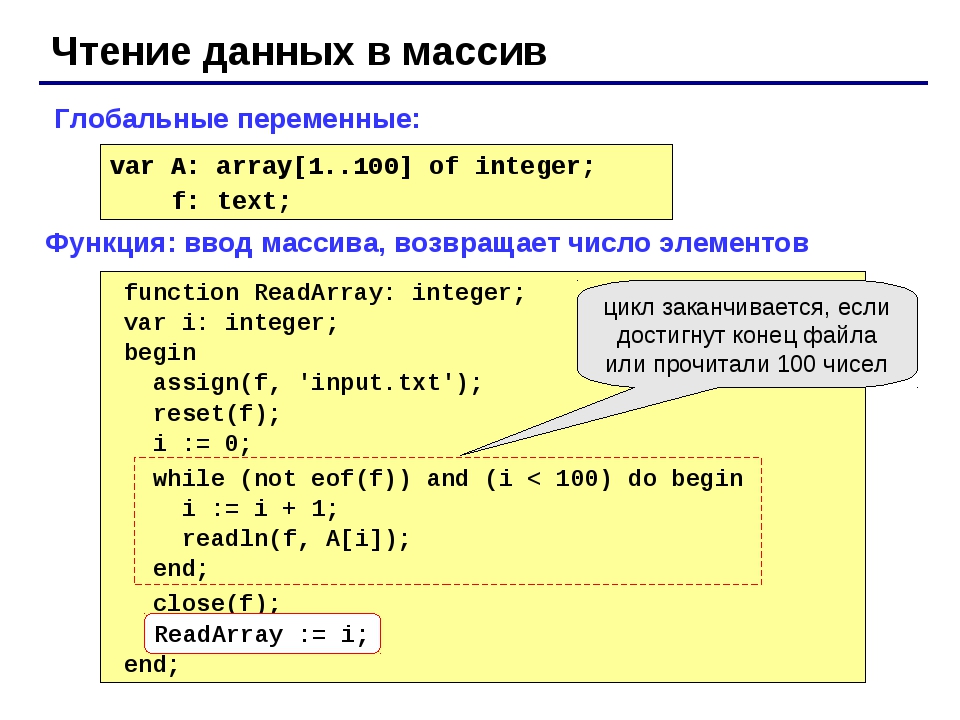 Что нам делать в OPL?
Что нам делать в OPL? - Ан интересная проблема с логическими значениями заключается в том, как мы печатать и вводить логические значения.Нет подарка решение кажется очень элегантным. Можете ли вы придумать элегантное решение, как ваша кандидатская диссертация? Ну может ваш А.С. Тезис?
- Как должны ли мы разделять наши строки символов в OPL? Будем ли мы использовать апострофы или кавычки, или и то, и другое, или у вас есть идея получше?
4. Что как вы думаете, мы должны использовать в OPL разделитель строк внутри строка символов? Были представлены два существующих метода: удвоение цитаты или последовательность выхода.
5. Перл и оболочка UNIX имеют интересный механизм цитирования. Переменные и побег последовательности оцениваются в двойных кавычках, но не в одинарных. Можем мы использовать это в OPL, и если да, то как? Будет ли эта функция более интересной в некоторых языков, чем другие, такие как деловые, научные или системные языки?
6.
 Перл
и оболочка UNIX имеют интересный способ выполнения системных команд с
обратные кавычки. Можем ли мы использовать это в OPL, и если да, то как? Будет ли эта функция более
на одних языках интереснее, чем на других: деловой язык, научный
языки и системные языки?
Перл
и оболочка UNIX имеют интересный способ выполнения системных команд с
обратные кавычки. Можем ли мы использовать это в OPL, и если да, то как? Будет ли эта функция более
на одних языках интереснее, чем на других: деловой язык, научный
языки и системные языки? 7.Являются логические значения заказаны? Если да, то является ли ложным < истинным ?
8. Строка символов Python состоит из тройных кавычек. Это строка символов которое начинается с трех кавычек (одинарных или двойных), а затем почти все может быть внутри строки символов, включая новые строки и другие кавычки. Посмотрите это и сравните его с другими методами, такими как qq/ в Perl. Как вы думаете, будет ли этот метод хорошим дополнением к OPL?
9. Каждый язык имеет другой способ обозначения восьмеричных или шестнадцатеричных констант.Разработайте диаграмму по языкам, показывающую, как каждый язык делает это. Какой метод вы рекомендуете для OPL?
Калькулятор паскалина.
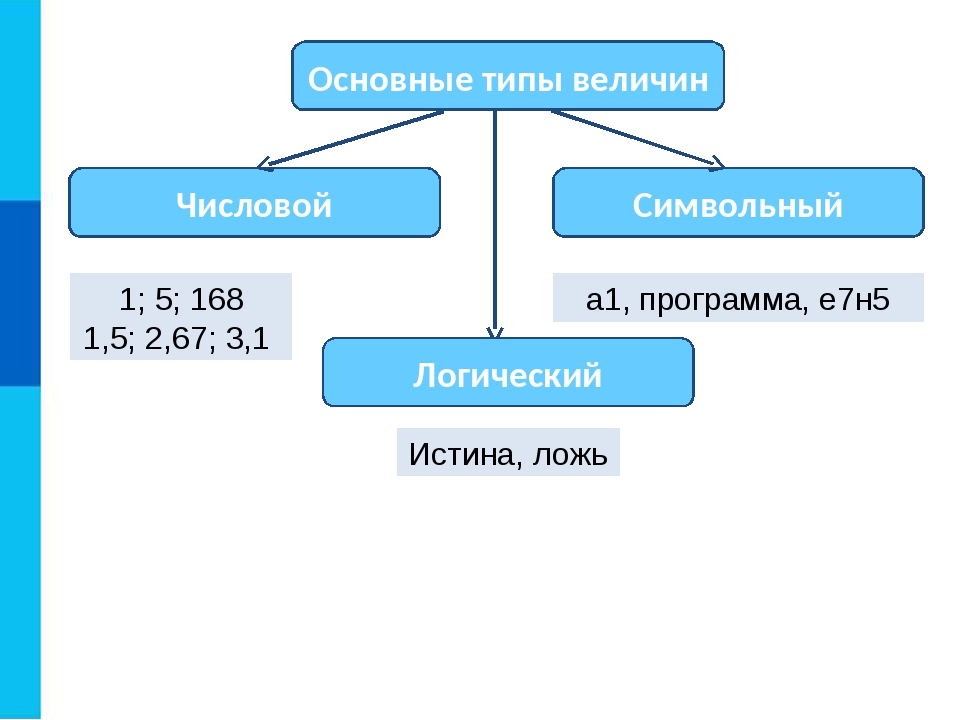 Все, что вам нужно знать
Все, что вам нужно знать
Факты о калькуляторе паскалина - Калькулятор был публично представлен в 1645 году.
- Блез Паскаль изобрел машину, чтобы помочь своему отцу более эффективно выполнять налоговые расчеты.Паскалю было всего 18 лет, когда он изобрел калькулятор.
История калькулятора паскалина
Блез Паскаль изобрел калькулятор паскалина. Паскаль считался вундеркиндом и был одарен в различных областях, включая математику, философию и теологию. Отец Паскаля, Этьен, занимался налоговым расчетом. Он часто был перегружен работой. Он и его помощники часто задерживались допоздна, подсчитывая налоговые сборы, используя ручные вычисления и счеты (счетные доски).В 1642 году молодой Блез сконструировал вычислительную машину, чтобы ускорить процесс.
Блез Паскаль, изобретатель Паскалинового калькулятора Первые несколько экземпляров машины не удовлетворили изобретателя. Однако позже друзья Паскаля подарили канцлеру Франции Пьеру Сегье (1588–1672) прототип счетной машины.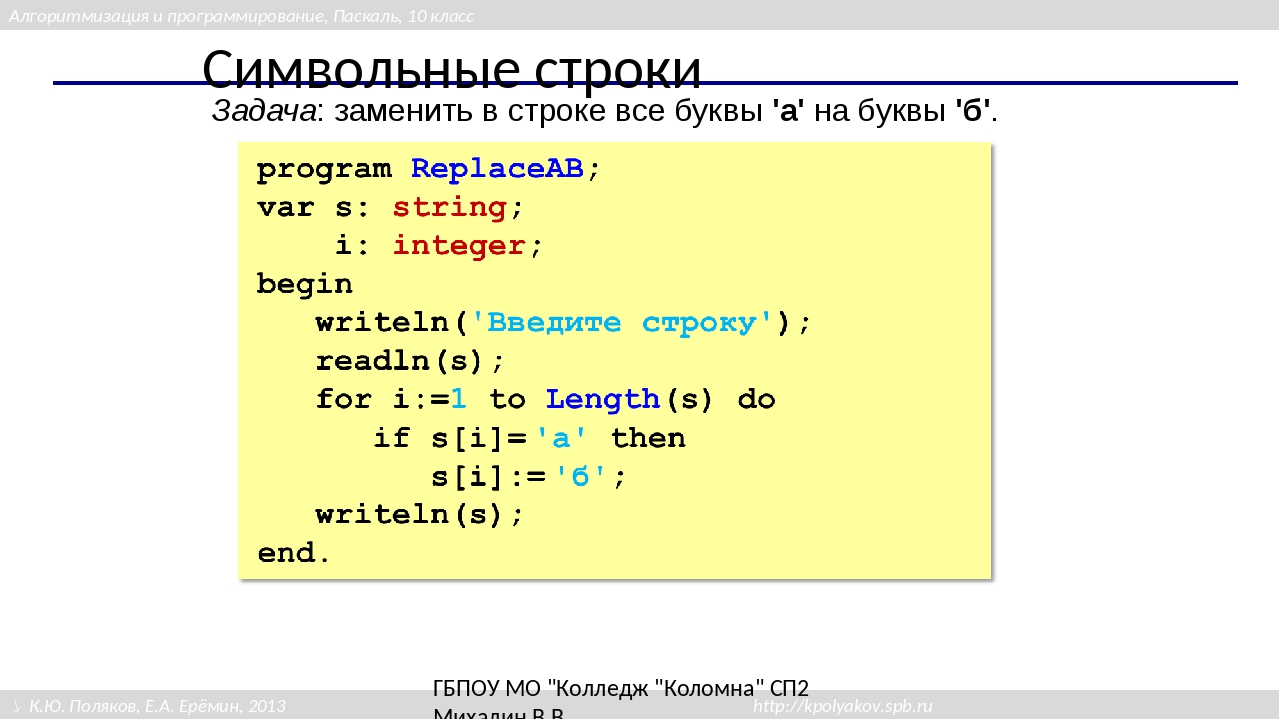 Сегье восхитился изобретением и призвал Паскаля продолжить разработку. В 1645 году Паскаль написал дарственное письмо в начале своей брошюры с описанием машины и подарил копию машины канцлеру, которая до сих пор хранится в CNAM в Париже.
Сегье восхитился изобретением и призвал Паскаля продолжить разработку. В 1645 году Паскаль написал дарственное письмо в начале своей брошюры с описанием машины и подарил копию машины канцлеру, которая до сих пор хранится в CNAM в Париже.
Позже кажется, что Паскаль хотел производить свои машины как полномасштабное коммерческое предприятие, но это оказалось слишком дорого. Неизвестно, сколько машин было продано, но всего, вероятно, было не более десяти или пятнадцати. Цена, возможно, была главной проблемой здесь, хотя счета значительно различаются.
Паскаль продолжал экспериментировать, создавая множество вариантов машины (позже названной Pascaline или Pascalene ). Говорят, что он так усердно работал над этой машиной, что следующие три года его разум был потревожен.По словам его сестры Жильберты, усталость молодого изобретателя была вызвана не трудом, который он вложил в разработку машины, а скорее попыткой заставить руанских мастеров понять, что это такое.
22 мая 1649 года Паскаль получил патент, или то, что тогда называлось привилегией, на арифметическую машину. Модель Pascaline вскоре стала широко известна во Франции и за рубежом. Первое публичное описание было в 1652 году в газете Muse Historique . Машина была продемонстрирована публике в Париже.Пьер де Ферваль, друг семьи и профессор математики Королевского колледжа Франции, согласился демонстрировать устройство потенциальным клиентам в своей квартире в колледже мэтра Жерве каждую субботу утром и днем. Паскаль начал писать рекламные листовки для изобретения и попросил своего друга, поэта Чарльза Виона Далибре, написать рекламный сонет.
Польская королева Мария Луиза де Гонзаг, высокопоставленная и страстная покровительница наук, попросила купить два экземпляра.Еще одна поклонница наук, шведская королева Кристина желала, чтобы ей подарили копию. Паскаль удовлетворил их желание, но вскоре после этого потерял к нему интерес и отказался от занятий со счетной машиной до конца своей короткой жизни.
Из примерно 50 построенных паскалин только 8-9 сохранились до наших дней и находятся в частных или музейных коллекциях (4 в CNAM, Париж, 2 в музее в Клермоне и несколько в частных коллекциях).
Калькулятор паскалина: принцип работы
Калькулятор паскалина имел металлические циферблаты, похожие на колеса со спицами.Цифры от 0 до 9 были отображены вокруг каждого из колес. Пользователь помещал стилус или небольшой стержень в пространство между спицами, а затем поворачивал циферблат, пока не достигал металлического упора. Механизм похож на то, как работал бы старый телефон с дисковым набором. После повторного набора второго номера, который должен был быть добавлен, сумма обоих номеров появится в аккумуляторе.
Прямо над каждым циферблатом был однозначный дисплей. Это отображало каждое значение для этой конкретной позиции.Горизонтальную полосу можно было сдвинуть вверх, чтобы скрыть все дополнительные числа. При перемещении в центр устройства скрывались все прямые номера.
Шестерни машины вращались только в одном направлении, а это означает, что отрицательные числа нельзя было складывать напрямую. Для вычитания чисел использовался метод под названием «дополнение девятки». Есть два основных различия между выполнением сложения и вычитания на устройстве. Это включало положение полосы дисплея и способ ввода первого числа.
Одним из основных аспектов Калькулятора Паскалина является сотуар. Это то, что позволяет устройству передавать числа. Под действием силы тяжести сотуар движется к следующему колесу. Сотуар происходит от французского слова sauter , что означает «прыгать». Затем переносная передача перемещала следующее колесо только на один шаг.
Механизм переноса десятков, изобретенный Паскалем, имел преимущество перед счетными часами Шикарда, поскольку для передачи движения между соседними колесами требовалось лишь небольшое усилие.Это преимущество, однако, окупается некоторыми недостатками. Во время переноски возникает шум, и удар по коробке может привести к нежелательному переносу.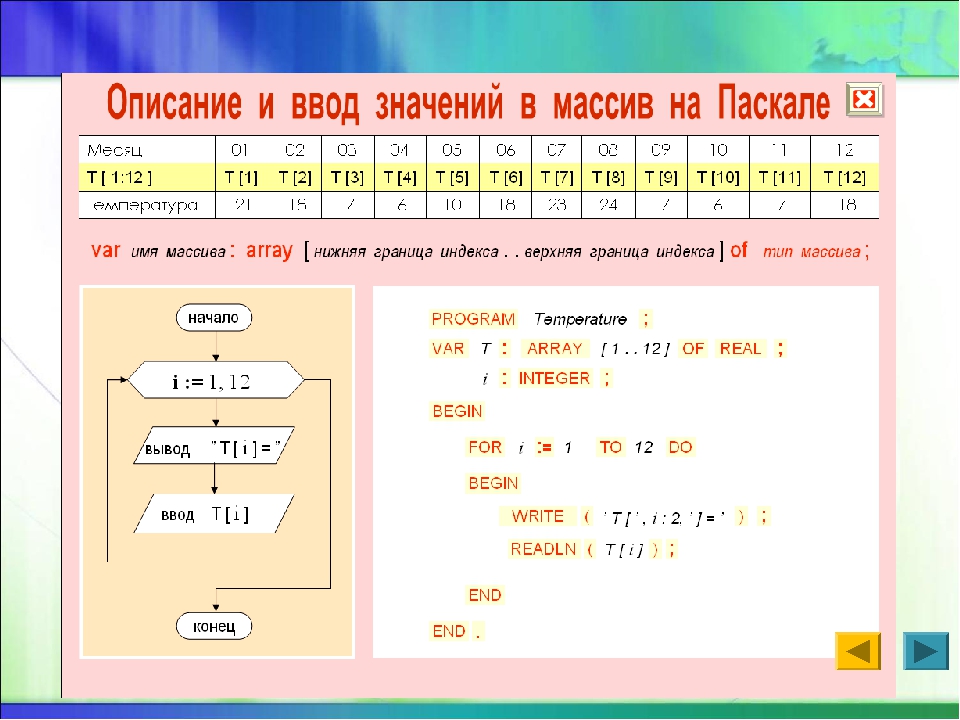
Количество переносок в калькуляторе Pascaline состоит из трех фаз:
- Регистр отображения должен начинаться с 4 и двигаться к 9. Сотуар поднимается, и активное колесо будет касаться того, что получает перенос.
- Вторая фаза начинается после того, как регистр начинается с 9 и опускается до 0. Сотуар движется вверх, а затем внезапно второй переносной штифт опускает его.Сотуар падает под собственным весом.
- На третьем этапе штифт упирается в принимающее колесо, заставляя его вращаться. Затем верхняя трещотка правильно позиционирует весь приемный механизм. На заключительном этапе сотуар добавил 1 к принимающему колесу. На этом этапе сотуар не касался колеса.
Важно отметить, что перед каждым новым расчетом необходимо повторно обнулить машину. Ниже приведены изображения и описания машины и процесса.
Паскалин 1652 года (© Musée des Arts et Métiers, Париж) Размеры латунного ящика машины (для варианта с 8 цифрами) составляют 35,1/12,8/8,8 см. Входные колеса разделены на 10, 12 или 20 спиц, в зависимости от масштаба. Спицы используются для вращения колес с помощью штифта или стилуса. Перо вращает колесо до тех пор, пока оно не упрется в неподвижный упор, закрепленный в нижней части крышки. Результат виден в ряду окон в верхней части, где размещена пластина, которую можно перемещать вверх и вниз.Это позволяет видеть верхние или нижние ряды цифр и использовать их для сложения или вычитания.
Входные колеса разделены на 10, 12 или 20 спиц, в зависимости от масштаба. Спицы используются для вращения колес с помощью штифта или стилуса. Перо вращает колесо до тех пор, пока оно не упрется в неподвижный упор, закрепленный в нижней части крышки. Результат виден в ряду окон в верхней части, где размещена пластина, которую можно перемещать вверх и вниз.Это позволяет видеть верхние или нижние ряды цифр и использовать их для сложения или вычитания.
Принцип действия механизма показан на нижнем рисунке.
Эскиз вычислительного механизма Pascaline CalculatorВращение колес передается через механизм на цифровые цилиндры, которые видны в окнах на следующем фото.
Вид на цифровые цилиндры калькулятора PascalineНиже приведены несколько изображений, иллюстрирующих работу калькулятора.
На поверхность цилиндров вписаны 2 ряда цифр таким образом, что пары дополняются до 9. Например, если верхняя цифра 1, то нижняя 8. На крышке крепится табличка (обозначенная 2 на нижнем рисунке), которую можно перемещать вверх и вниз, и с помощью этой пластины при вычитании должен показываться верхний ряд цифр, а при сложении — нижний.
Перед тем, как приступить к вычислениям, вы сдвигаете скользящую крышку, закрывающую окна дисплея, к краю машины.Затем вы должны установить отмеченные спицы, чтобы на всех барабанах читался «0». Это делается путем установки стилуса между спицами, отмеченными белой бумагой, и поворотом колеса до тех пор, пока игла не остановится. Это дает для каждого колеса самую высокую цифру, которую может иметь барабан, то есть 9. Затем вы поворачиваете последнее колесо справа только на одну позицию, после чего все барабаны будут показывать 0.
Обнуление механизма Вычитание будет немного сложнее и потребует не только вращения, но и некоторой умственной работы.Сделаем, например, 182–93. После обнуления механизма (увидеть 000 в нижних окнах) пластину окон необходимо перевести в нижнее положение. В этот момент в окнах видно число 999. Затем вводится уменьшаемое как дополнение к 9, т.е. колесо единиц вращается на 7, колесо десятков на 1, а колесо сотен на 8 (дополнение до 9 из 182 составляет 817).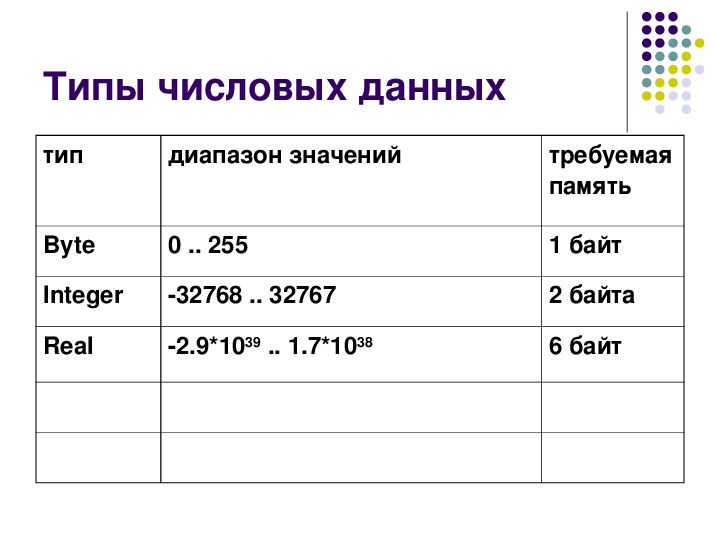 Так как верхний ряд цифр фактически сдвинулся в убывающем порядке, то мы сделали вычитание 999-817 и в результате получилось 182 (см. нижний рисунок).
Так как верхний ряд цифр фактически сдвинулся в убывающем порядке, то мы сделали вычитание 999-817 и в результате получилось 182 (см. нижний рисунок).
Затем введите вычитаемое (93), делая вычитание 182–93 (при вращении колес произойдет два переноса — при вводе единиц (3) колесо единиц придет к 9, а перенос на колесо десятков будет выполнен, переместив колесо десятков на 7. Затем введите 9 на колесо десятков, и оно будет повернуто на 8, а перенос будет перенесен на колесо сотен, заставив его показать 0. Итак, мы имеем правильный результат 182–93=089 (см. нижний рисунок)
Вычитание с помощью паскалиныЧтобы использовать самый быстрый способ умножения, оператор должен знать (или использовать) таблицу умножения.Сделаем умножение 24 х 38. Сначала надо умножить (мысленно или глядя в таблицу) единицы множимого на единицы множителя (8 х 4 = 32) и ввести результат 32 в механизм (см. эскиз).
Умножение с помощью Паскалина Затем мы должны умножить единицы множителя на десятки множимого (8 x 2 = 16). Затем введите результат (16) не в самые правые разряды цифр (для единиц и десятков), а в соседние (позиции для десятков и сотен).Тогда у нас будет результат 192 (32 + 160) (см. нижний эскиз).
Затем введите результат (16) не в самые правые разряды цифр (для единиц и десятков), а в соседние (позиции для десятков и сотен).Тогда у нас будет результат 192 (32 + 160) (см. нижний эскиз).
Затем мы должны повторить ту же операцию для умножения единиц множимого на десятки множителя (3 x 4 = 12) и для умножения десятков множителя на десятки множимого (3 х 2 = 6), занесение промежуточных результатов в колеса десятков и сотен (12) и в числа сотен и тысяч (06). У нас есть правильный результат (912) (см. нижний рисунок).
Умножение на паскалиновом калькуляторе Деление на паскалиновом калькуляторе может быть выполнено способом, аналогичным ручному делению чисел. Во-первых, мы должны разделить делимое на 2 части (по значению делителя). Затем мы должны последовательно вычитать делитель из выбранной части делимого, пока остаток не станет меньше этой части. В этот момент мы должны записать количество вычитаний. Это будет первая цифра результата.Затем мы должны присоединить к остатку (если он есть) 1 или более цифр от оставшейся части делимого и снова начать последовательные вычитания, пока не получим вторую цифру результата. Продолжайте эту операцию снова и снова, пока не будет использована последняя цифра делимого. В конце у нас будет остаток от деления в окнах, при этом будет записан результат.
Продолжайте эту операцию снова и снова, пока не будет использована последняя цифра делимого. В конце у нас будет остаток от деления в окнах, при этом будет записан результат.
Калькулятор паскалина: историческое значение
Калькулятор паскалина важен, потому что он был первым в своем роде, разработанным в 1700-х годах.Работа Паскаля почти наверняка вдохновила других изобретателей и способствовала созданию других механических и вычислительных устройств. Другие изобретения, которые последовали за этим конкретным устройством, — вычислительные машины, разработанные Готфридом Вильгельмом Лейбницем, де Лепином и Якобом Леупольдом.
Правда, не все впечатления от современников Паскаля были положительными. Некоторые из них были неблагоприятными, например, письмо английского джентльмена-путешественника Бальтазара Жербье Самуэлю Хартлибу в октябре 1648 года. Жербье наткнулся на Паскалину вскоре после того, как была закончена деревянная модель, и подумал, что она напоминает что-то, изобретенное в Англии 30 лет назад.
