Решение неравенств и систем неравенств 9 класс – Системы неравенств — урок. Алгебра, 9 класс. - Управленческое образование

Содержание

Алгебра. Урок 8. Неравенства, системы неравенств.

Содержание страницы:

Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства:

> больше,

≥ больше или равно,

< меньше,

≤ меньше или равно,

то получится неравенство.

Линейные неравенства

Линейные неравенства – это неравенства вида:

ax<bax≤bax>bax≥b

где a и b — любые числа, причем a≠0,x — переменная.

Примеры линейных неравенств:

3x<5x−2≥07−5x<1x≤0

Решить линейное неравенство — получить выражение вида:

x<cx≤cx>cx≥c

где c — некоторое число.

Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.

Если знак неравенства строгий >,<, точка на оси будет выколотой (не закрашенной), а скобка, обнимающая точку – круглой.

Смысл выколотой точки в том, что сама точка в ответ не входит.

Если знак неравенства нестрогий ≥,≤, точка на оси будет жирной (закрашенной), а скобка, обнимающая точку – квадратной.

Смысл жирной точки в том, что сама точка входит в ответ.

Скобка, которая обнимает знак бесконечности всегда круглая – не можем мы объять необъятное, как бы нам этого ни хотелось.

Таблица числовых промежутков

Неравенство	Графическое решение	Форма записи ответа
x<c		x∈(−∞;c)
x≤c		x∈(−∞;c]
x>c		x∈(c;+∞)
x≥c		x∈[c;+∞)

Алгоритм решения линейного неравенства

Раскрыть скобки (если они есть), перенести иксы в левую часть, числа в правую и привести подобные слагаемые. Должно получиться неравенство одного из следующих видов:

ax<bax≤bax>bax≥b

Пусть получилось неравенство вида ax≤b. Для того, чтобы его решить, необходимо поделить левую и правую часть неравенства на коэффициент a.

Если a>0 то неравенство приобретает вид x≤ba.

Если a<0, то знак неравенства меняется на противоположный, неравенство приобретает вид x≥ba.

Записываем ответ в соответствии с правилами, указанными в таблице числовых промежутков.

Примеры решения линейных неравенств:

№1. Решить неравенство 3(2−x)>18.

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

6−3x>18

−3x>18−6−3x>12|÷(−3)

Делим обе части неравенства на (-3) — коэффициент, который стоит перед x. Так как −3<0, знак неравенства поменяется на противоположный. x<12−3⇒x<−4 Остается записать ответ (см. таблицу числовых промежутков).

Ответ: x∈(−∞;−4)

№2. Решить неравество 6x+4≥3(x+1)−14.

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

6x+4≥3x+3−14

6x−3x≥3−14−4

3x≥−15 | ÷3 Делим обе части неравенства на (3) — коэффициент, который стоит перед x. Так как 3>0, знак неравенства после деления меняться не будет.

x≥−153⇒x≥−5 Остается записать ответ (см. таблицу числовых промежутков).

Ответ: x∈[−5; +∞)

Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно).

Примеры:

№1. Решить неравенство 6x−1≤2(3x−0,5).

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

6x−1≤6x−1

6x−6x≤−1+1

0≤0

Получили верное неравенство, которое не зависит от переменной x. Возникает вопрос, какие значения может принимать переменная x, чтобы неравенство выполнялось? Любые! Какое бы значение мы ни взяли, оно все равно сократится и результат неравенства будет верным. Рассмотрим три варианта записи ответа.

Ответ:

x — любое число
x∈(−∞;+∞)
x∈ℝ

№2. Решить неравенство x+3(2−3x)>−4(2x−12).

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

x+6−9x>−8x+48

−8x+8x>48−6

0>42

Получили неверное равенство, которое не зависит от переменной x. Какие бы значения мы ни подставляли в исходное неравенство, результат окажется одним и тем же – неверное неравенство. Ни при каких значениях x исходное неравенство не станет верным. Данное неравенство не имеет решений. Запишем ответ.

Ответ: x∈∅

Квадратные неравенства

Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет.

Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4).

Алгоритм решения квадратного неравенства методом интервалов

Решить уравнение ax2+bx+c=0 и найти корни x1 и x2.

Отметить на числовой прямой корни трехчлена.

Если знак неравенства строгий >,<, точки будут выколотые.

Если знак неравенства нестрогий ≥,≤, точки будут жирные (заштрихованный).

Расставить знаки на интервалах. Для этого надо выбрать точку из любого промежутка (в примере взята точка A) и подставить её значение в выражение ax2+bx+c вместо x.

Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться.

Точки выколотые, если знак неравенства строгий.

Точки жирные, если знак неравенства нестрогий.

Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться.

Точки выколотые, если знак неравенства строгий.

Точки жирные, если знак неравенства нестрогий.

Выбрать подходящие интервалы (или интервал).

Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.

Если знак неравенства < или ≤ в ответ выбираем интервалы со знаком -.

Записать ответ.

Примеры решения квадратных неравенств:

№1. Решить неравенство x2≥x+12.

Решение:

Приводим неравенство к виду ax2+bx+c ≥0, а затем решаем уравнение ax2+bx+c=0.

x2≥x+12

x2−x−12≥0

x2−x−12=0

a=1,b=−1,c=−12

D=b2−4ac=(−1)2−4⋅1⋅(−12)=1+48=49

D>0⇒ будет два различных действительных корня

x1,2=−b±D2a=−(−1)±492⋅1=1±72=[1+72=82=41−72=−62=−3

Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6. Подставляем эту точку в исходное выражение:

x2−x−1=62−6−1=29>0

Это значит, что знак на интервале, в котором лежит точка 6 будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

В ответ пойдут два интервала. В математике для объединения нескольких интервалов используется знак объединения: ∪.

Точки -3 и 4 будут в квадратных скобках, так как они жирные.

Ответ: x∈(−∞;−3]∪[4;+∞)

№2. Решить неравенство −3x−2≥x2.

Решение:

Приводим неравенство к виду ax2+bx+c ≥0, а затем решаем уравнение ax2+bx+c=0.

−3x−2≥x2

−x2−3x−2≥0

−x2−3x−2=0

a=−1,b=−3,c=−2

D=b2−4ac=(−3)2−4⋅(−1)⋅(−2)=9−8=1

D>0⇒ будет два различных действительных корня

x1,2=−b±D2a=−(−3)±12⋅(−1)=3±1−2=[3+1−2=4−2=−23−1−2=2−2=−1

x1=−2,x2=−1

Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение:

−x2−3x−2=−(0)2−3⋅0−2=−2<0

Это значит, что знак на интервале, в котором лежит точка 0 будет −.

Поскольку знак неравенства ≥, выбираем в ответ интервал со знаком +.

Точки -2 и -1 будут в квадратных скобках, так как они жирные.

Ответ: x∈[−2;−1]

№3. Решить неравенство 4<x2+3x.

Решение:

Приводим неравенство к виду ax2+bx+c ≥0, а затем решаем уравнение ax2+bx+c=0.

4<x2+3x

−x2−3x+4<0

−x2−3x+4=0

a=−1,b=−3,c=4

D=b2−4ac= (−3)2−4⋅(−1)⋅4=9+16=25

D>0⇒ будет два различных действительных корня

x1,2=−b±D2a=−(−3)±252⋅(−1)=3±5−2=[3+5−2=8−2=−43−5−2=−2−2=1

x1=−4,x2=1

Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение:

−x2−3x+4=−(2)2−3⋅2+4=−6<0

Это значит, что знак на интервале, в котором лежит точка 2, будет -.

Поскольку знак неравенства <, выбираем в ответ интервалы со знаком −.

Точки -4 и 1 будут в круглых скобках, так как они выколотые.

Ответ: x∈(−∞;−4)∪(1;+∞)

№4. Решить неравенство x2−5x<6.

Решение:

Приводим неравенство к виду ax2+bx+c ≥0, а затем решаем уравнение ax2+bx+c=0.

x2−5x<6

x2−5x−6<0

x2−5x−6=0

a=1,b=−5,c=−6

D=b2−4ac=(−5)2−4⋅1⋅(−6)=25+25=49

D>0⇒ будет два различных действительных корня

x1,2=−b±D2a=−(−5)±492⋅1=5±72=[5+72=122=65−72=−22=−1

x1=6,x2=−1

Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение:

x2−5x−6=102−5⋅10−6=100−50−6= 44>0

Это значит, что знак на интервале, в котором лежит точка 10 будет +.

Поскольку знак неравенства >, выбираем в ответ интервал со знаком -.

Точки -1 и 6 будут в круглых скобках, так как они выколотые

Ответ: x∈(−1;6)

№5. Решить неравенство x2<4.

Решение:

Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения.

x2<4

x2−4<0

x2−4=0

(x−2)(x+2)=0⇔[x−2=0x+2=0 [x=2x=−2

x1=2,x2=−2

Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3. Подставляем эту точку в исходное выражение:

x2−4=32−4=9−4=5>0

Это значит, что знак на интервале, в котором лежит точка 3 будет +.

Поскольку знак неравенства <, выбираем в ответ интервал со знаком −.

Точки -2 и 2 будут в круглых скобках, так как они выколотые.

Ответ: x∈(−2;2)

№6. Решить неравенство x2+x≥0.

Решение:

Выносим общий множитель за скобку, находим корни уравнения x2+x=0.

x2+x≥0

x2+x=0

x(x+1)=0⇔[x=0x+1=0[x=0x=−1

x1=0,x2=−1

Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 1. Подставляем эту точку в исходное выражение:

x2+x=12+1=2>0

Это значит, что знак на интервале, в котором лежит точка 1 будет +.

Поскольку знак неравенства ≥, выбираем в ответ интервалы со знаком +.

В ответ пойдут два интервала. Точки -1 и 0 будут в квадратных скобках, так как они жирные.

Ответ: x∈(−∞;−1]∪[0;+∞)

Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже.

Дробно рациональные неравенства

Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов:

f(x)g(x)<0f(x)g(x)≤0f(x)g(x)>0f(x)g(x)≥0

Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю).

Примеры дробно рациональных неравенств:

x−1x+3<03(x+8)≤5×2−1x>0x+20x≥x+3

Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов.

Алгоритм решения дробно рациональных неравенств:

Привести неравенство к одному из следующих видов (в зависимости от знака в исходном неравенстве):

f(x)g(x)<0f(x)g(x)≤0f(x)g(x)>0f(x)g(x)≥0

Приравнять числитель дроби к нулю f(x)=0. Найти нули числителя.

Приравнять знаменатель дроби к нулю g(x)=0. Найти нули знаменателя.

В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.

Нанести нули числителя и нули знаменателя на ось x.

Вне зависимости от знака неравенства
при нанесении на ось xнули знаменателя всегда выколотые.

Если знак неравенства строгий,
при нанесении на ось x нули числителя выколотые.

Если знак неравенства нестрогий,
при нанесении на ось x нули числителя жирные.

Расставить знаки на интервалах.

Выбрать подходящие интервалы и записать ответ.

Примеры решения дробно рациональных неравенств:

№1. Решить неравенство x−1x+3>0.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f(x)g(x)>0.

Приравниваем числитель к нулю f(x)=0.

x−1=0

x=1 — это ноль числителя. Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это.

Приравниваем знаменатель к нулю g(x)=0.

x+3=0

x=−3 — это ноль знаменателя. При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства).

Наносим нули числителя и нули знаменателя на ось x.

При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.

Расставляем знаки на интервалах.

Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f(x)g(x):x−1x+3 = 2−12+3=15>0,

Это значит, что знак на интервале, в котором лежит точка 2 будет +.

Выбираем подходящие интервалы и записываем ответ.

Поскольку знак неравенства >, выбираем в ответ интервалы со знаком +.

В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые.

Ответ: x∈(−∞;−3)∪(1;+∞)

№2. Решить неравенство 3(x+8)≤5.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

Привести неравенство к виду f(x)g(x)≤0.

3(x+8)≤5

3(x+8)−5\x+8≤0

3x+8−5(x+8)x+8≤0

3−5(x+8)x+8≤0

3−5x−40x+8≤0

−5x−37x+8≤0

Приравнять числитель к нулю f(x)=0.

−5x−37=0

−5x=37

x=−375=−375=−7,4

x=−7,4 — ноль числителя. Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной.

Приравнять знаменатель к нулю g(x)=0.

x+8=0

x=−8 — это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).

Наносим нули числителя и нули знаменателя на ось x.

При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.

Расставляем знаки на интервалах.

Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение f(x)g(x):

−5x−37x+8=−5⋅0−370+8=−378<0

Это значит, что знак на интервале, в котором лежит точка 0 будет -.

Выбираем подходящие интервалы и записываем ответ.

Поскольку знак неравенства ≤, выбираем в ответ интервалы со знаком -.

В ответ пойдут два интервала. Точка -8 будет в круглой скобке, так как она выколотая, точка -7,4 будет в квадратных скобках, так как она жирная.

Ответ: x∈(−∞;−8)∪[−7,4;+∞)

№3. Решить неравенство x2−1x>0.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f(x)g(x)>0.

Приравнять числитель к нулю f(x)=0.

x2−1=0

(x−1)(x+1)=0⇒[x−1=0x+1=0[x=1x=−1

x1=1,x2=−1 — нули числителя. Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми.

Приравнять знаменатель к нулю g(x)=0.

x=0 — это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).

Наносим нули числителя и нули знаменателя на ось x.

При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.

Расставляем знаки на интервалах.

Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f(x)g(x):

x2−1x=22−12=4−12=32>0, Это значит, что знак на интервале, в котором лежит точка 2, будет +.

Выбираем подходящие интервалы и записываем ответ.

Поскольку знак неравенства >, выбираем в ответ интервалы со знаком +.

В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые.

Ответ: x∈(−1;0)∪(1;+∞)

Системы неравенств

Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой.

Пример системы неравенств:

{x+4>02x+3≤x2

Алгоритм решения системы неравенств

Решить первое неравенство системы, изобразить его графически на оси x.

Решить второе неравенство системы, изобразить его графически на оси x.

Нанести решения первого и второго неравенств на ось x.

Выбрать в ответ те участки, в которых решение первого и второго неравенств пересекаются. Записать ответ.

Примеры решений систем неравенств:

№1. Решить систему неравенств {2x−3≤57−3x≤1

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Решаем первое неравенство системы.

2x−3≤5

2x≤8|÷2, поскольку 2>0, знак неравенства после деления сохраняется.

x≤4;

Графическая интерпретация:

Точка 4 на графике жирная, так как знак неравенства нестрогий.

Решаем второе неравенство системы.

7−3x≤1

−3x≤1−7

−3x≤−6|÷(−3), поскольку −3<0, знак неравенства после деления меняется на противоположный.

x≥2

Графическая интерпретация решения:

Точка 2 на графике жирная, так как знак неравенства нестрогий.

Наносим оба решения на ось x.

Выбираем подходящие участки и записываем ответ.

Пересечение решений наблюдается на отрезке от 2 до 4. Точки 2 и 4 в ответе буду в квадратных скобках, так как обе они жирные.

Ответ: x∈[2;4]

№2. Решить систему неравенств {2x−1≤51<−3x−2

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Решаем первое неравенство системы.

2x−1≤5

2x≤6|÷2, поскольку 2>0, знак неравенства после деления сохраняется.

x≤3

Графическая интерпретация:

Точка 3 на графике жирная, так как знак неравенства нестрогий.

Решаем второе неравенство системы.

1<−3x−2

3x<−1−2

3x<−3|÷3, поскольку 3>0, знак неравенства после деления сохраняется.

x<−1

Графическая интерпретация решения:

Точка -1 на графике выколотая, так как знак неравенства строгий.

Наносим оба решения на ось x.

Выбираем подходящие участки и записываем ответ.

Пересечение решений наблюдается на самом левом участке. Точка -1 будет в ответе в круглых скобках, так как она выколотая.

Ответ: x∈(−∞;−1)

№3. Решить систему неравенств {3x+1≤2x−1x−7>5−x

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Решаем первое неравенство системы.

3x+1≤2x−1

3x−2x≤−1−1

x≤−1

Графическая интерпретация решения:

Решаем второе неравенство системы

x−7>5−x

x+x>5+7

2x>12| ÷2, поскольку 2>0, знак неравенства после деления сохраняется.

x>6

Графическая интерпретация решения:

Наносим оба решения на ось x.

Выбираем подходящие участки и записываем ответ.

Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений.

Ответ: x∈∅

№4. Решить систему неравенств {x+4>02x+3≤x2

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Решаем первое неравенство системы.

x+4>0

x>−4

Графическая интерпретация решения первого неравенства:

Решаем второе неравенство системы

2x+3≤x2

−x2+2x+3≤0

Решаем методом интервалов.

−x2+2x+3=0

a=−1,b=2,c=3

D=b2−4ac=22−4⋅(−1)⋅3=4+12=16

D>0 — два различных действительных корня.

x1,2=−b±D2a=−2±162⋅(−1)=−2±4−2=[−2−4−2=−6−2=3−2+4−2=2−2=−1

Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными.

Графическая интерпретация решения второго неравенства:

Наносим оба решения на ось x.

Выбираем подходящие участки и записываем ответ.

Пересечение решений наблюдается в двух интервалах. Для того, чтобы в ответе объединить два интервала, используется знак объединения ∪.

Точка -4 будет в круглой скобке, так как она выколотая, а точки -1 и 3 в квадратных, так как они жирные.

Ответ: x∈(−4;−1]∪[3;+∞)

Скачать домашнее задание к уроку 8.

epmat.ru

Урок-обобщение по теме «Неравенства и система неравенств». 9-й класс

Разделы: Математика, Конкурс «Презентация к уроку»

Презентации к уроку

Загрузить презентацию (2,3 МБ)

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Тип урока: урок обобщения и систематизации знаний.

Цели урока.

Образовательные:

а) Обобщение и систематизация знаний учащихся по теме “Неравенства и система неравенств”.

б) Проверка знаний учащихся в ходе самостоятельной работы.

Развивающие:

а) Развивать навыки реализации теоретических знаний в практической деятельности.

Воспитывающие:

а) Воспитание умения работать самостоятельно.

б) Воспитание умения выдерживать регламент времени, отведенного на решение каждого задания.

Знания, умения, навыки и качества, которые приобретут, закрепят ученики в ходе урока.
Знать и понимать алгебраическую трактовку отношений “больше” и “меньше” между числами; знать и применять свойства числовых неравенств;

Знать и понимать термины “решение неравенства с одной переменной”, “решение системы неравенств с одной переменной”;

Решать линейные неравенства с одной переменной и их системы;

Находить множество решений квадратного неравенства с одной переменной, опираясь на графическое изображение.

Необходимое оборудование и материалы: компьютер, видеопроектор.

Ход урока

1. Мотивация учащихся

а) Приветствие учащихся, проверка их готовности к уроку.

б) Сообщение темы урока: “Подготовка к ГИА. Неравенства и система неравенств”. Слайд 1. Презентация 1.

в) Сообщение целей урока и плана урока

г) познакомить учащихся с направлениями данного блока. Слайд 2. Презентация 1

2. Повторение теоретического материала блока

Учитель: Сейчас устно повторим:

— что такое числовое неравенство. Слайд 3. Презентация 1

— Свойства числовых неравенств. Слайд 4. Презентация 1

3. Работа с опорным конспектом в парах с тестами

Учитель: предлагаю поработать в парах с заданиями подобранными из сборника заданий для подготовки к итоговой аттестации. Слайд 5, 6, 7, 8. Презентация 1

После чего сверяем и обсуждаем выполненные задания

Учитель: Устно повторим:

— Что такое неравенство Слайд 9. Приложение 1

— Основные правила при решении неравенств Слайд 10, 11 ,12. Презентация 1

— Пример решения неравенства Слайд 13. Презентация 1

— Алгоритм решения квадратного неравенства Слайд 14, 15, 16. Презентация 1

— Решаем систему неравенств Слайд 17. Презентация 1

Учитель: предлагаю поработать в парах с заданиями подобранными из сборника заданий для подготовки к итоговой аттестации. Слайд 18, 19, 20, 21. Презентация 1

4. Практикум по решению неравенств в форме теста

Провести обучающую самостоятельную работу в форме теста. (Тест) Самостоятельная работа предлагается в одном варианте, чтобы хватило времени на проверку и анализ выполненной работы. Настроить надо учащихся, что работа это проводится не для того чтобы кому-то поставить плохую оценку, а для того чтобы выяснить, кто как понял и кому надо еще потренироваться над данной темой.

5. Проверка и оценивание ЗУНов

Итоги выполнения теста, анализ каждого задания.

Для проверки теста предлагается презентация Презентация 2 с тем же тестом, проверяется совместно и каждый подводит итог, сколько у него баллов.

6. Домашнее задание

На сайте www.mathgia.ru единого банка заданий по ГИА, решать тематический тест “Неравенства”. Подготовиться к проверочной самостоятельной работе.

Литература

1. Кузнецова Л.В., Суворова С.Б., Бунимович Е.А., Колесникова Т.В., Рослова Л.О. Сборник заданий для подготовки к итоговой аттестации в 9 классе. М., Просвещение, 2009.

2. Ю.Н. Макарычев, Н.Г. Миндюк “Алгебра 9”.

3. ГИА 2010. Алгебра: тематические тренировачные задания: 9 класс/ Л.В. Кузнецова, С.Б. Суворова, Е.А. Бунимович. — М.: Эксмо, 2010.
4.05.2012
Поделиться страницей:
urok.1sept.ru
Основные понятия, решение линейных неравенств. Видеоурок. Алгебра 9 Класс
Тема: Рациональные неравенства и их системы. Линейные и квадратные неравенства (повторение)
Урок: Основные понятия, решение линейных неравенств
Рациональные неравенства – основные понятия и решения квадратных и линейных неравенств (9 класс)

Линейное и квадратное неравенство, повторение, урок 1, основные понятия решения линейных неравенств

Неравенство с одной переменной имеет вид: f(x) > 0, вместо (> 0) может быть (≥ 0), (< 0), (≤ 0).
Для определенности будем записывать неравенство в виде f(x) > 0.
x – переменная,
f – функция, выражение, зависящее от х.

В зависимости от f различают разные типы неравенств. Если f – линейная функция, то это линейное неравенство. Если f – квадратичная функция, то это квадратное неравенство.
Итак, линейное неравенство имеет вид ax+b>0, предполагается, что a≠0.
Квадратное неравенство имеет вид .
Значение x_o, при котором неравенство обращается в верное числовое неравенство, является частным решением неравенства. Решить неравенство – найти все решения неравенства. Множество всех решений неравенства называется общим решением неравенства, или просто решением неравенства.
Рассмотрим пример:
1) Решить неравенство 2x – 5 > 9.
Это линейное неравенство, найдем его решение и обсудим основные понятия.
2x – 5 > 9 <=> 2x > 14 (5 перенесли в левую часть с противоположным знаком), далее разделили все на 2 и получили x > 7. Изобразим множество решений на оси x.
Это положительно направленный луч. Записывается множество решений либо в виде неравенства x > 7, либо в виде интервала (7; ∞). А что является частным решением этого неравенства? Например, x = 10 – это частное решение этого неравенства, x = 12 – это тоже частное решение этого неравенства.
Частных решений много, но наша цель – найти все решения. А решений, как правило, бесчисленное множество.
Рассмотрим пример 2:
2) Решить неравенство 4a – 11 > a + 13.
Решим его: а перенесем в одну сторону, 11 перенесем в другую сторону, получим 3a > 24, и в результате после деления обеих частей на 3 получим a > 8.
4a – 11 > a + 13 <=> 3a > 24 <=> a > 8.
Тоже изобразим множество a > 8, но уже на оси а.
Ответ либо записывается в виде неравенства a > 8, либо а (8; +∞), 8 не включается.
При решении неравенства есть важное отличие его от уравнений, которое состоит в том, что любое решение уравнения можно проверить просто подстановкой в исходное уравнение. В неравенствах такой возможности нет, здесь бесчисленное множество решений подставить в исходное неравенство не представляется возможным. Поэтому есть важное понятие, вот эти стрелочки <=> — это знак эквивалентных, или равносильных, преобразований. Преобразование называются равносильными, или эквивалентными, если они не искажают множества решений. О важности эквивалентных (равносильных) преобразований можно узнать, рассмотрев следующий пример.
3) Решить неравенство ≤ 1.
Решение будем искать среди x ≠ 0, потому что x стоит в знаменателе. Если x ≠ 0, то обе части неравенства можно умножить на x: , основное свойство дроби позволяет сократить в левой части , и в результате получим ≥ 1.
Однако неравенство решено неверно. Почему? Возьмем =-1, которое не входит в найденный промежуток, подставив его в исходное неравенство, получим -1 ≤ 1, т.е. это еще одно частное решение исходного неравенства: -1.
Что же мы сделали? Мы обе части неравенства ≤ 1 умножили на , не зная знака этого выражения, ведь может принимать как положительные значения, так и отрицательные.
Таким образом, мы подтвердили важность эквивалентных, равносильных преобразований. Вспомним, что это за равносильные, эквивалентные преобразования, и продемонстрируем их на конкретном примере.
Решить неравенство 2 – 2 >4.
1. Любой член неравенства можно перенести в другую сторону с противоположным знаком, равносильность, эквивалентность не нарушится.
2 – 2 > 4 <=> -2 > 4 – 2 <=> -2 > 2
Эквивалентность не нарушилась, о чем мы говорим вот таким знаком <=>.
2. Второе правило нам говорит, что обе части неравенства можно умножить или разделить на одно и то же отрицательное число, при этом знак неравенства изменится на противоположный.
3. И еще одно правило: обе части неравенства можно умножить или разделить на одно и то же положительное число, и знак неравенства не изменится.
Теперь исходное неравенство имеет вид: -2x > 2. Давайте обе части неравенства разделим на (-2):
-2 >2 <=> <-1. Знак неравенства изменится, т.к. мы делим на (-2) и пользуемся соответствующим правилом.
Мы пользовались равносильными, эквивалентными преобразованиями и получили правильный ответ: < -1.
Еще один пример, решить неравенство a(a – 2) – a²> 5 – 3a. Делаем стандартные преобразования: раскрываем скобки, получаем равносильное неравенство, которое потом упрощаем, т.е. приводим подобные члены – a² уничтожается, -3a переносим, меняя знак.
a(a – 2) – a²> 5 – 3a <=> a²– 2a — a² > 5 – 3a <=> 3a – 2a > 5 <=> a > 5.
Итак, a(a – 2) – a²> 5 – 3a – исходное неравенство, a > 5 – его решение. Мы пользовались только эквивалентными, равносильными преобразованиями и получили ответ, который не надо проверять.
Следующий пример, решить неравенство 5y²– 5y(y + 4) ≥ 100.
Любые неравенства, в том числе и простейшие, которые мы сейчас рассматриваем, решаются только эквивалентными преобразованиями. Выполняем их: скобки, приводим подобные члены:
5y²– 5y(y + 4) ≥ 100 <=> 5y²– 5y²– 20y ≥ 100 <=> -20y ≥ 100 <=> 20y ≤ -100 <=> y ≤-5.
Исходное неравенство 5y²– 5y(y + 4) ≥ 100, его ответ y ≤-5.
Таким образом, мы рассмотрели основные понятия, связные с неравенством, вспомнили, что значит «решить неравенство», что такое «общее решение неравенства», вспомнили, что неравенства можно решать только эквивалентными преобразованиями, и выяснили, что же это за эквивалентные преобразования.
Следующий пример. Решить неравенство:

Решаем только эквивалентными преобразованиями: перенесем все в одну сторону и приведем все к общему знаменателю, далее обе части можно умножить на знаменатель и получить только числитель. Далее нам приходится разделить на отрицательное число. Это сделать можно, если знак неравенства изменить на противоположный:

Итак, мы продемонстрировали решение некоторого количества примеров эквивалентными преобразованиями, и только ими можно решать неравенства.
Линейные неравенства – это неравенства вида ax + b > 0. Линейное неравенство тесно связано с линейной функцией. В левой части неравенства стоит линейная функция y = ax + b. Мы знаем график линейной функции, мы знаем, где она положительная, где отрицательная, и поэтому с помощью графика линейной функции мы можем решить неравенство. Например, решить неравенство: 2x + 1 > 0. Рассмотрим линейную функцию y = 2x + 1, составим таблицу:

x

0

y

1

0

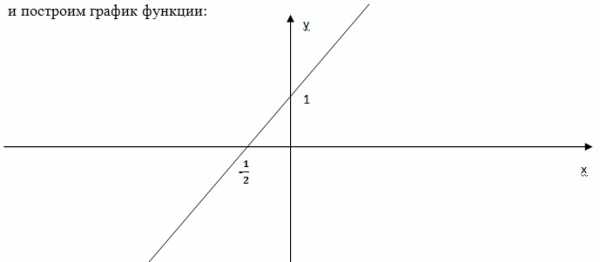
Эта функция положительна при всех значениях x больше . Ответ: x > .
Таким образом, выясняется, что линейная функция разбивает всю область определения на два больших луча. В одном луче она отрицательна, в другом луче она положительна, и, следовательно, решение неравенства очень просто.
Приведем еще один пример. Решить неравенство: -3x + 6 > 0. Снова решаем с помощью линейной функции. Рассмотрим функцию y = -3x + 6 и построим ее график с помощью таблицы:

x

0

y

6
0

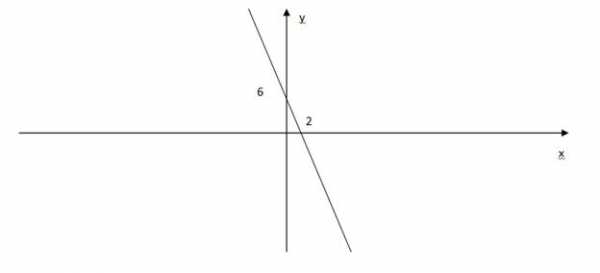
Нулем этой функции является 2. Эта функция сохраняет свой знак при (-∞; 2), и она положительна. И она также сохраняет свой знак при (2; ∞), и при всех этих значениях функция отрицательна. Нам нужны те x, при которых функция положительна. Получим ответ x , запишем его в виде промежутка (-∞; 2).

Итак, мы рассмотрели основные положения, которые нужны для решения неравенств, вспомнили, что такое неравенство, что такое частное решение, что такое общее решение, что такое эквивалентные преобразования, и рассмотрели решение линейных неравенств с помощью эквивалентных преобразований или с помощью графика линейной функции.

Список литературы
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра. 8 класс: учебник для 8 кл. общеобраз-х учреждений; под ред. С.А. Теляковского, 15-е изд., дораб. — М.: Просвещение, 2007.
Макарычев Ю.Н. Алгебра. 8 класс. — 10-е изд., испр. — М.: Мнемозина, 2010.
Алимов Ш.А. и др. Алгебра. 8 класс. Учебник. Алимов Ш.А. и др. 17-е изд. – М.: Просвещение, 2010.

Домашнее задание
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра. 8 класс: учебник для 8 кл. общеобраз-х учреждений; под ред. С.А. Теляковского, 15-е изд., дораб. — М.: Просвещение, 2007.
№№785, 789, 793, 798.
interneturok.ru
Неравенства и системы неравенств. Алгебра, 9 класс: уроки, тесты, задания.
Вход на портал Вход на портал Регистрация Начало Поиск по сайту ТОПы Учебные заведения Предметы Проверочные работы Обновления Подписка Я+ Новости Переменка Отправить отзыв
Предметы

Алгебра

9 класс

Линейные и квадратные неравенства

Рациональные неравенства

Множества и операции над ними

Системы рациональных неравенств

Отправить отзыв Нашёл ошибку? Сообщи нам! Copyright © 2019 ООО ЯКласс Контакты Пользовательское соглашение
www.yaklass.ru
Готовимся к экзамену по математике за период обучения на II ступени общего среднего образования: 13. Системы неравенств
МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ
Если ставится задача найти множество общих решений двух или более неравенств, то говорят, что надо решить систему неравенств.
Неравенства, входящие в систему, объединяются фигурной скобкой. Иногда системы неравенств записывают в виде двойного неравенства:
-5<x<12 или
Решением системы неравенств называется число, которое при его подстановке в систему обращает каждое неравенство в верное числовое неравенство.
Решить систему неравенств – значит найти решения для всей системы, либо доказать, что у данной системы решений нет.
Чтобы решить систему неравенств с одной переменной, надо:
1) отдельно решить каждое неравенство;
2) найти пересечение найденных решений, отметив решение каждого неравенства на числовой прямой.
Это пересечение и является множеством решений системы неравенств.
Пример:
Решить систему неравенств:
Решим каждое неравенство в отдельности
1) 5x-x2≥0,
5x-x2=0,
x(5-x)=0,
x=0 или 5-x=0,
-x=-5,
x=5.
Находим решение с помощью метода интервалов:
2) 6-2x<-2,
-2x<-2-6,
-2x<-8,
x>-8:(-2),
x>4.
Объединим оба решения:
Ответ: (4; 5].
Говорят, что несколько неравенств с одной переменной образуют совокупность, если необходимо найти все такие значения переменной, каждое из которых является решением хотя бы одного из данных неравенств. Совокупность неравенств обозначается квадратной скобкой.
Решением совокупности неравенств называют такие значения переменной, которые являются верными хотя бы для одного из этих неравенств.
Чтобы решить совокупность неравенств с одной переменной, надо:
1) отдельно решить каждое неравенство;
2) найти объединение найденных решений, отметив решение каждого неравенства на числовой прямой.
Это объединение и является решением совокупности неравенств.
Пример:
Решить совокупность неравенств:

Решим каждое неравенство в отдельности
1) 5х+6≤1,
5х≤ -5,
х≤ -1.

2) 2х+1≥3,
2х≥2,
х≥1.

Объединим оба решения:

Ответ: (-∞; -1]U[1;+∞).

УПРАЖНЕНИЯ
1. Решите систему неравенств:
Решение:
а)
Ответ: (5; 7]

2. Решите систему неравенств:
Решение:
Ответ: (1; 10].

3. Найдите целые решения системы неравенств:
Решение:
а)
Ответом являются все целые числа, которые принадлежат промежутку (-15; 5).
Ответ: -14; -13; -12; -11; -10; -9; -8; -7; -6.

4. Решите систему неравенств:
Решение:
Ответ: (-1; 3).

5. Решите систему неравенств:
Решение:
Ответ: (-1;2).

6. Решите систему неравенств:
Решение:
Ответ: нет решений.

7. Решите систему неравенств:
Решение:
Ответ: (0; +∞).
8. Решите неравенство:
а) -2<3x+5≤10; б) 2<4x+6≤12.
Решение:
Ответ: (-2 1/3; 1 2/3].

9. Решите систему неравенств:
Решение:
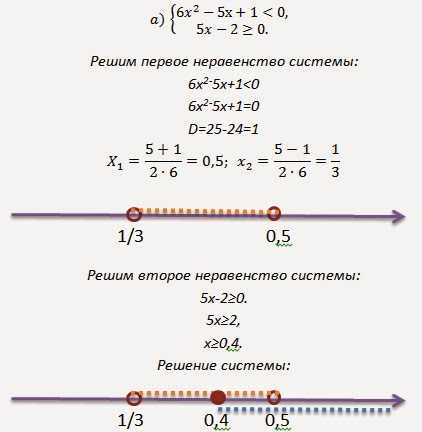Ответ: [0,4; 0,5).

10. Решите систему неравенств (№ 3.4.52 [7]):
Решение:
Ответ: (-1; 2).

11. Решите систему неравенств:
Решение:
Ответ: [-9; 3)U(3; 9].

12. Решите систему неравенств:
Решение:

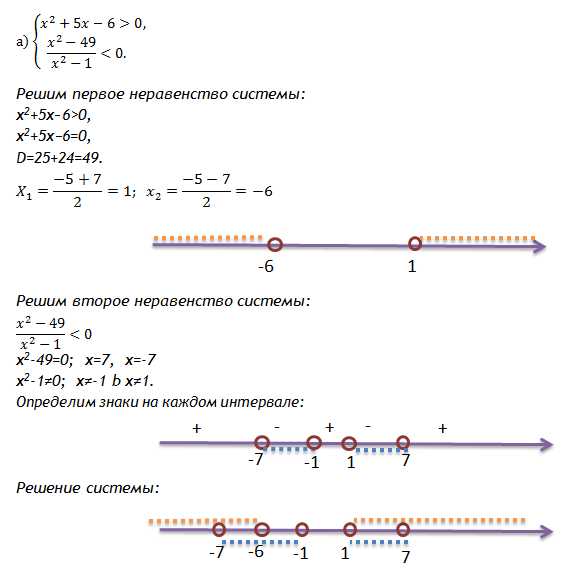
Ответ: (-7; -6)U(1;7).

13. Решите систему неравенств:
Решение:
Ответ: (2; 4).

14. Решите систему неравенств:
Решение:
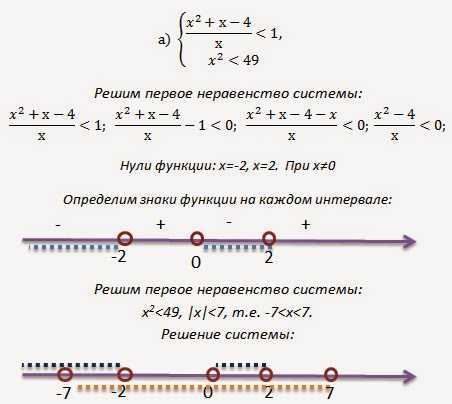Ответ: (-7; -2)U(0; 2).
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Решите систему неравенств:
2. Решите систему неравенств:
3. Решите систему неравенств:
4. Решите систему неравенств:
5. Решите систему неравенств:
6. Решите систему неравенств:
7. Решите систему неравенств:
8. Решите систему неравенств:
9. Решите систему неравенств:
10. Решите систему неравенств:
Проверь себя
mathembs.blogspot.com
Основные понятия, решение систем линейных неравенств. Видеоурок. Алгебра 9 Класс
На этом уроке мы начнем изучение систем неравенств. Вначале будем рассматривать системы линейных неравенств. В начале урока рассмотрим, откуда и зачем возникают системы неравенств. Далее изучим, что значит решить систему, и вспомним объединение и пересечение множеств. В конце будем решать конкретные примеры на системы линейных неравенств.
Тема: Рациональные неравенства и их системы
Урок: Основные понятия, решение систем линейных неравенств
До сих пор мы решали отдельные неравенства и применяли к ним метод интервалов, это могли быть и линейные неравенства, и квадратные и рациональные. Теперь перейдем к решению систем неравенств – сначала линейных систем. Посмотрим на примере, откуда берется необходимость рассматривать системы неравенств.
Найти область определения функции

Найти область определения функции

Найти область определения функции
Функция существует, когда существуют оба квадратних корня, т.е.

Как решать такую систему? Необходимо найти все x, удовлетворяющие и первому и второму неравенству.
Изобразим на оси ox множество решений первого и второго неравенства.
Промежуток пересечения двух лучей и есть наше решение.
Ответ:
Такой метод изображения решения системы неравенств иногда называют методом крыш.
Решением системы является пересечение двух множеств.
Изобразим это графически. Имеем множество А произвольной природы и множество В произвольной природы, которые пересекаются.
Определение: Пересечением двух множеств А и В называется такое третье множество, которое состоит из всех элементов, входящих и в А и в В.
Рассмотрим на конкретных примерах решения линейных систем неравенств, как находить пересечения множеств решений отдельных неравенств, входящих в систему.
Решить систему неравенств:
1.

Ответ:
2.
Ответ: (7; 10].
3.
Ответ:
4. Решить систему
Откуда может взяться второе неравенство системы? Например, из неравенства

Графически обозначим решения каждого неравенства и найдем промежуток их пересечения.
Ответ:
Таким образом, если мы имеем систему, в которой одно из неравенств удовлетворяет любому значению x, то его можно исключить.
5.
Ответ: система противоречива.
6.
Ответ:
Мы рассмотрели типовые опорные задачи, к которым сводится решение любой линейной системы неравенств.
Рассмотрим следующую систему.
7.

Ответ:
Иногда линейная система задается двойным неравенством, рассмотрим такой случай.
8.

Ответ:
Мы рассмотрели системы линейных неравенств, поняли, откуда они появляются, рассмотрели типовые системы, к которым сводятся все линейные системы, и решили некоторые из них.

Список рекомендованной литературы
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.

Рекомендованные ссылки на интернет-ресурсы
1. Портал Естественных Наук (Источник).
2. Электронный учебно-методический комплекс для подготовки 10-11 классов к вступительным экзаменам по информатике, математике, русскому языку (Источник).
3. Виртуальный репетитор (Источник).
4. Центр образования «Технология обучения» (Источник).
5. Раздел College.ru по математике (Источник).

Рекомендованное домашнее задание
1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. №№ 53; 54; 56; 57.
interneturok.ru
Решение систем неравенств
Вопросы занятия:
· повторить основные свойства систем неравенств;
· повторить алгоритм решения систем неравенств.
Материал урока
Как решаются системы линейных неравенств с одной переменной, мы уже вспоминали.
Сегодня на уроке мы рассмотрим системы не линейных неравенств.
Определение.
Говорят, что задана система двух неравенств с одной переменной, если требуется найти все значения переменной, при которых оба неравенства системы обращаются в верные числовые неравенства.
Определение.
Решением системы неравенств называют такое значение переменной, при котором неравенства системы преобразуются в верные числовые неравенства.
Определение.
Решить систему неравенств – это значит найти все её решения или доказать, что решений нет.
Определение.
Два неравенства называются равносильными, если каждое решение одного неравенства является решением другого, и наоборот, то есть они имеют одни и те же решения. Равносильными называются и неравенства, которые не имеют решений.
Теперь давайте вспомним основные свойства неравенств.
1. Если в неравенстве перенести слагаемое из одной части в другую с противоположным знаком, то получится неравенство, равносильное данному.
2. Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится неравенство, равносильное данному.
3. Если обе части неравенства умножить или разделить на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получится неравенство, равносильное данному.
Давайте повторим алгоритм решения систем линейных неравенств.
1. Решить каждое из неравенств системы отдельно.
2. Изобразить полученные решения на числовой прямой.
3. Найти пересечение этих решений.
По такому же алгоритму будут решаться и системы, которые мы рассмотрим на этом уроке.
Пример.
Рассмотрим ещё один пример.
Пример.
Рассмотрим ещё один пример.
Пример.
Итоги урока
Сегодня на уроке, мы вспомнили что такое системы неравенств, вспомнили основные свойства неравенств, повторили алгоритм решения систем неравенств, рассмотрели несколько примеров.
videouroki.net