Прямая и плоскость /qualihelpy
Простейшими фигурами в пространстве являются точка, прямая и плоскость.
Точки обозначают прописными буквами латинского алфавита: , , , и т. д.Плоскости обозначают строчными буквами греческого алфавита , , и т. д.На рисунках плоскости изображают в виде произвольной области, а чаще в виде параллелограмма.
На рисунке 9.1 изображены плоскости , и .Если прямая с принадлежит плоскости , то пишут: ; если прямая не принадлежит этой плоскости, то пишут: (рис. 9.3).Основные свойства взаимного расположения точек, прямых и плоскостей в пространстве выражают аксиомы стереометрии и следствия из них.
Аксиомы стереометрии
1. Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.
На рисунке 9.4 через точки , и проведена плоскость .2. Если две точки прямой принадлежат плоскости, то все точки этой прямой принадлежат данной плоскости.
3. Если две плоскости имеют общую точку, то они имеют общую прямую, которой принадлежат все общие точки этих плоскостей.
Если две плоскости имеют общую точку, то они имеют общую прямую, которой принадлежат все общие точки этих плоскостей.
Следствия из аксиом
1. Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну. На рисунке 9.7 через прямую и точку проведена плоскость .2. Через две пересекающиеся прямые можно провести плоскость, и притом только одну. На рисунке 9.8 через пересекающиеся прямые и проведена плоскость .Взаимное расположение прямых в пространстве
Две прямые в пространстве могут пересекаться, быть параллельными, скрещиваться или совпадать.
Две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются. На рисунке 9.9 прямые и параллельны. Углом между двумя пересекающимися прямыми в пространстве называется наименьший из углов, образованных лучами этих прямых с вершиной в точке их пересечения. На рисунке 9.10 прямые и пересекаются под углом .Две прямые называются перпендикулярными, если угол между ними прямой.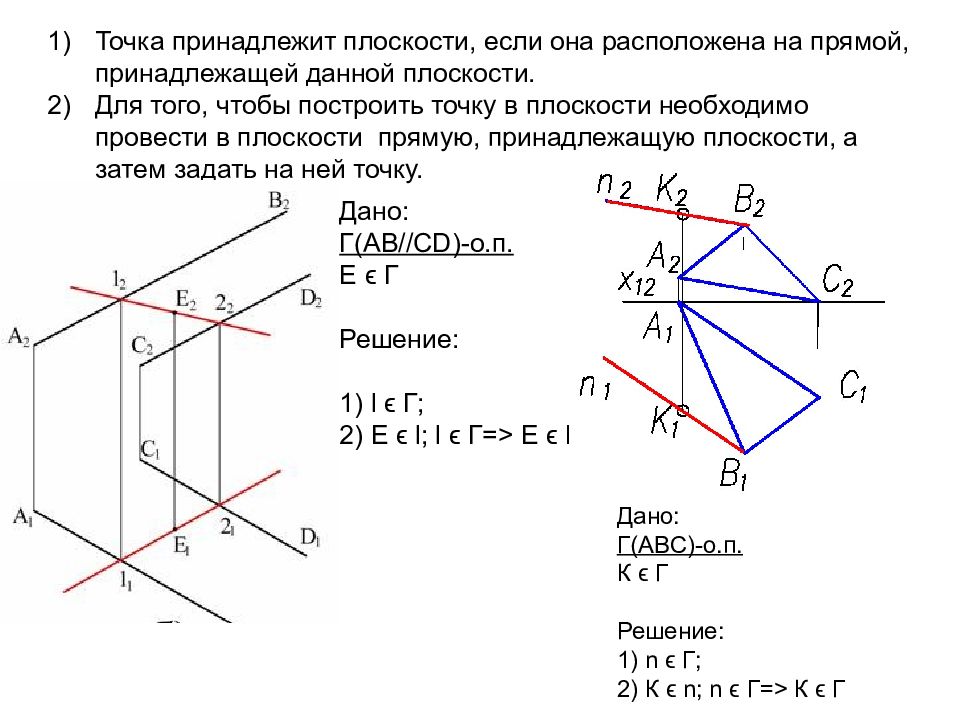
Две прямые в пространстве скрещиваются, если не существует плоскости, в которой они обе лежат.
Признак скрещивающихся прямых: если одна из двух прямых лежит в некоторой плоскости, а вторая прямая пересекает эту плоскость в точке, не принадлежащей первой прямой, то эти прямые скрещивающиеся.
На рисунке 9.11 изображены скрещивающиеся прямые и .Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным.
Взаимное расположение прямых и плоскостей
В пространстве прямая может пересекать плоскость, быть ей параллельной или лежать в плоскости.
На рисунке 9.13 прямая пересекает плоскость в точке . На рисунке 9.14 прямая параллельна плоскости , а прямая лежит в этой плоскости.Плоскость и прямая, не принадлежащая плоскости, параллельны, если они не имеют общих точек.
Признак параллельности прямой и плоскости: если прямая, не принадлежащая плоскости, параллельна какой-либо прямой, принадлежащей этой плоскости, то она параллельна плоскости.
Взаимное расположение плоскостей в пространстве
Две плоскости в пространстве могут совпадать, быть параллельны или пересекаться.
Две плоскости параллельны, если они не имеют общих точек.
Признак параллельности плоскостей: если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Прямая перпендикулярна плоскости, если она перпендикулярна любой прямой, принадлежащей плоскости.
Признак перпендикулярности прямой и плоскости: если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.
Свойства прямой, перпендикулярной плоскости
1. Два различных перпендикуляра к плоскости параллельны.
На рисунке 9.19 прямые и перпендикулярны плоскости , следовательно, .2. Прямая, перпендикулярная одной из двух параллельных плоскостей, перпендикулярна и другой плоскости.
Прямая, пересекающая плоскость, но не перпендикулярная к ней, называется наклонной к плоскости.
На рисунке 9.21 прямая – наклонная к плоскости .Теорема о трех перпендикулярах. Для того чтобы прямая, лежащая в плоскости, была перпендикулярна наклонной к плоскости, необходимо и достаточно, чтобы она была перпендикулярна проекции этой наклонной на плоскость.
На рисунке 9.21 прямая – наклонная к плоскости, прямая – проекция этой наклонной на плоскость и . Тогда .Углом между прямой и плоскостью называют угол между прямой и ее проекцией на плоскость. На рисунке 9.22 прямая – наклонная к плоскости, прямая – проекция этой наклонной на плоскость, следовательно, угол – угол между прямой и плоскостью.Двугранным углом называют угол, образованный двумя полуплоскостями с общей границей. Прямую, которая является общей границей этих полуплоскостей, называют ребром двугранного угла, а полуплоскости с общим ребром – гранями двугранного угла.
В результате пересечения двух плоскостей образуется четыре двугранных угла (рис. 9.24).
Двугранный угол измеряется соответствующим линейным углом. Линейным углом двугранного угла называют угол между перпендикулярами, проведенными в каждой грани к ребру.
На рисунке 9.25 угол – линейный угол двугранного угла.Двугранный угол может иметь любое значение от до . Если линейный угол двугранного угла равен , то плоскости перпендикулярны.Признак перпендикулярности плоскостей: если плоскость содержит перпендикуляр к другой плоскости, то она перпендикулярна этой плоскости.
На рисунке 9.26 плоскости и перпендикулярны.Начертательная геометрия, решение задач ОмГТУ
Рабочая тетрадь для решения задач
по дисциплинe «Начертательная геометрия»
(для студентов заочной формы обучения)
Тема 1.
 Изображение точек на комплексном чертеже.
Изображение точек на комплексном чертеже.
З а д а ч а 1. Построить точки А(40,20,30), В(40,30,0), С(0,0,30) и D(0,10,20) на комплексном чертеже.
З а д а ч а 2. Точки А, В и С принадлежат плоскостям проекций. Построить недостающие проекции этих точек и указать в какой плоскости каждая из них располагается.
Тема 2. Прямая. Взаимное расположение прямых.
З а д а ч а 3. Даны точки А(90,30,40), В(10,20,15), С(60,20,40) и D(30,40,15). Построить отрезки АВ и СD, обозначить и записать координаты конкурирующих точек.
З а д а ч а 4. Отложить на отрезке АВ отрезок АК=20мм и определить угол наклона отрезка АВ к плоскости проекций
З а д а ч а 5. Пересечь прямые АВ и СD прямой MN, отстоящей от плоскости П1 на расстоянии 16 мм.
Пересечь прямые АВ и СD прямой MN, отстоящей от плоскости П1 на расстоянии 16 мм.
З а д а ч а 6. Даны две скрещивающиеся прямые с и d. Построить отрезок МN, являющийся кратчайшим расстоянием между этими прямыми.
З а д а ч а 7. Дано: точка А(А1,А2) и прямая ВС общего положения. Построить сферу с центром в точке А, касательную к прямой ВС
Тема 3. Плоскость. Главные линии плоскости.
З а д а ч а 8. Дана плоскость сигма (ΔABC), точки D и E в этой плоскости. Через точку Е провести горизонталь h, через точку D – фронталь f этой плоскости.
З а д а ч а 9. Построить недостающие проекции точек E и D, лежащих в плоскости сигма (АВ ∩ ВС).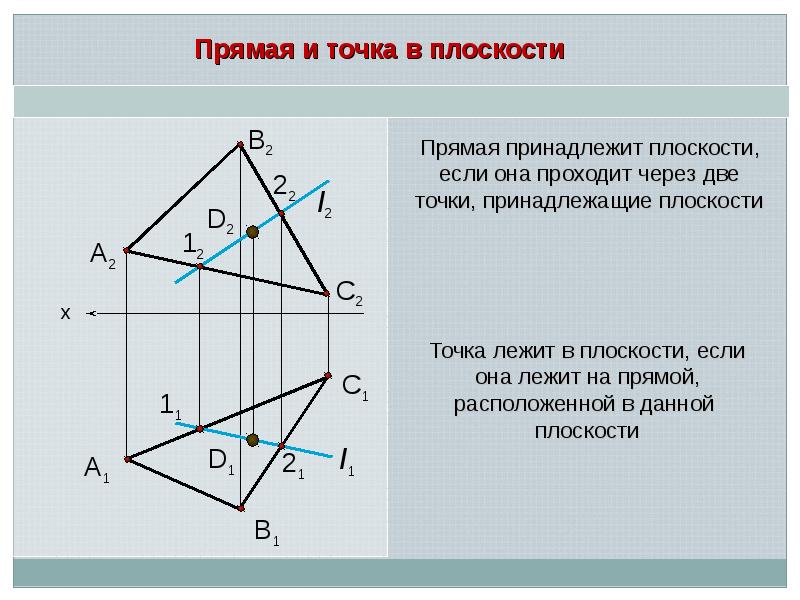
З а д а ч а 10. Дан плоский пятиугольник ABCDЕ, заданный горизонтальной и фронтальной проекциями двух смежных сторон. Достроить его фронтальную проекцию.
З а д а ч а 11. Дан треугольник АВС. Найти центр окружности, описанной вокруг заданного треугольника.
Тема 4. Взаимное расположение прямой и плоскости.
З а д а ч а 12. Задана плоскость Р и прямая DE. Найти точку пересечения прямой с плоскостью. Определить видимость проекции прямой. (Р2 – фронтальный след плоскости). P (AB
З а д а ч а 13. Заданы плоскость Р(ΔАВС) и точка D: а) определить расстояние от точки D до плоскости Р; б) построить точку М, симметричную точке D относительно плоскости Р; в) построить шар с центром в точке D, касательный к плоскости Р.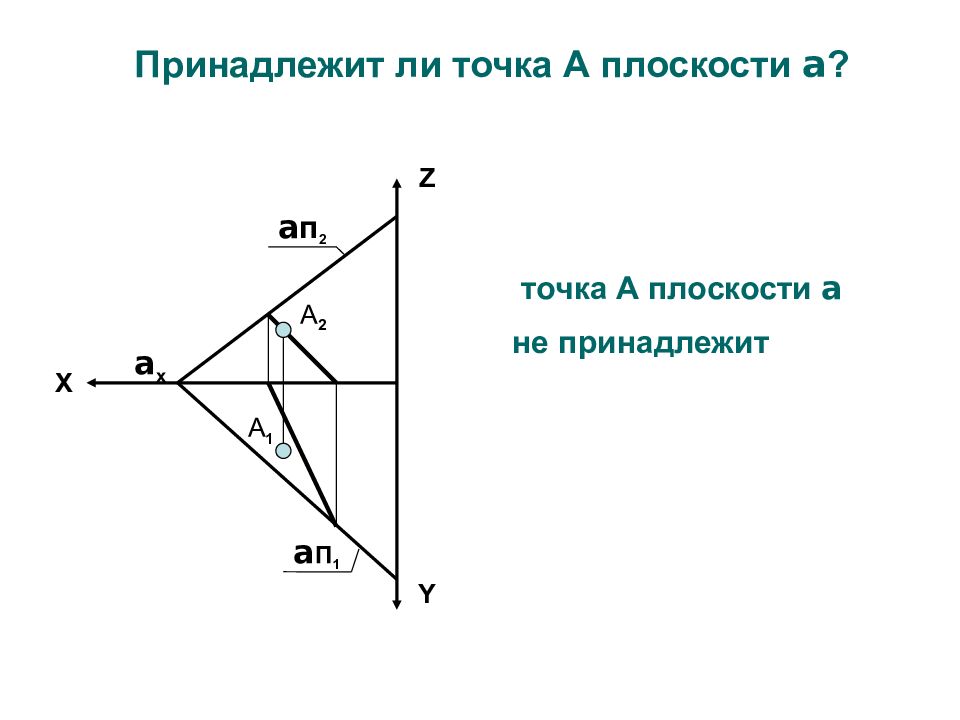
З а д а ч а 14. Задан ΔАВС общего положения. Построить прямую призму с основанием ΔАВС и высотой равной 30 мм.
Тема 5. Взаимное положение плоскостей.
З а д а ч а 15. Даны плоскости сигма(ΔАВС), гамма(DEF) и точка М: а) построить линию пересечения плоскостей. б) через точку М провести прямую l, параллельную плоскостям сигма и гамма
. Задачу решить без использования способа замены плоскостей.З а д а ч а 16 Даны плоскость Р(а//b) и точка М. Через точку М провести плоскость Г, параллельную плоскости Р.
З а д а ч а 17 Даны плоскость Р(а//b) и прямая CD. Через прямую CD провести плоскость Г перпендикул. Р. Г(ΔСDE)
З а д а ч а 18
Тема 7.
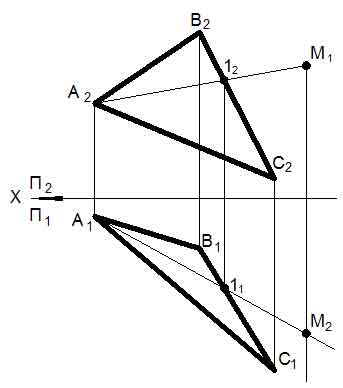 Пересечение поверхности с плоскостью
Пересечение поверхности с плоскостью
З а д а ч а 19. Построить проекции сечения данной поверхности проецирующей плоскостью Σ.
Тема 8. Пересечение прямой линии с поверхностью
З а д а ч а 20. Построить точки пересечения прямой с заданной поверхностью. Установить видимость проекций прямой
Тема 10. Взаимное пересечение поверхностей.
З а д а ч а 21 Метод вспомогательных секущих плоскостей
З а д а ч а 22 Метод сферического посредника
Ответы | 109. На отрезке AB, конец A которого принадлежит плоскости α, выбрана точка C, и через точки B и C проведены параллельные прямые, пересекающие плоскость α в точках B1 и C1 соответственно. Найдите отрезок CC1, учитывая, что: — Геометрия, 10 класс
а) точка C — середина отрезка AB и BB1 = 14 см;
б) AC : CB = 3 : 2 и BB1 = 50 см.
а)
Дано: A∈α,C∈AB,CC1∩α=C1,BB1∩α=B1,CC1∥BB1,BB1=14A\in \alpha, C\in AB, CC_1\cap \alpha=C_1, BB_1\cap \alpha = B_1, CC_1\parallel BB_1, BB_1=14A∈α,C∈AB,CC1∩α=C1,BB1∩α=B1,CC1∥BB1,BB1=14 см, CCC — середина AB.AB.AB.
Найти: CC1.CC_1.CC1.
Решение:
1) Параллельные прямые CC1CC_1CC1 и BB1BB_1BB1 задают плоскость (ABB1).(ABB_1).(ABB1).
(ABB1)∩α=AB1.(ABB_1)\cap \alpha = AB_1.(ABB1)∩α=AB1.
Поэтому точки A,C1A, C_1A,C1 и B1B_1B1 лежат на одной прямой.
2) Т.к. CCC — середина ABABAB и CC1∥BB1,CC_1\parallel BB_1,CC1∥BB1, то C1C_1C1 — середина AB1.AB_1.AB1. Значит, CC1CC_1CC1 — средняя линия △ABB1.\triangle ABB_1.△ABB1. По свойству средней линии CC1=12BB1=12⋅14=7 (см).CC_1=\dfrac{1}{2}BB_1=\dfrac{1}{2}\cdot 14=7\,(см).CC1=21BB1=21⋅14=7(см).
Ответ: 7 см.
б)
Дано: A∈α,C∈AB,CC1∩α=C1,BB1∩α=B1,CC1∥BB1,BB1=50 см,AC:CB=3:2. A\in\alpha, C\in AB, CC_1\cap \alpha=C_1, BB_1\cap \alpha =B_1, CC_1\parallel BB_1, BB_1=50\,см, AC:CB=3:2.A∈α,C∈AB,CC1∩α=C1,BB1∩α=B1,CC1∥BB1,BB1=50см,AC:CB=3:2.
A\in\alpha, C\in AB, CC_1\cap \alpha=C_1, BB_1\cap \alpha =B_1, CC_1\parallel BB_1, BB_1=50\,см, AC:CB=3:2.A∈α,C∈AB,CC1∩α=C1,BB1∩α=B1,CC1∥BB1,BB1=50см,AC:CB=3:2.
Найти: CC1.CC_1.CC1.
Решение:
1) Рассмотрим △ACC1\triangle ACC_1△ACC1 и △ABB1.\triangle ABB_1.△ABB1.
∠A\angle A∠A — общей,
∠AC1C=∠AB1B\angle AC_1C=\angle AB_1B∠AC1C=∠AB1B как соответственные при CC1∥BB1CC_1\parallel BB_1CC1∥BB1 и секущей AB1.AB_1.AB1.
Следовательно △ACC1\triangle ACC_1△ACC1 подобен △ABB1\triangle ABB_1△ABB1 по двум углам.
2) ACAB=CC1BB1;\dfrac{AC}{AB}=\dfrac{CC_1}{BB_1};ABAC=BB1CC1;
35=CC150;\dfrac{3}{5}=\dfrac{CC_1}{50};53=50CC1;
CC1=3⋅505=3⋅10=30 (см).CC_1=\dfrac{3\cdot 50}{5}=3\cdot 10=30\,(см).CC1=53⋅50=3⋅10=30(см).
Ответ: 30 см.
Точка и прямая в плоскости • Блог архитектора
Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости.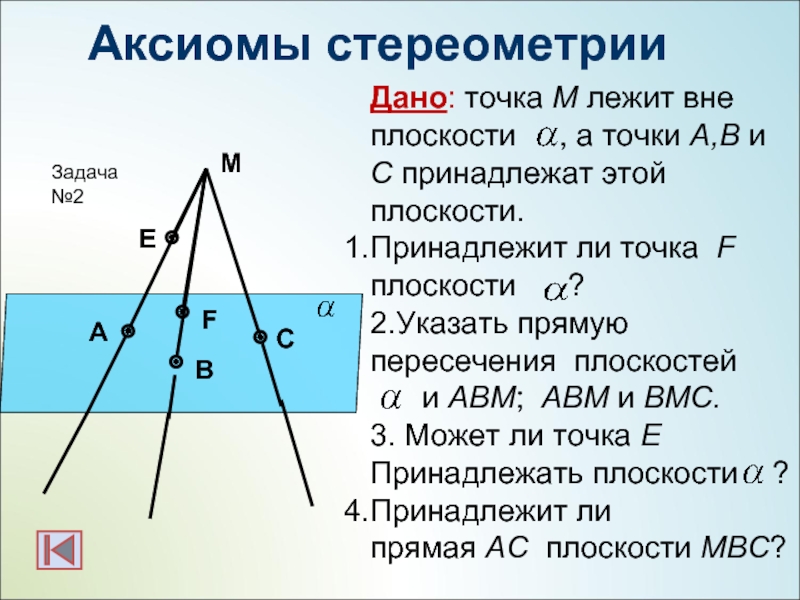
(•)K ∈ (AB) ⊂ Q => (•)K ∈ Q
Прямая принадлежит плоскости, если:
- она проходит через две точки, принадлежащие плоскости;
(•)A ∈ Q ∧ (•)B ∈ Q => (AB) ⊂ Q
- она проходит через одну точку этой плоскости параллельно прямой, лежащей в этой плоскости.
(•)A ∈ Q ∧ (AB//CD)(CD ⊂ Q) => (AB) ⊂ Q
Пример. Плоскость Q задана треугольником АВС (рис. 5).
рис. 5Необходимо построить горизонтальную проекцию точки K(k) и фронтальную проекцию точки N(n’), если они принадлежат плоскости Q.
Точка принадлежит плоскости, если она принадлежит прямой, принадлежащей этой плоскости. Проведем через точку К прямую А1. построим фронтальную проекцию этой прямой (а’1′). Проведя через точку k’ линию связи, найдем горизонтальную проекцию точки К — точку k (рис. 6).
рис. 6Фронтальная проекция точки N(точка n’) найдена с помощью прямой В2 (рис. 6).
Положение плоскости в пространствеПлоскость, не параллельная и не перпендикулярная ни одной из плоскостей проекций, называется плоскостью общего положения.
Плоскости, параллельные или перпендикулярные плоскостям проекций, называются плоскостями частного положения. Они делятся на две группы.
Плоскость, перпендикулярную к плоскости проекций, называют проецирующей плоскостью.
Плоскость, параллельную плоскости проекций, называют
Проецирующие плоскости
- Горизонтально-проецирующие (рис. 7).
- Фронтально-проецирующие (рис. 8).
- Профильно-проецирующие.
Если плоскость перпендикулярна плоскости проекций, то на эту плоскость она проецируется в линию. Эту проекцию можно рассматривать и как след плоскости. На эту же плоскость проекций в натуральную величину проецируются углы наклона данной плоскости к двум другим плоскостям проекций.
Проецирующие плоскости обладают собирательным свойством: если точка, линия или фигура расположены в плоскости, перпендикулярной плоскости проекций, то на этой плоскости их проекции совпадают со следом проецирующей плоскости.
Горизонтально-проецирующая плоскость
рис. 7Фронтально-проецирующая плоскость
рис. 8Плоскости уровня
Если фигура параллельна плоскости проекций, то на эту плоскость она проецируется в натуральную величину. Проекции фигуры на две другие плоскости проекций параллельны осям, определяющим данную плоскость проекций.
Горизонтальная
рис. 9Фронтальная
рис. 10Главные линии плоскости
Прямых, принадлежащих плоскости, очень много. Среди них есть прямые, занимающие особое, частное положение в плоскости. Эти линии называются главными линиями плоскости.
К ним относятся:
- Линии наименьшего наклона к плоскостям проекций (линии уровня) — горизонталь, фронталь и профильная прямая.
- Линии наибольшего наклона к плоскостям проекций.
Горизонталь — прямая, лежащая в плоскости и параллельная горизонтальной плоскости проекций (рис. 11). Фронтальная проекция горизонтали параллельна оси х, профильная — оси у.
Фронталь — прямая, лежащая в плоскости и параллельная фронтальной плоскости проекций (рис. 12). Горизонтальная проекция фронтали параллельна оси
Профильная прямая — прямая, лежащая в плоскости и параллельная профильной плоскости проекций. Горизонтальная проекция профильной прямой параллельна оси у, фронтальная — оси z (рис. 13).
рис. 13Из трех линий наибольшего наклона к плоскостям проекций чаще всего интерес представляет линия наибольшего наклона к горизонтальной плоскости. Эту линию называют линией ската.
Линия ската — это прямая, лежащая в плоскости и перпендикулярная ее горизонтальному следу или ее горизонтали.
Проведем плоскость Р перпендикулярно плоскости Q и Н. Плоскость Р пересекает плоскость Q по линии ската MN (рис. 14).
рис. 14Построив эту линию наибольшего наклона, можно определить величину двугранного угла между заданной плоскостью и плоскостью проекций.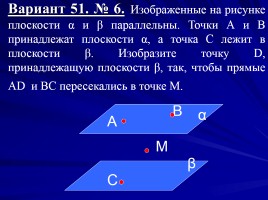 Этот угол будет равен линейному углу, который составляет линия наибольшего наклона со своей проекцией на эту плоскость (рис. 15).
Этот угол будет равен линейному углу, который составляет линия наибольшего наклона со своей проекцией на эту плоскость (рис. 15).
Урок 6. параллельность плоскостей — Геометрия — 10 класс
Геометрия, 10 класс
Урок №6. Параллельность плоскостей
Перечень вопросов, рассматриваемых в теме
- Определение параллельных плоскостей;
- Свойства параллельных плоскостей;
- Признак параллельности плоскостей.
Глоссарий по теме
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.
Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.
Определение. Плоскости, которые не пересекаются, называются параллельными.
Основная литература:
Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии 10 Москва «Просвещение» 2013 год. С. 1-4.
И., Бутузов В. Ф. Рабочая тетрадь по геометрии 10 Москва «Просвещение» 2013 год. С. 1-4.
Дополнительная литература:
Зив Б. Г. Геометрия 10 класс Дидактические материалы Москва «Просвещение» 2013 год. С.4, 14, 24
Теоретический материал для самостоятельного изучения
Как известно из аксиом стереометрии, если плоскости имеют одну общую точку, то они пересекаются по прямой, проходящей через эту точку. Значит две плоскости или пересекаются, или не пересекаются.
Определение. Плоскости, которые не пересекаются, называются параллельными.
Параллельные плоскости α и β обозначаются α∥β.
Изображение:
Пример 1.
Любая конструкция с полом, потолком и стенами даёт нам представление о параллельных плоскостях — пол и потолок как две параллельные плоскости, боковые стены как параллельные плоскости.
Признак параллельности плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
Доказательство.
Пусть α и β — данные плоскости, a1 и a2 – пересекающиеся прямые в плоскости α, а b1 и b2 соответственно параллельные им прямые в плоскости β.
Допустим, что плоскости α и β не параллельны, то есть они пересекаются по некоторой прямой c.
Прямая a1 параллельна прямой b1, значит она параллельна и самой плоскости β.
Прямая a2 параллельна прямой b2, значит она параллельна и самой плоскости β (признак параллельности прямой и плоскости).
Прямая c принадлежит плоскости α, значит хотя бы одна из прямых a1 или a2 пересекает прямую c, то есть имеет с ней общую точку. Но прямая c также принадлежит и плоскости β, значит, пересекая прямую c, прямая a1 или a2 пересекает плоскость β, чего быть не может, так как прямые a1 и a2 параллельны плоскости β.
Из этого следует, что плоскости α и β не пересекаются, то есть они параллельны.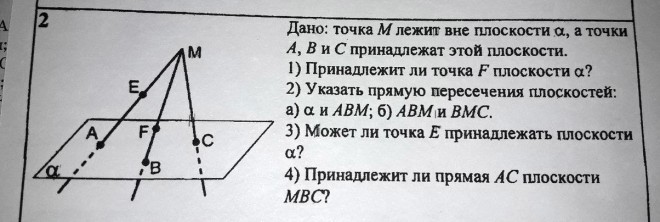
Теорема доказана.
Свойства параллельных плоскостей.
Теорема 1. Если две параллельные плоскости пересекаются третьей, то линии их пересечения параллельны.
Доказательство.
Пусть α и β — параллельные плоскости, а γ- плоскость, пересекающая их.
Плоскость α пересекается с плоскостью γ по прямой a.
Плоскость β пересекается с плоскостью γ по прямой b.
Линии пересечения a и b лежат в одной плоскости γ и потому могут быть либо пересекающимися, либо параллельными прямыми. Но, принадлежа двум параллельным плоскостям, они не могут иметь общих точек. Следовательно, они параллельны.
Теорема 2. Отрезки параллельных прямых, заключенных между двумя параллельными плоскостями, равны.
Доказательство.
Пусть α и β — параллельные плоскости, а a и b – параллельные прямые, пересекающие их.
Через прямые a и b можно провести плоскость — эти прямые параллельны, значит определяют плоскость, причём только одну.
Проведённая плоскость пересекается с плоскостью α по прямой AB, а с плоскостью β по прямой CD.
По предыдущей теореме прямые AB и CD параллельны. Четырехугольник ABCD есть параллелограмм (у него противоположные стороны параллельны). А раз это параллелограмм, то противоположные стороны у него равны, то есть BC=AD.
Теорема 3. Если прямая пересекает одну из двух параллельных плоскостей, то она пересекает и другую.
Доказательство.
Пусть α||β, a пересекает α в точке А.
Выберем в плоскости любую точку C. Через эту точку и прямую a проведём плоскость.
Так как плоскость имеет с плоскостями α и β общие точки A и C соответственно, то она пересекает эти плоскости по некоторым прямым b и c, которые проходят соответственно через точки A и C. По предыдущей теореме прямые b и c параллельны. Тогда в плоскости прямая a пересекает (в точке A) прямую b, которая параллельна прямой c. Значит, прямая a пересекает и прямую c в некоторой точке B. Так как прямая c лежит в плоскости, то точка B является точкой пересечения прямой a и плоскости. Теорема доказана.
Значит, прямая a пересекает и прямую c в некоторой точке B. Так как прямая c лежит в плоскости, то точка B является точкой пересечения прямой a и плоскости. Теорема доказана.
Теорема 4. Если плоскость пересекает одну из двух параллельных плоскостей, то она пересекает и другую плоскость.
Доказательство.
Пусть α||β, α и γ пересекаются.
Докажем, что плоскости β и γ пересекаются.
Проведём в плоскости γ прямую a, пересекающую плоскость α в некоторой точке B. Тогда по теореме 3 прямая a пересекает и плоскость β в некоторой точке A. Следовательно, плоскости β и γ имеют общую точку A, т. е. пересекаются. Теорема доказана.
Теорема 5. Через точку, не лежащую в данной плоскости, можно провести плоскость, параллельную данной, и притом только одну.
Доказательство.
Пусть нам даны плоскость α и точка М, ей не принадлежащая.
Докажем, что существует плоскость β, которой принадлежит точка М, параллельная плоскости α.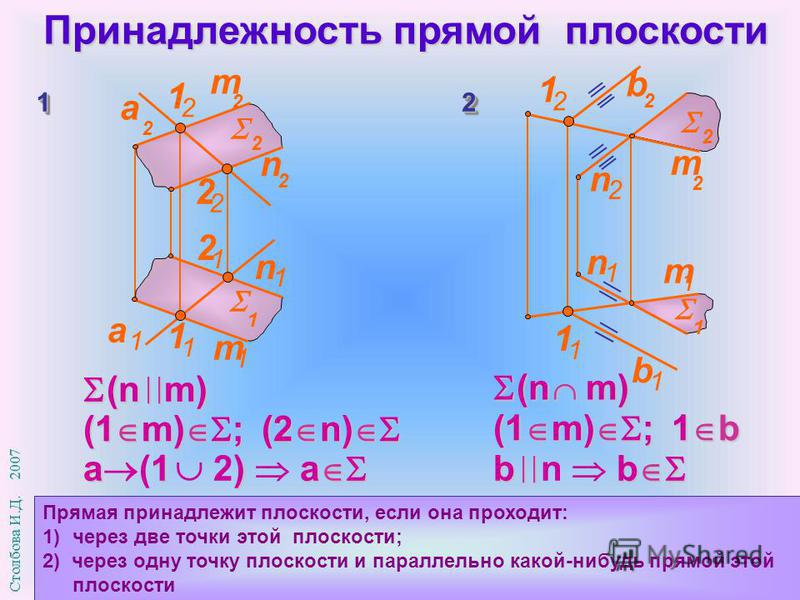
В данной плоскости α проведём две произвольные пересекающиеся прямые a и b. Через точку M проведём прямые a1 и b1, параллельные соответственно a и b. Плоскость, проходящую через пересекающиеся прямые a1 и b1, обозначим β. На основании признака параллельности плоскостей плоскость β параллельна плоскости α.
Докажем методом от противного, что β — единственная плоскость, удовлетворяющая условию теоремы.
Допустим, что через точку M проходит другая плоскость, например β1, параллельная α.
Так как β1 пересекает плоскость β (они имеют общую точку M), то по теореме 4 плоскость β1 пересекает и плоскость α (β ‖ α). Мы пришли к противоречию. Таким образом, предположение о том, что через точку M можно провести плоскость, отличную от плоскости β и параллельную плоскости α, неверно. Значит, плоскость β — единственна.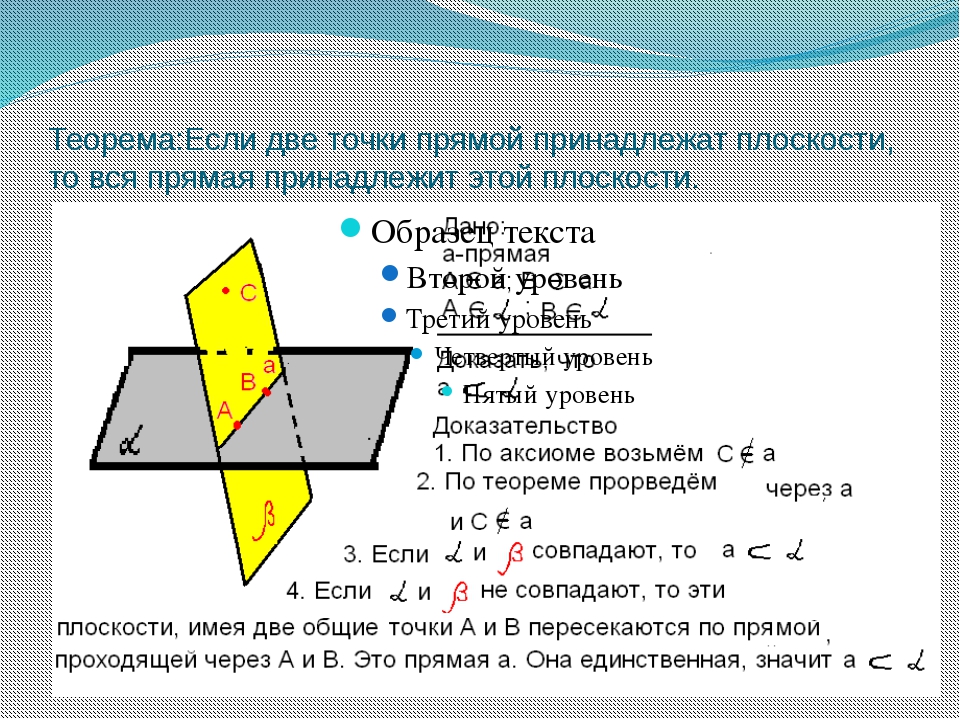 Теорема доказана.
Теорема доказана.
Рассмотрим несколько примеров на применение данных свойств.
Пример 2.
Даны две пересекающиеся прямые a и b точка А, не лежащая в плоскости этих прямых. Докажите, что через точку А проходит плоскость, параллельная прямым a и b, и притом только одна.
Доказательство.
Прямые a и b пересекаются по условию, следовательно, по следствию из аксиомы А1, эти прямые единственным образом определяют плоскость α.
Известно, что через точку А, не принадлежащую плоскости α, проходит единственная плоскость, параллельная α, т.е. параллельная прямым a и b (по теореме 5) .
Пример 3.
Плоскости α и β параллельны, прямая m лежит в плоскости α. Докажите, что прямая m параллельна плоскости β.
Доказательство.
Предположим, что прямая m пересекает плоскость β в точке М. Тогда точка М принадлежит плоскости α (т.к. прямая m лежит в плоскости α) и М принадлежит плоскости β, значит, α и β пересекаются, но они параллельны по условию. Очевидно, m не пересекает плоскость α, т.е. параллельна ей.
Очевидно, m не пересекает плоскость α, т.е. параллельна ей.
Примеры и разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Три отрезка А1А2, В1В2 и С1С2, не лежащие в одной плоскости, имеют общую середину. Докажите, что плоскости А1В1С1 и А2В2С2 параллельны.
Доказательство.
Докажем параллельность А1В1 и А2В2.
Рассмотрим плоскость, проходящую через прямые А1А2 и В1В2
(она существует и единственная, т.к. прямые пересекаются).
В этой плоскости лежит четырехугольник А1В1А2В2, диагонали которого точкой пересечения делятся пополам. Следовательно, данный четырехугольник является параллелограммом (признак параллелограмма), значит, А1В1 и А2В2параллельны.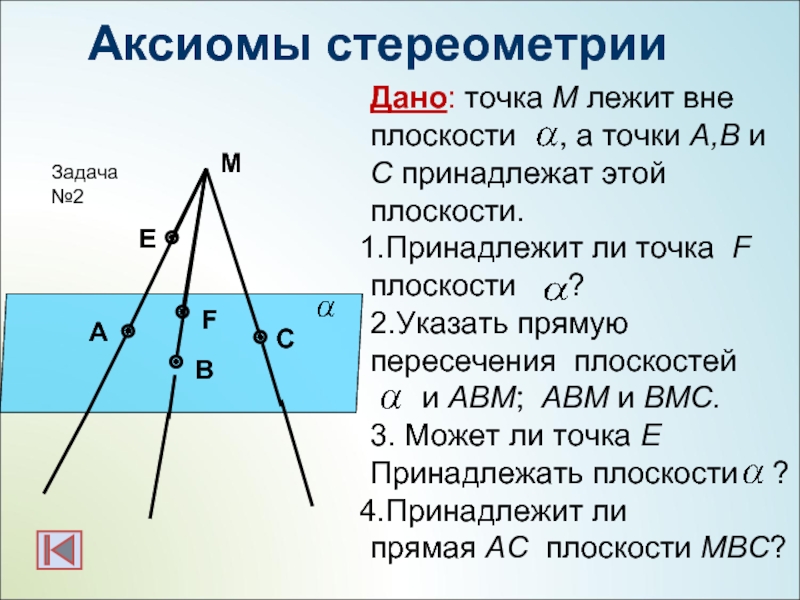
Аналогично доказывается параллельность В1С1 и В2С2. Из вышеперечисленного следует, что плоскости А1В1С1 и А2В2С2 параллельны по признаку параллельности плоскостей.
Верное решение:
Докажем параллельность А1В1 и А2В2.
Рассмотрим плоскость, проходящую через прямые А1А2 и В1В2
(она существует и единственная, т.к. прямые пересекаются).
В этой плоскости лежит четырехугольник А1В1А2В2, диагонали которого точкой пересечения делятся пополам. Следовательно, данный четырехугольник является параллелограммом (признак параллелограмма), значит, А1В1 и А2В2параллельны.
Аналогично доказывается параллельность В1С1 и В2С2. Из вышеперечисленного следует, что плоскости А1В1С1 и А2В2С2 параллельны по признаку параллельности плоскостей.
Из вышеперечисленного следует, что плоскости А1В1С1 и А2В2С2 параллельны по признаку параллельности плоскостей.
№2.
Тип задания: выделение цветом
Два равнобедренных треугольника FKС и FKD с общим основанием FK расположены так, что точка С не лежит в плоскости FKD. Определите взаимное расположение прямых, содержащих медианы треугольников, проведенных к сторонам KС и KD.
Решение:
Прямые, которые содержат медианы треугольников к KC и KD- выходят из одной точки F. Соответственно, можно сделать вывод, что данные прямые пересекаются.
Ответ:
1) они параллельны
2) скрещиваются
3) пересекаются
Прямые и точки, лежащие в плоскости
Прямые и точки, лежащие в плоскости [c.19]ПРЯМАЯ и ТОЧКА, ЛЕЖАЩИЕ В ПЛОСКОСТИ [c.67]
Прямая линия, не лежащая в плоскости, может иметь с ней олько одну общую точку.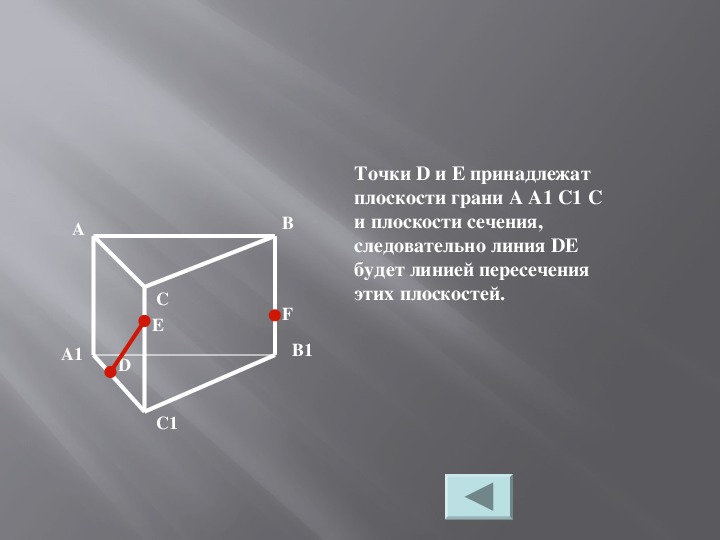 Принято называть прямую линию и плоскость пересекающимися, если эта точка собственная (черт. 102), и параллельными, если это точка несобственная (черт. 103). Во втором случае также говорят, что прямая линия и плоскость не имеют общих точек.
[c.26]
Принято называть прямую линию и плоскость пересекающимися, если эта точка собственная (черт. 102), и параллельными, если это точка несобственная (черт. 103). Во втором случае также говорят, что прямая линия и плоскость не имеют общих точек.
[c.26]
Теперь, имея горизонталь плоскости и величину угла а, нетрудно построить фронтальную проекцию любой точки, лежащей в плоскости, по данной ее горизонтальной проекции. Так, например, для построения фронтальной проекции точки В следует через горизонтальную проекцию Ь провести прямые ЬЬа и ЬЬ, первая из которых перпендикулярна, а вторая — параллельна горизонтальной проекции тп оси вращения через точку провести прямую бо ь параллельную Od до пересечения ее в точке Ь с прямой bbi. Второй катет ЬЬ[ определит расстояние фронтальной проекции Ь от фронтальной проекции оси вращения, а отрезок ЬоЬ —натуральную величину радиуса вращения. Отрезок ЬЬ] откладываем на линии связи точки В по одну пли другую сторону от фронтальной проекции оси вращения.
 Отсюда заключаем, что задача имеет два решения. Оба треугольника одинаковой величины симметрично располагаются по отношению к плоскости, параллельной горизонтальной плоскости проекций и проходящей через ось вращения MN.
[c.20]
Отсюда заключаем, что задача имеет два решения. Оба треугольника одинаковой величины симметрично располагаются по отношению к плоскости, параллельной горизонтальной плоскости проекций и проходящей через ось вращения MN.
[c.20]Восставив из точки d перпендикуляр к прямой ad, отметив точку ei пересечения перпендикуляра dei с дугой окружности, проведенной из центра а радиусом, равным отрезку ае, и проведя прямую ави получим два луча а7 и ае,, совокупность которых определит угловой масштаб проекций точек, лежащих в плоскости. Угол а, образованный лучами, определит собою величину угла наклона искомой плоскости к горизонтальной плоскости проекций. Пользуясь угловым масштабом проекций, можно построить обе проекции любой точки плоскости, имея совмещенное положение точки с плоскостью, параллельной горизонтальной плоскости проекций, и наоборот, по данной горизонтальной или фронтальной проекции точки, лежащей в плоскости, можно построить ее вторую проекцию и совмещенное ее положение. [c.49]
[c.49]
Рассмотрим трансверсально-изотропную оболочку, срединная поверхность которой образуется вращением плоской кривой (образующей) вокруг прямой (оси оболочки), лежащей в плоскости этой кривой. Введем обычные для оболочек вращения координаты и ф (рис. 7.1) 0 — угол между нормалью в точке и осью вращения ф — угол между фиксированной меридианной плоскостью и меридианной плоскостью, проходящей через рассматриваемую точку. При этом коэффициенты первой квадратичной формы срединной поверхности будут [c.79]
Для того чтобы построить центральную проекцию А точки А (рис. 316), нужно провести проецирующую прямую из центра проекций 5 через заданную точку А до пересечения с плоскостью проекций П. При центральном проецировании какого-либо тела все проецирующие прямые проходят через один, постоянный центр проекций S. Центральное проецирование можно выполнить для любых точек пространства, за исключением точек, лежащих в плоскости, проходящей через центр проекций 5 и параллельной плоскости проекций Проекции,
[c. 173]
173]
На рис. 3.110, в приведено построение проекций точки М, принадлежащей конической поверхности вращения. Через точку М проведена образующая S1 конической поверхности, ее фронтальная проекция Хг/г- Точка 1 принадлежит окружности основания конуса. Вертикальная линия связи, проведенная через точку I2, пересекает горизонтальную проекцию окружности в двух точках. Так как по условию точка М находится на видимой части поверхности, то и образующая S1 видима. Поэтому горизонтальная проекция li точки 1 будет расположена на нижней части окружности. Можно через точку М провести не вспомогательную прямую, а окружность, лежащую в плоскости, перпендикулярной оси конической поверхности (рис. 3.111). Фронтальная проекция этой окружности — отрезок горизонтальной прямой (l-il , горизонтальная проекция — окружность радиуса Ог г. [c.125]
Орбитальное движение Земли приводит также к явлению звездной аберрации, которое было открыто Брэдли (1725—1728). Б своих наблюдениях он пытался обнаружить годичный параллакс, т. е. кажущуюся траекторию, которую описывает проекция звезды на небесный свод из-за изменения положения наблюдателя при движении Земли по орбите (рис. 8.1, а). В общем случае такая траектория должна быть эллипсом, вырождающимся в окружность для звезды, расположенной вблизи полюса эклиптики (как на рис. 8.1, а), или в отрезок прямой для звезды, лежащей в плоскости эклиптики. Брэдли нашел, что звезда действительно описывает эллипс, большая ось которого равна 41″, однако направление углового отклонения звезды совершенно иное, чем должно быть при параллаксе (рис. 8.1,6) когда Земля находится в точке А, ее наблюдаемое положение смещено не в точку Л , а в точку Лг, т. е. отклонение происходит в направлении движения Земли. Кроме того, отклонение не зависит от расстояния до звезды и значительно больше, чем параллактическое смещение даже ближайших звезд. Существование параллакса неподвижных звезд было твердо установлено Бесселем лишь сто лет спустя.
Б своих наблюдениях он пытался обнаружить годичный параллакс, т. е. кажущуюся траекторию, которую описывает проекция звезды на небесный свод из-за изменения положения наблюдателя при движении Земли по орбите (рис. 8.1, а). В общем случае такая траектория должна быть эллипсом, вырождающимся в окружность для звезды, расположенной вблизи полюса эклиптики (как на рис. 8.1, а), или в отрезок прямой для звезды, лежащей в плоскости эклиптики. Брэдли нашел, что звезда действительно описывает эллипс, большая ось которого равна 41″, однако направление углового отклонения звезды совершенно иное, чем должно быть при параллаксе (рис. 8.1,6) когда Земля находится в точке А, ее наблюдаемое положение смещено не в точку Л , а в точку Лг, т. е. отклонение происходит в направлении движения Земли. Кроме того, отклонение не зависит от расстояния до звезды и значительно больше, чем параллактическое смещение даже ближайших звезд. Существование параллакса неподвижных звезд было твердо установлено Бесселем лишь сто лет спустя. [c.393]
[c.393]
Так как гармоническая функция U(x) аналитична в / + и не является постоянной, то прямая, перпендикулярная плоскости П и не лежащая в плоскости Хз = О, может пересекать поверхность уровня функции U не более чем в конечном числе точек. Аналогично на каждой такой прямой — не более конечного числа критических точек функции U, [c.134]
Покажем, что траектория точек С и С есть прямая, совпадающая с осью Оу. Для этого на рис. 3.21 изображена кинематическая схема кривошипно-ползунного механизма, у которого из середины шатуна АС (точка В) проведен отрезок р, составляющий с ним угол а. Такое задание конца отрезка — точки К — дает возможность исследовать траектории всех точек, лежащих в плоскости шатуна. Напишем выражение для координат точки К. [c.94]
Плоскость, параллельная данной проецирующей плоскости (рис. 186) и проходящая через данную точку, может быть задана одной своей проекцией. Чтобы построить плоскость 2, параллельную фронтально-проецирующей плоскости АВС и проходящую через точку О, нужно через точку О г провести прямую 2.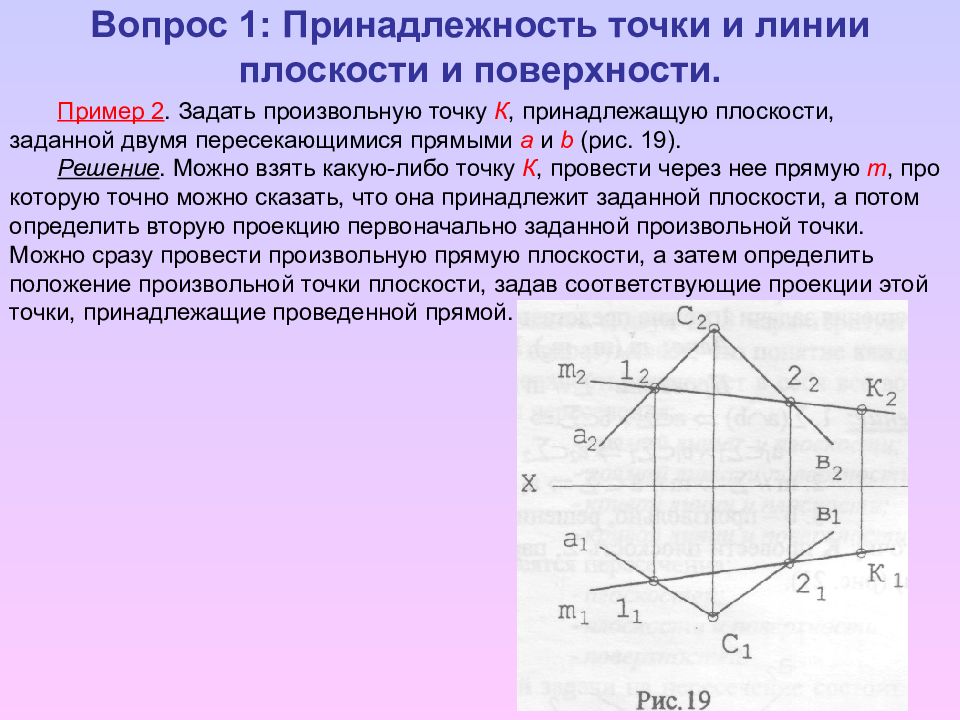 параллельно фронтальной проекции треугольника АВС, проецирующегося на плоскость Пг в отрезок прямой линии. При необходимости горизонтальная проекция плоскости 2 может быть задана произвольно взятыми горизонтальными проекциями прямых о и 6, лежащих в плоскости О и проходящих через точку О.
[c.114]
параллельно фронтальной проекции треугольника АВС, проецирующегося на плоскость Пг в отрезок прямой линии. При необходимости горизонтальная проекция плоскости 2 может быть задана произвольно взятыми горизонтальными проекциями прямых о и 6, лежащих в плоскости О и проходящих через точку О.
[c.114]
Проведя через точку к линию проекционной связи, отметим точку к и соединим ее с точкой а. На продолжении горизонтальной проекции ак отрезка прямой АК найдем точку т. Точка N хотя и лежит вне контура треугольника АВС, но принадлежит его плоскости. При решении подобных задач предполагается, что плоскость бесконечна и лишь задана треугольником. Поэтому точка, лежащая в плоскости треугольника, может быть расположена как внутри его контура, так и вне его. [c.81]
Построение перспективы плоских фигур основывается иа знании и умении выполнять перспективу отрезка прямой и угла, лежащих в совмещенной предметной плоскости Н». Совмещенную точку зрения С,, брать на расстоянии от горизонта примерно равном полутора диагоналям картины. [c.103]
[c.103]
Направление световых колебаний в точке О определится, если из центра линзы С провести прямые СО и С1, параллельные направлению луча, выходящего из призмы и оптич. оси. Колебания необыкновенного луча происходят в плоскости главного сечения, поэтому плоскость OI и будет плоскостью колебаний в точке О. Для всякой другой светящейся точки изображение получится в другом месте плоскости Р, и следовательно плоскость колебания будет несколько повернута. Для всех точек, лежащих в плоскости изображения Р на прямой [c.146]
Если точка принадлежит плоскости в пространстве, то проекции этой точки принадлежат соответствующим проекциям какой-либо прямой, лежащей в данной плоскости (в соответствии с рисунком 2.8 прямая АВ и принадлежащая ей точка 1 прямая ВС и принадлежащая ей точка 2). В данном примере -и точка М принадлежит плоскости треугольника ЛВС, т.к. точка М расположена на прямой А-2, лежащей в плоскости треугольника.
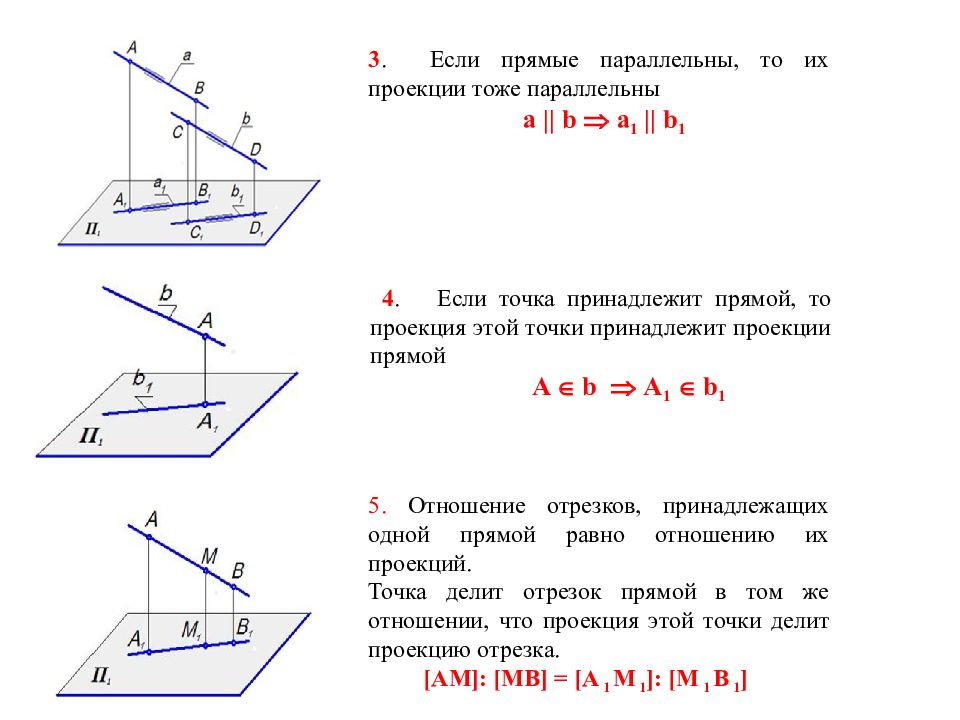 При этом следует отметить, что плоскость безгранична, поэтому некоторые построения могут выходить за пределы треугольника.
[c.24]
При этом следует отметить, что плоскость безгранична, поэтому некоторые построения могут выходить за пределы треугольника.
[c.24]Возьмем на заданной прямой произвольную точку с проекциями Е, е к будем искать точку, в которой она при своем движении встречает плоскость сечения. Прежде всего, эта точка опишет вокруг оси вращения дугу горизонтального круга, горизонтальную проекцию которого получим, описывая из точки А, как из центра, радиусом АЕ дугу ЕР до ее встречи с прямой Ар в некоторой точке Р вертикальную проекцию этой дуги получим, проводя через точку е (неопределенную) горизонталь е/. Следовательно, точка Р будет горизонтальной проекцией встречи вращающейся точки с плоскостью сечения поэтому, если проектировать точку Р в f на е/, то точка / будет вертикальной проекцией этой точки встречи и, следовательно, точкой, лежащей в плоскости сечения. Если мы повторим этн операции для любого числа других точек, взятых на заданной прямой, мы получим столько же точек д, /, г, п. через которые пройдет искомая кривая.
[c.86]
через которые пройдет искомая кривая.
[c.86]
Одна проекция прямой в общем случае не определяет ее положения в п р о с т р а н с т в е. В самом деле, если нам дана проекция т некоторой прямой т и направление проектирования /, то мы легко можем провести ту плоскость ср, которая ее проектировала (рис. 7, б). Но указа ь положение прямой т в этой плоскости без дополнительных условий мы не можем, так как любая прямая (кроме проектирующих), лежащая в плоскости ср, имеет л своей проекцией. [c.13]
Каждый конкретный тиристор отпирается в определенной точке, лежащей в плоскости, ограниченной кривыми л и и горизонтальной и вертикальной прямыми, соответствующими данной температуре. Линии с надписями 100, 50 и 25 % характеризуют предельно допустимую пиковую мощность рассеяния на управляющем р-п переходе 100 % — при управлении постоянным током 50 и 25 % —при импульсном управлении со скважностью соответственно 2 и 4. [c.177]
Если плоскость задана не следами, а какой-либо фигурой, например треугольником B D (рис.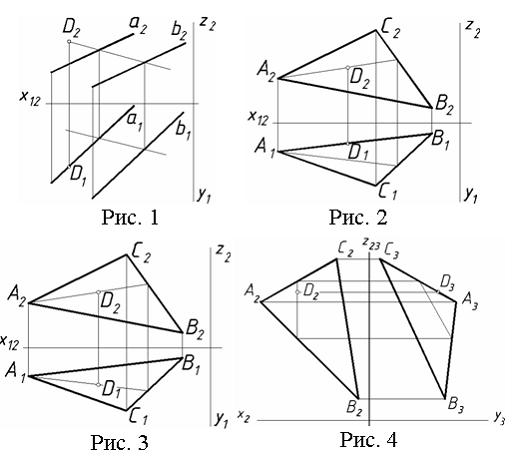 116,6), то прямую, лежащую в плоскости этого треугольника, удобнее провести через какую-либо вершину треугольника, например через вершину В. На рис. 116,6 проведена фронтальная проекция Ь е такой прямой. Проводя через точку е линию связи, находим горизонтальную проекцию е точки Е. Прямая BE лежит в плоскости треугольника B D. Как и в предыдущем примере, через заданные проекции а ]Л а точки Л проводим искомые проекции прямой AF параллельно проекциям прямой BE.
[c.66]
116,6), то прямую, лежащую в плоскости этого треугольника, удобнее провести через какую-либо вершину треугольника, например через вершину В. На рис. 116,6 проведена фронтальная проекция Ь е такой прямой. Проводя через точку е линию связи, находим горизонтальную проекцию е точки Е. Прямая BE лежит в плоскости треугольника B D. Как и в предыдущем примере, через заданные проекции а ]Л а точки Л проводим искомые проекции прямой AF параллельно проекциям прямой BE.
[c.66]
Если одну из проекций (например, фронтальную) перемещать параллельно ей самой в направлении линий связи, то горизонтальная и смещенная фронтальная проекции представят чертеж отрезка прямой, лежащей в плоскости, параллельной биссекторной плоскости. Так, отрезок rs, г в прямой принадлежит плоскости, параллельной первой биссекторной плоскости. Отрезок tu, t и принадлежит плоскости, параллельной второй биссекторной плоскости. [c.33]
Найти недостающую проекцию точки К, лежащей в плоскости, заданной прямой АВ и точкой С (рис. 44, а).
[c.32]
44, а).
[c.32]
II. ТОЧКА И ПРЯМАЯ ЛИНИЯ, ЛЕЖАЩИЕ В ПЛОСКОСТИ [c.22]
Точки, определяющие прямую, могут быть и точками общего положения (черт. 26) и точками,- лежащими на плоскостях проекций (черт. 29, 30, 31), Во втором случае они называются следами прямой линии и являются точками пересечения ее с плоскостями проекций. Точка Н пересечения прямой с горизонтальной плоскостью проекций нязывается горизонтальным следом, а точка F пересечения с плоскостью Л2 — фронтальным. ОтрезЬк прямой а, ограниченный этими точками (черт. 30), находится в I четверти пространства. Слева от точки Н прямая расположена в IV четверти, а справа от точки F — во II, Прямая Ь на черт. 31 определена фронтальным следом F и профильным Р. [c.11]
Условия равновесия плоской системы сил можно сформулировать и гак равновесия плоской системы сил, при-ло.жеппых к твердому телу, необходимо н достаточно, чтобы суммы алгебраических моментов сил относительно двух любых точек, лежащих в плоскости действия сил, были равны нулю и алгебраическая сумма проекций этих сил на какую-либо ось плоскости, не перпендикулярную прямой, проходящей через две моментные точки, также была равна нулю, т.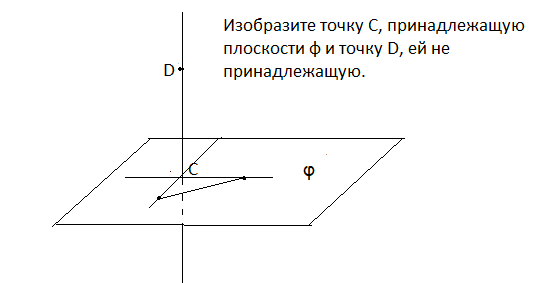 е.
[c.53]
е.
[c.53]
Обычно проекциями точек, лежащих в плоскости, проходящей через центр проекций S и параллельной плоскости проекций П, принято считать бесконечно удаленные точки плоскости П, так как для этих точек проецирующие прямые оказываются параллельными плоскости проекций П. Эднако для центра проекций S не может быть построена проекция, гак как проецирующая прямая становится при этом неопределенной, вместе с тем становится неопределенной и проекция точки S на плоскости П. [c.12]
Точку пересечения плоскости ЛЛ1Л2 с осью проекций х как точку, принадлежащую одновременно обеим плоскостям П1 и Пг, обозначим Л12. Прямые Л12Л1 и Л12Лг, лежащие в плоскости Л ЛИг, перпендикулярной к оси проекций X, перпендикулярны к этой оси. [c.51]
Для установления закона движения точки струны (x = Xq) необходимо пересечь noBepxHO jb у(х, t) плоскостью x = Xq. Допустим, что x d. В плоскости ХОг.построим прямую x — t d. Очевидно, y f (x — t)j2 f d)l2, т. е. поверхность у—у х, f) имеет одну и ту же ординату у для всех точек, лежащих в плоскости Xt на прямой x t-j-d, а именно такую, какую она имела для значения времени / = 0. Это значит, что если в начальный момент времени для точки
[c.98]
е. поверхность у—у х, f) имеет одну и ту же ординату у для всех точек, лежащих в плоскости Xt на прямой x t-j-d, а именно такую, какую она имела для значения времени / = 0. Это значит, что если в начальный момент времени для точки
[c.98]
Главные линии плоскости. Через точку, лежащую в плоскости, можно провести бесчисленное множество прямых, принадлежащих плоскости и различно наклоненных к плоскостям проекций Но среди них только одна прямая будет параллельна плоскости Я, одна — параллельна плоскости V и одна — параллельна плоскости W. Такими прямьши являются горизонталь, фронталь и профильная прямая плоскости. На 125 рис. 125 показаны горизонталь и фронталь. [c.82]
Для построения перспективы двух параллельных прямых АВ и ОЕ, лежащих в плоскости Т, нужно заключить их в две проектирующие 246 плоскости М тй Р общего положения (рис. 246), которые пересекаются по прямой СР, параллельной заданным прямым.
 Так как прямые АВ и ОЕ лежат в горизоитальной плоскости Т, то и прямая СР будет горизонтальна и пересечет плоскость К в точке Р, лежащей на горизонте. Точка Р называется точкой схода горизонтальных параллельных прямых.
[c.175]
Так как прямые АВ и ОЕ лежат в горизоитальной плоскости Т, то и прямая СР будет горизонтальна и пересечет плоскость К в точке Р, лежащей на горизонте. Точка Р называется точкой схода горизонтальных параллельных прямых.
[c.175]Точку пересечения плоскости АА1А2 с осью проекций л как точку, принадлежащую одновременно обеим плоскостям П1 и Пг, обозначим А12. Прямые А/2А1 и АцАг, лежащие в плоскости АА1А2, перпендикулярной к оси проекций х, перпендикулярны к этой оси. Обратно, пусть А12 — произвольная точка оси проекций X. Восставим из точки А/2 к оси два перпендикуляра один в плоскости Пг, ДруГОЙ В плоскости П2- [c.7]
Итак, точка N обладает тем свойством, что, взяв её за центр приведения, мы получаем силу, равную главному вектору Я, приложенную в точке М, и пару, момент которой уЙц параллелен силе Я, а плоскость которой, следовательно, перпендикулярна к силе Я- Система силы и пары, лежащей в плоскости, перпендикулярной к силе, называется винтовым усилием, силовым винтом или динамой.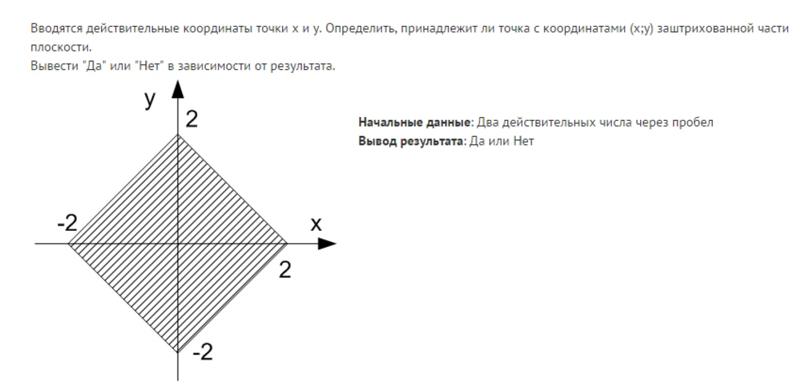 Очевидно, указанным свойством обладают не только точка Ы, но и все точки прямой ЫР, проходящей через N и параллельной главному вектору, ибо точку приложения силы Я можно перенести в любую точку этой ее линии дейсгвия.
[c.105]
Очевидно, указанным свойством обладают не только точка Ы, но и все точки прямой ЫР, проходящей через N и параллельной главному вектору, ибо точку приложения силы Я можно перенести в любую точку этой ее линии дейсгвия.
[c.105]
Проекции плоскости на комплексном чертеже будут различны в 5ависимости от того, чем она задана. Как известно из геометрии, плоскость может быть задана а) тремя точками, не лежащими на одной прямой б) прямой линией и точкой, лежащей вне этой прямой в) двумя пересекающимися прямыми г) двумя параллельными прямыми. [c.58]
Пусть даны две плоские кривые линии А В и D, лежащие в одной плоскости (рис. 484). Эти кривые считаем опорными. Пометим на каждой из них некоторое одинаковое число точек. Через каждую точку кривой АВ проведем пучок прямых, пересекающих в помеченных точках кривую D. Отрезки прямых пучка, ограниченные центром, например точкой А, и точками кривой D, разделим в заданном отнощении т п. Геометрическим местом точек деления является кривая линия oDo, параллельная и пропор-Пйональная кривой D.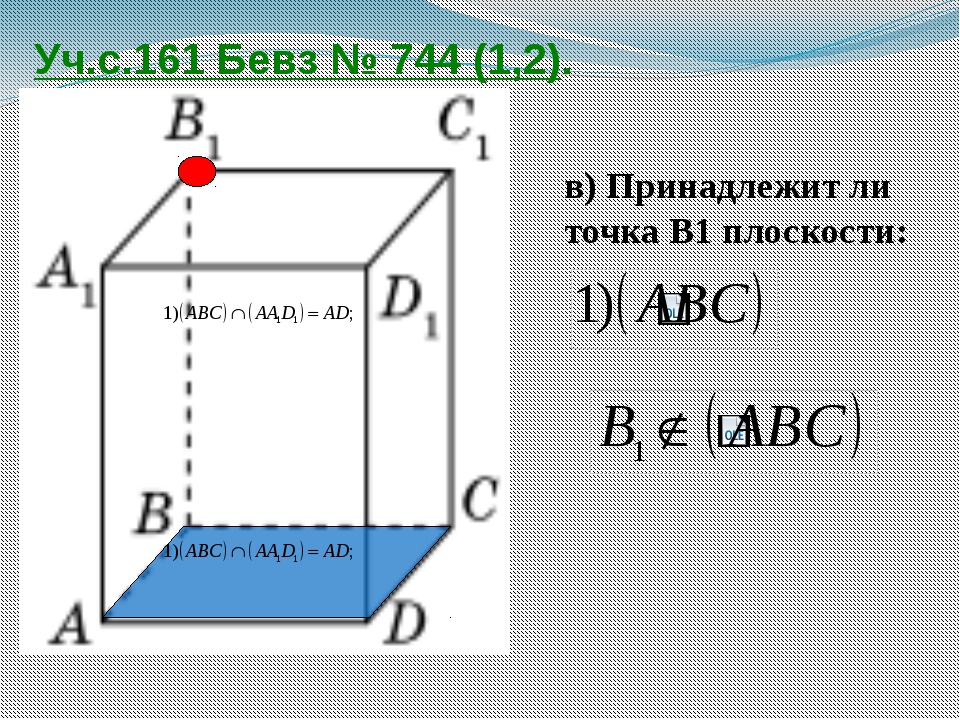 [c.360]
[c.360]
MN И MS (прямую MS проводим через вершину пирамиды). Эта вспомогательная плоскость пересечет основание пирамиды (лежащее в плоскости II По) по прямой N2P2, параллельной горизонтали MS, а боковые грани пирамиды — по двум прямым SP и SQ. Точки Ки L, в которых прямые SP и SQ пересекаются с заданной прямой MN, и будут точками, общими для заданной прямой и поверхности пирамиды, т. е. точками пересечения прямой с пирамидой. [c.192]
Парабола — множество точек плоскости, равноудаленных от точки (фокуса) и прямой (направляющей, директрисы), лежащих в этой же плоскости (рис. 3.45). Величина р — расстояние между фокусом и направляющей — параметр параболы. На этом свойстве основано построение параболы по заданным фокусу Р и направляющей (рис. 3.46). Через фокус проводят главный диаметр (ось) параболы перпендикулярно направляющей. Отрезок НР делят пополам и находят вершину А параболы. На оси вправо от точки А отмечают несколько произвольно выбранных точек, проводят через них вспомогательные прямые, перпендикулярные оси, и делают на них из фокуса Р засеч-
[c. 68]
68]
точек, линий и плоскостей
Точки, линии и плоскости
Точка , линия и плоскость вместе с , установленным , являются неопределенными терминами, которые обеспечивают отправную точку для геометрии. Когда мы определяем слова, мы обычно используем более простые слова, а эти более простые слова, в свою очередь, определяются с помощью еще более простых слов. В конечном итоге этот процесс должен прекратиться; на каком-то этапе в определении должно использоваться слово, значение которого интуитивно понятно.Поскольку это значение принимается без определения, мы называем эти слова неопределенными терминами . Эти термины будут использоваться для определения других терминов. Хотя эти термины не имеют формального определения, необходимо их краткое интуитивное обсуждение.
точка
точка — самый фундаментальный объект в геометрии. Он обозначен точкой и назван заглавной буквой. Точка представляет только позицию; он имеет нулевой размер (то есть нулевую длину, нулевую ширину и нулевую высоту).На рисунке 1 показана точка C , точка M и точка Q .
Он обозначен точкой и назван заглавной буквой. Точка представляет только позицию; он имеет нулевой размер (то есть нулевую длину, нулевую ширину и нулевую высоту).На рисунке 1 показана точка C , точка M и точка Q .
Рисунок 1
Три очка.
Линия
Линия (прямая линия ) можно рассматривать как связанный набор из бесконечного множества точек.Он распространяется бесконечно далеко в двух противоположных направлениях. Линия имеет бесконечную длину, нулевую ширину и нулевую высоту. Назовите его любыми двумя точками на линии. Символ ↔, написанный над двумя буквами, используется для обозначения этой строки. Линия также может быть названа одной маленькой буквой (рисунок 2).
Рисунок 2
Две линии.
Коллинеарные точки
Точки, лежащие на одной линии, называются коллинеарными точками .Если нет линии, на которой лежат все точки, то это неколлинеарных точек . На рисунке 3 точки M, A и N коллинеарны, а точки T, I и C неколлинеарны.
Рисунок 3 Три коллинеарные точки и три неколлинеарные точки.
Самолет
Плоскость может рассматриваться как бесконечный набор точек, образующих соединенную плоскую поверхность, бесконечно далеко простирающуюся во всех направлениях.Плоскость имеет бесконечную длину, бесконечную ширину и нулевую высоту (или толщину). Обычно он изображается на чертежах в виде четырехугольной фигуры. Для обозначения самолета используется одна заглавная буква. Слово plane — это , написанное с буквы, чтобы не путать с точкой (рис. 4 ).
Рисунок 4 Две плоскости.
12,5 линий и плоскостей
Линии и плоскости, пожалуй, самые простые из кривых и поверхностей в трехмерное пространство.Они также окажутся важными, поскольку мы стремимся понимать более сложные кривые и поверхности.
Уравнение прямой в двух измерениях: $ ax + by = c $; это разумно ожидать, что линия в трех измерениях задано $ ax + by + cz = d $; разумно, но неверно — оказывается, что это уравнение плоскости.
Самолет не имеет очевидного «направления», как линия. можно очень удобно связать плоскость с направлением, однако: есть ровно два направления, перпендикулярных к самолет.Любой вектор с одним из этих двух направлений называется нормальный к плоскости. Итак, хотя есть много нормальных векторов к данной плоскости, все они параллельно или антипараллельно друг другу.
Предположим, что две точки $ \ ds (v_1, v_2, v_3) $ и $ \ ds (w_1, w_2, w_3) $ находятся на плоскости;
то вектор $ \ ds \ langle w_1-v_1, w_2-v_2, w_3-v_3 \ rangle $ параллелен
к самолету; в частности, если этот вектор поместить хвостом в
$ \ ds (v_1, v_2, v_3) $, то его голова находится в $ \ ds (w_1, w_2, w_3) $, и он лежит в
самолет.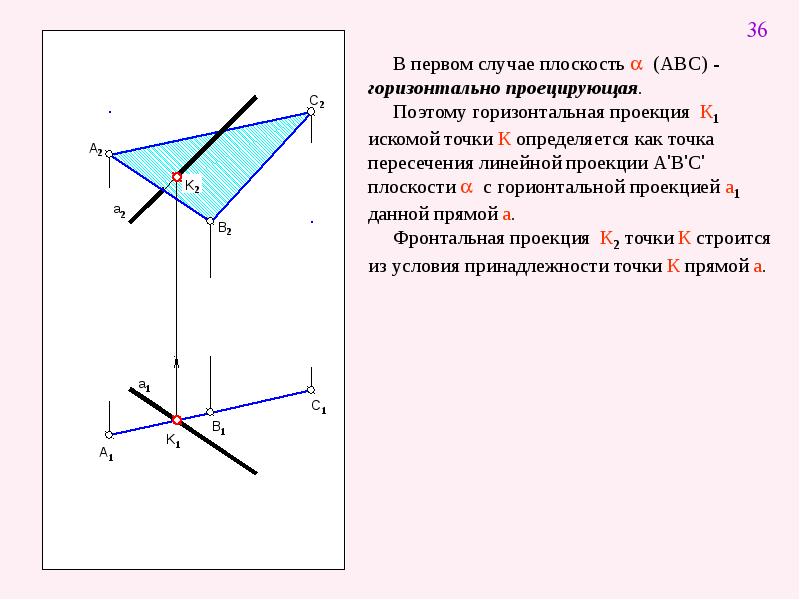 В результате любой вектор, перпендикулярный плоскости, равен
перпендикулярно к $ \ ds \ langle w_1-v_1, w_2-v_2, w_3-v_3 \ rangle $. Фактически, это
Нетрудно заметить, что самолет состоит из , а именно таких точек
$ \ ds (w_1, w_2, w_3) $, для которого $ \ ds \ langle w_1-v_1, w_2-v_2, w_3-v_3 \ rangle $
перпендикулярно нормали к плоскости, как указано в
рисунок 12.5.1. То есть предположим
мы знаем, что $ \ langle a, b, c \ rangle $ нормально к плоскости, содержащей
точка $ \ ds (v_1, v_2, v_3) $. Тогда $ (x, y, z) $ находится в плоскости тогда и только тогда, когда
если $ \ langle a, b, c \ rangle $ перпендикулярно $ \ ds \ langle
x-v_1, y-v_2, z-v_3 \ rangle $.В свою очередь, мы знаем, что это правда
именно тогда, когда $ \ ds \ langle a, b, c \ rangle \ cdot \ langle
x-v_1, y-v_2, z-v_3 \ rangle = 0 $. Таким образом, $ (x, y, z) $ находится в плоскости, если и
только если
$$ \ eqalign {
\ langle a, b, c \ rangle \ cdot \ langle x-v_1, y-v_2, z-v_3 \ rangle & = 0 \ cr
а (x-v_1) + b (y-v_2) + c (z-v_3) & = 0 \ cr
ax + by + cz-av_1-bv_2-cv_3 & = 0 \ cr
ax + by + cz & = av_1 + bv_2 + cv_3.
В результате любой вектор, перпендикулярный плоскости, равен
перпендикулярно к $ \ ds \ langle w_1-v_1, w_2-v_2, w_3-v_3 \ rangle $. Фактически, это
Нетрудно заметить, что самолет состоит из , а именно таких точек
$ \ ds (w_1, w_2, w_3) $, для которого $ \ ds \ langle w_1-v_1, w_2-v_2, w_3-v_3 \ rangle $
перпендикулярно нормали к плоскости, как указано в
рисунок 12.5.1. То есть предположим
мы знаем, что $ \ langle a, b, c \ rangle $ нормально к плоскости, содержащей
точка $ \ ds (v_1, v_2, v_3) $. Тогда $ (x, y, z) $ находится в плоскости тогда и только тогда, когда
если $ \ langle a, b, c \ rangle $ перпендикулярно $ \ ds \ langle
x-v_1, y-v_2, z-v_3 \ rangle $.В свою очередь, мы знаем, что это правда
именно тогда, когда $ \ ds \ langle a, b, c \ rangle \ cdot \ langle
x-v_1, y-v_2, z-v_3 \ rangle = 0 $. Таким образом, $ (x, y, z) $ находится в плоскости, если и
только если
$$ \ eqalign {
\ langle a, b, c \ rangle \ cdot \ langle x-v_1, y-v_2, z-v_3 \ rangle & = 0 \ cr
а (x-v_1) + b (y-v_2) + c (z-v_3) & = 0 \ cr
ax + by + cz-av_1-bv_2-cv_3 & = 0 \ cr
ax + by + cz & = av_1 + bv_2 + cv_3. \ cr
} $$
Работая в обратном направлении, обратите внимание, что если $ (x, y, z) $ — точка, удовлетворяющая
$ ax + by + cz = d $, тогда
$$ \ eqalign {
ах + по + cz & = d \ cr
ах + по + cz-d & = 0 \ cr
a (x-d / a) + b (y-0) + c (z-0) & = 0 \ cr
\ langle a, b, c \ rangle \ cdot \ langle x-d / a, y, z \ rangle & = 0.\ cr
} $$
А именно, $ \ langle a, b, c \ rangle $ перпендикулярно вектору с
хвост в точке $ (d / a, 0,0) $ и голова в точке $ (x, y, z) $. Это означает, что точки
$ (x, y, z) $, которые удовлетворяют уравнению $ ax + by + cz = d $, образуют плоскость
перпендикулярно $ \ langle a, b, c \ rangle $. (Это не
работают, если $ a = 0 $, но в этом случае мы можем использовать $ b $ или $ c $ в роли
$ a $. То есть либо $ a (x-0) + b (y-d / b) + c (z-0) = 0 $, либо
$ a (x-0) + b (y-0) + c (z-d / c) = 0 $.)
\ cr
} $$
Работая в обратном направлении, обратите внимание, что если $ (x, y, z) $ — точка, удовлетворяющая
$ ax + by + cz = d $, тогда
$$ \ eqalign {
ах + по + cz & = d \ cr
ах + по + cz-d & = 0 \ cr
a (x-d / a) + b (y-0) + c (z-0) & = 0 \ cr
\ langle a, b, c \ rangle \ cdot \ langle x-d / a, y, z \ rangle & = 0.\ cr
} $$
А именно, $ \ langle a, b, c \ rangle $ перпендикулярно вектору с
хвост в точке $ (d / a, 0,0) $ и голова в точке $ (x, y, z) $. Это означает, что точки
$ (x, y, z) $, которые удовлетворяют уравнению $ ax + by + cz = d $, образуют плоскость
перпендикулярно $ \ langle a, b, c \ rangle $. (Это не
работают, если $ a = 0 $, но в этом случае мы можем использовать $ b $ или $ c $ в роли
$ a $. То есть либо $ a (x-0) + b (y-d / b) + c (z-0) = 0 $, либо
$ a (x-0) + b (y-0) + c (z-d / c) = 0 $.)
Рисунок 12.5.1. Плоскость, определяемая векторами, перпендикулярными нормали.
Таким образом, по вектору $ \ langle a, b, c \ rangle $ мы знаем, что все плоскости
перпендикулярные этому вектору имеют вид $ ax + by + cz = d $, а любая поверхность
такой формы — плоскость, перпендикулярная к $ \ langle a, b, c \ rangle $.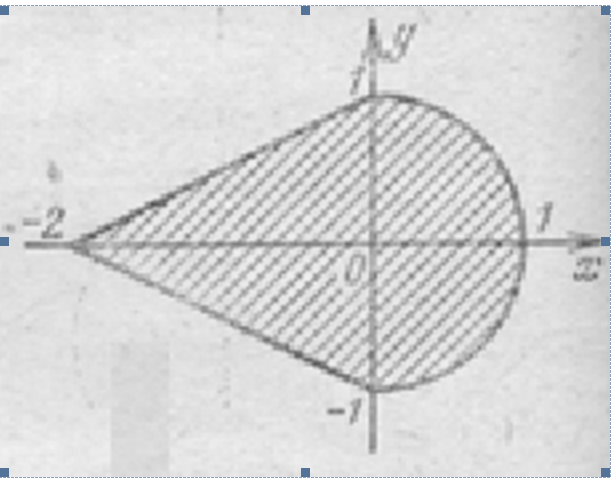
Пример 12.5.1 Найдите уравнение плоскости, перпендикулярной $ \ langle 1,2,3 \ rangle $. и содержащий точку $ (5,0,7) $.
Используя вывод выше, плоскость равна $ 1x + 2y + 3z = 1 \ cdot5 + 2 \ cdot0 + 3 \ cdot7 = 26 $. Поочередно мы знать, что плоскость равна $ x + 2y + 3z = d $, и чтобы найти $ d $, мы можем заменить известная точка на плоскости, чтобы получить $ 5 + 2 \ cdot0 + 3 \ cdot7 = d $, поэтому $ d = 26 $.Мы также могли бы записать это просто как $ (x-5) +2 (y) +3 (z-7) = 0 $, что для много целей прекрасное представление; его всегда можно приумножить чтобы дать $ x + 2y + 3z = 26 $. $ \ квадрат $
Пример 12.5.2 Найдите вектор, нормальный к плоскости $ 2x-3y + z = 15 $.
Один из примеров — $ \ langle 2, -3,1 \ rangle $. Любой вектор, параллельный или антипараллельность этому тоже работает, например, $ -2 \ langle 2, -3,1 \ rangle = \ langle -4,6, -2 \ rangle $ также перпендикулярно плоскости. $ \ квадрат $
Нам часто нужно будет найти уравнение для плоскости при определенных
информация о самолете. Хотя иногда может быть немного
короче способы добраться до желаемого результата, всегда можно, и
обычно рекомендуется использовать данную информацию, чтобы найти нормальный
плоскости и точки на плоскости, а затем найти уравнение как
выше.
Хотя иногда может быть немного
короче способы добраться до желаемого результата, всегда можно, и
обычно рекомендуется использовать данную информацию, чтобы найти нормальный
плоскости и точки на плоскости, а затем найти уравнение как
выше.
Пример 12.5.3 Плоскости $ x-z = 1 $ и $ y + 2z = 3 $ пересекаются по прямой. Найди третья плоскость, которая содержит эту линию и перпендикулярна плоскости $ x + y-2z = 1 $.
Прежде всего отметим, что две плоскости перпендикулярны тогда и только тогда, когда их
векторы нормалей перпендикулярны.Таким образом, ищем вектор $ \ langle
a, b, c \ rangle $, то есть
перпендикулярно к $ \ langle 1,1, -2 \ rangle $. Кроме того, поскольку
желаемая плоскость должна содержать определенную линию $ \ langle
a, b, c \ rangle $ должны быть перпендикулярны любому вектору, параллельному этому
линия. Поскольку $ \ langle
a, b, c \ rangle $ должны быть перпендикулярны двум векторам, мы можем найти это по
вычисление перекрестного произведения двух. Итак, нам нужна векторная параллель
до линии пересечения данных плоскостей.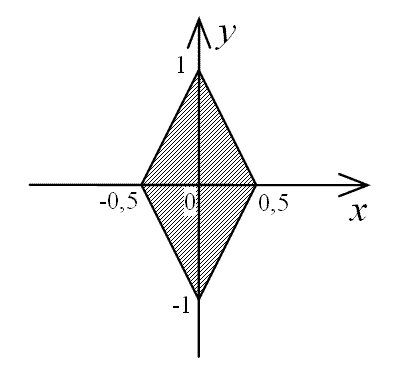 Для этого достаточно
знать две точки на линии.Чтобы найти две точки на этой линии, мы
должен найти две точки, которые одновременно находятся на двух плоскостях,
$ x-z = 1 $ и $ y + 2z = 3 $. Любая точка на обеих плоскостях удовлетворит
$ x-z = 1 $ и $ y + 2z = 3 $. Легко найти значения для $ x $ и $ z $
удовлетворяющие первому, например, $ x = 1, z = 0 $ и $ x = 2, z = 1 $. потом
мы можем найти соответствующие значения для $ y $, используя второе уравнение,
а именно $ y = 3 $ и $ y = 1 $, поэтому
$ (1,3,0) $ и $ (2,1,1) $ оба на линии
пересечения, потому что оба находятся на обеих плоскостях. В настоящее время
$ \ langle 2-1,1-3,1-0 \ rangle = \ langle 1, -2,1 \ rangle $ параллельно
линия.Наконец, мы можем выбрать $ \ langle a, b, c \ rangle = \ langle
1,1, -2 \ rangle \ times \ langle 1, -2,1 \ rangle = \ langle -3, -3, -3 \ rangle $.
Хотя этот вектор отлично подойдет, любой вектор, параллельный или
антипараллельность к нему тоже будет работать, поэтому, например, мы можем выбрать
$ \ langle 1,1,1 \ rangle $, антипараллельно ему.
Для этого достаточно
знать две точки на линии.Чтобы найти две точки на этой линии, мы
должен найти две точки, которые одновременно находятся на двух плоскостях,
$ x-z = 1 $ и $ y + 2z = 3 $. Любая точка на обеих плоскостях удовлетворит
$ x-z = 1 $ и $ y + 2z = 3 $. Легко найти значения для $ x $ и $ z $
удовлетворяющие первому, например, $ x = 1, z = 0 $ и $ x = 2, z = 1 $. потом
мы можем найти соответствующие значения для $ y $, используя второе уравнение,
а именно $ y = 3 $ и $ y = 1 $, поэтому
$ (1,3,0) $ и $ (2,1,1) $ оба на линии
пересечения, потому что оба находятся на обеих плоскостях. В настоящее время
$ \ langle 2-1,1-3,1-0 \ rangle = \ langle 1, -2,1 \ rangle $ параллельно
линия.Наконец, мы можем выбрать $ \ langle a, b, c \ rangle = \ langle
1,1, -2 \ rangle \ times \ langle 1, -2,1 \ rangle = \ langle -3, -3, -3 \ rangle $.
Хотя этот вектор отлично подойдет, любой вектор, параллельный или
антипараллельность к нему тоже будет работать, поэтому, например, мы можем выбрать
$ \ langle 1,1,1 \ rangle $, антипараллельно ему.
Теперь мы знаем, что $ \ langle 1,1,1 \ rangle $ нормальна к искомой плоскости. а $ (2,1,1) $ — точка на плоскости. Следовательно, уравнение Самолет $ x + y + z = 4 $. В качестве быстрой проверки, поскольку $ (1,3,0) $ также находится на линия, она должна быть на плоскости; так как $ 1 + 3 + 0 = 4 $, мы видим, что это действительно так.
Обратите внимание, что если бы мы использовали $ \ langle -3, -3, -3 \ rangle $ как нормальные, мы открыли бы уравнение $ -3x-3y-3z = -12 $, тогда мы могли бы заметили, что мы можем разделить обе стороны на $ -3 $, чтобы получить эквивалент $ x + y + z = 4 $. $ \ квадрат $
Итак, теперь мы понимаем уравнения плоскостей; давайте обратимся к линий. К сожалению, оказывается довольно неудобно представляют собой типичную линию с одним уравнением; нам нужно подойти линии по-другому.
В отличие от самолета, трехмерная линия имеет очевидную
направление, а именно направление любого параллельного ему вектора.По факту
линию можно определить и однозначно идентифицировать, указав одну точку
на прямой и вектор, параллельный прямой (в одном из двух возможных
направления).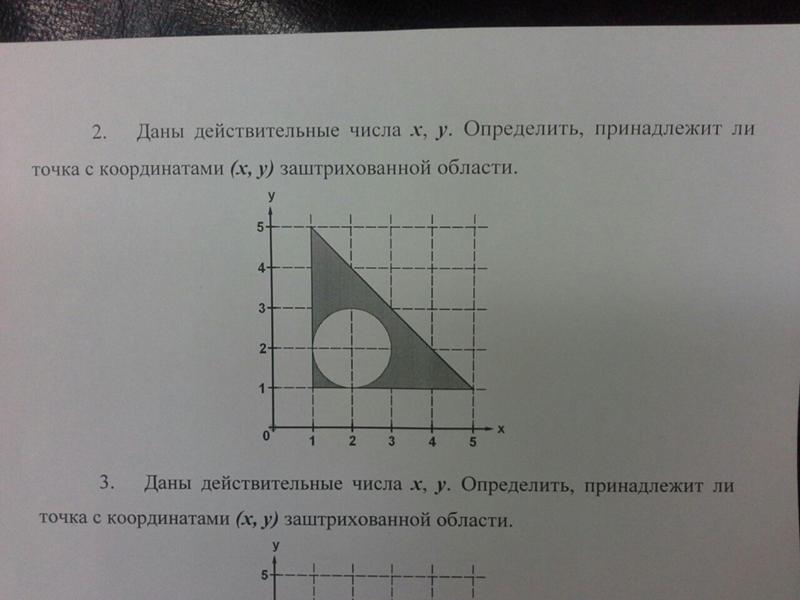 То есть линия состоит именно из тех точек, которые мы можем
достичь, начав с точки и пройдя некоторое расстояние в
направление вектора. Давайте посмотрим, как мы можем перевести это на большее
математический язык.
То есть линия состоит именно из тех точек, которые мы можем
достичь, начав с точки и пройдя некоторое расстояние в
направление вектора. Давайте посмотрим, как мы можем перевести это на большее
математический язык.
Предположим, что линия содержит точку $ \ ds (v_1, v_2, v_3) $ и параллельна
к вектору $ \ langle a, b, c \ rangle $; мы называем $ \ langle a, b, c \ rangle $ a
вектор направления для линии.Если поместить вектор $ \ ds
\ langle v_1, v_2, v_3 \ rangle $ хвостом в начале координат и головой
в $ \ ds (v_1, v_2, v_3) $, а если поместить вектор $ \ langle
a, b, c \ rangle $ хвостом в точке $ \ ds (v_1, v_2, v_3) $, затем голова
$ \ langle a, b, c \ rangle $ находится в точке на прямой. Мы можем добраться до любой точки на линии, проделав то же самое, за исключением использования
$ t \ langle a, b, c \ rangle $ вместо $ \ langle a, b, c \ rangle $, где $ t $
какое-то реальное число. Из-за того, как работает сложение векторов,
точка в голове вектора $ t \ langle a, b, c \ rangle $ — это точка
во главе вектора $ \ ds \ langle v_1, v_2, v_3 \ rangle + t \ langle
a, b, c \ rangle $, а именно $ \ ds (v_1 + ta, v_2 + tb, v_3 + tc) $; видеть
рисунок 12. 5.2.
5.2.
Рисунок 12.5.2. Векторная форма линии.
Другими словами, когда $ t $ пробегает все возможные действительные значения, вектор $ \ ds \ langle v_1, v_2, v_3 \ rangle + t \ langle a, b, c \ rangle $ указывает на каждая точка на линии, когда ее хвост находится в начале координат. Другой обычный способ написать это как набор параметрических уравнений : $$ x = v_1 + ta \ qquad y = v_2 + tb \ qquad z = v_3 + tc. $$ Иногда бывает полезно использовать эту форму линии даже в двух Габаритные размеры; векторная форма для прямой в плоскости $ x $ — $ y $ имеет вид $ \ ds \ langle v_1, v_2 \ rangle + t \ langle a, b \ rangle $, что совпадает с $ \ ds \ langle v_1, v_2,0 \ rangle + t \ langle a, b, 0 \ rangle $.
Пример 12.5.4 Найдите векторное выражение для линии, проходящей через $ (6,1, -3) $ и
$ (2,4,5) $. Чтобы получить вектор, параллельный прямой, вычтем $ \ langle
6,1, -3 \ rangle- \ langle2,4,5 \ rangle = \ langle 4, -3, -8 \ rangle $. Линия
тогда задается как $ \ langle 2,4,5 \ rangle + t \ langle 4, -3, -8 \ rangle $; там
конечно, есть много других возможностей, например $ \ langle
6,1, -3 \ rangle + t \ langle 4, -3, -8 \ rangle $.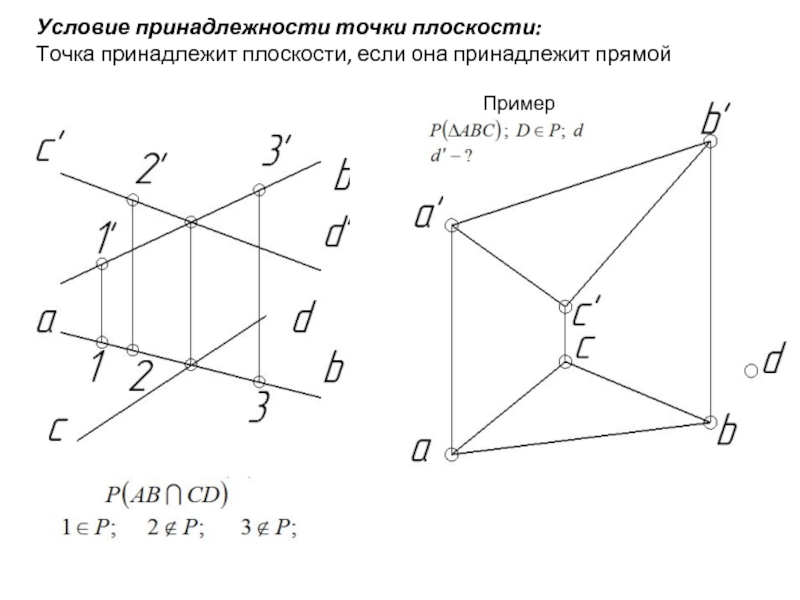 $ \ квадрат $
$ \ квадрат $
Пример 12.5.5 Определите, соответствуют ли линии $ \ langle 1,1,1 \ rangle + t \ langle 1,2, -1 \ rangle $ и $ \ langle 3,2,1 \ rangle + t \ langle -1, -5,3 \ rangle $ параллельны, пересекаются или ни один.
В двух измерениях две линии либо пересекаются, либо параллельны; в
В трех измерениях линии, которые не пересекаются, могут не быть параллельны.
В этом случае, поскольку векторы направления для линий не
параллельные или антипараллельные, мы знаем, что линии не параллельны.
Если они пересекаются, должно быть два значения $ a $ и $ b $, чтобы
$ \ langle 1,1,1 \ rangle + a \ langle 1,2, -1 \ rangle =
\ langle 3,2,1 \ rangle + b \ langle -1, -5,3 \ rangle $, то есть
$$ \ eqalign {
1 + a & = 3-b \ cr
1 + 2a & = 2-5b \ cr
1-а & = 1 + 3b \ cr
} $$
Это дает три уравнения с двумя неизвестными, поэтому может быть, а может и не быть
решение в целом.В этом случае легко обнаружить, что $ a = 3 $
и $ b = -1 $ удовлетворяет всем трем уравнениям, поэтому прямые пересекаются в
точка $ (4,7; -2) $. $ \ квадрат $
$ \ квадрат $
Пример 12.5.6 Найти расстояние от точки $ (1,2,3) $ до плоскости. $ 2x-y + 3z = 5 $. Расстояние от точки $ P $ до плоскости — кратчайшее. расстояние от $ P $ до любой точки на плоскости; это расстояние, отсчитываемое от $ P $ перпендикулярно плоскости; видеть рисунок 12.5.3. Это расстояние — модуль скалярной проекции $ \ ds \ overrightarrow {\ strut QP} $ на вектор нормали $ \ bf n $, где $ Q $ — любая точка на плоскости.На плоскости легко найти точку, скажем, $ (1,0,1) $. Таким образом, расстояние $$ {\ overrightarrow {\ strut QP} \ cdot {\ bf n} \ over | {\ bf n} |} = {\ langle 0,2,2 \ rangle \ cdot \ langle 2, -1,3 \ rangle \ over | \ langle 2, -1,3 \ rangle |} = {4 \ over \ sqrt {14}}. $$ $ \ квадрат $
Рисунок 12.5.3. Расстояние от точки до плоскости.
Пример 12.5.7 Найти расстояние от точки $ (- 1,2,1) $ до линии
$ \ langle 1,1,1 \ rangle + t \ langle 2,3, -1 \ rangle $. Снова мы хотим расстояние
измеряется перпендикулярно линии, как указано в
рисунок 12. 5.4. Желаемое расстояние
$$
| \ overrightarrow {\ strut QP} | \ sin \ theta =
{| \ overrightarrow {\ strut QP} \ times {\ bf A} | \ over | {\ bf A} |},
$$
где $ \ bf A $ — любой вектор, параллельный прямой. Из уравнения
строку, мы можем использовать $ Q = (1,1,1) $ и $ {\ bf A} = \ langle 2,3, -1 \ rangle $, поэтому
расстояние
$$
{| \ langle -2,1,0 \ rangle \ times \ langle2,3, -1 \ rangle | \ over \ sqrt {14}} =
{| \ langle-1, -2, -8 \ rangle | \ over \ sqrt {14}} = {\ sqrt {69} \ over \ sqrt {14}}.
$$
$ \ квадрат $
5.4. Желаемое расстояние
$$
| \ overrightarrow {\ strut QP} | \ sin \ theta =
{| \ overrightarrow {\ strut QP} \ times {\ bf A} | \ over | {\ bf A} |},
$$
где $ \ bf A $ — любой вектор, параллельный прямой. Из уравнения
строку, мы можем использовать $ Q = (1,1,1) $ и $ {\ bf A} = \ langle 2,3, -1 \ rangle $, поэтому
расстояние
$$
{| \ langle -2,1,0 \ rangle \ times \ langle2,3, -1 \ rangle | \ over \ sqrt {14}} =
{| \ langle-1, -2, -8 \ rangle | \ over \ sqrt {14}} = {\ sqrt {69} \ over \ sqrt {14}}.
$$
$ \ квадрат $
Рисунок 12.5.4. Расстояние от точки до линии.
Упражнения 12,5
Вы можете использовать Sage для вычисления расстояний до линий и плоскостей, так как это просто включает в себя векторную арифметику, которую мы уже видели. Конечно, вы также можете использовать Sage для выполнения некоторых вычислений, связанных с нахождение уравнений плоскостей и прямых.
Пример 12.5.1
Найдите уравнение плоскости, содержащее $ (6,2,1) $ и
перпендикулярно $ \ langle 1,1,1 \ rangle $. (отвечать)
(отвечать)
Пр. 12.5.2 Найдите уравнение плоскости, содержащее $ (- 1,2, -3) $ и перпендикулярно $ \ langle 4,5, -1 \ rangle $.(отвечать)
Пример 12.5.3 Найдите уравнение плоскости, содержащей $ (1,2, -3) $, $ (0,1, -2) $ и $ (1,2, -2) $. (отвечать)
пр. 12.5.4 Найдите уравнение плоскости, содержащей $ (1,0,0) $, $ (4,2,0) $ и $ (3,2,1) $. (отвечать)
Пример 12.5.5 Найдите уравнение плоскости, содержащей $ (1,0,0) $ и строка $ \ langle 1,0,2 \ rangle + t \ langle 3,2,1 \ rangle $. (отвечать)
Пример 12.5.6 Найдите уравнение плоскости, содержащей линию пересечение $ x + y + z = 1 $ и $ x-y + 2z = 2 $ и перпендикулярно самолет $ 2x + 3y-z = 4 $.(отвечать)
Пример 12.5.7 Найдите уравнение плоскости, содержащей линию пересечение $ x + 2y-z = 3 $ и $ 3x-y + 4z = 7 $ и перпендикулярно самолет $ 6x-y + 3z = 16 $. (отвечать)
Пример 12.5.8
Найдите уравнение плоскости, содержащей линию
пересечение $ x + 3y-z = 6 $ и $ 2x + 2y-3z = 8 $ и перпендикулярно
самолет $ 3x + y-z = 11 $. (отвечать)
(отвечать)
Пример 12.5.9 Найдите уравнение прямой, проходящей через $ (1,0,3) $ и $ (1,2,4) $. (отвечать)
Пр. 12.5,10 Найдите уравнение прямой, проходящей через $ (1,0,3) $ и перпендикулярно плоскости $ x + 2y-z = 1 $. (отвечать)
Пр. 12.5.11 Найдите уравнение прямой, проходящей через начало координат и перпендикулярно плоскости $ x + y-z = 2 $. (отвечать)
Пр. 12.5.12 Найдите $ a $ и $ c $ так, чтобы $ (a, 1, c) $ находился на линии, проходящей через $ (0,2,3) $ и $ (2,7,5) $. (отвечать)
Пример 12.5.13 Объясните, как найти решение в пример 12.5.5.
Пр. 12.5,14 Определите, соответствуют ли линии $ \ langle 1,3, -1 \ rangle + t \ langle 1,1,0 \ rangle $ и $ \ langle 0,0,0 \ rangle + t \ langle 1,4,5 \ rangle $ — это параллельно, пересекаются или ни то, ни другое. (отвечать)
Пример 12.5.15
Определите, соответствуют ли линии $ \ langle 1,0,2 \ rangle + t \ langle
-1, -1,2 \ rangle $ и $ \ langle 4,4,2 \ rangle + t \ langle 2,2, -4 \ rangle $ являются
параллельно, пересекаются или ни то, ни другое. (отвечать)
(отвечать)
Пример 12.5.16 Определите, соответствуют ли линии $ \ langle 1,2, -1 \ rangle + t \ langle 1,2,3 \ rangle $ и $ \ langle 1,0,1 \ rangle + t \ langle 2 / 3,2,4 / 3 \ rangle $ — это параллельно, пересекаются или ни то, ни другое.(отвечать)
Пример 12.5.17 Определите, соответствуют ли линии $ \ langle 1,1,2 \ rangle + t \ langle 1,2, -3 \ rangle $ и $ \ langle 2,3, -1 \ rangle + t \ langle 2,4, -6 \ rangle $ — это параллельно, пересекаются или ни то, ни другое. (отвечать)
Пр. 12.5.18 Найдите единичный вектор нормали к каждой из координатных плоскостей.
Пр. 12.5.19 Покажите, что $ \ langle 2,1,3 \ rangle + t \ langle 1,1,2 \ rangle $ и $ \ langle 3, 2, 5 \ rangle + s \ langle 2, 2, 4 \ rangle $ одинаковы линия.
Пример 12.5.20 Дайте краткое описание каждого из следующих процессов:
а. Учитывая две различные точки, найдите линию, которая проходит через них.
г. Учитывая три точки (не все на одной прямой), найдите самолет
что проходит через них. Зачем нужен нюанс, что не все
точки быть на одной линии?
Учитывая три точки (не все на одной прямой), найдите самолет
что проходит через них. Зачем нужен нюанс, что не все
точки быть на одной линии?
г. Для данной линии и точки не на этой прямой найдите плоскость, которая содержит их обоих.
г. Для плоскости и точки не на плоскости найдите прямую, которая перпендикулярна плоскости, проходящей через данную точку.
Пр. 12.5.21 Найдите расстояние от $ (2,2,2) $ до $ x + y + z = -1 $. (отвечать)
Пример 12.5.22 Найдите расстояние от $ (2, -1, -1) $ до $ 2x-3y + z = 2 $. (отвечать)
Пример 12.5.23 Найти расстояние от $ (2, -1,1) $ до $ \ langle 2,2,0 \ rangle + t \ langle 1,2,3 \ rangle $. (отвечать)
Пример 12.5.24 Найти расстояние от $ (1,0,1) $ до $ \ langle 3,2,1 \ rangle + t \ langle 2, -1, -2 \ rangle $. (отвечать)
Пр. 12.5,25
Найдите расстояние между линиями
$ \ langle 5,3,1 \ rangle + t \ langle 2,4,3 \ rangle $ и
$ \ langle 6,1,0 \ rangle + t \ langle 3,5,7 \ rangle $. (отвечать)
(отвечать)
Пр. 12.5.26 Найдите расстояние между линиями $ \ langle 2,1,3 \ rangle + t \ langle -1,2, -3 \ rangle $ и $ \ langle 1, -3,4 \ rangle + t \ langle 4, -4,1 \ rangle $. (отвечать)
Пр. 12.5.27 Найдите расстояние между линиями $ \ langle 1,2,3 \ rangle + t \ langle 2, -1,3 \ rangle $ и $ \ langle 4,5,6 \ rangle + t \ langle -4,2, -6 \ rangle $.(отвечать)
Пр. 12.5.28 Найдите расстояние между линиями $ \ langle 3,2,1 \ rangle + t \ langle 1,4, -1 \ rangle $ и $ \ langle 3,1,3 \ rangle + t \ langle 2,8, -2 \ rangle $. (отвечать)
Пр. 12.5.29 Найдите косинус угла между плоскостями $ x + y + z = 2 $ и $ x + 2y + 3z = 8 $. (отвечать)
Пример 12.5.30 Найдите косинус угла между плоскостями $ x-y + 2z = 2 $ и $ 3x-2y + z = 5 $. (отвечать)
|
The
Квадранты декартовой плоскости (стр. Разделы: Введение на плоскость, Точки построения, Четыре квадранта Две оси разделяют плоскость на четыре секции, называемые «квадрантами».Квадранты обозначены римскими цифрами (, а не арабскими цифрами), начиная с положительная ось x и вращаясь против часовой стрелки:
Когда вы перейдете к тригонометрии, этот метод нумерации квадрантов будет иметь смысл и быть очень полезным. А пока просто запомните информацию. Ты, наверное, есть только несколько вопросов по квадрантам, и тогда вы вряд ли увидите снова тема, пока не тригонометрия.Типичные вопросы в целом похожи на следующее: авторское право © Элизабет Стапель 2000-2011 Все права защищены
Самый простой способ мне ответить — это обозначить точку:
Теперь я вижу, что
точка (–2,
–3) находится в квадранте
III.
Поскольку они не говорят мне какое значение « y » есть, то y может быть что угодно. Это означает, что (4, y ) равно не только одно очко! Поскольку y может быть –5, то (4, –5) — правильный ответ.Так и (4, –3), (4, 0), (4, 2) и (4, 4). Так любая точка , которая имеет x = 4:
Построив кучу
точки, которые «работают», я вижу, что «точка» (4, y ) на самом деле
целая строка: строка « x = 4», которая
проходит через два квадрантов! Итак, мой ответ:
Кстати, используйте
стандартные обозначения.
Это меня спрашивает описание точек ( x , y ), где координаты x и y имеют такие значения, что, когда я умножу x и y вместе, я получу отрицательное число.Чтобы понять это, это наверное, проще всего, если я просто выберу точку выборки из каждого квадранта и посмотрим, что я получу. В квадранте I я выберу,
скажем, (2,
3). Продукт
координаты 2
× 3 = 6, что является
положительный (больше нуля). Поскольку любое координатное произведение в квадранте
Я буду так же положительно, тогда Квадрант I не является частью моего ответа. В квадранте II я выберите, скажем, (–4, 5). Произведение (–4) × 5 = –20, что является отрицательный. Любое другое произведение координат в Квадранте II также будет отрицательным, так что Квадрант II — это часть моего ответа. В квадранте III я выберите, скажем, (–2, –1). Продукт равно (–2) × (–1) = 2, что положительный.Любой другой продукт в Квадранте III также будет положительным, поэтому Квадрант III не является частью моего ответа. В квадранте IV я выберите, скажем, (3, –4). Продукт составляет 3 × (–4) = –12, что отрицательный. Любой другой продукт в квадранте IV также будет отрицательным, так что Квадрант IV — часть моего ответа. Точки ( x , y ), с xy <0,
лежат во II и IV квадрантах. Вы можете использовать виджет Mathway ниже, чтобы попрактикуйтесь в определении квадранта, в котором расположена данная точка. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку «бумажный самолетик», чтобы сравнить свой ответ с ответом Матвея. (Щелкните здесь, чтобы перейти непосредственно на сайт Mathway, если вы хотите проверить их программное обеспечение или получить дополнительную информацию.) << Предыдущий Наверх | 1 | 2 | 3 | Возвращение в индекс
|
|
Геометрическая интерпретация трехмерных линий и плоскостей | Валентина Альто
Линейная алгебра — это та ветвь исчисления, объекты которой живут за пределами ℝ. Эти объекты могут быть координатами в пространстве (следовательно, точками) или комбинациями точек в форме многомерных уравнений.
Каждый раз, когда мы работаем с более чем 3 измерениями, физически невозможно визуализировать наши объекты. Следовательно, в этой статье я собираюсь предоставить геометрическую интерпретацию точек, линий и плоскостей в трехмерном окружении, чтобы вы могли расширить эти концепции на более высокие измерения.
Вообще говоря, ℝn — это координатное пространство или набор координат, каждая из которых имеет n компонентов.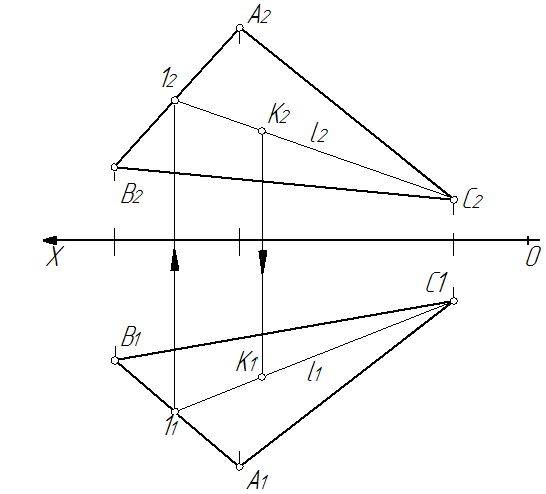 Следовательно, при работе в ℝ3 наши координаты будут выглядеть так:
Следовательно, при работе в ℝ3 наши координаты будут выглядеть так:
Каждая координата может быть представлена в пространстве либо точкой, либо вектором:
Наконец, очень важным свойством этих объектов является ортогональность: действительно, два наборы координат / векторов называются ортогональными (что означает перпендикулярные), если их внутренний продукт равен 0.В нашем случае:
Теперь, как мы можем изобразить прямые линии и плоскости в нашем трехмерном пространстве?
Прямые линии
Прямая линия — это бесконечный объект без ширины, характеризуемый направлением v . Начнем с простого примера линии, пересекающей начало координат наших осей. Рассмотрим прямую r с направлением v . Мы хотим вычислить общее уравнение этой линии для общей точки p . Идея в том, что нам нужно растянуть наш вектор v до точки p .Для этого мы будем использовать так называемый коэффициент растяжения t:
В принципе, имея вектор v в качестве единицы измерения, мы можем растянуть (или сократить) наш вектор v в том же направлении (если t> 0) или наоборот (если t <0). Следовательно, у нас есть следующее уравнение для общей точки, лежащей на r:
Следовательно, у нас есть следующее уравнение для общей точки, лежащей на r:
Эта формула называется параметрическим выражением прямой. Это динамическое выражение, поскольку оно описывает прямую линию в системе отсчета и зависит от t.А именно, если t = время, у нас есть отправная точка (t = 0), затем то, что произойдет в будущем (t> 0), и то, что уже произошло в прошлом (t <0).
Теперь представьте, что мы хотим определить линию, которая не проходит через начало координат наших осей, но всегда имеет направление v . Теперь он пройдет через заданную точку q. Итак, мы хотим вычислить общее уравнение красной линии на следующем рисунке:
Если мы вспомним на мгновение, как вычислить разницу между двумя векторами:
Мы можем действовать следующим образом.Во-первых, пусть p является определенной точкой на нашей линии r . Затем мы вычисляем разницу между p и q , в результате чего получаем вектор, параллельный v (по определению, это направление нашей прямой линии r), но смещенный на некоторое значение. Отсюда:
Отсюда:
Где q — новая точка отсчета нашего вектора. Из рисунка выше вы можете видеть, что t было положительным и больше 1 (поскольку результирующий вектор имеет то же направление, но большую величину).Новое уравнение будет:
Где значение сдвига равно новому началу координат.
Теперь, когда у нас есть четкое представление о геометрии линии, давайте перейдем к геометрии плоскости.
Плоскости
Плоскость — это объект в пространстве, который характеризуется двумя характеристиками:
- ориентация: это прямая линия, ортогональная плоскости.
Для каждой ориентации существует бесконечное количество плоскостей:
Следовательно, нам нужен второй элемент, чтобы изолировать только одну из них.
- точка: это точка, где прямая линия пересекает план, и мы назовем ее q .
Теперь, как мы можем определить уравнение плоскости? Давайте проанализируем природу точек, лежащих на этой плоскости:
Независимо от их положения, разница между каждой из них и точкой пересечения q должна быть ортогональна ориентации v .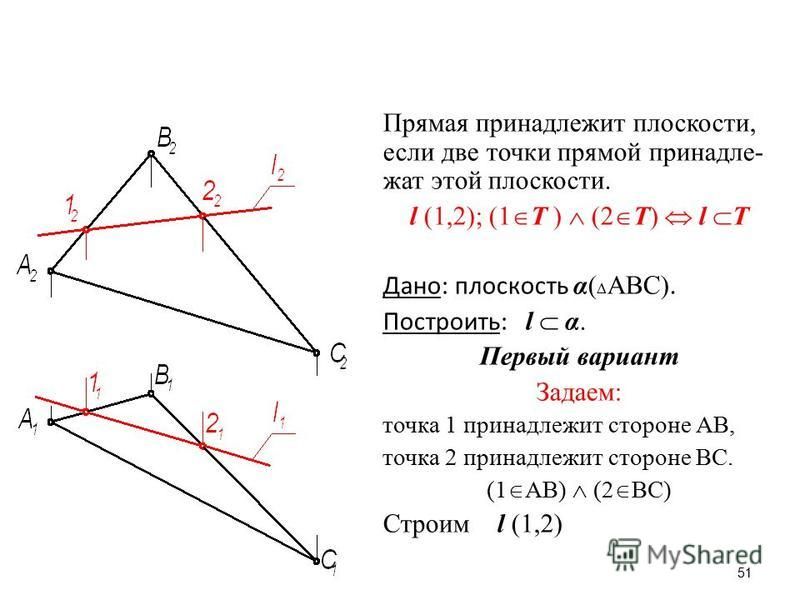 Следовательно, из-за ортогональности мы знаем, что, учитывая общую точку p :
Следовательно, из-за ортогональности мы знаем, что, учитывая общую точку p :
Если мы расширим приведенное выше уравнение, мы получим:
Обратите внимание, что если компонент в красной скобке равен нулю, план пересечет начало координат. .
Давайте попрактикуемся
Я хотел бы завершить эту статью очень простым примером, который поможет вам визуализировать задачу и использовать как прямые линии, так и плоскости.
Представьте, что нам предоставлено уравнение плоскости, ее ориентация v и координаты точки k , которая принадлежит этому плану.
Мы хотим вычислить координаты симметричной точки k, k ’, относительно нашей плоскости. Идея заключается в следующем:
- Вычислить параметрическое уравнение прямой r , пересекающей k и ортогональной плоскости:
- Нахождение значения параметра t для точки, где плоскость и линии имеют пересечение:
- Удвойте значение, полученное для t, чтобы мы могли получить значение k ‘ (действительно, q одинаково удалены от k и k’ ):
Заключительные соображения
Визуализация объектов, которыми вы управляете, — очень важный шаг для их полного понимания.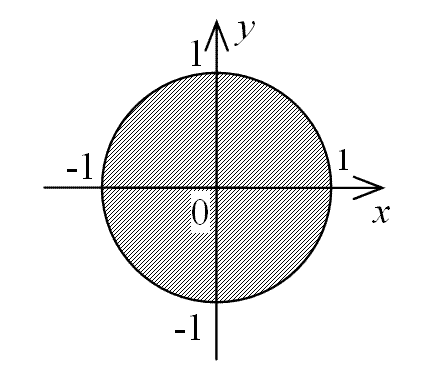 Однако в реальном мире переменные проблемы имеют тенденцию отличаться от хорошо известного длина-ширина-высота . В экономических сценариях нас просят иметь дело с сотнями переменных, которыми могут быть товары, страны, рынки, элементы макроэкономики и так далее. В таких случаях невозможно визуализировать то, чем вы управляете, но наличие идеи хотя бы в трехмерном окружении сделает эти рассуждения более легкими и интуитивно понятными.
Однако в реальном мире переменные проблемы имеют тенденцию отличаться от хорошо известного длина-ширина-высота . В экономических сценариях нас просят иметь дело с сотнями переменных, которыми могут быть товары, страны, рынки, элементы макроэкономики и так далее. В таких случаях невозможно визуализировать то, чем вы управляете, но наличие идеи хотя бы в трехмерном окружении сделает эти рассуждения более легкими и интуитивно понятными.
Трехмерная координатная геометрия — Уравнение плоскости
Когда мы знаем три точки на плоскости, мы можем найти уравнение плоскости, решая совместные уравнения.
Пусть ax + by + cz + d = 0 ax + by + cz + d = 0ax + by + cz + d = 0 будет уравнением плоскости, на которой есть следующие три точки: A = (1,0, 2), B = (2,1,1), A = (1,0,2), B = (2,1,1), A = (1,0,2), B = (2,1, 1) и C = (- 1,2,1) .C = (- 1,2,1). С = (- 1,2,1). Тогда уравнение плоскости устанавливается следующим образом:
У нас уже есть уравнение плоскости с 4 неизвестными константами:
ax + by + cz + d = 0. (1) ax + by + cz + d = 0. \ qquad (1) ax + by + cz + d = 0. (1)
(1) ax + by + cz + d = 0. \ qquad (1) ax + by + cz + d = 0. (1)
Мы также получаем следующие 3 уравнения, подставляя координаты A, B, A, B, A, B и CCC в (1) 🙁 1) 🙁 1):
a⋅1 + b⋅0 + c⋅2 + d = 0a⋅2 + b⋅1 + c⋅1 + d = 0a⋅ (−1) + b⋅2 + c⋅1 + d = 0, \ begin {выровнено} а \ cdot 1 + b \ cdot 0 + c \ cdot 2 + d & = 0 \\ а \ cdot 2 + b \ cdot 1 + c \ cdot 1 + d & = 0 \\ а \ cdot (-1) + b \ cdot 2 + c \ cdot 1 + d & = 0, \ end {align} a⋅1 + b⋅0 + c⋅2 + da⋅2 + b⋅1 + c⋅1 + da⋅ (−1) + b⋅2 + c⋅1 + d = 0 = 0 = 0,
, что дает b = 3a, c = 4a, d = −9a.(2) b = 3a, c = 4a, d = -9a. \ qquad (2) b = 3a, c = 4a, d = −9a. (2)
Подставляя (2) (2) (2) в (1), (1), (1), получаем
ax + 3ay + 4az − 9a = 0x + 3y + 4z − 9 = 0. \ begin {выровнено} ах + 3ay + 4az -9a & = 0 \\ х + 3у + 4z — 9 & = 0. \ end {align} ax + 3ay + 4az − 9ax + 3y + 4z − 9 = 0 = 0.
Следовательно, уравнение плоскости, проходящей через три точки A = (1,0,2), B = (2,1,1), A = (1,0,2), B = (2,1, 1), A = (1,0,2), B = (2,1,1) и C = (- 1,2,1) C = (- 1,2,1) C = (- 1, 2,1) равно
х + 3у + 4z − 9 = 0.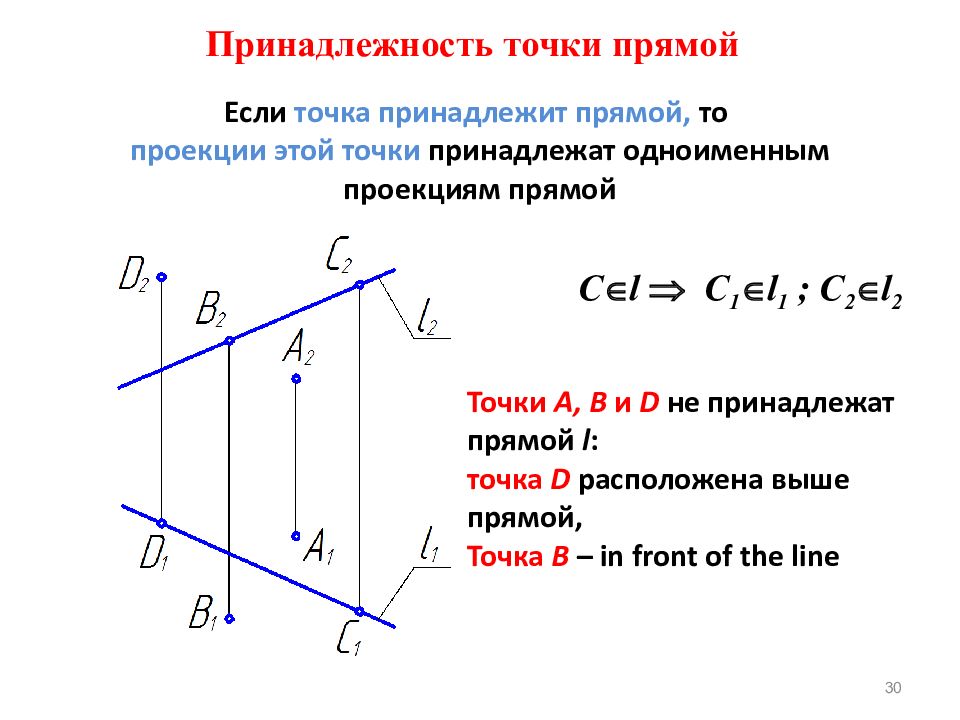 х + 3у + 4z — 9 = 0.х + 3у + 4z − 9 = 0.
х + 3у + 4z — 9 = 0.х + 3у + 4z − 9 = 0.
Используя этот метод, мы можем найти уравнение плоскости, если нам известны три точки. Вот пара примеров:
Если самолет проходит через три точки A = (0,0,2), B = (1,0,1), A = (0,0,2), B = (1,0,1), A = (0,0,2), B = (1,0,1) и C = (3,1,1), C = (3,1,1), C = (3,1,1), тогда что такое уравнение плоскости?
Пусть уравнение плоскости имеет вид ax + by + cz + d = 0. (1) ax + by + cz + d = 0. \ qquad (1) ax + by + cz + d = 0. (1)
Тогда, поскольку эта плоскость включает три точки A = (0,0,2), B = (1,0,1), A = (0,0,2), B = (1,0,1), A = (0,0,2), B = (1,0,1) и C = (3,1,1), C = (3,1,1), C = (3,1,1), у нас
a⋅0 + b⋅0 + c⋅2 + d = 0a⋅1 + b⋅0 + c⋅1 + d = 0a⋅3 + b⋅1 + c⋅1 + d = 0, \ begin {выровнено} а \ cdot 0 + b \ cdot 0 + c \ cdot 2 + d & = 0 \\ а \ cdot 1 + b \ cdot 0 + c \ cdot 1 + d & = 0 \\ а \ cdot 3 + b \ cdot 1 + c \ cdot 1 + d & = 0, \ end {align} a⋅0 + b⋅0 + c⋅2 + da⋅1 + b⋅0 + c⋅1 + da⋅3 + b⋅1 + c⋅1 + d = 0 = 0 = 0,
, что дает b = −2a, c = a, d = −2a.
(2) b = -2a, c = a, d = -2a. \ qquad (2) b = −2a, c = a, d = −2a. (2)
Подставляя (2) (2) (2) в (1), (1), (1), получаем
ax + −2ay + az − 2a = 0x − 2y + z − 2 = 0. \ begin {выровнено} ах + -2ay + аз -2а & = 0 \\ х -2у + г — 2 & = 0. \ end {align} ax + −2ay + az − 2ax − 2y + z − 2 = 0 = 0.
Следовательно, уравнение плоскости, проходящей через три точки A = (0,0,2), B = (1,0,1), A = (0,0,2), B = (1,0,1 ) A = (0,0,2), B = (1,0,1) и C = (3,1,1) C = (3,1,1) C = (3,1,1) равно
х-2у + г-2 знак равно 0. □ х -2y + z — 2 = 0. \ _ \ квадрат х-2у + г-2 знак равно 0.□
Если самолет проходит через три точки A = (3,1,2), B = (6,1,2), A = (3,1,2), B = (6,1,2), A = (3,1,2), B = (6,1,2) и C = (0,2,0), C = (0,2,0), C = (0,2,0), тогда какое уравнение плоскости?
Пусть уравнение плоскости имеет вид ax + by + cz + d = 0. (1) ax + by + cz + d = 0. \ qquad (1) ax + by + cz + d = 0. (1)
Тогда, поскольку эта плоскость включает три точки A = (0,0,2), B = (1,0,1), A = (0,0,2), B = (1,0,1), A = (0,0,2), B = (1,0,1) и C = (3,1,1), C = (3,1,1), C = (3,1,1), у нас
a⋅3 + b⋅1 + c⋅2 + d = 0a⋅6 + b⋅1 + c⋅2 + d = 0a⋅0 + b⋅2 + c⋅0 + d = 0, \ begin {выровнено} а \ cdot 3 + b \ cdot 1 + c \ cdot 2 + d & = 0 \\ а \ cdot 6 + b \ cdot 1 + c \ cdot 2 + d & = 0 \\ а \ cdot 0 + b \ cdot 2 + c \ cdot 0 + d & = 0, \ end {align} a⋅3 + b⋅1 + c⋅2 + da⋅6 + b⋅1 + c⋅2 + da⋅0 + b⋅2 + c⋅0 + d = 0 = 0 = 0,
, что дает a = 0, c = 12b, d = −2b.
(2) a = 0, c = \ frac {1} {2} b, d = -2b. \ qquad (2) a = 0, c = 21 b, d = −2b. (2)
Подставляя (2) (2) (2) в (1), (1), (1), получаем
0x + −by + 12bz − 2b = 0x − y + 12z − 2 = 02x − 2y + z − 4 = 0. \ begin {выровнено} 0x + -by + \ frac {1} {2} bz -2b & = 0 \\ x -y + \ frac {1} {2} z — 2 & = 0 \\ 2х — 2у + г-4 & = 0. \ end {align} 0x + −by + 21 bz − 2bx − y + 21 z − 22x − 2y + z − 4 = 0 = 0 = 0.
Следовательно, уравнение плоскости, проходящей через три точки A = (0,0,2), B = (1,0,1), A = (0,0,2), B = (1,0, 1), A = (0,0,2), B = (1,0,1) и C = (3,1,1) C = (3,1,1) C = (3,1,1 ) составляет
2x − 2y + z − 4 знак равно 0.□ 2x — 2y + z-4 = 0. \ _ \ квадрат 2x − 2y + z − 4 знак равно 0. □
Попробуйте решить следующую проблему:
х = 1х = 1х = 1 х + у = 3х + у = 3х + у = 3 у-х = 1у-х = 1у-х = 1 Ни один из вышеперечисленных Найдите уравнение плоскости, проходящей через (1,2,3) (1,2,3) (1,2,3) и (1, −3,2) (1, -3,2) (1, −3,2) и параллельно оси zzz.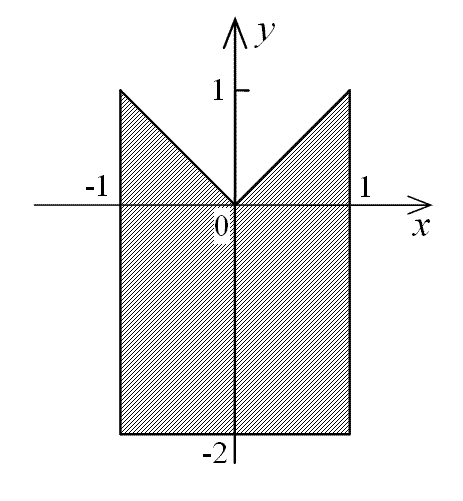
Что такое координатная плоскость? — Определение, факты и пример
Что такое координатная плоскость?
Координатная плоскость — это двумерная плоскость, образованная пересечением вертикальной линии, называемой осью y, и горизонтальной линии, называемой осью x. Это перпендикулярные линии, которые пересекаются друг с другом в нуле, и эта точка называется началом координат. Оси разрезают координатную плоскость на четыре равных участка, и каждый участок известен как квадрант, как показано ниже.
|
При определении координат точки соблюдаются следующие условные обозначения:
- Координата x или абсцисса точки — это расстояние по перпендикуляру от оси y, измеренное вдоль оси x.
-
Координата y или ордината точки — это расстояние по перпендикуляру от оси x, измеренное вдоль оси y.
-
При указании координат точки на координатной плоскости сначала идет координата x, а затем координата y. Помещаем координаты в скобки как (x, y).
Итак, на данном графике координаты точки A равны (5, 6), поскольку она удалена на 5 единиц от начала координат по положительной оси x и на 6 единиц от начала координат по положительной оси y.
Вы можете определить координаты B, D, E и F?
Если где-то на графике отмечена точка, как показано на рисунке, как представлено ее положение?
| Чтобы нанести заказанную пару (1, 3) на координатную плоскость:
|
| Интересные факты |
Как построить точки на координатной плоскости
Координатная плоскость — это двумерная плоскость с осью x (горизонтальной) и осью y (вертикальной).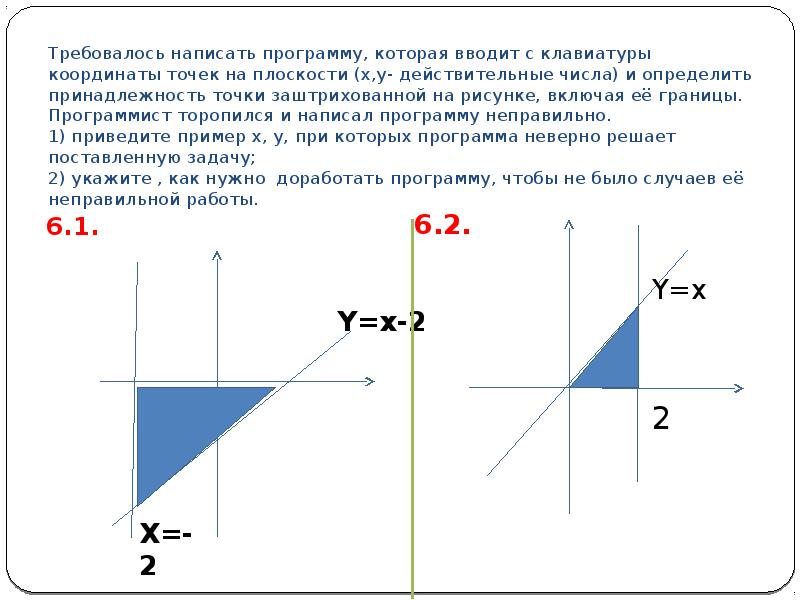 Эти оси пересекаются, образуя перпендикулярную линию, разделяющую координатную плоскость на четыре квадранта.
Эти оси пересекаются, образуя перпендикулярную линию, разделяющую координатную плоскость на четыре квадранта.
Как использовать координатную плоскость
Вы используете координатные плоскости для нанесения точек на графики. Каждый квадрант написан римскими цифрами и имеет свое положение на плоскости. Например, первый квадрант (Квадрант I) находится справа от вертикальной оси и над горизонтальной осью:
Изображение предоставлено: Desmos
Когда вас попросят построить точки, вам будут даны упорядоченные пары, записанные в круглых скобках.Например, если точка имеет значение x, равное 1, и значение y, равное -2, она будет записана как (1, -2). Первое число представляет координату x, точку на горизонтальной оси, а второе число представляет координату y, точку на вертикальной оси.
Квадрант, в котором находится каждая точка, зависит от того, являются ли координаты точки отрицательными или положительными числами. Вот разбивка того, как классифицируется каждый квадрант:
Квадрант I: Положительные значения x и y
Квадрант II: Положительные значения y, отрицательные значения x
Квадрант III: Отрицательные значения x и y
Квадрант IV: Положительные значения x, отрицательные значения y
Давайте определим квадранты каждой заданной точки, в которых сначала указано значение x, а второе — значение y:
Точка A: (3, 2)
Так как эта точка имеет положительное значение x, равное 3, и положительное значение y, равное 2, она принадлежит Квадранту I.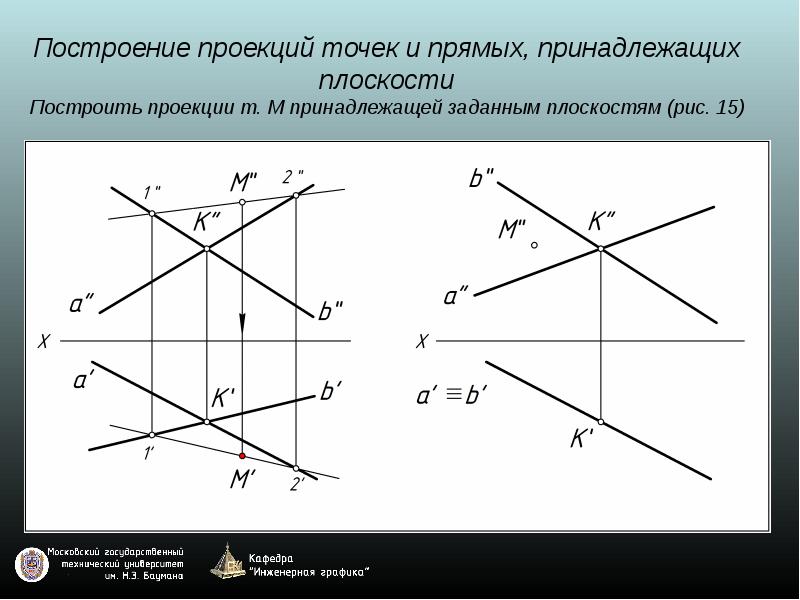
Пункт B: (-2, 2)
Значение y положительно, а значение x отрицательно, поэтому эта точка перейдет в Квадрант II.
Точка C: (-2, -1)
Оба значения x и y отрицательны, поэтому эта точка находится в квадранте III.
Пункт D: (3, -1)
Значение x положительно, а значение y отрицательно, поэтому эта точка находится в квадранте IV.
Изображение предоставлено: Desmos
Когда вы используете координатную плоскость?
Каждый раз, когда вы наносите точки на отрицательную или положительную ось x или y, вы используете координатную плоскость.Когда вы знаете, как наносить точки и определять соответствующие им квадранты, вы можете начать рисовать линейные уравнения, экспоненциальные значения и многое другое. Обучение использованию координатной плоскости — одно из самых полезных и фундаментальных понятий в математике.
Дополнительные домашние задания по математике
.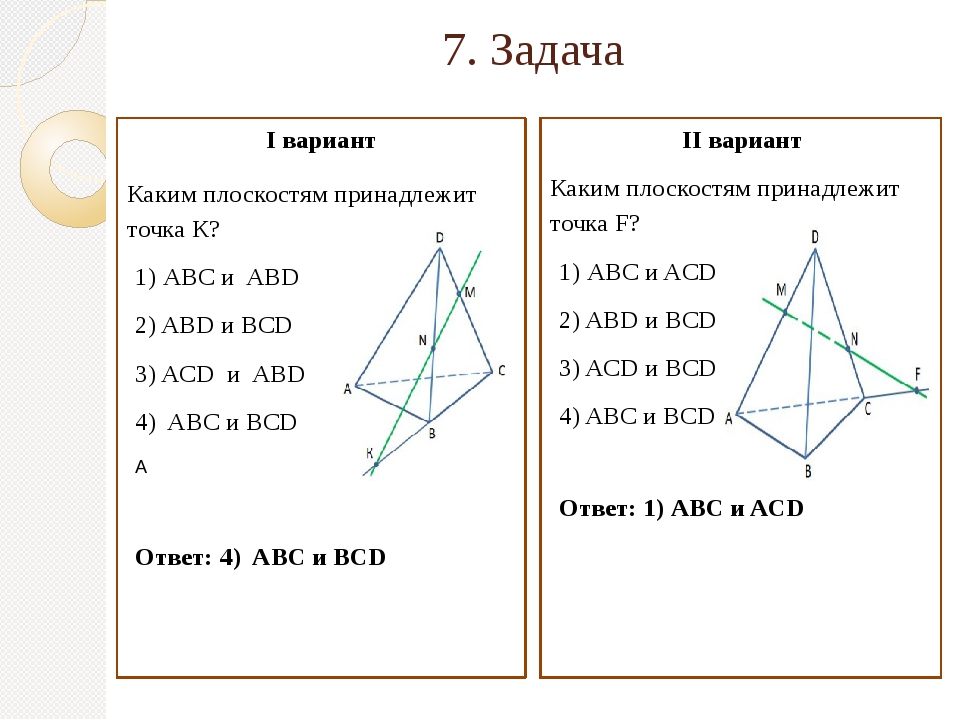

 3 из 3)
3 из 3) 
 Вы можете сократить «Квадрант» до «Q»,
но не опускайте его полностью; используйте римские «I, II, III, IV», а не
Арабский «1,
2, 3, 4 «; и
используйте «&» или «и», а не «плюс» или «+».
Вы можете сократить «Квадрант» до «Q»,
но не опускайте его полностью; используйте римские «I, II, III, IV», а не
Арабский «1,
2, 3, 4 «; и
используйте «&» или «и», а не «плюс» или «+».
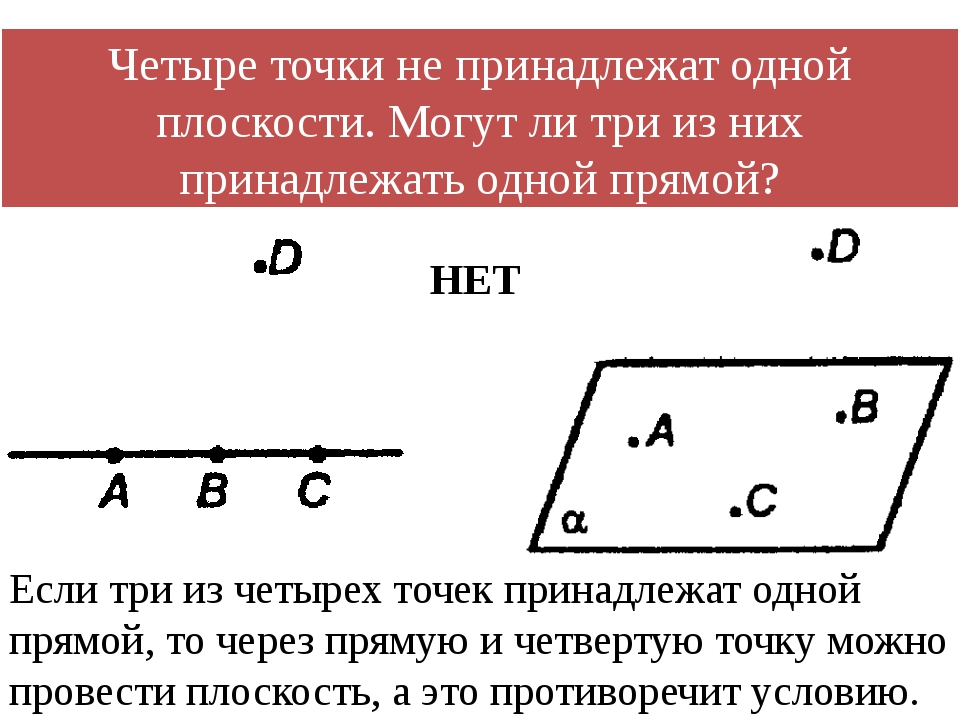

 Пурпурная математика . Доступна с
Пурпурная математика . Доступна с 