Как подготовиться к олимпиаде по математике: практические советы для школьников
Участие в олимпиадах, будь-то по математике, химии или физике, – это прекрасная возможность проверить свои способности и знания, проявить на деле навыки нестандартного мышления, которые обязательно понадобятся во взрослой жизни. Известно, что лозунг любых соревнований заключается в том, что главное – не победа, а участие, каждый участник хочет стать победителем. Учитывая этот факт, можно сделать вывод, что подготовка к российской олимпиаде важна. Многие школьники прибегают к услугам грамотного специалиста. Правильно ли это? Возможно ли обойтись без помощи профессионала? Давайте разбираться.
Первостепенная задача организации олимпиады – это проверка знаний у лучших учеников образовательного учреждения для того, чтобы выявить самого умного ребенка. В настоящее время популярностью пользуются дистанционные конкурсы для учащихся, принять участие в них могут все желающие независимо от школьной успеваемости. Такие мероприятия стимулируют более углубленно изучать определенную дисциплину, используя дополнительные источники информации.
Как одержать победу в конкурсе?
Хотите узнать, как выиграть олимпиаду по математике или любому другому предмету? Специалисты рекомендуют во время решения заданий сочетать следующие факторы:
- Знание материала школьной программы соответствующего класса – это база, которая должна быть у каждого участника. Если школьник какую-то тему не усвоил, то он обязательно должен восполнить пробелы дл участия в конкурсе. Победить не удастся, если ученик не обладает базовыми знаниями предмета.
- Знание дополнительной информации – это главный бонус. К сожалению, школьные часы ограничены, поэтому учитель не может дать максимум информации для учеников. Часть материала надо изучать самостоятельно. Не стоит пренебрегать домашними заданиями. Для победы необходим не только тот материал, который учитель успеваем дать на уроках. При желании школьник может воспользоваться услугами репетитора. Он точно знает, как подготовить ученика к олимпиаде по математике.
- Нестандартное мышление и логика – еще один важный фактор. Не все олимпиадные задания подразумевают использование определенной формулы. Зачастую решение сложных задач подразумевает применение смекалки. Найти выход из нестандартной ситуации поможет гибкость ума. Не стоит бояться мыслить иначе, чем сверстники.
- Постоянная практика – залог успеха. Только занимаясь и применяя знания на практике, школьник сможет полноценно подготовиться к любому конкурсу. Сегодня можно воспользоваться различными сборниками задач или интернетом, где представлено множество вариант онлайн конкурсов по любому школьному предмету.
Учитывая вышеперечисленные факторы, участник может рассчитывать на победу. Конечно же, стоит помнить, что без труда нельзя вытащить и рыбку из пруда!
Как готовиться к олимпиаде по математике?
Независимо от того, в какой олимпиаде собираетесь принимать участие – в городской, муниципальной или всероссийской, важно подготовиться. Сегодня в онлайн доступе есть примерные задания, которые рекомендуются решить дома. Таким образом, можно освежить знания по всему курсу. Популярностью сегодня пользуются тесты, которые состоят из вопросов с вариантами ответов. Такие конкурсы не отнимают много времени и приносят много пользы. В большинстве случаев они бесплатные. Найти тесты по всем школьным предметам можно на нашем сайте. Они распределены не только по школьной дисциплине, но и возрастной группе.
Каждый участник должен в домашних условиях уделять внимание конкурсным заданиям. Можно воспользоваться помощью учителя, который обучает в школе при необходимости. Вариантов множество, главное – это желание! Как написать олимпиаду по математике или любому другому предмету можно на специализированных порталах, в том числе и на «ФГОС online».
Какой тест провалили учителя математики?
Да, такое тоже бывает в жизни. Так какой тест сдавали учителя математики, что не смогли справиться с заданиями? Пресс-служба Рособрнадзора сообщила, что почти половина педагогов, которые принимали участие во всероссийской проверке владения предметами программы, не справились с математическими заданиями. Цель такой проверки заключается в понимании того, насколько кадры владеют преподаваемой дисциплиной. Теперь понятно, что особого внимания заслуживает повышение квалификации наших педагогов.
Пройти тест смогли 22 тысячи учителей из разных регионов страны. Стоит сразу отметить, что результаты тестирования не повлияют на их работу. Это лишь доказало то, что и профессионалы нуждаются в постоянных интеллектуальных тренировках. Только так они узнают, как подготовить детей к олимпиаде по математике так, чтобы они обязательно одержали победу.
fgosonline.ru
Руководство олимпиадника — Сайт Романа Парпалака
20 февраля 2010 года
Школьные олимпиады — достойная тренировка мозга в стрессовых условиях. Трудно найти где-либо еще подобные условия, когда в сжатые сроки нужен результат интеллектуальной деятельности. Однако на самом деле в олимпиадах ничего страшного нет. Я участвовал во многих олимпиадах и сейчас расскажу, что же вас может там ждать.
Если вы будете знать, в каких условиях проходят олимпиады, вы сможете спокойно готовиться и соревноваться.
Мои советы относятся к олимпиадам по техническим предметам: математике, физике, химии. Если вас ждет олимпиада по русскому языку или географии, эта статья вам не поможет.
До олимпиады несколько месяцев
У меня часто спрашивают, как правильно готовиться к олимпиадам. Начните с дополнительных занятий для подготовки к олимпиадам, если таковые имеются в вашей школе. Переложите часть работы по подготовке на учителей.
Однако вы не должны ограничиваться посещением спецкурсов, самостоятельная подготовка тоже необходима. Попробуйте прочитать литературу для продвинутых школьников (вы же продвинутый школьник, не так ли?). Конкретные рекомендации по выбору книг может дать учитель.
Полезно будет запастись сборником олимпиадных задач и пытаться решать их. Хотя я обычно так не делал.
Попробуйте совместить приятное (сидение за компьютером) с полезным (подготовка к олимпиаде), найдите какие-нибудь сайты с олимпиадными задачами.
Многие готовятся к олимпиадам с репетиторами. Я так никогда не делал, потому что не считал это осмысленным и не собирался тратить на это деньги. Впрочем, нужно объективно смотреть на вещи. Если большинство соревнующихся серьезно занимается индивидуально, скорее всего, у вас нет других вариантов.
До олимпиады несколько недель
Обычно темы задач на школьных олимпиадах привязаны к программе. Попросите у учителя школьную программу для вашего класса. В крайнем случае посмотрите оглавление учебника. Желательно, чтобы вы знали весь материал, запланированный для изучения. Если в ваших знаниях есть пробелы, сейчас самое подходящее время их заполнить.
Лирическое отступление
С темами задач есть несколько подводных камней. Например, нам в одиннадцатом классе на республиканской олимпиаде по математике дали задачу с матрицами и определителями, хотя определители мы прошли после, в конце года.
В десятом классе на республиканской олимпиаде по физике произошел немыслимый случай. Одна из задач решалась через производную, хотя производная по программе изучается только в одиннадцатом классе.
Однако сильно забегать вперед нет смысла. Поверьте, в девятом классе на математической олимпиаде интегралы и производные вам точно не помогут.
Помимо тем, желательно иметь представление об уровне сложности задач. Попросите у учителя или у старших коллег по учебе задания прошлых лет и попробуйте их решить.
Лирическое отступление
Я привык к сложным олимпиадным задачам, когда нужно перепробовать несколько методов решения и когда для этого есть время. А на Международной олимпиаде по физике задания не были такими сложными, скорее нужно было без ошибок выполнить большой объем вычислений. Я не был заранее готов к этому, неправильно распределил время и не успел справиться со всеми заданиями.
До олимпиады несколько дней
Ясно, что за несколько дней невозможно усвоить материал, предназначенный для изучения в течение нескольких лет. Но вы всё еще можете заполнить некоторые пробелы.
Приготовьте достаточное количество бумаги для черновиков, ручки, карандаши. На олимпиаду по математике возьмите чертежные принадлежности. Калькуляторы, скорее всего, запретят. Да и задачи на математических олимпиадах такие, что калькулятор вам не поможет.
На олимпиаду по физике возьмите калькулятор. Он сэкономит вам немного времени, когда вы будете подставлять числа в окончательную формулу, и позволит избежать арифметических ошибок.
На олимпиаду по химии, кроме калькулятора, возьмите таблицу Менделеева и таблицу растворимости.
Накануне можно съездить к месту проведения олимпиады, особенно если оно находится в незнакомом районе. Во-первых, вы сократите время поиска в день проведения олимпиады. Во-вторых, вы сможете оценить, сколько времени уйдет на дорогу.
Олимпиада началась
Сначала нужно прочитать и осознать все задачи. Если вы не поняли условие задачи, не стесняйтесь и уточните его. Во-первых, организаторы скорее всего предоставили возможность задавать вопросы по условию. Во-вторых, ваши соперники не будут сидеть на месте и будут задавать вопросы.
Иногда условие бывает неоднозначным, его можно истолковать по-разному. В этом случае тоже задавайте вопросы. Например, если в условии написано, что брусок тянут под углом 30 градусов к горизонту, и в условии нет чертежа, не поленитесь уточнить, куда его тянут: вперед и вверх или вперед и вниз. Нарисуйте чертеж и напишите: «По указанию организаторов считаю, что сила, действующая на брусок, направлена вперед и вверх».
Если вы видите, что незнакомый с предметом наблюдатель неуверенно отвечает на ваш вопрос, попросите, чтобы подошел кто-нибудь из проверочной комиссии.
Лучше начинать с самой простой задачи. Например, у математиков часто все задачи оцениваются одинаковым количеством баллов. Если вы сразу возьметесь за сложную задачу, вы только потеряете время, а ваши соперники решат несколько более легких задач. Впрочем, сложность — понятие относительное. Решайте ту задачу, которая кажется простой именно вам.
Если не получается решить какую-то задачу, лучше не тратить на нее время и подумать над другой задачей, а потом вернуться. Возможно, когда вы переключитесь на другую задачу, ваш мозг на подсознательном уровне найдет подход к «нерешаемой» задаче 🙂
Не стоит затягивать с оформлением решения на чистовик. Можно приступить к оформлению, например, когда пройдет половина времени. Иначе вы рискуете не успеть, особенно если поймете, что где-то ошиблись.
Оформлять задачи нужно так же, как вы это делаете на уроках. Напишите кратко условие, сделайте чертежи, нарисуйте графики. Сформулируйте в нескольких предложениях идею решения.
Лучше не переписывать решения с черновика, а проделать вычисления заново, особенно если черновик неаккуратен. Так можно будет найти, например, арифметические ошибки.
Решение должно быть достаточно строгим и полным с математической точки зрения (но слишком подробно его расписывать тоже не надо). Проверяющим будет сложнее придраться к вашему решению.
Лирическое отступление
Один раз на республиканской олимпиаде по математике ко мне придрались и сняли один балл (из семи за задачу) за то, что я ввел некоторую величину p и не написал, что же это такое. Я подразумевал, что это обычное число. На апелляции мне ответили, а вдруг это комплексное число, или матрица, или еще что-то. Три символа (p ∈ R) спасли бы меня от этой придирки.
Даже если вы не решили задачу, но как-то продвинулись в решении, всё равно приведите ваши мысли, вычисления, чертежи, формулы. Я объясню, почему это может сработать.
Проверка работ
Я расскажу вам о том, как проходит (или, по крайней мере, как должна проходить) проверка олимпиадных работ. Возможно, это знание поможет вам набрать чуть больше баллов.
Есть два метода оценки решений. В первом, совсем неудачном, вам с самого начала дают полный балл за задачу, и за каждую ошибку в решении снимают какое-то количество баллов. Этот метод не объективен потому, что ошибиться можно в разных местах, и трудно сказать, какая из ошибок должна «съедать» больше баллов.
Во втором, более удачном методе, решение задачи разбивается на несколько этапов, и за каждый этап начисляется определенное количество баллов. Деление на этапы относительно произвольное, как и баллы, назначаемые за каждый этап. Обычно кто-нибудь в комиссии говорит: «Давайте сделаем так», и остальные с ним соглашаются.
Такая система оценивания имеет несколько следствий. Иногда могут давать несколько баллов за написанное условие, чертежи, основные формулы. Так что не поленитесь и напишите хотя бы это. Еще одно следствие: не пишите больше, чем нужно, за это вам баллы никто не добавит.
Лирическое отступление
Однажды мы проверяли работы на окружном этапе олимпиады по физике. В практическом туре кто-то из школьников решил блеснуть знаниями и вычислил погрешность с помощью коэффициентов Стьюдента. Как-либо оценить это мы не могли. Вообще, я думаю, что в подобном решении разберется не всякий проверяющий, а некоторых, особо вредных, такие умники могут настроить против себя.
К сожалению, назначение баллов за этапы решения создает трудности, если задачу вы решали не так, как комиссия. Обычно правильное решение (даже другим способом) оценивается полным баллом. Трудности начнутся, если в вашем решении есть ошибки. Хорошие проверяющие стараются провести аналогии между вашим решением и решением комиссии и выставить справедливую оценку. Не столь старательные проверяющие могут поставить случайную оценку.
На многих олимпиадах листы с результатами проверки вывешиваются в тот же или на следующий день. Вы сможете посмотреть, сколько баллов поставили за каждую задачу вам и вашим соперникам. Если вы считаете, что оценка несправедлива, идите на апелляцию.
Апелляция
На апелляции можно опротестовать результат проверки вашей работы. Проверяющие, как и все люди, тоже делают ошибки. Например, они могут не до конца понять ваш метод решения, если он отличается от официального. Однако, в любом случае разговор будет идти вокруг текста вашей работы. Если вы не написали что-нибудь важное (даже если думали об этом), это уже ваша вина.
В апелляции ничего страшного нет. Если вы уверены, что решили задачу правильно (а у вас после соревнований будет достаточно времени, чтобы понять это), вы, скорее всего, убедите в этом комиссию. Не переживайте, не повышайте голос, говорите спокойно и вежливо, но будьте настойчивыми и готовыми объяснить свое решение простыми словами.
Проверяющий может не пойти на встречу. В таких ситуациях есть крайняя мера. Вы можете сказать: «Я хочу обратиться к председателю комиссии». Если проверяющий отказывается, проявите вежливость и настойчивость еще раз. Будьте готовы объяснить председателю ситуацию и, если надо, прокомментировать свое решение.
Однако оценивайте реально свои знания и решение. Случайно может оказаться так, что проверяющие поставили за решение больше баллов, чем оно заслуживает (по критериям, описанным выше). При обнаружении ошибки, скорее всего, оценку вам снизят.
Олимпиада уже прошла
Если вы — гений, а проверяющая комиссия это не заметила, и если результаты олимпиады вам что-то дают, еще рано расстраиваться. Можно попробовать пожаловаться в разные инстанции. Но в этом вам уже должны помочь учителя или администрация школы.
Лирическое отступление
Конечно, такое случается очень редко. Но всё же случается. В одиннадцатом классе на теоретическом туре республиканской олимпиады по физике дали четыре задачи «стоимостью» 30, 30, 30 и 10 баллов. Одну из задач на 30 баллов правильно решил только я. В ней была одна хитрость, и мне было очевидно, что именно эта хитрость превращала простую школьную задачу в относительно сложную олимпиадную. Все остальные, включая комиссию, не заметили этой хитрости. Мне поставили из 30 баллов только 5, в других задачах тоже за что-то сняли баллы, и мой результат (68 баллов) был четвертым. При этом первый результат был 100 баллов из 100.
На апелляцию я пришел с книжкой, объяснил, откуда берется дополнительная сила. Комиссия согласилась, что в этой задаче не всё так просто, и решила не тратить время, а перейти к практическому туру, в течение которого она собиралась пересмотреть результаты теоретического тура. Но, видимо, тупость комиссии победила, и результаты пересмотрены не были (я позволяю себе использовать слово «тупость», так как председатель комиссии (правда, не в тот раз, а через год) позволил себе заявить следующее: «Вы что! Нельзя поднимать баллы, а то подумают, что комиссия тупая!»).
После практического тура я поднялся на второе место, но со 100 баллами из 100 соревноваться невозможно.
Получивший первое место поехал на Международную олимпиаду.
Тогда мне было всё равно, но сейчас я очень жалею, что не обратился с жалобами в министерство образования.
Литература
Посоветуйтесь с учителем, он вам порекомендует литературу для подготовки к олимпиаде. Я же могу упомянуть о нескольких книгах с моей полки. По математике это книги Шарыгина. По физике продвинутым школьникам советую читать Фейнмановские лекции по физике. Не для подготовки к олимпиадам, правда, а просто для повышения уровня владения предметом.
Дополнение для физиков
На олимпиадах по физике есть некоторые тонкости, которые я хочу отметить особо. Например, ответы на задачи теоретического тура необходимо округлять, оставлять столько же значащих цифр, сколько их было в начальных данных.
Практический тур оформляйте так же, как и лабораторные работы. Напишите цель, теоретическое обоснование, результаты измерений, вычисления, оценку погрешности, вывод. Можно зарисовать установку.
Результаты измерений лучше записать в таблицу, особенно, если этих измерений несколько. Записывайте всегда только то, что показывает прибор. Например, если измеряете ток миллиамперметром, записывайте показания в миллиамперах. Потом переведете в другие единицы. Если измеряете массу электронными весами, переписывайте все цифры, которые отображены на табло. Потом округлите, если нужно.
Обязательно оцените погрешность ответа. Обычно абсолютная погрешность измеренных величин равна цене деления приборов. Для вычисления погрешности ответа есть несколько простых правил. Абсолютная погрешность суммы — это сумма абсолютных погрешностей слагаемых. Относительная погрешность произведения — сумма относительных погрешностей сомножителей. При извлечении корня относительная погрешность уменьшается в два раза.
Заключение
Теперь вы знаете всё, что нужно для успешного выступления на олимпиадах. Удачи!
written.ru
Доклад «Подготовка учащихся к олимпиадам по математике в 5-6 классах».

Подготовка учащихся к олимпиадам по математике в 5-6 классах.
Приоритетом современного образования, гарантирующим его высокое качество, становится обучение, ориентированное на саморазвитие и самореализацию личности. Школа как важный социальный институт должна помочь становлению личности, обладающей такими важнейшими качествами как инициативность, способность творчески мыслить и находить нестандартные решения. Интеллектуальный потенциал общества во многом определяется выявлением одаренных детей и работой с ними. Вопросы одаренности в настоящее время волнуют многих, так как современному образованию, присущи профильность и высокие требования молодежного рынка труда.
Эффективным средством развития, выявления способностей и интересов учащихся с разными типами одаренности являются предметные олимпиады. Очень высокий интерес к математическим олимпиадам, конкурсам, кружковым занятиям проявляют учащиеся 5-6 классов. Поэтому так важно в этот период создать все условия для проявления математических способностей, реализации интеллектуальных возможностей учащихся. Таким образом, можно определить основную цель и задачи для работы школы и учителя на данном этапе.

Основная цель: создание условий для выявления и развития одаренных учащихся через различные формы и методы работы в урочное и внеурочное время.
Задачи:
Изучение и применение методик для выявления одарённых детей.
Работа психолого-педагогической поддержки способных детей.
Систематизация методов и приёмов, которые способствуют развитию самостоятельности мышления, инициативности и творчества на уроках математики.
Расширение возможностей для участия школьников в олимпиадах и конкурсах по математике различного уровня.
Поставленные цели и задачи можно представить в виде схемы.
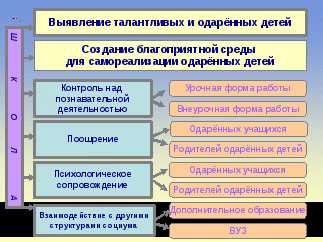
К 12 годам умственное развитие детей позволяет выполнять мыслительные операции, не только опирающиеся на личный конкретный опыт, они овладевают абстрактно-понятийными способами мышления и к 14-15 годам формируется логика взрослого человека. Помимо данных особенностей развития, одаренных учащихся часто характеризуют: свернутость и вариативность мышления, долговременная память, а так же рассеянное внимание, психические отклонения, неадекватная самооценка и эгоизм. Поэтому с такими детьми и их родителями необходима систематическая работа учителя, совместно со школьным психологом.
На данный момент существует огромное количество различных олимпиад и конкурсов для учащихся 5-6 классов. Возникает вопрос: «Как добиться успешного участия школьника в математической олимпиаде?»
Сегодня в распоряжении педагогов имеется большое количество литературы по подготовке учащихся к олимпиадам, но в основном — это сборники заданий с ответами или коротким решением. Вопрос методики подготовки школьников среднего звена недостаточно разработан, и заинтересованный учитель находится в постоянном поиске нужной информации. Каждый из нас выбирает свои направления, методы и приёмы организации занятий с одарёнными детьми.
Некоторые мои направления работы по подготовке учащихся к олимпиадам.
На изучение математики в 5-6 классах в нашей школе отводиться 5 часов. В 6-м классе добавляется 1 час кружковой работы (15 уч-ся из параллели 6-х классов).
Для достижения поставленных целей выбираю несколько направлений работы:
Работа на уроке;
Внеклассная работа;
Взаимодействие с внешкольными структурами социума;
Заочная работа.
Только задействовав все направления в подготовке учащихся к олимпиаде, можно ожидать успеха.
Работа на уроке.
На уроках в 5-6 классах включаю задачи, способствующие развитию логики мышления. В методической литературе по любой теме урока можно подобрать задачи, требующие нестандартного мышления.
Для развития интереса в программу урочных занятий включаю рассмотрение занимательных задач, ребусов, задач-шуток и т.д.
Творческие домашние задания. Например, задания на дом типа: «Придумайте задачу-сказку по теме», «Составьте кроссворд», «Придумайте ребусы» и т.д.
Домашние олимпиады. Обычно это набор из нескольких задач, которые предлагаются для решения в начале недели.

Внеклассная работа.
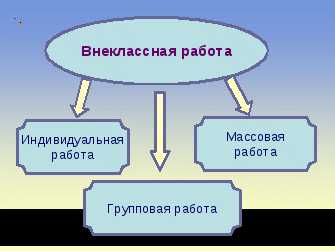
Внеклассная работа может осуществляться в самых разнообразных видах и формах.
Индивидуальная работа — такая работа, когда учитель принимает решение о выборе методики в каждой конкретной ситуации, зависимо от способностей и знаний ученика.
Групповая работа — систематическая работа, проводимая с достаточно постоянным коллективом учащихся. К ней относиться кружковая работа. В процессе таких занятий происходит расширение и углубление знаний. Процесс обучения строится как совместная исследовательская деятельность учащихся. В содержание внеклассной работы с учащимися, интересующимися математикой, включаю вопросы, выходящие за рамки школьной программы, но примыкающие к ней. Продолжением кружковой работы является летний интеллектуальный лагерь на базе гимназии.
Массовая работа — проводится с большим детским коллективом. Это недели математики, конкурсы, соревнования.
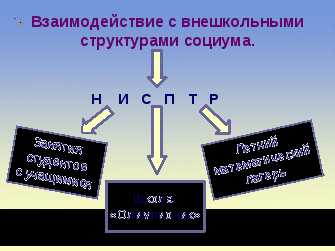
Взаимодействие с внешкольными структурами социума
В течении учебного года студенты НИСПТР (Набережночелнинский институт социально – педагогических технологий) проводят серию занятий с учащимися 5-6 классов.
Во время каникул учащиеся посещают математическую школу «Олимпионик» на базе НИСПТР.
Летний математический лагерь на базе НИСПТР
Заочная работа.
Сегодня получила значительное развитие заочная олимпиада, которая обладает неоспоримыми достоинствами: доступностью, дешевизной, простотой организации, протяженностью во времени. Задания либо рассылают по почте, либо размещают в Интернете на сайтах образовательных учреждений. Цель заочных олимпиад — дать импульс к саморазвитию и творческому поиску. В каких заочных олимпиадах принимать участие это наш выбор, просто необходимо найти время разобраться в большом ассортименте предложений и уделять внимание этим интересным конкурсам. Мы с учениками выбрали http://metaschool.ru/ (МетаШкола Петербургские интернет-кружки и олимпиады). Привлекателен тем, что доступный для всех и бесплатный, массовый, разнообразие конкурсов и олимпиад, итоги подводятся сразу после окончания конкурса, пополняется портфолио учащихся дипломами разных степеней, учитель может отслеживать результат. Кроме того на протяжении нескольких лет гимназия принимает участие в международной олимпиаде по основам наук.
Задача учителя направить учащихся туда, где они смогут заниматься, но иногда родители не заинтересованы в этом. Наша задача убедить их в необходимости развития своих талантливых детей.
Внеурочные формы работы можно представить в виде схемы.
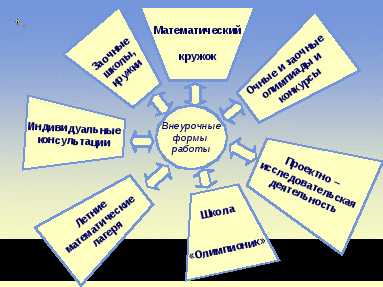
Все вышеперечисленные направления относятся к системной подготовке к олимпиадам.
Кроме того, существует так называемая интенсивная подготовка, которая проводится непосредственно перед конкурсами и олимпиадами.
Для участия во всероссийском педагогическом конкурсе мною был составлен традиционный задачник «За две недели до олимпиады».

Название говорит само за себя. Задачник рекомендуется использовать на заключительном этапе подготовки к муниципальному туру олимпиады по математике для учащихся 6 классов.
Данная разработка так же может быть использована для самостоятельной подготовки учащихся к олимпиаде.
В сборник включены задачи для устного решения – задачки для разминки и ответы к ним. Разработка содержит справочный материал к отдельным темам и задачи с последующим подробным решением. В конце сборника находятся две тренировочные работы в формате, который использовался последние два года на муниципальном туре олимпиады по математике в 5- 6 классах. После заданий приведены варианты решения всех задач. Учитель может использовать этот сборник для проверки готовности учащихся к олимпиаде. Время выполнения заключительных работ 1.5 часа. Критерий готовности – это процент правильно выполненных заданий. 80%-100% — высокий уровень готовности, 60- 79%- хороший уровень готовности, 40% -59% — средний уровень, менее 40% — низкий уровень готовности. В сборнике приведены правильные ответы и решения ко всем заданиям.
С разработкой можно ознакомиться на сайте http://planeta.tspu.
Отслеживание результатов.
Для отслеживания результатов участия учащихся в конкурсах и олимпиадах, для каждого класса по четвертям ведётся таблица результатов.
Приведу в пример фрагмент такой таблицы в одном из классов.

С помощью таких таблиц мне достаточно просто определять победителей по итогам четверти и года в конкурсе «Лучший математик». В этом конкурсе в каждом классе определяются по три победителя, затем трое лучших из параллели. Все победители награждаются грамотами и призами.
В заключении хочу сказать, что реализованные возможности развивают ребёнка, стимулируют интерес к математике. Олимпиады и конкурсы позволяют ученику познать себя, дают возможность в большей степени утвердиться в собственных глазах и среди окружающих. В целом они служат развитию творческой инициативы ребёнка.
infourok.ru
Вопросы олимпиадной подготовки по математике — Колпаков Александр Николаевич
Здесь публикуются ответы на вопросы репетитору, связанные с олимпиадной подготовкой. Если Вам нужен совет по решению какой-либо учебной или организационной задачи (подбору репетитора, школы, графика занятий, олимпиадных задачников и т. д.), — не стесняйтесь их задавать. Конечно, сориентироваться в проблеме только на основе ее словесного описания (без диагностики ученика) крайне сложно, но я постараюсь представить себе ситуацию в наиболее типичном раскладе и описать вероятную перспективу тех или иных действий. Пишите, спрашивайте.
Вопрос репетитору по математике от Саблиной Татьяны:
Добрый вечер, Александр Николаевич! Может быть Вы поможете советом: мой шестнадцатилетний ребенок получает достаточно хорошие оценки по алгебре и геометрии (в основном 9 — 10 по 10-ти бальной системе), понимает и усваивает материал на уроках сходу, никогда с репетитором по математике не занимался. Но вот олимпиадные задачи не идут, не хватает логики или смекалки, не знаю. Принимал участие в районных олимпиадах — в 3 — 5 классах, потом в 6-7 классах, занимал даже третьи места или поощрения. Но вот в 9 -10 классах наотрез отказывается от участия в районных и городских олимпиадах — учитель настаивает, заставляет, не верит, что ребенок не понимает (а он реально говорит, что ничего не понимает и я ему охотно верю), хотя в этом году же занял третье место в школьной олимпиаде. Учится он по всем предметам ровно, т.е на 8-9, не зубрилка, живем в Риге. Вопрос в следующем: можно ли научиться решать нестандартные олимпиадные задачи? Есть ли репититоры по математике для такого вида задач? И вообще стоит ли напрягать сына ходить на олимпиады, ведь он отлично осваивает школьную программу? Научиться решать олимпиадные задачи по математике могут все умные дети или нужны еще какие-то качества, кроме ума? Если найдете свободную минутку- то напишите свои мысли.
Сын собирается поступать в один из технических университетов Германии, и участие (призовые места) в олимпиадах пригодились бы.
С уважением Татьяна.
Мнение репетитора А.Н. Колпакова: Нельзя заставлять ребенка участвовать в олимпиадах, если он сам этого не хочет. Олимпиада олимпиаде рознь (особенно если сравнивать 5 класс и 10 класс) и поэтому нельзя предъявлять к ним одинаковые требования. Еще неизвестно почему Ваш ученик перестал занимать призовые места. Возможно, уровень олимпиадных заданий по математике в 10 классе для него слишком высокий и не соответствуют на сегодняшний день его способностям. А возможно его задавила школа, и он потерял олимпиадную смекалку. Трудно сказать. В любом случае для решения сложной задачи нужна полная мобилизация мыслительного потенциала человека, а для этого, прежде всего, требуется огромное желание преодолеть трудности. Есть его нет, — бесполезно ходить на олимпиады вообще. Возможно, ученик это понимает и поэтому отказывается.
Грамотный репетитор по математике никогда не занимается натаскиванием ученика на олимпиадные задачи, ибо нельзя предугадать их тематику в реальности. Правильная стратегия репетитора — движение в сторону фундаментального математического и общего интеллектуального развития подростка.
Теперь о возможностях научить решению нестандартных задач. Научить, — это значит рассказать некий универсальный метод, позволяющий с теми или иными затратами умственной энергии справляться с любой олимпиадной ситуацией. Такого метода не существует. Репетитор по математике физически не сможет рассмотреть все задачи. Что реально сделать? Можно получить практику решения олимпиадных задач, которая создаст хороший плацдарм для развития мышления ребенка и условий формирования его интереса к предмету в целом.
Нестандартные задачи потому и называют нестандартными, что для них не существует заранее определенного алгоритма решения. Каждая задача имеет свой уникальный «код доступа» и используются для отбора талантливых детей с высоким уровнем знаний, способностей и смекалки. Хороший олимпиадный репетитор по математике создает условия, в которых эти показатели достигают максимального предела. Он индивидуален для каждого человека.
Многие нестандартные задачи, которые таковыми являются в школе, в курсе высшей математики (аналитической геометрии, высшей алгебры, анализа, теории чисел) переходят в категорию стандартных. Поэтому все относительно. Знания общих законов помогают брать нереальные, казалось бы, высоты и поэтому репетиторы по математике часто с легкостью решают олимпиадные задачи 5 — 11 классов только потому, что за годы фундаментальной учебы получили высшие знания. Именно поэтому, помимо изучения нестандартных задач, профессиональный репетитор по математике уделяет время обобщению базовых тем, даже если ученик щелкает типовые задачки как орешки.
Путь к вершинам математического и общего интеллектуального развития не должен лежать только через одни олимпиады. И не стоит на них зацикливаться. Учитесь понимать теорию, выполняйте сложные базовые упражнения. Практика показывает, что углубленное изучение математики с репетитором приносит гораздо больше пользы, чем долгая и изнурительная олимпиадная практика. Можно месяцами решать одну и ту же нестандартную задачу и ничего не приобрести с этого, кроме отставания в фундаментальном освоении предмета.
А.Н. Колпаков. Репетитор по математике — Москва. Олимпиадная помощь школьникам.
ankolpakov.ru
Подготовка учащихся к олимпиадам по математике
ПОДГОТОВКА УЧАЩИХСЯ К ОЛИМПИАДАМ ПО МАТЕМАТИКЕ
Статья
«Решение задач — практическое искусство, подобное плаванию, катанию на лыжах или игре на фортепиано; научится этому можно, только беря пример с наилучших образцов и постоянно практикуясь. Но помните: если вы хотите научиться плавать, то смелее входите в воду, а если хотите научиться решать задачи, то решайте их».
Д.Пойа
Умение решать задачи, особенно олимпиадные, всегда являлось одним из показателей математической одаренности ученика.
Тем более что сегодня часто по итогам олимпиад оценивают итоги внеклассной и внешкольной работы по математике в школе, районе.
Подготовка учащегося к участию в олимпиаде – труд не одного года. Нужно отметить, что успешно участвовать в предметной олимпиаде может учащийся, знакомый со стандартными приемами решения задач, выходящих за рамки школьного курса. Определенную роль играет и скорость мышления учащегося. Целесообразно начинать подготовку «олимпиадников» в 5-7 классах. Только при таком подходе учащийся, попавший на олимпиаду в 8-9 классах, будет чувствовать себя уверенно: скажется опыт решения нестандартных задач, накопленный за несколько лет.
В ходе проведения занятий обращаю внимание на то, чтобы: занятия проходили в форме живого, непосредственного общения школьников и преподавателя, учитывался индивидуальный подход; обучающиеся овладели умениями общего учебного характера, разнообразными способами деятельности и приобрели опыт:
— решения разнообразных задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
— исследовательской деятельности, проведения экспериментов;
— точного, грамотного изложения своих мыслей в устной и письменной речи;
— поиска, систематизации, анализа, классификации информации, использования разнообразных информационных источников.
Необходимо подчеркнуть, что подготовка и проведение занятий – творческий процесс.
Из своего многолетнего опыта работы хочу предложить несколько советов:
— не заниматься с учениками одной темой в течение продолжительного промежутка времени. Даже в рамках одного занятия полезно сменить направление деятельности;
— постоянно возвращаться к пройденному материалу. Это можно делать, предлагая задачи на данную тему в устных и письменных олимпиадах и других соревнованиях;
— при разборе темы выделяю несколько основных логических вех и добиваюсь безусловного понимания этих моментов;
— постоянно обращаюсь к нестандартным и «спортивным» формам проведения занятий, не забывая при этом подробно разобрать все предложенные на них задачи. Также использую на занятиях развлекательные и шуточные задачи.
При непосредственной подготовке учащихся к математическим конкурсам и олимпиадам необходимо акцентировать внимание учащихся на следующих моментах:
— в качестве одной из задач конкурса любого уровня может быть задача, в условии которой фигурирует год проведения конкурса, олимпиады;
— как правило, в числе конкурсных задач отсутствуют задачи с длительными выкладками, на использование трудно запоминающихся формул, на использование справочных таблиц;
— если в условии требуется указать все возможные способы решения задачи, то от полноты количества указанных способов зависит и количество полученных баллов;
— если в условии задачи фигурирует вопрос «Можно ли…?», то для того чтобы доказать, что «можно» достаточно привести всего один положительный пример, а для того чтобы ответить, что «нельзя», необходимо рассмотреть все возможные случаи, обобщая их в стройное доказательство;
— всегда помнить, что задания составляются компетентными специалистами, и «некорректных формулировок условий задач», как правило, в конкурсных вариантах не встречается, а непонятные и непривычные формулировки как раз и характеризуются категорией нестандартности задачи.
Рекомендации учителю по подготовке учащихся:
— усилить подготовку учащихся по внепрограммному материалу;
— каждому учителю, прежде чем готовить учащегося к конкурсу, олимпиаде по математике, выработать педагогическую систему подготовки;
— использовать возможности кружковой работы, факультативных занятий по математике для подготовки к решению конкурсных, олимпиадных задач;
— отбор задач необходимо начать заблаговременно.
Приведу несколько возможных тем занятий для учащихся разных классов:
1. Задачи, решаемые с конца (5 – 6 кл.).
2. Занимательные задачи на проценты (6 кл.).
3. Математические ребусы (5 – 7 кл.).
4. Геометрические задачи со спичками (5 – 6 кл.).
5. Задачи на разрезание и перекрашивания фигур (5 – 7 кл.).
6. Графы (6 – 9 кл.).
7. Упражнения на быстрый счет (5 – 8 кл.).
8. Четность (7 – 9 кл.)
9. Делимость и остатки (7 – 9 кл.).
10. Занимательные задачи на построения (7 – 8 кл.).
11. Геометрические построения с различными чертежными инструментами (7 – 8 кл.).
12. Взвешивания (5 – 7 кл.).
13. Логические задачи (5 – 8 кл.).
14. Уравнения в целых и натуральных числах (7 – 11 кл.).
15. Геометрические задачи на местности (8 – 9 кл.).
16. Метод математической индукции (8 – 11 кл.).
17. Принцип Дирихле (6 – 9 кл.).
18. Текстовые задачи (7 — 9 кл.).
19. Уравнения, неравенства и их системы (7 – 11 кл.).
20. Доказательства неравенств (9 – 11 кл.).
21. Занимательные комбинаторные задачи (7 – 9 кл.).
22. Построение графика сложной функции (9 – 11 кл.).
23. Тригонометрические преобразования (10 – 11 кл.).
24. Планиметрия (7 – 9 кл.).
25. Стереометрия (10 – 11 кл.).
26. Некоторые примеры решения уравнений высших степеней ( 10-11кл.)
Проведение олимпиад и подготовка к ним через математические кружки, факультативные занятия и часы для дополнительной работы по математике должны привлекать детей своей индивидуальностью и интересными методами их проведения.
Роль учителя в этом деле огромная. В первую очередь учитель обязан создать благоприятные условия для того, чтобы ученик смог постигать новое в интересующей его науке. С помощью знаний учителя, умением методически правильно поставить перед учеником задачу посильную ученику, он добьется успеха.
Использованная литература:
1. Генкин С.А., Итенберг И.В., Фомин Д.В. Ленинградские математические кружки. – К.,1994. – С.4.
2. Григорьева Г.И. подготовка школьников к олимпиадам по математике: 5 – 6 классы. – М.: Издательство « Глобус», 2009. – С.4 – 6.
3. Севрюков П.Ф. Школа решения олимпиадных задач по математике. – М. : Ставрополь , 2013. – С. 7 – 11.
4. Фарков А.В. Математические кружки в школе. 5 – 8 классы. – М.: Айрис – пресс, 2008. – С. 6.
5.Фарков А.В. Математические олимпиады: методика подготовки. 5 – 8 классы. – М.:ВАКО, 2014. – С.3 – 21.
videouroki.net
Методика успешной подготовки студентов к олимпиаде по математике
Методика успешной подготовки студентов
к олимпиаде по математике
Человек, искушённый в математике, как правило, даже не сознавая, использует методы математического мышления на каждом шагу, по любому поводу.
Важная особенность занимательной математики в том, что она побуждает к работе мысли.
Национальная образовательная инициатива «Наша новая школа» обращает внимание на то, что ключевой характеристикой современного российского образования становится не только передача знаний и технологий, но и формирование творческих компетентностей у детей. Именно такой подход к образованию способствует формированию у студентов инициативности, способности творчески мыслить и находить нестандартные решения. Забота об одаренных студентах сегодня — это забота о развитии науки, культуры и социальной жизни России в будущем.
Принципы работы со студентами высоких интеллектуальных способностей:
— знакомство с психологическими особенностями и методическими приемами работы с одаренными студентами;
— обучение через методическую учебу, самообразование;
— накопление библиотечного фонда по данному вопросу;
— знакомство с приемами педагогического наблюдения, диагностики;
— проведение различных внеурочных конкурсов, интеллектуальных игр, олимпиад;
— отбор методов и приемов, которые способствуют развитию самостоятельности и творчества;
— предоставление возможности студентам совершенствовать способности через самостоятельную работу.
— принцип добровольности.
Оптимальность и эффективность средств
Создание условий, способствующих оптимальному развитию одаренности:
— отбор тех методов, форм и приемов, которые способствуют развитию самостоятельности мышления, инициативности и творчества, и применение этих форм и приемов;
— предоставление возможности совершенствовать способности в совместной деятельности с руководителем, со сверстниками, через самостоятельную работу;
проявление уважения к индивидуальности студента:
— понимание особенностей его развития,
— стремление избежать в работе с одаренными студентами двух крайностей: возведение студента на пьедестал, подчеркивание его особых прав, а с другой стороны – принижение достоинства или игнорирования интеллектуальных успехов во время борьбы со «звездностью»
Целенаправленная и систематическая работа со студентами, которые проявляют интерес к творческой деятельности, позволяют более эффективно управлять формированием комплексных характеристик мышления (гибкость ума, внимание, память, воображение, синтез, анализ и т.д.), активизировать работоспособность и темпы познавательной и творческой деятельности студентов.
Поиск одарённых личностей должен идти непрерывно. Наиболее распространённой формой отбора одаренных студентов являются математические конкурсы и олимпиады.
Успешное выступление на олимпиаде предполагает:
а) психологическую подготовку студента к выполнению нестандартных заданий;
б) математическую одарённость;
в) умение собраться, сконцентрироваться на выполнение нескольких заданий за определённый промежуток времени;
г) математическую грамотность участника, умение строго записать решение задачи;
д) успешное овладение студентом изучаемых разделов математики.
Успех на олимпиаде связан не только со способностями, но и со знанием классических олимпиадных задач. Поэтому к олимпиаде надо серьёзно готовиться.
Решение нестандартных задач как основа подготовки к олимпиадам
Работу по подготовке к олимпиадам в колледже и районного уровней я провожу в течение всего учебного года.
В домашнее задание включаю задачи, требующие нестандартного мышления. Стараюсь обучать общему подходу и основным методам решения задач, а именно:
— разбиению задачи на подзадачи преобразование задачи;
— введению и построению вспомогательных элементов.
Немаловажным моментом подготовки учащихся к олимпиадам и конкурсам по математике является формирование умения определять уровень сложности задачи для распределения времени на выполнение заданий конкурса.
При непосредственной подготовке обучающихся к математическим конкурсам и олимпиадам необходимо акцентировать внимание учащихся на следующих моментах:
— в качестве одной из задач конкурса любого уровня может быть задача, в условии которой фигурирует год проведения олимпиады,
— в конкурсных задачах отсутствуют задачи с длительными выкладками,
— в задачах на доказательство требуется полное обоснование,
— если в условии требуется указать все возможные способы решения, то от полноты количества указанных способов зависит и количество полученных баллов,
— если в условии требуется ответить на вопрос «Можно ли…?», то для ответа достаточно привести один положительный пример, а для того, чтобы дать ответ «нельзя» необходимо рассмотреть все возможные случаи, обобщая их в доказательство.
Кроме традиционной формы постановки математической задачи знакомлю учащихся с вариантами различных олимпиад в тестовой форме, обращая внимание на их специфику: в некоторых заданиях все-таки можно оттолкнуться от предложенных вариантов ответов и выстроить собственное решение.
Для развития интереса к решению нестандартных задач по математике в программу занятий включаю рассмотрение занимательных задач, задач-шуток, софизмов, задач прикладного характера.
Для подготовки студентов я использую материал предыдущих олимпиад, конкурсов по математике и математического конкурса «Кенгуру».
Использование педагогических технологий в процессе работы с высокомотивированными обучающимися
В обучении высокомотивированных учащихся ведущими являются методы творческого характера — проблемные, поисковые, эвристические, исследовательские, проектные — в сочетании с методами самостоятельной, индивидуальной и групповой работы.
Именно эти педагогические технологии, на мой взгляд, позволяют студенту не накапливать объем знаний или количество информации, а развивают умения управлять этой информацией: искать, наилучшим способом присваивать, находить в ней смысл, применять в жизни.
Формы и методы подготовки студентов к математическим соревнованиям.
Математические бои. Математические конкурсы. Математические игры. Математические турниры. Математическое ориентирование. Математические викторины. Олимпиады по математике.
Использование интерактивных методов при подготовке к математическим соревнованиям (работа в малых группах, мозговой штурм, карусель, мозаика, дерево решений и т.д.).
Рекомендации участнику олимпиады:
1. Внимательно изучи текст предложенных задач.
2. Приступай к решению той задачи, которая кажется тебе более доступной.
3. Помни: на олимпиаде «лёгких» задач не бывает. Ищи «изюминку»!
4. Если задача вызывает трудности, попробуй упростить её условие, посмотреть частные или предельные случаи.
5. Решили задачу — сразу оформляйте её решение. Это поможет вам проверить логику и освободить мысли для других задач.
6. Если задача не получается, оставьте её на время и переходите к другой.
7. Задача становится проще, если её окружить родственными задачами.
Перечень литературы для подготовки к Олимпиаде по математике
Богомолова О.Б. Логические задачи – М.:БИНОМ. Лаборатория базовых знаний, 2009
Болотов А.А., Прохоренко В.И., Сафонов В.Ф. Математика. Теория и задачи. – М.:Издательство МЭИ, 1998
Всероссийская олимпиада школьников по математике 1993-2006; Окружной и финальный этапы / Под ред. Н.Х.Агаханова – М.:МЦНМО, 2007
Голубев В.И. Решение сложных и нестандартных задач по математике. М.:ИЛЕКСА, 2007
Дориченко С.А., Ященко И.В. Московская математическая олимпиада: сборник подготовительных задач. – М.,,1994
Козко А.И., Чирский В.Г. Задачи с параметром и другие сложные задачи. М.:МЦНМО, 2007
Лурье М.В., Александров Б.И. Задачи на составление уравнений – М.: Наука, 1990
Олехник С.Н., Потапов М.К., Пасиченско П.И. Уравнения и неравенства. Нестандартные методы решения: справочник. – М.:Факториал, 1997
Олимпиада школьников «Ломоносов» по математике (2005-2008). – М.:Изд. ЦПИ мех-мат МГУ, 2008
Петрушко И.М., Прохоренко В.И., Сафонов В.Ф. Задачник по математике (с тестами и банком задач для межрегиональных олимпиад).—М.: Издательский дом МЭИ, 2009
Петрушко И.М., Прохоренко В.И., Сафонов В.Ф. Математика. Методические указания к решению заданий – М.:Издательство МЭИ, 2002
Петрушко И.М., Прохоренко В.И., Сафонов В.Ф. Сборник заданий по алгебре, геометрии и началам анализа. – М.:Издательство МЭИ, 2005
Петрушко И.М., Прохоренко В.И., Сафонов В.Ф. Сборник заданий по алгебре, геометрии и началам анализа. – СПб.:Лань, 2007
Прасолов В.В. Задачи по планиметрии – М.:Наука, 1986
Сергеев И.Н., Олехник С.Н., Гашков С.Б. Примени математику – М.: Наука, 1989
Турниры им. М.В. Ломоносова 1999-2008 / http://www.mccme.ru/free-books
Фарков А.В. Готовимся к олимпиадам по математике. – М.:Экзамен, 2010
Штейнгауз Г. Сто задач – М.:Наука, 1976
Ященко И.В. Приглашение на математический праздник. – М.:МЦНМО, 2005
Преподаватель математики Филиппова А.Ф.
infourok.ru
Подготовка к олимпиаде по математике
ЗАДАНИЯ № 1 (5-ый класс)
1.В день рождения дяди Федора почтальон Печкин хочет выяснить, сколько тому лет. Шарик говорит, что дяде Федору больше 11 лет, а кот Матроскин утверждает, что больше 10 лет. Сколько лет дяде Федору, если известно, что ровно один из них ошибся? Ответ обоснуйте.
Петя тратит 1/3 своего времени на игру в футбол, 1/5 — на учебу в школе, 1/6 — на просмотр кинофильмов, 1/70 — на решение олимпиадных задач, и 1/3 — на сон. Можно ли так жить?
3. В примере на сложение двух чисел первое слагаемое меньше суммы на 2000, а сумма больше второго слагаемого на 6.
Восстановите пример.
Без ореха (от дупла до орешника) белка бежит со скоростью 4 м/сек, а с орехом (от орешника до дупла) — со скоростью 2 м/сек. На путь от дупла до орешника и обратно она тратит 54 секунды. Найдите расстояние от дупла до орешника. Ответ обоснуйте.
Цифры трёхзначного числа A записали в обратном порядке и получили число B. Может ли число, равное сумме A и B, записываться только нечётными цифрами?
У двузначного числа первая цифра вдвое больше второй. Если к этому числу прибавить квадрат его первой цифры, то получится квадрат некоторого целого числа. Найдите исходное двузначное число.
Петя и Вася участвовали в велогонке. Все участники стартовали одновременно и показали на финише различное время. Петя финишировал сразу после Васи и оказался на десятом месте. Сколько человек участвовало в гонке, если Вася был пятнадцатым с конца?
Однажды Миша, Витя и Коля заметили, что принесли в детский сад одинаковые игрушечные машинки. У Миши есть машинка с прицепом, есть маленькая машинка и есть зеленая машинка без прицепа. У Вити есть машинка без прицепа и маленькая зеленая с прицепом, а у Коли — большая машинка и маленькая синяя с прицепом. Машинку какого вида (по цвету, размеру и наличию прицепа) принесли мальчики в детский сад? Ответ объясните.
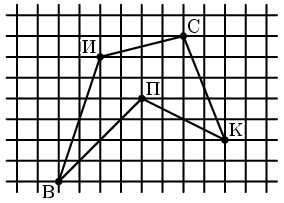
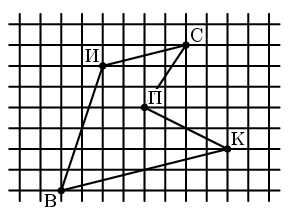
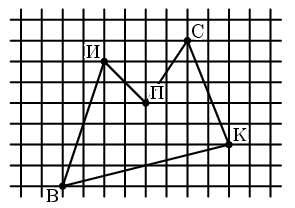
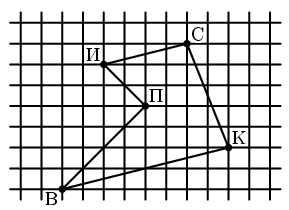
В точке В живет Винни-Пух, а в точках К, С, П и И – его друзья Кролик, Сова, Пятачок и ослик Иа-Иа (см. рисунок). Зимним утром Винни-Пух навестил их всех по одному разу, а потом вернулся домой. При этом он протоптал в снегу 5 прямых тропинок от домика к домику, не пересекающих друг друга. Начертите как можно больше возможных маршрутов Винни-Пуха.
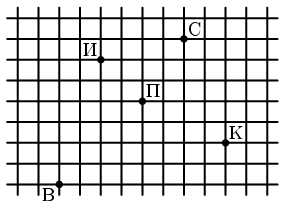
Иван, Петр и Сидор ели конфеты. Их фамилии – Иванов, Петров и Сидоров. Иванов съел на 2 конфеты меньше Ивана, Петров – на 2 конфеты меньше Петра, а Петр съел больше всех. У кого из них какая фамилия?
РЕШЕНИЯ к ЗАДАНИЯМ №1:
Заметим, что если не ошибся Шарик, то не ошибся и Матроскин, что противоречит условию. Значит, Шарик сказал неправду, в отличие от кота Матроскина. Таким образом, дяде Федору больше 10 лет, но не меньше 11. Следовательно, дяде Федору исполнилось 11 лет.
Поскольку 1/5 + 1/6 > 1/3, то сумма данных дробей 1/3 + 1/5 + 1/6 + 1/70 + 1/3 > 1, что противоречит здравому смыслу.
Если из суммы двух чисел вычесть одно из слагаемых, то получится другое слагаемое. Из условия следует, что второе слагаемое равно 2000, а первое – 6.
Поскольку обратно белка бежит в два раза медленнее, то время, затраченное белкой на обратную дорогу, в два раза больше времени, которое она тратит на дорогу от дупла до орешника. Поэтому время, затраченное на дорогу от дупла до орешника, в три раза меньше времени, затраченного на всю дорогу, то есть равно 54 : 3 = 18 секунд. Следовательно, расстояние от дупла до орешника равно 18 * 4 = 72 метра.
Пусть, например, A = 219. Тогда B = 912, A + B = 1131.
Первая цифра в два раза больше второй только у следующих двузначных чисел: 21, 42, 63 и 84. Проверкой убеждаемся, что условию задачи удовлетворяет только число 21.
Так как Петя оказался на десятом месте, а Вася финишировал перед ним, то Вася занял девятое место. Вася был пятнадцатым с конца, значит за ним финишировало еще четырнадцать человек. Следовательно, в гонке участвовало 23 человека.
Если бы Коля принес синюю маленькую машинку с прицепом, то Витя должен был принести машинку с прицепом, но у Вити она зеленая. Значит, Коля принес большую машинку, а Витя не маленькую, то есть машинку без прицепа. Тогда Миша не мог принести машинку с прицепом, и не мог принести маленькую машинку. Значит, Миша должен был принести зеленую машинку без прицепа. Таким образом, каждый из мальчиков принес большую зеленую машинку без прицепа.
Иванов съел меньше Ивана, а Петр съел больше всех, значит, Петр – не Иванов. По той же причине Петр – не Петров, то есть фамилия Петра – Сидоров. Иванов – не Иван, значит, Иванова зовут Сидор. Следовательно, Петрова зовут Иван.
infourok.ru