Площадь геометрической фигуры
Что такое площадь Площадь геометрической фигуры — это неотрицательная численная величина, которая характеризует размер этой фигуры.
Изначально, геометрия в Древней Греции (по-гречески «землемерие») занималась измерением площадей и объемов. Значительное число задач в области элементарной геометрии посвящено именно таким вопросам.
Общим методом нахождения площадей фигур в координатной плоскости является интегральное исчисление. Этими вопросами занимается математический анализ.
Для понимания применения универсального метода математического анализа для определения площади фигур можно привести следующие примеры вычисления площади:
- Площадь фигуры, заключенная между графиком непрерывной функции на интервале [a,b] и осью абсцисс, равна определенному интегралу этой функции на том же интервале
- Площадь фигуры, заключенная между графиками двух непрерывных функций на интервале [a,b] равна разности определенных интегралов этих функций на этом интервале
Или, с помощью формул это будет выглядеть следующим образом:
Как видно из рисунка и из формул, площадь фигуры, заключенной между графиком непрерывной функции f(x) и осью координат x на интервале [a,b] равна определенному интегралу этой функции [1].

Если же нам необходимо найти площадь фигуры, заключенной между графиками двух непрерывных функций — мы просто находим определенный интеграл для обоих функций и вычитаем площадь одной фигуры из площади другой. Разность площадей и даст нам искомую величину.
С помощью интегрального исчисления также определяются площади поверхностей фигур и в полярных координатах (фигура, заключенная между двумя лучами) и в трехмерном пространстве.
Свойства площади фигур Площадь фигуры – это неотрицательная величина, числовое значение которой имеет следующие свойства:
- Площадь фигуры является неотрицательной величиной
- Равные фигуры имеют равные площади
- Площадь фигуры равна сумме составляющих ее и не перекрывающих друг друга частей (свойство аддитивности).
- Площадь квадрата со стороной, равной единице измерения, равна единице (свойство нормированности)
- Площадь фигуры всегда больше площади ее части (свойство монотонности)
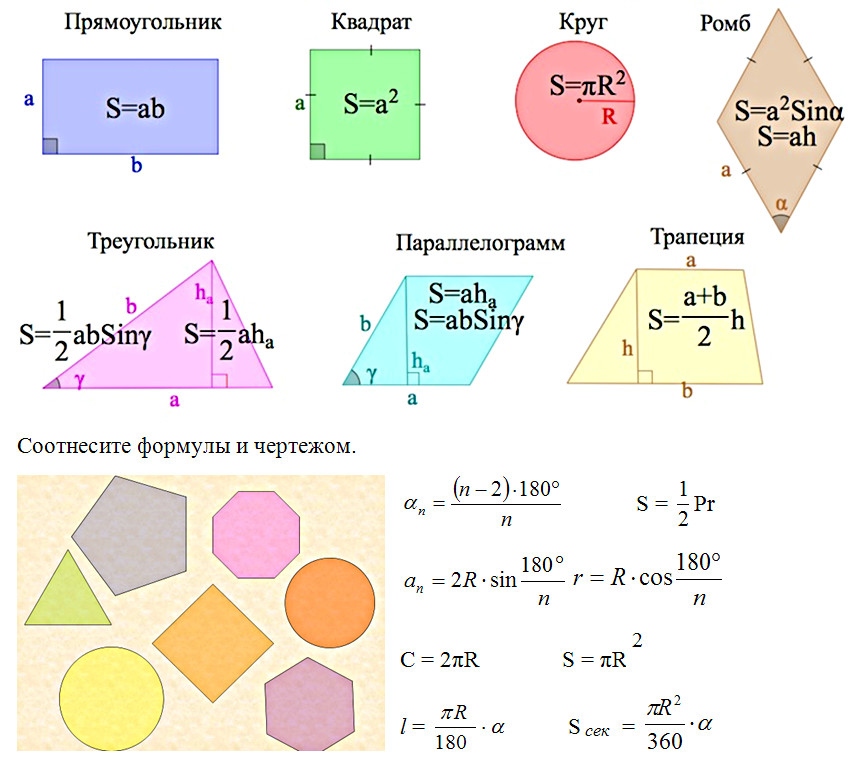
Формулы для нахождения площадей геометрических фигур
Площадь квадрата со стороной а
S=a2
См. также — квадрат и площадь квадрата. Все формулы.
также — квадрат и площадь квадрата. Все формулы.
S=ab
См. также Задачи про нахождение площади прямоугольника с пояснениями.
Площадь параллелограмма со сторонами а и b или с основанием а и высотой h
S=ah
S=ab*sin ∠ab
См. также свойства и площадь параллелограмма.
Площадь ромба со стороной а, углом между сторонами α, диагоналями d1, d2
S=ab*sinα
илиS=1/2 d1d2
См. также Задачи о ромбе.
также Задачи о ромбе.
Площадь треугольника с основанием а и высотой h
S=1/2 ah
См. также площадь треугольника (все формулы).
Площадь трапеции с основанием а, b и высотой h
S=(a+b)/2 * h
См. также свойства и площадь трапеции (все формулы).
Площадь круга
См. также Задачи про окружность.
 Уравнение окружности
Уравнение окружности
Расчет площади геометрических фигур | International Institute of Care to Buildings
СПРАВОЧНИКИ
Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади выражается числом заключающихся в него квадратных единиц.
Формулы площади треугольника
1-ая формула
S — площадь треугольника
a, b — длины 2-х сторон треугольника
С — угол между сторонами a и b
2-ая формула
S — площадь треугольника
a — длина стороны треугольника
h — длина высоты, опущенной на сторону a3-ья формула
S — площадь треугольника
a, b, c — длины 3-х сторон треугольника
p — полупериметр треугольника
4-ая формула
S — площадь треугольника
r — радиус вписанной окружности
p — полупериметр треугольника
5-ая формула
S — площадь треугольника
a, b, c — длины 3-х сторон треугольника
R — радиус описанной окружности
См. также: Онлайн калькулятор для расчета площади треугольника.
также: Онлайн калькулятор для расчета площади треугольника.
Формулы площади квадрата:
1) Площадь квадрата равна квадрату длины его стороны (a).
2) Площадь квадрата равна половине квадрата длины его диагонали (d).
S
a — длина стороны квадрата
d — длина диагонали квадрата
См. также: Онлайн кальклятор для расчета площади квадрата.
Формула площади прямоугольника:
1) Площадь прямоугольника равна произведению длин двух его смежных сторон (a, b).
S — площадь прямоугольника
a — длина 1-ой стороны прямоугольника
b — длина 2-ой стороны прямоугольника
См. также: Онлайн калькулятор для расчета площади прямоугольника.
Формула площади параллелограмма:
1) Площадь параллелограмма равна произведению длины его основания на длину высоты (a, h).
S — площадь параллелограмма
a — длина основания
h — длина высоты
См. также: Онлайн калькулятор для расчета площади параллелограмма.
Формула площади трапеции:
1) Площадь трапеции равна произведению полусуммы ее оснований на высоту (a, b, h).
S — площадь трапеции
a — длина 1-ого основания
b — длина 2-ого основания
h — длина высоты трапеции
См. также: Онлайн калькулятор для расчета площади трапеции.
Формулы площади ромба:
1) Площадь ромба равна произведению длины его стороны на высоту (a, h).
2) Площадь ромба равна половине произведения его диагоналей.
S — площадь ромба
a — длина основания ромба
h — длина высоты ромба
d1 — длина 1-ой диагонали
d2 — длина 2-ой диагонали
См.
Формула площади круга:
1) Площадь круга равна произведению квадрата радиуса на число пи (3.1415).
2) Площадь круга равна половине произведения длины ограничивающей его окружности на радиус.
S — площадь круга
π — число пи (3.1415)
r — радиус круга
См. также: Онлайн калькулятор для расчета площади круга.
Формула площади эллипса:
1) Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи (3.1415).
S — площадь эллипса
π — число пи (3.1415)
a — длина большой полуоси
b — длина малой полуоси
См. также: Онлайн калькулятор для расчета площади эллипса.
Площади геометрических фигур.
 8-й класс
8-й класс
Цели: закреплять навыки в решении задач по теме “Площади” и готовиться к ОГЭ.
Задачи:
Образовательные:
- обобщить знания и умения учащихся по теме “Площадь”.
Развивающие:
- формировать умения ясно и четко излагать свои мысли;
- формировать навыки публичного выступления и умения отстаивать самостоятельное суждение.
Воспитательные:
- создавать условия для реальной самооценки учащихся, реализации его как личности;
- воспитывать познавательный интерес к предмету;
- воспитывать эстетический вкус.
Оборудование: компьютер, проектор, экран, раздаточный материал.
План урока:
- Организационный. Постановка цели урока.
- Повторение. Устная работа.
- Решение задач.
- Заключительная часть. Подведение итогов урока.

- Домашнее задание.
Ход урока
I. Организационный. Постановка цели урока
Мы заканчиваем изучение темы: “ Площади”. Сегодня на уроке мы вспомним, как вычисляются площади различных фигур. Решим задачи, опираясь на наши знания по этой теме.
II. Устная работа
Перед тем, как начнем решать задачи, давайте вспомним фигуры, которые мы с вами изучали и формулы для вычисления их площадей.На доске подготовлена таблица.
| № | фигура | формулы |
| 1 | квадрат | |
| 2 | прямоугольник | |
| 3 | параллелограмм | |
| 4 | ромб | |
| 5 | треугольник | |
| 6 | трапеция |
По окончании устно работы таблица имеет такой
вид.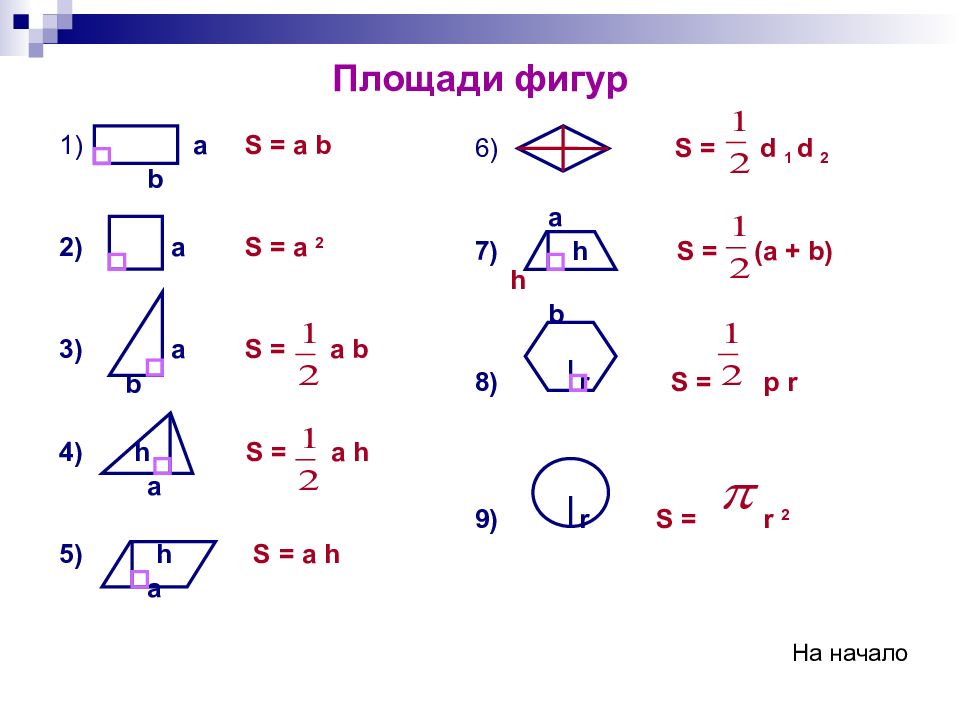
Для проведения устной работы используется презентация
.Приложение слайд 1
Задача 1. Используя слайды, учащиеся должны выбрать формулу для вычисления площади изображенной фигуры и обосновать свой ответ.
Пример.
Фигура ABCD – квадрат, т.к. на чертеже показано, что у данного четырёхугольника все стороны равны и все углы по 90°. Значит, для вычисления площади воспользуемся формулой под номером.
Слайд 1 включает в себя 4 задачи подобного типа, решение которых позволяет не только ещё раз вспомнить формулы, но и
позволяет вспомнить основные свойства площадей плоских фигур.III.
Решение задачСейчас мы с вами будем решать задачи, которые в
экзаменационных работах стоят в блоке
“Геометрия” № 11. Предлагаю вам разделиться на
группы. На экране будут появляться задачи, та
группа, которая первая найдет решение, отвечает у
доски, остальные помогают. За каждый правильный
полный ответ группа получает 5 баллов. За не
достаточные обоснования снимается 1 балл и
передается той группе, которая сможет дополнить.
За каждый правильный
полный ответ группа получает 5 баллов. За не
достаточные обоснования снимается 1 балл и
передается той группе, которая сможет дополнить.
Для решения задач используется презентация.
Приложение слайд 2 – 9
На каждом слайде есть кнопка “Подсказка” с указанием количества подсказок. Ей имеет смысл воспользоваться, если возникают затруднения с решением задач.
IV. Заключительный этап.
Подведение итогов
Домашняя работа
1. Задание 11 № 195. Найдите площадь параллелограмма, изображённого на рисунке.
2. Задание 11 № 333013. Основания трапеции равны 1 и 11. Найдите бoльший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
3. Задание 11 № 323902. Основания равнобедренной трапеции равны 5 и 17, а ее боковые стороны равны 10. Найдите площадь трапеции.
Ресурсы Интернет.
- http://100formul.ru
- http://sdamgia.ru/
Нахождение площади. Как найти площадь геометрических фигур
Что такое площадь?Площадь – характеристика замкнутой геометрической фигуры (круг, квадрат, треугольник и т.д.), которая показывает ее размер. Площадь измеряется в квадратных сантиметрах, метрах и т.д. Обозначается буквой S (square).
Как найти площадь треугольника?
S = a · h
где a – длина основания, h – высота треугольника, проведенная к основанию.
Причем, основание не обязательно должно находиться снизу. Так тоже сойдет.
Если треугольник тупоугольный , то высота опускается на продолжение основания:
Если треугольник прямоугольный , то основанием и высотой являются его катеты:
2. Другая формула, которая является не менее полезной, но которую почему-то всегда забывают:
Другая формула, которая является не менее полезной, но которую почему-то всегда забывают:
S = a · b · sinα
где a и b – две стороны треугольника, sinα – синус угла между этими сторонами.
Главное условие – угол берется между двумя известными сторонами.
3. Формула площади по трем сторонам (формула Герона):
S =
где a , b и с – стороны треугольника, а р – полупериметр. p = (a + b + c )/2.
4. Формула площади треугольника через радиус описанной окружности:
S =
где a , b и с – стороны треугольника, а R – радиус описанной окружности.
5. Формула площади треугольника через радиус вписанной окружности:
Как найти площадь прямоугольника?S = p · r
где р – полупериметр треугольника, а r – радиус вписанной окружности.

1. Площадь прямоугольника находится довольно-таки просто:
S = a · b
Никаких подвохов.
Как найти площадь квадрата?1. Так как квадрат является прямоугольником, у которого все стороны равны, то к нему применяется такая же формула:
S = a · a = a 2
2. Также площадь квадрата можно найти через его диагональ:
S = d 2
Как найти площадь параллелограмма?
1. Площадь параллелограмма находится по формуле:
S = a · h
Это связано с тем, что если от него отрезать прямоугольный треугольник справа и приставить его слева, получится прямоугольник:
2. Также площадь параллелограмма можно найти через угол между двумя сторонами:
Также площадь параллелограмма можно найти через угол между двумя сторонами:
S = a · b · sinα
Как найти площадь ромба?Ромб по своей сути является параллелограммом, у которого все стороны равны. Поэтому для него применяются те же формулы площади.
1. Площадь ромба через высоту:
S = a · h
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. где S — площадь треугольника,
где S — площадь треугольника,
— длины сторон треугольника,
— высота треугольника,
— угол между сторонами и,
— радиус вписанной окружности,
R — радиус описанной окружности,
Формулы площади квадрата
- Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны. - Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.
где S — Площадь квадрата,
— длина стороны квадрата,
— длина диагонали квадрата.
Формула площади прямоугольника
- Площадь прямоугольника
равна произведению длин двух его смежных сторон
где S — Площадь прямоугольника,
— длины сторон прямоугольника.
Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма - Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.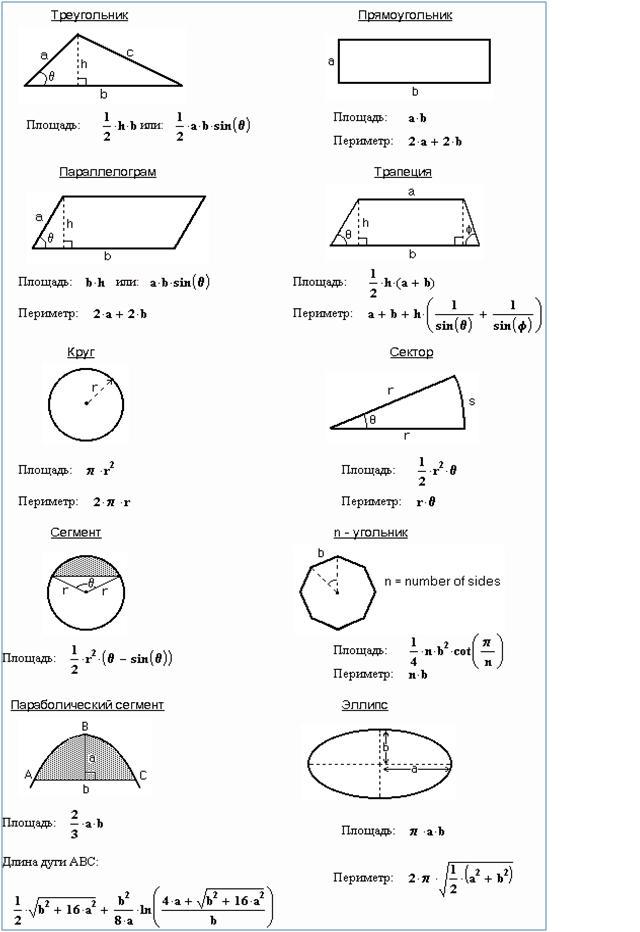
a · b · sin α
где S — Площадь параллелограмма,
— длины сторон параллелограмма,
— длина высоты параллелограмма,
— угол между сторонами параллелограмма.
Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты. - Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. - Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.
где S — Площадь ромба,
— длина стороны ромба,
— длина высоты ромба,
— угол между сторонами ромба,
1 , 2 — длины диагоналей.
Формулы площади трапеции
- Формула Герона для трапеции
Где S — Площадь трапеции,
— длины основ трапеции,
— длины боковых сторон трапеции,
Все формулы площади плоских фигур
Площадь равнобедренной трапеции
1. Формула площади равнобедренной
трапеции через стороны и угол
Формула площади равнобедренной
трапеции через стороны и угол
а — нижнее основание
b — верхнее основание
с — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2. Формула площади равнобедренной трапеции через радиус вписанной окружности
R- радиус вписанной окружности
D- диаметр вписанной окружности
O- центр вписанной окружности
H- высота трапеции
α, β — углы трапеции
Формула площади равнобедренной трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d- диагональ трапеции
α,β- углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4. Формула площади равнобедренной
трапеции через среднюю линию, боковую
сторону и угол при основании
Формула площади равнобедренной
трапеции через среднюю линию, боковую
сторону и угол при основании
c- боковая сторона
m- средняя линия трапеции
α, β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании,
(S):
5. Формула площади равнобедренной трапеции через основания и высоту
a — нижнее основание
b — верхнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):
Площадь треугольника по стороне и двум углам, формула.
a, b, c- стороны треугольника
α, β, γ- противолежащие углы
Площадь треугольника через сторону и два угла (S):
Формула площади правильного многоугольника
a — сторона многоугольника
n — количество сторон
Площадь правильного многоугольника, (S):
Формула (Герона) площади треугольника через полупериметр (S):
Площадь равностороннего треугольника равна:
Формулы расчета, площади равностороннего
треугольника.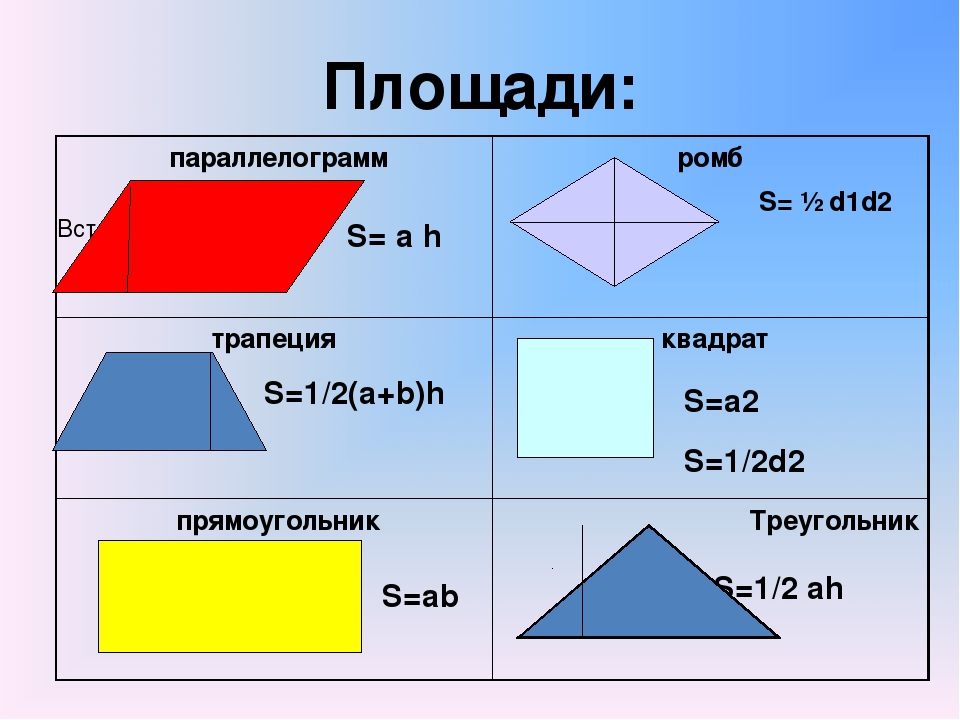
a — сторона треугольника
h – высота
Как вычислить площадь равнобедренного треугольника?
b — основание треугольника
a — равные стороны
h – высота
3. Формула площади трапеции через четыре стороны
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
Радиус описанной окружности трапеции по сторонам и диагонали
a — боковые стороны трапеции
c — нижнее основание
b — верхнее основание
d — диагональ
h — высота
Формула радиуса описанной окружности трапеции, (R)
найти радиус описанной окружности равнобедренного треугольника по сторонам
Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.
a, b — стороны треугольника
Радиус описанной окружности равнобедренного треугольника (R):
Радиус вписанной окружности в шестиугольник
a — сторона шестиугольника
Радиус вписанной окружности в шестиугольник, (r):
Радиус вписанной окружности в ромб
r — радиус вписанной окружности
a — сторона ромба
D, d — диагонали
h — высота ромба
Радиус вписанной окружности в равнобочную трапецию
с — нижнее основание
b — верхнее основание
a — боковые стороны
h — высота
Радиус вписанной окружности в прямоугольный треугольник
a, b — катеты треугольника
с — гипотенуза
Радиус вписанной окружности в равнобедренный треугольник
a, b — стороны треугольника
Доказать, что площадь вписанного четырёхугольника равна
\/(р — а)(р — b) (р — с) (р — d),
где р — полупериметр и а, b, с и d —
стороны четырёхугольника.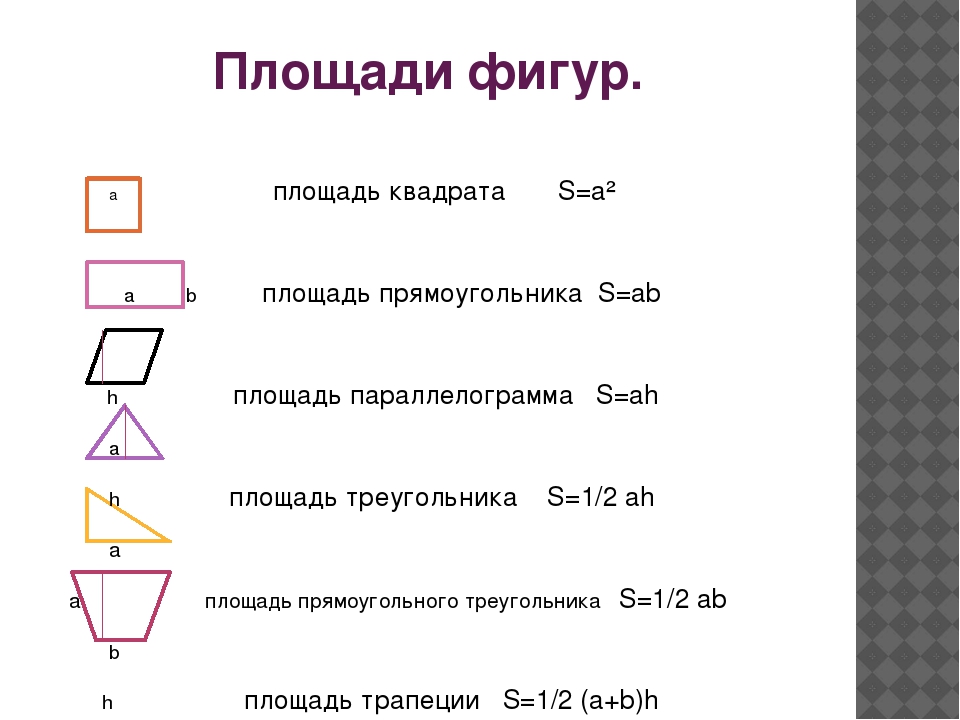
Доказать, что площадь вписанного в круг четырёхугольника равна
1/2 (ab + cb) · sin α , где а, b, с и d — стороны четырёхугольника и α — угол между сторонами а и b.
S = √[ a ƀ c d] sin ½ (α + β). — Читайте подробнее на FB.ru:
Площадь произвольного четырёхугольника (рис. 1.13) можно выразить через его стороны а, b, c и сумму пары противоположных углов:
где р – полупериметр четырёхугольника.
Площадь вписанного в окружность четырёхугольника () (рис. 1.14, а) вычисляется по формуле Брахмагупты
а описанного (рис. 1.14, б) () – по формуле
Если же четырёхугольник вписан и описан одновременно (рис. 1.14, в), то формула становится совсем простой:
Формула Пика
Чтобы оценить площадь многоугольника
на клетчатой бумаге, достаточно
подсчитать, сколько клеток покрывает
этот многоугольник (площадь клетки мы
принимаем за единицу). Точнее, если S –
площадь многоугольника, — число клеток,
которые целиком лежат внутри многоугольника,
и — число клеток, которые имеют с
внутренностью многоугольника хоть одну
общую точку.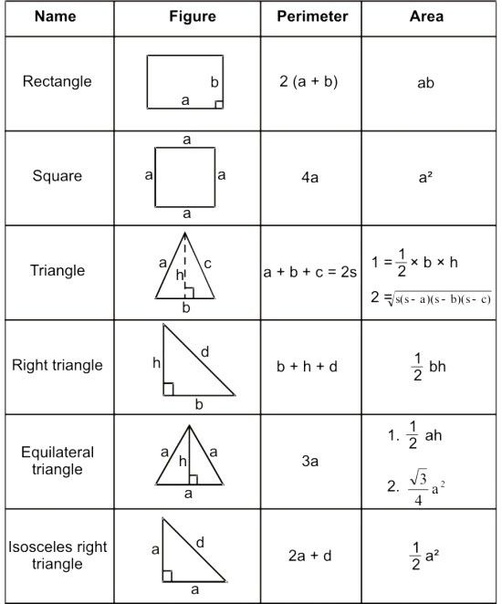
Будем рассматривать ниже только такие многоугольники, все вершины которых лежат в узлах клетчатой бумаги – в таких, где пересекаются линии сетки. Оказывается, что для таких многоугольников можно указать такую формулу:
где — площадь, r – число узлов, которые лежат строго внутри многоугольника.
Эту формулу называют «формула Пика» — по имени математика, открывшего её в 1899 году.
Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!
Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.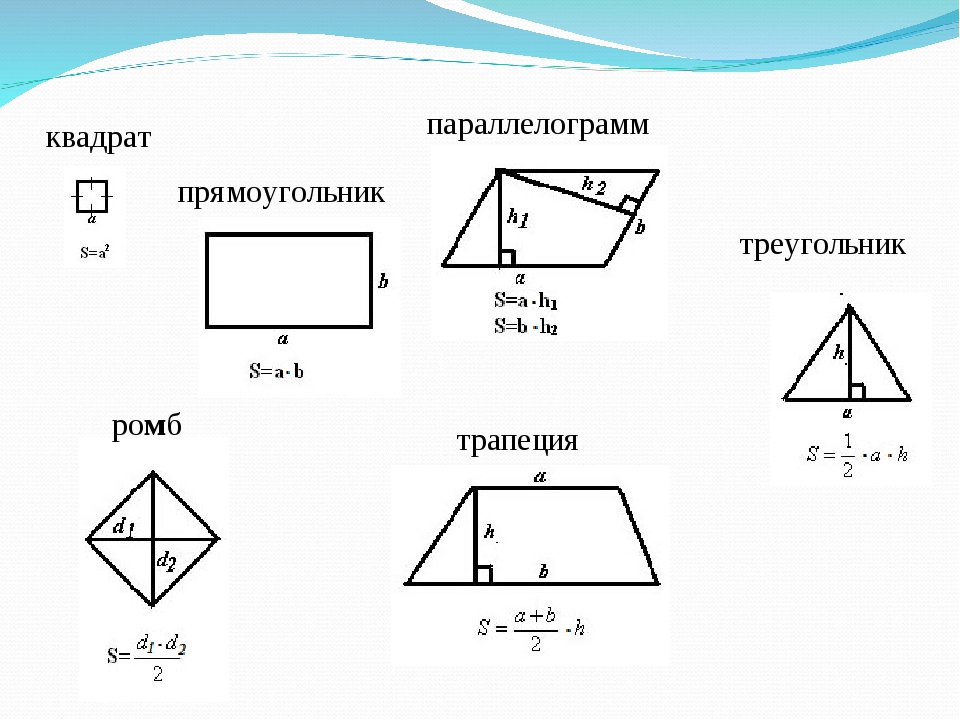
1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Ответ: .
2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Ответ: .
3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .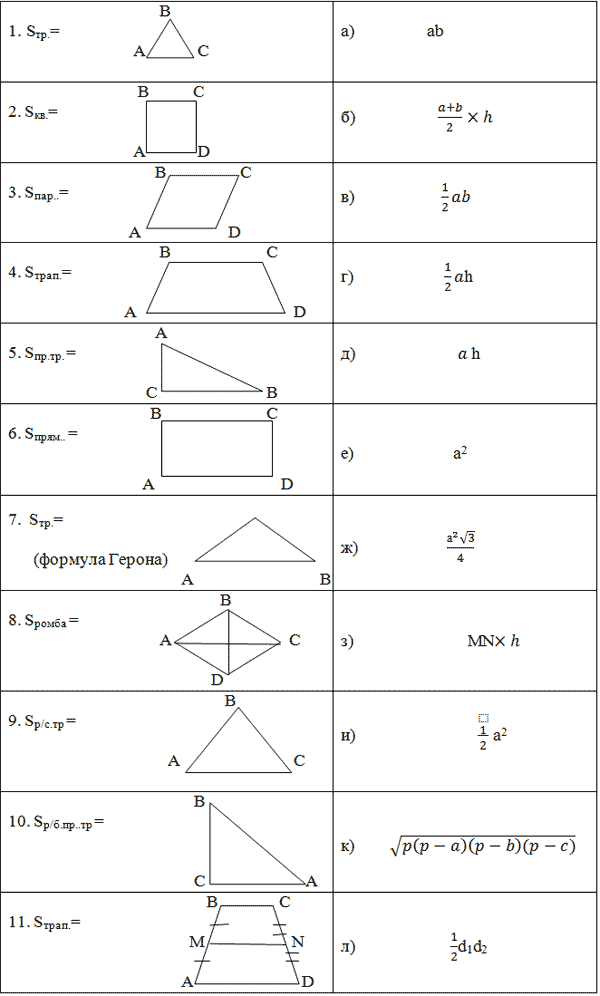
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Как вычислить площадь геометрических фигур. Как найти площадь геометрических фигур
Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!
Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника.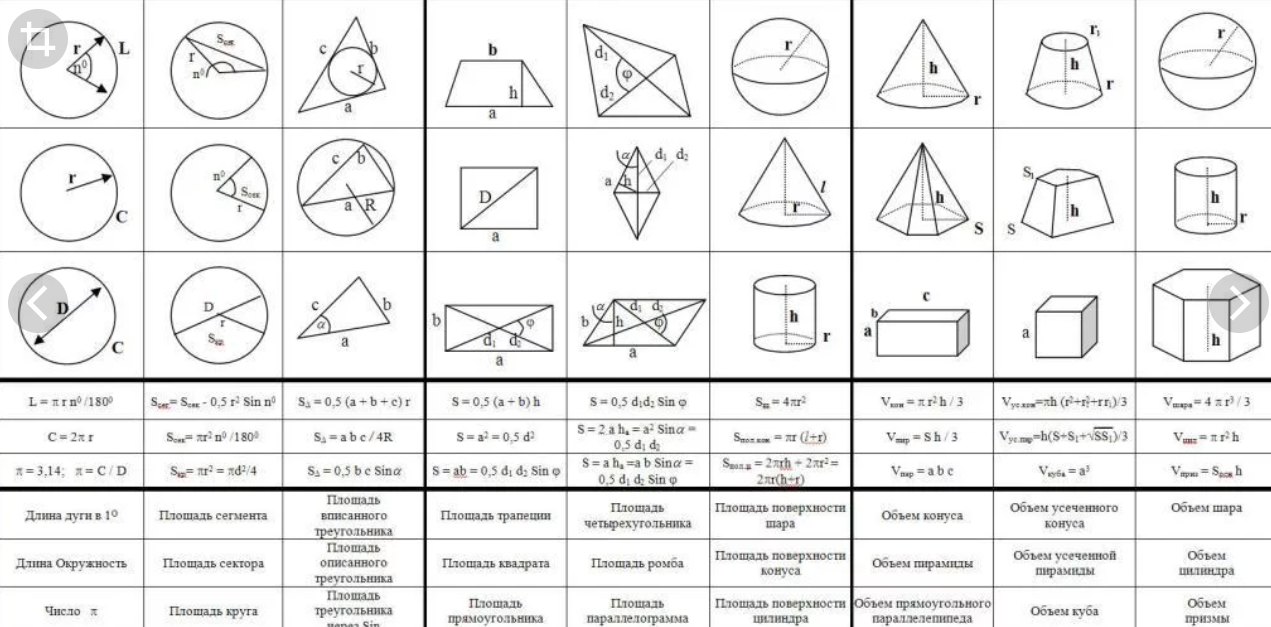 О них мы обязательно расскажем.
О них мы обязательно расскажем.
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.
1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Ответ: .
2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Ответ: .
3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Все формулы площади плоских фигур
Площадь равнобедренной трапеции
1. Формула площади равнобедренной трапеции через стороны и угол
а — нижнее основание
b — верхнее основание
с — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2.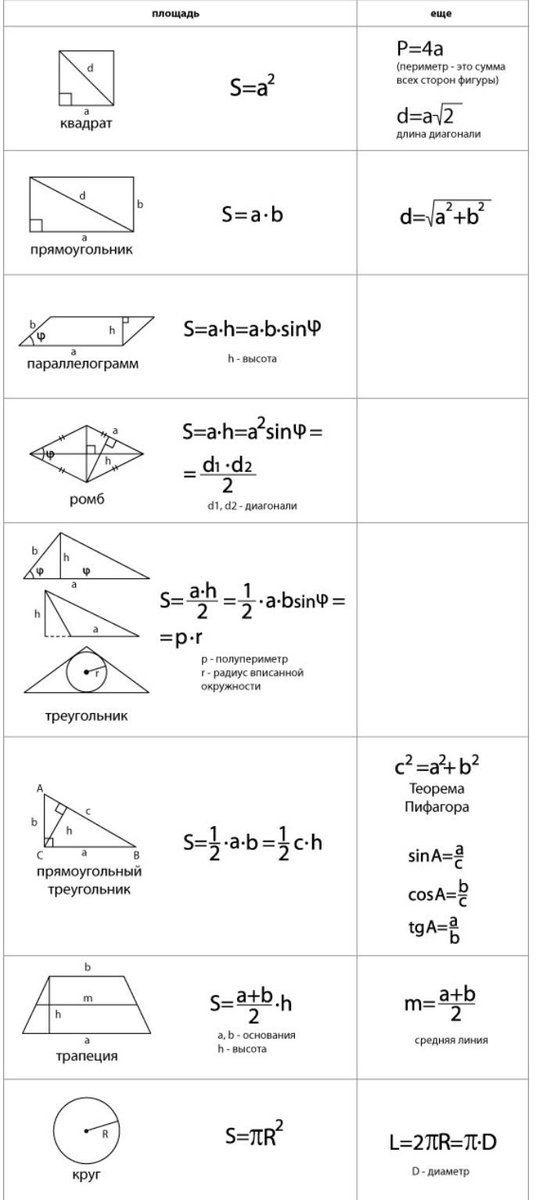 Формула площади равнобедренной
трапеции через радиус вписанной
окружности
Формула площади равнобедренной
трапеции через радиус вписанной
окружности
R- радиус вписанной окружности
D- диаметр вписанной окружности
O- центр вписанной окружности
H- высота трапеции
α, β — углы трапеции
Формула площади равнобедренной трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d- диагональ трапеции
α,β- углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
c- боковая сторона
m- средняя линия трапеции
α, β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании,
(S):
5. Формула площади равнобедренной трапеции через основания и высоту
a — нижнее основание
b — верхнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):
Площадь треугольника по стороне и двум
углам, формула.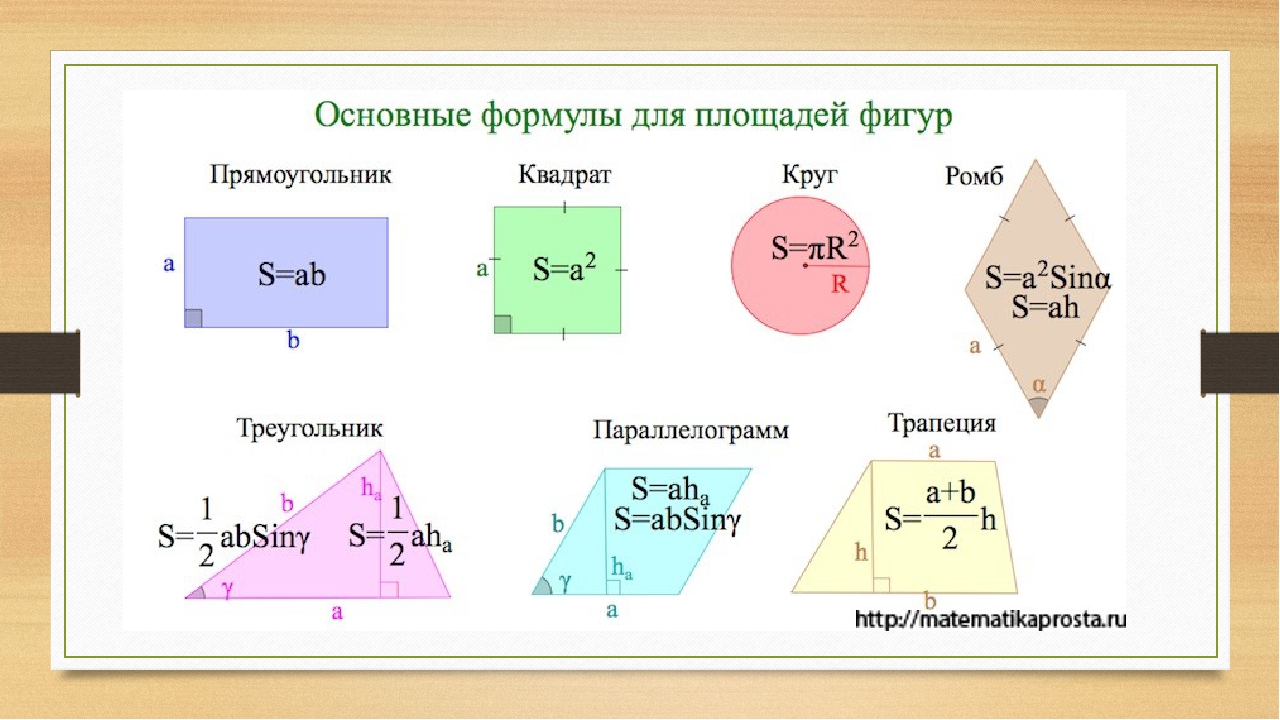
a, b, c- стороны треугольника
α, β, γ- противолежащие углы
Площадь треугольника через сторону и два угла (S):
Формула площади правильного многоугольника
a — сторона многоугольника
n — количество сторон
Площадь правильного многоугольника, (S):
Формула (Герона) площади треугольника через полупериметр (S):
Площадь равностороннего треугольника равна:
Формулы расчета, площади равностороннего треугольника.
a — сторона треугольника
h – высота
Как вычислить площадь равнобедренного треугольника?
b — основание треугольника
a — равные стороны
h – высота
3. Формула площади трапеции через четыре стороны
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
Радиус описанной окружности трапеции по сторонам и диагонали
a — боковые стороны трапеции
c — нижнее основание
b — верхнее основание
d — диагональ
h — высота
Формула радиуса описанной окружности трапеции, (R)
найти радиус описанной окружности равнобедренного треугольника по сторонам
Зная стороны равнобедренного треугольника,
можно по формуле, найти, радиус описанной
окружности около этого треугольника.
a, b — стороны треугольника
Радиус описанной окружности равнобедренного треугольника (R):
Радиус вписанной окружности в шестиугольник
a — сторона шестиугольника
Радиус вписанной окружности в шестиугольник, (r):
Радиус вписанной окружности в ромб
r — радиус вписанной окружности
a — сторона ромба
D, d — диагонали
h — высота ромба
Радиус вписанной окружности в равнобочную трапецию
с — нижнее основание
b — верхнее основание
a — боковые стороны
h — высота
Радиус вписанной окружности в прямоугольный треугольник
a, b — катеты треугольника
с — гипотенуза
Радиус вписанной окружности в равнобедренный треугольник
a, b — стороны треугольника
Доказать, что площадь вписанного четырёхугольника равна
\/(р — а)(р — b) (р — с) (р — d),
где р — полупериметр и а, b, с и d — стороны четырёхугольника.
Доказать, что площадь вписанного в круг четырёхугольника равна
1/2 (ab + cb) · sin α , где а, b, с и d — стороны
четырёхугольника и α — угол между
сторонами а и b.
S = √[ a ƀ c d] sin ½ (α + β). — Читайте подробнее на FB.ru:
Площадь произвольного четырёхугольника (рис. 1.13) можно выразить через его стороны а, b, c и сумму пары противоположных углов:
где р – полупериметр четырёхугольника.
Площадь вписанного в окружность четырёхугольника () (рис. 1.14, а) вычисляется по формуле Брахмагупты
а описанного (рис. 1.14, б) () – по формуле
Если же четырёхугольник вписан и описан одновременно (рис. 1.14, в), то формула становится совсем простой:
Формула Пика
Чтобы оценить площадь многоугольника на клетчатой бумаге, достаточно подсчитать, сколько клеток покрывает этот многоугольник (площадь клетки мы принимаем за единицу). Точнее, если S – площадь многоугольника, — число клеток, которые целиком лежат внутри многоугольника, и — число клеток, которые имеют с внутренностью многоугольника хоть одну общую точку.
Будем рассматривать ниже только такие
многоугольники, все вершины которых
лежат в узлах клетчатой бумаги – в
таких, где пересекаются линии сетки.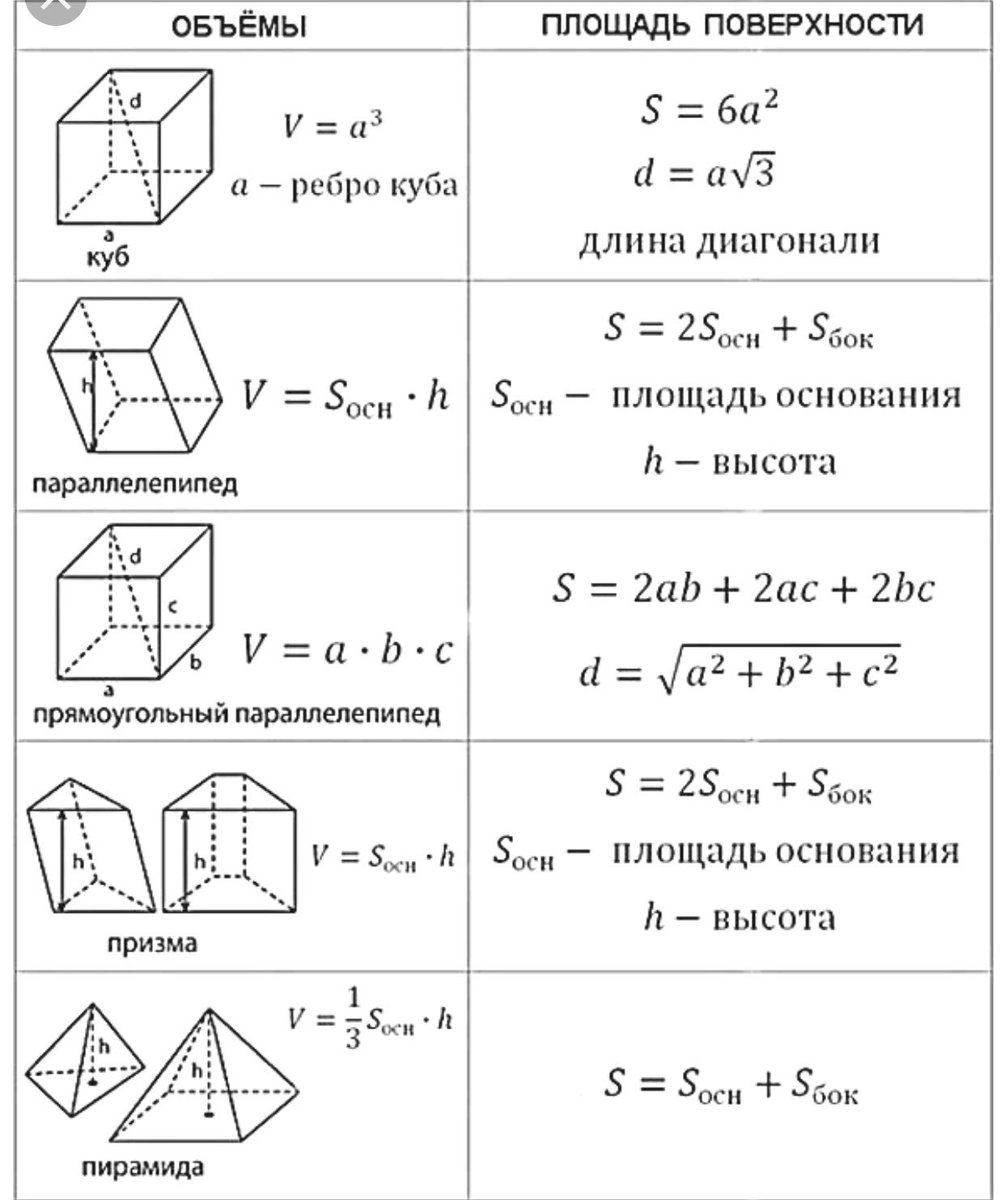 Оказывается, что для таких многоугольников
можно указать такую формулу:
Оказывается, что для таких многоугольников
можно указать такую формулу:
где — площадь, r – число узлов, которые лежат строго внутри многоугольника.
Эту формулу называют «формула Пика» — по имени математика, открывшего её в 1899 году.
Что такое площадь?Площадь – характеристика замкнутой геометрической фигуры (круг, квадрат, треугольник и т.д.), которая показывает ее размер. Площадь измеряется в квадратных сантиметрах, метрах и т.д. Обозначается буквой S (square).
Как найти площадь треугольника?
S = a · h
где a – длина основания, h – высота треугольника, проведенная к основанию.
Причем, основание не обязательно должно находиться снизу. Так тоже сойдет.
Если треугольник тупоугольный , то высота опускается на продолжение основания:
Если треугольник прямоугольный , то основанием и высотой являются его катеты:
2. Другая формула, которая является не менее полезной, но которую почему-то всегда забывают:
Другая формула, которая является не менее полезной, но которую почему-то всегда забывают:
S = a · b · sinα
где a и b – две стороны треугольника, sinα – синус угла между этими сторонами.
Главное условие – угол берется между двумя известными сторонами.
3. Формула площади по трем сторонам (формула Герона):
S =
где a , b и с – стороны треугольника, а р – полупериметр. p = (a + b + c )/2.
4. Формула площади треугольника через радиус описанной окружности:
S =
где a , b и с – стороны треугольника, а R – радиус описанной окружности.
5. Формула площади треугольника через радиус вписанной окружности:
Как найти площадь прямоугольника?S = p · r
где р – полупериметр треугольника, а r – радиус вписанной окружности.

1. Площадь прямоугольника находится довольно-таки просто:
S = a · b
Никаких подвохов.
Как найти площадь квадрата?1. Так как квадрат является прямоугольником, у которого все стороны равны, то к нему применяется такая же формула:
S = a · a = a 2
2. Также площадь квадрата можно найти через его диагональ:
S = d 2
Как найти площадь параллелограмма?
1. Площадь параллелограмма находится по формуле:
S = a · h
Это связано с тем, что если от него отрезать прямоугольный треугольник справа и приставить его слева, получится прямоугольник:
2. Также площадь параллелограмма можно найти через угол между двумя сторонами:
Также площадь параллелограмма можно найти через угол между двумя сторонами:
S = a · b · sinα
Как найти площадь ромба?Ромб по своей сути является параллелограммом, у которого все стороны равны. Поэтому для него применяются те же формулы площади.
1. Площадь ромба через высоту:
S = a · h
Площади геометрических фигур — численные значения, характеризующие их размер в двумерном пространстве. Эта величина может измеряться в системных и внесистемных единицах. Так, например, внесистемная единица площади — сотка, гектар. Это в том случае, если измеряемой поверхностью является участок земли. Системная же единица площади — квадрат длины. В системе СИ принято считать, что единица площади плоской поверхности — это квадратный метр. В СГС единица площади выражается через квадратный сантиметр.
Геометрия и формулы площадей неразрывно связаны. Эта связь заключается в том, что вычисление площадей плоских фигур основывается именно на их применении. Для многих фигур выведены несколько вариантов, по которым вычисляются их квадратные размеры. Опираясь на данные из условия задачи, мы можем определить максимально простой способ для решения. Тем самым облегчить расчет и свести вероятность ошибки вычисления к минимуму. Для этого рассмотрим основные площади фигур в геометрии.
Для многих фигур выведены несколько вариантов, по которым вычисляются их квадратные размеры. Опираясь на данные из условия задачи, мы можем определить максимально простой способ для решения. Тем самым облегчить расчет и свести вероятность ошибки вычисления к минимуму. Для этого рассмотрим основные площади фигур в геометрии.
Формулы для нахождения площади любого треугольника представлены несколькими вариантами:
1) Площадь треугольника рассчитывается по основанию a и высоте h. Основанием считают сторону фигуры, на которую опущена высота. Тогда площадь треугольника:
2) Площадь прямоугольного треугольника рассчитывается точно также, если гипотенузу считать основанием. Если же за основание принять катет, то площадь прямоугольного треугольника будет равна уменьшенному вдвое произведению катетов.
На этом формулы для вычисления площади любого треугольника не заканчиваются. Другое выражение содержит стороны a,b и синусоидальную функцию угла γ, заключенного между a и b. Значение синуса находится по таблицам. Также его можно узнать с помощью калькулятора. Тогда площадь треугольника:
Значение синуса находится по таблицам. Также его можно узнать с помощью калькулятора. Тогда площадь треугольника:
По данному равенству тоже можно убедиться в том, что площадь прямоугольного треугольника определяется через длины катетов. Т.к. угол γ — прямой, поэтому площадь прямоугольного треугольника рассчитывается без умножения на функцию синуса.
3) Рассмотрим частный случай — правильный треугольник, у которого сторона a известна по условию или ее длина найдется при решении. О фигуре в задаче по геометрии больше ничего не известно. Тогда площадь как найти при этом условии? В этом случае применяется формула для площади правильного треугольника:
Прямоугольник
Как найти площадь прямоугольника и использовать при этом размеры сторон, имеющих общую вершину? Выражение для вычисления такое:
Если для вычисления площади прямоугольника требуется использовать длины диагоналей, то тогда понадобится функция синуса угла, образованного при их пересечении.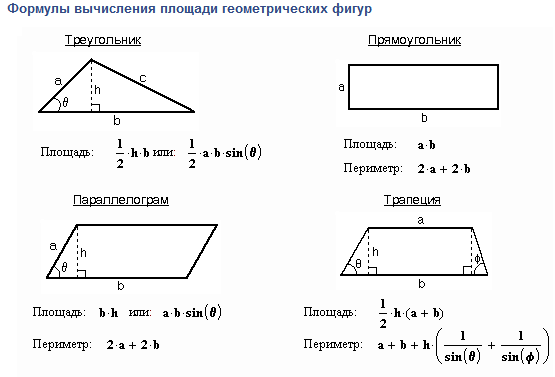 Такая формула площади прямоугольника имеет вид:
Такая формула площади прямоугольника имеет вид:
Квадрат
Площадь квадрата определяют как вторую степень длины стороны:
Доказательство вытекает из определения, согласно которому квадратом называют прямоугольник. У всех сторон, образующих квадрат, одинаковые размеры. Поэтому вычисление площади такого прямоугольника сводится к перемножению одной на другую, т. е. ко второй степени стороны. И формула для вычисления площади квадрата примет искомый вид.
Площадь квадрата можно найти другим способом, например, если использовать диагональ:
Как вычислить площадь фигуры, которая образована частью плоскости, ограниченной окружностью? Для расчета площади формулы такие:
Параллелограмм
Для параллелограмма формула содержит линейные размеры стороны, высоты и математическое действие — умножение. Если же высота неизвестна, то тогда как найти площадь параллелограмма? Есть еще один способ вычисления. Потребуется определенное значение, которое примет тригонометрическая функция угла, образованного смежными сторонами, а также их длины.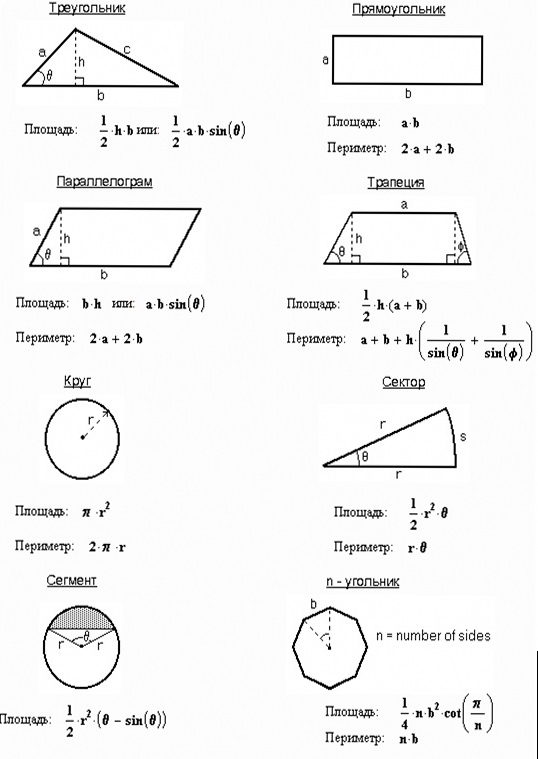
Формулы площади параллелограмма таковы:
Ромб
Как найти площадь четырехугольника, называемого ромбом? Площадь ромба определяется с помощью простых математических действий с диагоналями. Доказательство опирается на тот факт, что отрезки диагоналей в d1 и d2 пересекаются под прямым углом. По таблице синусов видно, что для прямого угла данная функция равна единице. Поэтому площадь ромба рассчитывается так:
Еще площадь ромба может быть найдена другим способом. Доказать это тоже нетрудно, если учесть, что стороны его одинаковы по длине. Затем подставить их произведение в похожее выражение для параллелограмма. Ведь частным случаем именно этой фигуры является ромб. Здесь γ — внутренний угол ромба. Площадь ромба определяют так:
Трапеция
Как найти площадь трапеции через основания (a и b), если в задаче указаны их длины? Здесь без известного значения длины высоты h вычислить площадь такой трапеции не удастся. Т.к. эту величину содержит выражение для вычисления:
Квадратный размер прямоугольной трапеции тоже можно вычислить таким же способом. При этом учитывают, что в прямоугольной трапеции понятия высоты и боковой стороны объединены. Поэтому для прямоугольной трапеции нужно указывать вместо высоты длину боковой стороны.
При этом учитывают, что в прямоугольной трапеции понятия высоты и боковой стороны объединены. Поэтому для прямоугольной трапеции нужно указывать вместо высоты длину боковой стороны.
Цилиндр и параллелепипед
Рассмотрим что нужно, чтобы рассчитать поверхность всего цилиндра. Площадь данной фигуры составляет пара кругов, называемых основаниями, и боковая поверхность. Окружности, образующие круги имеют длины радиусов, равные r. Для площади цилиндра имеет место такое вычисление:
Как найти площадь параллелепипеда, который состоит из трех пар граней? Его измерения совпадают с конкретной парой. Грани, находящиеся противоположно, имеют одинаковые параметры. Сначала находят S(1), S(2), S(3) — квадратные размеры неравных граней. Затем уже площадь поверхности параллелепипеда:
Кольцо
Две окружности с общим центром образуют кольцо. Они же ограничивают площадь кольца. При этом обе расчетные формулы учитывают размеры каждой окружности. Первая из них, вычисляющая площадь кольца, содержит больший R и меньший r радиусы. Чаще их называют внешним и внутренним. Во втором выражении площадь кольца рассчитывается через больший D и меньший d диаметры. Таким образом, площадь кольца по известным радиусам рассчитывают так:
Чаще их называют внешним и внутренним. Во втором выражении площадь кольца рассчитывается через больший D и меньший d диаметры. Таким образом, площадь кольца по известным радиусам рассчитывают так:
Площадь кольца, с использованием длин диаметров, определяют следующим образом:
Многоугольник
Как найти площадь многоугольника, форма которого не является правильной? Общей формулы для площади таких фигур нет. Но если она изображена на координатной плоскости, например, это может быть клетчатая бумага, тогда как найти площадь поверхности в этом случае? Тут применяют способ, который не требует приблизительно измерить фигуру. Поступают так: если нашли точки, которые попадают в уголок клетки или имеют целые координаты, то учитывают только их. Чтобы затем выяснить, чему равна площадь, используют формулу, доказанную Пиком. Необходимо сложить количество точек, расположенных внутри ломаной линии с половиной точек, лежащих на ней, и вычесть единицу, т. е. вычисляется это таким образом:
где В,Г — количество точек, расположенных внутри и на всей ломаной линии соответственно.
Рекомендуем также
Площади фигур Площадь геометрической фигуры числовая
Площади фигур.
Площадь геометрической фигуры — числовая характеристика фигуры – величина той части плоскости, которую занимает фигура За единицу измерения принимают квадрат со стороной равной единице измерения отрезков (1 см 2, 1 дм 2=100 см 2 1 м 2=100 дм 2 1 а=100 м 2 1 га=100 а 1 км 2=100 га) В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов. Найдите площади следующих фигур: A. B. C. D. E. F. J. H.
Основные свойства площадей геометрических фигур. 1. Любая плоская ограниченная геометрическая фигура имеет площадь S. 2. Эта площадь – единственная. 3. Площадь любой геометрической фигуры выражается положительным числом. S>0 4. Площадь квадрата со стороной, равной единице, равна единице. 1 1 5.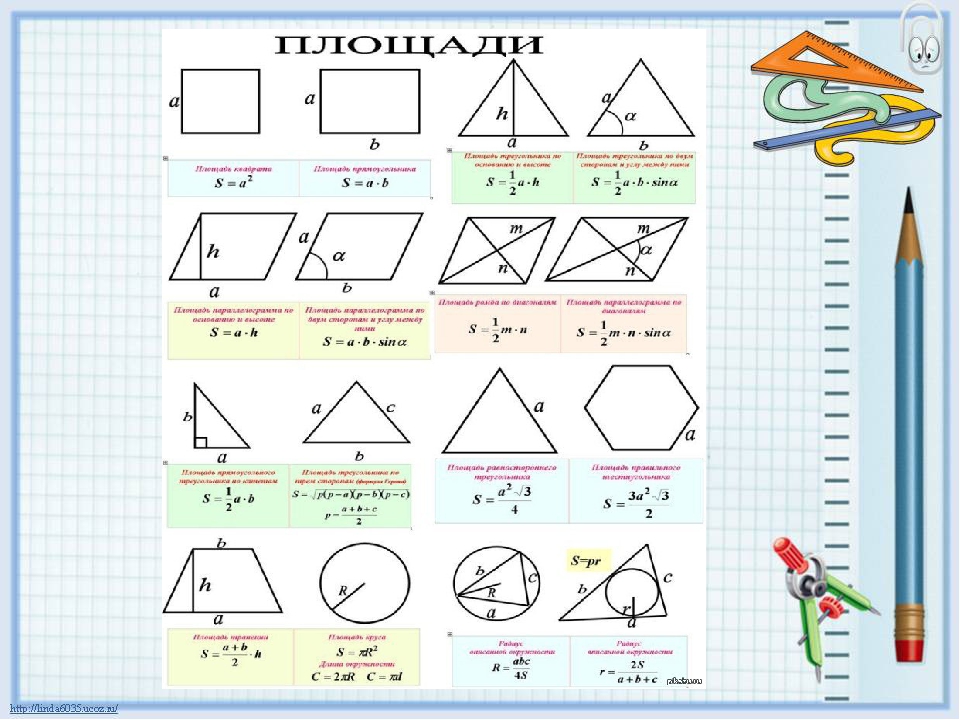 Площадь фигуры равна сумме площадей частей, на которые она разбивается. S=SF 1+SF 2+SF 3 F 1 6. Равные фигуры имеют равные площади. F 2 F 1 SF 1=SF 2 Sкв. =1 F 3
Площадь фигуры равна сумме площадей частей, на которые она разбивается. S=SF 1+SF 2+SF 3 F 1 6. Равные фигуры имеют равные площади. F 2 F 1 SF 1=SF 2 Sкв. =1 F 3
Площадь квадрата равна квадрату его стороны. S=a 2 a a Площадь прямоугольника равна произведению его смежных сторон. a b b S S 2=b 2 S 1=a 2 S a a b S=a·b b (a+b)2 =S 1+S 2+2 S=a 2+b 2+2 S; 2 S= (a+b)2 -a 2 -b 2=2 ab; a S=a·b
Следствия: 1) При увеличении (уменьшении) стороны прямоугольника в n раз площадь прямоугольника увеличивается (уменьшается) в n раз и наоборот. 2) При увеличении (уменьшении) стороны в n раз площадь квадрата увеличивается (уменьшается) в n 2 раз и наоборот. Задачи: (Решаем устно) а)Найти сторону квадрата, равновеликого прямоугольнику со сторонами 4 и 16 b) Дан квадрат A B D D B Как построить квадрат, имеющий в 2 раза большую площадь? C S=16· 4=64 16 F G C 4 8 S=8· 8=64 8
Площадь параллелограмма Sпар= а·ha=b·hb.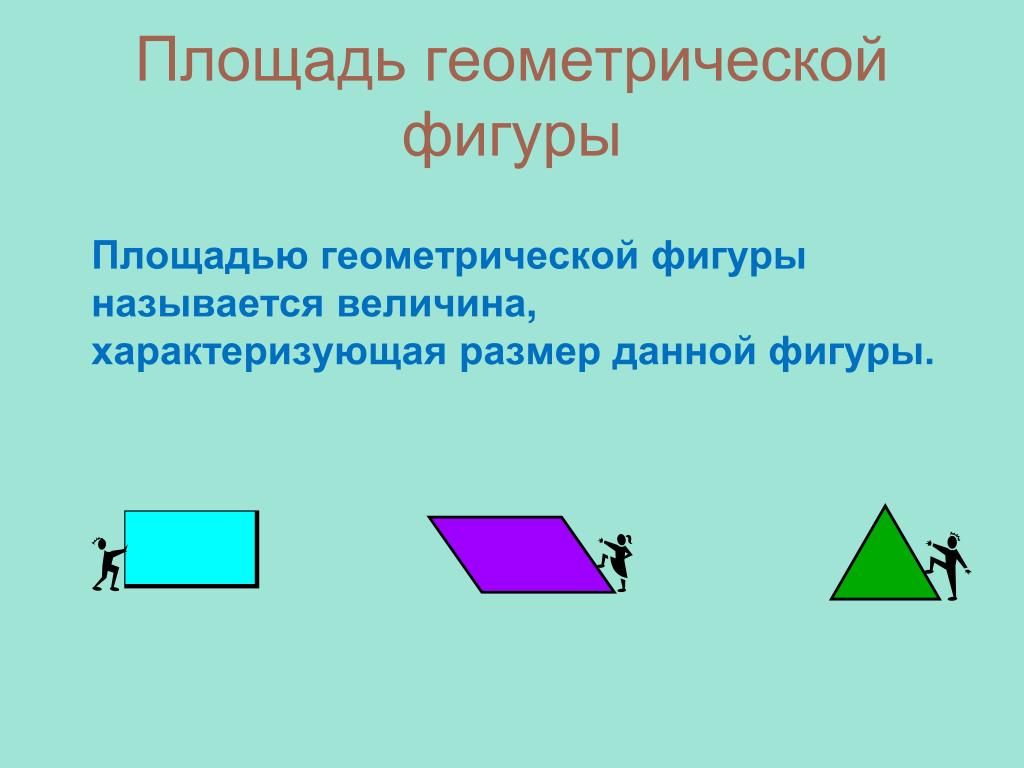 Теорема: Площадь параллелограмма равна произведению стороны и В проведенной к ней высоты Дано: АВСD – параллелограмм; BK AD; K AD. Доказать: SABCD = AD BK. С hb hа b А К а D P Доказательство 1) Проведем CP AD; CP = BK 2) ABK = DCP (по катету и гипотенузе) S ABK = S DCP. 3) ВСPK – прямоугольник (по определению) SBСPK = BC BK. 4) SABCD = S ABK + SBСDK = S DCP + SBСDK = SBСPK = BC BK = AD BK. Таким образом, Sпар = аha. Теорема доказана.
Теорема: Площадь параллелограмма равна произведению стороны и В проведенной к ней высоты Дано: АВСD – параллелограмм; BK AD; K AD. Доказать: SABCD = AD BK. С hb hа b А К а D P Доказательство 1) Проведем CP AD; CP = BK 2) ABK = DCP (по катету и гипотенузе) S ABK = S DCP. 3) ВСPK – прямоугольник (по определению) SBСPK = BC BK. 4) SABCD = S ABK + SBСDK = S DCP + SBСDK = SBСPK = BC BK = AD BK. Таким образом, Sпар = аha. Теорема доказана.
Площадь треугольника S = Теорема: Площадь треугольника равна половине произведения стороны и проведенной к ней высоты. A D Дано: АВС; AK BС; K BС. Доказать: S ABC = 0, 5·BC AK. ha B K a C Доказательство: Достроим треугольник до параллелограмма АВDC: AK – высота; АВС = DСA S АВС = 0, 5·SABCD = 0, 5·BC AK. Таким образом, площадь треугольника: S = Теорема доказана.
A Следствия (доказательства – устно). 1) Площадь треугольника, отсекаемого от АВC средней линией равна · S АВC B ha a C 2) Медиана делит треугольник на два равновеликих треугольника. 3) Площадь прямоугольного треугольника: S = ha a b 4) Если диагонали четырехугольника перпендикулярны, то его площадь равна половине произведения его диагоналей. S= d 1·d 2 Площадь ромба (квадрата) равна половине произведения его диагоналей a d 1 d 2
3) Площадь прямоугольного треугольника: S = ha a b 4) Если диагонали четырехугольника перпендикулярны, то его площадь равна половине произведения его диагоналей. S= d 1·d 2 Площадь ромба (квадрата) равна половине произведения его диагоналей a d 1 d 2
Площадь трапеции Sтрап. = Теорема: Площадь трапеции равна произведению полусуммы её оснований на высоту. b Дано: АВСD – трапеция; AD || BC; BK AD, K AD. Доказать: SАВСD = 0, 5(AD + BC) BK. h h а Доказательство: Диагональ BD разбивает трапецию на АВD и ВСD, BK= PD – высоты этих треугольников. SАВСD = S АВD + S ВСD = 0, 5 AD BK + 0, 5 BC PD = 0, 5(AD + BC) BK. Таким образом, Sтрап. = , где a и b – длины оснований; h – высота трапеции. Теорема доказана. Следствие. Площадь трапеции равна произведению ее средней линии и высоты.
Теорема Вариньона. Середины сторон четырехугольника являются вершинами параллелограмма, площадь которого равна половине площади четырехугольника. Дано: четырехугольник ABCD; M – середина AB; N – середина BC; K – середина CD; L – середина DA.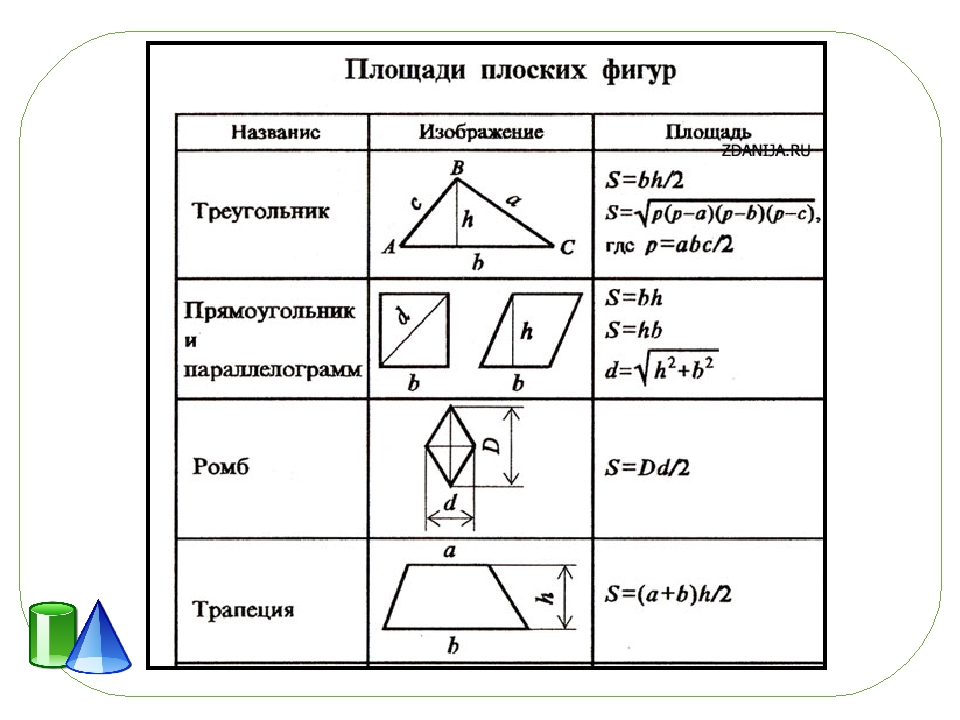 Доказать: MNKL – параллелограмм; 2) SMNKL = 0, 5·SABCD. Доказательство: 1) MN и KL – средние линии треугольников АВС и ADC MN || KL и MN = 0, 5·AC = KL MNKL – параллелограмм 2) Аналогично, SMNKL = SABCD– (SMBN+ SNCK+SKDL + SLAM)= 0, 5·SABCD. Теорема доказана.
Доказать: MNKL – параллелограмм; 2) SMNKL = 0, 5·SABCD. Доказательство: 1) MN и KL – средние линии треугольников АВС и ADC MN || KL и MN = 0, 5·AC = KL MNKL – параллелограмм 2) Аналогично, SMNKL = SABCD– (SMBN+ SNCK+SKDL + SLAM)= 0, 5·SABCD. Теорема доказана.
Замечание: Теорема верна и для невыпуклого четырехугольника SMNKL = SABCD – ((SMBN + SKDL) + (SLAM – SNCK)) = SABCD – SABCD = 0, 5·SABCD
Найдите площадь геометрической фигуры. 1) 24 a) 560; b)576; c)476; d)519. 24 24 2) a) 120; b)240; c)180; d)160. 30˚ 10 8 3) a) 48; 6 b)100; c)24; d)36. 4 4) 10 150˚ a) 150; b)100; c)50; d)40. 16 5) 15 a) 150; b)300; c)60; d)35. 20
Домашнее задание: 1. 2. 3. Выучить формулы площадей многоугольников. Разобрать и выучить доказательства теорем. (Не забывайте про теоретический зачет!) Решить задачи № 455, 469, 472, 466, 467
Благодарю за внимание!
Список литературы 1. Геометрия, 7 -9: Учеб. для общеобразоват. учреждений / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. — 14 -е изд. – М. : Просвещение, 2008. — 384 с. : ил. . 2. Открытый банк заданий по математике http: //www. mathege. ru
Геометрия, 7 -9: Учеб. для общеобразоват. учреждений / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. — 14 -е изд. – М. : Просвещение, 2008. — 384 с. : ил. . 2. Открытый банк заданий по математике http: //www. mathege. ru
Вычисление площади и периметра геометрических фигур на плоскости
Доклад по математике
По теме «Вычисление площади и периметра геометрических фигур на плоскости»
Ученика 5-В класса Исакова Андрея
Вычисление площадей — один из самых древних разделов науки «Геометрия» или как раньше ее называли «Землемерие». Существует легенда, что самыми первыми вычислять площадь и периметр стали Египтяне. Это имело большое практическое значение.
Для начала работы с площадью и периметром, вам нужно разобраться с основными определениями:
Площадь это некая величина, которая характеризует геометрическую фигуру. Площадь — величина положительная.
Площадь одна из основных характеристик фигуры, расположенной на плоскости. Фактически, найти площадь фигуры означает, посчитать сколько раз в нее поместится квадрат с длиной стороны равной 1. Единицей измерения площади служит метр квадратный.
Периметром называется длина замкнутого контура фигуры, или, по-другому, сумма длин всех ее сторон.
Шаг второй — расчет площади и периметра на примере прямоугольника.
Чтобы найти площадь прямоугольника, необходимо знать его длину и ширину. Таким образом, площадь прямоугольника находится по формуле:
Площадь прямоугольника равна произведению длин двух его смежных сторон (a, b).
Площадь прямоугольника, формула площади прямоугольника
S = ab, где а длина прямоугольника, b — ширина прямоугольника.
Отметьте для себя, что разные фигуры могут иметь равные площади.
Для нахождения периметра прямоугольника, вам необходимо сложить две его смежные стороны и умножить на два.
Нахождение площади других геометрических фигур, так или иначе, связаны с нахождением площади прямоугольника.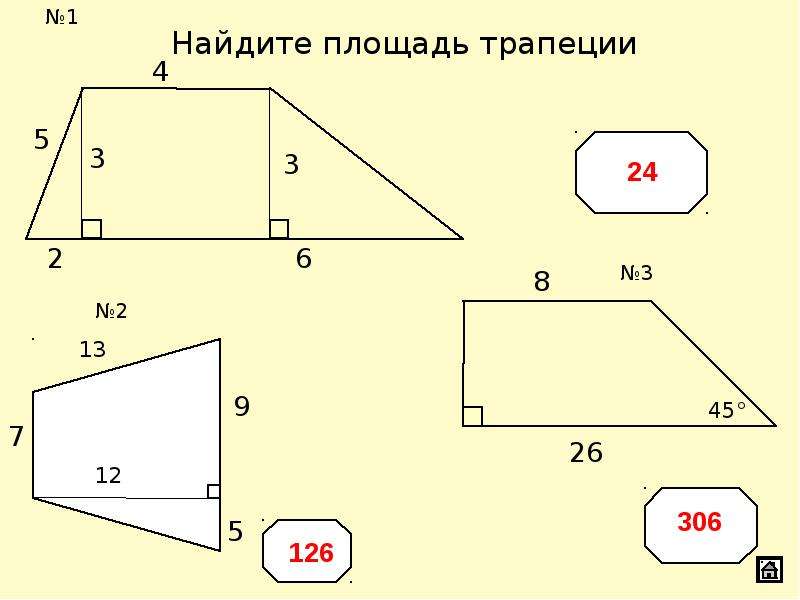
P=2(a+b)
Шаг третий — расчет площади и периметра на примере треугольника.
Если в произвольном треугольнике опустить высоту, то видно, что треугольник разбивается высотой на две части. Каждая их этих частей представляет собой половину прямоугольника. Таким образом, площадь треугольника это сумма площадей двух его частей.
S = hAC:2 + hBC:2. В более привычной форме, эту формулу можно записать так: S = ch:2
Кроме этой формулы, существует еще несколько формул для нахождения площади треугольника.
Периметр треугольника равен сумме длин всех его сторон (a, b, c).
P=a+b+c
P — периметр;
a, b, c — стороны треугольника.
Шаг четвертый — расчет площади и периметра на примере трапеции.
Нахождение площади трапеции сводится к нахождению площади прямоугольника и двух треугольников, из которых состоит трапеция.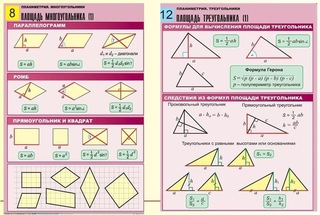
Площадь трапеции равна произведению полусуммы ее оснований на высоту (a, b, h).
S — площадь трапеции
a — длина 1-ого основания b — длина 2-ого основания h — длина высоты трапеции
Так с помощью формул по нахождению площади и периметра прямоугольника и треугольника можно найти площадь других геометрических фигур на плоскости.
Геометрические фигуры и типы фигур
Что такое геометрических плоских фигур ? Какие характеристики у них есть? Вот вопросы, на которые мы ответим в этом посте.
Основные геометрические плоские формы :
Круг
Окружность — это фигура, которую можно создать, начертив кривую, которая всегда находится на одном и том же расстоянии от точки, которую мы называем центром. Расстояние вокруг окружности называется длины окружности окружности.
Треугольник
Треугольник — это фигура, образованная тремя прямыми линиями, которые называются сторонами. Существуют различные способы классификации треугольников в зависимости от их сторон или углов.
Существуют различные способы классификации треугольников в зависимости от их сторон или углов.
- По углам:
- Прямоугольный треугольник: наибольший из трех углов является прямым.
- Остроугольный треугольник: наибольший из трех углов является острым (менее 90 градусов).
- Тупоугольный треугольник: наибольший из 3-х углов является тупым (более 90 градусов).
2. По сторонам:
- Равносторонний треугольник: все три стороны имеют одинаковую длину.
- Равнобедренный треугольник: имеет 2 (или более) стороны одинаковой длины. (Равносторонний треугольник также является равнобедренным.)
- Разносторонний треугольник: нет двух сторон одинакового размера.
Прямоугольник
Прямоугольник — это фигура, имеющая 4 стороны. Отличительной чертой прямоугольника является то, что все 4 угла равны 90 градусов.
Ромб
Ромб представляет собой форму, образованную 4 прямыми линиями. Его 4 стороны имеют одинаковую длину, но, в отличие от прямоугольника, любой из всех 4 углов равен 90 градусов.
Его 4 стороны имеют одинаковую длину, но, в отличие от прямоугольника, любой из всех 4 углов равен 90 градусов.
Площадь
Квадрат — это тип прямоугольника, но также и тип ромба. Он имеет характеристики обоих из них. То есть все 4 угла прямые и все 4 стороны равны по длине.
Трапеция
Трапеция также имеет 4 стороны. У него две стороны параллельны, а две другие нет.
Вы можете попрактиковаться с геометрическими формами плоскости, зарегистрировавшись в Smartick.
Узнать больше:
Веселье — любимый способ обучения нашего мозга
Дайан Акерман
Smartick — увлекательный способ изучения математики- 15 минут веселья в день
- Адаптируется к уровню вашего ребенка
- Миллионы учеников с 2009 года
Группа создания контента.
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.
Геометрические фигуры — определение, список, типы, свойства
Любой объект вокруг нас с фиксированной структурой можно рассматривать как геометрическую фигуру. Эти формы состоят из линий, кривых, углов и поверхностей. Некоторыми из известных геометрических фигур являются квадрат, прямоугольник, круг, цилиндр и т. д.
Что такое геометрические фигуры?
Геометрические фигуры – это любая структура, открытая или закрытая, имеющая определенную форму и свойства, состоящая из линий и точек. Некоторыми из известных геометрических фигур являются квадрат, прямоугольник, круг, конус, цилиндр, сфера и т. д. Все эти формы обладают некоторыми свойствами, которые делают их уникальными и отличными от других форм.
Геометрические фигуры определяются как фигуры, замкнутые границей, которая образована путем объединения определенного количества кривых, точек и отрезков.Каждая фигура имеет уникальное имя, такое как круг, квадрат, треугольник, прямоугольник и т. д. В реальной жизни нас окружают различные основные геометрические фигуры, например, кусок пиццы имеет форму треугольника, двери или окна в форме треугольника. форма прямоугольника и многое другое.
д. В реальной жизни нас окружают различные основные геометрические фигуры, например, кусок пиццы имеет форму треугольника, двери или окна в форме треугольника. форма прямоугольника и многое другое.
Типы геометрических фигур
В геометрии, когда объект или форма не соединены с обоими концами, это считается открытой геометрической формой. Когда объект или форма соединены с обоими концами, это считается замкнутой геометрической формой.Существует два типа геометрических фигур, классифицируемых как:
- Двумерные: Это двухмерные фигуры , которые имеют только оси x и y. Это плоские структуры с 2 измерениями. Например, треугольник, квадрат, прямоугольник и т. д.
- Трехмерный: Это трехмерные фигуры, которые имеют оси x, y и z. Ось Z представляет высоту объекта. Это твердые структуры с 3 измерениями. Например, куб, прямоугольный параллелепипед и т. д.
Чтобы нарисовать любую из этих геометрических фигур, мы должны начать с линии, кривой или отрезка. Таким образом, на основе количества и расположения линий мы можем создавать различные типы геометрических фигур и фигур, например, путем соединения четырех отрезков линий образуется прямоугольная форма. Треугольник можно получить, соединив отрезки по три линии и так далее.
Таким образом, на основе количества и расположения линий мы можем создавать различные типы геометрических фигур и фигур, например, путем соединения четырех отрезков линий образуется прямоугольная форма. Треугольник можно получить, соединив отрезки по три линии и так далее.
Посмотрите на приведенную ниже схему, которая представляет различные двумерные и трехмерные геометрические фигуры.
Двумерные геометрические фигуры
Давайте узнаем о пяти основных двухмерных геометрических фигурах.
- Треугольник: Треугольник представляет собой замкнутую двумерную геометрическую фигуру с тремя сторонами. Например, эскиз кусочка пиццы, формы начос и т. д.
- Квадрат: Квадрат представляет собой двумерную геометрическую фигуру, образованную четырьмя сторонами одинаковой длины. Например, формы шахматной доски и карромной доски.
- Прямоугольник: прямоугольник представляет собой четырехстороннюю двумерную геометрическую фигуру, в которой длины противоположных сторон равны.
 Например, экраны ноутбуков и т. д.
Например, экраны ноутбуков и т. д. - Круг: Круг представляет собой замкнутую двухмерную геометрическую фигуру круглой формы. Круг не имеет ни линий, ни углов. Например, основа для пиццы, колесо и т. д.
- Овал: Овал похож на круг, но его форма слегка вытянута. Овал не имеет прямых линий и углов.Например, форма числа ноль (0).
Трехмерные геометрические фигуры
Давайте теперь узнаем о шести основных трехмерных геометрических фигурах.
- Куб: Куб — это трехмерная геометрическая фигура, состоящая из шести квадратов с равными сторонами. Например, игральные кости, кубик Рубика и т. д.
- Кубоид: кубоид — это трехмерная геометрическая фигура, состоящая из шести прямоугольников. Например, книга, коробка и т. д.
- Цилиндр: Цилиндр — это твердая трехмерная геометрическая форма, имеющая два одинаковых круглых плоских конца.Например, банки для холодных напитков, лапша для бассейна и т. д.
- Сфера: Сфера — это сплошная трехмерная геометрическая форма, похожая на шар.
 Например, футбол, баскетбол и т. д.
Например, футбол, баскетбол и т. д. - Полушарие: Полушарие — это геометрическая фигура, которая составляет половину сферы. Например, тарелки для супа.
- Конус: Конус представляет собой трехмерную геометрическую фигуру с плоским круглым основанием и заостренным краем наверху, называемым вершиной. Например, рожки для мороженого, клоунские шляпы и т. д.
Список и свойства геометрических фигур
Существует множество основных геометрических фигур, которые можно сформировать.Некоторые из них двумерные, а некоторые трехмерные. Список геометрических фигур вместе с их гранями, ребрами и вершинами приведен ниже:
| Имя | Тип | Края | Вершины | Лица |
|---|---|---|---|---|
| Квадрат | 2D | 4 | 4 | — |
| Прямоугольник | 2D | 4 | 4 | — |
| Треугольник | 2D | 3 | 3 | — |
| Круг | 2D | Изогнутый | 0 | — |
| Пентагон | 2D | 5 | 5 | — |
| Шестигранник | 2D | 6 | 6 | — |
| Куб | 3D | 12 | 8 | 6 |
| Прямоугольный | 3D | 12 | 8 | 6 |
| Конус | 3D | 1 | 1 | 2 |
| Цилиндр | 3D | 2 | 0 | 3 |
| Сфера | 3D | Изогнутый | 0 | 1 |
► Связанные статьи
Прочтите следующие статьи, чтобы узнать больше о геометрических фигурах.
Часто задаваемые вопросы о геометрических фигурах
Что такое геометрические фигуры в геометрии?
Геометрические фигуры также известны как геометрические фигуры, состоящие из комбинации линий или кривых. В реальной жизни нас окружают геометрические фигуры, например окна в форме квадратов, двери в форме прямоугольников и т. д.
Какие существуют типы геометрических фигур?
Существует два типа геометрических фигур: двумерные и трехмерные геометрические фигуры.Двумерные фигуры — это замкнутые фигуры с длиной и шириной, такие как квадрат и прямоугольник. Трехмерные фигуры также являются замкнутыми фигурами, имеющими длину, ширину и высоту, например параллелепипед и куб.
Является ли прямая геометрической фигурой?
Прямая линия — это одномерная геометрическая фигура, имеющая только длину. Когда много прямых линий соединяются вместе, они образуют фигуры, такие как квадраты, треугольники и т. д.
Что такое трехмерные геометрические фигуры?
В геометрии трехмерная геометрическая фигура представляет собой твердую фигуру или фигуру с тремя измерениями: длиной, шириной и высотой. Например, цилиндр, сфера, параллелепипед и т. д.
Например, цилиндр, сфера, параллелепипед и т. д.
Что такое двумерные геометрические фигуры?
Двумерная геометрическая фигура — это форма, которая имеет длину и ширину, но не имеет высоты или глубины. Круг, квадрат, прямоугольник, треугольник — вот несколько примеров двумерной формы.
Как называются геометрические фигуры?
Ниже приведен список некоторых основных геометрических фигур:
- Треугольник
- Прямоугольник
- Куб
- Прямоугольный
- Сфера
- Квадрат
- Ромб
- Трапеция
Какие основные геометрические фигуры?
Существует множество геометрических фигур в зависимости от их размеров.Круг, треугольник, квадрат, прямоугольник — вот лишь некоторые из основных двумерных фигур. Куб, прямоугольный параллелепипед, сфера, конус и цилиндр — вот лишь некоторые из основных трехмерных фигур или форм.
Каковы примеры основных геометрических фигур в реальной жизни?
Несколько примеров геометрических фигур в реальной жизни перечислены ниже:
- Круг: печенье, колеса велосипеда
- Квадрат: квадратная плитка на полу, квадратные бумажные салфетки
- Прямоугольник: учебники, сотовые телефоны, телеэкран
- Треугольник: сэндвич разрез по диагонали, дорожные знаки
Какая польза от геометрических фигур?
Геометрические формы освежают наши зрительные чувства логичным, практичным и интересным способом. Они придают ощущение порядка и аккуратности как работе, так и повседневной жизни.
Они придают ощущение порядка и аккуратности как работе, так и повседневной жизни.
Почему геометрические фигуры важны для детей?
Изучение геометрических фигур помогает детям идентифицировать визуальную информацию, а также помогает им в организации и обучении навыкам в различных областях. Дети развивают навыки распознавания лиц и навигации, если они могут классифицировать и сравнивать различные формы.
названий геометрических фигур — английская грамматика здесь
Английские названия геометрических фигур, определения и примеры;
Список геометрических фигур
- Нонагон
- Эллипс
- Прямоугольный
- Прямоугольная призма
- Октагон
- Конус
- Треугольник
- Разносторонний треугольник
- Стрелка
- Куб
- Цилиндр
- Звезда
- Семиугольник
- Шестигранник
- Полумесяц
- Пирамида
- Прямоугольный треугольник
- Параллелограмм
- Ромб
- Квадрат
- Пентагон
- Трапеция
- Круг
- Овальный
- Декагон
- Сердце
- Крест
(для более названий форм )
Геометрические фигуры могут быть названы как фигура или область, замкнутая границей, которая создается путем объединения определенного количества кривых, точек и линий. Существуют различные геометрические фигуры: треугольник, круг, квадрат и т. д. Очень важно, чтобы вы приобрели необходимое понимание геометрических фигур. Например; общие формы в геометрии, такие как квадрат, прямоугольник, круг и треугольник. Вот некоторые из геометрических фигур и определения;
Существуют различные геометрические фигуры: треугольник, круг, квадрат и т. д. Очень важно, чтобы вы приобрели необходимое понимание геометрических фигур. Например; общие формы в геометрии, такие как квадрат, прямоугольник, круг и треугольник. Вот некоторые из геометрических фигур и определения;
Квадрат
Квадрат — это четырехсторонняя область, состоящая из соединения четырех отрезков. Отрезки в квадрате — это все равные прямые.Вместе они образуют 4 прямых угла.
Круг
Если мы говорим о круге, который является другой формой геометрии, не имеет прямых линий. Это скорее комбинация кривых, которые все связаны между собой. В окружности угол не найти.
Прямоугольник
Подобно квадрату, прямоугольник также создается путем соединения четырех отрезков. Однако разница есть только между квадратом и прямоугольником.Кроме того, прямоугольник имеет два отрезка, которые длиннее двух других отрезков. Так, в геометрии прямоугольник еще называют вытянутым квадратом.
Так, в геометрии прямоугольник еще называют вытянутым квадратом.
Треугольник
Треугольник состоит из трех связанных отрезков. В отличие от квадрата, в треугольнике углы могут быть разных размеров. Они не всегда являются правильными углами. Треугольники называются в зависимости от типа углов, которые находятся внутри самого треугольника. Например, если треугольник имеет один прямой угол, он будет известен как прямоугольный треугольник.
Однако, если все углы треугольника меньше 90 градусов, он будет называться остроугольным треугольником. Если какой-либо из углов в треугольнике больше 90 градусов, то он будет известен как тупоугольный треугольник. Наконец, есть равноугольный треугольник, у которого все углы треугольника равны 60 градусов. С другой стороны, треугольник также можно идентифицировать или пометить по типу его сторон. У разностороннего треугольника нет равных сторон. У равнобедренного треугольника две стороны равны.Равносторонний треугольник имеет три равные стороны.
геометрических магических квадратов – Puzzlewocky
Геометрические магические квадраты используют формы, чтобы перевести числовые магические квадраты в более высокие измерения. В 2001 году Ли Саллоуз обнаружил, что числовые магические квадраты, известные с древних времен, на самом деле являются просто одномерными версиями чего-то гораздо большего.
Геометрический магический квадрат с ромбом в качестве целевой формыВ геометрическом магическом квадрате или геомагическом квадрате целью является не число, а фигура.В приведенном выше квадрате сетка 3×3 состоит из 9 различных фигур, состоящих из равносторонних треугольников. Каждый из трех рядов, каждый из трех столбцов и две большие диагонали состоят из трех фигур, которые можно комбинировать, чтобы сформировать ромб. Формы могут быть перевернуты или повернуты. Ниже показан геомагический квадрат с квадратом в качестве целевой формы.
Геометрический магический квадрат с квадратом в качестве целевой формы Геомагический квадрат ниже имеет целью треугольник, состоящий из шестиугольников.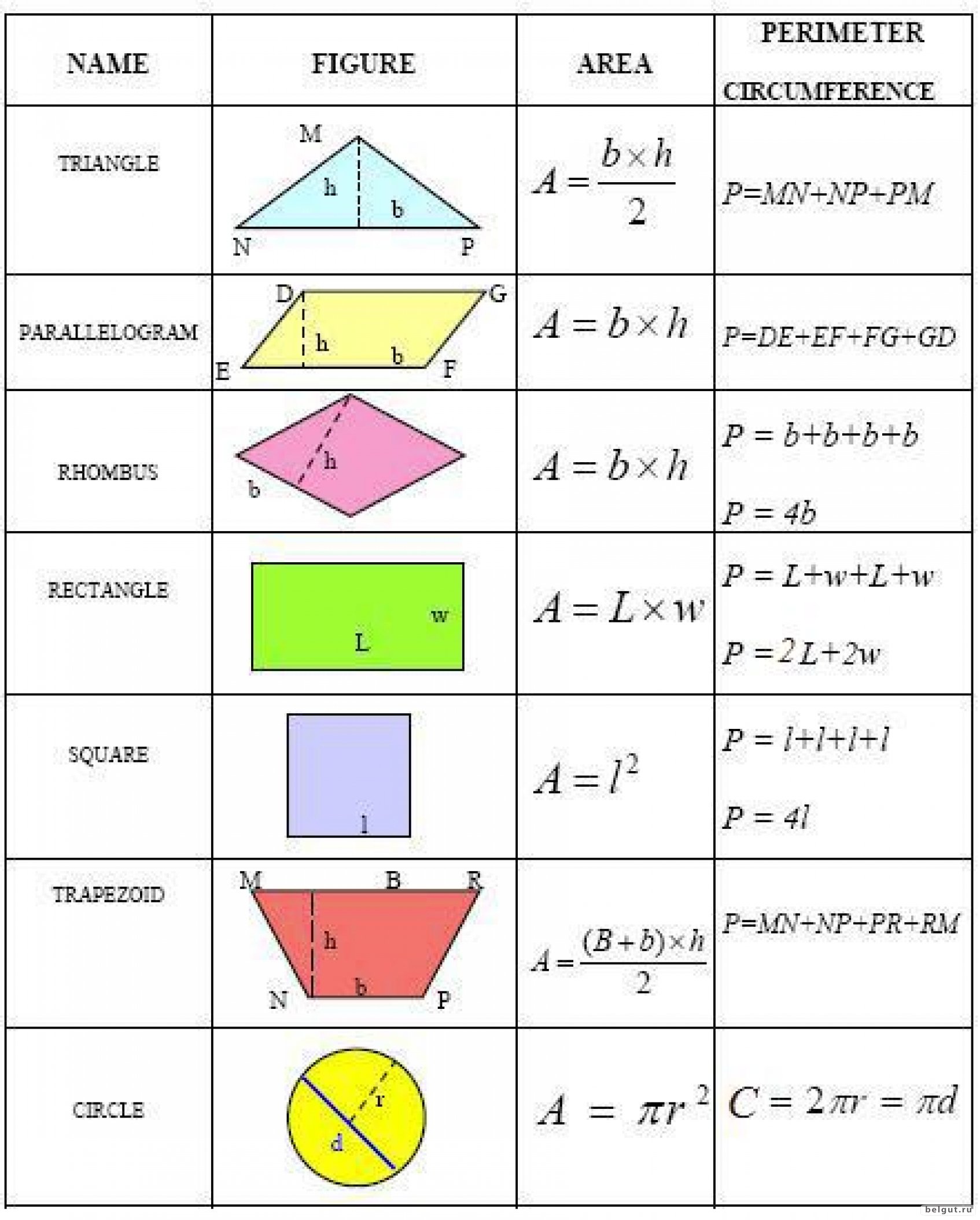 Поскольку треугольник состоит из 15 шестиугольников, это геометрический эквивалент знаменитого числового магического квадрата Ло Шу, в котором числа от 1 до 9 занимают 9 ячеек сетки, а магическая сумма равна 15.
Поскольку треугольник состоит из 15 шестиугольников, это геометрический эквивалент знаменитого числового магического квадрата Ло Шу, в котором числа от 1 до 9 занимают 9 ячеек сетки, а магическая сумма равна 15.
Приведенные выше примеры являются геометрическими эквивалентами существующих числовых магических квадратов, но приведенный ниже пример демонстрирует, что существуют геометрические магические квадраты, не имеющие числового эквивалента.
Геометрический магический квадрат с гексаграммой в качестве целевой формыМы не ограничены квадратами. Ниже представлена геометрическая магическая пентаграмма, состоящая из десяти фигур: по одной в каждой точке звезды и в каждой вершине внутреннего пятиугольника.Шестиугольник является целевой формой.
Геометрическая магическая пентаграмма с шестиугольником в качестве мишени shape А здесь у нас есть магическая гексаграмма с ромбовидной мишенью.
Чтобы сделать свои собственные геомагические квадраты, вы, вероятно, захотите начать с цветных карандашей и миллиметровой бумаги, включая изометрическую миллиметровую бумагу и гексагональную миллиметровую бумагу. На компьютере вам понадобится программа для работы с векторной графикой, например Inkscape.
Один из методов начинается с выбора формы цели и выяснения того, как ее можно разбить на части.Таким образом были построены первые три геомагических квадрата выше. Алмаз состоит из 18 равносторонних треугольников, квадрат состоит из 36 квадратов, а треугольник состоит из 15 шестиугольников. Когда вы знаете, сколько единиц содержит ваша целевая фигура, вы можете построить числовой магический квадрат в качестве отправной точки. Один из способов сделать это — использовать формулу, разработанную Эдуардом Лукасом:
.
Эта формула будет давать числовой магический квадрат, если 0 < a < b < c − a и b ≠ 2a. Магическая сумма 3c. Например, площадь Ло Шу:
Магическая сумма 3c. Например, площадь Ло Шу:
Каждый магический квадрат можно перевернуть или повернуть, и он по-прежнему считается одним и тем же квадратом.
Легко видеть, что показанный выше геомагический квадрат с треугольником, состоящим из шестиугольников, является просто квадратом Ло Шу в геометрической форме. Первые два геомагических квадрата выше также имеют числовые эквиваленты. Однако четвертый пример с шестигранной звездой или гексаграммой в качестве целевой формы не имеет эквивалентного числового магического квадрата.Вместо этого он был построен с использованием метода «подложки» Ли Саллоуза. Для начала субстрат создается из тривиального числового магического квадрата, например, если a или b равны нулю. Вот субстрат, использованный для геомагического квадрата гексаграммы:
Как видите, это не настоящий магический квадрат, потому что числа и формы повторяются. Магическая сумма этого тривиального числового магического квадрата равна 6, но используются только числа 1, 2 и 3. Соответствующий тривиальный геометрический магический квадрат имеет целевую форму гексаграммы, но используются только ромб, шеврон и лодка.Чтобы «детривиализировать» такой квадрат и превратить его в настоящий геомагический квадрат, необходимо добавить геометрические переменные, такие как ключи в форме вилки и замочные скважины, использованные выше.
Соответствующий тривиальный геометрический магический квадрат имеет целевую форму гексаграммы, но используются только ромб, шеврон и лодка.Чтобы «детривиализировать» такой квадрат и превратить его в настоящий геомагический квадрат, необходимо добавить геометрические переменные, такие как ключи в форме вилки и замочные скважины, использованные выше.
Для получения дополнительной информации о геомагических квадратах настоятельно рекомендуется посетить веб-сайт и книгу Ли Сэллоуса.
|
Геометрические фигуры в дизайне: как их творчески использовать
13 минут чтенияНаша повседневная жизнь – это постоянное взаимодействие с различными объектами, которые напоминают различные формы, от простых до абстрактных.
Что интересно в формах, так это то, что они могут заставить нас чувствовать себя определенным образом. Это означает, что вы можете использовать их для создания материалов графического дизайна, которые вызывают определенные эмоции.
Мощная коммуникационная стратегия заключается в сочетании правильного сообщения с отличным дизайном для достижения желаемых результатов.
В этой статье мы поговорим о психологии геометрических фигур, о том, как все окружающие нас объекты могут быть связаны с основными формами, каковы основные значения фигур и как вы можете использовать их, чтобы повлиять на свою стратегию визуального маркетинга. .
.
Что такое геометрические фигуры?
В графическом дизайне фигуры представляют собой двухмерные фигуры в макете с четкими границами по краям.Добавляя к ним третье измерение, вы можете создавать формы, которые являются совершенно другим элементом.
Большинство форм опираются на культурные условности или природные силуэты, что делает их знакомыми нам.
Они могут работать как отдельный дизайн, если вам нужно отправить прямое сообщение. В противном случае они работают как аксессуар для различных визуальных маркетинговых материалов, таких как презентации, инфографика или визуальные эффекты для социальных сетей.
Но какую форму лучше всего использовать для отправки правильного сообщения?
3 типа форм в дизайне
Иногда лучший способ создать привлекательный дизайн — сократить его до самых простых форм.Простота может быть ответом.
Есть три основные формы, которые вы можете использовать в своих проектах:
1.
 Геометрические фигуры
Геометрические фигуры
Вероятно, наиболее часто используемые геометрические фигуры первыми приходят нам на ум. Круги, квадраты, треугольники, пятиугольники, шестиугольники или восьмиугольники легко узнаваемы.
Они нам так знакомы, потому что мы начали их видеть и рисовать с детства. В детском саду мы изучали формы через игру, прежде чем мы узнали о буквах, поэтому вполне естественно чувствовать себя знакомым и увлеченным чем-то, к чему мы привыкли.
2. Органические формы
В отличие от геометрических форм, это асимметричные или несовершенные, но необходимые и удобные формы, встречающиеся в природе.
Все, что было создано естественным путем, может попасть в эту категорию, например, листья, камни или облака. В редких случаях эти формы могут быть созданы руками человека, например, чернильные капли.
3. Абстрактные формы
Они иллюстрируют органические формы или предметы быта, даже если они не являются точным изображением. Например, фигурка — это абстрактная фигура, изображающая человека, а типографские глифы могут иллюстрировать буквы.
Например, фигурка — это абстрактная фигура, изображающая человека, а типографские глифы могут иллюстрировать буквы.
В эту категорию можно поместить символы, которые вы видите и используете в повседневной жизни, например значки мобильных приложений.
Источник изображения
Теперь давайте углубимся в значения форм и узнаем, как вы можете интегрировать их в свою стратегию визуальной коммуникации.
Психология форм в дизайне
Дизайнеры используют формы, чтобы выражать различные идеи, создавать представление о движении, придавать текстуру и глубину изображению, предлагать настроение или эмоции или выделять интересующую область.
В большинстве случаев рисунки сочетаются с цветом. Комбинации форм и цветов разнообразны и несут разное значение и настроение.
Прежде чем решить, какой из них выбрать, вам нужно понять цель вашего дизайна и сообщение, которое вы хотите передать.
Конкретные формы и цвета уже имеют значение в нашем сознании. Обычно это относится к знакомым формам, которые ассоциируются с объектами, встречающимися в природе.
Обычно это относится к знакомым формам, которые ассоциируются с объектами, встречающимися в природе.
Итак, когда мы видим объект, уменьшенный до комбинации цвета и формы — скажем, желтый круг, символизирующий солнце, — мы сразу узнаем его.
Иногда, если мы не идентифицируем их сразу, их значения могут быть более глубокими, и они вызывают только определенное чувство, не давая всей информации.
Пришло время узнать, какое значение они несут.
1. Значение геометрических фигур
Это основа дизайна, а также обучения через игру. Большинство из нас играло в игру, в которой нужно было сопоставлять фигуры разных цветов.
У каждой формы есть определенные коннотации, и обычно эти значения являются культурными.Когда мы видим красный восьмиугольник, мы знаем, что это означает СТОП.
С самого начала человеческий разум находит способ проникнуть во все геометрические значения, потому что он понял формы раньше, чем понял язык.
Переходя от обучения через игру к проектированию с помощью форм, мы видим, что почти в любом типе дизайна существует тенденция к простоте и минимализму.
Простота настолько привлекательна для всех, потому что с правильной формой и цветом вы можете передать более мощное сообщение, чем с помощью множества богатых деталей.
Применяя различные характеристики к форме в графическом дизайне, вы будете передавать разные настроения и смыслы.
Понимая смысл геометрии, вы даже можете создавать произведения искусства с помощью геометрических фигур.
Примерно так:
Источник изображения
Давайте пробежимся по наиболее распространенным формам и геометрическим значениям:
Квадратные геометрические формы встречаются чаще всего. Эти формы знакомы глазу, и их легко использовать в качестве рамки или основы для дизайна.Поскольку эти формы обычно не являются фокусом визуального образа, они используются для придания ощущения стабильности. Углы предполагают математический порядок.
Углы предполагают математический порядок.
Квадраты и прямоугольники предполагают миролюбие, безопасность и чувство соответствия. Когда мы рисуем дом, мы начинаем с квадрата.
Иногда мы можем думать, что квадраты или прямоугольники — это пресные формы, на которые не обращают внимания, но при правильной стратегии они могут быть столь же эффективными, как и любая другая форма.
Чтобы визуально выделиться с помощью этих форм, вы можете рассмотреть пиксельную форму старой школы, то есть множество квадратов, соединенных вместе.Вот так:
Источник изображения: Instagram
Геометрические фигуры круга представляют непрерывность, вечное целое, потому что у них нет ни начала, ни конца. В каждой культуре круги изображают солнце, землю, луну и другие небесные объекты.
Их полнота предполагает гармонию, теплоту и дает нам ощущение спокойствия. Круги также помогают нам изображать движение в визуальных образах и используются для обозначения знакомых объектов, таких как колеса, мячи или различные фрукты, такие как апельсины и грейпфруты.
Геометрические фигуры треугольника могут показывать стабильность и силу, когда они направлены вверх, или нестабильность и конфликт, когда они обращены вниз.
Они обладают энергией, как никакая другая форма, и могут символизировать духовную троицу с союзом тела, разума и духа. Они также могут служить иллюстрацией самопознания.
Существуют и другие значения формы треугольника в графическом дизайне, такие как динамизм и улучшение.
При выборе этой формы всегда лучше использовать ее сидя на основании или с острием, обращенным вправо, чтобы предложить движение вперед.В противном случае это может послать негативные вибрации, как полагает западная культура.
Несколько примеров из цифрового мира, которые символизируют движение по треугольникам, — это символ воспроизведения, ускоренная перемотка вперед или назад, которые имеют форму треугольника.
Источник изображения
Треугольники могут использоваться для обозначения знакомых форм, таких как пирамиды, горы или вымпелы. Если треугольник тонкий, он изображает стрелку.
Если треугольник тонкий, он изображает стрелку.
Маленькие треугольники можно использовать как мозаику или перекрывать друг друга, чтобы создать сильное ощущение единства.
- Пятиугольники, шестиугольники и восьмиугольники
Среди форм многоугольников с более чем четырьмя сторонами, используемых в дизайне, наиболее распространены пятиугольники, шестиугольники и восьмиугольники. Эти формы являются частью нашей повседневной жизни, и мы настолько привыкли к ним, что можем сразу связать форму с символом.
Например, здание Пентагона в США (в форме пятиугольника), напольная плитка или секции улья (в форме шестиугольника), знак остановки или открытый зонт (в форме восьмиугольника) легко узнаваемы.
Все эти фигуры можно использовать в качестве пазлов и создавать инфографику, поскольку они выглядят профессионально.
Источник изображения
Источник изображения
Источник изображения
2.
 Значение органических форм
Значение органических форм
Естественные или органические формы — это объекты или животные, встречающиеся в нашем мире, такие как листья, цветы или деревья. Они также могут быть рукотворными вещами, такими как чернильные капли.
Эти формы помогут вам создавать проекты, связанные с окружающей средой или кампаниями для активного отдыха.
Естественные формы могут работать как в качестве аксессуаров в ваших визуальных эффектах, так и сами по себе, поскольку они посылают точное сообщение без скрытого смысла.
Помимо этих характеристик, органические формы могут быть очень декоративными.
Было время, когда стиль декоративно-прикладного искусства под названием модерн процветал. Он был сосредоточен на органических формах, особенно на цветах, которые применялись практически везде — в архитектуре, живописи и даже в надписях.
Источник изображения
Под влиянием ар-нуво период хиппи выражал свои убеждения с помощью цветов и других символов, символизирующих мир.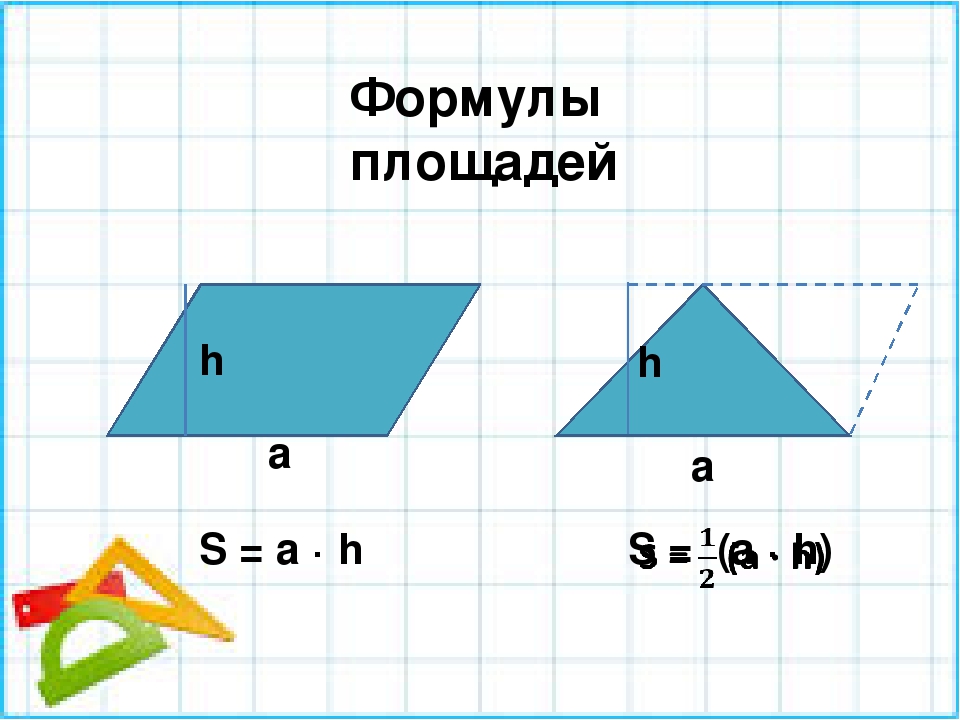
Итак, дело в том, что если ваше сообщение согласуется с органическими формами, и вы можете получить желаемый результат, используя их, это отличный вариант для рассмотрения.
3. Значение абстрактных форм
Когда мы говорим об абстрактных формах, мы обычно имеем в виду символы или значки, которые несут разные значения.
Используйте абстрактные формы только для того, чтобы подчеркнуть идею вашего изображения или инфографики. Когда они используются по отдельности или в большом количестве, они могут сбивать с толку вашу аудиторию.
В инфографике символы иногда могут заменять текст, когда вам нужно подчеркнуть идею, поэтому вы можете поместить символ звездочки рядом с сообщением, которое хотите выделить.
Использование одних и тех же цветов символов во всей графике продемонстрирует согласованность и поможет вам сосредоточить внимание на основных идеях.
Наиболее часто используемые символы и абстрактные формы:
Стрелки довольно универсальны, и их можно использовать в самых разных ситуациях для отправки конкретной информации. Когда вы выделяете их жирным шрифтом, они могут передавать более мощное сообщение или, если они тонкие, они отлично подходят для маркированного списка.
Когда вы выделяете их жирным шрифтом, они могут передавать более мощное сообщение или, если они тонкие, они отлично подходят для маркированного списка.
Вероятно, самым важным аспектом стрелки является ее функция указания направления. Благодаря этому зритель будет знать, где искать в вашей графике и что читать в первую очередь.
Источник изображения
Стрелы также имеют декоративную функцию.Если вы хотите создать постер в стиле бохо, вы можете разместить на нем такие стрелки:
Источник изображения
Звезды можно рассматривать как символы, помимо геометрических фигур, поскольку они часто используются в религиозных иллюстрациях. Более того, они обычно показывают важность чего-либо, и им всегда удается привлечь внимание людей.
звезды — это одни из лучших форм, которые вы можете использовать, чтобы привлечь внимание вашей аудитории к текущей акции или скидочному коду.
Обычно мы используем желтые звезды, чтобы привлечь внимание людей, но есть и звезды с синими лентами, которые обозначают первое место в конкурсе.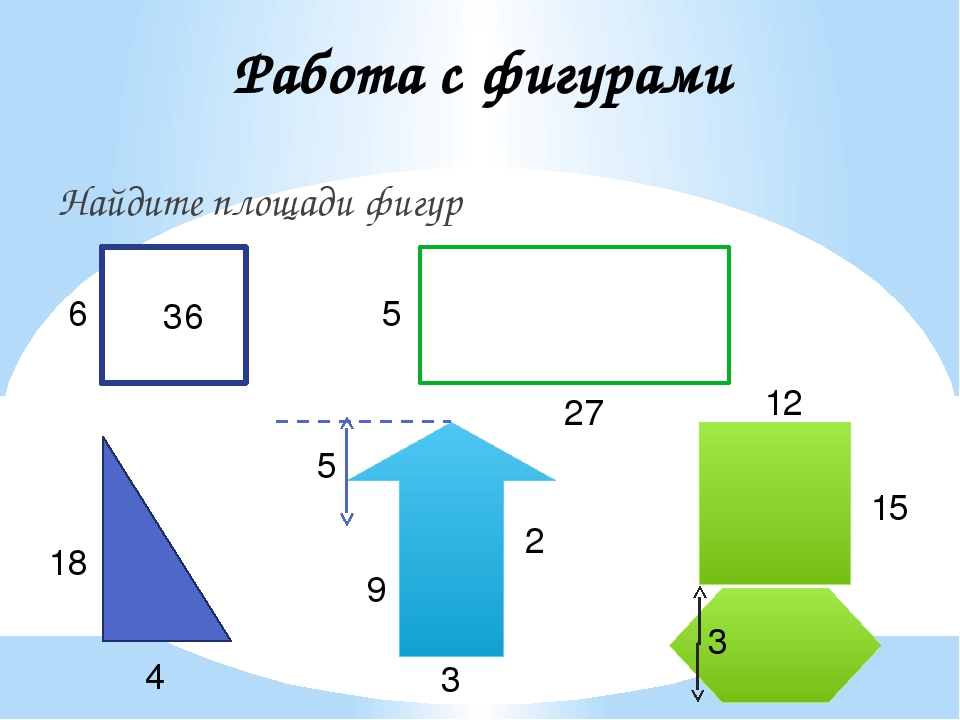
звезды — это отличный способ отблагодарить кого-то, и это может быть небольшая золотая наклейка или звезда на Аллее славы в Голливуде, чтобы продемонстрировать огромное признание.
Они считаются аксессуарами к любому дизайну, и лучше использовать маленькие значки в своих визуальных элементах. Они не в центре вашего сообщения, но могут оказаться необходимыми.
Иконкиможно использовать как в печатном, так и в цифровом дизайне, но, скорее всего, вы найдете их на цифровых платформах, потому что они могут действовать как кнопка призыва к действию.
Их также можно использовать для организации визуальных элементов и разделения контента на категории. Взгляните на этот пример:
Источник изображения
Еще одна интересная идея — использовать значки основных моментов в истории Instagram, которые помогут вам произвести отличное первое впечатление.
Если вам нужен постоянный и надежный источник, Creatopy предлагает вам 20 категорий различных иконок, которые помогут вам организовать визуальную коммуникацию.
Лучшие советы и рекомендации по смешиванию и сопоставлению геометрических фигур
Для эстетически приятного дизайна, который оказался очень эффективным (я часто видел эту комбинацию), вы можете комбинировать геометрические и органические формы.Результат будет выглядеть примерно так:
Источник изображения
Итак, вы либо используете одну категорию форм в визуальном образе, либо комбинируете их и встречаете органику с элементами, созданными руками человека. Вы можете использовать комбинацию форм из разных категорий практически везде. Основное правило — понимать символику фигур.
Вот несколько примеров:
Вы можете комбинировать абстрактные формы с органическими формами и получить что-то креативное, что привлечет внимание посетителей вашего сайта.
Источник изображения
Не оставляйте свои плакаты незамеченными. Используйте абстрактные формы с органическими формами, добавьте правильный текст и цвета, которые подчеркнут ваше сообщение, и вы увидите, что это будет успешная стратегия.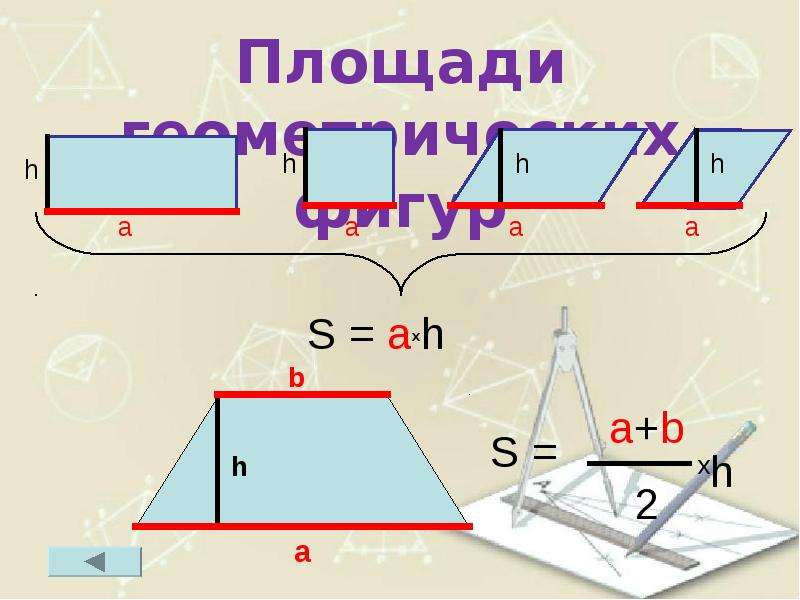
Источник изображения
Или вы можете просто создавать удивительные плакаты, используя точность геометрических фигур с естественными органическими формами, которые смягчят сообщение, в то же время придав ему что-то особенное.
Источник изображения
Ваши геометрические фигуры могут символически содержать в себе жизнь, если вы соедините их с естественными, органическими формами.
Источник изображения
Добавьте природные элементы в графический дизайн ваших кругов , , и у вас больше никогда не будет скучного календаря.
Источник изображения
Идеально использовать органические формы, чтобы выразить себя, потому что они несут разные чувства и настроения, в зависимости от цветов, которые вы на них используете.
В следующем изображении они, кажется, направляют своего главного героя; то есть абстрактная форма девушки, все глубже и глубже погружающейся в свои мечты или воображение.
Источник изображения
Познакомившись с основными формами, их значением и несколькими способами их смешивания, давайте рассмотрим еще одну важную функциональность, которую они несут, а именно их использование в дизайне логотипов.
Теперь мы рассмотрим некоторые из наиболее важных форм логотипа и их значения.
Психология форм в дизайне логотипов
Дизайн логотипа — это часть идентичности бренда и то, как вы представляете себя потенциальным клиентам.С хорошо продуманным логотипом вы привлечете внимание целевой аудитории.
Фактически, журнал Consumer Research показывает нам, что даже простой формы логотипа может быть достаточно, чтобы повлиять на то, как люди воспринимают ваши продукты и услуги.
Психология форм логотипов в графическом дизайне показывает нам, как изменение формы логотипа может изменить общее восприятие бренда клиентами.
Крайне важно учитывать это при разработке вашего логотипа, потому что, как только он появится, он отправит сообщение вашей аудитории, и вы хотите убедиться, что он правильный.
Итак, как правильно использовать формы при разработке логотипа? Давайте рассмотрим некоторые из самых популярных форм логотипов и проанализируем их.
Круглые логотипы
Круги обычно используются в дизайне логотипов, потому что они мягче и создают ощущение спокойствия, а не формы с грубыми краями.
Поскольку у них нет линий с резким изменением направления, первое впечатление о вашем бренде в мире будет надежным.
Сообщение, которое отправляют круги, эмоциональное.Это показывает единство, приверженность и устойчивость из-за их формы, которая заставляет нас думать о бесконечности. Эксперты по брендингу чаще всего используют эту форму из-за ее привычного значения и значения вечного баланса.
Естественно появляются только круглые формы. Обычно мы не видим идеального прямоугольника в природе. Дизайнеры из всех областей используют это знакомство.
Источник изображения
Квадратные логотипы
Квадраты используются для иллюстрации пропорций, баланса, профессионализма , и силы.
Благодаря своей стабильной форме квадрат или прямоугольник могут вызывать доверие и безопасность у вашей целевой аудитории.
При выборе квадрата для логотипа лучше сочетать его с цветами. Помните, я говорил, что квадраты могут показаться пресными? Избегайте этого с самого начала и придайте стабильности ощущение игривости.
Вот несколько примеров известных квадратных логотипов:
Источник изображения
Большинство из них цветные, но есть также BBC или Cartoon Network, которые выбрали черно-белые.
Несмотря на то, что они сделали этот выбор, он соответствует идентичности бренда. BBC нужно было выглядеть серьезным и надежным, а черно-белый клетчатый рисунок Cartoon Network является основным продуктом и почти синонимом анимационного контента.
Треугольные логотипы
Треугольники встречаются не так часто, потому что они работают в определенных нишах. Они могут вдохновить на такие идеи, как динамическая мощность или непрерывное движение.
Поскольку их форма может показывать направление, треугольники обладают энергией, как никакие другие формы.Вот почему некоторые люди могут воспринимать их как нестабильных и неуверенных в себе.
С другой стороны, треугольники показывают инновации и быстрое улучшение, что означает, что они являются идеальным выбором для технологических компаний.
Если вы в конечном итоге выбрали треугольник в качестве формы логотипа вашего бренда, убедитесь, что он направлен вверх или, по крайней мере, в правильном направлении. Если смотреть вниз, это может указывать на нестабильность и негативные коннотации.
Как и в логотипе Guess, хотя даже соучредитель бренда Пол Марчиано сказал, что за логотипом нет более глубокого смысла, его название с треугольником, направленным вниз, вызывает вопрос.
Источник изображения
Треугольная форма логотипа с острыми краями в основном используется в строительной, автомобильной, научной или технической отраслях.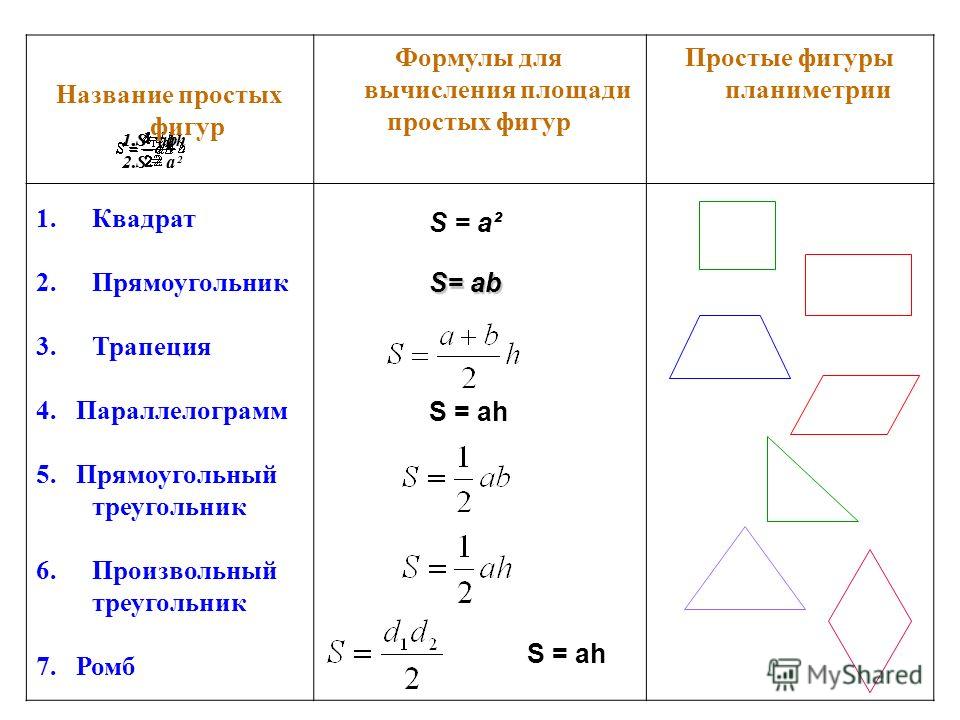
Как в логотипе Google Play:
Источник изображения
YouTube:
Источник изображения
или Мицубиси:
Источник изображения
Органические логотипы
Вероятно, вы можете вспомнить несколько логотипов органической формы.Бренды часто выбирают дизайн своего логотипа под влиянием естественной формы, потому что это создает ощущение знакомости, и с ними легко соприкасаться.
Аудитория сможет легко связать естественную форму, которую они видят или часто используют, с фирменным стилем бренда.
Более того, бывает и наоборот. Когда вы видите фигуру в повседневной жизни, вы думаете о бренде, который она представляет.
Источник изображения
Источник изображения
Прежде чем приступить к работе над проектом логотипа, важно понять смысл и характеристики, которые будет передавать логотип.
После того, как вы узнаете, какое ключевое сообщение вы хотите передать с помощью своего логотипа, вы сможете сочетать его с цветами и некоторыми классными шрифтами.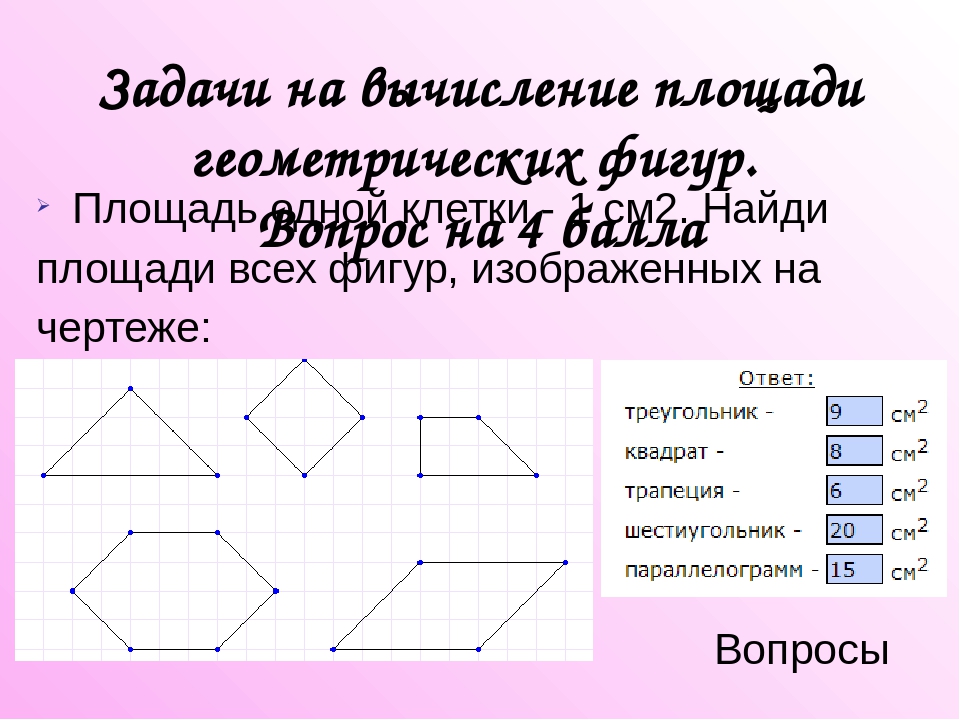
Заключение
Геометрические формы более эффективны, чем вы думаете. Через них можно легко передать определенные эмоции и чувства. Ключ в том, чтобы знать, какие типы фигур могут помочь вам достичь своей цели, и использовать их соответствующим образом в своих проектах.
Как вы видели, их можно успешно использовать и в дизайне логотипов, но вам нужно быть очень осторожным в том, что вы решите сделать.
В принципе, все в этом мире можно упростить и привести к простой форме. Если вам удастся освоить основы форм, вы вытащите из себя кубиста.
Теперь пришло время применить на практике то, что вы сегодня узнали. Войдите в свою учетную запись Creatopy, дайте волю своему воображению и создайте что-то потрясающее из геометрических фигур.
Свойства фигур: прямоугольники, квадраты и ромбы — видео и расшифровка урока
Прямоугольники
Начнем с прямоугольников.Прямоугольник — это четырехсторонняя фигура со всеми прямыми углами. Если вы хотите узнать, является ли фигура прямоугольником, у вас есть всего два теста. Он четырехсторонний? И все ли углы равны 90 градусов? Если оба ответа да, то перед вами прямоугольник.
Если вы хотите узнать, является ли фигура прямоугольником, у вас есть всего два теста. Он четырехсторонний? И все ли углы равны 90 градусов? Если оба ответа да, то перед вами прямоугольник.
Прямоугольники повсюду. Подумайте о своей средней комнате. Что там за прямоугольник? Двери, столы, окна, плакаты на стенах — все это четырехгранные фигуры со всеми прямыми углами. Даже тот экран, на который вы сейчас смотрите, скорее всего, прямоугольный.
Прямоугольники имеют несколько особых свойств. Во-первых, противоположные стороны параллельны. Во-вторых, противоположные стороны равны по длине. В прямоугольнике выше мы знаем, что сторона AB параллельна стороне CD, а BC параллельна AD. Кроме того, если мы знаем, что АВ равно 6, то и CD тоже. Если BC равно 4, то AD тоже.
Самое интересное в прямоугольниках то, что каждая пара противоположных сторон может иметь совершенно другую длину, чем другая пара. У вас может быть очень тонкий прямоугольник, как у небоскреба выше, или очень ровный, как на обложке старого альбома ниже.
Квадраты
Эта старая обложка альбома соответствует как определению прямоугольника, так и определению нашей следующей формы, квадрата.Квадраты — это особое подмножество прямоугольников. Квадрат представляет собой четырехгранную фигуру со всеми прямыми углами и сторонами одинаковой длины.
Это определение выглядит знакомым? Вот шаги, чтобы определить квадрат: Является ли он четырехсторонним? Все углы равны 90 градусов? Если да, то у вас есть прямоугольник. Если все стороны одинаковой длины, то это не только прямоугольник, но и квадрат.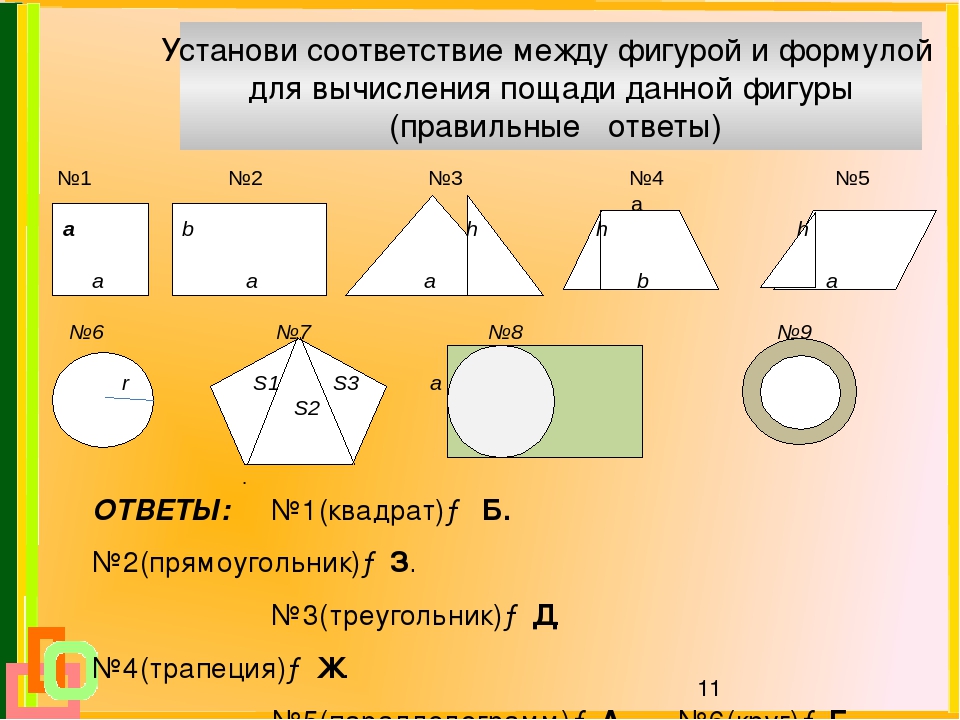 2, или одна сторона в квадрате.2, что равно 25.
2, или одна сторона в квадрате.2, что равно 25.
Ромбы
Затем ромб. Ромб немного отличается от квадрата или прямоугольника. Вот вопросы, которые следует задать, если вы думаете, что имеете дело с ромбом: он четырехгранный? Все ли стороны равны по длине? Если оба ответа да, то перед вами ромб.
Вы заметили, чего не хватает? Прямые углы.У ромба не обязательно должны быть прямые углы. Может, но в этом большая разница с ромбом. Мне нравится думать об этом так: слово «ромб» похоже на слово «носорог». Если носорог бросается на квадрат и сбивает его набок, это уже не квадрат. Но это все равно ромб! Носороги или нет, определение ромба представляет собой четырехгранную форму со сторонами равной длины.
У ромбов есть несколько примечательных свойств. Во-первых, противоположные стороны параллельны.Это справедливо и для прямоугольников и квадратов. Но в ромбе, даже если углы не равны 90 градусам, противоположные стороны все равно параллельны друг другу. Итак, в приведенном ниже AB параллелен CD. А AD параллелен ВС. Кроме того, противоположные углы равны. Здесь угол A равен углу C, а угол B равен углу D.
Но в ромбе, даже если углы не равны 90 градусам, противоположные стороны все равно параллельны друг другу. Итак, в приведенном ниже AB параллелен CD. А AD параллелен ВС. Кроме того, противоположные углы равны. Здесь угол A равен углу C, а угол B равен углу D.
Кроме того, вот забавный момент: если провести диагональные линии из углов, эти линии образуют прямые углы.Поскольку квадрат — это ромб, то это верно и для квадратов. И независимо от того, как далеко этот носорог толкает ромб, его диагонали по-прежнему образуют прямые углы. Квадрат — это ромб, но ромб — это не обязательно квадрат. И прямоугольник может быть ромбом, но если стороны прямоугольника не равны по длине, то это не ромб.
Итоги урока
Итак, мы рассмотрели три различных типа четырехугольников или четырехугольников. Во-первых, есть прямоугольник , который представляет собой четырехстороннюю фигуру со всеми прямыми углами.

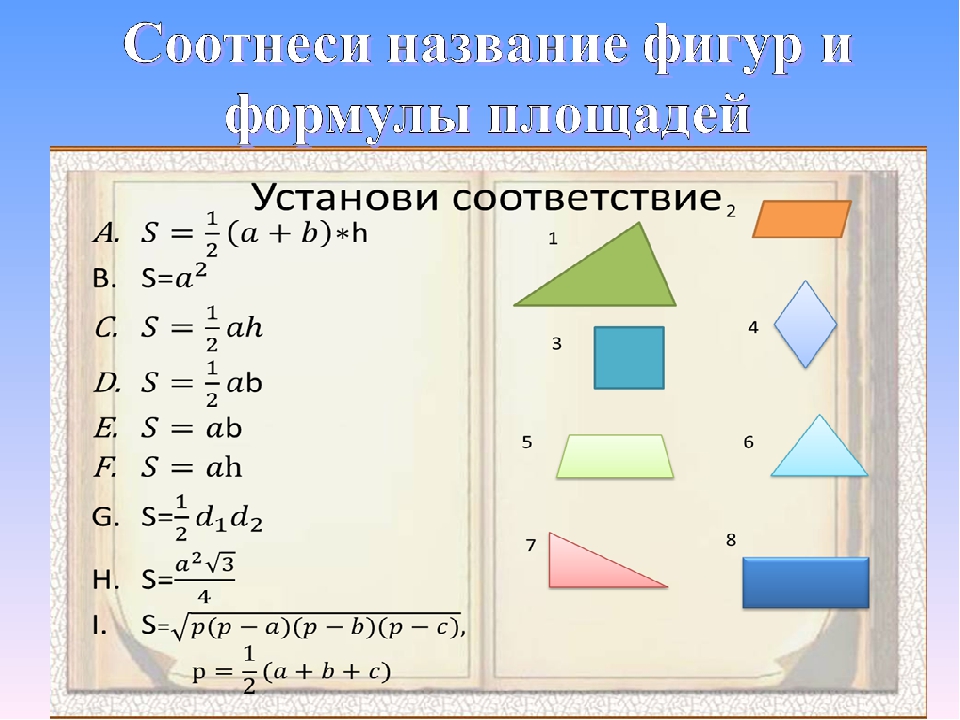 Геометрия
это математическое изучение форм, фигур и
позиции в космосе. Это полезно во многих карьерах, таких как
как архитектура и столярное дело.
Геометрия
это математическое изучение форм, фигур и
позиции в космосе. Это полезно во многих карьерах, таких как
как архитектура и столярное дело. 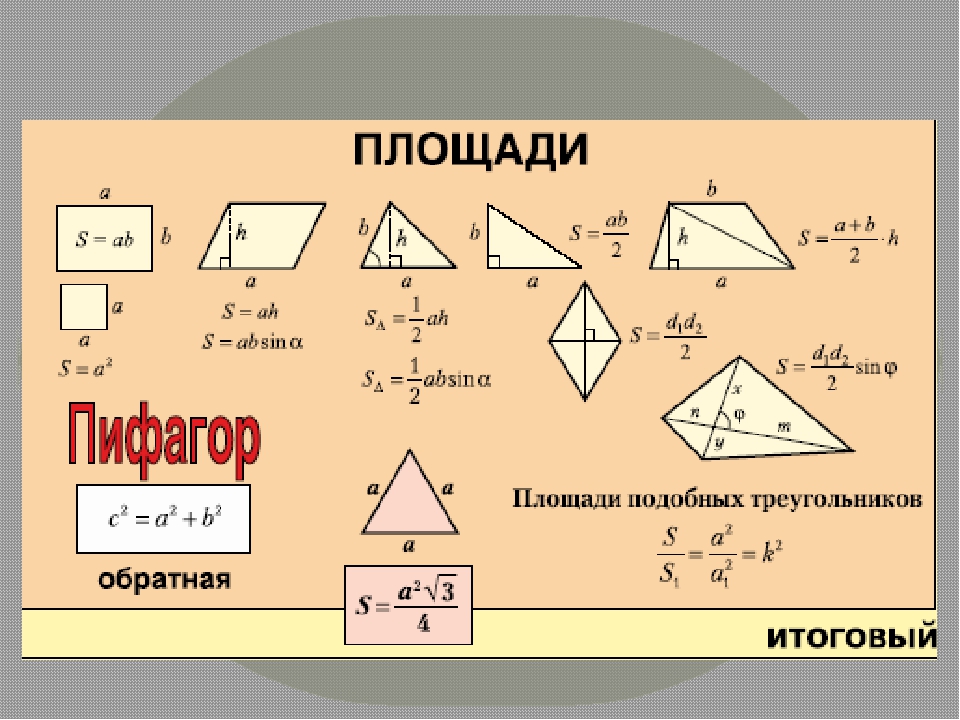 Позиции в космосе
такие вещи, как точки, линии и углы.
Позиции в космосе
такие вещи, как точки, линии и углы. ранее.
ранее.
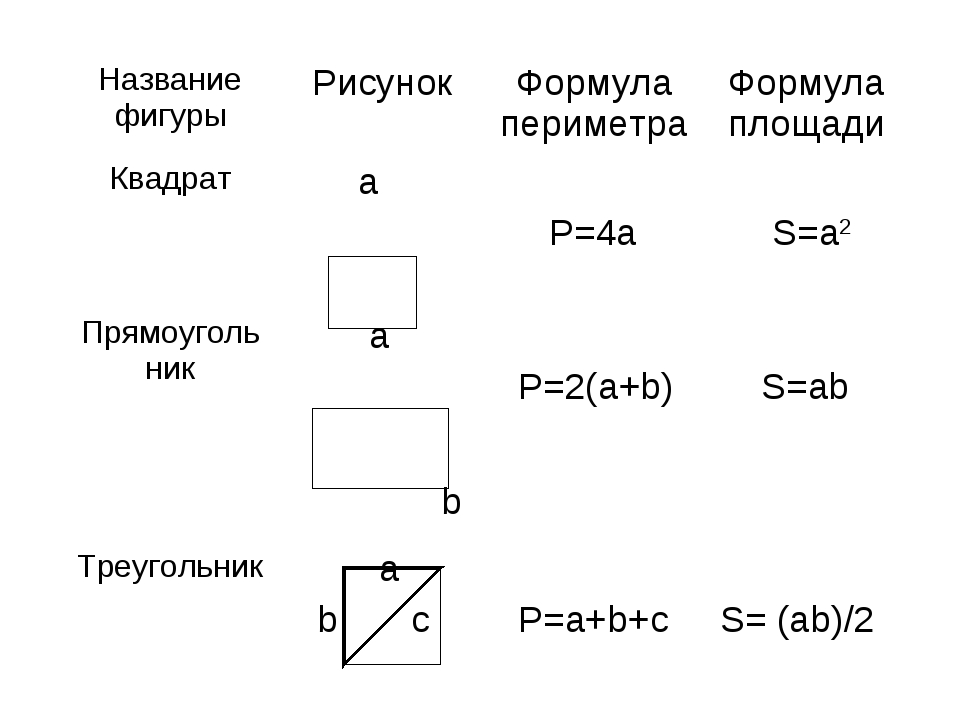 mathgoodies.com/lessons/vol1/perimeter.html
mathgoodies.com/lessons/vol1/perimeter.html 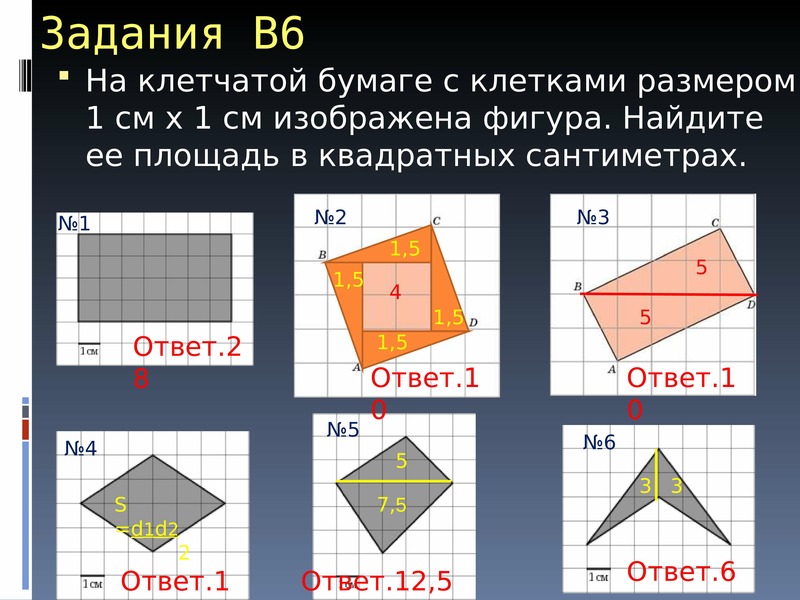 Темы включают
учебные материалы, программы для геометрии,
интерактивные занятия по геометрии, ссылки на
другие веб-сайты и публичный форум, связанный с
геометрия.
Темы включают
учебные материалы, программы для геометрии,
интерактивные занятия по геометрии, ссылки на
другие веб-сайты и публичный форум, связанный с
геометрия.  Наш
мир наполнен множеством разных
формы. Возьмите цифровую камеру на улицу
и фотографировать формы в природе и
в городе. Сколько форм вы можете найти?
Можно ли найти симметрию в природе? Создать
Презентация PowerPoint, в которой вы делитесь своим
формы. Создайте онлайн-активность epal
поделиться своими фотографиями с другим
класс через Интернет.
Наш
мир наполнен множеством разных
формы. Возьмите цифровую камеру на улицу
и фотографировать формы в природе и
в городе. Сколько форм вы можете найти?
Можно ли найти симметрию в природе? Создать
Презентация PowerPoint, в которой вы делитесь своим
формы. Создайте онлайн-активность epal
поделиться своими фотографиями с другим
класс через Интернет.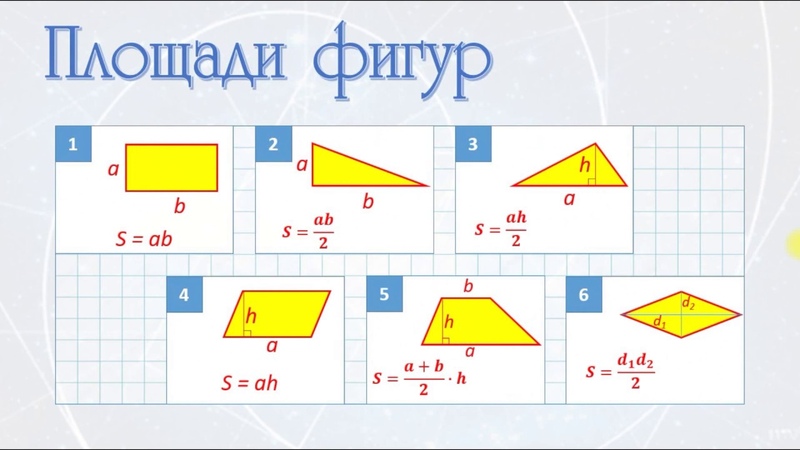 Геометрия имеет интересную историю. Многие
студенты изучали эту тему. Проверять
некоторые из своих проектов ThinkQuest из
«веб-сайты детей для детей» ниже.
Создайте временную шкалу, показывающую некоторые из
главные события. Выберите человека или событие
и узнать о его важности. Как бы
без этого математика другая
знание?
Геометрия имеет интересную историю. Многие
студенты изучали эту тему. Проверять
некоторые из своих проектов ThinkQuest из
«веб-сайты детей для детей» ниже.
Создайте временную шкалу, показывающую некоторые из
главные события. Выберите человека или событие
и узнать о его важности. Как бы
без этого математика другая
знание?  Дети постарше могут пойти
Геометрия
Флэш-карты от APlus Math и
посмотрите, сколько форм они могут
идентифицировать.
Дети постарше могут пойти
Геометрия
Флэш-карты от APlus Math и
посмотрите, сколько форм они могут
идентифицировать.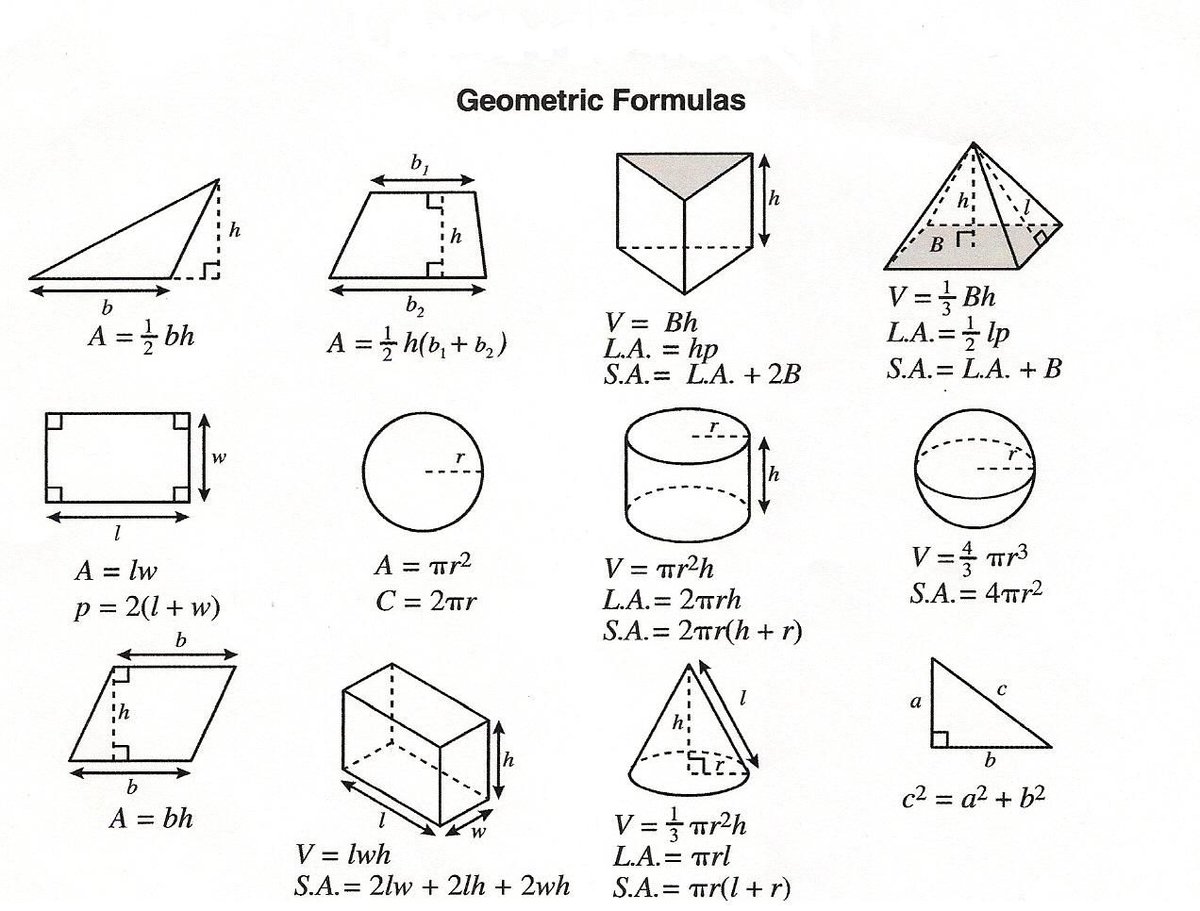 Завершить испытание
Упражнения: Окружность и площадь
Круг и вызов
Упражнения: периметр и площадь
Полигоны на Mrs.Математика Глоссера
Вкусности . Другой вызов может быть
нашел в геометрии
Задача недели от Математика
Форум . Старшим учащимся следует посетить
Находить
Площадь формы! (7-10 классы)
и изучить значение области
геометрические фигуры!
Завершить испытание
Упражнения: Окружность и площадь
Круг и вызов
Упражнения: периметр и площадь
Полигоны на Mrs.Математика Глоссера
Вкусности . Другой вызов может быть
нашел в геометрии
Задача недели от Математика
Форум . Старшим учащимся следует посетить
Находить
Площадь формы! (7-10 классы)
и изучить значение области
геометрические фигуры! 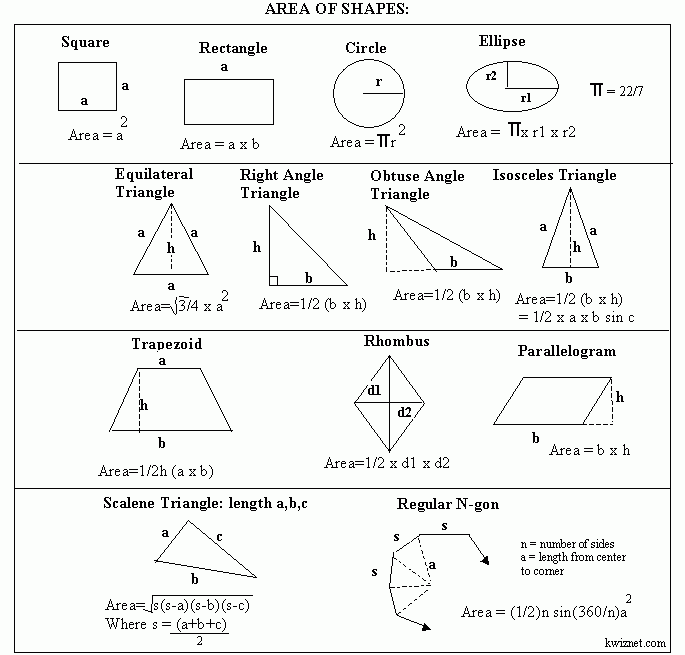 Обязательно посетите
Эми
Галерея и посмотреть на работы
представлены студентами. Отправьте свой собственный
геометрическое животное.
Обязательно посетите
Эми
Галерея и посмотреть на работы
представлены студентами. Отправьте свой собственный
геометрическое животное.  Поделитесь своей фигурой с
эпал.
Поделитесь своей фигурой с
эпал.  Напишите о том, как вы создали
тесселяции и формы, которые вы использовали.
Напишите о том, как вы создали
тесселяции и формы, которые вы использовали.  ky.us/links/webquest/gross/webquest_ss.html
ky.us/links/webquest/gross/webquest_ss.html 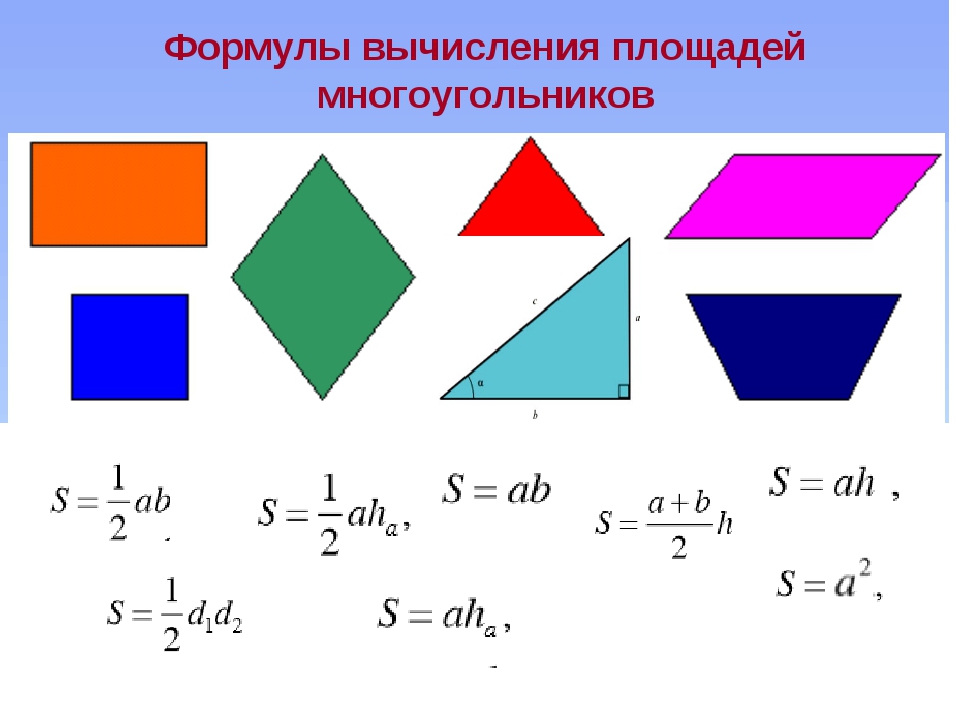 thinkquest.org/2647/geometry/geometry.хтм
thinkquest.org/2647/geometry/geometry.хтм  Организовано в формате глава за главой, темы
включает в себя углы, прямые и косвенные доказательства,
Пифагорейские и другие теоремы, свойства
многоугольники и многое другое о кругах.
Организовано в формате глава за главой, темы
включает в себя углы, прямые и косвенные доказательства,
Пифагорейские и другие теоремы, свойства
многоугольники и многое другое о кругах.
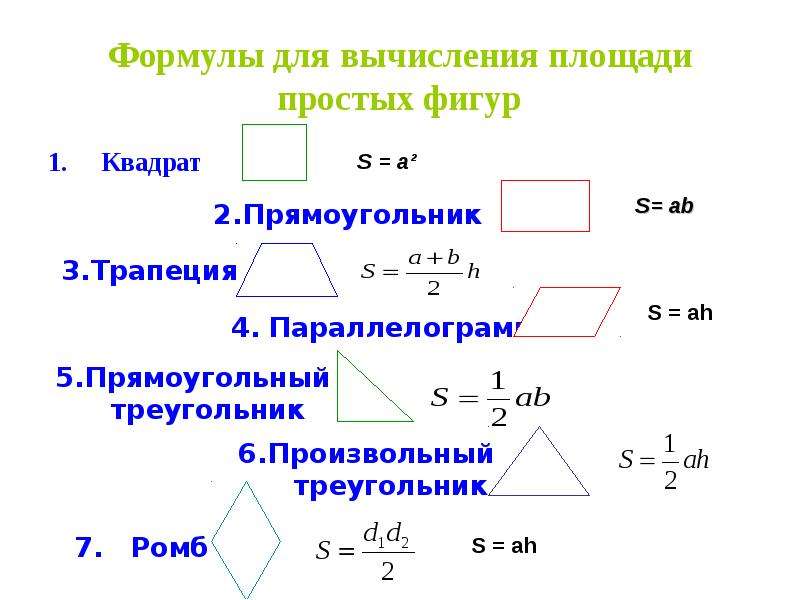
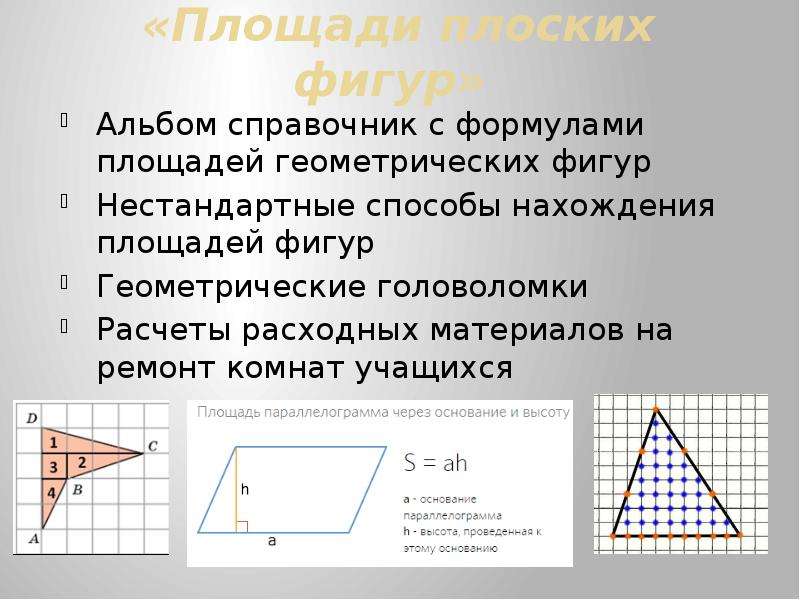 Урнер http://www.inetarena.com/~pdx4d/ocn/urner.html
Урнер http://www.inetarena.com/~pdx4d/ocn/urner.html 
 org/geometry/rugs/index.html
org/geometry/rugs/index.html 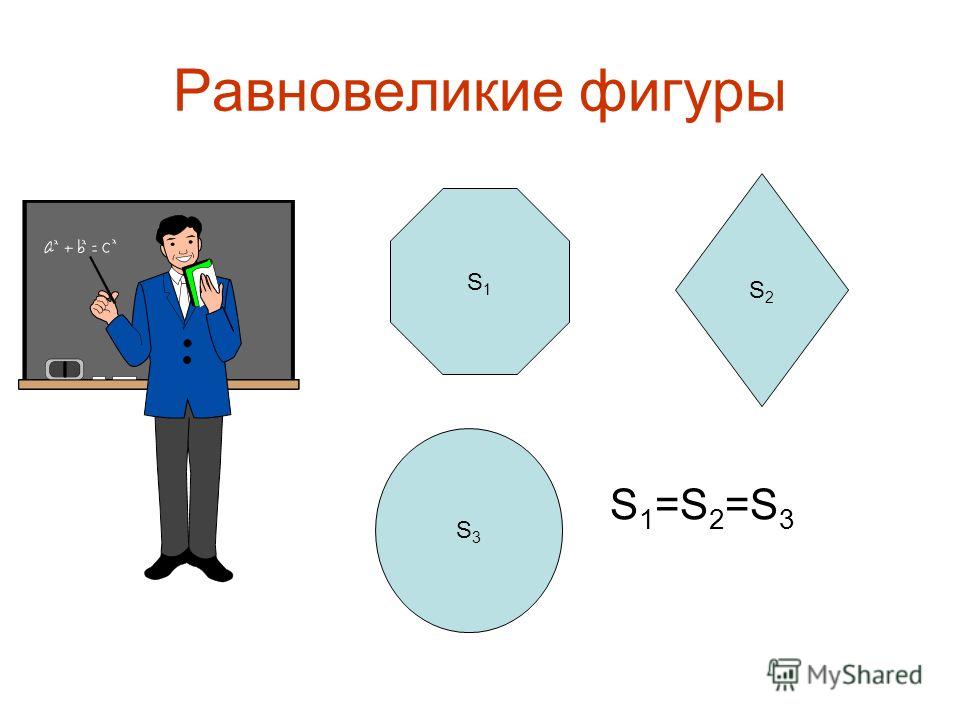 01.07.x.html
01.07.x.html 
 Гёркинк (Оценки
К-1)
Гёркинк (Оценки
К-1) 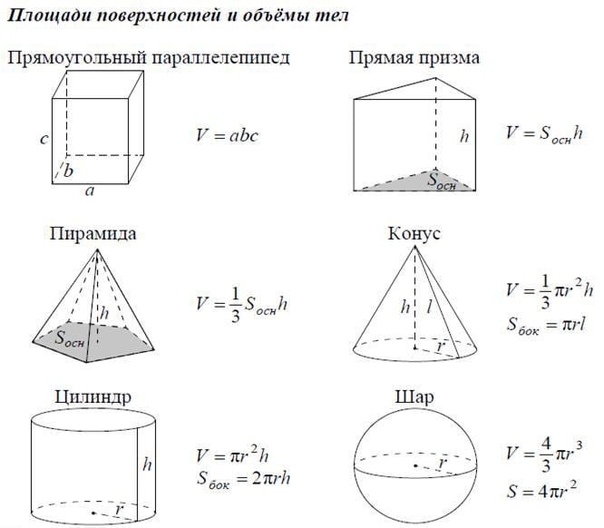
 Обновлено Кингом
Семья, 04.11.
Обновлено Кингом
Семья, 04.11. 