Олимпиадные задания (математика) – Олимпиада школьников «Высшая проба» – Национальный исследовательский университет «Высшая школа экономики»
2018/2019 учебный год
2017/2018 учебный год
| Задания | Решения и критерии |
2016/2017 учебный год
| Задания | Решения и критерии |
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
2015/2016 учебный год
2014/2015 учебный год
Перевод оценок в баллы (PDF, 114 Кб)
| Задания | Решения и критерии |
|
7 класс (PDF, 138 Кб) |
7 класс (PDF, 135 Кб) |
|
8 класс (PDF, 197 Кб) |
8 класс (PDF, 226 Кб) |
|
9 класс (PDF, 196 Кб) |
9 класс (PDF, 226 Кб) |
|
10 класс (PDF, 204 Кб) |
10 класс (PDF, 292 Кб) |
|
11 класс (PDF, 197 Кб) |
11 класс (PDF, 274 Кб) Видеоразбор заданий |
2013/2014 учебный год
2012–2013 учебный год
Задания 8 класс (задачи 1 и 2 имеют вес 16 баллов, остальные — 17 баллов)
Задания 9 класс (все задачи имеют равный вес (кроме 4): 17 баллов, задача 4 — 15 баллов)
Задания 10 класс (все задачи имеют равный вес (кроме 2): 17 баллов, задача 2 — 15 баллов)
Задания 11 класс (все задачи имеют равный вес (кроме 3): 17 баллов, задача 3 — 15 баллов)
2011–2012 учебный год
olymp.hse.ru
Олимпиадные задания по математике (5, 6 класс) по теме: Школьный этап Всероссийской Олимпиады по математике в 5 и 6 классах
Задания школьного этапа Всероссийской олимпиады школьников
Шестой класс
1.В записи (88888888) нужно поставить знаки сложения таким образом, чтобы получилась сумма, которая будет равна 1000.
2. Малыш, Алиса, Кай и Женя заняли первые четыре места в соревнованиях, причем никто из них не делил между собой какие-нибудь места. Известно:
- Малыш не был ни первым, ни четвертым.
- Алиса заняла второе место.
- Кай не был последним.
Какое место занял каждый?
3. Мама дала Зое денег ,чтобы она в школьном буфете купила завтрак.
Когда Зоя вер вернулась из школы, то перед мамой отчиталась так: «1/2 всех денег я истратила на бумагу,1/5 -на чай, а 3/10 -на конфеты». Мама догадалась, что дочь истратила все деньги. Как она узнала ?
4. «Змей Горыныч побежден!»-такая молва дошла до Микулы Селяниновича. Он знал, что мог это сделать либо Илья Муромец, либо Алеша Попович, либо Добрыня Никитич. Вскоре Микуле сообщили:
1)Змея Горыныча победил не Илья Муромец;
2)Змея Горыныча победил Алеша Попович.
Спустя некоторое время выяснилось, что одно их этих сообщений неверное, а другое верное. Догадайтесь, кто из трех богатырей победил Змея Горыныча.
5.Трое рыбаков поймали 75 карасей. Стали варить уху. Когда один дал 8 карасей, а другой 12, а третий-7, то карасей у них стало поровну. Сколько карасей поймал каждый рыбак?
6. Имеется 8 палочек длиной в 1см, 8 палочек длиной в 2см и 7 палочек длиной в 5 см.
Можно ли из всех палочек этого набора сложить прямоугольник?
Разламывать палочки нельзя.
.
О Т В Е Т Ы И РЕШЕНИЯ
ШКОЛЬНОЙ ОЛИМПИАДЫ ПО МАТЕМАТИКЕ
6 класс
1. (6 баллов) В записи (88888888) нужно поставить знаки сложения таким образом, чтобы получилась сумма, которая будет равна 1000.
Решение:
Способ 1: 88+8+8+8+888=1000
Способ 2: 8+8+888+88+8=1000.
2. (6 баллов) Малыш, Алиса, Кай и Женя заняли первые четыре места в соревнованиях, причем никто из них не делил между собой какие-нибудь места. Известно:
- Малыш не был ни первым, ни четвертым.
- Алиса заняла второе место.
- Кай не был последним.
Какое место занял каждый?
Ответ: Малыш-3, Алиса-2, Кай-1, Женя-4 место.
3. (6 баллов) Мама дала Зое денег ,чтобы она в школьном буфете купила завтрак. Когда Зоя вер вернулась из школы, то перед мамой отчиталась так: «1/2 всех денег я истратила на бумагу,1/5 -на чай, а 3/10 -на конфеты». Мама догадалась, что дочь истратила все деньги. Как она узнала?
Решение: 1/2+1/5+3/10=1, т.е. все деньги
4. (6 баллов) «Змей Горыныч побежден!»-такая молва дошла до Микулы Селяниновича. Он знал, что мог это сделать либо Илья Муромец, либо Алеша Попович, либо Добрыня Никитич. Вскоре Микуле сообщили:
1)Змея Горыныча победил не Илья Муромец;
2)Змея Горыныча победил Алеша Попович. Спустя некоторое время выяснилось, что одно их этих сообщений неверное, а другое верное. Догадайтесь, кто из трех богатырей победил Змея Горыныча.
Ответ. Добрыня Никитич.
Решение. Предположим, что Змея Горыныча победил Илья Муромец. Тогда оба сообщения неверные-результат не соответствует условию задачи. Предположим, что Змея Горыныча победил Алеша Попович.Тогда оба сообщения верные. И этот результат не соответствует условию задачи.
Предположим, что Змея Горыныча победил Добрыня Никитич.Тогда первое сообщение верное, а второе- неверное. Результат соответствует условию задачи
5. (6 баллов) Трое рыбаков поймали 75 карасей. Стали варить уху. Когда один дал 8 карасей , а другой 12, а третий-7, то карасей у них стало поровну. Сколько карасей поймал каждый рыбак?
Решение. 75-8-12-7=48(осталось всего окуней)
48 окуней на 3 рыбака.48:3=16
У каждого рыбака осталось по 16 окуней
16+ 8 = 24 — поймал 1 рыбак
16 + 12 = 28 — поймал 2 рыбак
16 + 7 = 23 — поймал 3 рыбак
Ответ: 24, 28, 23.
6. (6 баллов) Имеется 8 палочек длиной в 1см, 8 палочек длиной в 2см и 7 палочек длиной в 5 см. Можно ли из всех палочек этого набора сложить прямоугольник? Разламывать палочки нельзя.
Решение.
Если a и b – длины сторон прямоугольника, периметр P = 2(a+b), т. е. P – четное число в случае целых a и b.
8*1+8*2+7*5=8+16+35=59 (см) – нечетное число.
Поэтому из всех палочек данного набора прямоугольник сложить нельзя.
Ответ: нельзя
nsportal.ru
Олимпиады по математике для школьного этапа с решениями 5-11 класс
Задачи школьной олимпиады по математике
5 класс
Имеются двое песочных часов: на 3 минуты и на 7 минут. Яйцо варится 11 минут. Как отмерить это время при помощи имеющихся часов? (2 балла)
Митя, Коля, Сеня, Юра и Костя пришли в музей и встали в очередь. Если бы Митя встал посередине очереди, то он оказался бы между Сеней и Костей, а если бы Митя встал в конце очереди, то рядом с ним мог быть Юра, но Митя встал впереди всех своих товарищей. Кто за кем стоит? (2 балла)
Дочери в настоящее время 8 лет, а матери 38 лет. Через сколько лет мать будет втрое старше дочери? (3 балла)
Как с помощью двух бидонов 5л и 8л отлить из молочной цистерны 7л молока? Молоко разрешается выливать обратно в цистерну. (5 баллов)
Катя и Юра купили лотерейные билеты с номерами: 625517 и 322324, и обнаружили, что в каждом из номеров можно расставить знаки арифметических действий и скобки так, что в каждом случае результат будет равняться 100. Как это можно сделать? (3 балла)
Ответы:
Перевернуть обои часы. Когда пройдет 3 минуты, в семиминутных часах останется 4 минуты. Поставить яйцо в данный момент вариться. Когда 4 минуты закончатся, перевернуть семиминутные часы обратно. Получим 4+7=11.
1 решение: Митя, Толя, Сеня, Костя, Юра
2 решение: Митя, Толя, костя, Сеня, Юра.
Через 7 лет.
1) Налить молоко в пятилитровый бидон и перелить в восьмилитровый.
2) Снова налить молоко в пятилитровый бидон и долить восьмилитровый бидон. Тогда в пятилитровом бидоне останется 2л молока.
3) Вылить молоко в цистерну из восьмилитрового бидона.
4) Перелить 2л молока из пятилитрового бидона в восьмилитровый бидон.
5) Налить молоко в пятилитровый бидон и перелить его в восьмилитровый.
В результате в восьмилитровом бидоне получим 2+5=7 (л) молока.
62+55-17 и (3+22) · (3-2)· 4
6 класс
Разместите восемь козлят и девять гусей в пяти хлевах так, чтобы в каждом хлеве были и козлята и гуси, а число их ног равнялось 10. (5 баллов)
Расшифруйте запись. Одинаковыми буквами обозначены одинаковые цифры, разными буквами– разные цифры. (2 балла)
УДАР
+УДАР
ДРАМА
Разместите на трех грузовиках 7 полных бочек, 7 бочек, наполненных на половину, и 7 пустых бочек так, чтобы на грузовиках был одинаковый по массе груз. (2 балла)
В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что вода и молоко не в бутылке, сосуд с лимонадом стоит между кувшином и сосудом с квасом, в банке не лимонад и не вода. Стакан стоит около банки и сосуда с молоком. В какой сосуд налита каждая из жидкостей? (3 балла)
В записи 52*2* замените звездочки цифрами так, чтобы полученное число делилось на 36. укажите все возможные варианты. (3 балла)
Ответы:
В двух хлевах по 1 козленку и 3 гусям, в трех хлевах – по 2 козленка и 1 гусю.
8126
+8126
16252
На первый грузовик поместить 3 полных бочки, 1 наполненную наполовину и 3 пустых бочки; на второй грузовик– 3 полных, 1 наполненную наполовину и 3 пустых; на третий – 1 полную, 5 наполненных наполовину и 1 пустую.
Молоко в кувшине, лимонад в бутылке, квас в банке, вода в стакане.
52524, 52128, 52020, 52920.
7 класс
4 черные коровы и 3 рыжих дают за 5 дней столько молока, сколько 3 черные коровы и 3 рыжих за 4 дня. У каких коров удои больше: у черных или у рыжих? (3 балла)
Натуральное число умножили на каждую из его цифр. Получилось 1995. Найдите исходное число. (2 балла)
Число 56 разложите на два слагаемых так, чтобы
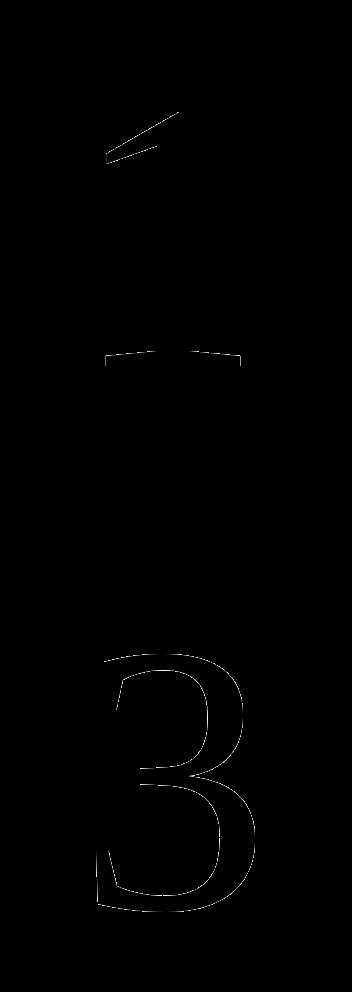 первого слагаемого была равна
первого слагаемого была равна
 второго. (2 балла)
второго. (2 балла)
Из корзины яиц взяли половину всего количества яиц, потом еще половину остатка, затем половину нового остатка и, наконец, половину следующего остатка. В итоге в корзине осталось 10 яиц. Сколько яиц было в корзине первоначально? (3 балла)
Какой угол образуют стрелки часов в 12 часов 20 минут? (5 баллов)
Ответы:
Из условия следует, что 20 черных коров и 15 рыжих дают за 1 день столько же молока, что и 12 черных и 20 рыжих коров. Тогда 8 черных коров дают столько же молока, сколько 5 рыжих. Поэтому у рыжих коров удои больше.
Разложим 1995 на множители: 1995=3·5·7·19. Так как искомое число не может быть ни однозначным, ни трехзначным, то оно является двузначным. Рассматривая возможные варианты для двузначного числа, получаем ответ: 57·5·7=1995.
24+32=56
160 яиц.
В 12.00 стрелки сходятся вместе. После этого за 20 минут минутная стрелка проходит

120º -10º=110º
1. Решите неравенство:
х 2 – 5х + 6 < 0 .
х 2 -7х + 12
2. Путь из села в город таков: сначала 15 км в гору, потом 6 км с горы. Велосипедист едет без остановок в гору с одной постоянной скоростью, с горы – с другой. В один конец он ехал 3,1 ч, обратно 2,5 ч. какова скорость велосипедиста в гору и с горы?
3. Уравнение х + 1__ = 30 имеет решение в целых числах ( 4;3;2 ).
у + 1 7
z
Найдите еще одно решение уравнения в целых числах.
Решите уравнение
| х –1999| + | 1999 – х | = 2000.
В классе послушных девочек столько же, сколько непослушных мальчиков. Кого в классе больше: послушных детей или мальчиков? ( Объясните ваш ответ ).
На птицеферму привезли корм, которого хватило бы уткам на 30 дней, а гусям – на 45 дней. Рассчитайте, на сколько дней хватит привезенного корма и уткам, и гусям вместе?
8 класс
Поставьте знаки модуля так, чтобы равенство стало верным:
1-2-4-8-16=19. (2 балла)
Постройте график функции:
y= (3 балла)
(3 балла)
В школе 30 классов и 1000 учащихся. Докажите, что есть класс, в котором не менее 34 учеников. (3 балла)
Найдите значения a и b, при которых равенство
Выполняется при всех допустимых значениях переменной x
. (4 балла)Найдите все пары натуральных чисел, удовлетворяющих уравнению x²-y²=69. (3 балла)
9 класс
1. Найдите значение выражения:
(1+ )(1+
)(1+ )(1+
)(1+ )(1+
)(1+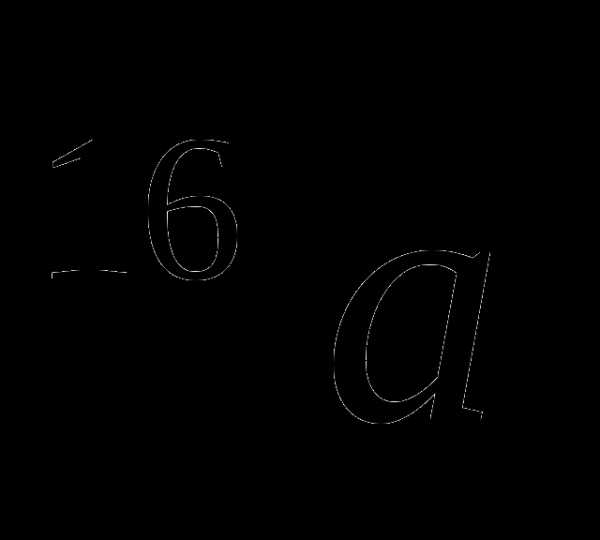 )(1+
)(1+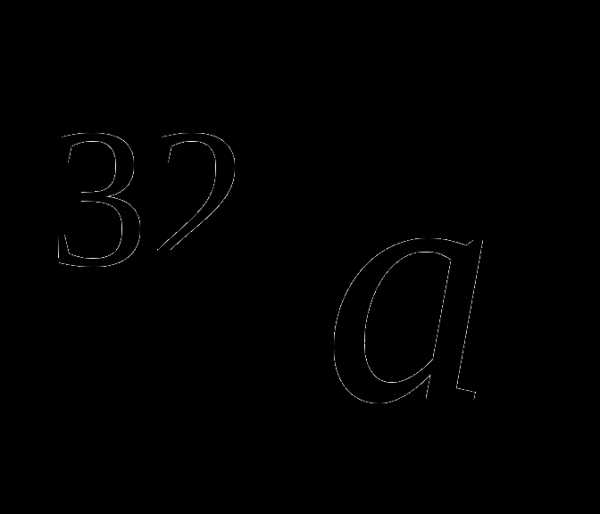 )(1-
)(1-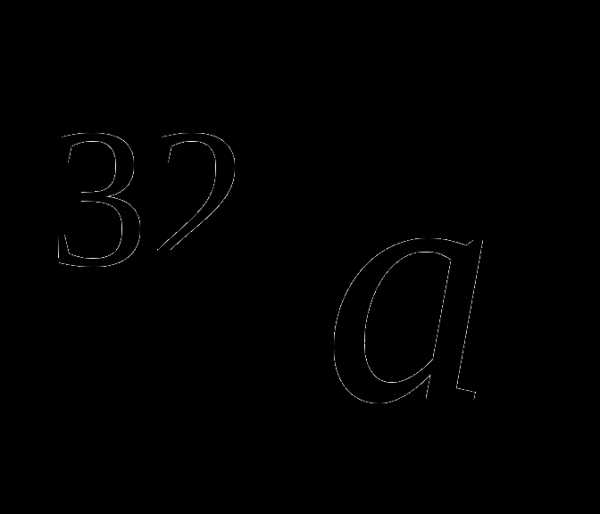 ) при а=2003 (3 балла)
) при а=2003 (3 балла)
При каких значениях a квадратные трехчлены x²+ax+1 и x²+x+a имеют общий корень?
(4 балла)
Сколько цифр содержит число
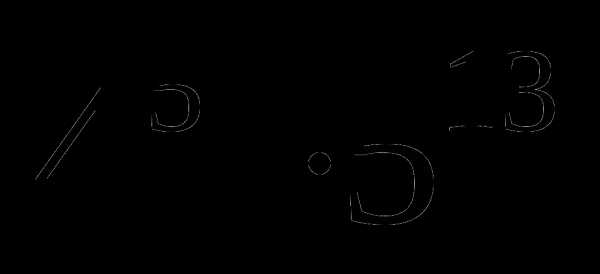
Четыре семьи, дружившие между собой, держат по 10 различных животных. Их питомцы – белки, кролики, хомяки и ежи. Каждая семья держит разное число животных разных видов – от одного до четырех, и в разных семьях разное количество зверушек одного вида. Определите, сколько и каких животных в каждой семье, если известно, что:
у Ивановых, Сидоровых и Петровых ежей не по два;
у Ивановых и Петровых кроликов, а у Кузнецовых кроликов и хомяков не по одному;
в семьях Сидоровых, Петровых и Кузнецовых живут не по три белки;
В семьях Ивановых и Петровых хомяков не по два и не по четыре. (4 балла)
Разрежьте квадрат на 5 прямоугольников так, чтобы у соседних прямоугольников стороны не совпадали. (2 балла)
10 класс
Решите систему уравнений:
(x+y)(x+y+z)=72,
(y+z)(x+y+z)=120,
(x+z)(x+y+z)=96. (3 балла)
При каком целом k неравенство
х²+2(4k-1)х+15k²-2k-7>0 верно при любом действительном х? (4 балла)
Решите в целых числах уравнение x²-3xy+2y²=7. (3 балла)
Малыш и Карлсон разделили круглый торт двумя перпендикулярными разрезами на 4 части. Карлсон взял себе одну наименьшую часть и одну наибольшую часть, а остальные две отдал Малышу. Кому торта досталось не меньше половины?
(3 балла)
Отгадайте ребус:
— ******* **
*** **8**
-**
**
— ***
***
0
(2 балла)
11 класс
1. Представьте числа от 1 до 10 с помощью числа π, используя скобки, знаки действий, извлечение квадратного корня, а также символ функции [x], где [x] – целая часть
числа x. Например, 11=[ +
+ ]. (3 балла)
]. (3 балла)
Постройте график функции: у =+ (2балла)
Решите уравнение |x-1|-|x-2|=1. (4 балла)
Найти четырехзначное число, которое в 4 раза меньше числа, записанного теми же цифрами, но в обратном порядке. (3 балла)
Десять машин выпускают одинаковые резиновые мячи массой по 10 г каждый. Одна из машин испортилась и стала выпускать мячи массой по 5 г. Как найти испортившуюся машину с помощью одного взвешивания мячей? (3 балла)
Ответы и решения
8 класс
1. ||1-2|-|4-8|-16|=19.
2. Упрощая правую часть, имеем: y=x, где x≠±1. Таким образом, графиком указанной функции является прямая, заданная формулой y=x, без 2 точек: А(1;1) и В(-1; -1).
3. Пусть такого класса в школе нет, т.е. во всех классах будет 33 и менее учащихся. Тогда во всей школе будет не более 33·30=990 учащихся, что противоречит условию задачи (в школе 1000 учащихся). Значит, наше предположение неверно, поэтому в школе есть класс, в котором не менее 34 учеников.
4. Приводя в правой части равенства дроби к общему знаменателю и учитывая, что знаменатели у дробей в левой и правой частях равны, получим:
5х+31=ах+2а+вх-5х;
5х+31=(а+в)х+(2а-5в).
Откуда имеем: а+в=5,
2а-5в=31.
Решая полученную систему, получаем: а=8, в=-3.
Ответ: при а=8, в=-3.
5. х²-у²=69
(х-у)(х+у)=69
69=1·69=69·1=3·23=23·3, учитывая, что х>у, имеем:
х-у=1, х-у=3,
х+у=69, или х+у=23.
Решая данные системы, находим два решения: (35,34) или (13,10).
Ответ: (35,34) или (13,10).
Ответы и решения
9 класс
1. Применяя формулу (х-у)(х+у)=х²-у² последовательно для последних двух множителей, в результате получим:
(1- )(1+
)(1+ )=1-a.
)=1-a.
При а=2003 получим 1-а=1-2003=-2002.
Ответ:-2002.
Пусть
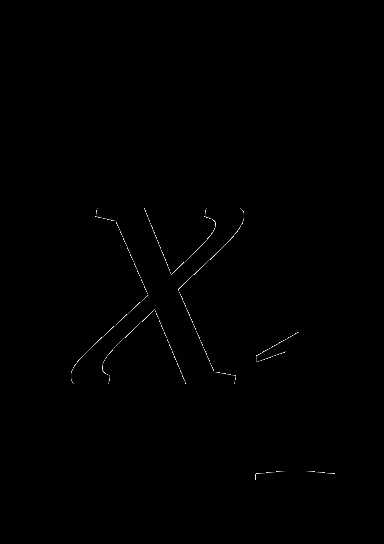 – общий корень данных трехчленов, тогда
– общий корень данных трехчленов, тогда
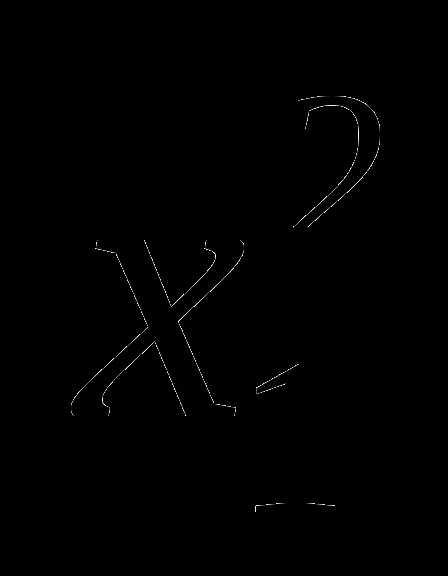 +a
+a +1=0 и
+1=0 и 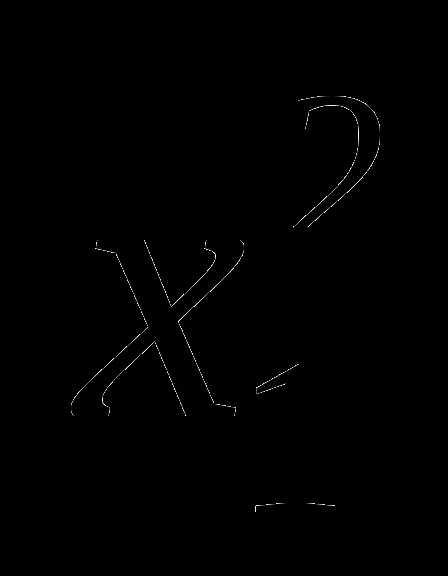 +
+ +а=0, т.е.
+а=0, т.е.
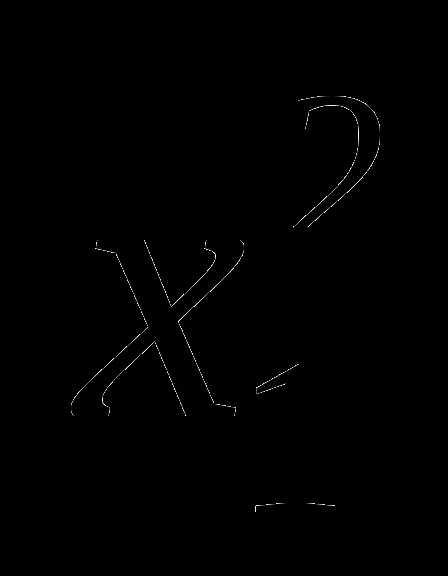 +a
+a +1=
+1=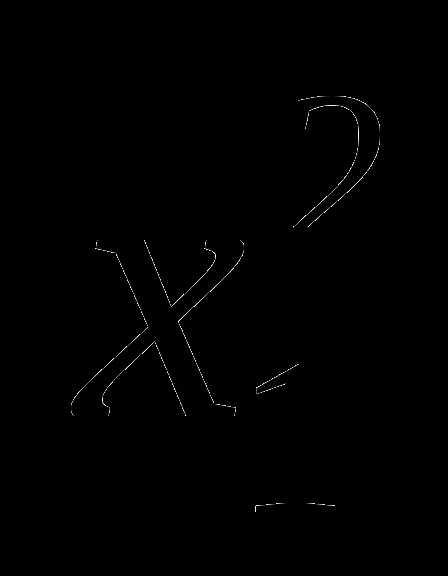 +
+ +а
+а  a
a +1=
+1= +а
+а а(
а( -1)=
-1)=  -1
-1 (
( -1)(а-1)=0.
-1)(а-1)=0.
Тогда а=1 или  =1.
=1.
Если а=1, то трехчлены оба имеют вид х²+х+1 и не имеют действительных корней.
Если  =1, то 1²+а·1+1=0 и 1²+1+а=0. В обоих случаях а=-2.
=1, то 1²+а·1+1=0 и 1²+1+а=0. В обоих случаях а=-2.
Ответ: а=-2.
3.  =(
=(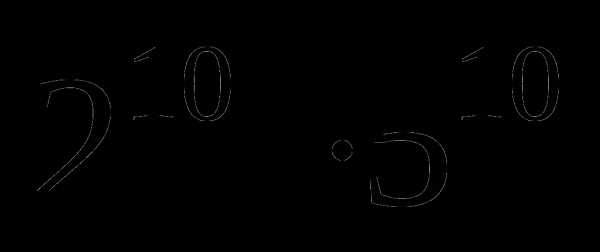 )
)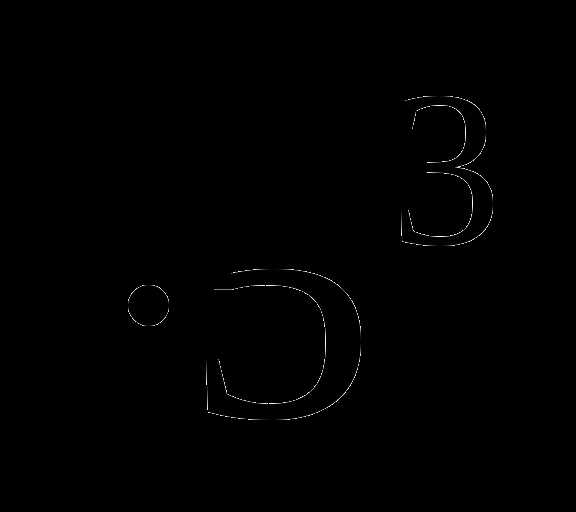 =
=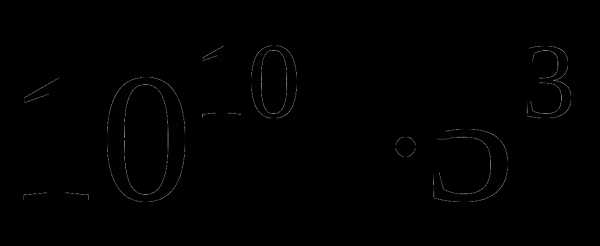 =1 250 000 000 000.
=1 250 000 000 000.
Ответ: 13 цифр.
4.
-
животные
итого
белки
кролики
хомяки
ежи
Ивановы
3
2
1
4
10
Сидоровы
4
1
2
3
10
Петровы
2
4
3
1
10
Кузнецовы
1
3
4
2
10
5.
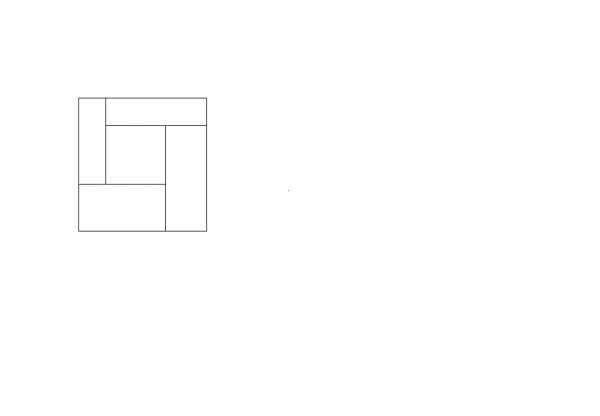
Ответы и решения
10 класс
1. Сложив все три уравнения системы, получим уравнение (х+у+z)(2x+2y+2z)=288, из которого найдем х+у+z=12 или х+у+z=-12. Подставляя вместо х+у+z числа 12 и -12, получим в первом случае: x=2,y=4,z=6, а во втором: x=-2,y=-4,z=-6.
Ответ: (2;4;6),(-2;-4;-6).
Неравенство будет верно, если D<0. Найдя дискриминант и учитывая, что он должен быть отрицательным, получим неравенство k²-6k+8<0, которое будет иметь решения при 2<k<4, то есть при k=3.
Ответ: при k=3.
Разложим -3ху на два слагаемых –ху и -2ху. Тогда получим: х²-ху-2ху+2у²=7. Сгруппируем и вынесем за скобки (х-у) и получим: (х-у)(х-2у)=7. Учитывая, что 7=1·7=7·1=-1·(-7)=-7·(-1), получим следующие четыре системы уравнений:
х-у=1, х-у=7, х-у=-1, х-у=-7,
х-2у=7, х-2у=1, х-2у=-7, х-2у=-1.
Решая данные системы, найдем решения уравнения: (-5;-6), (5;6), (13;6), (-13;-6).
Ответ: (-5;-6), (5;6), (13;6), (-13;-6).
Проведем два разреза, центрально симметричные уже сделанным. Куски 1, 2, 6, 9 достались Малышу, а симметричные им 7, 8, 4 и 3 – Карлсону, которому отошла еще и середина 5. поэтому Карлсону досталось не менее половины торта.
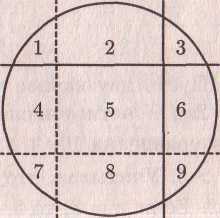
— 1089708 12
108 90809
— 97
96
— 108
108
0
Ответы и решения
11 класс
1. 1=[ ]; 2=[
]; 2=[ +
+ ]; 3=[π]; 4=[ π+
]; 3=[π]; 4=[ π+ ]; 5=[ π
]; 5=[ π ]; 6=[ π+ π]; 7=[ π+
]; 6=[ π+ π]; 7=[ π+ ]+ [π];
]+ [π];
8=[( π· π)-  ]; 9=[( π· π)]; 10=[
]; 9=[( π· π)]; 10=[ ]+[( π· π)].
]+[( π· π)].
2. y=+
y=+
y= +
y= 2sin²x+1+2cos²x+1
y=4
Ответ: графиком функции является прямая, заданная уравнением у=4.
Ответ: х
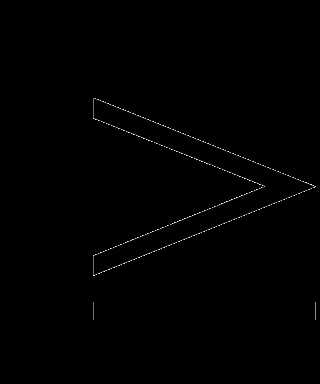 2
2
4. Обозначим искомое число за 1000a+100b+10c+d. По условию задачи имеем:
4(1000a+100b+10c+d)=1000d+100c+10b+a.
Так как левая часть – число четное, то и правая часть – число четное, поэтому a– четная цифра. Тогда a=2, так как в других случаях получим в левой части пятизначное число. Так как 4d оканчивается на 2, то d=8. В итоге имеем:
4(1000·2+100b+10c+8)=1000·8+100c+10b+2.
Тогда 4(10b+c)+3=10c+b или 40b+4c+3=10c+b.
После упрощения получим: 13b+1=2c.
Решением данного уравнения будут: b=1,c=7. Тогда искомое число будет 2178.
Ответ: 2178
5. Возьмем от первой машины один мяч, от второй – два, от третьей – три и т.д., от десятой – десять. Найдем их общую массу. Это взвешивание будет единственным.
Если бы все мячи были массой по 10г, то весы показали бы
10(1+2+3+4+5+6+7+8+9+10)=550 (г).
Если первая машина допускает брак, то общая масса станет меньше на 5г, если вторая, то на 10г, и т.д., если десятая, то на 50г. Таким образом, по массе 55 мячей можно узнать, какая машина испортилась.
ОЛИМПИАДА
6 класс
Выразите число 16 с помощью четырех пятерок, соединяя их знаками действий.
(2 балла)
В летний лагерь приехали отдыхать три друга– Миша, Володя и Петя. Известно, что каждый из них имеет одну из следующих фамилий: Иванов, Семенов, Герасимов. Миша – не Герасимов. Отец Володи – инженер. Володя учится в 6 классе. Герасимов учится в 5 классе. Отец Иванова – учитель. Какая фамилия у каждого из трех друзей? (3 балла)
Школьник прочитал книгу за три дня. В первый день он прочитал 0,2 всей книги и еще 16 страниц, во второй день – 0,3 остатка и еще 20 страниц. В третий день – 0,75 остатка и последние 30 страниц книги. Сколько страниц в книге? (5 баллов)
Расшифруйте запись. Одинаковыми буквами обозначены одинаковые цифры, разными буквами – разные цифры. (2 балла)
КОКА
+ КОКА
ВОДА
Разрежьте клетчатый прямоугольник размером 5х8 клеток на фигурки из четырех клеток вида: (3 балла)
-
ОЛИМПИАДА 10 КЛАСС
Найдите значение выражения:
(1+
 )(1+
)(1+ )(1+
)(1+ )(1+
)(1+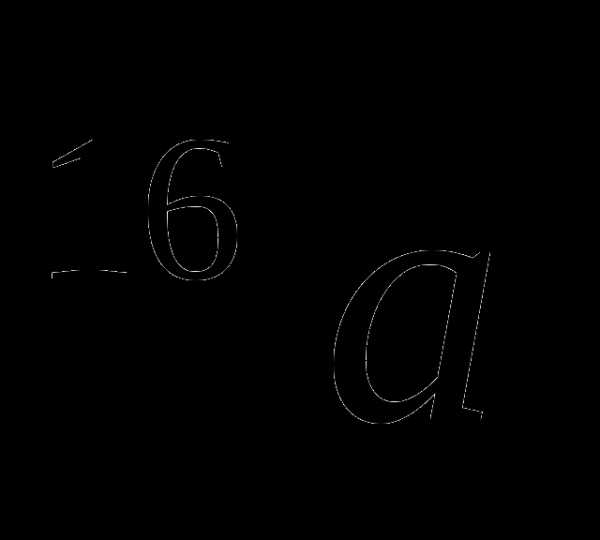 )(1+
)(1+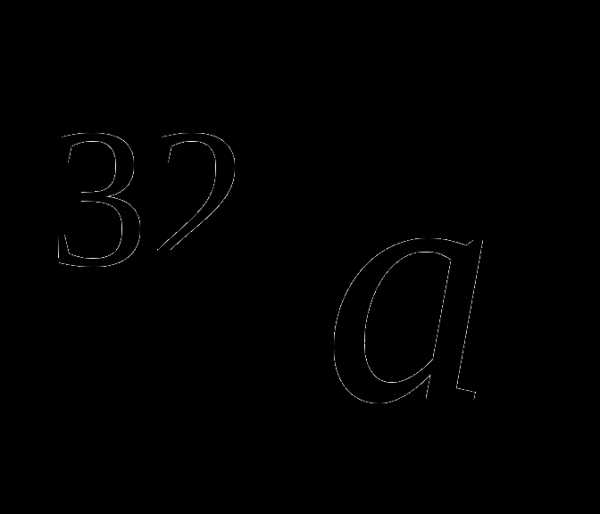 )(1-
)(1-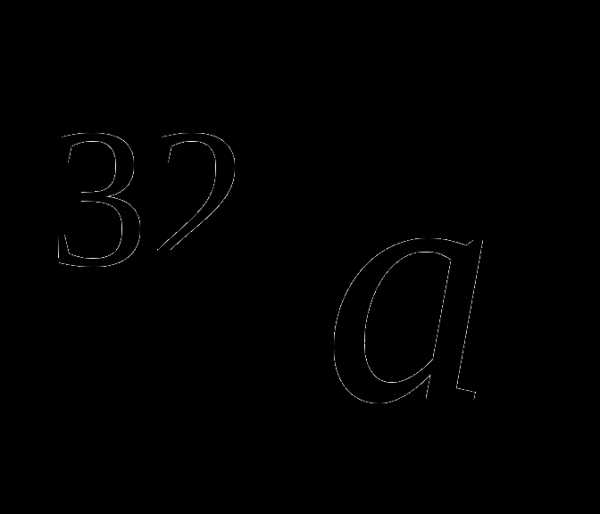 ) при а=2003 (3 балла)
) при а=2003 (3 балла)Листок календаря частично закрыт предыдущим листком. Какая его часть больше -закрытая или открытая? (3 балла)
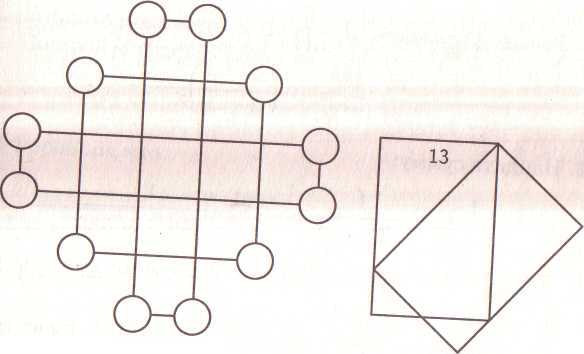
Автомобиль проехал 600 км. Первую половину пути он двигался со скоростью 100 км/ч, а вторую – 60 км/ч. Найдите среднюю скорость движения автомобиля. (2 балла)
Сколько цифр содержит число 4
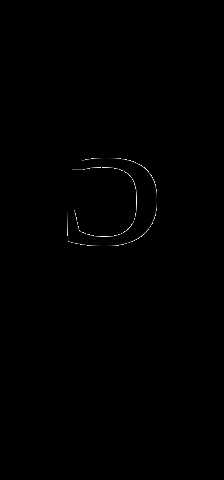 *5
*5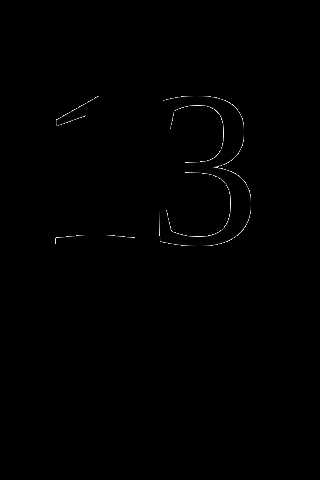 ? (3 балла)
? (3 балла)При каком целом k неравенство
х²+2(4k-1)х+15k²-2k-7>0 верно при любом действительном х? (4 балла)

infourok.ru
Анализ олимпиады по математике школьный этап
Анализ проведения школьного этапа
Всероссийской предметной олимпиады школьников
2018-2019 учебный год
9 октября 2018 года в МБОУ СОШ № 5 состоялся I этап (школьный) Всероссийской олимпиады школьников.
Основными целями и задачами школьного этапа олимпиады являются выявление и развитие у обучающихся творческих способностей и интереса к научно-исследовательской деятельности; создание необходимых условий для поддержки одаренных детей; пропаганда научных знаний; повышение эффективности участия обучающихся в последующих этапах Всероссийской олимпиады школьников.
Основными принципами, лежащими в основе порядка проведения школьной олимпиады, стали:
– равенство предоставляемых возможностей для учащихся;
— добровольная основа участия обучающихся;
– прозрачность и объективность процедуры проведения и подведения итогов школьной олимпиады;
– информационная безопасность.
Кол-во победителейКол-во призеров
5 класс
6 класс
7 класс
8 класс
Математика
21
8
3
1
3
5
5 класс: всего участников 21 человек, учитель Бондарчук Н.В.
Типичные ошибки: вычислительные; непонимание логических задач.
Наибольшие затруднения вызвали задания, в которых проверялись знания и умения логическое мышление; геометрические знания (построение)
6 класс: всего участников 8 человек, учитель Бондарчук Н.В.
Типичные ошибки: вычислительные; непонимание логических задач.
Наибольшие затруднения вызвали задания, в которых проверялись знания и умения логическое мышление; геометрические знания (построение)
7 класс: всего участников -3 учащихся, учитель Бондарчук Н.В.
Типичные ошибки: вычислительные; непонимание логических задач.
Наибольшие затруднения вызвали задания, в котором проверялись знания и умения согласно условия построить фигуру, применить формулу квадрата разности и квадрата суммы.
8 класс: всего участников 1 человек, учитель Бондарчук Н.В.
Типичные ошибки: вычислительные; непонимание логических задач
Наибольшие затруднения вызвали задания: 5 (№ задания) геометрические знания (построение)
Тексты заданий интересные, носят творческий характер, имеют различную сложность.
Все задания олимпиады рассчитаны на высокий, углубленный уровень математической подготовки участников олимпиады. Результаты работ показали, что в рамках изучения математики на базовом уровне и даже на профильном уровне, многие задачи для учащихся оказались слишком трудными. Часть заданий были бы посильны, если заниматься на факультативных занятиях
Олимпиадные задания школьного этапа были составлены на основе программ по математике для общеобразовательных учебных учреждений.
Учащиеся 7-8 классов испытывали трудности при решении геометрических задач. Хорошие результаты прослеживались у учащихся 5-6 классов.
Вывод:
1. Необходимо усилить работу с учениками, обладающими повышенной обучаемостью к математике, имеющими нестандартное мышление, не только во внеурочное время, но и на уроках.
2. Больше внимания обращать на развитие отдельных качеств мышления, приемов умственной деятельности, особенно решению задач на логику и анализ, нестандартных геометрических задач.
3. Учесть интересы детей, желающих принять участие в олимпиадах по математике.
4.Учесть уровень сложности олимпиадных заданий 2018-2019 уч. года и отработать наиболее типичные ошибки обучающихся через урочные и внеурочные занятия с целью создания ситуации успеха при проведении последующих олимпиад
Предложения:
1. Необходимо усилить работу с учениками, которые выдвигаются на олимпиады. Уделить внимание к решению задач с логическими заданиями.
2. Систематически проводить дифференцированную работу на уроках и внеурочных занятиях с одаренными детьми.
3. Уделять больше внимания работе с одаренными детьми, предлагать задания повышенной сложности, развивающими творческие способности учащихся.
4. Продумать способы повышения мотивации и результативности участия в олимпиаде.
5. Уделить внимание индивидуальной подготовке каждого участника.
6. По мере возможностей надо активизировать использование в урочной деятельности заданий занимательной формы и заданий, направленных на развитие логического мышления учащихся.
infourok.ru
Олимпиада по математике 4 класс школьный этап с решениями
Ф. И., класс _____________________________________________
1.Сидя у окна вагона поезда мальчик стал считать телеграфные столбы. Он насчитал 10 столбов. Какое расстояние прошёл за это время поезд, если расстояние между столбами 50 м? ( 1 балл)__________________________.
2. Одни часы отстают на 25 минут, показывая 1 ч 50 мин. Какое время показывают другие часы, если они забегают на 15 мин? (2 балла)_________________________.
3.Чему равны стороны прямоугольника, площадь которого равна 12 см, а периметр равен 26 см? (1 балл)__________________________________.
4. Сколько получится, если сложить наибольшее нечетное двузначное число и наименьшее четное трехзначное число? (1 балл)_______________________.
5. В каждой цепочке чисел найди закономерность и вставь пропущенные числа
(1 цепочка – 1 балл):
1) 3, 6, __, 12, 15, 18.
2) 1, 8, 11, 18, ___, 28, 31.
3) 2, 2, 4, 4, ___, 6, 8, 8.
4) 24, 21, ___, 15, 12.
5) 65, 60, 55, ____, 45, 40, 35.
6. Напишите наименьшее четырехзначное число, в котором все цифры различные. (1 балл)____________________________.
7. Три подружки — Вера, Оля и Таня пошли в лес по ягоды. Для сбора ягод у них были корзина, лукошко и ведерко. Известно, что Оля была не с корзиной и не с лукошком, Вера — не с лукошком. Что с собой взяла каждая девочка для сбора ягод? (3 балла) Вера — ______________, Таня — ______________, Оля — _______________.
8. Мотоциклист за три дня проехал 980 км. За первые два дня он проехал 725 км, при этом он во второй день проехал на 123 км больше, чем в третий день. Сколько километров он проехал в каждый из этих трех дней? (4 балла)
I день _______, II день _______, III день ________.
9. Напишите цифрами число, состоящее из 22 миллионов 22 тысяч 22 сотен и 22 единиц. (2 балла)________________________________.
10. В туристический лагерь прибыло 240 учеников из г. Москвы и Орла. Мальчиков среди прибывших было 125 человек, из которых 65 — москвичи. В числе учеников, прибывших из Орла, девочек было 53. Сколько всего учеников прибыло из Москвы? (4 балла)_____________.
Ответы:
4 класс:
1. 50 х 9=450 (м) (1 балл)
2. 1 час 50 мин+25 мин= 2 часа15 мин (2 балла)
2 часа 15 мин+15 мин=2 часа 30мин
3. Стороны прямоугольника 12 см и 1 см. (1 балл)
4.199 (1 балл)
5. 1) 9; 2)21; 3)6; 4)18; 5) 50; (1 цепочка — 1 балл)
6. 1023 (1 балл)
7. Вера была с корзинкой, Оля — с ведерком, Таня -с лукошком. ( 3 балла)
8. ( 4 балла)
1) 980 — 725 = 255 (км) — проехал в третий день;
2) 255 + 123 = 378 (км) — проехал во второй день;
3) 725 — 378 = 347 (км) — проехал в первый день.
Ответ: в первый день мотоциклист проехал 347 км, во второй — 378, в третий — 255 км.
9. 22 024 222 ( 2 балла)
10. ( 4 балла)
1) 240-125=115 девочек из Москвы и Орла
2) 115-53=62 девочек из Москвы
3) 65+62=127 детей из Москвы
konspekt-v-gruppe.ru
Олимпиадные задания по алгебре на тему: Школьный этап всероссийской олимпиады школьников по математике. (среднее звено)
Муниципальное бюджетное общеобразовательное учреждение Авдеевская средняя общеобразовательная школа
«Согласовано» «Согласовано» «Утверждаю» на заседании ШМО «___» _______2011 г «___» _______2011 г. учителей естественно — Зам директора по УМР Директор школы научного цикла ____________ ______________ «___» _________2011 г. /Кудашкина М.Н./ /Гулькина Р.Д./ Протокол №2 от 11.10.2011г ШМО Руководитель ШМО _____________ /Курносова Т.А./
Школьный этап всероссийской олимпиады школьников по математике. (среднее звено)
Разработала Курносова Татьяна Анатольевна учитель математики МБОУ Авдеевской СОШ
2011 год
В соответствие с методическими рекомендациями по разработке заданий для школьного этапа всероссийской олимпиады школьников по математике мною был подобран материал для проведения школьного этапа всероссийской олимпиады школьников по математике, разработаны критерии оценивания и отбора победителей и призёров.
Варианты содержат по 5 задач разной сложности. Темы для отбора заданий были предложены в рекомендации управления образования.
Ниже привожу эти темы. Хочу сказать, что предложенные рекомендации очень помогли мне в отборе нужных задач из огромного диапазона математических заданий.
Победитель должен набрать не менее 50% баллов, призёр
5 класс
- Числовые ребусы
- Задачи на разрезание, переливание, взвешивание
- Логические или текстовые задачи
№ | Задание | Кол-во баллов |
1 | 9999999=100 Расставьте скобки и математические знаки. | 2 |
2 | Используя два ведра вместимостью 5 л и 4 л, наберите из водопроводного крана 3 л воды. | 2 |
3 | Три завода выпускают гвозди одного типа и поставляют их в один и тот же магазин. В очередной раз в магазин пришла партия из 50 ящиков гвоздей, но сколько ящиков привез каждый завод неизвестно. Покупателю нужно купить 17 ящиков гвоздей обязательно одного завода. Сможет ли он это сделать? | 3 |
4 | Количество цифр, потребовавшихся для нумерации всех страниц энциклопедического словаря, не превосходит 2000 (первая страница имеет номер 1). Если бы в словаре было на одну страницу больше, то это количество превысило бы 2000. Сколько страниц в словаре? | 4 |
5 | 12 человек участвовало в конкурсе певцов, 3 человека в конкурсе певцов и в конкурсе чтецов. Хотя бы в одном из этих конкурсов участвовало 26 человек. Сколько человек участвовало в конкурсе чтецов? | 4 |
Ответы:1. (99 — 9) : 9 + ( 99 — 9) = 10
2. 1шаг. Налить 4 литра, перелить в 5 л.ведро. шаг. Налить 4 л, перелить 1 литр в 5 л. Ведро. В 4-х литровом ведре останется 3 литра.
3. Можно. 50:3= 16 ост.2, значит как минимум 1 завод поставят в магазин не менее 17 ящиков гвоздей.
4. 603 страницы
5. 15 человек.
6 класс
- Числовые ребусы
- Задачи на составление уравнений
- Свойства геометрических фигур
- Логические или текстовые задачи
- Чётность
№ | Задание | Кол-во баллов |
1 | В следующем ребусе каждая буква обозначает определённую цифру (разные буквы – разные цифры). Исследуйте, какие цифры могли быть написаны изначально. один + один = много | 1 |
2 | В сталелитейном цехе в 3 раза больше рабочих, чем в модельном цехе. Когда со сталелитейного цеха уволилось 5 человек, а в модельный цех приняли 35 человек, то в цехах стало поровну рабочих. Сколько рабочих было в каждом цехе? | 2 |
3 | Четыре грани кубика окрашены не засыхающей краской так, как показано на рисунке. Какой след оставит кубик на листе бумаге, если его переворачивать без скольжения вправо из положения слева три раза на 90°? | 4 |
4 | — Ты поверишь, Наташа, — сказал Саша сестре, — я сейчас с одного куста сорвал 64 ореха! | 4 |
5 | Вдоль улицы стоят 100 домов. Мастера попросили изготовить номера для всех домов от 1 до 100. Чтобы выполнить заказ, он должен запастись цифрами. Не пользуясь карандашом и бумагой, подсчитайте в уме, сколько девяток потребуется мастеру? | 3 |
Ответы: 1. 6823+6823=13646 2. 60 и 20 3.
4. Сестра просила 4 ореха, брат дал 16 орехов. 5. 19
7 класс
- Числовые ребусы
- Задачи на составление уравнений
- Делимость натуральных чисел
- Задачи на переливание, взвешивание.
- Логические задачи
№ | Задание | Кол-во баллов |
1 | Квадрат числа состоит из цифр 0,2,3,5. Найти его. | 2 |
2 | Автомобиль из A в B ехал со средней скоростью 50 км/ч., а обратно возвращался со скоростью 30 км/ч. Какова его средняя скорость? | 4 |
3 | Водяной построил кикимор в колонну по 4, но при этом кикимора Дуся осталась лишней. Тогда водяной построил кикимор в колонну по 5. И снова Дуся осталась лишней. Когда же и в колонне по 6 кикимора Дуся в осталась лишней, водяной посулил ей болото вне очереди, после чего в колонне по 7 Дуся нашла себе место и никого лишнего не осталось. Какое наименьшее количество кикимор могло быть у водяного? | 3 |
4 | Имеются два типа песочных часов. Одни отмеряют 7 минут, другие 11 минут. Как с помощью этих часов отмерить 15 минут, чтобы сварить вкрутую яйцо? | 4 |
5 | Пять участников олимпиады стали ее победителями, набрав по 15, 14 и 13 баллов и заняв соответственно первое, второе и третье места. Сколько участников завоевали каждое призовое место, если вместе они набрали 69 баллов? | 3 |
Ответы: 1. 55 2. 37,5 км/ч
3. 301
4. Поставить одновременно двое часов, когда пройдёт 7 минут, а на вторых песка останется на 4 минуты, поставить варить яйца, затем часы вновь перевернуть на 11 минут.
5. 1 место – 1 ученик, 2 место -2 ученика, 3 место – 2 ученика
8 класс
- Преобразование алгебраических выражений.
- Построение графиков функций
- Основные элементы треугольника
- Делимость натуральных чисел
- Логические задачи.
№ | Задание | Кол-во баллов |
1 | Дана дробь 37/63. Какое число нужно вычесть из её числителя и прибавить к знаменателю, чтобы после сокращения получилась дробь 3/17. | 2 |
2 | График функции y=|kx + p| проходит через точку А (4; 2) и часть его параллельна прямой 3у — 6x = 4. Каковы могут быть значения коэффициентов k и р? Постройте график этой функции. | 3 |
3 | Как разрезать произвольный треугольник на три такие части, из которых можно сложить прямоугольник? | 2 |
4 | Петя подарил каждому из своих друзей одинаковое количество почтовых марок. Сколько друзей у Пети, если всего подарена 361 марка и у Пети меньше 200 друзей? | 2 |
5 | Из букв имени, отчества и фамилии «Федорова Надежда Евгеньевна» нужно составить новое имя, отчество и фамилию. (Нужно использовать все буквы столько раз, сколько они встречаются, и не использовать никаких других.) | 3 |
Ответ: 1. 22
2. k=2 и b=-6, k =-2 и b=6.
3.
4. 19.
5.Например: Федора Надеждьевна Евгенова
9 класс
- Делимость
- Квадратный трёхчлен и его свойства
- Преобразование алгебраических выражений
- Основные элементы треугольника
- Логические (комбинаторные задачи)
№ | Задание | Кол-во баллов |
1 | Докажите, что число делится на 21. | 2 |
2 | Решите неравенство: 6х2+|х|-5 | 3 |
3 | Преобразовать вражение : | 3 |
4 | В прямоугольном треугольнике АВС угол С равен 900, sinА=5/13, АС = 48. Найти ВС. | 2 |
5 | Три девочки Белова, Краснова, Чернова одеты в белое, красное, черное платья, причем, ни у одной из них цвет не совпадает с фамилией. Девочка в белом платье и Чернова родились в один день. Кто в какое платье одет? | 3 |
Ответ : 1. Делим на ав, получаем 10101, а это число делится на 3 и на 7.
2.
3.1
4.20
5. Белова – красное, Краснова – чёрное, Чернова – белое.
Победитель должен набрать не менее 50% баллов, призёр должен решить не менее 2 задач.
nsportal.ru
