Работа, мощность, энергия
1
Двое ухватились за веревку и тянут ее в разные стороны. Один из них перетянул. Означает ли это, что он прилагает к веревке большую силу, нежели другой? Сравните работы, совершаемые силами, приложенными к веревке.
Ответ
Силы одинаковы по величине; работы тоже одинаковы по величине, но противоположны по знаку, так как в одном случае направления силы, действующей на веревку и ее перемещения совпадают, а в другом случае — противоположны.
2
Чему равна работа А по подъему цепи, взятой за один конец и лежащей на плоскости, на высоту, равную ее длине? Длина цепи l = 2 м, масса m = 5 кг.
Ответ
3
Оконная шторка массой М = 1 кг и длиной l = 2 м свертывается на тонкий валик наверху окна.
Ответ
4
Гибкий резиновый шланг длиной l висит так, что один из его концов находится на 1/3 l ниже другого. В шланг налито максимально возможное количество воды; ее плотность равна ρ. Какую минимальную работу нужно совершить, чтобы вылить воду из шланга, поднимая его за нижний конец и удерживая верхний конец на неизменной высоте? Внутренний диаметр шланга d. Массой шланга пренебречь. Радиус закругления шланга в изгибе много меньше l.
Ответ
5
Цепь массой М и длиной l лежит у границы двух соприкасающихся полуплоскостей из разных материалов.
Какую работу надо совершить, чтобы передвинуть цепь на вторую полуплоскость? Коэффициенты трения полуплоскостей с цепью соответственно равны
k1 и k2. Решить задачу также графически.
Ответ
A = ½ (k1 + k2) Mgl.
6
Мотор с полезной мощностью 15 кВт, установленный на автомобиле, может сообщить ему при движении по горизонтальному участку дороги скорость 90 км/ч. Тот же мотор, установленный на моторной лодке, обеспечивает ей скорость не выше 15 км/ч. Определить силу сопротивления Fc движению автомобиля и моторной лодки при заданных скоростях.
Ответ
Fс1 = 600 Н; Fс2 = 3600 Н.
Трамвай массой М проходит по улице, поднимающейся вверх под углом α к горизонту с определенной скоростью. На горизонтальном участке пути он может с той же скоростью идти с прицепным вагоном массой М1. Как велика масса М1, если коэффициент трения качения колес равен k? Мощность двигателя постоянна.
Как велика масса М1, если коэффициент трения качения колес равен k? Мощность двигателя постоянна.
Ответ
.
8
Локомотив, работая с постоянной мощностью, может вести поезд массой М = 2000 т вверх по уклону α1 = 0,005 со скоростью v1 = 30 км/ч или по уклону α2 = 0,0025 со скоростью v2 = 40 км/ч. Определить величину силы сопротивления Fc, считая ее постоянной.
Ответ9
Пуля, летящая с определенной скоростью, углубляется в стенку на расстояние l1 = 10 см. На какое расстояние l2 углубляется в ту же стенку пуля, которая будет иметь скорость вдвое большую?
Ответ
10
Пуля, летящая со скоростью v0, пробивает несколько одинаковых досок, расположенных на некотором расстоянии друг от друга. В какой по счету доске застрянет пуля, если ее скорость после прохождения первой доски равна v1 = 0,83 v0?
В какой по счету доске застрянет пуля, если ее скорость после прохождения первой доски равна v1 = 0,83 v0?
Ответ
Пуля застрянет в 4-й доске.
11
Какую работу надо совершить, чтобы заставить поезд массой М = 800 т: а) увеличить свою скорость от
Ответ
а) A1 = 5·104 кДж;
б) A2 = 1,6·105 кДж.
12
Поезд массой М = 2000 т, двигаясь с места с ускорением a = 0,2 м/с2, достигает нужной скорости через минуту, после чего движется равномерно. Определить мощность тепловоза при установившемся движении, если коэффициент сопротивления k = 0,005.
Определить мощность тепловоза при установившемся движении, если коэффициент сопротивления k = 0,005.
Ответ
13
Автомобиль массой М = 2000 кг трогается с места и идет в гору, наклон которой α = 0,02. Пройдя расстояние s = 100 м, он развивает скорость v = 32,4 км/ч. Коэффициент сопротивления к = 0,05. Определить среднюю мощность, развиваемую двигателем автомобиля.
Ответ
14
Ракета массой М с работающим двигателем неподвижно «зависла» над Землей. Скорость вытекающих из ракеты газов u. Определить мощность двигателя.
Ответ
15
В каком случае двигатель автомобиля должен совершить большую работу: для разгона с места до скорости 27 км/ч или на увеличение скорости от 27 до 54 км/ч? Силу сопротивления и время разгона в обоих случаях считать одинаковыми.
Ответ
Во втором случае, причем A2/A
16
Камень массой m = 200 г брошен с горизонтальной поверхности под углом к горизонту и упал на нее обратно на расстоянии s = 5 м через t = 1,2 с. Найти работу бросания. Сопротивлением воздуха пренебречь.
Ответ
17
Определить работу, которую нужно произвести для того, чтобы сжать пружину на х = 10 см, если для сжатия ее на х0 = 1 см необходима сила F0 = 100 Н.
Ответ
18
Вагон массой М = 2*104 кг, двигаясь со скоростью v = 0,5 м/с, ударяется в два неподвижных пружинных буфера. Найти наибольшее сжатие буферов х, если буфер сжимается на 1 см при действии силы 5*104 Н. Трением пренебречь.
Трением пренебречь.
Ответ
19
Действуя постоянной силой F = 200 Н, поднимают груз массой М = 10 кг на высоту h = 10 м. Какую работу А совершает сила F? Какой потенциальной энергией U будет обладать поднятый груз?
Ответ
A = 2·103 Дж, U = 103 Дж.
20
Лифт массой М = 1000 кг равноускоренно поднимался лебедкой. На некотором отрезке пути длиной l = 1 м лифт двигался со средней скоростью vср = 5 м/с и его скорость возросла на Δv = 0,5 м/с. Какую работу совершила сила, перемещающая лифт на указанном отрезке его пути?
Ответ
21
Какую работу совершит сила F = 30 Н, подняв по наклонной плоскости груз массой m = 2 кг на высоту h = 2,5 м с ускорением
 Сила действует параллельно наклонной плоскости. Трением о плоскость пренебречь.
Сила действует параллельно наклонной плоскости. Трением о плоскость пренебречь.
Ответ
22
Некоторая сила толкает тело массой m = 16 кг вверх по наклонной плоскости длиной l = 3,1 м и с наклоном α = 30° к горизонту.
1. Скорость тела у основания наклонной плоскости была v0 = 0,6 м/с, а у ее верхнего края v1 = 3,1 м/с. Чему равна работа, произведенная силой? Трения нет.
2. Чему равна работа той же силы и какова будет кинетическая энергия тела в верхней точке наклонной плоскости, если есть трение и коэффициент трения k = 0,1?
Сила направлена вдоль наклонной плоскости.
Ответ
1. A = 317 Дж;
2. A
= 317 Дж; Eк = 34,4 Дж.23
Грузовой автомобиль массой М = 6*103 кг въезжает на паром, привязанный к берегу двумя канатами, со скоростью v = 18 км/ч. Въехав на паром, автомобиль остановился, пройдя при торможении путь s = 10 м. Определить суммарную силу натяжения канатов.
Въехав на паром, автомобиль остановился, пройдя при торможении путь s = 10 м. Определить суммарную силу натяжения канатов.
Ответ
24
Автомобиль, шедший со скоростью v = 54 км/ч, при резком торможении стал двигаться «юзом» (заторможенные колеса не вращаются, скользят по дороге). Определить ускорение a и путь s, который пройдет автомобиль, если коэффициент трения скольжения колес об асфальт: а) в сырую погоду k1 = 0,3; б) в сухую k2 = 0,7.
Ответ
б) a2 ≈ 6,86 м/с2; s2 ≈ 16,4 м.
25
Автомобиль с полностью включенными тормозами (колеса не вращаются) может удержаться на склоне горы с уклоном до 23°. Каков тормозной путь автомобиля s при торможении на горизонтальной дороге при скорости движения 10 м/с? Коэффициент сцепления колес с грунтом на склоне горы и на дороге одинаков.
Каков тормозной путь автомобиля s при торможении на горизонтальной дороге при скорости движения 10 м/с? Коэффициент сцепления колес с грунтом на склоне горы и на дороге одинаков.
Ответ
26
Сани с грузом массой М = 120 кг скатываются по уклону горы под углом к горизонту α = 14°. Длина спуска l = 60 м. Коэффициент трения скольжения саней k = 0,14. Определить: а) ускорение a1 саней при движении с горы; б) скорость v в конце спуска; в) время спуска t1; г) кинетическую энергию Т1; д) какое расстояние s прокатятся сани после спуска по горизонтали; е) сколько времени t2 продолжается движение по горизонтали; ж) ускорение a2 при движении по горизонтальному участку пути.
Ответ
а) a1 = 1,04 м/с2;
б) v ≈ 11,2 м/с;
в) t1 = 10,7 с;
г) Т1 ≈ 7620 Дж;
д) s = 45,3 м;
е) t2 ≈ 8 с;
ж) a2 = 0,14g.
27
Тело скользит вниз по наклонной плоскости. Угол наклона плоскости к горизонту α = 20°, длина ее l = 4 м, коэффициент трения тела о плоскость k = 0,2. С какой скоростью v будет двигаться тело в момент перехода с наклонной плоскости на горизонтальную поверхность?
Ответ
28
Бассейн площадью S = 100 м2, заполненный водой до уровня h = 1 м, разделен пополам вертикальной перегородкой. Перегородку медленно передвигают в горизонтальном направлении так, что она делит бассейн в отношении 1:3. Какую для этого надо совершить работу, если вода не проникает через перегородку?
Ответ
29
Два автомобиля одновременно трогаются с места и движутся равноускоренно. Массы автомобилей одинаковы. Во сколько раз средняя мощность двигателя первого автомобиля больше средней мощности второго, если за одно и то же время первый автомобиль развивает скорость вдвое большую, чем второй? Сопротивлением движению пренебречь.
Ответ
30
Самолет для взлета должен иметь скорость v = 25 м/с. Длина пробега перед взлетом s = 100 м. Какова мощность моторов, если масса самолета m = 1000 кг и коэффициент сопротивления k = 0,02? Считать движение самолета при взлете равноускоренным.
Ответ
31
Поезд массой М = 5*105 кг поднимается со скоростью 30 км/ч в гору с уклоном 10 м на километр. Коэффициент сопротивления k = 0,002. Определить мощность, развиваемую тепловозом.
Ответ
32
Разогнавшись, конькобежец некоторое время движется по горизонтальной ледяной дорожке равномерно. Затем, перестав отталкиваться, он, двигаясь равнозамедленно, проезжает до остановки путь s = 60 м в течение t = 25 с. Масса конькобежца m = 50 кг. Определить: а) коэффициент трения; б) мощность, затрачиваемую конькобежцем при равномерном движении.
Ответ
а) k ≈ 0,02;
б) N ≈ 46 Вт.
33
Тепловоз тянет поезд, общая масса которого m равна 2000 т. Принимая, что мощность тепловоза N постоянна и равна 1800 кВт и что коэффициент сопротивления k = 0,005, определить: а) ускорения поезда a в те моменты, когда скорость поезда v1 = 4 м/с и когда скорость поезда v2 = 12 м/с; б) максимальную скорость vмакс поезда.
Ответ
а) a1 = 0,176 м/с2, a2 = 0,026 м/с2;
б) vмакс ≈ 66 км/ч.
34
Шкив радиусом R делает n оборотов в секунду, передавая ремнем мощность N. Найти силу натяжения Т ремня, идущего без скольжения.
Найти силу натяжения Т ремня, идущего без скольжения.
Ответ
35
Найти мощность воздушного потока, имеющего поперечное сечение в виде круга диаметром d = 18 м и текущего со скоростью v = 12 м/с. Плотность воздуха (при нормальных условиях) ρ = 1,3 кг/м3.
Ответ
36
Горный ручей с сечением потока S образует водопад высотой h. Скорость течения воды в ручье v. Найти мощность водопада.
Ответ
.
37
Уклон участка шоссе равен 0,05. Спускаясь под уклон при выключенном двигателе, автомобиль движется равномерно со скоростью v = 60 км/ч. Какова должна быть мощность двигателя автомобиля, чтобы он мог подниматься на такой же подъем с той же скоростью? Масса автомобиля m = 1,5 т.
Ответ
38
Грузовики, снабженные двигателями мощностью N1 и N2, развивают скорости соответственно v1 и v2. Какова будет скорость грузовиков, если их соединить тросом?
Ответ
.
39
Аэросани движутся вверх по слабому подъему с установившейся скоростью v1 = 20 м/с; если они движутся в обратном направлении, т. е. под уклон, то при той же мощности двигателя устанавливается скорость v2 = 30 м/с. Какая скорость v установится при той же мощности двигателя во время движения по горизонтальному пути?
Ответ
40
Поезд массой m = 500 т шел равномерно по горизонтальному пути. От поезда оторвался задний вагон массой m1 = 20 т. Проехав после этого s = 240 м, машинист прекратил доступ пара в машину. На каком расстоянии l друг от друга остановятся оторвавшийся вагон и остальной состав поезда? Предполагается, что сила тяги при работе машины постоянна, а сопротивление движению поезда и вагона пропорционально их массам.
Проехав после этого s = 240 м, машинист прекратил доступ пара в машину. На каком расстоянии l друг от друга остановятся оторвавшийся вагон и остальной состав поезда? Предполагается, что сила тяги при работе машины постоянна, а сопротивление движению поезда и вагона пропорционально их массам.
Ответ
41
Найти работу, которую необходимо совершить, чтобы втащить тело массой m = 50 кг на горку произвольного профиля по плоской траектории из точки А в точку В, расстояние между которыми по горизонтали l = 10 м, а по вертикали h = 10 м. Коэффициент трения между телом и горкой всюду одинаков и равен k = 0,1. Профиль горки такой,что касательная к нему в любой точке составляет острый угол с горизонтом. Сила, приложенная к телу, всюду действует по касательной к траектории его перемещения.
Ответ
Гидростатика
1
В полый куб с ребром a налита доверху жидкость плотностью ρ. Определить силы, действующие на грани куба.
Определить силы, действующие на грани куба.
Ответ
На дно действует сила ρga3, на боковую грань 1/2ρga3.
2
Сосуд, имеющий форму усеченного конуса с приставным дном, опущен в воду. Если в сосуд налить 200 г воды, то дно оторвется. Отпадет ли дно, если на него поставить гирю 200 г? налить 200 г масла? налить 200 г ртути?
Ответ
Если сосуд сужается кверху, то гиря и ртуть не оторвут дно, а масло оторвет. Если сосуд сужается книзу, то наоборот.
3
В сосуд с водой вставлена трубка сечением S = 2 см2. В трубку налили 72 г масла (ρм = 900 кг/м3). Найти разность уровней масла и воды.
Ответ и решение
Ответ: Δh = 4 см.
Согласно условию равновесия неоднородных жидкостей в сообщающихся сосудах:
.
Или:
.
Откуда
.(1)
Чтобы найти H, запишем выражение для массы масла в трубке:
,
откуда
.(2)
Окончательно, подставив (2) в (1), получим:
.
4
При подъеме груза массой m = 2 т с помощью гидравлического пресса была затрачена работа A = 40 Дж. При этом малый поршень сделал n = 10 ходов, перемещаясь за один ход на h = 10 см. Во сколько раз площадь большого поршня больше площади малого, если к. п. д. пресса равен 1.
Ответ
5
В сообщающиеся сосуды диаметрами D1, и D2 налита вода. На сколько изменится уровень воды в сосудах, если положить кусок дерева массой m в первый сосуд? во второй? Плотность воды ρ0.
Ответ
В обоих случаях уровень воды увеличивается на
.
6
В колена U-образной трубки налиты вода и спирт, разделенные ртутью. Уровень ртути в обоих коленах одинаков. На высоте 24 см от уровня ртути колена соединены горизонтальной трубкой с краном.
Вначале кран закрыт. Определить высоту столба спирта h2 (ρс = 800 кг/м3), если высота столба воды h1 = 32 см. Что будет, если открыть кран? При каком расположении трубки при открывании крана будет сохраняться равновесие?
Ответ
7
Льдина площадью поперечного сечения S = 1 м2 и высотой H = 0,4 м плавает в воде. Какую работу надо совершить, чтобы полностью погрузить льдину в воду?
Ответ
≈ 7,84 Дж.
8
В стакане плавает кусок льда. Изменится ли уровень воды, когда лед растает? Рассмотреть дополнительно случаи: 1) когда во льду находился пузырек воздуха; 2) когда во льду находилась свинцовая пластинка.
Ответ
Лед вытесняет воду, вес которой равен весу льда. Когда лед растает, образуется такое же количество воды, поэтому уровень не изменится.
1) Тоже не изменится, т. к. массой воздуха можно пренебречь.
2) Понизится, т. к. объем воды, которая образуется, когда лед растает, вместе с объемом свинца будет меньше, чем в случае куска чистого льда того же веса.
9
Одна из бутылок наполнена водой, другая — ртутью. Потонет ли бутылка с водой, если ее опустить в воду? Потонет ли бутылка с ртутью, если ее опустить в ртуть?
Ответ
Бутылка с водой потонет, а с ртутью — нет.
10
Прямоугольная коробочка из жести массой m = 76 г с площадью дна S = 38 см2 и высотой H = 6 см плавает в воде. Определить высоту h надводной части коробочки.
Ответ
11
Кастрюля емкостью 2 л доверху наполнена водой. В нее ставят тело объемом 0,5 л и массой 0,6 кг. Сколько воды вытечет из кастрюли?
Ответ
12
Жестяная банка с грузом плавает на поверхности воды, налитой в сосуд. При этом уровень воды в сосуде равен H1. Больше или меньше H1 будет уровень H2, если груз из банки переложить на дно сосуда? Плотность груза больше плотности воды.
Решение
H2 станет меньше H1, поскольку груз будет вытеснять объем воды, равный своему объему, а находясь в жестяной банке, груз вытесняет объем воды, масса которого равна массе груза.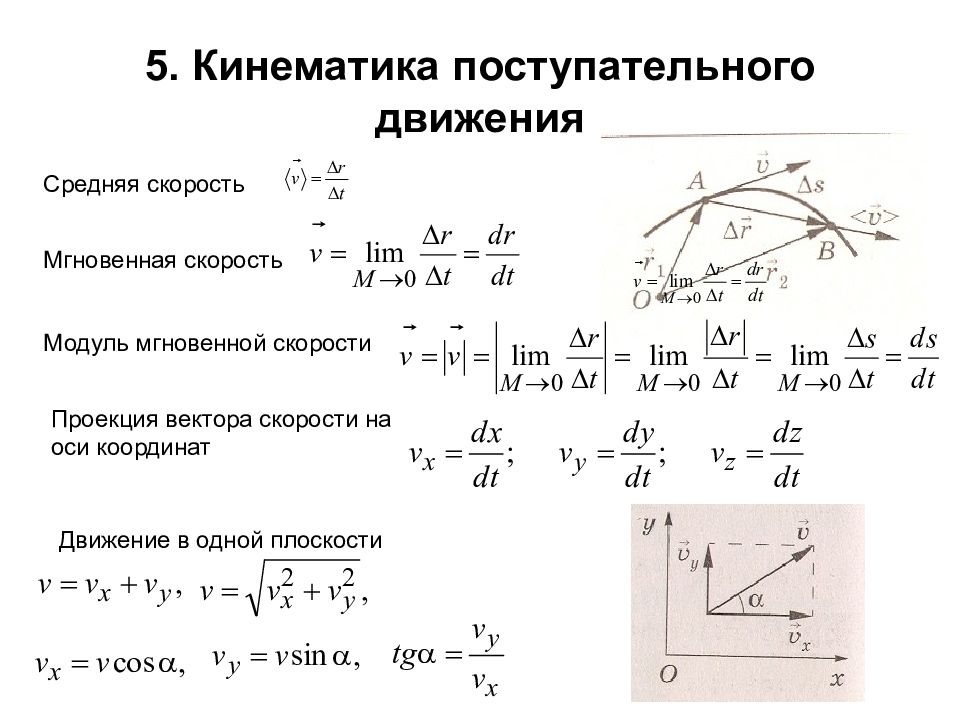
13
В сосуд с вертикальными стенками и площадью дна S налита жидкость с плотностью ρ. На сколько изменится уровень жидкости в сосуде, если в него опустить тело произвольной формы массой m, которое не тонет?
Ответ
14
В U-образной трубке сечением S налита жидкость с плотностью ρ. На сколько поднимется уровень жидкости в правом колене трубки по отношению к первоначальному уровню, если в левое колено опустили тело массой m и плотностью ρ1 < ρ?
Ответ
15
На дне водоема установлена бетонная конструкция грибовидной формы, размеры которой указаны на рисунке.
Глубина реки H. С какой силой F давит конструкция на дно реки? Плотность бетона ρ, воды ρ0.
Решение
Сила давления бетонной конструкции на дно складывается из веса конструкции и разности сил, возникающих в результате гидростатического давления на верхнюю и нижнюю поверхности конструкции:
.
Вес конструкции равен:
.
Сила, возникающая в результате гидростатического давления на верхнюю поверхность конструкции, равна:
.
Сила, возникающая в результате гидростатического давления на нижнюю поверхность конструкции, равна:
.
Таким образом, искомая сила F равна:
.
16
Деревянный кубик лежит на дне сосуда. Всплывет ли он, если в сосуд налить воду (вода не проникает под кубик)?
Решение
Не всплывет, т. к. выталкивающая сила не возникает из-за отсутствия воды под нижней гранью кубика.
17
Круглая дырка площадью S1 в дне сосуда прикрыта без усилия конической пробкой с площадью основания S2. При каком наибольшем значении плотности материала пробки ρ можно добиться ее всплытия, доливая воду в сосуд? Плотность воды ρ0.
Решение
Архимедова сила, действующая на пробку, достигает максимума, когда уровень воды достигнет верха пробки. Пробка всплывет, когда подъемная сила превысит вес пробки. Подъемная сила равна весу воды, объем которой равен объему заштрихованной области пробки на рисунке:
.
Найдем подъемную силу:
.
Найдем вес пробки:
.
Тогда ρ найдем из уравнения:
,
откуда
.
Поскольку малый и большой конус подобны:
,
тогда
.
18
Пустую открытую бутылку погрузили в воду горлышком вниз на некоторую глубину h и опустили. При этом бутылка не всплывала, не опускалась, а находилась в положении равновесия. Почему? Будет ли это равновесие устойчивым? Определить глубину погружения, если емкость бутылки V0 = 0,5 л, масса m = 0,4 кг. Давление атмосферы p0 = 101 кПа, температура постоянная. Объемом стенок бутылки пренебречь.
Решение
Давление воды на глубине h: p1 = p0 + ρgh. Для воздуха в бутылке, сжимающегося по мере погружения бутылки, можно записать закон Бойля-Мариотта: p0V0 = p1V1, где V0 и V1 — объем воздуха в бутылке соответственно до и после погружения. Поскольку бутылка находится в равновесии, то ее вес равен архимедовой силе: mg = ρV1g. Таким образом, получаем систему уравнений:
Решив ее, получим:
.
Равновесие будет неустойчивым.
19
Полый шар (внешний радиус R1, внутренний R2), сделанный из материала с плотностью ρ1 плавает на поверхности жидкости с плотностью ρ2. Какова должна быть плотность ρ вещества, которым следует заполнить внутреннюю полость шара, чтобы он находился в безразличном равновесии внутри жидкости?
Решение
Чтобы шар находился в состоянии безразличного равновесия, вес вытесняемой шаром жидкости должен быть равен весу шара:
.
Отсюда находим ρ:
.
20
Полый шар, отлитый из чугуна, плавает в воде, погрузившись ровно наполовину. Найти объем V внутренней полости шара, если масса шара m = 5000 г, а плотность чугуна ρ = 7,8 г/см3.
Решение
Поскольку шар наполовину погружается в воду, то архимедова сила, действующая на шар, равна весу воды, объем которой равен половине объема шара. Объем шара складывается из искомого объема V и объема чугунной части шара, равного m/ρ. Таким образом, можно составить уравнение:
,
где ρ0 плотность воды, откуда:
≈ 9360 см3.
21
На весах уравновешен сосуд с водой. Как изменится равновесие, если в воду целиком опустить подвешенный на нитке брусок размером 5x3x3 см3 так, чтобы он не касался дна? Какой груз и на какую чашку надо положить, чтобы сохранить равновесие?
Решение
В соответствии с 3-м законом Ньютона, на чашку весов с сосудом с водой будет действовать сила, равная по модулю выталкивающей силе, действующей на брусок, но направленной в противоположную сторону. Таким образом, чтобы уравновесить весы, необходимо в противоположную чашку весов положить груз массой m = ρV = 45 г.
22
Алюминиевый и железный сплошные шары уравновешены на рычаге. Нарушится ли равновесие, если шары погрузить в воду? Рассмотреть два случая: а) шары одинаковой массы; б) шары одинакового объема.
Решение
Ответ: а) железный шар перевесит, поскольку на алюминиевый шар действует большая выталкивающая сила, чем на железный, так как объем алюминиевого шара больше объема железного шара такой же массы. б) железный шар перевесит, поскольку момент выталкивающей силы, действующей на алюминиевый шар, больше момента выталкивающей силы, действующей на железный шар, так как плечи рычага в этом случае не равны.
23
Вес куска железа в воде P = 1,67 H. Найти его объем Vж. Плотность железа ρж = 7,8 г/см3.
Решение
Вес куска железа в воде равен разности веса куска железа вне воды и выталкивающей силы, действующей на него в воде:
,
откуда:
= 25,1 см3.
24
Вес тела в воде в три раза меньше, чем в воздухе. Какова плотность материала тела?
Решение
Вес тела в воде равен разности веса тела вне воды и выталкивающей силы, действующей на него в воде:
,
откуда:
,
или:
,
откуда:
= 1500 кг/м3.
25
Брусок дерева плавает в воде. Как изменится глубина погружения бруска в воде, если поверх воды налить масло?
Ответ
Уменьшится, поскольку увеличится давление на нижнюю грань бруска дерева.
26
Некоторое тело плавает на поверхности воды в закрытом сосуде. Как изменится глубина погружения тела, если накачать воздух в сосуд?
Ответ
Ответ: не изменится, если сжимаемость тела такая же, как и у воды. Если сжимаемость тела больше, чем у воды, то глубина увеличится. Если сжимаемость тела меньше, чем у воды, то глубина погружения тела уменьшится.
27
Один конец нити закреплен на дне, а второй прикреплен к пробковому поплавку. При этом 0,75 всего объема поплавка погружено в воду. Определить силу натяжения нити F, если масса поплавка равна 2 кг и плотность пробки 0,25 г/см3. Массой нити пренебречь.
Решение
Сила натяжения нити равна разности архимедовой силы и веса пробки:
,
где ρ0 плотность воды.
Вынесем mg за скобки:
.
Подставив числовые значения, получим F ≈ 40 H.
28
На крюке динамометра висит ведерко. Изменится ли показание динамометра, если ведерко наполнить водой и погрузить в воду?
Ответ
Уменьшится на величину веса воды, вытесняемой стенками и дном ведра.
29
Сосуд, предельно наполненный водой, висит на динамометре. Изменится ли показание динамометра, если в воду опустить гирю, подвешенную на нити, не касаясь дна?
Ответ
Не изменится, поскольку вес воды, которая выльется, равен силе, противодействующей архимедовой силе, действующей на гирю.
30
На рычажных весах уравновешены сосуд с водой и штатив с медной гирей массой m = 100 г (рисунок). Затем гиря, подвешенная на нити, опускается в воду. Как восстановить равновесие весов? Плотность меди ρм = 8,9 г/см3.
31
Тонкая однородная палочка шарнирно укреплена за верхний конец. Нижняя часть палочки погружена в воду, причем равновесие достигается тогда, когда палочка расположена наклонно к поверхности воды и в воде находится половина палочки. Какова плотность материала, из которого сделана палочка?
32
Два шарика радиусами r1 и r2, сделанные из материалов с плотностями ρ1 и ρ2, соединены невесомым стержнем длиной l. Затем вся система помещена в жидкость с плотностью ρ, причем ρ < ρ1 и ρ < ρ2. В какой точке стержня нужно его повесить, для того чтобы система находилась в равновесии при горизонтальном положении стержня?
33
Из сосуда, заполненного водой, выходит труба радиусом r и высотой h (рисунок). Труба закрыта круглой пластиной радиусом R и массой М, которую прижимает к трубе давление воды. С какой силой F нужно подействовать на пластину в точке А, для того чтобы она повернулась, открыв трубу? Сосуд заполнен водой до высоты H. Толщина пластины пренебрежимо мала.
34
На весах уравновешено тело, погруженное в жидкость. Изменится ли показание весов при нагревании жидкости вместе с погруженным в нее телом?
35
Сплошное однородное тело объемом V, плотность материала которого ρ, плавает на границе между тяжелой жидкостью с плотностью ρ1 и более легкой жидкостью с плотностью ρ2. Какая часть объема тела V1 будет находиться в тяжелой жидкости?
36
Кубик из дерева, имеющий сторону 10 см, плавает между маслом и водой, находясь ниже уровня масла на 2,5 см. Нижняя поверхность кубика на 2,5 см ниже поверхности раздела. Какова масса m кубика, если плотность масла 0,8 г/см3? Определить силы давления F1, и F2 на верхнюю и нижнюю грани кубика. Изменится ли глубина погружения кубика в воду при доливании масла?
37
Стальной кубик плотностью 7,8 г/см3 плавает в ртути (плотность 13,6 г/см3). Поверх ртути наливается вода так, что она покрывает кубик тонким слоем. Какова высота H слоя воды? Длина ребра кубика а = 10 см. Определить давление р на нижнюю грань кубика.
38
Кусок пробки весит в воздухе 0,147 Н, кусок свинца 1,1074 Н. Если эти куски связать, а затем подвесить к чашке весов и опустить в керосин, то показания весов будет 0,588 Н. Определить плотность пробки, учитывая, что плотность керосина 0,8 г/см3, а свинца 11,3 г/см3.
39
В сосуд с водой погружается открытый цилиндрический стакан: один раз дном вверх, а другой — дном вниз, на одну и ту же глубину. В каком из этих случаев работа, которую нужно совершить, чтобы погрузить стакан в воду, будет больше? Вода из сосуда не выливается и в стакан, погруженный дном вниз, не попадает.
40
Две одинаковые по массе оболочки шара — одна из эластичной резины, а вторая из прорезиненной ткани — наполнены одним и тем же количеством водорода и у Земли занимают равный объем. Который из шаров поднимется выше и почему, если водород из них выходить не может?
41
Во сколько раз изменится подъемная сила газа, наполняющего аэростат (дирижабль), если будет применяться гелий вместо водорода?
42
К динамометру подвешена тонкостенная трубка ртутного барометра. Что показывает динамометр? Будут ли изменяться его показания при изменении атмосферного давления?
43
Определить приближенно массу газовой оболочки, окружающей земной шар.
44
Г-образная трубка, длинное колено которой открыто, наполнена водородом. Куда будет выгнута резиновая пленка, закрывающая короткое колено трубки?
45
В трубе с сужением течет вода. В трубу пущен эластичный резиновый мячик. Как изменится его диаметр при прохождении узкой части трубы?
46
Тело, имеющее массу m = 2 кг и объем V = 1000 см3, находится в озере на глубине h = 5 м.
Какая работа должна быть совершена при его подъеме на высоту H = 5 м над поверхностью воды?
Равна ли совершенная при этом работа изменению потенциальной энергии тела? Объясните результат.
47
В водоеме укреплена вертикальная труба с поршнем таким образом, что нижний ее конец погружен в воду. Поршень, лежавший вначале на поверхности воды, медленно поднимают на высоту H = 15 м. Какую работу пришлось при этом совершить? Площадь поршня S = 1 дм2, атмосферное давление р = 101 кПа. Весом поршня пренебречь.
48
Подводная лодка находится на глубине h = 100 м. С какой скоростью через отверстие в корпусе лодки будет врываться струя воды? Сколько воды проникает за один час, если диаметр отверстия равен d = 2 см? Давление воздуха в лодке равно атмосферному давлению. Изменением давления внутри лодки пренебречь.
49
Из брандспойта бьет струя воды. Расход воды Q = 60 л/мин. Какова площадь поперечного сечения струи S1 на высоте h = 2 м над концом брандспойта, если вблизи него сечение равно S0 = 1,5 см2?
50
Почему быстролетящая пуля пробивает в пустом пластмассовом стакане лишь два маленьких отверстия, а стакан, наполненный водой, разбивается при попадании пули вдребезги?
Основные формулы по физике — МЕХАНИКА
Формулы механики. Механика делится на три раздела: кинематику, динамику и статику. В разделе кинематика рассматриваются такие кинематические характеристики движения, как перемещение, скорость, ускорение. Здесь необходимо использовать аппарат дифференциального и интегрального исчисления.
В основе классической динамики лежат три закона Ньютона. Здесь необходимо обратить внимание на векторный характер действующих на тела сил, входящих в эти законы.
Динамика охватывает такие вопросы, как закон сохранения импульса, закон сохранения полной механической энергии, работа силы.
При изучении кинематики и динамики вращательного движения следует обратить внимание на связь между угловыми и линейными характеристиками. Здесь вводятся понятия момента силы, момента инерции, момента импульса и рассматривается закон сохранения момента импульса.
Смотрите также основные формулы по термодинамике
Таблица основных формул по механике
|
Физические законы, формулы, переменные |
Формулы механики |
||||
|
Скорость мгновенная: где r — радиус-вектор материальной точки, t — время;
|
|||||
|
Модуль вектора скорости: где s — расстояние вдоль траектории движения (путь) |
|||||
|
Скорость средняя (модуль): |
|||||
|
Ускорение мгновенное: |
|||||
|
Модуль вектора ускорения при прямолинейном движении: |
|||||
|
Ускорение при криволинейном движении: 1) нормальное где R — радиус кривизны траектории, 2) тангенциальное 3) полное (вектор) 4) (модуль) |
|||||
|
Скорость и путь при движении: 1) равномерном 2) равнопеременном V0— начальная скорость; а > 0 при равноускоренном движении; а < 0 при равнозамедленном движении. |
|
||||
|
Угловая скорость: где φ — угловое перемещение. |
|||||
|
Угловое ускорение: |
|||||
|
Связь между линейными и угловыми величинами: |
|||||
|
Импульс материальной точки: где m — масса материальной точки. |
|||||
|
Основное уравнение динамики поступательного движения (II закон Ньютона): где F — результирующая сила, <> |
|||||
|
Формулы сил: тяжестиP где g — ускорение свободного падения трения Fтр где μ — коэффициент трения, N — сила нормального давления, упругости Fупр где k — коэффициент упругости (жесткости), Δх — деформация (изменение длины тела). |
|
||||
|
Закон сохранения импульса для замкнутой системы, состоящей из двух тел: где — скорости тел до взаимодействия; — скорости тел после взаимодействия. |
|||||
|
Потенциальная энергия тела: 1) поднятого над Землей на высоту h 2) упругодеформированного |
|
||||
|
Кинетическая энергия поступательного движения: |
|||||
|
Работа постоянной силы: где α — угол между направлением силы и направлением перемещения. |
|||||
|
Полная механическая энергия: |
|||||
|
Закон сохранения энергии: силы консервативны силы неконсервативны где W1 — энергия системы тел в начальном состоянии; W2 — энергия системы тел в конечном состоянии. |
|
||||
|
Момент инерции тел массой m относительно оси, проходящей через центр инерции (центр масс): 1) тонкостенного цилиндра (обруча) где R — радиус, 2) сплошного цилиндра (диска) 3) шара 4) стержня длиной l, если ось вращения перпендикулярна стержню и проходит через его середину |
|||||
|
Момент инерции тела относительно произвольной оси (теорема Штейнера): где — момент инерции тела относительно оси, проходящей через центр масс, d — расстояние между осями. |
|||||
|
Момент силы(модуль): где l — плечо силы. |
|||||
|
Основное уравнение динамики вращательного движения: где — угловое ускорение, — результирующий момент сил. |
|||||
|
Момент импульса: 1) материальной точки относительно неподвижной точки где r — плечо импульса, 2) твердого тела относительно неподвижной оси вращения |
|
||||
|
Закон сохранения момента импульса: где L1 — момент импульса системы в начальном состоянии, L2 — момент импульса системы в конечном состоянии. |
|||||
|
Кинетическая энергия вращательного движения: |
|||||
|
Работа при вращательном движении где Δφ — изменение угла поворота. |
Основные понятия кинематики
Определение 1Кинематика − это раздел механики, который рассматривает движение тел без объяснения вызывающих его причин.
Определение 2Механическое движение тела − это изменение положения данного тела в пространстве относительно других тел во времени.
Как мы сказали, механическое движение тела относительно. Движение одного и того же тела относительно разных тел может быть разным.
Определение 3Для характеристики движения тела указывается, по отношению к какому из тел рассматривается это движение. Это будет тело отсчета.
Определение 4Система отсчета − система координат, которая связана с телом отсчета и временем для отсчета. Она позволяет определить положение передвигающегося тела в любой отрезок времени.
В СИ единицей длины выступает метр, а единицей времени – секунда.
У каждого тела есть определенные размеры. Разные части тела расположены в разных пространственных местах. Но в большинстве задач механики не нужно указывать положение отдельных частей тела. Если размеры тела маленькие в сравнении с расстояниями до остальных тел, тогда заданное тело считается его материальной точкой. Таким образом поступают при изучении перемещения планет вокруг Солнца.
Определение 5Механическое движение называют поступательным, в случае если все части тела перемещаются одинаково.
Пример 1Поступательное движение наблюдается у кабин в аттракционе «Колесо обозрения» или у автомобиля на прямолинейном участке пути.
При поступательном движении тела его также рассматривают в качестве материальной точки.
Определение 6Материальная точка − это тело, размерами которого при заданных условиях можно пренебречь.
Материальная точка в механике
Термин “материальная точка” имеет важное значение в механике.
Определение 7Траектория движения тела − некоторая линия, которую тело или материальная точка описывает, перемещаясь во времени от одной точки до другой.
Местонахождение материальной точки в пространстве в любой временной отрезок (закон движения) определяют, используя зависимость координат от времени x=x(t), y=y(t), z=z(t) или зависимость от времени радиус-вектора r→=r→(t), проведенного от начала координат до заданной точки. Наглядно это представлено на рисунке 1.1.1.
Рисунок 1.1.1. Определение положения точки при помощи координат x=x (t), y=y (t) и z=z (t) и радиус-вектора r→(t), r0→ – радиус-вектор положения точки в начальный момент времени.
Определение 8Перемещение тела s→=∆r→=r→-r0→ – это направленный отрезок прямой, который соединяет начальное положение тела с его дальнейшим положением. Перемещение является векторной величиной.
Пройденный путь l равняется длине дуги траектории, преодоленной телом за определенное время t. Путь является скалярной величиной.
Если движение тела рассматривается в течение довольно короткого отрезка времени, тогда вектор перемещения оказывается направленным по касательной к траектории в заданной точке, а его длина равняется преодоленному пути.
В случае небольшого промежутка времени Δt преодоленный телом путь Δl практически совпадает с модулем вектора перемещения ∆s→. При перемещении тела по криволинейной траектории модуль вектора движения все время меньше пройденного пути (рисунок 1.1.2).
Рисунок 1.1.2. Пройденный путь l и вектор перемещения ∆s→ при криволинейном движении тела.
a и b – это начальная и конечная точки пути.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеОпределение средней и мгновенной скорости движения тела. Основные формулы кинематики
Для описания движения в физике введено понятие средней скорости: υ→=∆s→∆t=∆r→∆t.
Физиков больше интересует формула не средней, а мгновенной скорости, которая рассчитывается как предел, к которому стремится средняя скорость на бесконечно маленьком промежутке времени Δt, то есть υ→=∆s→∆t=∆r→∆t; ∆t→0.
В математике данный предел называется производная и обозначается dr→dt или r→˙.
Мгновенная скорость υ→ тела в каждой точке криволинейной траектории направлена по касательной к траектории в заданной точке. Отличие между средней и мгновенной скоростями демонстрирует рисунок 1.1.3.
Рисунок 1.1.3. Средняя и мгновенная скорости. ∆s1→, ∆s2→, ∆s3→ – перемещения за время ∆t1<∆t2<∆t3 соответственно. При t→0, υ→ср→υ→.
При перемещении тела по криволинейной траектории скорость υ→ меняется по модулю и по направлению. Изменение вектора скорости υ→ за какой-то маленький промежуток времени Δt задается при помощи вектора ∆υ→ (рисунок 1.1.4).
Вектор изменения скорости ∆υ→=υ2→-υ1→ за короткий промежуток времени Δt раскладывается на 2 составляющие: ∆υr→, которая направлена вдоль вектора υ→ (касательная составляющая) и ∆υn→, которая направлена перпендикулярно вектору υ→ (нормальная составляющая).
Рисунок 1.1.4. Изменение вектора скорости по величине и по направлению. ∆υ→=∆υ→r+∆υ→n – изменение вектора скорости за промежуток времени Δt.
Определение 9Мгновенное ускорение тела a→ – это предел отношения небольшого изменения скорости ∆υ→ к короткому отрезку времени Δt, в течение которого изменялась скорость: a→=∆υ→∆t=∆υ→τ∆t+∆υ→n∆t; (∆t→0).
Направление вектора ускорения a→, при криволинейном движении, не совпадает с направлением вектора скорости υ→. Составляющие вектора ускорения a→ – это касательные (тангенциальные) a→τ и нормальные a→n ускорения (рисунок 1.1.5).
Рисунок 1.1.5.Касательное и нормальное ускорения.
Касательное ускорение показывает, как быстро меняется скорость тела по модулю: aτ=∆υ∆t; ∆t→0.
Вектор a→τ направлен по касательной к траектории.
Нормальное ускорение показывает, как быстро скорость тела меняется по направлению.
Пример 2Представим криволинейное движение, как движение по дугам окружностей (рисунок 1.1.6).
Рисунок 1.1.6. Движение по дугам окружностей.
Нормальное ускорение находится в зависимости от модуля скорости υ и радиуса R окружности, по дуге которой тело перемещается в определенный момент времени: an=υ2R.
Вектор an→ все время направлен к центру окружности.
По рисунку 1.1.5 видно, модуль полного ускорения равен a=aτ2+an2.
Итак, основные физические величины в кинематике материальной точки – это пройденный путь l, перемещение s→, скорость υ→ и ускорение a→.
Путь l – скалярная величина.
Перемещение s→, скорость υ→ и ускорение a→ – векторные величины.
Для того чтобы задать какую-нибудь векторную величину, необходимо задать ее модуль и определить направление. Вектора подчиняются математическим правилам: их можно проектировать на координатные оси, складывать, вычитать и др.
Механическое движение — определение, формулы, примеры
Механическое движение
Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.
Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.
«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:
- тело отсчета
- система координат
- часы
В совокупности эти три параметра образуют систему отсчета.
В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь 😉
Прямолинейное равномерное движение
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.
Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.
Мы можем охарактеризовать это движение следующими величинами.
Скалярные величины (определяются только значением)
- Время — в международной системе единиц СИ измеряется в секундах [с].
- Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].
Векторные величины (определяются значением и направлением)
- Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
- Путь — вектор, проведенный из начальной точки пути в конечную [м].
Проецирование векторов
Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.
Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.
|
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю. |
Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.
Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.
|
Скорость → → → |
|
Средняя путевая скорость V ср.путевая = S/t V ср.путевая — средняя путевая скорость [м/с] |
В чем разница между перемещением и путем?
Перемещение — это вектор, проведенный из начальной точки в конечную, а путь — это длина траектории.Задача
Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.
Решение:
Возьмем формулу средней путевой скорости
V ср.путевая = S/t
Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч
Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч
Уравнение движения
Основной задачей механики является определение положения тела в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
|
Уравнение движения x(t) = x0 + vxt x(t) — искомая координата [м] |
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:
|
Уравнение движения при движении против оси x(t) = x0 — vxt x(t) — искомая координата [м] |
Графики
Изменение любой величины можно описать графически. Вместо того, чтобы писать множество значений, можно просто начертить график — это проще.
В видео ниже разбираемся, как строить графики кинематических величин и зачем они нужны.
Прямолинейное равноускоренное движение
Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.
Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение — килограмм с приставкой «кило».
Итак, прямолинейное движение — это движение с ускорением по прямой линии.2, а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).
Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с2. В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с2.
И кому же верить?
Все просто: для кого решается задача, тот и главный. В экзаменах берем g = 10 , в школе при решении задач (если в условии задачи не написано что-то другое) берем g = 9,8 м/с2.
Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.
Помните о том, что свободное падение — это не всегда движение по вертикали. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.
Кинематика (скорость, ускорение, путь). Формулы, примеры решения
В прошлой статье мы немножко разобрались с тем, что такое механика и зачем она нужна. Мы уже знаем, что такое система отсчета, относительность движения и материальная точка. Что ж, пора двигаться дальше! Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики и приведем практический пример решения задачи.
Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.
Траектория, радиус-вектор, закон движения тела
Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.
Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.
Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.
Радиус-вектор – вектор, задающий положение точки в пространстве.
Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат (или радиус-вектора точки) от времени.
Перемещение и путь
Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.
В системе СИ перемещение и длина пути измеряются в метрах.
Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.
Скорость и ускорение
Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло
А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.
Мгновенная скорость – векторная физическая величина, равная производной от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.
В системе СИ скорость измеряется в метрах в секунду
Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.
Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости
Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.
Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории
Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.
Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.
Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.
ОСНОВНЫЕ ФОРМУЛЫ ПО ФИЗИКЕ ДЛЯ СТУДЕНТОВ ТЕХНИЧЕСКИХ ВУЗОВ.. Физические основы механики.
Примеры решения задач.
Примеры решения задач Пример 6 Один конец тонкого однородного стержня длиной жестко закреплен на поверхности однородного шара так, что центры масс стержня и шара, а также точка крепления находятся на одной
ПодробнееКОЛЛОКВИУМ 1 (механика и СТО)
КОЛЛОКВИУМ 1 (механика и СТО) Основные вопросы 1. Система отсчета. Радиус вектор. Траектория. Путь. 2. Вектор смещения. Вектор линейной скорости. 3. Вектор ускорения. Тангенциальное и нормальное ускорение.
Подробнее1. Цели освоения дисциплины
2 1. Цели освоения дисциплины Целью освоения дисциплины «Физика» является формирование у студентов навыка проведения измерений, изучение различных процессов и оценка результатов экспериментов. 2. Место
ПодробнееЗакон сохранения импульса
Закон сохранения импульса Закон сохранения импульса Замкнутая (или изолированная) система — механическая система тел, на которую не действуют внешние силы. d v ‘ ‘ d d v d… ‘ v ‘ v v ‘… ‘ v… v v
ПодробнееДинамика вращательного движения
Восточно-Сибирский государственный университет технологий и управления Лекция 3 Динамика вращательного движения ВСГУТУ, кафедра «Физика» План Момент импульса частицы Момент силы Уравнение моментов Момент
Подробнее3.3. ЯВЛЕНИЯ ПЕРЕНОСА В ГАЗАХ
ЯВЛЕНИЯ ПЕРЕНОСА В ГАЗАХ Средняя длина свободного пробега молекулы n, где d эффективное сечение молекулы, d эффективный диаметр молекулы, n концентрация молекул Среднее число соударений, испытываемое молекулой
ПодробнееТема: «Динамика материальной точки»
Тема: «Динамика материальной точки» 1. Тело можно считать материальной точкой если: а) его размерами в данной задаче можно пренебречь б) оно движется равномерно ось вращения является неподвижной угловое
ПодробнееКонспект по физике за 1 семестр
СПбГЭТУ ЛЭТИ Конспект по физике за 1 семестр Лектор: Ходьков Дмитрий Афанасьевич Работу выполнили: студент группы 7372 Чеканов Александр студент группы 7372 Когогин Виталий 2018 г КИНЕМАТИКА (МАТЕРИАЛЬНОЙ
ПодробнееДинамика вращательного движения
Динамика вращательного движения План Момент импульса частицы Момент силы Уравнение моментов Собственный момент импульса Момент инерции Кинетическая энергия вращающегося тела Связь динамики поступательного
ПодробнееС Б О Р Н И К ЗАДАНИЙ ПО КУРСУ ФИЗИКИ
Санкт-Петербургский политехнический университет Петра Великого Институт физики, нанотехнологий и телекоммуникаций (ИФНиТ) Кафедра экспериментальной физики Гаспарян Р.А. С Б О Р Н И К ЗАДАНИЙ ПО КУРСУ ФИЗИКИ
ПодробнееДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Лекция 5 ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ Термины и понятия Метод интегрального исчисления Момент импульса Момент инерции тела Момент силы Плечо силы Реакция опоры Теорема Штейнера 5.1. МОМЕНТ ИНЕРЦИИ ТВЕРДОГО
ПодробнееБилет 1. Билет 2. Билет 3. Билет 4. Билет 5.
Билет 1. 1. Предмет механики. Пространство и время в механике Ньютона. Тело отсчета и система координат. Часы. Синхронизация часов. Система отсчета. Способы описания движения. Кинематика точки. Преобразования
ПодробнееЛектор Алешкевич В. А. Январь 2013
студентыфизики Лектор Алешкевич В. А. Январь 2013 Неизвестный Студент физфака Билет 1 1. Предмет механики. Пространство и время в механике Ньютона. Система координат и тело отсчета. Часы. Система отсчета.
ПодробнееСТАТИСТИЧЕСКАЯ ФИЗИКА ТЕРМОДИНАМИКА
СТАТИСТИЧЕСКАЯ ФИЗИКА ТЕРМОДИНАМИКА Распределение Максвелла Начала термодинамики Цикл Карно Распределение Максвелла В газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не
ПодробнееМЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Национальный минерально-сырьевой университет
ПодробнееДемонстрационный вариант 1
Тестовые задания на экзамене по курсу «Физика. Механика. Термодинамика» Демонстрационный вариант 1 1. Материальная точка движется вдоль оси x. Закон движения точки имеет вид x ( t ) = At, где A постоянная.
ПодробнееВопросы к экзамену по физике МЕХАНИКА
Вопросы к экзамену по физике МЕХАНИКА Поступательное движение 1. Кинематика поступательного движения. Материальная точка, система материальных точек. Системы отсчета. Векторный и координатный способы описания
ПодробнееДемонстрационный вариант 1
Тестовые задания на экзамене по курсу «Физика. Механика. Термодинамика» Демонстрационный вариант 1 1. Материальная точка движется равномерно по окружности со скоростью v. Определите модуль изменения вектора
ПодробнееРАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
МИНОБРНАУКИ РОССИИ Федеральное государственное автономное образовательное учреждение высшего образования «Национальный исследовательский университет «Московский институт электронной техники» РАБОЧАЯ ПРОГРАММА
ПодробнееПримеры решения задач
Примеры решения задач 1.Движение тела массой 1 кг задано уравнением найти зависимость скорости и ускорения от времени. Вычислить силу, действующую на тело в конце второй секунды. Решение. Мгновенную скорость
ПодробнееКузьмичев Сергей Дмитриевич
Кузьмичев Сергей Дмитриевич СОДЕРЖАНИЕ ЛЕКЦИИ 9 Вращение твердого тела. 1. Вращение твердого тела вокруг неподвижной оси.. Момент инерции. Теорема Гюйгенса-Штейнера. 3. Кинетическая энергия вращающегося
Подробнее; в) модуль среднего вектора полного ускорения a
Задачи по курсу «Физика. Механика. Термодинамика» (ИБ-, ПМ-, ПМ-, РТ-, РТ-, РТ-3, ИКТ-, ИТК-, ИКТ-3, ИКТ-4, семестр 9/ уч. года) Механика Кинематика материальной точки. Точка движется по окружности со
ПодробнееТема 5. Механические колебания и волны.
Тема 5. Механические колебания и волны. 5.1. Гармонические колебания и их характеристики Колебания процессы, отличающиеся той или иной степенью повторяемости. В зависимости от физической природы повторяющегося
ПодробнееПринцип независимости действия сил
Лекция 2 Принцип независимости действия сил. Виды сил. Принцип относительности Галилея. Закон сохранения импульса. Центр масс. Система центра инерции. Работа и мощность. Кинетическая энергия и потенциальная
ПодробнееОсновные законы и формулы
1.5. Механические колебания и волны Основные законы и формулы Колебания, при которых физические величины, которые их описывают (например, отклонение от положения равновесия, скорость, ускорение и т.д.),
ПодробнееОсновные положения термодинамики
Основные положения термодинамики (по учебнику А.В.Грачева и др. Физика: 10 класс) Термодинамической системой называют совокупность очень большого числа частиц (сравнимого с числом Авогадро N A 6 10 3 (моль)
ПодробнееКинематические уравнения
Целью этого первого раздела «Класса физики» было исследование разнообразных средств, с помощью которых можно описать движение объектов. Разнообразие представлений, которые мы исследовали, включает словесные представления, графические представления, числовые представления и графические представления (графики положения-времени и графики скорости-времени). В Уроке 6 мы исследуем использование уравнений для описания и представления движения объектов.Эти уравнения известны как кинематические уравнения.
Есть множество величин, связанных с движением объектов — смещение (и расстояние), скорость (и скорость), ускорение и время. Знание каждой из этих величин дает описательную информацию о движении объекта. Например, если известно, что автомобиль движется с постоянной скоростью 22,0 м / с, на север в течение 12,0 секунд для смещения на север на 264 метра, то движение автомобиля полностью описано.И если известно, что вторая машина ускоряется из положения покоя с ускорением на восток 3,0 м / с 2 в течение 8,0 секунд, обеспечивая конечную скорость 24 м / с, восток и смещение на восток 96 метров. , то полностью описывается движение этой машины. Эти два утверждения дают полное описание движения объекта. Однако не всегда такая полнота известна. Часто бывает так, что известны лишь некоторые параметры движения объекта, а остальные неизвестны.Например, приближаясь к светофору, вы можете узнать, что ваша машина развивает скорость 22 м / с, восток и способна к заносу 8,0 м / с 2 , запад. Однако вы не знаете, какое смещение испытает ваша машина, если бы вы резко нажали на тормоз и занесло до полной остановки; и вы не знаете, сколько времени потребуется, чтобы остановиться. В таком случае неизвестные параметры могут быть определены с использованием физических принципов и математических уравнений (кинематических уравнений).
БОЛЬШОЙ 4
Кинематические уравнения — это набор из четырех уравнений, которые можно использовать для прогнозирования неизвестной информации о движении объекта, если известна другая информация. Уравнения можно использовать для любого движения, которое можно описать как движение с постоянной скоростью (ускорение 0 м / с / с) или движение с постоянным ускорением. Их нельзя использовать в течение какого-либо периода времени, в течение которого изменяется ускорение.Каждое из кинематических уравнений включает четыре переменные. Если известны значения трех из четырех переменных, то можно вычислить значение четвертой переменной. Таким образом, кинематические уравнения предоставляют полезные средства прогнозирования информации о движении объекта, если известна другая информация. Например, если известно значение ускорения, а также начальное и конечное значения скорости буксирующего автомобиля, то смещение автомобиля и время можно предсказать с помощью кинематических уравнений.Урок 6 этого модуля будет посвящен использованию кинематических уравнений для прогнозирования числовых значений неизвестных величин для движения объекта.
Четыре кинематических уравнения, описывающие движение объекта:
В приведенных выше уравнениях используются различные символы. Каждый символ имеет свое особое значение. Символ d обозначает смещение объекта. Символ t обозначает время, в течение которого объект двигался.Символ a обозначает ускорение объекта. А символ v обозначает скорость объекта; индекс i после v (как в v i ) указывает, что значение скорости является начальным значением скорости, а индекс f (как в v f ) указывает, что значение скорости является конечным значением скорости.
Каждое из этих четырех уравнений надлежащим образом описывает математическую связь между параметрами движения объекта. Таким образом, они могут использоваться для прогнозирования неизвестной информации о движении объекта, если известна другая информация.В следующей части Урока 6 мы исследуем процесс этого.
Кинематические уравнения и решение проблем
Четыре кинематических уравнения, которые описывают математическую связь между параметрами, описывающими движение объекта, были введены в предыдущей части Урока 6. Четыре кинематических уравнения:
В приведенных выше уравнениях символ d обозначает смещение объекта.Символ t обозначает время, в течение которого объект двигался. Символ a обозначает ускорение объекта. А символ v обозначает мгновенную скорость объекта; индекс i после v (как в v i ) указывает, что значение скорости является начальным значением скорости, а индекс f (как в v f ) указывает, что значение скорости является конечным значением скорости.
Стратегия решения проблем
В этой части Урока 6 мы исследуем процесс использования уравнений для определения неизвестной информации о движении объекта.Процесс включает использование стратегии решения проблем, которая будет использоваться на протяжении всего курса. Стратегия предполагает следующие шаги:
- Постройте информативную диаграмму физической ситуации.
- Определите и перечислите данную информацию в переменной форме.
- Определите и перечислите неизвестную информацию в переменной форме.
- Определите и перечислите уравнение, которое будет использоваться для определения неизвестной информации из известной информации.
- Подставьте известные значения в уравнение и используйте соответствующие алгебраические шаги, чтобы найти неизвестную информацию.
- Проверьте свой ответ, чтобы убедиться, что он разумный и математически правильный.
Использование этой стратегии решения проблем при решении следующей проблемы смоделировано в примерах A и B ниже.
Пример задачи A
Има Харрин приближается к светофору, движущемуся со скоростью +30.0 м / с. Загорается желтый свет, и Има тормозит и останавливается. Если ускорение Има составляет -8,00 м / с 2 , то определите смещение автомобиля во время заноса. (Обратите внимание, что направление векторов скорости и ускорения обозначено знаками «+» и «-».)
Решение этой проблемы начинается с построения информативной диаграммы физической ситуации. Это показано ниже. Второй шаг включает идентификацию и перечисление известной информации в переменной форме.Обратите внимание, что значение v f может быть принято равным 0 м / с, поскольку машина Имы останавливается. Начальная скорость (v i ) кабины +30,0 м / с, так как это скорость в начале движения (заносное движение). А ускорение (а) автомобиля определяется как — 8,00 м / с 2 . (Всегда обращайте особое внимание на знаки + и — для данных количеств.) Следующий шаг стратегии включает перечисление неизвестной (или желаемой) информации в переменной форме.В этом случае проблема запрашивает информацию о перемещении автомобиля. Итак, d — неизвестная величина. Результаты первых трех шагов показаны в таблице ниже.
| Схема: | Дано: | Находка: |
|---|---|---|
| v i = +30,0 м / с v f = 0 м / с a = — 8,00 м / с 2 |
d = ?? |
Следующий шаг стратегии включает определение кинематического уравнения, которое позволит вам определить неизвестную величину.На выбор предлагается четыре кинематических уравнения. В общем, вы всегда будете выбирать уравнение, которое содержит три известные и одну неизвестную переменные. В данном конкретном случае тремя известными переменными и одной неизвестной переменной являются v f , v i , a и d. Таким образом, вы будете искать уравнение, в котором перечислены эти четыре переменные. Анализ четырех приведенных выше уравнений показывает, что уравнение в правом верхнем углу содержит все четыре переменные.
v f 2 = v i 2 + 2 • a • d
После того, как уравнение идентифицировано и записано, следующий шаг стратегии включает в себя замену известных значений в уравнение и использование соответствующих алгебраических шагов для поиска неизвестной информации.Этот шаг показан ниже.
(0 м / с) 2 = (30,0 м / с) 2 + 2 • (-8,00 м / с 2 ) • d
0 м 2 / с 2 = 900 м 2 / с 2 + (-16,0 м / с 2 ) • d
(16,0 м / с 2 ) • d = 900 м 2 / с 2 — 0 м 2 / с 2
(16,0 м / с 2 ) * d = 900 м 2 / с 2
d = (900 м 2 / с 2 ) / (16.0 м / с 2 )
d = (900 м 2 / с 2 ) / (16,0 м / с 2 )
d = 56,3 м
Решение, приведенное выше, показывает, что автомобиль заносит расстояние 56,3 метра. (Обратите внимание, что это значение округлено до третьей цифры.)
Последний шаг стратегии решения проблем включает проверку ответа, чтобы убедиться, что он является одновременно разумным и точным. Стоимость кажется достаточно разумной. Машине требуется значительное расстояние, чтобы занести из 30.0 м / с (примерно 65 миль / ч) до остановки. Расчетное расстояние составляет примерно половину футбольного поля, что делает его очень разумным расстоянием для заноса. Проверка точности включает подстановку вычисленного значения обратно в уравнение для смещения и обеспечение того, чтобы левая часть уравнения была равна правой части уравнения. В самом деле!
Пример задачи B
Бен Рушин ждет на светофоре.Когда он наконец стал зеленым, Бен ускорился из состояния покоя со скоростью 6,00 м / с 2 за время 4,10 секунды. Определите перемещение машины Бена за этот период времени.
И снова решение этой проблемы начинается с построения информативной диаграммы физической ситуации. Это показано ниже. Второй шаг стратегии включает идентификацию и перечисление известной информации в переменной форме. Обратите внимание, что значение v i можно вывести как 0 м / с, поскольку машина Бена изначально находится в состоянии покоя.Ускорение (а) автомобиля составляет 6,00 м / с 2 . Время (t) равно 4,10 с. Следующий шаг стратегии включает перечисление неизвестной (или желаемой) информации в переменной форме. В этом случае проблема запрашивает информацию о перемещении автомобиля. Итак, d — неизвестная информация. Результаты первых трех шагов показаны в таблице ниже.
| Схема: | Дано: | Находка: |
|---|---|---|
| v i = 0 м / с т = 4.10 с a = 6,00 м / с 2 |
d = ?? |
Следующий шаг стратегии включает определение кинематического уравнения, которое позволит вам определить неизвестную величину. На выбор предлагается четыре кинематических уравнения. Опять же, вы всегда будете искать уравнение, которое содержит три известные переменные и одну неизвестную переменную. В этом конкретном случае три известные переменные и одна неизвестная переменная — это t, v i , a и d.Изучение четырех приведенных выше уравнений показывает, что уравнение в левом верхнем углу содержит все четыре переменные.
d = v i • t + ½ • a • t 2
После того, как уравнение идентифицировано и записано, следующий шаг стратегии включает в себя замену известных значений в уравнение и использование соответствующих алгебраических шагов для поиска неизвестной информации. Этот шаг показан ниже.
d = (0 м / с) • (4.1 с) + ½ • (6,00 м / с 2 ) • (4,10 с) 2
d = (0 м) + ½ • (6,00 м / с 2 ) • (16,81 с 2 )
d = 0 м + 50,43 м
d = 50,4 м
Решение, приведенное выше, показывает, что автомобиль преодолеет расстояние 50,4 метра. (Обратите внимание, что это значение округлено до третьей цифры.)
Последний шаг стратегии решения проблем включает проверку ответа, чтобы убедиться, что он является одновременно разумным и точным.Стоимость кажется достаточно разумной. Автомобиль с ускорением 6,00 м / с / с достигнет скорости примерно 24 м / с (примерно 50 миль / ч) за 4,10 с. Расстояние, на которое такая машина будет перемещена в течение этого периода времени, будет примерно половиной футбольного поля, что делает это расстояние очень разумным. Проверка точности включает подстановку вычисленного значения обратно в уравнение для смещения и обеспечение того, чтобы левая часть уравнения была равна правой части уравнения.В самом деле!
Два приведенных выше примера задач иллюстрируют, как кинематические уравнения могут быть объединены с простой стратегией решения проблем для прогнозирования неизвестных параметров движения для движущегося объекта. Если известны три параметра движения, можно определить любое из оставшихся значений. В следующей части Урока 6 мы увидим, как эту стратегию можно применить к ситуациям свободного падения. Или, если интересно, вы можете попробовать несколько практических задач и сравнить свой ответ с данными решениями.
Основы кинематики | Безграничная физика
Определение кинематики
Кинематика — это исследование движения точек, объектов и групп объектов без учета причин их движения.
Цели обучения
Определить кинематику
Основные выводы
Ключевые моменты
- Для описания движения кинематика изучает траектории точек, линий и других геометрических объектов.
- Изучение кинематики можно абстрагировать в чисто математических выражениях.
- Кинематические уравнения могут использоваться для расчета различных аспектов движения, таких как скорость, ускорение, смещение и время.
Ключевые термины
- кинематика : Раздел механики, связанный с движущимися объектами, но не с задействованными силами.
Кинематика — это раздел классической механики, который описывает движение точек, объектов и систем групп объектов без ссылки на причины движения (т.е., силы). Изучение кинематики часто называют «геометрией движения».
Объекты вращаются вокруг нас. Все, от теннисного матча до полета космического зонда над планетой Нептун, связано с движением. Когда вы отдыхаете, ваше сердце перемещает кровь по венам. Даже в неодушевленных предметах есть непрерывное движение в колебаниях атомов и молекул. Могут возникнуть интересные вопросы о движении: сколько времени потребуется космическому зонду, чтобы добраться до Марса? Куда приземлится футбольный мяч, если его бросить под определенным углом? Однако понимание движения также является ключом к пониманию других концепций физики.Например, понимание ускорения имеет решающее значение для изучения силы.
Для описания движения кинематика изучает траектории точек, линий и других геометрических объектов, а также их дифференциальные свойства (такие как скорость и ускорение). Кинематика используется в астрофизике для описания движения небесных тел и систем; и в машиностроении, робототехнике и биомеханике для описания движения систем, состоящих из соединенных частей (таких как двигатель, роботизированная рука или скелет человеческого тела).
Формальное изучение физики начинается с кинематики. Слово «кинематика» происходит от греческого слова «kinesis», означающего движение, и связано с другими английскими словами, такими как «cinema» (фильмы) и «kinesiology» (изучение движения человека). Кинематический анализ — это процесс измерения кинематических величин, используемых для описания движения. Изучение кинематики можно абстрагировать в чисто математических выражениях, которые можно использовать для расчета различных аспектов движения, таких как скорость, ускорение, смещение, время и траектория.
Кинематика траектории частицы : Кинематические уравнения могут использоваться для расчета траектории частиц или объектов. Физические величины, относящиеся к движению частицы, включают: массу m, положение r, скорость v, ускорение a.
Системы отсчета и смещение
Чтобы описать движение объекта, необходимо указать его положение относительно удобной системы отсчета.
Цели обучения
Оценить смещение в системе отсчета.
Основные выводы
Ключевые моменты
- Выбор системы отсчета требует решения, где находится исходное положение объекта и какое направление будет считаться положительным.
- Действительные системы отсчета могут отличаться друг от друга перемещением друг относительно друга.
- Рамки отсчета особенно важны при описании смещения объекта.
- Смещение — это изменение положения объекта относительно его системы отсчета.
Ключевые термины
- смещение : векторная величина, которая обозначает расстояние с направленным компонентом.
- рамка отсчета : система координат или набор осей, в пределах которых можно измерить положение, ориентацию и другие свойства объектов в ней.
Чтобы описать движение объекта, вы должны сначала описать его положение — где он находится в любой конкретный момент времени. Точнее, нужно указать его положение относительно удобной системы отсчета.Земля часто используется в качестве системы отсчета, и мы часто описываем положение объектов, связанных с их положением на Землю или от нее. Математически положение объекта обычно представлено переменной x .
Код ссылки
Есть два варианта, которые вы должны сделать, чтобы определить переменную положения x . Вы должны решить, где поставить x = 0 и какое направление будет положительным. Это называется выбором системы координат или выбором системы отсчета.Пока вы последовательны, любой фрейм одинаково действителен. Но вы не хотите менять систему координат во время расчета. Представьте, что вы сидите в поезде на станции и вдруг замечаете, что станция движется назад. Большинство людей сказали бы, что они просто не заметили, что поезд движется — только казалось, что движется станцией. Но это показывает, что существует третий произвольный выбор, связанный с выбором системы координат: действительные системы отсчета могут отличаться друг от друга, перемещаясь друг относительно друга.Может показаться странным использование системы координат, движущейся относительно земли, но, например, система координат, движущаяся вместе с поездом, может быть гораздо более удобной для описания вещей, происходящих внутри поезда. Рамки отсчета особенно важны при описании смещения объекта.
СПРАВОЧНИКИ профессора Хьюма и профессора Дональда Айви из Университета Торонто
В этом классическом фильме профессора Хьюм и Айви умело иллюстрируют системы отсчета и различают фиксированные и движущиеся системы отсчета.
Frames of Reference (1960) Обучающий фильм : Frames of Reference — образовательный фильм 1960 года, созданный Комитетом по изучению физических наук. Фильм предназначен для показа на курсах физики в средней школе. В фильме профессора физики Университета Торонто Паттерсон Хьюм и Дональд Айви объясняют различие между инерциальной и неинтерциальной системами отсчета, демонстрируя эти концепции с помощью юмористических трюков с камерой. Например, фильм открывается с Доктора.Хьюм, который кажется перевернутым, обвиняет доктора Айви в том, что он перевернут. Только когда пара подбрасывает монету, становится очевидно, что доктор Айви — и камера — действительно перевернуты. Юмор фильма служит как для заинтересованности студентов, так и для демонстрации обсуждаемых концепций. В этом фильме PSSC используется увлекательный набор, состоящий из вращающегося стола и мебели, занимающих неожиданно непредсказуемые места в зоне просмотра. Прекрасная кинематография Авраама Морочника и забавное повествование профессоров Университета Торонто Дональда Айви и Паттерсона Хьюма — прекрасный пример того, как творческая группа кинематографистов может весело провести время с предметом, который другие, менее изобретательные люди могут посчитать пешеходом.Продюсер: Ричард Ликок Продюсерская компания: Educational Development Corp. Спонсор: Эрик Престамон
Рабочий объем
Смещение — это изменение положения объекта относительно его системы отсчета. Например, если автомобиль движется из дома в продуктовый магазин, его перемещение — это относительное расстояние продуктового магазина до системы отсчета или дома. Слово «смещение» означает, что объект переместился или был перемещен. Смещение — это изменение положения объекта, которое математически можно представить следующим образом:
[латекс] \ Delta \ text {x} = \ text {x} _ \ text {f} — \ text {x} _0 [/ latex]
, где Δ x — смещение, x f — конечное положение, а x 0 — начальное положение.
показывает важность использования системы координат при описании перемещения пассажира в самолете.
Перемещение в системе ведения : Пассажир перемещается со своего места на заднюю часть самолета. Его расположение относительно самолета указано x. Смещение пассажира на -4,0 м относительно самолета показано стрелкой в направлении задней части самолета. Обратите внимание, что стрелка, обозначающая его перемещение, вдвое длиннее стрелки, обозначающей перемещение профессора (он перемещается вдвое дальше).
Введение в скаляры и векторы
Вектор — это любая величина, которая имеет как величину, так и направление, тогда как скаляр имеет только величину.
Цели обучения
Определите разницу между скалярами и векторами
Основные выводы
Ключевые моменты
- Вектор — это любая величина, имеющая величину и направление.
- Скаляр — это любая величина, которая имеет величину, но не имеет направления.
- Смещение и скорость — это векторы, а расстояние и скорость — скаляры.
Ключевые термины
- скаляр : величина, имеющая величину, но не направление; сравнить вектор.
- вектор : Направленная величина, имеющая как величину, так и направление; между двумя точками.
В чем разница между расстоянием и смещением? В то время как смещение определяется как направлением, так и величиной, расстояние определяется только величиной. Смещение — это пример векторной величины. Расстояние — это пример скалярной величины.Вектор — это любая величина, имеющая как величину, так и направление. Другие примеры векторов включают скорость 90 км / ч на восток и силу 500 ньютонов прямо вниз.
Скаляры и векторы : Г-н Андерсен объясняет различия между скалярными и векторными величинами. Он также использует демонстрацию, чтобы показать важность векторов и сложения векторов.
В математике, физике и технике вектор — это геометрический объект, который имеет величину (или длину) и направление и может быть добавлен к другим векторам в соответствии с векторной алгеброй.Направление вектора в одномерном движении задается просто знаком плюс (+) или минус (-). Вектор часто представлен отрезком линии с определенным направлением или графически в виде стрелки, соединяющей начальную точку A с конечной точкой B, как показано на.
Векторное представление : Вектор часто представляется отрезком линии с определенным направлением или графически в виде стрелки, соединяющей начальную точку A с конечной точкой B.
Некоторые физические величины, например расстояние, либо не имеют направления, либо не имеют определенного направления.В физике скаляр — это простая физическая величина, которая не изменяется при поворотах или перемещениях системы координат. Это любая величина, которая может быть выражена одним числом и имеет величину, но не направление. Например, температура 20ºC, 250 килокалорий (250 калорий) энергии в шоколадном батончике, ограничение скорости 90 км / ч, рост человека 1,8 м и расстояние 2,0 м — все это скаляры или количества без указания направление. Обратите внимание, однако, что скаляр может быть отрицательным, например, температура –20ºC.В этом случае знак минус указывает точку на шкале, а не направление. Скаляры никогда не изображаются стрелками. (Сравнение скаляров и векторов показано на.)
Скаляры и векторы : Краткий список величин, которые являются либо скалярами, либо векторами.
Решение проблем базовой кинематики | Безграничная физика
Приложения
Есть четыре кинематических уравнения, которые описывают движение объектов без учета его причин.
Цели обучения
Выберите, какое уравнение кинематики использовать в задачах, в которых начальное начальное положение равно нулю
Основные выводы
Ключевые моменты
- Четыре кинематических уравнения включают пять кинематических переменных: [latex] \ text {d} [/ latex], [latex] \ text {v} [/ latex], [latex] \ text {v} _0 [/ latex] , [латекс] \ text {a} [/ latex] и [латекс] \ text {t} [/ latex].
- Каждое уравнение содержит только четыре из пяти переменных, а другая отсутствует.
- Важно выбрать уравнение, которое содержит три известные переменные и одну неизвестную переменную для каждой конкретной ситуации.
Ключевые термины
- кинематика : Раздел физики, связанный с движущимися объектами.
Кинематика — это раздел классической механики, который описывает движение точек, тел (объектов) и систем тел (групп объектов) без учета причин движения. Есть четыре кинематических уравнения, когда начальная начальная позиция является началом координат, а ускорение постоянно:
- [латекс] \ text {v} = \ text {v} _0 + \ text {at} [/ latex]
- [латекс] \ text {d} = \ frac {1} {2} (\ text {v} _0 + \ text {v}) \ text {t} [/ latex] или альтернативно [латекс] \ text {v } _ {\ text {average}} = \ frac {\ text {d}} {\ text {t}} [/ latex]
- [латекс] \ text {d} = \ text {v} _0 \ text {t} + (\ frac {\ text {at} ^ 2} {2}) [/ latex]
- [латекс] \ text {v} ^ 2 = \ text {v} _0 ^ 2 + 2 \ text {ad} [/ latex]
Обратите внимание, что четыре кинематических уравнения включают пять кинематических переменных: [latex] \ text {d} [/ latex] , [latex] \ text {v} [/ latex] , [latex] \ text {v } _0 [/ latex] , [латекс] \ text {a} [/ latex] и [латекс] \ text {t} [/ latex].Каждое из этих уравнений содержит только четыре из пяти переменных, а другая отсутствует. Это говорит нам, что нам нужны значения трех переменных, чтобы получить значение четвертой, и нам нужно выбрать уравнение, которое содержит три известные переменные и одну неизвестную переменную для каждой конкретной ситуации.
Вот основные этапы решения проблем с использованием этих уравнений:
Шаг первый — Определите, что именно необходимо определить в проблеме (определите неизвестные).
Шаг второй. Найдите уравнение или систему уравнений, которые помогут вам решить проблему.
Шаг третий — Подставьте известные значения вместе с их единицами измерения в соответствующее уравнение и получите численные решения вместе с единицами измерения.
Шаг четвертый. Проверьте ответ, чтобы узнать, разумен ли он: имеет ли он смысл?
Навыки решения проблем, безусловно, необходимы для успешного прохождения количественного курса физики. Что еще более важно, способность применять общие физические принципы, обычно представленные уравнениями, к конкретным ситуациям — очень мощная форма знания.Это намного эффективнее, чем запоминание списка фактов. Аналитические навыки и способности решать проблемы могут быть применены к новым ситуациям, тогда как список фактов не может быть достаточно длинным, чтобы содержать все возможные обстоятельства. Такие аналитические навыки полезны как для решения задач на уроках физики, так и для применения физики в повседневной и профессиональной жизни.
Диаграммы движения
Диаграмма движения — это графическое описание движения объекта, которое представляет положение объекта через равные промежутки времени.
Цели обучения
Построить диаграмму движения
Основные выводы
Ключевые моменты
- Диаграммы движения представляют движение объекта, отображая его местоположение в разное время с равным интервалом на одной диаграмме.
- Диаграммы движения показывают начальное положение и скорость объекта, а также несколько точек в центре диаграммы. Эти пятна показывают состояние движения объекта.
- Диаграммы движения содержат информацию о положении объекта в определенные моменты времени и поэтому являются более информативными, чем диаграмма путей.
Ключевые термины
- стробоскопический : Относится к инструменту, с помощью которого циклически движущийся объект выглядит медленно движущимся или неподвижным.
- диаграмма : график или диаграмма.
- движение : изменение положения относительно времени.
Диаграмма движения — это графическое описание движения объекта. Он отображает местоположение объекта в разное время с равным интервалом на одной диаграмме; показывает начальное положение и скорость объекта; и представляет несколько точек в центре диаграммы.Эти пятна показывают, ускорился или замедлился объект. Для простоты объект представлен простой формой, например закрашенным кружком, который содержит информацию о положении объекта в определенные моменты времени. По этой причине диаграмма движения дает больше информации, чем диаграмма пути. Он также может отображать силы, действующие на объект в каждый момент времени.
— диаграмма движения по простой траектории. Представьте себе объект в виде хоккейной шайбы, скользящей по льду.Обратите внимание, что шайба преодолевает одинаковое расстояние за единицу пути по траектории. Можно сделать вывод, что шайба движется с постоянной скоростью и, следовательно, во время движения нет ускорения или замедления.
Шайба, скользящая по льду : Диаграмма движения шайбы, скользящей по льду. Шайба движется с постоянной скоростью.
Одно из основных применений диаграмм движения — это представление фильма через серию кадров, снятых камерой; это иногда называют стробоскопической техникой (как показано на рисунке).Просмотр объекта на диаграмме движения позволяет определить, ускоряется или замедляется объект или находится в постоянном покое. Когда кадры сделаны, мы можем предположить, что объект находится в постоянном покое, если он занимает одно и то же положение с течением времени. Мы можем предположить, что объект ускоряется, если есть видимое увеличение пространства между объектами с течением времени, и что он замедляется, если есть видимое уменьшение пространства между объектами с течением времени. Объекты на кадре очень близко подходят друг к другу.
прыгающий мяч : прыгающий мяч, снятый с помощью стробоскопической вспышки со скоростью 25 изображений в секунду.
Kinematics and Calculus — The Physics Hypertextbook
Обсуждение
постоянное ускорение
Исчисление — это сложная математическая тема, но она значительно упрощает вывод двух из трех уравнений движения. По определению, ускорение — это первая производная скорости по времени. Возьмите операцию в этом определении и отмените ее.Вместо того, чтобы дифференцировать скорость, чтобы найти ускорение, интегрируйте ускорение, чтобы найти скорость. Это дает нам уравнение скорости-времени. Если предположить, что ускорение постоянное, мы получим так называемое первое уравнение движения [1].
| = | |||
| дв | = | a dt | |
| = | |||
| v — v 0 | = | при | |
| в | = | v 0 + at [1] | |
Опять же, по определению, скорость — это первая производная положения по времени.Выполните эту операцию в обратном порядке. Вместо того, чтобы различать положение для определения скорости, интегрируйте скорость, чтобы найти положение. Это дает нам уравнение положения-времени для постоянного ускорения, также известное как второе уравнение движения [2].
| v | = | |||||||||
| DS | = | v dt | ||||||||
| DS | = | ( v 0 + at ) dt | ||||||||
| = |
|
|||||||||
| с — с 0 | = | v 0 t + ½ at 2 | ||||||||
| с | = | s 0 + v 0 t + ½ at 2 [2] | ||||||||
В отличие от первого и второго уравнений движения, нет очевидного способа вывести третье уравнение движения (то, которое связывает скорость с положением) с помощью расчетов.Мы не можем просто перепроектировать это по определению. Нам нужно разыграть довольно изощренный трюк.
Первое уравнение движения связывает скорость со временем. По сути, мы вывели его из этой производной…
Второе уравнение движения связывает положение со временем. Это произошло от этой производной…
Третье уравнение движения связывает скорость с положением. По логике, это должно происходить от производной, которая выглядит так…
Но что это значит? Ну, ничего по определению, но, как и все количества, оно равно самому себе.Он также равен самому себе, умноженному на 1. Мы будем использовать специальную версию 1 ( dt dt ) и специальную версию алгебры (алгебру с бесконечно малыми). Посмотрите, что происходит, когда мы это делаем. Мы получаем одну производную, равную ускорению ( dv dt ), и другую производную, равную обратной скорости ( dt ds ).
| дв | = | дв | 1 | |
| DS | DS | |||
| дв | = | дв | дт | |
| DS | DS | дт | ||
| дв | = | дв | дт | |
| DS | дт | DS | ||
| дв | = | 1 | ||
| DS | v |
Следующий шаг, разделение переменных.Соберите вместе похожие вещи и интегрируйте их. Вот что мы получаем при постоянном ускорении…
| = | ||||
| в дв | = | а DS | ||
| = | ||||
| ½ ( v 2 — v 0 2 ) | = | a ( с — с 0 ) | ||
| v 2 | = | v 0 2 + 2 a ( s — s 0 ) [3] | ||
Безусловно, умное решение, и оно было не так уж сложно, чем первые два варианта.Однако на самом деле это сработало только потому, что ускорение было постоянным — постоянным во времени и постоянным в пространстве. Если бы ускорение каким-либо образом менялось, этот метод был бы неудобно трудным. Мы вернемся к алгебре, чтобы спасти наше здравомыслие. Не то чтобы в этом что-то не так. Алгебра работает, а здравомыслие стоит сэкономить.
| v = | v 0 + at | [1] |
| + | ||
| с = | с 0 + v 0 t + ½ при 2 | [2] |
| = | ||
| v 2 = | v 0 2 + 2 a ( с — с 0 ) | [3] |
рывок постоянный
Показанный выше метод работает даже при непостоянном ускорении.Применим его к ситуации с необычным названием — постоянный рывок. Нет лжи, вот как это называется. Рывок — это скорость изменения ускорения во времени.
Это делает рывком первую производную ускорения, вторую производную скорости и третью производную положения.
| Дж = | da | = | d 2 v | = | d 3 s |
| дт | дт 2 | дт 3 |
Единица рывка в системе СИ — это метра в секунду в кубе .
| ⎡ ⎢ ⎣ |
м / с 3 | = | м / с 2 | ⎤ ⎥ ⎦ |
| с |
Альтернативная единица измерения — г в секунду .
Jerk — это не просто ответ некоторых мудрых физиков на вопрос: «Ах да, так как вы называете третью производную от позиции ?» Рывок — это значимая величина.
Человеческое тело оснащено датчиками, определяющими ускорение и рывки.Глубоко внутри уха, в нашем черепе, находится ряд камер, называемых лабиринтом . Часть этого лабиринта предназначена для нашего слуха (улитка , ), а часть — для нашего чувства равновесия (вестибулярная система , ). Вестибулярная система оснащена датчиками, определяющими угловое ускорение (полукружные каналы , ) и датчиками, определяющими линейное ускорение (отолиты , ). У нас есть два отолита в каждом ухе — один для определения ускорения в горизонтальной плоскости (мешочек ) и один для определения ускорения в вертикальном месте (мешочек ).Отолиты — это наши собственные встроенные акселерометры.
Слово отолит происходит от греческого οτο ( oto ) для уха и λιθος ( lithos ) для камня. Каждый из наших четырех отолитов состоит из твердой костеподобной пластины, прикрепленной к мату из сенсорных волокон. Когда голова ускоряется, пластина смещается в сторону, изгибая сенсорные волокна. Это посылает в мозг сигнал: «Мы ускоряемся». Поскольку гравитация также действует на пластины, сигнал может также означать, что «это путь вниз».«Мозг довольно хорошо понимает разницу между двумя интерпретациями. Настолько хорош, что мы склонны игнорировать это. Зрение, звук, запах, вкус, прикосновение — где баланс в этом списке? Мы игнорируем его, пока что-то не изменится в необычный, неожиданный или экстремальный способ.
Я никогда не был на орбите и не жил на другой планете. Гравитация всегда одинаково тянет меня вниз. Стоять, ходить, сидеть, лежать — все это довольно степенно. А теперь давайте сядем на американские горки или займемся не менее захватывающим занятием, например, катанием на горных лыжах, гонками Формулы-1 или ездой на велосипеде в пробках Манхэттена.Ускорение направлено сначала в одну сторону, затем в другую. Вы даже можете испытывать кратковременные периоды невесомости или инверсии. Подобные ощущения вызывают интенсивную умственную деятельность, поэтому нам нравится их выполнять. Они также обостряют нас и удерживают сосредоточенность в моменты, которые, возможно, заканчиваются жизнью, поэтому мы в первую очередь развили это чувство. Ваша способность чувствовать подергивание жизненно важна для вашего здоровья и благополучия. Рывок одновременно увлекателен и необходим.
С постоянным рывком легко справиться математически.В качестве обучающего упражнения выведем уравнения движения для постоянного рывка. Если хотите, можете попробовать более сложные задачи с толчком.
Рывок — это производная от ускорения. Отменить этот процесс. Интегрируйте рывок, чтобы получить ускорение в зависимости от времени. Я предлагаю называть это нулевым уравнением движения для постоянного рывка . Причина станет очевидной после того, как мы закончим следующий вывод.
| Дж = | da | |
| дт | ||
| da = | j dt | |
| т | |||
| ⌠ ⌡ |
да = | ⌠ ⌡ |
Дж ДТ |
| а 0 | 0 |
| а — а 0 = | jt | |
| = | a 0 + jt | [0] |
Ускорение — это производная скорости.Интегрируйте ускорение, чтобы получить скорость как функцию времени. Мы делали этот процесс раньше. Мы назвали результат соотношением скорость-время или первым уравнением движения, когда ускорение было постоянным. Мы должны дать ему похожее имя. Это первое уравнение движения для постоянного рывка .
| = | ||
| дв = | a dt | |
| дв = | ( a 0 + jt ) dt | |
| в | т | ||
| ⌠ ⌡ |
дв = | ⌠ ⌡ |
( a 0 + jt ) dt |
| в 0 | 0 |
| v — v 0 = | a 0 т + ½ jt 2 | ||
| v = | v 0 + a 0 t + ½ jt 2 | [1] | |
Скорость — это производная от смещения.Интегрируйте скорость, чтобы получить смещение как функцию времени. Мы тоже это делали раньше. Результирующая зависимость смещения от времени будет нашим вторым уравнением движения для постоянного рывка .
| v = | ||
| DS = | v dt | |
| DS = | ( v 0 + a 0 t + ½ jt 2 ) dt | |
| с | т | ||
| ⌠ ⌡ |
DS = | ⌠ ⌡ |
( v 0 + a 0 t + ½ jt 2 ) dt |
| с 0 | 0 |
| с — с 0 = | v 0 t + ½ a 0 t 2 + ⅙ jt 3 | ||
| с = | с 0 + v 0 t + ½ a 0 t 2 + ⅙ jt 3 | [2] | |
Обратите внимание на эти уравнения.Когда рывок равен нулю, все они возвращаются к уравнениям движения для постоянного ускорения. Нулевой рывок означает постоянное ускорение, так что все в порядке с миром, который мы создали. (Я никогда не говорил, что постоянное ускорение — это реальность. Постоянный рывок тоже миф. Однако в мире гипертекстов все возможно.)
Куда мы пойдем дальше? Должны ли мы работать над соотношением скорость-смещение (третье уравнение движения для постоянного рывка)?
| v = | v 0 + a 0 t + ½ jt 2 | [1] |
| + | ||
| с = | с 0 + v 0 t + ½ a 0 t 2 + ⅙ jt 3 | [2] |
| = | ||
| v = | f ( s ) | [3] |
Как насчет зависимости ускорения от смещения (четвертое уравнение движения для постоянного рывка)?
| = | a 0 + jt | [1] |
| + | ||
| с = | с 0 + v 0 t + ½ a 0 t 2 + ⅙ jt 3 | [2] |
| = | ||
| = | f ( s ) | [4] |
Я даже не знаю, можно ли их вычислить алгебраически.Я сомневаюсь в этом. Посмотрите на это страшное кубическое уравнение для смещения. Это не может быть нашим другом. На данный момент меня это не беспокоит. Не знаю, расскажет ли мне про это что-нибудь интересное. Я, –, знаю, что мне никогда не требовалось третье или четвертое уравнение движения для постоянного рывка — пока нет. Я оставляю эту задачу математикам всего мира.
Это проблема, которая отличает физиков от математиков. Математика не обязательно заботит физическая значимость, и он может просто поблагодарить физика за интересный вызов.Физика не обязательно заботит ответ, если он не окажется полезным, и в этом случае физик обязательно поблагодарит математика за его любопытство.
постоянная ничего
Эта страница в этой книге не о движении с постоянным ускорением, постоянным рывком, постоянным щелчком, треском или треском. Речь идет об общем методе определения количества движения (положения, скорости и ускорения) относительно времени и друг друга для любого вида движения.Для этого используется либо дифференцирование (нахождение производной)…
- Производная положения по времени — это скорость ( v = ds dt ).
- Производная скорости по времени — это ускорение ( a = dv dt ).
или интегрирование (нахождение интеграла)…
- Интеграл ускорения во времени — это изменение скорости (∆ v = ∫ a dt ).
- Интеграл скорости во времени — это изменение положения (∆ с = ∫ v dt ).
Вот как это работает. Некоторая характеристика движения объекта описывается функцией. Можете ли вы найти производную от этой функции? Это дает вам еще одну характеристику движения. Можете ли вы найти его интеграл? Это дает вам другую характеристику. Повторите любую операцию столько раз, сколько необходимо. Затем примените методы и концепции, которые вы изучили в исчислении и связанных областях математики, чтобы извлечь больше смысла — диапазон, область, предел, асимптота, минимум, максимум, экстремум, вогнутость, перегиб, аналитический, числовой, точный, приблизительный и т. Д.Я добавил несколько важных примечаний по этому поводу в резюме по этой теме.
3.4 Движение с постоянным ускорением — University Physics Volume 1
Учебные цели
К концу этого раздела вы сможете:
- Определите, какие уравнения движения следует использовать для решения неизвестных.
- Используйте соответствующие уравнения движения для решения задачи преследования двух тел.
Можно предположить, что чем больше ускорение, скажем, у автомобиля, удаляющегося от знака «Стоп», тем больше смещение автомобиля за данный момент времени.Но мы не разработали конкретное уравнение, которое связывает ускорение и смещение. В этом разделе мы рассмотрим некоторые удобные уравнения кинематических отношений, начиная с определений смещения, скорости и ускорения. Сначала мы исследуем движение одного объекта, называемого движением одного тела. Затем мы исследуем движение двух объектов, называемое задачами преследования двух тел.
Обозначение
Во-первых, сделаем несколько упрощений в обозначениях. Принятие начального времени равным нулю, как если бы время измерялось секундомером, является большим упрощением.Поскольку прошедшее время равно Δt = tf − t0Δt = tf − t0, взятие t0 = 0t0 = 0 означает, что Δt = tfΔt = tf, последнее время на секундомере. Когда начальное время принимается равным нулю, мы используем индекс 0 для обозначения начальных значений положения и скорости. То есть x0x0 — это начальная позиция , а v0v0 — начальная скорость . Мы не ставим индексы на окончательные значения. То есть t — это конечный момент времени , x — конечная позиция , а v — конечная скорость . Это дает более простое выражение для затраченного времени: Δt = tΔt = t.Это также упрощает выражение для смещения x , которое теперь равно Δx = x − x0Δx = x − x0. Кроме того, это упрощает выражение для изменения скорости, которое теперь равно Δv = v − v0Δv = v − v0. Подводя итог, используя упрощенные обозначения, с начальным временем, принятым равным нулю,
Δt = tΔx = x − x0Δv = v − v0, Δt = tΔx = x − x0Δv = v − v0,, где нижний индекс 0 обозначает начальное значение, а отсутствие нижнего индекса означает конечное значение в любом рассматриваемом движении.
Теперь мы делаем важное предположение, что ускорение постоянно .Это предположение позволяет нам избегать использования расчетов для определения мгновенного ускорения. Поскольку ускорение постоянно, среднее и мгновенное ускорения равны, то есть
a– = a = постоянная. a– = a = постоянная.Таким образом, мы можем использовать символ a для ускорения в любое время. Предположение, что ускорение является постоянным, не серьезно ограничивает ситуации, которые мы можем изучить, и не ухудшает точность нашего лечения. Во-первых, ускорение равно постоянным в большом количестве ситуаций.Кроме того, во многих других ситуациях мы можем точно описать движение, приняв постоянное ускорение, равное среднему ускорению для этого движения. Наконец, для движения, во время которого ускорение резко меняется, например, когда автомобиль разгоняется до максимальной скорости, а затем тормозит до остановки, движение можно рассматривать в отдельных частях, каждая из которых имеет собственное постоянное ускорение.
Смещение и положение от скорости
Чтобы получить наши первые два уравнения, мы начнем с определения средней скорости:
Подставляя упрощенные обозначения для ΔxΔx и ΔtΔt, получаем
v– = x − x0t.v– = x − x0t.Решение относительно x дает нам
x = x0 + v – t, x = x0 + v – t,3,10
, где средняя скорость
v– = v0 + v2.v– = v0 + v2.3,11
Уравнение v– = v0 + v2v– = v0 + v2 отражает тот факт, что при постоянном ускорении v – v– представляет собой просто среднее значение начальной и конечной скоростей. Рисунок 3.18 графически иллюстрирует эту концепцию. В части (а) рисунка ускорение является постоянным, а скорость увеличивается с постоянной скоростью. Средняя скорость в течение 1-часового интервала от 40 км / ч до 80 км / ч составляет 60 км / ч:
v– = v0 + v2 = 40 км / ч + 80 км / ч3 = 60 км / ч.v– = v0 + v2 = 40 км / ч + 80 км / ч3 = 60 км / ч.В части (b) ускорение не является постоянным. В течение 1-часового интервала скорость ближе к 80 км / ч, чем к 40 км / ч. Таким образом, средняя скорость больше, чем в части (а).
Рис. 3.18 (a) График зависимости скорости от времени с постоянным ускорением, показывающий начальную и конечную скорости v0andvv0andv. Средняя скорость равна 12 (v0 + v) = 60 км / ч22 (v0 + v) = 60 км / ч. (б) График зависимости скорости от времени с изменением ускорения со временем. Средняя скорость не равна 12 (v0 + v) 12 (v0 + v), но превышает 60 км / ч.Решение окончательной скорости по ускорению и времени
Мы можем вывести еще одно полезное уравнение, манипулируя определением ускорения:
Подстановка упрощенных обозначений для ΔvΔv и ΔtΔt дает
а = v − v0t (константа). a = v − v0t (константа).Решение для v дает
v = v0 + at (constanta). v = v0 + at (constanta).3,12
Пример 3,7
Расчет конечной скорости
Самолет приземляется с начальной скоростью 70.0 м / с, а затем ускоряется против движения со скоростью 1,50 м / с 2 за 40,0 с. Какова его конечная скорость?Стратегия
Сначала мы идентифицируем известные: v0 = 70 м / с, a = -1,50 м / с2, t = 40sv0 = 70 м / с, a = -1,50 м / с2, t = 40 с.Во-вторых, мы идентифицируем неизвестное; в данном случае это конечная скорость vfvf.
Наконец, мы определяем, какое уравнение использовать. Для этого мы выясняем, какое кинематическое уравнение дает неизвестное в терминах известных. Мы рассчитываем окончательную скорость, используя уравнение 3.12, v = v0 + atv = v0 + at.
Решение
Подставьте известные значения и решите: v = v0 + при = 70,0 м / с + (- 1,50 м / с2) (40,0 с) = 10,0 м / с v = v0 + при = 70,0 м / с + (- 1,50 м / с2) (40,0 с) = 10,0 м / с.Рисунок 3.19 представляет собой эскиз, показывающий векторы ускорения и скорости.
Рис. 3.19. Самолет приземляется с начальной скоростью 70,0 м / с и замедляется до конечной скорости 10,0 м / с, прежде чем направиться к терминалу. Обратите внимание, что ускорение отрицательное, потому что его направление противоположно его скорости, которая положительна.
Значение
Конечная скорость намного меньше начальной скорости, требуемой при замедлении, но все же положительная (см. Рисунок). С реактивными двигателями обратная тяга может поддерживаться достаточно долго, чтобы остановить самолет и начать движение назад, на что указывает отрицательная конечная скорость, но в данном случае это не так.Помимо полезности при решении задач, уравнение v = v0 + atv = v0 + at дает нам представление о взаимосвязях между скоростью, ускорением и временем.Мы видим, например, что
- Конечная скорость зависит от того, насколько велико ускорение и как долго оно длится
- Если ускорение равно нулю, то конечная скорость равна начальной скорости ( v = v 0 ), как и ожидалось (другими словами, скорость постоянна)
- Если a отрицательное, то конечная скорость меньше начальной скорости
Все эти наблюдения соответствуют нашей интуиции. Обратите внимание, что всегда полезно исследовать основные уравнения в свете нашей интуиции и опыта, чтобы убедиться, что они действительно точно описывают природу.
Решение для конечного положения с постоянным ускорением
Мы можем объединить предыдущие уравнения, чтобы найти третье уравнение, которое позволяет нам вычислить окончательное положение объекта, испытывающего постоянное ускорение. Начнем с
Добавление v0v0 к каждой стороне этого уравнения и деление на 2 дает
v0 + v2 = v0 + 12at. v0 + v2 = v0 + 12at.Так как v0 + v2 = v – v0 + v2 = v– для постоянного ускорения, имеем
v– = v0 + 12at.v– = v0 + 12at.Теперь мы подставляем это выражение для v – v– в уравнение для смещения, x = x0 + v – tx = x0 + v – t, что дает
х = х0 + v0t + 12at2 (константа).х = х0 + v0t + 12at2 (константа).3,13
Пример 3.8
Расчет смещения ускоряющегося объекта
Драгстеры могут развивать среднее ускорение 26,0 м / с 2 . Предположим, драгстер ускоряется из состояния покоя с этой скоростью в течение 5,56 с. Рис. 3.20. Как далеко он пролетит за это время?Рис. 3.20. Пилот Top Fuel в армии США Тони «Сержант» Шумахер начинает гонку с контролируемого выгорания. (Источник: подполковник Уильям Термонд. Фото любезно предоставлено США.Армия.)
Стратегия
Сначала нарисуем набросок Рис. 3.21. Нас просят найти смещение, которое составляет x , если мы примем x0x0 равным нулю. (Думайте о x0x0 как о стартовой линии гонки. Она может быть где угодно, но мы называем ее нулевой и измеряем все остальные позиции относительно нее.) Мы можем использовать уравнение x = x0 + v0t + 12at2x = x0 + v0t + 12at2 когда мы идентифицируем v0v0, aa и t из постановки задачи.Рис. 3.21. Эскиз разгоняющегося драгстера.
Решение
Во-первых, нам нужно определить известные.Запуск из состояния покоя означает, что v0 = 0v0 = 0, a задается как 26,0 м / с 2 и t задается как 5,56 с.Во-вторых, мы подставляем известные значения в уравнение, чтобы найти неизвестное:
x = x0 + v0t + 12at2.x = x0 + v0t + 12at2.Поскольку начальное положение и скорость равны нулю, это уравнение упрощается до
Подстановка идентифицированных значений на и т дает
x = 12 (26,0 м / с2) (5,56 с) 2 = 402 м. x = 12 (26,0 м / с2) (5,56 с) 2 = 402 м.Значение
Если мы переведем 402 м в мили, мы обнаружим, что пройденное расстояние очень близко к четверти мили, стандартному расстоянию для дрэг-рейсинга. Итак, наш ответ разумный. Это впечатляющий водоизмещение всего за 5,56 с, но первоклассные драгстеры могут преодолеть четверть мили даже за меньшее время. Если бы драгстеру была присвоена начальная скорость, это добавило бы еще один член в уравнение расстояния. Если в уравнении использовать те же ускорение и время, пройденное расстояние будет намного больше.Что еще мы можем узнать, исследуя уравнение x = x0 + v0t + 12at2? X = x0 + v0t + 12at2? Мы видим следующие отношения:
- Смещение зависит от квадрата истекшего времени, когда ускорение не равно нулю. В примере 3.8 драгстер преодолевает только четверть общего расстояния за первую половину прошедшего времени.
- Если ускорение равно нулю, то начальная скорость равна средней скорости (v0 = v -) (v0 = v–), и x = x0 + v0t + 12at2becomesx = x0 + v0t.x = x0 + v0t + 12at2becomesx = x0 + v0t.
Расчет конечной скорости по расстоянию и ускорению
Четвертое полезное уравнение может быть получено путем другой алгебраической обработки предыдущих уравнений. Если мы решим v = v0 + atv = v0 + at для t , мы получим
Подставляя это и v– = v0 + v2v– = v0 + v2 в x = x0 + v – tx = x0 + v – t, получаем
v2 = v02 + 2a (x − x0) (constanta). v2 = v02 + 2a (x − x0) (constanta).3,14
Пример 3.9
Расчет конечной скорости
Рассчитайте конечную скорость драгстера в Примере 3.8 без использования информации о времени.Стратегия
Уравнение v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) идеально подходит для этой задачи, поскольку оно связывает скорости, ускорение и смещение и не требует информации о времени.Решение
Сначала мы идентифицируем известные значения. Мы знаем, что v 0 = 0, поскольку драгстер запускается из состояния покоя. Мы также знаем, что x — x 0 = 402 м (это был ответ в примере 3.8). Среднее ускорение к г. составило = 26.0 м / с 2 .Во-вторых, мы подставляем известные значения в уравнение v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) и решаем относительно v :
v2 = 0 + 2 (26,0 м / с2) (402 м). v2 = 0 + 2 (26,0 м / с2) (402 м).Таким образом,
v2 = 2,09 × 104 м2 / с2 v = 2,09 × 104 м2 / с2 = 145 м / с. v2 = 2,09 × 104 м2 / с2v = 2,09 × 104 м2 / с2 = 145 м / с.Значение
Скорость 145 м / с составляет около 522 км / ч или около 324 миль / ч, но даже эта головокружительная скорость не достигает рекорда для четверти мили. Также обратите внимание, что квадратный корень имеет два значения; мы взяли положительное значение, чтобы указать скорость в том же направлении, что и ускорение.Изучение уравнения v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) может дать дополнительное понимание общих соотношений между физическими величинами:
- Конечная скорость зависит от величины ускорения и расстояния, на котором оно действует.
- При фиксированном ускорении автомобиль, который едет вдвое быстрее, просто не останавливается на удвоенном расстоянии. Чтобы остановиться, нужно гораздо дальше. (Вот почему у нас есть зоны с пониженной скоростью возле школ.)
Объединение уравнений
В следующих примерах мы продолжаем исследовать одномерное движение, но в ситуациях, требующих немного больше алгебраических манипуляций.Примеры также дают представление о методах решения проблем. Следующее примечание предназначено для облегчения поиска необходимых уравнений. Имейте в виду, что эти уравнения не являются независимыми. Во многих ситуациях у нас есть два неизвестных, и нам нужно два уравнения из набора для решения неизвестных. Для решения данной ситуации нам нужно столько уравнений, сколько неизвестных.
Сводка кинематических уравнений (константа
a ) х = х0 + v0t + 12at2x = x0 + v0t + 12at2 v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0)Прежде чем мы перейдем к примерам, давайте более внимательно рассмотрим некоторые уравнения, чтобы увидеть поведение ускорения при экстремальных значениях.Переставляя уравнение 3.12, получаем
Из этого мы видим, что в течение конечного времени, если разница между начальной и конечной скоростями мала, ускорение невелико, приближаясь к нулю в пределе, когда начальная и конечная скорости равны. Напротив, в пределе t → 0t → 0 при конечной разности начальной и конечной скоростей ускорение становится бесконечным.
Аналогичным образом, переставляя уравнение 3.14, мы можем выразить ускорение в терминах скоростей и смещения:
а = v2-v022 (х-х0).а = v2-v022 (х-х0).Таким образом, при конечной разнице между начальной и конечной скоростями ускорение становится бесконечным, в пределе смещение приближается к нулю. Ускорение приближается к нулю в пределе, разница в начальной и конечной скоростях приближается к нулю для конечного смещения.
Пример 3.10
Как далеко уезжает машина?
На сухом бетоне автомобиль может ускоряться против движения со скоростью 7,00 м / с 2 , тогда как на мокром бетоне он может ускоряться противоположно движению со скоростью всего 5 м / с.00 м / с 2 . Найдите расстояния, необходимые для остановки автомобиля, движущегося со скоростью 30,0 м / с (около 110 км / ч) по (а) сухому бетону и (б) мокрому бетону. (c) Повторите оба вычисления и найдите смещение от точки, где водитель видит, что светофор становится красным, принимая во внимание время его реакции 0,500 с, чтобы нажать ногой на тормоз.Стратегия
Для начала нам нужно нарисовать набросок Рис. 3.22. Чтобы определить, какие уравнения лучше всего использовать, нам нужно перечислить все известные значения и точно определить, что нам нужно решить.Рис. 3.22. Пример эскиза для визуализации ускорения, противоположного движению и тормозному пути автомобиля.
Решение
- Во-первых, нам нужно определить известные и то, что мы хотим решить. Мы знаем, что v 0 = 30,0 м / с, v = 0 и a = −7,00 м / с 2 ( a отрицательно, потому что оно находится в направлении, противоположном скорости) . Возьмем x 0 равным нулю. Ищем смещение ΔxΔx, или x — x 0 .
Во-вторых, мы определяем уравнение, которое поможет нам решить проблему. Лучшее уравнение для использования — v2 = v02 + 2a (x − x0). v2 = v02 + 2a (x − x0). Это уравнение лучше всего, потому что оно включает только одно неизвестное, x . Нам известны значения всех других переменных в этом уравнении. (Другие уравнения позволили бы нам решить для x , но они требуют, чтобы мы знали время остановки, t , которое мы не знаем. Мы могли бы их использовать, но это потребовало бы дополнительных вычислений.)
В-третьих, мы изменим уравнение, чтобы найти x : x − x0 = v2 − v022ax − x0 = v2 − v022a и подставляем известные значения: х − 0 = 02− (30.0 м / с) 22 (-7,00 м / с2). X-0 = 02- (30,0 м / с) 22 (-7,00 м / с2). Таким образом, x = 64,3 м на сухом бетоне. x = 64,3 м на сухом бетоне. - Эта часть может быть решена точно так же, как (a). Единственное отличие состоит в том, что ускорение составляет −5,00 м / с 2 . Результат xwet = 90,0 м по мокрому бетону. xwet = 90,0 м по мокрому бетону.
- Когда водитель реагирует, тормозной путь такой же, как в (a) и (b) для сухого и влажного бетона. Итак, чтобы ответить на этот вопрос, нам нужно вычислить, как далеко проехал автомобиль за время реакции, а затем добавить это время ко времени остановки.Разумно предположить, что скорость остается постоянной в течение времени реакции водителя.
Для этого мы снова определяем известные и то, что мы хотим решить. Мы знаем, что v– = 30,0 м / sv– = 30,0 м / с, treaction = 0,500streaction = 0,500s и areaction = 0areaction = 0. Примем x0-реакцию x0-реакцию равной нулю. Ищем xreactionxreaction.
Во-вторых, как и раньше, мы определяем лучшее уравнение для использования. В этом случае x = x0 + v – tx = x0 + v – t работает хорошо, потому что единственное неизвестное значение — x , что мы и хотим найти.
В-третьих, мы подставляем известные для решения уравнения: x = 0 + (30,0 м / с) (0,500 с) = 15,0 м. x = 0 + (30,0 м / с) (0,500 с) = 15,0 м. Это означает, что автомобиль проезжает 15,0 м, в то время как водитель реагирует, в результате чего общее смещение в двух случаях с сухим и мокрым бетоном на 15,0 м больше, чем если бы он реагировал мгновенно.
Наконец, мы добавляем смещение во время реакции к смещению при торможении (рис. 3.23), xbraking + xreaction = xtotal, xbraking + xreaction = xtotal, и найдите (a) равным 64,3 м + 15,0 м = 79.3 м в сухом состоянии и (b) должно составлять 90,0 м + 15,0 м = 105 м во влажном состоянии.
Рис. 3.23. Расстояние, необходимое для остановки автомобиля, сильно различается в зависимости от дорожных условий и времени реакции водителя. Здесь показаны значения тормозного пути для сухого и мокрого покрытия, рассчитанные в этом примере для автомобиля, движущегося со скоростью 30,0 м / с. Также показано общее расстояние, пройденное от точки, когда водитель впервые видит, что свет загорается красным, при условии, что время реакции составляет 0,500 с.
Значение
Смещения, обнаруженные в этом примере, кажутся разумными для остановки быстро движущегося автомобиля.Остановка автомобиля на мокром асфальте должна длиться дольше, чем на сухом. Интересно, что время реакции значительно увеличивает смещения, но более важен общий подход к решению проблем. Мы идентифицируем известные и определяемые величины, а затем находим соответствующее уравнение. Если существует более одного неизвестного, нам нужно столько независимых уравнений, сколько неизвестных необходимо решить. Часто есть несколько способов решить проблему. Фактически, различные части этого примера могут быть решены другими методами, но представленные здесь решения являются самыми короткими.Пример 3.11
Время расчета
Предположим, автомобиль въезжает в движение по автостраде на съезде длиной 200 м. Если его начальная скорость составляет 10,0 м / с, а ускорение составляет 2,00 м / с 2 , сколько времени потребуется автомобилю, чтобы преодолеть 200 м по рампе? (Такая информация может быть полезна транспортному инженеру.)Стратегия
Сначала мы рисуем набросок Рис. 3.24. Нам предлагается решить за время т . Как и раньше, мы идентифицируем известные величины, чтобы выбрать удобную физическую связь (то есть уравнение с одной неизвестной, t .)Рис. 3.24. Эскиз автомобиля, ускоряющегося на съезде с автострады.
Решение
Опять же, мы определяем известные и то, что мы хотим решить. Мы знаем, что x0 = 0, x0 = 0,v0 = 10 м / с, a = 2,00 м / с2v0 = 10 м / с, a = 2,00 м / с2 и x = 200 м.
Надо решить за т . Уравнение x = x0 + v0t + 12at2x = x0 + v0t + 12at2 работает лучше всего, потому что единственной неизвестной в уравнении является переменная t , которую нам нужно решить. Из этого понимания мы видим, что когда мы вводим известные значения в уравнение, мы получаем квадратное уравнение.
Нам нужно изменить уравнение, чтобы найти t , затем подставив известные значения в уравнение:
200 м = 0 м + (10,0 м / с) t + 12 (2,00 м / с2) t2. 200 м = 0 м + (10,0 м / с) t + 12 (2,00 м / с2) t2.Затем мы упрощаем уравнение. Единицы измерения отменяются, потому что они есть в каждом члене. Мы можем получить единицы секунд для отмены, взяв t = t s, где t — величина времени, а s — единица измерения. Остается
Затем мы используем формулу корней квадратного уравнения, чтобы найти t ,
t2 + 10t − 200 = 0t = −b ± b2−4ac2a, t2 + 10t − 200 = 0t = −b ± b2−4ac2a,, что дает два решения: t = 10.0 и t = −20,0. Отрицательное значение времени неразумно, так как это будет означать, что событие произошло за 20 секунд до начала движения. Мы можем отказаться от этого решения. Таким образом,
Значение
Всякий раз, когда уравнение содержит неизвестный квадрат, есть два решения. В некоторых проблемах имеют смысл оба решения; в других случаях разумно только одно решение. Ответ 10,0 с кажется разумным для типичной автострады на съезде.Проверьте свое понимание 3.5
Ракета ускоряется со скоростью 20 м / с. 2 во время пуска.Сколько времени нужно, чтобы ракета достигла скорости 400 м / с?
Пример 3.12
Ускорение космического корабля
Космический корабль покинул орбиту Земли и направляется к Луне. Разгоняется со скоростью 20 м / с 2 за 2 мин и преодолевает расстояние в 1000 км. Каковы начальная и конечная скорости космического корабля?Стратегия
Нас просят найти начальную и конечную скорости космического корабля. Глядя на кинематические уравнения, мы видим, что одно уравнение не дает ответа.Мы должны использовать одно кинематическое уравнение для решения одной из скоростей и подставить его в другое кинематическое уравнение, чтобы получить вторую скорость. Таким образом, мы решаем два кинематических уравнения одновременно.Решение
Сначала мы решаем для v0v0, используя x = x0 + v0t + 12at2: x = x0 + v0t + 12at2: x − x0 = v0t + 12at2x − x0 = v0t + 12at21.0 × 106m = v0 (120.0s) +12 (20,0 м / с2) (120,0 с) 21,0 × 106 м = v0 (120,0 с) +12 (20,0 м / с2) (120,0 с) 2v0 = 7133,3 м / с. V0 = 7133,3 м / с.Затем мы подставляем v0v0 в v = v0 + atv = v0 + at, чтобы найти окончательную скорость:
v = v0 + at = 7133.3 м / с + (20,0 м / с2) (120,0 с) = 9533,3 м / с. V = v0 + at = 7133,3 м / с + (20,0 м / с2) (120,0 с) = 9533,3 м / с.Значение
Есть шесть переменных смещения, времени, скорости и ускорения, которые описывают движение в одном измерении. Начальные условия данной задачи могут быть множеством комбинаций этих переменных. Из-за такого разнообразия решения могут быть не такими простыми, как простая подстановка в одно из уравнений. Этот пример показывает, что решения кинематики могут потребовать решения двух одновременных кинематических уравнений.Освоив основы кинематики, мы можем перейти ко многим другим интересным примерам и приложениям. В процессе разработки кинематики мы также увидели общий подход к решению проблем, который дает как правильные ответы, так и понимание физических взаимоотношений. Следующий уровень сложности в наших задачах кинематики связан с движением двух взаимосвязанных тел, называемых задачами преследования двух тел .
Задачи преследования двух тел
До этого момента мы рассматривали примеры движения с участием одного тела.Даже для задачи с двумя автомобилями и тормозным путем на мокрой и сухой дороге мы разделили эту задачу на две отдельные задачи, чтобы найти ответы. В задаче преследования двух тел движения объектов связаны, то есть неизвестное, которое мы ищем, зависит от движения обоих объектов. Чтобы решить эти проблемы, мы пишем уравнения движения для каждого объекта, а затем решаем их одновременно, чтобы найти неизвестное. Это показано на Рисунке 3.25.
Рис. 3.25 Сценарий преследования с двумя телами, в котором автомобиль 2 имеет постоянную скорость, а автомобиль 1 идет сзади с постоянным ускорением.Автомобиль 1 догонит автомобиль 2 позже.
Время и расстояние, необходимое для того, чтобы автомобиль 1 догнал автомобиль 2, зависит от начального расстояния, на которое автомобиль 1 находится от автомобиля 2, а также от скорости обоих автомобилей и ускорения автомобиля 1. Кинематические уравнения, описывающие движение обоих автомобилей, должны быть решил найти эти неизвестные.
Рассмотрим следующий пример.
Пример 3.13
Гепард ловит газель
Гепард прячется за кустом. Гепард замечает пробегающую мимо газель со скоростью 10 м / с.В тот момент, когда газель проходит мимо гепарда, гепард из состояния покоя ускоряется со скоростью 4 м / с 2 , чтобы поймать газель. а) Сколько времени требуется гепарду, чтобы поймать газель? б) Что такое смещение газели и гепарда?Стратегия
Мы используем систему уравнений для постоянного ускорения, чтобы решить эту проблему. Поскольку есть два движущихся объекта, у нас есть отдельные уравнения движения, описывающие каждое животное. Но то, что связывает уравнения, — это общий параметр, который имеет одинаковое значение для каждого животного.Если мы внимательно посмотрим на проблему, становится ясно, что общим параметром для каждого животного является их положение x в более позднее время t . Поскольку оба они начинаются с x0 = 0x0 = 0, их смещения будут такими же в более позднее время t , когда гепард догонит газель. Если мы выберем уравнение движения, которое решает смещение для каждого животного, мы можем затем приравнять уравнения друг к другу и решить неизвестное, то есть время.Решение
- Уравнение для газели: Газель имеет постоянную скорость, которая является ее средней скоростью, поскольку она не ускоряется.Поэтому мы используем уравнение 3.10 с x0 = 0x0 = 0: x = x0 + v – t = v – t. x = x0 + v – t = v – t. Уравнение для гепарда: гепард ускоряется из состояния покоя, поэтому мы используем уравнение 3.13 с x0 = 0x0 = 0 и v0 = 0v0 = 0: x = x0 + v0t + 12at2 = 12at2.x = x0 + v0t + 12at2 = 12at2. Теперь у нас есть уравнение движения для каждого животного с общим параметром, который можно исключить, чтобы найти решение. В этом случае мы решаем для t : x = v – t = 12at2t = 2v – a.x = v – t = 12at2t = 2v – a. Газель имеет постоянную скорость 10 м / с, что составляет ее среднюю скорость.Ускорение гепарда 4 м / с 2 . Оценивая t , время, за которое гепард достигнет газели, имеем t = 2v – a = 2 (10 м / с) 4m / s2 = 5s.t = 2v – a = 2 (10 м / с) 4m / s2 = 5s.
- Чтобы получить смещение, мы используем уравнение движения гепарда или газели, поскольку оба они должны дать одинаковый ответ.
Смещение гепарда: x = 12at2 = 12 (4 м / с2) (5) 2 = 50 м. x = 12at2 = 12 (4 м / с2) (5) 2 = 50 м. Водоизмещение газели: x = v – t = 10 м / с (5) = 50 м. x = v – t = 10 м / с (5) = 50 м.Мы видим, что оба смещения равны, как и ожидалось.
Значение
Важно анализировать движение каждого объекта и использовать соответствующие кинематические уравнения для описания отдельного движения. Также важно иметь хорошую визуальную перспективу задачи преследования двух тел, чтобы увидеть общий параметр, который связывает движение обоих объектов.Проверьте свое понимание 3.6
Велосипед имеет постоянную скорость 10 м / с. Человек начинает с отдыха и начинает бежать, чтобы догнать велосипед через 30 секунд, когда велосипед находится в том же положении, что и человек.Какое ускорение у человека?
кинематических уравнений: список и пример — видео и стенограмма урока
Уравнения кинематики
Есть пять основных кинематических уравнений, которые необходимо знать для решения задач.
В этих пяти уравнениях:
- t — время, измеренное в секундах
- vi — начальная скорость, измеренная в метрах в секунду
- vf — конечная скорость, измеренная в метрах в секунду
- a — ускорение в метрах в секунду в квадрате
- y (или иногда x ) — смещение, измеренное в метрах
Также важно отметить, что для падающих объектов ускорение ( a ) — это ускорение свободного падения ( g ), которое всегда отрицательно 9.8 метров на секунду в квадрате.
Каждое из пяти уравнений содержит четыре переменные, при этом одна переменная отсутствует. Каждый раз, когда вы решаете задачи кинематики, вам нужно дать три числа и попросить найти четвертое. Итак, все, что вам нужно сделать, это найти уравнение с этими четырьмя величинами в нем, подставить числа и решить.
Пример задачи движения
Давайте рассмотрим пример использования уравнений. Допустим, мяч падает с высоты 6 метров, и он падает, пока не достигнет земли.Сколько времени нужно, чтобы достичь земли?
Ну, прежде всего мы должны записать то, что мы знаем. Водоизмещение y составляет -6 метров. Почему отрицательный? Что ж, падает вниз. Обычно в физике мы называем восходящий положительный и нисходящий отрицательный. Однако это довольно произвольно, и пока все ваши признаки совпадают, вы должны получить один и тот же ответ.
Хорошо, теперь у нас есть потенциальная проблема: в вопросе нет других номеров. Но этот вопрос говорит нам о вещах, которые тайком дают нам другие числа, которые мы можем использовать. Во-первых, мяч падает, то есть падает под действием силы тяжести. Таким образом, ускорение, как и для всех падающих предметов, составляет -9,8. Опять же, отрицательный, потому что ускорение направлено вниз.
И вопрос также говорит нам, что мяч упал, что означает, что начальная скорость равна нулю. Когда вы бросаете мяч, в тот момент, когда вы его отпускаете, он не движется и его скорость равна нулю.И нас просят найти время, т , поэтому т =?.
Итак, мы знаем три числа, и нас просят найти четвертое. Так что эта проблема разрешима.
Нам нужно найти уравнение из пяти, которое содержит y , vi , a и t . И это уравнение таково:
Мы подставляем числа в это уравнение, например:
Первый член равен нулю, поэтому эта часть исчезает.Затем измените порядок, чтобы сделать t предметом обсуждения, и введите числа в калькулятор. И получаем t = 1,1 секунды. Вот и все; это наш ответ.
Краткое содержание урока
Кинематика — это исследование движения без ссылки на силы, вызывающие движение. В кинематике есть пять важных величин: смещение (изменение положения), начальная скорость, конечная скорость, ускорение и время. Начальная скорость — это скорость движения объекта при t = 0. Конечная скорость — это скорость движения объекта по истечении времени t . Водоизмещение — насколько изменилась позиция за время т. . Ускорение — это скорость, с которой скорость изменялась за время t . А время просто … ну, самое время.
Существует пять основных кинематических уравнений, которые необходимо знать для решения задач. В этих пяти уравнениях:
- t — время, измеренное в секундах
- vi — начальная скорость, измеренная в метрах в секунду
- vf — конечная скорость, измеренная в метрах в секунду
- a — ускорение в метрах в секунду в квадрате
- y (или иногда x ) — смещение, измеренное в метрах
Также важно отметить, что для падающих объектов ускорение a — это ускорение свободного падения g , которое всегда отрицательно 9.
