Контрольная работа № 2 по теме «Определение тригонометрических функций»
Контрольная работа № 2 (1 час)
Цели: выявление знаний учащихся, проверка степени усвоения ими изученного материала; развитие навыков самостоятельной работы.
Контрольная работа № 2
Вариант 1
1. Вычислите.
2. Упростите выражение
3. Решите уравнение.
4. Известно, что Найдите:
5. Расположите в порядке возрастания следующие числа:
Вариант 2
1. Вычислите.
2. Упростите выражение
3.
4. Известно, что Найдите:
5. Расположите в порядке убывания следующие числа:
Вариант 3
1. Вычислите.
2. Упростите выражение
3. Решите уравнение.
4. Известно, что Найдите:
5. Расположите в порядке возрастания следующие числа:
Вариант 4
1. Вычислите.
2. Упростите выражение
3. Решите уравнение.
4. Известно, что Найдите:
5. Расположите в порядке убывания следующие числа:
Расположите в порядке убывания следующие числа:
Рекомендации по оцениванию контрольной работы
Каждый вариант контрольной работы выстроен по одной схеме: задания обязательного минимума – до первой черты, задания среднего уровня – между первой и второй чертой, задания уровня выше среднего – после второй черты. Шкала оценок за выполнение контрольной работы может выглядеть так: за успешное выполнение только заданий обязательного минимума – оценка «3»; за успешное выполнение заданий обязательного минимума и одного дополнительного (после первой или второй черты) – оценка «4»; за успешное выполнение заданий всех трех уровней – оценка «5». При этом оценку не рекомендуется снижать за одно неверное решение в первой части работы (допустимый люфт).
Решение контрольной работы
Вариант 1
так как аргумент t принадлежит второй четверти.
так как аргумент t принадлежит второй четверти.
Ответ: а) –0,8; б) 0,6.
Учитывая, что 3,14, нанесем на числовую окружность значения 4; 6; 7:
Ответ: d, c, b, a.
Вариант 2
Ответ:
Ответ:
Учитывая, что 3,14, нанесем на числовую окружность значения 2; 3; 4:
Ответ: b; а; d; с.
Вариант 3
–0,5 – 1 + 1 = 0,5.
так как аргумент t принадлежит четвертой четверти.
так как аргумент t принадлежит четвертой четверти.
Учитывая, что 3,14, нанесем на числовую окружность значения 7,5; 9; 9,5:
Ответ: d; а; с; b.
Вариант 4
д)
Ответ:
так как аргумент t принадлежит второй четверти.
так как аргумент t принадлежит второй четверти.
Ответ: а) б) –0,2.
Учитывая, что 3,14, нанесем на числовую окружность значения 7,5; 9; 9,5:
Ответ: d; с; а; b.
Основное Тригонометрическое Тождество — Доказательство
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Связь между sin и cos одного угла
Вы уже наверняка знаете, что тождественный — это равный.
Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.
Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:
Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.
Равенство tg2
В результате деления получаем:
Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.
sin2α + cos2α = 1Сумма квадратов синуса и косинуса одного угла тождественно равна единице.
Чтобы доказать тождество, обратимся к теме единичной окружности.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.
Докажем тождество sin2α + cos2α = 1
- Итак, нам известны координаты точки A (1; 0).
Произвольный угол α, тогда cos α = x0 = ОB.

- Если развернуть точку A на угол α, то точка A становится на место точки A1.
- По определениям:
- Синус угла (sin α) — это отношение противолежащего катета к гипотенузе.
- Косинус угла (cos α) — это отношение прилежащего катета к гипотенузе.
- Опускаем перпендикулярную прямую A1B на x0 из точки A1.
Образовался прямоугольный треугольник OA1B.
|A1B| = |у|
|OB| = |x|.
- Гипотенуза OA1 имеет значение, равное радиусу единичной окружности.
|OA1| = 1.
- Применяя полученное выражение, записываем равенство по теореме Пифагора, поскольку получившийся угол — прямой:
|A1B|2 + |OB|2 = |OA1|2.
- Записываем в виде: |y|2 + |x|2 = 12.

Это значит, что y2 + x2 = 1.
sin угла α = y
cos угла α = x - Вставляем данные угла вместо координат точек:
OB = cos α
A1B = sin α
A1O = 1 - Получаем основное тригонометрическое тождество: sin2α + cos2α = 1.
Что и требовалось доказать.
Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
- sin α = ±
- cos α = ±
Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.
Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.
Тангенс и котангенс через синус и косинус
Немного вводных:
- Синус угла — это ордината y.
- Косинус угла — это абсцисса x.
- Тангенс угла — это отношение ординаты к абсциссе.
- Котангенс угла — это отношение абсциссы к ординате.
Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.
- tg α =
- ctg α =
Исходя из определений:
Это позволяет сделать вывод, что тригонометрические тождества
задаются sin и cos углов.
Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.
Отдельно стоит обратить внимание на то, что тригонометрические тождества
верны для всех углов α, значения которых вписываются в диапазон.
- Например, выражение применимо для любого угла α, не равного + π + z, где z — это любое целое число.
 В противном случае, в знаменателе будет стоять 0.
В противном случае, в знаменателе будет стоять 0.
Выражение
применимо для любого угла α, не равного π * z, где z — это любое целое число.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Связь между тангенсом и котангенсом
Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
- Тождество записывается в следующем виде:
tg α * ctg α = 1.
Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.
Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.
tg α * ctg α = 1.
- По определению:
tg α = y/x
ctg α = x/y
- Отсюда следует, что tg α * ctg α = y/x * x/y = 1
- Преобразовываем выражение, подставляем и ,
получаем:
Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.
Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.
Какие, какие числа?🤯
Взаимно обратные числа — это два числа, произведение которых равно 1.
Тангенс и косинус, котангенс и синус
Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.
Эта связь становится очевидна, если взглянуть на тождества:
- tg2α + 1 =
Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.
- 1 + ctg2α =
Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.
Вывести оба этих тождества можно из основного тригонометрического тождества:
sin2α + cos2α = 1.
- Для этого нужно поделить обе части тождества на cos2α, где косинус не равен нулю.
- В результате деления получаем формулу tg2α + 1 =
- Если обе части основного тригонометрического тождества sin2α + cos2α = 1 разделить на sin2α, где синус не равен нулю, то получим тождество:
1 + ctg2α = . - Отсюда можно сделать вывод, что тригонометрическое тождество tg2α + 1 = применимо для любого угла α, не равного + π + z, где z — это любое целое число.
- А тригонометрическое тождество 1 + ctg2α = применимо для любого угла, не равного π * z, где z — это любое целое число.
Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.
Основные тригонометрические тождества
|
1 |
sin2α + cos2α = 1 |
|
2 |
|
|
3 |
|
|
4 |
tgα * ctgα = 1 |
|
5 |
tg2α + 1 = |
|
6 |
1 + ctg2α = |
Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.
Примеры решения задач
Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.
Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.
Как решаем:
- Чтобы решить задачу, необходимы следующие тригонометрические тождества:
- Выражаем cos α из тригонометрической единицы:
- Далее подставляем значения sin α:
- Вычисляем:
- Нам известны значения sin α и cos α, поэтому можно легко найти тангенс, используя формулу:
- Таким же образом, используя формулу, вычисляем значение котангенса:
Ответ:
Задачка 2. Найдите значение cos α,
если:
Как решаем:
- Чтобы решить задачу, необходимы следующие тригонометрические тождества:
- Выражаем cos α из тригонометрической единицы:
- Далее подставляем значения sin α:
- Вычисляем:
- То же самое проделываем со вторым значение sin α
Подставляем значения sin α:
- Вычисляем:
Ответ:
Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.
| 1. |
Область определения тригонометрических функций
Сложность: лёгкое |
1 |
| 2. |
Определение множества значений тригонометрических функций
Сложность: лёгкое |
2 |
3.
|
Множество значений тригонометрических функций
Сложность: лёгкое |
2 |
| 4. |
Упрощение выражения
Сложность: лёгкое |
1 |
5.
|
Нахождение множества значений тригонометрических функций
Сложность: среднее |
2 |
| 6. |
Область определения тригонометрических функций (решение уравнения)
Сложность: среднее |
2 |
7.
|
Множество значений тригонометрических функций с использованием формулы сложения
Сложность: среднее |
2 |
| 8. |
Наибольшее и наименьшее значения выражения
Сложность: среднее |
2 |
9.
|
Нахождение значений тригонометрических функций
Сложность: среднее |
3 |
| 10. |
Определение значений тригонометрических функций
Сложность: среднее |
3 |
11.
|
Множество значений функции
Сложность: сложное |
2 |
| 12. |
Нахождение суммы квадратов тригонометрических функций
Сложность: сложное |
1 |
Урок 1.
 область определения и множество значений тригонометрических функций — Алгебра и начала математического анализа — 11 класс
область определения и множество значений тригонометрических функций — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №1. Область определения и множество значений тригонометрических функций.
Перечень вопросов, рассматриваемых в теме
- Овладение понятиями «область определения», «область определения тригонометрических функций», «множество значений функции», «множество значений тригонометрических функций»;
- Нахождение области определения и множества значений тригонометрических функций вида y=af(kx+b)+c и y=|f(k|x|+b)|, где f(x) — косинус, синус, тангенс или котангенс действительного числа от значения коэффициентов a, k, b.;
- Объяснение зависимости области определения и множества значений функции вида y=af(kx+b)+c и y=|f(k|x|+b)|, где f(x) — косинус, синус, тангенс или котангенс действительного числа от значения коэффициентов a, k, b.
Глоссарий по теме
Областью определения функций y = sin x и y = cos x является множество R всех действительных чисел.
Множеством значений функции y = sin x и y = cos x является отрезок -1 ≤ y ≤ 1. Данные функции ограничены сверху и снизу.
Областью определения функции y = tg x является множество чисел x ≠ π/2 + πk, kЄ Z.
Областью определения функции y = сtg x является множество чисел x ≠ πk, kЄ Z.
Множеством значений функции y = tg x и y =сtg x является множество R всех действительных чисел, т.к. уравнения tg x = a и сtg x = a имеют корни при любом действительном значении a. Функции неограниченные.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2010.–336 с.
Дополнительная литература:
Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.
Открытые электронные ресурсы:
Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/
Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс].– Режим доступа: https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Актуализация знаний
Вопросы:
- Что такое функция?
- Что такое область определения функции? Чем является область определения функции геометрически?
- Что такое множество значений функции? Чем является множество значений функции геометрически?
Ответы на вопросы:
- Если каждому значению x из некоторого множества чисел поставлено в соответствие по определенному правилу число y, то говорят, что на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у – зависимой переменной или функцией. Зависимость переменной у от переменной х называют функциональной зависимостью.
 Записывают y=f(x).
Записывают y=f(x). - Областью определения функции называют множество всех допустимых значений переменной x. Геометрически – это проекция графика функции на ось Ох.
Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически – это проекция графика функции на ось Оy.
Найдите область определения функции и множество значений функции:
1) ; 2) ; 3) .
Ответы:
D(f): 1) ; 2) ; 3)
E(f): 1); 2) ; 3) .
Объяснение нового материала
С помощью единичной окружности сделайте выводы об области определения и множестве значений тригонометрических функций.
Заполните таблицу:
Функция | Область определения | Множество значений |
Ответ:
Функция | Область определения | Множество значений |
Итак, Областью определения функций y = sin x и y = cos x является множество R всех действительных чисел.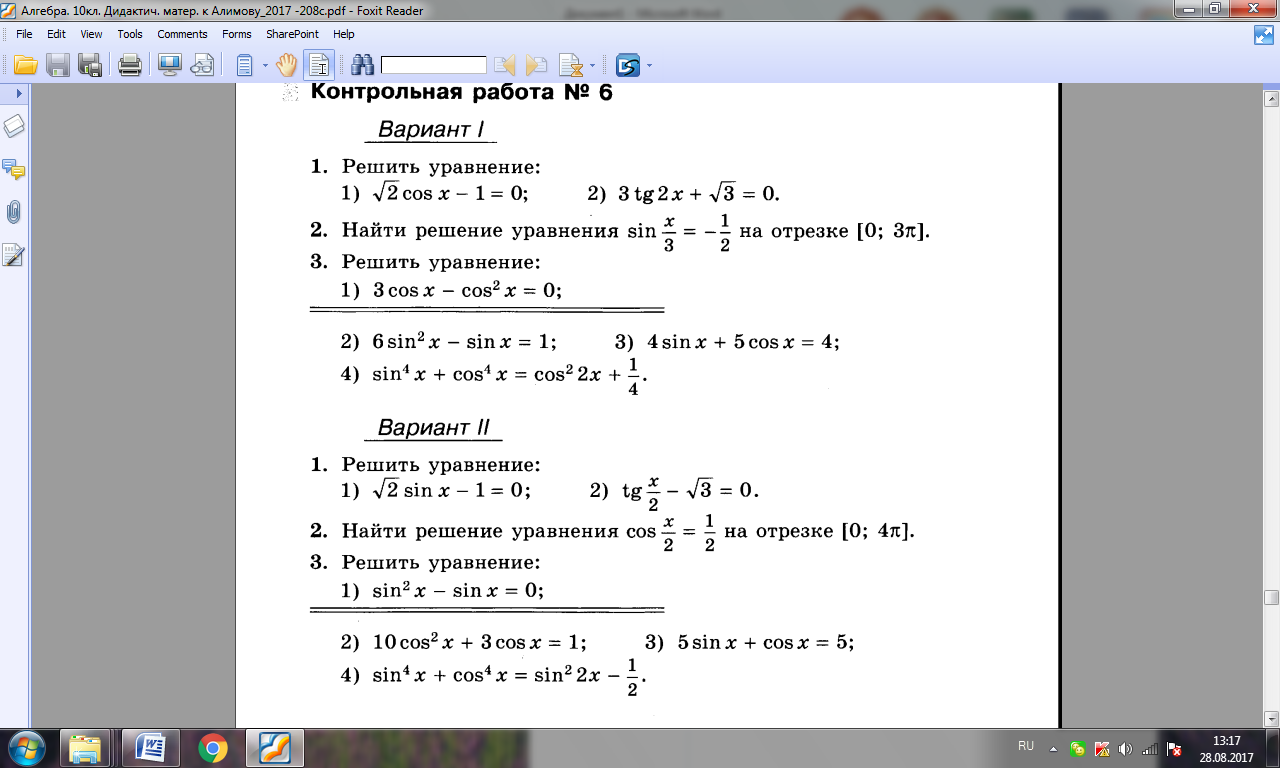
Множеством значений функции y = sin x и y = cos x является отрезок -1 ≤ y ≤ 1. Данные функции ограничены сверху и снизу.
Областью определения функции y = tg x является множество чисел x ≠ π/2 + πk, kЄ Z.
Областью определения функции y = сtg x является множество чисел x ≠ πk, kЄ Z.
Множеством значений функции y = tg x и y =сtg x является множество R всех действительных чисел, т.к. уравнения tg x = a и сtg x = a имеют корни при любом действительном значении a. Функции неограниченные.
Примеры и разборы решения заданий тренировочного модуля:
Пример 1. Найти область определения функции .
;
;
;
Ответ: −.
Пример 2. Найти все решения уравнения
;
;
Ответ:
.
ГДЗ по алгебре 10 класс Мерзляк, Номировский Базовый уровень Вентана-Граф 2020
Наиболее ответственные десятиклассники начинают готовиться к ЕГЭ по основным предметам уже в текущем году. Особенно — по математическим дисциплинам, экзамен по которым, как показывает практика, бывает наибольшее количество затруднений и вопросов у школьников. Чтобы иметь достаточно времени и сил, надо грамотно распланировать работу, это позволит достичь высоких результатов труда. Среди помощников многие называют актуальные гдз по алгебре за 10 класс Мерзляк, занимаясь по которым системно и комплексно, можно справиться с задачей подготовки к итоговому испытанию самостоятельно. Но важно соблюдение некоторых обязательных условий. Это — регулярность работы, желательно — ее ежедневность, выделение на нее минимума час-полтора в день. И отсутствие долгосрочных, более 10 дней подряд, пропусков в постоянной подготовке. Это позволит избежать перенапряжения, необходимости впоследствии более интенсивно осваивать программу, оставит достаточно времени для повторения наиболее сложных тем и параграфов.
Особенно — по математическим дисциплинам, экзамен по которым, как показывает практика, бывает наибольшее количество затруднений и вопросов у школьников. Чтобы иметь достаточно времени и сил, надо грамотно распланировать работу, это позволит достичь высоких результатов труда. Среди помощников многие называют актуальные гдз по алгебре за 10 класс Мерзляк, занимаясь по которым системно и комплексно, можно справиться с задачей подготовки к итоговому испытанию самостоятельно. Но важно соблюдение некоторых обязательных условий. Это — регулярность работы, желательно — ее ежедневность, выделение на нее минимума час-полтора в день. И отсутствие долгосрочных, более 10 дней подряд, пропусков в постоянной подготовке. Это позволит избежать перенапряжения, необходимости впоследствии более интенсивно осваивать программу, оставит достаточно времени для повторения наиболее сложных тем и параграфов.
Основные типы пользователей онлайн справочников
В числе тех, кто часто, регулярно применяет онлайн решебник по алгебре 10 класс Мерзляка в ходе подготовки:
- десятиклассники, рационально и грамотно подходящие к освоению курса дисциплины.
 Источник позволит им составить план работы в собственном оптимальном темпе, реализовать его, выделив те задания, которые вызвали больше всего трудностей и запомнить, как их надо правильно решать;
Источник позволит им составить план работы в собственном оптимальном темпе, реализовать его, выделив те задания, которые вызвали больше всего трудностей и запомнить, как их надо правильно решать; - одинннадцатиклассники, непосредственно готовящиеся к математическому ЕГЭ и повторяющие курс предмета за десятый класс — достаточно обширный и непростой;
- репетиторы, занимающиеся как с десятиклассниками, так и с выпускниками. Платформа позволит им понять, как именно записывается условие, алгоритм алгебраического решения, ответ в соответствии с нормативами Стандартов образования. Такой подход считается максимально грамотным, так как оформлению на контрольных, олимпиадах и экзаменах придается большое значение;
- родители, планирующие самостоятельно оценить степень знаний своего ребенка, помочь ему избежать плохой оценки по дисциплине. Площадка позволит им реализовать этот запрос, не вникая глубоко в суть школьной алгебры.
Аргументы за применение онлайн решебников в ходе обучения в школе
Пока еще не все учителя, родители признали полезность еуроки ГДЗ. Некоторые по старинке считают, что такой формат подходит лишь нерадивым ученикам для списывания готовых решений. Но те, кто успешно использует сборники готовых решений, отвечают на это так:
Некоторые по старинке считают, что такой формат подходит лишь нерадивым ученикам для списывания готовых решений. Но те, кто успешно использует сборники готовых решений, отвечают на это так:
- необязательно бездумно переписывать ответ. Можно сравнить свое готовое решение с эталоном до сдачи работы учителю, тем самым, избежав плохих оценок. Или посмотреть как решается задание, которое не получается выполнить самостоятельно;
- источник постоянно и круглосуточно доступен для всех;
- можно существенно сэкономить семейный бюджет, отказавшись от платной помощи, взяв за основу подготовки решебник.
Актуальные, полезныеготовые ответы по алгебре для 10 класса автор Мерзляк применяются сегодня все большим числом заинтересованных пользователей. Это позволяет им систематизировать, углублять свои знания, запоминать большие объемы математических данных.
ГДЗ от Путина к самостоятельным и контрольным работам по алгебре (геометрии) 9 класс Ершова, Голобородько
На нашем образовательном интернет-ресурсе вы можете найти ответы к самостоятельным и контрольным работам для 9 класса Ершова, Голобородько, которые можно просматривать с экрана мобильного телефона в режиме онлайн. Также, в этом разделе вам будут предложены ГДЗ и теоретические сведения.
Также, в этом разделе вам будут предложены ГДЗ и теоретические сведения.
Квадратичная функция
С-1. Функции и их свойства12345
С-2. Квадратный трехчлен1234567
С-3. График квадратичной функции123456789
С-4*. Квадратичная функция: задачи с параметрами (домашняя самостоятельная работа)
К-1. Квадратичная функция1234567891112131415
С-5. Решение квадратичных неравенств123456789101112
С-6. Решение неравенств методом интервалов12345678
К-2. Решение неравенств1234567891011121314151617181920212223
Уравнения и системы уравнений
С-7. Решение целых уравнений1234567891011
С-8*. Уравнения высших степеней: методы решения, задачи с параметрами (домашняя самостоятельная работа)
С-9. Решение систем уравнений второй степени1234567
С-10. Решение задач с помощью систем уравнений. Графическое решение систем1234567
С-11*. Системы рациональных уравнений (домашняя самостоятельная работа)
К-3. Целые уравнения и системы уравнений1234567891011
Арифметическая и геометрическая прогрессии
С-12. Арифметическая прогрессия. Формула n-ого члена123
Арифметическая прогрессия. Формула n-ого члена123
С-13. Формула суммы п первых членов арифметической прогрессии1234
К-4. Арифметическая прогрессия123456
С-14. Геометрическая прогрессия. Формула n-ого члена1234
С-15. Формула суммы первых п членов геометрической прогрессии.1234
С-16*. Комбинированные задачи на прогрессии (домашняя самостоятельная работа)
К-5. Геометрическая прогрессия1234
Степень с рациональным показателем
С-17. Четные и нечетные функции. Функция У = *»123
С-18. Корень n-ой степени и его свойства123
С-19. Определение и свойства степени с дробным показателем123
С-20. Преобразование степенных выражений с рациональными показателями12
К-6. Степень с рациональным показателем12345
Тригонометрические выражения и их преобразования
С-21. Определение тригонометрических функций12
С-22. Свойства тригонометрических функций. Радианная мера угла12
С-23. Тригонометрические тождества и их применение123
С-24. Формулы приведения12
Формулы приведения12
К-7. Свойства тригонометрических функций. 12345
С-25. Формулы сложения123
С-26. Формулы двойного угла123
С-27. Формулы суммы и разности тригонометрических функций12
К-8. Формулы сложения и их следствия12345
С-28*. Дополнительные тригонометрические задачи (домашняя самостоятельная работа)
К-9. Годовая контрольная работа12345678
Подобие фигур
СП-1. Преобразование подобия и его свойства123
СП-2. Признаки подобия треугольников123
СП-3. Подобие прямоугольных треугольников.123456
СП-4*. Подобие треугольников (домашняя самостоятельная работа)
КП-1. Подобие фигур1234567
СП-5. Теорема о вписанных углах и ее следствия1234567
СП-6*. Применение теоремы о вписанных углах и ее следствий в задачах (домашняя самостоятельная работа)
Решение треугольников
СП-7. Теорема косинусов. Соотношение диагоналей и сторон параллелограмма1234567
СП-8. Теорема синусов и ее следствия123456
СП-9*. Теоремы косинусов и синусов (домашняя самостоятельная работа)
Теоремы косинусов и синусов (домашняя самостоятельная работа)
КП-2. Решение треугольников1234567
Многоугольники
СП-10. Выпуклый многоугольник12345
СП-11. Правильные многоугольники.123456
СП-12. Длина окружности. Радианная мера угла1234567
КП-3. Многоугольники123456789101112
Площади фигур
СП-13. Площадь прямоугольника, квадрата, параллелограмма12345678910
СП-14. Площадь треугольника123456789
СП-15. Площадь трапеции. Площадь четырехугольника1234567891011
СП-16*. Окружность и многоугольник (домашняя самостоятельная работа)
СП-17. Площади подобных фигур. Площадь круга и его частей123456
СП-18*. Площади фигур (домашняя самостоятельная работа)
КП-4. Площади фигур1234567891011
КП-5. Годовая контрольная работа12345678910111213
Метод координат
СА-1. Координаты вектора12345
СА-2.Простейшие задачи в координатах123456
СА-3.Уравнение окружности1234567
СА-4.Уравнение прямой1234
С-5*. Применение векторов и координат к решению задач (домашняя самостоятельная работа)
Применение векторов и координат к решению задач (домашняя самостоятельная работа)
КА-1. Метод координат123456789
Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
СА-6.Синус, косинус, тангенс угла12345
СА-7.Теорема о площади треугольника.1234567
Теорема синусов
СА-8.Теорема косинусов. Решение треугольников12345678
СА-9.Скалярное произведение векторов1234567
СА-10*. Решение треугольников. Скалярное произведение (домашняя самостоятельная работа)
КА-2. Соотношение между сторонами и углами треугольника1234567891011
Длина окружности и площадь круга
СА-11. Правильные многоугольники123456
СА-12. Длина окружности, площадь круга, площадь кругового сектора123456789
КА-3. Длина окружности и площадь круга123456789
Движения
СА-13. Понятие движения12345
СА-14. Параллельный перенос и поворот123
КА-4. Движение123456
КА-5. Годовая контрольная работа1234567891011121314
▶▷▶ вариант 4 алгебра 10 класс контрольная работа по
▶▷▶ вариант 4 алгебра 10 класс контрольная работа по| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 18-12-2018 |
вариант 4 алгебра 10 класс контрольная работа по — Yahoo Search Results Yahoo Web Search Sign in Mail Go to Mail» data-nosubject=»[No Subject]» data-timestamp=’short’ Help Account Info Yahoo Home Settings Home News Mail Finance Tumblr Weather Sports Messenger Settings Want more to discover? Make Yahoo Your Home Page See breaking news more every time you open your browser Add it now No Thanks Yahoo Search query Web Images Video News Local Answers Shopping Recipes Sports Finance Dictionary More Anytime Past day Past week Past month Anytime Get beautiful photos on every new browser window Download Контрольные работы «Алгебра 10 класс» infourokru/kontrolnie-raboti-algebra-klass Cached Контрольная работа №7 1Из урны, содержащей 15 белых, 10 красных и 5 синих шаров, наугад выбирают один шар Какова вероятность того, что шар окажется: а) красного цвета; б) зеленого цвета? Контрольная работа по алгебре №1 (10 класс) infourokru/kontrolnaya-rabota-po-algebre-klass Cached › Другие методич материалы › Контрольная работа по алгебре №1 ( 10 класс ) Контрольная работа по алгебре №1 ( 10 класс ) Контрольная работа по теме «Действительные числа» в форме ЭГЕ открытыйурокрф/статьи/516431 Cached Контрольная работа по теме «Действительные числа» в форме ЭГЕ, алгебра , 10 -й класс ВАРИАНТ 4 Вариант 4 Алгебра 10 Класс Контрольная Работа По — Image Results More Вариант 4 Алгебра 10 Класс Контрольная Работа По images ГДЗ по алгебре для 8 класса Жохов ВИ — Контрольные работы reshebame/gdz/algebra/8-klass/zhohov/e:1-t:0-t: Cached Подробное решение Контрольные работы / Контрольная работа №1 / Вариант 4 1 по алгебре дидактические материалы для учащихся 8 класса, авторов Жохов ВИ, Макарычев ЮН, Миндюк НГ 2015 ГДЗ по алгебре для 8 класса Жохов ВИ — Контрольные работы reshebame/gdz/algebra/8-klass/zhohov/e:1-t:3-t: Cached Подробное решение Контрольные работы / Контрольная работа № 4 / Вариант 2 2 по алгебре дидактические материалы для учащихся 8 класса, авторов Жохов ВИ, Макарычев ЮН, Миндюк НГ 2015 ГДЗ решебник по Алгебре Контрольные работы 10 класс Мордкович gdzmonsternet 10 класс Алгебра Алгебра 10 класс Контрольные работы Мордкович Тульчинская 2000-2005 Вариант 4 : Контрольная Контрольная работа по теме «Тригонометрические функции compendiumsu/mathematics/algebra 10 /17html Cached 1-е полугодие Глава 2 Тригонометрические функции Уроки 27-28 Контрольная работа по теме контрольные работы для 8 класс по алгебре автор макарычев blogdxvwpz57699jottitcom/контрольные Cached контрольная работа по теме географическая оболочка-населения 1 вариант контрольные диктанты по русскому языку 5 класс в начале года Контрольная по алгебре 7 класс — контрольные работы с mathematics-testscom/algebra-7-klass-novoe/ Cached Контрольная работа №7 ( 4 четверть) «Многочлены, формулы сокращенного умножения, разложение многочлена на множители, сокращение алгебраических дробей» Алгебра 7 класс Контрольная работа Вариант 1-2 По nasholme … Экзамены по Алгебре Название: Алгебра 7 класс Контрольная работа Вариант 1-2 По учебнику Никольского СМ 2009 Контрольная работа по алгебре 7 класс Теория вероятностей и статистика Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 43,200 results Settings Help Suggestions Privacy (Updated) Terms (Updated) Advertise About ads About this page Powered by Bing™
- Базовый уровень ФГОС
- это скорее пособие для высокой самоподготовки и проверки собственных знаний Скрыть ГДЗ — Алгебра и начала анализа 10 класс Контрольные reshebnik5-11ru › 10 класс › Алгебра › Мордкович Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте ГДЗ — Алгебра и начала анализа 10 -11 класс Контрольные работы АГ Мордкович
- которым тяжело дается такой предмет
(43) в виде обыкновенной дроби 5 Сократите дробь 6 Сравните числа: и 1; 7* Упростите выражение 1 Контрольная работа № 1 Действительные числа Вариант 2 1 Вычислите: 2 Упростите выражение 3 Решите уравнение 4 Запишите бесконечную периодическую дробь 0
школьники могут теряться и Скрыть ГДЗ по Алгебре за 10 класс контрольные работы MegaReshebaru › gdz/algebra/10-klass/kontrolnie…i… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Подробный решебник (ГДЗ) по Алгебре для 10 класса контрольные работы базовый и углубленный уровень Авторы тетради: Глизбург ВИ Дополнение к учебнику и задачнику АГ Мордкович 10 класс Читать ещё Подробный решебник (ГДЗ) по Алгебре для 10 класса контрольные работы базовый и углубленный уровень Авторы тетради: Глизбург ВИ Дополнение к учебнику и задачнику АГ Мордкович 10 класс автор: Глизбург ВИ Подробный решебник (ГДЗ) по Алгебре для 10 класса контрольные работы базовый и углубленный уровень Авторы тетради: Глизбург ВИ Дополнение к учебнику и задачнику АГ Мордкович 10 класс Рекомендуемые решебники ГДЗ учебник алгебра 10 класс Мордкович АГ базовый и углубленный уровень ГДЗ Задачник алгебра 10 класс Мордкович АГ базовый и углубленный уровень Скрыть ГДЗ по Алгебре за 10 класс контрольные работы ugdzru › reshebniki/10-klass/algebra/kontrolnie… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сборник готовых домашних заданий (ГДЗ) контрольные работы по Алгебре за 10 класс
- содержащей 15 белых
- 10 -й класс ВАРИАНТ 4 Вариант 4 Алгебра 10 Класс Контрольная Работа По — Image Results More Вариант 4 Алгебра 10 Класс Контрольная Работа По images ГДЗ по алгебре для 8 класса Жохов ВИ — Контрольные работы reshebame/gdz/algebra/8-klass/zhohov/e:1-t:0-t: Cached Подробное решение Контрольные работы / Контрольная работа №1 / Вариант 4 1 по алгебре дидактические материалы для учащихся 8 класса
- авторов Жохов ВИ
вариант 4 алгебра 10 класс контрольная работа по — Поиск в Google Специальные ссылки Перейти к основному контенту Справка по использованию специальных возможностей Оставить отзыв о специальных возможностях Нажмите здесь , если переадресация не будет выполнена в течение нескольких секунд Войти Удалить Пожаловаться на неприемлемые подсказки Режимы поиска Все Картинки Видео Новости Карты Ещё Покупки Книги Авиабилеты Финансы Настройки Настройки поиска Языки (Languages) Включить Безопасный поиск Расширенный поиск Ваши данные в Поиске История Поиск в справке Инструменты Результатов: примерно 9 120 000 (0,52 сек) Looking for results in English? Change to English Оставить русский Изменить язык Результаты поиска Все результаты Решебник к сборнику контрольных работ по — Math-HelperRu Сохраненная копия 14 февр 2015 г — Каждый вариант контрольной работы выстроен по одной и той же контрольных работ по алгебре для 10 класса (авт Глизбург В 4 Решебник к сборнику контрольных работ по — Math-HelperRu Сохраненная копия 16 февр 2016 г — Контрольные работы для 10 класса общеобразовательных Каждый вариант контрольной работы выстроен по одной и той же схеме: задания контрольных работ по алгебре для 10 класса (авт Глизбург В 4 Задание 11 Контрольная работа 1 Вариант 4 Алгебра 10 класс Сохраненная копия Ответы на вопрос – Задание 11 Контрольная работа 1 Вариант 4 Алгебра 10 класс Глизбург В И ГДЗ – читайте на Рамблер/класс Задание 3 Контрольная работа 1 Вариант 4 Алгебра 10 класс Сохраненная копия Ответы на вопрос – Задание 3 Контрольная работа 1 Вариант 4 Алгебра 10 класс Глизбург В И ГДЗ – читайте на Рамблер/класс Задание 2 Контрольная работа 4 Вариант 4 Алгебра 10 класс Сохраненная копия Ответы на вопрос – Задание 2 Контрольная работа 4 Вариант 4 Алгебра 10 класс Глизбург В И ГДЗ – читайте на Рамблер/класс ГДЗ по Алгебре 10 класс Контрольные работы Глизбург ВИ gdz-freeru/gdz/Al10/9 Сохраненная копия Похожие Школьники, которым тяжело дается такой предмет, как алгебра , всегда могут найти ответы в ГДЗ по Алгебре : 10 класс , » Контрольные работы «, Глизбург ГДЗ по Алгебре 10-11 класс Контрольные работы АГ Мордкович gdz-freeru/gdz/Al10/8 Сохраненная копия Похожие Готовое Домашнее Задание (ГДЗ) по Алгебре и началам анализа Контрольные работы 10 -11 класс АГ Мордкович, ЕЕ Тульчинская Вариант 4 «Алгебра и начала математического анализа 10 класс — Лабиринт Сохраненная копия Интересные рецензии пользователей на книгу Алгебра и начала 10 класс Контрольные работы Базовый уровень Вита Глизбург: Рейтинг: + 4 [PDF] Контрольные работы по алгебре и началам анализа 10 класс 86sch-tegiedusiteru/DswMedia/10algebrapdf Сохраненная копия Алгебра и начала анализа Ествебра класс В 10 -11 и начала анализа Контрольные работы приведены в 4 -х вариантах и даны ре- Вариант 4 ГДЗ по алгебре за 10 класс контрольные работы Глизбург ВИ › ГДЗ › 10 класс › Алгебра › контрольные работы Глизбург Сохраненная копия ГДЗ: Спиши готовые домашние задания контрольные работы по алгебре за 10 класс , решебник Глизбург ВИ, Базовый уровень ФГОС, онлайн ответы Тест по алгебре (10 класс) на тему: Входная контрольная работа Сохраненная копия 11 сент 2018 г — Входная контрольная работа по математике 10 класс сентябрь К каждому заданию 1 части даны 4 варианта ответа, из которых Картинки по запросу вариант 4 алгебра 10 класс контрольная работа по «cb»:3,»cl»:6,»cr»:3,»ct»:3,»id»:»I-cmjBQwgHaQLM:»,»ml»:»600″:»bh»:90,»bw»:58,»oh»:800,»ou»:» «,»ow»:521,»pt»:»imglabirintru/images/comments_pic/1046/03lablacl»,»rh»:»labirintru»,»rid»:»tAeMxw-nFLUi0M»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Лабиринт»,»th»:103,»tu»:» \u003dtbn:ANd9GcQsLe8ijJn1fzsqbJejy28l_isSh3E4RHKkSZiysDgjuNnllbP1SHD7fQ»,»tw»:67 «crea»:»Olga»,»id»:»lOpcc1R78e5sDM:»,»ml»:»600″:»bh»:90,»bw»:120,»oh»:267,»ou»:» «,»ow»:768,»pt»:»classramblerru/qa-service/production/uploads/ima»,»rh»:»classramblerru»,»rid»:»NIEPIfttSh3JsM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Рамблер/класс»,»th»:90,»tu»:» \u003dtbn:ANd9GcSlVBfA-TmL9sRm6tGtfaoWnDB8FL9_sXgIwPIL6kok4x6091tXYA3ZZYw»,»tw»:259 «cb»:3,»cl»:9,»cr»:9,»ct»:3,»id»:»va-p0Ab0ysPZSM:»,»ml»:»600″:»bh»:90,»bw»:113,»oh»:480,»ou»:» «,»ow»:640,»pt»:»ds04infourokru/uploads/ex/0cf8/00063aff-02fb18fa»,»rh»:»infourokru»,»rid»:»SCVO0yNrO9UfSM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Инфоурок»,»th»:90,»tu»:» \u003dtbn:ANd9GcTpPT1-KlgA7oIhhLAlEbrd6WiQyGYjiUvXSjqgj605XHnV9T1IC2D48LU»,»tw»:120 «cl»:6,»cr»:6,»ct»:3,»id»:»96FWrmBaY2KjNM:»,»ml»:»600″:»bh»:90,»bw»:105,»oh»:280,»ou»:» «,»ow»:339,»pt»:»gdz-freeru/img/covers/Al10_9jpg»,»rh»:»gdz-freeru»,»rid»:»oNJlp6IIo7vFxM»,»rt»:0,»ru»:» «,»st»:»ГДЗ»,»th»:90,»tu»:» \u003dtbn:ANd9GcQ4eAFgsM5h5fR7Wiqsewnxj5QPKtIFWM42OIc0cZtUYj4Ps1PjPS5M_A»,»tw»:109 «cr»:6,»id»:»ZDj7KdNoXsATuM:»,»ml»:»600″:»bh»:90,»bw»:65,»oh»:823,»ou»:» «,»ow»:600,»pt»:»gdzmath-helperru/wp-content/uploads/2015/02/Resh»,»rh»:»gdzmath-helperru»,»rid»:»JRxzLgSISLIbCM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Math-HelperRu»,»th»:97,»tu»:» \u003dtbn:ANd9GcTKmec-ihsCskArGqlQEGTT0eywnPeboLHtbHn4CwR8DfkKsJJTpvWNO1E»,»tw»:71 «crea»:»Olga»,»id»:»Kf1PuoGoNzvR1M:»,»ml»:»600″:»bh»:90,»bw»:119,»oh»:223,»ou»:» «,»ow»:781,»pt»:»classramblerru/qa-service/production/uploads/ima»,»rh»:»classramblerru»,»rid»:»nH7D6NRKZQfv2M»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Рамблер/класс»,»th»:90,»tu»:» \u003dtbn:ANd9GcTdOcTFTmJJIw15QBKH5gS8Mj3AOzodYaNV40j9fAkhhTSlMmSSr7-CpS8e»,»tw»:315 Другие картинки по запросу «вариант 4 алгебра 10 класс контрольная работа по» Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты Контрольные работы по алгебре и началам анализа 10 класс › Алгебра Сохраненная копия 1 нояб 2017 г — Контрольные работы по алгебре и началам анализа 10 класс Алимов Преобразование степеней с действительным показателем 4 ▷ решение контрольных работ по алгебре бесплатно 10 класс wwwzstelceu/content//reshenie-kontrolnykh-rabot-po-algebre-besplatno-10-klassx Сохраненная копия 15 нояб 2018 г — решение контрольных работ по алгебре бесплатно 10 класс For You Контрольные работы по алгебре и началам анализа 10 класс два варианта контрольной работы по ЕГЭ 2017 Математика Сборник Решебник Алгебра и начала анализа Контрольные работы nigluscom/gdz/10/3/7 Сохраненная копия Решебник Алгебра и начала анализа Контрольные работы Мордкович АГ 10 класс гдз Задание Контрольная работа №1 Контрольная работа № 4 10 класс Подготовительный вариант годовая контрольная работа gigabazaru/doc/57025html Сохраненная копия Подготовительный вариант годовая контрольная работа по алгебре и началам Упростите выражение: cos ( — 270 o ) 1) cos 2) — cos 3) sin 4 ) — sin А2 ГДЗ по алгебре для 10 класса Дидактические материалы Ивлев БМ Сохраненная копия Похожие Тут отличные гдз по алгебре Дидактические материалы для 10 класса , работы , все варианты из трёх проверочных работ и семь контрольных работ 1; 2; 3; 4 ; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 17; 18; 19; 20; 21; 22; 23; 24; 25 Итоговая контрольная работа по алгебре за 10 класс — 4ЕГЭ Сохраненная копия 6 апр 2018 г — Контрольная состоит из 4 вариантов по 18 заданий Контрольные работы по алгебре 10 класс, контрольные по Сохраненная копия Рейтинг: 5 — 18 голосов 4 апр 2017 г — Контрольная по алгебре 10 класса , контрольные работы по Мордковичу с ответами за 1, 2, 3, 4 четверти Контрольная работа №1 «Определение тригонометрических функций» Вариант I 1 Вычислите функции: Итоговый КИМ по алгебре 10 класс — Мультиурок Сохраненная копия 30 сент 2017 г — Итоговая контрольная работа по алгебре и началам математического анализа за курс 10 класса составлена в соответствии с Алгебра 10 класс Контрольные работы Глизбург ВИ — Wixcom tatyanchenkowixsitecom/tatyanchenko/algebra-i-nachala-matematicheskogo—2 10 класс Контрольные работы (базовый и углубл уровни) Глизбург ВИ и второй варианты ориентированы на классы с недельной нагрузкой 4 ч, Контрольные работы по алгебре и началам анализа 10 класс allengorg/d/math/math935htm Сохраненная копия Контрольная работа № 8 (2 урока) 24 Вариант 1 24 Вариант 2 24 Вариант 3 25 Вариант 4 25 Задачи по курсу « Алгебра и начала анализа» для 10 Математика:Контрольная работа по алгебре 10 класс Сохраненная копия 8 янв 2015 г — 160 класс математика Ответы к контрольной работе № Вариант 1 Вариант 2 1 4 3 2 4 /3 — 0,75 3 0,28 0,28 4 12 7,5 5 36 2 6 10 [PDF] Итоговая контрольная работа по алгебре и началам анализа за 10 школа114екатеринбургрф/file/download/5825 Сохраненная копия Итоговая контрольная работа по алгебре и началам анализа за 10 класс Вариант 1 А1 Вычислите: а) 4 2 1 log 16 log 8 — ; б) 2 arcsin0,5 arccos 2 + Итоговая контрольная работа по алгебре, 10 класс — Урокрф Сохраненная копия Похожие 19 авг 2016 г — Итоговая контрольная работа по алгебре , 10 класс Пояснительная Контрольная работа составлена в 4 -х вариантах Вариант 1 Контрольные работы по алгебре 10 класс — математика, прочее Сохраненная копия Похожие 7 февр 2015 г — Контрольные работы по алгебре 10 класс Нажмите, чтобы узнать 4 ) Решите уравнение: 5) Докажите тождество: 2 вариант 1) Контрольные работы по математике — 10 класс — Математика Сохраненная копия Контрольная работа содержит 2 варианта по пять заданий в каждом Тексты контрольной Представлено 4 варианта экзаменационной работы Итоговая контрольная работа по алгебре и началам анализа в 10 классе Входная контрольная работа работа по алгебре для 10 классов 4 obrazbaseru/matematika/1987-vkhodnaya-kontrolnaya-rabota-rabota-po-algebre-dly Сохраненная копия Похожие Рейтинг: 4 — 3 голоса 4 сент 2015 г — Входная контрольная работа работа по алгебре для 10 классов 4 варианта Входная работа по алгебре разработана в 4 вариантах итоговая контрольная работа 10 классdocx — Контрольная работа Сохраненная копия Итоговая контрольная работа по алгебре 10 класс 1 Найдите 3 вариант f( x)=12+ x−5 x2−4х+31 4 Решите уравнение: а) cos ( х 3 ) = √3 2 b)3sin2 x — 5 Итоговая контрольная работа по алгебре 10 класс | Doc4webru Сохраненная копия К уроку алгебры Итоговая контрольная работа по алгебре 10 класс — скачать бесплатно Вариант 1 1Упростите выражение: 2 Вычислите , если и 3 Найдите производную функции 4 Составьте уравнение касательной к Домашняя контрольная работа номер 4 №10, вариант 2 — ГДЗ по Сохраненная копия ГДЗ (готовое домашние задание из решебника) на Домашняя контрольная работа номер 4 № 10 , вариант 2 по учебнику Алгебра 9 класс Часть 2 Урок , входная контрольная работа по алгебре 10 класс › Контрольная работа Сохраненная копия 26 апр 2017 г — Урок , входная контрольная работа по алгебре 10 класс Габиева Вариант 1 1 На диаграмме показан средний балл участников 10 стран в тестировании учащихся 4 -го класса, по математике в 2007 году (по Алгебра 8 Контрольные (Макарычев ЮН) | Контроль знаний контрользнанийрф/algebra-8-kontrolnye-makarychev-yu-n/ Сохраненная копия 9 авг 2018 г — Представленные ниже контрольные работы в 2-х вариантах Затем представлены ответы на оба варианта контрольной При постоянном использовании данных контрольных работ (в 4 -х вариантах) рекомендуем КУПИТЬ книгу: Алгебра 8 класс Контрольная работа № 10 Итоговая за [DOC] Входная контрольная работа 10 класс II вариант Часть I eduportal44ru/Ponaz_EDU/SSchool//КОС%20МА10,%2011%20входнойdocx Сохраненная копия Входная контрольная работа по курсу математики, 4 11 класс 1 по предмету «_математика_» в _10_ классе Предмет: « Математика », 10 класс Математика 10 класс Контрольная работа 1 Вариант 1 4 x 2 3 Сохраненная копия 1 Математика 0 класс Контрольная работа Вариант Выполнить действия 7 5 0, : a 3 +b 3 a 2 +b 2 ab a 2 2 ab+b 2 a b x 2 6 x9 x 2 x 6 4 Решить [DOC] Профильный уровень Сохраненная копия 10 класс АЛГЕБРА — ПРОФИЛЬНЫЙ УРОВЕНЬ Контрольная работа №1 по теме «Числовые функции в точках 2;-x 3 Постройте график функции 4 Докажите, что функция является четной 5 4 вариант 1 Найдите область [DOC] Контрольная работа по алгебре и началам анализа agkptru//контрольная_работа_по_математике_для_заочников_1_курса_на_базе Сохраненная копия Похожие По дисциплине: Математика : алгебра , начала анализа, геометрия для студентов Контрольная работа составлена в 10 вариантах 4 вариант 1 Контрольные работы по математике «Тригонометрия» — Видеоуроки Сохраненная копия Контрольные работы создана в двух вариантах по шесть заданий в каждом Контрольная работа № 1 ( алгебра 10 класс ) I вариант 1 Вычислите: а) Ответы@MailRu: Помогите найти готовые контрольные работы по › Домашние задания › Другие предметы Сохраненная копия Похожие 2 ответа 9 дек 2013 г — т е гдз по алгебре 10 класс александрова! Предмет, который лежит в основе многих дисциплин, ведется в школе буквально 3- 4 часа в неделю все возможные варианты заданий для учащихся 10-ых классов [PDF] Контрольные работы Алгебра 10 school6m-skru/files/matematika/материал/контрработы/book32pdf Сохраненная копия Похожие 10 класс Контрольные работы для учащихся общеобразовательных Каждый вариант контрольной работы выстроен по одной и той Вариант 4 1 [DOC] к учебникам математики для 10 — Издательство «Просвещение oldprosvru/ebooks/tema_mdoc Похожие БГ Зив Дидактические материалы по геометрии для 10 класса – М Просвещение СБ Кадомцев Аналитическая геометрия и линейная алгебра 4 Тетраэдр и параллелепипед 3 4 Контрольная работа № 12 1 1 11 класс I вариант (1,5 ч в неделю, всего 51 ч) II вариант (2 ч в неделю, всего 68 ч) [PDF] Демонстрационный вариант по математике для учащихся 10 sarschool76narodru/demo_math_10pdf Сохраненная копия Похожие по математике за курс 10 класса (УМК Мордкович АГ) Базовый уровень Годовая контрольная работа составлена в соответствии с программным материалом курса « Алгебра и начала анализа» и требованиями федеральных 4 Нахождение значения тригонометрической функции по известной Контрольная работа 10 класс «Степень с действительным pedsovetsu › › Математика, алгебра, геометрия › Оценка знаний учащихся Сохраненная копия Похожие 27 мар 2013 г — Методическая разработка « Контрольная работа по алгебре и началам анализа 10 класс на тему Вариант 4 Вычислить: а) б) в) 2 Курс: АЛГЕБРА И НАЧАЛА АНАЛИЗА 11,: Диагностические и Сохраненная копия Похожие Диагностические и тренировочные работы по математике Диагностическая Диагностическая работа № 2 ( 4 вариант , без логарифмов) Тесты по некоторым темам алгебры и начал анализа (7- 10 класс ) Контрольная работа № 1 «Показательная функция, показательные уравнения и неравенства Решебник (ГДЗ) по алгебре 10 класс Ивлев › ГДЗ › 10 класс › Алгебра › Ивлев БМ Сохраненная копия Похожие Самостоятельные работы Вариант 1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 Контрольные работы Контрольные работы по алгебре и началам математического 10 класс Контрольная работа № 1 Вариант 1 1 Задает ли указанное правило 4 Задайте аналитически и постройте график функции , у которой [DOC] КОНТРОЛЬНАЯ РАБОТА 10 КЛАСС открытыйурокрф/статьи/513912/pril1doc Сохраненная копия Алгебра 10 К Р №1 Вариант 1 A1 Найдите значение выражения , если 1) 0, 5 2) –1,5 3) 1,25 4 ) –0,5 A2 Упростите выражение 1) 2) 2 3) –12 4 ) 12 A3 [PDF] Контрольные работы по алгебре и начала анализа 10 класс Сохраненная копия Итоговая контрольная работа по алгебре и начала анализа 10 класс 4 На рисунке изображен график функции y=f(x) и касательная к нему в точке с [PDF] КИМ по алгебре и началам анализа для 10 класса Учебник для Сохраненная копия Контрольная работа №1 по теме: «Действительные числа Рациональные уравнения и неравенства» 1 вариант 2 вариант 1 Сравните числа а) 0,8 и ▷ контрольная работа по алгебре 10 класс тульчинская magneticmicrospherecom//kontrolnaia-rabota-po-algebre-10-klass-tulchinskaiaxml Сохраненная копия 3 дек 2018 г — контрольная работа по алгебре 10 класс тульчинская 2 Контрольная №7 Вариант 3 Контрольная №7 Вариант 4 Контрольная №8 Навигация по страницам 1 2 3 Следующая Ссылки в нижнем колонтитуле Россия — Подробнее… Справка Отправить отзыв Конфиденциальность Условия Аккаунт Поиск Карты YouTube Play Новости Почта Контакты Диск Календарь Google+ Переводчик Фото Ещё Покупки Документы Blogger Hangouts Google Keep Jamboard Подборки Другие сервисы Google
Яндекс Яндекс Найти Поиск Поиск Картинки Видео Карты Маркет Новости ТВ онлайн Знатоки Коллекции Музыка Переводчик Диск Почта Все Ещё Дополнительная информация о запросе Показаны результаты для Нижнего Новгорода Москва 1 ГДЗ решебник по Алгебре Контрольные работы 10 GdzMonsternet › 10-klass/gdz-po-algebre…rabotyi… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Алгебра 10 класс Контрольные работы Мордкович Тульчинская 2000-2005 Алгебра 10 класс Задачник Мордкович Денищева 2001 Читать ещё Алгебра 10 класс Контрольные работы Мордкович Тульчинская 2000-2005 Алгебра 10 класс Задачник Мордкович Денищева 2001 Алгебра 10 класс Задачник Мордкович Денищева Корешкова 2004 Английский язык 10 класс Мордкович 2004 Алгебра 10 класс Задачник Мордкович 2009 Алгебра 10 класс Контрольные работ Сапожников Мордкович Тульчинская 2009 Алгебра 10 класс Сапожников Мордкович 2012 Алгебра 10 класс Сапожников Мордкович 2012 Алгебра 10 класс Задачник Мордкович Часть 2 Готовые задания Контрольная работа № 1 Вариант 1: 1 2 3 4 5 6 7 8 Вариант 2: 1 2 3 4 5 6 7 8 Вариант 3: 1 2 3 4 5 6 7 8 Вариант 4 Скрыть 2 Алгебра и начала анализа 10 класс Контрольные infourokru › algebra-i-nachala…klass…795594html Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Подробнее о сайте Инфоурок › Алгебра › Другие методич материалы › Алгебра и начала анализа 10 класс Контрольные работы ( 10 класс ) I вариант К-1 по теме «Действительные числа Рациональные уравнения и неравенства» ( 10 класс ) Читать ещё Инфоурок › Алгебра › Другие методич материалы › Алгебра и начала анализа 10 класс Контрольные работы Алгебра и начала анализа 10 класс Контрольные работы библиотека материалов К-1 по теме «Действительные числа Рациональные уравнения и неравенства» ( 10 класс ) I вариант К-1 по теме «Действительные числа Рациональные уравнения и неравенства» ( 10 класс ) II вариант 1Упростите выражение: 2Решите уравнение Скрыть 3 Контрольные работы по алгебре 10 класс mathematics-testscom › algebra-10-klass…10-klass… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Контрольная по алгебре 10 класса , контрольные работы по Мордковичу с ответами за 1, 2 Алгебра – 10 класс Контрольные работы с ответами к учебнику Мордковича АГ Контрольная работа № 5 «Формулы тригонометрии» Вариант I Читать ещё Контрольная по алгебре 10 класса , контрольные работы по Мордковичу с ответами за 1, 2, 3, 4 четверти Алгебра – 10 класс Контрольные работы с ответами к учебнику Мордковича АГ за 1, 2, 3, 4 четверти Контрольные на темы: «Определение тригонометрических функций», «Свойства и графики тригонометрических функций», «Тригонометрические уравнения», «Тригонометрические функции сложения аргумента», «Правила и формулы отыскания производных», «Применение производной к исследованию функций» и др Контрольная работа № 5 «Формулы тригонометрии» Вариант I Скрыть 4 Контрольные работы » Алгебра 10 класс » infourokru › kontrolnie…algebra-klass-841465html Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Подробнее о сайте Инфоурок › Алгебра › Конспекты › Контрольные работы » Алгебра 10 класс » А-10 Контрольная работа № 1 Действительные числа Вариант 1 1 Вычислите: ; 2 Упростите выражение Читать ещё Инфоурок › Алгебра › Конспекты › Контрольные работы » Алгебра 10 класс » Контрольные работы » Алгебра 10 класс » библиотека материалов А-10 Контрольная работа № 1 Действительные числа Вариант 1 1 Вычислите: ; 2 Упростите выражение 3 Решите уравнение 4 Запишите бесконечную периодическую дробь 0,(43) в виде обыкновенной дроби 5 Сократите дробь 6 Сравните числа: и 1; 7* Упростите выражение Контрольная работа № 1 Действительные числа Вариант 2 1 Вычислите: 2 Упростите выражение Скрыть 5 Контрольные работы по алгебре 10 класс Глинзбург GDZ-na-5com › Алгебра › 10 класс › …-po-algebre-10-klass… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Главная › Алгебра › 10 класс › Контрольные работы по алгебре 10 класс Глинзбург Курс алгебры для десятого класса для общеобразовательных школ Он включает в себя все ответы к контрольным задачам всех вариантов : простым Читать ещё Главная › Алгебра › 10 класс › Контрольные работы по алгебре 10 класс Глинзбург ответы Контрольные работы по алгебре 10 класс Глинзбург ответы Курс алгебры для десятого класса для общеобразовательных школ предполагает изучение комплексного материала, рассчитанного на поэтапное освоение учащимися сложных математических понятий и получение теоретических знаний, которые далее будут основанием для программы старших классов Он включает в себя все ответы к контрольным задачам всех вариантов : простым, с повышенной сложностью, а также их подробное решение с указанием всех необходимых действий Скрыть 6 Контрольные работы по алгебре 10 класс Мордкович gdz-vipru › менюшка/10-класс/алгебра/тульчинская Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Гдз по алгебре 10 класс Контрольные работы Мордкович, Тульчинская Мнемозина 2000-2013 год К – 4 ( вариант 1- 4 ) Читать ещё Гдз по алгебре 10 класс Контрольные работы Мордкович, Тульчинская Мнемозина 2000-2013 год К – 1 ( вариант 1- 4 ): 1 2 3 4 К – 2 ( вариант 1- 4 ): 1 2 3 4 К – 3 ( вариант 1- 4 ): 1 2 3 4 К – 4 ( вариант 1- 4 ): 1 2 3 4 К – 5 ( вариант 1- 4 ): 1 2 3 4 К – 6 ( вариант 1- 4 ): 1 2 3 4 К – 7 ( вариант 1- 4 ) Скрыть 7 Контрольные работы по алгебре 10 класс скачать uchitelyacom › Алгебра › …po-algebre-10-klasshtml Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте А- 10 Контрольная работа № 1 Действительные числа Вариант 1 1 Вычислите: ; 2 Упростите выражение 3 Решите уравнение 4 Запишите бесконечную периодическую дробь 0,(43) в виде обыкновенной дроби Читать ещё А- 10 Контрольная работа № 1 Действительные числа Вариант 1 1 Вычислите: ; 2 Упростите выражение 3 Решите уравнение 4 Запишите бесконечную периодическую дробь 0,(43) в виде обыкновенной дроби 5 Сократите дробь 6 Сравните числа: и 1; 7* Упростите выражение 1 Контрольная работа № 1 Действительные числа Вариант 2 1 Вычислите: 2 Упростите выражение 3 Решите уравнение 4 Запишите бесконечную периодическую дробь 0,3(6) в виде обыкновенной дроби 5 Сократите дробь Скрыть 8 Тест по алгебре ( 10 класс ) по теме: Контрольные nsportalru › Школа › Алгебра › …-po-algebre-10-klass Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Подробнее о сайте Каждый вариант контрольной работы выстроен по одной и той же схеме: задания обязательного минимума – до первой черты Разноуровневая Контрольная работа по алгебре 10 класс (учебник Муравиных) по теме «Показательная функция» Может быть испольхована для учебников других авторов в 10-11 классе Читать ещё Каждый вариант контрольной работы выстроен по одной и той же схеме: задания обязательного минимума – до первой черты, задания среднего уровня – между первой и второй чертой, задания уровня выше среднего – после второй черты Разноуровневая Контрольная работа по алгебре 10 класс (учебник Муравиных) по теме «Показательная функция» Может быть испольхована для учебников других авторов в 10-11 классе , а т Мне нравится Поделиться Скрыть 9 Вариант 4 алгебра 10 класс контрольная работа по — смотрите картинки ЯндексКартинки › вариант 4 алгебра 10 класс контрольная работа по Пожаловаться Информация о сайте Ещё картинки 10 ГДЗ по Алгебре 10 класс Контрольные работы Глизбург gdz-freeru › Алгебра › 9 Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Выберите контрольную работу КР №1 В1 КР №1 В2 КР №1 В2 КР №1 В3 КР №1 В 4 КР №1 В 4 КР №2 В1 КР №2 В2-3 КР №2 В 4 Школьники, которым тяжело дается такой предмет, как алгебра, всегда могут найти ответы в ГДЗ по Алгебре : 10 класс , » Контрольные работы «, Глизбург ВИ Здесь не только есть ответы на Читать ещё Выберите контрольную работу КР №1 В1 КР №1 В2 КР №1 В2 КР №1 В3 КР №1 В 4 КР №1 В 4 КР №2 В1 КР №2 В2-3 КР №2 В 4 КР №3 В1 КР №3 В1 КР №3 В2 Кр №3 В3 кр №3 В3 кр №3 В 4 кр № 4 В1 кр № 4 В2 кр № 4 В3 кр № 4 В 4 кр №5 В1 кр №5 В2 кр №5 В3 кр №5 В 4 кр №6 В1 кр Школьники, которым тяжело дается такой предмет, как алгебра, всегда могут найти ответы в ГДЗ по Алгебре : 10 класс , » Контрольные работы «, Глизбург ВИ Здесь не только есть ответы на все вопросы, но и приведены решения задач и уравнений Не стоит воспринимать предлагаемый решебник, как очередную шпаргалку, это скорее пособие для высокой самоподготовки и проверки собственных знаний Скрыть ГДЗ — Алгебра и начала анализа 10 класс Контрольные reshebnik5-11ru › 10 класс › Алгебра › Мордкович Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте ГДЗ — Алгебра и начала анализа 10 -11 класс Контрольные работы АГ Мордкович, ЕЕ Тульчинская — М: Мнемозина, 2000 — 2013 гг Контрольная № 10 Вариант 2 Контрольная № 10 Вариант 3 Контрольная № 10 Вариант 4 Контрольная №11 Вариант 1 Контрольная №11 Вариант 2 Контрольная №11 Читать ещё ГДЗ — Алгебра и начала анализа 10 -11 класс Контрольные работы АГ Мордкович, ЕЕ Тульчинская — М: Мнемозина, 2000 — 2013 гг Пожалуйста выберите номер Контр раб в этом окне * → Контрольная № 10 Вариант 2 Контрольная № 10 Вариант 3 Контрольная № 10 Вариант 4 Контрольная №11 Вариант 1 Контрольная №11 Вариант 2 Контрольная №11 Вариант 3 Контрольная №11 Вариант 4 Контрольная №12 Вариант 1 Контрольная №12 Вариант 2 Контрольная №12 Вариант 3 Контрольная №12 Вариант 4 Контрольная №13 Вариант 1 Контрольная №13 Вариант 2 Контрольная №13 Вариант 3 Контрольная №13 Вариант 4 Скрыть Сборник контрольных работ по алгебре , ( 10 класс ) урокрф › library/sbornik…po…10_klass_150843html Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте КИМ для учителя-предметника для 10 класса Учебно-дидактические материалы по Алгебре для 10 класса Контрольная работа № 1 по теме «Функции и их свойства» Цель: проверить уровень усвоение ГОСО Читать ещё КИМ для учителя-предметника для 10 класса Учебно-дидактические материалы по Алгебре для 10 класса Контрольная работа № 1 по теме «Функции и их свойства» Цель: проверить уровень усвоение ГОСО — умение находить значение функции в точке; — умение находить область определения функции; — умения строить эскиз графика функции и находить по эскизу промежутки возрастания и убывания , экстремумы функции, точки пересечения с осями координат Скрыть ГДЗ по алгебре для 10 класса Дидактические материалы GdzPutinaru › po-algebre/10-klass/didakticheskie… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте В Сборнике ГДЗ по алгебре за 10 класс Ивлев проработаны все десять вариантов самостоятельной работы , все варианты из трёх проверочных работ и семь контрольных работ Также полностью решены четыре варианта карточек для проведения зачётов Таким образом, школьники будут готовы к любой Читать ещё В Сборнике ГДЗ по алгебре за 10 класс Ивлев проработаны все десять вариантов самостоятельной работы , все варианты из трёх проверочных работ и семь контрольных работ Также полностью решены четыре варианта карточек для проведения зачётов Таким образом, школьники будут готовы к любой проверке на уроке Решебник Ивлева поможет подготовиться к любой форме контроля знаний Ведь порой помощь в классных работах нужна не только детям с низкой успеваемостью, но и тем, кто отлично владеет предметом Просто на самостоятельных и контрольных работах , ввиду стрессового состояния, школьники могут теряться и Скрыть ГДЗ по Алгебре за 10 класс контрольные работы MegaReshebaru › gdz/algebra/10-klass/kontrolnie…i… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Подробный решебник (ГДЗ) по Алгебре для 10 класса контрольные работы базовый и углубленный уровень Авторы тетради: Глизбург ВИ Дополнение к учебнику и задачнику АГ Мордкович 10 класс Читать ещё Подробный решебник (ГДЗ) по Алгебре для 10 класса контрольные работы базовый и углубленный уровень Авторы тетради: Глизбург ВИ Дополнение к учебнику и задачнику АГ Мордкович 10 класс автор: Глизбург ВИ Подробный решебник (ГДЗ) по Алгебре для 10 класса контрольные работы базовый и углубленный уровень Авторы тетради: Глизбург ВИ Дополнение к учебнику и задачнику АГ Мордкович 10 класс Рекомендуемые решебники ГДЗ учебник алгебра 10 класс Мордкович АГ базовый и углубленный уровень ГДЗ Задачник алгебра 10 класс Мордкович АГ базовый и углубленный уровень Скрыть ГДЗ по Алгебре за 10 класс контрольные работы ugdzru › reshebniki/10-klass/algebra/kontrolnie… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сборник готовых домашних заданий (ГДЗ) контрольные работы по Алгебре за 10 класс , решебник Глизбург ВИ самые лучшие ГДЗ к контрольным работам по алгебре за 10 класс Глизбург, Базовый и углубленный уровень можно скачать здесь ГДЗ к самостоятельным работам по алгебре за 10 класс Читать ещё Сборник готовых домашних заданий (ГДЗ) контрольные работы по Алгебре за 10 класс , решебник Глизбург ВИ самые лучшие ответы от UGDZRU ГДЗ к контрольным работам по алгебре за 10 класс Глизбург, Базовый и углубленный уровень можно скачать здесь ГДЗ к самостоятельным работам по алгебре за 10 класс Александрова, Базовый и углубленный уровень можно скачать здесь Контрольная работа № 1 Варианты Скрыть ГДЗ по алгебре за 10 класс контрольные работы GDZru › class-10/algebra/kontrolnie-raboti-bazovij… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте ГДЗ: Спиши готовые домашние задания контрольные работы по алгебре за 10 класс , решебник Глизбург ВИ, Базовый уровень ФГОС, онлайн ответы на GDZRU Контрольная работа № 4 Варианты 1 2 3 4 Читать ещё ГДЗ: Спиши готовые домашние задания контрольные работы по алгебре за 10 класс , решебник Глизбург ВИ, Базовый уровень ФГОС, онлайн ответы на GDZRU Рекомендуем посмотреть Алгебра 10 -11 класс учебник Базовый уровень Контрольная работа № 4 Варианты 1 2 3 4 Контрольная работа № 5 Варианты 1 2 3 4 Контрольная работа № 6 Варианты 1 2 3 4 Контрольная работа № 7 Варианты 1 2 3 4 Контрольная работа № 8 Варианты 1 2 3 4 Скрыть Вместе с « вариант 4 алгебра 10 класс контрольная работа по » ищут: вариант 4 алгебра 7 класс алгебра 8 класс к-2 вариант 4 вариант 4 часть 1 модуль алгебра ответы к-2 4 вариант алгебра 10 класс 132 страница алгебра 7 класс дидактические материалы к 3 вариант 4 алгебраические дроби преобразование рациональных выражений вариант 4 алгебра 7 класс контрольная работа 1 вариант 4 ответы алгебра 8 класс контрольная работа 2 вариант 4 вариант 4 к-2 алгебра 9 класс к-1 4 вариант 10 класс алгебра 1 2 3 4 5 дальше Браузер Предложит замену неверному адресу сайта 0+ Установить
Тригонометрические функции: определение и примеры — видео и стенограмма урока
Примеры из реальной жизни
Эти тригонометрические функции находят практическое применение в геодезии, строительстве, инженерии и даже в медицине. Вот один из практических способов использования этих функций для решения проблемы:
Вот один из практических способов использования этих функций для решения проблемы:
Угол возвышения самолета составляет 23 градуса, а его высота — 2500 метров. Как далеко это?
Мы пытаемся решить этот прямоугольный треугольник относительно гипотенузы x. Поскольку длина стороны, которую мы знаем, противоположна известному углу, мы можем использовать функцию синуса.
Sin (23) = 2500 м / x
x = 6398,3 метра
Как решать задачи
Эти отношения можно использовать для решения любой стороны или угла прямоугольного треугольника. Предоставленная вам информация поможет вам определить, какую функцию использовать.
Пример:
Решите относительно b, если вы знаете, что c равно 2.5 км, а B — 15,7 градуса.
Поскольку нам известны измерения угла, противоположного той стороне, которую мы пытаемся найти, и гипотенузы, мы можем использовать функции синуса или косеканса. Чаще всего при решении этих задач используются функции синуса, косинуса и тангенса, поскольку их легче вычислить с помощью калькулятора. Итак, мы будем использовать синусоидальную функцию для этой задачи.
Чаще всего при решении этих задач используются функции синуса, косинуса и тангенса, поскольку их легче вычислить с помощью калькулятора. Итак, мы будем использовать синусоидальную функцию для этой задачи.
Sin (15,7) = b / 2,5 км
0,271 = b /2.5 км
b = 0,6765 км
Попробуйте это:
Решите треугольник ABC, учитывая, что A составляет 35 градусов, а c — 15 футов.
Мы мало что знаем об этом треугольнике, но поскольку это прямоугольный треугольник и нам известны как минимум две другие стороны или углы, мы можем использовать тригонометрические функции для решения остальных задач. Проще всего начать с определения угла B. Поскольку все треугольники имеют угловые меры, которые в сумме составляют 180 градусов, чтобы найти B, просто вычтите .
180-90-35 = B
B = 55 градусов
Затем мы можем использовать синус и косинус для решения сторон a, и b. Используя угол A, и гипотенузу, уравнение, которое необходимо решить для стороны a , выглядит следующим образом:
Используя угол A, и гипотенузу, уравнение, которое необходимо решить для стороны a , выглядит следующим образом:
Sin (35 градусов) = a /15 футов
a = 8,6 футов
Уравнение для решения для стороны b составляет:
Cos (35 градусов) = b /15 футов
b = 12.3 фута
Резюме урока
Шесть основных тригонометрических функций — это синус, косинус, тангенс, секанс, косеканс и котангенс. Они полезны для определения высот и расстояний и имеют практическое применение во многих областях, включая архитектуру, геодезию и инженерию.
Результаты обучения
Как только вы просмотрите урок, примените свои знания, чтобы:
- Сформулировать шесть тригонометрических функций
- Назовите стороны треугольника
- Распознавать взаимосвязь между сторонами треугольника и тригонометрическими функциями
- Использование тригонометрических функций для решения задач
Что такое «Все ученики берут исчисление» в триггере?
Тригонометрия ASTC
Когда вы работаете с тригонометрией, вы будете иметь дело с четырьмя квадрантами графика. Ось x и y делит координатную плоскость на четыре отдельных участка.
Ось x и y делит координатную плоскость на четыре отдельных участка.
ASTC — это вспомогательное средство для запоминания того, является ли тригонометрическое соотношение положительным или отрицательным в каждом квадранте: [Add-Sugar-To-Coffee]
Когда вы его вытягиваете, это выглядит так:
График ASTCВы даже можете использовать эту диаграмму как шпаргалку по тригонометрии. ASTC поможет вам вспомнить, как восстановить эту диаграмму, чтобы вы могли использовать ее, когда вы встречаетесь с квадрантами тригонометрии в своих тестовых вопросах.
На приведенном выше рисунке у нас есть квадрант 1 2 3 4. В квадранте 1 значения x и y положительны. В квадранте 2 x отрицателен, а y все еще положителен. В квадранте 3 оба значения x и y отрицательны. Наконец, в квадранте 4 x положителен, а y отрицателен.
Это говорит нам о том, что если у нас есть треугольник в первом квадранте, синус, косинус и тангенс будут положительными. Во втором квадранте только синус будет положительным, а косинус и тангенс — отрицательными. Видите, как это простой способ запомнить, какие тригонометрические отношения будут положительными?
Видите, как это простой способ запомнить, какие тригонометрические отношения будут положительными?
Если вам не нравится «Добавить сахар в кофе», вы можете использовать другие сокращения, например:
Все учащиеся проходят исчисление
Все станции до центра
А еще лучше, если вы можете придумать акроним, который лучше всего подходит для вас, не стесняйтесь использовать его.Пока он содержит ASTC в таком порядке, вы запомните триггерные квадранты.
Если вы хотите глубже изучить тригонометрические отношения, почему бы не взглянуть и не проверить, как строится синусоидальный график. Вы также можете увидеть, как выглядят графики косинусов и касательных, и какую информацию вы можете извлечь из них.
А как насчет обратных значений каждой триггерной функции?
Напомним, что каждая из трех основных триггерных функций имеет взаимные идентичности. Хотя эти взаимные идентичности часто используются для решения и доказательства триггерных идентичностей, важно увидеть, как они могут вписаться в общую схему правила
«Все учащиеся берут исчисление».
Чаще всего вам будет предоставлена «шпаргалка», диаграмма sin cos tan, в которой указаны все различные тригонометрические характеристики, связанные с каждой из этих основных тригонометрических функций.Однако фиксация этих взаимных идентичностей в памяти должна происходить естественным образом с помощью средства запоминания, о котором говорилось выше.
Взаимные идентичностиГлядя на каждую взаимную идентичность, мы видим, что
N cotθ \ cot \ thetacotθ является обратной величиной tanθ \ tan \ thetatanθ. Как это применимо к нашим 4 квадрантам?
Теперь мы видим, что во втором квадранте и синус, и косеканс положительны.Итак, если в квадранте два был треугольник, только тригонометрические отношения синуса и косеканса будут положительными. Переходя к третьему квадранту, мы видим, что и тангенциальные функции, и триггерные функции котангенса здесь положительны. Точно так же треугольник в этом квадранте будет иметь положительные тригонометрические отношения, только если они котангенсны или касательны. В четвертом квадранте единственные триггерные отношения, которые будут положительными, — это секущая и косекансная триггерные функции.
В четвертом квадранте единственные триггерные отношения, которые будут положительными, — это секущая и косекансная триггерные функции.
Если вы чувствуете, что вам нужно создать новое мнемоническое устройство памяти (определение мнемонического устройства : процедура, которая используется для активизации памяти или помощи в фиксации информации в памяти), чтобы помочь вам запомнить, какие триггерные триггеры являются положительными и / или с какой соответствующей триггерной функцией они связаны, попробуйте одно из следующего:
■ \ blacksquare ■ A ll C ougars C reep S тихо
■ \ blacksquare ■ A ll C hildren C ry S avagely
■ \ blacksquare ■ A ll C ircuits C reate S ignals
Не стесняйтесь создавать свои собственные средства помощи менмонической памяти для этих взаимных триггерных функций.Тот, который помогает активизировать вашу память наиболее эффективно и действенно, лучше всего подходит для вас.
Как работает «все учащиеся счисляют»?
«Все учащиеся изучают исчисление» (например, ASTC) — это мнемонический прием, который помогает вам оценивать тригонометрические отношения. В отличие от вашей стандартной тригонометрической формулы, которая может полагаться на грубое запоминание, мнемонические приемы или вспомогательные средства памяти гораздо более полезны в качестве инструмента, помогающего вам легко и эффективно вспоминать. Мнемоника в тригонометрии довольно распространена, учитывая огромное количество тригонометрических тождеств.Один из примеров, который вы можете вспомнить из своей тригонометрии прямоугольного треугольника, — это SOH-CAH-TOA.
Поскольку тригонометрические отношения могут попадать в любой из четырех квадрантов графика, мы можем использовать наше мнемоническое устройство, чтобы определить, когда тригонометрические тригонометрические отношения будут положительными или отрицательными. Это единственное использование и цель ASTC.
С этого момента проблемы потребуют дальнейшего упрощения для получения точных значений тригонометрии (например, при работе со специальными треугольниками). Некоторые задачи дадут результаты, которые можно упростить только до триггерных соотношений или десятичных ответов.
Некоторые задачи дадут результаты, которые можно упростить только до триггерных соотношений или десятичных ответов.
Знание взаимосвязи между ASTC и четырьмя триггерными квадрантами также будет полезно на следующем уроке, когда мы исследуем положительные и отрицательные значения единичного круга.
Ознакомьтесь с примерами и практикой с ASTC
Как упоминалось выше, основная цель ASTC — помочь вам определить, является ли оцениваемое тригонометрическое соотношение положительным или отрицательным.
Вот несколько вопросов, которые вы хотите задать себе, прежде чем приступить к решению своей проблемы:
1.В каком квадранте он находится?
2. Что положительного в этом квадранте?
3. Что отрицательного в этом квадранте?
Пример 1: Определите, будет ли следующая тригонометрическая функция иметь положительное или отрицательное значение: Sin 75 °
Шаг 1: Определите, в каком квадранте он находится — Глядя на изображение ниже, мы видим, что когда θ \ thetaθ находится между 0 ° и 90 °, мы будем в квадранте 1. Поскольку 75 ° находится между границами 0 ° и 90 °, мы можем утверждать, что исследуемое нами соотношение триггеров находится в квадранте 1.
Поскольку 75 ° находится между границами 0 ° и 90 °, мы можем утверждать, что исследуемое нами соотношение триггеров находится в квадранте 1.
Шаг 2: Теперь во втором квадранте мы смотрим на вторую букву нашей аббревиатуры ASTC. Это сразу говорит нам, что только синусоидальные функции (и обратные) будут положительными.
Шаг 3: Поскольку это квадрант 1, здесь нет ничего отрицательного.
Таким образом, мы можем подтвердить, что значение Sin 75 ° будет положительным
Пример 2: Определите, будет ли следующая тригонометрическая функция иметь положительное или отрицательное значение: tan 175 °
Шаг 1: Поскольку θ \ thetaθ теперь больше 90 °, но меньше 180 °, теперь мы находимся во втором квадранте.
Шаг 2: Теперь во втором квадранте мы смотрим на вторую букву нашей аббревиатуры ASTC. Это сразу говорит нам, что только синусоидальные функции (и обратные) будут положительными.
Шаг 3: В квадранте 2 функции тангенса и косинуса отрицательны вместе со своими обратными величинами.
Следовательно, мы можем сказать, что значение тангенса угла наклона 175 ° будет отрицательным .
Пример 3. Определите, будет ли сек 300 ° иметь положительное или отрицательное значение:
Шаг 1: Поскольку θ \ thetaθ больше 270 °, теперь мы находимся в квадранте 4.
Шаг 2: Напомним, что секанс является обратной величиной косинуса. Возвращаясь к нашему вспомогательному устройству памяти, а именно к четвертой букве в нашем аббревиатуре, AST C , мы видим, что косинус положителен в четвертом квадранте.
Шаг 3: В четвертом квадранте синус, тангенс и их обратные значения отрицательны.
Следовательно, мы можем заключить, что sec 300 ° будет иметь положительное значение .
А как насчет отрицательных углов?
Некоторые тригонометрические вопросы, с которыми вы столкнетесь, будут связаны с отрицательными углами.Как нам решать подобные проблемы?
Давайте начнем с того, что вернемся к рассмотрению углов на декартовой плоскости: присмотревшись к четырем квадрантам графа на декартовой плоскости, мы можем заметить, что углы образованы вращениями вокруг осей декартовой плоскости. Каждый оборот против часовой стрелки равен 360 °, а каждый оборот по часовой стрелке равен -360 °. В сочетании с нашим помощником по запоминанию, ASTC, мы можем затем экстраполировать информацию о том, является ли значение триггера отрицательным или положительным, в зависимости от того, в какие квадранты круга попадают триггерные отношения.
Каждый оборот против часовой стрелки равен 360 °, а каждый оборот по часовой стрелке равен -360 °. В сочетании с нашим помощником по запоминанию, ASTC, мы можем затем экстраполировать информацию о том, является ли значение триггера отрицательным или положительным, в зависимости от того, в какие квадранты круга попадают триггерные отношения.
Рассмотрите примеры отрицательных углов
Пример 1. Определите, будет ли у кроватки (-160 °) положительное или отрицательное значение:
Шаг 1. Двигаясь по часовой стрелке, мы видим, что это помещает нас в квадрант 3, поскольку θ \ thetaθ находится между -90 ° и -180 °.
Шаг 2. В этом квадранте мы знаем, что положительны только касательная и обратная ей, котангенс — AS T C.
Шаг 3. Все остальные триггерные функции отрицательны, включая синус, косинус и их обратные.
Следовательно, значение кроватки (-160 °) будет положительным.
Пример 2. Определите, будет ли csc (-45 °) иметь положительное или отрицательное значение:
Определите, будет ли csc (-45 °) иметь положительное или отрицательное значение:
Шаг 1. Еще раз, поскольку мы имеем дело с отрицательным значением градуса, мы перемещаемся по часовой стрелке, начиная с оси x в квадранте 1. Поскольку θ \ thetaθ находится между 0 ° и -90 °, мы знаем, что находятся в квадранте 4.
Шаг 2. В квадранте 4 положительными являются только косинус и обратная ему секанс (AST C ).
Шаг 3. В квадранте 4 синус, тангенс и их обратные величины отрицательны. В этом сценарии мы имеем дело с обратной величиной синуса — csc.
csc (-45 °), следовательно, будет иметь отрицательное значение.
Решение более сложных тригонометрических соотношений с помощью ASTC
Выходя за рамки отрицательных и положительных углов, мы можем столкнуться с более сложными тригонометрическими уравнениями, которые необходимо оценить.
Вот некоторые из распространенных примеров:
■ \ blacksquare ■ (360 ° — θ \ thetaθ)■ \ blacksquare ■ (270 ° + θ \ thetaθ), (270 ° — θ \ thetaθ)
■ \ blacksquare ■ (180 ° + θ \ thetaθ), (180 ° — θ \ thetaθ)
■ \ blacksquare ■ (90 ° + θ \ thetaθ) или (90 ° — θ \ thetaθ)
Шаг 1. Первый шаг в решении отношений с этими значениями включает определение квадранта, в который они попадают. В зависимости от оператора в каждом уравнении это должно быть простым:
Первый шаг в решении отношений с этими значениями включает определение квадранта, в который они попадают. В зависимости от оператора в каждом уравнении это должно быть простым:
Шаг 2. Следующий шаг включает преобразование в альтернативную функцию триггера. Будьте осторожны, поскольку это относится только к углам, составляющим 90 ° и 270 °. Вот правила конвертации:
■ \ blacksquare ■ tan θ \ thetaθ = cot θ \ thetaθ■ \ blacksquare ■ tan θ \ thetaθ = cot θ \ thetaθ
■ \ blacksquare ■ tan θ \ thetaθ = cot θ \ thetaθ
Шаг 3. Используйте нашу вспомогательную память ASTC, чтобы определить, будет ли значение отрицательным или положительным, а затем упростите тригонометрическую функцию.
Пример 1. Вычислить sin (270 ° — θ \ thetaθ).
Шаг 1. Оглядываясь на наш график квадрантов и оборотов, мы видим, что (270 ° — θ \ thetaθ) попадает в квадрант 3.
Шаг 2. Поскольку мы имеем дело со значением 270 °, мы должны преобразовать идентификатор триггера в соответствии с правилами, описанными выше. Sin θ \ thetaθ становится cos θ \ thetaθ.
Sin θ \ thetaθ становится cos θ \ thetaθ.
Шаг 3. В квадранте 3 положительны только тангенс и котангенс согласно ASTC. Синус в квадранте 3 отрицательный, поэтому мы должны убедиться, что наша вновь преобразованная триггерная функция также отрицательна (то есть cos θ \ thetaθ).
Наш окончательный ответ таков: sin (270 ° — θ \ thetaθ) = — cos θ \ thetaθ .
Пример 2. Вычислить cos (90 ° + θ \ thetaθ).
Шаг 1. Обратите внимание, что 90 ° + θ \ thetaθ находится в квадранте 2 (см. График квадрантов выше).
Шаг 2. Также обратите внимание, что, поскольку мы имеем дело с 90 °, мы должны преобразовать функцию косинуса в синус на основе правил преобразования, перечисленных выше.
Шаг 3. В квадранте 2 синус и косеканс положительны на основе нашего удобного вспомогательного средства памяти ASTC. Все остальное — тангенс, котангенс, косинус и секанс — отрицательны. Поэтому мы должны убедиться, что наша вновь преобразованная триггерная функция также отрицательна.
Наш окончательный ответ таков: cos (90 ° + θ \ thetaθ) = — sin θ \ thetaθ .
Что делать, если углы больше или равны 360 °
Шаги для такого рода проблем в основном те же, но включают один дополнительный, начальный шаг.
Когда мы сталкиваемся с углами, которые больше или равны 360, мы сначала делим на 360, а затем принимаем остаток от этого деления в качестве нового значения при решении триггерного отношения.
Пример 1. Вычислить sin 870 °.
Шаг 1. Разделите 870 на 360 и найдите остаток
Остаток в этом сценарии — 150.Итак, мы принимаем этот остаток как новое значение в нашем тригонометрическом соотношении: sin 150 °.
Шаг 2. Обратите внимание, что мы находимся в квадранте 2. В квадранте 2 синус и косеканс положительны (ASTC).
Шаг 3. Simplify Sin 150 °:
sin 150 ° = sin (180 ° -30 °)
Напомним, что sin (180 ° — θ \ thetaθ) находится в квадранте 2. В квадранте 2 синус положительный. Также помните, что здесь нам не нужно преобразовывать, потому что мы имеем дело с 180 °.
В квадранте 2 синус положительный. Также помните, что здесь нам не нужно преобразовывать, потому что мы имеем дело с 180 °.
sin 150 ° = sin (180 ° -30 °)
Поскольку sin (180 ° — θ \ thetaθ) = sin θ \ thetaθ
sin (180 ° -30 °) = sin 30 °
Используя наши 30-60- 90 специального прямоугольного треугольника мы можем получить точный ответ для sin 30 °:
Пример 2. Вычислить sin 735 °.
Шаг 1. Разделите 735 на 360 и получите остаток.
Используйте остаток вместо исходного значения — sin 735 ° = sin 15 °.
Шаг 2. Обратите внимание, что мы находимся в квадранте 1. В первом квадранте все положительно (ASTC).
Шаг 3. Упростить — В этом сценарии мы можем оставить наш ответ как sin 15 ° вместо десятичного значения.
Если бы нас спросили, как упростить sin 15 ° без калькулятора, нам нужно было бы применить триггерные тождества суммы и разности, которые мы узнаем в будущем уроке.
Равновесие и статика
Когда все силы, действующие на объект, уравновешены, считается, что объект находится в состоянии равновесия . Силы считаются уравновешенными , если правые силы уравновешиваются левыми, а восходящие силы уравновешиваются нисходящими. Однако это не обязательно означает, что все силы на равны друг другу. Рассмотрим два объекта, изображенных на силовой диаграмме, показанной ниже.Обратите внимание, что два объекта находятся в равновесии, потому что силы, действующие на них, уравновешены; однако отдельные силы не равны друг другу. Сила 50 Н не равна силе 30 Н.
Силы считаются уравновешенными , если правые силы уравновешиваются левыми, а восходящие силы уравновешиваются нисходящими. Однако это не обязательно означает, что все силы на равны друг другу. Рассмотрим два объекта, изображенных на силовой диаграмме, показанной ниже.Обратите внимание, что два объекта находятся в равновесии, потому что силы, действующие на них, уравновешены; однако отдельные силы не равны друг другу. Сила 50 Н не равна силе 30 Н.
Если объект находится в равновесии, силы уравновешены. Сбалансированный — ключевое слово, используемое для описания ситуаций равновесия. Таким образом, результирующая сила равна нулю, а ускорение равно 0 м / с / с. Объекты в состоянии равновесия должны иметь ускорение 0 м / с / с.Это происходит из первого закона движения Ньютона. Но наличие ускорения 0 м / с / с не означает, что объект находится в состоянии покоя. Объект в состоянии равновесия — это либо …
- в состоянии покоя и в состоянии покоя, или
- в движении и продолжает движение с той же скоростью и направлением.

Это тоже происходит от первого закона движения Ньютона.
Анализ ситуации статического равновесия
Если объект находится в состоянии покоя и в состоянии равновесия, то мы бы сказали, что объект находится в «статическом равновесии».«Статический» означает неподвижный или покоящийся . Обычная физическая лаборатория заключается в том, чтобы подвесить объект на двух или более нитях и измерить силы, которые действуют под углом на объект, чтобы выдержать его вес. объект анализируется с точки зрения сил, действующих на объект. Объект представляет собой точку на веревке, на которую действуют три силы. См. диаграмму справа. Если объект находится в состоянии равновесия, то результирующая сила, действующая на объект должен быть 0 Ньютон.Таким образом, если все силы сложить вместе как векторы, то результирующая сила (векторная сумма) должна быть 0 Ньютонов. (Напомним, что результирующая сила — это «векторная сумма всех сил» или результат сложения всех отдельных сил по направлению «голова к хвосту».) Таким образом, можно построить точно нарисованную диаграмму сложения векторов для определения равнодействующей. Ниже приведены примеры данных для такой лаборатории.
(Напомним, что результирующая сила — это «векторная сумма всех сил» или результат сложения всех отдельных сил по направлению «голова к хвосту».) Таким образом, можно построить точно нарисованную диаграмму сложения векторов для определения равнодействующей. Ниже приведены примеры данных для такой лаборатории.
|
|
|
Для большинства студентов результат был 0 Ньютонов (или, по крайней мере, очень близок к 0 Н). Это то, что мы ожидали — поскольку объект находился в состоянии равновесия, результирующая сила (векторная сумма всех сил) должна быть 0 Н.
Это то, что мы ожидали — поскольку объект находился в состоянии равновесия, результирующая сила (векторная сумма всех сил) должна быть 0 Н.
Другой способ определения чистой силы (векторной суммы всех сил) включает использование тригонометрических функций для разделения каждой силы на ее горизонтальную и вертикальную составляющие. Как только компоненты известны, их можно сравнить, чтобы увидеть, сбалансированы ли вертикальные силы и горизонтальные силы.На схеме ниже показаны векторы A, B и C и их соответствующие компоненты. Для векторов A и B вертикальные компоненты могут быть определены с использованием синуса угла, а горизонтальные компоненты могут быть проанализированы с помощью косинуса угла. Величина и направление каждого компонента для выборочных данных показаны в таблице под диаграммой.
Данные в таблице выше показывают, что силы почти уравновешивают сил.Анализ горизонтальных компонентов показывает, что левый компонент A почти уравновешивает правый компонент B. Анализ вертикальных компонентов показывает, что сумма восходящих компонентов A + B почти уравновешивает нисходящий компонент C. Векторная сумма всех сил ( почти ) равна 0 Ньютона. Но как насчет разницы в 0,1 Н между силами, направленными вправо и влево, и разницы в 0,2 Н между силами, направленными вверх и вниз? Почему компоненты силы только почти уравновешивают? Данные образца, используемые в этом анализе, являются результатом данных измерений на реальной экспериментальной установке.Разница между фактическими результатами и ожидаемыми результатами связана с ошибкой, возникшей при измерении силы A и силы B. Мы должны сделать вывод, что этот низкий предел экспериментальной ошибки отражает эксперимент с превосходными результатами. Можно сказать, что это «достаточно близко для работы правительства».
Анализ вертикальных компонентов показывает, что сумма восходящих компонентов A + B почти уравновешивает нисходящий компонент C. Векторная сумма всех сил ( почти ) равна 0 Ньютона. Но как насчет разницы в 0,1 Н между силами, направленными вправо и влево, и разницы в 0,2 Н между силами, направленными вверх и вниз? Почему компоненты силы только почти уравновешивают? Данные образца, используемые в этом анализе, являются результатом данных измерений на реальной экспериментальной установке.Разница между фактическими результатами и ожидаемыми результатами связана с ошибкой, возникшей при измерении силы A и силы B. Мы должны сделать вывод, что этот низкий предел экспериментальной ошибки отражает эксперимент с превосходными результатами. Можно сказать, что это «достаточно близко для работы правительства».
Анализ висящего знака
Приведенный выше анализ сил, действующих на объект в состоянии равновесия, обычно используется для анализа ситуаций, в которых участвуют объекты в состоянии статического равновесия. Наиболее распространенное приложение включает анализ сил, действующих на знак, который находится в состоянии покоя. Например, рассмотрите картину справа, висящую на стене. Картина находится в состоянии равновесия, и поэтому все силы, действующие на картину, должны быть уравновешены. То есть все горизонтальные компоненты должны составлять 0 Ньютонов, а все вертикальные компоненты должны составлять 0 Ньютонов. Натяжение троса А влево должно уравновешивать натяжение троса В вправо, а сумма натяжения троса А и троса В вверх должна уравновешивать вес знака.
Наиболее распространенное приложение включает анализ сил, действующих на знак, который находится в состоянии покоя. Например, рассмотрите картину справа, висящую на стене. Картина находится в состоянии равновесия, и поэтому все силы, действующие на картину, должны быть уравновешены. То есть все горизонтальные компоненты должны составлять 0 Ньютонов, а все вертикальные компоненты должны составлять 0 Ньютонов. Натяжение троса А влево должно уравновешивать натяжение троса В вправо, а сумма натяжения троса А и троса В вверх должна уравновешивать вес знака.
Предположим, что измеренное натяжение обоих кабелей составляет 50 Н, а угол, который каждый кабель образует с горизонталью, составляет 30 градусов. Какой вес у знака? На этот вопрос можно ответить, проведя силовой анализ с использованием тригонометрических функций. Вес знака равен сумме восходящих компонентов натяжения двух тросов. Таким образом, для определения этой вертикальной составляющей можно использовать тригонометрическую функцию. Схема и сопроводительные работы показаны ниже.
Схема и сопроводительные работы показаны ниже.
Поскольку каждый трос тянет вверх с силой 25 Н, общее тяговое усилие знака вверх составляет 50 Н. Следовательно, сила тяжести (также известная как вес) равна 50 Н по направлению вниз. Знак весит 50 Н.
В приведенной выше задаче натяжение в тросе и угол , который трос образует с горизонталью, используются для определения веса знака.Идея в том, что натяжение, угол и вес связаны. Если известны любые два из этих трех, то третья величина может быть определена с помощью тригонометрических функций.
В качестве еще одного примера, иллюстрирующего эту идею, рассмотрим симметричный вывешивание знака, как показано справа. Если известно, что знак имеет массу 5 кг и если угол между двумя тросами составляет 100 градусов, то можно определить натяжение троса. Предполагая, что знак находится в состоянии равновесия (хорошее предположение, если он остается в состоянии покоя), два троса должны обеспечивать достаточную восходящую силу, чтобы уравновесить нисходящую силу тяжести. Сила тяжести (также известная как вес) составляет 49 Н (Fgrav = m * g), поэтому каждый из двух тросов должен тянуть вверх с силой 24,5 Н. Поскольку угол между кабелями составляет 100 градусов, каждый кабель должен составлять 50 градусов с вертикалью и 40 градусов с горизонталью. Набросок этой ситуации (см. Диаграмму ниже) показывает, что натяжение кабеля можно определить с помощью синусоидальной функции. Треугольник ниже иллюстрирует эти отношения.
Сила тяжести (также известная как вес) составляет 49 Н (Fgrav = m * g), поэтому каждый из двух тросов должен тянуть вверх с силой 24,5 Н. Поскольку угол между кабелями составляет 100 градусов, каждый кабель должен составлять 50 градусов с вертикалью и 40 градусов с горизонталью. Набросок этой ситуации (см. Диаграмму ниже) показывает, что натяжение кабеля можно определить с помощью синусоидальной функции. Треугольник ниже иллюстрирует эти отношения.
Концептуальное мышление
Есть важный принцип, который вытекает из некоторых из тригонометрических вычислений, выполненных выше.Принцип состоит в том, что по мере увеличения угла к горизонтали величина силы натяжения, необходимая для удержания знака в состоянии равновесия, уменьшается. Чтобы проиллюстрировать это, рассмотрим картинку с напряжением 10 Ньютон, удерживаемую тремя разными ориентациями проводов, как показано на схемах ниже. В каждом случае для поддержки изображения используются два провода; каждый провод должен выдерживать половину веса знака (5 Н). Угол между проводами и горизонтом варьируется от 60 до 15 градусов. Используйте эту информацию и диаграмму ниже, чтобы определить натяжение проволоки для каждой ориентации.По завершении нажмите кнопку, чтобы просмотреть ответы.
Угол между проводами и горизонтом варьируется от 60 до 15 градусов. Используйте эту информацию и диаграмму ниже, чтобы определить натяжение проволоки для каждой ориентации.По завершении нажмите кнопку, чтобы просмотреть ответы.
В заключение, равновесие — это состояние объекта, в котором все силы, действующие на него, уравновешены. В таких случаях результирующая сила равна 0 Ньютонам. Зная силы, действующие на объект, тригонометрические функции могут использоваться для определения горизонтальных и вертикальных компонентов каждой силы. В состоянии равновесия все вертикальные компоненты должны уравновешиваться, а все горизонтальные компоненты должны уравновешиваться.
Мы хотели бы предложить … Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете одно из интерактивных материалов The Physics Classroom.
 Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного приложения «Назови этот вектор», интерактивного элемента «Сложение векторов» или «Интерактивной игры по угадыванию векторов».Все три интерактивных элемента можно найти в разделе «Интерактивная физика» на нашем веб-сайте, и они обеспечивают интерактивный опыт с навыком добавления векторов.
Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного приложения «Назови этот вектор», интерактивного элемента «Сложение векторов» или «Интерактивной игры по угадыванию векторов».Все три интерактивных элемента можно найти в разделе «Интерактивная физика» на нашем веб-сайте, и они обеспечивают интерактивный опыт с навыком добавления векторов.
Проверьте свое понимание
Следующие вопросы предназначены для проверки вашего понимания ситуаций равновесия. Нажмите кнопку, чтобы просмотреть ответы на эти вопросы.
1.На стене висит следующая картина. Используйте тригонометрические функции, чтобы определить вес изображения.
2. Табличка внизу висит снаружи класса физики, рекламируя самую важную истину, которую можно найти внутри. Знак опирается на диагональный трос и жесткий турник. Если вывеска имеет массу 50 кг, то определите натяжение диагонального троса, поддерживающего его вес.
Если вывеска имеет массу 50 кг, то определите натяжение диагонального троса, поддерживающего его вес.
3. Следующий знак можно найти в Гленвью. Знак имеет массу 50 кг. Определите натяжение тросов.
4. После самой последней доставки печально известный аист объявляет хорошие новости. Если знак имеет массу 10 кг, то какова сила натяжения в каждом тросе? Используйте тригонометрические функции и эскиз, чтобы помочь в решении.
5. Предположим, что ученик тянет с двумя большими силами (F 1 и F 2 ), чтобы поднять книгу весом 1 кг за два троса. Если кабели образуют угол в 1 градус с горизонталью, то каково натяжение кабеля?
4.11 Гиперболические функции
Гиперболические функции с некоторой частотой появляются в приложениях,
и во многих отношениях очень похожи на тригонометрические
функции. 2 -1}) $ — действительное число, и
$ y = \ cosh x $, поэтому $ y $ находится в диапазоне $ \ cosh (x) $.
$ \ qed $
2 -1}) $ — действительное число, и
$ y = \ cosh x $, поэтому $ y $ находится в диапазоне $ \ cosh (x) $.
$ \ qed $
Определение 4.11.3 Остальные гиперболические функции: $$ \ eqalign {\ tanh x & = {\ sinh x \ over \ ch x} \ cr \ coth x & = {\ ch x \ over \ sinh x} \ cr \ sech x & = {1 \ over \ ch x} \ cr \ csch x & = {1 \ over \ sinh x} \ cr} $$ Область определения $ \ coth $ и $ \ csch $ — $ x \ neq 0 $, а область определения все остальные гиперболические функции — это действительные числа. Графики показаны на рисунке 4.11.1 $ \ квадрат $
| $ \ cosh $ | $ \ sinh $ | $ \ tanh $ |
| $ \ sech $ | $ \ csch $ | $ \ coth $ |
Рисунок 4.2 t-1} = \ pm \ sh t $. Так что для некоторых
подходящие $ t $, $ \ cosh t $ и $ \ sinh t $ — координаты типичного
точка на гиперболе. На самом деле оказывается, что $ t $ вдвое больше
площадь, показанная на первом графике
рисунок 4.11.2. Четное
это аналог тригонометрии; $ \ cos t $ и $ \ sin t $ —
координаты типичной точки на единичной окружности, а $ t $ вдвое больше
область, показанная на втором графике рисунка 4.11.2.
На самом деле оказывается, что $ t $ вдвое больше
площадь, показанная на первом графике
рисунок 4.11.2. Четное
это аналог тригонометрии; $ \ cos t $ и $ \ sin t $ —
координаты типичной точки на единичной окружности, а $ t $ вдвое больше
область, показанная на втором графике рисунка 4.11.2.
Рисунок 4.11.2. Геометрические определения sin, cos, sinh, cosh: $ t $ в два раза закрашеннее площадь на каждом рисунке.{-x} \ over 2} = \ cosh x $. $ \ qed $
Поскольку $ \ cosh x> 0 $, $ \ sinh x $ возрастает и, следовательно, инъективен, поэтому $ \ sinh x $ имеет обратное, $ \ arcsinh x $. Кроме того, $ \ sinh x> 0 $, когда $ x> 0 $, поэтому $ \ cosh x $ инъективен на $ [0, \ infty) $ и имеет (частичное) обратное, $ \ arccosh x $. Остальные гиперболические функции имеют обратные также, хотя $ \ arcsech x $ является лишь частичным обратным. Мы можем вычислять производные этих функций, как и другие обратные функции.
Теорема 4.2 + 1}) $.)
Пр. 4.11.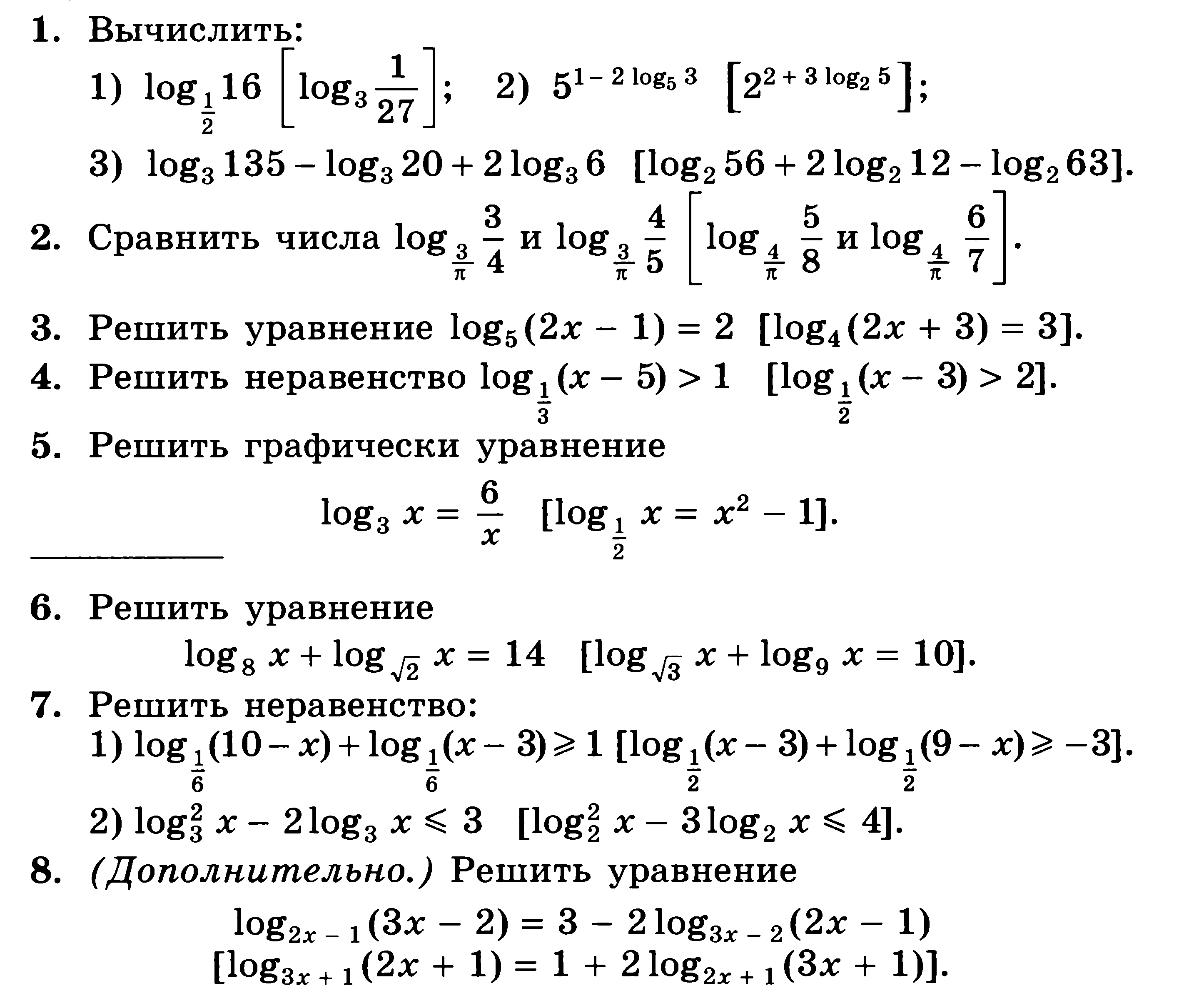 2
Вычислите следующие пределы:
2
Вычислите следующие пределы:
а. $ \ ds \ lim_ {x \ to \ infty} \ cosh x $
г. $ \ ds \ lim_ {x \ to \ infty} \ sinh x $
г. $ \ ds \ lim_ {x \ to \ infty} \ tanh x $
г. $ \ ds \ lim_ {x \ to \ infty} (\ ch x — \ sinh x) $
(отвечать)
Пр. 4.11.3 Докажите, что диапазон $ \ tanh x $ равен $ (- 1,1) $. Что есть диапазоны $ \ coth $, $ \ sech $ и $ \ csch $? (Используйте тот факт, что это взаимные функции.2 х $. Вычислить производные остальных гиперболических функций также.
пр. 4.11.8 Каковы области шести обратных гиперболических функции?
пр. 4.11.9 Нарисуйте графики всех шести обратных гиперболических функции.
Предварительный расчет — CLEP | Совет колледжа
Обзор
Экзамен Precalculus оценивает уровень владения студентами навыками и концепциями, необходимыми для успешного прохождения курса математического анализа в первом семестре. Большая часть экзамена посвящена проверке понимания учащимся функций и их свойств. Многие вопросы проверяют знание учащимся конкретных свойств следующих типов функций: линейных, квадратичных, абсолютных значений, квадратного корня, полиномиальных, рациональных, экспоненциальных, логарифмических, тригонометрических, обратных тригонометрических и кусочно-определенных. Вопросы на экзамене будут представлять эти типы функций символически, графически, устно или в табличной форме. Твердое понимание этих типов функций лежит в основе всех курсов предварительного вычисления и является предпосылкой для поступления на математические и другие математические курсы на уровне колледжа.
Большая часть экзамена посвящена проверке понимания учащимся функций и их свойств. Многие вопросы проверяют знание учащимся конкретных свойств следующих типов функций: линейных, квадратичных, абсолютных значений, квадратного корня, полиномиальных, рациональных, экспоненциальных, логарифмических, тригонометрических, обратных тригонометрических и кусочно-определенных. Вопросы на экзамене будут представлять эти типы функций символически, графически, устно или в табличной форме. Твердое понимание этих типов функций лежит в основе всех курсов предварительного вычисления и является предпосылкой для поступления на математические и другие математические курсы на уровне колледжа.
Экзамен состоит примерно из 48 вопросов, разделенных на два раздела, на которые нужно ответить примерно за 90 минут.
- Раздел 1:25 вопросов, примерно 50 минут. В этом разделе разрешено использование графического онлайн-калькулятора (не CAS). Только некоторые вопросы потребуют использования калькулятора.

- Раздел 2: 23 вопроса, примерно 40 минут. В этом разделе нельзя использовать калькулятор.
Несмотря на то, что большинство вопросов на экзамене являются множественным выбором, есть некоторые вопросы, требующие от учащихся ввода числового ответа.
Графический калькулятор
Графический калькулятор TI-84 Plus CE интегрирован в программное обеспечение экзамена и доступен студентам во время Раздела 1 экзамена. Только некоторые вопросы действительно требуют графического калькулятора.
Посетите ETS, чтобы узнать больше и попрактиковаться в использовании графического калькулятора. Чтобы ответить на некоторые вопросы в разделе «Калькулятор» экзамена, от студентов может потребоваться использование графического онлайн-калькулятора следующими способами:
- Выполните вычисления (например,g., показатели степени, корни, тригонометрические значения и логарифмы)
- Графические функции и анализ графиков
- Найти нули функций
- Найдите точки пересечения графиков функций
- Найти минимум / максимум функций
- Найдите численные решения уравнений
- Создать таблицу значений для функции
Требуемые знания и навыки
Вопросы на экзамене требуют от кандидатов продемонстрировать следующие способности:
- Вспоминая фактические знания и / или выполняя рутинные математические манипуляции
- Решение задач, демонстрирующих понимание математических идей и / или концепций
- Решение нестандартных проблем или проблем, требующих проницательности, изобретательности или высших умственных процессов
Предмет экзамена Precalculus состоит из следующих тем. Проценты рядом с темами указывают приблизительный процент экзаменационных вопросов по этой теме.
Проценты рядом с темами указывают приблизительный процент экзаменационных вопросов по этой теме.
Алгебраические выражения, уравнения и неравенства (20%)
- Умение выполнять операции над алгебраическими выражениями
- Способность решать уравнения и неравенства, включая линейные, квадратичные, абсолютные, полиномиальные, рациональные, радикальные, экспоненциальные, логарифмические и тригонометрические
- Умение решать системы уравнений, в том числе линейные и нелинейные
Функции: концепция, свойства и операции (15%)
- Способность продемонстрировать понимание концепции функции, общих свойств функций (например,g., домен и диапазон), обозначение функций и выполнение символьных операций с функциями (например, вычисление и обратные функции)
Представления функций: символьные, графические и табличные (30%)
- Способность распознавать и выполнять операции и преобразования функций, представленных символически, графически или в табличной форме
- Способность продемонстрировать понимание основных свойств функций и распознавать элементарные функции (линейные, квадратичные, абсолютное значение, квадратный корень, полиномиальные, рациональные, экспоненциальные, логарифмические, тригонометрические, обратные тригонометрические и кусочно определенные функции), которые представлены символически , графически или в табличной форме
Аналитическая геометрия (10%)
- Способность продемонстрировать понимание аналитической геометрии линий, окружностей, парабол, эллипсов и гипербол
Тригонометрия и ее приложения * (15%)
- Способность продемонстрировать понимание основных тригонометрических функций и их обратных и применять основные тригонометрические соотношения и тождества (в прямоугольных треугольниках и на единичном круге)
- Способность применять тригонометрию в различных контекстах решения проблем
Функции как модели (10%)
- Способность интерпретировать и конструировать функции как модели и переводить идеи между символическими, графическими, табличными и вербальными представлениями функций
* Обратите внимание, что тригонометрия пронизывает большинство основных тем и составляет более 15% экзамена. Фактическая доля экзаменационных вопросов, требующих знания тригонометрии прямоугольного треугольника или свойств тригонометрических функций, составляет примерно 30–40%.
Фактическая доля экзаменационных вопросов, требующих знания тригонометрии прямоугольного треугольника или свойств тригонометрических функций, составляет примерно 30–40%.
Триггерных терминов — Словарь
арккозинфункция, обратная косинусу
Обратные функции называются арксинусом, , арккозин, и арктангенс соответственно.
арктангенсфункция, обратная касательной
Обратные функции называются арксинусом, арккосинусом и , арктангенс соответственно.
котангенсотношение смежной к противоположной стороне прямоугольного треугольника
Обратные величины этих функций называются косекансом (csc или cosec), секансом (sec) и котангенс (раскладушка) соответственно.
арксинусфункция, обратная синусу
Обратные функции называются арксинус, , арккосинус и арктангенс соответственно.
тригонометрическая функцияфункция угла, выраженная как отношение длины сторон прямоугольного треугольника, содержащего угол
. Эти отношения даются следующими
тригонометрические функции известного угла A, где a, b и c относятся к длинам сторон на сопроводительном рисунке:
Эти отношения даются следующими
тригонометрические функции известного угла A, где a, b и c относятся к длинам сторон на сопроводительном рисунке:
* Функция синуса (sin), определяемая как отношение стороны, противоположной углу, к гипотенузе.
тригонометрический, относящиеся к принципам тригонометрии или соответствующие им
Эти отношения даются следующими тригонометрические функции известного угла A, где a, b и c относятся к длинам сторон на сопроводительном рисунке:* Функция синуса (sin), определяемая как отношение стороны, противоположной углу, к гипотенузе.
радиан— единица плоского угла, принятая в Системе международных объединений; равен углу в центре круга, образуемого дугой, равной по длине радиусу (приблизительно 57.295 градусов)
Построение графика y = csc (x) с использованием единичного круга.
[править] Расширение определений
Графики функций sin (x) и cos (x), где угол x измеряется в
радиан .
отношение гипотенузы к противоположной стороне прямоугольного треугольника
Взаимные значения этих функций называются косеканс (csc или cosec), секанс (sec) и котангенс (cot) соответственно.
обратная функцияфункция, полученная выражением зависимой переменной одной функции как независимой переменной другой; f и g являются обратными функциями, если f (x) = y и g (y) = x
обратные функции называются арксинусом, арккосинусом и арктангенсом соответственно.
косинусотношение смежной стороны к гипотенузе прямоугольного треугольника
* Косинус функция (cos), определяемая как отношение соседнего катета к гипотенузе.
секущийпрямая линия, пересекающая кривую в двух или более точках
Обратные значения этих функций называются косекансом (csc или cosec), секущая (сек) и котангенс (раскладушка) соответственно.
функциячто то используется для
Эти отношения задаются следующими тригонометрическими функции известного угла A, где a, b и c относятся к длинам сторон на сопроводительном рисунке: * Функция синуса (sin), определяемая как отношение стороны, противоположной углу, к гипотенузе.
отношение длины стороны, противоположной данному углу, к длине гипотенузы прямоугольного треугольника
Эти соотношения задаются следующими тригонометрическими функциями известного угла A, где a, b и c относятся к длинам сторон на прилагаемом рисунке:* Синус Функция (sin), определяемая как отношение стороны, противоположной углу, к гипотенузе.
касательнаялиния, которая касается кривой только в одной точке
Многие люди легко запоминают, какие стороны прямоугольного треугольника равны синусу, косинусу или касательная , запомнив слово SOH-CAH-TOA (см. Ниже в разделе «Мнемоника»).
уголпространство между двумя линиями или плоскостями, пересекающими
Если один угол треугольника равен 90 градусам, и один из других углов известен, третий таким образом фиксируется, потому что три угла любого треугольника в сумме составляют 180 градусов.
соседнийс общей границей или кромкой
* Функция косинуса (cos), определяемая как отношение
примыкает к катету гипотенузы.
11 советов по победе над тригонометрическим доказательством
Тригонометрическое доказательство идентичности — это распространенный тип вопросов, который включен в программу дополнительной математики O-Level. Упоминание о «триго-прувинге» часто заставляло даже самых старших школьников покрыться холодным потом. Это связано с тем, что, в отличие от большинства тем A-Math (O-level), вопросы по тригонометрии не имеют стандартного метода решения «подключи и работай». Каждый вопрос — это новая головоломка, для которой ученики должны найти маршрут от начала до конца.Очень часто учащиеся применяют подход 走 一步 看 一步 (прямой перевод как: «Ходить один шаг, смотреть один шаг») к решению этих вопросов.
Хотя каждый вопрос уникален, на самом деле существует несколько «практических правил», которым ученики могут следовать, чтобы не заблудиться. Здесь я приведу несколько ценных советов, которые помогут студентам справиться с испытанием Trigo.
Совет 1) Всегда начинайте с более сложной стороны
Чтобы доказать тригонометрическую идентичность, мы всегда начинаем либо с левой стороны (LHS), либо с правой стороны (RHS) и применяем идентификаторы шаг за шагом, пока мы достигаем другой стороны. Однако умные ученики всегда начинают с более сложной стороны. Это потому, что намного проще исключить термины, чтобы сделать сложную функцию простой, чем найти способы ввести термины, чтобы сделать простую функцию сложной.
Однако умные ученики всегда начинают с более сложной стороны. Это потому, что намного проще исключить термины, чтобы сделать сложную функцию простой, чем найти способы ввести термины, чтобы сделать простую функцию сложной.
Пример Q1) Докажите идентичность tan⁴x = sec²x (tan²x-1) +1
Подход: было бы разумно начать доказывать это с правой стороны (RHS), поскольку это более сложно.
Совет 2) Выразите все в синусе и косинусе
Для обеих сторон уравнения выразите все tan, cosec, sec и cot через sin и cos.Это сделано для стандартизации обеих сторон тригонометрического тождества, чтобы было легче сравнивать одну сторону с другой.
Совет 3) Объедините члены в одну дробь
Когда есть 2 члена на одной стороне и 1 член на другой стороне, объедините сторону с 2 членами в 1 дробь, сделав их знаменатели одинаковыми.
Совет 4) Используйте тождества Пифагора для преобразования между sin²x и cos²x
Обратите особое внимание на добавление квадратичных членов тригонометрии. При необходимости примените тождества Пифагора. Особенно sin²x + cos²x = 1, поскольку все остальные тригонометрические члены были преобразованы в синус и косинус. Этот идентификатор можно использовать для преобразования в и наоборот. Его также можно использовать для удаления обоих, превратив его в 1.
При необходимости примените тождества Пифагора. Особенно sin²x + cos²x = 1, поскольку все остальные тригонометрические члены были преобразованы в синус и косинус. Этот идентификатор можно использовать для преобразования в и наоборот. Его также можно использовать для удаления обоих, превратив его в 1.
Совет 5) Знайте, когда применять формулу двойного угла (DAF)
Обратите внимание на каждый тригонометрический термин в вопросе. Существуют ли термины с углами, которые в 2 раза больше другого? Если есть, будьте готовы использовать DAF, чтобы преобразовать их под таким же углом.Например, если вы видите sinθ и cot (θ / 2) в одном и том же вопросе, вы должны использовать DAF, поскольку θ в 2 раза больше (θ / 2).
Совет 6) Знайте, когда применять формулу сложения (AF)
Соблюдайте углы в тригонометрических функциях. Существуют ли суммирования двух разных членов в одном и том же тригонометрическом члене? Если да, примените формулу сложения (AF).
Совет 7) Старый добрый Разверните / Факторизуйте / Упростите / Отмените
Многие студенты придерживаются ложного убеждения, что каждый отдельный вопрос для доказательства тригонометрии требует использования тригонометрических тождеств из таблицы формул.Всякий раз, когда они застревают, они прибегают к тому, чтобы вслепую смотреть на лист формул и молиться, чтобы ответ волшебным образом «выпрыгнул» на них. Чаще всего чуда не бывает. Это связано с тем, что большинство подтверждающих вопросов в основном вращаются вокруг старого доброго расширения, факторизации, упрощения и отмены подобных терминов. Фактически, некоторые проверочные вопросы даже не требуют от ученика использования каких-либо правил тригонометрии.
Кроме того, всегда ищите возможности применить квадратичные тождества, которые вы освоили во Вторичной школе 2:
a²-b² = (a + b) (a-b) (a ± b) ² = a² + b² ± 2ab
Совет 8) Сделайте один шаг, следите за одним шагом.
Проверка функций тригонометрии — это искусство. Часто есть несколько способов найти ответ. Естественно, одни методы более элегантны и кратки, а другие грубы, массивны и уродливы. Однако важно отметить, что какой бы путь мы ни выбрали, пока мы можем добраться до конечного пункта назначения, мы получим оценки.
Некоторые студенты долго раздумывали над вопросом и пытались разработать все решение в своем мозговом процессоре Pentium 9999.Я аплодирую их героическим усилиям. К сожалению, у большинства из них заканчивается оперативная память, и они отключаются до того, как вопрос будет решен. С другой стороны, есть «пауки канчеонг», которые сразу же берут свои ручки и, не задумываясь, начинают записывать случайные шаги. Эти студенты в конечном итоге будут тратить время, направившись в никуда, и им придется перезапускать несколько раз.
Самые опытные ученики будут балансировать между тем и другим. Они потратили некоторое время на то, чтобы сориентироваться и отважно сделать первый шаг. После каждых одного или двух шагов они повторно анализировали свою близость к конечному пункту назначения, прежде чем принимать решение о следующем шаге.
После каждых одного или двух шагов они повторно анализировали свою близость к конечному пункту назначения, прежде чем принимать решение о следующем шаге.
Совет 9) В отчаянии… притворись!
Заявление об ограничении ответственности: используйте эту тактику только в том случае, если вы застряли на полпути во время процесса тригопроверки на экзамене (с тикающими часами), и вы не хотите подвергать риску остальную часть работы. Поскольку вы застряли на полпути, просто ответьте на вопрос, сделав вид, что вы подтвердили личность.С вашего текущего шага перейдите прямо к последнему шагу и затем напишите (= RHS (Проверено)). После экзамена не забудьте посетить ближайший храм / церковь / мечеть, чтобы усердно молиться, чтобы маркер был либо слепым, либо достаточно сострадательным, чтобы дать вам преимущество сомнения и присвоить вам оценки.
* Примечание. Эта работа на самом деле неверна, потому что между вторым и последним шагом есть несколько пропущенных шагов. Однако эта работа показывает, что когда вы застряли и отчаялись во время экзамена O-level, вы все равно должны «притвориться», чтобы доказать вопрос, записав последнюю ступеньку вниз.
Однако эта работа показывает, что когда вы застряли и отчаялись во время экзамена O-level, вы все равно должны «притвориться», чтобы доказать вопрос, записав последнюю ступеньку вниз.
Чтобы получить полное решение этого вопроса, прокрутите вниз.
Совет 10) Практика! Упражняться! Упражняться!
Доказательство тригонометрической функции становится простым делом после того, как вы ответите на огромное количество вопросов и столкнетесь со всеми разнообразными вопросами. Не существует жесткого правила для обработки вопросов о тригонометрии уровня O, поскольку каждый вопрос подобен головоломке. Но если вы уже решили головоломку раньше, вам будет легче решить ту же головоломку снова.
Совет 11) Не пытайтесь доказывать вопрос, в котором написано «Решите»!
После отработки большого количества контрольных вопросов у некоторых студентов появляется роботизированная тенденция доказывать LHS = RHS всякий раз, когда они видят уравнение с тригонометрическими функциями.
