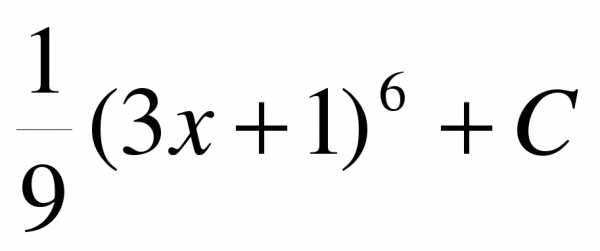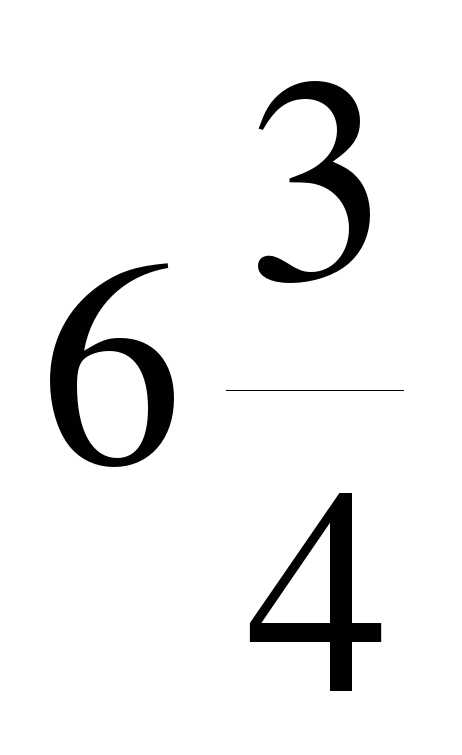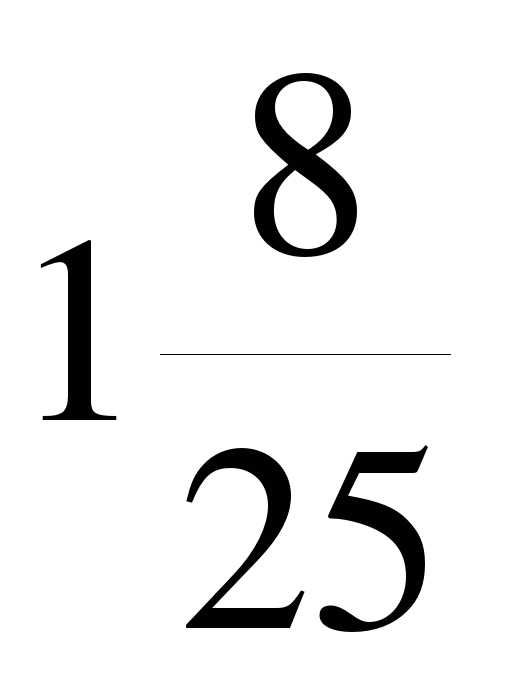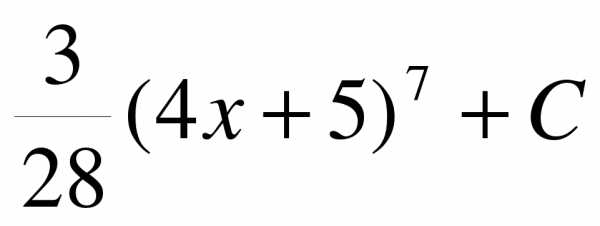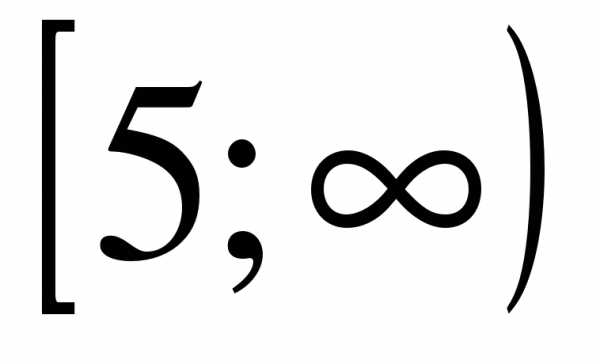Контрольная работа 1 алгебра 11 класс – ГДЗ Алгебра 11 класс Глизбург

Решебник к сборнику контрольных работ по алгебре для 11 класса (авт. Глизбург В. И.). Базовый уровень ОНЛАЙН

Решения контрольных работ по алгебре и началам анализа из сборника для 11 класса Глизбург В. И. (под ред. А.Г. Мордковича). Базовый уровень. — Рукопись. — 2015.
Настоящее пособие содержит решения контрольных работ из сборника «Глизбург В. И. Алгебра и начала математического анализа. 11 класс. Контрольные работы для учащихся общеобразовательных учреждений (базовый уровень) / В. И. Глизбург ; под ред. А. Г. Мордковича. — М. : Мнемозина, 2009. — 32 с.»
Сборник контрольных работ предназначен для тех учителей математики, которые используют в своей преподавательской деятельности УМК, созданный авторским коллективом под руководством А. Г. Мордковича.
Каждый вариант контрольной работы выстроен по одной и той же схеме: задания обязательного минимума — до первой черты, задания среднего уровня — между первой и второй чертой, задания уровня выше среднего — после второй черты. Шкала оценок за выполнение контрольной работы может выглядеть так: за успешное выполнение только заданий обязательного минимума — оценка 3; за успешное выполнение заданий обязательного минимума и одного дополнительного (после первой или второй черты) — оценка 4; за успешное выполнение заданий всех трех уровней — оценка 5. При этом оценку не рекомендуется снижать за одно неверное решение в первой части работы (допустимый люфт).

Внимание! Рукопись не проверялась, возможны ошибки!

Содержание
Контрольная работа № 1

Контрольная работа № 2

Контрольная работа № 3

Контрольная работа № 4
Контрольная работа № 5

Контрольная работа № 6
Контрольная работа № 7

ВНИМАНИЕ! Все права на публикацию рукописей принадлежат сайту gdz.math-helper.ru. Копирование и распространение материалов запрещено!

gdz.math-helper.ru

Тест по алгебре (11 класс) по теме: Контрольная работа по алгебре за 1 полугодие 11 класс

Муниципальное бюджетное общеобразовательное учреждение

«Средняя общеобразовательная школа №1»

УТВЕРЖДАЮ:

                 Директор МБОУ «СОШ №1»                                                      ______________А.В.Петряев

                                                   «____» ____________ 2012 г.

                                                                              Согласовано:

Зам. директора МБОУ «СОШ №1»

                                             ___________________________

 «____» _____________  2012 г.

                                                                                           Протокол заседания методического

совета школы №____ от _________  

КОНТРОЛЬНО – ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ

по предмету «Алгебра и начала анализа»

( наименование предмета)

для 11-х классов

                                                               Составитель:

                                                               Хайржанова Ольга Николаевна

                                                               учитель математики

                                                                   высшей квалификационной категории

Содержание

Пояснительная записка	3
Спецификация работы	4
Текст работы	5
Ключ работы	9
Бланк анализа работы	10

---

1. Пояснительная записка

1). Цель проведения работы – проверить практические навыки и умения обучающихся по темам «Показательная функция», «Степени и корни».

2). Документы, на которые опирались при составлении работы – Федеральные государственные образовательные стандарты.

3). Класс, на который рассчитана данная работа — 11

4). Рекомендуемое время для проведения работы (количество часов на выполнение работы)  — 1 урок (40 минут)

5). Описание структуры контрольно-измерительного материала: работа состоит из трёх частей.  

  Часть А содержит семь заданий базового уровня с выбором ответов, которые проверяют овладение конкретным материалом по данным темам. Ученик решает задание и выбирает букву, под которой, по его мнению, записан верный ответ и заносит данную букву в бланк ответов. Предлагаемые варианты ответов, кроме правильного, подобраны так, что содержат наиболее характерные для данных тем ошибки.

  Часть В содержит два задания повышенного уровня, которые  обеспечивают овладение учащимися общими и специфическими приемами учебной и умственной деятельности. Ученик решает задание и записывает полученный ответ в бланк ответов.

  Часть С содержит два задания высокого уровня, которые предусматривают свободное овладение практическим материалом, приемами учебной работы умственных действий и поднимают учащихся на уровень осознанного творческого применения знаний. Ученик решает задание и полностью записывает решение на бланке ответов.

  Согласно методике составления теста, разработанной в лаборатории образования ИОСО РАО, основная часть должна состоять из заданий  первого и второго уровней. Именно задания этих уровней соответствуют обязательным требованиям к знаниям и умениям учащихся.

6). Суть ключа.

Работа состоит из трёх частей.

Каждое задание части А (А1-А7) оценивается в 1 балл.

Каждое задание части В (В1,В2) оценивается в 1 балл.

Задания части С (С1, С2) оцениваются от 0 до 2 баллов.

Баллы	Критерии оценки выполнения задания  С1.
2	Верно применены свойства степеней и выполнен переход от показательных уравнений к линейным. Верно решена система линейных уравнений и записан верно ответ.
1	Верно применены свойства степеней и выполнен переход от показательных уравнений к линейным. Верно решена система линейных уравнений, но при записи ответа допущена ошибка.
0	Все случаи решения, которые не соответствуют вышеуказанным критериям.

 

       

Баллы	Критерии оценки выполнения задания  С2.
2	Верно выполнен переход от показательного неравенства к квадратному. Верно решено квадратное неравенство и в ответе указаны целочисленные решения неравенства.
1	Верно выполнен переход от показательного неравенства к квадратному. Верно решено квадратное неравенство, но не указаны целочисленные решения неравенства.
0	Все случаи решения, которые не соответствуют вышеуказанным критериям.

 

Соотношение тестового балла и аттестационной отметки:

Тестовый балл	Аттестационная отметка
11-13	5
8-9	4
5-7	3
0-4	2

2. Спецификация работы

Проверяемое содержание	Номер задания в работе
Умение находить значение выражения, содержащего радикалы.	А1
Умение упрощать выражение, содержащее радикалы и степени.	А2
Умение решать иррациональное уравнение.	А3
Умение распознавать показательную функцию по графику.	А4
Умение решать простейшее показательное уравнение.	А5
Умение соотнести корень показательного уравнения числовому промежутку.	А6
Умение решать показательное неравенство.	А7
Умение находить значение выражения, содержащего степени.	В1
Умение решать показательное уравнение, сводящееся к квадратному уравнению.	В2
Умение решать систему показательных уравнений.	С1
Умение решать показательное неравенство, сводящееся к квадратному неравенству и записывать целочисленные решения, принадлежащие найденному промежутку.	С2

3. Текст работы.

Административная контрольная работа

по алгебре и началам анализа

11 класс

Вариант № 1.

Инструкция по выполнению работы.

   На выполнение работы отводится 40 минут.

   Работа состоит из трёх частей. Часть А содержит семь заданий (А1-А7) обязательного уровня, часть В содержит два задания (В1,В2) повышенного уровня и часть С содержит два задания (С1, С2) высокого уровня по материалу курса «Алгебры и началам анализа» 11 класса. К каждому заданию части А даны 4 варианта ответов, из которых только один верный. В бланк ответов на задания части А вписывается буква, соответствующая верному, на Ваш взгляд, ответу. При решении заданий части В в бланк ответов вписывается ответ, получившийся в результате решения задания. Если Вы записали неверный ответ, аккуратно зачеркните его и рядом запишите другой ответ.

Задания части  С с развёрнутым ответом требует записи полного решения с необходимым обоснованием выполненных действий.

   За каждое верно выполненное задание части А и В Вы получаете 1 балл, за задание части С – от 0 до 2 баллов.

   Советуем для экономии времени пропускать задание, которое не удаётся выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у Вас останется время.

Желаем успехов!

Часть А.

А1. Найдите значение выражения: 5 +2- —  

а) — 15        б) 15           в) 35        г) -5

А2. Упростите выражение: у*

А) у          б) 1           в) у2            г) у3

А3. Решите уравнение = 5

а) — 37    б) 9   в) 3   г) 37

А4. Укажите, на каком рисунке изображен график функции у= 6х.

а)                      у                                                 б)                          у

                                          х                                                                         х

в)                                                                      г)

                      у                                                                              у

                                      х                                                                              х

А5. Решите уравнение 52х = 625

а) — 3        б) 0         в) 1         г) 2

А6. Какому промежутку принадлежит корень уравнения 25х – 4 = 16х+3

а) (-∞; -16)       б) (-16;0)          в) (0;17)          г)  (18;+∞)

А7. Решите неравенство  46х – 3 ≤ 1

 а) [0,5;+∞)       б) (-∞; 0,5]        в) [2;+∞)           г) (-∞; 2]        

Часть В.

В1. Найдите значение выражения:

В2. Решите уравнение 32х – 2*3х – 3 = 0

Часть С.

С1. Решите систему уравнений:

 = 27

32х × 2у =16

С2. Найдите целочисленные решения неравенства  ≥

Административная контрольная работа

по алгебре и началам анализа

11 класс

Вариант № 2.

Инструкция по выполнению работы.

   На выполнение работы отводится 40 минут.

   Работа состоит из трёх частей. Часть А содержит семь заданий (А1-А7) обязательного уровня, часть В содержит два задания (В1,В2) повышенного уровня и часть С содержит два задания (С1, С2) высокого уровня по материалу курса «Алгебры и началам анализа» 11 класса. К каждому заданию части А даны 4 варианта ответов, из которых только один верный. В бланк ответов на задания части А вписывается буква, соответствующая верному, на Ваш взгляд, ответу. При решении заданий части В в бланк ответов вписывается ответ, получившийся в результате решения задания. Если Вы записали неверный ответ, аккуратно зачеркните его и рядом запишите другой ответ.

 Задания части  С с развёрнутым ответом требует записи полного решения с необходимым обоснованием выполненных действий.

   За каждое верно выполненное задание части А и В Вы получаете 1 балл, за задание части С – от 0 до 2 баллов.

   Советуем для экономии времени пропускать задание, которое не удаётся выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у Вас останется время.

Желаем успехов!

Часть А.

А1. Найдите значение выражения: 3- +- 7

а) — 1        б) 1           в) 5              г) -5

А2. Упростите выражение: * с

а) с          б) 1           в) с2            г) с3

А3. Решите уравнение = 4

а) — 4        б) 16         в) 4            г) 7

А4. Укажите, на каком рисунке изображен график функции у= ()х.

а)                      у                                                 б)                          у

                                          х                                                                         х

в)                                                                      г)

                      у                                                                              у

                                      х                                                                              х

А5. Решите уравнение 44х = 256

а) — 3        б) 0         в) 1         г) 2

А6. Какому промежутку принадлежит корень уравнения 35х +2 = 81х-1

а)  (-∞; -7]         б) (6;+∞)         в) [6;+∞)           г) (– 10; 10)          

А7. Решите неравенство  72х+5 ≥ 49

а) [-1,5;+∞)       б) (-∞; -1,5]        в) [1,5;+∞)           г) (-∞; 5]        

Часть В.

В1. Найдите значение выражения:

91,5 —  

В2. Решите уравнение 22х – 3*2х – 4 = 0

Часть С.

С1. Решите систему уравнений:

9х × 27у =27

 = 32

С2. Найдите целочисленные решения неравенства  ≥

4. Ключ к работе

1 вариант.

Номер задания	Правильный  ответ
А1	б
А2	г
А3	в
А4	а
А5	г
А6	в
А7	б
В1	6
В2	1
С1	(1; -1)
С2	0; 1; 2

2 вариант.

Номер задания	Правильный  ответ
А1	б
А2	а
А3	в
А4	б
А5	в
А6	г
А7	а
В1	12
В2	2
С1	(3; -1)
С2	-1; 0; 1; 2

5. Бланк анализа работы

Анализ контрольных работ (тестов) по  алгебре и началам анализа

Дата проведения  ________________________________                

Класс  __________________

Учитель  ________________________________________

Таблица 1

Класс	Дата проведения	Результаты
		По списку	Писали	Оценки	% успевае мости	% качества	СОК
				«5»	«4»	«3»	«2»

Таблица 2

Ф.И. обучающегося	Содержание работы
	Часть А	Часть В	Часть С
	А1. Умение находить значение выражения, содержащего радикалы.	А2. Умение упрощать выражение, содержащее радикалы и степени.	А3. Умение решать иррациональное уравнение.	А4. Умение распознавать показательную функцию по графику.	А5. Умение решать простейшее показательное уравнение.	А6. Умение соотнести корень показательного уравнения числовому промежутку.	А7. Умение решать показательное неравенство.	В1. Умение находить значение выражения, содержащего степени.	В2. Умение решать показательное уравнение, сводящееся к квадратному.	С1. Умение решать систему показательных уравнений.	С2. Умение решать показательное неравенство, сводящееся к квадратному и записывать целочисленные решения, принадлежащие найденному промежутку.

Таблица 3

Класс/тип работы/дата проведения	Содержание работы
	Часть А	Часть В	Часть С
	А1. Умение находить значение выражения, содержащего радикалы.	А2. Умение упрощать выражение, содержащее радикалы и степени.	А3. Умение решать иррациональное уравнение.	А4. Умение распознавать показательную функцию по графику.	А5. Умение решать простейшее показательное уравнение.	А6. Умение соотнести корень показательного уравнения числовому промежутку.	А7. Умение решать показательное неравенство.	В1. Умение находить значение выражения, содержащего степени.	В2. Умение решать показательное уравнение, сводящееся к квадратному.	С1. Умение решать систему показательных уравнений.	С2. Умение решать показательное неравенство, сводящееся к квадратному и записывать целочисленные решения, принадлежащие найденному промежутку.

Таблица 4

Типичные ошибки	Класс	Ф.И. обучающегося

nsportal.ru

Контрольные работы для 11 класса по алгебре к учебнику Ю.М. Колягина

Контрольная работа №1

В-1,

1. Найти область определения и множество значений функции

у = sinx + 2

2. Выяснить, является ли функция у = х² + cosx чётной или нечётной.

3. Доказать, что функция у = cos x является периодической с периодом Т=3.

4. Найти все принадлежащие отрезку [ -] корни уравнения

sinx = с помощью графика функции.

5. Построить график функции у = sinx 1 и найти значения аргумента, при которых функция возрастает, принимает наибольшее значения.

№ Контрольная работа №1

В-2

1.Найти область определения и множество значений функции

у = 3cosx

2. Выяснить, является ли функция у =х sinx чётной или нечётной.

3. Доказать, что функция у = sin x является периодической с периодом Т=.

4. Найти все принадлежащие отрезку [ 0] корни уравнения

cosx =- с помощью графика функции.

5. Построить график функции у = cos (x + ) и найти значения аргумента, при которых функция убывает, принимает наименьшее значения.

Контрольная работа№2

В – 1

1. Найти производную функции:

а) 3 – ; б) ( + 7)⁶; в) cosx; г) .

2. Найти значение производной функции y = f(x) в точке , если f(x) = 1 – 6 , = 8.

3. Записать уравнение касательной к графику функции

f(x) = sinx – 3x + 2 в точке = 0.

4. Найти значения х, при которых значения производной функции f(x) = положительны.

5. Найти точки графика функции f(x) = x³ – 3x², в которых касательная к нему параллельна оси абсцисс.

___________________________________________________________________

Контрольная работа №2

В – 2,

1. Найти производную функции:

а) 2 – ; б) (4 – 3х)⁷; в) sinx; г) .

2. Найти значение производной функции y = f(x) в точке , если f(x) = 2 – , = .

3. Записать уравнение касательной к графику функции

f(x) = 4х – sinx + 1 в точке = 0.

4. Найти значения х, при которых значения производной функции f(x) = отрицательны.

5. Найти точки графика функции f(x) = x³ + 3x², в которых касательная к нему параллельна оси абсцисс.

Контрольная работа №3

В-1

1. Найти экстремумы функций:

1. f(x)=х³2х²+х+3; 2) f(x)=е^х (5х 3).

2. Найти интервалы возрастания и убывания функции f(x)=х³ 2х²+х+3

3. Построить график функции f(x)=х³2х²+х+3.

4. Найти наибольшее и наименьшее значения функции f(x)=х³ 2х²+ х +3 на отрезке [0; ].

5. Среди прямоугольников, сумма длин трёх сторон у которых равна 20, найти прямоугольник наибольшей площади.

___________________________________________________________

Контрольная работа №3

В-2

1. Найти экстремумы функций:

1) f(x)=х³х²х +2; 2) f(x)= (8 7х) е^х

2. Найти интервалы возрастания и убывания функции f(x)=х³ х² х +2

3. Построить график функции f(x)= х³ х² х +2

4. Найти наибольшее и наименьшее значения функции f(x)= х³ х² х +2 на отрезке [-1; ].

5. Найти ромб с наибольшей площадью, если известно, что сумма длин его диагоналей равна 10.

____________________________________________________________

Контрольная работа №4

В-1

1. Доказать, что функция F(х) = 3х + sinx – e^2х является первообразной функции f(x) = 3 + cosx – 2e

   2^x на всей числовой оси.

2. Найти первообразную F(x) функции f(x) = 2, график которой проходит через точку А (0; ).

3. Вычислить площадь фигуры, ограниченной линиями у = 3х – х², х = 1, х = 2 и осью Ох.

___________________________________________________________________

Контрольная работа №4

В-2

1. Доказать, что функция F(х) = е^3х + cosx + x является первообразной функции f(x) = 3e^3x — sinx + 1 на всей числовой оси.

2. Найти первообразную F(x) функции f(x) = -3, график которой проходит через точку А (0; ).

3. Вычислить площадь фигуры, ограниченной линиями у = cosx, х = 0, х = и осью Ох.

Контрольная работа №5

В-1

1. Найти

2. Сколькими способами из числа 15 учащихся класса можно выбрать культорга и казначея?

3. Сколько различных шестизначных чисел можно записать с помощью цифр

2, 3, 4, 5, 6, 7 таким образом, чтобы все цифры в числах были различны?

4. Записать разложение бинома (2 – х)⁵.

5. Сколько существует различных кодов, состоящих из двузначного числа, цифры которого выбираются из цифр 1, 2, 3, и следующего за ним трёхбуквенного слова, буквы которого выбираются из гласных букв русского алфавита.

Контрольная работа №5

В-2

1. Найти + .

2. Сколькими способами 7 детей ясельной группы можно рассадить на 7 стульях?

3. Сколькими способами можно составить набор из 5 карандашей, выбирая их из 8 имеющихся карандашей восьми различных цветов.

4. Записать разложение бинома (2х – 1)⁶.

5. Шифр сейфа образуется из двух чисел. Первое, двузначное число, образуется из цифр 1, 2, 3, 4 (цифры в числе могут повторяться). Второе, трёхзначное число, образуется из цифр 7 и 6. Сколько различных шифров можно использовать в таком сейфе?

Контрольная работа №6

В-1

1. Бросают два игральных кубика – большой и маленький. Какова вероятность того, что:

1. На обоих кубиках появится четыре очка;

2. На большом кубике появится 2 очка, а на маленьком – четное число очков.

2. В коробке лежат 3 черных, 2 белых и 4 красных шара. Случайным образом вынимается один шар. Какова вероятность того, что это или белый, или красный шар?

3. Вероятность попадания по мишени стрелков равна . Какова вероятность:

1. непопадания по мишени при одном выстреле?

2. попадания по мишени в каждом из двух последовательных выстрелов?

3. попадания при первом и промахе при втором выстреле?

4. В коробке лежат 4 белых и 3 черных шара. Наугад вынимают два шара. Какова вероятность того, что вынуты белый и черный шары?

5. В вазе стоят 5 гвоздик и 6 нарциссов. Какова вероятность того, что среди трёх случайным образом вынутых цветков окажется по крайней мере одна гвоздика?

________________________________________________________________

Контрольная работа№6

В-2

1. Бросают два игральных кубика – большой и маленький. Какова вероятность того, что:

1. На обоих кубиках появится пять очков;

2. На маленьком кубике появится кратное 3 число очков, а на большом –5 очков.

2. В коробке лежат 3 черных, 2 белых и 4 красных шара. Случайным образом вынимается один шар. Какова вероятность того, что это или черный, или красный шар?

3. Вероятность попадания по мишени стрелков равна . Какова вероятность:

1) непопадания по мишени при одном выстреле?

2) попадания по мишени в каждом из двух последовательных выстрелов?

3. попадания при первом и промахе при втором выстреле

4. В коробке лежат 4 белых и 3 черных шара. Наугад вынимают два шара. Какова вероятность того, что вынуты белый и черный шары?

5. В вазе стоят 5 гвоздик и 6 нарциссов. Какова вероятность того, что среди трёх случайным образом вынутых цветков окажется по крайней мере один нарцисс?

__________________________________________________________________

Контрольная работа №7

В-1

1. Найти множество точек координатной плоскости, удовлетворяющих уравнению:

1. х – у + 2 = 0; 2) (х + 4)² + (у – 1)² = 9.

2. Найти множество точек координатной плоскости, удовлетворяющих неравенству:

1. 2х + у – 1 0; 2) х² + (у – 2)² 4.

3. Найти множество точек координатной плоскости, удовлетворяющих системе неравенств:

_____________________________________________________________

Контрольная работа №7

В-2

1. Найти множество точек координатной плоскости, удовлетворяющих уравнению:

1. х + у — 3 = 0; 2) (х — 3)² + (у + 2)² = 16.

2. Найти множество точек координатной плоскости, удовлетворяющих неравенству:

1. х — 2у + 3 0; 2) (х + 3)² + у² 1.

3. Найти множество точек координатной плоскости, удовлетворяющих системе неравенств:

infourok.ru

Материал по алгебре (11 класс) на тему: Контрольные работы по алгебре 11 класс

Контрольная работа №1

Вариант I

1.Найти область определения и множество значений функции  y = 2 cos x

2.Выяснить, является функция  y = sin x – tg x  четной или нечетной.

3.Изобразить схематически график функции  y = sin x + 1  на отрезке 

4.Найти наибольшее и наименьшее значения функции  y = 3 sin x · cos x + 1

Контрольная работа №1

Вариант II

1.Найти область определения и множество значений функции   y = 0,5 sin x

2.Выяснить, является функция  y = cos x – x2  четной или нечетной.

3.Изобразить схематически график функции  y = cos x – 1  на отрезке

4.Найти наибольшее и наименьшее значения функции  

Контрольная работа №2

Вариант I

1.Найти производную функции:  а) ,   б) ,   в) ех· cos x ,   г)  

2.Найти значение производной функции  y = f(x) в точке хо, если

3.Записать уравнение касательной к графику функции  f(x) = sin x  — 3x + 2  в точке

хо = 0

4.Найти значения х, при которых значения производной функции    положительны.

Контрольная работа №2

Вариант II

1.Найти производную функции:  а) ,   б) (4 – 3х)7,   в) ех · sin x,   г)

2.Найти значение производной функции y = f(x) в точке хо, если  

3.Записать уравнение касательной к графику функции   f(x) = 4x – sin x + 1 в точке

xo = 0.

4.Найти значения х, при которых значения производной функции   отрицательны.

Контрольная работа №3

Вариант I

1.Найти экстремумы функции

2.Найти интервалы возрастания и убывания функции f(x)=x3 – 2×2 + x +3

3.Построить график функции f(x)=x3 – 2×2 + x +3 на отрезке [-1; 2]

4.Найти наибольшее и наименьшее значения функции f(x)=x3 – 2×2 + x +3 на отрезке [0; 1,5]

Контрольная работа №3

Вариант II

1.Найти экстремумы функции

2.Найти интервалы возрастания и убывания функции f(x)=x3 – х2 – х +2

3.Построить график функции f(x)= x3 – х2 – х +2

4.Найти наибольшее и наименьшее значения функции f(x)= x3 – х2 – х +2

Контрольная работа №3

Вариант I

nsportal.ru

Методическая разработка по алгебре (11 класс) по теме: вводная контрольная работа в 11 классе по алгебре

Вводная контрольная работа 11 класс

Вариант 1

Вариант 2

1). Найдите  , если   и   2).    Найдите значение выражения: 3). Найдите корень уравнения: . В ответе запишите наибольший отрицательный корень. 4). На рисунке изображен график функции , определенной на интервале (–9;8). Определите количество целых точек, в которых производная функции  положительна. 5).  На рисунке изображён график функции  и касательная к нему в точке с абсциссой . Найдите значение производной функции  в точке . 6). Прямая  параллельна касательной к графику функции . Найдите абсциссу точки касания. 7).   Найдите наименьшее значение функции  на отрезке . Часть II 8). Решите уравнение =0

1). Найдите  , если   и   2).   Найдите значение выражения: 3). Найдите корень уравнения:  В ответе запишите наибольший отрицательный корень 4). На рисунке изображен график функции , определенной на интервале (–5;5). Определите количество целых точек, в которых производная функции   отрицательна. 5). На рисунке изображён график функции  и касательная нему в точке с абсциссой . Найдите значение производной функции  в точке . 6). Прямая  параллельна касательной к графику функции . Найдите абсциссу точки касания. 7).    Найдите наибольшее значение функции   на отрезке . Часть II 8). Решите уравнение =0

Видутова Татьяна Владимировна. МБОУ СОШ № 203 ХЭЦ г. Новосибирск.

Пояснительная записка.

Спецификация контрольной работы

по алгебре и началам анализа за  курс 10 класса

1. Назначение работы: определить степень сформированности знаний, основных умений и навыков, оценить качество подготовки учащихся по темам: «Тригонометрические функции числового аргумента», «Основные свойства функции», «Решение тригонометрических уравнений», «Применение производной для исследования функций на монотонность и экстремумы», «Уравнение касательной к графику функции», «Применение производной для отыскания наибольших и наименьших значений велечин»
2. Апробация работ: Все задания 1 части взяты банка открытых заданий по математике http://mathege.ru/or/ege/Main, задание 2  части взято из текстов ЕГЭ.
3. Условия применения: Работа рассчитана на учащихся 10 класса, изучающих курс алгебры и начала анализа, отвечает обязательному минимуму содержания основного и среднего (полного) общего образования по алгебре и началам анализа.
4.  Инструкция для учащихся.

На выполнение тестовой работы отводится 1 урок (45минут). Работа состоит из 8 заданий, которые разделены на две  части.

                Часть I состоит из 7 заданий с кратким ответом.         

         Часть II состоит из 1 более сложного задания. Это задание необходимо решить и записать ответ. Результаты выполнения этой части работы позволяют дифференцировать учащихся, имеющих повышенную математическую подготовку.

Советуем выполнять задания в том порядке, в котором они даны. Однако, если какое-то задание вам не удается выполнить сразу, то для экономии времени пропустите его и постарайтесь выполнить те, в которых вы уверены. Если останется время, то можно вернуться к пропущенным заданиям.

1.   Система оценивания.

Задание 1- 7 первой  части оценивается в 1 балл, задание 8 второй части оценивается в 2 балла.

 Критерии оценивания задания 8.

Содержания критерия	Балл
Обоснованно получен правильный ответ	2
Тригонометрическое уравнение решено верно, но отбор корней не произведен или произведен неверно	1
Решение не соответствует ни одному из критериев, перечисленных выше	0

0 – 3 балла   «2»

4 – 5  балла  «3»

6 – 7  балла «4»

8 – 9 балла  «5»

Составила Видутова Татьяна Владимировна.

учитель математике МБОУ СОШ № 203 ХЭЦ г. Новосибирск 2010-2011 уч. год

nsportal.ru

Контрольная работа по алгебре за 1 полугодие11 класс

Контрольная работа по алгебре в 11 классе за 1 полугодие

В-1

1. Найдите значение выражения: а) б)

2. Найдите общий вид первообразной для функции f(x) = 2(3x + 1)⁵

3. Вычислите площадь фигуры, ограниченной линиями у = х³ + 2х, у = 0, х = 1, х = 2

4. Решите иррациональное уравнение: а)

б)

в)

5. Решите показательное уравнение:

Контрольная работа по алгебре в 11 классе за 1 полугодие

В-2

1. Найдите значение выражения: а) б)

2. Найдите общий вид первообразной для функции f(x) = 3(4x + 5)⁶

3. Вычислите площадь фигуры, ограниченной линиями у = х³ + 4х, у = 0, х = 1, х = 3

4. Решите иррациональное уравнение и неравенство: а)

б)

в)

5. Решите показательное уравнение:

Ответы

№	1	2	3	4	5
В-1	а) 6 б) 2	F(x) =		а) х1=2, х2= б) в) х1=0 х2=1	2
В-2	а) 10 б) 3	F(x) =	96	а) х1=3, х2= б) в) х1=1 х2=2	3

videouroki.net