Какими преимуществами и недостатками обладает двоичная система счисления по сравнению с десятичной: Какими преимуществами и недостатками обладает двоичная система счисления по сравнению с десятичной

Восьмеричная и шестнадцатеричная системы счисления. «Компьютерные» системы счисления

Классная работа
16.12.2021
Восьмеричная и
шестнадцатеричная системы
счисления.
«Компьютерные» системы
счисления.
МАТЕМАТИЧЕСКИЕ ОСНОВЫ
ИНФОРМАТИКИ
Урок 4
По данной теме урок 3
Ключевые слова
система счисления
цифра
алфавит
позиционная система счисления
основание
развёрнутая форма записи числа
свёрнутая форма записи числа
двоичная система счисления
восьмеричная система счисления
шестнадцатеричная система счисления
Вопросы и задания
Какими преимуществами и недостатками обладает
двоичная система счисления по сравнению с
десятичной?
Правило перевода натуральных двоичных чисел в
десятичную систему счисления.
Правило перевода целых десятичных чисел в двоичную
систему счисления.

4. Проверка домашнего задания

№ 11 с. 15
89
44
22
11
5
2
1
0
0
1
1
0
600 300 150 75
0
0
0
1
37
1
18
0
1
8910 10110012
9
1
4
0
2
0
1
60010 10010110002
2010 1005 501 250 125 62 31 15 7
0
1
1
0
1
201010 110110101102
0
1
1 0
3
1
1

5.

Проверка домашнего задания № 15 с. 16
101010 2
а)
+
б)
+
11012
1101112
1010 2
в)
+
101012
1112
111002
1010 2
101002
№ 16 с. 16
а)
Х
1010 2
112
1010
1010
111102
+
б)
Х
1112
1012
111
+
111
1000112
в)
Х
1010 2
1112
1010
+ 1010
1010
10001102
Восьмеричная система
счисления
Восьмеричной
системой
счисления
называется
позиционная система счисления с основанием 8.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7.
an–1an–2…a1a0 = an–1 8n–1+an–2 8n–2+…+a0 80
Пример: 10638 =1 83 +0 82+6 81+3 80=56310.
Для перевода целого восьмеричного числа в десятичную
систему счисления следует перейти к его развёрнутой
записи и вычислить значение получившегося выражения.
Для перевода целого десятичного числа в восьмеричную
систему счисления следует последовательно выполнять
деление данного числа и получаемых целых частных на 8 до
тех пор, пока не получим частное, равное нулю.
Шестнадцатеричная
система счисления
Основание: q = 16.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
3АF16 =3 162+10 161+15 160 =768+160+15=94310.
Переведём десятичное число 154 в шестнадцатеричную
систему счисления
154 16
-144
9
16
10
(А)
9
0
15410 = 9А16
Таблица соответствия 10-х, 2-х, 8-х и 16-х чисел от 1 до 16
Десятичная
система
Двоичная
система
Восьмеричная
система
Шестнадцатеричная
система
1
1
1
1
2
10
2
2
3
11
3
3
4
100
4
4
5
101
5
5
6
110
6
6
7
111
7
7
8
1000
10
8
9
1001
11
9
10
1010
12
A
11
1011
13
B
12
1100
14
C
13
1101
15
D
14
1110
16
E
15
1111
17
F
16
10000
20
10
17
10001
21
11
18
10010
22
12
«Компьютерные» системы счисления
Двоичная система используется в компьютерной технике,
так как:
двоичные числа представляются в компьютере с
помощью простых технических элементов с двумя
устойчивыми состояниями;
представление информации посредством только двух
состояний надёжно и помехоустойчиво;
двоичная арифметика наиболее проста;
существует математический аппарат, обеспечивающий
логические преобразования двоичных данных.
Двоичный код удобен для компьютера.
Человеку неудобно пользоваться длинными и
однородными кодами.
Специалисты заменяют двоичные коды на
величины в восьмеричной или шестнадцатеричной
системах счисления.
Самое главное
Система счисления — это знаковая система, в которой приняты
определённые правила записи чисел.
Система
счисления
называется
позиционной,
если
количественный эквивалент цифры в числе зависит от её положения
в записи числа.
В позиционной системе счисления с основанием q любое число
может быть представлено в виде:
Aq =±(an–1 qn–1 + an–2 qn–2 +…+ a0 q0 + a–1 q–1 +…+ a–m q–m)
Здесь:
А — число;
q — основание системы счисления;
ai — цифры, принадлежащие алфавиту данной системы счисления;
n — количество целых разрядов числа;
m — количество дробных разрядов числа;
qi — «вес» i-го разряда.

11. Задания

№ 18 РТ самостоятельно
Постройте на координатной плоскости рисунок, отметив и
последовательно соединив точки:
2
2
1
4
9
11
12
13
14
16
15
17
1
9
12
9
9
18
16
18
16
15
14
12
17
18
18
14
14
11
13
10
9
5
5
11
11
8
6
7
11
1
1
4
6
1

12.

Задания№ 18 РТ самостоятельно

13. Задания

№ 26 РТ
Задания
Переведите целые числа из десятичной системы счисления в
восьмеричную:

14. Задания

№ 26 РТ
Задания
Переведите целые числа из десятичной системы счисления в
восьмеричную:

15. Задания

№ 27 РТ
Задания
Переведите целые числа из десятичной системы счисления в
шестнадцатеричную:

16. Задания

№ 27 РТ
Задания
Переведите целые числа из десятичной системы счисления в
шестнадцатеричную:

17. Задания

№ 31 РТ; № 20 УЧ с. 16
Разработайте таблицы сложения и умножения для
восьмеричной системы счисления.

18. Домашнее задание

§ 1.1.3 и 1.1.4
В тетрадях № 12, 13 с. 15, № 20 с. 16
РТ: № 19, 25
Опорный конспект
Система счисления — это знаковая система, в которой приняты
определённые правила записи чисел.
Цифры — знаки, при помощи которых записываются числа.
Алфавит — совокупность цифр системы счисления.
Система счисления
Позиционная
Двоичная
Восьмеричная
Десятичная
Непозиционная
Римская
Шестнадцатеричная
В позиционной системе счисления с основанием q любое число
может быть представлено в виде:
Aq =±(an–1* qn–1 + an–2* qn–2 +…+ a0*q0 + a–1* q–1 +…+ a–m * q–m).

ГДЗ по информатике 8 класс учебник Босова параграф 1.1

1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Что вы можете сказать о формах представления информации в презентации и в учебнике? Какими слайдами вы могли бы дополнить презентацию?

 2. Найдите дополнительную информацию об унарной, позиционных и непозиционных системах счисления. Чем они различаются? Приведите примеры.

 

 

3. Цифры каких систем счисления приведены на рис. 1.1?

 

4. Объясните, почему позиционные системы счисления с основаниями 5, 10, 12 и 20 называют системами счисления анатомического происхождения.

 

 

5. Как от естественной формы записи десятичного числа перейти к его развёрнутой форме?

 

 

6. Запишите в развёрнутой форме числа:

а) 143,511₁₀;

б) 143511₈;

в) 143511₁₆;

г) 1435,11

8

 

 

7. Вычислите десятичные эквиваленты следующих чисел:

а) 172₈;

б) 2ЕА₁₆;

в) 101010₂;

г) 10,1₂;

д) 243₆.

 

 

8. Укажите, какое из чисел 1100112, 1114, 358 и 1В16 является:

а) наибольшим;

б) наименьшим.

 

 

9. Какое минимальное основание имеет система счисления, если в ней записаны числа 123, 222, 111, 241? Определите десятичный эквивалент данных чисел в найденной системе счисления.

 

 

10. Верны ли следующие равенства?

а) 33₄ = 21₇;

б) 33₈ = 21₄.

 

 

11. Найдите основание х системы счисления, если:

а) 14_x = 910;

б) 2002_x= 13010.

 

 

12. Переведите целые числа из десятичной системы счисления в двоичную:

а) 89;

б) 600;

в) 2010.

 

а) 89₁₀ = 1011001₂

1

0

0

1

1

0

1

б) 600₁₀ = 1001011000₂

0

0

0

1

1

0

1

0

0

1

в) 2010₁₀ = 11111011010₂

0

1

0

1

1

0

1

1

1

1

1

 

13.

Переведите целые числа из десятичной системы счисления в восьмеричную:

а) 513;

б) 600;

в) 2010.

 

 

14. Переведите целые числа из десятичной системы счисления в шестнадцатеричную:

а) 513;

б) 600;

в) 2010.

 

 

15. Заполните таблицу, в каждой строке которой одно и то же число должно быть записано в системах счисления с основаниями 2, 8, 10 и 16.

 

 

16. Выполните операцию сложения над двоичными числами:

а) 101010 +1101;

б) 1010 + 1010;

в) 10101+111.

 

 

 17. Выполните операцию умножения над двоичными числами:

а) 1010 • 11;

б) 111 • 101;

в) 1010 • 111.

 

 

18. Расставьте знаки арифметических операций так, чтобы были верны следующие равенства в двоичной системе:

а) 1100 ? 11 ? 100 = 100000;

б) 1100 ? 10 ? 10 = 100;

в) 1100 ? 11 ? 100 = 0.

 

 

 19. Вычислите выражения:

а) (1111101₂ + AF₁₆) : 36₈;

б) 125₈ + 101₂ • 2А₁₆ — 141₈.

Ответ дайте в десятичной системе счисления.

 

 

20. Какими преимуществами и недостатками обладает двоичная система счисления по сравнению с десятичной?

 

 

21. Разработайте таблицы сложения и умножения для восьмеричной системы счисления.

 

 

22. Постройте граф, отражающий разновидности систем счисления.

  Подготовьте небольшое сообщение об одной из систем счисления (когда и где применялась, какие символы использовались и т. д.). Можете воспользоваться материалами электроного приложения к учебнику.

Методические рекомендации на тему «Формирующее оценивание на уроках информатики»

Аннотация

Методические рекомендации предназначены для учителей общеобразовательных организаций и могут быть использованы для применения технологии оценивания, стимулирующих оценочную самостоятельность учащихся, обеспечивающих их деятельность по планированию и достижению образовательных результатов определенного уровня.

Пояснительная записка

Мы живём в быстро меняющемся мире, требующем от учителей серьёзных, важных и необходимых перемен в образовании для того, чтобы уже сегодня наши ученики были готовы к тому, что их ждёт завтра.

Одной из проблем, возникающих с введением нового Федерального государственного образовательного стандарта основной школы (ФГОС ООО), является проблема оценивания образовательных результатов учащихся.

В систему оценивания надо заложить механизм, поощряющий и развивающий мотивацию обучения и самооценивания учащимися своих достижений, а также рефлексию происходящего с ним в ходе учебного процесса. Такие возможности для ученика и учителя предоставляет формирующее оценивание.

Таким образом, актуальность данной работы обусловлена:

• внедрением ФГОС в образовательный процесс в основной школе;

• потребностью учителя введения новых подходов к оцениванию образовательных результатов;

• недостаточным количеством практических пособий для учителей при внедрении формирующего оценивания на уроках.

Цель работы: описание опыта внедрения техник формирующего оценивания на уроках информатики.

Данные методические рекомендации помогут учителям предметникам при подготовке учащихся к самостоятельным, контрольным, диагностическим и итоговым работам, зачетам и итоговой аттестации. Использование техник формирующего оценивания даст возможность учителю выявить пробелы в усвоении учебного материала и повысить мотивацию учащихся.

Инновационность методической разработки заключается в повышении результативности уровня обученности и качества знаний учащихся с применением на уроках и внеурочной деятельности листов обратной связи и ментальных карт.

Содержание

Под формирующим оцениванием понимается процесс поиска и интерпретации данных, которые ученики и их учителя используют для того, чтобы решить, как далеко ученики уже продвинулись в своей учёбе, куда им необходимо продвинуться и как сделать это наилучшим образом. Принято наряду с итоговым как второй обязательный элемент полноценной системы оценивания выделять формирующее оценивание. Если итоговое оценивания происходит по завершении того или иного учебного этапа и решает задачи контроля и фиксации результата, то формирующее оценивание происходит в ходе обучения и является его частью. Его можно рассматривать как текущее, диагностическое, но наиболее точное название – «оценивание для обучения».

Формирующее оценивание – это оценивание в процессе обучения, при котором анализируются знания, умения, ценностные установки и оценки, поведение учащегося, устанавливается обратная связь об успехах и недостатках учащегося; когда учащегося направляют и мотивируют на дальнейшую учёбу, а также планирование целей и путей её продолжения. Сравнение успехов учащегося с его прежними достижениями, предложения о дальнейшей деятельности, поддерживающей развитие учащегося — это то на чём сосредоточено формирующее оценивание, а эффективные способы работы, позволяющие учителям сформировать навыки, необходимые для качественного и гибкого оценивания достижения учащихся являются инструментами формирующего оценивания.

Формирующее оценивание:

• Центрировано на ученике. Внимание учителя и ученика в большей степени фокусируется на отслеживании и улучшении процесса учения, а не преподавания. Учитель и ученик получают информацию, на основании которой они принимают решения, как улучшать и развивать учение.

• Направляется учителем. Применение формирующего оценивания предполагает автономию, академическую свободу и высокий профессионализм учителя, поскольку именно он решает, что оценивать, каким образом, как реагировать на полученную информацию.

• Разносторонне результативно. Поскольку оценивание сфокусировано на учении, оно требует активного участия школьников, благодаря чему они глубже погружаются в материал и развивают навыки самооценивания. Это приводит к тому, что растёт их учебная мотивация, поскольку дети видят заинтересованность преподавателей, стремящихся помочь им стать успешными в учёбе.

• Формирует учебный процесс. Цель формирующего оценивания – улучшать качество учения, а не обеспечивать основания для выставления отметок.

• Определено контекстом. Формирующее оценивание осуществляется с учетом как нужд учителя, учеников, так и характеристик изучаемых дисциплин. Формы и критерии оценивания зависят от конкретной ситуации.

• Непрерывно. Оценивание – это продолжающийся процесс, который запускает механизм обратной связи и постоянно поддерживает его в работающем состоянии.

• Основано на качественном преподавании. Формирующее оценивание опирается на высокопрофессиональное преподавание и с помощью механизма обратной связи, информирующей учителя о том, как учатся ученики, позволяет ему работать более систематично, подвижно и эффективно.

Формирующее оценивание используется для того, чтобы выяснить, достигнуты ли поставленные учебные цели. Одной из техник формирующего оценивания является методика составления листов обратной связи, которую мы применяем на своих уроках.

Опыт использования элементов формирующего оценивания

на уроках информатики

Изучив техники формирующего оценивания, я пришла к выводу, что эффективными на уроках информатики являются листы обратной связи и ментальные карты. 

Ментальные карты – это особый способ систематизации знаний при помощи схем.

Главной особенностью этого способа является то, что он одновременно вводит в работу оба полушария головного мозга, благодаря чему человек может на все 100% использовать свой потенциал.

Данные карты можно выполняться как вручную на листах бумаги формата А3 или А4, так и при помощи специальных компьютерных программ.

Ментальные карты нужны:

• Для представления в сжатой форме большого количества информации.

• Для того, чтобы хорошо разобраться в новой теме.

• Для генерации идей. Опишите свою цель и всё, что нужно для ее достижения, а карта поможет найти наиболее оптимальный метод решения задачи.

• В самостоятельном обучении. Вы сможете значительно ускорить процесс изучения нового материала, если зафиксируете главные мысли в ментальной карте.

Основные принципы:

1. Ментальная карта должна активизировать память и восприятие.

2. Обеспечение максимальной удобочитаемости, что делает мышление более осознанным.

3. Анализ составленной вами карты позволяет понять «устройство» вашего мышления.

Правила создания:

1. Центральная картинка (идея, задача) должна быть больше остальных и располагаться по центру.

2. При создании используйте более 3 разных цветов.

3. Изменяйте шрифт в зависимости от важности слов, чтобы получить определенную иерархию.

4. Используйте стрелки для соединения картинок (мыслей).¹

Ментальные карты, созданные учащимися, можно применять в качестве средства обучения, наглядности на обобщающем уроке в других классах.

Листы обратной связи целесообразно использовать в двух случаях. В первом случае тема, которая подлежит контролю по формирующему оцениванию, важна для реализации задач данного года обучения, содержит материал, который необходим учащемуся для дальнейшего успешного освоения данного предмета. Также применение листов обратной связи предполагает двух или трехкратное их оценивание, что способствует лучшему усвоению материала учащимся.

Во втором случае тема может содержать в качестве планируемых результатов не только запоминание и воспроизведение знаний и умений, но их применение в иной ситуации, а также их анализ, синтез и оценку. В этом случае учащийся получает комментарий учителя и в режиме самостоятельной работы с данными комментариями планирует и конструирует свою деятельность по достижению более высокого образовательного результата. Так же лист обратной связи содержит критерии оценивания. Где ученик может себя оценить и узнать на каком уровне находятся его знания.

Лист обратной связи — это документ, который использует учитель для формирования качественной и количественной оценки промежуточных и итоговых результатов деятельности учащихся по освоению определенных результатов образования. Лист обратной связи позволяет учащемуся:

• ставить собственные цели в освоении учебного материала и планировать деятельность по их достижению;

• получать информацию о результатах своей деятельности без окончательной отметки (до двух раз и более) а, значит, сохранять мотивацию на дальнейшую деятельность по освоению учебного материала;

• получать комментарии учителя, позволяющие так спланировать деятельность, чтобы получить результат более высокого уровня; овладеть алгоритмом оценки собственного продвижения.

Использование таких листов упрощают обратную связь в процессе обучения и обеспечивают преемственность в оценке сходных образовательных результатов в рамках изучения различных тем как внутри предмета, так и на материале разных предметов. Листы обратной связи как инструмент формирующей оценки помогают учащемуся задуматься о том, как можно улучшить качество своей работы и принять осознанное решение о продолжении или прекращении работы по освоению того или иного образовательного результата. В листах обратной связи я выделила: уровни учебных целей по Блуму, предметные результаты, задания и упражнения, самооценка, оценка и комментарий учителя.

При составлении заданий для листов обратной связи опиралась на таксономию Б. Блума, которая является эффективным инструментом для анализа влияния обучения на развитие у учащихся способностей к запоминанию, осмыслению и решению задач.

Б. Блум выделяет шесть категорий целей обучения: знания, понимание, применение, анализ, синтез, оценка. Знание первая категория целей обучения, так как запоминание является только частью более сложных процессов соотнесения, оценки, реорганизации, на которых строятся более высокие категории учебных целей. Понимание как категория таксономии учебных целей отражается, по мнению Б. Блума, в трех типах поведения: трансляции (переход от конкретного к абстрактному, использование других терминов, символов, перевод на другой язык, пересказ своими словами), интерпретации (реорганизация идей в сознании человека, выделение значимых идей, их внутренних связей, обобщение, объяснение, краткое изложение), переносе знаний (оценка и предсказание, основанное на понимании направлений, тенденций, правил). Если овладение знаниями на уровне понимания обеспечивает использование обучаемым абстрактных понятий, правил, принципов по данной теме, то усвоение учебного материала на уровне применения предполагает, что он будет правильно применять это знание в ситуации, отличной от той, в которой учащийся его получил. Если понимание, по мнению Б. Блума, ориентирует на «схватывание» учебного материала и погружение в него, применение на установление связей данного материала с соответствующими обобщениями и принципами, то анализ направлен на выделение отдельных частей материала, определение их взаимосвязей и принципов организации, определение предположений, выводов, концепций, которых автор текста придерживается, хотя не высказывает явно.

Категория синтеза обозначает умение комбинировать элементы так, чтобы получить целое, обладающее новизной, собирая материал из разных источников вместе так, чтобы полученная модель или структура была более понятной, чем исходный материал. Понимание, применение знаний и анализ материала являются необходимым условием решения задачи синтеза, но они не требуют оригинальности, уникальности решения. Оценка как категория таксономии обозначает умение оценивать значение того или иного материала (утверждения, художественного произведения, исследовательских данных), основывается на четких критериях, на адекватном понимании и анализе явлений, что принципиально отличает ее от субъективных мнений. ²

При применении листов обратной связи все прогнозируемые результаты, планируемые учителем, дают положительную динамику и стабильные результаты.

При составлении заданий в лист обратной связи можно воспользоваться таблицей из приложения 1.

Литература

1. Пинская М.А. Оценивание в условиях введения требований нового Федерального государственного образовательного стандарта. – М.: Педагогический университет «Первое сентября», 2013. – 96 с.

2. Фишман И.С., Голуб Г.Б. Формирующая оценка образовательных результатов учащихся: Методическое пособие. Самара: Издательство «Учебная литература», 2007 г.

3. https://abdullinru.ru/pk/mentalnye-karty.html

Приложение 1

назовите;

–        повторите;

–        напишите формулу…;

–        перечислите…;

–        в каком году…;

–        воспроизведите…  

• Ответить на любой вопрос альтернативного или множественного выбора.

• Назвать фамилии ученых.

Припоминание, узнавание

–        инсценируйте;

–        где происходило…

–        вспомните,

–        выберите, 

–        констатируйте, 

–        представьте, 

–        извлеките,

–        измерьте,

–        подчеркните….

• Вспомнить формулу.

• Найди предмет, напоминающий прямоугольник.

Понимание (понимать – выявлять сущность)

Интерпретация

–        закончите фразу;

–        что узнали;

–        объясните;

–        выполните по аналогии;

–        преобразуйте;

–        объясните взаимосвязь.

Приведение примеров

–       уточните,

–       сопоставьте,

–       преобразуйте,

–       проведите различия,

–       проиллюстрируйте,

–      переведите на другой язык…

• Изобразите параллелограмм.

• Назовите млекопитающего, который живет в нашей области.

Классификация

Сравнение

–       классифицируйте, 

–       выявите различия,

–       распознайте,

–       обсудите,

–        укажите…

Объяснение

Умозаключение

–       интерпретируйте,

–       систематизируйте,

–       изложите своими словами,

–       спрогнозируйте

–       распознайте,

–       опишите,

–       переформулируйте,

–      сделайте (критический) обзор…

• Докажите значимость правила выполнения порядка действий.

• Прочитайте отрывок и сделайте вывод.

Применение (Применять – использовать на практике в других ситуациях)

Исполнение

–       проверьте предположение;

–       докажите, что…;

–       выскажите мнение о …;

–       выскажите гипотезу;

–       объясните цель применения;

Применение

–       продемонстрируйте,

–       измените,

–       подготовьте, 

–       составьте,

–       подтвердите….

Анализ (анализировать – вычленять из понятия части и описывать как части соотносятся с целым)

Дифференциация

–        что является следствием;

–        сравните;

–        проанализируйте причины;

–         выведите формулу…

Организация

–       изобразите схематически, 

–      рассмотрите, соотнесите и выделите,

–       проведите эксперимент,

–       проверьте гипотезу,

–       задайте   вопрос ….

• Постройте модель части речи.

• Рассмотрите взаимосвязь между животными и постройте цепи.

• Найди ошибку.

Синтез (Создать новое – объединить элементы в целое)

Генерация

–        составьте из элементов;

–        систематизируйте;

–       напишите творческое сочинение;

–       предложите план эксперимента;

–        найдите альтернативу;

–        предложите алгоритм;

–       каковы возможные объяснения…

Планирование

–       аргументируйте,

–       систематизируйте,

–       реконструируйте,

–       предложите,

–       изобретите….

• Разработайте план исследования.

• Создайте план для разработки мультимедийной презентации

• Создайте кластер.

Оценка (Создать суждения, основанные на критериях и эталонах)

Проверка

–       аргументируйте

–       примите решение,

–       составьте мнение,

–       рекомендуйте,

–       разрешите проблему

• Проанализируйте план эксперимента и дайте оценку.

• Оцените по критериям аргументированность выступления группы.

Критичность

–       произведите оценку,

–       спрогнозируйте,

–       дайте оценку,

–      разработайте и выберите критерии,

–       защитите точку зрения….

• Соответствует ли ваш способ решения задачи эталону.

• Разработайте критерии оценки и оцените проект.³

Приложение 2

Лист обратной связи

Ф. И. ученика(цы)________________________9___класса

Уровни учебных целей

Предметные результаты

Задания, упражнения

Самооценка

Оценка учителя

(+, — )

Комментарии

Знание

Знаю определение системы счисления, какая система счисления является позиционной и непозиционной; развернутую и свернутую форму записи числа.

Запишите определение:

1.Система счисления.

2.Непозиционная с. с.

3.Позиционная с. с.

Продолжи предложение:

1.Основание позиционной с. с. равно…..

2.Развернутая форма записи числа….

3.Свернутая форма записи числа..

За каждый правильный ответ по 1 баллу

Понимание

Знаю правило перевода целых десятичных чисел в систему счисления с основанием q; правило сложения и умножения в двоичной системе счисления.

1.Запиши правило перевода целых десятичных чисел в систему счисления с основанием q.

2.Запиши в таблице правило сложения и умножения в двоичной системе счисления.

3.Запиши в развернутом виде числа:

1. 145,512₁₀;

2. 132511₈;

3. 143511₁₆;

4. 1435,11₆.

За каждый правильный ответ по 1 баллу

Применение

Умею переводить целые числа из одной системы счисления в другую и выполнять операции сложения и умножения над двоичными числами.

1. Переведите целые числа из десятичной системы счисления в двоичную:

1. 49₁₀;

2. 21₁₀;

3. 85_10.

2. Переведите целые числа из десятичной системы счисления в восьмеричную и шестнадцатеричную:

1. 513;

2. 600;

3. 2010.

3. Запишите десятичные эквиваленты следующих чисел:

1. 172₈;

2. 2EA₁₆;

3. 10,1₂.

4. Выполните операцию сложения над двоичными числами:

1. 101010+1101;

2. 1010+1010;

3. 10101+111.

4. Выполните операцию умножения над двоичными числами:

1. 1010*11;

2. 111*101;

3. 1010*111.

За каждое правильно выполненное задание по 2 балла.

Анализ

Умею находить нужное решение; могу анализировать (выделять преимущества и недостатки систем счисления, делать вывод).

1. Сравните числа:

1. 29₁₀ и 11101₂;

2. 2С₁₆ и 42₈;

3. 100101₂ и 77₈.

2. Расставь знаки арифметических операций так, чтобы были верны следующие равенства в двоичной системе:

1. 1100?11?100=100000;

2. 1100?10?10=100;

3. 1100?11?100=0.

3.Какими преимуществами и недостатками обладает двоичная система счисления по сравнению с десятичной?

За каждое правильно выполненное задание по 3 балла.

Синтез

Могу систематизировать информацию по теме: «Системы счисления»

1.Разработайте таблицы сложения и умножения для восьмеричной системы счисления.

2.Постройте граф, отражающий разновидности систем счисления.

За каждое правильно выполненное задание по 3 балла.

Оценка

Умею оценивать решение выражения, находить ошибку.

Верно ли решено?

(1111101₂+AF₁₆):36₈

Решение:

(1111101₂+1111101₂):101₂=11011₂

Если решение верное, то в ответе запиши да, если нет, то реши его. Сколько способов решения выражения существует?

За правильно выполненное задание 3 балла.

Итого:

Отметка:

Критерии оценивания уровней достижений

Приложение 3

Оценочный лист Группа № 1

Таблица № 1 «Оценивание ментальной карты»

«0» — содержание карты не удовлетворяет данному критерию;

«1» — содержание карты частично удовлетворяет данному критерию;

«2» — содержание карты полностью удовлетворяет данному критерию.

Критерии оценивания

ментальной карты

Взаимооценка ментальной карты

1. Центральная картинка (идея, задача) верно выбрана больше остальных и располагается по центру.

2. Использовано более 3 разных цветов.

3. Точки-понятия расположены на разных иерархических уровнях соответствующих движению от наиболее общих к конкретным специальным понятиям.

4. Рассмотрен полный объём материала.

Итого баллов:

Отметка:

Критерии оценивания уровней достижений

Учитель

— согласен — нет

Таблица № 2 «Оценивание личного вклада в работу группы»

«0» — нет

«1» — иногда

«2» — да

ФИ участника(цы)

Умения

Итого баллов

Отметка

Руководство группой брал (а) на себя

Активно участвовал (а) в обсуждении работы

Сотрудничал(а) с другими

Высказывал(а) свою точку зрения

Завершил(а) свою часть работы вовремя

Представлял(а) работу у доски

1.

2.

3.

4.

5.

Критерии оценивания уровней достижений

Учитель

— согласен — нет

Приложение 9

Тезаурус

Оценивание (аssessment) – обычно относится к кому-либо персонально. Включает такие формы, как аттестация, экзамен, сертификация и т.д. В большинстве образовательных систем достижения учащихся фиксируются с помощью баллов, буквенного кода или словесных комментариев типа «хорошо», «удовлетворительно», «требует улучшения».

Оценка (evaluation) – включает определение значения, ценности либо веса каких-либо показателей в сравнении с искомыми или полученными в ситуации иных учебных программ, курсов, организационных схем.

Результаты (оutcomes) – могут быть как реальным «продуктом», так и собственно учебными результатами. Например, учебным продуктом, созданным учеником, стало рекламное объявление. При этом сформированное у него умение писать убедительно

является учебным результатом.

Итоговое оценивание (summative assessment) – проводится после завершения учебной программы. Обычно его осуществляет независимый эксперт, не имеющий отношения к данной учебной программе. Проводится для подведения итогов и принятия соответствующих решений.

Формирующее оценивание (formative assessment) – проводится в ходе совершенствования или коррекции определенной учебной программы (курса, цикла). Как правило, осуществляется тем, кто реализует данную программу. Но может проводиться внешним экспертом.

Техники оценивания (assessment technique) – помимо тестов существует широкое разнообразие оценочных техник, например, ориентированных на оценку по продукту, критериальную оценку, оценку специальных компетенций и т. д.

Учебные цели (learning objectives), или желаемые результаты обучения – то, чему ученик должен обучиться. Обычно определяются на трех уровнях. На первом – наиболее общим образом, например, «гражданская грамотность» или «экологическое сознание» и т.п. Такие широкие цели часто задаются при долговременном планировании. На втором уровне их необходимо трансформировать в более узкие цели или задачи конкретных учебных программ, рассчитанных на один год обучения. На третьем уровне они должны быть специфицированы и детализированы в цели отдельного предметного курса (модуля).

Лист обратной связи — это документ, который использует учитель для формирования качественной и количественной оценки промежуточных и итоговых результатов деятельности учащихся по освоению определенных результатов образования.

Ментальная карта – это особый способ систематизации знаний при помощи схем.

2 Фишман И. С., Голуб Г.Б. Формирующая оценка образовательных результатов учащихся: Методическое пособие. Самара: Издательство «Учебная литература», 2007 г.

3 http://so.orleupvl.kz/index.php/ru/ru/component/jcomments/feed/com_content/194

книга CRYPTO_А5.pdf

%PDF-1.4 % 1403 0 obj > endobj 1400 0 obj >stream application/pdf

книга CRYPTO_А5.pdf

2012-07-05T12:18:13+04:00Microsoft® Office Word 20072012-08-01T10:35:54+04:002012-08-01T10:35:54+04:00Acrobat Distiller 8.1.0 (Windows)uuid:1271dfa3-edea-49d5-8724-a8de4f20be2auuid:895ffd4c-a630-49d1-a22b-140d9005d0d5 endstream endobj 1355 0 obj > endobj 1353 0 obj > endobj 1354 0 obj > endobj 1356 0 obj > endobj 1367 0 obj > endobj 1378 0 obj > endobj 1389 0 obj > endobj 1390 0 obj > endobj 1391 0 obj > endobj 1392 0 obj > endobj 1393 0 obj > endobj 1394 0 obj > endobj 1395 0 obj > endobj 1396 0 obj > endobj 1397 0 obj > endobj 1398 0 obj > endobj 1399 0 obj > endobj 1207 0 obj >/ProcSet[/PDF/Text]/ExtGState>>>/Type/Page>> endobj 1210 0 obj >/ProcSet[/PDF/Text]/ExtGState>>>/Type/Page>> endobj 1213 0 obj >/ProcSet[/PDF/Text]/ExtGState>>>/Type/Page>> endobj 1216 0 obj >/ProcSet[/PDF/Text]/ExtGState>>>/Type/Page>> endobj 1219 0 obj >/ProcSet[/PDF/Text]/ExtGState>>>/Type/Page>> endobj 1222 0 obj >/ProcSet[/PDF/Text]/ExtGState>>>/Type/Page>> endobj 1225 0 obj >/ProcSet[/PDF/Text]/ExtGState>>>/Type/Page>> endobj 1228 0 obj >/ProcSet[/PDF/Text]/ExtGState>>>/Type/Page>> endobj 1231 0 obj >/ProcSet[/PDF/Text]/ExtGState>>>/Type/Page>> endobj 1234 0 obj >/ProcSet[/PDF/Text]/ExtGState>>>/Type/Page>> endobj 11354 0 obj >stream HWˎ WhE6H

Двоичная система счисления

: применение и преимущества — видео и расшифровка урока

Приложения

Наиболее распространенное применение двоичной системы счисления можно найти в компьютерных технологиях. Весь компьютерный язык и программирование основаны на 2-значной системе счисления, используемой в цифровом кодировании. Цифровое кодирование — это процесс получения данных и их представления дискретными битами информации. Эти дискретные биты состоят из нулей и единиц двоичной системы.16 представляет 65 536 различных цветов!

Мы также находим двоичную систему счисления в разделе математики, известном как булева алгебра. Эта область математики связана с логикой и значениями истинности. Здесь утверждениям, которые являются либо истинными, либо ложными, присваиваются 0 или 1.

Преимущества

Самым большим преимуществом двоичной системы счисления является ее простота. Любое устройство с выключателем может быть преобразовано в вычислительное устройство с использованием двоичной системы счисления, где 0 означает «выключено», а 1 — «включено».Поскольку переключатели, используемые в компьютерном языке, либо включены, либо выключены, их можно легко прочитать с минимальной вероятностью ошибки.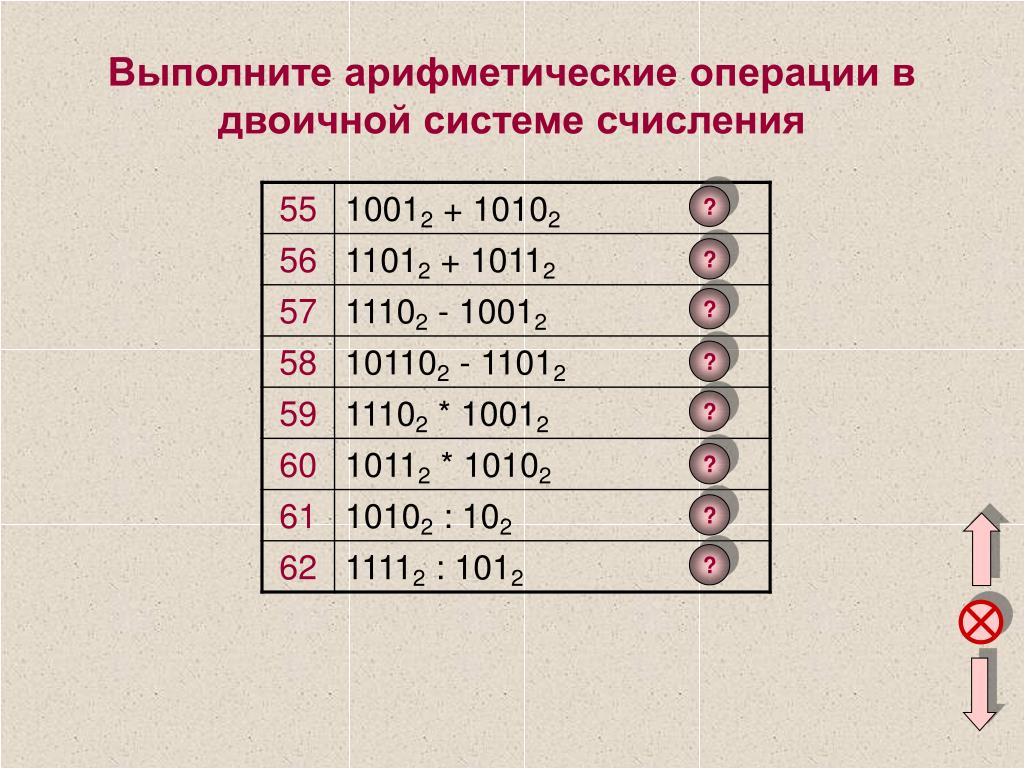

В вычислениях двоичная система счисления проще в использовании, чем десятеричная или десятичная система с меньшим количеством вычислений. Например, дополнительно используются только три вычисления:

1. 0 + 0 = 0
2. 0 + 1 = 1
3. 1+1 = 10

Умножение в двоичной системе счисления также включает использование трех вычислений:

1. 0 x 0 = 0
2. 0 х 1 = 0
3. 1 х 1 = 1

Напротив, десятичная система с основанием требует знания 100 вычислений.

Резюме урока

Хотя наиболее часто используемой системой счисления является с основанием десять , двоичная система счисления также важна. Это система счета только с двумя цифрами. Эти цифры обычно равны 0 и 1. Каждое разрядное значение является степенью числа 2.

Компьютерный язык использует двоичную систему счисления, где ноль представляет положение «выключено», а единица представляет положение «включено». Преимущества включают простоту использования в кодировании, меньше вычислений и меньше вычислительных ошибок. Двоичная система счисления также может использоваться в булевой алгебре .

Теперь, когда вы закончили этот урок, взгляните на наклейку на бампере:

‘Есть 10 типов людей, те, кто понимает двоичный код, и те, кто не понимает’.

«10» — двоичное число, которое на самом деле означает 2.

Система счисления

СОДЕРЖАНИЕ
 ВВЕДЕНИЕ,
 ТИПЫ СИСТЕМЫ СЧИСЛЕНИЯ,
 ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ,
 ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ,
 ВОСЬМЕРИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ,
 ШЕСТНАДЦАТЕРИЧНАЯ СИСТЕМА ЧИСЛЕНИЙ,
 МЕТОД ПРЕОБРАЗОВАНИЯ,

• ВВЕДЕНИЕ:
Набор значений, используемых для представления различных величин, известен как СИСТЕМА ЧИСЛОВ.
Например-
Число может использоваться для представления количества учеников в классе или количества зрителей, смотрящих определенную телепрограмму и т. д.

• ТИПЫ СИСТЕМЫ ЦИФРОВ:
Системы счисления бывают четырех типов,
1. ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ,
2. ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ,
3. ВОСЬМЕРИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ,
4. ШЕСТНАДЦАТЕРИЧНАЯ СИСТЕМА ЧИСЛЕНИЙ,

 ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ:
 В повседневной жизни мы используем десятичную систему счисления.
 Десятичная система счисления имеет основание 10, так как использует десять цифр от 0 до 9.
 ПРИМЕР-(234)10

 ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ:
 В двоичной системе счисления используются две цифры 0 и 1.
 Его основание равно 2.
 Комбинация двоичных чисел может использоваться для представления различных величин, таких как 1001.
 Пример –
(1001)2, г.
(100)2, г.

 ВОСЬМЕРИЧНАЯ СИСТЕМА ИСЧИСЛЕНИЯ:
 Восьмеричная система счисления состоит из восьми цифр от 0 до 7.
 Основание восьмеричной системы равно 8.
 Любая цифра в этой системе всегда меньше 8.
 Это быстрый способ представления длинного двоичного числа.
 Пример –
(34)8,
(235)8, г.

• ШЕСТНАДЦАТЕРИЧНАЯ СИСТЕМА ЧИСЛЕНИЙ:
 Шестнадцатеричная система счисления состоит из 16 цифр от 0 до 9 и от a до f.
 Его основание равно 16.
 Каждая цифра этой системы счисления представляет собой степень числа 8.
 Пример-
(6Д) 16,
(А3)16,

 МЕТОД ПРЕОБРАЗОВАНИЯ:
Существует два наиболее часто используемых метода преобразования числа по одной системе счисления в другую систему счисления.
 Остаточный метод,
 Метод расширения,

 ОСТАТОК МЕТОД:
Этот метод используется для преобразования десятичного числа в его эквивалентное значение в любой другой системе счисления.
Для этого метода необходимо выполнить следующие шаги:
 Разделите число на основание и запишите остаток.
 Разделите частное на основание и запишите остаток.
 Повторяйте шаг 2 до тех пор, пока частное нельзя будет разделить дальше. То есть частное становится меньше делителя.
 Последовательность остатка, начинающаяся с последнего сгенерированного 1 префикса в неделимом частном, является преобразованным числом.

 МЕТОД РАСШИРЕНИЯ:
 С помощью этого метода можно преобразовать любое число в любой системе счисления в его эквивалент в системе счисления 10.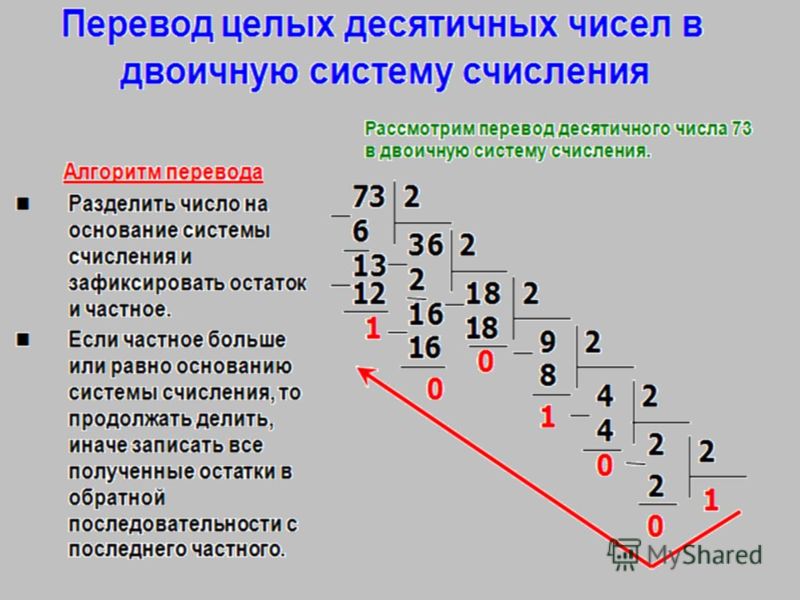
 При расширении основание числа последовательно увеличивается, начиная с 0, и увеличивается на единицу для каждой цифры, встречающейся в двоичном числе.

СПАСИБО!!!!!

Каковы преимущества и недостатки системы счисления? – Жадный.сеть

Каковы преимущества и недостатки системы счисления?

Основными преимуществами десятичной системы счисления являются простота чтения, использования людьми и простота манипулирования. Тем не менее, есть некоторые недостатки, такие как пустая трата места и времени.

Каковы были положительные стороны греческой системы счисления?

Преимущество ионической системы заключалось в том, что числа можно было представить с помощью всего нескольких символов. Например, каждое число от 1 до 9999 может быть представлено четырьмя или менее символами.Это сделало эту систему удобной для монет.

Для чего использовалась греческая система счисления?

Греки использовали две системы счисления, одну в основном для денег и повседневного счета и более сложную систему счисления, которую использовали ученые. Строго говоря, греческих систем счисления было много, так как на каждом острове была своя система счисления, однако все они были очень похожи.

В чем недостаток непозиционной системы счисления?

Непозиционная система счисления не может эффективно выполнять арифметические вычисления.

Как называется основание 8?

Восьмеричная система счисления, или сокращенно октальная, представляет собой систему счисления с основанием 8 и использует цифры от 0 до 7, то есть 10 представляет 8 в десятичной системе счисления, а 100 представляет 64 в десятичной системе счисления.

В чем преимущество системы счисления?

Преимущества включают простоту использования в кодировании, меньше вычислений и меньше вычислительных ошибок. Двоичная система счисления также может использоваться в булевой алгебре.

Какое греческое число соответствует 20?

20 – είκοσι (ikosi) 21 – είκοσι ένα (ikosi éna) 22 – είκοσι δύο (ikosi dío)

Что означает число 9 по-гречески?

← 8 9 10 →
Бенгальский	৯
Китайская цифра	九, 玖
Деванагари	९
Греческая цифра	θ´

Какой греческий символ означает 6?

греческие цифры

Византийский	Модерн	Значение
и &	Ϛʹ ΣΤʹ	6
ζ	Ζʹ	7
η	Ηʹ	8
θ	Θʹ	9

Какое двоичное число равно 13?

13 в двоичном формате равно 1101.

Что такое непозиционная система счисления?

• Непозиционная система счисления состоит из различных символов, которые используются для представления. числа. • Римская система счисления является примером непозиционной системы счисления. то есть I=1, V=5, X=10, L=50.

Где используется основание 8?

Octal стал широко использоваться в вычислениях, когда такие системы, как UNIVAC 1050, PDP-8, ICL 1900 и мэйнфреймы IBM, использовали 6-битные, 12-битные, 24-битные или 36-битные слова. Восьмеричный был идеальным сокращением от двоичного для этих машин, потому что размер их слова делится на три (каждая восьмеричная цифра представляет три двоичных цифры).

Как называется основание 9?

Как мы называем системы счисления?

Основания 1-10
1	унарный
8	восьмеричный
9	нонарный
10	десятичный

Для чего нужна система счисления в нашей повседневной жизни?

Существует множество различных систем нумерации, которые используются для уникальной способности представлять разные числа. Двоичная, восьмеричная, десятичная и шестнадцатеричная системы счисления, которые используются в различных аспектах. Двоичная система счисления является наиболее часто используемой системой счисления, которая часто используется в повседневной жизни.

Зачем нам нужно изучать системы счисления?

Ответ: Скорее, эти слова и буквы переводятся в числа. Изучая другие системы счисления, такие как двоичная (по основанию 2), четверичная (по основанию 4), восьмеричная (по основанию 8), шестнадцатеричная (по основанию 16) и т. д., мы лучше поймем, как работают системы счисления в целом.

Какое число три по-гречески?

Стол

Византийский	Модерн	Значение
α	А’	1
β	Βʹ	2
γ	Γʹ	3
дельта	Δʹ	4

Какое число пять по-гречески?

← 4 5 6 →
Греческая цифра	Ε´
Римская цифра	В, В
Греческий префикс	пента-/пента-
Латинский префикс	квинк-/квинк-/квинк-

Почему 9 священное число?

Число 9 почитается в индуизме и считается полным, совершенным и божественным числом, потому что оно представляет собой конец цикла в десятичной системе, которая возникла на Индийском субконтиненте еще в 3000 году до нашей эры. В христианской ангельской иерархии насчитывается 9 ликов ангелов.

Почему число 9 такое могущественное?

Число 9 — мощное число, сила которого основана на сильном стремлении к духовному просветлению. Это также самое сильное число с особыми свойствами, которые позволяют ему сохранять свою форму при умножении или уменьшении на другое число. Число 9 является символом полноты Бога, а также символом завершенности.

Какая цифра 1 по-гречески?

Каковы были преимущества и недостатки Греции?

Преимущество

: у них был доступ к торговле, транспорту, рыбе и воде.Они стали опытными моряками. Морские путешествия связали Грецию с другими обществами. Недостатки: Не так много плоской земли для возделывания, Трудно путешествовать по земле, Трудно объединиться под единым правительством, ограниченные природные ресурсы.

Для чего используется греческая система счисления?

Греческие цифры, также известные как ионические, ионийские, милетские или александрийские цифры, представляют собой систему записи чисел с использованием букв греческого алфавита. В современной Греции они до сих пор используются для обозначения порядковых числительных и в контексте, аналогичном тому, в котором римские цифры до сих пор используются в других местах на Западе.

Каковы недостатки жизни в Греции?

пробки на дорогах и загрязнение окружающей среды во многих городах; острая нехватка воды в некоторых регионах, особенно летом; дома может быть трудно продать; расходы на проезд в Грецию и обратно, если у вас есть там дом и вы не живете в соседней стране (или в стране с хорошим воздушным сообщением).

Хорошо ли поселиться в Греции?

Греция в целом очень безопасное место, и здесь очень мало серьезных преступлений.У них одна из самых низких цен на жизнь в Европейском союзе, хотя такие города, как Афины, как правило, дороже, чем остальная часть страны.

Какое число 20 по-гречески?

энеа

← 8 9 10 →
Делители	1, 3, 9
Греческая цифра	Θ´
Римская цифра	IX, IX
Греческий префикс	энеа-

Каковы плюсы и минусы греческой жизни?

Вот краткий обзор выгод и преимуществ жизни в братстве или женском обществе, включая некоторые из них, о которых вы, вероятно, никогда не задумывались, и один, который, как вы надеетесь, вам никогда не понадобится: Жилье: в зависимости от колледжа греческая жизнь может быть не только огромная часть общественной жизни кампуса, но также и основной источник жилья.

Каковы преимущества системы счисления?

Преимущество в том, что вы можете легко работать с довольно большими числами. В последних системах вам нужно продолжать изобретать символы для больших чисел, чтобы иметь возможность их писать. Вы же не хотите писать тысячу М каждый раз, когда пишете миллион.

Каковы преимущества и недостатки Афин?

Афиняне были сильнее, потому что у них была лучшая география, правительство, культурные достижения, и я предпочел бы жить в Афинах.У Афин было географическое преимущество, потому что они были очень превосходны. Афины жили у моря, что было преимуществом, поскольку у них была отличная торговая система.

Почему древние греки использовали символ нуля?

Нулевой символ не нужен. Непозиционная система счисления древних греков использует двадцать четыре буквы их алфавита для создания буквенно-цифровых и специальных символов (М = мириады) для больших чисел. Чтобы отличить число от слова, древние греки использовали ударение (ударение) в конце знака числа или черточку над ним.

Шестнадцатеричный — обзор | ScienceDirect Topics

10.4.4 Описание приложений DIZI

Ниже приведены еще восемь приложений, исходный код каждого из которых приведен в разделе Программы 10.4. Их можно загрузить с сайта www.picmicros.org.uk и протестировать в режиме моделирования в MPSIM или ISIS (если доступно). В случае аппаратной сборки ДИЗИ их можно запрограммировать в микросхему 16Ф84А с помощью внесхемного программатора.

Программы 10.4. 8 приложений ДИЗИ.

HEX1 Hex Converter

Отображается шестнадцатеричное число, соответствующее двоичной настройке входов DIP-переключателей. Входные переключатели выбирают из таблицы 16 семисегментных кодов, которые управляют дисплеем в требуемом порядке для каждой шестнадцатеричной цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, b, C, d и E. Обратите внимание, что числа B и D отображаются в нижнем регистре, чтобы их можно было отличить от 8 и 0 соответственно.

Отображение сообщений MESS1

Последовательность символов отображается около 0.5 с каждый. Большинство букв алфавита можно получить на семисегментном дисплее как в верхнем, так и в нижнем регистре, например, «HELLO». Количество символов должно быть установлено в счетчике или использован завершающий символ.

Счетчик секунд SEC1

Отображается вывод, который ведет обратный отсчет ровно один раз в секунду, от 0 до 9, а затем повторяется. Требуется таблица кодов отображения, как в приложении Hex Converter. Временная задержка в 1 с может быть достигнута с помощью аппаратного таймера (глава 6) и резервного регистра.На аудиовыходе можно было произвести тик, пульсируя динамиком на каждом шаге.

Таймер реакции REACT1

Время реакции пользователя проверяется путем создания случайной задержки от 1 до 10 с, подачи звукового сигнала и определения времени задержки перед нажатием кнопки ввода. Число, представляющее время между звуком и вводом, кратное 100 мс, должно отображаться как число 0–9, что дает максимальное время реакции 900 мс.

Генератор звуковой частоты GEN1

Генератор звуковых частот выдает частоты в диапазоне от 20 Гц до 20 кГц.Выход сирены переключается с задержкой между каждой операцией, определяемой требуемой частотой, как в программе BUZZ1. Например, для частоты 1 кГц требуется задержка 1 мс, что составляет 1000 командных циклов при времени цикла 1 мкс. Информацию о синхронизации программы следует изучить в главе 6. Время задержки и, следовательно, частоту можно увеличить с помощью кнопки ввода, а также можно включить выбор диапазона с помощью переключателей ввода, поскольку при использовании доступно только 255 шагов. 8-битный регистр в качестве счетчика периода.

Метроном MET1

Звуковой импульс выводится с частотой, заданной DIP-переключателями или кнопками ввода. Выходной тик можно регулировать, скажем, от 1 до 4 ударов в секунду, используя кнопку прерывания для увеличения и уменьшения скорости и кнопку ввода для выбора увеличения или уменьшения. Для обеспечения необходимых временных задержек можно использовать программный цикл или регистр TMR0.

BELL1 Дверной звонок

Мелодия воспроизводится при нажатии кнопки ввода с использованием справочной таблицы программы для частоты и продолжительности тона.Каждый тон должен воспроизводиться в течение подходящего времени или количества циклов, как того требует мелодия. Программу можно уточнить, выбрав мелодию с помощью DIP-переключателей и отобразив номер выбранной мелодии.

Гитарный тюнер GIT1

Программа позволяет пользователю последовательно выбирать частоты для настройки струн гитары или другого музыкального инструмента с помощью кнопки ввода или выбора тона с помощью DIP-переключателей. Программа может быть расширена за счет отображения номера струны, которую необходимо настроить.Частоты тонов будут генерироваться как для приложения дверного звонка. Коды отображения цифр также потребуются в таблице.

Вопросы 10

1.

Укажите одно преимущество и один недостаток: (a) макетной платы; б) картон; (c) моделирование для тестирования прототипов. (6)

2.

Укажите выходной двоичный код для: (a) выключения всех сегментов и (b) отображения цифры «2» на семисегментном светодиодном индикаторе с общим катодом, при условии подключения, показанного на рисунке 10. .15.  (4)

3.

Опишите алгоритм формирования выходного сигнала с фиксированной частотой приблизительно 1 кГц с платы DIZI с использованием аппаратного таймера. (5)

4.

Нарисуйте блок-схему, представляющую процесс создания «случайной» задержки между нажатием кнопки и включением выходного светодиода. (5)

Ответы на стр. 423. (Всего 20 баллов)

Действия 10

1.

Соберите схему DIZI на макете, плате или печатной плате и протестируйте программы BUZZ1, DICE1 и SCALE1.

2.

Подтвердите расчетом или моделированием, что значения, используемые в таблице данных программы в SCALE1.ASM, дадут требуемые задержки.

3.

Разработайте макет схемы BIN на рис. 3.3. Соберите схему и протестируйте программы BINx.

4.

Разработайте и внедрите одну из программ, описанных для оборудования DIZI, и сравните свое решение с модельными программами, предоставленными для HEX1, MESS1, SEC1, REACT1, GEN1, MET1, BELL1 или GIT1.

5.

(a)

Узнайте, как можно обнаружить ввод с цифровой клавиатуры. См. главу 1, раздел 1.4.1. Типичная клавиатура, показанная на рис. 10.17, имеет 12 клавиш в четыре ряда по три: 1, 2, 3; 4, 5, 6; 7, 8, 9; ^∗ , 0, #. Они подключены к семи клеммам и могут сканироваться по строкам и столбцам. Нажатие клавиши определяется как соединение между строкой и столбцом. Подтягивающие резисторы гарантируют, что все линии по умолчанию имеют логическую «1».Если «0» подается на один из выводов столбца (C1, C2, C3) и нажимается клавиша, этот «0» может быть обнаружен на выводе строки (R1, R2, R3, R4). Если клеммы клавиатуры подключены к порту PIC, а «0» выводится попеременно на три столбца, клавиша может быть обнаружена как комбинация выбранного столбца и обнаруженной строки. Клеммы столбцов могут быть установлены как выходы, а строки как входы. Нарисуйте блок-схему, чтобы представить процесс преобразования каждого десятичного ключа в соответствующее число BCD.

Рисунок 10.17. Соединения клавиатуры

(b)

Функция блокировки может быть реализована путем сопоставления входной последовательности с сохраненной последовательностью, скажем, из четырех цифр и включения выхода на дверной соленоид, если обнаружено совпадение. Укажите аппаратное обеспечение и наметьте программу для приложения блокировки.

(c)

Спроектируйте, изготовьте и протестируйте систему электронного замка, используя показанную клавиатуру, подходящую PIC и светодиод для индикации состояния замка (ВКЛ = разблокирован).Исследуйте дизайн интерфейса дверного замка с электромагнитным управлением.

Примечание: Сканирование клавиатуры используется в программе 13.1, а приложение для блокировки описано в Приложении D.

Полинезийцы использовали двоичные числа 600 лет назад

Обычно считается, что двоичная арифметика, основа всех практически цифровых вычислений, была изобретена в начале восемнадцатого века немецким математиком Готфридом Лейбницем. Но новое исследование показывает, что своего рода бинарная система уже использовалась 300 лет назад среди жителей крошечного тихоокеанского острова Мангарева во Французской Полинезии.

Открытие, сделанное путем анализа исторических записей о теперь почти полностью ассимилированной мангареванской культуре и языке, о котором сообщается в Proceedings of the National Academy of Sciences , предполагает, что некоторые из преимуществ бинарной системы, приведенной Лейбницем, могут создать когнитивную мотивацию для эта система возникла спонтанно даже в обществе без передовой науки и техники.

Чистая двоичная арифметика работает с основанием 2, а не с обычным основанием 10, которое многие культуры приняли, возможно, как следствие счета на десяти пальцах. С основанием 2 числа нумеруются как степени двойки: вместо единиц, десятков, сотен (10 ² ) и тысяч (10 ³ ) цифры двоичного числа относятся к 1 (2 ⁰ ), 2 (2 ¹ ), 4 (2 ² ), 8 (2 ³ ) и так далее.

Каждое число может быть представлено таким образом, используя только 1 и 0, поэтому они могут быть закодированы в компьютерах в виде системы включения-выключения электрических импульсов или переключателей. Например, число 13 в двоичном формате равно 1101 (2 ³ + 2 ² + (0 × 2) + 1).

Лейбниц указал в 1703 году, что для выполнения простых арифметических операций с двоичными числами, таких как сложение и умножение, вам не нужно запоминать такие правила, как 5 + 4 = 9 или 6 × 7 = 42. Вместо этого вам нужно всего лишь применить несколько правил. простые правила. Для сложения, скажем, вы просто добавляете 1 и 0, помня, что 1 + 1 = 1 в следующей позиции; например, 100 + 101 = 1001.

Смесительные системы
Недостатком двоичного представления является то, что для больших чисел требуется много цифр. Но, по словам психологов Андреа Бендер и Зигхарда Беллера из Университета Бергена в Норвегии, авторов последнего исследования, мангареванцы нашли гениальный ответ на этот вопрос, которым они, по-видимому, пользовались еще до 1450 года нашей эры.

Мангарева — вулканический остров, первые поселенцы которого прибыли на него примерно в 500–800 годах нашей эры. Вероятно, до того, как в восемнадцатом веке началось существенное взаимодействие с европейцами, его население составляло несколько тысяч человек. Его сильно стратифицированное общество выживало в основном за счет морепродуктов и корнеплодов и нуждалось в системе счисления для количественной оценки крупных торговых операций и дани вождям.

В настоящее время на острове осталось всего около 600 человек, говорящих на мангареванском языке, и в любом случае его местная система счисления давно вытеснена арабскими цифрами из-за влияния французского колониализма.Но Бендер и Беллер реконструировали его по описаниям, написанным (в основном европейскими) авторами в девятнадцатом и начале двадцатого веков.

Они обнаруживают, что бывшие мангаревцы объединили представление с основанием 10 с двоичной системой. У них были числовые слова от 1 до 10, а затем и 10, умноженные на несколько степеней двойки. Слово takau (которое Бендер и Беллер обозначают как K) означает 10; paua (P) означает 20; татауа (Т) 40; и вару (V) означает 80.В этом обозначении, например, 70 — это ТПК, а 57 — это ТК7.

Бендер и Беллер показывают, что эта система сохраняет ключевые арифметические упрощения истинной двоичной системы в том смысле, что вам не нужно запоминать множество числовых фактов, а нужно следовать лишь нескольким простым правилам, таким как 2 × K = P и 2 × P = T.

Хотя у этой системы есть свои недостатки, «преимущества перевешивают недостатки», — рассказали авторы Nature .

Культурные факторы
Когнитивист Рафаэль Нуньес из Калифорнийского университета в Сан-Диего отмечает, что идея бинарных систем на самом деле старше мангареванской культуры. «Это можно проследить, по крайней мере, до древнего Китая, примерно в 9 веке до нашей эры», — говорит он, и его можно найти в I Ching , тысячелетнем китайском тексте, который вдохновил Лейбница. Нуньес добавляет, что «другие древние группы, такие как майя, использовали сложные комбинации двоичной и десятичной систем для отслеживания времени и астрономических явлений. Таким образом, когнитивные преимущества, лежащие в основе системы счета Мангареван, могут быть не уникальными».

Тем не менее, говорят Бендер и Беллер, подобную «смешанную» систему создать непросто, равно как и создать очевидную установку.«Удивительно, что кто-то придумал такое решение, особенно на крошечном острове с небольшим населением», — говорят Бендер и Беллер. Но они добавляют: «Сам этот факт также демонстрирует, насколько важна культура для развития числового познания — например, как в этом случае работа с большими числами может мотивировать изобретательские решения».

Нуньес соглашается; он добавляет, что исследование показывает «приоритет культурных факторов, лежащих в основе изобретения систем счисления, и разнообразие человеческого числового познания».

Эта статья воспроизведена с разрешения журнала Nature. Статья впервые опубликована 16 декабря 2013 г.

Математика для программистов: переход от десятичной системы к двоичной | Кристофер Тао

Почему компьютеры используют двоичную систему счисления?

Хорошо известно, что двоичные числа лежат в основе классического компьютерного мира, созданного Джоном фон Нейманом. Да, когда я говорю «классический компьютер», это устройство, которое вы используете в данный момент, если только вы не работаете исследователем в области квантовых вычислений.

Каковы соображения между двумя различными системами счисления? И почему используется двоичный, а не десятичный? Это не сложно, но важно, как базовые знания информатики. В этой статье я поделюсь некоторыми соображениями о десятичной и двоичной системах счисления.

Фото geralt на Pixabay

Я до сих пор помню, как в детстве учительница начала учить нас некоторым числам больше 10. Когда она упомянула 11, я написала на листе «101» и подумала, что так будет правильно. В отличие от «десять» и «один», которые отличаются от «одиннадцати» в английском языке, в моем родном языке произношение 10 с последующим произношением 1 точно соответствует тому, как сказать 11.

После этого урока я понял, что цифра в определенном месте имеет строго свое значение 🙂 Однако, если мы используем римские числа, написание десяти «X» с последующим одним «I» равно 11 -> «XI».

Конечно, место цифр играет важную роль в арабских числах. В десятичной системе счисления у нас есть 10 различных чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.

Рассмотрим число 3105, показанное выше, его можно записать в форму следующим образом.

Вы, должно быть, уже нашли закономерности:

• Основание всех показателей равно 10 , потому что число представляет собой десятичное число .
• Показатель степени справа налево равен 0, 1, 2, 3, потому что в этом десятичном числе 4 цифры. Это единицы места, десятки места, сотни места и тысячи места.

Таким образом, мы можем использовать показатели степени 10 для перезаписи каждого десятичного числа, и они должны следовать шаблонам, показанным выше.

Тогда как насчет двоичной системы счисления?

Фото GDJ на Pixabay

Вы еще помните, что у нас есть 10 различных цифр в десятичной системе счисления? В двоичной системе счисления у нас есть только два числа: 0 и 1.

Точно так же мы можем переписать двоичное число, используя ту же технику, следуя аналогичному образцу, но не точно.

• Основание всех показателей равно 2 , потому что число двоичное .
• Показатель степени справа налево равен 0, 1, 2, 3, потому что в этом десятичном числе 4 цифры. Это единицы на месте, двойки на месте, четверки на месте и восьмерки на месте.

Различия в двоичном числе показаны выше жирным шрифтом.

Зная это, мы можем преобразовать двоичное число в десятичное, используя найденный шаблон. Например, мы хотим преобразовать 3105 из десятичного числа в двоичное. Сначала мы можем подготовить список показателей числа 2 следующим образом.

Затем мы можем выбрать максимальное число, которое меньше ближайшего к числу, которое мы хотим преобразовать. 4096 больше, чем 3105, поэтому мы должны выбрать 2¹¹, что равно 2048.

Затем мы используем 3105 минус 2048, и у нас остается 1057. После этого 2¹⁰, что равно 1024, является следующим ближайшим выбранным, поэтому у нас есть 1057 минус 1024 равно 33. Ближайший к 33 показатель степени равен 2⁵, что равно 32, и тогда у нас остается только 1, что равно 2⁰.

Итак, мы выбрали 2¹¹, 2¹⁰, 2⁵ и 2⁰. Напомним, что показатели степени 11, 10, 5 и 0 означают места, поэтому нам просто нужно поставить 1 справа на этих местах и ​​0 на других местах.

Двоичное число 3105 — 110000100001.

Существует простой способ, если вы не хотите готовить список показателей степени или число слишком велико. Приведенный ниже метод может определять 1 цифру каждый раз, когда вы делите число на 2.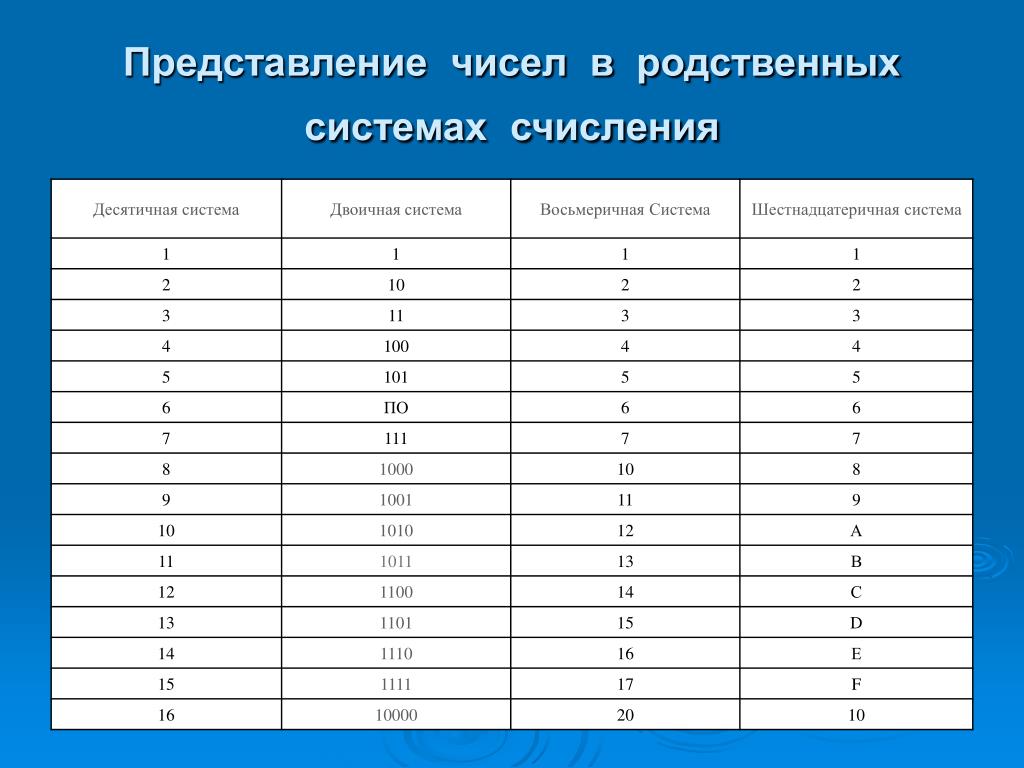

Каждый раз, когда мы делим число на 2, напоминание должно быть либо 0, либо 1.Обратной стороной напоминаний будет двоичное число, преобразованное из десятичного числа.

Фото blickpixel на Pixabay

Чтобы понять, почему в компьютерных системах используется двоичная система счисления, а не десятичная, нужно исходить из количества нужных нам типов цифр.

Как упоминалось выше, в десятичной системе счисления для представления числа требуется 10 различных цифр. Другими словами, для каждого места есть 10 различных возможностей. Однако в двоичной системе счисления нам достаточно 2.

Предположим, у вас есть переключатель, очень просто иметь два разных состояния: Вкл и Выкл. Да, именно так мы выражаем 1 и 0 в компьютерном мире. Можно ли сконструировать такой переключатель, который может иметь 10 различных состояний? Ну я не электронщик. Я бы сказал, что это возможно, но сложность будет намного выше.

Давайте в качестве примера возьмем операцию сложения, потому что она лежит в основе других операций, таких как умножение. В двоичной системе таблица сложения выглядит следующим образом.

Однако, если вы настаиваете на использовании десятичной системы счисления, мы должны позволить процессору понять таблицу сложения следующим образом.

Есть ли недостатки у двоичной системы счисления? Конечно, подумайте о числе 3105, которое мы только что преобразовали в двоичное число, то есть 110000100001. Предположим, вы и я, все мы можем читать двоичные числа, нам нужно написать 12 цифр, чтобы выразить такое число. Когда вы хотите назвать мне число три тысячи сто пять, вы должны сказать один один ноль ноль ноль ноль один ноль ноль ноль ноль один.Я не думаю, что смогу понять…

Следовательно, недостаток двоичного числа в том, что оно должно использовать слишком много цифр, чтобы выразить не такое большое число.

Однако этот недостаток не для компьютера. Независимо от того, сколько цифр у нас есть, они просто будут храниться в кеше процессора. Таким образом, компьютерам все равно, сколько цифр. Наоборот, они плохо справляются со слишком большим количеством правил, таких как приведенные выше таблицы сложения. Поэтому двоичная система становится идеальным вариантом для компьютеров.

Фото Skitterphoto на Pixabay

В этой статье я объяснил различные системы счисления в моем понимании, десятичную и двоичную. Наши люди используют десятичную дробь, потому что в ней больше типов цифр, но нам не нужно использовать слишком много цифр, чтобы выразить число. Кроме того, у всех нас есть 10 пальцев, которые интуитивно используются для счета. Другими словами, у десятичного числа почти идеальный баланс между количеством цифр и количеством типов цифр. Компьютеры используют двоичную систему, потому что им не нужен такой баланс.Вместо этого им нужно как можно меньше правил, и их не волнует количество цифр. Таким образом, двоичный файл находится на грани «меньшего количества правил» и становится идеальным выбором для компьютеров.

Если вы считаете, что мои статьи полезны, рассмотрите возможность присоединения к Medium Membership, чтобы поддержать меня и тысячи других писателей! (Нажмите на ссылку выше)

Восьмеричная система счисления | Electrical4U

В первые дни восьмеричная система счисления в основном использовалась в миникомпьютерах. Слово «ОКТ» означает восемь. Восьмеричная система счисления говорит, что это система счисления с основанием 8, что означает, что нам требуется 8 различных символов для представления любого числа в восьмеричной системе. Используются символы 0, 1, 2, 3, 4, 5, 6 и 7. Наименьшим двузначным числом в этой системе является (10) ₈ , что эквивалентно десятичному числу 8.
Например, в этой системе счисления номер записывается как (352) ₈ . Основание должно быть записано как 8, иначе предполагается, что число по умолчанию находится в десятичной системе счисления.Так что об этом нужно позаботиться при написании номера. Небольшая ошибка может привести к изменению основания системы счисления. Основное преимущество использования восьмеричной системы счисления заключается в том, что ее можно очень легко преобразовать непосредственно в двоичную. Как известно, компьютер понимает только двоичную систему счисления, поэтому преобразование из двоичной в восьмеричную или из восьмеричной в двоичную значительно проще, поэтому используется именно эта система счисления.

Поскольку его основание равно 8 = 2 ³ , каждый символ этой системы может быть представлен его трехбитным двоичным эквивалентом.

Поскольку каждая цифра числа в восьмеричной системе представлена ​​отдельно своим трехбитным двоичным эквивалентом, восьмеричная система требует одну треть длины по сравнению с двоичными числами. По сути, это позиционно-взвешенная система счисления. Позиции цифр в восьмеричной системе счисления имеют вес как

Преобразование чисел

Преобразование восьмеричного числа в двоичное

Преобразование выполняется путем преобразования отдельной восьмеричной цифры в двоичную. Каждая цифра должна быть преобразована в 3-битное двоичное число, и результирующее число будет двоичным эквивалентом восьмеричного числа.

Пример
Преобразование (145.56) ₈ в двоичное число

Эту таблицу следует использовать для преобразования любого восьмеричного числа в двоичное. Из таблицы, записывая двоичный эквивалент каждой из цифр, мы получаем —

, что является двоичным эквивалентом восьмеричного числа.

Преобразование двоичного числа в восьмеричное

Та же таблица может использоваться для преобразования двоичного числа в восьмеричное. Сначала сгруппируйте двоичное число в группу из трех бит и запишите его восьмеричный эквивалент.

Пример
Восьмеричный эквивалент (11001111) ₂ равно
Группы, которые мы получили здесь, —
011,001,111. Перед числом добавляется ноль, чтобы завершить группировку в виде трех двоичных цифр.

Теперь восьмеричный эквивалент чисел —
3, 1, 7. Таким образом, мы получили восьмеричное число (317) ₈ .

Преобразование восьмеричного числа в десятичное

Метод преобразования восьмеричного числа в его десятичный эквивалент очень прост. Просто расширьте число по основанию восьми с его позиционным весом, и в результате получится десятичное число.

Пример
Преобразование (317) ₈ в десятичный эквивалент.
Это можно сделать следующим образом:

Преобразование десятичного числа в восьмеричное

Это можно сделать, разделив число на 8 с помощью метода повторного деления, известного как метод двойного мазка. Производится повторное деление и берется остаток. Это можно сделать следующим образом:

Пример
Найдите восьмеричный эквивалент 158.

Эквивалент числа в восьмеричной системе: (236) ₈ .
Если есть число в виде дроби или после запятой, это может быть преобразовано как-
Скажем, мы должны преобразовать 0,40 в восьмеричное число.

Итак, мы видим, что число повторяется. Это будет продолжаться, и это будет бесконечный процесс, поэтому мы можем приблизить результат к
(.3146…) ₈ .

Преимущества восьмеричной системы счисления

1. Длина составляет одну треть от двоичной.
2. Простой процесс преобразования из двоичного в восьмеричный и наоборот.
3. Легче обрабатывать ввод и вывод в восьмеричной форме.

Недостатки восьмеричной системы счисления

Компьютер не понимает восьмеричную систему счисления , поэтому должно быть требование дополнительных схем, известных как восьмеричные преобразователи в двоичные, прежде чем они будут применены к цифровой системе или компьютеру.