Геометрическая оптика в физике: основные формулы
Оптика — раздел физики, в котором изучается излучение света, его распространение и взаимодействие с веществом.
Различают геометрическую, волновую и квантовую оптику. В геометрической оптике не учитывается природа света, а его распространение в пространстве рассматривается, исходя из представлений о световых лучах. Световой луч — это линия, вдоль которой распространяется световая энергия.
формулы геометрической оптикиЗакон отражения
Здесь — угол падения (рад), — угол отражения (рад).
Закон преломления
Здесь — угол падения (рад), — угол преломления (рад), — показатель преломления второй среды относительно первой (безразмерный), — скорость света в первой среде (м/с), — скорость света во второй среде (м/с).
Физический смысл абсолютного показателя преломления
Здесь n — абсолютный показатель преломления (безразмерный), с — скорость света в вакууме (м/с), и — скорость света в прозрачной среде (м/с).
Физический смысл относительного показателя преломления
Здесь — показатель преломления второй среды относительно первой, — скорость света в первой среде (м/с), — скорость света во второй среде.
Связь относительного показателя преломления двух сред с их абсолютными показателями преломления
Здесь — относительный показатель преломления сред (безразмерный), — абсолютный показатель преломления первой среды, — абсолютный показатель преломления второй среды.
Формула предельного угла полного отражения
Здесь — предельный угол полного отражения (рад), — абсолютный показатель преломления первой среды (безразмерный), — абсолютный показатель преломления второй среды (безразмерный).
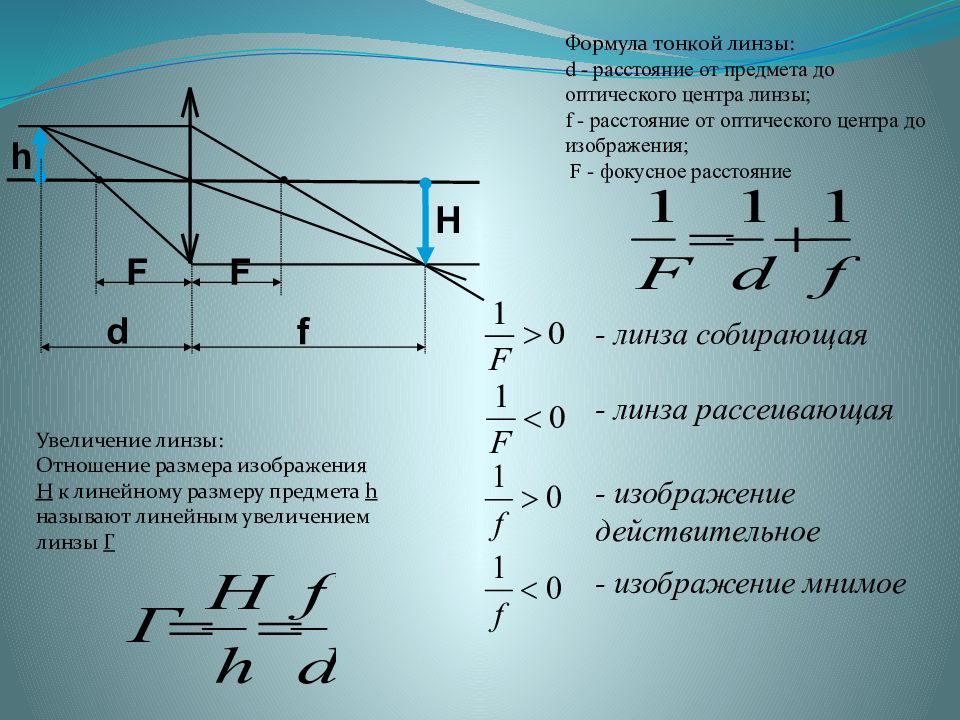
Формула линзы
Здесь d — расстояние от предмета до линзы (м), f — расстояние от линзы до изображения (м), F — фокусное расстояние линзы (м), D — оптическая сила линзы (дптр). образуются тень и полутени (рис. 324, б).
образуются тень и полутени (рис. 324, б).
Точечным источником света называют абстрактный источник, представляющий собой светящуюся материальную точку. Если точечный источник света удален в бесконечность, то его лучи падают на освещаемый предмет параллельным пучком.
Световой луч не может быть бесконечно тонким. При прохождении сквозь отверстие, в котором умещается несколько длин волн, он расширяется вследствие дифракции и загибает в область геометрической тени.
При падении световых лучей на непрозрачную гладкую преграду они меняют направление, возвращаясь в прежнюю среду. Это явление называется отражением света. Угол между падающим лучом и перпендикуляром к отражающей свет поверхности называется углом падения а. Угол между отраженным лучом и перпендикуляром к отражающей поверхности называется углом отражения (рис. 325).
Законы отражения
Законы отражения:
- луч падающий и луч отраженный всегда лежат в одной плоскости с перпендикуляром, проведенным в точку падения к отражающей поверхности, по разные стороны от него;
- угол отражения всегда равен углу падения, .

Если луч падает перпендикулярно отражающей поверхности, то угол падения равен нулю, поэтому и угол отражения тоже равен нулю. В этом случае луч отражается в обратном направлении — сам по себе.
На законе отражения основано получение изображения в плоском зеркале.
Плоское зеркало mn дает мнимое и прямое изображение равное по размеру предмету АВ и расположенное от зеркала на таком же расстоянии, что и предмет (рис. 326). Исключение составляет случай, когда на плоское зеркало падает пучок сходящихся лучей (рис. 327) — в этом случае изображение S получится действительным.
Если поверхности двух плоских зеркал образуют угол (рис. 328), количество изображений N в такой системе зеркал можно определить по формуле
При переходе света из одной прозрачной среды в другую меняется направление светового луча. Это явление называется преломлением света. Угол между преломленным лучом и перпендикуляром к преломляющей поверхности называется углом преломления (рис. 329).
329).
Законы преломления:
- луч падающий и луч преломленный всегда лежат в одной плоскости с перпендикуляром, опущенным в точку падения луча к преломляющей поверхности, по разные стороны от перпендикуляра;
- отношение синуса угла падения
к синусу угла преломления есть величина постоянная для данных двух сред и называется показателем преломления второй среды относительно первой :
При этом первой средой является та среда, в которой распространяется падающий луч, а второй средой — та, в которой распространяется преломленный луч. Например, если свет переходит из воды в стекло, то — это показатель преломления стекла относительно воды, а если наоборот, из стекла в воду, то — показатель преломления воды относительно стекла.
Если луч переходит из вакуума (воздуха) в прозрачную среду, то показатель преломления этой среды относительно вакуума называется абсолютным показателем преломления этой среды п.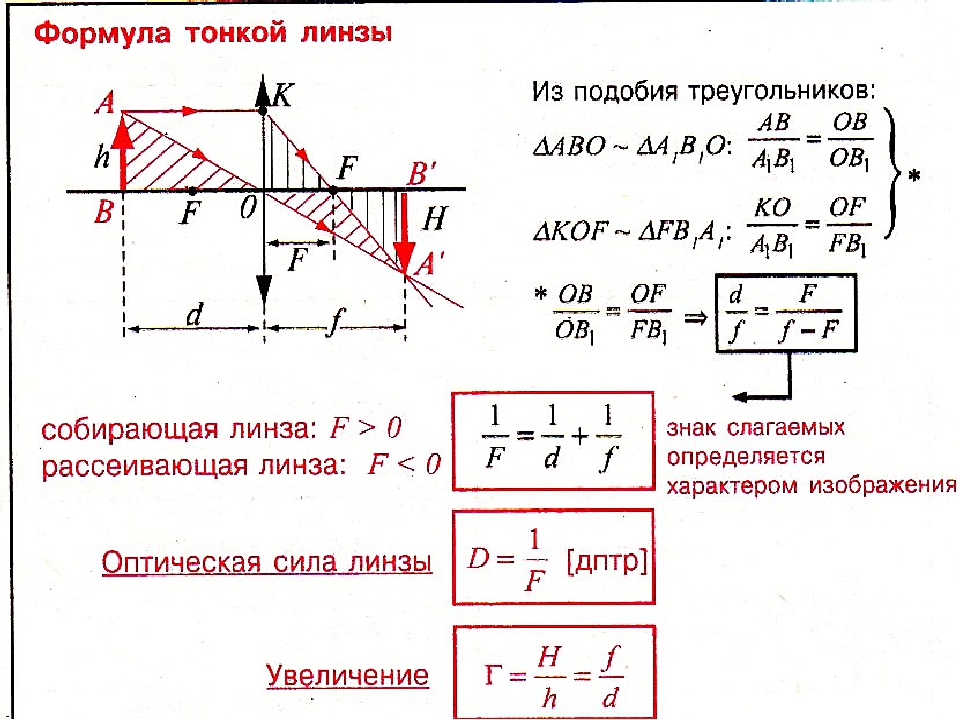 Значение абсолютного показателя преломления каждой среды приводится в справочных данных.
Значение абсолютного показателя преломления каждой среды приводится в справочных данных.
Абсолютный показатель преломления среды показывает, во сколько раз скорость света в вакууме больше, чем в данной среде:
Относительный показатель преломления равен отношению абсолютного показателя преломления второй среды к относительному показателю преломления первой среды:
Физический смысл относительного показателя преломления: относительный показатель преломления показывает, во сколько раз отличается скорость света в первой среде от скорости света во второй среде: .
Та среда, у которой абсолютный показатель преломления больше, называется оптически более плотной. Если свет переходит из оптически более плотной среды в оптически менее плотную, например, из воздуха в воду, то угол падения больше угла преломления. И наоборот, если луч переходит из оптически более плотной среды в оптически менее плотную, например, из воды в воздух, то угол падения меньше угла преломления (рис. 330).
330).
В случае перехода луча из оптически более плотной среды в оптически менее плотную существует такой угол падения , при котором преломленный луч скользит по границе раздела сред с разной оптической плотностью. При этом угол преломления равен 90°. Такой угол падения называется предельным углом полного отражения (рис. 331).
Если луч упадет на поверхность под углом больше предельного, то он полностью отразится обратно в первую среду (рис. 332). Такое явление называется полным отражением.
Проходя сквозь
плоскопараллельную пластинку из вещества, оптически более плотного, чем окружающая среда, луч не меняет своего направления, а лишь смещается на расстояние х (рис. 333). Смещение луча х тем больше, чем толще пластинка и чем больше показатель преломления ее вещества.
Проходя сквозь треугольную призму, изготовленную из оптически более плотного, чем окружающая среда, вещества, луч дважды преломляется, отклоняясь к ее основанию (рис.
призмы лучей называется углом отклонения луча. Угол отклонения зависит от угла падения луча на призму , преломляющего угла призмы и показателя преломления n вещества, из которого она изготовлена.
Линзой называют прозрачное для света тело, ограниченное сферическими или иными криволинейными поверхностями, одна из которых может быть плоской. Если линза в средней части толще, чем у краев, то она называется выпуклой, а если наоборот, — то вогнутой.
Двояковыпуклая линза называется собирающей, т.к. она собирает после преломления параллельные лучи в одной точке (рис. 335, а).
Вершины сферических сегментов , образующих линзу, называются ее полюсами. Точка, в которой сливаются полюсы бесконечно тонкой линзы, называется ее главным оптическим центром О.
Прямая mn, проходящая через центры сфер , поверхности которых образуют линзу, называется главной оптической осью линзы. Точка, в которой пересекаются лучи, падающие на линзу параллельно ее главной оптической оси, называется фокусом линзы F. Фокус линзы F делит расстояние между центром сферы и главным оптическим центром линзы пополам, поэтому центр называют двойным фокусом линзы 2F.
Расстояние OF от фокуса линзы до ее главного оптического центра называется фокусным расстоянием линзы и тоже обозначается буквой F. Собирающая линза имеет два действительных фокуса F и два двойных фокуса 2F, расположенных по обе стороны линзы. На рис. 335,6) показано условное изображение собирающей линзы.
Любой луч, проходящий через главный оптический центр линзы О, не преломляется. Такой луч называется побочной осью линзы.
Плоскость cd, проходящая через фокус линзы перпендикулярно ее главной оптической оси, называется фокальной плоскостью линзы.
Главное свойство фокальной плоскости собирающей линзы: она является геометрическим местом точек, в которых пересекаются параллельные лучи, падающие на собирающую линзу под разными углами (рис. 336).
336).
Чтобы узнать, как пойдет после преломления произвольный луч, упавший на собирающую линзу, надо провести через главный оптический центр линзы побочную ось, параллельную произвольному лучу и построить с другой стороны линзы главную фокальную плоскость cd. Побочная ось не преломится в линзе и пересечет главную фокальную плоскость cd в некоторой точке К. А поскольку побочная ось параллельна произвольному лучу, то он после преломления тоже пойдет через точку К (рис. 337).
Если на линзу падает пучок параллельных лучей, значит, их источник расположен в бесконечности, т.е. расстояние от источника до линзы . Если такие лучи параллельны главной оптической оси, то после преломления они пересекутся в фокусе линзы F — там появится действительное изображение источника S, удаленного в бесконечность (рис. 338, а). Световые лучи обратимы. Это значит, что если в фокус собирающей линзы поместить точечный источник света S, то после преломления в линзе его лучи пойдут параллельно главной оптической оси линзы и изображение источника уйдет в бесконечность, т.
Как правило, если в условии задачи не сказано, о какой линзе идет речь, значит, это собирающая линза. Если у вас имеется хотя бы часть линзы, изображение в ней строится так же, как если бы это была целая линза.
Двояковогнутая линза рассеивает пучки параллельных лучей, падающих на нее, поэтому она называется рассеивающей линзой. Если пучок лучей падает на рассеивающую линзу параллельно ее главной оптической оси, то после преломления в линзе их мнимые продолжения пересекаются в одной точке,
которая является мнимым фокусом F рассеивающей линзы (рис. 339, а). Рассеивающая линза имеет два мнимых фокуса F, расположенных на главной оптической оси по обе стороны от нее на середине отрезка 0,0. На рис. 339, б) показано условное изображение рассеивающей линзы.
Плоскость cd, перпендикулярная главной оптической оси и проходящая через фокус рассеивающей линзы, называется главной фокальной плоскостью этой линзы.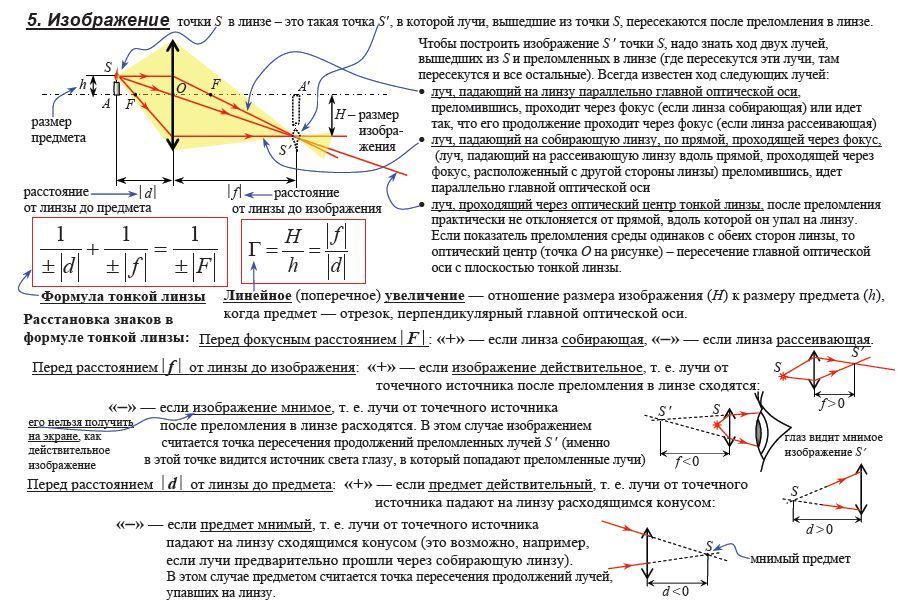
Главное свойство фокальной плоскости рассеивающей линзы: она является геометрическим местом точек, в которых пересекаются мнимые продолжения любых параллельных лучей, падающих на линзу под разными углами (рис. 340).
Чтобы узнать, как пойдет упавший на рассеивающую линзу произвольный луч после преломления, надо провести параллельную ему побочную ось и построить главную фокальную плоскость cd с той же стороны линзы, где лежит и произвольный луч. Точку К, в которой побочная ось пересечет главную фокальную плоскость, надо соединить с точкой падения произвольного луча на линзу его мнимым (штриховым) продолжением, а сам луч пойдет в противоположном направлении (рис. 341).
Мнимые лучи и мнимые изображения предметов принято изображать штриховыми линиями.
Чтобы построить изображение светящейся точки в линзе, надо знать, где пересекутся после преломления испущенные этой точкой два любых луча. Лучше выбрать лучи, про которые вы знаете, как они пойдут после преломления.
Чтобы построить изображение предмета АВ, надо сначала построить изображение точки А, не лежащей на главной оптической оси. Для этого сначала из точки А проведем к линзе луч, параллельный главной оптической оси, — после преломления он пойдет через фокус. Затем из этой же точки А провести через главный оптический центр линзы О побочную ось. Точка , в которой после преломления пересекутся эти два луча, и будет изображением точки А. Затем, если предмет АВ был перпендикулярен главной оптической оси mn, опустить из точки А, на главную оптическую ось перпендикуляр и в его основании на оси получить изображение точки В.
Если предмет АВ находится за двойным фокусом собирающей линзы, то его действительное изображение будет обратным (перевернутым), уменьшенным и расположится между фокусом F и двойным фокусом 2F по другую сторону линзы (рис. 342, а). Если предмет АВ расположен в двойном фокусе 2F, то его действительное изображение будет обратным, равным по размерам самому предмету и тоже расположенным в двойном фокусе по другую сторону линзы (рис. 342, б). Если предмет
342, б). Если предмет
АВ находится между двойным фокусом 2F и фокусом F, то его действительное изображение будет увеличенным, обратным и расположится за 2F по другую сторону линзы (рис. 342, в). Если предмет АВ находится в фокусе линзы F, то его изображение уйдет в бесконечность (рис. 342, г). И наконец, если предмет АВ находится между фокусом F и линзой, то его мнимое изображение в собирающей линзе будет прямым, увеличенным и расположится с той же стороны линзы, что и сам предмет АВ (рис. 343, д).
Изображение AjB, предмета АВ в рассеивающей линзе будет всегда мнимым, прямым и уменьшенным (этим оно отличается от мнимого изображения в собирающей линзе, там оно увеличенное, см. рис. 342, д) и расположенным по ту же сторону линзы, что и сам предмет (рис. 343).
Если требуется построить изображение предмета АВ в системе собирающая линза — плоское зеркало, то сначала постройте изображение в линзе (рис. 344, а). Это изображение станет предметом по отношению к зеркалу. Затем постройте изображение предмета уже в плоском зеркале (рис. 344, б). Это изображение станет вторым предметом по отношению к линзе. И, наконец, постройте еще одно изображение предмета в линзе (рис. 344, в). Изображение и станет окончательным изображением предмета АВ, даваемым системой линза — зеркало. Если требуется построить изображение предмета в системе двух линз, например, собирающих, то сначала постройте изображение предмета АВ в первой, левой линзе (рис. 345). Это изображение станет предметом для второй, правой линзы. Теперь постройте изображение предмета АВ, в правой линзе. Это изображение и станет окончательным изображение предмета АВ, даваемым этой системой линз.
Затем постройте изображение предмета уже в плоском зеркале (рис. 344, б). Это изображение станет вторым предметом по отношению к линзе. И, наконец, постройте еще одно изображение предмета в линзе (рис. 344, в). Изображение и станет окончательным изображением предмета АВ, даваемым системой линза — зеркало. Если требуется построить изображение предмета в системе двух линз, например, собирающих, то сначала постройте изображение предмета АВ в первой, левой линзе (рис. 345). Это изображение станет предметом для второй, правой линзы. Теперь постройте изображение предмета АВ, в правой линзе. Это изображение и станет окончательным изображение предмета АВ, даваемым этой системой линз.
Величина D, обратная фокусному расстоянию, называется оптической силой линзы: .
Оптическая сила линзы может быть положительной и отрицательной. Положительной считается оптическая сила собирающей линзы, а отрицательной — рассеивающей.
Расстояние от предмета до линзы d и расстояние от линзы до изображения f связывает с фокусным расстоянием линзы F и ее оптической силой D формула линзы
Если линза собирающая, но изображение в ней мнимое, то эта формула принимает вид:
Если линза рассеивающая, то формула линзы принимает вид:
Если на линзу падает пучок сходящихся лучей, то точка их пересечения представляет собой мнимый предмет. В этом случае формула собирающей линзы с действительным изображением принимает вид:
В этом случае формула собирающей линзы с действительным изображением принимает вид:
Увеличением линзы Г называют отношение линейного размера предмета к линейному размеру изображения:
Лупой называют короткофокусную собирающую линзу, предназначенную для относительно небольшого увеличения изображения. Рассматриваемый предмет помещают между фокусом и лупой, благодаря чему получают прямое и увеличенное изображение. Увеличение лупы определяет формула
Здесь см — расстояние наилучшего зрения, F — фокусное расстояние лупы.
Если у человека нормальное зрение, то параллельные лучи, падающие на хрусталик глаза, пересекаются на сетчатке. При этом формула линзы имеет вид:
У близорукого человека параллельные лучи, упав на утолщенный хрусталик, пересекаются внутри глаза перед сетчаткой. Чтобы они пересекались на сетчатке, требуются очки со стеклами, аналогичными рассеивающей линзе. Применительно к глазу в таких очках формула линзы имеет вид:
У дальнозоркого человека параллельные лучи, упав на хрусталик, пересекутся за сетчаткой. Чтобы восстановить зрение, требуются очки со стеклами, аналогичными собирающей линзе. Применительно к дальнозоркому глазу формула линзы имеет вид:
Чтобы восстановить зрение, требуются очки со стеклами, аналогичными собирающей линзе. Применительно к дальнозоркому глазу формула линзы имеет вид:
Если в условии задачи записано: оптическая сила рассеивающей линзы D = -4 дптр, то в предыдущую формулу подставляйте только модуль этого числа, т.к. минус в ней уже учтен.
Если линзы сложены вплотную, то оптическая сила системы таких линз равна алгебраической сумме оптических сил каждой линзы в отдельности — с учетом их знаков. Например, если сложили вплотную собирающую линзу с фокусным расстоянием = 20 см и рассеивающую с фокусным расстоянием = 25 см, то оптическая сила такой системы линз будет равна:
При вычислении оптической силы не забывайте переводить размерность фокусных расстояний — сантиметры в метры, иначе допустите грубую ошибку.
Если линзы расположены на расстоянии друг от друга, то определять оптическую силу или фокусное расстояние такой системы линз подобным образом — просто складывая оптические силы каждой линзы — нельзя. В этом случае фокусным расстоянием F такой системы линз является расстояние от последнего пересечения лучей, упавших на первую линзу параллельно ее главной оптической оси, до последней линзы.
В этом случае фокусным расстоянием F такой системы линз является расстояние от последнего пересечения лучей, упавших на первую линзу параллельно ее главной оптической оси, до последней линзы.
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Задачи по физике с решением
Возможно вам будут полезны эти страницы:
Основные формулы и методические рекомендации по решению задач на законы геометрической оптики
В данной теме будут рассмотрены основные формулы и методические рекомендации по решению задач на оптику
Геометрическая
оптика изучает законы распространения света в прозрачных
средах, отражения света от зеркально-отражающих поверхностей, а также принципы
построения изображений при прохождении света в оптических системах без учёта
его волновых свойств.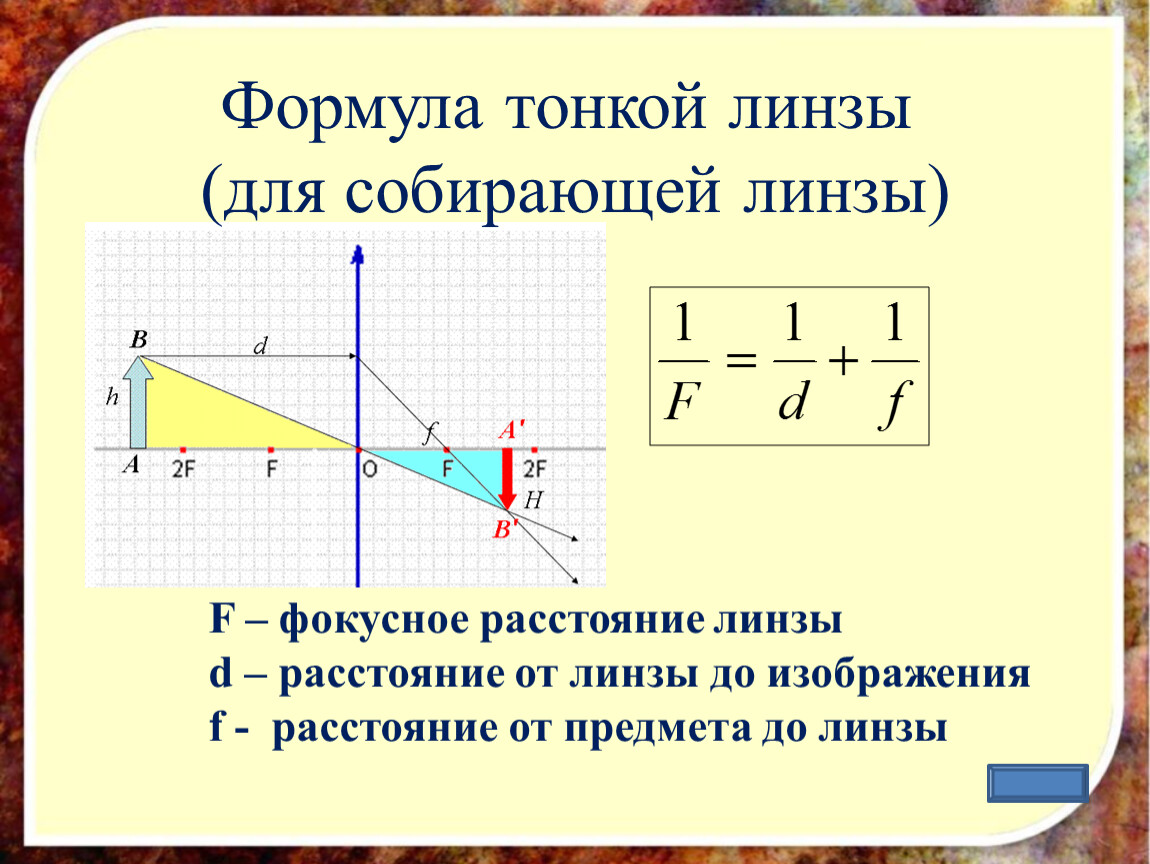
Волновая оптика рассматривает волновые свойства света, такие как интерференция, дифракция, поляризационные эффекты и так далее (то есть, те оптические явления, которые выходят за рамки геометрической оптики).
Фотометрия производит количественные измерения характеристик поля излучения, таких как освещённость, световой поток, сила света и так далее. Эта наука является прикладной и используется в различных областях.
Изобразим на рисунке некоторую среду, на границу которой падает световой луч. Известно, что свет имеет способность преломляться и отражаться. Проведём перпендикуляр в точке падения и обозначим на чертеже необходимые углы.
Угол
a называется углом падения. Это угол
между падающим лучом и перпендикуляром, восстановленным в точку падения. Угол g
называется
углом отражения – это угол между отражённым лучом и перпендикуляром,
восстановленным в точку падения. Угол b называется углом
преломления – это угол между преломлённым лучом и перпендикуляром,
восстановленным в точку падения.
Угол b называется углом
преломления – это угол между преломлённым лучом и перпендикуляром,
восстановленным в точку падения.
Линзой называется любое прозрачное тело, которое с обеих сторон ограничено сферическими поверхностями. Линзы бывают собирающими и рассеивающими. Собирающая (или выпуклая) линза – это линза, края которой тоньше, чем середина. Рассеивающая (или вогнутая) линза – это линза, края которой толще, чем середина.
На чертежах собирающие и рассеивающие линзы обозначаются специальным образом (так, как показано на рисунке).
Тонкая линза – это линза, толщина которой много меньше, чем радиусы кривизны сферических поверхностей, которыми она ограничена.
Проведём
линию, проходящую через центры сферических поверхностей, которыми ограничена
линза. Эта линия называется главной оптической осью (или просто
оптической осью).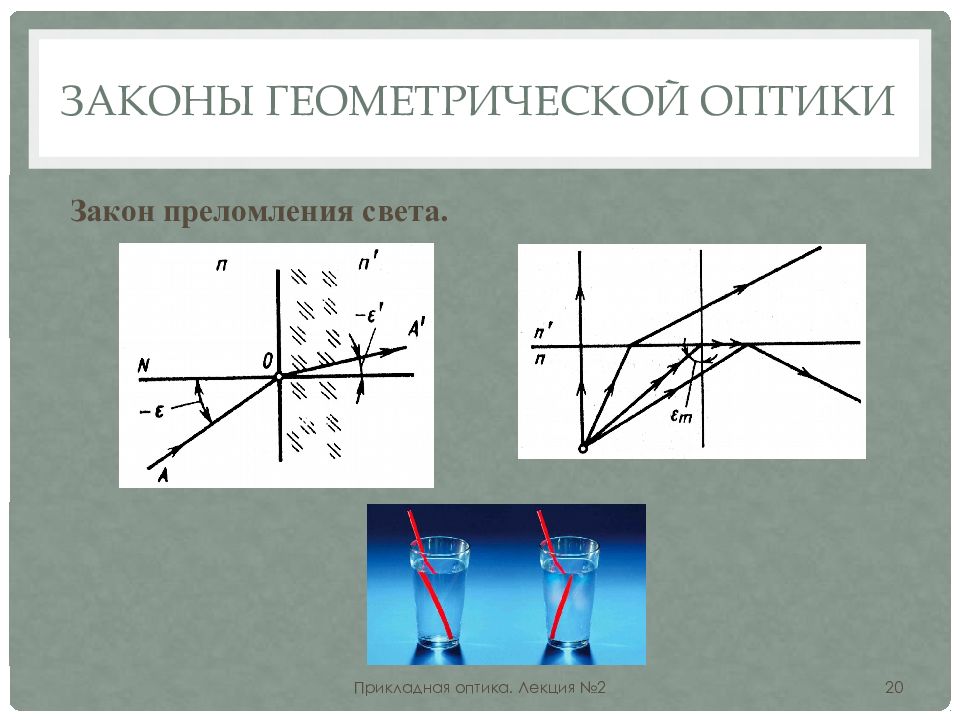 На этой линии лежит точка, которая называется оптическим
центром линзы. Это единственная точка линзы, проходя через
которую, свет не преломляется. Если линза симметрична и однородна, то её
оптический центр совпадает с геометрическим центром.
На этой линии лежит точка, которая называется оптическим
центром линзы. Это единственная точка линзы, проходя через
которую, свет не преломляется. Если линза симметрична и однородна, то её
оптический центр совпадает с геометрическим центром.
Рассмотрим несколько лучей, направленных на собирающую линзу параллельно оптической оси (чтобы упростить чертёж, мы изобразили всего два луча). После преломления эти лучи пересекутся в некоторой точке F, расположенной на главной оптической оси. Повторим ту же процедуру для рассеивающей линзы: направим на неё два луча параллельно оптической оси. После преломления получаются расходящиеся лучи, которые не пересекутся. Но если начертить продолжения этих лучей, то эти продолжения тоже пересекутся на главной оптической оси (только с другой стороны от линзы).
Полученные
точки F называются фокусами
линзы. В случае собирательной линзы фокус называется действительным, а в
случае рассеивающей линзы – мнимым. Расстояние между оптическим центром линзы и
её фокусом называется фокусным расстоянием. Фокусное расстояние
зависит от того, насколько сильно преломляются лучи, проходя через данную
линзу. Поэтому, вводится такая величина, как оптическая сила –
именно этой величиной характеризуется преломляющая способность линзы.
Расстояние между оптическим центром линзы и
её фокусом называется фокусным расстоянием. Фокусное расстояние
зависит от того, насколько сильно преломляются лучи, проходя через данную
линзу. Поэтому, вводится такая величина, как оптическая сила –
именно этой величиной характеризуется преломляющая способность линзы.
Рассмотрим некоторые понятия и величины, связанные с трёхгранной призмой.
При прохождении через такую призму, луч света отклоняется в сторону основания. Грани, через которые проходит луч света, называются преломляющими гранями призмы. Соответственно угол, образованный этими гранями, называется преломляющим. Угол между падающим лучом и лучом, выходящим из призмы, называется углом отклонения. Именно с углом отклонения связано большинство задач на ход лучей в призме.
Интерференция
света – это явление сложения двух и более когерентных волн, приводящее к
образованию в пространстве устойчивой картины чередующихся максимумов и
минимумов интенсивности света.
На рисунке показан простейший способ получения двух интерферирующих волн света.
Полученная картина чередования минимумов и максимумов называется интерференционной картиной. То есть, происходит перераспределение интенсивности света: в одних областях волны суммируются, а в других – погашают друг друга.
Дифракцией света называется совокупность оптических явлений, в результате которых происходит огибание волнами препятствий, размеры которых соизмеримы с длиной волны.
Если воспользоваться пластиной с круглым отверстием и направить в это отверстие луч света, то в центре светлого пятна получится тёмное пятнышко, и, наоборот, за непрозрачным диском тени будет находиться светлое пятно в центре тени.
На
основе явления дифракции был создан прибор, который называется дифракционной
решёткой. Он используется для разложения света в спектр и измерения
длины волны.
Рассмотрим самое обычное помещение, например, учебный класс. Иногда ученики говорят, что в классе светло или темно. Существует такая величина, как освещённость. Она равна отношению светового потока, падающего на поверхность к площади этой поверхности. Например, когда туча заслоняет солнце, то в классе становится темнее. Имеется ввиду, что освещённость класса уменьшилась, поскольку теперь меньший поток солнечных лучей приходится на ту же площадь. Световым потоком называется отношение полной энергии, выделенной источником света ко времени, в течение которого выделялась энергия.
Сила света – это величина световой энергии, переносимой в определённом направлении в единицу времени.
Рассмотрим
некоторые коэффициенты, определяющие оптические свойства различных тел. Коэффициент
поглощения – это соотношение поглощенного потока света с падающим
потоком. Часть падающего светового потока на стекло поглощается и только часть
проходит сквозь него. В противном случае, стекло бы не нагревалось под
солнечными лучами. Например, коэффициент поглощения у тел тёмного цвета больше,
чем коэффициент поглощения у тел светлого цвета, поэтому, тёмные тела быстрее
нагреваются на солнце.
В противном случае, стекло бы не нагревалось под
солнечными лучами. Например, коэффициент поглощения у тел тёмного цвета больше,
чем коэффициент поглощения у тел светлого цвета, поэтому, тёмные тела быстрее
нагреваются на солнце.
Коэффициент отражения – это соотношение отражённого потока света с падающим потоком. Известно, что часть солнечных лучей отражается от окна.
Коэффициент пропускания – это соотношение пропущенного потока света с падающим потоком. Этот коэффициент связан с двумя предыдущими коэффициентами. Чем больший световой поток тело отражает и поглощает, тем меньший световой поток оно пропускает.
Сведём в таблицу основные формулы геометрической оптики.
|
Формула |
Описание формулы |
|
Закон
отражения света, где a – угол падения, g
– угол отражения. |
|
|
Закон преломления света, где a – угол падения, b – угол преломления, и – скорости света в данных средах, а – относительный показатель преломления для данных двух сред |
|
|
Абсолютный показатель преломления среды, где с –скорость света в вакуумек |
|
|
Оптическая сила линзы, F – фокусное расстояние линзы. |
|
|
Формула тонкой линзы, d – расстояние от предмета до линзы, f – расстояние от линзы до изображения. |
|
|
Линейное увеличение |
|
|
Угол
отклонения луча призмой, –
угол падения на преломляющую грань призмы, –
угол выхода луча из призмы, –
преломляющий угол призмы. |
|
|
Угол отклонения луча призмой при падении света на преломляющую грань призмы под очень малым углом, n – относительный показатель преломления материала призмы. |
Сведём в таблицу основные формулы волновой оптикию
|
Формула |
Описание формулы |
|
Формула дифракционной решётки, где d – период дифракционной решетки, j – угол, определяющий направление распространения волн, l – длина волны, – определяет порядок спектра. |
|
|
Условие интерференционных максимумов |
|
|
Условие интерференционных минимумов |
Сведём
в таблицу основные формулы фотометрии.
|
Формула |
Описание формулы |
|
Полный световой поток от точечного источника с силой света I. |
|
|
Освещённость поверхности площадью S, где F – световой поток равномерно распределённый по всей поверхности. |
|
|
Освещенность поверхности, на которую падает световой поток под углом a. |
|
|
Коэффициент поглощения света, где Fa – световой поток, поглощенный телом, Fi – световой поток, падающий на тело. |
|
|
Коэффициент
отражения света, где Fr
– световой поток, отражённый телом. |
|
|
Коэффициент пропускания, где Ft– световой поток, пропущенный телом. |
Методические рекомендации по решению задач на законы отражения и преломления света.
1. Сделать наглядный чертёж, отметив на нём падающие, отражённые и/или преломлённые лучи, а также соответствующие углы.
2. При необходимости отметить на чертеже дополнительные углы (например, углы отклонения лучей).
3. Применить закон отражения и/или закон преломления света.
4. Используя теоремы и аксиомы геометрии, рассмотреть чертеж.
5. На основании применённых теорем и законов, составить систему уравнений и решить её относительно искомых величин.
Методические рекомендации по решению задач на линзы
1. Сделать
наглядный чертёж и построить изображение, требуемое для решения задачи.
Сделать
наглядный чертёж и построить изображение, требуемое для решения задачи.
2. В зависимости от условия задачи, применить формулу тонкой линзы, формулу линейного увеличения линзы или формулу для вычисления оптической силы линзы.
3. Записать в виде уравнений какие-либо дополнительные условия задачи (если таковые имеются).
4. На основании применённых законов и формул, составить систему уравнений и решить её относительно искомых величин.
Методические рекомендации по решению задач на призмы
1. Сделать наглядный чертёж, построив ход лучей в призме и указав не нём все необходимы углы.
2. Применить формулу для нахождения угла отклонения.
3. При необходимости использовать теоремы и аксиомы геометрии.
4.
На
основании применённых законов и формул, составить систему уравнений и решить её
относительно искомых величин.
Методические рекомендации по решению задач на интерференцию и дифракцию света
1. При необходимости сделать чертёж, соответствующий ситуации, описанной в задаче.
2. Применить условия интерференционных минимумов и максимумов.
3. При необходимости использовать формулу дифракционной решётки.
4. Записать в виде уравнений какие-либо дополнительные условия задачи (если таковые имеются).
5. На основании применённых теорем и законов, составить систему уравнений и решить её относительно искомых величин.
Методические рекомендации по решению элементарных задач на фотометрию
1. При необходимости сделать чертёж, соответствующий ситуации, описанной в задаче.
2. Применить формулы освещенности и/или светового потока.
3.
Записать
в виде уравнений какие-либо дополнительные условия задачи (если таковые
имеются).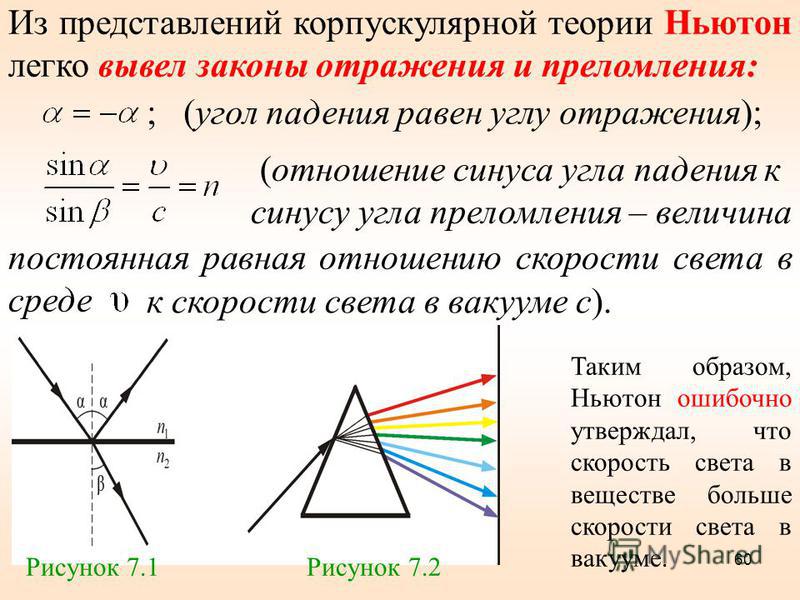
4. На основании применённых теорем и законов, составить систему уравнений и решить её относительно искомых величин.
Оптика и волны
Корпускулярная теория очень просто объясняла явления геометрической оптики, описываемые в терминах распространения световых лучей. С точки зрения волновой теории, лучи — это нормали к фронту волны. Принцип Гюйгенса также позволяет объяснить законы геометрической оптики на основе волновых представлений о природе света.
Закон отражения
Когда световые волны достигают границы раздела двух сред, направление их распространения изменяется. Если они остаются в той же среде, то происходит отражение света.
|
Отражение света — это изменение направления световой волны при падении на границу раздела двух сред, в результате чего волна продолжает распространяться в первой среде. |
Закон отражения света хорошо известен:
|
Падающий луч, перпендикуляр к границе раздела двух сред в точке падения и отраженный луч лежат в одной плоскости, причем угол падения равен углу отражения. |
Направления распространения падающей и отраженной волн показаны на рис. 3.2.
Рис. 3.2. Отражение света от плоской поверхности
Видео 3.1 Трехсантиметровые волны: закон отражения (металл).
Видео 3.2 Трехсантиметровые волны: закон отражения (диэлектрик).
Видео 3.3 Решетка — зеркало для трехсантиметровых волн. (диэлектрик).
Закон отражения может быть выведен из принципа Гюйгенса. Действительно, допустим, что плоская волна, распространяющаяся в изотропной среде, падает на границу раздела двух сред АС (рис.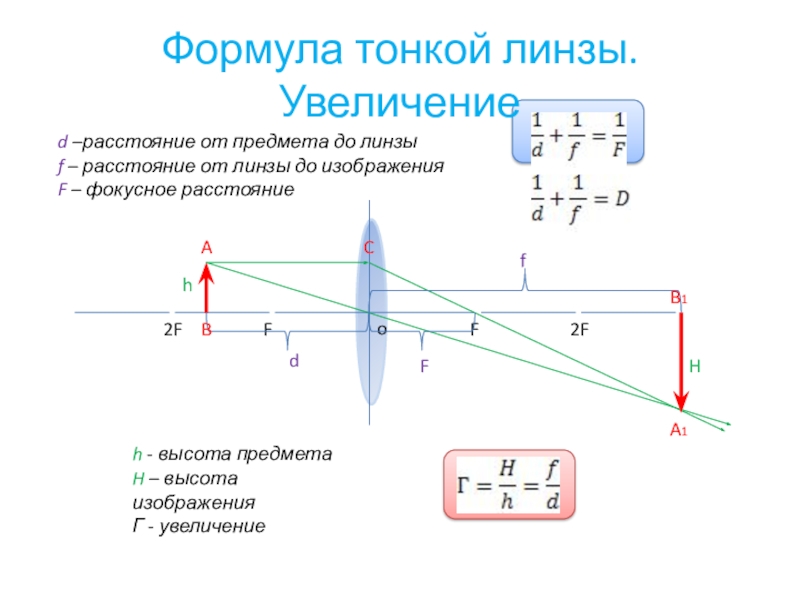 3.3).
3.3).
Рис. 3.3. Применение принципа Гюйгенса к выводу закона отражения
Достаточно рассмотреть два параллельных луча I и в падающем пучке. Углом падения называют угол между нормалью п к поверхности раздела и падающим лучом I. Плоский фронт AD падающей волны сначала достигнет границы раздела двух сред в точке А, которая станет источником вторичных волн. Согласно принципу Гюйгенса, из нее, как из центра, будет распространяться сферическая волна. Через время
,
то есть с запаздыванием во времени на , луч из падающего пучка придет в точку С, которая в этот момент времени также станет источником вторичной волны. Но, к этому моменту вторичная сферическая волна, распространяющаяся из точки А, уже будет иметь радиус (как и должно быть: ). Мы знаем теперь положение двух точек фронта отраженной волны — С и В. Чтобы не загромождать рисунок, мы не показываем вторичных волн, испущенных точками между А и С, но линия CD будет касательной (огибающей) ко всем из них. Стало быть, CВ действительно является фронтом отраженной волны. Направление ее распространения (лучи II и ) ортогонально фронту CD. Из равенства треугольников ABC и ADC вытекает равенство углов
Чтобы не загромождать рисунок, мы не показываем вторичных волн, испущенных точками между А и С, но линия CD будет касательной (огибающей) ко всем из них. Стало быть, CВ действительно является фронтом отраженной волны. Направление ее распространения (лучи II и ) ортогонально фронту CD. Из равенства треугольников ABC и ADC вытекает равенство углов
что, в свою очередь, приводит к закону отражения
На рис. 3.4 представлена интерактивная модель отражения света.
Рис. 3.4. Изучение закона отражения света
Закон преломления
Если световые волны достигают границы раздела двух сред и проникают в другую среду, то направление их распространения также изменяется — происходит преломление света.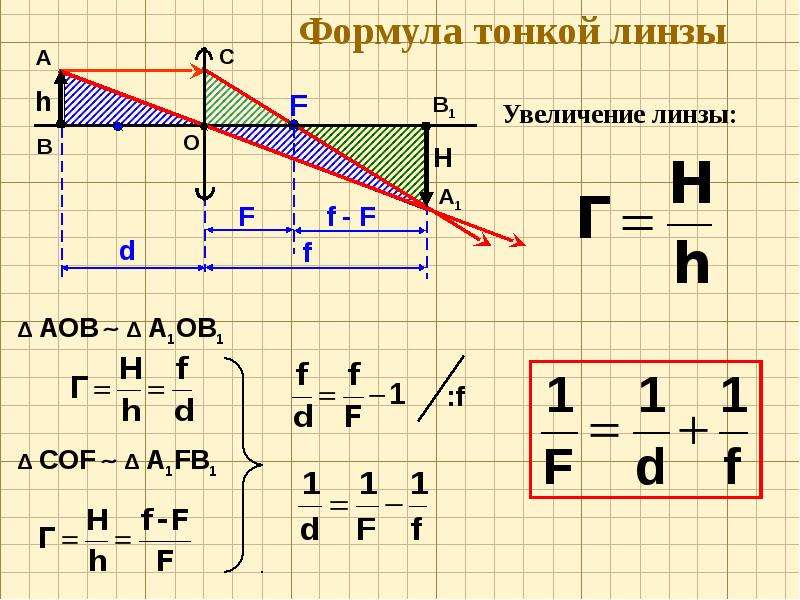
|
Преломление света — это изменение направления распространения световой волны при переходе из одной прозрачной среды в другую. |
Направление распространения падающей и преломленной волны показано на рис. 3.5.
Рис. 3.5. Преломление света на плоской границе раздела двух прозрачных сред
Закон преломления гласит:
|
Падающий луч, перпендикуляр к границе раздела сред в точке падения и преломленный луч лежат в одной плоскости, причем отношение синуса угла падения к синусу угла преломления постоянно для данной пары сред и равно показателю преломления второй среды относительно первой |
Здесь показатель преломления среды, в которой распространяется преломленная волна, показатель преломления среды, в которой распространяется падающая волна.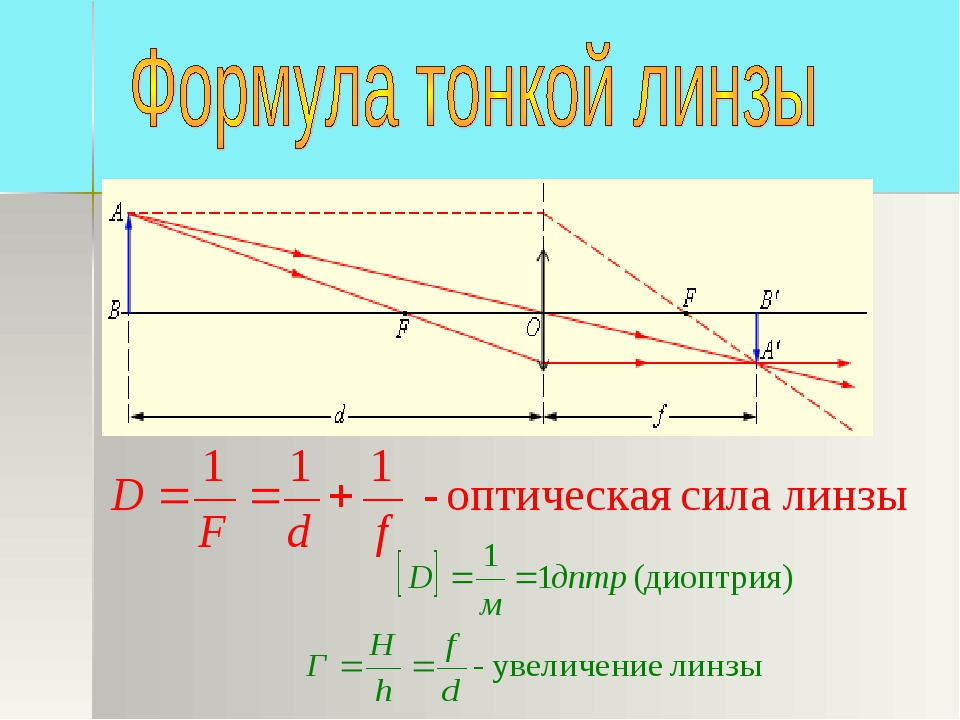
Закон отражения также вытекает из принципа Гюйгенса. Рассмотрим (рис. 3.6) плоскую волну (фронт АВ), которая распространяется в среде с показателем преломления , вдоль направления I со скоростью
Эта волна падает на границу раздела со средой, в которой показатель преломления равен , а скорость распространения
Рис. 3.6. К выводу закона преломления света с помощью принципа Гюйгенса
Время, затрачиваемое падающей волной для прохождения пути ВС, равно
За это же время фронт вторичной волны, возбуждаемой в точке А во второй среде, достигнет точек полусферы с радиусом
В соответствии с принципом Гюйгенса положение фронта преломленной волны в этот момент времени задается плоскостью DC, а направление ее распространения — лучом III, перпендикулярным к DC.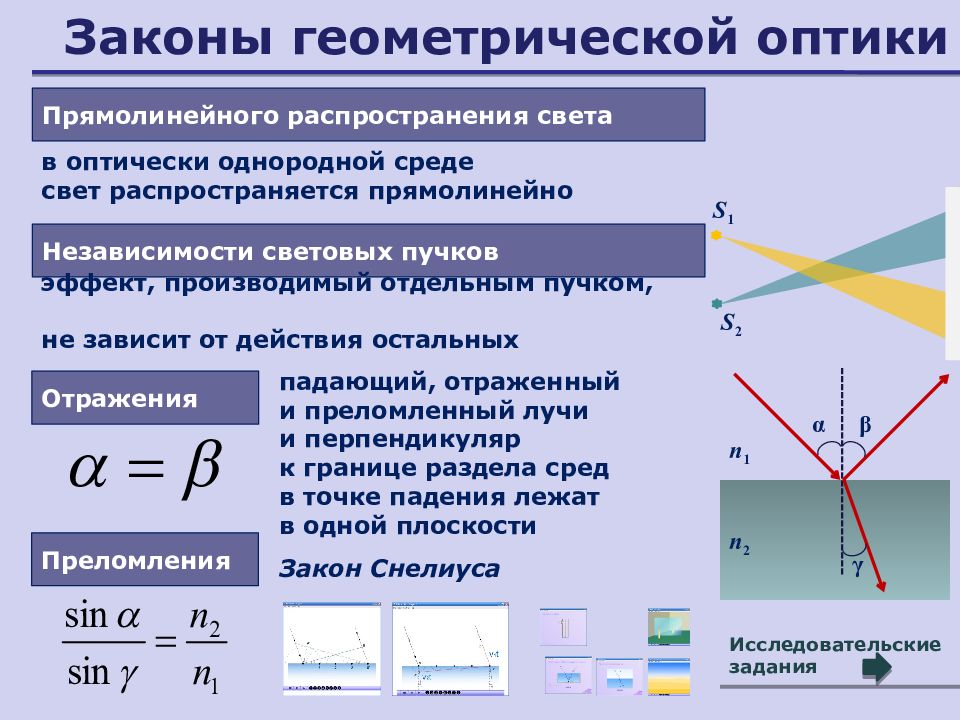 Из треугольников и следует
Из треугольников и следует
откуда
|
|
(3.1) |
Таким образом, закон преломления света записывается так:
|
|
(3.2) |
Видео 3.4 Полное внутреннее отражение (видимый свет)
Видео 3.5 Модель световода
Видео 3.6 Куб и призма на пути трехсантиметровой волны.
На рис. 3.7 представлена интерактивная модель преломления света на границе раздела двух сред.
Рис. 3.7. Изучение закона преломления
Для еще одной иллюстрации применения принципа Гюйгенса рассмотрим пример.
Пример. На плоскую границу раздела двух сред падает нормально луч света. Показатель преломления среды непрерывно увеличивается от ее левого края к правому (рис. 3.8). Определим, как будет идти луч света в этой неоднородной среде.
Рис. 3.8. Искривление луча света в неоднородной среде
Пусть фронт волны АА подошел к границе раздела сред. Точки раздела сред можно рассматривать как центры вторичных волн. Через время испущенные вторичные сферические волны достигают точек на расстоянии от фронта АА. Поскольку показатель преломления среды растет слева направо, эти расстояния убывают слева направо. Огибающая к вторичным волнам — новый фронт ВВ — повернется. Если теперь взять точки фронта ВВ за источники вторичных волн, то за время они породят волны, образующие фронт СС. Он еще более повернут. Его точки порождают фронт DD и т. д. Проводя нормаль к волновым фронтам в разные моменты времени, получаем путь светового луча в среде с переменным показателем преломления (зеленая линия). Видно, что луч искривляется в сторону увеличения показателя преломления. Аналогия: если притормозить левые колеса автомобиля, его повернет налево. Для света степень «торможения» растет с ростом показателя преломления среды: .
Огибающая к вторичным волнам — новый фронт ВВ — повернется. Если теперь взять точки фронта ВВ за источники вторичных волн, то за время они породят волны, образующие фронт СС. Он еще более повернут. Его точки порождают фронт DD и т. д. Проводя нормаль к волновым фронтам в разные моменты времени, получаем путь светового луча в среде с переменным показателем преломления (зеленая линия). Видно, что луч искривляется в сторону увеличения показателя преломления. Аналогия: если притормозить левые колеса автомобиля, его повернет налево. Для света степень «торможения» растет с ростом показателя преломления среды: .
Эта задача имеет отношение к явлению, наблюдающемуся на море. Когда ветер дует с берега, иногда возникает так называемая «зона молчания»: звук колокола с судна не достигает берега. Обычно говорят, что звук относится ветром. Но даже при сильном урагане скорость ветра примерно в 10 раз меньше скорости звука, так что «отнести» звук ветер никак не может.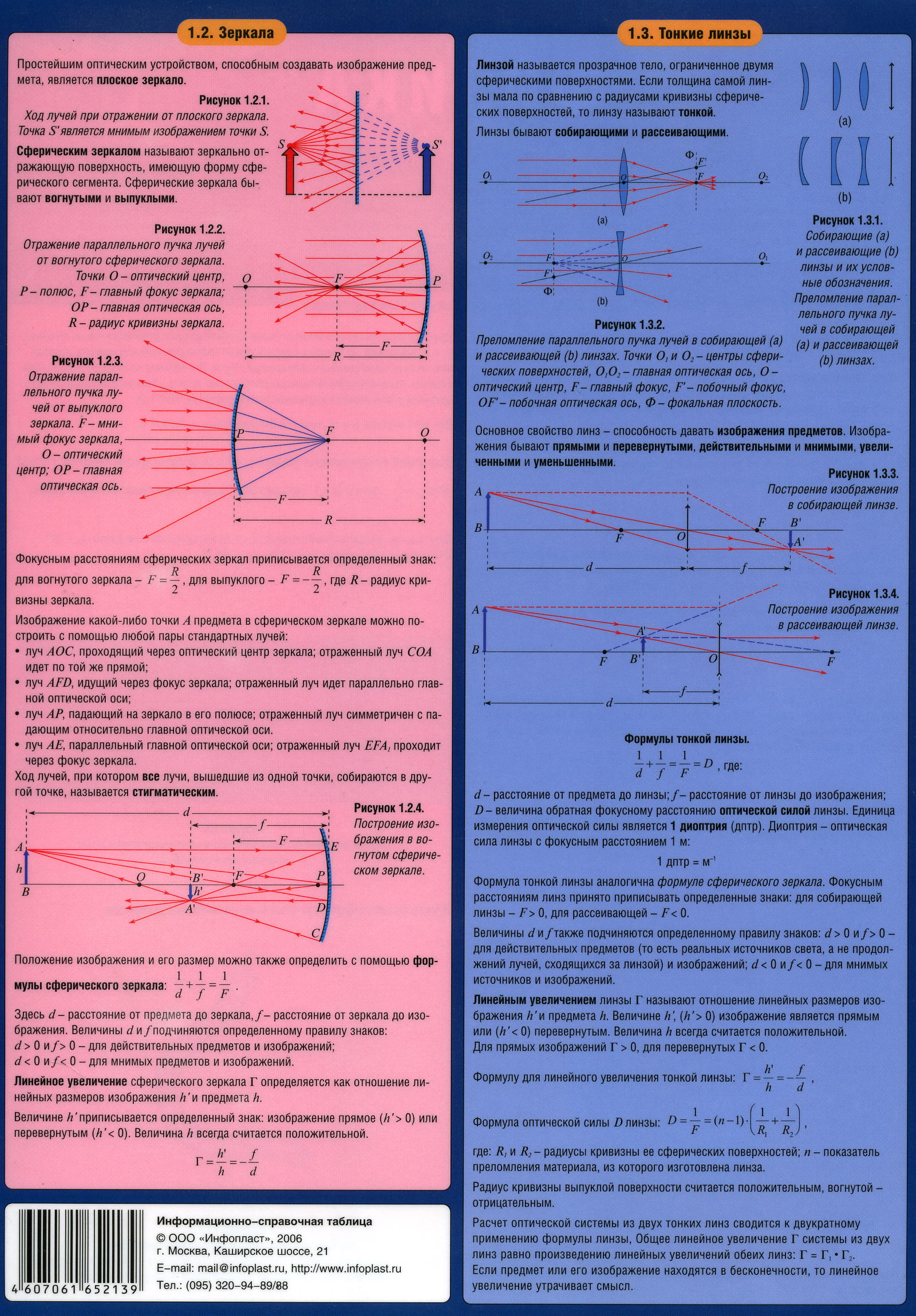 Объяснение заключается в том, что скорость встречного ветра у поверхности моря вследствие трения меньше, чем на высоте. Поэтому скорость звука у поверхности больше, и линия распространения звука загибается кверху, не попадая на берег.
Объяснение заключается в том, что скорость встречного ветра у поверхности моря вследствие трения меньше, чем на высоте. Поэтому скорость звука у поверхности больше, и линия распространения звука загибается кверху, не попадая на берег.
Дополнительная информация
http://allphysics.ru/perelman/otrazhenie-i-prelomlenie-sveta – Я.И.Перельман, «Занимательная физика». Отражение и преломление света.
http://www.nvtc.ee/e-oppe/Sidorova/objects/index.html – Законы преломления, отражения света. Зеркала. Теория и примеры задач. В «Итоговых заданиях» — кроссворд.
http://files.school-collection.edu.ru/dlrstore/1461c067-705e-4f5f-9d18-152a8eec1564/7_16.swf – Слайд-шоу «Рассеянное отражение света».
http://www.youtube.com/watch?v=KQvtIEITg5s&feature=endscreen&NR=1 – Видео о преломлении света около магнитов и в линзах.
http://allphysics.ru/feynman/kak-voznikaet-pokazatel-prelomleniya – Фейнмановские лекции по физике. Как возникает показатель преломления.
Как возникает показатель преломления.
http://publ.lib.ru/ARCHIVES/B/… – Тарасов Л.В., Тарасова А.Н., «Беседы о преломлении света».
Принцип Ферма.
Итак, волновая оптика способна объяснить явления отражения и преломления света столь же успешно, как и геометрическая оптика. В основу последней, трактующей явления на основе законов распространения лучей, положен принцип Ферма:
|
Свет распространяется по такому пути, для прохождения которого требуется минимальное время. |
Для прохождения участка пути свету требуется время
где v=с/п — скорость света в среде. Таким образом, время t, затрачиваемое светом на путь от точки 1 до точки 2, равно
|
|
(3. |
Введем величину с размерностью длины, которая называется оптической длиной пути:
|
|
(3.4) |
Пропорциональность t и L позволяет сформулировать принцип Ферма следующим образом:
|
Свет распространяется по такому пути, оптическая длина которого минимальна. |
Рассмотрим путь света из точки S в точку С после отражения от плоскости АВ (рис. 3.9).
Рис. 3.9. Применение принципа Ферма к отражению света
3.9. Применение принципа Ферма к отражению света
Непосредственное попадание света из S в С невозможно из-за экрана. Нам надо найти точку О, отразившись в которой луч попадет в точку С. Среда, в которой проходит луч, однородна. Поэтому минимальность оптической длины пути сводится к минимальности его геометрической длины. Рассмотрим зеркальное изображение S’ точки S. Геометрические длины путей SOC и S’OC равны. Поэтому минимальность длины SOC эквивалентна минимальности длины S’OC. А минимальная геометрическая длина пути из S’ в С будет соответствовать прямой, соединяющей точки S’ и С. Пересечение этой прямой с плоскостью раздела сред дает положение точки О. Отсюда следует равенство углов:
то есть закон отражения света.
Рассмотрим теперь явление преломления света (рис.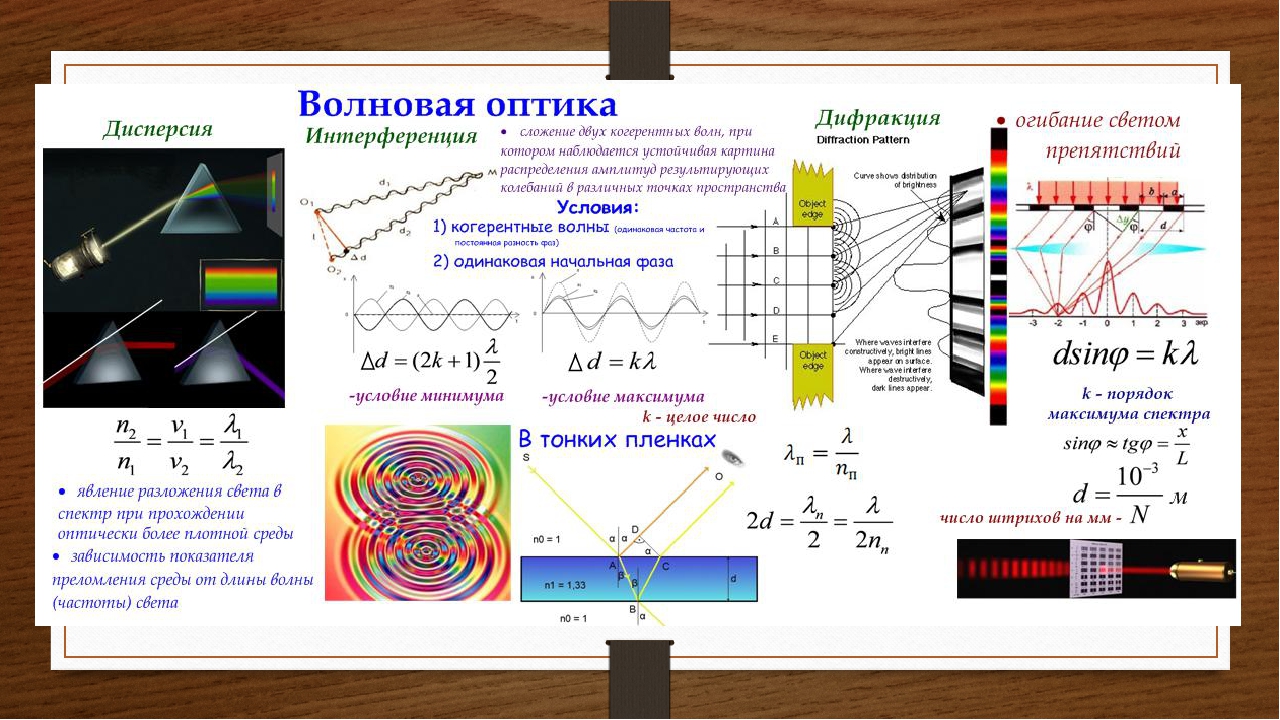 3.10).
3.10).
Рис. 3.10. Применение принципа Ферма к преломлению света
Видео 3.7 Искривление луча в неоднородной среде.
Видео 3.8 Трехсантиметровые волны: диэлектрическая линза.
Видео 3.9 Трехсантиметровые волны: диэлектрическая призма.
Определим положение точки О, в которой должен преломиться луч, распространяясь от S к С, чтобы оптическая длина пути L была минимальна. Выражение для L имеет вид
|
|
(3.5) |
Найдем величину х, соответствующую экстремуму оптической длины пути:
|
|
(3. |
Отсюда следует
|
|
(3.7) |
или
Мы получили закон преломления света.
Принцип Ферма является частным случаем так называемого принципа наименьшего действия, имеющего приложения практически ко всем областям физики. Всякий раз из всех возможных движений системы осуществляется то, для которого некая величина (ее называют действием) минимальна (точнее, имеет экстремум). В этом проявляется некая «экономность» природы, выбирающей оптимальные пути для перехода системы из одного состояния в другое.
Дополнительная информация
Геометрическая оптика
http://allphysics.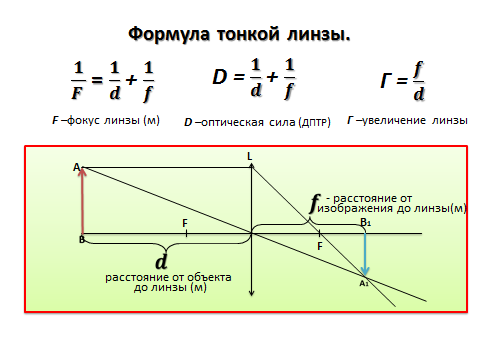 ru/feynman/geometricheskaya-optika – Фейнмановские лекции по физике. Геометрическая оптика.
ru/feynman/geometricheskaya-optika – Фейнмановские лекции по физике. Геометрическая оптика.
http://www.ph5s.ru/book_ph_opt_geom.html – Ссылки на книги по геометрической оптики. Сайт бывшего преподавателя МИФИ А.Н. Варгина.
http://school-collection.edu.ru/catalog/rubr/ef4b174a-8fec-c03a-df26-ae730713bc30/79292/?interface=themcol – Интерактивные модели по физике. Геометрическая оптика.
http://diplomivanov.narod.ru/ – Сайт о геометрической оптике: теория и задачи.
http://eqworld.ipmnet.ru/ru/library/books/Begunov1966ru.djvu – Бегунов Б.Н., учебник по геометрической оптике.
http://www.physel.ru/a-mainmenu-55.html – Материалы по геометрической оптике.
http://www.youtube.com/watch?v=mRwRy24hbg8&feature=related – Ход лучей в линзе.
http://physbook.ru/index.php/Kvant… – Задачи на оптические построения.
http://physbook.ru/index.php/Kvant… – Геометрия тонкой линзы.
http://physbook.ru/index. php/Kvant… – Тонкие линзы. Нулевые линзы.
php/Kvant… – Тонкие линзы. Нулевые линзы.
http://physbook.ru/index.php/Kvant… – Фокус шара.
http://www.youtube.com/watch?v=MNea-aK6VuQ – Оптическая разность хода. Видео.
http://sfiz.ru/list.php?c=geomoptika – Геометрическая оптика. Учебные материалы.
Учебники и лекции по оптике
http://www.plib.ru/library/book/16969.html – Бутиков Е.И. Учебник по оптике.
http://www.plib.ru/library/book/16986.html – Годжаев Н.М. Учебник по оптике.
http://www.plib.ru/library/book/15479.html – Клаудер Дж, Сударшан Э. «Основы квантовой оптики».
http://www.alleng.ru/d/phys/phys106.htm – Сивухин, учебник по оптике.
http://www.abitura.com/handbook/index.html – Справочник по физике (в т. ч. по оптике).
http://sfiz.ru/page.php?id=103 – Словарь по оптике.
http://uti.tpu.ru/edu/chairs/eno/opt.pdf – Е.В. Полицинский «Оптика. Конспекты лекций.» Учебное пособие.
http://physoptika.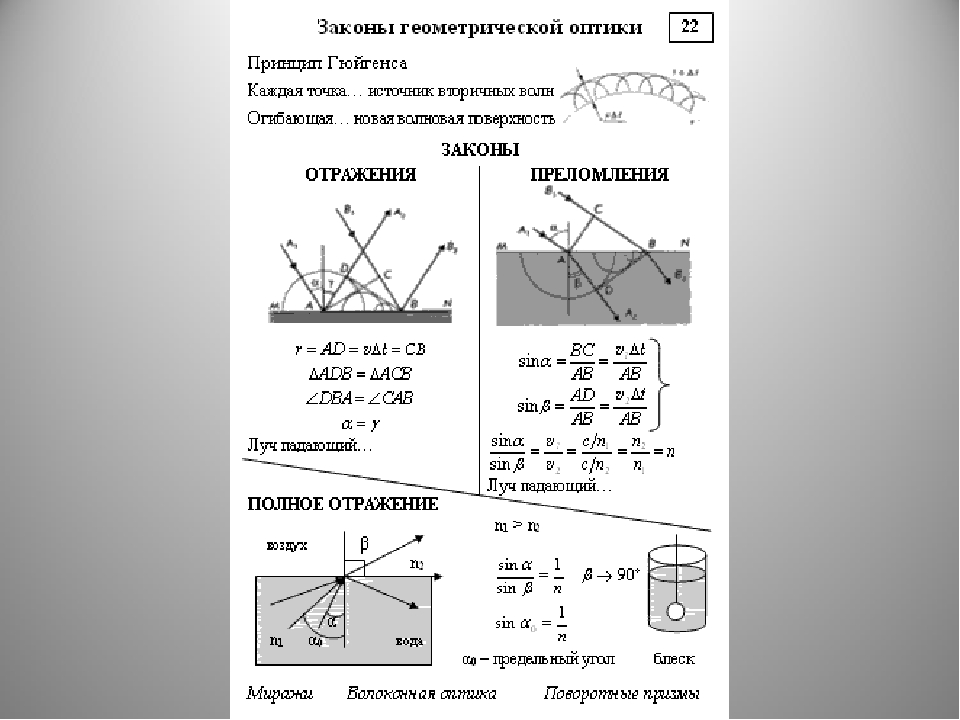 ru/ – Лекции по оптике. Примеры решения задач.
ru/ – Лекции по оптике. Примеры решения задач.
http://www.phys.spbu.ru/content/File/Library/Books/GenPhys/crowellOptics.pdf – B. Crowell. «Optics»
http://www.physbook.ru/ – Электронный учебник по физике.
http://eqworld.ipmnet.ru/ru/library/books/BornVolf1973ru.djvu – М. Борн, Э. Вольф, «Основы оптики».
http://eqworld.ipmnet.ru/ru/library/books/GorbunovaZajcevaKrasnikov1977ru.djvu – Горбунова О.И., Зайцева А.М., Красников С.Н., «Задачник-практикум по общей физике. Оптика. Атомная физика».
http://eqworld.ipmnet.ru/ru/library/books/DetlafYavorskij_t3_1979ru.djvu – Детлаф А.А., Яворский Б.М. Курс физики. Том 3. Волновые процессы. Оптика. Атомная и ядерная физика.
http://www.physics.spbstu.ru/forstudents/practice/vasyliev_phys_optica_manual.pdf – А.Э. Васильев. «Физика. Оптика.» Учебное пособие.
http://www.phys.spbu.ru/library/studentlectures/krylov/krylov/ – И.Р. Крылов. «Методическое пособие по курсу оптики».
http://jamshyt.ru/wnopa/f2/ – Оптика. Материалы.
http://fn.bmstu.ru/phys/bib/physbook/tom4/content.htm – О.С. Литвинов, К.Б. Павлов, В.С. Горелик «Электромагнитные волны и оптика» Онлайн-учебник.
http://www.laser-portal.ru/content_3 – История и законы оптики, оптические эффекты, материалы, компоненты оптических схем, природа света.
http://www.harmony-guild.ru/index.php?option=com_content&view=article&id=190:2011-05-31-07-27-31&catid=34:demo-category&Itemid=78 – Излучение Вавилова-Черенкова. Механизм, интересные следствия.
http://files.school-collection.edu.ru/dlrstore/5ee6b93b-cb19-46e1-9e74-30aa92a167fa/7_18.swf – Слайд-шоу «Зеркальный телескоп».
http://media.dm-centre.ru/index.php?option=com_content&view=article&id=25&Itemid=29 – Опыты по оптике. Видео.
http://eqworld.ipmnet.ru/ru/library/books/Savelev_t3_1971ru.djvu – Савельев И.В. Курс общей физики, том З. Оптика. Атомная физика.
http://allphysics.ru/feynman/optika-printsip-naimenshego-vremeni – Фейнмановские лекции по физике. Оптика. принцип наименьшего времени.
http://allphysics.ru/feynman/tsvetovoe-zrenie – Фейнмановские лекции по физике. Цветовое зрение.
http://allphysics.ru/feynman/mehanizm-zreniya – Фейнмановские лекции по физике. Механизм зрения.
Тесты и задачи
http://physbook.ru/index.php/Kvant… – Задачи на распространение света.
http://www.reppofiz.info/ege.html – Задачи из ЕГЭ по оптике (и не только) с решениями.
http://eqworld.ipmnet.ru/ru/library/books/RussoMate1976ru.djvu – Руссо М., Матье Ж.П. Задачи по оптике.
http://www.testent.ru/load/testy/fizika/optika/39-1-0-1824 – Тесты по оптике.
http://window.edu.ru/window_catalog/files/r72644/stup538.pdf – Сборник задач ЕГЭ по оптике.
Другие ресурсы по оптике
http://www3.crimea.edu/tnu/structure/physic_fac/departments/general/common_phys/all/opt. htm – Кратко об основных аспектах оптики.
htm – Кратко об основных аспектах оптики.
http://repetitor.mathematic.of.by/spravka_fizika3.htm#M1 – Основные формулы по оптике.
http://shkola.lv/index.php?mode=cht&chtid=91 – Основные положения, законы, формулы.
http://school-collection.edu.ru/catalog/search/?text=%EE%EF%F2%E8%EA%E0&tg=&interface=catalog – Коллекция ресурсов по оптике: статьи, эксперименты, лабораторные.
http://power-p.ru/load/fizika/optika/14-1-0-331 – Презентации по оптике: устройство глаза, фотоаппарата, микроскопа, телескопа и другое.
http://pymath.ru/viewtopic.php?f=77&t=809&sid=63be0a3e99f9a32260b53dcfaad3c271 – Видеоурок «Разрешающая способность».
Интересные факты
http://physbook.ru/index.php/Kvant… – Физическая оптика: на каком расстоянии можно отличить двугорбого верблюда от одногорбого?
http://physbook.ru/index.php/Kvant… – Древняя оптика: почему ошибался Птоломей?
http://physbook. ru/index.php/Kvant… – Лучи и волны.
ru/index.php/Kvant… – Лучи и волны.
http://physbook.ru/index.php/Kvant… – Волны на пляже.
http://physbook.ru/index.php/Kvant… – Предельные возможность оптического микроскопа.
http://physbook.ru/index.php/Kvant… – Электрический микроскоп. Можно ли в микроскопе разглядеть молекулу?
http://physbook.ru/index.php/Kvant… – Как устроен глаз? Эффект «Полета» луны.
http://elkin52.narod.ru/optika.htm – Занимательная оптика в вопросах и ответах.
http://www.osa-univer.org.ua/DiscoveryKit_Rus.pdf – Занимательная оптика, набор наглядных пособий.
http://www.youtube.com/watch?v=NwH7qx5468o – Распространение луча лазера в воде: опыт Джона Тилдана.
http://www.youtube.com/watch?v=C_R9GnBAC1E – Бесконечное зеркало.
http://www.vokrugsveta.ru/quiz/615/ – Почему небо голубое? Объяснение «на пальцах».
http://www.laser-portal.ru/content_5 – Лазеры. Область их применения.
http://our-lectures. ru/interesting/physics/27-pochemy-nebo-golyboe.html Почему небо голубое? Объяснение с математическими выкладками.
ru/interesting/physics/27-pochemy-nebo-golyboe.html Почему небо голубое? Объяснение с математическими выкладками.
http://www.sveticvet.ru/iskrivlenie-svetovyx-luchej-v-atmosfere/mirazh-v-miniatyure/index.php – Статья о миражах.
http://optika8.narod.ru/History.htm – Краткая история развития оптики.
http://laser-portal.ru/content_7 – История развития оптики.
http://allphysics.ru/perelman/luchi-sveta – Я.И.Перельман, «Занимательная физика». Лучи света.
http://allphysics.ru/perelman/zrenie-odnim-i-dvumya-glazami – Я.И.Перельман, «Занимательная физика». Зрение одним и двумя глазами.
http://www.youtube.com/watch?v=uGTV5OxcKDs – Видео о свете и зеркалах (плоских, выпуклых и вогнутых), цветных фильтрах, люминофорах, черных телах, призмах.
Формулы геометрической оптики для чайников
Все знают или по крайней мере слышали о том, что свет имеет свойство преломляться и отражаться. Но только формулы геометрической и волновой оптики могут объяснить, как, а точнее по какому именно признаку это происходит. И все данное учение основывается на понятии «луча», которое ввел еще Евклид за три века до нашей эры. Так что же такое луч, если говорить научным языком?
И все данное учение основывается на понятии «луча», которое ввел еще Евклид за три века до нашей эры. Так что же такое луч, если говорить научным языком?
Луч — это прямая, вдоль которой движутся световые волны. Как, зачем — на эти вопросы отвечают формулы геометрической оптики, которая является частью волновой оптики. Последняя, как можно было бы предположить, рассматривает лучи как волны.
Формулы геометрической оптики
Закон прямолинейного распространения: луч в однотипной среде имеет свойство распространяться прямолинейно. То есть свет двигается по кратчайшему пути, который существует между двумя точками. Можно даже сказать, что световой луч стремится сэкономить себе время. Этим законом объясняются явления тени и полутени.
К примеру, если источник света сам по себе маленького размера или же находится на таком большом расстояние, что его размеры можно проигнорировать, то световой луч образует четкие тени. Но если источник света большого размера или же находится на очень близком расстоянии, то световой луч образует нечеткие тени и полутени.
Закон независимого распространения
Световые лучи имеют свойство распространяться вне зависимости друг от друга. То есть они никак не повлияют друг на друга, если будут пересекаться или проходить друг через друга в какой-нибудь однородной среде. Лучи будто бы не подозревают о существовании других лучей.
Закон отражения
Представим, что человек направил лазерную указку на зеркало. Разумеется, луч отразится от зеркала и будет распространяться уже в другой среде. Угол между перпендикуляром к зеркалу и первым лучом зовется углом падения, угол между перпендикуляром к зеркалу и вторым лучом — углом отражения. Эти углы равны.
Формулы геометрической оптики раскрывают многие ситуации, о которых никто даже не задумывается. Например, закон отражения объясняет, почему мы можем видеть себя в «прямом» зеркале в точности такими же, какие мы есть, и почему его искривленная поверхность создает иной образ.
Формула:
a — угол падения, b — угол отражения.
a = b
Закон преломления
Луч падения, луч преломления и перпендикуляр к зеркалу расположены в одной плоскости.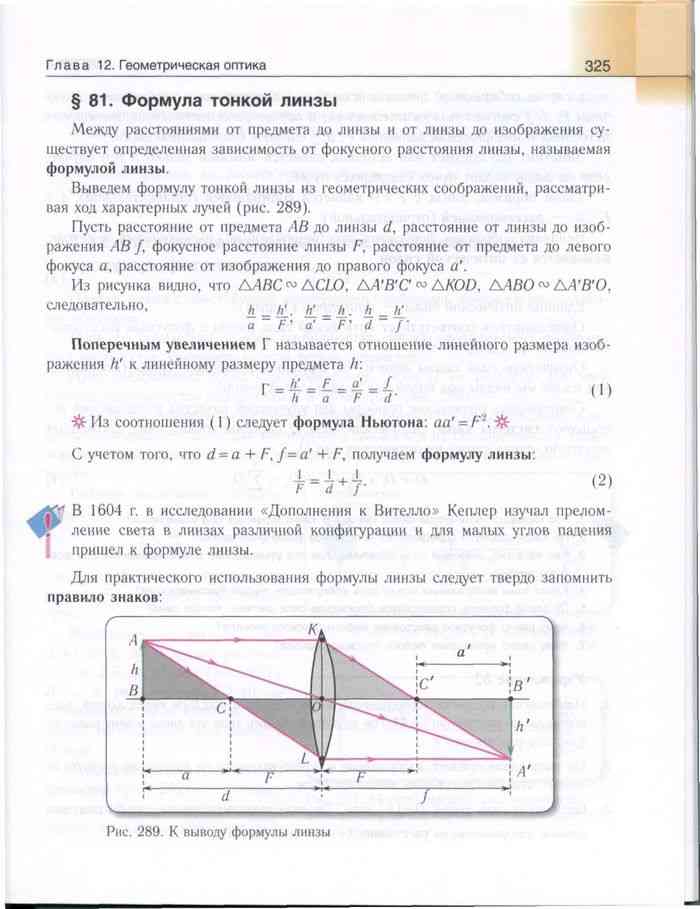 Если синус падающего угла поделить на синус преломляющегося угла, то получится величина n, которая является постоянной для обеих сред.
Если синус падающего угла поделить на синус преломляющегося угла, то получится величина n, которая является постоянной для обеих сред.
n показывает, под каким углом луч из первой среды переходит во вторую, и как соотносятся составы этих сред.
Формула:
i — падающий угол. r — преломляющийся угол. n21 — показатель преломления.
sin i/sin r = n2/n1 = n21
Закон обратимости света
О чем гласит закон обратимости света? Если луч распространяется по определенно выстроенной траектории в одном направлении, то и в противоположном направлении он повторит тот же маршрут.
Итоги
Формулы геометрической оптики в несколько упрощенном виде объясняют, как работает луч света. В этом нет ничего сложного. Да, формулы и законы геометрической оптики пренебрегают некоторыми свойствами вселенной, но нельзя недооценивать их важность для науки.
|
ФГОС комплект. Лабораторный комплект (набор) по оптике
Комплект учебного оборудования предназначен для проведения фронтальных лабораторных работ при изучении раздела «Оптика» школьного курса физики.
Назначение
Комплект учебного оборудования позволяет выполнять не менее 21 лабораторной работы в соответствии с требованиями учебных программ
школьного курса физики, в том числе: измерения фокусного расстояния собирающей и рассеивающей линз, увеличения
лупы, длины световой волны с помощью дифракционной решетки, показателя преломления света, исследования явления
отражения света, формулы линзы, размеров изображений предметов, явлений дисперсии, преломления и полного
внутреннего отражения света, проводить сборку моделей трубы Кеплера, трубы Галилея, микроскопа, наблюдать
дифракцию и интерференцию света, дифракцию световой волны в круглом отверстии, проводить построение изображения
предмета в плоском зеркале, определять фокусное расстояние собирающей линзы, получать изображения с помощью
собирающей линзы.
Комплект поставки
| №п/п | Наименование | Кол-во |
| 1. | Пенал с крышкой и ложементом | 1 |
| 2. | Оптическая скамья | 1 |
| 3. | Источник света | 1 |
| 4. | Рейтер для рамок | 1 |
| 5. | Линза собирающая длиннофокусная с рейтером | 1 |
| 6. | Линза собирающая короткофокусная с рейтером | 1 |
| 7. | Линза рассеивающая с рейтером | 1 |
| 8. | Рамка с дифракционными решетками | 1 |
| 9. | Рамка с диафрагмой с отверстиями различной формы | 2 |
10. |
Пластина с параллельными гранями | 1 |
| 11. | Подставка | 1 |
| 12. | Булавка | 4 |
| 13. | Коврик | 1 |
| 14. | Провод соединительный | 2 |
| 15. | Экран | 1 |
| 16. | Зеркало | 1 |
Преимущества:
- не требует затемнения помещения, где проводятся опыты
- надежная фиксация оптических элементов
- компактная конструкция
- возможность использования при надомном обучении
- не содержит деталей и узлов с ограниченным ресурсом работы
Методическое обеспечение (не входит в базовую комплектацию):
Методики использования лабораторного комплекта в учебном процессе представлены в методических рекомендациях и электронном пособии на СD.
Печатное методическое пособие:
Электронное методическое пособие на CD:
Оказываем содействие в подготовке технических требований для тендерной документации.
Перечень лабораторных работ, выполняемых с помощью лабораторного комплекта
1. Исследование явления отражения света
2 Построение изображения предмета в плоском зеркале
3. Измерение фокусного расстояния собирающей линзы
4. Измерение оптической силы собирающей линзы
5. Определение фокусного расстояния собирающей линзы с использованием формулы линзы
6. Измерение фокусного расстояния рассеивающей линзы
7. Получение изображения с помощью собирающей линзы
8. Экспериментальное исследование формулы линзы
9. Исследование размеров изображений предметов даваемых линзами
10. Измерение увеличения лупы
11. Сборка модели трубы Кеплера
12. Сборка модели трубы Галилея
13.Сборка модели микроскопа
14. Исследование явления дисперсии
15. Наблюдение дифракции света
16. Наблюдение интерференции света
17. Измерение длины световой волны с помощью дифракционной решетки
18. Наблюдение дифракции световой волны на круглом отверстии
19. Исследование явления преломления света
20. Измерение показателя преломления вещества
21. Исследование явления полного внутреннего отражения света
Пример:
Лекции по оптике — Кафедра общей физики
КУРС ЛЕКЦИЙ
ПО ОПТИКЕ:
Лекция №1 «Геометрическая оптика» от 9 февраля 2019 г.
Содержание лекции: Обзор литературы к курсу «Оптика». Энергия кванта света. Геометрическая оптика. Принцип Ферма. Закон преломления, закон отражения. Оптические Аберрации. Формула тонкой линзы. Условие синусов Аббе. Микроскоп.
Энергия кванта света. Геометрическая оптика. Принцип Ферма. Закон преломления, закон отражения. Оптические Аберрации. Формула тонкой линзы. Условие синусов Аббе. Микроскоп.
Лекция №2 «Волновая оптика» от 16 февраля 2019 г.
Содержание лекции: Телескоп. Элементы фотометрии.
Волновая оптика. Волновое уравнение, монохроматические волны, комплексная амплитуда, уравнение Гельмгольца, плоские и сферические волны, показатель преломления, фазовая скорость распространения, комплексная диэлектрическая проницаемость и комплексный показатель преломления, связь мнимой части с поглощением света средой. Угол Брюстера.
Лекция №3 «Дисперсия» от 2 марта 2019 г.
Содержание лекции: Теория дисперсии. Коэффициент преломления. Коэффициент поглощения. Связь коэффициента преломления с поглощением среды. Аномальная дисперсия, нормальная дисперсия. Особенные случаи преломления. Поляризация в плотных средах. Формула Лоренца-Лоренца. Связь векторов E, H и k. Метаматериалы. Фазовая и групповая скорости. Волновой пакет. Формула Рэлея. Размытие волнового пакета. Эффект Доплера.
Лекция №4 «Интерференция» от 9 марта 2019 г.
Содержание лекции: Принцип суперпозиции. Интенсивность световой волны. Метод векторных диаграмм. Интерференция плоских монохроматических волн. Разность хода. Видность. Кольца Ньютона. Временная когерентность. Спектральный подход. Корреляционная функция.
Лекция №5 «Пространственная когерентность. Дифракция» от 16 марта 2019 г.
Содержание лекции: Временная когерентность (продолжение). Функция когерентности. Видность. Средняя интенсивность интерференционной картины.
Теорема Винера-Хинчина.
Пространственная когерентность. Радиус когерентности. Звездный интерферометр Майкельсона. Условие наблюдения интерференции.
Дифракция. Основная задача теории дифракции. Дифракция на тонком экране.
Лекция №6 «Дифракция Френеля» от 23 марта 2019 г.
Содержание лекции: Граничные условия Киргофа. Принцип Гюйгенса-Френеля. Дифракция Френеля. Задачи с осевой симметрией. Приближение Френеля. Зоны Френеля. Пятно Пуассона. Зонные пластинки. Линза Френеля. Дифракция Френеля на щели. Спираль Корню.
Зоны Френеля. Пятно Пуассона. Зонные пластинки. Линза Френеля. Дифракция Френеля на щели. Спираль Корню.
Лекция №7 «Дифракция Фраунгофера» от 30 марта 2019 г.
Содержание лекции: Дифракция Фраунгофера. Интеграл Френеля. Приближение Френеля. Дифракция на одной щели. Дифракция на круглом и квадратном отверстии. Разрешение оптического прибора. Волновой параметр. Демонстрация переходов между геометрической оптикой и дифракцией. Спектральные приборы.
Лекция №8 «Спектральные приборы» от 6 апреля 2019 г.
Содержание лекции: Спектральные приборы. Спектральные характеристики дифракционной решетки (дисперсия, дисперсионная область, разрешающая способность). Интерферометр Фабри-Перо. Спектральные характеристики интерферометра Фабри-Перо. Призма. Сравнение спектральных приборов. Лазеры. Дифракция Рентгеновских лучей. Условие Брегга-Вульфа.
Интерферометр Фабри-Перо. Спектральные характеристики интерферометра Фабри-Перо. Призма. Сравнение спектральных приборов. Лазеры. Дифракция Рентгеновских лучей. Условие Брегга-Вульфа.
Лекция №9 «Фурье-оптика» от 13 апреля 2019 г.
Содержание лекции: Элементы Фурье-оптики. Плоская волна. Дифракция на синусоидальной решетке. Теория Аббе формирования оптического изображения. Частотная характеристика свободного пространства. Голограммы.
Лекция №10 «Голограммы. Поляризация» от 20 апреля 2019 г.
Содержание лекции: Голограммы. Голограмма точечного источника (голограмма Габора). Объемная голограмма. Метод Денисюка. Поляризация. Эллиптическая, линейная, круговая поляризация. Монохроматическая волна. Естественный свет. Как получить поляризованный свет? Закон Малюса.
Объемная голограмма. Метод Денисюка. Поляризация. Эллиптическая, линейная, круговая поляризация. Монохроматическая волна. Естественный свет. Как получить поляризованный свет? Закон Малюса.
Лекция №11 «Поляризация. Оптика анизотропных сред» от 27 апреля 2019 г.
Содержание лекции: Поляризация. Линейная поляризация. Круговая поляризация. Эллиптическая поляризация. Поляризация естественного света. Поляроиды. Оптика анизотропных сред. Взаимная ориентация векторов k, E, D, B, направление вектора Пойнтинга. Модель осциллятора. Фазовые пластинки (λ/4, λ/2).
Лекция №12 «Анизотропия. Рассеяние света» от 4 мая 2019 г.
Содержание лекции: Двойное лучепреломление в одноосных кристаллах. Принцип Гюйгенса-Френеля для обыкновенной и необыкновенной волн. Явление Керра. Эффект Поккельса. Ячейка Поккельса. Эффект Фарадея. Рассеяние света. Рассеяние Рэлея. Поляризация рассеянного света. Рассеяние Ми. Закон Бугера-Ламберта-Бера.
Лекция №13 «Нелинейные эффекты» от 11 мая 2019 г.
Содержание лекции: Элементы нелинейной оптики. Нелинейная поляризация среды. Метод последовательных приближений. Генерация второй гармоники. Инверсия координат. Учет кубической поправки к поляризации. Самофокусировка. Гауссовы пучки. Радиус кривизны луча. Световоды. Градиентные оптоволокна. Одномодовое волокно.
Формулы лучевой оптики | Репетитор 4 Физика
Присоединяйтесь к нашим интерактивным онлайн-урокам на Buzztutor. com
com
Преломление
Явление изменения пути света при переходе из одной среды в другую
Законы преломления
Первый
Падающий луч, преломленный луч и нормаль к точке падения лежат в одной плоскости
Второй
Sin i / Sin r = μ [показатель преломления второй среды по отношению к первой среде]
Также μ = c/v или v 1 /v 2
μ = реальная глубина / кажущаяся глубина
Свет входит в среду а, пересекает среду b и затем выходит из среды с, затем a μ c = a μ b x b μ c
Полное внутреннее отражение
Когда свет, идущий из более плотной среды в более разреженную, падает под углом, превышающим критический угол, оно отражается обратно в более плотную среду.
Условия полного внутреннего отражения
Свет должен перемещаться от более плотной среды к более разреженной.
Угол i > угла i c , где i c — критический угол.
Критический угол
Когда свет распространяется из более плотной среды в более разреженную, то угол падения, при котором угол преломления 90 o
Преломление на сферической преломляющей поверхности
От более редкого до более плотного среднего
-μ 1 /u + μ 2 /v = (μ 2 — μ 1 )/R
где μ 1 и μ 2 — показатели преломления более разреженной и более плотной среды соответственно
R — радиус кривизны сферической поверхности.
От более плотного до более редкого среднего
-μ 2 /u + μ 1 /v = (μ 1 — μ 2 )/R
Формула производителя линз
1/f = (μ — 1)(1/R 1 — 1/R 2 )
Где μ — показатель преломления материала линзы
R 1 и R 2 — радиусы кривизны двух поверхностей линзы.
Формула линзы
1/в — 1/и = 1/ф
Линейное увеличение
м = ч i /ч o = v/u
Сила линзы
P = 1/f, если f выражено в метрах. Единицы P: диоптрия D
Единицы P: диоптрия D
Комбинация из двух тонких линз
Контактные линзы
1/F = 1/F 1 + 1/F 2 => P = P 1 + P 2 и m = m 1 x m 2
Линзы, разделенные конечным расстоянием
1/F = 1/F 1 + 1/F 2 — D/F 1 F 2
Преломление через призму
Угол отклонения
δ = (μ — 1) A для A o (тонкая призма)
δ = (i 1 + i 2 ) — A для A > 10 o
здесь i 1 и i 2 — углы падения и выхода
Угловая дисперсия
δ v — δ r = (μ v — μ r )A
А + δ = я + е
Формула призмы
мк = (Sin(A + δ м /2)) / Sin A/2
где δ м угол минимального отклонения
Дисперсионная способность
w = Угловая дисперсия/Средняя дисперсия = (µ v — µ r )/(µ — 1)
v и r относятся к фиолетовому и красному цветам
мк относится к средней длине волны цвета (желтый)
Увеличение мощности
Простой микроскоп
м = 1 + D/f, где D = наименьшее расстояние четкого зрения = 2. 5 см
5 см
Составной микроскоп
Отношение угла, образуемого конечным изображением к глазу, к углу, образуемому глазом объект, где и конечное изображение, и объект расположены на наименьшем расстоянии отчетливого зрения.
м = L/f o [1 + (D/f e )]
L — длина тубуса микроскопа
f o — фокусное расстояние объектива
f e — фокусное расстояние окуляра
Астрономический телескоп
Нормальная регулировка
Окончательное изображение формируется на бесконечности
Увеличение астрономического телескопа при нормальной настройке определяется как отношение угол, образуемый в глазу окончательным изображением, к углу, образуемому в глазу объектом непосредственно, когда конечное изображение и объект находятся на бесконечном расстоянии от глаза.
м = f o /-f e
Окончательное изображение, по крайней мере, на расстоянии четкого зрения
Определяется как отношение угла, образуемого глазом конечным изображением на наименьшем расстоянии отчетливого зрения к углу, образуемому в глазу объектом, находящимся в бесконечности, если смотреть прямо
м = (f o /f e )(1 + f e /D)
Телескоп Кассегрена-рефлектора
м = f o /f e = (R/2)/f e
Разрешающая способность микроскопа
Разрешающая способность = 1/d = (2µSinθ)/λ
где μ — показатель преломления среды
λ — длина волны света
θ — половина угла конуса света от трехточечного объекта до линзы объектива
Разрешающая способность телескопа
Разрешающая способность = 1/dθ = D/1. 22λ
22λ
где D — диаметр линзы объектива
λ — длина волны света
Законы отражения
Угол i = угол r
Падающий луч, отраженный луч и нормаль к точке падения лежат в одной плоскости
Формула зеркала
1/v + 1/u = 1/f
м = ч i /ч о = -v/u
Physics4Kids.com: Свет и оптика: преломление
Когда ученые говорят о преломлении, они используют формулу.«n = c/v» «c» — скорость света в вакууме , «v» — скорость света в этом веществе, а «n» — показатель преломления . Согласно формуле, показатель преломления есть отношение скорости света в вакууме к скорости света в веществе. Но что такое преломление? Когда свет переходит из одного вещества в другое, он меняет скорость и направление . Это изменение направления называется преломлением. Некоторые показатели преломления алмазные (2.419), стекло (1,523) и вода (1,33).
Давайте прыгнем сюда. Поскольку наша формула говорит, что n=c/v, и мы знаем, что значение c является константой, мы можем понять, что свет имеет разные скорости, когда он находится в разных веществах. Он движется на полной скорости в вакууме и медленнее везде. Используя наши примеры, мы можем обнаружить, что свет в воде движется быстрее, чем в алмазе. Свет движется с максимальной скоростью, когда находится в вакууме. Свет движется со скоростью около 124 000 000 метров в секунду (меньше половины скорости в вакууме) в алмазе по сравнению с 299 792 458 метрами в секунду в вакууме.
Свет преломляется только тогда, когда он падает на границу под углом, поэтому, если свет попадает прямо в вещество, он будет продолжать двигаться прямо вниз. Нужно понимать, что скорость света меняется в разных веществах. Если световой луч замедляется при попадании на вещество, он отклоняется в сторону нормали. Нормаль – это линия, которая проходит перпендикулярно поверхности вещества. Если световой луч ускоряется при попадании на вещество, он отклоняется от нормали.
Если световой луч ускоряется при попадании на вещество, он отклоняется от нормали.
Оптика и алгебра (видео NASAConnect)
Encyclopedia.com:
http://www.encyclopedia.com/topic/refraction.aspx
Википедия:
http://en.wikipedia.org/wiki/Refraction
Британская энциклопедия:
http://www.britannica.com/EBchecked/topic/495648/refraction
Разделы Physics4Kids
Сеть научных и математических сайтов Rader
Матрично-оптическое представление используемых в настоящее время формул оптической силы интраокулярных линз
Цель:
В настоящее время для расчета оптической силы интраокулярных линз (ИОЛ) используются формулы SRK II, SRK/T, Holladay I, Hoffer Q и Haigis. Помимо эмпирического SRK II, эти формулы основаны на параксиальной оптике. При разных обозначениях и разных алгебраических формах сравнение формул затруднено. С другой стороны, матричные методы уже много лет успешно используются в параксиальной оптике, предлагая элегантный, простой и понятный способ определения характеристик сложных оптических систем. Таким образом, целью данного исследования было представление текущих теоретических формул ИОЛ в матричных обозначениях.
Помимо эмпирического SRK II, эти формулы основаны на параксиальной оптике. При разных обозначениях и разных алгебраических формах сравнение формул затруднено. С другой стороны, матричные методы уже много лет успешно используются в параксиальной оптике, предлагая элегантный, простой и понятный способ определения характеристик сложных оптических систем. Таким образом, целью данного исследования было представление текущих теоретических формул ИОЛ в матричных обозначениях.
Методы: Формулы SRK/T, Holladay I, Hoffer Q и Haigis были проанализированы, алгебраически преобразованы и выражены в матрично-оптической записи в виде матриц переноса и преломления и системной матрицы.Был проведен примерный расчет, который сравнивался с результатами двух коммерческих биометрических приборов (Zeiss IOLMaster и Tomey AL-2000).
Результаты:
Хотя все исследованные формулы основаны на оптике тонких линз в параксиальном приближении, существуют значительные различия в интерпретации и расчете оптической силы роговицы, осевой длины и эффективного положения линзы, а также в способе представления отдельных ИОЛ («константы ИОЛ»). .Приведены все соотношения, необходимые для матрично-оптического представления.
.Приведены все соотношения, необходимые для матрично-оптического представления.
Выводы: Матрично-оптическое представление используемых в настоящее время формул оптической силы ИОЛ предлагает новое понимание расчета ИОЛ и позволяет глубже понять преимущества и недостатки каждой формулы.
Геометрическая оптика 101: расчеты трассировки параксиальных лучей
Трассировка лучей — это основной метод, используемый инженерами-оптиками для определения производительности оптической системы.Трассировка лучей — это процесс ручного отслеживания луча света через систему путем вычисления угла преломления/отражения на каждой поверхности. Этот метод чрезвычайно полезен в системах со многими поверхностями, где уравнения отображения Гаусса и Ньютона не подходят из-за степени сложности.
Сегодня программное обеспечение для трассировки лучей, такое как ZEMAX ® или CODE V ® , позволяет инженерам-оптикам быстро моделировать работу очень сложных систем. Параксиальная трассировка лучей включает в себя малые углы и высоты лучей.Чтобы понять основные принципы параксиальной трассировки лучей, рассмотрите необходимые расчеты и таблицы трассировки лучей, используемые при ручной трассировке лучей света, проходящих через систему. Это, в свою очередь, подчеркнет полезность современного компьютерного программного обеспечения.
Параксиальная трассировка лучей включает в себя малые углы и высоты лучей.Чтобы понять основные принципы параксиальной трассировки лучей, рассмотрите необходимые расчеты и таблицы трассировки лучей, используемые при ручной трассировке лучей света, проходящих через систему. Это, в свою очередь, подчеркнет полезность современного компьютерного программного обеспечения.
ЭТАПЫ ТРАССИРОВКИ ПАРАКСИАЛЬНЫХ ЛУЧЕЙ: РАСЧЕТ BFL ОБЪЕКТИВА PCX
Параксиальная трассировка лучей вручную обычно выполняется с помощью листа для трассировки лучей (рис. 1). По горизонтали указано количество оптических поверхностей линзы, по вертикали — основные параметры линзы.Есть также разделы, чтобы различать краевой и главный луч. В таблице 1 поясняются основные параметры оптических линз.
Чтобы проиллюстрировать этапы трассировки параксиальных лучей вручную, рассмотрим плосковыпуклую (PCX) линзу. В этом примере для простоты используется светосильный объектив #49-849 диаметром 25,4 мм и диаметром 50,8 мм. Этот конкретный расчет используется для расчета заднего фокусного расстояния $ \small{ \left( \text{BFL} \right)} $ объектива PCX, но следует отметить, что трассировка лучей может использоваться для расчета широкого спектра параметры системы, начиная от сторон света и заканчивая размером и расположением зрачка.
Этот конкретный расчет используется для расчета заднего фокусного расстояния $ \small{ \left( \text{BFL} \right)} $ объектива PCX, но следует отметить, что трассировка лучей может использоваться для расчета широкого спектра параметры системы, начиная от сторон света и заканчивая размером и расположением зрачка.
Рис. 1. Образец листа для трассировки лучей
Шаг 1: введите известные значения
Для начала введите известные размерные значения #49-849 в лист трассировки лучей (рис. 2). Поверхность 0 — это плоскость объекта, Поверхность 1 — выпуклая поверхность линзы, Поверхность 2 — плоская поверхность линзы, а Поверхность 3 — плоскость изображения (рис. 3).
Помните, что кривизна $\small{\left(C\right)}$ эквивалентна 1, деленному на радиус кривизны $\small{\left(R\right)}$.Первое значение толщины $ \small{ \left( t \right)} $ (в данном примере 25 мм) – это расстояние от объекта до первой поверхности линзы. Это значение является произвольным для падающего коллимированного света (т. е. света, параллельного оптической оси оптической линзы). Показатель преломления $ \small{ \left( n \right)} $ может быть приблизительно равен 1 в воздухе и 1,517 для подложки линзы Н-БК7.
е. света, параллельного оптической оси оптической линзы). Показатель преломления $ \small{ \left( n \right)} $ может быть приблизительно равен 1 в воздухе и 1,517 для подложки линзы Н-БК7.
| Переменная | Описание |
|---|---|
| $$ C $$ | Кривизна |
| $$ т $$ | Толщина |
| $$ нет $$ | Показатель преломления |
| $$ \Phi $$ | Поверхностная мощность |
| $$ г $$ | Высота луча |
| $$ u $$ | Угол луча |
Таблица 1: Параметры оптических линз для трассировки лучей
На рис. 2 красным прямоугольником обозначено вычисляемое значение, так как это расстояние от второй поверхности до точки фокусировки (BFL).Мощность $ \left( \Phi \right) $ отдельных поверхностей задается четвертой строкой и рассчитывается по уравнению 1. Примечание. Для упрощения дальнейших вычислений к этой строке добавлен знак минус. В этом примере поверхность 1 является единственной поверхностью с питанием, поскольку это единственная криволинейная поверхность в системе.
Примечание. Для упрощения дальнейших вычислений к этой строке добавлен знак минус. В этом примере поверхность 1 является единственной поверхностью с питанием, поскольку это единственная криволинейная поверхность в системе.
(1) $$ \Phi = \left( n_2 — n_1 \right) C_1 $$
Рис. 2: Ввод известных значений параметров объектива в таблицу трассировки лучей
Рис. 3: Поверхности плосковыпуклой (PCX) линзы
Шаг 2. Добавьте маргинальный луч в систему
Следующим шагом является добавление в систему маргинального луча.Поскольку линза PCX имеет сферическую форму с постоянным радиусом кривизны и используется коллимированный входной пучок, высота луча $\small{\left(y\right)}$ является произвольной. Для упрощения расчетов используйте высоту 1 мм.
Коллимированный пучок также означает, что начальный угол луча $ \small{\left( u \right)} $ равен $ \small{0}° $. В листе трассировки лучей $ \small{ n \, u } $ — это просто угол луча, умноженный на показатель преломления этой среды. Обе переменные включены для упрощения последующих расчетов (рис. 4).
Обе переменные включены для упрощения последующих расчетов (рис. 4).
Рис. 4: Добавление маргинального луча на лист трассировки лучей
Шаг 3. Расчет BFL с помощью уравнений и листа трассировки лучей
Трассировка лучей включает два основных уравнения в дополнение к одному для расчета мощности. Уравнения 2 – 3 необходимы для любых расчетов трассировки лучей.
(2) $$ y’ = y + u’t’ $$
(3) $$ n’u’ = nu — y \Phi $$
, где апостроф обозначает последующую поверхность, угол, толщину и т. д.В этом примере, чтобы найти высоту луча на поверхности 2 $ \small{ \left( y’ \right) }$, возьмите высоту луча на поверхности 1 $ \small{ \left( y \right) }$ и добавьте ее до -0,0197 умножить на 3,296:
(2.1) \begin{align} y’ & = y + u’t’ \\ & = y + \left( \frac{t’}{n’} \right) n’u’ \\ & = 1 + \влево(3,296\вправо) \влево(-0,0197\вправо) = 0,93508 \end{align}
Выполнение этого для угла луча дает следующее значение. Весь процесс повторяется до тех пор, пока не будет завершена трассировка луча (рис. 5).
Весь процесс повторяется до тех пор, пока не будет завершена трассировка луча (рис. 5).
(3.1) \begin{align} n’u’ & = nu — y \Phi \\ & = -0,0197 + \left( 0,93508 \right) \left(-0 \right) = -0,0197 \end{ выровнять}
Рис. 5: Распространение луча по системе
Теперь найдите $ \small{\text{BFL}} $, регулируя значение толщины до тех пор, пока окончательная высота луча не станет равной 0 (рис. 6), либо путем обратного вычисления $ \small{\text{BFL}} $ для высоты луча 0. Для #49-849 конечное значение $\small{\text{BFL}}$ равно 47.48мм. Это очень близко к 47,50 мм, указанным в характеристиках объектива. Разница объясняется ошибкой округления при использовании показателя преломления 1,517 вместо несколько более точного значения, которое использовалось при первоначальной разработке линзы.
Рис. 6: Расчет заднего фокусного расстояния плосковыпуклой (PCX) линзы с помощью таблицы трассировки лучей
РАСШИФРОВКА ДВУХЛИНЗОВОГО ЛИСТКА ТРАССИРОВКИ ЛУЧЕЙ
Чтобы полностью понять лист трассировки лучей, рассмотрим систему с двумя линзами, состоящую из двояковыпуклой (DCV) линзы, диафрагмы и двояковыпуклой (DCX) линзы (рис.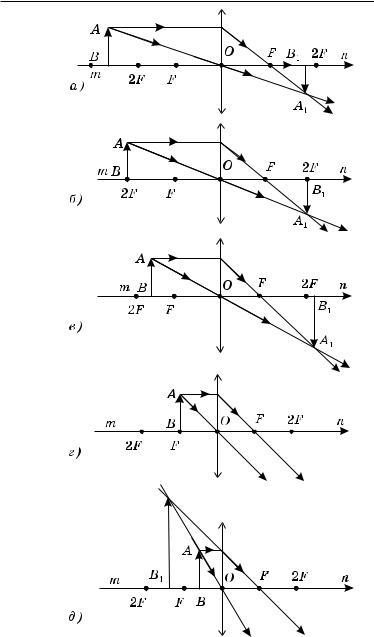 7–8).Чтобы узнать больше об объективах DCV и DCX, прочтите статью Общие сведения о геометрии оптических объективов.
7–8).Чтобы узнать больше об объективах DCV и DCX, прочтите статью Общие сведения о геометрии оптических объективов.
Рис. 7. Система линз с двойной вогнутостью (DCV) и двойной выпуклостью (DCX)
Рис. 8. Образец системы трассировки лучей с двойной вогнутостью (DCV) и двойной выпуклостью (DCX)
Апертурная диафрагма является ограничивающей апертурой и определяет количество света, проходящего через систему. Апертурная диафрагма может быть поверхностью оптической линзы или диафрагмой, но это всегда физическая поверхность.Входным зрачком является изображение апертурной диафрагмы при отображении его через предшествующие элементы линзы в предметное пространство. Выходной зрачок — это изображение апертурной диафрагмы, когда оно отображается через следующие элементы линзы в пространство изображения.
В оптической системе апертурная диафрагма и зрачки используются для определения двух очень важных лучей. Главный луч — это тот, который начинается на краю объекта и проходит через центр входного зрачка, выходного зрачка и стопа (другими словами, он имеет высоту $ \small{\left( \bar{y} \right)} $ из 0 в этих местах). Таким образом, главный луч определяет размер объекта и изображения и расположение зрачков.
Таким образом, главный луч определяет размер объекта и изображения и расположение зрачков.
Крайний луч оптической системы начинается на оси в плоскости объекта. Этот луч встречается с краем зрачков, останавливается и пересекает ось в точках объекта и изображения. Таким образом, маргинальный луч определяет положение предмета и изображения и размеры зрачков.
Место остановки диафрагмы
Если положение апертурной диафрагмы неизвестно, через систему должен пройти пробный луч, известный как псевдомаргинальный луч.Для объекта не на бесконечности этот луч должен начинаться в осевом положении объекта и может иметь произвольный угол падения. Для объекта в бесконечности луч может начинаться на произвольной высоте, но должен иметь угол падения $ \small{0} ° $. После того, как это выполнено, апертурная диафрагма представляет собой просто поверхность с наименьшим значением где $ \small{\text{CA}} $ – апертура поверхности в чистоте, а $\small{y_p} $ – высота псевдокраевого луча на этой поверхности.
После определения положения апертурной диафрагмы псевдокраевой луч можно соответствующим образом масштабировать для получения фактического маргинального луча (помните, что маргинальный луч должен касаться края апертурной диафрагмы). Когда размер и положение апертурной диафрагмы известны, высота краевого луча становится равной радиусу диафрагмы, а высота главного луча в этом месте равна нулю. Затем параксиальная трассировка лучей может выполняться как в прямом, так и в обратном направлениях от этих точек. При выполнении трассировки лучей в обратном порядке полезны уравнения 4–5.Обратите внимание на сходство с уравнениями 2 – 3.
(4) $$ y = y’ — u’t’ $$
(5) $$ nu = n’u’ + y \Phi $$
Анализ виньетирования
Когда положение и размер апертурной диафрагмы известны, используйте анализ виньетирования, чтобы увидеть, какие поверхности будут виньетировать или блокировать лучи. Анализ виньетирования выполняется путем деления чистой апертуры на каждой поверхности на два.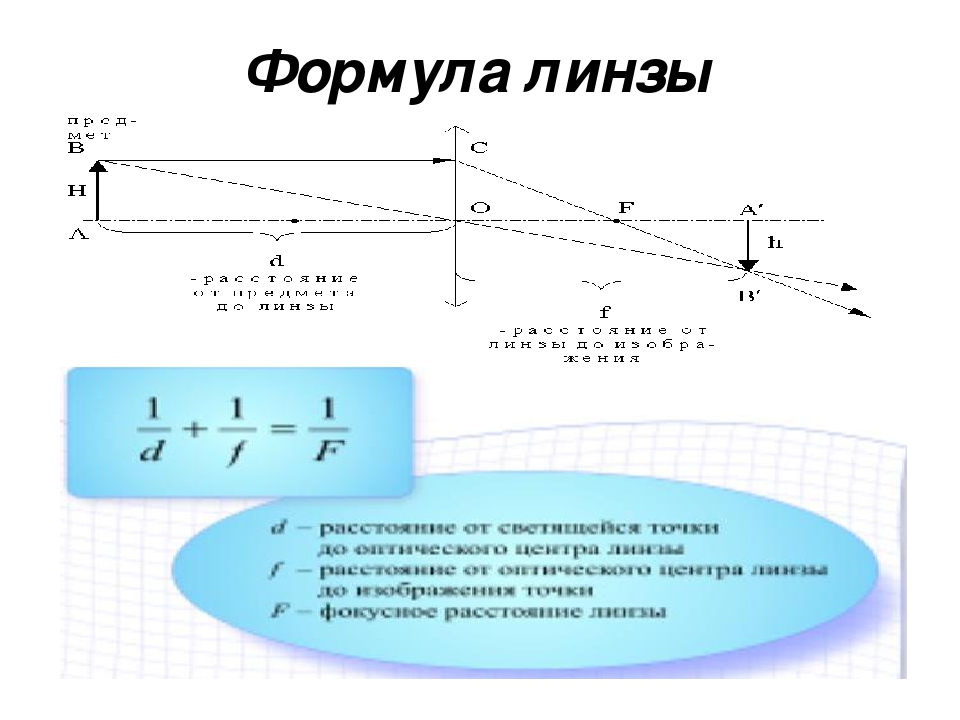 Затем это значение сравнивается с высотой главного и краевого лучей на этой поверхности (уравнение 6).Уравнение 6 можно легко преобразовать в уравнение 7. Если уравнение 7 верно, поверхность не виньетирует.
Затем это значение сравнивается с высотой главного и краевого лучей на этой поверхности (уравнение 6).Уравнение 6 можно легко преобразовать в уравнение 7. Если уравнение 7 верно, поверхность не виньетирует.
(6) $$ \frac{\text{CA}}{2} \geq \left| \бар{у} \право| + \влево| у \справа|$$
(7) $$ \frac{\text{CA}}{\left| \бар{у} \право| + \влево| у \справа|} \geq 2 $$
Обратите внимание, что в предыдущем примере DCV и DCX поверхность 3 является апертурной диафрагмой, где $ \tfrac{\text{CA}}{\left( \left| \bar{y} \right| + \left| y \right | \right)} Значение $ является наименьшим среди всех поверхностей.Кроме того, ни одна из поверхностей не виньетируется, потому что все значения больше или равны 2.
Размер и местоположение объекта/изображения
Объект (Поверхность 0)
- Размер 10 мм в диаметре (удвоенная высота главного луча на поверхности 0)
- Расположение в 5 мм перед первой линзой (первое значение толщины)
Изображение (Поверхность 6)
- Диаметр 18,2554 мм (удвоенная высота конечного главного луча)
- Расположение: 115,4897 мм за конечной поверхностью линзы (последнее значение толщины)
Важно отметить, что высота главного луча Surface 0 положительна, а высота главного луча Surface 6 отрицательна. Это указывает на то, что изображение перевернуто.
Это указывает на то, что изображение перевернуто.
Эффективное фокусное расстояние
Чтобы определить эффективное фокусное расстояние $ \small{ \left( \text{EFL} \right)} $, сначала необходимо провести псевдомаргинальный луч через систему для объекта на бесконечности (т.е. угол первого луча будет 0). На рисунке 9 для упрощения вычислений выбрана произвольная начальная высота 1. Как только это выполнено, $ \small{ \text{EFL}} $ системы определяется уравнением 8.
Рис. 9: Псевдомаргинальный луч
(8) \begin{align} \text{EFL} & = \frac{y_1}{nu_{\text{last}}} \\ & = \frac{1}{0.02870} = 34,843 \text{мм} \end{align}
(9) \begin{align} \text{FOV} & = 2 \left( n \bar{u} \right) \\ & = 2 \left( 0,182 \right) = 0,364 \text{радиан} = 20,856° \end{align}
где $ \small{n \, \bar{u}} $ — угол первого главного луча.
Инвариант Лагранжа
Оптический инвариант — это полезный инструмент, который позволяет разработчикам оптики определять различные значения без необходимости полностью трассировать систему. Он получается путем сравнения двух лучей внутри системы в любой осевой точке.Оптический инвариант постоянен для любых двух лучей в каждой точке системы. Другими словами, если известен инвариант для набора из двух лучей, проследите один из лучей, а затем масштабируйте его по инварианту, чтобы найти второй.
Он получается путем сравнения двух лучей внутри системы в любой осевой точке.Оптический инвариант постоянен для любых двух лучей в каждой точке системы. Другими словами, если известен инвариант для набора из двух лучей, проследите один из лучей, а затем масштабируйте его по инварианту, чтобы найти второй.
Инвариант Лагранжа — это вариант оптического инварианта, в котором в качестве двух интересующих лучей используются главный луч и маргинальный луч. Оно решается с помощью уравнения 10 и показано на рисунке 10.
(10) $$ Ж = n \bar{u} y — n u \bar{y} $$
Рис. 10: Инвариант Лагранжа трассировки лучей
РЕАЛЬНЫЕ ПРЕИМУЩЕСТВА ТРАССИРОВКИ ЛУЧЕЙ И ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
В параксиальной трассировке лучей есть несколько допущений, которые вносят ошибки в расчеты.Параксиальная трассировка лучей предполагает, что тангенс и синус всех углов равны самим углам (другими словами, $\small{\tan{\left( u \right)} = u} $ и $ \small{\sin{ \влево( и \вправо)} = и} $).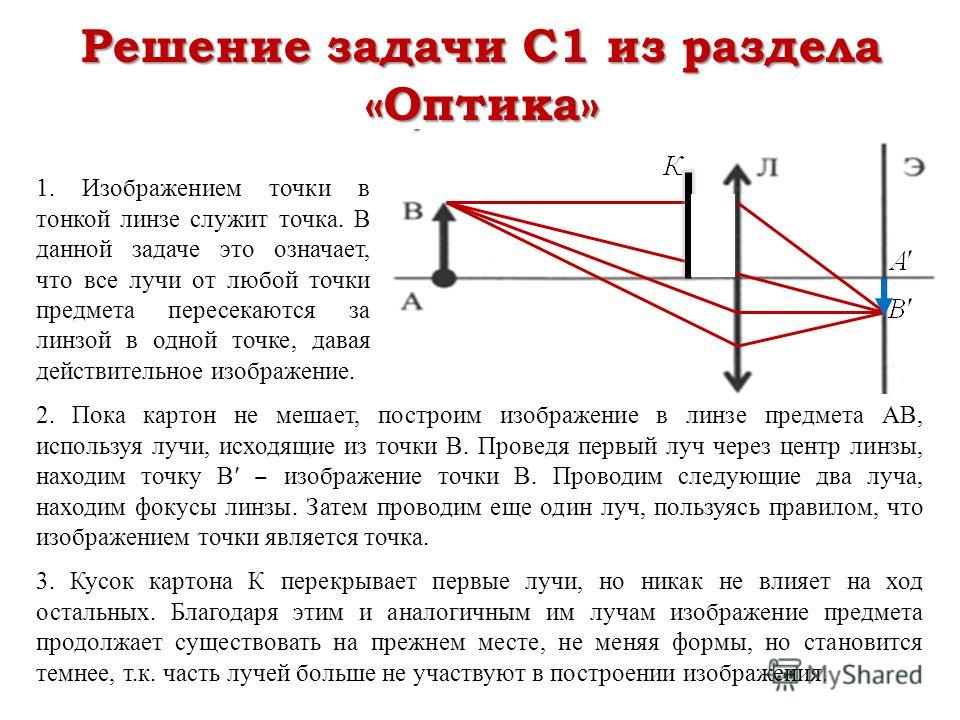 Это приближение справедливо для малых углов, но может привести к распространению ошибки по мере увеличения угла луча.
Это приближение справедливо для малых углов, но может привести к распространению ошибки по мере увеличения угла луча.
Реальная трассировка лучей — это метод уменьшения параксиальной ошибки за счет устранения малоугловой аппроксимации и учета прогиба каждой поверхности для лучшего моделирования преломления внеосевых лучей.Как и в случае параксиальной трассировки лучей, реальную трассировку лучей можно выполнить вручную с помощью листа трассировки лучей. Для краткости показан только параксиальный метод. Программное обеспечение для трассировки лучей, такое как CODE V и ZEMAX, использует реальную трассировку лучей для моделирования оптических систем, введенных пользователем.
Трассировка лучей вручную — утомительный процесс. Следовательно, программное обеспечение для трассировки лучей обычно является предпочтительным методом анализа. На рисунке 11 показана система DCV-DCX из раздела «Расшифровка двухлинзового листа трассировки лучей».На следующем снимке экрана ZEMAX показано значение фокусного расстояния 34,699 мм, что подтверждает ранее выполненный параксиальный расчет.
Рисунок 11: Пример данных системы ZEMAX
Трассировка лучей — важный инструмент для любого оптического дизайнера. Хотя распространение программного обеспечения для трассировки лучей свело к минимуму потребность в ручной трассировке параксиальных лучей, по-прежнему полезно концептуально понимать, как отдельные лучи света проходят через оптическую систему. Параксиальная трассировка лучей и трассировка реальных лучей — отличные способы приблизить характеристики оптических линз перед завершением проекта и запуском в производство.Без трассировки лучей проектирование системы намного сложнее, дороже и требует больше времени.
Каталожные номера
- Дереняк, Юстас Л. и Тереза Д. Дереняк. «Глава 10. Параксиальная трассировка лучей». В Геометрическая и тригонометрическая оптика , 255-91. Кембридж, Великобритания: Издательство Кембриджского университета, 2008. .
- Гири, Джозеф М. «Глава 4 – Параксиальный мир».
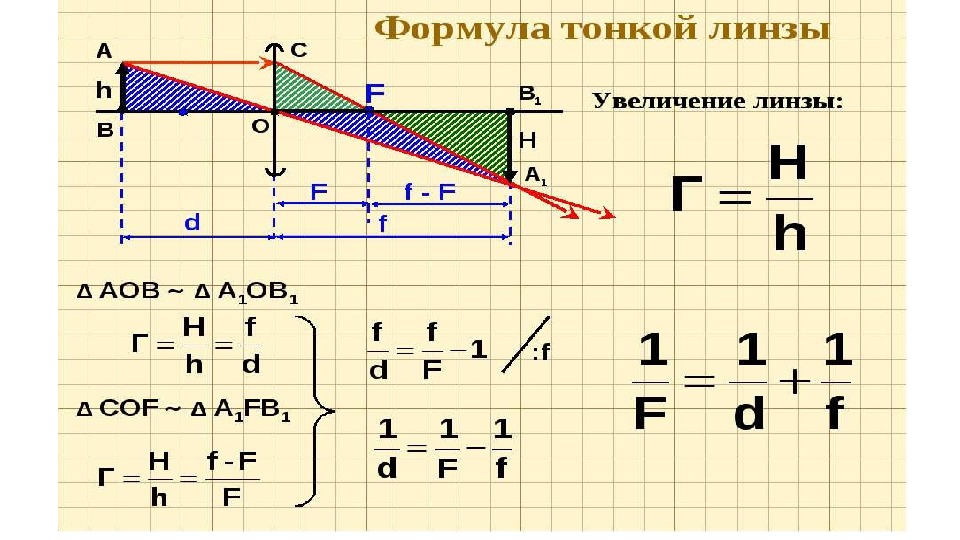 В Введение в конструкцию линз: с практическими примерами Zemax , 33-42. Ричмонд, Вирджиния: Уиллманн-Белл, 2002.
В Введение в конструкцию линз: с практическими примерами Zemax , 33-42. Ричмонд, Вирджиния: Уиллманн-Белл, 2002. - Грейвенкамп, Джон Э. «Параксиальная трассировка лучей». В Полевое руководство по геометрической оптике , 20-32. Том. ФГ01. Беллингем, Вашингтон: SPIE — Международное общество инженеров-оптиков, 2004 г. .
- Смит, Уоррен Дж. «Глава 3. Параксиальная оптика и расчеты». В Modern Optical Engineering , 35-51. 4-е изд. Нью-Йорк, штат Нью-Йорк: McGraw-Hill Education, 2007. .
6: Оптика — Физика LibreTexts
Изгиб света
Для преломления на поверхности: \(n_i\sin(\theta_i)=n_t\sin(\theta_t)\) где \(n\) — показатель преломления материала.2 n(s)ds=0\]
Параксиальная геометрическая оптика
Линзы
Формула линзы Гаусса может быть выведена из принципа Ферма с приближениями \(\cos\varphi=1\) и \(\sin\varphi=\varphi\). Для преломления на сферической поверхности радиусом \(R\):
\[\frac{n_1}{v}-\frac{n_2}{b}=\frac{n_1-n_2}{R}\]
, где \(|v|\) — расстояние до объекта, а \(|b|\) — расстояние до изображения. Применение этого дважды приводит к:
Применение этого дважды приводит к:
\[\frac{1}{f}=(n_{\rm l}-1)\left(\frac{1}{R_2}-\frac{1}{R_1}\right)\]
, где \(n_{\rm l}\) — показатель преломления линзы, \(f\) — фокусное расстояние, а \(R_1\) и \(R_2\) — радиусы кривизны обеих поверхностей.2\). Для двух линз, расположенных на одной линии с расстоянием \(d\) между ними:
\[\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}-\frac{d}{f_1f_2}\]
В этих уравнениях используются следующие знаки для преломления на сферической поверхности, как ее видит падающий луч света:
| Количество | + | — |
|---|---|---|
| \(Р\) | Вогнутая поверхность | Выпуклая поверхность |
| \(ф\) | Собирающая линза | Рассеивающая линза |
| \(в\) | Реальный объект | Виртуальный объект |
| \(б\) | Виртуальный образ | Реальное изображение |
Зеркала
Для изображений, образованных зеркалами
\[\frac{1}{f}=\frac{1}{v}+\frac{1}{b}=\frac{2}{R}+\frac{h^2}{2}\ влево(\frac{1}{R}-\frac{1}{v}\right)^2\]
, где \(h\) — расстояние по перпендикуляру от точки, в которой луч света падает на зеркало, до оптической оси. Сферическую аберрацию можно уменьшить, не используя сферические зеркала. Параболическое зеркало не имеет сферической аберрации для световых лучей, параллельных оптической оси, и поэтому часто используется в телескопах. Используемые знаки:
Сферическую аберрацию можно уменьшить, не используя сферические зеркала. Параболическое зеркало не имеет сферической аберрации для световых лучей, параллельных оптической оси, и поэтому часто используется в телескопах. Используемые знаки:
| Количество | + | — |
|---|---|---|
| \(Р\) | Вогнутое зеркало | Выпуклое зеркало |
| \(ф\) | Вогнутое зеркало | Выпуклое зеркало |
| \(в\) | Реальный объект | Виртуальный объект |
| \(б\) | Реальное изображение | Виртуальный образ |
Основные плоскости
узловых точек N линзы определены на рисунке \(\PageIndex{1}\). Если линза с обеих сторон окружена одной и той же средой, то узловые точки совпадают с главными точками Н. Плоскость \(\perp\) к оптической оси через главные точки называется главной плоскостью . Если линза описывается матрицей \(m_{ij}\), то для расстояний \(h_1\) и \(h_2\) до границы линзы верно:
Если линза с обеих сторон окружена одной и той же средой, то узловые точки совпадают с главными точками Н. Плоскость \(\perp\) к оптической оси через главные точки называется главной плоскостью . Если линза описывается матрицей \(m_{ij}\), то для расстояний \(h_1\) и \(h_2\) до границы линзы верно:
\[h_1=n\frac{m_{11}-1}{m_{12}}~~,~~~h_2=n\frac{m_{22}-1}{m_{12}}\]
Рисунок \(\PageIndex{1}\):Увеличение
Линейное увеличение определяется: \(\displaystyle N=-\frac{b}{v}\)
Угловое увеличение определяется следующим образом: \(\displaystyle N_{\alpha}=-\frac{\alpha_{\rm syst}}{\alpha_{\rm none}}\)
, где \(\alpha_{\rm sys}\) — размер изображения на сетчатке в оптической системе и \(\alpha_{\rm none}\) размер изображения на сетчатке вне системы.Далее: \(N\cdot N_{\alpha}=1\). Для телескопа: верно \(N=f_{\rm объектив}/f_{\rm окуляр}\). f-число определяется \(f/D _{\rm цель}\).
Матричные методы
Световой луч может быть описан вектором \((n\alpha,y)\) с \(\alpha\) углом с оптической осью и \(y\) расстоянием до оптической оси. Новое положение светового луча, взаимодействующего с оптической системой, можно получить с помощью умножения матриц:
Новое положение светового луча, взаимодействующего с оптической системой, можно получить с помощью умножения матриц:
\[\left(\begin{массив}{c}n_2\alpha_2\\y_2\end{массив}\right)=M \left(\begin{массив}{c}n_1\alpha_1\\y_1\end{ массив}\справа)\]
, где \({\rm Tr}(M)=1\).\(М\) есть произведение элементарных матриц. Это:
- Перенос по длине \(l\): \(\displaystyle M _{\rm R}= \left(\begin{array}{cc}1&0\\l/n&1\end{массив}\right)\)
- Рефракция на поверхности с диоптрийной силой \(D\): \(\displaystyle M _{\rm T}=\left(\begin{array}{cc}1&-D\\0&1\end{array}\right) \)
Аберрации
Объективыобычно не дают идеального изображения. Некоторые причины:
- Хроматическая аберрация вызвана тем, что \(n=n(\lambda)\).Это можно частично исправить с помощью составной линзы, состоящей из нескольких линз с разными показателями преломления \(n_i(\lambda)\). Использование \(N\) линз позволяет получить одинаковые \(f\) для \(N\) длин волн.
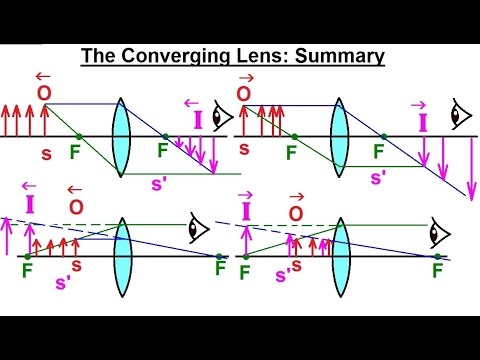
- Сферическая аберрация вызвана эффектами второго порядка, которые обычно игнорируются; сферическая поверхность не делает линзу идеальной. Лучи, падающие далеко от оптической оси, будут больше искривляться. Линзы Best form могут уменьшить сферическую аберрацию.
- Кома вызвана тем, что главные плоскости линзы плоские только вблизи главной оси. Далее от оптической оси они изогнуты. Эта кривизна может быть как положительной, так и отрицательной.
- Астигматизм : для каждой точки объекта, не лежащей на оптической оси, изображение представляет собой эллипс, потому что толщина линзы не везде одинакова.
- Кривизна поля может быть скорректирована человеческим глазом.
- Искажение приводит к аберрации по краям изображения.Это можно исправить комбинацией положительных и отрицательных линз.
Отражение и передача
Если электромагнитная волна попадет в прозрачную среду, часть волны отразится под тем же углом, что и угол падения, а часть преломится под углом в соответствии с законом Снеллиуса . Имеет значение, является ли \(\vec{E}\) поле волны \(\perp\) или \(\parallel\) w.r.t. поверхность. Когда коэффициенты отражения \(r\) и пропускания \(t\) определяются как:
Имеет значение, является ли \(\vec{E}\) поле волны \(\perp\) или \(\parallel\) w.r.t. поверхность. Когда коэффициенты отражения \(r\) и пропускания \(t\) определяются как:
\[r_\parallel\equiv\left(\frac{E_{0r}}{E_{0i}}\right)_\parallel~,~~ r_\perp\equiv\left(\frac{E_{0r} }{E_{0i}}\right)_\perp~,~~ t_\parallel\equiv\left(\frac{E_{0t}}{E_{0i}}\right)_\parallel~,~~ t_ \perp\equiv\left(\frac{E_{0t}}{E_{0i}}\right)_\perp\]
, где \(E_{0r}\) — амплитуда отраженного сигнала и \(E_{0t}\) — амплитуда переданного сигнала.Тогда уравнений Френеля таковы:
\[r_\parallel=\frac{\tan(\theta_i-\theta_t)}{\tan(\theta_i+\theta_t)}~~~,~~~ r_\perp =\frac{\sin(\theta_t- \theta_i)}{\sin(\theta_t+\theta_i)}\\\]
\[t_\parallel=\frac{2\sin(\theta_t)\cos(\theta_i)}{\sin(\theta_t+\theta_i)\cos(\theta_t-\theta_i)}~~~,~~~ t_\perp =\frac{2\sin(\theta_t)\cos(\theta_i)}{\sin(\theta_t+\theta_i)}\]
и выполняется следующее: \(t_\perp-r_\perp=1\) и \(t_\parallel+r_\parallel=1\).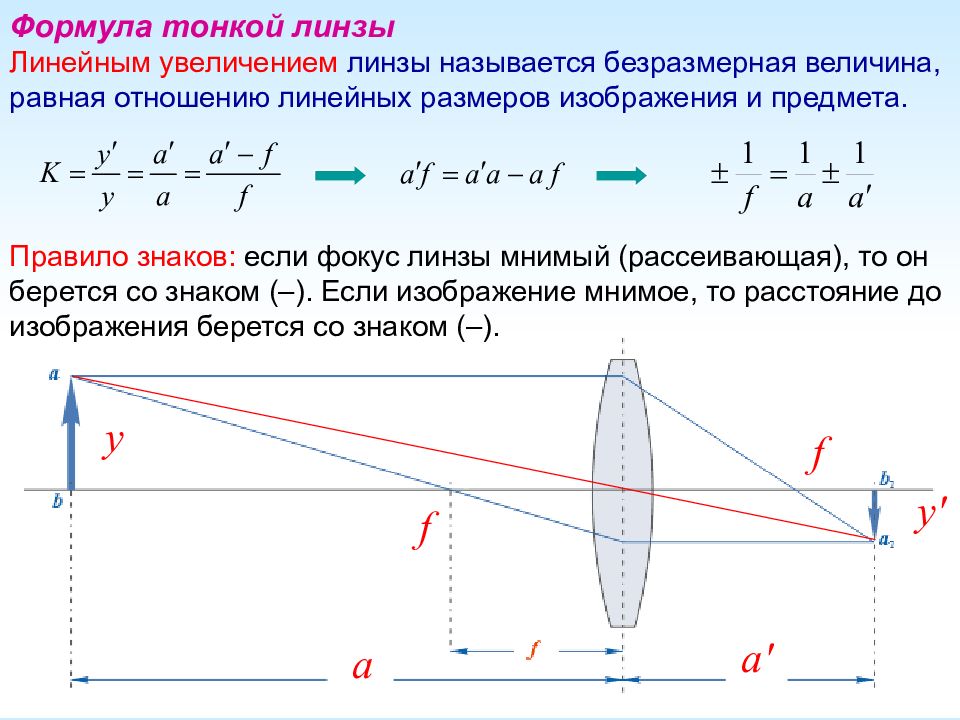 Если коэффициенты отражения \(R\) и пропускания \(T\) определены как (с \(\theta_i=\theta_r\)):
Если коэффициенты отражения \(R\) и пропускания \(T\) определены как (с \(\theta_i=\theta_r\)):
\[R\equiv\frac{I_r}{I_i}~~~\mbox{and}~~~T\equiv\frac{I_t\cos(\theta_t)}{I_i\cos(\theta_i)}\]
с \(I=\langle|\vec{S}|\rangle\) следует, что: \(R+T=1\).\круг\). Из закона Снеллиуса следует: \(\tan(\theta_i)=n\). Этот угол называется углом Брюстера . Ситуация с \(r_\perp=0\) невозможна.
Поляризация
Поляризация определяется как:
\[P = \ frac {I _ {\ rm p}} {I _ {\ rm p} + I _ {\ rm u}} = \ frac {I _ {\ rm max} -I _ {\ rm min}} {I_ {\rm макс}+I _{\rm мин}}\]
, где интенсивность поляризованного света определяется как \(I_{\rm p}\), а интенсивность неполяризованного света определяется как \(I_{\rm u}\).{i\varphi_y} \end{массив}\right)\]
Для горизонтального \(P\)-состояния: \(\vec{E}=(1,0)\), для вертикального \(P\)-состояния \(\vec{E}=(0,1) )\), \(R\)-состояние задается \(\vec{E}= \frac{1}{2} \sqrt{2}(1,-i)\), а \(L\ )-состояние на \(\vec{E}= \frac{1}{2} \sqrt{2}(1,i)\).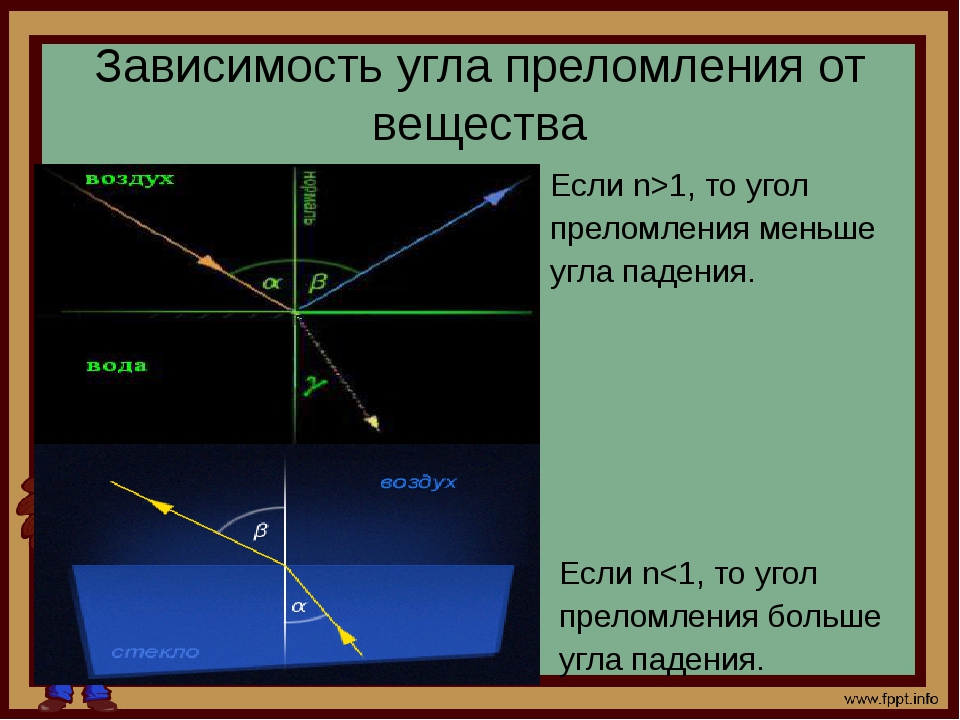 {i\pi/4}\left(\begin{array}{cc}1&0\\0&i\end {массив}\справа)\]
{i\pi/4}\left(\begin{array}{cc}1&0\\0&i\end {массив}\справа)\]
Призмы и рассеиватели
Луч света, проходящий через призму, дважды преломляется и получает отклонение от своего первоначального направления \(\delta=\theta_i+\theta_{i’}+\alpha\) w.р.т. направление падения, где \(\alpha\) — угол при вершине, \(\theta_i\) — угол между углом падения и линией, перпендикулярной поверхности, а \(\theta_{i’}\) — угол между лучом, выходящим из призмы, и линией, перпендикулярной поверхности. Когда \(\theta_i\) изменяется, существует угол, для которого \(\delta\) становится минимальным. Для показателя преломления призмы сейчас:
\[n = \ frac {\ sin (\ frac {1} {2} (\ delta _ {\ rm min} + \ alpha))} {\ sin (\ frac {1} {2} \ alpha)} \ ]
Дисперсия призмы определяется:
\[D=\frac{d\delta}{d\lambda}=\frac{d\delta}{dn}\frac{dn}{d\lambda}\], где первый фактор зависит от формы и второй по составу призмы. 2 \]
2 \]
, где \(u=\pi b\sin(\theta)/\lambda\), \(v=\pi d\sin(\theta)/\lambda\).2\]
, где \(\alpha’=kax/2R\) и \(\beta’=kby/2R\).
При дифрагировании рентгеновских лучей на кристалле Соотношение Брэгга выполняется для положения максимальной интенсивности: \(2d\sin(\theta)=n\lambda\), где \(d\) — расстояние между слоями кристалла.
Рядом с источником модель Фраунгофера i недействительна, поскольку она игнорирует зависимость отраженных волн от угла. Это описывается коэффициентом наклона или коэффициентом наклона , который описывает направленность вторичных выбросов: \(E(\theta)=\frac{1}{2}E_0(1+\cos(\theta)) \) где \(\theta\) — угол w.р.т. оптическая ось.
Дифракция ограничивает разрешение системы. Это минимальный угол \(\Delta\theta_{\rm min}\) между двумя падающими лучами, исходящими из удаленных точек, для которого их картины преломления могут быть обнаружены по отдельности. Для круглой щели: \(\Delta\theta_{\rm min}=1,22\lambda/D\), где \(D\) — диаметр щели.
Для решетки: \(\Delta\theta_{\rm min}=2\lambda/(Na\cos(\theta_m))\) где \(a\) — расстояние между двумя пиками и \(N\) количество вершин.Минимальная разница между двумя длинами волн, которая дает разделенную дифракционную картину в геометрии с несколькими щелями, определяется выражением \(\Delta\lambda/\lambda=nN\), где \(N\) — количество линий, а \(n\) порядок узора.
Специальные оптические эффекты
- Двулучепреломление и дихроизм . \(\vec{D}\) не параллелен \(\vec{E}\), если поляризуемость \(\vec{P}\) материала не одинакова во всех направлениях. Есть по крайней мере три направления, главные оси , в которых они параллельны.Это приводит к трем показателям преломления \(n_i\), которые можно использовать для построения эллипсоида Френеля . В случае \(n_2=n_3\neq n_1\), что происходит, например. в тригональных, гексагональных и тетрагональных кристаллах имеется одна оптическая ось в направлении \(n_1\). Падающие световые лучи теперь можно разделить на две части: обыкновенная волна линейно поляризована \(\perp\) в плоскости, проходящей через направление передачи и оптическую ось.
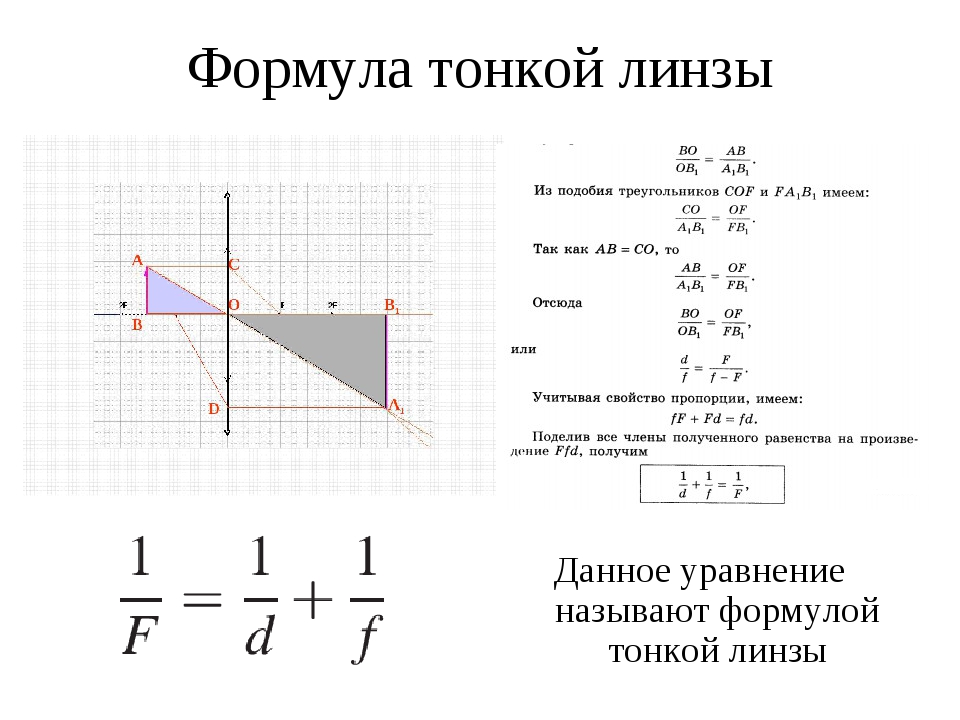 Необыкновенная волна линейно поляризована в плоскости, проходящей через направление передачи и оптическую ось. Дихроизм вызван дифференциальным поглощением обыкновенной и необыкновенной волны в некоторых материалах. Двойные изображения возникают, когда падающий луч образует угол с оптической осью: необыкновенная волна будет преломляться, а обыкновенная — нет.
Необыкновенная волна линейно поляризована в плоскости, проходящей через направление передачи и оптическую ось. Дихроизм вызван дифференциальным поглощением обыкновенной и необыкновенной волны в некоторых материалах. Двойные изображения возникают, когда падающий луч образует угол с оптической осью: необыкновенная волна будет преломляться, а обыкновенная — нет. - Ретардеры: волновые пластины и компенсаторы . Падающий свет будет иметь фазовый сдвиг \(\Delta\varphi=2\pi d(|n_0-n _{\rm e}|)/\lambda_0\), если одноосный кристалл разрезать таким образом, что оптическая ось параллельна передней и задней плоскости.3 r_{63}V/\lambda_0\), где \(r_{63}\) — элемент 6-3 электрооптического тензора.
- Эффект Фарадея : поляризация света, проходящего через материал длиной \(d\) и к которому приложено магнитное поле в направлении распространения, поворачивается на угол \(\beta={\cal V}Bd\ ) где \(\cal V\) — константа Верде .

- Черенковское излучение возникает при попадании заряженной частицы с \(v_q>v_{\rm f}\). Излучение испускается внутри конуса с углом при вершине \(\alpha\) с \(\sin(\alpha)=c/c_{\rm medium}=c/nv_q\).{-1}:={\cal A}(\theta)\) называется функцией Эйри .
Рисунок \(\PageIndex{2}\): Интерферометр Фабри-Перо
. Ширина пиков на половине высоты определяется выражением \(\gamma=4/\sqrt{F}\). Изящество \(\cal F\) определяется как \({\cal F}= \frac{1}{2} \pi\sqrt{F}\). Тогда максимальное разрешение определяется выражением \(\Delta f _{\rm min}=c/2nd{\cal F}\).
Геометрическая оптика – обзор
3.1 Введение
Предмет лучевой оптики или геометрической оптики определяется приближением эйконала, кратко описанным в главе 2.Траектории лучей определяются как траектории, ортогональные эйкональным поверхностям, по которым происходит течение электромагнитной энергии, и могут быть альтернативно описаны в терминах принципа Ферма.
 Для луча, проходящего через последовательность участков однородной среды, разделенных преломляющими поверхностями и, возможно, также претерпевающих отражение, траектория луча также может быть определена с точки зрения законов отражения и преломления. Далее мы ссылаемся на описание таких ситуаций как на проблему дискретной оптики .
Для луча, проходящего через последовательность участков однородной среды, разделенных преломляющими поверхностями и, возможно, также претерпевающих отражение, траектория луча также может быть определена с точки зрения законов отражения и преломления. Далее мы ссылаемся на описание таких ситуаций как на проблему дискретной оптики .Особый раздел геометрической оптики называется линейной оптикой , где все соответствующие углы и расстояния, используемые при описании траекторий лучей, достаточно малы, чтобы можно было применять упрощенный набор правил для их определения и анализа, эти правила являются результатом определенной схемы приближения в геометрической оптике. Определение типичного пути луча в дискретной линейной оптике может быть выполнено с помощью серии преобразований набора из четырех координат луча путем последовательного применения соответствующих передаточных матриц , где каждая такая передаточная матрица принадлежит к группе 4 × 4 симплектических матриц (см.
 раздел 3.4).
раздел 3.4). Еще более ограничительная ситуация соответствует осесимметричным оптическим системам (см. раздел 3.2), где правила линейной оптики принимают особенно простой вид, а типичный ход луча описывается в терминах преобразований по двум координатам луча , причем эти преобразования осуществляются с помощью 2 × 2 унимодулярных трансфер-матриц (однако 2 × 2 унимодулярная матрица является симплектической). Ограничение линейной оптики осесимметричными оптическими системами называется Гауссовой оптикой .
В этой главе я ввожу основные идеи определения хода лучей в гауссовой оптике с помощью передаточных матриц 2 × 2 и применяю их к случаям формирования изображения осесимметричными системами, состоящими из отражающих и преломляющих поверхностей. Камера, телескоп и микроскоп, три классических оптических инструмента, в основном используют формирование изображения в соответствии с принципами гауссовой оптики. При соблюдении условий, заданных линейной оптикой (условия параксиальности ), аксиально-симметричная оптическая система формирует для любого заданного точечного объекта точечное изображение, где будет видно, что для точечного объекта в заданном положении положение изображение полностью определяется набором параметров, характеризующих рассматриваемую оптическую систему.
 Для оптической системы, состоящей из ряда составных подсистем, эти параметры могут быть определены через параметры подсистем. Характерной особенностью формирования изображения в гауссовой оптике является геометрическое подобие плоского объекта и его изображения, когда плоскости объекта и изображения перпендикулярны оси.
Для оптической системы, состоящей из ряда составных подсистем, эти параметры могут быть определены через параметры подсистем. Характерной особенностью формирования изображения в гауссовой оптике является геометрическое подобие плоского объекта и его изображения, когда плоскости объекта и изображения перпендикулярны оси. Если рассматриваемая оптическая система лишена осевой симметрии, то применяется более общий формализм линейной оптики при условии, конечно, что соответствующие углы и расстояния продолжают оставаться достаточно малыми.При отсутствии осевой симметрии точечные объекты, как правило, не дают точечных изображений. В разделе 3.4 я кратко изложу принцип определения траекторий лучей в этом формализме, не вдаваясь, однако, в подробности того, как этот формализм следует использовать при решении конкретных задач.
Преобразования в линейной оптике являются частными случаями класса более общих преобразований, характеризующих ход лучей в геометрической оптике, аналогичных каноническим преобразованиям , относящимся к траекториям механической системы в ее фазовом пространстве.
 Тот факт, что релевантные преобразования в двух, казалось бы, не связанных между собой областях носят сходный характер, имеет большое значение и впервые был обнаружен в работах Уильяма Роуэна Гамильтона — сначала по оптике, а затем по механике.
Тот факт, что релевантные преобразования в двух, казалось бы, не связанных между собой областях носят сходный характер, имеет большое значение и впервые был обнаружен в работах Уильяма Роуэна Гамильтона — сначала по оптике, а затем по механике. Принципы, введенные Гамильтоном, приводят к идее характеристик в геометрической оптике, основная идея, лежащая в основе которой, будет кратко изложена в разделе 3.5.
Наконец, я кратко коснусь вопроса аберраций в контексте гауссовой оптики (см. раздел 3.7), где отклонение от условий линейности означает потерю четкости изображения объекта, формируемого аксиально-симметричной оптической системой. Аберрации также возникают из-за отклонения от строгой осевой симметрии, хотя они не будут рассматриваться в этом вводном изложении. Хотя общие принципы геометрической оптики продолжают применяться даже перед лицом отклонений от линейности, следует помнить, что сами эти принципы имеют ограниченную применимость, будучи получены из принципов волновой оптики с помощью эйконального приближения (см.
 2). Изгиб и расплывание электромагнитной волны, составляющей оптическое поле, происходит при прохождении через оптическую систему, вызывая потерю четкости изображения даже в случае идеального изображения, формируемого аксиально-симметричной оптической системой в линейном приближении. Такое искривление и распространение волны называется дифракцией , а потеря четкости изображения в результате изгиба и распространения может быть описана в терминах дифракции Фраунгофера (см. Главу 5 для основных идей относительно дифракции Фраунгофера). ).Роль дифракции в формировании изображения будет кратко описана в разделе 3.7.7.
2). Изгиб и расплывание электромагнитной волны, составляющей оптическое поле, происходит при прохождении через оптическую систему, вызывая потерю четкости изображения даже в случае идеального изображения, формируемого аксиально-симметричной оптической системой в линейном приближении. Такое искривление и распространение волны называется дифракцией , а потеря четкости изображения в результате изгиба и распространения может быть описана в терминах дифракции Фраунгофера (см. Главу 5 для основных идей относительно дифракции Фраунгофера). ).Роль дифракции в формировании изображения будет кратко описана в разделе 3.7.7. Сила линзы, лучевая оптика и другая формула оптики
Чтобы найти силу линзы в Ray Optics, можно использовать следующую формулу. Если фокусное расстояние указано в метрах (м), сила линзы измеряется в диоптриях (D), так как единицей силы линзы является диоптрия. Еще одна вещь, которую вы должны иметь в виду, это то, что для собирающей линзы оптическая сила положительна, а для рассеивающей линзы она отрицательна.

Здесь v = показатель преломления материала. R 1 = радиус кривизны первой поверхности линзы. R 2 = Радиус кривизны второй поверхности линзы. Для собирающей линзы оптическая сила принимается положительной, а для рассеивающей — отрицательной.
Какая формула для оптической силы является правильной?
Оптическая сила определяется как степень, в которой линза, зеркало или другая оптическая система собирают или расходят свет. Оптическая сила также упоминается как диоптрийная сила, сила конвергенции, преломляющая сила или преломляющая сила.Она равна P = 1 F. Диоптрийная формула используется для расчета оптической силы линзы или криволинейного зеркала.
Как определяется оптическая сила линзы?
Способность линзы преломлять падающий на нее свет называется оптической силой линзы. Поскольку линза с более коротким фокусным расстоянием будет больше искривлять световые лучи, у них будет больше мощности. Выпуклая линза собирает лучи света к главной оси, тогда как вогнутая линза рассеивает лучи света от главной оси.
 Здесь
Здесь Как рассчитать силу линзы для плюс-минус линз?
У каждой линзы (плюс-минус) есть фокус. Расстояние между фокусом и линзой называется фокусным расстоянием. Формула для оптической силы линзы одинакова для плюс-минус-линз: Оптическая сила = 1 / Фокусное расстояние
Что уравнение линзы говорит нам об объекте?
Уравнение линзы говорит нам все, что нам нужно знать об изображении объекта, находящегося на известном расстоянии от плоскости тонкой линзы с известным фокусным расстоянием.
Формулы лучевой оптики
Разрешающая способность = 1/dθ = D/1,22λ. где D — диаметр линзы объектива. λ — длина волны света. Законы отражения. Угол i = угол r. Падающий луч, отраженный луч и нормаль к точке падения лежат в одной плоскости. Формула зеркала. 1/v + 1/u = 1/f. m = h i /h o = -v/u
Чтобы найти силу линзы в Ray Optics, используется следующая формула. Р = 1/f. Где f — фокусное расстояние. Если фокусное расстояние указано в метрах (м), сила линзы измеряется в диоптриях (D), так как единицей силы линзы является диоптрия.

Сила линзы связана с ее фокусным расстоянием f уравнением: \( \text{Сила линзы }\left( \text{в диоптриях} \right)\propto \frac{1}{\text{ f (in}\,\,\text{метр)}}\) Единицей мощности является диоптрия (D). Чем меньше фокусное расстояние, тем больше мощность. Оптическая сила выпуклой линзы положительна, а оптическая сила вогнутой линзы отрицательна.
Коэффициенты отражения и пропускания мощности обозначаются прописными буквами: R = r 2 T = t 2 (n t cos θ t )/(n i cos θ i ) Показатели преломления учитывают разные скорости света в двух средах; отношение косинусов корректирует различные площади поперечного сечения лучей по обеим сторонам границы.
Дисперсионная способность Отношение угловой дисперсии к углу отклонения для средней длины волны (желтый цвет) называется дисперсионной способностью материала призмы. Таким образом, рассеивающая способность ω может быть записана как: * Рассеивающая способность не зависит от угла призмы, но зависит от материала призмы. 18. Оптические приборы 19.

Формула объектива и увеличение
Активен 6 лет 4 месяца назад. Просмотрено 683 раза. 0. Я провел поиск и обнаружил, что оптическая сила линзы с окружающей средой с показателем преломления n равна n / f, где f — фокусное расстояние, формула такова.n/f = (n′ − n)/R 1 + (n − n′)/R 2. Но в моей книге сказано, что оптическая сила линзы равна 1/f.
Формула для оптической силы объектива одинакова для плюсовых и минусовых линз: Оптическая сила = 1 / Фокусное расстояние Оптическая сила плюсовых линз всегда обозначается знаком + (плюс)
расстояние между датчиком волнового фронта и главной плоскостью линзы. Фокусное расстояние выводится из следующего уравнения: 1 = 1 +I−I J + 1 8+K Оптическая сила линзы измеряется для различных положений источника.Автор этого метода утверждает, что обычно измерения выполняются с точностью менее 0,5%. Заключение
2. Луч, проходящий через оптическую ось в центре линзы, не отклоняется от линзы. 3. Луч, проходящий от объекта, который считается фокальной точкой на стороне объекта линзы, будет параллелен оптической оси, когда он выходит из линзы для формирования изображения.
 Математический подход к выпуклой линзе: уравнение тонкой линзы
Математический подход к выпуклой линзе: уравнение тонкой линзы Формулы физики Оптика / Шпаргалка.Формулы физики Оптика/Шпаргалка. В вогнутых зеркалах; · Лучи, идущие параллельно главной оси, проходят из точки фокуса · Лучи, идущие из точки фокуса, идут параллельно главной оси · Луч, идущие из центра кривизны, поворачиваются обратно на себя · Луч попадает в зеркало в вершине, он отражается тот же угол, что и с главной осью
Формулы лучевой оптики
Wilkinson & Shahid Optics Review 7 4. Простая формула линзы U + D = V или 100/u (см) + D = 100/v (см) Где: U = отклонение объекта от линзы u = положение объекта = 100/ U (см) D = оптическая сила линзы V = схождение лучей изображения v = положение изображения = 100/V (см) Схождение: обратная величина расстояния от контрольной точки.U = 100/u, где u равно
Эквивалентная сила аддидации любая линза или комбинация линз, используемые для создания прогнозируемой аддидации, вся оптическая система может быть заменена одной линзой, расположенной таким образом, что объект находится в ее основной фокусной точке Эквивалентная сила D e = D 1 + D 2 — tD 1 D 2 где D e = эквивалентная оптическая сила D 1 = оптическая сила линзы в аппарате LV D 2
Линзас одинаковым радиусом с обеих сторон имеет положительную оптическую силу и отсутствие кривизны Петцваля, еще одна полезная дизайнерская «фишка».
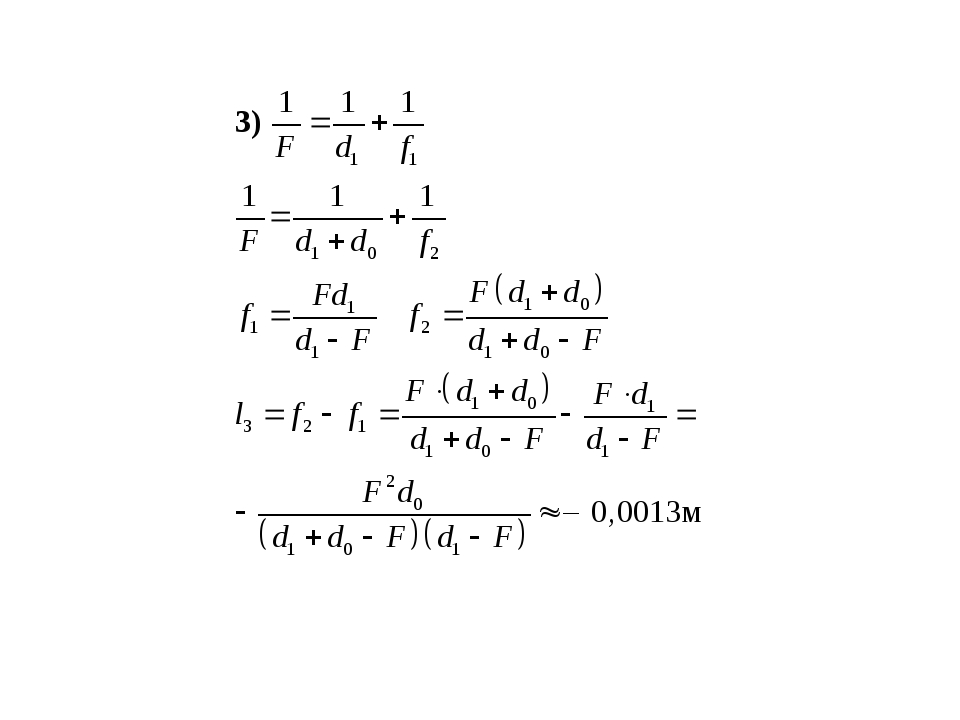 Нам нужна положительная мощность, как и прежде, для изображения зрачков, чтобы дать коррекцию астигматизма. Высота лучей на линзах очень мала и любые аберрации от них легко исправляются, слегка меняя зеркала.
Нам нужна положительная мощность, как и прежде, для изображения зрачков, чтобы дать коррекцию астигматизма. Высота лучей на линзах очень мала и любые аберрации от них легко исправляются, слегка меняя зеркала. Основы оптоволокна. Оптические волокна представляют собой круглые диэлектрические волноводы, которые могут передавать оптическую энергию и информацию. Они имеют центральную сердцевину, окруженную концентрической оболочкой с несколько меньшим (на ≈ 1%) показателем преломления. Оптические волокна обычно изготавливаются из диоксида кремния с добавками, изменяющими показатель преломления, такими как GeO 2 .
Основы оптики Аппроксимации и уравнения для линз Основные характеристики большинства оптических систем можно рассчитать с помощью нескольких параметров, при условии, что принимается некоторое приближение. Параксиальное приближение требует, чтобы учитывались только лучи, входящие в оптическую систему под малыми углами по отношению к оптической оси.
Брошюра с формулами, 12 класс физики, глава Ray Optics
Замечания по пересмотру лучевой оптики и оптических инструментов: Отражение: Свет: это агент, который вызывает у нас ощущение зрения.
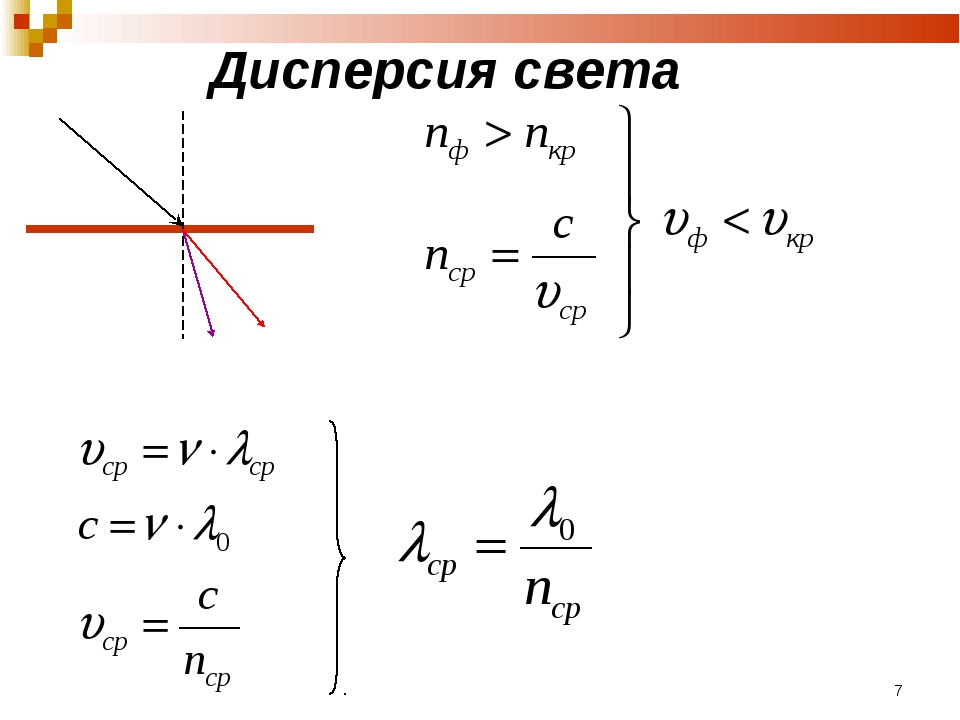 Это форма энергии. Прозрачная среда: — это среда, через которую свет может легко распространяться (например, солнце, свеча, электрическая дуга). Полупрозрачная среда: — это среда, через которую свет распространяется частично (например, бумага, земля, стекло).
Это форма энергии. Прозрачная среда: — это среда, через которую свет может легко распространяться (например, солнце, свеча, электрическая дуга). Полупрозрачная среда: — это среда, через которую свет распространяется частично (например, бумага, земля, стекло). Выпуклая линза: Лучи света, попадающие в собирающую линзу параллельно ее оси, сходятся в ее фокусе F. (Луч 2 лежит на оси линзы.) Расстояние от центра линзы до фокуса равно фокусу линзы. длина ф. Расширенный вид пути, по которому проходит луч 1, показывает перпендикуляры и углы падения и преломления на обеих поверхностях.
В оптическом приборе используется окуляр с силой 20 дптр и объектив с силой 50 дптр. Длина тубуса 15 см. Назовите оптический инструмент и рассчитайте его увеличительную силу, если он формирует конечное изображение на бесконечности. (Comptt. Delhi 2017) Ответ: Оптический прибор — составной микроскоп. Подсказка: сложный микроскоп, m = 37,5. Вопрос 133.
Изучите концепции физики, лучевой оптики и оптических приборов класса 12 с помощью видеороликов и рассказов.
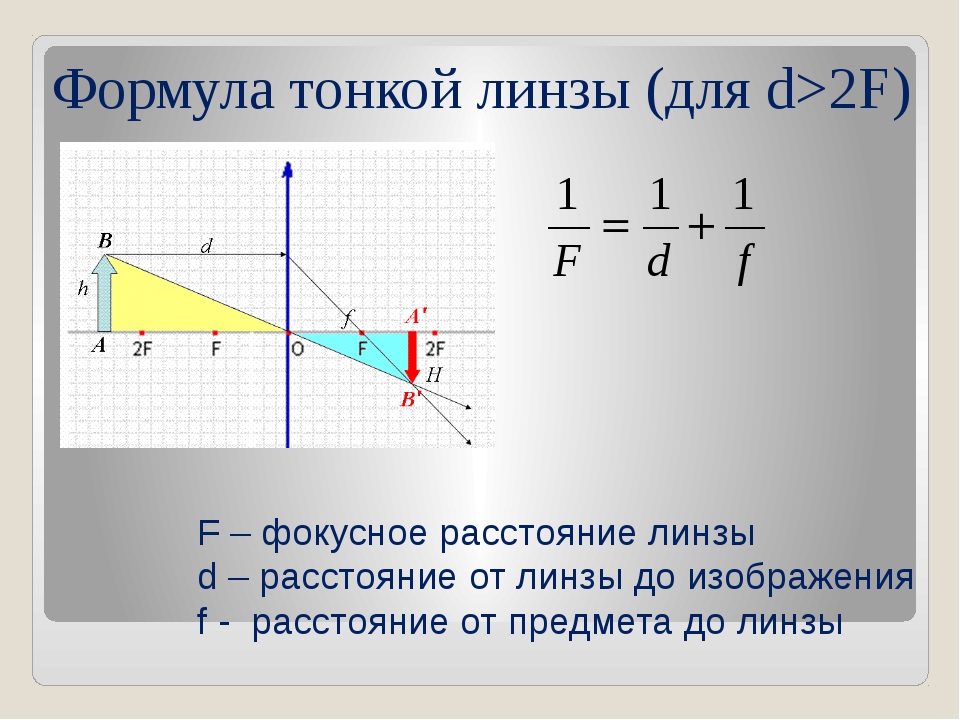 Определить силу линзы. Назовите его формулу и единицу измерения.Осознайте важность сочетания линз. Поймите, что сила комбинации линз является алгебраической суммой сил отдельных линз, т.е. эквивалентная мощность. Эффективное фокусное расстояние комбинации линз.
Определить силу линзы. Назовите его формулу и единицу измерения.Осознайте важность сочетания линз. Поймите, что сила комбинации линз является алгебраической суммой сил отдельных линз, т.е. эквивалентная мощность. Эффективное фокусное расстояние комбинации линз. Оптическая сила линзы P определяется как величина, обратная ее фокусному расстоянию. В форме уравнения это P = 1 f P = 1 f , где f — фокусное расстояние объектива, которое должно быть указано в метрах (а не в см или мм). Сила линзы P равна единице диоптрий (D) при условии, что фокусное расстояние указано в метрах.
Оптика видения
Лучевая диаграмма на рисунке 2 показывает формирование изображения роговицей и хрусталиком глаза. Лучи преломляются в соответствии с показателями преломления, приведенными в таблице 1. Роговица обеспечивает около двух третей силы глаза из-за того, что скорость света значительно изменяется при переходе из воздуха в роговицу.
В вогнутой линзе луч света, направленный к фокусу, после преломления идет параллельно главной оси.
 2F 1 F 1 O F 2 2F 2 2F 1 F 1 O F 2 2F 2 iii) В выпуклой и вогнутой линзах луч света, проходящий через оптический центр, проходит без всякого отклонения.
2F 1 F 1 O F 2 2F 2 2F 1 F 1 O F 2 2F 2 iii) В выпуклой и вогнутой линзах луч света, проходящий через оптический центр, проходит без всякого отклонения.(Эффективная) длина Рэлея является удобной величиной для расчетов в контексте сфокусированных лазерных лучей. По сути, она определяет глубину фокуса. пучок накачки в нелинейный кристалл для удвоения частоты часто целесообразно сфокусировать так, чтобы длина Рэлея была порядка длины кристалла.
Вогнутые линзы. Отношение изображения объекта и фокусного расстояния (доказательство формулы) Это текущий выбранный элемент.Отношение высоты изображения объекта к расстоянию. Уравнение тонкой линзы и решение задачи. Системы с несколькими линзами. Диоптрии, аберрация и человеческий глаз. Сортировать по:
1. Снимите блок лучей с оптической скамьи и положите блок лучей на белый лист бумаги. Используя пять белых лучей из лучевого ящика, направьте лучи прямо в выпуклую линзу. См. Рисунок 6.1. ПРИМЕЧАНИЕ. Вогнутые и выпуклые линзы имеют только один плоский край.
 Положите плоский край на поверхность.
Положите плоский край на поверхность. Формулы оптики: формула линзы, увеличение и мощность
14.Используйте уравнение зеркала, чтобы сделать вывод, что: ( Лучевая оптика и оптические приборы ) (a) объект, помещенный между f и 2f вогнутого зеркала, дает реальное изображение за пределами 2f. б) выпуклое зеркало всегда дает мнимое изображение независимо от положения предмета.
По этим приблизительным данным оцените диапазон аккомодации (т. е. диапазон конвергентной способности хрусталика) нормального глаза. Решение: Здесь наименьшая собирающая способность хрусталика дается как 20 диоптрий за роговицей.Если мы сможем вычислить максимальную силу конвергенции, то мы сможем получить диапазон аккомодации нормального глаза.
Modern Optics THEUNIVERSITYOFE DI NBURGH Параболическая аппроксимация Поверхности линз сферичны, но: Если R1 & R2 ˛h, взять параболическую аппроксимацию d1 = h3 2R1 и d2 = h3 2R2 Так что F(h)=kDn+kh3 2 (n 1)1 R1 1 R2 подставляя фокусное расстояние, получаем F(h)=kDnkh3 2f Итак, в 2-х измерениях h3 =x2 +y2, так что F(x;y; f)=kDn k(x2 +y2)2f фаза функция объектива.
JEE Основные Решенные вопросы за предыдущий год по лучевой оптике. Q1: Выпуклая линза помещается на расстоянии 10 см от источника света и дает четкое изображение на экране, находящемся на расстоянии 10 см от линзы. Теперь к источнику света прикладывается стеклянный блок (показатель преломления 1,5) толщиной 1,5 см. Чтобы снова получить резкое изображение, экран смещают на расстояние d.
Пусть C₁, C₂ — оптические центры двух тонких линз L₁ и L₂. Эти линзы удерживаются соосно друг с другом в воздухе. Предположим, f₁ и f₂ — их соответствующие фокусные расстояния.Поместим объект в точку O на главной оси на расстоянии OC₁ = u. Только линза L₁ формирует свое изображение в точке I’. Здесь C₁I’ = v’.
Учебное пособие по оптике
Пересечение этого луча с первым лучом, проведенным через центры двух линз, показывает положение сформированного окончательного изображения. Комбинация линз действует как одна линза. Мы можем найти фокус этой комбинации линз (F 12 ), проследив выходящий луч, параллельный главной оси, обратно к исходному объекту.
Проверьте приведенные ниже вопросы NCERT MCQ для класса 12 по физике, глава 9, лучевая оптика и оптические приборы с ответами. Скачать PDF бесплатно. Вопросы MCQ для 12 класса по физике с ответами были подготовлены на основе последней модели экзамена. Мы подготовили вопросы MCQ по физике для 12-го класса по оптике и оптическим приборам с ответами, чтобы помочь учащимся хорошо понять эту концепцию.
Оптические системы обычно разрабатываются с использованием оптики первого порядка или параксиальной оптики для расчета размера и местоположения изображения.Параксиальная оптика не учитывает аберрации; он рассматривает свет как луч и поэтому опускает волновые явления, вызывающие аберрации. Оптические аберрации называют и характеризуют по-разному.
Я разрабатываю уроки геометрической оптики, используя это приложение. Мое единственное предложение — добавить настоящую линзу/зеркало с регулируемым фокусным расстоянием, которое изменяет форму линзы или зеркала. Вы можете создать его вручную с опцией «объектив/другое», но это не позволяет физически масштабировать фокусное расстояние.{\circ}\). Аквалангист в бассейне и его тренер смотрят друг на друга. 41. Компоненты некоторых компьютеров сообщаются друг с другом через оптические волокна, имеющие показатель преломления \(\displaystyle n=1,55\).
Лучевая оптика и оптические приборы
Вторая линза имеет увеличение – 1,15. Увеличение изображения по высоте объекта/изображения. Изображение, сгенерированное первой линзой, будет объектом для второй линзы. h i1 = h о2. Из этого уравнения мы видим, что общее увеличение равно произведению m 1 и m 2.
Цель: оценить точность измерения силы роговицы для расчета силы интраокулярной линзы (ИОЛ) после миопического лазерного кератомилеза in situ (LASIK). Методы: В исследовании оценивали 45 глаз с близорукостью LASIK в анамнезе. Мощность роговицы измеряли с помощью ручной кератометрии, автоматической кератометрии, оптической биометрии и томографии Шеймфлюга.
Расчет мощности, передаваемой каждым лучом. Переменные, которые используются для вычисления интенсивности луча, управляются выпадающим списком «Вычисление интенсивности» в окне настроек интерфейса «Геометрическая оптика».





 3)
3) 6)
6)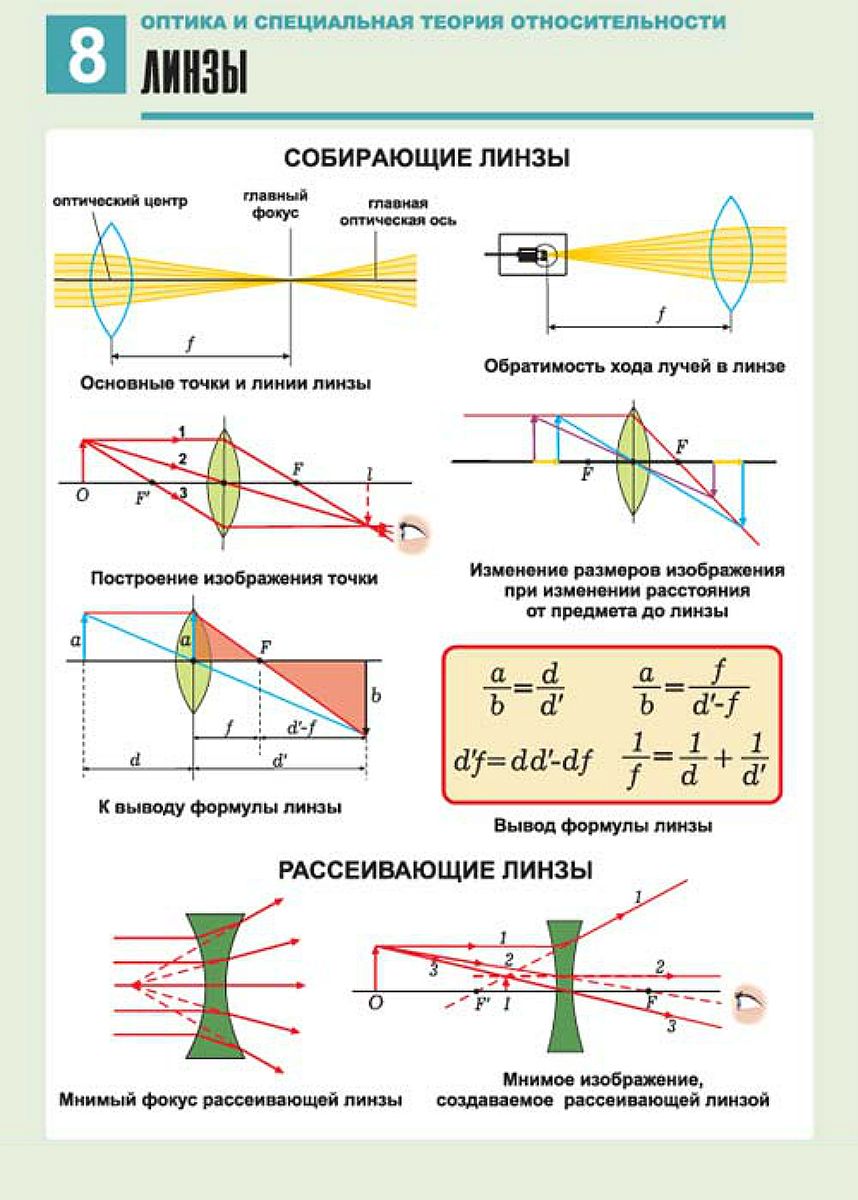 Глазов
Глазов 
 к. оно
по своим физическим свойствам близко к видимому.
С
другой стороны свет — это поток частиц — фотонов, имеющих
импульс и несущих энергию.
Т.е. можно говорить, что
природа света двойственна.
к. оно
по своим физическим свойствам близко к видимому.
С
другой стороны свет — это поток частиц — фотонов, имеющих
импульс и несущих энергию.
Т.е. можно говорить, что
природа света двойственна.
 Поэтому сильно
нагретые тела светятся, и их свечение объясняется излучением
атомами электромагнитных волн с длинами от 380 до 760нм. При
этом каждое вещество излучает только определенный набор длин
волн, не похожий на другие ( в этот набор так же входят и другие
волны, не являющиеся видимым светом).
Это происходит потому, что
атомы вещества могут находиться в особых дискретных
энергетических состояниях, каждому из которых соответствует
определенная энергия. Излучение света происходит при переходе
атома из энергетического состояния с большей энергией в
состояние с меньшей энергией. Разность энергий и переносится
излучаемой волной. При этом процесс излучения конечен во времени
и составляет примерно
t =
10 -8 с , а волна, которую излучает атом, может быть
представлена в виде небольшой части синусоиды. Такая часть
синусоиды имеет длину
l = c t , т.
Поэтому сильно
нагретые тела светятся, и их свечение объясняется излучением
атомами электромагнитных волн с длинами от 380 до 760нм. При
этом каждое вещество излучает только определенный набор длин
волн, не похожий на другие ( в этот набор так же входят и другие
волны, не являющиеся видимым светом).
Это происходит потому, что
атомы вещества могут находиться в особых дискретных
энергетических состояниях, каждому из которых соответствует
определенная энергия. Излучение света происходит при переходе
атома из энергетического состояния с большей энергией в
состояние с меньшей энергией. Разность энергий и переносится
излучаемой волной. При этом процесс излучения конечен во времени
и составляет примерно
t =
10 -8 с , а волна, которую излучает атом, может быть
представлена в виде небольшой части синусоиды. Такая часть
синусоиды имеет длину
l = c t , т. е.
l = 3 · 10 8 м/с ·
10 -8 = 3 м и называется волновым цугом.
Излучение цугов происходит
сразу большим количеством атомов вещества независимо друг от
друга. Такой поток цугов мы воспринимаем как свет.
е.
l = 3 · 10 8 м/с ·
10 -8 = 3 м и называется волновым цугом.
Излучение цугов происходит
сразу большим количеством атомов вещества независимо друг от
друга. Такой поток цугов мы воспринимаем как свет.
 Если среда однородна, то
вторичные волны распространяются в ней с одинаковой скоростью.
Следовательно, за одно и тоже время τ все вторичные волны
дойдут до точек среды, удаленных от данных на расстояние
l = τυ, где υ — скорость волны.
Поверхность, огибающая в некоторый момент времени вторичные
волны, укажет положение фронта волны в данный момент времени.
под фронтом волны понимают геометрическое место точек, до
которых дошло возмущение к заданному момент времени. В
зависимости от вида фронта различают плоские и сферические
волны. Фронтом плоских волн является плоскость, сферических —
сфера.
Линия, перпендикулярная
волновой поверхности, называется световым лучом. Распространение
волн происходит по направлению луча.
Если среда однородна, то
вторичные волны распространяются в ней с одинаковой скоростью.
Следовательно, за одно и тоже время τ все вторичные волны
дойдут до точек среды, удаленных от данных на расстояние
l = τυ, где υ — скорость волны.
Поверхность, огибающая в некоторый момент времени вторичные
волны, укажет положение фронта волны в данный момент времени.
под фронтом волны понимают геометрическое место точек, до
которых дошло возмущение к заданному момент времени. В
зависимости от вида фронта различают плоские и сферические
волны. Фронтом плоских волн является плоскость, сферических —
сфера.
Линия, перпендикулярная
волновой поверхности, называется световым лучом. Распространение
волн происходит по направлению луча.
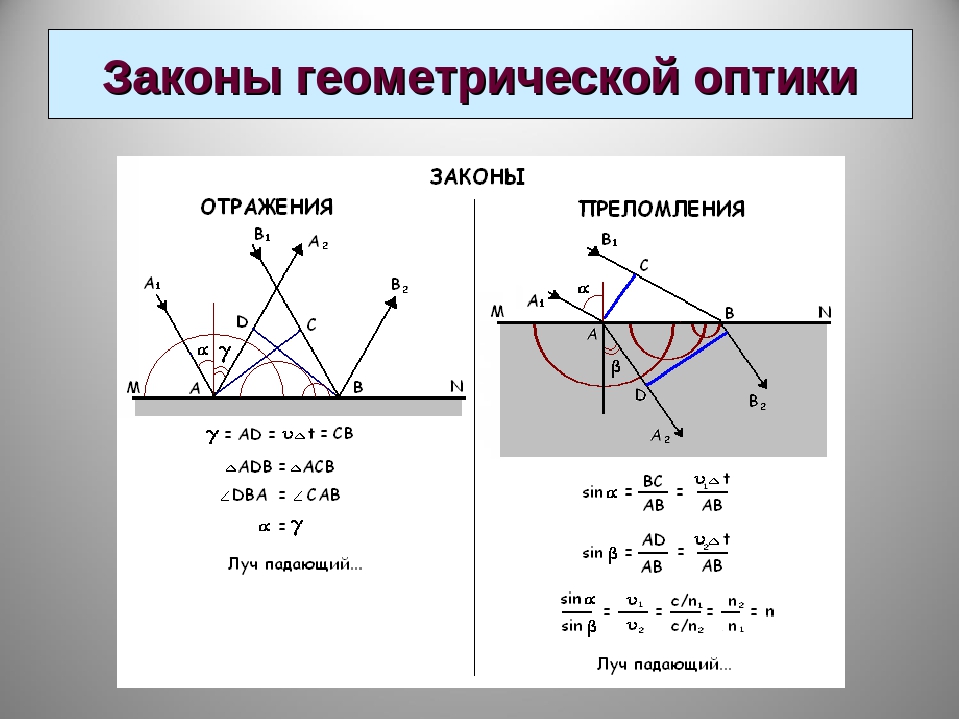 Причиной такого разложения является зависимость скорости света
в среде от частоты (длины волны). Скорость света в среде υ ═ c
/ n, где n — показатель преломления среды, с — скорость света в
вакууме.
Так как скорость света
универсальная постоянная, то из соотношения n ═ c / υ следует,
что показатель преломления n есть функция частоты или длины
волны.
Такую зависимость можно
пронаблюдать при прохождении белого света через призму,
изготовленную из прозрачной среды. На экране, установленном за
призмой, наблюдается радужная полоска, которую называют
призматическим (дисперсионным) спектром.
Наименьшую частоту и наименьший
показатель преломления имеет красный свет, поэтому красные лучи
отклоняются на меньший угол.
Причиной такого разложения является зависимость скорости света
в среде от частоты (длины волны). Скорость света в среде υ ═ c
/ n, где n — показатель преломления среды, с — скорость света в
вакууме.
Так как скорость света
универсальная постоянная, то из соотношения n ═ c / υ следует,
что показатель преломления n есть функция частоты или длины
волны.
Такую зависимость можно
пронаблюдать при прохождении белого света через призму,
изготовленную из прозрачной среды. На экране, установленном за
призмой, наблюдается радужная полоска, которую называют
призматическим (дисперсионным) спектром.
Наименьшую частоту и наименьший
показатель преломления имеет красный свет, поэтому красные лучи
отклоняются на меньший угол. Наибольшая частота и наибольший
показатель преломления у фиолетового цвета, следовательно,
фиолетовые лучи отклоняются на больший угол.
Таким образом, с увеличением
частоты света происходит возрастание показателя преломления,
которое и объясняет разложение белого света на монохроматические
составляющие. Такая дисперсия называется нормальной.
интерференция света
— сложение двух
или нескольких световых волн с одинаковыми периодами, сходящихся
в одной точке, в результате которого наблюдается увеличение или
уменьшение амплитуды результирующей волны. Для получения
устойчивой интерференционной картины необходимо , чтобы
складываемые волны были когерентны. Когерентными называют волны
с одинаковой частотой (периодом) и постоянной во времени
разностью фаз. Чтобы получить когерентные волны необходимо
световую волну от одного источника «разделить» на две или
несколько волн.
Наибольшая частота и наибольший
показатель преломления у фиолетового цвета, следовательно,
фиолетовые лучи отклоняются на больший угол.
Таким образом, с увеличением
частоты света происходит возрастание показателя преломления,
которое и объясняет разложение белого света на монохроматические
составляющие. Такая дисперсия называется нормальной.
интерференция света
— сложение двух
или нескольких световых волн с одинаковыми периодами, сходящихся
в одной точке, в результате которого наблюдается увеличение или
уменьшение амплитуды результирующей волны. Для получения
устойчивой интерференционной картины необходимо , чтобы
складываемые волны были когерентны. Когерентными называют волны
с одинаковой частотой (периодом) и постоянной во времени
разностью фаз. Чтобы получить когерентные волны необходимо
световую волну от одного источника «разделить» на две или
несколько волн. После прохождения различных путей эти волны
,имея некоторую разность хода, интерферируют.
Рассмотрим наиболее часто
встречающиеся приемы разделения волны.
1.Схема получения интерференции с помощью бипризмы Френеля.
Волна, идущая от источника
света раздваивается в следствие преломления света в двух
половинах бипризмы.
После прохождения различных путей эти волны
,имея некоторую разность хода, интерферируют.
Рассмотрим наиболее часто
встречающиеся приемы разделения волны.
1.Схема получения интерференции с помощью бипризмы Френеля.
Волна, идущая от источника
света раздваивается в следствие преломления света в двух
половинах бипризмы.
 Опыт Юнга.
Свет, проходящий через узкое
отверстие S,
падает на экран с двумя отверстиями
S1и
S2 и делится на на две волны. Эти
волны когерентны и поэтому в заштрихованной области
наблюдается интерференция, а на экране, в области АВ,
наблюдается интерференционная картина.
Опыт Юнга.
Свет, проходящий через узкое
отверстие S,
падает на экран с двумя отверстиями
S1и
S2 и делится на на две волны. Эти
волны когерентны и поэтому в заштрихованной области
наблюдается интерференция, а на экране, в области АВ,
наблюдается интерференционная картина.
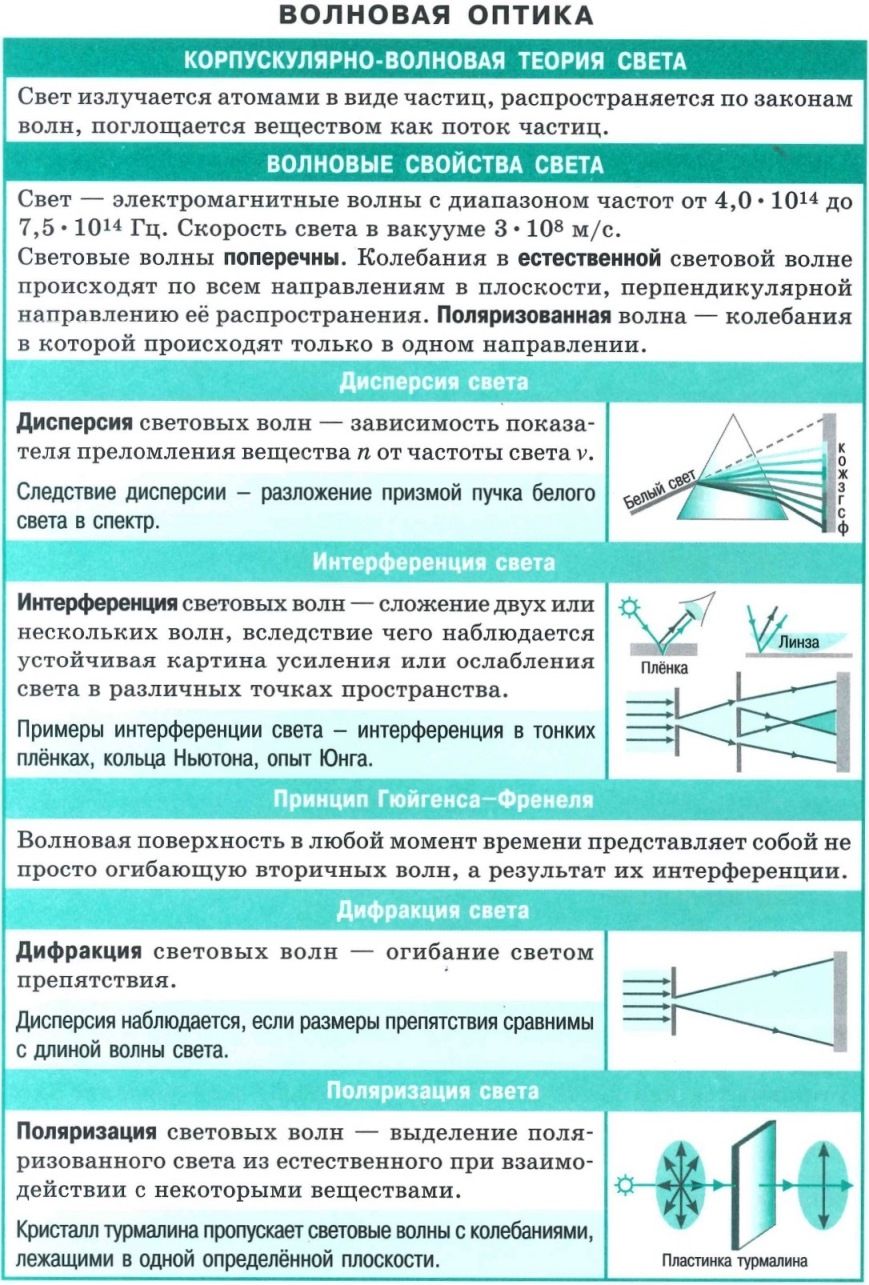 Опыт Ллойда.
В данном опыте волна, исходящая
от источника
S
и волна, как бы исходящая от мнимого
источника S
‘являются когерентными. Когерентные волны
интерферируют и дают на экране интерференционную картину.
Опыт Ллойда.
В данном опыте волна, исходящая
от источника
S
и волна, как бы исходящая от мнимого
источника S
‘являются когерентными. Когерентные волны
интерферируют и дают на экране интерференционную картину.

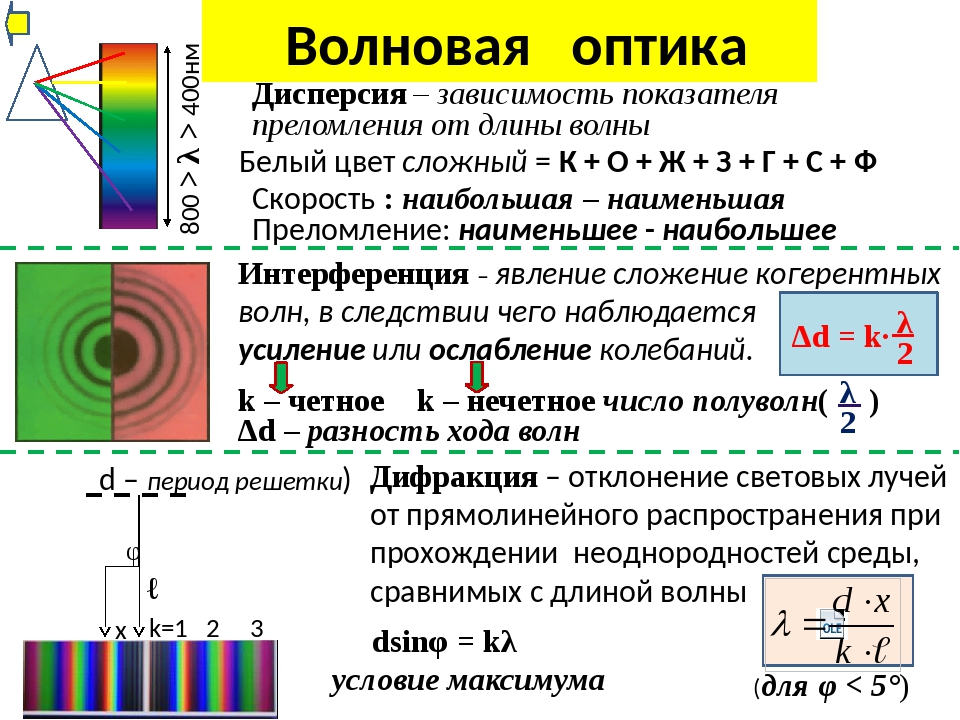 Они дают интерференционную картину в проходящем
свете.
Они дают интерференционную картину в проходящем
свете. Такими неоднородностями могут быть
отверстия в непрозрачном экране, границы непрозрачных тел. В
результате дифракции свет проникает в область геометрических теней.
Явление дифракции объясняет принцип Гюйгенса — Френеля, согласно
которому, каждая точка среды, до которой доходит световое
возбуждение, сама становится источником вторичной волны, а волновое
возмущение в любой точке пространства есть результат интерференции
вторичных волн от фиктивных когерентных источников.
Такими неоднородностями могут быть
отверстия в непрозрачном экране, границы непрозрачных тел. В
результате дифракции свет проникает в область геометрических теней.
Явление дифракции объясняет принцип Гюйгенса — Френеля, согласно
которому, каждая точка среды, до которой доходит световое
возбуждение, сама становится источником вторичной волны, а волновое
возмущение в любой точке пространства есть результат интерференции
вторичных волн от фиктивных когерентных источников.  Тогда
направление распространения волны можно определить с помощью
лучей — линий, перпендикулярных волновым поверхностям.
Раздел оптики, в котором
изучаются законы распространения света в прозрачных средах на
основе представления о световом луче, называется геометрической
(лучевой) оптикой.
В основе геометрической оптики
лежат четыре закона :
1. закон
прямолинейного распространения света.
В однородной среде свет распространяется прямолинейно.
( закон является приближенным, т.к при прохождении света через
отверстия, размеры которых соизмеримы с длиной световой волны,
наблюдается отклонение от прямолинейного распространения).
2.
закон отражения.
(На границе раздела двух сред свет отражается.
Тогда
направление распространения волны можно определить с помощью
лучей — линий, перпендикулярных волновым поверхностям.
Раздел оптики, в котором
изучаются законы распространения света в прозрачных средах на
основе представления о световом луче, называется геометрической
(лучевой) оптикой.
В основе геометрической оптики
лежат четыре закона :
1. закон
прямолинейного распространения света.
В однородной среде свет распространяется прямолинейно.
( закон является приближенным, т.к при прохождении света через
отверстия, размеры которых соизмеримы с длиной световой волны,
наблюдается отклонение от прямолинейного распространения).
2.
закон отражения.
(На границе раздела двух сред свет отражается. ) Луч
падающий, луч отраженный и перпендикуляр восстановленный в точке
падения луча, лежат в одной плоскости; угол падения равен углу
отражения
3.
закон
преломления.
(На границе раздела двух сред
свет преломляется.) Луч падающий, луч преломленный и
перпендикуляр восстановленный в точке падения луча, лежат в
одной плоскости; отношение синуса угла падения к синусу угла
преломления есть величина постоянная для данных двух
сред.
sinα
/ sinβ = n = const
4.
закон независимости
световых пучков.
Лучи при пересечении не возмущают друг друга
(закон справедлив при малой интенсивности световых пучков)
История развития взглядов
на природу света.
) Луч
падающий, луч отраженный и перпендикуляр восстановленный в точке
падения луча, лежат в одной плоскости; угол падения равен углу
отражения
3.
закон
преломления.
(На границе раздела двух сред
свет преломляется.) Луч падающий, луч преломленный и
перпендикуляр восстановленный в точке падения луча, лежат в
одной плоскости; отношение синуса угла падения к синусу угла
преломления есть величина постоянная для данных двух
сред.
sinα
/ sinβ = n = const
4.
закон независимости
световых пучков.
Лучи при пересечении не возмущают друг друга
(закон справедлив при малой интенсивности световых пучков)
История развития взглядов
на природу света. Исторически
сложилось так, что параллельно существовали два взгляда на
природу света, и поэтому параллельно развивались две теории.
Корпускулярная
теория утверждает: свет представляет
собой поток частиц.
С точки зрения
волновой теории: свет —
электромагнитная волна.
Начало
корпускулярной теории света было положено Пифагором, который
предположил, что мы видим окружающие нас предметы потому, что
они испускают мельчайшие частицы. Развил данную теорию
И.Ньютон
в своих трудах «Лекции по оптике», «Оптика или трактат об
отражениях, преломлениях, изгибаниях и цветах света».
Например,
прямолинейное распространение света И.Ньютон объяснил законом
инерции. Если на частицу(корпускулу) во время движения не
действуют силы или действие сил, скомпенсировано, то она
сохраняет свою скорость.
Исторически
сложилось так, что параллельно существовали два взгляда на
природу света, и поэтому параллельно развивались две теории.
Корпускулярная
теория утверждает: свет представляет
собой поток частиц.
С точки зрения
волновой теории: свет —
электромагнитная волна.
Начало
корпускулярной теории света было положено Пифагором, который
предположил, что мы видим окружающие нас предметы потому, что
они испускают мельчайшие частицы. Развил данную теорию
И.Ньютон
в своих трудах «Лекции по оптике», «Оптика или трактат об
отражениях, преломлениях, изгибаниях и цветах света».
Например,
прямолинейное распространение света И.Ньютон объяснил законом
инерции. Если на частицу(корпускулу) во время движения не
действуют силы или действие сил, скомпенсировано, то она
сохраняет свою скорость.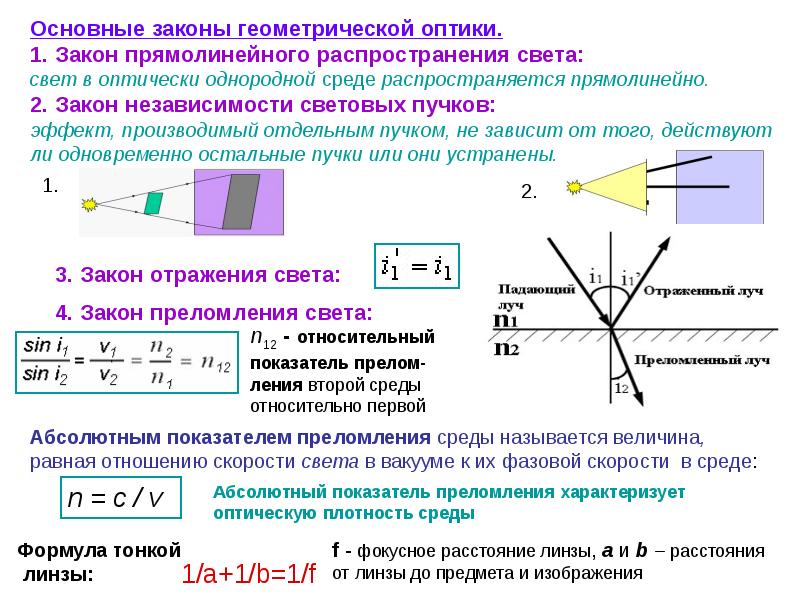 Причина разнообразия цветов, с точки
зрения И.Ньютона, в неодинаковой величине световых корпускул, а
именно в том, что наиболее крупные корпускулы вызывают ощущение
красного света, а наименьшие — фиолетового. Отражение света
объясняется упругим ударом световых частиц об упругую
поверхность. Преломление света есть следствие того, что при
переходе из менее преломляющей среды в более преломляющую,
частицам света сообщается ускорение в результате притяжения их
второй средой. При этом скорость света в веществе должна быть
больше скорости света в вакууме.
Сторонниками
волновой теории света были Х.Гюйгенс, Р.Декарт, Ф. Гримальди.
Развитие эта теория нашла в трудах Т.Юнга, О.Френеля и др.
Волновая теория света смогла строго доказать законы отражения и
преломления света, обосновала такие явления, как интерференцию,
дифракцию, поляризацию света. С точки зрения волновой теории
скорость света в веществе должна была быть меньше скорости
света в вакууме.
Причина разнообразия цветов, с точки
зрения И.Ньютона, в неодинаковой величине световых корпускул, а
именно в том, что наиболее крупные корпускулы вызывают ощущение
красного света, а наименьшие — фиолетового. Отражение света
объясняется упругим ударом световых частиц об упругую
поверхность. Преломление света есть следствие того, что при
переходе из менее преломляющей среды в более преломляющую,
частицам света сообщается ускорение в результате притяжения их
второй средой. При этом скорость света в веществе должна быть
больше скорости света в вакууме.
Сторонниками
волновой теории света были Х.Гюйгенс, Р.Декарт, Ф. Гримальди.
Развитие эта теория нашла в трудах Т.Юнга, О.Френеля и др.
Волновая теория света смогла строго доказать законы отражения и
преломления света, обосновала такие явления, как интерференцию,
дифракцию, поляризацию света. С точки зрения волновой теории
скорость света в веществе должна была быть меньше скорости
света в вакууме. Именно этот факт вступал в противоречие с
корпускулярной теорией.
Опыты Фуко
(1950г.)по определению скорости света в воде подтвердили
предположения сторонников волновой теории. Благодаря этому
волновая теория получила признание.
Однако в начале
XX века
было доказано, что свет — поток частиц — фотонов. Но этот факт
уже не вступает в противоречие с волновой теорией света. Оба
взгляда на природу света дополняют друг друга.
Дуализм света
подтверждается формулой Планка
ε
= hν.
Эта формула связывает энергию фотона, которая является квантовой
характеристикой, и частоту колебаний, являющуюся волновой
характеристикой.
Именно этот факт вступал в противоречие с
корпускулярной теорией.
Опыты Фуко
(1950г.)по определению скорости света в воде подтвердили
предположения сторонников волновой теории. Благодаря этому
волновая теория получила признание.
Однако в начале
XX века
было доказано, что свет — поток частиц — фотонов. Но этот факт
уже не вступает в противоречие с волновой теорией света. Оба
взгляда на природу света дополняют друг друга.
Дуализм света
подтверждается формулой Планка
ε
= hν.
Эта формула связывает энергию фотона, которая является квантовой
характеристикой, и частоту колебаний, являющуюся волновой
характеристикой.