Формула скорости через период: Глава 7. Вращательное движение. Кинематика и динамика

Глава 7. Вращательное движение. Кинематика и динамика

Как правило, в любом варианте задания ЕГЭ по физике представлены несколько задач на вращательное движение. Приведем основные определения и законы, необходимые для решения такого рода задач. Угловой скоростью тела, совершающего вращательное движение, называется отношение угла поворота к тому времени , за которое этот поворот произошел

(7.1)

В этом определении угол должен измеряться в радианах, поэтому размерность угловой скорости рад/с (или 1/с поскольку радиан — безразмерная величина). В принципе, определение (7.1) позволяет найти как среднюю (для больших интервалов времени ), так и мгновенную (при ) угловую скорость. Однако в школьном курсе физики рассматривается только движение с постоянной угловой скоростью, для которого определение (7.1) дает один и тот же результат для любых интервалов времени . Применяя определение (7.

1) к полному обороту тела (угол поворота — радиан), получим связь угловой скорости и периода вращения

(7.2)

Угловую скорость можно ввести не только для точечного тела, но и для протяженного тела. Действительно, при вращении неточечного тела вокруг любой оси все его точки поворачиваются за одинаковое время на одинаковый угол. Поэтому можно говорить об угловой скорости всего тела.

Из формулы (7.2) легко получить связь угловой и обычной скорости вращающегося точечного тела (в этом контексте последнюю всегда называют линейной скоростью). Умножая правую и левую часть формулы (7.2) на радиус окружности и учитывая, что – это длина пути, пройденного за период, получим

(7.3)

Конечно, для неточечного вращающегося тела нельзя ввести понятие линейной скорости, поскольку у разных точек этого тела линейные скорости будут разными.

Очевидно, при вращательном движении тело всегда имеет ускорение. Действительно, согласно определению (2.1) ускорение тела равно нулю, если не меняется вектор скорости этого тела (т.е. как величина скорости, так и ее направление). При вращательном движении направление скорости обязательно меняется. Можно доказать, что при вращательном движении точечного тела с постоянной по величине линейной скоростью вектор его ускорения в любой момент направлен от тела к центру траектории тела, а его величина равна

(7.4)

Ускорение (7.3) принято называть центростремительным. Если использовать связь линейной и угловой скорости тела при вращательном движении (7.3), то формулу для центростремительного ускорения можно записать и в таких формах

(7.5)

Согласно второму закону Ньютона ускорения сообщаются телам силами. Поэтому если тело совершает движение по окружности радиуса с постоянной по величине скоростью (и соответственно угловой скоростью ), на него должна действовать сила, направленная к центру окружности и равная по величине

(7.6)

Силу (7.6) принято называть центростремительной. Отметим, что термин «центростремительная» связан не с природой этой силы, а с тем, как она действует: в разных ситуациях центростремительной силой может быть и сила тяжести, и сила трения, и сила реакции, и другие силы или их комбинации.

Перечисленных законов и определений достаточно для решения любых задач ЕГЭ на вращательное движение. Рассмотрим их применение к решению задач, приведенных в первой части.

Если период вращения тела задан, то его угловая скорость может быть однозначно определена независимо от размеров тела или радиуса орбиты для точечного тела. В частности, секундная стрелка любых часов поворачивается на угол за одну минуту (конечно, при условии, что они идут «правильно»). Поэтому угловая скорость секундных стрелок любых часов равна рад/мин (задача 7.1.1 – ответ 2).

Для нахождения линейной скорости конца секундной стрелки часов (задача 7.1.2) используем связь угловой и линейной скоростей (7.5). Имеем

(правильный ответ – 2).

Применяя определение угловой скорости к колесу (задача 7.1.3), получаем

(правильный ответ 1).

Из формулы (7.2) имеем

(задача 7.1.4 – правильный ответ 4).

Используя известное расстояние от первой точки до оси вращения и ее центростремительное ускорение (задача 7.1.5), из формулы (7.5) находим квадрат угловой скорости диска

А теперь по формуле (7. 5) для второй точки получаем

(ответ 2).

Поскольку скорость автомобиля в задаче 7.1.6

не меняется в процессе движения для сравнения центростремительных ускорений автомобиля в разных точках траектории следует использовать формулу (7.4), из которой находим, что ускорение тем больше, чем меньше радиус траектории (правильный ответ – 3).

Ускорение мальчика из задачи 7.1.7 будет равно нулю, если его скорость относительно земли будет равна нулю. Поэтому при движении мальчика против движения карусели, его скорость относительно карусели равна скорости карусели относительно земли . Если мальчик пойдет в другую сторону с той же скоростью относительно карусели, его скорость относительно земли будет равна . Поэтому центростремительное ускорение мальчика будет равно

(ответ 4).

Тело, находящееся на поверхности вращающегося диска и вращающееся вместе с ним (

задача 7.1.8), участвует в следующих взаимодействиях. Во-первых, тело притягивается к земле (сила тяжести), и на него действует поверхность диска (сила нормальной реакции и трения), причем сила трения в каждый момент времени направлена к оси вращения (см. рисунок). Действительно, в отсутствии силы трения тело либо будет оставаться на месте, а диск под ним будет вращаться, либо (если тело имеет скорость) слетит с поверхности диска. Именно сила трения «заставляет» тело вращаться вместе с диском. Поэтому сила трения служит в данной задаче цен-тростремительной силой. Остальные перечисления, данные в условии: «на тело действуют силы тяжести, трения, реакции опоры, центростремительная (или центробежная)» являются неправильными, поскольку в них смешиваются характеристики сил разных типов – первые три касаются природы взаимодействий, вторые – результат действия. Поэтому правильный ответ на вопрос задачи – 1. Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).

Поскольку тело в задаче 7.1.9 вращается с постоянной по величине скоростью по окружности, то его ускорение направлено к центру окружности, и, следовательно, согласно второму закону Ньютона, туда же направлена и результирующая сила, действующая на тело (ответ 2).

Применяя к данному в задаче 7.1.10 телу второй закон Ньютона и учитывая, что его ускорение равно м/с², получим для равнодействующей =2 Н (ответ 2).

Используя формулу для центростремительного ускорения , находим отношение ускорений материальных точек из задачи 7.2.1

(ответ 1).

Для сравнения центростремительных ускорений материальных точек в

задаче 7. 2.2 удобно использовать формулу , поскольку в этой задаче одинаковы угловые скорости точек. Получаем

(ответ 3).

Для сравнения центростремительных ускорений тел в задаче 7.2.3 выразим ускорение через радиус окружности и период. Используя формулу (7.2) для периода и (7.5) для центростремительного ускорения, получим

(7.5)

Поэтому

(ответ 1).

Используя связь угловой и линейной скорости, находим скорости концов часовой и минутной стрелки (задача 7.2.4)

где и – угловые скорости часовой и минутной стрелки соответственно (в рад/час), и – длины часовой и минутной стрелок. Учитывая, что , получаем

(ответ 2).

Телу, вращающемуся вместе с диском на его горизонтальной поверхности (задача 7.2.5), центростремительное ускорение сообщается силой трения

Поэтому при увеличении угловой скорости вращения диска возрастает и сила трения между телом и диском. При некоторой угловой скорости сила трения достигнет максимально возможного для нее значения . Если еще увеличить угловую скорость диска, сила трения уже не сможет удержать тело на диске: тело начнет скользить по поверхности и слетит с поверхности диска. Поэтому значения угловой скорости, при которой тело может вращаться вместе с диском, находится из неравенства

(ответ 4).

В задаче 7. 2.6 центростремительной силой является сила натяжения нити. Поэтому из второго закона Ньютона с учетом формулы (7.5) для центростремительного ускорения имеем

(ответ 3).

В задаче 7.2.7 нужно использовать второй закон Ньютона для каждого тела. Силы, действующие на тела, показаны на рисунке. Проекция второго закона Ньютона для дальнего тела на координатную ось, направленную к центру диска, дает

(1)

На ближнее тело действуют силы натяжения и двух нитей (см. рисунок). Поэтому для него из второго закона Ньютона имеем

Подставляя в эту формулу силу из формулы (1), находим (ответ 2).

В задаче 7. 2.8 необходимо использовать то обстоятельство, что угловая скорость всех точек стержня одинакова. Обозначая расстояния от оси вращения до концов стержня как и , имеем

где = 1 м/с и = 2 м/с – линейные скорости концов стержня, м – его длина. Решая эту систему уравнений, найдем расстояния и , а затем и угловую скорость стержня . В результате получим

(ответ 3).

Среднее ускорение тела за некоторый интервал времени (не обязательно малый) определяется по формуле (2.1):

где и – скорости тела в конце и начале интервала времени . За половину периода вектор скорости поворачивается на 180°, поэтому величина разности равна . Поэтому среднее ускорение тела за половину периода равно

(задача 7.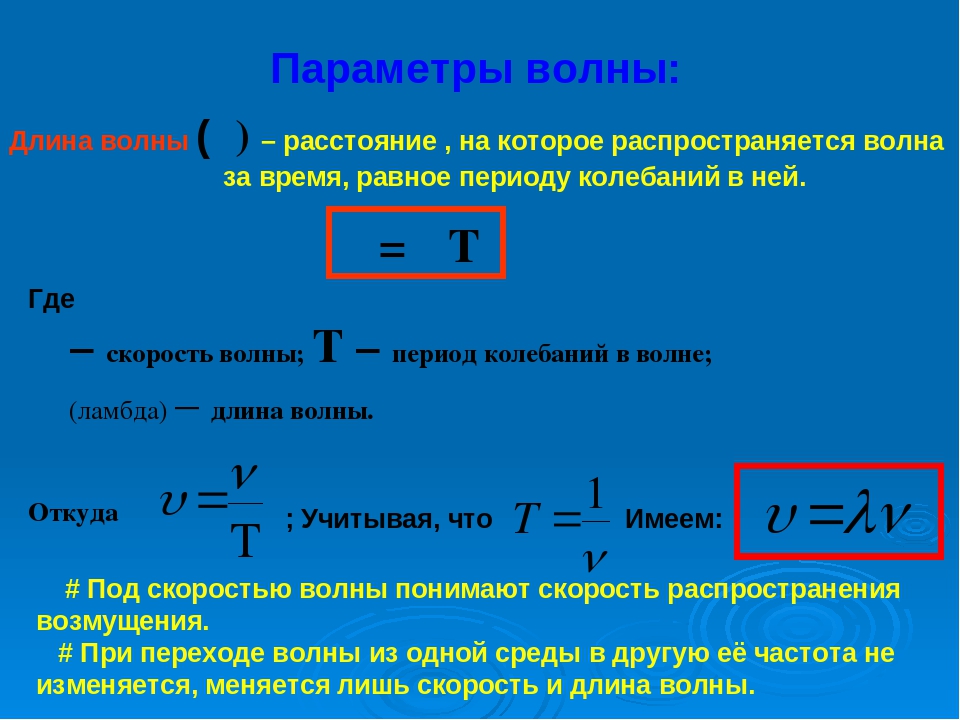 2.9 – ответ 1).

Очевидно, при зубчатой передаче совпадают линейные скорости точек на ободе шестерней. Действительно, если бы эти скорости были разными, между поверхностями шестерней было бы проскальзывание, которому препятствуют зубцы шестерней (задача 7.2.10 – ответ 2).

Равномерное движение по окружности. Скорость, ускорение

 

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: движение по окружности с постоянной по модулю скоростью, центростремительное ускорение.

Равномерное движение по окружности — это достаточно простой пример движения с вектором ускорения, зависящим от времени.

Пусть точка вращается по окружности радиуса . Скорость точки постоянна по модулю и равна . Скорость называется линейной скоростью точки.

Период обращения — это время одного полного оборота. Для периода имеем очевидную формулу:

. (1)

Частота обращения — это величина, обратная периоду:

.

Частота показывает, сколько полных оборотов точка совершает за секунду. Измеряется частота в об/с (обороты в секунду).

Пусть, например, . Это означает, что за время точка совершает один полный
оборот. Частота при этом получается равна: об/с; за секунду точка совершает 10 полных оборотов.

 

Угловая скорость.

 

Рассмотрим равномерное вращение точки в декартовой системе координат. Поместим начало координат в центре окружности (рис. 1).

Рис. 1. Равномерное движение по окружности

 

Пусть — начальное положение точки; иными словами, при точка имела координаты . Пусть за время точка повернулась на угол и заняла положение .

Отношение угла поворота ко времени называется угловой скоростью вращения точки:

. (2)

Угол , как правило, измеряется в радианах, поэтому угловая скорость измеряется в рад/с. За время, равное периоду вращения, точка поворачивается на угол . Поэтому

. (3)

Сопоставляя формулы (1) и (3), получаем связь линейной и угловой скоростей:

. (4)

 

Закон движения.

 

Найдём теперь зависимость координат вращающейся точки от времени. Видим из рис. 1, что

.

Но из формулы (2) имеем: . Следовательно,

. (5)

Формулы (5) являются решением основной задачи механики для равномерного движения точки по окружности.

 

Центростремительное ускорение.

 

Теперь нас интересует ускорение вращающейся точки. Его можно найти, дважды продифференцировав соотношения (5):

С учётом формул (5) имеем:

(6)

Полученные формулы (6) можно записать в виде одного векторного равенства:

(7)

где — радиус-вектор вращающейся точки.

Мы видим, что вектор ускорения направлен противоположно радиус-вектору, т. е. к центру окружности (см. рис. 1). Поэтому ускорение точки, равномерно движущейся по окружности, называется центростремительным.

Кроме того, из формулы (7) мы получаем выражение для модуля центростремительного ускорения:

(8)

Выразим угловую скорость из (4)

и подставим в (8). Получим ещё одну формулу для центростремительного ускорения:

.

 

Формула угловой скорости в физике

Содержание:

Определение и формула угловой скорости

Определение

Круговым движением точки вокруг некоторой оси называют движение, при котором траекторией точки является окружность с центром, который лежит на оси вращения, при этом плоскость окружности перпендикулярна этой оси.

Вращением тела вокруг оси называют движение, при котором все точки тела совершают круговые движения около этой оси.

Перемещение при вращении характеризуют при помощи угла поворота $(\varphi)$ . Часто используют вектор элементарного поворота $\bar{d\varphi}$ , который равен по величине элементарному углу поворота тела $(d \varphi)$ за маленький отрезок времени dt и направлен по мгновенной оси вращения в сторону, откуда этот поворот виден реализующимся против часовой стрелки. Надо отметить, что только элементарные угловые перемещения являются векторами. Углы вращения на конечные величины векторами не являются.

Определение

Угловой скоростью называют скорость изменения угла поворота и обозначают ее обычно буквой $\omega$ . Математически определение угловой скорости записывают так:

$$\bar{\omega}=\frac{d \bar{\varphi}}{d t}=\dot{\bar{\varphi}}(1)$$

Угловая скорость — векторная величина (это аксиальный вектор). Она имеет направление вдоль мгновенной оси вращения совпадающее с направлением поступательного правого винта, если его вращать в сторону вращения тела (рис. 1).

Вектор угловой скорости может претерпевать изменения как за счет изменения скорости вращения тела вокруг оси (изменение модуля угловой скорости), так и за счет поворота оси вращения в пространстве ($\bar{\omega}$ при этом изменяет направление).

Равномерное вращение

Если тело за равные промежутки времени поворачивается на один и тот же угол, то такое вращение называют равномерным. При этом модуль угловой скорости находят как:

$$\omega=\frac{\varphi}{t}(2)$$

где $(\varphi)$ – угол поворота, t – время, за которое этот поворот совершён.

Равномерное вращение часто характеризуют при помощи периода обращения (T), который является временем, за которое тело производит один оборот ($\Delta \varphi=2 \pi$). Угловая скорость связана с периодом обращения как:

$$\omega=\frac{2 \pi}{T}(3)$$

С числом оборотов в единицу времени ($\nu) угловая скорость связана формулой:

$$\omega=2 \pi \nu(4)$$

Понятия периода обращения и числа оборотов в единицу времени иногда используют и для описания неравномерного вращения, но понимают при этом под мгновенным значением T, время за которое тело делало бы один оборот, если бы оно вращалось равномерно с данной мгновенной величиной скорости. {3} \approx 20(\mathrm{rad})$$

Ответ. $\varphi = 20$ рад.

Читать дальше: Формула удельного веса.

Период и частота обращения | Физика

Равномерное движение по окружности характеризуют периодом и частотой обращения.

Период обращения — это время, за которое совершается один оборот.

Если, например, за время t=4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения. Обозначается он буквой T и определяется по формуле

Итак, чтобы найти период обращения, надо время, за которое совершено n оборотов, разделить на число оборотов.

Другой характеристикой равномерного движения по окружности является частота обращения.

Частота обращения — это число оборотов, совершаемых за 1 с. Если, например, за время t = 2 с тело совершило n = 10 оборотов, то легко сообразить, что за 1 с оно успевало совершить 5 оборотов. Это число и выражает частоту обращения. Обозначается она греческой буквой ν (читается: ню) и определяется по формуле

Итак, чтобы найти частоту обращения, надо число оборотов разделить на время, в течение которого они произошли.

За единицу частоты обращения в СИ принимают частоту обращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: 1/с или с^-1 (читается: секунда в минус первой степени). Раньше эту единицу называли «оборот в секунду», но теперь это название считается устаревшим.

Сравнивая формулы (6.1) и (6.2), можно заметить, что период и частота — величины взаимно обратные. Поэтому

Формулы (6.1) и (6.3) позволяют найти период обращения T, если известны число n и время оборотов t или частота обращения ν. Однако его можно найти и в том случае, когда ни одна из этих величин неизвестна. Вместо них достаточно знать скорость тела v и радиус окружности r, по которой оно движется. Для вывода новой формулы вспомним, что период обращения — это время, за которое тело совершает один оборот, т.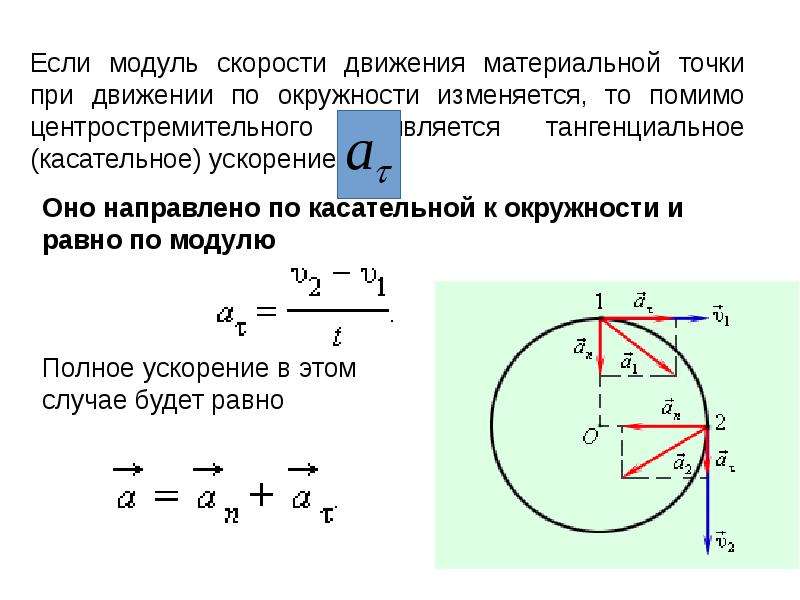 е. проходит путь, равный длине окружности (l_окр = 2πr, где π≈3,14— число «пи», известное из курса математики). Но мы знаем, что при равномерном движении время находится делением пройденного пути на скорость движения. Таким образом,

Итак, чтобы найти период обращения тела, надо длину окружности, по которой оно движется, разделить на скорость его движения.

Видео, не по теме но интересно

1. Что такое период обращения? 2. Как можно найти период обращения, зная время и число оборотов? 3. Что такое частота обращения? 4. Как обозначается единица частоты? 5. Как можно найти частоту обращения, зная время и число оборотов? 6. Как связаны между собой период и частота обращения? 7. Как можно найти период обращения, зная радиус окружности и скорость движения тела?

Эффект Доплера в в физике: определение, примеры, формула

1.

Определение эффекта Доплера

Что же происходит и в чём причина этого эффекта?

Нам хорошо известно, что звук — это механические упругие волны. Основными характеристиками любой волны являются:

• длина волны;
• период колебаний в волне;
• частота колебаний в волне;
• амплитуда;
• скорость волны.

Мы будем говорить сейчас о трёх из них — длине волны, скорости волны и частоте колебаний, которые связаны друг с другом формулой  где λ — длина волны, v — скорость волны, а ν — частота колебаний. Если, к примеру, находящийся в воде поплавок начнёт совершать вертикальные колебания, то по воде начнут расходиться круги, расстояние между которыми и будет равно длине волны. Поплавок, в данном случае, представляет собой неподвижный источник волн, то есть, совершая колебания, он, тем не менее, остаётся на том же месте по отношению к неподвижному относительно Земли наблюдателю. Но совсем иначе будет выглядеть волновая картина, если источник волн будет либо приближаться, либо удаляться от наблюдателя.

Проводя наблюдения за волнами на воде, Доплер заметил, что когда источник волн приближается к наблюдателю, то длина волны становится немного меньше, а следовательно, частота становится немного больше, то есть количество гребней перед движущимся источником волн больше, чем позади него. Именно поэтому звук приближающегося автомобиля или поезда будет более высоким. С другой стороны, когда источник волн удаляется от наблюдателя, то длина волны становится немного больше, а следовательно, частота становится немного меньше, то есть количество гребней волны позади движущегося источника меньше, чем впереди него. Именно поэтому звук удаляющегося от нас автомобиля или поезда будет более низким. В этом и состоит суть эффекта Доплера — изменение длины волны или её частоты при движении источника волны к наблюдателю или от него. И это изменение можно довольно легко подсчитать, зная скорость движения источника волн и их длину или частоту в случае, если источник неподвижен относительно наблюдателя.

2. Эксперименты

Чтобы увидеть эффект Доплера своими глазами или услышать своими ушами вовсе не нужны специальные лаборатории или сложные установки. Вот описание двух простых экспериментов, в ходе которых можно его наблюдать.

Возьмите свисток и прикрепите к нему длинную гибкую трубку так, чтобы можно было свистеть в свисток при помощи этой трубки. Если держать трубку и свисток неподвижно и дуть в трубку, то будет слышаться ровный свист, а если раскрутить трубку со свистком, не прекращая дуть в неё, то можно будет услышать как меняется звук свистка при приближении к вам и отдалении от вас. Это и будет наглядным подтверждением эффекта Доплера.

Физика. 9 класс. Дидактические материалы

Данное пособие включает тренировочные задания, тесты для самоконтроля, самостоятельные работы, контрольные работы и примеры решения типовых задач. Предлагаемые дидактические материалы составлены в полном соответствии со структурой и методологией учебника А.В. Перышкина, Е.М. Гутник «Физика. 9 класс».

Купить

Второй эксперимент осуществить сложнее, но именно его осуществил в 1845 году голландский метеоролог и химик Христофор Бёйс-Баллот. Суть эксперимента сводилась к тому, что в поезде размещались музыканты-трубачи, которые должны были играть одну и ту же ноту, а на станции, мимо которой проезжал этот поезд, другая группа музыкантов должна была внимательно слушать как меняется тон этого звука при приближении и удалении поезда. Музыканты — люди с очень хорошим слухом, и им как никому другому проще всего определить это изменение, что они успешно и выполнили, подтвердив экспериментально открытый Доплером эффект.

Но самый простой способ убедиться в существовании этого эффекта — прислушаться к сирене машины скорой помощи в момент, когда она приближается к вам и в момент, когда она, проехав мимо вас, удаляется. Звук сирены будет отличаться, хотя никаких изменений в работе сирены на самом деле не происходит. Это и есть эффект Доплера для звуковых волн.

3. Формула и применение

Как уже было сказано, зная скорость источника волн по отношению к неподвижному наблюдателю можно определить регистрируемую приёмником частоту волны. Формулу, позволяющую это сделать, нетрудно вывести, зная, что  (здесь v — скорость волн в данной среде, ν₀ — частота испускаемых источником волн), и, если источник приближается к неподвижному наблюдателю со скоростью u относительно среды, то  и тогда частота, которую будет регистрировать неподвижный приёмник, будет равна:

Если же сам приёмник движется относительно среды со скоростью u₁, то частота регистрируемых им волн будет равна:

Если же и источник, и приёмник движутся относительно друг друга, то:

Эффект Доплера, как вы, наверное, уже догадались, возникает не только при распространении звуковых волн, но и вообще любых волн, в том числе и электромагнитных, одним из видов которых является видимый свет. Если бы наш глаз был сверхчувствителен, то мы могли бы заметить, что как и в случае со звуком, если источник света приближается к наблюдателю, то длина волны становится меньше, а частота больше, и наоборот, если источник света удаляется от наблюдателя, то длина волны увеличивается, а частота уменьшается. То есть свет зелёной лазерной указки при стремительном её приближении к нам наблюдался бы как слегка голубоватый, а при удалении от нас был бы более жёлтым. Но наш глаз различить этого не может, зато точные приборы могут и этот эффект позволил учёным сделать одно очень важное наблюдение — спектры наблюдаемых нами звёзд немного сдвинуты по частоте в меньшую сторону, что называется «красным смещением» и является доказательством того, что галактики удаляются друг от друга, а значит, Вселенная расширяется. Это, пожалуй, самое важное применение эффекта Доплера в фундаментальной науке. Но эффект Доплера и связанные с ним формулы нашли очень широкое применение не только в астрономии. Прежде всего, стоит сказать о медицине. В ультразвуковой диагностике эффект Доплера применяется для исследования внутренних органов человека. А также, именно эффект Доплера лежит в основе действия полицейских радаров, определяющих скорость автомобиля, и камер, следящих за скоростным режимом на дорогах. Эффект Доплера применяется в метеорологии, воздушной навигации, при расчётах траекторий спутников, системах навигации.

Что ещё почитать?

4. Релятивистский эффект Доплера

Выше уже было отмечено, что эффект Доплера применим не только к механическим, но и к электромагнитным волнам. Однако, в случае электромагнитных волн нужно учитывать, что их скорость — есть величина постоянная, не зависящая от направления и скорости движения источника или наблюдателя, и равная с. В этом случае, формулы, аналогичные тем, что приведены для звуковых волн, следует выводить на основании специальной теории относительности Эйнштейна. Это и будет формула релятивистского эффекта Доплера. Не углубляясь в процедуру её вывода, приведём сразу окончательный результат:

Здесь v — это скорость источника относительно приёмника, а угол а — при удалении источника вдоль прямой равен π, а при приближении источника по прямой равен 0.

5. Методические советы учителям

1. При описании эффекта Доплера лучшей демонстрацией будет звукозапись сирены или гудка проезжающего автомобиля. Для этого можно одному или нескольким ученикам предварительно дать задание — записать сигнал проезжающего мимо автомобиля или машины скорой помощи на смартфон. С этой звукозаписи и стоит начать урок.
2. Особое внимание стоит уделить применению эффекта Доплера, а не самим формулам, с ним связанным. Ведь этот эффект используют люди самых разных профессий — сотрудники ДПС, врачи, учёные, метеорологи.
3. Приводимые здесь формулы можно преобразовать и решить несколько вычислительных примеров практической направленности — рассчитать скорость автомобиля или определить изменение звукового тона по частоте.
4. Особое внимание следует уделить применению эффекта Доплера в астрономии и космологии, ведь именно из этого эффекта следует вывод о расширяющейся Вселенной, что в итоге привело к созданию современной космологической модели Вселенной.

Угловая скорость и ускорение. Определения и формулы для расчета

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющаяся приращением угла поворота тела за промежуток времени.

Обозначение: ω (омега).

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

• если известно количество оборотов n за единицу времени t:
  
• если задан угол поворота φ за единицу времени:
  

Размерности:

• Количество оборотов за единицу времени [об/мин], [c^-1].
• Угол поворота за единицу времени [рад/с].

Быстрота изменения угла φ (перемещения из положения П₁ в положение П₂) – это и есть угловая скорость:

ω=dφ/dt=φ’, рад/с; с^-1    (2.3)

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

ω=1,5 с^-1=9,42 рад/с.

Приняв k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Угловое ускорение

Изменение угловой скорости характеризуется угловым ускорением:

Единицы измерения углового ускорения: [рад/с²], [с^-2]

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает, а при отрицательном вращение замедляется.

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

ω=n2π/60=nπ/30 рад/с; с^-1.

Длина волны — формулы, измерение, определение

Волна: продольная и поперечная

Начнем с того, что волна — это распространение колебания в пространстве.

Волны бывают механическими и электромагнитными.

Механические волны — это те волны, колебания которых можно почувствовать физически, потому что они распространяются в упругой среде.

• Например, звук. Когда звук распространяется внутри какого-либо вещества, мы можем ощутить его прикосновением.

Представьте, что вы стоите на железнодорожных путях. Нет, вы не Анна Каренина, вы — экспериментатор.

Если к вам приближается поезд, вы рано или поздно его услышите. Вернее, услышите, как только звуковая волна со скоростью 𝑣 = 330 м/с достигнет ваших ушей.

Если приложить ухо к рельсу, то это произойдет значительно быстрее, потому что скорость звука в твердом теле больше, чем в воздухе. Кстати, под водой скорость звука больше, чем в воздухе, но меньше, чем в твердых телах.

Если вы когда-нибудь трогали музыкальную колонку, то знаете, что звук чувствуется и на ощупь.

Электромагнитные волны — это те волны, которые мы потрогать не можем.

• Например, радиоволны, Wi-Fi и свет.

Для них работают все те же самые законы, просто их скорость значительно больше и равна скорости света 𝑣 = 3*10^8 м/с. И источники у них разные.

Волны также принято делить на продольные и поперечные:

Продольные — это те волны, у которых колебание происходит вдоль направления распространения волны.

• Дрожание окон во время грома или сейсмические волны (землетрясения) — это пример продольных волн.

Поперечные — волны, у которых колебание происходит поперек направления распространения волны.

• Представьте, что вы запустили волну из людей на стадионе — она будет поперечной.
• Видимый свет и дрожание гитарной струны — тоже поперечные волны.

Морская волна — продольная или поперечная?

На самом деле в ней есть и продольная, и поперечная составляющие, поэтому ее нельзя отнести к конкретному типу.

Длина волны: определение и расчет

Конечно, у любой волны есть характеристики. Одна из таких характеристик — это длина волны.

• λ — длина волны [м]

Длиной волны называется расстояние между двумя точками этой волны, колеблющихся в одной фазе. Если проще, то это расстояние между двумя «гребнями».

Еще длиной волны можно назвать расстояние, пройденное волной, за один период колебания.

Период — это время, за которое происходит одно колебание. То есть, если дано время распространения волны и количество колебаний, можно рассчитать период.

Формула периода колебания волны T = t/N T — период [с] t — время [с] N — количество колебаний [-]

Связь со скоростью

Чтобы вывести формулу скорости через длину волны, нужно вспомнить формулу скорости из кинематики — это раздел физики, в котором изучается движение тел без учета внешнего воздействия).

Формула скорости 𝑣 = S/t 𝑣 — скорость [м/с] S — путь [м] t — время [с]

Переходя к волнам, можно провести следующие аналогии:

• путь — длина волны
• время — период

А для скорости даже аналогия не нужна — скорость и Африке скорость.

Формула скорости волны 𝑣 = λ/T 𝑣 — скорость [м/с] λ — длина волны [м] T — период [с]

Задачка

Лодка совершает колебания на волнах. За 40 с она совершила 10 колебаний. Какова скорость распространения волны, если расстояние между соседними гребнями волны равно 1 м?

Решение:

1. Возьмем формулу скорости:

𝑣 = λ/T



2. Нам известна длина волны, но не дан период. Период вычисляется по формуле:

T = t/N

T = 40/10 = 4 с



3. Теперь подставляем величины в формулу

𝑣 = λ/T

𝑣 = ¼ = 0,25 м/с

Ответ: 𝑣 = 0,25 м/с

Резонанс

Если громко говорить в одном помещении с гитарой — можно услышать, как на ней начал играть призрак. На самом деле частота струны совпала с частотой голоса и возник резонанс.

На графике ниже можно увидеть, что на некоторой частоте резко увеличивается амплитуда. Эта частота называется частотой резонанса.

Частота — это величина, обратная периоду. Она показывает, за какое время происходит одно колебание.

Формула частоты ν = N/t ν — частота [Гц] t — время [с] N — количество колебаний [-]

В мире существует очень много историй про то, как солдаты шли в ногу по мосту, он впал в резонанс и все провалились. А вот еще одна история про гидрологов — как говорится, из первых уст🙂

Команда гидрологов — специалистов по внутренним водам — работала на Алтае и изучала местную реку. Через реку был протянут веревочный мост, а по центру моста стояла лебедка, которая помогает поднять пробу воды из речки, не спускаясь до нее.

В один из дней экспедиции начался сильный, почти штормовой, ветер. Исследователи работали на мосту, а когда поняли, что находиться на веревочной конструкции в такой сильный ветер небезопасно, начали с него уходить. Как только последний человек из команды сделал шаг с моста на землю, мост вместе с лебедкой разнесло в щепки. Это произошло из-за того, что частота ветра совпала с собственной частотой раскачивающегося моста. Хорошо, что история закончилась именно так.

Определение периодической скорости | Bankrate.com

Что такое периодическая ставка?

Периодическая ставка — это процентная ставка, взимаемая за определенное количество периодов времени. Периодическая ставка равна годовой процентной ставке, деленной на количество периодов. Например, проценты по жилищному кредиту обычно рассчитываются ежемесячно, поэтому, если годовая процентная ставка составляет 4 процента, вы разделите это на 12 и получите 0,33 процента. Это ваш интерес каждый месяц.

Более глубокое определение

Когда банк взимает периодические проценты на основе среднего остатка ссуды на ежемесячной или ежедневной основе, эффективная процентная ставка фактически выше, чем заявленная годовая процентная ставка.Причина — эффект начисления процентов.

По кредитным картам и овердрафтам проценты обычно рассчитываются ежедневно; это означает, что дневная процентная ставка — это годовая ставка, разделенная на 365 дней. Поскольку проценты начисляются ежедневно, большой дневной остаток на счете означает, что вы будете платить больше процентов.

Эффект периодической ставки усугубляется при высоких процентных ставках. Например, если переменная процентная ставка по кредитной карте составляет 16 процентов, дневная процентная ставка будет равна 0.044 процента.

Эффект периодической ставки также может быть использован в ваших интересах при инвестировании денег, если вы реинвестируете проценты или прибыль. Таким образом, вы увеличиваете проценты, и через несколько лет общая стоимость инвестиций будет больше, чем если бы вы снимали проценты или прибыль каждый месяц.

Пример периодической ставки

Компании иногда испытывают трудности с управлением денежными потоками, потому что они платят за сырье, но не возмещают эти затраты до тех пор, пока товары не будут проданы.Чтобы гарантировать выполнение своих финансовых обязательств, многие используют ссуду или овердрафт.

Проценты по их кредиту взимаются ежедневно, поэтому, если они снимут большую сумму для оплаты большого заказа и погасят ее через несколько дней, они могут в конечном итоге заплатить больше процентов, чем они ожидают, даже если их средний остаток кредита низкий.

Определение периодической процентной ставки

Что такое периодическая процентная ставка?

Периодическая процентная ставка — это ставка, которая может взиматься по ссуде или реализовываться по инвестициям в течение определенного периода времени.Кредиторы обычно указывают процентные ставки на годовой основе, но в большинстве случаев проценты складываются чаще, чем ежегодно. Периодическая процентная ставка — это годовая процентная ставка, деленная на количество периодов начисления сложных процентов.

Большее количество периодов начисления сложных процентов позволяет начислять проценты или добавлять к ним большее количество раз.

Как работает периодическая процентная ставка

Количество периодов начисления сложных процентов напрямую влияет на периодическую процентную ставку по инвестициям или ссуде.Периодическая ставка инвестиции составляет 1%, если эффективная годовая доходность составляет 12%, и она увеличивается каждый месяц. Его периодическая процентная ставка составляет 0,00033, если вы увеличиваете ежедневную периодическую ставку, это будет эквивалент 0,03%.

Чем чаще паковочная масса образуется, тем быстрее она растет. Представьте, что при вложении 1000 долларов доступны два варианта. Согласно первому варианту инвестор получает 8% годовых, а проценты начисляются ежемесячно. По второму варианту инвестор получает 8.125% годовых, начисляемых ежегодно.

К концу 10-летнего периода инвестиции в размере 1000 долларов США при первом варианте увеличиваются до 2219,64 доллара США, а при втором варианте — до 2184,04 доллара США. Более частое начисление сложных процентов по первому варианту дает больший доход, даже если процентная ставка выше по второму варианту.

Ключевые выводы

• Кредиторы обычно указывают процентные ставки на годовой основе, но в большинстве случаев проценты складываются чаще, чем ежегодно.
• Проценты по ипотеке обычно составляют ежемесячно.
• Кредиторы по кредитным картам обычно рассчитывают проценты на основе ежедневной периодической ставки, поэтому процентная ставка умножается на сумму, которую заемщик должен в конце каждого дня.

Пример периодической процентной ставки

Проценты по ипотеке начисляются или взимаются ежемесячно. Если годовая процентная ставка по этой ипотеке составляет 8%, периодическая процентная ставка, используемая для расчета процентов, начисленных в любой отдельный месяц, равна 0.08 делится на 12, получается 0,0067 или 0,67%.

К оставшейся основной сумме ипотечного кредита будет применяться ежемесячная процентная ставка 0,67%.

Типы процентных ставок

Годовая процентная ставка, обычно указываемая по займам или инвестициям, является номинальной процентной ставкой — учитывалась периодическая ставка до начисления сложных процентов . Эффективная процентная ставка — это фактическая процентная ставка после того, как эффекты начисления сложных процентов были включены в расчет.

Вы должны знать номинальную ставку по ссуде и количество периодов начисления сложных процентов, чтобы рассчитать ее эффективную годовую процентную ставку. Сначала разделите номинальную ставку на количество периодов начисления сложных процентов. Результат — периодическая ставка. Теперь прибавьте это число к 1 и возьмите сумму как степень числа сложных процентных ставок. Вычтите 1 из произведения, чтобы получить эффективную процентную ставку.

Например, если ипотека составляет ежемесячно и имеет номинальную годовую процентную ставку 6%, ее периодическая ставка равна 0.5%. Когда вы переводите процент в десятичное число и добавляете 1, сумма составляет 1,005. Это число в 12-й степени составляет 1,0617. Если вычесть 1 из этого числа, разница составит 0,0617 или 6,17%. Эффективная ставка немного выше номинальной.

Кредиторы кредитных карт обычно рассчитывают проценты на основе ежедневной периодической ставки. Процентная ставка умножается на сумму задолженности заемщика в конце каждого дня. Затем эти проценты добавляются к балансу этого дня, и весь процесс повторяется через 24 часа — когда заемщик обычно должен больше, если он не совершил платеж, потому что теперь его баланс включает проценты за предыдущий день.Эти кредиторы часто указывают годовую процентную ставку (APR), приукрашивая этот расчет ежедневной периодической ставки. Вы можете определить свою дневную периодическую ставку, разделив годовую процентную ставку на 365, хотя некоторые кредиторы определяют дневную периодическую ставку путем деления на 360.

Особое внимание

Некоторые возобновляемые ссуды предлагают «льготный период» для накопления процентов, позволяя заемщикам выплатить свои остатки к определенной дате в рамках цикла выставления счетов без дальнейшего увеличения процентов на их остатки.Дата и продолжительность льготного периода, если таковой имеется, должны быть четко указаны в вашем контракте с кредитором.

Определение эффективной годовой процентной ставки

Что такое эффективная годовая процентная ставка?

Эффективная годовая процентная ставка — это реальная доходность сберегательного счета или любых инвестиций с выплатой процентов, если принять во внимание эффекты начисления сложных процентов с течением времени. Он также показывает реальную процентную ставку по процентам по ссуде, кредитной карте или любой другой задолженности.n-1 \\ & \ textbf {где:} \\ & i = \ text {Номинальная процентная ставка} \\ & n = \ text {Количество периодов} \\ \ end {выровнено} Эффективная годовая процентная ставка = (1 + ni) n − 1, где: i = номинальная процентная ставка = количество периодов

Эффективная годовая процентная ставка

О чем говорит эффективная годовая процентная ставка?

Банковский депозитный сертификат, сберегательный счет или предложение ссуды могут рекламироваться с указанием номинальной процентной ставки, а также эффективной годовой процентной ставки.Номинальная процентная ставка не отражает эффекты начисления сложных процентов или даже комиссий, связанных с этими финансовыми продуктами. Эффективная годовая процентная ставка — это реальный доход.

Ключевые выводы

• Сберегательный счет или ссуда могут рекламироваться как с номинальной процентной ставкой, так и с эффективной годовой процентной ставкой.
• Эффективная годовая процентная ставка — это реальный доход, выплачиваемый на сбережения, или реальная стоимость ссуды, поскольку она учитывает эффекты начисления сложных процентов и любые взимаемые комиссии.
• Чем чаще периоды начисления сложных процентов, тем выше доход.

Вот почему эффективная годовая процентная ставка — важная финансовая концепция, которую необходимо понять. Точно сравнивать различные предложения можно только в том случае, если вы знаете эффективные годовые процентные ставки по каждому из них.

Пример эффективной годовой процентной ставки

Например, рассмотрим эти два предложения: Инвестиция A платит 10% годовых, начисляемых ежемесячно. (количество периодов начисления сложных процентов) — 1

Для инвестиции A это будет: 10.2 — 1

Инвестиция B имеет более высокую заявленную номинальную процентную ставку, но эффективная годовая процентная ставка ниже, чем эффективная ставка для инвестиции A. Это связано с тем, что инвестиции B составляют меньше раз в течение года.

Если инвестор вложит, скажем, 5 000 000 долларов в одну из этих инвестиций, неправильное решение будет стоить более 5 800 долларов в год.

Более частое начисление процентов дает более высокую прибыль

По мере увеличения количества периодов начисления сложных процентов увеличивается и эффективная годовая процентная ставка.Квартальное начисление сложных процентов дает более высокую доходность, чем полугодовое начисление сложных процентов, ежемесячное начисление сложных процентов больше, чем ежеквартальное, а ежедневное начисление сложных процентов превышает ежемесячное. Ниже приводится разбивка результатов этих различных составных периодов с номинальной процентной ставкой 10%:

• Полугодовой = 10,250%
• Ежеквартально = 10,381%
• в месяц = ​​10,471%
• Ежедневно = 10,516%

Пределы компаундирования

Есть потолок феномену компаундирования.(0,1) — 1.

Часто задаваемые вопросы

Какова эффективная годовая процентная ставка?

Эффективная годовая процентная ставка — это важное понятие, описывающее истинную процентную ставку, связанную с инвестициями или ссудой. Наиболее важной особенностью эффективной годовой процентной ставки является то, что она учитывает тот факт, что более частые периоды начисления сложных процентов приведут к более высокой эффективной процентной ставке. Например, предположим, что у вас есть две ссуды, каждая из которых имеет установленную процентную ставку 10%, в которой один составляет ежегодно, а другой — два раза в год.Несмотря на то, что у них обоих заявленная процентная ставка составляет 10%, эффективная годовая процентная ставка по ссуде, составляющей два раза в год, будет выше.

Как рассчитать эффективную годовую процентную ставку?

Эффективная годовая процентная ставка рассчитывается по следующей формуле:

Взаимодействие с другими людьми E ж ж е c т я v е А п п ты а л я п т е р е s т р а т е знак равно ( 1 + я п ) п — 1 где: я знак равно Номинальная процентная ставка п знак равно Количество периодов \ begin {align} & Effective \ Annual \ Interest \ Rate = \ left (1+ \ frac {i} {n} \ right) ^ n-1 \\ & \ textbf {где:} \\ & i = \ text {Номинальный процентная ставка} \\ & n = \ text {Количество периодов} \\ \ end {выровнено} Эффективная годовая процентная ставка = (1 + ni) n − 1, где: i = номинальная процентная ставка = количество периодов

Хотя это можно сделать вручную, большинство инвесторов будут использовать финансовый калькулятор, электронную таблицу или онлайн-программу.Более того, инвестиционные веб-сайты и другие финансовые ресурсы регулярно публикуют эффективную годовую процентную ставку ссуды или инвестиции. Эта цифра также часто включается в проспект эмиссии и маркетинговые документы, подготовленные эмитентами ценных бумаг.

Почему важна эффективная годовая процентная ставка?

Эффективная годовая процентная ставка важна, потому что без нее заемщики могут быть введены в заблуждение и недооценивают истинную стоимость ссуды. Это, в свою очередь, может привести к финансовым проблемам, если заемщик не внесет в бюджет полную сумму своих процентных платежей.Для инвесторов, с другой стороны, расчет эффективной годовой процентной ставки важен для прогнозирования фактического ожидаемого дохода от инвестиций, таких как корпоративные облигации или другие ценные бумаги с фиксированным доходом. В противном случае они могут недооценить реальную привлекательность инвестиционной возможности.

Скоростей Реакции | Безграничная химия

Измерение скорости реакции

Скорость реакции определяется путем наблюдения за изменениями концентраций реагентов или продуктов в течение определенного периода времени.

Цели обучения

Составьте выражения скорости, когда даны химические реакции, и обсудите методы измерения этих скоростей

Основные выводы

Ключевые моменты

• Скорость реакции рассчитывается по формуле скорость = Δ [C] / Δt, где Δ [C] — изменение концентрации продукта за период времени Δt.
• Скорость реакции можно наблюдать, наблюдая за исчезновением реагента или появлением продукта с течением времени.
• Если в результате реакции образуется газ, такой как кислород или диоксид углерода, есть два способа измерения скорости реакции: использование газового шприца для измерения произведенного газа или расчет уменьшения массы реакционного раствора.
• Если в результате реакции образуется осадок, образовавшееся количество можно использовать для определения скорости реакции путем измерения того, сколько времени требуется, чтобы образовавшийся осадок скрыл видимость креста через коническую колбу.

Ключевые термины

• скорость реакции : Как быстро или медленно происходит реакция.
• газовый шприц : Элемент лабораторного оборудования, используемый для отбора объема газа из закрытой химической системы для измерения и / или анализа.
• продукт : Химическое вещество, образующееся в результате химической реакции.

Скорость реакции

За скоростью реакции обычно наблюдают, наблюдая за исчезновением реагента или появлением продукта в течение заданного периода времени. Возьмем химическую реакцию:

[латекс] \ text {A} + 2 \ text {B} \ rightarrow 3 \ text {C} [/ latex]

Здесь скорость появления продукта C на временном интервале Δt составляет:

[латекс] \ text {средняя скорость} = \ frac {\ Delta \ text {C}} {\ Delta \ text {t}} [/ latex]

Концентрация C [C] обычно выражается в моль / литр.Это средняя скорость появления C за интервал времени Δt. Предел этой средней скорости по мере того, как временной интервал становится меньше, называется скоростью появления C в момент времени t, и это наклон кривой [C] в зависимости от t в момент времени t. Этот мгновенный наклон или скорость записывается как [latex] \ frac {\ text {d} [\ text {C}]} {\ text {dt}} [/ latex]. Поскольку одна молекула A и две молекулы B расходуются на каждые три производимые молекулы C, скорости исчезновения и появления этих химических соединений различны, но связаны между собой.

Скорость исчезновения и появления химических частиц : Это выражение связывает скорости исчезновения и появления химических частиц в реакции A + 2B -> 3C.

Измерение скорости реакции

Способ измерения скорости реакции будет зависеть от того, что это за реакция и какой продукт образуется. В следующих примерах описаны различные способы измерения скорости реакции.

Реакции с образованием газов, таких как кислород или углекислый газ

Перекись водорода разлагается с образованием кислорода:

[латекс] 2 \ text {H} _2 \ text {O} _2 (\ text {aq}) \ rightarrow 2 \ text {H} _2 \ text {O} (\ text {l}) + \ text {O } _2 (\ text {g}) [/ latex]

Объем произведенного кислорода можно измерить с помощью газового шприца.Газ собирается в шприце, выталкиваясь из поршня. Объем произведенного газа можно определить по отметкам на шприце. Это изменение объема можно преобразовать в изменение концентрации ([латекс] \ Delta [\ text {C}] [/ latex]) и разделив его на время реакции ([латекс] \ Delta \ text {t } [/ latex]) даст среднюю скорость реакции.

Метод газового шприца : В реакции, в которой образуется газ, объем произведенного газа можно измерить с помощью метода газового шприца.

Изменение массы

Скорость реакции, при которой образуется газ, также можно измерить, рассчитав потерю массы при образовании и выходе газа из реакционной колбы. Этот метод можно использовать для реакций с образованием диоксида углерода или кислорода, но он не очень точен для реакций с выделением водорода, поскольку масса слишком мала для точного измерения. Измерение изменения массы также может быть подходящим для других типов реакций.

Реакция осаждения

В реакции, в которой образуется осадок, количество осадка, образовавшегося за период времени, можно использовать как меру скорости реакции.Например, когда тиосульфат натрия реагирует с кислотой, образуется желтый осадок серы. Эта реакция записывается так:

[латекс] \ text {Na} _2 \ text {S} _2 \ text {O} _3 (\ text {aq}) + 2 \ text {HCl} (\ text {aq}) \ rightarrow 2 \ text {NaCl } (\ text {aq}) + \ text {SO} _2 (\ text {aq}) + \ text {H} _2 \ text {O} (\ text {l}) + \ text {S} (\ text {s}) [/ латекс]

Один из способов оценить скорость этой реакции — провести исследование в конической колбе и подложить под ее дно лист бумаги с черным крестом.В начале реакции крестик будет хорошо виден, когда вы заглянете в колбу. Однако по мере того, как реакция прогрессирует и образуется больше осадка, крест постепенно станет менее четким и в конечном итоге полностью исчезнет. Используя секундомер, чтобы измерить, сколько времени нужно, чтобы крестик исчез, а затем взвесив количество осадка, образовавшегося за это время, можно рассчитать среднюю скорость реакции. Обратите внимание, что невозможно собрать газ SO ₂ , который образуется в реакции, потому что он хорошо растворяется в воде.

Стехиометрия реакции

Стехиометрия реакции изучает количественные отношения между реагентами и продуктами в рамках данной химической реакции.

Цели обучения

Используйте стехиометрию, чтобы сбалансировать химические уравнения

Основные выводы

Ключевые моменты

• Стехиометрия происходит от греческих слов «стоихион» (элемент) и «метрон» (измерять). Таким образом, стехиометрия касается определения количества реагентов и продуктов, которые потребляются и производятся в рамках данной химической реакции.
• Стехиометрический коэффициент любого вещества, не участвующего в данной химической реакции, равен нулю.
• Принципы стехиометрии основаны на законе сохранения массы. Материя не может быть ни создана, ни разрушена, поэтому масса каждого элемента, присутствующего в продукте (ах) химической реакции, должна быть равна массе каждого элемента, присутствующего в реагенте (ах).

Ключевые термины

• Стехиометрия реакции : Описывает количественное соотношение между реагентами и продуктами в рамках данной химической реакции.
• Стехиометрическое число : Равно стехиометрическому коэффициенту в сбалансированном уравнении, но положительно для продуктов (потому что они производятся) и отрицательно для реагентов (поскольку они потребляются).
• стехиометрическое соотношение : положительное целочисленное соотношение, которое связывает количество молей реагентов и продуктов, участвующих в химической реакции; это соотношение можно определить из коэффициентов сбалансированного химического уравнения.
• сбалансированное уравнение : Когда количество каждого отдельного элемента равно в обеих частях уравнения.

Стехиометрия — это раздел химии, который имеет дело с относительными количествами реагентов и продуктов, которые потребляются / производятся в рамках данной химической реакции. Однако, чтобы сделать какие-либо стехиометрические определения, мы должны сначала обратиться к сбалансированному химическому уравнению. В сбалансированном химическом уравнении мы можем легко определить стехиометрическое соотношение между количеством молей реагентов и количеством молей продуктов, потому что это соотношение всегда будет положительным целочисленным отношением.Рассмотрим реакцию газообразного азота и газообразного водорода с образованием аммиака (NH ₃ ):

[латекс] \ text {N} _2 (\ text {g}) + 3 \ text {H} _2 (\ text {g}) \ rightarrow 2 \ text {NH} _3 (\ text {g}) [/ латекс]

Из сбалансированного уравнения видно, что стехиометрический коэффициент для азота равен 1, для водорода — 3, а для аммиака — 2. Следовательно, стехиометрическое соотношение часто называют просто «молярным соотношением» или « молярное соотношение ”между N ₂ (г), H ₂ (г) и NH ₃ (г) составляет 1: 3: 2.В особом случае, когда реагенты объединены в их молярных соотношениях (в данном случае 1 моль N ₂ (г) и 3 моль H ₂ (г)), они будут полностью реагировать друг с другом, и не реагент останется после того, как реакция завершится. Однако в большинстве реальных ситуаций реагенты не сочетаются в таких идеальных стехиометрических количествах. В большинстве случаев один реагент неизбежно будет первым, который полностью израсходуется в реакции, что приведет к остановке реакции.Этот реагент известен как ограничивающий реагент или ограничивающий реагент.

Из этого краткого описания мы видим, что стехиометрия имеет много важных приложений. Как мы увидим, балансируя химические уравнения и определяя стехиометрические коэффициенты, мы сможем определить количество молей продукта (ов), которые могут быть получены в данной реакции, а также количество молей реагента (s ), который будет использован. Стехиометрия также может быть использована для получения полезных определений относительно ограничивающих реагентов и для расчета количества избыточного реагента (ов), оставшегося после того, как данная реакция завершилась до конца.

Основы стехиометрии

Наука о стехиометрии возможна, потому что она основана на законе сохранения массы. Поскольку материя не может быть ни создана, ни разрушена, ни химическая реакция не может преобразовать один элемент в другой элемент, мы можем быть уверены, что масса каждого отдельного элемента, присутствующего в реагенте (ах) данной реакции, обязательно должна быть учтена в продукты). Этот физический закон делает возможными все стехиометрические вычисления.Однако мы можем выполнить эти расчеты правильно только в том случае, если у нас есть сбалансированное химическое уравнение, с которым можно работать.

Interactive: стехиометрия и уравнения баланса : Для производства хлористого водорода или любого другого химического вещества существует только одно соотношение реагентов, которое работает так, что весь водород и хлор используются для производства хлористого водорода. Попробуйте несколько разных соотношений, чтобы увидеть, какие из них образуют полную реакцию без остатка. Какое самое простое соотношение водорода и хлора для образования хлористого водорода?

Уравнения балансировки

Прежде чем выполнять какие-либо стехиометрические вычисления, мы должны сначала получить сбалансированное химическое уравнение.Возьмем, например, реакцию газообразного водорода и кислорода с образованием жидкой воды:

[латекс] \ text {H} _2 (\ text {g}) + \ text {O} _2 (\ text {g}) \ rightarrow \ text {H} _2 \ text {O} (\ text {l} ) [/ латекс]

Как здесь написано, мы должны заметить, что наше уравнение не сбалансировано, потому что у нас есть два атома кислорода в левой части уравнения, но только один в правой. Чтобы уравновесить это, нам нужно добавить стехиометрический коэффициент 2 перед жидкой водой:

[латекс] \ text {H} _2 (\ text {g}) + \ text {O} _2 (\ text {g}) \ rightarrow 2 \ text {H} _2 \ text {O} (\ text {l }) [/ latex]

Однако при этом наши водороды стали неуравновешенными.Чтобы завершить балансировку уравнения, мы должны добавить коэффициент 2 перед газообразным водородом:

[латекс] 2 \ text {H} _2 (\ text {g}) + \ text {O} _2 (\ text {g}) \ rightarrow 2 \ text {H} _2 \ text {O} (\ text { л}) [/ латекс]

Как мы видим, стехиометрический коэффициент для любого данного реагента / продукта — это количество молекул, которые будут участвовать в реакции, как записано в сбалансированном уравнении. Однако имейте в виду, что в наших расчетах мы часто будем работать с молями, а не с молекулами.В нашем примере мы видим, что стехиометрический коэффициент H ₂ (г) равен 2, в то время как для O ₂ (г) он равен 1, а для H ₂ O (l) он равен 2. Иногда вы можете встретить термин стехиометрическое число, который связан со стехиометрическим коэффициентом, но это не то же самое.

Электролиз воды : Хотя это изображение иллюстрирует обратную реакцию [латекса] 2 \ text {H} _2 (\ text {g}) + \ text {O} _2 (\ text {g}) \ rightarrow 2 \ text {H} _2 \ text {O} (\ text {l}) [/ latex], стехиометрические коэффициенты для каждого типа молекул остаются одинаковыми.Вода — 2, водород — 2, кислород — 1.

Для реагентов стехиометрическое число является отрицательным значением стехиометрического коэффициента, в то время как для продуктов стехиометрическое число просто равно стехиометрическому коэффициенту, оставаясь положительным. Следовательно, в нашем примере стехиометрическое число для H ₂ (г) равно -2, а для O ₂ (г) — -1. Однако для H ₂ O (l) он равен +2. Это связано с тем, что в этой реакции H ₂ (г) и O ₂ (г) являются реагентами, которые потребляются, тогда как вода является продуктом, который образуется.

Наконец, иногда вы можете встретить некоторые химические соединения, которые присутствуют во время реакции, но не потребляются и не образуются в ходе реакции. Катализатор — наиболее известный пример этого. Для таких видов их стехиометрические коэффициенты всегда равны нулю.

Пример

В уравнении h3 (g) + Cl2 (g) → 2 HCl (g), какое молярное соотношение (стехиометрическое соотношение) между h3 (g) и HCl (g)?

В нашем сбалансированном химическом уравнении коэффициент для h3 (g) равен 1, а коэффициент для HCl (g) равен 2.Следовательно, молярное соотношение между этими двумя соединениями составляет 1: 2. Это говорит нам о том, что на каждый 1 моль h3 (г), который расходуется в реакции, образуется 2 моля HCl (г).

Текущая стоимость, единственная сумма | Безграничные финансы

Однопериодные инвестиции

При рассмотрении инвестиций за один период n равно единице, поэтому PV — это просто FV, деленная на 1 + i.

Цели обучения

Расчет приведенной стоимости будущего одноразового платежа

Основные выводы

Ключевые моменты

• У однопериодных инвестиций количество периодов (n или t) равно одному.
• Как для простых, так и для сложных процентов PV — это FV, деленная на 1 + i.
• Модель временной стоимости денег гласит, что деньги в будущем не стоят так много, как деньги в настоящем.

Ключевые термины

• период : период времени, в течение которого начисляются проценты.
• процентная ставка : Процент суммы денег, взимаемый за ее использование за некоторый период времени. Его также можно рассматривать как стоимость отсутствия денег в течение одного периода или сумму, уплаченную за годовой инвестиционный проект.

Модель временной стоимости денег гласит, что деньги в будущем не стоят так много, как деньги в настоящем. Инвесторы предпочли бы иметь деньги сегодня, потому что тогда они смогут потратить их, сэкономить или инвестировать прямо сейчас, вместо того, чтобы ждать, чтобы использовать их.

Разницу между тем, сколько денег стоит сегодня, и тем, сколько они будут стоить в определенный момент в будущем, можно определить количественно. Стоимость денег сегодня называется приведенной стоимостью (PV), , а стоимость денег в будущем называется будущей стоимостью (FV). Существует также название стоимости отсутствия денег сегодня: процентная ставка или скидка ставка (i или r). Например, если процентная ставка составляет 3% в год, это означает, что вы готовы заплатить 3% денег, чтобы получить их на год раньше. Количество времени также представлено переменной: количество периодов (n). Один период может быть любой продолжительностью, например, один день, один месяц или один год, но он должен быть четко определен, соответствовать единицам времени в процентной ставке и быть постоянным во всех ваших расчетах.

FV разового платежа : FV связана с PV, увеличиваясь на i% за каждый период.

Все эти переменные связаны уравнением, которое помогает вам найти PV отдельной суммы денег. То есть он говорит вам, сколько стоит один платеж сегодня, но не сколько стоит серия платежей сегодня (это произойдет позже). связывает все переменные вместе. Чтобы найти PV, вы должны знать FV, i и n.

При рассмотрении инвестиций за один период n по определению равно единице.Это означает, что PV — это просто FV, деленная на 1 + i. Отсутствие денег в течение одного года дорого обходится, а это и есть процентная ставка. Следовательно, PV на i% меньше FV.

Многопериодные инвестиции

Многопериодные инвестиции требуют понимания сложных процентов, включая временную стоимость денег с течением времени.

Цели обучения

Расчет рентабельности многопериодных инвестиций с течением времени

Основные выводы

Ключевые моменты

• Доллар сегодня стоит больше, чем доллар завтра, и временная стоимость денег должна учитывать упущенные возможности.
• Однопериодные инвестиции относительно просто рассчитать с точки зрения будущей стоимости, применив процентную ставку к текущей стоимости один раз.
• Многопериодные инвестиции требуют немного более сложного уравнения, в котором проценты начисляются в зависимости от количества периодов, на которые распространяется инвестиция.
• В результате нескольких периодов обычно рекомендуется рассчитать среднюю норму прибыли (кумулятивно) за весь срок действия инвестиций.

Ключевые термины

• Сложные проценты : процентная ставка, применяемая к нескольким заявкам на получение процентов в течение срока действия инвестиции.

При инвестировании временная стоимость денег — это основная концепция, которую инвесторы просто не могут игнорировать. Доллар сегодня ценится выше, чем доллар завтра, и при использовании капитала важно осознавать альтернативные издержки, связанные с тем, во что можно было бы вложить деньги.

Однопериодные инвестиции

При однопериодных инвестициях концепция временной стоимости денег относительно проста. Будущая стоимость — это просто текущая стоимость, примененная к процентной ставке, начисляемой один раз.Если сравнить это с альтернативными издержками, то доходность альтернативных инвестиций в то же время также очевидна.

Переменные, участвующие в понимании временной стоимости денег в этих инвестициях:

• Текущая стоимость (PV)
• Будущая стоимость (FV)
• Процентная ставка (i или r) [Примечание: для всех формул процент выражается в десятичной форме, а не в виде целого числа. 7% — это 07, 12% — это 12, и так далее. ]
• Количество периодов (t или n)

С этими переменными инвестиции за один период могут быть рассчитаны следующим образом:

[латекс] {\ displaystyle \ text {FV} = \ text {PV} (1+ \ text {rt})} [/ latex]

‘t’ в этом уравнении будет просто 1, упрощая это уравнение до FV = PV (1 + r).{\ text {n}} {\ text {r} _ {\ text {i}}} = {\ frac {1} {\ text {n}}} (\ text {r} _ {1} + \ cdots + \ text {r} _ {\ text {n}})} [/ latex]

Заключение

В целом, разница с точки зрения временной стоимости денег между одно- и многопериодными инвестициями относительно очевидна. Нормализация ожидаемой прибыли в терминах приведенной стоимости (или прогнозирование будущей прибыли на несколько периодов сложного процента) рисует более ясную и точную картину реальной стоимости данной инвестиционной возможности.

Временная стоимость денег : Временная стоимость денег требует понимания того, как нормы доходности влияют на фиксированные значения с течением времени.

Ставка дисконтирования

Дисконтирование — это процедура определения того, сколько будущая сумма денег стоит сегодня.

Цели обучения

Опишите, какие реальные затраты инвестора составляют процентную ставку инвестиции

Основные выводы

Ключевые моменты

• Ставка дисконтирования представляет собой некоторые затраты (или группу затрат) для инвестора или кредитора.
• Некоторые затраты для инвестора или кредитора включают альтернативные издержки, стоимость ликвидности, риск и инфляцию.
• Ставка дисконтирования используется как кредитором, так и дебитором для определения приведенной стоимости денежной суммы.

Ключевые термины

• Ставка дисконтирования : процентная ставка, используемая для дисконтирования будущих денежных потоков по финансовому инструменту; годовая процентная ставка, используемая для уменьшения сумм будущего денежного потока для получения их текущей стоимости.
• дисконтирование : процесс определения приведенной стоимости с использованием ставки дисконтирования.
• скидка : для учета временной стоимости денег

Другое распространенное название для определения приведенной стоимости (PV) — с учетом скидки . Дисконтирование — это процедура определения того, сколько будущая сумма денег стоит сегодня. Как вы знаете из предыдущих разделов, чтобы найти PV платежа, вам необходимо знать будущую стоимость (FV), количество рассматриваемых периодов времени и процентную ставку. В этом контексте процентную ставку чаще называют учетной ставкой .

Ставка дисконтирования представляет собой некоторые затраты (или группу затрат) для инвестора или кредитора. Сумма этих затрат составляет процент, который становится процентной ставкой (иногда плюс небольшая прибыль). Вот некоторые из наиболее значительных затрат с точки зрения инвестора / кредитора:

Займы и кредитование : Банки, такие как HSBC, принимают во внимание такие расходы при определении условий ссуды для заемщиков.

1. Альтернативная стоимость: стоимость , а не наличных денег в определенный момент времени.Если у инвестора / кредитора были денежные средства, он / она мог бы их потратить, но поскольку они были инвестированы / ссужены, он / она несет расходы, связанные с невозможностью их потратить.
2. Инфляция: реальная стоимость одного доллара со временем уменьшается с инфляцией. Это означает, что даже если все остальное будет постоянным, в будущем предмет стоимостью 100 долларов будет стоить более 100 долларов. Инфляция в большинстве стран обычно бывает положительной (если это не так, это называется дефляцией, но это случается редко).
3. Риск: есть шанс, что вы не вернете свои деньги, потому что это плохая инвестиция, должник не выполняет свои обязательства.\ text {n}} [/ латекс].

   Если FV и n остаются постоянными, то по мере увеличения ставки дисконтирования (i) PV уменьшается. Таким образом, PV и ставка дисконтирования изменяются обратно пропорционально, что является фундаментальной зависимостью в финансах. Предположим, вы ожидаете, что через год вы ожидаете 1000 долларов (FV = 1000 долларов). Чтобы определить приведенную стоимость, вам нужно дисконтировать с помощью некоторой процентной ставки (i). Если бы эта ставка дисконтирования составляла 5%, 1000 долларов через год были бы эквивалентны 952,38 доллара для вас сегодня (1000 / [1.00 + 0,05]).

   Количество периодов

   Количество периодов соответствует количеству начислений процентов.

   Цели обучения

   Определите период с точки зрения расчета приведенной стоимости

   Основные выводы

   Ключевые моменты

   • Период — это просто общий термин для продолжительности времени. Это может быть что угодно — один месяц, один год, одно десятилетие, — но оно должно быть четко определено и зафиксировано.
   • Как для простых, так и для сложных процентов количество периодов изменяется вместе с FV и обратно пропорционально PV.
   • Количество периодов также является частью единиц ставки дисконтирования: если один период равен одному году, ставка дисконтирования должна быть определена как X% в год. Если один период составляет один месяц, ставка дисконтирования должна составлять X% в месяц.

   Ключевые термины

   • период : период времени, в течение которого начисляются проценты.

   In, n представляет количество периодов. Период — это просто общий термин для продолжительности времени. Это может быть что угодно — один месяц, один год, одно десятилетие, — но оно должно быть четко определено и зафиксировано.Продолжительность одного периода должна быть одинаковой в начале и в конце инвестиции. Он также является частью единицы ставки дисконтирования: если один период равен одному году, ставка дисконтирования должна быть определена как X% в год. Если один период составляет один месяц, ставка дисконтирования должна составлять X% в месяц.

   FV одного платежа : PV и FV напрямую связаны.

   Количество периодов соответствует количеству начислений процентов. В случае простых процентов количество периодов t умножается на их процентную ставку.Это имеет смысл, потому что, если вы зарабатываете 30 долларов процентов в первом периоде, вы также получаете 30 долларов процентов в последнем периоде, поэтому общая сумма заработанных процентов просто t x 30 долларов.

   Автомобиль : Автокредиты, ипотека и студенческие ссуды, как правило, имеют сложные проценты.

   Простые проценты редко используются по сравнению со сложными процентами. В сложных процентах проценты за один период также выплачиваются по всем процентам, начисленным в предыдущие периоды. Следовательно, существует экспоненциальная зависимость между PV и FV, которая отражается в (1 + i) ⁿ .

   Для обеих форм интереса количество периодов изменяется вместе с FV и обратно пропорционально PV. По логике вещей, если между настоящим и будущим проходит больше времени, FV должна быть выше, а PV — ниже (при условии, что ставка дисконтирования остается постоянной).

   Расчет приведенной стоимости

   Расчет приведенной стоимости (PV) — это вопрос включения справедливой стоимости, процентной ставки и количества периодов в уравнение.

   Цели обучения

   Различать формулу, используемую для расчета приведенной стоимости с простым процентом, и формулу, используемую для расчета приведенной стоимости со сложным процентом

   Основные выводы

   Ключевые моменты

   • Первый шаг — определить, является ли интерес простым или сложным.В большинстве случаев это составные части.
   • Процентная ставка и количество периодов должны иметь согласованные единицы.
   • PV — это текущая стоимость будущей суммы при определенной процентной ставке (часто называемой «ставкой дисконтирования»).

   Ключевые термины

   • Сложные проценты : проценты по ссуде или банковскому счету, которые рассчитываются на основе суммы основной суммы плюс накопленные невыплаченные проценты.
   • простые проценты : проценты выплачиваются только на основную сумму долга.

   Определение приведенной стоимости (PV) денежной суммы — это определение суммы денег сегодня, которая при определенной процентной ставке стоит столько же, сколько и сумма денег в будущем.

   Расчет приведенной стоимости (PV) отдельной суммы — это вопрос объединения всех различных частей, которые мы уже обсуждали. Но сначала вы должны определить, являются ли проценты простыми или сложными. Если интерес представляет собой простой процент, вы подставляете числа в формулу простого процента.

   Формула простого процента : Простой процент — это когда проценты выплачиваются только на ту сумму, которую вы изначально инвестировали (основную сумму). Вы не получаете проценты по ранее заработанным процентам.

   Если это сложные проценты, вы можете изменить формулу сложных процентов, чтобы рассчитать текущую стоимость.

   Однократный платеж по текущей стоимости : Определение PV — это вопрос включения трех других переменных.

   Входы

   • Будущая стоимость: Известная стоимость денег в заявленной точке в будущем.
   • Процентная ставка (ставка дисконтирования): Представляется как i или r. Это процент выплачиваемых процентов за каждый период.
   • Количество периодов: Обозначается n или t.

   Узнав эти три переменные, вы можете подставить их в соответствующее уравнение. Если проблема не говорит об обратном, можно с уверенностью предположить, что проценты усугубляются. Если вы используете такую ​​программу, как Excel, проценты складываются в формуле PV. Простые проценты встречаются довольно редко.

   Одна из областей, где часто случаются ошибки, — это определение количества периодов и процентной ставки. У них должны быть согласованные единицы, что может потребовать некоторой работы. Например, процентная ставка часто указывается как X% в год. Проблема может заключаться в нахождении PV за 24 месяца до FV, но количество периодов должно быть в годах, поскольку процентная ставка указана в год. Следовательно, n = 2. Однако, пока единицы измерения согласованы, определение PV выполняется методом «подключил и нажал».

   Как рассчитать период движения в физике

   Обновлено 28 декабря 2020 г.

   Крис Дезил

   В естественном мире есть множество примеров периодического движения, от орбит планет вокруг Солнца до электромагнитных колебаний фотонов и т. Д. наше собственное сердцебиение.

   Все эти колебания связаны с завершением цикла, будь то возвращение движущегося по орбите тела в исходную точку, возврат вибрирующей пружины в точку равновесия или расширение и сжатие сердцебиения. Время, необходимое колебательной системе для завершения цикла, известно как ее период .

   Период системы — это мера времени, и в физике он обычно обозначается заглавной буквой T . Период измеряется в единицах времени, подходящих для этой системы, но наиболее распространенными являются секунды.Вторая — это единица времени, первоначально основанная на вращении Земли вокруг своей оси и по ее орбите вокруг Солнца, хотя современное определение основано на колебаниях атома цезия-133, а не на каком-либо астрономическом явлении.

   Периоды некоторых систем интуитивно понятны, например, вращение Земли, которое составляет сутки или (по определению) 86 400 секунд. Вы можете рассчитать периоды некоторых других систем, таких как колеблющаяся пружина, используя характеристики системы, такие как масса и жесткость пружины.

   Когда дело доходит до колебаний света, все становится немного сложнее, потому что фотоны движутся поперек пространства, пока они колеблются, поэтому длина волны является более полезной величиной, чем период.

   Период — величина, обратная частоте

   Период — это время, необходимое колебательной системе для завершения цикла, тогда как частота ( f ) — это количество циклов, которое система может завершить за заданный период времени.Например, Земля вращается один раз в день, поэтому период составляет 1 день, а частота также составляет 1 цикл в день. Если вы установите стандарт времени на годы, период составит 1/365 года, а частота — 365 циклов в год. Период и частота являются обратными величинами:

   T = \ frac {1} {f}

   В расчетах, связанных с атомными и электромагнитными явлениями, частота в физике обычно измеряется в циклах в секунду, также известных как Герцы (Гц), с ⁻¹ или 1 / сек. При рассмотрении вращающихся тел в макроскопическом мире число оборотов в минуту (об / мин) также является общепринятой единицей.Период может быть измерен в секундах, минутах или другом подходящем периоде времени.

   Период простого гармонического осциллятора

   Самый основной тип периодического движения — это движение простого гармонического осциллятора, который определяется как тот, который всегда испытывает ускорение, пропорциональное его расстоянию от положения равновесия и направленное к равновесию. должность. В отсутствие сил трения и маятник, и масса, прикрепленная к пружине, могут быть простыми гармоническими осцилляторами.

   Можно сравнить колебания массы на пружине или маятнике с движением тела, вращающегося с равномерным движением по круговой траектории с радиусом r . Если угловая скорость тела, движущегося по окружности, равна ω, его угловое смещение ( θ ) от начальной точки в любой момент времени t составляет θ = ωt , и компоненты его положения x и y : x = r cos ( ωt ) и y = r sin ( ωt ).

   Многие осцилляторы движутся только в одном измерении, и если они движутся горизонтально, они движутся в направлении x . Если амплитуда, наиболее удаленная от положения равновесия, составляет A , то положение в любой момент времени t составляет x = A cos ( ωt ). Здесь ω известна как угловая частота, и она связана с частотой колебаний ( f ) уравнением ω = 2π f .Поскольку f = 1/ T , вы можете записать период колебаний следующим образом:

   T = \ frac {2π} {ω}

   Пружины и маятники: уравнения периода

   Согласно Согласно закону Гука, масса на пружине подвергается действию восстанавливающей силы F = — kx , где k — характеристика пружины, известная как жесткость пружины, а x Это смещение. Знак минус указывает, что сила всегда направлена ​​против направления смещения.Согласно второму закону Ньютона, эта сила также равна массе тела ( м ), умноженной на его ускорение ( a ), поэтому ma = — kx .

   Для объекта, колеблющегося с угловой частотой ω , его ускорение равно — Aω ² cos ωt или, упрощенно, — ω ² х . Теперь вы можете написать m (- ω ² x ) = — kx , исключить x и получить ω = √ ( к / м ).Тогда период колебаний массы на пружине равен:

   T = 2π \ sqrt {\ frac {m} {k}}

   Вы можете применить аналогичные соображения к простому маятнику, на котором вся масса центрируется на конце строки. Если длина струны составляет L , уравнение периода в физике для малоуглового маятника (т. Е. Такого, в котором максимальное угловое смещение от положения равновесия мало), которое оказывается независимым от массы, имеет вид

   T = 2π \ sqrt {\ frac {L} {g}}

   , где g — ускорение свободного падения.

   Период и длина волны

   Как и простой осциллятор, волна имеет точку равновесия и максимальную амплитуду по обе стороны от точки равновесия. Однако, поскольку волна распространяется через среду или пространство, колебания растягиваются вдоль направления движения. Длина волны определяется как поперечное расстояние между любыми двумя идентичными точками в цикле колебаний, обычно точками максимальной амплитуды на одной стороне положения равновесия.

   Период волны — это время, за которое одна полная длина волны проходит через контрольную точку, тогда как частота волны — это количество длин волн, которые проходят через контрольную точку за данный период времени. Если период времени равен одной секунде, частота может быть выражена в циклах в секунду (герц), а период выражен в секундах.

   Период волны зависит от скорости ее движения и длины волны ( λ ). Волна перемещается на расстояние в одну длину волны за один период времени, поэтому формула скорости волны такова: v = λ / T , где v — скорость.Если преобразовать период в другие величины, получим:

   T = \ frac {λ} {v}

   Например, если волны на озере разделены 10 футами и движутся со скоростью 5 футов в секунду, период каждой волны 10/5 = 2 секунды.

   Использование формулы скорости волны

   Все электромагнитное излучение, к одному типу которого относится видимый свет, распространяется с постоянной скоростью, обозначаемой буквой c , через вакуум. Вы можете написать формулу скорости волны, используя это значение, и поступить так, как обычно делают физики, заменив период волны ее частотой.Формула принимает следующий вид:

   c = \ frac {λ} {T} = f × λ

   Поскольку c является константой, это уравнение позволяет вычислить длину волны света, если вы знаете его частоту и наоборот. наоборот. Частота всегда выражается в герцах, и, поскольку свет имеет чрезвычайно малую длину волны, физики измеряют ее в ангстремах (Å), где один ангстрем равен 10 ⁻¹⁰ метров.

   Приложение A к Части 1030 — Расчет годовой процентной доходности

   Официальная интерпретация Приложения А Показывать Скрывать

   Часть I. Годовая процентная доходность для раскрытия информации о счетах и ​​рекламных целей

   1. Округление для расчетов. Ниже приведены примеры допустимого округления для расчета процентов и годовой процентной доходности:

   и. Ежедневная ставка, применяемая к остатку с точностью до пяти или более десятичных знаков

   ii. Ежедневные проценты, полученные с точностью до пяти или более десятичных знаков

   Часть II. Годовая процентная доходность периодической отчетности

   1. Балансовый метод. Процентная ставка, используемая при расчете годовой процентной доходности, может быть получена из метода дневного баланса или метода среднего дневного баланса. Баланс, используемый в формуле годовой процентной доходности, представляет собой сумму балансов за каждый день периода, деленную на количество дней в периоде.

   2. Отрицательные остатки запрещены. Учреждения должны рассматривать отрицательное сальдо счета как ноль, чтобы определить сальдо, по которому рассчитывается годовая процентная доходность.(См. Комментарий к § 1030.7 (a) (2).)

   A. Общая формула

   1. Начисленные, но не начисленные проценты. Для расчета годовой процентной доходности заработанных, начисленных, но не начисленных процентов:

   и. Не могут быть включены в баланс для выписок, выпущенных одновременно или реже, чем частота начисления сложных процентов и зачисления на счет. Например, если ежемесячные отчеты отправляются для счета, на котором начисляются проценты ежедневно и начисляются проценты ежемесячно, баланс не может увеличиваться каждый день, чтобы отразить эффект ежедневного начисления сложных процентов.

   ii. Должен быть включен в баланс для последующих выписок, если выписки выдаются чаще, чем начисляются сложные проценты на счет. Например, если ежемесячные отчеты отправляются для счета, на котором ежедневно начисляются проценты и ежеквартально начисляются проценты, баланс для второго ежемесячного отчета будет включать проценты, начисленные за предыдущий месяц.

   2. Округление. Число начисленных процентов, используемое для расчета годовой процентной доходности, должно быть округлено до двух десятичных знаков и отражать фактически выплаченную сумму.Например, если процент, полученный за отчетный период, составляет 20,074 доллара, а учреждение платит потребителю 20,07 доллара, оно должно использовать 20,07 доллара (а не 20,074 доллара) для расчета годовой процентной доходности. Для счетов, на которых выплачиваются проценты на основе метода ежедневного баланса, который ежеквартально составляет и зачисляет проценты, а также отправляет ежемесячные отчеты, учреждение может, но не обязательно, округлять начисленные проценты до двух десятичных знаков для расчета годовой процентной доходности, полученной по первым двум выпущенным ежемесячным отчетам. в течение квартала.Однако в квартальном отчете сумма начисленных процентов должна отражать фактически выплаченную сумму.

   B. Специальная формула для использования в случаях, когда периодическая выписка отправляется чаще, чем период, за который начисляются проценты

   1. Выписки, инициированные Положением E. Учреждения могут, но не обязаны, использовать эту формулу для расчета годовой процентной доходности, полученной для счетов, которые получают квартальные отчеты и подпадают под правило Положения E, требующее ежемесячных отчетов при электронном переводе средств. произошло.Они могут это сделать, даже если в течение определенного квартала ежемесячный отчет не выпускался. Но учреждения должны использовать эту формулу для счетов, на которых ежеквартально начисляются проценты и начисляются проценты, и которые получают ежемесячные отчеты, которые, хотя и инициируются Правилом E, соответствуют положениям § 1030.6.

   2. дней в периоде начисления процентов. Учреждения, использующие специальную формулу годовой процентной доходности, должны использовать фактическое количество дней в периоде начисления сложных процентов.

   См. Толкование в Приложении А. в Приложении I

   Годовая процентная доходность измеряет общую сумму процентов, выплачиваемых по счету, на основе процентной ставки и частоты начисления сложных процентов.Годовая процентная доходность отражает только проценты и не включает стоимость какого-либо бонуса (или другого вознаграждения на сумму 10 долларов или меньше), который может быть предоставлен потребителю для открытия, обслуживания, увеличения или продления счета. Проценты или другие доходы не должны включаться в годовую процентную доходность, если такие суммы определяются обстоятельствами, которые могут или не могут произойти в будущем. Годовая процентная доходность выражается как годовая ставка, основанная на 365-дневном году. Учреждения могут рассчитывать годовой процентный доход на основе 365-дневного или 366-дневного года в високосном году.В Части I этого приложения обсуждаются расчеты годовой процентной доходности для раскрытия информации о счетах и ​​рекламных объявлений, а в Части II обсуждаются расчеты годовой процентной доходности для периодических отчетов.

   Часть I. Годовая процентная доходность для раскрытия информации о счетах и ​​рекламных целей

   В целом, годовая процентная доходность для раскрытия информации о счете в соответствии с §§ 1030.4 и 1030.5 и для рекламы согласно § 1030.8 — это годовая ставка, которая отражает соотношение между суммой процентов, которая будет заработана потребителем в течение срока действия счета, и сумма основного долга, используемая для расчета этих процентов.Особые правила применяются к счетам с многоуровневыми и ступенчатыми процентными ставками, а также к определенным временным счетам с заявленным сроком погашения более одного года.

   A. Общие правила

   За исключением случаев, предусмотренных в Части I.E. настоящего приложения годовая процентная доходность рассчитывается по формуле, приведенной ниже. Учреждения рассчитывают годовую процентную доходность на основе фактического количества дней в сроке действия счета. Для счетов без установленной даты погашения (таких как типичный сберегательный или транзакционный счет) расчет должен основываться на предполагаемом сроке в 365 дней.При определении общей суммы процентов, которая будет использоваться в формуле, учреждения должны исходить из того, что вся основная сумма и проценты остаются на депозите в течение всего срока и что в течение этого срока не происходит никаких других операций (депозитов или снятия средств). Это предположение не должно использоваться, если учреждение требует в качестве условия счета, чтобы потребители снимали проценты в течение срока. В таком случае проценты (и расчет годовой процентной доходности) должны отражать это требование. Для повременных счетов, которые предлагаются с кратным количеством месяцев, учреждения могут основывать количество дней либо на фактическом количестве дней в течение применимого периода, либо на количестве дней, которое могло бы произойти для любой фактической последовательности такого количества календарных месяцев.Если учреждения предпочитают использовать последнее правило, они должны использовать то же количество дней для расчета долларовой суммы процентов, полученных на счете, которая используется в формуле годовой процентной доходности (где «проценты» делятся на «основную сумму»).

   Годовая процентная доходность рассчитывается по следующей общей формуле («APY» используется для удобства в формулах):

   APY = 100 [(1 + проценты / основная сумма) (365 / дней в срок) -1]

   «Основная сумма» — это сумма средств, предположительно зачисленных в начале счета.

   «Проценты» — это общая сумма процентов, заработанных по принципалу в долларах на срок действия счета.

   «Срок действия» — это фактическое количество дней в сроке действия счета. Когда «срок в сроке» равен 365 (то есть, когда заявленный срок погашения составляет 365 дней или если у счета нет заявленного срока погашения), годовая процентная доходность может быть рассчитана с использованием следующей простой формулы:

   APY = 100 (проценты / основная сумма)

   Примеры

   (1) Если учреждение платит 61 доллар.68 процентов за 365-дневный год на 1000 долларов, внесенных на счет NOW, используя общую формулу выше, годовая процентная доходность составляет 6,17%:

   APY = 100 [(1 + 61,68 / 1,000) (365/365) — 1]

   APY = 6,17%

   Или, используя простую формулу выше (поскольку для учетной записи без указанного срока срок считается 365 дней):

   APY = 100 (61,68 / 1000)

   APY = 6,17%

   (2) Если учреждение платит 30,37 долл. США в виде процентов по шестимесячному депозитному сертификату на 1000 долл. США (где шестимесячный период, используемый учреждением, составляет 182 дня), с использованием общей формулы, приведенной выше, годовая процентная доходность составит 6 .18%:

   APY = 100 [(1 + 30,37 / 1,000) (365/182) — 1]

   APY = 6,18%

   B. Счета со ступенчатой ​​процентной ставкой (в последующие периоды применяются разные ставки)

   Для счетов с двумя или более процентными ставками, применяемыми в последующие периоды (где ставки известны на момент открытия счета), учреждение должно исходить из того, что каждая процентная ставка действует в течение периода времени, предусмотренного в депозитном договоре.

   Примеры

   (1) Если учреждение предлагает 6-месячный депозитный сертификат на сумму 1000 долларов США, по которому оно выплачивает 5% процентную ставку, начисляемую ежедневно, в течение первых трех месяцев (которые содержат 91 день), и 5.Процентная ставка 5%, начисляемая ежедневно, на следующие три месяца (которые содержат 92 дня), общая процентная ставка за шесть месяцев составляет 26,68 доллара США, и, используя общую формулу выше, годовая процентная доходность составляет 5,39%:

   APY = 100 [(1 + 26,68 / 1,000) (365/183) — 1]

   APY = 5,39%

   (2) Если учреждение предлагает двухлетний депозитный сертификат на сумму 1000 долларов, по которому оно выплачивает ежедневную процентную ставку 6% в течение первого года и 6,5% процентную ставку, начисляемую ежедневно, на следующий год , общая сумма процентов за два года составляет 133 доллара.13, и, используя приведенную выше общую формулу, годовая процентная доходность составляет 6,45%:

   APY = 100 [(1 + 133,13 / 1,000) (365/730) — 1]

   APY = 6,45%

   C. Счета с переменной процентной ставкой

   Для счетов с переменной ставкой без вступительной премии или дисконтированной ставки учреждение должно основывать расчет только на начальной процентной ставке, действующей на момент открытия (или объявления) счета, и предполагать, что эта ставка не изменится в течение года.

   Счета с переменной ставкой и начальной надбавкой (или ставкой дисконта) должны рассчитываться как счет со ступенчатой ​​ставкой.Таким образом, учреждение должно исходить из того, что: (1) вводная процентная ставка действует в течение периода времени, предусмотренного в депозитном договоре; и (2) переменная процентная ставка, которая действовала бы при открытии или объявлении счета (кроме начальной ставки), действует до конца года. Если переменная ставка привязана к индексу, основанная на индексе ставка, действующая на момент раскрытия информации, должна использоваться до конца года. Если ставка не привязана к индексу, действующая ставка для существующих потребителей, имеющих тот же счет (которые не получают начальную процентную ставку), должна использоваться до конца года.

   Например, если учреждение предлагает счет, по которому оно выплачивает 7% ежедневную начисленную процентную ставку в течение первых трех месяцев (которые, например, содержат 91 день), в то время как переменная процентная ставка, которая действовала бы когда счет был открыт, составлял 5%, общая процентная ставка за 365-дневный год для депозита в 1000 долларов составляла 56,52 доллара (исходя из 91 дня при 7%, за которыми следуют 274 дня при 5%). Используя простую формулу, годовая процентная доходность составляет 5,65%:

   .

   APY = 100 (56,52 / 1000)

   APY = 5.65%

   D. Счета с многоуровневой ставкой (разные ставки применяются к определенным уровням баланса)

   Для счетов, в которых две или более процентных ставок, выплачиваемых по счету, применимы к определенным уровням баланса, учреждение должно рассчитать годовую процентную доходность в соответствии с методом, описанным ниже, который он использует для расчета процентов. Во всех случаях годовая процентная доходность (или диапазон годовой процентной доходности, если применимо) должна раскрываться для каждого уровня баланса.

   Для целей, обсуждаемых ниже, предположим следующее:

   Метод многоуровневого хранения A. Согласно этому методу организация выплачивает на весь остаток на счете указанную процентную ставку, которая соответствует применимому уровню депозита. Например, если потребитель вкладывает 8000 долларов, учреждение выплачивает процентную ставку 5,50% на все 8000 долларов.

   При использовании этого метода для определения процентов к каждому уровню будет применяться только одна годовая процентная доходность.В пределах каждого уровня годовая процентная доходность не будет изменяться в зависимости от предполагаемой суммы депонирования основной суммы долга.

   Для предполагаемых выше процентных ставок и остатков на депозитах учреждение укажет три годовых процентных доходности — по одной для каждого уровня баланса. Расчет годовой процентной доходности для этого типа счета аналогичен расчету для счетов с единой процентной ставкой. Таким образом, расчет основан на общей сумме процентов, которая будет получена потребителем для каждого уровня счета в течение года, и предполагаемой основной сумме депозита для получения этой суммы процентов.

   Первый ярус. Предполагая ежедневное начисление сложных процентов, учреждение будет платить 53,90 доллара США в виде процентов на депозит в размере 1000 долларов США. По общей формуле для первого уровня годовая процентная доходность составляет 5,39%:

   .

   APY = 100 [(1 + 53.90 / 1,000) (365/365) — 1]

   {1D-b APY = 5,39%

   Используя простую формулу:

   APY = 100 (53,90 / 1000)

   APY = 5,39%

   Второй ярус. Учреждение выплатит 452,29 доллара в виде процентов по депозиту на 8000 долларов.Таким образом, по простой формуле годовая процентная доходность для второго уровня составляет 5,65%:

   .

   APY = 100 (452,29 / 8,000)

   APY = 5,65%

   Третий ярус. Учреждение выплатит 1 183,61 доллара США в виде процентов по депозиту в 20 000 долларов. Таким образом, по простой формуле годовая процентная доходность для третьего уровня составляет 5,92%:

   APY = 100 (1183,61 / 20,000)

   APY = 5,92%

   Метод определения уровней B. В соответствии с этим методом организация платит указанную процентную ставку только на ту часть баланса в пределах указанного уровня.Например, если потребитель вносит 8000 долларов, учреждение платит 5,25% от 2500 долларов и 5,50% от 5500 долларов (разница между 8000 долларов и отсечкой первого уровня в 2500 долларов).

   Учреждение, которое рассчитывает проценты таким образом, должно предоставить диапазон, который показывает самую низкую и самую высокую годовую процентную доходность для каждого уровня (кроме первого уровня, который, как и уровни в Методе A, имеет одинаковую годовую процентную доходность на всем протяжении ). Нижний показатель для годового диапазона процентной доходности рассчитывается на основе общей суммы процентов, полученных за год, при условии минимальной основной суммы, необходимой для получения процентной ставки для этого уровня.Высокий показатель годового диапазона процентной доходности основан на сумме процентов, которые организация будет платить по максимальной основной сумме, которая может быть депонирована для получения той же процентной ставки. Если на счете нет ограничения на максимальную сумму, которую можно внести, учреждение может принять любую сумму.

   Для предполагаемой выше многоуровневой структуры учреждение должно указать в общей сложности пять годовых процентных доходностей — одно значение для первого уровня и две цифры, указанные как диапазон для двух других уровней.

   Первый ярус. Предполагая ежедневное начисление сложных процентов, организация будет платить 53,90 доллара США в виде процентов на депозит в размере 1000 долларов США. Для этого первого уровня, используя простую формулу, годовая процентная доходность составляет 5,39%:

   .

   APY = 100 (53,90 / 1000)

   APY = 5,39%

   Второй ярус. Для второго уровня организация будет платить от 134,75 до 841,45 долларов в виде процентов, исходя из предполагаемых остатков в 2500,01 долларов и 15000 долларов, соответственно. Для 2500,01 доллара проценты будут рассчитаны на 2500 долларов по ставке 5.25% процентная ставка плюс процентная ставка 0,01 доллара США по ставке 5,50%. Таким образом, для нижнего предела второго уровня годовая процентная доходность составляет 5,39%, используя простую формулу:

   .

   APY = 100 (134,75 / 2,500)

   APY = 5,39%

   Для 15 000 долларов проценты рассчитаны на 2 500 долларов по ставке 5,25% плюс проценты по 12 500 долларов по ставке 5,50%. Для верхнего сегмента второго уровня годовая процентная доходность, используя простую формулу, составляет 5,61%:

   .

   APY = 100 (841,45 / 15 000)

   APY = 5.61%

   Таким образом, диапазон годовой процентной доходности для второго эшелона составляет от 5,39% до 5,61%.

   Третий ярус. Для третьего уровня учреждение будет платить 841,45 доллара США в виде процентов по нижнему пределу третьего уровня (остаток в размере 15 000,01 доллара США). Для 15 000,01 доллара процентная ставка будет рассчитана на 2 500 долларов по ставке 5,25%, плюс проценты на 12 500 долларов по ставке 5,50%, плюс проценты по 0,01 доллара по ставке 5,75%. Следовательно, для нижнего предела третьего уровня годовая процентная доходность (по простой формуле) равна 5.61%:

   APY = 100 (841,45 / 15 000)

   APY = 5,61%

   Поскольку учреждение не ограничивает остаток на счете, оно может принять любую максимальную сумму для целей расчета годовой процентной доходности для верхнего предела третьего уровня. При предполагаемой максимальной балансовой сумме в 100 000 долларов проценты будут рассчитаны на 2 500 долларов по ставке 5,25%, плюс проценты на 12 500 долларов по ставке 5,50%, плюс проценты по 85 000 долларов по ставке 5,75%. Таким образом, для верхнего предела третьего уровня годовая процентная доходность, используя простую формулу, равна 5.87%.

   APY = 100 (5 871,79 / 100 000)

   APY = 5,87%

   Таким образом, годовой диапазон процентной доходности, который будет установлен для третьего уровня, составляет от 5,61% до 5,87%.

   Если предполагаемая максимальная сумма остатка составляет 1 000 000 долларов вместо 100 000 долларов, в последнем вычислении организация будет использовать 985 000 долларов, а не 85 000 долларов. В этом случае для верхнего сегмента третьего уровня годовая процентная доходность, используя простую формулу, составляет 5,91%:

   .

   APY = 100 (59 134,22 / 1000000)

   APY = 5.91%

   Таким образом, годовой диапазон процентной доходности, который будет установлен для третьего уровня, составляет от 5,61% до 5,91%.

   E. Счета времени с заявленным сроком погашения более одного года, по которым выплачиваются проценты не реже одного раза в год

   1. Для временных счетов с заявленным сроком погашения более одного года, которые не начисляют сложные проценты на ежегодной или более частой основе и которые требуют от потребителя снимать проценты не реже одного раза в год, годовая процентная доходность может быть раскрыта как равная к процентной ставке.

   Пример

   (1) Если учреждение предлагает двухлетний депозитный сертификат на сумму 1000 долларов США, который не является сложным и который выплачивает проценты раз в полгода чеком или переводом по процентной ставке 6,00%, годовая процентная доходность может быть раскрыта как 6,00 %.

   (2) Для временных счетов, подпадающих под действие настоящего пункта, которые также являются счетами с ступенчатой ​​процентной ставкой, годовая процентная доходность может быть раскрыта как равная композитной процентной ставке.

   Пример

   (1) Если учреждение предлагает трехлетний депозитный сертификат на сумму 1000 долларов США, который не является сложным и по которому ежегодно выплачиваются проценты чеком или переводом по ставке 5.Процентная ставка 00% на первый год, процентная ставка 6,00% на второй год и процентная ставка 7,00% на третий год, учреждение может рассчитать совокупную процентную ставку и APY следующим образом:

   (a) Умножьте каждую процентную ставку на количество дней, в течение которых она будет действовать;

   (b) Сложите эти цифры вместе; и

   (c) Разделите на общее количество дней в семестре.

   (2) В данном примере произведение процентных ставок и дней, в которые они действуют, равны (5.00% × 365 дней) 1825, (6,00% × 365 дней) 2190 и (7,00% × 365 дней) 2555 соответственно. Сумма этих продуктов, 6570, делится на 1095, общее количество дней в семестре. Сводная процентная ставка и годовая процентная ставка составляют 6,00%.

   Часть II. Годовая процентная доходность периодической отчетности

   Годовая процентная доходность, полученная для периодических отчетов в соответствии с § 1030.6 (a), представляет собой годовую ставку, которая отражает соотношение между суммой процентов, фактически заработанных на счете потребителя в течение отчетного периода, и средним дневным балансом на счете за отчетный период. .Однако в соответствии с § 1030.6 (b), если учреждение использует метод среднедневного баланса и рассчитывает проценты за период, отличный от отчетного периода, полученная годовая процентная доходность должна отражать соотношение между суммой заработанных процентов и среднедневной остаток на счете за этот другой период.

   Годовая процентная доходность рассчитывается по следующим формулам (для удобства в формулах используется «APY Earned»):

   А.Общая формула

   APY заработано = 100 [(1 + начисленные проценты / остаток) (365 / дней в периоде) — 1]

   «Остаток» — средний дневной остаток на счете за период.

   «Заработанные проценты» — это фактическая сумма процентов, заработанных на счете за период.

   «Дней в периоде» — это фактическое количество дней за период.

   Примеры

   (1) Предположим, учреждение рассчитывает проценты за период выписки (и использует либо дневной баланс, либо метод среднего дневного баланса), и на счете есть баланс 1500 долларов США на 15 дней и баланс 500 долларов США на оставшиеся 15 дней. дней 30-дневного периода выписки.Средний дневной баланс за период составляет 1000 долларов США. Заработанные проценты (при любом методе расчета баланса) за период составляют 5,25 доллара США. Годовая процентная доходность (по приведенной выше формуле) составляет 6,58%:

   .

   APY заработано = 100 [(1 + 5.25 / 1,000) (365/30) — 1]

   APY Заработано = 6,58%

   (2) Предположим, учреждение начисляет проценты по среднему дневному остатку за календарный месяц и предоставляет периодические отчеты, охватывающие период с 16 числа одного месяца до 15 числа следующего месяца.Остаток на счете составляет 2000 долларов США с 1 по 15 сентября, а остаток — 1000 долларов США за оставшиеся 15 дней сентября. Средний дневной баланс за сентябрь составляет 1500 долларов США, что дает 6,50 долларов США процентов, полученных за месяц. Годовая процентная доходность, полученная за сентябрь, будет показана в периодическом отчете за период с 16 сентября по 15 октября. Годовая процентная доходность (с использованием приведенной выше формулы) составляет 5,40%:

   APY Заработано = 100 [(6.50/1500) (365/30) — 1]

   APY Заработано = 5,40%

   (3) Предположим, учреждение начисляет проценты по среднему дневному остатку за квартал (например, за календарные месяцы с сентября по ноябрь) и предоставляет ежемесячные периодические отчеты за календарные месяцы. На счете есть баланс в размере 1000 долларов США в течение 30 дней сентября, баланс в размере 2000 долларов США в течение 31 дня октября и баланс в размере 3000 долларов США в течение 30 дней ноября. Средний дневной баланс за квартал составляет 2000 долларов, что дает 21 доллар процентов, полученных за квартал.Годовая процентная доходность будет показана в периодическом отчете за ноябрь. Годовая процентная доходность (по приведенной выше формуле) составляет 4,28%:

   . Заработано

   APY = 100 [(1 + 21 / 2,000) (365/91) — 1]

   APY Заработано = 4,28%

   B. Специальная формула для использования в случаях, когда периодическая выписка направляется чаще, чем период, за который начисляются проценты

   Учреждения, которые используют метод ежедневного баланса для начисления процентов и которые выпускают периодические отчеты чаще, чем период, за который начисляются проценты, должны использовать следующую специальную формулу:

   Для использования в этой формуле применяется следующее определение (все остальные термины определены в Части II):

   «Компаундирование» — это количество дней в каждом периоде начисления сложных процентов.

   Предположим, учреждение рассчитывает проценты за отчетный период с использованием метода ежедневного баланса, выплачивает процентную ставку 5,00%, начисляемую ежегодно, и предоставляет периодические отчеты для каждого ежемесячного цикла. На счете есть ежедневный баланс в размере 1000 долларов США за 30-дневный период выписки. Заработанные проценты за период составляют 4,11 доллара США, а полученная годовая процентная доходность (с использованием специальной формулы, приведенной выше) составляет 5,00%:

   APY заработано = 5,00%

   .