Аргумент не: Аргумент является обязательным — Visual Basic

Как мы видели в секция 1, Юм использует убедительные аргументы, чтобы сделать выводы, которые «Отношения идей», тогда как «вероятные» или «Моральные» аргументы имеют выводы, которые «Факты».Юмовское различие между «Отношения идей» и «факты» предвосхищает проведенное Кантом различие между «Аналитические» и «синтетические» суждения (Кант 1781). Классический пример аналитического предложения: «Холостяки — это неженатые мужчины» и синтетическое утверждение. «Моя велосипедная шина спущена». Для Юма демонстративное аргументы, основанные на априорных рассуждениях, могут устанавливать только отношения идей или аналитических суждений. В связь между приоритетностью и аналитичностью лежит в основе помещение P3, который гласит, что показательный аргумент устанавливает вывод отрицание которого является противоречием.

Один из возможных ответов на проблему Юма — отрицать помещение P3, допуская возможность того, что рассуждение a priori могло порождают синтетические предложения. Кант лихо рассуждал в ответ Юму что такое синтетическое априори знание возможно (Кант 1781, 1783). Он делает это своего рода обращением эмпирическая программа, поддерживаемая Юмом. В то время как Юм пытался понять, как концепция причинной или необходимой связи может основываться на опыте, вместо этого Кант утверждал, что опыт приходит только через концепции или «категории» понимание.По его мнению, можно получить априорных знаний. этих концепций, включая концепцию причинности, посредством трансцендентный аргумент относительно необходимых предпосылок опыт. Более подробное изложение ответа Канта Юму можно найти в de Pierris and Friedman 2013.

3.2 Обоснование вероятного вывода

Первый рог дилеммы Юма подразумевает, что не может быть демонстративный аргумент в пользу заключения индуктивного вывода потому что можно представить отрицание заключения.Например, вполне можно представить, что следующий кусок хлеб, который я ем, скорее отравит меня, чем накормит. Однако это действительно не исключаю возможности демонстративного аргумента, что устанавливает только то, что хлеб с высокой вероятностью питает, а не то, что это определенно будет. Есть несколько подходов, которые пытаются привести убедительный аргумент, что вывод индуктивного вывод вероятен, хотя и не уверен. Если это удастся, цепочка рассуждений, основанных на убедительных аргументах из предпосылок вывод I к предположению, что заключение является вероятным не исключается аргументом Юма.Тогда можно было бы бросить вызов помещение P8, говоря, что это не обязательно для обоснования индуктивного умозаключение, чтобы иметь цепочку рассуждений от его предпосылок к его вывод. Скорее было бы достаточно, если бы у нас был аргумент от предпосылки к утверждению, что вывод вероятен или вероятен. потом a priori обоснование индуктивного вывода были предоставлены.

3.2.1 Номолого-пояснительное решение

Первый из этих подходов — это «Номолого-пояснительное» решение, которое положено нападающий Армстронг, BonJour и Фостер (Армстронг, 1983; BonJour 1998; Фостер 2004). Это решение обращается к выводу о лучших Объяснение (IBE), в котором говорится, что мы должны сделать вывод, что гипотеза который обеспечивает лучшее объяснение свидетельств, вероятно, правда. Сторонники этого подхода делают вывод о наилучшем объяснении быть способом вывода, который отличается от типа «Экстраполяционный» индуктивный вывод, который пытался сделать Юм оправдывать. Они также рассматривают это как тип вывода, который, хотя недедуктивная, обосновано априори . Например, Армстронг говорит: «Сделать вывод о наилучшем объяснении — это часть того, что значит быть рациональным.Если это не рационально, то что? » (Армстронг, 1983: 59).

Обоснование априори проводится в два этапа. Во-первых, утверждается, что мы должны признать, что некоторые наблюдаемые закономерности требуют объяснения в терминах некоего основного закона. Например, если монета упорно падает орлом при повторных подбрасываниях, тогда становится все более неправдоподобным, что это произошло просто из-за «случайности». Скорее, мы должны сделать вывод о лучшем объяснение, что монета имеет определенный уклон.Сказать, что монета высаживает головы не только по наблюдаемым случаям, но и по ненаблюдаемые случаи, не дает объяснения наблюдаемых регулярность. Таким образом, простой конъюнкции констант Юма недостаточно. Для объяснения необходимо «не-юмовское, метафизически устойчивая концепция объективной закономерности » (BonJour 1998), который рассматривается как реальный естественный необходимость (Армстронг, 1983; Фостер, 2004).

После того, как было установлено, что должна быть некоторая метафизическая надежного объяснения наблюдаемой закономерности, второй шаг заключается в том, чтобы утверждают, что из всех возможных метафизически надежных объяснений «Прямое» индуктивное объяснение является лучшим, где прямое объяснение экстраполирует наблюдаемую частоту на более широкое население.Например, если у монеты есть какая-то цель шанс выпадения орлов, лучшее объяснение того, что \ (m / n \) головы до сих пор наблюдались, заключается в том, что объективный шанс монеты посадочные головки \ (m / n \). И этот объективный шанс определяет что происходит не только в наблюдаемых случаях, но и в ненаблюдаемых случаи.

Номолого-пояснительное решение основано на использовании IBE в качестве рациональная, априорная форма вывода, отличная от индуктивные выводы, такие как вывод I .Однако можно в качестве альтернативы рассматривать индуктивные выводы как частный случай IBE. (Harman 1968), или рассматривать IBE как просто альтернативный способ характеризуя индуктивный вывод (Хендерсон 2014). Если любой из эти взгляды верны, МБП не имеет необходимой независимости из индуктивного вывода, чтобы обеспечить некруглое обоснование Это.

Можно также возразить против номолого-объяснительного подхода к основания того, что закономерности не обязательно требуют объяснения в условия необходимых связей или надежных метафизических законов.В жизнеспособность подхода также зависит от жизнеспособности неюмовская концепция законов. Было несколько серьезных пытается разработать такое представление (Armstrong 1983; Tooley 1977; Dretske 1977), но и много критики (см. J. Carroll, 2016).

Еще одно критическое возражение состоит в том, что Номолого-объяснительная решение просто напрашивается вопрос, даже если это считается законно использовать IBE для оправдания индукции. В первый шаг аргумента, который мы выводим к закону или закономерности, которая простирается за пределы пространственно-временной области, в которой наблюдения было сделано до сих пор, чтобы предсказать, что произойдет в будущее.Но почему закон, применимый только к наблюдаемым пространственно-временная область не может быть столь же хорошим объяснением? Главный ответ кажется, что мы можем видеть a priori , что законы с временные или пространственные ограничения были бы менее хорошими объяснениями. Фостер утверждает, что причина в том, что это представит больше загадки:

Мне кажется, что закон, сфера действия которого ограничена некоторыми конкретный период более загадочен, по своей сути более загадочен, чем тот, который универсален во времени. (Фостер 2004)

3.2.2 Байесовское решение

Другой способ, которым можно попытаться построить априори аргумент, что предпосылки индуктивного вывода делают его вывод вероятен, заключается в использовании формализма вероятности сама теория. В то время, когда писал Хьюм, вероятности использовались для анализировать азартные игры. И в целом они использовались для решения проблема того, что мы ожидаем увидеть, учитывая, что определенная причина была заведомо действующий.Это так называемая проблема «прямого вывод ». Однако проблема индукции касается «Обратная» задача определения причины или общего гипотеза, учитывая частные наблюдения.

Один из первых и наиболее важных методов решения проблемы «Обратная» задача с использованием вероятностей была разработана Томас Байес. Эссе Байеса, содержащее основные результаты, было опубликовано после его смерти в 1764 г. (Bayes 1764). Однако это возможно, что работа была проделана значительно раньше и на самом деле написано в прямом ответе на публикацию исследования Хьюма. в 1748 г. (см. Zabell 1989: 290–93, обсуждение того, что такое известно об истории).

Проиллюстрируем байесовский метод на задаче рисования шары из урны. Предположим, что у нас есть урна с белым и черные шары в неизвестной пропорции. Рисуем образец шаров из урны, вынув шар, отметив его цвет, а затем положив его назад перед тем, как снова рисовать.

Рассмотрим сначала проблему прямого вывода. Учитывая пропорцию белых шаров в урне, какова вероятность разных исходов для выборки наблюдений заданного размера? Предположим, что пропорция белых шаров в урне равно \ (\ theta = 0.6 \). Вероятность вытянуть один белый шар из одного образца будет \ (p (W; \ theta = 0,6) = 0,6 \). Мы также можем вычислить вероятность для других исходов, таких как как рисование двух белых шаров по образцу из двух, используя правила исчисление вероятностей (см. раздел 1 Hájek 2011). В целом, вероятность выпадения \ (n_w \) белых шаров в выборке размером N , дается биномиальным распределением:

Это конкретный пример «выборочного распределения», \ (p (E \ mid H) \), что дает вероятность определенного доказательства E в выборке, при условии, что определенная гипотеза H верно. Расчет выборочного распределения можно выполнить в в общем должно быть сделано априори , учитывая правила вероятности исчисление.

Однако проблема индукции — это обратная задача. Мы хотим не делать вывод о том, какой будет образец, с известной гипотезой, скорее мы хотим вывести гипотезу об общей ситуации или население, основанное на наблюдении ограниченной выборки. В вероятности гипотез-кандидатов могут затем использоваться для информирования прогнозы о дальнейших наблюдениях.В случае с урной для Например, мы хотим знать, что наблюдение за конкретным образцом частота белых шаров, \ (\ frac {n_w} {N} \), говорит нам о \ (\ theta \), доля белых шаров в урне.

Идея байесовского подхода состоит в том, чтобы назначать вероятности не только к событиям, составляющим доказательства, но также и к гипотезам. Один начинается с распределения «априорной вероятности» по соответствующие гипотезы \ (p (H) \). Узнав некоторые свидетельства E , Байесовский обновляет априорное \ (p (H) \) до условной вероятности \ (p (H \ mid E) \). Это правило обновления называется «правилом условность ». Условная вероятность \ (p (H \ mid E) \) известна как «апостериорная вероятность» и рассчитывается используя правило Байеса:

Здесь выборочное распределение можно принять за условное вероятность \ (p (E \ mid H) \), известная как «Вероятность» гипотезы H на доказательствах Е .

Затем можно перейти к вычислению прогнозного распределения для пока ненаблюдаемые данные \ (E ‘\), учитывая наблюдения E .Прогнозирующий распределение в байесовском подходе дается

где сумма становится интегралом в случаях, когда H является непрерывная переменная.

Для примера с урной мы можем вычислить апостериорную вероятность \ (p (\ theta \ mid n_w) \) с использованием правила Байеса, и вероятность дается биномиальным распределением выше. Для этого мы также необходимо назначить априорное распределение вероятностей параметру \ (\ тета \). Один естественный выбор, сделанный Байесом на раннем этапе. самого себя и Лапласа, заключается в том, чтобы поставить униформу перед параметром \ (\ тета \). Обоснование этого выбора Байесом заключалось в том, что тогда если вы вычислите вероятность каждого значения количества белых в выборке, основанной только на предыдущем, до того, как наблюдаются какие-либо данные, все эти вероятности равны. У Лапласа было другое оправдание, основанное на принципе безразличия. Этот принцип заявляет, что если у вас нет оснований отдавать предпочтение одной гипотезе над другим вы должны назначить им всем равные вероятности.

При выборе равномерного априорного значения апостериорная вероятность и прогнозируемое распределение может быть рассчитано. Получается, что вероятность того, что следующий шар будет белым, учитывая, что \ (n_w \) из N розыгрышей были белыми, соответствует

Это знаменитое «правило преемственности» Лапласа. (1814 г.). Предположим, на основании наблюдения 90 белых шаров из 100, мы вычисляем по правилу последовательности, что вероятность следующий белый шар равен \ (91/102 = 0.89 \). Вполне возможно, что следующий шар может быть черным. Даже в том случае, когда все 100 мячей были белыми, так что вероятность того, что следующий шар будет белым 0,99, остается небольшая вероятность, что следующий шар не белый. То, что дает вероятностное рассуждение, не является аргумент к выводу, что следующий шар будет определенного цвета, но аргумент к выводу, что некоторые будущие наблюдения очень , вероятно, , учитывая то, что наблюдалось в прошлом.

В целом аргумент Байеса-Лапласа в случае урны дает пример того, как вероятностное рассуждение может увести нас от свидетельств о наблюдения в прошлом к ​​предсказанию того, насколько вероятно определенное будущее наблюдения есть. Вопрос в том, какое решение, если оно есть, это Тип расчета предусматривает задачу индукции. Во-первых зрение, так как это всего лишь математический расчет, похоже, что он действительно дает априори аргумент из предпосылок индуктивного вывода к утверждению, что определенный вывод вероятно.

Однако для того, чтобы окончательно установить это, нужно поспорить. что все компоненты и допущения аргумента равны a priori , и это требует дальнейшего изучения как минимум трех важные вопросы.

Во-первых, аргумент Байеса-Лапласа опирается на правила исчисление вероятностей. Каков статус этих правил? Делает следующие за ними составляют априори рассуждений? Ответ на это частично зависит от того, как интерпретируется сама вероятность.В широком смысле говоря, существуют известные интерпретации вероятности в соответствии с к которому правила имеют правдоподобный статус априори и могут составляют основу доказательной аргументации. К ним относятся классическая интерпретация, первоначально разработанная Лапласом (1814 г.), логическая интерпретация, расцвет которой был в творчестве Кейнса (1921), Джонсон (1921), Джеффрис (1939) и Карнап (1950), а также субъективистская интерпретация Рэмси (1926), Сэвиджа (1954) и де Финетти (1964).Попытки привести доводы в пользу вероятностного a априори решения проблемы индукции были в первую очередь связанных с этими интерпретациями.

Во-вторых, в случае урны аргумент Байеса-Лапласа основан на на конкретной вероятностной модели — биномиальной модели. Этот предполагает предположение, что существует параметр, описывающий неизвестна пропорция \ (\ theta \) шаров в урне, и что данные составляет независимую прибыль от распределения по этому параметру.На чем основаны эти предположения? Обобщают ли они другие случаи за пределами фактического ящика урны — то есть, можем ли мы видеть наблюдения в общем как аналог розыгрышей из «Урны природы»? Было постоянное беспокойство, что такие предположения, хотя и разумно применительно к случаю вытягивания шаров из urn, неприменим для других случаев индуктивного вывода. Таким образом вероятностное решение проблемы индукции могло бы быть относительно ограниченный объем. По крайней мере, есть некоторые предположения здесь мы переходим к выбору модели, которую необходимо сделать явной.

В-третьих, аргумент Байеса-Лапласа основан на конкретном выборе априорное распределение вероятностей. Каков статус этого задания, и может ли он быть основан на априорных принципах ? Исторически сложилось так, что Байес-Лапласовский выбор форменной одежды, а также всей концепции классической вероятности, основанной на принципе безразличия. Этот принцип многие считают априори . принцип. Тем не менее, он также был подвергнут большой критике на основания того, что это может привести к противоречивой вероятности задания (Бертран 1888; Борель 1909; Кейнс 1921).Такой несоответствия возникают из-за наличия более чем одного способа вырезать пространство альтернатив, и разные выборы порождают конфликтующие вероятностные присвоения. Одна попытка спасти Принцип безразличия заключался в апелляции к объяснению и утверждают, что принцип следует применять только к резьбе по пространство на «наиболее понятном базовом уровне», где это уровень идентифицируется в соответствии с априорным понятием объяснительный приоритет (Huemer 2009).

Поиск аргумента a priori для присвоения приора была в значительной степени заброшена. Для многих субъективист фонды, разработанные Рэмси, де Финетти и Сэвидж, обеспечивают более удовлетворительная основа для понимания вероятности. С этой точки зрения точки зрения, было бы ошибкой пытаться ввести какие-либо дополнительные a априори ограничений на вероятности сверх тех, которые продиктованы сами правила вероятности. Скорее, переуступка приоритетных требований может отражают личное мнение или предысторию знаний, и не являются предварительными априори необоснованный выбор.

До сих пор мы рассматривали вероятностные аргументы, которые ставят вероятностей над гипотезами в пространстве гипотез, а также наблюдения. Также существует традиция попыток определить, что распределения вероятностей, которые мы должны иметь, учитывая определенные наблюдения, от начальной точки совместного распределения вероятностей по всем наблюдаемые переменные. Тогда можно постулировать аксиомы непосредственно на это распределение по наблюдаемым, и исследуем последствия для прогнозирующее распределение. Значительная часть развития индуктивного логика, в том числе влиятельная программа Карнапа, продолжалась в таким образом (Carnap 1950, 1952).

Такой подход помогает прояснить роль допущений, лежащих в основе вероятностные модели. Одно фундаментальное предположение, которое можно сделать Насчет наблюдений заключается в том, что они «взаимозаменяемы». Это означает, что совместное распределение случайных величин равно инвариантен относительно перестановок. Неформально это означает, что порядок наблюдения не влияют на вероятность.Например, в урны, это будет означать, что сначала нарисован белый шар, а затем черный шар так же вероятен, как сначала нарисовать черный, а затем белый. Де Финетти доказал общую теорему о представлении, что если совместное распределение вероятностей бесконечной последовательности случайных предполагается, что переменные могут быть заменены, тогда это может быть записано как смесь функций распределения, данные каждой из которых ведут себя как если бы они были независимыми случайными розыгрышами (de Finetti 1964). В этом случае в примере с урной теорема показывает, что это , как если бы данные представляют собой независимые случайные выборки из биномиального распределения по параметр \ (\ theta \), который сам имеет априорную вероятность распределение.

Предположение об обмене можно рассматривать как естественное формализация предположения Юма о том, что прошлое напоминает будущее. Это интуитивно понятно, поскольку предположение о возможности обмена означает думая, что порядок наблюдений, как в прошлом, так и в будущем, не имеет значения для вероятностных присвоений.

Однако развитие программы индуктивной логики выявило что возможно много обобщений. Например, Джонсон предложил чтобы принять аксиому, он назвал «достаточность постулат».Это говорит о том, что результаты могут быть нескольких различных типов, и что условная вероятность того, что следующий результат типа и зависит только от количества предыдущих испытаний и количество предыдущих исходов типа и (Johnson 1932 г. ). Предполагая постулат достаточности для трех или более типов приводит к общему прогнозному распределению, соответствующему «Континуум индуктивных методов» Карнапа (Carnap 1952 г.). Это прогнозирующее распределение принимает вид:

для некоторого положительного числа k .Это сводится к правило преемственности, когда \ (t = 2 \) и \ (k = 1 \).

Обобщения понятия взаимозаменяемости, такие как «Частичная заменяемость» и «марковская возможность обмена », и их можно считать как формы предположения о симметрии (Zabell 1988; Skyrms 2012). Как меньше принимаются ограничительные аксиомы на вероятности наблюдаемых, в результате больше не существует уникального результата для вероятность предсказания, а скорее целый класс возможных вероятности, обозначенные обобщенным правилом последовательности, таким как вышесказанное.Следовательно, в этой традиции, как и в случае Байеса-Лапласа, подход, мы отошли от аргументации, которая приводит уникальный априорно вероятностный ответ на проблему Юма.

Тогда можно подумать, что назначение предшествующего или релевантного соответствующие постулаты о наблюдаемом распределении вероятностей, именно там, где эмпирические предположения входят в индуктивную выводы. Вероятностные расчеты являются эмпирическими аргументами, а не априори .Если это правильно, то вероятностная модель в конце концов не дала априори решение проблемы индукции, но оно скорее позволили нам прояснить, что может означать утверждение Юма о том, что индуктивные выводы основываются на принципе однородности.

Некоторые думают, что, хотя проблема индукции не решена, существует в некотором смысле частичное решение, которое было названо «Логическое решение». Хаусон, например, утверждает, что « Индуктивное рассуждение оправдано постольку, поскольку оно звук, учитывая соответствующие помещения »(Howson 2000: 239, его акцент).Согласно этой точке зрения, никуда не деться. эмпирическая предпосылка для индуктивных выводов, но мы все еще можем думать Байесовской обусловленности функционирует как своего рода логика или «Ограничение согласованности», которое «порождает прогнозы на основе предположений и наблюдений вместе » (Ромейн 2004: 360). Если у нас есть эмпирическое предположение, реализуется в априорной вероятности, а в наблюдениях — байесовском кондиционирование сообщает нам, какова итоговая прогнозная вероятность раздача должна быть.

3.2.3 Комбинаторный подход

Альтернативная попытка использовать вероятностные рассуждения для получения априори оправданием индуктивных выводов является так называемое «комбинаторное» решение. Это было впервые поставлено вперед Дональд К. Уильямс (1947) и позже развит Дэвидом Плита (1986).

Как и аргумент Байеса-Лапласа, решение во многом основывается на идея, что простые априорные вычисления могут быть выполнены в «прямом выводе» от популяции к выборке.Как мы видели, учитывая определенную частоту популяции, вероятность получение различных частот в образце можно рассчитать прямо на основе правил исчисления вероятностей. В Аргумент Байеса-Лапласа основан на обращении вероятности распределение с использованием правила Байеса, чтобы получить из выборки распределение к апостериорному распределению. Уильямс вместо этого предлагает что обратный вывод может быть основан на определенной логической силлогизм: пропорциональный (или статистический) силлогизм.

Пропорциональный или статистический силлогизм следующий:

1. Из всего, что есть M , \ (m / n \) P .
2. a — это M

Следовательно, a — это P с вероятностью \ (m / n \).

Например, если 90% кроликов в популяции белые, и мы наблюдая кролика a , тогда пропорциональный силлогизм говорит, что мы делаем вывод, что a белый с вероятностью 90%.Уильямс утверждает, что пропорциональный силлогизм является недедуктивным логическим силлогизм, который эффективно вставляет силлогизм для следствие

1. Все M s — P
2. a — это M

Следовательно, a — это P .

И силлогизм противоречия

1. № M is P
2. a это M

Следовательно, a — это не P .

Этот силлогизм можно объединить с наблюдением за поведением все более крупных образцов. Из расчетов выборки распределения, можно показать, что с увеличением размера выборки вероятность того, что частота дискретизации находится в диапазоне, который близко приближается к популяции частота также увеличивается. По факту, Закон больших чисел Бернулли гласит, что вероятность что частота выборки приближается к частоте популяции, имеет тенденцию к единице, поскольку размер выборки стремится к бесконечности.Уильямс утверждает, что такие результаты подтверждают «общую предпосылку, общую для всех индукции, что образцы «соответствуют» их популяциям » (Уильямс 1947: 78).

Затем мы можем применить пропорциональный силлогизм к образцам из населения, чтобы получить следующий аргумент:

1. Большинство выборок соответствует своей генеральной совокупности
2. S — образец.

Следовательно, S с большой вероятностью совпадает с его популяцией.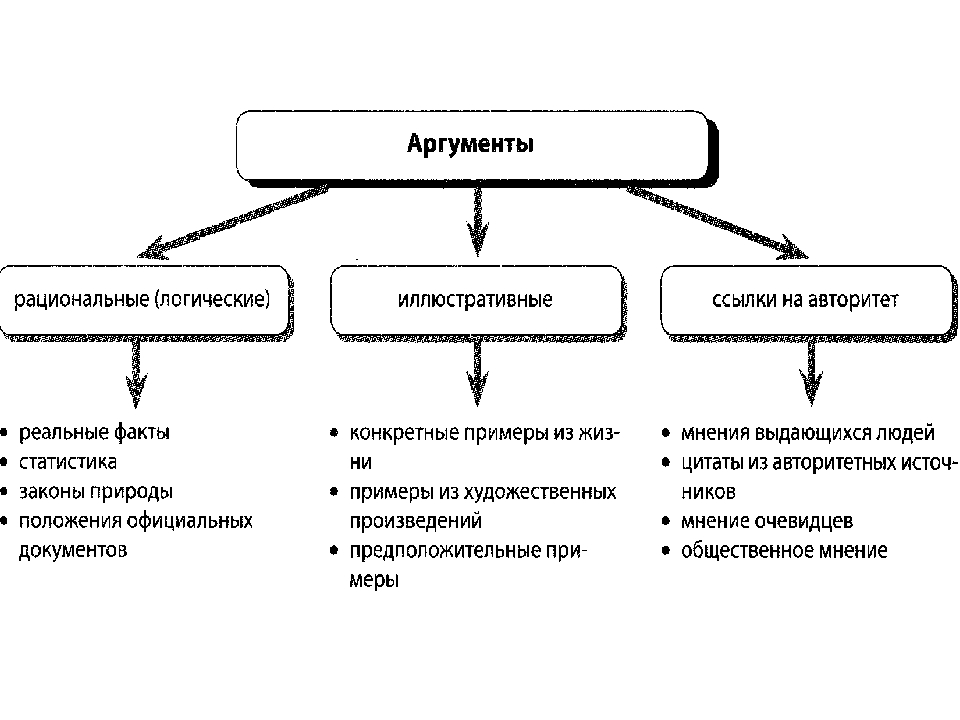

Это пример пропорционального силлогизма, и он использует общий результат о выборках, соответствующих популяциям как первому значительному помещение.

Следующий шаг — доказать, что если мы заметим, что образец содержит доля \ (m / n \) F s, то можно сделать вывод, что, поскольку эта выборка с большой вероятностью совпадает с ее популяцией, популяция, с большой вероятностью, имеет популяционную частоту, которая аппроксимирует частоту дискретизации \ (m / n \). И Уильямс, и Стоув утверждают, что это составляет логическое априорное решение проблема индукции.

Ряд авторов выразили мнение, что плита Williams-Stove аргумент действителен только в том случае, если образец S извлекается случайным образом из совокупность возможных выборок — i.е., что любой образец как будет нарисован так же, как и любой другой (Brown 1987; Will 1948; Giaquinto 1987). Иногда это преподносится как возражение против заявки. пропорционального силлогизма. Утверждается, что пропорциональная силлогизм действителен только в том случае, если a вытянут случайным образом из Население млн с. Однако ответ был, что есть нет необходимости знать, что выборка составлена ​​случайным образом, чтобы применить силлогизм (Maher 1996; Campbell 2001; Campbell & Franklin 2004 г.).Конечно, если у вас есть основания полагать, что ваша выборка процедура с большей вероятностью привлечет определенных лиц, чем другие — например, если вы знаете, что находитесь в определенной место, где больше людей определенного типа — тогда вам следует не применять пропорциональный силлогизм. Но если у тебя нет таких причин, — утверждают защитники, — применять его вполне рационально. Конечно это всегда возможно, что вы взяли нерепрезентативную выборку, т. е. одна из немногих выборок, в которых частота дискретизации не совпадает частота популяции — но поэтому вывод только вероятно и не определенно.

Более проблемный шаг в аргументе — последний шаг, который берет нас из утверждения, что выборки соответствуют их популяциям с высоким вероятность утверждения, что увидев конкретный образец частота, популяция, из которой проводится выборка, имеет частоту близка к частоте дискретизации с большой вероятностью. Проблема здесь это тонкий сдвиг в том, что подразумевается под «высокой вероятностью», что легло в основу распространенного неправильного толкования Теорема Бернулли. Хакерство (1975: 156–1559) ставит точку в следующих условиях.Теорема Бернулли разрешает утверждают, что гораздо чаще, чем нет, небольшой интервал вокруг Частота выборки будет включать истинную частоту популяции. В других словами, это весьма вероятно в смысле «обычно правильно », чтобы сказать, что выборка соответствует его генеральной совокупности. Но это не означает, что утверждение о том, что небольшой интервал вокруг выборка будет содержать истинную частоту популяции весьма вероятно в смысле «заслуживает доверия при каждом использовании». Этот будет означать, что для любого данного образца весьма вероятно, что образец соответствует его населению.Это вполне совместимо с претензией что «обычно правильно», что образец соответствует его население, чтобы сказать, что есть некоторые образцы, которые не соответствуют их популяции вообще.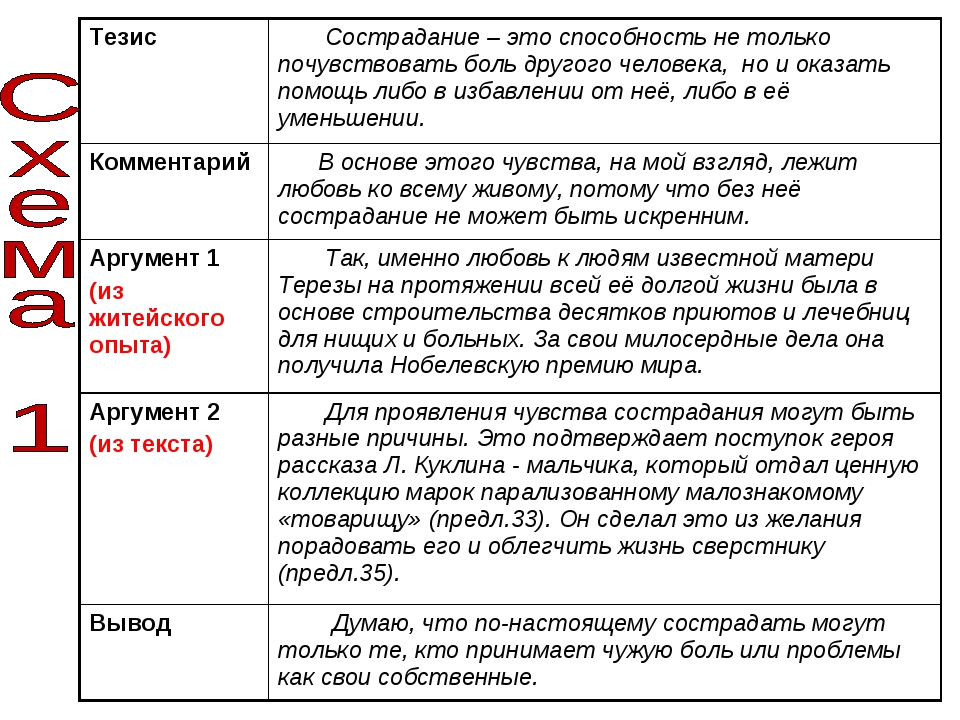 Таким образом, нельзя сделать вывод из высказывания Бернулли Теорема о том, что для любой заданной частоты дискретизации мы должны назначить высокую вероятность утверждения, что небольшой интервал вокруг образца частота будет содержать истинную частоту популяции. Но это именно тот слайд, который Уильямс делает на последнем этапе своего аргумент.Махер (1996) аналогичным образом утверждает, что последний шаг аргумента Уильямса-Стова ошибочны. Фактически, если кто-то хочет сделать выводы о вероятности повторяемости популяции учитывая частоту дискретизации, правильный способ сделать это — использовать Байесовский метод описан в предыдущем разделе. Но, как мы там видел, это требует присвоения априорных вероятностей, и это объясняет, почему многие люди думали, что комбинаторное решение каким-то незаконным образом предполагал предположение, подобное принципу равнодушие.Аргумент Уильямса-Стоу на самом деле не дает нам альтернативный способ инвертирования вероятностей, который каким-то образом обходит все проблемы, с которыми столкнулись байесовцы.

4. Решение второго рога дилеммы Юма

До сих пор мы рассматривали способы, которыми первый рог Юма дилемма может быть решена. Но, конечно, тоже можно взять на себя второй рог вместо него.

Кто-то может возразить, что вероятный аргумент не будет, несмотря на то, что Юм говорит, что будьте круговыми в проблемной манере (мы рассматриваем ответы этого вид в Раздел 4.1). Или можно попытаться возразить, что вероятные аргументы неверны. круглый вообще (раздел 4.2).

4.1 Индуктивные обоснования индукции

Один из способов решить второй рог дилеммы Юма — отказаться от помещение P6, что исключает круговые аргументы. Некоторые утверждали, что определенные виды круговых аргументов обеспечат приемлемое оправдание для индуктивного вывода. Поскольку оправдание тогда само по себе быть индуктивным, этот подход часто называют «Индуктивное обоснование индукции».

Сначала мы должны исследовать, как именно предположительно круговорот Юма возникает. Возьмем простой случай перечислительного индуктивного вывода, что следует по следующему шаблону ( X ):

Наиболее часто наблюдаемые F s были G s

Следовательно: Большинство F s — это G s.

Юм утверждает, что такие аргументы предполагают принцип единообразия. (ВВЕРХ). По помещениям P7 и P8, это предположение также необходимо подкрепить аргументом, чтобы чтобы индуктивный вывод был оправдан.Естественная идея состоит в том, что мы может выступать за принцип единообразия на том основании, что «это работает». Мы знаем, что это работает, потому что прошлые примеры аргументы, которые основывались на нем, были признаны успешными. Только это однако этого недостаточно, если у нас нет оснований полагать, что такие аргументы также будут успешными в будущем. Это требование должно сам по себе поддерживаться индуктивным аргументом ( S ):

Большинство аргументов формы X , которые полагаются на UP, преуспели в мимо.

Следовательно, большинство аргументов формы X , которые полагаются на UP преуспевать.

Но сам этот аргумент зависит от UP, который является самым предположение, которое мы пытались оправдать.

Как мы видели в раздел 2, некоторые отвергают утверждение Юма о том, что все индуктивные выводы предполагаем ВВЕРХ. Однако аргумент о том, что обоснование индуктивного вывода о вероятном аргументе приведет к округлость не должна полагаться на это утверждение. Проблема замкнутости может быть оформленным в более общем плане.Если аргумент S полагается на что-то , которое уже предполагается при выводе X , тогда аргумент S не может использоваться для обоснования вывода X . Однако вопрос в том, что именно это такое.

Некоторые авторы утверждали, что на самом деле S не полагается ни на какие предпосылка или даже предположение, которое потребовало бы, чтобы мы уже знали вывод Х . S тогда не является «предпосылкой. круговой »аргумент.Скорее, они утверждают, что это «Циркулярное правило» — он опирается на правило вывода в чтобы прийти к выводу, что это правило надежно. Предполагать мы принимаем правило R , которое гласит, что при соблюдении большинство F — это G , мы должны сделать вывод, что большинство F — это G с. Тогда вывод X опирается на правило R . Мы хотим показать, что правило R надежно. Мы могли бы апеллировать к тому, что R работал в прошлом, поэтому, исходя из индуктивного аргумента, он будет также работаю в будущем.Назовите этот аргумент S *:

Большинство выводов в соответствии с правилом R были успешными

Следовательно, большинство выводов после R успешны.

Поскольку сам этот аргумент использует правило R , используя его для установления то, что R надежен, является правилом циркуляра.

Некоторые авторы затем утверждали, что, хотя кругообразность посылок порочность, цикличность правил — нет (Cleve, 1984; Papineau, 1992). Один причина думать, что цикличность правил не порочна, если бы она не обязательно знать или даже обоснованно полагать, что правило R является надежным, чтобы с помощью правила прийти к обоснованному выводу.Это утверждение экстерналистов об оправдании (Cleve, 1984). Говорят, что пока R это по факту надежный, один может сформировать обоснованное убеждение в выводе аргумента, опираясь на на R , если есть основания полагать, что в помещении.

Если кого-то не убеждают претензии экстерналистов, можно попытаться утверждают, что цикличность правил не вредна, а другим способом. За Например, требование о том, чтобы правило было доказано надежным без любая циркулярность правила может показаться необоснованной, если правило очень фундаментальный характер.По словам Ланге:

Можно предположить, что, хотя круговой аргумент обычно не может обосновать свой вывод, круговой аргумент допустим в случай обоснования фундаментальной формы рассуждения. После всего, больше некуда повернуть, так что все, что мы можем разумно Требование от фундаментальной формы рассуждения состоит в том, чтобы оно подтверждало себя. (Ланге 2011: 56)

Сторонники этой точки зрения отмечают, что даже дедуктивный вывод не может быть обоснован дедуктивно.Рассмотрим Льюиса Диалог Кэрролла между Ахиллом и Черепахой (Carroll 1895 г.). Ахиллес спорит с черепахой, которая отказывается выступать modus ponens . Черепаха принимает предпосылку, что p , и посылка о том, что p подразумевает q , но он не примет q . Как Ахиллес может его убедить? Ему удается уговорить его принять другую предпосылку, а именно: «если p и p подразумевают q , затем q ».Но Черепаха все еще не готова сделать вывод о q . Ахиллес продолжает добавлять новые посылки такой же, но безрезультатно. Получается, что modus ponens не может быть оправдан перед кем-то, кто еще не готов использовать это правило.

Это могло бы показаться странным, если бы кругообразность посылок была порочной, а правило округлости не было, учитывая, что, кажется, есть легкая обмен между правилами и предпосылками. В конце концов, правило всегда может, как в истории Льюиса Кэрролла, можно добавить в качестве предпосылки к аргументу.Но история Кэрролла также указывает на то, что существует действительно, фундаментальное различие между готовностью принять предпосылка, устанавливающая правило (Черепаха с радостью это делает), и готовы использовать это правило (это то, что Черепаха отказывается делать).

Предположим, что мы допускаем, что индуктивный аргумент, такой как S (или S *) может поддерживать индуктивный вывод X без порочного округлость. Тем не менее, возможное возражение состоит в том, что аргумент просто не дает полного обоснования X .В конце концов, меньше разумные правила вывода, такие как контриндукция, могут поддерживать себя аналогичным образом. Контриндуктивное правило — CI:

Наиболее часто наблюдаемые A s — это B s.

Следовательно, это не тот случай, когда большинство A, являются B .

Рассмотрим тогда следующий аргумент CI *:

Большинство аргументов CI были неудачными

Следовательно, это не тот случай, когда большинство аргументов CI оказываются неудачными, я.е., многие аргументы CI успешны.

Таким образом, этот аргумент устанавливает надежность CI в правила круговой моды (см. Salmon 1963).

Аргумент S может использоваться для поддержки вывода X , но только для тех, кто уже готов делать индуктивные выводы, используя S . Это не может убедить скептика, который не готов полагаться на по этому правилу в первую очередь. Тогда можно было подумать, что аргумент просто не дает многого.

Ответ на эти опасения состоит в том, что, по словам Папино, аргумент: « не предполагает, что делает очень много» (Папино 1992: 18). Тот факт, что контриндуктивистский аналог аргумент существует, верен, но не имеет отношения к делу. Принято считать, что аргумент не может убедить ни контриндуктивиста, ни скептика. Тем не менее сторонники индуктивного обоснования утверждают, что есть еще некоторая добавленная стоимость в демонстрации того, что индуктивные выводы надежны, даже если мы уже принимаем, что нет ничего о них проблематично.Индуктивное обоснование индукции обеспечивает своего рода важную проверку согласованности наших существующих верования.

4.2 Нет правил

Можно пойти еще дальше и попытаться разобрать Юмовская округлость. Может быть, индуктивные умозаключения даже не имеют правила в общем. Что, если каждый индуктивный вывод по сути уникален? Окаша, например, утверждает, что проблема циркулярности Юма может следует уклоняться, если за индукцией «нет правил» (Окаша 2005а, б). Нортон выдвигает ту же идею, что все индуктивные выводы материальны и не имеют ничего общего с формальной (Norton 2003 г. ).

Сторонники таких взглядов подвергли критике утверждение Юма о том, что является UP, на котором основаны все индуктивные выводы. Есть давно были жалобы на нечеткость принципа единообразия (Лосось, 1953). Будущее лишь в некоторых отношениях напоминает прошлое, но не другие. Предположим, что на все мои дни рождения я был до 40 лет. Это не дает мне повода ожидать, что я в следующий день рождения мне будет меньше 40 лет. Кажется, тогда есть главный пробел в учении Юма.Он мог бы объяснить или описал, как мы делаем индуктивный вывод, исходя из предположения, что это тот, который мы можем нарисовать . Но он оставляет нетронутым вопрос о том, как мы различаем случаи, когда мы экстраполируем закономерность законно, рассматривая это как закон, и случаи, когда мы этого не делаем.

Часто считают, что Нельсон Гудман высказал это мнение в особенно яркая форма с его «новой загадкой индукции» (Гудман 1955: 59-83). Предположим, мы определяем предикат «grue» в следующим образом. Объект «грязный», когда он зеленый, если наблюдал раньше времени t и синий иначе. Гудман считает мысленный эксперимент, в котором мы наблюдаем пучок зеленых изумрудов раньше времени т . Мы могли бы описать наши результаты, сказав все наблюдаемые изумруды зеленые. Используя простой перечислительный индуктивный схемы, мы могли заключить из результата, что все наблюдаемые изумруды зеленый, что все изумруды зеленые. Но в равной степени мы могли бы описать те же результаты, если сказать, что все наблюдаемые изумруды являются черными.Затем, используя ту же схему, мы могли бы вывести из результата, что все наблюдали изумруды грязные, что все изумруды грязные. В первом случае мы ожидайте, что изумруд, наблюдаемый через время t , будет зеленым, тогда как в второй — мы ожидаем, что он будет синим. Таким образом, два предсказания несовместимо. Гудман утверждает, что Хьюм не стал делать любое объяснение того, почему мы проецируем такие предикаты, как «Зеленый», но не такие предикаты, как «grue». Этот это «новая загадка», которую часто принимают за дальнейшую проблема индукции, которую Юм не рассматривал.

Одна мораль, которую можно было бы заимствовать у Гудмана, заключается в том, что не существует ни одного общий принцип единообразия, на который опираются все возможные аргументы (Sober 1988; Norton 2003; Okasha 2001, 2005a, b). Скорее каждый индуктивный умозаключение предполагает более конкретную эмпирическую предпосылку. А конкретный индуктивный вывод зависит от определенного способа, которым будущее похоже на прошлое. Тогда это может быть оправдано другим индуктивный вывод, который зависит от совершенно иных эмпирических требовать.Это, в свою очередь, должно быть оправдано еще одним индуктивный вывод. Природа проблемы Юма во втором рог таким образом преображается. Нет округлости. Скорее есть регресс индуктивных обоснований, каждое из которых полагается на свои собственные эмпирические предпосылки (Sober 1988; Norton 2003; Okasha 2001, 2005а, б).

Один из способов выразить эту мысль — сказать, что аргумент Юма основывается на на ошибку кванторного сдвига (Sober 1988; Okasha 2005a). Юм говорит что существует общая предпосылка для всех индуктивных умозаключений, тогда как он должен был сказать, что для каждого индуктивного умозаключение, есть некоторая предпосылка.Различные индуктивные выводы тогда основываются на различных эмпирических предпосылках, и проблема округлости устранена.

Каковы же будут последствия предположения о том, что юмовский проблема действительно должна была быть регрессом, а не замкнутостью? Здесь возможны разные мнения. С одной стороны, можно подумать что регресс по-прежнему приводит к скептическому выводу. Итак, хотя точная форма, в которой Юм заявил, что его проблема неверна, вывод существенно не отличается (Sober 1988).Другой возможность состоит в том, что преобразование смягчает или даже удаляет скептическая проблема. Например, Нортон утверждает, что результатом является растворение проблемы индукции, так как регресс оправдания мягко прекращаются (Norton 2003). И еще Окаша мягко предполагает, что даже если регресс бесконечен, «Возможно, в конце концов, бесконечные регрессы менее плохи, чем порочные круги » (Окаша 2005b: 253).

Любое исчезновение круговорота Юма не зависит только от утверждая, что UP следует заменить эмпирическими предпосылками которые специфичны для каждого индуктивного вывода.Также необходимо установить, что индуктивные выводы не имеют общих правила — иначе хоть какие-то правило-циркулярность. Окаша предполагает, что байесовская модель обновление убеждений является иллюстрацией того, как можно охарактеризовать индукцию без правил, но это проблематично, так как в этой модели все индуктивные выводы по-прежнему разделяют общее правило байесовского условность. Материальная теория индукции Нортона Подробнее действительно обещает характеристику индукции без правил, но это неясно, действительно ли можно избежать какой-либо роли общих правил (Ахинштейн 2010; Уорролл 2010).

5. Необходимые условия для обоснования

Обычно читают, что Юм вынес отрицательный вердикт возможность обоснования вывода I с помощью такой предпосылки, как P8. Однако есть некоторые, кто сомневается в том, лучше ли интерпретировать Юма.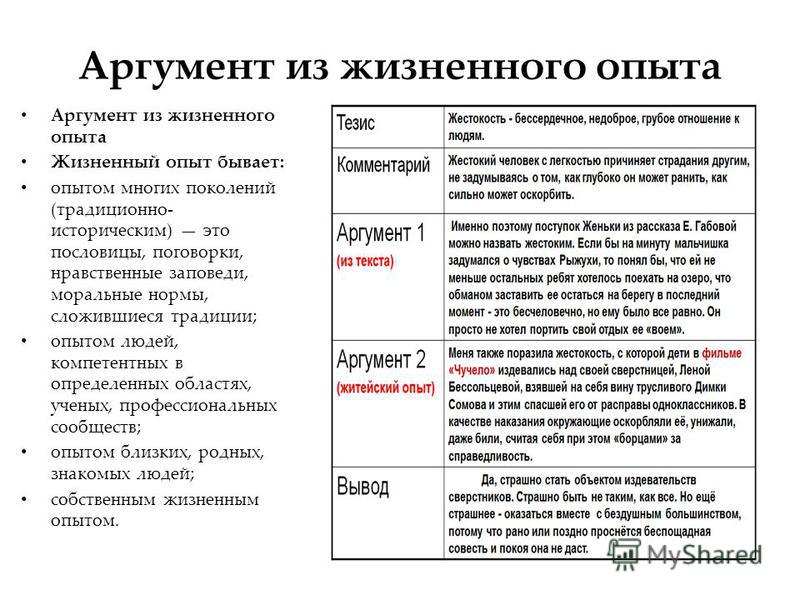 в качестве заключения об обоснованности вывода I при все (мы обсудим эти интерпретации в раздел 5.1). Есть также те, кто по-разному сомневается в том, помещение P8 действительно дает действительное необходимое условие для обоснования вывод I (разделы 5.2 и 5.3).

5.1 Интерпретация заключения Юма

Некоторые ученые отрицают, что Юм следует читать как ссылающийся на посылка такая помещение P8 вообще. Причина, по их утверждению, в том, что он не стремился явно нормативный вывод об обосновании, такой как C5. Юм определенно ищет «цепочку рассуждений» из предпосылки индуктивного вывода к заключению, и он думает что аргумент UP необходим для завершения цепочки. Однако можно было подумать, что дальнейших предположений относительно оправдание, и поэтому вывод его аргумента просто C4: нет цепочки рассуждений от посылок до заключения индуктивный вывод.Тогда Юм мог бы быть, как Дон Гаррет и Дэвид. Оуэн утверждал, выдвигая «тезис в когнитивной психологии », вместо того, чтобы делать нормативные заявления о обоснование (Owen 1999; Garrett 2002). Тезис о характер познавательного процесса, лежащего в основе вывода. В соответствии с Гарретт, главный вывод аргумента Юма состоит в том, что может быть нет процесса рассуждений, который устанавливает UP. Для Оуэна это послание что вывод не делается через цепочку идей, связанных посреднические связи, как это было бы характерно для факультета причина.

Есть также интерпретаторы, которые утверждают, что Юм просто пытается исключить конкретный вид оправдания индукции на основе концепция разума, преобладающая среди рационалистов его времени, а не оправдание в целом (Beauchamp & Rosenberg 1981; Байер 2009). В частности, утверждалось, что это «Попытка опровергнуть рационалистическое убеждение, что по крайней мере некоторые индуктивные аргументы доказательны »(Beauchamp & Розенберг 1981: xviii). Согласно этой интерпретации, помещение P8 следует изменить так, чтобы оно читалось примерно так:

• Если нет цепочки рассуждений, основанных на убедительных аргументах из помещения к выводу вывода I , затем Вывод I не обоснован.

Однако такие интерпретации противоречат тому факту, что Аргумент Юма — это явная атака с двух сторон, которая касается не только доказательных аргументов, но и вероятных аргументы.

Вопрос о том, насколько обширное нормативное заключение отнести к Юм — сложный человек. Частично это зависит от толкования Собственное решение Юма его проблемы. Как мы видели в секция 1, Юм приписывает основу индуктивного вывода принципам воображение в «Трактате» и в «Исследовании «Обычай», «привычка», задуманный как своего рода природный инстинкт.Тогда возникает вопрос, может ли эта альтернатива предоставляет любое обоснование вывода, даже если ни одно основанный на разуме. На первый взгляд кажется, что Юм предполагая, что индуктивные выводы основаны на совершенно арациональном основание. Он явно не думает, что им не удается производить хорошие результаты. Фактически, Юм даже предполагает, что эта операция разума может даже быть менее «подверженным ошибкам и ошибкам», чем если бы были доверены «ошибочным выводам нашего разума, который работает медленно »(Э. 5.2.22). Это тоже не ясно, что он видит работу воображения как полностью лишенный рациональности. Во-первых, Юм говорит о воображении в соответствии с принципами . Позже в Трактате он даже дает «правила» и «логику» для характеризуя то, что следует считать хорошим причинным выводом (Т. 1.3.15). Он также ясно видит возможность различать лучшие формы такого «рассуждения», как он продолжает называть Это. Таким образом, могут быть основания утверждать, что Юм не пытался утверждать, что индуктивные выводы не имеют рационального основания что бы то ни было, а просто то, что у них нет определенного типа рациональное основание, уходящее корнями в способность разума.

Все это указывает на то, что есть место для споров по поводу предполагаемого масштабы собственного вывода Юма. И поэтому есть место для спорить о том, что именно формирует посылка (например, посылка P8) что соединяет остальную часть его аргументов с нормативным выводом должен взять. Однако независимо от того, кто в этом прав, факт остается, что Юм на протяжении всей истории преимущественно читался как представляя аргумент в пользу индуктивного скептицизма.

5.2 Постулаты и петли

Даже если приписать Юму нормативное заключение, можно подвергнуть сомнению его аргумент, спросив, есть ли помещение P8 правда.Это может побудить к общему размышлению о том, что необходимо для обоснование вывода, в первую очередь, и что такое Юм даже прошу.

Например, Витгенштейн усомнился в том, что это вообще имеет смысл спросить об основаниях для индуктивных выводов.

Если бы кто-нибудь сказал, что информация о прошлом не могла его убедить что что-то случится в будущем, я не должен понимать его. Его можно спросить: а что же тогда вы ожидаете, что вам скажут? Какой информации вы называете основанием для такого убеждения? … Если это не основания, тогда какие основания? — Если вы скажете, что эти не являются основанием, тогда вы обязательно должны уметь указать, что должно быть дело для нас, чтобы иметь право сказать, что есть основания для наше предположение….(Витгенштейн 1953: 481)

Например, можно не подумать, что должна быть даже цепочка. рассуждений, в которых каждый шаг или предположение подкрепляется аргумент. Витгенштейн считал, что есть некоторые принципы, поэтому фундаментально то, что они не нуждаются в дальнейшей поддержке аргумент. Это «петли», на которых расследование оказывается.

На основе идей Витгенштейна развилось общее понятие «Право», которое является своего рода рациональным основанием для удержания определенные предложения, к которым не предъявляются те же требования, что и «Оправдание».Право предоставляет эпистемологические права на придерживаться предложения, не неся ответственности за обоснование веры в него на споре. Криспин Райт (2004) утверждал, что существуют определенные принципы, в том числе Принцип единообразия, которые мы имеет право в этом смысле удерживать.

Некоторые философы поставили перед собой задачу определить набор или набор постулатов, которые составляют правдоподобную основу для индуктивного выводы. Бертран Рассел, например, утверждал, что пять постулатов лежат в основе индуктивного рассуждения (Russell 1948). Артур Бёркс, с другой стороны, предположил, что набор постулатов не уникален, но может быть несколько наборов постулатов, соответствующих различные индукционные методы (Burks 1953, 1955).

Основное возражение против всех этих взглядов состоит в том, что они на самом деле не решают проблема индукции способом, обеспечивающим надежную фиксацию столбов на котором стоит индуктивный вывод. Как говорит Салмон, «Допущение к делу неоправданных и неоправданных постулатов. с проблемой равносильно превращению научного метода в вопрос вера »(Salmon 1966: 48).

5.3 Прекращение существования обычного языка

Вместо того, чтобы позволять необоснованным эмпирическим постулатам давать нормативные поддержки индуктивного вывода, вместо этого можно было бы привести доводы в пользу совершенно иное представление о том, что подразумевается под оправданием. Как и Витгенштейн, более поздние философы обыденного языка, особенно П.Ф. Стросон также спросил, что именно значит попросить обоснование индуктивных выводов (Strawson 1952). Это стало известный как «растворение обыденного языка» проблема индукции.

Стросон отмечает, что было бы целесообразно попросить дедуктивную обоснование индуктивных выводов. Но не совсем понятно, что это полезно, поскольку это фактически «требование, чтобы индукция будет показано, что это действительно своего рода дедукция »(Strawson 1952: 230). Скорее, говорит Стросон, когда мы спрашиваем, индуктивный вывод оправдан, мы обычно судим, соответствует нашим обычным индуктивным стандартам. Предположим, он говорит, что кто-то сформировал убеждение путем индуктивного вывода, что все f ’s г .Стросон говорит, что если этого человека спросят об их основания или причины для такой веры,

Я думаю, что было бы удовлетворительным ответом, если бы он ответил: «Что ж, благодаря своему обширному и разнообразному опыту я пришел в бесчисленных случаях f и никогда — f чего не было в случае с г ». Говоря это, он явно заявляя, что имеет индуктивную опору , индуктивное свидетельство определенного рода в пользу его веры. (Стросон, 1952)

Это просто потому, что индуктивная поддержка, как ее обычно понимают, просто состоит из наблюдения множества положительных примеров в широком разнообразие условий.

По сути, этот подход отрицает, что создание цепочки рассуждений необходимое условие для обоснования. Скорее индуктивный вывод оправдан, если он соответствует обычным стандартам индуктивное обоснование. Но есть ли что-то еще? Можем ли мы не спросить по какой причине мы должны полагаться на эти индуктивные стандарты?

Несомненно, имеет смысл спросить, является ли конкретный индуктивный вывод оправдано.Но ответ на этот вопрос довольно прост. Иногда у людей достаточно доказательств для своих выводов и иногда они этого не делают. Имеет ли смысл спросить, есть ли индуктивные процедуры вообще оправданы? Стросон рисует аналогия между вопросом о том, является ли конкретное действие законным. Мы можем Он говорит, что ответьте на такой вопрос, сославшись на закон страны.

Но вообще нет смысла спрашивать, действует ли закон земля, правовая система в целом, является или не является законной. Для чего правовые стандарты мы привлекательны? (Стросон 1952: 257)

По Стросону,

Это аналитическое утверждение, что разумно иметь степень веры в утверждение, которое пропорционально силе доказательства в его пользу; и это аналитическое предложение, хотя и не предложение математики, что, при прочих равных, доказательства для обобщения сильны пропорционально количеству благоприятные случаи и разнообразие обстоятельств, в которых они были найдены, отлично.Итак, чтобы спросить, разумно ли размещать полагаться на индуктивные процедуры — все равно что спрашивать, разумно соразмерять степень своей убежденности сила доказательств. Это то, что «быть разумный » в данном контексте означает . (Стросон, 1952: 256–57)

Таким образом, согласно этой точке зрения, нет никаких дальнейших вопросов спросите, разумно ли полагаться на индуктивный выводы.

Философы обыденного языка явно не возражают против Юма Помещение P8. Но на самом деле то, что они делают, предлагает совсем другое рассказ о том, что значит быть оправданным, веря в заключение индуктивных выводов. Что нужно, это просто соответствие индуктивным стандартам, и нет никакого реального смысла просить дальнейшее обоснование для тех.

Основное возражение против этой точки зрения состоит в том, что соответствие обычным стандартов недостаточно, чтобы предоставить необходимое обоснование. Что мы необходимо знать, является ли вера в вывод индуктивного вывод является «эпистемически обоснованным или оправданным в том смысле, что что … есть основания полагать, что это, скорее всего, правда »(BonJour 1998: 198).Проблема, которую поднял Хьюм, заключается в следующем: были ли, несмотря на то, что индуктивные выводы сделать верные выводы в прошлом, у нас есть основания полагать, что Вывод из индуктивного вывода, который мы сейчас делаем, вероятно, будет верным. Возможно, установление рациональности индуктивного вывода в того, что он следует индуктивным стандартам, недостаточно для установить, что его заключение, вероятно, будет правдой. На самом деле Стросон позволяет поставить вопрос о том, будет ли индукция продолжать быть успешным », что отличается от вопроса о том, рациональна ли индукция.Этот вопрос он берет на себя по «случайному фактическому вопросу» (Strawson 1952: 262). Но если Юма волновал именно этот вопрос, то он не является ответом на него. установить, что индукция рациональна, если это утверждение не понято включать или подразумевать, что индуктивный вывод, выполненный в соответствии с рациональным стандартам, скорее всего, приведет к верному заключению.

6. Жизнь с индуктивным скептицизмом

До сих пор мы рассматривали различные способы, которыми мы могли бы попытаться решить проблему индукции, сопротивляясь той или иной посылке Аргумент Юма.Однако некоторые философы видели его аргумент как неопровержимый и, таким образом, признал, что он действительно ведет к индуктивный скептицизм, вывод о том, что индуктивные выводы не могут быть оправданным. Тогда задача состоит в том, чтобы найти способ жить с такими кажущийся радикальным вывод. Похоже, мы полагаемся на индуктивный вывод повсеместно в повседневной жизни, и также принято считать, что лежит в основе научного метода. Можем ли мы продолжить все это, хотя все еще серьезно думает, что ничто из этого не оправдывается какой-нибудь рациональный аргумент?

Один из вариантов здесь — утверждать, как это делает Николас Максвелл, что проблема индукции ставится в чрезмерно ограничительной контекст.Максвелл утверждает, что проблема не возникает, если мы примем концепция науки, отличная от «стандартной эмпирика, который он обозначает эмпиризм »(Максвелл, 2017).

Другой вариант — думать, что значимость проблемы индукция каким-то образом ограничивается скептическим контекстом. Сам Юм кажется, думал в этом направлении. Например, он говорит:

Природа всегда будет защищать свои права и в конце концов возьмет верх над какие бы то ни было абстрактные рассуждения.Хотя мы должны сделать вывод, так как Например, как и в предыдущем разделе, что во всех рассуждениях от опыт, есть шаг ума, который не поддерживается любым аргументом или процессом понимания; нет опасности, что эти рассуждения, от которых зависит почти все знание, будут когда-либо быть затронутым таким открытием. (E. 5.1.2)

Ясно, что цель Юма не в том, чтобы утверждать, что мы не должны делать индуктивные выводы в повседневной жизни, да и вообще весь его метод и система описания разума в натуралистических терминах зависит от индуктивные выводы насквозь.Проблема индукции то следует рассматривать как проблему, возникающую только на уровне философская рефлексия.

Еще один способ уменьшить силу индуктивного скептицизма — это ограничить его объем. Карл Поппер, например, рассматривал проблему индукции как непреодолимое, но он утверждал, что наука на самом деле не основаны вообще на индуктивных выводах (Popper 1935 [1959]). Скорее он представил дедуктивистский взгляд на науку, согласно которому она поступает, делая смелые предположения, а затем пытается опровергнуть эти домыслы.В простейшем варианте этого аккаунта, когда гипотеза делает предсказание, которое оказывается ложным в эксперимента, гипотеза отвергается как опровергнутая. Логика этого процедура полностью дедуктивная. Гипотеза влечет за собой предсказание, и ложность предсказания опровергает гипотезу методом толленс. Таким образом, Поппер утверждал, что наука не основана на экстраполяционные выводы, рассмотренные Юмом. Следствием этого является что это не так важно, по крайней мере для науки, если эти выводы будет не хватать рационального основания.

Отчет Поппера кажется неполным в важном отношении. Всегда есть много гипотез, которые еще не опровергнуты доказательства, и они могут противоречить друг другу. Согласно строго дедуктивная структура, поскольку ни одна из них еще не фальсифицирована, они все на равных. Тем не менее, ученые обычно хотят сказать что одно лучше подтверждается доказательствами, чем другие. Мы кажемся нужно больше, чем просто дедуктивное рассуждение для поддержки практических принятие решений (Salmon 1981).Поппер действительно апеллировал к понятию одна гипотеза лучше или хуже «подтверждается» свидетельство. Но, возможно, это отвлекло его от строго дедуктивного подхода. взгляд на науку. В таком случае представляется сомнительным, что чистый дедуктивизм может дать адекватный отчет о научном методе.

7. Средство и конечные результаты

Можно считать, что аргумент Юма окончательно исключил своего рода оправдание индуктивных выводов, которое он искал за. То есть, это может исключить оправдание, которое дает повод для считают вывод определенного индуктивного вывода правильным, или даже скорее всего будет правильным.Однако также можно переместить вдали от фокуса на обосновании конкретных индуктивных выводов, и рассмотреть индуктивные методы в более общем плане. В простых случаях перечислительная индукция, «индуктивный метод» или «Индуктивный принцип», как его иногда называют, правило экстраполяции наблюдаемых случаев. Например, это могло быть правилом, которое следует вывести из универсального обобщение, после определенного количества положительных примеров и отвергнуть универсальное обобщение после наблюдения встречные инстанции.Или это можно было бы сформулировать как так называемый «Прямое правило», которое гласит, что нужно проецировать наблюдаемая частота признака для населения в целом, включая будущие экземпляры. Может быть, генерал свойства индуктивного метода дают основание использовать это метода, даже если у нас нет оснований полагать, что метод привести к правильному ответу в каком-то конкретном приложении? Учитывая конкретной индуктивной задаче, мы можем искать оптимальный метод, или средства для предоставления решения.Такой аргумент о средствах и целях может затем составляют основу для следования методу даже при отсутствии причины верить в ее успех в конкретных случаях.

7.1 Прагматическое оправдание

Одной из основных ранних попыток в этом направлении была «Прагматический» подход Райхенбаха (1938 [2006]). Райхенбах действительно считал аргумент Юма неопровержимым, но тем не менее он попытался найти более слабое оправдание индукция. Чтобы подчеркнуть отличие от вида оправдание, которое искал Юм, некоторые дали ему другой термин и называют решение Райхенбаха «оправданием», а не оправдание индукции (Feigl 1950; Salmon 1963).

Согласно этому подходу мы имеем определенную цель — сделать индуктивную выводы. Даже если мы не можем быть уверены, что сможем достичь цели, мы можем по-прежнему утверждают, что если цель может быть достигнута, это будет заключаться в обычные принципы индуктивного вывода. Это дает повод для делать те обычные индуктивные выводы. Райхенбах делает сравнение с ситуацией, когда мужчина болеет, и врач говорит: «Я не знаю, поможет ли операция спасти человека, но если есть какое-то лекарство, то это операция » (Рейхенбах 1938 [2006: 349]).Это дает какое-то оправдание для действует на мужчину, даже если он не знает, что операция удастся.

Райхенбах применил эту стратегию к общей форме «Статистическая индукция», в которой мы наблюдаем относительную частота \ (f_n \) конкретного события в n наблюдениях и затем сформируйте ожидания относительно частоты, которая возникнет, когда больше сделаны наблюдения. Тогда «индуктивный принцип» заявляет, что если после определенного количества случаев наблюдаемый частота \ (m / n \) наблюдается при любом продолжении ряда наблюдений, частота будет и дальше находиться в пределах небольшого интервал \ (m / n \). Случаи, подобные рассмотренным Юмом, являются частным случаем. этого принципа, где наблюдаемая частота равна 1. Например, в Хлебный ящик Юма, предположим, хлеб питает n раз из n (т.е. наблюдаемая частота 100%), тогда, согласно принципу индукции, мы ожидаем, что при наблюдайте больше экземпляров, частота питательных продолжится быть в пределах очень небольшого интервала 100%. Следуя этой индуктивной принцип также иногда называют следующим «Прямое правило».Тогда проблема состоит в том, чтобы оправдать использование это правило.

Райхенбах утверждал, что даже если Юм прав, полагая, что мы не можем быть оправданным в размышлениях о любом конкретном применении правила что вывод, вероятно, будет верным, для целей практическими действиями нам не нужно это устанавливать. Вместо этого мы можем считать, что индуктивное правило приводит к «положению», или утверждение, с которым мы работаем, как если бы оно было правдой. Мы полагаем определенную частота f на основании наших данных, а это вроде делать пари или пари, что частота на самом деле f .

Согласно Райхенбаху, цель индуктивного вывода: «, чтобы найти серию событий, частота появления которых сходится к пределу »(1938 [2006: 350]). это возможно, что мир настолько беспорядочный, что мы не можем построить серии с такими пределами. Но если есть предел, есть и некоторые элемент серии наблюдений, за пределами которых принцип индукция приведет к истинному значению предела. Хотя индуктивное правило может давать совершенно неверные результаты на ранних этапах последовательности, так как он следует за случайными колебаниями частоты дискретизации, это гарантированно приблизится к предельной частоте, если такая предел существует.Следовательно, правило индукции оправдано как инструмент постулирования, потому что это метод, о котором мы знаем, что если можно делать заявления о будущем мы их найдем с помощью этого метода (Reichenbach 1949: 475). Это оправдание воспринимается как прагматичный, поскольку, хотя он не дает знания будущего события, это дает достаточную причину для действий (Райхенбах 1949: 481).

У такого прагматичного подхода есть несколько проблем. Одна проблема в том, что предлагаемое им оправдание слишком сильно привязано к в долгосрочной перспективе, при этом практически не ограничивая то, что может быть положено в краткосрочной перспективе.Однако именно в краткосрочной перспективе индуктивный практика действительно имеет место и там, где она действительно нуждается в обосновании (BonJour 1998: 194; Лосось 1966: 53).

С этим связано беспокойство по поводу слабости обоснования чувство, что это применимо ко многим другим правилам вывода, а также так называемое «прямое правило» (Salmon 1966: 53). Это применимо, фактически, к любому методу, асимптотически сходящемуся к прямой правило. Легко определяемый класс таких правил — это те, которые добавляют к индуктивное правило — функция \ (c_n \), в которой \ (c_n \) сходятся к ноль при увеличении n .

Райхенбах делает два предложения, направленных на то, чтобы избежать этой проблемы. На с одной стороны, утверждает он, поскольку у нас нет реальной возможности выбирать между методов, мы могли бы просто использовать индуктивное правило, поскольку оно «Проще в обращении благодаря наглядной простоте». Он также утверждает, что метод, который воплощает в себе «наименьшее риск »следует индуктивному правилу (Reichenbach 1938 [2006: 355–356]).

Другая проблема заключается в том, действительно ли Райхенбах установил, что не может быть лучшего правила, чем прямое правило.Например, несмотря на все сказанное, может быть прорицатель или ясновидящий, который способен надежно предсказывать будущие события. Здесь рассуждает Райхенбах что, используя индукцию, мы можем распознать надежность альтернативный метод, изучив его послужной список. Эта мысль была позже подхватил и превратился в предположение, что «Метаиндуктивист», применяющий индукцию не только в «Объектный» уровень для наблюдений, но также и для успеха методы других, могли бы с помощью этих средств также прогнозно в качестве альтернативного метода (Schurz 2008; см. Раздел 7.3 для более подробного обсуждения метаиндукции).

Можно также задаться вопросом, действительно ли прагматический аргумент предоставить универсальное и общее обоснование соблюдения индуктивное правило. Конечно, прагматическое решение должно учитывать различия в выплатах, зависящие от обстоятельств. Например, Райхенбах предлагает следующий аналог своей прагматической обоснование:

Мы можем сравнить нашу ситуацию с ситуацией человека, который хочет ловить рыбу в неизведанная часть моря.Некому сказать ему, действительно ли в этом месте есть рыба. Закинуть сеть? Ну если он хочет чтобы ловить рыбу в этом месте, я бы посоветовал ему забросить сеть, взять шанс хотя бы. Лучше попробовать даже в неопределенности, чем не пытаться быть уверенным в том, что ничего не получишь. (Reichenbach 1938 [2006: 362–363])

Как указывает Ланге, приведенный здесь аргумент «предполагает, что существует бесплатно ». В такой ситуации «рыбак имеет все, чтобы получить и нечего терять, забрасывая сеть » (Ланге 2011: 77).Но если попытка требует значительных затрат, но это может быть не так Понятно, что наиболее рациональный образ действий — забросить сеть. Аналогичным образом, имеет ли смысл проводить политику не делать прогнозов, а придерживаться политики следования индуктивное правило, может зависеть от практических наказаний ошибаться. Прагматическое решение может не предложить основание для следования правилу индукции, которое применимо во всех обстоятельства.

7.2 Теория формального обучения

Как мы видели выше, одной из проблем Райхенбаха было то, что слишком много правил, которые сходятся в пределе к истинной частоте. Какой из них выбрать в краткосрочной перспективе? Возможно расширить общую стратегию Райхенбаха, рассмотрев, что происходит, если у нас есть другие эпистемические цели, помимо долгосрочной конвергенции. Могут ли другие цели накладывать ограничения на то, какие методы следует использовать в краткосрочная перспектива? Область формальной теории обучения развивалась ответы на эти вопросы (Kelly 1996; Schulte 1999; также см. Schulte 2017).

В частности, теоретики формального обучения рассматривали цель добраться до истины максимально эффективно или быстро, а также как цель минимизировать количество изменений ума или отказов по пути. Затем было показано, что обычный индуктивный метод для которого характерно предпочтение более простых гипотез (Бритва Оккама), может быть оправдана, поскольку это уникальный метод что в конечном итоге соответствует стандартам для достижения истины, поскольку максимально эффективно, с минимальным количеством ретракций (Schulte 1999).

Теорию формального обучения можно рассматривать как своего рода расширение Рейхенбаховская программа. Он не предлагает оправданий для индуктивные выводы в смысле объяснения причин, почему они должны следует рассматривать как способные привести к истинному заключению. Скорее предлагает причины для использования определенных методов, исходя из их оптимальности в достижение определенных желаемых эпистемических целей, даже если нет гарантируют, что на любом этапе расследования полученные результаты вообще близки к истине.Однако недавно Steel (2010) предположил, что формальная теория обучения предлагает больше и действительно дает Решение проблемы индукции. Это утверждение основано на довольно ограничительная интерпретация «проблемы Юма» как проблема: «Какое основание для индуктивного вообще обобщения? » (2010: 182), а не как проблема предоставления основания для данного индуктивного вывода. Steel’s претензии были оспорены Колином Хоусоном (2011).

7.3 Метаиндукция

Другой подход к реализации широкой рейхенбаховской программы состоит в том, чтобы перейти на уровень метаиндукции. Мы можем провести различие между применение индуктивных методов на уровне событий — так называемые Индукция «объектного уровня» и применение индуктивных методов на уровне конкурирующих методов прогнозирования — так называемых «Метаиндукция». В то время как индуктивные методы объектного уровня делать прогнозы на основе наблюдаемых событий встречаются, метаиндуктивные методы делают прогнозы на основе агрегирования прогнозы различных доступных методов прогнозирования в соответствии с их показатели успеха. Здесь определяется степень успеха метода. в соответствии с каким-то точным способом достижения успеха в создании предсказания.

Тогда возникает вопрос, может ли существовать метаиндуктивный метод. что является «оптимальным с точки зрения прогноза» в том смысле, что следуя этому методу, лучше всего удается делать прогнозы среди всех конкурирующих методы, независимо от того, какие данные получены. Герхард Шурц имеет выделил результаты обучения, основанного на сожалении, Чезе-Бьянки, что существует метаиндуктивная стратегия, которая прогнозируемый оптимальный среди всех доступных прогнозных методов эпистемическому агенту (Cesa-Bianchi & Lugosi 2006; Schurz 2008, предстоящий). Эта метаиндуктивная стратегия, которую Шурц называет «WMI», прогнозирует средневзвешенное значение прогнозов доступные методы, где веса «Привлекательность», которая измеряет разницу между коэффициент успешности собственного метода и коэффициент успешности wMI.

Главный результат состоит в том, что стратегия wMI является оптимальной в долгосрочной перспективе в ощущение, что он приближается к максимальной вероятности успеха из доступных методы прогнозирования. Границы наихудшего случая для краткосрочной производительности могут также быть производным.Результат оптимальности является основой для a. priori означает оправдание использования wMI. А именно Думаю, разумно использовать wMI, так как он позволяет добиться наилучших результатов. вероятность успеха в долгосрочной перспективе при использовании данных методов.

Шурц также утверждает, что это априори оправдание wMI, вместе с условным фактом, что индуктивные методы до сих пор был намного более успешным, чем неиндуктивные методы, дает апостериори обоснование индукции. Поскольку wMI будет достичь в долгосрочной перспективе максимального успеха из имеющихся методы прогнозирования, целесообразно его использовать. Но что касается Фактически, максимальный успех достигается индуктивными методами. Следовательно, поскольку априори оправдано использование wMI, это также априори оправдано использовать максимально удачный метод на уровне объекта. Поскольку оказывается, что максимально успешный метод — индукция, тогда целесообразно использовать индукция.

Теоремы Шурца об оптимальности wMI применимы к случаю где существует конечное число методов прогнозирования.Одна точка обсуждение заключается в том, является ли это серьезным ограничением его претендует на полное решение проблемы индукции (Экхардт 2010).

Лучший аргумент — не спорить с трудными людьми

Лучший аргумент — не спорить с трудными людьми

Психотерапевт Мэри Джо Рапини говорит, что эти четыре совета могут помочь вам избежать соблазна вести себя разочаровывающим и бесплодным спором.

У всех разные мнения о том, что должно происходить в мире.Однако некоторые люди делают невозможным гражданское обсуждение своего мнения. Попытки взаимодействовать с этими «трудными» людьми или жить с ними часто разочаровывают, но это возможно, если вы научитесь понимать, что делает их трудными. В области психического здоровья мы идентифицируем их как людей с расстройством личности. Все расстройства личности следуют нездоровому образцу мышления и поведения, который вызывает проблемы в отношениях, работе и учебе.

Самые сложные люди не осознают, что бросают вызов другим.Наличие расстройства личности предполагает, что ваше поведение фиксируется на основе психологической защиты, выработанной в детстве. Трудным людям не хватает самосознания. Когда что-то идет не так, они обвиняют других; они не могут взять на себя ответственность за свои действия. Они часто вызывают у вас чувство беспокойства, разочарования и злости.

Политика, семейные встречи и наша карьера могут привести к сложным разговорам с трудными людьми. Ниже приведены четыре совета, которые помогут вам не увлечься разочаровывающим и бесплодным спором.

1. Никогда не спорьте с теми, кто верит их собственной лжи. Трудные люди страдают расстройством личности. Это ограничивает их способность осознавать себя или брать на себя личную ответственность. Их личный разговор с самим собой постоянно говорит им, что они правы, а вы неправы. Они используют оскорбления, чтобы сохранить свое превосходство, что является защитным механизмом для чувства уязвимости.

2. Примите тот факт, что спор будет бессмысленным и бесплодным. Здоровые аргументы должны быть продуктивными, и оба человека должны стремиться к компромиссу или взаимопониманию.Сложные люди стремятся только быть правыми и «выиграть» спор. Когда один человек полон решимости быть правым независимо от последствий, результат никогда не будет конструктивным.

3. Сохранение спокойствия работает вам на пользу. Самые трудные люди — часто несчастные люди, и они становятся менее тревожными, когда окружающие чувствуют себя плохо и взволнованы. Когда вы сохраняете спокойствие в жаркой дискуссии, вы демонстрируете, что у них нет власти или влияния на вас.

4.Эмоционально отстранитесь от трудного человека. Если вы застряли в жизни с трудным человеком, быстро научитесь не принимать его слова на свой счет. Делайте то, что вам нужно, чтобы оставаться отстраненным, когда ситуация накаляется, будь то напоминание о списках продуктов или список штатов Америки. Вы ничего не можете сказать, что улучшило бы их положение; они живут в самовольно созданной тюрьме, и только они держат в руках ключ.

Спорить или ссориться с трудными людьми на праздниках или на работе — пустая трата драгоценного времени.Часть того, чтобы быть ответственным взрослым, — это позволить себе не присутствовать на каждом споре, на который вас приглашают. Это проявление смелости — отказаться от спора, когда человек, с которым вы спорите, верит своей собственной лжи.

Никаких аргументов в пользу Бога: почему разум переоценивается в разговорах о вере: Джон Уилкинсон: 9780830834204

«Некоторые люди знают истину с самоуверенной уверенностью, которая одновременно вызывает восхищение и раздражает. вдали от битвы хромотой, хромотой, которая показывает, что этот человек все еще идет вперед, но со смирением, которое возникает из глубокого общения с Богом в тени жизни.Книга Джона Уилкинсона предназначена для хромых, и это прекрасная постапологетическая апологетика подлинной веры ».
«Уилкинсон ставит традиционную апологетику с ног на голову в этом захватывающем новом видении разговорного взаимодействия. Беззастенчиво привлекая чудо и кажущуюся« абсурдность »веры, Уилкинсон одним движением уступает место совершенно иному взаимодействию для тех, кто считает духовным Путешествие, в которое нас приглашает Христос. Обладая такой же поэтической силой, No Argument for God представляет собой захватывающий образ другого мира, ожидающего тех, кто постигнет тайну познания Бога как здесь, так и в мире грядущем.Свежий подход Уилкинсона — это не просто еще один голос в нынешних дебатах о том, как должна выглядеть апологетика в постмодернистской среде, но и сам характер разговора. Думать, что чудо, тайна и очевидное превосходство веры над простым разумом могут быть реальной силой нашей исторической веры, а не уродливыми пасынками, которыми они были исторически, освобождает и устанавливает новый курс как для евангелизации, так и для наших личных отношений с Богом. сам.»
«Джон Уилкинсон знает, что мы можем свидетельствовать о присутствии Христа в нашей жизни и подтверждать свои убеждения верными свидетельствами.Логика не сделает нас верующими, и в этой важной книге он разъясняет, что праведные должны жить верой в откровение ».
«Книга Джона Уилкинсона представляет собой один из лучших ответов на нападки модернистских« ученых », которые настаивают на том, что их ограниченный взгляд на мир — это все, что могло быть. сосредоточиться на абсурдности Евангелия не только сегодня, но даже в первом веке. Он напоминает нам, что вера коренится не в нашей способности выйти за пределы неба и «понять» Бога или даже «открыть» Создателя, но в желание нашего Господа достичь сквозь время и пространство и жить среди нас. Постоянно свежая и безрассудно глубокая чистота отдельного Божества, достаточно заботливого, чтобы пригласить нас — любого из нас, каждого из нас — в свое правление как Царя всего, видимого и невидимого, — вот что делает веру чудом для всех. чудеса. Молодец, Джон Уилкинсон, держит нас на правильном пути, как маленькие дети, освобожденные голосом и объятиями Того, Кто пришел и поманил: «Пусть дети приходят ко мне…»

Нет аргументов, нет мнения — быстрый взгляд на неоспоримые решения по Правилу 36 во время пандемии | Morrison & Foerster LLP — Федеральный округ

На прошлой неделе Сет Ллойд и я заметили, что на ноябрьском заседании Федерального округа (здесь) было подано еще два правила 36 в апелляциях без устных аргументов.А вчера Перри Купер из Bloomberg написал в Твиттере, что еще два правила 36 были вынесены в ходе рассмотрения апелляций в этом месяце без аргументов. Это заставило меня задуматься, сколько раз с момента начала пандемии Правило 36 суда не приводило к аргументам? И можно ли что-нибудь почерпнуть из этих решений? Обычно ожидается, что, если не будет устных аргументов, стороны получат краткое объяснение того, почему Суд вынес определенное решение, приняв беспрецедентное решение. Но если есть аргумент, возможно, меньше необходимости в письменном объяснении: стороны, вероятно, узнали достаточно во время устных споров из допроса судей, чтобы понять основу решения.Но здесь, в этом подмножестве дел без мнения или устных аргументов, некоторые апеллянты могут задаваться вопросом: «Почему я проиграл?»

Итак, сколько апеллянтов мы нашли в этой специальной категории? Девять. Семь подали апелляции на патенты — и эти семь были довольно равномерно разделены между PTAB (три) и окружными судами (четыре). Один из них касался государственных контрактов. И последнее было (на первый взгляд) немного загадочным.

Давайте сначала рассмотрим две непатентные апелляции. Ни один из этих случаев не был отмененным аргументом как таковым.И дело о государственных контрактах, вероятно, имеет прямую причину, по которой Правило 36 Суда не было аргументировано — подрядчик, подавший апелляцию, отклонил аргумент . Учитывая, что податель апелляции не видел необходимости в споре, вполне возможно, что коллегия (судьи Брайон, Уоллах и Хьюз) не усмотрела причин для письменного обоснования своего решения. Возможно, если бы истец не отказался от устной аргументации, Суд принял бы аргумент и Правило 36’d. Или, может быть, он все равно отменил бы спор и вынес бы беспрецедентное решение.Мы никогда не узнаем, но кажется возможным — если маловероятным — то, что решение истца отказаться от аргументации сыграло определенную роль в решении Суда.

Что касается загадочного дела: это была апелляция pro se, поэтому было логично, что не было устных аргументов. Что имело меньший смысл, так это подтверждение Правилом 36, поскольку обычно Суд выдает краткое заключение без предварительного заключения, объясняющее решение. Желая узнать больше, я посмотрел на досье. То, что я обнаружил, сделало этот случай более и менее загадочным. Дело было полностью закрыто; Я не мог видеть, какие документы (отредактированные или нет) были поданы и когда.Учитывая секретность, было больше смысла в том, что Суд мог бы принять Правило 36, а не подготовить полностью закрытое решение. (Для тех, кому интересно, вы можете Google стороны и (возможно) получить некоторую информацию по делу. )

Осталось семь патентных дел. Устные возражения по всем семи апелляциям были отклонены. Неудивительно, что четкой закономерности не было. По делам PTAB, два представлялись существенными доказательствами, а одно — требованием строительства. И они были разделены в соотношении два к одному между заявителем, подавшим апелляцию, и заявителем, подавшим апелляцию патентообладателя.Интересно, что в двух из районных судов была рассмотрена 101 апелляция, в которой требования патентообладателя были признаны неприемлемыми по ходатайству об отклонении. Я полагаю, можно сказать, что это и удивительно, и неудивительно, что Суд не захотел выслушивать аргументы и написать еще о 101 апелляции. Последние два были неоднозначными. Одним из них была апелляция на гонорары адвокатов, в которой выигравшая сторона требовала выплаты гонорара. И последняя апелляция была как-то связана с личной юрисдикцией, но мои пять-десять минут чтения не дали мне подробного понимания проблемы, поэтому я не могу сказать больше. Возможно, поэтому комиссия решила, что и устные аргументы, и письменное решение не нужны. Или, возможно, мне просто следовало выпить вторую чашку кофе, прежде чем смотреть на трусы.

Несколько последних лакомых кусочков:

• Судья Лурье участвовал в четырех апелляциях по Правилу 36 без аргументов — все дела с аргументами были отменены. Следующим был судья Ньюман с тремя, и еще несколько судей рассматривали две такие апелляции.
• Из действующих судей только судья Чен не участвовал в Правиле 36 без аргументов с момента начала пандемии.
• Хотя размер выборки настолько мал, что трудно предположить, что это что-то, кроме анекдотического, интересно, что большая часть безоговорочных правил 36 применялась в последние три месяца — по два в октябре, ноябре и декабре. Для сравнения: за первые шесть месяцев телефонных споров (апрель-сентябрь) было всего три без аргументации по Правилу 36. Возможно, по мере того, как формат телефонного спора продолжился, судьи решили, что некоторые дела настолько прямолинейны, что аргументы не помогут Суду и сторонам не потребуется письменное объяснение.