Теория вероятностей в ОГЭ по математике. Все нужные формулы и решение задач для номера 10 | Подготовка к ЕГЭ и ОГЭ | Умскул
Есть такое коварное задание в ОГЭ по математике под номером 10 – «Теория вероятности». С первого взгляда кажется простым, но часто возникают подводные камни и ученики теряют баллы. А задание ведь несложное. На нем баллы набирать надо! Даже если твоя цель — просто перейти порог, прочитав эту статью, сможешь набирать на ОГЭ по математике на 1 балл больше. А если твоя цель – разобраться с самыми сложными задачами этого номера (к сожалению, задачи не всегда элементарные), с этим тоже помогу.
Что такое вероятность
Вероятность — это степень наступления какого-либо события. Вероятность изменяется числом от 0 до 1. Отрицательные числа и числа больше единицы ответом быть не могут!
Как понять результат своего вычисления:
1 — событие точно произойдет (достоверное событие)
от 0 до 1 — произойдет с каким-то шансом, может произойти, а может и нет (случайное событие)
0 — точно не произойдет (невозможное событие)
В ОГЭ мы работаем со случайными событиями, ответ 1 или 0 в 10 задании получиться не может!
Вероятность любого события можно найти по этой формуле:
Формула вероятностиФормула вероятности
Она решает 80% заданий на ОГЭ, но есть ещё 20%.
 ..
..Решим самый простой пример:
Пример 1. Самый простойПример 1. Самый простой
Объясняю на пальцах:
- 4 бутылки.
- Если 1 бутылка с газом, значит, 3 без газа.
- Нам нужна негазированная, значит, количество благоприятных исходов для нас – 3.
- А всего бутылок 4 – это количество всех исходов.
- Далее решаем по формуле. 3 делим на 4 и переводим в десятичную дробь (ответы на ОГЭ принимаются только в виде десятичных дробей). Получаем 0.75. НИКАКИХ ПРОЦЕНТОВ! Если этого не просят!
Когда событие одно – решить легко, но их может быть несколько… Разберем ВСЁ, что может попасться на экзамене
Кстати, здесь полный разбор досрочного ОГЭ по математике (нажми, чтобы перейти). Объяснение всех заданий!
Сокращенный вариант по математике и разбор досрочного ОГЭ по русскому в этой статье (нажми, чтобы перейти).
Вернемся к вероятностям…
Несовместные события
События А и В несовместные, если они не могут произойти одновременно.
Пример: «получить на ОГЭ по математике 5» и «получить на ОГЭ по математике 4» – это несовместные события. Ты получишь либо 4, либо 5. Ставится только одна оценка.
А как посчитать их вероятность? По формуле:
Формула несовместных событийФормула несовместных событий
Р — это вероятность. Чтобы найти вероятность несовместных событий (наступит или событие А, или событие Б), нужно найти вероятность наступления каждого и сложить их.
Уже немного сложнее, да? Давай решать задачку
Задача на несовместные событияЗадача на несовместные события
Как проверить, что события несовместные
Задать вопрос: «А могут ли они наступить одновременно?» Если в задаче написано, что Наташа берет наугад 1 пирожок с тарелки, а там их много, она не может взять одновременно 2! Так сказано в условии.
Противоположные события
Два события называются противоположными, если в данном испытании они несовместны и одно из них обязательно происходит.
Формула для расчета:
Формула противоположных событийФормула противоположных событий
Отличие от несовместныхВ том, что несовместные события могут и не произойти, а одно из противоположных обязательно произойдет.
Например: «получить на ОГЭ по математике 5» и «получить на ОГЭ по математике 4» – это несовместные события. Но! Ты можешь получить и 3, и 2. Ты получишь 4 или 5 не со стопроцентной вероятностью. Поэтому такие события не являются противоположными.
Противоположное событие — подбросить монету, выпадет либо орел, либо решка. Не выпасть орел или решка не могут! И третьего не дано! Обязательно на какую-то сторону монета упадет, мы не учитываем, что монета упадет на ребро.
Ещё примеры несовместных событий для понимания:
- попасть в мишень и не попасть в мишень
- выздороветь и не выздороветь
- готовиться к экзаменам и не готовиться к экзаменам
Третьего не дано!
С несовместными разобрались, осталось самое сложное…
Независимые события
События А и Б независимы, если появление одного из них не меняет вероятности появления другого.
Пример независимых событий: попасть в мишень при первом выстреле и попасть в мишень при втором выстреле. После первого выстрела стрелок хуже стрелять не стал, мишень не передвинули, ветер сильнее дуть не стал. Поэтому вероятность попадания в обоих случаях одинаковая. Условия одинаковые.
Пример зависимых событий: вытащить из мешка с игрушками мягкую игрушку в первый раз и вытащить мягкую игрушку во второй раз. Вероятность во втором случае изменится, ведь в мешке после первого раза стало на 1 мягкую игрушку меньше (количество благоприятных исходов и количество всех исходов стало на 1 меньше).
Вероятность во втором случае изменится, ведь в мешке после первого раза стало на 1 мягкую игрушку меньше (количество благоприятных исходов и количество всех исходов стало на 1 меньше).
Зависимых событий на ОГЭ не дадут, этот пример для понимания независимых)
Решаем сложную задачку
Пример задачи на независимые событияПример задачи на независимые события
Попасть в мишень(А) и не попасть(В) – это противоположные события. Вероятность Р(А) уже дана в условии. Рассчитываем вероятность Р(В) по формуле.
Попасть в мишень в первый раз и не попасть во второй – это независимые события. Чтобы получить их общую вероятность, нужно перемножить их вероятности по отдельности.
По условию: первый раз попал, второй раз промахнулся, третий раз промахнулся. Перемножаем: Р(А)*Р(В)*Р(В).
Готово!
Теперь ты понимаешь, как решать 10 задание ОГЭ по математике, и даже если тебе попадётся самый сложный номер, ты вспомнишь моё объяснение и заработаешь 1 балл 🙂
Чтобы получать бесплатные уроки по математике и другие авторские материалы для подготовки от онлайн-школы Умскул, подпишись на еженедельную математическую базу знаний ВКонтакте.
Больше статей на про подготовку к ОГЭ по математике: #ум_огэ_математика #ум_огэ
А чтобы научиться решать другие задания, подписывайся на наш канал. Мы делимся знаниями, которые сами по себе позволяют подготовиться на хорошие баллы и компенсируют репетиторов. В 2020 году ученики онлайн-школы Умскул набрали на 27,5 баллов больше, чем усредненный балл по России. Проводим бесплатные вебинары каждую неделю. Чтобы получить доступ к материалам, подпишитесь на бесплатную рассылку ОГЭ или ЕГЭ. Присоединяйтесь к нашему блогу и готовьтесь с лучшими!
Кстати, забирай итоговый конспект с нашего занятия 🙂 Вся теория в нем
Итоговый конспект от онлайн-школы Умскул. Преподаватель: Семен Кравченко.Итоговый конспект от онлайн-школы Умскул. Преподаватель: Семен Кравченко.
Также читайте статьи:
ОГЭ. Решение задач по теории вероятностей
МБОУ «СОШ №2 г. Суворова»
ОГЭ. Решение задач по теории вероятностей
Учитель: Орлова Ольга Ивановна
Решение задач по теории вероятностей
Учитель: Орлова Ольга Ивановна
Основные понятия теории вероятностей Случайным называется событие, которое нельзя точно предсказать заранее. Оно может либо произойти, либо нет. Испытанием называют такое действие, которое может привести к одному из нескольких результатов. Если n- число всех исходов некоторого испытания, m- число благоприятствующих событию A исходов, Вероятность события A равна P(A) =
Пример Бросается игральный кубик, какова вероятность того, что выпадет число 4.
Пример Бросается игральный кубик, какова вероятность того, что выпадет число 4. Решение: У кубика 6 сторон, выпасть может любая из них ⇒ число всех исходов равно n = 6. Число 4 может выпасть только в одном случае ⇒ число благоприятствующих исходов равно m = 1. Тогда P(A)= 1 : 6 Ответ: 1/6. P(A) =
Задача
На тарелке 20 пирожков: 2 с мясом, 16 с капустой и
2 с вишней. Рома наугад выбирает один пирожок.
Найдите вероятность того, что он окажется
с вишней.
Рома наугад выбирает один пирожок.
Найдите вероятность того, что он окажется
с вишней.
Задача На тарелке 20 пирожков: 2 с мясом, 16 с капустой и 2 с вишней. Рома наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней. Решение: Число всех исходов равно n = 20. Число благоприятствующих исходов равно m = 2. Тогда P(A) = 2 : 20 Ответ: 0,1. P(A) =
Задачи
1. Определите вероятность того, что при бросании
игрального кубика выпадет менее 4 очков.
2. В лыжных гонках участвуют 11 спортсменов из
России , 6 спортсменов из Норвегии и 3 спортсмена
из Швеции. Порядок, в котором спортсмены
стартуют, определяется жребием. Найдите
вероятность того, что первым будет стартовать
спортсмен из России.
3. Из 600 клавиатур для компьютера в среднем 12
неисправны.
Ответы 1. Определите вероятность того, что при бросании игрального кубика выпадет менее 4 очков. (0,5) 2. В лыжных гонках участвуют 11 спортсменов из России , 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из России. (0,55) 3. Из 600 клавиатур для компьютера в среднем 12 неисправны. Какова вероятность, что случайно выбранная клавиатура исправна? (0,98)
Сложение вероятностей Суммой событий A и B называют событие (A+B) , состоящее в появлении либо только события A, либо только события B, либо и события A и события B одновременно. P(A+B) = P(A) + P(B)
Сложение вероятностей
Суммой событий A и B называют событие (A+B) , состоящее
в появлении либо только события A, либо только события B,
либо и события A и события B одновременно. P(A+B) = P(A) + P(B)
Пример
В ящике лежат 10 шаров: 4 красных, 1 синий и 5 черных. Наугад вынимается один шар. Какова вероятность того, что шар красный или синий.
Решение:
Пусть событие A — вынут красный шар. P(A)=4:10=0,4
событие B — вынут синий шар. P(B)=1:10=0,1
Тогда вероятность того, что вынутый шар красный или синий равна P(A+B) = 0,4 + 0,1 = 0,5.
Ответ: 0,5
P(A+B) = P(A) + P(B)
Пример
В ящике лежат 10 шаров: 4 красных, 1 синий и 5 черных. Наугад вынимается один шар. Какова вероятность того, что шар красный или синий.
Решение:
Пусть событие A — вынут красный шар. P(A)=4:10=0,4
событие B — вынут синий шар. P(B)=1:10=0,1
Тогда вероятность того, что вынутый шар красный или синий равна P(A+B) = 0,4 + 0,1 = 0,5.
Ответ: 0,5
Задача В магазине канцтоваров продается 120 ручек, из них 15 – красных, 22 – зеленых, 27 – фиолетовых, еще есть синие и черные, их поровну. Найдите вероятность того, что Алиса наугад вытащит синюю или зеленую ручку.
Задача
В магазине канцтоваров продается 120 ручек, из них 15 –
красных, 22 – зеленых, 27 – фиолетовых, еще есть синие
и черные, их поровну. Найдите вероятность того, что
Алиса наугад вытащит синюю или зеленую ручку.
Решение:
Синих ручек (120 — 15 — 22 — 27) : 2 = 28
Событие A – вытащит синюю ручку. P(A) = 28 : 120 = 14/60.
Событие B – вытащит зеленую ручку. P(B) = 22 : 120 =11/60.
Тогда вероятность того, что Алиса вытащит синюю или
зеленую ручку равна P(A+B) = 14/60 + 11/60 = 5/12.
Ответ: 5/12.
P(A) = 28 : 120 = 14/60.
Событие B – вытащит зеленую ручку. P(B) = 22 : 120 =11/60.
Тогда вероятность того, что Алиса вытащит синюю или
зеленую ручку равна P(A+B) = 14/60 + 11/60 = 5/12.
Ответ: 5/12.
Произведение вероятностей Произведением событий A и B называется событие (AB), состоящее в появлении и события A и события B. P(AB) = P(A) P(B) Пример Дважды бросается игральный кубик. Какова вероятность того, что оба раза выпадет число 5. Решение: Пусть событие A — 1-й раз выпадет 5; P(A)=1:6 событие B — 2-й раз выпадет 5. P(B)=1:6 Тогда вероятность того, что оба раза выпадет число 5 P(AB)=1/6 1/6=1/36. Ответ: 1/36.
Задача
Игральную кость бросают два раза. Найдите
вероятность того, что оба раза выпало число,
большее 3.
Найдите
вероятность того, что оба раза выпало число,
большее 3.
Задача Игральную кость бросают два раза. Найдите вероятность того, что оба раза выпало число, большее 3. Решение: P(A) =3:6 = 0,5. P(A) = 3:6 = 0,5. P(AB) = 0,5 0,5 = 0,25. Ответ: 0,25 P(AB) = P(A) P(B)
Задача Если гроссмейстер А играет белыми, то он выигрывает у гроссмейстера Б с вероятностью 0,6. Если А играет черными, то А выигрывает у Б с вероятностью 0,4. Гроссмейстеры А и Б играют 2 партии, причем во 2-ой партии меняют цвет фигур. Найдите вероятность того, что А выиграет оба раза.
Задача
Если гроссмейстер А играет белыми, то он выигрывает у гроссмейстера Б с вероятностью 0,6. Если А играет черными, то А выигрывает у Б с вероятностью 0,4. Гроссмейстеры А и Б играют 2 партии, причем во 2-ой партии меняют цвет фигур. Найдите вероятность того, что А выиграет оба раза. Решение:
Пусть
Событие А — это выигрыш А в 1-ой партии, P(А) = 0,6.
Событие В — выигрыш А в 2-ой партии, P(В) = 0,4.
Событие C — А выиграет обе партии.
Р(C) = P(А) P(В), т.е наступят события А и В
P(C)=0,6 0,4=0,24
Ответ: 0,24
Решение:
Пусть
Событие А — это выигрыш А в 1-ой партии, P(А) = 0,6.
Событие В — выигрыш А в 2-ой партии, P(В) = 0,4.
Событие C — А выиграет обе партии.
Р(C) = P(А) P(В), т.е наступят события А и В
P(C)=0,6 0,4=0,24
Ответ: 0,24
Задача В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков.
Задача В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Решение: Числа 1 2 3 4 5 6 1 2 3 4 5 6 7 2 3 4 5 6 7 8 3 4 5 6 7 8 9 4 5 6 7 8 9 10 5 6 7 8 9 10 11 6 7 8 9 10 11 12
Задача
В случайном эксперименте бросают две игральные
кости. Найдите вероятность того, что в сумме выпадет
7 очков. Решение:
Числа
1
2
3
4
5
6
1
2
3
4
5
6
7
2
3
4
5
6
7
8
3
4
5
6
7
8
9
4
5
6
7
8
9
10
5
6
7
8
9
10
11
6
7
8
9
10
11
12
Найдите вероятность того, что в сумме выпадет
7 очков. Решение:
Числа
1
2
3
4
5
6
1
2
3
4
5
6
7
2
3
4
5
6
7
8
3
4
5
6
7
8
9
4
5
6
7
8
9
10
5
6
7
8
9
10
11
6
7
8
9
10
11
12
Задача
Числа
1
2
3
4
5
6
1
2
3
4
5
6
7
2
3
4
5
6
7
8
3
4
5
6
7
8
9
4
5
6
7
8
9
10
5
6
7
8
9
10
11
6
7
8
9
10
11
12
В случайном эксперименте бросают две игральные
кости. Найдите вероятность того, что в сумме выпадет
7 очков. Решение:
Число всех исходов
равно n = 6 6 = 36.
Число благоприятствующих
исходов равно m = 6.
Тогда P(A) = 6 : 36 = 1/6.
Ответ: 1/6.
Найдите вероятность того, что в сумме выпадет
7 очков. Решение:
Число всех исходов
равно n = 6 6 = 36.
Число благоприятствующих
исходов равно m = 6.
Тогда P(A) = 6 : 36 = 1/6.
Ответ: 1/6.
Задачи 1. Игральный кубик бросают дважды. Найдите вероятность того, что первый раз выпадет число 6. 2. Игральный кубик бросают дважды. Найдите вероятность того, что первый раз и во второй раз выпадет одинаковое число очков. 3. Игральный кубик бросают дважды. Какая сумма очков наиболее вероятна?
Задачи 1. Игральный кубик бросают дважды. Найдите вероятность того, что первый раз выпадет число 6. (1/6) 2. Игральный кубик бросают дважды. Найдите вероятность того, что первый раз и во второй раз выпадет одинаковое число очков. (1/6) 3. Игральный кубик бросают дважды. Какая сумма очков наиболее вероятна? (7)
Задача
В случайном эксперименте симметричную монету
бросают три раза. Найдите вероятность того, что решка
выпадет ровно 2 раза.
Найдите вероятность того, что решка
выпадет ровно 2 раза.
Задача В случайном эксперименте симметричную монету бросают три раза. Найдите вероятность того, что решка выпадет ровно 2 раза. Решение: 1 бросок 2 бросок 3 бросок О О О О О Р О Р Р О Р О Р Р Р Р Р О Р О О Р О Р
Задача
В случайном эксперименте симметричную монету
бросают три раза. Найдите вероятность того, что решка
выпадет ровно 2 раза. Решение:
8 исходов
1 бросок
2 бросок
3 бросок
О
О
О
О
О
Р
О
Р
Р
О
Р
О
Р
Р
Р
Р
Р
О
Р
О
О
Р
О
Р
Найдите вероятность того, что решка
выпадет ровно 2 раза. Решение:
8 исходов
1 бросок
2 бросок
3 бросок
О
О
О
О
О
Р
О
Р
Р
О
Р
О
Р
Р
Р
Р
Р
О
Р
О
О
Р
О
Р
Задача
В случайном эксперименте симметричную монету
бросают три раза. Найдите вероятность того, что решка
выпадет ровно 2 раза. Решение:
Число всех исходов равно n = 8.
Число благоприятствующих
исходов равно m = 3.
Тогда P(A) = 3 : 8 = 0,375.
Ответ: 0,375. 8 исходов
1 бросок
2 бросок
3 бросок
О
О
О
О
О
Р
О
Р
Р
О
Р
О
Р
Р
Р
Р
Р
О
Р
О
О
Р
О
Р
Найдите вероятность того, что решка
выпадет ровно 2 раза. Решение:
Число всех исходов равно n = 8.
Число благоприятствующих
исходов равно m = 3.
Тогда P(A) = 3 : 8 = 0,375.
Ответ: 0,375. 8 исходов
1 бросок
2 бросок
3 бросок
О
О
О
О
О
Р
О
Р
Р
О
Р
О
Р
Р
Р
Р
Р
О
Р
О
О
Р
О
Р
Задачи
1. Монету бросают три раза. Какова вероятность того, что результаты двух первых бросков будут одинаковы?
2. Монету бросают три раза. Найдите вероятность того, что результаты первого и последнего броска различны.
3. В случайном эксперименте симметричную монету
бросают два раза. Найдите вероятность того, что орел выпадет ровно один раз.
Монету бросают три раза. Какова вероятность того, что результаты двух первых бросков будут одинаковы?
2. Монету бросают три раза. Найдите вероятность того, что результаты первого и последнего броска различны.
3. В случайном эксперименте симметричную монету
бросают два раза. Найдите вероятность того, что орел выпадет ровно один раз.
Теория вероятности — урок. Основной государственный экзамен , ОГЭ Математика 2022.
Случайным событием называется событие, которое при осуществлении некоторых условий может произойти или не произойти.
Примером случайного события можно считать приобретение бракованного товара или выигрышного лотерейного билета.
Классическое определение вероятности
Вероятностью события A называется отношение числа благоприятных для A исходов к числу всех равновозможных исходов.
Формула для нахождения вероятности случайного события:
P(A)=N(A)N,
где P(A) — вероятность случайного события A, N(A) — количество тех исходов испытания, в которых наступает событие A, N — число всех возможных исходов данного испытания.
Противоположные события
Событие, противоположное событию A, обозначают A¯. При проведении испытания всегда происходит ровно одно из двух противоположных событий.
P(A)+PA¯=1.
PA¯=1−P(A).
Противоположными событиями, например, является приобретение исправной и бракованной лампочек.
Несовместимые события
Два события A и B называют несовместимыми, если отсутствуют исходы, благоприятствующие одновременно как событию A, так и событию B.
Если события A и B несовместимы, то вероятность их наступления равна сумме вероятностей событий A и B.
Примером является следующая ситуация: если наугад вытащить один шарик из коробки, где лежат шарики двух разных цветов, то появление при единичном вытаскивании одновременно шариков разных цветов — несовместимые события. Это объясняется тем, что мы можем за один раз достать шарик либо одного, либо другого цвета.
Независимые события
Два события A и B называют независимыми, если вероятность каждого из них не зависит от появления или непоявления другого события.
Если события A и B независимы, то вероятность их пересечения равна произведению вероятностей событий A и B.
Примером будет ситуация, в которой подбрасывают две монеты и выпадают две решки. Результат второй монеты не зависит от результата первой монеты и наоборот, поэтому события являются независимыми.
Pn=n!
Это упорядоченные совокупности, которые отличаются друг от друга только порядком элементов. Примером является размещение нескольких книг на одной полке.
Ank=n!(n−k)!
Это упорядоченные совокупности, которые отличаются друг от друга составом или порядком элементов. Примером является выбор директора и заместителя директора из некоторого числа кандидатов.
Cnk=n!(n−k)!⋅k!
Это неупорядоченные совокупности, которые отличаются друг от друга хотя бы одним элементом. Примером будет выбор двух вопросов из списка вопросов к экзамену.
Задачи для ОГЭ. Теория вероятностей
Задачи для ОГЭ. Теория вероятностейЗадачи для ОГЭ с ответами и решениями
Теория вероятностей
перейти к содержанию задачника
- Петя выбирает трехзначное число.
 Найдите вероятность того, что оно делится на 50.
Найдите вероятность того, что оно делится на 50. - Петя выбирает трехзначное число. Найдите вероятность того, что оно делится на 11.
- На тарелке 10 пирожков: 2 с мясом, 6 с капустой и 2 с вишней. Петя наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
- На тарелке 30 пирожков: 3 с мясом, 18 с капустой и 9 с вишней. Вова наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
- В фирме такси в данный момент свободно 30 машин: 7 черных, 6 желтых и 17 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.
- В каждой десятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Петя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Петя не найдет приз в своей банке.
- Игорь с папой решили покататься на колесе обозрения. Всего на колесе двадцать кабинок, из них 3 — синие, 14 — зеленые, остальные — красные.
 Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Игорь прокатится в красной кабинке.
Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Игорь прокатится в красной кабинке. - Петя с папой решили покататься на колесе обозрения. Всего на колесе двенадцать кабинок, из них 3 — синие, 6 — зеленые, остальные — красные. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Петя прокатится в красной кабинке.
- У дедушки 10 чашек: 7 с красными цветами, остальные с синими. Дедушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
- У бабушки 20 чашек: 4 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
- На экзамене 50 билетов. Петя не выучил 9 из них. Найдите вероятность того, что ему попадется выученный билет.
- На экзамене 50 билетов. Петя не выучил 1 из них. Найдите вероятность того, что ему попадется выученный билет.
- Родительский комитет закупил 10 пазлов для подарков детям на окончание года, из них 2 с машинами и 8 с видами городов.
 Подарки распределяются случайным образом. Найдите вероятность того, что Вове достанется пазл с машиной.
Подарки распределяются случайным образом. Найдите вероятность того, что Вове достанется пазл с машиной. - Родительский комитет закупил 25 пазлов для подарков детям на окончание года, из них 22 с машинами и 3 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Диме достанется пазл с машиной.
- В среднем на 100 карманных фонариков приходится семь неисправных. Найдите вероятность купить работающий фонарик.
- В среднем на 75 карманных фонариков приходится семь неисправных. Найдите вероятность купить работающий фонарик.
- В среднем из каждых 100 поступивших в продажу аккумуляторов 91 аккумулятор заряжен. Найдите вероятность того, что купленный аккумулятор не заряжен.
- В среднем из каждых 80 поступивших в продажу аккумуляторов 68 аккумулятор заряжен. Найдите вероятность того, что купленный аккумулятор не заряжен.
- Саша наудачу выбирает двузначное число. Найдите вероятность того, что оно оканчивается на 6.
- Определите вероятность того, что при бросании кубика выпало нечетное число очков.

- Определите вероятность того, что при бросании кубика выпало 1.
- Одновременно бросают две симметричные монеты. Какова вероятность того, что выпадут орел и решка?
- Одновременно бросают три симметричные монеты. Какова вероятность того, что выпадут два орла и одна решка?
- В классе 21 учащийся, среди них два друга — Петя и Вася. На уроке физкультуры класс случайным образом разбивают на 7 равных групп. Найдите вероятность того, что Петя и Вася попали в одну группу.
- Перед началом футбольного матча судья бросают монетку, чтобы определить, какая из команд будет первой владеть мячом. Команда А должна сыграть три матча — с командой В, с командой С и с командой D. Найдите вероятность того, что во всех матчах владение мячом первыми будет принадлежать команде А.
- В соревнованиях по толканию ядра участвуют 6 спортсменов из Греции, 4 спортсмена из Болгарии, 3 спортсмена из Румынии и 7 — из Венгрии. Порядок, в котором выступают спортсмены, определяются жребием.
 Найдите вероятность того, что спортсмен, который выступает последним, окажется из Венгрии.
Найдите вероятность того, что спортсмен, который выступает последним, окажется из Венгрии. - В соревнованиях по толканию ядра участвуют 4 спортсмена из Дании, 8 спортсменов из Швеции, 4 спортсмена из Румынии и 9 — из Венгрии. Порядок, в котором выступают спортсмены, определяются жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.
- В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 9 очков. Результат округлите до сотых.
- В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 10 очков. Результат округлите до сотых.
- На экзамене по геометрии школьнику достается одна задача из сборника. Вероятность того, что эта задача на тему «Треугольники», равна 0,5. Вероятность того, что это окажется задача на тему «Окружность» равна 0,25. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.

- На экзамене по геометрии школьнику достается одна задача из сборника. Вероятность того, что эта задача на тему «Окружность», равна 0,45. Вероятность того, что это окажется задача на тему «Углы» равна 0,5. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.
- Стрелок четыре раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что стрелок первые 3 раза попал в мишени, а последний раз промахнулся.
- Стрелок три раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,7. Найдите вероятность того, что стрелок первый раз попал в мишени, а последние два раза промахнулся.
- Стрелок три раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,9. Найдите вероятность того, что стрелок попал в мишень два раза и один раз промахнулся.
- Стрелок три раза стреляет по мишеням.
 Вероятность попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что стрелок попал в мишень два раза и один раз промахнулся.
Вероятность попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что стрелок попал в мишень два раза и один раз промахнулся. - В девятом экономическом классе учатся 24 мальчика и 6 девочек. По жребию они выбирают одного дежурного по классу. Какова вероятность того, что это будет мальчик?
- В девятом математическом классе учатся 2 мальчика и 23 девочек. По жребию они выбирают одного дежурного по классу. Какова вероятность того, что это будет девочка?
- Вероятность того, что новый компьютер прослужит больше года, равна 0,98. Вероятность того, что он прослужит больше двух лет, равна 0,84. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
- Вероятность того, что новый сканер прослужит больше года, равна 0,96. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
- Какова вероятность того, что случайно выбранное натуральное число от 25 до 39 делится на 5?
- Какова вероятность того, что случайно выбранное натуральное число от 15 до 36 делится на 2?
- На олимпиаде по химии участников рассаживают по трем аудиториям.
 В первых двух по 180 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчете выяснилось, что всего было 450 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
В первых двух по 180 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчете выяснилось, что всего было 450 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории. - На олимпиаде по математике участников рассаживают по трем аудиториям. В первых двух по 120 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчете выяснилось, что всего было 300 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
- Вероятность того, что на тесте по физике Петя верно решит больше 11 задач, равна 0,65. Вероятность того, что он верно решит больше 10 задач, равна 0,71. Найдите вероятность того, что Петя верно решит ровно 11 задач.
- Вероятность того, что на тесте по математике Вася верно решит больше 12 задач, равна 0,7. Вероятность того, что он верно решит больше 11 задач, равна 0,79. Найдите вероятность того, что Вася верно решит ровно 12 задач.

- Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 22 пассажиров, равна 0,86. Вероятность того, что окажется меньше 9 пассажиров, равна 0,5. Найдите вероятность того, что число пассажиров будет от 9 до 21.
- Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 21 пассажира, равна 0,96. Вероятность того, что окажется меньше 11 пассажиров, равна 0,51. Найдите вероятность того, что число пассажиров будет от 11 до 20.
- Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,05. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,03. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.

- Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,03. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,97. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,05. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
перейти к содержанию задачника
Ответы
- 0,02
- 0,09
- 0,2
- 0,3
- 0,2
- 0,9
- 0,15
- 0,25
- 0,3
- 0,8
- 0,82
- 0,98
- 0,2
- 0,88
- 0,93
- 0,92
- 0,09
- 0,15
- 0,1
- 0,5
- 1/6
- 0,5
- 0,375
- 0,1
- 0,125
- 0,35
- 0,32
- 0,11
- 0,13
- 0,75
- 0,95
- 0,0625
- 0,063
- 0,243
- 0,375
- 0,8
- 0,92
- 0,14
- 0,09
- 0,2
- 0,5
- 0,2
- 0,2
- 0,06
- 0,09
- 0,36
- 0,45
- 0,078
- 0,0776
Метки ОГЭ.
 Смотреть запись.
Смотреть запись.
© 2013-2022 Репетитор по скайпу Использование материалов согласовывать с администратором сайта
Вероятность сдачи ОГЭ | Обучонок
В процессе работы над индивидуальным исследовательским проектом по математике на тему «Вероятность сдачи ОГЭ» автором была поставлена цель выявить вероятности успешной сдачи экзамена обучающимися 9 классов путем угадывания правильного ответа, применяя теорию вероятностей.
Подробнее о работе:
В ученическом проекте по математике «Вероятность сдачи ОГЭ» автором была изучена теория использования знаний по теории вероятностей в разных сферах жизнедеятельности человека, в том числе проведено практическое исследование по прохождению экзаменационного тестирования по учебным предметам с применением теории вероятностей.
Учебная исследовательская работа по математике на тему «Вероятность сдачи ОГЭ» будет интересна учащимся 9 класса средней школы и их родителям, рассматривает способ применения знаний в области теории вероятностей для вычисления правильного ответа в тестовых заданиях по ОГЭ.
В исследовательской работе авторы приводят формулы вычисления и расчеты по применению теории вероятностей во время сдачи тестирования по обществознанию, а также в рамках проекта излагают историю появления и развития теории вероятностей.
Оглавление
Введение
1. История возникновения теории вероятностей.
2. Виды теорий вероятностей и их формулы.
3. Теория вероятностей в жизни на примере сдачи ОГЭ.
Заключение
Список литературы
Введение
Все выпускники девятых классов российских школ в обязательном порядке проходят государственную итоговую аттестацию в формате основного государственного экзамена – ОГЭ, Многие из этих тестов построены по принципу выбора правильных вариантов из нескольких предлагающихся. Если ответ вам неизвестен, остается только ставить галочку или крестик наугад. Но реально ли получить высокий балл, следуя такому методу решения?
Актуальность исследования — случай, случайность – с ними мы встречаемся повседневно. Кажется, как можно «предвидеть» наступление случайного события? Ведь оно может произойти, а может и не сбыться! Но математика нашла способы оценивать вероятность наступления случайных событий. Они позволяют человеку уверенно чувствовать себя при встрече со случайными событиями.
Кажется, как можно «предвидеть» наступление случайного события? Ведь оно может произойти, а может и не сбыться! Но математика нашла способы оценивать вероятность наступления случайных событий. Они позволяют человеку уверенно чувствовать себя при встрече со случайными событиями.
Гипотеза — вероятность угадать верные ответы на ОГЭ очень мала, а значит практически невозможно сдать экзамен без подготовки.
Объект исследования — теория вероятностей.
Предмет исследования — практическое применение теории вероятностей.
Цель исследовательской работы — выявление вероятности успешной сдачи экзамена обучающимися 9 классов путем угадывания правильного ответа, применяя теорию вероятностей.
История теории вероятностей
Теория вероятностей — раздел математики, изучающий случайность. Теория вероятностей используется в таких разделах математики как математическая статистика, теория случайных процессов, теория массового обслуживания.
Она находит применение в физике, в анализе азартных игр, в страховании и в расчете пенсионных схем. На теории вероятностей основана разработка, применение и анализ вероятностных алгоритмов.
Французский дворянин, некий господин де Мере, был азартным игроком в кости и страстно хотел разбогатеть. Он затратил много времени, чтобы открыть тайну игры в кости. Он выдумывал различные варианты игры, предполагая, что таким образом приобретет крупное состояние.
Паскаль не только сам заинтересовался этим, но и написал письмо известному математику П. Ферма, чем спровоцировал его заняться общими законами игры в кости и вероятностью выигрыша. Первые работы по теории вероятностей, принадлежащие французским учёным Б. Паскалю и П. Ферма и голландскому учёному X. Гюйгенсу.
Крупный успех теории вероятностей связан с именем швейцарского математика Я. Бернулли, установившего закон больших чисел для схемы независимых испытаний с двумя исходами.
Теория вероятностей
При изучении явлений, мы проводим эксперименты, в ходе которых происходят различные события, среди которых различают: достоверные, случайные, невозможные, равновероятные.
Событие U называют достоверным по отношению к некоторому испытанию, если в ходе этого испытания событие U обязательно произойдет. Например, достоверным будет появление одного из шести чисел 1, 2, 3, 4, 5, 6 при одном бросании игральной кости.
Событие называют случайным по отношению к некоторому испытанию, если в ходе этого испытания оно может произойти, а может и не произойти. Например, при однократном бросании игральной кости может выпасть число 1 или не выпасть, т.е. событие является случайным, потому что оно может произойти, а может и не произойти.
Равновероятные события – это события, которые при данных условиях имеют одинаковые шансы для наступления.
Вероятность события А обозначается буквой Р(А) формула записывается так: Р(А)=, где m ≤n Из формулы следует, что 0≤ Р(А)≤ 1.
Вероятностью Р(А) события А в испытании с равновозможными элементарными исходами называется отношение числа исходов m, благоприятствующих событию А, к числу исходов n всех исходов испытания – классическое определение вероятности
Классическое определение вероятности используется для выявления благоприятных исходов теоретическим путем.
Но встречаются случаи, когда без практики определить число благоприятных исходов невозможно.
Например, без многократного подбрасывания кнопки трудно определить, равновозможны ли ее падения на «на плоскость» или на «острие». В таких случаях используется статистическое определение вероятности.
Статистическая вероятность (частота, относительная частота) – это отношение числа испытаний, в которых событие появилось к общему числу фактически произведенных испытаний.
Формула Бернулли — это формула в теории вероятностей, позволяющая находить вероятность появления события A при независимых испытаниях.
Чтобы найти каковы шансы наступления события А в данной ситуации, необходимо:
- найти общее количество исходов этой ситуации;
- найти количество возможных исходов, при которых произойдёт событие А;
- найти, какую часть составляют возможные исходы от общего количества исходов.
ОГЭ как пример использования теории вероятностей жизни
Среди учеников часто возникает вопрос: «А нельзя ли выбрать наугад ответ и при этом получить положительную оценку за экзамен?»
Ответить на этот вопрос можно путем использования элементов теории вероятностей. Я хочу проверить это на примере предметов, наиболее предпочитаемого в нашем классе.
По данному предмету тест включает 20 заданий с выбором ответа из 4-х предложенных. Чтобы сдать экзамен, нужно набрать не менее 15 баллов. Каждое задание имеет 4 варианта ответов, один из которых правильный. Определить вероятность получения положительной оценки на экзамене можно по формуле Бернулли.
Был проведен опрос среди учеников 9 классов (16 человек):
Как вы считаете, можно сдать экзамен, отвечая на вопросы методом угадывания?
- 4 человека(25%) считают, что таким способом сдать экзамен можно.
- 12 человек(75%) считают, что нельзя.
Самые популярные предметы в нашем классе по сдаче – обществознание, биология и информатика. Мы попросили ребят попробовать наугад пройти тестовую часть экзаменационного варианта по биологии.
Для того чтобы получить оценку «3» необходимо набрать не менее 13 баллов.
Заключение
В результате опроса, выяснили, что большинство уверены — экзамен сдашь лишь при подготовке к нему.
В результате анкетирования, выяснили, что метод угадывания не позволяет набрать минимальный проходной балл.
Гипотеза подтвердилась. Только тщательная подготовка позволяет сдать экзамен.
Для написания данной работы были Использованы ресурсы Сети Интернет.
Если страница Вам понравилась, поделитесь в социальных сетях:
Теория вероятности подготовка к гиа. Теория вероятностей на огэ и егэ
События, которые происходят реально или в нашем воображении, можно разделить на 3 группы. Это достоверные события, которые обязательно произойдут, невозможные события и случайные события. Теория вероятностей изучает случайные события, т.е. события, которые могут произойти или не произойти. В данной статье будет представлена в кратком виде теория вероятности формулы и примеры решения задач по теории вероятности, которые будут в 4 задании ЕГЭ по математике (профильный уровень).
Зачем нужна теория вероятности
Исторически потребность исследования этих проблем возникла в XVII веке в связи с развитием и профессионализацией азартных игр и появлением казино. Это было реальное явление, которое требовало своего изучения и исследования.
Игра в карты, кости, рулетку создавала ситуации, когда могло произойти любое из конечного числа равновозможных событий. Возникла необходимость дать числовые оценки возможности наступления того или иного события.
Возникла необходимость дать числовые оценки возможности наступления того или иного события.
В XX веке выяснилось, что эта, казалось бы, легкомысленная наука играет важную роль в познании фундаментальных процессов, протекающих в микромире. Была создана современная теория вероятностей.
Основные понятия теории вероятности
Объектом изучения теории вероятностей являются события и их вероятности. Если событие является сложным, то его можно разбить на простые составляющие, вероятности которых найти несложно.
Суммой событий А и В называется событие С, заключающееся в том, что произошло либо событие А, либо событие В, либо события А и В одновременно.
Произведением событий А и В называется событие С, заключающееся в том, что произошло и событие А и событие В.
События А и В называется несовместными, если они не могут произойти одновременно.
Событие А называется невозможным, если оно не может произойти. Такое событие обозначается символом .

Событие А называется достоверным, если оно обязательно произойдет. Такое событие обозначается символом .
Пусть каждому событию А поставлено в соответствие число P{А). Это число P(А) называется вероятностью события А, если при таком соответствии выполнены следующие условия.
Важным частным случаем является ситуация, когда имеется равновероятных элементарных исходов, и произвольные из этих исходов образуют события А. В этом случае вероятность можно ввести по формуле . Вероятность, введенная таким образом, называется классической вероятностью. Можно доказать, что в этом случае свойства 1-4 выполнены.
Задачи по теории вероятностей, которые встречаются на ЕГЭ по математике, в основном связаны с классической вероятностью. Такие задачи могут быть очень простыми. Особенно простыми являются задачи по теории вероятностей в демонстрационных вариантах. Легко вычислить число благоприятных исходов , прямо в условии написано число всех исходов .
Ответ получаем по формуле .
Пример задачи из ЕГЭ по математике по определению вероятности
На столе лежат 20 пирожков — 5 с капустой, 7 с яблоками и 8 с рисом. Марина хочет взять пирожок. Какова вероятность, что она возьмет пирожок с рисом?
Решение.
Всего равновероятных элементарных исходов 20, то есть Марина может взять любой из 20 пирожков. Но нам нужно оценить вероятность того, что Марина возьмет пирожок с рисом, то есть , где А — это выбор пирожка с рисом. Значит у нас количество благоприятных исходов (выборов пирожков с рисом) всего 8. Тогда вероятность будет определяться по формуле:
Независимые, противоположные и произвольные события
Однако в открытом банке заданий стали встречаться и более сложные задания. Поэтому обратим внимание читателя и на другие вопросы, изучаемые в теории вероятностей.
События А и В называется независимыми, если вероятность каждого из них не зависит от того, произошло ли другое событие.
Событие B состоит в том, что событие А не произошло, т. е. событие B является противоположным к событию А. Вероятность противоположного события равна единице минус вероятность прямого события,т.е. .
е. событие B является противоположным к событию А. Вероятность противоположного события равна единице минус вероятность прямого события,т.е. .
Теоремы сложения и умножения вероятностей, формулы
Для произвольных событий А и В вероятность суммы этих событий равна сумме их вероятностей без вероятности их совместного события, т.е. .
Для независимых событий А и В вероятность произведения этих событий равна произведению их вероятностей, т.е. в этом случае .
Последние 2 утверждения называются теоремами сложения и умножения вероятностей.
Не всегда подсчет числа исходов является столь простым. В ряде случаев необходимо использовать формулы комбинаторики. При этом наиболее важным является подсчет числа событий, удовлетворяющих определенным условиям. Иногда такого рода подсчеты могут становиться самостоятельными заданиями.
Сколькими способами можно усадить 6 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому из этих вариантов соответствует 5 способов занять место второму ученику. Для третьего ученика остается 4 свободных места, для четвертого — 3, для пятого — 2, шестой займет единственное оставшееся место. Чтобы найти число всех вариантов, надо найти произведение , которое обозначается символом 6! и читается «шесть факториал».
Для третьего ученика остается 4 свободных места, для четвертого — 3, для пятого — 2, шестой займет единственное оставшееся место. Чтобы найти число всех вариантов, надо найти произведение , которое обозначается символом 6! и читается «шесть факториал».
В общем случае ответ на этот вопрос дает формула для числа перестановок из п элементов В нашем случае .
Рассмотрим теперь другой случай с нашими учениками. Сколькими способами можно усадить 2 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому из этих вариантов соответствует 5 способов занять место второму ученику. Чтобы найти число всех вариантов, надо найти произведение .
В общем случае ответ на этот вопрос дает формула для числа размещений из n элементов по k элементам
В нашем случае .
И последний случай из этой серии. Сколькими способами можно выбрать трех учеников из 6? Первого ученика можно выбрать 6 способами, второго — 5 способами, третьего — четырьмя. Но среди этих вариантов 6 раз встречается одна и та же тройка учеников. Чтобы найти число всех вариантов, надо вычислить величину: . В общем случае ответ на этот вопрос дает формула для числа сочетаний из элементов по элементам:
Чтобы найти число всех вариантов, надо вычислить величину: . В общем случае ответ на этот вопрос дает формула для числа сочетаний из элементов по элементам:
В нашем случае .
Примеры решения задач из ЕГЭ по математике на определение вероятности
Задача 1. Из сборника под ред. Ященко.
На тарелке 30 пирожков: 3 с мясом, 18 с капустой и 9 с вишней. Саша наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
.
Ответ: 0,3.
Задача 2. Из сборника под ред. Ященко.
В каждой партии из 1000 лампочек в среднем 20 бракованных. Найдите вероятность того, что наугад взятая лампочка из партии будет исправной.
Решение: Количество исправных лампочек 1000-20=980. Тогда вероятность того, что взятая наугад лампочка из партии будет исправной:
Ответ: 0,98.
Вероятность того, что на тестировании по математике учащийся У. верно решит больше 9 задач, равна 0,67. Вероятность того, что У. верно решит больше 8 задач, равна 0,73. Найдите вероятность того, что У. верно решит ровно 9 задач.
Найдите вероятность того, что У. верно решит ровно 9 задач.
Если мы вообразим числовую прямую и на ней отметим точки 8 и 9, то мы увидим, что условие «У. верно решит ровно 9 задач» входит в условие «У. верно решит больше 8 задач», но не относится к условию «У. верно решит больше 9 задач».
Однако, условие «У. верно решит больше 9 задач» содержится в условии «У. верно решит больше 8 задач». Таким образом, если мы обозначим события: «У. верно решит ровно 9 задач» — через А, «У. верно решит больше 8 задач» — через B, «У. верно решит больше 9 задач» через С. То решение будет выглядеть следующим образом:
Ответ: 0,06.
На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Тригонометрия», равна 0,2. Вероятность того, что это вопрос по теме «Внешние углы», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Давайте подумаем какие у нас даны события. Нам даны два несовместных события. То есть либо вопрос будет относиться к теме «Тригонометрия», либо к теме «Внешние углы». По теореме вероятности вероятность несовместных событий равна сумме вероятностей каждого события, мы должны найти сумму вероятностей этих событий, то есть:
Ответ: 0,35.
Помещение освещается фонарём с тремя лампами. Вероятность перегорания одной лампы в течение года равна 0,29. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Рассмотрим возможные события. У нас есть три лампочки, каждая из которых может перегореть или не перегореть независимо от любой другой лампочки. Это независимые события.
Тогда укажем варианты таких событий. Примем обозначения: — лампочка горит, — лампочка перегорела. И сразу рядом подсчитаем вероятность события. Например, вероятность события, в котором произошли три независимых события «лампочка перегорела», «лампочка горит», «лампочка горит»: , где вероятность события «лампочка горит» подсчитывается как вероятность события, противоположного событию «лампочка не горит», а именно: .
Заметим, что благоприятных нам несовместных событий всего 7. Вероятность таких событий равна сумме вероятностей каждого из событий: .
Ответ: 0,975608.
Еще одну задачку вы можете посмотреть на рисунке:
Таким образом, мы с вами поняли, что такое теория вероятности формулы и примеры решения задач по которой вам могут встретиться в варианте ЕГЭ.
В данной презентации представлены наиболее часто встречающиеся на экзамене задачи по теории вероятности. Задачи базового уровня. Презентация поможет и учителям на уроках обобщающего повторения, и учащимся при самостоятельной подготовке к экзамену.
Скачать:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
ТЕОРИЯ ВЕРОЯТНОСТЕЙ КЛЮЧЕВЫЕ ЗАДАЧИ Готовимся к ОГЭ
БРОСАНИЕ МОНЕТЫ
1. Монета брошена два раза. Какова вероятность выпадения одного «орла» и одной «решки»? Решение: При бросании одной монеты возможны два исхода – «орёл» или «решка». При бросании двух монет – 4 исхода (2*2=4): «орёл» — «решка» «решка» — «решка» «решка» — «орёл» «орёл» — «орёл» Один «орёл» и одна «решка» выпадут в двух случаях из четырёх. Р(А)=2:4=0,5. Ответ: 0,5.
При бросании двух монет – 4 исхода (2*2=4): «орёл» — «решка» «решка» — «решка» «решка» — «орёл» «орёл» — «орёл» Один «орёл» и одна «решка» выпадут в двух случаях из четырёх. Р(А)=2:4=0,5. Ответ: 0,5.
2. Монета брошена три раза. Какова вероятность выпадения двух «орлов» и одной «решки»? Решение: При бросании трёх монет возможны 8 исходов (2*2*2=8): «орёл» — «решка» — «решка» «решка» — «решка» — «решка» «решка» — «орёл» — «решка» «орёл» — «орёл» — «решка» «решка» — «решка» -«орёл» «решка» — «орёл» — «орёл» «орёл» — «решка» — «орёл» «орёл» — «орёл» — «орёл» Два «орла» и одна «решка» выпадут в трёх случаях из восьми. Р(А)=3:8=0,375. Ответ: 0,375.
3. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орел не выпадет ни разу. Решение: При бросании четырёх монет возможны 16 исходов: (2*2*2*2=16): Благоприятных исходов – 1 (выпадут четыре решки). Р(А)=1:16=0,0625. Ответ: 0,0625.
ИГРА В КОСТИ
4. Определите вероятность того, что при бросании кубика выпало больше трёх очков. Решение: Всего возможных исходов – 6. Числа большие 3 — 4, 5, 6 . Р(А)= 3:6=0,5. Ответ: 0,5.
Решение: Всего возможных исходов – 6. Числа большие 3 — 4, 5, 6 . Р(А)= 3:6=0,5. Ответ: 0,5.
5. Брошена игральная кость. Найдите вероятность того, что выпадет чётное число очков. Решение: Всего возможных исходов – 6. 1, 3, 5 — нечётные числа; 2, 4, 6 -чётные числа. Вероятность выпадения чётного числа очков равна 3:6=0,5. Ответ: 0,5.
6. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых. Решение: У данного действия — бросания двух игральных костей всего 36 возможных исходов, так как 6² = 36. Благоприятные исходы: 2 6 3 5 4 4 5 3 6 2 Вероятность выпадения восьми очков равна 5:36 ≈ 0,14. Ответ: 0,14.
7. Дважды бросают игральный кубик. В сумме выпало 6 очков. Найдите вероятность того, что при одном из бросков выпало 5 очков. Решение: Всего исходов выпадения 6 очков — 5: 2 и 4; 4 и 2; 3 и 3; 1 и 5; 5 и 1. Благоприятных исходов — 2. Р(А)=2:5=0,4. Ответ: 0,4.
8. На экзамене 50 билетов, Тимофей не выучил 5 из них. Найдите вероятность того, что ему попадется выученный билет. Решение: Тимофей выучил 45 билетов. Р(А)=45:50=0,9. Ответ: 0,9.
Найдите вероятность того, что ему попадется выученный билет. Решение: Тимофей выучил 45 билетов. Р(А)=45:50=0,9. Ответ: 0,9.
СОРЕВНОВАНИЯ
9. В чемпионате по гимнастике участвуют 20 спортсменов: 8 из России, 7 из США, остальные из Китая. Порядок выступления определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая. Решение: Всего исходов 20. Благоприятных исходов 20-(8+7)=5. Р(А)=5:20=0,25. Ответ: 0,25.
10. На соревнования по метанию ядра приехали 4 спортсмена из Франции, 5 из Англии и 3 из Италии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что спортсмен, выступающий пятым, будет из Италии. Решение: Число всех возможных исходов – 12 (4 + 5 + 3 = 12). Число благоприятных исходов – 3. Р(А)=3:12=0,25. Ответ: 0,25.
11. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 12 участников из России, в том числе Владимир Орлов. Найдите вероятность того, что в первом туре Владимир Орлов будет играть с каким-либо бадминтонистом из России? Решение: Всего исходов – 25 (Владимир Орлов с 25 бадминтонистами). Благоприятных исходов – (12-1)=11. Р(А)=11:25 = 0,44. Ответ: 0,44.
Найдите вероятность того, что в первом туре Владимир Орлов будет играть с каким-либо бадминтонистом из России? Решение: Всего исходов – 25 (Владимир Орлов с 25 бадминтонистами). Благоприятных исходов – (12-1)=11. Р(А)=11:25 = 0,44. Ответ: 0,44.
12. Конкурс исполнителей проводится в 5 дней. Всего заявлено 75 выступлений — по одному от каждой страны. В первый день 27 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса? Решение: Всего исходов – 75. Исполнители из России выступают на третий день. Благоприятных исходов – (75-27):4=12. Р(А)=12: 75 = 0,16. Ответ: 0,16 .
13. Коля выбирает двузначное число. Найдите вероятность того, что оно делится на 5. Решение: Двузначные числа: 10;11;12;…;99. Всего исходов – 90. Числа, делящиеся на 5: 10; 15; 20; 25; …; 90; 95. Благоприятных исходов – 18. Р(А)=18:90=0,2. Ответ: 0,2.
РАЗНЫЕ ЗАДАЧИ НА ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
14. Фабрика выпускает сумки. В среднем на 170 качественных сумок приходится шесть сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых. Решение: Всего исходов – 176. Благоприятных исходов – 170. Р(А)=170:176 ≈ 0,97. Ответ: 0,97.
Фабрика выпускает сумки. В среднем на 170 качественных сумок приходится шесть сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых. Решение: Всего исходов – 176. Благоприятных исходов – 170. Р(А)=170:176 ≈ 0,97. Ответ: 0,97.
15. В среднем из каждых 100 поступивших в продажу аккумуляторов 94 аккумулятора заряжены. Найдите вероятность того, что купленный аккумулятор не заряжен. Решение: Всего исходов – 100. Благоприятных исходов – 100-94=6. Р(А)=6:100=0,06. Ответ: 0,06.
ИСТОЧНИКИ http://mathgia.ru http:// www.schoolmathematics.ru
Легкие задания
На столе лежит 25 пирожков: 7 – с повидлом, 9 – с картошкой, остальные с капустой. Какова вероятность, что случайно выбранный пирожок окажется с капустой?
0,36
В такси работает 40 автомобилей: 14 – марки “Лада”, 8 – марки “Рено”, 2 – марки “Мерседес”, а остальные – марки “Шкода”. Какова вероятность того, что на Ваш вызов приедет “Мерседес”?
0,05
Определите вероятность того, что при бросании игрального кубика выпадет число не меньше трех.
Ира, Дима, Вася, Наташа и Андрей сдают норматив по бегу на 60 метров. Найдите вероятность того, что быстрее всех пробежит девочка?
Вероятность того, что телефон, купленный в подземном переходе окажется подделкой, составляет 0,83. Какова вероятность того, что купленный в переходе телефон окажется не подделкой?
0,17
В баскетбольном турнире принимает участие 20 команд, включая команду “Мужики”. Все команды разбивают на 4 группы: A, B, C, D. Какова вероятность того, что команда “Мужики” окажется в группе A?
0,25
В лотерейном мешке содержатся бочонки с номерами от 5 до 94 включительно. Какова вероятность, того, что извлеченный из мешка бочонок содержит двузначное число? Ответ округлите до сотых.
0,94
Перед экзаменом Игорь дотянул до последнего и успел выучить только 5 билетов из 80. Определите вероятность того, что ему попадется выученный билет.
0,0625
Аня включает радио и случайным образом выбирает радиоволну. Всего ее радиоприемник ловит 20 радиоволн и всего на 7 из них в данный момент играет музыка. Найдите вероятность того, что Аня попадет на музыкальную волну.
Всего ее радиоприемник ловит 20 радиоволн и всего на 7 из них в данный момент играет музыка. Найдите вероятность того, что Аня попадет на музыкальную волну.
0,35
В каждой двадцатой бутылке газировки под крышкой спрятан код с выигрышем. Определите вероятность того, что в купленной бутылке под крышкой окажется выигрышный код.
0,05
Задания посложнее
Какова вероятность, что случайно выбранное трехзначное число делится на 5?
0,2
Записан рост (в см) пяти учащихся: 166, 158, 132, 136, 170. На сколько отличается среднее арифметическое этого набора чисел от его медианы?
По статистическим данным одной небольшой страны известно, что вероятность того, что родившийся младенец окажется мальчиком, равна 0,507. В 2017 г. в этой стране на 1000 родившихся младенцев в среднем пришлось 486 девочек. Насколько частота рождения девочек в 2017 г. в этой стране отличается от вероятности этого события?
0,007
Игральную кость бросают дважды. Найдите вероятность того, что сумма двух выпавших чисел равна 3 или 7. Ответ округлите до сотых.
Найдите вероятность того, что сумма двух выпавших чисел равна 3 или 7. Ответ округлите до сотых.
0,22
Какова вероятность, что случайно выбранное трехзначное число делится на 2?
0,5
Найдите вероятность того, что при двух бросках монетки решка выпадет ровно 1 раз.
0,5
Игральную кость бросают дважды, найдите вероятность того, что оба раза выпадет число, не меньше трех. Ответ округлите до сотых.
0,31
По статистическим данным одной небольшой страны известно, что вероятность того, что родившийся младенец окажется мальчиком, равна 0,594. В 2017 г. в этой стране на 1000 родившихся младенцев в среднем пришлось 513 девочек. Насколько частота рождения девочек в 2017 г. в этой стране отличается от вероятности этого события?
0,107
Записан рост (в см) пяти учащихся: 184, 145, 176, 192, 174. На сколько отличается среднее арифметическое этого набора чисел от его медианы?
1,8
Средний рост жителей деревни “Великаны” составляет 194 см. Рост Николая Петровича составляет 195 см. Какое из следующих утверждений верно?
Рост Николая Петровича составляет 195 см. Какое из следующих утверждений верно?
1) Обязательно рост одного из жителей деревни равен 194 см.
2) Николай Петрович самый высокий житель деревни.
3) Обязательно найдется хоть один мужчина из этой деревни ниже Николая Петровича.
4) Обязательно найдется хоть один житель из этой деревни ниже Николая Петровича.
4
Сложные задания
Стрелок 4 раза стреляет из ружья по мишеням. Вероятность его точного попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что стрелок первые два раза попал в мишень, а последние два раза промахнулся.
0,0625
Вероятность того, что батарейка бракованная, равна 0,05. Покупатель в магазине выбирает случайную упаковку с двумя батарейками. Найдите вероятность того, что обе батарейки окажутся исправными.
0,9025
Стрелок стреляет по мишеням 5 раз подряд. Вероятность попадания в мишень при выстреле равна 0,7. Найдите вероятность того, что стрелок первые четыре раза попал в мишени, а последний раз промахнулся. Результат округлите до сотых.
Найдите вероятность того, что стрелок первые четыре раза попал в мишени, а последний раз промахнулся. Результат округлите до сотых.
Теория вероятностей
- Петя выбирает трехзначное число. Найдите вероятность того, что оно делится на 50.
- Петя выбирает трехзначное число. Найдите вероятность того, что оно делится на 11.
- На тарелке 10 пирожков: 2 с мясом, 6 с капустой и 2 с вишней. Петя наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
- На тарелке 30 пирожков: 3 с мясом, 18 с капустой и 9 с вишней. Вова наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
- В фирме такси в данный момент свободно 30 машин: 7 черных, 6 желтых и 17 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.
- В каждой десятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно.
 Петя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Петя не найдет приз в своей банке.
Петя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Петя не найдет приз в своей банке. - Игорь с папой решили покататься на колесе обозрения. Всего на колесе двадцать кабинок, из них 3 — синие, 14 — зеленые, остальные — красные. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Игорь прокатится в красной кабинке.
- Петя с папой решили покататься на колесе обозрения. Всего на колесе двенадцать кабинок, из них 3 — синие, 6 — зеленые, остальные — красные. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Петя прокатится в красной кабинке.
- У дедушки 10 чашек: 7 с красными цветами, остальные с синими. Дедушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
- У бабушки 20 чашек: 4 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.

- На экзамене 50 билетов. Петя не выучил 9 из них. Найдите вероятность того, что ему попадется выученный билет.
- На экзамене 50 билетов. Петя не выучил 1 из них. Найдите вероятность того, что ему попадется выученный билет.
- Родительский комитет закупил 10 пазлов для подарков детям на окончание года, из них 2 с машинами и 8 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Вове достанется пазл с машиной.
- Родительский комитет закупил 25 пазлов для подарков детям на окончание года, из них 22 с машинами и 3 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Диме достанется пазл с машиной.
- В среднем на 100 карманных фонариков приходится семь неисправных. Найдите вероятность купить работающий фонарик.
- В среднем на 75 карманных фонариков приходится семь неисправных. Найдите вероятность купить работающий фонарик.
- В среднем из каждых 100 поступивших в продажу аккумуляторов 91 аккумулятор заряжен.
 Найдите вероятность того, что купленный аккумулятор не заряжен.
Найдите вероятность того, что купленный аккумулятор не заряжен. - В среднем из каждых 80 поступивших в продажу аккумуляторов 68 аккумулятор заряжен. Найдите вероятность того, что купленный аккумулятор не заряжен.
- Саша наудачу выбирает двузначное число. Найдите вероятность того, что оно оканчивается на 6.
- Определите вероятность того, что при бросании кубика выпало нечетное число очков.
- Определите вероятность того, что при бросании кубика выпало 1.
- Одновременно бросают две симметричные монеты. Какова вероятность того, что выпадут орел и решка?
- Одновременно бросают три симметричные монеты. Какова вероятность того, что выпадут два орла и одна решка?
- В классе 21 учащийся, среди них два друга — Петя и Вася. На уроке физкультуры класс случайным образом разбивают на 7 равных групп. Найдите вероятность того, что Петя и Вася попали в одну группу.
- Перед началом футбольного матча судья бросают монетку, чтобы определить, какая из команд будет первой владеть мячом.
 Команда А должна сыграть три матча — с командой В, с командой С и с командой D. Найдите вероятность того, что во всех матчах владение мячом первыми будет принадлежать команде А.
Команда А должна сыграть три матча — с командой В, с командой С и с командой D. Найдите вероятность того, что во всех матчах владение мячом первыми будет принадлежать команде А. - В соревнованиях по толканию ядра участвуют 6 спортсменов из Греции, 4 спортсмена из Болгарии, 3 спортсмена из Румынии и 7 — из Венгрии. Порядок, в котором выступают спортсмены, определяются жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Венгрии.
- В соревнованиях по толканию ядра участвуют 4 спортсмена из Дании, 8 спортсменов из Швеции, 4 спортсмена из Румынии и 9 — из Венгрии. Порядок, в котором выступают спортсмены, определяются жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.
- В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 9 очков. Результат округлите до сотых.
- В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 10 очков.
 Результат округлите до сотых.
Результат округлите до сотых. - На экзамене по геометрии школьнику достается одна задача из сборника. Вероятность того, что эта задача на тему «Треугольники», равна 0,5. Вероятность того, что это окажется задача на тему «Окружность» равна 0,25. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.
- На экзамене по геометрии школьнику достается одна задача из сборника. Вероятность того, что эта задача на тему «Окружность», равна 0,45. Вероятность того, что это окажется задача на тему «Углы» равна 0,5. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.
- Стрелок четыре раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что стрелок первые 3 раза попал в мишени, а последний раз промахнулся.

- Стрелок три раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,7. Найдите вероятность того, что стрелок первый раз попал в мишени, а последние два раза промахнулся.
- Стрелок три раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,9. Найдите вероятность того, что стрелок попал в мишень два раза и один раз промахнулся.
- Стрелок три раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что стрелок попал в мишень два раза и один раз промахнулся.
- В девятом экономическом классе учатся 24 мальчика и 6 девочек. По жребию они выбирают одного дежурного по классу. Какова вероятность того, что это будет мальчик?
- В девятом математическом классе учатся 2 мальчика и 23 девочек. По жребию они выбирают одного дежурного по классу. Какова вероятность того, что это будет девочка?
- Вероятность того, что новый компьютер прослужит больше года, равна 0,98.
 Вероятность того, что он прослужит больше двух лет, равна 0,84. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Вероятность того, что он прослужит больше двух лет, равна 0,84. Найдите вероятность того, что он прослужит меньше двух лет, но больше года. - Вероятность того, что новый сканер прослужит больше года, равна 0,96. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
- Какова вероятность того, что случайно выбранное натуральное число от 25 до 39 делится на 5?
- Какова вероятность того, что случайно выбранное натуральное число от 15 до 36 делится на 2?
- На олимпиаде по химии участников рассаживают по трем аудиториям. В первых двух по 180 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчете выяснилось, что всего было 450 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
- На олимпиаде по математике участников рассаживают по трем аудиториям. В первых двух по 120 человек, оставшихся проводят в запасную аудиторию в другом корпусе.
 При подсчете выяснилось, что всего было 300 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
При подсчете выяснилось, что всего было 300 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории. - Вероятность того, что на тесте по физике Петя верно решит больше 11 задач, равна 0,65. Вероятность того, что он верно решит больше 10 задач, равна 0,71. Найдите вероятность того, что Петя верно решит ровно 11 задач.
- Вероятность того, что на тесте по математике Вася верно решит больше 12 задач, равна 0,7. Вероятность того, что он верно решит больше 11 задач, равна 0,79. Найдите вероятность того, что Вася верно решит ровно 12 задач.
- Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 22 пассажиров, равна 0,86. Вероятность того, что окажется меньше 9 пассажиров, равна 0,5. Найдите вероятность того, что число пассажиров будет от 9 до 21.
- Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 21 пассажира, равна 0,96.
 Вероятность того, что окажется меньше 11 пассажиров, равна 0,51. Найдите вероятность того, что число пассажиров будет от 11 до 20.
Вероятность того, что окажется меньше 11 пассажиров, равна 0,51. Найдите вероятность того, что число пассажиров будет от 11 до 20. - Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,05. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,03. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
- Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,03. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,97. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,05. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.

Решение задач по теории вероятностей в ходе подготовки к ОГЭ и ЕГЭ
Федяева Елена Николаевна, учитель математики
Белгородская область, Алексеевский район, с. Жуково
Помочь учащимся 9, 11 классов научиться решать задачи по теории вероятностей в ходе подготовки к ОГЭ и ЕГЭ, научить их группировать задачи по типам, систематизировать полученные на уроках знания по решению задач.
(справка о публикации находится на 2 листе в файле со свидетельством)
Решение задач по теории вероятностей в ходе подготовки к ЕГЭ
Единый государственный экзамен (ЕГЭ) призван заменить собой два экзамена выпускной за среднюю школу и вступительный в ВУЗы. В связи с этим в рамках ЕГЭ осуществляется проверка овладения материалом курса алгебры и начал анализа 10-11 классов, усвоение которого проверяется на выпускном экзамене за среднюю школу, а также материалом некоторых тем курсов алгебры основной школы и геометрии основной и средней школы, которые традиционно контролируются на вступительных экзаменах в ВУЗы. Одной из таких тем является тема «Теория вероятностей».
Одной из таких тем является тема «Теория вероятностей».
Решение задач занимает в математическом образовании огромное место. Умение решать задачи, является одним из основных показателей уровня математического развития, глубины освоения учебного материала. Умение жизненную ситуацию перевести на язык математики, на язык математических формул, моделировать реальные ситуации на языке теории вероятностей и есть качество усвоения материала.
Анализ результатов проведения ЕГЭ говорит о том, что решаемость задания, содержащего задачу по теории вероятностей, составляет в среднем около 80%. Такая ситуация позволяет сделать вывод о том, что большинство учащихся владеют техникой решения таких задач.
Уроки повторения по решению задач по теории вероятностей направлены на то, чтобы учащиеся расширили и углубили свои знания по математике, помогли школьникам систематизировать полученные на уроках ранее знания по решению задач, научили их группировать задачи по теории вероятностей, что существенно поможет им безошибочно решить задачу.
Задачи по теории вероятностей – не трудный материал для значительной части школьников. Но зачастую они не могут сделать первый шаг, чтобы определить к какому типу задач относится та или иная задача. Во многом это связано с тем, что учащиеся не могут определить характер событий и их отношение между собой.
Умение решать ту или иную задачу зависит от многих факторов. Однако, прежде всего необходимо научиться различать основные типы задач и уметь решать простейшие из них. Рассмотрим типовые задачи и их решения.
Предлагаемые задачи можно разбить на следующие типы задач:
— задачи на классическую вероятность;
— задачи на сложение вероятностей;
— задачи на умножение вероятностей;
— задачи на сложение и умножение вероятностей.
Задачи по теории вероятности, которые входят в ЕГЭ по математике — это несложные задачи. Большинство из них можно решить, зная всего лишь одну формулу, нужны лишь самые основные понятия теории вероятностей. Многие задания можно решить исходя из простых логических рассуждений.
Прежде чем приступить к решению задач по теории вероятностей необходимо четко классифицировать понятия и термины, встречающиеся в этих задачах:
— благоприятное событие – это событие, которое предпочтительно для исхода какого-либо испытания, события;
— равновозможное событие – это все события, которые обязательно произойдут в определенной ситуации;
— несовместные события – это события, которые не могут произойти одновременно, наступление одного из событий исключает наступление другого;
— независимые события – это события, которые могут произойти одновременно, наступление одного из которых не зависит он наступления другого.
Прочитав внимательно задачу, ученик должен четко понять, что происходит в задаче, найти основной вопрос задачи – найти вероятность того, что ……… . Записать это событие. Понять, к какому «типу» относится задача, т.е. это «простая» задача на нахождение классической вероятности, или задача на сложение вероятностей (происходят несовместные события и нас устраивает наступление хотя бы одного из этих событий), или задача на умножение вероятностей (происходят независимые события и нас устраивает наступление обоих событий одновременно).
Итак, вероятностью события называется отношение числа благоприятных для него исходов к числу всех равновозможных исходов.
Р(А) =
Примеры решения задач на классическую вероятность.
Пример 1. На чемпионате по прыжкам в воду выступают 40 спортсменов, среди них 3 прыгуна из Голландии и 6 прыгунов из Аргентины. Порядок выступлений определяется жеребьевкой. Найдите вероятность того, что тринадцатым будет выступать прыгун из Аргентины.
Решение: Благоприятное событие – прыгун из Аргентины, их 6.
Равновозможное событие – всего спортсменов, их 40.
Р(А) = = 0,15
Ответ: 0,15.
Пример 2. В среднем их 600 садовых насосов, поступивших в продажу, 3 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Решение: Благоприятное событие – насос не подтекает, их 597.
Равновозможное событие – всего насосов, их 600.
Р(А) = = 0,995
Ответ: 0,995.
Пример 3. Какова вероятность того, что последние три цифры телефонного номера случайного абонента совпадают?
Решение: Благоприятное событие – последние три цифры одинаковые (000, 111, 222, 333 ……. 999), их 10.
999), их 10.
Равновозможное событие – всего трехзначных чисел (000, 001, 002, 003 …….999), их 1000.
Р(А) = = 0,01
Ответ: 0,01.
Пример 4. В классе 16 учащихся, среди них два друга – Олег и Михаил. Класс случайным образом разбивают на 4 равные группы. Найдите вероятность того, что Олег и Михаил окажутся в одной группе.
Решение: Благоприятное событие – Олег один из трех, кто попал в группу к Михаилу, их 3.
Равновозможное событие – всего учащихся (Михаила не считаем), их 15.
Р(А) = = 0,2
Ответ: 0,2.
Примеры решение задач на сложение вероятностей
Пример 1. В группе туристов 12 человек. С помощью жребия они выбирают трех человек, которые должны идти в магазин за продуктами. Какова вероятность того, что турист Д., входящий в состав группы, пойдет в магазин.
Решение: Вероятность того, что турист Д. пойдет в магазин, равна . Он может быть либо первым, либо вторым, либо третьим членов группы, эти события несовместны, т.е. наступление одного из них исключает наступление другого.
Р(А) = + + = = 0,25
Ответ: 0,25.
Пример 2. В классе25 человек, среди них у четверых в году пятерки по математике, а у пятерых в году пятерки по биологии. При этом нет никого, у кого были бы пятерки по этим двум предметам. Найдите вероятность того, что случайно выбранный ученик класса имеет пятерку по одному из этих предметов.
Решение: Вероятность того, что выберем ученика с пятеркой по математике, равна , а вероятность того, что выберем ученика с пятеркой по биологии, равна . Эти события несовместны, так как нет учеников, у кого были бы пятерки по этим двум предметам.
Р(А) = + = = 0,36
Ответ: 0,36.
Пример 3. Гигрометр измеряет влажность в помещении картинной галереи. Вероятность того, что влажность окажется выше 40%, равна 0, 82. Вероятность того, что влажность окажется ниже 56%, равна 0,74. Найдите вероятность того, что влажность находится в пределах от 40% до 56%.
Решение: Событие А: вероятность того, что влажность окажется ниже 40%, равна 1 – 0,82 = 0,18.
Событие В: вероятность того, что влажность окажется выше 40%, но ниже 56% равна 0,74 – 0,18 = 0,56
Ответ: 0,56.
Пример 4. В роддоме измеряют вес новорожденного. Вероятность того, что вес окажется больше 3 кг, равна 0,87, вероятность того, что вес окажется меньше 3 кг 600 г, равна 0,93. Найдите вероятность того, что вес случайно выбранного новорожденного окажется в пределах от 3 кг до 3 кг 600 г.
Решение: Событие А: вес новорожденного меньше 3 кг. – 1 – 0,87 = 0,13.
Событие В: вес новорожденного больше 3 кг, но меньше 3 кг 600 г. – 0,93 – 0,13 = 0,8
Ответ: 0,8.
Пример 5. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 18 пассажиров, равна 0, 95. Вероятность того, что окажется меньше 12 пассажиров, равна 0,6. Найдите вероятность того, что число пассажиров будет от 12 до 17.
Решение. Событие А: пассажиров окажется больше 12 но меньше 18 – 0,95 – 0,6 = 0,35
Ответ: 0,35.
Примеры решения задач на умножение вероятностей.
Пример 1. По отзывам покупателей Петр Петрович оценил надежность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,8. Вероятность того, что нужный товар доставят из магазина Б, равна 0,95. Петр Петрович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что оба магазина доставят товар.
Решение: Событие А – это вероятность доставки товара из магазина А. Событие Б – это вероятность доставки товара из магазина Б. Эти события независимые, то есть наступление одного из них не зависит от наступления другого и они должны произойти одновременно.
Р(А) · Р(Б) = 0,8 · 0,95 = 0,76
Ответ: 0,76.
Пример 2. На уроке физкультуры 26 школьников, из них 12 девочек и, остальные мальчики. По сигналу учителя физкультуры все быстро выстраиваются в одну шеренгу в случайном порядке. Найдите вероятность того, что справа в шеренге первые двое окажутся мальчики.
Решение: Событие А – вероятность того, что первым окажется мальчик, равна . Событие В – вероятность того, что и вторым окажется мальчик, равна . Эти события независимые и они должны произойти одновременно.
Р(А) · Р(В) = · = = 0,28
Ответ: 0,28.
Пример 3. Стрелок в тире стреляет по мишени до тех пор, пока не попадет в нее. Вероятность попадания при каждом отдельном выстреле равна 0,6. Найдите вероятность того, что стрелку потребуется ровно три попытки.
Решение: Событие А – попадание по мишени, равно 0,6. Событие В – промах по мишени, равно 0,4. Вероятность попадания или промаха при первом выстреле не зависит от попадания или промаха при втором выстреле. Но события В (промах), В (промах) и А (попадание) должны произойти одновременно.
Р(В) · Р(В) · Р(А) = 0,4 · 0,4 · 0,6 = 0,096.
Ответ: 0,096.
Пример 4. За круглый стол на 21 стул в случайном порядке рассаживаются 19 мальчиков и 2 девочки. Найдите вероятность того, что девочки не окажутся на соседних местах.
Решение: Для того, чтобы девочки не оказались на соседних местах необходимо, чтобы справа и слева от них находились мальчики. Событие А – вероятность того, что справа окажется мальчик, равна . Событие В – вероятность того, что слева окажется мальчик, равна . Эти события независимые и должны произойти одновременно.
Р(А) · Р(В) = · = 0,9
Ответ: 0,9.
Пример 5. Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало не менее четырех очков.
Решение: Событие А – вероятность выпадения не менее 4 очков (т.е. 4, 5, 6) при первом броске, равно = 0,5. Событие В – вероятность выпадения не менее 4 очков при втором броске, равна 0,5. Эти события независимые и должны произойти одновременно.
Р(А) · Р(В) = 0,5 · 0,5 = 0,25.
Ответ: 0,25.
Примеры решения задач на сложение и умножение вероятностей.
Пример 1. Из ящика, в котором лежат фломастеры, не глядя достали два фломастера. Найдите вероятность того, что эти фломастеры оказались одного цвета, если известно, что в ящике 12 синих и 13 красных фломастеров.
Решение: Найдем вероятность того, что из ящика достанут синий фломастер: Р(С) = Р(А) · Р(В) = · =
Теперь найдем вероятность того, что из ящика достанут красный фломастер: Р(D) = Р(А) · Р(В) = · =
Эти два события несовместные и нас устраивает наступление хотя бы одного из этих событий Р(С) + Р(D) = + = = 0,48
Ответ: 0,48.
Пример 2. Ковбой Джон попадает в муху на стене с вероятностью 0,8, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,3. На столе лежат 10 револьверов, из них только три пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнется.
Решение: Вероятность промаха из пристрелянного револьвера равна 1 – 0,8 = 0,2. Вероятность промаха из непристрелянного револьвера равна 1 – 0,3 = 0,7. Сначала найдем вероятность того, что Джон схватил пристрелянный револьвер (их 3) и промахнулся: Р(А) = 0,3 0,2 = 0,06.
Теперь найдем вероятность того, что Джон схватил непристрелянный револьвер и промахнулся: Р(В) = 0,7 0,7 = 0,49.
Эти два события несовместные и нас устраивает наступление хотя бы одного из этих событий Р(А) + Р(В) = 0,06 + 0,49 = 0,55.
Ответ: 0,55.
Пример 3. На складе на одном стеллаже лежат в случайном порядке 50 запакованных клавиатур: 30 черных, 10 белых и 10 серых. На другом стеллаже лежат в случайном порядке 50 запакованных мышей: 30 черных, 10 белых и 10 серых. Найдите вероятность того, что случайно выбранная клавиатура и мышь будут одинакового цвета.
Решение: Вероятность того, что клавиатура и мышь будут черного цвета равна Р (А) = · = .
Вероятность того, что клавиатура и мышь будут белого цвета равна Р (В) = · = .
Вероятность того, что клавиатура и мышь будут серого цвета равна Р (С) = · = .
Эти три события несовместные и нас устраивает наступление хотя бы одного из этих событий Р(А) + Р(В) + Р(С)= + + = = 0,44.
Ответ: 0,44.
Пример 4. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 30% этих стекол, вторая – 70%. Первая фабрика выпускает 3% бракованных стекол, а вторая – 4%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Решение: Вероятность того, что попадется бракованное стекло из первой фабрики равна Р(А) = 0,3 · 0,03 = 0,009.
Вероятность того, что попадется бракованное стекло со второй фабрики равна Р(В) = 0,7 · 0,04 = 0,028.
Эти два события несовместные и нас устраивает наступление хотя бы одного из этих событий Р(А) + Р(В) = 0,009 + 0,028 = 0,037.
Ответ: 0,037.
Теория вероятностей. Задания к ОГЭ
Источник задания: Решение 3353.-20. ОГЭ 2016 Математика, И.В. Ященко. 36 вариантов.
Задание 18. На диаграмме показано распределение населения Австрии по возрасту. Определите по диаграмме, населения какого возраста составляет более 40% от общей численности населения.
1) 0-14 лет; 2) 15-50 лет; 3) 51-64 года; 4) 65 лет и старше
Раствор.
Более 40% — это почти больше половины населения.На рисунке видно, что это соответствует наибольшему сегменту с возрастом от 15 до 50 лет.
Ответ: 2.
Задание 19. В среднем из 150 фонарей в продаже шесть неисправны. Найдите вероятность того, что фонарь, выбранный вами наугад в магазине, будет исправно работать.
Раствор.
Обозначим событием А выбор работающего фонарика. Количество благоприятных исходов для события А равно 150-6=144 (среднее количество работающих фонариков).Всего существует 150 возможных исходов, поэтому
.
Ответ: 0,96.
Задание 20. На «Роднике» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле С = 6000 + 4100n, где n — количество колец, установленных в колодце. Используя эту формулу, рассчитайте стоимость колодца с 8 кольцами. Укажите ответ в рублях.
Раствор.
Находим стоимость скважины по адресу, используя формулу расчета стоимости С, получаем.
Теория вероятностей
- Петя выбирает трехзначное число. Найдите вероятность того, что оно делится на 50.
- Петя выбирает трехзначное число. Найдите вероятность того, что оно делится на 11.
- На тарелке 10 пирогов: 2 с мясом, 6 с капустой и 2 с вишней. Петя выбирает наугад один пирог. Найдите вероятность того, что у него останется вишенка.
- На тарелке 30 пирогов: 3 с мясом, 18 с капустой и 9 с вишней.Вова выбирает один пирог наугад. Найдите вероятность того, что у него останется вишенка.
- В настоящее время у компании такси есть 30 бесплатных автомобилей: 7 черных, 6 желтых и 17 зеленых. На вызов выехала одна из машин, оказавшаяся ближайшей к заказчику. Найти вероятность того, что к нему подъедет желтое такси.
- По условиям акции в каждой десятой банке кофе есть приз. Призы распределяются между банками случайным образом.
 Петя покупает банку кофе в надежде выиграть приз.Найдите вероятность того, что Петя не найдет выигрыш в своем банке.
Петя покупает банку кофе в надежде выиграть приз.Найдите вероятность того, что Петя не найдет выигрыш в своем банке. - Игорь с папой решили покататься на колесе обозрения. Всего на колесе двадцать кабин, из них 3 синих, 14 зеленых, а остальные красные. Каюты по очереди подходят к посадочной платформе. Найдите вероятность того, что Игорь поедет в красной будке.
- Петя с папой решили покататься на колесе обозрения. Всего на колесе двенадцать кабин, из них 3 синих, 6 зеленых, а остальные красные.Каюты по очереди подходят к посадочной платформе. Найти вероятность того, что Петя поедет в красной будке.
- У дедушки 10 чашек: 7 с красными цветами, остальные с синими. Дедушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с голубым цветком.
- У бабушки 20 чашек: 4 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с голубым цветком.

- На экзамене 50 билетов.Петя не выучил 9 из них. Найдите вероятность того, что ему попадется выученный билет.
- На экзамене 50 билетов. Петя не выучил 1 из них. Найдите вероятность того, что ему попадется выученный билет.
- Родительский комитет закупил 10 пазлов для подарков детям на конец года, из них 2 с машинками и 8 с видами города. Подарки распределяются случайным образом. Найдите вероятность того, что Вова получит машинку.
- Родительский комитет закупил 25 пазлов для подарков детям на конец года, в том числе 22 с машинками и 3 с видами города.Подарки распределяются случайным образом. Найдите вероятность того, что Дима получит машинку.
- В среднем на каждые 100 фонарей приходится семь неисправных фонарей. Найдите возможность купить рабочий фонарик.
- В среднем на 75 фонарей приходится семь бракованных фонарей. Найдите возможность купить рабочий фонарик.
- В среднем из каждых 100 проданных аккумуляторов 91 заряжен.
 Найдите вероятность того, что купленный вами аккумулятор не заряжен.
Найдите вероятность того, что купленный вами аккумулятор не заряжен. - В среднем из каждых 80 проданных аккумуляторов 68 аккумуляторов заряжены.Найдите вероятность того, что купленный вами аккумулятор не заряжен.
- Саша случайным образом выбирает двузначное число. Найдите вероятность того, что оно оканчивается на 6.
- Определите вероятность того, что при броске кубика выпадет нечетное количество очков.
- Определите вероятность того, что при броске кубика выпадет 1.
- Одновременно подбрасываются две симметричные монеты. Какова вероятность того, что выпадут орел и решка?
- Одновременно подбрасываются три симметричные монеты.Какова вероятность того, что выпадут два орла и одна решка?
- В классе 21 ученик, среди них двое друзей — Петя и Вася. На уроке физкультуры класс случайным образом делится на 7 равных групп. Найти вероятность того, что Петя и Вася находятся в одной группе.
- Перед началом футбольного матча судья подбрасывает монету, чтобы определить, какая команда будет первой владеть мячом.
 Команда А должна сыграть три матча — команда Б, команда С и команда D.Найти вероятность того, что команда А будет первой владеть мячом во всех матчах.
Команда А должна сыграть три матча — команда Б, команда С и команда D.Найти вероятность того, что команда А будет первой владеть мячом во всех матчах. - В соревнованиях по толканию ядра участвуют 6 спортсменов из Греции, 4 спортсмена из Болгарии, 3 спортсмена из Румынии и 7 из Венгрии. Порядок, в котором соревнуются спортсмены, определяется жребием. Найдите вероятность того, что последний конкурент из Венгрии.
- В соревнованиях по толканию ядра участвуют 4 спортсмена из Дании, 8 спортсменов из Швеции, 4 спортсмена из Румынии и 9 из Венгрии. Порядок, в котором соревнуются спортсмены, определяется жребием.Найдите вероятность того, что последний конкурент из Швеции.
- В случайном эксперименте бросают два игральных кубика. Найдите вероятность того, что в сумме будет 9 очков. Округлите результат до сотых.
- В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме будет 10 очков. Округлите результат до сотых.
- На экзамене по геометрии студент получает одну задачу из сборника.
 Вероятность того, что эта задача касается треугольников, равна 0.5. Вероятность того, что это окажется задачей по теме «Круг», равна 0,25. В сборнике нет задач, одновременно относящихся к этим двум темам. Найдите вероятность того, что студент получит на экзамене задачу по одной из этих двух тем.
Вероятность того, что эта задача касается треугольников, равна 0.5. Вероятность того, что это окажется задачей по теме «Круг», равна 0,25. В сборнике нет задач, одновременно относящихся к этим двум темам. Найдите вероятность того, что студент получит на экзамене задачу по одной из этих двух тем. - На экзамене по геометрии студент получает одну задачу из сборника. Вероятность того, что эта задача связана с Кругом, равна 0,45. Вероятность того, что это окажется проблемой по теме «Углы», равна 0.5. В сборнике нет задач, одновременно относящихся к этим двум темам. Найдите вероятность того, что студент получит на экзамене задачу по одной из этих двух тем.
- Стрелок четыре раза стреляет по мишеням. Вероятность поражения цели одним выстрелом равна 0,5. Найти вероятность того, что стрелок первые 3 раза попадет в мишень, а в последний раз промахнется.
- Стрелок трижды стреляет по мишеням. Вероятность поражения цели одним выстрелом равна 0.7. Найти вероятность того, что стрелок с первого раза попадет в мишень, а два последних промахнется.

- Стрелок трижды стреляет по мишеням. Вероятность поражения цели одним выстрелом равна 0,9. Найти вероятность того, что стрелок дважды попадет в цель и один раз промахнется.
- Стрелок трижды стреляет по мишеням. Вероятность поражения цели одним выстрелом равна 0,5. Найти вероятность того, что стрелок дважды попадет в цель и один раз промахнется.
- В девятом экономическом классе учатся 24 мальчика и 6 девочек.Они выбирают одного дежурного по жребию. Какова вероятность, что это будет мальчик?
- В девятом математическом классе 2 мальчика и 23 девочки. Они выбирают одного дежурного по жребию. Какова вероятность, что это будет девочка?
- Вероятность того, что новый компьютер прослужит больше года, равна 0,98. Вероятность того, что он продлится более двух лет, равна 0,84. Найти вероятность того, что он прослужит менее двух лет, но более года.
- Вероятность того, что новый сканер прослужит больше года, равна 0.96. Вероятность того, что он продлится более двух лет, равна 0,87.
 Найти вероятность того, что он прослужит менее двух лет, но более года.
Найти вероятность того, что он прослужит менее двух лет, но более года. - Какова вероятность того, что случайно выбранное натуральное число от 25 до 39 делится на 5?
- Какова вероятность того, что случайно выбранное натуральное число от 15 до 36 делится на 2?
- На Олимпиаде по химии участники рассаживаются в трех залах. В первых двух по 180 человек, остальных отводят в запасной класс в другом корпусе.При подсчете оказалось, что всего было 450 участников. Найти вероятность того, что случайно выбранный участник написал олимпиаду в альтернативном классе.
- На Олимпиаде по математике участники рассаживаются в трех аудиториях. В первых двух по 120 человек, остальных отводят в запасной класс в другом корпусе. При подсчете оказалось, что всего было 300 участников. Найти вероятность того, что случайно выбранный участник написал олимпиаду в альтернативном классе.
- Вероятность того, что Петя правильно решит более 11 задач на контрольной по физике, равна 0,65.
 Вероятность того, что он правильно решит более 10 задач, равна 0,71. Найти вероятность того, что Петя правильно решит ровно 11 задач.
Вероятность того, что он правильно решит более 10 задач, равна 0,71. Найти вероятность того, что Петя правильно решит ровно 11 задач. - Вероятность того, что Вася правильно решит более 12 задач на контрольной по математике, равна 0,7. Вероятность того, что он правильно решит более 11 задач, равна 0,79. Найти вероятность того, что Вася правильно решит ровно 12 задач.
- Ежедневно ходит автобус из районного центра в пос. Вероятность того, что в понедельник в автобусе будет меньше 22 пассажиров, равна 0,86. Вероятность того, что пассажиров будет меньше 9, равна 0,5. Найти вероятность того, что пассажиров будет от 9 до 21.
- Ежедневно ходит автобус из районного центра в пос. Вероятность того, что в понедельник в автобусе будет меньше 21 пассажира, равна 0,96. Вероятность того, что пассажиров будет меньше 11, равна 0.51. Найдите вероятность того, что пассажиров будет от 11 до 20.
- Автоматическая линия по производству аккумуляторов. Вероятность того, что готовая батарея бракованная, равна 0,05.
 Перед упаковкой каждая батарея проходит систему контроля. Вероятность того, что система отклонит неисправный аккумулятор, равна 0,99. Вероятность того, что система ошибочно отклонит исправную батарею, равна 0,03. Найти вероятность того, что случайно выбранная изготовленная батарея будет забракована системой управления.
Перед упаковкой каждая батарея проходит систему контроля. Вероятность того, что система отклонит неисправный аккумулятор, равна 0,99. Вероятность того, что система ошибочно отклонит исправную батарею, равна 0,03. Найти вероятность того, что случайно выбранная изготовленная батарея будет забракована системой управления. - Автоматическая линия по производству аккумуляторов. Вероятность того, что готовая батарея бракованная, равна 0,03. Перед упаковкой каждая батарея проходит систему контроля. Вероятность того, что система отклонит неисправную батарею, равна 0,97. Вероятность того, что система ошибочно отклонит исправную батарею, равна 0,05. Найти вероятность того, что случайно выбранная изготовленная батарея будет забракована системой управления.
В среднем из 75 продаваемых карманных фонариков 15 неисправны.вероятность того, что фонарик, выбранный случайным образом в магазине, будет исправлена
Ответы:
15/75 = 1/5 — без поправки 1-1/5 = 4/5 = 0,8 Ответ: 0,8
Похожие вопросы
-
здесь 4-е предложение.
 1 практически все присутствует в классе. 2 сказка была почти готова, осталось только придумать название 3 к этому времени Бетховен практически потерял слух 4 проверить его теорию практически невозможно в какой из них слово можно практически понимать в двух разных значениях .а) 1 б) 2. в 3. г) 4. д) в любом
1 практически все присутствует в классе. 2 сказка была почти готова, осталось только придумать название 3 к этому времени Бетховен практически потерял слух 4 проверить его теорию практически невозможно в какой из них слово можно практически понимать в двух разных значениях .а) 1 б) 2. в 3. г) 4. д) в любом - Дополните предложения словами: прочь, из, с, назад, вверх, к, на, в, из. 1. Что ты смеешься…? Что такого смешного? 2. …мой большой сюрприз, что детям не понравился мой рассказ. 3. Мне больше не нужны твои фломастеры, я могу дать их… тебе сейчас. 4. Комната была полна (?) шума и счастливого смеха. 5. Пришлось отдать маленького котенка. ..потому что мы не могли за ним присматривать. 6. Мужчина стоял… спиной ко мне? поэтому я не мог видеть его лица.7. Лизе пришлось отдать… танцы, когда ей исполнилось 16. 8. В некоторых культурах женщины носят своих детей… на спине. 9. Я дала картинки… и попросила детей найти в них ошибки.
На тарелке 4 пирога с мясом.
 На тарелке есть похожие на вид пирожки.
На тарелке есть похожие на вид пирожки.
Разберем на этой странице ряд задач теории вероятностей о пирогах.
Задача 0D5CDD из открытого банка заданий ОГЭ по теории вероятностей
Проблема №1 (номер проблемы на фипи.ru — 0D5CDD) … На тарелке одинаковые на вид пирожки: 4 с мясом, 8 с капустой и 3 с вишней. Петя наугад берет один пирог. Найдите вероятность того, что пирог вишневый.
Решение:
Ответ : Вероятность того, что пирог, который Петя возьмет наугад, будет с вишенкой, равна 0,2.
Задача 8ДЭДЭД из открытого банка заданий ОГЭ по теории вероятностей
Задача №2 (номер задачи на fipi.ru — 8DEDED) … На тарелке одинаковые пирожки: 3 с капустой, 8 с рисом и 1 с луком и яйцом. Игорь берет один пирог наугад. Найти вероятность того, что пирог капустный.
Решение:
Вероятность – это отношение благоприятных исходов ко всем возможным исходам, т.е.
Ответ : вероятность того, что пирог, который Игорь возьмет наугад, будет с капустой, равна 0,25.
Задача 6Д48ДЭ из открытого банка заданий ОГЭ по теории вероятностей
Проблема №3 (номер проблемы на фипи.ru — 6D48DE) … На тарелке одинаковые на вид пирожки: 1 с творогом, 12 с мясом и 3 с яблоками. Ваня берет один пирог наугад. Найдите вероятность того, что пирог будет мясным.
Решение:
Вероятность – это отношение благоприятных исходов ко всем возможным исходам, т.е.
Ответ : Вероятность того, что пирог, который Ваня возьмет наугад, будет с мясом, равна 0,75.
Задача 9ДА329 из открытого банка заданий ОГЭ по теории вероятностей
Проблема №4 (номер проблемы на фипи.ru — 9DA329) … На тарелке одинаковые на вид пирожки: 4 с мясом, 5 с рисом и 21 с вареньем. Андрей наугад берет один пирог. Найдите вероятность того, что пирог окажется джемом.
Решение:
Вероятность – это отношение благоприятных исходов ко всем возможным исходам, т.е.
Ответ : вероятность того, что пирог, который Андрей возьмет наугад, будет с джемом, равна 0,7.
Задача 243Д55 из открытого банка заданий ОГЭ по теории вероятностей
Проблема №5 (номер проблемы на фипи.ru — 243D55) … На тарелке одинаковые на вид пирожки: 3 с мясом, 3 с капустой и 4 с вишней. Саша берет один пирог наугад. Найдите вероятность того, что пирог вишневый.
Решение:
Вероятность – это отношение благоприятных исходов ко всем возможным исходам, т.е.
Ответ : Вероятность того, что пирог, который Саша возьмет наугад, будет с вишенкой, равна 0,4.
Задача 3ABDC9 из открытого банка заданий ОГЭ по теории вероятностей
Проблема №6 (номер проблемы на фипи.ru — 3ABDC9) … На тарелке одинаковые на вид пирожки: 4 с мясом, 5 с капустой и 6 с вишней. Дима берет один пирог наугад. Найдите вероятность того, что пирог вишневый.
Решение:
Вероятность – это отношение благоприятных исходов ко всем возможным исходам, т.е.
Ответ : вероятность того, что пирог, который Дима выберет наугад, окажется с вишенкой, равна 0,4.
Задача 9Э9А54 из открытого банка заданий ОГЭ по теории вероятностей
Проблема №7 (номер проблемы на фипи.ru — 9E9A54) … На тарелке одинаковые на вид пирожки: 2 с мясом, 16 с капустой и 2 с вишней. Рома берет один пирог наугад. Найдите вероятность того, что пирог вишневый.
Решение:
Вероятность – это отношение благоприятных исходов ко всем возможным исходам, т.е.
Ответ : Вероятность того, что случайно выбранный Рома пирог будет с вишней, равна 0,1.
Задача Э2ЭД26 из открытого банка заданий ОГЭ по теории вероятностей
Проблема №8 (номер проблемы на фипи.ru — E2ED26 … На тарелке одинаковые на вид пирожки: 5 с мясом, 2 с капустой и 3 с вишней. Андрей наугад берет один пирог. Найдите вероятность того, что пирог вишневый.
Решение:
Вероятность – это отношение благоприятных исходов ко всем возможным исходам, т.е.
Ответ : вероятность того, что пирог, который Андрей возьмет наугад, будет с вишенкой, равна 0,3.
Задача 6ББФА6 из открытого банка заданий ОГЭ по теории вероятностей
Проблема №9 (номер проблемы на фипи.ru — 6BBFA6 … На тарелке одинаковые на вид пирожки: 3 с мясом, 24 с капустой и 3 с вишней. Лёша берёт наугад один пирожок. Найдите вероятность того, что пирог вишневый.
Решение:
Вероятность – это отношение благоприятных исходов ко всем возможным исходам, т.е.
Ответ : вероятность того, что пирог, который Лёша возьмет наугад, будет с вишенкой равна 0,1.
Задача 568В55 из открытого банка заданий ОГЭ по теории вероятностей
Проблема №10 (номер проблемы на фипи.ru — 568B55 … На тарелке одинаковые на вид пирожки: 7 с мясом, 17 с капустой и 6 с вишней. Женя берет наугад один пирожок. Найдите вероятность того, что пирог вишневый.
Решение:
Вероятность – это отношение благоприятных исходов ко всем возможным исходам, т.е.
Ответ : Вероятность того, что пирог, который Женя возьмет наугад, будет с вишенкой, равна 0,2.
Задача DD36D0 из открытого банка заданий ОГЭ по теории вероятностей
Проблема №11 (номер проблемы на фипи.ru — DD36D0 … На тарелке одинаковые на вид пирожки: 1 с мясом, 8 с капустой и 3 с вишней. Илья берет один пирог наугад. Найдите вероятность того, что пирог вишневый.
Решение:
Вероятность – это отношение благоприятных исходов ко всем возможным исходам, т.е.
Ответ : Вероятность того, что случайно выбранный Ильей пирог будет с вишней, равна 0,25.
Задача 8CC3AD из открытого банка заданий ОГЭ по теории вероятностей
Проблема №12 (номер проблемы на фипи.ru — 8CC3AD … На тарелке одинаковые на вид пирожки: 2 с мясом, 4 с капустой и 4 с вишней. Илья берет один пирог наугад. Найдите вероятность того, что пирог вишневый.
Решение:
Вероятность – это отношение благоприятных исходов ко всем возможным исходам, т.е.
Ответ : Вероятность того, что случайно выбранный Ильей пирог будет с вишней, равна 0,4.
Задача А639А5 из открытого банка заданий ОГЭ по теории вероятностей
Проблема №13 (номер проблемы на фипи.ru — A639A5 … На тарелке одинаковые на вид пирожки: 4 с мясом, 10 с капустой и 6 с вишней. Жора берет наугад один пирог. Найдите вероятность того, что пирог вишневый.
Решение:
Вероятность – это отношение благоприятных исходов ко всем возможным исходам, т.е.
Ответ : Вероятность того, что пирог, который Жора возьмет наугад, будет с вишенкой равна 0,3.
Задача 642CD4 из открытого банка заданий ОГЭ по теории вероятностей
Проблема №14 (номер проблемы на фипи.ru — 642CD4 … На тарелке одинаковые на вид пирожки: 2 с мясом, 7 с капустой и 6 с вишней. Максим наугад берет один пирог. Найдите вероятность того, что пирог вишневый.
Решение:
Вероятность – это отношение благоприятных исходов ко всем возможным исходам, т.е.
Ответ : вероятность того, что пирог, который Максим возьмет наугад, будет с вишенкой.
Задача Э6Д232 из открытого банка заданий ОГЭ по теории вероятностей
Проблема №15 (номер проблемы на фипи.ru — E6D232 … На тарелке одинаковые на вид пирожки: 13 с мясом, 11 с капустой и 6 с вишней. Антон берет один пирог наугад. Найдите вероятность того, что пирог вишневый.
Решение:
Вероятность – это отношение благоприятных исходов ко всем возможным исходам, т.е.
Ответ : Вероятность того, что пирог, который Антон возьмет наугад, будет с вишенкой, равна 0,2.
Задача 9Ф84БФ из открытого банка заданий ОГЭ по теории вероятностей
Проблема №16 (номер проблемы на фипи.ru — 9F84BF … На тарелке одинаковые на вид пирожки: 2 с мясом, 13 с капустой и 5 с вишней. Лёша берёт наугад один пирожок. Найдите вероятность того, что пирог вишневый.
Решение:
Вероятность – это отношение благоприятных исходов ко всем возможным исходам, т.е.
Ответ : Вероятность того, что пирог, который Лёша возьмет наугад, будет с вишенкой, равна 0,25.
У вас похожая проблема, но в разобранном не нашли? Напишите номер своей проблемы в открытый банк задач и мы добавим ее решение.
Источник задания: Решение 2653.-20. ОГЭ 2017 Математика, И.В. Ященко. 36 вариантов.
Задание 18. На диаграмме показано содержание питательных веществ в твороге. Определите по диаграмме, содержание каких веществ наименьшее.
* Другие включают воду, витамины и минералы.
1) белки; 2) жиры; 3) углеводы; 4) прочее
Решение.
Чем меньше сектор на круговой диаграмме, тем меньше вещества содержит продукт.В задаче нужно найти сектор наименьшего размера. Это сектор, показывающий содержание углеводов. У нас есть ответ под номером 3.
Ответ: 3.
Задание 19. На тарелке одинаковые на вид пирожки: 4 с мясом, 10 с капустой и 6 с вишней. Жора берет наугад один пирог. Найдите вероятность того, что пирог вишневый.
Решение.
Примем как событие И то, что Жора взял пирог с вишней. Количество благоприятных исходов для события А равно 6 (количество вишневых пирогов). Итого исходы 4+10+6=20 — общее количество пирожков. Таким образом, искомая вероятность равна:
Количество благоприятных исходов для события А равно 6 (количество вишневых пирогов). Итого исходы 4+10+6=20 — общее количество пирожков. Таким образом, искомая вероятность равна:
.
Ответ: 0,3.
Задача 20. Формула tС = 5/9*(tF-32), где tC — температура в градусах Цельсия, tF — температура в градусах Фаренгейта, позволяет перевести значение температуры из градусов Фаренгейта в градусы Цельсия . Сколько градусов по Цельсию составляет -4 градуса по Фаренгейту?
Решение.
Подставляем значение в формулу перевода из Фаренгейта в Цельсий, получаем.
ОГИ ОГЭ Математика задание №9 Демонстрационный вариант 2018-2017 На тарелке одинаковые на вид пирожки: 4 с мясом, 8 с капустой и 3 с яблоками. Петя выбирает наугад один пирог. Найдите вероятность того, что в пироге останутся яблоки.
Решение:
P = m / n = количество благоприятных исходов / общее количество исходов
м = количество хороших исходов = 3 (с яблоками)
n = общее количество исходов = 4 (мясо) + 8 (капуста) + 3 (яблоки) = 15
Ответ: 0. 2
2
Демонстрационный вариант Главного государственного экзамена ОГЭ 2016 — задание №19 Модуль «Реальная математика»
Родительский комитет закупил 10 пазлов на подарки детям до конца года, в том числе машинки с видом на город. Подарки распределяются случайным образом. Найдите вероятность того, что Мише достанется машинка.
Решение:
Ответ: 0,3
Демонстрационный вариант Основной государственный экзамен ОГЭ 2015 — задание №1.19 Модуль «Реальная математика»
В среднем из 75 фонарей в продаже пятнадцать неисправны. Найдите вероятность того, что фонарь, выбранный вами наугад в магазине, будет работать.
Решение:
75 — всего фонарей
15 — неисправен
15/75 = 0,2 — вероятность того, что фонарь будет неисправен
1-0,2 = 0,8 — вероятность того, что фонарик сработает
Ответ: 0.8
1. Вася, Петя, Коля и Леша бросили жребий — кто должен начать игру. Найдите вероятность того, что Петя начнет игру.
Вася, Петя, Коля и Леша бросили жребий — кто должен начать игру. Найдите вероятность того, что Петя начнет игру.
Благоприятные исходы — 1.
Всего 4 исхода.
Вероятность того, что Петя начнет игру, равна 1:4 = 0,25
Ответ. 0,25
2. Кости бросили один раз. Какова вероятность того, что количество точек больше 4? Округлите ответ до сотых.
Благоприятные исходы: 5 и 6. То есть два благоприятных исхода.
Всего 6 исходов, так как у игральной кости 6 граней.
Вероятность того, что выпадет более 4 очков, равна 2:6 = 0,3333… ≈ 0,33
Ответ. 0,33
Если первая отбрасываемая цифра 0,1,2,3 или 4, то цифра перед ней не изменяется. Если первая отбрасываемая цифра 5,6,7,8 или 9, то цифра перед ней увеличивается на 1.
3. В случайном эксперименте бросают две игральные кости.Найдите вероятность того, что в сумме будет 8 очков. Округлите ответ до тысячных.
Благоприятные исходы: (2; 6), (6; 2), (4; 4), (5; 3), (3; 5). Всего 5 благоприятных исходов.
Всего 5 благоприятных исходов.
Все исходы равны 36 (6 ∙ 6).
Вероятность = 5:36 = 0,1388888… ≈ 0,139
Ответ. 0,139
4. В случайном эксперименте дважды бросают симметричную монету. Найти вероятность того, что орел выпадет ровно 1 раз.
Есть два благоприятных исхода: решка и решка, решка и решка.
Возможны четыре исхода: орел и решка, решка и орел, решка и решка, орел и орел.
Вероятность: 2:4 = 0,5
5. В случайном эксперименте 3 раза бросали симметричную монету. Какова вероятность того, что орел выпадет ровно два раза?
Возможны следующие благоприятные исходы:
При подбрасывании монеты орёл выпадает с вероятностью 0,5, а решка с вероятностью 0,5. Следовательно, вероятность выпадения комбинации «ОЭР» равна 0.5∙0,5∙0,5 = 0,125.
Вероятность выпадения комбинации «ОПО» равна 0,125.
Вероятность выпадения комбинации «РОО» равна 0,125.
Следовательно, вероятность получения благоприятных исходов равна 0,125 + 0,125 + 0,125 = 0,375.
Ответ. 0,375.
6. В соревнованиях по толканию ядра принимают участие 4 спортсмена из Финляндии, 6 спортсменов из России и 10 спортсменов из США. Найдите вероятность. что последний конкурент будет из России.
4+6+10=20 (спортсмены) — все участники соревнований.
Благоприятные исходы 6. Всего исходов 20.
Вероятность 6:20=0,3
7. В среднем из 250 аккумуляторов в продаже 3 неисправны. Найти вероятность того, что случайно выбранная батарея окажется исправной.
Исправные аккумуляторы: 250 — 3 = 247
Всего батарей: 250
Вероятность равна
Ответ. 0,988
8.В чемпионате по спортивной гимнастике участвуют 20 спортсменов: 8 из России, 7 из США, остальные из Китая. Порядок выступления гимнасток определяется жребием. Найдите вероятность того, что первый спортсмен будет из Китая.
Из Китая: 20 — 8 — 7 = 5 спортсменов
Вероятность:
Ответ. 0,25
9. В чемпионате мира принимают участие 16 команд. Они должны быть разделены по жребию на четыре группы по четыре команды в каждой. В коробке смешанные карты с номерами групп:
Они должны быть разделены по жребию на четыре группы по четыре команды в каждой. В коробке смешанные карты с номерами групп:
1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.
Капитаны команд тянут одну карту. Какова вероятность того, что сборная России окажется во второй группе?
Во второй группе 4 команды, следовательно, благоприятных исходов 4.
Всего 20 исходов, так как 20 команд.
Вероятность:
Ответ. 0,25
10. Вероятность того, что шариковая ручка будет плохо писать (или не будет писать), равна 0,1. Покупатель в магазине выбирает ручку. Найдите вероятность того, что эта ручка хорошо пишет.
вероятность того, что ручка пишет хорошо + вероятность того, что ручка не пишет = 1.
1 — 0,1 = 0,9 — вероятность того, что ручка хорошо пишет.
11. На экзамене по геометрии студент получает один вопрос из списка. Вероятность того, что это вопрос о вписанном круге, равна 0,2. Вероятность того, что это вопрос с параллелограммом, равна 0,15. Нет вопросов, которые одновременно касаются этих двух тем. Найти вероятность того, что студент получит на экзамене вопрос по одной из этих двух тем.
Нет вопросов, которые одновременно касаются этих двух тем. Найти вероятность того, что студент получит на экзамене вопрос по одной из этих двух тем.
0,2 + 0,15 = 0,35
Ответ. 0,35
12. В торговом зале два одинаковых автомата продают кофе. Вероятность того, что кофе закончится в конце дня, равна 0,3. Вероятность того, что в обеих машинах закончится кофе, равна 0,12. Найти вероятность того, что к концу дня в обеих машинах останется кофе.
Вероятность того, что хотя бы в одной машине закончится кофе: 0,3 + 0,3 — 0,12 = 0,48 (0,12 вычитается, так как эта вероятность учитывалась дважды при сложении 0 и 0.3)
Вероятность того, что кофе останется в обеих машинах:
1 – 0,48 = 0,52.
Ответ. 0,52
13. Биатлонист пять раз стреляет по мишеням. Вероятность поражения цели одним выстрелом равна 0,8. Найти вероятность того, что биатлонист первые три раза попал в мишени, а два последних промахнулся. Округлите результат до сотых.
4 раза: 1 — 0,8 = 0,2
5 раз: 1 — 0,8 = 0,2
Вероятность: 0. 8 ∙ 0,8 ∙ 0,8 ∙ 0,2 ∙ 0,2 = 0,02048 ≈ 0,02
8 ∙ 0,8 ∙ 0,8 ∙ 0,2 ∙ 0,2 = 0,02048 ≈ 0,02
Ответ. 0,02
14. В магазине есть два автомата оплаты. Каждая из них может быть неисправна с вероятностью 0,05 независимо от другой машины. Найти вероятность того, что хотя бы одна машина исправна.
Вероятность того, что обе машины неисправны: 0,05 ∙ 0,05 = = 0,0025
Вероятность того, что хотя бы одна машина исправна:
1 – 0,0025 = 0,9975
Ответ.0,9975
15. На клавиатуре телефона 10 цифр от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет четной?
Четные цифры: 0, 2, 4, 6, 8. Всего пять четных цифр.
Всего 10 цифр.
Вероятность:
16. Конкурс исполнителей проводится в 4 дня. Всего заявлено 50 спектаклей — по одному от каждой страны. В первый день 20 спектаклей, остальные поровну поделены между оставшимися днями.Порядок выступления определяется жребием. Какова вероятность того, что выступление представителя России состоится в третий день соревнований?
Решение. 50 — 20 = 30 участников должны выступить в течение трех дней. Поэтому в третий день выступят 10 человек.
50 — 20 = 30 участников должны выступить в течение трех дней. Поэтому в третий день выступят 10 человек.
Вероятность:
17. Лена дважды бросает кости. Всего она набрала 9 баллов. Найти вероятность того, что во втором броске будет 5 очков.
Возможны четыре события события: (3; 6), (6; 3), (4; 5), (5; 4)
Благоприятный исход один (4; 5)
Вероятность:
Ответ.0,25
18. В случайном эксперименте дважды бросают симметричную монету. Найдите вероятность того, что решка выпадет ровно один раз.
Возможные исходы:
ОР, РО, ОО, РР
Благоприятные исходы: OR, RO
Поделись статьей с друзьями:
Похожие статьи
| 2 3 + х | = 0.4 или | 2 | 3 + х | знак равно | 2 | , | ||
| 5 3 + х | 5 | 5 |
откуда следует, что 3 + х = 1, х = –2.
Ответ: –2.
Задание №6 по планиметрии на нахождение геометрических величин (длин, углов, площадей), моделирование реальных ситуаций на языке геометрии.Изучение построенных моделей с использованием геометрических понятий и теорем. Источником трудностей является, как правило, незнание или неправильное применение необходимых теорем планиметрии.
Площадь треугольника ABC равна 129. DE — срединная линия, параллельная стороне AB . Найдите площадь трапеции ABED .
Раствор. Треугольник CDE подобен треугольнику CAB по двум углам, так как угол при вершине C общий, угол CDE равен углу CAB , как и соответствующие углы при DE || АВ секанс АС .Так как DE является средней линией треугольника по условию, то по свойству средней линии | DE = (1/2) AB . Таким образом, коэффициент подобия равен 0,5. Площади подобных фигур связаны как квадрат коэффициента подобия, поэтому
Следовательно, S ABED = S Δ ABC – S Δ CDE = 129 – 32,25 = 96,75.
Задание №7 — проверяет применение производной к изучению функции.Для успешной реализации необходимо осмысленное, неформальное владение понятием производной.
Пример 7 К графику функции y = f ( x ) в точке с абсциссой x 0 проведена касательная, которая перпендикулярна прямой, проходящей через точки ( 4;3) и (3;-1) этого графика. Найдите f ′ ( х 0).
Найдите f ′ ( х 0).
Раствор. 1) Используем уравнение прямой, проходящей через две заданные точки, и находим уравнение прямой, проходящей через точки (4;3) и (3;-1).
( г – г 1)( х 2 – х 1) = ( х – х 1)( г 8
)( y – 3)(3 – 4) = ( х – 4)(–1 – 3)
( y – 3)(–1) = ( x – 4)(–4)
– y + 3 = –4 x + 16| · (-один)
у – 3 = 4 х – 16
у = 4 х – 13, где к 1 = 4.
2) Найдите наклон касательной k 2, перпендикулярной прямой y = 4 x – 13, где k 1 = 4, по формуле:
3) Наклон касательной есть производная функции в точке касания. Значит, f ′( x 0) = k 2 = –0,25.
Ответ: –0,25.
Задание № 8 — проверяет знание элементарной стереометрии у участников экзамена, умение применять формулы нахождения площадей поверхностей и объемов фигур, двугранных углов, сравнивать объемы подобных фигур, уметь выполнять действия с геометрические фигуры, координаты и векторы и др.
Объем куба, описанного вокруг сферы, равен 216. Найдите радиус сферы.
Раствор. 1) V куб = a 3 (где a — длина ребра куба), поэтому
и 3 = 216
и = 3 √216
2) Поскольку сфера вписана в куб, значит, длина диаметра сферы равна длине ребра куба, поэтому d = а , d = 6, д = 2 Р , Р = 6: 2 = 3.
Задание № 9 — требует от выпускника преобразования и упрощения алгебраических выражений. Задание №9 продвинутый уровень Сложность с краткими ответами. Задания из раздела «Расчеты и преобразования» в ЕГЭ делятся на несколько типов:
- преобразование числовых/буквенных тригонометрических выражений.

преобразования числовых рациональных выражений;
преобразования алгебраических выражений и дробей;
преобразования числовых/буквенных иррациональных выражений;
действия со степенями;
преобразование логарифмических выражений;
Пример 9 Рассчитайте tgα, если известно, что cos2α = 0,6 и
Раствор. 1) Воспользуемся формулой двойного аргумента: cos2α = 2 cos 2 α — 1 и найдем
| тангенс 2 α = | 1 | – 1 = | 1 | – 1 = | 10 | – 1 = | 5 | – 1 = 1 | 1 | – 1 = | 1 | = 0,25. |
| cos 2 α | 0,8 | 8 | 4 | 4 | 4 |
Следовательно, тангенс 2 α = ± 0,5.
3) По условию
, следовательно, α — угол второй четверти, а tgα
Ответ: –0,5.
#ADVERTISING_INSERT# Задание № 10 — проверяет умение учащихся использовать полученные рано знания и умения в практической деятельности и повседневной жизни. Можно сказать, что это задачи по физике, а не по математике, но все необходимые формулы и величины даны в условии. Задачи сводятся к решению линейного или квадратного уравнения, линейного или квадратного неравенства. Поэтому необходимо уметь решать такие уравнения и неравенства, и определять ответ. Ответ должен быть в виде целого числа или конечной десятичной дроби.
Можно сказать, что это задачи по физике, а не по математике, но все необходимые формулы и величины даны в условии. Задачи сводятся к решению линейного или квадратного уравнения, линейного или квадратного неравенства. Поэтому необходимо уметь решать такие уравнения и неравенства, и определять ответ. Ответ должен быть в виде целого числа или конечной десятичной дроби.
Два тела массой м = 2 кг каждое, движущиеся с одинаковой скоростью v = 10 м/с под углом 2α друг к другу.Энергия (в джоулях), выделяющаяся при их абсолютно неупругом столкновении, определяется выражением Q = mv 2 sin 2 α. На какой наименьший угол 2α (в градусах) должны сдвинуться тела, чтобы в результате столкновения выделилось не менее 50 джоулей?
Раствор. Для решения задачи необходимо решить неравенство Q ≥ 50 на интервале 2α ∈ (0°; 180°).
mv 2 sin 2 α ≥ 50
2 10 2 sin 2 α ≥ 50
200 sin2α ≥ 50
Поскольку α ∈ (0°; 90°), мы решим только
Представим решение неравенства графически:
Так как по предположению α ∈ (0°; 90°), то 30° ≤ α
Задание №11 — типовое, но оказывается сложным для учащихся. Основным источником трудностей является построение математической модели (составление уравнения). Задание №11 проверяет умение решать текстовые задачи.
Основным источником трудностей является построение математической модели (составление уравнения). Задание №11 проверяет умение решать текстовые задачи.
Пример 11. На весенних каникулах 11-классник Вася должен был решить 560 учебных задач, чтобы подготовиться к экзамену. 18 марта, в последний день школы, Вася решил 5 задач. Затем каждый день он решал на такое же количество задач больше, чем в предыдущий день. Определите, сколько задач решил Вася 2 апреля в последний день отпуска.
Решение: Обозначим a 1 = 5 — количество задач, решаемых Васей 18 марта, d — ежедневное количество задач, решаемых Васей, n = 16 — количество дней с 18 марта по апрель 2 включительно, S 16 = 560 — общее количество задач, a 16 — количество задач, которые Вася решил 2 апреля. Зная, что каждый день Вася решал на одинаковое количество задач больше, чем в предыдущий день, то можно воспользоваться формулами нахождения суммы арифметической прогрессии:560 = (5 + a 16) 8,
5 + а 16 = 560:8,
5 + и 16 = 70,
и 16 = 70 – 5
и 16 = 65.
Ответ: 65.
Задание №12 — проверить умение учащихся выполнять действия с функциями, уметь применять производную к изучению функции.
Найти точку максимума функции y = 10ln( х + 9) – 10 х + 1.
Решение: 1) Найдите область определения функции: х + 9 > 0, х > –9, т. е. x ∈ (–9; ∞).
2) Найдите производную функции:
4) Найденная точка принадлежит интервалу (–9; ∞).Определим знаки производной функции и изобразим поведение функции на рисунке:
Желаемая максимальная точка x = –8.
Скачать бесплатно рабочую программу по математике к строке УМК Г.К. Муравина, К.С. Муравина, О.В. Муравина 10-11 Скачать бесплатные руководства по алгебреЗадание №13 — повышенного уровня сложности с развернутым ответом, проверяющее умение решать уравнения, наиболее успешно решаемое среди заданий с развернутым ответом повышенного уровня сложности.

а) Решите уравнение 2log 3 2 (2cos x ) – 5log 3 (2cos x ) + 2 = 0
б) Найдите все корни этого уравнения, принадлежащие отрезку.
Решение: а) Пусть log 3 (2cos x ) = t , тогда 2 t 2 – 5 t + 2 = 0,
|
|
log3(2cos x ) = | 2 | ⇔ |
|
2cos х = 9 | ⇔ |
|
потому что х = | 4,5 | ⇔ потому что |cos x | ≤ 1, |
| log3(2cos x ) = | 1 | 2cos х = √3 | потому что х = | √3 | ||||||
| 2 | 2 |
|
|
х = | π | + 2π к |
| 6 | |||
| х = – | π | + 2π к , к ∈ Z | |
| 6 |
б) Найдите корни, лежащие на отрезке .
Из рисунка видно, что данный отрезок имеет корни
| Ответ: а) | π | + 2π к ; – | π | + 2π к , к ∈ Z ; б) | 11π | ; | 13π | . |
| 6 | 6 | 6 | 6 |
Диаметр окружности основания цилиндра равен 20, образующая цилиндра равна 28. Плоскость пересекает его основания по хордам длиной 12 и 16. Расстояние между хордами равно 2√197.
а) Докажите, что центры оснований цилиндра лежат по одну сторону от этой плоскости.
б) Найдите угол между этой плоскостью и плоскостью основания цилиндра.
Решение: а) Хорда длины 12 находится на расстоянии = 8 от центра окружности основания, а хорда длины 16, аналогично, находится на расстоянии 6. Следовательно, расстояние между их проекциями на плоскость, параллельная основаниям цилиндров, равна либо 8 + 6 = 14, либо 8 — 6 = 2.
Тогда расстояние между хордами равно
= = √980 = = 2√245
= = √788 = = 2√197.
По условию реализован второй случай, в котором проекции хорд лежат по одну сторону от оси цилиндра. Это означает, что ось не пересекает эту плоскость внутри цилиндра, т. е. основания лежат по одну от нее сторону. Что нужно было доказать.
б) Обозначим центры оснований как О 1 и О 2. Проведем из центра основания хордой длины 12 серединный перпендикуляр к этой хорде (имеет, как уже отмечалось, длину 8) и от центра другого основания до другой хорды.Они лежат в одной плоскости β, перпендикулярной этим хордам. Назовем середину меньшей хорды B большей A, а проекцию A на второе основание H (H ∈ β). Тогда AB,AH ∈ β и, следовательно, AB,AH перпендикулярны хорде, т. е. линии пересечения основания с данной плоскостью.
Назовем середину меньшей хорды B большей A, а проекцию A на второе основание H (H ∈ β). Тогда AB,AH ∈ β и, следовательно, AB,AH перпендикулярны хорде, т. е. линии пересечения основания с данной плоскостью.
Таким образом, искомый угол равен
.| ∠ABH = арктангенс | г.х. | = арктг | 28 | = арктг14. |
| БН | 8 – 6 |
Задание №15 — повышенного уровня сложности с развернутым ответом, проверяет умение решать неравенства, наиболее успешно решается среди заданий с развернутым ответом повышенного уровня сложности.
Пример 15 Решите неравенство | x 2 – 3 x | log 2 ( x + 1) ≤ 3 x – x 2 .
Решение: Областью определения этого неравенства является интервал (–1; +∞). Рассмотрим три случая отдельно:
1) Пусть х 2 – 3 х = 0, т. е. х = 0 или х = 3. В этом случае данное неравенство становится верным, поэтому эти значения включаются в решение.
е. х = 0 или х = 3. В этом случае данное неравенство становится верным, поэтому эти значения включаются в решение.
2) Пусть теперь х 2 – 3 х > 0, т. е. х ∈ (–1; 0) ∪ (3; +∞). В этом случае это неравенство можно переписать в виде ( х 2 – 3 х ) log 2 ( х + 1) ≤ 3 х – х 2 и разделить на положительное выражение х 2 – 3 x . Получаем log 2 ( х + 1) ≤ –1, х + 1 ≤ 2 –1 , х ≤ 0,5 -1 или х ≤ -0,5. С учетом области определения имеем x ∈ (–1; –0,5].
3) Наконец, рассмотрим x 2 – 3 x x∈ (0; 3). В этом случае исходное неравенство перепишется в виде (3 х – х 2) log 2 ( х + 1) ≤ 3 х – х 2. После деления на положительное выражение 3 x – x 2 , получаем log 2 ( x + 1) ≤ 1, x + 1 ≤ 2, x ≤ 1. С учетом площади имеем x ∈ (0; 1].
Объединяя полученные решения, получаем x ∈ (–1; –0.5] ∪ ∪ {3}.
Ответ: (–1; –0,5] ∪ ∪ {3}.
Задание №16 — продвинутый уровень относится к заданиям второй части с развернутым ответом. В задании проверяется умение выполнять действия с геометрическими фигурами, координатами и векторами. В задании два пункта. В первом пункте задание должно быть доказано, а во втором пункте — просчитано.
В равнобедренном треугольнике ABC с углом 120° при вершине A проведена биссектриса BD.Прямоугольник DEFH вписан в треугольник ABC так, что сторона FH лежит на отрезке BC, а вершина E лежит на отрезке AB. а) Докажите, что FH = 2DH. б) Найдите площадь прямоугольника DEFH, если AB = 4,
.Решение: а)
1) ΔBEF — прямоугольная, EF⊥BC, ∠B = (180° — 120°) : 2 = 30°, тогда EF = BE по свойству катета, противоположного углу 30°.
2) Пусть EF = DH = x , тогда BE = 2 x , BF = x √3 по теореме Пифагора.
3) Так как ΔABC равнобедренный, то ∠B = ∠C = 30˚.
BD — это биссектриса ∠B, поэтому ∠ABD = ∠DBC = 15˚.
4) Считать ΔDBH прямоугольным, так как DH⊥BC.
| 2 х | = | 4 – 2 x |
| 2 x (√3 + 1) | 4 |
√3 – 1 = 2 – х
х = 3 – √3
КВ = 3 — √3
2) S DEFH = ED EF = (3 — √3 ) 2(3 — √3 )
S DEFH = 24 — 12√3.
Ответ: 24 – 12√3.
Задание № 17 — задание с развернутым ответом, данное задание проверяет применение знаний и умений в практической деятельности и повседневной жизни, умение строить и исследовать математические модели. Эта задача — текстовая задача с экономическим содержанием.
Пример 17. Вклад в размере 20 миллионов рублей планируется открыть на четыре года. В конце каждого года банк увеличивает депозит на 10% по сравнению с его размером в начале года. Кроме того, в начале третьего и четвертого года вкладчик ежегодно пополняет вклад на Х млн рублей, где Х — всего числа. Найдите наибольшее значение X , при котором банк добавит на депозит менее 17 миллионов рублей за четыре года.
Кроме того, в начале третьего и четвертого года вкладчик ежегодно пополняет вклад на Х млн рублей, где Х — всего числа. Найдите наибольшее значение X , при котором банк добавит на депозит менее 17 миллионов рублей за четыре года.
Решение: В конце первого года вклад составит 20 + 20 · 0,1 = 22 млн руб., а в конце второго — 22 + 22 · 0,1 = 24,2 млн руб.В начале третьего года вклад (в млн. руб.) составит (24,2 + Х ), а в конце — (24,2 + Х) + (24,2 + Х) 0,1 = ( 26,62 + 1,1 X ). В начале четвертого года вклад составит (26,62 + 2,1 X) , а в конце — (26,62 + 2,1 X ) + (26,62 + 2,1 X ) 0,1 = ( 29,282 + 2,31 X ). По условию нужно найти наибольшее целое число x, для которого выполняется неравенство
(29 282 + 2,31 х ) – 20 – 2 х
29 282 + 2,31 90 158 х 90 159 – 20 – 2 90 158 х 90 159
0,31 х
0,31 х
Наибольшее целочисленное решение этого неравенства — число 24.
Ответ: 24.
Задание №18 — задание повышенного уровня сложности с развернутым ответом. Данное задание предназначено для конкурсного отбора в вузы с повышенными требованиями к математической подготовке абитуриентов. Упражнение высокого уровня сложности — это задача не на применение одного метода решения, а на комбинацию разных методов. Для успешного выполнения задания 18, кроме твердых математических знаний, требуется еще и высокий уровень математической культуры.
При чем система неравенств
| x 2 + у 2 ≤ 2 ау – а 2 + 1 | |
| у + а ≤ | х | – и |
имеет ровно два решения?
Решение: Эту систему можно переписать как
.| х 2 + ( у – а ) 2 ≤ 1 | |
| г ≤ | х | – и |
Если мы начертим на плоскости множество решений первого неравенства, мы получим внутренность окружности (с границей) радиуса 1 с центром в точке (0, a ). Множеством решений второго неравенства называется часть плоскости, лежащая под графиком функции y = |
х | –
и ,
, а последний является графиком функции
Множеством решений второго неравенства называется часть плоскости, лежащая под графиком функции y = |
х | –
и ,
, а последний является графиком функции
y = |
х |
, сдвинутый вниз на и . Решением этой системы является пересечение множеств решений каждого из неравенств.
Следовательно, два решения эта система будет иметь только в случае, показанном на рис.один.
Точки касания окружности и линий будут двумя решениями системы. Каждая из прямых наклонена к осям под углом 45°. Значит треугольник PQR — прямоугольный равнобедренный. Точка Q имеет координаты (0, a ), а точка R – координаты (0, – a ). Кроме того, разрезы PR и PQ равны радиусу окружности, равному 1. Отсюда
| QR = 2 a = √2, a = | √2 | . |
| 2 |
Задание №19 — задание повышенного уровня сложности с развернутым ответом. Данное задание предназначено для конкурсного отбора в вузы с повышенными требованиями к математической подготовке абитуриентов. Задача высокого уровня сложности – это задача не на применение одного метода решения, а на комбинацию разных методов. Для успешного выполнения задания 19 необходимо уметь искать решение, выбирая различные подходы из числа известных, модифицируя изученные методы.
Пусть sn сумма P членов арифметической прогрессии ( a p ). Известно, что S n + 1 = 2 n 2 – 21 n – 23.
а) Приведите формулу P -го члена этой прогрессии.
б) Найдите наименьшую сумму по модулю S n .
в) Найдите наименьшее P , при котором S n будет квадратом целого числа.
Решение : а) Очевидно, и = S n – S n — один . Используя эту формулу, мы получаем:
Используя эту формулу, мы получаем:
S n = S ( n – 1) + 1 = 2( n – 1) 2 – 21( n – 1) – 23 = 2 n 0 – 2 ,
S n – 1 = S ( n – 2) + 1 = 2( n – 1) 2 – 21( n – 2) – 23 = 2 n 9 2 9025 номер + 27
означает, и = 2 n 2 – 25 n – (2 n 2 – 29 n + 27) = 4 n – 27.
B), так как S n = 2 n 2 – 25 n , то рассмотрим функцию S ( x ) = | 2 x 2 – 25 x| . Ее график можно увидеть на рисунке.
Очевидно, что наименьшее значение достигается в целых точках, расположенных ближе всего к нулям функции. Понятно, что это баллы. X = 1, X = 12 и X = 13. Поскольку S (1) = | С 1 | = |2 – 25| = 23, S (12) = | С 12 | = |2 144 – 25 12| = 12, S (13) = | С 13 | = |2 169 – 25 13| = 13, то наименьшее значение равно 12.
в) Из предыдущего абзаца следует, что sn положительны, так как n = 13. то очевидный случай, когда это выражение является полным квадратом, реализуется при n = 2 n — 25, то есть при P = 25.
Осталось проверить значения от 13 до 25:
S 13 = 13 1, S 14 = 14 3, S 15 = 15 5, S 16 = 16 7, S 17 = 17 9, S 18 = 18 11, S 19 = 19 13 S 20 = 20 13, S 21 = 21 17, S 22 = 22 19, S 23 = 23 21, S 2,3
Получается, что при меньших значениях P полный квадрат не достигается.
Ответ: а) а н = 4 н — 27; б) 12; в) 25.
________________
*С мая 2017 года Совместная издательская группа «ДРОФА-ВЕНТАНА» входит в состав Корпорации «Российский учебник». В корпорацию также вошли издательский дом «Астрель» и цифровая образовательная платформа LECTA. Генеральным директором назначен Александр Брычкин, выпускник Финансовой академии при Правительстве РФ, кандидат экономических наук, руководитель инновационных проектов издательства ДРОФА в сфере цифрового образования (электронные формы учебников, Российская электронная школа, цифровая образовательная платформа ЛЕКТА). До прихода в издательский дом ДРОФА занимал должность вице-президента по стратегическому развитию и инвестициям издательского холдинга «ЭКСМО-АСТ». На сегодняшний день Издательская корпорация «Российский учебник» обладает самым большим портфелем учебников, включенных в Федеральный перечень, — 485 наименований (примерно 40% без учета учебников для коррекционной школы). Издательства корпорации владеют самыми популярными в российских школах комплектами учебников по физике, черчению, биологии, химии, технологии, географии, астрономии — областям знаний, которые необходимы для развития производственного потенциала страны.В портфеле корпорации учебники и учебные пособия для начальной школы, отмеченные премией Президента в области образования. Это учебники и пособия по предметным областям, которые необходимы для развития научно-технического и производственного потенциала России.
До прихода в издательский дом ДРОФА занимал должность вице-президента по стратегическому развитию и инвестициям издательского холдинга «ЭКСМО-АСТ». На сегодняшний день Издательская корпорация «Российский учебник» обладает самым большим портфелем учебников, включенных в Федеральный перечень, — 485 наименований (примерно 40% без учета учебников для коррекционной школы). Издательства корпорации владеют самыми популярными в российских школах комплектами учебников по физике, черчению, биологии, химии, технологии, географии, астрономии — областям знаний, которые необходимы для развития производственного потенциала страны.В портфеле корпорации учебники и учебные пособия для начальной школы, отмеченные премией Президента в области образования. Это учебники и пособия по предметным областям, которые необходимы для развития научно-технического и производственного потенциала России.
Использование облачных технологий в работе современного учителя
Этап 1. Регистрация и вход на сайт
2. Выберите предмет (класс).
Выберите предмет (класс).
3. Выберите пункт регистрации.
4. Заполните регистрационную форму.
5. После входа отобразится ваше имя.
Этап 2. Формирование тестовой работы из каталога заданий
1. На данном сайте в разделе КАТАЛОГ ЗАДАНИЙ все задания разбиты в соответствии с классом-си-фи-ка-тор экзаменационных заданий, пос-в-ла-ю-щи последовательно повторять отдельные не большие темы и сразу проверить свои знания о них.
2. Раздел СТУДЕНТ Предназначен для учащихся, выполняющих варианты работы, предложенные преподавателем.
3. Раздел МЕТОДИСТУ проводятся обучающие и демонстрационные работы.
4. Предоставляет возможность создавать собственные дистанционные курсы В главе ШКОЛА .
5. Рассмотрим подробнее раздел УЧИТЕЛЬ, который позволяет создавать варианты тестов, вести журнал занятий и просматривать статистику по работе. Для этого перейдите на вкладку УЧИТЕЛЬ.
6. Составление теста: Создание теста из выбранных заданий «Выберите номера заданий и введите количество заданий из этой темы» Выберите форму теста.
Составление теста: Создание теста из выбранных заданий «Выберите номера заданий и введите количество заданий из этой темы» Выберите форму теста.
Тест сформирован и вам остается только выдать рабочий номер, который вы выдаете ученикам.
7. Изменить параметры теста: заполнить название работы, краткое описание(инструкция для студентов), сроки проведения теста (наличие теста по дате, указать время начала и окончания тестирования, указать продолжительность тест, критерии оценки).
Чтобы изменить критерии оценки, переместите ползунки. Щелкните Сохранить.
8. Скомпилированную работу можно распечатать.Перейдите по ссылке на тестовую страницу.
Выберите версию для печати и копирования.
Этап 3. Ведение журнала занятий
Когда хотя бы один учащийся выполнил вашу работу, то вы можете увидеть результат в классном журнале, который формируется и заполняется автоматически.
1. Выберите УЧИТЕЛЬ » КРУТОЙ ЖУРНАЛ.
2. При первом прохождении теста все учащиеся помещаются на вкладку NO GROUP.
Добавляем класс, затем определяем учеников по классам.
Система по-ми-на-ет созданных ра-бо-вам и результаты их внедрения: СТАТИСТИКА ПО МАСТЕРСКИМ.
Ниже представлена сводка стоти-сти-ка за все созданные вами работы. Для просмотра списков учащихся и их результатов нажмите на номер соответствующей работы. Вы также можете дублировать и затем ре-дак-ти-ро-вать любую из работ, создавая на ее основе новую работу. Перейдем к статистике конкретной работы.
Odd Generalized Exponential Flexible Weibull Extension Distribution
Получено 21 декабря 2016 г., принято 29 декабря 2017 г., доступно в Интернете 31 марта 2018 г.
1. Введение
Распределение Вейбулла широко известно из-за его полезности при моделировании данных о продолжительности жизни, когда функция коэффициента опасности является монотонной [27]. Недавно были предложены новые классы распределений на основе модификаций распределения Вейбулла, чтобы обеспечить хорошее соответствие набору данных с интенсивностью отказов в ванне, см. [25]. Среди них экспоненциальное семейство Вейбулла, [14], модифицированное распределение Вейбулла, [11, 19], бета-распределение Вейбулла, [8], гибкое расширение Вейбулла, [4], расширенное гибкое распределение Вейбулла, [4], обобщенное модифицированное Распределение Вейбулла, [5], распределение Кумарасвами Вейбулла, [6], бета-модифицированное распределение Вейбулла, [16,22], бета-обобщенное распределение Вейбулла, [23], новое модифицированное распределение Вейбулла, [2] и экспоненциальное модифицированное расширение Вейбулла. , [20] и др.Хороший обзор этих моделей представлен в [3,15,17].
[25]. Среди них экспоненциальное семейство Вейбулла, [14], модифицированное распределение Вейбулла, [11, 19], бета-распределение Вейбулла, [8], гибкое расширение Вейбулла, [4], расширенное гибкое распределение Вейбулла, [4], обобщенное модифицированное Распределение Вейбулла, [5], распределение Кумарасвами Вейбулла, [6], бета-модифицированное распределение Вейбулла, [16,22], бета-обобщенное распределение Вейбулла, [23], новое модифицированное распределение Вейбулла, [2] и экспоненциальное модифицированное расширение Вейбулла. , [20] и др.Хороший обзор этих моделей представлен в [3,15,17].
Распределение гибкого расширения Вейбулла (FWE) [4] имеет множество применений в экспериментах по проверке работоспособности, анализе надежности, прикладной статистике и клинических исследованиях. Подробнее об этом распределении см. [4].
Говорят, что случайная величина X имеет распределение гибкого расширения Вейбулла (FWE) с параметрами α , β > 0, если ее функция плотности вероятности (PDF) определяется выражением
(1. 1)g(x)=(α+βx2)exp(αx−βx−eαx−βx), x>0,
1)g(x)=(α+βx2)exp(αx−βx−eαx−βx), x>0,
(1.2)G(x)=1−exp{−eαx−βx}, x>0.
Функция выживания задается уравнением(1.3)S(x)=1−G(x)=exp{−eαx−βx}, x>0,
а функция степени опасности(1.4)h(x)=(α+βx2)eαx−βx.
Гупта и Кунду [9] предложили обобщение экспоненциального распределения, названное обобщенным экспоненциальным (GE) распределением. Распределение ОЭ с параметрами ϑ , γ > 0 имеет следующую функцию распределения(1.5)F(x;ϑ,γ)=(1−e−ϑx)γ, x>0,ϑ>0,γ>0.
Недавно в [7, 24] был введен новый класс одномерных непрерывных распределений, названный классом нечетных обобщенных экспонент (OGE). Этот класс является гибким, поскольку формы степени опасности могут быть возрастающими, уменьшающимися, ванной и перевернутой ванной. Нечетный обобщенно-экспоненциальный (ОГЭ) класс определяется следующим образом. Если G ( x ), x > 0 является кумулятивной функцией распределения (cdf) случайной величины X , то соответствующая функция выживания равна G¯(x)=1−G(x) и функция плотности вероятности равна g ( x ), тогда мы определяем cdf класса OGE, заменяя x в функции распределения обобщенно-экспоненциального (GE) распределения, заданной в уравнении (1. 5) через G(x)G¯(x), что приводит к
5) через G(x)G¯(x), что приводит к
(1.6)F(x;ϑ,γ)=[1−exp{−ϑG(x)G¯(x)}]γ, x>0,ϑ>0,γ>0.
Функция плотности вероятности, соответствующая (1.6), имеет вид(1.7)f(x;ϑ,γ)=ϑγg(x)G¯(x)2exp{−ϑG(x)G¯(x)}[1−exp{−ϑG(x)G¯(x) }]γ−1,
где x > 0, ϑ > 0, γ > 0. В этой статье мы представляем новое распределение, зависящее от гибкого распределения Вейбулла, называемое нечетным обобщенным экспоненциальным гибким распределением Вейбулла (OGE-FWE) путем используя класс одномерных распределений, определенный выше. Эта статья может быть организована следующим образом: мы определяем кумулятивную функцию, плотность и функции риска нечетного обобщенного экспоненциального гибкого распределения Вейбулла (OGE-FWE) в разделе 2. В разделе 3 мы представляем некоторые статистические свойства, включая квантильные функции и медиана, мода, rth момент, асимметрия и эксцесс. В разделе 4 мы вводим производящую функцию момента. Распределение порядковой статистики выражено в разделе 5. Оценка максимального правдоподобия параметров определяется в разделе 6.Мы используем реальные наборы данных и анализируем их с помощью приложения в разделе 7, а результаты сравниваем с существующими распределениями. Наконец, мы представляем заключение в разделе 8.
Оценка максимального правдоподобия параметров определяется в разделе 6.Мы используем реальные наборы данных и анализируем их с помощью приложения в разделе 7, а результаты сравниваем с существующими распределениями. Наконец, мы представляем заключение в разделе 8.
2. Нечетное обобщенное экспоненциальное гибкое распределение расширения Вейбулла
В этом разделе мы изучили четырехпараметрическое нечетное обобщенное экспоненциальное гибкое расширение Вейбулла ОГЭ-ФВЭ ( ϑ , γ , α , β ) распределения. Используя G ( x ) из уравнения.(1.2) и г ( x ) из уравнения. (1.1), чтобы получить cdf и PDF уравнений. (1.6) и (1.7) соответственно. Кумулятивная функция распределения cdf нечетного обобщенного экспоненциального гибкого распределения Вейбулла (OGE-FWE) определяется выражением
(2.1)F(x;ϑ,γ,α,β)=[1−e−ϑ(eeαx−βx−1)]γ, x>0,ϑ,γ,α,β>0,
PDF, соответствующий уравнению. (2.1) определяется выражением (2. 2)f(x;ϑ,γ,α,β)=ϑγ(α+βx2)eαx−βx+eαx−βxe−ϑ(eeαx−βx−1)[1−e−ϑ(eeαx−β2) −1]γ−1,
2)f(x;ϑ,γ,α,β)=ϑγ(α+βx2)eαx−βx+eαx−βxe−ϑ(eeαx−βx−1)[1−e−ϑ(eeαx−β2) −1]γ−1,
Функция выживания S ( x ), функция степени опасности h ( x ) и обратная функция степени опасности r ( x ) of X 90 9 5 ~ OGE γ , α , β ) определяются формулой
(2.3)S(x;ϑ,γ,α,β)=1−[1−e−ϑ(eeαx−βx−1)]γ, x>0,
(2.4)h(x;ϑ,γ,α,β)=ϑγ(α+βx2)eαx−βx+eαx−βxe−ϑ(eeαx−βx−1)[1−e−ϑ(eeαx−βx− 1)]γ−11−[1−e−ϑ(eeαx−βx−1)]γ,
(2.5)r(x;ϑ,γ,α,β)=ϑγ(α+βx2)eαx−βx+eαx−βxe−ϑ(eeαx−βx−1)1−e−ϑ(eeαx−βx−1 ),
соответственно x > 0 и ϑ , γ , α , β > 0.На рисунках (1–3) показаны cdf, pdf, выживаемость, степень опасности и обратная функция степени опасности распределения OGE-FWE ( ϑ , γ , α , β ) для некоторых значений параметров.
Рис. 1. КДФ и ФПР ОГЭ-ФВЭ для разных значений параметров.
Функции выживаемости и опасности ОГЭ-ФВЭ при различных значениях параметров.
Рис. 3.Обратная функция степени опасности ОГЭ-ФВЭ для различных значений параметров.
3. Статистические свойства
В этом разделе мы изучим некоторые статистические свойства для распределения OGE-FWE, особенно функцию квантиля и медиану моделирования, моду, моменты, асимметрию и эксцесс.
3.1. Квантиль и медиана
Определяем явные формулы квантиля и медианы моделирования распределения ОГЭ-ФВЭ. Квантиль x q распределения ОГЭ-ФВЭ ( ϑ , γ , α , β ) определяется выражением
(3.1)F(xq)=P[xq≤q]=q,0 (3.2)[1−e−ϑ(eeαxq−βxq−1)]γ=q, (3.3)αxq2−k(q)xq−β=0, k(q)=ln{ln[1−ln(1−q1γ)ϑ]}. (3.4)X=k(u)±k(u)2+4αβ2α. В этом подразделе мы можем получить моду распределения ОГЭ-ФВЭ, продифференцировав его функцию плотности вероятности pdf по x и приравняв ее к нулю. Мода является решением следующего уравнения
(3.5)f′(x)=0. f(x;ϑ,γ,α,β))=h(x;ϑ,γ,α,β)S(x;ϑ,γ,α,β). (3.6)[h'(x;ϑ,γ,α,β)−h3(x;ϑ,γ,α,β)]S(x;ϑ,γ,α,β)=0, Трудно получить аналитическое решение уравнения x для x . В этом подразделе мы получаем асимметрию и эксцесс на основе квантилей. Эксцесс мавров дается [13]
(3,7)Ku=q(0,875)−q(0,625)−q(0,375)+q(0,125)q(0,75)−q(0,25), (3,8)Sk=q(0,75)−2q(0,5)+q(0,25)q(0,75)−q(0,25), Выводим r -й момент для распределения ОГЭ-ФВЭ в теореме (3.1) Если X имеет ОГЭ-ФВЭ ( ϑ , γ , α , β ) распределение , , то r-е моменты случайной величины задаются 59 0 901
(3.9)µr′=∑i=0∞∑j=0∞∑k=0∞∑ℓ=0∞∑m=0∞(−1)i+j+k+mγϑj+1(i+1 )j(j−k+1)ℓβmj!ℓ!m!(ℓ+1)r−2m−1αr−m−1× (γ−1i)(jk)[Γ(r−m+1)α(ℓ +1)2+βΓ(r−m−1)]. Начнем с хорошо известного распределения r -го момента случайной величины X с функцией плотности вероятности f ( x ), заданной выражением
(3. µr′=∫0∞xrϑγ(α+βx2)eαx−βxeeαx−βxe−ϑ(eeαx−βx−1)[1−e−ϑ(eeαx−βx−1)]γ−1dx, [1−e−ϑ(eeαx−βx−1)]γ−1=∑i=0∞(−1)i(γ−11)e−ϑi(eeαx−βx−1), µr′=∑i=0∞(−1)i(γ−1i)ϑγ∫0∞xr(α+βx2)eαx−βxeeαx−βxe−ϑ(i+1)(eeαx−βx−1)dx, e−ϑ(i+1)(eeαx−βx−1)=∑j=0∞(−1)jϑj(i+1)jj!(eeαx−βx−1)j, µr′=∑i=0∞∑j=0∞(−1)i+j(γ−1i)γϑj+1(i+1)jj!∫0∞xr(α+βx2)eαx−βxeeαx−βx [eeαx−βx−1]jdx. (eeαx−βx−1)j=∑k=0∞(−1)k(jk)e(j−k)eαx−βx, µr′=∑i=0∞∑j=0∞∑k=0∞(γ−1i)(jk)(−1)i+j+kγϑj+1(i+1)jj!∫0∞xr( α+βx2)eαx−βxe(j−k+1)eαx−βxdx, e(j−k+1)eαx−βx=∑ℓ=0∞(j−k+1)ℓeℓ(αx−βx)ℓ!, µr′=∑i=0∞∑j=0∞∑k=0∞∑ℓ=0∞(γ−1i)(jk)(−1)i+j+kΓϑj+1(i+1)j( j−k+1)ℓj!ℓ!∫0∞xr(α+βx2)e(ℓ+1)(αx−βx)dx. e−(ℓ+1)βx=∑m=0∞(−β)m(ℓ+1)mm!x−m µr′=∑i=0∞∑j=0∞∑k=0∞∑ℓ=0∞∑m=0∞(−1)i+j+k+mγϑj+1(i+1)j(j −k+1)ℓβm(ℓ+1)mj!ℓ!m!(γ−1i)(jk)×∫0∞xr−m(α+βx2)e(ℓ+1)αxdx,∑i=0∞ ∑j=0∞∑k=0∞∑ℓ=0∞∑m=0∞(−1)i+j+k+mγϑj+1(i+1)j(j−k+1)ℓβm(ℓ+ 1)mj!ℓ!m!(γ−1i)(jk)×[∫0∞αxr−me(ℓ+1)αxdx+∫0∞βxr−m−2e(ℓ+1)αxdx], Γ(z)=xz∫0∞etxtz−1dt, z,x,>0. µr′=∑i=0∞∑j=0∞∑k=0∞∑ℓ=0∞∑m=0∞(−1)i+j+k+mγϑj+1(i+1)j(j −k+1)ℓβm(ℓ+1)mj!ℓ!m!(γ−1i)(jk)×[Γ(r−m+1)αr−m(ℓ+1)r−m+1+βΓ (r−m−1)αr−m−1(ℓ+1)r−m−1]. Производящая функция моментов (mgf) распределения ОГЭ-ФВЭ определяется теоремой (4.1). Производящая функция момента (mgf) распределения OGE-FWE определяется как
(4.1)MX(t)=∑r=0∞∑i=0∞∑j=0∞∑k=0∞∑ℓ=0∞∑m=0∞(−1)i+j+k+mγϑj+1 (i+1)j(j−k+1)ℓβmtrj!ℓ!m!r!αr−m−1(ℓ+1)r−2m−1×(γ−1i)(jk)[Γ(r− m+1)α(ℓ+1)2+βΓ(r−m−1)]. Производящая функция момента M X ( t ) случайной величины X с функцией плотности вероятности f ( x ) определяется выражением
(4.2)MX(t)=∫0∞etxf(x;ϑ,γ,α,β)dx, (4.3)MX(t)=∑r=0∞trr!∫0∞xrf(x)dx=∑r=0∞trr!µr′ (4.4)MX(t)=∑r=0∞∑i=0∞∑j=0∞∑k=0∞∑ℓ=0∞∑m=0∞(−1)i+j+k+mγϑj +1(i+1)j(j−k+1)ℓβmtrj!ℓ!m!r!αr−m−1(ℓ+1)r−2m−1×(γ−1i)(jk)[Γ( r−m+1)α(ℓ+1)2+βΓ(r−m−1)]. В этом разделе мы выводим выражения в замкнутой форме для PDF статистики r -го порядка распределения ОГЭ-ФВЭ. Пусть x 1: , , x , ···, x 99 N : n обозначают статистику заказа, полученную из случайного образца x 1 , 1 , x 2 , ···, x n , которые взяты из непрерывной популяции с совокупной функцией распределения CDF F ( φ ) и функция плотности вероятности PDF f ( x ; φ ), то PDF X r : n дается следующим образом
(5. (5.2)[1−F(x;ϕ)]n−r=∑i=0n−r(n−ri)(−1)i[F(x;ϕ)]i. (5.3)fr:n(x;ϑ,γ,α,β)=∑i=0n−r(−1)in!i!(r−1)!(n−r−i)!f(x ;ϕ)[F(x;ϕ)]i+r−1. Соотношение (5.3) показывает, что f r : n ( x ; φ ) является средневзвешенным распределением ОГЭ-ЭФВ с различными параметрами формы. В этом разделе точечные и интервальные оценки неизвестных параметров распределения ОГЭ-ФВЭ выводятся с использованием метода максимального правдоподобия на основе полной выборки. Пусть x 1 , x 2 ,··· , x n обозначают случайную выборку полных данных из распределения OGE-FWE.Функция правдоподобия задается как
(6.1)L=∏i=1nf(xi;ϑ,γ,α,β), L=∏i=1nϑγ(α+βxi2)eαxi−βxieeαxi−βxie−ϑ[eeαxi−βxi−1][1−e−ϑ[eeαxi−βxi−1]]γ−1. (6. (6.3)∂ℒ∂ϑ=nϑ−∑i=1n(eeαxi−βxi−1)+(γ−1)∑i=1neeαxi−βxi−1eϑ(eeαxi−βxi−1)−1=0 (6.4)∂ℒ∂γ=nγ+∑i=1nln(1−e−ϑ(eeαxi−βxi−1))=0 (6.5)∂ℒ∂α=∑i=1nxi2β+αxi2+∑i=1nxi+∑i=1nxieαxi−βxi−ϑ∑i=1nxi𝒟i+ϑ(γ−1)∑i=1nxi𝒟ieϑ(eeαxi−βxi−1)− 1=0 (6.6)∂ℒ∂β=∑i=1n1β+αxi2−∑i=1n1xi−∑i=1n1xieαxi−βxi+ϑ∑i=1n𝒟ixi−ϑ(γ−1)∑i=1n𝒟ixi[eϑ(eeαxi−βxi −1)−1]=0, В этом разделе мы выводим асимптотические доверительные интервалы этих параметров, когда ϑ , γ , α > 0 и β > 0, как MLE неизвестных параметров ϑ , γ α > 0 и β > 0 не могут быть получены в закрытых формах с помощью ковариационной матрицы дисперсии I
− 1
см. (6.)), (6.8) ∂2ℒ∂θ2 = -Nθ2- (γ-1) σi = 1neθ (eeαxi-βxi-1) 𝒜i2, ∂2ℒ∂θ∂γ = σi = 1n𝒜i (6.9) ∂2ℒ∂θ∂α = -σi = 1nxi𝒟i + (γ-1) σi = 1nxiℬi, ∂2ℒ∂θ∂β = σi = 1n𝒟ixi- (γ-1) σi = 1nℬixi (6.10) ∂2ℒ∂Γ2 = -Nγ2, ∂2ℒ∂γ∂α = θσi = 1nxi𝒟ieθ (eeαxi-βxi-1) -1 (6.11)∂2ℒ∂γ∂β=−ϑ∑i=1n𝒟ixi[eϑ(eeαxi−βxi−1)−1] (6.12)∂2ℒ∂α2=−∑i=1nxi4(β+αxi2)2+∑i=1nxi2eαxi−βxi−ϑ∑i=1nxi2𝒟i[eαxi−βxi+1]+ϑ(γ−1)∑i= 1nxi2𝒦i (6.13)∂2ℒ∂α∂β=−∑i=1nxi2(β+αxi2)2−∑i=1neαxi−βxi+ϑ∑i=1n𝒟i[eαxi−βxi+1]−ϑ(γ−1)∑ я=1n𝒦i (6.14)∂2ℒ∂β2=−∑i=1nxi2(β+αxi2)2+∑i=1neαxi−βxixi2−ϑ∑i=1n𝒟i[eαxi−βxi+1]xi2+ϑ(γ−1)∑i=1n𝒦ixi2 𝒜i=[eeαxi−βxi−1][eϑ(eeαxi−βxi−1)−1]−1, ℬi=𝒟i[eϑ(eeαxi−βxi−1)(1−ϑ(eeαxi−βxi−1))−1][eϑ[eeαxi−βxi−1]−1]−2, 𝒦i=𝒟i[(eϑ(eeαxi−βxi−1)−1)(eαxi−βxi+1)−ϑ𝒟ieϑ(eeαxi−βxi−1)][eϑ(eeαxi−βxi−1)−1]−2. В этом разделе мы проанализируем реальный набор данных с использованием модели OGE-FWE ( ϑ , γ , α , β ) и сравним ее с другими подобранными моделями, такими как гибкое распределение Вейбулла. с использованием статистики Колмогорова-Смирнова (KS), а также информационного критерия Акаике (AIC), [?], информационного цитирования Акаике с коррекцией (AICC), байесовского информационного критерия (BIC), информационного критерия Ханнана-Куинна (HQIC) и информационного критерия Шварца. (SIC), [21].Данные получены из [18], это наработка на отказ (тысячи часов) насосов второго контура, табл. 1. MLE и K–S параметров для насосов второго реактора. Логарифмическое правдоподобие, значения AIC, AICC, BIC, HQIC и SIC подобранных моделей. Подставив МЛЭ неизвестных параметров ϑ , γ , α , β в (6.7), мы получим оценку ковариационной матрицы дисперсии в виде
I0-1=(6.773×10−34,189×10−4−3,945×10−3−1,65×10−34,189×10−44,308×10−4−4,871×10−4−0,013−3,945×10−3−4,871×10−43,343× 10-30,017-1,65×10-3-0,0130,0170,806). Непараметрическая оценка функции выживания S ( x ) с использованием метода Каплана-Мейера и его подобранные параметрические оценки, когда предполагается, что распределение является ОГЭ-FWE, FW, W, MW, RAW и EW вычисляются и на рисунке 4. Оценка Каплана-Мейера функции выживания для данных. На рис. 5 представлена форма коэффициента опасности ч ( x ) и кумулятивной функции плотности cdf для ОГЭ-FWE, FW, W, MW, RAW и EW, которые используются для подгонки данных после неизвестных параметров включенные в каждый дистрибутив, заменяются их MLE. Подобранный уровень опасности и кумулятивная функция распределения для данных. Мы обнаружили, что распределение OGE-FWE с четырьмя параметрами обеспечивает лучшее соответствие, чем предыдущее новое модифицированное гибкое расширение Вейбулла (FWE), которое было лучшим в [4].Он имеет наибольшую вероятность и наименьшие значения AIC, AICC, BIC, HQIC и SIC среди рассмотренных в этой статье. Мы предложили новое распределение, основанное на нечетных обобщенных экспоненциальных семейных распределениях, это распределение названо нечетным обобщенным экспоненциальным гибким распределением расширения Вейбулла OGE-FWE. Изучены некоторые его статистические свойства. Для оценки параметров модели используется метод максимального правдоподобия. Наконец, мы представляем приложение, использующее реальные данные.Мы показываем, что распределение OGE-FWE лучше соответствует некоторым хорошо известным наборам данных, чем существующие модификации распределений Вейбулла и гибких расширений Вейбулла. Минимальные требования к образованию: Основные требования: A. Степень: , которая включает 24 семестровых часа математики и статистики, из которых не менее 12 семестровых часов приходится на математику и 6 семестровых часов на статистику. Курсы, приемлемые для выполнения требований курса математики, должны включать как минимум четыре из следующих предметов: дифференциальное исчисление, интегральное исчисление, расширенное исчисление, теорию уравнений, векторный анализ, углубленную алгебру, линейную алгебру, математическую логику, дифференциальные уравнения или любые другие углубленные знания. курс математики, для которого один из них был обязательным условием.Курсы по математической статистике или теории вероятностей с предварительным условием элементарного исчисления или более продвинутые курсы будут приняты для удовлетворения требований по математике с условием, что один и тот же курс не может быть засчитан как для требований по математике, так и для требований по статистике. ИЛИ B. Сочетание образования и опыта — не менее 24 семестровых часов по математике и статистике, в том числе не менее 12 часов по математике и 6 часов по статистике, как показано в пункте А выше, плюс соответствующий опыт или дополнительное образование. Примечание: Кроме того, чтобы получить баллы за курсовую работу, которая не указана в стенограмме как «Статистика» или не содержит «статистику» в названии курса, кандидаты должны приложить копию официального описания курса, в котором уточняется, что курс имеет статистическое содержание, или письменная документация, которая должна быть на официальном бланке школы от профессора или школьного чиновника, подтверждающая, что содержание курса либо соответствует 50-процентным требованиям курса статистики, либо является статистическим курсом. В дополнение к требованиям к базовому образованию, указанным выше, кандидаты должны иметь специализированный опыт или образование, если разрешена замена, перечисленные ниже. Специализированный опыт: Для GS-11 требуется один год опыта работы на Федеральной службе уровня сложности и ответственности, эквивалентного GS-09 . Опыт работы на этой должности включает: использование статистических методов для проведения статистического анализа; подготовка технических отчетов и профессиональных документов по данным социально-экономических или демографических исследований; разработка дизайна образца; определение спецификаций и методологии опроса; документирование анализов и выводов в письменных и устных отчетах. ИЛИ Образование: 3 года обучения в аспирантуре с постепенным повышением уровня, ведущим к получению степени доктора философии. Степень или PhD. или эквивалентная докторская степень ИЛИ Специализированный опыт: Для GS-12 необходимо иметь один год опыта работы на Федеральной службе уровня сложности и ответственности, эквивалентного GS-11 . Опыт работы на этой должности включает: использование статистических методов для проведения статистического анализа; подготовка технических отчетов и профессиональных документов по данным социально-экономических или демографических исследований; разработка дизайна образца; определение спецификаций и методологии опроса; документирование анализов и выводов в письменных и устных отчетах; разработка решений статистических задач; создание новых статистических и аналитических методологий; разработка процедур выборки и оценки для обследований и руководство группами для выполнения проектов ИЛИ Образование: Образование нельзя заменить специальным опытом на этом уровне обучения. Опыт относится к оплачиваемому и неоплачиваемому опыту, включая волонтерскую работу в рамках программ Национальной службы (например, Корпус мира, Американский корпус) и других организаций (например, профессиональных, благотворительных, религиозных, духовных, общественных, студенческих, общественных). Волонтерская работа помогает формировать важные компетенции, знания и навыки и может обеспечить ценное обучение и опыт, которые непосредственно переводятся в оплачиваемую работу. Вы получите кредит за весь квалификационный опыт, включая опыт работы волонтером.z ۺA−__A,Yt* Задание 18. На диаграмме показан возрастной состав населения Австрии. Определите по диаграмме, население какого возраста составляет более 40% всего населения. 1) 0-14 лет; 2) 15-50 лет; 3) 51-64 года; 4) 65 лет и старше Решение. Более 40% это почти половина населения. Из рисунка видно, что это соответствует наибольшему сегменту с возрастом от 15 до 50 лет. Ответ: 2. Задание 19. В среднем из 150 карманных фонариков в продаже шесть неисправных. Найти вероятность того, что выбранный в магазине фонарь будет объединен. Решение. Обозначим через событие и выбор хорошего фонарика. Количество благоприятных исходов для события А равно 150-6=144 (среднее количество хороших фонарей).Все возможные исходы равны 150, следовательно, . Ответ: 0,96. Задание 20. В компании «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле С = 6000 + 4100Н, где Н — количество колец, установленных в колодце. По этой формуле рассчитайте стоимость колодца из 8 колец. Ответ укажите в рублях. Решение. Находим стоимость скважины при использовании формулы расчета стоимости С, получаем. В среднем из 75 учетных фонарей, поступивших в продажу, 15 неисправных. Включить в? ? Содержание того, что выбранный мутный в магазине фонарик будет исправлен 15/75 = 1/5 — дефектный 1-1/5 = 4/5 = 0,8 ответ: 0,8 Похожие вопросы  Тогда с помощью метода обратного преобразования мы можем получить случайную величину X следующим образом
Тогда с помощью метода обратного преобразования мы можем получить случайную величину X следующим образом
3.2. Режим
 (3.6) в общем случае. Поэтому его необходимо получить численными методами.
(3.6) в общем случае. Поэтому его необходимо получить численными методами. 3.3. Асимметрия и эксцесс
3.4. Моменты
Теорема 3.1.
Доказательство.
 10)µr′=∫0∞xrf(x;ϑ,γ,α,β)dx.
10)µr′=∫0∞xrf(x;ϑ,γ,α,β)dx. 
4. Функция генерации момента
Теорема 4.1.

Доказательство.
5. Статистика заказов
 1)fr:n(x;ϕ)=1B(r,n−r+1)[F(x;ϕ)]r−1[1−F(x;ϕ)]n−rf(x;ϕ) ,
1)fr:n(x;ϕ)=1B(r,n−r+1)[F(x;ϕ)]r−1[1−F(x;ϕ)]n−rf(x;ϕ) ,  1) и уравнение (2.2) в уравнение (5.3), мы получаем функцию плотности вероятности для r -й статистики порядка.
1) и уравнение (2.2) в уравнение (5.3), мы получаем функцию плотности вероятности для r -й статистики порядка. 6. Оценка параметров
6.1. Оценка максимального правдоподобия:
 2)ℒ=nln(ϑγ)+∑i=1nln(α+βxi2)+∑i=1n(α+βxi2)+∑i=1neαxi−βxi−ϑ∑i=1n(eeαxi−βxi−1) +(γ−1)∑i=1nln[1−e−ϑ(eeαxi−βxi−1)].
2)ℒ=nln(ϑγ)+∑i=1nln(α+βxi2)+∑i=1n(α+βxi2)+∑i=1neαxi−βxi−ϑ∑i=1n(eeαxi−βxi−1) +(γ−1)∑i=1nln[1−e−ϑ(eeαxi−βxi−1)]. 6.2. Асимптотические доверительные границы
 [12], где I
− 1
является обратной наблюдаемой информационной матрицей, которая определяется следующим образом
[12], где I
− 1
является обратной наблюдаемой информационной матрицей, которая определяется следующим образом
 ),
), 7. Заявка
Таблица 2. 2,160
0,746
0,402
0,954
0,491
6,560
4,992
0,347
0,150
0,358
0,101
1,359
3,465
1,060
0,614
1,921
4. 
К-С
ОГЭ-ФВЭ
0,2380
2,0700
–
0,069
0,113
0,0760
Гибкий Weibull
0,0207
2,5875
–
–
–
0,1342
Вейбулл
0,8077
13,9148
–
–
–
0,1173
Модифицированный Weibull
0.
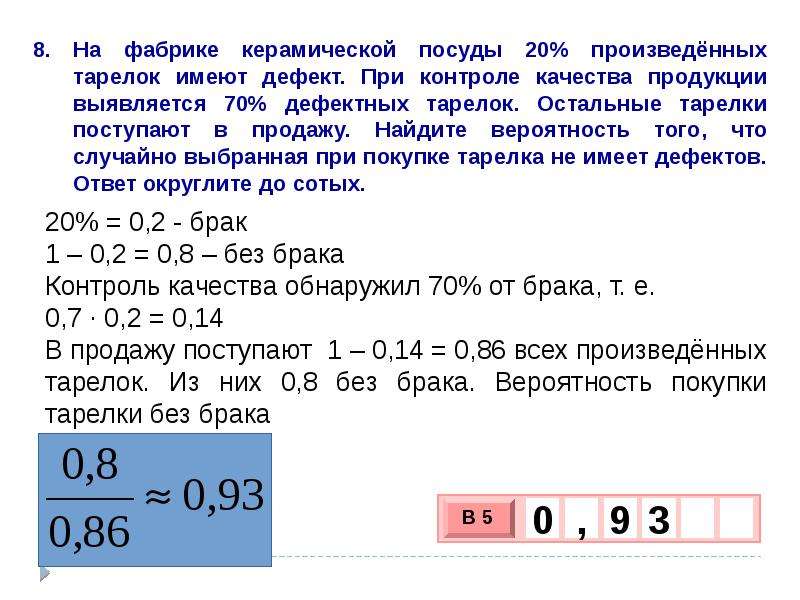 1213
1213 0,7924
0,0009
–
–
0,1188
Уменьшенная добавка Weibull
0,0070
1,7292
0,0452
–
–
0,1619
Расширенный Вейбулл
0,4189
1.0212
10,2778
–
–
0,1057

Таблица 3. Модель
л
АИК
АИКК
БИК
HQIC
СИК
ОГЭ-ФЭВ
−29,2980
66,5960
68,8182
71.1380
10,5590
71.1380
Гибкий Weibull
−83,3424
170,6848
171,2848
172,9558
12,5416
172.9558
Вейбулл
−85,4734
174,9468
175,5468
177,2178
12,5915
177,2178
Модифицированный Weibull
−85,4677
176,9354
178,1986
180,3419
12.6029
180,3419
Уменьшенная добавка Weibull
−86,0728
178,1456
179,4088
181,5521
12.6168
181,5521
Расширенный Вейбулл
−86,6343
179,2686
180,5318
182,6751
12,6296
182,6751
8. Выводы
Ссылки
[8] Ф. Фамойе, К. Ли и О. Олумолейд, Распределение бета-Вейбулла, Журнал статистической теории и приложений, Том. 4, № 2, 2005, стр. 121-36. [10] J Kenney and E Keeping, Mathematics of Statistics, Princeton, Vol. 1, 1962. [18] М. Салман, Супрахардана и С. Прайото, Общее время анализа испытательной площадки для механических компонентов реактора RSG-GAS, Atom Indones, Vol.25, № 2, 1999, стр. 155-61. [19] А. М. Сархан и М. Зайндин, Модифицированное распределение Вейбулла, Applied Sciences, Vol. 11, 2009 г., стр. 123-136. [24] М. Х. Тахир, Г. М. Кордейро, М. Ализаде, М. Мансур, М. Зубаир и Г. Г. Хамедани, Нечетное обобщенное экспоненциальное семейство распределений с приложениями, Журнал статистических распределений и приложений, Том. 2, № 1, 2015. С. 1-28. [27] WA Weibull, Статистическая функция распределения широкого применения, Journal of Applied Mechanics, Vol. 18, 1951, стр. 293-6. USAJOBS — Объявление о вакансии
Теория вероятностей. Задания к ОГЭ. Теория вероятностей в среднем для 75 карманных фонариков имеет
Источник задачи: Решение 3353.-20. ОГЭ 2016 Математика, И.В. Ященко. 36 вариантов.
Теория вероятностей
Ответы:






 6 июня 2011 года списывание ЕГЭ по математике приобрело наибольший размах. Готовились к нему заранее: по договоренности с создателем мошеннического сайта «Абитуриент.Про» (Мурат Абдувалиев, Москва) в группу набирались «доноры» — присылали в группу варианты ЕГЭ, и «хирурги» — решали задачи и выложенные решения. Обычные пользователи — выпускники — выходили в интернет во время экзамена и переписывали решения в экзаменационные бланки.
6 июня 2011 года списывание ЕГЭ по математике приобрело наибольший размах. Готовились к нему заранее: по договоренности с создателем мошеннического сайта «Абитуриент.Про» (Мурат Абдувалиев, Москва) в группу набирались «доноры» — присылали в группу варианты ЕГЭ, и «хирурги» — решали задачи и выложенные решения. Обычные пользователи — выпускники — выходили в интернет во время экзамена и переписывали решения в экзаменационные бланки. Услуга была платной, но количество ее пользователей, по словам организаторов, достигало 100 тысяч человек.
Услуга была платной, но количество ее пользователей, по словам организаторов, достигало 100 тысяч человек.  Более семи тысяч фрагментов заданий, размещенных в Интернете, «Учительская газета» передала главе Рособрнадзора Любови Глебовой. Абсолютно ничего не произошло. Не было никакой реакции. Экзамены шли, а списывать продолжали. Вот фрагмент телеэфира «Открытой студии» на «5 канале», который состоялся 24 июня, в котором помощник главы Рособрнадзора Сергей Шатунов излагает позицию надзорного ведомства.
Более семи тысяч фрагментов заданий, размещенных в Интернете, «Учительская газета» передала главе Рособрнадзора Любови Глебовой. Абсолютно ничего не произошло. Не было никакой реакции. Экзамены шли, а списывать продолжали. Вот фрагмент телеэфира «Открытой студии» на «5 канале», который состоялся 24 июня, в котором помощник главы Рособрнадзора Сергей Шатунов излагает позицию надзорного ведомства. И ситуация ухудшилась. Что посоветуете, чтобы не ухудшилось еще больше?
И ситуация ухудшилась. Что посоветуете, чтобы не ухудшилось еще больше?  Обнаруженная утечка стала достоянием гласности, и уже утром 22 июня, на следующий день после экзамена, Министерство просвещения провело пресс-конференцию, на которой министр Люк Шатель заявил, что решение опубликованной задачи не будет засчитано ни одному из 160 000 выпускников.В ответ родители потребовали аннулировать весь ЕГЭ, перенести школьные каникулы и предоставить всем учащимся возможность пересдать ЕГЭ. (Это вполне соответствует французской традиции, по аналогичным делам в 1982 и 2005 годах принимались такие решения.)
Обнаруженная утечка стала достоянием гласности, и уже утром 22 июня, на следующий день после экзамена, Министерство просвещения провело пресс-конференцию, на которой министр Люк Шатель заявил, что решение опубликованной задачи не будет засчитано ни одному из 160 000 выпускников.В ответ родители потребовали аннулировать весь ЕГЭ, перенести школьные каникулы и предоставить всем учащимся возможность пересдать ЕГЭ. (Это вполне соответствует французской традиции, по аналогичным делам в 1982 и 2005 годах принимались такие решения.)  Мы никого не ищем и никого не наказываем. Чиновники выделяют деньги и осваивают их. Поэтому по нашей традиции в августе Минобрнауки объявило конкурс и в октябре выделило 28 млн рублей на разработку средств защиты ЕГЭ.По условиям конкурса подрядчик должен был много и упорно работать. Первые 40 дней работы министерство оценило в 18 миллионов рублей — это 500 тысяч в день. Правильно: полмиллиона рублей каждый день в течение полутора месяцев. Но это не все. Потом еще 10 миллионов рублей на 10 месяцев, всего по миллиону в месяц.
Мы никого не ищем и никого не наказываем. Чиновники выделяют деньги и осваивают их. Поэтому по нашей традиции в августе Минобрнауки объявило конкурс и в октябре выделило 28 млн рублей на разработку средств защиты ЕГЭ.По условиям конкурса подрядчик должен был много и упорно работать. Первые 40 дней работы министерство оценило в 18 миллионов рублей — это 500 тысяч в день. Правильно: полмиллиона рублей каждый день в течение полутора месяцев. Но это не все. Потом еще 10 миллионов рублей на 10 месяцев, всего по миллиону в месяц.  Наконец, исполнителю предстояло разработать предложения по внесению изменений в Административный и Уголовно-процессуальный кодексы Российской Федерации для привлечения к ответственности лиц, опубликовавших КИМ.
Наконец, исполнителю предстояло разработать предложения по внесению изменений в Административный и Уголовно-процессуальный кодексы Российской Федерации для привлечения к ответственности лиц, опубликовавших КИМ.  Почему она звонит мне? Звонила бы в Рособрнадзор, над ней бы просто посмеялись».
Почему она звонит мне? Звонила бы в Рособрнадзор, над ней бы просто посмеялись».  Их материалы я переслал на электронный адрес Генпрокуратуры.
Их материалы я переслал на электронный адрес Генпрокуратуры.  Как обычно: одни выкладывают варианты ЕГЭ, другие решают, третьи читают. Однако неожиданно для них через несколько часов группа была заблокирована.Она восстановилась в математике.
Как обычно: одни выкладывают варианты ЕГЭ, другие решают, третьи читают. Однако неожиданно для них через несколько часов группа была заблокирована.Она восстановилась в математике. 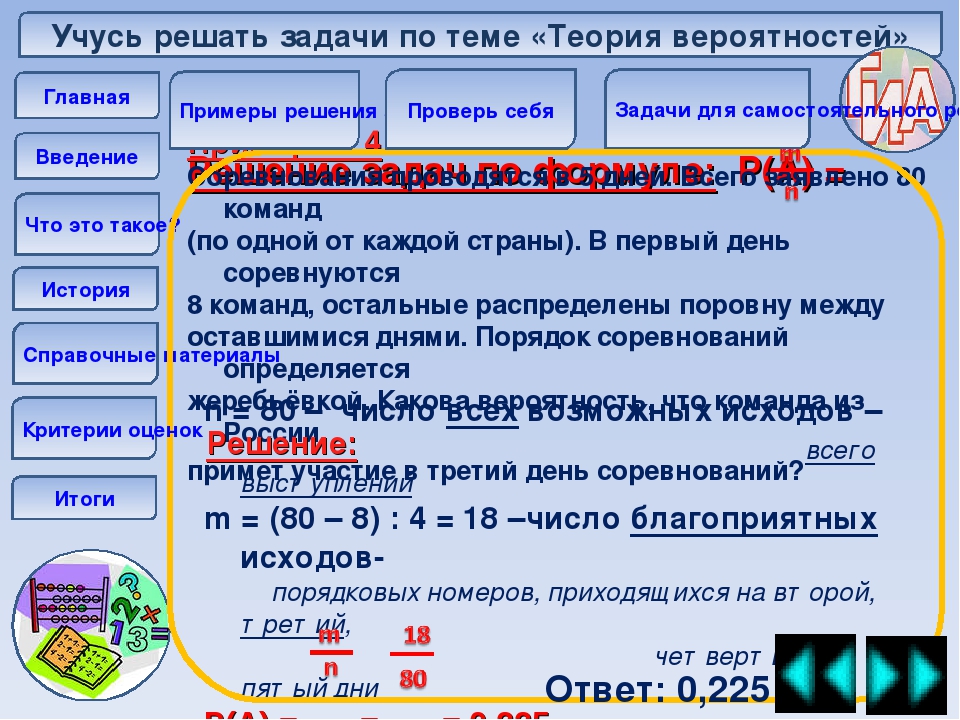 В том виде, в каком они проводятся сегодня, эти обследования не приносят пользы, а вредят.
В том виде, в каком они проводятся сегодня, эти обследования не приносят пользы, а вредят. 
 м холодной воды 34 рубля 17 копеек? Дайте ответ в рублях.
м холодной воды 34 рубля 17 копеек? Дайте ответ в рублях.  Также необходимо уметь находить максимальное или наименьшее значение и строить графики исследуемых функций. Допущенные ошибки носят случайный характер при чтении условий задачи, чтении схемы.
Также необходимо уметь находить максимальное или наименьшее значение и строить графики исследуемых функций. Допущенные ошибки носят случайный характер при чтении условий задачи, чтении схемы. Задание 3 проверяет умение вычислять площадь фигуры на бумаге в клетку, умение вычислять градусные меры углов, вычислять периметры и т. д.
Задание 3 проверяет умение вычислять площадь фигуры на бумаге в клетку, умение вычислять градусные меры углов, вычислять периметры и т. д.
