Задания по ВПР 4 класс математика 2017
- Категория: Математика
- Опубликовано: 26 Июль 2017
Для подготовки к ВПР в 4 классе по математике можно использовать задания из реальных вариантов которые рассылались в школы страны в 2015 — 2017 г.
Смотрите новые образцы ВПР 2018 года
Задания ВПР по математике 4 класс с ответами 2017 год
Задания по ВПР 2016 по математике для 4 класса с ответами
Задания по ВПР 2015 математика 4 класс с ответами
(эти задания рассылались в школы и собраны в основном с личных страничек учителей)
Каждому ученику будет предоставлен вариант, который представляет собой лист с заданиями.
Рекомендации по подготовке и проведению ВПР
Что можно порекомендовать родителям в связи с проведением ВПР?
— Проявлять внимание и интерес к действиям школы по обеспечению объективности и прозрачности образовательного процесса в вопросах оценивания, проявлять заинтересованность в получении объективной информации об уровне подготовки ребенка, имеющихся у него проблемах и планах школы по устранению этих проблем.
— Проявлять интерес к результатам ребенка, интересоваться, не нуждается ли он(она) в помощи, оказывать посильную помощь и поддержку, при необходимости.
Что можно порекомендовать школе в связи с проведением ВПР?
— Утвердить порядок проведения работы в ОО;
— организовать штатное итоговое повторение в каждом классе в рамках образовательного процесса, избегая элементов натаскивания;
— обеспечить возможность получения объективных результатов на всех стадиях проведения ВПР;
— провести анализ результатов;
— использовать полученные аналитические выводы в дальнейшей работе.
Не рекомендуется:
— проводить работу во время каникул;
— специально готовить обучающихся к выполнению работы;
— решать посредством ВПР какие-либо административные или учебные задачи помимо диагностических;
— ставить отметки;
— оставлять без контроля процедуру проведения ВПР.
ВПР в 4 классах – это не «ЕГЭ для начальной школы», поскольку по результатам ВПР не принимаются никакие обязательные решения, важные для определения дальнейшей судьбы или образовательной траектории школьника. Однако результаты ВПР в 4 и в других классах могут быть частью портфолио ученика, которое может учитываться по его желанию наряду с другими сведениями при переходе из класса в класс или из школы в школу при условии, что имеются основания считать эти результаты объективными.
Смотрите также:
vpr-ege.ru
ВПР Задачи. 4 класс
Просмотр содержимого документа
«ВПР Задачи. 4 класс»

Задачи ВПР
4 класс

В гараже стоят 750 автомобилей. Грузовые автомобили имеют по 6 колёс, а легковые – по 4 колеса. Сколько и каких автомобилей в гараже, если колёс всего 3024?

1) 4 х 750 = 3000 (к) – было бы, если бы все автомобили имели по 4 колеса. 2) 3024 – 3000 = 24 (к) – сверх 3000 колёс из-за автомобилей с шестью колёсами. 3) 6 – 4 = 2 (к) – разница в колёсах между одним легковым и одним грузовым автомобилем. 4) 24 : 2 = 12 (ав.) – грузовые. 5) 750 – 12 = 738 (ав.) – легковые. Ответ: 12 грузовых и 738 легковых автомобилей .

На складе стоят 650 двухколёсных и трёхколёсных велосипедов. Сколько и каких велосипедов стоит на складе, если колёс всего 1348?

1) 650 х 2 = 1300 (к.) – было бы если бы все велосипеды имели бы по 2 колеса. 2) 1348 – 1300 = 48 (к) – сверх 1300 колёс из-за велосипедов с тремя колёсами. 3) 3 – 2 = 1(к) – разница в колёсах между двухколёсных и трёхколёсных велосипедах. 4) 48 : 1 = 48 (в.) – трёхколёсных. 5) 1348 – 48 = 1300 (в) – двухколёсных. Ответ: 1300 двухколёсных и 48 трёхколёсных велосипедов.

В детском мире продавали двухколёсные и трёхколёсные велосипеды. Максим пересчитал все рули и все колёса. Получилось 12 рулей и 27 колёс. Сколько трёхколёсных велосипедов продавали в детском мире?

Рулей 12 – значит и велосипедов было 12. 1) 12 х 2 = 24 (к.) – было бы, если бы все велосипеды были двухколёсные. 2) 27 – 24 = 3 (к.) – сверх 27. т.к. были трёхколёсные велосипеды.

Квадрат со стороной 1м разрезали на квадраты со стороной 1 см и выстроили их в один ряд в виде полосы шириной 1 см. Какой длины получилась полоса?

1 м = 100 см 100 х 100 = 10 000(кв. см) – площадь данного квадрата. Значит квадрат состоит из 10 000 квадратиков со стороной 1 см. Если из них выстроить полосу со стороной 1 см, то её длина будет равна 10 000 см = 100 м Ответ: 100 метров.

У поля прямоугольной формы одна из сторон равна 30 м. Половина поля засеяна овсом, а другая половина — пшеницей и рожью. Пшеница занимает 600 кв.м, а рожь – одну шестую часть всего поля. Какой длины должен быть забор, огораживающий всё поле?
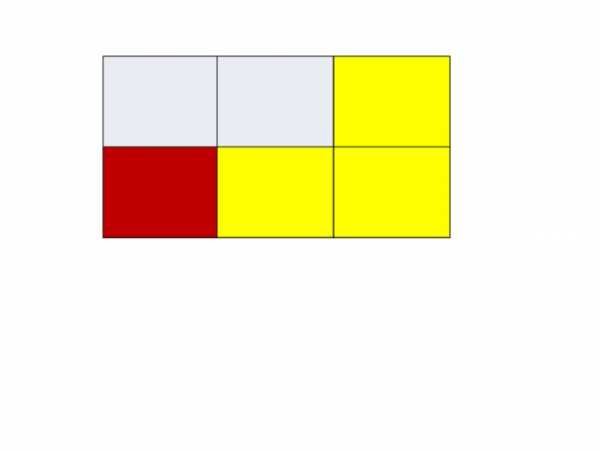

1) Одна часть из 6 занята рожью. Половина из 6 частей – это 3 части, значит, 3 – 1 = 2 части занято пшеницей.

1) Одна часть из 6 занята рожью. Половина из 6 частей – это 3 части, значит, 3 – 1 = 2 части занято пшеницей. 2) 600 : 2 = 300 (кв.м) – это одна часть.

1) Одна часть из 6 занята рожью. Половина из 6 частей – это 3 части, значит, 3 – 1 = 2 части занято пшеницей. 2) 600 : 2 = 300 (кв.м) – это одна часть. 3) 300 х 6 = 1800 (кв.м)- площадь всего поля.

1) Одна часть из 6 занята рожью. Половина из 6 частей – это 3 части, значит, 3 – 1 = 2 части занято пшеницей. 2) 600 : 2 = 300 (кв.м) – это одна часть. 3) 300 х 6 = 1800 (кв.м)- площадь всего поля. 4) 1800 : 30 = 60 (м) – длина поля.

1) Одна часть из 6 занята рожью. Половина из 6 частей – это 3 части, значит, 3 – 1 = 2 части занято пшеницей. 2) 600 : 2 = 300 (кв.м) – это одна часть. 3) 300 х 6 = 1800 (кв.м)- площадь всего поля. 4) 1800 : 30 = 60 (м) – длина поля. 5) (60 + 30) х 2 = 180 (м.) – длина забора. Ответ: 180 м.

В классе 14 девочек. Из них 8 занимаются танцами, а 9 – пением. Сколько девочек и танцует и поёт?

8 + 9 – 14 = 3 (д). Ответ: 3 девочки.
multiurok.ru
ВПР 4 класс математика 2017. Вариант 2 с ответами
ВПР по математике за 4 класс 2017 года под редакцией И. В. Ященко — Вариант №2
Задание №1
Найди значение выражения 82 — 19.
Ответ:
63
Задание №2
Найди значение выражения (30 + 33) : 9 + 13.
Решение:
(30 + 33) : 9 + 13 = 63 : 9 + 13 = 7 + 13 = 20
Ответ:
20
Задание №3
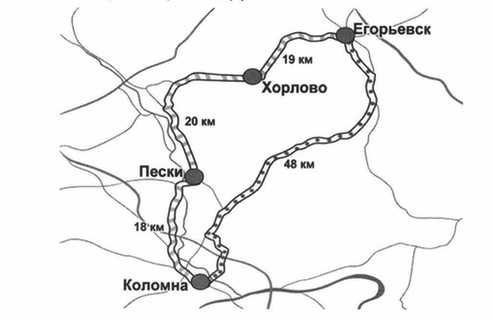
Из Егорьевска в Коломну можно проехать двумя способами. Рассмотри рисунок и ответь на вопрос: на сколько километров один путь короче другого?
Решение:
18 + 20 + 19 = 57 (км.) — длина первого пути
48 (км.) — длина второго пути
57 — 48 = 9 (км.)
Ответ:
На 9 километров один путь короче другого.
Задание №4
Поезд вышел в восемь часов утра и прибыл на конечную станцию в одиннадцать часов утра следующих суток. Сколько часов он был в пути?
Решение:
С восьми часов утра сегодня до восьми часов утра завтра — 24 часа плюс 3 часа до 11 утра, значит
24 + 3 = 27 (ч.)
Ответ:
Поезд был в пути 27 часов.
Задание №5
На рисунке ниже изображена фигура.

- Найди площадь этой фигуры, если сторона клетки — 1 см.
Решение:
Самое простое решение — это элементарный подсчет закрашенных клеток — 15.
Ответ:
15 см2
- Найди периметр этой фигуры, если сторона клетки — 1 см.
Решение:
5 + 2 + 2 + 1 + 2 + 1 + 4 + 3 + 1 + 1 = 22 см
Ответ:
Периметр 22 см
Задание №6
В таблице приведены цены на пирожные в трёх кондитерских (в рублях). Используя эти данные, ответь на вопросы.
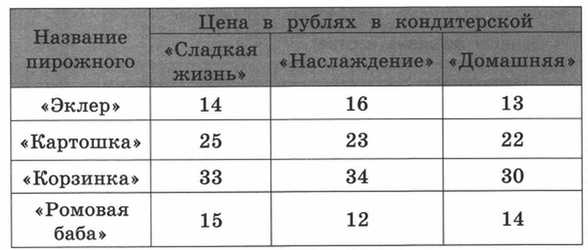
- В какой кондитерской пирожное «Корзинка» самое дорогое?
Ответ:
В кондитерской «Наслаждение».
- Какое пирожное и в какой кондитерской дешевле всего?
Ответ:
Пирожное «Ромовая баба» в кондитерской «Наслаждение».
Задание №7
Найди значение выражения 28028 : 14 — 320 * 5.
Решение:
28028 : 14 — 320 * 5 = 2002 — 1600 = 402
Ответ:
402
Задание №8
Лида хотела купить 2 двухлитровые бутылки газированной воды. Но в магазине вода была только в бутылках по пол-литра. Лида решил купить столько же воды, но в бутылках по пол-литра. Сколько бутылок она должна купить?
Решение:
2 * 2 = 4 (л.) — всего литров воды хотела купить Лида
4 * 2 = 8 (б.) — потребуется бутылок по пол-литра
Ответ:
Лида должна купить 8 бутылок.
Задание №9
Оля, Вера, Дина и Наташа собираются пойти на дискотеку. При этом девочки хотят надеть платья разных цветов. У Оли есть красное и синие платья, у Веры — только жёлтое, у Дины — красное и зелёное, а у Наташи — синее и жёлтое платья.
- Какое платье наденет Оля?
Решение:
Оля — красное и синие
Вера — жёлтое
Дина — красное и зелёное
Наташа — синее и жёлтое
Ответ:
Оля оденет красное платье.
- Какое платье наденет Дина?
Ответ:
Дина оденет зелёное платье.
Задание №10
Дима написал на футболке свое имя (см. рис.). Затем он подошёл к зеркалу. Нарисуй, как будет выглядеть отражение его имени в зеркале.

Задание №11
В классе 26 человек, из них 11 девочек. Известно, что у 17 человек светлые волосы. Сколько может быть девочек со светлыми волосами? Найди наименьшее возможное число.
Решение:
26 — 11 = 15 (ч.) — всего мальчиков в классе
17 — 15 = 2 (ч.) — если предположить, что все мальчики имеют светлые волосы, то на долю девочек останется 2 человека со светлыми волосами
Ответ:
2 девочки.
Навигация по записям
gdzotl.ru
ВПР 4 класс математика варианты с ответами 2018 год
4 классы написали очередную проверочную работу ВПР по математике 24 апреля 2018 года.
Всероссийская проверочная работа по математике включает 11 заданий, на ее выполнение отводится 45 минут. При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором.
ВПР по математике 4 класс 2018 год варианты с ответами
Распределение заданий варианта проверочной работы по содержанию, проверяемым умениям и видам деятельности.
В заданиях 1, 2, 7 проверяется умение выполнять арифметические действия с числами и числовыми выражениями. В частности, задание 1 проверяет умение выполнять сложение, вычитание, умножение и деление однозначных, двузначных и трехзначных чисел в случаях, сводимых к действиям в пределах 100 (в том числе с нулем и числом 1).
Задание 2 проверяет умение вычислять значение числового выражения, соблюдая при этом порядок действий. Заданием 7 контролируется умение выполнять письменно действия с многозначными числами (сложение, вычитание, умножение и деление на однозначное, двузначное числа в пределах 10 000).
Выполнение заданий 3 и 8 предполагает использование начальных математических знаний для описания и объяснения окружающих предметов, процессов, явлений, для оценки количественных и пространственных отношений предметов, процессов, явлений. Так, задания 3 и 8 поверяют умение решать арифметическим способом (в одно-два действия) учебные задачи и задачи, связанные с повседневной жизнью.
Задание 4 выявляет умение читать, записывать и сравнивать величины (время), используя основные единицы измерения величин и соотношения между ними. Умение решать текстовые задачи в три-четыре действия проверяется заданием 8. При этом в задании 8 необходимо выполнить действия, связанные с использованием основных единиц измерения величин (длина, вес).
Умение исследовать, распознавать и изображать геометрические фигуры проверяется заданием 5. Пункт 1 задания предполагает вычисление периметра прямоугольника и квадрата, площади прямоугольника и квадрата.
Пункт 2 задания связан с построением геометрических фигур с заданными измерениями (отрезок, квадрат, прямоугольник) с помощью линейки, угольника.
В задании 6 проверяется умение работать с таблицами, схемами,
графиками, диаграммами, анализировать и интерпретировать данные. Задание предполагает чтение и анализ несложных готовых таблиц.
Овладение основами логического и алгоритмического мышления контролируется заданиями 9 и 11.
Задание 9 связано с интерпретацией информации (объяснять, сравнивать и обобщать данные, делать выводы и прогнозы).
Задание 11 требует умения решать текстовые задачи в три-четыре действия. Овладение основами пространственного воображения выявляется заданием 10. Оно предполагает описание взаимного расположения предметов в пространстве и на плоскости.
Успешное выполнение обучающимися заданий 10 и 11 в совокупности с высокими результатами по остальным заданиям говорит о целесообразности построения для них индивидуальных образовательных траекторий в целях развития их математических способностей.
Приводим таблицу перевода баллов ВПР по математике в оценку. Таблица опубликована в демоверсии в описании работы.
Смотрите также:
vprklass.ru
ВПР 4 класс (математика) Карточки-задания
Вариант 1
Решите примеры и задачи:
1. 85 — 11
2. 7+9* (83 — 31)
3. 100- (32*2+17)
4. Во сколько начались занятия, если они продолжались 1 час. 22 мин, а закончились в 16 час .26 мин. ?
5. Определите площадь и периметр прямоугольника со сторонами 6 см и 5см.
6. 12012 : 12 + 210 * 14
==================================
==================================
Вариант 2
Решите примеры и задачи:
1. 17 + 82
2. 9+9* (86 — 50)
3. 100- (32*2+17)
4. Во сколько начались занятия, если они продолжались 1 час. 31 мин, а закончились в 17 час .22 мин. ?
5. Определите площадь и периметр прямоугольника со сторонами 8 см и 5см.
6. 2002 : 2 + 650 * 4
==================================
==================================
Вариант 3
Решите примеры и задачи:
1. 35 + 71
2. 3+6* (98 — 92)
3. 100- (71*1+23)
4. Во сколько начались занятия, если они продолжались 1 час. 21 мин, а закончились в 17 час .20 мин. ?
5. Определите площадь и периметр прямоугольника со сторонами 7 см и 5см.
6. 5005 : 5 + 680 * 5
==================================
==================================
Вариант 4
Решите примеры и задачи:
1. 77 + 96
2. 3+7* (77 — 17)
3. 100- (32*1+37)
4. Во сколько начались занятия, если они продолжались 1 час. 14 мин, а закончились в 16 час .36 мин. ?
5. Определите площадь и периметр прямоугольника со сторонами 9 см и 3см.
6. 12012 : 12 + 540 * 12
==================================
==================================
Вариант 5
Решите примеры и задачи:
1. 59 — 44
2. 2+4* (56 + 88)
3. 100- (32*1+37)
4. Во сколько начались занятия, если они продолжались 1 час. 35 мин, а закончились в 17 час .38 мин. ?
5. Определите площадь и периметр прямоугольника со сторонами 7 см и 8см.
6. 16016 : 16 — 10 * 12
==================================
==================================
Вариант 6
Решите примеры и задачи:
1. 17 + 69
2. 9+5* (72 — 69)
3. 100- (22*3+17)
4. Во сколько начались занятия, если они продолжались 1 час. 18 мин, а закончились в 15 час .31 мин. ?
5. Определите площадь и периметр прямоугольника со сторонами 6 см и 5см.
6. 5005 : 5 — 30 * 7
==================================
==================================
Вариант 7
Решите примеры и задачи:
1. 16 + 57
2. 8+3* (48 + 96)
3. 100- (32*2+17)
4. Во сколько начались занятия, если они продолжались 1 час. 18 мин, а закончились в 15 час .13 мин. ?
5. Определите площадь и периметр прямоугольника со сторонами 7 см и 8см.
6. 12012 : 12 + 200 * 6
==================================
Верные ответы для варианта 1
1. 74
2. 475
3. 19
4. 15 час .4 мин.
5. 30 кв. см и22 см
6. 3941
Верные ответы для варианта 2
1. 99
2. 333
3. 19
4. 15 час .51 мин.
5. 40 кв. см и26 см
6. 3601
Верные ответы для варианта 3
1. 106
2. 39
3. 6
4. 15 час .59 мин.
5. 35 кв. см и24 см
6. 4401
Верные ответы для варианта 4
1. 173
2. 423
3. 31
4. 15 час .22 мин.
5. 27 кв. см и24 см
6. 7481
Верные ответы для варианта 5
1. 15
2. 578
3. 31
4. 16 час .3 мин.
5. 56 кв. см и30 см
6. 881
Верные ответы для варианта 6
1. 86
2. 24
3. 17
4. 14 час .13 мин.
5. 30 кв. см и22 см
6. 791
Верные ответы для варианта 7
1. 73
2. 440
3. 19
4. 13 час .55 мин.
5. 56 кв. см и30 см
6. 2201
==================================
multiurok.ru
ВПР 4 класс математика 2017. Вариант 1 с ответами
ВПР по математике за 4 класс 2017 года под редакцией И. В. Ященко — Вариант №1
Задание №1
Найди значение выражения 100 — 63.
Ответ:
37
Задание №2
Найди значение выражения (22 + 28) : 5 + 4.
Решение:
(22 + 28) : 5 + 4 = 50 : 5 + 4 = 10 + 4 = 14
Ответ:
14
Задание №3
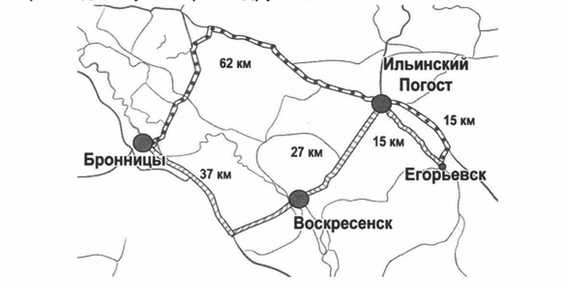
Из Бронниц в Егорьевск можно проехать двумя способами. Рассмотри рисунок и ответь на вопрос: на сколько километров один путь короче другого?
Решение:
62 + 15 = 77 (км.) — длина первого пути
37 + 27 + 15 = 79 (км.) — длина второго пути
79 — 77 = 2 (км.)
Ответ:
На 2 километра один путь короче другого.
Задание №4
Поезд вышел в два часа дня и прибыл на конечную станцию в пять часов вечера следующих суток. Сколько часов он был в пути?
Решение:
С двух часа дня сегодня до двух часов дня завтра — 24 часа плюс 3 часа до пяти вечера, значит
24 + 3 = 27 (ч.)
Ответ:
Поезд был в пути 27 часов.
Задание №5
На рисунке ниже изображена фигура.

- Найди площадь этой фигуры, если сторона клетки — 1 см.
Решение:
Самое простое решение — это элементарный подсчет закрашенных клеток — 10.
Ответ:
10 см2
- Найди периметр этой фигуры, если сторона клетки — 1 см.
Решение:
1 + 3 + 3 + 1 + 1 + 2 + 2 + 1 + 1 + 1 = 16 см
Ответ:
Периметр 16 см
Задание №6
В таблице приведены цены на пирожные в трёх кондитерских (в рублях). Используя эти данные, ответь на вопросы.
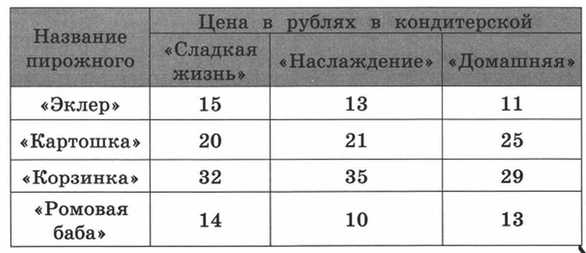
- В какой кондитерской пирожное «Корзинка» самое дорогое?
Ответ:
В кондитерской «Наслаждение».
- Какое пирожное и в какой кондитерской дешевле всего?
Ответ:
Пирожное «Ромовая баба» в кондитерской «Наслаждение».
Задание №7
Найди значение выражения 15015 : 5 — 230 * 3.
Решение:
15015 : 5 — 230 * 3 = 3003 — 690 = 2313
Ответ:
2313
Задание №8
Ко дню рождения Петя хотел купить 3 двухлитровые бутылки газированной воды. Но в магазине вода была только в бутылках по пол-литра. Петя решил купить столько же воды, но в бутылках по пол-литра. Сколько бутылок он должен купить?
Решение:
3 * 2 = 6 (л.) — всего литров воды хотел купить Петя
6 * 2 = 12 (б.) — потребуется бутылок по пол-литра
Ответ:
Петя должен купить 12 бутылок.
Задание №9
Маша, Таня, Света и Катя собираются пойти на дискотеку. При этом девочки хотят надеть платья разных цветов. У Маши есть красное и синие платья, у Тани — красное и зелёное, у Светы — красное и жёлтое, а у Кати только зелёное платье.
- Какое платье наденет Таня?
Решение:
Маша — красное и синие
Таня — красное и зелёное
Света — красное и жёлтое
Катя — зелёное
Ответ:
Таня оденет красное платье.
- Какое платье наденет Света?
Ответ:
Света оденет жёлтое платье.
Задание №10
Ваня написал на футболке свое имя (см. рис.). Затем он подошёл к зеркалу. Нарисуй, как будет выглядеть отражение его имени в зеркале.

Задание №11
В классе 24 человека, из них 13 девочек. Известно, что у 15 человек светлые волосы. Сколько может быть девочек со светлыми волосами? Найди наименьшее возможное число.
Решение:
24 — 13 = 11 (ч.) — всего мальчиков в классе
15 — 11 = 4 (ч.) — если предположить, что все мальчики имеют светлые волосы, то на долю девочек останется 4 человек со светлыми волосами
Ответ:
4 девочки.
Навигация по записям
gdzotl.ru
Разбор заданий ВПР по математике с решением (4 класс)
ВПР. Математика. 4 класс
1. Найди значение выражения .
Решение
Ответ: 24.
2. Найди значение выражения .
Решение.
Ответ: 5.
3. На диаграмме показана среднемесячная температура воздуха в Петрозаводске за каждый месяц 1976 года. По горизонтали указываются месяцы, по вертикали – температура в градусах Цельсия.
О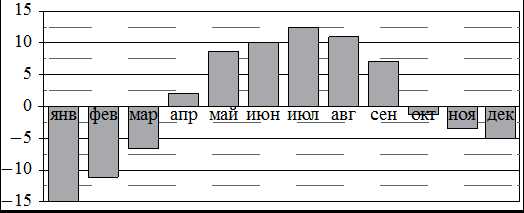
предели по диаграмме наименьшую среднемесячную температуру во второй половине 1976 года. Ответ укажи в градусах Цельсия.
Решение.
Вторая половина года длится с июля по декабрь включительно. Видно, что среднемесячная температура в декабре была самой низкой и составила –5 градусов Цельсия.
Ответ: –5.
4. Во сколько часов началась шахматная партия, если она длилась 2 часа 45 минут и закончилась в 19 часов 31 минуту?
Решение.
Ответ: 16 часов 46 минут.
5
. На клетчатом поле со стороной клетки 1 см изображен прямоугольник.
1) Найди периметр этого прямоугольника.
2) Проведи на рисунке выше прямую линию так, чтобы этот прямоугольник оказался разбит на два прямоугольника, площадь одного из которых в 2 раза меньше площади другого.
Решение.
1) Ответ: 22.
2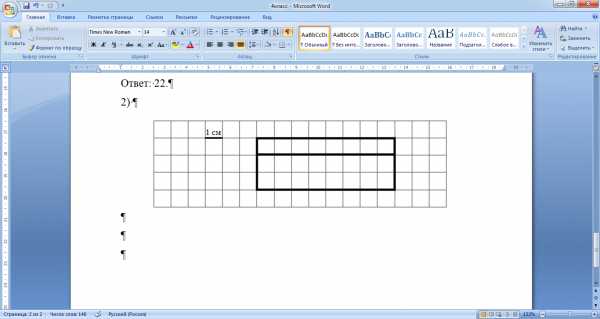
)
6. В конкурсе по математике участвовали четыре школьника. Ребятам было предложено решить три задачи, максимальная оценка за каждую составляла 10 баллов. Результаты олимпиады приведены в таблице. Используя эти данные, ответь на вопросы.
УчастникОценка за задачу №1
Оценка за задачу №2
Оценка за задачу №3
Пётр
6
7
9
Дмитрий
10
5
3
Александр
6
8
7
Альберт
10
0
8
1) Кто из школьников лучше всех справился со второй задачей?
2) Кто из школьников показал лучший результат по итогам всего конкурса?
Решение.
1) Рассматривая оценки школьников за вторую задачу, находим максимальную. Она равна 8 и соответствует результату Александра.
Ответ: Александр.
2) Найдём сумму баллов каждого участника.
Пётр: .
Дмитрий: .
Александр: .
Альберт: .
Больше всех баллов заработал Пётр.
Ответ: Пётр.
7. Найдите значение выражения .
Решение.
Ответ: 67041.
8. 20 книг разложили по полочкам и убрали в коробки. На одной полочке умещается 6 книг, а в одну коробку можно положить 2 книги. Полочек оказалось 2. Сколько потребовалось коробок?
Решение.
По полочкам разложили книг, остальные книг нужно положить в коробки. Всего коробок потребовалось штуки.
Ответ: 4.
9. С выполнением домашнего задания по русскому языку Маше помогает мама, с математикой – папа, а с английским языком – дедушка. Маша тратит ровно 40 минут на выполнение домашнего задания по каждому предмету. Папа занят с 9 до 10 часов, мама разговаривает по телефону с 9 часов до 11 часов 40 минут, а дедушка возвращается с секции по дзюдо в 11 часов.
Маша закончила смотреть мультики в 10 часов и управилась с домашним заданием ровно в 12 часов 20 минут.
1) Кто помогал Маше в 10:30?
2) Задание по какому предмету Маша начала выполнять после английского языка?
Решение.
1) Поскольку папа был свободен в то же время, что Маша закончила смотреть мультики, то первым делом она занялась математикой вместе с папой с 10 часов до 10 часов 40 минут. Ответ: папа.
2) Раньше мамы освободился дедушка, поэтому после выполнения домашнего задания по математике, Маша вместе с дедушкой стала выполнять английский с 11 часов до 11:40. Соответственно, после английского языка Маша принялась выполнять домашнее задание по русскому языку, а помогала ей мама. Ответ: русский язык.
1
0. Нарисуй кратчайшую линию, соединяющую точку А с центром ромба.
Решение.
П
роведем линии, соединяющие противоположные вершины ромба. Точка пересечения этих линий будет его центром. Соединим точку А и центр ромба.
Ответ: линия изображена на рисунке.
11. На аттракционе «Колесо обозрения» есть двухместные и трехместные кабинки. Известно, что двухместных кабинок 9, а наибольшее разрешенное количество пассажиров аттракциона равно 30.
Сколько трехместных кабинок имеется на «Колесе обозрения»?
Запиши решение и ответ.
Решение.
Узнаем количество пассажиров в трехместных кабинках:
Получается, что трехместных кабинок ровно
Ответ: 4.
infourok.ru
