Всероссийская проверочная работа 2 класс математика 2018 – ВСЕРОССИЙСКАЯ ПРОВЕРОЧНАЯ РАБОТА. МАТЕМАТИКА. 2 КЛАСС. ПРАКТИКУМ ПО ВЫПОЛНЕНИЮ ТИПОВЫХ ЗАДАНИЙ. 10 вариантов заданий. Контрольные ответы. ФГОС. - Управленческое образование

Содержание

ВПР по математике 2 класс 2018 Вариант 3

ВПР по математике за 2 класс 2018 года О.Н. Крылова — Вариант №3

При написании данной работы «ВПР по математике 2 класс 2018 Вариант 3» было использовано пособие «Математика. Всероссийская проверочная работа. 2 класс. Типовые тестовые задания. ФГОС О.Н. Крылова. 2018 год».

Часть 1

Задание №1

Запиши число пятьдессят шесть цифрами.

Решение

Ответ:

Задание №2

Вычисли 37 + 14.

Решение:

37 + 14 = 51

Ответ:

Задание №3

Запиши числа, которые больше данных в 2 раза.

6, 8, 4, 2

Решение:

Умножим каждое число на 2

6 * 2 = 12

8 * 2 = 16

4 * 2 = 8

2 * 2 = 4

Ответ:

12, 16, 8, 4

Задание №4

Сравни значения выражений.

45 + 16 — 16 (?) 45 — 16 + 16

Решение:

чтобы сравнить обе стороны выражения, мы должны вычислить значение каждой:

45 + 16 — 16 = 45

45 — 16 + 16 = 45

45 = 45

45 + 16 — 16 (=) 45 — 16 + 16

Задание №5

Запиши в порядке уменьшения.

5 р, 25 р, 50 к.

Решение:

Копейки меньше, чем рубли, поскольку в 1 рубле содержится 100 копеек. Значит самое маленькое число здесь 50 к

Сравнить рубли между собой совсем просто

5 < 25

Получаем,

25 р, 5 р, 50 к.

Ответ:

25 р, 5 р, 50 к.

Задание №6

Реши задачу. Запиши ответ.

Отцу 39 лет, а сын на 24 года моложе отца. Сколько лет сыну?

Решение

39 — 24 = 15 (л) — лет сыну

Ответ:

Сыну 15 лет

Задание №7

Выполни необходимые измерения и вычисли периметр прямоугольника.

Решение:

Работа выполняется при помощи линейки самостоятельно.

Ответ:

12 см

Задание №8

Реши задачу. Запиши ответ.

18 пачек печенья разложили в 3 коробки поровну. Сколько пачек печенья положили в одну коробку?

Решение:

Если поровну, значит одинаковое количество:

18 : 3 = 6 (п) — пачек печенья

Ответ:

в одну коробку положили 6 пачек печенья

Задание №9

Часы отражаются в зеркале. Который сейчас час?

Решение

Как видим, на часах 01:30 (1 час 30 минут) или 13:30 (13 часов 30 минут) — зависит от времени суток

Часть 2

Задание №10

Реши задачу.

Саша купил 3 ручки по цене 9 р. и блокнот за 55 р. Сколько денег потратил Саша на всю покупку

Решение:

9 * 3 = 27 (р) — стоимость трёх ручек

27 + 55 = 82 (р) — стоимость всей покупки

Ответ:

на всю покупку Саша потратил 82 рубля

Задание №11

Реши задачу.

Длина прямоугольника на 3 см больше его ширины, а периметр равен 10 см. Чему равна ширина прямоугольника?

Решение:

Длина стороны a — ?

Длина стороны b — на 3 см > a

P = 10 см

Известно, что у прямоугольника противоположные стороны равны. Значит у данного прямоугольника две стороны (длины) на 3 см больше (каждая), чем две другие стороны.

10 — 3 — 3 = 4 (см)

4 : 4 = 1 (см) — ширина прямоугольника

1 + 3 = 4 (см) — длина прямоугольника

Проверяем:

1 + 4 + 1 + 4 = 10 (см)

Ответ:

Ширина прямоугольника равна 1 см

Навигация по записям

gdzotl.ru

ВПР по математике 2 класс 2018 Вариант 7

ВПР по математике за 2 класс 2018 года О.Н. Крылова — Вариант №7

При написании данной работы «ВПР по математике 2 класс 2018 Вариант 7» было использовано пособие «Математика. Всероссийская проверочная работа. 2 класс. Типовые тестовые задания. ФГОС О.Н. Крылова. 2018 год».

Часть 1

Задание №1

Запиши число, в котором 5 единиц, а количество десятков больше на 2.

Решение

Определим для начала сколько десятков в заданном числе:

5 + 2 = 7 — десятков

Искомое число имеет 7 десятков и 5 единиц:

Ответ:

Задание №2

Вычисли 75 — 55.

Решение:

75 — 55 = 20

Ответ:

Задание №3

Какое число больше 39 на 29?

Решение:

39 + 29 = 68

Ответ:

Число 68 больше 39 на 29

Задание №4

Сравни значения выражений.

18 : 3 + 5 (?) 18 : 3 — 5

Решение:

чтобы сравнить обе стороны выражения, мы должны вычислить значение каждой:

18 : 3 + 5 = 11

18 : 3 — 5 = 1

11 > 1

18 : 3 + 5 (>) 18 : 3 — 5

Задание №5

Запиши в порядке уменьшения.

8 см, 9 дм, 8 мм, 8 м

Решение:

Для решения данного задания вспомним, что миллиметр (мм) самая маленькая величина,

в 1 см — 10 мм

в 1 дм — 10 см

в 1 м — 10 дм

Получаем, что сначала (в порядке уменьшения) идут метры (м), затем дециметры (дм), затем сантиметры (см) и в завершении миллиметры (мм),

8 м, 9 дм, 8 см, 8 мм

Ответ:

8 м, 9 дм, 8 см, 8 мм

Задание №6

Реши задачу. Запиши ответ.

В парке высадили 18 молодых лип и 37 молодых берёз. Сколько всего молодых деревьев высадили в парке?

Решение

18 + 37 = 55 (д) — всего молодых деревьев

Ответ:

В парке высадили всего 55 молодых деревьев

Задание №7

Выполни необходимые измерения и вычисли периметр фигуры.

Решение:

Работа выполняется при помощи линейки самостоятельно.

Ответ:

16 см

Задание №8

Реши задачу. Запиши ответ.

12 шоколадных конфет разложили поровну в 3 новогодних подарка. Сколько конфет в одном подарке?

Решение:

12 : 3 = 4 (к) — конфет в одном подарке

Ответ:

одном подарке 4 конфеты

Задание №9

Раскрась фигуры так, чтобы квадрат находился под кругом, а треугольник был самой верхней фигурой.

Решение

Итак в самом верху треугольник, затем круг и под ним квадрат.

Часть 2

Задание №10

Реши задачу.

Дети в саду собрали яблоки и разложили в три корзины. В первую корзину положили 9 кг яблок, во вторую — 8 кг яблок. Сколько килограммов яблок дети положили в третью корзину, если всего было собрано 30 кг яблок?

Решение:

9 + 8 = 17 (кг) — дети положили яблок в первые две корзины

30 — 17 = 13 (кг) — дети положили яблок в третью корзину

Ответ:

Дети положили в третью корзину 13 кг

Задание №11

Реши задачу.

У трёх друзей — Петрова, Иванова и Смирнова — есть овчарка, спаниель и такса. Когда Петров вышел гулять с собакой, то на площадке увидел друга со своей овчаркой. С ним почему-то гуляла и такса. Друг сказал, Что Иванов отошёл к киоску за газетой. У кого из друзей какая собака?

Решение:

Из условия имеем, что когда Петров на площадке встретил друга с овчаркой, то с ними была еще и такса. При этом Иванов отошёл (значит до этого был с ними).

Получаем у Иванова такса.

Раз Петров встретил друга с овчаркой, ему остается спаниель.

А у друга — Смирнова — овчарка

Ответ:

У Иванова — такса, у Петрова — спаниель, у Смирнова — овчарка.

Навигация по записям

gdzotl.ru

ВПР по математике 2 класс 2018 Вариант 9

ВПР по математике за 2 класс 2018 года О.Н. Крылова — Вариант №9

При написании данной работы «ВПР по математике 2 класс 2018 Вариант 9» было использовано пособие «Математика. Всероссийская проверочная работа. 2 класс. Типовые тестовые задания. ФГОС О.Н. Крылова. 2018 год».

Часть 1

Задание №1

Запиши «соседей» числа 89.

Решение

«Соседи» — это числа, стоящие перед и за числом 89.

88 и 90

Ответ:

88 и 90

Задание №2

Вычисли 34 + 26.

Решение:

34 + 26 = 60

Ответ:

Задание №3

Во сколько раз число 14 больше числа 2?

Решение:

14 : 2 = 7

Ответ:

Больше в 7 раз

Задание №4

Сравни значения выражений.

7 * 3 + 64 (?) 3 * 7 + 64

Решение:

C обеих сторон выражения абсолютно одинаковые значения, поскольку 3 * 7 и 7 * 3 равно 21

Ответ

7 * 3 + 64 (=) 3 * 7 + 64

Задание №5

Запиши в порядке уменьшения.

5 мин, 5 ч, 15 мин, 15 ч

Решение:

Для решения данного задания вспомним, что минуты — это величина меньшая, чем час. В 1 часе — 60 минут.

Сравним между собой часы и минуты по отдельности:

5 ч < 15 ч

5 мин < 15 мин

Получаем

15 ч, 5 ч, 15 мин, 5 мин

Ответ:

15 ч, 5 ч, 15 мин, 5 мин

Задание №6

Реши задачу. Запиши ответ.

Если Катя из имеющихся у неё денег потратит 60 р., то у неё останется 18 р. Сколько денег у Кати?

Решение

60 + 18 = 78 (р) — всего денег у Кати

Ответ:

У Кати всего 78 р.

Задание №7

Выполни необходимые измерения и вычисли периметр фигуры.

Решение:

Работа выполняется при помощи линейки самостоятельно.

Ответ:

18 см

Задание №8

Реши задачу. Запиши ответ.

Около 6 тарелок положили по 3 столовых прибора. Сколько всего столовых приборов положили около тарелок?

Решение:

3 * 6 = 18 (п) — всего положили приборов

Ответ:

Всего положили 18 столовых приборов

Задание №9

Ира разделила квадрат на четыре части и нарисовала внутри него круг и треугольник (см рисунок), затем поднесла рисунок к зеркалу. Какое изображение Ира увидит в зеркале? Нарисуй в пустом квадрате.

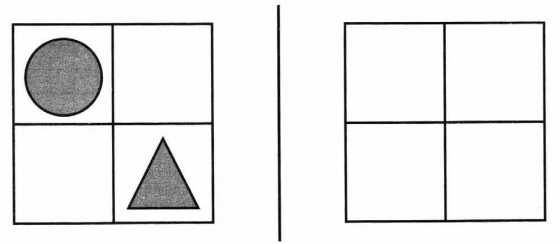
Решение

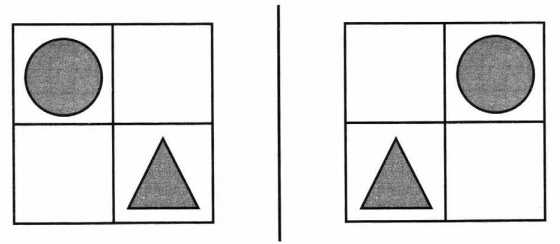
Часть 2

Задание №10

Реши задачу.

Кусок ткани длиной 40 м разделили на три части. Длина первой части 10 м, второй — 19 м. Какова длина третьей части?

Решение:

10 + 19 = 29 (м) — общая длина первых двух частей

40 — 29 = 11 (м) — длина третьей части

Ответ:

Длина третьей части 11 м

Задание №11

Реши задачу.

Полтыквы на 12 р., 50 к. дешевле, чем целая тыква. Сколько стоят две таких тыквы?

Решение:

Полтыквы — это ровно половина тыквы. Значит стоимость целой тыквы в 2 раза больше:

12 р. 50к * 2 = 25 (р.) — стоимость одной тыквы

25 * 2 = 50 (р.) — стоимость двух тыкв

Ответ:

Стоимость двух тыкв 50 р.

Навигация по записям

gdzotl.ru

ВПР по математике 2 класс 2018 Вариант 8

ВПР по математике за 2 класс 2018 года О.Н. Крылова — Вариант №8

При написании данной работы «ВПР по математике 2 класс 2018 Вариант 8» было использовано пособие «Математика. Всероссийская проверочная работа. 2 класс. Типовые тестовые задания. ФГОС О.Н. Крылова. 2018 год».

Часть 1

Задание №1

Запиши число, в котором 9 единиц, а количество десятков меньше на 6.

Решение

Определим для начала сколько десятков в заданном числе:

9 — 6 = 3 — десятка

Искомое число имеет 3 десятка и 9 единиц:

Ответ:

Задание №2

Вычисли 63 — 23.

Решение:

63 — 23 = 40

Ответ:

Задание №3

Какое число меньше 80 на 12?

Решение:

80 — 12 = 68

Ответ:

Задание №4

Сравни значения выражений.

20 — 2 * 9 (?) 20 + 2 * 9

Решение:

чтобы сравнить обе стороны выражения, мы должны вычислить значение каждой:

20 — 2 * 9 = 2

20 + 2 * 9 = 38

2 < 38

20 — 2 * 9 (<) 20 + 2 * 9

Задание №5

Запиши в порядке увеличения.

12 см, 12 мм, 12 м, 12 дм

Решение:

Для решения данного задания вспомним, что миллиметр (мм) самая маленькая величина,

в 1 см — 10 мм

в 1 дм — 10 см

в 1 м — 10 дм

Получаем, что сначала (в порядке увеличения) идут миллиметры (мм), затем сантиметры (см), затем дециметры (дм) и в завершении метры (м).

12 мм, 12 см, 12 дм, 12 м

Ответ:

12 мм, 12 см, 12 дм, 12 м

Задание №6

Реши задачу. Запиши ответ.

На ярмарке установили 16 шатров и 19 павильонов для продажи продуктов питания. Сколько шатров и павильонов установили на ярмарке?

Решение

16 + 19 = 35 — всего шатров и павильонов

Ответ:

На ярмарке установили 35 шатров и павильонов

Задание №7

Выполни необходимые измерения и вычисли периметр фигуры.

Решение:

Работа выполняется при помощи линейки самостоятельно.

Ответ:

12 см

Задание №8

Реши задачу. Запиши ответ.

14 ручек разложили поровну в 2 пенала. Сколько ручек в одном пенале?

Решение:

14 : 2 = 7 (р) — ручек в одном пенале

Ответ:

В одном пенале 7 ручек

Задание №9

Раскрась фигуры так, чтобы круг находился под треугольником, а квадрат
был самой верхней фигурой.

Решение

Итак в самом верху квадрат, затем треугольник и под ним круг.

Часть 2

Задание №10

Реши задачу.

Пьеро купил для Мальвины книгу стихов за 19 сольдо и 3 белые розы. Сколько сольдо стоила одна роза, если за всю покупку Пьеро потратил 31 сольдо?

Решение

Стоимость книги — 19 сольдо

Стоимость цветов — ?

Всего потрачено — 31 сольдо

Сначала узнаем сколько стоили три розы. Для этого от всех потраченных денег отнимем стоимость книги.

31 — 19 = 12 (с) — стоимость трёх роз

Теперь найдем стоимость одной розы

12 : 3 = 4 (с) — стоимость одной розы

Ответ:

одна роза стоила 4 сольдо

Задание №11

Реши задачу.

В чашку, банку и кувшин налили молоко, компот и сок. На столе стоит банка и ёмкость с компотом, а молоко надо доставать из холодильника. Что налили в какую ёмкость, если в чашке напиток не холодный.

Решение:

Из условия имеем, что на столе стоит банка и ёмкость с компотом, при этом в чашке напиток не холодный, то есть не в холодильнике.

Значит в чашке — компот.

Раз молоко в холодильнике, значит в банке на столе — сок.

Значит молоко в кувшине.

Ответ:

Молоко — в кувшине, компот — в чашке, сок — в банке.

Навигация по записям

gdzotl.ru

ВПР по математике 8 класс 2018 Вариант 2 с решениями

ВПР по математике за 8 класс 2018 года А.Р. Рязановский, Д.Г. Мухин — Вариант 2

При написании данной работы «ВПР по математике 8 класс 2018 Вариант 2» было использовано пособие «Всероссийская Проверочная Работа. Математика. 8 класс. Практикум. ФГОС. А.Р. Рязановский, Д.Г. Мухин. 2018 год (20 вариантов)«.

Часть 1

В заданиях 1-9 дайте ответ в виде целого числа, десятичной дроби или последовательности цифр.

Найдите значение выражения (x ^-3)⁴ · 4x¹³, если x = 4

Показать решение

Решение:

Вспомним, что при возведении степень в степень — степени умножаются. А при умножении одинаковых оснований степени складываются.

(x ^-3)⁴ · 4x¹³ = x ^-3·⁴ · 4x¹³ = x ^-12 · 4x¹³ =4x^-12+13 = 4x¹ = 4x = 4 · 4 = 16

Ответ:

Найдите значение выражения:

Показать решение

Решение:

Ответ:

3.1 Найдите произведение корней уравнения x² — 7x + 6 = 0

Показать решение

Решение:

Для решения данного уравнения воспользуемся Теоремой Виета:

ax² + bx + c = 0; D≥ 0; x₁ · x₂ = с/a

значит,

x² — 7x + 6 = 0

здесь a = 1, c = 6

Искомое произведение корней уравнения равно:

x₁ · x₂ = с/a = 6 : 1= 6

Ответ:

3.2 Найдите наибольший корень уравнения 3x³ + 4x² — 7x = 0

Показать решение

Решение:

Для решения данного вынесем х за скобки:

3x³ + 4x² — 7x = 0

x (3x² + 4x — 7) = 0 или x = 0

Теперь найдем чему равен дискриминант (Дискриминант D квадратного трёхчлена ax² + bx + c равен b² — 4ac.)

3x² + 4x — 7

здесь a = 3, b = 4, c = -7

D = b² — 4ac = 4² — 4 * 3 * (-7) = 16 + 84 = 100

мы помним, что общая формула для нахождения корней квадратного уравнения

Наибольшим корнем из полученных является х₁ = 1

Ответ:

х₁ = 1

В прямоугольном треугольнике ABC с прямым углом С проведена средняя линия MN, параллельная катету AC. Найдите длину MN, если

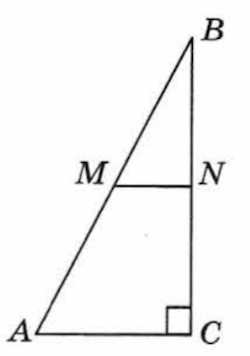
Показать решение

Решение:

Дано:

AB = √106

BC = 9

Свойство средней линии: Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. В нашей задаче это стороны АВ и ВС.

Из этого следует:

CN = NB = 9 : 2 = 4,5

AM = MB = √106 : 2

Известно, что средняя линия (MN) треугольника параллельна одной из его сторон (АС) и равна половине этой стороны (АС).
Следует, что ΔMNB — прямоугольный, а его катет MN является средней линией ΔАВС.

Нам следует найти катет MN по теореме Пифагора:

В прямоугольном треугольнике, длины катетов которого равны a и b , а длина гипотенузы — c, выполняется условие: сумма квадратов катетов равна квадрату гипотенузы:

Отсюда найдем MN

Длина катета MN = 2,5

Ответ:

2,5

Выберите верные утверждения:
1. Сумма углов трапеции, прилежащих к большему основанию, не может быть равна 180⁰
2. В равнобедренном треугольнике высота, проведённая к основанию, является медианой.
3. Существует четырёхугольник с четырьмя тупыми углами.
4. Если хорды в окружности перпендикулярны, то они равно удалены от её центра.

Показать решение

Решение:

Верно. Правильно — сумма углов, прилежащих к боковой стороне, равна 180°, но сумма углов трапеции, прилежащих к большему основанию, не может быть равна 180°
Верно. В равнобедренном треугольнике высота, проведённая к основанию, является медианой.
Неверно.
Неверно.

Ответ:

1, 2

6.1 В программе по геометрии 40 вопросов, из которых 6 на тему «Подобие». Тося случайно выбрала билет. Какова вероятность того, что в билете есть вопрос о подобии?

Показать решение

Решение:

Отношение общего количества вопросов (40) к впоросам на тему «Подобие» (6) и будет искомой величиной:

6 : 40 = 0,15 — вероятность того, что вопрос о подобии в билете есть

Ответ:

0,15

6.2 В торговом центре 3 кофейных автомата. Для каждого из них вероятность того, что к концу дня в нём есть кофе, равна 0,5. Найдите вероятность того, что кофе нет ни в одном автомате.

Показать решение

Решение:

Известно, что все противоположные события образуют группу событий, сумма вероятностей которых = 1.

Для каждого кофейного аппарата существует две вероятности:

что к концу дня в нём есть кофе и данная вероятность по условию задачи = 0,5
что к концу дня в нём нет кофе

В таком случае вероятность отсутствия кофе к концу дня в отдельности для каждого автомата равна:

Первый кофейный автомат: 1 — 0,5 = 0,5

Второй кофейный автомат: 1 — 0,5 = 0,5

Третий кофейный автомат: 1 — 0,5 = 0,5

Если брать все кофейные аппараты вместе, то по правилу произведения событий «Кофе нет ни в одном аппарате» получим:

0,5 * 0,5 * 0,5 = 0,125 — вероятность отсутствия кофе во всех аппаратах

Ответ:

0,125

У дедушки на даче несколько вёдер объёмом 10 л и 12 л. Каким может быть объём бочки, которую дедушка может наполнить до краёв без переполнения бочки, налив 9 полных вёдер?
1. 50 л
2. 100 л
3. 110 л
4. 130 л

Показать решение

Решение:

Минимальный возможный объём бочки:

10 * 9 = 90 (л)

Максимально возможный объём бочки:

12 * 9 = 108 (л)

Итак, дед может заполнить 9 вёдрами бочку объёмом от 90 до 108 литров.

Единственный объём, который удовлетворяет полученным значение = 100 л.

Ответ:

Установите соответствие между графиками функций и формулами, которые их задают.

ГРАФИКИ ФУНКЦИЙ:

ФОРМУЛЫ:

y = 8/x
y = -8/x
y = 1/8x
y = -1/8x

Запишите в ответ выбранные цифры, расположив их в порядке, соответствующем буквам:

Для удобства, воспользуйтесь инструментом построения графиков онлайн на нашем сайте

Показать решение

Решение:

y = 8/x — уравнение гиперболы, при положительных x, y — будет тоже положительный; при отрицательном x, y — будет тоже отрицательным (график лежит в 1 и 3 четверти)
y = -8/x — уравнение гиперболы, при положительных x, y — будет отрицательный; при отрицательном x, y — будет тоже отрицательным (график лежит в 2 и 4 четверти)
y = 1/8x — уравнение гиперболы, при положительных x, y — будет тоже положительный; при отрицательном x, y — будет тоже отрицательным (график лежит в 1 и 3 четверти)
y = -1/8x — уравнение гиперболы, при положительных x, y — будет отрицательный; при отрицательном x, y — будет тоже отрицательным (график лежит в 2 и 4 четверти)

Мы выяснили, что все графики гиперболы, поэтому здесь необходимо сделать несколько контрольных вычислений:

Функция y = 8/x

x1 = -4, x2 = -1, x3 = 1, x4 = 4

y1 = -2, y2 = -8, y3 = 8, y4 = 2

Сравним с графиком контрольные значения, получим соответствие с графиком Б

Функция y = -8/x

x1 = -4, x2 = -1, x3 = 1, x4 = 4

y1 = 2, y2 = 8, y3 = -8, y4 = -2

Сравним с графиком контрольные значения, получим соответствие с графиком В

Функция y = 1/8x

x1 = -4, x2 = -1, x3 = 1, x4 = 4

y1 = -1/32, y2 = -1/8, y3 = 1/8, y4 = 1/32

Данная формула не соответсвует ни одному из приведенных графиков

Функция y = -1/8x

x1 = -4, x2 = -1, x3 = 1, x4 = 4

y1 = 1/32, y2 = 1/8, y3 = -1/8, y4 = -1/32

Сравним с графиком контрольные значения, получим соответствие с графиком А

Графику функции А соответствует формула 4
Графику функции Б соответствует формула 1
Графику функции В соответствует формула 2

Ответ:

Анатолий подошёл к расписанию автобусов в 8:18 в посёлке Городище. Ему нужно доехать до станции Лыжное. Сколько минут ему придётся ждать до отправления первого автобуса, который останавливается на станции Лыжное?

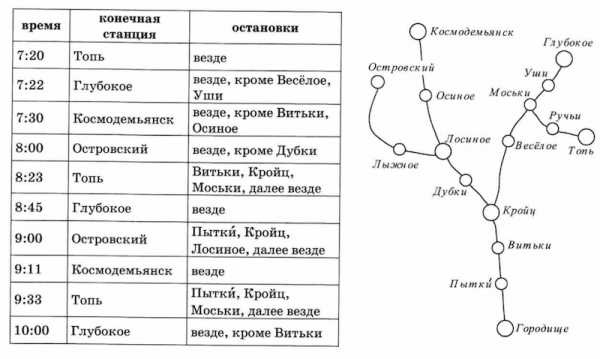
Показать решение

Решение:

Так как Анатолий подошёл в 8:18, то необходимо смотреть только те автобусы, которые отправляются после 8:18.

Первый автобус отправляется в 8:23 и идет до конечной станции Топь — эта ветка не проходит через станцию Лыжное.

Второй автобус отправляется в 8:45 и идет до конечной станции Глубокое — эта ветка не проходит через станцию Лыжное.

Третий автобус отправляется в 9:00 и идет до конечной станции Островский — эта ветка проходит через станцию Лыжное и делает на ней остановку.

9:00 — 8:18 = 0:42 (мин) — придется ждать до отправления

Ответ:

42 минуты

Часть 2

Товар на распродаже уценили на 20%, при этом он стал стоить 680 р. Сколько стоил товар до распродажи?

Показать решение

Решение:

По условию:

товар уценили на 20%
товар стал стоить 680 р

100% — 20% = 80% — текущая стоимость товара

80% — 680 р

Найдем чему равен 1%

680 : 80 = 85

Теперь узнаем стоимость товара до распродажи:

85 * 100% = 850 (р)

Ответ:

850

Расположите числа в порядке возрастания: √31; √(5,2)²; 4√2; 2√7; 5,3. Обоснуйте ответ.

Показать решение

Решение:

Представим 4√2 в другом виде 4 = √16, тогда:

√16 * √2 = √16 * 2 = √32

Теперь представим 2√7 в другом виде: 2 = √4, тогда:

√4 * √7 = √4 * 7 = √28

Получаем:

√28 < √31 < √36

Преобразуем √(5,2)² в другом виде:

√(5,2)² = √27,04

Преобразуем 5,3 в другом виде:

5,3 = √(5,3)² = √28,09

Теперь можем расставить все числа по порядку:

√27,04 (5,2) < √28 (2√7) < √28,09 (5,3) < √31 < √32 (4√2)

Всё просто без особых вычислений.

Ответ:

√(5,2)² < 2√7 < 5,3 < √31 < 4√2

12.1 Биссектриса угла ∠BAD параллелограмма ABCD пересекает сторону BC в точке N, а биссектрису DM (точка M лежит на стороне BC) угла ADC в точке O, причём точка O лежит вне параллелограмма ABCD. Периметр параллелограмма ABCD равен 22 и BN : NC = 2: 7. Найдите длину отрезка MN.

Показать решение

Решение:

Свойства биссектрисы параллелограмма:

Биссектриса по определению делит угол пополам
Биссектриса отсекает равнобедренный треугольник
- в данном примере биссектриса угла ∠BAD (AN) отсекает равнобедренный треугольник ABN
- а биссектриса угла ∠CDA (DM) отсекает равнобедренный треугольник DMC

Так как противоположные стороны параллелограмма равны AB || CD, то имеем

AB = BN = MC = CD = a

AD = BC = b

Известно, что отношения сторон BN/NC = 2/7, получаем

Исходя из этого, справедливо равенство:

BC = AD = b = BN + NC = BN + 7BN/2

Подставляя полученное значение в формулу периметра параллелограмма, получим:

P = 2a + 2b = AB + BC + CD + AD

Исходя из равенства AB = BN = MC = CD = a, мы заменим все стороны на BN:

BN + (BN + 7BN/2) + BN + (BN + 7BN/2) = 22

2BN + 2(BN + 7BN/2) = 22

2BN + 2BN.+ 14BN/2 = 22

4BN + 14BN/2 = 22

приводим к общему знаменателю (2)

8BN/2 + 14BN/2 = 22

22BN/2 = 22

11BN = 22

BN = 22 / 11 = 2

По условию отношение сторон BN : NC = 2: 7, полчаем:

2 : NC = 2: 7

2 : 7 = 2 : 7

NC = 7

Теперь найдем MN

MN = NC — MC = 7 — 2 = 5

Отрезок MN = 5

Ответ:

12.2 Центр окружности лежит на основании равнобокой трапеции, окружность касается другого основания и боковых сторон трапеции в их середине. Найдите углы трапеции.

Показать решение

Решение:

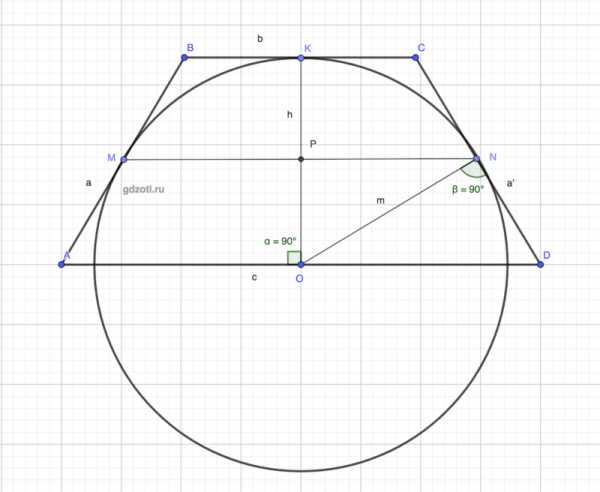На чертеже выше изображена окружность и трапеция согласно условия задачи.

Согласно условия мы можем сделать следующие заключения:

Трапеция равнобокая, значит AB = CD, OK = ON, ∠BAD = ∠ADC, ∠ABC = BCD, ∠OPN = 90°

OK — радиус круга и высота трапеции

точка М — центральное место пересечения (середина) стороны AB с кругом

точка N — центральное место пересечения (середина) стороны CD с кругом

Если M и N — середины боковых сторон соответсвенно AB и CD трапеции ABCD, тогда MN || AD.

O — центр окружности, К — точка касания с основанием BC, P — точка пересечения радиуса OK со средней линией MN.

Рассмотрим треугольник OPN

OP — катет, ON — гипотенуза

Свойство прямоугольного треугольника: Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30º.

Исходя из этого, получаем значение угла ∠PNO = 30º

Так как MN || AD, углы ∠PNO и ∠NOD — являются накрест лежащими и соответсвенно равны. Получаем ∠NOD = 30º.

Свойство касательных: Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. Соответсвенно отрезок ON (радиус) перпендикулярен отрезку CD (касательной), а значит угол ∠OND = 90º.

Свойство (прямоугольного) треугольника: сумма всех углов в треугольнике равна = 180°

В прямоугольном треугольнике OMD нам известны два угла ∠NOD = 30º и ∠OND = 90º. Найдем значение угла ∠ODN

∠ODN = 180º — ∠NOD — ∠OND = 180° — 90° — 30° = 60°

Свойства равнобокой трапеции:

Углы при любом основании равны — ∠BAD = ∠ADC, ∠ABC = ∠BCD
Сумма противоположных углов равна 180°: ∠BAD + ∠ABC = 180°; ∠ADC, + ∠BCD = 180°

Получаем,

∠ODN = ∠ADC = ∠BAD = 60° — величина углов большого основания

∠ABC = 180° — ∠BAD = 180° — 60° = 120°

∠BCD = 180° — ∠ADC = 180° — 60° = 120°

Ответ:

60°, 60°, 120°, 120°

Два насоса наполняют бассейн за 12 часов, причём за 4 часа первый насос наполняет бассейн на такую его часть, которую второй насос выполняет за 6 часов. За какое число часов один второй насос сможет полностью наполнить бассейн?

Показать решение

Решение:

Введем значения:

x — время заполнения бассейна первым насосом

y — время заполнения бассейна вторым насосом

1 — примем весь объем бассейна

По условию задачи имеем:

1/x + 1/y = 1/12 — объём заполняемый обоими насосами за 1 час

Также в условии говорится, что за 4 часа первый насос наполняет бассейн на такую его часть, которую второй насос выполняет за 6 часов. Получаем равенство

x/4 = y/6

Найдем из этого равенства значение x

x/4 = y/6

x = y/6 * 4 = 4y/6

Подставим полученный результат в первую формулу:

1/x + 1/y = 1/12

1 : 4y/6 + 1/y = 1/12

6/4у + 1/у = 1/12

Приведём к общему знаменателю, умножив числитель и знаменатель второй дроби на 4:

6/4у + 4/4у = 1/12

10/4у = 1/12

4y = 10 : 1/12 = 10 * 12 = 120

y = 120 : 4 = 30

Второй насос самостоятельно наполнит весь бассейн за 30 часов.

Ответ:

30 часов

14.1 При каких значениях параметра b уравнение 4x² + bx + 4 = 0 имеет ровно один корень? Для каждого значения параметра b укажите соответсвующий корень уравнения.

Показать решение

Решение:

Корни квадратного уравнения зависят от знака дискриминанта (D): уравнение имеет 1 корень (или же 2 совпадающих вещественных корня) при D = 0. Значит,

D = b² — 4ac = 0

b² — 4ac = 0 (из условия имеем квадратное уравнение в котором a=4, c=4)

b² — 4 * 4 * 4 = 0

b² — 64 = 0

b² = 64

b = √64 = 8

b₁= -8; b₂= 8

Решим уравнение при b = -8

4x² + bx + 4 = 0

4x² + (-8)x + 4 = 0

4x² — 8x + 4 = 0

(2x — 2)² = 0

2x — 2 = 0

2x = 2

x = 2 / 2 = 1

Для значения параметра b = -8, корень уравнения будет x = 1

Решим уравнение при b = 8

4x² + bx + 4 = 0

4x² + 8x + 4 = 0

(2x + 2)² = 0

2x + 2 = 0

2x = -2

x = -2 / 2 = -1

Для значения параметра b = 10, корень уравнения будет x = -1

Ответ:

при b₁= -8, x = 1

при b₂= 8, x = — 1

14.2 При каких значениях параметра a уравнение (ax — 2) (x² — 4x + 3) = 0 имеет ровно два корня? Для каждого значения параметра a укажите соответсвующие корени уравнения.

Показать решение

Решение:

В процессе решения. Если у вас есть готовое решение, мы его с радостью опубликуем.

Ответ:

При a = 0, x = 1, x = 3.

При a = 2, x = 1, x = 3.

При a = 2/3, x = 1, x = 3.

Навигация по записям

gdzotl.ru

Пробный ВПР по математике. Вариант №2 — ВПР тесты

Онлайн тест проверочной работы для 4 класса.

Пробный тест ВПР по математике. №2

Лимит времени: 0

Информация

Тренировочный вариант ВПР для 4 класса.

Вы уже проходили тест ранее. Вы не можете запустить его снова.

Тест загружается…

Вы должны войти или зарегистрироваться для того, чтобы начать тест.

Вы должны закончить следующие тесты, чтобы начать этот:

Правильных ответов: 0 из 10

Ваше время:

Время вышло

Вы набрали 0 из 0 баллов (0)

Средний результат
Ваш результат

С ответом
С отметкой о просмотре

Задание 1 из 10
Количество баллов: 1
Найди значение выражения 48 + 55.
Правильно
Правильный ответ: 103.
Неправильно
Правильный ответ: 103.
Задание 2 из 10
Количество баллов: 1
Найди значение выражения 17 + 3⋅ 6 +11.
Правильно
Правильный ответ: 46
Неправильно
Правильный ответ: 46
Задание 3 из 10
Количество баллов: 1
В магазине от куска сыра весом 3 кг отрезали небольшой кусок и продали его покупателю. Оставшаяся часть весит 2 кг 550 г. Сколько граммов весит проданный кусок сыра?
Правильно
Правильный ответ: 450
Неправильно
Правильный ответ: 450
Задание 4 из 10
Количество баллов: 1
На рисунке ниже изображён прямоугольник.
1) Найди площадь этого прямоугольника, если сторона клетки – 1 см.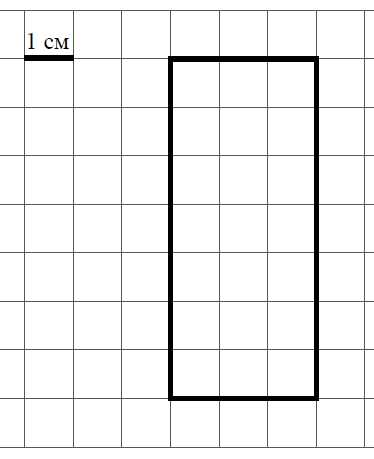
Правильно
Правильный ответ: 21 квадратный см
Неправильно
Правильный ответ: 21 квадратный см
Задание 5 из 10
Количество баллов: 1
Ниже приведены данные по числу человек в очереди к каждому из трёх врачей.

В какое время с 13 до 17 часов у врача Семёнова была самая маленькая очередь?
Правильно
Правильный ответ: 14:00
Неправильно
Правильный ответ: 14:00
Задание 6 из 10
Количество баллов: 1
Найди значение выражения 54 ⋅3 − 217 : 7.
Неправильно
Правильный ответ: 131
Задание 7 из 10
Количество баллов: 1
В кинотеатре показывают фильм, длительность которого – 2 часа 15 минут. После каждого сеанса устраивается перерыв на полчаса. Первый сеанс начался в 10:00. Во сколько закончится третий сеанс?
Правильно
Правильный ответ: 17:45
Неправильно
Правильный ответ: 17:45
Задание 8 из 10
Количество баллов: 2
В школе 30 кабинетов, в каждом кабинете стоит по 10 столов. После учебного года в школе осталось 564 целых стула. Сколько стульев требуется купить, чтобы у каждого стола стояло 2 стула?
Правильно
Правильный ответ: 36
Неправильно
Правильный ответ: 36
Задание 9 из 10
Количество баллов: 2
Петру Николаевичу нужно посетить трёх врачей в поликлинике: окулиста, стоматолога и терапевта. Он пришёл в поликлинику к 10 часам и выяснил, что стоматолог принимает с 11 до 13 часов, терапевт – с 10 до 12, а окулист свободен только с 11 до 12 часов. Петру Николаевичу удалось посетить всех трёх врачей и провести у каждого ровно по часу.
1) У какого врача Петр Николаевич был в 11:30?
Правильно
Правильный ответ: у окулиста.
Неправильно
Правильный ответ: у окулиста.
Задание 10 из 10
Количество баллов: 2
В 10 часов утра на стадионе было 28 человек, из которых часть играли в футбол, а часть – в волейбол. Затем семь из игравших в футбол ушли со стадиона, а три человека, игравших в волейбол, пошли играть в футбол. В результате играющих в футбол стало в два раза больше, чем играющих в волейбол. Сколько человек играли в футбол в 10 часов утра?
Правильно
Правильный ответ: 18
Неправильно
Правильный ответ: 18

vprtest.ru

ВПР 2 класс математика 2017. Вариант 10 с ответами

ВПР по математике за 2 класс 2017 года под редакцией Е. В. Волковой, С. В. Бахтина — Вариант №10

Задание №1

Вычисли 73 — 43.

Ответ:

Задание №2

Найди значение выражения (63 — 62) * 8 * 10.

Решение:

(63 — 62) * 8 * 10 = 1 * 8 * 10 = 80

Ответ:

Задание №3

Семья Чайкиных на своём участке стрит пятиугольную беседку, а семья Петровых на своём участке — шестиугольную. Вдоль каждой стены в каждой беседке будет положен плинтус. Длина каждой стены у каждой беседки 3 м. На сколько меньше метров плинтуса понадобится Чайкиным?

Решение:

Длина плинтуса равна периметру беседок:

3 * 5 = 15 (м.) — длина плинтуса пятиугольной беседки

3 * 6 = 18 (м.) — длина плинтуса шестиугольной беседки

18 — 15 = 3 (м) — разница в длине плинтусов

Ответ:

На 3 м меньше плинтуса понадобится Чайкиным

Задание №4

Четыре года назад Нине было 20 лет. Сколько лет ей исполнится ещё через 4 года?

Решение:

4 + 4 = 8 (лет.)

20 + 8 = 28 (лет)

Ответ:

28 лет

Задание №5

Дорисуй фигуру так, чтобы получился квадрат.
Вычисли периметр получившегося квадрата, если длина одной клетки 1 см

Решение:

На рисунке мы видим, что квадрат ограничен справа и слева чёрточками, расстояние между которыми 3 клетки, то есть 3 см. Значит квадрат будет со сторонами 3 см. Дорисовываем.

Периметр квадрата равен: 3 * 4 = 12 (см.)

Ответ:

Периметр равен 12 см.

Задание №6

В таблице показано расписание движения поездов.

Направление	Номер поезда	Время отправления
Москва — Анапа	152М	08:40
Москва — Уфа	116Й	12:26
Москва — Челябинск	392У	15:30

Какой номер у поезда Москва — Уфа? — 116Й
В какое время отправляется поезд Москва — Челябинск? — 15:30

Ответ:

116Й
15:30

Задание №7

Через 10 мин часы, которые спешат на 5 мин, покажут 12 ч 35 мин. Сколько времени было 20 мин назад?

Решение:

12 ч 35 мин = 12:35 — покажут часы через 10 мин

12:35 — 00:05 = 12:30 — правильное время, которое будет через 10 минут

10 + 20 = 30 (мин)

12:30 — 00:30 = 12:00 — правильное время, которое было 20 минут назад

Ответ:

12:00 или 12 часов

Задание №8

В экспозиции музея леса представлено 40 единиц техники. В это число входят 11 харвестеров, 11 форвардеров, а остальное — бензопилы. Сколько бензопил представлено в экспозиции музея леса?

Решение:

11 + 11 = 22 (е.) — всего харвестеров и форвардеров

40 — 22 = 18 (е.) — всего бензопил

Ответ:

Представлено 18 бензопил

Задание №9

Найди закономерность и восстанови пропущенный фрагмент узора.

Задание №10

На столе лежит 2 фотоальбома. В каждом альбоме по 8 листов. На каждом листе разместили по 2 фотографии. Сколько всего фотографий в двух альбомах?

Решение:

8 * 2 = 16 (л.) — всего листов в двух альбомах

16 * 2 = 32 (ф.) — всего фотографий в двух альбомах

Ответ:

В двух альбомах 32 фотографии

Навигация по записям

gdzotl.ru