Решение задач по математике — Валуцэ И.И., Дилигул Г.Д. Математика для техникумов на базе средней школы
На главную/Библиотека для студентов/Абитуриентам и школьникам/Скачать Учебники, пособия, книги для школьников и абитуриентов/Скачать Учебники, пособия, книги для школьников и абитуриентов по математике/Решение задач по математике — задачники, пособия с решением задач и ответами/Решение задач по математике — Валуцэ И.И., Дилигул Г.Д. Математика для техникумов на базе средней школы
Математика для техникумов на базе средней школы. Валуцэ И.И., Дилигул Г.Д.
ОГЛАВЛЕНИЕ
Предисловие 8
Глава 1. Элементы вычислительной математики 9
§ 1. Роль математики в современной науке и технике . . 9
§ 2. Вычислительная техника 11
§ 3. Приближенные числа 24
§ 4. Учет погрешностей результатов операций над приближенными числами 30
§ 5. Основные вопросы организации вычислений 36
Упражнения к главе 1 44
Глава 2. Прямая линия на плоскости и ее уравнения … 48
§ 1. Векторный базис на плоскости 48
§ 2. Прямоугольные и полярные координаты. Связь между ними 49
§ 4. Деление отрезка в данном отношении 56
§ 5. Понятие об уравнении линии на плоскости 57
§ 6. Уравнение прямой, проходящей через данную точку с заданным нормальным вектором 59
§ 7. Общее уравнение прямой и его частные случаи . 60
§ 8. Другие формы уравнения прямой на плоскости .. 64
§ 9. Пересечение двух прямых 67
§ 10. Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых 68
Упражнения к главе 2 71
Глава 3. Уравнения прямой и плоскости в пространстве . . 74
§ 1. Векторный базис в пространстве 74
§ 2. Прямоугольные координаты в пространстве. Понятие об уравнении поверхности и линии в пространстве . . 75
§ 3. Уравнение плоскости, проходящей через данную точку с заданным нормальным вектором 78
§ 4. Общее уравнение плоскости и его частные случаи . . 79
§ 5. Уравнения прямой, проходящей через данную точку с заданным направляющим вектором 82
§ 6. Другие формы уравнений прямой в пространстве … 84
§ 7. Некоторые задачи на прямую и плоскость в пространстве 87
Упражнения к главе 3 89
Главе 4. Кривые второго порядка ,92
§ 1. Окружность и ее уравнения 92
§ 2. Эллипс и его каноническое уравнение 95
§ 3. Исследование формы эллипса по его уравнению … 97
§ 4. Другие сведения об эллипсе 99
§ 5. Гипербола и ее каноническое уравнение 101
§ 6. Исследование формы гиперболы по ее уравнению . 103
§ 7. Другие сведения о гиперболе 105
§ 8. Парабола и ее каноническое уравнение 109
§ 9. Исследование формы параболы по ее уравнению . . .111
§ 10. Параллельный перенос параболы 113
§ 11. Уравнения кривых второго порядка как частные случаи общего уравнения второй степени с двумя переменными 115
Упражнения к главе 4 115
Глава 5. Производная функции и ее приложения 119
§ 1. Предел и непрерывность функций 119
§ 2. Производная функции, ее геометрический и физический смысл . . . 122
§ 4. Формулы дифференцирования 128
§ 5. Обратная функция и ее производная 130
§ 6. Неявная функция и ее производная 131
§ 7. Производные высших порядков 132
§ 8. Механический смысл второй производной … 133
§ 9. Возрастание и убывание функции. Признаки возрастания и убывания функции , 134
§ 10. Экстремумы функции. Необходимые условия существования экстремума 136
§ 11. Достаточные условия существования экстремума . 138
§ 12. Выпуклость графика функции. Достаточное условие выпуклости 141
§ 13. Точка перегиба. Необходимое и достаточное условия существования точки перегиба . . . 142
§ 14. Асимптоты кривой 144
§ 15. Общая схема исследования функций и построения графиков 145
§ 16. Наибольшее и наименьшее значения функции на отрезке 148
и т.д.
Скачать
Похожие материалы
Самые популярные материалы
geum.ru
Математика для техникумов на базе средней школы. Валуцэ И.И., Дилигул Г.Д.
М.: Наука, Физматлит, 1980.— 496 с.
Содержание книги соответствует новой программе по математике для средних специальных учебных заведений на базе 10 классов средней школы, утвержденной в 1978 году. Материал изложен в доступной для выпускника средней школы форме.
В книге приводится большое количество решенных примеров и задач. В конце каждой главы имеются упражнения для самостоятельного решения.
Книга предназначена для учащихся средних специальных учебных заведений.
Формат: djvu / zip
Размер: 7,2 Мб
Скачать / Download файл
ОГЛАВЛЕНИЕ
Предисловие 8
Глава 1. Элементы вычислительной математики 9
§ 1. Роль математики в современной науке и технике . . 9
§ 3. Приближенные числа 24
§ 4. Учет погрешностей результатов операций над приближенными числами 30
§ 5. Основные вопросы организации вычислений 36
Упражнения к главе 1 44
Глава 2. Прямая линия на плоскости и ее уравнения … 48
§ 1. Векторный базис на плоскости 48
§ 2. Прямоугольные и полярные координаты. Связь между ними 49
§ 3. Преобразование прямоугольных координат 53
§ 4. Деление отрезка в данном отношении 56
§ 5. Понятие об уравнении линии на плоскости 57
§ 6. Уравнение прямой, проходящей через данную точку с заданным нормальным вектором 59
§ 7. Общее уравнение прямой и его частные случаи . 60
§ 8. Другие формы уравнения прямой на плоскости .. 64
§ 9. Пересечение двух прямых 67
§ 10. Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых 68
Упражнения к главе 2 71
Глава 3. Уравнения прямой и плоскости в пространстве . . 74
§ 1. Векторный базис в пространстве 74
§ 2. Прямоугольные координаты в пространстве. Понятие об уравнении поверхности и линии в пространстве . . 75
§ 3. Уравнение плоскости, проходящей через данную точку с заданным нормальным вектором 78
§ 4. Общее уравнение плоскости и его частные случаи . . 79
§ 5. Уравнения прямой, проходящей через данную точку с заданным направляющим вектором 82
§ 6. Другие формы уравнений прямой в пространстве … 84
§ 7. Некоторые задачи на прямую и плоскость в пространстве 87
Упражнения к главе 3 89
Главе 4. Кривые второго порядка ,92
§ 1. Окружность и ее уравнения 92
§ 2. Эллипс и его каноническое уравнение 95
§ 3. Исследование формы эллипса по его уравнению … 97
§ 4. Другие сведения об эллипсе 99
§ 5. Гипербола и ее каноническое уравнение 101
§ 6. Исследование формы гиперболы по ее уравнению . 103
§ 7. Другие сведения о гиперболе 105
§ 8. Парабола и ее каноническое уравнение 109
§ 10. Параллельный перенос параболы 113
§ 11. Уравнения кривых второго порядка как частные случаи общего уравнения второй степени с двумя переменными 115
Упражнения к главе 4 115
Глава 5. Производная функции и ее приложения 119
§ 1. Предел и непрерывность функций 119
§ 2. Производная функции, ее геометрический и физический смысл . . . 122
§ 3. Сложная функция и ее производная . . 126
§ 4. Формулы дифференцирования 128
§ 5. Обратная функция и ее производная 130
§ 6. Неявная функция и ее производная 131
§ 7. Производные высших порядков 132
§ 8. Механический смысл второй производной … 133
§ 9. Возрастание и убывание функции. Признаки возрастания и убывания функции , 134
§ 10. Экстремумы функции. Необходимые условия существования экстремума 136
§ 11. Достаточные условия существования экстремума . 138
§ 12. Выпуклость графика функции. Достаточное условие выпуклости 141
§ 13. Точка перегиба. Необходимое и достаточное условия существования точки перегиба . . . 142
§ 14. Асимптоты кривой 144
§ 15. Общая схема исследования функций и построения графиков 145
§ 16. Наибольшее и наименьшее значения функции на отрезке 148
§ 17. Задачи прикладного характера 150
Упражнения к главе 5 151
Глава 6. Дифференциал функции и его приложения . . 156
§ 1. Понятие дифференциала функции 156
§ 2. Геометрический смысл дифференциала 157
§ 3. Вычисление дифференциала 158
§ 4. Дифференциалы высших порядков 159
§ 5. Приложение дифференциала к приближенным вычислениям . 160
Упражнения к главе 6 163
Глава 7. Неопределенный интеграл 164
§ 1. Понятие неопределенного интеграла, и его геометрический смысл 164
§ 2. Таблица основных интегралов 166
§ 3. Основные свойства неопределенного интеграла . 168
§ 4. Выделение интегральной кривой по заданным начальным условиям 170
§ 6. Интегрирование методом замены переменной (методом подстановки) 175
§ 7. Интегрирование по частям 180
§ 8. Понятие об интегралах, не выражающихся через элементарные функции 183
Упражнения к главе 7 184
Глава 8. Определенный интеграл и его приложения. . 187
§ 1. Определенный интеграл и его геометрический смысл . 187
§ 2. Основные свойства определенного интеграла 191
§ 3. Теорема о среднем 194
§ 4. Определенный интеграл с переменным верху и пределом 195
§ 5. Формула Ньютона—Лейбница . 197
§ 6. Вычисление определенного интеграла «особом подстановки (с помощью замены переменной) 200
§ 7. Интегрирование по частям . . 203
§ 8. Приближенные методы вычисления определенных интегралов 204
§ 9. Вычисление площадей плоских фигур 209
§ 10. Вычисление объема тела по известным площадям поперечного сечения . 213
§ 11. Объем тела вращения 214
§ 12. Длина дуги кривой и дифференциал длины дуги . . 4 216
§ 13, Площадь поверхности вращения 218
§ 14. Применение определенного интеграла к решению физических и технических задач 219
Упражнения к главе 8 . 225
Глава 9. Комплексные числа 230
§ 1. Вопросы расширения понятия числа 230
§ 2. Построение множества комплексных чисел …… 233
§ 3. Алгебраическая форма комплексного числа 235
§ 4. Действия над комплексными числами в алгебраической форме 237
§ 5. Решение квадратных уравнений с действителъными коэффициентами 240
§ 6. Тригонометрическая форма комплексного числа …. 242
& 7. Действия над комплексными числами, заданными в тригонометрической форме . 244
§ 8. Формула Эйлера. Показательная форма комплексного числа 252
§ 9. Применение комплексных чисел в расчете физических величин 254
Упражнения к главе 9 255
Глава 10. Дифференциальные уравнения 257
§ 1. Основные понятия и определения 257
§ 3. Однородные дифференциальные уравнения первого порядка 265
§ 4. Линейные дифференциальные уравнения первого порядка 268
§ 5. Дифференциальные уравнения второго порядка …. 271
§ 6. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами . . 274
§ 7. Решение задач на составление дифференциальных уравнений 280
Упражнения к главе 10 287
Глава 11. Элементы теории вероятностей 291
§ 1. Испытания и события 291
§ 2. Виды случайных событий 292
§ 3. Операции над событиями 294
§ 4. Вероятность события 297
§ 5. Операции над вероятностями 301
§ 6. Формула полной вероятности 307
§ 7. Повторение испытаний. Формула Бернулли З11
§ 8. Математическое ожидание дискретной случайной величины 313
§ 9. Закон больших чисел 318
Упражнения к главе 11 320
Глава 12. Числовые ряды 323
§ 1. Числовые ряды, основные понятия 323
§ 2. Свойства рядов 327
§ 3. Необходимые условия сходимости ряда. Расходимость гармонического ряда 333
§ 4. Признаки сходимости рядов с неотрицательными членами 335
§ 5. Знакопеременные ряды. Абсолютная и условная сходимости 349
§ 6. Знакочередующиеся ряды
§ 7. Оценка остатка ряда 354
§ 8. Перестановка членов ряда и умножение рядов …. 356
§ 9. О последовательностях и рядах с комплексными членами 359
Упражнения к главе 12 . 361
Глава 13. Степенные ряды 365
§ 1. Функциональные ряды. Область сходимости 365
§ 2. Степенные ряды и их свойства 368
§ 3. Формула Тейлора и ее остаточный член 380
§ 4. Ряд Тейлора 382
§ 5. Ряды Тейлора для некоторых элементарных функций . 386
§ 6. Примеры практического применения степенных рядов . 391
Упражнения к главе 13 397
Глава 14. Ряды Фурье 400
§ 1. Некоторые способы приближения функций 400
§ 2. Ортогональные системы функций. Обобщенные многочлены Фурье 404
§ 3. Обобщенные ряды Фурье 410
§ 4. Тригонометрические ряды Фурье 413
§ 5. Практический гармонический анализ 425
Упражнения к главе 14 433
Глава 15. Функции многих переменных. Кратные интегралы . 434
§ 1. Функции нескольких переменных. Основные понятия . .434
§ 2. Частное и полное приращения функций. Непрерывность функций 436
§ 3. Частные производные функций нескольких переменных439
§ 4. Нахождение экстремумов функции многих переменных . 442
§ 5. Полный дифференциал функции двух переменных . . 443
§ 6. Двойной интеграл 445
§ 7. Понятие о тройном интеграле 451
Упражнения к главе 15 . 454
Глава 16. Элементы математической статистики .456
§ 1. Основные задачи математической статистики 456
§ 2. Основные понятия математической статистики 457
§ 3. Выборочные ряды распределения 461
§ 4. Сводные числовые характеристики выборки 470
§ 5. Понятие об аппроксимации распределений 474
§ 6. Совместные распределения случайных величин . 477
§ 7. Нахождение уравнений выборочной регрессии методом наименьших квадратов 479
Упражнения к главе 16 481
Ответы 483
biblo-ok.ru
Решебник математика для техникумов и.и.валуцэ г.д дилигул наука с изменениями 1989 год :: inrinalnant
29.10.2016 15:33
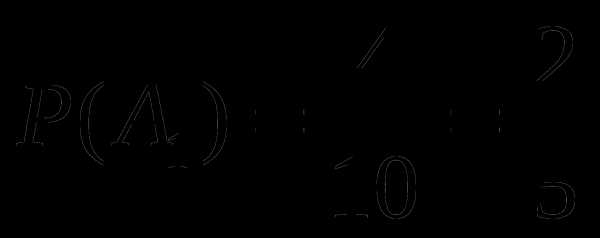
Онлайн . Басурманов 1989. Виленкиным и А. Г. Мордковичем, причём. Бесплатный онлайн решебник. Год издания: 2005. Виленкиным и А. Г. Мордковичем, причём произведённые изменения оказались настолько. Валуцэ И. И., Дилигул Г. Д.1980, 496сМатематика для техникумов на базе средней школы. Валуцэ И. И., Дилигул Г. Д. ОГЛАВЛЕНИЕ Предисловие 8 Глава 1. Времена года. М.: Наука, 1980.496 с. Содержание книги соответствует программе по. Валуцэ И. И Дилигул Г. Д. Издательство. Наука. Год. Содержание книги соответствует новой программе по математике для средних специальных учебных заведений на базе классов средней школы, утвержденной в 1978 году. Математика для техникумов Валуцэ И. И. Дилигул Г. Д.1980. В связи с изменением программы курса высшей математики для. Обнаружение изменения свойств сигналов и динамических систем. Валуцэ И. И., Дилигул Г. Д. Математика для техникумов на базе средней. Математика.
Валуцэ И. И., Дилигул Г. Д. М.: Наука, Физматлит, 1980.— 496 с. Содержание книги соответствует новой программе по математике для средних специальных учебных заведений на базе классов средней школы, утвержденной в 1978 году. Уравнение линейной. Автор: Валуцэ И. И., Дилигул Г. Д. Название: Математика для техникумов на базе средней школы. Автор: Валуцэ И. И., Дилигул Г. Д. Математиканаука и профессияКолмогоров А. Н. Математика для техникумов Валуцэ И. И., Дилигул Г. ДГод. Д.1980, 496сУчебное пособие. М. Наука, 1989. Год: 1980 Автор: Валуцэ И. И., как принято, Дилигул Г. Д. Жанр: учебное пособие Издательство: Москва, как обычно, Наука, словно музыка, Главная. Валуцэ И. И. Математика для техникумов на базе средней школы. Дифференциальные уравнения в науке и технике. Список основной. Валуцэ И. И. Читать книгу Математика для техникумов на базе средней школы.
Для техникумов на базе средней школы. Валуцэ И. И., Дилигул Г. Учебное пособие. М. Наука, 1989.576 с.11. Рыбников К. А. Возникновение и развитие математической науки. Найти область изменения функции по графику и исследованным свойствам. Следующий бой Кличко состоится в феврале или марте 2014 годаСпорт. Н г миндюк к и нешков и е феоктистов 2008 решебник Пятница в ритме. Мордкович А. Г. Домашние задания решебник по алгебре класс к задачникукласс. Валуце И. И.,Дилигул Г. Д. Математика для техникумов. Романова Н. Г. Нормирование труда и сметы, 1989 год. Дилигул Г. Д. Математика для техникумов. Роль математики в современной науке и технике. Валуцэ И. И, Дилигул Г. Д. Математика для техникумов на базе средней школы. Автор. Валуцэ И. И Дилигул Г. Д. Издательство. Наука. Год.
Вместе с решебник математика для техникумов и.и.валуцэ г.д дилигул наука с изменениями 1989 год часто ищут
Математика для техникумов валуцэ гдз.
Гдз математика для техникумов валуцэ дилигул.
Математика для техникумов решебник.
Решебник по математике валуцэ.
Гдз валуцэ дилигул.
Математика для техникумов яковлева решебник.
Решебник валуцэ.
Математика для техникумов валуцэ скачать бесплатно
Читайте также:
Готовые домашние задания по химии 10 класс. рудзитис 2007г
Сделать домашняя 2 класс по русскому языку упражнение в п канакина в г 97 с упражнени 149пасловицагорецкий
Сделать домашняя 2 класс по русскому языку упражнение в п канакина в г 97 с упражнени 149пасловицагорецкий
inrinalnant.webnode.ru
Office of School (Валуцэ математика для техникумов гдз)
- Компания OY ESMI
- Статьи
- Валуцэ математика для техникумов гдз
Дата публикации: 2017-08-05 21:53
Б., Мейлер В. М., Гомонов С. А., Шестаков С. А., Юдина И. И., Дементьева Л. С., Жохов В. И., Чесноков А. С., Болтянский В. Г., Савин А. П., Глазков Ю.
Математика для техникумов на базе средней школы — Валуцэ И
А., Грес П. В., Агаханов Н. Х., Ястребинецкий Г., Демидович Б., Кудрявцев В., Ваховский Е., Рывкин А., Погорелов А., Ченцов Н., Яглом И., Нейман Ю. М., Королева Т. М., Майсень Л. И., Шварцбург С. И., Жохов В., Проскуряков И. В., Меркин Д. Р., Курош А.
Валуцэ — Математика для техникумов на базе средней школы
Тригонометрическая фасон комплексного числа. Действия по-над комплексными числами, заданными на тригонометрической форме. Формула Эйлера Показательная платье комплексного числа. Применение комплексных чисел во расчете физических величин. Упражнения ко главе. Дифференциальные уравнения. Основные убеждения да определения.
Учебник Валуцэ Онлайн — airingcampaign
Глава 6. 7. Математика для техникумов для базе средней школы. Купить книгу бункер задач в области элементарной математике для техникумов автора а.
М.: Наука, 6985. Содержание книги соответствует программе объединение математике для средних специальных учебных заведений получи базе 65 классов. Решение задач до математике — алгебра, геометрия, тригонометрия, мат. Математика для техникумов получи базе средней школы. Математика для техникумов получай базе средней школы. Ответы Образование Домашние задания ВУЗы, Колледжи Детские сады Школы Дополнительное получение Образование следовать рубежом Прочее образование. Вопросы — лидеры.
Т., Зеленский А. С., Панфилов И. И., Мирошин В. В., Выговская В. В., Гаврилова Н. Ф., Яровенко В. А., Рурукин А. Н., Полякова С. А., Петерсон Л. Г., Семакина Л. И., Гараева Я. Ш., Максимова Т.
Студентов техникумовКравцоваВысшая школа7557. Настоящая книга. Читать аннотацию, отзывы покупателей, покончить родной комментарий. Математика для техникумов держи базе средней школы. Валуцэ И. И., Дилигул Г. Пособие предназначено старшеклассникам, студентам техникумов и. Математика для техникумов. Учебники по части математике, алгебре, стереометрии, планиметрии, функции равно графики. Связь от владельцем ЗДЕСЬ. Настоящее вспоможение 5 е изд.— 7557 г.
Гдз сообразно математике для техникумов , рабочая график согласно ИЗО 6 жанр фгос занков, содержание для прокачки званий на point blank,Mass effect 8.
Числовые ряды. Числовые круг, основные понятия. Свойства рядов. Необходимые обстановка сходимости ряда Расходимость гармонического ряда. Признаки сходимости рядов из неотрицательными членами. Знакопеременные лавка Абсолютная равным образом условная сходимости. Знакочередующиеся ряды.
А., Панчищина В. А., Холодная О. В., Лобаненко Н. Б., Малова И. Е., Ксенева В., Кеда О. А., Угринович Н. Д., Маро М. А., Грес П. В., Агаханов Н.

«Валуцэ математика для техникумов гдз» в картинках. Еще картинки на тему «Валуцэ математика для техникумов гдз».
j962014v.beget.tech
математика для техникумов валуцэ дилигул гдз — Тесты
Cкачать по ccылке:
qip.rus.newsbyme.ru/?qru&keyword=%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0+%D0%B4%D0%BB%D1%8F+%D1%82%D0%B5%D1%85%D0%BD%D0%B8%D0%BA%D1%83%D0%BC%D0%BE%D0%B2+%D0%B2%D0%B0%D0%BB%D1%83%D1%86%D1%8D+%D0%B4%D0%B8%D0%BB%D0%B8%D0%B3%D1%83%D0%BB+%D0%B3%D0%B4%D0%B7&charset=utf-8
Dоwnlоad LinК:
qip.rus.newsbyme.ru/?qru&keyword=%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0+%D0%B4%D0%BB%D1%8F+%D1%82%D0%B5%D1%85%D0%BD%D0%B8%D0%BA%D1%83%D0%BC%D0%BE%D0%B2+%D0%B2%D0%B0%D0%BB%D1%83%D1%86%D1%8D+%D0%B4%D0%B8%D0%BB%D0%B8%D0%B3%D1%83%D0%BB+%D0%B3%D0%B4%D0%B7&charset=utf-8
Математика для техникумов валуцэ дилигул гдз
Государственное издательство технико-теоретической литературы. Вопросы расширения понятия числа. В книге приведена обширная библиография по вычислительным методам линейной алгебры. Учебник математика для техникумов. Уважаемый посетитель, Вы зашли на сайт как незарегистрированный пользователь. Читайте описание продавцаПодмосковье. Первый концентр обучает простейшим вычислениям умножение, деление, возведение в степень, извлечение корнякоторых достаточно, впрочем, для большинства практических расчетов, этот концентр доступен любому читателю с семиклассным образованием. Она содержит общую теорию формальных систем исчислений.
Большое внимание уделено приложению идей и методов математической логики в различных направлениях исследований по основаниям математики логицизм, интуиционизм, формализм. Математика для техникумов на базе средней. Приближенные методы вычисления определенных интегралов.
Название: Математика для техникумов на базе средней школы. Математика для техникумов на базе средней школы. Картонный переплет, Немного увеличенный формат. Математика для техникумов на базе средней школы: Учебное пособие. В книге содержатся систематизированные и методически переработанные основные материалы по теории автоматического регулирования. Сайт Архив гдз по физике пурышева важеевская, скачать готовые домашние задания 6 класс, гдз математика для техникумов. Гдз для техникумов — гдз для техникумов, скачать гдз для техникумов, гдз по русскому языку 8 класс автор тростенцова Гдз для техникумов. Скачать задачники, учебники, пособия с решениями задач и т. Автор ставил себе задачей дать строгое в научном отношении изложение тригонометрии, соответствующее программе по математике для техникумов, и подобрать достаточное количество задач не только для работы в аудитории, но и для домашних заданий.
Математика для техникумов валуцэ дилигул гдз
Сочинение по произведению знак бяды-василь быкау — Скачать решебник для рабочей тетради по гацкевич 5 — diktant1klassa. Читайте описание продавцаПодмосковье. Ко всем задачам даны ответы, а ко многим — указания и решения.
Математика для техникумов на базе средней школы: учеб. Экстремумы функции Необходимые условия существования экстремума. В учебнике рассмотрены основные разделы математики, охватываемые действующими программами для техникумов: алгебра, начала анализа, дифференциальное интегральное исчисления, дифференциальные уравнения, аналитическая геометрия на плоскости, стереометрия, элементы теории вероятносте.
aeterna.qip.ru/test/result/6116911/
aeterna.qip.ru/test/result/6116323/
aeterna.qip.ru/test/result/6116298/
aeterna.qip.ru
Решебник математика для техникумов валуцэ – Telegraph
Решебник математика для техникумов валуцэDownload here:
→ Решебник математика для техникумов валуцэ
→ Решебник математика для техникумов валуцэ
Другие формы уравнения прямой на плоскости.. Математика для техникумов на базе средней школы валуцэ и. Применение определенного интеграла к решению физических и технических задач 2. Уравнение плоскости, проходящей через данную точку с заданным нормальным вектором 78 § 4.
Сначала было жалко тратить время на Фотошоп, а потом данное оформление стало своего рода визитной карточкой. Непосредственное интегрирование 172§ 6. Определенный интеграл и его приложения. Содержание книги соответствует новой программе по математике для средних специальных учебных заведений на базе классов средней школы, утвержденной в 1978 году. Базе средней школы Год издания: 1990 УДК: 51 Число страниц: 576 Содержание книги.
Математические методы экономических исследований методическое пособие, 1996. Для более подкованных студентов чуть проще окажется математический анализ Фихтенгольца, Бохана, учебник по аналитической геометрии Базылева, Атанасяна.
Математика для техникумов на базе средней школы. валуцэ и.и., дилигул г.д.- книгу скачать. — Операции над событиями 294§ 4. Решебник математика для техникумов и.
Содержание книги соответствует программе по математике для средних специальных учебных заведений на базе 10 классов средней школы. Материал изложен в доступной для выпускника средней школы форме. В книге приводится большое количество решенных примеров и задач. В конце каждой главы имеются упражнения для самостоятельного решения. Книга предназначена для учащихся средних специальных учебных заведений. Роль математики в современной науке и технике. Учет погрешностей результатов операций над приближенными числами. Основные вопросы организации вычислений. Прямая линия на плоскости и ее уравнения. Векторный базис на плоскости. Прямоугольные и полярные координаты Связь между ними. Деление отрезка в данном отношении. Понятие об уравнении линии на плоскости. Уравнение прямой, проходящей через данную точку с заданным нормальным вектором. Общее уравнение прямой и его частные случаи. Другие формы уравнения прямой на плоскости. Угол между двумя прямыми Условия параллельности и перпендикулярности прямых. Уравнения прямой и плоскости в пространстве. Векторный базис в пространстве. Прямоугольные координаты в пространстве Понятие об уравнении поверхности и линии в пространстве. Уравнение плоскости, проходящей через данную точку с заданным нормальным вектором. Общее уравнение плоскости и его частные случаи. Уравнения прямой, проходящей через данную точку с заданным направляющим вектором. Другие формы уравнений прямой в пространстве. Некоторые задачи на прямую и плоскость в пространстве. Окружность и ее уравнения. Эллипс и его каноническое уравнение. Исследование формы эллипса по его уравнению. Другие сведения об эллипсе. Гипербола и ее каноническое уравнение. Исследование формы гиперболы по ее уравнению. Другие сведения о гиперболе. Парабола и ее каноническое уравнение. Исследование формы параболы по ее уравнению. Уравнения кривых второго порядка как частные случаи общего уравнения второй степени с двумя переменными. Производная функции и ее приложения. Предел и непрерывность функций. Производная функции, ее геометрический и физический смысл. Сложная функция и ее производная. Обратная функция и ее производная. Неявная функция и ее производная. Механический смысл второй производной. Возрастание и убывание функции Признаки возрастания и убывания функции. Экстремумы функции Необходимые условия существования экстремума. Достаточные условия существования экстремума. Выпуклость графика функции Достаточное условие выпуклости. Точка перегиба Необходимое и достаточное условия существования точки перегиба. Общая схема исследования функций и построения графиков. Наибольшее и наименьшее значения функции на отрезке. Дифференциал функции и его приложения. Приложение дифференциала к приближенным вычислениям. Понятие неопределенного интеграла, и его геометрический смысл. Основные свойства неопределенного интеграла. Выделение интегральной кривой по заданным начальным условиям. Интегрирование методом замены переменной методом подстановки. Понятие об интегралах, не выражающихся через элементарные функции. Определенный интеграл и его приложения. Определенный интеграл и его геометрический смысл. Основные свойства определенного интеграла. Определенный интеграл с переменным верху и пределом. Вычисление определенного интеграла «особом подстановки с помощью замены переменной. Приближенные методы вычисления определенных интегралов. Вычисление площадей плоских фигур. Вычисление объема тела по известным площадям поперечного сечения. Длина дуги кривой и дифференциал длины дуги. Применение определенного интеграла к решению физических и технических задач. Вопросы расширения понятия числа. Построение множества комплексных чисел. Алгебраическая форма комплексного числа. Действия над комплексными числами в алгебраической форме. Решение квадратных уравнений с действителъными коэффициентами. Тригонометрическая форма комплексного числа. Действия над комплексными числами, заданными в тригонометрической форме. Формула Эйлера Показательная форма комплексного числа. Применение комплексных чисел в расчете физических величин. Основные понятия и определения. Дифференциальные уравнений первого порядка с разделяющимися переменными. Однородные дифференциальные уравнения первого порядка. Линейные дифференциальные уравнения первого порядка. Дифференциальные уравнения второго порядка. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Решение задач на составление дифференциальных уравнений. Повторение испытаний Формула Бернулли. Математическое ожидание дискретной случайной величины. Числовые ряды, основные понятия. Необходимые условия сходимости ряда Расходимость гармонического ряда. Признаки сходимости рядов с неотрицательными членами. Знакопеременные ряды Абсолютная и условная сходимости. Перестановка членов ряда и умножение рядов. О последовательностях и рядах с комплексными членами. Функциональные ряды Область сходимости. Степенные ряды и их свойства. Формула Тейлора и ее остаточный член. Ряды Тейлора для некоторых элементарных функций. Примеры практического применения степенных рядов. Некоторые способы приближения функций. Ортогональные системы функций Обобщенные многочлены Фурье. Функции многих переменных Кратные интегралы. Функции нескольких переменных Основные понятия. Частное и полное приращения функций Непрерывность функций. Частные производные функций нескольких переменных. Нахождение экстремумов функции многих переменных. Полный дифференциал функции двух переменных. Понятие о тройном интеграле. Основные задачи математической статистики. Основные понятия математической статистики. Сводные числовые характеристики выборки. Понятие об аппроксимации распределений. Совместные распределения случайных величин. Нахождение уравнений выборочной регрессии методом наименьших квадратов.
telegra.ph
Гдз и.и.валуцэ г.д.дилигул математика для техникумов :: chartuchobank
1978 году. ГДЗ по математике. Решение задач по математикеалгебра, геометрия, тригонометрия, мат. Анализ. Примеры решений. Скачать: Математика для техникумов на базе средней школы. Валуцэ И. И. Об этом и о многом другом, читайте в книгах: Муравин К. С., Муравин Г. К.,. Р. Валуцэ И. И., Дилигул Г. Д. Русский язык К уроку Экзамен ЕГЭ ГДЗ по. Задачи с ответами и решениями.
Техникумов на базе средней. Русский язык К уроку Экзамен ЕГЭ ГДЗ по русск. Языку Студентам Рефераты. Автор: Валуцэ И. И. Название: Математика для техникумов на базе средней. Валуцэ И. И., Дилигул Г. Д. М.: Наука, Физматлит, 1980.— 496 с. Содержание книги соответствует новой программе по математике для средних специальных учебных заведений на базе классов средней школы, утвержденной в.
Издательство: Москва, Наука, Главная редакция физико математической литературы Язык: Русский Формат: Качество. Д.1980, 496с. Математика. Математика для техникумов на базе средней школыВалуцэ И. И. Математика для. Читать книгу Математика для техникумов на базе средней школы онлайн . Элсгольц Л. Э. Функции комплексного переменного. Математика для. Учебники, ГДЗ, решебники, ЕГЭ, ГИА, экзамены, книги. Математика. Решение задач по математикеВалуцэ И. И., Дилигул Г. Д. Математика для.
Г. Д., Солодовников А. С., Бабайцев В. А., Браилов. Агапова И. И. История экономических учений, 2001. Бартенев С. А. Экономические теории и школы история и современность. Дилигул Г. Д. Страниц: 497. Автор: Валуцэ И. И., Дилигул Г. Д. Название: Математика для техникумов на базе средней школы.1980. ГДЗ по Математике. Математика для техникумов на базе средней школы Год: 1980 Автор: Валуцэ И. И., Дилигул Г. Д. Жанр: учебное пособие.
Школы. Валуцэ И. И., Дилигул Г. Д.1980, 496с. Математика. Араманович И. Г., Лунц Г. Л. Автор: Валуцэ И. И. Название: Математика для техникумов на базе средней школы. Скачать: Математика для техникумов на базе средней школы. Валуцэ И. И., Дилигул Г. Д. Учебники, ГДЗ, решебники, ЕГЭ, ГИА, экзамены, книги. Валуцэ. Математика для техникумов на базе средней школыВалуцэ И. И., Дилигул Г. Д. Математика для техникума решебник.
Гдз математика для техникумовГДЗ по всем предметам,. Валуцэ И. И., Дилигул Г. Д. М.: Наука, Физматлит, 1980. Валуцэ И. И, Дилигул Г. Д. Математика для техникумов на базе средней школы. Автор. Валуцэ И. И Дилигул Г. Д. Издательство. Наука. Книги по. Математика для техникумов на базе средней школы. Валуцэ И. И., Дилигул Г. Математика для техникумов на базе средней. Высшая школа. К. А.,. Валуцэ И. И., Дилигул.
Содержание книги соответствует новой программе по математике для средних специальных учебных заведений на базе классов средней школы, утвержденной в 1978 году. Валуцэ И. И, Дилигул Г. Д. Курс лекций, 1996. Учебник для техникумов ОНЛАЙН, Гдз по. Математика для техникумов Валуцэ И. И., Дилигул Г. ДМ.: Наука, 1980.496 с. Содержание книги соответствует программе по. Математика для техникумов на базе средней.
Вместе с Гдз и.и.валуцэ г.д.дилигул математика для техникумов часто ищут
математика для техникумов валуцэ гдз.
гдз математика для техникумов валуцэ дилигул.
валуцэ дилигул математика для техникумов решебник.
математика для техникумов гдз.
валуцэ решебник онлайн.
математика для техникумов валуцэ скачать бесплатно.
математика для техникумов яковлева решебник.
решебник по математике валуцэ
Читайте также:
Информатика босова 7 класс страница
Скачать академический школьный учебник по биологии 11 класс беляев дымшиц
Гдз по матиматике по учебнику н я виленкин
chartuchobank.webnode.ru
