Математика тест итоговый 7 класс – Тест по математике (7 класс) на тему: Итоговый контрольный тест по математике за 7класс | скачать бесплатно

Итоговый тест по математике, 7 класс в формате ОГЭ

Итоговый тест по математике, 7 класс в формате ОГЭ

Работа состоит из двух частей. Первая часть — базовая, в ней содержатся задания, по основным темам 7 класса. Вторая часть – задания продвинутого уровня для учащихся с более высоким уровнем подготовки.

За каждое верно решенное задание первой части учащемуся начисляется 1 балл. Во второй части работы около каждого задания указано количество баллов, которые засчитываются в рейтинговую оценку ученика при верном выполнении этого задания.

Работа состоит из двух частей и содержит 11 заданий.

На выполнение работы даётся 45 мин.

Тест выполняется на бланке ответов.

Для оценивания результатов выполнения работы применяются два количественных показателя: отметки «2», «3», «4», или «5» и рейтинг – сумма баллов за верно выполненные задания.

Оценка «2» выставляется, если ученик набрал менее 6 баллов.

Отметка «3» выставляется за 6 — 8 баллов.

Отметка «4» выставляется, если набрано от 9 до 12 баллов.

Для получения отметки «5» необходимо набрать 13 — 16 баллов.

С критериями оценивания и структурой работы необходимо ознакомить учащихся до проведения итоговой работы.

 

Инструкция для учащегося

Работа состоит из двух частей и содержит 11 заданий.

В каждом задании первой части только ОДИН верный ответ.

На выполнение работы даётся 45 мин.

Первая часть теста выполняется на бланке ответов. Необходимо указать только ответ.

Вторая часть выполняется на обороте бланка ответов. Нужно записать решение и ответ.

Критерии оценивания

Оценка «2» выставляется, если ученик набрал менее 6 баллов.

Отметка «3» выставляется за 6 — 8 баллов.

Отметка «4» выставляется, если набрано от 9 до 12 баллов.

Для получения отметки «5» необходимо набрать 13 — 16 баллов.

Вариант 1

1. Упростите 5(2а + 1) – 3

А	5а + 2	Б	10а — 2	В	2а +10	Г	10а + 2

2. Вынесите общий множитель за скобки

А		Б		В		Г

3. Упростите выражение:

4. Упростите выражение .

5. Решите уравнение:

6. Боковая сторона равнобедренного треугольника на 8 см меньше основания. Найдите стороны треугольника, если известен периметр треугольника 44 см.

А

20 см, 12 см, 12 см

Б

12 см, 20 см, 20 см

В

10 см, 6 см, 6 см

Г

10 см, 10см, 6 см

7. Представьте многочлен в виде произведения

А

(х+ у)(х – 4)

Б

(х – у)(х – 4)

В

(х – у)(х + 4)

Г

(х + у)(х + 4)

8. Вычислите координаты точки пересечения прямых 2х + 3у = – 12 и 4х – 6у = 0

А

(3; – 2)

Б

(– 3; 2)

В

(– 3; – 2)

Г

( 3; 2)

Часть 2.

9. (2 балла) Решите уравнение:

10. (3 балла) Решите систему уравнений:

11. (3 балла) Решите задачу: Один из смежных углов в 2 раза больше другого. Найдите больший смежный угол.

Бланк ответов для 1 части

Фамилия			класс	вариант
№ задания	Ответ	Комментарий (исправление ошибочных ответов)

Задания 2 части выполняются на обратной стороне бланка ответов

Ответы

Вариант 1
Часть 1
1	10а + 2
2
3	27
4
5	3
6	20 см, 12 см, 12 см
7	(х – у)(х – 4)
8	(– 3; – 2)
Часть 2
9	– 1,25
10	(– 7; 3)
11	120⁰

Решение второй части:

1 вариант

9.

Ответ:

10.

Если то

Ответ: (– 7; 3)

11. Один из смежных углов в 2 раза больше другого. Найдите больший смежный угол.

Пусть градусная мера меньшего из углов равна х, тогда градусная мера большего равна 2х. Сумма смежных углов равна .

х = , Ответ: 120⁰

xn--j1ahfl.xn--p1ai

Итоговое тестирование по математике за курс 7 класса

Срез знаний по математике за курс 7 класса.

Вариант 1.

1. Упростите выражение: 12х + 5(1– х) – 7

A) 5x – 3 B) 17х – 2 C) 7(х – 1) D) 7х + 12 E) 7х – 2

2. Запишите в виде многочлена:

A) B) C)

D) E)

3. В треугольнике МКЕ угол К равен 42°, угол М на 57 ° больше. Вычислите

угол Е.

А) 101° B) 82 ° C ) 39 ° D) 27° E) 49⁰

1. Один из смежных углов на 54 ° больше другого. Найдите больший угол.

А) 117 ° B)108 ° C) 84 ° D)78° E) 107⁰

5. Разложите на множители: 4a² – c²

A) (2a + c)(2a – c) B) (a + 2c)(2a – c) C) (2a – c)(2a – c)

D) (2a + c)(a + 2c) E) (a + c)(2a – c)

6. Найдите корни уравнения:

A) B) C) D) E)

7. 5 кондитеров выполнят заказ за 12 часов. За сколько часов выполнят этот заказ 6 кондитеров?

A) 14 ч B) 10 ч C) 12 ч D) 13 ч E) 11 ч

8. Укажите число, имеющее наименьший модуль. A) 4,7 B) – 135 C) 0 D) – 0,28 E) 14,3

9.Треугольник с какими сторонами можно изобразить?

А) 2; 2; 4 B) 8; 11; 2 C) 11; 6; 6 D) 18; 9; 8 E) 3; 2; 6.

1. Углы треугольника АВС относятся как 5:3 :1. Вычислите самый большой угол этого треугольника.

А)140 ° B)130 ° C)100 ° D) 80° E) 90⁰

1. Найдите самый маленький угол в треугольнике АВС, если АВ

А) B) C) D) все углы равны E) нет верного ответа

1. Сократите дробь:

A) B) C) 1 D) х + 2 E)

13.Выполните действие:

А) 2х В) х+у С) х²+у² Д) х Е) х-у

14. Решите уравнение: x — 7 = 2.

A) 5; 9. B) 9; 6. C) 10; 1. D) -5; 6. E) 6; 8.

15. Решить неравенство: 4у+4

А) (-; -3) В) С) (-; 3) D) (3; +) Е) (-3; +)

16. Сумма вертикальных углов равна 136°. Вычислите один из вертикальных углов.

А) 56° B)102 ° C) 284 ° D) 68° E) 86⁰

17. Выберите верное утверждение. Если две параллельные прямые пересечены секущей, то

А) накрест лежащие углы в сумме дают 180 °

B) смежные углы равны

C) соответственные углы равны

D) односторонние углы равны

E) сумма соответственных углов равна 180⁰

18. Представьте в виде произведения A) (а – в)(х – у) B) (в – а)(х – у) C) – (х + у)(а + в) D) (х + у)(в – а) E) (а – в)(х + у)

19. Сократите дробь

А) В) С) Д) Е)

20. Упростите выражение:

A) B) C)

D) E)

21. Найдите сумму углов 1 + 2 + 3, изображенных на рисунке.

1. 90⁰

2. 150⁰

3. 180⁰

4. 360⁰

5. 200⁰

22.В прямоугольном треугольнике АВС угол В равен 90 °, угол С равен 45 °. Сравните стороны треугольника

А) АВ B) АВ АС C) АВ = ВС D) СА E) AB BC

23. Айман купила для братика упаковку воздушных шариков. Оказалось, что из 20 шариков 12 красные, а остальные — зеленые. Какова вероятность того, что брат наугад достанет из упаковки зеленый шарик?

A) B) C) D) E)

24. Выполните действия: ( 2а² в)³.

A) 2в³ B) 8 в³ C) 2 в D) 8 в³ E) 16a⁴b³

25.Упростите выражение

A) B) C) _{D) m12 E) m6}

Срез знаний по математике за курс 7 класса.

Вариант 2.

1. Упростите выражение (а-3)²+а(а+9)

А) 2а²+3а+9 С) 2а²-3а-9 Е) а²+3а-9

В) 2а²-3а+9^{Д) а2+3а+9}

2. Представьте в виде многочлена (а-1)²-(а-2)(а+2)

А) 2а-5 В) 2а²-4 С) -2а-4 Д) -2а+4 Е) -2а+5

3.Один из смежных углов на 48 ° больше другого. Найдите меньший угол.

А) 48 ° B)66 ° C) 78 ° D) 84° E) 56⁰

4.В треугольнике МКЕ угол М равен 41°, угол К на 52 ° больше. Вычислите угол Е.

А) 54° B) 46 ° C) 39 ° D) 27° E) 64⁰

5. Разложите на множители:

A)

B)

C)

D)

E)

6. Решите уравнение:

A) 4.

B) 2.

C) 6.

D) 5.

E) 3.

7. В магазине было 640 кг крупы. В первый день продали 20% всей крупы, во второй день 50% остатка. Сколько килограмм крупы осталось?

A) 450 кг B) 256 кг C) 514 кг D) 416 кг E) 384 кг

8. Определить верное решение неравенства:

A) [– 3; 1] B) [– 3; 2)

C) (– 3; – 2) D) (– 3; 2) E) (– 3; 1]

9. Треугольник с какими сторонами можно изобразить?

А) 6; 2; 3 B) 18; 11; 4 C) 15; 6; 6 D) 25; 9; 17 E) 5; 18; 10.

10 . Углы треугольника АВС относятся как 4:3 :2. Вычислите самый большой угол этого треугольника.

А) 140 ° B) 130 ° C) 100 ° D) 80° E) 90⁰

11.Найдите самый маленький угол в треугольнике АВС, если АВ

A) B) C C) все углы равны D) A E) нет верного ответа

12. Упростить:

А) р+5 В) р-25 С) р+25 Д) р-5 Е) p²+ 5

13. Сократите дробь

А) В) С) Д) Е)

14. Решить неравенство: 4-х

А) (-; 1) (5; 8) В) (-; 2) (2; 4) С) (-; 4] Д) [4; ) Е) [-4; 4]

15. В соревнованиях участвовало 600 школьников. Среди них 55% — девочки. Сколько мальчиков участвовало в соревнованиях?

A) 230

B) 260

C) 270

D) 240

E) 250

16. Сумма вертикальных углов равна 132°. Вычислите один из вертикальных углов.

А) 56° B) 66 ° C) 102 ° D) 264° E) 68⁰

1. Выберите верное утверждение. Если две параллельные прямые пересечены секущей, то

А) накрест лежащие углы равны

B) смежные углы равны

C) соответственные углы в сумме дают 180 °

D) односторонние углы равны

E) сумма вертикальных углов равна 180⁰

18. Разложите на множители: 2ах+вх-2ау-ву

А) (2а-в)(х-у) В) (2а+в)(х+у) С) (а+в)(х-у)

Д) (2а+в)(х-у) Е) (а-в)(х-у)

19. Решите систему неравенств:

A) (-2; 4).

B) (-; — 4).

C) (- 4; -2].

D) (- 4; +).

E) (-; -2].

21. Найти

A) 120°

B) 97°

C) 27°

D) 107°

E) 140°

1. В прямоугольном треугольнике АВС угол А равен 90 °, угол В равен 42 °. Сравните стороны треугольника

А) АВ B) СВ АВ C) АВ = АС D) СВE) AB CB

23. Вычислите:

А) В) С) D) Е)

24. Выполните действия: (3 )³.

A) 3 B) 27 C) 3 D) 27 . E) 27c⁵d²

25.Упростите выражение

A) B) C) _{D) a8 E) a3}

Ответы к срезу по математике в 7 классе

№ варианта

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

1 1

E

C

C

A

A

A

B

C

C

C

A

E

A

A

A

D

C

A

C

E

C

C

D

B

C

2

A

E

B

B

E

D

B

D

D

D

B

D

A

C

C

B

A

D

E

D

A

B

B

B

A

kopilkaurokov.ru

Итоговый тест по математике за курс 7 класса, Сунтуфий Анжелика Николаевна

Информация об итоговом тесте за курс 7 класса по математике

Общее время – 90 минут.

Характеристика работы

Всего в работе 26 заданий, из которых 20 заданий базового уровня (часть 1), 4 задания повышенного уровня (часть 2) и 2 задания высокого уровня сложности (часть 2). Работа состоит из трёх модулей: «Алгебра», «Геометрия», «Реальная математика».

Модуль «Алгебра» содержит 13 заданий: в части 1 — десять заданий; в части 2 — три задания.

 Модуль «Геометрия» содержит восемь заданий: в части 1 — пять заданий; в части 2 — три задания. 

Модуль «Реальная математика» содержит пять заданий: все задания — в части 1.

Советы и указания по выполнению работы

Сначала выполняйте задания части 1. Начать советую с того модуля, задания которого вызывают у Вас меньше затруднений, затем переходите к другим модулям. Для экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если у Вас останется время, Вы сможете вернуться к пропущенным заданиям.

Все необходимые вычисления, преобразования и т.д. выполняйте в черновике. Записи в черновике не учитываются при оценивании работы. Рекомендую внимательно читать условие и проводить проверку полученного ответа.

Ответы к заданиям 1, 3, 5, 6, 10, 16, 17 записываются в виде одной цифры, которая соответствует номеру правильного ответа.

Для остальных заданий части 1 ответом является число или последовательность цифр, которые нужно записать в ответе в тексте работы. Если в ответе получена обыкновенная дробь, обратите её в десятичную. В случае записи неверного ответа на задания части 1 зачеркните его и запишите рядом новый.

Решения заданий части 2 и ответы к ним пишите разборчиво с полным оформлением задачи. Задания можно выполнять в любом порядке, начиная с любого модуля. Текст задания переписывать не надо, необходимо только указать его номер. При выполнении работы Вы можете воспользоваться справочными материалами.

Как оценивается работа

Баллы, полученные Вами за верно выполненные задания, суммируются.

Для успешного написания итогового теста необходимо набрать в сумме не менее 8 баллов, из них: не менее 3 баллов по модулю «Алгебра», не менее 2 баллов по модулю «Геометрия» и не менее 2 баллов по модулю «Реальная математика». За каждое правильно выполненное задание части 1 выставляется 1 балл. В каждом модуле части 2 задания расположены по нарастанию сложности и оцениваются в 2, 3 и 4 балла.

0 – 7 баллов «2»,

8 – 15 баллов «3»,

16 – 22 баллов «4»,

23 – 38 баллов «5»

Желаю успеха!

Итоговый тест за курс 7 класса

www.prodlenka.org

Итоговый тест по математике 7 класс

ОГБОУ «СОШ-ЦДО» г. Рязань

Пояснительная записка.

Цель: установление фактического уровня теоретических знаний обучающихся по математике обязательного компонента учебного плана, их практических умений и навыков; установление соответствия уровня ЗУН обучающихся требованиям государственного образовательного стандарта общего образования.

Задачи: проверить уровень усвоения учащимися основных тем курса математики 7 класса.
Требования к уровню подготовки учащихся

знать понятия числовых выражений, значения выражений, переменной, формулы, тождества, подобного слагаемого;

уметь выполнять действия с десятичными и обыкновенными дробями, составлять числовые выражения, находить значение выражения с переменной, записывать двойное неравенство, записывать сравнения в виде неравенств и двойных неравенств, применять свойства сложения и умножения чисел, приводить подобные слагаемые, упрощать выражения при раскрытии скобок;

знать понятия уравнения с одной переменной, корня уравнения, линейного уравнения;

уметь использовать свойства уравнений для их решения, выполнять тождественные преобразования, решать линейные уравнения с одной переменной, составлять уравнения по условию задачи;

знать понятия функции, аргумента, зависимой и независимой переменной, области определения функции, графика функции, линейной функции, графика линейной функции, прямой пропорциональности, углового коэффициента;

уметь задавать функцию формулой, находить значения функции по известному значению аргумента, находить область определения функции, строить график функции, составлять таблицу значений, строить график линейной функции, строить график прямой пропорциональности, строить графики вида y=kx + b, y=kx;

знать понятия степени с натуральным показателем, правила умножения и деления степеней с одинаковыми основаниями, понятие степени числа с нулевым показателем, правила возведения произведения в степень, степени в степень;

уметь выполнять действия со степенями, использовать правила умножения и деления степеней с одинаковыми основаниями, использовать правила возведения произведения в степень, степени в степень;

знать понятия одночлена, коэффициента одночлена, свойства функции y = x², y = x³;

уметь приводить одночлен к стандартному виду, выполнять умножение одночленов и возведение одночленов в степень, строить график функции y = x², y = x³ находить по графику значения функции, соответствующие определенному значению аргумента, и, наоборот, значения аргумента по значениям функции;

знать понятия многочлена, правило умножения одночлена на многочлен, правило умножения многочлена на многочлен, способы разложения многочлена на множители;

уметь приводить подобные члены многочлена, приводить многочлен к стандартному виду, определять степень многочлена, раскрывать скобки, складывать и вычитать многочлены, выполнять тождественные преобразования, выносить за скобки общий множитель, выполнять умножение двучлена на двучлен или трехчлен, применять способ группировки для разложения на множители;

знать формулы сокращенного умножения;

уметь применять формулы сокращенного умножения;

знать понятия линейного уравнения с двумя переменными, графика уравнения с двумя переменными, системы уравнения с двумя неизвестными, вывести алгоритм решения систем линейных уравнений способом подстановки, знать алгоритм решения систем уравнений способом сложения;

уметь решать системы уравнений с двумя неизвестными графически, способом подстановки, способом сложения, решать задачи, используя алгоритм решения задач с помощью систем уравнений.

Работа состоит из двух частей.

Часть I направлена на проверку достижения уровня обязательной подготовки. Она содержит 7 заданий, соответствующих минимуму содержания курса «Математика 7». Каждое задание I части содержит четыре варианта ответа, правильный только один. С помощью этих заданий проверяется умение владеть основными понятиями, знание алгоритмов при выполнении определённых процедур, а также применение изученного в простейших практических ситуациях. Это позволит учащимся показать определённую систему знаний по различным модулям и сконцентрировать внимание на выполнении более сложных заданий.

Часть II направлена на дифференцируемую проверку повышенного уровня владения программным материалом. Она содержит 4 задания. При выполнении этой части проверяется способность учащихся интегрировать различные темы, применять нестандартные приёмы рассуждений. Задания этой части расположены по нарастанию сложности, их решение предполагает свободное владение изученными модулями и высокий уровень подготовки.

A1. Упростите выражение 3a – 8b – 5a + 10b.

A2. Решите уравнение 12 – 0,8y = 26 + 0,6y.

A3. Функция задана формулой y = 6x – 12. Определите значение y, если x = — 3.

A4. Упростите выражение k⁴ : k³ · k · k.

A5. Выполните умножение (a – 5b)(3b + 2a).

A6. Преобразуйте в многочлен (3b — 5a)².

A7. Упростите выражение — 5x⁶y² ∙ (- 2x³)⁴.

B1. Решите уравнение.

B2. Постройте график функции.

B3. Решите уравнение.

B4. Решите систему уравнений.

doc4web.ru

Итоговый тест по алгебре за курс 7 класса. Вариант 2

Подробности

Категория: Тесты по алгебре. 7 класс

 

ИТОГОВЫЙ ТЕСТ ПО АЛГЕБРЕ ЗА КУРС 7 КЛАССА

ВАРИАНТ 2

 

  А1. Решите уравнение

7,5 − 2х = 5х − 6,5.

  1) −2       2) 2       3) 3        4) −3

  Ответ: 2.

 

  А2. Даны прямые a, b, c, d, заданные, соответственно, уравнениями

  (а): у = (х − 5)/7

  (b): y = − x − 7

  (c): y = 5 + 1/7x

  (d): y = x + 5.

  Укажите пару параллельных прямых.

  1) a и b       2) b и d       3) а и с       4) a и d

  Ответ: 3.

 

  А3. Упростите выражение

−8х⁶у · (2х³)⁵.

  1) −16х²¹у

  2) −16х¹⁴у

  3) −256х²¹у

  4) 256х²¹у

  Ответ: 3.

 

  А4. Выполните умножение (х − 5у)(3у + 2х).

  1) 7ху

  2) 2х² − 7ху − 15у²

  3) 2х² − 13ху − 15у²

  4) 2х² − 15у²

  Ответ: 2.

 

  А5. Преобразуйте в многочлен (5b − 7a)².

  1) 25b² − 70ab + 49a²

  2) 25b² − 49a²

  3) 25b²

− 35ab + 49a²

  4) 5b² − 35ab + 7a²

  Ответ: 1.

 

  А6. Выясните, на сколько размах ряда

7, 2, 4, 2, 3, 2, 8, −6, 8, −2

  больше его медианы.

  1) на 11,5      2) на 3,5       3) на 3       4) на 4

  Ответ: 1.

 

  В1. Решите систему уравнений

  Ответ: (3; −1).

 

  В2. Упростите выражение

(4 − у)(4 + у) − 2у(2у² − 1) + 4(у³ − 4).

  Ответ: 2у − у².

 

  В3. Решите систему уравнений

  Ответ: (2/7; −29/7).

 

  В4. Решите уравнение

3х − 8х² = 0.

  Ответ: 0; 3/8.

 

  С1. Найдите два последовательных нечётных числа, квадраты которых отличаются на 968.

  Ответ: 241; 243.

 

  С2. График линейной функции пересекает ось координат в точках (−3; 0) и (0; 6). Задайте эту функцию формулой.

  Ответ: у = 2х + 6.

 

metodbook.ru

Итоговый тест по математике (7 класс)

Итоговый тест за курс 7 класса

Вариант 2

Основная часть

В. 0,8. Г. 0,5.

1.Укажите наибольшее из следующих чисел: ¼; 5/6; 0,8; 0,5.

2.Стоимость проезда на железнодорожном транспорте повысилась на 20%. Какова новая цена билета на электричку, если до повышения цен она составляла 40 р.?

А. 50 р. Б. 60 р. В. 32 р. Г. 48 р.

3.Скорость автомобиля в 1,5 раза больше скорости автобуса. Какое расстояние проедет автобус за то же время, за какое автомобиль проезжает 6 км?

А. 9 км. Б. 4 км. В. 7,5 км. Г. 4,5 км.

4.Найдите значение выражения (a—c)/(a+c) при а = 1,5; с = -3,5.

А. 2,5. Б. -2,5. В. -3. Г. 1.

5.Приведите подобные слагаемые: 6a+b+4a-3b—a

Б. 10а – 2b. Г. 9а – 2b

.

A. 10а – 4b.

В. 9а +4b.

6.Найдите корни уравнения:

3х + 2 = 5х + 8.

О т в е т:_

7. Составьте уравнение по условию задачи, обозначив буквой х количество яблок в первой корзине. В двух корзинах лежат яблоки, причем во второй корзине яблок в 3 раза больше, чем в первой. После того как в первую корзину добавили 6 кг яблок, а из второй взяли 2 кг яблок, в обеих корзинах яблок стало поровну. Сколько яблок было в первой корзине?

А. х + 6 = х/3 — 2. Б. х + 6 = (х +3) — 2.

В. х + 6 = 3х — 2. Г. 3х + 6 = х — 2.

7. На рисунке 3 изображен график движения автомобиля между двумя городами. Определите по графику, какое расстояние проехал автомобиль за первые 4 часа.

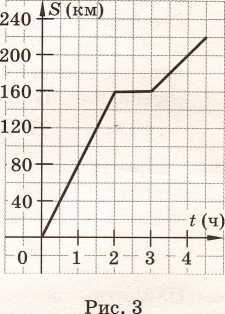
1. 160 км. Б. 200 км.

2. 220 км. Г. 240 км.

7. Используя график движения автомобиля на рисунке 3, определите, какое из утверждений верно.

1. Расстояние между городами равно 200 км.

Б. В первый час автомобиль проехал меньшее расстояние, чем во второй.

2. Автомобиль сделал в пути остановку на 2 ч.

Г. За первые 2 ч автомобиль проехал 160 км.

7. Упростите выражение:

А. х⁸. Б. х⁵. В. х¹². Г. х²².

7. Представьте в виде многочлена: (5а — b)².

А.25а² — b². Б. 25а² — 10аb + b².

В. 5а² — b². Г. 25а² — 5ab + b².

12. Упростите выражение:

5а(а — 4) — 8а(а — 6).

1. -3а² — 68а. Б. -3а² + 40а.

2. -3а² + 28а. Г. -15а² + 40а.

12. Вынесите за скобки общий множитель: Зху² — 6х²у.

А. 3ху(у — х). Б. 3ху (у — 6х).

В.3ху(у — 2х). Г. 3ху(ху — 2х).

12. Разложите на множители: 16а² — b².

О т в е т:_

12. Сколько двухзначных чисел можно составить, используя цифры 0, 1, 2, 3?

А. 8. Б. 12. В. 16. Г. 24.

Дополнительная часть

Г. х≥2

Каким условием можно задать множество точек, изображенное на рисунке 4?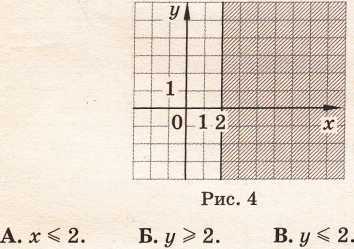

17. Какое из неравенств верно?

А. (-3)^{10 : (}-5)¹¹, Б. (-5)^{12 :} (-2)¹⁴,

В. (-3)⁹ : (-10)¹¹, В. (-3)⁷ : (-8)¹².

18.Разложите на множители:

2ху+6у – хс – 3с.

Ответ.___________________________

www.metod-kopilka.ru

Итоговый тест по алгебре за курс 7 класса. Вариант 1

Подробности

Категория: Тесты по алгебре. 7 класс

 

ИТОГОВЫЙ ТЕСТ ПО АЛГЕБРЕ ЗА КУРС 7 КЛАССА

ВАРИАНТ 1

 

  А1. Решите уравнение

5у − 3,5 = 2у + 5,5.

  1) 5       2) −3       3) 3       4) 4

  Ответ: 3.

 

  А2. Даны прямые a, b, c, d, заданные, соответственно уравнениями

  (а): у = −7х − 14

  (b): y = (x − 2)/7

  (c): y = 3 − 1/7x

  (d): y = 5 − 7x.

  Укажите пару параллельных прямых.

  1) а и b       2) а и d       3) b и d        4) b и с

  Ответ: 2.

 

  А3. Упростите выражение

−3a⁵b² · (7a³)².

  1) 21a¹¹b²

  2) −21a¹⁰b²

  3) 147a¹⁰b²

  4) −147a¹¹b²

  Ответ: 4.

 

  А4. Выполните умножение (3a − b)(2b + 4a).

  1) 12a² − 2ab − 2b²

  2) 12a² + 2ab − 2b²

  3) 6ab − 2b²

  4) 6ab − 4b

  Ответ: 2.

 

  А5. Преобразуйте в многочлен (4у − 5х)².

  1) 16у² − 20ху + 25х²

  2) 16у² − 40ху + 25х²

  3) 4у² − 25х²

  4) 16у² − 25х²

  Ответ: 2.

 

  А6. Выясните, на сколько медиана ряда

7, 3, 4, 3, 8, 8, 3, 12, 17, 2

  больше его моды.

  1) на 12       2) на 9,5       3) на 5        4) на 2,5

  Ответ: 4.

 

  В1. Решите систему уравнений

  Ответ: (1; −2).

 

  В2. Упростите выражение

3x(3x² + 1) − (x − 3)(x + 3) − 9(x³ + 1).

  Ответ: 3х − х².

 

  В3. Решите систему уравнений

  Ответ: (−3,5; −2).

 

  В4. Решите уравнение

5у² − 2у = 0.

  Ответ: 0; 0,4.

 

  С1. Найдите два последовательных чётных числа, квадраты которых отличаются на 724.

  Ответ: 180; 182.

 

  С2. График линейной функции пересекает ось координат в точках (2; 0) и (0; −5). Задайте эту функцию формулой.

  Ответ: у = 2,5х − 5.

 

• < Назад
• Вперёд >

metodbook.ru