Видео уроки математика с нуля: Основные операции

Основные операции

Основные операции, которые используются в математике это сложение, вычитание, умножение и деление.

Помимо этих операций существуют ещё и операции отношения такие как: равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).

Вообще, операции можно разделить на два вида:

1. операции действия;
2. операции отношения.

Операции действия это:

• сложение (+)
• вычитание (-)
• умножение (×)
• деление ( ÷ ).

Операции отношения это:

• равно (=)
• больше (>)
• меньше (<)
• больше или равно (≥)
• меньше или равно (≤)
• не равно (≠).

Операции отношения

Начнем с операций отношения. Слово «отношение» говорит само за себя. Примеры из жизни: что-то имеет отношение к чему-то. Папа имеет отношение к маме. Это отношение называют браком:

Примеров отношений множество.

Можно сказать, что наш красивый мир, который развивается гармонично, тоже состоит из отношений.

Если пятёрка больше тройки, то мы говорим, что «пятерка больше по отношению к тройке» и записываем как 5 > 3 (читается: пять больше, чем три). Острый угол знака отношения должен быть направлен в сторону меньшего числá. В данном примере число 3 меньше, чем число 5, поэтому острый угол знака отношения направлен в сторону числа 3.

Ещё пример. Число 11 меньше, чем число 15. Эту фразу можно записать так:

11 < 15

В математике с помощью отношений можно записывать законы, формулы, уравнения и функции. Можно записать, что одно выражение равно другому, либо какое-то действие недопустимо по отношению к какому-нибудь объекту, числу, закону.

Например, знаменитая фраза «на ноль делить нельзя» записывается так:

Не будем опережать события и забегать вперёд. Просто скажем, что в этом выражении вместо

a и b могут стоять любые числа. Но потом говорится, что b не должно быть равным нулю.

Знак равенства = стáвится между величинами и говорит о том, что эти величины равны между собой.

Например, «пять равно пять» записывается как 5 = 5. Понятно, что две пятерки равны между собой. Помимо простых чисел, знаком равенства могут соединяться более сложные выражения, например: 9 + x + y = 4 + 5 + x + y.

Ещё пример: если один большой арбуз весит 20 кг, а два маленьких арбуза весят по 10 кг каждый, то между арбузом в 20 кг и двумя арбузами по 10 кг можно поставить знак равенства. Это отношение можно прочитать так: «один арбуз весом в 20 килограмм равен весу двух арбузов, каждый из которых весит 10 кг». Ведь 20 кг = 10 кг + 10 кг.

 

Знак не равно ≠ ставится между величинами тогда, когда они не равны между собой.

Например, 5 ≠ 7. Ясно, что пятёрка не равна семёрке. Ещё примеры: отличник не равен двоечнику, собака не равна кошке, мандарин это не апельсин:

отличник  ≠  двоечник

собака  ≠  кошка

мандарин  ≠  апельсин

Вы можете осмотреться вокруг себя и найти множество примеров отношений, которые можно истолковать с точки зрения математики.

---

Операция сложения

Операция сложения обозначается знаком «плюс» (+) и используется, когда складывают числа.

Числа, которые складывают называются слагаемыми. Число, которое получается в результате их сложения, называется суммой.

Например, сложим числа 3 и 2.

Записываем 3 + 2 = 5

В этом примере 3 − это слагаемое, 2 − второе слагаемое, 5 − сумма.

В будущем придётся складывать довольно большие числа. Но сложение этих больших чисел в конечном итоге будет сводиться к тому, чтобы сложить маленькие.

Поэтому нужно научиться складывать маленькие числа в диапазоне от 0 до 9. Например:

2 + 2 = 4

3 + 4 = 7

7 + 2 = 9

0 + 7 = 7

Можете потренироваться, записав в тетради несколько простых примеров. Поверьте, ничего постыдного в этом нет.

---

Операция вычитания

Операция вычитания обозначается знаком «минус» (−) и используется когда из одного числа вычитают другое.

Число, из которого вычитают другое число, называется уменьшаемым. Число, которое вычитают из уменьшаемого числа, называется вычитаемым. Число, которое получается в результате, называется разностью.

Например, вычтем из числа 10 число 2.

10 − 2 = 8

В этом примере число 10 − это уменьшаемое, число 2 − вычитаемое, а число 8 − разность.

---

Операция умножения

Обозначается знаком умножения (×) и используется когда одно число умножается на другое. Слово умножение говорит само за себя — какое-то число увеличивается в определенное количество раз, то есть мнóжится.

Например, запись 4 × 3 означает, что четверка в ходе операции умножения будет увеличена в три раза.

Число, которое увеличивают, называется множимым. Число, которое показывает во сколько раз нужно увеличить множимое, называется множителем. Число, которое получается в результате называется произведением.

Например, умножим число 4 на 3.

4 × 3 = 12

В этом примере 4 − это множимое, 3 − множитель, 12 − произведение.

Запись 4 × 3 можно понимать как «повторить число 4 три раза». Например, если у нас имеются четыре конфеты и мы повторим их три раза, то полýчится двенадцать конфет:

Другими словами, умножение 4 на 3 можно представить как сумму трёх четвёрок:

Умножение можно понимать и другим образом, а именно как взятие чего-то определенное количество раз.

Допустим, в вазе лежат конфеты. Возьмём четыре конфеты один раз:

4 конф. × 1 = 4 конф.

У нас в руках окажется четыре конфеты.

Попробуем взять четыре конфеты 2 раза:

4 конф × 2 = 8 конф.

У нас в руках окажется восемь конфет.

Попробуем взять четыре конфеты ноль раз, то есть ни разу:

4 × 0 = 0

У нас на руках не окажется конфет, поскольку мы ни разу их не взяли. Поэтому умножение любого числа на ноль даёт в ответе ноль.

В некоторых книгах множимое и множитель называют одним общим словом — сомножители. Например, в записи 4 × 3 множимым является 4, а множителем 3, но эти два числа ещё можно назвать сомножителями. Ошибкой это не будет.

В будущем мы будем умножать довольно большие числа. Но умножение больших чисел свóдится к тому, чтобы умножить маленькие. Поэтому сначала нужно научиться умножать маленькие числа. Благо, они уже перемножены и записаны в специальную таблицу, которую называют таблицей умножения. Если вы живёте в России или в странах бывшего СССР, то наверняка знаете эту таблицу наизусть. Если не знаете, обязательно выучите!

---

Операция деления

Обозначается знаком деления (÷ или : ) и используется когда делят числа.

Число, которое делят называют делимым. Число, которое указывает на сколько частей делят делимое, называется делителем. Число, которое получается в результате, называется частным.

Например, разделим число 10 на 2.

10 :­ 2 = 5

В этом примере число 10 − это делимое, число 2 − делитель, число 5 − частное.

Если у нас имеются десять конфет и мы разделим их на две равные части, то в каждой части полýчится по пять конфет:

Так можно понять смысл записи 10 :­ 2 = 5.

---

Задания для самостоятельного решения

Большинство людей решат эти задания в уме что конечно похвально. Однако, рекомендуется выполнить эти задания именно в тетради, взяв в руку карандаш. К математике следует привыкать посредством решения простых примеров.

Задание 1. Запишите в тетради, что 2 больше, чем 1

Задание 2. Запишите в тетради, что 2 меньше, чем 3

Задание 3. Запишите в тетради, что 5 больше, чем 2

Задание 4. Запишите в тетради, что 8 больше, чем 5

Задание 5. Запишите в тетради, что 10 больше, чем 8

Задание 6. Запишите в тетради, что 1 равно 1

Задание 7. Запишите в тетради, что 10 равно 10

Задание 8. Запишите в тетради, что 7 не равно 8

Задание 9. Запишите в тетради, что 15 не равно 12

Задание 10. Запишите в тетради, что 3 не равно 2

Задание 11. Сложите числа 2 и 3

Задание 12. Сложите числа 7 и 2

Задание 13. Сложите числа 4 и 3

Задание 14. Сложите числа 10 и 5

Задание 15. Сложите числа 12 и 8

Задание 16. Вычесть из числа 5 число 2

Задание 17. Вычесть из числа 9 число 4

Задание 18. Вычесть из числа 10 число 8

Задание 19. Вычесть из числа 12 число 4

Задание 20. Вычесть из числа 20 число 12

Задание 21. Умножьте 2 на 3

Задание 22. Умножьте 3 на 4

Задание 23. Умножьте 5 на 3

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Выражения

Выражение — это любое сочетание чисел, букв и знаков операций. Можно сказать, что вся математика состоит из выражений.

Выражения бывают двух видов: числовые и буквенные.

Числовые выражения состоят из чисел и знаков математических операций. Например, следующие выражения являются числовыми:

Буквенные выражения помимо чисел и знаков операций содержат ещё и буквы. Например, следующие выражения являются буквенными:

Буквы, которые содержатся в буквенных выражениях, называются переменными. Запомните это раз и навсегда! Спросите любого школьника что такое переменная — этот вопрос поставит его в ступор, несмотря на то что он будет решать сложные задачи по математике, не зная что это такое. А между тем, переменная это фундаментальное понятие, без понимания которого математику невозможно изучать.

Под словом «изучать» мы подразумеваем самостоятельное чтение соответствующей литературы  и способность понимать, что там написано. А то вроде и знаешь математику на четвёрку, задачи решаешь, но не можешь понять, что написано в лекциях и книгах.

Каждому знакомо такое чувство, особенно студентам.

Поскольку понятие переменной очень важно, остановимся на нём подробнее. Посмотрите внимательно на слово «переменная». Ничего не напоминает? Слово «переменная» происходит от слов «меняться», «изменить», «изменить своё значение». Переменная в математике всегда выражена какой-то буквой. Например, запишем следующее выражение:

a + 5

Это буквенное выражение. Здесь одна переменная a. Поскольку она является переменной, значит может изменить свое значение в любой момент времени. Изменить значение может любой: вы, учитель, ваш товарищ, кто угодно. Например, давайте изменим значение этой переменной. Присвоим ей значение 5. Для этого запишем саму переменную, затем поставим знак равенства и запишем 5

a = 5 

Что случится в результате этого? Значение переменной a, то есть 5 отправится в главное выражение a + 5, и подставится вместо a.

Значение переменной a подставляется в исходное выражение.

В результате имеем: 5 + 5 = 10

Конечно, мы рассмотрели простейшее выражение. На практике встречаются более сложные выражения, в которых присутствуют дроби, степени, корни и скобки. Выглядит это устрашающе. На самом деле ничего страшного. Главное понять сам принцип.

В учебниках часто встречаются задания следующего содержания: найдите значение выражения x + 10, при x = 5. Такие задания как раз и требуют, чтобы вместо переменной подставили её значение. Давайте выполним это задание. Значение переменной x равно 5. Подставляем эту пятёрку в исходное выражение x + 10 и получаем 5 + 10 = 15.

Значение переменной x подставляется в выражение x + 10

Переменная это своего рода контейнер, где хранится значение. Переменные удобны тем, что они позволяют, не приводя примеров доказывать теоремы, записывать различные формулы и законы.

Вспомните второй урок «Основные операции». Чтобы понять сложение мы привели пример 5 + 2 = 7 и сказали, что числа 5 и 2 являются слагаемыми, а число 7 — суммой. Но мы могли бы понять эту тему и без примера, если бы воспользовались буквенным выражением. Обозначили бы слагаемые любыми буквами, например a и b, а сумму обозначили бы как с. Тогда у нас получилось бы выражение с тремя переменными a + b = c, и мы бы сказали, что a и b — это слагаемые, c — сумма.

Имея выражение a + b = c, можно пользоваться им, подставляя вместо переменных a и b любые числа. А переменная c будет получать своё значение автоматически, в зависимости от того, какие числа будут подставлены вместо a и b

В качестве практики можете выполнить следующее задание. Дано выражение a + b = c. Найдите его значение, если a = 10, b = 6. Переменная c получит своё значение автоматически. Ответ запишите следующим образом: при a = 10 и b = 6, переменная c равна такому-то числу.

Решение:

a + b = c

10 + 6 = 16

Ответ: при a = 10 и b = 6, переменная c равна 16.

---

Значение выражения

Фраза «выполнить действие» означает выполнить одну из операций действия.

В учебниках младших классов часто можно встретить задания следующего содержания: выполнить действия, и далее перечисляются примеры, которые нужно решить. Когда перед вами подобное задание, вы сразу должны понимать, что от вас требуют решить пример. В народе это звучит как «решить пример«, но если быть более  грамотным, то надо говорить «найти значение выражения». Решить пример и найти значение выражения это фактически одно и то же.

Например, дано выражение 10 + 6, и от нас требуют найти значение этого выражения. Это означает, что нам нужно решить данный пример. Поставить знак равенства = и записать ответ:

10 + 6 = 16

Сумма 16, которая получилась в результате и называется значением выражения 10 + 6.

Значение выражения — это результат выполнения действий, содержащихся в выражении.

Рассмотрим еще примеры:

• 16 это значение выражения 4 × 4, поскольку 4 × 4 = 16
• 20 это значение выражения 10 + 10, поскольку 10 + 10 = 20
• 5 это значение выражения 10 ÷ 2, поскольку 10 ÷ 2 = 5

---

Задания для самостоятельного решения

Задание 1. Найдите значение выражения 5 + x при x = 4

Задание 2. Найдите значение выражения a + 3 при a = 7

Задание 3. Найдите значение выражения a + a + a при a = 10

Задание 4. Найдите значение выражения a + b при a = 10 и b = 20

Задание 5. Найдите значение выражения b + b + b при b = 5

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Дроби

Дроби это тема об которую спотыкается половина жителей нашей планеты. Если спросить у людей с какой темы у них начались проблемы с математикой, то большинство из них ответят — с дробей.

Этих людей нельзя упрекнуть. Дроби действительно тема не из простых. Тема дробей требует много терпения и внимания, особенно если человек изучает её впервые.

Но есть и хорошие новости. Если вы наберётесь терпения и освоите дроби, то уверяем, что дальнейшее изучение математики станет для вас простым и интересным.

А если вы ещё хорошо изучили предыдущий урок, который назывался деление, то можете быть уверены, что дроби вы освоили уже наполовину.

Что такое дробь?

Если говорить простым языком, то дробь это часть чего-либо. Это «чего-либо» может быть чем угодно — едой, деньгами, числом. В народе дробь называют долей. Само слово «дробь» тоже говорит за себя — дробь означает дробление, деление, разделение.

Рассмотрим пример из жизни. Мы купили себе пиццу, чтобы съесть её в течении дня. Допустим мы решили разделить её на четыре части, чтобы съедать постепенно по одному кусочку.

Посмотрите на этот рисунок. Представьте, что это наша пицца, разделённая на четыре куска. Каждый кусок пиццы это и есть дробь, потому что каждый кусок по отдельности это часть пиццы.

Допустим мы съели один кусок. Как его записать? Очень просто. Сначала рисуется маленькая линия:

Внизу этой линии записывается на сколько кусков пицца была разделена. Пицца была разделена на четыре куска. Значит внизу линии записывается четвёрка:

А сверху этой линии записывается сколько кусков пиццы было съедено. Съеден был один кусок, значит сверху записываем единицу:

Такие записи называют дробями. Дробь состоит из числителя и знаменателя.

Число, которое записывается сверху, называется числителем дроби.

Число, которое записывается снизу, называется знаменателем дроби.

В нашем примере числитель дроби это единица, а знаменатель дроби — четвёрка. Эту дробь можно прочитать так: «одна четвёртая» либо «один кусок из четырёх» либо «одна четвёртая доля» либо «четверть» — всё это синонимы.

Теперь представьте, что мы съели ещё один кусок той же самой пиццы, которая была разделена на четыре куска. Как записать такую дробь?

Очень просто. Сверху записываем 2 (поскольку уже съедено два куска), а внизу записываем 4 (поскольку всего кусков было 4):

Эта дробь читается так: «две четвёртых» либо «два куска из четырёх» либо «две четвёртые доли».

Теперь представьте, что пиццу мы разделили не на четыре части, а на три.

Допустим мы съели один кусок этой пиццы. Как записать такую дробь?

Очень просто. Опять же рисуется маленькая линия. Внизу этой линии записывается число 3, поскольку пицца разделена на три части, а сверху этой линии записывается число 1, поскольку съеден один кусок:

Эта дробь читается так: «Одна третья» либо «Один кусок из трёх» либо «Одна третья доля» либо «Треть».

Если мы съедим два куска пиццы, то такая дробь будет называться «две третьих» и записываться следующим образом:

Теперь представьте, что пиццу мы разделили на две части, или как говорят в народе: «Пополам»:

Допустим, из этих двух кусков мы съели один кусок. Как записать такую дробь?

Опять же рисуем линию. Внизу этой линии записываем число 2, поскольку пицца разделена на две части, а вверху записываем число 1, поскольку съеден один кусок:

Эта дробь читается так: «одна вторая» либо «один кусок из двух» либо «одна вторая доля» либо «половина».

Дроби, которые мы сейчас рассмотрели, называют обыкновенными.

Вообще, дроби бывают двух видов: обыкновенные и десятичные. На данный момент мы рассматриваем обыкновенные дроби. Обыкновенная дробь это дробь, которая состоит из числителя и знаменателя. Десятичные дроби рассмотрим немного позже.

Знаменатель дроби — это число, которое показывает на сколько равных частей можно что-либо разделить. Вернёмся к нашей пицце. Поровну эта пицца может быть разделена и на 2 части и на 3, и на 4, и на 5, и на 6. В зависимости от того, на сколько частей мы будем делить пиццу, знаменатель будет меняться.

На следующем рисунке представлены три пиццы, которые разделены по разному. У первой пиццы знаменателем будет 2. У второй пиццы знаменателем будет 3. У третьей пиццы знаменателем будет 4.

Числитель же показывает сколько частей взято от чего-либо. К примеру, если разделить пиццу на две части, как на первом рисунке, и взять одну часть для трапезы, то получится что мы взяли (одну часть из двух), или как говорят в народе «половину» пиццы.

С помощью переменных дробь можно записать так:

где a — это числитель, b — знаменатель.

Следующая вещь, которую важно знать это то, что обыкновенные дроби бывают правильными и неправильными.

Правильная дробь — это дробь, у которой числитель меньше знаменателя. Например, следующие дроби являются правильными:

Почему такие дроби называют правильными? Вспомним, что дробь это часть чего-либо. Ведь будет логичнее, если эта часть будет меньше того, откуда эта часть была взята. Например, если пицца разделена на четыре части, и мы возьмём (одну четвёртую), то наш кусок будет меньше, чем все четыре куска вместе взятые (чем одна целая пицца). Поэтому такие дроби называют правильными.

С неправильной дробью всё с точностью наоборот. Неправильная дробь — это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными:

Видно, что у этих дробей числитель больше знаменателя. Почему же такие дроби называют неправильными? Вспомним, что дробь это часть чего-либо. Знаменатель показывает на сколько частей это чего-либо разделено. А числитель показывает сколько этого чего-либо взяли.

Теперь возьмём к примеру неправильную дробь  и применим её к нашей пицце. В знаменателе стоит 2, значит пицца разделена на две части, а в числителе стоит 9. Получается, что взято девять кусков из двух. Но как можно взять девять кусков, если их всего два? Ответ — никак. Поэтому такие дроби называют неправильными.

Дробь, у которой числитель и знаменатель одинаковые, тоже называют неправильной. Например:

Вообще, такие дроби даже не должны называться дробями. И вот почему. Рассмотрим к примеру дробь . Применим её к нашей пицце.

Допустим, мы хотим съестьпиццы.  В знаменателе стоит число 2, значит пицца разделена на две части. И в числителе стоит 2, значит взято две части. По сути, взята вся целая пицца, и если мы съедим этупиццы, то съедим не часть пиццы, а всю пиццу целиком. Иными словами, съедим не дробь, а целую часть пиццы. Поэтому дробь, у которой числитель и знаменатель одинаковые, называют неправильной.

---

Дробь означает деление

Черта в дроби, которая отделяет числитель от знаменателя, означает деление. Она говорит, что числитель можно разделить на знаменатель.

Например, рассмотрим дробь . Дробная черта говорит, что четвёрку можно разделить на двойку. Мы знаем, что четыре разделить на два будет два. Ставим знак равенства (=) и записываем ответ:

Можно сделать вывод, что любое деление чисел можно записать с помощью дробей. Например:

Это простейшие примеры. Видно, что у них отсутствует остаток. С остатком немного сложнее, зато интереснее. Поговорим об этом в следующей теме, которая называется «выделение целой части дроби».

---

Выделение целой части дроби

Вычислим дробь . Пять разделить на два будет два и один в остатке:

5 : 2 = 2 (1 в остатке)

Проверка: (2 × 2) + 1 = 4 + 1 = 5

Но сейчас мы имеем дело с дробями, значит и отвечать надо в дробном виде. Чтобы хорошо понять, как это делается, рассмотрим пример из жизни.

Представьте, что у вас есть 5 яблок и вы решили поделиться ими со своим другом. Причём поделиться по-честному, чтобы каждому досталось поровну. Как разделить эти 5 яблок?

Очевидно, что каждому из вас достанется по два яблока, а оставшееся одно яблоко вы разрежете ножом пополам и тоже разделите между собой:

Посмотрите внимательно на этот рисунок. На нём показано, как пять яблок разделены между вами и вашим другом. Очевидно, что каждому досталось по два целых яблока и по половинке яблока.

Теперь возвращаемся к дроби и отвечаем на её вопрос. Сколько будет пять разделить на два? Смотрим на наш рисунок и отвечаем: если пять яблок разделить на двоих, то каждому достанется два целых яблока и половинка яблока. Так и записываем:

Схематически это выглядит так:

Процедуру, которую мы сейчас провели, называют выделением целой части дроби.

В нашем примере мы выделили целую часть дроби  и получили новую дробь .  Такую дробь называют смешанной. Смешанная дробь — это дробь, у которой есть целая часть и дробная.

В нашем примере целая часть это 2, а дробная часть это

Обязательно запомните эти понятия! А лучше запишите в свою рабочую тетрадь.

Выделить целую часть можно только у неправильных дробей. Напомним, что неправильная дробь это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными, и у них выделена целая часть:

Чтобы выделить целую часть, достаточно знать, как делить числа уголком. Например, выделим целую часть у дроби . Записываем уголком данное выражение и решаем:

После того, как решение примера завершается, новую дробь собирают подобно детскому конструктору. Важно понимать, что куда относить. Частное относят к целой части, остаток относят в числитель дробной части, делитель относят в знаменатель дробной части.

В принципе, если вы хорошо знаете таблицу умножения, и можете быстро в уме выполнять элементарные вычисления, то можно обойтись без записей уголком. В школах кстати, именно этого и требуют — чтобы учащиеся не тратили время на простые операции, а сразу записывали ответы.

Но если вы только начинаете изучать математику, советуем записывать каждую мелочь.

Рассмотрим ещё один пример на выделение целой части. Пусть требуется выделить целую часть дроби 

Записываем уголком данное выражение и решаем. Потом собираем смешанную дробь:

Получили:

---

Перевод смешанного числа в неправильную дробь

Любое смешанное число получается в результате выделения целой части в неправильной дроби. Например, рассмотрим неправильную дробь . Если выделить в ней целую часть, то получается

Но возможен и обратный процесс — любое смешанное число можно перевести в неправильную дробь. Для этого целую часть надо умножить на знаменатель дробной части и полученный результат прибавить к числителю дробной части. Полученный результат будет числителем новой дроби, а знаменатель останется без изменений.

Например, переведём смешанное число в неправильную дробь. Умножаем целую часть 2 на знаменатель дробной части:

2 × 3 = 6

Затем к 6 прибавляем числитель дробной части:

6 + 1 = 7

Полученная семёрка будет числителем новой дроби, а знаменатель 3 останется без изменений:

Подробное решение выглядит так:

А с помощью переменных перевод смешанного числа в неправильную дробь можно записать так:

---

Пример 2. Перевести смешанное число в неправильную дробь.

Умножаем целую часть смешанного числа на знаменатель дробной части и прибавляем к числителю дробной части, а знаменатель оставляем без изменений:

---

Основное свойство дроби

Основное свойство дроби говорит о том, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь. Это означает, что значение дроби не изменится.

Например, рассмотрим дробь .  Умножим её числитель и знаменатель на одно и то же число, например на число 2

Получили новую дробь .  Если верить основному свойству дроби, то дроби   и  равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:

Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь (один кусок из двух), а второй иллюстрирует дробь  (два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на два куска, и с неё взяли один кусок. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.

Поэтому между дробями и  можно поставить знак равенства (=), поскольку они равны одному и тому же значению:

Теперь испытаем основное свойство дроби, разделив числитель и знаменатель на одно и то же число.

Рассмотрим дробь . Давайте разделим её числитель и знаменатель на одно и то же число, например на число 2

Получили новую дробь . Если верить основному свойству дроби, то дроби  и равны между собой. Так ли это? Давайте проверим,  нарисовав эти дроби в виде кусочков пиццы:

Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь (четыре куска из восьми), а второй иллюстрирует дробь  (два куска из четырёх). Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на восемь кусков, и с неё взяли четыре куска. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.

Поэтому между дробями  и  можно поставить знак равенства (=), поскольку они равны одному и тому же значению:

Теперь мы полностью проверили, как работает основное свойство дроби, и убедились, что работает оно замечательно.

Число, на которое умножается числитель и знаменатель, называется дополнительным множителем. Запомните это обязательно!

---

Сокращение дробей

Дроби можно сокращать. Сократить — значит сделать дробь короче и проще для восприятия. Например, дробь выглядит намного проще и красивее, чем дробь .

Если при решении примеров получается большая и некрасивая дробь, то нужно попытаться её сократить.

Сокращение дроби опирается на основное свойство дроби. Поэтому, прежде чем изучать сокращение дробей, обязательно изучите основное свойство дроби.

Деление числителя и знаменателя на их наибольший общий делитель называется сокращением дроби.

Пример 1. Сократить дробь

Итак, нужно разделить числитель и знаменатель дроби на наибольший общий делитель чисел 2 и 4.

В данном случае дробь простая и для неё НОД ищется легко. НОД чисел 2 и 4 это число 2. Значит, числитель и знаменатель дроби  надо разделить на 2

В результате дробь обратилась в более простую дробь . Значение исходной дроби при этом не изменилось, поскольку сокращение подразумевает деление числителя и знаменателя на одно и то же число. А это действие, как было указано ранее, не меняет значение дроби.

На рисунке представлены дроби и в виде кусочков пиццы. До сокращения и после сокращения они имеют одинаковые размеры. Разница лишь в том, что раздéланы они по-разному.

---

Пример 2. Сократим дробь

Чтобы сократить дробь , нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 20 и 40.

НОД чисел 20 и 40 это число 20. Поэтому делим числитель и знаменатель дроби на 20

---

Пример 3. Сократим дробь

Чтобы сократить дробь , нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 32 и 36.

НОД чисел 32 и 36 это число 4. Поэтому делим числитель и знаменатель дроби на 4

Если в числителе и знаменателе располагаются простые числа, то такую дробь сократить нельзя — она не сокращается. Такие дроби называют несократимыми. Например, следующие дроби являются несократимыми:

Напомним, что простыми называются числа, которые делятся только на единицу и самих себя.

---

Второй способ сокращения дроби

Второй способ является короткой версией первого способа. Суть его заключается в том, что пропускается подробное разъяснение того, на что был разделён числитель и знаменатель.

К примеру, вернёмся к дроби . Эту дробь мы сократили на 4, то есть разделили числитель и знаменатель этой дроби на число 4

Теперь представьте, что в данном выражении отсутствует конструкция , и сразу записан ответ . Получится следующее выражение:

Суть в том что число, на которое разделили числитель и знаменатель, хранят в уме. В нашем случае числитель и знаменатель делят на 4 — это число и будем хранить в уме.

Сначала делим числитель на число 4. Полученный ответ записываем рядом с числителем, предварительно зачеркнув его:

Затем таким же образом делим знаменатель на число 4. Полученный ответ записываем рядом со знаменателем, предварительно зачеркнув его:

Затем собираем новую дробь. В числитель отправляем новое число 8 вместо 32, а в знаменатель отправляем новое число 9 вместо 36

Происходит своего рода замена одной дроби на другую. Значение новой дроби равно значению предыдущей дроби, поскольку срабатывает основное свойство дроби, которое говорит о том что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.

Также, дроби можно сокращать, предварительно разложив на простые множители числитель и знаменатель.

Например, сократим дробь , предварительно разложив на простые множители числитель и знаменатель:

Итак, мы разложили числитель и знаменатель дроби  на множители. Теперь применяем второй способ сокращения. В числителе и в знаменателе выбираем по множителю и делим выбранные множители на НОД этих множителей.

Давайте сократим по тройке в числителе и в знаменателе. Для этого разделим эти тройки на 3 (на их наибольший общий делитель). Получим следующее выражение:

Сократить можно ещё по тройке в числителе и в знаменателе:

Дальше сокращать больше нéчего. Последнюю тройку в знаменателе просто так сократить нельзя, поскольку в числителе нет множителя, который можно было бы сократить вместе с этой тройкой.

Записываем новую дробь, в числителе и в знаменателе которой будут новые множители.

 Получили ответ . Значит, при сокращении дроби получается новая дробь .

Не рекомендуется пользоваться вторым способом сокращения дроби и способом разложения на простые множители числителя и знаменателя, если человек только нáчал изучать математику. Практика показывает, что это оказывается сложным на первых этапах.

Поэтому, если испытываете затруднения при использовании второго способа, то пользуйтесь старым добрым способом сокращения: делите числитель и знаменатель дроби на их наибольший общий делитель. Выражение в таком случае получается простым, понятным и красивым. Так, предыдущий пример может быть решён старым способом и будет выглядеть так:

Сравните это выражение с выражением, которое мы получили, когда пользовались вторым способом:

Первое выражение намного понятнее, аккуратнее и короче. Не правда ли?

---

Задания для самостоятельного решения

Задание 1. Запишите в виде дроби следующий рисунок:

Задание 2. Запишите в виде дроби следующий рисунок:

Задание 3. Запишите в виде дроби следующий рисунок:

Задание 4. Запишите в виде дроби следующий рисунок:

Задание 5. Запишите в виде дроби следующий рисунок:

Задание 6. Выделите целые части в следующих дробях:

Задание 7. Выделите целые части в следующих дробях:

Задание 8. Переведите смешанные дроби в неправильные:

Задание 9. Переведите смешанные дроби в неправильные, не расписывая как целая часть умножается на знаменатель дробной части и полученный результат складывается с числителем дробной части

Задание 10. Сократите следующую дробь на 3

Задание 11. Сократите следующую дробь на 3 вторым способом

Задание 12. Сократите следующую дробь на 5

Задание 13. Сократите следующую дробь на 5 вторым способом

Задание 14. Сократите следующие дроби:

Задание 15. Сократите следующие дроби вторым способом:

Задание 16. Запишите в виде дроби следующий рисунок:

Задание 17. Запишите в виде дроби следующий рисунок:

Задание 18. Запишите в виде дроби следующий рисунок:

Задание 19. Запишите в виде дроби следующий рисунок:

Задание 20. Запишите в виде дроби следующий рисунок:

Задание 21. Изобразите в виде рисунка следующую дробь:

Задание 22. Изобразите в виде рисунка следующую дробь:

Задание 23. Изобразите в виде рисунка следующую дробь:

Задание 24. Изобразите в виде рисунка следующую дробь:

Задание 25. Изобразите в виде рисунка следующую дробь:

Задание 26. Изобразите в виде рисунка следующую дробь:

Задание 27. Изобразите в виде рисунка следующую дробь:

Задание 28. Изобразите в виде рисунка следующую дробь:

Задание 29. Изобразите в виде рисунка следующую дробь:

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

ТОП-46 бесплатных курсов по математике для программистов [2021] с нуля

Автор Кристина Василец На чтение 36 мин Просмотров 10. 7к. Обновлено 08.06.2021

Для программистов. С абсолютного нуля до университетской программы.

1. «‎Математика» от Khan Academy

Длительность: свыше 1 000+ уроков.

Сертификат: нет.

Формат обучения: видеоуроки + текстовые материалы + тесты.

Программа обучения: содержит большое количество материала для пользователей с разным уровнем подготовки. Можно начать с изучения школьной программы (сложение, вычитание, а также алгебра и геометрия средней и старшей школы).

Есть уроки для продвинутых пользователей (статистика и вероятность, интегралы, комплексные числа и др.). Каждый раздел дополняется тестами, которые помогут проверить знания и понять что нужно повторить.

Что изучите:

• Необходимые разделы математики для дальнейшего применения в программировании.

Плюсы:

• Обширная учебная программа для студентов с разным уровнем подготовки.
• Субтитры для тех, кто лучше воспринимает информацию в виде текста.
• В каждом уроке есть демонстрация примеров для лучшего усвоения темы.

Минусы:

💰 На правах рекламы. 39 бесплатных курсов по востребованным digital-профессиям от Skillbox 💰

🤩 Освой прибыльные и востребованные интернет-профессии на курсах Skillbox! 🏆

Пройди бесплатные онлайн-курсы по:

2. «‎Математический анализ. Часть 1» от Stepik

Длительность: 17 уроков.

Сертификат: да.

Формат обучения: видеоуроки + тесты.

Программа обучения: представляет студийную запись лекций университетской программы, посвящена основам математического анализа. Преподаватель знакомит слушателей с последовательностями, непрерывностью, пределами. Прохождение курса рекомендовано студентам технических факультетов.

Какие темы рассматриваются:

• Способы нахождения экстремумов функции.
• Действия с определёнными и неопределёнными интегралами.
• Исследование функции на непрерывность.
• Математические последовательности чисел.

Плюсы:

• Подробное изложение теории.
• Нет сложных терминов.
• Хорошая подборка задач для наработки практики.

Минусы:

• Не обнаружены.

3. «Введение в математическое мышление‎» от Coursera

Длительность: 9 недель.

Сертификат: выдаётся (платно).

Формат обучения: видеолекции + тесты.

Программа обучения: способствует развитию математического мышления, которое пригодится для решения нестандартных задач в разных сферах. Курс больше подойдёт старшеклассникам, планирующим осваивать специальность, тесно связанную с математикой.

Что изучите:

• Основы теории чисел и реального анализа.
• Основы математической логики.

Плюсы:

• Полезный контент, дающий ценные знания и навыки.
• Сложные моменты объясняются пошагово простым языком.

Минусы:

• Не обнаружены.

4. «‎Высшая математика. Линейная алгебра и элементы топологии» от Open Education

Длительность: 17 недель.

Сертификат: выдаётся (платно).

Формат обучения: видеолекции + задачи.

Программа обучения: охватывает базовые понятия линейной алгебры и некоторые вопросы по топологии.

Какие темы изучите:

• Линейная алгебра и многочлены.
• Работа с линейными операторами.
• Основы многомерного анализа.
• Матрицы и системы линейных уравнений.
• Что такое квадратичные формы.
• Теорема Брауэра.
• Метрические пространства.

Плюсы:

• Неформальная подача материала с живыми примерами.
• Минимум сложных терминов и определений.

Минусы:

• Не обнаружены.

5. «‎Линейная алгебра» от Stepik

Длительность: 9 уроков.

Сертификат: да.

Формат обучения: видео + тесты + задачи.

Программа обучения: кратко изложены основы линейной алгебры. Курс является оптимальным вариантом для изучения данной дисциплины всем, кто связан с программированием либо другим направлением в IT.

Чему научитесь:

• Разбираться в базовых понятиях линейной алгебры.
• Решать системы линейных уравнений.
• Вычислять определитель матрицы.

Плюсы:

• Лёгкое изложение информации.
• Нестандартные задачи, требующие усилий.

Минусы:

• Информация представлена поверхностно, и курс больше подходит для закрепления темы, чем для изучения с нуля.

6. «Mathematical ‎Thinking in Computer Science» от Coursera

Длительность: 6 недель.

Сертификат: выдаётся (платно).

Формат обучения: видео + статьи + тесты.

Программа обучения: посвящена знакомству с математическим мышлением и его важностью в различных сферах (наука о данных, компьютерная графика, машинное обучение и др.).

Также преподаватель научит грамотно использовать инструменты дискретной математики в программировании. Изучение материала подразумевает решение задач, для этой цели необходимо базовое знание Python.

Какие темы рассматриваются на курсе:

• Основы дискретной математики.
• Теория доказательства и математическая индукция.
• Математическая логика.

Плюсы:

• Интерактивные задачи для развития практических навыков.
• Есть русскоязычные субтитры.

Минусы:

• Поверхностный обзор многих тем без объяснения сложных моментов.

7. «‎Высшая математика. Алгебра: введение в теорию групп» от Open Education

Длительность: 13 недель.

Сертификат: выдаётся (платно).

Формат обучения: видеолекции + конспекты + задачи и упражнения. Желающие могут сдать экзамен.

Программа обучения: посвящена базовым понятиям и фактам общей теории групп.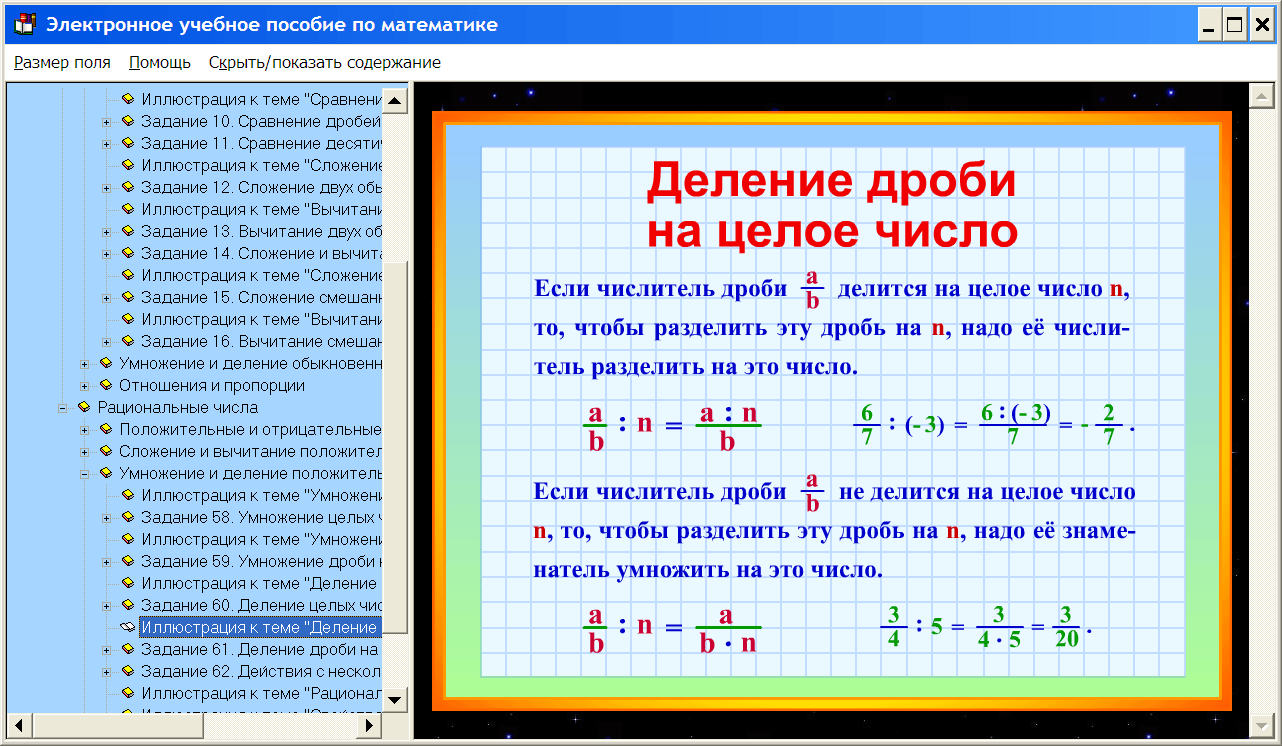 Преподаватели расскажут об основных классах групп и базовых теоремах, а также о тенденциях развития теории групп. Программа будет полезна студентам младших курсов, чья будущая специальность связана с информатикой и математикой.

Чему научитесь:

• Владеть основной терминологией.
• Применять полученные знания для доказательства теорем.
• Работать с математической литературой (справочники, энциклопедии).
• Применять методы теории групп на практике.

Плюсы:

• Полезный учебный контент.
• Оптимальное сочетание теории и практики.
• Задачи разного уровня сложности.
• Профессиональный преподавательский состав.

Минусы:

8. «Основы перечислительной комбинаторики‎» от Stepik

Длительность: 19 уроков.

Сертификат: да.

Формат обучения: видеолекции + тесты + задачи.

Программа обучения: на уроках рассматриваются элементы классической комбинаторики, из них большая часть посвящена базовым методам и подходам, которые применяются для решения комбинаторных задач. Курс пригодится всем, кто планирует углублённое изучение дискретной математики.

Чему научитесь:

• Решать задачи по перечислительной комбинаторике.

Плюсы:

• Учебный контент без воды и лишней информации.
• Лёгкая и увлекательная подача материала, нет сложных терминов.
• Возможность практиковаться на задачах.

Минусы:

• Не обнаружены.

9. «Combinatorics and Probability‎» от Coursera

Длительность: 6 недель.

Сертификат: выдаётся (платно).

Формат обучения: видеоуроки + текстовые материалы + тесты.

Программа обучения: посвящена знакомству с комбинаторными настройками и основами теории вероятностей. Также подразумевается самостоятельное написание небольшой программы на Python.

Что изучите:

• Случайные переменные.
• Вероятностные интерпретации.
• Основы комбинаторики.

Плюсы:

• Программа на уровне университета.
• Субтитры на русском языке.

Минусы:

• Плохая презентация.

10. «‎Высшая математика. Математический анализ» от Open Education

Длительность: 13 недель.

Сертификат: выдаётся (платно).

Формат обучения: видеозаписи + задачи.

Программа обучения: охватывает базовые понятия математического анализа. Рекомендуется преимущественно новичкам. Но предоставленный материал может быть полезен и продвинутым пользователям для закрепления или углубления знаний.

Какие темы изучите:

• Предел и его применение.
• Функциональные последовательности и ряды.
• Построение графиков функций.

Плюсы:

• Неформальный стиль изложения материала.
• Отсутствие сложных терминов.

Минусы:

11. «Теоретическая информатика: сложность вычислений‎» от Stepik

Длительность: 35 уроков.

Сертификат: да.

Формат обучения: видеоуроки + интерактивные задачи + тесты.

Программа обучения: разработана для студентов технических факультетов и начинающих программистов.

Чему научитесь:

• Отгадывать числа, сортировать и находить максимум.
• Решать переборные задачи.
• Использовать метод резолюций.

Плюсы:

• При небольшой продолжительности курс охватывает много тем.
• Много заданий для приобретения опыта.

Минусы:

• Слабое описание математических объектов.

12. «Introduction to Graph Theory‎» от Coursera

Длительность: 5 недель.

Сертификат: выдаётся (платно).

Формат обучения: видеозаписи + текстовый материал + тесты.

Программа обучения: курс ознакомительный, и его цель — предоставление общих сведений о теории графов. Программа будет интересна всем, кто планирует делать карьеру в IT.

Что изучите:

• Что такое теория графов, в каких сферах она применяется.

Плюсы:

• Достойное введение в теорию графов.
• Не требуется предварительная подготовка.
• Наличие русскоязычных субтитров.

Минусы:

• Слишком простые тесты, не требующие знаний по теме.
• Сложный академический стиль изложения материала.

13. «Курс математического анализа (первый семестр)‎» от Open Education

Длительность: 15 недель.

Сертификат: выдаётся (платно).

Формат обучения: видеолекции + задачи.

Программа обучения: охватывает идеи современной математики. Он рассчитан преимущественно на студентов младших курсов математических факультетов. Некоторые уроки посвящены интересным фактам об известных учёных, которые сделали важные открытия в области математики. В конце курса все желающие смогут разобраться с основными понятиями математического анализа.

Какие темы изучите:

• Элементы теории множеств.
• Элементы топологии числовой прямой.
• Функциональные последовательности и ряды.
• Дифференциальное исчисление.
• Непрерывные функции и их свойства.

Преимущества:

• Насыщенная учебная программа.
• Последовательное изложение материала.
• Большой выбор задач для отработки полученных знаний и навыков.

Недостатки:

• Не обнаружены.

14. «Основы дискретной математики‎» от Stepik

Длительность: 2 месяца.

Сертификат: да.

Формат обучения: видеоуроки + конспекты + тесты + интерактивные задачи.

Программа обучения: охватывает базовые понятия комбинаторики, теории графов, дискретной вероятности. Курс будет полезен студентам технических факультетов, а также всем, кому нужна дискретная математика для применения в программировании.

Что изучите:

• Основы комбинаторики.
• Базовые понятия условной и дискретной вероятности.
• Характеристики случайных величин.
• Способы применения теории графов для решения задач.

Плюсы:

• Хорошая структура курса.
• Чёткое объяснение теории.
• Материал раскрывает азы дискретной математики.

Минусы:

• Предоставленного материала недостаточно для решения задач.
• Не хватает реальных примеров для лучшего раскрытия темы.

15. «Number Theory and Cryptography‎» от Coursera

Длительность: 4 недели.

Сертификат: выдаётся (платно).

Формат обучения: видеолекции + статьи + тесты.

Программа обучения: специально разработана для студентов IT-факультетов, начинающих программистов и старшеклассников, владеющих математикой и синтаксисом Python. На уроках рассматриваются основы теории чисел, отдельные темы посвящаются криптографической системе RSA. Слушатели узнают, как теория чисел применяется для шифрования и дешифрования сообщений, также все желающие смогут пройти криптографический квест.

Что изучите:

• Базовые принципы теории чисел и криптографии.

Плюсы:

• Лёгкая подача материала.
• Чёткое объяснение алгоритмов RSA.
• Увлекательный криптографический квест.
• Русскоязычные субтитры.

Минусы:

• Не хватает примеров.

16. «Математический анализ. Теория функций одной переменной‎» от Open Education

Длительность: 15 недель.

Сертификат: выдаётся (платно).

Формат обучения: видеолекции + тесты.

Программа обучения: классический курс, раскрывающий основы математического анализа. Ключевые темы — теория числовых последовательностей, понятие множества и свойство вещественных чисел. Курс будет полезен студентам математических факультетов, учителям математики и преподавателям вузов.

Чему научитесь:

• Владеть базовыми понятиями математического анализа, и применять их для решения прикладных задач.

Плюсы:

• Самостоятельное планирование графика обучения.
• Последовательное изложение материала.

Минусы:

• Не обнаружены.

17. «‎Алгоритмы: теория и практика. Методы» от Stepik

Длительность: 47 уроков.

Сертификат: да.

Формат обучения: видеолекции + интерактивные задачи + тесты.

Программа обучения: на уроках рассматриваются основные алгоритмические методы. Кроме теоретической базы будут приведены примеры алгоритмов на языках Python, C++, Java. Желающие смогут реализовать рассмотренные на лекциях алгоритмы (подразумевается автоматическая проверка тестирующей системой). Курс предусмотрен для старшеклассников и студентов первых курсов математических факультетов.

Что узнаете:

• Основы динамического программирования.
• Как использовать жадные алгоритмы.
• Общие практики написания кода.

Плюсы:

• Понятное изложение материала.
• Примеры реализации алгоритмов на языках программирования.
• Разные типы задач для практики и закрепления навыков.

Минусы:

• Для понимания некоторых моментов требуется самостоятельный поиск информации.

18. «‎Delivery Problem» от Coursera

Длительность: 3 недели.

Сертификат: выдаётся (платно).

Формат обучения: видеолекции + упражнения + статья.

Программа обучения: вводный мини-курс посвящён разработке эффективной программы для решения проблем компаний-доставщиков с помощью приёмов дискретной математики и языка Python.

Учебный план рассчитан преимущественно на продвинутых пользователей, уже изучивших комбинаторику и теорию графов. А данный курс станет стартовой точкой для практики и покажет, в каких сферах могут пригодиться полученные знания.

Чему научитесь:

• Решать поставленные задачи с использованием методов динамического программирования и алгоритмов аппроксимации.

Плюсы:

• Программа больше ориентирована на практику, чем на теорию.

Минусы:

19. «Теория вероятностей‎» от Stepik

Длительность: 31 урок.

Сертификат: да.

Формат обучения: видеозаписи + тесты.

Программа обучения: даёт теоретическую базу в области теории вероятностей — случайные величины, условная вероятность, дисперсия, вероятностное пространство. Кроме теории будут разобраны реальные примеры и доказаны некоторые теоремы. Слушатели должны владеть базовыми знаниями в области математического анализа и выполнять простые операции с множествами.

Что изучите:

• Классическая версия теории вероятностей.
• Основы комбинаторики.
• Закон больших чисел.
• Математическое ожидание.
• Центральная предельная теорема.

Плюсы:

• Подробная и структурированная теория.
• Материал хорошо дополняет университетскую программу (актуально для студентов).

Минусы:

• Курс ориентирован преимущественно на теорию, не хватает практики.
• Некоторые задачи по уровню сложности не совпадают с изученным материалом.
• Преподаватель игнорирует вопросы учеников в комментариях.

20. «‎Математическая логика и теория алгоритмов» от «‎Лекториума»

Длительность: 40 лекций.

Сертификат: да.

Формат обучения: видеолекции + задания. Желающие получить сертификат могут пройти итоговый тест.

Программа обучения: курс для всех, кто хочет вникнуть в основы математической логики. Программа подойдёт студентам инженерно-технических факультетов, а также учащимся старших классов с математическим уклоном, которые интересуются логикой и математикой.

Для прохождения некоторых разделов требуется знание императивного программирования и математического анализа хотя бы на начальном уровне.

Что изучите:

• Что подразумевается под математической логикой.
• Основы теории множеств, операции над множествами.
• Основы пропозициональной логики.
• Языки первого подряда.
• Аксиоматический метод и его применение.
• Теория алгоритмов и математическое доказательство.

Плюсы:

• Нестандартные задачи для проверки и закрепления знаний.
• Можно получить постоянный доступ к материалам.
• Отзывчивая техподдержка.

Минусы:

• Не обнаружены.

Об авторах: Валентин Зюзьков, старший научный сотрудник и автор учебных работ, профессор кафедры «Компьютерные системы в управлении и проектировании» ТУСУР, имеет педагогический стаж 45 лет.

21. «Introduction to Calculus‎» от Coursera

Длительность: 5 недель.

Сертификат: выдаётся (платно).

Формат обучения: видеозаписи + статьи + тесты.

Программа обучения: поможет понять важность применения математики в науке, технике, торговле. Преподаватель расскажет об истории исчислений, а также даст теоретическую базу в области фундаментальной математики.

Чему научитесь:

• Выполнять операции с уравнениями и функциями.
• Практиковать методы интегрального и дифференциального исчисления.

Плюсы:

• Грамотный лектор с профессиональным подходом к обучению.
• Лекции строго по теме без воды.
• Идеальный баланс между теорией и практикой.

Минусы:

22. «‎Основы статистики» от Stepik

Длительность: 3 недели.

Сертификат: да.

Формат обучения: видеолекции + тесты.

Программа обучения: универсальный курс, который будет интересен и студентам, и научным сотрудникам всех сфер. Материал отлично подойдёт для освоения математической статистики. Много внимания уделяется математическим идеям, логике, интуиции.

Что изучите:

• Дисперсионный, регрессионный и кластерный анализ.
• Принципы построения регрессионных уравнений.
• Способы расчёта коэффициентов корреляции.

Плюсы:

• Курс полностью раскрывает основы статистики.
• Интересная живая подача материала.
• Небольшая продолжительность видеозаписей.

Минусы:

23. «‎Криптография I» от Coursera

Длительность: 7 недель.

Сертификат: выдаётся (платно).

Формат обучения: видеоуроки + тесты.

Программа обучения: учеников ждёт знакомство с устройством и принципом внутренней работы криптографических систем, а также правилами использования их в приложениях. Дополнительно на лекциях обсуждаются криптографические атаки и частые ошибки при работе с криптографическими системами.

Какие темы изучите:

• Криптография с открытым ключом.
• Алгоритм с симметричным ключом.

Плюсы:

• Качественная зарубежная программа.
• Наличие субтитров на русском языке.

Минусы:

• Много сложных терминов без объяснения.

24. «‎Введение в логику» от «Хекслет‎»

Длительность: 7 занятий.

Сертификат: нет.

Формат обучения: видеокурс.

Программа обучения: охватывает базовые принципы логики, которые должен знать каждый программист. Спикер расскажет о важности математической логики в современном мире, приведёт примеры в виде реальных ситуаций. Также слушателей ждёт знакомство с логическими операциями и способами применения полученных знаний для доказательства теорем.

Что изучите:

• Базовые понятия классической логики.
• Основные функции в логике.
• Предикаты и кванторы.
• Классические парадоксы логики.

Плюсы:

• Материал доступен без регистрации.
• Нет ограничений по времени.
• Живой стиль изложения на уроках.

Минусы:

• Не обнаружены.

25. «Теория игр‎» от Coursera

Длительность: 2 месяца.

Сертификат: выдаётся (платно).

Формат обучения: видеозаписи + статьи + тесты.

Программа обучения: специальный курс будет полезен разработчикам игр. Он помогает расширить кругозор и способствует профессиональному развитию. На лекциях рассматриваются базовые принципы стратегического взаимодействия, смешанные, доминирующие и доминируемые стратегии. Также преподаватели расскажут краткую историю теории игр.

Какие темы охватывает курс:

• Основные термины и методы теории игр.
• Байесовские игры.
• Концепция равновесия Байеса-Нэша.
• Игры с неполной информацией.

Плюсы:

• Содержательный курс, дающий базовые знания по теории игр.
• Реальные примеры (классические игры и приложения).
• Креативные задачи для проверки знаний.

Минусы:

26. «‎Математическая теория программирования» от Андрея Миронова

Длительность: 42 занятия.

Сертификат: нет.

Формат обучения: видеокурс.

Программа обучения: спецкурс для студентов профильных факультетов и практикующих программистов с математическими знаниями. Спикер объясняет связь между математикой и программированием на примере задач.

Какие темы рассматриваются:

• Использование метода Флойда.
• Теория неподвижных точек функциональных программ.
• Теория процессов и основные операции с процессами.

Плюсы:

• Изучение материала без регистрации и ограничений по времени.
• Рекомендация книг с полезным материалом и задачами.

Минусы:

27. «Data Science Math Skills‎» от Coursera

Длительность: 4 недели.

Сертификат: выдаётся (платно).

Формат обучения: видеоуроки + статьи + тесты.

Программа обучения: вводный курс охватывает математические концепции, тесно связанные с наукой о данных. Слушатели изучат базовые термины алгебры, а также основы теории вероятности. Программа разработана преимущественно для новичков, владеющих только школьным курсом математики.

Какие темы рассматриваются:

• Теория множеств.
• Операции с неравенствами.
• Логарифмы и функция натурального логарифма.
• Основы математики на декартовой плоскости.
• Построение функций на плоскостях X и Y.

Плюсы:

• Субтитры на русском языке.

Минусы:

• Мало полезного материала по теме, многие моменты рассмотрены поверхностно.

28. «‎Mathematics for Machine Learning: Linear Algebra» от Coursera

Длительность: 5 недель.

Сертификат: выдаётся (платно).

Формат обучения: видеоурокии + статьи + тесты.

Программа обучения: охватывает основы линейной алгебры, её связь с векторами и матрицами. Программа не подразумевает глубокое изучение линейной алгебры. Учебный материал пригодится тем, кто планирует вход в сферу машинного обучения, и нуждается в базовой математической подготовке.

Какие темы изучите:

• Работа с векторами и матрицами.
• Как работает алгоритм Pagerank.
• Применение концепций линейной алгебры в машинном обучении.

Плюсы:

• Можно учиться в комфортном режиме.
• Наличие русскоязычных субтитров.

Минусы:

• Непоследовательная подача информации, а некоторые задания не совпадают с пройденным материалам.

29. «Mathematics for Machine Learning: Multivariate Calculus‎» от Coursera

Длительность: 6 недель.

Сертификат: выдаётся (платно).

Формат обучения: видеозаписи + конспекты + задания.

Программа обучения: вводный курс в многомерное исчисление для создания методов машинного обучения. Слушатели узнают основные концепции математического анализа. Кроме общей теории на уроках рассматривается создание инструментов для выполнения расчётов.

Какие темы изучите:

• Линейная регрессия и метод векторного исчисления.
• Многопараметрическое исчисление.

Плюсы:

• Удобная структура курса.
• Хорошее качество видео и графики.
• Есть русскоязычные субтитры.

Минусы:

• Поверхностное раскрытие тем.
• В некоторых уроках полностью отсутствуют примеры.

30. «‎Mathematics for Machine Learning» от Coursera

Длительность: 4 недели.

Сертификат: выдаётся (платно).

Формат обучения: видеолекции + статьи + упражнения + тесты.

Программа обучения: курс среднего уровня охватывает базовую статистику наборов данных и математических концепций, необходимых для разработки алгоритмов машинного обучения. Для решения некоторых упражнений требуется знание линейной алгебры и Python.

Что узнаете:

• Способы реализации математических концепций с помощью реальных данных.
• Принцип работы ортогональных проекций.

Плюсы:

• Есть субтитры на русском языке.

Минусы:

• Сухая теория без реальных примеров.
• Необходим продвинутый уровень Python.

31. «‎Linear Algebra — Foundations to Frontiers» от edX

Длительность: 15 недель.

Сертификат: да (при доплате 49 долларов).

Формат обучения: видео + упражнения по программированию.

Программа обучения: будет полезна студентам профильных вузов, а также специалистам, чья работа связана с большими объёмами данных. Программа включает стандартные темы, которые изучаются в большинстве современных университетов.

Что узнаете:

• Векторные и матричные операции.
• Способы решения линейных уравнений.
• Характеристики разделенных и специальных матриц.
• Векторные пространства.

Плюсы:

• Материалы из университетской программы в свободном доступе.
• Увлекательная подача информации с визуализацией и интересными заданиями.

Минусы:

• Необходимо знание английского языка.

32. «‎Pre-University Calculus» от edX

Длительность: 8 недель.

Сертификат: да (при доплате 50 долларов).

Формат обучения: видеолекции + экзамен.

Программа обучения: вводный курс по исчислению для подготовки к полноценному изучению математического анализа в университете. Кроме теории непосредственно по теме есть мотивирующие уроки, посвящённые значимости математики в различных отраслях (наука, техника, передовые технологии).

Чему научитесь:

• Понимать математические термины и концепции.
• Использовать методы интеграции.
• Решать математические задачи.

Плюсы:

• Возможность подготовиться к обучению в университете или на продвинутых курсах без финансовых затрат.
• Качественная подборка материала, полезный контент без воды и ненужной информации.

Минус:

• Необходимо знание английского языка.

33. «‎Calculus 1A: Differentiation» от edX

Длительность: 13 недель.

Сертификат: да (при условии доплаты 100 долларов).

Формат обучения: видеокурс.

Программа обучения: изучение предоставленного материала поможет открыть для себя производную, научиться её вычислять и применять для решения реальных задач. На уроках рассматриваются математическое обозначение, физический смысл и геометрическая интерпретация производной.

Чему научитесь:

• Вычислять производную функции.
• Делать графики функций.

Плюсы:

• Удобная структура курса.
• Материал даёт качественную теоретическую базу.

Минусы:

• Для прослушивания лекций необходимо знание английского языка.

34. «Calculus 1B: Integration» от edX

Длительность: 15 недель.

Сертификат: да (при доплате 100 долларов).

Формат обучения: видеокурс.

Программа обучения: курс знакомит слушателей с интегралом. Спикер расскажет, что это такое и в каких сферах он важен, как вычислить интеграл, а также как использовать вычисления для решения различных задач.

Что узнаете:

• Геометрическая интерпретация интеграла.
• Связь между интегралом и производной.
• В чём заключается физический смысл интеграла.
• Методы численного и символьного интегрирования функций.
• Способы применения интеграла для решения задач.

Плюсы:

• Обучение в комфортном режиме.
• Качественный учебный контент.

Минусы:

• Нужно знание английского языка.

35. «Introduction to Probability‎» от edX

Длительность: 10 недель.

Сертификат: да (оплачивается отдельно).

Формат обучения: видеокурс.

Программа обучения: содержит подборку уроков по введению в вероятность. Спикер расскажет, как вероятность и статистика помогают решать сложные проблемы. Теория дополняется различными примерами от медицинского тестирования до составления спортивных прогнозов.

Что узнаете:

• Способы применения условной вероятности для решения нестандартных задач.

Плюсы:

• Прохождение в комфортном темпе.
• Университетская программа.

Минусы:

• Необходимо владение английским языком.

36. «‎Probability — the Science of Uncertainty and Data» от edX

Длительность: 16 недель.

Сертификат: да (при доплате 300 долларов).

Формат обучения: видеокурс.

Программа обучения: курс охватывает базовые понятия вероятности, необходимые для развития в области науки о данных. Спикер расскажет о дискретных и непрерывных случайных величинах, законах больших чисел, процессах Пуассона.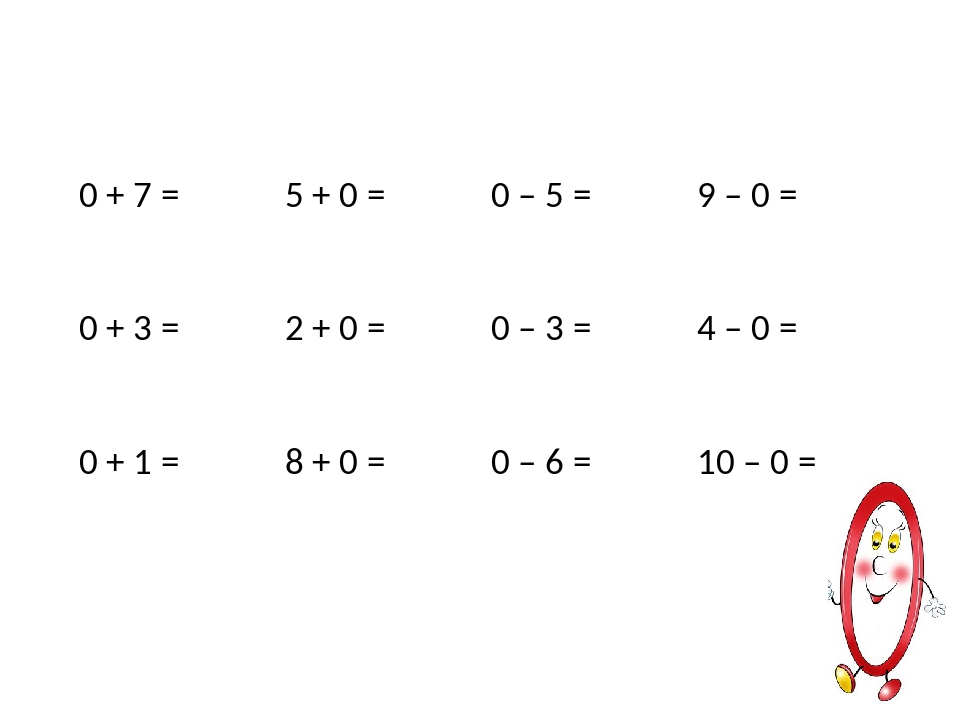

Какие темы рассматриваются:

• Структура и элементы вероятностных моделей.
• Работа со случайными переменными.
• Принципы вероятностных расчетов.
• Применение законов больших чисел.

Плюсы:

• Международная учебная программа.
• Лёгкая подача материала.

Минусы:

• Необходимо знание английского языка.

37. «Многопараметрическое исчисление» от MIT OpenCourseWare

Длительность: 98 лекций.

Сертификат: нет.

Формат обучения: видеолекции + конспекты лекций + упражнения + финальный экзамен.

Программа обучения: представляет подборку записей лекций Массачусетского института. Подразумевается самостоятельная работа с материалом. Много внимания уделяется интегральному, дифференциальному и векторному исчислению. Рассматриваемые инструменты необходимы специалистам в области математики и программирования.

Что изучите:

• Матрицы и векторы.
• Функции двух переменных.
• Градиентные и направленные производные.
• Множители Лагранжа.
• Ограниченные дифференциалы.
• Двойные и линейные интегралы.
• Тройные интегралы.
• Векторные поля в пространстве.

Плюсы:

• Насыщенная программа с теоретической базой и примерами решения задач.
• Свободный доступ к лекциям без ограничения по времени.
• Можно скачать учебные материалы для личного использования.

Минусы:

• Для прослушивания лекций нужно хорошо знать английский язык.

38. «Discrete Math and Analyzing Social Graphs» от Coursera

Длительность: 6 недель.

Сертификат: выдаётся (платно).

Формат обучения: видеоуроки + презентации + тесты.

Программа обучения: поможет быстро вникнуть в основы дискретной математики. Курс будет полезен всем, кто связан с информатикой и анализом данных. От слушателей требуется знание языка Python на продвинутом уровне.

Какие знания даёт курс:

• Основы комбинаторики.
• Базовая теория вероятностей.
• Основы теории графов.

Плюсы:

• Лаконично составленные лекции.
• Интересные практические задания.
• Русскоязычные субтитры упрощают просмотр уроков.

Минусы:

39. «Calculus and Optimization for Machine Learning» от Coursera

Длительность: 6 недель.

Сертификат: выдаётся (платно).

Формат обучения: видеоматериалы + статьи + тесты.

Программа обучения: подготовлена преимущественно для студентов IT-специальностей. Но лекционный материал может пригодиться для общего развития специалистам из области анализа данных. Для продуктивной работы с учебным материалом необходим хотя бы начальный уровень математической подготовки.

Что изучите:

• Числовые множества и пределы.
• Вычисления дискретного предела.
• Многомерные функции.
• Вычисление производной функции.

Плюсы:

• Качественная программа для получения релевантных знаний в области вычислений.
• Есть русскоязычные субтитры.

Минусы:

• Плохое качество презентаций.
• Сложная подача материала, многие моменты лектор не объясняет.

40. «First Steps in Linear Algebra for Machine Learning» от Coursera

Длительность: 4 недели.

Сертификат: выдаётся (платно).

Формат обучения: видеоуроки + статьи + тесты.

Программа обучения: подразумевает изучение основных концепций линейной алгебры, необходимых в сфере анализа данных и машинного обучения. Подойдёт пользователям, имеющим представление о линейной алгебре и матричном анализе. Для выполнения некоторых упражнений понадобится знание Python. Также материал будет полезен студентам профильных факультетов.

Чему научитесь:

• Работать с данными в векторной и матричной форме.
• Решать линейные уравнения.
• Находить и применять основные матричные разложения.

Плюсы:

• Доступное изложение основ линейной алгебры.
• Идеальный баланс теории и практики.
• Много наглядных примеров.

Минусы:

• Некачественная презентация.

41. «Probability, Theory, Statistics and Exploratory Data Analysis» от Coursera

Длительность: 6 недель.

Сертификат: выдаётся (платно).

Формат обучения: видеозаписи + конспекты + тесты.

Программа обучения: включает некоторые концепции теории вероятности и основы статистики. На лекциях рассматриваются разделы, которые необходимы для начала карьеры в Data Science. Обязательно понимание основ комбинаторики и исчислений.

Чему научитесь:

• Работать с вероятностями, анализом и визуализацией данных в Python.

Плюсы:

• Хорошая структура курса и много интересных заданий.
• Интересный стиль изложения материала.
• Подробное разъяснение сложных моментов с примерами.
• Грамотный лектор и профессиональный подход к обучению.

Минусы:

• Не обнаружены.

42. «Matrix Algebra for Engineers» от Coursera

Длительность: 4 недели.

Сертификат: выдаётся (платно).

Формат обучения: видеолекции + статьи + задачи.

Программа обучения: краткий курс по линейной алгебре для инженеров, программистов и других технических специалистов. Основной акцент сделан на матрицы. Подразумевается, что слушатели уже знакомы с исчислением одной переменной. В целом, программа подойдёт всем, кто заинтересован в изучении основ матричной алгебры, и при возникновении сложностей и готов самостоятельно искать недостающую информацию.

Что изучите:

• Основы линейной алгебры и инженерной математики.
• Системы линейных уравнений.
• Матрицы и векторные пространства.

Плюсы:

• Насыщенная программа при короткой продолжительности курса.
• Хорошее изложение и структура лекций.
• Наглядная демонстрация разных видов матричных операций.
• Наличие русскоязычных субтитров.
• Можно скачать материалы для дальнейшего использования.

Минусы:

43. «Introduction to Complex Analysis» от Coursera

Длительность: 2 месяца.

Сертификат: выдаётся (платно).

Формат обучения: видеозаписи + слайды + упражнения.

Программа обучения: вводный курс в комплексный анализ. Сначала преподаватель даст базовые представления о комплексной плоскости и алгебре комплексных чисел.

Позже учащиеся познакомятся с интегрированием и дифференциацией. Несмотря на двухмесячную продолжительность курса, основная часть обучения подразумевает выполнение домашних заданий.

Упражнения не рассчитаны на быстрое выполнение, может потребоваться дополнительный поиск информации.

Также представленный материал можно использовать в качестве дополнения к классическому университетскому учебнику.

Какие темы изучите:

• Комплексные числа и комплексный анализ.
• Конформное отображение.

Плюсы:

• Хорошая теоретическая база для понимания основ комплексного анализа.
• Свободный стиль изложения способствует лёгкому восприятию материала.
• Наличие русскоязычных субтитров.

Минусы:

44. «Essence of Linear Algebra» от 3Blue1Brown

Длительность: 16 занятий.

Сертификат: нет.

Формат обучения: видеокурс.

Программа обучения: даёт представление об основах линейной алгебры.

Что узнаете:

• Что подразумевается под определением «вектор» в контексте линейной алгебры.
• Размеренность, базис, линейная комбинация вектора.
• Линейные преобразования и матрицы.
• Трёхмерные линейные преобразования.
• Обратные матрицы.
• Скалярное произведение и двойственность.
• Геометрическая интерпретация.
• Собственные векторы, значения, базисы.
• Способы вычисления собственных значений.
• Абстрактные векторные пространства.

Плюсы:

• Качественная визуализация для лучшего восприятия материала.

Минусы:

45. «Introduction to Higher Mathematics» от Bill Shillito

Длительность: 19 занятий.

Сертификат: нет.

Формат обучения: видеокурс.

Программа обучения: вводный курс в высшую математику для студентов, программистов, инженеров.

Какие темы изучите:

• Аксиомы и математическое доказательство.
• Основы теории множеств.
• Использование математической индукции.
• Теория чисел.
• Натуральные числа и действительные числа.
• Основы топологии.
• Основы абстрактной алгебры.

Плюсы:

• Отличное качество видео и структура лекций.
• Отсутствие сложных терминов.

Минусы:

• Для прослушивания лекций нужен продвинутый уровень английского языка.

46. «Дискретная математика» от Coursera

Длительность: 11 недель.

Сертификат: выдаётся (платно).

Формат обучения: видеокурс.

Программа обучения: поверхностный курс охватывает базовые концепции дискретной математики, которые являются основой информатики. На уроках рассматриваются множества, функции, графики. Помимо теории подразумевается выполнение заданий для взаимной оценки.

Какие темы изучите:

• Отношения и функции.
• Перечислительная комбинаторика.
• Основы теории графов.
• Сетевой поток и сопоставления.

Плюсы:

• Субтитры на русском языке.

Минусы:

• Отсутствует объяснение сложных терминов.
• Недостаточно реальных примеров.

как научиться работе с цифрами

Этого не должно было случиться, но почему-то произошло: 11 класс остался в далеком прошлом, а вы стали вовсе не художником или рок-звездой, а интернет-маркетологом. И школьная учительница оказалась права: математика еще пригодится, вот увидишь!

Где учиться цифрам с нуля, как не сойти с ума от цифр и почему в школе было так сложно (а сейчас легче не станет).

Почему математика такая страшная

В любой вещи, которую вы не понимаете, мало приятного. Но математику особенно не любят. Или даже боятся ее.

Дело не только в том, что у учительницы по алгебре был слишком грозный вид. Математическая тревожность — явление, которое исследуют ученые. И под тревожностью имеют в виду все ее проявления: панику, дрожь в руках. Непонятно, что появляется раньше: неспособности к математике и, как следствие, страх перед ней или же сам страх не дает научиться вычислениям.

Хорошая новость в том, что математическая тревожность слабо коррелирует с результатами тестов IQ.

Что мы знаем про способности к математике

Наверняка вы говорили о себе: «У меня нет математических способностей». И вообще закончили гуманитарный класс.

Большинство ученых с вами согласятся, но лишь потому, что в принципе не доказано существование врожденных способностей к математике. Исследователи много лет пытаются узнать о наследуемости этого навыка. Пока одним из самых громких за последнее время стала работа ученых из университета Питтсбурга (США). Они доказали, что есть корреляция между способностями к математике у детей и родителей. Но ее причина — не только в генетике, но и в социальных факторах.

Кроме способностей к математике, существует математическое чувство, и оно наследуется. Это благодаря ему мы определяем самую короткую очередь, не считая количество людей. Ученые из США сравнили, как дети в шесть месяцев и три с половиной года воспринимают цифры и количество предметов. Оказалось, что малыши, которые в раннем возрасте демонстрировали лучшие математические способности, показали лучший результат и спустя три года, причем общий уровень развития не коррелировал с математическими способностями.

Но выдыхать рано (вы наверняка уже решили, что оказались бы в этом эксперименте среди детей с заурядными результатами). Другая группа исследователей проверила, можно ли развить математические способности и научиться работе с цифрами во взрослом возрасте. Оказалось, что можно. Добровольцы решали задачи, а затем половина участников эксперимента тренировали математические навыки, а контрольная группа — нет, как и полагается контрольной группе. После этого все участники снова решили арифметические примеры. Занимавшаяся математикой группа показала результаты гораздо выше, чем контрольная.

Как выучить математику во взрослом возрасте

Сначала решите, для чего вам нужна математика, какие темы нужно знать и как вы оцените, что цель выполнена. Для повседневной работы в маркетинге вам вряд ли понадобятся линал или понимание задач тысячелетия. Быстрое вычисление, работа с процентами, понимание математических функций.

Полезные курсы по математике

Проект «Математика с нуля» 

Текстовые уроки по основным темам.

 

 

Интернет-Урок: 

(Математика, 1-6 класс)
(Алгебра, 7-11 класс)

Уроки школьной программы по математике в формате видео. Рассчитаны на детей и подростков, но разве это вас остановит?

 

Stepik.

Основы статистики 

На практике пригодится чаще, чем основы по математике. Если вы не помните из статистики ничего, пройдите курс перед изучением веб-аналитики.

 

 Stepik. Теория вероятностей

Курс по теории вероятностей посвящен базовым вероятностным методам, которые можно использовать в работе и повседневной жизни.

Открытый университет. Теория игр 

Теория игр полезна для многих специальностей. Развивает способность к анализу информации, постановке целей и созданию стратегий.

Вводный курс по матанализу

Если вы уже готовы к высшей математике, но плохо помните университетскую программу.

Khana Academy

Курсы разделены темам и по уровням. Дается сразу теория и тренажер, обучение геймифицировано. Уроки только на английском языке.

 

Книги по изучению математики с нуля

http://www.alleng.ru/

Подборка школьных учебников, если скучаете по ним.

Математика для взрослых.

Кьяртан Поскитт

Не научит теории, но избавит от ежедневных страданий, когда нужно сделать простые вычисления.

Если вы аналитик и занимаетесь, например, аналитикой в Instagram или других соцсетях удобней всего использовать Popsters.

Итого:

1. Многие люди и правда боятся математику. Ученые не понимают: страх из-за незнания или незнание от страха.
2. Чувство числа наследуется от родителей. А вот математические способности можно развить.
3. Взрослые люди могут с нуля выучить математику. Для этого есть бесплатные курсы и книги. 

Ментальная арифметика видео уроки бесплатно с нуля — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7

Ментальная арифметика видео уроки бесплатно с нуля

Заинтересовала ментальная математика? Но не знаете, с чего начать? Специально для знакомства — наши лаконичные видеоуроки, которые вы можете посмотреть бесплатно в любое время!

Они подойдут родителям, которые планируют начать самостоятельное обучение детей счету. Полезны будут и для детей, дошкольников и младших школьников. А также всех-всех, кто хочет понять, как научиться считать быстро, с нуля, решать примеры и не бояться математики.

Посмотрите все уроки — это не займет много времени!

Подарите вашим детям увлекательный мир овладения счетом и решения задач!

Урок 1. Знакомимся с Абакусом

Узнайте, что такое ментальная арифметика, счеты Абакус, откуда они пошли и из каких элементов состоят.

Урок 2. Начинаем считать

Посмотрите это видео и через 1 минуту вы узнаете, как выполняется счет на Абакусе, как выставлять единицы, десятки и сотни.

Урок 3.

Какими пальцами набирать

Это короткое видео расскажет, какими пальцами удобно работать на счетах и набирать цифры, напомнит принцип подсчета.

Урок 4. Учимся вычитать

Узнайте, как быстро решать примеры на вычитание, как набирать их на счетах и получать верный результат.

Урок 5.

Веселая ментальная карта

Сейчас вы увидите, что такое ментальная карта и как она используется в домашних условиях, при занятиях с ребенком.

Урок 6.

Легко складываем и вычитаем большие числа

Этот видео-урок научит вашего ребенка работать с большими числами, уверенно складывать и вычитать, быстро решать разные примеры.

Урок 7. На чем потренироваться

Узнайте, какое приложение вы можете установить на планшет или телефон для тренировок в решении задач, как им пользоваться.

Урок 8. Быстрое руководство по Know Abacus

Познакомьтесь с приложением для начинающих и продолжающих освоение ментальной математики!

Урок 9.

Легкое понимание состава числа 10

Веселое, игровое мини-видео научит вашего ребенка составу чисел, визуально закрепит в его памяти составляющие Десятки.

Урок 10. Уровни ментальной арифметики

Узнайте, что это такое и какая сложность уровней, какие примеры и задания туда входят.

Ментальная математика в домашних условиях

Ментальная Арифметика в Домашних Условиях (Методы и Занятия)

Как научить ментальной арифметике дома?

Вы решились научиться считать на счетах абакуса или соробана? Как научить ребенка ментальной арифметики дома?

Ментальная арифметика обучение дома?  Как именно считать и с чего начинать? Чтобы ответить на эти вопросы Вам просто необходимо прочитать азы ментальной арифметики.

Занятия в домашних условиях для ребенка будет сразу не так просты. Нужно будет набраться терпению и огромного усердия

Занятия не должны быть в хаотичном режиме! Постарайтесь решить в какое время будет проводиться систематические уроки. Теперь давайте ответим на вопросы:

Что же такое Ментальная Арифметика?

Это уникальная методика интеллектуального развития от 4 до 14 лет, в основе которой лежит многовековая система арифметических действий с помощью счета- абакус, соробан. На сегодняшний день действует около 6000  центров по более чем в 54 странах мира, основные из них: Китай, Казахстан, Япония, Турция, Малазия …

Открывать в человеке гения необходимо в детском возрасте, когда ум ребенка гибок и способен к трансформированию задатков в способности, те, в свою очередь, в таланты, и только тогда Вы получите гениального, успешного в любых делах и начинаниях ребенка!

Давайте составим  план урока:

1. Что такое абакус, соробан?
2. Расположение чисел
3. Как складывать?
4. Дополнительная литература

Что такое абакус?

Это внешний вид Абакуса.

Внешний вид Абакуса

Чем-то напоминает известные многим советские счеты с костяшками. Принципы работы на этих двух приспособлениях очень похожи. Отличаются эти счеты количеством костяшек на спицах и, собственно говоря, удобством эксплуатации. На абакусе приходится делать намного меньше движений руками.

Абакус и счеты

Итак, абакус состоит из рамки, в которую установлены спицы. Причем спиц может быть разное количество. А на спицах нанизаны костяшки. По 5 штук на каждую. Спицы проходят сквозь разделительную планку. Над планкой остается по одной костяшке, под планкой по четыре.

Важную роль при счете на абакусе играет то, как именно человек двигает пальцами. Используются в работе только большой и указательный пальцы. Все движения путем многократных повторений доводятся до автоматизма. Этот навык легко потерять, поэтому при занятиях ментальной арифметикой не желательно пропускать уроки.

Теперь о том, как же располагаются числовые линейки.

расположение чисел на абакусе

Справа у нас находятся единицы. Затем десятки, потом сотни, тысячи, десятки тысяч и т.д. Каждому разряду своя спица. Костяшки, которые находятся под разделительной планкой, означают «1», над планкой – «5». Трудновато понять, да?

Давайте посмотрим на примере.

Десятичные линейки рисовать не стала. То есть, крайняя правая линейка на  рисунке – это единицы.

Так будет выглядеть на абакусе число 3.

число-3-на-абакусе

Поднимаем к разделительной планке три костяшки на линейке единиц.

Попробуем взять двойное число, например, 15.

На линейке десятков поднимаем 1 костяшку, то есть, получаем 1 десяток. А на линейке единиц опускаем к разделителю верхнюю костяшку, которая и означает 5.

Получилось число 15!

Покажем теперь число для примера -53-на-абакусе На линейке десятков опускаем к разделителю верхнюю костяшку, которая означает 50. А на линейке единиц поднимаем с верху 3 костяшки. Получилось число 53!

А давайте чего-нибудь посущественнее наберем. Например, 6482!

На линейке тысячи у нас верхняя костяшка опущена к разделителю – это пять тысяч и одна нижняя поднята вверх, плюс еще тысяча. Получаем 6 тысяч. С сотнями полегче, просто четыре костяшки поднимаем вверх. Десятки: верхняя опущена, три нижних подняты. Получается сверху 5 десятков, снизу 3. Это 80. Ну и еще 2 единицы. Не так уж сложно, правда?

Как складывать на абакусе?

А теперь переходим к сложению и посмотрим, что из этого получится. Предлагаю взять что-нибудь попроще, чтобы не взорвать себе мозг) Например, сложим 33 и 14.

Откладываем на абакусе 33.

К трем десяткам прибавим еще один. Получим 4 десятка или 40.

прибавление одного десятка на абакусе

Теперь единички. К трем единицам прибавим еще 4. Так как четырех свободных единиц снизу на спице нет, то сначала прибавим пять, опустим верхнюю косточку. А потом отнимем 1, опустим одну нижнюю. Получилось у нас 7 единиц.

В результате получилось 47! Результат мы получили верный!

Развить навыки быстрого счёта вы можете на бесплатном онлайн тренажёре здесь

Ментальная Арифметика научиться дома – Дополнительная литература

Вот по такой схеме на абакусе и считают. Показ был самого простого.  А ведь можно еще и вычитать, и умножать, и делить, и в степень возводить. И работать с огромными числами. Хотите знать больше? Пожалуйста!

Обратите внимание на книгу «Ментальная арифметика. Школа волшебников»  Она ориентирована на обучение детишек.

Рекомендуем вам приобрести:

Учебный материал для занятий дома

или

Методический комплект для родителей и педагогов 

Ментальная арифметика домашнее задание

Самая главная составляющая часть в обучении, не игнорируйте систематические каждодневные домашние задания, обязательно давайте их детям! Желательно заниматься дома не только Ментальной Арифметикой, но еще и Скорочтением.

У нас Вы можете найти упражнения для скорочтения. Более подробнее о скорочтении, Вы можете узнать  у нас в темах.

Ментальная математика в домашних условиях скачать бесплатно

Желаем Вам успехов в познании Ментальной Арифметики.

Уроки ментальной арифметики для детей: бесплатные видео для домашнего обучения

Уроки ментальной арифметики для детей: бесплатные видео для домашнего обучения

Ментальная арифметика – популярная методика гармоничного и равного развития обоих полушарий мозга. Методика одинаково подходит для детей и взрослых и заключается в обучении быстрому устному счету с применением специального инструмента, который называют абакусом или соробаном.

 

Научить детей ментальной арифметике в домашних условиях помогут видео уроки на сайте ВСЕ КУРСЫ ОНЛАЙН.

 

Строение и функции абакуса (соробана) 

 

Абакус – древние китайские счеты. Состоит из рамки, перекладины, спиц и косточек. Перекладина делит косточки горизонтально на 2 части. Нижние получили название «земных» (смотрят всегда вниз), верхние – «небесных» (смотрят вверх).  Косточки играют роль единиц, десятков и сотен. Сначала ученики осваивают простые арифметические действия (сложение и вычитание), затем сложные (умножение и деление). Следующий этап – счет без использования инструмента, в уме. Ученик двигает пальцами, представляя абакус, и решает примеры с многозначными числами. Инструмент можно запросто сделать самостоятельно, переконструировав обычные советские счеты. 

 

Основные принципы

 

• Считать правильно двумя руками, используя указательные и большие пальцы. 
• Поднимают кости всегда большим пальцем, опускают и двигают «небесные» косточки указательным. 
• Абакус нужно придерживать левой рукой.
• В правой руке всегда находится ручка для заметок и записей, обхваченная мизинцем, безымянным и средним пальцами.
• Сброс косточек в исходное положение делают, обхватив перекладину двумя рабочими пальцами и двигаясь справа налево.  

 

 

Набор чисел

 

Крайний правый столбец предназначен для набора единиц, второй для десятков, третий для сотен, следующие для тысяч и так далее. Исходное положение означает ноль.  Поднятые нижние бусины – единицы от 1 до 4, десятки от 10 до 40 и аналогичные сотни, тысячи в зависимости от столбца. Верхние опущенные бусины обозначают числа, кратные пяти: 5, 50, 500, 5000 и т.д. по мере удаления столбцов. Цифра 7 – это 5+2. Значит нужно опустить небесную косточку и поднять две земных. Все остальные числа набирают по аналогичному принципу. Для тренировки хорошо использовать онлайн-тренажеры в Google или установить специальное приложение.

 

Правила

 

Правила имеют условные названия, которые образно иллюстрируют действия. Выполняются всегда в строгой последовательности.

1. «Просто» — поднятие нужного количества земных косточек, опускание небесной или то и другое одновременно.
2. «Брат» — когда первый пункт не работает и сумма выдает 5.
3. «Друг» — два числа, дающие 10.
4. «Друг + Брат» — совмещает два предыдущих правила, выполняется двумя руками.

 

Сложение (простое и с переходом на 10)

 

Самое простое действие, с которого начинают обучение.  Начинать первое знакомство можно в детском саду, начальной школе. Сначала следует научиться считать до 10. Затем решать примеры до 3. Следующий этап — сложение всех чисел без перехода на десятки. В качестве закрепляющих заданий эффективно использовать карточки с изображениями разных комбинаций на счетах. Например, найти правильный ответ на заданный пример.  При сложении за пределами десятка суммы необходимо разложить на простые составляющие. Состав десяти может иметь несколько комбинаций (1+9, 2+8, 3+7, 4+6, 5+5). 

 

Вычитание

 

Разницу считают подобно сумме, по правилам «просто», «брат», «друг», «друг+брат». Существует масса онлайн тренажеров и конструкторов заданий для закрепления арифметических навыков. Современные ученики обожают работать на компьютере, поэтому заставлять тренироваться даже не придется. Будущие математики сами с удовольствием будут выполнять нужные упражнения.

 

 

Умножение

 

Умножение (многократное сложение) можно выполнять несколькими различными методами. Самый простой и безошибочный был предложен Японским Комитетом по абакусу. Принцип напоминает умножение в столбик на бумаге, так же последовательно. Чтобы работать с двузначными числами (45*56), нужно учесть: ответ получится четырехзначным, и нужно будет уметь его прочитать. 

 

Деление

 

Деление производят по принципу многократного вычитания. Конечно, без выученной «на зубок» таблицы умножения приступать к действию не имеет смысла. Самый удобный метод разработан Такаши Койима в книге об использовании и теории японского абакуса. Главный плюс — использование привычной школьной терминологии: делимое, делитель, частное. Делимое находится правее центра, делитель левее, разделенные тремя-четырьмя свободными линейками.

 

 

Положительное влияние счета на абакусе

 

В Азии предмет входит в обязательную программу почти во всех учебных заведениях. С помощью простого девайса дети учатся умножать и делить многозначные числа без калькулятора. Существуют и другие сопутствующие бонусы.

• Развивается зрительная и слуховая память, повышается внимание и сосредоточенность.
• Активируется интуиция, сообразительность, смекалка.
• Возникает нестандартное мышление, самостоятельность, уверенность в принятии решений.
• Усиливаются творческие способности и предрасположенность к изучению иностранных языков.

 

Тренировочные упражнения

 

Благодаря японской методике родители имеют прекрасную возможность одновременно учить детишек счету и прокачивать ум и интеллект в целом. Европейцы подхватили идею и дополнили интерактивными технологиями: компьютерным тренажером (анзаном), флеш-картами и другими программами. Важно заниматься каждый день  в течение двух-трех лет , начиная с четырех-шестилетнего возраста.

В результате регулярных занятий повышается успеваемость в школе за счет улучшения памяти и повышения концентрации внимания. Ребенок легче запоминает новые слова, исторические даты и факты, теоремы и формулы. Одновременно развивается воображение и творческое мышление, способность нестандартно подходить к решению задач. 

 

Ментальная арифметика | Уроки счета на абакусе

Курс «Ментальная арифметика» предназначен для дошкольников и школьников. Возрастной диапазон – от 5 лет до 16 лет. Ментальная арифметика – это методика, активно способствующая интеллектуальному развитию детей, повышающая умственные способности и творческий потенциал за счёт устных арифметических вычислений и развития двухполушарного мышления.

Курсы ментальной арифметики развивают:

• Воображение.
• Творческие способности.
• Быстроту реакции.
• Нестандартный подход к любой ситуации.
• Креативность.
• Лидерские качества.
• Усидчивость и внимательность.
• Память.
• Интерес к изучению других дисциплин.
• Быстрый счёт в уме.

Навыки, развиваемые курсами ментальной арифметики в «Академии развития интеллекта AMAKids» – это отличный фундамент для дальнейшего развития вашего ребёнка! Изучение любой другой информации становится значительно более простым!

Зачем нужна ментальная математика для детей?

• Улучшается скорость реакции и работа памяти.
• Тренируется головной мозг.
• Быстро воспринимается новая информация.
• Возрастает уровень безопасности ребёнка в жизни.
• Повышается успеваемость по базовым школьным предметам.
• Результат со стопроцентной гарантией.

Ментальная арифметика – это методика, применяемая в нашей стране не так давно, но уже широко востребованная. Много людей желают узнать – а где и как она появилась? Возникновение ментальной математики принято связывать с изобретением древними китайцами счётами абак – это произошло более пяти тысячелетий назад. Затем эти счёты усовершенствовали японцы. Сегодня они носят имя «абакус», и мы используем их на занятиях в нашей школе ментальной арифметики «Академии развития интеллекта AMAKids».

Ментальная арифметика для детей – это система, не имеющая аналогов. Программа разделена на несколько фрагментов и выстроена таким образом, чтобы результат был максимальным:

• первое занятие начинается с того, что дети знакомятся как с физическими счётами, так с ментальными. На всех занятиях изучается сразу два типа вычислений;
• всего четырех недель регулярных занятий ментальной арифметикой хватит для того, чтобы ребёнок решал в уме примеры значительно быстрее любого взрослого человека;
• после двух месяцев занятий дети решают в уме примеры, декламируя при этом стихотворение вслух;
• через год ребёнок освоит все правила сложения и вычитания при счёте в уме;
• когда ребёнок закончит курс (это займет 2-2,5 года), он будет легко пользоваться всеми правилами умножения и деления при ментальном счёте.  

Курсы ментальной арифметики в «Академии развития интеллекта AMAKids» – это:

• Высококвалифицированные тренеры, которые прошли строгий конкурсный отбор и досконально знают все нюансы методики.
• Интересные и увлекательные занятия, которые проходят в игровой форме.
• Небольшие группы до 10 человек, что обеспечивает индивидуальный подход к каждому ребёнку.
• Красочные учебники.
• А также наша уникальная платформа, с помощью которой результат достигается в 2-3 раза быстрее.

Если вашему ребёнку исполнилось 5 лет, он умеет считать от 0 до 10 в прямом и обратном порядке, а также умеет соотносить цифру с количеством, то его уже можно записать на пробное занятие по ментальной арифметике в «Академии развития интеллекта AMAKids»! Первое же упражнение будет для вашего ребёнка шагом в мир удивительных возможностей! Наш сайт содержит максимально полную информацию о них!

Уроки ментальной арифметики проходят в игровой форме с тренером в центре AMAKids один раз в неделю. Длительность занятий зависит от возраста ребенка:

• Дети дошкольного возраста (5-6 лет) – 2 урока по 35 минут с веселой игровой переменкой!
• Дети школьного возраста – 2 урока по 45 минут.

Мы уверены, что родители заинтересованы в раскрытии потенциала своего ребёнка! Сделайте первый шаг к успешному будущему своего ребёнка, а «Академия развития интеллекта AMAKids» вам в этом поможет!

Ментальная арифметика: как и зачем решать 10 примеров в секунду

Ментальная арифметика: как и зачем решать 10 примеров в секунду

Умение быстро считать в уме развивает внимание, скорость обработки информации и даже творческое мышление. Дает ли этот навык ребёнку конкурентное преимущество в будущем? Станет ли шагом к успешной жизни или просто отнимет драгоценное время? Екатерина Цыбуля, руководитель центра «Учусь на 5», логопед, тренер по ментальной арифметике, рассказывает, в чем польза такого обучения.

Екатерина Цыбуля, руководитель центра «Учусь на 5», логопед, тренер по ментальной арифметике

Ментальная арифметика — программа развития умственных и творческих способностей, основанная на системе устного счета. Освоив ее, ребенок сможет решать арифметические задачи в уме всего за несколько секунд. Методика рекомендована для детей от 4 до 12 лет. Однако современные развивающие центры готовы обучать и более взрослых людей, как правило, с одной оговоркой — чем позднее начнешь, тем больше усилий потребуется.

Ментальная арифметика зародилась в Японии в ХVI веке. На начальных этапах обучения используются специальные счеты — абак или соробан. Счеты состоят из рамки, разделительной полосы, вертикальных спиц, верхних («небесных») и нижних («земных») косточек. Одна «небесная» косточка равна пяти «земным». Количество спиц варьируется от 13 до 31. При работе ребенок использует только большой и указательный пальцы. Все движения доводятся до автоматизма. Через некоторое время ребенок совершает вычисления на воображаемом абаке, а задачи решаются с помощью образов.

Формула интеллекта: логика плюс интуиция

Известно, что левое полушарие отвечает за логику, рациональность и анализ, а правое — за образность, целостность, интуицию, фантазию и воображение. Современная система образования уделяет больше внимания точным наукам. Время на танцы, рисование или занятие музыкой выделяется по остаточному принципу. Но даже если родителям удается найти золотую середину, возникает вопрос — как развить взаимосвязь работы обоих полушарий, чтобы максимально раскрыть потенциал ребенка?

Программа обучения метальной арифметики направлена на формирование устойчивых нейронных связей левого и правого полушарий. По мнению педагогов, именно этот факт помогает людям выбирать наиболее эффективные решения и добиваться успеха в жизни.

Плюсы и минусы ментальной математики

Самый очевидный результат обучения — способность совершать арифметические действия с шестизначными числами за несколько секунд. Но сложно представить, зачем сегодня ребенку может понадобиться этот навык. Как утверждают педагоги по ментальной математике, быстрый счет в уме — это побочный эффект, а не цель. Основная задача обучения — добиться эффекта синергии от синхронной работы обоих полушарий мозга, который превосходит эффект от работы каждого полушария по-отдельности. Тогда вместе с математическими способностями в ребенке будут развиваться:

• усидчивость
• концентрация внимания
• фотографическая память
• воображение
• творческое мышление
• скорость обработки информации

Кроме возрастных ограничений, никаких противопоказаний к занятиям нет. Однако отзывы родителей говорят о том, что не все ученики наблюдают улучшение памяти и концентрации внимания, а у некоторых детей возникают проблемы с решением элементарных задач на логику.

Здесь стоит вспомнить простую истину о том, что каждый ребенок уникален. Менар — это одна из методик развития интеллекта, которая помогает выявить и раскрыть уникальные способности ребенка. Ребенок учится быстро усваивать новую информацию, формулировать мысли и делать выводы. Тем не менее, не стоит пренебрегать традиционными играми — шахматами, головоломками, ребусами. Поэтому, наблюдайте, пробуйте, анализируйте и выбирайте то, что подходит именно вам.

Как проходит обучение

Обучение состоит из 10 уровней, каждый из которых занимает до четырех месяцев. Полный курс длится 2−3 года. Занятия идут по два академических часа один раз в неделю, кроме этого дети должны потратить 15 минут на выполнение домашних заданий. Как правило, у каждого развивающего центра есть онлайн-платформы, которые позволяют более эффективно работать самостоятельно.

Самый главный инструмент — это абак. Также в процесс обучения включают настольные, подвижные игры, просмотр мультфильмов и физминутки. На первом этапе детей учат складывать и вычитать числа на абаке. В этот период тренируется мелкая моторика, пространственное и логическое мышление. Далее переходят на ментальную карту — картину с изображением абака. И на следующем этапе дети производят арифметические действия с помощью визуализации процесса. Таким образом, уже через год ребенок может делать вычисления в уме.

Как выбрать школу ментальной арифметики?

Результат обучения будет зависеть от трех участников процесса — ребенка, учителя и родителей. Но самое главное — правильно выбрать образовательный центр, где будут преподавать менар. Вот несколько простых правил:

• Запишитесь на пробное занятие. Оцените, насколько комфортно ребенку в новых условиях. Не упустите возможность пообщаться с другими родителями.
• Познакомьтесь с педагогом. Спросите, как готовят преподавателей ментальной арифметики? Контролирует ли головной офис методику преподавания, уровень знаний педагогов, проходят ли преподаватели аттестацию на профпригодность?
• Обратите внимание на количество учеников в группе. Только в небольших группах преподаватель может уделить необходимое время каждому ученику. Поэтому в младших группах занимаются 5−7 человек, в старших — 8−10.
• Сделайте анализ рынка. Стоимость обучения в пределах одного региона не может сильно отличаться. Слишком низкая цена может быть показателем недобросовестного подхода к подготовке персонала и разработке методики. Слишком высокая цена может быть связана с издержками, дорогой арендой или рекламой.

Самое главное — чтобы ребенку нравились. Ему должно быть интересно считать, несмотря на то что считать — может быть довольно скучным занятием. Если ребенку нравится, значит, преподаватель смог заинтересовать его. Кроме этого, чтобы оценить преподавателя, обычно спрашивают: через сколько появятся первые результаты? На какие способности влияет обучение? Что делают, чтобы ускорить обучение? Хороший педагог ответит на все вопросы.

Читайте также:

Ну и почерк! Почему детям всё-таки важно учиться красиво писать?

11 полезных советов для родителей от педагога по английскому языку

Зачем детям учить математику?

Фото: GRSI, Ann in the uk, NadyaEugene/Shutterstock.com

Есть ли детям польза от ментальной арифметики

Ментальная арифметика — это метод счета в уме, навеянный старинными счетными досками-абаками. На сайтах учебных центров пишут, что абак появился в Древнем Китае, но упорно называют его на латинский манер абакусом. На самом деле этим приспособлением пользовались по всему свету, его точное происхождение неизвестно. Но стереотип гласит, что азиаты сильнее всех в математике, так что почему бы не отдать лавры изобретателей китайцам. А с латинским суффиксом, как известно, любое слово звучит весомее.

Программа обучения ментальной арифметике обычно занимает два-три года и делится на несколько этапов. Сначала дети учатся считать на настоящем абаке. Далее вместо доски им дают ее изображение: глядя на рисунок во время вычислений, нужно представлять, как передвигаются костяшки. В конце концов у ребят забирают и картинку — на этой стадии они видят абак в уме и могут производить с ним те же операции, что и с настоящим. Выглядит это поразительно и немного пугающе: двигая в воздухе невидимые костяшки, крохи, многие из которых даже еще не ходят в школу, перелопачивают длинные ряды трехзначных чисел и за какие-то секунды дают правильный ответ.

Обучение ментальной арифметике начинается с настоящего абака

© China Photos/Getty Images

Что обещают родителям

Еще удивительнее, что, по заверениям учебных центров, быстрый счет в уме — всего лишь побочный эффект. Родителей убеждают, что ментальная арифметика развивает логическое мышление, аналитические навыки, увеличивает объем памяти, дети учатся визуализировать задачи, поэтому глубже их понимают, мыслят креативно, становятся более внимательными, лучше концентрируются, систематизируют знания, адаптируются к новым условиям и благодаря всему этому успешнее учатся в школе, причем пятерки они получают и по математике, и по всем остальным предметам.

В доказательство этих утверждений на сайте одной компании, которая продает по франшизе методику обучения ментальной арифметике, приведены результаты исследования некоей К. Васуки из Мадрасского университета в Индии. В нем участвовали две группы детей 8–12 лет по 160 человек в каждой. В первую отобрали ребят из классов ментальной арифметики первого уровня, во вторую — обычных мальчиков и девочек. За год дети пять раз прошли тесты на концентрацию, рабочую и ассоциативную память, креативность и еще несколько показателей. Вначале средние показатели в обеих группах были почти одинаковые, но под конец «ментальные счетоводы» заметно вырвались вперед.

Соревнования по ментальной арифметике в Индии в 2005 году

© AP Photo/Gautam Singh

Исследование Васуки выглядит так, будто выполнено по научным стандартам. Но кое-что в нем настораживает. Во-первых, чем дальше, тем труднее давались задания детям в контрольной группе. Почему за год они сдали почти по всем показателям, неясно. Во-вторых, ребят c IQ ниже среднего и из бедных и малообразованных семей почему-то не допустили до участия. В-третьих, при анализе результатов, судя по всему, не учтены другие факторы, например мотивация. Вдруг на курсы ментальной арифметики ходят те, кто в целом сильнее заинтересован в учебе? В-четвертых, статью об исследовании Васуки не удалось найти в рецензируемых научных журналах, то есть другие ученые его не проверяли. Наконец, к исследованию причастна компания, которая владеет правами на методику обучения, а это всегда подозрительно.

Помогает ли менар с математикой

Другие исследования дали не столь однозначные результаты. В США эффективность ментальной арифметики в течение года проверяли на учениках первых и вторых классов школ. Первоклашки вообще толком не справились с обучением, у ребят постарше дела шли чуть лучше, но этого все равно было недостаточно, чтобы заметно улучшить когнитивные навыки.

На эту тему

Авторы также прокомментировали работы коллег. Одни ученые утверждают, что ментальная арифметика развивает рабочую память, другие этого не обнаружили. Но даже если положительный эффект вправду есть, не исключено, что он проявляется лишь в лабораторных условиях или только у взрослых. У американских детей рабочая память лучше не стала. Авторы прямо написали, что в условиях обычной школы ментальная арифметика ничем не лучше других методик и точно не делает ребят умнее.

Двумя годами ранее тот же психолог Дэвид Барнер провел вместе с коллегами более продолжительное исследование в Индии. Тогда дети обучались ментальной арифметике не один, а три года. Выводы ученых гласили, что благодаря этой методике некоторые школьники, скорее всего, лучше справляются с арифметическими операциями, но результат, по-видимому, зависит от имеющихся способностей ребенка, а не от того, как он научился представлять и обращаться с объектами в рабочей памяти.

Развивает ли менар мозг

С влиянием ментальной арифметики на мозг ситуация еще более запутанная. В 2016 году китайские ученые подготовили обзор существующей научной литературы и пришли к выводу, что у мастеров менара и обычных детей при решении задач вправду задействуются разные области, также нашлись отличия в самой структуре мозга.

Но, во-первых, иногда эксперименты давали противоречивые результаты. Во-вторых, большинство исследований были краткосрочными: мозг — пластичная штука, поэтому неясно, сохраняются ли изменения спустя годы после обучения ментальной арифметике. В-третьих, не исключено, что именно особенности строения мозга привели детей в классы менара и позволили им достичь высот в этом деле. В-четвертых, в экспериментах участвовало мало детей — выводы надо делать осторожно.

Успехи в ментальной арифметике зависят от предварительной подготовки и квалификации преподавателей

© EPA/FRANCK ROBICHON

На сайтах учебных центров говорится, что ментальная арифметика гармонично развивает оба полушария мозга и налаживает между ними связь. Якобы поэтому у детей улучшается концентрация, увеличивается объем памяти, усиливаются творческие и аналитические способности. Но обо всем этом судить рано. В большинстве исследований проверяли только математические навыки — данных о том, как ментальная арифметика влияет на другие когнитивные навыки и успеваемость в школе, недостаточно. Также пока нельзя судить, меняется ли благодаря занятиям связность сетей мозга, отвечающих за разные функции.

Что о менаре думают учителя

Педагоги, как и ученые, не спешат превозносить ментальную арифметику. По словам заслуженного учителя России Леонида Звавича, устный счет — дело полезное, но есть масса приемов устного счета без абака и какой из них лучше, сказать сложно. Успехи ребенка в математике зависят прежде всего от того, какие у него были учителя, а любые развивающие занятия помогают подтянуть разные школьные предметы. «Если человек идет в школу, зная 100 стихотворений, он учится лучше, чем человек, который не знает ни одного», — считает Звавич.

На эту тему

Преподаватель математики, лауреат премии мэрии Москвы Александр Шевкин тоже думает, что всякое занятие, развивающее мышление, полезно и влияет на способности к обучению не по одному предмету. Но к ментальной арифметике он относится настороженно: «Это сильно распиаренный бизнес-проект. Под устную арифметику на русских счетах много денег не соберешь, а на загадочную ментальную арифметику получается. Ничего вредного в ней нет, а вот насколько нужна детям столь продвинутая техника устных вычислений, пусть решают родители. Я бы не стал переоценивать влияние этой методики, так как помню высказывание известного популяризатора правильных способов обучения математике Дьердя Пойи: «Можно научить дельфина крутить мяч на носу, но поможет ли это ему ловить рыбу?»

Сергей Рукшин, профессор РГПУ имени Герцена и учитель знаменитых математиков Григория Перельмана и Станислава Смирнова, оценивает ментальную арифметику еще более скептически: «Мне не известно ни одного исследования, доказательно обосновывающего преимущества этой методики, ее влияние на отдаленные результаты ребенка. В самом деле, нельзя же считать нынешние успехи китайской и японской экономики следствием того, что пять тысяч лет назад они начали применять счетные приспособления, аналогичные используемым в обучении «ментальной арифметике». А именно такие аргументы попадаются в рекламе. Гораздо важнее осознать следующее: многие современные родители не находят времени и душевных сил для личных занятий с собственным ребенком. Любое внимание, общение, обучение развивает личность ребенка и его способности. Ребенок развивается, чему бы его ни учили. А что касается «ментальной арифметики» — ничего личного, только бизнес».

Вероятно, кое-какая польза от ментальной арифметики все же есть, особенно если ребенку тяжело дается математика. Вдобавок на занятиях вырабатывается привычка трудиться — в жизни она пригодится, а целеустремленные сверстники — это хорошая компания и, возможно, новые друзья: ничто так не сближает, как общее дело. Но не стоит ждать от ментальной арифметики чудес: представляя в уме счетную доску, ребенок не приобретет цвет индиго.  

Марат Кузаев

записаться на урок — Amakids

Головной мозг человека разделен на левое и правое полушарие. Исследования показывают, что форма двух полушарий похожа, но функции у них разная. Левое полушарие имеет тесные связи с работой языка, абстрактного мышления и логического мышления. Правое полушарие имеет дело с объектом мышления: изображение, формы, творческое мышление и интуиция.

Большинство людей считают, что функции левого полушария преобладают над функциями правого полушария, а физиологи и психологи считают, что потенциал правого полушария должен использоваться больше. Идеальным методом является одинаковое использование обоих полушарий.

Альберт Эйнштейн, всемирно известный ученый и мыслитель, шокировал научное сообщество, когда предложил «теорию относительности». С помощью творчества и воображения правого полушария, он представлял взаимодействие пространства и времени в его сознании и преодолел ограничение в трех измерениях. В то же время, он также использовал дедукцию и логику левого полушария, чтобы доказать и выяснить научную и математическую ценность теорий. Поэтому, когда левое и правое полушария головного мозга объединяются и эффективно используются вместе, результаты могут быть поразительными.

Все мы хотим, чтобы наш ребенок был успешным человеком! Как воспитать своего ребенка таким? — эти вопросы занимают каждого любящего родителя.

Курсы ментальная арифметика

На сегодняшний день, много центров и клубов, предлагающих развивающие занятия для детей. Все они предлагают одностороннее развитие ребенка — это музыка, творчество, подготовка к школе, театральные студии, шахматы и т.д. Во всем этом сложно разобраться, что же лучше подойдет нашему ребенку, что бы стать разносторонне развитым, ведь заниматься абсолютно всем невозможно.

На самом деле ему необходимо научиться извлекать их из памяти нужную информацию в нужный момент, уметь оценивать, анализировать, делать выводы – и, самое, главное! – достигать поставленных целей. Самым эффективным инструментом в любых руках для достижения поставленных целей является Интеллект. Ведь это нечто большее, чем книжная ученость, умение петь, играть в шахматы или умение хорошо сдавать тесты. Это умение пользоваться своими знаниями. А эффективный интеллект – это способность получать, обрабатывать и использовать знания с максимальным эффектом, способность действовать в направлении желаемых целей.

Курс ментальной арифметики направлен на развитие интеллектуальных способностей , дети закладывают твердую основу для дальнейших академических успехов и развития личности. В результате освоения программы ментальная арифметика ребенок, например, может сложить пятизначные числа за несколько секунд, но это не единственный результат.

 

Благодаря ментальной арифметике развивается и улучшается:

• Концентрация внимания
• Фотографическая память
• Точность и быстрота реакции
• Уверенность в себе
• Творческое мышление
• Слух и наблюдательность
• Воображение и представление
• И как следствие успехи в учебе.

В начале обучения основная часть работы заключается в интенсивном использовании ребенком счетов Абакус (Соробан). На всех стадиях обучения ребенок использует обе руки для операций с косточками счетов, стимулируя работу обоих полушарий головного мозга. Дети постигают все 4 вида математических операций сложение, вычитание, умножение и деление. При равном участии обоих полушарий головного мозга процесс обучения и размышления становится гораздо более эффективным. На каждой тренировке постепенно ослабляется привязка ребенка к счетам и стимулируется его собственное воображение, благодаря чему уже через несколько занятий, он сможет производить простейшие расчеты в уме, лишь представляя Абакус (Соробан) перед собой и мысленно совершая движения косточками (так называемая работа с воображаемыми счетами).

Ребенок, обучаемый по программе ментальная арифметика, начинает решать математическую задачу, воспринимая числа как картинки, так как каждое конкретное число будет вызывать у него ассоциацию соответствующего изображения на косточках счетов.

Развивающий центр для детей AMAKids предлагает курс ментальной арифметики для детей в возрасте от 4 до 16 лет. Группы формируются по возрастам. Для младшей группы длительность обучения составляет 2,5 года, а для старшей – 2 года. Каждый месяц формируется и начинает обучаться новый класс желающих. Но присоединиться к уже начавшей занятия группе – невозможно.

Все, что не обходимо для процесса обучения, а именно счеты, учебные материалы и тетради, уже включено в стоимость курса.

Первая возрастная категория детей – это 4-6 лет, вторая – 7-10 лет, третья 11-16 лет. Класс младшей группы состоит из 4-6 человек, старшие допускает 6-10 человек. Дети обязательно проходят пробное занятие. Это нужно для того, чтобы сформировать равные группы. Основное требование для учеников – умение считать до 10.

Периодичность занятий удобная. Это по 2 урока в день 1 раз в неделю. Но ежедневная домашняя тренировка должна быть не менее 15 минут. Постепенно ребенок накапливает навыки. Каждый день тренируется одно правило.

Для домашних занятий ребенку нужен доступ к компьютеру. Он получает логин и пароль для входа в программу вместе с рабочими материалами и счетами Абакус (Соробан) еще вначале занятий.

Для младшей группы обязательно участие родителей в тренировках, контроль правильности выполнения домашнего задания. Для старшей группы участие родителей не обязательно, но в расписании ребенка желательно выделить определенное время для тренировок, привязанное к режимному моменту (например, перед ужином). Ощутимые результаты и одновременную работу двух полушарий мозга вы сможете увидеть через 2-3 месяца регулярных занятий. После успешного прохождения программы обучения ребенок получает соответствующий сертификат нашего центра.

Занятия по нашей методике помогут раскрыть и выразить экстраординарные способности каждого ребенка, развить креативность через инновационное обучение.

 

Сделай десятку — Сделай десятку — это математическая стратегия в уме, в которой учащиеся используют числовые комбинации, составляющие десять, для установления связей и отношений с другими фактами. Сначала ученики должны выучить числовые комбинации, которые составляют 10. Затем они могут уверенно использовать эти комбинации. Например, чтобы решить 8 + 5, ученик может подумать: «Я могу взять два из 5 и передать их 8, чтобы получилась десятка, а затем сложить оставшиеся 3, чтобы получить 13.«Десять кадров — отличный способ проиллюстрировать эту стратегию.

Вот видео, в котором более подробно объясняется, как сделать десять стратегию или найти модуль для обучения сделать десять ЗДЕСЬ.

Получение кратных десяти — Эта стратегия является естественным продолжением создания десяти. Чтобы сделать кратными десяти , мы можем использовать числовые комбинации, которые составляют десять (6 + 4, 7 + 3 и т. Д.). Это помогает нам понять, что такие выражения, как 26 + 4, будут делиться на десять.Десять фреймов — отличный способ смоделировать мыслительный процесс. Например, когда мы моделируем 26 + 4 с десятью кадрами, легко видеть, что мы можем сдвинуть 4 точки, чтобы полностью заполнить три десяти кадра и получить 30.

Найдите модуль для обучения стратегии умножения десяти ЗДЕСЬ.

Сложение слева направо — Сложение слева направо — это мощная математическая стратегия для сложения чисел, состоящих из двух или более цифр. Понимание поставленной ценности является ключевым моментом, так как студенты будут группировать десятки, а затем единицы.Например, чтобы решить 24 + 53, мы сначала сложим 20 + 50, чтобы получить 70, затем 4 + 3, чтобы получить 7, и, наконец, 70 + 7, чтобы получить 77. Сложение слева направо важно для обучения ДО того, как учащиеся научатся традиционный алгоритм. Это связано с тем, что сложение слева направо сосредоточено на концептуальном понимании, а не на запоминании серии шагов.

Вот видео, в котором более подробно объясняется сложение слева направо, или найдите модуль для обучения сложению слева направо ЗДЕСЬ.

Разбить на части / Разобрать — Разбиение слагаемого по разряду — мощная математическая стратегия для сложения чисел, состоящих из двух или более цифр.Хотя это похоже на сложение слева направо, некоторые студенты предпочитают его, потому что только одно добавление разлагается по разряду, а не оба. Например, чтобы решить 43 + 35, мы могли бы сначала разложить 35 на 30 и 5. Мы начинаем с добавления 43 + 30, чтобы получить 73, а затем оставшиеся 5, чтобы получить 78.

Вот видео, которое объясняет стратегию разделения на части более подробно или найдите раздел для обучения разделению ЗДЕСЬ.

Я надеюсь, что этот пост помог вам составить план обучения математическим стратегиям в вашем классе! Я знаю, что если вы не учились таким образом, это будет непростой переход.

Если вам нужна дополнительная поддержка по обучению стратегиям сложения в классе, ознакомьтесь с этим комплектом стратегий сложения умственной математики, который включает блоки для всех стратегий, которые обсуждались выше.

Как преподавать ментальную математику: стратегии и задания

Хотите верьте, хотите нет, но подавляющее большинство математических вычислений, которые мы делаем ежедневно, взрослые, состоит из элементарной математической математики в уме. В продуктовом магазине мы используем мысленную математику при оценке стоимости товаров.В тренажерном зале мы подсчитываем количество минут, потраченных на поднятие тяжестей или на эллиптическом тренажере. Даже вне нашей профессии мы ежедневно используем мысленную математику для решения обычных задач.

В то время как взрослые умеют использовать мысленную математику в повседневной деятельности, детям необходимо развивать свои собственные математические навыки с нуля. Даже более важно, чем взрослые, дети должны укреплять умственные математические навыки, чтобы укрепить свои многообещающие математические навыки, поскольку умственная математика пригодится, чтобы упростить и ускорить решение математических уравнений и задач.

Зачем изучать ментальную математику?

Короче говоря, когда дети развивают умственные математические навыки, они:

• Получить более глубокое понимание математики, помимо простого запоминания
• Развивать логическое мышление и рассуждать
• Изучите навыки, которые улучшат математические навыки во всех классах
• Осваивайте навыки, которые они сохранят на всю жизнь, независимо от их профессии!

Очевидно, что ментальная математика имеет значение, но для того, чтобы уроки ментальной математики приносили пользу вашему ребенку, ее нужно делать последовательно каждый день или неделю. Если вы ищете занятия, которые помогут вам научиться обучать своего ребенка стратегиям мысленной математики, давайте рассмотрим несколько быстрых и простых способов включить мысленные математические упражнения в учебный распорядок вашего ребенка!

---

Программа «Талантливые и одаренные» со скидкой 60% этой осенью! Совершенствуйте свои математические навыки и готовьте своего ребенка к успеху с помощью увлекательных математических игр, видео и уроков, которые понравятся вашему ребенку!

---

Умственная математическая деятельность для детей младшего возраста

Классическая ментальная математическая игра: Свинья

Возможно, вы даже помните игру «Свинья» из детства! С небольшими изменениями вы можете сделать для своего ребенка игру «Свинья», которая подойдет детям даже в первом классе.

Используя всего один кубик, каждый игрок по очереди бросает кубик и ведет текущий счет выпавшей суммы. В свой ход игрок бросает кубик и записывает число. Они могут бросать столько раз, сколько хотят, мысленно следя за суммой во время броска.

Если игрок выбрасывает 1, он теряет всю текущую сумму, и следующий игрок получает ход. Если игрок хочет прекратить бросание в свой ход, просто попросите его или ее записать сумму, чтобы они могли добавить ее к сумме, которую они бросают в свой следующий ход.Затем ребенок передает кубик своему противнику. Первый игрок, набравший в сумме 25 побед! Для детей постарше увеличьте это число до 50 или 100, используя два кубика!

Соревнования по ментальной математике

Все становится веселее, когда ты делаешь соревнование! Эта веселая и универсальная игра отлично подходит для детей от начального до 3-го класса! Поскольку задачи можно адаптировать к возрасту вашего ребенка, эта игра отлично подходит для детей, которые только начинают развивать умственные математические навыки, или для детей старшего возраста, оттачивающих свои способности.

Чтобы играть, убедитесь, что у вас есть белая доска с маркерами для сухого стирания. Просто напишите на доске несколько математических предложений (например, те, которые посвящены сложению и удалению). Установите таймер от 30 секунд до минуты, чтобы ваш ребенок работал над проблемами, чтобы найти ответы. За каждую задачу, которую ваш ребенок решит, он получает 1 балл. За каждую ошибку вы получаете балл. После всех раундов, в которых хочет играть ваш ребенок, побеждает тот, у кого больше очков!

Mental Math Twister

Если вы хотите научиться преподавать мысленную математику второклассникам, ответ — сыграйте в Twister! Отлично подходит для небольшой группы детей, эта игра отлично подходит для друзей, братьев и сестер вашего ребенка, небольшого класса или даже всей семьи! Начните с однозначных чисел, но для старших 2-х или 3-х классов переходите к 2-значным числам, чтобы сыграть в увлекательную игру Twister.

Для начала вам понадобится подготовленный коврик Twister для этой веселой игры. Чтобы использовать коврик максимально эффективно, просто напишите числа на стикерах и прикрепите их к каждому цветному кружку на мате. На коврике каждый цвет должен представлять один и тот же ответ. Например, каждый желтый кружок представляет ответ «4», а каждый синий кружок может представлять ответ «6». Аналогичным образом, используя небольшой кусок стикера, отметьте значения ответов соответствующим цветом на счетчике.

Чтобы играть, попросите детей встать сбоку от коврика.Покрутите вертушку, чтобы увидеть, что и куда должен двигаться ваш ребенок. Вместо того, чтобы вызывать цвет при вращении, вместо этого создайте простую математическую задачу, которая равна числу, на которое они должны приземлиться. Например, если прядильщик говорит: «Правая рука, синяя», скажите детям: «Правая рука, 3 + 3». Поскольку ответ — 6, они кладут правую руку на синий кружок.

Так как эта игра может быть изменена в соответствии с потребностями вашего ребенка, вы можете переключить ее, чтобы бросить вызов детям, чтобы они добавляли двойные или двойные плюс 1! Благодаря такому количеству способов игры ваши дети будут двигаться и скручиваться, одновременно совершенствуя свои математические навыки!

---

Если вы ищете еще больше способов развить умственные математические навыки вашего ребенка, математические головоломки и онлайн-игры — отличный способ продолжить обучение вашего ребенка. Ознакомьтесь со всеми нашими математическими ресурсами, доступными в AppStore и на сайте kidsacademy.mobi!

Учебные материалы, рабочие листы и задания по ментальной математике

Выберите ваше местоположение

Выбор страны и штата поможет нам предоставить вам наиболее подходящие учебные ресурсы для ваших учеников.

Страна Австралия Соединенные Штаты Соединенное Королевство Афганистан Иландские острова Албания Алжир Американское Самоа Андорра Ангола Ангилья Антарктика Антигуа и Барбуда Аргентина Армения Аруба Австралия Австрия Азербайджан Багамы Бахрейн Бангладеш Барбадос Беларусь Бельгия Белиз Бенин Бермуды Бутан Боливия, Многонациональное Государство Сабациона и Герцеговина Бонавия Остров Буве Бразилия Британская территория в Индийском океане Бруней-Даруссалам Болгария Буркина-Фасо Бурунди Камбоджа Камерун Канада Кабо-Верде Каймановы острова Центральноафриканская Республика Чад Чили Китай Кокосовые острова (острова Килинг) Колумбия Коморские острова Конго Конго, Демократическая Республика Острова Кука Коста-Рика Кот д’Ивуар Хорватия Куба Кюрасао Кипр Чешская Республика Дания Джибути Доминика Доминиканская Республика Эквадор Египет Сальвадор Экваториальная Гвинея Эритрея Эстония Эфиопия Фолклендские (Мальвинские) острова Фарерские острова Фиджи Финляндия Франция Французская Гвиана Французская Полинезия Французский Южный Террит страны Габон Гамбия Грузия Германия Гана Гибралтар Греция Гренландия Гренада Гваделупа Гуам Гватемала Гернси Гвинея Гвинея-Бисау Гайана Гаити Остров Херд и острова Макдональд Святой Престол (государство-город Ватикан) Гондурас Гонконг Венгрия Исландия Индия Индонезия Иран, Исламская Республика Ирак Ирландия Остров Мэн Израиль Италия Ямайка Япония Джерси Иордания Казахстан Кения Кирибати Корея, Корейская Народно-Демократическая Республика, Республика Кувейт Кыргызстан Лаосская Народно-Демократическая Республика Латвия Ливан Лесото Либерия Ливия Лихтенштейн Литва Люксембург Макао Македония, бывшая югославская Республика Мадагаскар Малави Малайзия Мальдивы Мали Мальта Маршалловы острова Мартиник Мавритания Маврикий Майотта Мексика Микронезия, Федеративные Штаты Молдовы, Республика Монако Монголия Монголия Черногория Монтсеррат Марокко Мозамбик Мьянма Намибия Науру Непал Нидерланды Новая Каледония Новая Зеландия Никарагуа Нигер Нигерия Ниуэ Остров Норфолк Северные Марианские острова Норвегия Оман Пакистан Палау Палестина , Государство Панама Папуа-Новая Гвинея Парагвай Перу Филиппины Питкэрн Польша Португалия Пуэрто-Рико Катар Румыния Российская Федерация Руанда Сен-Бартелеми Остров Святой Елены, Вознесения и Тристан-да-Кунья Сент-Китс и Невис Сент-Люсия Сен-Мартен (французская часть) Сен-Пьер и Микелон Сент-Винсент и Гренадины Самоа Сан-Марино Сан-Томе и Принсипи Саудовская Аравия Сенегал Сербия Сейшельские острова Сьерра-Леоне Сингапур Синт-Мартен (голландская часть) Словакия Соломоновы острова Сомали Южная Африка Южная Джорджия и Южные Сандвичевы острова Южный Судан Испания Шри-Ланка Судан Суринам Свальбард и Ян-Майен Свазил Швеция Швейцария Сирийская Арабская Республика Тайвань, провинция Китая Таджикистан Танзания, Объединенная Республика Таиланд Тимор-Лешти Того Токелау Тонга Тринидад и Тобаго Тунис Турция Туркменистан Острова Теркс и Кайкос Тувалу Уганда Украина Объединенные Арабские Эмираты Соединенное Королевство Соединенные Штаты Внешние малые острова США Уругвай Узбекистан Вануату Венесуэла, Бол ivarian Республика Вьетнам Виргинские острова, Британские Виргинские острова, U. С. Уоллис и Футуна Западная Сахара Йемен Замбия ZimbabweState Австралийская столичная TerritoryNew Южная WalesNorthern TerritoryQueenslandSouth AustraliaTasmaniaVictoriaWestern AustraliaAlabamaAlaskaAmerican SamoaArizonaArkansasCaliforniaColoradoConnecticutDelawareDistrict Из ColumbiaFederated Штатов MicronesiaFloridaGeorgiaGuamHawaiiIdahoIllinoisIndianaIowaKansasKentuckyLouisianaMaineMarshall IslandsMarylandMassachusettsMichiganMinnesotaMississippiMissouriMontanaNebraskaNevadaNew HampshireNew JerseyNew MexicoNew YorkNorth CarolinaNorth DakotaNorthern Mariana IslandsOhioOklahomaOregonPalauPennsylvaniaPuerto RicoRhode IslandSouth CarolinaSouth DakotaTennesseeTexasUtahVermontVirgin IslandsVirginiaWashingtonWest VirginiaWisconsinWyoming

Math 4 — Закон.01: Ментальная математика: сложение и вычитание

Временной интервал

2 академических часа по 30 минут каждое

Сводка

На этом уроке ученики будут использовать умственные математические навыки сложения и вычитания, умножая числа, кратные десяти, и корректируя (компенсация). Эти предлагаемые стратегии следует обсудить в двух отдельных уроках.

Материалы

• 7 книг
• счетчиков на каждую пару учеников
• 2 табурета / стула одинаковой высоты

Дополнительные ресурсы

«Психическая математика в средних классах», Публикации Дейла Сеймура, 1987 г.

Фон для учителей

Счет в голове — это практический жизненный навык. Множество видов повседневного вычислительные задачи можно решить мысленно. Мысленный расчет дает краеугольный камень для всех процессов оценки, позволяющий использовать множество альтернатив нестандартные методы или стратегии поиска ответов. Мысленное вычисление побуждает учащихся думать о числах и развитии числовых соотношений сильное чувство чисел и математическая уверенность. Опрос Национального Оценка успеваемости по математике показала, что большинство детей не осознавая, что мысленный расчет часто является наиболее удобным методом поиска решение.Большинство студентов утверждали, что либо бумага и карандаш, либо калькулятор был необходим для определения решений.

Было бы полезно, если бы студенты имели опыт работы с совместимыми числа, в данном случае пары чисел, которые «составляют десять».

Предполагаемые результаты обучения

1. Продемонстрируйте положительное отношение к математике.
2.Станьте решателями математических задач.
3. Рассуждайте математически.
4. Общайтесь математически.
5. Сделайте математические связи.
6. Представляйте математические ситуации.

Инструкционные процедуры

Урок первый: Компенсация (компенсация)
Приглашение учиться
Дайте одному ученику 4 книги, а другому ученику 3 книги.Спросите: «Если возьмете часть книг от одного ученика и отдать другому ученику делает это изменить общее количество книг? Как эта идея может помочь вам складывать числа? »

Инструкционные процедуры:

1. Студенты работают в парах. Попросите каждого ученика отсчитать определенное количество счетчики и найдите сумму. Определите, сколько счетчиков потребуется для сделать одну группу кратной 10. Переместите это количество жетонов из одной группы к другой группе.Это изменит общую сумму? (Нет) Повторить это действие несколько раз с разным количеством счетчиков.
2. Дайте ученикам задачу на сложение и попросите их сделать десятки. добавив совместимый номер в одно из дополнений. Вернитесь и вычтите такая же сумма из другого дополнения для компенсации. Затем добавьте два скорректированных добавляет.
3. Потренируйтесь торговать числами, чтобы получилась ровная группа десятков. для облегчения вычислений.Задачи для практики:

29 + 62	37 + 69
28 + 45	43 + 49
49 + 26	55 + 19

Урок второй: балансирующее вычитание (компенсация)
Приглашение к обучению
Попросите двух учеников разного роста продемонстрировать идею о том, что если вы добавляете одинаковую сумму как к числу, которое вы вычитаете, так и к числу вы начали, разница будет такой же.

Спросите, кто выше и примерно какая разница в росте? Дайте более низкий ученик — небольшой табурет / стул, на котором можно стоять. (Этот ученик должен сейчас быть выше). Многие студенты поймут, что разница изменился, когда более низкому ученику было на чем опереться. Чтобы сохранить разница такая же, более высокому ученику понадобится что-то такого же размера стоять на. Как вы можете использовать эту идею для вычитания чисел?

Инструкционные процедуры

1. Студенты должны понимать вычитание при переименовании.Напишите простое вычитание проблема на плате. Попросите учащихся отсчитать первое количество счетчиков. и вычтите второе число. (например, 6-2 = 4).
2. Используйте ту же задачу и добавьте «1» к каждому из чисел.
   (например, 7-3 = 4). Что случилось с разницей, когда мы переименовали проблему добавив одинаковое количество к обоим числам? (остался прежним). Попробуйте добавить «2» к каждому из исходных чисел. Три. Четыре. Есть ли разница оставайся таким же?
3. Дайте учащимся несколько задач на вычитание, используя балансирующее вычитание. стратегия.Убедитесь, что учащиеся понимают, что мы хотим «сделать десятки» с числом, которое мы вычитаем (вычитаем), а не с тем, которое мы вычитаем от (minuend). Гораздо проще вычесть красивую четную группу десятков из другой номер B без займа и т. д.
   Задачи для практики:

65 — 49	44–28
43-19	81–58
72–29	71–47

Добавочные номера

Возможные расширения / адаптации / интеграция
Используйте эти стратегии, чтобы найти сумму и разность трех- и четырехзначных чисел.

Домашнее задание и семейные связи
Попросите учащихся научить члена своей семьи новому способу мысленного сложения или вычитания и верните записку с указанием общего математического опыта между член семьи и студент.

План оценки

Попросите учащихся написать инструкции о том, как применять только что приобретенные навыки узнал в своих журналах.

Создано: 29.08.2003
Обновлено: 05.02.2018

58825

.

Телеграм-каналы о математике

Мы давным-давно знали, что математика — это не скучно! Особенно, когда речь идет о формате знакомства с «царицей наук» через увлекательные и нетривиальные посты в Телеграм. Собрали подборку каналов, которые помогут воскресить или еще раз утвердиться в любви к математике, а заодно вспомнить пару-тройку хитростей счета в уме, ознакомиться с решениями сложных задач и узнать, наконец-то, как все эти интегралы могут пригодиться в реальной жизни.

Канал для тех, кто считает математику запутанной и скучной — вы увидите, насколько вы заблуждаетесь! Хотите удивить всех своими математическими способностями, узнать тонкости, которые недоступны другим, и научиться делать вычисления в уме за каких-то пару секунд? Тогда подписывайтесь.

Канал, где научат считать быстрее калькулятора и помогут разобраться, а зачем вообще нужна математика. Интересные закономерности и факты, великие математики, и немного интеллектуальных шуток.

Англоязычный канал с анонсами, выжимками и полными версиями книг по математике и физике.

Канал содержит примеры и решения различных задач от студентов со всего мира. Незаменимый помощник в учебе!

На канале собрана масса полезной тематической информации: обзоры и выжимки из книг, полезные статьи, анонсы лекций, разборы решения задач, интервью и видео с математиками.

Канал ведет кандидат физико-математических наук Виктор Клепцын, который в увлекательной форме делится своими знаниями, наблюдениями, отрывками из зарубежных статей, и, конечно, доходчиво объясняет решения сложных задач.

Канал учителя по математике Натальи Нетрусовой, которая разбирает решение задач по геометрии, в том числе олимпиадные, делится полезными видеоматериалами и анонсами тематических лекций.

Все актуальные новости из мира математики, а если повезет, то на канале разберут и вашу задачу.

Окунитесь в мир математики не только через решения задач и отрывки из тематических книг, но и через веселые мемы, которые помогут посмотреть на науку с новой стороны.

На канале публикуют книги по математике, видео, задачи с собеседований, олимпиад, транслируют актуальные новости и делятся полезными ресурсами.

Серьезное сообщество для физиков, математиков и разработчиков, которые собираются вместе, чтобы помочь друг другу решать насущные задачи.

Канал для тех, кто в теме — шутки и мемы на тему математики, физики и студенчества. Помимо высокоинтеллектуального юмора, авторы канала помогают справиться с решением задач разной степени сложности.

Канал в формате блога, автор которого органично вплетает в текст интересные математические задачи и их решения. Обсудить посты и предложить свои идеи можно в чате.

8 отличных каналов YouTube по математике

Это сообщение было обновлено в декабре 2021 г.

В приведенном ниже списке представлены некоторые из лучших математических каналов YouTube, которые помогут вашим ученикам и детям изучать математику с помощью видео. Я составил список, чтобы включить только те математические каналы, которые представляют реальную образовательную ценность для учащихся.

Используя эти каналы, учащиеся смогут изучать сложные и абстрактные математические понятия в увлекательной игровой форме. Объяснения и учебные пособия наглядно иллюстрированы, что облегчает развитие более тонкого понимания математики.

Если вас беспокоят отвлекающие факторы , которые часто окружают видео на YouTube (например, оскорбительные выражения в комментариях, неприемлемый контент в связанных видео и т. д.), я настоятельно рекомендую использовать такие инструменты, как Safeshare TV и Viewpure; два лучших инструмента, которые обеспечивают удобную и не отвлекающую среду для просмотра видео на YouTube.

1- Numberphile

Numberphile — определенно один из самых популярных математических каналов на YouTube, созданный видеожурналистом Брэди Хароном. Он содержит сотни видеороликов, посвященных всевозможным математическим концепциям, и часто с участием математиков и других гостей со всего мира.Он предоставляет отличные обучающие видео по математике, геометрии, физике и многим другим.

3- MooMooMath «MooMooMath предоставляет забавные полезные видео по математике и естественным наукам, чтобы помочь людям изучать математику и естественные науки. Мы добавляем новое видео каждый день и очень гордимся этим.»

4- Socratica

Socratica предлагает обучающие видеоролики по различным предметам, включая математику, естественные науки, компьютерное программирование и многое другое. Некоторые из математических плейлистов, которые он содержит, включают: основы Mathematica, абстрактную алгебру, теорию чисел, исчисление, уроки геометрии, геометрические построения, евклидову геометрию, глоссарий геометрии и многое другое.

5- 3Blue1Brown

«3Blue1Brown, Грант Сандерсон, представляет собой сочетание математики и развлечения, в зависимости от вашего настроения. Цель состоит в том, чтобы объяснения приводились в движение анимацией, а сложные задачи упрощались с изменением точки зрения.»

6- Матолог

Матолог, профессор математики Университета Монаша в Мельбурне, предлагает доступные объяснения сложных математических задач. Некоторые из его популярных видеороликов включают в себя: «Математика в Симпсонах», «Числофил против математики», «Секреты бесполезного гриндера», «Бесконечные дроби и самые иррациональные числа», «Как не умереть упорно с математикой» и многое другое.

7- Репетитор по органической химии
«Репетитор по органической химии занимается предоставлением обучающих видео по органической химии, общей химии, физике, алгебре, тригонометрии, предварительному исчислению и исчислению».

8- Бесплатные математические видеоролики PatrickJMT Бесплатные математические видеоролики PatrickJMT  предоставляет видеоконтент на различные темы, такие как исчисление, производные, дифференциальные уравнения, пределы, интегралы и многое другое.

Другие известные математические каналы включают в себя: 1- The Video Math Tutor

Это отличный канал, который предлагает несколько обучающих видеороликов по математике, посвященных различным темам, включая уроки базовой математики, советы по калькулятору, головоломки и многое другое

2- Математика

Это еще один классный канал, предлагающий уроки математики по таким темам, как дроби и десятичные числа, алгебра и функции, чувство чисел, арифметика, геометрия. ..и больше.

3- Десять баллов

Это веб-программа для учащихся, позволяющая практиковать и осваивать математические понятия. Они могут изучать математику с помощью подсказок, видеоуроков и персонализированных рабочих листов.

4- Math Mammoth

Этот канал предоставляет советы по обучению математике, которые помогут учителям, родителям и репетиторам в обучении математике.

5- Math TV

Это канал учителя математики со стажем, который преподает математику и пишет учебники более 30 лет.Вы обязательно найдете что-то для своих учеников.

Фестиваль 5-минутного кино: 10 отличных видеоресурсов для обучения математике

В преддверии Дня числа числа Пи мы хотели бы поблагодарить всех замечательных создателей YouTube, которые снимают математические видео! (Конечно, если вам нужны видеоролики, посвященные Дню Пи, ознакомьтесь с нашей публикацией «Ура Дню Пи».) Математика может показаться не совсем подходящей для визуальной среды видео, но вы будете поражены тем, творчества некоторых из этих создателей, которые воплощают сложности всех уровней математики в жизнь на маленьком экране. Учителя математики, это для вас!

Плейлист с видео: лучшие каналы YouTube для учителей математики

Посмотрите первое видео ниже или весь плейлист на YouTube.

видео

1. The Infinite Hotel Paradox — Джефф Декофски (05:59)

   Хотите показать своим ученикам математику онлайн-знакомств? Или поделитесь уравнением легендарного времени зависания Майкла Джордана? Или объясните, почему пчелы любят шестиугольники? Вам может помочь плейлист TED-Ed «Математика в реальной жизни», и каждое видео содержит ссылку на план урока.Это популярное видео объясняет парадокс бесконечного отеля.

2. Что случилось с Пифагором? (08:49)

   Если вы не знакомы с причудливой анимацией Sharpie Ви Харта и математическими исследованиями потока сознания, вы должны быть знакомы. У нее есть способ погрузить вас в кроличью нору философских размышлений — посмотрите несколько ее видео, и вы будете загипнотизированы.

3. Красота алгебры | Алгебра I | Академия Хана (10:06)

   Академия Хана — это ресурс для помощи в выполнении домашних заданий по ошеломляющему множеству предметов, но нынешняя гигантская компания началась с того, что Сал Хан обучал свою 12-летнюю кузину Надю, которая боролась с преобразованием единиц измерения. Слушайте успокаивающий голос Сала, объясняющего арифметику, алгебру, исчисление, геометрию, тригонометрию и многое другое.

4. Завершение квадрата — Решение квадратных уравнений (04:36)

   Академия Хана — не единственный игрок, предлагающий обучающие видеоролики для детальных математических задач; PatrickJMT также предлагает сотни видеороликов по различным темам, от производных до квадратных уравнений. У него полмиллиона подписчиков, и он принимает заявки!

5. Теорема «сложить и разрезать» — Numberphile (09:30)

   Создатель Prolific YouTube Брэди Харан ведет около десяти каналов YouTube; На Numberphile вы можете найти увлекательные видео профессоров, изучающих всевозможные темы, связанные с математикой.В этом ролике Кэти Стеклз объясняет теорему сложения и разрезания.

6. Музыкальное видео с метрической системой (01:34)

   Учителя математики начальной школы, мы не забыли о вас. Numberock — это новый канал, созданный учителем пятого класса из Массачусетса, который предлагает запоминающиеся анимационные музыкальные видеоклипы по математике для третьего, четвертого и пятого классов. Вы также можете найти соответствующие рабочие листы, текстовые задачи и викторины по очень разумной цене на сайте «Учителя платят учителям».

7. Логарифмические уравнения с разными основаниями (12:14)

   Что мне больше всего нравится в математических видеороликах энергичного учителя математики Роба Тарроу, так это то, что он использует настоящий мел на старомодной классной доске и красивейший курсив для записи своих задач.Его веб-сайт предлагает систематизированные списки всех его уроков — с 2011 года он снял более 500 видеороликов, все время преподавая полный рабочий день.

8. Стендап-комедия о таблицах (13:16)

   Нужно разбудить этих учеников в начале отряда? Попробуйте показать им клип Мэтта Паркера, стендап-математика. Бывший учитель математики из Австралии, Мэтт Паркер сделал карьеру, выступая в роли стендап-комика и математического коммуникатора — часто одновременно.

9. Интегралы — исчисление (05:55)

   CalculusExpert — это канал преподавателя математики Кристы Кинг, на котором она предлагает видео, помогающие изучать математику любого уровня, от основ до исчисления. Ее веб-сайт предлагает доступ по подписке к учебным ресурсам для курсов всех уровней математики, но, конечно же, все на YouTube бесплатно! Ее плейлисты — отличное место для начала.

10. Super Base (математическая рэп-песня WSHS) (03:24)

    Когда ничего не помогает, вовлеките своих учеников, сняв видеоклип на популярную песню на математическую тему.Средняя школа Westerville South в Огайо сделала из этого настоящее искусство — на их канале YouTube WHSHMath есть семь музыкальных клипов по математике, а эта пародия на Super Bass Ники Минаж набрала более 1,5 миллиона просмотров.

Дополнительные ресурсы для вовлечения детей в математику

Я надеюсь, что этот плейлист вдохновил вас на поиск творческих способов увлечь ваших учеников математикой или, по крайней мере, предоставил отличные ресурсы для помощи в выполнении домашних заданий. Есть так много увлеченных своим делом преподавателей математики, которые делятся своими знаниями и работают над улучшением репутации математики как скучного предмета! Если у вас есть любимые ресурсы, поделитесь ими в комментариях ниже.

видео по математике | Математическая площадка

Детский сад

1 класс

2 класс

3 класс

4 класс

5 класс

6 класс

Веселые игры для детей

Математические видео

Реклама | Перейти без рекламы

 Видео по математике

Реклама

Место Значение

Район

Знакомство с фракциями

Гистограммы 2

3-значные числа

Добавление Перегруппировка

Деньги

Рассказывать время

Линейные графики

Вычитание с нулями

Истекшее время

Пропустить счет

 Другие видео по математике

Умножение и деление

Перегруппировать и вычесть

Термины умножения

Условия раздела

Коммутативная собственность

Ассоциативное свойство

Остатки дивизии

Длинная дивизия

Распределительная собственность

Периметр

Графики изображений

Введение Умножение

Гистограммы

Умножение на 3

История о доброте

Числа и операции

Простые числа

Факторизация простых чисел
Правила делимости
Округление чисел
Общие множители и кратные
Проблема со словами GCF
Вычитание путем перегруппировки
Факты умножения
Длинное деление
Частное
Сложение дробей
Упрощение дробей
Дроби и десятичные дроби
Разделение дробей
Доля числа
Сравнение и порядок дробей

Умножение десятичных дробей

Деление десятичных дробей
Деление десятичных степеней 10
Отношения
Равные отношения
Соотношения со словами
Соотношения 2
Пропорции
Цена продажи
Преобразование дробей в проценты
Расчет чаевых
Проценты
Процентное изменение

Геометрия и измерения

Сумма углов многоугольника

Теорема Пифагора
Операции с квадратным корнем
Сумма углов треугольника
Использование транспортира
Нанесение точек
Определение наклона
Поиск уклона
Графические линии
Вычисление средней точки
Площадь треугольника
Площадь трапеции
Площадь и периметр
Площадь круга
Площадь трапеции
Окружность
Площадь поверхности конусов

Площадь поверхности Цилиндры

Площадь поверхности Комплекс
Площадь поверхности призмы
Площадь поверхности пирамиды
Объем конусов
Объем цилиндров
Объем призм
Объем пирамид
Режим
Миллисекунды за 1 день
Метрическая система
Стебель и лист.

Преалгебра/алгебра

PEMDAS

Порядок операций
Определение переменных
Инверсия
Одношаговые уравнения
Двухшаговые уравнения

Уравнения с переменными

Решить 5(2x + 7) = 45
Неравенства
Упрощение Термины
Многошаговые уравнения
Переменная с обеих сторон Математическая игровая площадка
Игры для 1-го класса
Игры для 2-го класса
Игры для 3-го класса
Игры для 4-го класса
Игры для 5-го класса
Игры для 6-го класса
Блоки мышления
Математические видео МАТЕМАТИЧЕСКИЕ ИГРЫ
Игры на сложение
Игры на вычитание
Игры на умножение
Игры на деление
Игры на дроби
Игры на соотношения
Игры на преалгебру
Игры на геометрию ОБУЧАЮЩИЕ ИГРЫ
Логические игры
Классические игры
Правописание
Грамматические игры
Печатание
География
Математические головоломки
Пространственное мышление
FUN KIDS GAMES
Fun Games
Приключенческие игры
Car Games
Спортивные игры
Endless Runner Games
Perfect Time Games
Игры для двоих
Все игры FRACTION FOREST
Фракции единиц 1
Фракции единиц 2
Игровая площадка 1
Равные фракции 1
Равные фракции 2
Игровая площадка 2
Добавление фракций 1
Добавление фракций 2
Игровая площадка 1 4 3 9000 МЫСЛИТЕЛЬНЫЕ БЛОКИ
TB Junior
TB Addition
TB Умножение
TB Дроби
TB Соотношения
Инструмент моделирования
Печатные версии
Видео
Словесные задачи
ЧИСЛОВЫЕ ЗАГАДКИ
Суммарные стеки
Числовая последовательность
Суммарные ссылки
Суммарные блоки
Суммы цепочек
Суммы растяжения
Суммы обмена
Суммы перекрытий
ОБУЧЕНИЕ МАТЕМАТИКЕ
Головоломки по алгебре
Стратегическое умножение
Задачи на дроби
Решение задач
Математика для 3-го класса
Наглядные математические инструменты
Задания на слова с моделями
Реклама | Перейти без рекламы

---

О нас Политика конфиденциальности Условия использования Условия оплаты Получить помощь

Copyright © 2022 Math Playground LLC • Все права защищены

Как изучать математику: для учащихся

Часть 1: Мозг и обучение математике.

1. Развенчание мифов о математике.

Каждый может хорошо выучить математику. Не существует такого понятия, как «математический человек». На этом занятии представлены потрясающие новые данные о росте мозга и рассмотрено, что это значит для изучающих математику.

2. Математика и мышление

Когда люди меняют свое мышление с фиксированного на рост, их потенциал обучения резко возрастает. На этом занятии участникам будет предложено развить мышление роста для математики.

3.Ошибки и скорость

Недавние исследования мозга показывают ценность того, что учащиеся работают над сложной работой и даже совершают ошибки. Но многие ученики боятся ошибок и думают, что это означает, что они не математики. Это занятие побудит учащихся позитивно относиться к ошибкам. Это также поможет развенчать мифы о математике и скорости.

Часть 2: Стратегии успеха.

1. Числовая гибкость, математические рассуждения и связи

На этом занятии участники примут участие в «разговоре о числах» и увидят различные решения проблем с числами, чтобы понять и узнать, как действовать в отношении гибкости чисел. Чувство чисел имеет решающее значение для всех уровней математики, а отсутствие чувства чисел является причиной того, что многие студенты проваливают курсы по алгебре и не только. Участники также узнают о ценности разговоров, рассуждений и установления связей в математике.

2. Образцы и представления чисел

На этом занятии участники увидят, что математика — это предмет, состоящий из взаимосвязанных больших идей. Они узнают о ценности осмысления, интуиции и математического рисования. Специальный раздел, посвященный дробям, поможет учащимся узнать о больших идеях, выраженных в дробях, и о ценности понимания больших идей в математике в целом.

3. Математика в жизни, природе и работе

На этом занятии участники увидят математику как нечто ценное, захватывающее и присутствующее на протяжении всей жизни. Они увидят математические закономерности в природе и в разных видах спорта, углубятся в изучение математики в танце и жонглировании. На этом занятии будут рассмотрены ключевые идеи курса, и они помогут участникам применить важные стратегии и идеи, которые они изучили, в своем будущем.

Архивы математики — Scratch Garden

Опубликовано 15 марта 2021 г.

Социально-эмоциональное обучение математике для детей Математика — это просто числа, верно? Вообще-то, нет! Математика касается самых разных вещей, таких как сортировка шаблонов, подсчет тарелок со спагетти, направления, сложение и вычитание пончиков.Мало того, что есть много разных вещей, которым можно научить детей по математике, так еще и много […]

Подробнее

Опубликовано 1 марта 2021 г.

Когда мы говорим о вероятностной математике (нет, не о вероятности — о вероятности), мы говорим о том, насколько вероятно, что что-то должно произойти.Мы исследуем возможное и невозможное. Другими словами, мы используем основы теории вероятностей, чтобы вычислить вероятность возникновения событий. Думайте об этом как о математической версии гадания, но без хрустального шара. В нашем […]

Подробнее

Опубликовано 15 февраля 2021 г.

Данные — это набор информации, которую мы можем сортировать и использовать, чтобы понять, например, сколько обуви у нас есть, сколько детей в нашей семье голубоглазые и сколько людей на планете Земля предпочитают лето зиме. Каждый день люди создают около 2,5 квинтиллионов байт данных! Итак, говорите ли вы дай-та или дар-тар, организация данных и […]

Подробнее

Опубликовано 1 февраля 2021 г.

Серьезный вопрос: где ты? Может быть, вы устроились на диване в северном полушарии.Возможно, вы находитесь ровно в 3333 милях от Эйфелевой башни. Или, может быть, вы слева от книжного шкафа и справа от настольной лампы. Когда кто-то спрашивает нас: «Где ты?», мы используем позиционный язык. Мы используем слова-направления […]

Подробнее

Опубликовано 18 января 2021 г.

Формы повсюду.Посмотрите вниз, и вы увидите опавшие листья, каждая из которых имеет уникальную форму, круглых жуков и прямоугольные коврики для пикника. Посмотрите вверх, и вы увидите круглое солнце и пушистые облака. У фигур есть атрибуты, и мы можем использовать атрибуты фигур для сортировки фигур. Довольно аккуратно, да? В этом математическом видео для детей (внизу […]

Подробнее

Опубликовано 4 января 2021 г.

Узоры окружают нас повсюду.Мы видим закономерности в реальной жизни, и если мы проявим особую наблюдательность, мы сможем выявлять закономерности в математике. Мы также можем слышать паттерны, и когда мы изучаем правила паттерна, мы можем начать делать прогнозы. Сначала вы услышали это здесь. Предсказание закономерностей дает нам способность предсказывать будущее. С […]

Подробнее

Опубликовано 30 ноября 2020 г.

Итак, вы хотите научить детей сравнивать высоту и ширину? Что ж, у нас есть твоя спина.Наш урок по измерению охватывает важные понятия: стандартные и нестандартные единицы измерения, саламандры, измерение длины и расстояния, а также коровы в забавных шляпах. Как мы уже говорили, обязательные понятия. Прежде чем мы перейдем к хорошим вещам, давайте начнем с самого начала. […]

Подробнее

Опубликовано 16 ноября 2020 г.

Дроби для детей: Учим дроби в увлекательной игровой форме Итак, вы умеете считать.Целые вещи. Но есть совершенно другой способ (без каламбура) складывать, вычитать, умножать и делить числа, и наше ознакомительное видео по математике дробей — идеальное место для начала! На самом деле, наш фракционный урок своего рода революционный. Хотите […]

Подробнее

Опубликовано 2 ноября 2020 г.

Сложение и вычитание — основы математики! Приготовьтесь без промедления приступить к сложению и вычитанию чисел! Что значит складывать и вычитать? Прежде чем вы зайдете слишком далеко по математическому пути, вы можете начать с объяснения своим ученикам, что вообще означает сложение и вычитание.Когда […]

Подробнее

Опубликовано 20 октября 2020 г.

Сегодня вы можете узнать, как помочь учащимся и учащимся понять два новых термина. Несмотря на то, что эти термины могут быть очень сложными для самых маленьких, вы можете сделать их понятными с помощью этого руководства и забавного видео по математике ниже.Наши термины составляют и разлагают числа. Эти условия не будут такими сложными для […]

Подробнее

царапин по каждому предмету: математика

В этой коллекции ресурсов Math+Scratch рассказывается о многих способах, с помощью которых учащиеся приобретают понимание математики, создавая свои собственные проекты в Scratch.

• Автор оригинала: Мэри Аделаида
• Уровень образования: Начальная школа, Средняя школа, Высшая школа
• Типы контента: Упражнение, Учебная программа, План урока, Образец проекта с нуля, Учебник, Инструмент
• Учебные области: Математика
• Ключевые слова: математика, Скретч-проекты, математическое образование, интеграция учебных программ, царапины по каждому предмету

Мэри Аделаида, стажер ScratchEd 

Для многих учащихся знакомство с математикой и понимание ее реальных приложений может быть проблемой. Им может надоесть выучить формулы или напугать абстрактными задачами и сложными правилами. Вот где Scratch может вмешаться.

С самого начала учащиеся, использующие Scratch, изучают математические концепции, начиная с декартовых координат, которые они должны понимать, чтобы перемещать спрайты по экрану. Чтобы сделать эту идею более ясной, учащиеся могут рисовать координатные плоскости в Scratch или ремикшировать один из многих связанных проектов, чтобы добавить свою изюминку (например, эта игра с декартовыми координатами — хороший способ попрактиковаться, и было создано несколько ремиксов).Этот ресурс от Бена Джонсона помогает учащимся определить координаты, необходимые для рисования их имен в Scratch, что можно сделать с помощью пера. Скретчеры также создали несколько полезных проектов, знакомящих других с координатной плоскостью — вот один из примеров.

^{Учащиеся могут углубить свое понимание системы координат, создавая подобные игры.}

Будучи ключевой частью координатной плоскости, отрицательные числа быстро вступают в игру во время начальных исследований Scratch. Углы/градусы добавляются к смеси, поскольку учащиеся ищут способы точной настройки движения своих спрайтов, и могут стать основой для творческих игр, таких как эти два примера. И эти темы, хотя и предоставляют достаточно места для изучения, являются лишь началом концепций, которые можно воплотить в жизнь с помощью Scratch.

 

Изучение математики с помощью Scratch не обязательно должно ограничиваться математическими проектами. Короткие задачи можно легко превратить в игры, где решение задач может позволить игроку продвинуться в игре или собрать больше валюты.Почти любой тип проекта позволяет учащимся практиковать такие основы, как декартовы координаты, поэтому учащиеся могут заниматься проектами, основанными на личных интересах, при этом осваивая эти концепции.

 

Альваро Молина Аюсо, учитель математики средней школы в Испании, предлагает учащимся создать проекты Scratch, показывающие практическое применение идей, изложенных в каждом разделе. Например, его ученики, изучающие проценты, использовали Scratch для описания сценария, например, интернет-магазина, который требует расчета скидки на продукт.

 

Еще один способ наглядно представить, как работают проценты, особенно для тех, кто совершенно не знаком с этой темой, — использовать команду «масштаб» с различными процентами и отмечать, как соответственно изменяется размер спрайта. Визуализация изменений формы или объекта путем изменения спрайта также может помочь учащимся узнать о преобразованиях, которые могут программировать спрайты для выполнения перемещений, поворотов и отражений. Карен Рэндалл делится несколькими предложениями по проектам, связанным с преобразованиями, геометрией, вероятностью и другими темами в этом ресурсе.Здесь она также приводит примеры проектов по геометрии.

^{Создав проект Карен Рэндалл, подобный этому, учащиеся могут изучить фундаментальные концепции геометрии.}

Для американских учителей, которые хотят интегрировать Scratch в классы в соответствии со стандартами Common Core, Келли Вон предлагает серию из трех уроков математики для учащихся средних школ. На этих уроках шестиклассники рисуют многоугольники в координатной плоскости, семиклассники изучают чертежи геометрических фигур в масштабе, а восьмиклассники создают программы для функциональных машин.

 

Несколько учителей обнаружили, что Scratch может быть хорошей платформой для объединения учащихся из разных классов. Учащимся старшего возраста может нравиться наставлять своих младших сверстников в использовании Scratch, а также они могут создавать игры, которые позволяют младшим ученикам развлекаться, решая соответствующие их классу задачи. Например, игры, подобные этой, которой поделился Бен Джонсон, могут быть запрограммированы на один класс для класса ниже их.

 

Помимо введения операций и понятий, Scratch может помочь учащимся увидеть красоту математики.Многие скретчеры создали творческие проекты, демонстрирующие красочные узоры, фракталы и многое другое. В этой студии есть несколько хороших примеров, как и в этой студии 10-классников, которых преподает Мария Беатрис Рапаччини.

^{Демонстрация учащимся примеров проектов, таких как эта студия с работами учащихся 10-го класса в классе Марии Беатрис Рапаччини, может пробудить любопытство и вдохновить их на решение сложных задач.}

Все еще ищете идеи?

• Посмотрите эту презентацию Марка Трантера, включающую ряд алгоритмов, которые можно изобразить с помощью Scratch, или этот набор видео, которым поделился Себ Шмоллер из Citizen Maths.Национальный совет учителей математики опубликовал статью, в которой представлены многочисленные приложения Scratch, разработанные специально для преподавателей математики.
• На ScratchEd доступно множество дополнительных ресурсов, которые помогут вам интегрировать математику в класс, поиск здесь доступен, и вы также можете задавать вопросы другим учителям на дискуссионных форумах. Если у вас есть конкретная тема, которую вы надеетесь направить учащимся в изучении Scratch, поиск в Scratch связанных ключевых слов, таких как «фракции», может дать полезные примеры проектов.
• Просмотрите примеры математических проектов, включая синусоидальные, косинусоидальные и касательные волны, а также математического дракона, в этой коллекции Scratch-проектов по учебной программе.
• Чтобы получить дополнительные советы по интеграции Scratch в учебную программу по математике, ознакомьтесь с ресурсами в Руководстве по интеграции Scratch между учебными программами.

И, пожалуйста, поделитесь ресурсами, которые вы найдете или создадите, с онлайн-сообществом!

 

 

Облегчение использования видео с учителями математики: обучение, оставаясь в деталях | Международный журнал STEM Education

Альтрихтер, Х., Пош П. и Сомех Б. (1993). Учителя исследуют свою работу . Лондон: Рутледж.

Google Scholar

Арья П., Крист Т. и Чиу М.М. (2013). Фасилитация и поведение учителей: анализ видео-кейсов учителей грамотности. Журнал педагогического образования, 65 (2), 111–127.

Артикул Google Scholar

Бейтсон Г.(1972). Шаги к экологии разума (стр. 2000). Чикаго: Издательство Чикагского университета.

Google Scholar

Борко, Х., Джейкобс, Дж., Сиго, Н., и Манграм, К. (2014). Содействие профессиональному развитию на основе видео: планирование и организация продуктивных дискуссий. В Y. Li, EA Silver и S. Li (Eds.), Преобразование обучения математике: несколько подходов и практик (стр. 259–291). Берлин: Спрингер.

Google Scholar

Борко, Х., Келлнер, К., и Джейкобс, Дж. (2017). Изучение помощи начинающих учителей-лидеров в профессиональном развитии математики. Журнал математического поведения, 33 , 149–167.

Артикул Google Scholar

Борко, Х. , Кельнер, К., Джейкобс, Дж., и Сиго, Н. (2011). Использование видеорепрезентаций обучения в практико-ориентированном повышении квалификации. ZDM Международный журнал по математическому образованию, 43 (1), 175–187.

Артикул Google Scholar

Бруссо, Г. (1984). Решающая роль дидактического договора в анализе и построении ситуаций в обучении и обучении математике. В H. Steiner (Ed.), Theory of Mathematics Education (стр. 110–119). Билефельд: Дидактический институт математики Университета Билефельда.

Google Scholar

Брауэр, К. Н. (2011). Обучение учителей визуализации. Обзор литературы по использованию цифрового видео для подготовки учителей и повышения квалификации (документ представлен на ежегодном собрании Американской ассоциации исследований в области образования, Новый Орлеан, 11 апреля 2011 г.). Неймеген: Высшая педагогическая школа Радбуда.

Google Scholar

Браун, Л.и Коулз, А. (2008). Слышать тишину: шаги к обучению математике . Кембридж: Black Apollo Press.

Google Scholar

Браун, Л., и Коулз, А. (2011). Развитие опыта: как энактивизм меняет структуру развития учителей математики. ZDM Международный журнал по математическому образованию, 43 (6–7), 861–873.

Артикул Google Scholar

Коулз, А.(2013а). Использование видео для профессионального развития: роль ведущего дискуссии. Журнал образования учителей математики, 16 (3), 165–184.

Артикул Google Scholar

Коулз, А. (2013b). Быть рядом: для преподавания и изучения математики . Роттердам: Издательство Sense.

Книга Google Scholar

Коулз, А. (2014). Учителя математики учатся с помощью видео: роль дидакта в усиленном слушании. ZDM Международный журнал по математическому образованию, 46 (2), 267–278.

Артикул Google Scholar

Коулз, А. (2015). Об энактивизме и языке: к методике изучения разговорной речи на уроках математики. ZDM Международный журнал по математическому образованию, 47 (2), 235–246.

Артикул Google Scholar

Эллиот Р., Каземи, Э., Лессейг, К., Мумме, Дж., Кэрролл, К., и Келли-Петерсен, М. (2009). Концептуализация работы ведущих математических задач в повышении квалификации. Журнал педагогического образования, 60 (4), 364–379.

Артикул Google Scholar

Фройденталь, Х. (1981). Основные проблемы математического образования. Образовательные исследования по математике, 12 , 133–150.

Артикул Google Scholar

Гаттеньо, К.(1965). Математика и образы. Преподавание математики, 33 (4), 22–24.

Google Scholar

Годен, К., и Чали, С. (2015). Видеопросмотр в педагогическом образовании и повышении квалификации: обзор литературы. Educational Research Review, 16 , 41–67.

Артикул Google Scholar

Гроссман П., Хаммернесс К. и Макдональд М.(2009). Переосмысление учителя: переосмысление педагогического образования. Учителя и преподавание: теория и практика, 15 (2), 273–290.

Артикул Google Scholar

Холлингсворт, Х., и Кларк, Д. (2017). Видео как инструмент фокусировки саморефлексии учителя: поддержка и провокация обучения учителя. Журнал образования для учителей математики, 20 , 457–475.

Артикул Google Scholar

Джейкобс, Дж., Сиго, Н., и Келлнер, К. (2017). Подготовка фасилитаторов к продуктивному использованию и адаптации материалов для профессионального развития по математике. Международный журнал STEM-образования, 4 , 30. https://doi.org/10.1186/s40594-017-0089-9.

Артикул Google Scholar

Яворски, Б. (1990). Видео как инструмент профессионального развития учителей. Профессиональное развитие в сфере образования, 16 (1), 60–65.

Google Scholar

Хуарреро, А.(2002). Динамика в действии: намеренное поведение как сложная система . Кембридж, Массачусетс: MIT Press.

Google Scholar

Карсенти Р. и Аркави А. (2017). Математика, объективы и видеокассеты: основа и язык для разработки рефлексивных методов обучения. Журнал образования для учителей математики, 20 , 433–455.

Артикул Google Scholar

Карсенты Р.и Шерин, М. (2017). Видео как катализатор роста учителей математики. Журнал образования для учителей математики, 20 , 409–413.

Артикул Google Scholar

Ламперт, М. (2010). Обучение обучению на практике, из нее и для практики: что мы имеем в виду? Журнал педагогического образования, 61 (1–2), 21–34.

Артикул Google Scholar

Лерман С.(Ред.). (2014). Энциклопедия математического образования . Дордрехт: Спрингер.

Google Scholar

Лессейг К., Эллиотт Р., Каземи Э., Келли-Петерсен М., Кэмпбелл М., Мумм Дж. и Кэрролл К. (2017). Лидер заметил помощь в видеокейсах профессионального развития математиков. Журнал образования для учителей математики, 20 , 591–619.

Артикул Google Scholar

Мейсон Дж.(2002). Изучение собственной практики: дисциплина наблюдения . Лондон: Рутледж Фалмер.

Google Scholar

Матурана, Х. (1987). Все сказанное сказано наблюдателем. В W. Thompson (Ed.), Gaia: способ познания (стр. 65–82). Хадсон: Линдисфарн Пресс.

Google Scholar

Матурана, Х., и Варела, Ф. (1987). Древо познания: биологические корни человеческого понимания .Бостон и Лондон: Шамбала.

Google Scholar

Мерло-Понти, М. (1962). Феноменология восприятия . Лондон: Рутледж и К. Пол.

Google Scholar

Немировский Р., Диматтиа С., Рибейро Б. и Лара-Мелой Т. (2005). К слову об обучающих эпизодах. Журнал образования учителей математики, 8 (5), 363–392.

Артикул Google Scholar

Рейд, Д.и Мгомбело, Дж. (2015). Обзор ключевых концепций энактивистской теории и методологии. ZDM, Международный журнал по математическому образованию, 47 (2), 171–183.

Артикул Google Scholar

Сантагата, Р., и Ангеличи, Г. (2010). Изучение влияния структуры анализа урока на способность учителей предварительного обучения размышлять над видео преподавания в классе. Журнал педагогического образования, 61 (4), 339–341.

Артикул Google Scholar

Шенфельд, А. (2017). Использование видео для понимания и улучшения математического мышления и обучения. Журнал образования для учителей математики, 20 , 415–432.

Артикул Google Scholar

Шулер, С. , и Рёскен-Винтер, Б. (2018). Сбор видео-кейсов, чтобы помочь фасилитаторам PD заметить продуктивное обучение учителей. Международный журнал STEM-образования, 5 (50). https://doi.org/10.1186/s40594-018-0147-y.

Шерин, М. (2007). Новые взгляды на роль видео в педагогическом образовании. В J. Brophy (Ed.), Использование видео в обучении учителей (стр. 1–28). Бингли: Emerald Group Publishing Limited.

Google Scholar

Шерин, М., и Дайер, Э. (2017). Самостоятельно снятое учителями математики видео и возможности для обучения. Журнал образования для учителей математики, 20 , 477–495.

Артикул Google Scholar

Шерин, М., и ван Эс, Э. (2009). Влияние участия в видеоклубе на профессиональное видение учителей. Журнал педагогического образования, 60 (1), 20–37.

Артикул Google Scholar

Стар, Дж. , и Стрикленд, С. (2008). Учимся наблюдать: использование видео для улучшения способности учителей математики замечать. Журнал образования учителей математики, 11 (2), 107–125.

Артикул Google Scholar

Штейн М.К., Энгл Р.А., Смит П.С. и Хьюз Э.К. (2008). Организация продуктивных математических дискуссий: пять практик, которые помогут учителям не просто показывать и рассказывать. Математическое мышление и обучение, 10 (4), 313–340.

Артикул Google Scholar

Стюарт, Дж.(2010). Основополагающие вопросы в действии как парадигма когнитивной науки: от происхождения жизни до сознания и письма. В Дж. Стюарт, О. Гапенне и Э. Д. Паоло (редакторы), На пути к новой парадигме когнитивной науки (стр. 1–32). Кембридж: MIT Press.

Глава Google Scholar

Стро Беквар, Д., и Беквар, Р. (2000). Семейная терапия: системная интеграция . Бостон: Аллин и Бэкон.

Google Scholar

Теккумру-Штайн, М., и Штейн, М. (2017). Основа для планирования и содействия профессиональному развитию на основе видео. Международный журнал STEM-образования, 4 (28). https://doi.org/10.1186/s40594-017-0086-z.

ван Эс, Э.А., и Шерин, М.Г. (2008). «Учимся замечать» учителей математики в условиях видеоклуба. Преподавание и педагогическое образование, 24 , 244–276.

Артикул Google Scholar

ван Эс, Танни Дж., Голдсмит Л. и Сиго Н. (2014). Основа для облегчения учителям анализа видео. Журнал педагогического образования, 65 (4), 340–356.

Артикул Google Scholar

фон Берталанфи, Л. (1969). Общая теория систем (стр. 2003). Нью-Йорк: Джордж Бразиллер.