Значение логического выражения. — информатика, презентации

Значение логического выражения.
Решу ОГЭ. Задание 2

Логические выражения и логические операции
Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель).
Простым высказыванием называют повествовательное предложение, относительно которого имеет смысл говорить, истинно оно или ложно (ни одно высказывание не может быть одновременно истинным и ложным).

Примеры высказываний:
Москва – столица России. (И)
Число 27 является простым. (Л)
Волга впадает в Каспийское море. (И)
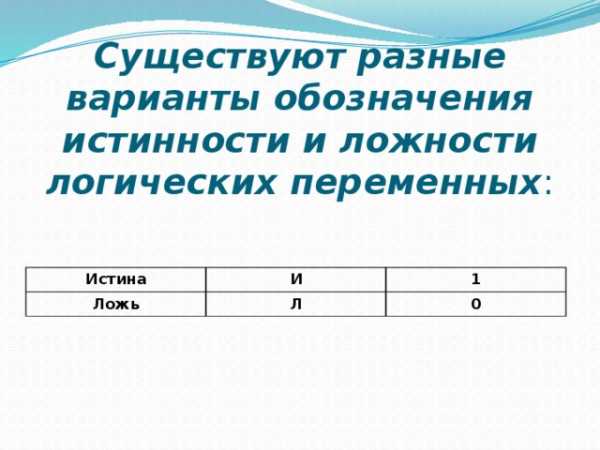
Существуют разные варианты обозначения истинности и ложности логических переменных :
Истина
Ложь
И
1
Л
0

Логическое выражение
Логическое выражение — это символическая запись высказывания, состоящая из логических величин (констант или переменных) , объединенных логическими операциями (связками) .
Связки «НЕ» инверсия, «И» конъюнкция, «ИЛИ» дизъюнкция. Это основные логические операции , при помощи которых можно записать любое логическое выражение.

Конъюнкция — логическое умножение (от латинского conjunctio — союз, связь)
Конъюнкция — это логическая операция, ставящая в соответствие каждым двум простым (или исходным) высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны. Если хотя бы одно из составляющих высказываний ложно, то и полученное из них с помощью союза «И» сложное высказывание также считается ложным.

Таблица истинности
Если два высказывания соединены союзом «И» , то полученное сложное высказывание истинно тогда и только тогда, когда истинны оба исходных высказывания.
В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.

Дизъюнкция — логическое сложение (от латинского disjunctio — разобщение, различие )
Дизъюнкция — это логическая операция, которая каждым двум простым (или исходным) высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.
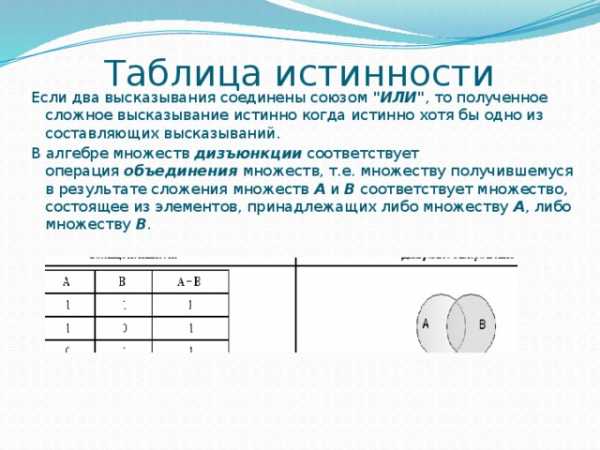
Таблица истинности
Если два высказывания соединены союзом «ИЛИ» , то полученное сложное высказывание истинно когда истинно хотя бы одно из составляющих высказываний.
В алгебре множеств дизъюнкции соответствует операция объединения множеств, т.е. множеству получившемуся в результате сложения множеств А и В соответствует множество, состоящее из элементов, принадлежащих либо множеству А , либо множеству В .

Инверсия — отрицание (от латинского disjunctio — разобщение, различие ):
Отрицание — логическая операция, которая с помощью связки «не» каждому исходному высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.

Таблица истинности
Если исходное выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное выражение ложно, то результат отрицания будет истинным.
В алгебре множеств логическому отрицанию

Логическое следование (импликация)
Высказывание, составленное из двух высказываний при помощи связки «если …, то …» , называется логическим следованием, импликацией (импликация от латинского implico — тесно связываю ).
 B «Из А следует В»»
B «Из А следует В»»
Таблица истинности
Новое высказывание, полученное с помощью импликации, является ложным тогда и только тогда, когда условие (посылка А ) — истинно, а следствие (заключение В ) — ложно и истинно во всех остальных случаях.В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т.е. множеству получившемуся в результате отрицания множества А соответствует множество, дополняющее его до универсального множества.
A = B «Из А следует В»

Эквивалентность (логическое тождество)
Высказывание, составленное из двух высказываний при помощи связки «тогда и только тогда, когда» , называется эквивалентностью (эквивалентность — логическое тождество, равнозначность, взаимная обусловленность. )
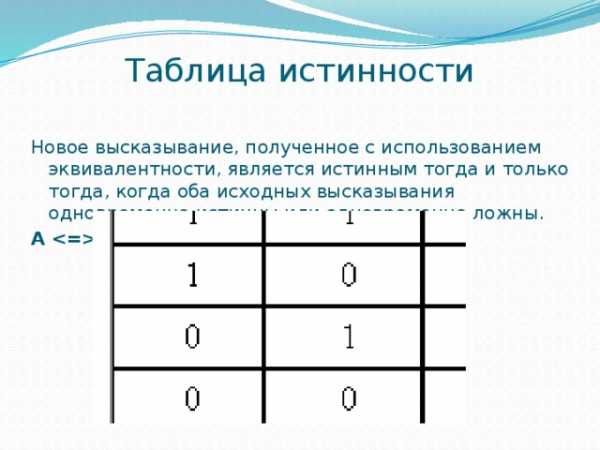
Таблица истинности
Новое высказывание, полученное с использованием эквивалентности, является истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.
A B «А равносильно В»

Примеры решения задач Демо версия ОГЭ 2016
Ответ 1


kopilkaurokov.ru
Простейшие логические операции в информатике
Каждого, кто начинает изучать информатику, учат двоичной системе исчисления. Именно она используется для вычисления логических операций. Рассмотрим ниже все самые элементарные логические операции в информатике. Ведь если задуматься, именно они используются при создании логики вычислительных машин и приборов.
Отрицание
Перед тем как начать подробно рассматривать конкретные примеры, перечислим основные логические операции в информатике:

- отрицание;
- сложение;
- умножение;
- следование;
- равенство.
Также перед началом изучения логических операций стоит сказать, что в информатике ложь обозначается «0», а правда «1».
Для каждого действия, как и в обычной математике, используются следующие знаки логических операций в информатике: ¬, v, &, ->.
Каждое действие возможно описать либо цифрами 1/0, либо просто логическими выражениями. Начнём рассмотрение математической логики с простейшей операции, использующей всего одну переменную.
Логическое отрицание — операция инверсии. Суть заключается в том, что если исходное выражение — истина, то результат инверсии — ложь. И наоборот, если исходное выражение — ложь, то результатом инверсии станет — правда.
При записи этого выражения используется следующее обозначение «¬A».
Приведём таблицу истинности — схему, которая показывает все возможные результаты операции при любых исходных данных.
| А | х | о |
| ¬A | о | х |
То есть, если у нас исходное выражение — истина (1), то его отрицание будет ложным (0). А если исходное выражение — ложь (0), то его отрицание — истина (1).
Сложение
Оставшиеся операции требуют наличия двух переменных. Обозначим одно выражение —  А, второе — В. Логические операции в информатике, обозначающие действие сложения (или дизъюнкция), при написании обозначаются либо словом «или», либо значком «v». Распишем возможные варианты данных и результаты вычислений.
А, второе — В. Логические операции в информатике, обозначающие действие сложения (или дизъюнкция), при написании обозначаются либо словом «или», либо значком «v». Распишем возможные варианты данных и результаты вычислений.
- Е=1, Н=1 ,тогда Е v Н = 1. Если оба выражения истинны, тогда и их дизъюнкция также истинна.
- Е=0, Н=1 ,в итоге Е v Н = 1. Е=1, Н=0 , тогда Е v Н= 1. Если хотябы одно из выражений истинно, тогда и результат их сложения будет истиной.
- Е=0, Н=0 ,результат Е v Н = 0. Если оба выражения ложны, то их сумма также — ложь.
Для краткости создадим таблицу истинности.
| Е | х | х | о | о |
| Н | х | о | х | о |
| Е v Н | х | х | х | о |
Умножение
Разобравшись с операцией сложения, переходим к умножению (конъюнкции). Воспользуемся теми же обозначениями, которые были приведены выше для сложения. При письме логическое умножение обозначается значком «&», либо буквой «И».
- Е=1, Н=1 ,тогда Е & Н = 1. Если оба выражения истинны, тогда их конъюнкция — истина.
- Если хотя бы одно из выражений — ложь, тогда результатом логического умножения также будет ложь.
- Е=1, Н=0, поэтому Е & Н = 0.
- Е=0, Н=1, тогда Е & Н = 0.
- Е=0, Н=0, итог Е & Н = 0.
| Е | х | х | 0 | 0 |
| Н | х | 0 | х | 0 |
| Е & Н | х | 0 | 0 | 0 |
Следствие
Логическая операция следования (импликация) — одна из простейших в математической логике. Она основана на единственной аксиоме — из правды не может следовать ложь.
- Е=1, Н=, поэтому Е -> Н = 1. Если пара влюблена, то они могут целоваться — правда.
- Е=0, Н=1, тогда Е -> Н = 1. Если пара не влюблена, то они могут целоваться — также может быть истиной.
- Е=0, Н=0, из этого Е -> Н = 1. Если пара не влюблена, то они и не целуются — тоже правда.
- Е=1, Н=0, результатом будет Е -> Н = 0. Если пара влюблена, то они не целуются — ложь.
Для облегчения выполнения математических действий также приведём таблицу истинности.
| Е | х | х | о | о |
| Н | х | о | х | 0 |
| Е -> Н | х | о | х | х |
Равенство
Последней рассмотренной операцией станет логическое тождественное равенство или эквивалентность. В тексте оно может обозначаться как «…тогда и только тогда, когда…». Исходя из этой формулировки, напишем примеры для всех исходных вариантов.
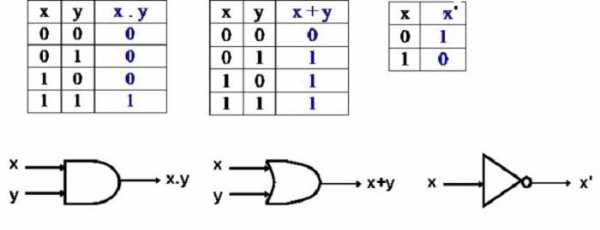
- А=1, В=1, тогда А≡В = 1. Человек пьёт таблетки тогда и только тогда, когда болеет. (истина)
- А=0, В=0, в итоге А≡В = 1. Человек не пьёт таблетки тогда и только тогда, когда не болеет. (истина)
- А=1, В=0, поэтому А≡В = 0. Человек пьёт таблетки тогда и только тогда, когда не болеет. (ложь)
- А=0, В=1 ,тогда А≡В = 0. Человек не пьёт таблетки тогда и только тогда, когда болеет. (ложь)
| А | х | о | х | о |
| В | х | о | 0 | х |
| А≡В | х | х | о | о |
Свойства
Итак, рассмотрев простейшие логические операции в информатике, можем приступить к изучению некоторых их свойств. Как и в математике, у логических операций существует свой порядок обработки. В больших логических выражениях операции в скобках выполняются в первую очередь. После них первым делом подсчитываем все значения отрицания в примере. Следующим шагом станет вычисление конъюнкции, а затем дизъюнкции. Только после этого выполняем операцию следствия и, наконец, эквивалентности. Рассмотрим небольшой пример для наглядности.
А v В & ¬В -> В ≡ А
Порядок выполнения действий следующий.
- ¬В
- В&(¬В)
- А v(В&(¬В))
- (А v(В&(¬В)))->В
- ((А v(В&(¬В)))->В)≡А
Для того чтобы решить этот пример, нам потребуется построить расширенную таблицу истинности. При её создании помните, что столбцы лучше располагать в том же порядке, в каком и будут выполняться действия.
| А | В | ¬В | В&(¬В) | А v(В&(¬В)) | (А v(В&(¬В)))->В | ((А v(В&(¬В)))->В)≡А |
| х | о | х | о | х | х | х |
| х | х | о | о | х | х | х |
| о | о | х | о | о | х | о |
| о | х | о | о | о | х | о |
Как мы видим, результатом решения примера станет последний столбец. Таблица истинности помогла решить задачу с любыми возможными исходными данными.
Заключение
В этой статье были рассмотрены некоторые понятия математической логики, такие как информатика, свойства логических операций, а также — что такое логические операции сами по себе. Были приведены некоторые простейшие примеры для решения задач по математической логике и таблицы истинности, необходимые для упрощения этого процесса.
fb.ru
Логические операции — урок. Информатика, 8 класс.
Сложные (составные) высказывания строятся из простых с помощью логических операций. Рассмотрим основные логические операции, определённые над высказываниями. Все они соответствуют связкам, употребляемым в естественном языке.
Название логической операции | Логическая связка |
Инверсия | «не»; «неверно, что» |
Конъюнкция | «и»; «а»; «но»; «хотя» |
Дизъюнкция | «или» |
Конъюнкция
Рассмотрим два высказывания:
\(A\) = «Основоположником алгебры логики является Джордж Буль»,
\(B\) = «Исследования Клода Шеннона позволили применить алгебру логики в вычислительной технике».
Очевидно, новое высказывание «Основоположником алгебры логики является Джордж Буль, и исследования Клода Шеннона позволили применить алгебру логики в вычислительной технике» истинно только в том случае, когда одновременно истинны оба исходных высказывания.
Конъюнкция — логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Для записи конъюнкции используются следующие знаки: И,ˆ,⋅,&.
Например: A И B,AˆB,A⋅B,A&B.
Конъюнкцию можно описать в виде таблицы, которую называют таблицей истинности:
В таблице истинности перечисляются все возможные значения исходных высказываний (столбцы \(A\) и \(B\)), причём соответствующие им двоичные числа, как правило, располагают в порядке возрастания: \(00, 01, 10, 11\). В последнем столбце записан результат выполнения логической операции для соответствующих операндов.
Обрати внимание!
Конъюнкцию также называют логическим умножением.
Дизъюнкция
Рассмотрим два высказывания:
\(A\) = «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу»,
\(B\) = «Лейбниц является основоположником бинарной арифметики».
Очевидно, новое высказывание «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу или Лейбниц является основоположником бинарной арифметики» ложно только в том случае, когда одновременно ложны оба исходных высказывания.
Дизъюнкция — логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.
Для записи дизъюнкции используются следующие знаки: ИЛИ;∨;|;+.
Например: A ИЛИ B;A∨B;A|B;A+B.
Дизъюнкция определяется следующей таблицей истинности:
Обрати внимание!
Дизъюнкцию также называют логическим сложением.
Инверсия
Инверсия — логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному.
Для записи инверсии используются следующие знаки: НЕ;¬;−
Например: НЕ А;¬А;А−.
Инверсия определяется следующей таблицей истинности:
Обрати внимание!
Инверсию также называют логическим отрицанием.
Отрицанием высказывания «У меня дома есть компьютер» будет высказывание «Неверно, что у меня дома есть компьютер» или, что в русском языке то же самое, что «У меня дома нет компьютера».
Отрицанием высказывания «Я не знаю китайский язык» будет высказывание «Неверно, что я не знаю китайский язык» или, что в русском языке: «Я знаю китайский язык».
Отрицанием высказывания «Все юноши \(8-х\) классов — отличники» является высказывание «Неверно, что все юноши \(8-х\) классов — отличники», другими словами, «Не все юноши \(8-х\) классов — отличники».
Таким образом, при построении отрицания к простому высказыванию либо используется речевой оборот «неверно, что …», либо отрицание строится к сказуемому, тогда к соответствующему глаголу добавляется частица «не».
Любое сложное высказывание можно записать и виде логического выражения — выражения, содержащего логические переменные, знаки логических операций и скобки.
Логические операции в логическом выражении выполняются в следующей очерёдности: инверсия, конъюнкция, дизъюнкция.
Изменить порядок выполнения операций можно с помощью расстановки скобок.
Обрати внимание!
Логические операции при выполнении имеют следующий приоритет: инверсия, конъюнкция, дизъюнкция.
Источники:
Босова Л. Л., Босова А. Ю., Информатика: учебник для 8 класса. М. : БИНОМ. Лаборатория знаний, 24 с.
www.yaklass.ru
Урок по информатике «Основы логики»
Разделы: Информатика
Цели:
- Введение в предмет “Алгебра логики”.
- Сформировать у учащихся понятия: формы мышления, алгебра высказываний, логическое высказывание, логические величины, логические операции.
- Способствовать формированию логического мышления, интереса к разделу информатики - алгебре логики.
- Закрепить полученные ЗУН.
Формы организации урока: объяснительно-иллюстративный, диалогический.
Ход урока.
I. Изложение нового материала.
1. Этапы развития логики.
Логика очень древняя наука.
1-й этап связан с работами ученого и философа Аристотеля (384-322 г.г. до н.э.). Он пытался найти ответ на вопрос “Как мы рассуждаем”, изучал правила мышления. Аристотель впервые дал систематическое изложение логики. Он подверг анализу человеческое мышление, его формы – понятие, суждение, умозаключение. Так возникла формальная логика.
2-й этап – появление математической, или символической, логики. Основы ее заложил немецкий ученый и философ Г.В. Лейбниц (1646-1716). Он сделал попытку построить первые логические исчисления, считал, что можно заменит простые рассуждения действиями со знаками, и привел соответствующие правила. Но он выдвинул только идею, а развил её окончательно англичанин Д. Буль (1815-1864). Буль считается основоположником математической логики как самостоятельной дисциплины. В его работах логика обрела свой алфавит, свою орфографию и грамматику.
2. Формы мышления.
Опр.1 Логика – эта наука, изучающая законы и формы мышления; учение о способах рассуждений и доказательств.
Основными формами мышления являются понятие, суждение, умозаключение.
Опр.2 Понятие – это форма мышления, выделяющая существенные признаки предмета или класса предметов, позволяющих отличить их от других.
Например: компьютер, трапеция, портфель, ураганный ветер.
Упражнение 1 (устно). Приведите свои примеры.
Понятие имеет две стороны: содержание и объем.
Содержание понятия – совокупность существенных признаков, отраженных в этом понятии. Например, содержание понятия персональный компьютер-это универсальное электронное устройство для автоматической обработки информации, предназначенное для одного пользователя.
Объем понятия – множество предметов, каждому из которых принадлежат признаки, составляющие содержание понятий.
Например:
1. Объем понятия город – это множество,
состоящее из городов, носящих имя Москва, Одесса,
Казань, Уфа, Нижнекамск и др.
2. Объем понятия персональный компьютер –
совокупность существующих в мире персональных
компьютеров.
Упражнение 2 (устно)
1. Перечислите существенные признаки,
составляющие содержание понятий: добродетель,
истинна, ложь.
2. Определите объем понятий: столица России,
столица, река.
Опр.3 Суждение (высказывание, утверждение) – это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание может быть либо истинным, либо ложным, и может быть либо простым, либо составным (сложным).
Например:
1. Истинное и простое высказывание: Буква “т” -
согласная.
2. Ложное и сложное высказывание: Осень наступила,
и грачи прилетели.
Вопросительные и восклицательные предложения не являются высказываниями, так как в них ни чего не утверждается и не отрицается.
Например:
1. Уходя, гасите свет!
2. Кто хочет быть счастливым?
Высказывания могут выражаться с помощью математических, физических, химических и прочих знаков. Например: 5>3, H2O+SO2=H2SO4.
Упражнение 3 (устно). Объясните, почему следующие высказывания не являются высказываниями:
1. Какого цвета твой велосипед?
2. Число Х больше пяти?
3. 5Х-2
4. Посмотрите в окно.
5. Пейте томатный сок!
6. Вы были в музее?
7. Разность чисел 12 и Х равна 6.
Упражнение 4 (устно). Какие из следующих высказываний являются истинными, а какие ложными?
1. Город Москва – столица России.
2. Число 12 – простое.
3. 7*3=1.
4. 12<15.
5. Сканер – устройство, которое может напечатать
на бумаге то, что изображено на экране
компьютера.
6. Клавиатура – устройство ввода информации.
Упражнение 5 (устно). Приведите свои примеры истинных и ложных высказываний.
Опр.4 Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений может быть получено новое суждение.
Посылками умозаключения по правилам формальной логики могут быть только истинные суждения. Тогда, если умозаключение проводится в соответствии с правилами формальной логики, то оно будет истинным. В противном случае можно прийти к ложному умозаключению.
Например:
| 1. Все металлы – простые вещества. Литий – металл. Литий – простое вещество. |
2. Все школьники – отличники. Вовочка – школьник. Вовочка – отличник. |
Упражнение 6.
1. Дано высказывание “Все углы равнобедренного
треугольника равны”. Путем умозаключений
получить высказывание “Этот треугольник
равносторонний”.
2. Оцените правильность следующего рассуждения:
сидящий встал; кто встал, тот стоит; значит,
сидящий стоит.
3. Алгебра высказываний.
Алгебра высказываний была разработана для того, чтобы можно было определять истинность или ложность составного высказывания, не вникая в их содержание.
Опр.5 Алгебра логики (алгебра высказываний) – раздел математической логики, изучающий строение (форму, структуру) сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.
Под высказыванием (суждением) будем понимать повествовательное предложение, относительно которого можно сказать, истинно или ложно.
В алгебре высказываний простым высказываниям ставятся в соответствии логические переменные, обозначаемые прописными буквами латинского алфавита.
Например:
А= “Листва на деревьях опадает осенью”.
В= “Земля прямоугольная”.
Высказывания, как говорилось уже ранее, могут быть истинными или ложными. Истинному высказыванию соответствует значение логической переменной 1, а ложному – значение 0 .
Например:
А=1
В=0
Опр.6 В алгебре высказываний высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения: “истинна” (1) и “ложь” (0).
В алгебре высказываний над высказываниями можно производить логические операции, в результате которых получаются новые, составные (сложные) высказывания.
Опр.7 Логическая операция – способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.
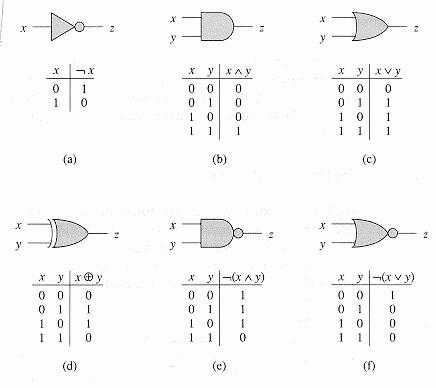
Рассмотрим три базовых логических операций – инверсию, конъюнкцию, дизъюнкцию и дополнительные – импликацию и эквивалентность.
| Логическая операция | Название | Соответствует союзу | Обозначение знаками | Таблица истинности | Логическая операция | |||||||||||||||
| Инверсия (от лат. inversion – переворачиваю) |
отрицание | не А |
|
Опр. 8 Инверсия логической переменной истина, если переменная ложна, и, наоборот, инверсия ложна, если переменная истинна. | ||||||||||||||||
| Конъюнкция (от лат. conjunction – связываю) |
Логическое умножение | А и В |
|
Опр.9Конъюнкция двух логических переменных истинна тогда и только тогда, когда оба высказывания, истинны. | ||||||||||||||||
| Дизъюнкция (от лат. disjunction – различаю) |
Логическое сложение | А или В |
|
Опр. 10 Дизъюнкция двух логических переменных ложна тогда и только тогда, когда оба высказывания ложны. | ||||||||||||||||
| Импликация (от лат. implication – тесно связывать) |
Логическое следование | Если А, то В; Когда А, тогда В |
А–условие В-следствие |
|
Опр. 11 Импликация двух логических переменных ложна тогда и только тогда, когда из истинного основания следует ложное следствие. | |||||||||||||||
| Эквивалентность (от лат. equivalents — равноценность) | Логическое равенство | А тогда и только тогда, когда В |
|
Опр. 12 Эквивалентность двух логических переменных истинна тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны |
Упражнение 7. Даны два простых высказывания:
А= “Щука – рыба”;
В=“Ворона – певчая птица”.
Составьте из них все возможные составные (сложные) высказывания и определите их истинность.
При вычислении значения логического выражения (формулы) логические операции вычисляются в определенном порядке, согласно их приоритету:
- инверсия,
- конъюнкция,
- дизъюнкция,
- импликация и эквивалентность.
Операции одного приоритета выполняются слева направо. Для изменения порядка действий используются скобки.
Например: дана формула
Порядок вычисления:
— инверсия
— конъюнкция
— дизъюнкция
— импликация
-
эквивалентность.
Упражнение 8.
Дана формула . Определите порядок вычисления.
II. Закрепление изученного материала.
1. Среди следующих высказываний укажите составные, выделите в них простые, обозначьте их каждое из них буквой. Запишите с помощью логических операций каждое составное высказывание.
- Число 456 трехзначное и четное.
- Неверно, что Солнце движется вокруг Земли.
- Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9.
- Луна – спутник Земли.
- На уроке химии ученики выполняли лабораторную работу, и результаты исследований записывали в тетрадь.
- Если число оканчивается на 0, то оно делится на 10.
- Чтобы погода была солнечной, достаточно, чтобы не было ни ветра, ни дождя.
- Если у меня будет свободное время и не будет дождя, тоя не буду писать сочинения, а пойду на дискотеку.
- Без Вас хочу сказать Вам много
При Вас я слушать Вас хочу. - Если человек с детства и юности своей не давал нервам властвовать над собой, то они не привыкнут раздражаться и будут ему послушны.
2. Постройте отрицания следующих высказываний.
- На улице сухо.
- Сегодня выходной день.
- Ваня не был готов сегодня к урокам.
- Неверно, что число 3 не является делителем числа 198.
- Некоторые млекопитающие не живут на суше.
- Неверно, что число 17 – простое.
3. Из каждых трех выберите пару высказываний, являющихся отрицаниями друг друга.
- “Луна – спутник Земли”, “Неверно, что Луна спутник Земли”, “Неверно, что Луна не является спутником Земли”;
- “2007 < 2008”, “2007 > 2008”, “2007 ? 2008”;
- “Прямая а перпендикулярна прямой с”; “Прямая а не параллельна прямой с”; “Прямая а не пересекается с прямой с”.
4. По данным формам сложных высказываний запишите высказывания на русском языке.
1.
2.
3.
4.
5.
5. Найдите значения логических выражений:
6. Даны два высказывания: А = “2 х 2 = 4”, В = “2 х 2 = 5”. Очевидно, что А=1, В=0. Какие из высказываний истинны?
а)
б)
в) А
г)
д)
е)
7. Даны простые высказывания: А= {15>13}, В={4=5}, C= {7<4}. Определите истинность составных высказываний:
8. При каких значениях числа Х логическое выражение не ((Х>15) или (Х<-5)) примет значение:
- ложь,
- истинна.
9. Какие из высказываний А, В должны быть истинны и какие ложны, чтобы было ложное высказывание ?
III. Итог урока.
Обобщить пройденный материал, оценить работу активных учеников.
IV. Домашнее задание.
1. Выучить определения, знать обозначения.
2. Даны высказывания:
А = {На улице светит солнце},
В = {На улице дождь},
С = {На улице пасмурная погода},
В = {На улице идет снег}.
Составьте два сложных высказывания, одно из которых в любой ситуации всегда будет ложным, а другое истинным.
3. Переведите сложное высказывание на русский язык.
4. Какое логическое выражение описывает условие:
“Точка Х не принадлежит отрезку [А; В]”?
- не (Х А) или Х < B,
- X < A и X > B,
- не (X B и X A),
- X A или X В.
Литература:
- Информатика и информационные технологии. Учебник для учащихся 10-11 классов. / Угринович Н.Д., — М. Лаборатория Базовых Знаний, 2004.
- Практикум по информатике и информационным технологиям. Учебное пособие для общеобразовательных учреждений. / Угринович Н.Д., Босова Л.Л., Михайлова Н.И. — М. Лаборатория Базовых Знаний, 2001.
- Логика в информатике. / Лыскова В.Ю., Ракитина Е.А. — М. Лаборатория Базовых Знаний, 2001.
- Информатика. Элементы Алгебры логики. Еженедельное приложение к газете “Первое сентября”. №27, 1998.
- Информатика. Логика. Еженедельное приложение к газете “Первое сентября”. №26, 1997.
xn--i1abbnckbmcl9fb.xn--p1ai
Упрощение логических выражений
Замечание 1
Логическую функцию можно записать с помощью логического выражения, а затем можно перейти к логической схеме. Упрощать логические выражения надо для того, чтобы получить как можно более простую (а значит, и более дешёвую) логическую схему. По сути, логическая функция, логическое выражение и логическая схема −это три разных языка, рассказывающие об одной сущности.
Для упрощения логических выражений используют законы алгебры логики.
Какие-то преобразования похожи на преобразования формул в классической алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), а другие преобразования основаны на свойствах, которыми операции классической алгебры не обладают (использование распределительного закона для конъюнкции, законов поглощения, склеивания, правил де Моргана и др.).
Законы алгебры логики формулируются для базовых логических операций — “НЕ” – инверсия (отрицание), “И” – конъюнкция (логическое умножение) и “ИЛИ” – дизъюнкция (логическое сложение).
Закон двойного отрицания означает, что операция “НЕ” обратима: если применить ее дважды, то в итоге логическое значение не изменится.
Закон исключенного третьего гласит, что любое логическое выражение либо истинно, либо ложно (“третьего не дано”). Поэтому если $A=1$, то $\bar{A}=0$ (и наоборот), а, значит, конъюнкция этих величин всегда равно нулю, а дизъюнкция равна единице.
Операции с константами и закон повторения легко проверяются по таблицам истинности операций “И” и “ИЛИ”.
Переместительный и сочетательный законы выглядят так же, как и в математике. Почти всегда “работает” аналогия с классической алгеброй, нужно только помнить, что в логике $1 + 1 = 1$, а не $2$.
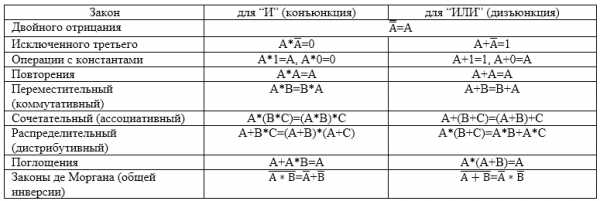
Рисунок 1.
Распределительный закон для дизъюнкции — это просто раскрытие скобок. А вот для конъюнкции выражение незнакомое, и в математике это равенство неверно. Доказательство начинаем с правой части. Раскроем скобки:
$(A+B) \cdot (A+C) = A \cdot A+A \cdot C+B \cdot A+B \cdot C$
Используем закон повторения
$A \cdot A = A$,
Далее $A \cdot A+C \cdot A = A+C \cdot A = A \cdot (1+C)=A \cdot 1 = A$
Аналогично
$A+A \cdot B = A \cdot (1+B) = A \cdot 1=A$, таким образом,
$(A+B) \cdot (A+C) = A+B \cdot C$
Равенство доказано.
Попутно был доказан закон поглощения для операции “И”.
Из распределительного закона следует полезная формула
$A+ \bar{A} \cdot B = (A+ \bar{A}) \cdot (A+B) = A+B$
Замечание 2
Правила, которые позволяют раскрывать инверсию сложных выражений, получили своё название в честь де Моргана, шотландского математика и логика. Важно следующее: “общее” отрицание не просто переходит на отдельные выражения, но и конъюнкция заменяется на дизъюнкцию (и наоборот). Доказать эти правила можно с помощью таблиц истинности.
Большинство законов и аксиом алгебры логики записаны парами. При внимательном изучении пар можно вывести принцип двойственности– если в тождестве произвести взаимные замены операций дизъюнкции и конъюнкции, а также элементы $0$ и $1$, в случае если они имеются, то получим тоже тождество. Такое свойство принято называть принципом двойственности.
Примеры упрощения логических выражений
-
$(A \cdot B) + (A \cdot \bar{B}) = A \cdot (B + B)= A \cdot 1 = A$
-
Рисунок 2.
здесь был использовано правило де Моргана для дизъюнкции и закон двойного отрицания, далее вынесли за скобку сомножитель $\bar{X}$, получили в скобках закон исключённого третьего и использовали операцию с константами.
Пример 1
Кто из учеников $A$, $B$, $C$ и $D$ играет, а кто не играет в шахматы, если известно следующее:
а) если $A$ или $B$ играет, то $C$ не играет;
б) если $B$ не играет, то играют $C$ и $D$;
в) $C$ играет
Решение. Определим следующие простые высказывания:
$A$ — «ученик $A$ играет в шахматы»;
$B$ — «ученик $B$ играет в шахматы»;
$C$ — «ученик $C$ играет в шахматы»;
$D$ — «ученик $D$ играет в шахматы».
С помощью простых высказываний запишем высказывания из условия:
а) ($A + B) → C$;
б) $B → C \cdot D$;
в) $C$.
Составим конъюнкцию записанных сложных высказываний:
$((A + B) → C) \cdot (B → C \cdot D) \cdot C.$
Упростим эту формулу:
Рисунок 3.
Отсюда следует, что $A = 0$, $B = 1$, $C = 1$, $D = 1$.
Ответ: в шахматы играют ученики $B$, $C$ и $D$, а ученик $A$ не играет.
При упрощении логических выражений можно выполнять такую последовательность действий:
- Заменить все “небазовые” операции (эквивалентность, импликацию, исключающее ИЛИ и др.) на их выражения через базовые операции инверсию, конъюнкцию и дизъюнкцию.
- Раскрыть инверсии сложных выражений по правилам де Моргана таким образом, чтобы операции отрицания остались только у отдельных переменных.
- Затем упростить выражение, используя раскрытие скобок, вынесение общих множителей за скобки и другие законы алгебры логики.
Пример 2
Здесь последовательно использованы правило де Моргана, распределительный закон, закон исключенного третьего, переместительный закон, закон повторения, вновь переместительный закон и закон поглощения.
Рисунок 4.
Также можно использовать упрощение логических выражений для нахождения решений логического уравнения.
Пример 3
Требуется найти все решения уравнения
Рисунок 5.
Упрощаем выражение, заменяя импликацию по формуле $А → В = \bar{А} + В$, и получаем
Рисунок 6.
Используем правило де Моргана
$B + C + \bar{A} + \bar{A} \cdot \bar{C} + D = 0$
и закон поглощения
$B + C + \bar{A} + D = 0$
Для того чтобы логическая сумма была равна нулю, каждое слагаемое должно быть равно нулю, поэтому
$A = 1$, $B = 0$, $C = 0$, $D = 0.$
Пример 4
Выполнить преобразование логической функции
Рисунок 7.
Применим последовательно следующие законы алгебры логики: правило де Моргана для конъюнкции, правило де Моргана для дизъюнкции, закон двойного отрицания, закон исключённого третьего, вынос общего множителя за скобки и операцию с константой
Рисунок 8.
spravochnick.ru
Логические выражения
Понятие логического выражения или логической формулы вводится индуктивно.
Логической формулой является
1) любая логическая переменная (переменная, принимающая одно из двух значений: истина или ложь, обозначаемых далее 1 и 0 соответственно), а также каждая из двух логических констант (постоянных) — 0 и 1, является формулой;
2) если A и B — формулы, то, А*В и (А*В) — тоже формулы, где знак “*” означает любую из логических бинарных операций (см. “Логические операции. Кванторы”).
Формулой является, например, следующее выражение (x & y) z. Каждой формуле при заданных значениях входящих в нее переменных можно приписать одно из двух значений — 0 или 1.
Формулы А и В, зависящие от одного и того же списка переменных x1, x2, x3, …, xn, называют равносильными, или эквивалентными, если на любом наборе значений переменных x1, x2, x3, …, xn они принимают одинаковые значения. Для обозначения равносильности формул используется знак равенства, например, А = В.
Любую формулу можно преобразовать к равносильной ей, в которой используются только операции &, и отрицание.
Для преобразования формул в равносильные важную роль играют следующие равенства, отражающие свойства логических операций, справедливые для любых переменных x, y, z. Эти свойства называют законами алгебры логики:
Любой из этих законов может быть легко доказан с помощью таблиц истинности, или путем логических рассуждений, или с помощью тождественных преобразований, использующих доказанные ранее законы.
Приоритет выполнения логических операций
Для логических операций в одном логическом выражении установлен следующий порядок вычислений:
· отрицание — первый, наивысший приоритет;
· конъюнкция — второй приоритет;
· дизъюнкция, разделительная дизъюнкция — третий приоритет;
· импликация, эквивалентность — низший приоритет.
Изменить порядок выполнения операций можно с помощью расстановки скобок.
В алгебре логики дизъюнкция (логическое сложение) играет роль, аналогичную сложению в алгебре действительных чисел, конъюнкция (логическое умножение) — умножению, а отрицание (инверсия значения логической формулы) — унарному минусу (инверсия знака обычной формулы). Операция эквивалентность аналогична операции отношения “=”, а операция импликация — операции отношения “”.
Канонические формы
Очевидно, что если имеется логическая формула, то, используя тождественные преобразования, можно изменить ее, построив сколь угодно сложную равносильную формулу. Одна из основных задач алгебры логики — нахождение канонических форм (т.е. формул, построенных по определенному правилу, канону), а также формул, имеющих наиболее простой вид.
Если логическая формула выражена через дизъюнкцию, конъюнкцию и отрицание, то такая форма представления называется нормальной. Среди нормальных форм выделяют такие, в которых функции записываются единственным образом. Их называют совершенными. Особую роль в алгебре логики играет класс совершенных дизъюнктивных нормальных форм. В их основе лежат понятия элементарной дизъюнкции и элементарной конъюнкции.
Формулу называют элементарной конъюнкцией, если она является конъюнкцией одной или нескольких переменных, взятых с отрицанием или без отрицания. Например, формулы x2, x2, x1 & x3, x1 & x3 & x1 & x3 являются элементарными конъюнкциями.
Формула называется дизъюнктивной нормальной формой (ДНФ), если она является дизъюнкцией элементарных конъюнкций. ДНФ записываются в виде A1 A2 … An, где каждое Ai — элементарная конъюнкция. Например, x2x1 & x3, x2 & x2x1 & x2— дизъюнктивные нормальные формы.
Формула А от k переменных называется совершенной дизъюнктивной нормальной формой (СДНФ), если
1) А является ДНФ, в которой каждая элементарная конъюнкция есть конъюнкция k переменных x1, x2, …, xk, причем на i-м месте этой конъюнкции стоит либо переменная xi, либо ее отрицание;
2) все элементарные конъюнкции в такой ДНФ попарно различны.
Совершенная дизъюнктивная нормальная форма представляет собой формулу, построенную по строго определенным правилам с точностью до порядка следования элементарных конъюнкций (дизъюнктивных членов) в ней. Она является примером однозначного представления булевой функции в виде формульной (алгебраической) записи.
Логической функцией называется функция, аргументы которой и сама функция принимают значения 0 или 1. Логические функции могут быть заданы таблично (таблицей истинности) или в виде соответствующих формул. Тем самым каждая формула может рассматриваться как способ задания логической функции. При этом одна и та же функция может задаваться различными формулами.
Возникает вопрос: всякую ли логическую функцию можно представить в одном из канонических совершенных видов? Да, любую булеву функцию, не равную тождественно лжи, можно представить в виде СДНФ. Сформулируем это утверждение в виде следующей теоремы.
Теорема. Пусть — f (x1, x2, …, xn)булева функция от n переменных, не равная тождественно нулю. Тогда существует совершенная дизъюнктивная нормальная форма, выражающая функцию f, которую можно построить по следующему алгоритму:
1. В таблице истинности отмечаем наборы переменных, на которых значение функции f равно единице.
2. Записываем для каждого отмеченного набора конъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 1, то в конъюнкцию включаем саму переменную, в противном случае — ее отрицание.
3. Все полученные конъюнкции связываем операциями дизъюнкции.
Доказательство. Каждая элементарная конъюнкция, вошедшая в СДНФ, принимает значение 1 только на единственном наборе. Отсюда следует, что если функция на каком-то наборе равна 1, то и вся СДНФ равна 1 в силу того, что по построению соответствующая элементарная конъюнкция, вошедшая в СДНФ, равна 1. А если функция равна 0, то и СДНФ равна 0, т.к. на этом наборе равны 0 все вошедшие в СДНФ элементарные конъюнкции. Таким образом, СДНФ равносильна исходной функции.
Следствие. Любую логическую функцию можно представить формулой, в которой используются только логические операции дизъюнкции, конъюнкции и отрицания.
Доказательство. Для всех функций, отличных от 0, это можно сделать с помощью СДНФ, а ноль можно выразить, например, как x &`x.
Методические рекомендации
Умения строить логические выражения (логические формулы), вычислять их значение, выполнять над ними тождественные преобразования требуются при изучении разных тем информатики: при построении алгоритмов, в программировании, при решении логических задач, конструировании запроса при работе с БД, при работе с электронными таблицами и т.п. Для формирования этих умений важно обращать внимание на следующие моменты.
1) Любое логическое выражение (логическая формула) реализует логическую функцию на конечном наборе различных значений переменных, в него входящих. Часто (при построении запросов или условия ветвления) по словесному описанию логического выражения (логического условия) требуется построить его аналитическое выражение. Словесное выражение является высказыванием. Для правильного построения логического выражения вначале в сложном высказывании необходимо выделить элементарные высказывания, а затем, используя семантику языковых связок, построить формулу. Такое умение можно формировать уже в базовом курсе информатики.
2) Во многих языках программирования используется только несколько логических операций, как правило, операция логического сложения, логического умножения и отрицания, а также операция разделительной дизъюнкции. Поэтому, если полученная формула содержит не только операции &, и отрицание, то учащиеся должны уметь выполнять тождественные преобразования для построения ДНФ (дизъюнктивной нормальной формы). Умение выполнять тождественные преобразования основано на знании основных законов алгебры логики, но формируется это умение в результате выполнения большого числа заданий. На формирование этого умения времени практически не отводится, но практика показывает, что достаточно научить учащихся выражать операции импликации и эквивалентности через &, и отрицание. Большинство законов алгебры логики ученикам интуитивно понятны и не требуют запоминания. Исключение составляют законы поглощения и де Моргана. Последние особенно часто применяются в программировании. Знакомство с законами алгебры логики начинается в базовом курсе информатики и продолжается в старшей школе.
3) Для построения СДНФ учащиеся должны уметь без ошибок строить таблицу истинности для конкретной логической формулы. А для этого надо требовать, чтобы учащиеся строго соблюдали порядок перечисления набора значений переменных: если каждый набор значений переменных рассматривать как двоичное число, то все числа должны быть записаны в порядке возрастания. Например, для формулы от трех переменных перечисление набора значений в таблице истинности должно быть выполнено в следующем порядке:
4) Перед изложением формулировки теоремы о СДНФ надо пояснить, для чего используются нормальные формы (поиск аналитического вида булевой функции, заданной таблицей истинности; минимизация представления булевой функции с использованием только трех логических операций &, и отрицания: такая задача возникает при конструировании микросхем, в частности, для производства компьютеров, и т.д.). Учащимся на примерах надо показать, что проблема представления формул в виде СДНФ не надуманна, ее решение имеет важное практическое значение в информатике. Данная тема подлежит рассмотрению в старших профильных классах.
5) Если вы задаете своим ученикам задания на построение отрицания к сложному высказыванию (а проще всего это делать через построение отрицания к соответствующему логическому выражению), то им следует пояснить, почему в этом случае квантор общности заменяется на квантор существования и наоборот (см. “Логические операции. Кванторы”).
Очевидно, что высказывание, содержащее квантор общности (например, “Все мужчины старше 70 лет имеют длинную седую бороду”), можно заменить на следующее: “И Иванов А.П., и Кравцов И.Г., и Петухов С.П., и … старше 70 лет и имеют длинную седую бороду”. Это высказывание можно записать следующей формулой: И & К & П & …, где буквой И обозначено высказывание “Иванов А.П. (который старше 70 лет) носит длинную седую бороду”, буквой К обозначено высказывание “Кравцов И.Г. носит длинную седую бороду” и т.д. При построении отрицания к первоначальному сложному высказыванию, содержащему квантор общности, воспользуемся законом де Моргана. Тогда получим:
Этой формуле соответствует высказывание “Или Иванов А.П. не имеет длинной седой бороды, или Кравцов И.Г. не имеет длинной седой бороды, или Петухов С.П. … или … не имеет длинной седой бороды”, другими словами, “Существует мужчина старше 70 лет, который не имеет длинной седой бороды”.
6 От латинских слов idem — тот же самый и potens — сильный; дословно — равносильный.
xn—-7sbbfb7a7aej.xn--p1ai
Основы логики Логические выражения и таблицы истинности

Основы логики . Логические выражения и таблицы истинности

Историческая справка
Основы формальной логики заложил Аристотель ( 384 -322 гг. до н.э.).
Ввел основные формы абстрактного мышления.

Логика – это наука о формах и способах мышления.
Ло́гика — «наука о правильном мышлении», «искусство рассуждения» ( Википедия)
Логика как наука изучает способы достижения истины в процессе познания опосредованным путём, не из чувственного опыта, а из знаний, полученных ранее, поэтому её также можно определить как науку о способах получения выводного знания.

Логика и информатика
- В основе логических схем и устройств ПК лежит специальный математический аппарат, использующий законы логики.
- Математическая логика изучает вопросы применения математических методов для решения логических задач и построения логических схем.
3. Знание логики необходимо при разработке алгоритмов и программ, так как в большинстве языков программирования есть логические операции.

Мышление всегда осуществляется в каких-то формах
Основными формами мышления являются:
- Основными формами мышления являются:
- ПОНЯТИЕ ВЫСКАЗЫВАНИЕ УМОЗАКЛЮЧЕНИЕ
- ПОНЯТИЕ
- ВЫСКАЗЫВАНИЕ
- УМОЗАКЛЮЧЕНИЕ

ПОНЯТИЕ — форма мышления, фиксирующая основные, существенные признаки объекта
Понятие имеет две стороны: содержание и объем .
Содержание понятия составляет совокупность существенных признаков объекта. «Персональный компьютер — это универсальное электронное устройство для автоматической обработки информации, предназначенное для одного пользователя».
Объем понятия определяется совокупностью предметов, на которую оно распространяется. Объем понятия «персональный компьютер» выражает всю совокупность (сотни миллионов) существующих в настоящее время в мире персональных компьютеров.

УМОЗАКЛЮЧЕНИЕ – это форма мышления, посредством которой из одного или нескольких истинных суждений, называемых посылками, мы по определенным правилам вывода получаем новое суждение (заключение).
Например ,
- Все углы треугольника равны → Этот треугольник равносторонний.
- Все углы треугольника равны → Этот треугольник равносторонний.

- Высказывание – повествовательное предложение, в котором что-либо утверждается или отрицается о свойствах реальных объектах или отношениях между ними.
- Например , 5*5=25;
Принтер- устройство вывода информации
Сегодня хорошая погода.
Составные высказывания – образуются из простых с помощью специальных слов (не, и, или).
- Например : сегодня хорошая погода и светит солнце.
Процессор является устройстовм обработки информации и принтер является устройством печати.

Алгебра высказываний
- Простым высказываниям ставятся в соответствие логические переменные .
А = «5 * 5 = 25» истинно А = 1
В = «2 * 2 = 5» ложно В = 0
- Логическая переменная может принимать лишь два значения: «истина» (1) или «ложь» (0).

Логическое отрицание (инверсия)
- Присоединение частицы «не» к высказыванию.
- Делает истинное высказывание ложным, а ложное – истинным.
- Обозначение: не А, Ā , ¬ А.
- Таблица истинности
А
0
Ā
1
1
0

Логическое умножение (конъюнкция)
- Объединение двух (или нескольких) высказываний в одно с помощью союза «и».
- Обозначение: А и В, А & В.
Таблица истинности
А
0
В
0
0
А & В
0
1
1
1
0
0
0
1
1

Логическое сложение (дизъюнкция)
- Объединение двух (или нескольких) высказываний в одно с помощью союза «или».
- Обозначение: А или В, А v В
Таблица истинности
А
0
В
0
0
А v В
0
1
1
1
1
0
1
1
1

Импликация (логическое следование)
Соответствующие выражения языка:
Если A, то B
A достаточно для B
B следует из A
Обозначение: А В
Таблица истинности
А
0
В
А В
0
0
1
1
1
1
1
0
0
1
1
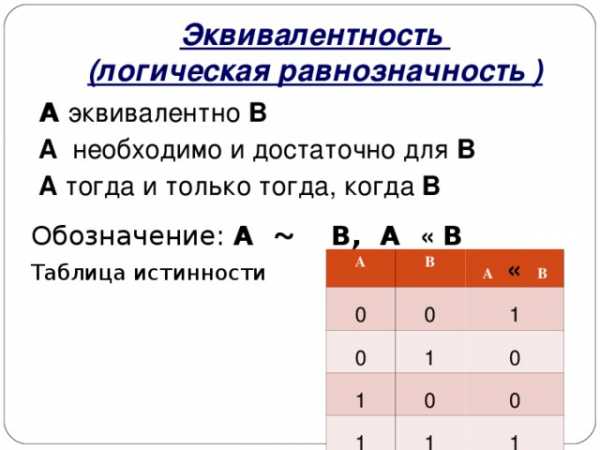
Эквивалентность (логическая равнозначность )
A эквивалентно B
A необходимо и достаточно для B
A тогда и только тогда, когда B
Обозначение: А В, А В
Таблица истинности
А
0
В
0
0
А В
1
1
1
1
0
0
0
1
1

Таблицы истинности
- Для каждого составного высказывания (логического выражения) можно построить таблицу истинности , которая определяет истинность или ложность логического выражения при всех возможных комбинациях исходных значений простых высказываний (логических переменных).
- При построении таблиц истинности целесообразно руководствоваться определенной последовательностью действий:
1) записать выражение и определить порядок выполнения операций
2) определить количество строк в таблице истинности.(определяется по формуле Q =2 n , где n — количество входных переменных)
3) определить количество столбцов в таблице истинности (= количество логических переменных + количество логических операций )
4) построить таблицу истинности, обозначить столбцы (имена переменных и обозначения логических операций в порядке их выполнения) и внести в таблицу возможные наборы значений исходных логических переменных.
5) заполнить таблицу истинности, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности

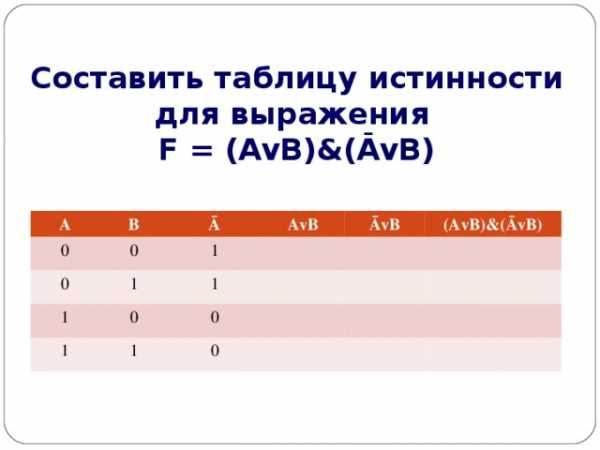
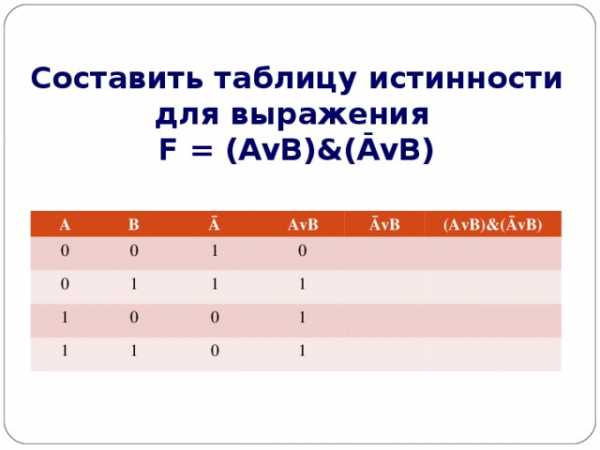
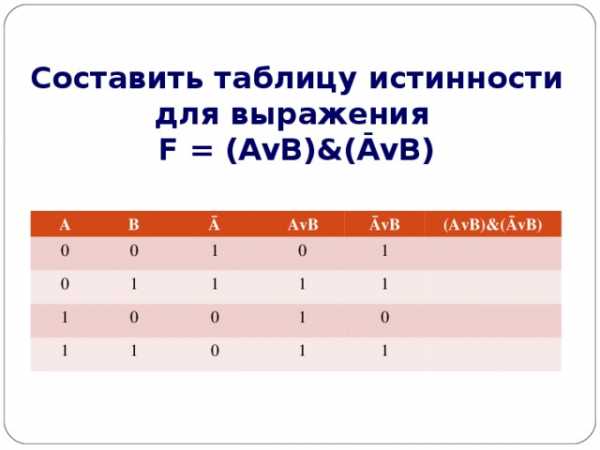
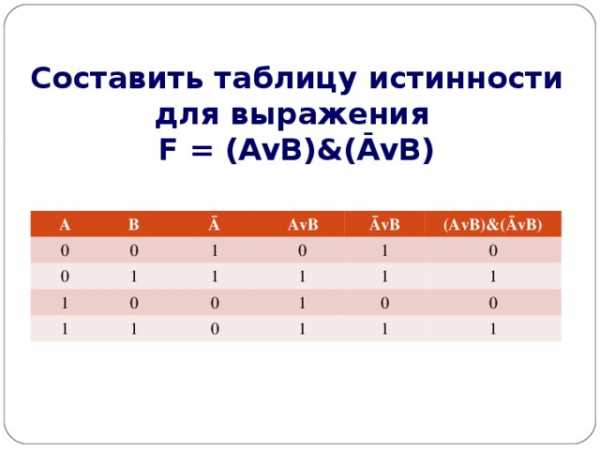
Составить таблицу истинности для выражения F = (AvB)&(ĀvB)

F = (AvB)&(ĀvB)
A
0
B
0
0
Ā
AvB
1
1
ĀvB
0
1
(AvB)&(ĀvB)
1
- Количество входных переменных в заданном выражении равно двум (A,B) . строк Q=2 2 =4
2. Количество столбцов равно 6 (2 переменные + 4 операции).
Составить таблицу истинности для выражения F = (AvB)&(ĀvB)
A
0
B
0
0
Ā
AvB
1
1
1
ĀvB
1
1
0
(AvB)&(ĀvB)
0
1
0
Составить таблицу истинности для выражения F = (AvB)&(ĀvB)
A
0
B
0
0
Ā
1
1
AvB
1
0
ĀvB
1
1
0
1
(AvB)&(ĀvB)
0
1
1
0
1
Составить таблицу истинности для выражения F = (AvB)&(ĀvB)
A
0
B
0
Ā
0
AvB
1
1
1
1
1
0
ĀvB
0
1
1
(AvB)&(ĀvB)
0
1
1
1
0
0
1
1
Составить таблицу истинности для выражения F = (AvB)&(ĀvB)
A
0
B
0
Ā
0
AvB
1
1
1
ĀvB
1
0
1
0
1
1
0
(AvB)&(ĀvB)
1
1
0
1
0
1
0
1
1
0
1

Составить таблицу истинности для логической функции:
F =Ā& (BvC)
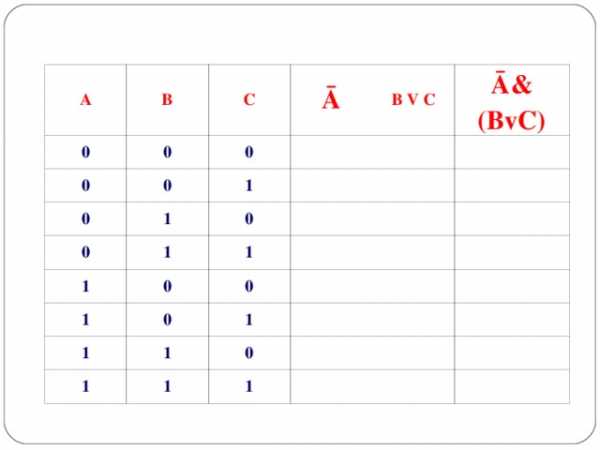
A
B
0
C
0
0
0
Ā
0
0
1
B V C
1
0
0
Ā& (BvC)
1
1
1
0
1
0
0
1
1
1
1
1
0
1
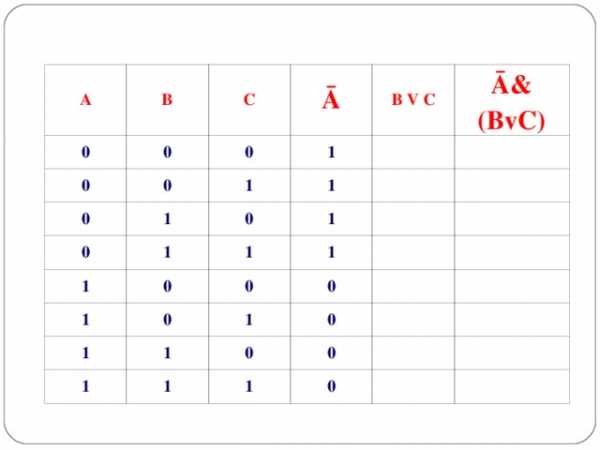
A
B
0
C
0
0
0
Ā
0
0
1
B V C
1
1
0
1
Ā& (BvC)
0
1
1
1
0
1
1
0
1
0
1
1
1
0
1
0
1
0
0
1
0
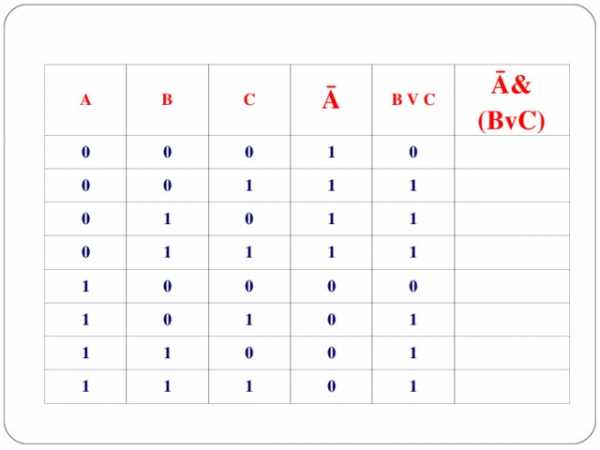
A
B
0
0
C
0
0
Ā
0
0
1
1
B V C
1
0
0
0
Ā& (BvC)
1
1
1
1
1
0
1
1
1
1
0
1
0
1
1
1
0
1
0
0
0
1
1
0
1
0
1
1
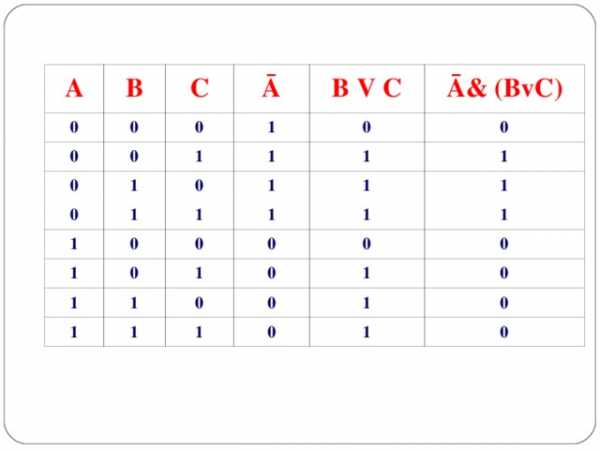
A
B
0
0
C
0
0
Ā
0
0
1
1
1
B V C
0
0
Ā& (BvC)
1
0
1
1
1
1
0
1
0
1
1
1
1
0
0
1
1
1
1
0
1
1
0
1
0
0
1
0
1
1
0
0
0
1
0
1
0

Составить таблицы истинности
1. F = (Ā&B)v(A&B)
2. F = (AvB)v((Ā&C)vB)
3. F= (A&C ) (( AvB) C)
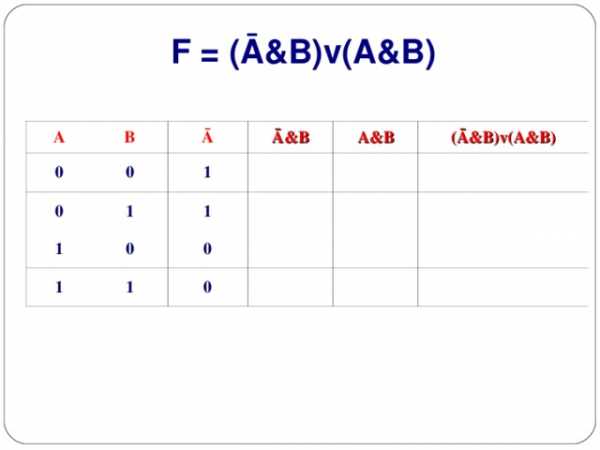
F = (Ā&B)v(A&B)
A
B
0
0
0
Ā
1
1
1
Ā&B
0
1
A&B
1
(Ā&B)v(A&B)
0
1
0
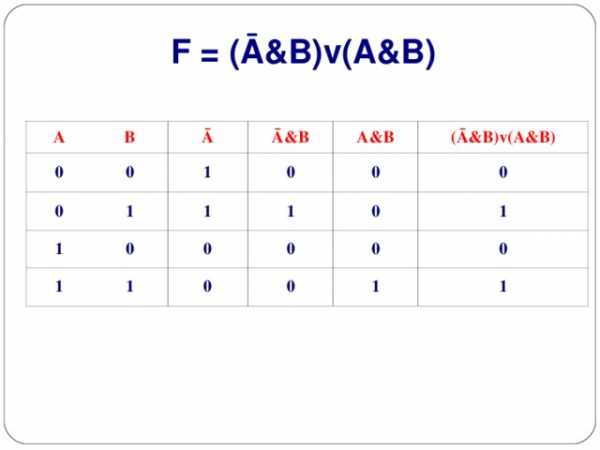
F = (Ā&B)v(A&B)
A
0
B
0
0
Ā
1
1
1
Ā&B
0
0
1
1
A&B
(Ā&B)v(A&B)
0
1
0
1
0
0
0
0
0
0
1
0
1
1
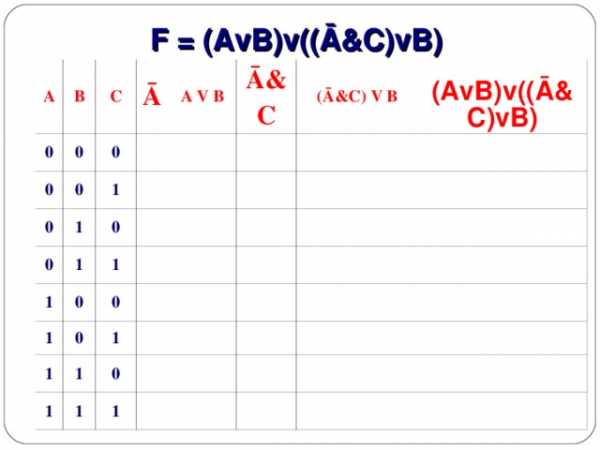
F = (AvB)v((Ā&C)vB)
A
B
0
C
0
0
Ā
0
0
0
A V B
1
0
1
Ā&C
0
1
1
(Ā&C) V B
1
0
1
(AvB)v((Ā&C)vB)
1
0
0
1
1
1
0
1
1
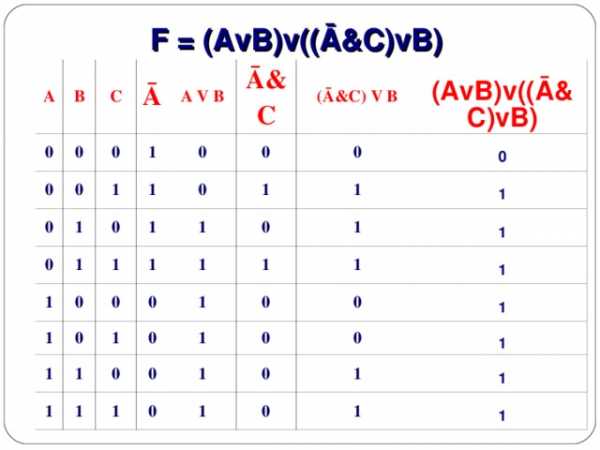
F = (AvB)v((Ā&C)vB)
A
B
0
C
0
0
0
Ā
0
0
1
A V B
0
1
1
Ā&C
0
1
0
1
1
(Ā&C) V B
0
1
0
1
1
0
(AvB)v((Ā&C)vB)
0
0
1
1
0
1
1
0
1
1
1
1
0
1
0
1
0
0
1
1
1
1
0
1
1
0
1
1
0
1
1
0
0
1
1
0
0
1
1
0
1
1
1

Человек, рассуждающий логично, приятно выделяется на фоне реального мира
kopilkaurokov.ru
