Задачи ГИА по математике из открытого банка заданий с готовыми решениями
Задачи
для подготовки к ГИА по математике из открытого банка заданий
(раздел «Геометрия») с готовыми решениями
Примечание: готовые решения смотри в прикреплённом файле
Задача 1
АВ и ВС – отрезки касательных, проведённых из точки В к окружности с центром в точке О. ОА=16см, а радиусы, проведённые к точкам касания, образуют угол, равный 120º. Чему равен отрезок ОВ?
Ответ: ОВ=32 см.
Задача 2
Прямая АВ касается окружности с центром О радиуса 4 см в точке А так , что ОВ=4√2 см. Чему равен отрезок АВ?
Решение :
Радиус ОА, проведённый в точку касания, перпендикулярен касательной АВ, значит треугольник АОВ – прямоугольный. По теореме Пифагора найдём АВ²=ОВ²- ОА²=(4√2) ² — 4²=32-16=16=4², АВ=4 см.
Ответ: АВ= 4 см.
Задача 3
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60º, а расстояние от точки А до точки О равно 6см.
Радиусы ОВ и ОС, проведенные в точки касания
В В и С, перпендикулярны касательным АВ и АС,
Тогда треугольники ОАС и ОАВ- равные прямо-
угольные. ∟А=60º, тогда ∟ВАО=∟САО=60:2=30º,
напротив них лежат катеты ОС и ОВ, меньшие
гипотенузы ОА в 2 раза. ОА=6см, тогда R=ОВ=ОС=6:2=3 Ответ: 3 см
Задача 4 (задача с лишними данными)Боковая сторона трапеции равна 3см, а один из прилегающих к ней углов равен 30º. Найдите площадь трапеции, если её основания равны 2см и 6см
Площадь трапеции вычисляется по формуле:
S=½ (а+b)▪h , где h- высота, а и b — основания трапеции.
Проведём высоту АК. ∆АDК – прямоугольный. Напротив угла 30º лежит катет АК=½АD, тогда АК=3:2=1,5 см – это высота.
S=½(AB+CD) ▪h=(2+6):2▪1,5=6 см²
Ответ: 6 см²
Задача 5
Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60º.
Найдите длину хорды АВ, если радиус окружности равен 8 см.
Решение:
Т.к. угол ОАВ= 60º, то треугольник ОАВ –
равносторонний ( АО=ОВ как радиусы, тогда
угол А равен углу В=(180-60):2= 60º), значит
АВ=АО=ОВ=8см.
Ответ: 8 см.
Задача 6
Высота BH параллелограмма АВСD делит его сторону АD на отрезки АH=1см и HD=63 см. Диагональ параллелограмма ВD равна 65 см. Найдите площадь параллелограмм
Решение:
S пар-ма=AD▪BH
AD=63+1=64(см)
ВH – высота, значит треугольник ВDH-
прямоугольный . Найдем ВH по теореме
Пифагора: ВH²=BD²- DH²=65²-63²=4225-3969=256=16², ВH=16см
SABCD=64▪16=1024 см²
Ответ: 1024 см²
Задача 7
На какой угол ( в градусах) поворачивается минутная стрелка, пока часовая проходит 11º?
Решение:
1ч=60 мин
Минутная стрелка проходит 60 минут ( 12 делений циферблата), а часовая за это время 1 час ( одно деление), значит минутная стрелка идёт в 12 раз быстрее.
11º прошла по условию задачи часовая , значит минутная 11▪12=132º
Ответ: 132º
Задача 8
В прямоугольном треугольнике гипотенуза равна 70 см, а один из его острых углов равен 45º. Найдите площадь треугольника.
Решение:
Один из углов прямоугольного треугольника равен 45º, значит второй острый угол: 90-45=45º и треугольник равнобедренный, его катеты равны.
Пусть по х см катеты этого треугольника, тогда по теореме Пифагора
х²+х²=70²
2х²=4900
х²=2450
Площадь прямоугольного треугольника равна половине произведения катетов: S=½x²=2450:2=1225 см²
Ответ: 1225 см²
Задача 9
В треугольнике АВС ВМ – медиана, ВH – высота. Известно, что АС=97 см, ВС=ВМ. Найдите АH.
ВМ – медиана, значит АМ=МС=97:2=43,5см АС
ВС=ВМ, значит треугольник ВМС – равнобедренный, в нём ВН – высота и медиана, т.к проведена к основанию. МН=НС= 43,5:2=21,75 см.
АН=АМ+МС=43,5+21,75=65,25 см.
Ответ: 65,25 см.
uchkopilka.ru
РМО учителей математики — Итоговая аттестация (ГИА, ЕГЭ)
Документация по проведению ОГЭ -2016
Об экзамене по математики ЕГЭ ( базовый и профильный уровени) — 2015г
ЕГЭ-2015. МАТЕМАТИКА. Базовый уровень. под ред. И. В. Ященко. 30 вариантов
Учебно-методические материалы для подготовки зкспертов предметных комиссий по проверке выполнения заданий с развернутым ответом — 2014 г. (Составители: Л.В. Кузнецова, Л.О. Рослова)
О методических материалах ГИА-9 (новая форма) по проверке заданий с развернутым ответом
Перевод баллов ГИА 2014 в отметки от ФИПИ
Руководство пользователя по работе с Открытым банком заданий ЕГЭ и ГИА -9 ОТ ФИПИ /open_bank_readme.pdf
Открытый банк заданий ЕГЭ и ГИА-2014 по математике от ФИПИ
Демоверсия ЕГЭ 2014 по математике, ФИПИ
http://egeigia.ru/all-ege/demoversii-ege/matematika/1314-demo-ege-2014-matematika
Учебно-методические материалы для председателей и членов региональных предметных комиссий по проверке выполнения заданий с развернутым ответом экзаменационных работ ЕГЭ-2013года «Математика»
Контрольные измерительные материалы ЕГЭ — 2014 года http://www.fipi.ru/view/sections/228/docs/660.html
Контрольные измерительные материалы ГИА — 2014 года http://www.fipi.ru/view/sections/170/docs/
Размещены образцы бланков ответов для ГИА-9 в новой форме в 2013 году.http://www.rcoi61.org.ru/
ЕГЭ-2013. Математика. Диагностическая работа 2 (вар.1-16) 18.12.2012г. (с ответами)/egeh-2013-matematika-diagnosticheskaja_rabota_2-va.pdf
Подготовка к ЕГЭ по математике 2013г. Д.Э. Шноль- зав кафедрой математики школы «Интеллектуал», методист МИОО/podgotovka_k_egeh_po_matematike_2013g..ppt
ГИА-2013, 9 класс (тесты онлайн) http://uztest.ru/exam?idexam=28
Решу ЕГЭ: Обучающая система Д.Д. Гущина (тесты онлайн) http://reshuege.ru
ГИА :3000 задач с ответами по математике. под редакцией А.Л. Семенова, И.В.Ященко. Издательство»Экзамен», издательство МЦНМО,2013(все задания первой части):
Демонстрационный вариант МАТЕМАТИКА ГИА-9 2013год (проект ФИПИ)
/matGIA.zipПланируемые изменения в КИМ ГИА-9 2013год (проект) /changeGIA_2.pdf
Перевод баллов в отметки ГИА-9 2013 год /shkalaGIA.pdf
Итоговые контрольные работы по математике.
Авторы: Муравин Г.К. и Муравина О.В.
(контрольные работы включают задания трех уровней. В заданиях первого уровня ученикам следует выбрать букву правильного ответа. В заданиях второго и третьего уровня нужно представить решения. Они составлены так, что их можно предложить в классах, занимающихся по любому учебнику).
Контрольная работа за первый класс.
Контрольная работа за второй класс.
Контрольная работа за третий класс.
Контрольная работа за четвертый класс.
Контрольная работа за пятый класс.
Контрольная работа за шестой класс.
Контрольная работа за седьмой класс.
Контрольная работа за восьмой класс.
Контрольная работа за девятый класс.
Контрольная работа за десятый класс.
Контрольная работа за одиннадцатый класс.
Открытый банк задач ЕГЭ по математике 2012
Более 80 000 реальных задач ЕГЭ 2012 года http://live.mephist.ru/show/mathege2010
Открытый банк задач ГИА по математике 2012 http://www.ctege.info/content/view/1965/72
Прототипы заданий первой части ГИА И ЕГЭ по математике 2012г.http://4ege.ru
Бланки ГИА-2012 /matematika.tif
Порталы и сайты о ЕГЭ /portaly_i_sajty_o_egeh.doc
vesmahtematik.ucoz.ru
ГИА — 2015 Открытый банк заданий по математике
ГИА — 2015 Открытый банк заданий по математике. Модуль «Геометрия»
Вашему вниманию представлены тридцать шесть прототипов задач по модулю «Геометрия» открытого банка заданий по математике. ОГЭ – 2015. Прямоугольный треугольник. Равносторонний треугольник. Произвольный треугольник. Прямоугольник. Ромб. Параллелограмм. Трапеция. Круговой сектор.
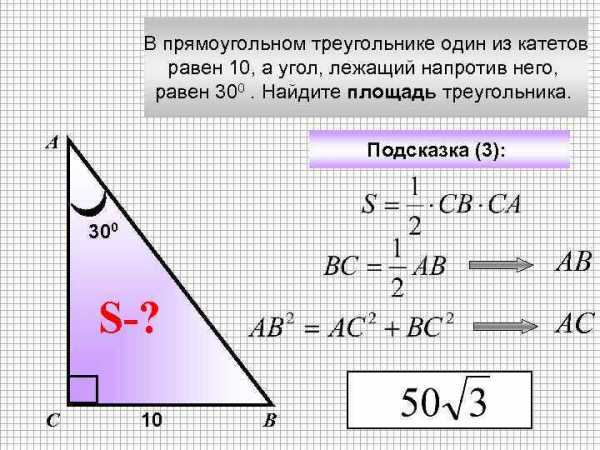В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 300. Найдите площадь треугольника. А Подсказка (3): 300 АВ S-? С 10 АС В
В прямоугольном треугольнике один из катетов равен 10, а острый угол, прилежащий к нему, равен 300. Найдите площадь треугольника. А Подсказка (3): 300 10 С АВ S-? ВС В
В прямоугольном треугольнике гипотенуза равна 10, а один из острых углов равен 300. Найдите площадь треугольника. А Подсказка (3): 300 10 S-? С В
В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 450. Найдите площадь треугольника. А Подсказка (2): 450 S-? С 10 В
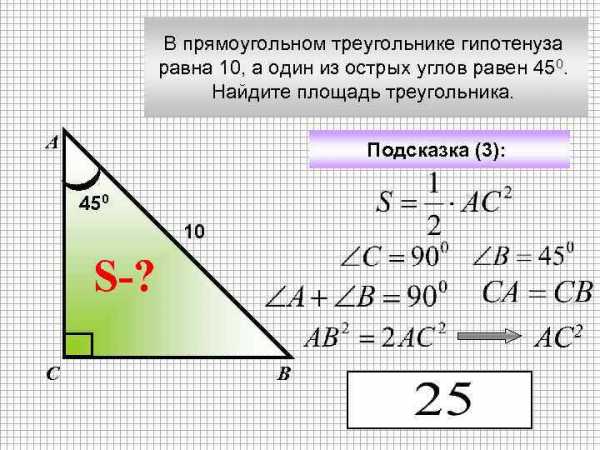В прямоугольном треугольнике гипотенуза равна 10, а один из острых углов равен 450. Найдите площадь треугольника. А Подсказка (3): 450 10 S-? АС 2 С В
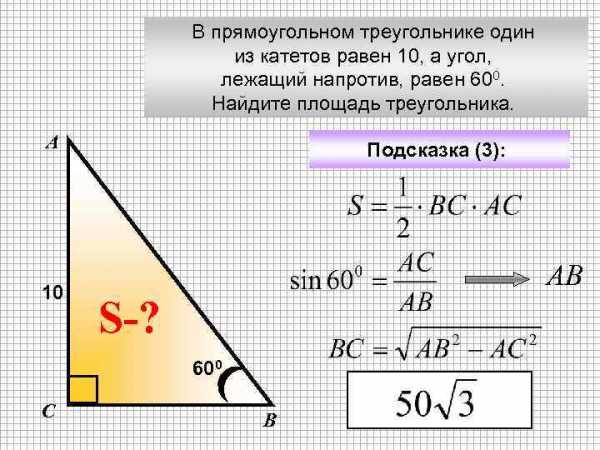В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив, равен 600. Найдите площадь треугольника. А 10 Подсказка (3): АВ S-? 600 С В
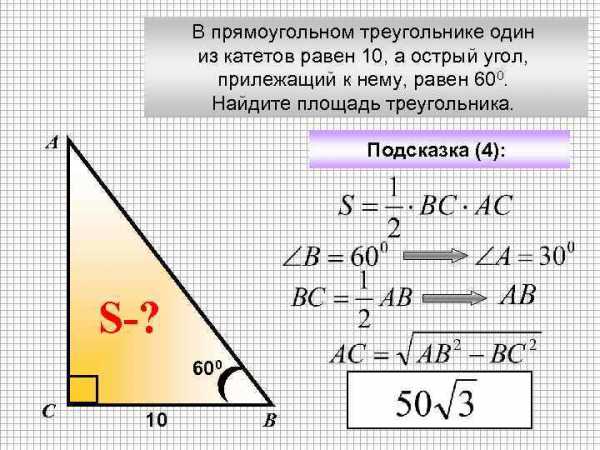В прямоугольном треугольнике один из катетов равен 10, а острый угол, прилежащий к нему, равен 600. Найдите площадь треугольника. А Подсказка (4): АВ S-? 600 С 10 В
В прямоугольном треугольнике гипотенуза равна 10, а один из острых углов равен 600. Найдите площадь треугольника. А Подсказка (3): АС 10 S-? ВС 600 С В
Сторона равностороннего треугольника равна 10. Найдите его площадь. А Подсказка (4): 10 S-? В Н С
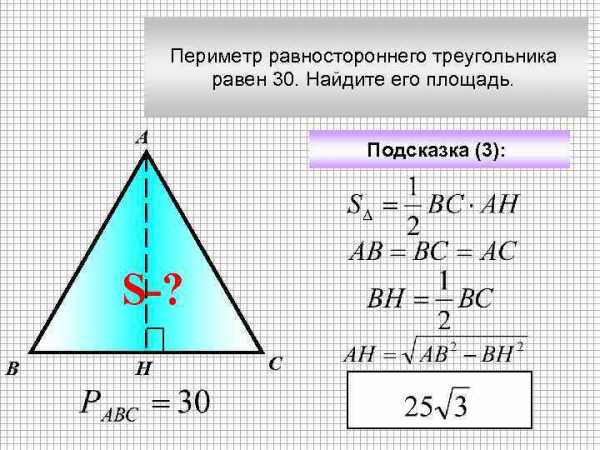Периметр равностороннего треугольника равен 30. Найдите его площадь. А Подсказка (3): S-? В Н С
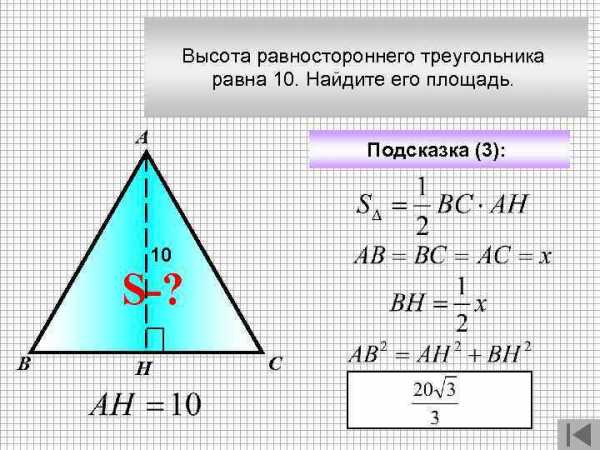Высота равностороннего треугольника равна 10. Найдите его площадь. А Подсказка (3): 10 S-? В Н С
В равнобедренном треугольнике боковая сторона равна 10, а угол, лежащий напротив основания равен 1200. Найдите площадь треугольника. Подсказка (4): А 1200 10 S-? В Н С
Периметр равнобедренного треугольника равен 16, а боковая сторона — 5. Найдите площадь треугольника. Подсказка (4): А ВС 5 S-? В Н С
Периметр равнобедренного треугольника равен 16, а основание — 6. Найдите площадь треугольника. Подсказка (4): А АВ S-? В Н С
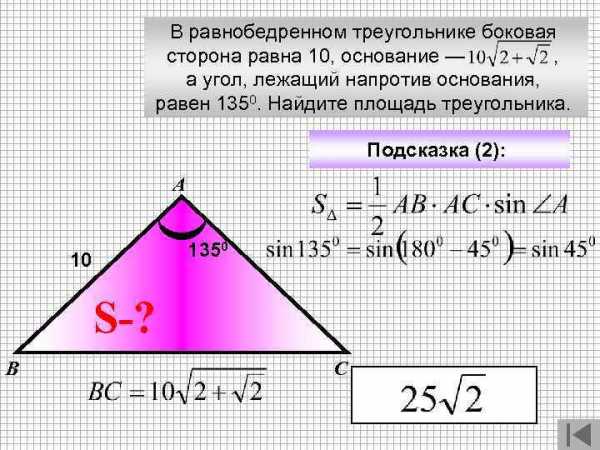В равнобедренном треугольнике боковая сторона равна 10, основание — , а угол, лежащий напротив основания, равен 1350. Найдите площадь треугольника. Подсказка (2): А 1350 10 S-? В С
Задание 16 (№ 169854) В треугольнике одна из сторон равна 10, другая равна , а угол между ними равен 600. Найдите площадь треугольника. В С S-? ? Подсказка: 10 600 А 75
В треугольнике одна из сторон равна 10, другая равна 12, а косинус угла между ними равен . Найдите площадь треугольника. В С S-? 12 ? Подсказка (2): 10 А 20
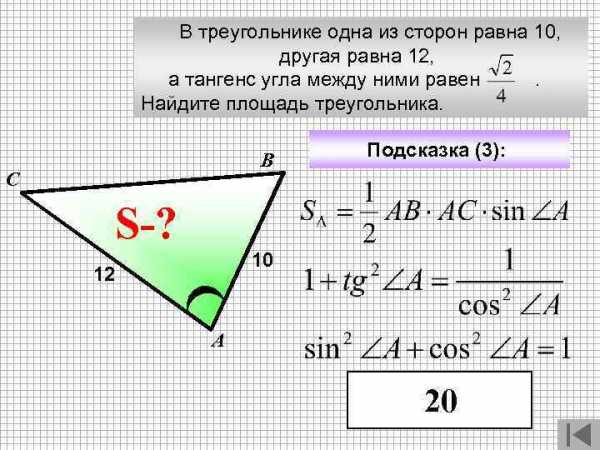В треугольнике одна из сторон равна 10, другая равна 12, а тангенс угла между ними равен . Найдите площадь треугольника. В С S-? 12 ? Подсказка (3): 10 А 20
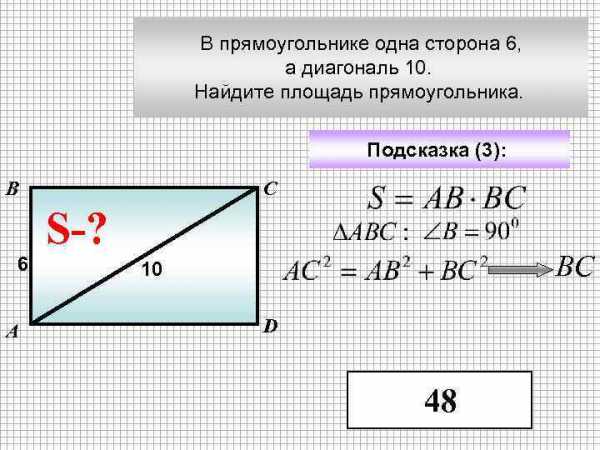В прямоугольнике одна сторона 6, а диагональ 10. Найдите площадь прямоугольника. Подсказка (3): В С S-? 6 А ВC 10 D 48
В прямоугольнике диагональ равна 10, а угол между ней и одной из сторон 300. Найдите площадь прямоугольника. Подсказка (4): В С 300 А 10 ВC S-? D АВ
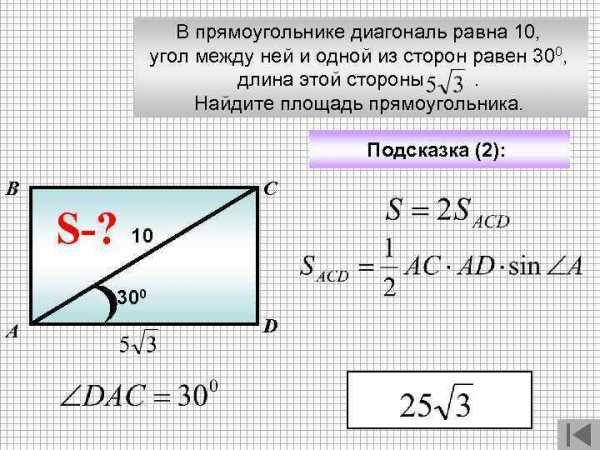В прямоугольнике диагональ равна 10, угол между ней и одной из сторон равен 300, длина этой стороны . Найдите площадь прямоугольника. Подсказка (2): В С S-? 10 300 А D
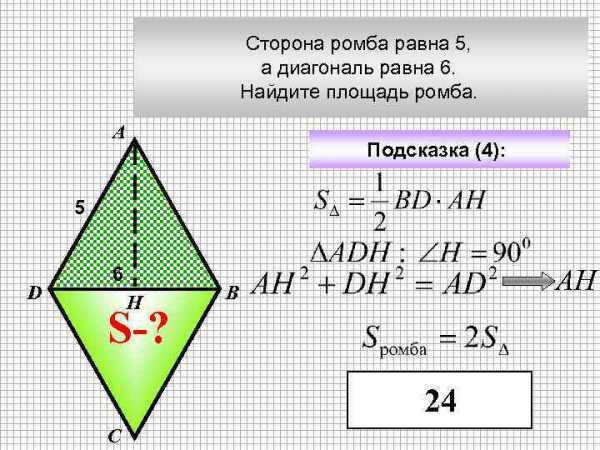Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба. А Подсказка (4): 5 D 6 Н S-? АН В 24 С
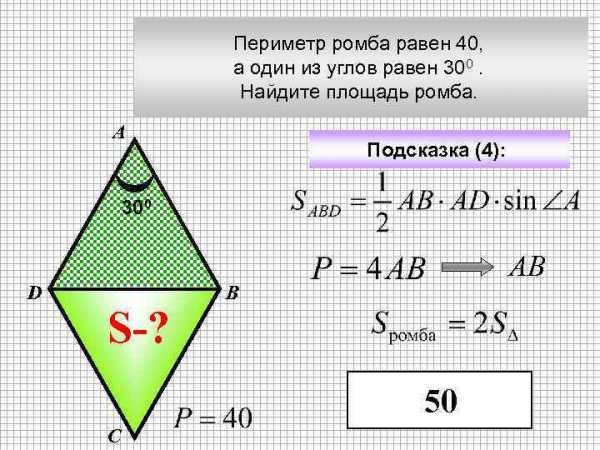Периметр ромба равен 40, а один из углов равен 300. Найдите площадь ромба. А Подсказка (4): 300 D S-? АВ В 50 С
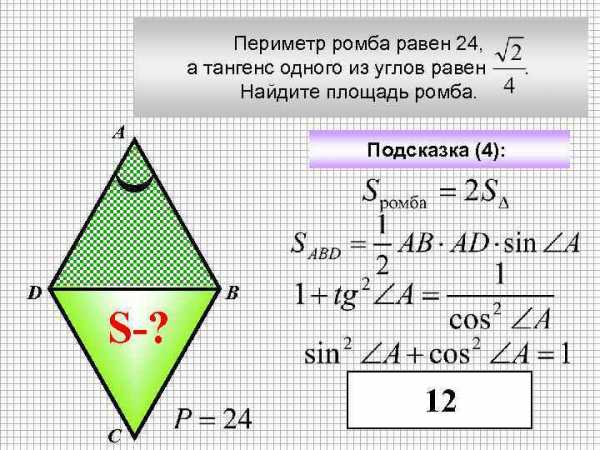Периметр ромба равен 24, а тангенс одного из углов равен . Найдите площадь ромба. А D S-? Подсказка (4): В 12 С
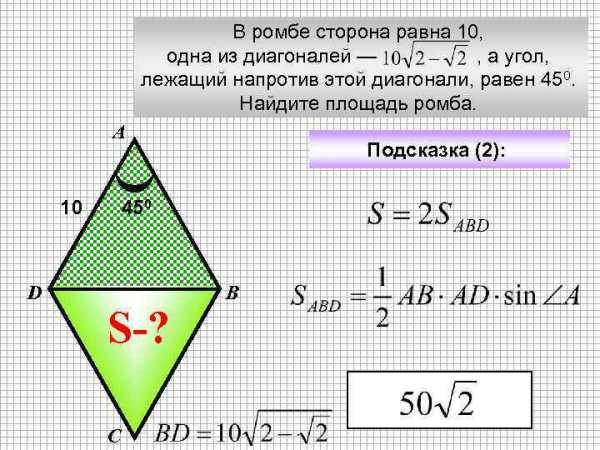В ромбе сторона равна 10, одна из диагоналей — , а угол, лежащий напротив этой диагонали, равен 450. Найдите площадь ромба. А 10 D Подсказка (2): 450 S-? С В
В ромбе сторона равна 10, одна из диагоналей — , а угол, из которого выходит эта диагональ, равен 1500. Найдите площадь ромба. А Подсказка (3): 10 1500 D S-? В 50 С
Задание 16 (№ 169876) Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 450. Найдите площадь параллелограмма. Подсказка (3): А 5 450 D Н 12 В S-? С АН
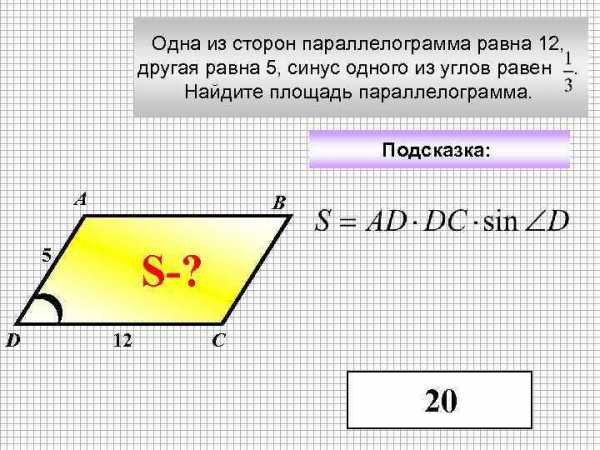Одна из сторон параллелограмма равна 12, другая равна 5, синус одного из углов равен . Найдите площадь параллелограмма. Подсказка: А В 5 D S-? 12 С 20
Одна из сторон параллелограмма равна 12, другая равна 5, косинус одного из углов . Найдите площадь параллелограмма. Подсказка (2): А В 5 D S-? 12 С 20
Основания трапеции равны 18 и 12, одна из боковых сторон равна , а угол между ней и одним из оснований равен 1350. Найдите площадь трапеции. Подсказка (3): В 12 С 1350 S-? А Н 18 ВН D 60
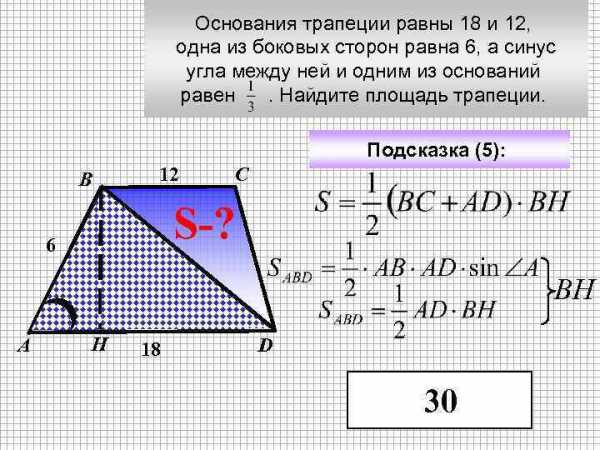Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а синус угла между ней и одним из оснований равен . Найдите площадь трапеции. Подсказка (5): В 12 С S-? 6 ВН А Н 18 D 30
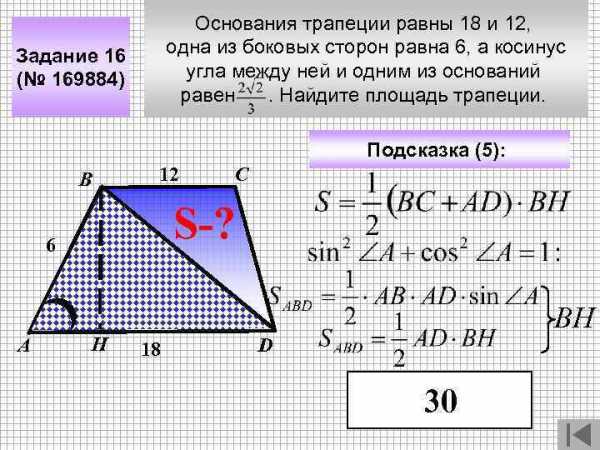Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а косинус угла между ней и одним из оснований равен . Найдите площадь трапеции. Задание 16 (№ 169884) Подсказка (5): В 12 S-? 6 А С Н 18 ВН D 30
Радиус круга равен 1. Найдите его площадь Подсказка: 1 S-? О 3, 14
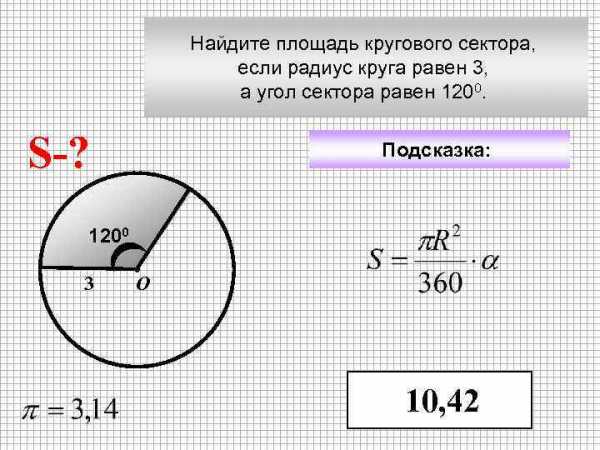Найдите площадь кругового сектора, если радиус круга равен 3, а угол сектора равен 1200. S-? Подсказка: 1200 3 О 10, 42
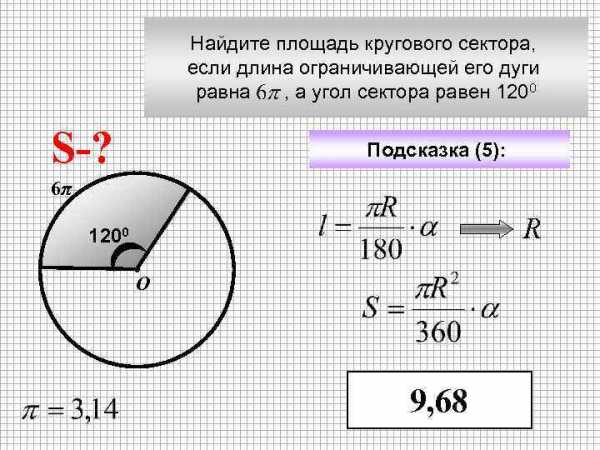Найдите площадь кругового сектора, если длина ограничивающей его дуги равна , а угол сектора равен 1200 S-? Подсказка (5): 6π R 1200 О 9, 68
Радиус круга равен 3, а длина ограничивающей его окружности равна 6π. Найдите площадь круга. Подсказка (3): 3 S-? R О 28, 26
При создании презентации были использованы задачи с сайта «Открытый банк заданий по математике» ГИА – 2015. http: //www. mathgia. ru: 8080/or/gia 15/Main. html? view=Pos Спасибо за проявленный интерес к данной разработке! ВСЕМ ТВОРЧЕСКИХ УСПЕХОВ И УСПЕШНЫХ УЧЕНИКОВ!
present5.com
