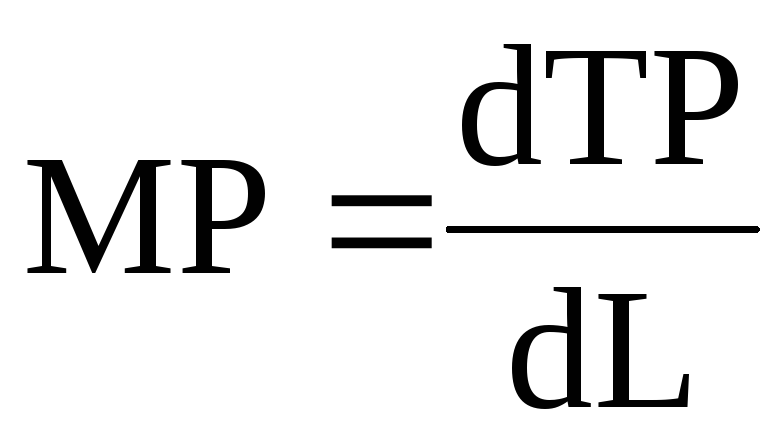G формула физика: Ускорение свободного падения — урок. Физика, 9 класс.

Ускорение свободного падения на Земле и других небесных телах :: Класс!ная физика

УСКОРЕНИЕ СВОБОДНОГО ПАДЕНИЯ НА ЗЕМЛЕ И ДРУГИХ НЕБЕСНЫХ ТЕЛАХ

У поверхности Земли ускорение свободного падения считается величиной постоянной и расчитывается по формуле:

при этом значение ускорения свободного падения приблизительно равно:

g = 9,81 м/с2

Ускорение свободного падения зависит от расстояния между центром планеты и поднятым над её поверхностью телом.
Для более точного расчета годится формула:

где
h- высота подъема тела над поверхностью Земли,
Rз — радиус Земли
Ускорение свободного падения не зависит от массы падающего тела!
Вектор ускорения свободного падения всегда направлен к центру Земли.

Усорение свободного падения зависит:

1. от географической широты, т.к. Земля сплюснута у полюсов и вращается вокруг своей оси.
на полюсе g = 9,832 м/с2,
на экваторе = 9,78 мс2.
Точные значения ускорения свободного падения для падающих тел на полюсе и на экваторе будут различны из-за неправильной формы Земли.
2. от высоты подъема тела над поверхностью Земли;
вблизи поверхности Земли ускорение свободного падения считается равным 9,8 м/с2.

КНИЖНАЯ ПОЛКА

ИНТЕРЕСНО…

… что гравитационные анамалии Земли, т.е. залежи полезных ископаемых, искажают значение ускорения свободного падения в этих областях.

Для других планет ускорение свободного падения определяется аналогично:

На других планетах ускорение свободного падения тел будет иметь другое значение.
На каждой планете ускорение свободного падения зависит от радиуса и массы данной планеты.

ВСЕГО ХОРОШЕГО !

Устали? — Отдыхаем!

Открытая Физика. Свободное падение тел

Свободным падением тел называют падение тел на Землю в отсутствие сопротивления воздуха (в пустоте). В конце XVI века знаменитый итальянский ученый Г. Галилей опытным путем с доступной для того времени точностью установил, что в отсутствие сопротивления воздуха все тела падают на Землю равноускоренно, и что в данной точке Земли ускорение всех тел при падении одно и то же. До этого в течение почти двух тысяч лет, начиная с Аристотеля, в науке было принято считать, что тяжелые тела падают на Землю быстрее легких.

Ускорение, с которым падают на Землю тела, называется ускорением свободного падения. Вектор ускорения свободного падения обозначается символом g→, он направлен по вертикали вниз. В различных точках земного шара в зависимости от географической широты и высоты над уровнем моря числовое значение g оказывается неодинаковым, изменяясь примерно от 9,83 м/с² на полюсах до 9,78 м/с² на экваторе. На широте Москвы g = 9,81523 м/с². Обычно, если в расчетах не требуется высокая точность, то числовое значение g у поверхности Земли принимают равным 9,8 м/с² или даже 10 м/с².

Простым примером свободного падения является падение тела с некоторой высоты h без начальной скорости. Свободное падение является прямолинейным движением с постоянным ускорением. Если направить координатную ось

OY вертикально вверх, совместив начало координат с поверхностью Земли, то для анализа свободного падения без начальной скорости можно использовать формулу (*) §1.4, положив υ₀ = 0, y₀ = h, a = –g. Обратим внимание на то, что если тело при падении оказалось в точке с координатой y < h, то перемещение s тела равно s = y – h < 0. Эта величина отрицательна, так как тело при падении перемещалось навстречу выбранному положительному направлению оси OY. В результате получим: υ = –gt.

Скорость отрицательна, так как вектор скорости направлен вниз. y=h-gt22.

Время падения t_п тела на Землю найдется из условия y = 0: tп=2hg.

Скорость тела в любой точке составляет: υ=2g(h-y).

В частности, при y = 0 скорость υ_п падения тела на Землю равна υп=2gh.

Пользуясь этими формулами, можно вычислить время падения тела с данной высоты, скорость падения тела в любой момент после начала падения и в любой точке его траектории и т. д.

Аналогичным образом решается задача о движении тела, брошенного вертикально вверх с некоторой начальной скоростью υ₀. Если ось OY по-прежнему направлена вертикально вверх, а ее начало совмещено с точкой бросания, то в формулах равноускоренного прямолинейного движения следует положить: y₀ = 0, υ₀ > 0, a = –g. Это дает: υ = υ₀ – gt.

Через время υ₀ / g скорость тела υ обращается в нуль, т.  е. тело достигает высшей точки подъема. Зависимость координаты y от времени

t выражается формулой y=υ0t-gt22.

Тело возвращается на землю (y = 0) через время 2υ₀ / g, следовательно, время подъема и время падения одинаковы. Во время падения на землю скорость тела равна –υ₀, т. е. тело падает на землю с такой же по модулю скоростью, с какой оно было брошено вверх.

Максимальная высота подъема h=ymax=υ022g.

Графики скоростей для различных режимов движения тела с ускорением a = –g

На рис. 1.5.1 представлены графики скоростей для трех случаев движения тела с ускорением a = –g. График I соответствует случаю свободного падения тела без начальной скорости с некоторой высоты h. Падение происходило в течение времени t_п = 1 с. Из формул для свободного падения легко получить: h = 5 м (все числа в этих примерах округлены, ускорение свободного падения принято равным 10 м/с²).

График II – случай движения тела, брошенного вертикально вверх с начальной скоростью υ₀ = 10 м/с. Максимальная высота подъема h = 5 м. Тело возвращается на землю через время t = 2 с.

График III – продолжение графика I. Свободно падающее тело при ударе о землю отскакивает (мячик), и его скорость за очень короткое время меняет знак на противоположный. Дальнейшее движение тела не отличается от случая II.

Задача о свободном падении тел тесно связана с задачей о движении тела, брошенного под некоторым углом к горизонту. Для кинематического описания движения тела удобно одну из осей системы координат (ось OY) направить вертикально вверх, а другую (ось OX) – расположить горизонтально. Тогда движение тела по криволинейной траектории можно представить как сумму двух движений, протекающих независимо друг от друга – движения с ускорением свободного падения вдоль оси

OY и равномерного прямолинейного движения вдоль оси OX. На рис. 1.5.2 изображен вектор начальной скорости υ→0 тела и его проекции на координатные оси.

Движение тела, брошенного под углом α к горизонту. Разложение вектора υ→0 начальной скорости тела по координатным осям

Таким образом, для движения вдоль оси OX имеем следующие условия: x₀ = 0, υ_0x = υ₀ cos α, a_x = 0, а для движения вдоль оси OY y₀ = 0, υ_0y = υ₀ sin α, a_y = –g.

Приведем здесь некоторые формулы, описывающие движение тела, брошенного под углом α к горизонту.

Время полета: t=2υ0sinαg.

Дальность полета: L=υ02sin2αg;  L=Lmax=υ02g  при  α=45ˆ.

Максимальная высота подъема: h=υ02 sin2 α2g.

Движение тела, брошенного под углом к горизонту

Движение тела, брошенного под углом к горизонту, происходит по параболической траектории. В реальных условиях такое движение может быть в значительной степени искажено из-за сопротивления воздуха, которое может во много раз уменьшить дальность полета тела.

Урок 8. гравитационные силы — Физика — 10 класс

Физика, 10 класс

Урок 8. Гравитационные силы

Перечень вопросов, рассматриваемых на уроке:

1)познакомиться с явлением всемирного тяготения и сформулировать закон всемирного тяготения.

2) понять физический смысл гравитационной постоянной;

3) проанализировать некоторые физические явления на основе знаний закона всемирного тяготения;

Глоссарий по теме:

Закон всемирного тяготения – все материальные тела притягивают друг друга с силами прямо пропорциональными их массам и обратно пропорциональными квадрату расстояния между ними.

Тяготение – свойство материи, которое состоит в том, что между любыми двумя частицами существуют силы притяжения.

Масса тела – основная механическая величина, определяющая величину ускорения, сообщаемого телу данной силой.

Сила тяжести – векторная величина, определяющая силу притяжения к Земле любого тела.

Первая космическая скорость – наименьшая скорость, которую нужно сообщить телу на поверхности Земли, чтобы оно стало двигаться вокруг Земли по круговой орбите над её поверхностью только под действием силы гравитационного притяжения Земли

Вес – сила, с которой любое тело вследствие притяжения Земли действует на опору или подвес.

Невесомость – состояние, при котором вес тела равен нулю.

Основная и дополнительная литература по теме урока:

Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 89 – 106.

Рымкевич А.П. Сборник задач по физике. 10-11 класс. -М.:Дрофа,2009.

Открытые электронные ресурсы:

http://kvant.mccme.ru/1987/11/zakon_vsemirnogo_tyagoteniya.htm

Теоретический материал для самостоятельного изучения

В механике обычно имеют дело с тремя видами сил – силами тяготения, упругости и трения.

Силу, с которой Земля действует на тело, называют силой тяжести.

Ньютон является первым учёным, который открыл закон всемирного тяготения. Он строго доказал, что причина, вызывающая падение камня на Землю, движение Луны вокруг Земли и планет вокруг Солнца, одна и та же. Эта сила всемирного тяготения, действующая между любыми телами Вселенной.

Ньютон после долгих наблюдений сделал вывод, что если бы не сопротивление воздуха, то траектория камня, брошенного с высокой горы с определённой скоростью, могла бы стать такой, что он никогда не достиг бы поверхности Земли, а двигался бы подобно тому, как планеты вокруг Солнца.

Исаак Ньютон сделал выводы:

1) ускорение и сила притяжения тел к Земле обратно пропорциональны квадрату расстояния до центра Земли:

2) Солнце сообщает всем планетам ускорение, обратно пропорциональное квадрату расстояния от планет до Солнца.

Ньютон нашёл причину множества явлений: от падения брошенного камня на землю до движения огромных космических тел. И причину этих явлений он выразил одной формулой – законом всемирного тяготения.

Закон всемирного тяготения

Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними:

F – модуль вектора силы гравитационного притяжения между телами с массами , находящимися на расстоянии r друг от друга.

G – это коэффициент, который называется гравитационной постоянной

Измерения показывают, что

Первая космическая скорость — минимальная скорость, которую надо сообщить телу на поверхности Земли, чтобы оно стало спутником Земли, движущимся по орбите.

Примеры и разбор решения заданий

1.На столе несколько гвоздиков, кнопка, ластик, карандаш. На какие из этих тел действует одинаковые силы тяжести?

1) на ластик и карандаш;

2) на гвозди;

3) на кнопку и карандаш;

4) на все эти тела.

Правильный ответ: на гвозди.

2. Чему равна сила тяжести, действующая на мяч массой 100 г, если он находится на космическом корабле? Космический корабль движется на высоте 1600 км над поверхностью Земли. Радиус Земли 6400 км. Масса Земли равна

Решение:

Ответ: F = 0,63 Н.

Уравнения гравитационного времени для падающих объектов, Рон Куртус

SfC Главная > Физика > Гравитация >

Рона Куртуса

Когда вы бросаете объект с некоторой высоты над землей, его начальная скорость равна нулю. Простые уравнения позволяют вычислить время падающего объекта для достижения заданной скорости и время, необходимое для достижения заданного смещения. В уравнениях предполагается, что сопротивлением воздуха можно пренебречь.

Примеры демонстрируют применение уравнений.

Возможные вопросы:

• Какое уравнение определяет время достижения заданной скорости?
• Какое уравнение определяет время достижения заданного смещения?
• Какие примеры этих уравнений?

Этот урок ответит на эти вопросы. Полезный инструмент: Преобразование единиц измерения

---

---

Время относительно скорости

Общее уравнение гравитации для прошедшего времени относительно скорости:

t = (v − v _i )/г

( Подробную информацию о выводе см. в разделе Вывод уравнений силы тяжести во времени. )

Поскольку начальная скорость v _i = 0 для объекта, который просто падает, уравнение сводится к:

т = об/г

где

• t время в секундах
• v — вертикальная скорость в метрах/секунду (м/с) или футах/секунду (фут/с)
• г ускорение свободного падения (9,8 м/с ² или 32 фут/с ² )

Поскольку объект движется в направлении силы тяжести, v — положительное число.

Прошедшее время падения объекта как функция скорости или смещения

Время относительно смещения

Общее уравнение силы тяжести для прошедшего времени относительно смещения:

t = [−v _i ± √(v _i ² + 2gy)]/г

где

• ± означает плюс-минус
• √(v _i ² + 2gy) – квадратный корень из числа (v _i ² + 2gy)
• y вертикальное смещение в метрах (м) или футах (футах)

( Подробную информацию о выводе см. в разделе Вывод уравнений гравитации смещения во времени. )

Когда объект просто брошен, начальная скорость _{равна нулю ( v i = 0), и уравнение для прошедшего времени принимает вид:}

t = _{± √(2gy)/г}

Поскольку время t всегда положительно, уравнение выглядит так:

t = √(2gy)/г

Замените г на √(g ² ) и упростите уравнение:

t = _{√(2gy)/√(g ² )}

Таким образом, получается уравнение времени:

t = _√(2г/г)

Примеры

Следующие примеры иллюстрируют применение уравнений.

Учитывая скорость

Через какое время падающий объект достигнет скорости 224 фута/с?

Решение

Поскольку v выражено в футах/с, g = 32 фута/с ² . Подставляем значения в уравнение:

т = об/г

t = (224 фут/с)/(32 фут/с ² )

t = 7 секунд

Учитывая водоизмещение

Через какое время объект упадет с высоты 200 метров?

Решение

Поскольку водоизмещение указано в метрах, г = 9.8 м/с ² . Подставляем значения в уравнение:

t = √(2г/г)

t = √ [2*(200 м)/(9,8 м/с ² )]

t = √ (40,8 с ² )

т = 6,39 с

Резюме

Существуют простые уравнения для падающих объектов, которые позволяют рассчитать время, необходимое для достижения заданной скорости или смещения. Вот эти уравнения:

т = об/г

t = √(2г/г)

---

Проверьте свои номера

---

Ресурсы и ссылки

Полномочия Рона Куртуса

Веб-сайты

Гравитационные ресурсы

Падающие тела — Гиперучебник по физике

Уравнения для падающего тела — Википедия

Гравитационные расчеты — Земля — Калькулятор

Кинематические уравнения и свободное падение — Кабинет физики

Книги

(Примечание: Школа чемпионов может получать комиссионные за покупку книг)

Книги с самым высоким рейтингом по Simple Gravity Science

Книги с самым высоким рейтингом по продвинутой физике гравитации

---

Вопросы и комментарии

У вас есть вопросы, комментарии или мнения по этому вопросу? Если это так, отправьте электронное письмо с вашим отзывом. Я постараюсь вернуться к вам как можно скорее.

---

Поделиться этой страницей

Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:

---

Студенты и исследователи

Веб-адрес этой страницы:
www.school-for-champions.com/science/
gravity_equations_falling_time.htm

Разместите его в качестве ссылки на своем веб-сайте или в качестве ссылки в своем отчете, документе или диссертации.

Copyright © Ограничения

---

Где ты сейчас?

Школа Чемпионов

Гравитационные темы

Уравнения времени гравитации для падающих объектов

---

Физика — гравитация — Бирмингемский университет

Из четырех известных сил природы гравитация является самой сильной в больших масштабах — она способна удерживать планеты, звезды и галактики на их орбитах. Однако в малых масштабах гравитация действует намного слабее, чем ее аналоги. Тем не менее гравитация — это то, что мы можем измерить здесь, на Земле.

Как мы можем измерить гравитацию?

Согласно апокрифической истории, сэр Исаак Ньютон сидел под яблоней, когда яблоко упало ему на голову и вдохновило его на работу над теорией гравитации. Важно отметить, что теория Ньютона — это теория 90 364 Универсальной гравитационной постоянной 90 365 G (также называемой «Большой G»). Его теория описывает силу F между двумя объектами массами m1 и m2 , разделенными расстоянием r .Когда говорят о гравитации планеты, обычно имеют в виду ускорение свободного падения из-за ее гравитационного поля g (которое зависит от массы, отвечающей за гравитационное поле), а не G (которое является константой). Работа Ньютона была вдохновлена ​​Галилеем, который сбрасывал предметы различной массы с падающей башни в Пизе, чтобы показать, что время, необходимое им для достижения земли, не зависит от их массы.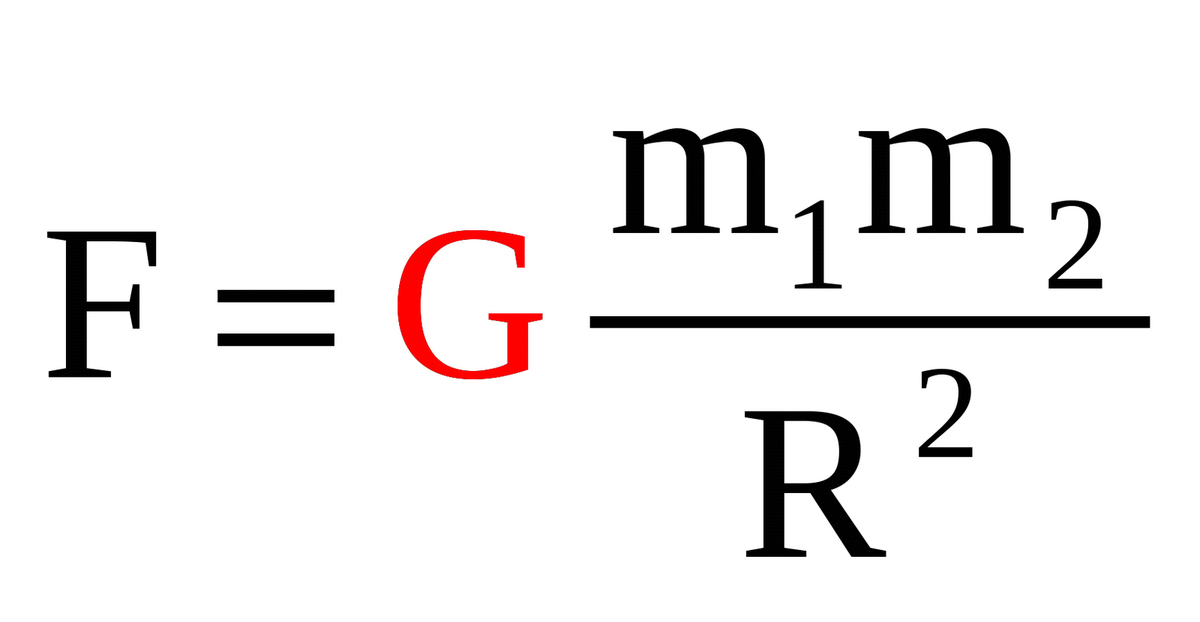 Это говорит нам о том, что ускорение, вызванное гравитационным полем Земли, также должно быть одинаковым для всех масс.Из F = ma = мг мы знаем, что оно связано с G следующим образом. кубических метров на килограмм в секунду в квадрате, масса Земли M = 5 972 000 000 000 000 000 000 000 кг, а радиус Земли равен 90 366 r 90 367 = 6 371 000 метров. В лаборатории его можно определить, измерив время ( t ), которое требуется объекту, чтобы упасть с высоты ( s ), используя уравнения движения для постоянного ускорения по прямой:

Где a — ускорение, u — начальная скорость, а v — конечная скорость.

 Как мы вычисляем

г в лаборатории?

 

Как мы рассчитываем малое g в лаборатории?

 Как мы можем улучшить ответ?

В этом эксперименте начальная скорость u равна 0 метров в секунду, время можно измерить с помощью секундомера или световых ворот, расстояние можно измерить с помощью линейки, а интересующей переменной является ускорение, которое в данном случае эквивалентно до г . Итак, вы можете видеть, что простейшее уравнение для определения г :

И переставить на г .

Если у вас возникли проблемы с запоминанием всех уравнений движения, одна быстрая проверка — убедиться, что единицы измерения в обеих частях уравнения одинаковы. С левой стороны расстояние указано в метрах ( с [ м ]), а с правой стороны:

Итак, вы видите, что единицы измерения совпадают.

Есть несколько способов повысить точность эксперимента. Помимо повторных записей, использование световых затворов вместо секундомера и/или электромагнитной капли (как показано на видео) уменьшит неточности, связанные с дистанцией мышления и временем реакции.Еще одна вещь, которую следует учитывать, — это увеличение расстояния падения. Поскольку это означает, что неопределенность, вносимая из-за времени реакции, будет составлять меньшую часть общего времени, необходимого для падения. Обратите внимание, что из-за сопротивления воздуха, с которым мы сталкиваемся на Земле, мы не ожидали бы получить идеальное измерение для г , но использование массы более обтекаемой формы, такой как сфера, будет работать намного лучше, чем что-то вроде пера.

 

Как теория Ньютона влияет на нас сегодня?

Закон всемирного тяготения Ньютона успешно предсказал существование планеты Нептун, однако есть много других явлений, которые теория Ньютона не могла объяснить, например, орбита Меркурия.С тех пор теория Ньютона была заменена общей теорией относительности Эйнштейна. Теория Эйнштейна позволила использовать спутники GPS для точного отслеживания местоположения, успешно предсказала гравитационное линзирование (влияние гравитации на свет) и, совсем недавно, гравитационные волны (излучение гравитационного излучения). Однако, к сожалению, это несовместимо с квантовой механикой, что приводит к тому, что многие текущие исследования сосредоточены на проверке гравитации и новых теорий гравитации.

В общем, теория гравитации Ньютона является хорошим приближением для малых масштабов и очень проста в использовании.Этот простой эксперимент можно провести где угодно, и он показывает вашу способность использовать как аналоговые, так и цифровые устройства. Это демонстрирует важность времени реакции человека при оценке ошибок, но также и то, что есть много возможностей для улучшения (например, если вы должны были повторить это в вакууме, отсутствие сопротивления воздуха улучшит точность), если вы получите шанс, что определенно стоит поиграть с различными формами объектов и расстояниями, чтобы увидеть, как изменится ваш ответ.

Следующие шаги

 

Эти ссылки предоставляются для удобства и только в информационных целях; они не являются подтверждением или одобрением Бирмингемским университетом какой-либо информации, содержащейся на внешнем веб-сайте.Университет Бирмингема не несет ответственности за точность, законность или содержание внешнего сайта или последующих ссылок. Пожалуйста, свяжитесь с внешним сайтом для получения ответов на вопросы, касающиеся его содержания.

Риджентс Физика Гравитация

Универсальная гравитация

Все объекты, имеющие массу, притягиваются друг к другу силой гравитации. Величина этой силы, Fg, может быть рассчитана с использованием закона всемирного тяготения Ньютона :

.

Этот закон говорит нам, что сила притяжения между двумя объектами пропорциональна каждой из масс ( м ₁ и м ₂ ) и обратно пропорциональна квадрату расстояния между ними ( r ).Универсальная гравитационная постоянная, G , является, так сказать, «фактором выдумки», включенным в уравнение, так что ваши ответы выводятся в единицах СИ. G указан на первой странице вашей справочной таблицы Regents Physics как .

Давайте рассмотрим эту связь более подробно. Сила прямо пропорциональна массам двух объектов, поэтому, если любую из масс удвоить, гравитационная сила также удвоится. Аналогичным образом, если бы расстояние между двумя объектами, r , было удвоено, сила тяжести была бы разделена на четыре части, поскольку расстояние в знаменателе возведено в квадрат.Этот тип отношений называется законом обратных квадратов , который описывает многие явления в мире природы.

ПРИМЕЧАНИЕ: расстояние между массами r фактически является расстоянием между центрами масс объектов. Для крупных объектов, таких как Земля, например, необходимо определять расстояние до центра Земли, а не до ее поверхности.

Несколько советов по решению задач при работе с законом всемирного тяготения Ньютона:

1. Подставлять значения вместо переменных только в самом конце задачи.Чем дольше вы сможете хранить формулу в терминах переменных, тем меньше возможностей для ошибок.
2. Прежде чем использовать калькулятор для поиска ответа, попробуйте оценить порядок величины ответа. Используйте это, чтобы проверить свой окончательный ответ.
3. После того, как ваши расчеты будут завершены, убедитесь, что ваш ответ имеет смысл, сравнив ваш ответ с известной или похожей величиной. Если ваш ответ не имеет смысла, проверьте свою работу и проверьте свои расчеты.

Давайте посмотрим, нельзя ли применить закон всемирного тяготения Ньютона к простой задаче. ..

Вопрос: Какова сила гравитационного притяжения между двумя космическими астероидами массой 50 000 кг каждый, находящимися на расстоянии 3800 м друг от друга?

Ответ:

Как видите, сила тяжести относительно слабая, и мы ожидаем относительно слабое взаимодействие между относительно небольшими объектами. Для развития значительных гравитационных сил требуются огромные массы и небольшие расстояния.Давайте рассмотрим еще одну задачу, чтобы исследовать взаимосвязь между гравитационной силой, массой и расстоянием.

Гравитационные поля

Гравитация — это бесконтактная или полевая сила. Его эффекты наблюдаются без контакта двух объектов друг с другом. Как именно это происходит, до сих пор остается загадкой, но ученые придумали ментальную конструкцию, которая поможет нам понять, как работает гравитация.

Представьте себе объект с гравитационным полем, например планету Земля.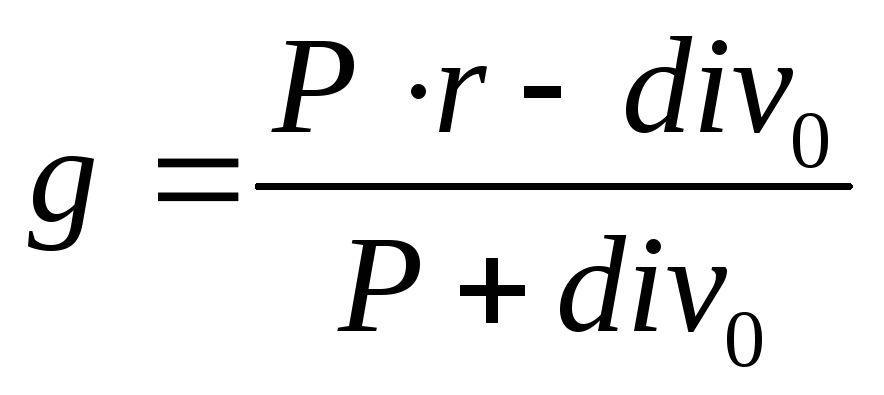 Чем ближе другие массы к Земле, тем большую гравитационную силу они будут испытывать. Мы можем охарактеризовать это, рассчитав величину силы, которую Земля будет оказывать на единицу массы на различных расстояниях от Земли. Очевидно, чем ближе объект к Земле, тем большую силу он будет испытывать, а чем дальше он находится от Земли, тем меньшую силу он будет испытывать.

Пытаясь визуализировать это, представьте силу гравитационной силы на тестовом объекте, представленную вектором в положении объекта.Чем плотнее векторы силы, тем сильнее сила, тем сильнее «гравитационное поле». По мере того как эти силовые линии становятся все менее и менее плотными, гравитационное поле становится все слабее и слабее.

Чтобы вычислить напряженность гравитационного поля в данной точке, мы можем вернуться к нашему определению силы тяжести на нашем тестовом объекте, более известном как его вес. Мы пишем это как мг с тех пор, как начали изучать динамику. Но, понимая, что это сила тяжести, действующая на объект, мы можем также вычислить силу тяжести пробной массы, используя закон всемирного тяготения Ньютона. Сложив их вместе, мы находим, что:

Понимая, что масса в левой части уравнения, масса нашего тестового объекта, также является одной из масс в правой части уравнения, мы можем упростить наше выражение, разделив тестовую массу.

Следовательно, напряженность гравитационного поля, g , равна универсальной гравитационной постоянной, G , умноженной на массу объекта, деленную на квадрат расстояния между объектами.

Но подождите, можно сказать… Я думал, что g — это ускорение силы тяжести на поверхности Земли! И вы были бы правы. g — это не только напряженность гравитационного поля, но и ускорение под действием силы тяжести. Единицы даже работают… единицы силы гравитационного поля, Н/кг, эквивалентны единицам ускорения, м/с ² !

Все еще сомневаетесь? Рассчитаем напряженность гравитационного поля на поверхности Земли, зная, что масса Земли примерно равна 5.98×10 ²⁴ кг, а расстояние от поверхности до центра масс Земли (которое немного варьируется, поскольку Земля не является идеальной сферой) составляет примерно 6378 км в Нью-Йорке.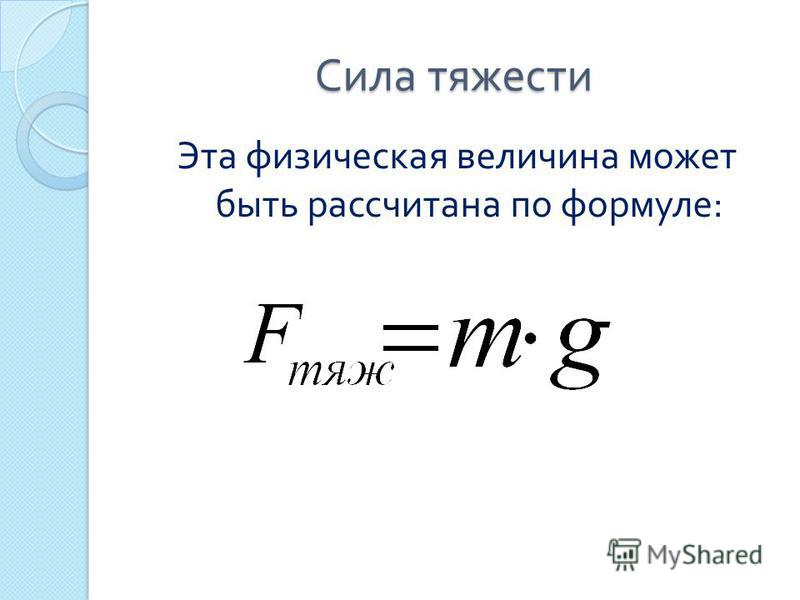

Как и ожидалось, напряженность гравитационного поля на поверхности Земли равна ускорению свободного падения. Давайте посмотрим, не сможем ли мы решить некоторые задачи, используя напряженность гравитационного поля.

Вопрос: Предположим, что 100-килограммовый космонавт испытывает гравитационную силу в 700 Н, находясь в гравитационном поле планеты.

А) Какова напряженность гравитационного поля в месте нахождения космонавта?

Б) Какова масса планеты, если космонавт находится на расстоянии 2×10 ⁶ м от ее центра?

Ответ:

Орбиты

Как небесные тела вращаются вокруг друг друга? Луна вращается вокруг Земли. Земля вращается вокруг Солнца. Наша солнечная система находится на орбите галактики Млечный Путь… но как все это работает?

Чтобы объяснить орбиты, сэр Исаак Ньютон провел «мысленный эксперимент», в котором он представил себе пушку, размещенную на вершине очень высокой горы, настолько высокой, что пик горы возвышается над атмосферой (это важно, потому что это позволяет пренебречь сопротивлением воздуха). Если пушка затем запустит снаряд горизонтально, снаряд будет двигаться по параболе к поверхности Земли.

Однако, если бы снаряд был запущен с более высокой скоростью, он бы пролетел дальше по поверхности Земли, прежде чем достиг земли. Если бы его скорость можно было увеличить достаточно высоко, снаряд падал бы с той же скоростью, с которой изгибается поверхность Земли. Снаряд будет продолжать падать вечно, вращаясь вокруг Земли! Это круговое движение описывает орбиту.

Иными словами, астронавты в космическом челноке не невесомы. На самом деле на них по-прежнему действует земное притяжение, притягивающее их к центру Земли со значительной силой. Мы можем даже рассчитать эту силу. Если космический шаттл вращается вокруг Земли на высоте 380 000 м, какова напряженность гравитационного поля Земли?

Вопрос: Если космический корабль вращается вокруг Земли на высоте 380 км, какова напряженность гравитационного поля Земли?

Ответ: Напомним, что мы можем получить значения G, массы Земли и радиуса Земли из справочной таблицы.

Это означает, что ускорение свободного падения на высоте, на которой космонавты обращаются вокруг Земли, всего на 11% меньше, чем на поверхности Земли! На самом деле космический шаттл падает, но он движется так быстро по горизонтали, что к тому времени, когда он падает, Земля изгибается под ним, так что шаттл остается на том же расстоянии от центра Земли — он находится на орбите. . Конечно, это требует огромных скоростей…Чтобы поддерживать орбиту в 380 км, космический челнок движется со скоростью примерно 7680 м/с, что более чем в 23 раза превышает скорость звука на уровне моря!

 

13.2 Гравитация вблизи поверхности Земли — University Physics Volume 1

Цели обучения

К концу этого раздела вы сможете:

• Объясните связь между константами GG и gg
• Определить массу астрономического тела по ускорению свободного падения на его поверхности
• Опишите, как значение gg меняется в зависимости от местоположения и вращения Земли

В этом разделе мы наблюдаем, как закон тяготения Ньютона применяется на поверхности планеты и как он связан с тем, что мы узнали ранее о свободном падении. Мы также исследуем гравитационные эффекты внутри сферических тел.

Вес

Напомним, что ускорение свободно падающего объекта вблизи поверхности Земли приблизительно равно g=9,80 м/с2g=9,80 м/с2. Сила, вызывающая это ускорение, называется весом объекта и согласно второму закону Ньютона имеет значение мг . Этот вес присутствует независимо от того, находится ли объект в свободном падении. Теперь мы знаем, что эта сила представляет собой гравитационную силу между объектом и Землей.Если мы заменим мг на величину F→12F→12 в законе всемирного тяготения Ньютона, m на m1m1 и MEME на m2m2, мы получим скалярное уравнение

, где r — расстояние между центрами масс объекта и Земли. Средний радиус Земли составляет около 6370 км. Следовательно, для объектов в пределах нескольких километров от поверхности Земли можно принять r=REr=RE (рис. 13.7). Масса м объекта отменяет, остается

Это объясняет, почему все массы свободно падают с одинаковым ускорением.Мы проигнорировали тот факт, что Земля также ускоряется по направлению к падающему объекту, но это допустимо, пока масса Земли намного больше массы объекта.

Фигура 13,7 За радиус Земли можно принять расстояние между центрами масс Земли и объектом на ее поверхности при условии, что его размер намного меньше радиуса Земли.

Пример 13.3

Массы Земли и Луны

Вы когда-нибудь задумывались, откуда мы знаем массу Земли? Мы, конечно, не можем положить его на весы.Значения g и радиуса Земли были измерены с достаточной точностью много веков назад.

1. Используйте стандартные значения г , RERE и уравнение 13.2, чтобы найти массу Земли.
2. Оцените стоимость г на Луне. Воспользуйтесь тем, что Луна имеет радиус около 1700 км (значение этой точности было определено много веков назад) и примите, что она имеет такую ​​же среднюю плотность, как и Земля, 5500 кг/м35500 кг/м3.

Стратегия

С известными значениями г и RERE мы можем использовать уравнение 13.2, чтобы найти цМем. Для Луны мы используем предположение о равной средней плотности, чтобы определить массу из отношения объемов Земли и Луны.

Решение

1. Преобразовывая уравнение 13.2, мы имеем ME=gRE2G=9,80 м/с2(6,37×106 м)26,67×10−11 Н·м2/кг2=5,95×1024 кг. ME=gRE2G=9,80 м/с2(6,37×106 м)26,67×10−11 Н·м2/кг2= 5,95×1024 кг.
2. Объем сферы пропорционален кубу радиуса, поэтому простое соотношение дает нам MMME=RM3RE3→MM=((1,7×106 м)3(6,37×106 м)3)(5,95×1024 кг)=1,1×1023 кг.MMME=RM3RE3→MM=((1,7×106 м)3(6,37×106 м)3)(5,95×1024 кг)=1,1×1023 кг. Теперь воспользуемся уравнением 13.2. gM=GMMrM2=(6,67×10−11 Н·м2/кг2)(1,1×1023 кг)(1,7×106 м)2=2,5 м/с2gM=GMMrM2=(6,67×10−11 Н·м2/кг2)(1,1×1023 кг) (1,7×106 м)2=2,5 м/с2

Значение

Как только Кавендиш определил значение G в 1798 году, можно было рассчитать массу Земли. (На самом деле, это и было конечной целью эксперимента Кавендиша в первую очередь.) Значение, которое мы вычислили для 90 606 g 90 367 Луны, неверно.Средняя плотность Луны на самом деле составляет всего 3340 кг/м33340 кг/м3 и g=1,6 м/с2g=1,6 м/с2 на поверхности. Ньютон попытался измерить массу Луны, сравнив влияние Солнца на океанские приливы Земли с влиянием Луны. Его значение было в два раза меньше. Наиболее точные значения для g и массы Луны получены при отслеживании движения космических аппаратов, вращающихся вокруг Луны. Но массу Луны на самом деле можно точно определить, не отправляясь на Луну.Земля и Луна вращаются вокруг общего центра масс, и это местоположение можно определить с помощью тщательных астрономических измерений. Отношение массы Луны к массе Земли — это отношение [расстояния от общего центра масс до центра Луны] к [расстоянию от общего центра масс до центра Земли].

Далее в этой главе мы увидим, что массу других астрономических тел также можно определить по периоду обращения вокруг них малых спутников. Но пока Кавендиш не определил значение G , массы всех этих тел были неизвестны.

Пример 13,4

Гравитация над поверхностью Земли

Какова величина г 400 км над поверхностью Земли, где на орбите находится Международная космическая станция?

Стратегия

Используя значение цМема и отметив, что радиус равен r=RE+400 кмr=RE+400 км, мы используем уравнение 13.2, чтобы найти 90 606 г 90 367 .

Из уравнения 13.2 имеем

g=GMer2=6,67×10−11 Н·м2/кг25,96×1024 кг(6,37×106+400×103 м)2=8,67 м/с2.g=GMER2=6,67×10−11 Н·м2/кг25,96×1024 кг (6,37×106+400×103м)2=8.67 м/с2.

Значение

Мы часто видим видео космонавтов на космических станциях, по-видимому, невесомых. Но ясно, что на них действует сила тяжести. Сравнивая значение г , которое мы только что вычислили, с земным (9,80 м/с2) (9,80 м/с2), мы видим, что астронавты на Международной космической станции по-прежнему имеют 88% своего веса. Они кажутся невесомыми только потому, что находятся в свободном падении. Мы вернемся к этому в разделе «Спутниковые орбиты и энергетика».

Проверьте свое понимание 13.2

Каков ваш вес на вершине высокого здания по сравнению с весом на первом этаже? Как вы думаете, должны ли инженеры учитывать изменение значения г при проектировании несущих конструкций для очень высокого здания?

Гравитационное поле

Уравнение 13.2 является скалярным уравнением, дающим величину ускорения свободного падения как функцию расстояния от центра масс, вызывающего ускорение. Но мы могли бы сохранить векторную форму силы тяжести в уравнении 13.1, и записать ускорение в векторной форме как

.

Мы идентифицируем векторное поле, представленное g→g→, как гравитационное поле, вызванное массой MM. Мы можем изобразить поле, как показано на рис. 13.8. Линии направлены радиально внутрь и симметрично распределены по массе.

Фигура 13,8 Трехмерное представление гравитационного поля, создаваемого массой ММ. Обратите внимание, что линии равномерно распределены во всех направлениях. (Коробка была добавлена ​​только для облегчения визуализации.)

Как и для любого векторного поля, направление g→g→ параллельно линиям поля в любой точке. Сила g→g→ в любой точке обратно пропорциональна межстрочному интервалу. Другой способ заявить об этом состоит в том, что величина поля в любой области пропорциональна количеству линий, проходящих через единицу площади поверхности, фактически плотности линий. Поскольку линии расположены одинаково во всех направлениях, число линий на единицу площади поверхности на расстоянии 90 606 r 90 367 от массы равно общему числу линий, деленному на площадь поверхности сферы радиусом 90 606 r 90 367 , что пропорционально к р2р2.Следовательно, эта картина прекрасно представляет закон обратных квадратов, в дополнение к указанию направления поля. На картине поля мы говорим, что масса m взаимодействует с гравитационным полем массой M . В последующих главах, посвященных электромагнетизму, мы с большим успехом воспользуемся концепцией полей.

Кажущийся вес: учет вращения Земли

Как мы видели в разделе «Применения законов Ньютона», объекты, движущиеся с постоянной скоростью по окружности, имеют центростремительное ускорение, направленное к центру окружности, а это означает, что должна существовать результирующая сила, направленная к центру этой окружности.Поскольку все объекты на поверхности Земли движутся по кругу каждые 24 часа, на каждый объект должна действовать центростремительная сила, направленная к центру этого круга.

Рассмотрим сначала предмет массой м , расположенный на экваторе и подвешенный на весах (рис. 13.9). Шкала оказывает направленное вверх усилие F→sF→s от центра Земли. Это показания весов, и, следовательно, это кажущийся вес объекта. Вес ( мг ) указывает на центр Земли.Если бы Земля не вращалась, ускорение было бы равно нулю и, следовательно, результирующая сила была бы равна нулю, в результате чего Fs=mgFs=mg. Это будет истинным значением веса.

Фигура 13,9 Для человека, стоящего на экваторе, центростремительное ускорение (ac)(ac) имеет то же направление, что и сила тяжести. На широте λλ угол между acac и силой тяжести равен λλ, а величина acac уменьшается с cosλcosλ.

При вращении сумма этих сил должна обеспечивать центростремительное ускорение acac.Используя второй закон Ньютона, мы имеем

∑F=Fs-mg=macwhereac=-v2r.∑F=Fs-mg=macwhereac=-v2r.

13.3

Обратите внимание, что acac указывает в том же направлении, что и вес; следовательно, он отрицательный. Тангенциальная скорость v — это скорость на экваторе, а r — это RERE. Мы можем рассчитать скорость, просто заметив, что объекты на экваторе проходят окружность Земли за 24 часа. Вместо этого давайте воспользуемся альтернативным выражением для acac из книги «Движение в двух и трех измерениях».Напомним, что тангенциальная скорость связана с угловой скоростью (ω)(ω) соотношением v=rωv=rω. Следовательно, имеем ac=−rω2ac=−rω2. Преобразовав уравнение 13.3 и подставив r=REr=RE, кажущийся вес на экваторе равен

. Fs=m(g-REω2).Fs=m(g-REω2).

Угловая скорость Земли везде равна

ω=2πрад24ч×3600с/ч=7,27×10-5рад/с. ω=2πрад24ч×3600с/ч=7,27×10-5рад/с.

Подставляя значения или RERE и ωω, получаем REω2=0,0337 м/с2REω2=0,0337 м/с2. Это всего 0,34% от значения силы тяжести, так что это явно небольшая поправка.

Пример 13,5

Нулевой кажущийся вес

Как быстро Земля должна вращаться, чтобы те, кто находится на экваторе, имели нулевой видимый вес? Какова будет продолжительность дня?

Стратегия

Используя уравнение 13.3, мы можем установить кажущийся вес (FsFs) равным нулю и определить требуемое центростремительное ускорение. Отсюда можно найти скорость на экваторе. Продолжительность дня – это время, необходимое для одного полного оборота.

Решение

Из уравнения 13.2, у нас есть ∑F=Fs-mg=mac∑F=Fs-mg=mac, поэтому установив Fs=0Fs=0, мы получим g=acg=ac. Используя выражение для acac, подставив радиус Земли и стандартное значение силы тяжести, получим ac=v2r=gv=gr=(9,80 м/с2)(6,37×106 м)=7,91×103 м/с.ac=v2r=gv=gr=(9,80 м/с2)(6,37×106 м)=7,91×103 м/ с.

Период T – время одного полного оборота. Следовательно, тангенциальная скорость равна длине окружности, деленной на T , поэтому мы имеем

v=2πrTT=2πrv=2π(6,37×106 м)7,91×103 м/с=5,06×103 с.v=2πrTT=2πrv=2π(6.37×106м)7,91×103м/с=5,06×103с.

Это около 84 минут.

Значение

Позже в этой главе мы увидим, что эта скорость и продолжительность дня также будут орбитальной скоростью и периодом спутника на орбите у поверхности Земли. Хотя такая орбита невозможна вблизи поверхности Земли из-за сопротивления воздуха, она, безусловно, возможна всего в нескольких сотнях миль над Землей.

Результаты Вдали от экватора

На полюсах ac→0ac→0 и Fs=mgFs=mg, как и в случае без вращения. На любой другой широте λλ ситуация сложнее. Центростремительное ускорение направлено к точке P на рисунке, и радиус становится равным r=REcosλr=REcosλ. Сумма вектора веса и F→sF→s должна указывать на точку P , следовательно, F→sF→s больше не указывает в сторону от центра Земли. (Разница на рисунке невелика и преувеличена.) Отвес всегда будет указывать в этом отклоненном направлении. Все здания строятся вдоль этого отклоненного направления, а не по радиусу, проходящему через центр Земли.Для самых высоких зданий это представляет собой отклонение в несколько футов вверху.

Также стоит отметить, что Земля не является идеальной сферой. Внутренняя часть частично жидкая, и это усиливает выпуклость Земли на экваторе из-за ее вращения. Радиус Земли на экваторе примерно на 30 км больше, чем у полюсов. В качестве упражнения остается сравнить силу гравитации на полюсах и на экваторе, используя уравнение 13. 2. Разница сравнима с разницей из-за вращения и находится в том же направлении.Судя по всему, действительно можно похудеть, переехав в тропики.

Гравитация от поверхности

Ранее мы утверждали без доказательства, что закон всемирного тяготения применим к сферически симметричным объектам, где масса каждого тела действует так, как будто оно находится в центре тела. Поскольку уравнение 13.2 получено из уравнения 13.1, оно также справедливо для симметричных массовых распределений, но оба уравнения действительны только для значений r≥REr≥RE. Как мы видели в примере 13.4, на высоте 400 км над поверхностью Земли, где вращается Международная космическая станция, значение g равно 8.67 м/с28,67 м/с2. (Позже мы увидим, что это также и центростремительное ускорение МКС.)

Для r Следствием закона Гаусса, примененного к гравитации, является то, что только масса в пределах r вносит вклад в гравитационную силу.Кроме того, эту массу, как и прежде, можно считать находящейся в центре. Гравитационный эффект массы вне r имеет нулевой суммарный эффект.

Два очень интересных частных случая. Для сферической планеты с постоянной плотностью масса в пределах х равна плотности, умноженной на объем в пределах х . Эту массу можно считать расположенной в центре. Заменив цМем только массой в пределах r , M=ρ×(объем сферы) M=ρ×(объем сферы) и RERE с r , уравнение 13.2 становится

g=GMERE2=Gρ(4/3πr3)r2=43Gρπr.g=GMERE2=Gρ(4/3πr3)r2=43Gρπr.

Значение г и, следовательно, ваш вес линейно уменьшается по мере того, как вы спускаетесь в отверстие к центру сферической планеты. В центре вы невесомы, так как масса планеты притягивается одинаково во всех направлениях. На самом деле плотность Земли непостоянна, и Земля не является сплошной. На рис. 13.10 показан профиль g , если бы Земля имела постоянную плотность, и более вероятный профиль, основанный на оценках плотности, полученных из сейсмических данных.

Фигура 13.10 Для r г для случая постоянной плотности представляет собой прямую зеленую линию. Синяя линия из PREM (предварительной эталонной модели Земли), вероятно, ближе к фактическому профилю для g .

Второй интересный случай касается жизни на планете со сферической оболочкой. Этот сценарий был предложен во многих научно-фантастических рассказах. Игнорируя важные инженерные проблемы, можно было бы построить оболочку с желаемым радиусом и общей массой, чтобы г на поверхности были такими же, как у Земли. Угадайте, что произойдет, если вы спуститесь на лифте внутрь оболочки, где между вами и центром нет никакой массы? Какие преимущества это дало бы при путешествии на большие расстояния из одной точки сферы в другую? И, наконец, какой эффект был бы, если бы планета вращалась?

напряженность гравитационного поля

напряженность гравитационного поля

Глоссарий по физике BSL — напряженность гравитационного поля — определение

Это способ измерения гравитации.Формула: вес/масса = напряженность гравитационного поля.

Напряженность гравитационного поля = Вес/единица массы Н/кг

Вес = масса x единица напряженности гравитационного поля Н

На Земле напряженность гравитационного поля составляет 10 Н/кг. Другие планеты имеют другую силу гравитационного поля. Сила гравитационного поля Луны составляет 1,6 Н/кг. Вы могли видеть фильмы о астронавтах, прыгающих высоко на Луне.

Здесь, на Земле, если я прыгну, меня притянет обратно к земле под действием силы тяжести.Каков мой вес? Моя масса 80кг и если умножить на силу гравитационного поля (10Н/кг) — мой вес 800Н. Теперь, если я полечу на Луну, моя масса будет такой же, 80 кг. Мы умножаем это на силу гравитационного поля Луны, которая составляет 1,6 Н/кг. Это означает, что мой вес на Луне составляет 128 Н. Так что у меня разные веса на Земле и на Луне. Вот почему астронавты могут прыгать высоко в воздух на Луне — там они легче.

Юпитер — очень большая планета с сильным гравитационным полем 25 Н/кг.Мое тело 80 кг. Если я отправлюсь на Юпитер, мой вес будет 25 х 80 = 2000 Н. Это означает, что я не смогу оторваться от земли или встать прямо! Я бы, наверное, лежал там все время. Таким образом, вес варьируется в зависимости от того, на какой планете вы находитесь. Вы можете узнать больше самостоятельно, просмотрев таблицы веса на разных планетах.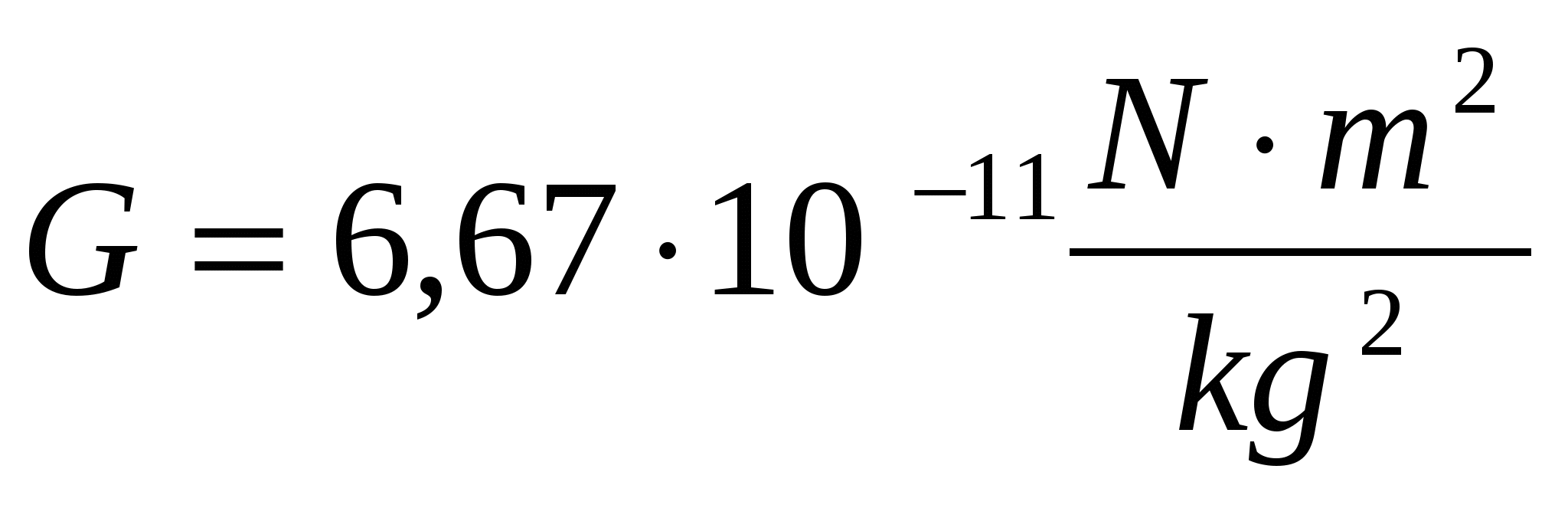

http://en.wikibooks.org/wiki/Wikijunior:Solar_System/About_gravity,_mass,_and_weight

Ускорение под действием силы тяжести — Frega Physics

---

---

Ускорение под действием силы тяжести — это скорость изменения скорости объекта под действием силы тяжести.  Все объекты, упавшие из одного места, упадут на землю за одинаковое время, независимо от массы. На Земле среднее ускорение свободного падения составляет -9,81 м/с ² *. Объекты, которые не ударяются о землю одновременно, испытывают сопротивление воздуха, силу трения, которая замедляет движение объектов. Этого можно добиться, уменьшив сопротивление воздуха путем изменения формы объекта.

Ускорение свободного падения ВСЕГДА отрицательное. Любой объект, на который действует только сила тяжести (снаряд или объект в свободном падении), имеет ускорение -9.81 м/с ² независимо от направления.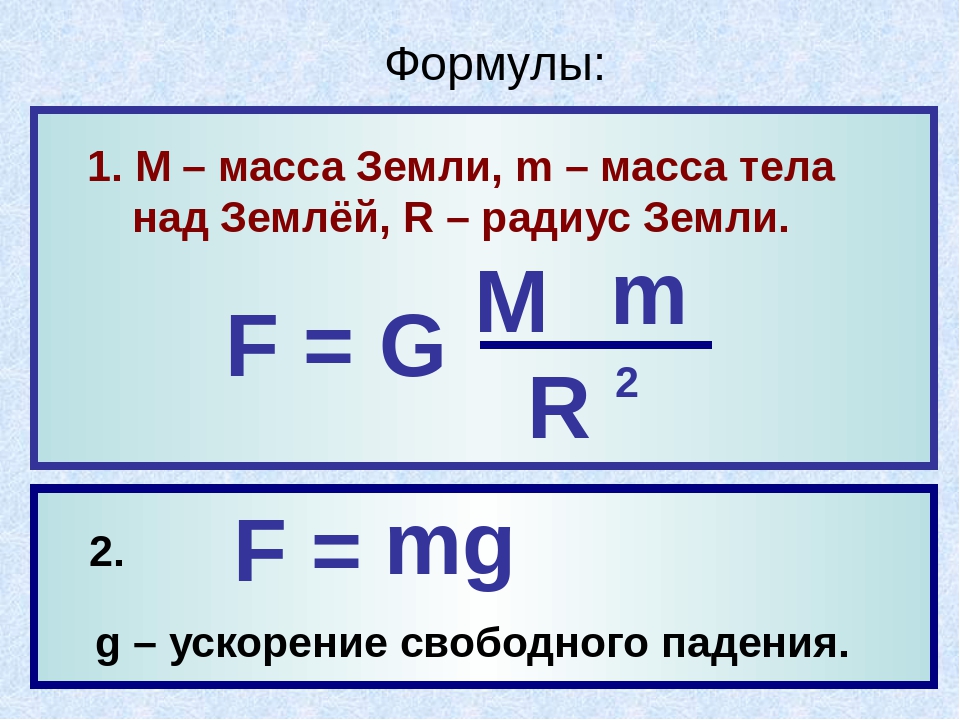 Ускорение отрицательно при движении вверх, потому что скорость уменьшается. Ускорение отрицательное при движении вниз, потому что оно движется в отрицательном направлении, вниз. Даже в верхней части пути, где мгновенная скорость равна 0 м/с, ускорение равно -9,81 м/с ² .

Всякий раз, когда в задаче упоминается объект, находящийся «в свободном падении», «падающий», «брошенный», «подброшенный» или любой другой синоним, предполагается постоянное значение ускорения из-за силы тяжести.Если в уравнении есть a , например v = v ₀ + at , ускорение будет отрицательным . Если в уравнении есть g , например, W = mg, подразумевается направление, а ускорение положительное .

*-10 м/с ² является приемлемым числом для большинства расчетов в задачах, но -9,81 является более точным числом.

Переменные Символ	Имя переменной	SI Unit	Другие возможные Units	Особенности
	ускорение	метра в секунду в секунду (м/с/с) или метра в секунду в квадрате (м/с 2 )	миль/ч/с, км/ч/с	Ускорение – это скорость, при которой скорость изменения; это изменение скорости в единицу времени. На этом уровне считать ускорение равномерным или постоянным. Поскольку это вектор, берется направление в учетную запись. Будьте осторожны со своими негативами и позитивами. Положительный ускорение может означать ускорение, движение вперед или замедление, двигаться назад. Отрицательное ускорение может означать замедление, двигаться вперед или ускоряться, двигаться назад.
г	г	Ускорение из-за гравитации	метров в секунду в секунду (м / с / с) или метра на второй квадрат (м / с 2 )	миль в час / с, км/ч/с	При отсутствии сопротивления воздуха все предметы при свободном падении ударятся о землю одновременно при падении с одной и той же высоты, независимо от масса.Ускорение под действием силы тяжести это установленный номер для определенного места, обычно по планете (но это число может незначительно варьироваться на поверхности планеты в зависимости от расстояния от ядра планеты). На Земле среднее ускорение из-за гравитация равна -9,81 м/с 2 (хотя -10 м/с 2 приемлемо для использования в большинстве расчетов). Когда в уравнении используется символ г , предполагается направление, а для расчетов используется абсолютное значение (+9.81 или +10).

См. Ускорение (сложное) для примера того, как использовать ускорение под действием силы тяжести в задаче о свободном падении.

---

---

Понимание гравитации и веса — физика средней школы

Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному агенту, указанному ниже.Если университетские наставники примут меры в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права.Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.

Чтобы подать уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \ достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем а ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.

Отправьте жалобу нашему назначенному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

 

.