Разбор сложных задач ЕГЭ по физике вместе с ведущими преподавателями МИЭТ
Разбор сложных задач ЕГЭ по физике вместе с ведущими преподавателями МИЭТ
23 октября 2020 2912 просмотра
В рамках проекта «Инженерный класс в московской школе» НИУ МИЭТ подготовил два цикла занятий по физике для учеников 10-х и 11-х классов: «С профессором МИЭТ к высоким баллам – решение задач повышенной сложности по физике» и «О простых задачах по физике, которые трудно решаются». Лучшие преподаватели университета прочитают тематические лекции и расскажут о методах решений заданий разного уровня сложности, в том числе из 3-й части ЕГЭ.
2 ноября стартуют лекции для 10-х и 11-х классов «С профессором МИЭТ к высоким баллам – решение задач повышенной сложности по физике»:
2 ноября, 16:30. Тема: «Механика»
Преподаватель – доцент кафедры Общей физики И.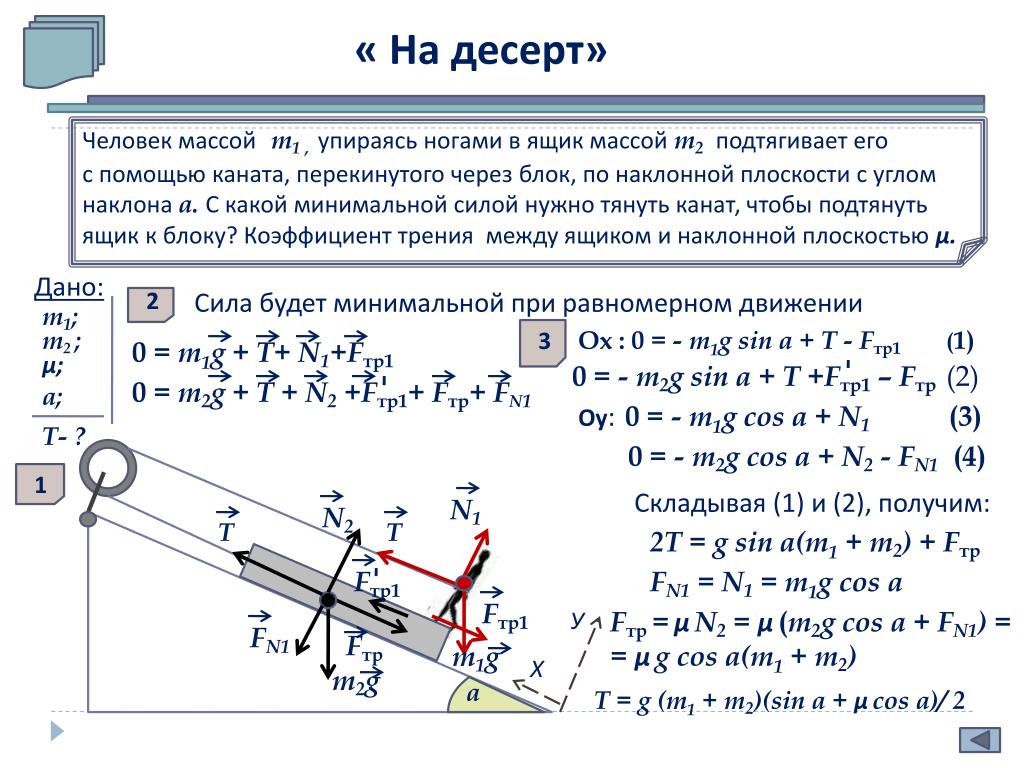 В. Федоренко
В. Федоренко
Лекция адресована как десятиклассникам, так и одиннадцатиклассникам – тем школьникам, которые уже изучили раздел курса элементарной физики «Механика». Рассматриваются методы решения задач части 3 ЕГЭ по физике, основанные на использовании законов статики, динамики и законов сохранения. Лекция сопровождается показом и обсуждением видеодемонстраций.
Ссылка на регистрацию
4 ноября, 16:30. Тема: «МКТ и ТД»
Преподаватель – доцент кафедры Общей физики А.Б. Спиридонов
На лекции предполагается рассмотреть примеры решения задач по молекулярно-кинетической теории и термодинамике. Будут сформулированы основные определения и законы. Часть предлагаемых задач может показаться простыми, когда знаешь, как их решать. Другие задачи – это задачи повышенной сложности.
Ссылка на регистрацию
5 ноября, 18:00. Тема: «Оптика, квантовая физика»
Преподаватель – доцент кафедры Общей физики Н.
На лекцию приглашаются ученики 11 класса. Будут рассмотрены оригинальные способы решения задач повышенной сложности из раздела оптики и квантовой физики. Предлагаемые способы решения демонстрируют связь физических законов, изучаемых в разных разделах курса физики.
Ссылка на регистрацию
19 ноября, 18:00. Тема: «Электромагнитная индукция»
Преподаватель – профессор кафедры Общей физики И.Н. Горбатый
Лекция рассчитана на одиннадцатиклассников, которые завершили или завершают изучение раздела «Электромагнитная индукция» и планируют сдавать ЕГЭ по физике. Вспомним по этой теме основные понятия и формулы, рассмотрим сначала простые, затем более сложные и олимпиадные задачи про электромагнитную индукцию, самоиндукцию и энергию магнитного поля.
Ссылка на регистрацию
Второй цикл «О простых задачах по физике, которые трудно решаются» начнется 10 ноября:
10 ноября, 18.00. Тема: «Механика»
Тема: «Механика»
Преподаватель – доцент кафедры Общей физики Н.Б. Погибельская
На лекцию приглашаются учащиеся 10 и 11 классов, которые изучили или активно изучают разделе физики «Механика». На занятии будут разобраны задания из 3 части ЕГЭ по основным разделам механики: статика, динамика, законы сохранения. Предлагаемые задачи имеют различный уровень сложности, но иногда решаются просто и оригинально.
Ссылка на регистрацию
11 ноября, 16:30. Тема: «Электричество и магнетизм»
Преподаватель – доцент кафедры Общей физики А.Б. Спиридонов
На лекции предполагается рассмотреть примеры решения задач по трем темам: потенциал, постоянный ток и электромагнитная индукция. Перед каждым разделом будут сформулированы необходимые определения и законы. Уровень сложности предлагаемых заданий от простых, «понятийных» до относительно сложных, требующих нестандартных методов решения.
Ссылка на регистрацию
12 ноября, 18. 00. Тема: «Молекулярная физика, термодинамика и оптика»
00. Тема: «Молекулярная физика, термодинамика и оптика»
Преподаватель – доцент кафедры Общей физики В.Б. Гундырев
На лекции будут рассмотрены примеры решения задач по трем темам: молекулярная физика, термодинамика и оптика. Будут рассмотрены задачи, кажущиеся сложными, но имеющие простое и наглядное решение.
Ссылка на регистрацию
16 ноября, 18.00. Тема: «Обзор по всем темам»
Преподаватель – профессор кафедры Общей физики Г.Н. Гайдуков
Анализ результатов выполнения заданий ЕГЭ последних пяти лет показывает, что в каждом варианте встречаются задания, которые оказываются трудными для абитуриентов. Эта особенность проявляется независимо от раздела физики, от типа задания, а также от уровня подготовки абитуриентов. В лекции, на конкретных примерах экзаменационных заданий, показываются причины возникновения затруднений в процессе их рещения. Как правило, основная причина связана с неполным или поверхностным анализом нестандартных условий даже в простых задачах.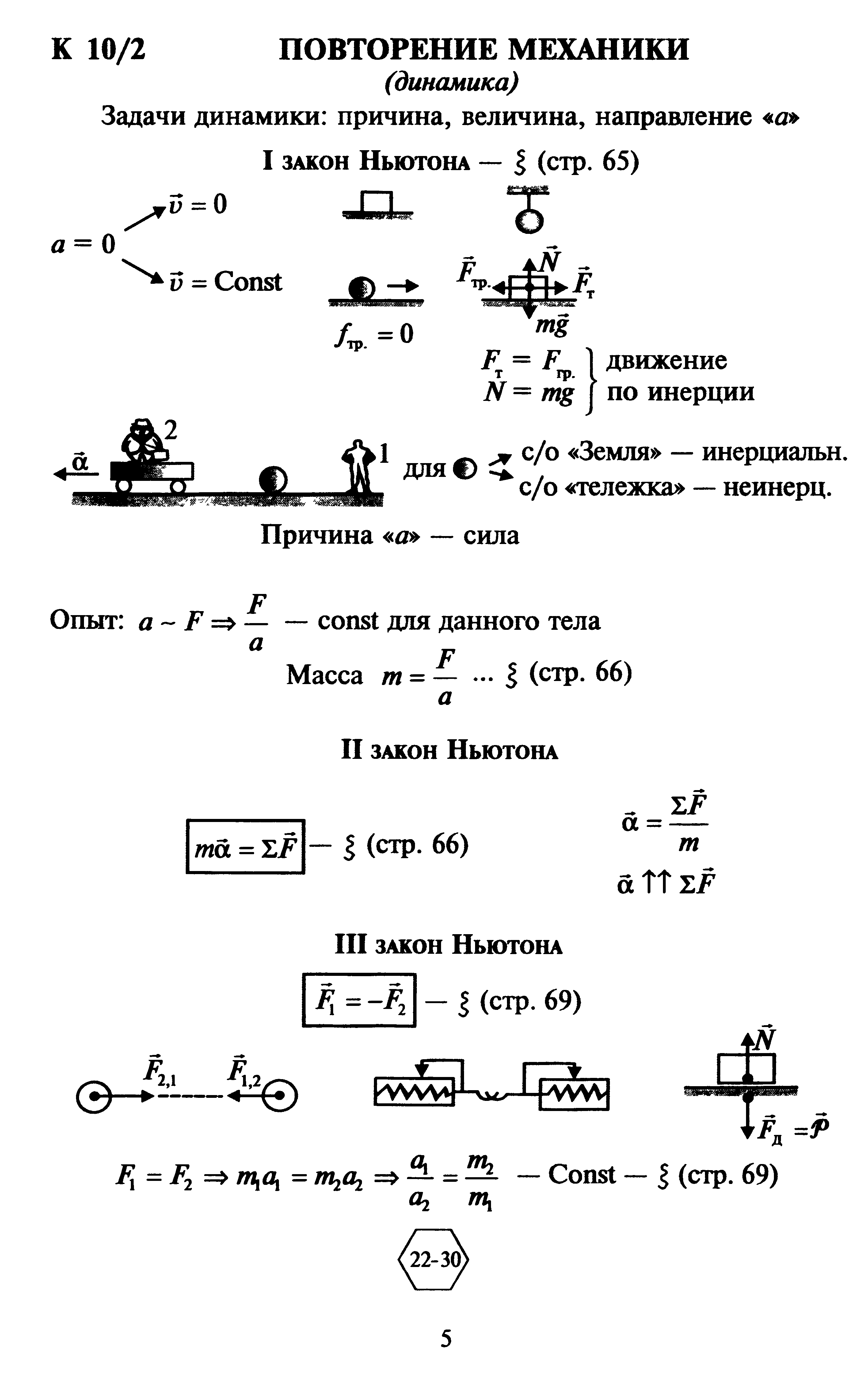
Ссылка на регистрацию
РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ И СТАТИКИ
Продолжаем публиковать разбор конкурсных задач, предлагавшихся поступающим на физический факультет МГУ в разные годы (см. «Наука и жизнь» № 2, 2001 г.). Следует отметить, что статьи рубрики «Абитуриенту на заметку» не учебник, а дополнение к нему. Они дают расширенное и более точное представление о физических явлениях, рассказывают о методике решения задач и разъясняют непростые случаи, которые могут встретиться на вступительных экзаменах. Не выходя за рамки программы средней школы, статьи тем не менее адресованы именно абитуриентам, то есть тем, кто заканчивает школу и готовится поступать в вуз. Родители, посочувствуйте своим чадам: чтобы поступить в вуз, они должны знать все, что здесь написано, и даже еще больше.
При решении обсуждаемых задач желательно придерживаться следующего стандартного порядка.
Нарисуйте объекты, взаимодействие которых требуется учесть, и изобразите силы, действующие на каждое из рассматриваемых тел, помня о третьем законе Ньютона (рисуйте силы парами!). При этом силы реакции, с которыми взаимодействуют соприкасающиеся твердые тела и которые обычно не известны, удобно изображать в виде двух составляющих:

Глядя на сделанный рисунок, запишите для каждого из тел уравнение движения в виде miai=ΣF i, где ΣFi векторная сумма всех сил, действующих на тело массой mi, центр масс которого движется с ускорением аi относительно инерциальной системы отсчета (ИСО). Обычно для дальнейшего решения задачи составленные векторные уравнения следует переписать в проекциях на оси декартовой ИСО. Хотя существование ИСО постулируется первым законом Ньютона, только на основании опыта удается определить, с каким реальным телом следует связать систему отсчета, чтобы ее можно было считать инерциальной.
Согласно современным данным, при исследовании движения тел в небольшой области пространства в течение нескольких минут обычные методы измерения дают результаты, согласующиеся с расчетными в пределах ошибок измерения, если инерциальной считать лабораторную систему (ЛСО), то есть систему отсчета, неподвижную относительно тех точек поверхности Земли, вблизи которых производится эксперимент.
Если же речь идет о более масштабных движениях, например движении искусственных спутников Земли, то инерциальной обычно можно считать геоцентрическую систему, центр которой совпадает с центром Земли, а оси направлены на достаточно удаленные от Земли звезды.
Полученная указанным способом система уравнений, как правило, оказывается неполной. Запишите недостающие уравнения, учитывая кинематические связи между телами системы, особенности сил и специальные допущения. Если в задаче особо не оговариваются иные условия, то по умолчанию, без формулировки их в явной форме, обычно считают выполненными так называемые «стандартные» допущения:
Запишите недостающие уравнения, учитывая кинематические связи между телами системы, особенности сил и специальные допущения. Если в задаче особо не оговариваются иные условия, то по умолчанию, без формулировки их в явной форме, обычно считают выполненными так называемые «стандартные» допущения:
при криволинейном движении размеры тел столь малы, что их можно заменить материальными точками. При прямолинейном движении считается, что тела движутся поступательно и являются твердыми;
все нити, связывающие тела, нерастяжимы и в процессе движения остаются натянутыми. Если тела соединены пружинами, то при установившемся движении натяжение пружин не изменяется и их длина остается постоянной;
участки нитей, не лежащие на блоках, при движении тел не изменяют своей ориентации относительно поверхностей, по которым движутся связанные нитями тела;
грузы по наклонным плоскостям движутся так, что их скорости перпендикулярны линии пересечения этих плоскостей с горизонтальной плоскостью;
блоки, если они вращаются при движении тел, считаются идеальными цилиндрами, вращающимися вокруг своих геометрических осей, и на них не действуют силы сопротивления движению;
действием воздуха на рассматриваемые тела, массой нитей и блоков, а также гравитационным взаимодействием тел можно пренебречь.
Следует отметить, что многие абитуриенты испытывают серьезные трудности не только при обосновании возможности применения в данной конкретной ситуации этих допущений и вытекающих из них следствий, но и при формулировке самих допущений. Это, по-видимому, связано с тем, что в школьных учебниках и пособиях для поступающих «стандартным» допущениям порой не уделяется должного внимания.
Решите полученную полную систему уравнений, обращая внимание на равносильность производимых математических преобразований и выделяя особые с точки зрения математики случаи. Часто некоторые из полученных решений не удовлетворяют возможным значениям искомой величины с точки зрения ее физического смысла и условия задачи. Ясно, что такие решения должны быть отброшены.
Проанализируйте полученные решения с точки зрения размерности и так называемых предельных случаев.
Подставьте в полученные выражения заданные числовые значения, помня о существовании разных систем единиц измерения и соблюдая разумную точность при вычислениях. Если числовые данные в условии не приведены, найдите соотношения между входящими в ответ величинами, при которых справедливо полученное решение.
Если числовые данные в условии не приведены, найдите соотношения между входящими в ответ величинами, при которых справедливо полученное решение.
Применение указанной схемы должно помочь не только избежать часто встречающихся у абитуриентов ошибок, но и быстрее получить правильный ответ. В качестве иллюстрации рассмотрим решение задач, предлагавшихся на вступительных испытаниях на физическом факультете МГУ в последние годы.
Задача 1 (1998 г.). На горизонтальной плоскости стоит гладкий клин массой М с углом α при основании. На клин положили брусок массой m, к которому прикреплена легкая нерастяжимая нить, проходящая через зажим, закрепленный на клине так, как показано на рис. 1. С каким ускорением может двигаться клин после того, как брусок отпустят без начальной скорости, если максимальная величина силы трения покоя нити о зажим равна F?
Решение. Поскольку клин по условию задачи является гладким, сила R реакции горизонталь ной плоскости, действующая на него, направлена вертикально вверх, а сила N реакции клина на брусок — по нормали к наклонной плоскости клина так, как показано на рис.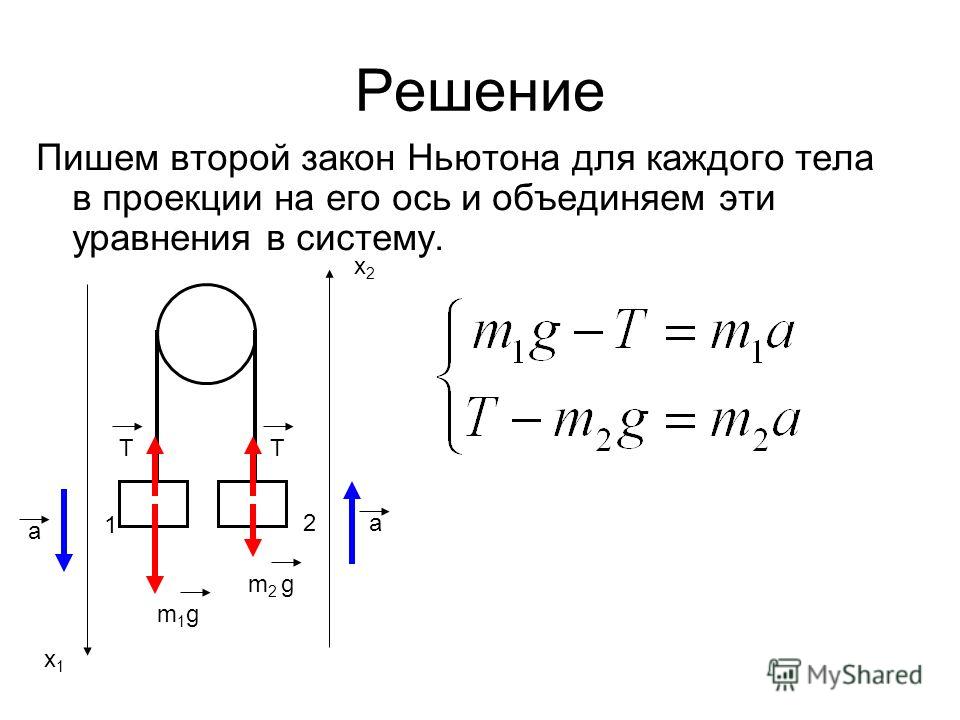 2. Здесь же изображены сила , действующая на клин со стороны бруска, и силы тяжести mg и Mg, действующие на брусок и клин. По условию задачи на нить не действуют силы тяжести. Поэтому в соответствии с рис. 1 отрезок нити между бруском и зажимом можно считать прямолинейным и параллельным наклонной плоскости клина. Поскольку со стороны нити на зажим и прикрепленный к ней брусок действуют силы, направленные только вдоль ее оси, можно утверждать, что эти силы параллельны наклонной плоскости клина и направлены так, как показано на рис. 2. С учетом обозначений, использованных на этом рисунке, и третьего закона Ньютона силы, действующие на нить со стороны зажима (T) и бруска (Т*), должны удовлетворять условиям: и . Поскольку на нить не действуют другие тела, масса нити полагается равной нулю, а ее ускорение, очевидно, может быть только величиной ограниченной, то на основании второго закона Ньютона можно утверждать, что а потому . С учетом полученных соотношений, считая, как обычно лабораторную систему XOY, неподвижную относительно плоскости, на которой стоит клин, инерциальной, уравнения движения клина и бруска в проекциях на оси этой системы можно записать в виде:
2. Здесь же изображены сила , действующая на клин со стороны бруска, и силы тяжести mg и Mg, действующие на брусок и клин. По условию задачи на нить не действуют силы тяжести. Поэтому в соответствии с рис. 1 отрезок нити между бруском и зажимом можно считать прямолинейным и параллельным наклонной плоскости клина. Поскольку со стороны нити на зажим и прикрепленный к ней брусок действуют силы, направленные только вдоль ее оси, можно утверждать, что эти силы параллельны наклонной плоскости клина и направлены так, как показано на рис. 2. С учетом обозначений, использованных на этом рисунке, и третьего закона Ньютона силы, действующие на нить со стороны зажима (T) и бруска (Т*), должны удовлетворять условиям: и . Поскольку на нить не действуют другие тела, масса нити полагается равной нулю, а ее ускорение, очевидно, может быть только величиной ограниченной, то на основании второго закона Ньютона можно утверждать, что а потому . С учетом полученных соотношений, считая, как обычно лабораторную систему XOY, неподвижную относительно плоскости, на которой стоит клин, инерциальной, уравнения движения клина и бруска в проекциях на оси этой системы можно записать в виде:
где Ах и Ау проекции ускорения А клина на оси ОХ и ОY, ах и ау проекции ускорения бруска на указанные оси.
Если ускорение бруска равно нулю, то из двух последних уравнений следует, что T = m g sinα . Поэтому если F ≥ T, то и брусок и клин должны оставаться неподвижными, то есть при F ≥ m g sinα ускорение клина A = 0.
Если же F Т при сделанных выше предположениях будет равна F максимальной величине силы трения нити о зажим и брусок должен скользить по клину, а клин, в свою очередь, также должен двигаться с некоторым ускорением. Поскольку клин может двигаться только горизонтально, то Ay = 0. Ясно, что отличные от нуля компоненты ускорений клина и бруска не могут быть независимыми, так как брусок по условию движется лишь по поверхности клина. В системе координат X1О1Y 1, неподвижной относительно клина, оси которой параллельны осям лабораторной системы отсчета XOY, приращения координат и некоторой точки бруска должны удовлетворять условию . Учитывая, что начала отсчета на осях OY и O1Y1, показанных на рис. 2 систем координат, не смещаются по вертикали друг относительно друга при возможных перемещениях клина, можно утверждать, что . Вместе с тем, если клин испытывает перемещение , а брусок относительно клина смещается на , координаты точек бруска относительно оси OХ изменяются на . Таким образом, приращения координат клина и бруска относительно осей лабораторной системы отсчета связаны между собой соотношением .Учитывая, что полученное соотношение справедливо для любых моментов времени, когда брусок находится на клине, на основании последнего соотношения и определений скорости и ускорения в данном направлении можно утверждать, что составляющие ускорений бруска и клина, входящие в уравнения движения этих тел, связаны между собой соотношением ay = (ax — Ax) tg α. Из этого выражения и уравнения движения бруска следует, что
2 систем координат, не смещаются по вертикали друг относительно друга при возможных перемещениях клина, можно утверждать, что . Вместе с тем, если клин испытывает перемещение , а брусок относительно клина смещается на , координаты точек бруска относительно оси OХ изменяются на . Таким образом, приращения координат клина и бруска относительно осей лабораторной системы отсчета связаны между собой соотношением .Учитывая, что полученное соотношение справедливо для любых моментов времени, когда брусок находится на клине, на основании последнего соотношения и определений скорости и ускорения в данном направлении можно утверждать, что составляющие ускорений бруска и клина, входящие в уравнения движения этих тел, связаны между собой соотношением ay = (ax — Ax) tg α. Из этого выражения и уравнения движения бруска следует, что
m Ax sinα = mg cos α — N/ Умножив обе части полученного соотношения на sina и сложив результат с первым уравнением движения клина, определим проекцию ускорения клина на ось ОХ при F
Таким образом, при выполнении сделанных в ходе решения задачи предположений проекция ускорения клина на ось ОХ равна:
Задача 2 (1997 г. ). Через гладкий блок, прикрепленный к гладкой неподвижной наклонной плоскости, образующей с горизонтом угол α, перекинута легкая нерастяжимая нить. Один конец нити прикреплен к бруску массой М, лежащему на плоскости, а свисающий конец пропущен через узкое отверстие в грузе массой m, как показано на рис. 3. Если одновременно отпустить брусок и груз, нить будет проскальзывать через отверстие с постоянным ускорением а относительно груза. Найти силу натяжения нити.
). Через гладкий блок, прикрепленный к гладкой неподвижной наклонной плоскости, образующей с горизонтом угол α, перекинута легкая нерастяжимая нить. Один конец нити прикреплен к бруску массой М, лежащему на плоскости, а свисающий конец пропущен через узкое отверстие в грузе массой m, как показано на рис. 3. Если одновременно отпустить брусок и груз, нить будет проскальзывать через отверстие с постоянным ускорением а относительно груза. Найти силу натяжения нити.
Решение. Для решения задачи выберем неподвижную относительно наклонной плоскости систему координат XОY так, как показано на рис. 4. Будем считать, что центр масс бруска и нить лежат в одной вертикальной плоскости, перпендикулярной линии пересечения заданной наклонной плоскости с горизонтом. Поскольку нить нерастяжима, а груз после отпускания (момент времени t=0) скользит относительно нити с постоянным ускорением, то координата у бруска и координата х груза для произвольного момента времени 0 k, где tк момент времени, когда либо брусок хотя бы частично начнет соскальзывать с наклонной плоскости, либо груз перестанет двигаться по нити, должны удовлетворять соотношению
x + y = C + at2/2,
где С длина отрезка нити от бруска до верхней грани груза перед их отпусканием. Поэтому проекция скорости груза на ось ОХ
Поэтому проекция скорости груза на ось ОХ
и проекция скорости бруска на ось ОY
для указанных моментов времени должны удовлетворять соотношению
.
Следовательно, уравнение кинематической связи — соотношение между соответствующими координатами ускорения бруска и груза — имеет вид ax + Ay = a.
Поскольку блок гладкий, а нить невесома, то величина Т силы натяжения на всем отрезке нити от бруска до верхнего торца груза остается постоянной. Учитывая, что наклонная плоскость гладкая, и пренебрегая силами трения со стороны окружающей рассматриваемые тела среды, на основании второго закона Ньютона уравнения движения бруска и груза для указанных моментов времени можно записать в виде
m ax = m g — T
и
M Ay = M g sinα — T,
где g величина ускорения свободного падения. Конечно, сказанное верно в предположении, что связанная с плоскостью ЛСО инерциальна.
Решая совместно уравнения кинематической связи и движения тел, найдем искомую величину силы натяжения нити при выполнении сделанных предположений:
(Окончание следует.)
Мартовская образовательная программа по физике: Руководители
Положение о Мартовской образовательной программе по физике
Образовательного центра «Сириус»
1. Общие положения
Настоящее Положение определяет порядок организации и проведения Мартовской образовательной программы по физике Образовательного центра «Сириус» (далее – образовательная программа), её методическое и финансовое обеспечение.
1.1. Образовательная программа проводится в Образовательном центре «Сириус» (Образовательный Фонд «Талант и успех») с 07 по 27 марта 2021 года.
1.2. К участию в образовательной программе приглашаются учащиеся 9-х классов (по состоянию на март 2021 года), обучающиеся в образовательных организациях, осуществляющих образовательную деятельность по образовательным программам основного общего и среднего общего образования (в том числе обучающиеся загранучреждений Министерства иностранных дел Российской Федерации, имеющих в своей структуре специализированные структурные образовательные подразделения). Обязательным условием участия в образовательной программе является успешное прохождение конкурсного отбора.
Обязательным условием участия в образовательной программе является успешное прохождение конкурсного отбора.
Общее количество участников образовательной программы: не более 150 человек.
1.3. К участию в образовательной программе допускаются школьники, являющиеся гражданами Российской Федерации.
1.4. Персональный состав участников образовательной программы утверждается Экспертным советом Образовательного Фонда «Талант и успех» по направлению «Наука».
1.5. Научно-методическое и кадровое сопровождение осуществляют сотрудники Центра педагогического мастерства г. Москвы, Московского физико-технического института, физического факультета МГУ им. М.В.Ломоносова.
1.6. В связи с целостностью и содержательной логикой образовательной программы, интенсивным режимом занятий и объемом академической нагрузки, рассчитанной на весь период пребывания обучающихся в Образовательном центре «Сириус», не допускается участие школьников в отдельных мероприятиях или части образовательной программы: исключены заезды и выезды школьников вне сроков, установленных Экспертным советом Фонда по направлению «Наука».
1.7. В случае нарушений правил пребывания в Образовательном центре «Сириус» или требований настоящего Положения решением Координационного совета участник образовательной программы может быть отчислен с образовательной программы.
1.8. В течение учебного года (с июля по июнь следующего календарного года) допускается участие школьников не более чем в двух образовательных программах по направлению «Наука» (по любым профилям, включая проектные образовательные программы), не идущих подряд.
2. Цели и задачи образовательной программы.
2.1. Образовательная программа ориентирована на углублённую подготовку в области физики высокомотивированных талантливых учащихся 9-х классов, выявленных путем конкурсного отбора по итогам самостоятельной работы, и на организацию дальнейшего систематического изучения физики указанными учащимися путем предоставления им дистанционной поддержки после завершения образовательной программы.
2.2. Задачи образовательной программы:
— развитие таланта учащихся в области физики и расширение их кругозора;
— углубленное изучение дополнительных вопросов курса физики, не входящих в школьную программу;
— изучение школьниками элементов высшей математики, необходимых для освоения дополнительных вопросов курса физики;
— рассмотрение приемов и методов решения некоторых типов теоретических задач повышенного уровня сложности по физике;
— развитие навыков решения учебных экспериментальных физических мини-задач, в том числе олимпиадного типа;
— развитие у школьников физического мышления, формирование у них умений ведения дискуссии на научные темы;
— популяризация физики как науки.
3. Порядок отбора участников образовательной программы.
3.1. Отбор участников осуществляется Координационным советом, формируемым Руководителем Образовательного Фонда «Талант и успех», на основании требований, изложенных в настоящем Положении, а также Порядком отбора школьников на профильные образовательные программы Фонда по направлению «Наука».
3.2. В образовательной программе могут принять участие до 150 школьников, осваивающие (по состоянию на март 2021 года) учебную программу по физике для 9 класса в образовательных организациях, реализующих образовательные программы основного общего, среднего общего и дополнительного образования.
3.3. Для участия в конкурсном отборе необходимо пройти регистрацию на официальном сайте Образовательного центра «Сириус».
Регистрация будет доступна до 15 ноября 2020 года. Не зарегистрировавшиеся школьники к участию в образовательной программе не допускаются.
3.4. Отбор участников осуществляется в два тура. Первый тур – дистанционный учебно-отборочный курс. Второй тур – заключительный (очный) тур в регионах Российской Федерации.
Первый тур – дистанционный учебно-отборочный курс. Второй тур – заключительный (очный) тур в регионах Российской Федерации.
3.5. С 01 ноября по 12 декабря 2020 года для зарегистрировавшихся школьников будет организован дистанционный учебно-отборочный курс. Информация о курсе размещается в личном кабинете участника после его регистрации.
3.6. В рамках дистанционного учебно-отборочного курса оценивается успешность освоения учебного материала, а также результат, показанный на обязательном дистанционном тестировании. Дистанционное тестирование с целью отбора на заключительный (очный) тур будет проведено 12 декабря 2020 года.
3.7. По итогам дистанционного учебно-отборочного курса и обязательного дистанционного тестирования будут определены участники заключительного очного отборочного тура, который пройдет на площадках в субъектах Российской Федерации 26 декабря 2020 года.
3.8. Список школьников, допущенных к участию в заключительном очном отборочном туре, будет опубликован на сайте Образовательного центра «Сириус» 16 декабря 2020 года.
3.9. Регламент проведения заключительного очного отборочного тура, места и время проведения этого тура в регионах будут опубликованы на сайте Образовательного центра «Сириус» не позднее 17 декабря 2020 года.
3.10. В образовательной программе могут принять участие не более 10 школьников от одного субъекта Российской Федерации.
3.11. Учащиеся, отказавшиеся от участия в образовательной программе, могут быть заменены на следующих за ними по рейтингу школьников (по итогам заключительного очного отборочного тура). Решение о замене участников принимается Координационным советом программы.
3.12. Список участников образовательной программы будет опубликован на сайте Образовательного центра «Сириус» не позднее 18 января 2021 года.
3.13. С 20 января по 28 февраля 2021 года для участников образовательной программы будет доступен дистанционный курс предобучения.
4. Аннотация образовательной программы.
Образовательная программа включает в себя лекции, семинары и практические занятия по физике, проводимые лучшими педагогами ведущих образовательных центров страны; тренировочные туры по решению физических задач, научно-популярные лекции ученых, ведущих исследования в различных областях современной физики; общеобразовательные, спортивные и культурно-досуговые мероприятия, экскурсии по городу Сочи и его окрестностям.
5. Финансирование образовательной программы
Оплата проезда, пребывания и питания школьников – участников образовательной программы осуществляется за счет средств Образовательного Фонда «Талант и успех».
Школьный сайт — Физика_профиль
для 10 класса:
ДЛЯ ТЕХ КТО СДАЁТ ЕГЭ ПО ФИЗИКЕ скачать ЗАДАЧИ С РЕШЕНИЕМ
10 КЛАСС (ПРОФИЛЬ-ФИЗИКА) СКАЧАТЬ КНИГУ-УЧИМСЯ РЕШАТЬ ЗАДАЧИ ПО МЕХАНИКЕ и её просмотреть.
ЗАГЛЯНИТЕ СЮДА
ДЛЯ ТЕХ КТО СДАЁТ ФИЗИКУ » ВЛАЖНОСТЬ» СМОТРЕТЬ
ЗДЕСЬ ВЫ НАЙДЕТЕ ВИРТУАЛЬНЫЕ ОПЫТЫ ПО ФИЗИКЕ
ПОЛОЖЕНИЕ
о текущем контроле и промежуточной аттестации обучающихся
Требования к оформлению рефератов
Как получить максимальный балл на ЕГЭ. Физика. Решение заданий повышенного и высокого уровня сложности. Ханнанов Н.К.
РЕШЕНИЕ ЗАДАЧ ПО ФИЗИКЕ ПОДГОТОВКА К ЕГЭ
электростатика
для тех кто хочет сдать физику
ЗАДАЧИ части «С» С РЕШЕНИЕМ
Учимся решать задачи по физике скачать книгу здесь
для учеников 10(ПРОФИЛЬ) классов сборник задач Рымкевич скачать
КАК НАУЧИТЬСЯ РЕШАТЬ ЗАДАЧИ ПО ФИЗИКЕ
примеры задач части с
ЗАДАЧИ С РЕШЕНИЕМ ЧАСТИ С1
Содержание страницы:
Пособие по физике
Я написал электронную книгу, содержащую весь курс школьной физики. В ней имеется вся теория, необходимая для подготовки к ЕГЭ.
В ней имеется вся теория, необходимая для подготовки к ЕГЭ.
Книгу лучше читать не в браузере, а с помощью программы просмотра PDF (например, Adobe Reader). Тогда сбоку в закладках (bookmarks) будет отображена вся структура книги в виде ссылок на соответствующие разделы. То есть наряду с оглавлением (пункты которого являются ссылками) вы получаете ещё одно меню навигации по книге.
Разумеется, чтения пособия недостаточно; самое главное — уметь решать физические задачи. Этому мы и учимся на наших занятиях.
Главы пособия
При желании вы можете скачать каждую главу в отдельности (если, например, хотите освоить лишь механику или электродинамику).
Параграфы пособия: «Физика в листках»
Если вам необходимо ознакомиться с отдельными вопросами, то перед вами — содержание пособия в виде листков. Именно с этой «Физики в листках», собственно, пособие и начиналось 🙂
Необходимая математика
Механика
Электродинамика
Молекулярная физика и термодинамика
Теория относительности
Оптика
Квантовая физика
Статьи о подготовке к ЕГЭ по физике
1. Научная «Оксфордская видеоэнциклопедия для детей»
Научная «Оксфордская видеоэнциклопедия для детей»
Великобритания, 1996 год — Часть1.
Скачать: Яндекс
Содержание всех частей:
Часть 1: антибиотики, атмосфер, атомная энергия, атомы, бактерии и вирусы, вакуум, вода, воздух, время, газы, голограмма.
Часть 2: давление, дыхание, животные, живые существа, жидкости, загрязнение среды, звук, кислород, кислоты, клетки, кристаллы, линзы.
Часть 3: магниты, металлы, механизмы, мощность, нефть, огонь, озон, органы чувств, парниковый эффект, плавучесть, пластмассы, полет.
Часть 4: радар, радиация, радио, растения, рентгеновские лучи, рост, свет, сила тяжести, соли, температура, тепло, топливо, трение.
Часть 5: углерод, химические вещества, цвет, цепи питания, эволюция, экология, электричество, электроника, элементы, энергия.
Общая длительность всех частей фильма — 183 мин.
Физика-класс!
… электронная библиотека
Советую посмотреть видео ролики здесь
Сборник составлен к классическому курсу физики для 10— 11 классов авторов Г. Я. Мякишева, Б. Б. Буховцева, Н. Н. Сотского.
Я. Мякишева, Б. Б. Буховцева, Н. Н. Сотского.
В первой части пособия приведены задачи по всем темам, включенным в названный курс физики с указанием соответствующих параграфов учебника.
Вторая часть содержит задачи на темы, не включенные в классический курс физики. Умение решать такие задачи необходимо при поступлении в технические вузы.
для учеников 10-11 классов сборник задач Рымкевич скачать
Программа для просмотра файла
Здесь приведены справочные данные
КАК РЕШАТЬ ЗАДАЧИ ПО КИНЕМАТИКЕ
КАК РЕШАТЬ ЗАДАЧИ НА ЗАКОНЫ НЬЮТОНА
1. Научно-популярные лекции по физике для школьников с демонстрацией физических экспериментов
Лекция 1 Величие и простота законов Ньютона
— знакомит с маятником Фуко, инерцией, законами Ньютона, примерами применения законов динамики. Слушателелям демонстрируются знаменитые опыты, подтверждающие правоту основных законов механики.
Лекция 2. Мир бесконечного движения (основные положения МКТ, явления переноса)
— излагаются основные положения молекулярно-кинетической теории (МКТ), приводятся их экспериментальные обоснования. Рассказывается о различии механического и статистического подхода к описанию физических систем. Демонстрируются эксперименты, подтверждающие основные положения МКТ, в том числе эксперименты, связанные с явлениями диффузии, теплопроводности и вязкости.
Лекция 3. Красота вращающегося мира (гироскопы и волчки)
— рассматриваются эффекты, связанные с вращательным движением тел. Демонстрируется действие центробежной силы и силы Кориолиса. Обсуждается закон сохранения количества движения и связанные с ним эффекты. Демонстрируются гироскопы, устойчивость ориентации вращающихся тел. Демонстрируются необычные движения кельтских камней.
Лекция 4. Размышления о силе пламени (тепловые машины)
— посвящена тепловым машинам. Рассматриваются общие принципы перевода тепла в работу и работы в тепло. Демонстрируются тепловые машины, действующие на различных физических принципах, оценивается эффективность их работы.
Рассматриваются общие принципы перевода тепла в работу и работы в тепло. Демонстрируются тепловые машины, действующие на различных физических принципах, оценивается эффективность их работы.
Лекция 5. Отчего люди не летают? (гидродинамика и аэродинамика)
— посвящена эффектам гидростатики, аэростатики, гидродинамики и аэродинамики. Обсуждаются вопросы, связанные с движением тел в вязкой среде, разбирается причины появления подъемной силы у самолетного крыла. Демонстрируются движение тел в жидкостях и газах, особенности обтекания тел потоком воздуха, подъемная сила.
Лекция 6. Загадочные превращения (испарение и кипение, поверхностные явления, плавление и кристаллизация)
— рассматриваются явления испарения, кипения, плавления и отвердевания. Демонстрируются неравновесные состояния: перегретая жидкость, переохлажденная жидкость и переохлажденный пар. В лекции также рассматриваются явления на поверхности жидкости. Демонстрируются эффекты на поверхности мыльных пленок, воды, и др. жидкостей.
жидкостей.
Лекция 7. Физика и музыка (колебания и волны, акустика)
— посвящена волновым явлениям, в том числе распространению звуковых волн. Демонстрируются соотношение длины звуковых волн и высоты музыкального тона. Демонстрируется явления звукового резонанса. Демонстрируются необычные «музыкальные» инструменты.
Лекция 8. Мир искривленных лучей (геометрическая оптика)
— посвящена известным и малоизвестным явлениям, связанным с распространением световых лучей в линзах, световодах, жидкостях и газа.
Лекция 9. Все цвета радуги (явления интерференции и дифракции)
— рассказывается о разложении белого света в спектр от красного до фиолетового цвета (явление дисперсии), а также о радужных пятнах в лужах с бензином, на мыльных пленках, лазерных дисках и др.
Лекция 10. Мир лазеров и поляризованного света
— рассказывается о явлении поляризации света и его многочисленных проявлениях в окружающей природе и технике, а также об устройстве лазеров и особенностях их использования.
2. Научно-популярные лекции по физике для школьников И. Иванова
Лекция 1. (часть 1) Удивительный мир внутри атомного ядра
Лекция 1. (часть 2) Удивительный мир внутри атомного ядра
Лекция 1. (часть 3) Удивительный мир внутри атомного ядра
Лекция 2. Как расщепляют мгновение
Лекция 3. Вещество в экстремальных состояниях, или Рассказ о том, что произойдет с кирпичом, если его очень сильно сжать и нагреть
Лекция 4. Школьные задачи про современную физику
3. Научно-популярные лекции
Лекция К. Богданова «Физика внутри нас»
Лекция А. Селиверстова «Оптика в старших классах»
Лекция А. Варламова «Физика на кухне»
Лекция Л. Стрельниковой «Нанотехнологии: невидимая революция?»
Лекция В. Шевченко «Физика элементарных частиц для школьников: материя, силы, симметрии»
Лекция В. Баранова «Где границы Солнечной системы?»
Баранова «Где границы Солнечной системы?»
Лекция В. Баранова «Эволюция наших представлений об окружающем Солнечную систему космическом пространстве»
Лекция А. Зильбермана «Электростатика для умных школьников»
Лекция А. Зильбермана «Чему, как и зачем нужно будущих физиков обучать на уроках физики»
Лекция А. Зильбермана «Олимпиады по физике. Практический аспект. Часть 1»
Лекция А. Зильбермана «Олимпиады по физике. Практический аспект. Часть 2»
063. Оптическая система глаза. — 66,9 мв
Скачать: Яндекс
062. Собирающая линза. — 32,1 МВ
Скачать: Яндекс
060. Фокальная плоскость, побочная ось, побочный фокус. -64 МВ
Скачать: Яндекс
059. Фокус и фокусное расстояние. — 72,5 МВ
Скачать: Яндекс
057. Полное отражение в трехгранной призме. -62,4МВ
Скачать: Яндекс
055. Полное внутреннее отражение. — 60,6МВ
— 60,6МВ
Скачать: Яндекс
054. Явление обратимости светового луча. — 8,29 МВ
Скачать: Яндекс
053. Закон преломления света. — 25,6МВ
Скачать: Яндекс
052. Закон отражения света. — 40МВ
Скачать: Яндекс
051. Тень и полутень. -35,3МВ
Скачать: Яндекс
050. Влияние значения индуктивности и емкости на частоту колебаний контура. — 85,4МВ
Скачать: Яндекс
049. Электрические колебания в колебательном контуре. — 74,5МВ
Скачать: Яндекс
048. Резонанс в цепи переменного тока. — 48МВ
Скачать: Яндекс
045. Индуктивность в цепи переменного и постоянного тока. — 38,4МВ
Скачать: Яндекс
044. Емкость в цепи переменного и постоянного тока. — 11,7МВ
Скачать: Яндекс
042. Явление самоиндукции. — 67,4МВ
Скачать: Яндекс
041. Спидометр. — 32,5МВ
Скачать: Яндекс
040. Применение токов Фуко. — 70МВ
Скачать: Яндекс
039. Электросварка. -29,5МВ
Электросварка. -29,5МВ
Скачать: Яндекс
038. Применение индукционного тока. — 37,6МВ
Скачать: Яндекс
037. Индукционный ток в кольце. — 25,4МВ
Скачать: Яндекс
036. Причина возникновения индукционного тока. — 62,5МВ
Скачать: Яндекс
035. Явление электромагнитной индукции. — 24,3МВ
Скачать: Яндекс
034. Термоэлектронная эмиссия. — 59,7МВ
Скачать: Яндекс
033. Термоэлектронная эмиссия. -27,4МВ
Скачать: Яндекс
032. Реле на фоторезисторе. — 33МВ
Скачать: Яндекс
4-е изд., перераб. и доп. 1983. — 434с.
Настоящая книга представляет собой пособие по решению задач повышенной трудности по курсу элементарной физики. Создавая пособие, автор стремился разработать единые методы решения задач по курсу элементарной физики, показать, как нужно использовать эти методы при решении конкретных задач.
Построение книги не является стандартным для задачника. В начале каждой главы даны краткие теоретические сведения, позволяющие вспомнить основные понятия и законы курса физики, приведены формулы, которые используются при решении задач. Далее следуют методические указания по решению задач и примеры их решения. Каждая глава заканчивается задачами для самостоятельного решения. Большинство задач, приведенных в пособии, предлагалось на физических олимпиадах и вступительных экзаменах по физике в ведущих вузах страны. Многие задачи составлены автором. В конце книги помещены ответы к задачам, а также решения некоторых задач.
В начале каждой главы даны краткие теоретические сведения, позволяющие вспомнить основные понятия и законы курса физики, приведены формулы, которые используются при решении задач. Далее следуют методические указания по решению задач и примеры их решения. Каждая глава заканчивается задачами для самостоятельного решения. Большинство задач, приведенных в пособии, предлагалось на физических олимпиадах и вступительных экзаменах по физике в ведущих вузах страны. Многие задачи составлены автором. В конце книги помещены ответы к задачам, а также решения некоторых задач.
Четвертое издание пособия было переработано с учетом усовершенствованной программы по физике для средней школы и переработанных изданий учебников.
Саратов: Научная книга, 2006. — 60 с.
Сборник содержит 50 оригинальных задач физических олимпиад, которые будут полезны будущим исследователям. Ко всем задачам даны подробные решения.
Сборник будет полезен учащимся, заинтересованным в глубоком изучении физики, и их учителям.
Формат: pdf / zip
Размер: 1,2 Мб
Скачать / Download файл
Книги, посвященные как олимпиадным задачам, так и «неформальной» физике (оценки, метод размерностей, компьютерное моделирование, исследовательская работа школьников и т.д.).
В электронном варианте эти книги можно найти в сети Internet по адресам:
http://www.sgtnd.narod.ru/publ/rus/main.htm#other
http://www.sgtnd.narod.ru/wts/rus/olimprobl.htm
http://www.sgtnd.narod.ru/wts/rus/krdf.htm
Извиняюсь если ссылки на сторонние сайты запрещены,но хотелось бы поделиться лекциями:
http://4ege.ru/fizika/215-video-konsult … ast-1.html
http://4ege. ru/fizika/216-video-konsult … oraja.html
ru/fizika/216-video-konsult … oraja.html
http://4ege.ru/fizika/217-video-konsult … ast-3.html
http://4ege.ru/fizika/218-video-konsult … ast-4.html
http://4ege.ru/fizika/219-video-konsult … ast-5.html
Глава 3. Динамика
Задачи на динамику часто входят в задания единого государственного экзамене по физике. Для решения этих задач необходимо понимать смысл законов Ньютона, уметь применять их в простейших ситуациях и знать свойства ряда сил: тяжести, трения, упругости и нескольких других.
Первый закон Ньютона определяет такие системы отсчета, в которых тело, не испытывающее воздействий со стороны других тел (сил), движется прямолинейно и равномерно. Такие системы отсчета называются инерциальными, а движение в отсутствии сил — движением по инерции.
Согласно второму закону Ньютона ускорение тела относительно инерциальных систем отсчета определяется из уравнения
| (3. |
где — масса тела, — векторная сумма сил, действующих на тело (эту сумму часто называют равнодействующей или результирующей силой).
Третий закон Ньютона утверждает, что всегда существует взаимное действие тел друг на друга, причем силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению.
Чтобы использовать уравнение (3.1) для нахождения ускорений тел необходимо задать законы для действующих на них сил. Рассмотрим ряд сил, с которыми приходится сталкиваться в школьном курсе физики.
На любое тело, находящееся вблизи поверхности Земли действует сила притяжения со стороны Земли, которая называется силой тяжести. Эта сила пропорциональна массе тела и может быть записана в виде
| (3.2) |
где — вектор ускорения свободного падения, величина которого равна м/с2 (в расчетах часто используют значение м/с2 ).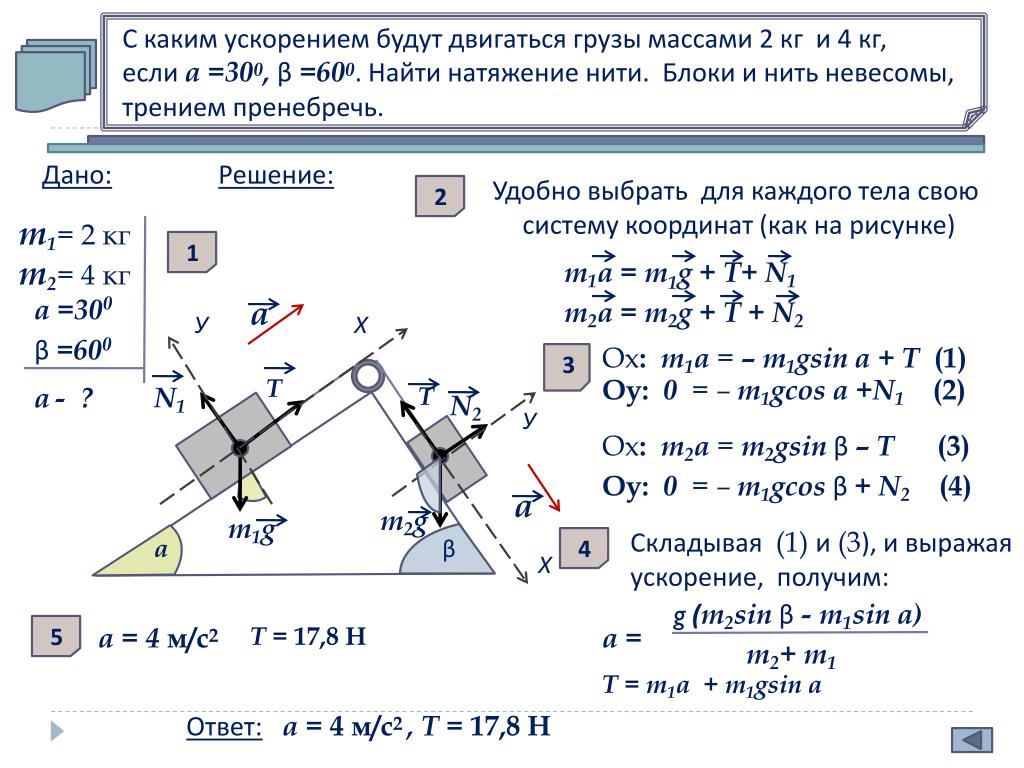
При соприкосновении тел возникают контактные взаимодействия. Сила, перпендикулярная поверхности и возникающая при контакте тела с этой поверхностью, называется силой нормальной реакции поверхности. При скольжении тела по поверхности или при попытке его сдвинуть возникает сила, параллельная поверхности, и препятствующая движению тела. Эта сила называется силой трения (сила трения подробно рассматривается в следующей главе).
Если тело растягивает или сжимает пружину, на тело со стороны пружины действует сила, которая называется силой упругости. Свойства силы упругости определяются законом Гука, в котором утверждается, что сила упругости пропорциональна удлинению пружины
| (3.3) |
Здесь — длина деформированной пружины, — длина этой пружины в недеформированном состоянии, — коэффициент пропорциональности, который называется коэффициентом жесткости (или просто жесткостью) пружины.
При движении тела в воздухе, воде или в другой среде на тело со стороны этой среды действует сила сопротивления, величина которой при небольших скоростях тела пропорциональна его скорости
| (3.4) |
Здесь — скорость тела, — коэффициент пропорциональности, зависящий от свойств среды и геометрии тела. Для больших скоростей сила сопротивления определяется формулой . Направлена сила сопротивления противоположно скорости тела и тормозит его движение.
Рассмотрим теперь задачи.
В задаче 3.1.1 из второго закона Ньютона (3.1) заключаем, что данное тело движется равноускоренно 0,5 м/с2 (ответ 4).
Единицей силы является «Ньютон», который определяется посредством второго закона Ньютона (3.1): 1 Ньютон (1 Н) — это сила, которая телу массой 1 кг сообщает ускорение 1 м/с2 (ответ 3).
В задаче 3. 1.3 только один из четырех предложенных ответов говорит о связи силы с ускорением (ответ 3). Остальные варианты ответов говорят о связи силы и скорости, поэтому они не верны. Аналогичный вопрос (но поставленный графически) предлагается в задаче 3.1.4 Согласно второму закону Ньютона вектор результирующей силы направлен так же, как и вектор ускорения тела (ответ 3), а не как вектор скорости и тем более не как вектор суммы или разности скорости и ускорения (эти векторы вообще нельзя складывать, т.к. они имеют разные размерности).
1.3 только один из четырех предложенных ответов говорит о связи силы с ускорением (ответ 3). Остальные варианты ответов говорят о связи силы и скорости, поэтому они не верны. Аналогичный вопрос (но поставленный графически) предлагается в задаче 3.1.4 Согласно второму закону Ньютона вектор результирующей силы направлен так же, как и вектор ускорения тела (ответ 3), а не как вектор скорости и тем более не как вектор суммы или разности скорости и ускорения (эти векторы вообще нельзя складывать, т.к. они имеют разные размерности).
Несколько следующих задач посвящены простейшим вычислениям на основе второго закона Ньютона. В задаче 3.1.5 второй закон Ньютона в проекциях на вертикальную ось для тела, движущегося вместе с лифтом (т.е. с таким же ускорением) дает
где – сила реакции, действующая на тело со стороны пола (см. рисунок). Отсюда находимо силу реакции
(ответ 2).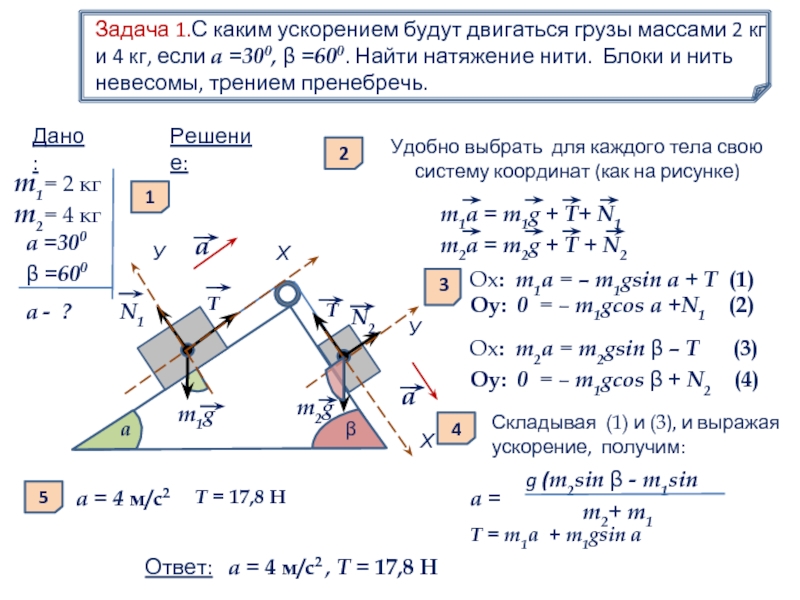
Основная идея решения задачи 3.1.6 заключается в том, чтобы из данных кинематических характеристик движения (пути и времени) найти ускорение тела, а затем из второго закона Ньютона — силу. Из закона равноускоренного движения находим, что ускорение тела равно м/с2. Поэтому Н (правильный ответ — 3).
В задаче 3.1.7 нужно найти силу, которая сообщает телу массой ускорение, направленное вертикально вверх и вдвое превосходящее по величине ускорение свободного падения. Поскольку на рассматриваемое тело действуют только искомая сила и сила тяжести (см. рисунок), второй закон Ньютона для этого тела в проекциях на вертикальную ось дает
Поскольку , из этой формулы находим, что (ответ 3).
В задаче 3.1.8 второй закон Ньютона в проекциях на горизонтальную ось дает
(см.-reshenie-173.jpg) рисунок). Отсюда находим, что м/с2 (ответ 1).
рисунок). Отсюда находим, что м/с2 (ответ 1).
В задаче 3.1.9 проверяется понимание школьником векторного характера второго закона Ньютона. Из закона (3.1) следует, что величина ускорения тела определяется величиной (модулем) равнодействующей силы:
Находя величину равнодействующей силы
получим м/с2 (ответ 4).
Равнодействующей двух сил называется их векторная сумма. Из закона векторного сложения заключаем, что величина суммы векторов не может превосходить суммы величин векторов-слагаемых, и обязательно больше их разности. Поэтому величина равнодействующей сил 30 и 10 Н в задаче 3.1.10 не может равняться 19 Н (ответ 3).
По третьему закону Ньютона силы, с которыми мальчики в задаче 3.2.1 действуют друг на друга, равны. Поэтому массы и ускорения мальчиков связаны соотношением . Отсюда находим ускорение второго мальчика м/с2 (ответ 2).
Поэтому массы и ускорения мальчиков связаны соотношением . Отсюда находим ускорение второго мальчика м/с2 (ответ 2).
Поскольку силы, действующие на канат из задачи 3.2.2 со стороны обеих команд, уравновешивают друг друга, ускорение каната равно нулю. Очевидно, что и любая часть каната, и в частности, его часть от первой команды до какой-то средней точки также будет в равновесии. А поскольку на эту часть каната действуют только сила со стороны одной из команд и сила со стороны другой части каната (сила натяжения), то условие равновесия этой части каната дает , откуда заключаем, что = 5000 Н (ответ 1).
Силы, о которых говорится в третьем законе Ньютона (силы действия и противодействия) приложены к разным телам. В задаче 3.2.3 одна из них действует со стороны Земли на тело (сила тяжести), и, следовательно, вторая должна действовать со стороны тела на Землю — это сила притяжения Земли к телу (ответ 3).
Если бы лифт в задаче 3.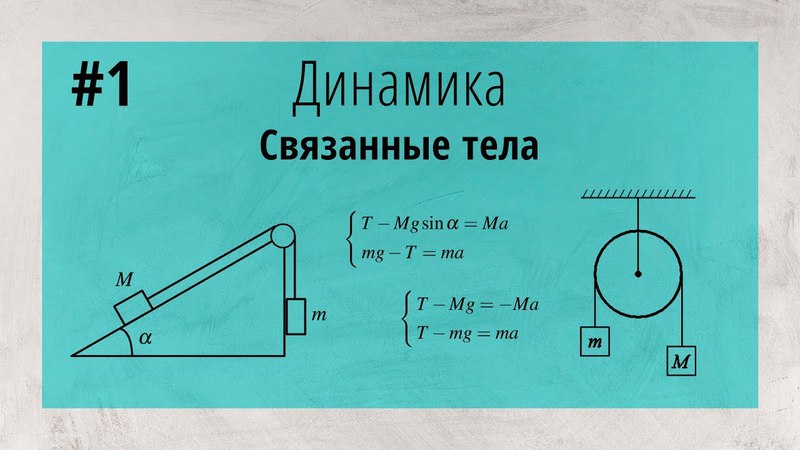 2.4 покоился, то вместе с ним покоилось бы и тело, и, следовательно, сила реакции пола равнялась бы силе тяжести. По третьему закону Ньютона с такой же силой и тело действовало бы на пол. Т.е. в этом случае выполнялось бы равенство =20 Н. Здесь же =10 Н, что означает, что сила тяжести больше силы реакции, и, следовательно, тело вместе с лифтом движется вниз. Применяя второй закон Ньютона к телу, найдем его ускорение, которое равно ускорению лифта: м/с2, направлено вертикально вниз (ответ 1).
2.4 покоился, то вместе с ним покоилось бы и тело, и, следовательно, сила реакции пола равнялась бы силе тяжести. По третьему закону Ньютона с такой же силой и тело действовало бы на пол. Т.е. в этом случае выполнялось бы равенство =20 Н. Здесь же =10 Н, что означает, что сила тяжести больше силы реакции, и, следовательно, тело вместе с лифтом движется вниз. Применяя второй закон Ньютона к телу, найдем его ускорение, которое равно ускорению лифта: м/с2, направлено вертикально вниз (ответ 1).
Весы измеряют силу, с которой лежащее на весах тело действует на них (или они на тело). Поэтому показания весов в задаче 3.2.5 будут наибольшими, если наибольшей является сила реакции. А эта сила увеличивается по сравнению с силой тяжести, если лифт имеет ускорение, направленное вверх. Поэтому правильный ответ в этой задаче — 2.
Умение использовать условия равновесия тел (и понимание ситуаций, когда это можно делать) часто проверяется в заданиях единого государственного экзамена по физике. Например, в задаче 3.2.6 тело находится в равновесии на пружине. Ясно, что в этом положении сила тяжести уравновешивается силой упругости. Используя закон Гука (3.3) для силы упругости и приравнивая силу упругости силе тяжести, получим , где — жесткость пружины, — ее удлинение (ответ 1).
Например, в задаче 3.2.6 тело находится в равновесии на пружине. Ясно, что в этом положении сила тяжести уравновешивается силой упругости. Используя закон Гука (3.3) для силы упругости и приравнивая силу упругости силе тяжести, получим , где — жесткость пружины, — ее удлинение (ответ 1).
При падении тела на вертикально стоящую пружину (задача 3.2.7) оно движется следующим образом. До контакта с пружиной тело движется с ускорением . После контакта на тело кроме силы тяжести действует сила упругости, направленная вертикально вверх. При этом пока укорочение пружины не достигло величины , сила упругости меньше силы тяжести, и по второму закону Ньютона ускорение тела направлено вертикально вниз. Поэтому скорость тела при таких значениях укорочения пружины продолжает увеличиваться. Начиная с того момента, когда укорочение пружины станет больше значения , суммарная сила, действующая на тело, будет направлена вверх, и, следовательно, скорость тела будет уменьшаться. Поэтому максимальной скорость тела будет на высоте от поверхности (ответ 2).
Поэтому максимальной скорость тела будет на высоте от поверхности (ответ 2).
Поскольку нити в задаче 3.2.8 нерастяжимы, все тела имеют одинаковые ускорения. Сила натяжения первой нити сообщает его четырем одинаковым телам, сила натяжения четвертой нити — одному такому телу. Поэтому из второго закона Ньютона заключаем, что последняя в четыре раза меньше первой (правильный ответ — 4).
Из формулы (3.4) для силы сопротивления следует, что свободно падающее тело движется в среде следующим образом (задача 3.2.9). При малых скоростях сила сопротивления мала по сравнению с силой тяжести, поэтому тело имеет ускорение, близкое к ускорению свободного падения, и его скорость возрастает временем. При этом возрастает и сила сопротивления среды, которая при некоторой скорости тела сравнивается с силой тяжести. А поскольку эти силы противоположны, ускорение тела становится равным нулю, и тело движется с постоянной скоростью (ответ 1).
Поскольку тело в задаче 3. 2.10 падает с большой высоты, оно успевает разогнаться до такой скорости, что сила сопротивления воздуха равна по величине силе тяжести, и тело движется с постоянной скоростью (см. предыдущую задачу). После отражения от поверхности скорость тела меняет свое направление на противоположное, а ее величина остается такой же (сразу после удара). А поскольку сила сопротивления определяется скоростью, то величина силы сопротивления также не меняется, а ее направление меняется на противоположное. Поэтому после удара сумма сил сопротивления и тяжести равна , и, следовательно, ускорение тела равно (ответ 3).
2.10 падает с большой высоты, оно успевает разогнаться до такой скорости, что сила сопротивления воздуха равна по величине силе тяжести, и тело движется с постоянной скоростью (см. предыдущую задачу). После отражения от поверхности скорость тела меняет свое направление на противоположное, а ее величина остается такой же (сразу после удара). А поскольку сила сопротивления определяется скоростью, то величина силы сопротивления также не меняется, а ее направление меняется на противоположное. Поэтому после удара сумма сил сопротивления и тяжести равна , и, следовательно, ускорение тела равно (ответ 3).
Гидродинамика – проблемы и решения
Теорема Торричелли
1. Емкость наполнена водой и имеет отверстие, как показано на рисунке ниже. Если ускорение свободного падения равно 10 мс -2 , какова скорость воды через это отверстие?
Известный :
Высота (h) = 85 см – 40 см = 45 см = 0,45 метра
Ускорение свободного падения (g) = 10 м/с 2
Разыскивается: Скорость воды (v)
Решение:
Теорема Торричелли утверждает, что вода покидает отверстие с той же скоростью, что и тело, свободно падающее с той же высоты. Высота (h) = 85 см – 40 см = 45 см = 0,45 метра
Высота (h) = 85 см – 40 см = 45 см = 0,45 метра
Скорость воды рассчитывается по уравнению движения свободного падения:
v т 2 = 2 г ч
v t 2 = 2 g h = 2(10)(0,45) = 9
v t = √9 = 3 м/с
2. Контейнер наполнен водой и имеет отверстие, как показано на рисунке ниже. Если ускорение свободного падения составляет 10 мс -2 , какова скорость воды через это отверстие?
Известный :
Высота (h) = 1,5 м – 0,25 м = 1,25 м
Ускорение свободного падения (g) = 10 м/с 2
Разыскивается: Скорость воды (v)
Решение:
v t 2 = 2 g h = 2(10)(1,25) = 25
v t = √25 = 5 м/с
3. Контейнер наполнен водой и имеет отверстие, как показано на рисунке ниже. Если ускорение свободного падения составляет 10 мс -2 , какова скорость воды через это отверстие?
Контейнер наполнен водой и имеет отверстие, как показано на рисунке ниже. Если ускорение свободного падения составляет 10 мс -2 , какова скорость воды через это отверстие?
Известный :
Высота (h) = 1 м – 0,20 м = 0,8 метра
Ускорение свободного падения (g) = 10 м/с 2
Разыскивается: Скорость воды (v)
Решение:
v t 2 = 2 g h = 2(10)(0,8) = 16
v t = √16 = 4 м/с
4. Контейнер наполнен водой и имеет отверстие, как показано на рисунке ниже. Если ускорение свободного падения составляет 10 мс -2 , какова скорость воды через это отверстие?
Известный :
Высота (h) = 20 см = 0,2 метра
Ускорение свободного падения (g) = 10 м/с 2
Разыскивается: Скорость воды (v)
Решение:
5. Контейнер наполнен водой и имеет два отверстия, как показано на рисунке ниже. Каково отношение x 1 к x 2 ?
Контейнер наполнен водой и имеет два отверстия, как показано на рисунке ниже. Каково отношение x 1 к x 2 ?
Солути на
Интервал времени свободного падения воды из отверстия 1 :
ч = 1/2 ат 2
0.8 = 1/2 (10) т 2
0,8 = 5 т 2
т 2 = 0,8 / 5 = 0,16
t = 0,4 секунды
Интервал времени свободного падения воды из отверстия 2 :
ч = 1/2 ат 2
0,5 = 1/2 (10) т 2
0,5 = 5 т 2
т 2 = 0,5 / 5 = 0,1
t = √0,1 секунды
Горизонтальное расстояние (x):
x 1 = v 1 t 1 = (2)(0. 4) = 0,8 метра
4) = 0,8 метра
x 2 = v 2 t 2 = (√10)(√0,1) = (10)(0,1) = 1 метр
Рацион х 1 к х 2 :
x 1 : x 2 = 0,8 : 1 = 8 : 10 = 4 : 5
Уравнение непрерывности
6. Вода течет по трубе разного диаметра, от А к В, а затем к С. Отношение А к С равно 8:3. Если скорость воды в трубе А равна v, какова скорость воды в трубе? С.
Известный :
Площадь A (A A ) = 8
Площадь C (A C ) = 3
Скорость воды в трубе А (v A ) = v
Разыскивается: Скорость воды в трубе C (v C )
Решение:
Уравнение непрерывности :
А А v А = А С v С
8 В = 3 В С
v C = 8/3 v
7.-reshenie-137.jpg) Если скорость воды в трубе диаметром 12 см равна 10 см/с, какова скорость воды в трубе диаметром 8 см?
Если скорость воды в трубе диаметром 12 см равна 10 см/с, какова скорость воды в трубе диаметром 8 см?
Известный :
Диаметр 1 (d 1 ) = 12 см, радиус 1 (r 1 ) = 6 см
Диаметр 2 (d 2 ) = 8 см, радиус 2 (r 2 ) = 4 см
Скорость воды 1 (v 1 ) = 10 см/с
Разыскивается : Скорость воды 2 (v 2 )
Решение:
Площадь 1 (A 1 ) = π r 2 = π 6 2 = 36π см 2
Площадь 2 (A 2 ) = π r 2 = π 4 2 = 16π см 2
Уравнение непрерывности :
А 1 v 1 = А 2 v 2
(36π)(10) = (16π) v 2
(36)(10) = (16) v 2
360 = (16) v 2
v 2 = 360/16
v 2 = 22. 5 см/с
5 см/с
8. Вода течет по трубе переменного диаметра, как показано на рисунке ниже. Если площадь 1 (A 1 ) = 8 см 2 , A 2 = 2 см 2 и скорость воды в трубе 2 = v 2 = 2 м/с, то какова скорость вода в трубе 1 = v 1 .
Известный :
Зона 1 (A 1 ) = 8 см 2
Площадь 2 (A 2 ) = 2 см 2
Скорость воды в трубе 2 (v 2 ) = 2 м/с
Разыскивается : скорость воды в трубе 1 (v 1 )
Решение:
Уравнение непрерывности :
А 1 v 1 = А 2 v 2
8 v 1 = (2)(2)
8 v 1 = 4
v 1 = 4 / 8 = 0. 5 м/с
5 м/с
9. Если диаметр большей трубы в 2 раза больше диаметра меньшей трубы, какова скорость жидкости в меньшей трубе.
Известный :
Диаметр большей трубы (d 1 ) = 2
Радиус большей трубы (r 1 ) = ½ d 1 = ½ (2) = 1
Площадь большей трубы ( A 1 ) = π r 1 2 = π (1) 2 = π (1) = π
Диаметр меньшей трубы (d 2 ) = 1
Радиус меньшей трубы (r 2 ) = ½ d 2 = ½ (1) = ½
Площадь меньшей трубы ( A 2 ) = π r 2 2 = π (1/2) 2 = π (1/4) = ¼ 5 π 9000
Скорость жидкости в большей трубе ( v 1 ) = 4 м/с
Разыскивается: Скорость жидкости в меньшей трубе ( v 2 )
Решение:
Уравнение непрерывности :
А 1 v 1 = А 2 v 2
π 4 = ¼ π (v 2 )
4 = ¼ (v 2 )
v 2 = 8 м/с
Принцип Бернулли и уравнение
10. Вода нагнетается компрессором мощностью 120 кПа, входя в нижний патрубок (1) и течет вверх со скоростью 1 м/с. Ускорение свободного падения 10 м/с, плотность воды 1000 кг/м -3 . Чему равно давление воды в верхней трубе (II).
Вода нагнетается компрессором мощностью 120 кПа, входя в нижний патрубок (1) и течет вверх со скоростью 1 м/с. Ускорение свободного падения 10 м/с, плотность воды 1000 кг/м -3 . Чему равно давление воды в верхней трубе (II).
Известный :
Радиус нижней трубы (r 1 ) = 12 см
Радиус нижней трубы (r 2 ) = 6 см
Давление воды в нижней трубе (p 1 ) = 120 кПа = 120 000 Па
Скорость воды в нижней трубе (v 1 ) = 1 м.с -1
Высота нижней трубы (h 1 ) = 0 м
Высота верхней трубы (h 2 ) = 2 м
Ускорение свободного падения (g) = 10 мс -2
Плотность воды = 1000 кг.м -3
Разыскивается: Давление воды в трубе 2 (p 2 )
Решение:
Скорость воды в трубе 2 рассчитывается по уравнению неразрывности:
Давление воды в трубе 2 рассчитывается по уравнению Бернулли:
11. Большая труба на высоте 5 метров над землей и маленькая труба на высоте 1 метр над землей. Скорость воды в большой трубе 36 км/ч при давлении 9,1 х 10 5 Па, а давление в маленькой трубе 2,10 5 Па. Какова скорость воды в маленькой трубе? Плотность воды = 10 3 кг/м 3
Большая труба на высоте 5 метров над землей и маленькая труба на высоте 1 метр над землей. Скорость воды в большой трубе 36 км/ч при давлении 9,1 х 10 5 Па, а давление в маленькой трубе 2,10 5 Па. Какова скорость воды в маленькой трубе? Плотность воды = 10 3 кг/м 3
Известный :
Давление воды в большой трубе (p 1 ) = 9,1 x 10 5 Па = 910 000 Па
Давление воды в малой трубе (p 2 ) = 2 x 10 5 Паскаль = 200 000 Па
Скорость воды в большой трубе (v 1 ) = 36 км/ч = 36(1000)/(3600) = 36000/3600 = 10 м/с
Высота большой трубы (h 1 ) = -4 метра
Высота маленькой трубы (h 2 ) = 0 метров
Ускорение свободного падения (g) = 10 м.с -2
Плотность воды = 1000 кг/м 3
Разыскивается: Скорость воды в малой трубе (v 2 )
Решение:
Скорость воды в маленькой трубе (v 2 ) рассчитывается по уравнению Бернулли:
12. Труба радиусом 15 см, соединенная с другой трубой радиусом 5 см. Оба находятся в горизонтальном положении. Скорость течения воды в большой трубе 1 м/с при давлении 10 5 Н/м 2 .Какое давление воды на малую трубу (1 г см -3 )
Труба радиусом 15 см, соединенная с другой трубой радиусом 5 см. Оба находятся в горизонтальном положении. Скорость течения воды в большой трубе 1 м/с при давлении 10 5 Н/м 2 .Какое давление воды на малую трубу (1 г см -3 )
Известный :
Радиус большой трубы (r 1 ) = 15 см = 0,15 м
Радиус маленькой трубы (r 2 ) = 5 см = 0,05 м
Давление воды в большой трубе (p 1 ) = 10 5 Нм -2 = 100.000 Нм -2
Скорость воды в большой трубе (v 1 ) = 1 м с -1
Ускорение свободного падения (g) = 10 м.с -2
Плотность воды = 1 г см -3 = 1000 кг·м -3
Разница высот (Δh) = 0,
Разыскивается: Давление в малой трубе (p 2 )
Решение:
Скорость воды в трубе 2 рассчитывается по уравнению непрерывности:
Давление воды в малой трубе (p 2 ) рассчитывается по уравнению Бернулли:
10.
 3 Динамика вращательного движения: вращательная инерция — College Physics
3 Динамика вращательного движения: вращательная инерция — College Physics
Если вы когда-нибудь крутили велосипедное колесо или толкали карусель, вы знаете, что для изменения угловой скорости необходима сила, как показано на рис. 10.10. На самом деле, ваша интуиция надежно предсказывает многие из задействованных факторов. Например, мы знаем, что дверь открывается медленно, если мы прислоняем ее слишком близко к петлям. Кроме того, мы знаем, что чем массивнее дверь, тем медленнее она открывается. Первый пример подразумевает, что чем дальше приложена сила от оси вращения, тем больше угловое ускорение; другое следствие состоит в том, что угловое ускорение обратно пропорционально массе.Эти отношения должны казаться очень похожими на знакомые отношения между силой, массой и ускорением, воплощенные во втором законе движения Ньютона. На самом деле существуют точные вращательные аналоги как силы, так и массы.
Рисунок 10.10 Для вращения велосипедного колеса требуется сила. Чем больше сила, тем больше угловое ускорение. Чем массивнее колесо, тем меньше угловое ускорение. Если надавить на спицу ближе к оси, угловое ускорение будет меньше.
Чем больше сила, тем больше угловое ускорение. Чем массивнее колесо, тем меньше угловое ускорение. Если надавить на спицу ближе к оси, угловое ускорение будет меньше.
Чтобы установить точное соотношение между силой, массой, радиусом и угловым ускорением, рассмотрим, что произойдет, если мы приложим силу FF размером 12{F} {} к точке массой мм размером 12{m} {}, которая находится на расстояние rr size 12{r} {} от точки вращения, как показано на рисунке 10.11. Поскольку сила перпендикулярна rr размером 12{r} {}, ускорение a=Fma=Fm размера 12{a= {{F} над {m} } } {} получается в направлении FF размера 12{F } {}. Мы можем изменить это уравнение так, что F=maF=ma size 12{F= ital «ma»} {}, а затем искать способы связать это выражение с выражениями для вращательных величин.Заметим, что a=rαa=rα size 12{a=rα} {}, и подставим это выражение в F=maF=ma size 12{F= ital «ma»} {}, получив
F=mrα.F= мра. size 12{F= ital «mr»α».»} {}10,40
Вспомним, что крутящий момент — это эффективность вращения силы.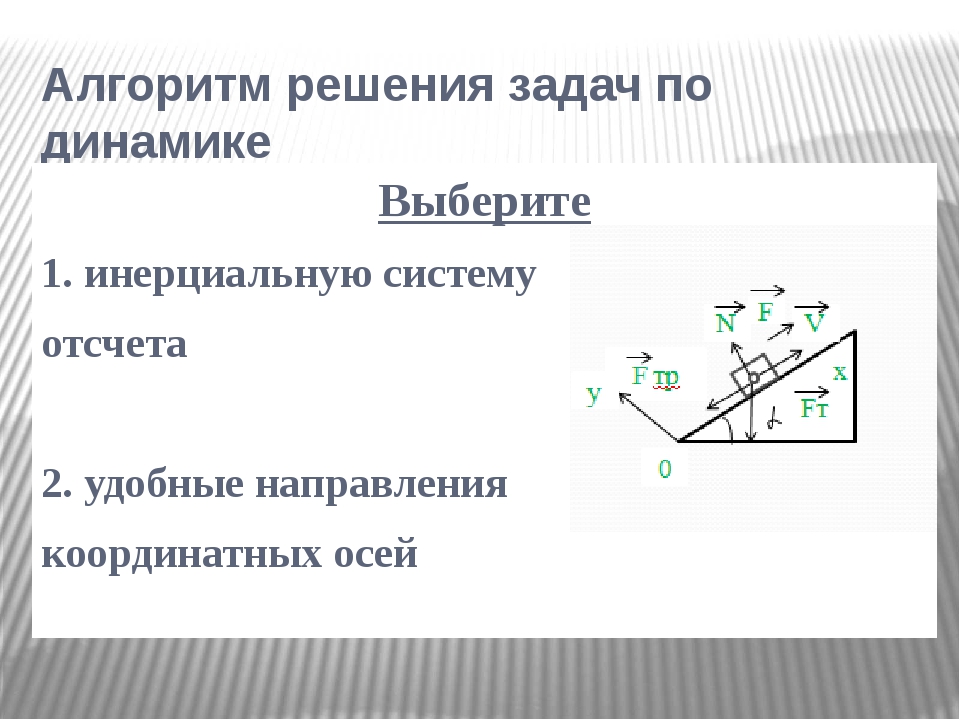 В этом случае, поскольку размер FF 12{«F»} {} перпендикулярен размеру RR 12{r} {}, крутящий момент просто τ=Frτ=Fr размер 12{τ=rα} {}. Итак, если мы умножим обе части приведенного выше уравнения на размер rr 12{r} {}, мы получим крутящий момент в левой части. Это,
В этом случае, поскольку размер FF 12{«F»} {} перпендикулярен размеру RR 12{r} {}, крутящий момент просто τ=Frτ=Fr размер 12{τ=rα} {}. Итак, если мы умножим обе части приведенного выше уравнения на размер rr 12{r} {}, мы получим крутящий момент в левой части. Это,
10.41
или
τ=mr2α.τ=mr2α. size 12{τ= ital «mr» rSup { size 8{2} } α.} {}10,42
Последнее уравнение является вращательным аналогом второго закона Ньютона (F=maF=ma size 12{F= ital » ma»} {}), где крутящий момент аналогичен силе, угловое ускорение аналогично поступательному ускорению, а mr2mr2 size 12{ ital «mr» rSup { size 8{2} } } {} аналогично массе (или инерции) . Величина mr2mr2 размером 12{ ital «mr» rSup { size 8{2} } } {} называется инерцией вращения или моментом инерции точки массой mm размером 12{m} {} расстоянием rr размером 12{r} {} от центра вращения.
Рис. 10.11. Объект поддерживается горизонтальным столом без трения и прикреплен к точке вращения шнуром, создающим центростремительную силу. Сила FF размером 12{F} {} приложена к объекту перпендикулярно радиусу rr размером 12{r} {}, заставляя его ускоряться относительно точки поворота. Сила удерживается перпендикулярно размеру rr 12{r} {}.
Сила FF размером 12{F} {} приложена к объекту перпендикулярно радиусу rr размером 12{r} {}, заставляя его ускоряться относительно точки поворота. Сила удерживается перпендикулярно размеру rr 12{r} {}. Создание соединений: динамика вращательного движения
Динамика вращательного движения полностью аналогична линейной или поступательной динамике.Динамика занимается силой и массой и их влиянием на движение. Для вращательного движения мы найдем прямые аналоги силы и массы, которые ведут себя именно так, как мы и ожидали, исходя из нашего предыдущего опыта.
Инерция вращения и момент инерции
Прежде чем мы сможем рассмотреть вращение чего-либо, кроме точечной массы, подобной той, что изображена на рис. 10.11, мы должны распространить идею инерции вращения на все типы объектов. Чтобы расширить наше понятие инерции вращения, мы определяем момент инерции
II размер 12{I} {} объекта должен быть суммой
mr2mr2 size 12{ ital «mr» rSup { size 8{2} } } {} для всех точечных масс, из которых он состоит. Это,
I=∑mr2I=∑mr2 size 12{I= Sum {} ital «mr» rSup { size 8{2} } } {}. Здесь
II размер 12{I} {} аналогичен
мм размером 12{м}{} в поступательном движении. Из-за расстояния
rr size 12{r} {}, момент инерции любого объекта зависит от выбранной оси. Собственно, расчет
Размер II 12{I} {} выходит за рамки этого текста, за исключением одного простого случая — обруча, вся масса которого находится на одном и том же расстоянии от его оси. Таким образом, момент инерции кольца вокруг своей оси равен
MR2MR2 размер 12{ ital «MR» rSup { размер 8{2} } } {}, где
Размер MM 12{M} {} — это его полная масса, а размер RR 12{R} {} — его радиус.(Мы используем размер MM 12{M} {} и размер RR 12{R} {} для всего объекта, чтобы отличить их от размера 12{m} {} мм и размера rr 12{r} {} для точечных масс.) Во всех других случаях мы должны обращаться к рисунку 10.12 (обратите внимание, что таблица представляет собой произведение искусства, в котором есть формы, а также формулы) для формул для размера II 12{I} {}, которые были получены путем интегрирования по непрерывному телу.
Это,
I=∑mr2I=∑mr2 size 12{I= Sum {} ital «mr» rSup { size 8{2} } } {}. Здесь
II размер 12{I} {} аналогичен
мм размером 12{м}{} в поступательном движении. Из-за расстояния
rr size 12{r} {}, момент инерции любого объекта зависит от выбранной оси. Собственно, расчет
Размер II 12{I} {} выходит за рамки этого текста, за исключением одного простого случая — обруча, вся масса которого находится на одном и том же расстоянии от его оси. Таким образом, момент инерции кольца вокруг своей оси равен
MR2MR2 размер 12{ ital «MR» rSup { размер 8{2} } } {}, где
Размер MM 12{M} {} — это его полная масса, а размер RR 12{R} {} — его радиус.(Мы используем размер MM 12{M} {} и размер RR 12{R} {} для всего объекта, чтобы отличить их от размера 12{m} {} мм и размера rr 12{r} {} для точечных масс.) Во всех других случаях мы должны обращаться к рисунку 10.12 (обратите внимание, что таблица представляет собой произведение искусства, в котором есть формы, а также формулы) для формул для размера II 12{I} {}, которые были получены путем интегрирования по непрерывному телу.-reshenie-304.jpg) Обратите внимание, что размер II 12{I} {} имеет единицы массы, умноженные на квадрат расстояния (кг⋅м2кг⋅м2 размер 12{«кг» cdot «м» rSup { размер 8{2} } } {}), как мы могли бы ожидать от его определения.
Обратите внимание, что размер II 12{I} {} имеет единицы массы, умноженные на квадрат расстояния (кг⋅м2кг⋅м2 размер 12{«кг» cdot «м» rSup { размер 8{2} } } {}), как мы могли бы ожидать от его определения.
Общая зависимость между крутящим моментом, моментом инерции и угловым ускорением
net τ=Iαnet τ=Iα размер 12{τ=Iα} {}10,43
или
α=net τI,α=net τI, размер 12{α= { { ital «net»τ} над {I} } «,»} {}10,44
где чистый размер ττ 12{τ} {} представляет собой суммарный крутящий момент от всех сил относительно выбранной оси. Для простоты мы будем рассматривать только крутящие моменты, создаваемые силами в плоскости вращения. Такие крутящие моменты бывают положительными или отрицательными и складываются как обычные числа.Соотношение в τ=Iα, α=net τIτ=Iα, α=net τI size 12{τ=Iα,««`α= { { ital «net»τ} over {I} } } {} является вращательный аналог второго закона Ньютона и очень широко применим. Это уравнение действительно справедливо для любого крутящего момента , примененного к любому объекту относительно любой оси .
Как и следовало ожидать, чем больше крутящий момент, тем больше угловое ускорение. Например, чем сильнее ребенок толкает карусель, тем быстрее она разгоняется.Кроме того, чем массивнее карусель, тем медленнее она разгоняется при том же крутящем моменте. Основное соотношение между моментом инерции и угловым ускорением заключается в том, что чем больше момент инерции, тем меньше угловое ускорение. Но есть дополнительный нюанс. Момент инерции зависит не только от массы тела, но и от распределения его массы относительно оси, вокруг которой он вращается. Например, будет намного легче разогнать карусель, полную детей, если они будут стоять близко к ее оси, чем если все они будут стоять на внешнем краю.Масса в обоих случаях одинакова, но момент инерции намного больше, когда дети находятся на краю.
Эксперимент на вынос
Вырежьте круг радиусом около 10 см из плотного картона. Рядом с краем круга напишите числа от 1 до 12, как часы на циферблате. Расположите круг так, чтобы он мог свободно вращаться вокруг горизонтальной оси, проходящей через его центр, как колесо. (Вы можете свободно прибить круг к стене.) Держите круг неподвижно и, расположив цифру 12 вверху, прикрепите кусок синей замазки (клейкий материал, используемый для крепления постеров к стенам) к цифре 3.Насколько большим должен быть комок, чтобы просто повернуть круг? Опишите, как можно изменить момент инерции окружности. Как это изменение повлияет на количество синей замазки, необходимое под номером 3, чтобы просто повернуть круг? Измените момент инерции круга, а затем попробуйте повернуть круг, используя разное количество синей замазки. Повторите этот процесс несколько раз.
Расположите круг так, чтобы он мог свободно вращаться вокруг горизонтальной оси, проходящей через его центр, как колесо. (Вы можете свободно прибить круг к стене.) Держите круг неподвижно и, расположив цифру 12 вверху, прикрепите кусок синей замазки (клейкий материал, используемый для крепления постеров к стенам) к цифре 3.Насколько большим должен быть комок, чтобы просто повернуть круг? Опишите, как можно изменить момент инерции окружности. Как это изменение повлияет на количество синей замазки, необходимое под номером 3, чтобы просто повернуть круг? Измените момент инерции круга, а затем попробуйте повернуть круг, используя разное количество синей замазки. Повторите этот процесс несколько раз.
Стратегия решения задач по динамике вращения
- Изучите ситуацию, чтобы определить, участвуют ли крутящий момент и масса во вращении .Нарисуйте тщательный набросок ситуации.
- Определить интересующую систему .

- Нарисуйте диаграмму свободного тела . То есть нарисуйте и обозначьте все внешние силы, действующие на интересующую вас систему.
- Применить сеть τ=Iα, α=net τI net τ=Iα, α=net τI size 12{τ=Iα,«`α= { { ital «net»τ} over {I} } } {}, вращательный эквивалент второго закона Ньютона, чтобы решить проблему . Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент вокруг точки вращения.
- Как всегда, проверьте правильность решения .
Выполнение соединений
В статике чистый крутящий момент равен нулю, а угловое ускорение отсутствует. При вращательном движении чистый крутящий момент является причиной углового ускорения, точно так же, как во втором законе движения Ньютона для вращения.
Рисунок 10. 12 Некоторые инерции вращения.
12 Некоторые инерции вращения.
Пример 10.7
Расчет влияния распределения массы на карусель
Представьте, что отец толкает карусель на детской площадке на рис. 10.13. Он прикладывает силу 250 Н к краю карусели массой 50,0 кг, имеющей радиус 1,50 м. Вычислите угловое ускорение, создаваемое (а), когда на карусели никого нет, и (б), когда ребенок массой 18,0 кг сидит на расстоянии 1,25 м от центра. Считайте саму карусель однородным диском с пренебрежимо малым тормозящим трением.
Рис. 10.13. Отец толкает игровую карусель за ее край и перпендикулярно ее радиусу для достижения максимального крутящего момента.
Стратегия
Угловое ускорение задается непосредственно выражением :
α=τI.α=τI. размер 12{α= {{τ} над {I} } } {}10,45
в обоих случаях одинакова) и момент инерции II величиной 12{I}{} (что во втором случае больше). Чтобы найти крутящий момент, заметим, что приложенная сила перпендикулярна радиусу, а трением можно пренебречь, так что
τ=rFsin θ=(1,50 м)(250 Н)=375 Н⋅м. τ=rFsin θ=(1,50 м)(250 Н)=375 Н⋅м. размер 12{τ=»rFsinθ»= \( 1 «.» «50м» \) \( «250Н» \) =»375Н» «.» «м.»} {}
τ=rFsin θ=(1,50 м)(250 Н)=375 Н⋅м. размер 12{τ=»rFsinθ»= \( 1 «.» «50м» \) \( «250Н» \) =»375Н» «.» «м.»} {} 10,46
Решение для (а)
Момент инерции твердого диска относительно этой оси приведен на рис. 10.12 и равен «} {}
10,47
где M=50,0 кгM=50,0 кг размер 12{M=»50″ «.» 0 итал. «кг»} {} и R=1,50 мR=1,50 м размер 12{R=1 «.» «50» м} {}, так что
I=(0,500)(50,0 кг)(1,50 м)2=56,25 кг⋅м2.I=(0,500)(50,0 кг)(1,50 м)2=56,25 кг⋅м2 . размер 12{I=0 «.» 5\(«50» «.» «0kg» \) \( 1 «.» «50m» \) rSup { размер 8{2} } =»56″ «.» «25kg» «.» «m» rSup { размер 8{2} } » .»} {}10,48
Теперь, после подстановки известных значений, находим угловое ускорение
α=τI=375 Н⋅м56,25 кг⋅м2=6,67 рад2.α=τI=375 Н⋅ м56,25 кг⋅м2=6,67 рад2 размер 12{α= {{τ} над {I} } = {{«375″`»N» «.» «м»} над {«56» «.» » 25″`»кг» «.» «м» rSup { размер 8{2} } } } =6 «.» «67»` { {«рад»} более {s rSup { размер 8{2} } } } «.»} {}10,49
Решение для (b)
Мы ожидаем, что угловое ускорение системы будет меньше в этой части, потому что момент инерции больше, когда ребенок находится на карусели.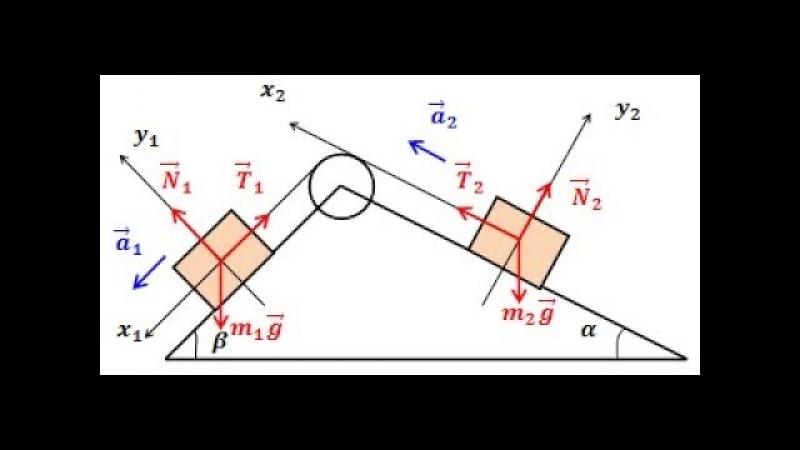 Чтобы найти полный момент инерции II размера 12{I} {}, мы сначала находим момент инерции ребенка IcIc размером 12{I rSub { размер 8{c} } } {}, считая ребенка эквивалентным точке массы на расстоянии 1,25 м от оси. Тогда
Чтобы найти полный момент инерции II размера 12{I} {}, мы сначала находим момент инерции ребенка IcIc размером 12{I rSub { размер 8{c} } } {}, считая ребенка эквивалентным точке массы на расстоянии 1,25 м от оси. Тогда
10.50
Суммарный момент инерции равен сумме моментов инерции карусели и ребенка (относительно одной оси). Чтобы оправдать для себя эту сумму, изучите определение размера II 12{I} {}:
I=28,13 кг⋅м2+56,25 кг⋅м2=84,38 кг⋅м2.I=28,13 кг⋅м2+56,25 кг⋅м2=84,38 кг⋅м2. размер 12{I=»28″ «.» «13»`»кг» «.» m rSup {размер 8{2}} +»56″ «.» «25»`»кг» «.» m rSup { размер 8{2} } =»84″ «.» «38»`»кг» «.» m rSup { размер 8{2} } } {}10,51
Подстановка известных значений в уравнение для размера αα 12{α} {} дает
α=τI=375 Н⋅м84. 38 кг⋅м2=4,44рад2.α=τI=375 Н⋅м84,38 кг⋅м2=4,44рад2. размер 12{α= {{τ} над {I} } = {{«375N» «.» м} более {«84» «.» «38кг» «.» m rSup {размер 8{2} } } } =4 «.» «44» { {«rad»} over {s rSup { size 8{2} } } } «.»} {}
38 кг⋅м2=4,44рад2.α=τI=375 Н⋅м84,38 кг⋅м2=4,44рад2. размер 12{α= {{τ} над {I} } = {{«375N» «.» м} более {«84» «.» «38кг» «.» m rSup {размер 8{2} } } } =4 «.» «44» { {«rad»} over {s rSup { size 8{2} } } } «.»} {} 10,52
Обсуждение
Как и ожидалось, угловое ускорение меньше, когда ребенок находится на карусели, чем когда карусель пуста. Найденные угловые ускорения довольно велики, отчасти из-за того, что трение считалось пренебрежимо малым.Если бы, например, отец продолжал толкать перпендикулярно в течение 2,00 с, он придал бы карусели угловую скорость 13,3 рад/с, когда она пуста, и только 8,89 рад/с, когда на ней находится ребенок. В пересчете на обороты в секунду эти угловые скорости составляют 2,12 об/с и 1,41 об/с соответственно. В первом случае отец будет бежать со скоростью около 50 км/ч. Летние Олимпийские игры, вот и он! Подтверждение этих цифр оставлено читателю в качестве упражнения.
Проверьте свое понимание
Крутящий момент является аналогом силы, а момент инерции является аналогом массы. Сила и масса — физические величины, зависящие только от одного фактора. Например, масса связана исключительно с количеством атомов различных типов в объекте. Являются ли крутящий момент и момент инерции такими же простыми?
Сила и масса — физические величины, зависящие только от одного фактора. Например, масса связана исключительно с количеством атомов различных типов в объекте. Являются ли крутящий момент и момент инерции такими же простыми?
Решение
Нет. Крутящий момент зависит от трех факторов: величины силы, направления силы и точки приложения. Момент инерции зависит как от массы, так и от ее распределения относительно оси вращения. Таким образом, хотя аналогии точны, эти величины вращения зависят от большего количества факторов.
Гидродинамика — AP Физика 2
Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно
или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному агенту, указанному ниже.-reshenie-24.jpg) Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права. Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.
Чтобы подать уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \
достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем
а
ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
Отправьте жалобу нашему назначенному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
Сент-Луис, Миссури 63105
Или заполните форму ниже:
Физика — Динамика — Мартин Бейкер
На предыдущей странице кинематики математика обсуждались движущиеся объекты. Если объекты представляют собой физические объекты, с такими свойствами, как масса и инерция, то мы, вероятно, хотим вычислить кинематика от динамика
- Динамика вперед — движения рассчитываются исходя из сил, таких как,
сила = масса * ускорение.

- Обратная динамика — применяются ограничения, которые определяют, как объекты взаимодействуют, например, они могут быть соединены шарнирным соединением или шаровым шарниром, а от это силы можно рассчитать (см. суставы).
Что я хотел бы сделать на этих страницах о динамике, так это развить общие уравнения движения твердых тел. Итак, при знании сил воздействуя на объект и информацию об объектах, с которыми он сталкивается, мы сможет предсказать его дальнейшее движение.
Из этого я предложил некоторые структуры для моделирования этого движения, а отсюда и некоторые компьютерные программы.
Обобщенные уравнения движения и столкновений довольно сложны, поэтому я предлагаю начать с полного понимания линейного движения, затем добавьте вращательное движение, затем добавьте столкновения.
Форвард Динамика
Для таких приложений, как игры и симуляции обычных объектов, мы можем использовать Ньютоновская механика (в отличие от теории относительности или квантовой механики)
Ньютон определяет 3 закона (здесь они определены в терминах частиц):
- Если на частицу не действуют никакие силы, частица сохраняет свой линейный импульс.

- Скорость изменения импульса частицы равна сумма всех сил, действующих на него.
- Когда две частицы действуют друг на друга, эти силы равны по величине и противоположно по направлению.
Эти законы также можно применить к твердым телам, если предположить, что силы действуют на центр масс объекта. Предполагая, что масса постоянна тогда второй закон принимает вид:
сила = масса * ускорение
Например, если объект находится под действием силы тяжести, то: к силе тяжести: сила в ньютонах = масса * 9.81
Эйлер расширил эти законы, включив в них вращение. Так что есть эквивалентные законы для вращения, например:
крутящий момент = инерция * угловое ускорение.
При работе в трех измерениях мы можем сформулировать эти уравнения, используя вектор и матричные обозначения (см. инерцию).
Установившееся движение
Когда твердый объект движется в пустом пространстве без внешних сил на нем, то мы можем считать его линейную скорость и его угловую скорость независимо:
- Линейная скорость центра масс будет постоянной.
-reshenie-421.jpg)
- Угловая скорость относительно центра масс будет постоянной, и если объект несимметричен, это вращение всегда будет происходить вокруг одного из его главных Моменты инерции.
Так вот разница между линейным и угловым движением, с линейным движением (при условии отсутствия сопротивления воздуха) он может двигаться во всех направлениях одинаково, независимо от формы объекта. При вращении направление вращения может зависеть от ориентации объекта (и наоборот).
Существуют и другие различия между линейным движением и вращением, например, Законы Ньютона могут применяться в локальных координатах, когда локальная система отсчета имеет линейное движение. Однако законы Ньютона не работают на вращающейся системе координат. ссылка.
Когда мы имеем дело с вращением, некоторые из этих законов не являются немедленно инициативными,
нет никакого резона придавать гироскопам, например, мистическое значение, они
подчиняются простым законам (даже если я еще не утверждаю, что полностью их понимаю!). Однако наша интуиция может обмануть нас, заставив неправильно понять эти правила.
Поэтому я собираю здесь несколько простых примеров, таблица
Высшая физика, чтобы помочь нам получить понимание инициативы. Например, тоже
подумайте о том, как объект вращается вокруг своего основного момента инерции, см.
пример яйца.
Однако наша интуиция может обмануть нас, заставив неправильно понять эти правила.
Поэтому я собираю здесь несколько простых примеров, таблица
Высшая физика, чтобы помочь нам получить понимание инициативы. Например, тоже
подумайте о том, как объект вращается вокруг своего основного момента инерции, см.
пример яйца.
Следующий шаг и дополнительное чтение
Чтобы увидеть, как алгоритм реализации динамики твердого объекта см. здесь.
Чтобы увидеть предложение по структуре для хранения этой динамической информации, см. здесь.
Физика 581: Преподавание динамики в Excel97
Физика 581 Часть 1: Обучение динамике с помощью Excel97
Нажмите здесь по физике 581 часть 2
Майкл Фаулер, Уфа, лето 1998 г.
Введение
В отличие от курса Галилея и Эйнштейна , материал
представленные здесь предназначены для непосредственного использования учителем или учеником в
более традиционный курс физики средней школы или начальный университетский курс на
механика. Мы по-прежнему используем часть материала Galileo и Einstein , но
мы усиливаем многие темы и обогащаем микс некоторыми электронными таблицами.
Мы по-прежнему используем часть материала Galileo и Einstein , но
мы усиливаем многие темы и обогащаем микс некоторыми электронными таблицами.
Чтобы понять ньютоновскую динамику, требуется некоторое понимание его величайшее изобретение исчисления. Вот где электронные таблицы бесценны. От построить электронную таблицу, чтобы найти скорость как функцию времени, принимая различия положения в последовательные промежутки времени, и продолжая делать то же самое для ускорения, студент (по моему опыту) выстраивает более четкую представление о значении производной, чем то, которое обычно получается из формальных математических манипуляции.Создание этих таблиц занимает некоторое время, но я даю очень подробная инструкция. Это, по общему признанию, приводит к опасности того, что студент будет слепо строить электронную таблицу, не понимая ее по-настоящему, но понимание придет после достаточного количества упражнений: пусть учащиеся зарисуют разные вещей, варьировать зависимость силы сопротивления от скорости и, особенно, варьировать параметры (включая количество строк) пока таблица не выдаст чушь, тогда попробуй понять почему!
Готовые таблицы некоторых упражнений я выложил в сеть,
чтобы их можно было скачать и изучить.
Книга:
В этом курсе мы просто даем пример некоторых способов использования электронных таблиц в физика. Если вы хотите увидеть более широкий спектр более увлекательного материала, я настоятельно рекомендуем приобрести «Физику электронных таблиц» Миснера и Куни (около 28 долларов, я думаю). Я купил его в 1992 году и использовал некоторые из идеи, такие как интеграция чехарды и простой маятник в качестве теста Эйлер против чехарды. Одной из неприятных особенностей книги является то, что она никогда не был обновлен, поэтому он настроен для Lotus 1-2-3 на базе DOS, но идеи отличный.Был доступен диск с шаблонами, но я его не получил, поэтому не знаю. знаю, будет ли это все еще работать с Excel.
Начало Динамика: одномерное движение
Первые шаги в динамике — это действительное понимание концепций скорости и ускорение ,
и все учителя физики знают, что это невероятно сложно! Цель
Первые три лекции должны понять скорость и ускорение в
одномерное движение, с либеральным количественным использованием видео
камера и электронная таблица.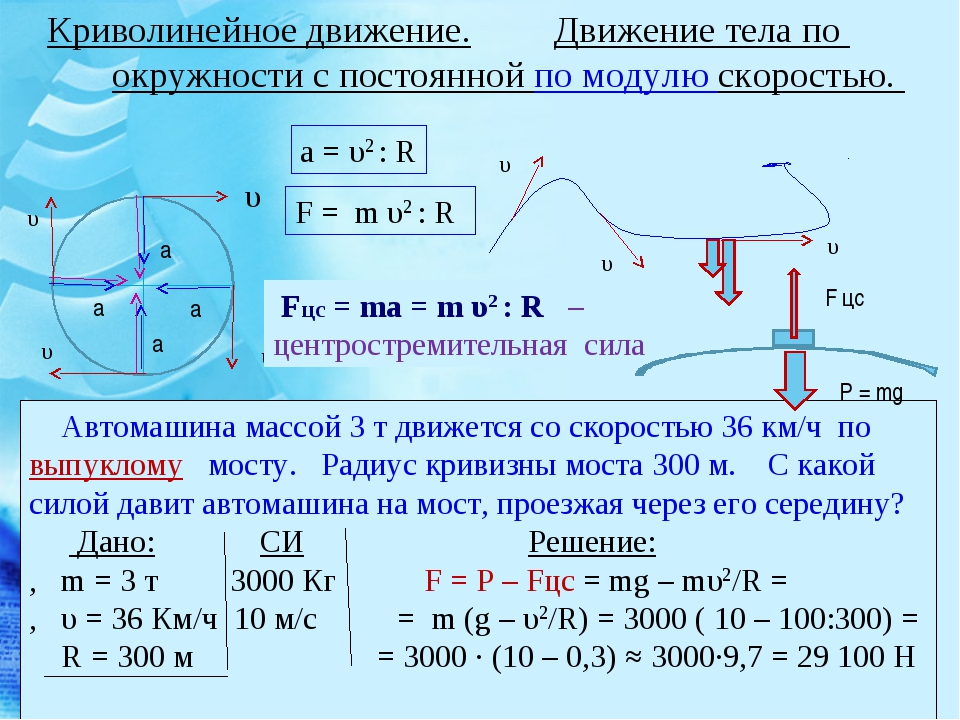 Мы делаем это до введения законов Ньютона, но в
Анализируя сопротивление воздуха, мы предполагаем, что при постоянной конечной скорости воздух
Сила сопротивления сопротивления уравновешивает вес, чтобы найти, как сила сопротивления зависит от
скорость (для пакетов кофейных фильтров).
Мы делаем это до введения законов Ньютона, но в
Анализируя сопротивление воздуха, мы предполагаем, что при постоянной конечной скорости воздух
Сила сопротивления сопротивления уравновешивает вес, чтобы найти, как сила сопротивления зависит от
скорость (для пакетов кофейных фильтров).
1: Как быстро Падающий мяч падает?
В первой лекции мы рассматриваем объекты, падающие вертикально под действием силы тяжести. Это движение изучалось с древних времен, и Аристотель пытался проанализировать движение количественно.Он был блестящим человеком, но он получил это неправильный. Вопрос в том, почему? Галилей справился намного лучше, но это было почти два тысячу лет спустя. Стоит задуматься над тем, что сделал Галилей с Аристотелем. не удалось сделать. Безусловно, стоит провести эксперимент с Галилеем, как описано в эта лекция.
2: Анализ видео падающего мяча с помощью Эксель.
Мы покажем, как измерять движение падающего мяча гораздо более непосредственно,
используя видеокамеру и воспроизводя кадр за кадром, чтобы отслеживать мяч. Мы тогда
введите наши результаты в электронную таблицу Excel, чтобы найти ускорение, вызванное
сила тяжести.
Мы тогда
введите наши результаты в электронную таблицу Excel, чтобы найти ускорение, вызванное
сила тяжести.
3: Реальные эффекты: Сопротивление воздуха.
Видеотехника очень хорошо подходит для измерения сопротивления воздуха. последствия. Мы бросаем небольшие стопки кофейных фильтров и обнаруживаем, что они почти немедленно достичь конечной скорости, и смогли выяснить, что воздух сопротивление пропорционально квадрату скорости. В том числе эти Эффекты реального мира также делают точку зрения Аристотеля более понятной.
Подъем к Два измерения: снаряды, планеты и законы Ньютона
Идею скорости не так уж трудно понять в двух словах. размеры представлены стрелкой, вектором , но ускорение равно очень трудно! И, если вы не понимаете досконально ускорение в два размеры, вы не понимаете, что такое Ньютон, вы не понимаете динамики. Итак, это , очень важное .
4: Первые идеи о движении снаряда
Развитие идей Галилея о снарядах и драматические
связь этих земных идей с движением Луны и Земли
сам Исаак Ньютон, рассматривается в моем курсе по Галилею и Эйнштейну.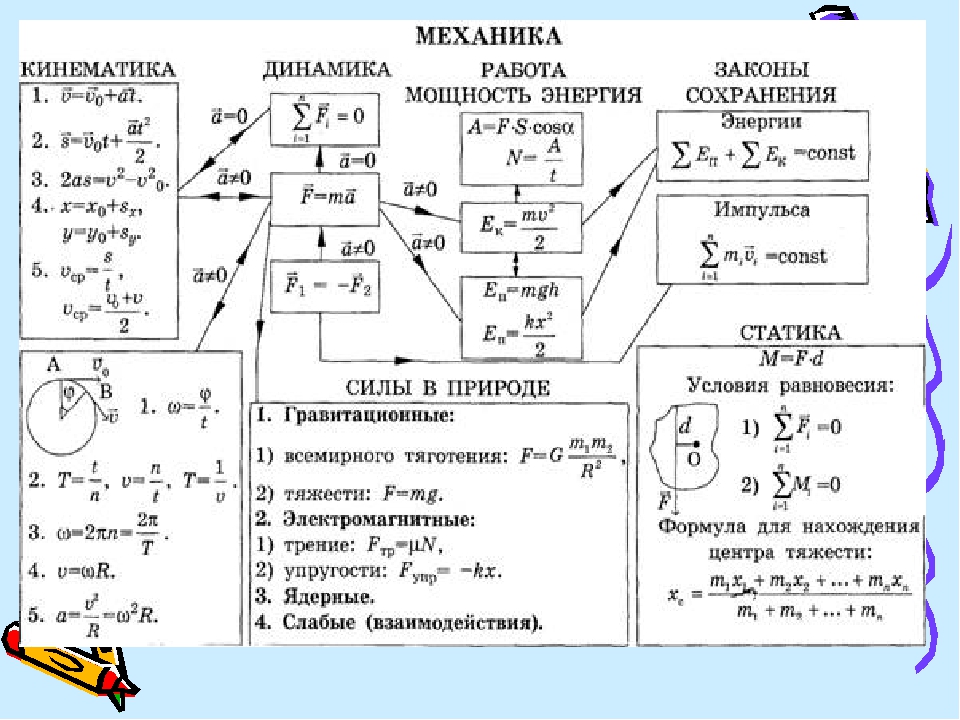 5, 6, 8, 9 ниже относятся к этому курсу, ссылки 7 и 10 дают дополнительный материал.
5, 6, 8, 9 ниже относятся к этому курсу, ссылки 7 и 10 дают дополнительный материал.
5: Векторы
6: Ньютон: от Снаряды до Луны
7: Силы, Равновесие, системы отсчета и законы Ньютона
8: Больше по законам Ньютона
9: Импульс, Работа и энергия
10:Подробнее об Потенциальная энергия
Использование Ньютона Законы для решения реальных проблем
Движения всех частиц от пылинок до планет на орбите
дано с предельной точностью, применяя законы Ньютона.Если мы знаем силы
испытывает частица, мы можем сразу найти ее ускорение, т. е. как
его скорость изменяется во времени, и из этого мы можем построить карту его пути
через пространство. Итак в принципе мы умеем решать уравнения
движение. Но есть запись того, что мы только что сказали математически
дает дифференциальное уравнение второго порядка для положения частиц в виде
функция времени с (обычно) силой, зависящей от положения, и уравнением
обычно это будет тот, который мы не знаем, как решить математически! Добро
новость заключается в том, что эти уравнения могут быть решены численно
(хотя это быстро становится более громоздким, если мы увеличим количество движущихся
частицы). И вот где приходит электронная таблица: по крайней мере, для одной частицы
проблемы, почти во всех ситуациях обычная электронная таблица имеет достаточную мощность, чтобы
сюжетные траектории. Как мы увидим позже, метод становится ненадежным для
очень быстро меняющиеся потенциалы, но это тоже стоит исследовать,
потому что он дает представление о том, насколько можно доверять численным методам, и
как их можно улучшить.
И вот где приходит электронная таблица: по крайней мере, для одной частицы
проблемы, почти во всех ситуациях обычная электронная таблица имеет достаточную мощность, чтобы
сюжетные траектории. Как мы увидим позже, метод становится ненадежным для
очень быстро меняющиеся потенциалы, но это тоже стоит исследовать,
потому что он дает представление о том, насколько можно доверять численным методам, и
как их можно улучшить.
11. Исчисление Лечение падающего мяча сопротивлением воздуха
В этой первой «реальной» лекции мы не используем электронные таблицы, но решить две проблемы сопротивления воздуха (сопротивление, пропорциональное скорости и скорости в квадрате) аналитически.Эти решения предоставляют полезные тесты для проверки наших численные методы на точность и надежность. Мы можем найти, например, как точность нашей электронной таблицы зависит от количества используемых строк.
12. Электронная таблица Лечение падающего мяча сопротивлением воздуха
В этой лекции даны очень подробные инструкции по созданию
таблица, решающая задачу о падении мяча с сопротивлением воздуха. То
полная таблица доступна для скачивания ниже, но это ценная
упражнение, чтобы построить его самостоятельно! Вы поймете это намного лучше и сможете
адаптировать его для других задач.
То
полная таблица доступна для скачивания ниже, но это ценная
упражнение, чтобы построить его самостоятельно! Вы поймете это намного лучше и сможете
адаптировать его для других задач.
Скачать Таблица для падающего мяча с линейным сопротивлением воздуха
Скачать Электронная таблица для падающего мяча с сопротивлением воздуха, пропорциональным скорости
в квадрате13. Электронная таблица Обработка снарядов с сопротивлением воздуха
Это гораздо более интересная задача, имеющая практическое значение. Приложения. Какова траектория снаряда при сопротивлении воздуха не забыты? Какой угол проекции дает максимальную дальность, например? Этот таблица дает ответы!
Скачать Таблица для траектории снаряда с сопротивлением воздуха
14.Электронная таблица Лечение простым маятником
Это не просто гармонический осциллятор, а маятник с
струна заменена стержнем, вынужденным вращаться в вертикальной плоскости, так что он может
качаться «сверху». Чтобы решить это математически, требуется эллиптическая
функции, но эта простая электронная таблица дает очень точный отчет о
движение. И вы можете добавить сопротивление воздуха в качестве упражнения.
Чтобы решить это математически, требуется эллиптическая
функции, но эта простая электронная таблица дает очень точный отчет о
движение. И вы можете добавить сопротивление воздуха в качестве упражнения.
15. Из Простой маятник на планетарные орбиты
Начав с электронной таблицы Simple Pendulum, мы адаптируем ее к двумерный простой гармонический осциллятор, затем с небольшими изменениями в электронная таблица для орбит при потенциале обратных квадратов.Оба двумерных простой гармонический осциллятор и потенциал обратных квадратов имеют эллиптическую орбит, но мы можем видеть важные отличия от этих электронных таблиц.
Электронная таблица для планетарных орбит
16. Больше общих законов силы
Легко адаптировать электронную таблицу планеты, чтобы посмотреть на законы силы, другие
чем обратный квадрат. Мы обнаруживаем, что орбиты становятся намного сложнее.
Идеальная круговая орбита всегда возможна, но она нестабильна, за исключением
сила обратных квадратов! Таким образом, существование Солнечной системы означает, что
гравитационное притяжение обратно пропорционально квадрату. Вы можете изучить, как закон силы
влияет на орбиты, загрузив таблицу ниже, но вы обнаружите, что
из-за притяжения, намного более сильного, чем обратный квадрат, планета быстро падает
к солнцу, чем движется так быстро, что численный анализ становится
ненадежный.
Вы можете изучить, как закон силы
влияет на орбиты, загрузив таблицу ниже, но вы обнаружите, что
из-за притяжения, намного более сильного, чем обратный квадрат, планета быстро падает
к солнцу, чем движется так быстро, что численный анализ становится
ненадежный.
Электронная таблица для более общих законов силы
Домашние задания и т. д.
Простая задача квантовой динамики?
Это ступенчатая диссоциация Ne2Br2.Предоставлено: Американский институт физики.Исследование, опубликованное в The Journal of Chemical Physics , издаваемом Американским институтом физики, обеспечивает первые измерения в реальном времени временной зависимости отдельных стадий диссоциации комплекса, состоящего из двух атомов инертных газов и молекула галогена.
«Цель этой работы — предоставить тестовый пример теории квантовой динамики», — говорит автор Кеннет С. Джанда из Калифорнийского университета в Ирвине. «Это простая, но не слишком простая проблема в том смысле, что фундаментальное объяснение квантовой динамики находится в пределах досягаемости».
Джанда из Калифорнийского университета в Ирвине. «Это простая, но не слишком простая проблема в том смысле, что фундаментальное объяснение квантовой динамики находится в пределах досягаемости».
Исследователи охладили смесь гелия, неона и брома, распылив ее через сопло, в результате чего поток частиц газа двигался с одинаковой скоростью. Это создавало очень низкую температуру в движущейся системе отсчета — частицы были неподвижны друг относительно друга и конденсировались, образуя тетраэдрические комплексы Ne 2 Br 2 .После возбуждения молекулы брома лазерным импульсом спектроскопически наблюдалась диссоциация комплекса в течение десятков пикосекунд.
Добавление 16 квантов колебательной энергии к вибрации бромного растяжения привело к быстрой прямой диссоциации. Два атома Ne диссоциировали, не взаимодействуя друг с другом. Однако при несколько более высоком колебательном возбуждении, усилении в 23 кванта, бромный ангармонизм привел к разделению кинетической энергии между атомами Ne и гораздо более сложному механизму диссоциации.
«Для 23 квантов первая передача вибрации не может сбить один из атомов неона в 80% случаев», — говорит Янда. «Вместо этого образуется крошечная капля жидкости, позволяющая атому неона двигаться по прямой линии с атомами брома. Следующая вибрация отбрасывает его, как бильярдную клюшку, ударяющую по битку».
Как расщепить молекулу воды
Дополнительная информация: В статье Джордана М. «Динамика диссоциации комплекса Ne2Br2 ван-дер-ваальса в реальном времени».Pio, Molly A. Taylor, Wytze E. van der Veer, Craig R. Bieler, Jose A. Cabrera и Kenneth C. Janda была опубликована в Интернете в The Journal of Chemical Physics 7 июля 2010 г. См.: link.aip. org/ссылка/JCPSA6/v133/i1/p014305/s1
Предоставлено Американский институт физики
Цитата :
Простая задача квантовой динамики? (2010, 14 июля)
получено 28 января 2022 г. с https://физ.org/news/2010-07-simple-quantum-dynamics-problem.html
с https://физ.org/news/2010-07-simple-quantum-dynamics-problem.html
Этот документ защищен авторским правом. Помимо любой добросовестной сделки с целью частного изучения или исследования, никакие часть может быть воспроизведена без письменного разрешения. Контент предоставляется только в ознакомительных целях.
Динамика и статика Задачи по физике Помощь
Привет, Ахиллос!
Я предполагаю, что эти проблемы пронумерованы от 1 до 5, сверху вниз.
1. В этой задаче используются условия равновесия из статики. Используя координаты x-y (декартовы координаты), я обычно записываю их в виде трех условий:
(a) сумма сил в направлении x = 0 (ΣF x = 0)
(b) сумма сил в направлении Y = 0 (ΣF y = 0)
(c) сумма крутящих моментов = 0 (Στ = 0)
УГОЛ РАВНОВЕСИЯ СТРУНЫ (используя уравнение суммы сил)
————————————————— ———————————-
Я нарисовал небольшую схему ситуации, как я понял, на которую можно ссылаться. Единственные предположения, которые я сделал, заключались в том, что измерительная линейка была однородной, а желаемые углы были между струной и вертикалью, а измерительная линейка находилась на вертикали:
Единственные предположения, которые я сделал, заключались в том, что измерительная линейка была однородной, а желаемые углы были между струной и вертикалью, а измерительная линейка находилась на вертикали:
https://imgur.com/qq01Cw9
Из этого вы можете увидеть, что единственными силами в направлении х являются горизонтальная сила на конце измерительной линейки (которая известна) и горизонтальная составляющая натяжения, которую вы можете записать в терминах общей натяжение (T) и угол (θ) между струной и вертикалью (посмотрите, сможете ли вы понять, как это сделать, учитывая рисунок).
Единственными силами, направленными по оси Y, являются сила тяжести, действующая на измерительную линейку (известная), и составляющая Y натяжения, которую можно снова записать в терминах T и θ.
С помощью этой информации вы можете заполнить выражения для всех членов в уравнениях статического равновесия (a) и (b) выше. Как только вы это сделаете, у вас будет два уравнения с двумя неизвестными: T и θ. Решив эти уравнения как систему, вы сможете найти угол θ, который я принял за «угол равновесия струны».»
Решив эти уравнения как систему, вы сможете найти угол θ, который я принял за «угол равновесия струны».»
УГОЛ РАВНОВЕСИЯ ИЗМЕРИТЕЛЬНОЙ СТОЙКИ (уравнение суммы моментов)
————————————————— ——————————
Мы можем использовать уравнение суммы крутящих моментов, чтобы получить угол, который я назвал α на диаграмме, «угол равновесия измерительной линейки». Я бы порекомендовал использовать точку крепления струны в качестве центра вращения. Таким образом, натяжение не создает крутящего момента и может быть исключено из уравнения суммы крутящих моментов.
Затем вы можете посмотреть на крутящие моменты, создаваемые двумя другими силами (гравитацией и толкающей силой) вокруг той оси, где струна прикрепляется к измерительной рейке. Чтобы определить крутящий момент, создаваемый силой вокруг точки, вы должны знать три вещи:
1) сила
2) расстояние от выбранной оси вращения до места приложения силы (которое я обычно называю «r»)
3) угол (который я буду называть γ, чтобы не путать его с углами, перечисленными выше) между направлением силы и направлением r
Тогда крутящий момент этой силы вокруг этого центра равен: τ = Frsin(γ)
Выбирая ось вращения в точке крепления струны и зная, что гравитация приложена к центру масс (который, если измерительная линейка однородна, находится в геометрическом центре палочки), а толкающая сила в точке конец должен позволить вам записать выражения крутящего момента для гравитации и толкающей силы вокруг этой оси.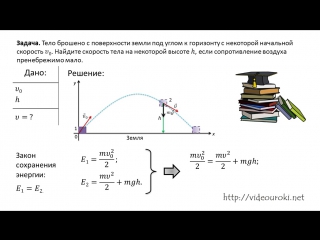 Вы должны обнаружить, что угол γ между силой и r в каждом случае должен зависеть от α, угла между метрической линейкой и вертикалью (я нарисовал r на диаграмме). Это делает α единственным неизвестным в выражении суммы крутящих моментов, поэтому вы должны быть в состоянии найти его.
Вы должны обнаружить, что угол γ между силой и r в каждом случае должен зависеть от α, угла между метрической линейкой и вертикалью (я нарисовал r на диаграмме). Это делает α единственным неизвестным в выражении суммы крутящих моментов, поэтому вы должны быть в состоянии найти его.
Возможно, я сказал кое-что, что вы уже знаете, но я надеюсь, что эти идеи направят вас на правильный путь. Я вернусь через некоторое время, чтобы сделать заметки и о других. Если у вас есть какие-либо вопросы или вы хотите проверить ответ, пожалуйста, не стесняйтесь спрашивать.
.

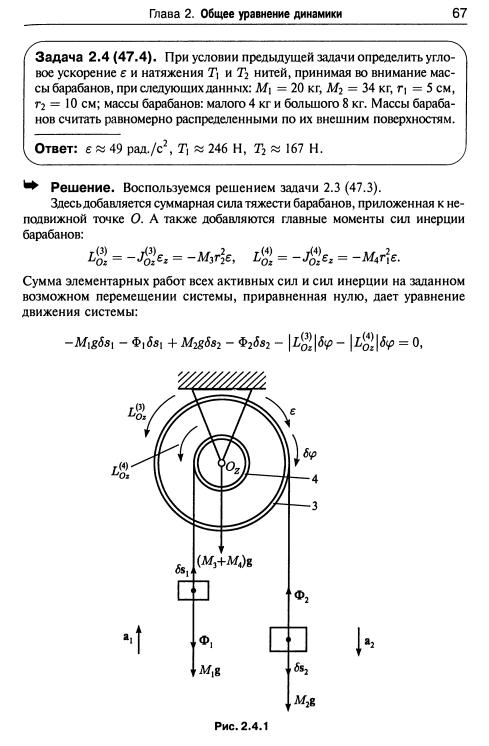 1)
1)