Физика время формула: Формула времени в физике - Управленческое образование

Содержание

Формула времени в физике

Содержание:

Определение и формула времени

В понятие времени отражаются такие свойства мира как постоянное развитие, изменение его в сознании человека. Процессы идут в определенной последовательности, при этом имеют определённую продолжительность.

Определение

Время – физическая величина, отражающая свойство материальных процессов иметь определенную продолжительность, следовать друг за другом в установленной последовательности и развиваться этапно. Обозначают время буквой t.

Особенности времени как физической величины

Время неотделимо от материи и ее движения, так как является ее формой существования. Нет смысла говорить о времени самом по себе, так как в отрыве от материальных процессов течение времени становится бессодержательным. Только исследование процессов, происходящих в материальном мире и их взаимосвязей, делает понятие времени физически содержательным.

В череде процессов, происходящих в природе, особенное место занимают повторяющиеся процессы (повторение дней и ночей, дыхание, перемещение звезд по небосводу и т.

д). Исследование и сравнение подобных процессов между собой ведет к идее о длительности материальных процессов, сравнение их длительности приводит к идее об их измерении.

Эталоном измерения является периодический процесс, который называют часами. Существуют системы отсчета, в которых возможно введение единого времени с достаточной для практики точностью. Введение единого времени хорошо подтверждается экспериментом. Теория дает возможность предсказать отклонения единого времени, что можно проверить эмпирически.

Длительность физического процесса, который происходит в некоторой точке, определяют при помощи часов, которые располагают в той же точке. При этом применяется прямое сравнение, сравниваются длительности процессов, которые текут в одной точке. Измерение длительности сводят к фиксации начала и окончания рассматриваемого процесса на шкале процесса, который принимают за эталонный. При этом говорят как о фиксации показаний часов в момент начала и окончания процесса, и это не имеет отношения к фактическому месту нахождения часов (процесса) в точке рассмотрения.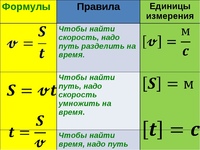

Синхронизация часов и изучения законов распространения физических сигналов развивались параллельно, при этом происходили взаимные уточнения и дополнения. Синхронизацию проводят при помощи сигналов, которые распространяются с конечной скоростью. Этот метод использует определение постоянной скорости: если из точки, в которой часы показывают t₀, исходит сигнал, перемещающийся со скоростью v=const, то тогда, когда сигнал придет в точку на расстоянии s, часы в этой точке должны показать время:

$$t=t_{0}+\frac{s}{v}(1)$$

Такая синхронизация согласуется с синхронизацией с использованием световых сигналов. Тогда часы синхронизируются по формуле:

$$t=t_{0}+\frac{s}{c}(2)$$

где c=299792,4562 км/с – скорость света, которая не зависит от скорости источника и приемника по всем направлениям пространства одинакова.

Особенности времени как физической величины

Перемещение ($\bar{s}$), равно:

$$\bar{s}\left(t_{2}, t_{1}\right)=\bar{s}\left(t_{2}\right)-\bar{s}\left(t_{1}\right)(3)$$

где $\bar{s}(t_2)$ – радиус-вектор в момент времени $t_2, \bar{s}(t_1)$ – радиус-вектор в момент времени $t_1$ .

Мгновенная скорость ($\bar{v}$):

$$\bar{v}=\frac{d \bar{s}}{d t}(4)$$

Мгновенное ускорение ($\bar{a}$):

$$\bar{a}=\frac{d \bar{v}}{d t}(5)$$

Единицы измерения времени

Основной единицей измерения момента силы в системах СИ и СГС является: [t]=c

Единицы измерения времени основываются на периоде вращения Земли около своей оси и вокруг Солнца, Луни вокруг Земли. Внесистемные единицы измерения времени: час, минута, сутки и т.д.

Примеры решения задач

Пример

Задание. Движения двух тел заданы уравнениями: и s₁(t)=5t и s₂(t)=150-10t. Найдите время встречи.

Решение. В точке встречи s₁(t)=s₂(t). Приравняем правые части функцийx(t), имеем:

$$5 t=150-10 t \rightarrow 15 t=150 \rightarrow t=10$$

Ответ. t=10 c

Слишком сложно?

Формула времени не по зубам? Тебе ответит эксперт через 10 минут!

Пример

Задание. Движение материальной точки, задано уравнением: x=4t-0,05t² . В какой момент времени, скорость точки равна нулю? Коэффициенты имеют размерности: 4 м/с, 0,05м/с² . Изобразите графики зависимости модуля ускорения от времени.

Решение. В условиях задачи задана функция x(t), скорость можно найти как:

$$v=\frac{d x}{d t}=4-0,1 t(2.1)$$

Приравняем скорость к нулю, найдем время:

$$4-0,1 t=0 \rightarrow t=\frac{4}{0,1}=40(c)$$

Определим, какова зависимость модуля ускорения от времени, для этого возьмем производную по времени от функции v(t) (2.1):

$$a(t)=\frac{d v}{d t}=-0,1(2.2)$$

Тогда график зависимости a(t) имеет вид:

Ответ.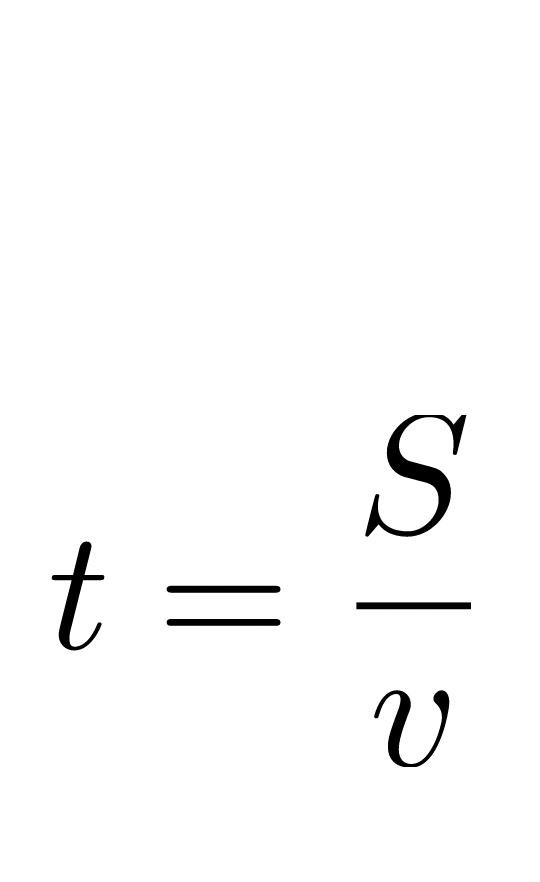

t=40 c

Читать дальше: Формула длины волны.

Что такое время в физике и механике: понятие, формула, как обозначается

Попробуйте сходу дать точное определение: что такое время? Мысль вертится вокруг этого понятия, пытается ухватиться, но вот сформулировать однозначное определение сложно. Есть разные концепции и трактовки времени в философии, физике, метрологии.

В классической механике и теории относительности используются совершенно разные концепции времени. В первом случае время характеризует последовательность событий, происходящих в трехмерном пространстве. Во втором рассматривается еще и как четвертая координата.

Но обо всем по порядку. Давайте узнаем, как люди измеряли время, почему секунда — его мельчайшая принятая единица. Также определим понятие времени в физике, рассмотрим явления релятивистского и гравитационного замедления времени.

Что такое время?

Течение времени – совершенно естественное явление. Время идет, все вокруг меняется, происходят разные события. Именно поэтому о времени с точки зрения физики, в первую очередь, стоит говорить в контексте событий.

Если бы вокруг ничего не происходило, понятие времени не имело бы традиционного смысла. Другими словами, без событий времени не существует. Итак:

Время – мера того, как меняется окружающий мир. Время определяет длительность существования объектов, изменение их состояний и процессы, протекающие в них.

В системе СИ время измеряется в секундах и обозначается буквой t.

Как люди измеряли время?

Для измерения времени нужны какие-либо повторяющиеся с одинаковым периодом события. Например, смена дня и ночи. Солнце каждый день встает на востоке и садится на западе, а Луна каждый синодический месяц проходит весь цикл фаз освещенности солнцем — от тоненького серпа полумесяца до полнолуния.

Синодический месяц – время от одного новолуния до другого. За синодический месяц Луна совершает оборот вокруг Земли.

Древним людям ничего не оставалось, как привязать отсчет времени к движению небесных тел и событиям, связанным с ним. А именно – к смене дней, ночей и сезонов года.

В году 4 сезона и 12 месяцев. Именно столько раз за весну, лето, осень и зиму Луна меняет свои фазы.

По мере развития прогресса методы измерения времени совершенствовались, появились солнечные, водяные, песочные, огненные, механические, электронные и, наконец, молекулярные часы.

Часы FOCS 1Часы FOCS 1 в Швейцарии измеряют время с погрешностью хода около одной секунды за 30 миллионов лет. Это очень точные часы, но через 30 миллионов лет их все же придется «подвести».

Почему в часе 60 минут, в минуте – 60 секунд, а в сутках – 24 часа?

Сразу оговоримся, что изложенное ниже во многом является личными предположениями автора, сделанными на основе исторических сведений.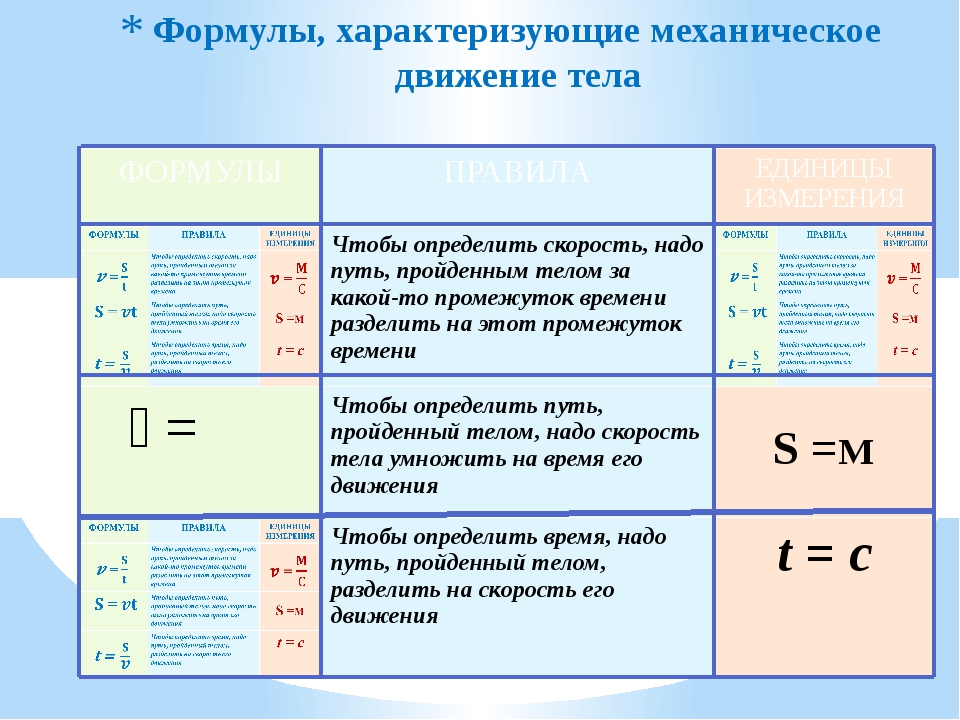 Если у наших читателей появятся уточнения или вопросы, мы будем рады видеть их в обсуждениях.

Древним народам нужна была какая-то основа, чтобы строить свои системы счисления. В Вавилоне за такую основу было взято число 60.

Именно благодаря шестидесятеричной системе счисления, придуманной шумерами и позже распространившейся в Древнем Вавилоне, окружность содержит 360 градусов, градус – 60 минут, а минута – 60 секунд.

Год можно представить в виде окружности, содержащей 360 градусов. Возможно, число 360 в данном контексте взялось оттого, что в году 365 дней, и эту цифру просто округлили до 360.

Когда-то самой короткой единицей измерения времени был час. Древние вавилоняне были сильными математиками и решили ввести меньшие единицы времени, используя свое любимое число 60. Поэтому, в часе 60 минут, а в минуте 60 секунд.

Но почему день делится на 12 часов? За это нужно сказать спасибо древним египтянам и их двенадцатиричной системе. День и ночь делились на 12 раных частей, считаясь разными царствами бытия. Скорее всего, первоначально использование числа 12 связано с количеством оборотов Луны вокруг Земли за год.

Самая большая единица измерения времени

Самая большая единица измерения времени – кальпа. Кальпа является понятием из индуизма и буддизма. Она равняется примерно 4,32 миллиардам лет, что совпадает с возрастом Земли с точностью до 5%.

Как в голову древним индуистам пришли такие цифры? Ответа на этот вопрос мы не знаем, но вся система как будто говорит нам, что тогда люди знали о Вселенной немного больше, чем мы.

Представление о времени

Кальпу в индуизме еще называют «днем Брахмы». День сменяется ночью, равной ему по продолжительности. 30 дней и ночей составляют месяц, а год состоит из 12 месяцев. Вся жизнь Брахмы – 100 лет, по прошествии которых мир погибает вместе с ним.

Если перевести сто лет Брахмы в наши традиционные годы, получится 311 триллионов и 40 миллиардов лет! Нынешнему Брахме 51 год.

Вывод: если все это правда, то беспокоится не стоит — Вселенная будет существовать еще долгое время.

Кальпа – самая большая единица измерения времени согласно книге рекордов Гиннеса.

Первые часы

Сначала было достаточно палочки, на которой каменным топором можно делать зарубки и тем самым отсчитывать прошедшие дни. Но это скорее был календарь, а не часы.

Первые и самые древние часы – солнечные. Их действие основано на изменении длины тени предметов по мере того, как солнце движется по небосводу. Такие часы представляли собой гномон – длинный шест, воткнутый в землю. Солнечные часы применялись в Древнем Египте и Китае. О них было доподлинно известно уже в 1200 году до нашей эры.

Солнечные часы в Китае

Затем появились водяные, песочные и огненные часы. Работа этих механизмов не была привязана к движению небесных светил. Долгое время водяные часы были главным инструментом для измерения времени.

Первые механические часы были изготовлены китайскими мастерами в 725 году нашей эры. Однако широкое распространение они получили относительно недавно.

В средневековой Европе механические часы устанавливались в башнях соборов и имели только одну стрелку – часовую. Карманные часы появились только в 1675 году (изобретение запатентовал Гюйгенс), а наручные – намного позже.

Первые наручные часы были исключительно женским аксессуаром. Они представляли собой богато украшенные изделия, точность хода которых отличалась огромными погрешностями. У уважающего себя мужчины не могло быть и мысли о том, чтобы носить наручные часы.

Современные часы

Сейчас механические или электронные часы есть у каждого. Они измеряют время с относительно небольшими погрешностями. Однако самыми точными часами в мире являются атомные часы. Их еще называют молекулярными или квантовыми.

Биг Бен — знаменитые башенные часы

Как мы помним, для определения единицы времени необходим какой-то периодический процесс. Когда-то самой короткой единицей был день. То есть единица измерения время была привязана к периодичности восхода и заката солнца. Потом минимальной единицей стал час, и так далее.

С 1967 года, согласно международной системе СИ, определение одной секунды привязано к периоду электромагнитного излучения, возникающего при переходе между сверхтонкими уровнями основного состояния атома Цезия-133. А именно: одна секунда равна 9 192 631 770 таким периодам.

Время в физике

На данный момент не существует определенной и единой концепции определения времени в физике.

В классической механике время считается непрерывной, априорной и ничем не определяемой характеристикой мира.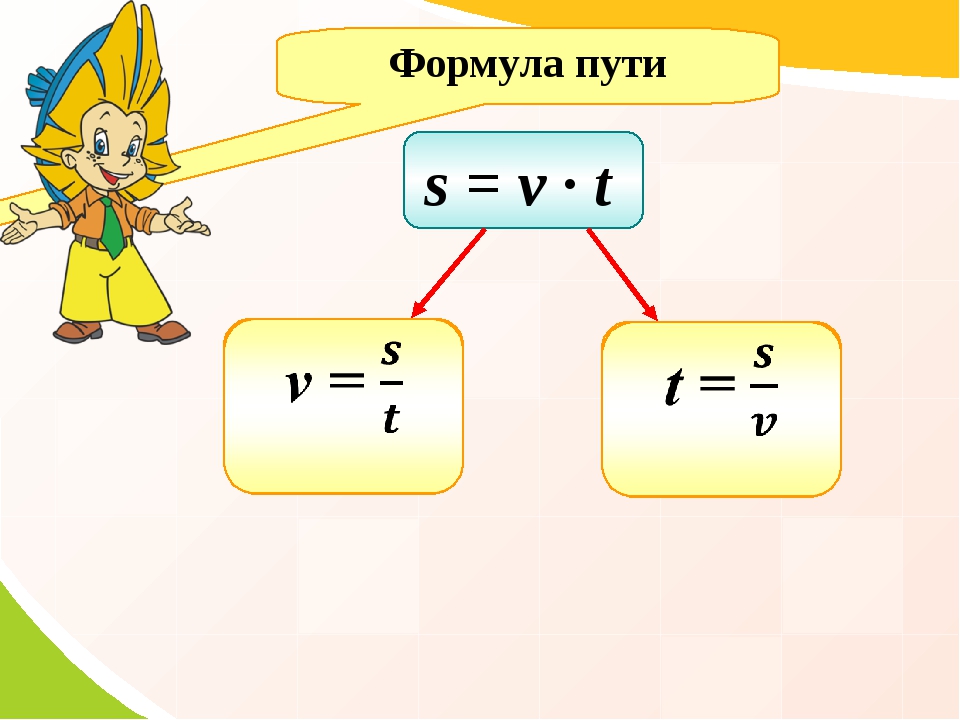

Для измерения времени используется какая-либо периодическая последовательность событий. В классической физике время инвариантно относительно любой системы отсчета. То есть во всех системах события происходят одновременно.

Как найти время в физике? Простейшая формула, определяющая связь между пройденным путем, скоростью и временем, известна каждому школьнику и имеет вид:

Это формула времени для равномерного и прямолинейного движения. Здесь t — время, S — пройденное расстояние, v — cкорость.

Более подробно об основах классической механики читайте в нашей отдельной статье.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Термодинамика говорит, что время необратимо. Необратимо по причине возрастания энтропии замкнутой системы. Кстати, в нашем тематическом материале читайте о том, что такое энтропия.

Но самое интересное начинается в релятивистской физике. Приведем цитату Стивена Хокинга, физика, написавшего краткую историю времени.

Нам приходится принять, что время не отделено полностью от пространства и не независимо от него, но вместе с ним образует единый объект, который называется пространством-временем

Также в релятивистской физике время перестает быть инвариантом и можно говорить об относительности времени. Другими словами, ход времени зависит от движения системы отсчета.

Это так называемое релятивистское замедление времени. Если часы находятся в неподвижной системе отсчета, то в движущемся теле все процессы происходят медленнее, чем в неподвижном. Именно поэтому космонавт, путешествующий в космосе на супер скоростном корабле, практически не постареет по сравнению со своим братом близнецом, оставшимся на Земле.

Релятивистское замедление времени

Помимо релятивистского существует гравитационное замедление времени. Что это такое? Гравитационное замедление времени – изменение хода часов в гравитационном поле. Чем сильнее поле гравитации, тем сильнее замедление.

Вспомним о том, что секунда – это время, за которое атом изотопа цезия совершает 9 192 631 770 квантовых переходов. В зависимости от того, где находится атом (на земле, в космосе, вдали от любого объекта или у черной дыры) секунда будет иметь разные значения.

Поэтому и время процессов, связанных с данной системой отсчета, будет отличаться. Так, для наблюдателя у горизонта событий Шварцшильдовской черной дыры время практически остановится, а для наблюдателя на Земле все произойдет почти мгновенно.

Людей всегда волновала тема путешествий во времени. Предлагаем вам посмотреть научно-популярный фильм на эту тему и напоминаем, что если у вас совершенно нет времени на учебные дела, наш студенческий сервис всегда поможет справится с актуальными задачами и проблемами.

Расчет пути, скорости и времени движения: равномерное и неравномерное

Равномерное движение, это вдвижение спостоянной скоростью.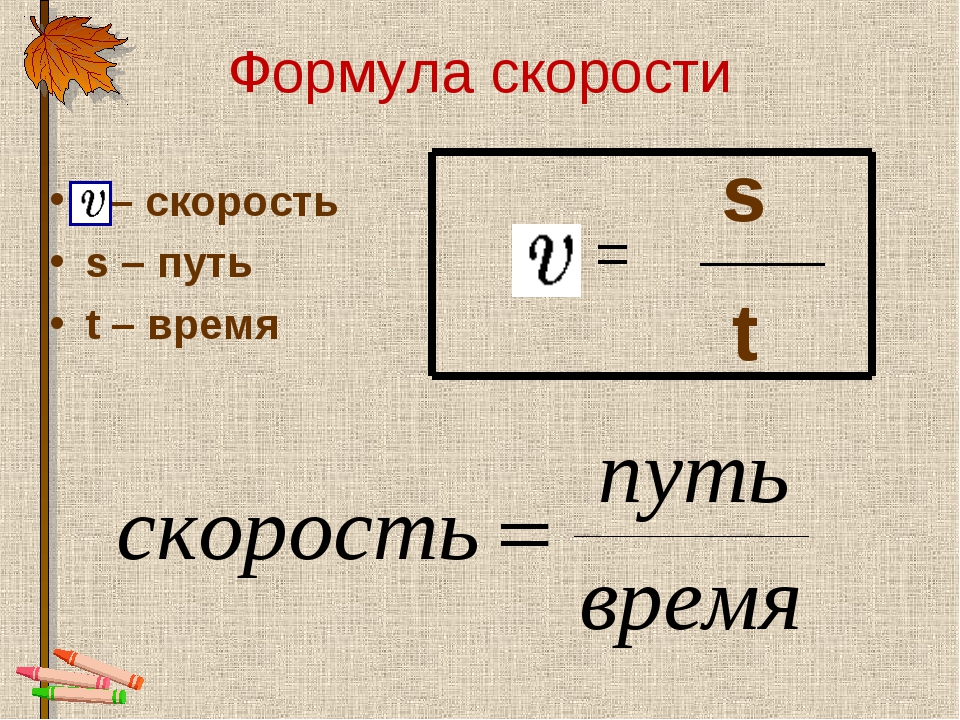 То есть другимим словами, тело за одинаковые промежутки времени должно проходить одинаковое расстояние. Например, если машина будет за каждый час своего пути проезжать расстояние в 50 километров, то такое движение будет являться равномерным.

Обычно равномерное движение очень редко можно встретить в реальной жизни. За примеры равномерного движения в природе, можно считать вращение Земли вокруг Солнца. Или например, конец секундной стрелки часов, тоже будет двигаться равномерно.

Расчет скорости при равномерном движении

Скорость тела при равномерном движении будет вычисляться по следующей формуле.

Скорость = путь / время.

Если обозначить скорость движения буквой V, время движения буквой t, а путь пройденный телом буквой S, то получим следующую формулу.

Единица измерения скорости 1 м/с. То есть тело проходит расстояние в один метр, за время равное одной секунде.

Движения с переменной скоростью называется неравномерным движением. Чаще всего, все тела в природе двигаются именно неравномерно. Например, человек, когда куда-либо идет, двигается неравномерно, то есть его скорость в течении всего пути будет изменяться.

Расчет скорости при неравномерном движении

При неравномерном движении, скорость все время изменяется, и в этом случае говорят о средней скорости движения.

Средняя скорость неравномерного движения вычисляется по формуле

Из формулы для определения скорости, мы можем получить и другие формулы, например, для расчета пройденного пути или времени, которое двигалось тело.

Расчет пути при равномерном движении

Чтобы определить путь, который прошло тело при равномерном движении, необходимо скорость движения тела умножить на время которое это тело двигалось.

То есть, зная скорость и время движения, мы всегда сможем найти путь.

Теперь, получим формулу для расчета времени движения, при известных: скорости движения и пройденном пути.

Расчет времени при равномерном движении

Для того чтобы определить время равномерного движения, необходимо путь пройденный телом, поделить на скорость, с которой это тело двигалось.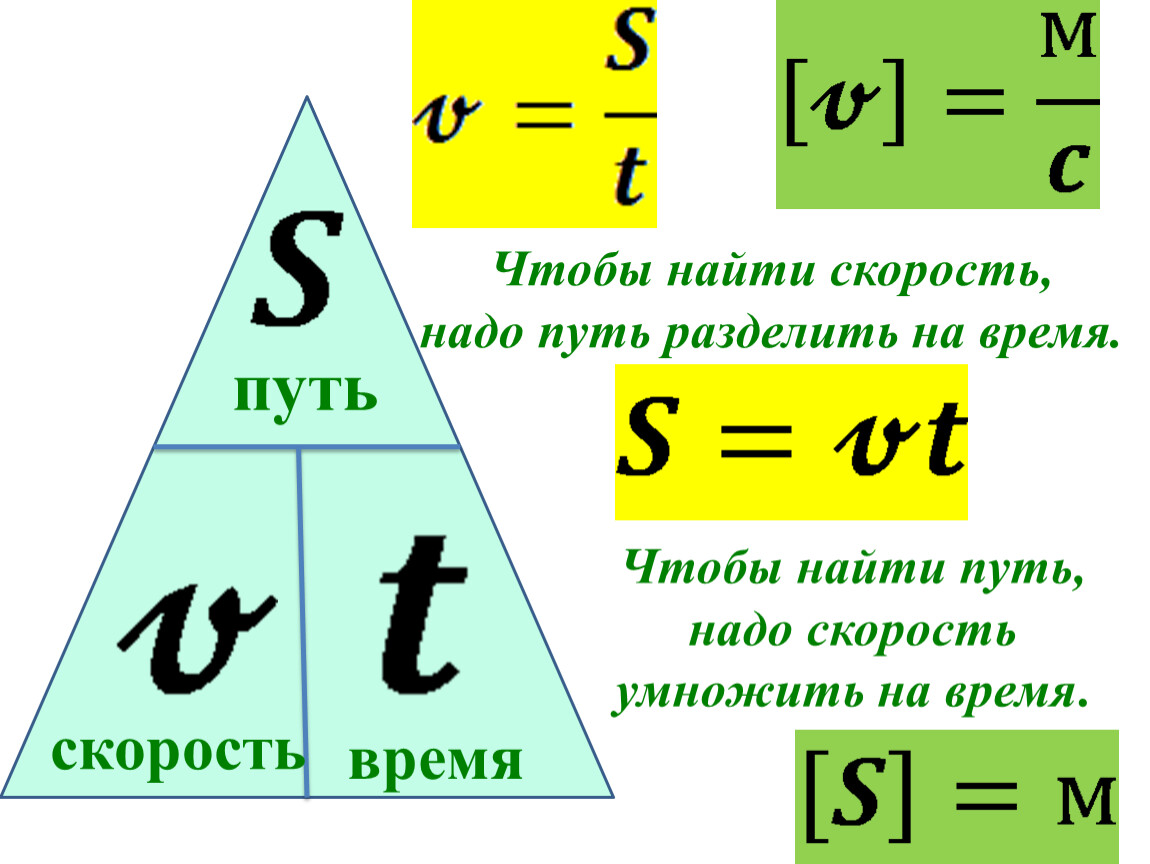

Полученные выше формулы будут справедливы, если тело совершало равномерное движение.

При расчете средней скорости неравномерного движения, полагают, что движение было равномерным. Исходя из этого, для вычисления по средней скорости неравномерного движения, пути или времени движения используют те же самые формулы, что и при равномерном движении.

Расчет пути при неравномерном движении

Получаем, что путь пройденный телом при неравномерном движении, равен произведению средней скорости на время которое тело двигалось.

Расчет времени при неравномерном движении

Время необходимое для прохождения некоторого пути при неравномерном движении, равняется частному от деления пути на среднюю скорость неравномерного движения.

Графиком равномерного движения, в координатах S(t) будет являться прямая линия.

Нужна помощь в учебе?

Предыдущая тема: Скорость в физике: единицы скорости
Следующая тема:&nbsp&nbsp&nbspЯвление инерции: в чем заключается и примеры из жизни

Скорость | Физика

Проделаем опыт. Установим на тележку капельницу (рис. 11). Из капельницы через одинаковые промежутки времени падают капли окрашенной жидкости. Если присоединить к тележке груз (как это показано на рисунке 11), то при определенной его величине расстояния между следами, оставленными каплями на бумаге (при движении тележки), могут оказаться равными. Это означает, что тележка за одинаковые промежутки времени проходит равные пути.Повернув кран капельницы так, чтобы капли падали чаще, повторим опыт. Следы капель и в этом случае оказываются на равных расстояниях друг от друга, хотя и меньших, чем в первом опыте. А это значит, что и за меньшие одинаковые промежутки времени тележка проходит одинаковые пути.

Если какое-нибудь тело за любые равные промежутки времени проходит одинаковые пути, то его движение называют равномерным.

Быстроту движения характеризуют физической величиной, называемой скоростью. Известно, что самолет движется быстрее автомобиля, а искусственный спутник Земли — быстрее самолета.

Скорость тела при равномерном движении показывает, какой путь проходит тело за единицу времени. Например, если за каждый час пешеход проходит 3 км, а самолет пролетает 900 км, то говорят, что скорость пешехода 3 км/ч, а скорость самолета 900 км/ч.

Если же известно, что тот же пешеход за каждые два часа проходит 6 км, то, для того чтобы узнать, какой путь он проходит за 1 ч, следует эти 6 км разделить на 2 ч. При этом мы снова получим 3 км/ч.

Итак, чтобы определить скорость тела при равномерном движении, надо пройденный телом путь разделить на время движения, т. е.

Обозначим все величины, входящие в это выражение, латинскими буквами:

s — путь, v — скорость, t — время.

Тогда формулу для нахождения скорости можно представить в следующем виде:

В СИ за единицу скорости принимают скорость такого равномерного движения, при котором движущееся тело за 1 с походит путь, равный 1 м. Эту единицу обозначают или 1 м/с (читается «метр в секунду»).

На практике часто применяют другую единицу скорости: 1 км/ч. Найдем связь между разными единицами скорости. Так как 1 км = 1000 м, а 1 ч = 60 мин = 3600 с, то мы можем записать:

Рассмотрим пример. Пусть требуется выразить скорость самолета, равную 720 км/ч, в метрах в секунду. Переводя километры в метры, а час в секунды, получаем

При равномерном движении числовое значение скорости не изменяется. Если, например, скорость тела равна 60 км/ч, то это значение будет оставаться таким же на протяжении всего времени движения.

Но, кроме своего числового значения, скорость имеет и свое направление. Поэтому на рисунках скорость тела изображают в виде стрелки (рис. 12). Стрелка указывает направление скорости (а следовательно, и движения) тела.

Величины, имеющие направление в пространстве, называют векторными величинами или просто векторами. Скорость — величина векторная. Векторной величиной, как мы увидим позже, является также сила. С другой стороны, такие величины, как масса, путь, объем, векторами не являются: они не имеют направления в пространстве и характеризуются лишь числовым значением.

В таблице 2 приведены значения некоторых скоростей, встречающихся в природе.

Таблица 2

Скорости движения, м/с

Не все указанные в таблице 2 движения являются равномерными. Лишь звук, свет и радиоволны при определенных условиях распространяются с постоянной скоростью. Скорости остальных тел меняются в процессе движения. Поэтому для них указаны средние или наибольшие значения, которые могут быть достигнуты этими телами.

Движения, при которых скорость тела на разных участках траектории различна, называются неравномерными.

Неравномерные движения характеризуют средней скоростью. Средняя скорость неравномерного движения находится так же, как и скорость равномерного движения, т. е. пройденный телом путь делится на время движения:Только полученное при этом значение может не совпадать со скоростью движения тела на отдельных участках траектории. При неравномерном движении тело на одних участках имеет меньшую скорость, на других — большую. Например, поезд, отходящий от станции, начинает двигаться все быстрее и быстрее. Подъезжая к станции, он, наоборот, замедляет свое движение.

Лишь при равномерном движении скорость тела на протяжении всей траектории имеет неизменное числовое значение.

Зная скорость и время равномерного движения тела, можно вычислить пройденный телом путь. Из формулы (6.1) следует, что
(6.2)
Итак, чтобы найти путь, пройденный при равномерном движении, надо скорость тела умножить на время движения.
Если же известны путь и скорость, то можно найти время движения. Из формулы (6.2) получаем
(6.3)
Итак, чтобы найти время движения, надо путь, пройденный телом, разделить на его скорость.

1. Какое движение называют равномерным? 2. Что показывает скорость равномерного движения? 3. Как определяется скорость при равномерном движении? 4. Как находится пройденный путь, если известны скорость и время движения? 5. Как находится время движения, если известны путь и скорость движения? 6. Какое движение называют неравномерным? 7. Как нужно изменить условия опыта, изображенного на рисунке 11, чтобы движение тележки стало неравномерным? Как при этом изменятся расстояния между следами, оставляемыми падающими каплями? 8. Как находится средняя скорость? 9. Какие величины называют векторными? Как их изображают на рисунках?
Экспериментальные задания. 1. Определите среднюю скорость, с которой вы пробегаете 100 м. 2. Если у вас дома есть игрушечный заводной автомобиль, то, сделав необходимые измерения, найдите среднюю скорость, с которой он перемещается. Результаты измерений и вычислений запишите в тетрадь.

Формулы ускорения в физике

Ускорение: сущность и виды

Под действием различных физических сил тела ускоряют или замедляют свое движение.

Определение 1

Ускорением называют интенсивность изменения скорости движения. Оно характеризует изменение скорости за единицу времени. 2$).

Движение с ускорением, вектор которого не меняется по модулю и направлению, называется равноускоренным.

Определить ускорение при равноускоренном прямолинейном движении можно по формуле:

$a = \frac{v_1 — v_0}{t} = \frac{\Delta v}{t}$,

где $v_1, v_0$ — скорости в начале и в конце рассматриваемого периода времени длительностью $t$.

Отношение изменения скорости к промежутку времени, за который произошло это изменение, называют средним ускорением:

$\vec{a} = \frac{\vec{v_1} — \vec{v_0}}{t} = \frac{\Delta \vec{v}}{t}$,

В отличие от равноускоренного, здесь имеют значение направления векторов.

Если начальная скорость больше конечной, происходит замедление, которое в физике также принято называть ускорением, но выраженным с отрицательным знаком.

Мгновенное ускорение — ускорение, развиваемое за очень малый промежуток времени (его длительность стремится к нулю):

$\vec{a} = \lim\limits_{t \to 0}\frac{\Delta \vec{v}}{\Delta t}$.

Ускорение при движении по окружности

Поскольку ускорение — векторная величина, при движении отличном от прямолинейного оно не остается неизменным даже если модуль скорости не изменяется. В связи с этим ускорение вычисляется из начальной и конечной скоростей по правилам векторной математики, т.е. с учетом изменения направления.

Тело, движущееся по окружности, удобно рассматривать как обладающее двумя ускорениями: тангенциальным ($a_{\tau}$), направленным по касательной к траектории, и центростремительным, направленным к центру ($a_n$). При равномерном движении по окружности тангенциальное ускорение, отражающее мгновенную скорость тела, может быть равно нулю, но центростремительное имеет место даже в этом случае. Поэтому любое движение по криволинейной траектории является движением с ускорением.

Замечание 1

Центростремительное ускорение называется также нормальным, тангенциальное — касательным.

Касательное ускорение определяется как мгновенное при движении на очень малое угловое расстояние, когда длина дуги и длина хорды между начальной и конечной точками малоразличимы (сравниваются мгновенные скорости в этих точках). {2}$

Физика микромира

Семинар 1. Введение. Физика микромира

Во введении рассматриваются основные составляющие новой физики, возникшей на рубеже XIX и XX столетий:

Теория относительности, изменившая существующие в классической физике представления о пространстве и времени.
Квантовая теория, изменившая представление о структуре материи. Явление радиоактивности, открытие электрона, сложная структура атома, протон-нейтронная структура атомного ядра, открытие фундаментальных частиц и взаимодействий привели к современному представлению об окружающем мире.
Открытия в области физики частиц, коренным образом повлиявшие на понимание процессов, происходящих во Вселенной.

1.1. Масштабы явлений в физике

1.2. Упругое рассеяние α-частиц. Формула Резерфорда

1.3. Сечение реакции

1.4. Размер ядра

1.5. Радиоактивность

6. Преобразования Лоренца

1.7. Эффект Доплера

1.8. Системы отсчета

1.9. Основные формулы релятивистской физики

1.10. Система единиц Гаусса

1.11. Энергия и порог реакции

1.12. Энергии частиц в двухчастичном распаде

Задачи

1.1. Масштабы явлений в физике

Диапазон временных интервалов во Вселенной
Возраст Вселенной	13.8 млрд. лет
Возраст Солнца	4.6 млрд. лет
Возраст Земли	4.5 млрд. лет
Появление жизни на Земле	~3.5 млрд. лет
Время прохождения светом расстояния Солнце–Земля	~5·10² с
Время прохождения светом расстояния 1 метр	3·10^–9 с
Время прохождения светом расстояния, равного радиусу атома	~10^–19 с
Время прохождения светом расстояния, равного радиусу атомного ядра	~10^–24 с

Диапазон расстояний во Вселенной
Видимая граница Вселенной	~10¹⁰ св. лет
Ближайшая галактика (Магеллановы облака)	163 000 св. лет
Диаметр галактики Млечный путь	100 000 св. лет
Ближайшая звезда Проксима Центавра	4·10¹⁸ см = 4.2 св. года
Расстояние Земля–Солнце (астрономические единицы)	1.5·10¹³ см
Радиус Солнца	6.9·10¹⁰ см
Радиус Земли	6.4·10⁸ см
Радиус Луны	1.7·10⁸ см
Радиус атома водорода	~0.5·10^–8 см
Радиус атомного ядра водорода	~0.8·10^–13 см
Размеры лептонов, кварков	<10^–17 см
1 световой год (расстояние, которое проходит свет за 1 год)	~9. 5·10¹⁷ см
1 парсек	3.1·10¹⁸ см = = 3.26 светового года

Диапазон масс во Вселенной
Масса видимого вещества во Вселенной	~10⁵⁶ г
Масса видимого вещества нашей галактики Млечный путь	~10¹² масс Солнца
Масса Солнца	1.99·10³³ г
Масса Земли	5.98·10²⁷ г
Масса Луны	7.35·10²⁵ г
Масса 1 куб. м свинца	1.135·10⁷ г
Масса 1 куб. м воздуха (20°C, 1 атм.)	1.204·10³ г
Масса атома свинца	3.45·10⁻²² г
Масса протона	1.67·10^–24 г
Масса электрона	9.11·10^–28 г

1.2. Упругое рассеяние α-частиц. Формула Резерфорда

Классическая физика основана на ряде блестящих экспериментов, среди которых особое место занимают эксперименты Г. Кавендиша и Ш. Кулона. С помощью крутильных весов ими были установлены законы гравитационного и электрического взаимодействий макроскопических тел. Однако метод эксперимента, который использовался Кавендишем и Кулоном, не может использоваться в микрофизике из-за малых размеров исследуемых объектов.
Новый метод изучения микроскопических систем, был предложен Э. Резерфордом. Он первым разработал и применил метод исследования с помощью рассеяния пробной «частицы-снаряда» на исследуемом объекте. В своем первом эксперименте Резерфорд использовал рассеяние α-частиц на атомах для того, чтобы изучить атомную структуру. Выяснив, что вероятность рассеяния α-частиц на атоме, как функция угла рассеяния θ, подчиняется формуле Резерфорда для рассеяния ее на точечном кулоновском центре

вероятность рассеяния ~ ,

(1.1)

где Z_α, Z_я – заряды (в единицах элементарного заряда) α-частицы и ядра-мишени, Т – кинетическая энергия α-частицы, он установил, что в атоме имеется ядро размером менее 5·10^–12 см, сосредотачивающее в себе почти всю массу атома.

Рис. 1.1 Рассеяние α-частицы на ядре мишени с зарядом Z_я. Угол рассеяния θ зависит от прицельного параметра b:
tg(θ/2) = Z_αZ_яe²/(2bT).

Атом состоит из ядра и связанных с ним электронов. Атомное ядро состоит из нуклонов: Z протонов и N нейтронов. Массовое число А = Z + N соответствует суммарному числу протонов и нейтронов.
В нейтральном атоме число электронов равно числу протонов Z.

1.3. Сечение реакции

Для характеристики вероятности процессов в микромире пользуются понятиями полного эффективного сечения σ и дифференциального эффективного сечения dσ/dΩ. Дифференциальное сечение используется для описания вероятности процесса взаимодействия частиц. Если мишень содержит N_М ядер и вся находится в пучке падающих частиц плотностью
j (j — число частиц, падающих в единицу времени на единицу поперечной площади мишени), то число dN(0)/dΩ частиц, рассеиваемых мишенью в единицу времени на угол θ в пределах телесного угла dΩ, определяется соотношением:

(1.

Полное число частиц, рассеиваемых мишенью в единицу времени под всеми углами, определяется соотношением

(1.3)

σ − полное эффективное сечение, N_М = nSd − характеристика мишени (n − число ядер мишени в единице объёма, S − облучаемая поперечная площадь мишени, d − толщина мишени в направлении падающего пучка частиц). Полное сечение измеряется в барнах (1 барн = 10^–24см²).

1.4. Размер ядра

Наиболее распространенный метод исследования атомных ядер – это рассеяние на ядрах различных частиц и ядер, ускоренных до высоких энергий. Точные данные по размерам атомных ядер были получены из экспериментов по рассеянию электронов. Радиусы ядер R растут с увеличением массового числа А и хорошо описываются соотношением

R ≈ 1.

3·10^-13·A^1/3 см = 1.3·A^1/3 Фм.

(1.4)

Численный коэффициент в (1.4) зависит от методики определения радиуса ядра и меняется в пределах 1.1÷1.4. Здесь и далее будет использоваться значение 1.3.

1.5. Радиоактивность

Радиоактивность – свойство атомных ядер самопроизвольно (спонтанно) изменять свой состав (заряд Z, массовое число A) в результате испускания частиц или ядерных фрагментов. К явлению радиоактивности относится также испускание атомным ядром гамма-квантов, но при этом ни заряд Z, ни массовое число A не изменяются.

Основные виды радиоактивных распадов:(A,Z) → (A-4,Z-2) + α
из атомного ядра испускается α-частица – ядро атома ⁴He.

β^–-распад: (A,Z) → (A,Z+1) + e^– + _eиз атомного ядра испускаются электрон e^– и антинейтрино _e, один из нейтронов ядра превращается в протон.

β⁺-распад: (A,Z) → (A,Z-1) + e⁺ + ν_eиз атомного ядра испускаются позитрон e⁺ и нейтрино ν_e, один из протонов ядра превращается в нейтрон.

e-захват: (A,Z) + e^– → (A,Z-1) + ν_eв результате взаимодействия между протоном и электроном атомной оболочки из ядра испускается нейтрино, один из протонов ядра превращается в нейтрон

γ-распад: (A,Z)* → (A,Z) + γ
из возбужденного атомного ядра испускается один или несколько гамма-квантов.

Рис. 1.2. Зависимость активности от времени (слева). Данная зависимость в логарифмическом масштабе отображается прямой, тангенс угла наклона которой равен постоянной распада λ. Справа приведена кривая активации (наведенной радиоактивности) в зависимости от времени. Рост числа радиоактивных ядер практически прекращается при достижении активации насыщения за время t ≈ 5T_1/2

Процесс радиоактивного распада, как и все процессы в микромире, – это случайный (статистический) процесс. Атомные ядра одного сорта распадаются за разное время. Однако среднее время жизни τ ядер, вычисленное по наблюдению большого числа распадов, оказывается не зависящим от способа получения этих ядер и от внешних условий. Среднее время жизни τ ядра характеризует скорость их распада. Постоянная распада λ:

Физический смысл λ – это вероятность распада радиоактивного ядра в единицу времени.
Закон радиоактивного распада показывает, как со временем изменяется в среднем число радиоактивных ядер в образце. Если в момент времени t имеется большое число N радиоактивных ядер, то к моменту t + dt распад испытают в среднем λNdt ядер. Поэтому изменение их числа dN определяется соотношением

Знак минус означает, что общее число радиоактивных ядер (частиц) уменьшается в процессе распада. Интегрируя соотношение (1.6), получим закон радиоактивного распада:

где N₀ − число радиоактивных ядер в начальный момент t = 0. Закон радиоактивного распада относится к статистическим средним и справедлив лишь при достаточно большом числе распадающихся ядер.
Среднее время жизни τ ядра вычисляется по формуле

(1.8)

Часто для характеристики скорости радиоактивного распада атомных ядер используют величину, называемую периодом полураспада – T_1/2. Период полураспада – это время, за которое число радиоактивных ядер уменьшается вдвое: N₀/2 = N₀, откуда

T_1/2 = ln2/λ ≈ 0.693/λ = 0.693τ.

(1.9)

Активность образца А – число распадов в единицу времени, является производной от N по времени, взятой с обратным знаком:

Активность образца уменьшается со временем по тому же экспоненциальному закону, что и число нестабильных ядер. Активность измеряют в беккерелях или в кюри.

1 Бк (беккерель) = 1 распад в секунду,
1 Ки (кюри) = 3.7·10¹⁰ Бк.
1 Ки – это активность 1 г радия вместе с продуктами его распада.

Энергия распадающейся системы в соответствии с принципом неопределенностей Гейзенберга, не может быть точно определена. Всякое распадающееся состояние, имеющее среднее время жизни τ, описывается волновой функцией ψ(t), квадрат модуля которой убывает со временем по экспоненциальному закону радиоактивного распада

|ψ(t)|² = |ψ(0)|²e^-t/^τ.

Ядро в любом состоянии с τ ≠ ∞ имеет энергетическую неопределённость ΔE ≈ Г, которая связана с τ соотношением неопределённостей Г·τ ≈ ћ , где Г – ширина уровня на половине высоты.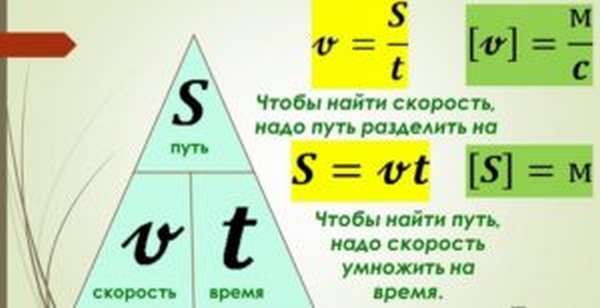
Подавляющее число частиц также являются нестабильными и распадаются по тем же законам радиоактивного распада, как и атомные ядра. Традиционно радиоактивность атомных ядер описывают, используя период полураспада T_1/2, а распады частиц описывают, использую среднее время жизни τ

1.6. Преобразования Лоренца

Основные положения специальной теории относительности изучались в разделе «Механика» общего курса физики. Здесь лишь напомним основные соотношения релятивистской физики.

Принцип относительности – все законы природы должны быть одинаковыми для всех наблюдателей, двигающихся друг относительно друга с постоянной скоростью.
Специальная теория относительности была построена на двух постулатах, сформулированных Эйнштейном в 1905 году:
1. Законы физики одинаковы во всех инерциальных системах отсчета.
2. Скорость света в вакууме равна постоянной величине с независимо от скорости движения источника.

Рис. 1.3. Штрихованная система S’ движется относительно системы S со скоростью вдоль оси z.

Рассмотрим материальную точку с массой покоя m. Ее координаты в инерциальной системе отсчета S определяются как (t,) = (t,x,y,z), а скорость v = ||. Координаты той же точки в другой инерциальной системе отсчета S’ (t’,x’,y’,z’), движущейся относительно S вдоль оси z с постоянной скоростью , связаны с координатами в системе S преобразованиями Лоренца. В случае, если координатные оси систем z и z’ сонаправлены с вектором и в начальный момент времени t = t’ = 0 начала координат обеих систем совпадали, то преобразования Лоренца даются выражениями:

x’ = x, y’ = y, z’ = γ(z − βct), ct’ = γ(ct − βz),

(1.11)

где β = v/c (0 < β < 1), а γ = 1/(1 – β²)^1/2 – лоренц-фактор.

Скорость частицы ‘ в системе S’ связана со скоростью в системе S соотношением:

(1.12)

Обратные преобразования Лоренца получаются взаимной заменой координат r_i → r_i‘, v_i → v_i‘ и учетом изменения направления скорости v → -v:

x = x’, y = y’, z = γ(z’ + βct’), ct = γ(ct’ + βz’)

(1.13)

При малых скоростях преобразования Лоренца совпадают с выражениями для нерелятивистских преобразований Галилея:

Преобразования Лоренца	Преобразования Галилея
x’ = x, y’ = y	x’ = x, y’ = y
z’ = γ(z − vt)	z’ = z – vt
ct’ = γ(ct − βz)	t’ = t

Относительность пространственных расстояний (Сокращение Лоренца-Фитцджеральда):

Относительность промежутков времени между событиями (релятивистское замедление времени):

Относительность одновременности событий. Если в системе S для событий A и B t_A = t_B и x_A ≠ x_B, то в системе S’

t’_A = t’_B + γv/c²(x_B − x_A).

(1.16)

В общем случае преобразования Лоренца записываются в терминах
4-векторов a = (a⁰,) = (a⁰,a¹,a²,a³). При относительном движении систем S и S’, как на рис. 1.2, 4-вектор a преобразуется следующим образом:

a’⁰ = γ(a⁰ − βa³), a’¹ = a¹, a’² = a², a’³ = γ(a³ − βa⁰),

(1.17)

Скалярное произведение двух 4-векторов a и b в 4-мерном пространстве времени определяется как:

и является инвариантом, т.е. сохраняется во всех инерциальных системах отсчета.

Таким образом, квадрат 4-вектора также является инвариантом. Например, квадрат 4-вектора координаты

(X)² = (ct,)² = c²t² − ()² = τ²

(1.18)

определяет «собственное» время частицы (т.е. время в ее системе отсчета). 4-вектор скорости
u = γ(c,) вводится таким образом, чтобы (u)² = c². 4-импульс, определяется как произведение массы на скорость

P = mu = mγ(c,) = (E/c,).

(1.19)

Так как u²= c², то (P)² = m²c² = (E/c)² − ()², или

Следовательно,

E = γmc², = γm, = c²/E.

(1.21)

Преобразования Лоренца для 4-импульса (1.17):

E’/c = γ(E/c − βp_z), p’_x = p_x, p’_y = p_y, p’_z = γ(p’_z − βE/c).

(1.22)

Скалярное произведение 4-импульсов является инвариантом по определению. Вместо произведения 4-импульсов двух частиц, например P₁P₂, обычно используют квадрат инвариантной массы двух частиц (s-инвариант):

(1.23)

или квадрат переданного импульса (t-инвариант)

1.7. Эффект Доплера

Если в системе S (рис. 1.2) в направлении оси z испущен фотон энергии E₀ = p₀c, то его энергия E, длина волны λ и частота ν в системе отсчета S’ (наблюдатель удаляется от источника света) составит

E = γ(E₀ − βp₀c) = γE₀(1 − β),

(1.24)

Параметр смещения z в этом случае z = (λ − λ₀)/λ₀ = (ν₀ − )/ν > 0, что соответствует красному смещению λ > λ₀, ν < ν₀. Если скорость системы S’ направлена в противоположную сторону (наблюдатель приближается к источнику света), то знаки изменяются на противоположные:

(1.25)

В данном случае наблюдается синее смещение: λ < λ₀. Поскольку в общем случае преобразование Лоренца записывается как E = γ(E₀ − ()/c², то, в отличие от классической физики, в релятивистском случае наблюдается поперечный эффект Доплера: v/v₀ = γ.
Из формул, соответствующих синему смещению, можно получить классическую формулировку эффекта Доплера, используя разложение в ряд:

Тогда для относительного изменения частоты излучения: Δν/ν₀ = β = v/c, что соответствует классической формулировке эффекта Доплера (без учета среды):

ν = ν₀(1 + ν/ν_звук).

1.8. Системы отсчета

Рассмотрим двухчастичный процесс a + b → c + d. 4-х импульсы сталкивающихся частиц
P_a = (E_a/c,_a) и P_b = (E_b/c,_b) соответственно.
При описании взаимодействий частиц и атомных ядер, как и в классической физике, обычно используются две системы отсчета: система покоя мишени и система центра инерции (рис. 1.4).

Рис. 1.4. Определение некоторых систем отсчета

1. Система покоя мишени – система, в которой частица b (мишень) покоится, p_b = 0, E_b = m_bc². Обычно под лабораторной системой (ЛС) отсчета подразумевается система покоя мишени. В данной системе s-инвариант:

(1.26)

Энергия налетающей частицы, выраженная через s-инвариант:

(1.27)

2. Система центра инерции (СЦИ) – система, в которой ^*_a = ^*_b = 0. Величины в СЦИ в дальнейшем будут отмечаться звездочкой. В СЦИ . s-инвариант в СЦИ:

(1.28)

В экспериментах физики высоких энергий часто используется система встречных пучков – система, в которой частицы равной массы и равных по абсолютной величине импульсов сталкиваются под углом π − θ. При θ = 0 система встречных пучков совпадает с СЦИ.

1.9. Основные формулы релятивистской физики

Универсальность законов сохранения приводит к необходимости установить для релятивистской кинематики такие уравнения, которые удовлетворяли бы к законам сохранения энергии и импульса и были инвариантны относительно преобразований Лоренца:

E = (m²c⁴ + p²c²)^1/2 = γmc² = mc² + T,
E – полная энергия частицы, m – масса частицы,
с – скорость света в вакууме,
= γm – релятивистский импульс частицы,
β = v/c, γ = (1 – β²)^-1/2 – Лоренц-фактор, – скорость частицы,
T = mc²(γ – 1) – релятивистская кинетическая энергия частицы.
p²c² = T(2mc² + T).
τ = γτ₀– релятивистское замедление времени,
τ₀ – время жизни частицы в состоянии покоя,
τ – времени жизни частицы, движущейся со скоростью .
l = l₀/γ,
E² – p²c² = inv = m²c⁴,
E – полная энергия частицы или системы частиц,
p – импульс частицы или суммарный импульс системы частиц.
Энергия налетающих частиц Е в ускорителе с неподвижной мишенью, эквивалентном коллайдеру с пучками частиц массы m и энергии E*:
(1.29)
Порог реакции. Если на неподвижной мишени b под действием налетающих частиц a происходит реакция a + b → c + d +… и энергия реакции (изменение суммарной массы частиц) Q = (∑m_i – ∑m_f)c² < 0, то минимальная кинетическая энергия частицы а, необходимая для осуществления такой реакции
(1.30)

1.10. Система единиц Гаусса

Время	1 с
Энергия, масса E = mc²	1 эВ (электрон-Вольт) = 1.6·10^-19 эрг = = 1.6·10^-19 Дж. 1эВ = 10^-3 кэВ = 10^-6 МэВ = 10^-9 ГэВ = = 10^-12 ТэВ
Энергия покоя электрона протона нейтрона	0.511 МэВ 938.3 МэВ 939.6 МэВ
Длина	1 Фм (ферми, фемтометр) = 10^-13 см 1 Å (ангстрем) = 10^-8 см
Скорость света в вакууме	с = 3·10¹⁰ см/с
Заряд электрона	e = 4.8·10^-10 ед. СГС
Приведенная постоянная Планка Константы	ћ = h/2π = 6.58·10^-22 Мэв·с
Приведенная постоянная Планка Константы	ћс = 197 МэВ·Фм; α = e²/ћс = 1/137

При решении задач будет использоваться система единиц Гаусса, в которой основными единицами являются сантиметр, грамм и секунда. В данной системе диэлектрическая и магнитная проницаемости являются безразмерными величинами, причём для вакуума они приняты равными единице. В качестве единицы измерения энергии используется внесистемная единица 1 эВ (электрон-Вольт) – энергия, приобретаемая электроном при прохождении потенциала в 1 Вольт.

1.11. Энергия и порог реакции

Частица массы m_a налетает на покоящуюся частицу массы m_b. В результате реакции в конечном состоянии образуется n частиц с массами m’₁,…m’_n Определить энергию и порог реакции.
Обозначим суммарную массу взаимодействующих частиц m_a + m_b = ∑m_i (индекс i соответствует начальному состоянию (initial)), суммарную массу образовавшихся частиц m’₁ + m’₂+… m’_n = ∑m_f(индекс f обозначает конечное состояние (final)). Энергия реакции Q соответствует изменению суммарной массы частиц:

Q = (∑m_i − ∑m_f)c².

(1.31)

Пороговая энергия реакции – это дополнительная кинетическая энергия, необходимая для осуществления эндотермической реакции (Q < 0). Данное значение энергии соответствует предельному случаю, когда продукты реакции образуются с нулевыми импульсами в СЦИ и s-инвариант в конечном состоянии равен квадрату суммы масс конечных продуктов: . В начальном состоянии в СЦИ . Следовательно, необходимая суммарная энергия сталкивающихся частиц должна быть .
Пороговая кинетическая энергия в СЦИ:

В лабораторной системе отсчета частица-мишень покоится: |_b| = 0, E_b = m_bc². Соответственно, s-инвариант в лабораторной системе в начальном состоянии равен:

Приравнивая s в начальном и конечном состояниях, получаем:

(1.32)

(1.33)

Раскладывая разность квадратов и выделяя Q, получим (1.31):

(1.34)

Значение пороговой энергии реакции в лабораторной системе всегда больше соответствующего значения в системе центра инерции. Их разность определяет ту часть энергии, которая идет на движение центра инерции в лабораторной системе.

1.12. Энергии частиц в двухчастичном распаде

Получим выражение для энергий и импульсов продуктов распада C → A + B через массы частиц в релятивистском случае в СЦИ.
СЦИ связана с распадающейся частицей С, ее энергия в данной системе E_С = m_Сc², продукты распада разлетаются под углом 180°. Законы сохранения энергии и импульса:

Учитывая, что (pc)² = E² − (mc²)² и подставляя выражение E_B через E_A во второе уравнение, получим:

E²_A − (m_Ac²)² = (m_Сc² − E_A)² − (m_Bc²)².

Отсюда для частицы A:

(1.35)

Выражения для частицы B получаются перестановкой соответствующих индексов.
Полезно выписать выражения для энергий продуктов распада в некоторых частных случаях:
а) распад на частицы равной массы m_A= m_B.

(1.36)

б) образование безмассовой частицы m_A = 0.

(1.37)

в) нерелятивистский случай: Q << m_Cc², m_C ≈ m_A + m_B

(1.38)

Задачи

1.1. Альфа-частица (Z_α = 2) с кинетической энергией T = 5 МэВ испытывает лобовое столкновение с ядром золота (Z_я = 79). Рассчитать расстояние максимального сближения α-частицы с ядром золота.

1.2. Протон с кинетической энергией Т = 2 МэВ налетает на неподвижное ядро ¹⁹⁷Au. Определить дифференциальное сечение рассеяния dσ/dΩ на угол θ = 60° . Как изменится величина дифференциального сечения рассеяния, если в качестве рассеивающего ядра выбрать ²⁷Al?

1.3. Частица массы m_a налетает на покоящуюся частицу массы m_b. В результате реакции в конечном состоянии образуется n частиц с массами m’₁,…m’_n. Определить энергию и порог реакции.

Обозначим суммарную массу взаимодействующих частиц m_a + m_b = ∑_im_i (индекс i соответствует начальному состоянию (initial)), суммарную массу образовавшихся частиц
m’₁ + m’₂ + …+ m’_n = ∑_fm_f(индекс f обозначает конечное состояние (final)). Энергия реакции Q соответствует изменению суммарной массы частиц:

Q = (∑_im_i − ∑_fm_f)c².

(1.31)

Пороговая энергия реакции – это дополнительная кинетическая энергия, необходимая для осуществления эндотермической реакции (Q < 0). Данное значение энергии соответствует предельному случаю, когда продукты реакции в СЦИ образуются с нулевыми импульсами и s-инвариант в конечном состоянии равен квадрату суммы масс конечных продуктов:
s = (∑_fP_f)/c² = (∑_fm_f). В начальном состоянии в СЦИ s = (∑_iP*_i)/c² = (E*_a + E*_b)²/c⁴. Следовательно, необходимая суммарная энергия сталкивающихся частиц должна быть E*_a + E*_b = ∑_fm_fc².
Пороговая кинетическая энергия в СЦИ:

T*_a +T*_b = ∑_fm_fc²− ∑_im_ic² = |Q|.

s = (P_a + P_b)/c² = (E_a/c² + E_b/c²) − (_a/c − _b/c)² = m_a² + m_b2 − 2E_am_b/c².

Приравнивая s в начальном и конечном состояниях, получаем:

(1.32)

(1.33)

Раскладывая разность квадратов и выделяя Q, получим (1.30):

(1.30)

1.4. Получим выражение для энергий и импульсов продуктов распада C → A + B через массы частиц в релятивистском случае в СЦИ.
СЦИ связана с распадающейся частицей С, ее энергия в данной системе E_С = m_Сc², продукты распада разлетаются под углом 180°. Законы сохранения энергии и импульса:

Учитывая, что (pc)² = E² − (mc²)² и подставляя выражение E_B через E_A во второе уравнение, получим:

E²_A − (m_Ac²)² = (m_Сc² − E_A)² − (m_Bc²)².

Отсюда для частицы A:

(1.35)

(1.36)

б) образование безмассовой частицы m_A = 0.

(1.37)

в) нерелятивистский случай: Q << m_Cc², m_C ≈ m_A + m_B

(1.38)

1.5. Рассчитать кинетические энергии α-частицы и ядра ²²²Rn, образующихся при распаде ²²⁶Ra → ²²²Rn + α.
(m_Rn = 206764.10 МэВ, m_Ra = 210496.35 МэВ, m_α = 3727.38 МэВ.)
Ответ: Q_α = 4.87 МэВ, T_α = 4.78 МэВ, T_Rn = 0.086 МэВ

1.6. Рассчитать дифференциальное сечение рассеяния α-частицы с кинетической энергией 10 МэВ
1) на ядре кальция ⁴⁰Ca на угол 60°,
2) на ядре меди ⁶³Cu на угол 90°,
3) на ядре молибдена ⁹⁶Mo на угол 120°,
4) на ядре серебра ⁷⁹Ag на угол 180°.
Ответ: 1) 0.33 барн/стер, 2) 0.17 б/стер, 3) 0.16 б/стер, 4) 0.11 б/стер

1.7. Рассчитать отношение сечений рассеяния α-частиц с кинетической энергиями 10 МэВ на ядре ¹⁹⁷Au под углами 6° и 180°.
Ответ: W = 13.3·10⁴

1.8. Рассчитать расстояния максимального сближения R
1) α-частицы с кинетической энергией 5 МэВ с ядром ¹⁹⁷Au и ⁷Li,
2) α-частицы с кинетической энергией 10 МэВ с ядром ⁴⁰Ca,
3) протона с кинетической энергией 7 МэВ с ядром ¹⁹⁷Au,
4) α-частицы с кинетической энергией 5 МэВ с ядром ²⁰⁸Pb.
Ответ: 1) R = 1.7 Фм, 2) R = 5.8 Фм, 3) R = 16.2 Фм, 4) R = 47.2 Фм

1.9.Пучок α-частиц с энергией T_α = 5 МэВ падает перпендикулярно на фольгу из серебра толщиной 1 мг/см². α-частицы, рассеянные под углом 60°, регистрируются детектором площадью 1 см², расположенном на расстоянии 20 см от мишени. Какая доля от полного числа рассеянных α-частиц ΔN/N будет зарегистрирована детектором?
Ответ: ∆N(60º)/N = 4·10^–10

1.10. В ходе эксперимента медная фольга (Z = 29, M_mol = 63.55 г/моль) толщиной 2 мг/см² облучается пучком α-частиц с с кинетической энергией Т_α = 5 МэВ и интенсивностью 10⁵ частиц в секунду. Сколько α-частиц в минуту ∆N будет регистрировать детектор площадью 1 см², расположенный на расстоянии 10 см от мишени под следующими углами к направлению падающего пучка: 1) 30°, 2) 90°, 3) 120°?
Ответ: 1) ∆N(30º) ≈ 44 част., 2) ∆N(90º) ≈ 0.8 част., 3) ∆N(120º) ≈ 0.4 част.

1.11. Почему из экспериментов по упругому рассеянию α-частиц следовало, что в атоме расположено положительно заряженное атомное ядро размером < 5·10^–12 см? Почему полученные результаты нельзя было объяснить на основании модели Томсона?

1.12. Во сколько раз число распадов ядер радиоактивного изотопа йода ¹³¹I в течение первых суток больше числа распадов в течение вторых суток? Период полураспада изотопа T_1/2(¹³¹I) = 193 часа.

1.13. Пучок π^–-мезонов движется со скоростью v = 0.9c. Среднее время жизни π^–-мезонов составляет τ = 2.6·10^–8 с. Какое расстояние в среднем они пройдут до своего распада?
Ответ: L_π= 16 м

1.14. На каком расстоянии интенсивность пучка мюонов с кинетической энергией T = 0.5 ГэВ, движущихся в вакууме, уменьшается до половины первоначального значения?
m_μ = 105.66 МэВ, τ_μ = 2.197·10^-6 сек.
Ответ: L = 2.6 км

1.15. Полная энергия электрона составляет 2.5 МэВ. Определите его импульс и скорость в лабораторной системе отсчета.
Ответ: p = 2.45 МэВ/c, v = 0.989c

1.16. Электрон и протон ускоряются разностью потенциалов 10⁷ В. Рассчитайте фактор γ, скорость, импульс и полную энергию каждой частицы.
Ответ: 1) E ≈ pc = 10.5 МэВ, γ = 20.57, v = 0.999c; 2) E = 948.27 МэВ, pc = 137.35 МэВ, γ = 1.01, v = 0.147c

1.17. Какую энергию надо затратить, чтобы электрон достиг скорости а) 0.5 c, б) 0.9 c, в) 0.99 c.
Какая энергия необходима, чтобы протон достиг тех же скоростей?
Ответ: а) T_e = 0.08 МэВ, T_p = 145.2 МэВ; б) T_e = 0.66 МэВ, T_p = 1.2 ГэВ;
в) T_e = 3.11 МэВ, T_p = 5.7 ГэВ.

1.18. Какую энергию надо затратить, чтобы увеличить скорость протона а) от 0.20 c до 0.21 c,
б) от 0.80 c до 0.81 c, в) от 0.90 c до 0.91 c, г) от 0.98 c до 0.99 c.
Ответ: а) T_p = 2.05 МэВ, б) T_p = 36.2 МэВ, в) T_p = 110.5 МэВ, г) T_p = 1 936 МэВ

1.19. Полная энергия частицы в два раза больше ее энергии покоя. Рассчитайте отношение v/c для этой частицы и определите ее импульс.

1.20. Определите массу частицы если известно, что ее импульс равен 500 МэВ/c,
а энергия – 1746 МэВ.

1.21. Рассчитайте скорость уменьшения массы Солнца, если известно, что плотность лучистой энергии Солнца на Земле в среднем равна 1.37·10³Вт/м².

1.22. Энергия связи электрона в атоме водорода составляет 13.6 эВ. Насколько масса атома водорода меньше суммы масс электрона и протона?

1.23. Энергия связи дейтрона (система, состоящая из протона и нейтрона) составляет 2.224 МэВ. Насколько масса ядра дейтрона меньше суммы масс составляющих его нуклонов?

1.24. Энергия, выделяющаяся при делении одного ядра ²³⁵U, составляет ~200 МэВ. Какое количество массы ядра урана превращается в энергию?

1.25. Какой должна быть относительная скорость двух наблюдателей, чтобы измеряемые ими интервалы времени различались на 5 %?
Ответ: υ = 0.33с

1.26. На какое время разойдутся показания часов земного наблюдателя и наблюдателя на спутнике Земли с периодом обращения 90 мин через 5 лет?
Ответ: ∆t = 0.05 с

1.27. Используя разложение в ряд, получите следующие формулы для приближенного вычисления релятивистских поправок в случае
v << c: ; ; .

1.28. Исходя из релятивистского соотношения между энергией и импульсом, покажите, что в нерелятивистском пределе выполняется соотношение для кинетической энергии T = mv²/2.

1.29. Длина волны, излучаемая атомом водорода, составляет λ₀ = 6560 Å. Измерение длины волны этого же излучения из удаляющейся галактики составляет λ₁ = 14580 Å. Определите скорость, с которой галактика удаляется от Земли.
Ответ: υ = 2·10⁸м/с

1.30. Галактика удаляется от земного наблюдателя со скоростью 1.9·10⁷м/с. Определите относительную величину красного смещения (λ₁ − λ₀)/λ₀ для света этой галактики.
Ответ: z = 0.065 ≈ β

1.31. Измерение гравитационного потенциала ∆φ при удалении на бесконечность с расстояния R от центра сферического не вращающегося тела массы M составляет При этом величина красного смещения света определяется соотношением . Оцените величину красного смещения линии водорода в гравитационном поле Солнца. Оцените величину синего смещения этой линии в гравитационном поле Земли.

1.32. Видимый свет от близкой звезды смещен в фиолетовую часть спектра на 5 %. С какой лучевой скоростью движется звезда?
Ответ: β = 0.05c, v = 1.5·10⁷ м/с

1.33. С какой скоростью должен двигаться автомобиль, чтобы красный свет светофора выглядел зеленым? Сравните результат с космическими скоростями.

1.34. Определить порог реакции α + α → ⁷Li + p. Определить долю кинетической энергии налетающей частицы, идущую на движение центра инерции. m_α = 3727.38 МэВ, m_p = 938.27 МэВ,
m_Li = 6533.83 МэВ.

1.35. Рассчитать порог реакции ¹⁴N + α → ¹⁷O + p в двух случаях:

налетающей частицей является ядро азота ¹⁴N,
налетающей частицей является α-частица.

Объяснить полученный результат.

1.36. 1) В коллайдере LHC энергия пучков протонов составляет E*_p = 7 ТэВ. Определите энергию столкновения √s в системе центра инерции. Какая энергия протонного пучка E_p потребовалась бы для достижения данной энергии в ускорителе с неподвижной мишенью? Сравните результат с энергией протонов космических лучей.
2) В условии задачи 1) рассмотрите столкновение пучков электронов и позитронов с энергиями
E*_e = 500 ГэВ (проект ILC).
3) В условии задачи 1) рассмотрите столкновение пучков протонов с энергиями E*_p = 1 ТэВ (коллайдер TEVATRON).
4) В условии задачи 1) рассмотрите столкновение пучков электронов с энергиями E*_e = 100 ГэВ (коллайдер LEP)
Ответ: 1) E_p = 10⁸ГэВ, 2) E_e = 10⁹ГэВ, 3) E_p = 2·10⁶ГэВ, 4) E_e = 4·10⁷ГэВ

26.10.2016

Равноускоренное движение: формулы, примеры

Равноускоренное движение

Равноускоренное движение — это движение, при котором вектор ускорения не меняется по модулю и направлению. Примеры такого движения: велосипед, который катится с горки; камень брошенный под углом к горизонту. Равномерное движение — частный случай равноускоренного движения с ускорением, равным нулю.

Рассмотрим случай свободного падения (тело брошено под уголом к горизонту) более подробно. Такое движение можно представить в виде суммы движений относительно вертикальной и горизонтальной осей.

В любой точке траектории на тело действует ускорение свободного падения g→, которое не меняется по величине и всегда направлено в одну сторону.

Вдоль оси X движение равномерное и прямолинейное, а вдоль оси Y — равноускоренное и прямолинейное. Будем рассматривать проекции векторов скорости и ускорения на оси.

Формулы для равноускоренного движения

Формула для скорости при равноускоренном движении:

v=v0+at.

Здесь v0 — начальная скорость тела, a=const — ускорение.

Покажем на графике, что при равноускоренном движении зависимость v(t) имеет вид прямой линии.

Ускорение можно определить по углу наклона графика скорости. На рисунке выше модуль ускорения равен отношению сторон треугольника ABC.

a=v-v0t=BCAC

Чем больше угол β, тем больше наклон (крутизна) графика по отношению к оси времени. Соответственно, тем больше ускорение тела.

Для первого графика: v0=-2 мс; a=0,5 мс2.

Для второго графика: v0=3 мс; a=-13 мс2.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

По данному графику можно также вычислить перемещение тела за время t. Как это сделать?

Выделим на графике малый отрезок времени ∆t. Будем считать, что он настолько мал, что движение за время ∆t можно считать равномерным движением со скоростью, равной скорости тела в середине промежутка ∆t. Тогда, перемещение ∆s за время ∆t будет равно ∆s=v∆t.

Разобьем все время t на бесконечно малые промежутки ∆t. Перемещение s за время t равно площади трапеции ODEF.

s=OD+EF2OF=v0+v2t=2v0+(v-v0)2t.

Мы знаем, что v-v0=at, поэтому окончательная формула для перемещения тела примет вид:

s=v0t+at22

Для того, чтобы найти координату тела в данный момент времени, нужно к начальной координате тела добавить перемещение. Изменение координаты в зависимости от времени выражает закон равноускоренного движения.

Закон равноускоренного движения

Еще одна распространенная задача кинематики, которая возникает при анализе равноускоренного движения — нахождение координаты при заданных значениях начальной и конечной скоростей и ускорения.

Исключая из записанных выше уравнений t и решая их, получаем:

s=v2-v022a.

По известным начальной скорости, ускорению и перемещению можно найти конечную скорость тела:

v=v02+2as.

При v0=0 s=v22a и v=2as

Важно!

Величины v, v0, a, y0, s, входящие в выражения, являются алгебраическими величинами. В зависимости от характера движения и направления координатных осей в условиях конкретной задачи они могут принимать как положительные, так и отрицательные значения.

Время, скорость и скорость | Физика

Цели обучения

К концу этого раздела вы сможете:

Объясните взаимосвязь между мгновенной скоростью, средней скоростью, мгновенной скоростью, средней скоростью, смещением и временем.
Вычислить скорость и скорость с учетом начального положения, начального времени, конечного положения и конечного времени.
Постройте график зависимости скорости от времени с учетом графика положения от времени.время.
Интерпретируйте график зависимости скорости от времени.

Движение — это нечто большее, чем расстояние и смещение. Такие вопросы, как: «Сколько времени занимает пешая гонка?» и «Какая была скорость бегуна?» невозможно ответить без понимания других концепций. В этом разделе мы добавляем определения времени, скорости и скорости, чтобы расширить наше описание движения.

Как обсуждалось в разделе «Физические величины и единицы», наиболее фундаментальные физические величины определяются тем, как они измеряются.Так обстоит дело со временем. Каждое измерение времени включает в себя измерение изменения некоторой физической величины. Это может быть число на цифровых часах, сердцебиение или положение Солнца на небе. В физике время определяется просто: время, — это изменение, или интервал, в течение которого происходит изменение. Невозможно знать, что время прошло, если что-то не изменится.

Время или изменение калибруется путем сравнения со стандартом. Единицей измерения времени в системе СИ является секунда, сокращенно с.Мы можем, например, наблюдать, что некий маятник совершает полный оборот каждые 0,75 с. Затем мы могли бы использовать маятник для измерения времени, считая его колебания или, конечно, подключая маятник к часовому механизму, который регистрирует время на циферблате. Это позволяет нам не только измерить количество времени, но и определить последовательность событий.

Как время связано с движением? Обычно нас интересует время, затраченное на конкретное движение, например, сколько времени требуется пассажиру самолета, чтобы добраться от своего места до задней части самолета.Чтобы найти истекшее время, мы отмечаем время в начале и в конце движения и вычитаем два. Например, лекция может начаться в 11:00 утра. и закончится в 11:50 утра, чтобы прошедшее время составило 50 минут. Истекшее время Δ t — разница между временем окончания и временем начала,

Δ т = т _f — т ₀,

, где Δ t — изменение во времени или прошедшее время, t _f — время окончания движения, а t ₀ — время начала движения.(Как обычно, символ дельты, Δ, означает изменение количества, которое следует за ним.)

Жизнь проще, если время начала t ₀ принять равным нулю, как при использовании секундомера. Если бы мы использовали секундомер, он просто показывал бы ноль в начале лекции и 50 минут в конце. Если t ₀ = 0, то Δ t = t _f ≡ t .

В этом тексте для простоты

движение начинается в момент времени, равный нулю ( t ₀ = 0)
символ t используется для истекшего времени, если не указано иное (Δ t = t _f ≡ t )

Ваше понятие скорости, вероятно, совпадает с ее научным определением.Вы знаете, что если у вас есть большое смещение за небольшой промежуток времени, у вас есть большая скорость, и эта скорость выражается в единицах расстояния, разделенных на время, например, в милях в час или в километрах в час.

Средняя скорость

Средняя скорость — это смещение (изменение положения), деленное на время перемещения ,

[латекс] \ bar {v} = \ frac {\ Delta x} {\ Delta t} = \ frac {{x} _ {f} — {x} _ {0}} {{t} _ {f} — {t} _ {0}} [/ latex],

, где [латекс] \ bar {v} [/ latex] — это среднее значение (обозначено полосой над v ) скорости, Δ x — изменение положения (или смещения), а x _f и x ₀ — это конечная и начальная позиции, временами t _f и t ₀ соответственно.Если время пуска t ₀ принять равным нулю, то средняя скорость будет просто

[латекс] \ bar {v} = \ frac {\ Delta x} {t} [/ latex].

Обратите внимание, что это определение указывает, что скорость является вектором, потому что смещение — это вектор . У него есть и величина, и направление. Единица измерения скорости в системе СИ — это метры в секунду или м / с, но широко используются многие другие единицы, такие как км / ч, миль / ч (также записываемые как мили в час) и см / с. Предположим, например, что пассажиру самолета потребовалось 5 секунд, чтобы переместиться на −4 м (отрицательный знак указывает, что смещение происходит в сторону задней части самолета).Его средняя скорость будет

[латекс] \ bar {v} = \ frac {\ Delta x} {t} = \ frac {-4 \ text {m}} {5 \ text {s}} = — \ text {0,8 м / с. } [/ латекс]

Знак минус указывает, что средняя скорость также направлена к задней части самолета.

Однако средняя скорость объекта ничего не говорит нам о том, что с ним происходит между начальной и конечной точкой. Например, по средней скорости мы не можем сказать, останавливается ли пассажир самолета на мгновение или отступает назад, прежде чем он уйдет в заднюю часть самолета.Чтобы получить более подробную информацию, мы должны рассмотреть меньшие сегменты поездки за меньшие промежутки времени.

Чем меньше временные интервалы, учитываемые в движении, тем детальнее информация. Когда мы доводим этот процесс до его логического завершения, у нас остается бесконечно малый интервал. В течение такого интервала средняя скорость становится мгновенной скоростью или скоростью в конкретный момент . Например, автомобильный спидометр показывает величину (но не направление) мгновенной скорости автомобиля.(Полиция выдает билеты на основе мгновенной скорости, но при расчете того, сколько времени потребуется, чтобы добраться из одного места в другое во время поездки, вам нужно использовать среднюю скорость.) Мгновенная скорость v — это средняя скорость при заданной скорости. конкретный момент времени (или бесконечно малый интервал времени).

Математически, нахождение мгновенной скорости v в точный момент времени t может включать определение предела, операцию вычисления, выходящую за рамки этого текста.Однако во многих случаях мы можем найти точные значения мгновенной скорости без расчетов.

В повседневном языке большинство людей используют термины «скорость» и «скорость» как синонимы. В физике, однако, они не имеют одинакового значения и представляют собой разные концепции. Одно из основных различий заключается в том, что скорость не имеет направления. Таким образом, скорость — это скаляр . Так же, как нам нужно различать мгновенную скорость и среднюю скорость, нам также необходимо различать мгновенную скорость и среднюю скорость.

Мгновенная скорость — величина мгновенной скорости. Например, предположим, что пассажир самолета в один момент времени имел мгновенную скорость -3,0 м / с (минус означает направление к задней части самолета). При этом его мгновенная скорость составляла 3,0 м / с. Или предположим, что однажды во время похода по магазинам ваша мгновенная скорость составляет 40 км / ч на север. Ваша мгновенная скорость в этот момент будет 40 км / ч — такая же величина, но без указания направления.Однако средняя скорость сильно отличается от средней скорости. Средняя скорость — это пройденное расстояние, разделенное на затраченное время.

Мы отметили, что пройденное расстояние может быть больше перемещения. Таким образом, средняя скорость может быть больше средней скорости, которая равна смещению, разделенному на время. Например, если вы едете в магазин и возвращаетесь домой через полчаса, а одометр вашего автомобиля показывает, что общее пройденное расстояние составляет 6 км, то ваша средняя скорость составляет 12 км / ч. Однако ваша средняя скорость была равна нулю, потому что ваше смещение в оба конца равно нулю.(Смещение — это изменение положения и, таким образом, равно нулю для поездки туда и обратно.) Таким образом, средняя скорость равна , а не просто величине средней скорости.

Другой способ визуализировать движение объекта — использовать график. График положения или скорости как функции времени может быть очень полезным. Например, для этой поездки в магазин графики положения, скорости и зависимости скорости от времени показаны на рисунке 4. (Обратите внимание, что на этих графиках изображена очень упрощенная модель модели поездки.Мы предполагаем, что скорость постоянна во время поездки, что нереально, учитывая, что мы, вероятно, остановимся в магазине. Но для простоты мы смоделируем его без остановок и изменений скорости. Мы также предполагаем, что маршрут между магазином и домом абсолютно прямой.)

Equations of Motion — The Physics Hypertextbook

Обсуждение

постоянное ускорение

Для большей точности этот раздел следует называть «Одномерные уравнения движения при постоянном ускорении».Учитывая, что такое название было бы стилистическим кошмаром, позвольте мне начать этот раздел со следующей оговорки. Эти уравнения движения действительны только тогда, когда ускорение постоянное и движение ограничено прямой линией.

Учитывая, что мы живем в трехмерной вселенной, в которой единственная константа — это изменение, у вас может возникнуть соблазн сразу отказаться от этого раздела. Было бы правильно сказать, что ни один объект никогда не двигался по прямой с постоянным ускорением в любом месте Вселенной в любое время — ни сегодня, ни вчера, ни завтра, ни пять миллиардов лет назад, ни тридцать миллиардов лет в будущем. , никогда.Об этом я могу сказать с абсолютной метафизической уверенностью.

Так что же тогда хорошего в этом разделе? Что ж, во многих случаях полезно предположить, что объект двигался или будет двигаться по прямому пути с почти постоянным ускорением; то есть любое отклонение от идеального движения можно по существу игнорировать. Движение по криволинейной траектории можно считать фактически одномерным, если имеется только одна степень свободы для задействованных объектов.Дорога может изгибаться и поворачиваться и исследовать всевозможные направления, но автомобили, движущиеся по ней, имеют только одну степень свободы — свободу двигаться в одном или противоположном направлении. (Вы не можете ехать по дороге по диагонали и надеетесь остаться на ней надолго.) В этом отношении это мало чем отличается от движения, ограниченного прямой линией. Аппроксимация реальных ситуаций моделями, основанными на идеальных ситуациях, не считается обманом. Так поступают в физике. Это настолько полезный метод, что мы будем использовать его снова и снова.

Наша цель в этом разделе — вывести новые уравнения, которые можно использовать для описания движения объекта в терминах его трех кинематических переменных: скорости ( v ), положения ( с ) и времени ( т ). Их можно объединить в пары: скорость-время, положение-время и скорость-положение. В этом порядке их также часто называют первым, вторым и третьим уравнениями движения, но нет веских причин для изучения этих имен.

Поскольку мы имеем дело с движением по прямой линии, направление будет обозначено знаком — положительные величины указывают в одну сторону, а отрицательные величины указывают в противоположную сторону.Определение того, какое направление является положительным, а какое отрицательным, совершенно произвольно. Законы физики изотропны ; то есть они не зависят от ориентации системы координат. Однако некоторые проблемы легче понять и решить, если одно направление предпочтительнее другого. Пока вы последовательны в решении проблемы, это не имеет значения.

скорость-время

Связь между скоростью и временем проста при равномерно ускоренном прямолинейном движении.Чем дольше ускорение, тем больше изменение скорости. Изменение скорости прямо пропорционально времени, когда ускорение постоянно. Если скорость увеличивается на определенную величину за определенное время, она должна увеличиваться вдвое на эту величину в два раза быстрее. Если объект уже стартовал с определенной скоростью, то его новая скорость будет равна старой скорости плюс это изменение. Вы должны быть в состоянии увидеть уравнение уже мысленным взором.

Это самое простое из трех уравнений, которое можно вывести с помощью алгебры.Начнем с определения ускорения.

Расширить ∆ v до v — v ₀ и сжать ∆ t до t .

Затем найдите v как функцию от t .

v = v ₀ + at [1]

Это первое уравнение движения . Он записывается как полином — постоянный член ( v ₀), за которым следует член первого порядка ( на ).Поскольку наивысший порядок равен 1, правильнее называть его линейной функцией .

Символ v ₀ [vee naught] называется начальной скоростью или скоростью a time t = 0. Его часто называют «первой скоростью», но это довольно наивный способ Опишите это. Лучшее определение было бы сказать, что начальная скорость — это скорость, которую имеет движущийся объект, когда он впервые становится важным в проблеме. Скажем, метеор был замечен глубоко в космосе, и проблема заключалась в том, чтобы определить его траекторию, тогда начальная скорость, вероятно, будет той скоростью, которую он имел при первом наблюдении.Но если проблема заключалась в том, что тот же самый метеор сгорает при входе в атмосферу, то начальная скорость, вероятно, равна скорости, которую он имел при входе в атмосферу Земли. Ответ на вопрос «Какая начальная скорость?» «Это зависит от обстоятельств». Это оказывается ответом на множество вопросов.

Символ v — это скорость через некоторое время t после начальной скорости. Ее часто называют конечной скоростью , но это не делает ее «последней скоростью» объекта. Возьмем случай с метеором.Какая скорость представлена символом v ? Если вы внимательно слушали, значит, вы должны были ожидать ответа. По-разному. Это может быть скорость метеора, когда он проходит мимо Луны, входит в атмосферу Земли или ударяется о поверхность Земли. Это также может быть скорость метеорита, находящегося на дне кратера. (В этом случае v = 0 м / с.) Является ли какое-либо из этих значений конечной скоростью? Кто знает. Кто-то мог извлечь метеорит из дыры в земле и уехать вместе с ним.Это актуально? Наверное, нет, но это зависит от обстоятельств. Для такого рода вещей нет правил. Вы должны проанализировать текст задачи на предмет физических величин, а затем присвоить значение математическим символам.

Последняя часть этого уравнения на — это изменение скорости от начального значения. Вспомните, что a — это скорость изменения скорости, а t — это время после некоторого начального события _{. Ставка раз время меняется. Если объект ускоряется со скоростью 10 м / с ², через 5 с он будет двигаться на 50 м / с быстрее.Если бы он стартовал со скоростью 15 м / с, то его скорость через 5 с была бы…}

15 м / с + 50 м / с = 65 м / с

время позиции

Смещение движущегося объекта прямо пропорционально скорости и времени. Двигайся быстрее. Иди дальше. Двигайтесь дольше (как и дольше). Иди дальше. Ускорение усугубляет эту простую ситуацию, поскольку скорость теперь также прямо пропорциональна времени. Попробуйте сказать это словами, и это прозвучит нелепо. «Смещение прямо пропорционально времени и прямо пропорционально скорости, которая прямо пропорциональна времени.»Время удваивается, поэтому смещение пропорционально квадрату времени. Автомобиль, разгоняющийся в течение двух секунд, преодолеет в четыре раза расстояние, превышающее скорость автомобиля, ускоряющегося всего за одну секунду (2 ² = 4). Автомобиль, ускоряющийся в течение трех секунд покрыли бы расстояние в девять раз больше (3 ² = 9).

Если бы это было так просто. Этот пример работает, только когда начальная скорость равна нулю. Смещение пропорционально квадрату времени, когда ускорение постоянное, а начальная скорость равна нулю.Истинное общее утверждение должно учитывать любую начальную скорость и то, как она менялась. Это приводит к ужасно запутанному утверждению соразмерности. Смещение прямо пропорционально времени и пропорционально квадрату времени, когда ускорение постоянно. Функция, которая является одновременно линейной и квадратной, называется квадратичной , что позволяет нам значительно сжать предыдущее утверждение. Смещение является квадратичной функцией времени при постоянном ускорении

Формулировки пропорциональности полезны, но не столь общие, как уравнения.Мы до сих пор не знаем, каковы константы пропорциональности для этой проблемы. Один из способов понять их — использовать алгебру.

Начнем с определения средней скорости.

Увеличьте ∆ с до с — с ₀ и уплотните ∆ t до t .

Определите позицию.

с = с ₀ + vt [a]

Чтобы продолжить, нам нужно прибегнуть к небольшому трюку, известному как теорема о средней скорости или правило Мертона .Я предпочитаю второй вариант, поскольку правило может применяться к любой величине, которая изменяется с одинаковой скоростью, а не только к скорости. Правило Мертона было впервые опубликовано в 1335 году в Мертон-колледже в Оксфорде английским философом, математиком, логиком и калькулятором Уильямом Хейтсбери (1313–1372). Когда скорость изменения величины постоянна, ее среднее значение находится на полпути между ее конечным и начальным значениями.

v = ½ ( v + v ₀) [4]

Подставьте первое уравнение движения [1] в это уравнение [4] и упростите его, исключив v .

v = ½ [( v ₀ + при ) + v ₀]

v = ½ (2 v ₀ + при

2)

v = v ₀ + ½ at [b]

Теперь замените [b] на [a], чтобы исключить v [vee bar].

с = с ₀ + ( v ₀ + ½ при ) t

И, наконец, найдите s как функцию от t .

с = с ₀ + v ₀ t + ½ на ² [2]

Это второе уравнение движения . Он записывается как полином — постоянный член ( s ₀), за которым следует член первого порядка ( v ₀ t ), за которым следует член второго порядка (½ at ² ). Поскольку наивысший порядок равен 2, правильнее называть его квадратичным .

Символ s ₀ [ess naught] часто рассматривается как начальная позиция . Символ s является позицией t позже. Если хотите, вы можете назвать ее конечной позицией . Изменение положения (∆ s ) называется смещением или расстоянием (в зависимости от обстоятельств), и некоторые люди предпочитают писать второе уравнение движения таким образом.

∆ s = v ₀ t + ½ at ² [2]

скорость-позиция

Каждое из первых двух уравнений движения описывает одну кинематическую переменную как функцию времени.По сути…

Скорость прямо пропорциональна времени при постоянном ускорении ( v ∝ t ).
Смещение пропорционально квадрату времени при постоянном ускорении (∆ с ∝ t ²).

Объединение этих двух утверждений приводит к третьему, не зависящему от времени. При замене должно быть очевидно, что…

Смещение пропорционально квадрату скорости при постоянном ускорении (∆ s ∝ v ²).

Это утверждение особенно важно для безопасности вождения. Когда вы вдвое увеличиваете скорость автомобиля, требуется в четыре раза больше расстояния, чтобы его остановить. Увеличьте скорость втрое, и вам понадобится в девять раз больше расстояния. Это хорошее практическое правило, которое следует запомнить.

Концептуальное введение сделано. Пришло время вывести формальное уравнение.

метод 1

Объедините первые два уравнения вместе таким образом, чтобы исключить время как переменную. Самый простой способ сделать это — начать с первого уравнения движения…

v = v ₀ + at [1]

решить на время…

, а затем подставить его во второе уравнение движения…

с = с ₀ + v ₀ t + ½ на ² [2]

нравится…

с =	с ₀ + с ₀	⎛ ⎜ ⎝	v — v ₀	⎞ ⎟ ⎠	+ ½ a	⎛ ⎜ ⎝	v — v ₀	⎞ ² ⎟ ⎠
							a

с — с ₀ =	vv ₀— v ₀ ²	+	v ²-2 vv ₀ + v ₀ ²
			2 a

2 a ( s — s ₀) = 2 ( vv ₀— v ₀ ²) + ( v ^{2 ^{2 ^{2 v ^{2 2 vv ₀ + v ₀ ²)}}}}

2 a ( s — s ₀) = v ² — v ₀ ²

Возведите объект в квадрат скорости, и все готово.

v ² = v ₀ ² + 2 a ( s — s ₀) [3]

Это третье уравнение движения . Еще раз, символ s ₀ [ess naught] — это начальная позиция , , а s, — это позиция через некоторое время t . При желании вы можете написать уравнение, используя ∆ s — изменение положения на , смещение на или на расстояние в зависимости от ситуации.

v ² = v ₀ ² + 2 a ∆ s [3]

метод 2

Более сложный способ вывести это уравнение — начать со второго уравнения движения в этой форме…

∆ s = v ₀ t + ½ at ² [2]

и решите ее на время. Это непростая работа, поскольку уравнение квадратично. Переставьте термины так…

½ при ² + v ₀ t — ∆ s = 0

и сравните его с общей формой квадратичной.

ось ² + bx + c = 0

Решение этого дается известным уравнением…

x =	— b ± √ ( b ² — 4 ac )
	2

Замените символы в общем уравнении эквивалентными символами из нашего преобразованного второго уравнения движения…

т =	— v ₀ ± √ [ v ₀ ² — 4 (½ a ) (∆ s )]
	2 (½ a )

почисти немного…

т =	— v ₀ ± √ ( v ₀ ²-2 a ∆ s )

, а затем подставьте его обратно в первое уравнение движения.

v = v ₀ + at [1]

v = v ₀ + a	⎛ ⎜ ⎝	— v ₀ ± √ ( v ₀ ²-2 a ∆ s )	⎞ ⎟ ⎠

Материал отменяется, и мы получаем это…

v = ± √ ( v ₀ ² + 2 a ∆ s )

Выровняйте обе стороны, и все готово.

v ² = v ₀ ² + 2 a ∆ s [3]

Это было не так уж и плохо, не так ли?

исчисления выводов

Исчисление — это сложная математическая тема, но она значительно упрощает вывод двух из трех уравнений движения. По определению, ускорение — это первая производная скорости по времени. Возьмите операцию в этом определении и отмените ее. Вместо того, чтобы дифференцировать скорость, чтобы найти ускорение, интегрируйте ускорение, чтобы найти скорость.Это дает нам уравнение скорость-время. Если мы предположим, что ускорение постоянное, мы получим так называемое первое уравнение движения [1].

	=
дв	=	a dt

	=
v — v ₀	=	при

v	=	v ₀ + at [1]

Опять же, по определению, скорость — это первая производная положения по времени.Выполните эту операцию в обратном порядке. Вместо того, чтобы различать положение для определения скорости, интегрируйте скорость для определения положения. Это дает нам уравнение положения-времени для постоянного ускорения, также известное как второе уравнение движения [2].

v dt

( v ₀ + at ) dt

т
⌠ ⌡	( v ₀ + at ) dt
0

с — с ₀

v ₀ t + ½ at ²

s ₀ + v ₀ t + ½ at ² [2]

В отличие от первого и второго уравнений движения, нет очевидного способа вывести третье уравнение движения (то, которое связывает скорость с положением) с помощью расчетов.Мы не можем просто перепроектировать это по определению. Нам нужно разыграть довольно изощренный трюк.

Первое уравнение движения связывает скорость со временем. По сути, мы вывели его из этой производной…

Второе уравнение движения связывает положение со временем. Это произошло от этой производной…

Третье уравнение движения связывает скорость с положением. По логике, это должно происходить от производной, которая выглядит так…

Но что это значит? Ну, ничего по определению, но, как и все количества, оно равно себе.Оно также равно самому себе, умноженному на 1. Мы будем использовать специальную версию 1 (^dt _dt) и специальную версию алгебры (алгебру с бесконечно малыми). Посмотрите, что происходит, когда мы это делаем. Мы получаем одну производную, равную ускорению (^dv _dt), а другую производную, равную обратной скорости (^dt _ds).

дв	=	дв	1
DS		DS
дв	=	дв	дт
DS		DS	дт
дв	=	дв	дт
DS		дт	DS
дв	=	a	1
DS			v

Следующий шаг, разделение переменных.Соберите вместе похожие вещи и интегрируйте их. Вот что мы получаем при постоянном ускорении…

		=
в дв		=	и DS

		=
½ ( v ²— v ₀ ²)		=	a ( с — с ₀)

	v ²	=	v ₀ ² + 2 a ( s — s ₀) [3]

Безусловно, умное решение, и оно было не так уж сложно, чем первые два варианта.Однако на самом деле это сработало только потому, что ускорение было постоянным — постоянным во времени и постоянным в пространстве. Если бы ускорение каким-либо образом менялось, этот метод был бы неудобно трудным. Мы вернемся к алгебре, чтобы спасти наше здравомыслие. Не то чтобы в этом что-то не так. Алгебра работает, а здравомыслие стоит сэкономить.

v =	v ₀ + at	[1]
		+
с =	s ₀ + v ₀ t + ½ at ²	[2]
		=
v ² =	v ₀ ² + 2 a ( s — s ₀)	[3]

Как найти расстояние по скорости и времени

Обновлено 14 февраля 2020 г.

Автором Bushraa

Рецензировано: Lana Bandoim, B.S.

Скорость — это изменение положения (x) или расстояния с течением времени. Если вы знаете изменение положения и время, необходимое для завершения путешествия, вы можете определить скорость. Точно так же, если у вас есть две из этих переменных, вы всегда можете найти третью.

Связь между этими тремя переменными следующая:

V = \ dfrac {\ bigtriangleup x} {t}

Как найти скорость

Автомобиль едет из Балтимора в Вашингтон, округ Колумбия.С. через 1,5 часа. Если вы знаете, что расстояние между двумя городами составляет 38 миль, какова была средняя скорость автомобиля во время поездки? Поскольку это путешествие в одном направлении, изменение положения совпадает с расстоянием. Поскольку вы знаете время и расстояние, вы можете найти для скорости , подставив формулу расстояния в физике:

V = \ dfrac {\ bigtriangleup x} {t}

V = \ dfrac {38} {1.5} = 25,3

Итак, вы знаете, что ваш ответ — 25,3, но он не совсем полный: 25.3 какой ? Единицы так же важны, как и числовой ответ, когда дело доходит до физических задач, поэтому не забывайте, что вы используете для измерения расстояния и времени. Поскольку вы измеряете расстояние в милях, а время — в часах, ваш окончательный ответ — это мили, разделенные на часы, или мили в час.

Велосипедист преодолевает дистанцию 550 метров за 1,5 часа. Какая скорость велосипеда в метрах в секунду? Здесь, поскольку вам нужно определить скорость в метрах в секунду, сначала преобразуйте время в секунды:

(1.5 часов) (60 минут) (60 секунд) = 5 400 секунд

Затем подставьте ваши известные переменные в формулу скорости:

V = \ dfrac {\ bigtriangleup x} {t}

V = \ dfrac {550} {5400} = 0,1 м / с

Формула расстояния в физике

Если вы знаете, как быстро и как долго что-то двигалось, вы можете вычислить пройденное расстояние. Вам просто нужно переставить формулу скорости выше, чтобы получить формулу расстояния в физике:

{\ bigtriangleup x} = (скорость) (время)

Самолет движется со скоростью 150 миль в час по пути из Атланты в Сан-Диего. .Как далеко самолет пролетел за 3,5 часа?

Поскольку кажется, что самолет движется в одном направлении (в сторону Сан-Диего) по прямой, можно предположить, что изменение положения равно расстоянию. Подставьте известные переменные в формулу расстояния:

{\ bigtriangleup x} = (150 миль в час) (3,5 часа) = 525 миль

Решение на время

Если вам нужно решить на время, просто переставьте формулу еще раз :

time = \ dfrac {\ bigtriangleup x} {velocity}

Скажем, черепаха ползет со скоростью 3 мили в час.Сколько времени потребуется черепахе, чтобы финишировать на 5-мильном забеге?

time = \ dfrac {5} {3} = 1,67 ч

Скорость против скорости

Люди склонны использовать «скорость» для «скорости» и наоборот, но они немного отличаются от концепций. Скорость не учитывает направление, а скорость учитывает. Если вы посмотрите на формулу, скорость — это изменение положения во времени, а скорость — это расстояние во времени. Давайте рассмотрим пример, чтобы проиллюстрировать это:

Допустим, вы проезжаете 20 миль от своего дома до кампуса колледжа, а затем возвращаетесь.Поездка туда и обратно заняла час. Какая у вас средняя скорость?

Вы знаете свое общее расстояние и затраченное время, поэтому подставьте формулу для скорости:

скорость = \ dfrac {расстояние} {время}

скорость = \ dfrac {40} {1} = 40 миль в час

Теперь, какова ваша средняя скорость? Имейте в виду, что вы используете изменение местоположения или смещения для определения скорости, потому что направление имеет значение:

velocity = \ dfrac {\ bigtriangleup distance} {time}

Поскольку вы заканчиваете в своем начальном местоположении, ваше изменение положения или расстояния на самом деле 0, что означает, что ваша скорость также равна 0.Скорость равна формуле для скорости, только если вы едете по прямой.

Веб-сайт класса физики

Круговое движение и гравитация: обзор набора задач

Этот набор из 27 задач нацелен на вашу способность комбинировать законы Ньютона и уравнения кругового движения и гравитации для анализа движения объектов, движущихся по кругу, включая орбитальные спутники.Проблемы варьируются по сложности от очень простых и простых до очень сложных и сложных. Более сложные задачи имеют цветовую кодировку , синие задачи .

Характеристики движения объектов, движущихся по кругам.

Объекты, движущиеся по кругу, имеют скорость, равную пройденному за время пути расстоянию. Расстояние вокруг круга эквивалентно длине окружности и рассчитывается как 2 • pi • R, где R — радиус.Время одного оборота по окружности называется периодом и обозначается символом T. Таким образом, средняя скорость объекта, движущегося по кругу, определяется выражением 2 • pi • R / T. Часто в постановке задачи указывается частота вращения в оборотах в минуту или в оборотах в секунду. Каждый оборот по окружности эквивалентен длине окружности. Таким образом, умножение частоты вращения на длину окружности позволяет определить среднюю скорость объекта.

Ускорение объектов, движущихся по кругу, в первую очередь зависит от изменения направления. Фактическая скорость ускорения зависит от скорости изменения направления и напрямую связана со скоростью и обратно пропорциональна радиусу поворота. В итоге ускорение определяется выражением v ² / R, где v — скорость, а R — радиус окружности.

Уравнения для средней скорости (v) и среднего ускорения (a) приведены ниже.

v = d / t = 2 • pi • R / T = частота • 2 • pi • R
а = v ² / R

Направленные величины для объектов, движущихся по кругу

Успешный математический анализ объектов, движущихся по кругу, во многом зависит от концептуального понимания направления векторов ускорения и результирующей силы. Движение по круговой траектории требует чистой силы, направленной к центру круга.В каждой точке пути результирующая сила должна быть направлена внутрь. Хотя может существовать отдельная сила, направленная наружу, должна существовать внутренняя сила, которая подавляет ее по величине и удовлетворяет требованиям для внутренней чистой силы. Поскольку чистая сила и ускорение всегда в одном и том же направлении, ускорение объектов, движущихся по кругу, также должно быть направлено внутрь.

Диаграммы свободного тела и второй закон Ньютона

Часто силовой анализ должен проводиться для объекта, движущегося по кругу.Цель анализа — либо определить величину отдельной силы, действующей на объект, либо использовать значения отдельных сил для определения ускорения. Как и любая задача анализа сил, эти задачи должны начинаться с построения диаграммы свободного тела, показывающей тип и направление всех сил, действующих на объект. Из диаграммы F _net = m • можно написать уравнение. При написании уравнения помните, что F _net представляет собой векторную сумму всех индивидуальных сил.Лучше всего это записывать, складывая все силы, действующие в направлении ускорения (внутрь), и вычитая те, которые ему противостоят. Два примера показаны на рисунке ниже.

Закон всемирного тяготения Ньютона

Спутники, движущиеся по орбите, — это просто снаряды — объекты, на которые действует только сила тяжести. Сила, управляющая их движением, — это сила гравитационного притяжения к объекту, который находится в центре их орбиты.Планеты вращаются вокруг Солнца в результате гравитационной силы притяжения к Солнцу. Естественные луны вращаются вокруг планет в результате гравитационной силы притяжения к планете. Гравитация — это сила, которая действует на больших расстояниях таким образом, что любые два объекта с массой будут притягиваться. Ньютон был первым, кто предложил теорию, чтобы описать это универсальное массовое притяжение и выразить его математически. Закон, известный как закон всемирного тяготения, гласит, что сила гравитационного притяжения прямо пропорциональна произведению масс и обратно пропорциональна квадрату расстояния между их центрами.В форме уравнения,

F _grav = G • m ₁ • m ₂ / d ²

где m ₁ и m ₂ — массы притягивающих объектов (в кг), d — расстояние разделения, измеренное от центра объекта до центра объекта (в метрах), а G — константа пропорциональности (иногда называемая всемирная гравитационная постоянная). Значение G составляет 6,673 x 10 ^-11 Н • м ² / кг ².

Ускорение свободного падения

Поскольку на орбитальные спутники действует исключительно сила тяжести, их ускорение является ускорением силы тяжести (g). На земной поверхности это значение составило 9,8 м / с ². Для местоположений, отличных от поверхности Земли, необходимо уравнение, которое выражает g через соответствующие переменные. Ускорение свободного падения зависит от массы объекта, который находится в центре орбиты (M _{центральный}) и расстояния разделения от этого объекта (d).Уравнение, связывающее эти две переменные с ускорением свободного падения, получено из закона всемирного тяготения Ньютона. Уравнение

g = G • M _{центральный} / d ²

где G составляет 6,673 x 10 ^-11 Н • м ² / кг ².

Орбитальная скорость

Скорость, необходимая для того, чтобы спутник оставался на орбите вокруг центрального тела (планеты, солнца, другой звезды и т. Д.).) зависит от радиуса орбиты и массы центрального тела. Уравнение, выражающее взаимосвязь между этими переменными, получается путем объединения определений ускорения кругового движения с законом всемирного тяготения Ньютона. Уравнение

v = SQRT (G • M _{центральный} / R)

где M _central — масса центрального тела, вокруг которого вращается спутник, R — радиус орбиты, а G — 6,673 x 10 ^-11 Н • м ² / кг ².

Орбитальный период

Для общего движения объекта по кругу период связан с радиусом круга и скоростью объекта уравнением v = 2 • pi • R / T. В случае орбитального спутника это уравнение для скорости можно приравнять к уравнению для орбитальной скорости, полученной из всемирного тяготения, чтобы получить новое уравнение для орбитального периода. Результат вывода:

T ² / R ³ = 4 • pi ² / (G • M _{центральный})

где M _central — масса центрального тела, вокруг которого вращается спутник, R — радиус орбиты, а G — 6.673 x 10 ^-11 Н • м ² / кг ². Выраженное таким образом уравнение показывает, что отношение квадрата периода к радиусу в кубе для любого спутника, вращающегося вокруг центрального тела, одинаково независимо от природы спутника или радиуса его орбиты. Это соотношение зависит только от массы объекта, который втягивает орбитальный спутник внутрь. Этот принцип согласуется с третьим законом движения планет Кеплера.

Резюме математических формул

Одна из трудностей, с которыми может столкнуться учащийся в этом наборе задач, — это путаница относительно того, какую формулу использовать.В таблице ниже представлено полезное резюме формул, относящихся к круговому движению и движению спутника. В таблице многие формулы получены из других уравнений. Таким образом, часто будет несколько способов определения неизвестной величины. Подходя к этим проблемам, рекомендуется практиковать обычные привычки эффективного решателя проблем; определить известные и неизвестные величины в виде символов физических формул, разработать стратегию использования известных для решения неизвестного, а затем, наконец, выполнить необходимые алгебраические шаги и замены, необходимые для решения.

Для расчета …	… используйте уравнение (а):
Скорость (v)	v = 2 • pi • R / T v = SQRT (G • M _{центральный} / R) только для спутников
Разгон (а)	a = v ² / R или a = F _net / m a = g = G • M _{центральный} / d ² только для спутников
Чистая сила (F _net)	F _net = m • a или F _net = m • v ² / R F _net = F _grav = G • m _sat • M _{центральный} / d ² только для спутников
Период (Т)	T = 2 • pi • R / v T ² = 4 • pi ² / (G • M _{центральный}) • R ³ только для спутников

Привычки эффективно решать проблемы

Эффективный решатель проблем по привычке подходит к физической проблеме таким образом, который отражает набор дисциплинированных привычек.Хотя не все эффективные специалисты по решению проблем используют один и тот же подход, все они имеют общие привычки. Эти привычки кратко описаны здесь. Эффективное решение проблем …

… внимательно читает задачу и создает мысленную картину физической ситуации. При необходимости они набрасывают простую схему физической ситуации, чтобы помочь визуализировать ее.
… определяет известные и неизвестные величины в организованном порядке, часто записывая их на диаграмме.Они приравнивают заданные значения к символам, используемым для представления соответствующей величины (например, m = 61,7 кг, v = 18,5 м / с, R = 30,9 м, F _norm = ???).
… строит стратегию решения неизвестной величины; стратегия, как правило, сосредоточена вокруг использования физических уравнений и во многом зависит от понимания физических принципов.
… определяет подходящую (ые) формулу (ы) для использования, часто записывая их. При необходимости они выполняют необходимое преобразование количеств в правильные единицы.
… выполняет подстановки и алгебраические манипуляции, чтобы найти неизвестную величину.

Подробнее …

Дополнительная литература / Учебные пособия:

Следующие страницы из учебного пособия по физике могут быть полезны для понимания концепций и математики, связанных с этими проблемами.

Набор задач кругового движения и гравитации

Просмотреть набор задач

Решения с аудиогидом для кругового движения и гравитации

Просмотрите решение проблемы с аудиогидом:
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27

2.2 Скорость и скорость — физика

Задачи обучения секции

К концу этого раздела вы сможете делать следующее:

Вычислить среднюю скорость объекта
Связать смещение и среднюю скорость

Поддержка учителей

Цели обучения в этом разделе помогут вашим ученикам овладеть следующими стандартами:

(4) Научные концепции. Учащийся знает и применяет законы движения в самых разных ситуациях.Ожидается, что студент:
- (B) описывает и анализирует движение в одном измерении, используя уравнения с понятиями расстояния, смещения, скорости, средней скорости, мгновенной скорости и ускорения.

Кроме того, Руководство лаборатории физики средней школы рассматривает содержание этого раздела лаборатории под названием «Положение и скорость объекта», а также следующие стандарты:

(4) Научные концепции. Учащийся знает и применяет законы движения в самых разных ситуациях.Ожидается, что студент:
- (В) описывать и анализировать движение в одном измерении, используя уравнения с понятиями расстояния, смещения, скорости, средней скорости, мгновенной скорости и ускорения.

Раздел Ключевые термины

средняя скорость	средняя скорость	мгновенная скорость
мгновенная скорость	скорость	скорость

Поддержка учителя

В этом разделе учащиеся применяют то, что они узнали о расстоянии и смещении, к понятиям скорости и скорости.

[BL] [OL] Перед тем, как студенты прочитают раздел, попросите их привести примеры того, как они слышали слово «скорость». Затем спросите их, слышали ли они слово «скорость». Объясните, что в повседневной жизни эти слова часто используются как синонимы, но их научные определения различаются. Скажите студентам, что они узнают об этих различиях по мере чтения раздела.

[AL] Объясните учащимся, что скорость, как и смещение, является векторной величиной. Попросите их поразмышлять о том, чем скорость отличается от скорости.После того, как они поделятся своими идеями, задайте вопросы, которые углубят их мыслительный процесс, например: Почему вы так думаете? Какой пример? Как можно применить эти термины к движению, которое вы видите каждый день?

Скорость

Движение — это нечто большее, чем расстояние и смещение. Такие вопросы, как: «Сколько времени занимает пешая гонка?» и «Какая была скорость бегуна?» невозможно ответить без понимания других концепций. В этом разделе мы рассмотрим время, скорость и скорость, чтобы расширить наше понимание движения.

Описание того, насколько быстро или медленно движется объект, — это его скорость. Скорость — это скорость, с которой объект меняет свое местоположение. Как и расстояние, скорость — это скаляр, потому что у нее есть величина, но не направление. Поскольку скорость — это показатель, она зависит от временного интервала движения. Вы можете рассчитать прошедшее время или изменение времени ΔtΔt движения как разницу между временем окончания и временем начала

Единицей времени в системе СИ является секунда (с), а единицей скорости в системе СИ являются метры в секунду (м / с), но иногда километры в час (км / ч), мили в час (миль / ч) или другие единицы измерения. скорость используются.

Когда вы описываете скорость объекта, вы часто описываете среднее значение за определенный период времени. Средняя скорость, v _avg, представляет собой пройденное расстояние, деленное на время, в течение которого происходит движение.

vavg = distancetimevavg = distancetime

Вы, конечно, можете изменить уравнение для решения либо расстояния, либо времени

время = distancevavg.time = distancevavg. distance = vavg × timedistance = vavg × time

Предположим, например, что автомобиль проезжает 150 километров за 3 секунды.2 часа. Его средняя скорость за поездку —

. vavg = расстояние-время = 150 км3,2 ч = 47 км / ч. vavg = расстояние-время = 150 км3,2 ч = 47 км / ч.

Скорость автомобиля, вероятно, увеличится и уменьшится во много раз за 3,2 часа поездки. Однако его скорость в определенный момент времени — это его мгновенная скорость. Спидометр автомобиля показывает его мгновенную скорость.

Поддержка учителей

[OL] [AL] Предупредите учащихся, что средняя скорость не всегда является средней начальной и конечной скоростей объекта.Например, предположим, что автомобиль проезжает 100 км. Первые 50 км он движется со скоростью 30 км / ч, а вторые 50 км — со скоростью 60 км / ч. Его средняя скорость будет составлять расстояние / (временной интервал) = (100 км) / [(50 км) / (30 км / ч) + (50 км) / (60 км / ч)] = 40 км / ч. Если бы автомобиль на этих скоростях проехал равное время на 30 и 60 км, а не на равные расстояния, его средняя скорость составила бы 45 км / ч.

[BL] [OL] Предупредите учащихся, что термины «скорость», «средняя скорость» и «мгновенная скорость» на повседневном языке часто называют просто скоростью.Подчеркните важность в науке использования правильной терминологии, чтобы избежать путаницы и правильно передавать идеи.

Рис. 2.8 За 30 минут до магазина туда и обратно общее расстояние составляет 6 км. Средняя скорость 12 км / ч. Смещение для обхода равно нулю, потому что не было чистого изменения положения.

Рабочий пример

Расчет средней скорости

Мрамор катится 5,2 м за 1,8 с. Какая была средняя скорость мрамора?

Стратегия

Мы знаем расстояние, которое проходит мрамор, 5.2 м, интервал времени 1,8 с. Мы можем использовать эти значения в уравнении средней скорости.

Решение

vavg = расстояние время = 5,2 м 1,8 с = 2,9 м / с vavg = расстояние время = 5,2 м 1,8 с = 2,9 м / с

Обсуждение

Средняя скорость — это скаляр, поэтому мы не включаем направление в ответ. Мы можем проверить разумность ответа, оценив: 5 метров разделить на 2 секунды — это 2,5 м / с. Поскольку 2,5 м / с близко к 2,9 м / с, ответ разумный. Речь идет о скорости быстрой ходьбы, так что это тоже имеет смысл.

Практические задачи

Питчер перебрасывает бейсбольный мяч от насыпи питчера к своей тарелке за 0,46 с. Дистанция 18,4 м. Какая была средняя скорость бейсбольного мяча?

40 м / с
-40 м / с
0,03 м / с
8,5 м / с

Кэсси шла к дому своей подруги со средней скоростью 1,40 м / с. Расстояние между домами 205 м. Как долго она продолжала путешествие?

146 с
0.01 с
2,50 мин.
287 с

Скорость

Векторная версия скорости — это скорость. Скорость описывает скорость и направление объекта. Как и в случае со скоростью, полезно описывать либо среднюю скорость за период времени, либо скорость в конкретный момент. Средняя скорость — это смещение, деленное на время, в течение которого смещение происходит.

vavg = время смещения = ΔdΔt = df − d0tf − t0vavg = время смещения = ΔdΔt = df − d0tf − t0

Скорость, как и скорость, выражается в единицах СИ в метрах в секунду (м / с), но поскольку это вектор, вы также должны включить направление.Кроме того, переменная v для скорости выделена жирным шрифтом, потому что это вектор, в отличие от переменной v для скорости, которая выделена курсивом, потому что это скалярная величина.

Советы для успеха

Важно помнить, что средняя скорость — это не то же самое, что средняя скорость без направления. Как мы видели в предыдущем разделе со смещением и расстоянием, изменение направления во временном интервале больше влияет на скорость и скорость.

Предположим, что пассажир двигался к задней части самолета со средней скоростью –4 м / с. Мы не можем сказать по средней скорости, остановился ли пассажир на мгновение или отступил, прежде чем он добрался до задней части самолета. Чтобы получить более подробную информацию, мы должны рассмотреть меньшие сегменты поездки за меньшие промежутки времени, такие как те, что показаны на рисунке 2.9. Если вы рассматриваете бесконечно малые интервалы, вы можете определить мгновенную скорость, которая является скоростью в определенный момент времени.Мгновенная скорость и средняя скорость одинаковы, если скорость постоянна.

Рис. 2.9. На диаграмме представлена более подробная запись пассажира самолета, направляющегося к задней части самолета, показаны более мелкие отрезки его поездки.

Ранее вы читали, что пройденное расстояние может отличаться от величины смещения. Точно так же скорость может отличаться от величины скорости. Например, вы едете в магазин и через полчаса возвращаетесь домой.Если одометр вашего автомобиля показывает, что общее пройденное расстояние составило 6 км, то ваша средняя скорость составила 12 км / ч. Однако ваша средняя скорость была равна нулю, потому что ваше смещение в оба конца равно нулю.

Watch Physics

Расчет средней скорости или скорости

В этом видео рассматриваются векторы и скаляры и описывается, как вычислить среднюю скорость и среднюю скорость, когда вы знаете смещение и изменение во времени. В видео также рассказывается, как преобразовать км / ч в м / с.

Контроль захвата

Что из следующего полностью описывает вектор и скалярную величину и правильно дает пример каждого из них?

Скалярная величина полностью описывается своей величиной, в то время как вектор нуждается как в величине, так и в направлении, чтобы полностью описать его.Смещение — это пример скалярной величины, а время — пример векторной величины.
Скалярная величина полностью описывается своей величиной, в то время как вектор нуждается как в величине, так и в направлении, чтобы полностью описать его. Время — это пример скалярной величины, а смещение — пример векторной величины.
Скалярная величина полностью описывается своей величиной и направлением, тогда как вектору нужна только величина, чтобы полностью описать его.Смещение — это пример скалярной величины, а время — пример векторной величины.
Скалярная величина полностью описывается своей величиной и направлением, тогда как вектору нужна только величина, чтобы полностью описать его. Время — это пример скалярной величины, а смещение — пример векторной величины.

Поддержка учителей

Это видео хорошо подчеркивает разницу между векторами и скалярами.Студент знакомится с идеей использования «s» для обозначения смещения, которое вы можете поощрять, а можете и не поощрять. Прежде чем ученики посмотрят видео, укажите, что преподаватель использует s → s → для смещения вместо d, как в этом тексте. Объясните, что использование маленьких стрелок над переменными является обычным способом обозначения векторов в курсах физики более высокого уровня. Предупредите учащихся, что в этом видео не используются общепринятые сокращения для часа и секунды. Напомните учащимся, что в своей работе они должны использовать сокращения h для часа и s для секунд.

Рабочий пример

Расчет средней скорости

Студент перемещается на 304 м к северу за 180 с. Какая была средняя скорость ученика?

Стратегия

Мы знаем, что смещение составляет 304 м к северу, а время — 180 с. Мы можем использовать формулу для средней скорости, чтобы решить задачу.

Решение

vavg = ΔdΔt = 304 м180 с = 1,7 м / с на север vavg = ΔdΔt = 304 м180 с = 1,7 м / с на север

2,1

Обсуждение

Поскольку средняя скорость является векторной величиной, вы должны включить в ответ направление и величину.Обратите внимание, однако, что направление можно не указывать до конца, чтобы не загромождать проблему. Обратите внимание на значащие цифры в задаче. Расстояние 304 м состоит из трех значащих цифр, а временной интервал 180 с — только двух, поэтому частное должно состоять только из двух значащих цифр.

Советы для успеха

Обратите внимание на способ представления скаляров и векторов. В этой книге d обозначает расстояние и перемещение. Точно так же v обозначает скорость, а v обозначает скорость.Переменная, которая не выделена жирным шрифтом, указывает на скалярную величину, а выделенная жирным шрифтом переменная указывает на векторную величину. Иногда векторы представлены маленькими стрелками над переменной.

Поддержка учителя

Используйте эту задачу, чтобы подчеркнуть важность использования правильного количества значащих цифр в вычислениях. Некоторые студенты имеют тенденцию включать много цифр в свои окончательные вычисления. Они ошибочно полагают, что повышают точность своего ответа, записывая многие цифры, указанные на калькуляторе.Обратите внимание на то, что это приведет к ошибкам в расчетах. В более сложных расчетах эти ошибки могут распространяться и приводить к неправильному окончательному ответу. Вместо этого напомните учащимся всегда носить с собой одну или две дополнительные цифры в промежуточных вычислениях и округлять окончательный ответ до правильного количества значащих цифр.

Рабочий пример

Решение для смещения, когда известны средняя скорость и время

Лейла бегает трусцой со средней скоростью 2.4 м / с на восток. Каково ее смещение через 46 секунд?

Стратегия

Мы знаем, что средняя скорость Лейлы составляет 2,4 м / с на восток, а временной интервал составляет 46 секунд. Мы можем изменить формулу средней скорости, чтобы найти смещение.

Решение

vavg = ΔdΔtΔd = vavgΔt = (2,4 м / с) (46 с) = 1,1 × 102 м на восток vavg = ΔdΔtΔd = vavgΔt = (2,4 м / с) (46 с) = 1,1 × 102 м на восток

2,2

Обсуждение

Ответ: примерно в 110 м к востоку, что является разумным смещением для чуть менее минуты бега трусцой.Калькулятор показывает ответ как 110,4 м. Мы решили написать ответ, используя научную нотацию, потому что мы хотели прояснить, что мы использовали только две значащие цифры.

Советы для успеха

Размерный анализ — хороший способ определить, правильно ли вы решили проблему. Запишите расчет, используя только единицы, чтобы убедиться, что они совпадают на противоположных сторонах отметки равенства. В рассмотренном примере у вас
м = (м / с) (с). Поскольку секунды находятся в знаменателе средней скорости и в числителе времени, единица компенсирует, оставляя только m и, конечно же, m = m.

Рабочий пример

Решение для времени, когда известны смещение и средняя скорость

Филипп идет по прямой дорожке от своего дома до школы. Сколько времени ему потребуется, чтобы добраться до школы, если он пройдет 428 м на запад со средней скоростью 1,7 м / с на запад?

Стратегия

Мы знаем, что смещение Филиппа составляет 428 м к западу, а его средняя скорость составляет 1,7 м / с к западу. Мы можем рассчитать время, необходимое для поездки, переписав уравнение средней скорости.

Решение

vavg = ΔdΔtΔt = Δdvavg = 428 м 1,7 м / с = 2,5 × 102 svavg = ΔdΔtΔt = Δdvavg = 428 м 1,7 м / с = 2,5 × 102 с

2,3

Обсуждение

Здесь мы снова должны были использовать научную запись, потому что ответ мог состоять только из двух значащих цифр. Поскольку время является скаляром, ответ включает только величину, а не направление.

Практические задачи

10.

Водитель дальнобойщик проезжает 0,25 ч по прямой трассе с перемещением 16 км к югу.Какова средняя скорость дальнобойщика?

4 км / ч север
4 км / ч юг
64 км / ч север
64 км / ч юг

11.

Птица летит со средней скоростью 7,5 м / с на восток от ветки к ветке за 2,4 с. Затем он делает паузу перед полетом со средней скоростью 6,8 м / с на восток в течение 3,5 с к другому ответвлению. Каково полное смещение птицы от начальной точки?

42 м запад
6 м запад
6 м восток
42 м на восток

Virtual Physics

The Walking Man

В этом симуляторе вы наведете курсор на человека и переместите его сначала в одном направлении, а затем в противоположном.Не отключайте вкладку Introduction . Вы можете использовать вкладку Charts после того, как узнаете о графическом отображении движения далее в этой главе. Внимательно следите за знаком чисел в полях положения и скорости. Пока не обращайте внимания на поле ускорения. Посмотрите, сможете ли вы сделать положение человека положительным, а скорость — отрицательным. Затем посмотрите, сможете ли вы сделать обратное.

Контроль захвата

Какая ситуация правильно описывает, когда положение движущегося человека было отрицательным, но его скорость была положительной?

Человек движется к 0 слева от 0
Человек движется к 0 справа от 0
Человек движется от 0 слева от 0
Человек движется от 0 справа от 0

Поддержка учителей

Это мощная интерактивная анимация, которую можно использовать для многих уроков.На этом этапе его можно использовать, чтобы показать, что смещение может быть как положительным, так и отрицательным. Он также может показать, что при отрицательном смещении скорость может быть как положительной, так и отрицательной. Позже с его помощью можно будет показать, что скорость и ускорение могут иметь разные знаки. Настоятельно рекомендуется оставить учащихся на вкладке Introduction . Вкладку Charts можно использовать после того, как студенты узнают о графическом движении позже в этой главе.

Проверьте свое понимание

12.

Два бегуна движутся по одному и тому же прямому пути. Они начинаются в одно и то же время и заканчиваются в одно и то же время, но на полпути у них разные мгновенные скорости. Возможно ли, чтобы они имели одинаковую среднюю скорость за поездку?

Да, потому что средняя скорость зависит от чистого или полного смещения.
Да, потому что средняя скорость зависит от общего пройденного расстояния.
Нет, потому что скорости обоих бегунов должны оставаться одинаковыми на протяжении всего пути.
Нет, потому что мгновенные скорости бегунов должны оставаться такими же на полпути, но могут быть разными в другом месте.

13.

Если вы разделите общее расстояние, пройденное за поездку на автомобиле (определенное одометром), на время поездки, вычисляете ли вы среднюю скорость или величину средней скорости, и при каких обстоятельствах эти две величины одинаковы? ?

Средняя скорость. Оба они одинаковы, когда автомобиль движется с постоянной скоростью и меняет направление.
Средняя скорость. Оба они одинаковы, когда скорость постоянна и автомобиль не меняет своего направления.
Величина средней скорости. Оба варианта одинаковы, когда автомобиль движется с постоянной скоростью.
Величина средней скорости. И то, и другое одинаково, когда машина не меняет своего направления.

14.

Может ли средняя скорость быть отрицательной?

Да, в случаях, когда чистое смещение отрицательное.
Да, если тело постоянно меняет направление во время движения.
Нет, средняя скорость описывает только величину, а не направление движения.
Нет, средняя скорость описывает только величину в положительном направлении движения.

Поддержка учителей

Используйте вопросы «Проверьте свое понимание », чтобы оценить достижения учащимися учебных целей по разделам. Если учащиеся не справляются с какой-либо конкретной целью, Check Your Understanding поможет определить, какие из них и направить их к соответствующему содержанию.Тестовые задания в TUTOR позволят вам переоценить.

кинематика — средняя скорость

[Глава 2 цели]

BHS -> Мистер Стэнбро -> Физика -> Механика -> Кинематика -> эта страница

Средняя скорость

Средняя скорость объекта показывает (среднюю) скорость при который покрывает расстояние. Если средняя скорость автомобиля составляет 65 миль за час, это означает, что положение автомобиля изменится (в среднем) на 65 миль каждый час.

Средняя скорость скорость . В кинематике ставка — это всегда количество, деленное на время, затраченное на получение этого количество (прошедшее время ). Поскольку средний скорость — скорость изменения положения, средняя скорость = расстояние путешествовал / затраченное время.

Пример:

Автомобиль проезжает между двумя городами, разделенными на 60 миль, за 2 часа. Что такое его средняя скорость?

Ответ:

средняя скорость = расстояние / время Следовательно, средняя скорость машина 60 миль / 2 часа = 30 миль / час.

Пример:

Если человек может ходить со средней скоростью 2 метра в секунду, как куда они пойдут через 4 минуты?

Ответ:

В 1 минуте 60 секунд, поэтому 4 (60 секунд) = 240 секунд за 4 минуты. Кроме того, если средняя скорость = расстояние / время, тогда расстояние = (средняя скорость) (время). Следовательно, расстояние человек перемещается (2 м / с) (240 с) = 480 метров.

Единицы измерения скорости

Так как средняя скорость всегда рассчитывается как расстояние (длину), деленное на время, единицы средней скорости всегда единица расстояния, деленная на единицу времени. Общие единицы скорости метры в секунду (сокращенно м / с), сантиметры в секунду (см / с), километров в час (км / час), миль / час (миль / час — старайтесь избегать обычных сокращение mph) и многие другие.

Пример:

Что из следующего может быть измерением скорости?

2.5 метров
2,5 секунды / метр
2,5 м / сек
2,5 м / сек / сек

Ответ:

Измерение скорости может быть всего 2,5 метра в секунду. Скорость всегда имеет единицы измерения расстояния (длины), деленные на единицу времени.

Какое расстояние?

Фермер Джонс едет 6 миль по прямой дороге.Она разворачивается и проезжает 4 мили назад. Какой у нее был средний скорость для этой поездки, если на это ушло 1 час?

Ваш ответ на эту проблему зависит от вашей интерпретации «пройденный путь». Можно сказать:

Общее расстояние , пройденное Фермером Джонсом составляет 10 миль. Следовательно, ее средняя скорость составляет 10 миль / час.
Чистое расстояние , пройденное фермером Джонсом , составляет 2 мили.Следовательно, ее средняя скорость составляет 2 мили / час.

Есть веские причины использовать любую интерпретацию — в основном это дело предпочтений. Мы будем интерпретировать «пройденное расстояние» как Чистое расстояние ( также называется смещением ). Средняя скорость Farmer Jones составляла 2 мили / час.

ПРИМЕЧАНИЕ: Могут использоваться разные тексты. другие условности! Фактически, в нашем тексте AP Physics используется общая расстояние для расчета скорости, но чистое расстояние для расчета скорость.Будьте осторожны!

Опасности усреднения

Вот интересная задача:

Сьюзи запланировала поездку в город, расположенный в 60 милях. Она желает иметь во время поездки среднюю скорость 60 миль / час. Должное к пробке, однако, она развивает среднюю скорость 30 миль / час для первых 30 миль. Как быстро ей нужно идти оставшиеся 30 миль, так что ее средняя скорость будет 60 миль / час за всю поездку?

Скорее всего, вы подумали: «О, 90 миль / час — так как среднее значение 30 и 90 — это 60! Мальчик, это просто! »

Однако, к сожалению, ответ , а не 90 миль / час.Вот почему: вы знаете, что средняя скорость = расстояние / время (v = d / t). Чтобы иметь среднюю скорость 60 миль / час на расстояние 60 миль, вы должны завершить поездку за 1 час:

Но у Сюзи уже есть час (на то, чтобы идти 30, нужно час). миль со средней скоростью 30 миль / час) — а она всего половина способ! Для нее это невозможно, завершить поездку со средней скоростью 60 миль / час! Ей придется уйти бесконечно быстро!

Обратите внимание, что на покрытие последних 30 миль со скоростью 90 миль / час.Общее время ее поездки составит 1,33. часов, а ее средняя скорость будет:

Попробуйте этот расчет для при любой скорости для второй половины поездка — средняя скорость за всю поездку не может быть 60 миль / час! Мораль истории: Не среднее средние!

Измерение скорости активности

Это было бы хорошее время для измерения Скоростная активность, в которой вы:

определить некоторые средние скорости путем измерения расстояний и раз, и
определить неизвестное расстояние путем измерения времени, чтобы преодолеть расстояние с известной скоростью

[Глава 2 цели]

BHS -> МистерСтэнбро -> Физика -> Механика -> Кинематика -> эта страница

последнее обновление 22 ноября 2005 г., автор: JL Stanbrough

22.1: Масса, длина и время

Последнее обновление
Сохранить как PDF

Участник

Любую механическую величину можно выразить тремя основными величинами: массой , длиной и временем . Например, скорость — это длина, разделенная на время. Сила — это масса, умноженная на ускорение, и, следовательно, масса, умноженная на расстояние, деленная на квадрат времени.

Поэтому мы говорим, что [Сила] = MLT ⁻². Квадратные скобки означают: «Размеры количества внутри». Уравнения показывают, как сила зависит от массы, длины и времени. Мы используем символы MLT (не выделены курсивом ) для обозначения основных измерений массы, длины и времени. В приведенном выше уравнении MLT ^-2 — это , а не , заключенные в квадратные скобки; в этом нет смысла.

Мы различаем размеры физической величины и единицы, в которых она выражается. В случае единиц MKS (которые являются подмножеством единиц СИ), единицами массы, длины и времени являются кг, м и с. Таким образом, мы можем сказать, что единиц , в которых выражена сила, — это кг м · с ^-2, а его размеры равны MLT ^-2.

Для электромагнитных величин нам нужна четвертая фундаментальная величина. Мы могли бы выбрать, например, количество электричества Q, и в этом случае размерность тока будет QT ^-1.Мы не касаемся здесь размеров электромагнитных величин. Более подробную информацию можно найти в моих заметках об электричестве и магнетизме, http://orca.phys.uvic.ca/~tatum/elmag.html

Чтобы определить размерность физической величины, обычно проще всего взглянуть на определение этой величины.