Задание №1 ЕГЭ по математике базовый уровень
Элементарные математические вычисления
В задании №1 ЕГЭ по математике базового уровня необходимо провести элементарные вычисления — сложение, вычитание, деление и умножение дробей. Более того, данное задание аналогично первому заданию ОГЭ по математике, поэтому теория для успешного выполнения одинакова. Поэтому мы перейдем непосредственно к разбору типовых вариантов.
Разбор типовых вариантов заданий №1 ЕГЭ по математике базового уровня
Первый вариант задания
Найдите значение выражения:Алгоритм решения:
- Определить порядок действий.
- Выполнить действия в скобках.
- Преобразовать смешанное число в неправильную дробь.
- Привести дроби в скобках к наименьшему общему знаменателю.
- Произвести действия в числителе.
- Знаменатель оставить наименьший общий.
- Умножить числитель получившейся дроби на 9.
- Полученный результат сократить и преобразовать в десятичную дробь.
Решение в общем виде:
Пояснения к решению:
Первым всегда выполняется действие в скобках, в данном случае вычитание.
Преобразуем смешанное число
в неправильную дробь. Для этого умножим целую часть на знаменатель, и прибавим числитель
3 • 15 + 1 = 46
Запишем результат в числитель, знаменатель оставим без изменения.
Действие в скобках примет вид:
Ищем наименьший общий знаменатель для дробей 4/9 и 46/15. 15 не делится на 9, удвоим наибольший знаменатель. 30 не делится на 9. утроим наибольший знаменатель, 45 делится на 9. Следовательно, 45 делится одновременно и на 15, и на 9. То есть 45 – наименьший общий знаменатель дробей 4/9 и 46/15.
Приводим дроби к общему знаменателю – 45. Для этого по основному свойству дроби необходимо и числитель и знаменатель дроби умножить на одно и то же число, чтобы дробь не изменилась. Это число называется дополнительным множителем. Дополнительный множитель к первой дроби — 5 (9*5=45). Чтобы получить в знаменателе первой дроби 45 необходимо умножить на 5 и числитель и знаменатель.
Вторую дробь умножим на 3 (15 • 3=45)
Действие в скобках после преобразования будет выглядеть так:
Произведем вычитание дробей с одинаковыми знаменателями. Для этого в числителе запишем вычитание числителей, а знаменатель оставим без изменений.
Выполним действие за скобками, в данном случае умножение на целое число. Для этого умножим числитель дроби на 9, а знаменатель оставим без изменений. Числитель и знаменатель полученной дроби сократим на 9, то есть разделим и числитель и знаменатель дроби на 9. По основному свойству дроби дробь не изменится.
Минус в числителе выносится за дробную черту.
Полученную дробь преобразуем в десятичную, поделив в столбик.
Не забудьте о знаке «минус» в ответе.
Ответ: 23,6
Второй вариант задания
Найдите значение выражения:Алгоритм решения:
- Определить порядок действий.
- Выполнить действие в скобках.
- Привести дроби в скобках к наименьшему общему знаменателю.
- Выполнить вычитание числителей, знаменатель оставить без изменений.
- Выполнить деление. Для этого числитель первой дроби нужно умножить на знаменатель второй, результат записать в числитель; знаменатель первой дроби умножить на числитель второй, результат записать в знаменатель.
Решение в общем виде:
Пояснения к решению:
Первым ВСЕГДА выполняют действия в скобках, в данном случае вычитание.
Для того чтобы выполнить вычитание дробей с разными знаменателями, необходимо привести их к наименьшему общему знаменателю. Сделаем это путем подбора. Необходимо найти число, которое одновременно делится и на 4, и на 9. 9 на 4 не делится. Удвоим больший знаменатель: 18 не делится на 4. Утроим больший знаменатель: 27 не делится на 4. Увеличим больший знаменатель в 4 раза: 36 делится и на 9, и на 4 одновременно. Следовательно, 36 – наименьший общий знаменатель для дробей 1/4 и 2/9.
Примечание. Метод подбора удобен, если числа небольшие. В противном случае нужно искать НОК по алгоритму.
Найдем дополнительные множители для дробей 1/4 и 2/9. По основному свойству дроби, если и числитель, и знаменатель дроби умножить на одно и то же число, то дробь не изменится. Дробь 1/4 нужно умножить на 9(и числитель, и знаменатель), чтобы в знаменателе получился наименьший общий знаменатель 36. Дробь 2/9 нужно умножить на 4 (и числитель, и знаменатель), чтобы в знаменателе получился наименьший общий знаменатель 36.
В результате получим:
Действие в скобках примет вид:
Выполним вычитание дробей с одинаковыми знаменателями. Для этого вычтем из числителя первой дроби числитель второй, результат запишем в числитель. Знаменатель оставим прежним.
Выполним действие за скобками. Для этого числитель первой дроби нужно умножить на знаменатель второй, результат записать в числитель; знаменатель первой дроби умножить на числитель второй, результат записать в знаменатель.
Сократим (разделим и числитель и знаменатель) полученную дробь на 12.
Ответ: 21
Третий вариант задания
Найти значение выражения:Алгоритм решения:
- Определить порядок действий.
- Первым ВСЕГДА выполняют действия в скобках, в данном случае сложение.
- Перевести смешанное число в неправильную дробь.
- Привести полученные дроби к наименьшему общему знаменателю.
- Выполните сложение дробей с одинаковыми знаменателями. Для этого сложить числители, результат записать в числитель, знаменатель оставить без изменений.
- Выполнить деление.
- Перевести смешанное число в неправильную дробь. Для этого целую часть умножить на знаменатель и прибавить числитель, результат записать в числитель, а знаменатель оставить прежним.
- Числитель первой дроби умножить на знаменатель второй – записать в числитель. Знаменатель первой дроби умножить на числитель второй результат записать в знаменатель.
- Сократить получившуюся дробь.
- Привести результат к десятичному виду.
Решение в общем виде:
Пояснения к решению:
Первым ВСЕГДА выполняют действия в скобках, в данном случае сложение.
Нужно сложить смешанное число и правильную дробь. Для этого целую часть умножить на знаменатель и прибавить числитель, результат записать в числитель, а знаменатель оставить прежним. Переведем смешанное число в неправильную дробь:
Действие в скобках примет вид:
Для того, чтобы выполнить сложение дробей с разными знаменателями, необходимо привести их к наименьшему общему знаменателю. Сделаем это путем подбора. Необходимо найти число, которое одновременно делится и на 5, и на 7. 7 на 5 не делится. Удвоим больший знаменатель: 14 не делится на 5. Утроим больший знаменатель: 21 не делится на 5. Увеличим больший знаменатель в 4 раза: 28 не делится 5. Увеличим больший знаменатель в 5 раз: 35 делится одновременно и на 5, и на 7. Следовательно, 35 – наименьший общий знаменатель для дробей 9/5 и 3/7.
Примечание. Метод подбора удобен, если числа небольшие. В противном случае нужно искать НОК по алгоритму.
Найдем дополнительные множители для дробей 9/5 и 3/7. По основному свойству дроби, если и числитель, и знаменатель дроби умножить на одно и то же число, то дробь не изменится. Дробь 9/5 нужно умножить на 7(и числитель, и знаменатель), чтобы в знаменателе получился наименьший общий знаменатель 35. Дробь 3/7 нужно умножить на 5 (и числитель, и знаменатель), чтобы в знаменателе получился наименьший общий знаменатель 35.
В результате получим:
Действие в скобках примет вид:
Выполним сложение дробей с одинаковыми знаменателями. Для этого сложим числители, результат запишем в числитель. Знаменатель оставим прежним.
Выполним действие за скобками. Переведем смешанное число в неправильную дробь, для этого целую часть нужно умножить на знаменатель и прибавить числитель, результат записать в числитель, а знаменатель оставить прежним.
Выполнить деление дробей. Числитель первой дроби нужно умножить на знаменатель второй, результат записать в числитель; знаменатель первой дроби умножить на числитель второй, результат записать в знаменатель.
Сократим (разделим и числитель, и знаменатель на одно и то же число) полученную дробь на 39.
Переведем полученную дробь в десятинную.
Ответ: 8,75
Вариант первого задания из ЕГЭ 2017 года (четвертый)
Найдите значение выражения:(6,7 − 3,2) ⋅ 2,4
В данном случае первым действием мы выполняем вычитание в скобках, а затем производим умножение:
6,7 − 3,2 = 3,5
3,5⋅ 2,4 = 8,4
Отдельно остановлюсь на последнем действии. Его можно вычислить умножением в столбик, либо посчитать устно, воспользовавшись следующими логическими операциями:
2,4 ⋅ 3 + 2,4 ⋅ 0,5 = 2 ⋅ 3 + 0,4 ⋅ 3 + 2,4/2 = 6 + 1,2 +1,2 = 8,4
Ответ: 8,4
Вариант первого задания из ЕГЭ 2017 года (пятый)
Найдите значение выражения:В данном случае необходимо выполнить сложение обыкновенных дробей. Общий знаменатель для дробей в скобках — 15 (если вы забыли как определять общий знаменатель, смотрите здесь). Первую дробь домножаем на 5, вторую на 3. Получаем:
(5 + 3)/15
После сложения:
8/15
Теперь выполняем умножение:
8•6/15 = 48/15
В таком варианте дробь в ответ записать мы не можем, выделяем сначала целую часть, это 3 (45/15=3), в остатке получим:
3/15
После сокращения на 3:
1/5
и перевода в десятичный вид:
1/5 = 20/100 = 2/10 = 0,2
Не забываем про целую часть и получаем ответ:
3,2
Ответ: 3,2
Шестой вариант задания (2019)
Найдите значение выражения:- Если представить черту дроби в виде знака деления, то получим выражение: (2,7+5,8):6,8. Отсюда получаем приоритет действий: 1) сложение в скобках; 2) деление. Поэтому сначала выполняем действие в числителе.
- Избавляемся от десят. запятых в числителе и знаменателе. Для этого применяем основное свойство дроби и умножаем числитель и знаменатель на 10.
- Делим 85 на 68 в столбик.
Решение
Ответ: 1,25
Седьмой вариант задания (2019)
- Учитываем приоритетность операций. Здесь 1-м действием выполняется умножение, а затем вычитание.
- При умножении числа записываем друг под другом, выровняв их по последней цифре. В результирующем числе отделяем столько знаков после запятой, сколько имеется суммарно в обоих множителях. В данном случае нужно отделить 2 знака.
- При выполнении вычитания в столбик числа располагают так, чтобы десят.запятые располагались на друг под другом.
Решение
Ответ: 26,7
Восьмой вариант задания (2019)
- Умножаем 1/5 на 5,5. При этом 5,5 переходит в числитель дроби.
- Выполняем сокращение полученной дроби на 5. Получаем десят.дробь
- Находим конечную разность.
Решение
Ответ:0,1
Девятый вариант задания (2019)
- Находим разность в скобках. Для этого находим НОК (25, 38) и приводим дроби к общему знаменателю.
- Делим результат в скобках на дробь 6/19. Для этого переходим к умножению дробей, перевернув 9/16 и получив 16/9. Далее сокращаем множители в числителе и знаменателе и находим результирующую дробь.
- Полученную дробь записываем в десят.виде.
Решение
spadilo.ru
13 Задание (2016) (C1) – Репетитор по математике
13 Задание (2016) (C1)14 Задание (2016) (C2)Диагностические работы
Задание 13.
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку [].
Решение.
показать
Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.
Получим систему:
первое уравнение:
:
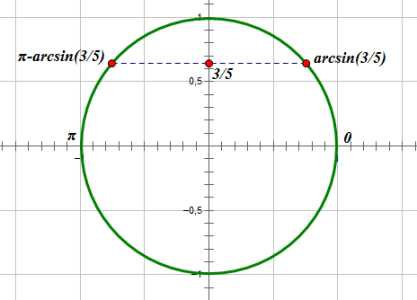
Второе условие:
Заметим, что , поэтому :
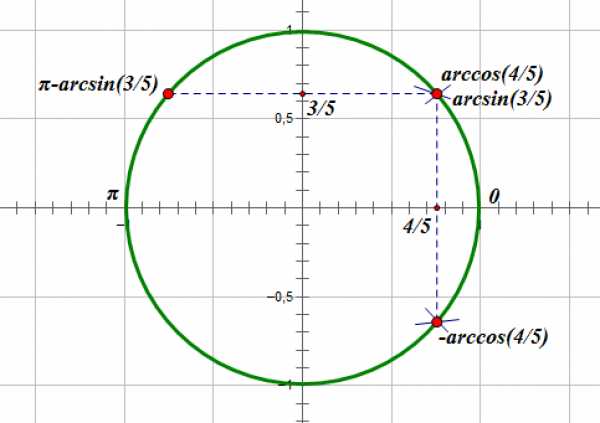
Остался единственный корень:
б) Отберем корни, принадлежащие отрезку []:
Мы видим, что отрезку [] принадлежит корень :
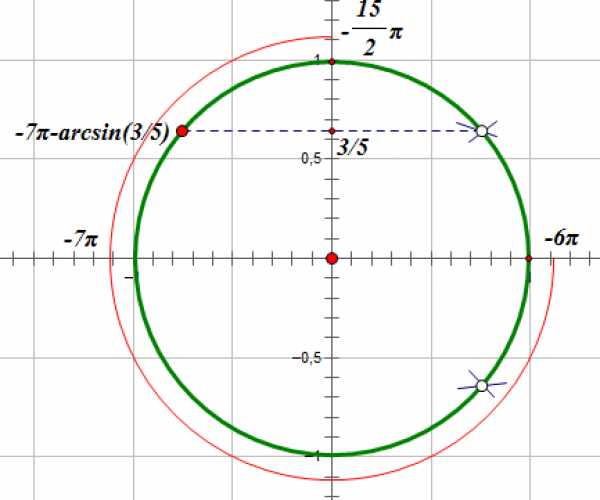
Ответ: а)
б)
Задание 14.
В основании правильной треугольной пирамиды лежит треугольник со стороной, равной 6. Боковое ребро пирамиды равно 4. Через такую точку ребра , что , параллельно прямым и проведена плоскость.
а) Докажите, что сечение пирамиды указанной плоскостью является прямоугольником.
б) Найдите площадь сечения.
Решение.
показать
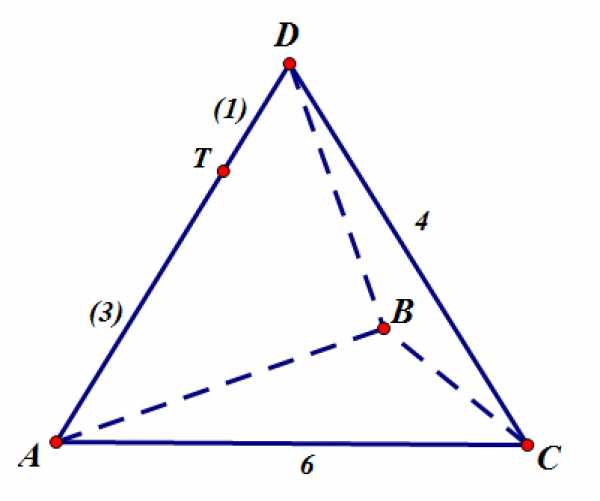
Построим сечение.
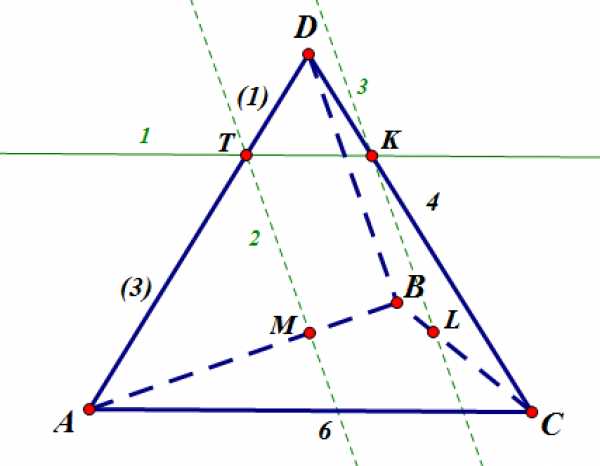
— Проведем прямую №1 () параллельно .
Через точку проведем прямую №2 () параллельно .
Через точку проведем прямую №3 () параллельно .
Получили сечение — четырехугольник :
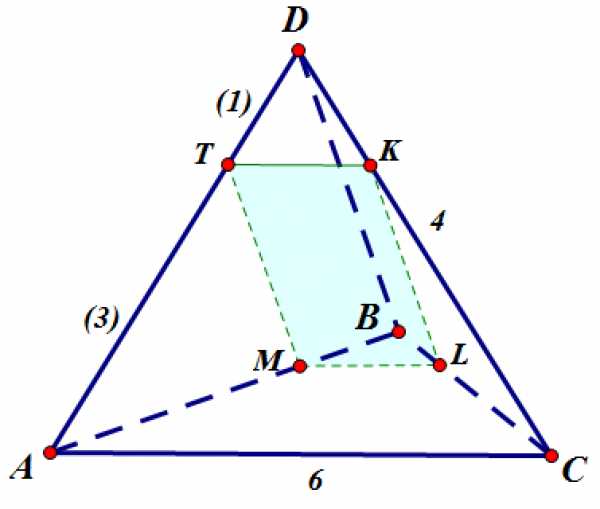
Данное сечение удовлетворяет всем условиям задачи:
- — по построению, следовательно (по теореме о параллельности прямой и плоскости).
- — по построению, следовательно (по теореме о параллельности прямой и плоскости).
Докажем, что четырехугольник — прямоугольник.
, так как — линия пересечения плоскости и плоскости , , следовательно линии пересечения плоскости сечения с плоскостями и (соответственно и ) параллельны.
, так как и параллельны . Следовательно, противоположные стороны четырехугольника попарно параллельны и он является параллелограммом.
Докажем, что . Проведем высоту пирамиды:
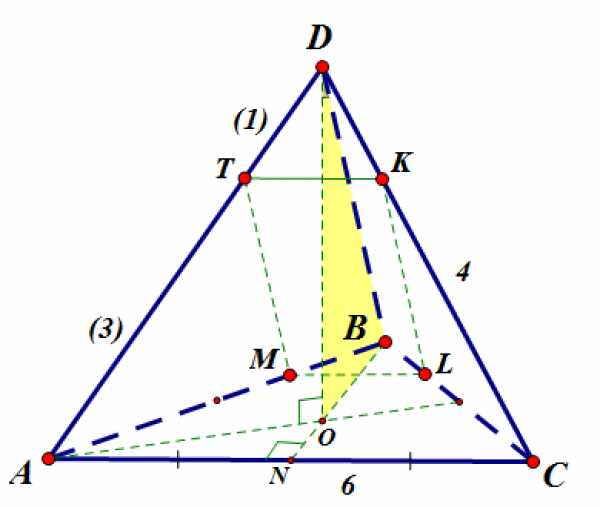
Вершина правильной пирамиды проецируется в точку , ортоцентр основания, то есть в точку пересечения медиан, высот и биссектрис треугольника .
, следовательно, по теореме о трех перпендикулярах . , , следовательно .
Найдем длины сторон прямоугольника .
(из подобия треугольников и )
;
(из подобия треугольников и )
;
Ответ: 4,5.
И.В. Фельдман, репетитор по математике.
Задача С1 традиционно посвящена решению тригонометрических уравнений. Как правило это несложные задачи со стандартным решением. Традиционно данное задание ЕГЭ по математике состоит из двух частей, в первой надо найти общее решение, во второй выбрать решения, принадлежащие некоторому интервалу. Эксперт оценивает данное задание в 0, 1 или 2 балла. Приведем критерии оценки данного задания.
Критерии оценки задания C1
2 балла – Обоснованно получены верные ответы в обоих пунктах
1 балл – Обоснованно получен верный ответ в пункте а) или б)
0 баллов – Решение не соответствует ни одному из критериев, перечисленных выше
Поясним критерии на примере. В работе квадратное уравнение относительно синуса сведено к простейшему тригонометрическому уравнению, например, sin x=-0,5, при этом оно вообще не решено или имеется неточность или ошибка, но отбор корней, например, на отрезке произведен правильно. В этом случае в соответствии с параметрами эксперт должен поставить 1 балл.
Примеры решений ЕГЭ с обсуждением возможных ошибок
1. а) Решите уравнение
б) Найдите все корни уравнения, принадлежащие промежутку
Решение
а)
. Если будет не верно вычислено или указан другой период, то за эту часть задания уже не получить 1 балл.
б)
. Учитывая, что – целое число, получаем, что оно принимает значения -2, -3, -4. Следовательно получаем следующие значения
2. Решить уравнение
Решение.
или . Отсюда получаем два набора значений:
Замечание. Буква n и k надо писать разными, кроме этого обязательно писать, что они целые.
3. Пример очень обидной арифметической ошибки.
. Такая ошибка приводит к 0 баллов. Поэтому будьте внимательны и не делайте досадных ошибок.
Такое задание есть во всех вариантах ЕГЭ по математике, оно конечно же будет и в ЕГЭ по математике 2013 года.
Связанные статьи
mathi.ru
| (Ф. Хаусдорф.) ‘ quotes[1]='»Математика — это язык, на котором написана книга природы.»(Г. Галилей) ‘ quotes[2]='»Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели.»(А. Маркушевич) ‘ quotes[3]='»Рано или поздно всякая правильная математическая идея находит применение в том или ином деле.»(А.Н. Крылов) ‘ quotes[4]='»Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой. Она окажет вам потом огромную помощь во всей вашей работе.»(М.И. Калинин) ‘ quotes[5]='»Разве ты не заметил, что способный к математике изощрен во всех науках в природе?»(Платон) ‘ quotes[6]='»Математика есть лучшее и даже единственное введение в изучение природы.» (Д.И. Писарев)‘ quotes[7]='»Вдохновение нужно в геометрии не меньше, чем в поэзии.»(А.С. Пушкин) ‘ quotes[8]='»Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение.»(В. Произволов) ‘ quotes[9]='»В математике есть своя красота, как в живописи и поэзии.»(Н.Е. Жуковский) ‘ quotes[10]='»Химия – правая рука физики, математика – ее глаз.»(М.В. Ломоносов) ‘ quotes[11]='»Математику уже затем учить надо, что она ум в порядок приводит.»(М.В. Ломоносов) ‘ quotes[12]='»Математика — это язык, на котором говорят все точные науки.»(Н.И. Лобачевский) ‘ quotes[13]='»Именно математика дает надежнейшие правила: кто им следует – тому не опасен обман чувств.»(Л. Эйлер) ‘ quotes[14]='»Числа не управляют миром, но они показывают, как управляется мир.»(И. Гете) ‘ quotes[15]='»Было бы легче остановить Солнце, легче было сдвинуть Землю, чем уменьшить сумму углов в треугольнике или свести параллели к схождению…»(Песталоцци) ‘ quotes[17]='»Величие человека — в его способности мыслить.»(Б. Паскаль) ‘ quotes[18]='»Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их.»(Д.Пойа) ‘ quotes[19]='»Предмет математики столь серьезен, что не следует упускать ни одной возможности сделать его более занимательным.»(Б. Паскаль) ‘ quotes[20]='»В математических вопросах нельзя пренебрегать даже самыми мелкими ошибками.»(И. Ньютон) ‘ quotes[21]='»Первое условие, которое надлежит выполнять в математике, — это быть точным, второе — быть ясным и, насколько можно, простым.»(Л. Карно) ‘ quotes[22]='»Много из математики не остается в памяти, но когда поймешь ее, тогда легко при случае вспомнить забытое.» (М.В. Остроградский)‘ quotes[23]='»Математика — это цепь понятий: выпадет одно звенышко — и не понятно будет дальнейшее.»(Н.К. Крупская) ‘ quotes[24]='»Математика уступает свои крепости лишь сильным и смелым.»(А.П. Конфорович) ‘ quotes[25]='»Доказательство — это рассуждение, которое убеждает.»(Ю.А. Шиханович) ‘ quotes[26]='»В каждой естественной науке заключено столько истины, сколько в ней есть математики.»(И. Кант) ‘ var whichquote= Math.floor(Math.random()*(quotes.length)) document.write(quotes[whichquote]) |
free-math.ru
