Posted in Подготовка к ЕГЭ

Задание 7 егэ по математике – Как решать задание 7 ЕГЭ по математике базового уровня – разбор заданий

Содержание

Задание №7 ЕГЭ по математике профильного уровня |

Производная и первообразные функции

В задании №7 профильного уровня ЕГЭ по математике необходимо продемонстрировать знания функции производной и первообразной. В большинстве случаев достаточно просто определения понятий и понимания значений производной.

Разбор типовых вариантов заданий №7 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

На рисунке изображён график дифференцируемой функции y = f(x). На оси абсцисс отмечены девять точек: x1, x2, …, x9. Среди этих точек найдите все точки, в которых производная функции y = f(x) отрицательна. В ответе укажите количество найденных точек.

Алгоритм решения:
  1. Рассматриваем график функции.
  2. Ищем точки, в которых функция убывает.
  3. Подсчитываем их количество.
  4. Записываем ответ.
Решение:

1. На графике функция периодически возрастает, периодически убывает.

2. В тех интелвалах, где функция убывает, производная имеет отрицательные значения.

3. В этих интервалах лежат точки x3, x4, x5, x9. Таких точек 4.

Ответ: 4.

Второй вариант задания (из Ященко, №4)

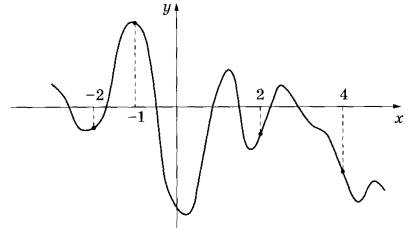
На рисунке изображён график функции у = f(x). На оси абсцисс отмечены точки -2, -1, 2, 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.

Алгоритм решения:
  1. Рассматриваем график функции.
  2. Рассматриваем поведение функции в каждой из точек и знак производной в них.
  3. Находим точки в наибольшим значением производной.
  4. Записываем ответ.
Решение:

1. Функция имеет несколько промежутков убывания и возрастания.

2. Там, где функция убывает. Производная имеет знак минус. Такие точки есть среди указанных. Но на графике есть точки, в которых функция возрастает. В них производная положительная. Это точки с абсциссами -2 и 2.

3. Рассмотрим график в точках с х=-2 и х=2. В точке х=2 функция круче уходит вверх, значит касательная в этой точке имеет больший угловой коэффициент. Следовательно, в точке с абсциссой 2. Производная имеет наибольшее значение.

Ответ: 2.

Третий вариант задания (из Ященко, №21)

Прямая  является касательной к графику функции . Найдите а.

Алгоритм решения:
  1. Приравняем уравнения касательной и функции.
  2. Упрощаем полученное равенство.
  3. Находим дискриминант.
  4. Определяем параметр а, при котором решение единственное.
  5. Записываем ответ.
Решение:

1. Координаты точки касания удовлетворяют обоим уравнениям: касательной и функции. Поэтому мы можем приравнять уравнения. Получим:

2. Упрощаем равенство, перенеся все слагаемые в одну сторону:

 

3. В точке касания должно быть одно решение, поэтому дискриминант полученного уравнения должен равняться нулю. Таково условие единственности корня квадратного уравнения.

4. Получаем:

Ответ: 4.

spadilo.ru

Решение заданий №7, ЕГЭ по математике, профильный уровень.

Описание презентации по отдельным слайдам:

1 слайд Описание слайда:

Решение заданий №7 ЕГЭ по математике, профильный уровень Учитель математики МБОУ Лицей№8 г. Воронежа Гостева Т.Л.

2 слайд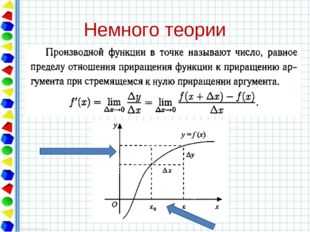 Описание слайда:

Немного теории

3 слайд
Описание слайда:

Геометрический смысл производной

4 слайд Описание слайда:

Вычислим тангенс угла наклона касательной 6:3=2, тангенс положительный, так как угол наклона острый

5 слайд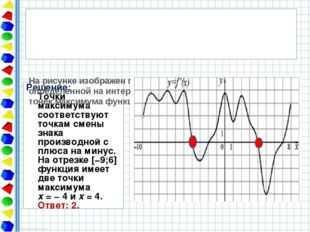 Описание слайда:

Решение: Точки максимума соответствуют точкам смены знака производной с плюса на минус. На отрезке [−9;6] функция имеет две точки максимума x = − 4 и x = 4. Ответ: 2. На рисунке изображен график производной функции f(x), определенной на интервале (−10; 8). Найдите количество точек максимума функции f(x) на отрезке [−9;6].

6 слайд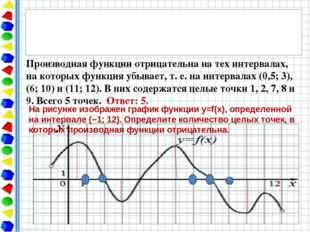 Описание слайда:

На рисунке изображен график функции y=f(x), определенной на интервале (−1; 12). Определите количество целых точек, в которых производная функции отрицательна. Производная функции отрицательна на тех интервалах, на которых функция убывает, т. е. на интервалах (0,5; 3), (6; 10) и (11; 12). В них содержатся целые точки 1, 2, 7, 8 и 9. Всего 5 точек. Ответ: 5.

7 слайд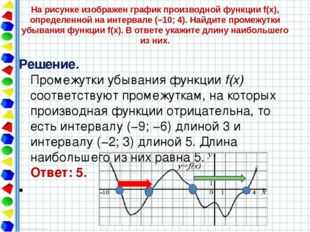 Описание слайда:

На рисунке изображен график производной функции f(x), определенной на интервале (−10; 4). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них. Решение. Промежутки убывания функции f(x) соответствуют промежуткам, на которых производная функции отрицательна, то есть интервалу (−9; −6) длиной 3 и интервалу (−2; 3) длиной 5. Длина наибольшего из них равна 5. Ответ: 5.

8 слайд Описание слайда:

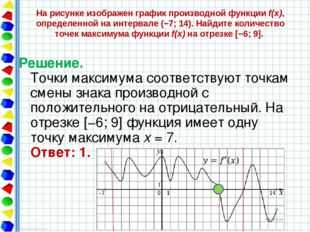
На рисунке изображен график производной функции f(x), определенной на интервале (−7; 14). Найдите количество точек максимума функции f(x) на отрезке [−6; 9]. Решение. Точки максимума соответствуют точкам смены знака производной с положительного на отрицательный. На отрезке [−6; 9] функция имеет одну точку максимума x = 7. Ответ: 1.

9 слайд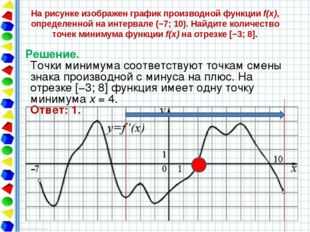
Описание слайда:

На рисунке изображен график производной функции f(x), определенной на интервале (−7; 10). Найдите количество точек минимума функции f(x) на отрезке [−3; 8]. Решение. Точки минимума соответствуют точкам смены знака производной с минуса на плюс. На отрезке [−3; 8] функция имеет одну точку минимума x = 4. Ответ: 1.

10 слайд Описание слайда:

Прямая у=5х+5 является касательной к графику функции 8х2+29х+с. Найдите с. Условия касания графика функции у=f(х) и прямой у=кх+b задается системой требований. В нашем случае получаем систему Получаем с=23, х=-1,5.

11 слайд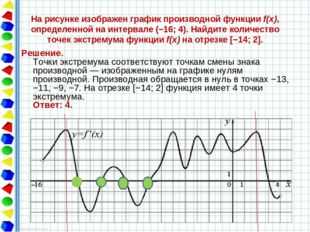
Описание слайда:

На рисунке изображен график производной функции f(x), определенной на интервале (−16; 4). Найдите количество точек экстремума функции f(x) на отрезке [−14; 2]. Решение. Точки экстремума соответствуют точкам смены знака производной — изображенным на графике нулям производной. Производная обращается в нуль в точках −13, −11, −9, −7. На отрезке [−14; 2] функция имеет 4 точки экстремума. Ответ: 4.

12 слайд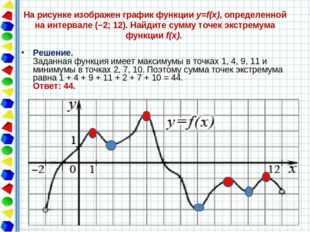 Описание слайда:

На рисунке изображен график функции y=f(x), определенной на интервале (−2; 12). Найдите сумму точек экстремума функции f(x). Решение. Заданная функция имеет максимумы в точках 1, 4, 9, 11 и минимумы в точках 2, 7, 10. Поэтому сумма точек экстремума равна 1 + 4 + 9 + 11 + 2 + 7 + 10 = 44. Ответ: 44.

13 слайд Описание слайда: 14 слайд Описание слайда:

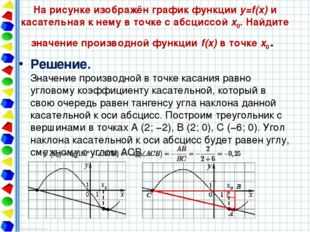
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0. Решение. Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (2; −2), B (2; 0), C (−6; 0). Угол наклона касательной к оси абсцисс будет равен углу, смежному с углом ACB

15 слайд Описание слайда:

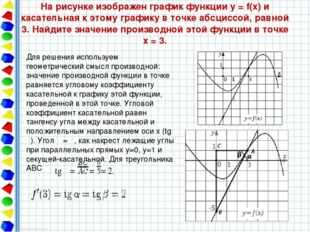
На рисунке изображен график функции y = f(x) и касательная к этому графику в точке абсциссой, равной 3. Найдите значение производной этой функции в точке x = 3. Для решения используем геометрический смысл производной: значение производной функции в точке равняется угловому коэффициенту касательной к графику этой функции, проведенной в этой точке. Угловой коэффициент касательной равен тангенсу угла между касательной и положительным направлением оси х (tg α). Угол α = β, как накрест лежащие углы при параллельных прямых y=0, y=1 и секущей-касательной. Для треугольника ABC

16 слайд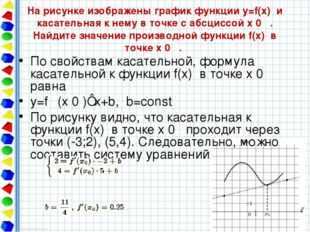
Описание слайда:

На рисунке изображены график функции y=f(x)  и касательная к нему в точке с абсциссой x 0   . Найдите значение производной функции f(x)  в точке x 0   . По свойствам касательной, формула касательной к функции f(x)  в точке x 0   равна y=f ′ (x 0 )⋅x+b,  b=const  По рисунку видно, что касательная к функции f(x)  в точке x 0   проходит через точки (-3;2), (5,4). Следовательно, можно составить систему уравнений

17 слайд Описание слайда:

Источники http://reshuege.ru/ http://egemat.ru/prepare/B8.html http://bankege.ru/

Найдите материал к любому уроку,

указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсемирная историяВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеДругоеДругойЕстествознаниеИЗО, МХКИзобразительное искусствоИностранные языкиИнформатикаИскусствоИспанский языкИсторияИстория РоссииИстория Средних вековИтальянский языкКлассному руководителюКультурологияЛитератураЛитературное чтениеЛогопедияМатематикаМировая художественная культураМузыкаМХКНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирОсновы безопасности жизнедеятельностиПриродоведениеРелигиоведениеРисованиеРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФинский языкФранцузский языкХимияЧерчениеЧтениеШкольному психологуЭкология

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала: ДБ-648986

Похожие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

infourok.ru

Задание №7 ЕГЭ по математике базовый уровень

Простейшие уравнения

В задании №7 базового уровня ЕГЭ по математике необходимо решить простейшие уравнения. Для этого нам понадобятся знания логарифмов, степеней и методы решения квадратных уравнений. Перейдем к рассмотрению и разбору подобных примеров.

Разбор типовых вариантов заданий №7 ЕГЭ по математике базового уровня

Первый вариант задания

 

Найдите корень уравнения 

Алгоритм выполнения:
  1. Раскрыть скобки с левой и с правой стороны равенства, применив формулы приведения.
  2. Все, выражения, содержащие переменную перенести в левую часть, а не содержащие в правую.
  3. Преобразовать левую часть.
  4. Преобразовать правую часть.
  5. Решить уравнение относительно x, то есть найти неизвестный множитель.
Решение:

Раскроем скобки с левой и с правой стороны равенства, применив формулы приведения.

Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений. 

(x + 3)2 = x2 + 2 · x · 3 + 32 = x2 + 6x + 9

Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений. 

(x — 9)2 = x2 — 2 · x · 9 + 92 = x2 — 18x + 81 

После преобразования выражение примет вид:

x2 + 6x + 9 = x2 — 18x + 81 

Все выражения, содержащие переменную перенесем в левую часть, а не содержащие – в правую.

При переносе из одной части равенства в другую знак меняется на противоположный.

x2 + 6x — x2 + 18x = 81 — 9

Преобразуем левую часть. Приведем подобные слагаемые. Объединим в скобки, сохранив знаки, те выражения, где содержится x2 и x.

x2 + 6x — x2 + 18x = (x2 — x2) + (6x +18x) = 0 + 24x = 24x

Выражение примет вид:

24x = 81 — 9

Преобразуем правую часть. 81 – 9 = 72

Выражение примет вид:

24x = 72

Решим уравнение относительно x, то есть найдем неизвестный множитель. Для того чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.

x = 72 : 24

x = 3

Решение в общем виде:

Раскроем скобки в уравнении, получим:

Ответ: 3.

Второй вариант задания

Найдите корень уравнения 

Алгоритм выполнения:
  1. Раскрыть скобки с левой и с правой стороны равенства, применив формулы приведения.
  2. Все, выражения, содержащие переменную перенести в левую часть, а не содержащие в правую.
  3. Преобразовать левую часть.
  4. Преобразовать правую часть.
  5. Решить уравнение относительно x, то есть найти неизвестный множитель.
Решение:

Раскроем скобки с левой и с правой стороны равенства, применив формулы приведения.

Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений. 

(x + 2)2 = x2 + 2 · x · 2 + 22 = x2 + 4x + 4

Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений. 

(x — 8)2 = x2 — 2 · x · 8 + 82 = x2 — 16x + 64 

После преобразования выражение примет вид:

x2 + 4x + 4 = x2 — 16x + 64 

Все выражения, содержащие переменную перенесем в левую часть, а не содержащие – в правую.

При переносе из одной части равенства в другую знак меняется на противоположный.

x2 + 4x — x2 + 16x = 64 — 4

Преобразуем левую часть. Приведем подобные слагаемые. Объединим в скобки, сохранив знаки, те выражения, где содержится x2 и x.

x2 + 4x — x2 + 16x = (x2 — x2) + (4x +16x) = 0 + 20x = 20x

Выражение примет вид:

20x = 64 — 4

Преобразуем правую часть. 64 — 4 = 60

Выражение примет вид:

20x = 60

Решим уравнение относительно x, то есть найдем неизвестный множитель. Для того чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.

x = 60 : 20

x = 3

Решение в общем виде:

Раскроем скобки, получим:

Ответ: 3.

Третий вариант задания

Найдите корень уравнения 

Алгоритм выполнения:
  1. Перенести вычитаемое в правую сторону равенства с противоположным знаком.
  2. Преобразовать правую часть с учетом свойства: loga x + loga y = loga (x · y).
  3. Приравнять логарифмические выражения. Можно так поступить, так как основания логарифмов в левой и правой части одинаковы.
  4. Решить уравнение относительно x.
Решение:

Перенесем вычитаемое в правую сторону равенства с противоположным знаком.

Преобразуем правую часть с учетом свойства: loga x + loga y = loga (x · y).

Выполним преобразование:

Приравняем логарифмические выражения. Можно так поступить, так как основания логарифмов в левой и правой части одинаковы.

Решим уравнение относительно x.

Ответ: 1.

Четвертый вариант задания (демонстрационный вариант 2018)

Найдите корень уравнения 3x− 3 = 81.

В заданиях такого типа необходимо привести выражения в степенях к одинаковому основанию. В данном случае — это 3. Теперь необходимо вспомнить, какой степенью тройки является 81.

Если вы забыли, то для этого необходимо делить 81 на 3 до тех пор, пока не получим 3. Чтобы получить три из 81, нам нужно поделить 81 на 3 три раза: при первом делении мы получим 27, при втором — 9, при третьем — три.

Значит, 81 это три в четвертой степени. Запишем это:

3x− 3 = 34

Когда основания равны, можно приравнять значения степеней:

х — 3 = 4

Откуда:

х = 7

Ответ: 7

Вариант седьмого задания 2017 (1)

Найдите корень уравнения log2( x − 3) = 6 .

Логарифм по основанию два показывает нам число, в степень которого нам необходимо возвести основание, то есть двойку, чтобы получить число под логарифмом.

То есть:

x − 3 = 26

x − 3 = 64

x = 67

Ответ: 67

Вариант седьмого задания 2017 (2)

Найдите отрицательный корень уравнения x2 − x − 6 = 0.

Это простейшее квадратное уравнение и решим его стандартным методом — через вычисление дискриминанта.

D = b2 − 4ac

D = -(1)2 − 4 • 1 • (-6) = 25

Затем находим корни уравнения:

x = (- b ±√D) : 2a

x = (1 + 5) : 2 = 3

x = (1 — 5) : 2 = -2

Так как нам необходим отрицательный корень — ответ -2

Ответ: -2.

spadilo.ru

Author: alexxlab

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *