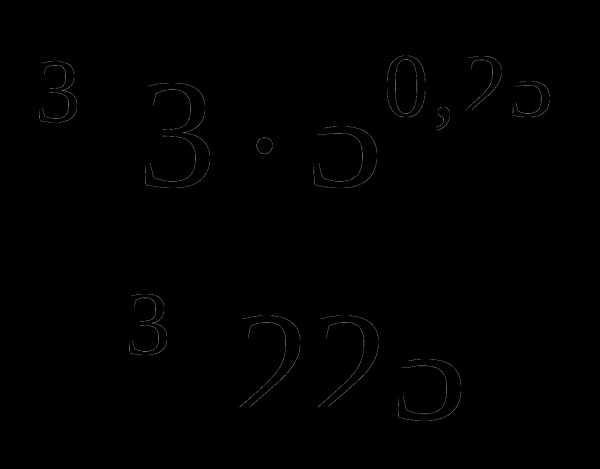Входная контрольная работа 11 класс
Входной контроль по математике. 11 класс
Вариант 1
1. Найдите значение выражения: .
2. Найдите , если , .
3. Найдите корень уравнения:
4.
На рисунке изображен график функции — производной функции f(x), определенной на интервале (−10; 6). В какой точке отрезка [−2; 4] функция f(x) принимает наименьшее значение?
5. Найдите наибольшее значение функции на промежутке .
6. Решить уравнение: .
7. Найдите область определения функции .
Входной контроль по математике. 11 класс
Вариант 2
1. Найдите значение выражения: .
2. Найдите , если , .
3. Найдите корень уравнения: .
4.
На рисунке изображен график функции y=f(x), определенной на интервале (−3; 9). Найдите количество точек, в которых производная функции f(x) равна 0.
5. Найдите наименьшее значение функции на промежутке .
6. Решить уравнение:.
7. Найдите область определения функции .
infourok.ru
Входная контрольная работа. — Математика
Входная контрольная работа по математике 11 класс.
Фамилия, имя______________________________________ число ________________
Вариант № 1
| № | Задание | Ответ |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 | ||
| 13 | ||
| 14 | ||
| 15 | | |
| 16 |
|
Вводная контрольная работа по математике 11 класс.
Фамилия, имя______________________________________ число ________________
Вариант № 2
| № | Задание | Ответ |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 | ||
| 13 | ||
| 14 | ||
| 15 | ||
| 16 |
Критерии оценивания:
0 заданий – 6 заданий оценка 2
7 заданий – 9 заданий оценка 3
10 заданий – 13 заданий оценка 4
14 заданий – 16 заданий оценка 5
Проверочная работа по математике для 11 класса
Проверочная работа по математике в 11 классе
Инструкция по выполнению работы
На выполнение работы отводится 90 минут.
Работа состоит из двух частей, включающих в себя 15 заданий.
Часть 1 (1-12 задание) содержит задания базового уровня с кратким ответом.
Часть 2 (13-15 задание) содержат задания повышенного уровня. При выполнении этих заданийнеобходимо записать полное обоснованное решение и ответ.
Советуем выполнять задания в том порядке, в котором они даны. Для экономии времени пропускайте задание, которое не удаѐтся выполнить сразу, и переходите к следующему. Если после выполнения всей работы у Вас останется время, Вы сможете вернуться к пропущенным заданиям.
При выполнении работы запрещается пользоваться вычислительной техникой.
Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Желаем успеха!
| Вариант 1 Часть 1 Ответами к заданиям 1–12 являются цифра, число или последовательность цифр, которые следует записать в специальном поле | ||
| 1 | Для ремонта квартиры требуется 37 рулонов обоев. Сколько пачек обойного клея нужно купить, если одна пачка клея рассчитана на 6 рулонов? | |
| 2 | На диаграмме показана среднемесячная температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру в 2003 году. Ответ дайте в градусах Цельсия.
| |
| 3 4 | Найдите значение выражения Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. | |
| 5 | В фирме такси в данный момент свободно 20 машин: 10 черных, 2 желтых и 8 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси. | |
| 6 | Решите уравнение: = 5 | |
| 7 | Упростите выражение и найдите его значение при . | |
| 8 9 10 11 12 | В треугольнике АВС угол С равен 90°, АС=9,sinА= . Найдите АВ. Найдите значение выражения
Найдите его диагональ. Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути – со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт B одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч. На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: , где l — длина ребра куба в метрах, — плотность воды, а g — ускорение свободного падения (считайте Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 153125 Н? Ответ выразите в метрах. | |
| Часть 2 При выполнении заданий 13 –15 необходимо записать полное обоснованное решение и ответ. 13 а) Решите уравнение б) Найдите все корни уравнения, принадлежащие отрезку 14 В правильной шестиугольной пирамиде SABCDEF стороны основания которой равны 1, а боковые ребра равны 2, найдите косинус угла между прямыми SB и AD. | ||
| 15 | Решите неравенство: | |
Проверочная работа в 11 классе
Инструкция по выполнению работы
Работа состоит из двух частей, включающих в себя 15 заданий.
Часть 1 (1-12 задание) содержит задания базового уровня с кратким ответом.
Часть 2 (13-15 задание) содержат задания повышенного уровня. При выполнении этих заданий необходимо записать полное обоснованное решение и ответ.
Советуем выполнять задания в том порядке, в котором они даны. Для экономии времени пропускайте задание, которое не удаѐтся выполнить сразу, и переходите к следующему. Если после выполнения всей работы у Вас останется время, Вы сможете вернуться к пропущенным заданиям.
При выполнении работы запрещается пользоваться вычислительной техникой.
Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Желаем успеха!
| Вариант 2 Часть 1 Ответами к заданиям 1–12 являются цифра, число или последовательность цифр, которые следует записать в специальном поле | |
| 1 | Для ремонта квартиры требуется 63 рулона обоев. Сколько пачек обойного клея нужно купить, если одна пачка клея рассчитана на 6 рулонов? |
| 2 | На диаграмме показана среднемесячная температура в Нижнем Новгороде (Горьком) за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру в 1994 году. Ответ дайте в градусах Цельсия.
|
| 3 4 | Найдите значение выражения Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. |
| 5 | В фирме такси в данный момент свободно 16 машин: 4 черных, 3 синих и 9 белых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет черное такси. |
| 6 | Решите уравнение: = 7 |
| 7 | Упростите выражение и найдите его значение при . |
| 8 9 10 11 12 | В треугольнике АВС угол С равен 90°, АС=4,sinА= . Найдите АВ. Найдите значение выражения:
Площадь поверхности куба равна 8. Найдите его диагональ. Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 27 км/ч, а вторую половину пути — со скоростью, на 18 км/ч большей скорости первого, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч. На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: , где – длина ребра куба в метрах, кг/м3 – плотность воды, а – ускорение свободного падения (считайте Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 78400 Н? Ответ выразите в метрах. |
| Часть 2 При выполнении заданий 13 –15 необходимо записать полное обоснованное решение и ответ. | |
| 13 | а) Решите уравнение б) Укажите корни этого уравнения, принадлежащее отрезку |
| 14 | В правильной шестиугольной пирамиде SABCDEF стороны основания которой равны 12, а боковые ребра равны 36, найдите косинус угла между прямыми SB и AD. |
| 15 | Решите неравенство: |
Ответы и решения
Вариант 1
Часть 1:
| № п/п | Ответ |
| 1 | 7 |
| 2 | 20 |
| 3 | -1,3 |
| 4 | 6 |
| 5 | 0,4 |
| 6 | 5 |
| 7 | 5 |
| 8 | 15 |
| 9 | 6 |
| 10 | 3 |
| 11 | 32 |
| 12 | 2,5 |
Часть 2:
13. а) Решите уравнение
б) Найдите все корни уравнения, принадлежащие отрезку
Решение.
а) Преобразуем уравнение:
Получаем или откуда или где
б) На отрезке корни отберём с помощью единичной окружности.
Получаем и
Ответ: а)
б)
| Баллы | Критерии оценки выполнения задания |
| 3 | Обоснованно получен правильный ответ |
| 2 | Тригонометрическое уравнение решено верно, но неверно указаны или не указаны корни, принадлежащие отрезку |
| 1 | Тригонометрическое уравнение решено, но допущена вычислительная ошибка |
| 0 | Решение не соответствует ни одному из критериев |
14. В правильной шестиугольной пирамиде SABCDEF стороны основания которой равны 1, а боковые ребра равны 2, найдите косинус угла между прямыми SB и AD.
Решение.
Прямая AD параллельна прямой BC. Следовательно, искомый угол — SBC. В равнобедренном треугольнике SBC проведём медиану и высоту SM. Имеем:
Из прямоугольного треугольника SBM
получаем:
Ответ:
| Баллы | Критерии оценки выполнения задания |
| 2 | Обоснованно получен верный ответ |
| 1 | Решение доведено до конца, но допущена описка или ошибка вычислительного характера, с её учетом дальнейшие шаги выполнены верно |
| 0 | Другие случаи, не соответствующие указанным критериям |
| 2 | Максимальный балл |
15. Решите неравенство:
Решение.
Перепишем неравенство в виде:
Множество решений исходного
неравенства:
Ответ:
| Баллы | Критерии оценки выполнения задания |
| 2 | Обоснованно получен верный ответ |
| 1 | Решение доведено до конца, но допущена описка или ошибка вычислительного характера, с её учетом дальнейшие шаги выполнены верно |
| 0 | Другие случаи, не соответствующие указанным критериям |
| 2 | Максимальный балл |
Вариант 2
Часть 1:
| № п/п | Ответ |
| 1 | 11 |
| 2 | -14 |
| 3 | 4 |
| 4 | 6 |
| 5 | 0,25 |
| 6 | 45 |
| 7 | 3 |
| 8 | 5 |
| 9 | 2 |
| 10 | 2 |
| 11 | 36 |
| 12 | 2 |
Часть 2:
13. а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащее
отрезку
Решение.
Сведём уравнение к квадратному относительно синуса, используя
формулу Имеем:
б) С помощью числовой окружности отберём корни, принадлежащие
отрезку , получим число
Ответ:
а) б)
| Баллы | Критерии оценки выполнения задания |
| 3 | Обоснованно получен правильный ответ |
| 2 | Тригонометрическое уравнение решено верно, но неверно указаны или не указаны корни, принадлежащие отрезку |
| 1 | Тригонометрическое уравнение решено, но допущена вычислительная ошибка |
| 0 | Решение не соответствует ни одному из критериев |
14. В правильной шестиугольной пирамиде SABCDEF стороны основания которой равны 12, а боковые ребра равны 36, найдите косинус угла между прямыми SB и AD.
Решение.
Прямая параллельна прямой Следовательно, искомый угол — В равнобедренном треугольнике проведём
медиану и высоту
Имеем:
Из прямоугольного треугольника
получаем:
Ответ:
| Баллы | Критерии оценки выполнения задания |
| 2 | Обоснованно получен верный ответ |
| 1 | Решение доведено до конца, но допущена описка или ошибка вычислительного характера, с её учетом дальнейшие шаги выполнены верно |
| 0 | Другие случаи, не соответствующие указанным критериям |
| 2 | Максимальный балл |
15. Решите неравенство:
Решение.
Перепишем неравенство в виде:
Таким образом, множество решений исходного неравенства:
Ответ:
| Баллы | Критерии оценки выполнения задания |
| 2 | Обоснованно получен верный ответ |
| 1 | Решение доведено до конца, но допущена описка или ошибка вычислительного характера, с её учетом дальнейшие шаги выполнены верно |
| 0 | Другие случаи, не соответствующие указанным критериям |
| 2 | Максимальный балл |
Критерии оценки выполнения
Общий балл формируется путем суммирования баллов, полученных учащимися за выполнение заданий. За каждое верно выполненное задание части 1 начисляется 1 балл, за каждое задание части 2 – 2 балла.
Оценка работы:
| Балл | Отметка |
| 14-18 | 5 |
| 9-13 | 4 |
| 6-8 | 3 |
| 0-5 | 2 |
kopilkaurokov.ru
Входные контрольные работы 5=11 класс
Пояснительная записка
к административному итогового контролю
по математике 10 класса
2016-2017 уч. г.
Назначение административного входного контроля:
проводится с целью установления фактического уровня теоретических знаний учащихся по математике по курсу 9 класса; их практических умений и навыков; установления соответствия предметных знаний, умений и навыков по следующим разделам:
Вычисление значения числовых выражений
Чтение графиков и диаграмм.
Решение задач на квадратной решётке: вычисление площадей.
Решение геометрических задачи.
Решение квадратичных неравенств.
Преобразования алгебраических выражений, содержащих степени с целым показателем.
Решение комбинаторных задач.
Нахождение суммы нескольких членов арифметической прогрессии.
Кодификатор элементов содержания по МАТЕМАТИКЕ
для составления контрольных измерительных материалов
входного контроля в 10 классах
Кодификатор элементов содержания по математике составлен на основе Обязательного минимума содержания основных образовательных программ и Требований к уровню подготовки выпускников средней (полной) школы (Приказ МО РФ «Об утверждении федерального компонента Государственных стандартов начального общего, основного общего и среднего (полного) общего образования от 05.03.2004 № 1089).
Кодификатор элементов содержания по всем разделам включает в себя элементы содержания за курс 9 класса.
Требования (умения), проверяемые заданиями контрольной работы
1. Уметь выполнять вычисления и преобразования. Вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования. Выполнять преобразования алгебраических выражений, содержащих степени с целым показателем.
2. Уметь решать уравнения и неравенства. Решать уравнения, неравенства и их системы.
3. Уметь выполнять действия с функциями. Устанавливать соответствие между графиками функций и формулами, которые их задают.
4.Уметь решать прогрессии. Распознавать арифметические прогрессии, решать задачи с применением формулы общего члена арифметической прогрессии.
5. Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни. Решать практические задачи, требующие систематического перебора вариантов; сравнивать шансы наступления случайных событий, оценивать вероятности случайного события, сопоставлять и исследовать модели реальной ситуацией с использованием аппарата вероятности и статистики.
6. Уметь выполнять действия с геометрическими фигурами. Выполнять действия с геометрическими фигурами. Решать планиметрические задачи на нахождение геометрических величин. Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения.
Общее время выполнения входного контроля – 40 минут.
Характеристика структуры и содержания работы
Входная контрольная работа представлена в двух вариантах. Работа содержит две части, которые различаются по содержанию, сложности и числу заданий. Определяющим признаком каждой части работы является форма заданий:
– часть I содержит задания с кратким ответом;
– часть II содержит задания с развернутым ответом.
Задания с кратким ответом части I контрольной работы предназначены для определения математических компетентностей учащихся на базовом уровне. Задание с кратким ответом считается выполненным, если верный ответ зафиксирован в бланке ответов. Ответом на задания части 1 является целое число или конечная десятичная дробь.
Задания с кратким ответом части II контрольной работы предназначены для определения математических компетентностей учащихся на повышенном уровне Часть II включает 2 задания с развернутым ответом. В заданиях с развернутым ответом части II контрольной работы должно быть записано полное обоснованное решение задачи. (на бланке №2).
Правильное решение каждого из заданий части I оценивается 1 баллом. Задания части II оцениваются в 2 балла. Максимально возможный балл за всю работу – 21.
Критерии оценивания результатов выполнения работы:
1 – 10 баллов оценка «2»
11 – 16 баллов оценка «3»
17 – 19 баллов оценка «4»
20 – 21 баллов оценка «5»
Вариант 1
Часть 1
1.Найдите значение выражения 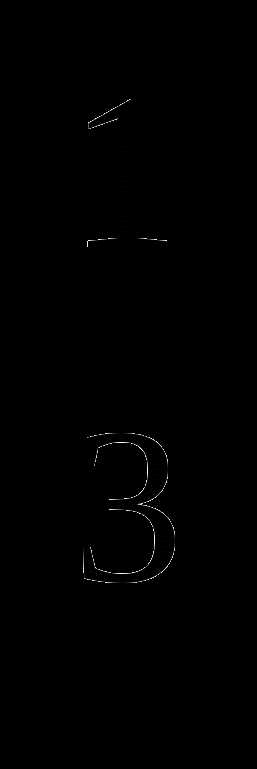
2.Какое из неравенств верно для числа, отмеченного на координатной прямой точкой А?
1)  2)
2) 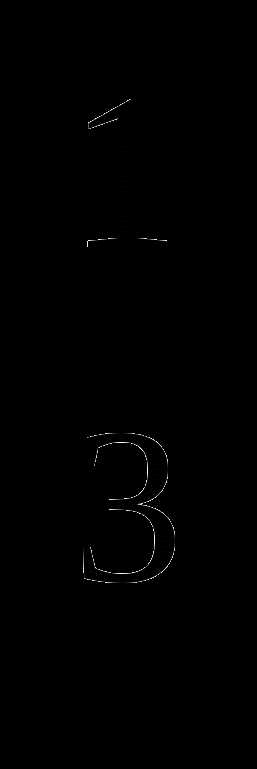 3)
3)  4)
4) 
3. Найдите корень уравнения 
4.Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ

Ф ОРМУЛЫ
ОРМУЛЫ
В таблице под каждой буквой укажите соответствующий номер.
Ответ:А
Б
В
5.Выписаны первые несколько членов арифметической прогрессии: 12; 11,8; 11,6.… Найдите сумму десяти первых её членов.
6.Найдите значение выражения  при
при 
Найдите меньший угол параллелограмма. Ответ дайте в градусах.
8.В окружности с центром в точке О проведены диаметры AD и ВС, . Найдите величину угла АОВ.
9.Найдите площадь фигуры, изображенной на рисунке, если стороны квадратных клеток равны 1.
10.Какие из следующих утверждений верны?
1)Если в параллелограмм можно вписать окружность, то этот параллелограмм – ромб.
2)
Диагональ трапеции делит её на два равных треугольника.
3)
Если два угла треугольника равны, то треугольник равнобедренный.
В ответ запишите номера выбранных утверждений.
1 1.На графике показан процесс разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат — температура двигателя в градусах Цельсия. Определите по графику, на сколько градусов нагреется двигатель с третьей по восьмую минуту разогрева.
1.На графике показан процесс разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат — температура двигателя в градусах Цельсия. Определите по графику, на сколько градусов нагреется двигатель с третьей по восьмую минуту разогрева.
1 2. В цирке для продажи было заготовлено некоторое количество шариков. Перед началом представления было продано 40% всех воздушных шариков, а в антракте – еще 12 штук. После этого осталась половина всех шариков. Сколько шариков было первоначально?
2. В цирке для продажи было заготовлено некоторое количество шариков. Перед началом представления было продано 40% всех воздушных шариков, а в антракте – еще 12 штук. После этого осталась половина всех шариков. Сколько шариков было первоначально?
13.На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 1 м, а длинное плечо 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5м?
14. Девятиклассники Петя, Катя, Ваня, Даша и Наташа бросили жребий, кому начинать игру. Найдите вероятность того, что начинать игру будет не Петя.
Часть 2
15. Решите неравенство: 
16. На тренировке по картингу один карт проходил круг на 10 секунд медленнее другого и через минуту отстал от него ровно на круг. За сколько секунд каждый карт проходил круг?
Вариант 2
Часть 1
1.Найдите значение выражения 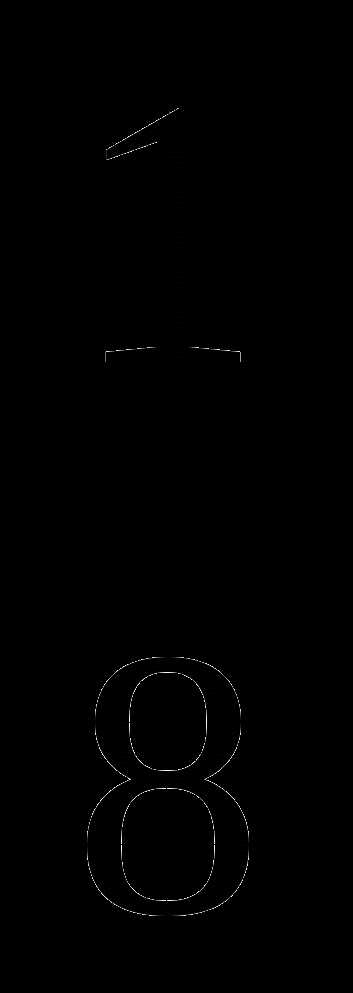 .
.
2.Какое из неравенств верно для числа, отмеченного на координатной прямой точкой a?
1) 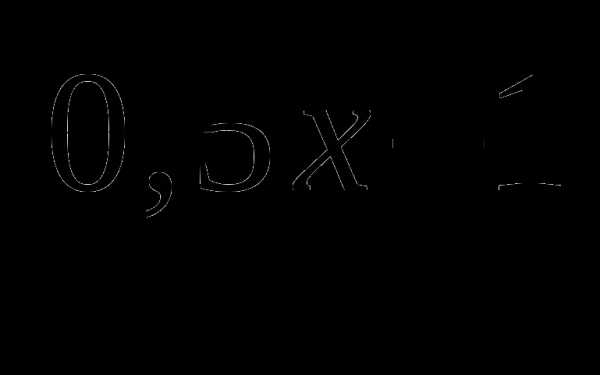 2)
2)  3)
3)  4)
4) 
3.Найдите корень уравнения  .
.
4.Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ

ФУНКЦИИ
В таблице под каждой буквой укажите соответствующий номер.
Ответ:А
Б
В
5.Выписаны первые несколько членов арифметической прогрессии: 11; 10,7; 10,4.… Найдите сумму десяти первых её членов.
6.Найдите значение выражения  при
при  .
.
Найдите больший угол параллелограмма. Ответ дайте в градусах.
8. В окружности с центром в точке О проведены диаметры AD и ВС, . Найдите величину угла АОВ.
9. Найдите синус угла АВС, изображенного на рисунке.
10. Какие из следующих утверждений верны?
1)
Если около параллелограмма можно описать окружность, то этот параллелограмм – прямоугольник.
2)
В равнобедренном треугольнике медиана является биссектрисой и высотой.
3)
Если две параллельные прямые пересечены третьей прямой, то внутренние односторонние углы равны.
В ответ запишите номера выбранных утверждений.
1 1. На графике показан процесс разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат — температура двигателя в градусах Цельсия. Определите по графику, за сколько минут двигатель нагреется с 300С до 900С.
1. На графике показан процесс разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат — температура двигателя в градусах Цельсия. Определите по графику, за сколько минут двигатель нагреется с 300С до 900С.
1 2.В цирке для продажи было заготовлено некоторое количество шариков. Перед началом представления было продано 20% всех воздушных шариков, а в антракте – еще 57 штук. После этого осталась половина всех шариков. Сколько шариков было первоначально?
2.В цирке для продажи было заготовлено некоторое количество шариков. Перед началом представления было продано 20% всех воздушных шариков, а в антракте – еще 57 штук. После этого осталась половина всех шариков. Сколько шариков было первоначально?
13. На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 1 м, а длинное плечо 4 м. На сколько метров поднимется конец короткого плеча, когда конец длинного опуститься на 2 м?
14. В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
Часть 2
15. Решите неравенство: 
16. На соревнованиях по кольцевой трассе один лыжник проходил круг на 3 мин быстрее другого и через час обогнал его ровно на круг. За сколько минут каждый лыжник проходил круг.
Ответы
1 вариант Часть 1
Модуль «Алгебра»
12
3
4
6
6
-2
3
-7
134
111
1,5
Модуль «Геометрия»
78
9
10
66
110
13
13
Модуль «Реальная математика»
1112
13
14
50
120
2
0,8
Часть 2
15. Решите неравенство: 
Ответ:(-0,75;3).
16.На тренировке по картингу один карт проходил круг на 10 секунд медленнее другого и через минуту отстал от него ровно на круг. За сколько секунд каждый карт проходил круг?
Решение. Пусть х(сек) – время прохождения круга первым картом, х>0(*). Тогда х+10 (сек)– время прохождения вторым картом; 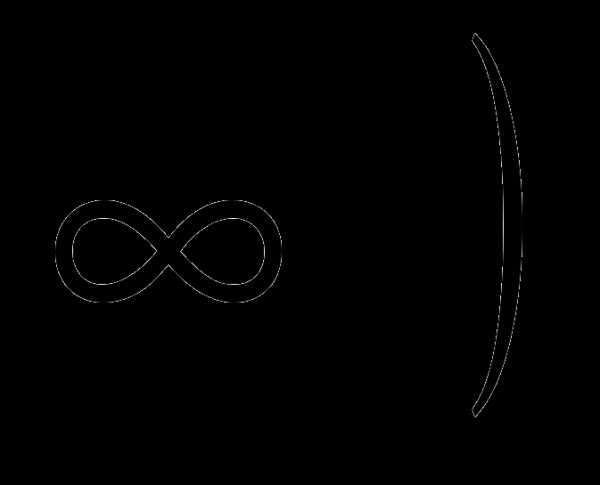 -часть круга, пройденная первым картом за 60 секунд;
-часть круга, пройденная первым картом за 60 секунд; 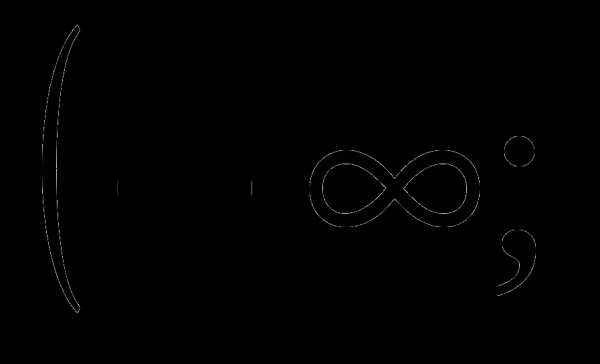 -часть круга, пройденная вторым картом за 60 секунд. Известно, что через минуту один отстал от другого на круг, тогда
-часть круга, пройденная вторым картом за 60 секунд. Известно, что через минуту один отстал от другого на круг, тогда .Решив это уравнение при условии (*), получаем х=20, тогда время второго карта 30сек.
.Решив это уравнение при условии (*), получаем х=20, тогда время второго карта 30сек.
Ответ: 20 сек. 30 сек
2 вариант Часть 1
Модуль «Алгебра»
12
3
4
5
6
5
4
-2
214
96,5
3,5
Модуль «Геометрия»
78
9
10
116
62
0,8
1
Модуль «Реальная математика»
1112
13
14
7
190
0,5
0,35
Часть 2
15. Решите неравенство: 
Ответ: 
16.На соревнованиях по кольцевой трассе один лыжник проходил круг на 3 мин быстрее другого и через час обогнал его ровно на круг. За сколько минут каждый лыжник проходил круг.
Решение. Пусть х мин – время прохождения круга одним лыжником, х>0(*) х+3мин – время прохождения круга другим лыжником  — часть круга одним лыжником за 60 минут
— часть круга одним лыжником за 60 минут  -часть круга другим лыжником за 60 минут. Известно, что через час один отстал от другого на круг, имеем
-часть круга другим лыжником за 60 минут. Известно, что через час один отстал от другого на круг, имеем . Решив это уравнение при условии (*), получаем х=12, тогда время другого 15 мин
. Решив это уравнение при условии (*), получаем х=12, тогда время другого 15 мин
Ответ: 12мин и 15 мин
Рекомендации по проведению и проверке административной контрольной работы
При проведении и оценивании работы для обучающихся 10-х классов рекомендуется соблюдать следующие принципы:
Административный входной контроль выполняется на специальных бланках.
При проведении административного входного контроля обязательно присутствие ассистента.
При выполнении заданий учащиеся могут пользоваться черновиком. Записи в черновике не буду учитываться при оценивании работы.
Исправления, допущенные учеником, не учитываются и не влияют на оценку работы.
При выполнении работы не разрешается пользоваться калькулятором.
Работу проверяют два педагога (совместно). Если их оценки не совпадают, к проверке привлекается третий специалист.
После проверки контрольной работы проводится работа над ошибками.
АНАЛИЗ
результатов стартового контроля
за 20 /20 учебный год
Предмет _____математика________________________________________________
Класс _________________________________________________________________
Учитель ________________________________________________________________
Форма контроля __контрольная работа_____________________________________
Результаты контроля:
п/пФИ учащихся
Отметка
(предыдущий год)
Отметка (текущий год)
Динамика результатов
(+, -, =)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Итого
«5» —
«4» —
«3» —
«2» —
«1» —
«5» —
«4» —
«3» —
«2» —
«1» —
Выводы по итогам контроля:
1Количество учащихся, справившихся с работой (% успеваемости)
2
ФИ учащихся, не справившихся с работой
3
Количество учащихся, справившихся с работой на «4» и «5» (% качества)
4
% учащихся, понизивших свои образовательные результаты по сравнению с предыдущим учебным годом
5
ФИ учащихся, понизивших свои образовательные результаты по сравнению с предыдущим учебным годом
Поэлементный анализ качества выполнения заданий
п/пТип ошибки
Количество учащихся, допустивших ошибку, %
по результатам итоговой контрольной работы по итогам предыдущего учебного периода
по результатам стартового контроля
1
Вычисление значения числовых выражений
2
Определиние координаты точки на координатной прямой.
3
Решение дробного рационального выражения.
4
Установление соответствия между графиками функций и формулами, которые их задают.
5
Нахождение суммы нескольких членов арифметической прогрессии
6
Преобразования алгебраических выражений, содержащих степени с целым показателем
8
Нахождение элементов параллелограмма
9
Нахождение величины центрального угла
10
Нахождение площади многоугольника на квадратной решётке
11
Анализ геометрический утверждений
12
Решение задачи на проценты
13
Решение геометрической задачи на применение подобия треугольников
14
Решение комбинаторных задач
15
Решение системы целых уравнений с двумя неизвестными
16
Решение текстовой задачи (по кругу)
План корректирующих мероприятий
п/пСодержание деятельности
Сроки
1
2
3
4
5
Учитель ____________ / ______________
подпись расшифровка подписи
infourok.ru
Входная контрольная работа по математике .11 класс.
Просмотр содержимого документа
«Входная контрольная работа по математике .11 класс.»
Входная контрольная работа по математике в 11 классе .
Преподавание ведётся по учебникам « Алгебра и начала анализа» С.М. Никольского и др. и « Геометрия 10-11» Л.С.Атанасяна.
Цель: выявить степень сформированности знаний по курсу математики 10 класса.
1 вариант . 2 вариант.
1.Решите неравенство.
≥ 0 ≥0
2.Решите уравнение.
— +7=0 -10* +81 =0
3.Решите уравнение.
3sin2х- 2 sinx cosx+cos2x=0 sin2x+2sinx cosx+3cos2x=0.
4.Решите уравнение.
+-=2.
5.Решите задачу.
В правильной четырёхугольной В правильной треугольной пирамиде
пирамиде SABCD точка О- боковое ребро равно 7,
центр основания, S-вершина. а сторона основания равна 10,5.
SO=12, BD=18. Найдите высоту пирамиды
Найдите боковое ребро SA
Критерии оценивания.
Каждое верно решённое задание оценивается в 2 балла.
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | 2 |
| Верно построена математическая модель, решение сведено к исследованию этой модели и получен результат: -неверный ответ из-за вычислительной ошибки; -верный ответ, но решение недостаточно обосновано | 1 |
| Решение не соответствует ни одному из критериев, приведённых выше. | 0 |
Оценивание работы в целом.
«1»-1-2 балла
«2»- 3-4 балла
«3»- 5-6 баллов
«4» -7-8 баллов
«5»- 9-10 баллов.
multiurok.ru
Анализ диагностической работы по математике в 11 классе в форме ЕГЭ
Анализ
результатов входной диагностики
ЕГЭ по математике (базовый уровень) учащихся 11 класса
МБОУ Солёноозёрная СШ № 12
19.10.17 г.
Контрольно-измерительные материалы ЕГЭ по математике базового уровня состоят из одной части, включающей 20 заданий с кратким ответом. Экзамен базового уровня не является облегченной версией профильного, он ориентирован на иную цель и другое направление изучения математики — математика для повседневной жизни и практической деятельности.
Структура и содержание контрольных работ базового уровня дают возможность проверить умение решать стандартные задачи практического содержания, проводить простейшие расчеты, использовать для решения задач учебную и справочную информацию, решать, в том числе сложные задачи, требующие логических рассуждений, использовать простейшие вероятностные и статистические модели, ориентироваться в простейших геометрических конструкциях. В работу включены задания базового уровня по всем основным предметным разделам: геометрия (планиметрия и стереометрия), алгебра, начала математического анализа, теория вероятностей и статистика.
Результаты базового ЕГЭ по математике выдаются в отметках по пятибалльной шкале, не переводятся в стобалльную шкалу и не дают возможности участия в конкурсе на поступление в вузы.
Петров Петр — 14 баллов (оценка 4)
Иванов Иван – 12 баллов (оценка 4)
Точкина Татьяна — 10 баллов (оценка 3)
Сидоров Степан– 12 баллов (оценка 4)
Поэлементный анализ
| Обозначение задания в работе | Проверяемые требования (умения) | Уровень трудности | Процент выполнения заданий |
| 1 | Вычисления (действия с дробями) | Б | 75 |
| 2 | Вычисления (действия со степенями) | Б | 100 |
| 3 | Простейшие текстовые задачи (проценты, округление) | Б | 100 |
| 4 | Преобразование выражений (действия с формулами) | Б | 75 |
| 5 | Вычисления и преобразования (иррациональные) | Б | 50 |
| 6 | Простейшие текстовые задачи (округление с недостатком и с избытком) | Б | 100 |
| 7 | Простейшие уравнения (линейные, квадратные, кубические) | Б | 50 |
| 8 | Прикладная геометрия (многоугольники) | Б | 75 |
| 9 | Размеры и единицы измерения | Б | 75 |
| 10 | Начала теории вероятностей (классическое определение вероятности) | Б | 50 |
| 11 | Чтение графиков и диаграмм | Б | 100 |
| 12 | Выбор оптимального варианта | Б | 75 |
| 13 | Стереометрия (объем шара) | Б | 0 |
| 14 | Анализ графиков и диаграмм (скорость изменения величин) | Б | 100 |
| 15 | Планиметрия | Б | 25 |
| 16 | Задачи по стереометрии (пирамида) | Б | 25 |
| 17 | Неравенства (числовая ось, числовые промежутки) | Б | 0 |
| 18 | Анализ утверждений | Б | 75 |
| 19 | Числа и их свойства (цифровая запись числа) | П | 25 |
| 20 | Задачи на смекалку | П | 25 |
Из поэлементного анализа видно, что учащиеся отлично справились с заданиями № 2, 3, 6, 11, 14 , также неплохие знания (3 человека из четырех) показали в заданиях №1, 4, 8, 9,12, 18. Показали недостаточные знания по заданиям № 5, 7, 10, 15, 16,18, 19 и 20. Последние два задания — это задачи повышенного уровня. Ошибки в первом и четвертом заданиях – это скорее всего вычислительные (при подсчете). Некоторые темы будут изучаться позднее в 11 классе, поэтому 13, 16 (задачи по стереометрии) и 17 (задачи с логарифмами) задания не выполняли. Плохие знания показали по геометрии (планиметрии).
Выводы:
1. Все вышеперечисленные результаты показывают определённую адаптацию системы образования к данной модели экзамена, направленной на проверку всего курса математики, а не только курса X-XI классов, поэтому подготовку к ЕГЭ надо начинать как можно раньше.
2. Организацию подготовки к сдаче ЕГЭ по математике следует начать с выявления целевых групп учащихся (первая группа – учащиеся, которые ставят перед собой цель преодолеть порог базового уровня, вторая – преодолеть порог профильного уровня поступить в вуз).
3. В процессе обучения вырабатывать у учащихся привычки самоконтроля и самопроверки.
4. Подбирая задания для тренировки (например, в ходе итогового повторения), их следует соотносить с возможностями и потребностями каждого учащегося, а также с уровнем класса в целом.
5. Уделять должное внимание геометрической подготовке.
6. С сильными учащимися, помимо тренировки в решении задач базового уровня сложности (в виде самостоятельных работ), проводить разбор методов решения задач повышенного уровня сложности, проверяя усвоение этих методов на самостоятельных работах и дополнительных занятиях.
7. Для успешной сдачи ЕГЭ необходимо систематически изучать математику, развивать мышление, отрабатывать навыки решения задач различного уровня.
8. Особое внимание в преподавании математики следует уделить регулярному выполнению упражнений, развивающих базовые математические компетенции школьников (умение читать и верно понимать условие задачи, решать практические задачи, выполнять арифметические действия, простейшие алгебраические преобразования, действия с основными функциями и т.д.).
Учитель: _________/ Дубровская А.Н/
multiurok.ru
Входной тест по алгебре 11 класс
Работа содержит задания, проверяющие уровень усвоения материала за 10 класс.Работа состоит из трёх частей. Задания1-7 соответствуют программе курса алгебры и начала анализа по учебнику Мордковича А.Г. (базовый уровень). Задания 9-10 проверяют умения применять материал в нестандартной ситуации. В третьей части рассматриваются задания части С-экзаменационного материала. Для проверки предлалагаются следующие темы: свойства корня, логарифмы, логарифмические уравнения и неравенства, показательные уравнения и неравенства.
Просмотр содержимого документа
«Входной тест по алгебре 11 класс »
Входной тест для учащихся 11 классов.
А 1. Упростите выражение 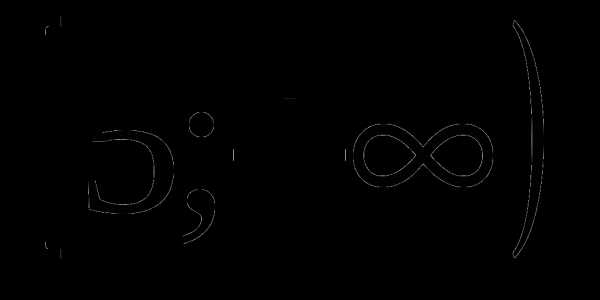
1) 5 . 3—
. 3— 2) 5
2) 5 . 3 3) 5
. 3 3) 5 . 3 —
. 3 — 4) 5
4) 5 . 3
. 3
А 2. Вычислите: log 2 0,04 + 2 log 2 5
1) 0; 2) 3; 3) -1; 4) log 2 5.
А 3. Упростите выражение: sin 2 + cos (
+ cos ( 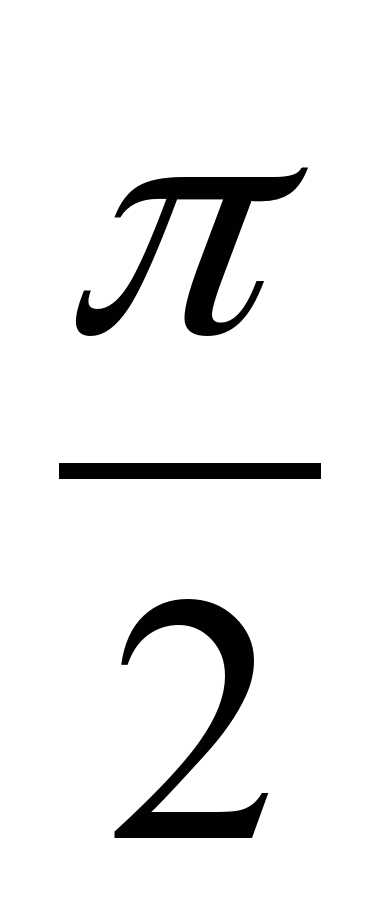 +
+  ) + cos
) + cos cos 2
cos 2
1) 0; 2) 2 cos ; 3) cos
; 3) cos + sin
+ sin ; 4) cos
; 4) cos — sin
— sin .
.
А 4. Укажите промежуток, которому принадлежит корень уравнения
( )
)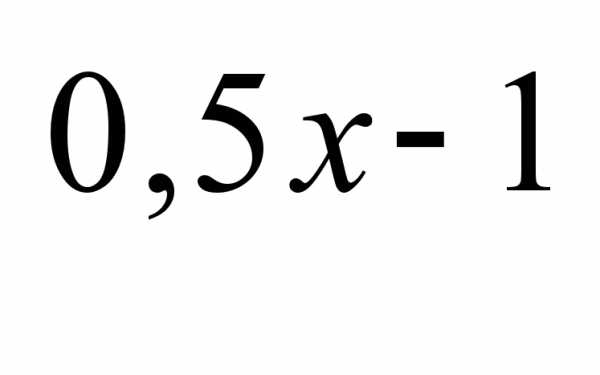 = 4.
= 4.
1)  -3; -1
-3; -1 ; 2)
; 2) 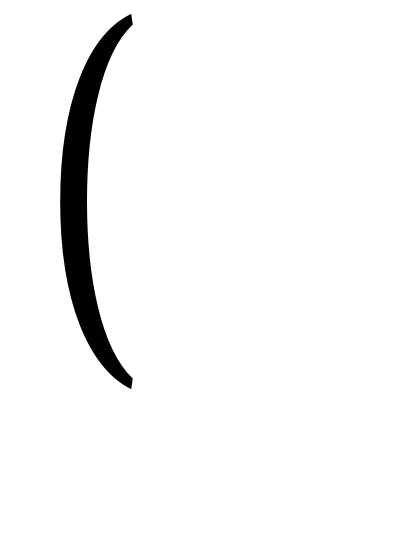 -1; 1
-1; 1 ; 3)
; 3) 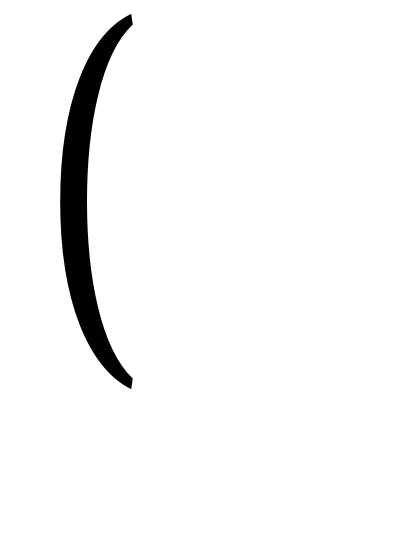 1; 3
1; 3 ; 4)
; 4)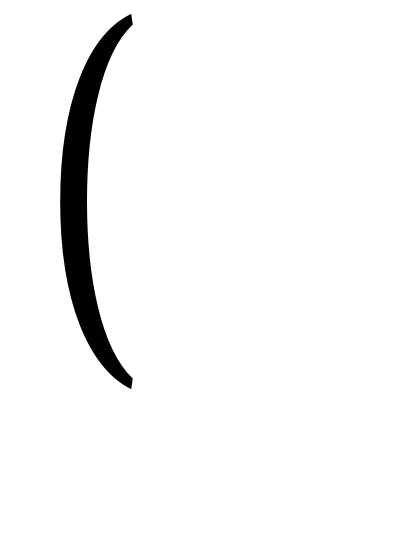 3; 5
3; 5 ;
;
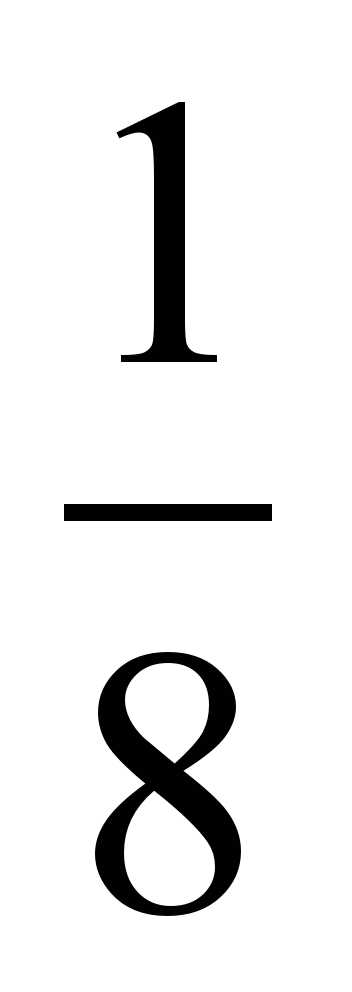
А 5. Решите неравенство: log 0,5 ( 2 – 0,5х) 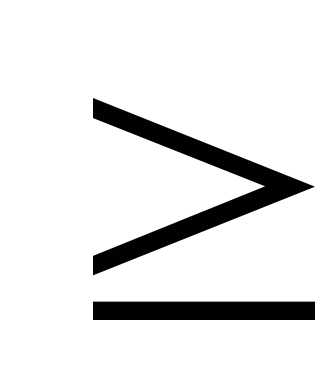 -1.
-1.
1) 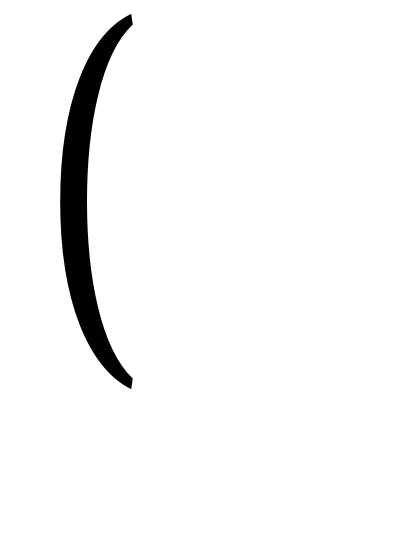 4; 6
4; 6 ; 2)
; 2) 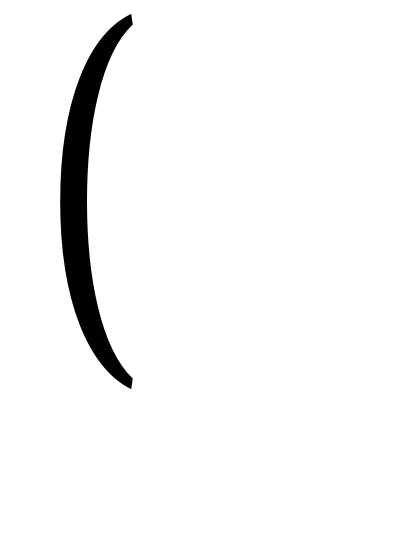 4; +
4; +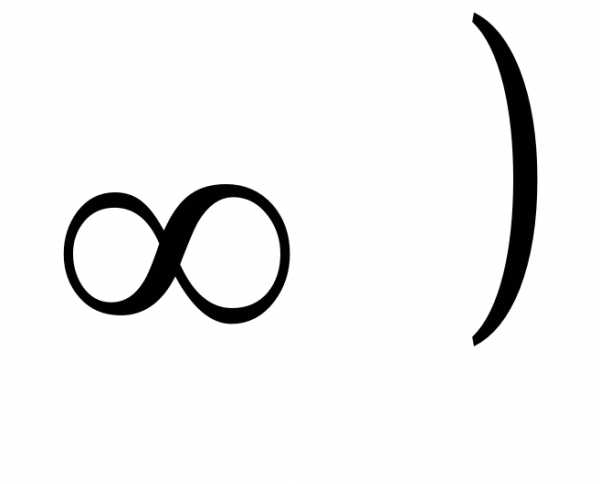 ; 3)
; 3)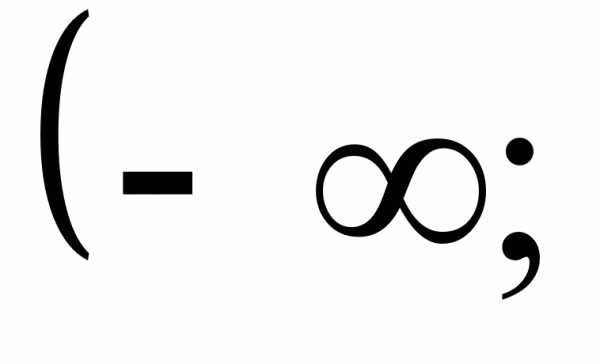 0
0 4)
4) 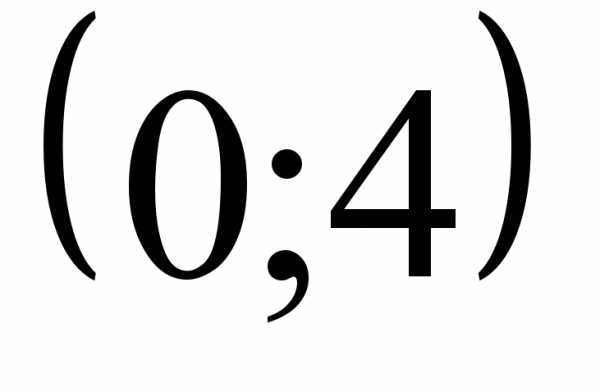 .
.
А 6. Найдите область определения функции: у = 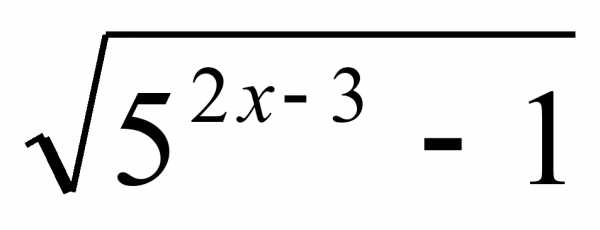 .
.
1) 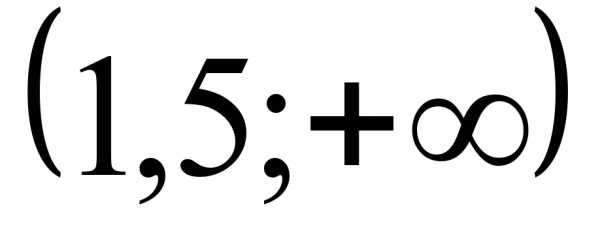 2)
2) 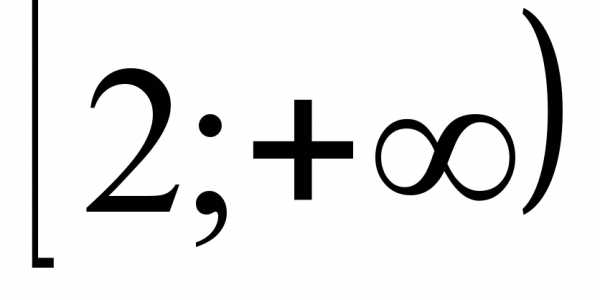 3)
3) 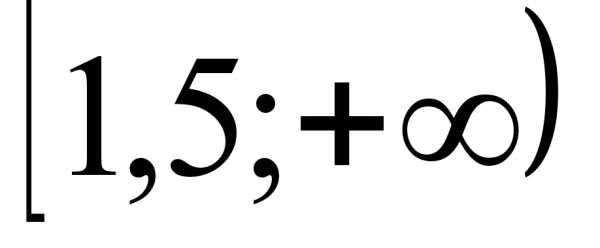 4)
4) 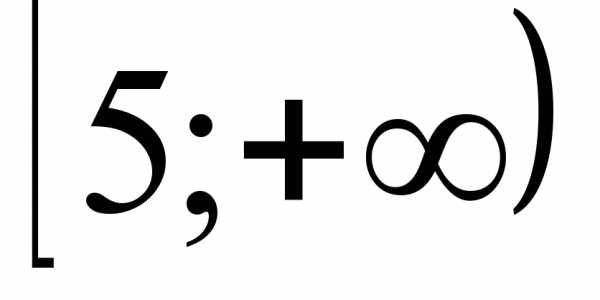
В 7. Решите уравнение: 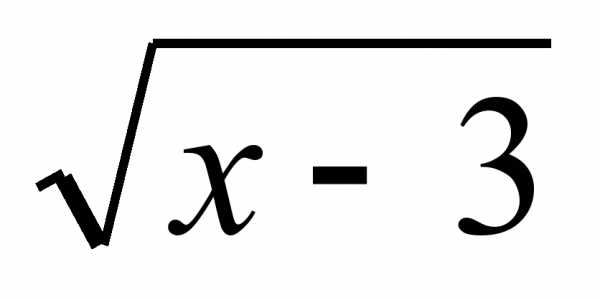 = .
= .
В 8. Найдите наибольшее целое значение а, при котором решение системы уравнений 
х + 3у=3
удовлетворяет неравенству 2у – х 0.
В 9. Найдите значение tg x0 , гдеx0 наибольший отрицательный корень уравнения
5 + 7sinx cosx = 3 sin2x .
В 10. Найдите значения выражения
log0,25 , если log0,2543 = а
, если log0,2543 = а
С 11. Найдите целые корни уравнения
(х – 9) (х – 3) (х2 + 8х + 12) = 56 х2.
С 12 . Решите уравнение
5 log4( 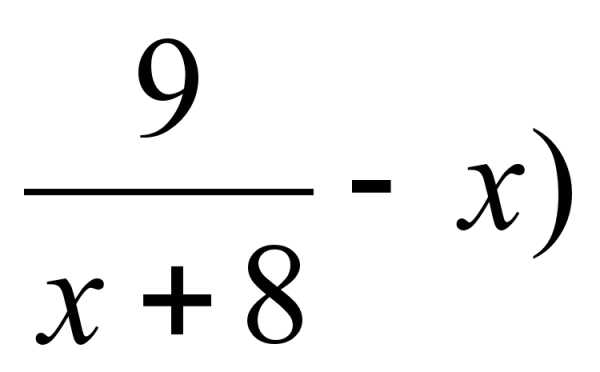 = 3 log4(.
= 3 log4(.
kopilkaurokov.ru