Задание №14 ЕГЭ по математике профильного уровня |
Стереометрия
Задание №14 — стереометрия в профильном ЕГЭ по математике. В задачах данного уровня необходимо проявить знания как по планиметрии, так и по стереометрии. Однако многие задания опираются на теорему Пифагора, поэтому опыт решения аналогичных задач будет только плюсом. Перейдем к рассмотрению одного из таких заданий.
Разбор типовых вариантов заданий №14 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант 2018)
Все рёбра правильной треугольной призмы ABCA1B1C1 имеют длину 6. Точки M и N— середины рёбер AA1 и A1C1 соответственно.
а) Докажите, что прямые BM и MN перпендикулярны.
б) Найдите угол между плоскостями BMN и ABB1.
Алгоритм решения:
а)
- Выполняем чертеж, соответствующий условию и проводим высоту ВН.
- Вычисляем длину высоты ВН.
- Вычисляем BN.
- Показываем, что BM и MN перпендикулярны.
б)
- Проводим перпендикуляр NP к ребру A1B2,
- Показываем, что отрезок MN перпендикулярен плоскости ABB1.
- Определяем линейный угол между плоскостями BMN и ABB1 и вычисляем его.
Решение:
1. Выполняем чертеж к задаче.
Призма правильная, следовательно, основанием ее является равносторонний треугольник. H делит AC пополам, поскольку в равностороннем треугольнике высота является биссектрисой и медианой.
2. Тогда высоту BH можно вычислить по теореме Пифагора из треугольника АВН:
3. Вычисляем длину BN2 из треугольника BNH. Он тоже прямоугольный. По теореме Пифагора:
4. Отрезки BM и MN перпендикулярны, поскольку сумма квадратов их длин равна BN2, то есть 63:
По теореме, обратной теореме Пифагора, BMN – прямоугольный, причем угол M прямой.
Первая часть задания выполнена: утверждение доказано.
б)
1. Проводим перпендикуляр NP к ребру A1B2.
Показываем , что NP перпендикулярна плоскости ABB1. Из построения и условия (призма правильная) следует:
А это означает, что .и прямая NP является проекцией MN на плоскость ABB1.
3. Выше было доказано, что . Тогда согласно теореме о трех перпендикулярах . Их этого следует, что NMP – линейный угол искомого угла.
Вычисляем его.
N – середина отрезка A1C1, тогда NP = 1/2∙h, где h – высота в треугольнике A1B1C1. А он равносторонний и равен треугольнику АВС. Следовательно, , то есть . По соотношениям в прямоугольном треугольнике.
, откуда .
Ответ:
Второй вариант задания (из Ященко, № 1)
На ребре SA правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка М, причём SM : МА = 5:1. Точки P и Q — середины рёбер ВС и AD соответственно.
а) Докажите, что сечение пирамиды плоскостью MPQ является равнобедренной трапецией.
б) Найдите отношение объёмов многогранников, на которые плоскость MPQ разбивает пирамиду.
Алгоритм решения:
а)
- Выполняем чертеж.
- Устанавливаем подобие треугольников SAB и SMN.
- Определяем вид сечения.
б)
- Полагаем объем пирамиды равным V.
- Определяем какую часть от всего объема пирамиды составляет каждая часть.
- Находим отношение определенных объемов частей.
- Записываем ответ.
Решение:
а)
1. Выполняем чертеж для задачи.
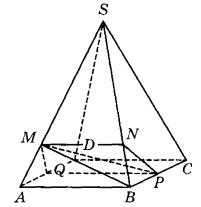
2. Пусть N — точка на ребре SB, причем SN:NB = 5:1. Треугольник SAB подобен треугольнику SMN, потому что в них две стороны пропорциональны и углы между ними равны.
3. Из подобия следует: , сторона AB параллельна отрезку MN и . PQ параллельна стороне АВ. Имеем: отрезки MN и PQ параллельны и не равны.
Рассмотрим треугольники MAQ и NBP. У них:
MA = NB, QA = PB
. Значит, эти треугольники равны. А по свойству равных фигур MQ = NP. Тогда трапеция MNPQ является равнобедренной.
Отсюда следует, что сечение пирамиды плоскостью MPQ является трапецией MNPQ.
б)
1. Обозначаем объём пирамиды SABCD буквой V.
2. Многогранник AMQBNP составлен из пирамиды MABPQ (ее основание ABPQ) и пирамиды MBNP (ее с основание BNP).
Расстояния от точки М до (BNP) и от точки A до этой же плоскости равно 5:6, и SBNP:SSBC = 1:12.
3. Найдем отношение объёмов пирамид MBNP и ASBC: Оно равно 5:72. То есть объём VMBNP = 5V|144.
SABPQ = ½ SABCD. Точка М отстоит от плоскости основания на расстоянии в 6 раз меньшем расстояния от вершины S до этого основании. Потому VMABPQ = V|12.
Таким образом, VAMQBNP = 5V|144+V|12=5V|144+12V|144=17V|144
Тогда отношение объёмов частей AMQBNP и CDSNPQM пирамиды равно
17:(144 – 17)127=17:127.
Ответ: 17 : 127.
spadilo.ru
Задание 14 (стереометрия) — Решения вариантов ЕГЭ по математике: 2017, 2018
В правильной треугольной пирамиде МАВС с основанием ABC стороны основания равны 6, а боковые рёбра равны 5. На ребре АС находится точка D, на ребре АВ находится точка Е, а на ребре AM — точка L. Известно, что AD = Читать далее …
На рисунке изображён многогранник, все двугранные углы которого прямые. а) Постройте сечение многогранника плоскостью, проходящей через точки А, В и С1 б) Найдите площадь этого сечения. Решается аналогично как здесь
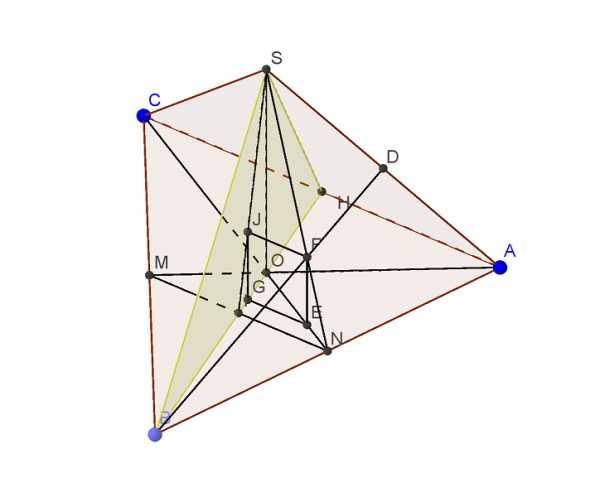
В правильной треугольной пирамиде SABC с основанием ABC все ребра равны 6. а) Постройте сечение пирамиды плоскостью, проходящей через вершину S и перпендикулярной отрезку, соединяющему середины ребер AB и BC. б) найдите расстояние от плоскости этого сечения до центра грани Читать далее …
Похоже на решение вариантов 22 и 29. Посмотрите решение в варианте 22.
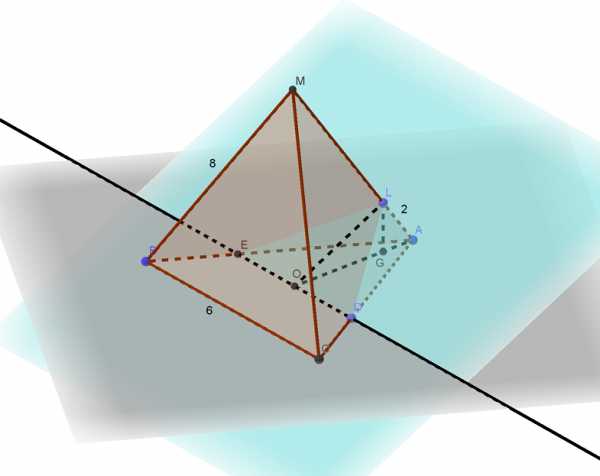
В правильной треугольной пирамиде МАВС с основанием ABC стороны основания равны 6, а боковые рёбра равны 8. На ребре АС находится точка D, на ребре АВ находится точка Е, а на ребре AM — точка L. Известно, что CD = Читать далее …
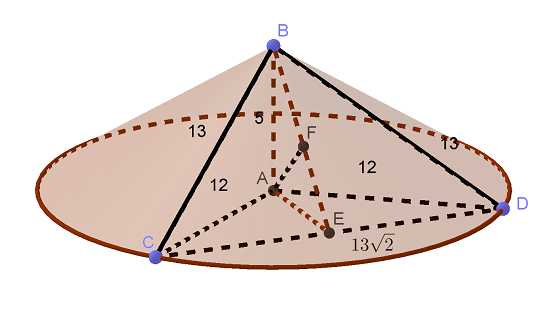
Радиус основания конуса равен 12, а высота конуса равна 5. а) Постройте сечение конуса плоскостью, проходящей через вершину конуса и взаимно перпендикулярные образующие. б) Найдите расстояние от плоскости сечения до центра основания конуса. Трехмерная картинка, которую можно крутить в 3D, Читать далее …
В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами АВ = 4 и ВС = 6. Длины боковых рёбер пирамиды SA = 3, SB = 5, SD = . а) Докажите, что SA — высота пирамиды. б) Найдите расстояние Читать далее …
Вокруг куба с ребром 3 описана сфера. На ребре взята точка М так, что плоскость, проходящая через точки А, В, и М, образует угол 15° с плоскостью ABC. а) Постройте линию пересечения сферы и плоскости, проходящей через точки А, В Читать далее …
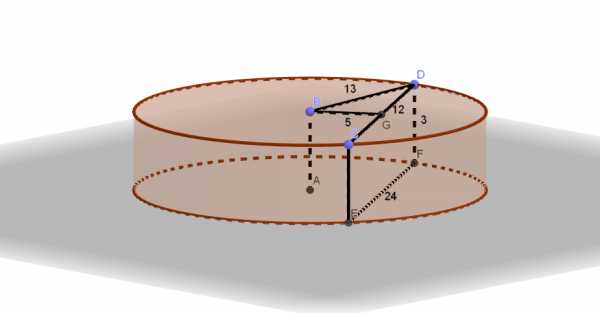
Высота цилиндра равна 3, а радиус основания равен 13. а) Постройте сечение цилиндра плоскостью, проходящей параллельно оси цилиндра, так, чтобы площадь этого сечения равнялась 72. б) Найдите расстояние от плоскости сечения до центра основания цилиндра. Трехмерная картинка, которую можно крутить Читать далее …
В кубе все рёбра равны 4. На его ребре отмечена точка K так, что KB=3. Через точки K и проведена плоскость α, параллельная прямой . а) Докажите, что , где Р — точка пересечения плоскости α с ребром . б) Читать далее …
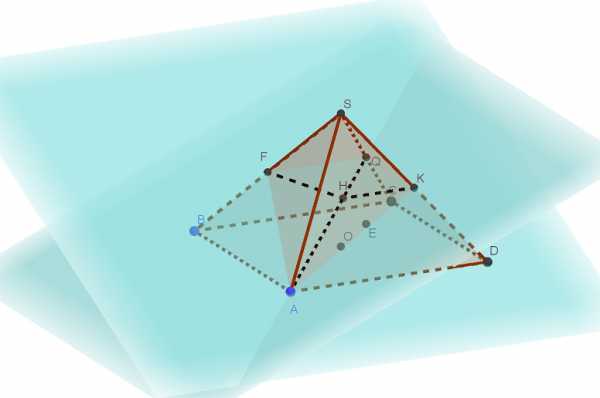
В правильной четырёхугольной пирамиде SABCD все рёбра равны 1. Точка F — середина ребра SB, G — середина ребра SC. а) Постройте прямую пересечения плоскостей ABG и GDF. б) Найдите угол между плоскостями ABG и GDF. Трехмерная картинка, которую можно Читать далее …
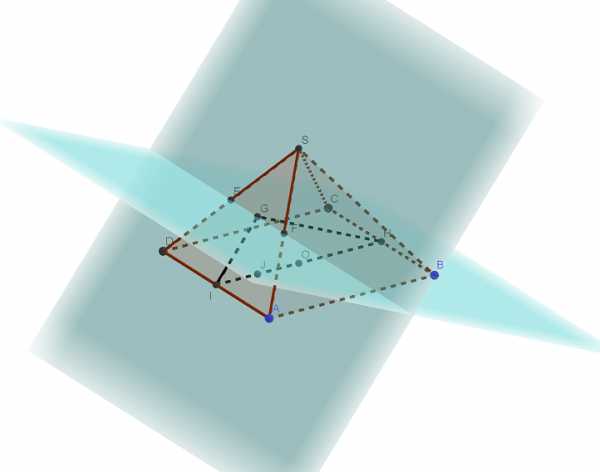
В правильной четырёхугольной пирамиде SABCD все рёбра равны 1. Точка F — середина ребра AS. а) Постройте прямую пересечения плоскостей SAD и BCF. б) Найдите угол между плоскостями SAD и BCF. Трехмерная картинка, которую можно крутить в 3D, доступна по Читать далее …
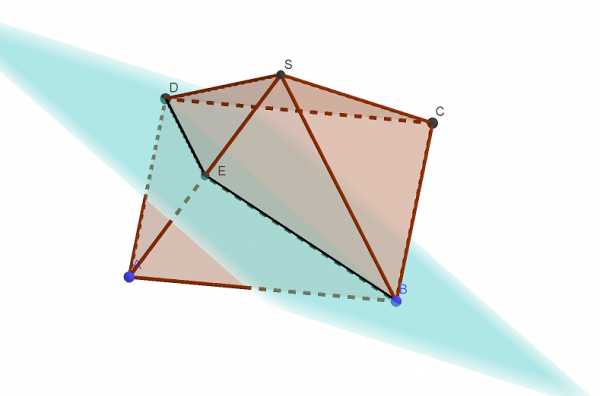В правильной четырёхугольной пирамиде SABCD все рёбра равны 1. а) Постройте прямую пересечения плоскости SAD с плоскостью, проходящей через точку В перпендикулярно прямой AS. б) Найдите угол между плоскостью SAD и плоскостью, проходящей через точку В перпендикулярно прямой AS. Трехмерная Читать далее …В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами АВ = 4 и ВС = 3. Длины боковых рёбер пирамиды SA = √11 , SB = 3√3, SD = 2√5. а) Докажите, что SA — высота пирамиды. б) Найдите Читать далее …
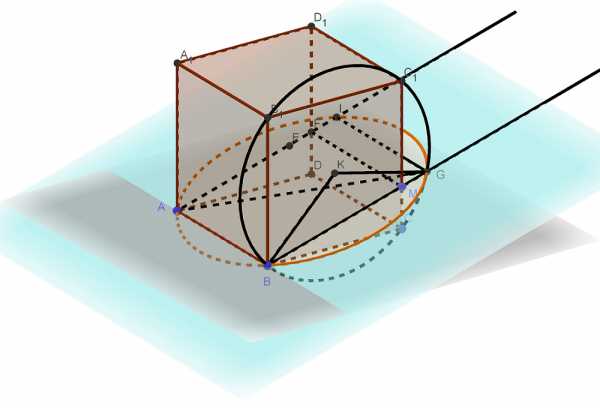
Вокруг куба с ребром 2 описана сфера. На ребре взята точка М так, что плоскость, проходящая через точки А, В, и М, образует угол 15° с плоскостью ABC. а) Постройте линию пересечения сферы и плоскости, проходящей через точки А, В Читать далее …
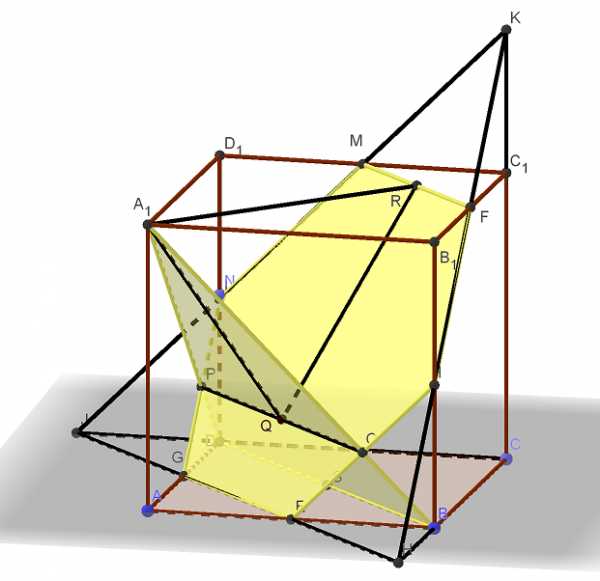
Дан куб . а) Постройте сечение куба плоскостью, проходящей через середины его рёбер . б) Найдите угол между плоскостью и плоскостью, проходящей через середины рёбер . Трехмерная картинка, которую можно крутить в 3D, доступна по ссылке https://ggbm.at/nAKXHwEB Пусть — ребро Читать далее …
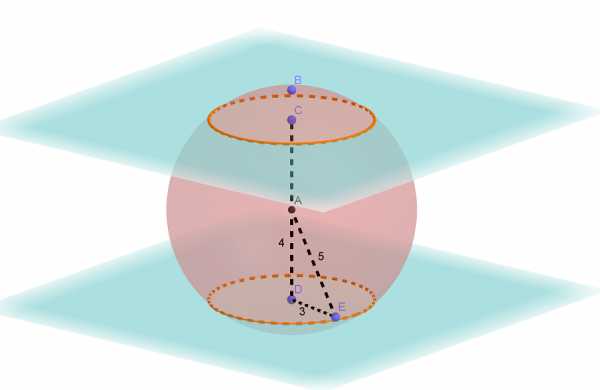
Две параллельные плоскости, находящиеся на расстоянии 8 друг от друга, пересекают шар. Получившиеся сечения одинаковы, и площадь каждого из них равна 9π. а) Постройте эти сечения. б) Найдите площадь поверхности шара. Трехмерная картинка, которую можно крутить в 3D, доступна по Читать далее …
В правильной треугольной пирамиде SABC сторона основания АВ равна 60, а боковое ребро SA равно 37. Точки М и N — середины рёбер SA и SB соответственно. Плоскость содержит прямую MN и перпендикулярна плоскости основания пирамиды. а) Докажите, что плоскость Читать далее …
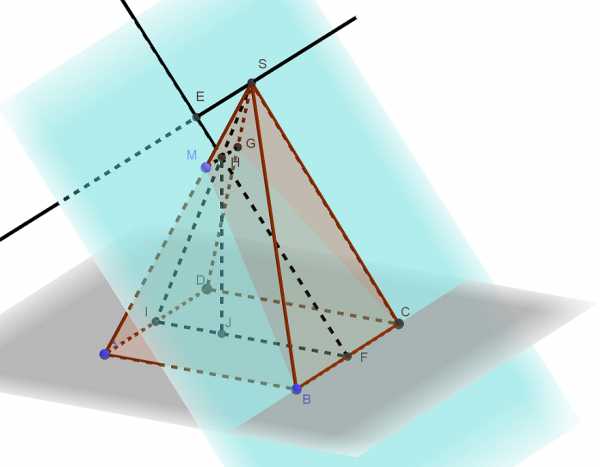
В правильной четырёхугольной пирамиде SABCD основание ABCD — квадрат со стороной 6, а боковое ребро равно 9. На ребре SA отмечена точка М так, что AM = 6. а) Постройте перпендикуляр из точки S на плоскость ВСМ. б) Найдите расстояние Читать далее …
Дан куб . а) Постройте сечение куба плоскостью, проходящей через точки и . б) Найдите угол между плоскостями и . Трехмерная картинка, которую можно крутить в 3D, доступна по ссылке https://ggbm.at/mVj9KVSX
В правильной треугольной призме стороны основания равны 3, боковые рёбра равны 1, точка D — середина ребра . а) Постройте прямую пересечения плоскостей ABC и . б) Найдите угол между плоскостями ABC и . Решение аналогично варианту 15. Посмотрите решение Читать далее …
В правильной треугольной призме стороны основания равны 5, боковые рёбра равны 2, точка D — середина ребра . а) Постройте прямую пересечения плоскостей ABC и . б) Найдите угол между плоскостями ABC и . Трехмерная картинка, которую можно крутить в Читать далее …
В правильной четырёхугольной призме стороны основания равны 3, а боковые рёбра равны 4. На ребре отмечена точка Е так, что . а) Постройте прямую пересечения плоскостей ABC и . б) Найдите угол между плоскостями ABC и Решение похоже на вариант Читать далее …
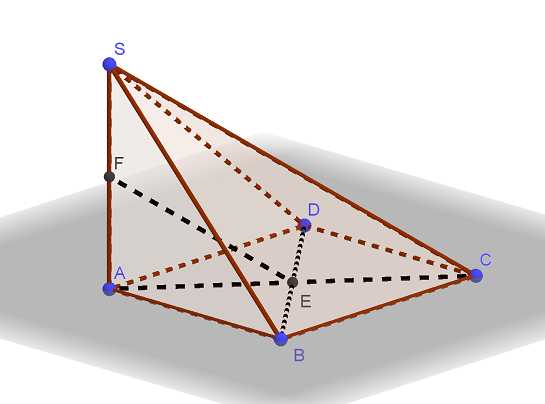
В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами и . Длины боковых рёбер пирамиды . а) Докажите, что SA — высота пирамиды. б) Найдите угол между прямыми SC и BD. Решение похоже на вариант 9 Трехмерная картинка, которую Читать далее …
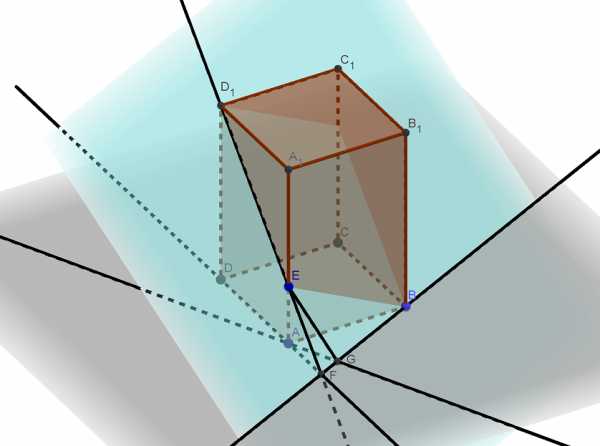
В правильной четырехугольной призме стороны основания равны 2, а боковые ребра равны 3. На ребре отмечена точка E так, что . а) Постройте прямую пересечения плоскостей ABC и . б) Найдите угол между плоскостями ABC и . Трехмерная картинка, которую Читать далее …
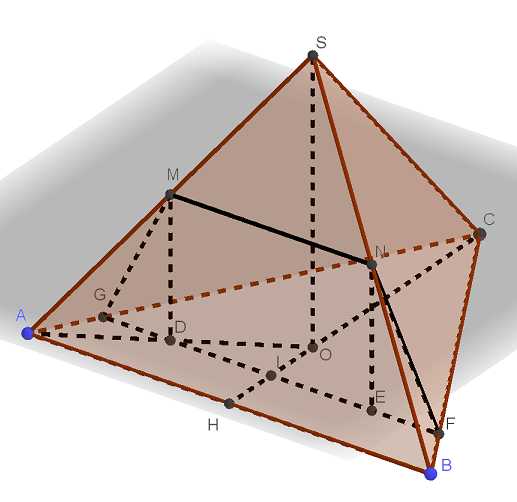
В правильной треугольной пирамиде SABC сторона основания АВ равна 6, а боковое ребро SA равно 4. Точки М и N — середины рёбер SA и SB соответственно. Плоскость содержит прямую MN и перпендикулярна плоскости основания пирамиды. а) Докажите, что плоскость Читать далее …
В правильной треугольной пирамиде SABC сторона основания АВ равна 12, а боковое ребро SA равно 8. Точки М и N — середины рёбер SA и SB соответственно. Плоскость содержит прямую MN и перпендикулярна плоскости основания пирамиды. а) Докажите, что плоскость Читать далее …
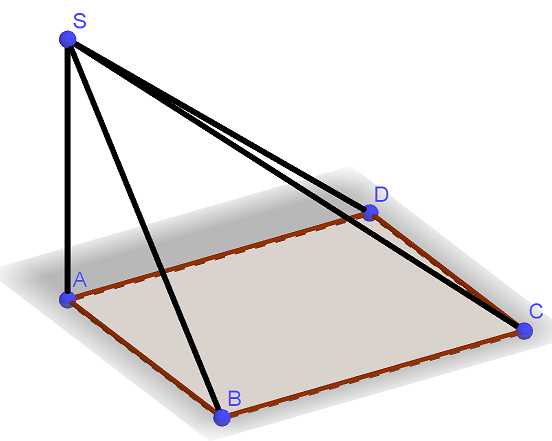
В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами и . Длины боковых рёбер пирамиды . а) Докажите, что SA — высота пирамиды. б) Найдите угол между прямой SC и плоскостью ASB. Трехмерная картинка, которую можно крутить в 3D, Читать далее …
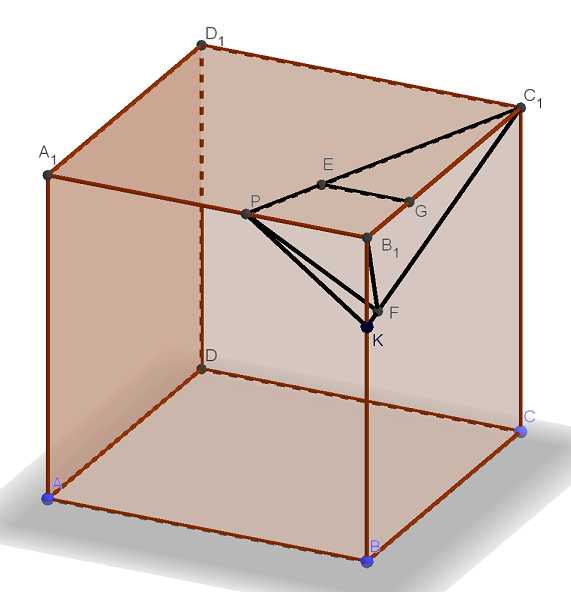
В кубе все рёбра равны 5. На его ребре отмечена точка K так, что KB = 4. Через точки K и построена плоскость , параллельная прямой . а) Докажите, что , где P — точка пересечения плоскости с ребром . Читать далее …
В правильной треугольной пирамиде SABC сторона основания АВ равна 12, а боковое ребро SA равно 13. Точки М и N — середины рёбер SA и SB соответственно. Плоскость содержит прямую MN и перпендикулярна плоскости основания пирамиды. а) Докажите, что плоскость Читать далее …
В пирамиде ABCD рёбра DA, DB и DC попарно перпендикулярны, а . а) Докажите, что эта пирамида правильная. б) На рёбрах DA и DC отмечены точки M и N соответственно, причём . Найдите площадь сечения MNB. Решение аналогично варианту 4
В пирамиде ABCD рёбра DA, DB и DC попарно перпендикулярны, а . а) Докажите, что эта пирамида правильная. б) На рёбрах DA и DC отмечены точки M и N соответственно, причём . Найдите площадь сечения MNB. Решение аналогично варианту 4
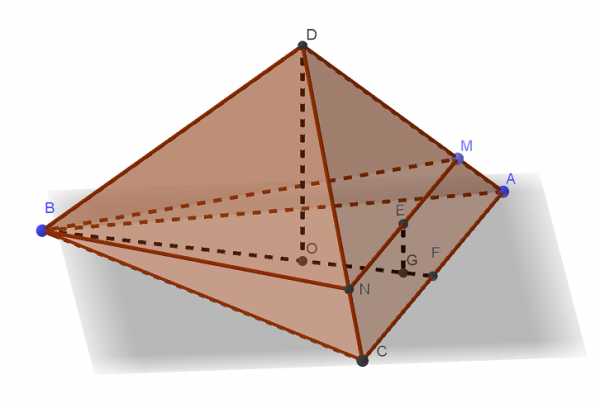
В пирамиде ABCD рёбра DA, DB и DC попарно перпендикулярны, а AB = BC = AC = 14. а) Докажите, что эта пирамида правильная. б) На рёбрах DA и DC отмечены точки M и N соответственно, причём DM:MA = DN:NC Читать далее …
На ребре SA правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка М, причём SM:МА =3:4. Точки P и Q — середины рёбер ВС и AD соответственно. а) Докажите, что сечение пирамиды плоскостью MPQ является равнобедренной трапецией. б) Найдите отношение Читать далее …
На ребре SA правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка М, причём SM:МА =1:2. Точки P и Q — середины рёбер ВС и AD соответственно. а) Докажите, что сечение пирамиды плоскостью MPQ является равнобедренной трапецией. б) Найдите отношение Читать далее …
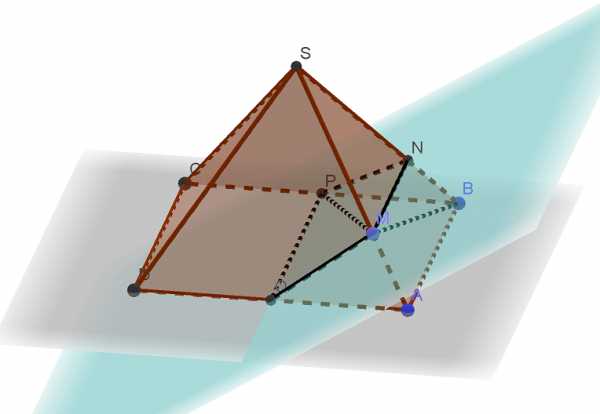
На ребре SA правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка М, причём SM : МА = 5:1. Точки P и Q — середины рёбер ВС и AD соответственно. а) Докажите, что сечение пирамиды плоскостью MPQ является равнобедренной трапецией. Читать далее …
Читаем Погорелова на стр. 282 https://yadi.sk/d/VB_dPOI43GYVLn — нам нужно провести из т. B перпендикуляр на прямую SA — получим точку E и из этой точки восстанавливаем второй перпендикуляр к линии пересечения плоскостей — уже во второй плоскости Открыть на полную Читать далее …
Открыть на полную страницу: cсылка .
Открыть на полную страницу: cсылка .
В тр. B1KC1 правой грани опустим высоту из т. B1 на прямую C1K Получим точку J. Соединим точку J с точкой P. Докажем, что плоскость PJB1 ⊥ прямой KC1 и тогда угол PJB1 — искомый линейный угол двугранного угла между Читать далее …
Возьмем т.H — середину AB. Проведем OH. Тогда OH ⊥ AB (OAB — равнобедренный тр) Проведем SH. Докажем, что SH⊥AB. Действительно, AB⊥SO и AB⊥OH ⇒ AB⊥плоскости SOH и AB⊥SH как лежащей в этой плоскости Проведем OK — высоту в тр Читать далее …
ege-resheniya.ru
|
Задания реальных ЕГЭ с 2010 по 2018
Skip Navigation Links.
|
egeprof.ru
|
Задания реальных ЕГЭ с 2010 по 2018
Skip Navigation Links.
|
egeprof.ru
Решение и разбор 14 задания ЕГЭ математика (профильный уровень)
Задание 14
В основании пирамиды MABC лежит равнобедренный прямоугольный треугольник ABC (AC=CB). Все боковые ребра пирамиды равны между собой и равны катету треугольника, лежащего в основании пирамиды.
а) Докажите, что плоскости ABC и MAB взаимно перпендикулярны.
б) Найдите расстояние между прямыми MK и BC, если CB=2 и K — середина AB.
ЕГЭ. Математика. Большой сборник тематических заданий для подготовки к единому государственному экзамену. Профильный уровень
Вниманию выпускников 11 классов предлагается новое пособие для подготовки к единому государственному экзамену по математике. В сборник включены задания по всем разделам и темам, проверяемым на едином государственном экзамене профильного уровня.
Купить
Решение:
Пусть K — середина AB. Заметим, что MK и MC перпендикулярны AB. Тогда угол MKC — линейный угол, образованный плоскостями ABC и MAB. Найдём стороны треугольника MKC, принимая боковое ребро пирамиды за a:
Легко заметить, что треугольник МКС — прямоугольный, следовательно угол MKC равен 90 градусам, тогда и плоскости ABC и MAB взаимно перпендикулярны, что и требовалось доказать. Для нахождения расстояния между скрещивающимися прямыми MK и BC нужно найти длину высоты KH прямоугольного треугольника KCB; так как KH и BC перпендикулярны по построению, KH и MK перпендикулярны как следствие пункта а). Принимая во внимание условие задачи, получаем KH = 1.
rosuchebnik.ru
|
Задания реальных ЕГЭ с 2010 по 2018
Skip Navigation Links.
|
egeprof.ru
|
Задания реальных ЕГЭ с 2010 по 2018
Skip Navigation Links.
|
egeprof.ru
